牛顿迭代在盲信号处理中的应用

合集下载

数学优化中的牛顿法和拟牛顿法

数学优化中的牛顿法和拟牛顿法在数学中，优化是一个非常重要的研究领域，其目的是找到使某个函数达到最大或最小值的变量集合。

在实际应用中，很多问题都可以转化为优化问题，如机器学习、经济学、物理学等。

在优化领域中，牛顿法和拟牛顿法是两种常见的方法。

本文将介绍这两种优化方法的基本原理、优缺点以及应用场景。

一、牛顿法牛顿法（Newton's method）是由数学家牛顿发明的非线性优化方法，其思想是利用函数的泰勒级数展开进行逼近。

具体来说，牛顿法先求出目标函数的一阶和二阶导数，然后使用二阶导数来逼近目标函数本身，进而得到近似最优解。

牛顿法的数学公式如下：$$\boldsymbol{x}_{k+1}= \boldsymbol{x}_{k} -{\boldsymbol{\nabla}^2 f(\boldsymbol{x}_k)^{-1}}\boldsymbol{\nabla} f(\boldsymbol{x}_k)$$其中，$\boldsymbol{x}_k$ 表示第 $k$ 次迭代的解，$\boldsymbol{\nabla} f(\boldsymbol{x}_k)$ 和$\boldsymbol{\nabla}^2 f(\boldsymbol{x}_k)$ 分别表示目标函数在$\boldsymbol{x}_k$ 处的一阶和二阶导数。

牛顿法的优点是收敛速度非常快，通常只需要很少的迭代次数即可达到最优解。

另外，牛顿法适用于连续可微、二阶可导的函数，因此适用范围广。

然而，牛顿法也存在一些缺点，例如无法处理不可导或一阶可导但二阶不可导的函数。

此外，牛顿法需要计算目标函数的二阶导数，因此在大规模问题上计算成本很高。

二、拟牛顿法拟牛顿法（quasi-Newton method）是一类基于牛顿法的优化算法，它通过逼近目标函数的海森矩阵来求解。

拟牛顿法没有计算海森矩阵的显式表达式，而是通过估计海森矩阵的变化来逼近。

最简单和最流行的拟牛顿法是BFGS算法和L-BFGS算法。

牛顿迭代法及其应用

牛顿迭代法及其应用牛顿迭代法是一种求解函数零点的迭代方法，具有快速收敛、精度高等优点，被广泛应用于计算机、数学、物理等领域。

本文将从理论和实际应用两方面介绍牛顿迭代法，并对其应用进行探讨。

一、理论基础牛顿迭代法是通过一点处的切线来逼近函数零点的方法。

设$f(x)$在$x_0$点有一个零点，且其导数$f'(x_0)$存在且不为零，那么该零点可以通过一点$(x_0,f(x_0))$处的切线与$x$轴的交点来逐步逼近。

假设切线的方程为$y=f'(x_0)(x-x_0)+f(x_0)$，则其中$x$轴上的交点为$x_1=x_0-\frac{f(x_0)}{f'(x_0)}$，这是零点的一个更好的近似值。

用$x_1$代替$x_0$，再利用同样的方法得到$x_2$，不断重复这个过程，即可逐步逼近零点。

这个过程可以用下面的公式表示：$$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$$这就是牛顿迭代法的基本公式。

从初始值$x_0$开始迭代，不断利用公式进行逼近，直到找到满足$f(x_n)=0$的解。

二、实际应用牛顿迭代法在实际应用中广泛存在，比如在计算机图形学中，通过牛顿迭代法可以精确计算出圆的周长、面积等参数，也可以实现快速的路径追踪和光线追踪。

在金融领域中，牛顿迭代法可以用来计算隐含波动率，即在期权定价模型中，寻找满足期权定价公式的波动率。

由于这个过程中往往要用到反函数，所以牛顿迭代法可以快速找到隐含波动率。

另外，在机器学习、神经网络中，多次用到牛顿迭代法进行梯度下降，智能化运用牛顿迭代法可以提高计算效率，降低误差。

三、应用探讨牛顿迭代法的应用范围较广，但在实际应用中也存在一些问题。

如何避免迭代过程中出现抖动、越界、阻尼等现象，可以通过设置收敛条件、调整步长等方式进行优化。

此外，当函数的导数存在零点或迭代公式不存在时，牛顿迭代法也会失效。

因此，在选择牛顿迭代法时，需要了解函数特性，根据情况选择适合的迭代方法。

牛顿迭代法在优化问题中的应用

牛顿迭代法在优化问题中的应用牛顿迭代法是一种基于泰勒级数的优化算法，可以有效地解决优化问题。

它的基本思想是从一个初始点出发，利用一阶导数和二阶导数信息，逐步找到函数的极值点。

在这篇文章中，我们将介绍牛顿迭代法在优化问题中的应用，并且通过实际例子来演示如何使用该方法求解问题。

一、牛顿迭代法的基本思想牛顿迭代法可以解决那些需要找到函数最值点的问题。

它的基本思想是从一个初始点 $x_0$ 出发，利用函数的一阶导数和二阶导数信息，逐步逼近函数的最值点。

具体的实现方式是通过求解下列方程来确定下一个迭代点 $x_k$：$$f(x_{k+1})=f(x_k)+f'(x_k)(x_{k+1}-x_k) +\frac{1}{2}f''(x_k)(x_{k+1}-x_k)^2 = 0$$其中，$f'(x_k)$ 和 $f''(x_k)$ 分别是函数 $f(x)$ 在点 $x_k$ 处的一阶导数和二阶导数。

这个方程可以通过牛顿迭代法一步一步地求解，直到达到预定的收敛条件。

二、例子说明现在我们通过一个例子来说明牛顿迭代法的运用。

假设我们要求解函数 $f(x)$ 的最小值，其中$$f(x)=x^3-2x^2+4$$首先我们需要求解 $f(x)$ 的一阶导数和二阶导数：$$f'(x) = 3x^2-4x$$$$f''(x) = 6x-4$$接下来设置初始点 $x_0=0$，然后运用牛顿迭代法求解下一个迭代点 $x_1$：$$f(x_1) = f(x_0) + f'(x_0)(x_1-x_0) + \frac{1}{2}f''(x_0)(x_1-x_0)^2=0$$化简得：$$x_1= \frac{4}{3}$$接下来我们将 $x_1$ 作为下一个初始点，并重复上述的操作，得到：$$x_2= 1.33333333...$$这个迭代过程是连续迭代的，当$x_k$ 的值趋近于最小值点时，函数值逐渐接近于 0。

盲信号总结

盲分离研究背景与数学模型简介：盲信号分离是当前信号处理领域最热门的技术之一。

由于其重要的理论价值和广泛的应用前景 ,盲信号分离在近 20 年引起了广泛的重视和研究。

盲信号分离起源于鸡尾酒会议问题 ,即在很多人同时说话的情况下(通常包含噪声),怎样从多个声音采集设备(如麦克风)采集到的声音信号中分离出所需要的各个说话者的声音?在这个过程中,各个信号源未知,信号混叠参数即传输信道的先验知识也未知,因此我们称这个过程是“盲”的。

目前,以盲信号分离为核心的盲信号处理技术已经成为重要的研究课题,并在许多领域,特别是在语音信号分离与识别、生物信号(如脑电图、心电图)处理、雷达、声纳、遥感、通信系统、噪声控制等领域,吸引了大量的研究和重视。

盲信号分离：是指在不知道源信号和传输信道特性的情况下,从一个传感器阵列的输出信号(也叫观测信号,混叠信号)中分离或估计出源信号的波形。

目标是如何最大化分离信号的独立性。

观测数据：是一组传感器的输出,其中每个传感器接收到的是源信号的不同混合。

源信号混合方式：有线性和非线性两种方式。

当混叠模型为非线性时,一般很难从混叠数据中恢复源信号,除非对信号和混叠模型有进一步的先验知识。

线性模型有三种：（1)线性瞬时混叠(2)延迟无回声混叠(3)回声混叠1，线性瞬时混叠模型：目前主要采用的工具是稀疏成分分析。

2，延迟无回声混叠模型：即每个传感器仅接收到每个源一次。

由于传输距离的远近及传输介质的影响，源信号到达每个传感器的时刻可能并不是同时的。

3，回声混叠：各个传感器不仅直接接收到每个源信号,而且还接收到每个源信号的回声信号。

根据混叠方式对盲信号分离进行分类：如果根据传感器个数M 和源信号个数N 来分类,则把M > N称为超定模型,M = N为适定模型,M < N称为欠定模型。

欠定模型比适定模型和超定模型更难求解。

对适定或者超定模型,只要能够估计出混叠矩阵,就能恢复源信号。

●按照未知信号源的混合形式，可以将盲处理分为线性混合和非线性混合两种类型，其中线性混合包括瞬时混合和卷积混合。

盲信号处理

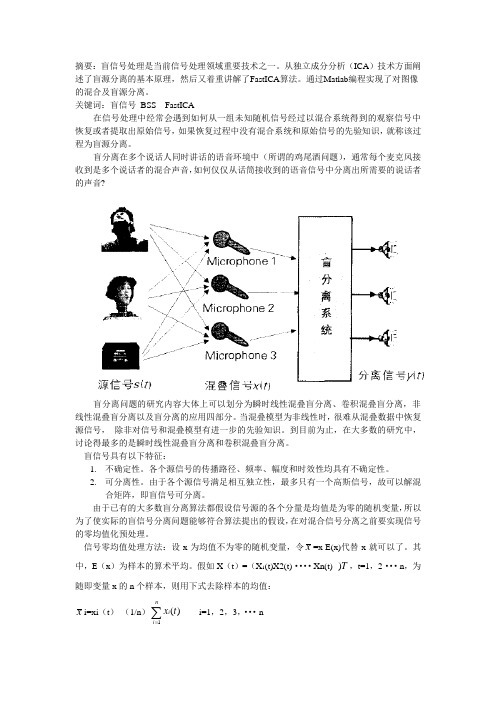
摘要：盲信号处理是当前信号处理领域重要技术之一。

从独立成分分析（ICA ）技术方面阐述了盲源分离的基本原理，然后又着重讲解了FastICA 算法。

通过Matlab 编程实现了对图像的混合及盲源分离。

关键词：盲信号 BSS FastICA在信号处理中经常会遇到如何从一组未知随机信号经过以混合系统得到的观察信号中恢复或者提取出原始信号，如果恢复过程中没有混合系统和原始信号的先验知识，就称该过程为盲源分离。

盲分离在多个说话人同时讲话的语音环境中（所谓的鸡尾酒问题），通常每个麦克风接收到是多个说话者的混合声音，如何仅仅从话筒接收到的语音信号中分离出所需要的说话者的声音?盲分离问题的研究内容大体上可以划分为瞬时线性混叠盲分离、卷积混叠盲分离，非线性混叠盲分离以及盲分离的应用四部分。

当混叠模型为非线性时，很难从混叠数据中恢复源信号，除非对信号和混叠模型有进一步的先验知识。

到目前为止，在大多数的研究中，讨论得最多的是瞬时线性混叠盲分离和卷积混叠盲分离。

盲信号具有以下特征：1. 不确定性。

各个源信号的传播路径、频率、幅度和时效性均具有不确定性。

2. 可分离性。

由于各个源信号满足相互独立性，最多只有一个高斯信号，故可以解混合矩阵，即盲信号可分离。

由于已有的大多数盲分离算法都假设信号源的各个分量是均值是为零的随机变量，所以为了使实际的盲信号分离问题能够符合算法提出的假设，在对混合信号分离之前要实现信号的零均值化预处理。

信号零均值处理方法：设x 为均值不为零的随机变量，令x =x-E(x)代替x 就可以了。

其中，E （x ）为样本的算术平均。

假如X （t ）=（X 1(t)X2(t)····Xn(t) T )，t=1，2···n ，为随即变量x 的n 个样本，则用下式去除样本的均值：x i=xi （t ）-（1/n ）)(1∑=ni i t x i=1，2，3，···n另外在实际中，信号在传输接收中混合信号的各个分量之间难免有一些相关成分，这时零均值x 的协方根矩阵}{T xx E Rxx 不是对角阵。

牛顿迭代法的应用

牛顿迭代法的应用1. 问题背景非线性方程求解是在很多工程问题上都会碰到的。

对于其精确解一般是很难求解到的，但是我们在工程中也并不需要精确解，近似解就可以达到我们的计算要求。

我们可以通过采取牛顿迭代法来求解非线性方程的近似解。

2. 数学模型非线性方程，就是因变量与自变量之间的关系不是线性的关系，这类方程很多，例如平方关系、对数关系、指数关系、三角函数关系等等。

比如下面这个函数。

3. 算法及流程牛顿迭代法公式如下:牛顿迭代法步骤如下：1. 前期阶段。

选初始点 0x ,并计算与这点相关的一阶导和函数值，以便在后面使用。

2. 迭代阶段。

按照迭代公式迭代一次，计算最新的近似函数值 1x ,并计算与最新点相关的一阶导以及函数值。

3. 验证阶段。

当误差值在允许误差范围内，则停止迭代，以最新点作为方程式的解，否则转 4。

4. 判断阶段。

如果迭代次数 N 已经达到预先设定的次数，则代表该次迭代没有成功，转5。

如果是另外一种情况，没有达到预先设定的迭代次数，那么就转到第2步，重新进入迭代阶段，进行迭代。

5.修改阶段。

重新选择迭代初始值进行迭代。

)()('1k k k k x f x f x x -=+10sin 2)(3-+-+=x x x e x f xmatlab程序fun=input('请输入求解函数f(x)=');a=input('请输入迭代初值x0=');e=input('请输入求解精度e=');%求解精度n=input('请输入最大求解次数n=');%最大求解次数f=inline(fun);%修改需要求解的inline函数的函数体x1=a;f1=diff(fun,x,1);%对原函数进行求导f2=inline(f1);x2=x1-f(a)/f2(a);n0=0;d=x1-x2;while n0<nif d>ex1=x2；x2=x1-f(x1)/f2(x1)n0=n0+1;d=x1-x2；elsebreak;endendif n0==ndisp('超过迭代次数，请重新选择初始值，进行迭代。

盲源分离问题综述

盲源分离问题综述盲源分离问题综述摘要：盲源分离，是从观测到的混合信号中恢复不可观测的源信号的问题。

作为阵列信号处理的一种新技术，近几年来受到广泛关注。

本文主要阐述了盲源分离问题的数学模型、典型算法以及盲源分离的应用，并结合盲源分离问题的研究现状，分析了其未来的发展方向。

主题词：盲源分离;盲源分离的典型算法1. 引言盲信号分离问题起源于人们对“鸡尾酒会”问题的研究。

在某个聚会上，我们正在相互交谈，同一时刻同一场景下其他人的交谈也在同时进行着，可能还有乐队的音乐伴奏，这时整个会场上是一片嘈杂。

但是非常奇妙的是，作为交谈对象的双方，我们能够在这混乱的众多声音中很清晰的听到对方的话语，当然，如果我们偶尔走神，将精力放在乐队奏出的音乐时，我们也同样可以听清楚音乐的主旋律。

这种可以从由许多声音所构成的混合声音中选取自己需要的声音而忽视其他声音的现象就是鸡尾酒会效应。

如何在这种从观察到的混合信号中分离出源信号的问题就是所谓的盲分离（Blind Signal Separation, BSS）问题，有时也被称为盲源分离（Blind Source Separation）问题。

1986年，法国学者Jeanny Herault和Christian Jutten提出了递归神经网络模型和基于Hebb学习律的学习算法，以实现两个独立源信号混合的分离，这一篇开创性论文的发表使盲源分离问题的研究有了实质性的进展。

随着数字信号处理理论和技术的发展以及相关学科的不断深入,大量有效的盲分离算法不断被提出,使盲分离问题逐渐成为当今信息处理领域中最热门的研究课题之一,在无线通信、图象处理、地震信号处理、阵列信号处理和生物医学信号处理等领域得到了广泛的应用。

2. 盲源分离问题的数学模型盲源分离是指在不知道源信号和信道传输参数的情况下,根据输入信号的统计特性,仅由观测信号恢复出源信号各个独立成分的过程。

盲源分离研究的信号模型主要有三种:线性混合模型、卷积混合模型和非线性混合模型。

牛顿迭代法在信号处理中的应用

牛顿迭代法在信号处理中的应用信号处理是一门广泛应用于通信、音频处理、图像处理等领域的技术。

而牛顿迭代法则是一种常用的数值解法之一，被广泛应用于求解非线性函数的根、最优化问题等。

本文将讨论牛顿迭代法在信号处理中的应用，包括信号匹配检测、音频降噪、图像增强等方面。

一、信号匹配检测在通信领域中，信号匹配检测是一种广泛应用于信号传输和接收的技术。

该技术主要通过比对传输数据与接收数据中的信号波形是否相同来检测数据是否正确传输或接收。

牛顿迭代法可以应用于信号匹配检测中，解决非线性函数的根。

在匹配检测中，传输数据与接收数据之间的误差往往受到噪声的影响，导致误差较大。

采用牛顿迭代法可以将误差逐步缩小，从而提高匹配检测的精度和可靠性。

二、音频降噪音频降噪是音频处理领域中的一个常见问题。

当音频信号中存在噪声时，会严重降低音频质量，影响人们对音乐或语音的感受。

牛顿迭代法可以应用于音频降噪中，通过不断迭代优化算法，去除音频信号中的噪声。

在音频降噪中，视频降噪一般采用卡尔曼滤波器、小波变换等算法。

牛顿迭代法是其中的一种有效算法，可以根据音频信号的特性，快速、有效地去除噪声。

三、图像增强图像增强是图像处理领域中的一个重要技术，它主要可以通过加强图像的对比度、清晰度等方面来提高图像的质量。

牛顿迭代法可以应用于图像增强中，通过逐步迭代搜索图像的最优解。

在图像增强中，常用的算法有拉普拉斯金字塔、均值滤波器等。

牛顿迭代法可以利用图像特征进行快速、有效搜索，提高图像增强的效果。

综上所述，牛顿迭代法在信号处理领域中的应用十分广泛。

通过不断优化算法、搜索最优解，可以有效地去除噪声、提高信号质量。

未来，随着技术的不断发展，牛顿迭代法在信号处理中的应用也将得到更广泛和深入的应用。

基于拟牛顿法的盲信号分离算法

法是ＳＯＢＩ算法… ；另一类基于高阶统计特性，典型
考虑以下的瞬时混合模型
的算法是ＪＡＤＥ算法Ｊ．这两类算法首先都要进行Ｘ（ｔ）＝Ａｓ（ｔ）＋ｓ（ｔ）＝［ｓ。（ｔ），… ，ｓ（ｔ）］。ｎ（ｔ），
白化（ｗｈｉｔｅｎｉｎｇ）预处理，然后求矩阵的正交对角算子（ｏｒｔｈｏｇｏｎａｌｄｉａｇｏｎａｌｉｚｅｒ）．但文献［３］指出，对基于最小二乘准则的盲信号分离算法，白化过程的存在可能会造成分离结果与期望值偏离很远的情况．
虽然对向量的处理拟牛顿法是一种好的最优化算法，但它不能直接用来处理矩阵．本文拟利用矩阵联合对角化方法构造代价函数，提出一种基于拟牛顿的处理矩阵的迭代算法，并通过计算机仿真来验证算法的有效性．
２构造代价函数
首先，定义时延相关矩阵Ｒ（ｒ），考虑到加性噪声在时间上是白的，即Ｅ｛ｎ（ｔ）ｎ（ｔ＋ｒ）。｝＝０，ｒ ≠０，那么
（ｒ）＝Ｅ｛（ｔ）ｘ（ｔ＋ｒ）。｝＝
收稿日期：２００６－１１－２３作者简介：蹇柯（１９８３－），男，硕士研究生，主要研究方向为信号与图像处理
维普资讯
广东工业大学学报
第２４卷
ＡＥ｛ｓ（ｔ）ｓ（ｔ＋ｆ）｝Ａ＝ＡＲ（ｆ）Ａ，（３）
Ｔ（ｆ）
（ｆ）＋ｄｉａｇ（（ｆ））
其中，（ｆ）＝Ｅ｛Ｓ（ｔ）Ｓｔ＋ｆ）｝是对角阵．若分离矩阵Ｗ＝ＰＡ一，其中Ｐ是广义置换矩阵，那么
ＷＲ（ｆ）ＷＴ—ｄｉａｇ（ＷＲ（ｆ）ＷＴ）＝

牛顿迭代法一致切线 -回复

牛顿迭代法一致切线-回复什么是牛顿迭代法？牛顿迭代法，也被称为牛顿-拉弗森法（Newton-Raphson method），是一种用于求解方程的迭代数值方法。

该方法通过不断逼近方程的根来达到求解方程的目的。

牛顿迭代法的核心思想是利用方程在某一点的切线来逼近方程的根，并不断更新切线与x轴的交点，从而逼近方程的根。

具体而言，假设方程为f(x)=0，我们需要求解方程在某一点x0附近的根。

首先，我们通过求解方程的切线来逼近方程的根。

方程的切线可以通过方程在x0处的导数来表示，切线的方程为y=f'(x0)(x-x0)+f(x0)。

然后，更新x轴上的交点x1=x0-f(x0)/f'(x0)，即新的逼近根，然后重复以上步骤直到达到所需的精度。

牛顿迭代法的初始值选择和迭代次数是影响该方法收敛效果的重要因素。

如果初始值的选择离真实根足够近，并且迭代次数足够多，则牛顿迭代法通常可以达到较高的迭代精度。

为什么牛顿迭代法有效？牛顿迭代法的有效性可以通过其几何意义进行解释。

在每一次迭代中，牛顿迭代法选取方程的切线与x轴的交点作为新的逼近根。

由于切线是方程在该点的近似线性表示，所以与真实根足够接近时，切线与x轴的交点也会足够接近真实根。

通过不断更新切线与x轴的交点，牛顿迭代法可以逐渐逼近方程的根。

值得注意的是，牛顿迭代法的有效性受到方程的性质的影响。

当方程具有良好的局部可导性和单调性时，牛顿迭代法通常能够得到较好的收敛效果。

然而，如果方程在初始点附近存在多个根或者迭代过程中出现振荡或发散现象，则牛顿迭代法的有效性会受到挑战。

牛顿迭代法的步骤是怎样的？牛顿迭代法的步骤可以总结为以下几个关键步骤：1. 选择初始值：选择一个初始点x0来开始迭代计算。

2. 计算切线斜率：求解方程在x0处的导数f'(x0)，并计算切线的斜率。

3. 计算切线与x轴的交点：通过切线与x轴的交点来逼近方程的根。

切线方程为y=f'(x0)(x-x0)+f(x0)，将y设置为0，解方程得到新的逼近根x1。

盲信号处理的分类

盲信号处理（Blind Signal Processing）是一种处理信号的方法，不依赖于关于信号和噪声统计信息的先验知识。

盲信号处理技术主要用于信号分离、信号检测和信号估计等场景。

盲信号处理的一些主要技术分类如下：
1. 盲源分离（Blind Source Separation, BSS）：是从混合信号中分离出原始信号的技术，包括独立成分分析（Independent Component Analysis, ICA）和主成分分析（Principal Component Analysis, PCA）等。

2. 盲均衡（Blind Equalization）：是一种消除或减小信道畸变的方法，只依赖于接收信号的统计特性。

常用算法有零引导（Zero Forcing）和最小均方误差（Minimum Mean Square Error, MMSE）等。

3. 盲信道估计（Blind Channel Estimation）：是在缺乏信道输入输出直接观测的情况下，使用接收信号的统计特性来估计信道参数。

这种方法在无线通信系统中尤为重要。

4. 盲多径消除（Blind Multi-path Fading Elimination）：是一种在缺乏信道状态信息的情况下，消除或减小多径效应的方法。

这种技术可以提高无线通信系统的性能。

5. 盲检测（Blind Detection）：是在没有关于信号和噪声统计信息的先验知识的情况下，实现信号检测和识别的技术。

这种方法在通信和雷达系统中具有广泛的应用。

上述技术只是盲信号处理的几个主要类别。

这些技术通常涉及复杂数学模型和算法，并在无线通信、音频处理、图像处理、生物医学信号处理等多个领域有广泛应用。

基于牛顿迭代盲源分离方法的磨床故障诊断

（ＳｔａｔｅＫｅｙＬａｂ．ｏｆＭｅｃｈａｎｉｃａｌＳｙｓｔｅｍａｎｄＶｉｂｒａｔｉｏｎ，ＳｈａｎｇｈａｉＪｉａｏｔｏｎｇＵｎｉｖｅｒｓｉｔｙ，Ｓｈａｎｇｈａｉ２００２４０，Ｃｈｉｎａ）
ｓｏｕｒｃｅｓ．Ｉｎｏｒｄｅｒｔｏｉｓｏｌａｔｅｔｈｅｍ，ｂｌｉｎｄｓｏｕｒｃｅｓｅｐａｒａｔｉｏｎ（ＢＳＳ）ａｌｇｏｒｉｔｈｍｗａｓｕｓｅｄｈｅｒｅｔｏｉｍｐｒｏｖｅｔｈｅａｃｃｕｒａｃｙｏｆ
较好地应用于工程实际中。关键词：牛顿迭代法；峭度；盲源分离；磨床；故障诊断
中图分类号：ＴＮ９１１．７１文献标识码：Ａ
Ｎｅｗｔｏｎｉｔｅｒａｔｉｏｎ－ｂａｓｅｄｂｌｉｎｄｓｏｕｒｃｅｓｅｐａｒａｔｉｏｎｆｏｒｇｒｉｎｄｉｎｇｍａｃｈｉｎｅｆａｕｌｔｄｉａｇｎｏｓｉｓＬＩＺｉｎｇ，ＤＵＷｅｎ — ｌｉａｏ，ＬＩＹａｈ— ｍｉｎｇ，ＷＡＮＧＳｈｕａｎｇ— ｙｕａｎ，ＬＩＵＣｈｅｎｇ— ｌｉａｎｇ
摘要：磨床的振动信号是由多个振动源混合而成的复杂信号，利用盲源分离技术分离混合信号成为各个振动源
的单独信号能更准确地实现设备的状态监控和故障诊断。基于峭度的不动点迭代法是一种常用的盲源分离方法，但存在

牛顿迭代法在图像处理中的应用

牛顿迭代法在图像处理中的应用随着计算机技术的发展，图像处理技术正变得越来越重要。

图像处理可以让我们更好地理解和分析图片中的信息。

其中，在图像处理中最常见的一个问题是：将一张图片缩放到需要的大小。

这时候就经常用到牛顿迭代法。

牛顿迭代法是一种求解方程的方法，而在图像处理中，它被用来求解一个像素点的新位置。

什么是牛顿迭代法？牛顿迭代法是一种求解方程的方法，用于计算一个函数的零点（函数零点就是函数值为零的位置）。

这种方法可以处理任何种类的函数，包括非线性函数。

它是一种迭代逼近方法。

其基本思想是：从一个猜测值开始，通过不断用函数的导数来逼近零点。

这个过程重复进行，直到求得相对精度足够高的零点或者达到最大迭代次数。

在图像处理中，牛顿迭代法被用来求解一个像素点的新位置，这个像素点的位置是通过对原始图像缩放所得到的像素位置进行插值计算得到的。

通常情况下，牛顿迭代法可以求解图像中任何一个像素点的位置，而且对于图像处理中的任何问题（如图像缩放、旋转、纠正等），都可以使用牛顿迭代法。

一个典型的例子是：我们知道图像中某一个像素点的位置和颜色值，但是我们想要得到缩放后该像素点的位置和颜色值。

这时候，通过插值计算，我们可以得到该像素点在缩放后的位置。

然而，插值计算得到的结果可能不是整数，而是一个小数。

因此，我们需要对其进行四舍五入，得到该像素点的最终位置。

对于这个问题，我们可以使用牛顿迭代法来得到更为精确的位置。

如何应用牛顿迭代法在使用牛顿迭代法时，需要注意一些细节。

首先，我们需要先计算导数。

其次，为了使牛顿迭代法能够得到更快的收敛结果，我们通常需要给出一个好的初始值。

最后，我们需要对迭代次数进行限制，以便避免无限循环和降低计算复杂度。

具体而言，我们可以使用以下公式进行牛顿迭代法计算：f(x)-y=0xn+1=xn-f(xn)/f'(xn)其中，xn 是第n 次迭代的结果，xn+1 是第n+1 次迭代的结果。

f(x) 是一个代表原始函数的方程，f'(x) 是 f(x) 的导数。

牛顿迭代法在深度学习中的应用

牛顿迭代法在深度学习中的应用深度学习是一种人工神经网络的延伸，是机器学习的一个分支，近年来被广泛应用于人脸识别、语音识别、自然语言处理等领域，取得了巨大的成功。

牛顿迭代法是一种求函数零点的方法，可以快速逼近函数的根，是一种高效的数值计算方法。

在深度学习中，牛顿迭代法也有着广泛的应用。

一、概述牛顿迭代法又称为牛顿-拉夫逊方法，是一种用于寻找实数或复数方程零点的高精度数值方法。

常用于解决无法通过代数解析求解的方程，例如超越方程。

牛顿迭代法的基本思想是：选取一点x0，通过一系列迭代计算，逐步改进求解结果，直到满足精度要求为止。

牛顿迭代法的优点是收敛速度快，通常只需要几步迭代即可逼近函数的根，是一种高效的数值计算方法。

在深度学习中，牛顿迭代法被广泛应用于模型的优化过程中。

在深度神经网络中，经常需要求解损失函数的最小值，以减小预测结果与实际结果之间的误差。

牛顿迭代法可以用于求解损失函数的最小值，从而提高深度学习的效率和准确性。

二、原理在深度学习中，通常采用的是反向传播算法来求解损失函数的最小值。

反向传播算法是一种计算梯度的方法，通过将误差反向传播至网络每一层，计算出每一层的梯度，并使用梯度下降法来更新网络的参数，以减小损失函数的值。

传统的梯度下降法通常有以下两种实现方式：1. 批量梯度下降法（Batch Gradient Descent）批量梯度下降法是在每一次迭代中，计算整个训练集的梯度，从而更新网络的参数。

由于需要计算整个训练集的梯度，因此在大数据集上，批量梯度下降法的计算开销非常大，训练速度很慢。

2. 随机梯度下降法（Stochastic Gradient Descent）随机梯度下降法是在每一次迭代中，计算一个样本的梯度，并更新网络的参数。

由于只需要计算一个样本的梯度，因此计算开销非常小，训练速度很快。

但是，由于每个样本的梯度存在噪声，因此随机梯度下降法的路径可能不是最优的，存在震荡现象。

为了解决上述方法的不足，通常采用更为先进的优化算法，例如牛顿法、拟牛顿法、共轭梯度法等。

牛顿迭代法在互联网技术中的应用

牛顿迭代法在互联网技术中的应用随着互联网技术的发展，越来越多的问题需要使用数值计算的方法来解决，而牛顿迭代法作为一种经典的数值优化算法，在互联网技术中发挥着重要的作用。

一、牛顿迭代法简介牛顿迭代法又称为牛顿-拉弗森方法，是一种求解非线性方程的数值方法。

该方法是基于泰勒级数展开的，通过一阶和二阶导数的信息来逼近函数，并迭代求解方程。

牛顿迭代法的特点是收敛速度快，但需要一定的初值估计和求解导数。

二、牛顿迭代法在互联网搜索中的应用在互联网搜索中，热词联想和智能提示是非常重要的功能。

其中，热词联想是指在用户输入关键词时，搜索引擎会根据用户输入的前缀，展示相关的热门关键词。

而智能提示则是在用户输入过程中，根据用户的输入和搜索历史，在下拉框中显示相关的搜索建议。

这些功能的实现涉及到字符串匹配和模式匹配，而牛顿迭代法可以用来求解这些问题。

针对热词联想，我们可以将搜索引擎已经存储的关键词定义为一个函数，通过牛顿迭代法来迭代优化这个函数的导数，来获得下一个热门关键词。

而对于智能提示，我们可以建立模型，并通过牛顿迭代法来求解优化问题，得到最合适的搜索建议。

三、牛顿迭代法在互联网广告投放中的应用在互联网广告投放中，广告主需要确定适当的广告出价才能在广告拍卖中获得流量。

而广告出价的确定需要考虑到竞价者的广告出价和广告质量得分等因素。

这时，我们可以使用牛顿迭代法来求解最优的出价。

我们可以将关键词的质量得分定义为一个函数，并通过求解这个函数的最优解来确定关键词的最佳出价。

同时，为了避免出价过高或过低，我们可以通过牛顿迭代法来逐步逼近最优解，以达到最优出价。

四、牛顿迭代法在机器学习中的应用在互联网技术中，机器学习是一个热门的研究领域，机器学习模型的拟合也是一个需要用到数值优化方法的场景。

牛顿迭代法作为一种优化算法，可以用来求解机器学习中的拟合问题。

在机器学习中，我们可以构建代价函数来评估模型的预测能力，然后通过牛顿迭代法来迭代优化模型参数，以提高模型的预测能力。

牛顿迭代法在天线定位上的运用概要

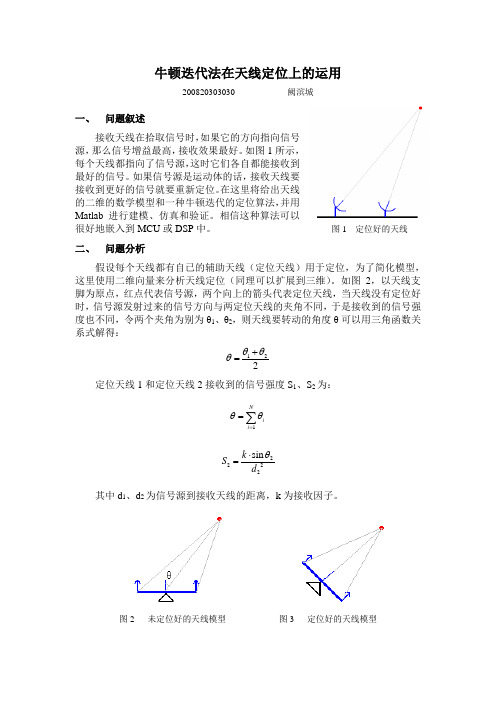
牛顿迭代法在天线定位上的运用200820303030 阙滨城一、问题叙述接收天线在拾取信号时，如果它的方向指向信号源，那么信号增益最高，接收效果最好。

如图1所示，每个天线都指向了信号源，这时它们各自都能接收到最好的信号。

如果信号源是运动体的话，接收天线要接收到更好的信号就要重新定位。

在这里将给出天线的二维的数学模型和一种牛顿迭代的定位算法，并用Matlab 进行建模、仿真和验证。

相信这种算法可以很好地嵌入到MCU 或DSP 中。

图1 定位好的天线二、问题分析假设每个天线都有自已的辅助天线（定位天线）用于定位，为了简化模型，这里使用二维向量来分析天线定位（同理可以扩展到三维）。

如图2，以天线支脚为原点，红点代表信号源，两个向上的箭头代表定位天线，当天线没有定位好时，信号源发射过来的信号方向与两定位天线的夹角不同，于是接收到的信号强度也不同，令两个夹角为别为θ1、θ2，则天线要转动的角度θ可以用三角函数关系式解得：122θθθ+=定位天线1和定位天线2接收到的信号强度S 1、S 2为：1Ni i θθ==∑2222sin k S d θ⋅=其中d 1、d 2为信号源到接收天线的距离，k 为接收因子。

图2 未定位好的天线模型图3 定位好的天线模型在这里涉及的变量较多，如果要全部求出这些变量，在这个模型下不太可能，而且没有必要。

但是这个模型可以很好地运用重定位后接收到的信号强度来迭代计算角度，并通过累加旋转角来计算出角度，当计算出角度时，此时的天线也定位好了。

由于变量多，条件少，在这里可以用辅助天线接收到的信号强度相同来判断天线是否定位好。

即：12S S ≈而在寻求两信号强度相等的同时，这些中间过程天线旋转的角度的累加可以计算出偏角θ：1Ni i θθ==∑其中θi 为第i 次旋转时的所旋转的角度，N 为从不稳定开始计数到转到定位好时的旋转次数，通过N 也可以算出这次从新定位所用的时间。

t N T =⋅下面用流程图来表示此过程：图4 算法流程图其中，流程图中的S 1==S 2 是在一定的容差情况下近似相等情况，为了加快迭代算法的收敛，这里的θ加减值可以根据S 1和S 2的比值大小来确定。

语音信号识别基于盲源信号分离的实现

语音信号识别基于盲源信号分离的实现张敏;于海燕;武克斌【摘要】The blind source separation (BSS) is usually used to distinguish two-channel sound signals of spectrum aliasing, but it is difficult to achieve in engineering practice. Therefore, a method which makes use of the principle and feature of blind source signal separation is introduced. The technological process to implement BSS with FastICA algorithm on ADSP_BF533 platform is described. The proposed scheme in this paper eonsumes less time, needs less memory and is high efficient.%为了识别两路频谱混叠语音信号,多采用盲信号分离的方法.但是该方法在工程实践中实现较困难.因此给出了一种利用盲源信号分离的原理及特点的实现方法,具体说明了用FastICA算法在ADSP_BF533平台上实现盲源信号分离时的具体流程.该设计方案所需时间短,效率高,而且占用内存较少.【期刊名称】《现代电子技术》【年(卷),期】2011(034)011【总页数】4页(P79-81,84)【关键词】盲信号分离;DSP;FastICA;ADSP_BF533平台【作者】张敏;于海燕;武克斌【作者单位】哈尔滨工业大学,威海,山东威海264209;哈尔滨工业大学,威海,山东威海264209;哈尔滨工业大学,威海,山东威海264209【正文语种】中文【中图分类】TN971.2-340 引言近年来，许多学者都针对盲信号分离不断地提出新的理论算法，盲信号分离(BSS)发展也日趋完善。

一种新的盲自适应拟Newton迭代Kalman滤波MUD检测器

一种新的盲自适应拟Newton迭代Kalman滤波MUD检测器高维廷;李辉;翟海天【期刊名称】《计算机工程与应用》【年(卷),期】2012(048)011【摘要】针对ISI、MAI并存情况下码分多址系统盲自适应Kalman滤波算法检测稳定性不足的问题进行了研究,结合Newton迭代法提出了一种适于多径信道下DS-CDMA系统的盲自适应拟Newton迭代Kalman滤波MUD算法.该算法能够在进行状态滤波的同时对未知噪声的统计特性进行在线估计,确保算法能够有效收敛于期望用户提高了检测算法在动态条件下的用户跟踪能力.仿真结果表明,BN-Kalman算法具有更好的收敛性和动态性能.%The blind multiuser detection algorithm of CDMA(Code Division Multiple Access) system is studied under the condition with ISI, MAI and FNP. A new BN-Kalman algorithm to multipath CDMA system is proposed. The algorithm can estimate the unknown noise statistics characteristics on-line while conducting state filtering, and an efficient iterative implementation that provides very fast convergence under this representation is presented. Simulation results show that the new algorithm has the better tracking capability under the dynamic environment and convergence ability than Kalman algorithm.【总页数】4页(P115-118)【作者】高维廷;李辉;翟海天【作者单位】西北工业大学电子信息学院,西安710072;西北工业大学电子信息学院,西安710072;西北工业大学电子信息学院,西安710072【正文语种】中文【中图分类】TP393【相关文献】1.一种盲自适应RLS多用户检测器 [J], 周义建;王永民2.一种基于盲自适应卡尔曼滤波的多用户检测器 [J], 史朋;李辉;任梦颖3.一种改进的kalman滤波器盲自适应多用户检测 [J], 苏锐;赵来定;王视环4.基于子空间的Kalman滤波盲自适应多用户检测器 [J], 杜晓宇;王华奎;史永超5.在新条件下拟Newton迭代方法的收敛性 [J], 李晓霞因版权原因，仅展示原文概要，查看原文内容请购买。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

牛顿迭代在盲信号处理中的应用
作者：徐勇
来源：《科教导刊》2013年第25期
摘要本文对盲信号处理中的ICA算法作了简要介绍，并主要关注了其中能实现快速收敛的FastICA算法，而该算法的核心其实就是利用了反演理论中的牛顿迭代法，指出了算法的优点。

最后进行了仿真以验证算法的实际效果。

关键词反演理论盲分离FastICA
中图分类号：TP301.6 文献标识码：A
0 引言
盲源分离（BSS：Blind source separation）一直信号处理中的热点问题。

BSS指在仅了解观测信号的情况下，利用一些算法恢复经混合系统混合的源信号的过程。

所谓的“盲”，指我们只知道观测值，没有其他先验信息。

也就是说，除了观测的结果外，没有其他信息帮助我们去寻找原始的信号。

这种情况下，想把原始信号准确地找到，显然是需要信号的一些其它特征的。

独立分量分析（ICA）是盲分离问题中的代表性方法。

它假设原始信号之间是独立的，然后利用一些算法从混合信号中恢复原始信号。

也就是说，ICA的前提是在任何时刻，源信号的各分量之间独立。

这就说明了盲信号的分离就是使分离的各信号满足独立性。

通常来说，ICA 问题通过目标函数寻优实现。

所谓的目标函数是指，为了将问题数值化，我们需要用函数来表现问题所需要达到的目标。

比如，我们在经济问题中，为了弄清楚最大利润问题，可以去设定一个表示利润的函数，通过寻找该函数的驻点来找到让利润最大的条件，该函数就是一个目标函数。

目标函数寻优与让问题得以解决是等价的。

简而言之，就是用函数的寻优来数值化实际问题的目标。

不过，想直接用函数的形式来表现信号的独立，从而产生目标函数是得不偿失的。

因为，在数学上表现信号的独立，不可避免地需要使用信号的密度函数。

由于先验信息的缺失，我们是不知道各信号的密度函数的。

有些可以估计信号密度函数的方法，但这些方法普遍过于复杂，会使得问题的表述十分繁琐，不便求解。

所以直接构造表现信号独立性的目标函数是不可行的，因此，一些等价于表现信号独立性，且计算方便可行的目标函数就显得尤为必要了。

比如，我们可以通过互信息函数来等价地表现信号的独立。

所谓的互信息，是指信号之间相互包含的信息，顾名思义，信号的独立性越强，互信息应该是越少的。

所以我们可以通过对互信息函数寻优（即寻找互信息的最小值点），来表现信号之间的独立性。

另外，我们还可以通过信息传输最大化来表现信号的独立性。

1 FastICA的原理
实际上FastICA是基于信息论的。

根据目标函数的不同和寻优的算法特点可以构成各种类型ICA算法。

ICA方法可归结为如下构成：ICA过程=目标函数+寻优算法。

1.1 数据的预处理
在实际问题中，获取的观测数据之间都具备相关性，因此一般都要求对观测数据进行白化或球化处理，因为白化处理可消除观测信号之间的相关性，因此简化了后面独立分量的提取。

从实际效果上说，对信号进行白化处理与不对信号进行白化处理相比，恢复算法的收敛性更好。

如果零均值的随机向量 = 满足{} = ，且为单位矩阵，称这个向量为白化（球化）向量。

白化的意义在于去除对象之间的相关性。

白化作为ICA过程中的预处理模块可以极大地降低问题的复杂度，并且实现数据的白化比较简单，用一般的主成分分析就可实现。

1.2 FastICA算法
FastICA算法，是一种能很快找到最优点的基于迭代思想的算法。

由于它利用了固定点迭代的思想，使得收敛更加快速、稳健。

FastICA算法将负熵最大化作为寻优目标。

对于一些独立的随机变量的线性组合，它们的任意线性组合较它们本身更接近高斯分布。

换句话说，原始信号比混合信号表现出的非高斯性会更强。

综上所述，在信号分离过程中，可通过对信号分离结果的非高斯性度量来表示恢复信号间的相互独立性，当非高斯性度量达到最大值时，表示各独立分量的分离已经实现。

如果要估计个独立分量，可以按以下流程完成：
（1）对观测数据进行零均值化，即使观（下转第201页）（上接第194页）测值的均值为0；
（2）对观测数据进行白化过程，记白化后的结果为；
（3）记录独立分量的个数和迭代次数，且初始化 = 1；
（4）随机选取一个初始权向量，记为，作为独立分量的初始值；
（5）令 = {（）}{（）}，其中为待定的非线性函数，关于的选取见[2]；
（6） = （）；
（7）令 = / ||||；
（8）若不收敛的话，返回（5）；
（9）令迭代次数 = + 1，若≤，返回（4）。

FastICA算法与其他的恢复信号算法相比，有这些优点：
（1）算法收敛速度相对于其他算法更快，初始值选取得当的话，4到5步迭代往往就能收敛，且运行时间很短。

（2）和一些需要选择步长参数的梯度算法不同，与步长参数无关，无需调整这些参数，从而使得算法便于实现。

（3）非线性函数的选择可以多样化，不影响分离非高斯性的独立分量的效果。

相对于其他算法而言，概率密度函数的估计可以省略，大大降低复杂度。

（4）算法结合神经算法的特点，是各分量并行的、分布式的算法，对机器内存要求很低。

2 针对FastICA算法的仿真
产生三个人工源信号（）,（）,（），分别服从均匀分布，拉普拉斯分布以及高斯分布。

先对三个源信号采取线性混合，其中以随机生成的三阶高斯矩阵为混合矩阵。

混合后，采取FastICA进行迭代，为使得结果的准确性，对源信号采样1000个点，迭代也进行1000次。

分离结果表明，尽管振幅，顺序与源信号不同，但波形得到了较好的恢复，我们也可以清晰地辨认分离信号与源信号之间的对应关系。

而振幅，顺序的不同正是FastICA算法的特征。

当然，如果想要更精确地知道分离效果，我们可以通过一些评价指标来评价分离效果，比如相似系数矩阵。

相似系数矩阵中各行不同列的那个绝对值最接近1的元素衡量了恢复信号与源信号的相似程度，在本例中我们计算三组信号的相似系数矩阵后得到，在三阶的相似系数矩阵中，位于三行且不同列的绝对值最接近1的三个元素分别是-0.9912,0.9994，-0.9967。

这说明分离效果已经相当好了。

当然，用来衡量分离效果的指标还有一些，比如我们也可以采用性能矩阵来表示分离效果。

牛顿迭代在此算法中最重要的作用是让计算变得简单，收敛非常快。

通常情况下，只要初值向量选择合适，只需3到4次迭代就可达到收敛的效果。

所以牛顿迭代极大地发展了ICA问题，使之向前迈进了一大步。

我们可以将这种方法与其他恢复信号的算法比较。

比如我们用被广泛认可的Infomax算法去恢复原始信号，实验表明，针对同样的原始信号，Infomax算法需要迭代到1000多步，其结果才趋于收敛。

这种差别使得牛顿迭代法的优势在原始信号较多时体现得更为明显。

这种快速收敛的算法的应用前景非常广阔。

接收器可视为一个混合系统，接收器收到的信号可视为观测信号，这也是我们能用来分析的唯一数据。

地质工作者需要从接收器接收的信号
中，去将各个地层或地质结构对应的反射信号分离出来，这样就可以让我们在不深入地表以下的情况下，仅由分离结果来判断地表以下的各地层是怎样的，各个地层的地质结构具有怎样的特征。

而这种分离过程，实际上就是我们前面所说的盲分离问题了。

鉴于地震信号的多样性，复杂性，快速稳健的分离算法就显得尤为重要了。

牛顿迭代正是满足这一要求的优良算法。