2011年普通高等学校招生全国统一考试数学卷(全国新课标.理)含答案

合集下载

2011年普通高等学校招生全国统一考试理科数学(必修+选修Ⅱ)

ＡＢ＝２ＡＣ＝ＢＤ＝１贝至平面，，０ＵＤ的
１．１）。３（一的二项展开式中，的系数与Ｘ
Ｘ的系数之差为０
．
— —
距离等于 … … … … … … … … … … … … 一（）
（Ａ）
；（）；（）；（）．ＢｃＤ１
（５已知Ｆ、Ｆ分别为双曲线：１）１２
Ｉ
一
２
＝
１的左、右焦点，Ａ ∈Ｃ，点点Ｍ的坐标
（４Ａ）种；（）０（）８（２种．Ｂ１种；Ｃ１种；Ｄ）０（）曲线＝ｅ＋１点（，２处的切８在０）
线与直线Ｙ＝０Ｙ＝围成的三角形的面积和
为（，）２０，
为ＦＦ的平分线，ＩＦｌｌ２则Ａ２＝
（６已知点、Ｆ分别在正方体Ａ１）ＢＣＤ
２
数学数学
２１年第７０１期
ＡＢ１１的棱ＢＢ、１且ＢＥ＝２Ｂ，１ＣＤ１１ＣＣ上，１ＥＦ＝２Ｃ，Ｆ１则面ＥＦ与面ＡＢＣ所成的二面角的正切值等于— — ．三、解答题：本大题共６小题，７分．解共０
（０１）已知抛物线Ｃ：Ｙ＝４的焦点为ｘＦ，直线Ｙ＝２ｘ一４与交于、Ｂ两点，则
ＣＳＡＦ＝……………………………………一）ＯＺＢ（
（）＿（Ｒ）（）Ａｙ ∈ ；Ｂ＝兰（）－＿ ≥０；（）＝４ ∈ ；（ｙ４Ｘ）ＣＹｘ（Ｒ）Ｄ）＿ｘ（≥０．－（）３下面四个条件中，使ａ＞６成立的充分而

2011年普通高等学校招生全国统一考试数学卷(湖南.理)含详解

2011年普通高等学校招生全国统一考试（湖南卷）数学（理工农医类）本试题卷包括选择题、填空题和解答题三部分，共6页，时量120分钟，满分150分。

参考公式：（1）()()()P AB P B A P A =，其中,A B 为两个事件，且()0P A >，（2）柱体体积公式V Sh =，其中S 为底面面积，h 为高。

（3）球的体积公式343V R π=，其中R 为求的半径。

一选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项符合题目要求的。

1.若,a b R ∈，i 为虚数单位，且()a i i b i +=+，则（）A ．1,1a b ==B ．1,1a b =-=C ．1,1a b =-=-D ．1,1a b ==- 答案：D解析：因()1a i i ai b i +=-+=+，根据复数相等的条件可知1,1a b ==-。

2.设{1,2}M =，2{}N a =，则“1a =”是“N M ⊆”则（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件 D ．既不充分又不必要条件答案：A解析：因“1a =”，即{1}N =，满足“N M ⊆”，反之“N M ⊆”，则2{}={1}N a =，或2{}={2}N a =，不一定有“1a =”。

3.设图一是某几何体的三视图，则该几何体的体积为（）A ．9122π+B ．9182π+C ．942π+D ．3618π+答案：B解析：有三视图可知该几何体是一个长方体和球构成的组合体，其体积3439+332=18322V ππ=⨯⨯+（）。

4.通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：男女总计爱好 40 20 60 不爱好 20 30 50 总计 60 50 110由22()()()()()n ad bc K a b c d a c b d -=++++算得22110(40302020)7.860506050K ⨯⨯-⨯=≈⨯⨯⨯ 附表：正视图侧视图俯视图图12()P K k ≥ 0.0500.010 0.001 k3.8416.63510.828参照附表，得到的正确结论是（）A ．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”B ．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”C ．有99%以上的把握认为“爱好该项运动与性别有关”D ．有99%以上的把握认为“爱好该项运动与性别有关” 答案：C解析：由27.8 6.635K ≈>，而2( 6.635)0.010P K ≥=，故由独立性检验的意义可知选C.5.设双曲线2221(0)9x y a a -=>的渐近线方程为320x y ±=，则a 的值为（） A ．4 B ．3 C ．2 D ．1答案：C解析：由双曲线方程可知渐近线方程为3y x a=±，故可知2a =。

2011年四川高考数学试题理科(含答案)

2011年普通高等学校招生全国统一考试(四川卷)数学(理工类)本试卷分第一部分(选择题)和第二部分(非选择题)。

第一部分1至2页，第二部分3至4页，共4页．考生作答时，须将答案答在答题卡上及试题卷，草稿纸上答题无效，满分150分，考试时间120分钟。

考试结束后，将本试卷和答题卡一并交回. 参考公式：如果事件A 、B 互斥，那么球的表面积公式 P(A+B) =P(A)+P(B) 24s R π= 如果事件A 、B 相互独立，那么其中R 表示球的半径 P(A·B)=P(A)·P(B) 球的体积公式如果事件A 在一次试验中发生的概率是p ，那么 243v R π=在n 次独立重复试验中事件A 恰好发生k 次的概率其中R 表示球的半径n ()(1)(0,1,2,...)k k n k n P k C p p k n -=-=第一部分（选择题共60分）注意事项：1.选择题必须使用2B 铅笔将答案标号填涂在答题卡上对应题目标号的位置上。

2.本部分共12小题，每小题5分，共60分。

一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

（11四川理1）有一个容量为66的样本，数据的分组及各组的频数如下： [11.5，15.5) 2 [15.5,19.5) 4 [19.5，23．5) 9 [23.5,27.5) 18 [27.5，31.5) 1l [31.5，35.5) 12 [35.5．39.5) 7 [39.5,43.5) 3 根据样本的频率分布估计，数据落在[31.5，43.5)的概率约是(A)16 (B)13 (C)12 （D ）23（11四川理2）复数1i i-+=(A)2i - （B ）12i （C ）0 （D ）2i（11四川理3）1l ，2l ，3l 是空间三条不同的直线，则下列命题正确的是 (A)12l l ⊥，23l l ⊥13l l ⇒ （B ）12l l ⊥，23l l ⇒13l l ⊥[来源:](C)233l l l ⇒ 1l ，2l ，3l 共面（D ）1l ，2l ，3l 共点⇒1l ，2l ，3l 共面（11四川理4）如图，正六边形ABCDEF 中，BA CD EF ++= (A)0 (B)BE (C)AD (D)CF（11四川理5）函数，()f x 在点0x x =处有定义是()f x 在点0x x =处连续的(A)充分而不必要的条件 (B)必要而不充分的条件 (C)充要条件 (D)既不充分也不必要的条件（11四川理6）在ABC ∆中．222sin sin sin sin sin B C B C ≤+-.则A 的取值范围是 (A)(0，6π] (B)[ 6π，π) (c)(0，3π] (D) [ 3π，π) （11四川理7）已知()f x 是R 上的奇函数，且当0x >时，1()()12xf x =+，则()f x 的反函数的图像大致是（11四川理8）数列{}n a 的首项为3，{}n b 为等差数列且1(*)n n n b a a n N +=-∈ .若则32b =-，1012b =，则8a =（A ）0 （B ）3 （C ）8 （D ）11（11四川理9）某运输公司有12名驾驶员和19名工人，有8辆载重量为10吨的甲型卡车和7辆载重量为6吨的乙型卡车.某天需运往A 地至少72吨的货物，派用的每辆车虚满载且只运送一次.拍用的每吨甲型卡车虚配2名工人，运送一次可得利润450元；派用的每辆乙型卡车虚配1名工人，运送一次可得利润350元.该公司合理计划党团派用两类卡车的车辆数，可得最大利润（A ）4650元（B ）4700元（C ）4900元（D ）5000元（11四川理10）在抛物线25(0)y x ax a =+-≠上取横坐标为14x =-，22x =的两点，过这两点引一条割线，有平行于该割线的一条直线同时与抛物线和圆225536x y +=相切，则抛物线顶点的坐标为（A ）(2,9)-- （B ）(0,5)- （C ）(2,9)- （D ）(1,6)- （11四川理11）已知定义在[)0,+∞上的函数()f x 满足()3(2)f x f x =+，当[)0,2x ∈时，2()2f x x x =-+.设()f x 在[)22,2n n -上的最大值为(*)n a n N ∈，且{}n a 的前n 项和为n S ，则lim n n S →∞=（A ）3 （B ）52 （C ）2 （D ）32（11四川理12）在集合{}1,2,3,4,5中任取一个偶数a 和一个奇数b 构成以原点为起点的向量(,)a b α=.从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形.记所有作成的平行四边形的个数为n ，其中面积不超过．．．4的平行四边形的个数为m ，则m n=（A ）415 （B ）13 （C ）25 （D ）23二、填空题：本大题共4小题，每小题4分，共16分.（11四川理13）计算121(lg lg 25)100=4--÷ .（11四川理14）双曲线22x y =1P 46436-上一点到双曲线右焦点的距离是，那么点P 到左准线的距离是 .（11四川理15）如图，半径为R 的球O 中有一内接圆柱.当圆柱的侧面积最大时，球的表面积与改圆柱的侧面积之差是 .（11四川理16）函数()f x 的定义域为A ，若12,x x A ∈且12()()f x f x =时总有12x x =，则称()f x 为单函数，例如，函数()21()f x x x R =+∈是单函数.下列命题： ① 函数2()()f x x x R =∈是单函数；② 若()f x 为单函数，12,x x A ∈且12x x ≠，则12()()f x f x ≠；③ 若f ：A →B 为单函数，则对于任意b B ∈，它至多有一个原象； ④ 函数()f x 在某区间上具有单调性，则()f x 一定是单函数. 其中的真命题是 .（写出所有真命题的编号）三、解答题（11四川理17）已知函数73()sin()cos(),44f x x x x R ππ=++-∈ (1)求()f x 的最小正周期和最小值；（2）已知44cos(),cos(),(0)552a πββααβ-=+=-<<≤，求证：2[()]20f β-=（11四川理18）本着健康、低碳的生活理念，租自行车骑游的人越来越多。

2011年高考数学文科试卷(全国1卷)(含答案)(新课标卷卷)

绝密★启用前2011年普通高等学校招生全国统一考试文科数学(必修+选修I)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。

第Ⅰ卷1至2页。

第Ⅱ卷3至4页。

考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷注意事项：1．答题前，考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚，并贴好条形码.请认真核准条形码上的准考证号、姓名和科目.2．每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动,用橡皮擦干净后，再选涂其他答案标号，在试．．题卷上作答无效．．．．．．．. 3．第Ⅰ卷共l2小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的.一、选择题(1)设集合U={}1,2,3,4,{}1,2,3,M ={}2,3,4,N =则U =（M N ）I ð （A ）{}12，（B ）{}23，（C ）{}2，4 （D ）{}1，4(2)函数2(0)y x x =≥的反函数为（A ）2()4x y x R =∈ （B ）2(0)4x y x =≥ （C ）24y x =()x R ∈ （D ）24(0)y x x =≥.(3)设向量,a b 满足||||1a b == ,12a b ⋅=-r r ,则2a b += （A ）2 （B ）3 （C ）5 （D ）7(4)若变量x ，y 满足约束条件63-21x y x y x +≤⎧⎪-≤⎨⎪≥⎩，则=23z x y +的最小值为（A ）17 （B ）14 （C ）5 （D ）3(5)下面四个条件中，使a b >成立的充分而不必要的条件是Cβαl A BD（A ）1a b +＞（B ）1a b -＞（C ）22a b ＞（D ）33a b ＞(6)设n S 为等差数列{}n a 的前n 项和，若11a =，公差2d =，224k k S S +-=，则k =（A ）8 （B ）7 （C ）6 （D ）5(7)设函数()cos (0)f x x ωω=>，将()y f x =的图像向右平移3π个单位长度后，所得的图像与原图像重合，则ω的最小值等于（A ）13（B ）3 （C ）6 （D ）9 (8)已知直二面角l αβ--,点A α∈，AC l ⊥,C 为垂足,B β∈，BD l ⊥,D 为垂足,若2,1AB AC BD ===，则CD =（A ） 2 （B ）3 （C ）2 （D ）1 (9) 4位同学每人从甲、乙、丙3门课程中选修1门，则恰有2人选修课程甲的不同选法共有(A) 12种 (B) 24种 (C) 30种 (D)36种 (10) 设()f x 是周期为2的奇函数，当01x ≤≤时，()f x =2(1)x x -,则5()2f -= (A) -12 (B)1 4- (C)14 (D)12 (11)设两圆1C 、2C 都和两坐标轴相切，且都过点（4，1），则两圆心的距离12C C =(A)4 (B)42 (C)8 (D)82(12)已知平面α截一球面得圆M ，过圆心M 且与α成060二面角的平面β截该球面得圆N .若该球面的半径为4，圆M 的面积为4π，则圆N 的面积为(A)7π (B)9π (C)11π (D)13π第Ⅱ卷注意事项：1答题前，考生先在答题卡上用直径0．5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚，然后贴好条形码。

2011年普通高等学校招生全国统一考试数学卷(广东.文)含详解

绝密★启用前试卷类型：B2011年普通高等学校招生全国统一考试（广东卷）线性回归方程 y bxa =+ 中系数计算公式121()()()niii nii x x y y b x x ==--=-∑∑ ， ay bx =- ，样本数据12,,,n x x x 的标准差，222121[()()()]n s x x x x x x n=-+-++- ，其中x ，y 表示样本均值．n 是正整数，则1221()()n n n n n n a b a b a a b ab b -----=-++++ ．一、选择题：本大题共10小题，每小题5分，满分50分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．设复数z 满足1iz =，其中i 为虚数单位，则z =A ．i -B ．iC ．1-D ．1 2．已知集合{(,)|,A x y x y =为实数，且221}x y +=，{(,)|,B x y x y =为实数，且1}x y +=，则A B ⋂的元素个数为A ．4B ．3C ．2D ．1 3．已知向量(1,2),(1,0),(3,4)===a b c ．若λ为实数，()λ+a b ∥c ，则λ=A ．14 B ．12C ．1D ．2 4．函数1()lg(1)1f x x x=++-的定义域是 A ．(,1)-∞- B ．(1,)+∞ C ．(1,1)(1,)-⋃+∞ D ．(,)-∞+∞5．不等式2210x x -->的解集是A ．1(,1)2-B ．(1,)+∞C ．(,1)(2,)-∞⋃+∞D ．1(,)(1,)2-∞-⋃+∞ 6．已知平面直角坐标系xOy 上的区域D 由不等式组0222x y x y⎧⎪⎨⎪⎩≤≤≤≤给定．若(,)M x y 为D 上的动点，点A的坐标为(2,1)，则z OM OA=⋅的最大值为A ．3B ．4C ．32D ．4223正视图图1侧视图图22 俯视图 2图37．正五棱柱中，不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线，那么一个正五棱柱对角线的条数共有A ．20B ．15C ．12D ．10 8．设圆C 与圆22(3)1x y +-=外切，与直线0y =相切，则C 的圆心轨迹为A ．抛物线B ．双曲线C ．椭圆D ．圆 9．如图1 ~ 3，某几何体的正视图（主视图），侧视图（左视图）和俯视图分别是等边三角形，等腰三角形和菱形，则该几何体的体积为 A ．43 B ．4 C ．23 D ．210．设(),(),()f x g x h x 是R 上的任意实值函数，如下定义两个函数()f g ()x 和()f g ()x ：对任意x ∈R ，()f g ()x =(())f g x ；()f g ()x =()()f x g x ，则下列等式恒成立的是A ．(()f g h )()x =(()f h ()g h )()xB ．(()f g h )()x =(()f h ()g h )()xC ．(()f g h )()x =(()f g ()g h )()xD ．(()f g h )()x =(()f g()g h )()x二、填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分．（一）必做题（9 ~ 13题）11．已知{}n a 是递增的等比数列，若22a =，434a a -=，则此数列的公比q = ．12．设函数3()cos 1f x x x =+．若()11f a =，则()f a -= ．13．为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系，下表记录了小李某月1号到5号每天打篮球时间x （单位：小时）与当天投篮命中率y 之间的关系：图4BAC DEF时间x 1 2 3 4 5 命中率y0.40.50.60.60.4小李这5天的平均投篮命中率为；用线性回归分析的方法，预测小李该月6号打6小时篮球的投篮命中率为．（二）选做题（14 ~ 15题，考生只能从中选做一题）14．（坐标系与参数方程选做题）已知两曲线参数方程分别为5cos sin x y θθ⎧=⎪⎨=⎪⎩(0)θπ<≤和254x t y t⎧=⎪⎨⎪=⎩(t ∈)R ，它们的交点坐标为___________．15．（几何证明选讲选做题）如图4，在梯形ABCD 中，AB ∥CD ，4AB =，2CD =，,E F 分别为,AD BC 上的点，且3EF =， EF ∥AB ，则梯形ABFE 与梯形EFCD 的面积比为________．三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 16．（本小题满分12分）已知函数1()2sin()36f x x π=-，x ∈R ．（1）求(0)f 的值；（2）设,0,2παβ⎡⎤∈⎢⎥⎣⎦，10(3)213f πα+=，6(32)5f βπ+=，求sin()αβ+的值．17．（本小题满分13分）在某次测验中，有6位同学的平均成绩为75分．用n x 表示编号为n (1,2,,6)n = 的同学所得成绩，且前5位同学的成绩如下：编号n 1 2 3 4 5 成绩n x7076727072（1）求第6位同学的成绩6x ，及这6位同学成绩的标准差s ；（2）从前5位同学中，随机地选2位同学，求恰有1位同学成绩在区间（68，75）中的概率．18．（本小题满分13分）图5所示的几何体是将高为2，底面半径为1的直圆柱沿过轴的平面切开后，将其中一半沿切面向右BAB 'A 'CC 'DD 'EE 'G H '1O2O1O '2O '图5水平平移后得到的．,,,A A B B ''分别为 CD , C D '', DE , D E ''的中点，1122,,,O O O O ''分别为CD ,C D '', DE ,D E ''的中点．（1）证明：12,,,O A O B ''四点共面；（2）设G 为AA '中点，延长1A O ''到H '，使得11O H A O ''''=．证明：2BO '⊥平面H B G ''．19．（本小题满分14分）设0a >，讨论函数2()ln (1)2(1)f x x a a x a x =+---的单调性． 20．（本小题满分14分）设0b >，数列{}n a 满足1a b =，111n n n nba a a n --=+-(n ≥2)．（1）求数列{}n a 的通项公式；（2）证明：对于一切正整数n ，2n a ≤11n b ++．21．（本小题满分14分）在平面直角坐标系xOy 上，直线l ：2x =-交x 轴于点A ．设P 是l 上一点，M 是线段OP 的垂直平分线上一点，且满足MPO AOP ∠=∠．（1）当点P 在l 上运动时，求点M 的轨迹E 的方程；（2）已知(1,1)T -，设H 是E 上动点，求HO HT +的最小值，并给出此时点H 的坐标；（3）过点(1,1)T -且不平行于y 轴的直线1l 与轨迹E 有且只有两个不同的交点，求直线1l 的斜率k 的取值范围．1．（A ）．1()iz i i i i -===-⨯- 2．（C ）．A B ⋂的元素个数等价于圆221x y +=与直线1x y +=的交点个数，显然有2个交点 3．（B ）．(1,2)λλ+=+a b ，由()λ+a b ∥c ，得64(1)0λ-+=，解得λ=124．（C ）．10110x x x -≠⎧⇒>-⎨+>⎩且1x ≠，则()f x 的定义域是(1,1)(1,)-⋃+∞5．（D ）．21210(1)(21)02x x x x x -->⇒-+>⇒<-或1x >，则不等式的解集为1(,)(1,)2-∞-⋃+∞6．（B ）．2z x y =+，即2y x z =-+，画出不等式组表示的平面区域，易知当直线2y x z =-+经过点(2,2)时，z 取得最大值，max 2224z =⨯+=7．（D ）．正五棱柱中，上底面中的每一个顶点均可与下底面中的两个顶点构成对角线，所以一个正五棱柱对角线的条数共有5210⨯=条8．（A ）．依题意得，C 的圆心到点(0,3)的距离与它到直线1y =-的距离相等，则C 的圆心轨迹为抛物线 9．（C ）．该几何体是一个底面为菱形的四棱锥，菱形的面积1223232S =⨯⨯=，四棱锥的高为3，则该几何体的体积112332333V Sh ==⨯⨯= 10．（B ）．11．2． 2243224422402(2)(1)0a a a q a q q q q q -=⇒-=⇒--=⇒-+=2q ⇒=或1q =-∵{}n a 是递增的等比数列，∴2q =12．9-3()cos 111f a a a =+=，即3()cos 10f a a a ==，则33()()cos()1cos 11019f a a a a a -=--+=-+=-+=- 13．0.5；0.53小李这5天的平均投篮命中率1(0.40.50.60.60.4)0.55y =++++= 3x =，1222221()()0.2000.1(0.2)0.01(2)(1)012()niii ni i x x y y bx x ==--++++-===-+-+++-∑∑ ， 0.47a y bx =-=∴线性回归方程 0.010.47y x =+，则当6x =时，0.53y = ∴预测小李该月6号打6小时篮球的投篮命中率为0.5314．25(1,)5．5cos sin x y θθ⎧=⎪⎨=⎪⎩表示椭圆2215x y +=(5501)x y -<≤≤≤且，254x t y t⎧=⎪⎨⎪=⎩表示抛物线245y x =,22221(5501)5450145x y x y x x x y x ⎧+=-<≤≤≤⎪⎪⇒+-=⇒=⎨⎪=⎪⎩且或5x =-（舍去），又因为01y ≤≤，所以它们的交点坐标为25(1,)515．75如图，延长,AD BC ，AD BC P =∵23CD EF =，∴49PCD PEF S S ∆∆= ∵24CD AB =，∴416PCD PEF S S ∆∆= ∴75ABEF EFCDS S =梯形梯形16．解：（1）(0)2sin()16f π=-=-（2）110(3)2sin[(3)]2sin 232613f πππααα+=+-==，即5sin 13α= 16(32)2sin[(32)]2sin()3625f ππβπβπβ+=+-=+=，即3cos 5β=∵,0,2παβ⎡⎤∈⎢⎥⎣⎦， ∴212cos 1sin 13αα=-=，24sin 1cos 5ββ=-= ∴5312463sin()sin cos cos sin 13513565αβαβαβ+=+=⨯+⨯=17．解：（1）61(7076727072)756x +++++=，解得690x = PBAC DEFxy O2x =-AP l MM标准差22222222212611[()()()](5135315)766s x x x x x x =-+-++-=+++++= （2）前5位同学中随机选出的2位同学记为(,)a b ，,{1,2,3,4,5}a b ∈且a b ≠则基本事件有(1,2)，(1,3)，(1,4)，(1,5)，(2,3)，(2,4)，(2,5)，(3,4)，(3,5)，(4,5)共10种这5位同学中，编号为1、3、4、5号的同学成绩在区间（68，75）中设A 表示随机事件“从前5位同学中随机选出2位同学，恰有1位同学成绩在区间（68，75）中” 则A 中的基本事件有(1,2)、(2,3)、(2,4)、(2,5)共4种，则42()105P A == 18．证明：（1）连接2,BO 22,O O '依题意得1122,,,O O O O ''是圆柱底面圆的圆心∴,,,CD C D DE D E ''''是圆柱底面圆的直径∵,,A B B ''分别为 C D '', DE , D E ''的中点∴1290A O D B O D ''''''∠=∠=∴1A O ''∥2BO '∵BB '//22O O '，四边形22O O B B ''是平行四边形∴2BO ∥2BO ' ∴1A O ''∥2BO ∴12,,,O A O B ''四点共面（2）延长1A O '到H ，使得11O H AO ''=，连接1,,HH HO HB '' ∵11O H A O ''''=∴1O H ''//2O B ''，四边形12O O B H ''''是平行四边形 ∴12O O ''∥H B ''∵1222O O O O '''⊥，122O O B O ''''⊥，2222O O B O O ''''= ∴12O O ''⊥面22O O B B ''∴H B ''⊥面22O O B B ''，2BO '⊂面22O O B B '' ∴2BO H B '''⊥易知四边形AA H H ''是正方形，且边长2AA '=∵11tan 2HH HO H O H '''∠==''，1tan 2A G A H G A H '''∠==''∴1tan tan 1HO H A H G ''''∠⋅∠=∴190HO H A H G ''''∠+∠= ∴1HO H G ''⊥易知12O O ''//HB ，四边形12O O BH ''是平行四边形∴2BO '∥1HO '∴2BO H G ''⊥，H G H B H ''''= ∴2BO '⊥平面H B G ''21．解：（1）如图所示，连接OM ，则PM OM =∵MPO AOP ∠=∠，∴动点M 满足MP l ⊥或M 在x 的负半轴上，设(,)M x yxy O 2x =-TN l HNH∙H xy O TA 1l 1l1l① 当MP l ⊥时，2MP x =+，22OM x y =+222x x y +=+，化简得244y x =+(1)x ≥-② 当M 在x 的负半轴上时，0y =(1)x <-综上所述，点M 的轨迹E 的方程为244y x =+(1)x ≥-或0y =(1)x <-（2）由（1）知M 的轨迹是顶点为(1,0)-，焦点为原点的抛物线和x 的负半轴0y =(1)x <- ① 若H 是抛物线上的动点，过H 作HN l ⊥于N由于l 是抛物线的准线，根据抛物线的定义有HO HN = 则HO HT HN HT +=+当,,N H T 三点共线时，HN HT +有最小值3TN =求得此时H 的坐标为3(,1)4--② 若H 是x 的负半轴0y =(1)x <-上的动点显然有3HO HT +>综上所述，HO HT +的最小值为3，此时点H 的坐标为3(,1)4-- （3）如图，设抛物线顶点(1,0)A -，则直线AT 的斜率12AT k =-∵点(1,1)T -在抛物线内部，∴过点T 且不平行于,x y 轴的直线1l 必与抛物线有两个交点则直线1l 与轨迹E 的交点个数分以下四种情况讨论： ① 当12k ≤-时，直线1l 与轨迹E 有且只有两个不同的交点 ② 当102k -<<时，直线1l 与轨迹E 有且只有三个不同的交点 ③ 当0k =时，直线1l 与轨迹E 有且只有一个交点 ④ 当0k >时，直线1l 与轨迹E 有且只有两个不同的交点综上所述，直线1l 的斜率k 的取值范围是1(,](0,)2-∞-+∞。

2011年高考数学文科试卷(全国1卷)(内含答案)(新课标卷卷)

2011年普通高等学校招生全国统一考试一、选择题(1)设集合U={}1,2,3,4,{}1,2,3,M ={}2,3,4,N =则U =（M N ）I ð （A ）{}12，（B ）{}23，（C ）{}2，4 （D ）{}1，4【答案】D【命题意图】本题主要考查集合交并补运算.【解析】{2,3},(){1,4}U M N M N =∴=ðQ I I(2)函数0)y x =≥的反函数为（A ）2()4x y x R =∈ （B ）2(0)4x y x =≥ （C ）24y x =()x R ∈ （D ）24(0)y x x =≥【答案】B【命题意图】本题主要考查反函数的求法. 【解析】由原函数反解得24y x =,又原函数的值域为0y ≥,所以函数0)y x =≥的反函数为2(0)4x y x =≥. (3)设向量,a b 满足||||1a b ==,12a b ⋅=-r r ,则2a b += （A（B（C（D【答案】B 【命题意图】本题主要考查平面向量的数量积与长度的计算方法.【解析】2221|2|||44||14()432a b a a b b +=+⋅+=+⨯-+=r r r r r u r ,所以2a b +=r r (4)若变量x ，y 满足约束条件63-21x y x y x +≤⎧⎪-≤⎨⎪≥⎩，则=23z x y +的最小值为（A ）17 （B ）14 （C ）5 （D ）3【答案】C【命题意图】本题主要考查简单的线性规划.【解析】作出不等式组表示的可行域，从图中不难观察当直线=23z x y +过直线x=1与x-3y=-2的交点（1，1）时取得最小值,所以最小值为5.(5)下面四个条件中，使a b >成立的充分而不必要的条件是（A ）1a b +＞（B ）1a b -＞（C ）22a b ＞（D ）33a b ＞【答案】A【命题意图】本题主要考查充要条件及不等式的性质.【解析】即寻找命题P ,使P a b ⇒>,且a b >推不出P ,逐项验证知可选A.(6)设n S 为等差数列{}n a 的前n 项和，若11a =，公差2d =，224k k S S +-=，则k =（A ）8 （B ）7 （C ）6 （D ）5【答案】D【命题意图】本题主要考查等差数列的基本公式的应用.【解析】解法一2(2)(1)(1)[(2)12][12]442422k k k k k k S S k k k +++--=+⨯+⨯-⨯+⨯=+=，解得5k =. 解法二: 221[1(1)2](12)4424k k k k S S a a k k k +++-=+=++⨯++⨯=+=，解得5k =.(7)设函数()cos (0)f x x ωω=>，将()y f x =的图像向右平移3π个单位长度后，所得的图像与原图像重合，则ω的最小值等于（A ）13（B ）3 （C ）6 （D ）9 【答案】C【命题意图】本题主要考查三角函数的周期性与三角函数图像变换的关系.【解析】由题意将()y f x =的图像向右平移3π个单位长度后，所得的图像与原图像重合，说明了3π是此函数周期的整数倍,得2()3k k Z ππω⨯=∈,解得6k ω=,又0ω>,令1k =,得min 6ω=.(8)已知直二面角l αβ--,点A α∈，AC l ⊥,C 为垂足,B β∈，BD l ⊥,D 为垂足,若2,1AB AC BD ===，则CD =（A ） 2 （B（C （D ）1 【答案】C【命题意图】本题主要考查二面角的平面角及解三角形.【解析】因为l αβ--是直二面角, AC l ⊥,∴AC ⊥平面β,AC BC ∴⊥BC ∴=又BD l ⊥,CD ∴=(9) 4位同学每人从甲、乙、丙3门课程中选修1门，则恰有2人选修课程甲的不同选法共有(A) 12种 (B) 24种 (C) 30种 (D)36种【答案】B【命题意图】本题主要考查两个原理与排列组合知识，考察考生分析问题的能力.【解析】第一步选出2人选修课程甲有246C =种方法，第二步安排剩余两人从乙、丙中各选1门课程有22⨯种选法，根据分步计数原理，有6424⨯=种选法.(10) 设()f x 是周期为2的奇函数，当01x ≤≤时，()f x =2(1)x x -,则5()2f -= (A) -12 (B)1 4- (C)14 (D)12【答案】A【命题意图】本题主要考查利用函数的周期性和奇偶性求函数值的方法. 关键是把通过周期性和奇偶性把自变量52-转化到区间[0,1]上进行求值. 【解析】由()f x 是周期为2的奇函数,利用周期性和奇偶性得:5511111()(2)()()2(1)2222222f f f f -=-+=-=-=-⨯⨯-=-(11)设两圆1C 、2C 都和两坐标轴相切，且都过点（4，1），则两圆心的距离12C C =(A)4 (B)【答案】C【命题意图】本题主要考查圆的方程与两点间的距离公式.【解析】由题意知圆心在直线y=x 上并且在第一象限,设圆心坐标为(,)(0)a a a >,则a =,即210170a a -+=,所以由两点间的距离公式可求出128C C ===.(12)已知平面α截一球面得圆M ，过圆心M 且与α成060二面角的平面β截该球面得圆N .若该球面的半径为4，圆M 的面积为4π，则圆N 的面积为(A)7π (B)9π (C)11π (D)13π【答案】D【命题意图】本题主要考查二面角的概念与球的性质.【解析】如图所示,由圆M 的面积为4π知球心O 到圆M 的距离OM =,在Rt OMN ∆中,30OMN ︒∠=, ∴12ON OM ==故圆N 的半径r ==,∴圆N 的面积为213S r ππ==.第Ⅱ卷注意事项：1答题前，考生先在答题卡上用直径0．5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚，然后贴好条形码。

2011年高考新课标卷文科数学试题(解析版)

2011年普通高等学校招生全国统一考试(新课标全国卷)文科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，其中第Ⅱ卷第22～24题为选考题，其他题为必考题第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{0,1,2,3,4}M =，{1,3,5}N =，P MN =，则P 的子集共有A ．2个B ．4个C ．6个D ．8个【答案】B 【解析】P M N =={1,3}，故P 的子集有224=个．2．复数5i12i=- A ．2i - B ．12i - C ．2i -+ D ．12i -+ 【答案】C 【解析】5i 5i(12i)2i 12i (12i)(12i)+==-+--+． 3．下列函数中，既是偶函数又在(0,)+∞单调递增的函数是A ．3y x =B ．||1y x =+C ．21y x =-+ D ．||2x y -=【答案】B【解析】3y x =为奇函数，21y x =-+在(0,)+∞上为减函数，||2x y -=在(0,)+∞上为减函数，故选B ．4．椭圆221168x y +=的离心率为A ．13 B ．12C D ．2【答案】D【解析】由221168x y +=可知216a =，28b =，∴2228c a b =-=，∴22212c e a ==，∴22e =． 5．执行右面的程序框图，如果输入的N 是6，那么输出的p 是A ．120B ．720C ．1440D ．5040 【答案】B【解析】由程序框图可得，输出的123456720p =⨯⨯⨯⨯⨯=，选B6．有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为 A ．13 B ．12 C ．23 D ．34【答案】A【解析】记三个兴趣小组分别为1、2、3，甲参加1组记为“甲1”，则基本事件为“甲1，乙1；甲1，乙2；甲1，乙3；甲2，乙1；甲2，乙2；甲2，乙3；甲3，乙1；甲3，乙2；甲3，乙3”，共9个．记事件A 为“甲、乙两位同学参加同一个兴趣小组”，其中事件A 有“甲1，乙1；甲2，乙2；甲3，乙3”，共3个．因此31()93P A ==． 7．已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线2y x =上，则cos2θ=A ．45-B ．35-C ．35D ．45【答案】B【解析】由题知tan 2θ=，222222cos sin 1tan 3cos2cos sin 1tan 5θθθθθθθ--===-++，选B ．8．在一个几何体的三视图中，正视图与俯视图如右图所示，则相应的侧视图可以为俯视图正视图DCB A【答案】D【解析】通过正视图及俯视图可看出该几何体为半个圆锥和一个三棱锥组合在一起，故侧视图为D ．9．已知直线l 过抛物线C 的焦点，且与C 的对称轴垂直，l 与C 交于,A B 两点，||AB =12，P 为C 的准线上一点，则ABP ∆的面积为_____．A ．18B ．24C ．36D ．48 【答案】C【解析】设抛物线方程为22y px =，则焦点坐标为(,0)2p ，将2px =代入22y px =可得22y p =，||AB =12，即2p =12，∴p =6．点P 在准线上，到AB 的距离为p =6，所以ABP ∆面积为1612362⨯⨯=． 10．在下列区间中，函数()43xf x e x =+-的零点所在的区间为_____． A ．1(,0)4- B ．1(0,)4 C ．11(,)42 D ．13(,)24【答案】C【解析】因为114411()432044f e e =+⨯-=-<，112211()431022f e e =+⨯-=->，所以()43xf x e x =+-的零点所在的区间为11(,)42．11．设函数()sin(2)cos(2)44f x x x ππ=+++，则 A ．()y f x =在(0,)2π单调递增，其图象关于直线4x π=对称 B ．()y f x =在(0,)2π单调递增，其图象关于直线2x π=对称 C ．()y f x =在(0,)2π单调递减，其图象关于直线4x π=对称 D ．()y f x =在(0,)2π单调递减，其图象关于直线2x π=对称【答案】D【解析】因为()sin(2)cos(2)44f x x x ππ=+++=2sin(2)2x π+=2cos 2x ，所以2cos 2y x =，在(0,)2π单调递减，对称轴为2x k π=，即2k x π=(k ∈Z )．12．已知函数()y f x =的周期为2，当[1,1]x ∈-时2()f x x =，那么函数()y f x =的图象与函数|lg |y x =的图象的交点共有_____．A ．10个B ．9个C ．8个D ．1个【答案】A【解析】画出两个函数图象可看出交点有10个．第Ⅱ卷本卷包括必考题和选考题两部分．第13题-第21题为必考题，每个试题考生都必须做答．第22题-第24题为选考题，考生根据要求做答．二、填空题：本大题共4小题，每小题5分．13．已知a 与b 为两个不共线的单位向量，k 为实数，若向量+a b 与向量k -a b 垂直，则k = ．【答案】1【解析】∵+a b 与k -a b 垂直，∴(+a b )·(k -a b ) =0，化简得(1)(1)0k -⋅+=a b ，根据a 、b 向量不共线，且均为单位向量得10⋅+≠a b ，得10k -=，即1k =． 14．若变量x ，y 满足约束条件32969x y x y ≤+≤⎧⎨≤-≤⎩，则2z x y =+的最小值是_________．【答案】－6【解析】画出区域图知，当直线2z x y =+过239x y x y +=⎧⎨-=⎩的交点(4，-5)时，min 6z =-．15．ABC ∆中，120,7,5B AC AB =︒==，则ABC ∆的面积为_________．153【解析】根据sin sin AB ACC B=得5353sin sin 7AB C B AC === 25311cos 1()1414C =-=，所以sin sin[()]sin cos sin cos A B C B C C B π=-+=+3111533321421414=⨯-⨯=．因此ABC S ∆=1133153sin 7522144AB AC A ⨯⨯⨯=⨯⨯⨯= 16．已知两个圆锥有公共底面，且两圆锥的顶点和底面的圆周都在同一个球面上．若圆锥底面面积是这个球面面积的316，则这两个圆锥中，体积较小者的高与体积较大者的高的比值为______________．【答案】13【解析】设球心为1O ，半径为1r ，圆锥底面圆圆心为2O ，半径为2r ，则有22123416r r ππ⨯=，即212r r =，所以1122r O O ==，设两个圆锥中，体积较小者的高与体积较大者的高分别为1h 、2h ，则1111211232r r h r h r -==+．三、解答题：解答应写文字说明，证明过程或演算步骤． 17．（本小题满分12分）已知等比数列{}n a 中，113a =，公比13q =．(Ⅰ)n S 为{}n a 的前n 项和，证明：12nn a S -=；(Ⅱ)设31323log log log n n b a a a =+++，求数列{}n b 的通项公式．【解析】（Ⅰ）因为.31)31(311n n n a =⨯=- ,2311311)311(31nn n S -=--= 所以,21nn a S --（Ⅱ）n n a a a b 32313log log log +++=)21(n +++-=2)1(+-=n n 所以}{n b 的通项公式为.2)1(+-=n n b n18．（本小题满分12分）如图，四棱锥P ABCD -中，底面ABCD 为平行四边形，60DAB ∠=︒，2AB AD =，PD ⊥底面ABCD ．(Ⅰ)证明：PA BD ⊥；(Ⅱ)若1PD AD ==，求棱锥D PBC -的高．【解析】（Ⅰ）因为60,2DAB AB AD ∠=︒=，由余弦定理得3BD AD =从而222BD AD AB +=，故BD ⊥AD 又PD ⊥底面ABCD ，可得BD ⊥PD 所以BD ⊥平面P AD. 故 P A ⊥BD（Ⅱ）如图，作DE ⊥PB ，垂足为E ．已知PD ⊥底面ABCD ，则PD ⊥BC ．由（Ⅰ）知BD ⊥AD ，又BC //AD ，所以BC ⊥BD ．故BC ⊥平面PBD ，BC ⊥DE ．则DE ⊥平面PBC ．由题设知，PD =1，则BD =3，PB =2，根据BE ·PB =PD ·BD ，得DE =23，即棱锥D —PBC 的高为.2319．（本小题满分12分）某种产品的质量以其质量指标值衡量，质量指标越大表明质量越好，且质量指标值大于或等于102的产品为优质品．现用两种新配方（分别称为A 配方和B 配方）做试验，各生产了100件这种产品，并测量了每件产品的质量指标值，得到时下面试验结果：A 配方的频数分布表B 配方的频数分布表(Ⅰ)分别估计用A 配方，B 配方生产的产品的优质品率；(Ⅱ)已知用B 配方生产的一种产品利润y （单位：元）与其质量指标值t 的关系式为2,942,941024,102t y t t -<⎧⎪=≤<⎨⎪≥⎩，估计用B 配方生产的一件产品的利润大于0的概率，并求用B配方生产的上述100件产品平均一件的利润．【解析】(Ⅰ)由试验结果知，用A 配方生产的产品中优质品的频率为2280.3100+=，所以用A 配方生产的产品的优质品率的估计值为0.3．由试验结果知，用B 配方生产的产品中优质品的频率为32100.42100+=，所以用B 配方生产的产品的优质品率的估计值为0.42．(Ⅱ)由条件知，用B 配方生产的一件产品的利润大于0当且仅当其质量指标值94t ≥，由试验结果知，质量指标值94t ≥的频率为0．96．所以用B 配方生产的一件产品的利润大于0的概率估计值为0．96．用B 配方生产的产品平均一件的利润为1[4(2)542424] 2.68100⨯⨯-+⨯+⨯=(元)．20．（本小题满分12分）在平面直角坐标系xOy 中，曲线261y x x =-+与坐标轴的交点都在圆C 上． (Ⅰ)求圆C 的方程；(Ⅱ)若圆C 与直线0x y a -+=交于,A B 两点，且OA OB ⊥，求a 的值．【解析】（Ⅰ）曲线162+-=x x y 与y 轴的交点为(0，1)，与x 轴的交点为（).0,223(),0,223-+故可设C 的圆心为（3，t ），则有,)22()1(32222t t +=-+解得t =1.则圆C 的半径为.3)1(322=-+t 所以圆C 的方程为.9)1()3(22=-+-y x（Ⅱ）设A (11,y x )，B (22,y x )，其坐标满足方程组：⎪⎩⎪⎨⎧=-+-=+-.9)1()3(,022y x a y x 消去y ，得到方程.012)82(222=+-+-+a a x a x由已知可得，判别式.0416562>--=∆a a因此，,441656)28(22,1a a a x --±-=从而2120,422121+-=-=+a a x x a x x①由于OA ⊥OB ，可得,02121=+y y x x 又,,2211a x y a x y +=+=所以.0)(222121=+++a x x a x x②由①，②得1-=a ，满足,0>∆故.1-=a21．（本小题满分12分）已知函数ln ()1a x bf x x x=++，曲线()y f x =在点(1,(1))f 处的切线方程为230x y +-=．(Ⅰ)求a ，b 的值；(Ⅱ)证明：当0x >，且1x ≠时，ln ()1xf x x >-．【解析】（Ⅰ）221(ln )'()(1)x x b x f x x x α+-=-+由于直线230x y +-=的斜率为12-，且过点(1,1)，故(1)1,1'(1),2f f =⎧⎪⎨=-⎪⎩即1,1,22b a b =⎧⎪⎨-=-⎪⎩解得1a =，1b =．（Ⅱ）由（Ⅰ）知ln 1f ()1x x x x=++，所以 )1ln 2(111ln )(22xx x x x x x f -+-=-=考虑函数()2ln h x x =+xx 12-(0)x >，则22222)1()1(22)(xx x x x x x h --=---=' 所以当1≠x 时，,0)1(,0)(=<'h x h 而故当)1,0(∈x 时，;0)(11,0)(2>->x h x x h 可得当),1(+∞∈x 时，;0)(11,0)(2>-<x h xx h 可得从而当.1ln )(,01ln )(,1,0->>--≠>x xx f x x x f x x 即且请考生在第（22）、（23）、（24）三题中任选一题做答，如果多做，则按所做的第一题记分．22．（本小题满分10分）选修4-1：几何证明选讲如图，D ，E 分别为ABC ∆的边AB ，AC 上的点，且不与ABC ∆的顶点重合．已知AE 的长为m ，AC 的长为n ，AD ，AB 的长是关于x 的方程2140x x mn -+=的两个根．EB(Ⅰ)证明：,,,C B D E 四点共圆；(Ⅱ)若90A ∠=︒，且4,6,m n ==求,,,C B D E 所在圆的半径．【解析】(Ⅰ)连结DE ，根据题意在ADE ∆和ACB ∆中，AD AB mn AE AC ⨯==⨯，即AD AEAC AB=．又DAE CAB ∠=∠，从而ADE ∆∽ACB ∆．因此ADE ACB ∠=∠．所以C ，B ，D ，E 四点共圆．(Ⅱ)4m =，6n =时，方程2140x x mn -+=的两根为12x =，212x =．故2AD =，12AB =．取CE 的中点G ，DB 的中点F ，分别过G ，F 作AC ，AB 的垂线，两垂线相交于H 点，连结DH ．因为C ，B ，D ，E 四点共圆，所以C ，B ，D ，E 四点所在圆的圆心为H ，半径为DH ．由于90A ∠=︒，故//GH AB ，//HF AC ，从而5HF AG ==，()112252DF =-=．故C ，B ，D ，E 四点所在圆的半径为23．（本小题满分10分）选修4-4：坐标系与参数方程在直角坐标系xOy 中，曲线1C 的参数方程为2cos (22sin x y ααα=⎧⎨=+⎩为参数），M 为1C 上的动点，P 点满足2OP OM =，点P 的轨迹为曲线2C ． (Ⅰ)求2C 的方程；ADB C GEM(Ⅱ)在以O 为极点，x 轴的正半轴为极轴的极坐标系中，射线3πθ=与1C 的异于极点的交点为A ，与2C 的异于极点的交点为B ，求||AB .【解析】(Ⅰ)设(),P x y ，则由条件知,22x y M ⎛⎫⎪⎝⎭，由于M 点在1C 上，所以2cos 222sin 2xy αα⎧=⎪⎪⎨⎪=+⎪⎩，即4cos 44sin x y αα=⎧⎨=+⎩．从而2C 的参数方程为4cos 44sin x y αα=⎧⎨=+⎩(α为参数)．(Ⅱ)曲线1C 的极坐标方程为4sin ρθ=，曲线2C 的极坐标方程为8sin ρθ=．射线3πθ=与1C 的交点A 的极径为14sin 3πρ=，射线3πθ=与2C 的交点B 的极径为28sin3πρ=，所以12AB ρρ=-=24．（本小题满分10分）选修4-5：不等式选讲设函数()||3f x x a x =-+，其中0a >． (Ⅰ)当1a =时，求不等式()32f x x ≥+的解集．(Ⅱ)若不等式()0f x ≤的解集为｛x |1}x ≤-，求a 的值．【解析】(Ⅰ)当1a =时，()32f x x ≥+可化为12x -≥由此可得3x ≥或1x ≤-，故不等式()32f x x ≥+的解集为{3x x ≥或}1x ≤-． (Ⅱ)由()0f x ≤得30x a x -+≤，此不等式化为不等式组 30x a x a x ≥⎧⎨-+≤⎩或30x a a x x ≤⎧⎨-+≤⎩即4x a a x ≥⎧⎪⎨≤⎪⎩或2x aa x ≤⎧⎪⎨≤-⎪⎩．由于0a >，所以不等式组的解集为2a x x ⎧⎫≤-⎨⎬⎭⎩．由题设可得12a-=-，故2a =．。

2011新课标全国卷数学(理科)(含答案)

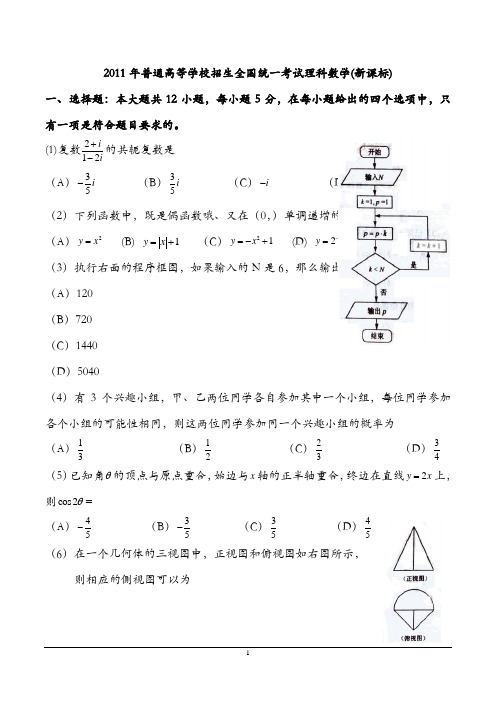
2011年普通高等学校招生全国统一考试理科数学(新课标)一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

(1)复数212ii+-的共轭复数是（A ）35i - （B ）35i （C ）i - （D ）i （2）下列函数中，既是偶函数哦、又在（0，）单调递增的函数是（A ）2y x = (B) 1y x =+ （C ）21y x =-+ (D) 2x y -= （3）执行右面的程序框图，如果输入的N 是6，那么输出的p 是（A ）120 （B ）720 （C ）1440 （D ）5040（4）有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为（A ）13（B ）12（C ）23（D ）34（5）已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线2y x =上，则cos2θ=（A ）45- （B ）35- （C ）35（D ）45（6）在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的侧视图可以为（7）设直线l 过双曲线C 的一个焦点，且与C 的一条对称轴垂直，l 与C 交于 A,B 两点，AB 为C 的实轴长的2倍，则C 的离心率为（A（B （C ）2 （D ）3（8）512a x x x x ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭的展开式中各项系数的和为2，则该展开式中常数项为（A ）-40 （B ）-20 （C ）20 （D ）40 （9）由曲线y =2y x =-及y 轴所围成的图形的面积为（A ）103 （B ）4 （C ）163（D ）6 （10）已知a 与b 均为单位向量，其夹角为θ，有下列四个命题12:10,3P a b πθ⎡⎫+>⇔∈⎪⎢⎣⎭ 22:1,3P a b πθπ⎛⎤+>⇔∈⎥⎝⎦3:10,3P a b πθ⎡⎫->⇔∈⎪⎢⎣⎭ 4:1,3P a b πθπ⎛⎤->⇔∈ ⎥⎝⎦其中的真命题是（A ）14,P P （B ）13,P P （C ）23,P P （D ）24,P P（11）设函数()sin()cos()(0,)2f x x x πωϕωϕωϕ=+++><的最小正周期为π，且()()f x f x -=，则（A ）()f x 在0,2π⎛⎫ ⎪⎝⎭单调递减（B ）()f x 在3,44ππ⎛⎫ ⎪⎝⎭单调递减（C ）()f x 在0,2π⎛⎫ ⎪⎝⎭单调递增（D ）()f x 在3,44ππ⎛⎫⎪⎝⎭单调递增 (12)函数11y x =-的图像与函数2sin (24)y x x π=-≤≤的图像所有焦点的横坐标之和等于（A ）2 (B) 4 (C) 6 (D)8 二、填空题：本大题共4小题，每小题5分。

2011年高考全国卷(有答案)

2011年普通高等学校招生全国统一考试(新课标全国卷)理科综合本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。

满分300分。

考试时间150分钟。

可能用到的相对原子质量：H －1 B －11 C －12 N －14 O －16 Na －23 S －32 Cl －35.5 Ca －40 Cu －64第Ⅰ卷(选择题共126分)一、选择题：本大题共13小题，每小题6分，共78分。

在每小题给出的四个选项中，只有一项是最符合题目要求的。

7．下列叙述正确的是( )A ．1.00 mol NaCl 中含有 6.02×1023个 NaCl 分子B ．1.00 mol NaCl 中，所有Na ＋的最外层电子总数为 8×6.02×1023C ．欲配制 1.00 L 1.00 mol·L －1的 NaCl 溶液，可将58.5 g NaCl 溶于1.00 L 水中 D ．电解58.5 g 熔融的 NaCl ，能产生22.4 L 氯气(标准状况)、23.0 g 金属钠解析：本题主要考查物质的量、物质的量的浓度、阿伏加德罗常数及相关计算，意在考查考生对概念的理解及推理、计算能力．NaCl 是离子化合物，故A 错误；Na ＋最外层有8个电子，所以1.00 mol Na ＋的最外层电子总数为8×6.02×1023，故B 正确；欲配制1.00 L NaCl 溶液，所需水的体积应小于1.00 L ，故C 错误；电解58.5 g 的熔融的NaCl ，根据电解方程式：2NaCl(熔融)=====电解2Na ＋Cl 2↑，得出生成标准状况下11.2 L 氯气，故D 错误．答案：B8．分子式为C 5H 11Cl 的同分异构体共有(不考虑立体异构)( ) A ．6种 B ．7种 C ．8种 D ．9种解析：本题考查同分异构体的书写，意在考查考生的分析能力．戊烷的一氯取代物有8种，方式如下：答案：C9．下列反应中，属于取代反应的是( )①CH 3CH===CH 2＋Br 2――→CCl 4CH 3CHBrCH 2Br②CH 3CH 2OH ――→浓H 2SO 4△CH 2===CH 2＋H 2O ③CH 3COOH ＋CH 3CH 2OH ――→浓H 2SO 4△ CH 3COOCH 2CH 3＋H 2O④C 6H 6＋HNO 3――→浓H 2SO 4△C 6H 5NO 2＋H 2O A ．①② B ．③④ C ．①③ D ．②④解析：本题考查有机反应类型，意在考查考生对有机化学反应的理解与区别能力．①是加成反应，②是消去反应，③、④都是取代反应．答案：B10．将浓度为 0.1 mol·L －1HF 溶液加水不断稀释，下列各量始终保持增大的是( )A ．c (H ＋) B ．K a (HF)C.c (F －)c (H ＋)D.c (H ＋)c (HF )解析：本题考查电离平衡，意在考查考生对电离平衡常数、电离的影响因素的掌握情况．在0.1 mol·L －1 HF 溶液中存在如下电离平衡：＋＋F －，加水稀释，平衡向右移动，但c (H ＋)减小；选项B, 电离平衡常数与浓度无关，其数值在稀释过程中不变；选项C ，加水后，平衡右移，n (F －)、n (H ＋)都增大，但由于水电离产生的n (H ＋)也增大，故C 项比值减小；选项D ，变形后得K a (HF )c (F －)，稀释过程中c (F －)逐渐减小，故其比值始终保持增大．答案：D11．铁镍蓄电池又称爱迪生电池，放电时的总反应为：Fe ＋Ni 2O 3＋3H 2O===Fe(OH)2＋2Ni(OH)2.下列有关该电池的说法不．正确的是( )A ．电池的电解液为碱性溶液，正极为Ni 2O 3、负极为FeB ．电池放电时，负极反应为 Fe ＋2OH －－2e －===Fe(OH)2 C ．电池充电过程中，阴极附近溶液的pH 降低D ．电池充电时，阳极反应为2Ni(OH)2＋2OH －－2e －===Ni 2O 3＋H 2O解析：本题考查充电电池的有关知识，意在考查考生对充电电池正负极的判断及书写电极反应的能力．在铁镍蓄电池中，Fe 是负极，Ni 2O 3是正极，由于生成Fe(OH)2，则电解液为碱性溶液，故A 正确；电池放电时，负极反应为：Fe ＋2OH －－2e －===Fe(OH)2，故B 正确；电池充电时，阴极反应式为：Fe(OH)2＋2e －===Fe ＋2OH －，阴极附近溶液pH 升高，故C 错误；由充电时的总反应式减去阴极反应式，可得到阳极反应式，D 正确．答案：C12．能正确表示下列反应的离子方程式为( )A ．硫化亚铁溶于稀硝酸中：FeS ＋2H ＋===Fe 2＋＋H 2S ↑ B ．NH 4HCO 3溶于过量的NaOH 溶液中：HCO －3＋OH －===CO 2－3＋H 2OC ．少量SO 2通入苯酚钠溶液中：C 6H 5O －＋SO 2＋H 2O===C 6H 5OH ＋HSO －3D 解析：本题考查离子方程式的书写，意在考查考生准确判断离子方程式是否符合客观事实、化学式的拆分是否准确等能力．选项A ，不符合事实，硝酸具有强氧化性，能将Fe 2＋、H 2S 氧化，故A 错误；选项B ，忽略了NH ＋4＋OH －===NH 3↑＋H 2O ，故B 错误；选项C ，SO 2少量，不会生成HSO －3，应生成SO 2－3，故C 错误.答案：D．大理石溶于醋酸中：CaCO 3＋2CH 3COOH===Ca 2＋＋2CH 3COO －＋CO 2↑＋H 2O13．短周期元素W 、X 、Y 和Z 的原子序数依次增大．元素W 是制备一种高效电池的重要材料，X 原子的最外层电子数是内层电子数的2倍，元素Y 是地壳中含量最丰富的金属元素，Z 原子的最外层电子数是其电子层数的2倍．下列说法错误的是( )A ．元素W 、X 的氯化物中，各原子均满足8电子的稳定结构B ．元素X 与氢形成的原子比为1∶1的化合物有很多种C ．元素Y 的单质与氢氧化钠溶液或盐酸反应均有氢气生成D ．元素Z 可与元素X 形成共价化合物XZ 2解析：本题考查物质结构、元素周期律的知识，意在考查考生对物质结构的推理能力、元素周期律的应用能力．首先根据题意，推断出W 是Li ，X 是C ，Y 是Al ，Z 是S.A 项，LiCl 中的Li 不满足8电子稳定结构，故A 错误；B 项，碳元素和氢元素可形成C 2H 2、C 6H 6、C 8H 8等多种化合物；C 项，Al 为两性金属，与强酸、强碱都能反应放出氢气；D 项，碳元素和硫元素能形成CS 2.答案：AⅡ卷(非选择题共174分)三、非选择题：包括必考题和选考题两部分。

2011年高考题、参考答案(全国卷)

2011年普通高等学校招生全国统一考试语文注意事项：1. 本试卷分第Ⅰ卷（阅读题）和第Ⅱ卷（表达题）两部分。

第Ⅰ卷1至8页，第Ⅱ卷9至10页。

2. 答题前，考生务必将自己的姓名、准考证号填写在本试题相应的位置。

3. 全部答案在答题卡上完成，答在本试题上无效。

4. 考试结束，将本试题和答题卡一并交回。

第Ⅰ卷（30分）一、（12分，每小题3分）1.下列词语中加点的字，读音全都正确的一组是（）A.逾．越（yú）鸟瞰．（kàn）一丘之貉．（luî）栩栩．．如生（xǔ）B.溃．败（kuì）凹．陷（wā）贻．笑大方（yí）兢兢．．业业（jīng）C.咀．嚼（zǔ）桧．柏（guì）罄．竹难书（qìng）饕餮．大餐（tiã）D.觊．觎（jì）攻讦．（jiã）光阴荏苒．（rǎn）心怀叵．测（pǒ）2.下列各句中，加点的成语便用恰当的一项是（）A.我读过弗莱的著作，很喜欢他那高屋建瓴．．．．的气势和包罗万象的体系，更欣赏他努力摆脱主观印象式品评的文学批评方法。

B.吴羽先生知道弟子写论文时强调，学术论文要有的放矢，论证严密，语言准确而简洁，不能模棱两可，也不能繁文缛节．．．．。

C.这是一家国家级出版社，近几年来，出版了很多深受读者尤其是在校大学生喜爱的精品图书，不少作家都对他趋之若鹜．．．．。

D.虽然已经是晚上了，但候车大厅里依然人来人往，热闹非凡，大喇叭的广播声、商贩的叫卖声、孩子的哭泣声不绝如缕．．．．。

3、下列各句中，没有语病的一句是（）A、不同的生活习俗、自然条件以及地理环境，使各地的民居在平面布局、结构方法、造型等方面呈现出淳朴自然，而又有着各自的特色。

B、历时三年的第六次全国人口普查是一次成功的国情大盘点，其数据将为我国社会经济发展规划的制定和政府的相关决策提供重要参考。

C、失眠是指因睡眠时间不足、质量不佳对身体产生损害而出现的不舒服的感觉，应对失眠需要了解相关的睡眠卫生知识，进行自我调护。

2011年全国普通高等学校招生统一考试上海数学试卷(理工农医类)

为— — ．
１．４已知点ｏ（，）ｏＯ１和Ｒ（，）记ｏ０、Ｑ（，）ｏ３１，
Ｑｏｏ中点为，Ｑ・１Ｐ０Ｒ的取ｃ和１中的一条，Ｐ
１的一个焦点，ｍ＝— 则４不等式．
—
． — ．
≤３的解为 —
记其端点为Ｑ１，、使之满足（ｌ［Ｉ）ＩＲ１ＯＱ１（）Ｉ一２（二２）＜０；记Ｑ１１Ｒ的中点为Ｐ，取Ｑ１２２Ｐ和
该圆锥的体积为—
—
．
１．若ａ５、ｂ∈Ｒ，０＞０则下列不等式且６，
８数一ｉ吾ｃ（一）．ｎ＋）ｓ１的函（ｏ７－
最大值为 — — ．９．马老师从课本上抄录一个随机变量 ∈ 的概率分布律如下表：
中，恒成立的是
［（）答］
二、选择题（本大题满分２分）０本大题共有
４题，每题有且只有一个正确答案，考生应在答题纸的相应编号上，将代表答案的小方格涂黑，
选对得５分，否则一律得零分．
６在相距２．千米的、Ｂ两点处测量目标点Ｃ，若Ｂ＝７。ＣＢＡ＝６。则、两５，０，点之间的距离为— — 千米．７若圆锥的侧面积为２，．丌底面面积为丌则，
（）ｌ０，，２一，Ｂ０，３ … ０他ｌ… ０，４・・２，２０，・０扎，是等比数列．（）１０，・０ｎ１… 和ｎ，４・・２，Ｃｎ，３・・２一，，２０，・０扎，均是等比数列．
已知数列｛ｎ和｛ｎ．０）ｂ】的通项公式分别是ａ３ｎ＋６ｂ，ｎ＝２＋７ｎ∈Ｎ．ｎ（）将集合｛＝Ｉａ，ｎ∈Ｎ．ｘｘ＝ｂ，］ｕ｛ｌｎ∈Ｎ［的元素从）ｐ

2011年普通高等学校招生全国统一考试数学卷(上海.理)含答案

2011年上海市高考数学试题（理科 2011-6-7）一、填空题（56分） 1、函数1()2f x x =-的反函数为1()fx -= 。

2、若全集U R =，集合{|1}{|0}A x x x x =≥≤ ，则U C A = 。

3、设m 为常数，若点(0,5)F 是双曲线2219yxm-=的一个焦点，则m = 。

4、不等式13x x+<的解为。

5、在极坐标系中，直线(2c o s sin )2ρθθ+=与直线c o s 1ρθ=的夹角大小为。

6、在相距2千米的A 、B 两点处测量目标C ，若075,60C A B C B A ∠=∠=，则A 、C 两点之间的距离是千米。

7、若圆锥的侧面积为2π，底面积为π，则该圆锥的体积为。

8、函数sin ()c o s()26y x x ππ=+-的最大值为。

9、马老师从课本上抄录一个随机变量ε的概率分布律如下表请小牛同学计算ε的数学期望，尽管“！”处无法完全看清，且两个“？”处字迹模糊，但能肯定这两个“？”处的数值相同。

据此，小牛给出了正确答案E ε= 。

10、行列式a b cd（,,,{1,1,2}a b c d ∈-）的所有可能值中，最大的是。

11、在正三角形A B C 中，D 是B C 上的点，3,1A B B D ==，则A B A D ⋅=。

12、随机抽取9个同学中，至少有2个同学在同一月出生的概率是（默认每月天数相同，结果精确到0.001）。

13、设()g x 是定义在R 上、以1为周期的函数，若()()f x x g x =+在[3,4]上的值域为[2,5]-，则()f x 在区间[10,10]-上的值域为。

14、已知点(0,0)O 、0(0,1)Q 和0(3,1)R ，记00Q R 的中点为1P ，取01Q P 和10P R 中的一条，记其端点为1Q 、1R ，使之满足11(||2)(||2)0O Q O R --<；记11Q R 的中点为2P ，取12Q P 和21P R 中的一条，记其端点为2Q 、2R ，使之满足22(||2)(||2)0O Q O R --<；依次下去，得到点12,,,,n P P P ，则0lim ||n n Q P →∞= 。

2011年普通高等学校招生全国统一考试数学试题(江苏卷,解析版)

- 1 - 2011年普通高等学校招生全国统一考试(江苏卷)数学I
参考公式：（1）样本数据12,,,n x x x 的方差2211()n i i s x x n ==-∑,其中11n i i x x n ==∑ （2）直柱体的侧面积S ch =，其中c 为底面周长，h 是高（3）柱体的体积公式V Sh =，其中S 为底面面积，h 是高一、填空题：本大题共14小题，每小题5分，共70分。

请把答案填写在答题卡相应位置上．．．．．．．．。

1、已知集合{1,1,2,4},{1,0,2},A B =-=- 则_______,=⋂B A 答案：{}1－，2 2、函数)12(log )(5+=x x f 的单调增区间是__________ 答案：+∞1（－）2 3、设复数i 满足i z i 23)1(+-=+（i 是虚数单位），则z 的实部是_________ 答案：1
4、根据如图所示的伪代码，当输入b a ,分别为2，3时，最后输出的m 的值是________ 答案：3
5、从1，2，3，4这四个数中一次随机取两个数，则其中一个数是另一个的两倍的概率是______ 答案：13
6、某老师从星期一到星期五收到信件数分别是10，6，8，5，6，则该组数据的方差___2=s
★此卷上交考点保存★ 姓名___________________ 准考证号___________________。

2011年安徽高考数学理科试卷(带详解)

2011年普通高等学校招生全国统一考试（安徽卷）数学（理科）第Ⅰ卷（选择题共50分)一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的.1.设i 是虚数单位,复数a 1+2-ii为纯虚数,则实数a 为 ( )A.2B.-2C.1-2D.12【测量目标】复数的基本概念及代数形式的四则运算.【考查方式】给出一个含未知数的复数,令其为纯虚数,运用公式求解. 【难易程度】容易【参考答案】A 【试题解析】法一：()()()()()a a a a 1+2+1+2-+2+1==2-2-2+5i i i ii i i 为纯虚数,所以,a a 2-=0=2；法二：设a b 1+=2-ii i得a b b 1+=+2i i ,所以,b a =1=2；法三：()a a -1+=2-2-i i i i i为纯虚数,所以a =2； 2.双曲线x y 222-=8的实轴长是( )A.2B.C. 4 【测量目标】双曲线的标准方程.【考查方式】给出一个双曲线方程,求出实轴长. 【难易程度】容易【参考答案】C【试题解析】双曲线方程可变为x y 22-=148,所以,a a 2=4=2,实轴长a 2=4. 3.设()f x 是定义在R 上的奇函数,当x 0…时,()f x x x 2=2-,则()f 1=( )A.-3B.-1C.1D.3 【测量目标】函数的奇偶性的综合运用.【考查方式】给出在某一区间上一个函数方程，已知函数是奇函数,求解函数值. 【难易程度】容易【参考答案】A【试题解析】法一:()f x 是定义在R 上的奇函数,且x 0…时, ()f x x x 2=2-()()()()2112113f f ∴=--=--+-=-,故选A.法二:设0x >,则0x -<,()f x 是定义在R 上的奇函数,且x 0…时,()f x x x 2=2-,()()()2222f x x x x x ∴-=---=+,(步骤1)又()()f x f x -=-,()22f x x x ∴=--,()212113f ∴=-⨯-=-,故选A. (步骤2) ４.设变量,x y 满足1,x y +…则2x y +的最大值和最小值分别为( )Ａ.1，－1 Ｂ.2，－2 Ｃ.1，－2 Ｄ.2，－1 【测量目标】二元线性规划求目标函数的最值.【考查方式】给出一个二元不等式，求目标函数的最值. 【难易程度】中等【参考答案】B【试题解析】法一：特值验证：当0,1x y ==时，22x y +=,故排除A ，C ；当0,1x y ==-时，22x y +=-,故排除D ，答案为B.法二:画出不等式1,x y +…表示的平面区域，平移目标函数线，易知当直线2x y u +=经过点B ，D 时分别对应u 的最大值和最小值，所以max min 2,2u u ==-.第4题图法三：已知条件是含绝对值的不等式，所以目标函数的最大值和最小值一定互为相反数，易知0,1x y ==时，22x y +=，故选B法四：绝对值不等式表示的区域是以(0,1),(1,0),(0,1),(1,0)--为顶点的正方形，线性规划一定在顶点处取得最优解，带入目标函数计算可得最大值、最小值分别为2,2-. 5.在极坐标系中，点(,)π23到圆2cos ρθ=的圆心的距离为( )A.2 【测量目标】极坐标与参数方程及点到圆心的距离.【考查方式】给出一个点坐标和参数方程，求出点到圆心之间的距离. 【难易程度】容易【参考答案】D【试题解析】极坐标(,)π23化为直角坐标：cos cos sin sin x y ρθρθπ⎧==2=1⎪⎪3⎨π⎪==2=⎪3⎩，即圆2cos ρθ=的方程为222x y x +=即22(1)0x y -+=，圆心到点(1故选D. 6.一个空间几何体的三视图如图所示，则该几何体的表面积（）第6题图A.48B.32+C.48+D.80 【测量目标】由三视图求几何体的表面积.【考查方式】给出三视图及其各边边长，求出其表面积. 【难易程度】中等【参考答案】C【试题解析】几何体是以侧视图等腰梯形为底面的直四棱柱,所以该几何体的表面积为12(24)44421642S =⨯⨯+⨯+⨯+⨯+⨯487=+故选C. 7命题“所有能被2整除的数都是偶数”的否定．．是 ( )A.所有不能被2整除的数都是偶数B.所有能被2整除的数都不是偶数C.存在一个不能被2整除的数都是偶数D.存在一个能被2整除的数不是偶数【测量目标】含有一个量词的命题的否定.【考查方式】给出含有一个量词的命题，求出其特称命题. 【难易程度】容易【参考答案】D【试题解析】全称命题的否定是特称命题，“所有”对于“存在一个”，同时否定结论，答案为D. 8.设集合{}1,2,3,4,5,6,A ={}4,5,6,7,8,B =则满足S A ⊆且S B ≠∅ 的集合S 的个数为( ) A.57 B.56 C.49 D.8 【测量目标】集合间的关系及基本运算.【考查方式】给出两个集合与他们之间的集合关系，求出其中一个集合的个数. 【难易程度】容易【参考答案】B【试题解析】法一：集合A 的子集有6264=个，满足S B =∅ 的子集就是集合{1,2,3}的所有子集，一共有328=个，所以集合S 的个数为632264856-=-=.法二：集合S 是集合A 的子集且至少含有集合{4,5,6}的一个元素，所以将S 看作集合{4,5,6}的非空子集与集合{1,2,3}的子集的并集，因此一共有33(21)256-⨯=个.9.已知函数()sin(2)f x x ϕ=+，其中ϕ为实数，若π()()6f x f …对x ∈R 恒成立，且π()(π)2f f >，则()f x 的单调递增区间是( )A.ππ[π,π]()36k k k -+∈Z B.π[π,π]()2k k k +∈Z C.π2π[π,π]()63k k k ++∈Z D.π[π,π]()2k k k -∈Z 【测量目标】三角函数的单调性、最值.【考查方式】给出一个三角函数及其最值，求出其单调递增区间. 【难易程度】较难【参考答案】C【试题解析】对x ∈R 时，π()()6f x f …恒成立，所以ππ()sin()163f ϕ=+=±，可得π5π2π2π66k k ϕϕ=+=-或，（步骤1）因为π()sin(π)sin (π)sin(2π)sin 2f f ϕϕϕϕ=+=->=+=，故sin 0ϕ<，所以5π2π6k ϕ=-，所以5π()sin 26f x x ⎛⎫=- ⎪⎝⎭，（步骤2）函数单调递增区间为π5ππ2π22π262k x k -+-+剟，所以π2π[π,π]()63x k k k ∈++∈Z ,答案为C. （步骤3） 10.函数()(1)mnf x ax x =-在区间[0,1]上的图象如图所示，则,m n 的值可能是 ( ) A.1,1m n == B.1,2m n == C.2,1m n == D.3,1m n ==第10题图【测量目标】函数图象的应用.【考查方式】给出一个含未知量的复合函数在某一区间的图象，求出未知量. 【难易程度】较难【参考答案】B【试题解析】由图得，原函数的极大值点小于0.5，当1,1m n ==时,()21(1)(),24a f x ax x a x =-=--+在12x =处有最值,所以A 不可能；(步骤1) 当1,2m n ==时,232()(1)(2),f x ax x a x x x =-=-+()(31)(1)f x a x x '∴=--，令()100,,3f x x x '=⇒==即函数在13x =处有最值所以B 可能；(步骤2) 当2,1m n ==时,223()(1)(),f x ax x a x x =-=-有2()(32)(23),f x a x x ax x '=-+=- 令()200,,3f x x x '=⇒==即函数在23x =处有最值,所以C 不可能；(步骤3) 当3,1m n ==时，343()(1)()f x ax x a x x =-=-+,有2()(43)f x ax x '=-+，令()300,,4f x x x '=⇒==即函数在34x =处有最值,所以D 不可能. (步骤4) 第II 卷（非选择题共100分）二、填空题：本大题共5小题，每小题5分，共25分.把答案填在答题卡的相应位置. 11.如图所示，程序框图（算法流程图）的输出结果是 .第11题图【测量目标】循环结构的程序框图.【考查方式】给出程序框图，阅读并运行程序，得出结果. 【难易程度】中等【参考答案】15【试题解析】第1次进入循环体有：00T =+，第2次有：01T =+，第3次有：012T =++，……第n 次有：012(1)T n =++++- ,（步骤1）令(1)1052n n T -=>，解得15n >（负值舍去），（步骤2）故16,n =此时输出15k =.（步骤3） 12.设()x a a x a x a x 2122101221-1=+++L ，则a a 1011+= .【测量目标】二项式定理.【考查方式】给出一个二项式，通过公式展开二项式，求出其中两项系数的和. 【难易程度】容易【参考答案】0【试题解析】,a a 1011分别是含x 10和x 11项的系数，所以C ,a 111021=-C a 101121=，所以a a 1011+=C C 10112121-=0.13.已知向量,a b 满足()()+2-=-6g a b a b ，且1=a ，2=b ，则a 与b 的夹角为 . 【测量目标】平面向量的夹角问题.【考查方式】给出两个向量之间的关系等式及各自的模长，求出它们之间的夹角. 【难易程度】中等【参考答案】π3【试题解析】设a 与b 的夹角为θ，依题意有：22(2)()272cos 6θ+-=+-=-+=- a b a b a a b b ，（步骤1）所以1cos =2θ，（步骤2）因为0πθ剟，故π=3θ.（步骤3） 14.已知ABC △的一个内角为120，并且三边长构成公差为4的等差数列，则ABC △的面积为 .【测量目标】余弦定理及三角形面积.【考查方式】给出一个三角形的内角度数及三边关系，求出三角形的面积. 【难易程度】中等【参考答案】【试题解析】不妨设角120,A c b =<，则4,4a b c b =+=-，于是222(4)(4)1cos1202(4)2b b b b b +--+==--，解得=10b ，所以1=sin1202S bc = .15.在平面直角坐标系中，如果x 与y 都是整数，就称点(,)x y 为整点，下列命题中正确的是 .（写出所有正确命题的编号）.①存在这样的直线，既不与坐标轴平行又不经过任何整点②如果k 与b 都是无理数，则直线y kx b =+不经过任何整点 ③直线l 经过无穷多个整点，当且仅当l 经过两个不同的整点④直线y kx b =+经过无穷多个整点的充分必要条件是：k 与b 都是有理数 ⑤存在恰经过一个整点的直线【测量目标】新定义，直线的性质，命题的判定.【考查方式】给出一个新定义，根据新定义判断给出五个命题的正确性. 【难易程度】较难【参考答案】①③⑤【试题解析】①正确，如直线12y =+，不经过任何整点（10,2x y ==；0x ≠，y 是无理数）(步骤1)②错误，直线y =k 与b 都是无理数，但直线经过整点（1,0）；(步骤2) ③正确，当直线经过两个整点时，它经过无数多个整点；(步骤3) ④错误，当10,2k b ==时，直线12y =不通过任何整点；(步骤4)⑤正确，比如直线y =只经过一个整点(0,0).(步骤5)三、解答题：本大题共6小题，共75分.解答应写出文字说明、证明过程或演算步骤.解答写在答题卡的指定区域内.16.（本小题满分12分）设2e ()1xf x ax =+，其中a 为正实数.（Ⅰ）当34=a 时，求)(x f 的极值点；（Ⅱ）若)(x f 为R 上的单调函数，求a 的取值范围【测量目标】导数的运算,利用导数求函数的极值，利用函数的单调性求参数范围. 【考查方式】给出一个含参数函数，（Ⅰ）给出参数的值求极值点，（Ⅱ）给出其单调性，求参数的取值范围.【难易程度】中等【试题解析】对)(x f 求导得22212()e (1)xax axf x ax +-'=+①（步骤1）（Ⅰ）当34=a 时，若0)(='x f ，则03842=+-x x ，解得21,2321==x x （步骤2）结合①，可知所以，21=x 是极小值点，22=x 是极大值点. （步骤3）（Ⅱ）若)(x f 为R 上的单调函数，则)(x f '在R 上不变号，结合①与条件0a >，知2210ax ax -+…（步骤4）在R 上恒成立，因此2444(1)0a a a a ∆=-=-…，由此并结合0a >，知01a <….（步骤5） 17.（本小题满分12分）如图，ABEDFC 为多面体，平面ABED 与平面ACFD 垂直，点O 在线段AD 上，1,2OA OD ==，,,,OAB OAC ODE ODF △△△△都是正三角形.（Ⅰ）证明直线BC EF ; （Ⅱ）求棱锥F OBED -的体积.第17题图【测量目标】线线平行的判定，棱锥的体积，空间向量及其运算.【考查方式】给出一个多面体，其中两个面互相垂直，有4个正三角形，证明两条直线平行和求解棱锥的体积.【难易程度】较难【试题解析】（Ⅰ）（综合法）证明：设G 是线段DA 与线段EB 延长线的交点，由于OAB △与ODE△都是正三角形，所以1,2OB DE=2OG OD =，（步骤1）同理，设G '是线段DA 与线段FC 延长线的交点，有2OG OD '==，又由于G 和G '都在线段DA 的延长线上，所以G 与G '重合. （步骤2）在GED △和GFD △中，由12OB DE 和12OC DF , 12OC DF =,12OB DE =可知,B C 分别是GE 和GF 的中点，所以BC 是GEF △的中位线，故BC EF .（步骤3）（向量法）过点F 作FQ AD ⊥,交AD 于点Q ，连QE ，由平面ABED ⊥平面ADFC ，知FQ ⊥平面ABED ,以Q 为坐标原点，QE 为x 轴正向，QD 为y 轴正向，QF 为z 轴正向，建立如图所示空间直角坐标系.由条件知E )，F （，B （3,022-），C （30,,22-）. （步骤1）则有)23,0,23(-=，)3,0,3(-=EF .（步骤2）所以2=，即得BC EF .（步骤3）第17题（Ⅰ）图（Ⅱ）由1,2,60OB OE EOB ==∠= ，知EOB S =（步骤4）而ODE △是边长为2的正三角形，故OED S =所以OBED EOB ODE S S S =+=233.（步骤5）过点F 作FQ AD ⊥，交AD 于点Q ，由平面ABED ⊥平面ACFD 知，FQ 就是四棱锥F OBED -的高，且FQ =，所以13.32F OBED OBED V FQ S -== （步骤6） 18.（本小题满分13分）在数1和100之间插入n 个实数，使得这2n +个数构成递增的等比数列，将这2n +个数的乘积记作n T ，再令n n T a lg =，1n …. （Ⅰ）求数列{}n a 的通项公式；（Ⅱ）设1tan tan n n n b a a += ，求数列{}n b 的前n 项和n S .【测量目标】对数和指数的运算，两角差的正切公式，等比和等差数列及其前n 项和. 【考查方式】考查灵活运用基本知识解决问题的能力，创新思维能力和运算求解能力. 【难易程度】较难【试题解析】（Ⅰ）设221,,,+n t t t 构成等比数列，其中100,121==+n t t ，则1212n n n T t t t t ++=①（步骤1）2121n n n T t t t t +⋅+= ②（步骤2）①×②并利用231210,(12)i n i n t t t t in +-+==+ 剟，得)2(2210+=n n T ，lg 2, 1.n n a T n n ∴==+…（步骤3）（Ⅱ）由题意和（Ⅰ）中计算结果，知tan(2)tan(3),1n b n n n =++ …（步骤4）另一方面，利用tan(1)tan tan1tan((1))1tan(1)tan k kk k k k+-=+-=-+得tan(1)tan tan(1)tan 1tan1k kk k +-+=- （步骤5）所以22133tan(1)tan tan(3)tan 3tan(1)tan (1)tan1tan1nn n n i i i i k k n S b k k n ++===+-+-==+=-=-∑∑∑ （步骤6）19.（本小题满分12分）（Ⅰ）设1,1,x y厖证明111x y xy xy x y++++…；（Ⅱ）设1,a bc <剟证明log log log log log log a b c b c a b c a a b c ++++….【测量目标】基本不等式证明不等式.【考查方式】考查对数函数的性质和对数换底公式, 不等式的性质等基本知识，考查代数式的恒等变形和推理论证能力. 【难易程度】中等【试题解析】证明：（Ⅰ）由于1,1,x y 厖所以111x y xy xy x y++++…（步骤1） 2()1()xy x y y x xy ⇔++++…（步骤2）将上式中的右式减左式，得22(())(()1)(()1)(()())y x xy xy x y xy xy x y x y ++-++=--+-+(1)(1)()(1)(1)(1)(1)(1)(1)xy xy x y xy xy xy x y xy x y =+--+-=---+=--- 既然1,1,x y 厖所以(1)(1)(1)0xy x y ---…，从而所要证明的不等式成立. （步骤3）（Ⅱ）设y c x b b a ==log ,log ，由对数的换底公式得xy c yb x a xy a ac b c ====log ,1log ,1log ,1log （步骤4）于是，所要证明的不等式即为111x y xy xy x y++++…（步骤5）其中log 1,log 1a b x b y c==厖，故由（Ⅰ）立知所要证明的不等式成立. （步骤6）20.（本小题满分13分）工作人员需进入核电站完成某项具有高辐射危险的任务，每次只派一个人进去，且每个人只派一次，工作时间不超过10分钟.如果前一个人10分钟内不能完成任务则撤出，再派下一个人，现在一共只有甲、乙、丙三个人可派，他们各自能完成任务的概率分别为123,,P P P ，假设123,,P P P 互不相等，且假定各人能否完成任务的事件相互独立.（Ⅰ）如果按甲最先、乙次之、丙最后的顺序派人，求任务能被完成的概率.若改变三个人被派出的先后顺序，任务能被完成的概率是否发生变化？（Ⅱ）若按某指定顺序派人，这三个人各自能完成任务的概率依次为321,,q q q ，其中321,,q q q 是123,,P P P 的一个排列，求所需派出人员数目X 的分布列和均值（数学期望）EX ；（Ⅲ）假定1231P P P >>>，试分析以怎样的先后顺序派出人员，可使所需派出的人员数目的均值（数学期望）达到最小.【测量目标】随机事件与概率，离散型随机变量的期望.【考查方式】考查相互独立事件的概率计算，考查离散型随机变量及其分布列、均值等基本知识，考查在复杂情境下处理问题的能力以及抽象概括能力、合情推理与演绎推理，分类讨论思想，应用意识与创新意识.【难易程度】较难【试题解析】（Ⅰ）无论以怎样的顺序派出人员，任务不能被完成的概率都是123(1)(1)(1)P P P ---，（步骤1）所以任务能被完成的概率与三个人被派出的先后顺序无关，并等于1231231213231231(1)(1)(1)P P P P P P PP PP P P PP P ----=++---+（步骤2）（Ⅱ）当依次派出的三个人各自完成任务的概率分别为321,,q q q 时，随机变量X 的分布列为所需派出的人员数目的均值（数学期望）EX 是EX =1q +21)1(q q -+)1)(1(21q q --=212123q q q q +--（步骤3）（Ⅲ）（方法一）由（Ⅱ）的结论知，当甲最先、乙次之、丙最后的顺序派人时，EX =212123q q q q +--根据常理，优先派出完成任务概率大的人，可减少所需派出的人员数目的均值.下面证明：对于123,,P P P 的任意排列321,,q q q ，都有121212123232q q q q P P PP --+--+…（＊）（步骤4）事实上， 12121212(32)(32)q q q q P P PP ∆=--+---+（步骤5）112212122()()P q P q PP q q =-+--+1122112122211122112122()()()()(2)()(1)()(1)[()()]0P q P q P q P q P q P P q q P q q P P q q =-+-----=--+---+-+……即（＊）成立. （步骤6）（方法二）（ⅰ）可将（Ⅱ）中所求的EX 改写为12121)(3q q q q q -++-，若交换前两人的派出顺序，则变为22121)(3q q q q q -++-.由此可见，当12q q >时，交换前两人的派出顺序可减少均值. （步骤4）（ⅱ）也可将（Ⅱ）中所求的EX 改写为211)1(23q q q ---，若交换后两人的派出顺序，则变为111)1(23q q q ---.由此可见，若保持第一个派出的人选不变，当12q q <时，交换后两人的派出顺序也可减少均值. （步骤5）综合（ⅰ）（ⅱ）可知，当123(,,)P P P =),,(321q q q 时，EX 达到最小.即完成任务概率大的人优先派出，可减少所需派出人员数目的均值，这一结论是合乎常理的. （步骤6）21.（本小题满分13分）设0>λ，点A 的坐标为（1,1），点B 在抛物线2x y =上运动，点Q 满足λ=，经过点Q 与x 轴垂直的直线交抛物线于点M ，点P 满足λ=，求点P 的轨迹方程.第21题图【测量目标】直线与抛物线的位置关系，圆锥曲线中的轨迹问题.【考查方式】考查直线和抛物线的方程，平面向量的概念，性质与运算，动点的轨迹方程等基本知识，考查灵活运用知识探究问题和解决问题的能力.【难易程度】较难【试题解析】由λ=知,,Q M P 三点在同一条垂直于x 轴的直线上，故可设(),,P x y ()0,,Q x y （步骤1）()2,,M x x 则)(202x y y x -=-λ,即y x y λλ-+=20)1( ①（步骤2）再设),(11y x B ，由QA BQ λ=，即)1,1(),(0101y x y y x x --=--λ，解得110(1),(1)x x y y λλλλ=+-⎧⎨=+-⎩ ②（步骤3）将①式代入②式，消去0y ，得1221(1),(1)(1)x x y x y λλλλλλ=+-⎧⎨=+-+-⎩ ③（步骤4）又点B 在抛物线2x y =上，所以211x y =，再将③式代入211x y =，得,))1(()1()1(222λλλλλλ-+=-+-+x y x （步骤5）整理得0)1()1()1(2=+-+-+λλλλλλy x 因0>λ，两边同除以)1(λλ+，得 012=--y x故所求点P 的轨迹方程为12-=x y .（步骤6）。

2011年普通高等学校招生全国统一考试数学卷山东.理含详解

2011年普通高等学校招生全国统一考试（山东卷）参考公式：柱体的体积公式：v sh =，其中s 表示柱体的底面积，h 表示柱体的高. 圆柱的侧面积公式：s cl =，其中c 是圆柱的底面周长，是圆柱的母线长.球的体积公式V=34R 3π, 其中R 是球的半径.球的表面积公式：S=4πR2,其中R 是球的半径.用最小二乘法求线性回归方程系数公式1221ˆˆˆ,ni ii ni i x y nx ybay bx x nx==-⋅==--∑∑ . 如果事件A B 、互斥，那么()()()P A B P A P B +=+.第1卷（共60分）一、选择题：本大题共l2小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）设集合 M ={x|x 2+x-6<0}，N ={x|1≤x ≤3},则M ∩N =（A ）[1,2) （B ）[1,2] （C ）( 2,3] （D ）[2,3]（2）复数z=22ii-+(为虚数单位)在复平面内对应的点所在象限为（A ）第一象限（B ）第二象限（C ）第三象限（D ）第四象限（3）若点（a,9）在函数3xy =的图象上，则tan=6a π的值为：（A ）0 （B ）（C ）1 （D(4)不等式|x-5|+|x+3|≥10的解集是（A ）[-5,7] (B)[-4,6] (C)(-∞,-5]∪[7，+∞) （D ）(-∞，-4]∪[6,+∞) （5）对于函数y=f （x ），x ∈R ，“y=|f(x)|的图像关于y 轴”是“y=f （x ）是奇函数”的（A ）充分而不必要条件（B ）必要而不充分条件（C ）充要条件（D ）既不充分也不必要条件（6）若函数()sin f x x ω= (ω>0)在区间0,3π⎡⎤⎢⎥⎣⎦上单调递增，在区间,32ππ⎡⎤⎢⎥⎣⎦上单调递减，则ω=（A ）3 （B ）2 （C ）32 （D ）23（7）某产品的广告费用x 与销售额y 的统计数据如下表根据上表可得回归方程ˆˆˆybx a =+中的ˆb 为9.4，据此模型预报广告费用为6万元时销售额为（A ）63.6万元（B ）65.5万元（C ）67.7万元（D ）72.0万元（8）已知双曲线22221x y a b-=（a>0,b>0）的两条渐近线均和圆C ：x 2+y 2-6x+5=0相切，且双曲线的右焦点为圆C 的圆心，则该双曲线的方程为（A ）22154x y -= （B ）22145x y -=（C ）221x y 36-= （D ）221x y 63-=（9）函数2sin 2xy x =-的图象大致是（10）已知f （x ）是R 上最小正周期为2的周期函数，且当0≤x ＜2时，f （x ）=x 3-x ，则函数y=f （x ）的图像在区间[0,6]上与x 轴的交点个数为（A ）6（B ）7（C ）8（D ）9（11）右图是长和宽分别相等的两个矩形．给定下列三个命题：①存在三棱柱，其正(主)视图、俯视图如右图；②存在四棱柱，其正(主)视图、俯视图如下图；③存在圆柱，其正(主)视图、俯视图如下图．其中真命题的个数是（A ）3 （B ）2（C ）1 （D ）0（12）设1A ，2A ，3A ，4A 是平面直角坐标系中两两不同的四点，若1312A A A A λ= (λ∈R)，1412A A A A μ= (μ∈R)，且112λμ+=,则称3A ，4A 调和分割1A ，2A ,已知点C(c ，o),D(d ，O) (c ，d∈R)调和分割点A(0，0)，B(1，0)，则下面说法正确的是（A ）C 可能是线段AB 的中点（B ）D 可能是线段AB 的中点（C ）C ，D 可能同时在线段AB 上（D ）C ，D 不可能同时在线段AB 的延长线上第II 卷（共90分）二、填空题：本大题共4小题，每小题4分，共16分.（13）执行右图所示的程序框图，输入2l =，m=3，n=5，则输出的y 的值是 .(14)若62x x ⎛- ⎝⎭展开式的常数项为60，则常数a 的值为 .（15）设函数()2xf x x =+（x ＞0），观察：()()12xf x f x x ==+ f 2 (x)=f(f 1（x ）)= 34xx +f 3 (x)=f(f 2（x ）)= 78xx +f 4 (x)=f(f 3（x ）)= 1516xx +……根据以上事实，由归纳推理可得：当n ∈N *且n ≥2时，f m （x ）=f （f m-1（x ））= . （16）已知函数f x （）=log (0a 1).a x x b a +-≠＞，且当2＜a ＜3＜b ＜4时，函数f x （）的零点*0(,1),,n=x n n n N ∈+∈则 .三、解答题：本大题共6小题，共74分. （17）（本小题满分12分）在 ABC 中，内角A ，B ，C 的对边分别为a ，b ，c.已知cos A-2cosC 2c-a=cos B b. （Ⅰ）求sin sin CA的值；（Ⅱ）若cosB=14，b=2, 求△ABC 的面积S.（18）（本小题满分12分）红队队员甲、乙、丙与蓝队队员A 、B 、C 进行围棋比赛，甲对A ，乙对B ，丙对C 各一盘，已知甲胜A ，乙胜B ，丙胜C 的概率分别为0.6,0.5,0.5，假设各盘比赛结果相互独立。

2011新课标全国卷数学理科含答案

2011年北京市高考数学试卷(理科)(含解析版)

；|a1|+|a2|+…+|an|=
．
12．（5 分）用数字 2，3 组成四位数，且数字 2，3 至少都出现一次，这样的四位数共有数字作答）
个．（用
13．（5 分）已知函数
若关于 x 的方程 f（x）=k 有两个不同的实根，则数 k
16．（14 分）如图，在四棱锥 P﹣ABCD 中，PA⊥平面 ABCD，底面 ABCD 是菱形，AB=2，∠BAD=60°．（Ⅰ）求证：BD⊥平面 PAC；（Ⅱ）若 PA=AB，求 PB 与 AC 所成角的余弦值；（Ⅲ）当平面 PBC 与平面 PDC 垂直时，求 PA 的长．
20．（13 分）若数列 An=a1，a2，…，an（n≥2）满足|ak+1﹣ak|=1（k=1，2，…，n﹣1），数列 An 为 E 数列，记 S（An）=a1+a2+…+an．
（Ⅰ）写出一个满足 a1=as=0，且 S（As）＞0 的 E 数列 An；（Ⅱ）若 a1=12，n=2000，证明：E 数列 An 是递增数列的充要条件是 an=2011；（Ⅲ）对任意给定的整数 n（n≥2），是否存在首项为 0 的 E 数列 An，使得 S（An）=0？如果存在，
．
三、解答题（共 6 小题，满分 80 分） 15．（13 分）已知 f（x）=4cosxsin（x+ ）﹣1．（Ⅰ）求 f（x）的最小正周期；（Ⅱ）求 f（x）在区间[﹣ ， ]上的最大值和最小值．
17．（13 分）以下茎叶图记录了甲、乙两组各四名同学的植树棵数．乙组记录中有一个数据模糊，无法确认，在图中以 X 表示．
绝密★启用前
2011 年普通高等学校招生全国统一考试
①AD+AE=AB+BC+CA；②AF•AG=AD•AE③△AFB～△ADG 其中正确结论的序号是（）

2011年高考新课标卷文科数学试题(解析版)

2011年普通高等学校招生全国统一考试(新课标全国卷）文科数学本试卷分第Ⅰ卷(选择题）和第Ⅱ卷（非选择题）两部分，其中第Ⅱ卷第22～24题为选考题，其他题为必考题第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{0,1,2,3,4}M =，{1,3,5}N =，P MN =，则P 的子集共有A ．2个B ．4个C ．6个D ．8个【答案】B 【解析】P M N =={1,3}，故P 的子集有224=个．2．复数5i12i=- A ．2i - B ．12i - C ．2i -+ D ．12i -+ 【答案】C 【解析】5i 5i(12i)2i 12i (12i)(12i)+==-+--+． 3．下列函数中，既是偶函数又在(0,)+∞单调递增的函数是A ．3y x = B ．||1y x =+ C ．21y x =-+ D ．||2x y -=【答案】B【解析】3y x =为奇函数，21y x =-+在(0,)+∞上为减函数，||2x y -=在(0,)+∞上为减函数，故选B ．4．椭圆221168x y +=的离心率为A ．13 B ．12C D ．2【答案】D【解析】由221168x y +=可知216a =，28b =，∴2228c a b =-=，∴22212c e a ==,∴22e =． 5．执行右面的程序框图，如果输入的N 是6，那么输出的p 是A ．120B ．720C ．1440D ．5040 【答案】B【解析】由程序框图可得，输出的123456720p =⨯⨯⨯⨯⨯=，选B6．有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为 A ．13 B ．12 C ．23 D ．34【答案】A【解析】记三个兴趣小组分别为1、2、3，甲参加1组记为“甲1”，则基本事件为“甲1,乙1；甲1，乙2；甲1，乙3；甲2，乙1;甲2，乙2；甲2,乙3；甲3,乙1；甲3,乙2；甲3，乙3”，共9个．记事件A 为“甲、乙两位同学参加同一个兴趣小组”,其中事件A 有“甲1，乙1;甲2，乙2；甲3，乙3”,共3个．因此31()93P A ==． 7．已知角θ的顶点与原点重合,始边与x 轴的正半轴重合，终边在直线2y x =上，则cos2θ=A ．45-B ．35-C ．35D ．45【答案】B【解析】由题知tan 2θ=，222222cos sin 1tan 3cos2cos sin 1tan 5θθθθθθθ--===-++,选B ．8．在一个几何体的三视图中，正视图与俯视图如右图所示，则相应的侧视图可以为俯视图正视图DCB A【答案】D【解析】通过正视图及俯视图可看出该几何体为半个圆锥和一个三棱锥组合在一起，故侧视图为D ．9．已知直线l 过抛物线C 的焦点，且与C 的对称轴垂直，l 与C 交于,A B 两点,||AB =12,P为C 的准线上一点，则ABP ∆的面积为_____．A ．18B ．24C ．36D ．48 【答案】C【解析】设抛物线方程为22y px =，则焦点坐标为(,0)2p ,将2px =代入22y px =可得22y p =，||AB =12，即2p =12,∴p =6．点P 在准线上，到AB 的距离为p =6,所以ABP∆面积为1612362⨯⨯=． 10．在下列区间中,函数()43xf x e x =+-的零点所在的区间为_____． A ．1(,0)4- B ．1(0,)4 C ．11(,)42 D ．13(,)24【答案】C【解析】因为114411()432044f e e =+⨯-=-<，112211()431022f e e =+⨯-=->，所以()43xf x e x =+-的零点所在的区间为11(,)42．11．设函数()sin(2)cos(2)44f x x x ππ=+++，则 A ．()y f x =在(0,)2π单调递增，其图象关于直线4x π=对称B ．()y f x =在(0,)2π单调递增,其图象关于直线2x π=对称C ．()y f x =在(0,)2π单调递减，其图象关于直线4x π=对称 D ．()y f x =在(0,)2π单调递减，其图象关于直线2x π=对称【答案】D【解析】因为()sin(2)cos(2)44f x x x ππ=+++=2sin(2)2x π+=2cos 2x ，所以2cos 2y x =，在(0,)2π单调递减，对称轴为2x k π=，即2k x π=(k ∈Z )．12．已知函数()y f x =的周期为2,当[1,1]x ∈-时2()f x x =，那么函数()y f x =的图象与函数|lg |y x =的图象的交点共有_____．A ．10个B ．9个C ．8个D ．1个【答案】A【解析】画出两个函数图象可看出交点有10个．第Ⅱ卷本卷包括必考题和选考题两部分．第13题—第21题为必考题，每个试题考生都必须做答．第22题-第24题为选考题，考生根据要求做答．二、填空题：本大题共4小题，每小题5分．13．已知a 与b 为两个不共线的单位向量，k 为实数，若向量+a b 与向量k -a b 垂直,则k = ．【答案】1【解析】∵+a b 与k -a b 垂直，∴（+a b ）·（k -a b ) =0，化简得(1)(1)0k -⋅+=a b ，根据a 、b 向量不共线，且均为单位向量得10⋅+≠a b ，得10k -=，即1k =． 14．若变量x ，y 满足约束条件32969x y x y ≤+≤⎧⎨≤-≤⎩，则2z x y =+的最小值是_________．【答案】－6【解析】画出区域图知,当直线2z x y =+过239x y x y +=⎧⎨-=⎩的交点(4,-5）时，min 6z =-．15．ABC ∆中,120,7,5B AC AB =︒==，则ABC ∆的面积为_________．153【解析】根据sin sin AB ACC B=得5353sin sin 7AB C B AC === 25311cos 1()1414C =-=, 所以sin sin[()]sin cos sin cos A B C B C C B π=-+=+3111533321421414=⨯-⨯=．因此ABC S ∆=1133153sin 7522144AB AC A ⨯⨯⨯=⨯⨯⨯= 16．已知两个圆锥有公共底面，且两圆锥的顶点和底面的圆周都在同一个球面上．若圆锥底面面积是这个球面面积的316，则这两个圆锥中，体积较小者的高与体积较大者的高的比值为______________．【答案】13【解析】设球心为1O ，半径为1r ，圆锥底面圆圆心为2O ，半径为2r ，则有22123416r r ππ⨯=，即212r r =,所以1122r O O ==，设两个圆锥中,体积较小者的高与体积较大者的高分别为1h 、2h ，则1111211232r r h r h r -==+．三、解答题:解答应写文字说明，证明过程或演算步骤． 17．(本小题满分12分）已知等比数列{}n a 中，113a =，公比13q =．（Ⅰ）n S 为{}n a 的前n 项和，证明：12nn a S -=；(Ⅱ）设31323log log log n n b a a a =+++，求数列{}n b 的通项公式．【解析】（Ⅰ）因为.31)31(311n n n a =⨯=- ,2311311)311(31nn n S -=--= 所以,21nn a S --（Ⅱ）n n a a a b 32313log log log +++=)21(n +++-=2)1(+-=n n 所以}{n b 的通项公式为.2)1(+-=n n b n18．（本小题满分12分)如图，四棱锥P ABCD -中，底面ABCD 为平行四边形，60DAB ∠=︒,2AB AD =,PD ⊥底面ABCD ．(Ⅰ）证明:PA BD ⊥；(Ⅱ）若1PD AD ==，求棱锥D PBC -的高．【解析】（Ⅰ)因为60,2DAB AB AD ∠=︒=，由余弦定理得3BD AD =从而222BD AD AB +=，故BD ⊥AD 又PD ⊥底面ABCD ,可得BD ⊥PD 所以BD ⊥平面P AD 。

2011年普通高等学校招生全国统一考试数学卷(全国新课标.理)含答案

2011年普通高等学校招生全国统一考试 理科数学(必修+选修Ⅱ)

2011年普通高等学校招生全国统一考试数学卷(湖南.理)含详解

2011年四川高考数学试题理科(含答案)

2011年高考数学文科试卷(全国1卷)(含答案)(新课标卷卷)

2011年普通高等学校招生全国统一考试数学卷(广东.文)含详解

2011年高考数学文科试卷(全国1卷)(内含答案)(新课标卷卷)

2011年高考新课标卷文科数学试题(解析版)

2011新课标全国卷数学(理科)(含答案)

2011年高考全国卷(有答案)

2011年高考题、参考答案(全国卷)

2011年全国普通高等学校招生统一考试 上海 数学试卷(理工农医类)

2011年普通高等学校招生全国统一考试数学卷(上海.理)含答案

2011年普通高等学校招生全国统一考试数学试题(江苏卷,解析版)

2011年安徽高考数学理科试卷(带详解)

2011年普通高等学校招生全国统一考试数学卷山东.理含详解

2011新课标全国卷数学理科含答案

2011年北京市高考数学试卷(理科)(含解析版)

2011年高考新课标卷文科数学试题(解析版)

2011年普通高等学校招生全国统一考试理科数学(必修+选修Ⅱ)

2011年全国普通高等学校招生统一考试上海数学试卷(理工农医类)