正弦余弦函数图像及其应用
正弦函数余弦函数的图象和性质

-1
o
-1 -
6
3
2
2 3
5 6
3 2
与x轴的交点 ( 2
5 3
11 6
2
x
-
,0) ( 32 ,0)
图象的最低点 ( ,1)
例1.画出下列函数的简图
1)y=-cosx
解:(1)按五个关键点列表 x cosx -cosx 0 1 -1
2
3 2
B
O1
A O
-1
3
2 3
4 3
5 3
2
x
正弦函数以2π为最小正周期 即: sin(x+2)=sinx, kZ y=sinx,xR y=sinx,x[0,2] 利用图象平移
y
1 -4 -3 -2 -
正弦曲 线
2 3 4 5 6
o
-1
x
三、余弦函数的图象
2 0
-1
y=sin2x,x∈[0,π] y=sin2x y=sinx
2
0
y=1+cosx的简图 x (2)作函数 y sin 的简图 2 y
2 1
-
y=1+cosx
-
o
-1
-
2
x 2
3 2
2
x
y=cosx
y sin
Y
1 0 -1
y sin x
y=cosx
2
X
(2)
1-
y=|sinx|
2
-1
o
-1
3 2
2
正弦余弦函数图像及其应用

A
B
C
D
例2.函数 y A sin( x )( 0, ) 的部分图 2 y 4sin( x ) 像如图所示,则函数表达式为______________. 8 4
y
4
2
o
4
6
x
变式训练1.(09’辽宁,8)已知函数 f ( x ) A cos( x )
y
2
7 12
o
2
4
5 4
x
2 y sin(2 x ) 图所示,则函数的解析式是_____________. 3
3. 函数 y sin( x )( 0,| | ) 的图像如
y
1
o
1
12
7 12
x
课堂小结
正弦线 1.利用_______作出正弦函数的图像;
A. [1,1]
B.
2 [ ,1] 2
cos x , sin x cos x f ( x) sin x , sin x cos x y
1
2 2 C. [1, ] D. [1, ] 2 2
o
1 -
2
x
巩固练习 1.(08’四川,15)已知函数 f ( x ) sin( x ) ( 0) 在 6 1 4 4 (0, ) 单调递增,在 ( , 2 ) 单调递减, 则_____. 2 3 3 分析: 4
2 的图像如图所示, ( ) , 则 f(0)等于( f 2 3
C )
1 D. 2
分析:
2 A. 3
1 B. 2
Hale Waihona Puke 2 T 3 3 11 ( , 0)是第二个关键点 12 11 2k , k Z 4 2 令k=1,则 4
正弦函数和余弦函数的图像与性质

3. 求最小正周期: (1) f ( x) 3sin x 4cos x (2) f ( x) sin 2 x (3) f ( x) sin 2 x cos 2 x
y cos x , x R 的值域是 [1,1],最大值是 1,最小值是 1.
当 cos x 1时,x 2k (k Z). 当 cos x 1 时,x (2k 1) (k Z).
(2)周期性
一般地,对于函数 f ( x),如果存在一个常数 T (T 0), 使得当 x 取定义域 D 内的任意值时,都有 f ( x T ) f ( x) 成立,那么函数 f ( x) 叫做周期函数,常数 T 叫做函数 f ( x) 的周期。对于一个周期函数 f ( x) 来说,如果在所有的周期中 存在一个最小正数,那么这个最小正数叫做函数 f ( x) 的 最小正周期。
解: 偶函数; (1)
(2) f ( x) cos 2 x,偶函数;
2 (k Z)
(3)sin x 1 x 2k
x
,但 x 可以取 ,即 f ( x)的定义域不关于原点对称, 2 2
f ( x) 是非奇非偶函数。
(4) f ( x)
1 sin 2 x sin x 1 1 sin 2 x sin x 1
5 3 增:k , k (k Z), 减:k , k (k Z) 8 8 8 8
(4) y log 1 2cos x 3
2
3 解: x cos x 2 k , 2 k 2 6 6
6.1_正弦函数和余弦函数的图像与性质
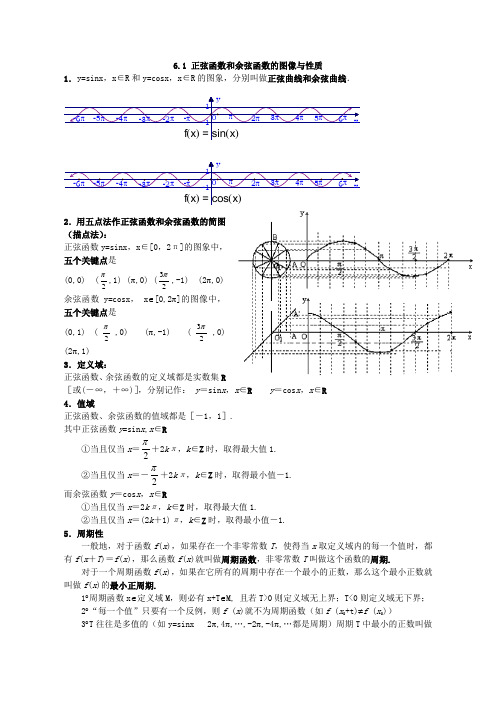
6.1 正弦函数和余弦函数的图像与性质1.y=sinx ,x ∈R 和y=cosx ,x ∈R 的图象,分别叫做正弦曲线和余弦曲线.2.用五点法作正弦函数和余弦函数的简图(描点法):正弦函数y=sinx ,x ∈[0,2π]的图象中,五个关键点是(0,0) (2π,1) (π,0) (23π,-1) (2π,0) 余弦函数y=cosx , x ∈[0,2π]的图像中,五个关键点是(0,1) (2π,0) (π,-1) (23π,0) (2π,1)3.定义域:正弦函数、余弦函数的定义域都是实数集R[或(-∞,+∞)],分别记作: y =sin x ,x ∈R y =cos x ,x ∈R4.值域正弦函数、余弦函数的值域都是[-1,1].其中正弦函数y =sin x ,x ∈R①当且仅当x =2π+2k π,k ∈Z 时,取得最大值1. ②当且仅当x =-2π+2k π,k ∈Z 时,取得最小值-1. 而余弦函数y =cos x ,x ∈R①当且仅当x =2k π,k ∈Z 时,取得最大值1.②当且仅当x =(2k +1)π,k ∈Z 时,取得最小值-1.5.周期性一般地,对于函数f (x ),如果存在一个非零常数T ,使得当x 取定义域内的每一个值时,都有f (x +T )=f (x ),那么函数f (x )就叫做周期函数,非零常数T 叫做这个函数的周期.对于一个周期函数f (x ),如果在它所有的周期中存在一个最小的正数,那么这个最小正数就叫做f (x )的最小正周期.1︒周期函数x ∈定义域M ,则必有x+T ∈M, 且若T>0则定义域无上界;T<0则定义域无下界; 2︒“每一个值”只要有一个反例,则f (x )就不为周期函数(如f (x 0+t)≠f (x 0))3︒T 往往是多值的(如y=sinx 2π,4π,…,-2π,-4π,…都是周期)周期T 中最小的正数叫做f (x )的最小正周期(有些周期函数没有最小正周期)正弦函数、余弦函数都是周期函数,2k π(k ∈Z 且k ≠0)都是它的周期,最小正周期是2π.6.奇偶性y =sin x 为奇函数,y =cos x 为偶函数正弦曲线关于原点O 对称,余弦曲线关于y 轴对称7.单调性 正弦函数在每一个闭区间[-2π+2k π,2π+2k π](k ∈Z )上都是增函数,其值从-1增大到1;在每一个闭区间[2π+2k π,23π+2k π](k ∈Z )上都是减函数,其值从1减小到-1. 余弦函数在每一个闭区间[(2k -1)π,2k π](k ∈Z )上都是增函数,其值从-1增加到1;在每一个闭区间[2k π,(2k +1)π](k ∈Z )上都是减函数,其值从1减小到-1.例1 求下列函数的周期:(1)y =3cos x ,x ∈R ;(2)y =sin2x ,x ∈R ;(3)y =2sin(21x -6π),x ∈R .一般地,函数y =A sin(ωx +ϕ),x ∈R 及函数y =A cos(ωx +ϕ),x ∈R (其中A 、ω、ϕ为常数,且A ≠0,ω>0)的周期T =ωπ2.根据这个结论,我们可以由这类函数的解析式直接写出函数的周期,如对于上述例子:(1)T =2π,(2)T =22π=π,(3)T =2π÷21=4π 例2不通过求值,指出下列各式大于0还是小于0.(1)sin(-18π)-sin(-10π); (2)cos(-523π)-cos(-417π).例3 求函数y =2cos 1cos 3++x x 的值域.例4.f (x )=sin x 图象的对称轴是 .例5.(1)函数y =sin(x +4π)在什么区间上是增函数?(2)函数y =3sin(3π-2x )在什么区间是减函数?【当堂训练】1.函数y =cos 2(x -12π)+sin 2(x +12π)-1是( )A.奇函数而不是偶函数B.偶函数而不是奇函数C.奇函数且是偶函数D.非奇非偶函数2.函数y =sin (2x +25π)图象的一条对称轴方程是( )A.x =-2πB.x =-4πC.x =8πD.x =45π3.设条件甲为“y =A sin(ωx +φ)是偶函数”,条件乙为“φ=23π”,则甲是乙的( )A.充分非必要条件B.必要非充分条件C.充要条件D.既不充分也不必要条件4.函数y =sin 4x +cos 4x 的最小正周期为 .5.函数y =sin2x tan x 的值域为 .6.函数y =x -sin x ,x ∈[0,π]的最大值为( ) A.0 B. 2π-1 C.π D. 2243-π7.求函数y =2sin 22x +4sin2x cos2x +3cos 22x 的最小正周期.8.求函数f (x )=sin 6x +cos 6x 的最小正周期,并求f (x )的最大值和最小值.9.已知f (x )=xx x x cos sin 1cos sin 1+-,问x 在[0,π]上取什么值时,f (x )取到最大值和最小值.10.给出下列命题:①y =sin x 在第一象限是增函数; ②α是锐角,则y =sin(α+4π)的值域是[-1,1]; ③y =sin |x |的周期是2π; ④y =sin2x -cos2x 的最小值是-1;其中正确的命题的序号是 .11.求下列函数的单调递增区间:①y =cos(2x +6π); ②y =3sin(3π-2π)12.求函数y =-|sin(x +4π)|的单调区间.13.函数y =sin(2x +25π)的图象的一条对称轴方程是( ) A.x =-2π B.x =-4π C.x =8π D.x =45π【家庭作业】1.在下列区间中函数y =sin(x +4π)的单调增区间是( ) A.[2π,π] B.[0,4π] C.[-π,0] D.[4π,2π] 2.若函数y =sin2x +a cos2x 的图象关于直线x =-8π对称,试求a 的值. .]4,3[sin 2)( .3的取值范围上递增,求在是正数,函数已知例ωππωω-=x x f4.求下列函数的定义域、值域:(1); (2) ; (3) .5.求下列函数的最大值,并求出最大值时 的集合:(1) , ; (2) , ; (3)(4) .6.要使下列各式有意义应满足什么条件?(1); (2) .37.函数,的简图是()8.函数的最大值和最小值分别为()A.2,-2 B.4,0 C.2,0 D.4,-4 9.函数的最小值是()A.B.-2 C. D.10.如果与同时有意义,则的取值范围应为()A. B. C.D.或11.与都是增函数的区间是()A., B.,C., D.,12.函数的定义域________,值域________,时的集合为_________.13.求证:(1)的周期为;(2)的周期为;(3)的周期为.参考答案:例1解:(1)∵y =cos x 的周期是2π∴只有x 增到x +2π时,函数值才重复出现.∴y =3cos x ,x ∈R 的周期是2π.(2)令Z =2x ,那么x ∈R 必须并且只需Z ∈R ,且函数y =sin Z ,Z ∈R 的周期是2π.即Z +2π=2x +2π=2(x +π).只有当x 至少增加到x +π,函数值才能重复出现.∴y =sin2x 的周期是π.(3)令Z =21x -6π,那么x ∈R 必须并且只需Z ∈R ,且函数y =2sin Z ,Z ∈R 的周期是2π,由于Z +2π=(21x -6π)+2π=21 (x +4π)-6π,所以只有自变量x 至少要增加到x +4π,函数值才能重复取得,即T =4π是能使等式2sin [21 (x +T)-6π]=2sin(21x -6π)成立的最小正数.从而y =2sin(21x -6π),x ∈R 的周期是4π. 从上述可看出,这些函数的周期仅与自变量x 的系数有关.例2解:(1)∵-2π<-10π<-18π<2π. 且函数y =sin x ,x ∈[-2π,2π]是增函数. ∴sin(-10π)<sin(-18π) 即sin(-18π)-sin(-10π)>0 (2)cos(-523π)=cos 523π=cos 53π cos(-417π)=cos 417π=cos 4π ∵0<4π<53π<π 且函数y =cos x ,x ∈[0,π]是减函数∴cos53π<cos 4π 即cos 53π-cos 4π<0 ∴cos(-523π)-cos(-417π)<0 例3解:由已知:cos x =⇒--y y 312|y y --312|=|cos x |≤1⇒(yy --312)2≤1⇒3y 2+2y -8≤0 ∴-2≤y ≤34∴y max =34,y min =-2 例4解:由图象可知:对称轴方程是:x =k π+2π(k ∈Z ) 例5解:(1)函数y =sin x 在下列区间上是增函数:2k π-2π<x <2k π+2π (k ∈Z ) ∴函数y =sin(x +4π)为增函数,当且仅当2k π-2π<x +4π<2k π+2π 即2k π-3π<x <2k π+4π(k ∈Z )为所求. (2)∵y =3sin(3π-2x )=-3sin(2x -3π) 由2k π-2π≤2x -3π≤2k π+2π 得k π-12π≤x ≤k π+125π (k ∈Z )为所求. 或:令u =3π-2x ,则u 是x 的减函数 又∵y =sin u在[2k π-2π,2k π+2π](k ∈Z )上为增函数, ∴原函数y =3sin(3π-2x )在区间[2k π-2π,2k π+2π]上递减. 设2k π-2π≤3π-2x ≤2k π+2π 解得k π-12π≤x ≤k π+125π(k ∈Z ) ∴原函数y =3sin(3π-2x )在[k π-12π,k π+125π](k ∈Z )上单调递减. 【当堂训练】 1.A 2.A 3.B 4.2π 5.[0,2) 6.C 7. 2π 8.T=2π 函数最大值为1 函数最小值为41. 9.x =4π时,f (x )取到最小值31; x =43π时,f (x )取到最大值3. 10.分析:①y =sin x 是周期函数,自变量x 的取值可周期性出现,如反例:令x 1=4π,x 2=6π+2π,此时x 1<x 2 而sin 3π>sin(6π+2π)∴①错误;②当α为锐角时,4π<α+4π<2π+4π 由图象可知22<sin(α+4π)≤1 ∴②错误;③∵y =sin |x |(x ∈R )是偶函数.其图象是关于y 轴对称,可看出它不是周期函数.∴③错误;④y =sin 2x -cos 2x =-cos2x ,最小值为-1∴④正确.答案:④11. 解:①设u=2x +6π,则y =cos u当2k π-π≤u≤2k π时y =cos u 随u 的增大而增大 又∵u=2x +6π随x ∈R 增大而增大 ∴y =cos(2x +6π)当2k π-π≤2x +6π≤2k π(k ∈Ζ) 即k π-127π≤x ≤k π-12π时,y 随x 增大而增大 ∴y =cos(2x +6π)的单调递增区间为: [k π-127π,k π-12π](k ∈Z ) ②设u=3π-2π,则y =3sin u 当2k π+2π≤u≤2k π+23π时,y =3sin u随x 增大在减小, 又∵u=3π-2x 随x ∈R 增大在减小 ∴y =3sin(3π-2x )当2k π+2π≤3π-2x ≤2k π+23π 即-4k π-37π≤x ≤-4k π-3π时,y 随x 增大而增大 ∴y =3sin(3π-2x )的单调递增区间为 [4k π-37π,4k π-3π](k ∈Z )12. 解:利用“五点法”可得该函数的图象为:显然,该函数的周期为π在[k π-4π,k π+4π](k ∈Z )上为单调递减函数;在[k π+4π,k π+43π](k ∈Z )上为单调递增函数. 13. 方法一:运用性质1′,y =sin(2x +25π)的所有对称轴方程为x k =2πk -π(k ∈Z ),令k =-1,得x -1=-2π,对于B 、C 、D 都无整数k 对应. 故选A.方法二:运用性质2′,y =sin(2x +25π)=cos2x ,它的对称轴方程为x k =2πk (k ∈Z ),令k =-1,得x -1=-2π,对于B 、C 、D 都无整数k 对应,故选A. 【家庭作业】 1.分析:函数y =sin(x +4π)是一个复合函数即y =sin [ϕ(x )],ϕ (x )=x +4π,欲求y =sin(x +4π)的单调增区间,因ϕ (x )=x +4π在实数集上恒递增,故应求使y 随ϕ (x )递增而递增的区间.方法一:∵ϕ (x )=x +4π在实数集上恒递增,又y =sin x 在[2k π-2π,2k π+2π](k ∈Z )上是递增的,故令2k π-2π≤x +4π≤2k π+2π ∴2k π-43π≤x ≤2k π+4π ∴y =sin(x +4π)的递增区间是[2k π-43π,2k π+4π] 取k =-1、0、1,分别得[-411π,47π]、[-43π,4π]、[45π,49π], 对照选择支,可知应选B像这类题型,上述解法属常规解法,而运用y =A sin(ωx +ϕ)的单调增区间的一般结论,由一般到特殊求解,既快又准确,如本题倘若运用对称轴方程求单调区间,则是一种颇具新意的简明而又准确、可靠的方法.方法二:函数y =sin(x +4π)的对称轴方程是: x k =k π+2π-4π=k π+4π (k ∈Z ),对照选择支,分别取k =-1、0、1,得一个递增或递减区间分别是[-43π,4π]或[4π,45π],对照选择支思考即知应选B. 注:一般运用正、余弦函数的对称轴方程求其单调区间,可先运用对称轴方程求其一个单调区间,然后在两端分别加上周期的整数倍即得.2. 解:显然a ≠0,如若不然,x =-8π就是函数y =sin2x 的一条对称轴,这是不可能的. 当a ≠0时,y =sin2x +a cos2x =)2cos(1)2sin 112cos 1(12222θ-+=++++x a x a x a aa其中cos θ=2211sin ,1aaa +=+θ即tan θ=a1cos sin =θθ 函数y =21a +cos(2x -θ)的图象的对称轴方程的通式为2x k =k π+θ(k ∈Z )∴x k =22πθk +,令x k =-⇒8π22πθk +=-8π∴θ=-k π-4π∴tan θ=tan(-k π-4π)=-1.即a1=-1,∴a =-1为所求. 3. 解:由题设得)(2222Z k k x k ∈+≤≤-ππωππ.230.42,32.2222,0⎪⎩⎪⎨⎧≤<≥-≤-∴+≤≤-∴>ωπωππωπωπωπωπωπω解得k x k故ω的取值范围为].23,0(4. 解:(1) ,(2)由 ()又∵ ,∴∴定义域为 (),值域为. (3)由 (),又由∴∴定义域为(),值域为 .指出:求值域应注意用到 或 有界性的条件.5.解:(1)当,即()时,取得最大值∴函数的最大值为2,取最大值时的集合为.(2)当时,即()时,取得最大值.∴函数的最大值为1,取最大值时的集合为.(3)若,,此时函数为常数函数.若时,∴时,即()时,函数取最大值,∴时函数的最大值为,取最大值时的集合为.(4)若,则当时,函数取得最大值.若,则,此时函数为常数函数.若,当时,函数取得最大值.∴当时,函数取得最大值,取得最大值时的集合为;当时,函数取得最大值,取得最大值时的集合为,当时,函数无最大值.指出:对于含参数的最大值或最小值问题,要对或的系数进行讨论.思考:此例若改为求最小值,结果如何?6.解:(1)由,∴当时,式子有意义.(2)由,即∴当时,式子有意义.7.B 8.B 9.A 10.C 11.D12.;;13.分析:依据周期函数定义证明.证明:(1)∴的周期为.(2)∴的周期为.(3)∴的周期为.。
正弦函数和余弦函数的图像与性质

10
18
(2) 因为
π < 2 π < 3 π <π ,
23
4
且
y =sin x
在[ π ,π] 上是减函数,
2
所以 sin 2 π > sin 3 π .
3
4
例8.判断f(x)=xsin(+x)奇偶性
解 函数的定义域R关于原点对称 f (x) xsin( x) xsin x
f (x) (x)sin(x) f (x) f (x) f (x)
y
1
-2 - o 2 3
-1
4 x
定义域
R
值域
[1,1]
x 2k (k Z ) 时
2
最
值
ymax=1 x 2k (k Z ) 时
2
ymin= 1
y= 0 x k (k Z)
R [1,1]
x 2k (k Z) 时 ymax=1 x 2k (k Z ) 时 ymin= 1
是减函数。
② 函数y=cos(x+/2),xR ( A )
A 是奇函数; B 是偶函数; C 既不是奇函数也不是偶函数; D 有无奇偶性不能确定。
2 不通过求值,比较下列各组中两个三角函数值的大小:
sin 250 >_ sin 260
cos15 / 8>_ cos14 / 9
cos515 >_ cos530
y
1-
-
o
π 6
π 3
π 2
2π 3
5π 6
π
7 6
4π 3
3π 2
5π 3
11π 6
2π
x
-1 -
图象的最高点: ( π ,1); 2
正弦函数和余弦函数的图像与性质.ppt

, 0), (2 ,1)
2
2
并注意-4 曲线的“凹凸”变化.
课堂练习
1.作函数 y sin x 与 y sin x 1在 [0, 2 ]
上的大致图像. 2.指出1.中各图像与正弦函数图像的位置关系.
3.作函数 y cos x, x [ , ]的大致图像.
4.利用3.解不等式:cos x sin x, x [ , ]
-2
五个关键点:(0, 0), ( ,1), ( , 0), (3 , 1), (2 , 0)
2
2
利用五个关-4键点作简图的方法称为“五点法”
10
三、余弦函数的图像
根据诱导公式
cos
8
x
sin(
x) 可知余弦函数
y
cos
6
x的图像可由
y
2 sin
x
的图像向左平移
2
4
个单位得到.
1
2
2
-10
3-5
0
2
1
-2
余弦函数的值域是[1,1] -4
当且仅当 x 2k , k Z 时, -6
余弦函数取得最大值1;-8
5
2
35
x10
2
yP
OM x
当且仅当 x 2k , k-10 Z 时,
余弦函数取得最小值-1-1.2例1.求下列函数的源自大值与最小值,及取到最值6
课堂练习答案
12
1. y sin x, x [0, 2 ] y4
10
x
0
2
3 2
2
2 8
5
-10
正弦函数余弦函数的图象完整版课件
y
1-
-
-
6
4
2
o
-1-
2
4
6
x
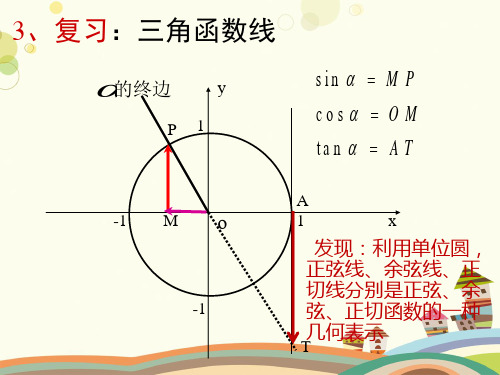
因为终边相同的角的三角函数值相同,所以y=sinx,x∈R的图象在
4,2 ,2,0, 0,2, 2,4,…与y=sinx,x∈[0,2π]的图象相同
正弦曲线:ysinx xRy
1
-1
x
-cosx -1 0
1
0 -1
y
y=-cosx x[0,2 ]
1
●
o
●
3●
2
x
2
2
-1 ●
●
思考:
1、函数y=1+sinx的图象与函数y=sinx的图象有什么关系? 2、函数y=-cosx的图象与函数y=cosx的图象有什么关系?
y 2
y=1+sinx x[0, 2]
1
o
3
2
-1
2
2
x
y=sinx x[0, 2]
1
●
●
●
●
●
7 4 3 5 11
6
6 3 2 3 6 2
●
2 0
2 5
●
11
6 32 3 6
●
●
x
●
5
6
-1
●
●
●
3
y
ysinx x [0 ,2 ]
1-
-
-1
o 6
3
2
2 3
5
7
6
6
4 3
3
5
2
3
11 6
2
-1 -
正弦函数余弦函数的图像与性质

三角函数在物理学中的应用
振动与波动
正弦和余弦函数是描述简谐振动和波动的基本函 数,广泛应用于声学、光学等领域。
交流电
交流电的电压和电流是时间的正弦或余弦函数, 用于驱动各种电器设备。
磁场与电场
在电磁学中,正弦和余弦函数用于描述磁场和电 场的分布和变工程中的许多振动问题都可以用 正弦和余弦函数来描述,如桥梁 振动、车辆振动等。
周期性
正弦函数具有周期性, 其周期为2π。
奇偶性
正弦函数是奇函数,满 足sin(-x) = -sin(x)。
余弦函数的定义
定义
余弦函数是三角函数的另一种形式,定义为直角三角形中锐角的邻边与斜边的比值,记作 cos(x)。
周期性
余弦函数也具有周期性,其周期为2π。
奇偶性
余弦函数是偶函数,满足cos(-x) = cos(x)。
奇偶性
总结词
正弦函数是奇函数,而余弦函数是偶 函数。
详细描述
奇函数满足$f(-x) = -f(x)$,偶函数满 足$f(-x) = f(x)$。对于正弦函数, $sin(-x) = -sin(x)$;对于余弦函数, $cos(-x) = cos(x)$。
最值与振幅
总结词
正弦函数和余弦函数都具有最大值和最小值,这取决于它们的振幅。
正弦函数余弦函数的图像与性质
目录
• 正弦函数与余弦函数的定义 • 正弦函数与余弦函数的图像 • 正弦函数与余弦函数的性质 • 正弦函数与余弦函数的应用 • 正弦函数与余弦函数的扩展知识
01 正弦函数与余弦函数的定 义
正弦函数的定义
定义
正弦函数是三角函数的 一种,定义为直角三角 形中锐角的对边与斜边 的比值,记作sin(x)。
1.4.1三角函数图象(正弦、余弦)

三、巩固提高,实战演练 巩固提高,
画出下列函数的简图( 例2.画出下列函数的简图(五点法作图) 画出下列函数的简图 五点法作图)
(请同学们在练习本上独立完成,邻桌对照) 请同学们在练习本上独立完成,邻桌对照) (1)y=2sinx , x∈[0,2π] ) 解: (1)列表 ) (2)描点作图 描点作图 Y 2 1 0
π
π
单调减区间: 单调减区间
π
3π [ + 2kπ , + 2kπ ](k ∈ Z ) 2 2
单调减区间: 单调减区间
[2kπ ,π + 2kπ ](k ∈ Z )
的集合: 【例2】求下列函数的最大值,并求出最大值时 的集合: 】求下列函数的最大值,并求出最大值时x的集合 (1)y=cos x ,x∈R ; (2) y=2-sin2x,x∈R ∈ ∈
正弦图像之应用: 正弦图像之应用:例子一 图像
正弦图像之应用:例子二 正弦图像之应用:例子二 图像
一、创设情境,引入新课 创设情境,
思考: 思考:角的集合与实数集合以及三角函数值之间有着怎 样的关系? 样的关系? 角
一 一对应
实数(角的弧度数) 实数(角的弧度数)
三角函数值
实数集与角的集合之间可以建立一一对应关系, 实数集与角的集合之间可以建立一一对应关系, 而一个确定的角又对应唯一确定的正弦(或余弦) 而一个确定的角又对应唯一确定的正弦(或余弦) 这样任意给定的一个实数x, 值。这样任意给定的一个实数 ,有唯一确定的的值 sinx(或cosx)与之对应。由这个对应法则所确定的函 ( )与之对应。 数y=sin x(或 y=cos x)叫做正弦函数(或余弦函数), ( )叫做正弦函数(或余弦函数), 其定义域为R. 其定义域为 .
正弦函数余弦函数的图像和性质

f ( x) = 3cos x = 3cos( x + 2π ) = f ( x + 2π )
所以T=2π
2、y=sin2x x ∈R 解、令z=2x,那么x∈R必须并且只需z∈R,且函 数y=sinz,z∈R的T=2π,即变量z只要并且至少 要增加到z+2π,函数y=sinz,z∈R的值才能重复 取得,而z+2π=2x+2π=2(x+π) 故变量x只要并且至少要增加到x+π,函数值 x x+π 就能重复取得,所以y=sin2x,x∈R的T=π 即 f ( x) = sin 2 x = sin(2 x + 2π ) = sin 2( x + π ) = f ( x + π ) 所以T=π
例1.画出下列函数的简图 .
(1)y= 2sinx ,x∈[0, 2π], ) ∈ π (2)y=sin2x , x∈[0,2π] ) 解: (1) 列表 ) Y 2 1 0
x y=2sinx
0 0
π
2
π 0
3π 2
2π π 0
2
-2
(2)描点作图 描点作图
y=2sinx y=sinx
π
2π
X
2、五点作图法 、
y = sin( x + ), x ∈ R 3 4
例4利用三角函数的单调性,比较下列各组数的大小:
(1) sin 250 (2) cos
15 π 8
o
与
sin 260o
与 cos 14 π 9
例5 求函数 y = sin( 2 x + 3 ), x ∈ [−2π , 2π ] 的单调递增区间. 解: 令
( 0 , 0 ) (π , 0 ) (2π ,0)
正余弦函数的图像与性质

o
-1
2
3
4
5
6
x
正弦函数的图象 y=sin(x+ )=cosx, xR 2 y 余弦函数的图象
(0,1) (0,1) 1 -4 -3 -2 -
(o 2 ,0) 2 -1
3 ( ,0) 2
形状完全一样 只是位置不同
正弦曲 线
,1) ,1) ((22
2 3 4
f ( x 2 ) sin( x 2 ) sin x f ( x) 最小正周期为2
余弦函数的性质
1、定义域 2、值域
3、对称性
xR y 1,1
( k∈Z)
对称轴方程 x= k
4、单调性
在x 2k ,2k 上是增函数;
当x 2k时,ymax 1
y
1
4 3
2
3 2
2
2
3
4
7 2
5 2
0
-1
2
3 2
5 2
7 2
x
y=sin x, x∈R
思考与交流:图中,起着关键作用的点
是那些?找到它们有什么作用呢? 3 0,0 ,1 ,0 , 1 2
正弦函数y=sinx(x R)的图象
5 6
2 3
2
3 6
11 6
y
1
● ● ● ● ●
y=sinx ( x[0, 2 ] )
●
7 6 4 3 5 3
7 4 3 5 11 6 6 3 2 3
2
●
2
0
6
正弦函数、余弦函数的图像及五点法作图

正弦函数、余弦函数的图像及五点法作图
【余弦函数y=cosx的图象】
用几何法作余弦函数的图象,可以用“反射法”将
角 与 终xx点的轴A余的作弦 正x轴线 半的“ 轴垂竖 成线立4,”角它[的把与直坐前线标面,轴所又向作过下的余平直弦移线线,交O过于1OAA1的′作,
那么 O1 A与AA′长度相等且方向同时为正,我们就 把余弦线 O1 A“竖立”起来成为AA′,用同样的方 法,将其它的余弦线也都“竖立”起来.再将它们 平移,使起点与x轴上相应的点x重合,则终点就是 余弦函数图象上的点.]
解:按五个关键点列表
利用正弦函数的特征描点画图:
正弦函数、余弦函数的图像及五点法作图
【变形训练】
1、作出 y cos x, x 0, 2 的简图
解:按五个关键点列表
x
0
2
π
3
2π
2
cosx 1
0
-1
0
1
-cosx -1
0
1曲线连接起来.
y=cosx的图象. 正弦函数y=sinx的图象和余弦函数y=cosx的图象 分别叫做正弦曲线和余弦曲线.
正弦函数、余弦函数的图像及五点法作图
【余弦函数y=cosx的图象】
-6 -5 -6 -5
-4 -3 -4 -3
-2 -
-2
-
y y=sinx
1
o
-1
y y=cosx
1
正弦函数、余弦函数的图像及五点法作图
【余弦函数y=cosx的图象】
也可以用“旋转法”把角 的余弦线“竖立”(把
角置诱x=x,导si的n则公x余的式O弦1图cM线o象s1与Ox向1OM左1sM按i平n长(逆移x度时 2相2针)单等方,还位,向可即方旋以得向转把余相2正弦同到弦函.O)函数1M根数1据位
正弦、余弦、正切函数图象及其性质
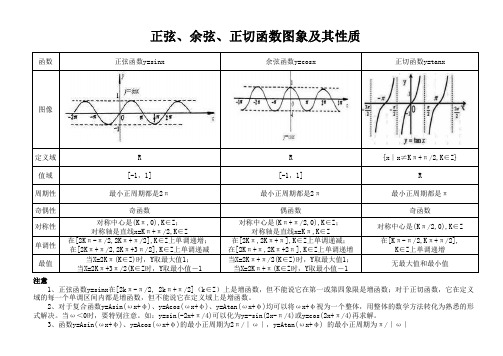
函数正弦函数y=sinx 余弦函数y=cosx 正切函数y=tanx图像定义域R R{x∣x≠Kπ+π/2,K∈Z}值域[-1,1][-1,1]R周期性最小正周期都是2π最小正周期都是2π最小正周期都是π奇偶性奇函数偶函数奇函数对称性对称中心是(Kπ,0),K∈Z;对称轴是直线x=Kπ+π/2,K∈Z对称中心是(Kπ+π/2,0),K∈Z;对称轴是直线x=Kπ,K∈Z对称中心是(Kπ/2,0),K∈Z单调性在[2Kπ-π/2,2Kπ+π/2],K∈Z上单调递增;在[2Kπ+π/2,2Kπ+3π/2],K∈Z上单调递减在[2Kπ,2Kπ+π],K∈Z上单调递减;在[2Kπ+π,2Kπ+2π],K∈Z上单调递增在[Kπ-π/2,Kπ+π/2],K∈Z上单调递增最值当X=2Kπ(K∈Z)时,Y取最大值1;当X=2Kπ+3π/2(K∈Z时,Y取最小值-1当X=2Kπ+π/2(K∈Z)时,Y取最大值1;当X=2Kπ+π(K∈Z时,Y取最小值-1无最大值和最小值正弦、余弦、正切函数图象及其性质注意1、正弦函数y=sinx在[2kπ-π/2, 2kπ+π/2](k∈Z)上是增函数,但不能说它在第一或第四象限是增函数;对于正切函数,它在定义域的每一个单调区间内都是增函数,但不能说它在定义域上是增函数。
2、对于复合函数y=Asin(ωx+φ)、y=Acos(ωx+φ)、y=Atan(ωx+φ)均可以将ωx+φ视为一个整体,用整体的数学方法转化为熟悉的形式解决。
当ω<0时,要特别注意。
如:y=sin(-2x+π/4)可以化为y=-sin(2x-π/4)或y=cos(2x+π/4)再求解。
3、函数y=Asin(ωx+φ)、y=Acos(ωx+φ)的最小正周期为2π/∣ω∣,y=Atan(ωx+φ) 的最小正周期为π/∣ω∣。
正弦函数、余弦函数的图像 课件

五点描出后,余弦函数y=cos x,x∈[0,2π]的图像的形状也
就基本上确定了.
2.利用三角函数图像解三角不等式的步骤: (1)作出相应的正弦函数或余弦函数的图像; (2)写出在[0,2π]上适合不等式的解集; (3)根据公式一写出定义域内的解集.
②描点:
③连线:用光滑的曲线依次连接各点,即得 所求的图像.
(2)画法:①列表:
x
0
sin x
0
-sin x
0
π 2
π
3π 2
2π
1 0 -1 0
-1 0 1 0
②描点: ③连线:用平滑曲线依次连接各点,即可得到所求图像.
[一点通] 作形如 y=asin x+b(或 y=acos x+b),x∈[0,2π] π
1.正弦曲线 正弦函数y=sin x,x∈R的图像叫正弦曲线.
2.正弦函数图像的画法
(1)几何法: ①利用 正弦线 画出y=sin x,x∈[0,2π]上的图像; ②将图像向左、向右 平行移动(每次2π个单位).
(2)五点法:
画出正弦曲线在[0,2π]上的图像的五个关键点 (0,0),
(
π
2 ,1),
集合为{x|π6 +2kπ≤x≤56π+2kπ,k∈Z}.
(12分)
法二:(利用单位圆中三角函数线)
如图(2),在0≤x<2π中,满足sin
x≥
1 2
的角x的集合为
{x|π6 ≤x≤5π6 }.
(10分)
因此当x∈R时,
集合为{x|π6 +2kπ≤x≤56π+2kπ,k∈Z}.
(12分)
[一点通] 正、余弦函数图像的作用主要有:解三角不 等式,确定交点个数及求定义域等,具体地确定范围时,应 先确定出[0,2π]上的范围,再向左向右扩展,即得整个实 数集上的范围.求交点个数时图像务必准确.
数学中的三角函数正弦余弦与正切的应用

数学中的三角函数正弦余弦与正切的应用在数学中,三角函数是一种基础的数学工具,常用于解决与角度和三角形相关的问题。
其中,正弦、余弦和正切是三角函数中最常见且广泛应用的三种。
它们在几何、物理、工程等领域中起到了重要的作用。
本文将介绍三角函数正弦、余弦和正切的定义、性质以及其在各个领域中的具体应用。
一、正弦函数的定义与性质在三角函数中,正弦函数(sin)是最基本且常见的函数之一。
它的定义如下:定义1:对于任意实数x,正弦函数sin(x)的值等于以x为角度的弧所对应的直角三角形中,斜边的长度与斜边所在直角的邻边的比值。
正弦函数的性质如下:性质1:正弦函数的周期为2π(或360°)。
即sin(x+2π) = sin(x),对于任意实数x。
性质2:正弦函数的取值范围为[-1,1]。
即-1≤ sin(x) ≤1,对于任意实数x。
正弦函数在几何、物理等领域中有许多应用。
1. 几何中的应用正弦函数在解决几何问题中起到了重要的作用,尤其是在三角形中。
其中,正弦定理是一项基于正弦函数的重要几何定理。
它可以用于计算三角形的边长或角度。
利用正弦函数,可以得到正弦定理的数学表达式如下:对于任意三角形ABC,边长分别为a, b, c,对应的角度分别为A, B, C,那么有:sin(A)/a = sin(B)/b = sin(C)/c根据这个定理,我们可以根据已知的两个边与它们夹角的关系,求解未知边长或角度。
2. 物理中的应用正弦函数在物理学中的应用非常广泛。
例如,振动和波动等现象均可以通过正弦函数进行描述和分析。
在简谐振动中,物体以正弦函数的形式来回振动。
振动的幅度、频率以及相位差等都可以通过正弦函数来表示。
在波动中,正弦函数也被广泛应用。
例如,声波、光波等均可以表示为正弦函数的形式。
通过正弦函数可以描述波的振幅、频率、波长等特征。
3. 工程中的应用正弦函数在工程领域中也有很多应用。
例如,在电工学中,交流电信号可以表示为正弦函数。
正弦,余弦函数的图像PPT课件

途径:利用单位圆中正弦、余弦线来解决。
描图:用光滑曲线
y
B
1
将这些正弦线的 终点连结起来
A
O1
O
2
4
5
2
x
3
3
3
3
-1
y=sinx
终边相同角的三角函数值相等 即: sin(x+2k)=sinx, kZ
x[0,2]
f(x2k)f(x)利用图象平移
y=sinx xR
正弦、余弦函数的图象
y 1
o
2
2
-1
y=sinx x[0,2]
y
y=sinx xR
1
-4 -3
-2
- o
-1
3
2
x
2
正弦曲 线
2
3
4
5 6 x
正弦、余弦函数的图象
如何作出正弦函数的图象(在精确度要求不太高时)?
y
五点画图法
1
(2
,1)
( 2 ,1)
( ,0)
( 2 ,0)
五点法——
2
(
(0,0)o
(0,0)
2
(0,0)
-1
(0,0)
汇报人:XXX 汇报日期:20XX年10月10日
2 ,0) x
2 ,0)
( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0)
正弦、余弦函数的图象
y
1
-4 -3
-2
- o
-1
2
3
4
5 6 x
正弦函数的图象 y=cosx=sin(x+ ), xR
2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 -(0,1)
-
(2 ,1) 最高点
o
1
-
( , 1)
( 32 ,0) 2 x
最低点
平衡点
用“五点法”与正弦余弦函数图 像解决有关的问题
例1:用“五点法”作 的简 y sin(2 x ) , x [ , ] 3 2 2 图. 3 2 4 2x 0 0 2 2
连州中学 黄淑霞
授课班级
高三(16)班
复习回顾 1.正弦线、余弦线 y 正弦线: MP
P
余弦线: OM
o
M
x
2.诱导公式
正弦余弦函数的图像及其应用
作正弦余弦函数的图像的方法 正弦线
作精确的图像
平移
正弦函数的图像
余弦函数的图像
作简图
“五点法”作图
利用正弦线作出正弦函数的图像
( 1)作y sin x (0 x 2 )的图像
在区间 [ , ] 上的最小值是-2,则ω的最小值等 于( B ) 2 A. 3
y
3 B. 2
3 2
C .2
D.3
2 2
3 2
o
x
3 即 2
2
巩固练习 1.(08’四川,15)已知函数 f ( x ) sin( x ) ( 0) 在 6 1 4 4 (0, ) 单调递增,在 ( , 2 ) 单调递减, 则_____. 2 3 3 分析: 4
图像平移 作余弦函数的图像; 2.利用_________
“五点法” 3.利用________ 作正弦余弦函数及
y A sin( x ) b 的简图;
4.用“五点法”与正弦余弦函数图 像解决有关的问题.
y
2
7 12
o
2
4
5 4
x
2 y sin(2 x ) 图所示,则函数的解析式是_____________. 3
3. 函数 y sin( x )( 0,| | ) 的图像如
y
1
o
1
12
7 12
x
课堂小结
正弦线 作出正弦函数的图像; 1.利用_______
8 ∵点(-2,0)是“五点” 中的第一个关键点 2k , k Z 4
2
o
4
6
x
4
即
4
2k , k Z . 又 | |
2
变式训练.(09’辽宁,8)已知函数 f ( x ) A cos( x )
2 的图像如图所示, f ( ) , 则 f(0)等于( 2 3
3 是最大值点
1 3k 4 2k , k Z 即 ,k Z 3 6 2 2
又T>2 且 >0
1 2
即 0< <1
2.(09’海南,16)已知函数 f ( x ) 2sin( x ) 的图像 7 0 . 如图所示,则 f ( ) _____ 12
6
12
2
3
3
2
3 2
)
3 2
1
0
1
y
2
1
2
o
1
x
y 课后作业:用“五点法”作
2 sin(2 x
4
) 1, x [
, ] 2 2
的简图.
变式:(2010’江西)如图, 四位同学在同一个坐标系中分别 选定了一个适当的区间, 各自作出三个函数 y sin 2 x, y sin( x ), y sin( x ) 的图像如下.结果发现其中有一
C )
1 D. 2
2 A. 3
1 B. 2
2 C. 3
解法二:
2 由图知T . 3 2 f (0) f ( ) 3
y
2
o
2 3
7 2 11 12 3 12
x
例3.(06’辽宁11)
1 1 已知函数 f ( x ) (sin x cos x ) sin x cos x , 2 2 则f(x)的值域是( C )
y cos x sin(
正弦曲线
x x)
1. y sin x (0 x 2 )的简图
y
1-
五点法
(2 , 0) 平衡点
2
( ,1) 最高点 2
o (0, 0)
-
( , 0)
3 2
x
最低点
1
-
( , 1)
( , 0) 2
2. y cos x (0 x 2 )的简图
位同学作出的图像有错误,那么有错误的图像是(C )
6
3
0
A
B
3 2 2
C
D
例2.函数 y A sin( x )( 0, ) 的部分图
8 ∵点(-2,0)是“五点” 中的第三个关键点 2 2k , k Z 4 4
2 y 4sin( x ) 像如图所示,则函数表达式为______________. 8 4 分析: 由图知ymax 4, T 16. y , 当A 4时, 8 4 则y 4sin( x )
(2)利用周期性作y=sinx的图像
y
1
-
正弦曲线
2
4
6
6
4
2
o
-
-1
x
利用图像平移作余弦函数的图像
y
1
-
余弦曲线
2
-
6
-
4
-
2
-
o
-
-1
4
-
6
-
x
2 2 y=cosx的图像可通过把y=sinx的图像 左平移____ 向__ 2 个单位长度而得到.
3
x
y sin(2 x
3
2
2 2
3
6 2
3 2
)
例1:用“五点法”作 的简 y sin(2 x ) , x [ , ] 3 2 2 图. 2 4 2x 0 3 2
3
x
y sin(2 x
3
2
5 12
)
1 D. 2
2 A. 3
1 B. 2
解法一:求出f(x)的 解析式,再求f(0)
y
2 C. 3
o
2 3
2
7 12
11 12
x
变式训练.(09’辽宁,8)已知函数 f ( x ) A cos( x )
2 的图像如图所示, f ( ) , 则 f(0)等于( 2 3
o
6
x
5 即 2k , k Z . 又 | | 4 2
无解
例2.函数 y A sin( x )( 0, ) 的部分图
2 y 4sin( x ) 像如图所示,则函数表达式为______________. 8 4 分析: 由图知ymax 4, T 16. y , 当A 4时, 8 4 则y 4sin( x )
A. [1,1]
B.
cos x , sin x cos x f ( x) sin x , sin x cos x y
1
2 [ ,1] 2
2 2 C. [1, ] D. [1, ] 2 2
o
1
-
2
x
变式训练.(06’福建9)已知函数
3 4
f ( x ) 2sin x( 0)
