频率分布直方图、折线图
频率分布直方图与折线图课件

优缺点分析
分别分析两种图表在展示 数据方面的优缺点,以便 在实际应用中选择合适的 图表。
实例对比
通过对比实际数据实例, 展示两种图表在展示数据 时的差异和效果。
感谢您的观看
THANKS
频率分布直方图的缺点
对于连续型数据或数据量较小的情况,直方图的表现力可能不够理想。
折线图的优点
能够直观地展示数据随时间或其他变量的变化趋势。能够清晰地展示 数据的趋势和变化。
折线图的缺点
对于数据点较少或数据变化不大的情况,折线图的表现力可能不够理 想。
05
实践练习
制作频率分布直方图
收集数据
首先需要收集一组数据,可以是 关于某班级学生的考试成绩、某
频率分布直方图与折线图课 件
目录
• 引言 • 频率分布直方图 • 折线图 • 比较频率分布直方图与折线图 • 实践练习
01
引言
课程目标
掌握频率分布直方图 和折线图的绘制方法
能够根据实际数据选 择合适的图表进行展 示
理解频率分布直方图 和折线图在数据分析 中的应用
学习内容概述
01
02
03
04
频率分布直方图的概念、特点 和绘制步骤
品牌产品的销售数据等。
确定组距
根据数据的特点和需求,确定 合适的组距,以便将数据分成 若干个区间。
计算频率
根据每个区间的数据个数,计 算出每个区间的频率。
绘制直方图
使用适当的图表软件,根据区间 和频率绘制出直方图,每个矩形
的高度代表该区间的频率。
制作折线图
01
02
03
04
准备数据
准备一组有序的数据点,可以 是时间序列数据或有序分类数
高二数学教案:频率分布直方图与折线图

高二数学教案:频率分布直方图与折线图总课题总体分布的估量总课时第14课时分课题频率分布直方图与折线图分课时第2 课时教学目标能列出频率分布表,能画出频数条形图、频率分布直方图及折线图;会用样本频率分布去估量总体分布.重点难点绘制频率直方图、条形图、折线图.引入新课1.列频率分布表的一样步骤是什么?能否依照频率分布表来绘制频率直方图?2.作频率分布直方图的方法为:3.假如将频率分布直方图中各相邻矩形的上底边中点并顺次连结起来,就得到_________,简称___________.4.频率折线图的优点是:__________________________.假如样本容量取得足够大,分组的组距取得足够小,那么相应的频率折线图将趋于一条光滑的曲线,我们称这条光滑的曲线为总体分布的___________.例题剖析例1 下表是某学校一个星期中收交来的失物件数,请将5天中收交来的失物数用条形图表示.星期一二三四五件数6 2 3 5 1累计6 8 11 16 17例2 作出例中数据的频率分布直方图.例3 为了了解一大片经济林生长情形,随机测量其中的株的底部周长,得到如下数据表(单位:cm)135 98 102 110 99 121 110 96 100 103125 97 117 113 110 92 102 109 104 112109 124 87 131 97 102 123 104 104 128105 123 111 103 105 92 114 108 104 102129 126 97 100 115 111 106 117 104 109111 89 110 121 80 120 121 104 108 118129 99 90 99 121 123 107 111 91 10099 101 116 97 102 108 101 95 107 101102 108 117 99 118 106 119 97 126 108123 119 98 121 101 113 102 103 104 108(1)编制频率分布表;(2)绘制频率分布直方图;(3)估量该片经济林中底部周长小于100cm的树木约占多少,周长不小于120cm的树木约占多少.巩固练习1.在频率分布直方图中,所有矩形的面积和为_________.2. 辆汽车通过某一段公路时的时速如下图所示,则时速在的汽车大约有______辆.课堂小结什么是频数条形图、频率直方图、折线图、密度曲线.课后训练班级:高二( )班姓名:____________一基础题1.在人中,有个学生,个干部,个工人,个农民,则是工人( )A.频数B.频率C.累计频率D.累计频数2.关于样本频率分布折线图与总体密度曲线的关系,下列说法中正确的是( )A.频率分布折线图与总体密度曲线无关;B.频率分布折线图确实是总体密度曲线;C.样本容量专门大的频率分布折线图确实是总体密度曲线;D.假如样本容量无限增大,分组的组距无限减小,那么频率分布折线图就会无限接近于总体密度曲折线.3.在频率分布直方图中,各个小长方形的面积表示( )A.落在相应各组的数据的频数B.相应各组的频率.C.该样本所分成的组数D.该样本的样本容量4.容量为的某个样本数据拆分为组,并填写频率分布表,若前七组频率之和为,而剩下的三组的频率依次差为,则剩下的三组中频率最大的一组的频率为_________.5.在一个小时内统计一传呼台接收到用户的呼吁次数,按每分钟统计如下:写出一分钟内传呼呼吁次数的频率分布表,并画出频率分布图.二提高题6.在一个容量为的样本,数据的分组及各组的频数如下:(1)列出样本的频率分布表;(2)画出频率分布直方图;(3)依照频率分布直方图估量,数据落在的可能性约是多少?7.姚明在赛季常规赛场竞赛的前场中,带领休斯顿火箭队取得了较好的战绩,提早锁定了季后赛资格.以下是姚明在这场竞赛中的得分表现:(1)假如将那个数据分为组,作出这组数据的频率分布表;(2)画出频率分布直方图并作出频率折线图;要练说,得练听。
频率分布直方图和折线图
频率分布直方图和折线图【学习导航】知识网络学习要求1.频率分布直方图的作法,频率分布直方图更加直观形象地反映出总体分布的情况;2.频率分布折线图的作法,优点是反映了数据的变化趋势,如果样本容量足够大,分组的组距足够小,则这条折线将趋于一条曲线,称为总体分布的密度曲线。
【课堂互动】自学评价案例1 下表是某学校一个星期中收交来的失物件数,请将5天中收交来的失物数用条(1)在EXCEL工作表中输入数据,光标停留在数据区中;(2)选择“插入/图表”,在弹出的对话框中点击“柱形图”;(3)点击“完成”,即可看到如下频数条形图.案例2 从某校高一年级的1002名新生中用系统抽样的方法抽取一个容量为100的身高样本,数据如下(单位:cm)。
试作出该样本的频率分布直方图和折线图.【解】上一课时中,已经制作好频率分布表,在此基础上, 我们绘制频率分布直方图.(1)作直角坐标系,以横轴表示身高,纵轴表示组距频率;(2)在横轴上标上150.5,153.5,156.5,…,180.5表示的点。
(为方便起见,起始点150.5可适当前移);(3)在上面标出的各点中,分别以连结相邻两点的线段为底作矩形,高等于该组的组距频率至此,就得到了这组数据的频率分布直方图,如下图150.5 153.5 156.5 159.5 162.5 165.5 168.5 171.5 174.5 177.5 180.8同样可以得到这组数据的折线图.150.5 153.5 156.5 159.5 162.5 165.5 168.5 171.5 174.5 177.5180.8【小结】1.利用直方图反映样本的频率分布规律,这样的直方图称为频率分布直方图(frequency histogram),简称频率直方图。
2. 频率直方图比频率分布表更直观、形象地反映了样本的分布规律。
3.如果将频率分布直方图中相邻的矩形的上底边的中点顺次连结起来,就得到一条折线,我们称这条折线为本组数据的频率折线图(frequency polygon)4.频率分布折线图的的首、尾两端如何处理: 取值区间两端点须分别向外延伸半个组距,并取此组距上的x轴上的点与折线的首、尾分别相连5.如果将样本容量取得足够大,分组的组距取得足够小,则这条折线趋于一条曲线,这一曲线称为总体分布的密度曲线。
2.2.2频率分布直方图与折线图课件

思考: 思考: 频率分布条形图和频率分布直方图是两个相同的概念吗? 频率分布条形图和频率分布直方图是两个相同的概念吗? 有什么区别? 有什么区别? 频率分布的条形图和频率分布直方图的区别 两者是不同的概念; 两者是不同的概念; 横轴:两者表示内容相同. 横轴:两者表示内容相同 相同 纵轴:两者表示的内容不相同 不相同. 纵轴:两者表示的内容不相同 频率分布条形图的纵轴 长方形的高)表示频数或频率; 的纵轴( 频率分布条形图的纵轴(长方形的高)表示频数或频率 频率分布直方图的纵轴(长方形的高) 频率分布直方图的纵轴(长方形的高)表示频率与组距 的纵轴 的比值.其相应组距上的频率等于该组距上长方形的面积 其相应组距上的频率等于该组距上长方形的面积. 的比值 其相应组距上的频率等于该组距上长方形的面积
(1)编制频率分布表 (1)编制频率分布表 ; (2)绘制频率分布直方图 ; (2)绘制频率分布直方图 (3)估计该片经济林中底部周长小于100cm的树木约占多 估计该片经济林中底部周长小于100cm (3)估计该片经济林中底部周长小于100cm的树木约占多 周长不小于120cm 120cm的树木约占多少 少,周长不小于120cm的树木约占多少 .
频率折线图的优点是它反映了数据的变化趋势 . 如果将样本容量取得足够大 , 分组的组距取得足够 小 , 则这条折线将趋于一条曲线 , 我们称这一曲线 为总体分布的密度曲线 为总体分布的密度曲线 . 如例 3 的频率分布密度曲线可近似地表示为下图 :
例4.为了了解一大片经济林的生长情况,随机测量其中的 4.为了了解一大片经济林的生长情况, 为了了解一大片经济林的生长情况 株的底部周长,得到如下数据表(长度单位:cm): 100 株的底部周长,得到如下数据表(长度单位:cm):
用excel画频率分布直方图、折线图、散点图方法

Excel在统计中的应用一、用excel来计算样本的数字特征(1)平均值法一:按定义来算,先算出所有数据的总和,然后在除以样本个数法二:直接用函数average计算(2)中位数法一:先排序(数据——排序),然后找出中间值法二:直接用函数median计算(3)众数(英文名mode)直接用函数mode来计算(4)方差(英文名variance)直接用函数var计算(5)标准差(英文名standard deviation)直接用函数stdev计算二、用excel画频率分布直方表和频率分布直方图(分析工具库属于扩展功能,应在工具——宏加载——分析工具库)①录入数据②求出最大值与最小值,确定组距(可接收范围)③工具——数据分析——直方图——确定——(输入区域:所录入的数据;接受区域:确定的分组数据;输出区域:可以在当前表格,也可在新表格)选择累计百分率和图表输出——确定观察所得出的图形?与课本上的频率分布直方图对比画频率分布表:①将接受改为分组,下面数据改为相应区间,将频率改为频数②在右侧增加一列频率和频率/组距,并用相应函数计算画频率分布直方图和频率分布折线图①选中分组下面的数据,按住ctrl,选择频率/组距和累积%下面相应的数据,然后插入——图表——柱形图②将累积%的柱形图改为折线图,(右键——图表类型——折线图)③将条形图变为直方图(右键——数据系列格式——选项——分类间距调整为0)④将累积%的折线图变为频率分布折线图(改变百分比)Excel中没有直接的函数计算茎叶图和总体密度曲线图,可以用专门的统计软件来作(R软件、SPSS软件等)三、画散点图和回归直线插入——图表——散点图——添加趋势线——线性——选项——显示公式——确定工具——数据分析——相关系数r。
频率分布直方图和折线图

频率折 线图
0.08
频率直方
0.06
图
0.04
0.02
150.5 153.5
162.5 165.5
180.5
身高/cm
折线图反映了数据的变化趋势;若组距取得越小,则
频率折线的光滑程度会怎样?
越光滑
频率折线图的 优点是它反映 了数据的变化
频率/组距 0.08
趋势.如果把样
0.06
本容量取得足
0.04
课堂小结
1、绘制频率分布直方图的步骤 2、绘制频率分布折线图的步骤 3、总体分布的密度曲线
4、频率分布表、频率分布直方图、 频率分布折线图各自的优点。
四、课堂练习 (1)教材56页第2题. (2)一个高中研究性学习小组对本地区2000年至2002年 快餐公司发展情况进行了调查,制成了该地区快餐公司个 数情况的条形图和快餐公司盒饭年销售量的平均数情况条 形图(如图),根据图中提供的信息可以得出这三年中该 地区每年平均销售盒饭 85 万盒.
快餐公司饭盒年平均数图
分组
频数
频率
频数/组距
[80,85)
1
0.01
0.002
[85,90)
2
0.02
0.004
[90,95)
4
0.04
0.008
[95,100)
14
0.14
0.028
[100,105)
24
0.24
0.048
[105,110)
15
0.15
0.03
[110,115)
12
0.12
0.024
[115,120)
9
162.5 165.5
频率分布表

例2、为了了解一大片经济林的生长情况,随机测量其中的100株的 底部周长,得到如下数据表(长度单位:cm):
135 98 102 110 99 121 110 96 100 103 125 97 117 113 110 92 102 109 104 112 109 124 87 131 97 102 123 104 104 128 105 123 111 103 105 92 114 108 104 102 129 126 97 100 115 111 106 117 104 109 111 89 110 121 80 120 121 104 108 118 129 99 90 99 121 123 107 111 91 100 99 101 116 97 102 108 101 95 107 101 102 108 117 99 118 106 119 97 126 108 123 119 98 121 101 113 102 103 104 108
合计
பைடு நூலகம்
100 1
频率分布表的制作
1、计算数据中最大值与最小值的差,
即全距。据此,决定组数和组距。
组距
全距 组数
2、分组:通常对组内数据所在区间取 左闭右开区间,最后一组取闭区间。
3、登记频数,计算频率,列出频率分 布表
练习1
1. 某电子元件厂生产一批同型号的电子元件,今 从中随机地抽取40个测得其电阻值如下:
168 165 171 167 170 165 170 152 175 174 165 170 168 169 171 166 164 155 164 158 170 155 166 158 155 160 160 164 156 162 160 170 168 164 174 171 165 179 163 172 180 174 173 159 163 172 167 160 164 169 151 168 158 168 176 155 165 165 169 162 177 158 175 165 169 151 163 166 163 167 178 165 158 170 169 159 155 163 153 155 167 163 164 158 168 167 161 162 167 168 161 165 174 156 167 166 162 161 164 166
频率分布表

B、1/14
C、0.03
D、3/14
3、将一个容量为50的样本数据分组后,组距和频数如下:
[12.5,15.5),3;[15.5,18.5),8;[18.5,21.5),9; [21.5,24.5),11;[24.5,27.5),10;[27.5,30.5),6; [30.5,33.5],3.
则估计小于30的数据大约占总体的( A)
161
165
174
156
167
166
162
161
164
166
168
165
171
167
170
165
170
152
175
174
165
170 160 180 151 177 178 167 161
170
155 170 174 168 158 165 163 165
168
166 168 173 158 175 158 164 174
练习1
1. 某电子元件厂生产一批同型号的电子元件,今 从中随机地抽取40个测得其电阻值如下:
101 101 107 92 99 97 102 98 99 113 93 106 103 101 90 87 95 99 98 103 102 96 94 100 94 97 110 103 99 103 108 102 102 100 94 105 98 97 107 101
问题情境
为了了解7月25日至8月24日北京地区的气温分布状况, 我们对以往年份此段时间的日最高气温进行抽样,得到如 下样本(单位:C )
7月25 日至8 月10 日
41.9 37.5 35.7 35.4 37.2 38.1 34.7 33.7 33.3 32.5 34.6 33.0 30.8 31.0 28.6 31.5 28.8 28.6 31.5 28.8 33.2 32.5 30.3 30.2 29.8 33.1 32.8 29.4 25.6 24.7 30.0 30.1 29.5 30.3
教你绘制频数分布图

教你绘制频数分布图教你绘制频数分布图频数分布直⽅图和频数分布折线统计图是描述数据的两种重要统计图,⽤这两种统计图把数据描述出来,就以直观地了解数据的分布情况及变化规律.下⾯谈谈这两种统计图的画法:⼀、频数分布直⽅图画频数分布直⽅图⼀般按下列步骤:1.计算极差(最⼤值与最⼩值的差).2.决定组数.3.列出频数分布表.4.画出频数分布直⽅图.例⼩明调查了他们班54名学⽣的⾝⾼,结果(单位:cm)如下:141 154 149 154 162 165 168 150 155 163 144 168 150 156 155 168 155 160 145 163 145 155 152 160 148 145 169 152 160 163 158 157 159 169 168 155 158 152 157 150 157 159 157 162 145 172 150 158 144 155 160 161 159 163 请将数据适当分组,并绘制相应的频数分布直⽅图.分析:要绘制频数分布直⽅图,需要把数据适当分组,数出每⼀组的频数,得出频数分布表,在此基础上绘制频数分布直⽅图.解:通过观察得到上⾯数据的最⼤值是172cm,最⼩值是141cm,它们的差是(172-141)=31cm.将该组数据按⾝⾼的范围分为141≤x<145,145≤x<149, ≤分成7组.整理可得下列统计表:⽤横轴表⽰⾝⾼,⽤纵轴表⽰频数,并在纵轴上等距离标出5,10,15,以各组学⽣⼈数为⾼画出与此组对应的长⽅形,得到频数分布直⽅图(如图1).图1⼆、频数折线图频数折线图画法如下:1.在频数分布直⽅图的基础上画频数折线图.(1)取频数分布直⽅图中每个长⽅形上边的中点;(2)在横轴上取两个频数为0的点,在直⽅图横轴的左边取点(139,0),在直⽅图横轴的右边取点(175,0);(3)将这些点⽤线段依次连接起来就得到了频数折线图(如图2).图22.根据已有的数据直接画频数折线图.(1)把数据分组,求出每个⼩组两端点的平均数,这些平均数称为组中值,如图141≤x<145这个⼩组的组中值为(141+145)÷2=143.(2)⽤横轴表⽰⾝⾼,⽤纵轴表⽰频数,以各⼩组的组中值为横坐标,各⼩组对应的频数为纵坐标描点,另取两个点(139,0)和(175,0).(3)依次连接这些点就得到了频数折线图(如图3).图3。
频率分布直方图与折线图

探究新知
条形图
人数 25 20 15 10 5 0 一号 二号 三号 四号
150.5153.5156.5 159.5162.5165.5168.5171.5 174.5 177.5 180.5 身高/cm 频率/组距 0.08
(3)条形图和直方图的有哪些区别?
直方图
0.06
一号 二号 0.04 三号 四号
实际应用
问题6.若两个研究小组分别抽样,是否得到相同的样 本?对总体估计是否一定相同?是否会有很大的差异? 问题7.比较一下几种表示频率分布的方法的优缺点.
名称
频率分布表 频率直方图 频率折线图
优点
数据清晰明了,便于查阅 形象直观,对比效果强烈 反映发展变化的趋势
不足
课堂小结
样本 频率分布表
频率分布直方图
频率分布折 线图
Байду номын сангаас
0.08 0.06 0.04 0.02
150.5153.5 156.5 159.5 162.5165.5168.5171.5174.5177.5 180.5
频率直方 图
身高/cm
频率/组距
频率分布 折线图
0.08 0.06 0.04 0.02
150.5 153.5
180.5
身高/cm
问题5.若组距取得越小,则频率折线光滑程度会怎 样?
问题3.类比频数条形图的画法,谈谈根据频率分布表 如何画出频率分布直方图!
名称 频数条形图 频率直方图
横轴 分类
纵轴 频数
探究新知
例1.从某校高一 年级的1002名新 生中用系统抽样 的方法抽取一个 容量为100的身高 样本,频率分布 表如下(单位: cm).试作出该 样本的频率分布 图.
12.9频率分布、直方图与概率密度曲线

x 1, 1 x,
x x
(1,0] (0,1]
0, x (1,)
⑴画出ξ 的概率密度曲线;
⑵根据所画曲线,求ξ 在区间(-0.5,0.5)内取值的概率.
例2.对某电子元件进行寿命追踪调查,情况如下: 寿命(h) 100~200 200~300 300~400 400~500 500~600
正 正正 正正正 正正正正正 正正正 正正
[25.475,25.505)
[25.505,25.535)
[25.535,25.565) 合计
频数 1 2 5 12 18 25 16 13 4 2 2 100
频率 0.01 0.02 0.05 0.12 0.18 0.25 0.16 0.13 0.04 0.02 0.02 1.00
总体密度曲 线与x轴围成 的面积为1.
连续型总体
总体密度曲线通常又叫概率密度曲线,以概率密度曲线为图像的 函数y=f(x)叫做概率密度函数.如图,连续型随机变量落在(a,b)内 的概率为阴影部分面积.即:
P(ab)S阴影
0, x (,1]
例1.已知随机变量ξ
的密度函数是
f
(x)
20
0.10
200~300
30
0.15
300~400
80
0.40
400~500
40
0.20
500~600
30
0.15
合计
200
1
⑸样本的期望为(总体均值) :
1 0 0 2 0 0 0 . 1 0 2 0 0 3 0 0 0 . 1 5 3 0 0 4 0 0 0 . 4 0 4 0 0 5 0 0 0 . 2 0 5 0 0 6 0 0 0 . 1 5 1 5 1 4 0 9 0 8 2 . 5 3 6 5 . 22 2 2 2
精美配套课件:第2章 2.2 第1课时 频率分布表 频率分布直方图与折线图

1. 从全校参加科技知识竞赛的学生试卷 中,抽取一个样本,考察竞赛的成绩 分布.将样本分成 5 组,绘成频率分 布直方图(如图),图中从左到右各小组 的小长方形的高的比是 1∶3∶6∶4∶2,最右边一组的 频数是 6. 请结合频率分布直方图提供的信息, 解答下列问题:
(1)样本的容量是多少? (2)列出频率分布表.
某制造商为 2013 年全运会生产一批直径为 40 mm 的乒 乓球,现随机抽样检查 20 只,测得每只球的直径(单位:mm, 保留两位小数)如下 40.03 40.01 40.02 40.00 39.98 39.98 39.98 39.99 40.00 40.00 40.00 39.99 39.99 39.99 40.00 40.00 39.95 39.96 39.98 40.01
解:(1)频率分布表如下:
分组 [-20,-15) [-15,-10) [-10,-5) [-5,0) [0,5) [5,10) [10,15) [15,20) 合计
频数 7 11 15 40 49 41 20 17 200
分布的表格称为频率分布表. (2)绘制的步骤: 全距 ①求全距,决定组数和组距,组距= . 组数
左闭右开 区间,最 ②分组,通常对组内数值所在区间取 _________
后一组取闭区间.
频率 ,列出频率分布表. ③登记_____ 频数 ,计算_____
2.频率分布直方图
频率分布规律 ,这样的 (1)定义:我们用直方图反映样本的_பைடு நூலகம்___________
解:(1)由于各组的组距相等,所以各组的频率与各小长方 形的高成正比且各组频率的和等于 1, 那么各组的频率分别 1 3 6 4 2 6 2 为 , , , , .设该样本容量为 n,则n= ,所以 16 16 16 16 16 16 样本容量为 n=48. (2)由以上得频率分布表如下:
怎么画频率分布折线图频数分布表茎叶图作频率分布直方图的步骤

频率分布:样本中所有数据(或者数据组)的频率和样本容量的比就是该数据的频率,所有数据(或者数据组)的频率的分布变化规律叫做频率分布,可以用频率分布表,频率分布折线图,茎叶图,频率分布直方图来表示.频率分布折线图:如果将频率分布直方图中各相邻的矩形的上底边的中点顺次连接起,就得到一条折线,称这条折线为本组数据的频率折线图。
频数分布表:反映总体频率分布的表格。
一般地,编制频率分布表的步骤如下:(1)求全距,决定组数和组距;(2)分组,通常对组内数值所在区间取左闭右开区间,最后一组取闭区间;(3)登记频数,计算频率,列出频率分布表。
茎叶图:(1)茎是指中间的一列数,叶是从茎的旁边生长出来的数。
(2)制作茎叶图的方法是:将所有两位数的十位数字作为“茎”,个位数字作为“叶”,茎相同者共用一个茎,茎按从小到大的顺序从上向下列出,共茎的叶一般按从大到小(或从小到大)的顺序同行列出;(3)茎叶图的性质:①茎叶图的优点是保留了原始数据,便于记录及表示,能反映数据在各段上的分布情况。
②茎叶图不能直接反映总体的分布情况,这就需要通过茎叶图给出的数据求出数据的数字特征,进一步估计总体情况。
1、频率分布样本中所有数据(或者数据组)的频率和样本容量的比就是该数据的频率,所有数据(或者数据组)的频率的分布变化规律叫做频率分布,可以用频率分布表,频率分布折线图,茎叶图,频率分布直方图来表示.2、频率分布折线图如果将频率分布直方图中各相邻的矩形的上底边的中点顺次连接起,就得到一条折线,称这条折线为本组数据的频率折线图。
3、频数分布表:反映总体频率分布的表格。
一般地,编制频率分布表的步骤如下:(1)求全距,决定组数和组距;(2)分组,通常对组内数值所在区间取左闭右开区间,最后一组取闭区间;(3)登记频数,计算频率,列出频率分布表茎叶图的性质:①茎叶图的优点是保留了原始数据,便于记录及表示,能反映数据在各段上的分布情况。
②茎叶图不能直接反映总体的分布情况,这就需要通过茎叶图给出的数据求出数据的数字特征,进一步估计总体情况。
高中数学知识点精讲精析 频率分布直方图与折线图

6.2.2 频率分布直方图与折线图画频率分布直方图的步骤:(1)计算最大值与最小值的差(知道这组数据的变动范围)(2)决定组距与组数(将数据分组)组数:将数据分组,当数据在100个以内时,按数据多少常分5-12组.组距:指每个小组的两个端点的距离.(4)决定分点.(5)列出频率分布表.(6)画出频率分布直方图.画频率分布直方图应注意的问题:(1)频率分布直方图的横轴和纵轴与前面学的直角坐标系中的横轴和纵轴有所不同,两轴的单位长度可以不同;两轴的交点也不一定是坐标为(0,0)的点.(2)各个小长方形的面积等于相应各组的频率;各小长方形的面积的和等于1.如果将频率分布直方图中各相临的矩形的上底边中点顺次连接起来,就得到频率分布折线图.当样本容量无限增大,组距无限缩小,这时与直方图相应的频率折线图将趋于一条光滑曲线——总体密度曲线.总体密度曲线反映了总体在各个范围内取值的概率,精确地反映了总体的分布规律.是研究总体分布的工具.100名年龄为17.5岁~18岁试根据上述数据画出样本的频率分布直方图,并对相应的总体分布作出估计.【解析】解:按照下列步骤获得样本的频率分布.(1)求最大值与最小值的差.在上述数据中,最大值是76,最小值是55,它们的差(又称为极差)是76-55=21.所得的差告诉我们,这组数据的变动范围有多大.(2)确定组距与组数.(3)决定分点.根据本例中数据的特点,第1小组的起点可取为54.5,第1小组的终点可取为56.5,为了避免一个数据既是起点,又是终点从而造成重复计算,我们规定分组的区间是“左闭右开”的.这样,所得到的分组是[54.5,56.5],[56.5,58.5],…,[74.5,76.5](4)列频率分布表.频率分布表(5)绘制频率分布直方图,频率分布直方图如图所示由于图中各小长方形的面积等于相应各组的频率,这个图形的面积的形式反映了数据落在各个小组的频率的大小.在反映样本的频率分布方面,频率分布表比较确切,频率分布直方图比较直观,它们起着相互补充的作用.在得到了样本的频率后,就可以对相应的总体情况作出估计.例如可以估计,体重在(64.5,66.5)kg的学生最多,约占学生总数的16%;体重小于58.5kg的学生较少,约占8%等等.2. 抽查某地区55名12岁男生的身高(单位:cm)的测量值如下:128.1 144.4 150.3 146.2 140.6 126.0 125.6 127.7 154.4 142.7 141.2 142.7 137.6 136.9 132.3 131.8 147.7 138.4 136.6 136.2 141.6 141.1 133.1 142.8 136.8 133.1 144.5 142.4 140.8 127.7 150.7 160.3 138.8 154.3 147.9 141.3 143.8 138.1 139.7 142.9 144.7 148.5 138.3 135.3 134.5 140.6 138.4 137.3 149.5 142.5 139.3 156.1 152.2 129.8 133.2试根据以上数据画出样本的频率分布直方图和折线图.【解析】3. 关于频率 分布直方图的下列说法中,正确的是( ) (A )、直方图的高表示某数的频率; (B )、直方图的高表示该组上的个体在样本中出现的频率; (C )、直方图的高表示该组上的个体与组距的比值; (D )、直方图的高表示该组上的个体在样本中出现的频率与组距的比值; 【解析】在频率分布直方图中,每一个小矩形都是等宽的,即等于组距,其面积表示数据的取值落在相应区间上的频率,因此每一个小矩形的高表示该组上的个体在样本中出现的频率与组距的比值,所以选(D ).4. 某校高一某班共有64名学生,下图是该班某次数学考试成绩的频率分布直方图,根据该图可知,成绩在110120间的同学大约有( )A 、 10B 、11C 、13D 、16 【解析】通过直方图可知:成绩在110120的频率是:2.023.015.01.005.01=----,所以成绩在110120之间的同学大约有:64×0.2=12.813≈人.故选择C点评:解决本题需要注意两点:所有小矩形的面积之和等于1;在分布图中若有高度相同的两个矩形,不能出现计算失误.5. 为了了解一大片经济林的生长情况,随机测量其中的100株的底部周长,得到如下数据表(长度单位:cm ):(1)编制频率分布表;(2)绘制频率分布直方图【分析】绘制频率分布直方图之前,一般地可先编制频率分布表,这样便于对数据进行分组及计算频数和频率. 分组一般以7~11组为宜.【解】(1)频率分布表(2)频率分布直方图:6. 如第5题,试画出树林底部周长的频率分布折线图.【分析】在频率分布直方图中,按照分组原则,在左边和右边各加一个区间,从所加的左边区间的中点开始,用线段依次连接各个矩形的顶端中点,直至右边所加区间的中点,这样得到的一条折线就是频率折线图.【解】取[75,80]的中点作为折线的起点,以(135,140)的中点作为折线的终点,连接各矩形上底中点所得折线即为所求(如图).。
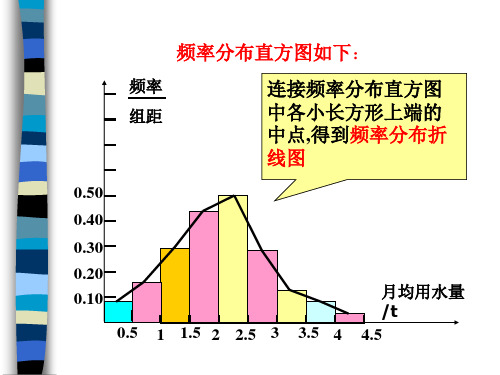
频率分布直方图如下
(1)解:如图:茎为成绩的整环数,叶为小数点后的数字
甲
乙
85 2 74
7
1
8
57
4
9
112 78
8751
10
11
(2)乙成绩大致对称,甲成绩的中位数为9.05, 乙成绩的中位数为9.15,所以乙成绩较甲好, 乙成绩较集中于峰值,甲成绩分散
所以乙发挥的稳定性好,甲波动大
练习2:课本71页练习第三题
作业:课本71页练习1,上面的练习1和2。
优化设计
小结:1.什么是频率折线图
2.什么是总体密度曲线及其意义 3.1)认识茎叶图,如何做茎叶图 2)分析茎叶图,3)茎叶图的优缺点
频率分布直方图如下:
频率
连接频率分布直方图
组距
中各小长方形上端的
中点,得到频率分布折
线图
0.50
0.40
0.30
0.20
0.10
月均用水量
/t
0.5 1 1.5 2 2.5 3 3.5 4 4.5
利用样本频率分布对总体分布进行相应估计
(1)上例的样本容量为100,如果增至1000, 其频率分布直方图的情况会有什么变化?假如增 至10000呢?
26
思考: 数据大于俩位数的整数时又如何选茎,叶?
数据为小数时又如何选茎,叶?
结论:1>当数据为整数时:通常个位数字在叶上, 其他位数在茎上(一位数时,茎为0)
2>当数据为小数时:通常小数部分在叶上, 整数部分在茎上
甲的茎叶图画法
也可以画一组数据的茎叶图,竖线左边为茎,
右边为叶。
茎
叶
08
1 364
甲的中位数为26,乙的中位数为36,所以乙较甲成绩要好, 另,乙的叶较甲的更集中于峰值附近,所以乙较甲发挥 更稳定
数学教材梳理频率分布直方图与折线图

庖丁巧解牛知识·巧学一、关于频率分布直方图的概念由于频率分布表数字较多,阅读困难,为了将频率分布表中的结果直观形象地表示出来,我们通常画频率分布直方图.画图时,应以横轴表示分组,纵轴表示频率与组距的比值。
以每个组距为底,以各频率除以组距的商为高,分别画成矩形,这样得到的直方图就是频率分布直方图.二、关于频率分布直方图的绘制方法频率分布直方图是在频率分布表的基础上绘制而成的,它的前期工作就是准确列出频率分布表,然后在平面直角坐标系中画出频率分布直方图,具体步骤如下:(1)求极差,即计算最大值与最小值的差。
(2)决定组距和组数。
组距与组数的确定没有固定标准,需要尝试、选择,力求有合适的组数,以能把数据的规律较清楚地呈现为准.太多或太少都不好,不利对数据规律的发现.组数应与样本的容量有关,样本容量越大组数越多。
(3)决定分点,将数据分组。
分组时,通常规定分组的区间是“左闭右开”的,避免数据被重复计算.(4)列频率分布表。
一般分“分组”“频数”“频率”三列,最后一行是“合计”。
注意频数的合计应是样本容量,频率合计应是1。
(5)画频率分布直方图。
建立直角坐标系,图中横轴为分组,图中的纵轴表示“频率/组距”。
各组数据以小长方形表示,其中,小长方形的宽为组距,小长方形的高=组距频率,频率=样本容量频率=组距×组距频率=小长方体的面积.各小长方形的面积总和为1。
由此可以看出,直方图中的各小长方形的面积表示相应的各组的频率。
这样频率分布直方图就以面积的形式反映了数据落在各个小组的频率的大小.误区警示 直方图中小长方形的高并不表示各组数据的频率,而是频率与组距之比,小长方形的面积才是各组数据的频率.辨析比较 频率分布表在数量表示上比较确切,但不够直观、形象,分析数据的总体态势不太方便,频率分布直方图形象、直观,与频率分布表相比较,频率直方图能直观地表明数据的分布形状,但原始数据不能在图中表示,说明直方图丢失了一些信息.从频率分布直方图可以清楚地看出数据分布的总体态势,但是从直方图本身得不出原始的数据内容。
扇形统计图,折线图,频率直方图

典型例题
解:用频率分布表表示.
分组
[80,90) [90,100) [100,110) [110,120) [120,130) [130,140) [140,150) [150,160]
合计
频数
2 3 9 12 7 4 2 1 40
频率
0.05 0.075 0.225 0.3 0.175 0.1 0.05 0.025
最大的是亚洲,面积最小的是大洋洲,亚洲和非洲的面积
为29.3%+20.2%=49.5%,
欧洲7.1% 大洋洲6%
南极洲
9.3%
南美洲 12%
亚洲 29.3%
北美洲 16.1%
非洲 20.2%
综合练习
练习1.根据地球陆地面积分布统计图,给出以下说法: ①全世界共有七大洲,其中面积最大的是亚洲; ②全世界共有七大洲,其中面积最小的是大洋洲; ③亚洲和非洲的面积接近地球陆地总面积的50%; ④最小的两个洲的面积还不到最大洲面积的一一半.
月平均收入/元 5000
4000
300020001000 打 务 养 其 项目
工 农殖 他
综合练习
练习3.某学生某月有零花钱a元,其支出情况如图
所示,那么下列说法错误的是( B ).
A.该学生捐赠款为0.6a元
B.捐赠款所对应的圆心角为240° C.捐赠款是购书款的2倍 D.其他支出占10%
捐赠款60%
50%; ④最小的两个洲的面积还不到最大洲面积的一
一半. 其中正确的说法共有( D ). A.1个 B.2个 C.3个 D.4个
综合练习
练习2.某地农村20户农民月平均收入如下(单位: 元):
项目
打工 务农 养殖 其他
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.2.2.频率分布直方图与折线图作业
一、填空题
1.从某小学随机抽取100名同学,将他们身高(单位:厘米)数据绘制成频率分布直方图(如图)。
由图中数据可知a 的值为( )
A. 0.033
B. 0.028
C. 0.030
D. 0.025
2.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
根据该折线图,下列结论错误的是( )
A .月接待游客量逐月增加
B .年接待游客量逐年增加
C .各年的月接待游客量高峰期大致在7,8月份
D .各年1月至6月的月接待游客量比7月至12月少;
3.某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直
方图,其中自习时间的范围是,样本数据分组为[17.5,20),[20,22.5),
[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是( )
A .56
B .60
C .120
D .
140
[17.5,30]
4.已知某地区中小学生人数和近视情况分别如图1和图2所示,为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别是( )
A.200,20 B.100,20 C.200,10 D.100,10
二、填空题
5.某校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们
在某一天各自课外阅读所用时间的数据,结果用下面的条形图表示.根据
条形图可得这50名学生这一天平均每天的课外阅读时间为__________.
6.某班50名学生在一次百米测试中,成绩全部
介于13秒与19秒之间,将测试结果按如下方式分成六组:
第一组,成绩大于等于13秒且小于14秒;
第二组,成绩大于等于14秒且小于15秒;……
第六组,成绩大于等于18秒且小于等于19秒.
右图是按上述分组方法得到的频率分布直方图.
设成绩小于17秒的学生人数占全班总人数的百分比为x,
成绩大于等于15秒且小于17秒的学生人数为y,
则从频率分布直方图中可分析出x和y分别为.
三、解答题
7.一个容量为100的样本,数据的分组和各组的一些相关信息如下,画出频率分布直方图和频率分布折线图.
8、我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用
水收费方案,拟确定一个合理的月用水量标准x(吨)、一位居民的月用水量不超过x的
部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得
了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
(I)求直方图中a的值;
(II)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(III)若该市政府希望使85%的居民每月的用水量不超过标准x(吨),估计x的值,
并说明理由.
2.2.2频率分布直方图与折线图作业答案:
1、C
2、A
3、D
4、A
5、0.9
6、x=0.9 y=35
6、频率分布表
7,、(I )由概率统计相关知识,各组频率之和的值为1 ∵频率=(频率/组距)*组距
∴()0.50.080.160.40.520.120.080.0421a ⨯+++++++= 得0.3a =.
(II )由图,不低于3吨人数所占百分比为()0.50.120.080.04=12%⨯++ ∴全市月均用水量不低于3吨的人数为:3012%=3.6⨯(万) (Ⅲ)由图可知,月均用水量小于2.5吨的居民人数所占百分比为: ()0.50.080.160.30.40.520.73⨯++++=
即73%的居民月均用水量小于2.5吨,
同理,88%的居民月均用水量小于3吨,故2.53x << 假设月均用水量平均分布,则()85%73%0.52.50.5 2.90.3x -÷=+⨯
=(吨). 分组
频数 频率 组距频率 [12,15)
6 0.06 0.02 [15,18)
8 0.08 0.027 [18,21)
16 0.16 0.053 [21,24)
21 0.21 0.07 [24,27)
18 0.18 0.06 [27,30)
16 0.16 0.053 [30,33)
10 0.10 0.033 [33,36]
5 0.05 0.017 合计 100 1.00 0.33。
