北师大版七年级数学下册第6课时探索三角形全等的条件
探索三角形全等的条件课件北师大版七年级数学下册

∴∠DAB=∠EAC
在ΔABD与ΔACE中
∠DAB=∠EAC
AB=AC
B
C
∠ABD=∠ACE
∴ΔABD≌ΔACE
∴BD=CE
三 角
01 三角形全等判定——SSS
形
全 02 三角形全等判定——SAS
等
的 判
03 三角形全等判定——AAS
定
条 件
04 三角形全等判定——SAS
判定两个三角形全等的思路:
针对练习:如图,已知OA=OC,OB=OD,∠AOC=∠BOD, 试说明:ΔAOB≌ΔCOD
D C
解:ΔAOB≌ΔCOD,理由如下:
∴∠AOC=∠BOD
∴∠AOC-∠AOD=∠BOD-∠AOD
∴∠COD=∠AOB
在ΔAOB与ΔCOD中
OA=OC
∠COD=∠AOB
OB=OD
O
∴ΔAOB≌ΔCOD
A B
A
全等判定——ASA
F
E
D
B
C
三角形全等的性质
全等判定——SSS
全等判定——SAS
选题背景
全等判定——AAS
针对练习:如图,AC=DC,AB=DE,CB=CE.
试说明:∠1=∠2
A
全等判定——ASA
解:∠1=∠2,理由如下: E 在ΔABC与ΔDEC中
AC=DC
AB=DE
CB=CE
B
∴ΔABC≌ΔDEC
E C
D
A
B
三角形全等的性质
全等判定——SSS
全等判定——SAS
选题背景
全等判定——AAS 全等判定——ASA
判定方法四: 两角及其夹边分别相等的两个三角形全等 ( 简写成“边角边”或“ASA”)
七年级数学下册《探索三角形全等的条件》练习题及答案(北师大版)
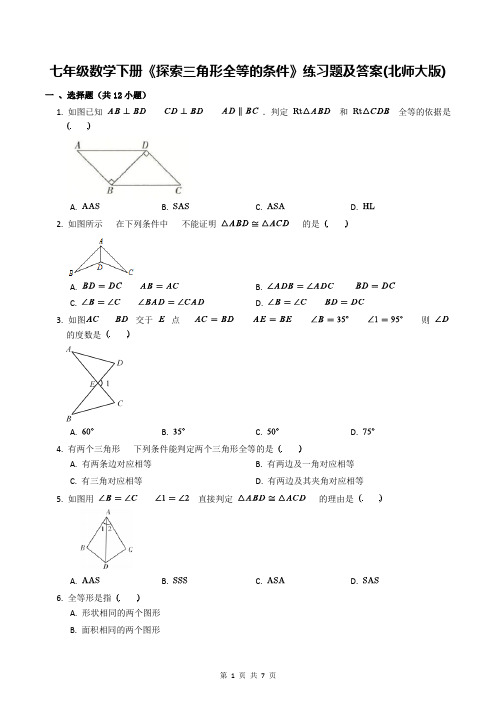
七年级数学下册《探索三角形全等的条件》练习题及答案(北师大版)一、选择题(共12小题)1. 如图已知.判定和全等的依据是A. B. C. D.2. 如图所示在下列条件中不能证明的是A. B.C. D.3. 如图交于点则的度数是A. B. C. D.4. 有两个三角形下列条件能判定两个三角形全等的是A. 有两条边对应相等B. 有两边及一角对应相等C. 有三角对应相等D. 有两边及其夹角对应相等5. 如图用直接判定的理由是A. B. C. D.6. 全等形是指A. 形状相同的两个图形B. 面积相同的两个图形C. 每个角均对应相等的两个平面图形D. 能够完全重合的两个平面图形7. 如图已知要得到还需要的条件是A. B. C. D.8. 在下列命题中真命题是A. 两个钝角三角形一定相似B. 两个等腰三角形一定相似C. 两个直角三角形一定相似D. 两个等边三角形一定相似9. 下列四组中一定是全等三角形的是A. 两条边对应相等的两个锐角三角形B. 面积相等的两个钝角三角形C. 斜边相等的两个直角三角形D. 周长相等的两个等边三角形10. 如图已知能直接判定的方法是A. B. C. D.11. 如图已知点在一直线上都是等边三角形连接和与相交于点与相交于点下列说法不一定正确的是A. B. C. D.12. 如图已知如果只添加一个条件使则添加的条件不能为A. B. C. D.二、填空题(共6小题)13. 如图已知则依据可以判定从而有再依据可以判定.14. 如图所示已知要推得若以" "为依据还缺条件.15. 全等三角形判定方法:在两个三角形中如果那么简记为.16. 全等三角形的判定方法:在两个三角形中如果有两个角及对应相等那么这两个三角形全等(简记为).17. 两个全等三角形的周长面积.18. 如图因为(已知)所以()因为(已知)所以()在和中所以().三解答题(共5小题)19. 如图是正方形的边上任意一点过点作交的延长线于点.求证:.20. 一天某校数学课外活动小组的同学们带着皮尺去测量某河道因挖沙形成的“圆锥形坑”的深度来评估这些深坑对河道的影响.如图是同学们选择(确保测量过程中无安全隐患)的测量对象测量方案如下:①先测量出沙坑坑沿圆周的周长约为米;②甲同学直立于沙坑坑沿圆周所在平面上经过适当调整自己所处的位置当他位于点时恰好他的视线经过沙坑坑沿圆上的一点看到坑底(甲同学的视线起点与点点三点共线).经测量:米米.根据以上测量数据求“圆锥形坑”的深度(圆锥的高).(取结果精确到米)21. 如图已知在同一条直线上求证:.22. 如图已知试说明和全等的理由.23. 如图矩形中对角线相交于点点是线段上一动点(不与点重合)的延长线交于点.(1)求证:四边形为平行四边形.(2)若从点出发.以的速度向点匀速运动.设点运动时间为秒问四边形能够成为菱形吗?如果能求出相应的值;如果不能说明理由.参考答案1. C2. D3. A4. D5. A6. D7. D8. D9. D10. A11. B【解析】A项可由得得到 C D项可由得得到而B 项不能由已知条件得到.12. A13.14.15. 略略略16. 略略17. 相等相等18. 略略略略略略略略略略19. 略20. 如图所示取圆锥底面圆圆心连接则......“圆锥形坑”的深度约为米.21. 因为(已知)所以(等式性质)即在与中所以所以(全等三角形的对应角相等)所以(同位角相等两直线平行).22. 在与中.23. (1)如图四边形是矩形在与中四边形为平行四边形.(2)点从点出发运动秒时.当四边形是菱形时.四边形是矩形在直角中即解得:点运动时间为秒时四边形能够成为菱形.。
北师大版七年级数学下册探索三角形全等的条件课件

②BC=EF ⑤∠B=∠E
F ③CA=FD ⑥∠C= ∠F
新课导入
即:三条边分别相等,三个角分别相等的两个三角形全等.
想一想:
如果只满足这些条件中的一部分,那么能保证△ABC ≌△DEF 吗?
自学探究
三角形全等的判定(“边边边”)
探究活动1: 一个条件可以 吗?
(1)有一条边相等的两个三角形;不一定全等 (2)有一个角相等的两个三角形. 不一定全等
证明:因为C是BF中点, 所以BC=CF.
在△ABC 和△DCF中, AB = DC (已知), AC = DF (已知), BC = CF (已证),
所以△ABC≌△DC(FSSS).
BB CC FF
AA DD
变式题:
如图,点B,E,C,F在同一直线上 , AB = DE , AC = DF ,BE = CF . 求证: (1)△ABC ≌ △DEF; (2)∠A=∠D.
自学探究 探究活动2:两个条件可以吗? (1)有两个角对应相等的两个三角形;不一定全等 (2)有两条边对应相等的两个三角形; 不一定全等
(3)有一个角和一条边对应相等的两个三角形.不一定全等
3cm
30
50
3°0°
°
50
°
3cm
30° 3cm
30 ° 3cm
自学探究 探究活动3:三个条件可以吗?
(1)有三个角对应相等的两个三角形;
只要三角形三条边的长度固定,这 个三角形的形状和大小也就完全确定, 三角形的这种性质叫做
三角形的稳定性
典例精析
例1 如图,有一个三角形钢架,AB =AC ,AD 是连接
点A 与BC 中点D 的支架.求证:△ABD ≌△ACD
专题探索三角形全等的条件(SSS和SAS)(知识讲解)数学七年级下册(北师大版)
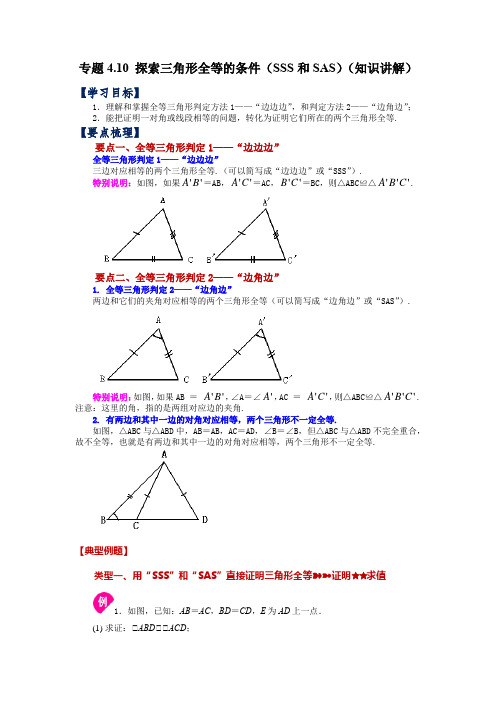
专题4.10 探索三角形全等的条件(SSS 和SAS )(知识讲解)【学习目标】1.理解和掌握全等三角形判定方法1——“边边边”,和判定方法2——“边角边”;2.能把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.【要点梳理】要点一、全等三角形判定1——“边边边”全等三角形判定1——“边边边”三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS ”).特别说明:如图,如果''A B =AB ,''A C =AC ,''B C =BC ,则△ABC ≌△'''A B C .要点二、全等三角形判定2——“边角边”1. 全等三角形判定2——“边角边”两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS ”).特别说明:如图,如果AB = ''A B ,∠A =∠'A ,AC = ''A C ,则△ABC ≌△'''A B C . 注意:这里的角,指的是两组对应边的夹角.2. 有两边和其中一边的对角对应相等,两个三角形不一定全等.如图,△ABC 与△ABD 中,AB =AB ,AC =AD ,∠B =∠B ,但△ABC 与△ABD 不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等.【典型例题】类型一、用“SSS”和“SAS”直接证明三角形全等➽➼证明✮✮求值1.如图,已知:AB =AC ,BD =CD ,E 为AD 上一点.(1) 求证:△ABD △△ACD ;(2) 若△BED =50°,求△CED 的度数.【答案】(1) 证明见分析 (2) 50CED ∠=︒【分析】(1)根据SSS 即可证明△ABD △△ACD ;(2)只要证明△EDB △△EDC (SAS ),即可推出△BED =△CED ,进而得到答案. (1)证明:在△ABD 和△ACD 中, AB ACBDCD AD AD ⎧⎪⎨⎪⎩===,△△ABD △△ACD (SSS );(2)解:△△ABD △△ACD ,△△ADB =△ADC ,在△EDB 和△EDC 中,DB DC BDE CDE DE DE ⎧⎪∠∠⎨⎪⎩===,△△EDB △△EDC (SAS ),△△BED =△CED ,△△BED =50°,△△CED =△BED =50°.【点拨】本题考查全等三角形的判定和性质,解题的关键是根据图形题意,熟练掌握两个三角形全等判定与性质.举一反三:【变式1】如图,点A 、M 、N 、C 在同一条直线上,AB CD =,BN DM =,AM CN =,求证:AB CD ∥.【分析】根据AB CD =,BN DM =,AM CN =,利用SSS 定理证明ABN CDM ≌,从而得到A C ∠=∠,再根据内错角相等,两直线平行,AB CD ∥得证.解:证明:∵AM CN =∴AM MN CN MN∴AN CM =在ABN 和CDM 中AB CD BN DM AN CM =⎧⎪=⎨⎪=⎩,∴()ABN CDM SSS △≌△∴A C ∠=∠∴AB CD ∥(内错角相等,两直线平行)【点拨】本题考查了三角形全等的判定方法和性质,以及平行线的判定,解题关键是掌握全等三角形的判定方法,运用全等三角形的性质证明线段和角相等.【变式2】如图,已知AB AC =,AD AE =,BD CE =,求证:312.【分析】利用SSS 可证明△ABD△△ACE ,可得△BAD=△1,△ABD=△2,根据三角形外角的性质即可得△3=△BAD+△ABD ,即可得结论.解:在△ABD 和△ACE 中,AB=AC AD=AE BD=CE ⎧⎪⎨⎪⎩,△△ABD△△ACE ,△△BAD=△1,△ABD=△2,△△3=△BAD+△ABD ,△△3=△1+△2.【点拨】本题考查全等三角形的判定与性质及三角形外角性质,熟练掌握判定定理及外角性质是解题关键.2.已知:如图,AB AC =,F ,E 分别是AB AC ,的中点,求证:ABE ACF ≌.在ABE 与△AB AC A A AE AF =⎧⎪∠=∠⎨⎪=⎩ABE △≌△【点拨】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:ASAAAS 、、【变式1】如图,点D 在BC 上,,ADB B BAD CAE ∠=∠∠=∠.(1) 添加条件:____________(只需写出一个),使ABC ADE ≅;(2) 根据你添加的条件,写出证明过程.【答案】(1) AC AE = (2) 见分析【分析】(1)根据已知条件可得AB AD =,BAC DAE ∠=∠,结合三角形全等的判定条件添加条件即可;(2)结合(1)的条件,根据三角形全等的判定条件添加条件进行证明即可.解:(1)添加的条件是:AC AE =,故答案为AC AE =;(2)△,ADB B ∠=∠△AB AD =,△BAD CAE ∠=∠△BAD DAC CAE DAC ∠+∠=∠+∠,即BAC DAE ∠=∠,又AC AE =△ABC ADE ≅【点拨】本题主要考查了三角形全等的判定,确定出三角形全等判定条件是解答本题的关键.【变式2】如图所示,DC CA ⊥,EA CA ⊥,CD AB =,CB AE =,求证:(1) BCD EAB ≌△△;(2) DB BE ⊥.【分析】(1)利用SAS 判定定理证明三角形全等即可;(2)由()≌DCB BAE SAS △△,可得∠=∠DBC BEA ,∠=∠BDC EBA ,再利用90DBC BDC ∠+∠=︒,可得90∠+∠=︒DBC EBA ,即90DBE ∠=︒,所以DB BE ⊥.解:(1)证明:△DC CA ⊥,EA CA ⊥,△90∠=∠=︒DCB BAE ,在DCB △和BAE 中,CD AB DCB BAE CB AE =⎧⎪∠=∠⎨⎪=⎩△()≌DCB BAE SAS △△. (2)证明:由(1)可知()≌DCB BAE SAS △△, △∠=∠DBC BEA ,∠=∠BDC EBA ,△90DBC BDC ∠+∠=︒,△90∠+∠=︒DBC EBA ,即90DBE ∠=︒,△DB BE ⊥.【点拨】本题考查全等三角形的判定定理及性质,垂直的定义,解题的关键是掌握全等三角形的判定定理及性质.类型二、用“SSS”和“SAS”间接证明三角形全等➽➼证明✮✮求值3.已知:如图,A 、C 、F 、D 在同一直线上,AF =DC ,AB =DE ,BC =EF ,求证:△ABC≌≌DEF .【分析】首先根据AF=DC ,可推得AF ﹣CF=DC ﹣CF ,即AC=DF ;再根据已知AB=DE ,BC=EF ,根据全等三角形全等的判定定理SSS 即可证明△ABC△△DEF .解:△AF=DC ,△AF ﹣CF=DC ﹣CF ,即AC=DF ;在△ABC 和△DEF 中AC DF AB DE BC EF =⎧⎪=⎨⎪=⎩△△ABC△△DEF (SSS )举一反三: 【变式1】如图,已知:PA=PB,AC =BD ,PC =PD ,△PAD 和△PBC 全等吗?请说明理由.【分析】由AC=BD ,利用线段的和差关系可得AD=BC ,利用SSS 即可证明△PAD△△PBC.解:△AC =BD ,△AC+CD=BD+CD ,即AD =BC ,又△PA =PB ,PC =PD ,△△PAD△△PBC(SSS)【点拨】本题考查全等三角形的判定与性质,熟练掌握全等三角形的判定定理是解题关键.【变式2】如图,点D ,A ,E ,B 在同一直线上,EF =BC ,DF =AC ,DA =EB .试说明:△F =△C .【分析】根据SSS 的方法证明△DEF△△ABC,即可得到结论.解:因为DA =EB , 所以DE =AB.在△DEF 和△ABC 中, 因为DE =AB ,DF =AC ,EF =BC ,所以△DEF△△ABC(SSS),所以△F =△C.【点拨】本题考查了全等三角形的判定和性质,属于简单题,找到证明全等的方法是解题关键.4.如图,在ABCD 中,点E 、F 在BD 上,ABE 与CDF 全等吗?若全等,写出证明过程;若不全等,请你添加一个条件使它们全等,并写出证明过程.(1) 你添加的条件是__________.(2) 证明过程: 【答案】(1) BE DF =,答案不唯一; (2) 证明见分析; 【分析】(1)根据选择的全等三角形判定方法添加合适的条件即可;(2)由四边形ABCD 是平行四边形得到AB CD ∥,AB CD =,得ABE CDF ∠=∠,再用上添加的条件,即可证明结论.(1)解:BE DF =(答案不唯一)故答案为:BE DF =(答案不唯一)(2)证明:△四边形ABCD 是平行四边形,△AB CD ∥,AB CD =,△ABE CDF ∠=∠,在ABE 和CDF 中,AB CD ABE CDF BE DF =⎧⎪∠=∠⎨⎪=⎩,△ABE CDF △≌△(SAS ).【点拨】此题考查了平行四边形的性质、全等三角形的判定等知识,熟练掌握全等三角形的判定是解题的关键.举一反三:【变式1】如图,在ABC 和ADE 中,AB AD =,AC AE =,且BAD CAE ∠=∠,求证:ABC ADE △≌△.【分析】根据BADCAE ∠=∠可得BAC DAE ∠=∠,再根据SAS 即可证明.证明:△BAD CAE ∠=∠,△BAD DAC CAE DAC ∠+∠=∠+∠,即BAC DAE ∠=∠,在ABC 和ADE 中,AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩,△()SAS ABC ADE △≌△.【点拨】本题主要考查了用SAS 证明三角形全等,解题的关键是通过BAD CAE ∠=∠得出BAC DAE ∠=∠.【变式2】图,BE CF =,AC DF =,AC DF ∥.求证:ABC DEF ≌△△.【分析】首先根据BE CF =可得BC EF =,再由AC DF ∥可得ACB F ∠=∠,然后利用定理证明ABC DEF ≌即可.证明:△BE CF =,△BE EC CF EC ++=,即BC EF =,△AC DF ∥,△ACB F ∠=∠, 在ACB △和DFE △中,BC EF ACB F AC DF =⎧⎪∠=∠⎨⎪=⎩,△()SAS ABC DEF ≌.【点拨】此题主要考查了全等三角形的判定和平行线的性质,判定两个三角形全等的一般方法有:SSS SAS ASA AAS HL 、、、、.注意:AAA SSA 、不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.类型三、全等的性质与“SSS”和“SAS”综合➽➼证明✮✮求值 5.已知:如图,在ABC 中,AB AC AD =,是BC 边上的中线.求证:AD BC ⊥(填空).证明:在三角形ABD ACD 和中,△()()()______________BD AB ⎧=⎪⎪=⎨⎪⎪⎩已知已知公共边,△ ≌ ( ).△ADB ∠= (全等三角形的对应角相等).△1902ADB BDC ∠∠︒==(平角的意义). △(垂直的意义).【答案】,,,,SSS DC AC AD AD ABD ACD ADC AD BC =∠⊥,△△,,【分析】证明()SSS ADB ADC ≌△△.推出ADB ADC ∠∠=,可得结论. 证明:△AD 是BC 边上的中线,△BD CD =,在三角形ABD △和ACD 中,【变式1】如图:AB AC =,BD CD =,若28B ∠=︒,求C ∠的度数.【答案】28︒ 【分析】连接AD ,利用“SSS ”证明ABD ACD △≌△,即可得到答案.解:连接AD ,在ABD △和ACD 中,AB AC BD CD AD AD =⎧⎪=⎨⎪=⎩,()SSS ABD ACD ∴≌C B ∴∠=∠,28B ∠=︒,28C ∴∠=︒.【点拨】本题考查了全等三角形的判定和性质,正确作辅助线构造全等三角形是解题关键.【变式2】已知:如图,AC BD =,AD BC =,AD ,BC 相交于点O ,过点O 作OE AB ⊥,垂足为E .求证:(1) ABC BAD ≌.(2) AE BE =.【分析】(1)利用SSS 证明ABC BAD ≌;(2)根据全等三角形的性质得出DAB CBA ∠=∠,则OA OB =,根据等腰三角形的性质可得出结论.(1)证明:在ABC 和BAD 中,AC BD BC AD AB BA =⎧⎪=⎨⎪=⎩,△ABC BAD ≌(2)证明:△ABC BAD ≌△CBA DAB ∠=∠,△OA OB =,△OE AB ⊥,△AE BE =.【点拨】此题考查了全等三角形的判定与性质,利用SSS 证明ABC BAD ≌是解题的关键.6.如图,在ABC 中,CM 是AB 边上的中线,8AC =,12BC =,求CM 的取值范围.【答案】210CM <<【分析】倍长中线CM 至点N ,构造BNM ,易得ACM BNM ≅△△,再利用三角形的三边关系找到CN 的取值范围,进而得到CM 的取值范围.解:如图,延长CM 到点N ,使CM MN =,连接BN ,在ACM △和BNM 中,CM NM AMC BMN AM BM =⎧⎪∠=∠⎨⎪=⎩,∴ACM BNM ≅△△(SAS ),∴8AC BN ==, 在BCN △中,BC BN CN BC BN -<<+,∴128128CN -<<+,即420CN <<,∴4220CM <<,即210CM <<.【点拨】本题考查了全等三角形的性质与判定以及三角形的三边关系,解决本题的关键是倍长中线构造全等三角形.举一反三:【变式1】如图,已知在ABC 与ADE 中,90BAC DAE AB AC AD AE ∠=∠=︒==,,,点C ,D ,E 三点在同一条直线上,连接BD .图中的CE BD 、有怎样的数量和位置关系?请证明你的结论.【答案】CE BD =,证明见分析【分析】根据SAS 证明ACE ABD ≌△△,即可得到CE BD =.解:CE BD =,证明:△90BAC DAE ∠=∠=︒,△BAC CAD DAE CAD ∠+∠=∠+∠,即BAD CAE ∠=∠,在ACE △和ABD △中AC AB CAE BAD AE AD =⎧⎪∠=∠⎨⎪=⎩△()SAS ACE ABD ≌△CE BD =.【点拨】此题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定方法是解题的关键.【变式2】如图已知AOB 和MON △都是等腰直角三角形.(1) 如图1,连接AM ,BM ,此时AM ,BN 的数量关系为___________请说明理由.(2) 若将MON △绕点O 顺时针旋转,如图2,当点N 恰好在AB 边上时,求证:222BN AN MN +=.【答案】(1) AM BN =,理由见分析(2) 见分析 【分析】(1)由AOB 和MON △都是等腰直角三角形,得到AOM BON ≌,即可得到AM BN =(2)连接AM ,由AOB 和MON △都是等腰直角三角形,得到AOM BON ≌,即可得到AM BN =,再求得90MAN ∠=︒,利用勾股定理即可得到222BN AN MN +=解:(1)AM BN =,理由如下:△AOB 和MON △都是等腰直角三角形,△OA OB =,OM ON =,90AOB MON ∠=∠=︒,△AOM BON ∠=∠,在AOM 和BON △中:OA OB OM ON AOM BON =⎧⎪=⎨⎪∠=∠⎩, △AOM BON ≌,△AM BN =(2)如下图,连接AM ,△AOB 和MON △都是等腰直角三角形,△OA OB =,OM ON =,90AOB MON ∠=∠=︒,45B BAO ∠=∠=︒,△AOM BON ∠=∠,在AOM 和BON △中:OA OB OM ONAOM BON =⎧⎪=⎨⎪∠=∠⎩, △AOM BON ≌,△AM BN =,45B MAO ∠=∠=︒,△90MAN MAO BAO ∠=∠+∠=︒,△222AM AN MN +=,△222BN AN MN +=【点拨】本题考查了旋转的性质、全等三角形的判定和性质、等腰直角三角形的性质及勾股定理,熟练掌握全等三角形的判定和性质是解决问题的关键。
北师大版七年级下册数学说课稿:4.3.1《探索三角形全等的条件》

北师大版七年级下册数学说课稿:4.3.1《探索三角形全等的条件》一. 教材分析《探索三角形全等的条件》这一节内容是北师大版七年级下册数学的一个重要部分。
在此之前,学生已经学习了三角形的性质、三角形的分类以及三角形的判定等知识。
本节课通过探索三角形全等的条件,让学生掌握三角形全等的判定方法,为后续学习三角形相似、解三角形等知识打下基础。
二. 学情分析七年级的学生已经具备了一定的逻辑思维能力和空间想象力,能够通过观察、操作、猜想、验证等方法探索数学问题。
但部分学生对几何图形的认识还不够清晰,对全等三角形的概念及判定方法的理解可能存在困难。
因此,在教学过程中,要关注学生的认知水平,引导学生逐步理解全等三角形的判定条件。
三. 说教学目标1.知识与技能:让学生掌握三角形全等的判定方法,能够运用这些方法判断两个三角形是否全等。
2.过程与方法:通过观察、操作、猜想、验证等方法,培养学生探索几何问题的能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养学生的团队合作意识,使学生感受到数学在生活中的应用。
四. 说教学重难点1.教学重点:三角形全等的判定方法。
2.教学难点:如何引导学生理解并掌握三角形全等的判定条件,以及如何运用这些判定方法解决实际问题。
五. 说教学方法与手段本节课采用讲授法、问答法、讨论法、操作活动法等教学方法。
利用多媒体课件、几何画板等教学手段,帮助学生直观地理解全等三角形的判定条件。
六. 说教学过程1.导入新课:通过复习三角形的相关知识,引导学生回顾已学过的三角形性质,为新课的学习做好铺垫。
2.探索全等三角形的判定条件:(1)让学生观察两个形状相同的三角形,引导学生发现全等三角形的特征。
(2)引导学生通过操作,尝试将一个三角形变换成另一个三角形,从而探索全等三角形的判定条件。
(3)学生进行讨论,总结全等三角形的判定方法。
3.讲解判定方法:(1)边边边(SSS)判定法:引导学生理解并掌握三角形三边分别相等,则两个三角形全等。
北师大版七年级数学下册探索三角形全等的条件

BD=CE
10
练一练
如图,AB∥CD,AD∥BC,那么
AB=CD吗?为什么?
AD与BC呢?
D
Cபைடு நூலகம்
A
B
重要思路:两直线平行,可以找到等角.
11
练一练
如图,D在AB上,DF交AC于点E,DE=FE, FC∥AB,若AB=4,CF=3, 则BD的长是( ) A.0.5 B.1 C.1.5 D.2
D
9
练一练 如图,AD=AE,∠B=∠C,
请证明:BD=CE.
D B
A 证明:∵在△ABE和△ACD中,
∠B=∠C (已知)
E
∠A=∠A (公共角)
AE=AD (已知)
C ∴ △ABE≌△ACD(AAS)
∴ BD=CE (全等三角形对应边相等)
不是三角 形的边 ∴ AD=AE(全等三角形对应边相等)
北师大版七年级下册
第四章 三角形
1
复习
两个三角形全等的判定方法1:
三边对应相等的两个三角形全等.简写为“边边边”或“SSS”.
用符号表达:
指明范围
A
在△ABC和△A′B′C′中,
三个条件
AB=A′B′, AC=A′C′,BC=B′C′
B
∴△ABC≌△A′B′C′ (SSS)
写出结论
C A'
B'
C'
∴ △AOC≌△BOD ( ASA )
8
练一练 图中的两个三角形全等吗?
请说明理由.
A
在△ABC和△DBC中,
110
_∠__A_B__C_=_∠__DBC(已知)B ∠__A__=_∠__D__(__已知)
数学北师大版七年级下册利用“边边边”判定三角形全等

BC=EF
∴△ABC≌△DEF(SSS)
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
You Know, The More Powerful You Will Be
全等?试说明理由. 解: △ABC≌△DCB. 理由如下:
AB = CD,
A = B
D =
C
AC = BD, BC = CB
△ABC≌ △DCB (SSS).
当堂练习
2.填空题: 如图,D、F是线段BC上的两点, AB=CE,AF=DE,要使△ABF≌△ECD , 还需要条件_B_F__=_C_D__或__B__D_=_F_C__.
有一个角对应相等的三角形 结论:不能保证所画的三角 形全等 不一定全等
30o
探究2
2个条件
(1) 三角形的一个角为30°,一条边为3cm;
不一定全等
30o 3cm
探究2
2个条件
(2)三角形的两个角分别是:30°,50°;
不一定全等
30o
50o
50o
探究2
2个全等
(重点) 2.由探索三角形全等条件的过程,体会由操作、归
纳获得数学结论的过程.(难点)
复习巩固
已知:如图,△ABC≌△A1B1C1,
找出图中相等的边和角
A1
A1
B1
C1
B1
C1
△ABC≌△ A1B1C1
AB A1B1, BC B1C1, AC A1C1
A A1, B B1, C C1
A
E
=
2023年北师大版七年级下册数学第四章三角形第6课时探索三角形全等的条件(1)

·数学
知识点二:三角形全等的条件(SSS)的应用 如图,AB=CD,BD=AC,用三角形全等的条件“SSS”可 说明 △ABC ≌ △DCB 或 △ABD ≌ △DCA .
方法指引:若已知两边对应相等, 则找它们的第三边.
·数学 2.(人教8上P44)如图,在△ABC中,AB=AC,BD=CD,试 说明:△ABD≌△ACD.
·数学
★12.如图,已知AB=AC,AD=AE,BD=CE,B,D,E三点 共线,试说明:∠3=∠1+∠2.
解:在△ABD和△ACE中, AB=AC
ቐAD=AE, BD=CE
所以△ABD≌△ACE(SSS). 所以∠BAD=∠1,∠ABD=∠2. 因为∠3=180°-∠BDA=180°-(180°-∠BAD-∠ABD) =∠BAD+∠ABD,所以∠3=∠1+∠2.
解:在△ABD和△ACD中,
AB=AC ቐBD=CD,
AD=AD 所以△ABD≌△ACD(SP6)如图,三角形具有 四边形具有 不稳定性 .
·数学 稳定性 ,
(2)三角形的稳定性在实际生活中有着广泛的应用,如钢架 桥、房屋架梁等,因此要使一些图形具有稳定的结构,往往 通过连接辅助线转化为三角形而获得.
解:因为BE=CF,所以BC=EF, 在△ABC和△DEF中,
AB=DE ቐAC=DF,
BC=EF 所以△ABC≌△DEF(SSS).
·数学
8.【例4】(北师7下P111改编、人教8上P44改编)如图,点A, D,C,F在同一直线上,AB=EF,AD=CF,BC=ED.试 说明:AB∥EF. 解:因为AD=CF, 所以AD+DC=CF+DC,即AC=FD, 在△ABC和△FED中, AB=FE,AC=FD,BC=ED, 所以△ABC≌△FED(SSS). 所以∠A=∠F,所以AB∥EF.
