4_2力矩 转动定律 转动惯量
合集下载
力矩转动定律转动惯量解析课件
02
CATALOGUE
转动惯量基础概念
转动惯量的定义
转动惯量
描述刚体绕固定轴转动的惯性大 小的物理量。
定义公式
I = Σ(m * r^2)，其中m为刚体的 质量，r为刚体上任意质点到转动 轴的距离。
转动惯量的性质
转动惯量只与刚体的质量分布 和转动轴的位置有关，与刚体 的运动状态无关。
对于同一刚体，不同的转动轴 位置，其转动惯量可能不同。
力矩转动定律转动 惯量解析课件
contents
目录
• 力矩转动定律概述 • 转动惯量基础概念 • 力矩与转动惯量的关系 • 转动惯量的计算方法 • 转动惯量的应用实例
01
CATALOGUE
力矩转动定律概述
力矩的定义
力矩是描述力的转动效果的物理量，其大小等于力和力臂的乘积。
力矩是一个向量，其大小等于力和力臂的乘积。力臂是从转动轴到力的垂直距离 。在二维平面中，力矩可以表示为M=F×r，其中F是力，r是力臂。
CATALOGUE
转动惯量的应用实例
飞轮的设计与优化
飞轮的设计
飞轮是利用转动惯量储存能量的重要 装置，其设计需要考虑转动惯量的大 小、质量分布、转速等因素。
飞轮的优化
为了提高飞轮的储能效率和稳定性， 需要对飞轮进行优化设计，如采用轻 质高强度的材料、优化飞轮的形状和 尺寸等。
陀螺仪的设计与优化
陀螺仪的设计
陀螺仪是利用角动量守恒原理工作的惯性导 航和姿态测量器件，其设计需要考虑转动轴 的稳定性、转动惯量的大小和分布等因素。
陀螺仪的优化
为了提高陀螺仪的测量精度和稳定性，需要 对陀螺仪进行优化设计，如采用高性能的轴 承材料、减小摩擦力矩等。
电机转子的设计与优化
4-2 力矩 转动定律 转动惯量
R
R
T
m1
m2
h
Mf
T
mg
yLeabharlann h第四章 刚体转动
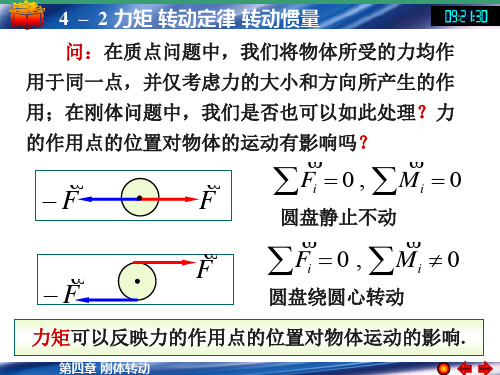
4 – 2 力矩 转动定律 转动惯量 已知：R 50cm h 2.0m
T
m1 8.0kg m2 4.0kg
Mf C
求：J
t2 25s
t1 16s
Mf
m1 g T1 m1a1
a1 T1 R M f J R
1 m1 m2 m r 2
m1 m2 gt
1 m1 m2 m r 2
第四章 刚体转动
4 – 2 力矩 转动定律 转动惯量 例 如图所示, A、B 为两个相同的定滑轮, A 滑 A 轮挂一质量为M的物体, B 滑轮受力F = Mg, 设 A、B 两滑轮的角加速度分别为 M αA和αB ,不计轴的摩擦,这两 个滑轮的角加速度的 大小关系为:
垂直于转轴方向的两个分量
F Fz F
方向垂直于轴，其效果是改变轴 的方位，在定轴问题中，与轴承 受到的约束力矩平衡。 第二项 M z r F 方向平行于轴，其效果是改变绕轴转动 状态，称为力对轴的矩，表为代数量：
第一项 M r F 1 z
1.06103 kg m2
m1 g T1 m1a1 m2 g T2 m2a2
a1 T1 R M f J R a2 T2 R M f J R
2
4 – 2 力矩 转动定律 转动惯量 例.长为L质量为m的匀质细杆，在水平粗糙桌面上 绕过其一端的竖直轴旋转，杆与桌面间的摩擦系数为 ，求摩擦力矩。 解1):
N
+
4-2 力矩 转动定律 转动惯量
19
物理学 第六版
4-2 力矩 转动定律 转动惯量
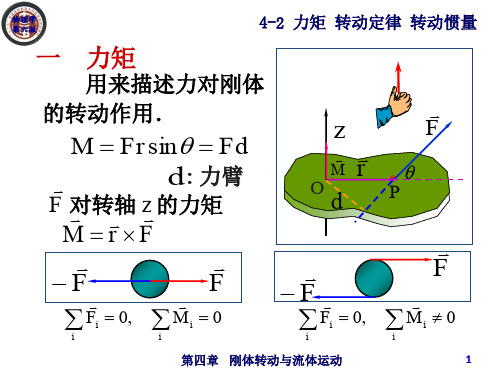
解 (1) 用隔离法分 别对各物体作受力分析， 取如图所示坐标系．
A
mA
FN
mA FT1
PA
O
x
C
mC
mB B
FT1
FC
PC
FT2
FT2
O
mB
PB y
第四章 刚体转动与流体运动
20
物理学 第六版
4-2 力矩 转动定律 转动惯量
第四章 刚体转动与流体运动
1
物理学 第六版
4-2 力矩 转动定律 转动惯量
讨论
（1）若力
F
不在转动平面内，把力分
解为平行 和垂 直于 转轴方向的两个分量
F
Fz
F
其中 Fz对转 轴的
力矩为零，故 F 对转
轴的力矩 M zk
r
F
z
F
k
O rFz
F
M z rF sin
索跨过一半径为R、质量为mC的圆柱形滑轮 C，并系在另一质量为mB 的物体B上，B 竖 直悬挂．滑轮与绳索间无滑动， 且滑轮与
轴承间的摩擦力可略去不计．(1)两物体的 线加速度为多少？ 水平和竖直两段绳索的
张力各为多少？(2) 物体 B 从静止落下距 离 y 时，其速率是多少？
第四章 刚体转动与流体运动
4
物理学 第六版
4-2 力矩 转动定律 转动惯量
解 设水深h，坝长L，在坝面上取面积 元 dA Ldy ，作用在此面积元上的力
dF pdA pLdy
力矩 刚体定轴转动的转动定律
dJ R dm
2
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
12
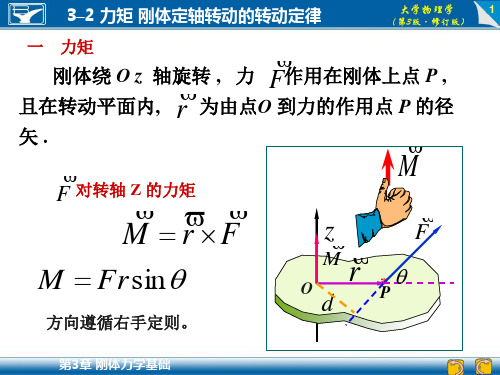
考虑到所有质元到转轴的距离均为R，所以细圆环对 中心轴的转动惯量为
J dJ R dm R
2 m
2
m
dm mR
2
(2)求质量为m，半径为R的圆盘对中心轴的转动惯量
m 如图 dS 2 rdr , , dm dS 2 rdr 2 R
l 2
o
P
d d d d dt d dt d
代入初始条件积分 得
第3章 刚体力学基础
3g d sin d 2l 3g (1 cos ) l
1 2 J x dx ml 0 3
l 2
由此看出，同一均匀细棒，转轴位置不同，转动惯 量不同.
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
11
例3.2 设质量为m，半径为R的细圆环和均匀圆盘分 别绕通过各自中心并与圆面垂直的轴转动，求圆环和 圆盘的转动惯量. 解 (1) 在环上任 取一质元，其质量 为dm，距离为R， 则该质元对转轴的 转动惯量为
解 (1)转轴通过棒的中心并与棒垂直
m l
dm dx
dJ x 2dm x 2dx
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
10
整个棒对中心轴的转动惯量为
J dJ
l 2 l 2
1 x dx ml 2 12
2
(2)转轴通过棒一端并与棒垂直时，整个棒对该轴的 转动惯量为
解 (1) M k 2 ，故由转动定律有
k k J 即 J 2 1 k0 0 3 9J
04-2转动定律(新)
n
M = r F sin θ
1. 力在转动平面内： ω F sin θ
0
力矩的方向判断
右手螺旋前进法则 F F cos θ
·
r
M
F r
·
θ
力矩的量值
M = r F sin θ
力矩量值的一般书写：
力矩的矢量式：
M = r ×F M = r F sin （r、 F）
2. 力不在转动平面内:
F
力矩的矢量式
点支△应设在离A 端35cm处 才能使该装置静止平衡。
二. 转动定律 研究刚体受外力矩作用时，外力矩与角加速度 之间的关系：刚体转动中的牛顿第二定律。
Fi 内力 fi 对△mi 质点进行
外力 受力分析并应用 牛顿第二定律有： 切向分力： 法向分力：
0
´ω
fi ri mi △
·
0
·j
θi
Fi
i
0
f i sinθ i + F i sin j i = △ m i a i t - f i cosθi - F i cosj i = △ m i r iω
2 2 圆盘
o
2
细棒
2
2
2
0
o
·
0.5L
m1
0.5L m2
2
同理：
J ＝J ＋ J
0
杆1
杆2
L 1 m （ ） J ＝ 3 2
杆1
1
L L 1 L ＋m（ ＋ ） J ＝ m（ ） 4 2 2 12
2
2 杆2
2
2
J ＝J ＋ J
0
杆1
杆2
1 m L＋ 7 m L ＝ 12 12
M = r F sin θ
1. 力在转动平面内： ω F sin θ
0
力矩的方向判断
右手螺旋前进法则 F F cos θ
·
r
M
F r
·
θ
力矩的量值
M = r F sin θ
力矩量值的一般书写：
力矩的矢量式：
M = r ×F M = r F sin （r、 F）
2. 力不在转动平面内:
F
力矩的矢量式
点支△应设在离A 端35cm处 才能使该装置静止平衡。
二. 转动定律 研究刚体受外力矩作用时，外力矩与角加速度 之间的关系：刚体转动中的牛顿第二定律。
Fi 内力 fi 对△mi 质点进行
外力 受力分析并应用 牛顿第二定律有： 切向分力： 法向分力：
0
´ω
fi ri mi △
·
0
·j
θi
Fi
i
0
f i sinθ i + F i sin j i = △ m i a i t - f i cosθi - F i cosj i = △ m i r iω
2 2 圆盘
o
2
细棒
2
2
2
0
o
·
0.5L
m1
0.5L m2
2
同理：
J ＝J ＋ J
0
杆1
杆2
L 1 m （ ） J ＝ 3 2
杆1
1
L L 1 L ＋m（ ＋ ） J ＝ m（ ） 4 2 2 12
2
2 杆2
2
2
J ＝J ＋ J
0
杆1
杆2
1 m L＋ 7 m L ＝ 12 12
4-2-力矩-转动定律-转动惯量jm
方向: 服从右手螺旋法则
2、刚体的定 轴 转动定律
M J
d: 力臂
Z
R Om
40
二 转动惯量
➢ 离散质点系 J miri2 ➢ 连续质点系 J r 2dm
* r: 质点到转轴的垂直距离
➢ 平行轴定理 J Jc md 2
41
➢ 常用的转动惯量公式
m质点：J r2m 圆盘(圆柱): J 1 mR2
7
（2）刚体内作用力和反作用力的力矩 互相抵消．
刚体对转轴的合内力矩为零。
Mij 0
Z
M
O
rj
i
j F
d ri F
M
Mij M M Fd Fd 0
8
5、求合力矩
M rF
M Frsin Fd
R+ T
r
R
T1
T2
对转轴：M TR 转对轴：M T2R T1r
9
FT1
2L
o d
26
➢ 转动定律应用 M J
说明
(1) M J , 与 M 方向相同
(2) 为瞬时关系
(3) 转动中M J与平动中F ma
地位相同
27
例: 一定滑轮的质量为 m ，半径为 r ，一轻绳
两边分别系 m1 和 m2 两物体挂于滑轮上，绳不伸
长，绳与滑轮间无相对滑动。不计轴的摩擦，初角 速度为零，求滑轮转动角速度随时间变化的规律。
圆环：J mR 2 更稳定ຫໍສະໝຸດ 飞轮的质量为什么 大都分布于外轮缘？
定轴转动定理
M J
M / J
25
定轴转动定理 M J
细棒绕其一端 J 1 mL2
竿 子
3
长
4-2-力矩-转动定律-转动惯量
0
2
第24页，共47页。
而 m π R2
所以 J 1 mR2 2
注意
刚体的转动惯量与以下三个因素有关： （1）与刚体的几何形状有关．
（2）与刚体的体密度 有关．
（3）与转轴的位置有关．
在定轴转动定律中，不论是对M还是对于J， 首先都要明确的是转轴的位置，只有轴确定，
M和J才有意义。
第25页，共47页。
为R＝0.100 m，一根不能伸长的轻绳，一端固定在定滑轮
上，另一端系有一质量为m＝5.00 kg的物体，如图所示．已
知定滑轮的初角速度 w0＝10.0 rad/s，方向垂直纸面向 里．求：
(1) 定滑轮的角加速度的大小和方向； (2) 定滑轮的角速度变化到0时，物体
0
R
上升的高度；
M
(3) 当物体回到原来位置时，定滑轮
PmA AO
FT1
x
FT1
PC
FC FT2
C
mC FT2
mB B
FT2
O
mB
PB y
解 （1）隔离物体分别 对物体A、B 及滑轮作受力 分析，取坐标如图，运用 牛顿第二定律 、转动定律 列方程 .
FT1 mAa
mBg FT2 mBa
RFT2 RFT1 J
a R
第34页，共47页。
y
x
dF y
O
Q
第12页，共47页。
dF [ p0 g(h y)]Ldy
dF对通过点Q的轴的力矩 dM ydF
h
M 0 y[ p0 g(h y)]Ldy
y
1 2
p0 Lh2
1 6
gLh3
h dF O
dy 代入数据，得：
§4.2 力矩 转动惯量 转动定律
Fi
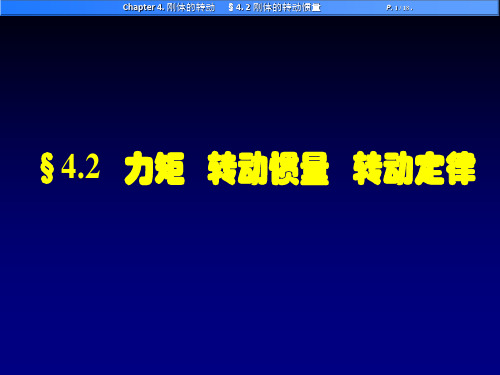
3. Mz、J、皆对同一轴而言。
fi
n
ri Fi ri fi ( miri2)
i
i
i 1
o ri
f
i
mi
Fi
n
ri Fi J i1
Mz J ( 转动定律 )
Chapte作r 4者. 刚：体杨的茂转田作动者：§杨4.茂2 田刚体的转动惯量
P. 27 / 18 .
1. Mz J 反映了力矩 Mz与角加速度 间的瞬时关系。
P. 29 / 18 .
例 已知细杆长l、质量 m，初角速度为0，细杆与桌面
间有摩擦，经 t0 时间后杆静止，求摩擦力矩 M阻。
解：细杆只受摩擦力矩，且为恒力矩，由 Mz J 可
知，细杆作匀变速转动：
m, l
而 J 1 ml 2 3
0 t
0 t0 0
0
t0
M阻 J
ml 2 3t 0
i 1
二、转动惯量
n
J miri2 i 1
mi
m3
ri
r3
r2
r1 m1
m2
1 2
(
n i1
mi ri2
) 2
Ek
1( 2
n i1
mi ri2
) 2
Chapte作r 4者. 刚：体杨的茂转田作动者：§杨4.茂2 田刚体的转动惯量
P. 9 / 18 .
n
可知： 一定时， miri2越大，刚体转动动能亦越大。
i 1
n
ri Fi J i1
Mz J
Fi fi
o ri
F ma
f
i
mi
Fi
( 转动定律 )
Chapte作r 4者. 刚：体杨的茂转田作动者：§杨4.茂2 田刚体的转动惯量
力矩转动定律转动惯量jm汇总课件
力矩的物理意义
总结词
力矩描述了力使物体绕某点转动的趋势或转动效果。
详细描述
力矩决定了物体绕某点转动的趋势或转动效果，其方向与力和力臂的乘积方向 相同。力矩越大，物体转动的趋势或转动效果越明显。
力矩的计算方法
总结词
力矩的大小等于力和力臂的乘积，计中力臂是从转动轴（或转动中心）到力的垂 直距离。计算公式为 M=FL，其中 M 为力矩，F 为力，L 为力臂。同时，力矩的 方向与力和力臂的乘积方向相同。
转动惯量的大小决定了物体旋转运动 的加速度、角速度和角动量等参数的 变化规律，进而影响物体的运动状态 和稳定性。
转动惯量的计算方法
转动惯量的计算方法主要包括平行轴定理和垂直轴定理。
平行轴定理指出，对于一个质量分布均匀的刚体，其相对于某固定轴的转动惯量，等于该刚体的质量乘以质心到该轴的距离 的平方，再加上所有相对于此轴的离散质量的转动惯量之和。垂直轴定理则说明，一个质量分布均匀的刚体相对于任一垂直 于其对称平面的轴的转动惯量，等于该刚体的质量乘以其对称轴到质心的距离的平方。
车辆工程
在车辆工程中，力矩转动定律用于分析车辆动力学和稳定性 问题。例如，通过分析车轮的力矩，可以研究车辆的操控性 能和行驶稳定性。
力矩转动定律在科研中的应用
物理学研究
力矩转动定律是物理学中分析转 动问题的基本原理，广泛应用于 分析天体运动、刚体动力学等问 题。
生物学研究
在生物学研究中，力矩转动定律 用于分析生物体的运动和平衡机 制，如动物的行走、飞行等。
动惯量。
实验步骤
2. 将刚体安装到实验装置上 ，调整力矩计和角位移传感
器的位置和角度。
1. 准备实验器材：刚体、力 矩计、角位移传感器、数据
42力矩转动定律转动惯量
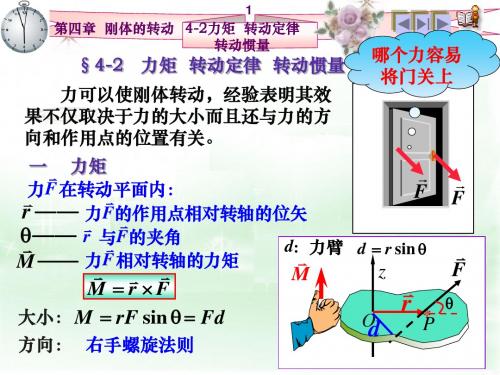
dm ——质量线密度 dl
dm r dl
r1
m1
J mr 2
m2
（2）质量离散分布刚体的转动惯量 J m j rj2 m1r12 m2r22 （3）质量连续分布刚体的转动惯量
J r 2 dm
j
r2
r3m3转轴来自dm：质量元15
第四章 刚体的转动 4-2力矩 转动定律 转动惯量
F ：垂直于转轴的分力；
F F F
k
O
F
F
r
P
F
M r F 大小： M rF sin rd
方向： 右手螺旋法则
4
第四章 刚体的转动 4-2力矩 转动定律 转动惯量
对于作定轴转动的刚体，一般规定： 如力矩使刚体沿逆时针方向转动，力矩为正； 如力矩使刚体沿顺时针方向转动，力矩为负； 讨论 1 力矩的三要素： （1）力的大小和方向； （2）力的作用点； （3）转轴位置 . 2. 若力F不在转动平面内： z
j
转动定律
M J
2 J m r jj 刚体的转动惯量：
刚体定轴转动的角 加速度与它所受的合外 力矩成正比 ，与刚体的 转动惯量成反比.
11
三 转动惯量 1. 物理意义 转动惯量与物体的惯性质量物理意义一致， 是物体转动惯性大小的量度。 2. 与转动惯量有关的因素： （3）转轴的位置； （2）质量分布； （1）刚体的总质量； 对所有质点求和：
j
第四章 刚体的转动 4-2力矩 转动定律 转动惯量
m2
2
r3
m3
（3）质量连续分布刚体的转动惯量
J r 2 dm
转轴
dm：质量元
定轴转动定律 转动惯量
一半径为R，质量为m均质圆盘 均质圆盘， 例4-6 一半径为 ，质量为 均质圆盘，平放在粗糙的 水平桌面上。 水平桌面上 。 设盘与桌面间摩擦因数为 µ ， 令圆盘最 绕通过中心且垂直盘面的轴旋转， 初以角速度ω0 绕通过中心且垂直盘面的轴旋转，问它 经过多少时间才停止转动？ 经过多少时间才停止转动？ 解： 把圆盘分成许多环形 质元，每个质元的质量 dm= ρ red θ dr， e是盘的厚 ， 是盘的厚 度 ， 质元所受到的阻力矩 为 rµdmg 。 圆盘所受阻力矩为
§4-2 定轴转动定律 转动惯量
一、力矩
r 点的力矩： 点的力矩 F 对O点的力矩：
r M
r r r M = r ×F
大小： 大小： 说明 1、只有垂直转轴的外力分量才产生 、 沿转轴方向的力矩M 沿转轴方向的力矩 z ，而平行于转 轴的外力分量产生的力矩 Mxy 则被 轴承上支承力的力矩所抵消。 轴承上支承力的力矩所抵消。
二、定轴转动定律
对刚体中任一质量元 ∆ m i
r r 受外力 Fi 和内力 F内 i
r r r Fi + F内i = ∆mi ai
应用牛顿第二定律， 应用牛顿第二定律，可得
采用自然坐标系， 采用自然坐标系，上式切向分量式为
Fi sin ϕi + F内i sin θi = ∆mi ait = ∆mi ri β
Fi ri sin ϕi + F内i ri sin θi = ∆mi ri β
2
对刚体内各个质点的相应式子， 对刚体内各个质点的相应式子，相加得
Fi ri sin ϕi + ∑ F内i ri sin θ i = ∑ (∆mi ri 2 )β ∑
i i i
对于成对的内力，对同一转轴的力矩之和为零， 对于成对的内力，对同一转轴的力矩之和为零，则
4-2力矩转动定律转动惯量
J r2dm
图1
图2
J1 J2
➢ 常用的转动惯量 （P110 表）
21
四 平行轴定理
质量为m 的刚体，
如果对其质心轴的转动 惯量为 JC ，则对任一与
该轴平行，相距为 d 的
转轴的转动惯量
JO JC md 2
d
C mO
J Jc
22
J Jc md2
圆盘对P 轴的转动惯量 P R O m
Fit Fit miait miri
11
➢ 质元绕Z轴转动的力矩
M i ri Fit ri Fit miri2
➢ 刚体绕Z轴转动的力矩
z
Fi内
Fi外
r O i m i 质量元
Mi riFit riFit
mi ri 2
M
r
F
M Frsin Fd
5
4、一对力偶的力矩
M Fd
F
F
o
l
F 0 M 0
M F l F l Fl
22
ro
F'
F
F 0
M 0
M Fr Fr 0
6
讨论
（1）若力 F不在转动平面内，把力分
解为平行和垂直于转轴方向的两个分量
41
➢ 常用的转动惯量公式
m质点：J r2m 圆盘(圆柱): J 1 mR2
2
杆：
Jc
1 12
mL2
J
端
1 3
mL2
R Om
O1
O1’
d=L/2
第4章-刚体转动
例1 如图, 有一半径为 R 质量为 m的匀质圆盘, 可绕
通过盘心 O 垂直盘面的水平轴转动. 转轴与圆盘之间的
摩擦略去不计. 圆盘上绕有轻而细的绳索, 绳的一端固
定在圆盘上, 另一端系质量为 m 的物体. 试求物体下落
时的加速度、绳中的张力和圆盘的角加速度.
m
Ro
m
oR
m
T
m
T'
Py
解：1） 分析受力 2）选取坐标
2 刚体定轴转动的角动量
L mirivi ( miri2 )
i
i
L J
单位：kg·m2·s-1，量纲：ML2T-1
二 刚体定轴转动的角动量定理
z
O ri
vi
mi
dL d(J) J d J M
dt dt
dt
t2
t1
Mdt t2 Mdt
t1
L2
L1
dL L2 dL
L1
J2 J1
➢ 角速度矢量 lim d
t t0 dt
方向: 右手螺旋方向
参考轴
6
4-1 刚体的定轴转动
➢ 刚体定轴转动（一维转动）的转动方向可以用角速
度的正负来表示 .
➢
角加速度
d
dt
z
z
定轴转动的特点
0 0
1） 2）
每任一一质 质点 点均 运作 动圆周 ,运动,，均圆相面同为，转但动v平,面a 不；同；
球体（沿任一直径）： 圆筒（沿几何中心轴）：
J 2 mR2 5
J m 2
R12 R22
21
4-2 力矩 转动定律 转动惯量
讨论 ➢ 有两个飞轮：一个是木制的，周围镶上铁制
大学物理刚体习题补充
班级 姓名 学号 批阅日期 月 日4-1 刚体的定轴转动 4-2 力矩 转动定律 转动惯量一、 选择题1、一自由悬挂的匀质细棒AB ，可绕A 端在竖直平面内自由转动，现给B 端一初速v 0，则棒在向上转动过程中仅就大小而言 [ ]A 、角速度不断减小，角加速度不断减少；B 、角速度不断减小，角加速度不断增加；C 、角速度不断减小，角加速度不变；D 、所受力矩越来越大，角速度也越来越大。
2、今有半径为R 的匀质圆板、圆环和圆球各一个，前二个的质量都为m ，绕通过圆心垂直于圆平面的轴转动；后一个的质量为2m ，绕任意一直径转动，设在相同的力矩作用下，获得的角加速度分别是β1、β2、β3，则有 [ ]A 、β3＜β1＜β2B 、β3＞β1＜β2C 、β3＜β1＞β2D 、β3＞β1＞β23、关于力矩有以下几种说法，其中正确的是 [ ]A 、内力矩会改变刚体对某个定轴的角动量（动量矩）；B 、作用力和反作用力对同一轴的力矩之和必为零；C 、角速度的方向一定与外力矩的方向相同；D 、质量相等、形状和大小不同的两个刚体，在相同力矩的作用下，它们的角加速度一定相等。
4、一轻绳跨过两个质量均为m 、半径均为R 的匀质圆盘状定滑轮。
绳的两端分别系着质量分别为m 和2m 的重物，不计滑轮转轴的摩擦。
将系统由静止释放，且绳与两滑轮间均无相对滑动，则两滑轮之间绳的张力。
[ ](A)mg ； (B)3mg /2； (C)2mg ； (D)11mg /8。
5、一根质量为m 、长度为L 的匀质细直棒，平放在水平桌面上。
若它与桌面间的滑动摩擦系数为μ，在t =0时，该棒绕过其一端的竖直轴在水平桌面上旋转，其初始角速度为0ω，则棒停止转动所需时间为 [ ](A)μωg L 3/20； (B) μωg L 3/0； (C) μωg L 3/40； (D) μωg L 6/0。
6、力kN j i F )53( +=，其作用点的矢径为m j i r )34(-=，则该力对坐标原点的力矩大小为 [ ](A)m kN ⋅-3； （B ）m kN ⋅29； (C)m kN ⋅19； (D)m kN ⋅3。
(完整版)转动定律讲解
d力臂:转轴到力作用线的垂直距离
方向: r F 的方向 单位: N m
对于定轴转动；
z
M
r
Od
F
P*
规定转动正方向,力矩使刚体绕
正方向转动, M 取正,反之取负。
第四章 刚体的定轴转动
4 – 2 力矩 转动定律 转动惯量
大学物理学
讨论 1）与转轴平行的力对转轴不产生力矩;
2）与转 轴垂直但通过转轴的力对转轴不产生力矩； 3）若力 F 不在转动平面内，把力分解为平行和垂
直于转轴方 向的两个分 量 F Fz F
其中 Fz 对转轴的力
矩为零，故 F 对转轴的
力矩
M r F
M z rF sin
4）合 力矩 等于各分力矩的矢量和
M M1 M2 M3
第四章 刚体的定轴转动
z
k
Fz
F
O r
F
定轴转动：（规定转动 正方向）
M Mi
i
4 – 2 力矩 转动定律 转动惯量
力矩可以反映力的作用点的位置对物体运动的影响.
第四章 刚体的定轴转动
4 – 2 力矩 转动定律 转动惯量
大学物理学
一 力矩
刚体绕 O z 轴旋 转 , 力 F 作用在刚体上点 P ,
r 且在转动平面内, 为由点O 到力的作用点 P 的径
矢 .
F 对转轴 Z 的力矩 M rF
M
力矩是矢量
大小: M Frsin Fd
M i Fitri (mi )atri
at ri
Mi (mi )ri2
z
Fit
O
ri
mi
M Mi (mi )ri2 (mi )ri2
➢ 转动惯量
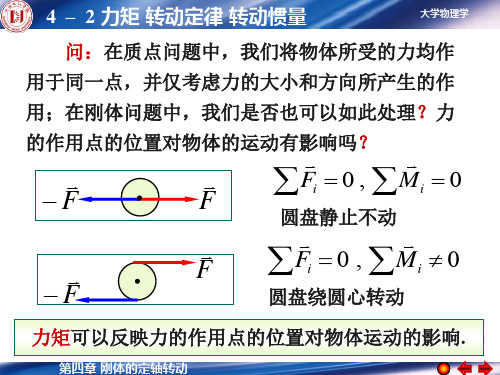
方向: r F 的方向 单位: N m
对于定轴转动；
z
M
r
Od
F
P*
规定转动正方向,力矩使刚体绕
正方向转动, M 取正,反之取负。
第四章 刚体的定轴转动
4 – 2 力矩 转动定律 转动惯量
大学物理学
讨论 1）与转轴平行的力对转轴不产生力矩;
2）与转 轴垂直但通过转轴的力对转轴不产生力矩； 3）若力 F 不在转动平面内，把力分解为平行和垂
直于转轴方 向的两个分 量 F Fz F
其中 Fz 对转轴的力
矩为零，故 F 对转轴的
力矩
M r F
M z rF sin
4）合 力矩 等于各分力矩的矢量和
M M1 M2 M3
第四章 刚体的定轴转动
z
k
Fz
F
O r
F
定轴转动：（规定转动 正方向）
M Mi
i
4 – 2 力矩 转动定律 转动惯量
力矩可以反映力的作用点的位置对物体运动的影响.
第四章 刚体的定轴转动
4 – 2 力矩 转动定律 转动惯量
大学物理学
一 力矩
刚体绕 O z 轴旋 转 , 力 F 作用在刚体上点 P ,
r 且在转动平面内, 为由点O 到力的作用点 P 的径
矢 .
F 对转轴 Z 的力矩 M rF
M
力矩是矢量
大小: M Frsin Fd
M i Fitri (mi )atri
at ri
Mi (mi )ri2
z
Fit
O
ri
mi
M Mi (mi )ri2 (mi )ri2
➢ 转动惯量
大学物理 第四章 刚体的转动 4-2 力矩 转动定律 转动惯量
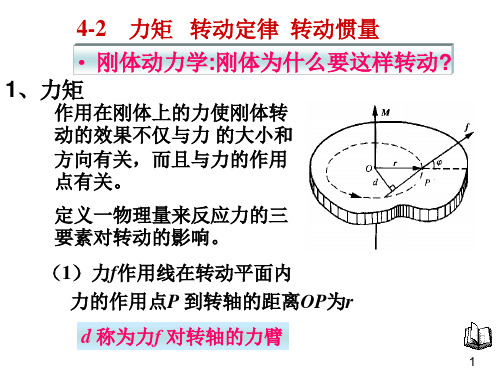
} ⇒ω
} ⇒θ
2、 M = Jα
F = ma
}⇒
17
m反映质点的平动惯性，J 反映刚体的转动惯性。 反映质点的平动惯性， 反映刚体的转动惯性。 反映质点的平动惯性
三 转动惯量
J 的计算方法 质量离散分布
J = ∑ ∆m r
j
2 j j
J = ∑ ∆m r = (∆m )r + (∆m2 )r + L+ (∆mN )r
质量为m，长为L的细棒绕其一端的 的细棒绕其一端的J 质量为 ，长为 的细棒绕其一端的
1 2 J c = mL 12
O1
O1’
L2 1 2 J = J c + m( ) = mL 2 3
d=L/2
O2 O2’
20
竿 子 长 些 还 是 短 些 较 安 全 ？
飞轮的质量为什么 大都分布于外轮缘？ 大都分布于外轮缘？
（3） ）
1 2 对M： T2 r − T1r = J α = M r α ： 2
4、运动学： 运动学：
rα = a
（4） ）
26
解以上四个联立方程式, 解以上四个联立方程式 可得
1 T2 ' ≠ T 、
原因： 原因：
' 1
' (1)若：T2 ' = T T2 ' r −T ' r = Jα v 1 1 FN v 1 T 1 ⇒ J = mr2 = 0 ⇒m = 0 2 m
21
例1（补充例题）：一个转动惯量为2.5 kg⋅m2 、 （补充例题） 一个转动惯量为 ⋅ 例题 直径为60cm 的飞轮，正以 的飞轮，正以130 rad⋅s−1 的角速度旋转。 直径为 ⋅ 的角速度旋转。 现用闸瓦将其制动, 现用闸瓦将其制动 如果闸瓦对飞轮的正压力为 500 N, 闸瓦与飞轮之间的摩擦系数为0.50。求： 闸瓦与飞轮之间的摩擦系数为 。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
d F
: 力臂
F
Fi 0 , Mi 0
F
F
1）若力 F 不在转动平面内，把力分解为平行和垂 直于转轴方向的两个分量 z F Fz F F 其中 Fz 对转轴的力 k Fz
矩为零，故 F 对转轴的 力矩
求：重物的加速度，系统中各绳的张力，轴承O的约束反力。
解：设个物体的数度如 图示，且：
R1 F Oy
1
m1 g
M
FOx
A
1 v3 v2 R22 R11 2
对系统进行受力分析如 图
v2
2
m2 g
B
R2
C
m3 g
v3
则整个系统对O点的动量矩为：
LO LOA LOB LOC J11 J 22 m2 v2 R2 m3v3 R2
o
l'
F
l
五、平面运动刚体的运动微分方程
刚体相对质心轴的转动定理为
J C M C Fi
maC F i
e
e
－－－－（1）
刚体质心运动的运动微分方程为
－－－－（2）
（1）、（2）式共同成为刚体平面运动的运动微 分方程为
例:
均质滑轮A、B的质量为 m1 与 m2 ，半径分别为 R1与 R2 ，
r dr
圆环对轴的转动惯量
dJ r dm 2π r dr R 3 4 J 2π r dr π R 0
2
而
m π R
2
所以
1 2 J mR 2
转动惯量的大小取决于刚体的质量、形 状及转轴的位置 . 四 平行轴定理 质量为 m 的刚体，如果对 其质心轴的转动惯量为 J C ，则 对任一与该轴平行，相距为 d 的转轴的转动惯量
三 转动惯量
I m r , I r dm
2 j j 2 j
rotational inertia
转动惯性的计算方法
物理意义：转动惯性的量度 .
质量离散分布刚体的转动惯量
2 j j 2 11
I m r m r m r
2 2 2 j
2 j j 2
质量连续分布刚体的转动惯量
二
转动定律 取质量元 m j
质量元受外力 F ，内力 F ij ej
M ej M ij Fejtrj Fijtrj m j a j rj
Fej Fij m j a j
Fejt Fijt mj a j t
Mej Mij m r
轮A绕固定轴转动,不计细绳的质量和轴承的摩擦
求:轮B下落时轮心C的加速度
及绳的拉力
R1
M A
T
TR1 I11
T R2 I 2 2
'
T’
C
m2 g T m2 ac
'
B
R2
R11 ac R2 2
例4：均质滑轮A、B的质量为 m1 与 m2 ，半径分别为 R1与R2 ， 物体C的质量为 m3 ；
R1 F Oy
1
m1 g
M
FOx
A
J11 M T2 R1
联合上述各式可求 得各未知量
T2 T1
I m r
j
2 j j
转动定律
M I
刚体定轴转动的角加速度与它所受的合外力矩成 正比 ，与刚体的转动惯量成反比 .
转动定律
d Lz Mz dt
(对 z 轴)
Lz I z
d Lz d( I z ) Mz dt dt d =I Z IZ dt
x
z
Ri
4.2 力矩 转动定律
力矩 刚体绕 O z 轴旋转 , 力 F 作用在刚体上点 P , 且在转动 为由点O 到力的 平面内, r 作用点 P 的径矢 . Z F 对转轴 的力矩
一
M
M
O
z
M Fr sin Fd
M r F
r
F
*
d
P
Fi 0 , Mi 0
1 2 J 1 m1 R1 2 1 2 J 2 m2 R2 2
1 LO 4m1 3m2 2m3 R2 v3 2
由动量矩定理得：
e d LO M O Fi dt
R1 F Oy
1
m1 g
M
FOx
A
2M m2 m3 gR2 a3 对细杆的约束力 F N
作用，由转动定律得
解
细杆受重力和
1 mgl sin J 2
1 mgl sin J 2 1 2 式中 J ml 3 3g sin 得 2l
由角加速度的定义
d d d d dt d dt d
代入初始条件积分 得
l/2 2
如转轴过端点垂直于棒
1 2 J r dr ml 0 3
l 2
例3 一质量为 m 、半径为 R 的均匀圆盘，求通 过盘中心 O 并与盘面垂直的轴的转动惯量 .
解 设圆盘面密度为 ， 在盘上取半径为 ，宽为 dr 的圆环
r
圆环质量
dm 2 π r dr
2 3
R R
O
A
mA FN FT1 mA O x PA
FT1
C
mC FT2
mB B
FT2
mB PB y
O
解 （1）隔离物体分 别对物体A、B 及滑轮作 受力分析，取坐标如图， 运用牛顿第二定律 、转 动定律列方程 .
FT1 mA a
mB g FT2 mBa
RFT2 RFT1 J
I m r r dm
j
dm
：质量元
质量连续分布刚体的转动惯量
I m r r dm
2 j j 2 j
dm
：质量元
对质量线分布的刚体： dm
dl
：质量线密度
对质量面分布的刚体： dm
：质量面密度
：质量体密度
dS
dV
对质量体分布的刚体：dm
mB B
mA (mB g M f / R) FT1 mA mB mC / 2
mB (mA mC 2) g M f R FT2 mA mB mC 2
例5 一长为 l 质量为 m 匀质细杆竖直放置，其 下端与一固定铰链 O 相接，并可绕其转动 . 由于此 竖直放置的细杆处于非稳定平衡状态，当其受到微小 扰动时，细杆将在重力作用下由静止开始绕铰链O 转 动 .试计算细杆转动到与竖直线成 角时的角加速度 和角速度 .
例2 一质量为 m 、长为 l 的均匀细长棒，求 通过棒中心并与棒垂直的轴的转动惯量 .
O
l 2
O
l 2
r
l
dr O´
dr O´
解 设棒的线密度为 ，取一距离转轴 OO´ 为 处的质量元 dm dr dJ r 2dm r 2dr
r
1 3 J 2 r dr l 0 12 1 ml 2 12
0，可得
（2） B由静止出发作匀加速直线运动，下落的速率
2mB gy v 2ay mA mB mC / 2
（3） 考虑滑轮与轴承间的摩 擦力矩 M f ，转动定律
FT1
Mf
RFT2 RFT1 M f J
结合（1）中其它方程
FT2
FN
FT1 mA a
FT1
PC
FC
FT2
a R
mB g a mA mB mC 2 mA mB g FT1 mA mB mC 2
(mA mC 2)mB g FT2 mA mB mC 2
如令 mC
A mA
FT1
C
mC FT2
mB B
mA mB g FT1 FT2 mA mB
2 j j
z
O
外力矩
内力矩
rj
Fej
m j
Fij
M ej M ij m j rj2
j j
z
O
M ij M ji
M ij 0
j
rj
m j
Fej
M
j
ej
( m r )
2 j j
Fij
I r dm
2
定义转动惯量
取分离体C：
v2
2
m2 g
B
R2
C
m3 g
v3
m3a3 T3 m3 g
v3
T3
C
m3 g
取分离体B：
T1
T2
B
m2 a2 T1 T2 T3 m2 g
J 2 2 T1 R2 T2 R2
取分离体C ：
v2 2
m2 g
R2
m1a1x FOx
m1a1 y 0
vi
m Δ i ri
y
Li
i
O
定轴
则：
M I
—转动定律矢量式
M I —转动定律
与牛顿第二定律
M 相应 F
F ma
相比，有： 。
，I 相应 m ， 相应 a
刚体绕某一固定轴的合外力矩,等于刚体对此 轴的转动惯量与刚体的角加速度的乘积 。 ----刚体的定轴转动定律
讨论
M z k r F M z rF sin