四川省成都石室中学高一数学4月月考试题
四川省成都市2023-2024学年高一下学期第一次月考数学试题含答案
武侯高中高2023级2023——2024下期第一次月考试题数学（答案在最后）学校：__________姓名：__________班级：__________考号：__________一、单选题1.如图，四边形ABCD 中，AB DC =，则必有（）A.AD CB= B.DO OB= C.AC DB= D.OA OC= 【答案】B 【解析】【分析】根据AB DC =，得出四边形ABCD 是平行四边形，由此判断四个选项是否正确即可．【详解】四边形ABCD 中，AB DC =，则//AB DC 且AB DC =，所以四边形ABCD 是平行四边形；则有AD CB =-，故A 错误；由四边形ABCD 是平行四边形，可知O 是DB 中点，则DO OB =，B 正确；由图可知AC DB≠，C 错误；由四边形ABCD 是平行四边形，可知O 是AC 中点，OA OC =-，D 错误．故选：B ．2.下列说法正确的是（）A.若a b ∥ ，b c ∥，则a c∥ B.两个有共同起点，且长度相等的向量，它们的终点相同C.两个单位向量的长度相等D.若两个单位向量平行，则这两个单位向量相等【答案】C 【解析】【分析】A.由0b =判断；B.由平面向量的定义判断；C.由单位向量的定义判断； D.由共线向量判断.【详解】A.当0b = 时，满足a b ∥ ，b c ∥，而,a c 不一定平行，故错误；B.两个有共同起点，且长度相等的向量，方向不一定相同，所以它们的终点不一定相同，故错误；C.由单位向量的定义知，两个单位向量的长度相等，故正确；D.若两个单位向量平行，则方向相同或相反，但大小不一定相同，则这两个单位向量不一定相等，故错误；故选：C3.若a b ，是平面内的一组基底，则下列四组向量中能作为平面向量的基底的是（）A.,a b b a --B.21,2a b a b++ C.23,64b a a b-- D.,a b a b+- 【答案】D 【解析】【分析】根据基底的知识对选项进行分析，从而确定正确答案.【详解】A 选项，()b a a b -=-- ，所以a b b a -- ，共线，不能作为基底.B 选项，1222a b a b ⎛⎫+=+ ⎪⎝⎭ ，所以12,2a b a b ++ 共线，不能作为基底.C 选项，()64223a b b a -=-- ，所以64,23a b b a --共线，不能作为基底.D 选项，易知a b a b +-，不共线，可以作为基底.故选：D4.将函数2cos 413y x π⎛⎫=-+ ⎪⎝⎭图象上各点的横坐标伸长到原来的2倍，再向左平移3π个单位，纵坐标不变，所得函数图象的一条对称轴的方程是（）A.12x π=B.6x π=-C.3x π=-D.12x π=-【答案】B 【解析】【分析】根据图像的伸缩和平移变换得到2cos(2)13y x π=++，再整体代入即可求得对称轴方程.【详解】将函数2cos 413y x π⎛⎫=-+ ⎪⎝⎭图象上各点的横坐标伸长到原来的2倍，得到2cos 213y x π⎛⎫=-+ ⎪⎝⎭，再向左平移3π个单位，得到2cos[2()]12cos(2)1333y x x πππ=+-+=++，令23x k π+=π，Z k ∈，则26k x ππ=-，Z k ∈.显然，=0k 时，对称轴方程为6x π=-，其他选项不符合.故选：B5.设a ，b 是非零向量，“a a bb =”是“a b =”的（）A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【答案】B 【解析】【分析】根据向量相等、单位向量判断条件间的推出关系，结合充分、必要性定义即知答案.【详解】由a a b b =表示单位向量相等，则,a b 同向，但不能确定它们模是否相等，即不能推出a b =，由a b =表示,a b 同向且模相等，则a a b b = ，所以“a a bb =”是“a b =”的必要而不充分条件.故选：B6.已知向量,a b ，且2,52,72AB a b BC a b CD a b =+=-+=+，则下列一定共线的三点是（）A.,,A B CB.,,B C DC.,,A B DD.,,A C D【答案】C 【解析】【分析】利用向量的共线来证明三点共线的．【详解】2,52,72AB a b BC a b CD a b =+=-+=+，则不存在任何R λ∈，使得AB BC λ=，所以,,A B C 不共线，A 选项错误；则不存在任何R μ∈，使得BC CD μ=，所以,,B C D 不共线，B 选项错误；由向量的加法原理知242BD BC CD a b AB =+=+=．则有//BD AB ，又BD 与AB有公共点B ，所以,,A B D 三点共线，C 选项正确；44AB BC a b AC ==-++，则不存在任何R t ∈，使得AC tCD = ，所以,,A C D 不共线，D 选项错误．故选：C ．7.已知sin α＝5，且α为锐角，tan β＝－3，且β为钝角，则角α＋β的值为（）A.4π B.34π C.3π D.23π【答案】B 【解析】【分析】先求出tan α12=，再利用两角和的正切公式求出tan(α＋β)＝－1，判断出角α＋β的范围，即可求出α＋β的值.【详解】sin α，且α为锐角，则cos α5=，tan αsin 1cos 2αα==.所以tan(α＋β)＝tan tan 1tan tan αβαβ+-＝13211(3)2--⨯-＝－1.又α＋β∈3(,22ππ，故α＋β＝34π.故选：B8.筒车亦称“水转筒车”，是一种以水流作动力，取水灌田的工具，唐陈廷章《水轮赋》：“水能利物，轮乃曲成.升降满农夫之用，低徊随匠氏之程.始崩腾以电散，俄宛转以风生.虽破浪于川湄，善行无迹；既斡流于波面，终夜有声.”如图，一个半径为4m 的筒车按逆时针方向每分钟转一圈，筒车的轴心O 距离水面的高度为2m .在筒车转动的一圈内，盛水筒P 距离水面的高度不低于4m 的时间为（）A.9秒B.12秒C.15秒D.20秒【答案】D 【解析】【分析】画出示意图，结合题意和三角函数值可解出答案.【详解】假设,,A O B 所在直线垂直于水面，且4AB =米，如下示意图，由已知可得12,4OA OB OP OP ====，所以1111cos 602OB POB POB OP ∠==⇒∠=︒，处在劣弧 11PP 时高度不低于4米，转动的角速度为360660︒=︒/每秒，所以水筒P 距离水面的高度不低于4m 的时间为120206=秒，故选：D.二、多选题9.已知函数()cos f x x x =+，则下列判断正确的是（）A.()f x 的图象关于直线π6x =对称 B.()f x 的图象关于点π,06⎛⎫- ⎪⎝⎭对称C.()f x 在区间2π,03⎡⎤-⎢⎥⎣⎦上单调递增 D.当π2π,33x ⎛⎫∈-⎪⎝⎭时，()()1,1f x ∈-【答案】BC 【解析】【分析】利用辅助角公式化简函数()f x 的解析式，利用正弦型函数的对称性可判断AB 选项；利用正弦型函数的单调性可判断C 选项；利用正弦型函数的值域可判断D 选项.【详解】因为()πcos 2sin 6f x x x x ⎛⎫=+=+ ⎪⎝⎭，对于A选项，ππ2sin 63f ⎛⎫==⎪⎝⎭，故函数()f x 的图象不关于直线π6x =对称，A 错；对于B 选项，π2sin 006f ⎛⎫-== ⎪⎝⎭，故函数()f x 的图象关于点π,06⎛⎫- ⎪⎝⎭对称，B 对；对于C 选项，当2π03x -≤≤时，πππ266x -≤+≤，则函数()f x 在区间2π,03⎡⎤-⎢⎥⎣⎦上单调递增，C 对；对于D 选项，当π2π33x -<<时，ππ5π666x -<+<，则1πsin 126x ⎛⎫-<+≤ ⎪⎝⎭，所以，()(]π2sin 1,26f x x ⎛⎫=+∈- ⎪⎝⎭，D 错.故选：BC.10.下图是函数()sin()(0π)f x A x ωϕϕ=+<<的部分图像，则（）A.2πT =B.π3ϕ=C.π,06⎛⎫-⎪⎝⎭是()f x 的一个对称中心 D.()f x 的单调递增区间为5πππ,π1212k k ⎡⎤-++⎢⎥⎣⎦（Z k ∈）【答案】BCD 【解析】【分析】由图象可得πT =，由2πT ω=可求出ω，再将π12⎛⎝代入可求出ϕ可判断A ，B ；由三角函数的性质可判断C ，D .【详解】根据图像象得35ππ3ππ246124T T =-=⇒=⇒=ω，故A 错误；π12x =时，πππ22π2π1223k k ⨯+=+⇒=+ϕϕ，0πϕ<< ，π3ϕ∴=，故()π23f x x ⎛⎫=+ ⎪⎝⎭，故B 正确；因为πππ20663f ⎡⎤⎛⎫⎛⎫-=⋅-+= ⎪ ⎪⎢⎝⎭⎝⎭⎣⎦，所以π,06⎛⎫- ⎪⎝⎭是()f x 的一个对称中心，C 正确；令πππ2π22π232k x k -+≤+≤+，解得5ππππ1212k x k -+≤≤+，Z k ∈．故D 正确．故选：BCD .11.潮汐现象是地球上的海水受月球和太阳的万有引力作用而引起的周期性涨落现象.某观测站通过长时间观察，发现某港口的潮汐涨落规律为πcos 63y A x ω⎛⎫=++ ⎪⎝⎭（其中0A >，0ω>），其中y （单位：m ）为港口水深，x （单位：h ）为时间()024x ≤≤，该观测站观察到水位最高点和最低点的时间间隔最少为6h ，且中午12点的水深为8m ，为保证安全，当水深超过8m 时，应限制船只出入，则下列说法正确的是（）A.π6ω=B.最高水位为12mC.该港口从上午8点开始首次限制船只出入D.一天内限制船只出入的时长为4h 【答案】AC 【解析】【分析】根据题意可求得6π=ω，可知A 正确；由12点时的水位为8m 代入计算可得4A =，即最高水位为10m ，B 选项错误；易知ππ4cos 663y x ⎛⎫=++⎪⎝⎭，解不等式利用三角函数单调性可得从上午8点开始首次开放船只出入，一天内开放出入时长为8h ，即可判断C 正确，D 错误.【详解】对于A ，依题意π62T ω==，所以6π=ω，故A 正确；对于B ，当12x =时，ππcos 126863y A ⎛⎫=⨯++=⎪⎝⎭，解得4A =，所以最高水位为10m ，故B 错误；对于CD ，由上可知ππ4cos 663y x ⎛⎫=++⎪⎝⎭，令8y ≥，解得812x ≤≤或者2024x ≤≤，所以从上午8点开始首次开放船只出入，一天内开放出入时长为8h ，故C 正确，D 错误.故选：AC.三、填空题12.设e为单位向量，2a =r ，当,a e 的夹角为π3时，a 在e 上的投影向量为______.【答案】e【解析】【分析】利用投影向量的定义计算可得结果.【详解】根据题意可得向量a 在e 上的投影向量为22π21cos 31a e e a e e e e ee e⨯⨯⋅⋅⋅=== .故答案为：e13.已知向量a 、b 满足5a = ，4b = ，a 与b 的夹角为120，若()()2ka b a b -⊥+ ，则k =________.【答案】45##0.8【解析】【分析】运用平面向量数量积公式计算即可.【详解】因为5a = ，4b = ，a 与b的夹角为120 ，所以1cos12054102a b a b ⎛⎫⋅==⨯⨯-=- ⎪⎝⎭.因为()2ka b -⊥()a b +r r ，所以()()()()222222521610215120ka b a b kab k a b k k k -⋅+=-+-⋅=-⨯--=-=，解得45k =.故答案为：45.14.已知1tan 3x =，则1sin 2cos 2x x +=______【答案】2【解析】【分析】根据二倍角公式以及齐次式即可求解.【详解】2222222211121sin 2cos sin 2sin cos 1tan 2tan 332cos 2cos sin 1tan 113x x x x x x x x x x x ⎛⎫++⨯ ⎪+++++⎝⎭====--⎛⎫- ⎪⎝⎭.故答案为：2四、解答题15.已知1a b a == ，与b 的夹角为45︒．（1）求()a b a +⋅的值；（2）求2a b -的值【答案】（1）2（2【解析】【分析】（1）先求2,a a b ⋅ ，再根据运算法则展开计算即可；（2）先计算2b，再平方，进而开方即可.【小问1详解】因为22||1,||||cos 451122a a a b a b ==⋅=︒=⨯=所以2()112a b a a a b ++⋅=⋅=+=【小问2详解】因为22||2b b ==，所以2222|2|(2)444242a b a b a b a b -=-=+⋅=+--=所以|2|a b -=16.已知函数()222cos 1f x x x =+-.（1）求函数()f x 的最小正周期；（2）若3π,π4θ⎛⎫∈⎪⎝⎭且()85f θ=-，求cos 2θ的值.【答案】（1）π（2）410-【解析】【分析】（1）利用辅助角公式化简，求出最小正周期；（2）将θ代入可求出πsin 26θ⎛⎫+ ⎪⎝⎭，结合π26+θ的范围，求出πcos 26θ⎛⎫+ ⎪⎝⎭，因为ππ2266θθ=+-，由两角差的余弦公式求出结果.【小问1详解】()2π22cos 12cos 22sin 26f x x x x x x ⎛⎫=+-=+=+ ⎪⎝⎭，所以()f x 的最小正周期2ππ2T ==【小问2详解】()π82sin 265f θθ⎛⎫=+=- ⎪⎝⎭，所以π4sin 265θ⎛⎫+=- ⎪⎝⎭，因为3π,π4θ⎛⎫∈⎪⎝⎭，1π25π3663π,θ⎛⎫∈ ⎪⎝⎭+，所以π3cos 265θ⎛⎫+== ⎪⎝⎭，所以ππππππcos 2cos 2cos 2cos sin 2sin 666666θθθθ⎛⎫⎛⎫⎛⎫=+-=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭3414525210-⎛⎫=⨯+-⨯=⎪⎝⎭.17.如图，在ABC 中，6AB =，60ABC ∠=︒，D ，E 分别在边AB ，AC 上，且满足2AD DB = ，3CE EA =，F 为BC 中点.（1）若DE AB AC λμ=+，求实数λ，μ的值；（2）若8AF DE ⋅=-，求边BC 的长.【答案】（1）23λ=-，14μ=.（2）8【解析】【分析】（1）根据向量的线性运算以及平面向量的基本定理求得正确答案.（2）利用转化法化简8AF DE ⋅=-，从而求得BC 的长.【小问1详解】∵2AD DB = ，3CE EA= ，∴23AD AB = ，14AE AC = ∴1243DE AE AD AC AB =-=- ，∴23λ=-，14μ=.【小问2详解】12AF BF BA BC BA =-=- ，()1212154343412DE AC AB BC BA BA BC BA =-=-+=+ ，22115115241282412AF DE BC BA BC BA BC BC BA BA ⎛⎫⎛⎫⋅=-⋅+=-⋅- ⎪ ⎪⎝⎭⎝⎭设BC a = ，∵6AB = ，60ABC ∠=︒，221115668824212AF DE a a ⋅=-⨯⨯-⨯=- ，即2560a a --=，解得7a =-（舍）或8a =，∴BC 长为8.18.设(,)P x y 是角θ的终边上任意一点，其中0x ≠，0y ≠，并记r =cot x y θ=，sec r xθ=，csc r y θ=．（Ⅰ）求证222222sin cos tan cot sec +csc θθθθθθ+--+是一个定值，并求出这个定值；（Ⅱ）求函数()sin cos tan cot sec +csc f θθθθθθθ=++++的最小值．【答案】（Ⅰ）定值为3；（Ⅱ）min ()1f θ=-；【解析】【分析】（Ⅰ）由题可知，分别将6个三角函数分别代入，进行简单的化简，即可得到定值3；(Ⅱ)将()f x 中的未知量均用sin ,cos θθ来表示，得到1sin cos ()sin cos sin cos sin cos g θθθθθθθθθ+=+++，运用换元法设sin cos t θθ+=，化简成2()111g t t θ=-++-，再利用对勾函数的性质即可得到最值．【详解】解：（Ⅰ）222222222222222222sin cos tan cot sec +csc =y x y x r r r x y r y xθθθθθθ+--++--++2222222221113x y r y r x r x y+--⇒++=++=；（Ⅱ）由条件，1cot tan x y θθ==，1sec cos x θ=，1csc sin θθ=令()sin cos tan cot sec +csc g θθθθθθθ=++++sin cos 11sin cos +cos sin cos sin θθθθθθθθ=++++1sin cos sin cos sin cos sin cos θθθθθθθθ+=+++，令sin cos t θθ+=，则sin cos =2sin()4t πθθθ=++[2,2]∈-，1t ≠±，且21sin cos 2t θθ-=，从而2222()11t g y t t t θ==++--22(1)1t t t +=+-221111t t t t =+=-++--，令1u t =-，则21y u u =++，[21,21]u ∈---，且0u ≠，2u ≠-．所以，(,122][322,)y ∈-∞-⋃++∞．从而()221f y θ=≥-，即min ()221f θ=-．19.已知函数()2000ππ2sin sin 2sin 266f x x x x C ωωω⎛⎫⎛⎫=+++-+ ⎪ ⎪⎝⎭⎝⎭（R C ∈）有最大值为2，且相邻的两条对称轴的距离为π2（1）求函数()f x 的解析式，并求其对称轴方程；（2）将()f t 向右平移π6个单位，再将横坐标伸长为原来的24π倍，再将纵坐标扩大为原来的25倍，再将其向上平移60个单位，得到()g t ，则可以用函数()sin()H g t A t B ωϕ==++模型来模拟某摩天轮的座舱距离地面高度H 随时间t （单位：分钟）变化的情况．已知该摩天轮有24个座舱，游客在座舱转到离地面最近的位置进仓，若甲、乙已经坐在a ，b 两个座舱里，且a ，b 中间隔了3个座舱，如图所示，在运行一周的过程中，求两人距离地面高度差h 关于时间t 的函数解析式，并求最大值．【答案】（1）()π2sin 26f x x ⎛⎫=- ⎪⎝⎭，ππ32k x =+，Z k ∈（2）ππ()50sin 126f x t ⎛⎫=-⎪⎝⎭，50【解析】【分析】（1）由二倍角公式与两角和与差的正弦公式化简得()0π2sin 216f x x C ω⎛⎫=-++ ⎪⎝⎭，再结合最值及周期即可得解析式；（2）由正弦型函数的平移变换与伸缩变换得变换后的解析式为ππ50sin 60122y t ⎛⎫=-+ ⎪⎝⎭，则ππ50sin 126h H H ⎛⎫=-==- ⎪⎝⎭甲乙，再求最值即可.【小问1详解】()00001cos 2π22sin 2cos 2cos 2126x f x x C x x C ωωωω-=⨯++=-++0π2sin 216x C ω⎛⎫=-++ ⎪⎝⎭，所以2121C C ++=⇒=-，因为相邻两条对称轴的距离为π2，所以半周期为ππ22T T =⇒=，故002ππ12=⇒=ωω，()π2sin 26f x x ⎛⎫=- ⎪⎝⎭令ππππ2π6232k x k x -=+⇒=+，Z k ∈【小问2详解】()f t 向右平移π6得到π2sin 22y t ⎛⎫=- ⎪⎝⎭，将横坐标伸长为原来的24π倍，得到ππ2sin 122y t ⎛⎫=- ⎪⎝⎭，将纵坐标扩大为原来的25倍，得到ππ50sin 122y t ⎛⎫=- ⎪⎝⎭，再将其向上平移60个单位，得到ππ50sin 60122y t ⎛⎫=-+ ⎪⎝⎭游客甲与游客乙中间隔了3个座舱，则相隔了2ππ4243⨯=，令ππ50sin 60122H t ⎛⎫=-+ ⎪⎝⎭甲，则π5π50sin 60126H t ⎛⎫=-+ ⎪⎝⎭乙，则πππ5π50sin sin 122126h H H t t ⎛⎫⎛⎫=-=--- ⎪ ⎪⎝⎭⎝⎭甲乙π1πcos 12212t t =-ππ50sin 126t ⎛⎫=- ⎪⎝⎭，π12ω=，24T =，024t ≤≤，故πππ11π61266t -≤-≤，当πππ1262t -=或3π82t ⇒=或20时，max 50h =。
2023-2024学年四川省成都市高一上册第一次月考数学模拟试题(含解析)
2023-2024学年四川省成都市高一上册第一次月考数学模拟试题一、单选题1．命题“x ∀∈R ，23230x x -->”的否定为（）A ．x ∀∈R ，23230x x --≤B ．x ∀∉R ，23230x x --≤C ．x ∃∈R ，23230x x --≤D ．x ∃∉R ，23230x x --≤【正确答案】C【分析】根据全称命题的否定选出答案即可.【详解】命题“x ∀∈R ，23230x x -->”的否定为x ∃∈R ，23230x x --≤故选：C2．集合{1,0,1,2,3}A =-，{0,2,4}B =，则图中阴影部分所表示的集合为（）A ．{0,2}B ．{1,1,3,4}-C ．{1,0,2,4}-D ．{1,0,1,2,3,4}-【正确答案】B【分析】求()()A B A B ð得解.【详解】解：图中阴影部分所表示的集合为()(){1,1,3,4}A B A B =- ð.故选：B3．若0a b >>，0c <，则有（）A ．a c b c ->-B ．b c a c+>+C ．ac bc>D ．a b c c>【正确答案】A【分析】利用不等式的性质直接判断即可．【详解】解：0a b >> ，a cbc ∴->-，a c b c +>+，所以A 选项正确，B 选项错误又0c < ，ac bc ∴<，a b c c<，所以C 选项，D 选项错误；故选：A.4．“10x ->”成立的一个必要不充分条件的是（）A ．1x >B ．2x >C ．3x <D ．0x >【正确答案】D【分析】根据充分必要条件的定义判断.【详解】因为101x x ->⇔>，所以A 为“10x ->”成立的充要条件；B 为“10x ->”成立的充分不必要条件；C 为“10x ->”成立的既不充分也不必要条件；D 为“10x ->”成立的必要不充分条件．故选：D5．若2x >，则函数42y x x =+-的最小值为（）A ．3B ．4C ．5D ．6【正确答案】D【分析】根据题意结合基本不等式运算求解.【详解】由题意可得：()442222y x x x x =+=-++--，∵2x >，则20x ->，故()422262y x x =-++≥+=-，当且仅当422x x -=-，即4x =时，等号成立.故选：D.6．不等式2110x x +-->的解集是（）A ．{2x x <-或}0x >B ．112x x ⎧⎫-<<⎨⎬⎩⎭C ．122x x x ⎧⎫<->-⎨⎬⎩⎭或D ．112x x x ⎧⎫<->⎨⎬⎩⎭或【正确答案】A【分析】分类讨论12x ≤-、112x -<<与1x ≥三种情况，将绝对值不等式转化一元一次不等式，解之即可.【详解】因为2110x x +-->，当12x ≤-时，210,10x x +≤-<，则不等式可化为()()2110x x -++->，解得<2x -，故<2x -；当112x -<<时，210,10x x +>-<，则不等式可化为()()2110x x ++->，解得0x >，故01x <<；当1x ≥时，210,10x x +>-≥，则不等式可化为()()2110x x +-->，解得2x >-，故1x ≥；综上：<2x -或0x >，即不等式2110x x +-->的解集为{2x x <-或}0x >.故选：A.7．已知函数()()2245413y k k x k x =+-+-+的图象都在x 轴的上方，求实数k 的取值范围为（）A ．{}119k k <<B ．{}119k k ≤<C ．{}119k k <≤D ．{}119k k ≤≤【正确答案】B【分析】分类讨论函数的平方项系数是否为零，根据常数函数、一次函数、二次函数的图象性质即可求出k 的取值范围.【详解】因为()()2245413y k k x k x =+-+-+的图象都在x 轴上方，①当2450k k +-=时，5k =-或1k =，当5k =-时，函数243y x =+为一次函数，不满足条件；当1k =时，函数3y =满足条件；故1k =；②当2450k k +-≠时，函数()()2245413y k k x k x =+-+-+为二次函数，则()()222450Δ16112450k k k k k ⎧+->⎪⎨=--+-<⎪⎩，解得119k <<；综上，119k ≤<，即实数k 的取值范围为{}119k k ≤<.故选：B.8．若关于x 的不等式()2330x m x m -++<的解集中恰有3个整数，则实数m 的取值范围为（）A ．(]6,7B ．[)1,0-C ．[)(]1,06,7-⋃D ．[]1,7-【正确答案】C【分析】由题设可得()()30x x m --<，讨论,3m 的大小关系求解集，并判断满足题设情况下m 的范围即可.【详解】不等式()2330x m x m -++<，即()()30x x m --<，当3m >时，不等式解集为()3,m ，此时要使解集中恰有3个整数，这3个整数只能是4，5，6，故67m <≤；当3m =时，不等式解集为∅，此时不符合题意；当3m <时，不等式解集为(),3m ，此时要使解集中恰有3个整数，这3个整数只能是0，1，2，故10m -≤<；故实数m 的取值范围为[)(]1,06,7-⋃．故选：C二、多选题9．已知集合{}2,3,4A =，集合{}1,2,3,4,5A B =U ，则集合B 可能为（）A ．{}1,2,5B ．{}2,3,5C ．{}0,1,5D ．{}1,2,3,4,5【正确答案】AD【分析】根据集合并集的概念可得选项．【详解】因为{}2,3,4A =，{}1,2,3,4,5A B =U ，所以集合B 可能为A 选项{}1,2,5，，D 选项{}1,2,3,4,5，而对于B 选项{}2,3,5，此时{}2,3,4,5A B ⋃=，不满足题意，对于C 选项{}0,1,5，此时{}01,2,3,4,5A B = ，，不满足题意，故选：AD ．本题考查并集的概念与运算，属于基础题．10．下列说法正确的是（）A ．“0xy >”是“0x y +>”的必要不充分条件B ．“22ac bc >”是“a b >”的充分不必要条件C ．命题“200R,10x x ∃∈+=”的的否定是“2R ,10x x ∀∈+≠”D ．“对任意一个无理数x ，2x 也是无理数”是真命题【正确答案】BC【分析】对于A ，举反例即可说明两者关系既不充分也不必要；对于B ，利用不等式的性质推导即可判断；对于C ，利用命题的否定即可判断；对于D ，举反例即可排除.【详解】对于A ，令1,1x y =-=-，则0xy >，但0x y +<，所以0xy >推不出0x y +>；令1,2x y =-=，则0x y +>，但0xy <，所以0x y +>推不出0xy >；综上：“0xy >”是“0x y +>”的既不充分也不必要条件，故A 错误；对于B ，当22ac bc >时，易知20c ≠，则20c >，故210c >，所以222211ac bc c c ⨯>⨯，即a b >，所以“22ac bc >”是“a b >”的充分条件；当a b >时，取0c =，则22ac bc =，即a b >推不出22ac bc >，所以“22ac bc >”是“a b >”的不必要条件；综上：“22ac bc >”是“a b >”的充分不必要条件，故B 正确；对于C ，特称命题的否定是全称命题，其步骤为：改量词，否结论；所以命题“200R,10x x ∃∈+=”的的否定是“2R ,10x x ∀∈+≠”，故C 正确；对于D ，取x 22x =，所以至少存在一个无理数x ，使得2x 不是无理数，故D 错误.故选：BC.11．已知关于x 的不等式20ax bx c ++>的解集为(1,3)-，则下列说法正确的是（）A ．0a >B ．0bx c ->的解集是32xx ⎧⎫>⎨⎩⎭∣C ．20cx ax b +->的解集是2|3x x ⎧<-⎨⎩或1}x >D ．a b c+<【正确答案】BCD【分析】由不等式的解集可得根与系数的关系，可将,b c 用a 表示，分别代入不等式求解即可．【详解】不等式20ax bx c ++>的解集(1,3)-，说明0133a b aca ⎧⎪<⎪⎪-=-+⎨⎪⎪=-⎪⎩，即023a b ac a <⎧⎪=-⎨⎪=-⎩0bx c ->即23230,,02ax a x cx ax b -+>∴>+->，即2320ax ax a -++>，即2320x x -->，解集是2|3x x ⎧<-⎨⎩或1}x >，=1x -属于2|3x x ⎧<-⎨⎩或1}x >，所以0c a b -->，即a b c+<故选：BCD12．早在公元前6世纪，毕达哥拉斯学派已经知道算术中项，几何中项以及调和中项，毕达哥拉斯哲学家阿契塔在《论音乐》中定义了上述三类中项，其中，算术中项，几何中项的定义与今天大致相同，而今我们称2a b+为正数a ，b为正数a ，b 的几何0,0)2a ba b +≤>>（叫做基本不等式，下列与基本不等式有关的命题中正确的是（）A ．若0,0,21a b a b >>+=，则1142a b+≥B ．若110,0,132a b a b a b >>+=++，则a b +的最小值为35+C ．若20,0,210a b b ab >>+-=，则2+a b的最小值为D ．若0,0,4a b a b >>+=，则2222+++a ba b 的最小值为2【正确答案】ABD【分析】对A ：根据21a b +=，由“1”的代换，利用基本不等式求解判断；对B ：令32a b ma b n+=⎧⎨+=⎩，得到111m n+=，由“1”的代换，利用基本不等式求解判断；对C ：由2210b ab +-=，得到212-=b a b ，利用基本不等式求解判断；对D ：令22a m b n +=⎧⎨+=⎩，得到8m n +=，由“1”的代换，利用基本不等式求解判断.【详解】对A ：因为0,0,21a b a b >>+=，所以()111122224222b a a b a b a b a b ⎛⎫+=++=++≥+= ⎪⎝⎭，当且仅当22b aa b=，即2b a =时，等号成立，A 正确；对B ：因为110,0,132a b a b a b>>+=++，令32a b m a b n +=⎧⎨+=⎩，则111m n +=，3525n m a m n b -⎧=⎪⎪⎨-⎪=⎪⎩，所以11111211(2)(2)33(355555n m a b m n m n m n m n ⎛⎛⎫⎛⎫+=+=++=++≥+=+ ⎪ ⎪⎝⎭⎝⎭⎝，当且仅当2n mm n=，即m =时，等号成立，B 正确；对C ：因为20,0,210a b b ab >>+-=，所以212-=b a b ，则221131112232222b b a b b b b b b -+⎛⎫+=+==+≥⨯ ⎪⎝⎭，当且仅当13b b =，即3b =时，等号成立，C 错误；D ．令22a m b n +=⎧⎨+=⎩，则2,482a m m n a b b n =-⎧+=++=⎨=-⎩，则2222(2)(2)44444422--+=+=+-++-=+++a b m n m n a b m n m n m n，而4411111()222222n m m n m n m n m n ⎛⎛⎫⎛⎫+=++=++≥+= ⎪ ⎪⎝⎭⎝⎭⎝，当且仅当n mm n=，即n m =时，等号成立，D 正确．故选：ABD.三、填空题13．不等式522x >+的解集为_________．【正确答案】122x x ⎧⎫-<<⎨⎬⎩⎭【分析】根据分式不等式运算求解.【详解】∵522x >+，则5122022xx x --=>++，等价于()()1220x x -+>，解得122x -<<，即不等式522x >+的解集为122x x ⎧⎫-<<⎨⎬⎩⎭.故答案为.122x x ⎧⎫-<<⎨⎬⎩⎭14．已知命题p ：x ∃∈R ，210x ax -+<，若命题p 是假命题，则实数a 的取值范围为_________．【正确答案】[]22-,【分析】对a 进行分类讨论，结合判别式求得a 的取值范围.【详解】若命题p 是假命题，则210x ax -+≥恒成立，则2Δ40a =-≤，解得22a -≤≤.故答案为.[]22-,15．运货卡车以每小时x 千米的速度匀速行驶130千米，按交通法规限制50100x ≤≤（单位：千米/时）．假设汽油的价格是每升6元，而汽车每小时耗油26360x ⎛⎫+ ⎪⎝⎭升，司机的工资是每小时24元．则这次行车的总费用最低为_________元．【正确答案】260【分析】先确定所用时间，再乘以每小时耗油与每小时工资的和得到总费用表达式，再利用基本不等式求最值即可得到结果.【详解】设所用时间为130()t h x=，则由题意知21301306624360x y x x ⎛⎫=⨯⨯++⨯ ⎪⎝⎭，[]50,100x ∈.所以这次行车总费用y 关于x 的表达式是7800136xy x =+，[]50,100x ∈7800132606x y x =+≥==，当且仅当7800136xx =，即60x =时等号成立.故当60x =千米/时，这次行车的总费用最低，最低费用的值为260元.故260.16．设函数()2f x x ax b =++(),a b R ∈，若关于x 的不等式()06f x x ≤≤-的解集为[]{}2,36⋃，则a b +=______【正确答案】9【分析】根据不等式的解集可得2,3,6应为不等式对应方程的根，故分析两个不等式对应方程的根，即可求解.【详解】由6x =满足不等式知0(6)0f ≤≤，即3660a b ++=，所以366b a =--，所以()22636(6)(6)0f x x ax b x ax a x x a =++=+--=-++≥，所以()0f x =的两根为6,6a --，而()6f x x ≤-可化为2(1)6(7)0x a x a ++-+≤，即(6)(7)0x x a -++≤，所以方程(6)(7)0x x a -++=的两根为6，7a --且76a a --<--，不等式()06f x x ≤≤-的解集为[]{}2,36⋃，可知7263a a --=⎧⎨--=⎩，解得9a =-，所以36618b a =--=，所以1899a b +=-=，故9关键点点睛：本题主要考查不等式与方程的关系，不等式解集的端点为对应方程的根，本题在理解2,3,6分别是(6)(6)0x x a -++=与(6)(7)0x x a -++=的根，而方程含有公共根6，所以必然2,3两根分别是7,6a a ----，即可求解,本题属于难题.四、解答题17．已知集合{}28120A x x x =-+=．(1)若集合B={a ，2a+2}，且A=B ，求a 的值；(2)若集合{}60C x ax =-=，且A C C ⋂=，求a 的取值．【正确答案】(1)2；(2)0a =或1a =或3a =．【分析】（1）求出{2A =，6}，解方程组2226a a =⎧⎨+=⎩或6222a a =⎧⎨+=⎩即得解；（2）由A C C ⋂=得C A ⊆，再利用集合子集的元素关系求解．【详解】（1）解：由28120x x -+=得2x =或6x =，{2A ∴=，6}，因为A B =，所以2226a a =⎧⎨+=⎩或6222a a =⎧⎨+=⎩，解得22a a =⎧⎨=⎩或60a a =⎧⎨=⎩，故2a =．（2）解：因为A C C ⋂=，所以C A ⊆．当C =∅时，0a =，满足题意；当{2}C =时，260a -=，解得3a =；当{6}C =时，660a -=，解得1a =．综上，a 的取值为0a =或1a =或3a =．18．设全集为R ，{|12}A x a x a =-<<，{|25}B x x =<≤．(1)若4a =，求A B ⋂，R ()A B ð；(2)请在①A B ⋂=∅，②A B B ⋃=，③A B B = 三个条件中，任选其中一个作为条件，并求在该条件下实数a 的取值范围．（若多个选择，只对第一个选择给分．）【正确答案】(1)A B ⋂{|35}x x =<≤；R ()A B ð{|35}x x x =≤或＞；(2)答案见解析【分析】（1）由已知，把4a =代入集合A ，然后根据集合A 、集合B 可以直接求解A B ⋂，然后利用A B ⋂再去求解R ()A B ð；（2）分别根据三个条件，找到集合A 、集合B 之间的关系，注意考虑空集的情况，可以列出关于参数a 的不等式，求解即可.【详解】（1）当4a =时，{|38}A x x =<<，而{|25}B x x =<≤，所以A B ⋂{|35}x x =<≤，R ()A B ð{|35}x x x =≤或＞；（2）若选①，因为{|12}A x a x a =-<<，{|25}B x x =<≤．当A B ⋂=∅时，1.当A =∅时，12a a -≥，即1a ≤-，此时满足A B ⋂=∅；2.当A ≠∅时，满足A B ⋂=∅，即需满足1222a a a -⎧⎨≤⎩＜或1215a a a -⎧⎨-⎩＜＞解得11a -≤＜或6a ＞综上所述：实数a 的取值范围为]()(16∞∞-⋃+，，.若选②，因为{|12}A x a x a =-<<，{|25}B x x =<≤．当A B B ⋃=时，1.当A =∅时，12a a -≥，即1a ≤-，此时满足A B B ⋃=；2.当A ≠∅时，满足A B B ⋃=，即需满足121225a a a a -⎧⎪-≥⎨⎪≤⎩＜，解得A =∅，综上所述，实数a 的取值范围为](1∞--，；若选③，因为{|12}A x a x a =-<<，{|25}B x x =<≤．当A B B = 时，需满足121225a a a a -⎧⎪-≤⎨⎪⎩＜＞，解得532a ≤＜.综上所述：实数a 的取值范围为]532⎛ ⎝.19．已知集合{}30,2111x A x B x m x m x ⎧⎫+=≤=-≤≤+⎨⎬-⎩⎭．(1)命题:p x A ∈，命题:q x B ∈，若p 是q 的必要不充分条件，求实数m 的取值范围．(2)命题“0:r x A ∃∈，使得0x B ∈”是真命题，求实数m 的取值范围．【正确答案】(1)10m -≤<或m>2；(2){}41m m -≤<．【分析】（1）先解分式不等式化简集合A ，再由条件得到集合B 是集合A 的真子集，从而分类讨论集合B 为空集与B 不为空集两种情况，利用数轴法即可得解；（2）先由条件得到B 为非空集合且A B ⋂≠∅，分别由B 为非空集合得到2m ≤，由A B ⋂≠∅得到41m -≤<或m>2，从而取交集即可得解.【详解】（1）因为由301x x +≤-得()()31010x x x ⎧+-≤⎨-≠⎩，解得31x -≤<，所以{}30311x A x x x x ⎧⎫+=≤=-≤<⎨⎬-⎩⎭，因为命题:p x A ∈，命题:q x B ∈，p 是q 的必要不充分条件，所以集合B 是集合A 的真子集，又{}211B x m x m =-≤≤+，当B 为空集时，121m m +<-，解得m>2，满足题意；当B 不是空集时，213112m m m -≥-⎧⎪+<⎨⎪≤⎩，解得10m -≤<，经检验，当10m -≤<时，满足题意；综上，m 的取值范围为10m -≤<或m>2；（2）因为命题“0:r x A ∃∈，使得0x B ∈”是真命题，所以B 为非空集合且A B ⋂≠∅，当B 为非空集合时，有121m m +≥-，则2m ≤，当A B ⋂=∅时，2112m m -≥⎧⎨≤⎩或132m m +<-⎧⎨≤⎩，解得12m ≤≤或4m <-，所以A B ⋂≠∅时，41m -≤<或m>2，所以B 为非空集合且A B ⋂≠∅时，41m -≤<，综上：m 的取值范围为：{}41m m -≤<．20．（1）已知0,0,0a b c d n >><<<，求证：22()()n n a c b d >--；（2）若实数x ，y 满足221x y xy ++=，求x y +的取值范围.【正确答案】（1）证明见解析；（2）33x x ⎧⎪-≤≤⎨⎬⎪⎪⎩⎭.【分析】（1）根据不等式的性质即得；（2）根据基本不等式结合条件可得22()12x y x y +⎛⎫+-≤ ⎪⎝⎭，进而即得.【详解】（1）因为0c d <<，所以0c d ->->，因为0a b >>，所以0a c b d ->->，所以22()()0a c b d ->->，所以222222()()0()()()()a c b d a c b d a c b d -->>----，所以22110()()b d a c >>--，因为0n <，所以22()()n n b d a c <--，即22()()n n a c b d >--；（2）∵2221()1x y xy xy x y ++=⇔=+-，又∵22x y xy +⎛⎫≤ ⎪⎝⎭，∴22()12x y x y +⎛⎫+-≤ ⎪⎝⎭，令x y t +=，则2244-≤t t ，∴t ≤33x y -≤+≤，当且仅当x y =时，取等号，∴x y +的取值范围是33x x ⎧⎪-≤≤⎨⎬⎪⎪⎩⎭.21．已知二次函数2y ax bx c =++的图象过点(0,0),(5,0)，且最小值为252-．(1)求函数的解析式；(2)当1t x t ≤≤+时，该函数的最小值为12-，求此时t 的值．【正确答案】(1)2021xy x -=(2)1或3【分析】（1）先根据题意设出二次函数的两点式形式，再由条件得到其顶点坐标，代入即可得解；（2）根据二次函数的图象性质，分类讨论32t ≤、3522t <<与52t ≥三种情况下2021x y x -=在[],1t t +的单调情况，从而得到关于t 的方程，解之即可.【详解】（1）由题意设函数的解析式为(5)(0)y ax x a =->，由已知可得二次函数的顶点坐标为525,22⎛⎫- ⎪⎝⎭，代入得2555222a ⎛⎫-=⨯⨯- ⎪⎝⎭，解得2a =，所以二次函数解析式为2(5)y x x =-，即2021x y x -=．（2）由（1）知22525102222y x x x ⎛⎫-=--⎪⎝⎭= ，则其图象的开口向上，对称轴为52x =，当512t +≤，即32t ≤时，2021x y x -=在[],1t t +上单调递减，所以当1x t =+时，2021x y x -=取得最小值，所以22(1)10(1)12t t +-+=-，解得1t =或2t =（舍去），所以1t =；当512t t <<+，即3522t <<时，2021x y x -=在对称轴52x =处取得最小值252-，不满足题意；当52t ≥时，2021x y x -=在[],1t t +上单调递增，所以当x t =时，2021x y x -=取得最小值，所以221012t t -=-，解得3t =或2t =（舍去）．综上所述：t 的值为1或3．22．已知函数()()()2111f x m x m x m =+--+-．(1)若不等式()1f x <的解集为R ，求m 的取值范围；(2)解关于x 的不等式()()1f x m x ≥+；(3)若不等式()0f x ≥对一切11,22x ⎡⎤∈-⎢⎥⎣⎦恒成立，求m 的取值范围．【正确答案】(1)m <(2)答案见解析；(3)1m ≥.【分析】（1）对二次项系数1m +进行分类讨论，结合二次函数的判别式即可容易求得结果；（2）()()()211210f x m x m x mx m ≥+⇔+-+-≥，对10m +=，10m +>与10+<m 分类讨论，可分别求得其解集；（3）()()()()222222211111011111x x x m x m x m m x x x x m x x x x ---++--+-≥⇔-+≥--+⇔≥=-+-+-+，通过分离常数与利用基本不等式结合已知即可求得m 的取值范围．【详解】（1）根据题意，①当10m +=，即1m =-时，()22f x x =-，不合题意；②当10m +≠，即1m ≠-时，()1f x <的解集为R ，即()()21120m x m x m +--+-<的解集为R ，()()()21014120m m m m +<⎧⎪∴⎨∆=--+-<⎪⎩，即213290m m m <-⎧⎨-->⎩，故1m <-时，13m -<或13m +>.故m <．（2）()()1f x m x ≥+，即()21210m x mx m +-+-≥，即()()()1110m x m x ⎡⎤+---≥⎣⎦，①当10m +=，即1m =-时，解集为{|1}x x ≥；②当10m +>，即1m >-时，()1101m x x m -⎛⎫--≥ ⎪+⎝⎭，121111m m m -=-<++ ，∴解集为1{|1m x x m -≤+或1}x ≥；③当10+<m ，即1m <-时，()1101m x x m -⎛⎫--≤ ⎪+⎝⎭，121111m m m -=->++ ，∴解集为1{|1}1m x x m -≤≤+．综上所述：当1m <-时，解集为1{|1}1m x x m -≤≤+；当1m =-时，解集为{|1}x x ≥；当1m >-时，解集为1{|1m x x m -≤+或1}x ≥.（3）()()21110m x m x m +--+-≥，即()2211m x x x x -+≥--+，210x x -+> 恒成立，()222211111x x x m x x x x ---+∴≥=-+-+-+，设1x t -=，则1322t ⎡⎤∈⎢⎣⎦，，1x t =-，()()222111111111x t t x x t t t t t t-∴===-+-+---++-，12t t+≥ ，当且仅当1t =时取等号，2111x x x -∴≤-+，当且仅当0x =时取等号，∴当0x =时，22max111x x x x ⎛⎫--+= ⎪-+⎝⎭，1m ∴≥．本题考查二次函数恒成立问题，以及含参二次函数不等式的求解，其中正确的分类讨论，是解决本题的关键，属综合困难题.。
四川省成都市青羊区石室中学2020届高三上学期4月月考数学(文)试题 Word版含解析
成都石室中学2019~2020学年度上期高2020届4月月考数学试卷（文科）一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{|(1)(2)0},{|0}=--≤=>M x x x N x x ，则（ ） A. N M ⊆B. M N ⊆C. M N ⋂=∅D.M N R =U【答案】B 【解析】 【分析】求解出集合M ，根据子集判定可得结果.【详解】由题意知：()(){}{}12012M x x x x x =--≤=≤≤，则M N ⊆ 本题正确选项：B【点睛】本题考查集合间的关系，属于基础题.2.已知i 为虚数单位，则232019i i i i ++++L 等于（ ） A. i B. 1 C. i - D. 1-【答案】D 【解析】 【分析】利用)ni n N *∈（的周期求解.【详解】由于234110i i i i i i +++=--+=， 且)ni n N *∈（的周期为4，2019=4504+3⋅， 所以原式=2311i i i i i ++=--=-. 故选：D【点睛】本题主要考查复数的计算和)ni n N *∈（的周期性，意在考查学生对这些知识的理解掌握水平和分析推理能力.3.已知命题p ：(),0x ∀∈-∞，22310x x -+>，命题q ：若0x ≥，则22310x x -+≤，则以下命题正确的为（ ）A. p 的否定为“[0,)x ∃∈+∞，22310x x -+≤”，q 的否命题为“若0x <，则22310x x -+>”B. p 的否定为“(,0)x ∃∈-∞，22310x x -+≤”，q 的否命题为“若0x <，则22310x x -+>”C. p 的否定为“[0,)x ∃∈+∞，22310x x -+≤”，q 的否命题为“若0x ≥，则22310x x -+>”D. p 的否定为“(,0)x ∃∈-∞，22310x x -+≤”，q 的否命题为“若0x ≥，则22310x x -+>”【答案】B 【解析】 【分析】根据命题的否定：全称变特称，只否结论；否命题：条件结论都要否。
四川省成都石室中学2017-2018学年高一4月月考数学试题 Word版含答案
成都石室中学高2020届2017～2018学年度下期4月月考数学试卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一个是符合题目要求的． 1.sin 20cos10cos160sin10︒︒-︒︒=（ ）A.12-B.12C.2.若sin cos αα+=，则sin 2α=（ ） A.257 B.51 C.51- D.257-3.若等差数列{}n a 的前n 项和为n S ，且满足525S =，则3a =（ ） A ．3 B ．5 C ．7 D ．84.设函数1()cos 2f x x x =，则下列结论错误的是（ ） A ．()f x 的一个周期为2π-B ．()y f x =的图象关于直线83x π=对称 C ．()f x π+的一个零点为6x π=D ．()f x 在(,)2ππ上单调递减5.已知角θ的顶点与原点重合，始边与x 轴的非负半轴重合，终边在直线2y x =-上，则23cos +sin 2θθ=（ ）A ．15-B ．15C ．75-D ．756.在ABC ∆中，若BA CA AB CB ⋅=⋅，则ABC ∆的形状为（ ）A ．等边三角形 B.等腰三角形 C.直角三角形 D.等腰直角三角形 7.已知等差数列{}n a 的前n 项和为n S ，55a =，515S =，则数列12n S ⎧⎫⎨⎬⎩⎭的前50项和为（ ） A.5051 B.4951 C.4950 D.51508.若θ是第二象限角，5tan +=312πθ⎛⎫- ⎪⎝⎭，则sin 2=6πθ⎛⎫+ ⎪⎝⎭（ ）A ．120169B ．119169C ．120169-D ．119169-9.设n S 为等比数列{}n a 的前n 项和，51S =，104S =，则2515S S -=（ ） A.36 B.90 C.108 D.11710.已知曲线1:sin C y x =，2:cos(2)6C y x π=-，则下面结论正确的是（ ）A ．把1C 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线2CB ．把1C 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π3个单位长度，得到曲线2CC ．把1C 上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移π6个单位长度，得到曲线2CD ．把1C 上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π3个单位长度，得到曲线2C11.已知ABC ∆的重心为点P 3sin sin 0A PA B PB C PC ⋅+⋅+⋅=，则角B 为（ ） A ．512π B ．3π C ．4π D ．6π12.设n S 为数列{}n a 的前n 项和，对任意的*n N ∈，都有212n n n a a a +++=，若()()37722018230a a ++++=，()3201220121201820150a a +++=，则2018S =（）A.3027-B.6054-C.2018D.4036二、填空题：本大题共4小题，每小题5分． 13.44sincos 88ππ+= _________.14.已知函数1()1f x x=-，数列{}n a 满足22a =，1()n n a f a +=，则2017a =_________.15.如图，一辆汽车在一条水平的公路上向正西行驶，到A 处时测得公路北侧一山顶D 在西偏北030的方向上，行驶300 m 后到达B 处，测得此山顶在西偏北075的方向上，仰角为030，则此山的高度CD ＝________m.16.在ABC ∆中，角,,A B C 所对的边分别为,,a b c ，若ABC ∆为锐角三角形，且满足22b a ac -=，则三、解答题：解答应写出文字说明，证明过程或演算步骤．17．（本小题10分）在等差数列{}n a 中，138a a +=，且4a 为2a 和9a 的等比中项，求数列{}n a 的首项、公差及前n 项和．18．（本小题12分）在ABC ∆中，角,,A B C 的对边分别为,,a b c ，且满足()cos 2cos 0++=b A c a B .（Ⅰ）求角B 的大小；（Ⅱ）若6=b ， ABC ∆ABC ∆的周长.19．（本小题12分）设()2sin cos cos 4f x x x x π⎛⎫=-+ ⎪⎝⎭.（Ⅰ）求函数()f x 的单调递增区间；（Ⅱ）在锐角ABC ∆中，角,,A B C 的对边分别为,,a b c ,若0,12A f a ⎛⎫== ⎪⎝⎭，求ABC ∆面积的最大值.20.（本小题12分）已知数列{}n a 是各项均为正数的等比数列，且122a a⋅=，3432a a ⋅=.（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）设数列{}n b *n N ∈），求数列{}n b 的前n 项和n T .21.（本小题12分）如图，在等腰直角三角形OPQ ∆中，090POQ ∠=，OP =点M 在线段PQ 上.（Ⅰ）若OM =PM 的长；（Ⅱ）若点N 在线段MQ 上，且030MON ∠=，问:当POM ∠取何值时，OMN ∆的面积最小？并求出面积的最小值.22.（本小题12分）已知数列{}n a 满足11a =，（Ⅰ）证明：数列1{1}na +为等比数列，并求数列{}n a 的通项公式；（Ⅱ）若数列{}n a 的前n 项和为n S ，证明：2n S <； （Ⅲ）若111n n na b n a =-++，求{}n b 的最大项.成都石室中学高2020届2017～2018学年度下期4月月考数学试卷 参考答案一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一个是符合题目要求的．二、填空题：本大题共4小题，每小题5分． 13.34 14. 12 15. 50 6 16. 1⎛ ⎝⎭ 三、解答题：解答应写出文字说明，证明过程或演算步骤． 17．（本小题10分）【解析】设等差数列{}n a 的公差为d ，前n 项和为n S ，由已知可得：11211122840(3)()(8)a d a d a d a d a d +==⎧⎧⇒⎨⎨=+=++⎩⎩或113a d =⎧⎨=⎩， 即数列{}n a 的首项是4，公差为0或首项是1，公差为3.……………………………6分所以数列{}n a 的前n 项和为4n S n =或232n n nS -=．……………………………10分18．（本小题12分）【解析】（Ⅰ）()cos 2cos 0++=b A c a B ，由正弦定理可得： ()sin cos 2sin sin cos B A C A B =--，∴()sin 2sin cos sin A B C B C +=-=.……………………………4分 又角C 为ΔABC 内角， sin 0C >，∴1cos 2B =- 又()0,πB ∈，∴2π3B =……………………………6分 ，得12=ac ……………………………8分 又()222236=++=+-=b a c ac a c ac ，∴10分所以ΔABC 12分19．（本小题12分） 【解析】（Ⅰ）由题意知()1cos 2sin 2222x x f x π⎛⎫++ ⎪⎝⎭=-sin 21sin 21sin 2222x x x -=-=- ……………………………3分由222,22k x k k Z ππππ-+≤≤+∈ 可得,44k x k k Z ππππ-+≤≤+∈所以函数()f x 的单调递增区间是(),44k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦. ………………5分（Ⅱ）由1sin 0,22A f A ⎛⎫=-= ⎪⎝⎭得1sin 2A =由题意知A 为锐角，所以cos 2A = 由余弦定理：2222cos a b c bc A =+-可得：2212b c bc =+≥ 即：2bc ≤ 当且仅当b c =时等号成立.因此12sin 24bc A +≤ 所以ABC ∆面积的最大值为24.……………12分 20.（本小题12分） 【解析】 （Ⅰ）设等比数列{}n a 的公比为q ，由已知得()4132432a a a a q ⋅=⋅=又∵10,0a q >>，解得112a q =⎧⎨=⎩ ∴12n na -=……………………3分（Ⅱ）由题意可得12211321n nb b b n +++=--① ()11122121323n n b b b n n --+++=-≥-②相减得1221n nb n -=-， ()1212n nb n -∴=-，（） ……………………6分当1n =时， 11b =，符合上式， ()1212n n b n -∴=- ……………………7分设()12113252212n nT n -=+⋅+⋅++-⋅则()()2312123252232212n n nT n n -=⋅+⋅+⋅++-⋅+-⋅，两式相减： ()()2112222212n n n T n --=+++--⋅ ∴()2323nn T n =-+．……12分21.（本小题12分）【解析】（Ⅰ）在OMP ∆中,45OPM ∠=︒,OM=OP =,由余弦定理得,2222cos 45OM OP MP OP MP =+-⨯⨯⨯︒,得2430MP MP -+=, 解得1MP =或3MP =. ……………………4分 （Ⅱ）设POM α∠=,060α︒≤≤︒, 在OMP ∆中,由正弦定理,得sin sin OM OPOPM OMP=∠∠, 所以()sin 45sin 45OP OM α︒=︒+,同理()sin 45sin 75OP ON α︒=︒+ ……………………6分故1sin 2OMNS OM ON MON ∆=⨯⨯⨯∠ ()()221sin 454sin 45sin 75OP αα︒=⨯︒+︒+ ()()1sin 45sin 4530αα=︒+︒++︒=====……………………10分因为060α︒≤≤︒,30230150α︒≤+︒≤︒,所以当30α=︒时,()sin230α+︒的最大值为1，此时OMN ∆的面积取到最小值.即30POM ∠=︒时,OMN ∆的面积的最小值为8-. …………………………………………12分22.（本小题12分） 【解析】（Ⅰ）由题意，1121n n a a +=+ 1111112(1),120n na a a +∴+=++=≠，∴1{1}na +是以2为首项，2为公比的等比数列. ……………………………………3分（Ⅱ）*11111()212112n n n n a n N -+=≤=∈--+， 111(1())1111212(1())21242212n n n n S --∴≤++++==-<-.……………………………………7分（Ⅲ） 1111111,111222n n n n n n a b b n a n n ++=-=-=-++++, 1111(1)(2)2n n n b b n n ++-=-++,易知，213243540,0,0,0b b b b b b b b ->->->-<，当4n ≥时11111(1)(2)(1)(1)(2)(1)(2)22n n n n n n n n ++++-=-++++记1(1)(2),2n n n n c +++=则12(2)(3)2n n n n c ++++= 1212(2)(3)(1)(2)(2)(1)0222n n n n n n n n n n n c c +++++++++--=-=<，∴当4n ≥时，{}n c 单减，即4301513216n c c ≤==<， 即当4n ≥时111110,(1)(2)2n n n n n b b b b n n +++-=-<<++，∴当4n =时，{}n b 最大，最大值411.80b =……………………………………12分。
四川省成都市石室中学(文庙校区)高一数学理测试题含解析
四川省成都市石室中学(文庙校区)高一数学理测试题含解析一、选择题：本大题共10小题，每小题5分，共50分。
在每小题给出的四个选项中，只有是一个符合题目要求的1. 已知六边形是边长为1的正六边形，则的值为A．B．C．D．参考答案：D2. 某教育集团对公司图书质量问卷调查，实行的是百分制，发出问卷后共收回1000份，右图是统计1000份问卷的分数的程序框图，若输出的结果是800，则这次问卷调查分数不低于90分的频率是 ( )A．0.20 B．0.30 C．0.80 D．0.70参考答案：C3. 函数y=|x﹣1|的图象为( )A．B．C．D．参考答案：A【考点】函数的图象．【专题】函数的性质及应用．【分析】由于x﹣1的符号不能确定，故应分x≥1与x＜1两种情况求出函数的解析式，取特殊点验证函数图象．【解答】解：当x≥1时，y=x﹣1，为递增的射线；当x＜1时，y=﹣x+1，为递减的射线；又f（1）=|1﹣1|=0，故函数的图象过（1，0）只有A符合，故选：A【点评】本题考查的是一次函数的图象，在解答此题时要注意分类讨论．4. 给出下列命题：①正切函数图象的对称中心是唯一的；②若函数f(x)的图像关于直线对称，则这样的函数f(x)是不唯一的；③若x1，x2是第一象限角，且x1＞x2，则；④若f(x)是定义在R上的奇函数，它的最小正周期是T，则．（A）1 （B）2 （C）3 （D）4参考答案：B5. 函数的值域为（）A． B． C． D．参考答案：B解析：,是的减函数，当6. 已知f（x）=x5﹣ax3+bx+2，且f（﹣5）=3，则f（5）+f（﹣5）的值为( ) A．0 B．4 C．6 D．1参考答案：B考点：函数奇偶性的性质．专题：计算题；转化思想；函数的性质及应用．分析：根据已知中f（x）=x5﹣ax3+bx+2，可得f（x）+f（﹣x）=4，解得答案．解答：解：∵f（x）=x5﹣ax3+bx+2，∴f（﹣x）=﹣（x5﹣ax3+bx）+2，∴f（x）+f（﹣x）=4，故选：B点评：本题考查的知识点是函数奇偶性的性质，熟练掌握函数奇偶性是性质是解答的关键7. 已知集合，，则=( )A．{2,4} B．{1,2,3,4,6} C．{3} D．{4,6}参考答案：A8. 为了得到函数的图象，只需把函数的图象()A、向左平移B、向左平移C、向右平移D、向右平移参考答案：B略9. （5分）下列命题正确的是（）A．有两个面平行，其余各面都是四边形的几何体叫棱柱B．有两个面平行，其余各面都是平行四边形的几何体叫棱柱C．有两个面平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱D．用一个平面去截棱锥，截面与底面之间的部分组成的几何体叫棱台参考答案：C考点：棱柱的结构特征．专题：阅读型．分析：对于A，B，C，只须根据棱柱的定义：有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的多面体叫做棱柱进行判断即可．对于D，则须根据棱锥的概念：棱锥的底面和平行于底面的一个截面间的部分，叫做棱台．进行判断．解答：对于A，它的每相邻两个四边形的公共边不一定互相平行，故错；对于B，也是它的每相邻两个四边形的公共边不一定互相平行，故错；对于C，它符合棱柱的定义，故对；对于D，它的截面与底面不一定互相平行，故错；故选C．点评：本题主要考查了棱柱、棱台的结构特征，由一个平面多边形沿某一方向平移形成的空间几何体叫做棱柱．当棱柱的一个底面收缩为一点时，得到的空间几何体叫做棱锥．棱锥被平行与底面的一个平面所截后，截面和底面之间的部分叫做棱台．10. 已知函数f（x）=m+log2x2的定义域是[1，2]，且f（x）≤4，则实数m的取值范围是（）A．（﹣∞，﹣2] B．（﹣∞，2] C．[2，+∞） D．（2，+∞）参考答案：B【考点】对数函数的单调性与特殊点；函数的定义域及其求法．【分析】先根据指数函数的单调性求出函数在[1，2]上的值域，然后根据f（x）≤4建立关于m 的不等式，解之即可．【解答】解：∵函数f（x）=m+log2x2在[1，2]单调递增，∴函数f（x）的值域为[m，2+m]，∵f（x）≤4，∴2+m≤4，解得m≤2，∴实数m的取值范围是（﹣∞，2]．故选：B．二、填空题:本大题共7小题,每小题4分,共28分11. 等边△ABC的边长为2，则___________;参考答案：2略12. 当a＞0且a≠1时，函数f (x)=a x－2－3必过定点 .参考答案：(2，－2).13. （4分）圆心是点（1，﹣2），且与直线2x+y﹣1=0相切的圆的方程是参考答案：．考点：圆的切线方程．专题：直线与圆．分析：直线与圆相切，则圆心到直线的距离即为圆的半径．利用点到直线的距离公式求出半径即可得到圆的方程．解答：解；圆心（1，﹣2）到直线2x+y﹣1=0的距离为=．∵圆与直线直线2x+y﹣1=0相切，∴半径r=．∴所求圆的方程为．故答案为：．点评：本题考查直线与圆相切的性质，圆的标准方程等知识的综合应用，属于基础题．14. 经过两点的直线倾斜角为▲ ．参考答案：略15. 设f（x）=，则f（f（2））的值为．参考答案：1【考点】对数的运算性质；函数的值．【专题】计算题；函数思想；综合法；函数的性质及应用．【分析】先求出f（2）的值，从而求出f（f（2））的值即可．【解答】解：f（2）==1，∴f（f（2））=f（1）=e1﹣1=1，故答案为：1．【点评】本题考察了求函数值问题．考察对数函数、指数函数的性质，是一道基础题．16. 在数列{a n}中，a1=1，a n=a n﹣1（n≥2，n∈N*），则数列{}的前n项和T n= ．参考答案：【考点】8E ：数列的求和．【分析】由条件可得=?，令b n =，可得b n =?b n ﹣1，由b n =b 1??…?，求得b n ，进而得到a n ，可得==2（﹣），再由数列的求和方法：裂项相消求和，即可得到所求和．【解答】解：在数列{a n }中，a 1=1，a n =a n ﹣1（n≥2，n∈N *），可得=?，令b n =，可得b n =?b n ﹣1，由b n =b 1??…?=1??…?=，可得a n =，即有==2（﹣），则前n 项和T n =2（1﹣+﹣+…+﹣）=2（1﹣）=．故答案为：．17. 设使不等式成立的的集合是参考答案：三、 解答题：本大题共5小题，共72分。
四川省成都市石室中学2023-2024学年高一下学期4月月考数学试卷
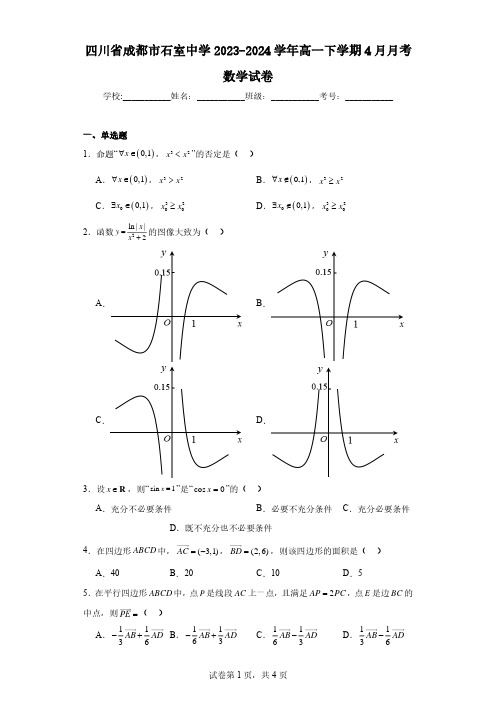
四川省成都市石室中学2023-2024学年高一下学期4月月考数学试卷学校:___________姓名：___________班级：___________考号：___________一、单选题1．命题“()0,1x ∀∈，32x x <”的否定是（ ） A ．()0,1x ∀∈，32x x >B ．()0,1x ∀∉，32x x ≥C ．()00,1x ∃∈，3200x x ≥D ．()00,1x ∃∉，3200x x ≥2．函数2ln ||2x y x =+的图像大致为（ ） A ． B ．C ．D ．3．设x ∈R ，则“sin 1x =”是“cos 0x =”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件D ．既不充分也不必要条件4．在四边形ABCD 中，(3,1)AC =−，(2,6)BD =，则该四边形的面积是（ ） A ．40B ．20C ．10D ．55．在平行四边形ABCD 中，点P 是线段AC 上一点，且满足2=AP PC ，点E 是边BC 的中点，则PE =（ ）A ．1136AB AD −+ B ．1163−+AB ADC ．1163AB AD −D ．1136AB AD −6．已知函数()cos2f x x x =−，将函数()f x 的图象向右平移m (0m >)个单位后与函数()g x =2cos2x 的图象重合，则m 的最小值为（ ） A ．π3B ．π12 C ．π4D ．π67．已知△ABC 的内角,,A B C 的对边分别为,,a b c ，且222b c a bc +−=−，若内角A 的平分线交BC 于点D ，2AD =，3b =，则c =（ ） A ．3B ．4C ．6D ．88．在边长为2的正三角形ABC 中，BM tBC =，t CN CA =，01t ≤≤，当MA NM ⋅取得最大值时，t =（ ） A ．13B ．16C ．12D ．14二、多选题9．下列函数中最小值为2的是（ ） A ．223y x x =++ B ．122x x y −=+ C ．1sin sin y x x=+D ．1ln ln y x x=+10．已知O 为坐标原点，点()1cos ,sin P αα，()2cos ,sin P ββ−，()()()3cos ,sin P αβαβ++，()1,0A ，则（ ）A ．12OP OP =B ．12AP AP =C ．312OA OP OP OP ⋅=⋅D ．123OA OP OP OP ⋅=⋅11．已知函数()sin 2cos 2f x x x =+，则（ ）A ．函数()f x 的最小正周期为πB ．函数()f x 在ππ,28⎡⎤−−⎢⎥⎣⎦上单调递增C ．对任意x ∈R ，函数()f x 满足()()πf x f x +=−D ．函数()f x 的最小值为12．若ABC 的内角,,A B C 所对的边分别为,,a b c ，且满足24sin22A Ba ab +=−，则（ ） A ．角C 可以为锐角 B ．tan 3tan C A =C ．2222a b c +=D ．角B 的最大值为π6三、填空题13．已知向量,a b 是两个不共线的向量，且4a mb −+与()38m a b −−共线，则实数m 的值为 ．14．已知函数()()()2cos 0,πf x x ωϕωϕ=+><的部分图象如图所示，则()0f = .15．已知ππsin cos 3cos sin 1212αα=−且π7sin cos π01212λαα⎛⎫⎛⎫−−+= ⎪ ⎪⎝⎭⎝⎭，则实数λ的值为 .16．在锐角ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，22a c a b −=−且1b =，则ABC 面积的取值范围为 .四、解答题17．设集合{}2|3100A x x x =−−<，{}|221,B x a x a a =−≤≤+∈R ，{}2|9C x x =<.(1)设全集U =R ，求()U A C ð； (2)若A B A ⋃=，求实数a 的取值范围．18．已知向量,a b 满足22a b ==，且()(2)2a b a b +⋅−=. (1)求向量a 在向量b 方向上的投影向量； (2)求cos 2,a b b +的值.19．某海域的东西方向上分别有A ，B 两个观测点（如图），它们相距一艘轮船在D 点发出求救信号，经探测得知D 点位于A 点北偏东45，B 点北偏西75，这时位于B 点南偏西45且与B 相距80海里的C 点有一救援船，其航行速度为35海里/小时．(1)求B 点到D 点的距离BD ；(2)若命令C 处的救援船立即前往D 点营救，求该救援船到达D 点需要的时间．20．已知函数()()3sin 02f x x x ωωω=>的图象的相邻两条对称轴的间距为π2，将函数()f x 的图象上的每一个点的纵坐标保持不变，横坐标变为原来的2倍，得到函数()g x 的图象.(1)求函数()g x 的单调递增区间；(2)若()3α=g ，求π6f α⎛⎫+ ⎪⎝⎭的值.21．记ABC 的内角A ，B ，C 的对边分别为a ，b ，c .已知2b ac =，点D 在边AC 上，且sin sin BD ABC a C ∠=.(1)证明：BD (2)若23AD AC =，求tan ABC ∠的值. 22．已知定义域为R 的函数()h x 满足：对于任意的x ∈R ，都有()()()2π2πh x h x h =++，则称函数()h x 具有性质P .(1)判断函数()2f x x =，()cos g x x =是否具有性质P ，并说明理由；(2)已知函数()()35πsin ,222f x x ωϕωϕ⎛⎫=+<<< ⎪⎝⎭，判断是否存在,ωϕ，使函数()f x 具有性质P ？若存在，请求出,ωϕ的值；若不存在，请说明理由.。
四川省成都石室中学2020学年度高三数学月考试卷 人教版
四川省成都石室中学2020学年度高三数学月考试卷一、选择题：只有唯一正确答案，每小题5分，共60分。
1．设集合M = {a ，b ，c }，N = {0，1}，映射f ：M →N 满足f (a ) + f (b ) = f (c )，则映射f ： M →N 的个数为 （ ）A ．1B ．2C ．3D ．4 2．函数)1(21)(x x x f --=的最大值是 （ ）A ．49B ．94C ．47D ．743．（理科）函数x x g x f )21()()(=与的图象关于y = x 对称，则f (4x －x 2)的单调递增区间为（ ）A ．（－∞，2）B ．（0，2）C ．（2，4）D ．（2，+∞）（文科）为得到函数100lg xy =的图象，可以把函数y = lg x 的图象 （ ）A ．向上平移两个单位B ．按向量)2,0(-=平移C ．向左平移两个单位D ．按向量)0,2(=a 平移4．如果2log |3|log 2121ππ≥-x ，那么sin x 的取值范围是 （ ）A ．]21,21[-B ．]1,21[-C ．]1,21()21,21[Y -D ．]1,23()23,21[Y -5．已知yxy x y x y x 则,lg lg 2lg )2lg()lg(++=++-的值为 （ ）A ．－1B ．2C ．21 D ．－1或26．设全集U 是实数集R ，}11|{},4|{2≥-=>=x x N x x M ，则图中阴影部分所表示的集合是（ ）A ．}12|{<≤-x x xB ．}22|{≤≤-x x xC ．}21|{≤<x xD ．}2|{<x x7．若方程0122=--x ax 在区间（0，1）内恰有一解，则实数a 的取值范围是 （ ）A ．a <－1B ．a >1C ．－1< a < 1D ．0≤a ＜18．（理科）若函数)0,(2)1(log )(223-∞++++=在x x b ax x f 上有最小值－5，（a ，b 为常数），则函数),0()(+∞在x f 上（ ）A ．有最大值5B ．有最小值5C ．有最大值3D ．有最大值9（文科）若函数f (x )的图象关于直线x =1对称，且当x >1时，x x x f -=32)(，则当x <1时，f (x )的表达式为（ ）A ．2)2(2)(3-+-=x x x fB ．x x x f --=3)2(2)(C ．1)1(2)(3-+-=x x x fD ．x x x f +=32)(9．定义在R 上的函数y = f (x + 1)的图象如图所示，且在定义域上， 是减函数，给出如下命题：①f (0) =1；②f (－1) =1；③若x >0， 则f (x ) <0；④若x <0，则f (x ) >0，其中正确的是 （ ）A ．②③B ．①④C ．②④D ．①③10．（理科）已知定义在R 上的偶函数f (x )满足)3()3(x f x f -=+，且当]4,3[∈x 时，x x f )21()(=，求当]2,3[--∈x 时，则函数f (x )的表达式为（ ）A ．6)21()(+=x x fB ．6)21()(-=x x f C ．x x f )21()(=D ．62)(+=x x f（文科）设f (x )是定义在实数集R 上以2为周期的奇函数，已知x x f x )21()(,)1,0(=∈时，则)12(log 2f 的值为（ ）A ．43 B ．43-C ．34-D ．34 11．设偶函数)0,(||log )(-∞-=在b x x f a 上递增，则)2()1(++b f a f 与的大小关系是（ ） A ．)2()1(+≥+b f a f B ．)2()1(+≤+b f a fC ．)2()1(+<+b f a fD ．)2()1(+>+b f a f12．（理科）设定义域为R 的函数⎪⎩⎪⎨⎧=≠-=1,11,|1|1)(x x x x f ，若关于x 的方程0)()(2=++c x bf x f 有三个不同的实数解x 1、x 2、x 3，则232221x x x ++等于（ ）A ．5B ．2222bb + C ．13 D ．2223c c +（文科）在正实数集上定义一种运算*，规则是：当a ≥b 时，a *b =b 3，当a ＜b 时，a *b =b 2，根据这一规则，方程a *b = b 3的解为 （ ）A ．3B ．33C ．3或33D ．3或9二、填空题：每小题4分，共16分。
四川省成都市石室中学2015-2016学年高一4月月考数学试题(PDF版)
C．锐角三角形 轴交于
D．等腰三角形 的直线与函数的图象
x
4
，
的图象与 ( )
点，过点
D.
4
12.在△ABC 中，E , F 分别是 AC , AB 的中点，且 3 AB 2 AC ，若 最小值为（ ） A．
BE t 恒成立，则 t 的 CF
3 4
B．
4 5
C．
6 7
D．
7 8
二、填空题（本大题共 4 个小题，每小题 5 分，共 20 分） 13.等边△ABC 的边长为 2，则 AB 在 BC 方向上的投影为 14.在△ ABC 中，已知 BC 8,
3 8
y f ( x) 的最大值 g (m) ，并解不等式 g (m) 5 m 1 .
第 4 页/共 4 页
命题、审题人：寇明珍、唐永明、漆星星
1
的值为（ ）
C．
13 24
D．
13 5
2 k ,
A．
1 1 a b 4 4
B．
1 1 a b 2 2
C． a
1 b 2
D．
3 3 a b 4 4
）
1 cos 50 2 tan 13 1 3 sin 6 ， b 7.设 a cos 6 ，c ，则有（ 2 2 2 1 tan 2 13
A、 c b a B、 a c b C、 a b c D、 b c a
第 1 页/共 4 页 命题、审题人：寇明珍、唐永明、漆星星
8．已知 | a | 2 | b | 0 ,且关于 x 的方程 x 2 | a | x a b 0 有实根,则 a 与 b 的夹角的取值 范围是( A.[0, )
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
四川省成都石室中学2017-2018学年高一数学4月月考试题一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一个是符合题目要求的．1.sin 20cos10cos160sin10︒︒-︒︒=（ ）A.12-B.12C.2.若sin cos αα+=sin2α=（ ） A.257 B.51 C.51- D.257-3.若等差数列{}n a 的前n 项和为n S ，且满足525S =，则3a =（ ） A ．3 B ．5 C ．7 D ．84.设函数1()cos 2f x x x =-，则下列结论错误的是（ ） A ．()f x 的一个周期为2π-B ．()y f x =的图象关于直线83x π=对称 C ．()f x π+的一个零点为6x π=D ．()f x 在(,)2ππ上单调递减5.已知角θ的顶点与原点重合，始边与x 轴的非负半轴重合，终边在直线2y x =-上，则23cos +sin 2θθ=（ ）A ．15-B ．15C ．75-D ．756.在ABC ∆中，若BA CA AB CB ⋅=⋅，则ABC ∆的形状为（ ）A ．等边三角形 B.等腰三角形 C.直角三角形 D.等腰直角三角形 7.已知等差数列{}n a 的前n 项和为n S ，55a =，515S =，则数列12n S ⎧⎫⎨⎬⎩⎭的前50项和为（ ） A.5051 B.4951 C.4950 D.51508.若θ是第二象限角，5tan +=312πθ⎛⎫- ⎪⎝⎭，则sin 2=6πθ⎛⎫+ ⎪⎝⎭（ ）A ．120169B ．119169C ．120169-D ．119169-9.设n S 为等比数列{}n a 的前n 项和，51S =，104S =，则2515S S -=（ ） A.36 B.90 C.108 D.117 10.已知曲线1:sin C y x =，2:cos(2)6C y x π=-，则下面结论正确的是（ ）A ．把1C 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线2CB ．把1C 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π3个单位长度，得到曲线2CC ．把1C 上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移π6个单位长度，得到曲线2CD ．把1C 上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π3个单位长度，得到曲线2C11.已知ABC ∆的重心为点P ，若3sin sin 0A PA B PB C PC ⋅+⋅+⋅=，则角B 为（ ） A ．512π B ．3π C ．4π D ．6π12.设n S 为数列{}n a 的前n 项和，对任意的*n N ∈，都有212n n n a a a +++=，若()()37722018230a a ++++=，()3201220121201820150a a +++=，则2018S =（）A.3027-B.6054-C.2018D.4036二、填空题：本大题共4小题，每小题5分． 13.44sin cos 88ππ+= _________.14.已知函数1()1f x x=-，数列{}n a 满足22a =，1()n n a f a +=，则2017a =_________.15.如图，一辆汽车在一条水平的公路上向正西行驶，到A 处时测得公路北侧一山顶D 在西偏北030的方向上，行驶300 m 后到达B 处，测得此山顶在西偏北075的方向上，仰角为030，则此山的高度CD ＝________m.16.在ABC ∆中，角,,A B C 所对的边分别为,,a b c ，若ABC ∆为锐角三角形，且满足三、解答题：解答应写出文字说明，证明过程或演算步骤．17．（本小题10分）在等差数列{}n a 中，138a a +=，且4a 为2a 和9a 的等比中项，求数列{}n a 的首项、公差及前n 项和．18．（本小题12分）在ABC ∆中，角,,A B C 的对边分别为,,a b c ，且满足()cos 2cos 0++=b A c a B .（Ⅰ）求角B 的大小；（Ⅱ）若6=b ， ABC ∆ABC ∆的周长.19．（本小题12分）设()2sin cos cos 4f x x x x π⎛⎫=-+⎪⎝⎭. （Ⅰ）求函数()f x 的单调递增区间；（Ⅱ）在锐角ABC ∆中，角,,A B C 的对边分别为,,a b c ,若0,12A f a ⎛⎫== ⎪⎝⎭，求ABC ∆面积的最大值.20.（本小题12分）已知数列{}n a 是各项均为正数的等比数列，且122a a⋅=，3432a a ⋅=.（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）设数列{}n b *n N ∈），求数列{}n b 的前n 项和n T .21.（本小题12分）如图，在等腰直角三角形OPQ ∆中，090POQ ∠=，OP =，点M在线段PQ 上.（Ⅰ）若OM =PM 的长；（Ⅱ）若点N 在线段MQ 上，且030MON ∠=，问:当POM ∠取何值时，OMN ∆的面积最小？并求出面积的最小值.22.（本小题12分）已知数列{}n a 满足11a =，（Ⅰ）证明：数列1{1}na +为等比数列，并求数列{}n a 的通项公式；（Ⅱ）若数列{}n a 的前n 项和为n S ，证明：2n S <； （Ⅲ）若111n n na b n a =-++，求{}n b 的最大项.参考答案一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一个是符合题目要求的．二、填空题：本大题共4小题，每小题5分． 13.34 14. 12 15. 50 6 16. 1⎛ ⎝⎭ 三、解答题：解答应写出文字说明，证明过程或演算步骤． 17．（本小题10分）【解析】设等差数列{}n a 的公差为d ，前n 项和为n S ，由已知可得：11211122840(3)()(8)a d a d a d a d a d +==⎧⎧⇒⎨⎨=+=++⎩⎩或113a d =⎧⎨=⎩， 即数列{}n a 的首项是4，公差为0或首项是1，公差为3.……………………………6分所以数列{}n a 的前n 项和为4n S n =或232n n nS -=．……………………………10分18．（本小题12分）【解析】（Ⅰ）()cos 2cos 0++=b A c a B ，由正弦定理可得： ()sin cos 2sin sin cos B A C A B =--，∴()sin 2sin cos sin A B C B C +=-=.……………………………4分 又角C 为ΔABC 内角， sin 0C >，∴1cos 2B =- 又()0,πB ∈，∴2πB =……………………………6分 ，得12=ac ……………………………8分 又()222236=++=+-=b a c ac a c ac ，∴10分 所以ΔABC 12分19．（本小题12分） 【解析】（Ⅰ）由题意知()1cos 2sin 2222x x f x π⎛⎫++ ⎪⎝⎭=-sin 21sin 21sin 2222x x x -=-=- ……………………………3分由222,22k x k k Z ππππ-+≤≤+∈ 可得,44k x k k Z ππππ-+≤≤+∈所以函数()f x 的单调递增区间是(),44k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦. ………………5分（Ⅱ）由1sin 0,22A f A ⎛⎫=-= ⎪⎝⎭得1sin 2A = 由题意知A为锐角，所以cos 2A =由余弦定理：2222cos a b c bc A =+-可得：2212b c bc =+≥即：2bc ≤ 当且仅当b c =时等号成立.因此12sin 24bc A ≤ 所以ABC ∆面积的最大值为24+.……………12分 20.（本小题12分） 【解析】 （Ⅰ）设等比数列{}n a 的公比为q ，由已知得()4132432a a a a q ⋅=⋅=又∵10,0a q >>，解得11 2a q =⎧⎨=⎩ ∴12n n a -=……………………3分 （Ⅱ）由题意可得12211321n n b b b n +++=--① ()11122121323n n b b bn n --+++=-≥-②相减得1221n n bn -=-， ()1212n n b n -∴=-，（） ……………………6分当1n =时， 11b =，符合上式， ()1212n n b n -∴=- ……………………7分设()12113252212n nT n -=+⋅+⋅++-⋅则()()2312123252232212n n nT n n -=⋅+⋅+⋅++-⋅+-⋅，两式相减： ()()2112222212n n n T n --=+++--⋅ ∴()2323nn T n =-+．……12分21.（本小题12分）【解析】（Ⅰ）在OMP ∆中,45OPM ∠=︒,OM =OP =,由余弦定理得,2222cos 45OM OP MP OP MP =+-⨯⨯⨯︒,得2430MP MP -+=, 解得1MP =或3MP =. ……………………4分 （Ⅱ）设POM α∠=,060α︒≤≤︒,在OMP ∆中,由正弦定理,得sin sin OM OP OPM OMP=∠∠, 所以()sin 45sin 45OP OM α︒=︒+, 同理()sin 45sin 75OP ON α︒=︒+ ……………………6分故1sin 2OMNS OM ON MON ∆=⨯⨯⨯∠ ()()221sin 454sin 45sin 75OP αα︒=⨯︒+︒+ ()()1sin 45sin 4530αα=︒+︒++︒=⎣⎦====……………………10分因为060α︒≤≤︒,30230150α︒≤+︒≤︒,所以当30α=︒时,()sin230α+︒的最大值为1，此时OMN ∆的面积取到最小值.即30POM ∠=︒时,OMN ∆的面积的最小值为8-. …………………………………………12分22.（本小题12分） 【解析】（Ⅰ）由题意，1121n n a a +=+ 1111112(1),120n na a a +∴+=++=≠，∴1{1}na+是以2为首项，2为公比的等比数列.……………………………………3分（Ⅱ）*11111()212112n n n na n N-+=≤=∈--+，111(1())1111212(1())21242212nnn nS--∴≤++++==-<-.……………………………………7分（Ⅲ）1111111,111222nn nn nnab bn a n n++=-=-=-++++,1111(1)(2)2n n nb bn n++-=-++,易知，213243540,0,0,0b b b b b b b b->->->-<，当4n≥时11111(1)(2)(1)(1)(2)(1)(2)22n nn nn n n n++++-=-++++记1(1)(2),2n nn nc+++=则12(2)(3)2n nn nc++++=1212(2)(3)(1)(2)(2)(1)222n n n n nn n n n n nc c+++++++++--=-=<，∴当4n≥时，{}nc单减，即4301513216nc c≤==<，即当4n≥时111110,(1)(2)2n n n nnb b b bn n+++-=-<<++，∴当4n=时，{}nb最大，最大值411.80b=……………………………………12分。