弹簧,轻杆,绳件模型
轻绳_轻杆_轻弹簧三种模型的特点及其应用

轻绳、轻杆、轻弹簧三种模型的特点及其应用在中学物理中,经常会遇到绳、杆、弹簧三种典型的模型,在这里将它们的特点归类,供同学们学习时参考。
一. 三种模型的特点1. 轻绳(或细绳)中学物理中的绳和线,是理想化的模型,具有以下几个特征:①轻:即绳(或线)的质量或重力可以视为等于零。
由此特点可知,同一根绳(或线)的两端及其中间各点的张力大小相等;②软:即绳(或线)只能受拉力,不能承受压力。
由此特点可知:绳(或线)与其他物体的相互间作用力的方向总是沿着绳子;③不可伸长:即无论绳(或线)所受拉力多大,绳子(或线)的长度不变。
由此特点可知:绳(或线)中的张力可以突变。
2. 轻杆具有以下几个特征:①轻:即轻杆的质量和重力可以视为等于零。
由此特点可知,同一轻杆的两端及其中间各点的张力大小相等;②硬:轻杆既能承受拉力也能承受压力,但其力的方向不一定沿着杆的方向;③轻杆不能伸长或压缩。
3. 轻弹簧中学物理中的轻弹簧,也是理想化的模型。
具有以下几个特征:①轻:即弹簧的质量和重力可以视为等于零。
由此特点可知,向一轻弹簧的两端及其中间各点的张力大小相等;②弹簧既能承受拉力也能承受压力,其方向与弹簧的形变的方向相反;③由于弹簧受力时,要发生形变需要一段时间,所以弹簧的弹力不能发生突变,但当弹簧被剪断时,它所受的弹力立即消失。
二. 三种模型的应用例1. 如图1所示,质量相等的两个物体之间用一轻弹簧相连,再用一细线悬挂在天花板上静止,当剪断细线的瞬间两物体的加速度各为多大?解析:分析物体在某一时刻的瞬时加速度,关键是分析瞬时前后的受力情况及运动状态,再由牛顿第二定律求出瞬时加速度。
此类问题应注意两种模型的建立。
先分析剪断细线前两个物体的受力如图2,据平衡条件求出绳或弹簧上的弹力。
可知,F mg 2=,F F mg mg 122=+='。
剪断细线后再分析两个物体的受力示意图,如图2,绳中的弹力F 1立即消失,而弹簧的弹力不变,找出合外力据牛顿第二定律求出瞬时加速度,则图2剪断后m 1的加速度大小为2g ,方向向下,而m 2的加速度为零。
盘点30条高中物理模型及隐含条件,解题关键所在!

盘点30条高中物理模型及隐含条件,解题关键所在!在物理学习中,事实上好多的物理模型,而每一种模型,都相伴着隐含条件,这些隐含条件会是解题的关键所在!下面是三十条大伙儿在做题中容易遇到的模型和隐含条件,不管你是高几,都期望大伙儿多体会体会,在审题做题过程中能够总结领会。
1、绳:只能拉,不能压,即受到拉力时F≠0,受压时F=0.2、杆:既能拉也能压,即受到拉力、压力时,有F≠0.3、绳刚要断:现在绳的拉力差不多达到最大值,即F=Fmax.4、光滑:意味着无摩擦力.5、长导线:意味着长度L可看成无穷大.6、足够大的平板:意味着平板的面积S可看成无穷大.7、轻杆、轻绳、轻滑轮:意味着质量m=0.8、物体刚要离开地面、物体刚要飞离轨道等物体和接触面之间作用力:FN=0.9、绳恰好被拉直,现在绳中拉力:F=0.10、物体开始运动、自由开释:表示初速度为0.11、锤打桩无反弹:碰撞后,锤与桩有共同速度.12、理想变压器:无功率损耗的变压器.13、细杆:体积为零,仅有长度.14、质点:具有质量,但可忽略其大小、形状和内部结构而视为几何点的物体.15、点电荷:在研究带电体间的相互作用时,假如带电体的大小比它们之间的距离小得多,即可认为分布在带电体上的电荷是集中在一点上的.16、差不多粒子如电子、质子、离子等是不考虑重力的粒子,而带电的质点、液滴、小球等(除说明不考虑重力外)则要考虑重力.17、“轻绳、弹簧、轻杆”模型:注意三种模型的异同点,常考查直线与圆周运动中三种模型的动力学问题和功能问题.18、“挂件”模型:考查物体的平稳问题、死结与活结问题,常采纳正交分解法,图解法,三角形法则和极值法解题.19、“追碰”模型:考查运动规律、碰撞规律、临界问题.常通过数学法(函数极值法、图像法等)和物理方法(参照物变换法、守恒法)等解题.20、“皮带”模型:注意摩擦力的大小和方向.常考查牛顿运动定律、功能关系及摩擦生热等问题.21、“平抛”模型:物体做平抛运动(或类平抛运动),考查运动的合成与分解、牛顿运动定律、动能定理等知识.22、“行星”模型:万有引力提供向心力.注意相关物理量、功能问题、数理问题(圆心、半径、临界问题).23、“人船”模型:不仅是动量守恒问题中典型的物理模型,也是最重要的力学综合模型之一.通过类比和等效方法,能够使许多动量守恒问题的分析思路和解答步骤变得简捷.24、“子弹打木块”模型:子弹和木块组成的系统动量守恒,机械能不守恒.系统缺失的机械能等于阻力乘以相对位移.25、“限流与分压器”模型:电路设计中经常遇到.考查串、并联电路规律及闭合电路的欧姆定律、电能、电功率以及实际应用等.26、“电路的动态变化”模型:考查闭合电路的欧姆定律.27、“回旋加速器”模型:考查带电粒子在磁场中运动的典型模型.注意加速电场的平行极板接的是交变电压,且它的周期和粒子的运动周期相同.28、电磁场中的“单杆”模型:导体棒要紧是以棒生电或电生棒的内容显现,从组合情形来看有棒与电阻、棒与电容、棒与电感、棒与弹簧等.导体棒所在的导轨有平面导轨、竖直导轨等.29、电磁场中的“双电源”模型:考查力学中的三大定律、闭合电路的欧姆定律、电磁感应定律等知识.30、“远距离输电变压器”模型. 注意变压器的三个制约问题.。
高中物理必考模型:轻绳、轻弹簧、轻杆联系与区别全解析

高中物理必考模型:轻绳、轻弹簧、轻杆联系与区别全解析轻绳特点轻绳模型的建立轻绳或称为细线,它的质量可忽略不计,轻绳是软的,不能产生侧向力,只能产生沿着绳子方向的力。
它的劲度系数非常大,以至于认为在受力时形变极微小,看作不可伸长。
轻绳模型的特点①轻绳各处受力相等,且拉力方向沿着绳子;②轻绳不能伸长;③用轻绳连接的系统通过轻绳的碰撞、撞击时,系统的机械能有损失;④轻绳的弹力会发生突变。
轻杆特点轻杆模型的建立轻杆的质量可忽略不计,轻杆是硬的,能产生侧向力,它的劲度系数非常大,以至于认为在受力时形变极微小,看作不可伸长或压缩。
轻杆模型的特点①轻杆各处受力相等,其力的方向不一定沿着杆的方向;②轻杆不能伸长或压缩;③轻杆受到的弹力的方式有拉力或压力。
轻弹簧特点轻弹簧模型的建立轻弹簧可以被压缩或拉伸,其弹力的大小与弹簧的伸长量或缩短量有关。
轻弹簧的特点①轻弹簧各处受力相等,其方向与弹簧形变的方向相反;②弹力的大小为F=kx,其中k 为弹簧的劲度系数,x为弹簧的伸长量或缩短量;③弹簧的弹力不会发生突变。
特别提醒:橡皮筋与轻弹簧极为相似,只是橡皮筋不能被压缩静止或匀速运动例1、如图所示,有一质量为m的小球用轻绳悬挂于小车顶部,小车静止或匀速直线运动时,求绳子对小球作用力的大小和方向。
解析:小车静止或匀速直线运动时,小球也处于静止或匀速直线运动状态。
由平衡条件可知,绳子对小球的弹力为F=mg,方向是沿着绳子向上。
若将轻绳换成轻弹簧,其结果是一样的。
例2、如图所示,小车上有一弯折轻杆,杆下端固定一质量为m的小球。
当小车处于静止或匀速直线运动状态时,求杆对球的作用力的大小和方向。
解析:以小球为研究对象,可知小球受到杆对它一个的弹力和重力作用,由平衡条件可知小球受力如图所示。
则可知杆对小球的弹力为F=mg,方向与重力的方向相反即竖直向上。
注意:在这里杆对小球的作用力方向不是沿着杆的方向。
以加速度a做匀加速直线运动时,求轻绳对小球的作用力的大小和方向。
轻绳、轻杆和轻弹簧模型(修)

轻绳、轻杆和轻弹簧模型的应用一、三个模型的相同点1、“轻”—不计质量,不受重力。
2、在任何情况下,沿绳、杆和弹簧伸缩方向的张力、弹力处处相等。
二、三个模型的不同点1、形变特点轻绳—可以任意弯曲,但不能伸长,即伸长形变不计。
轻杆—不能任意弯曲,不能伸长和缩短,即伸缩形变不计。
轻弹簧—可以伸长,也可以缩短,且伸缩形变不能忽略不计。
2、施力和受力特点轻绳—只能产生和承受沿绳方向的拉力。
轻杆—不仅能产生和承受沿杆方向的拉力和压力,还能产生和承受不沿杆方向的拉力和压力。
轻弹簧—可以产生和承受沿弹簧伸缩方向的拉力和压力。
3、力的变化特点轻绳—张力的产生、变化、或消失不需要时间,具有突变性和瞬时性。
轻杆—拉力和压力的产生、变化或消失不需要时间,具有突变性和瞬时性。
轻弹簧—弹力的产生、变化或消失需要时间,即只能渐变,不具有瞬时性,且在形变保持瞬间,弹力保持不变。
(注意:当弹簧的自由端无重物时,形变消失不需要时间)4、连接体的运动特点轻绳—轻绳平动时,两端的连接体沿绳方向的速度(或速度分量)总是相等,且等于省上各点的平动速度;轻绳转动并拉直时,连接体具有相同的角速度,而线速度与转动半径成正比。
轻杆—轻杆平动时,连接体具有相同的平动的速度;轻杆转动时,连接体具有相同的角速度,而线速度与转动半径成正比。
轻弹簧—在弹簧发生形变的过程中,两端连接体的速率不一定相等;在弹簧形变最大,即弹性势能最大时,两端连接体的速率相等;在弹簧转动时,连接体的转动半径随弹力变化,速度方向不一定垂直于弹力。
5、作功和能量转化特点轻绳—在连接体作匀速率和变速率圆周运动的过程中,绳的拉力都不作功;在绳突然拉直的瞬间,有机械能转化为绳的内能,即机械能不守恒。
轻杆—在连接体作匀速率和变速率圆周运动的过程中,轻杆的法向力对物体不作功,而切向力既可以对物体作正功,也可以对物体作负功,但系统机械能守恒。
轻弹簧—弹力对物体作功,系统机械能守恒;弹力作正功,弹性势能减少,物体动能增加;弹力作负功,弹性势能增加,物体动能减少。
“绳”与“弹簧”模型对比3页

“绳”与“弹簧”模型对比高中物理教学中经常会遇到细绳(轻杆)、弹簧模型,弄清楚两者的异同点,对于分析物体在某一时刻的瞬时加速度有着关键点作用。
一、两类模型的区别1.刚性绳(或杆)一种不发生明显形变就能产生弹力的物体,剪断(或脱离)后,弹力立即改变或消失,不需要形变恢复的时间,一般题目中的细绳、轻杆或接触面在不加特殊说明时,均可按此模型处理。
其中杆与绳模型中处理问题也有差别,如杆能承受拉力和压力,而轻绳只能承受拉力(不能起支撑作用)。
绳上的拉力只能沿绳,而杆上的作用力可以沿杆,也可以与杆成任意夹角。
2.弹簧(或橡皮绳)此类模型的特点是形变量大,形变恢复需要较长的时间,在剪断的瞬间可认为弹簧来不及恢复原长,因此弹力大小可近似认为保持不变。
二、两种模型的对比例1. 如图1所示,质量相等的两个物体之间用一轻弹簧相连,再用一细线悬挂在天花板上静止,当剪断细线的瞬间两物体的加速度各为多大?解析:分析物体在某一时刻的瞬时加速度,关键是分析瞬时前后的受力情况及运动状态,再由牛顿第二定律求出瞬时加速度。
此类问题应注意两种模型的建立。
先分析剪断细线前两个物体的受力如图2,据平衡条件求出绳或弹簧上的弹力。
可知,F2=mg,F1=F2'+mg=2mg。
剪断细线后再分析两个物体的受力示意图,如图3,绳中的弹力F1立即消失,而弹簧的弹力不变,找出合外力据牛顿第二定律求出瞬时加速度,则图3剪断后m1的加速度大小为2g,方向向下,而m2的加速度为零。
从上述解析过程中,我们不难发现,m1在细线剪断前后受力发生了变化,故其瞬时加速度不同;m2在剪断细线前后,由于弹簧弹力来不及发生变化,所以其瞬时加速度与剪断前相同。
例2如图4所示,一质量为m的物体系于长度分别为L1、L2的两根细线上,L1的一端悬挂在天花板上,与竖直方向夹角为θ,L2水平拉直,物体处于平衡状态。
求解下列问题:⑴现将L2线剪断,求剪断L2瞬间物体的加速度。
⑵若将图4中的细线L1改为长度相同、质量不计的轻弹簧,如图5所示,其他条件不变,求剪断L2瞬间物体的加速度。
(完整版)轻绳、轻杆和轻弹簧模型

浅析轻绳、轻杆和轻弹簧模型的应用山西泽州县第一中学成文荣李智涛 048000轻绳、轻杆和轻弹簧,是力学中三个重要的理想模型,在高中物理解题中有着重要的地位,为了帮助学生正确地分析和解决与轻绳、轻杆和轻弹簧有关的问题,笔者对三个模型的相同点和不同点进行了总结,并想通过一定的实例,对学生学习和应用给与启迪思考。
一、三个模型的相同点1、“轻”- 不计质量,不受重力。
2、在任何情况下,沿绳、杆和弹簧伸缩方向的张力、弹力处处相等.二、三个模型的不同点1、形变特点轻绳—可以任意弯曲,但不能伸长,即伸长形变不计。
轻杆—不能任意弯曲,不能伸长和缩短,即伸缩形变不计。
轻弹簧—可以伸长,也可以缩短,且伸缩形变不能忽略不计。
2、施力和受力特点轻绳 - 只能产生和承受沿绳方向的拉力.轻杆 - 不仅能产生和承受沿杆方向的拉力和压力,还能产生和承受不沿杆方向的拉力和压力。
轻弹簧—可以产生和承受沿弹簧伸缩方向的拉力和压力。
3、力的变化特点轻绳—张力的产生、变化、或消失不需要时间,具有突变性和瞬时性。
轻杆 - 拉力和压力的产生、变化或消失不需要时间,具有突变性和瞬时性.轻弹簧—弹力的产生、变化或消失需要时间,即只能渐变,不具有瞬时性,且在形变保持瞬间,弹力保持不变。
(注意 :当弹簧的自由端无重物时,形变消失不需要时间)4、连接体的运动特点轻绳 - 轻绳平动时,两端的连接体沿绳方向的速度(或速度分量)总是相等,且等于省上各点的平动速度;轻绳转动并拉直时,连接体具有相同的角速度,而线速度与转动半径成正比。
轻杆—轻杆平动时,连接体具有相同的平动的速度;轻杆转动时,连接体具有相同的角速度,而线速度与转动半径成正比.轻弹簧—在弹簧发生形变的过程中,两端连接体的速率不一定相等;在弹簧形变最大,即弹性势能最大时,两端连接体的速率相等;在弹簧转动时,连接体的转动半径随弹力变化,速度方向不一定垂直于弹力。
5、作功和能量转化特点轻绳 - 在连接体作匀速率和变速率圆周运动的过程中,绳的拉力都不作功;在绳突然拉直的瞬间,有机械能转化为绳的内能,即机械能不守恒.轻杆—在连接体作匀速率和变速率圆周运动的过程中,轻杆的法向力对物体不作功,而切向力既可以对物体作正功,也可以对物体作负功,但系统机械能守恒。
物理建模轻杆轻绳轻弹簧模型
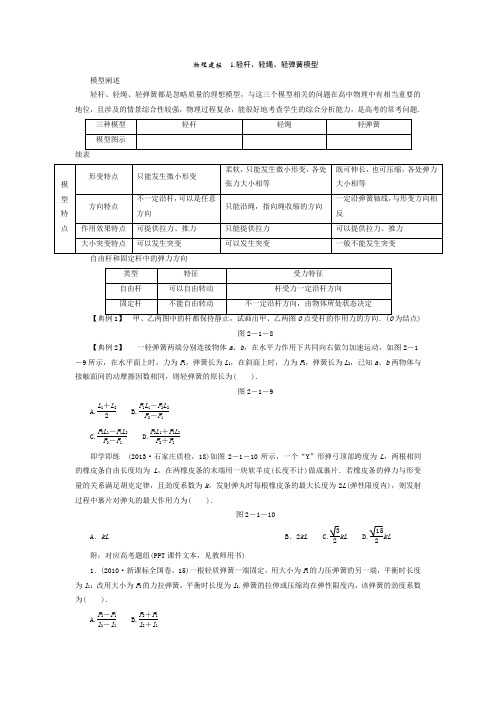
物理建模 1.轻杆、轻绳、轻弹簧模型模型阐述轻杆、轻绳、轻弹簧都是忽略质量的理想模型,与这三个模型相关的问题在高中物理中有相当重要的地位,且涉及的情景综合性较强,物理过程复杂,能很好地考查学生的综合分析能力,是高考的常考问题.为结点)图2-1-8【典例2】 一轻弹簧两端分别连接物体a 、b ,在水平力作用下共同向右做匀加速运动,如图2-1-9所示,在水平面上时,力为F 1,弹簧长为L 1,在斜面上时,力为F 2,弹簧长为L 2,已知a 、b 两物体与接触面间的动摩擦因数相同,则轻弹簧的原长为( ).图2-1-9A.L 1+L 22B.F 1L 1-F 2L 2F 2-F 1C.F 2L 1-F 1L 2F 2-F 1 D.F 2L 1+F 1L 2F 2+F 1即学即练 (2013·石家庄质检,18)如图2-1-10所示,一个“Y”形弹弓顶部跨度为L ,两根相同的橡皮条自由长度均为L ,在两橡皮条的末端用一块软羊皮(长度不计)做成裹片.若橡皮条的弹力与形变量的关系满足胡克定律,且劲度系数为k ,发射弹丸时每根橡皮条的最大长度为2L (弹性限度内),则发射过程中裹片对弹丸的最大作用力为( ).图2-1-10A .kLB .2kL C.32kL D.152kL 附:对应高考题组(PPT 课件文本,见教师用书)1.(2010·新课标全国卷,15)一根轻质弹簧一端固定,用大小为F 1的力压弹簧的另一端,平衡时长度为l 1;改用大小为F 2的力拉弹簧,平衡时长度为l 2.弹簧的拉伸或压缩均在弹性限度内,该弹簧的劲度系数为( ).A.F 2-F 1l 2-l 1 B.F 2+F 1l 2+l 1C.F 2+F 1l 2-l 1 D.F 2-F 1l 2+l 12.(2011·山东卷,19)如图所示,将两相同的木块a 、b 置于粗糙的水平地面上,中间用一轻弹簧连接,两侧用细绳系于墙壁.开始时a 、b 均静止,弹簧处于伸长状态,两细绳均有拉力,a 所受摩擦力F f a ≠0,b 所受摩擦力F f b =0.现将右侧细绳剪断,则剪断瞬间( ).A .F f a 大小不变B .F f a 方向改变C .F f b 仍然为零D .F f b 方向向右3.(2012·山东基本能力,85)力是物体间的相互作用,下列有关力的图示及表述正确的是( ).物理建模 1.轻杆、轻绳、轻弹簧模型模型阐述轻杆、轻绳、轻弹簧都是忽略质量的理想模型,与这三个模型相关的问题在高中物理中有相当重要的地位,且涉及的情景综合性较强,物理过程复杂,能很好地考查学生的综合分析能力,是高考的常考问题.为结点)图2-1-8解析 甲为自由杆,受力一定沿杆方向,如下图甲所示的F N1.乙为固定杆,受力由O 点所处状态决定,此时受力平衡,由平衡条件知杆的支持力F N2的方向与mg 和F 1的合力方向相反,如下图乙所示.答案 如解析图所示【典例2】 一轻弹簧两端分别连接物体a 、b ,在水平力作用下共同向右做匀加速运动,如图2-1-9所示,在水平面上时,力为F 1,弹簧长为L 1,在斜面上时,力为F 2,弹簧长为L 2,已知a 、b 两物体与接触面间的动摩擦因数相同,则轻弹簧的原长为( ).图2-1-9A.L 1+L 22B.F 1L 1-F 2L 2F 2-F 1C.F 2L 1-F 1L 2F 2-F 1 D.F 2L 1+F 1L 2F 2+F 1解析 设物体a 、b 的质量分别为m 1、m 2,与接触面间的动摩擦因数为μ,弹簧原长为L 0,在水平面上时,以整体为研究对象有F 1-μ(m 1+m 2)g =(m 1+m 2)a ,①隔离a 物体有k (L 1-L 0)-μm 1g =m 1a ,② 联立解得k (L 1-L 0)=m 1m 1+m 2F 1,③ 同理可得k (L 2-L 0)=m 1m 1+m 2F 2,④ 联立③④可得轻弹簧的原长为L 0=F 2L 1-F 1L 2F 2-F 1,C 对.答案 C反思总结 如何理解理想化模型——“轻弹簧”与“橡皮筋” (1)弹簧与橡皮筋产生的弹力遵循胡克定律F =kx ,x 是指形变量.(2)“轻”即指弹簧(或橡皮筋)的重力不计,所以同一弹簧的两端及中间各点的弹力大小相等. (3)弹簧既能受拉力,也能受压力(沿弹簧轴线),分析弹簧问题时一定要特别注意这一点,而橡皮筋只能受拉力作用.(4)弹簧和橡皮筋中的弹力均不能突变,但当将弹簧(或橡皮筋)剪断时,其弹力立即消失.即学即练 (2013·石家庄质检,18)如图2-1-10所示,一个“Y”形弹弓顶部跨度为L ,两根相同的橡皮条自由长度均为L ,在两橡皮条的末端用一块软羊皮(长度不计)做成裹片.若橡皮条的弹力与形变量的关系满足胡克定律,且劲度系数为k ,发射弹丸时每根橡皮条的最大长度为2L (弹性限度内),则发射过程中裹片对弹丸的最大作用力为( ).图2-1-10A .kLB .2kL C.32kL D.152kL 解析 对裹片受力分析,由相似三角形可得:kL2L=F2?2L ?2-⎝⎛⎭⎫L 22得:F =152kL 则裹片对弹丸的最大作用力为F 丸=F =152kL ,故选项D 正确. 答案 D附:对应高考题组(PPT 课件文本,见教师用书)1.(2010·新课标全国卷,15)一根轻质弹簧一端固定,用大小为F 1的力压弹簧的另一端,平衡时长度为l 1;改用大小为F 2的力拉弹簧,平衡时长度为l 2.弹簧的拉伸或压缩均在弹性限度内,该弹簧的劲度系数为( ).A.F 2-F 1l 2-l 1B.F 2+F 1l 2+l 1 C.F 2+F 1l 2-l 1 D.F 2-F 1l 2+l 1解析 设弹簧原长为l ,由题意知,F 1=k (l -l 1),F 2=k (l 2-l ),两式联立,得k =F 2+F 1l 2-l 1,选项C 正确. 答案 C2.(2011·山东卷,19)如图所示,将两相同的木块a 、b 置于粗糙的水平地面上,中间用一轻弹簧连接,两侧用细绳系于墙壁.开始时a、b均静止,弹簧处于伸长状态,两细绳均有拉力,a所受摩擦力F f a≠0,b所受摩擦力F f b=0.现将右侧细绳剪断,则剪断瞬间( ).A.F f a大小不变B.F f a方向改变C.F f b仍然为零D.F f b方向向右解析剪断右侧绳的瞬间,右侧细绳上拉力突变为零,而弹簧对两木块的拉力没有发生突变,与原来一样,所以b对地面有向左的运动趋势,受到静摩擦力F f b方向向右,C错误,D正确.剪断右侧绳的瞬间,木块a受到的各力都没有发生变化,A正确,B错误.答案AD3.(2012·山东基本能力,85)力是物体间的相互作用,下列有关力的图示及表述正确的是( ).解析由于在不同纬度处重力加速度g不同,旅客所受重力不同,故对飞机的压力不同,A错误.充足气的篮球平衡时,篮球壳对内部气体有压力作用,即内外气体对篮球壳压力的差值等于篮球壳对内部气体的压力,故B正确.书对桌子的压力作用在桌子上,箭尾应位于桌面上,故C错误.平地上匀速行驶的汽车,其主动轮受到地面的摩擦力是其前进的动力,地面对其从动轮的摩擦力是阻力,汽车受到的动力与阻力平衡时才能匀速前进,故D正确.答案BD。
1、轻杆、轻绳、轻弹簧模型

点评: 解答本题的关键是抓住:活结中轻绳上各点的拉力大小相
等,死结中几段绳子的张力不一定相等。固定轻杆(死杆)作
用力的方向不一定沿杆。当轻杆以铰链形式连接时(活杆), 要使轻杆处于平衡状态,则两段轻绳的作用力的合力必须沿轻 杆轴线方向。
四、建模启示
• (1)对于弹力方向的确定,一定要分清情景类型及相关结 论和规律尤其要注意结合物体运动状态分析。 • (2)轻杆对物体的弹力不一定沿杆,其具体方向与物体所
处的状态有关,一般应结合物体平衡或牛顿第三定律分析。
• (3)分析此类问题的关键是区别各模型的特点,分析发生 的物理过程,依据不同的物理场景,把握其运动状态,分 析其临界状态下的条件或突变问题中的“拐点”,弄清变化 和不变的物理量,只有如此才能更好的解决此类问题。
解析:杆与球相连,做非匀速圆周运动,其轨迹为圆的一部分, 只有重力做功,由机械能守恒,选取最低处为零势能面,则:
2 vB T mg m 由牛顿第二定律得 l 解得: T m g(3 2 sin )
1 2 mgl (1 sin ) mv B 2
[典例2]轻杆长为L,一端用光滑轴固定,另一端系一个可视为 质点,质量为的小球,把小球拉至图示的位置,无初速度地自 由释放到最低处的过程中,小球做什么运动?到最低处时速度 多大?弹力多少?若其它条件不变,把轻杆换为细绳,则释放 后小球做什么运动?到最低处时速度多大?弹力为多少?
由速度的分解得 由牛顿第二定律得 v1 v c cos
解得 T / 3.5mg
2 mv B T/ mg l
点评: 轻杆与球相连时,只有重力势能向动 能的转化;无能量损耗。轻绳与球相连时, 在绳突然拉紧的瞬间,沿径向的动能将耗
轻绳、轻杆、轻弹簧三种模型之比较
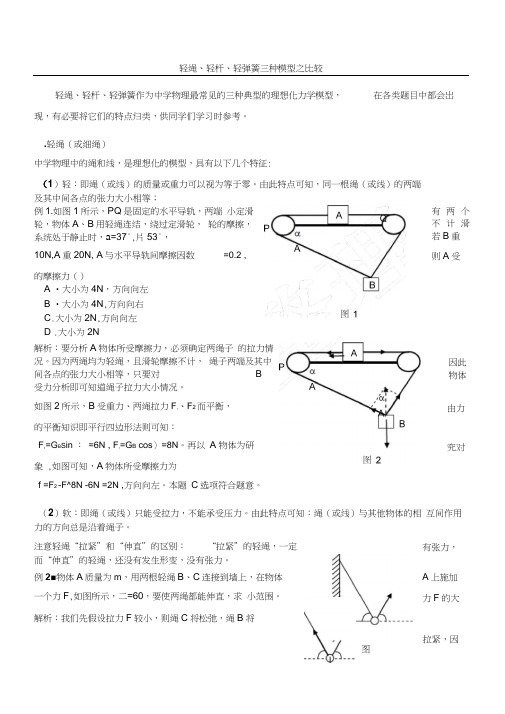
轻绳、轻杆、轻弹簧三种模型之比较轻绳、轻杆、轻弹簧作为中学物理最常见的三种典型的理想化力学模型, 在各类题目中都会出现,有必要将它们的特点归类,供同学们学习时参考。
.轻绳(或细绳)中学物理中的绳和线,是理想化的模型,具有以下几个特征:(1)轻:即绳(或线)的质量或重力可以视为等于零。
由此特点可知,同一根绳(或线)的两端及其中间各点的张力大小相等;例1.如图1所示,PQ 是固定的水平导轨,两端 小定滑轮,物体A 、B 用轻绳连结,绕过定滑轮, 轮的摩擦,系统处于静止时,a =37°,片53°,10N,A 重20N, A 与水平导轨间摩擦因数=0.2 ,的摩擦力()A •大小为4N ,方向向左B •大小为4N ,方向向右C .大小为2N ,方向向左D .大小为2N解析:要分析A 物体所受摩擦力,必须确定两绳子 的拉力情况。
因为两绳均为轻绳,且滑轮摩擦不计, 绳子两端及其中间各点的张力大小相等,只要对 B 受力分析即可知道绳子拉力大小情况。
如图2所示,B 受重力、两绳拉力F ,、F 2而平衡, 的平衡知识即平行四边形法则可知:F ,=G B S in : =6N , F ,=G B cos 〉=8N 。
再以 A 物体为研 象 ,如图可知,A 物体所受摩擦力为f =F 2 -F^8N -6N =2N ,方向向左。
本题 C 选项符合题意。
(2)软:即绳(或线)只能受拉力,不能承受压力。
由此特点可知:绳(或线)与其他物体的相 互间作用力的方向总是沿着绳子。
注意轻绳“拉紧”和“伸直”的区别:“拉紧”的轻绳,一定而“伸直”的轻绳,还没有发生形变,没有张力。
例2■物体A 质量为m ,用两根轻绳B 、C 连接到墙上,在物体 一个力F ,如图所示,二=60,要使两绳都能伸直,求 小范围。
解析:我们先假设拉力F 较小,则绳C 将松弛,绳B 将有两个 不计滑 若B 重 则A 受因此 物体由力究对 拉紧,因有张力,A 上施加力F 的大图此,拉力F 的最小值F min ,出现在绳C 恰好伸直无弹力,而绳B 张紧时。
轻绳、轻杆、轻弹簧三种模型之比较

轻绳、轻杆、轻弹簧三种模型之比较一. 三种模型的主要特点1. 轻绳(1)轻绳模型的建立轻绳或称为细线,它的质量可忽略不计,轻绳是软的,不能产生侧向力,只能产生沿着绳子方向的力。
它的劲度系数非常大,以至于认为在受力时形变极微小,看作不可伸长。
(2)轻绳模型的特点①轻绳各处受力相等,且拉力方向沿着绳子;②轻绳不能伸长;③用轻绳连接的系统通过轻绳的碰撞、撞击时,系统的机械能有损失;④轻绳的弹力会发生突变。
2. 轻杆(l)轻杆模型的建立轻杆的质量可忽略不计,轻杆是硬的,能产生侧向力,它的劲度系数非常大,以至于认为在受力时形变极微小,看作不可伸长或压缩。
(2)轻杆模型的特点①轻杆各处受力相等,其力的方向不一定沿着杆的方向;②轻杆不能伸长或压缩;③轻杆受到的弹力的方式有拉力或压力。
3. 轻弹簧(1)轻弹簧模型的建立轻弹簧可以被压缩或拉伸,其弹力的大小与弹簧的伸长量或缩短量有关。
(2)轻弹簧的特点①轻弹簧各处受力相等,其方向与弹簧形变的方向相反;②弹力的大小为F=kx,其中k为弹簧的劲度系数,x为弹簧的伸长量或缩短量;③弹簧的弹力不会发生突变。
二. 三种模型的主要区别1.静止或匀速直线运动时例1.如图1所示,有一质量为m的小球用轻绳悬挂于小车顶部,小车静止或匀速直线运动时,求绳子对小球作用力的大小和方向。
图1解析:小车静止或匀速直线运动时,小球也处于静止或匀速直线运动状态。
由平衡条件可知,绳子对小球的弹力为F mg=,方向是沿着绳子向上。
若将轻绳换成轻弹簧,其结果是一样的。
例2.如图2所示,小车上有一弯折轻杆,杆下端固定一质量为m的小球。
当小车处于静止或匀速直线运动状态时,求杆对球的作用力的大小和方向。
图2解析:以小球为研究对象,可知小球受到杆对它一个的弹力和重力作用,由平衡条件可知小球受力如图3所示。
则可知杆对小球的弹力为F mg=,方向与重力的方向相反即竖直向上。
图3注意:在这里杆对小球的作用力方向不是沿着杆的方向。
高中物理常见十种模型

a2=g(sin θ-μcos θ)=2 m/s2, x2=L-x1=5.25 m,
(2 分) (1 分)
x2=v0t2+12a2t22,
(2 分)
得 t2=0.5 s,(2 分) 则煤块从 A 到 B 的时间为 t=t1+t2=1.5 s.(1 分)
甲
乙
(2)第一过程痕迹长 Δx1=v0t1-12a1t21=5 m,(2 分)
物理模型——传送带模型中的动力学问题 1.模型特征 一个物体以速度v0(v0≥0)在另一个匀速运动的物体上开始运动 的力学系统可看做“传送带”模型,如图甲、乙、丙所示.
2.建模指导 传送带模型问题包括水平传送带问题和倾斜传送带问题. (1)水平传送带问题:求解的关键在于对物体所受的摩擦力进 行正确的分析判断.根据物体与传送带的相对速度方向判断 摩擦力方向.两者速度相等是摩擦力突变的临界条件. (2)倾斜传送带问题:求解的关键在于认真分析物体与传送带 的相对运动情况,从而确定其是否受到滑动摩擦力作用.如 果受到滑动摩擦力作用应进一步确定其大小和方向,然后根 据物体的受力情况确定物体的运动情况.当物体速度与传送 带速度相等时,物体所受的摩擦力有可能发生突变.
物理模型——两种运动的合成与分解实例 一、小船渡河模型 1.模型特点 两个分运动和合运动都是匀速直线运动,其中一个分运动的 速度大小、方向都不变,另一分运动的速度大小不变,研究 其速度方向不同时对合运动的影响.这样的运动系统可看做 小船渡河模型.
2.模型分析 (1)船的实际运动是水流的运动和船相对静水的运动的合运动. (2)三种速度:v1(船在静水中的速度)、v2(水流速度)、v(船的实际 速度). (3)两个极值
[审题点睛] (1)判断两者之间是否发生滑动,要比较两者之 间的摩擦力与最大静摩擦力的关系,若f<fm,则不滑动,反 之则发生滑动. (2)两者发生相对滑动时,两者运动的位移都是对地的,注意 找位移与板长的关系.
高中物理中“轻绳”、“轻杆”和“轻弹簧”问题的分析

高中物理中“轻绳” 、“轻杆”和“轻弹簧”的问题分析中学阶段常涉及到“轻绳” 、“轻杆”和“轻弹簧”模型,这三种模型都是由各种实际情况中的绳、杆和弹簧抽象出来的理想化物理模型。
但它们的成因和特性并不完全相同,由此导致这类模型在实际应用中有很多同学混淆出错,下面对这三种模型的特点及区别应用作一些简单的讨论和分析。
一、三个模型的正确理解1.轻绳模型轻绳也称细线,它的质量可忽略不计;轻绳是软的;同时它的劲度系数非常大,可认为在受外力作用时它的形变极微小,看作不可伸长;其弹力的主要特征是:①不能承受压力,不能产生侧向力,只能产生沿绳收缩方向的拉力。
②内部张力大小处处相等,且与运动状态无关。
③轻绳的弹力大小可发生突变。
2.轻杆模型轻杆的质量可忽略不计,轻杆是硬的,它的劲度系数非常大,可认为在受外力作用时形变极微小,看作不可伸长或压缩;其弹力的主要特征是:①轻杆既可产生压力、也可产生拉力,且能产生侧向力(力的方向不一定沿着杆的方向);②轻杆各处受力大小相等,且与运动状态无关;③轻杆的弹力可发生突变。
3.轻弹簧模型轻弹簧的质量可忽略不计,可以被压缩或拉伸。
其弹力的主要特征是:①轻弹簧能产生沿弹簧轴线伸缩方向的压力或拉力;②轻弹簧各处受力大小相等,且与弹簧形变的方向相反;③轻弹簧产生的弹力是连续变化的,不能发生突变,只能渐变(除弹簧被剪断外);④在弹性限度内,弹力的大小与弹簧的形变量成正比,即F=kx,其中 k 为弹簧的劲度系数, x 为弹簧的伸长量或缩短量。
二、三种模型的主要区别及应用下面结合例题分析它们的区别及应用:1.轻绳对物体只能产生沿绳收缩方向的拉力,而轻杆对物体的弹力不一定沿杆的方向。
【例1】如图1 所示,轻绳一端系着质量为m 的小球,另一端系在固定于小车上一直杆 AB 的上端;试求当小车以 a 的加速度水平向左匀加速度直线运动,轻绳对小球作用力的大小和方向?解析:如图 2 所示,小球受两个力作用:重力mg 和绳对小球弹力T。
经典高中物理模型--绳子、弹簧和杆产生的弹力特点

1.如图所示,有一质量为m的小球用轻绳悬挂于小车顶部,小车静止或匀速直线运动时,求绳子对小球作用力的大小和方向。
2.如图所示,小车上有一弯折轻杆,杆下端固定一质量为m的小球。当小车处于静止或匀速直线运动状态时,求杆对球的作用力的大小和方向。
3.如图所示,一质量为m的小球用轻绳悬挂在小车顶部,小车向左以加速度a做匀加速直线运动时,求轻绳对小球的作用力的大小和方向。
6.解析:在细线未剪断前,由平衡条件可得
水平细线的拉力
弹簧的拉力
当剪断细线的瞬时,,而弹簧形变不能马上改变,故弹簧弹力F保持原值。在图所示中,。所以在剪断细线的瞬时F和mg的合力仍等于原的大小,方向水平向右。则可知小球的加速度方向沿水平向右,即与竖直成角,其大小为。
(1)剪断前,两种情况小球受力一样,分别如图(1)、(2)所示,利用平衡条件,则mg与F2的合力与F1大小相等,方向相反,可以解得F1=mgtgθ。
(2)剪断后瞬间,绳OA产生的拉力F1消失,
对绳来说,其伸长量很微小,可以忽略不计,不需要形变恢复时间,因此,绳子中的张力也立即发生变化, 这时F2将发生瞬时变化,mg与F2的合力将不再沿水平方向,而是由于小球下一时刻做单摆运动沿圆弧的切线方向,与绳垂直,如图(3)所示,F合=mgsinθ,所以a=gsinθ。
绳子、弹簧和杆产生的弹力特点
模型特点:
1.轻绳
(1)轻绳模型的特点
“绳”在物理学上是个绝对柔软的物体,它只产生拉力(张力),绳的拉力沿着绳的方向并指向绳的收缩方向。它不能产生支持作用。
它的质量可忽略不计,轻绳是软的,不能产生侧向力,只能产生沿着绳子方向的力。它的劲度系数非常大,以至于认为在受力时形变极微小,看作不可伸长。
对弹簧来说,其伸长量大,形变恢复需要较长时间,认为弹簧的长度还没有发生变化。这时F2不发生变化,故mg与F2的合力仍然保持不变,与F1大小相等,方向相反,如图(4)所示,所以F合= F1=mgstgθ,
高中物理常见的物理模型

1专题:高中物理力学常见物理模型高考中常出现的物理模型:斜面模型、叠加体模型(包含滑块、子弹射入)、〔弹簧、轻绳、轻杆〕连接体模型、传送带模型、人船模型、碰撞模型等。
一、斜面模型每年各地高考卷中几乎都有关于斜面模型的试题。
以下结论有助于更好更快地理清解题思路和方法.1.自由释放的滑块能在斜面上(如右图)匀速下滑时,m 与M 之间的动摩擦因数μ=g tan θ.2.自由释放的滑块在斜面上(如右图所示):(1)静止或匀速下滑时,斜面M 对水平地面的静摩擦力为零; (2)加速下滑时,斜面对水平地面的静摩擦力水平向右; (3)减速下滑时,斜面对水平地面的静摩擦力水平向左.3.自由释放的滑块在斜面上(如右图所示)匀速下滑时,M 对水平地面的静摩擦力为零,这一过程中再在m 上加上任何方向的作用力,(在m 停止前)M 对水平地面的静摩擦力依然为零..4.悬挂有物体的小车在斜面上滑行(如右图所示):(1)向下的加速度a =g sin θ时,悬绳稳定时将垂直于斜面;(2)向下的加速度a >g sin θ时,悬绳稳定时将偏离垂直方向向上; (3)向下的加速度a <g sin θ时,悬绳将偏离垂直方向向下.5.在倾角为θ的斜面上以速度v 0平抛一小球(如右 图所示):(1)落到斜面上的时间t =2v 0tan θg;(2)落到斜面上时,速度的方向与水平方向的夹角α恒定,且tan α=2tan θ,与初速度无关;(3)经过t c =v 0tan θg 小球距斜面最远,最大距离d =(v 0sin θ)22g cos θ.6.如下图,当整体有向右的加速度a =g tan θ时,m 能在斜面上保持相对静止.7.在如以下图所示的物理模型中,当回路的总电阻恒定、导轨光滑时,ab 棒所能到达的稳定速度v m =mgR sin θB 2L 2.8.如以下图所示,当各接触面均光滑时,在小球从斜面顶端滑下的过程中,斜面后退的位移s =mm +ML .2v v tt二、叠加体模型叠加体模型〔包括滑块、子弹打木块、滑环直杆、传送带等模型,传送带另详述〕在高考中频现,常需求解摩擦力、相对滑动路程、摩擦生热、多次作用后的速度等。
浅析“轻绳”、“轻杆”和“轻弹簧”

复 习指 津
浅 析“ 绳" “ 轻 、 轻杆 ’ 轻 弹 簧" ’ 和“
广西 百 色凌 云县 中学 (3 1 0 黄宏 标 53 0 )
中学阶段 常 涉及 到 “ 绳” “ 杆” “ 弹 簧” 轻 、轻 和 轻 模 型, 这三种模 型都是 由各种 实际情 况 中的绳 、 杆和 弹簧 抽象出来的理想化物理模型. 但它们 的成因和特性 并不 完全相同 , 由此导致这类模 型在实 际应 用 中有很 多学生 混 淆 出 错 , 者 拟 对 这 三 种 模 型 的特 点 及 区 别 应 用 作 一 笔 些简单的讨论. 下面结合例题分析它们的区别及应用 : 轻 绳对 物 体 只 能 产 生 沿 绳 收 缩 方 向 的 拉 力 , 而 轻杆对物体 的弹 力不一定沿杆的方向 【 1 如 图 1 示 , 绳 一 端 系 着 质 量 为 的小 例 】 所 轻 球 , 一 端 系 在 固定 于小 车 上 一 直 杆 A_的上 端 ; 求 当 另 B 试 小车以加速度 “水平 向左做匀加速 运动时 , 求轻绳 对小 球 作 用 力 的 大 小 和方 向.
与重力 同 向; O 当 ≤
与重 力 反 向 , 选 项 C正 确 , 故 D
ZH ONGX J A UE I OXUE C ANKA O
解 题 方 法与技 巧
利 用 知 识 迁 移 巧 解 电 功 率 计 算
g
可见轻绳对小球 的作用 力大 小随着 加速 度 n的改
变 而改 变 , 它 的方 向一 定 是 在 绳 子 的 方 向上 . 但
【 2 如 图 3 示 , 车 上 固 例 】 所 小 定一 弯 折 硬 杆 AB C 端 固 定 一 质 C, 量 为 的小 球 , : 问 () 1 当小车向左匀速直线运动时, A B 杆 对小球作用力 的大 小和方 向. C () ( ) 小 车 以 加 速 度 水 平 向 2当 左做匀加速直线运 动时 , C杆对小 B 球作用力 的大小和方 向. 解析 : 以小 球 为研 究 对 象 进行 受 力分 析 , 球 受 两 个 力 作 用 : 力 m 小 重 g
物理经典模型(三:绳,弹簧与杆的不变与突变)最新修正版

物理经典模型(三:绳,弹簧与杆的不变与突变)绳子、弹簧和杆产生的弹力特点..............1. 轻绳:(1) 轻绳模型的特点:“绳”在物理学上是个绝对柔软的物体,它只产生拉力(张力),绳的拉力沿着绳的方向并指向绳的收缩方向。
它不能产生支持作用。
它的质量可忽略不计,轻绳是软的,不能产生侧向力,只能产生沿着绳子方向的力。
它的劲度系数非常大,以至于认为在受力时形变极微小,看作不可伸长。
(2) 轻绳模型的规律:①轻绳各处受力相等,且拉力方向沿着绳子;②轻绳不能伸长;③用轻绳连接的系统通过轻绳的碰撞、撞击时,系统的机械能有损失;④轻绳的弹力会发生突变。
2. 轻杆:(1) 轻杆模型的特点:轻杆的质量可忽略不计,轻杆是硬的,能产生侧向力,它的劲度系数非常大,以至于认为在受力时形变极微小,看作不可伸长或压缩。
(2)轻杆模型的规律:①轻杆各处受力相等,其力的方向不一定沿着杆的方向;②轻杆不能伸长或压缩;③轻杆受到的弹力的方式有拉力或压力。
3. 轻弹簧:(1)轻弹簧模型的特点:轻弹簧可以被压缩或拉伸,其弹力的大小与弹簧的伸长量或缩短量有关。
(2)轻弹簧的规律:①轻弹簧各处受力相等,其方向与弹簧形变的方向相反;②弹力的大小为F=kx ,其中k 为弹簧的劲度系数,x 为弹簧的伸长量或缩短量; ③弹簧的弹力不会发生突变。
esp1:如图所示,一质量为m 的物体系于长度分别为L 1、L 2的两根细绳OA 、OB 上,0B一端悬挂在天花板上,与竖直方向夹角为θ,OA 水平拉直,物体处于平衡状态,现在将OA 剪断,求剪断瞬间物体的加速度,若将绳OB 换为长度为L 2的弹簧,结果又如何?(1)剪断前,两种情况小球受力一样,分别如图(1)、(2)所示,利用平衡条件,则mg 与F 2的合力与F 1大小相等,方向相反,可以解得F 1=mgtg θ。
(2)剪断后瞬间,绳OA 产生的拉力F 1消失,力也立即发生变化,这时F 2将发生瞬时变化,mg 与F 2于小球下一时刻做单摆运动沿圆弧的切线方向,与绳垂直,如图(3)所示,F 合=mgsinθ,所以a=gsin θ。
力学中常见的三种模型--对“轻杆、轻绳、轻弹簧”理解与应用

【 中图分类号】 G 6 3 3 . 8
【 文献标识码 】 A
【 文章编号】 2 0 9 5 — 3 0 8 9 ( 2 0 1 3 ) 0 9 — 0 1 6 0 — 0 2
半径方 向的速度对应 的能量 转换成 绳的 内 能, 即此 极短 时间 内机械 能 不 守恒 : 高中阶段 只考虑拉伸形 变, 绳上的弹力表现 从 B至 c, 由机 械 能 守恒 :
。
V
辩 璺 图3
2 . 轻绳的形变 为拉 力 . 方 向在 绳 上 并指 向绳 子收 缩 的方 向 。 m g L( 1 一 s i n 0 ) :÷ m v 一÷ m 3 . 轻弹簧的形 变 高中阶段只考虑压缩与拉伸 两种情况, 弹 力表现为拉力或压力, 其大小根据胡克定律求解 。 ( 其中 v B = v B c o s 0 )
二 二
Байду номын сангаас
二、 弹 力作 用效 果与 实 际应 用 1 . 轻 绳 上 的弹 力 变化 具 有 瞬时性 ( 突变 ) 例 2 : 如图4 , 物体 的 质 量 为 i n . 由 两 绳 系住 处 于静 止 状 态 ,
‘ .
V c = 、 / 2 g L ( 1 一 s i n 0 ) +
一
、
图4
2 . 轻弹簧上的弹力变化具有缓慢性 ( 不 突变) 瞬 间 ,当引起 弹 簧形 变的原 因变化 后 ,弹簧
上的 弹 力不 可 能马 上恢 复 形 变 .导 致 弹 力的 变化 有一 时 间过程 。 例3 :将 例 2中的 B O 绳 换成 轻 弹簧 .剪 断 动。 O A绳瞬间. 求 绳上 的拉 力 大 小。 解析 : 剪 断 绳 OA 的 , 物体 受 两个 力 作 用 , 重力不变, 拉 力 来 解析 : ( 1 ) 小 车 匀速 运动 , 小球 受合 力 为零 , 所 以 小球 受 弹 力 不及 变化 , 所 以 BO 绳上 的拉 力仍 为 1 " 1 2 g / c o s e 。 与重 力等 大 、 反 向。 3 . 轻 绳 发 生形 变时可 能伴 随 着的 能 量 的 变化 ( 2 ) 小球也 向右匀加速运动, 根据牛顿第二定律 , 小球的弹力 应随加速度大小有多种情况 , 如图所示( 只显示两种情况) 。 例 4 : 如图 6 , 轻绳 长 L , 一 端 可 绕 。 转 动. 另 一端 系一质 量 为 m 的 小球 , 起 初将 绳 绷
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弹簧,轻杆,绳件模型
[模型概述]
挂件问题是力学中极为常见的模型,其中绳件、弹簧件更是这一模型中的主要模具,相关试题在高考中一直连续不断。
它们间的共同之处是均不计重力,但是它们在许多方面有较大的差别。
[模型回顾]
1. 轻绳
(1)轻绳模型的特点
“绳”在物理学上是个绝对柔软的物体,它只产生拉力(张力),绳的拉力沿着绳的方向并指向绳的收缩方向。
它不能产生支持作用。
它的质量可忽略不计,轻绳是软的,不能产生侧向力,只能产生沿着绳子方向的力。
它的劲度系数非常大,以至于认为在受力时形变极微小,看作不可伸长。
(2)轻绳模型的规律
①轻绳各处受力相等,且拉力方向沿着绳子;
②轻绳不能伸长;
③用轻绳连接的系统通过轻绳的碰撞、撞击时,系统的机械能有损失;
④轻绳的弹力会发生突变。
2. 轻杆
(l)轻杆模型的特点
轻杆的质量可忽略不计,轻杆是硬的,能产生侧向力,它的劲度系数非常大,以至于认为在受力时形变极微小,看作不可伸长或压缩。
(2)轻杆模型的规律
①轻杆各处受力相等,其力的方向不一定沿着杆的方向;
②轻杆不能伸长或压缩;
③轻杆受到的弹力的方式有拉力或压力。
3. 轻弹簧
(1)轻弹簧模型的特点
轻弹簧可以被压缩或拉伸,其弹力的大小与弹簧的伸长量或缩短量有关。
(2)轻弹簧的规律
①轻弹簧各处受力相等,其方向与弹簧形变的方向相反;
②弹力的大小为F=kx,其中k为弹簧的劲度系数,x为弹簧的伸长量或缩短量;
③弹簧的弹力不会发生突变。
[模型讲解]
1、如图1中a所示,一质量为m的物体系于长度分别为l1、l2的两根细线上,l1的一端悬挂在天花板上,与竖直方向夹角为θ,l2水平拉直,物体处于平衡状态。
现将l2线剪断,求剪断瞬时物体的加速度。
(a)a=gsinθ(b)a=gstgθ
2、一根细绳,长度为L ,一端系一个质量为m 的小球,在竖直面内做圆周运动,求小球通过最高点时的速度至少是多少?若将绳换为一根匀质细杆,结果又如何?
1)对绳来说,是个柔软的物体,
它只产生拉力,不能产生支持作用,
小球在最高点时,
弹力只可能向下,如图(1)所示。
这种情况下有
mg
L mv
mg F ≥=+2 即gL v ≥,否则不能通过最高点。
(2)对细杆来说,是坚硬的物体,它的弹力既可能向上又可能向下,速度大小v 可以取任意值。
可以进一步讨论:
①当杆对小球的作用力为向下的拉力时,如图(2)所示: F+mg=L mv 2
>mg 所以 v >gL
②当杆对小球的作用力为向上的支持力时,如图(3)所示:
mg -F=L mv 2
<mg 所以 v <gL
当N=mg 时,v 可以等于零。
③当弹力恰好为零时,如图(4)所示: mg=L
mv 2
所以 v=gL
3、如图所示,
m 的小球,已知α=30°恒定。
当小车水平向左以v=0.5m/s
的速度匀速运动时,BC 杆对小球的作用力的大小是
mg ,方向是垂直向上;当小车水平向左以a=g 的加速度
作匀加速运动时,BC 杆对小球的作用力的大小是 2mg ,方向是与水平方向夹角为450。
4、如图2所示,质量为m 的小球用长为L 的细绳系于O 点,把小球拿到O 点正上方且使细绳拉直的位置A 后,以的速度水平向右弹出(空气阻力不计)
(1)小球从弹出至下落到与O 点等高的位置这一过程中,小球做什么运动,请说明理由;平抛运动。
(2)求小球到达最低点时细绳上的拉力大小。
5、(2006年无锡统考)如图(a )轻绳AD 跨过固定在水平横梁BC 右端的定滑轮挂住一个质量为M1的物体。
∠ACB=30°;图(b )中轻杆HG 一端用铰链固定在竖直墙上,另一端G 通过细绳EG 拉住,EG 与水平方向也成30°,轻杆的G 点用细绳GF 拉住一个质量为M2的物体,求细绳AC 段的张力FTAC 与细绳EG 的张力FTEG 之比?
图5
解析:图(a )中绳AC 段的拉力FTAC =M1g
图(b )中由于FTEGsin30°=M2g ,解得:
212M M F F TEG TAC
=
在水平地面上放一重为30N 的物体,物体与地面间的滑动摩擦因数为33。
若要使物体在
地面上做匀速直线运动,问F 与地面的夹角为多大时最省力,此时的拉力多大?Fmin=
N mg
15)33
(
13033
122=+⨯=+μμ
6、如图所示,在水平桌面上叠放着质量均为M 的A 、B 两块木板,在木板A 的上面放着一个质量为m 的物块C ,木板和物块均处于静止状态.A 、B 、C 之间以及B 与地面之间的动摩擦因数都为μ.若用水平恒力F 向右拉动木板A ,使之从C 、B 之间抽出来,已知重力加速度为g ,则拉力F 的大小应该满足的条件是(已知最大静摩擦力的大小等于滑动摩擦力)( C )
A .F >μ(2m +M)g
B .F >μ(m +2M)g
C .F >2μ(m +M)g
D .F >2μmg
7、[2011·天津卷] 如图所示,A 、B 两物块叠放在一起,在粗糙的水平面上保持相对静止地向右做匀减速直线运动,运动过程中B 受到的摩擦力( A )
A .方向向左,大小不变
B .`方向向左,逐渐减小
C. 方向向右,大小不变
D. 方向向右,逐渐减小
8、(2005年烟台市检测题)如图1所示,将一根不可伸长、柔软的轻绳左、右两端分别系于A 、B 两点上,一物体用动滑轮悬挂在轻绳上,达到平衡时,两段绳子间的夹角为1θ,绳子张力为1F ;将绳子右端移到C 点,待系统达到平衡时,两段绳子间的夹角为2θ,绳子张力为2F ;将绳子右端再由C 点移到D 点,待系统达到平衡时,两段绳子间的夹角为3θ,
绳子张力为
3F ,不计摩擦,并且BC 为竖直线,则( A ) A.
321θθθ<= B. 321θθθ== C. 321F F F >> D. 3
21F F F >= 9、在图6所示的装置中,绳子与滑轮的质量不计,摩擦不计,
悬点a 与b 之间的距离远大于两轮的直径,两个物体的质量分
别为m1和m2,若装置处于静止状态,则下列说法错误的是
( C )
A. 2m 可以大于1m
B. 2m 必定大于21
m
C.
2m 必定等于1m D.
1θ与2θ必定相等。
