数字电路教程
数字电路与逻辑设计教程-第1章

1.2 数制和码制
【例1-4】求十进制数(26)10所对应的二进制数。
因此(26)10=(11010)2。
上一页 下一页 返回
1.2 数制和码制
【例1-5】求十进制数(357 ) 10所对应的八进制数。 解
因此(357 )10=(545)8。
上一页 下一页 返回
1.2 数制和码制
上一节介绍了数字信号的两种取值,实际生活中的数字表示 大多采用进位计数制。
下一页 返回
1.2 数制和码制
1.2.1 进位计数制与常用计数制
用数字量表示物理量大小时,仅用一位数码往往不够用,经 常需要用进位计数的方法组成多位数码表示。把多位数码中 每一位的构成方法以及从低位到高位的进位规则称为计数制 。在生产实践中除了人们最熟悉的十进制以外,还大量使用 各种不同的进位计数制,如八进制、十六进制等。在数字设 备中,机器只认识二进制代码,由于二进制代码书写长,所 以在数字设备中又常采用八进制代码或十六进制代码。
上一页 下一页 返回
1.2 数制和码制
任何进制数的值都可以表示为该进制数中各位数字符号值与 相应权乘积的累加和形式,该形式称为按权展开的多项式之 和。一个J进制数(N为按权展开的多项式的普遍形式可表示为 :
式中,K为任意进制数中第i位的系数,可以为0~ (J-1)数码中 的任何一个;i是数字符号所处位置的序号;m和n为整数,m为 小数部分位数(取负整数),n为整数部分位数(取正整数);.J为 进位基数,Ji为第i位的权值。例如,十进制数(123.75 )10表示 为:
第1章 微型计算机系统概述
1.1 数字电路概述 1.2 数制和码制 1.3 逻辑代数基础 本章小结
1.1 数字电路概述
数字电路基础教程

A
F ABC
B C
&F
(1-24)
或非:条件
A、B、C任一 具备,则F 不 发生。
A
F ABC B
C
异或:条件
A、B有一个具 备,另一个不 具备则F 发生。
F AB AB AB
A
B C
同或:条件
A、B相同,则 F 发生。
F AB A B A
B
A B
0010
0011 0100 0101 0110 0111 1000
1001
1010 1011 1100 1101 1110 1111
0
0
0
0
1
1
1
1
2
2
2
2
3
3
3
3
0
4
4
4
4
1
5
5
6
6
7
7
8
8
2
3
4
5
5
9
9
6
6
10
7
7
11
5
8
8
12
6
9
9
13
7
14
8
15
9
(1-17)
§1.2 基本逻辑关系
基本逻辑关系:与 ( and )、或 (or ) 非 ( not )。
• 信号放大及运算 (信号放大、功率放大) • 信号处理(采样保持、电压比较、有源滤波) • 信号发生(正弦究的问题
基本电路元件 基本数字电路
• 逻辑门电路 • 触发器
• 组合逻辑电路 • 时序电路(寄存器、计数器、脉冲发生器、
数字电子技术基础教程
第6页/共55页
2.2 逻辑代数的基本定律和规则
反演律 吸收律
A B AB
A AB A
A B A B A (A B) A
A B A B A
(A B)(A B) A
A AB A B
A(A B) AB
冗余律
AB AC BC AB AC
(A+B)(A+C)(B C) (A+B)(A+C)
F AB
2.或非逻辑
F AB
A
F
&
B
与非门
A
F
B
或非门
3. 与或非逻辑
&
F AB CD
第20页/共55页
异或逻辑与同或逻辑
4.异或逻辑
F A B AB AB
A
=1
F
B
5.同或逻辑 F=A ⊙ B= AB AB
A
=
F
B
AB F
00 0 01 1 10 1 11 0
AB F
00 1 01 0 10 0 11 1
② 任意两个i0最小项之积恒i为0A0B,C任·意AB两C个=最0大项之
和恒等于1 。
mi m j 0(i j)
Mi M j 1(i j)
③ n 变量的每一个最小(大)项有n 个相邻项
(相邻项是指两个最小项只有一个因子互为反变
量,其余因子均相同,又称为逻辑相邻项)。
第32页/共55页
2.6 逻辑代数的K诺图
ABC ABC ABC
最大项表达式:
F ( A B C)( A B C)( A B C)
第28页/共55页
最大项的Mi表示
n个变量可以构成2n个最大项。最大项用符号Mi表示。与 最小项恰好相反,对于任何一个最大项,只有一组变量 取值使它为0,而变量的其余取值均使它为1。
数字集成电路与eda设计基础教程

数字集成电路与eda设计基础教程数字集成电路与EDA设计基础教程数字集成电路(Digital Integrated Circuits, DIC)是由数字逻辑门电路组成的集成电路。
它们是现代电子设备中的核心组成部分,广泛应用于计算机、通信、控制系统等领域。
而EDA(Electronic Design Automation)设计则是指利用计算机辅助工具进行集成电路设计的过程。
数字集成电路的发展历程可以追溯到二十世纪四十年代。
随着半导体材料和工艺的不断进步,集成电路的规模和功能不断扩大,从最早的小规模集成电路(SSI)发展到现在的大规模集成电路(LSI)和超大规模集成电路(VLSI)。
这些数字集成电路的设计需要借助EDA工具进行。
EDA设计是通过计算机辅助设计软件实现的。
它可以帮助设计师在电路设计的不同阶段进行各种分析和验证,从而提高设计效率、降低成本。
EDA设计的主要任务包括逻辑设计、电路设计、布局设计和物理验证等。
逻辑设计是指根据电路功能要求,采用逻辑门电路来实现电路功能的设计过程。
逻辑设计常常采用硬件描述语言(HDL)来描述电路的行为,并通过逻辑综合工具将其转化为门级电路网表。
常用的HDL语言有VHDL和Verilog。
电路设计是指根据逻辑设计所得的门级电路网表,通过选择合适的器件和电路拓扑结构,设计出满足电路功能和性能要求的电路。
电路设计需要考虑到电路的功耗、延迟、面积等因素,并进行合适的优化。
布局设计是指根据电路设计所得的电路图,将电路各个组件和连线进行合理的排布,形成最终的版图。
布局设计需要考虑到电路的物理约束和制造工艺的要求,以保证电路的可制造性和可靠性。
物理验证是指通过各种验证手段,验证电路的功能、时序、功耗、电磁兼容等方面的性能。
常用的物理验证手段包括时序分析、功耗分析、电磁兼容分析等。
数字集成电路与EDA设计的基础知识包括布尔代数、组合逻辑电路、时序逻辑电路等。
布尔代数是描述逻辑门电路行为的数学工具,它可以用来分析和简化逻辑电路。
数电简明教程第一章 逻辑代数基础知识

10
第六章 脉冲产生与整形电路
概述 6.1 施密特触发器
11
12
概 述
一、逻辑代数(布尔代数、开关代数) 逻辑: 事物因果关系的规律 逻辑函数: 逻辑自变量和逻辑结果的关系
Z f ( A, B, C )
逻辑变量取值:0、1 分别代表两种对立的状态 一种状态 另一状态 高电平 真 低电平 假 是 非 有 无 … … 1 0 0 1
概述 3.1 3.2 3.3 3.4 3.5 组合电路的分析方法和设计方法 加法器和数值比较器 编码器和译码器 数据选择器和分配器 用 MSI 实现组合逻辑函数
8
第四章
概述
触发器
4.1 基本触发器 4.2 同步触发器 4.3 边沿触发器 4.4 触发器的电气特性
9
第五章
时序逻辑电路
概述 5.1 时序电路的基本分析和设计方法 5.2 计数器 5.3 寄存器和读/写存储器
( 26 )10 = 16 + 8 + 2 = 24 +23 + 21 = ( 1 1 0 1 0 )2
16 8 4 2 1
20
(3) 二-八转换: 每 3 位二进制数相当一位 8 进制数
( 0 10 101 111 ) 2 ( 257 )8
2 5 7
( 0 1 0 0 1 1 1 0 0 0 0 1. 0 0 0 1 1 0 )2 ( 2 3 4 1 . 0 6 )8
(4) 八-二转换: 每位 8 进制数转换为相应 3 位二进制数
( 31. 47 )8 ( 011 001 . 100 111
)2
)2
( 375.64 )8 ( 011 111 101 . 110 100
《数字电路》教学大纲

一、总则1.本课程的教学目的和要求:本课程是我院计算机科学与技术专业的一门专业基础课程。
通过本课程的学习,使学生熟悉数字电路的基础理论知识,理解基本数字逻辑电路的工作原理,掌握数字逻辑电路的基本分析和设计方法,具有应用数字逻辑电路,初步解决数字逻辑问题的能力,为以后学习计算机组成原理、微机原理、单片机原理等后续课程的学习以及从事数字电子技术领域的工作打下扎实的基础。
2.本课程的主要内容:逻辑代数的公式、定理,逻辑函数的化简方法。
半导体二极管、三极管、MOS管的开关特性。
CMOS、TTL集成逻辑门。
组合电路的基本分析和设计方法。
加法器、比较器、编码器和译码器、数据选择器和分配器,只读存储器。
基本、同步、主从、边沿触发器,时钟触发器功能分类及转换。
时序电路的基本分析和设计方法。
计数器、寄存器、读/写存储器、顺序脉冲发生器。
多谐振荡器、施密特触发器。
数模、模数转换器。
3.教学重点与难点:教学重点是:逻辑代数的基本概念、公式、定理,逻辑函数的化简方法。
各种门电路的逻辑功能,两种集成逻辑门的电气特性。
各类触发器的逻辑功能及触发方式。
组合、时序电路的分析、设计方法。
常用典型组合、时序电路的功能、特点和应用。
典型中、大规模集成电路器件的功能和应用。
多谐、施密特、单稳的特点、功能、参数及应用。
数模、模数转换器的典型电路原理、输出量与输入量间的定量关系,特点、参数。
教学难点:逻辑代数的公式、定理的正确应用,逻辑函数化简的准确性。
集成逻辑门的电气特性。
组合、时序电路的设计。
触发器的触发方式以及脉冲产生,整形电路、数模、模数转换电路的工作原理。
4.本课程的知识范围及与相关课程的关系本课程是计算机科学与技术专业的硬件基础课程,其先修课为高等数学、普通物理、电路基础、模拟电路,后读课程为计算机组成原理、微机原理、单片机原理、计算机接口技术、计算机网络技术等。
5.教材的选用:数字电子技术基础简明教程(第二版)清华大学电子学教研组编余孟尝主编高等教育出版社1999年10月第2版二、课程内容及学时分配:第一章逻辑代数基础1.教学内容:概述逻辑代数、数制及其转换、BCD码。
Orcad数字电路仿真简明教程
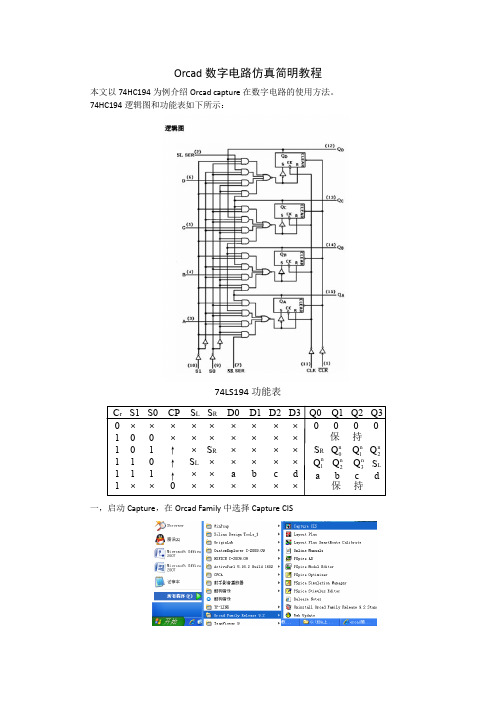
Orcad数字电路仿真简明教程本文以74HC194为例介绍Orcad capture在数字电路的使用方法。
74HC194逻辑图和功能表如下所示:74LS194功能表C r S1 S0 CP S L S R D0 D1 D2 D3Q0 Q1 Q2 Q30 1 1 1 1 1×11××11×××↑↑↑×××S L××××S R×××××××a×××××b×××××c×××××d×0 0 0 0保持S R nQ n1Q n2Qn1Q n2Q n3Q L Sa b c d保持一,启动Capture,在Orcad Family中选择Capture CIS二,启动软件后,在菜单栏中选择File>New>Project,新建一个工程三,在New Project窗口中选择Analog or Mixed A/, 键入工程名以及选择工作路径,点击OK四,选择Create a blank pro,点击OK五,进入如下图工作界面后,在最右侧工具栏中选择按钮添加元件六,在新窗口中选择Add Library添加74hc.olb和sourcstm.olb等所需库,点击打开七,在74HC中选取所需要的元件,点击OK后放置至图纸上八,右侧工具栏中的按钮可用于连线,若需对连线标号则用九,按照74HC194的逻辑图将电路完成(逻辑图中的SR触发器可暂时由74HC107的JK 触发器代替),若图纸大小不够可以通过菜单栏Options> Schemactic Page Properties调整(注意:所有元件的序号不能重复,在绘图时若用到复制,需修改复制后的元件序号,否则仿真时会出错!)十,电路完成后,在中选择SOURCSTM的DigStim1作为1位信号的激励源十一,选中激励右键选择Edit PSpice Stimulus可编辑激励源形式十二,Stimulus Editor中提供了多种激励形式,在此选择Digital型作为数字信号源,Clock 为时钟型,信号呈周期性变化,可跟据时钟频率,占空比,初值,信号延时等参数设定Signal为一般形式信号,先选定一个初值,然后可通过Stimulus Editor工具栏中的点击信号上的位置使之翻转添加新激励信号时也可选择Stimulus>New,添加后双击电路图激励源上的Implementation将value改为所对应的激励信号即可除此之外,还可通过编辑文本激励的方式完成,文件格式为<project_name.stl>,其中project_name为所建的工程名,编辑完后在Stimulus Editor打开即可十三,所有激励设定完毕后通过下图工具栏中的建立仿真文件十四,在中设置仿真条件十五,设置完成后点击进行仿真,给所需查看波形的信号加电压探针,观察仿真结果。
数字集成电路教程课程设计

数字集成电路教程课程设计一、课程设计简介本次数字集成电路教程课程设计的目的是让同学们通过实践掌握数字集成电路的基本概念和设计方法,为日后从事数字电路设计打下坚实的基础。
本次课程设计主要分为三个部分,分别是:1.设计基础电路:包括组合逻辑电路和时序逻辑电路的设计;2.器件的选型和仿真:通过工具对所选用的器件进行仿真,并进行性能分析;3.电路的综合:将前两个步骤中设计出来的电路进行综合,实现所需的功能。
本次课程设计需要利用Quartus II软件进行仿真和综合,并需要使用DE10-Lite开发板进行验证。
在设计过程中,需要注意电路自检功能以及实际调试时电路的稳定性和可靠性。
二、设计基础电路1. 组合逻辑电路1.1 电路设计目标将任意两个4位二进制数进行加法运算,并将结果以4位二进制码输出。
1.2 电路设计思路使用全加器电路将两个4位二进制数进行加法运算,并将其中一个4位二进制数作为初始值。
在这一过程中,由于进位的存在需要进行进位的判断。
最终,将运算结果转换为4位二进制码输出。
1.3 电路设计图4位全加器电路设计图1.4 电路仿真结果4位全加器电路仿真结果图2. 时序逻辑电路2.1 电路设计目标设计一个进行计数的电路,通过按键控制该电路的计数起始值和计数的步进值,并且在计数到一定值时能够自动清零。
2.2 电路设计思路本电路通过使用锁存器进行计数,根据不同按键输入进行计数的起始值和步进值的设置,并通过比较电路判断当前计数值是否达到所设定的上限,一旦达到则将计数器清零。
2.3 电路设计图计数器电路设计图2.4 电路仿真结果计数器电路仿真结果图三、器件的选型和仿真1. 器件的选型本次课程设计中使用的器件主要包括ALU、全加器、锁存器、按键、LED等。
其中,ALU和全加器的性能对电路的计算能力有很大的影响,因此需要特别注意其性能和功耗。
锁存器的选型需要考虑其在时序电路中的可靠性和时序准确性。
按键和LED的选型需要考虑其信号响应速度和使用寿命。
数字电子技术基础简明教程第三版

AB BC
与或非表达式
转换方法举例
与或式 与非式
或与式 或非式 与或非式
Y AB BC
Y ( A B)(B C )
AB BC 用还原律 AB BC 用摩根定律
( A B)(B C ) 用还原律 A B B C 用摩根定律
AB BC 用摩根定律
二、逻辑函数式化简的意义与标准
化
使逻辑式最简,以便设计出最简的逻辑电路,
简 意
从而节省元器件、优化生产工艺、降低成本和提
义 高系统可靠性。
不同形式逻辑式有不同的最简式,一般先求取 最简与 - 或式,然后通过变换得到所需最简式。
最简与 - 或式标准
(1)乘积项(即与项)的个数最少 (2)每个乘积项中的变量数最少
用与门个数最少 与门的输入端数最少
4 个输入
0
0
1
0
1
变量有 24
0 0
0 1
1 0
1 0
0 1
= 16 种取 0
1
0
1
1
值组合。 0
1
1
0
1
0
1
1
1
0
1
0
0
0
1
1
0
0
1
1
1
0
1
0
1
1
0
Байду номын сангаас
1
1
0
1
1
0
0
0
1
1
0
1
0
1
1
1
0
0
1
1
1
1
0
2. 逻辑函数式 表示输出函数和输入变量逻辑关系的 表达式。又称逻辑表达式,简称逻辑式。
VHDL数字电路设计教程第3讲 数据类型

7)自然数(natural)和正整数(positive)
natural是integer的子类型,表示非负整数。 positive是integer的子类型,表示正整数。
定义如下:
subtype natural is integer range 0 to integer’high; subtype positive is integer range 1 to integer’high;
bit_vector(0 to 15);
SUBTYPE语句格式:
subtype 子类型名 is 基本数据类型 约束范围; 例: subtype digits is integer range 0 to 9;
由subtype 语句定义的数据类型称为子类型。
22
3.4 数组(ARRAY)
数组是将相同数据类型的数据集合在一起形成 的一种新的数据类型。可以是1D、2D或1D*1D,更高 维数的数组往往是不可综合(即综合库中没有直接 可以调用的器件)的。 数组的结构:
20
3.3 子类型
子类型是已定义的类型或子类型的一个子集。 格式: subtype 子类型名 is 数据类型名[范围]; 例: bit_vector 类型定义如下:
type bit_vector is array (natural range <>) of bit;
如设计中只用16bit;可定义子类型如下: subtype my_vector is 注:子类型与基(父)类型具有相同的操作符和子 程序。可以直接进行赋值操作。 21
9
6)整数(integer)
integer 表示所有正的和负的整数。硬件实现时, 利用32位的位矢量来表示。可实现的整数范围为: -(231-1) to (231-1)
数字电子技术基础简明教程(第三版)余孟尝第三章-完成ok

第三章 组合逻辑电路【】 分析图P3.1电路的逻辑功能,写出Y 1、Y 2的逻辑函数式,列出真值表,指出电路完成了什么逻辑功能.Y 1【解】1()Y ABC A B C AB AC BC ABC ABC ABC ABC=+++•++=+++2Y AB BC AC =++由真值表可见,这是一个全加器电路。
A 、B 、C 为加数、被加数和来自低位的进位,Y 1是和,Y 2是进位输出。
【】 图3.2是对十进制数9求补的集成电路CC14561的逻辑图,写出当COMP=1;Z=0和COMP=0,Z=0时Y 1,Y 2,Y 3,Y 4的逻辑式,列出真值表。
Y 1Y 2Y 3Y 4A 1A 2A 3A 4Z【解】(1)COMP=1、Z=0时输出的逻辑式为11223234234Y A Y A Y A A Y A A A⎧=⎪=⎪⎨=⊕⎪⎪=++⎩ 〔2〕COMP=0、Z=0时输出的逻辑式为11223344Y A Y A Y A Y A =⎧⎪=⎪⎨=⎪⎪=⎩〔即不变换,真值表从略〕3个或3个以上为1时输出1,输入为其他状态时输出0。
【解】Y ABCD ABCD ABCD ABCD ABCD ABC ABD ACD BCD ABC ABD ACD BCD=++++=+++=•••B D Y【】 有一水箱由大、小两台水泵M L 、M S 供水,如图P3.4所示.水箱中设置了3个水位检测元件A、B 、C 。
水面低于检测元件时,检测元件给出高电平;水面高于检测元件时,检测元件给出低电平。
现要求当水位超过C 点时水泵停止工作;水位低于C 点高于B 点时M S 单独工作;水位低于B 点而高于A 点时M L 单独工作;水位低于A 点时M L 、M S 同时工作。
试用门电路设计一个控制两台水泵的逻辑电路,要求电路尽量简单。
【解】图P3.4M L真值表中的ABC 、ABC 、ABC 、ABC 为约束项,利用卡诺图【图A3.4(a)】化简后得到S L M A BCM B⎧=+⎪⎨=⎪⎩ 〔M S 、M L 的1状态表示工作,0状态表示停止〕 逻辑图如图A3.4(b).S M A BC =+L M B =〔a 〕(b)A B CM SM L【】。
数字电子技术基础简明教程第三版

注意
置 0 端 RD 和置 1 端 SD 低电平有效。
禁用 RD = SD = 0。
称约束条件
EXIT
[例] 设下图中触发器初始状态为 0,试相应输入波形 画出 Q 和 Q 旳波波形形。分析举例
RD R
Q RD
SD S
Q SD
保持 置 0保持置 1 初态为 0,故保持为 0。
解:
Q
Q
EXIT
(二)基本 RS 触发器旳两种形式
EXIT
一、基本 RS 触发器 Basic Flip - Flop
(一)由与非门互正构补常输工成出 作旳端时基,, 本 RS 触发器
1. 电路构它造们及旳逻输辑出符号 状态相反。
Q
Q
Q
Q
低电平有效
SR
G1
G2
SD
RD
SD 信号输入端 RD
置1端,也 置0端,也 称置位端。 称复位端。 S 即 Set R 即 Reset
触 CP 上升沿(或下降沿)时刻翻转。
发
这种触发方式称为边沿触发式。
器
EXIT
主从触发器和边沿触发器有何异同?
相
只能在 CP 边沿时刻翻转,所以都克服了
同
处 空翻,可靠性和抗干扰能力强,应用范围广。
电路构造和工作原理不同,所以电路功能 相 不同。为确保电路正常工作,要求主从 JK 触 异 处 发器旳 J 和 K 信号在 CP = 1 期间保持不变;而
Q
Q
Q
Q
1S C1 1R
1D C1
CP D CP
同步 D 触发器功能表
D
CP D Qn+1 ❖ 阐
明
称为 D 功能
VHDL数字电路设计教程第10讲 函数和过程

15
例 11.4(2): 在主代码中调用在包集中定义的函数。
---------------在主代码中调用包集中定义的函数------------------library ieee; use ieee.std_logic_1164.all; use work.my_package.all; entity dff is port(d, clk, rst: in std_logic; q: out std_logic ); end dff; architecture my_arch of dff is begin
声明信号 注意:在输入参数 列表中仍然不能指 定信号的范围 注意:虽然不知道输入信号 的范围,但可以函数被调用 时使用s’length来获取输入 参数的具体范围
function conv_integer (signal vector: std_logic_vector) return integer is variable result: integer range 0 to 2**vector’length-1; begin if (vector(vector’high)=‘1’) then result:=1; else result:=0; end if; for i in (vector’high-1) downto (vector’low) loop result:=result*2; if (vector(i)=‘1’) then result:=result+1; end if; end loop; return result; end conv_integer; ----------------函数的调用--------------........ y<=conv_integer (a); ....
数字电路 课程教学大纲

数字电路课程教学大纲一、课程的基本信息适应对象:本科,电子科学与技术、电子信息工程、通信工程课程代码:A7D00514学时分配:64赋予学分:4先修课程:电路分析、模拟电子技术后续课程:单片机原理、微机原理、自动控制原理、EDA技术二、课程性质与任务《数字电路》是电子信息类和电气类(包括电子类、电气类、自动控制类)各专业的专业基础课程,是一门实践性很强的技术基础课。
课程的任务是使学生获得数字电子技术方面的基本理论、基本知识和基本技能,培养学生分析问题和解决问题的能力。
即通过本课程的学习,使学生在理解数字电路的基本概念、基本电路的工作原理和基本分析方法的基础上,能熟悉数字集成电路的工作原理、外特性和功能,掌握数字电路的分析方法,具备正确运用数字集成电路设计和调试数字系统的能力,为深入学习后续相关课程以及今后从事专业工作打下良好的基础三、教学目的与要求1、课程教学目的:数字电路课程是电子科学与技术专业本科生的技术基础课程,它涉及数字技术中的基本原理、基本概念和基本方法,具有很强的工程实践性。
设置本课程的目的是使学生通过该课程的学习,理解和掌握数字电路的基本原理,基本概念和基本数字电路的分析和设计方法,掌握常用的中、小规模集成逻辑器件的功能应用,学会使用各种数字集成芯片设计各种数字电路,并通过实验学会使用常用电子仪器测量和调试各种数字电路的方法,更好地培养学生在工程实践方面独立分析问题和解决问题的能力。
2、课程教学基本要求在《数字电路》理论课程教学过程中,理论课程教学内容要新颖,信息量要大。
课程讲授要把握两个淡化:淡化电路的内部结构,强调电路的外部特性;淡化逻辑表达式的化简,强调电子设计自动化的优化作用。
三个注意:注意新技术的发展,引入可编程逻辑器件;注意描述方法的变化,引入Verilog HDL描述语言;注意系统分析方法,引入数字系统设计。
在《数字电路》实验课程教学过程中,实验课程内容的技术性、综合性和探索性的关系要做到处理得当。
数字电路技术教程

数字电路的应用与发展趋势
总结词
数字电路广泛应用于计算机、通信、控制等领域,随 着技术的发展,其发展趋势包括更高的集成度、更快 的速度和更低的功耗。
详细描述
数字电路因其可靠、精确、速度快和易于大规模集成等 特点,被广泛应用于各个领域,如计算机、通信、控制 等。随着技术的不断发展,数字电路也在不断进步和完 善。未来,数字电路的发展趋势包括更高的集成度、更 快的速度和更低的功耗。更高的集成度可以使得电子设 备更加小型化和高性能化;更快的速度可以满足高速信 号处理和高频通信的需求;更低的功耗则有助于降低设 备的运行成本和减少能源消耗。
数字电路与模拟电路的区别
总结词
数字电路和模拟电路在信号处理方式、电路结构和应 用领域等方面存在显著差异。模拟电路处理连续变化 的信号,而数字电路处理离散的二进制信号。此外, 数字电路具有更高的可靠性和精确度,且易于实现大 规模集成。
详细描述
模拟电路和数字电路在处理信号的方式上有根本的区别 。模拟电路处理的是连续变化的信号,这些信号的值可 以在一个连续的范围内变化。相比之下,数字电路处理 的是离散的二进制信号,这些信号的值只能是0或1。 由于数字电路处理的是离散信号,因此其具有很高的可 靠性和精确度,这使得数字电路在许多领域中取代了模 拟电路。此外,数字电路易于实现大规模集成,使得现 代电子设备能够实现高性能和小型化。
计算器的组成
计算器一般由键盘、显示器、微处理器、存储器等组成。
计算器的设计步骤
首先确定设计方案,然后选择合适的微处理器和存储器等器件,接着 进行电路设计,最后进行仿真和调试。
计算器的实现
根据设计好的电路图,将微处理器、存储器等器件连接起来,然后进 行测试和调整,确保计算器能够正常工作。
电工电子技术项目化教程项目数字电路基础

逻辑表达式的化简
公式化简
利用逻辑代数的基本定律,将表 达式化简为最简形式。
卡诺图化简
利用卡诺图(Karnaugh map)进 行化简,通过圈选最小项来得到最 简表达式。
吸收律和消去律
在化简过程中,利用吸收律和消去 律来消除多余的项。
逻辑函数的实现
基本门电路
利用与门、或门、非门等 基本门电路实现逻辑函数 。
控制技术
在自动化控制系统中,数字电 路被用于实现各种控制逻辑和 算法。
测量技术
在测量领域,数字电路被用于 实现各种测量和控制系统的数
字化处理和传输。
02
数字电路的基本元件
二极管
总结词
二极管是数字电路中的基本元件之一 ,它只允许电流单向流动。
详细描述
二极管由一个PN结组成,它有两个电 极,正极和负极。在Байду номын сангаас向偏置下,电 流可以从正极流向负极。在反向偏置 下,电流很小或几乎为零。
或门
逻辑或运算的电路实现
或门是数字电路中实现逻辑或运算的电路。当输入端中至少有一个为高电平时,输出端就为高电平;只有当所有输入端都为 低电平时,输出端才为低电平。
非门
逻辑非运算的电路实现
非门是数字电路中实现逻辑非运算的电路。非门只有一个输入端和一个输出端,当输入端为高电平时 ,输出端为低电平;当输入端为低电平时,输出端为高电平。
与非门
逻辑与非运算的电路实现
与非门是数字电路中实现逻辑与非运算的电路。与非门的逻 辑功能是:当所有输入端都为高电平时,输出端才为低电平 ;只要有一个输入端为低电平,输出端就为高电平。
或非门
逻辑或非运算的电路实现
或非门是数字电路中实现逻辑或非运算的电路。或非门的 逻辑功能是:当所有输入端都为低电平时,输出端才为高 电平;只要有一个输入端为高电平,输出端就为低电平。
数字电路简明教程

( 101. 11 ) 2 = 1 × 22 + 0 × 21 + 1 × 20 + 1 × 2−1 + 1 × 2−2
= 4 + 1 + 0. 5 + 0. 25 = ( 5. 75)10
(2) 十-二转换: 二转换: 降幂比较法 — 要求熟记 20 ∼ 210 的数值 。 20 1 21 2 22 4 23 8 24 16 25 32 26 27 28 29 210
十进 制数 0 1 2 3 4 5 6 7 8 9 权 8421 码 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 8421
几种常见的 BCD 代码
余 3 码 2421(A)码 5211 码 余3循环码 码 循环码 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 0000 0001 0010 0011 0100 1011 1100 1101 1110 1111 2421 0000 0001 0100 0101 0111 1000 1001 1100 1101 1111 5211 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010
( 2A. 7F )16 = 2 × 161 + 10 × 160 + 7 × 16 −1 + 15 × 16 −2
任意(N)进制数展开式的普遍形式: 任意 进制数展开式的普遍形式: 进制数展开式的普遍形式
D = ∑ki N i
ki — 第 i 位的系数
N — 第 i 位的权
i
4. 几种常用进制数之间的转换 (1) 二-十转换: 将二进制数按位权展开后相加 十转换: 十转换
【图文】数字电子技术经典教程 CMOS门电路

改进型CMOS门电路改进型CMOS门电路 CMOS CMOS门电路几种常见系列:门电路几种常见系列:门电路几种常见系列系列:(1)CD4000系列:基本系列,速度较慢)系列基本系列,(2)74HC系列:速度比系列:系列提高近10倍)系列速度比CD4000系列提高近倍系列提高近系列:(3)74HCT系列:与LSTTL门电路兼容)系列门电路兼容系列:(4)LVC系列:低电压系列)系列(5)BiCMOS系列)系列
改进型CMOS门电路改进型CMOS门电路 CMOS BiCMOS反相器反相器当vI输入高电平时,VTN1、VTN2和VT2导通,VTP、VTN3 和VT1截止,vO输出低电平。
当vI输入低电平时,VTP1、VTN3和VT1导通,VTN1、VTN2 和VT2截止,vO输出高电平。
输入和输出实现非逻辑。
改进型CMOS门电路改进型CMOS门电路 CMOS BiCMOS门电路的结构特点门电路的结构特点门的输出电路总是由两个NPN晶体管组成推(1)BiCMOS 门的输出电路总是由两个)门的输出电路总是由两个晶体管组成推拉式结构。
拉式结构。
2)连接上方(射随输出)(2)连接上方(射随输出)晶体管基极的
内部电路总是该门电路的基本功能电路部分。
门电路的基本功能电路部分。
(3)下方(反相输出)晶体管基极上的信号总是上方晶体)下方(反相输出)管基极信号的反。
管基极信号的反。
本节作业习题 1、2、3 、、。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(4)十六进制:基数N为16,十六进制有0…9、A、 B、C、D、E、F共16个数码, “逢十六进一,借一为十六”。下标16或H表示, 如(A1)16,(1F)H等。
(3AE.7F)16 =3×162+10×161+14×160+7×16-1+15×16-2 =(942.4960937)10
1.3 不同数制间的转换
同或逻辑 A B Y 0 0 1 0 1 0 1 0 0 1 1 1 异或逻辑 A B Y 0 0 0 0 1 1 1 0 1 1 1 0
2.2 逻辑代数的公式
1 基本公式 关于变量和常量的公式 0· 0=0 0+0=0 1· 1=1 1+1=1 0· 1=0 0+1=1 0 1 1 0 (1) 0· A=0 (2) 0+A=A (3) 1· A=A (4) 1+A=1 互补律 (5) A A 0 (6) A A 1
5211码
0000 0001 0010 0011 0111 1000 1100 1101 1110 1111
余3循环 码
0010 0110 0111 0101 0100 1100 1101 1111 1110 1010
三种常用的代码: 8421BCD码,格雷(Gray)码, ASCII码。 (1)8421BCD码:BCD (Binary Coded Decimal) 码,即二—十进制代码,用四 位二进制代码表示一位十进制 数码。 8421BCD码是有权码,四位 的权值自左至右依次为: 8、4、2、1。
2.1 逻辑代数的基本运算
逻辑代数基本运算有与、或、非三种,逻辑与、逻辑或 和逻辑非。 1.逻辑与 只有决定某事件的全部条件同时具备时,该事件 才发生,逻辑与,或称逻辑乘and。 开关A=B=1开关接通,电灯Y=1灯亮,A=B=0开关断开、灯 灭,逻辑与“·”,写成Y=A· 或Y=AB B
逻辑真值表(Truth Table) :自变量的各种可能取值与函数值 F的对应关系。 与逻辑真值表 与逻辑符号 and A B Y 0 0 0 0 1 0 1 0 0 1 1 1
4.其他常见逻辑运算 常见的复合逻辑运算有: 与非、或非、异或、同或等 运算的表达式: 与非: Y AB 先与后非 或非:Y A B 先或后非 与或非表达式: AB CD Y 先与再或后取非
与非逻辑 A 0 0 1 1 B 0 1 0 1 Y 1 1 1 0 或非逻辑 A 0 0 1 1 B 0 1 0 1 Y 1 0 0 0
• 数字信号有两种传输波形,电平型、脉冲型。 • 电平型数字信号以一个时间节拍内信号是高电平还 是低电平来表示“1”或“0”, • 脉冲型数字信号是以一个时间节拍内有无脉冲来表 示“1”或“0”。
1.2 几种常用的数制
数制中允许使用的数码个数称为数制的基数。 常用的进位计数制有十进制、二进制、八进制和十 六进制。 D=Σkj Ni ,ki是第j位的系数,N是基数, N =10,2,8,16; Ni称为第i位的权,10i, 2i ,8i,16i。 2345=2×103+3×102+4×101+5×100
数 余3码 值 0 1 2 3 4 5 6 7 8 9 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100
8421 BCD 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001
(2)格雷(Gray)码:格雷码是一种无权循环码,它的特点是: 相邻的两个码之间只有一位不同。
第二章 逻辑代数基础
• 逻辑代数是由英国数学家乔治· 布尔于1849年首先 提出的,称为布尔代数。 • 逻辑代数是研究逻辑变量间的因果关系,是分析 和设计逻辑电路的数学工具。 • 逻辑变量是使用字母表示的变量,只有两种取值1、 0, • 代表两种不同的逻辑状态:高低电平、有无脉冲、 真或假、1或0。
nand
ቤተ መጻሕፍቲ ባይዱ
nor
异或表达式: Y A B A B AB A、B不同,Y为1;A、B相同,Y为0。 异或逻辑 A B Y 0 0 0 0 1 1 1 0 1 1 1 0
可以证明:奇数个1相异或,等于1; 偶数个1相异或,等于0。
A⊕0=A A=1, 1⊕0=1; A 1 A A=1, 1⊕1=0 ; A A 1 A⊕A=0 A=0, A=0, 0⊕0=0; 0⊕1=1
(5)二—十六转换 【例1.12】( 10111010111101.101 )B =(0010 1110 1011 1101 . 1010 )B =(2EBD.A )H (6)十六—二转换 【例1.13】十六进制数:(1 C 9. 2 F )H 二进制数: ( 1 1100 1001 . 0010 1111 )B (7)二—八转换 【例1.14】 (010 111 011.101 100)B =(273 . 54)O (8)八—二转换 ( 361.72)O =(11 110 001.111 010)B
(1)十进制:十进制数一般用下标10或D表示,如2310, 87D等。 (2)二进制:基数N为2的进位计数制称为二进制 (Binary),它只有0和1两个有效数码, 进位关系 “逢二进一,借一为二”。 二进制数下标2或B,如1012,1101B等。 (1001.11)2=1×23+0×22+0×21+1×20+1×2-1+1×2-2 =(9.75)10 (3)八进制:基数N为8的进位计数制,共8个有效 数码,0 1 2 3 4 5 6 7,下标8或O。 (456.1)8=4×82+5×81+6×80+1×8-1=(302.125)10
3.逻辑非 在只有一个条件决定某事件的情况下,如果当条件 具备时,该事件不发生;而当条件不具备时,该事件反而发 生,称为逻辑非,也称为逻辑反not。 开关接通(A=1)时,电灯Y不亮(Y=0),而当开关断开 (A=0)时,电灯Y亮(Y=1)。 逻辑反,写成 Y A 非逻辑真值表 A 0 1 Y 1 0 非逻辑符号 inverter
(1)二—十转换:按位权展开,将所有值为1的数 位的位权相加。 【例1.1】 (11001101.11)B =1× 27+1× 26+0× 25+0× 24+1× 23+1× 22 +0× 21+1× 20+1× 2-1+1× 2-2 =128+64+8+4+1+0.5+ 0.25=(205.75)D
数字电路与逻辑设计
课程特点: 1、数字电路重要的专业基础课 2、数字电路不难,新的思维方法 3、重视应用,分析设计题为主。 4、只讲知识点、难点和重点,多讲习题 5、网上答疑 ymgao83@ 课件 /eeec/实验教学 教学要求: 1、多做习题、作业成绩20%,思考题3人一组。 2、 应用PSpice仿真
第一章 数制和码制
1.1 数字量和模拟量 • 数字量:时间上和数值上都离散变化的物理量, 最小数量单位△ • 模拟量:时间上和数值上都连续变化的物理量。 • 处理数字信号(Digital Signal)的电路称为数字电 路, • 处理模拟信号(Analog Signal)的电路称为模拟 电路。 • 数字信号传输可靠、易于存储、抗干扰能力强、 稳定性好。 • 数字信号是一种脉冲信号(Pulse Signal),边沿 陡峭、持续时间短,凡是非正弦信号都称为脉冲 信号。
1.5码制
• 在数字系统中,常用0和1的组合来表示不同的数 字、符号、事物,叫做编码,这些编码组合称为 代码(Code)。 • 代码可以分为数字型的和字符型的,有权的和无 权的。 • 数字型代码用来表示数字的大小,字符型代码用 来表示不同的符号、事物。 • 有权代码的每一数位都定义了相应的位权,无权 代码的数位没有定义相应的位权。 • 有权码:8421、2421、5421 、 5211码 • 无权码:余3码、余3循环码、格雷码。
重叠律 (7) A· A=A (8) A+A=A 交换律 (9) A· B=B· A (10)A+B=B+A 结合律 (11)A· C)=(A· C (B· B)· (12)A+(B+C)=(A+B)+C
0 1 0 1 1 1 1 1 1 0 1 0 1
同或表达式: Y=A⊙B= AB A B A、B相同,Y为1; A、B不同,Y为0。 A⊕B=
A⊙B= A B A⊙0= A A⊙1=A A⊙A=1 A⊙ A =0 A⊙B= A⊙ B A B A B A⊕B A B A⊙B=A⊙ B
十进制数 格雷码 十进制数 格雷码
0 1 2 3 4 5 6 7
0000 0001 0011 0010 0110 0111 0101 0100
8 9 10 11 12 13 14 15
1100 1101 1111 1110 1010 1011 1001 1000
(3)ASCII码 ASCII码,即美国信息交换标准码 (American Standard Code for Information Interchange), • 是目前国际上广泛采用的一种字符码。 • ASCII码用七位二进制代码来表示128个不同的字 符和符号。
【例1.3】 (0.8125)D=( 0.8125×2=1.625 0.625×2=1.25 0.25×2=0.5 0.5×2=1 (0.8125)D=( 0.1101 )B
)B 积的整数 1 MSB 1 0 1 LSB
(3)十六—十转换 按位权展开 【例1.7】 (1A7.C)H=1×162 +10×161+7×160+12×16-1 =1×256+10×16+7+12×0.0625 =(423.75)D (4)十—十六转换 与十—二转换方法相似,整数部分转换除 16取余法,小数部分转换乘以16取整法 【例1.8】(287)D= (11F)H 转换过程:287/16=17余15 17/16=1余1 【例1.9】 (0.62890625)D=(0.A1)H 转换过程:0.62890625×16=10.0625 0.0625×16=1
