传热学9-辐射换热计算
传热学第九章

9-1 辐射传热的角系数
(3)角系数的可加性
从表面1上发出而落到表面2上的总能量,等于落到表面2上 各部分的辐射能之和,于是有
注意,利用角系数可加性时,只有对角系数符号中第二个角码 是可加的,对角系数符号中的第一个角码则不存在类似的关系。
9-1 辐射传热的角系数 3. 角系数的计算方法
试计算: (1)板1的自身辐射; (2)板1的有效辐射; (3)板1的投入辐射; (4)板1的反射辐射; (5)板1,2的净辐射换热量。
§ 9-4 气体辐射的特点及其计算
辐射性气体: 具有发射和吸收辐射能的能力的气体。
工业上常见的温度范围内 常见的辐射性气体: 二氧化碳、水蒸气、二氧化硫、甲烷、氟里昂等三原子、多原子及 结构不对称的双原子气体(一氧化碳)
ቤተ መጻሕፍቲ ባይዱ
9.3.2 多表面封闭系统网络法求解的实施步骤
9.3.2 多表面封闭系统网络法求解的实施步骤
3. 求解代数方程组,计算各表面的有效辐射。
例如
已知三个表面温度T1, T2, T3;以及 A1, A2, A3, ε1, ε2, ε3, X1,2, X1,3, X2,3。
确定每个表面的有效辐射J1, J2, J3和 净辐射热量Φ1, Φ2, Φ3。
81
9.6 综合传热问题
82
9.6 综合传热问题
83
9.6 综合传热问题 解:
求解的结果为,
这样的测量误差在工业上是可以接受的。
84
85
9.6 综合传热问题 辐射传热系数
86
第9章 测试题
• 试述气体辐射的基本特点,气体能当做灰体来处 理吗?请说明原因。(2003年,华电,15分)
• 两块平行放置且相互靠得很近的灰体平壁,它们 的黑度均为0.8,壁1和2的温度分别为400和30℃ ,试计算壁2的(1)辐射换热量;(2)本身辐 射;(3)有效辐射。( 2003年,华电,15分)
传热学-第九章 辐射计算

X1, 2
1,2 1,2 A 1,2 B
X1, 2i
i 1
n
A1 Eb1 X 1,2 A1 Eb1 X 1,2 A A1 Eb1 X 1,2 B X 1,2 X 1,2 A X 1,2 B
再来看一下2 对 1 的能量守恒情况: 2 ,1 2 A ,1 2 B ,1
X 1,2 X 2,1
1 A1 1 A2
A1
A2
X d 1, d 2 dA1 X d 2, d 1dA2
A
A1 1
1
cos 1 cos 2 dA1dA2
A2
A1
1 A2
A2
A1
r cos 1 cos 2 dA1dA2
2
(9-4a)
A2
r
2
(9-4b)
的电流、电位差和电阻比拟热辐射中的热流、热势差与热
阻,用电路来比拟辐射热流的传递路径。但需要注意的是, 该方法也离不开角系数的计算,所以,必须满足漫灰面、 物性均匀以及投入辐射均匀的条件。
热势差与热阻
上节公式(9-12):
J Eb ( 1)q
1
改写为:
Eb J q 1
1, 2 A1 Eb1 X 1, 2 A2 Eb 2 X 2,1 A1 X 1, 2 ( Eb1 Eb 2 ) 的热辐射 到达表面 2的部分 的热辐射 到达表面 1的部分
图9-13 黑体系统的 辐射换热
表面1发出 表面 2发出
例题9-4 一直径d=0.75m的圆筒形埋地式加热炉采用电加热。 在操作过程中需要将炉子顶盖移去一段时间,设此时筒身温 度为 500K ,筒底为 650K 。环境温度为 300K 。试计算顶盖移 去期间单位时间内的热损失。设筒身及底面均可作为黑体。
§9-2 灰表面间的辐射换热概述

The Department
of Construction Engineering
Logo
考察表面温度均匀表面1(如图8-8所示)。根据有效辐 射的定义,表面1的有效辐射有如下表达式:
J1 E1 1G1 1Eb1 (1 1 )G1
在表面外能感受到的表面辐射 就是有效辐射,它也是用辐射探 测仪能测量到的单位表面积上的 辐射功率 W / m2 。
Logo
二、两灰表面组成的封闭腔的辐射换热
两个物体组成的辐射换热系统
Heat Transfer
建筑工程系
The Department
of Construction Engineering
Logo
下面来分析两个等温漫灰表面封闭系统内的辐射换热 情况。如图所示,两个表面的净换热量为:
1,2 A 1 J1 X1,2 A 2 J 2 X 2,1
E b1 J 1 1 Φ1 A1 ( E b1 J 1 ) 1 1 1 1 1 A1
1 1 1 A1
称之为表面热阻。
注意:式中的各个量均是对同一表面而言的,而且以 向外界的净放热量为正值。
Heat Transfer
建筑工程系
The Department
of Construction Engineering
建筑环境与设备工程专业主干课程之一 !
Heat Transfer
传热学
建筑环境与设备工程专业主干课程之一 !
第九章 辐射换热的计算
Chapter9 The Calculation of Radiation Heat Transfer
建筑工程系
The Department
of Construction Engineering
《传热学》第9章-辐射换热的计算

J = E + ρG = εEb + (1 − α )G
漫灰表面之间的辐射换热
单位面积的辐射换热量=?
应该等于有效辐射与投入辐射之差
Φ= A
也等于自身辐射力与吸收的投入辐射能之差
J− Φ A
G = εEb
α =ε
− αG
Φ
=
Aε 1−ε
X
1,
2
1 ε1
− 1
+1+
X
2.1
1 ε2
− 1
= ε s A1 X1,2 (Eb1 − Eb2 )
εs
=
X
1,
2
1 ε1
−1 + 1 +
X
2.1
1 ε2
− 1 −1
系统黑度
6
两个漫灰表面构成的封闭空腔中的辐射换热
两块平行壁面构成的封闭空腔
角系数的曲线图
(a)平行的等面积矩形
(c)垂直的两个矩形
2 角系数的性质
(1) 相对性 (2) 完整性
A1 X 1,2 = A2 X 2,1
-互换性
封闭空腔的所有表面的角系数之和等于1
n
∑ X i , j = X i ,1 + X i ,2 +L+ X i ,i +L + X i ,n = 1
j =1
黑体辐射
Lb
=
Eb π
角系数的定义式
∫ ∫ Φ1→2 =
A1
A2
Eb1
cosθ1 cosθ 2 πr 2
传热学 第九章 辐射换热的计算

9-2 两表面之间的辐射换热过程
1. 黑体表面之间的辐射换热
任意位置的两个黑体表面1、2,从表面1发出并直接投射
到表面2上的辐射能为
1 2 A1 X 1,2 E b1
从表面2发出并直接投射到表面1上的辐射能为
21 A2 X 2 ,1 E b 2
两个表面之间的直接辐射换热量为
X 1,2 X 2 ,1 1
A2 a
A1
9-1 角系数
4. 角系数的计算方法
(2) 代数法
由三个垂直于纸面方向无限长的非凹表面构成的封闭空腔,
三个表面的面积分别为A1、A2、A3 。
X i ,i 0
根据角系数的完整性
角系数的相对性
A1 X 1, 2 A1 X 1, 3 A1
A1 X 1,2 A2 X 2 ,1
Eb1 cos 1 cos 2 dA1dA2
1d 1
dd11
2
2 Lb1 dA1 cos
2
r
Eb1
dA2 cos 2
Lb1
d1
r2
9-1 角系数
2. 角系数的定义式
12
cos 1 cos 2
cos 1 cos 2
dA1dA2
E b1
dA1dA2 E b1
2
2
A1 A2
A1 A2
r
r
表面1对表面2的角系数为
X 1,2
12
A1 Eb1
1
A1
cos 1 cos 2
A1 A2 r 2 dA1dA2
1
A2
cos 1 cos 2
新大《传热学》复习题及解答第9章 辐射传热的计算

第9章辐射传热的计算(复习题解答)【复习题9-1]试述角系数的定义:”角系数是一个纯几何因子”的结论是在什么前提下得出的?答:表面1发出的辐射能中落到表面2的百分比称为表面1对表面2的角系数。
“角系数是一个纯几何因子”的结论成立的前提是(1)所研究的表面是漫射的;(2)在所研究表面的不同地点上向外发出的辐射热流密度是均匀的。
【复习题9-2】角系数有哪些特性?这些特性的物理背景是什么?答:角系数具有相对性、完整性和可加性。
相对性是在两物体处于热平衡时,净辐射换热量为零的条件下得出的。
完整性反映了一个由多表面组成的封闭系统中,任一表面所发出的辐射能,必全部落到封闭系统的各个表面上。
可加性表明从表面1发出的辐射,落到表面2的总能量,等于落到表面2上各部分的辐射能之和。
【复习题9-3]为什么计算一个表面与外界之间的净辐射传热量时要采用封闭腔的模型?答:因为任一表面与外界的辐射换热,包括该表面向空间各个方向发出的辐射,以及从空间各个方向投入到该表面上的辐射能。
【复习题9-4]实际表面系统与黑体系统相比,辐射传热计算增加了哪些复杂性?答:实际表面系统的辐射换热存在表面间的多次重复反射和吸收,光谱辐射力不服从普朗克定律,光谱吸收比与波长有关,辐射能在空间的分布不服从兰贝特定律,这都使辐射换热的计算更加复杂。
【复习题9-5】什么是一个表面的自身辐射、投入辐射及有效辐射?有效辐射的引入对于灰体表面系统辐射传热的计算有什么作用?答:由物体的内能转变而成的辐射能叫做自身辐射。
从外界投入到辐射表面的辐射能叫做投入辐射。
从一个辐射表面发出的辐射能(包括自身辐射和反射)叫做有效辐射。
引入有效辐射可避免实际物体辐射中出现的多次吸收和反射,从而简化计算。
【复习题9-6】对于温度已知的多表面系统,试总结求解每一表面净辐射传热量的基本步骤。
答:(1)画出等效的网络图;(2)列出节点的电流方程;(3)求解方程,得到各个节点电势;(4)确定每个表面的净辐射传热量。
第9章辐射换热的计算

传热学 Heat Transfer
对于两平行的黑体大平壁(A1=A2 =A),若略 去周边溢出的辐射热量,可以认为: X1, 2= X2, 1=1,
且由斯蒂芬-波尔兹曼定律知Eb=σbT4,此时:
传热学 Heat Transfer
传热学 Heat Transfer
一.积分法
直接用角系数的公式进行积分得出。
X dA1,A2
A2
cos
θ1 π
cos r2
θ
2
dA2
R2 2πxdx
A2 π (R2 x 2 )2
R2 D/ 2
dx 2
0 (R2 x2 )2
D2
4R2 D2
此法太烦,有人做成图表,供查阅P242、243图
三、多个黑体表面间的辐射换热
如图所示为n个黑体表面组成了封闭空腔。 1、封闭空腔某一黑体表面的净换热量:
2、角系数的完整性:
注意: 对于平面或凸表面等于0,对于凹面不等于0。
传热学 Heat Transfer
计算黑表面与所有其他黑表面的辐射换热:
n
n
i i, j (Ebi Ebj ) X i, j Ai
传热学 Heat Transfer
未加遮热板时: 在板间加入遮热板后:
【例9-7】
传热学 Heat Transfer
第三节 角系数的确定方法
漫射表面间的辐射换热计算,必须先要 知道它们之间的辐射角系数。求角系数 的常用方法有: (1)直接积分法 (2)数值计算方法 (3)图解方法 (4)代数方法 (5)几何投影方法(单位球法), 这里主要介绍积分法和代数法。
传热学 辐射换热计算

A2
表面1对表面2的角系数,
记为X1,2。
1. 与物体温度无关,对于表面性 质均匀的漫射表面,它是一个 纯几何因子。
A1
角系数定义
② 两黑体表面的辐射换热:(不存在重复反射)
1,2E b1A 1X 1,2E b2A 2X 2,1
3
热平衡时: T 1 T 2 1 ,2 0 A 1 X 1 ,2 A 2 X 2 ,1
1 X 1 , 2 A 1
1 2 2 A 2
辐射换热量:
1,211Eb1 1Eb2 11 2 A111Eb1 1 EbA 2112
A AX A X A 1 1
1 1,2 X 21 , 2 2A 1 1
1,2 2 2
1 A 11 s Eb1Eb2 1 A 1 1
1 2
12 A 2
解:由几何关系:cos1 cos2 s / l
l2 s2 r2
dA2 2 r dr 根据角系数定义式:
Xd1,2
Ld1Acosd
A2 d1AE1
(E1/)cosd
A2
E1
A2cosdA 2lc2osA2co2l2sdA 2
代入几何关系整理得:
dA 1
s
l
r
R0 A2
X R0 d1,2 0
2.角系数有哪些特性?这些特性的物理背景是什么?
答:角系数有相对性,完整性和可加性。相对性是在两物体处于 热平衡时,净辐射换热量为零的条件下导得的;完整性反映了一 个由几个表面组成的封闭系统中,任一表面所发生的辐射能必全 部落到封闭系统的各个表面上;可加性是说明从表面1发出而落 到表面2上的总能量等于落到表面2上各部份的辐射能之和。
能力,而在光带之外为热辐射的透明体,如图927。(气体不是灰体 ) ② 在整个容积中进行。
传热学第八章辐射换热的计算

02
辐射换热的计算方法
辐射换热的基本公式
斯蒂芬-玻尔兹曼方程
描述了物体在任意温度下的辐射功率,是辐射换热的基本公式。
辐射力方程
表示物体发射和吸收的辐射能与物体表面温度和周围环境温度之间 的关系。
辐射传递方程
表示在给定温度和光谱发射率下,物体表面发射和吸收的辐射能与 物体表面温度之间的关系。
辐射换热的角系数法
表面传热系数的计算方法
通过实验测定或经验公式计算表面传热系数, 需要考虑表面粗糙度和涂层的影响。
表面传热系数的应用
适用于简化模型或近似计算中的辐射换热计算。
辐射换热的积分方程法
积分方程的建立
根据斯蒂芬-玻尔兹曼方程和边界条件建立积分方程。
积分方程的求解方法
采用数值方法求解积分方程,如有限元法、有限差分 法等。
太阳能利用
通过优化太阳能集热器的设计,提高太阳能辐射的吸收和 转换效率,降低太阳能利用成本,有助于减少化石能源的 消耗和碳排放。
05
辐射换热的发展趋势与展 望
新型材料的辐射换热特性研究
总结词
随着科技的发展,新型材料不断涌现,对新型材料的辐射换热特性研究成为当 前热点。
详细描述
新型材料如碳纳米管、石墨烯等具有独特的物理和化学性质,其辐射换热特性 与传统材料有所不同。研究这些新型材料的辐射换热特性有助于发现新的传热 机制,提高传热效率。
感谢观看
THANKS
传热学第八章辐射 换热的计算
目 录
• 辐射换热的基本概念 • 辐射换热的计算方法 • 辐射换热的实际应用 • 辐射换热的优化与控制 • 辐射换热的发展趋势与展望
01
辐射换热的基本概念
定义与特性
定义
传热学 第9章-传热过程分析和换热器计算

第九章 传热过程分析和换热器计算在这一章里讨论几种典型的传热过程,如通过平壁、圆筒壁和肋壁的传热过程通过分析得出它们的计算公式。
由于换热器是工程上常用的热交换设备,其中的热交换过程都是一些典型的传热过程。
因此,在这里我们对一些简单的换热器进行热平衡分析,介绍它们的热计算方法,以此作为应用传热学知识的一个较为完整的实例。
9-1传热过程分析在实际的工业过程和日常生活中存在着的大量的热量传递过程常常不是以单一的热量传递方式出现,而多是以复合的或综合的方式出现。
在这些同时存在多种热量传递方式的热传递过程中,我们常常把传热过程和复合换热过程作为研究和讨论的重点。
对于前者,传热过程是定义为热流体通过固体壁面把热量传给冷流体的综合热量传递过程,在第一章中我们对通过大平壁的传热过程进行了简单的分析,并给出了计算传热量的公式 t kF Q ∆=, 9-1式中,Q 为冷热流体之间的传热热流量,W ;F 为传热面积,m 2;t ∆为热流体与冷流体间的某个平均温差,o C ;k 为传热系数,W/(⋅2m o C)。
在数值上,传热系数等于冷、热流体间温差t ∆=1 o C 、传热面积A =1 m 2时的热流量值,是一个表征传热过程强烈程度的物理量。
在这一章中我们除对通过平壁的传热过程进行较为详细的讨论之外,还要讨论通过圆筒壁的传热过程,通过肋壁的传热过程,以及在此基础上对一些简单的包含传热过程的换热器进行相应的热分析和热计算。
对于后者,复合换热是定义为在同一个换热表面上同时存在着两种以上的热量传递方式,如气体和固体壁面之间的热传递过程,就同时存在着固体壁面和气体之间的对流换热以及因气体为透明介质而发生的固体壁面和包围该固体壁面的物体之间的辐射换热,如果气体为有辐射性能的气体,那么还存在固体壁面和气体之间的辐射换热。
这样,固体壁面和它所处的环境之间就存在着一个复合换热过程。
下面我们来讨论一个典型的复合换热过程,即一个热表面在环境中的冷却过程,如图9-1所示。
传热学课件第六章辐射换热计算

X 1,3
A1 A3 A2 2 A1
X 2,1
A2
A1 A3 2 A2
X 2,3
A2
A3 A1 2 A2
X 3,1
A3 A1 A2 2 A3
X 3,2
A3
A2 2 A3
A1
3.查曲线图法
利用已知几何关系的角系数,确定
其它几何关系的角系数。 例:如图,确定X1,2 由相互垂直且具有公共边的长方形表面
• 若A2和A3的温度相等,则有
J2A2X2,1+J2A3X3,1 =J2 A2+3X(2+3),1 角系数的可加性
即 A2+3X(2+3),1=A2X2,1+A3X3,1
利用角系数的可加性,应注意只有对角系数
符号中第二个角码是可加的。
• 三、角系数的确定方法
角系数的确定方法很多,从角系数的定义直 接求解法、查曲线图法、代数分析法和几何图形 法,这里主要介绍定义直求法和代数分析法。
一、表面辐射热阻
对于任一表面A,其本身辐射为E=ε Eb, 投射辐射为G,吸收的辐射能为α G。向外 界发出的辐射能为
J E G Eb 1 G (a)
因此,表面A的净热流密度为
q = J-G
(b)
对于灰体表面α =ε ,联解(a)和(b),
消去G得
q
Eb J
1
第六章 辐射换热计算
例内 重 基 题容 点 本 赏精 难 要 析粹 点 求
基本要求
1.掌握角系数的意义、性质及确定方法。 2.掌握有效辐射的确定方法。 3.熟练掌握简单几何条件下透热介质漫灰
面间辐射换热的计算方法。 4.掌握遮热板的原理及其应用
传热学第九章辐射基本定律

绝对黑体(黑体) 吸收比 α=1 → 绝对黑体(黑体) 镜体(对于漫反射称为白体) 反射比 ρ=1 → 镜体(对于漫反射称为白体) 穿透比 τ=1 绝对透明体(透明体) → 绝对透明体(透明体)
10
2、黑体辐射 、
黑体的基本概念 辐射力和 辐射力和光谱辐射力 普朗克定律 维恩位移定律 斯蒂芬斯蒂芬-波尔兹曼定律 黑体辐射函数 兰贝特定律 小结
物体的黑度:ε=f(物质种类,表面温度,表面状况) 物体的黑度:ε=f(物质种类,表面温度,表面状况)
28
2)吸收热辐射的性质 2)吸收热辐射的性质
Eλ
E λ (T2 )
αλ
T1
λ
投入辐射与吸收辐射的关系
λ
29
光谱吸收比:物体对某一特定波长投入辐射能的吸收份额 份额。 光谱吸收比:物体对某一特定波长投入辐射能的吸收份额。 吸收比:物体对投入辐射在全波长范围内的吸收份额 吸收比: α=f(自身表面性质与温度T 辐射源性质与温度T α=f(自身表面性质与温度T1,辐射源性质与温度T2)
24
黑度: ① 黑度:
实际物体的辐射力与同温 度下黑体辐射力的比值 称为实际物体的黑度, 称为实际物体的黑度, 又称发射率 记为ε。 发射率, 又称发射率,记为 。
E ∫0 Eλ dλ ∫0 ελ Ebλ dλ ε= = = 4 Eb σT σT 4
∞ ∞
⇒ E = εEb = εσT 4
对于实际物体来说,黑度仍是温度的函数, 对于实际物体来说,黑度仍是温度的函数,即实 际物体的辐射力不满足四次方关系。 际物体的辐射力不满足四次方关系。
8
t>0K 内 的物体 能
热辐射传播速度c、波长 和频率 之间的关系c=f·λ 和频率f之间的关系 热辐射传播速度 、波长λ和频率 之间的关系 热辐射的主要波谱: 热辐射的主要波谱:
传热学-学习课件-9-1 辐射传热的角系数

A1 A2
由角系数相对性
A1 X 1,2 A2 X 2,1 A1 X 1,3 A3 X 3,1 A2 X 2,3 A3 X 3,2
A3
三表面封闭空间 角系数的确定
传热学 Heat Transfer
上述方程解得: X1,2
A1
A2 2 A1
A3
X 1,3
A1
A3 2A3
传热学 Heat Transfer
从表面2上发出而落到表面1上的辐射能,等于从 表面2的各部分发出而落到表面1上的辐射能之和,于 是有
A 2 E b 2 X 2 ,1 A 2 a E b 2 X 2 a ,1 A 2 b E b 2 X 2 b ,1
A2 X 2,1 A2a X 2a,1 A2b X 2b,1
X 2,1
X 2a,1
A2a A2
X 2b,1
A2b A2
角系数的上述特性可以用来求解许多情况下 两表面间的角系数值。
传热学 Heat Transfer
9.1.3 角系数的计算方法
求解角系数的方法
直接积分法 代数分析法
传热学 Heat Transfer
1、直接积分法
• 按角系数的基本定义通过求解多重积分而获得角 系数的方法
2、代数分析法
利用角系数的相对性、完整性及可加性,通过求解代数方 程而获得角系数的方法称为代数分析法。 (1)三个非凹表面组成的封闭系统
图9-10 三个非凹表面组成的封闭系统
传热学 Heat Transfer
由角系数完整性
X1,2 X1,3 1 X 2,1 X 2,3 1 X 3,1 X 3,2 1
传热学 Heat Transfer
第9章 辐射传热的计算(杨世铭,陶文栓,传热学,第四版,答案)
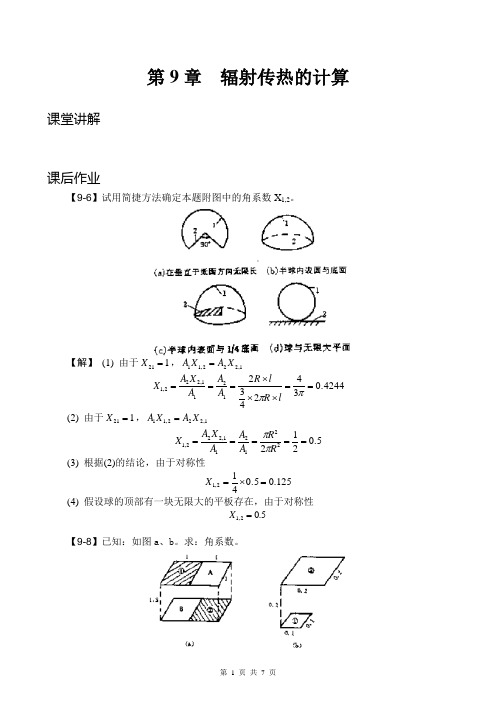
第9章 辐射传热的计算课堂讲解课后作业【9-6】试用简捷方法确定本题附图中的角系数X 1,2。
【解】 (1) 由于121=X ,1,222,11X A X A =0.42443424321211,222,1==⨯⨯⨯===ππl R l R A A A X A X(2) 由于121=X ,1,222,11X A X A =0.5212221211,222,1=====R R A A A X A X ππ (3) 根据(2)的结论,由于对称性125.00.5412,1=⨯=X(4) 假设球的顶部有一块无限大的平板存在,由于对称性0.52,1=X【9-8】已知:如图a 、b 。
求:角系数。
【解】(a) A,2A B A,A 1,21B 1,12B A,1A 1X A X A X A X A X A +++=+++由于对称性,则()1,21B 1,11,21B 1,12B A,1A 1222X A X A X A X A X A +=+=+++。
1A 12A A =+ ,1,2B 1,2B A,1X X X +=∴++B 1,2B A,11,2X X X -=++X =1,Y =2175.01,2=X(b) 扩充图(b),得1'由扩充图可知,2.021,='X ,由于对称性,可得:05.042.04121,1,2==='X X 1,222,11X A X A =2.005.041,21211,222,1=⨯===X A A A X A X【9-18】一管状电加热器内表面温度为900K 、ε=1,试计算从加热表面投入到圆盘上的总辐射能(见附图)。
【解】表面2发出而落到表面1上的辐射能应为2,11b 1X E A =Φ; 按角系数的对称性,1,222,11X A X A =;做虚拟表面3及4,则可有4,21,23,2X X X +=,即4,23,21,2X X X -=,其中3,2X ,4,2X 为两平行圆盘间辐射角系数。
传热学第九章辐射换热的计算

遮热罩的热平衡表达式
4 4 2 h T T TT f 3 3 3 2
联立求解以上两式可求得测温误差 Tf T ,结果为 44 K。可见,加 1 遮热罩后,相对测温误差由未加遮热罩的14.4%降低到4.4% 。
i 1 n
图9-2 角系数的完 整性
上式称为角系数的完整性。若表面1为非凹表面时,X1,1 = 0。
(3) 可加性
3 角系数的计算方法
4 求解角系数的方法通常有直接积分法、代数分析法。
(1) 直接积分法 dA1对A2角系数为:
X d 1 , 2
A 2
d 1 , d 2
d 1
9.3
辐射换热应用举例
1、控制表面热阻强化或削弱辐射换热:比如涂层(不同辐射 表面涂层的效果不同,为什么?举例说明); 2、控制空间热阻强化或削弱辐射换热:比如遮热板; 3、遮热板的原理。
遮热板的主要作用就是削弱辐射换热。下面以两块靠得很近
的大平壁间的辐射换热为例来说明遮热板的工作原理。 没有遮热板时,两块平 壁间的辐射换热有 2 个 表面辐射热阻、 1 个空 间辐射热阻。 在两块平壁之间加一块大 小一样、表面发射率相同 的遮热板3 如果忽略遮热板的导热热阻,则总辐射热阻增加了1倍, 辐射换热量减少为原来的1/2,即 12
d 1 , d 2 d 1
A 2
d 1 , d 2 X
A 2
A1对A2角系数为:
1 cos cos d A d A 1 2 1 2 1 X X d A 1 , 2 d 1 , d 2 1 2 A A A A A A r 1 1
1 2 1 2
传热学-辐射传热的计算

X1,2
=
A1 + A2 − 2A1
A3
X1,3
=
A1 + A3 − 2A1
A2
X 2,3
=
A2
+ A3 − 2A2
A1
相对性
A1 X1,2 = A2 X 2,1 A1 X1,3 = A3 X 3,1 A2 X 2,3 = A3 X 3,2
三个非凹表面组成的封闭系统
由于垂直纸面方向的长度相同,则有:
从表面内部观察,该表面与外界的辐射
换热量应为: q = E1 − α1G1
J1
=
q
+
E1 − α1
q
=
E1 α1
−
⎛ ⎜ ⎝
1 α1
−
1
⎞ ⎟
q
⎠
注意:式中的各个量均是对
J
=
E α
−1−α α
q
=
Eb
−
(1 ε
−1)q
同一表面而言的,而且以向 外界的净放热量为正值。
9.2.3 两漫灰表面组成的封闭腔的辐射传热
n
∑ Φ1 = Φ1− j j =1
∑ ∑ Φ n 1− j
Φ j =1
1
=
n
x1− j = 1
j =1
X1,1 + X1,2 + X1,3 + + X1,n = 1
9.1.2 角系数的性质
1.角系数的相对性
两个有限大小表面之间角系数的相对性 Φ1,2 = A1 Eb1 X 1,2 − A2 Eb2 X 2,1
E b1 − +1
Eb2 + 1− ε2
ε 1 A1
传热学重点、题型讲解第九章辐射换热计算

第九章 辐射换热计算 第一节 黑表面间的辐射换热一、任意位置两非凹黑表面间的辐射换热1.黑表面间的辐射换热图9-1 任意位置两非凹黑表面的辐射换热122dA dA b1111d d cos d ΦI A θω-= E b1=πI b1; 2221cos d d rA θω=12212dA dA b1122cos cos d d d πΦE A A r θθ-=21212dA dA b2122cos cos d d d πΦE A A r θθ-=12122122212dA ,dA dA dA dA dA b1b2122cos cos d d d ()d d πΦΦΦE E A A r θθ--=-=- 1212122121,2dA ,dA b1b2122cos cos d ()d d πA A A A ΦΦE E A A r θθ==-⎰⎰⎰⎰ (9-1)2.角系数12121122b1122dA dA 12dA ,dA 22dA b11cos cos d d d cos cos πd d d πE A A Φr X A ΦE A r θθθθ-===12122121122dA dA 2dA A 12dA ,A 22dA dA d d cos cos d d d πA A ΦΦX A ΦΦr θθ--===⎰⎰12121211122dA dAA A121,2122A A1dcos cos1d dπA AA AΦΦX A AΦΦA rθθ--===⎰⎰⎰⎰(9-2a)212212AAA1,2ddπcoscos121212AArAΦΦXAA⎰⎰==-θθ(9-2b)21,212,1AXAX=(9-3)3.辐射空间热阻图9-2 辐射空间热阻21,2b2b112,1b2b12,1)()(AXEEAXEEΦ-=-=(9-4)b1b21,21,211E EΦX A-=Φ1,2=(E b1-E b2)A = σb(T14- T24)A二、封闭空腔诸黑表面间的辐射换热图9-3 多个黑表面组成的空腔图9-4 三个黑表面组成空腔的辐射网络图9-5 例9-1附图:,1,2,,1ni i i i n i j j ΦΦΦΦΦ==++⋅⋅⋅⋅⋅⋅=∑将上式除以i Φ,按角系数定义,可得,1,2,n ,11ni i i i j j X X X X ==++⋅⋅⋅⋅⋅⋅=∑(9-5)∑∑∑∑====-=-==nj nj i j i nj i j i i j i nj j i i A X E A X E A X E E ΦΦ11,bj 1,bi ,bj bi 1,)(∑=-=nj j i j i i A X E A E Φ1,bj bi (9-6)【例9-1】∑=-=311,b 1b11j j j j A X E A E Φ (a )∑=-=312,b 2b22j j j j A X E A E Φ (b )0313,b 3b33=-=∑=j j j j A X E A E Φ (c )02,21,22,11,1====X X X X13,23,1==X X31,313,1A X A X =32,323,2A X A X =213,11,33,223/210.252A r X X X A r ππ==⨯==13,32,31,3=++X X X5.03,3=X033,3b323,2b213,1b13b3=---A X E A X E A X E A E4b b T E σ=2424143T T T +=T 3=415.6K 或者142.6℃1b11b11,11b22,12b33,1344b11b31,3111344311b 244()()()100100473415.61 5.67()()1801.0W 2100100b ΦE A E X A E X A E X A E A E X A A T T T T AC σπ=---=-=-⎡⎤=-⎢⎥⎣⎦⎡⎤=⨯⨯⨯-=⎢⎥⎣⎦【讨论】π411212121=+=+=∑A A A A A AR 4444b1b2121,2()π 5.67 4.73 3.13)1801.0W 4/π4b E E T T ΦRσ--===⨯⨯-=∑(第二节 灰表面间的辐射换热一、有效辐射图9-6 有效辐射示意图图9-7 辐射表面热阻1.有效辐射J 1=ε1E b1+ρ1G 1=ε1E b1+(1-α1)G 1 W/m 2(a )2. 辐射表面热阻11b111111G E G J A Φαε-=-= W/m 2 (b ) 1111b11b111111)(1A J E J E A Φεεεε--=--= W (9-7)二、组成封闭腔的两灰表面间的辐射换热图9-8 两个灰表面组成封闭腔的辐射换热网络图9-9 空腔与内包壁面间的辐射换热22212,1111b2b12,1111A A X A E E Φεεεε-++--=W (9-8a ))11(1)11()(2212,112b 1b 12,1-++--=εεA A X E E A Φ 1,2112()W s b b X A E E ε=- (9-8b ))11()11(1121,212,1s -+-+=εεεX X1.无限大平行灰平壁的辐射换热A 1=A 2=A ,且X 1,2=X 2,1=1,)(111)(4241b s 212b b12,1T T A E E A Φ-=-+-=σεεε W (9-9)1121s -+=εεε2.其中一个表面为平面或凸表面的辐射换热)11(1)(22112b 1b 12,1-+-=εεA A E E A Φ W (9-10)A 2 >>A 1,且ε2的数值较大Φ1,2=ε1 A 1(E b1-E b2)W (9-11)三、封闭空腔中诸灰表面间的辐射换热1.网络法求解图9-10三个灰表面组成封闭腔辐射换热网络图9-11 例9-4附图图9-12 例题9-5附图节点1013,11312,1121111b1=-+-+-A X J J A X J J A J E εε (a )节点2 011123,22321,2212222b2=-+-+--A X J J A X J J A J E εε (b )节点3 011132,33231,3313333b3=-+-+--A X J J A X J J A J E εε (c )【例9-4】X 1,2= X 2,1=0.38X 1,3=X 2,3=1-X 1,2=1-0.38=0.62计算网络中的各热阻值:A 1=A 2=π⨯0.32=0.283m 21.14283.02.02.011111=⨯-=-A εε m -23.5283.04.04.011222=⨯=--A εε m -23.9283.038.01112,1=⨯=A X m -27.5283.062.011123,213,1=⨯==A X A X m -2流入每个节点的电流总和等于零07.53.91.141b3121b1=-+-+-J E J J J E 07.53.93.52b3212b2=-+-+-J E J J J E 202447731067.5484b1=⨯⨯==-T E b σW/m 235445001067.5484b2=⨯⨯==-T E b σW/m24593001067.5484b3=⨯⨯==-T E b σW/m 2J 1=5129 W/m 2 J 2=2760W/m 2b1111112024451291072W 114.1E J ΦA εε--===- b22222235442760148W 1 5.3E J ΦA εε--===-312()(1072148)1220W ΦΦΦ=-+=-+=-【例9-5】1.1411111=-=A R εεm -23.512222=-=A R εεm -23.9112,12,1==A X R m -27.5113,13,23,1===A X R R m -2E b1=20244W/m 2 E b2=3544W/m 2∑++++=23,23,12,11111R R R R R R =14.1+5.243.57.57.513.911=+++m -2b1b21,2202443544682W 24.5E E ΦR --===∑J 1=E b1-Φ1,2⨯R 1=20244-682⨯14.1=10627.8 W/m 2J 2=E b2+Φ1,2⨯R 2=3544+682⨯5.3=7185.6 W/m 2J 3=(J 1+J 2)/2=8893.2 W/m 2J 3=G 3=E b3=σ b T 341/41/4b3388893.2629K5.6710b E T σ-⎛⎫⎛⎫=== ⎪⎪⨯⎝⎭⎝⎭2. 值解法图9-13 例9-6(a )(b )附图及其辐射换热网络∑==ni i j i i j j A X J G A 1,j j εα=∑=-+=ni i j i i j j j j j j A X J A E A J 1,b )1(εε(9-12)∑∑===ni i j i j n i i j i i X J A A X J 1,1,b ,1(1)nj j j j i j i i J E J X εε==+-∑(9-13)4b 1,11j j j j jni i j i T J X J σεεε⎥⎥⎦⎤⎢⎢⎣⎡-=--∑=(9-14)4111,121,231,31,b 1114212,122,232,32,b 2221,12,231()()111()()11n n n n n n n J X J X J X J X T J X J X J X J X T J X J X J X εσεεεσεε-+++⋅⋅⋅+=--+-++⋅⋅⋅+=--⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅++4,3,b 1()()11n n n n n n n J X T εσεε⎫⎪⎪⎪⎪⎬⎪⎪⎪+⋅⋅⋅+-=⎪--⎭ (9-15)ii i i i i A J E Φεε--=1b i =1,2,…n (9-16)【例9-6】1,11,21,31,400.150.540.31X X X X ====、、、;2,12,22,32,40.2500.500.25X X X X ====、、、;3,13,23,33,40.270.140.320.27X X X X ====、、、;4,14,24,34,40.310.150.540X X X X ====、、、;4432198.267.5931.054.015.010⨯⨯=---J J J J 4432183.267.5425.05.0525.0⨯⨯=--+-J J J J4432186.267.5427.068.414.027.0⨯⨯=-+--J J J J 4432184.267.55.15.254.015.031.0⨯⨯=+---J J J JJ 1=440.45 W/m 2; J 2=370.28 W/m 2; J 3=382.69 W/m 2 ; J 4=380.80 W/m 2。
工学传热学辐射传热的计算

3. 交叉线法
分析 确定表面A1,A2的角系数。
解:封闭空腔 abcd 中 :
c
X1,2 1 X1,1 X1,ac X1,bd
封闭空腔 abc ,abd中 :
X 1,ac
ab ac bc 2ab
a
X 1,bd
ab bd ad 2ab
因此:
X 1, 2
(bc
ad) (ac bd) 2ab
由 X1,2 1, A2 A1, A1 A2 0 得: 1,2 A11(Eb1 Eb2 )
A1
A2
1,2
(1
A1(Eb1 Eb2 ) 1) 1 A1 (
1
1)
1
X1,2 A2 2
9.3 多表面系统的辐射换热
辐射换热网络求解法:
应用有效辐射的概念,将辐射换热系统模拟 成相应的电路系统,借助于电学中基尔霍夫电流 定律求解该系统的辐射换热问题。
9.3.1 两漫灰表面间的辐射换热网络图
1, 2
1 1
Eb1
1
Eb 2
12
A11 A1 X1,2 A2 2
Φ 1,2
Eb1
1 1 A1 1
J1 1 A1 X 1,2
J2 1 2 A2 2
Eb2
9.3.2 多表面封闭系统网络法求解的实施步骤
1. 画出等效的网络图。 三个漫灰表面构成的封闭空腔中的辐射换热
传热学
第9章 辐射传热的计算
第9章 辐射传热的计算
内容要求
掌握辐射传热的角系数; 两表面封闭系统的辐射传热; 多表面系统的辐射传热; 辐射传热的控制; 综合传热问题分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
测仪能测量到的单位表面积上的
辐射功率,W/m2。
有效辐射示意图
从表面1外部来观察,其能量收支差额应等于有
效辐射J1与投入辐射G1之差,即
q J G
从表面内部观察,该表面
与外界的辐射换热量应为:
q E G
对漫灰表面:=ε
有效辐射示意图
上两式联立,消去G,
=ε
q E J q
(2)
(3)
(4)
热阻串联得:
1, 2 1 1 1 A1 Eb1 Eb 2 1 2 1 A 2 A2 1 X 1, 2
J1
J2
Eb1
1 1 1 A1
Eb 2
1 A1 X 1,2
1 2 2 A2
两封闭表面间的辐射换热网络图
1, 2
Eb1 Eb 2 1 1 1 2 1 1 A1 A1 X 1,2 2 A2
dω1
即
X 1, 2 1 A1 cos 1 cos 2 dA2 dA1 A1 A2 r 2
dA1 dA2
工程上已将大量几何结构角系数的求 解结果绘制成图线。见教材P242。
例题 9-9 9-10 P245
2、代数分析法
利用角系数的相对性、完整性及可加性,通
过求解代数方程而获得角系数的方法称为代数分析法。 (1)三个非凹表面组成的封闭系统
J为物体表面的有效辐射力W/m2;
有效辐射示意图
G为投入辐射力W/m2
自身辐射E 有效辐射
投入辐射 G 被反射辐射的部分ρG
(ρ:表面的反射比,可表示成1-α)
根据有效辐射的定义,表面1 的有效辐射有如下表
达式:
J E G Eb 1 G
在表面外能感受到的表面辐射
就是有效辐射,它也是用辐射探
Φ1,2 Eb1 Eb2 1 X 1,2 A1
辐射空间热阻
的热辐射 到达表面 1的部分
表面1发出 表面 2发出
黑体系统的辐射换热
二、两漫灰表面组成的封闭系统的辐射换热计算
1、有效辐射 (1)投入辐射:单位时间内投射 到单位面积上的总辐射能,记为G (2)有效辐射:单位时间内离
开单位面积的总辐射能,记为J
1 1 1 X1,2 1 X 2,1 1 1 2
两黑体表面组成的封闭腔
s A1 X1,2 (Eb1 Eb2 )
1
定义系统黑度(或称为系统发射率)
s
1 X 1, 2 ( 1 1) X 2,1 ( 1 1)
1
号中的第一个角码则不存在类似的关系。
n
X 1, 2 X 1, 2 i
i 1
角系数的可加性
从表面2上发出而落到表面1上的辐射能,等于从表
面2的各部分发出而落到表面1上的辐射能之和,于
是有:
A2 Eb2 X 2,1 A2a Eb2 X 2a,1 A2b Eb2 X 2b,1
A2 X 2,1 A2a X 2a,1 A2b X 2b,1
X d 1,d 2 cos 1 cos 2 dA2 r2
dω1
微元面积 dA1对A2的角系数为
cos 1 cos 2 dA2 X d 1, 2 A 2 2 r
dA1
dA2
上式积分可得
A1 X 1, 2 cos 1 cos 2 dA2 dA1 2 A1 A2 r
A1 E b1 X 1,2 A1 E b1 X 1, 2a A1 E b1 X 1, 2b
X 1, 2 X 1, 2 a X 1, 2 b
如把表面 2 进一步分成若干小块,则有
X 1, 2 X 1, 2 i
i 1
n
(6)
注意:利用角系数可加性(分解性)时,只有对角
系数符号中第二个角码是可加的,对角系数符
表面1发出的有 效辐射到达表 面 2的部分 表面2发出的有 效辐射到达表 面1的部分
根据下式及能量守恒有
J Eb ( 1)q
1
1 J 1 A1 A1 Eb1 11, 2 1 1 J A A E 1 2,1 2 2 2 b2 2 1, 2 2,1
若以A1为计算面积, 上式可改写为:
Φ1,2 Eb1 Eb2 1 X 1,2 A1
1, 2
A1 ( Eb1 Eb 2 ) A1 1 1 1 1 1 1 X 1,2 A2 2
A1 X1,2 ( Eb1 Eb 2 )
三表面封闭空间角 系数的确定
上述方程解得:
X 1, 2 X 1,3 X 2,3
A1 A2 A3 2 A1
A1 A3 A2 2 A1 A2 A3 A1 2 A2
A1
A2
A3
一个表面对另一个表面的角 系数可表示为两个参与表面 之和减去非参与表面,然后 除以二倍的该表面。
第九章
辐射换热计算
主要内容:
§9-1 角系数的定义、性质及计算 §9-2 被透明介质隔开的两固体表面间的辐射换热
§9-3 多表面系统辐射换热的计算
§9-4 辐射换热的强化与削弱 §9-5气体辐射与太阳辐射
§9-1 角系数的定义、性质及计算 两个表面之间的辐射换热量与两个表面之间的相 对位置有很大关系
1, 2 A1 Eb1 X 1, 2 A2 Eb 2 X 2,1
则有限大小表面间角系数的相对性/互换性的表 达式:
A1 X1, 2 A2 X 2,1
(4)
⑵ 角系数的完整性 从任何一个表面发射出的辐射能必全部落到封闭系统的 各表面上。因此,任何一个表面对封闭腔各表面的角系 数之间存在下列关系:
对于由几个表面组成的封闭系统,据能量守衡原理,
X1,1 X1,2 X1,3 X1,n 1
X
i 1
n
1, i
1
(5)
注:若表面1为非凹表面时,X1,1
= 0;若表面1为凹表面,X 1, 1 0
角系数的完整性
⑶ 角系数的分解性/可加性 从表面 1 上发出而落到表面 2 上的总能量,等 于落到表面 2 上各部分的辐射能之和,于是有
三个非凹表面组成的封闭系统
由角系数完整性
X 1, 2 X 1, 3 1 X 2 ,1 X 2 , 3 1 X 3 ,1 X 3 , 2 1
由角系数相对性
A1
A2 A3
A1 X 1, 2 A2 X 2,1 A1 X 1, 3 A3 X 3,1 A2 X 2, 3 A3 X 3, 2
表面相对位置的影响
A图中两表面无限接近,相互间的换热量最大;
B图中两表面位于同一平面上,相互间的辐射换热量
为零。
由图可以看出,两个表面间的相对位置不同时,一
个表面发出而落到另一个表面上的辐射能的百分数随 之而异,从而影响到换热量。
一、角系数的定义 定义:把表面 1 发出的辐射能中落 到表面 2 上的百分数称为表面 1 对表 面 2 的角系数,记为X1,2。 同理,表面 2 发出的辐射能中落到 表面 1 上的百分数称为表面 2 对表面 1 的角系数,记为X 2,1。 角系数是进行辐射换热计算时空间 热阻的主要组成部分。
T1 4 T2 4 s A1 5.67 100 100 其中系统发射率为:
1 s 1 A1 1 1 1 A2 2
(2)非凹,且表面积A1比表面积A2小得多,即A1/A2 0 于是 A1 ( Eb1 Eb 2 )
2
三种特殊情形
1, 2
A1 ( Eb1 Eb 2 ) A 1 1 1 1 1 1 1 X 1,2 A2 2
(1) 表面1为凸面或平面(非凹),此时,X1,2=1,
1,2 A1 ( Eb1 Eb 2 ) 1 A1 1 1 1 A2 2
二、角系数的性质
研究角系数的性质是用代数法(代数分析法)求
解角系数的前提:
定向辐射强度与空间方向无关
假定:(1)所研究的表面是漫射的;
(2)在所研究表面的不同地点上向外发射的
辐射热流密度是均匀的。
⑴ 角系数的相对性(互换性)
一个微元表面到另一个微元表面的角系数
X dA ,dA
1 2
由dA1发出的落到dA2上的辐射能 I b1 cos1dA1d 由dA1发出的辐射能 Eb1dA1
dA2 cos 1 cos 2 X dA1 ,dA2 r 2
Eb1 I b1
dAc dA2 cos 2 d 2 r r2
Eb1 : 辐射力,W m2
Ib1:定向辐射强度,W/(m2· sr) dΩ:立体角,sr( 球面度 )
两微元面间的辐射
dA2 cos 1 cos 2 X dA1 ,dA2 r 2
E 1 1 J q Eb ( 1)q
注意:式中的各个量均是对同一表面而言的,
而且以向外界的净放热量为正值。
Eb J 1 A
辐射表面热阻
2、两灰表面组成的封闭腔的辐射换热
两个物体组成的辐射换热系统
两个等温漫灰表面封闭系统内的辐射换热的净换热量为:
1, 2 A1 J1 X 1, 2 A2 J 2 X 2,1
三表面封闭空间角 系数的确定
由于垂直屏幕方向的长度相同,则有:
X 1, 2 X 1, 3 X 1, 2 l1 l 2 l 3 2l 1 l1 l 3 l 2 2l 1 l 3 l 2 l1 2l 2
注意:在垂直于屏幕方向为无限长,故从系统
