数学建模08 上机实验及简单综合编程
数学建模基础实验报告(3篇)

第1篇一、实验目的本次实验旨在让学生掌握数学建模的基本步骤,学会运用数学知识分析和解决实际问题。
通过本次实验,培养学生主动探索、努力进取的学风,增强学生的应用意识和创新能力,为今后从事科研工作打下初步的基础。
二、实验内容本次实验选取了一道实际问题进行建模与分析,具体如下:题目:某公司想用全行业的销售额作为自变量来预测公司的销售量。
表中给出了1977—1981年公司的销售额和行业销售额的分季度数据(单位:百万元)。
1. 数据准备:将数据整理成表格形式,并输入到计算机中。
2. 数据分析:观察数据分布情况,初步判断是否适合使用线性回归模型进行拟合。
3. 模型建立:利用统计软件(如MATLAB、SPSS等)进行线性回归分析,建立公司销售额对全行业的回归模型。
4. 模型检验:对模型进行检验,包括残差分析、DW检验等,以判断模型的拟合效果。
5. 结果分析:分析模型的拟合效果,并对公司销售量的预测进行评估。
三、实验步骤1. 数据准备将数据整理成表格形式,包括年份、季度、公司销售额和行业销售额。
将数据输入到计算机中,为后续分析做准备。
2. 数据分析观察数据分布情况,绘制散点图,初步判断是否适合使用线性回归模型进行拟合。
3. 模型建立利用统计软件进行线性回归分析,建立公司销售额对全行业的回归模型。
具体步骤如下:(1)选择合适的统计软件,如MATLAB。
(2)输入数据,进行数据预处理。
(3)编写线性回归分析程序,计算回归系数。
(4)输出回归系数、截距等参数。
4. 模型检验对模型进行检验,包括残差分析、DW检验等。
(1)残差分析:计算残差,绘制残差图,观察残差的分布情况。
(2)DW检验:计算DW值,判断随机误差项是否存在自相关性。
5. 结果分析分析模型的拟合效果,并对公司销售量的预测进行评估。
四、实验结果与分析1. 数据分析通过绘制散点图,观察数据分布情况,初步判断数据适合使用线性回归模型进行拟合。
2. 模型建立利用MATLAB进行线性回归分析,得到回归模型如下:公司销售额 = 0.9656 行业销售额 + 0.01143. 模型检验(1)残差分析:绘制残差图,观察残差的分布情况,发现残差基本呈随机分布,说明模型拟合效果较好。
《数学建模与数学实验》上机实验报告
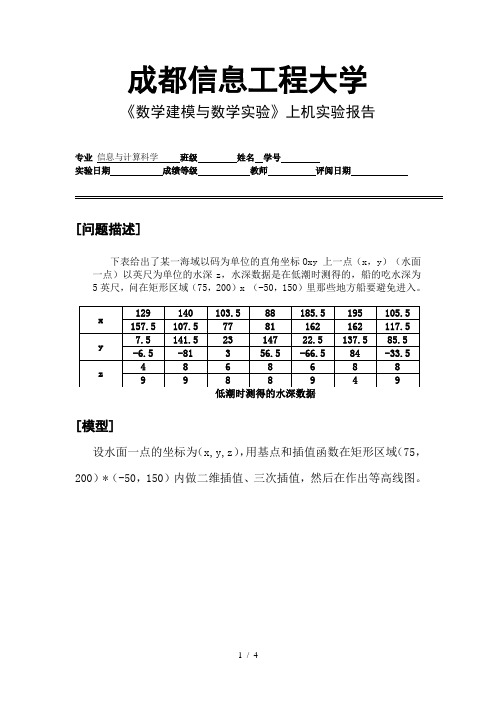
成都信息工程大学《数学建模与数学实验》上机实验报告专业信息与计算科学班级姓名学号实验日期成绩等级教师评阅日期[问题描述]下表给出了某一海域以码为单位的直角坐标Oxy 上一点(x,y)(水面一点)以英尺为单位的水深z,水深数据是在低潮时测得的,船的吃水深为5英尺,问在矩形区域(75,200)x (-50,150)里那些地方船要避免进入。
[模型]设水面一点的坐标为(x,y,z),用基点和插值函数在矩形区域(75,200)*(-50,150)内做二维插值、三次插值,然后在作出等高线图。
[求解方法]使用matlab求解:M文件:water.mx=[129 140 103.5 88 185.5 195 105.5 157.5 107.5 77 81 162 162 117.5];y=[7.5 141.5 23 147 22.5 137.5 85.5 -6.5 -81 3 56.5 -66.584 -33.5];z=[-4 -8 -6 -8 -6 -8 -8 -9 -9 -8 -8 -9 -4 -9];cx = 75:0.5:200;cy = -50:0.5:150;[cx,cy]=meshgrid(cx,cy);作出曲面图:代码如下:>> water>> cz=griddata(x,y,z,cx,cy,'cubic');>> meshz(cx,cy,cz)>> xlabel('X'),ylabel('Y'),zlabel('Z')>>作出等高线图:代码如下:>> water>> cz=griddata(x,y,z,cx,cy,'cubic');>> figure(2)>> contour(cx,cy,cz,[-5,-5],'r')>> hold on>> plot(x,y,'*')>> xlabel('X'),ylabel('Y')[结果]插值结果等值图:[结果分析及结论]根据等值图可看出:红色区域为危险区域,所以船只要避免进入。
数学的上机实验报告

实验题目:线性代数求解方程组一、实验目的1. 理解线性代数中方程组的求解方法。
2. 掌握利用计算机求解线性方程组的算法。
3. 熟悉数学软件(如MATLAB、Python等)在数学问题中的应用。
二、实验内容本次实验主要利用数学软件求解线性方程组。
线性方程组是线性代数中的一个基本问题,其求解方法有很多种,如高斯消元法、矩阵求逆法等。
本实验以高斯消元法为例,利用MATLAB软件求解线性方程组。
三、实验步骤1. 编写高斯消元法算法程序。
2. 输入方程组的系数矩阵和常数项。
3. 调用程序求解方程组。
4. 输出解向量。
四、实验代码及分析1. 高斯消元法算法程序```matlabfunction x = gaussElimination(A, b)[n, m] = size(A);assert(n == m, 'The matrix A must be square.');assert(n == length(b), 'The length of b must be equal to the number of rows in A.');% 初始化解向量x = zeros(n, 1);% 高斯消元for i = 1:n-1% 寻找最大元素[~, maxIdx] = max(abs(A(i:n, i)));maxIdx = maxIdx + i - 1;% 交换行A([i, maxIdx], :) = A([maxIdx, i], :);b([i, maxIdx]) = b([maxIdx, i]);% 消元for j = i+1:nfactor = A(j, i) / A(i, i);A(j, i:n) = A(j, i:n) - factor A(i, i:n); b(j) = b(j) - factor b(i);endend% 回代求解for i = n:-1:1x(i) = (b(i) - A(i, i+1:n) x(i+1:n)) / A(i, i); endend```2. 输入方程组的系数矩阵和常数项```matlabA = [2, 1, -1; 1, 2, 1; -1, 1, 2];b = [8; 5; 2];```3. 调用程序求解方程组```matlabx = gaussElimination(A, b);```4. 输出解向量```matlabdisp('解向量为:');disp(x);```五、实验结果与分析实验结果:```解向量为:2-13```实验分析:通过高斯消元法,我们成功求解了给定的线性方程组。
数学实验与数学建模上机实习任务

数学建模(1)第一次上机实习任务1、 写出分段函数00102010301020()30(20)/22040204050202(50)5060060x x x x f x x x x x x x ≤⎧⎪+<≤⎪⎪<≤⎪=--<≤⎨⎪<≤⎪--<≤⎪⎪>⎩ 的Mathematica 自定义函数形式,并画出其在[0,60]上的图形。
代码:f[x_]:=Which[x<=0,0,x<=10,10+2*x,x<=20,30,x<=40,30-(x-20)/2,x<=50,20,x<=60,20-2*(x-50),x>60,0]Plot[f[x],{x,0,60}]2、 分别用Do 语句、For 语句、While 语句三种循环控制语句完成1到100所有自然数求和运算。
代码1:s = 0; Do[s += i, {i, 100}]; s代码2:For[i = 0; s = 0, i <= 100, i++, s += i]; s代码3: i = 0; s = 0; While[i <= 100, s += i; i++]; s3、按要求绘制下列函数图形。
(1) s i n ()z x y =,1010,1010x y -≤≤-≤≤。
代码: Plot3D[Sin[x*y],{x,-10,10},{y,-10,10}](2)在同一坐标系中画出下列三个函数2sin(),,x y x x y e y x =+==的图形,并给坐标横轴和纵轴分别标记为x 和y ,自变量范围为:2020x -≤≤,第一个输出曲线是绿色且线宽为0.06,第二个输出曲线为蓝色,第三个输出曲线为虚线。
代码:Plot[{Sin[x]+x,Exp[x],x^2,x},{x,-20,20},AxesLabel->{"x","y"},PlotStyle->{{RGBColor[0,1,0],T hickness[0.06]},{Dashing[{0.5,0.3}]},{RGBColor[0,0,1]}}]。
数学建模实验教学大纲

数学建模实验教学⼤纲《数学建模》实验教学⼤纲课程名称:数学建模课程编号:011850课程类别:专业基础选修课学时/学分:32/2开设学期:第4、5学期开设单位:数学与统计学院适⽤专业:数学与应⽤数学说明⼀、课程性质专业任选课⼆、教学⽬标通过上机实验, 对⼀些数学模型进⾏实际计算, 可以达到熟悉数学软件, 提⾼解决问题的能⼒. 要求学⽣先理解问题, 弄懂模型, 对软件有⼀定了解, 然后上机操作编程和利⽤专门软件计算. 数模实验是进⾏数学建模的实践性环节, 学⽣以三⼈为⼀组组成兴趣⼩组进⾏研究. 经过⼀段时间的探讨, 完成⼀篇数模论⽂, 包括模型的假设、建⽴和求解、计算⽅法的设计和计算机实现、结果的分析和检验、模型的改进等⽅⾯内容.三、学时分配表四、实验⽅法与要求建议实验课教师不再讲授, 主要靠学⽣⾃学, 教师可以适当指导. 学⽣上机时⼀边学习Matlab 软件介绍, ⼀边仿照例题的格式进操作和运⾏并针对实验内容完成实验操作.五、考核⽅式及要求1.考核⽅式:考试;考查2.成绩评定:计分制:百分制;五级分制;两级分制成绩构成:总评成绩由平时考核成绩、中期考核成绩和期末考核成绩综合评定本⽂实验⼀⼈⼝的预测⼀、实验性质:实验类别:专业⽅向/选修实验类型:综合性计划学时:2学时实验分组:⼆、实验⽬的:1.了解数据拟合的基本原理;会⽤matlab 求解数据拟合问题;2.要求学⽣了解Matlab 软件的基本操作、基本功能、基本运算和作图.三、实验的基本内容和要求:1.熟习Matlab 软件的作图;2. 掌握利⽤Matlab 软件解决拟合问题的⽅法;3.对上机实验的内容写出算法步骤, 记录和分析计算结果, 写出实验报告. 四、实验仪器设备及材料:计算机, Matlab数学软件五、实验操作要点:1.上机时⼀边学习Matlab 软件介绍⼀边仿照例题的格式进操作和运⾏;2.对具体问题建⽴的模型进⾏求解.六、实验教学建议:实验课教师不再讲授, 主要靠学⽣⾃学, 教师可以适当指导.实验⼆炼油⼚的⽣产计划⼀、实验性质:实验类别:专业⽅向/选修实验类型:综合性计划学时:2学时实验分组:⼆、实验⽬的:1. 了解线性规划模型的建⽴⽅法;2. 会⽤Matlab 软件求解线性规划问题.三、实验的基本内容和要求:1. 要求学⽣掌握Matlab 软件的操作;2. 利⽤Matlab 软件求解炼油⼚的⽣产计划;3. 对上机实验的内容写出算法步骤, 记录和分析计算结果, 写出实验报告.四、实验仪器设备及材料:计算机, Matlab数学软件五、实验操作要点:1.上机时⼀边学习Matlab 软件介绍⼀边仿照例题的格式进操作和运⾏;2.对具体问题建⽴的模型进⾏求解.六、实验教学建议:实验课教师不再讲授, 主要靠学⽣⾃学, 教师可以适当指导.实验三⼈寿保险的影响因素⼀、实验性质:实验类别:专业⽅向/选修实验类型:综合性计划学时:2学时实验分组:⼆、实验⽬的:1.了解统计回归的基本原理;2. 掌握线性回归与⾮线性回归.三、实验的基本内容和要求:1. 会⽤matlab 求解统计回归问题;2. 要求学⽣进⼀步了解Matlab 软件的操作;3. 对上机实验的内容写出算法步骤, 记录和分析计算结果, 写出实验报告.四、实验仪器设备及材料:计算机, Matlab数学软件五、实验操作要点:1.上机时⼀边学习Matlab 软件介绍⼀边仿照例题的格式进操作和运⾏;2.利⽤Matlab 软件求解⼈寿保险的影响因素.六、实验教学建议:实验课教师不再讲授, 主要靠学⽣⾃学, 教师可以适当指导.实验四⽔塔流量的估计⼀、实验性质:实验类别:专业⽅向/选修实验类型:综合性计划学时:2学时实验分组:⼆、实验⽬的:1. 掌握模型的建⽴⽅法;2. 掌握值⽅法三、实验的基本内容和要求:1. 表述⽔塔流量问题的分析过程;2. 利⽤插值计算⽔塔的流量;利⽤曲线拟合计算⽔塔的流量;3. 对上机实验的内容写出算法步骤, 记录和分析计算结果, 写出实验报告四、实验仪器设备及材料:计算机, Matlab数学软件五、实验操作要点:⾸先在上机前写出源程序, 上机时进⼊matlab 语⾔运⾏环境输⼊源程序, 然后调试和运⾏.六、实验教学建议:实验课教师不再讲授, 主要靠学⽣⾃学, 教师可以适当指导.实验五微分⽅程实验⼀、实验性质:实验类别:专业⽅向/选修实验类型:综合性计划学时:2学时实验分组:⼆、实验⽬的:1. 认识微分⽅程的建模过程;2. 认识微分⽅程的数值解法.三、实验的基本内容和要求:1. 熟练应⽤Matlab的符号求解⼯具箱求解常微分⽅程;2. 掌握机理分析建⽴微分⽅程的⽅法和步骤;3. 提⾼Matlab的编程应⽤技能.四、实验仪器设备及材料:计算机, Matlab数学软件五、实验操作要点:1.上机时⼀边学习Matlab 软件介绍⼀边仿照例题的格式进操作和运⾏;2.对具体问题建⽴的模型进⾏求解.六、实验教学建议:实验课教师不再讲授, 主要靠学⽣⾃学, 教师可以适当指导.指导书与参考资料:[1]. 姜启源, 谢⾦星等.数学模型(第三版)[M].北京:⾼等教育出版社, 2003.8[2]. 张志涌等Matlab教程(2009年修订)[M].北京:北就航空航天⼤学出版社2009.8.[3]. 周义仓, 赫孝良.数学建模实验[M].西安:西安交通⼤学出版社, 1999.8.执笔:王汝军审核:朱睦正制(修)订时间:2011-10-20。
数学建模实验指导书08(一)

《数学建模》实验指导书《数学建模》实验指导书 数学建模》实验报告的格式 姓名: 姓名: 实验名称 实验目的 实验内容 模型 程序 结果 结果的分析 学号: 学号: 班级试验一: 试验一:数学软件 Matlab 的使用学时: 学时:2 学时 实验目的: 实验目的:了解 Matlab 软件的运行、基本操作、M 文件的建立与使用。
实验内容: 实验内容: (一) 1. 对以下问题,编制 M 文件: (1) 用起泡法对 10 个数由小到大排序。
即将相邻两个数比较,将小的调到前头; (2) 有一个 4×5 的矩阵,编程求出其最大值及其所处的位置; (3) 有一个函数 f ( x, y ) = x 2 + sin xy + 2 y ,写一程序,输入自变量的值,输出函数值。
2. 用 plot,fplot 绘制函数 y = cos(tan(πx )) 图形。
3. 用 ezplot 绘制摆线: x = a (t − sin t ) , t ∈ [0,2π ] 的图形 y = a (1 − cos t )4. 在同一平面中的两个窗口分别画出心形线和马鞍面。
要求: (1)在图形上加格栅、 图例和标注; (2)定制坐标; (3)以不同的角度观察马鞍面。
第1页《数学建模》实验指导书5. 画出圆锥面 z =x 2 + y 2 及旋转抛物面 z = 2 − x 2 − y 2 所围的立体图形(二) 编程练习:利用 Matlab 编程,求 “应急设施的位置问题的模型”的解。
以上(一)(二)可以任选其一。
、 参考资料: Malab 软件基础 赵静,但琦,数学建模与数学实验(第 2 版) ,高等教育出版社实验二 实验二:Matlab 微分方程的数值解学时: 学时:2 学时 实验目的: 实验目的:掌握用 matlab 进行微分方程的数值解。
实验内容: 实验内容: di dt = λsi − µi, i (0) = i0 进行数值计算输出结果,并在同一坐标系中画 1. 对传染病模型 ds = −λsi, s ( 0) = s 0 dt 出 i(t), s(t) 的图形。
2008年大学生数学建模竞赛A题优秀论文程序

本文件夹中共有7个m文件,分别为:m1.m:用边缘检测算法检测的圆的像的边缘点,并用多元线性回归求出椭圆的方程,然后按照我们的模型中提供的方法,求出每个圆心的像的位置moni.m:用计算机模拟的方法检验相机和标靶的距离对我们模型带来的影响,即统计不同距离下的误差值moni2.m:用计算机模拟的方法检验α的变化对我们模型带来的影响,即统计不同α下的误差值moni3.m:用计算机模拟的方法检验β的变化对我们模型带来的影响,即统计不同β下的误差值gongqiexian.m:计算圆的像的的公切线并根据这个算出圆心的像的坐标jiaodian.m:函数,用于计算分别由两个点确定的两条直线的交点jiaodian2.m:函数,用于计算由8个点确定的4条直线的交点连线的交点坐标说明:1.m1.m,moni.m,moni2.m,moni3.m,gongqiexian.m为可执行代码,直接运行即得结果(当然必须保证代码即本文件中的图片pictrue.bmp在matlab的当前工作区)2.执行m1.m时程序会将每个圆的像的边缘点以excel文件保存在D盘,而执行gongqiexian.m 需要这些文件文件顺序为:format long;[p1,txt1,raw1]=xlsread('d:/1.xls');[p2,txt2,raw2]=xlsread('d:/2.xls');[p3,txt3,raw3]=xlsread('d:/3.xls');[p4,txt4,raw4]=xlsread('d:/4.xls');[p5,txt5,raw5]=xlsread('d:/5.xls');qd=ones(6,4);P=imread('picture.bmp');imshow(P);hold on;%第1组圆1,3[min1 i]=min(p1(:,1));qd(1,1)=i;[min3 i]=min(p3(:,1));qd(1,2)=i;size1=size(p1);size3=size(p3);flag=1;while flag>0flag=0;for i=1:size1(1)ifp1(i,1)<(p1(qd(1,1),1)-p3(qd(1,2),1))/(p1(qd(1,1),2)-p3(qd(1,2),2))*(p1(i,2)-(p1(qd(1,1),2)))+p1(q d(1,1),1)qd(1,1)=i;flag=1;endendfor i=1:size3(1)ifp3(i,1)<(p1(qd(1,1),1)-p3(qd(1,2),1))/(p1(qd(1,1),2)-p3(qd(1,2),2))*(p3(i,2)-(p1(qd(1,1),2)))+p1(q d(1,1),1)qd(1,2)=i;flag=1;endendendfor i=1:1024y(i)=(p1(qd(1,1),1)-p3(qd(1,2),1))/(p1(qd(1,1),2)-p3(qd(1,2),2))*(i-(p1(qd(1,1),2)))+p1(qd(1,1),1) ;endplot([1:1024],y);hold on;%另一条切线[max1 i]=min(p1(:,1));qd(1,3)=i;[max3 i]=min(p3(:,1));qd(1,4)=i;size1=size(p1);size3=size(p3);flag=1;while flag>0flag=0;for i=1:size1(1)ifp1(i,1)>(p1(qd(1,3),1)-p3(qd(1,4),1))/(p1(qd(1,3),2)-p3(qd(1,4),2))*(p1(i,2)-(p1(qd(1,3),2)))+p1(q d(1,3),1)qd(1,3)=i;flag=1;endendfor i=1:size3(1)ifp3(i,1)>(p1(qd(1,3),1)-p3(qd(1,4),1))/(p1(qd(1,3),2)-p3(qd(1,4),2))*(p3(i,2)-(p1(qd(1,3),2)))+p1(q d(1,3),1)qd(1,4)=i;flag=1;endendendfor i=1:1024y(i)=(p1(qd(1,3),1)-p3(qd(1,4),1))/(p1(qd(1,3),2)-p3(qd(1,4),2))*(i-(p1(qd(1,3),2)))+p1(qd(1,3),1) ;endplot([1:1024],y);hold on;%第2组圆4,5[min4 i]=min(p4(:,1));qd(2,1)=i;[min5 i]=min(p5(:,1));qd(2,2)=i;size4=size(p4);size5=size(p5);flag=1;while flag>0flag=0;for i=1:size4(1)ifp4(i,1)<(p4(qd(2,1),1)-p5(qd(2,2),1))/(p4(qd(2,1),2)-p5(qd(2,2),2))*(p4(i,2)-(p4(qd(2,1),2)))+p4(q d(2,1),1)qd(2,1)=i;flag=1;endendfor i=1:size5(1)ifp5(i,1)<(p4(qd(2,1),1)-p5(qd(2,2),1))/(p4(qd(2,1),2)-p5(qd(2,2),2))*(p5(i,2)-(p4(qd(2,1),2)))+p4(q d(2,1),1)qd(2,2)=i;flag=1;endendendfor i=1:1024y(i)=(p4(qd(2,1),1)-p5(qd(2,2),1))/(p4(qd(2,1),2)-p5(qd(2,2),2))*(i-(p4(qd(2,1),2)))+p4(qd(2,1),1) ;endplot([1:1024],y);hold on;%另一条切线[max4 i]=min(p4(:,1));qd(2,3)=i;[max5 i]=min(p5(:,1));qd(2,4)=i;size4=size(p4);size5=size(p5);flag=1;while flag>0flag=0;for i=1:size4(1)ifp4(i,1)>(p4(qd(2,3),1)-p5(qd(2,4),1))/(p4(qd(2,3),2)-p5(qd(2,4),2))*(p4(i,2)-(p4(qd(2,3),2)))+p4(q d(2,3),1)qd(2,3)=i;flag=1;endendfor i=1:size5(1)ifp5(i,1)>(p4(qd(2,3),1)-p5(qd(2,4),1))/(p4(qd(2,3),2)-p5(qd(2,4),2))*(p5(i,2)-(p4(qd(2,3),2)))+p4(q d(2,3),1)qd(2,4)=i;flag=1;endendendfor i=1:1024y(i)=(p4(qd(2,3),1)-p5(qd(2,4),1))/(p4(qd(2,3),2)-p5(qd(2,4),2))*(i-(p4(qd(2,3),2)))+p4(qd(2,3),1) ;endplot([1:1024],y);hold on;%第3组圆1,4[min1 i]=min(p1(:,2));qd(3,1)=i;[min4 i]=min(p4(:,2));qd(3,2)=i;size1=size(p1);size4=size(p4);flag=1;while flag>0flag=0;for i=1:size1(1)ifp1(i,2)<(p1(qd(3,1),2)-p4(qd(3,2),2))/(p1(qd(3,1),1)-p4(qd(3,2),1))*(p1(i,1)-p1(qd(3,1),1))+p1(qd (3,1),2)qd(3,1)=i;flag=1;endendfor i=1:size4(1)ifp4(i,2)<(p1(qd(3,1),2)-p4(qd(3,2),2))/(p1(qd(3,1),1)-p4(qd(3,2),1))*(p4(i,1)-p1(qd(3,1),1))+p1(qd (3,1),2)qd(3,2)=i;flag=1;endendendfor i=1:1024y(i)=(p1(qd(3,1),1)-p4(qd(3,2),1))/(p1(qd(3,1),2)-p4(qd(3,2),2))*(i-p1(qd(3,1),2))+p1(qd(3,1),1); endplot([1:1024],y);hold on;%另一条切线[max1 i]=max(p1(:,2));qd(3,3)=i;[max4 i]=max(p4(:,2));qd(3,4)=i;size1=size(p1);size4=size(p4);flag=1;while flag>0flag=0;for i=1:size1(1)ifp1(i,2)>(p1(qd(3,3),2)-p4(qd(3,4),2))/(p1(qd(3,1),1)-p4(qd(3,4),1))*(p1(i,1)-p1(qd(3,3),1))+p1(qd (3,3),2)qd(3,3)=i;flag=1;endendfor i=1:size4(1)ifp4(i,2)>(p1(qd(3,3),2)-p4(qd(3,4),2))/(p1(qd(3,1),1)-p4(qd(3,4),1))*(p4(i,1)-p1(qd(3,3),1))+p1(qd (3,3),2)qd(3,4)=i;flag=1;endendendfor i=1:1024y(i)=(p1(qd(3,3),1)-p4(qd(3,4),1))/(p1(qd(3,3),2)-p4(qd(3,4),2))*(i-p1(qd(3,3),2))+p1(qd(3,3),1);endplot([1:1024],y);hold on;%第4组圆2,4[min2 i]=min(p2(:,2));qd(4,1)=i;[min4 i]=min(p4(:,2));qd(4,2)=i;size2=size(p2);size4=size(p4);flag=1;while flag>0flag=0;for i=1:size2(1)ifp2(i,2)<(p2(qd(4,1),2)-p4(qd(4,2),2))/(p2(qd(4,1),1)-p4(qd(4,2),1))*(p2(i,1)-p2(qd(4,1),1))+p2(qd (4,1),2)qd(4,1)=i;flag=1;endendfor i=1:size4(1)ifp4(i,2)<(p2(qd(4,1),2)-p4(qd(4,2),2))/(p2(qd(4,1),1)-p4(qd(4,2),1))*(p4(i,1)-p2(qd(4,1),1))+p2(qd (4,1),2)qd(4,2)=i;flag=1;endendendfor i=1:1024y(i)=(p2(qd(4,1),1)-p4(qd(4,2),1))/(p2(qd(4,1),2)-p4(qd(4,2),2))*(i-p2(qd(4,1),2))+p2(qd(4,1),1); endplot([1:1024],y);hold on;%另一条切线[max2 i]=max(p2(:,2));qd(4,3)=i;[max4 i]=max(p4(:,2));flag=1;while flag>0flag=0;for i=1:size4(1)ifp4(i,2)>(p2(qd(4,3),2)-p4(qd(4,4),2))/(p2(qd(4,1),1)-p4(qd(4,4),1))*(p4(i,1)-p2(qd(4,3),1))+p2(qd (4,3),2)qd(4,4)=i;flag=1;endendfor i=1:size2(1)ifp2(i,2)>(p2(qd(4,3),2)-p4(qd(4,4),2))/(p2(qd(4,1),1)-p4(qd(4,4),1))*(p2(i,1)-p2(qd(4,3),1))+p2(qd (4,3),2)qd(4,3)=i;flag=1;endendendfor i=1:1024y(i)=(p2(qd(4,3),1)-p4(qd(4,4),1))/(p2(qd(4,3),2)-p4(qd(4,4),2))*(i-p2(qd(4,3),2))+p2(qd(4,3),1); endplot([1:1024],y);hold on;%第5组圆2,5[min2 i]=min(p2(:,2));qd(5,1)=i;[min5 i]=min(p5(:,2));qd(5,2)=i;size2=size(p2);size5=size(p5);flag=1;while flag>0flag=0;for i=1:size2(1)p2(i,2)<(p2(qd(5,1),2)-p5(qd(5,2),2))/(p2(qd(5,1),1)-p5(qd(5,2),1))*(p2(i,1)-p2(qd(5,1),1))+p2(qd (5,1),2)qd(5,1)=i;flag=1;endendfor i=1:size5(1)ifp5(i,2)<(p2(qd(5,1),2)-p5(qd(5,2),2))/(p2(qd(5,1),1)-p5(qd(5,2),1))*(p5(i,1)-p2(qd(5,1),1))+p2(qd (5,1),2)qd(5,2)=i;flag=1;endendendfor i=1:1024y(i)=(p2(qd(5,1),1)-p5(qd(5,2),1))/(p2(qd(5,1),2)-p5(qd(5,2),2))*(i-p2(qd(5,1),2))+p2(qd(5,1),1); endplot([1:1024],y);hold on;%另一条切线[max2 i]=max(p2(:,2));qd(5,3)=i;[max5 i]=max(p5(:,2));qd(5,4)=i;flag=1;while flag>0flag=0;for i=1:size2(1)ifp2(i,2)>(p2(qd(5,3),2)-p5(qd(5,4),2))/(p2(qd(5,1),1)-p5(qd(5,4),1))*(p2(i,1)-p2(qd(5,3),1))+p2(qd (5,3),2)qd(5,3)=i;flag=1;endendfor i=1:size5(1)ifp5(i,2)>(p2(qd(5,3),2)-p5(qd(5,4),2))/(p2(qd(5,1),1)-p5(qd(5,4),1))*(p5(i,1)-p2(qd(5,3),1))+p2(qd (5,3),2)qd(5,4)=i;flag=1;endendendfor i=1:1024y(i)=(p2(qd(5,3),1)-p5(qd(5,4),1))/(p2(qd(5,3),2)-p5(qd(5,4),2))*(i-p2(qd(5,3),2))+p2(qd(5,3),1); endplot([1:1024],y);hold on;%第6组圆3,5[min3 i]=min(p3(:,2));qd(6,1)=i;[min5 i]=min(p5(:,2));qd(6,2)=i;size3=size(p3);size5=size(p5);flag=1;while flag>0flag=0;for i=1:size3(1)ifp3(i,2)<(p3(qd(6,1),2)-p5(qd(6,2),2))/(p3(qd(6,1),1)-p5(qd(6,2),1))*(p3(i,1)-p3(qd(6,1),1))+p3(qd (6,1),2)qd(6,1)=i;flag=1;endendfor i=1:size5(1)ifp5(i,2)<(p3(qd(6,1),2)-p5(qd(6,2),2))/(p3(qd(6,1),1)-p5(qd(6,2),1))*(p5(i,1)-p3(qd(6,1),1))+p3(qd (6,1),2)qd(6,2)=i;flag=1;endendfor i=1:1024y(i)=(p3(qd(6,1),1)-p5(qd(6,2),1))/(p3(qd(6,1),2)-p5(qd(6,2),2))*(i-p3(qd(6,1),2))+p3(qd(6,1),1); endplot([1:1024],y);hold on;%另一条切线[max2 i]=max(p3(:,2));qd(6,3)=i;[max5 i]=max(p5(:,2));qd(6,4)=i;flag=1;while flag>0flag=0;for i=1:size3(1)ifp3(i,2)>(p3(qd(6,3),2)-p5(qd(6,4),2))/(p3(qd(6,1),1)-p5(qd(6,4),1))*(p3(i,1)-p3(qd(6,3),1))+p3(qd (6,3),2)qd(6,3)=i;flag=1;endendfor i=1:size5(1)ifp5(i,2)>(p3(qd(6,3),2)-p5(qd(6,4),2))/(p3(qd(6,1),1)-p5(qd(6,4),1))*(p5(i,1)-p3(qd(6,3),1))+p3(qd (6,3),2)qd(6,4)=i;flag=1;endendendfor i=1:1024y(i)=(p3(qd(6,3),1)-p5(qd(6,4),1))/(p3(qd(6,3),2)-p5(qd(6,4),2))*(i-p3(qd(6,3),2))+p3(qd(6,3),1); endplot([1:1024],y);hold on;%求圆1的圆心X=jiaodian2(p1(qd(1,1),1),p1(qd(1,1),2),p3(qd(1,2),1),p3(qd(1,2),2),p1(qd(3,1),1),p1(qd(3,1),2),p 4(qd(3,2),1),p4(qd(3,2),2),p1(qd(1,3),1),p1(qd(1,3),2),p3(qd(1,4),1),p3(qd(1,4),2),p1(qd(3,3),1),p 1(qd(3,3),2),p4(qd(3,4),1),p4(qd(3,4),2))x=(X(2)-512)/3.78y=(384-X(1))/3.78%求圆2的圆心circle=2X=jiaodian2(p2(qd(4,1),1),p2(qd(4,1),2),p4(qd(4,2),1),p4(qd(4,2),2),p2(qd(5,1),1),p2(qd(5,1),2),p 5(qd(5,2),1),p5(qd(5,2),2),p2(qd(4,3),1),p2(qd(4,3),2),p4(qd(4,4),1),p4(qd(4,4),2),p2(qd(5,3),1),p 2(qd(5,3),2),p5(qd(5,4),1),p5(qd(5,4),2))x=(X(2)-512)/3.78y=(384-X(1))/3.78%求圆3的圆心circle=3X=jiaodian2(p1(qd(1,1),1),p1(qd(1,1),2),p3(qd(1,2),1),p3(qd(1,2),2),p3(qd(6,1),1),p3(qd(6,1),2),p 5(qd(6,2),1),p5(qd(6,2),2),p1(qd(1,3),1),p1(qd(1,3),2),p3(qd(1,4),1),p3(qd(1,4),2),p3(qd(6,3),1),p 3(qd(6,3),2),p5(qd(6,4),1),p5(qd(6,4),2))x=(X(2)-512)/3.78y=(384-X(1))/3.78%求圆4的圆心circle=4X=jiaodian2(p4(qd(2,1),1),p4(qd(2,1),2),p5(qd(2,1),1),p5(qd(2,1),2),p1(qd(3,1),1),p1(qd(3,1),2),p 4(qd(3,2),1),p4(qd(3,2),2),p4(qd(2,3),1),p4(qd(2,3),2),p5(qd(2,4),1),p5(qd(2,4),2),p1(qd(3,3),1),p 1(qd(3,3),2),p4(qd(3,4),1),p4(qd(3,4),2))x=(X(2)-512)/3.78y=(384-X(1))/3.78%求圆5的圆心circle=4X=jiaodian2(p4(qd(2,1),1),p4(qd(2,1),2),p5(qd(2,1),1),p5(qd(2,1),2),p3(qd(6,1),1),p3(qd(6,1),2),p 5(qd(6,2),1),p5(qd(6,2),2),p4(qd(2,3),1),p4(qd(2,3),2),p5(qd(2,4),1),p5(qd(2,4),2),p3(qd(6,3),1),p 3(qd(6,3),2),p5(qd(6,4),1),p5(qd(6,4),2))x=(X(2)-512)/3.78y=(384-X(1))/3.78function y = jiaodian(m1,n1,m2,n2,m3,n3,m4,n4)A=[n1-n2 m2-m1;n3-n4 m4-m3];B=[(n1-n2)*m1-(m1-m2)*n1;(n3-n4)*m3-(m3-m4)*n3];y=A\B;function y = jiaodian2(x1,y1,x2,y2,x3,y3,x4,y4,x5,y5,x6,y6,x7,y7,x8,y8) d1=jiaodian(x1,y1,x2,y2,x3,y3,x4,y4);d2=jiaodian(x5,y5,x6,y6,x7,y7,x8,y8);d3=jiaodian(x1,y1,x2,y2,x7,y7,x8,y8);d4=jiaodian(x5,y5,x6,y6,x3,y3,x4,y4);y=jiaodian(d1(1),d1(2),d2(1),d2(2),d3(1),d3(2),d4(1),d4(2));format longP=imread('picture.bmp');lefttop=[100 240142 244170 258450 545471 543];rightbutton=[200 368375 466591 685200 330537 624];for circle=1:5circleif(circle~=1)clear u;clear v;endk=1;for i=lefttop(circle,1):lefttop(circle,2)flag=0;for j=rightbutton(circle,1):rightbutton(circle,2) if flag==0 & P(i,j)<10u(k)=i;v(k)=j;k=k+1;flag=1;elseif flag==1 & P(i,j)<10 & P(i,j+1)>200u(k)=i;v(k)=j;k=k+1;endendendfor j=rightbutton(circle,1):rightbutton(circle,2) flag=0;for i=lefttop(circle,1):lefttop(circle,2)if flag==0 & P(i,j)<10f1=0;for temp=1:k-1if u(temp)==i & v(temp)==jf1=1;endendif f1==0u(k)=i;v(k)=j;k=k+1;flag=1;endelseif flag==1 & P(i,j)<10 & P(i+1,j)>200f1=0;for temp=1:k-1if u(temp)==i & v(temp)==jf1=1;endendif f1==0u(k)=i;v(k)=j;k=k+1;flag=1;endendendendaxis equal;axis([1 768 1 1024]);plot(u,v,'.');grid on ;hold on;x=ones(k-1,5);y=ones(k-1,1);for i=1:k-1x(i,:)=[1 v(i) u(i) u(i)*v(i) v(i)*v(i) ];y(i)=-u(i)*u(i);end[b,bint,r,rint,stats]=regress(y,x);bbintstatsA=[2 b(4);b(4) 2*b(5)];B=[-b(3);-b(2)];X=A\Bxo=(X(2)-512)/3.78yo=(384-X(1))/3.78xlswrite(strcat('d:/',num2str(circle),'.xls'),[u;v]'); endformat longclear;aa=140;bb=1000count=1;for t=aa:bbb=-0.7;r=0;a=0;L=3.78;f=1577/3.78;Tx=-t;Ty=0;Tz=-t;R1=[L*f 0 0 0;0 L*f 0 0;0 0 0 1];R2=[cos(b)*cos(r) sin(a)*sin(b)*cos(r)+cos(a)*sin(r) -cos(a)*sin(b)*cos(r)+sin(a)*sin(r) Tx;-cos(b)*sin(r) -sin(a)*sin(b)*sin(r)+cos(a)*cos(r) cos(a)*sin(b)*sin(r)+sin(a)*cos(r) Ty;sin(b) -sin(a)*cos(b) cos(a)*cos(b)Tz;0 0 01;];M=R1*R2;k=1;for w=0:2*pi/100:2*piX=12*cos(w);Y=12*sin(w);Zc=R2(3,1:3)*[X Y 0]'-Tz;u(k)=1/Zc*M(1,:)*[X Y 0 1]';v(k)=1/Zc*M(2,:)*[X Y 0 1]';k=k+1;endx=ones(k-1,5);y=ones(k-1,1);for i=1:k-1x(i,:)=[1 v(i) u(i) u(i)*v(i) v(i)*v(i) ];y(i)=-u(i)*u(i);end[b,bint,r,rint,stats]=regress(y,x);A=[2 b(4);b(4) 2*b(5)];B=[-b(3);-b(2)];X=A\B;M=M/(-Tz);F(count)=sqrt((X(1)-M(1,4))*(X(1)-M(1,4))+(X(2)-M(2,4))*(X(2)-M(2,4)));count=count+1;endplot(aa:bb,F);xlabel('k');ylabel('D')grid on;format longclear;count=1;for t=-pi/2:0.05:pi/2b=-0.7;r=0;a=t;L=3.78;f=1577/3.78;Tx=-350;Ty=0;Tz=-350;R1=[L*f 0 0 0;0 L*f 0 0;0 0 0 1];R2=[cos(b)*cos(r) sin(a)*sin(b)*cos(r)+cos(a)*sin(r) -cos(a)*sin(b)*cos(r)+sin(a)*sin(r) Tx;-cos(b)*sin(r) -sin(a)*sin(b)*sin(r)+cos(a)*cos(r) cos(a)*sin(b)*sin(r)+sin(a)*cos(r) Ty;sin(b) -sin(a)*cos(b) cos(a)*cos(b)Tz;0 0 01;];M=R1*R2;k=1;for w=0:2*pi/200:2*piX=12*cos(w);Y=12*sin(w);Zc=R2(3,1:3)*[X Y 0]'-Tz;u(k)=1/Zc*M(1,:)*[X Y 0 1]';v(k)=1/Zc*M(2,:)*[X Y 0 1]';k=k+1;endx=ones(k-1,5);y=ones(k-1,1);for i=1:k-1x(i,:)=[1 v(i) u(i) u(i)*v(i) v(i)*v(i) ];y(i)=-u(i)*u(i);end[b,bint,r,rint,stats]=regress(y,x);A=[2 b(4);b(4) 2*b(5)];B=[-b(3);-b(2)];X=A\B;M=M/(-Tz);F(count)=sqrt((X(1)-M(1,4))*(X(1)-M(1,4))+(X(2)-M(2,4))*(X(2)-M(2,4)));count=count+1;endplot(-pi/2:0.05:pi/2,F);xlabel('β');ylabel('D')grid on;format longclear;count=1;for t=-pi/2:0.05:pi/2b=t;r=0;a=0;L=3.78;f=1577/3.78;Tx=-350;Ty=0;Tz=-350;R1=[L*f 0 0 0;0 L*f 0 0;0 0 0 1];R2=[cos(b)*cos(r) sin(a)*sin(b)*cos(r)+cos(a)*sin(r) -cos(a)*sin(b)*cos(r)+sin(a)*sin(r) Tx;-cos(b)*sin(r) -sin(a)*sin(b)*sin(r)+cos(a)*cos(r) cos(a)*sin(b)*sin(r)+sin(a)*cos(r)Ty;sin(b) -sin(a)*cos(b) cos(a)*cos(b)Tz;0 0 01;];M=R1*R2;k=1;for w=0:2*pi/200:2*piX=12*cos(w);Y=12*sin(w);Zc=R2(3,1:3)*[X Y 0]'-Tz;u(k)=1/Zc*M(1,:)*[X Y 0 1]';v(k)=1/Zc*M(2,:)*[X Y 0 1]';k=k+1;endx=ones(k-1,5);y=ones(k-1,1);for i=1:k-1x(i,:)=[1 v(i) u(i) u(i)*v(i) v(i)*v(i) ];y(i)=-u(i)*u(i);end[b,bint,r,rint,stats]=regress(y,x);A=[2 b(4);b(4) 2*b(5)];B=[-b(3);-b(2)];X=A\B;M=M/(-Tz);F(count)=sqrt((X(1)-M(1,4))*(X(1)-M(1,4))+(X(2)-M(2,4))*(X(2)-M(2,4)));count=count+1;endplot(-pi/2:0.05:pi/2,F);xlabel('β');ylabel('D')grid on;。
上机实验题目 内容和要求 编程类

上机实验题目、内容和要求实验1:熟悉上机环境和顺序结构编程练习1. 键盘输入与屏幕输出练习问题1 要使下面程序的输出语句在屏幕上显示1, 2, 34,则从键盘输入的数据格式应为以下备选答案中的。
#include <stdio.h>main(){char a,b;int c;scanf("%c%c%d",&a,&b,&c);printf("%c,%c,%d\n",a,b,c);}A)1 2 34 B)1, 2, 34C)’1’,’2’,34D)12 34问题2 在与上面程序的键盘输入相同的情况下,要使上面程序的输出语句在屏幕上显示12 34,则应修改程序中的哪条语句?怎样修改?问题 3 要使上面程序的键盘输入数据格式为1,2,34,输出语句在屏幕上显示的结果也为1,2,34,则应修改程序中的哪条语句?怎样修改?问题4 要使上面程序的键盘输入数据格式为1,2,34,而输出语句在屏幕上显示的结果为'1', '2',34,则应修改程序中的哪条语句?怎样修改?[提示:利用转义字符输出字符单引号字符。
]问题5 要使上面程序的键盘输入无论用下面哪种格式输入数据,程序在屏幕上的输出结果都为'1', '2',34,则程序应修改程序中的哪条语句?怎样修改?第1种输入方式:1,2,34↙(以逗号作为分隔符)第2种输入方式:1 2 34↙(以空格作为分隔符)第3种输入方式:1 2 34↙(以Tab键作为分隔符)第4种输入方式:1↙2↙34↙(以回车符作为分隔符)[提示:利用忽略输入修饰符。
]2. 计算定期存款本利之和设银行定期存款的年利率rate为2.25%,并已知存款期为n年,存款本金为capital元,试编程计算n年后的本利之和deposit。
要求定期存款的年利率rate、存款期n和存款本金capital 均由键盘输入。
数学建模实验上机指导

数学建模实验指导书Experiment Instruction Book Of Mathematical Modeling数学与信息科学学院2008年2月前言数学建模实验是数学建模课程的一个重要组成部分,实验的设置是为了配合课堂教学,使学生亲自实践建模、求解、解释和结果分析的全过程,进一步掌握和理解课堂教学内容,培养动手能力,提高他们分析问题和解决问题能力。
同时,通过上机练习,也可以提高应用数学软件和计算机技术的能力。
实验一指导实验项目:初等模型实验实验目的:1.实践参数估计及多项式拟合的方法;2.学习掌握用数学软件包进行参数估计和多项式拟合的问题。
实验内容:1.建模实例,汽车刹车距离问题等; 2.编程计算 实例1.(汽车刹车距离问题)某司机培训课程中有这样的规则:正常驾驶条件下, 车速每增16公里/小时,后面与前车的距离应增一个车身的长度。
实现这个规则的简便办法是 “2秒准则” :后车司机从前车经过某一标志开始默数2秒钟后到达同一标志,而不管车速如何。
这个规则的合理性如何,是否有更合理的规则。
下表是测得的车速和刹车距离的一组数据。
实验方法与步骤:1.建立模型刹车距离的拟合多项式为v k v k d 221+=2.Matlab 计算求解 建立M 文件exp1.m v=[20:20:140]/3.6; v2=v.^2; x=[v;v2]‟;d=[6.5,17.8,33.6,57.1,83.4,118,153.5]‟; a=x\d; dd=x*a;ddd=[6.5,17.8,33.6,57.1,83.4,118,153.5]; b=polyfit(v,ddd,2) y=polyval(b,v)plot(v,ddd,‟ro ‟,v,dd,‟b ‟) t=y./vy = 6.2024 17.7571 34.5643 56.6238 83.9357 116.5000 154.3167t =1.1164 1.5981 2.0739 2.5481 3.0217 3.4950 3.96813.结果分析.0.02+=0851vvd6617实验一问题:举重比赛按照运动员的体重分组,在一些合理、简化的假设下建立比赛成绩与体重之间的关系。
08数学建模与数学实验习题6章

习题:某厂向用户提供发动机,合同规定,第一、二、三季度末分别交货40台、60台、80台.每季度的生产费用为f(x)=ax+bx^2(元),其中x是该季生产的台数.若交货后有剩余,可用于下季度交货,但需支付存储费,每台每季度c元.已知工厂每季度最大生产能力为100台,第一季度开始时无存货,设a=50、b=0.2、c=4,问工厂应如何安排生产计划,才能既满足合同又使总费用最低.讨论a、b、c变化对计划的影响,并作出合理的解释.设:第一季度生产x1台,第二季度生产x2台,第三季度生产x3台。
Min=50x1+0.2x2^2 +50x2+0.2x2 ^2+50x3+0.2x3^2+4(x1-40)+4(x1+x2-100)Stx1>=40;x1+x2>=100;x1+x2+x3=180;x1<=100;x2<=100;x3<=100;MATLAB运行:先建立M文件 cc1.m,定义目标函数:function f=cc1(x):f=50*x(1)+0.2*x(1)^2+50*x(2)+0.2*x(2)^2+50*x(3)+0.2*x(3)^2+4*(x(1)-40 )+4*(x(1)+x(2)-100);再建立M文件从此cc11.m定义非线性约束:x0=[60;60;60];A=[-1 -1 0];b=[-100];Aeq=[1 1 1];beq=[180];vlb=[40;0;0];vub=[100;100;100];[x,fval]=fmincon('cc1',x0,A,b,Aeq,beq,vlb,vub)结果:x =50.000060.000070.0000fval =11280lingo运行:model:min=50*x1+0.2*x1^2+50*x2+0.2*x2^2+50*x3+0.2*x3^2+(x1-40)*4+(x1+x2-100 )*4;x1>=40;x1+x2>=100;x1+x2+x3>=180;x1<=100;x2<=100;x3<=100;end结果:Local optimal solution found at iteration: 47Objective value: 11280.00Variable Value Reduced CostX1 50.00000 0.000000X2 60.00000 0.000000X3 70.00000 0.000000Row Slack or Surplus Dual Price1 11280.00 -1.0000002 10.00000 0.0000003 10.00000 0.0000004 0.000000 -78.000015 50.00000 0.0000006 40.00000 0.0000007 30.00000 0.000000进一步分析,讨论参数a,b,c对生产计划的影响:1)、固定b,c不变,a变化(分别取a=20、60),仍运行上述程序,结果为:由于生产总量是恒定的,而c x x x x x x b x x x a y )]100()40[()()(211232221321-++-++++++=,故a 的变化不会影响生产计划;b 是x 的二次项的系数,它反映了生产费用。
数学建模上机实验报告3

西华大学数学建模上机实验报告课程名称: 数学建模年级:2011级 上机实验成绩: 指导教师:蒲俊老师姓名:李国强 上机实验名称:函数图形设计学号:362011********* 上机实验日期:2013.03.22 上机实验编号:组号: 上机实验时间: 一、实验目的掌握函数图形设计的方法。
二、实验内容1. 在一幅图象中作出函数及其导函数的图形 :Y=x 3-3x+4 Y=3x 2-32. 作出函数Y=sin(x)/x 的图形;注意,x=0时,需要单独处理。
3. 无穷级数逼近:正弦函数Y=sin(X)与其Taylor 展开式的前几项构成的多项式函数的逼近关系;()()2111121!n n n x y n -+∞-==--∑ 4. 作出参数方程函数的图象5cos 615sin x t t y t =+⎧⎨=⎩。
5. 已知一个教室长为20米,宽为15米,在距离地面高2.5米的位置均匀的安放8个光源,假设各个光源到墙壁横纵向之间的距离是相等的,各个光源的光照强度均为一个单位。
光源对目标点的光照强度与该光源到目标点距离的平方成反比,与该光源的强度成正比。
三、使用环境MATLAB 7.0.1四、核心代码及调试过程1. >> x=-6:6;>> y=x.^3-3*x+4;>> y1=3*x.^2-3;>> plot(x,y,'k')>> hold on>> plot(x,y1,'g')2.-6-4-20246 -200-150-100-5050100150200250>> ezplot('sin(x)/x',[-20,20,-1,1.2]);-20-15-10-505101520 -1-0.8-0.6-0.4-0.20.20.40.60.81xsin(x)/x或者>> x=-20:0.1:20;n=length(x);for i=1:nif(abs(x(i)-0)<=0.0001)y(i)=1;elsey(i)=sin(x(i))/x(i);endendplot(x,y)-20-15-10-505101520-0.4-0.20.20.40.60.813. >> x=-3:0.2:3;>> y1=x;>> y2=x-x.^3/prod(1:3);>> y3=x-x.^3/prod(1:3)+x.^5/prod(1:5);>> y4=x-x.^3/prod(1:3)+x.^5/prod(1:5)-x.^7/prod(1:7); >> figure>> hold on>> plot(x,sin(x));>> plot(x,y1,'g');>> plot(x,y2,'b');>> plot(x,y3,'m');>> plot(x,y4,'r');-3-2-10123-3-2-11234. >> t=-2*pi:0.01:2*pi;x=5*cos(t)+6*t;y=15*sin(t);figurehold onplot(t,x,t,y);-8-6-4-202468-40-30-20-101020304050五、总结学会了怎样通过matlab 软件绘制一个函数的图象。
【VIP专享】AllExperiments__《数学建模实验》上机实验作业

数学科学学院 张勇
实验 1 1.1
实验 2 实验 3
3.1 3.2 3.3 实验 4 4.1 4.2 4.3 4.4 实验 5 5.1 5.2 实验 6 实验 7 7.1 实验 8 8.1 8.2 8.3
字符串与文本文件操作...............................................................................................1 实验题目:基因序列文件的读取 ............................................................................... 1 优化模型实验 1............................................................................................................2 优化建模实验 2............................................................................................................2 课堂练习.......................................................................................................................2 实验题目.......................................................................................................................3 课后练习题...................................................................................................................3 微分模型实验...............................................................................................................4 实验:狐狸与野兔问题...............................................................................................4 实验提示 1....................................................................................................................5 实验提示 2:欧拉法....................................................................................................5 课后学习.......................................................................................................................6 差分建模实验...............................................................................................................6 实验基础.......................................................................................................................6 实验题目:细菌繁殖...................................................................................................8 插值与拟合实验...........................................................................................................9 数据处理实验.............................................................................................................12 实验:施肥效果分析.................................................................................................12 随机系统模拟实验.....................................................................................................14 课堂练习题.................................................................................................................15 实验题目:电子管的寿命.........................................................................................15 实验题目:办公室电话系统(选作) ..................................................................... 15
数学建模实验报告Matlab的基本操作编程

wilyes11收集 博客(与学习无关):/u/1810231802MATLAB 基本操作、编程一、 实验目的及意义1.熟悉MATLAB 软件的用户环境; 2.了解MATLAB 软件的一般命令; 3.掌握MATLAB 向量操作与矩阵运算函数; 4.掌握MATLAB 软件的基本符号运算命令; 5. 掌握MATLAB 语言编程的循环、条件和选择结构。
二、实验内容1. MATLAB 软件的向量操作及矩阵运算练习;2. 使用MATLAB 软件进行符号运算练习;3. 用MA TLAB 语言编写命令M-文件和函数M-文件;三、实验步骤1.在D 盘建立一个自己的文件夹; 2.开启软件平台——MATLAB ,将你建立的文件夹加入到MA TLAB 的搜索路径中。
3.利用帮助了解函数max, min, sum, mean, sort, length ,rand, size 和diag 的功能和用法。
4.开启MATLAB 编辑窗口,键入你编写的M 文件(命令文件或函数文件); 5.保存文件(注意将文件存入你自己的文件夹)并运行; 6.若出现错误,修改、运行直到输出正确结果; 7. 写出实验报告,并浅谈学习心得体会。
四、实验要求与任务根据实验内容和步骤,完成以下具体实验,按要求写出实验报告。
1.设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦,其中E,R,O,S 分别为单位阵、随机阵、零阵和对角阵,试通过数值计算验证22E R RS A O S +⎡⎤=⎢⎥⎣⎦。
2.某零售店有9种商品的单件进价(元)、售价(元)及一周的销量如下表,问哪种商品的利润最大,哪种商品的利润最小;按收入由小到大,列出所有销量 568 1205 753 580 395 2104 1538 810 6943.建立一个命令M-文件:求所有的“水仙花数”,所谓“水仙花数”是指一个三位数,其各位数字的立方和等于该数本身。
例如,153是一个水仙花数,因为。
数学建模Matlab上机实训题目

数学建模Matlab上机实训题目一、矩阵及数组操作:1.利用基本矩阵产生3×3和15×8的单位矩阵、全1矩阵、全0矩阵、均匀分布随机矩阵([-1,1]之间)、正态分布矩阵(均值为1,方差为4)。
2.利用fix及rand函数生成[0,10]上的均匀分布的10×10的整数随机矩阵a,然后统计a中大于等于5的元素个数。
3.在给定的矩阵中删除含有整行内容全为0的行,删除整列内容全为0的列。
二、绘图:4.在同一图形窗口画出下列两条曲线图像:y1=2x+5;y2=x^2-3x+1,并且用legend标注。
5.画出下列函数的曲面及等高线:z=x^2+y^2+sin(xy).三、程序设计:6.编写程序计算(x在[-3,3],间隔0.01)7.有一列分数序列:求前15项的和。
8.用至少三种方法编写函数实现求任意整数n的阶乘。
9*.将任意偶数m写成两个素数p1、p2的和(试着写出所有的m=p1+p2的可能形式)。
10*.是否任意3的倍数m可以写成两个素数p1、p2、p3的和(试着写出所有的m=p1+p2+p3 的可能形式)?四、数据处理与拟合初步:分别采用y=c1+c2e^(-t)和y=d1+d2te^(-t)进行拟合,并画出拟合曲线进行对比。
12.计算下列定积分:13.微分方程组当t=0时,x1(0)=1,x2(0)=-0.5,求微分方程t在[0,25]上的解,并画出相空间轨道图像。
14.设通过测量得到时间t与变量y的数据:t=[0 0.3 0.8 1.1 1.6 2.3];y=[0.5 0.82 1.14 1.25 1.35 1.41];分别采用多项式:y=a0+a1t+a2t2和指数函数y=b0+b1e-t+b2te-t进行拟合,并计算均方误差、画出拟合效果图进行比较。
15.V an der Pol(范德堡)方程是典型的二阶非线性方程之一:y”-u(1-y^2)y’+y=0,y(0)=2,y‘(0)=0;其中u>0为标量。
数学建模上机实验报告4

西华大学数学建模基础实验报告课程名称: 数学建模基础 年级: 实验成绩: 指导教师姓名:实验名称:数据拟合与线性规划 学号: 实验日期: 实验编号: 组号:实验时间:一、实验目的学习简单的数据拟合与线性规划。
找出函数关系,解决最值问题。
二、实验内容1.已知飞机下轮廓线上数据如下(1)作数据的点图形。
(2)确定X 和 Y 之间的近似关系。
2.已知下列数据为录像机磁带的测试数据 试求出下列关系bn an t +=23.用MATLAB 或 Lingo 求解线性规划问题6543218121110913min x x x x x x z +++++=⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=≥≤++≤++=+=+=+6,,2,1,09003.12.15.08001.14.0500600400x ..654321635241 i x x x x x x x x x x x x t s i4.用MATLAB 或 Lingo 求解线性规划问题m a x 6543216.064.072.032.028.04.0x x x x x x z +++++=85003.003.003.001.001.001.0..654321≤+++++x x x x x x t s70005.002.041≤+x x 10005.002.052≤+x x 90008.003.063≤+x x6,2,10 =≥j x j 5.用MATLAB 或 Lingo 求解线性规划问题X 0 3 5 7 9 11 12 13 14 15 Y1.21.72.02.12.01.81.21.01.6321436min x x x z ++= 120..321=++x x x t s 301≥x5002≤≤x203≥x三、使用环境MATLAB7.0四、核心代码、调试过程及结果1.题(1)X=[0 3 5 7 9 11 12 13 14 15] Y=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6] plot(X,Y,'*')(2)x=polyfit(X,Y,2) x =-0.0249 0.4416 0.0683 >> x=polyfit(X,Y,3) x =0.0012 -0.0517 0.5939 -0.0541>> x=polyfit(X,Y,4) x =0.0004 -0.0123 0.0769 0.2146 0.03003.C=[13 9 10 11 12 8];A=[0.4 1.1 1 0 0 0;0 0 0 0.5 1.2 1.3];b=[800;900];Aeq=[1 0 0 1 0 0;0 1 0 0 1 0;0 0 1 0 0 1]; beq=[400;600;500];VLB=[0;0;0;0;0;0];VUB=[];[x,fval]=linprog(C,A,b,Aeq,beq,VLB,VUB) Optimization terminated.x =1.6518e-0126004.4013e-0134001.4351e-012500fval =138004.c=[-0.4 -0.28 -0.32 -0.72 -0.64 -0.6];A=[0.01 0.01 0.01 0.03 0.03 0.03;0.02 0 0 0.05 0 0;0 0.02 0 0 0.05 0;0 0 0.03 0 0 0.08];b=[850;700;100;900];Aeq=[]; beq=[];vlb=[0;0;0;0;0;0]; vub=[];[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)>> xxgh4Optimization terminated.x =1.0e+004 *3.50000.50003.00000.00000.00000.0000fval =-2.5000e+0045.c=[6 3 4]’;A=[0 1 0];b=[50];Aeq=[1 1 1];beq=[120];vlb=[30,0,20];vub=[];[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)>> xxgh5Optimization terminated.x =30.000050.000040.0000fval =490.0000五、总结通过这个上机,我对MA TLAB解决简单的线性规划问题只能说有初步的了解,但是还是编程起来很吃力。
数模第八次上机作业

0.0030 -0.5082 0.0500
>> f=curvefun1(x,tdata)
f =
0.0050 0.0056 0.0064 0.0073 0.0083
f =
0.0050 0.0056 0.0064 0.0073 0.0083
>> ezplot('0.0030*exp(0.5082*t)')
xdwc=[jdwc./y]
jdwc =
Columns 1 through 6
0.1609 0.0587 0.0951 0.2647 0.1195 0.1831
Column 7
0.0451
xdwc =
Columns 1 through 6
0.0021 0.0008 0.0012 0.0033 0.0015 0.0022
>> tdata=1790:10:1980
tdata =
Columns 1 through 4
1790 1800 1810 1820
Columns 5 through 8
1830 1840 1850 1860
Columns 9 through 12
1870 1880 1890 1900
Columns 13 through 16
20.48
25.13
26.15
30
26.1
20.3
19.35
试以年龄为横坐标,旋转定向能力为纵坐标描绘上述表格中数据的散点图,并根据其变化趋势选择适当的模型对其进行最小二乘逼近,建立旋转定向能力与年龄之间关系的数学模型并绘制拟合曲线
>> x=[17:2:29];
y=[20.48 25.13 26.15 30 26.1 20.3 19.35];
《数学建模》上机指导书(信科 数学)

《数学建模》上机指导书曾繁慧编著辽宁工程技术大学理学院目录数学模型概论 (2)MATLAB平台简介 (3)实验1 线性规划模型 (5)实验2 非线性规划模型 (7)实验3 一阶常微分方程模型 (8)实验4 高阶常微分方程模型 (9)实验5 时间序列模型 (10)实验6 多元线性回归模型 (11)数学模型概论应用数学学科的一项重要任务是从自然科学、社会科学、工程技术以及现代化管理中提出问题和解决问题。
这就要求我们学会如何将实际问题经过分析、简化,转化为一个数学问题,然后用适当的数学方法去解决。
在这个过程中,如何将所考察的实际问题转化为一个相应的数学问题,即建立该实际问题的数学模型,是重要的一步。
一、数学模型的概念和分类1、模型的概念模型是客观事物的一种简化的表示和体现。
模型可分为实物模型(形象)和抽象模型,抽象模型又可分为模拟模型和数学模型。
2、数学模型的概念以解决某个现实问题为目的,经过分析简化,从中抽象、归结出来的数学问题就是该问题的数学模型,这个过程称为数学建模。
3、数学模型的分类按照建模所用的数学方法的不同,可分为:初等模型、运筹学模型、微分方程模型、概率统计模型、控制论模型等。
按照数学模型应用领域的不同,可分为:人口模型、交通模型、经济预测模型、金融模型、环境模型、生态模型、企业管理模型、城镇规划模型等等。
按照人们对建模机理的了解程度的不同可分为:白箱模型、灰箱模型、黑箱模型。
按照模型的表现特性可分为:确定性模型与随机模型、静态模型与动态模型、离散模型与连续模型。
二、数学建模的方法与步骤1、数学建模的方法机理分析法:根据人们对现实对象的了解和已有的知识、经验等,分析研究对象中各变量(因素)之间的因果关系,找出反映其内部机理的规律的一类方法。
测试分析法:当人们对研究对象的机理不清楚时,可以把研究对象视为一个“黑箱”系统,对系统的输入输出进行观测,并以这些实测数据为基础进行统计分析来建立模型,这样的一类方法称为测试分析法。
数学模型实验报告-lingo软件的使用-习题代码

运筹学实验报告姓名:学号:班级:相关问题说明:一、实验性质和教学目的本实验是运筹学课内安排的上机操作实验。
目的在于了解、熟悉计算机Lingo软件在运筹学模型求解中的作用,激发学习兴趣,提高学习效果,增强自身的动手能力,提高实际应用能力。
二、实验基本要求要求学生:1. 实验前认真做好理论准备,仔细阅读实验指导书;2. 遵从教师指导,认真完成实验任务,按时按质提交实验报告。
三、主要参考资料1.LINGO软件2. LINGO8.0及其在环境系统优化中的应用,天津大学出版社,20053. 优化建模与LINDO/LINGO软件,清华大学出版社,20054.运筹学编写组主编,运筹学(修订版),清华大学出版社,19905.蓝伯雄主编,管理数学(下)—运筹学,清华大学出版社,19976.胡运权主编,运筹学习题集(修订版),清华大学出版社,19957.胡运权主编,运筹学教程(第二版),清华大学出版社,2003实验内容1、线性规划问题:⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤++=0,13119241171289..68max 2121212121x x x x x x x x t s x x z (1) 给出原始代码;(2) 计算结果(包括灵敏度分析,求解结果粘贴);(3) 回答下列问题(手写):a ) 最优解及最优目标函数值是多少;b ) 资源的对偶价格各为多少,并说明对偶价格的含义;c ) 为了使目标函数值增加最多,让你选择一个约束条件,将它的常数项增加一个单位,你将选择哪一个约束条件?这时目标函数值将是多少?d ) 对x 2的目标函数系数进行灵敏度分析;e ) 对第2个约束的约束右端项进行灵敏度分析;f ) 结合本题的结果解释“Reduced Cost ”的含义。
对偶价格就是说 约束方程右端变量增加1对目标函数值的影响 答案: (1)代码max =8*x1+6*x2; 9*x1+8*x2<=12; 7*x1+11*x2<=24; 9*x1+11*x2<=13; x1>=0; x2>=0;(2)计算结果Global optimal solution found.Objective value: 10.66667 Total solver iterations: 2Variable Value Reduced Cost X1 1.333333 0.000000 X2 0.000000 1.111111Row Slack or Surplus Dual Price 1 10.66667 1.000000 2 0.000000 0.8888889 3 14.66667 0.000000 4 1.000000 0.000000 5 1.333333 0.000000Ranges in which the basis is unchanged:Objective Coefficient RangesCurrent Allowable Allowable Variable Coefficient Increase Decrease X1 8.000000 INFINITY 1.250000 X2 6.000000 1.111111 INFINITYRighthand Side RangesRow Current Allowable Allowable RHS Increase Decrease 2 12.00000 1.000000 12.00000 3 24.00000 INFINITY 14.66667 4 13.00000 INFINITY 1.000000 5 0.0 1.333333 INFINITY 6 0.0 0.0 INFINITY(3)a) b) c) d) e) f)2、运输问题:(1) 给出原始代码;(2) 计算结果(决策变量求解结果粘贴)Min Z = Cij Xij∑=61i Xij <=bj (j=1...8) 销量约束∑=81j Xij = ai (i=1...6) 产量约束∑∑==6181i jXij ≥ 0(i=1...6;j=1...8)代码:model:!6发点8 model:!6发点8收点运输问题;sets:warehouses/wh1..wh6/: capacity;vendors/v1..v8/: demand;links(warehouses,vendors): cost, volume;endsetsmin=@sum(links: cost*volume); !目标函数;@for(vendors(J):@sum(warehouses(I): volume(I,J))<=demand(J)); !需求约束;@for(warehouses(I):@sum(vendors(J): volume(I,J))=capacity(I)); !产量约束; !这里是数据;data:capacity=55 47 42 52 41 32;demand=60 55 51 43 41 52 43 38;cost=6 2 9 7 4 2 5 94 5 5 3 8 5 3 25 2 1 3 7 4 8 37 6 7 9 9 2 7 12 3 6 5 7 2 6 55 9 2 2 8 1 4 3;enddataend答案Global optimal solution found.Objective value: 473.0000 Infeasibilities: 0.000000 Total solver iterations: 9Model Class: LPTotal variables: 48Nonlinear variables: 0Integer variables: 0Total constraints: 15Nonlinear constraints: 0Total nonzeros: 144Nonlinear nonzeros: 0Variable Value Reduced Cost CAPACITY( WH1) 55.00000 0.000000 CAPACITY( WH2) 47.00000 0.000000 CAPACITY( WH3) 42.00000 0.000000 CAPACITY( WH4) 52.00000 0.000000 CAPACITY( WH5) 41.00000 0.000000 CAPACITY( WH6) 32.00000 0.000000 DEMAND( V1) 60.00000 0.000000 DEMAND( V2) 55.00000 0.000000 DEMAND( V3) 51.00000 0.000000 DEMAND( V4) 43.00000 0.000000 DEMAND( V5) 41.00000 0.000000 DEMAND( V6) 52.00000 0.000000 DEMAND( V7) 43.00000 0.000000 DEMAND( V8) 38.00000 0.000000 COST( WH1, V1) 6.000000 0.000000 COST( WH1, V2) 2.000000 0.000000 COST( WH1, V3) 9.000000 0.000000 COST( WH1, V4) 7.000000 0.000000 COST( WH1, V5) 4.000000 0.000000 COST( WH1, V6) 2.000000 0.000000 COST( WH1, V7) 5.000000 0.000000 COST( WH1, V8) 9.000000 0.000000 COST( WH2, V1) 4.000000 0.000000 COST( WH2, V2) 5.000000 0.000000 COST( WH2, V3) 5.000000 0.000000 COST( WH2, V4) 3.000000 0.000000 COST( WH2, V5) 8.000000 0.000000 COST( WH2, V6) 5.000000 0.000000 COST( WH2, V7) 3.000000 0.000000 COST( WH2, V8) 2.000000 0.000000 COST( WH3, V1) 5.000000 0.000000 COST( WH3, V2) 2.000000 0.000000 COST( WH3, V3) 1.000000 0.000000 COST( WH3, V4) 3.000000 0.000000 COST( WH3, V5) 7.000000 0.000000 COST( WH3, V6) 4.000000 0.000000 COST( WH3, V7) 8.000000 0.000000 COST( WH3, V8) 3.000000 0.000000 COST( WH4, V1) 7.000000 0.000000COST( WH4, V4) 9.000000 0.000000 COST( WH4, V5) 9.000000 0.000000 COST( WH4, V6) 2.000000 0.000000 COST( WH4, V7) 7.000000 0.000000 COST( WH4, V8) 1.000000 0.000000 COST( WH5, V1) 2.000000 0.000000 COST( WH5, V2) 3.000000 0.000000 COST( WH5, V3) 6.000000 0.000000 COST( WH5, V4) 5.000000 0.000000 COST( WH5, V5) 7.000000 0.000000 COST( WH5, V6) 2.000000 0.000000 COST( WH5, V7) 6.000000 0.000000 COST( WH5, V8) 5.000000 0.000000 COST( WH6, V1) 5.000000 0.000000 COST( WH6, V2) 9.000000 0.000000 COST( WH6, V3) 2.000000 0.000000 COST( WH6, V4) 2.000000 0.000000 COST( WH6, V5) 8.000000 0.000000 COST( WH6, V6) 1.000000 0.000000 COST( WH6, V7) 4.000000 0.000000 COST( WH6, V8) 3.000000 0.000000 VOLUME( WH1, V1) 0.000000 4.000000 VOLUME( WH1, V2) 55.00000 0.000000 VOLUME( WH1, V3) 0.000000 7.000000 VOLUME( WH1, V4) 0.000000 5.000000 VOLUME( WH1, V5) 0.000000 2.000000 VOLUME( WH1, V6) 0.000000 0.000000 VOLUME( WH1, V7) 0.000000 3.000000 VOLUME( WH1, V8) 0.000000 8.000000 VOLUME( WH2, V1) 0.000000 1.000000 VOLUME( WH2, V2) 0.000000 2.000000 VOLUME( WH2, V3) 0.000000 2.000000 VOLUME( WH2, V4) 43.00000 0.000000 VOLUME( WH2, V5) 0.000000 5.000000 VOLUME( WH2, V6) 0.000000 2.000000 VOLUME( WH2, V7) 4.000000 0.000000 VOLUME( WH2, V8) 0.000000 0.000000 VOLUME( WH3, V1) 0.000000 4.000000 VOLUME( WH3, V2) 0.000000 1.000000 VOLUME( WH3, V3) 42.00000 0.000000 VOLUME( WH3, V4) 0.000000 2.000000 VOLUME( WH3, V5) 0.000000 6.000000 VOLUME( WH3, V6) 0.000000 3.000000VOLUME( WH4, V1) 0.000000 5.000000 VOLUME( WH4, V2) 0.000000 4.000000 VOLUME( WH4, V3) 0.000000 5.000000 VOLUME( WH4, V4) 0.000000 7.000000 VOLUME( WH4, V5) 0.000000 7.000000 VOLUME( WH4, V6) 14.00000 0.000000 VOLUME( WH4, V7) 0.000000 5.000000 VOLUME( WH4, V8) 38.00000 0.000000 VOLUME( WH5, V1) 41.00000 0.000000 VOLUME( WH5, V2) 0.000000 1.000000 VOLUME( WH5, V3) 0.000000 4.000000 VOLUME( WH5, V4) 0.000000 3.000000 VOLUME( WH5, V5) 0.000000 5.000000 VOLUME( WH5, V6) 0.000000 0.000000 VOLUME( WH5, V7) 0.000000 4.000000 VOLUME( WH5, V8) 0.000000 4.000000 VOLUME( WH6, V1) 0.000000 4.000000 VOLUME( WH6, V2) 0.000000 8.000000 VOLUME( WH6, V3) 0.000000 1.000000 VOLUME( WH6, V4) 0.000000 1.000000 VOLUME( WH6, V5) 0.000000 7.000000 VOLUME( WH6, V6) 32.00000 0.000000 VOLUME( WH6, V7) 0.000000 3.000000 VOLUME( WH6, V8) 0.000000 3.000000Row Slack or Surplus Dual Price1 473.0000 -1.0000002 19.00000 0.0000003 0.000000 0.0000004 9.000000 0.0000005 0.000000 0.0000006 41.00000 0.0000007 6.000000 0.0000008 39.00000 0.0000009 0.000000 1.00000010 0.000000 -2.00000011 0.000000 -3.00000012 0.000000 -1.00000013 0.000000 -2.00000014 0.000000 -2.00000015 0.000000 -1.0000003、一般整数规划问题:某服务部门各时段(每2h为一时段)需要的服务员人数见下表。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学建模与实验上机实验三
1.求下列方程组的解⎪⎪⎩⎪
⎪⎨⎧=+-+-=-+=++-=--+4
1025695842475412743w z y x w z x w z y x w z y x 。
2.设⎥⎥
⎥⎦
⎤⎢⎢⎢⎣⎡------=81272956313841A ,⎥⎥⎥⎦⎤
⎢⎢⎢⎣⎡-----=793183262345B ,求C1=A*B’; C2=A’*B; C3=A.*B, 并求上述所有方阵的逆阵。
3.设 ⎥⎦⎤
⎢⎣⎡++=)1(sin 35.0cos 2x x x y ,把x=0~2π间分为101点,画出以x 为横坐标,y 为纵坐标的曲线。
4.求代数方程3x 5+4x 4+7x 3+2x 2+9x+12=0的所有根。
5.⎪⎩
⎪
⎨⎧≤≤-+-<≤-+--<≤----=312/)34(1111
32/)34(222x x x x x x x x y ,画出在[]3,3-上的曲线。
.6. 设,求。
7.
⎰++dx x x x ))(1(1
22。
8. 矩阵A=[0 1 2; 1 2 0; 0 2 1 ], (1)编程将矩阵A 中的0和2互换;
(2)编程将A 中的0变为1,1变为2,2换为0. 9. 求微分方程的解析解, 并画出图形, y’= y + 2x, y(0) = 1, 0<x<1; 10. 计算⎥⎦⎤⎢
⎣⎡=572396a 与⎥⎦
⎤
⎢⎣⎡=864142b 的数组乘积。
11.
已知:⎥⎥⎥⎦
⎤
⎢⎢⎢⎣⎡=987654321a ,分别计算
a 的数组平方和矩阵平方,并观察其结果。
12. 将矩阵4257a ⎡⎤=⎢⎥⎣⎦
、⎥⎦⎤⎢⎣⎡=3817b 和⎥⎦⎤
⎢⎣⎡=2695c 组合成两个新矩阵: (1)组合成一个4⨯3的矩阵,第一列为按列顺序排列的a 矩阵元素,第二列为按列顺序排列的b 矩阵元素,第三列为按列顺序排列的c 矩阵元素,即
⎥⎥
⎥⎥⎦
⎤⎢⎢⎢
⎢⎣⎡237
912685
574
(2)按照a 、b 、c 的列顺序组合成一个行向量,即 []296531877254。
