时杨中学2012届高三数学小题训练013

合集下载

江苏省时杨中学高三数学模拟训练(8).pdf

江苏省时杨中学2012届高三数学模拟训练（8） 1．已知向量若则实数的值是． 2．从分别写有1，2，3，4，5的五张卡片中任取两张，求这两张卡片上的数字和为偶数的概率为． 3．已知函数是定义在上的奇函数，当时，则不等式的解集是__________． 4．已知复数，那么的最大值是． 5．设是定义域为R，最小正周期为的函数，若,则的值等于． 6．若函数的值域是，则函数的值域是：方程有一正根和一负根，命题：的图象与轴有公共点．若命题“或”为真命题，而命题“且”为假命题，则实数的取值范围是． 8．将正奇数按下表规律排成5列，那么2011应该在第行，第列．第1列第2列第3列第4列第5列第1行1357第2行1513119第3行17192123…………27259．设的解集为． 10．已知双曲线与椭圆的焦点相同，它们的离心率之和为则此双曲线的标准方程是． 11．已知函数，则． 12．已知各项都为正数的等差数列的公差也不为0，若正整数、、满足，且、、三项成等比数列，则此等比数列的公比．（用含、、的式子表示） 13．已知点F是椭圆的右焦点，过原点的直线交椭圆于点A、P，PF垂直于x轴，直线AF交椭圆于点B，，则该椭圆的离心率=___▲___. 14．已知函数在上是增函数，函数时，函数的最大值M与最小值m的差为，则=___▲___. 二、解答题本大题共6小题共90分解答应写出文字说明证明过程或演算步骤15.（本题满分14分）中，底面为菱形，⊥平面，为的中点，为的中点，求证：（Ⅰ）平面⊥平面；（Ⅱ）//平面.考资源网 16.（本题满分14分）如图，单位圆（半径为1的圆）的圆心为坐标原点，单位圆与轴的正半轴交与点，与钝角的终边交于点，设. （Ⅰ）用表示；（Ⅱ）如果,求点的坐标；（Ⅲ）求的最小值. 17.（本题满分14分）日产量808182 ……9899100次品率…P（）… 其中（为常数）.已知生产一件正品盈利元，生产一件次品损失元（为给定常数）.（Ⅰ）求出，并将该厂的日盈利额（元）表示为日生产量（件）的函数；（Ⅱ）为了获得最大盈利，该厂的日生产量应该定为多少件？ 18. (本题满分16分) 如图,设点P是椭圆上的任意一点(异于左,右顶点A,B). 若椭圆E的右焦点为F,上顶点为C,求以F为圆心且与直线AC相切的圆的半径; 设直线分别交直线与点M,N,求证:. 19. (本题满分16分) 设数列的前n项和为,已知,,数列是公差为d的等差数列,. 求d的值; 求数列的通项公式; 求证:. 20. (本题满分16分) 已知函数和函数. 若方程在上有两个不同的解,求实数m的取值范围; 若对任意,均存在,使得成立,求实数m的取值范围. 八 1．－3 2． 3． 4． 5． 6． 7． 8． 252 3 9． 10. 11. 12. 13． 14．二、解答题本大题共6小题,共90分,解答应写出文字说明,证明过程或演算步骤 ∵是菱形，∴，又，∴平面，又∵平面，∴平面平面． ……………………6分 ⑵取中点，连接,则， ∵是菱形，∴， ∵为的中点，∴， ∴．∴四边形是平行四边形，∴，又∵平面，平面．∴平面．…14分 16．（Ⅰ）如图. （Ⅱ）由，又,得 . 由钝角，知 . （Ⅲ）【法一】，又，,的最小值为. 【法二】为钝角，, ， ,,的最小值为. 17．角终边。

时杨中学2012届高三数学小题训练10

时杨中学2012届高三数学小题训练0101．复数z=12i+,则|z|= ． 2．已知函数()()223f x x m x =+++是偶函数，则=m ． 3克的苹果数约占苹果总数的％．4．若点P （1,1）到直线2sin cos =+αy αx 的距离为d ，则d 的最大值是．5．函数762)(23+-=x x x f 的单调减区间是．6．若函数)10(log )(<<=a x x f a 在区间[,2]a a 上的最大值是最小值的3倍，则a =7．已知两圆0822:,024102:222221=-+++=-+-+y x y x C y x y x C ，则以两圆公共弦为直径的圆的方程是 . 8．若cos 2π2sin 4αα=-⎛⎫- ⎪⎝⎭，则cos sin αα+的值为． 9．设等差数列{}n a 的公差d 不为0，19a d =．若k a 是1a 与2k a 的等比中项，则k = ． 10．在直角坐标系xOy 中，,i j 分别是与x 轴，y 轴平行的单位向量，若直角三角形ABC 中，AB i j =+，2AC i m j =+，则实数=m ．11．已知函数22(1),00,0(1),0x x y x x x ⎧->⎪==⎨⎪+<⎩，右图是计算函数值y 的流程图，在空白框中应该填上．12．已知m 、n 是两条不重合的直线，α、β、γ是三个两两不重合的平面，给出下列命题： ①若m∥β，n∥β，m 、n ⊂α，则α∥β；②若α⊥γ，β⊥γ，α∩β＝m ，n ⊂γ，则m⊥n；③若m⊥α，α⊥β，m∥n，则n∥β；④若n∥α，n∥β，α∩β＝m ，那么m∥n；其中所有正确命题的序号是．练习十答案1 2．－2 3．30 4．2＋ 2 5．[0，2] 6 7．5)1()2(22=-++y x 8．12 9．4 10．0或－2 11．x =0 12．②④。

时杨中学2012届高三数学小题训练15.doc

时杨中学2012届高三数学小题训练0151．设全集{2,1,0,1,2},{1,0,1},()S T ST =--=-=S 则C ． 2．命题:p 2{|0}a M x x x ∈=-<；命题:q {|||2}a N x x ∈=<，p 是q 的条件． 3．某学校共有师生2400人，现用分层抽样的方法，从所有师生中抽取一个容量为160的样本，已知从学生中抽取的人数为150，那么该学校的教师人数是．4．若复数12z a i =+, 234z i =-，且12z z 为纯虚数，则实数a 的值为． 5．在100ml 的水中有一个草履虫，现从中随机取出20ml 水样放到显微镜下观察，则发现草履虫的概率是．6．已知数列{}n a 的前n 项和为2,n S n =某三角形三边之比为234::a a a ，则该三角形最大角为．7．方程sin x ax =（a 为常数，0a ≠）的所有根的和为．8．若抛物线22y px =的焦点与双曲线22122x y -=的右焦点重合，则p 的值为．9．如图给出的是计算201614121+⋅⋅⋅+++的值的一个程序框图，其中判断框内应填入的条件是．10．已知1a =，2b =，()a a b ⊥+，则a 与b 夹角的度数为．11．已知函数)1(log )(+=x x f a 的定义域和值域都是[]0,1，则实数a 的值是． 12．一个小朋友按如图所示的规则练习数数，1大拇指，2食指，3中指，4无名指，5小指，6无名指，...，一直数到2008时，对应的指头是 (填指头的名称).第9题第12题练习十五答案1．{}2,2- 2．充分不必要 3．150 4．835．0.2 6．120 7．0 8．4 9．i>10 10．120 11．2 12．食指。

江苏省时杨中学高三数学模拟训练(12).pdf

江苏省时杨中学2012届高三数学模拟训练（12） 1．不等式的解集是__________. 2．抛物线的焦点坐标是__________.相切，且在两坐标轴上有相等截距的切线有__________条 4．已知向量, 将绕原点按逆时针方向旋转得到,则与同向的单位向量是__________. 5．已知椭圆以坐标轴为对称轴，且长轴是短轴的3倍，并且过点P（3，0），则椭圆的标准方程为_________________. 6．函数的值域是． 7．函数的递增区间为____________________． 8．实数满足，则取值范围是____________________． 9．关于的方程有解，则实数的取值范围是______________． 10．某同学在借助题设给出的数据求方程的近似数（精确到0.1）时，设,且，他用“二分法”又取到了4个值，计算到其函数值的正负，并得出判断：方程的近似解为，那么他所取的4个值中的第二个值为_________ . 11．依次写出数列：，，，…，，…，其中，从第二项起由如下法则确定：如果为自然数且未出现过，则用递推公式否则用递推公式，则． 12. 在复平面内，复数对应的点分别为A、B，O为坐标原点，若点P在第四象限内，则实数的取值范围是__________.13. 如图，在△ABC和△AEF中，B是EF的中点，AB＝1，若·＋·＝2，则与的夹角等于________．14. 已知l1和l2是平面内互相垂直的两条直线，它们的交点为A，动点B，C分别在l1和l2上，且BC＝3，则过A，B，C三点的动圆所形成的区域的面积为__________．二、解答题：本大题共6小题，共90分．解答时应写出必要的文字说明、证明过程或演算步骤． 15. (本小题满分14分) 设△ABC的角A、B、C所对的边分别为a，b，c，且acosC＋c＝b. (1) 求角A的大小； (2) 若a＝1，求△ABC面积的最小值．16. (本小题满分14分) 如图，ABEDFC为多面体，平面ABED与平面ACFD垂直，点O在线段AD上，OA＝1，OD＝2，△OAB，△OAC，△ODE，△ODF都是正三角形． (1) 求证：直线BC∥平面OEF； (2) 求点O到平面DEF的距离． 17. (本小题满分15分) 如图，所示是某水产养殖场的养殖大网的平面图，四周的实线为网衣，为避免混养，用筛网(图中虚线)把大网箱隔成大小一样的小网箱． (1) 若大网箱的面积为108平方米，每个小网箱的长、宽分别设计为多少米时，才能使围成的网箱中筛网总长度最小； (2) 若大网箱的面积为160平方米，网衣的造价为112元/米，筛网的造价为96元/米，且大网箱的长与宽都不超过15米，则小网箱的长、宽各为多少米时，可使总造价最低？ 18. (本小题满分15分) 已知数列{an}的首项a1＝4，前n项的和为Sn，且Sn＋1－3Sn－2n－4＝0. (1) 求数列{an}的通项公式； (2) 设函数f(x)＝anx＋an－1x2＋…＋a1xn，f′(x)是函数f(x)的导函数，令bn＝f′(1)，求数列{bn}的通项公式，并研究其单调性．19. (本小题满分16分) 如图，已知椭圆：＋＝1(a>0，b>0)和圆O：x2＋y2＝b2，过椭圆上一点P引圆O的两条切线，切点分别为A、B. (1) 若椭圆上存在点P，使得·＝0，求椭圆离心率e的取值范围； (2) 设直线AB与x轴、y轴分别交于点M、N，求证：＋为定值． 20. (本小题满分16分) 已知函数f(x)＝－1. (1) 求函数f(x)的单调区间； (2) 设m>0，求f(x)在[m,2m]上的最大值；(3) 试证明：对任意的n∈N*，不等式eln()<恒成立.2..3. 3条4.5. 或 6．7． 8． 9． 10． 11．31 12. 13. 90°　解析：(＋)＋(＋)(＋)＝2， 22＋·＋·＋·＋·＝2， ∵ B是EF的中点，AB＝1，∴ 2＝1，＝－， ∴ ·＋·＝0·＝0. 14. 18π　解析：分别以l1、l2为x轴、y轴建立直角坐标系，设线段BC中点为E，则过A、B、C三点的圆即为以E为圆心、为半径的圆， ∵ B、C分别在l1和l2上运动，∴ 圆心E在以A为圆心、AE＝为半径的圆上运动，所以，过A、B、C三点的动圆所形成的面积为以A为圆心、3为半径的圆的面积为18π. 15. 解：(1) 由正弦定理知：sinAcosC＋sinC＝sinB，(2分) ∴ sinAcosC＋sinC＝sin(A＋C)， ∴ sinC＝cosAsinC，cosA＝.(5分) ∵ 00，所以{bn}是单调递增数列．(15分) 19. (1) 解：∵ ·＝0PA⊥PB.(2分) 又PA，PB为圆O切线，∴ OA⊥PA，OB⊥PB. ∴ 四边形OAPB为正方形．(4分) ∴ OP＝b≤a，即a2≥2b2＝2(a2－c2)a2≤2c2，∴ ≤e<1.(7分) (2) 证明：设P(x0，y0)，A(x1，y1)，B(x2，y2)(x0≠0，y0≠0) 则＝－x0x1＋y0y1＝x＋y＝b2，(10分) 所以PA的方程：x1x＋y1y＝b2，同理，PB的方程：x2x＋y2y＝b2.(12分) ∴ AB方程为x0x＋y0y＝b2. ∴ ON＝，OM＝， ∴ ＋＝为定值．(16分) 20. (1) 解：函数f(x)的定义域是(0，＋∞)，由f′(x)＝，(1分) 令f′(x)＝0，得1－lnx＝0x＝e.(2分) 当0<x0；当x>e时，f′(x)＝<0；所以，函数f(x)在(0，e]上单调递增，在[e，＋∞)上单调递减．(4分) (2) 解：由(1)的结论知， ① 当0<2m≤e，即0<m≤时，f(x)在[m,2m]上单调递增，于是，f(x)max＝f(2m)＝－1.(6分) ② 当m≥e时，f(x)在[m,2m]上单调递减，于是，f(x)max＝f(m)＝－1.(8分) ③ 当m<e<2m，即<m0，≠e，所以ln<·lne<，即对任意的n∈N*，不等式lne<成立．(16分)。

江苏时杨中学2012高三数学模拟训练(4).

第11题江苏省时杨中学2012届高三数学模拟训练（4）１．2)11(iai-+为实数，则实数a 的值是．２．已知5()lg ,f x x =则(2)f = ．３．若角α的终边落在直线x y -=上，则ααααcos cos 1sin 1sin 22-+-的值等于_________．４．已知,αβ是两个不同平面，,m n 是两条不同直线．给出下列命题： ①若m ∥,,n m n αα⊥⊥则 ②若m ∥,,n m ααβ=则∥n③若,,m m αβα⊥⊥则∥β ④若,,m n m n α⊥⊥则∥α其中不正确．．．的是．（填写你认为正确的序号）５．过点)2,3(-的直线l 经过圆0222=-+y y x 的圆心，则直线l 的倾斜角大小为．６．已知x 、y 满足约束条件⎪⎩⎪⎨⎧≥+-≤--≥-+063201022y x y x y x ，则22)1(y x ++的最小值为．７．已知数列{}n a 的前n 项和n S 满足n S =n3－2，则它的一个通项公式为n a = ．８．若函数432--=x x y 的定义域为],0[m ，值域为]4,425[--，则m 的取值范围是．９．函数)34cos(x y -=π的单调递增区间为．１０．已知椭圆19822=++y a x 的离心率21=e ，则a 的值等于．１１．阅读流程图填空：（1）最后一次输出的i = ；（2）一共输出i 的个数为．１２．如图,在ABC △中，12021BAC AB AC ∠===，，°，D 是边BC 上一点，2DC BD =，则AD BC ⋅=_________．ABDC第12题13.设A 、B 分别为椭圆22221(0)x y a b a b +=>>和双曲线22221x y a b-=(0,0)a b >>的公共顶点，P 、M 分别是双曲线和椭圆上不同于A 、B 的两动点，且满足()AP BP AM BM λ+=+,其中,1,R λλ∈>设直线AP 、BP 、AM 、BM 的斜率分别为1k 、2k 、3k 、4k ，则1k +2k =5，则3k +4k = ▲ ．14.已知数列{}n a 为各项均为正的等比数列，其公比为q ．当q ＞1时，在数列{}n a 中，最多有 ▲ 项是100～1000之间的整数. 15.（本小题满分14分）在ABC ∆中，角,,A B C 的对边分别为,,a b c（1）若sin()2cos 6A Aπ+=，求A 的值；（2）若1cos ,33A b c==，求sin C 的值。

时杨中学2012届高三数学小题训练13

(第8题图)(第11题图)时杨中学2012届高三数学小题训练0131.已知集合{}2log 0|2≤≤=x x A ，集合{}321|≤≤=xx B ，则B A = .2．已知全集为实数集，2{|20},{|M x x x N x y =-<==，则)(N C M U = ____ _． 3．复数2i1iz =-(i 为虚数单位)的实部是 . 4．已知椭圆的中心在原点、焦点在y 轴上，若其离心率是12，焦距是8，则该椭圆的方程为．5．在等差数列{n a }中，若4681012120a a a a a ++++=，则数列{n a } 前15项的和为 .6.在ABC ∆中，如果sin A ∶sin B ∶sin C =5∶6∶8，那么此三角形最大角与最小角之和的余弦值是．7．若命题“x ∃∈R ，使得2(1)10x a x +-+<”是真命题，则实数a 的取值范围是 .89.在一个袋子中装有分别标注数字1,2,3,4,5的五个小球,的数字外完全相同.现从中随机取出两个小球,和为5或7的概率是 .10．若方程1n 2100x x +-=的解为0x ，则不小于0x 11．如图，函数)(x f y =的图象在点P 处的切线是l ，则(2)(2)f f '+= ．12.若数列}{n a 满足12 (01),1 (1).n n n n n a a a a a +≤≤⎧=⎨->⎩且167a =,则=2010a .练习十三答案1.{}3log 1|2≤≤x x 2． {|01}x x << 3. 1- 4. y 264 + x 248=15. 3606.8053- 7. (,1)-∞-∪(3,)+∞ 8.1320 9.25 10.511. 98 12.73。

江苏盐城市时杨中学高三12月月考数学试题

盐城市时杨中学2018届高三年级12月月考数学试题班级_____________ 姓名______________一、填空题（本大题共14小题，每小题5分，共70分，请将答案填写在答题纸相应的位置上）1．集合{}{}52|,7,5,3,2,1≤≤=x x B A ，则=⋂B A ▲ ． 2．已知i 是虚数单位，且复数,21,221i z bi z -=+=若21z z 是实数，则实数=b ▲ ． 3．设x ∈R ，则“30x -≥”是“|1|2x -≤”的 ▲ 条件. （用“充要”、“充分不必要”、“必要不充分”或“既不充分也不必要条件”填空）4．执行如图所示的算法流程图，则输出k 的值是 ▲ ．5．在各项均为正数的等比数列{}n a 中，若46822,1a a a a +==，则7a 的值是 ▲ ．6．若变量y x ,满足约束条件⎪⎩⎪⎨⎧-≥≤+≤11y y x xy ，且y x z +=2的最大值和最小值分别为m 和n,则=-n m ▲ ．7．3，,的夹角为 60-= ▲ ．8．函数()y f x =是定义在R 上的偶函数，且在(,0]-∞上是增函数，若()()4f a f ≥，则实数a 的取值范围是 ▲ ．9．在正三棱柱111C B A ABC -中，已知4,21==AA AB ,若F E ,分别是棱1BB 和1CC 上的点，则三棱锥EF A A 1-的体积是 ▲ ．10．在锐角三角形ABC ∆中，c b a ,,分别是角C B A ,,的对边，已知b a ,是方程03322=+-x x 的两个根，且03)sin(2=-+B A ,则=c ▲ ．11137cos sin =-x x ，则24sin cos cos x x x -的值为 ▲ ．12．已知函数⎩⎨⎧<≤-+>=04,30,log )(x x x x x f a ，其中0>a 且1≠a ，)(x f y =的图像上有且只有两对点关于y 轴对称，则实数a 的取值范围是 ▲ ．13．已知点P 为矩形ABCD 4231===，则PD = ▲ ．14．已知0x >，0y >，22x y +=，则222121x y x y --++的最大值为 ▲ ．二、解答题（本大题共6小题，共90分。

时杨中学2012届高三数学小题训练009

时杨中学2012届高三数学小题训练0091。

已知复数121,2z i z i =-=+，那么12z z ⋅的值是．2. 集合{}22,A xx x R=-≤∈，{}2|,12B y y x x ==--≤≤,则()RC A B = .3. 函数x y 2sin =的图像向右平移k 个单位后，所得图像的解析式是x y 2cos =，则正数k4. 他们分别射击了5次,1人入选，则入选的最佳人选应是。

5。

曲线在53123+-=x xy 在1=x 处的切线的方程为.6。

已知实数x ，y 满足22,052y x y x +=++那么的最小值为 .7。

已知nS 是数列}{na 的前n 项和,且有21nSn =+，则数列}{n a 的通项n a =．8。

设数列{}na 的首项127,5a a =-=，且满足22()n n a a n N ++=+∈，则13518a a a a ++++=.9. 已知tan()3πα-=则22sin cos 3cos 2sin αααα=- 。

10. 已知()()(2,3),(1,2),a b a b a b λ==+⊥-，则__________λ=． 11。

已知命题P: “对R m R x ∈∃∈∀,使0241=+-+m x x"，若命题P ⌝是假命题，则实数m 的取值范围是：_______ 12. 对于ABC ∆,有如下命题:(1)sin 2sin 2A B =若，则ABC ∆一定为等腰三角形．(2)sin sin ,A B ABC =∆若则一定为等腰三角形. 222sin sin cos 1A B C ABC ++<∆(3)若，则一定为钝角三角形. (4)tan tan tan 0,A B C ABC ++>∆若则一定为锐角三角形.则其中正确命题的序号是______________.（把所有正确的命题序号都填上）.精品资料。

欢迎使用。

江苏省盐城市时杨中学高三数学综合练习(十三)(文科)(附答案)

江苏省盐城市时杨中学高三数学综合练习（十三）（文科）一、填空题（本大题共14小题，每小题5分，共70分，请将答案填写在答题卡相应的位置上）1．已知集合A={a，b，c，d，e}，B={c，d，e，f}，全集U=A∪B，则集合C U（A∩B）中元素的个数为_________．2．设角α的终边经过点P（﹣3，4），那么tan（π﹣α）+2cos（﹣α）=_________．3．设S n为等差数列{a n}的前n项和，已知S5=5，S9=27，则S7=_________．4．函数y=sin（2x+ϕ）（0＜ϕ＜π）图象的一条对称轴是x=，则ϕ=_________．5．不等式x2+ax+b＜0的解集为（﹣2，3），则a+b=_________．6．若曲线y=x4的一条切线l与直线x﹣4y﹣8=0垂直，则l的方程是_________．7．函数f（x）=lnx+x﹣2的零点的个数为_________．8．已知函数f（x）是定义在R上的奇函数．当x＜0时，f（x）=x2﹣6，则x＞0时，不等式f（x）＜x的解集为_________．9．已知直线l的斜率为6，且被两坐标轴所截得的线段长为，则直线l的方程为_________．10．设函数f（x）=，若f（f（a））≤2，则实数a的取值范围是_________．11．函数的最小值是_________．12．已知数列{a n }是公差为1的等差数列，S n 是其前n 项和，若S 8是数列{S n }中的唯一最小项，则{a n }数列的首项a 1的取值范围是 _________ ．13.若正数x ，y 满足111x y +=，则4911x yx y +--的最小值为_______________． 14．已知f （x ）为定义在（0，+∞）上的可导函数，且f （x ）＞xf′（x ）恒成立，则不等式x 2f （）﹣f （x ）＞0的解集为 _________ ．1、___________________________________2、___________________________________3、___________________________________4、___________________________________5、___________________________________6、___________________________________7、___________________________________8、___________________________________9、___________________________________ 10、__________________________________ 11、___________________________________ 12、__________________________________ 13、___________________________________ 14、__________________________________ 二、解答题：本大题共6小题，共90分．解答应写出文字说明、证明过程或演算步骤． 15．已知函数f （x ）=Asin （ωx+ϕ）（A>0，0,2πωϕ><）的图象在y 轴上的截距为1，它在y 轴右侧的第一个最大值点和最小值点分别为（x 0，2）和（x 0+π，﹣2）．（1）求f （x ）的解析式；（2）若成立，求m 的取值范围．16．如图，已知三棱锥A ﹣BPC 中，AP ⊥PC ，AC ⊥BC ，M 为AB 中点，D 为PB 中点，且△PMB 为正三角形．（1）求证：DM ∥平面APC ；（2）求证：平面ABC ⊥平面APC ；（3）若BC=4，AB=20，求三棱锥D ﹣BCM 的体积．17．已知函数2f x msinxcosx mcos x n =++（）（m ，n ∈R ）在区间[0，4π]上的值域为[1，2]．（1）求函数f （x ）的单调递增区间；（2）在△ABC 中，角A ，B ，C 所对的边长分别为a ，b ，c ，当m ＞0时，若f （A ）=1，sinB=4sin （π﹣C ），△ABC 的面积为，求边长a 的值．18．如图，在半径为30cm 的圆形（O 为圆心）铝皮上截取一块矩形材料OABC ，其中点B 在圆弧上，点A 、C 在两半径上，现将此矩形铝皮OABC 卷成一个以AB 为母线的圆柱形罐子的侧面（不计剪裁和拼接损耗），设矩形的边长AB=xcm ，圆柱的体积为Vcm 3．（1）写出体积V 关于x 的函数关系式；（2）当x 为何值时，才能使做出的圆柱形罐子体积V 最大？19．设a ∈R ，函数2f x ax 2a 1x lnx =++（）﹣（）．（1）当a=1时，求f （x ）的极值；（2）设x g x e x 1=（）﹣﹣，若对于任意的12x 0x R ∈+∞∈（，），，不等式12f x g x ≤（）（）恒成立，求实数a 的取值范围．参考答案1．（2013•闵行区一模）已知集合A={a，b，c，d，e}，B={c，d，e，f}，全集U=A∪B，则集合C U（A∩B）中元素的个数为3．2．（2014•南充模拟）设角α的终边经过点P（﹣3，4），那么tan（π﹣α）+2cos（﹣α）=．，﹣﹣（﹣）（﹣．故答案为：．3．（2014•苏州一模）设S n为等差数列{a n}的前n项和，已知S5=5，S9=27，则S7=14．，∴=4．（2010•绍兴一模）函数y=sin（2x+φ）（0＜φ＜π）图象的一条对称轴是x=，则φ=．kπ+=2×+φ，．，5．不等式x2+ax+b＜0的解集为（﹣2，3），则a+b=﹣7．，解得6．若曲线y=x4的一条切线l与直线x﹣4y﹣8=0垂直，则l的方程是4x+y+3=0．，∴直线7．函数f（x）=lnx+x﹣2的零点的个数为1．：求导函数，可得，∴8．（2014•杨浦区三模）已知函数f（x）是定义在R上的奇函数．当x＜0时，f（x）=x2﹣6，则x＞0时，不等式f（x）＜x的解集为（2，+∞）．可化为9．已知直线l的斜率为6，且被两坐标轴所截得的线段长为，则直线l的方程为6x﹣y±6=0（﹣=3710．（2014•浙江）设函数f（x）=，若f（f（a））≤2，则实数a的取值范围是（﹣∞，]．=，它的图象如图所示：，a≤11．（2010•内江二模）函数的最小值是3+2．==0x=2+．故答案为：3+212．（2013•婺城区模拟）已知数列{a n}是公差为1的等差数列，S n是其前n项和，若S8是数列{S n}中的唯一最小项，则{a n}数列的首项a1的取值范围是（﹣8，﹣7）．=中的唯一最小项，∴，解得﹣14．（2014•福州模拟）已知f（x）为定义在（0，+∞）上的可导函数，且f（x）＞xf′（x）恒成立，则不等式x2f（）﹣f（x）＞0的解集为{x|x＞1}．，则，∵为定义域上的减函数，由不等式（＞，∴＜二．解答题（共8小题）15．（2014•湖南模拟）已知函数f（x）=Asin（ωx+φ）的图象在y轴上的截距为1，它在y轴右侧的第一个最大值点和最小值点分别为（x0，2）和（x0+π，﹣2）．（1）求f（x）的解析式；（2）若成立，求m的取值范围．）的图象，）的图象在，∵，∴x+）在时函数的最大值为：16．（2015•重庆一模）如图，已知三棱锥A﹣BPC中，AP⊥PC，AC⊥BC，M为AB中点，D为PB中点，且△PMB为正三角形．（1）求证：DM∥平面APC；（2）求证：平面ABC⊥平面APC；（3）若BC=4，AB=20，求三棱锥D﹣BCM的体积．DM=5，PC==217．（2015•资阳模拟）已知函数f（x）=msinxcosx+mcos2x+n（m，n∈R）在区间[0，]上的值域为[1，2]．（Ⅰ）求函数f（x）的单调递增区间；（Ⅱ）在△ABC中，角A，B，C所对的边长分别为a，b，c，当m＞0时，若f（A）=1，sinB=4sin（π﹣C），△ABC的面积为，求边长a的值．=，时，，则，解得，则（）的单调递增区间是，，则，解得．则）的单调递增区间是，时，由，所以面积为，所以，则．18．（2014•重庆模拟）如图，在半径为30cm的圆形（O为圆心）铝皮上截取一块矩形材料OABC，其中点B在圆弧上，点A、C在两半径上，现将此矩形铝皮OABC卷成一个以AB为母线的圆柱形罐子的侧面（不计剪裁和拼接损耗），设矩形的边长AB=xcm，圆柱的体积为Vcm3．（1）写出体积V关于x的函数关系式；（2）当x为何值时，才能使做出的圆柱形罐子体积V最大？，∴，，•x=）由．）上是增函数，在（所以当19．（2015•兴国县一模）设a∈R，函数f（x）=ax2﹣（2a+1）x+lnx．（Ⅰ）当a=1时，求f（x）的极值；（Ⅱ）设g（x）=e x﹣x﹣1，若对于任意的x1∈（0，+∞），x2∈R，不等式f（x1）≤g（x2）恒成立，求实数a的取值范围．1因此，当）有极大值，且时，时，时，时，0＜x1＜1，令f'（x）＞0，解得或x＞1；，解得时也不成立．综上所述：20．（2015•惠州模拟）已知数列{a n}中，a1=3，前n和S n=（n+1）（a n+1）﹣1．①求证：数列{a n}是等差数列；②求数列{a n}的通项公式③设数列{}的前n项和为T n，是否存在实数M，使得T n≤M对一切正整数n都成立？若存在，求M的最小值，若不存在，试说明理由．（，∴，=（=，时，M≥，．。

时杨中学2012届高三数学小题训练005

时杨中学2012届高三数学小题训练0051．在复平面内，复数错误! 对应的点位于____________．2．已知cos 0()(1)10x x f x f x x π->⎧⎪=⎨++≤⎪⎩，则)34()34(-+f f 的值等于____________． 3．已知,41)6sin(=+πx 则)3(sin )65sin(2x x -+-ππ= 。

4．已知函数cos ()cos()6xf x x π=-,则()()3f x f x π+-的值为． 5．)3,2(),1,(==b x a ，若a 与b 的夹角为锐角，则实数x 的范围是____________．6．已知椭圆)0(12222>>=+b a b y a x 的左、右焦点分别为1F 、2F ，点A 、B 分别为上下顶点，点C 为右顶点，若CB AF⊥2，则椭圆的离心率e 为__ __． 7．设奇函数()f x 在(0)+∞，上为增函数，且(1)0f =，则不等式()()0f x f x x--<的解集为．学科网8．已知向量1(3,1),(2,),2a b ==-直线l 过点(1,2)A 且与向量2a b +垂直，则直线l 的一般方程是____________．9．设{}n a 是正项数列，其前n 项和n S 满足：4(1)(3)n n n S a a =-+，则数列{}n a 的一个通项公式na =____________．10。

函数)24sin(3x y -=π图象是将函数x y 2sin 3-=的图象经过怎样的平移而得？答：_ ．11．已知,a b 是两条不重合的直线,,,αβγ是三个两两不重合的平面，给出下列四个命题：①若α⊥a 且β⊥a ,则βα// ②若γα⊥且βαγβ//,则⊥③若b a b a //,,,//则βαβα⊂⊂ ④若b a b a //,,,//则==γβγαβα其中正确命题的序号有____________．12. 下列四种说法:①命题“∃x∈R，使得x 2＋1＞3x”的否定是“∀x∈R，都有x 2＋1≤3x”;②“m=－2”是“直线(m ＋2)x ＋my ＋1=0与直线（m －2）x ＋（m＋2）y －3=0相互垂直”的必要不充分条件；③在区间［－2，2]上任意取两个实数a ，b,则关系x 的二次方程x 2＋2ax －b 2＋1=0的两根都为实数的概率为161π-； ④过点(12，1）且与函数y=1x图象相切的直线方程是4x ＋y －3=0．其中所有正确说法的序号是____________．.精品资料。

时杨中学2012届高三数学小题训练11

时杨中学2012届高三数学小题训练0111．已知集合2112{|lg 0},{|222,}x M x x N x x Z -+===<<∈,则M N = . 2．已知等差数列{}n a 中,,33,4,31521==+=n a a a a 则n 的值为 _ _. 3．“1x >”是“2x x >”的条件.4．在△ABC 中,1=BC ,2=AB ,1cos 4B =，则sin(2)A B +的值为 _. 5．直线0=++C By Ax 与圆422=+y x 相交于两点M 、N ，若222B A C +=，则OM ·ON 的值（O 为坐标原点）等于 _ _.6．设椭圆的两个焦点分别为1F 、2F ，过2F 作椭圆长轴的垂线交椭圆于点P ，若21F PF ∆为等腰直角三角形，则椭圆的离心率是 _.7．已知α,β均为锐角,且21sin sin -=-βα,1cos cos 3αβ-=,则cos()αβ-= _ _. 8．已知变量x 、y 满足条件620x y x y x y +≤⎧⎪-≤⎪⎨≥⎪⎪≥⎩，若目标函数z ax y =+ (其中0a >)，仅在(4，2)处取得最大值，则a 的取值范围是 _ _.9．在△ABC 中,若a ＝7,b ＝8,13cos 14C =,则最大内角的余弦值为 __. 10．如图是函数d cx bx x x f +++=23)(的大致图象,则2221x x +等于_________.11．已知双曲线2212y x -=的焦点为1F 、2F ，点M 在双曲线上且120,MF MF ⋅=则点M 到x 轴的距离为 _.12．设()y f x =是定义在R 上的函数，给定下列三个条件：（1）()y f x =是偶函数；（2）()y f x =的图象关于直线1x =对称；（3）2T =为()y f x =的一个周期．如果将上面（1）、（2）、（3）中的任意两个作为条件，余下一个作为结论，那么构成的三个命题中真命题的个数有个．练习十一答案1．{}1- 2．50 3．⇒ 4．16153 5．2- 61 7．5972 8．a>19．71-10．916 11 12．3。

江苏省盐城市时杨中学高考数学第13讲二项分布练习

【学习目标】1．理解n 次独立重复试验的模型（n 重伯努利试验）及其意义；2．能进行一些与事件独立有关的概率的计算．【问题情境】（1）射击n 次，每次射击可能击中目标，也可能击不中目标，而且当射击条件不变时，可以认为每次击中目标的概率p 是不变的；（2）抛掷一颗质地均匀的筛子n 次，每一次抛掷可能出现“5”，也可能不出现“5”，而且每次掷出“5”的概率p 都是61；（3）种植n 粒棉花种子，每一粒种子可能出苗，也可能不出苗，其出苗率是67%．问题：上述试验有什么共同特点？【我的疑问】备注第1页共4页备注【自主探究】1．求随机抛掷100次均匀硬币，正好出现50次正面的概率．2．一盒零件中有9个正品和3个次品，每次取一个零件，如果取出的次品不再放回，求在取得正品前已取出的次品数X的概率分布．第2页共4页【课堂检测】备注1．某种灯泡使用寿命在1000 h以上的概率为0.2，求3个灯泡使用1000 h后，至多只坏1个的概率．2．甲、乙、丙3人独立地破译某个密码，每人译出密码的概率均为0.25，设随机变量X表示译出密码的人数．（1）写出X的分布列；（2）密码被译出的概率是多少？【回标反馈】第3页共4页【巩固练习】备注1．制药厂组织2组技术人员分别独立地试制不同类型的新药，设每组试制成功的概率都是0.40．当第一组成功时，该组研制的新药的年销售额为400万元，若失败则没有收入；当第二组成功时，该组研制的新药的年销售额为600万元，若失败则没有收入．以X表示这两组新药的年销售总额，求X的概率分布．2. 批量较大的一批产品中有30%的一级品，进行重复抽样检查，共取5个样品，求：（1）取出的5个样品中恰有2个一级品的概率；（2）取出的5个样品中至少有2个一级品的概率．第4页共4页。

时杨中学高三数学小题训练12

时杨中学高三数学小题训练0121．不等式103x x -≥-的解集是__________. 2．抛物线212y x =-的焦点坐标是__________. 3．与圆22(3)(1)2x y -++=相切，且在两坐标轴上有相等截距的切线有__________条4．已知向量)12,5(=→--OA , 将→--OA 绕原点按逆时针方向旋转 90得到→--OB ,则与→--OB 同向的单位向量是__________.5．已知椭圆以坐标轴为对称轴，且长轴是短轴的3倍，并且过点P （3，0），则椭圆的标准方程为_________________.6．函数113x y -=的值域是．7．函数y =____________________．8．实数,x y 满足350,(1,3]x y x --=∈，则2y x -取值范围是____________________． 9．关于x 的方程3sin 4cos 21x x m +=-有解，则实数m 的取值范围是______________． 10．某同学在借助题设给出的数据求方程lg 2x x =-的近似数（精确到0.1）时，设()lg 2,f x x x =+-()10f <,且()0f >2，他用“二分法”又取到了4个值，计算到其函数值的正负，并得出判断：方程的近似解为 1.8x ≈，那么他所取的4个值中的第二个值为_________ .11．依次写出数列：1a ，2a ，3a ，…， n a ，…，其中11a =，从第二项起n a 由如下法则确定：如果2-n a 为自然数且未出现过，则用递推公式21-=+n n a a 否则用递推公式n n a a 31=+，则=10a ．12. 在复平面内，复数121,23z i z i =+=+对应的点分别为A 、B ，O 为坐标原点，,.OP OA OB R =+λλ∈若点P 在第四象限内，则实数λ的取值范围是__________.练习十二答案1. {}|13x x ≤<2.. 1(0,)2-3. 3条4. 125(,)1313- 5. 1922=+y x 或181922=+y x 6．(0,1)(1,)+∞ 7． 1(2,)2-8．(,2)[4,)-∞+∞ 9．[2,3]m ∈- 10．1.75 11．31 12.1123λ-<<-。

江苏省时杨中学2012届高三数学模拟训练(3)

江苏省时杨中学2012届高三数学模拟训练（3）1. 函数)1(log 23x x y ++-=的定义域为 .2.若命题“R x ∈∃，使得01)1(2<+-+x a x ”是真命题，则实数a 的取值范围为 . 3. “直线(a +2)x +3a y +1=0与直线(a －2)x +(a +2)y －3=0相互垂直”的充要条件是a = ．4.已知2()1f x ax bx =++是偶函数，定义域为[]a a 2,1-，则b a +的值为 .5.在等差数列{n a }中，22,16610a a x x --=是方程的两根，则5691213a a a a a ++++= .6. 已知{},2,1,0,1,2a b ∈--且b a ≠，则复数bi a z +=对应点在第二象限的概率为 .7. 直线1+=kx y 与曲线x y =3则b 的值为 .8. 9. 当20π<<x 时，函数()f x =最小值为 .10. 已知实数x,y 满足条件⎪⎩⎪⎨⎧≤+-x x x i yi x z (+=为虚数单位），则|21|i z +-的最大值和最小值分别是． 11.已知圆22(2)9x y -+=和直线y kx =交于A,B 两点,O 是坐标原点, 若2OA OB O +=,则||AB = .12.已知2()(0)f x ax bx c a =++≠，且方程()f x x =无实数根，下列命题： ①方程[()]f f x x =也一定没有实数根；②若0a >，则不等式x x f >)(对一切实数x 都成立； ③若0a <，则必存在实数0x ，使0)(00>-x x f 成立； ④若0a b c ++=，则不等式x x f <)(对一切实数x 都成立．中，正确命题的序号是．(把你认为正确的命题的所有序号都填上)13．若060=∠B ，O 为ABC ∆的外心，点P 在ABC ∆所在的平面上，→-→-→-→-++=OCOB OA OP且8=⋅→-→-BC BP ，则边AC 上的高h 的最大值为．14．已知二次函数q px x x f ++=2)(通过点)0,(),0,(βα。

江苏省时杨中学2012届高三数学模拟训练(2)

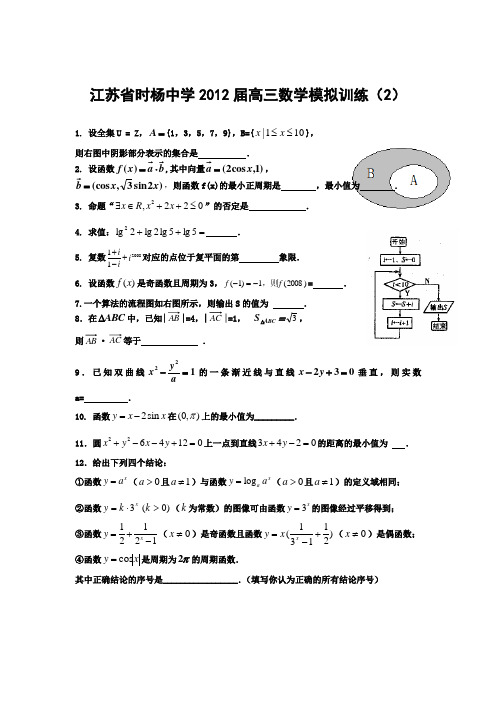
江苏省时杨中学2012届高三数学模拟训练（2）1. 设全集U = Z ，=A {1，3，5，7，9}，B={101|≤≤x x }，则右图中阴影部分表示的集合是．2. 设函数b a x f ⋅=)(,其中向量)1,cos 2(x a =，)2sin 3,(cos x x b =，则函数f(x)的最小正周期是，最小值为 .3. 命题“2,220x R x x ∃∈++≤”的否定是． 4. 求值：=++5lg 5lg 2lg 2lg 2．5. 复数200811i i i++-对应的点位于复平面的第象限． 6. 设函数)(x f 是奇函数且周期为3，)2008(1)1(f f ，则-=-= ． 7.一个算法的流程图如右图所示，则输出S 的值为． 8．在ABC ∆中，已知||=4，||=1， ABC S ∆=3，则AB ·等于．9．已知双曲线122=-ay x 的一条渐近线与直线032=+-y x 垂直，则实数a= ．10. 函数2sin y x x =-在(0,)π上的最小值为_________．11．圆2264120x y x y +--+=上一点到直线3420x y +-=的距离的最小值为． 12．给出下列四个结论：①函数xy a =（0a >且1a ≠）与函数log xa y a =（0a >且1a ≠）的定义域相同；②函数)0(3>⋅=k k y x（k 为常数）的图像可由函数3xy =的图像经过平移得到；③函数11221x y =+-（0≠x ）是奇函数且函数)21131(+-=x x y （0≠x ）是偶函数； ④函数x y cos =是周期为π2的周期函数．其中正确结论的序号是_________________．（填写你认为正确的所有结论序号）13．给出四个命题：①函数||sin x y =是周期函数，且周期为2π,②函数11221x y =+-与2(12)2x xy x +=⋅都是奇函数； ③函数)32cos(2π+=x y 的图象关于点)0,12(π对称； ④中，若sinA,sinB,sinC 成等差数列，则其中所有正确的序号是14．已知命题p ：对一切∈x ]1,0[，0)5(6241≠-+⋅-⋅+k k k x x，若命题p 是假命题，则实数k 的取值范围是．二、解答题：本大题共六小题，共计90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．15．将一颗骰子先后抛掷2次，观察向上的点数，求：（1）两数之和为5的概率；（2）以第一次向上点数为横坐标x ，第二次向上的点数为纵坐标y 的点(x,y)在圆x 2+y 2=15的内部的概率．16. 如图，在正三棱柱ABC －A 1B 1C 1中，点D 在边BC 上，AD ⊥C 1D ．（1）求证：AD ⊥平面BC C 1 B 1；（2）设E 是B 1C 1上的一点，当11BE EC 的值为多少时，A 1E ∥平面ADC 1？请给出证明． 17．（本题满分14分）如图，在平面直角坐标系xoy 中，椭圆C ：B1A 1ABCC 1D22221(0)x y a b a b +=>>的离心率为23，以原点为圆心，椭圆C 的短半轴长为半径的圆与直线x-y+2=0相切．（1）求椭圆C 的方程；（2）已知点P(0,1),Q(0,2),设M,N 是椭圆C 上关于y 轴对称的不同两点，直线PM 与QN 相交于点T 。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

(第8题图)
(第11题图)
时杨中学2012届高三数学小题训练013
1.已知集合{}2log 0|2
≤≤=x x A ，集合{}
32
1|≤≤
=
x
x B ，则B A = .
2．已知全集为实数集，2
{|20},{|M x x x N x y =-<==，则)(N C M U = ____ _．
3．复数2i 1i
z
=
-(i 为虚数单位)的实部是 .
4．已知椭圆的中心在原点、焦点在y 轴上，若其离心率是12
，焦距是8，则该椭圆的方程
为．
5．在等差数列{n a }中，若4681012120
a a a a a ++++=，则数列{n a }
前15项的和为 . 6.在A B C ∆中，如果sin
A ∶sin B
∶sin C =5∶6∶8，那么此三角形最大
角与最小角之和的余弦值是． 7．若命题“x ∃∈R ，使得2
(1)10
x a x +-+<”是真命题，则实数a 的
取值范围是 .
89.在一个袋子中装有分别标注数字1,2,3,4,5的五个小球,的数字外完全相同.现从中随机取出两个小球,和为5或7的概率是 . 10．若方程1n 2100
x x +
-=的解为0x ，则不小于0x 11．如图，函数)(x f y =的图象在点P 处的切线是l ，则(2)(2)
f f '+= ．
12.若数列}{n a 满足12 (01),1 (1).
n
n n n n a a a a a +≤≤⎧=⎨
->⎩且1
67
a =
,则=2010a .。