运筹学经典课件第8次 共22页
合集下载
运筹学课程课件

▪Involves different types of shipments
▪ Direct truck – Shipment made with no stops ▪ Less than truckload (LTL) – Smaller shipment combined with other loads
Copyright © 2016 Pearson Education, Inc.
8-8
Logistics Decision Areas
Water
▪Ideal for materials with high weight-to-value ratio, especially if delivery speed is not critical. ▪Examples of these materials include farm produce, timber, petroleum-based products. ▪Has one of the lowest ton-mile rates of any mode which helps to keep costs down.
▪ Warehousing can be used to:
▪ Reduce transportation costs ▪ Improve operational flexibility ▪ Shorten customer lead times ▪ Lower inventory-related costs.
Copyright © 2016 Pearson Education, Inc.
8-14
Logistics Decision Areas
▪ Reducing Transportation Costs
▪ Direct truck – Shipment made with no stops ▪ Less than truckload (LTL) – Smaller shipment combined with other loads
Copyright © 2016 Pearson Education, Inc.
8-8
Logistics Decision Areas
Water
▪Ideal for materials with high weight-to-value ratio, especially if delivery speed is not critical. ▪Examples of these materials include farm produce, timber, petroleum-based products. ▪Has one of the lowest ton-mile rates of any mode which helps to keep costs down.
▪ Warehousing can be used to:
▪ Reduce transportation costs ▪ Improve operational flexibility ▪ Shorten customer lead times ▪ Lower inventory-related costs.
Copyright © 2016 Pearson Education, Inc.
8-14
Logistics Decision Areas
▪ Reducing Transportation Costs
运筹学ppt课件
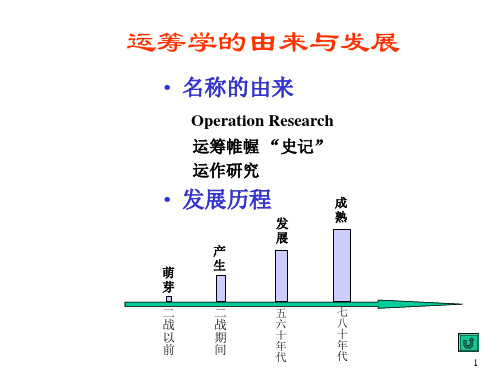
– 无穷多个最优解。若将例1中的目标函数变为 max z=50x1+50x2,则线段BC上的所有点都代表 了最优解;
– 无界解。即可行域的范围延伸到无穷远,目标 函数值可以无穷大或无穷小。一般来说,这说 明模型有错,忽略了一些必要的约束条件;
– 无可行解。若在例1的数学模型中再增加一个约 束条件4x1+3x2≥1200,则可行域为空域,不存在 满足约束条件的解,当然也就不存在最优解了。
• 交叉学科 --涉及经济、管理、数学、工程和系统等 多学科
• 开放性 --不断产生新的问题和学科分支
• 多分支 --问题的复杂和多样性
2
运筹学的主要内容
线性规划
数 非线性规划
学
整数规划
规
动态规划
划
多目标规划
学
双层规划
最优计数问题
科
组 合
网络优化
内
优 排序问题 化 统筹图
容
对策论
随 排队论
机 优 化
13
组织 宝洁公司 法国国家铁路
应用
Interface 每年节支 期刊号 (美元)
重新设计北美生产和分销系统以 1-2/1997 2亿 降低成本并加快了市场进入速 度
制定最优铁路时刻表并调整铁路 1-2/1998 1500万更多
日运营量
年收入
Delta航空公司 IBM
进行上千个国内航线的飞机优化 配置来最大化利润
负。当某一个右端项系数为负时,如 bi<0,则把该 等式约束两端同时乘以-1,得到:-ai1 x1-ai2 x2… -ain xn = -bi。
30
例:将以下线性规划问题转化为标准形式
则该极小化问题与下面的极大化问题有相同的最优解,
– 无界解。即可行域的范围延伸到无穷远,目标 函数值可以无穷大或无穷小。一般来说,这说 明模型有错,忽略了一些必要的约束条件;
– 无可行解。若在例1的数学模型中再增加一个约 束条件4x1+3x2≥1200,则可行域为空域,不存在 满足约束条件的解,当然也就不存在最优解了。
• 交叉学科 --涉及经济、管理、数学、工程和系统等 多学科
• 开放性 --不断产生新的问题和学科分支
• 多分支 --问题的复杂和多样性
2
运筹学的主要内容
线性规划
数 非线性规划
学
整数规划
规
动态规划
划
多目标规划
学
双层规划
最优计数问题
科
组 合
网络优化
内
优 排序问题 化 统筹图
容
对策论
随 排队论
机 优 化
13
组织 宝洁公司 法国国家铁路
应用
Interface 每年节支 期刊号 (美元)
重新设计北美生产和分销系统以 1-2/1997 2亿 降低成本并加快了市场进入速 度
制定最优铁路时刻表并调整铁路 1-2/1998 1500万更多
日运营量
年收入
Delta航空公司 IBM
进行上千个国内航线的飞机优化 配置来最大化利润
负。当某一个右端项系数为负时,如 bi<0,则把该 等式约束两端同时乘以-1,得到:-ai1 x1-ai2 x2… -ain xn = -bi。
30
例:将以下线性规划问题转化为标准形式
则该极小化问题与下面的极大化问题有相同的最优解,
运筹学课件PPT课件

整数规划的解法
总结词
整数规划的解法可以分为精确解法和近似解法两大类。
详细描述
整数规划的解法可以分为两大类,一类是精确解法,另一类是近似解法。精确解法包括割平面法、分支定界法等, 这些方法可以找到整数规划的精确最优解。而近似解法包括启发式算法、元启发式算法等,这些方法可以找到整 数规划的近似最优解,但不一定能保证找到最优解。
模拟退火算法采用Metropolis准则来 判断是否接受一个较差解,即如果新 解的能量比当前解的能量低,或者新 解的能量虽然较高但接受的概率足够 小,则接受新解。
模拟退火算法的应用
01
模拟退火算法在旅行商问题中得到了广泛应用。通过模拟退火算 法,可以求解旅行商问题的最优解,即在给定一组城市和每对城 市之间的距离后,求解访问每个城市恰好一次并返回出发城市的 最短路径。
动态规划的解法
确定问题的阶段和状态
首先需要确定问题的阶段和状态,以便将问 题分解为子问题。
建立状态转移方程
根据问题的特性,建立状态转移方程,描述 状态之间的转移关系。
求解子问题
求解每个子问题,并存储其解以供将来使用。
递推求解
从最后一个阶段开始,通过递推方式向前求 解每个阶段的最优解。
动态规划的应用
线性规划的解法
单纯形法
01
单纯形法是求解线性规划问题的经典方法,通过迭代过程逐步
找到最优解。
对偶理论
02
对偶理论是线性规划的一个重要概念,它通过引入对偶问题来
简化求解过程。
分解算法
03
分解算法是将大规模线性规划问题分解为若干个小问题,分别
求解后再综合得到最优解。
线性规划的应用
生产计划
线性规划可以用于生产计划问题, 通过优化资源配置和生产流程, 提高生产效率和利润。
运筹学经典课件第8 次共23页PPT

、纪律是管理关系的形式。——阿法 纳西耶 夫 2、改革如果不讲纪律,就难以成功。
3、道德行为训练,不是通过语言影响 ,而是 让儿童 练习良 好道德 行为, 克服懒 惰、轻 率、不 守纪律 、颓废 等不良 行为。 4、学校没有纪律便如磨房里没有水。 ——夸 美纽斯
5、教导儿童服从真理、服从集体,养 成儿童 自觉的 纪律性 ,这是 儿童道 德教育 最重要 的部分 。—— 陈鹤琴
21、要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
25、学习是劳动,是充满思想的劳动。——乌申斯基
3、道德行为训练,不是通过语言影响 ,而是 让儿童 练习良 好道德 行为, 克服懒 惰、轻 率、不 守纪律 、颓废 等不良 行为。 4、学校没有纪律便如磨房里没有水。 ——夸 美纽斯
5、教导儿童服从真理、服从集体,养 成儿童 自觉的 纪律性 ,这是 儿童道 德教育 最重要 的部分 。—— 陈鹤琴
21、要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
25、学习是劳动,是充满思想的劳动。——乌申斯基
第8章 动态规划《管理运筹学》PPT课件

Vk,n (sk , uk , , sn1) fk [sk , uk ,Vk 1,n (sk 1, uk 1, , 1)] ③函数 fk (sk , uk ,Vk 1,n ) 对于变量 Vk1,n 要严格单调。
8.2 动态规划模型建立
下面以投资问题为例介绍动态规划的建模条件。
【例8-2】 某公司现有资金20万元,若投资于三个
8.1 动态规划基础知识
(5)状态转移方程:状态转移方程是确定过程由一
个状态转移到另一个状态的演变过程。动态规划中某一状
态以及该状态下的决策,与下一状态之间具有一定的函数
关系,称这种函数关系的表达式为状态转移方程。如果第
k段的状态为 sk ,该阶段的决策为
的状态就可以用下式来表示:
uk
sk
,则第k+1段
阶段的指标函数,是该阶段最优的指标函数。
8.2 动态规划模型建立
建立动态规划模型,就是在分析实际问题的基础上建 立该问题的动态规划基本方程。成功地应用动态规划方法 的关键,在于识别问题的多阶段特征,将问题分解成为可 用递推关系式联系起来的若干子问题,或者说正确地建立 具体问题的基本方程,这需要经验与技巧。而正确建立基 本递推关系方程的关键又在于正确选择状态变量,保证各 阶段的状态变量具有递推的状态转移关系。
第8章 动态规划
动态规划(DYnamic Programming,缩写为DP)方法 ,是本世纪50年代初期由美国数学家贝尔曼(Richard E ,Bellman)等人提出,后来逐渐发展起来的数学分支, 它是一种解决多阶段决策过程最优化问题的数学规划法 。动态规划的数学模型和求解方法比较灵活,对于连续 的或离散的,线性的或非线性的,确定性的或随机性的 模型,只要能构成多阶段决策过程,便可用动态规划方 法求其最优解。因而在自然科学、社会科学、工程技术 等许多领域具有广泛的用途,甚至一定程度上比线性规 划(LP)、非线性规划(NLP)有成效,特别是对于某 些离散型问题,解析数学无法适用,动态规划方法就成 为非常有用的求解工具。
8.2 动态规划模型建立
下面以投资问题为例介绍动态规划的建模条件。
【例8-2】 某公司现有资金20万元,若投资于三个
8.1 动态规划基础知识
(5)状态转移方程:状态转移方程是确定过程由一
个状态转移到另一个状态的演变过程。动态规划中某一状
态以及该状态下的决策,与下一状态之间具有一定的函数
关系,称这种函数关系的表达式为状态转移方程。如果第
k段的状态为 sk ,该阶段的决策为
的状态就可以用下式来表示:
uk
sk
,则第k+1段
阶段的指标函数,是该阶段最优的指标函数。
8.2 动态规划模型建立
建立动态规划模型,就是在分析实际问题的基础上建 立该问题的动态规划基本方程。成功地应用动态规划方法 的关键,在于识别问题的多阶段特征,将问题分解成为可 用递推关系式联系起来的若干子问题,或者说正确地建立 具体问题的基本方程,这需要经验与技巧。而正确建立基 本递推关系方程的关键又在于正确选择状态变量,保证各 阶段的状态变量具有递推的状态转移关系。
第8章 动态规划
动态规划(DYnamic Programming,缩写为DP)方法 ,是本世纪50年代初期由美国数学家贝尔曼(Richard E ,Bellman)等人提出,后来逐渐发展起来的数学分支, 它是一种解决多阶段决策过程最优化问题的数学规划法 。动态规划的数学模型和求解方法比较灵活,对于连续 的或离散的,线性的或非线性的,确定性的或随机性的 模型,只要能构成多阶段决策过程,便可用动态规划方 法求其最优解。因而在自然科学、社会科学、工程技术 等许多领域具有广泛的用途,甚至一定程度上比线性规 划(LP)、非线性规划(NLP)有成效,特别是对于某 些离散型问题,解析数学无法适用,动态规划方法就成 为非常有用的求解工具。
《运筹学实用教程》PPT课件

7
服务系统的运行指标
队长(Ls)指系统中顾客数的数学期望值。 排队长(Lq)指系统内排队顾客数的数学期
望值。 很显然,Ls =Lq+正在被服务顾客数的期望
值。 逗留时间(Ws)指一个顾客在系统中停留时
间的数学期望值。 等待时间(Wq)指一个顾客在系统中排队等
待时间的数学期望值。 很显然,Ws=[等待时间]+[服务时间] 忙期 指服务员忙于服务的时间。与此相反
泊松过程是马尔科夫过程 本章主要考虑马尔科夫过程,即泊松流。
ppt课件
17
二、生灭过程的假设条件
系统状态N(t)得分布具有下列性质时,称 其为一个生灭过程:
当N(t)=n时,顾客到达的时间间隔服从参数
为 的负指数分布
当N(t)=n时,服务时间间隔服从参数为 的
负指数分布
在一个无限短的时间间隔里,最多只有一个 顾客到达或离去
ekt
E (T ) 1
1
D[T ] k 2
ppt课件
12
服务系统模型的符号表示法
为了使用上的方便,肯达(Kendal)在1953年归纳了一种服务 系统的符号表示法。它用[A/B/C]表示一个服务系统的特征。
其中 A处填写顾客到达的规律;
B处填写服务时间的分布规律;
C处填写服务通道的数目。
ppt课件
18
三、生灭过程的状态转移图
生灭过程的瞬时状态一般很难求得,但 可求得稳定状态分布
对于稳定的生灭状态,从平均意义上说 有:“流入=流出”
稳定的生灭过程可以用状态转移图表示
ppt课件
19
一般状态转移图示例
0 1
2
01
2
1 2 3
n2
n 1
运筹学教学课件(全)

实用举例
某公司通过市场调研,决定生产高中档新型拉杆箱。 某分销商决定买进该公司3个月内的全部产品。拉杆箱生 产需经过原材料剪裁、缝合、定型、检验和包装4过程。
通过分析生产过程,得出:生产中档拉杆箱需要用 7/10小时剪裁、5/10小时缝合、1小时定型、1/10小时检 验包装;生产高档拉杆箱则需用1小时剪裁、5/6小时缝合、 2/3小时定型、1/4小时检验包装。由于公司生产能力有限, 3月内各部的最大生产时间为剪裁部630小时、缝合部600 小时、定型部708小时、检验包装部135小时。
D {x | Ax b, x (x1,, xi ,, xn ) 0}
是凸集(凸多面体)。
引理2.1:线性规划的可行解 x (x1 ,, xn )T 为基本可行解的 充分必要条件是x的正分量所对应的系数列向量是线性无关的, 即每个正分量都是一个基变量。
定理2.2:线性规划问题的基本可行解x对应于可行域的顶点
通过分析生产过程,得出:生产中档拉杆箱需要用
7/10小时可剪裁以、通5/1过0小线时性缝合规、划1小求时定解型!、1/10小时
检验包装;生产高档拉杆箱则需用1小时剪裁、5/6小时 缝合、2/3小时定型、1/4小时检验包装。由于公司生产 能力有限,3月内各部的最大生产时间为剪裁部630小时、 缝合部600小时、定型部708小时、检验包装部135小时。
x2
L1:x1=6 L3:2x1+3x2=18
B 可行域
L2:x2=4 最优解
x1
4x1+3x2
解的特殊情况——解的特殊情况——无界解
线性规划的基本性质
若线性规划有最 优解,则最优解必在可 行域的顶点上达到。
X
可行域内部的点 • 可行解? 是 • 最优解? 不
运筹学全册精品完整课件

否则,目标函数等值线与可行域 将交于无穷远处,此时称无有限最 优解。
36
例2-2 考虑例2-1
某工厂拥有A、B、C 三种类型的设备,
生产甲、乙两种产品。每件产品在生产中 需要占用的设备机时数,每件产品可以获 得的利润以及三种设备可利用的时数如下 表所示。问题:工厂应如何安排生产可获 得最大的总利润?
一、线性规划问题的提出
在实践中,根据实际问题的要求,常常 可以建立线性规划问题数学模型。
例2-1 我们首先分析开篇案例提到的问题。 解:设变量 xi 为第 i 种(甲、乙)产品的 生产件数(i=1,2)。根据题意,我们知道 两种产品的生产受到设备能力(机时数)的 限制。对设备A:两种产品生产所占用的机时 数不能超过65,于是我们可以得到不等式:
运筹学是运用科学的方法(如 分析、试验、量化等)来决定如何 最佳地运营和设计各种系统的一门 学科。
4
运筹学概述
运筹学能够对经济管理系统中 的人力、物力、财力等资源进行统 筹安排,为决策者提供有依据的最 优方案,以实现最有效的管理。
通常以最优、最佳等作为决策 目标,避开最劣的方案。
5
运筹学的产生和发展
8பைடு நூலகம்
运筹学在管理中的应用
生产计划:生产作业的计划、日程表的
编排、合理下料、配料问题、物料管 理等。
库存管理:多种物资库存量的管理,库
存方式、库存量等。
运输问题:确定最小成本的运输线路、
物资的调拨、运输工具的调度以及建
厂地址的选择等。
9
运筹学在管理中的应用
• 人事管理:对人员的需求和使用的 预测,确定人员编制、人员合理分 配,建立人才评价体系等。
x1 ,x2 ,… ,xn ≥ 0
36
例2-2 考虑例2-1
某工厂拥有A、B、C 三种类型的设备,
生产甲、乙两种产品。每件产品在生产中 需要占用的设备机时数,每件产品可以获 得的利润以及三种设备可利用的时数如下 表所示。问题:工厂应如何安排生产可获 得最大的总利润?
一、线性规划问题的提出
在实践中,根据实际问题的要求,常常 可以建立线性规划问题数学模型。
例2-1 我们首先分析开篇案例提到的问题。 解:设变量 xi 为第 i 种(甲、乙)产品的 生产件数(i=1,2)。根据题意,我们知道 两种产品的生产受到设备能力(机时数)的 限制。对设备A:两种产品生产所占用的机时 数不能超过65,于是我们可以得到不等式:
运筹学是运用科学的方法(如 分析、试验、量化等)来决定如何 最佳地运营和设计各种系统的一门 学科。
4
运筹学概述
运筹学能够对经济管理系统中 的人力、物力、财力等资源进行统 筹安排,为决策者提供有依据的最 优方案,以实现最有效的管理。
通常以最优、最佳等作为决策 目标,避开最劣的方案。
5
运筹学的产生和发展
8பைடு நூலகம்
运筹学在管理中的应用
生产计划:生产作业的计划、日程表的
编排、合理下料、配料问题、物料管 理等。
库存管理:多种物资库存量的管理,库
存方式、库存量等。
运输问题:确定最小成本的运输线路、
物资的调拨、运输工具的调度以及建
厂地址的选择等。
9
运筹学在管理中的应用
• 人事管理:对人员的需求和使用的 预测,确定人员编制、人员合理分 配,建立人才评价体系等。
x1 ,x2 ,… ,xn ≥ 0
运筹学学习课件

8.1 引言
Preface
第8章 动态规划 Dynamic Programming
2018年4月15日星期日
Page 3
动态规划是运筹学的一个分支,适用于许多类型问题的数学 方法,即它是跨越数学规划的各个领域。一些线性规划,非线性 规划及整数规划等问题都可用动态规划的方法来求解。动态规划 是解决多阶段决策过程最优化的一种方法,它的特点是先将一个 复杂的问题分解成相互联系的若干阶段;每个阶段即为一个小问 题,然后逐个处理,当每一个阶段的决策一旦确定之后,整个过 程的决策也随之确定。由于阶段往往可以用时段表示,这就是 “动态”的含义和由来,当然,动态规划也可以解决一些与时间 无关的静态规划的最优化问题。 动态规划产生于50年代,1951年,美国数学家贝尔曼 (R.Bellman)等人提出了解决多阶段决策问题的“最优化原理”, 并研究了许多实际问题,从而创建了“动态规划”,1957年,出 版了著作“Dynamic Programming”,首次对动态规划的主要内容 作了系统的阐述。
10 13 7 2 8 6 10
5
v2
v7
5
v5
2 19 v1 5 13 v4 20 11 v6 8 14 7 v3
8 v8
8
v10 0
12
5 12 8 4 v9 4
阶段: 第1阶段
第2阶段 第3阶段 图8-1
第4阶段 第5阶段
8.1 动态规划数学模型 Mathematical Model of DP
第8章 动态规划 Dynamic Programming
2018年4月15日星期日
Page 7
用WinQSB软件计算时,需要对状态重新编号,如下图所示.
2
《高等运筹学》课件

动态规划的应用案例
总结词
列举几个动态规划在实际问题中的应用案例,包括生产与存储问题、背包问题、排程问 题等。
详细描述
动态规划的应用案例包括生产与存储问题,通过动态规划方法确定最佳的生产和存储策 略,以最小化总成本;背包问题,通过动态规划求解给定重量限制和价值总和最大的物 品组合;排程问题,通过动态规划安排任务或活动的最佳顺序,以最小化总完成时间。
详细描述
整数规划的数学模型可以表示为 在满足一系列约束条件下,最小 化或最大化一个目标函数,其中 决策变量是整数。约束条件可以 是等式或不等式,并且可以包含 其他决策变量。
整数规划的求解方法
总结词
整数规划的求解方法可以分为精确求解和近似求解两大类。
详细描述
精确求解方法包括分支定界法、割平面法等,这些方法可以找到整数规划问题的最优解,但计算复杂度较高,对 于大规模问题难以求解。近似求解方法包括启发式算法、元启发式算法等,这些方法可以在较短的时间内找到近 似最优解,但解的质量与问题的规模和约束条件有关。
整数规划的应用案例
总结词
整数规划在金融领域也有广泛应用, 如投资组合优化、风险管理等。
详细描述
在投资组合优化中,整数规划可以用 于确定最优的投资组合方案,实现风 险和收益的平衡。在风险管理中,整 数规划可以用于确定最优的风险控制 策略,降低风险损失。
04
非线性规划
非线性规划的定义与模型
总结词
非线性规划是一种数学优化方法,用于解决 目标函数和约束条件均为非线性函数的问题 。
06
动态规划
动态规划的定义与模型
总结词
详述动态规划的基本定义,包括其核心思想、特点以 及在优化问题中的应用。
详细描述
《运筹学》全套课件(完整版)

负指数分布、几何分布、爱尔朗分布等。
服务时间分布
负指数分布、确定型分布、一般分布等。
顾客到达和服务时间的独立性
假设顾客到达和服务时间是相互独立的。
单服务台排队系统
M/M/1排队系统
顾客到达服从泊松分布,服务时间服从负指 数分布,单服务台。
M/D/1排队系统
顾客到达服从泊松分布,服务时间服从确定 型分布,单服务台。
投资组合优化
确定投资组合中各种资产的最 优配置比例,以最大化收益或
最小化风险。
03
整数规划
整数规划问题的数学模型
01
整数规划问题的定 义
整数规划是数学规划的一个分支 ,研究决策变量取整数值的规划 问题。
02
整数规划问题的数 学模型
包括目标函数、约束条件和决策 变量,其中决策变量要求取整数 值。
03
Edmonds-Karp算法
介绍Edmonds-Karp算法的原理、步骤和实现方法,以及其与FordFulkerson算法的比较。
网络最大流问题的应用
列举网络最大流问题在资源分配、任务调度等领域的应用案例。
最小费用流问题
最小费用流问题的基本概 念
介绍最小费用流问题的定义、 分类和应用背景。
Bellman-Ford算法
优点是可以求解较大规模的整数规划问题,缺点是计算量较大,需 要较高的计算精度。
割平面法
割平面法的基本思想
通过添加新的约束条件(割平面)来缩小可行域的范围,从而逼 近最优解。
割平面法的步骤
包括构造割平面、求解子问题和更新割平面三个步骤,通过不断 迭代找到最优解。
割平面法的优缺点
优点是可以处理较复杂的整数规划问题,缺点是构造割平面的难 度较大,需要较高的数学技巧。
服务时间分布
负指数分布、确定型分布、一般分布等。
顾客到达和服务时间的独立性
假设顾客到达和服务时间是相互独立的。
单服务台排队系统
M/M/1排队系统
顾客到达服从泊松分布,服务时间服从负指 数分布,单服务台。
M/D/1排队系统
顾客到达服从泊松分布,服务时间服从确定 型分布,单服务台。
投资组合优化
确定投资组合中各种资产的最 优配置比例,以最大化收益或
最小化风险。
03
整数规划
整数规划问题的数学模型
01
整数规划问题的定 义
整数规划是数学规划的一个分支 ,研究决策变量取整数值的规划 问题。
02
整数规划问题的数 学模型
包括目标函数、约束条件和决策 变量,其中决策变量要求取整数 值。
03
Edmonds-Karp算法
介绍Edmonds-Karp算法的原理、步骤和实现方法,以及其与FordFulkerson算法的比较。
网络最大流问题的应用
列举网络最大流问题在资源分配、任务调度等领域的应用案例。
最小费用流问题
最小费用流问题的基本概 念
介绍最小费用流问题的定义、 分类和应用背景。
Bellman-Ford算法
优点是可以求解较大规模的整数规划问题,缺点是计算量较大,需 要较高的计算精度。
割平面法
割平面法的基本思想
通过添加新的约束条件(割平面)来缩小可行域的范围,从而逼 近最优解。
割平面法的步骤
包括构造割平面、求解子问题和更新割平面三个步骤,通过不断 迭代找到最优解。
割平面法的优缺点
优点是可以处理较复杂的整数规划问题,缺点是构造割平面的难 度较大,需要较高的数学技巧。
运筹学PPT完整版

优化炼油程序及产品供应、配送和营销
每年节约成本600万美元 每年节约成本7000万
优化商业用户的电话销售中心选址
控制成本库存(制定最优再定购点和定购 量确保安全库存) 制定最优铁路时刻表并调整铁路日运营量
优化员工安排,以最低成本服务客户
每年节约成本4.06亿美元,销 售额大幅增加 每年节约成本380万美元
s.t
n j1
aij
xj
bi
(i 1,2,,m)
(2)
xj 0, j 1,2,,n (3)
求解线性规划问题,就是从满足约束条件(2)、(3)的方程组 中找出一个解,使目标函数(1)达到最大值。
线性规划问题的数学模型
Page 28
可行解:满足约束条件②、③的解为可行解。所有可行解 的集合为可行域。
(5) 目标函数是最小值,为了化为求最大值,令z′=-z,得到max z′=-z,即当z达到最小值时z′达到最大值,反之亦然;
线性规划问题的数学模型
标准形式如下:
maxZ 2x1 x2 3(x3 x3)0x4 0x5
5x1 x2 (x3 x3) x4 7
1 2
1 0
0 1
r(A)=2,2阶子矩阵有10个,其中基矩阵只有9个,即
5 1
1 1 5 0 1 1
B 1 106 B 2 6 2 B 3 101 B 4 6 0
5 1 1 0
1 1 1 0
1 0
B 5 100 B 6 2 1 B 7 2 0 B 8 6 1 B 9 0 1
线性规划问题的数学模型
Page 17
2. 线性规划的数学模型由三个要素构成 决策变量 Decision variables 目标函数 Objective function 约束条件 Constraints
每年节约成本600万美元 每年节约成本7000万
优化商业用户的电话销售中心选址
控制成本库存(制定最优再定购点和定购 量确保安全库存) 制定最优铁路时刻表并调整铁路日运营量
优化员工安排,以最低成本服务客户
每年节约成本4.06亿美元,销 售额大幅增加 每年节约成本380万美元
s.t
n j1
aij
xj
bi
(i 1,2,,m)
(2)
xj 0, j 1,2,,n (3)
求解线性规划问题,就是从满足约束条件(2)、(3)的方程组 中找出一个解,使目标函数(1)达到最大值。
线性规划问题的数学模型
Page 28
可行解:满足约束条件②、③的解为可行解。所有可行解 的集合为可行域。
(5) 目标函数是最小值,为了化为求最大值,令z′=-z,得到max z′=-z,即当z达到最小值时z′达到最大值,反之亦然;
线性规划问题的数学模型
标准形式如下:
maxZ 2x1 x2 3(x3 x3)0x4 0x5
5x1 x2 (x3 x3) x4 7
1 2
1 0
0 1
r(A)=2,2阶子矩阵有10个,其中基矩阵只有9个,即
5 1
1 1 5 0 1 1
B 1 106 B 2 6 2 B 3 101 B 4 6 0
5 1 1 0
1 1 1 0
1 0
B 5 100 B 6 2 1 B 7 2 0 B 8 6 1 B 9 0 1
线性规划问题的数学模型
Page 17
2. 线性规划的数学模型由三个要素构成 决策变量 Decision variables 目标函数 Objective function 约束条件 Constraints
运筹课件

3
4 5 6 7 8
(0,1,0)
(0,1,1) (1,0,0) (1,0,1) (1,1,0) (1,1,1)
-2
3 3 8 1 6
no
no yes 3 yes 8 no no
增加约束条件(0)(Z 3)后实际做了24次运 算,而原问题需要计算 23*4=32次运算(3个变量, 4个约束条件)。
例5-9
求下列问题:
Max Z=3x1- 2x2 + 5x3
s.t. x1+2x2 - x3 2
x1+4x2 + x3 4 x1 + x2
(1)
(2) (3)3来自4x2 + x3 6 xj 0或1
(4) (5)
解: 容易看出(1,0,0)满足约束 条件,对应Z=3,对Max Z来说, 希望Z 3,所以增加约束条件: Z=3x1- 2x2 + 5x3 3 (0)
定界:把满足整数条件各分枝的 最优目标函数值作为上(下)界, 用它来判断分枝是保留还是剪枝。 剪枝:把那些子问题的最优值与 界值比较,凡不优或不能更优的 分枝全剪掉,直到每个分枝都查 清为止。
例5-6 用分枝定界法求解:
Max Z=4x1+3x2 4x1+2x2 9 x1,x2 0 整数
甲 2 4 6
乙 3 2 4
可利用 的资源 总量 100 120
加工时间(小时) 单位利润(百元)
如何安排生产,使利润达到最大。
用单纯形法求得最优解=(20,20)
最优值=200(百元)
问题:该厂提出如下目标 (1)利润达到280百元; (2)钢材不超过100吨,工时不 超过120小时; 如何安排生产?
运筹学PPT完整版

绪论
运筹学的历史与发展 “运筹学思想的出现可以追溯到很早—“田忌赛马” 。 齐王要与大臣田忌赛马,双方各出上、中、下马各一匹, 对局三次,每次胜负1000金。田忌在好友、著名的军事谋 略家孙膑的指导下,做出以下安排: 齐王 上 中 下
田忌
下
上
中
绪论
丁谓的皇宫修复工程
北宋年间,丁谓负责修复火毁的开封皇宫。他 的施工方案是:先将皇宫前的一条大街挖成一条大 沟,将大沟与汴水相通。使用挖出的土就地制砖, 令与汴水相连形成的河道承担繁重的运输任务;修 复工程完成后,实施大沟排水,并将原废墟物回填, 修复成原来的大街。丁谓将取材、运输及清废用 “一沟三用”巧妙地解决了,体现了系统规划的思 想。
2x1 + 2x2 ≤ 12
A 2
B 1
C 4
D 0
利润 (元)
Ⅰ
2
பைடு நூலகம்
Ⅱ
有效台时
2
12
2
8
0
16
4
12
3
x1 + 2x2 ≤ 8
4x1 ≤ 16 4x2 ≤ 12 x1 ≥ 0 , x2 ≥ 0
线性规划问题的数学模型
例1.4 某厂生产三种药物, 这些药物可以从四种不同的 原料中提取。下表给出了单 位原料可提取的药物量
3x1 +x2 +x3 +2 x4
x1、x2 、x3 、x4 ≥0
线性规划问题的数学模型
例1.5 某航运局现有船只种类、数量以及计划期内各条航 线的货运量、货运成本如下表所示:
航线号 船队 类型 1 1 2 3 2 4 1 1 2 编队形式 拖轮 1 A型 驳船 2 — 2 — B型 驳船 — 4 4 4 货运成本 (千元/队) 36 36 72 27 货运量 (千吨) 25 20 40 20
经济学运筹学PPT课件
2
第2页/共73页
数学规划中的模型都是线性函数时,称线性规划。 线性规划 (Linear Programming ——LP)
是数学规划的一个分支,是一种解决在线性约 束条件下追求最大或最小的线性目标函数的方 法。一般可以表达成以下两个问题中的一个: 1. 当资源给定时,要求完成的任务最多; 2. 当任务给定时,要求为完成任务所消耗的资源 最少。
LP解的可能情况:
有可行解
有最优解
唯一解 无穷多解
无最优解(可行域为无界)
无可行解(无解)
若LP问题有最优解,则要么最优解唯一,要么 有无穷多最优解。
9
第9页/共73页
x2
③
①
4, 6
②
多重解举例
Max Z=3X1+4X2
X1 ≤8 ①
2X2 ≤12
②
3X1+4X2≤36 ③
X1﹑X2≥0
963
4
x1 x2 x3 x4 x5 基本变量 非基变量
1 0 1 0 0 x1x2x3 x4x5
0 2 0 1 0 令x4,x5=0,得:
3
4
0
0
1
X=(4 6 4 0 0) z=42
5
x1 x2 x3 x4 x5 基本变量 非基变量
1 0 1 0 0 x1x3x4 x2x5
0 2 0 1 0 令x2,x5=0,得:
0 2 0 1 0 令x3,x4=0,得:
34001
X=(8 6 0 0 -12)
z=54
8
x1 x2 x3 x4 x5 基本变量 非基变量
1 0 1 0 0 x2x4x5 x1x3 0 2 0 1 0 ∵ 000 3 4 0 0 1 2 1 0 =0
第2页/共73页
数学规划中的模型都是线性函数时,称线性规划。 线性规划 (Linear Programming ——LP)
是数学规划的一个分支,是一种解决在线性约 束条件下追求最大或最小的线性目标函数的方 法。一般可以表达成以下两个问题中的一个: 1. 当资源给定时,要求完成的任务最多; 2. 当任务给定时,要求为完成任务所消耗的资源 最少。
LP解的可能情况:
有可行解
有最优解
唯一解 无穷多解
无最优解(可行域为无界)
无可行解(无解)
若LP问题有最优解,则要么最优解唯一,要么 有无穷多最优解。
9
第9页/共73页
x2
③
①
4, 6
②
多重解举例
Max Z=3X1+4X2
X1 ≤8 ①
2X2 ≤12
②
3X1+4X2≤36 ③
X1﹑X2≥0
963
4
x1 x2 x3 x4 x5 基本变量 非基变量
1 0 1 0 0 x1x2x3 x4x5
0 2 0 1 0 令x4,x5=0,得:
3
4
0
0
1
X=(4 6 4 0 0) z=42
5
x1 x2 x3 x4 x5 基本变量 非基变量
1 0 1 0 0 x1x3x4 x2x5
0 2 0 1 0 令x2,x5=0,得:
0 2 0 1 0 令x3,x4=0,得:
34001
X=(8 6 0 0 -12)
z=54
8
x1 x2 x3 x4 x5 基本变量 非基变量
1 0 1 0 0 x2x4x5 x1x3 0 2 0 1 0 ∵ 000 3 4 0 0 1 2 1 0 =0
运筹学PPT

某公司面临一个是外包协作还是自行生产的问 题。该公司有甲、乙、丙三种产品,这三种产品 都要经过铸造、机械加工和装配三道工序。甲、 乙两种产品的铸件可以外包协作,亦可以自行生 产,但产品丙必须由本厂铸造才能保证质量。有 关情况如图所示,公司中可利用的总工时为:铸 造8000小时,机械加工12000小时和装配 10000小时。为了获得最大利润,甲、乙、丙 三种产品各应生产多少件?甲、乙两种产品的铸 件有多少由本公司铸造?有多少为外包协作?
工时与成本
每件铸造工时/小时 每件机械加工工时/小时 每件装配工时/小时 5 6 3
甲
件每件成本/元 外包协作铸件每件成本/元
机械加工每件成本/元 装配每件成本/元 每件产品售价/元
3 5
2 3 23
5 6
1 2 18
4 --3 2 16
最优解如下
目标函数最优值为:29400 变量 最优解 相差值 ---------------------------X1 1600 0 X2 0 2 X3 0 13.1 X4 0 0.5 X5 600 0 约束 松弛/剩余变量 对偶价格 -------------------------------1 0 0.3 2 0 2.25 3 4000 0 目标函数系数范围: 变量 下限 当前值 上限 --------------------------X1 14 15 无上限 X2 无下限 10 12 X3 无下限 7 20.1 X4 无下限 13 13.5 X5 8.667 9 10 常数项数范围: 约束 下限 当前值 上限 ----------------------1 0 8000 10000 2 9600 12000 20000 3 6000 10000 无上限
Thank you
工时与成本
每件铸造工时/小时 每件机械加工工时/小时 每件装配工时/小时 5 6 3
甲
件每件成本/元 外包协作铸件每件成本/元
机械加工每件成本/元 装配每件成本/元 每件产品售价/元
3 5
2 3 23
5 6
1 2 18
4 --3 2 16
最优解如下
目标函数最优值为:29400 变量 最优解 相差值 ---------------------------X1 1600 0 X2 0 2 X3 0 13.1 X4 0 0.5 X5 600 0 约束 松弛/剩余变量 对偶价格 -------------------------------1 0 0.3 2 0 2.25 3 4000 0 目标函数系数范围: 变量 下限 当前值 上限 --------------------------X1 14 15 无上限 X2 无下限 10 12 X3 无下限 7 20.1 X4 无下限 13 13.5 X5 8.667 9 10 常数项数范围: 约束 下限 当前值 上限 ----------------------1 0 8000 10000 2 9600 12000 20000 3 6000 10000 无上限
Thank you
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、目标函数系数C(价格)变化 的灵敏度分析
对 max z CX s.t AX b
X 0
最优单纯形表:
检验行
XB XN
常数项
0 CN- CBB-1N Z- CBB-1b
XB
E B-1N
B-1b
当C变为C时,即 C B C N (C B C N )时
C NC BB 1N C NC BB 1N,ZC B B 1 b ZC B B 1 b
B C 拥有量 3 5 45 4 5 30
设x3 : xC1的 产A的量产,量,x2 B的产量, maxz 3x1 x2 4x3 s.t. 6x1 3x2 5x3 45
售价(元) 3 1 4
3x1 4x2 5x3 30
x1, x2, x3 0
最优单纯形表
原问题的最优基不变
其中 m 1 2ii i是 B1的i第 列b b bm , 1 2 B1b是最优单 s.t的 纯常 形数 表
例:某工厂准备生产A、B、C三种产品,他们都 消耗劳动力和材料,有关数据如下:
原料 产品 A
劳动力
6
材料
3
劳动力的数量在30至 60之间时生产计划不 变
期中练习题(20分):
某企业生产A、B、C 三种产品,他们都消耗甲、 乙、 丙三种资源,有关数据如下:
原料 产品
甲 乙 丙 售价(元)
AB
11 10 4 22 10 6
C 拥有 量
1 100 5 600 6 300 4
问: 一、如何安排生产,使企业的收入最多?
X 0
标准型 max z CX s.t AX X S b
X 0
设B是最优基
AXXS b
B NX XN BXS b
BB X NN X X S b
X B B 1 N N X B 1 X S B 1 b
最优单纯形表的s.t中 松弛变量的系数
maxbkk1
| k1
0
b1
minbkk1
|
k1
0
minbkk1
| k1 0
b 2 21
15
max
bk
k1
|
k1
0
b1 11
15
即 15b115
结论:当劳动力 量的 在 3拥 0至6有 0之间时,
仍然不生产B产品
2、若劳动力b1拥 增有 加2量 了 0个,求最优生
原料 产品 A B C
劳动力
635
材料
345
售价(元) 3 1 4
拥有量 45 30
最优单纯形表
B 1
X1 X2 X3 X4 X5 0 -2 0 -1/5 -3/5 ZZ-2371
变量 最优解 相差值
-------
-------- --------
x1
5
0
x2
0
2
x3
3
0
约束 松弛/剩余变量 对偶价格
------- ------------- --------
1
0
.2
2
0
.6
目标函数系数范围 :
变量 下限 当前值 上限
------- -------- -------- --------
ci在范围 ci i内时,最优解不
结论 2:若 ci是基变量的系 ci的 数改 ,变 则 ci在 量 当 范围
maxaijj |aij 0,Pj Nci minaijj |aij0,Pj N
内时,最优解不变
其中 aij是最优单纯 s.t中 形基 表变 的 xi 量 所在行对应x非 j的基 系变 数量
参考答案:
一、线性规划模型
max z 10 x1 6 x 2 4 x 3
x1 x 2 x 3 100
s.t.
120xx11
4x2
2x2
x
1,
x
,
2
5x3 6x3 x3 0
600 300
最优单纯形标为:
X1 X2 X3
X4
X5
X6
常数项
问题 变: 化 bi 设 时 bi , bi,其 原余 最不 优变 基 bi在 , 不什 则 变么范
即bi在什么范围内变化B时1b, 0
结论b: i的当 改 变 bi满量 足
maxbkki
| ki
0bi
minbkki
| ki0
例:某工厂准备生产A、B、C三种产品,他们都消耗 劳动力和材料,有关数据如下:
最 最优 优Z X值 解 ( 25, 70, 3, 0, 0)劳 材原动 料料力
产品
A 6 3
最优生产方案:
售价(元) 3
B C 拥有量 3 5 45 4 5 30 14
5个A,0个B,3个C
最优单纯形表
新问题: 由于特殊原因,要求至
0 -3 -1 0 -1 Z-30
X1 1 -2 5/3 0 X4 0 -5 -5 1
1/3 10 -2 5
最优X解 ( 10, 0, 0, 5, 0), 最优Z值 30
结论:最优生产方案:10个A,其余不生产
将最优解代入新的约束中:
(1)若满足新约束,则原最优解不变;
(2)若不满足新约束,则原最优解改变, 将新增的约束条件添入最终的单纯形 表中,并增加一个基变量,继续迭代。
X1 1 X3 0
-1/3 0 11
1/3 -1/3 355 / 3 -1/5 2/5 3 1
B1b 11//35
21//53
65 30
35
/3 1
ZCBB1bZ3,435/13
Z31
X1 X2 X3 X4 X5
X1 1 -1/3 0 1/3 -1/3 0 5 X3 0 1 1 -1/5 2/5 0 3 X6 0 1 0 -1/5 2/5 1 -3
X1 X2
0 -1
X3 X4 X5 X6
0 0 -1 -1 Z-24
X1 1 4/3 X3 0 0 X4 0 -5
00 10 01
1/3 5/3 0 0 -1 6 -2 -5 15
2、6,15 3、 4,5 。
4、10 , 2 ,0; 33
5、可以生产
6、 A 生产 95 3 , B 生产 1 75 3 , C 生产 10。
谢谢!
XB1b, 00不变,还是本 新可 问行 题解 的
若 C NC BB1N0:X B1b, 0还是最优解
若 CNCBB1N0:新问题还没取到最优
在原最优单纯形表上 用单纯形法继续迭代
任务:找出C的变化范围,使在该范围内, 原问题的最优解还是新问题的最优解
结论 1:若 ci是非基变量的当 系 ci的 数改 ,变 则量
X1 X2 X3 X4 X5 X6
0 -2 0 -1/5 -3/5 0 Z-27
少生产6个C产品,求最 X1 1 -1/3 0 1/3 -1/3 0 5
优生产方案 即x3 6
显然 x*3 36
X3 0
1
1
-1/5 2/5 0
3
X6 0
0
-1 0
0
1
-6
在最优单纯形表约中束增方加程 x3 :6 x3x66
最优 X*( 解 B1b, 0) , 最 优 Z*值 CBB1b
若B1b 0:在原最优单纯形表中, B 1b B 1 b , ZC B B 1b ZC B B 1b 用对偶单纯形法迭代求出最优解
B 1的求法:
对问题 max z CX s .t AX b
最优X解 ( 5, 0, 3, 0, 0),
X1 X2 X3 X4 X5
0 -2 0 -1/5 -3/5 Z-27
最优Z值 27
X1 1 X3 0
-1/3 0 11
1/3 -1/3 5 -1/5 2/5 3
最优生产方案: 5个A,0个B,3个C
问题 1、劳动力b拥 1的有 改量 变 b1量 在什么范围内 变化时,仍然品 不 B 生产产
并取x6为基变量
X1 X2 X3 X4 X5 X6
0 -2 0 -1/5 -3/5 0 Z-27
X1 1
-1/3 0
1/3 -1/3 0
5
X3 0
1
1
-1/5 2/5 0
3
X6 0 0 -1 0 0 1 -6
不是单纯形表
X1 X2 X3 X4 X5 X6
0 -2 0 -1/5 -3/5 0 Z-27
x1
2.4
3
4.8
x2
无下限 1
3
x3 约束
2.5
4
常数项数范围 :
下限
当前值
5 上限
------- -------- -------- --------
1
30
45
60
2
22.5
30
45
最大总收入:27 最优生产方案: 5个A,0个B,3个C
产品B的价格至少上 升2元才可考虑生产
影子价格
产品A的价格在2.4元 至4.8元之间时生产计 划不变
最优X解 ( 0, 0, 6, 1, 50,0) 最优Z值 24
最优生产方案: 0个A,0个B,6个C
管理运筹学软件
适应范围:变量个数≤100个,
约束方程个数≤50个
例:某工厂准备生产A、B、C三种产品,他们都 消耗劳动力和材料,有关数据如下:
原料 产品 A
对 max z CX s.t AX b
X 0
最优单纯形表:
检验行
XB XN
常数项
0 CN- CBB-1N Z- CBB-1b
XB
E B-1N
B-1b
当C变为C时,即 C B C N (C B C N )时
C NC BB 1N C NC BB 1N,ZC B B 1 b ZC B B 1 b
B C 拥有量 3 5 45 4 5 30
设x3 : xC1的 产A的量产,量,x2 B的产量, maxz 3x1 x2 4x3 s.t. 6x1 3x2 5x3 45
售价(元) 3 1 4
3x1 4x2 5x3 30
x1, x2, x3 0
最优单纯形表
原问题的最优基不变
其中 m 1 2ii i是 B1的i第 列b b bm , 1 2 B1b是最优单 s.t的 纯常 形数 表
例:某工厂准备生产A、B、C三种产品,他们都 消耗劳动力和材料,有关数据如下:
原料 产品 A
劳动力
6
材料
3
劳动力的数量在30至 60之间时生产计划不 变
期中练习题(20分):
某企业生产A、B、C 三种产品,他们都消耗甲、 乙、 丙三种资源,有关数据如下:
原料 产品
甲 乙 丙 售价(元)
AB
11 10 4 22 10 6
C 拥有 量
1 100 5 600 6 300 4
问: 一、如何安排生产,使企业的收入最多?
X 0
标准型 max z CX s.t AX X S b
X 0
设B是最优基
AXXS b
B NX XN BXS b
BB X NN X X S b
X B B 1 N N X B 1 X S B 1 b
最优单纯形表的s.t中 松弛变量的系数
maxbkk1
| k1
0
b1
minbkk1
|
k1
0
minbkk1
| k1 0
b 2 21
15
max
bk
k1
|
k1
0
b1 11
15
即 15b115
结论:当劳动力 量的 在 3拥 0至6有 0之间时,
仍然不生产B产品
2、若劳动力b1拥 增有 加2量 了 0个,求最优生
原料 产品 A B C
劳动力
635
材料
345
售价(元) 3 1 4
拥有量 45 30
最优单纯形表
B 1
X1 X2 X3 X4 X5 0 -2 0 -1/5 -3/5 ZZ-2371
变量 最优解 相差值
-------
-------- --------
x1
5
0
x2
0
2
x3
3
0
约束 松弛/剩余变量 对偶价格
------- ------------- --------
1
0
.2
2
0
.6
目标函数系数范围 :
变量 下限 当前值 上限
------- -------- -------- --------
ci在范围 ci i内时,最优解不
结论 2:若 ci是基变量的系 ci的 数改 ,变 则 ci在 量 当 范围
maxaijj |aij 0,Pj Nci minaijj |aij0,Pj N
内时,最优解不变
其中 aij是最优单纯 s.t中 形基 表变 的 xi 量 所在行对应x非 j的基 系变 数量
参考答案:
一、线性规划模型
max z 10 x1 6 x 2 4 x 3
x1 x 2 x 3 100
s.t.
120xx11
4x2
2x2
x
1,
x
,
2
5x3 6x3 x3 0
600 300
最优单纯形标为:
X1 X2 X3
X4
X5
X6
常数项
问题 变: 化 bi 设 时 bi , bi,其 原余 最不 优变 基 bi在 , 不什 则 变么范
即bi在什么范围内变化B时1b, 0
结论b: i的当 改 变 bi满量 足
maxbkki
| ki
0bi
minbkki
| ki0
例:某工厂准备生产A、B、C三种产品,他们都消耗 劳动力和材料,有关数据如下:
最 最优 优Z X值 解 ( 25, 70, 3, 0, 0)劳 材原动 料料力
产品
A 6 3
最优生产方案:
售价(元) 3
B C 拥有量 3 5 45 4 5 30 14
5个A,0个B,3个C
最优单纯形表
新问题: 由于特殊原因,要求至
0 -3 -1 0 -1 Z-30
X1 1 -2 5/3 0 X4 0 -5 -5 1
1/3 10 -2 5
最优X解 ( 10, 0, 0, 5, 0), 最优Z值 30
结论:最优生产方案:10个A,其余不生产
将最优解代入新的约束中:
(1)若满足新约束,则原最优解不变;
(2)若不满足新约束,则原最优解改变, 将新增的约束条件添入最终的单纯形 表中,并增加一个基变量,继续迭代。
X1 1 X3 0
-1/3 0 11
1/3 -1/3 355 / 3 -1/5 2/5 3 1
B1b 11//35
21//53
65 30
35
/3 1
ZCBB1bZ3,435/13
Z31
X1 X2 X3 X4 X5
X1 1 -1/3 0 1/3 -1/3 0 5 X3 0 1 1 -1/5 2/5 0 3 X6 0 1 0 -1/5 2/5 1 -3
X1 X2
0 -1
X3 X4 X5 X6
0 0 -1 -1 Z-24
X1 1 4/3 X3 0 0 X4 0 -5
00 10 01
1/3 5/3 0 0 -1 6 -2 -5 15
2、6,15 3、 4,5 。
4、10 , 2 ,0; 33
5、可以生产
6、 A 生产 95 3 , B 生产 1 75 3 , C 生产 10。
谢谢!
XB1b, 00不变,还是本 新可 问行 题解 的
若 C NC BB1N0:X B1b, 0还是最优解
若 CNCBB1N0:新问题还没取到最优
在原最优单纯形表上 用单纯形法继续迭代
任务:找出C的变化范围,使在该范围内, 原问题的最优解还是新问题的最优解
结论 1:若 ci是非基变量的当 系 ci的 数改 ,变 则量
X1 X2 X3 X4 X5 X6
0 -2 0 -1/5 -3/5 0 Z-27
少生产6个C产品,求最 X1 1 -1/3 0 1/3 -1/3 0 5
优生产方案 即x3 6
显然 x*3 36
X3 0
1
1
-1/5 2/5 0
3
X6 0
0
-1 0
0
1
-6
在最优单纯形表约中束增方加程 x3 :6 x3x66
最优 X*( 解 B1b, 0) , 最 优 Z*值 CBB1b
若B1b 0:在原最优单纯形表中, B 1b B 1 b , ZC B B 1b ZC B B 1b 用对偶单纯形法迭代求出最优解
B 1的求法:
对问题 max z CX s .t AX b
最优X解 ( 5, 0, 3, 0, 0),
X1 X2 X3 X4 X5
0 -2 0 -1/5 -3/5 Z-27
最优Z值 27
X1 1 X3 0
-1/3 0 11
1/3 -1/3 5 -1/5 2/5 3
最优生产方案: 5个A,0个B,3个C
问题 1、劳动力b拥 1的有 改量 变 b1量 在什么范围内 变化时,仍然品 不 B 生产产
并取x6为基变量
X1 X2 X3 X4 X5 X6
0 -2 0 -1/5 -3/5 0 Z-27
X1 1
-1/3 0
1/3 -1/3 0
5
X3 0
1
1
-1/5 2/5 0
3
X6 0 0 -1 0 0 1 -6
不是单纯形表
X1 X2 X3 X4 X5 X6
0 -2 0 -1/5 -3/5 0 Z-27
x1
2.4
3
4.8
x2
无下限 1
3
x3 约束
2.5
4
常数项数范围 :
下限
当前值
5 上限
------- -------- -------- --------
1
30
45
60
2
22.5
30
45
最大总收入:27 最优生产方案: 5个A,0个B,3个C
产品B的价格至少上 升2元才可考虑生产
影子价格
产品A的价格在2.4元 至4.8元之间时生产计 划不变
最优X解 ( 0, 0, 6, 1, 50,0) 最优Z值 24
最优生产方案: 0个A,0个B,6个C
管理运筹学软件
适应范围:变量个数≤100个,
约束方程个数≤50个
例:某工厂准备生产A、B、C三种产品,他们都 消耗劳动力和材料,有关数据如下:
原料 产品 A
