运筹学课件——第4讲 马尔可夫决策培训资料
马尔可夫决策过程简介

马尔可夫决策过程简介马尔可夫决策过程(Markov Decision Process,MDP)是一种在人工智能和运筹学领域广泛应用的数学模型。
它可以描述一类随机决策问题,并提供了一种优化决策的框架。
在现实世界中,许多问题都可以被建模为马尔可夫决策过程,比如自动驾驶车辆的路径规划、机器人的行为控制和资源分配等。
1. 马尔可夫决策过程的基本概念在马尔可夫决策过程中,问题被建模为一个五元组(S, A, P, R, γ):- S 表示状态空间,包括所有可能的状态;- A 表示动作空间,包括所有可能的动作;- P 表示状态转移概率,描述了在某个状态下采取某个动作后转移到下一个状态的概率分布;- R 表示奖励函数,描述了在某个状态下采取某个动作后获得的即时奖励;- γ(gamma)表示折扣因子,用于平衡当前奖励和未来奖励的重要性。
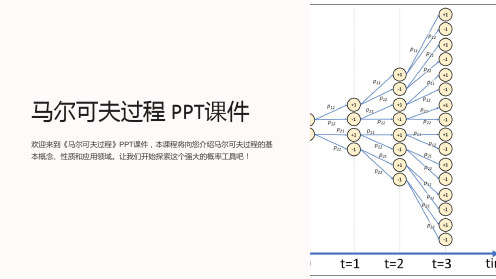
2. 马尔可夫决策过程的模型马尔可夫决策过程的模型可以用有向图表示,其中节点表示状态,边表示从一个状态到另一个状态的动作,边上的权重表示状态转移概率和即时奖励。
通过对模型进行分析和计算,可以找到最优的决策策略,使得在长期累积奖励最大化的情况下,系统能够做出最优的决策。
3. 马尔可夫决策过程的求解方法对于小规模的马尔可夫决策过程,可以直接使用动态规划方法进行求解,比如值迭代和策略迭代。
值迭代是一种迭代算法,通过不断更新状态值函数来找到最优策略;策略迭代则是一种迭代算法,通过不断更新策略函数来找到最优策略。
这些方法可以保证最终收敛到最优解,但是计算复杂度较高。
对于大规模的马尔可夫决策过程,通常采用近似求解的方法,比如蒙特卡洛方法、时序差分学习方法和深度强化学习方法。
蒙特卡洛方法通过对大量样本进行采样和统计来估计状态值函数和策略函数;时序差分学习方法则是一种在线学习算法,通过不断更新估计值函数来逼近真实值函数;深度强化学习方法则是一种基于神经网络的方法,通过端到端的学习来直接从环境中学习最优策略。
《马尔可夫过程 》课件
马尔可夫过程的应用实例
隐马尔可夫模型
隐马尔可夫模型是一种概率模型,常用于语音 识别、手写识别和自然语言处理等领域。
马尔可夫链蒙特卡罗法
马尔可夫链蒙特卡罗法是一种随机模拟方法, 用于估计复杂概率分布的数值解。
马尔可夫决策过程
马尔可夫决策过程是一种用来模拟决策问题的 数学框架,常应用于人工智能和运筹学领域。
马尔可夫过程的应用
自然语言处理
马尔可夫过程在自 然语言处理中被广 泛应用于语言模型 和信息检索等领域。
机器学习
马尔可夫过程是许 多机器学习算法中 的核心概念,如隐 马尔可夫模型和马 尔可夫决策过程。
金融市场分析
马尔可夫过程被用 于预测金融市场的 变化趋势和风险评 估。
生态学模型
马尔可夫过程能够 模拟生态系统中的 物种迁移和数量变 化,帮助研究者理 解生态系统的动态。
1 唯一性
2 可逆性
马尔可夫链的过渡概率是唯一确定的,无 论起始状态如何。
某些马尔可夫链具有可逆性,可以在时间 上逆转而保持同样的概率性质。
3 ቤተ መጻሕፍቲ ባይዱ态分布
4 马尔可夫链收敛于定态分布
马尔可夫链能够收敛于某个稳定的定态分 布。
随着时间的推移,马尔可夫链的状态会趋 向于定态分布,并在该分布上进行随机转 移。
PageRank算法
PageRank算法是根据网页之间的链接关系进行 排名的算法,被Google用于搜索引擎的搜索结 果排序。
结论
马尔可夫过程是一种强大的概率工具,它在不同的领域有着广泛的应用。深 入研究马尔可夫过程可能会带来更多的应用和发现。
参考文献
• [1] 马尔可夫过程 - 维基百科 • [2] 黄永宏《马尔可夫过程与随机游动》 • [3] 李航《统计学习方法》第10章
决策管理-马尔可夫决策基础理论教材(PDF36页)

马尔可夫决策基础理论内容提要本章介绍与研究背景相关的几类决策模型及算法。
模型部分,首先是最基本的马尔可夫决策模型,然后是在此基础上加入观察不确定性的部分可观察马尔可夫决策模型,以及进一步加入多智能体的分布式部分可观察马尔可夫决策模型和部分可观察的随机博弈模型。
算法部分,针对上述几类模型,我们均按照后向迭代和前向搜索两大类进行对比分析。
最后,我们介绍了半马尔可夫决策模型及Option理论,这一理论为我们后面设计分等级的大规模多智能体系统的决策模型及规划框架提供了重要基础。
2.1 MDP基本模型及概念马尔可夫决策过程适用的系统有三大特点:一是状态转移的无后效性;二是状态转移可以有不确定性;三是智能体所处的每步状态完全可以观察。
下面我们将介绍MDP基本数学模型,并对模型本身的一些概念,及在MDP模型下进行问题求解所引入的相关概念做进一步解释。
2.1.1 基本模型马尔科夫决策过程最基本的模型是一个四元组S,A,T,R(Puterman M, 1994):♦状态集合S:问题所有可能世界状态的集合;♦行动集合A:问题所有可能行动的集合;♦状态转移函数T: S×A×S’→[0,1]: 用T(s, a, s’)来表示在状态s,执行动作P s s a;a,而转移到状态s’的概率('|,)♦报酬函数R: S×A→R:我们一般用R(s,a)来表示在状态s执行动作a所能得到的立即报酬。
虽然有针对连续参数情况的MDP模型及算法,然而本文在没有特殊说明的情况都只讨论离散参数的情况,如时间,状态及行动的参数。
图2.1描述的是在MDP模型下,智能体(Agent)与问题对应的环境交互的过程。
智能体执行行动,获知环境所处的新的当前状态,同时获得此次行动的立即收益。
图 0.1 MDP 的基本模型2.1.2 状态状态是对于在某一时间点对该世界(系统)的描述。
最一般化的便是平铺式表示[],即对世界所有可能状态予以标号,以s 1,s 2,s 3,…这样的方式表示。
高中数学人教A版选修第四讲三长期准则下的马尔可夫型决策理论课件

P (n+1) 1
P (n+1) 2
=
P (n) 1
P (n) 2
0.95
0.6
0.05
0.4
假设初始分布
p (0) 1
p (0) 2
1
0
高 中 数 学 人 教A版选 修4-9 第 四讲 三 长 期 准 则 下的 马尔可 夫型决 策理论 课 件 ( 共27张 PPT四讲 三 长 期 准 则 下的 马尔可 夫型决 策理论 课 件 ( 共27张 PPT) 高 中 数 学 人 教A版选 修4-9 第 四讲 三 长 期 准 则 下的 马尔可 夫型决 策理论 课 件 ( 共27张 PPT)
则得各个时刻的分布表
0
1 0
1 0.9500 0.0500
2 0.9325 0.0675
3 0.9264 0.0736
…
50 0.9231 0.0769
…
100 0.9231 0.0769
高 中 数 学 人 教A版选 修4-9 第 四讲 三 长 期 准 则 下的 马尔可 夫型决 策理论 课 件 ( 共27张 PPT)
情感态度与价值观
通过长期准则下马尔可夫型决策的 学习,更加全面和清晰地了解马尔可夫型 决策,能解决长期准则下的马尔可夫型决 策案例.
当机器处于状态状态是对它进行检修, 在一小时内排除故障的概率为0.6.Xn表 示时刻n时的状态,试分析时刻n分布 的规律.
高 中 数 学 人 教A版选 修4-9 第 四讲 三 长 期 准 则 下的 马尔可 夫型决 策理论 课 件 ( 共27张 PPT)
高 中 数 学 人 教A版选 修4-9 第 四讲 三 长 期 准 则 下的 马尔可 夫型决 策理论 课 件 ( 共27张 PPT)
马尔柯夫预测法 PPT课件

3
在自然界和人类社会生活中普遍存在着两类现 象:
(1)确定性现象(在一定条件下必然出现);
(2)随机现象(掷硬币、射手打靶等)。
随机现象的统计规律性:
同一随机现象在大量重复出现时,其每种可能 的结果出现的频率却具有稳定性,从而表明随 机现象也具有其固有的规律性。
马尔柯夫预测法:
应用概率论中马尔柯夫链的理论和方法来研究 有关经济现象变化规律并藉以此预测未来状况 的一种方法。
6月份,甲厂有400户原来的顾客,上月的顾客有 50户转乙厂,50户转丙厂;乙厂有300户原来的顾 客,上月的顾客有20户转甲厂,80户转丙厂;丙厂 有80户原来的顾客,上月的顾客有10户转甲厂, 10户转乙厂。
试计算其状态转移概率。
2020/3/31
8
6月份顾客转移表
从到
甲
乙
丙
合计
甲
400
50
记为: P(xn j | x0 i) Pij (n)
并令
P11 (n) P12 (n)
P(n)
P21 (n)
PN1 (n)
P22 (n)
PN 2 (n)
则称P(n)为n步转移概率矩阵。
P1N (n)
P2N (n)
PNN (n)
当n=2时,为2步转移概率,P(2)为2步转移概率矩阵。
0.1
P32 100 0.1
P33
0.8 100
10
基本概念
3、状态转移概率矩阵
状态转移概率具有如下特征: 0 Pij 1 i, j 1,2, , N
N
Pij
1
i 1,2 , N
j1
并且,在一定条件下,系统只能在可能出现的状态 E1,
马氏决策规划简介上课讲义

i1,2,......N
称 Qq(1),q(2).....q(N)T
为一次转移的期望报酬向量。
记 V n ( i ) 为系统由状态i经过n次转移之后的 总期望报酬,则有
N
N
v n (i) j 1p ij r ij v n 1 (j) q (i) j 1p ijv n 1 (j)
i 1,2.....N
马氏决策规划简介
★
★
★
★★
马尔可夫过程
马尔可夫过程是一类特殊的随机过程, 它因伟大的俄国数学家马尔可夫而得名。 这种过程的特点是存在着确定的转移概 率,与系统先前的历史无关,有一个很 形象的比喻来形容这个过程:池塘里的 青蛙在荷叶上跳来跳去,如果将它在某 一时刻所在的荷叶称为状态,则青蛙未 来处于什么状态只有它现在所在的状态 有关,与它以前所处的状态无关。这种
状态1:顾客到A购物,0.9
状态2:顾客到B购物,0.1
2.状态转移概率矩阵
假定市场调查数据显示,在随后的一周 内,上周去A购物的顾客有90%仍然在A 购物,有10%的顾客则流向了B,去B购 物的顾客有80%继续在B购物,而20% 则流向了A,这些状态转移概率可用如下
矩阵表示
3.一步平稳转移概率
qd(i) N
pidj
fn1(j)
d1,2
j1
f1(i)maxqd(i) d1,2
n 2,...
❖ 由于
Q 1 q q 1 1 ( (1 2 ) ) (P 1 ) (R 1 ) 0 0 ..4 50 0 ..6 5 9 3 3 7 6 3
Q 2 q q 2 2 ( (1 2 ) ) (P 2 ) (R 2 ) 0 0 ..7 80 0 ..2 3 1 4 4 1 9 4 5
马尔可夫介绍PPT课件

100 0 5 15 70
合计 205 239 135
78
补充 100 305 339 235
178
这些数字怎么来的?如:175=250*0.7
8
2021/2/11
t=2
305 213 61 0 339 51 271 0 235 0 35 176 178 0 9 27
合计 264 376 203 补充 100 364 476 303
外部招聘
A
将提升到上一层次
退休+辞职
B
(提升受阻) 将提升到本层次
A现有人员 B可提升人员
11
2021/2/11
管理人员接替模型
12
2021/2/11
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
马尔可夫法
基本思路:通过收集历史数据,找出组织过去人事变动的规律
步骤
1.根据组织的历史资料,计算出人员流动的平均概率; 2.根据计算出来的概率,建立一个人员变动矩阵表; 3.根据期末的种类人数和所建立的变动矩阵表,预测下一期组
织可供给的人数。
例子:某企业在2000-2002年的三年时间中,管理人员从第二级提升到 第一级的人数分别为10人,12人和9人,而这三年中管理人员第二级的人 数分别是52、55和50。那么,这个企业管理人员从第二级提升到第一级 的概率是:(10+12+9/52+55+50)*100%=26.1%。同样可以计算出其他每 一类员工从一个级别流向另一个级别的平均概率。接着可以建立人员变 动矩阵表。
1
运筹学课件——第4讲马尔可夫决策(精)

例:人力资源预测
• 某高校1990年为编制师资发展规划,需要预测 为了教师队伍的结构。现在对教师状况进行如 下四个分类:青年,中年,老年和流退(流失 或退休)。根据历史资料以及调查分析,各类 教师按照一年一期的状态转移概率矩阵如下, 目前青年教师400人,中年教师360人,老年教 师300人。试分析3年后教师的结构以及为保持 编制不变,3年内应当多少硕士和博士毕业生 充实教师队伍?
0 . 4 0 .3 0 .3 0.3 0.5 0.2 P1 0.3 0.7 0 0.6 0.1 0.3 P 2 0.6 0.3 0.1 0.4 0.5 0.1 u= ( 0.5 ,0.25 , 0.25 )
u 1= ( 0.39 , 0.44 ,0.17 ) u2= ( 0.44 , 0.42 ,0.14 )
例:三品牌洗衣粉下月 购买意愿调查
A A B C 40 60 60 B 30 30 30 C 30 60 30 调查总数 100 150 120
• 求( 1 )一步状态转移概率矩阵 P ( 1 )=? • ( 2 )购买 C 品牌的顾客在未来第 2 个月购买 各品牌的概率? • ( 3 )二步状态转移概率矩阵 P ( 2 )=? • 您发现P(K)的一般规律了吗?
320 240 240 N 360 180 60 360 60 180
2
3
状态转移概率矩阵 P
• 从转移频数矩阵到状态转移概率矩阵 P : • 用各行总数分别去除转移频数矩阵 N 的每行 各元素,得到状态转移概率矩阵 P 如下:
320 240 240 /800 N 360 180 60 /600 360 60 180 /600
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020/8/10
例:人力资源预测
• 某高校1990年为编制师资发展规划,需要预测 为了教师队伍的结构。现在对教师状况进行如 下四个分类:青年,中年,老年和流退(流失 或退休)。根据历史资料以及调查分析,各类 教师按照一年一期的状态转移概率矩阵如下, 目前青年教师400人,中年教师360人,老年 教师300人。试分析3年后教师的结构以及为保 持编制不变,3年内应当多少硕士和博士毕业 生充实教师队伍?
p11
P
(
pi
)j n
Xn
p2 1 ... pn1
p12 ... p22 ... ... ... pn2 ...
p1n
p2n p..n.n
2020/8/10
多步状态转移概率 pij
• 一步状态转移概率:用 pij(1) 表示, pij(1) 即 pij ,表 示从状态 Si 经过一个时刻转移到状态 Sj 的概率,记 为:
0.6 0.1 0.3
0.5
0.25
0.25
0.5
0.25
0.25
正规概率矩阵
• 设 P 为马尔可夫链的一步状态转移概率矩阵,如果 存在自然数 k 使 Pk 的所有元素都是正数,则称 P 为正规概率矩阵。
• 正规概率矩阵的例子 • 正规概率矩阵的判断方法:看任意两状态之间是否
可以相互连通(彼此到达),若是,则为正规概率 矩阵,若否,则不是正规概率矩阵。
• P(k)=P · P · …· P= Pk
2020/8/10
例:通过 P ( 1 )计算 P ( 3 )
• 已知一步状态转移概率矩阵 P ( 1 )= P ,计算三步状态转移概率矩阵P ( 3 )=?
2020/8/10
固定概率向量 u
• 设 P 为马尔可夫( Markov )链的一步状态转移概率 矩阵,如果存在概率向量 u=( u1 , u2 ,…, un) 满足 于
2020/8/10
例:项目选址问题
• 某汽车维修公司有甲、乙、丙3个维修厂。由于公 司注重对员工的技术培训,树立顾客至上,信誉第
一的理念,管理模式先进,所以公司在本行业具有
良好的形象,形成了一定规模的客户群。对客户的 调查显示,客户在甲、乙、丙3个维修厂之间的转 移概率如下,由于资金的原因, 公司目前打算
引例:牛奶厂决策
• 最佳经营策略选择:
•
北京地区鲜牛奶由三个厂家提供,该地
区客户总数为 100 万户,假定厂家每年从每个
客户那里平均获利 50 元,客户资源每月都在三
个厂家之间相互流动,厂家 2 考虑从以下两套
候选方案之中选择一个实施:
• 方案一:吸引老客户,须花费 450 万元;
• 方案二:吸引厂家 1 和厂家 3 的客户,须花 费 400 万元。
• 您有什么好的建议来帮助厂家 2 决策?
2020/8/10
市场调查数据
•
今年一月份厂家 2 对 2000 名消费者进行了调
查,购买厂家 1 , 2 , 3 产品的消费者人数分别
为 800 , 600 和 600 ,得到市场占有率向量(概
率向量)为( 0.4 , 0.3 , 0.3 );
•
同时通过询问这 2000 名消费者下月的购买
来)的状态只与 t 时刻(现在)的状态有关而与 t 时刻 之前(过去)的状态无关,即 P{ Xk+1= Sik+1/ X1=Sik1 , X2=Sik2 ,… ,Xk=Sik}
=P{ Xk+1= Sik+1/Xk=Sik}
• 马尔可夫( Markov )链:具备无后效性的时间序列 。
2020/8/10
2020/8/10
马尔可夫链基本定理
• 定理:设 P 为马尔可夫链的一步状态转移概率矩 阵,如果 P 为正规概率矩阵,则存在唯一的由正 数组成的固定概率向量(均衡点) u ,并且对于 任意的初始概率向量 u0 ,向量序列:
•
u0 P , u0 P2 ,…, u0 Pk 以 u 为极
限,
• 即当 k→ ∞时,有 lim u0 Pk =u
相应的 k 步状态转移概率矩阵记为 P ( k )。
P(k) 与 P ( 1 )之间的关系如何?
2020/8/10
例:三品牌洗衣粉下月 购买意愿调查
A B C 调查总数
A
40 30 30
100
B
60 30 60
150
C
60 30 30
120
• 求( 1 )一步状态转移概率矩阵 P ( 1 )=?
•
倾向,得到如下1 转移频2数矩源自:3•320 240 240 1
N 360 180 60 2
360 60 180 3
2020/8/10
状态转移概率矩阵 P
• 从转移频数矩阵到状态转移概率矩阵 P :
•
用各行总数分别去除转移频数矩阵 N 的每行
各元素,得到状态转移概率矩阵 P 如下:
320 240 240 /800
•
u=0.25 , u1=0.44 , u2=0.42 ,
• 因此,如果采用方案一可获利:
•
100 Х (0.44- 0.25) Х 50 – 450=500 (万元)
•
如果采用方案二可获利:
•
100 Х (0.42- 0.25) Х 50 – 400=450 (万元)
结论:选择方案一,即吸引老客户的方案为佳。
( 2 )购买 C 品牌的顾客在未来第 2 个月购买
各品牌的概率?
•
( 3 )二步状态转移概率矩阵 P ( 2 )=?
• 您发现P(K)的一般规律了吗?
2020/8/10
规律:P(K)=Pk
• 定理: k 步状态转移概率矩阵 P ( k )等于一步状态转移概率矩阵 P ( 1 )= P 的k 次幂, 即
uP =u 则称 u 为 P 的固定概率向量或者均衡点 • 示例: u 为 P 的固定概率向量 • 引例中均衡状态时的市场占有率就是 P 的固定 概率向量(均衡点) u 。 • 均衡点是否一定存在,是否唯一?
2020/8/10
牛奶厂例:市场占有率变动 表及均衡状态
月份 k
0 1 2 3 4 5 6 7
• pij=pij(1)=P ( Xt+1= Sj/Xt= Si ),
相应的一步状态转移概率矩阵记为 P ( 1 )= P 。 • k 步状态转移概率:用 pij(k) 表示,表示从状态 Si 经
过 k 个时刻转移到状态 Sj 的概率,记为:
• pij(k)=P ( Xt+ k=Sj/Xt= Si ),
2020/8/10
马尔可夫( Markov )链
• 随机过程:不确定变化的随机变量序列 • 时间序列:{X1 , X2 ,…, Xt, …} ,指与时间相关
的离散随机变量序列 • 状态集合: S={S1 , S2 ,…, Sn} ,一般表示为
Xt= Si • 无后效性(马尔可夫性):时间序列在 t+1 时刻(将
• 均衡点举例
2020/8/10
均衡点 u 的求法
• 设概率向量 u 为状态转移矩阵 P 的均衡点,有:
uP =u 即 u ( P- I) =0 ,其中I为单位矩阵
等式两边取转置,得到:
( PT - I) uT =0
• 方法:联立求解以下线性方程组
( PT - I) uT =0
u1+u2+ … + un =1
2020/8/10
三个厂家的市场占有率
u1
u2
u3
0.4
0.3
0.3
0.52 0.496
0.24 0.252
0.24 0.252
0.4 0.3 0.3
0.5008 0.2496 0.2496 P 0.6 0.3 0.1
0.49984 0.25008 0.25008 0.500032 0.249984 0.249984
只对其中的一个 维修厂
进行改造,并且扩大 规 模。试决定应该
0.8 0.2
0
选择哪个维修厂? 0.2 0 0.8
0.2 0.2 0.6
2020/8/10
作业
• 作业本:习题1.6 • 预习:层次分析方法决策
2020/8/10
谢谢! 再 见!
2020/8/10
状态转移概率矩阵 P
• 状态转移概率: pij 表示从状态 Si 转移到状态 Sj 的概 率,记: pij= P ( Sj/ Si ) =P ( Xk+1=Sj/Xk= Si ) , 简称为从状态 i 到状态 j 的转移概率。
• 状态转移概率矩阵:由状态转移概率 pij ( i , j=1,2 ,…,n )构成的 n 阶方阵 P
N 360 180 60 /600
360 60 180 /600
0.4 0.3 0.3 P 0.6 0.3 0.1
0.6 0.1 0.3
2020/8/10
厂家 2 的方案选择
• 有了均衡状态时的市场占有率 u , u1 和 u2 ,厂家 2 就能够方便地进行分别方案选择,根据前面的数据, 我们知道:
