九年级数学下册第三章圆3.7切线长定理同步练习新版北师大版
北师大版九年级数学下册3.7 切线长定理(同步练习)

*3.7 切线长定理1. 如图,PA 、PB 分别切⊙O 于点A 、B ,AC 是⊙O 的直径,连结AB 、BC 、OP , 则与∠PAB 相等的角(不包括∠PAB 本身)有 ( )A .1个B .2个C .3个D .4个2.一个钢管放在V 形架内,右图是其截面图,O 为钢管的圆心.如果钢管的半径为25 cm ,∠MPN = 60︒,则OP =( )A .50 cmB .253cmC .3350cm D .503cm3.如图,一圆内切于四边形ABCD ,且AB=16,CD=10,则四边形ABCD 的周长为________.4.如图,在△ABC 中,5cm AB AC ==,cos B 35=.如果⊙O 的半径为10cm ,且经过点B 、C ,那么线段AO = cm .5.如图,PA 、PB 分别切⊙O 于点A 、B ,点E 是⊙O 上一点,且 60=∠AEB ,则=∠P __ ___度.P B AO6. 如图,AE 、AD 、BC 分别切⊙O 于点E 、D 、F ,若AD=20,求△ABC 的周长.7. 如图,PA 、PB 是⊙O 的两条切线,切点分别为点A 、B ,若直径AC= 12,∠P=60o ,求弦AB 的长.8. 如图,PA 、PB 是⊙O 的切线,A 、B 为切点,∠OAB =30°.(1)求∠APB 的度数;(2)当OA =3时,求AP 的长.9.已知:如图,⊙O内切于△ABC,∠BOC=105°,∠ACB=90°,AB=20cm.求BC、AC 的长.10.如图,在△ABC中,已知∠ABC=90o,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2 cm,AD=4 cm.(1)求⊙O的直径BE的长;(2)计算△ABC的面积.(赠品,不喜欢可以删除)数学这个家伙即是科学界的“段子手”,又是“心灵导师”一枚。
它要是给你讲起道理来,那可满满的都是人生啊。
2021-2022学年北师大版九年级数学下册《3-7切线长定理》同步练习题(附答案)

2021-2022学年北师大版九年级数学下册《3.7切线长定理》同步练习题(附答案)1.如图,P A、PB、CD分别切⊙O于A、B、E,CD交P A、PB于C、D两点,若∠P=40°,则∠P AE+∠PBE的度数为()A.50°B.62°C.66°D.70°2.如图,P A,PB切⊙O于A,B两点,CD切⊙O于点E,交P A,PB于C,D.若⊙O的半径为1,△PCD的周长等于2,则线段AB的长是()A.B.3C.2D.33.如图,P A,PB切⊙O于A,B两点,CD切⊙O于点E交P A,PB于C,D,若⊙O的半径为r,△PCD的周长为3r,连接OA,OP,则的值是()A.B.C.D.4.如图,P为⊙O外一点,P A,PB分别切⊙O于A,B,CD切⊙O于点E,分别交P A,PB于点C,D.若P A=5,则△PCD的周长和∠COD分别为()A.5,(90°+∠P)B.7,90°+C.10,90°﹣∠P D.10,90°+∠P5.已知⊙O1和⊙O2外切于M,AB是⊙O1和⊙O2的外公切线,A,B为切点,若MA=4cm,MB=3cm,则M到AB的距离是()A.cm B.cm C.cm D.cm6.如图,在平面直角坐标系xOy中,直线AB经过点A(6,0)、B(0,6),⊙O的半径为2(O为坐标原点),点P是直线AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为()A.B.3C.3D.7.如图,⊙O是四边形ABCD的内切圆,切点依次是E、F、G、H,下列结论一定正确的有()个①AF=BG②CG=CH③AB+CD=AD+BC④BG<CG.A.1B.2C.3D.48.如图,AB、AC是⊙O的切线,B、C为切点,∠A=50°,点P是圆上异于B、C,且在上的动点,则∠BPC的度数是()A.65°B.115°C.115°或65°D.130°或65°9.已知P为⊙O外一点,P A,PB为⊙O的切线,A、B为切点,∠P=70°,C为⊙O上一个动点,且不与A、B重合,则∠BCA=()A.35°、145°B.110°、70°C.55°、125°D.110°10.如图,直角梯形ABCD中,以AD为直径的半圆与BC相切于E,BO交半圆于F,DF 的延长线交AB于点P,连DE.以下结论:①DE∥OF;②AB+CD=BC;③PB=PF;④AD2=4AB•DC.其中正确的是()A.①②③④B.只有①②C.只有①②④D.只有③④11.已知:如图,AB为⊙O的直径,CD、CB为⊙O的切线,D、B为切点,OC交⊙O于点E,AE的延长线交BC于点F,连接AD、BD.以下结论:①AD∥OC;②点E为△CDB的内心;③FC=FE;④CE•FB=AB•CF.其中正确的只有()A.①②B.②③④C.①③④D.①②④12.如图△ABC内接于⊙O,P A,PB是⊙O的两条切线,已知AC=BC,∠ABC=2∠P,则∠ACB的弧度数为()A.B.C.D.13.如图,以正方形ABCD的边BC为直径作半圆O,过点D作直线切半圆于点F,交AB 于点E,则△ADE和直角梯形EBCD的周长之比为.14.如图,P A、PB、EF分别切⊙O于A、B、D,若P A=10cm,则△PEF的周长是cm,若∠P=35°,则∠AOB=(度),∠EOF=(度).15.如图,⊙O与△ABC的边AB、AC、BC分别相切于点D、E、F,如果AB=4,AC=5,AD=1,那么BC的长为.16.如图,四边形ABCD外切于⊙O,切点分别是E、F、G、H.(1)请探索四边形ABCD四边AB、BC、CD、AD之间的关系;(2)圆的外切平行四边形是形;(3)圆的外切矩形是形;(4)若AB:BC:CD:DA=1:3:4:x,且四边形ABCD的周长为20cm,则x=,AD=.17.如图,AB为⊙O直径,P A、PC分别与⊙O相切于点A、C,PQ⊥P A,PQ交OC的延长线于点Q.(1)求证:OQ=PQ;(2)连BC并延长交PQ于点D,P A=AB,且CQ=6,求BD的长.18.如图,在梯形ABCD中,AB∥CD,⊙O为内切圆,E为切点.(1)求证:AO2=AE•AD;(2)若AO=4cm,AD=5cm,求⊙O的面积.19.已知:AB为⊙O的直径,∠BAD=∠B=90°,DE与⊙O相切于E,⊙O的半径为,AD=2.①求BC的长;②延长AE交BC的延长线于G点,求EG的长.20.已知:以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,过点D作⊙O的切线交BC边于点E.(1)如图,求证:EB=EC=ED;(2)试问在线段DC上是否存在点F,满足BC2=4DF•DC?若存在,作出点F,并予以证明;若不存在,请说明理由.21.如图,P A、PB分别与⊙O相切于点A、B,PO的延长线交⊙O于点C,连接BC,OA.(1)求证:∠POA=2∠PCB;(2)若OA=3,P A=4,求tan∠PCB的值.参考答案1.解:∵P A、PB、CD分别切⊙O于A、B、E,CD交P A、PB于C、D两点,∴CE=CA,DE=DB,∴∠CAE=∠CEA,∠DEB=∠DBE,∴∠PCD=∠CAE+∠CEA=2∠CAE,∠PDC=∠DEB+∠DBE=2∠DBE,∴∠CAE=∠PCD,∠DBE=∠PDC,即∠P AE=∠PCD,∠PBE=∠PDC,∵∠P=40°,∴∠P AE+∠PBE=∠PCD+∠PDC=(∠PCD+∠PDC)=(180°﹣∠P)=70°.故选:D.2.解:∵P A,PB切⊙O于A、B两点,CD切⊙O于点E,交P A,PB于C,D,∴AC=EC,DE=DB,P A=PB,∵△PCD的周长等于2,∴P A+PB=2,∴P A=PB=,链接P A和AO,∵⊙O的半径为1,∴tan∠APO===,∴∠APO=30°,∴∠APB=60°,∴△APB是等边三角形,∴AB=P A=PB=.故选:A.3.解:∵P A,PB切⊙O于A,B两点,CD切⊙O于点E交P A,PB于C,D,∴CA=CF,DF=DB,P A=PB,∴PC+CF+DF+PD=P A=PB=2P A=3r,∴P A=r,则的值是:=.故选:D.4.解:∵P A、PB切⊙O于A、B,CD切⊙O于E,∴P A=PB=10,ED=AD,CE=BC;∴△PCD的周长=PD+DE+PC+CE=2P A,即△PCD的周长=2P A=10,;如图,连接OA、OE、OB.由切线性质得,OA⊥P A,OB⊥PB,OE⊥CD,DB=DE,AC=CE,∵AO=OE=OB,易证△AOC≌△EOC(SAS),△EOD≌△BOD(SAS),∴∠AOC=∠EOC,∠EOD=∠BOD,∴∠COD=∠AOB,∴∠AOB=180°﹣∠P,∴∠COD=90°﹣∠P.故选:C.5.解:如图,∵AB是⊙O1和⊙O2的外公切线,∴∠O1AB=∠O2BA=90°,∵O1A=O1M,O2B=O2M,∴∠O1AM=∠O1MA,∠O2BM=∠O2MB,∴∠BAM+∠AMO1=90°,∠ABM+∠BMO2=90°,∴∠AMB=∠BMO2+∠AMO1=90°,∴AM⊥BM,∵MA=4cm,MB=3cm,∴由勾股定理得,AB=5cm,由三角形的面积公式,M到AB的距离是=cm,故选:B.6.解:连接OP、OQ.∵PQ是⊙O的切线,∴OQ⊥PQ;根据勾股定理知PQ2=OP2﹣OQ2,∵当PO⊥AB时,线段PQ最短;又∵A(﹣6,0)、B(0,6),∴OA=OB=6,∴AB=6∴OP=AB=3,∵OQ=2,∴PQ==,故选:D.7.解:如图,连接OE、OF、OH、OG.①∵⊙O是四边形ABCD的内切圆,切点依次是E、F、G、H,∴BF=BG、AF=AE,只有当点F是边AB的中点时,AF=BF=BG,否则,等式AF=BG不成立;故本选项不一定正确;②根据题意,知,CG、CH都是⊙O的切线,∴CG=CH.故本选项正确;③根据题意,知AF=AE,DH=DE,BF=BG,CG=CH,则AF+BF+CH+DH=AE+BG+CG+DE,即AB+CD=AD+BC.故本选项正确;④当点G是边BC的中点时,BG=CG.故本选项错误;综上所述,正确的说法有2个;故选:B.8.解:如图,连接OB、OC,∵AB、AC是⊙O的切线,∴∠OBA=∠OCA=90°,∵∠A=50°,∴∠BOC=130°,∵∠BOC=2∠P,∴∠BPC=65°;故选:A.9.解:如图;连接OA、OB,则∠OAP=∠OBP=90°,∴∠BOA=180°﹣∠P=110°,∴∠AEB=∠AOB=55°;∵四边形AEBF是⊙O的内接四边形,∴∠AFB=180°﹣∠AEB=125°,①当C点在优弧AB上运动时,∠BCA=∠AEB=55°;②当C′点在劣弧AB上运动时,∠BC′A=∠AFB=125°;故选:C.10.解:∵BA,BE是圆的切线.∴AB=BE,BO是△ABE顶角的平分线.∴OB⊥AE∵AD是圆的直径.∴DE⊥AE∴DE∥OF故①正确;∵CD=CE,AB=BE∴AB+CD=BC故②正确;∵OD=OF∴∠ODF=∠OFD=∠BFP若PB=PF,则有∠PBF=∠BFP=∠ODF而△ADP与△ABO不一定相似,故PB=PF不一定成了.故③不正确;连接OC.可以证明△OAB∽△CDO∴即:OA•OD=AB•CD∴AD2=4AB•DC故④正确.故正确的是:①②④.故选:C.11.解:连接OD,DE,EB,CD与BC是⊙O的切线,∠ODC=∠OBC=90°,OD=OB,∵OC=OC∴Rt△CDO≌Rt△CBO,∴∠COD=∠COB,∴∠COB=∠DAB=∠DOB,∴AD∥OC,故①正确;∵CD是⊙O的切线,∴∠CDE=∠DOE,而∠BDE=∠BOE,∴∠CDE=∠BDE,即DE是∠CDB的角平分线,同理可证得BE是∠CBD的平分线,因此E为△CBD的内心,故②正确;若FC=FE,则应有∠OCB=∠CEF,应有∠CEF=∠AEO=∠EAB=∠DBA=∠DEA,∴弧AD=弧BE,而弧AD与弧BE不一定相等,故③不正确;设AE、BD交于点G,由②可知∠EBG=∠EBF,又∵BE⊥GF,∴FB=GB,由切线的性质可得,点E是弧BD的中点,∠DCE=∠BCE,又∵∠MDA=∠DCE(平行线的性质)=∠DBA,∴∠BCE=∠GBA,而∠CFE=∠ABF+∠F AB,∠DGE=∠ADB+∠DAG,∠DAG=∠F AB(等弧所对的圆周角相等),∴∠AGB=∠CFE,∴△ABG∽△CEF,∴CE•GB=AB•CF,又∵FB=GB,∴CE•FB=AB•CF故④正确.因此正确的结论有:①②④.故选:D.12.解:连接OA,OB.则OA⊥AP,OB⊥PB,∴在四边形APBO中,∠P+∠AOB=180°,又∵∠AOB=2∠ACB,∠ABC=2∠P,设∠ACB=180°﹣2∠ABC=180°﹣4∠P,∴∠AOB=360°﹣8∠P,∴∠P+∠AOB=∠P+(360°﹣8∠P)=180°,∴∠P=,∴∠ACB=180﹣4×=,∴∠ACB的弧度数为.故选:A.13.解:根据切线长定理得,BE=EF,DF=DC=AD=AB=BC.设EF=x,DF=y,则在直角△AED中,AE=y﹣x,AD=CD=y,DE=x+y.根据勾股定理可得:(y﹣x)2+y2=(x+y)2,∴y=4x,∴三角形ADE的周长为12x,直角梯形EBCD周长为14x,∴两者周长之比为12x:14x=6:7,故△ADE和直角梯形EBCD周长之比为:6:7.故答案为:6:7.14.解:∵P A、PB、EF分别切⊙O于A、B、D,∴P A=PB=10cm,ED=EA,FD=DB,∴PE+EF+PF=PE+ED+PF+FD=P A+PB=20(cm);∵P A、PB为⊙O的切线,∴∠P AO=∠PBO=90°,而∠P=35°,∴∠AOB=360°﹣90°﹣90°﹣35°=145°;连OD,如图,∴∠ODE=∠ODF=90°,易证得Rt△OAE≌Rt△ODE,Rt△OFD≌Rt△OFB,∴∠1=∠2,∠3=∠4,∴∠2+∠3=∠AOB=72.5°,∠EOF=72.5°.故答案为20;145;72.5.15.解:∵AB、AC、BC都是⊙O的切线,∴AD=AE,BD=BF,CE=CF,∵AB=4,AC=5,AD=1,∴AE=1,BD=3,CE=CF=4,∴BC=BF+CF=3+4=7.16.解:(1)∵四边形ABCD外切于⊙O,切点分别是E、F、G、H,∴AH=AE,BE=BF,CF=CG,DG=DH,∴AH+DH+CF+BF=DG+CG+AE+BE,即AD+BC=AB+DC;(2)由(1)得,圆的外切四边形对边和相等,则圆的外切平行四边形是:菱形;故答案为:菱;(3)由(1)得,圆的外切四边形对边和相等,则圆的外切矩形是正方形;故答案为:正方;(4)∵AB:BC:CD:DA=1:3:4:x,AD+BC=AB+DC,∴1+4=3+x,则x=2,∵四边形ABCD的周长为20cm,∴20÷(1+3+4+2)=2,∴AD=2×2=4(cm).故答案为:2,4cm.17.(1)证明:连接OP.∵P A、PC分别与⊙O相切于点A,C,∴P A=PC,OA⊥P A,∵OA=OC,OP=OP,∴△OP A≌△OPC(SSS),∴∠AOP=∠POC,∵QP⊥P A,∴QP∥BA,∴∠QPO=∠AOP,∴∠QOP=∠QPO,∴OQ=PQ.(2)设OA=r.∵OB=OC,∴∠OBC=∠OCB,∵OB∥QD,∴∠QDC=∠B,∵∠OCB=∠QCD,∴∠QCD=∠QDC,∴QC=QD=6,∵QO=QP,∴OC=DP=r,∵PC是⊙O的切线,∴OC⊥PC,∴∠OCP=∠PCQ=90°,在Rt△PCQ中,∵PQ2=PC2+QC2,∴(6+r)2=62+(2r)2,r=4或0(舍弃),∴OP==4,∵OB=PD,OB∥PD,∴四边形OBDP是平行四边形,∴BD=OP=4.18.(1)证明:根据切线长定理可知:∵∠OAE+∠ODA=(∠BAD+∠ADC)=90°,∴∠AOD=90°,∵∠OAE=∠OAE,∠AOD=∠AEO=90°,∴△AOE∽△ADO,∴=,即AO2=AE•AD;(2)解:在Rt△AOD中,OD==3(cm),∵S△AOD=×AD×EO=×AO×OD即5×EO=4×3,∴EO=(cm),∵OE是⊙O的半径,∴S圆O=πr2=π(cm2).19.解:①过点D作DF⊥BC于点F,∵AB为⊙O的直径,∠BAD=∠B=90°,∴四边形ABFD是矩形,AD与BC是⊙O的切线,∴DF=AB=2,BF=AD=2,∵DE与⊙O相切,∴DE=AD=2,CE=BC,设BC=x,则CF=BC﹣BF=x﹣2,DC=DE+CE=2+x,在Rt△DCF中,DC2=CF2+DF2,即(2+x)2=(x﹣2)2+(2)2,解得:x=,即BC=;②∵AB为⊙O的直径,∠BAD=∠B=90°,∴AD∥BC,∴△ADE∽△GCE,∴AD:CG=DE:CE,AE:EG=AD:CG,∵AD=DE=2,∴CG=CE=BC=,∴BG=BC+CG=5,∴AE:EG=4:5,在Rt△ABG中,AG==3,∴EG=AG=.20.(1)证明:连接BD.由于ED、EB是⊙O的切线,由切线长定理,得ED=EB,∠DEO=∠BEO,∴OE垂直平分BD.又∵AB是⊙O的直径,∴AD⊥BD.∴AD∥OE.即OE∥AC.又O为AB的中点,∴OE为△ABC的中位线,∴BE=EC,∴EB=EC=ED.(4分)(2)解:在△DEC中,由于ED=EC,∴∠C=∠CDE,∴∠DEC=180°﹣2∠C.①当∠DEC>∠C时,有180°﹣2∠C>∠C,即0°<∠C<60°时,在线段DC上存在点F满足条件.在∠DEC内,以ED为一边,作∠DEF,使∠DEF=∠C,且EF交DC于点F,则点F 即为所求.这是因为:在△DCE和△DEF中,∠CDE=∠EDF,∠C=∠DEF,∴△DEF∽△DCE.∴DE2=DF•DC.即(BC)2=DF•DC∴BC2=4DF•DC.(6分)②当∠DEC=∠C时,△DEC为等边三角形,即∠DEC=∠C=60°,此时,C点即为满足条件的F点,于是,DF=DC=DE,仍有BC2=4DE2=4DF•DC.(7分)③当∠DEC<∠C时,即180°﹣2∠C<∠C,60°<∠C<90°;所作的∠DEF>∠DEC,此时点F在DC的延长线上,故线段DC上不存在满足条件的点F.(8分)21.证明:(1)连接OB,∵P A、PB分别与⊙O相切于点A、B,∴P A=PB,∠OBP=∠OAP=90°,在Rt△POA和Rt△POB中,∵,∴Rt△POA≌Rt△POB(HL),∴∠POA=∠POB,∵∠POB=2∠PCB,∴∠POA=2∠PCB;(2)过B作BE⊥PC于E,∵PB=P A=4,OB=OA=3,∴PO=5,∴PO•BE=OB•PB,∴BE=,由勾股定理得:OE==,∴CE=OC+OE=3+=,在Rt△OBE中,tan∠PCB===.。
九年级数学下3.7切线长定理课时练习北师大有答案和解释

适用精选文件资料分享九年级数学下 3.7 切线长定理课时练习(北师大有答案和解说)北师大版数学九年级下册第 3 章第 7 节切线长定理同步检测一、选择题 1. 如图,一圆内切四边形 ABCD,且 BC=10,AD=7,则四边形的周长为() A .32 B.34 C.36 D.38 答案: B 解析:解答:由题意可得圆外切四边形的两组对边和相等,所以四边形的周长=2×( 7+10)=34.应选: B.解析:依据切线长定理,可以证明圆外切四边形的性质:圆外切四边形的两组对边和相等,从而可求得四边形的周长. 2. 以以以下图, P 为⊙O外一点, PA、PB分别切⊙O于A、B,CD切⊙O于点 E,分别交 PA、PB于点C、D,若 PA=15,则△ PCD的周长为() A .15 B.12 C.20 D.30 答案: D 解析:解答:∵P为⊙O外一点, PA、PB分别切⊙O于 A、B,CD切⊙O于点 E,分别交 PA、PB于点 C、D,∴AC=EC,BD=DE,AP=BP,∵PA=15,∴△ PCD的周长为: PA+PB=30.应选: D.解析:直接利用切线长定理得出AC=EC,BD=DE,AP=BP,从而求出答案. 3. 如图,△ ABC是一张三角形的纸片,⊙O是它的内切圆,点D是此中的一个切点,已知AD=10cm,小明准备用剪刀沿着与⊙O 相切的任意一条直线 MN剪下一块三角形(△ AMN),则剪下的△ AMN的周长为() A .20cmB.15cmC.10cm D.随直线 MN的变化而变化答案: A 解析:解答:如图:∵△ABC 是一张三角形的纸片,⊙O 是它的内切圆,点 D是此中的一个切点,AD=10cm,∴设E、F 分别是⊙O 的切点,故DM=MF,FN=EN,AD=AE,∴AM+AN+MN=AD+AE=10+10=20(cm).应选:A.解析:利用切线长定理得出DM=MF,FN=EN,AD=AE,从而得出答案. 4. 如图,⊙O内切于四边形ABCD,AB=10,BC=7,CD=8,则AD的长度为()A .8 B.9 C.10 D.11 答案:D 解析:解答:∵⊙O内切于四边形 ABCD,∴AD+BC=AB+CD,∵AB=10,BC=7,CD=8,∴AD+7=10+8,解得:AD=11.应选: D.解析:依据圆外切四边形的性质对边和相等从而得出 AD的长. 5. 圆外切等腰梯形的一腰长是 8,则这个等腰梯形的上底与下底长的和为() A .4 B.8 C.12 D.16 答案: D 解析:解答:∵圆外切等腰梯形的一腰长是8,∴梯形对边和为:8+8=16,则这个等腰梯形的上底与下底长的和为16.应选: D.解析:直接利用圆外切四边形对边和相等,从而求出即可. 6. 如图,⊙O是△ ABC的内切圆,点 D、E 分别为边 AB、 AC上的点,且 DE为⊙O的切线,若△ ABC的周长为 25,BC的长是 9,则△ ADE的周长是() A .7 B.8 C.9 D.16 答案: A 解析:解答:∵ AB、AC、BC、DE都和⊙O相切,∴BI=BG, CI=CH,DG=DF,EF=EH.∴BG+CH=BI+CI=BC=9,∴△ ADE 的周长 =AD+AE+DE=AD+AE+DF+EF=AD+DG+EH+AE=AG+AH=△ABC 的周长 - (BG+EH+BC)=25- 2×9=7.应选 A.解析:依据切线长定理,可得BI=BG,CI=CH,DG=DF,EF=EH,△ ADE的周长=AD+AE+DE=AD+AE+DF+EF=AD+DG+EH+AE=AG+AH=△ABC的周长 -(BG+EH+BC),据此即可求解. 7. 如图,从⊙O 外一点 P 引⊙O的两条切线 PA,PB,切点分别为 A,B.假如∠ APB=60°, PA=8,那么弦AB的长是()A .4 B.8 C.4 D.8 答案:B 解析:解答:∵PA、PB都是⊙O的切线,∴PA=PB,又∵∠ P=60°,∴△ PAB是等边三角形,即 AB=PA=8,应选 B.解析:依据切线长定理知 PA=PB,而∠P=60°,所以△PAB是等边三角形,由此求得弦AB的长.8. 如图,PA、PB分别是⊙O 的切线, A、B 为切点, AC是⊙O的直径,已知∠BAC=35°,∠P的度数为() A.35° B.45° C.60° D.70°答案: D 解析:解答:依据切线的性质定理得∠ PAC=90°,∴∠ PAB=90° - ∠BAC=90° - 35°=55°.依据切线长定理得 PA=PB,所以∠ PBA=∠PAB=55°,所以∠ P=70°.应选 D.解析:依据切线长定理得等腰△ PAB,运用内角和定理求解. 9. 如图, AB、AC是⊙O的两条切线,B、C是切点,若∠ A=70°,则∠ BOC的度数为()A.130° B.120° C.110° D.100°答案: C 解析:解答:∵AB、AC是⊙O的两条切线, B、C是切点,∴∠ B=∠C=90°,∠BOC=180° - ∠A=110°.应选 C.解析:利用切线的性质可得,∠B=∠C=90°,再用四边形的内角和为 360 度可解. 10. 如图, PA、PB是⊙O的两条切线,切点是 A、B.假如 OP=4,PA= ,那么∠ AOB等于() A .90° B.100° C.110° D.120°答案: D 解析:解答:∵△ APO≌△ BPO(HL),∴∠ AOP=∠BOP.∵sin∠AOP=AP:OP=2 :4= :2,∴∠ AOP=60°.∴∠ AOB=120°.应选 D.解析:由切线长定理知△ APO≌△ BPO,得∠ AOP=∠BOP.可求得 sin ∠AOP=:2,所以可知∠ AOP=60°,从而求得∠ AOB的值. 11. 如图, PA切⊙O于 A,PB切⊙O于 B,OP交⊙O于 C,以下结论中,错误的选项是()A.∠ 1=∠2 B. PA=PBC.AB⊥OPD. =PC?PO答案: D 解析:解答:连接 OA、OB,AB,∵PA切⊙O于 A,PB切⊙O于 B,由切线长定理知,∠1=∠2,PA=PB,∴△ ABP是等腰三角形,∵∠ 1=∠2,∴AB⊥OP(等腰三角形三线合一),故 A,B,C正确,依据切割线定理知: =PC? (PO+OC),所以 D错误.应选 D.解析:由切线长定理可判断出 A、B选项均正确.易知△ ABP是等腰三角形,依据等腰三角形三线合一的特色,可求出 AB⊥OP,故 C 正确.而 D选项明显不切合切割线定理,所以 D错误. 12. 如图, P为⊙O外一点, PA,PB分别切⊙O于A,B,CD切⊙O于点 E,分别交 PA,PB于点 C,D.若 PA=5,则△ PCD的周长和∠ COD分别为()A.5,(90°+∠P)B.7,90°+ C.10,90° - ∠P D. 10,90°+ ∠P 答案: C 解析:解答:∵ PA、PB切⊙ O于 A、B,CD切⊙O于 E,∴PA=PB=10,ED=AD,CE=BC;∴△ PCD 的周长 =PD+DE+PC+CE=2PA,即△ PCD的周长 =2PA=10,;如图,连接OA、OE、OB.由切线性质得,OA⊥PA,OB⊥PB,OE⊥CD,DB=DE,AC=CE,∵AO=OE=OB,易证△ AOC≌△ EOC( SAS),△ EOD≌△ BOD( SAS),∴∠ AOC=∠EOC,∠EOD=∠BOD,∴∠ COD=∠AOB,∴∠ AOB=180°- ∠P,∴∠ COD=90°- ∠P.应选: C.解析:依据切线长定理,即可获得 PA=PB,ED=AD,CE=BC,从而求得三角形的周长 =2PA;连接 OA、OE、OB依据切线性质,∠ P+∠AOB=180°,再依据 CD为切线可知∠ COD=∠AOB. 13. 圆外切等腰梯形的中位线等于8,则一腰长等于()A.4 B.6 C.8 D.10答案:C解析:解答:如图,设圆的外切梯形ABCD,切点分别为 E、H、N、中位线为 MN,∴MN= (AB+CD),依据切线长定理得: DE=DH,CF=CH,而且等腰梯形和圆都是轴对称图形,∴CD=DH+CH=DE+CF=(AB+CD),∴CD=MN,而 MN=8,∴CD=8.应选 C.解析:如图,设圆的外切梯形ABCD,切点分别为 E、H、N、中位线为 MN,依据中位线定理可以获得上下底之和,此后利用切线长定理可以获得一腰长等于中位线,由此即可解决问题. 14. 如图,⊙O为△ ABC的内切圆,AC=10,AB=8,BC=9,点 D,E分别为 BC,AC上的点,且 DE为⊙O的切线,则△ CDE 的周长为() A.9 B.7 C.11 D.8 答案: C 解析:解答:如图:设 AB,AC,BC和圆的切点分别是 P,N,M,CM=x,依据切线长定理,得CN=CM=x,BM=BP=9-,xAN=AP=10-x.则有9-x+10-x=8 ,解得:x=5.5 .所以△CDE的周长=CD+CE+QE+DQ=2x=11.应选:C.解析:设 AB,AC,BC和圆的切点分别是 P,N,M.依据切线长定理得到 NC=MC,QE=DQ.所以三角形 CDE的周长即是 CM+CN的值,再进一步依据切线长定原由三角形 ABC的三边进行求解即可. 15. 已知四边形 ABCD是梯形,且 AD∥BC,AD<BC,又⊙O与 AB、AD、CD分别相切于点 E、F、G,圆心 O在 BC上,则 AB+CD与 BC的大小关系是()A.大于 B .等于 C.小于 D.不可以确立答案:A解析:解答:连接OF,∵AD是切线,∴OF⊥AD,又∵ AD∥BC,∴AB≥OF,CD≥OF,又∵ AD<BC,∴AB≥OF,CD≥OF最多有一个成立.∴AB+CD>2OF,∵BC=2OF,∴AB+CD> BC.应选 A,解析:连接 OF,则 OF是梯形的高,则 AB≥OF,CD≥OF,而两个式子不可以同时成立,据此即可证得.二、填空题 16. 如图,PA、PB分别切圆 O于 A、B,并与圆 O的切线,分别订交于 C、D,已知△ PCD的周长等于 10cm,则 PA=cm. 答案: 5解析:解答:如图,设DC与⊙O的切点为 E;∵PA、PB分别是⊙O的切线,且切点为A、B;∴PA=PB;同理,可得: DE=DA,CE=CB;则△ PCD的周长 =PD+DE+CE+PC=PD+DA+PC+CB=PA+PB=10(cm);∴PA=PB=5cm,故答案为: 5.解析:因为 DA、DC、BC都是⊙O的切线,可依据切线长定理,将△PCD的周长变换为PA、PB的长,然后再进行求解. 17. 如图, PA、PB、DE分别切⊙O 于 A、B、C,DE分别交 PA,PB于 D、E,已知 P 到⊙O的切线长为 8cm,那么△ PDE的周长为答案: 16 解析:解答:∵ PA、 PB、DE分别切⊙O 于 A、 B、C,∴PA=PB,DA=DC,EC=EB;∴C△PDE=PD+DE+PE=PD+DA+EB+PE=PA+PB=8+8=16;∴△ PDE的周长为16.故答案为16.解析:因为PA、PB、DE都是⊙O的切线,可依据切线长定理将切线PA、PB的长转变成△PDE的周长.18. 如图,PA,PB切⊙O于 A,B 两点, CD切⊙O于点 E,交 PA,PB于 C,D,若⊙O的半径为 r ,△ PCD的周长等于 3r ,则 tan ∠APB的值是答案:解析:解答:连接 PO,AO,∵PA,PB切⊙O于 A,B 两点, CD切⊙O于点 E,交 PA,PB于 C,D,∴∠ APO=∠BPO,AC=EC,DE=BD,PA=PB,∴PA+PB=△PCD的周长 =3r ,∴,∴tan ∠APB=AO: PA=r :1.5r = ,故答案为:.解析:利用切线长定理得出,再联合锐角三角函数关系得出答案. 19. 如图,Rt△ABC的内切圆⊙O与两直角边 AB,BC分别相切于点 D、E,过劣弧 DE(不包含端点 D,E)上任一点 P 作⊙O的切线MN与 AB,BC分别交于点 M,N,若⊙O的半径为 4cm,则 Rt△MBN的周长为答案: 8cm 解析:解答:连接OD、OE,∵⊙O是 Rt△ABC的内切圆,∴OD⊥AB,OE⊥BC,∵∠ ABC=90°,∴∠ ODB=∠DBE=∠OEB=90°,∴四边形 ODBE是矩形,∵OD=OE,∴矩形 ODBE是正方形,∴BD=BE=OD=OE=4cm,∵⊙O切 AB于 D,切 BC于 E,切 MN于 P,NP与 NE是从一点出发的圆的两条切线,∴MP=DM, NP=NE,∴Rt△MBN的周长为:MB+NB+MN=MB+BN+NE+DM=BD+BE=4cm+4cm=8cm,故答案为:8cm.解析:连接 OD、OE,求出∠ ODB=∠DBE=∠OEB=90°,推出四边形 ODBE 是正方形,得出 BD=BE=OD=OE=4cm,依据切线长定理得出 MP=DM,NP=NE,代入 MB+NB+MN得出 BD+BE,求出即可. 20.如图,已知以直角梯形ABCD的腰 CD为直径的半圆 O与梯形上底 AD、下底BC以及腰AB均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰 AB为 5,则该梯形的周长是答案:14 解析:解答:依据切线长定理,得 AD=AE,BC=BE,所以梯形的周长是 5×2+4=14,故答案为:14.解析:由切线长定理可知: AD=AE,BC=BE,所以梯形的周长=2AB+CD,已知了AB和⊙O的半径,由此可求出梯形的周长.三、计算题 21. 已知四边形 ABCD外切于⊙ O,四边形 ABCD的面积为24,周长 24,求⊙O的半径.答案: 2 解析:解答:设四边形 ABCD 是⊙O的外切四边形,切点分别为: F,G,M,E,连接 FO,AO,OG,CO,OM,DO,OE,四边形 ABCD的面积为:×EO×AD+OM×DC+GO×BC+ FO×AB = EO(AD+AB+BC+DC)= EO×24 =24,解得:EO=2.故 r=2 .分析:利用切线的性质从而利用三角形面积求法得出⊙O 的半径. 22. 如图,AB为⊙O的直径,点 C在 AB的延长线上, CD、CE分别与⊙O相切于点D、E,若 AD=2,∠ DAC=∠DCA,求 CE. 答案: 2 解析:解答:∵CD、CE分别与⊙O相切于点 D、E,∴CD=CE,∵∠ DAC=∠DCA,∴AD=CD,∴AD=CE,∵AD=2,∴CE=2.故答案为: 2.解析:由条件可得 AD=CD,再由切线长定理可得: CD=CE,所以 AD=CE,问题得解. 23. 如图,已知 PA、PB分别切⊙O于点 A、B,∠P=90°,PA=3,求⊙O的半径 .答案:3解析:解答:连接OA、OB,则 OA=OB(⊙O的半径),∵PA、PB分别切⊙O于点 A、B,∴PA=PB,∠OAP=∠OBP=90°,已知∠ P=90°,∴∠ AOB=90°,∴四边形 APBO为正方形,∴OA=OB=PA=3,则⊙O的半径长是 3,故答案为: 3.解析:连接OA、OB,已知 PA、PB分别切⊙O于点 A、B,由切线的性质及切线长定理可得: PA=PB,∠ OAP=∠OBP=90°,再由已知∠ P=90°,所以得到四边形 APBO为正方形,从而得⊙O的半径长即 PA的长.24. 如图,P是⊙O的直径 AB的延长线上一点,PC、PD切⊙O于点 C、D.若 PA=6,⊙O的半径为 2,求∠ CPD. 答案: 60°解析:解答:∵ PA=6,⊙O的半径为 2,∴PB=PA-AB=6-4=2,∴OP=4,∵PC、PD切⊙O于点 C、D.∴∠ OPC=∠OPD,∴CO⊥PC,∴sin ∠OPC=2: 4 =0.5 ,∴∠OPC=30°,∴∠ CPD=60°,故答案为: 60°.解析:依据切线的性质定理和切线长定理求出 OP=4,∠ OPC=∠OPD,再利用解直角三角形的知识求出∠ OPC=30°,即可得出答案. 25. 如图,⊙O与△ ABC中 AB、AC的延长线及 BC边相切,且∠ ACB=90°,∠ A,∠ B,∠C所对的边长挨次为3,4,5,求⊙O的半径 . 答案:2 解析:解答:连接OD、OE,∵⊙O与△ ABC中 AB、AC的延长线及 BC边相切,∴AF=AD,BE=BF,CE=CD, OD⊥AD,OE⊥BC,∵∠ ACB=90°,∴四边形ODCE 是正方形,设 OD=r,则 CD=CE=r,∵BC=3,∴BE=BF=3-r ,∵AB=5,AC=4,∴AF=AB+BF=5+3-r ,AD=AC+CD=4+r,∴5+3-r=4+r ,r=2 ,则⊙O的半径是 2.故答案为: 2.解析:先连接 OD、OE依据⊙O与△ ABC中 AB、AC的延长线及 BC边相切,得出 AF=AD,BE=BF,CE=CD,再依据 OD⊥AD,OE⊥BC,∠ ACB=90°,得出四边形 ODCE是正方形,最后设 OD=r,列出 5+3-r=4+r ,求出 r=2 即可.。
北师大版九年级数学下册3.7切线长定理同步练习
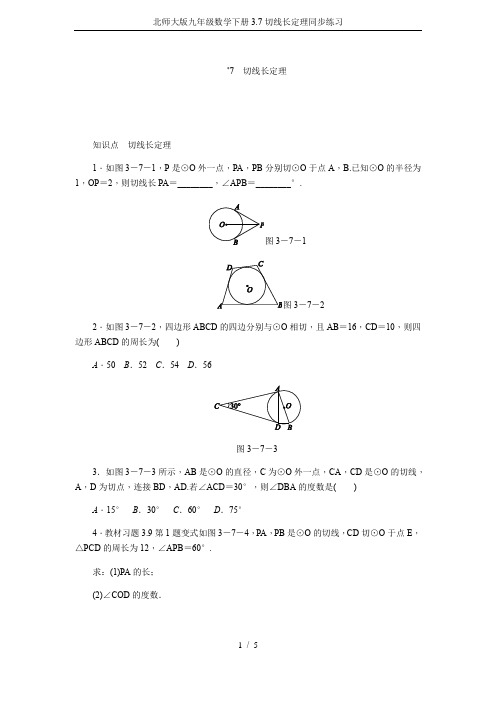
*7切线长定理知识点切线长定理1.如图3-7-1,P是⊙O外一点,PA,PB分别切⊙O于点A,B.已知⊙O的半径为1,OP=2,则切线长PA=________,∠APB=________°.3-7-13-7-22.如图3-7-2,四边形ABCD的四边分别与⊙O相切,且AB=16,CD=10,则四边形ABCD的周长为()A.50 B.52 C.54 D.56图3-7-33.如图3-7-3所示,AB是⊙O的直径,C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的度数是()A.15°B.30°C.60°D.75°4.教材习题3.9第1题变式如图3-7-4,PA,PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:(1)PA的长;(2)∠COD的度数.图3-7-45.如图3-7-5,PA ,PB 切⊙O 于A ,B 两点,CD 切⊙O 于点F 且分别交PA ,PB 于点C ,D ,若⊙O 的半径为r ,△PCD 的周长为3r ,连接OA ,OP ,则OAPA的值是( )A .213 13B .125C .32D .233-7-53-7-66.如图3-7-6,正方形ABCD 的边长为4 cm ,以正方形的一边BC 为直径在正方形ABCD 内作半圆,过点A 作半圆的切线,与半圆相切于点F ,与DC 相交于点E ,则△ADE 的面积为( )A .12 cm 2B .24 cm 2C .8 cm 2D .6 cm 2图3-7-77.如图3-7-7,△ABC 的周长为16,∠A =60°,BC =6.若⊙O 与BC ,AC ,AB 三边分别切于点E ,F ,D ,则DF 的长为________.8.[2017·孝感模拟]如图3-7-8,直线AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,OB=6 cm,OC=8 cm.求:(1)∠BOC的度数;(2)BE+CG的长;(3)⊙O的半径.图3-7-8详解详析1.3602.B[解析] 根据切线长定理可证AB+CD=AD+BC,∴四边形ABCD的周长=2×(16+10)=52.故选B.3.D [解析] 连接OD .∵CA ,CD 是⊙O 的切线, ∴OA ⊥AC ,OD ⊥CD ,∴∠OAC =∠ODC =90°.∵∠ACD =30°,∴∠AOD =360°-∠C -∠OAC -∠ODC =150°.∵OB =OD ,∴∠DBA =∠ODB =12∠AOD =75°.故选D.4.解:(1)∵CA ,CE 都是⊙O 的切线,∴CA =CE . 同理DE =DB ,P A =PB ,∴△PCD 的周长=PD +CD +PC =PD +PC +CA +BD =P A +PB =2P A =12,∴P A =6. (2)∵∠P =60°,∴∠PCE +∠PDE =120°, ∴∠ACD +∠CDB =360°-120°=240°. ∵CA ,CE 是⊙O 的切线, ∴∠OCE =∠OCA =12∠ACD .同理∠ODE =12∠CDB ,∴∠OCE +∠ODE =12(∠ACD +∠CDB )=120°,∴∠COD =180°-120°=60°.5.D [解析] ∵P A ,PB 切⊙O 于A ,B 两点,CD 切⊙O 于点F 且分别交P A ,PB 于点C ,D ,∴CA =CF ,DF =DB ,P A =PB ,∴PC +CF +DF +PD =P A +PB =2P A =3r , ∴P A =32r ,∴OA P A =r 32r =23.故选D.6.D [解析] 设DE =x cm ,则CE =(4-x )cm ,根据题意知EF =CE =(4-x )cm ,AF =AB =4 cm ,∴AE =(8-x )cm.在Rt △ADE 中,AD 2+DE 2=AE 2,即42+x 2=(8-x )2,解得x =3.∴△ADE 的面积=12×AD ×DE =12×4×3=6(cm 2).7.2.8.解:(1)如图,连接OF .根据切线长定理,得BE =BF ,CF =CG ,∠OBF =∠OBE ,∠OCF =∠OCG .∵AB ∥CD ,∴∠ABC +∠BCD =180°, ∴∠OBF +∠OCF =90°, ∴∠BOC =90°.(2)由(1)知,∠BOC =90°. ∵OB =6 cm ,OC =8 cm ,∴由勾股定理,得到BC =OB 2+OC 2=10 cm , ∴BE +CG =BC =10 cm.(3)由(1)知,OF ⊥BC ,OB ⊥OC , ∴OF =OB ·OCBC =4.8 cm.即⊙O 的半径为4.8 cm.。
九下第三章圆7切线长定理作业新版北师大版

6.如果四边形的四条边都与圆________,我们把这个四边形叫做圆的外切四边形,把这个圆叫做这个四边形的内切圆.圆外切四边形的两组__________相等.
相切
对边的和
7.【2023·中山六中模拟】如图所示,⊙O内切于四边形ABCD,AB=10,BC=7,CD=8,则AD的长度为( ) A.8 B.9 C.10 D.11
B
【点拨】如图所示,作CF⊥AB交AB的延长线于点F,连接DE, 易得∠FAD=∠ADC=∠F=90°,∴四边形ADCF为矩形, ∴AF=DC,AD=FC,易得AB为⊙D的切线. ∵BE为⊙D的切线,∴DE⊥BC,AB=BE. ∵ ,∴设AB=BE=a,则CD=3a, ∴BF=AF-AB=CD-AB=2a,设CE=x,
8.圆外切四边形的周长为32,相邻的三条边的比为2∶5∶6,则此四边形各边的长分别为______________.
4,10,12,6
9.如图,⊙O的半径为3,外切四边形ABCD中,AB=5,CD=3,则S四边形ABCD=________.
24
【点拨】如图,作圆心到各边的垂线,垂足分别为E,F,G,S,即E,F,G,S为切点.∵四边形ABCD是⊙O的外切四边形,∴AD+BC=AB+CD=8. ∴S四边形ABCD=S△AOB+S△BOC+S△COD+S△DOA = AB×OG+ BC×OF+ CD×OE+ AD×OS = (AB+BC+CD+AD)×OG= ×(8+8)×3=24.
则BC=BE+CE=a+x. 在Rt△DEC中,DE2=CD2-CE2=9a2-x2. 在Rt△BFC中,FC2=BC2-BF2=(a+x)2-(2a)2. ∵DE=DA=FC,∴9a2-x2=(a+x)2-(2a)2, 解得x=2a或x=-3a(不合题意,舍去), ∴CE=2a,∴DE= ∴sin C= ,故选B.
北师大版九年级数学下册《3.7切线长定理》同步测试题带答案

北师大版九年级数学下册《3.7切线长定理》同步测试题带答案学校:___________班级:___________姓名:___________考号:___________【基础达标】1.如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是()A.4B.4√3C.8D.8√32.如图,四边形ABCD的边AB,BC,CD,DA和☉O分别相切于点L,M,N,P.若四边形ABCD的周长为20,则AB+CD等于()A.5B.8C.10D.123.如图,PA,PB是☉O的切线,切点分别为A,B,若OP=4,PA=2√3,则∠AOB的度数为()A.60°B.90°C.120°D.无法确定4.如图,AB为☉O的直径,点C在AB的延长线上,CD,CE分别与☉O相切于点D,E,若AD=6,∠DAC=∠DCA,则CE=.5.如图,AB,AC,BD是☉O的切线,其切点分别为P,C,D,如果AB=5,AC=3,则BD的长为.6.如图,PA,PB分别与☉O相切于点A,B,AC为弦,BC为☉O的直径,若∠P=60°,PB=2 cm.(1)求证:△PAB是等边三角形.(2)求AC的长.【能力巩固】7.如图,有一张三角形纸片ABC,☉O是它的内切圆,D是其中的一个切点,已知AD=5 cm,小明准备用剪刀沿着与☉O相切的任意一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长为()A.20 cmB.15 cmC.10 cmD.随直线MN的变化而变化8.如图,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆☉O切AB,BC,AC于点D,E,F,则AF的长为()A.5B.10C.7.5D.49.如图,PA,PB是☉O的切线,其切点分别为A,B,点C,D在☉O上.若∠PAD+∠C=220°,则∠P的度数为°.10.如图,AB为☉O的直径,AD,BC分别与☉O相切于点A,B,CD经过☉O上一点E,AD=DE,若AB=12,BC=4,则AD的长为.11.如图,在△ABC中,∠C=90°,点O在BC上,以OC为半径的半圆切AB于点E,交BC于点D,若BE=4,BD=2,求☉O的半径和边AC的长.【素养拓展】12.如图,一位小朋友在不打滑的平面轨道上滚动一个半径为5 cm 的圆环,当滚到与坡面BC 开始相切时停止.AB=40 cm,BC 与水平面的夹角为60°.试问其圆心所经过的路线长是多少?(结果保留根号)参考答案【基础达标】1.C2.C3.C4.65.26.解:(1)证明:∵PA ,PB 分别与☉O 相切于点A ,B∴PA=PB ,且∠P=60° ∴△PAB 是等边三角形. (2)∵△PAB 是等边三角形∴PB=AB=2 cm,∠PBA=60°.∵BC 是☉O 的直径,PB 是☉O 的切线 ∴∠CAB=90°,∠PBC=90°,∴∠ABC=30° ∴AC=2×√33=2√33cm .【能力巩固】 7.C 8.A 9.100 10.9 11.解:如图,连接OE.∵AB 与☉O 相切 ∴OE ⊥AB ∴∠BEO=90°. 设☉O 的半径为r在Rt △BEO 中,由勾股定理得OB 2=OE 2+BE 2.∵BE=4,BD=2∴(2+r )2=r 2+42,解得r=3 ∴CD=6∴BC=BD+CD=2+6=8.∵∠C=90°,OC为☉O的半径∴AC与☉O相切∴AC=AE.设AC=AE=x∴AB=BE+AE=4+x.在Rt△ABC中,由勾股定理得AB2=AC2+BC2 ∴(4+x)2=x2+82,解得x=6∴AC=6.【素养拓展】12.解:如图,连接OD,BD,作DE⊥AB于点E.∵BC与水平面的夹角为60°∴∠DBE=60°,∴∠BDE=30°.设BE=x,则BD=2x∴由勾股定理得4x2-x2=25解得x=5√33∴OD=AE=40-5√3(cm).3)cm.答:其圆心所经过的路线长是(40−5√33。
北师大版九年级数学下册 3.7切线长定理 同步练习题(含答案)
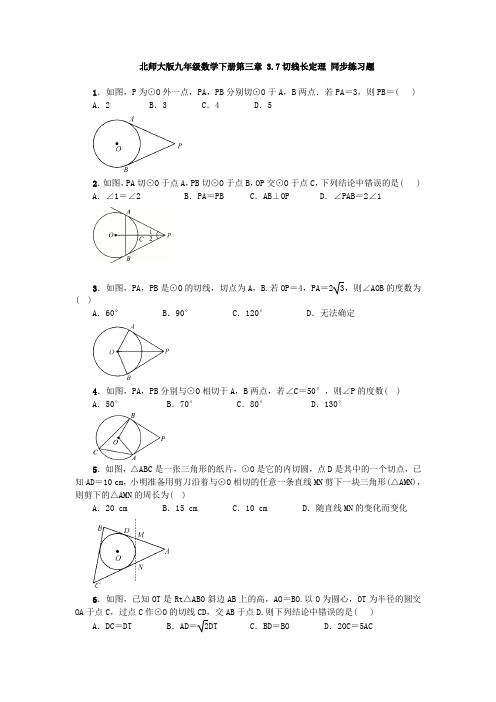
北师大版九年级数学下册第三章 3.7切线长定理同步练习题1.如图,P为⊙O外一点,PA,PB分别切⊙O于A,B两点.若PA=3,则PB=( ) A.2 B.3 C.4 D.52.如图,PA切⊙O于点A,PB切⊙O于点B,OP交⊙O于点C,下列结论中错误的是( ) A.∠1=∠2 B.PA=PB C.AB⊥OP D.∠PAB=2∠13.如图,PA,PB是⊙O的切线,切点为A,B.若OP=4,PA=23,则∠AOB的度数为( )A.60°B.90°C.120° D.无法确定4.如图,PA,PB分别与⊙O相切于A,B两点,若∠C=50°,则∠P的度数( )A.50° B.70° C.80° D.130°5.如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,已知AD=10 cm,小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长为( )A.20 cm B.15 cm C.10 cm D.随直线MN的变化而变化6.如图,已知OT是Rt△ABO斜边AB上的高,AO=BO.以O为圆心,OT为半径的圆交OA于点C,过点C作⊙O的切线CD,交AB于点D.则下列结论中错误的是( ) A.DC=DT B.AD=2DT C.BD=BO D.2OC=5AC7.如图,在△MBC中,∠B=90°,∠C=60°,MB=23,点A在MB上,以AB为直径作⊙O与MC相切于点D,则CD的长为( )A. 2B. 3 C.2 D.38.如图,一圆内切于四边形ABCD,AB=16,CD=10,则四边形ABCD的周长为( )A.50 B.52 C.54 D.569.如图,AB,AC,BD是⊙O的切线,P,C,D为切点.如果AB=5,AC=3,那么BD 的长为______.10.如图,在菱形ABCD中,∠B=60°,AB=4,⊙O内切于菱形ABCD,则⊙O的半径为______.11.如图,AB为⊙O的直径,点C在AB的延长线上,CD,CE分别与⊙O相切于点D,E.若AD=2,∠DAC=∠DCA,则CE=______.12.如图,P为⊙O外一点,PA,PB分别切⊙O于点A,B,CD切⊙O于点E且分别交PA,PB 于点C ,D.若PA =4,则△PCD 的周长为______.13.如图,菱形ABOC 的边AB ,AC 分别与⊙O 相切于点D ,E.若点D 是AB 的中点,则∠DOE =______.14.如图,PA ,PB 是⊙O 的切线,A ,B 为切点,AC 是⊙O 的直径,∠P =60°,OA =2,求BC 的长.B 组(中档题)15.如图,菱形ABCD 的边AB =20,面积为320,∠BAD <90°,⊙O 与边AB ,AD 都相切.若AO =10,则⊙O 的半径长为______.16.如图,AB 为半圆O 的直径,AD ,BC 分别切⊙O 于A ,B 两点,CD 切⊙O 于点E ,AD 与CD 相交于点D ,BC 与CD 相交于点C ,连接OD ,OC ,对于下列结论:①OD 2=DE ·CD ;②AD +BC =CD ;③OD =OC ;④S 梯形ABCD =12CD ·OA ;⑤∠DOC =90°.其中正确的是______.(只需填上正确结论的序号)17.如图,PA,PB分别切⊙O于点A,B,连接PO,与AB相交于D,C是⊙O上一点,∠C=60°.(1)求∠APB的大小;(2)若PO=20 cm,求△AOB的面积.18.在一个夹角为120°的墙角放置了一个圆柱体的容器,俯视图如图,在俯视图中圆与两边的墙分别切于B,C两点(圆柱体容器的直径不易直接测量).(1)写出此图中相等的线段;(2)请你设计一种可以通过计算求出直径的测量方法(写出主要解题过程).19.如图,边长为1的正方形ABCD的边AB是⊙O的直径,CF是⊙O的切线,E为切点,F点在AD上,BE是⊙O的弦,求△CDF的面积.C组(综合题)20.如图,AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,BO=6 cm,CO=8 cm.(1)求证:BO⊥CO;(2)求BE和CG的长.21.如图,P为⊙O外一点,PA,PB均为⊙O的切线,A和B是切点,BC是直径.求证:(1)∠APB=2∠ABC;(2)AC∥OP.22.如图,AB是⊙O的直径,AM和BN是它的两条切线,过⊙O上一点E作直线DC,分别交AM,BN于点D,C,且DA=DE.求证:(1)直线CD是⊙O的切线;(2)OA2=DE·CE.参考答案2020-2021学年北师大版九年级数学下册第三章 3.7切线长定理同步练习题A组(基础题)1.如图,P为⊙O外一点,PA,PB分别切⊙O于A,B两点.若PA=3,则PB=(B) A.2 B.3 C.4 D.52.如图,PA切⊙O于点A,PB切⊙O于点B,OP交⊙O于点C,下列结论中错误的是(D) A.∠1=∠2 B.PA=PB C.AB⊥OP D.∠PAB=2∠13.如图,PA,PB是⊙O的切线,切点为A,B.若OP=4,PA=23,则∠AOB的度数为(C)A.60°B.90°C.120° D.无法确定4.如图,PA,PB分别与⊙O相切于A,B两点,若∠C=50°,则∠P的度数(C)A.50° B.70° C.80° D.130°5.如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,已知AD=10 cm,小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长为(A)A.20 cm B.15 cm C.10 cm D.随直线MN的变化而变化6.如图,已知OT是Rt△ABO斜边AB上的高,AO=BO.以O为圆心,OT为半径的圆交OA于点C,过点C作⊙O的切线CD,交AB于点D.则下列结论中错误的是(D) A.DC=DT B.AD=2DT C.BD=BO D.2OC=5AC7.如图,在△MBC中,∠B=90°,∠C=60°,MB=23,点A在MB上,以AB为直径作⊙O与MC相切于点D,则CD的长为(C)A. 2B. 3 C.2 D.38.如图,一圆内切于四边形ABCD,AB=16,CD=10,则四边形ABCD的周长为(B)A.50 B.52 C.54 D.569.如图,AB,AC,BD是⊙O的切线,P,C,D为切点.如果AB=5,AC=3,那么BD 的长为2.10.如图,在菱形ABCD中,∠B=60°,AB=4,⊙O内切于菱形ABCD,则⊙O的半径11.如图,AB为⊙O的直径,点C在AB的延长线上,CD,CE分别与⊙O相切于点D,E.若AD=2,∠DAC=∠DCA,则CE=2.12.如图,P为⊙O外一点,PA,PB分别切⊙O于点A,B,CD切⊙O于点E且分别交PA,PB于点C,D.若PA=4,则△PCD的周长为8.13.如图,菱形ABOC的边AB,AC分别与⊙O相切于点D,E.若点D是AB的中点,则∠DOE=60°.14.如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,∠P=60°,OA=2,求BC的长.解:∵PA ,PB 是⊙O 的切线,∴AP =BP. 又∵∠P =60°,∴△ABP 是等边三角形. ∴∠PAB =60°. ∵PA 是⊙O 的切线, ∴∠PAC =90°.∴∠BAC =90°-60°=30°. 又∵AC 是⊙O 的直径, ∴∠ABC =90°. ∴BC =12AC =OA =2.B 组(中档题)15.如图,菱形ABCD 的边AB =20,面积为320,∠BAD <90°,⊙O 与边AB ,AD 都相切.若AO =10,则⊙O 的半径长为25.16.如图,AB 为半圆O 的直径,AD ,BC 分别切⊙O 于A ,B 两点,CD 切⊙O 于点E ,AD 与CD 相交于点D ,BC 与CD 相交于点C ,连接OD ,OC ,对于下列结论:①OD 2=DE ·CD ;②AD +BC =CD ;③OD =OC ;④S 梯形ABCD =12CD ·OA ;⑤∠DOC =90°.其中正确的是①②⑤.(只需填上正确结论的序号)17.如图,PA ,PB 分别切⊙O 于点A ,B ,连接PO ,与AB 相交于D ,C 是⊙O 上一点,∠C =60°.(1)求∠APB 的大小;(2)若PO =20 cm ,求△AOB 的面积.解:(1)∵∠C =60°, ∴∠AOB =120°.∵PA ,PB 分别切⊙O 于点A ,B , ∴∠PAO =∠PBO =90°.∴∠APB =360°-90°-90°-120°=60°. (2)∵PA ,PB 分别切⊙O 于点A ,B ,∴PA =PB.∴点P 在AB 的垂直平分线上. 同理,点O 在AB 的垂直平分线上. ∴PO 垂直平分AB.∵∠APB =60°,∠AOB =120°,∴∠OPB =∠OPA =30°,∠POB =∠POA =60°. ∵PO =20 cm ,∴OB =10 cm. ∴OD =OB ·cos ∠POB =5 cm , BD =OB ·sin ∠POB =5 3 cm. ∴AB =2BD =10 3 cm.∴S △AOB =12×103×5=253(cm 2).18.在一个夹角为120°的墙角放置了一个圆柱体的容器,俯视图如图,在俯视图中圆与两边的墙分别切于B ,C 两点(圆柱体容器的直径不易直接测量).(1)写出此图中相等的线段;(2)请你设计一种可以通过计算求出直径的测量方法(写出主要解题过程).解:(1)根据切线长定理,知AB =AC. (2)连接OB ,OA. ∵∠BAC =120°, ∴∠OAB =60°. 在Rt △AOB 中,OB =AB ·tan ∠OAB =3AB. ∴圆的直径为23AB.故只需测得AB 的长,就可求得圆的直径.19.如图,边长为1的正方形ABCD 的边AB 是⊙O 的直径,CF 是⊙O 的切线,E 为切点,F 点在AD 上,BE 是⊙O 的弦,求△CDF 的面积.解:设AF =x.∵四边形ABCD 是正方形, ∴∠DAB =∠CBA =90°. ∴DA ⊥AB ,CB ⊥AB.又∵OA ,OB 是⊙O 的半径, ∴AD ,BC 是⊙O 的切线.∵CF 是⊙O 的切线,E 为切点,∴EF =AF =x ,CE =CB =1.∴FD =1-x ,CF =CE +EF =1+x.在Rt △CDF 中,由勾股定理,得CF 2=CD 2+DF 2,即(1+x)2=1+(1-x)2,解得x =14. ∴DF =1-x =34. ∴S △CDF =12×1×34=38.C 组(综合题)20.如图,AB ,BC ,CD 分别与⊙O 相切于点E ,F ,G ,且AB ∥CD ,BO =6 cm ,CO =8 cm.(1)求证:BO ⊥CO ;(2)求BE 和CG 的长.解:(1)证明:∵AB ∥CD ,∴∠ABC +∠BCD =180°.∵AB ,BC ,CD 分别与⊙O 相切于点E ,F ,G ,∴BO 平分∠ABC ,CO 平分∠DCB.∴∠OBC =12∠ABC ,∠OCB =12∠DCB. ∴∠OBC +∠OCB =12(∠ABC +∠DCB)=12×180°=90°. ∴∠BOC =90°.∴BO ⊥CO.(2)连接OF ,则OF ⊥BC ,∴Rt △BOF ∽Rt △BCO.∴BF BO =BO BC. ∵在Rt △BOC 中,BO =6 cm ,CO =8 cm ,∴BC =BO 2+CO 2=10(cm).∴BF 6=610. ∴BF =3.6 cm.∵AB ,BC ,CD 分别与⊙O 相切,∴BE =BF =3.6 cm ,CG =CF.∴CG =CF =BC -BF =6.4 cm.21.如图,P 为⊙O 外一点,PA ,PB 均为⊙O 的切线,A 和B 是切点,BC 是直径.求证:(1)∠APB =2∠ABC ;(2)AC ∥OP.证明:(1)连接AO ,∵PA ,PB 均为⊙O 的切线,A 和B 是切点,∴∠APO =∠BPO ,OA ⊥AP ,PA =PB.∴∠APB =2∠BPO ,∠OBP =90°,PO ⊥AB.∴∠OBA +∠ABP =90°,∠ABP +∠BPO =90°.∴∠OBA =∠BPO.∴∠APB =2∠ABC.(2)设AB 交OP 于点F ,由(1)知,PO ⊥AB ,∴∠AFP =90°.∵BC 是⊙O 直径,∴∠CAB =90°.∴∠CAB =∠AFP.∴AC ∥OP.22.如图,AB 是⊙O 的直径,AM 和BN 是它的两条切线,过⊙O 上一点E 作直线DC ,分别交AM ,BN 于点D ,C ,且DA =DE.求证:(1)直线CD 是⊙O 的切线;(2)OA 2=DE ·CE.证明:(1)连接OE ,OD ,∵DA 是⊙O 的切线,∴∠OAD =90°.∵OA =OE ,DA =DE ,OD =OD ,∴△AOD ≌△EOD(SSS).∴∠OAD =∠OED =90°.∴OE ⊥CD.又∵OE 是⊙O 的半径,∴CD 是⊙O 的切线.(2)连接OC ,∵AM ,BN ,DC 是⊙O 的切线,∴∠OAD =∠OBC =∠DEO =∠OEC =90°,CE =CB ,OD 平分∠ADE ,OC 平分∠BCE. ∴AM ∥BN.∴∠ADE +∠BCE =180°.∴∠ODE +∠OCE =12(∠ADE +∠BCE)=12×180°=90°. 又∵∠ODE +∠DOE =90°,∴∠OCE =∠DOE.∴△DEO ∽△OEC.∴OECE=DEOE.∴OE2=DE·CE.又∵OA=OE,∴OA2=DE·CE.。
北师大版数学九年级下册3.7 初中数学 《切线长定理》同步练习3

《切线长定理》同步练习3
一、选择题
1.下列四个命题中正确的是( )
①与圆有公共点的直线是该圆的切线 ②垂直于圆的半径的直线是该圆的切线 ③到圆心的距离等于半径的直线是该圆的切线 ④过圆直径的端点,垂直于此直径的直线是该圆的切线
A.①②
B.②③
C.③④
D.①④
2.边长分别为3,4,5的三角形的内切圆半径与外接圆半径之比( )
(A)15∶ (B)25∶ (C)35∶ (D)54∶
二、填空题
3.如图1,点A ,B ,D 在O 上,25A =∠,OD 的延长线交直线BC 于点C ,且40OCB =∠,直线BC 与⊙O 的位置关系为
_________.
三、解答题
4.如图2,AB 是⊙O 的直径,C 为AB 延长线上的一点,CD 交⊙O 于点D ,且30A C ∠=∠=︒.
(1)说明CD 是⊙O 的切线;
(2)请你写出线段BC 和AC 之间的数量关系,并说明理由.
A B C
D O A O
B C D
参考答案
1.C 2. B 3.相切
4.解:(1)连结OD . AB ∵是直径,90ADB ∠=︒∴. 30A ∠=︒∵,
60ABD ∠=︒∴,OBD ∴△是等边三角形. 而ABD C BDC ∠=∠+∠, 30BDC ABD C ∠=∠-∠=︒∴, 90ODC ∠=︒∴,
即OD DC ⊥,故DC 是⊙O 的切线.
(2)13
BC AC =. OD DC ⊥∵,且30C ∠=︒,BD BC =∴. 又在ABD △Rt 中,30A ∠=︒, 12BD AB =
∴,12BC AB =∴, 13
BC AC =
∴.。
北师大版九年级数学下册3.7切线长定理同步练习

北师大版九年级数学下册3.7切线长定理同步练习*7切线长定理知识点切线长定理1.如图3-7-1,P是⊙O外一点,PA,PB分别切⊙O于点A,B.已知⊙O的半径为1,OP=2,则切线长PA=________,∠APB=________°.图3-7-13-7-22.如图3-7-2,四边形ABCD的四边分别与⊙O相切,且AB=16,CD=10,则四边形ABCD的周长为()A.50 B.52 C.54 D.56图3-7-33.如图3-7-3所示,AB是⊙O的直径,C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的度数是()4 cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过点A作半圆的切线,与半圆相切于点F,与DC相交于点E,则△ADE的面积为()A.12 cm2B.24 cm2C.8 cm2D.6 cm2图3-7-77.如图3-7-7,△ABC的周长为16,∠A=60°,BC=6.若⊙O与BC,AC,AB三边分别切于点E,F,D,则DF的长为________.8.[2019·孝感模拟]如图3-7-8,直线AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,OB=6 cm,OC=8 cm.求:(1)∠BOC的度数;(2)BE+CG的长;(3)⊙O的半径.图3-7-8详解详析1.3602.B[解析] 根据切线长定理可证AB+CD=AD+BC,∴四边形ABCD的周长=2×(16+10)=52.故选B.3.D[解析] 连接OD.∵CA,CD是⊙O 的切线,∴OA⊥AC,OD⊥CD,∴∠OAC=∠ODC =90°.∵∠ACD=30°,∴∠AOD=360°-∠C -∠OAC-∠ODC=150°.∵OB=OD,∴∠DBA=∠ODB=12∠AOD=75°.故选D.4.解:(1)∵CA,CE都是⊙O的切线,∴CA=CE.同理DE=DB,PA=PB,∴△PCD的周长=PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12,∴PA=6.(2)∵∠P=60°,∴∠PCE+∠PDE=120°,∴∠ACD+∠CDB=360°-120°=240°.∵CA ,CE 是⊙O 的切线,∴∠OCE =∠OCA =12∠ACD . 同理∠ODE =12∠CDB ,∴∠OCE +∠ODE =12(∠ACD +∠CDB )=120°, ∴∠COD =180°-120°=60°.5.D [解析] ∵PA ,PB 切⊙O 于A ,B 两点,CD 切⊙O 于点F 且分别交PA ,PB 于点C ,D ,∴CA =CF ,DF =DB ,PA =PB ,∴PC +CF +DF +PD =PA +PB =2PA =3r ,∴PA =32r ,∴OA PA =r 32r =23.故选D. 6.D [解析] 设DE =x cm ,则CE =(4-x )cm ,根据题意知EF =CE =(4-x )cm ,AF =AB =4 cm ,∴AE =(8-x )cm.在Rt△ADE中,AD2+DE2=AE2,即42+x2=(8-x)2,解得x=3.∴△ADE的面积=12×AD×DE=12×4×3=6(cm2).7.2.8.解:(1)如图,连接OF.根据切线长定理,得BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG.∵AB∥CD,∴∠ABC+∠BCD=180°,∴∠OBF+∠OCF=90°,∴∠BOC=90°.(2)由(1)知,∠BOC=90°.∵OB=6 cm,OC=8 cm,∴由勾股定理,得到BC=OB2+OC2=10 cm,∴BE+CG=BC=10 cm.(3)由(1)知,OF⊥BC,OB⊥OC,∴OF=OB·OCBC=4.8 cm.即⊙O的半径为4.8 cm.。
九年级数学下册第三章圆3.7切线长定理同步练习新版北师大版

课时作业(二十七)[第三章*7 切线长定理]一、选择题1.2017·红桥区期末如图K-27-1,PA,PB分别切⊙O于点A,B,PA=10,CD切⊙O 于点E,与PA,PB分别交于C,D两点,则△PCD的周长是链接听课例1归纳总结()图K-27-1A.10 B.18 C.20 D.222.如图K-27-2,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O与AB,BC,AC分别切于点D,E,F,则AF的长为()图K-27-2A.5 B.10 C.7.5 D.43.已知⊙O的半径是4,P是⊙O外一点,且PO=8,从点P引⊙O的两条切线,切点分别是A,B,则AB的长为()A.4 B.4 2 C.4 3 D.2 34.如图K-27-3,PA切⊙O于点A,PB切⊙O于点B,OP交⊙O于点C,下列结论中,错误的是( )链接听课例2归纳总结图K-27-3A.∠1=∠2 B.PA=PBC.AB⊥OP D.PA2=PC·PO5.如图K-27-4,AB为半圆O的直径,AD,BC分别切⊙O于A,B两点,CD切⊙O于点E,连接OD,OC.下列结论:①∠DOC=90°;②AD+BC=CD;③S△AOD∶S△BOC=AD2∶AO2;④OD∶OC=DE∶EC;⑤OD2=DE·CD.其中正确的有()图K-27-4A.2个 B.3个C.4个 D.5个二、填空题6.如图K-27-5,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为________.图K-27-57.2017·昌平区期末如图K-27-6所示,在Rt△ABC中,∠C=90°,AC长为8,BC 长为15,则△ABC的内切圆⊙O的直径是________.图K-27-68.如图K-27-7,P是⊙O的直径AB的延长线上的一点,PC,PD分别切⊙O于点C,D.若PA=6,⊙O的半径为2,则∠CPD=________°.图K-27-79.如图K-27-8所示,已知PA,PB,EF分别切⊙O于点A,B,D,若PA=15 cm,则△PEF的周长是________ cm;若∠P=50°,则∠EOF=________°.链接听课例1归纳总结图K-27-810.如图K-27-9所示,⊙O与△ABC中AB,AC的延长线及BC边相切,且∠ACB=90°,∠A,∠ABC,∠ACB所对的边长依次为3,4,5,则⊙O的半径是________.图K-27-9三、解答题11.如图K-27-10,PA,PB分别切⊙O于点A,B,连接PO与⊙O相交于点C,连接AC,BC.求证:AC=BC.链接听课例2归纳总结图K-27-1012.2017·孝感模拟如图K-27-11,直线AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,OB=6 cm,OC=8 cm.求:(1)∠BOC的度数;(2)BE+CG的长;(3)⊙O的半径.链接听课例1归纳总结图K-27-1113.如图K-27-12,△ABC外切于⊙O,切点分别为D,E,F,∠A=60°,BC=7,⊙O的半径为 3.求:(1)BF+CE;(2)△ABC的周长.图K-27-1214.如图K-27-13,AB为⊙O的直径,∠DAB=∠ABC=90°,DE与⊙O相切于点E,⊙O的半径为5,AD=2.(1)求BC的长;(2)延长AE交BC的延长线于点G,求EG的长.图K-27-13探究存在题如图K-27-14,以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,过点D作⊙O的切线交BC边于点E.(1)求证:EB=EC=ED.(2)在线段DC上是否存在点F,使得BC2=4DF·DC?若存在,求出点F,并予以证明;若不存在,请说明理由.图K-27-14详解详析【课时作业】[课堂达标]1.[解析] C∵PA,PB分别切⊙O于点A,B,CD切⊙O于点E,∴PA =PB =10,CA =CE ,DE =DB ,∴△PCD 的周长是PC +CD +PD =PC +AC +DB +PD =PA +PB =10+10=20.故选C.2.[解析] A 设AF =x ,根据切线长定理得AD =x ,BD =BE =9-x ,CE =CF =CA -AF =6-x ,则有9-x +6-x =5,解得x =5,即AF 的长为5.3.[解析] C 如图,PA ,PB 分别切⊙O 于A ,B 两点.∵OA =4,PO =8,∴AP =82-42APB =2∠APO =60°, ∴△PAB 是等边三角形,∴AB =AP 4.[解析] D 如图,连接OA ,OB .∵PA 切⊙O 于点A ,PB 切⊙O 于点B ,∴PA =PB , ∴△ABP 是等腰三角形.易证∠1=∠2,∴AB ⊥OP .故A ,B ,C 均正确.设OP 交AB 于点D ,易证△PAD ∽△POA ,∴PA ∶PO =PD ∶PA ,∴PA 2=PD ·PO .故D 错误.5.[解析] C 连接OE .∵AD ,BC ,CD 分别与⊙O 切于点A ,B ,E ,∴OA ⊥AD ,OB ⊥BC ,OE ⊥CD ,DA =DE ,EC =BC ,∠ADO =∠EDO ,∠ECO =∠BCO ,∴∠OAD =∠OED =∠OEC =∠OBC =90°,∴∠AOD =∠EOD ,∠BOC =∠EOC .①∵∠AOD +∠EOD +∠BOC +∠EOC =180°,∴∠DOC =∠EOD +∠EOC =90°,∴①正确;②∵DA =DE ,EC =BC ,∴AD +BC =DE +EC =CD ,∴②正确;③∵∠AOD +∠BOC =90°,∠AOD +∠ADO =90°,∴∠BOC =∠ADO .又∵∠OAD =∠CBO =90°,∴△OAD ∽△CBO ,∴S △AOD ∶S △BOC =AD 2∶BO 2=AD 2∶AO 2,∴③正确;④∵△OAD ∽△CBO ,∴OD OC =AD OB =DEOB.∵OB ≠EC ,∴④不正确;⑤∵∠DOC =∠OED =90°,∴∠EOD +∠EDO=90°,∠CDO +∠DCO =90°,∴∠EOD =∠DCO ,∴△OED ∽△COD ,∴OD CD =DEOD,即DE ·CD =OD 2,∴⑤正确.综上,正确的有①②③⑤.故选C.6.[答案] 44[解析] ∵四边形ABCD 是⊙O 的外切四边形,∴AD +BC =AB +CD =22,∴四边形ABCD 的周长=AD +BC +AB +CD =44. 7.[答案] 6[解析] ∵∠C =90°,AC =8,BC =15,∴AB =AC 2+BC 2=17,∴△ABC 的内切圆⊙O的直径为15×817+15+8×2=6.故答案为6.8.[答案] 60[解析] 连接OC .∵PA =6,⊙O 的半径为2,∴OP =PA -OA =6-2=4.∵PC ,PD 分别切⊙O 于点C ,D ,∴∠OPC =∠OPD ,OC ⊥PC ,∴sin ∠OPC =24=12,∴∠OPC =30°,∴∠CPD =60°.9.[答案] 3065[解析] ∵PA ,PB ,EF 分别切⊙O 于点A ,B ,D , ∴PA =PB =15 cm ,ED =EA ,FD =FB ,∴PE +EF +PF =PE +ED +PF +FD =PA +PB =30 cm ,即△PEF 的周长是30 cm ;连接OA ,OB ,OD .∵PA ,PB 为⊙O 的切线,∴∠PAO =∠PBO =90°,而∠P =50°,∴∠AOB =360°-90°-90°-50°=130°.易证得Rt △OAE ≌Rt △ODE ,Rt △OFD ≌Rt △OFB ,∴∠1=∠2,∠3=∠4,∴∠2+∠3=12∠AOB =65°,即∠EOF =65°.10.[答案] 2[解析] 如图,设⊙O 与AB ,AC 的延长线及BC 边分别相切于点F ,D ,E .连接OD ,OE .∵⊙O 与△ABC 中AB ,AC 的延长线及BC 边相切,∴AF =AD ,BE =BF ,CE =CD ,OD ⊥AD ,OE ⊥BC .∵∠ACB =90°,∴四边形ODCE 是正方形.设OD =r ,则CD =CE =r .∵BC =3,∴BE =BF =3-r .∵AB =5,AC =4,∴AF =AB +BF =5+3-r ,AD =AC +CD =4+r ,∴5+3-r =4+r ,解得r =2,则⊙O 的半径是2.11.证明:∵PA ,PB 分别切⊙O 于点A ,B , ∴PA =PB ,∠APC =∠BPC .又∵PC =PC ,∴△APC ≌△BPC ,∴AC =BC .12.解:(1)连接OF .根据切线长定理,得BE =BF ,CF =CG ,∠OBF =∠OBE ,∠OCF =∠OCG .∵AB ∥CD ,∴∠ABC +∠BCD =180°,∴∠OBF +∠OCF =90°, ∴∠BOC =90°.(2)由(1)知,∠BOC =90°. ∵OB =6 cm ,OC =8 cm ,∴由勾股定理,得BC =OB 2+OC 2=10 cm , ∴BE +CG =BC =10 cm.(3)∵OF ⊥BC ,由三角形的面积公式,得12OB ·OC =12BC ·OF ,∴OF =OB ·OCBC =4.8 cm.13.解:(1)∵△ABC 外切于⊙O ,切点分别为D ,E ,F ,∴BF =BD ,CE =CD ,∴BF +CE =BD +CD =BC =7.(2)如图,连接OE ,OF ,OA .∵△ABC 外切于⊙O ,切点分别为D ,E ,F , ∴∠OEA =90°,∠OAE =12∠BAC =30°,∴OA =2OE =2 3.由勾股定理,得AF =AE =OA 2-OE 2=3,∴△ABC 的周长是AB +BC +AC =AF +AE +CE +BF +BC =3+3+7+7=20, 即△ABC 的周长是20.14.[解析] (1)过点D 作DF ⊥BC 于点F ,由切线长定理可得DE =AD =2,CE =BC .设BC =x ,在Rt △DCF 中,DC 2=CF 2+DF 2,即可得方程(2+x )2=(x -2)2+(2 5)2,解此方程即可求得答案;(2)易证得△ADE ∽△GCE ,由相似三角形的对应边成比例,可得AE ∶EG =4∶5,由勾股定理即可求得AG 的长,继而求得答案.解:(1)过点D 作DF ⊥BC 于点F . ∵∠DAB =∠ABC =90°,∴四边形ABFD 是矩形,AD 与BC 是⊙O 的切线,∴DF =AB =2 5,BF =AD =2. ∵DE 与⊙O 相切, ∴DE =AD =2,CE =BC .设BC =x ,则CF =BC -BF =x -2,DC =DE +CE =2+x .在Rt △DCF 中,DC 2=CF 2+DF 2,即(2+x )2=(x -2)2+(2 5)2,解得x =52,即BC =52.(2)∵∠DAB +∠ABC =180°,∴AD ∥BC ,∴△ADE ∽△GCE , ∴AD GC =DE CE ,AE EG =ADGC.∵AD =DE =2,∴GC =CE =BC =52,∴BG =BC +CG =5,AE EG =45.在Rt △ABG 中,AG =AB 2+BG 2=3 5,∴EG =59AG =535.[点评] 此题考查了切线的性质与判定、切线长定理以及勾股定理等知识,难度适中,注意掌握辅助线的作法与方程思想的应用.[素养提升][解析] (1)连接BD ,已知ED ,EB 都是⊙O 的切线,由切线长定理可证得OE 垂直平分BD ,而BD ⊥AC (圆周角定理),则OE ∥AC .由于O 是AB 的中点,可证得OE 是△ABC 的中位线,即E 是BC 的中点,那么在Rt △BDC 中,DE 就是斜边BC 的中线,由此可证得所求的结论.(2)由(1)知:BC =2BE =2DE ,则所求的比例关系式可转化为(BC2)2=DF ·DC ,即DE 2=DF ·DC ,那么只需作出与△DEC 相似的△DFE 即可,这两个三角形的公共角为∠CDE ,只需作出∠DEF =∠C 即可.①当∠DEC >∠C ,即180°-2∠C >∠C ,0°<∠C <60°时,∠DEF 的EF 边与线段DC 相交,那么交点即为所求的点F ;②当∠DEC =∠C ,即180°-2∠C =∠C ,∠C =60°时,点F 与点C 重合,点F 仍在线段DC 上,此种情况也成立;③当∠DEC <∠C ,即180°-2∠C <∠C ,60°<∠C <90°时,∠DEF 的EF 边与线段DC 的延长线相交,与线段CD 没有交点,所以在这种情况下不存在符合条件的点F .解:(1)证明:连接BD .∵ED ,EB 是⊙O 的切线,由切线长定理,得ED =EB ,∠DEO =∠BEO , ∴OE 垂直平分BD . 又∵AB 是⊙O 的直径, ∴AD ⊥BD ,∴AD ∥OE ,即OE ∥AC . 又O 为AB 的中点,∴OE 为△ABC 的中位线, ∴EB =EC ,∴EB =EC =ED .(2)存在.在△DEC 中,∵ED =EC , ∴∠C =∠CDE ,∴∠DEC =180°-2∠C .①当∠DEC >∠C 时,有180°-2∠C >∠C ,即0°<∠C <60°时,在线段DC 上存在满足条件的点F .在∠DEC 内,以ED 为一边,作∠DEF ,使∠DEF =∠C ,且EF 交DC 于点F ,则点F 即为所求.证明:在△DCE 和△DEF 中,∠CDE =∠EDF ,∠C =∠DEF ,∴△DEF ∽△DCE ,∴DE DC =DF DE, ∴DE 2=DF ·DC ,即(12BC )2=DF ·DC ,∴BC 2=4DF ·DC .②当∠DEC =∠C 时,△DEC 为等边三角形,即∠DEC =∠C =60°,此时,点C 即为满足条件的点F , 于是,DF =DC =DE ,仍有BC 2=4DE 2=4DF ·DC . ③当∠DEC <∠C ,即180°-2∠C <∠C ,60°<∠C <90°时,所作的∠DEF >∠DEC ,此时点F 在DC 的延长线上,故线段DC 上不存在满足条件的点F.。
北师大版九年级数学下册3.7:切线长定理 同步测试

3.7 切线长定理同步测试一、选择题1.如图,直线AB 与半径为2的⊙O 相切于点C ,点D ,E ,F 是⊙O 上三个点,EF ∥AB ,若EF=2 3,则∠EDC 的度数为( )A. 60°B. 90°C. 30°D. 75°2.如图,PA 、PB 分别切⊙O 于点A 、B ,AC 是⊙O 的直径,连结AB 、BC 、OP ,则与∠PAB 相等的角(不包括∠PAB 本身)有( )A .1个B .2个C .3个D .4个3.如图,在Rt △ABC 中,∠ABC =90°,AB ==2,以AB 的中点O 为圆心,OA 的长为半径作半圆交AC 于点D,则图中阴影部分的面积为( )2π 2π C.π D.2π4.边长分别为3,4,5的三角形的内切圆半径与外接圆的半径之比为( ).A.1:5B.2:5C.3:5D. 4:55.一个钢管放在V形架内,右图是其截面图,O为钢管的圆心.如果钢管的半径为25 cm,∠MPN = 60 ,则OP =( )A.50 cm B.25cm C.cm D.50cm6. 一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于( )A.21 B.20 C.19 D.187.如图,AB是⊙O直径,点C在⊙O上,AE是⊙O的切线,A为切点,连接BC并延长交AE于点D.若∠AOC=80°,则∠ADB的度数为()A.40°B.50°C.60°D.20°8.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于( )A.21 B.20 C.19 D.189.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与图中4×7方格中的格点的连线中,能够与该圆弧相切的格点个数有()A.1个B.2个C.3个D. 4个10.如图,AB是⊙O的直径,PA切⊙O于点A,OP交⊙O于点C,连接BC.若∠P=20°,则∠B的度数是()A. 20°B. 25°C. 30°D. 35°二、填空题11.如图,在△ABC中,,cos B.如果⊙O的半径为cm,且经过点B、C,那么线段AO= cm.12.如图,PA、PB是⊙O的两条切线,切点分别是A、B,如果AP=4, ∠APB= 40 ° ,则∠APO= ,PB= .13.如图,已知点O是△ABC 的内心,且∠ABC= 60 °, ∠ACB= 80 °,则∠BOC= .14.如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________.15.如图,PA、PB是⊙O的切线,切点分别为A、B,点C在⊙O上,如果∠ACB=70°,那么∠OPA的度数是________度.三、综合题16. 如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30°.(1)求∠APB的度数;(2)当OA=3时,求AP的长.17.如图,AB是 O的直径,点P是BA延长线上一点,过点P作 O的切线PC,切点是C,过点C作弦CD⊥AB于E,连接CO,CB.(1)求证:PD是 O的切线;(2)若AB=10,tanB=1,求PA的长;218.如图,AB是⊙O的直径,BC是⊙O的弦,直线MN与⊙O相切于点C,过点B作BD⊥MN于点D.(1)求证:∠ABC=∠CBD;(2)若BC=45,CD=4,则⊙O的半径是.19.如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G 三点,过点D作⊙O的切线交BC于点M,切点为N,求DM的长.3.7 切线长定理同步测试答案一、选择题1.A2.C3.A4.C5.D6.B7.C8.C9.D 10.B二、填空题11.12.200 4 13.110014.5215.200三、综合题 16.解:(1)∵在△ABO 中,OA =OB ,∠OAB =30°∴∠AOB =180°-2×30°=120°∵PA 、PB 是⊙O 的切线∴OA ⊥PA ,OB ⊥PB .即∠OAP =∠OBP =90°∴在四边形OAPB 中,∠APB =360°-120°-90°-90°=60°.(2)如图①,连结OP∵PA 、PB 是⊙O 的切线∴PO 平分∠APB ,即∠APO =21∠APB =30° 又∵在Rt △OAP 中,OA =3, ∠APO =30°∴AP ==3.17.解:(1)连接OD,∵CD ⊥AB,∴CE =ED,∴PC =PD,∵OC =OD,∴△POC ≌△POD,∴∠PDO =∠PCO,∵PC 是 O 的切线,∴PC ⊥OC,∠PCO =90°,∴∠PDO =90°,∴PD ⊥DO,∴PD 是 O 的切线;(2)连接AC,∵tanB =12,∴设AC =x,则BC =2x,∵AB =10,∴AO =CO =5,在Rt △ABC 中,由勾股定理可求得:AC =25,BC =45,∴CE =4,EO =3,∵△COE ∽△POC,∴PO =253,∴AP =PO -AO =103; 18.(1)证明:连接OC ,∵MN 为⊙O 的切线,∴OC ⊥MN ,∵BD ⊥MN ,∴OC ∥BD ,∴∠CBD =∠BCO .又∵OC =OB ,∴∠BCO =∠ABC ,∴∠CBD =∠ABC .;(2)解:连接AC ,在Rt △BCD 中,BC =45,CD =4,∴BD =8,∵AB 是⊙O 的直径,∴∠ACB =90°,∴∠ACB =∠CDB =90°,∵∠ABC =∠CBD ,∴△ABC ∽△CBD , ∴BD CB BC AB ,即54AB =854,∴AB =10,∴⊙O 的半径是5,故答案为5.19.解:连接OE ,OF ,ON ,OG .∵四边形ABCD 是矩形,∴∠A =∠B =90°,CD =AB =4.∵AD ,AB ,BC 分别与⊙O 相切于E ,F ,G 三点,∴∠AEO =∠AFO =∠OFB =∠BGO =90°,OE =OF =OG ,∴四边形AFOE ,FBGO 是正方形,∴AF =BF =AE =BG =2,∴DE =3.∵DM 是⊙O 的切线,∴DN =DE =3,MN =MG ,∴CM =BC -BG -MG =5-2-MN =3-MN .在Rt △DMC 中,DM 2=CD 2+CM 2,∴(3+MN )2=42+(3-MN )2,∴MN =43,∴DM =3+43=133.。
北师大版九年级数学下《3.7切线长定理》同步习题含答案

北师大版九年级数学下册 第三章 圆 3.7切线长定理 同步俩习题一、选择题(9分×3=27分)1.如图,AD 、AE 、CB 均为⊙O 的切线,D 、E 、F 分别是切点,AD =8,则△ABC 的周长为( )A .8B .12C .16D .不能确定,第1题图) ,第2题图)2.如图,已知⊙O 分别与△ABC 的BC 边、AB 的延长线、AC 的延长线相切,则∠BOC 等于()A .∠AB .90°+∠AC .90°-12∠AD .180°-12∠A3.如图,Rt △ABC 的内切圆⊙O 与两直角边AB 、BC 分别相切于点D 、E ,过劣弧DE ︵(不包括端点D 、E)上任一点作⊙O 的切线MN 与AB 、BC 分别交于点M 、N.若⊙O 的半径为r ,则Rt △MBN 的周长为( )A .r B.32r C .2r D.52r二、填空题(9分×3=27分)4.如图所示,△ABC的内切圆I与AB、BC、CA分别切于D、E、F.若AB=10cm,BC=6cm,AC=8cm,则AD=__________,BD=________ ,CE=______ .5.如图,AC⊥BC于点C,BC=4,AC=3,⊙O与直线AB、BC、CA都相切,则⊙O的半径为______.,第5题图),第6题图)6.如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB.若∠ABC=30°,则AM=______.三、解答题(14分+15分+17分=46分)7.如图,PA、PB分别切⊙O于A、B,BC为⊙O的直径.(1)求证:AC∥OP;(2)若∠APB=60°,BC=10cm,求AC的长.8.如图,AB是⊙O的直径,AM和BN是它的两条切线,DE切⊙O于点E,交AM于点D,交BN于点C,F是CD的中点,连接OF.(1)求证:OD∥BE;(2)猜想:OF与CD有何数量关系?并说明理由.9.如图①,直线y =-34x +3与x 轴相交于点A ,与y 轴相交于点B ,点C(m ,n)是第二象限内一点,以点C 为圆心的圆与x 轴相切于点E ,与直线AB 相切于点F.(1)当四边形OBCE 是矩形时,求点C 的坐标;(2)如图②,若⊙C 与y 轴相切于点D ,求⊙C 的半径.答案:1. C2. C3. C4. 6cm4cm2cm5. 26. 337. 解:(1)连接OA ,∵PA 、PB 分别切⊙O 于A 、B ,∴OA ⊥PA ,OB ⊥PB ,∵OP 平分∠APB ,∴∠POA =∠POB ,而∠BOA =∠C +∠OAC ,而∠OAC =∠C ,∴∠POB =∠C ,∴AC ∥OP(2)证△PAB 为等边三角形,可求∠ABC =30°,又BC =10,∴AC =5cm8. 解:(1)连接OE ,∵AM 、DE 是⊙O 的切线,OA 、OE 是⊙O 的半径,∴∠ADO =∠EDO ,∠DAO =∠DEO =90°,∴∠AOD =∠EOD =12∠AOE ,∵∠ABE =12∠AOE ,∴∠AOD =∠ABE ,∴OD ∥BE.(2)OF =12CD.理由:连接OC ,∵BC 、CE 是⊙O 的切线,∴∠OCB =∠OCE.∵AM ∥BN ,∴∠ADO +∠EDO +∠OCB +∠OCE =180°,由(1)得∠ADO =∠EDO ,∴2∠EDO +2∠OCE =180°,即∠EDO +∠OCE =90°,在Rt △DOC 中,∵F 是DC 的中点,∴OF =12CD.9. 解:(1)连接CB、CE、CF、AC,则∠BAC=∠EAC=∠BCA,∴AB=BC=5,CE=OB=3,∴C的坐标为(-5,3)(2)连接CD、CE、CF,∵∠CEO=∠CDO=90°,又∠DOE=90°,∴四边形CEOD为矩形,又CE=CD,得正方形CEOD,∴CE=DO=R,又BO=3,∴BD=3-R,∵BF、BD为切线,∴FB=BD=3-R,同理AE=AF,即R+4=3-R+5,∴R=2.。
九下第3章圆7切线长定理作业新版北师大版

又∵弧 AE 所在圆与 BC 相切于点 E, ∴BC⊥DE,EB=AB=m,∠CBD=∠ABD. ∵AB∥CD,∴∠ABD=∠CDB, ∴∠CBD=∠CDB,∴CB=CD=3m, ∴CE=CB-EB=3m-m=2m. ∵∠CED=90°,∴DE= CD2-CE2= (3m)2-(2m)2= 5m, ∴sin C=DCDE= 35mm= 35.故选 B. 【答案】B
如图所示,则 AD=BD=12AB. 由(1)得△APB 是等边三角形,∴AB=PA=1.∴AD=12.
∵∠BAC=30°,∴AO=2OD.∴AD= 3OD.
∴OD=
63,即点
O
到弦
AB
的距离为
3 6.
【点方法】 切线长定理揭示了两个方面的内容,一是切线长相
等,揭示线段之间的数量关系;二是圆外一点与圆心的连 线平分两条切线的夹角.这两个方面的内容为证明线段之 间的关系或者角之间的关系提供了条件.
改变一下条件…… (3)若∠C=60°,用m,n表示△ABC的面积.
【解】过点 A 作 AG⊥BC 于点 G. 在 Rt△ACG 中,∠C=60°,则∠CAG=30°, ∴CG=12AC=12(x+m).∴AG= AC2-CG2= 23(x+m). ∴BG=BC-CG=(x+n)-12(x+m).
北师版 九年级下
第三章 圆
3.7 切线长定理
习题链接
温馨提示:点击 进入讲评
1B 2C 3 42
5B 6 6.9 7 8
答案呈现
9 10 11
1 (母题:教材P121总复习T13)如图,PA,PB是⊙O的切 线,A,B为切点,AC是⊙O的直径,若∠BAC=26°, 则∠P的度数为( ) A.32° B.52° C.64° D.72°
九年级数学下册 第3章 圆 3.7 切线长定理同步测试 (新版)北师大版-(新版)北师大版初中九年级

《切线长定理》◆基础题1.如图,PA、PB切⊙O于点A、B,PA=10,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是()A.10B.18C.20D.222.如图,PA,PB分别是⊙O的切线,A,B分别为切点,点E是⊙O上一点,且∠AEB=60°,则∠P为()A.120°B.60°C.30°D.45°3.已知P为⊙O外一点,PA,PB为⊙O的切线,A、B为切点,∠P=70°,C为⊙O上一个动点,且不与A、B重合,则∠BCA=()A.35°C、145°B.110°、70°C.55°、125°D.110°4.如图,一圆外切四边形ABCD,且BC=10,AD=7,则四边形的周长为()A.32B.34C.36D.385.如图,AB、AC、BD是⊙O的切线,P、C、D为切点,如果AB=5,AC=3,则BD的长为.6.如图,PA、PB是⊙O的两条切线,A、B是切点,若∠APB=60°,PO=2,则⊙O的半径等于.7.已知P是⊙O外一点,PA切⊙O于A,PB切⊙O于B.若PA=6,则PB=.8.如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为4cm,则Rt△MBN的周长为.9.如图所示,PA、PB是⊙O的切线,切点分别是A、B,Q为⊙O上一点,过Q点作⊙O 的切线,交PA、PB于E、F点,已知PA=8cm,求:△PEF的周长.10.如图,点B在⊙O外,以B点为圆心,OB长为半径画弧与⊙O相交于两点C,D,与直线OB相交A点.当AC=5时,求AD的长.◆能力题1.如图,直线AB、CD、BC分别与⊙O相切于E、F、G,且AB∥CD,若OB=6,OC=8,则BE+CG的长等于()A.13B.12C.11D.102.如图,正方形ABCD边长为4,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积()A.12B.24C.8D.63.如图中,CA,CD分别切圆O1于A,D两点,CB、CE分别切圆O2于B,E两点.若∠1=60°,∠2=65°,判断AB、CD、CE的长度,下列关系何者正确()A.AB>CE>CDB.AB=CE>CDC.AB>CD>CED.AB=CD=CE4.如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3cm,则此光盘的直径是cm.5.一位小朋友在不打滑的平面轨道上滚动一个半径为5cm的圆环,当滚到与坡面BC 开始相切时停止.其AB=40cm,BC与水平面的夹角为60°.其圆心所经过的路线长是cm(结果保留根号).6.如图,在矩形ABCD中,AB=5,BC=4,以BC为直径在矩形内作半圆,自点A作半圆的切线AE,则tan∠CBE=.7.如图,⊙O是梯形ABCD的内切圆,AB∥DC,E、M、F、N分别是边AB、BC、CD、DA 上的切点.(1)求证:AB+CD=AD+BC;(2)求∠AOD的度数.8.如图,PA、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:(1)PA的长;(2)∠COD的度数.◆提升题1.P是⊙O外一点,PA、PB分别与⊙O相切于点A、B,点C是劣弧AB上任意一点,经过点C作⊙O的切线,分别交PA、PB于点D、E.若PA=4,则△PDE的周长是()A.4B.8C.12D.不能确定2.如图,△ABC中,∠A=60°,BC=6,它的周长为16.若⊙O与BC,AC,AB三边分别切于E,F,D点,则DF的长为()A.2B.3C.4D.63.如图,AB是⊙O的直径,C是AB延长线上的一点,CD是⊙O的切线,D为切点,过点B作⊙O的切线交CD于点E,若AB=CD=2,则CE=.4.如图所示,⊙D的半径为3,A是圆D外一点且AD=5,AB,AC分别与⊙D相切于点B,C.G是劣弧BC上任意一点,过G作⊙D的切线,交AB于点E,交AC于点F.(1)△AEF的周长是;(2)当G为线段AD与⊙D的交点时,连结CD,则五边形DBEFC的面积是.5.如图,AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,BO=6,CO=8.(1)判断△OBC的形状,并证明你的结论;(2)求BC的长;(3)求⊙O的半径OF的长.6.已知:如图△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于D,过D作⊙O的切线交BC于点E,EF⊥AB,垂足为F.(1)求证:DE=12 BC;(2)若AC=6,BC=8,求S△ACD:S△EDF的值.答案和解析◆基础题1.【答案】C解:∵PA、PB切⊙O于点A、B,CD切⊙O于点E,∴PA=PB=10,CA=CE,DE=DB,∴△PCD 的周长是PC+CD+PD=PC+AC+DB+PD=PA+PB=10+10=20.2.【答案】B解:连接OA,BO,∵∠AOB=2∠E=120°,∴∠OAP=∠OBP=90°,∴∠P=180°﹣∠AOB=60°.3.【答案】C解:如图;连接OA、OB,则∠OAP=∠OBP=90°,∴∠BOA=180°﹣∠P=110°,∴∠AEB=1 2∠AOB=55°;∵四边形AEBF是⊙O的内接四边形,∴∠AFB=180°﹣∠AEB=125°,①当C 点在优弧AB上运动时,∠BCA=∠AEB=55°;②当C点在劣弧AB上运动时,∠BCA=∠AFB=125°.4.【答案】B解:由题意可得圆外切四边形的两组对边和相等,所以四边形的周长=2×(7+10)=34.5.【答案】2解:∵AC、AP为⊙O的切线,∴AC=AP,∵BP、BD为⊙O的切线,∴BP=BD,∴BD=PB=AB ﹣AP=5﹣3=2.6.【答案】1解:∵PA、PB是⊙O的两条切线,∴∠APO=∠BPO=12∠APB,∠PAO=90°,∵∠APB=60°,∴∠APO=30°,∵PO=2,∴AO=1.7.【答案】6解:∵PA、PB都是⊙O的切线,且A、B是切点;∴PA=PB,即PB=6.8.【答案】8cm解:连接OD、OE,∵⊙O是Rt△ABC的内切圆,∴OD⊥AB,OE⊥BC,∵∠ABC=90°,∴∠ODB=∠DBE=∠OEB=90°,∴四边形ODBE是矩形,∵OD=OE,∴矩形ODBE是正方形,∴BD=BE=OD=OE=4cm,∵⊙O切AB于D,切BC于E,切MN于P,NP与NE是从一点出发的圆的两条切线,∴MP=DM,NP=NE,∴Rt△MBN的周长为:MB+NB+MN=MB+BN+NE+DM=BD+BE=4cm+4cm=8cm.9.解:∵PA、PB是⊙O的切线,切点分别是A、B,Q为⊙O上一点,过Q点作⊙O的切线,交PA、PB于E、F点,∴PA=PB,EA=EQ,FB=FQ,∵PA=8cm,∴△PEF的周长为:PE+EF+PF=PA+PB=8+8=16(cm).10.解:连接OC、OD.∵OA是⊙B的直径,∴∠OCA=∠ODA=90°,∴AC、AD都是⊙O 的切线.∴AD=AC=5.◆能力题1.【答案】D解:∵AB∥CD,∴∠ABC+∠BCD=180°,∵CD、BC,AB分别与⊙O相切于G、F、E,∴∠OBC =12∠ABC ,∠OCB =12∠BCD ,BE =BF ,CG =CF ,∴∠OBC +∠OCB =90°,∴∠BOC =90°,∴BC =22OB OC =10,∴BE +CG =10.2.【答案】D解:∵AE 与圆O 切于点F ,显然根据切线长定理有AF =AB =4,EF =EC ,设EF =EC =x ,则DE =4﹣x ,AE =4+x ,在三角形ADE 中由勾股定理得:(4﹣x )2+42=(4+x )2,∴x =1,∴CE =1,∴DE =4﹣1=3,∴S △ADE =AD •DE ÷2=3×4÷2=6.3.【答案】A解:∵∠1=60°,∠2=65°,∴∠ABC =180°﹣∠1﹣∠2=180°﹣60°﹣65°=55°,∴∠2>∠1>∠ABC ,∴AB >BC >AC ,∵CA ,CD 分别切圆O 1于A ,D 两点,CB 、CE 分别切圆O 2于B ,E 两点,∴AC =CD ,BC =CE ,∴AB >CE >CD .4.【答案】63解:∵∠CAD =60°,∴∠CAB =120°,∵AB 和AC 与⊙O 相切,∴∠OAB =∠OAC ,∴∠OAB =12∠CAB =60°,∵AB =3cm ,∴OA =6cm ,∴由勾股定理得OB =33cm ,∴光盘的直径63cm .5.【答案】40﹣533解:连接OD 、BD ,作DE ⊥AB ,∵BC 与水平面的夹角为60°,∴∠DBE =60°,∴∠BDE =30°,设BE =x ,则BD =2x ,∴由勾股定理得4x 2﹣x 2=25,解得x =533,∴OD =AE =40﹣533.6.【答案】25解:设BC 的中点为O ,连接AO ,交BE 于F .由于AB 、AE 分别切⊙O 于B 、E ,则AB =AE ,且∠BAF=∠EAF.又∵AF=AF,∴△ABF≌△AEF.∴AO垂直平分BE.在Rt△ABO中,BF⊥AO,则∠FBO=∠BAO,易知BO=2,AB=5,∴tan∠BAO=tan∠CBE=25.7.(1)证明:∵⊙O切梯形ABCD于E、M、F、N,由切线长定理:AE=AN,BE=BM,DF=DN,CF=CM,∴AE+BE+DF+CF=AN+BM+DN+CM,∴AB+DC=AD+BC;(2)解:连OE、ON、OM、OF,∵OE=ON,AE=AN,OA=OA,∴△OAE≌△OAN,∴∠OAE=∠OAN.同理,∠ODN=∠ODF.∴∠OAN+∠ODN=∠OAE+∠ODE.又∵AB∥DC,∠EAN+∠CDN=180°,∴∠OAN+∠ODN=12×180°=90°,∴∠AOD=180°﹣90°=90°.8.解:(1)∵CA,CE都是圆O的切线,∴CA=CE,同理DE=DB,PA=PB,∴三角形PDE 的周长=PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12,即PA的长为6;(2)∵∠P=60°,∴∠PCE+∠PDE=120°,∴∠ACD+∠CDB=360°﹣120°=240°,∵CA,CE是圆O的切线,∴∠OCE=∠OCA=12∠ACD;同理:∠ODE=12∠CDB,∴∠OCE+∠ODE=12(∠ACD+∠CDB)=120°,∴∠COD=180﹣120°=60°.◆提升题1.【答案】B解:根据题意画出图形,如图所示,由直线DA和直线DC为圆O的切线,得到AD=DC,同理,由直线EC和直线EB为圆O的切线,得到EC=EB,又直线PA和直线PB为圆O的切线,所以PA=PB=4,则△PDE的周长C=PD+DE+PE=PD+DC+EC+PE=PD+DA+EB+PE=PA+PB=4+4=8.2.【答案】A解:∵⊙O与BC,AC,AB三边分别切于E,F,D点,∴AD=AF,BE=BD,CE=CF,∵BC=BE+CE=6,∴BD+CF=6,∵AD=AF,∠A=60°,∴△ADF是等边三角形,∴AD=AF=DF,∵AB+AC+BC=16,BC=6,∴AB+AC=10,∵BD+CF=6,∴AD+AF=4,∵AD=AF=DF,∴DF=AF=AD=1 2×4=2.3.【答案】55 2 -解:∵CD是⊙O的切线,∴CD2=CB•CA,∵AB=CD=2,∴4=BC(BC+2),解得BC=﹣1+5,∵CD是⊙O的切线,BE为⊙O的切线,∴∠CBE=∠CDO=90°,∴△BCE∽△DCO,∴OD CD BE BC=,即12215CE=--+,解得,CE=552-.4.【答案】8;9解:(1)如图1所示:连接ED,DG,FD,CD,∵AB,AC分别与⊙D相切于点B,C,∴AB=AC,∠ABD=∠ACD=90°,∵⊙D的半径为3,A是圆D外一点且AD=5,∴AB==4,∵过G 作⊙D的切线,交AB于点E,交AC于点F,∴BE=EG,FG=FC,则△AEF的周长是:AE+EG+FG+AF=AB+AC=8.(2)如图2,AG=AD﹣DG=5﹣3=2.∵在△AEG和△ADB中,∠ABD=∠AGD=90°,∠BAD=∠EAG,∴△AEG∽△ADB,∴EG AGBD AB=,∴EG=32,∴EF=2EG=3,∴S△AEF=12EF•AG=12×3×2=3.又∵S四边形ABDC=2S△ABD=AB•BD=3×4=12,∴S五边形DBEFC=12﹣3=9.word 11 / 115.解:(1)△OBC 是直角三角形.证明:∵AB 、BC 、CD 分别与⊙O 相切于E 、F 、G ,∴∠OBE =∠OBF =12∠EBF ,∠OCG =∠OCF =12∠GCF ,∵AB ∥CD ,∴∠EBF +∠GCF =180°,∴∠OBF +∠OCF =90°,∴∠BOC =90°,∴△OBC 是直角三角形;(2)∵在Rt △BOC 中,BO =6,CO =8,∴BC =10;(3)∵AB 、BC 、CD 分别与⊙O 相切于E 、F 、G ,∴OF ⊥BC ,∴OF =6810BO CO BC ⋅⨯==4.8. 6.(1)证明:∵EC 、ED 都是⊙O 的切线,∴EC =ED ,∠ECD =∠EDC .∵∠EDC +∠EDB =90°,∠ECD +∠B =90°,∴∠EDB =∠B .∴ED =BE .∴DE =BE =EC .∴DE =12BC . (2)解:在Rt △ABC 中,AC =6,BC =8,则AB =10,根据射影定理可得:AD =AC 2÷AB =3.6,∴BD =BC 2÷AB =6.4,∴S △ACD :S △BCD =AD :BD =9:16,∵ED =EB ,EF ⊥BD ,∴S △EDF =12S △EBD ,同理可得S △EBD =12S △BCD ,∴S △EDF =14S △BCD ,∴S △ACD :S △EDF =94.。
九年级数学下册 3.7 切线长定理同步练习 (新版)北师大版

3.7切线长定理一、选择题1. 一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于 ( ) A .21 B .20 C .19 D .182. 如图,PA 、PB 分别切⊙O 于点A 、B ,AC 是⊙O 的直径,连结AB 、BC 、OP , 则与∠PAB 相等的角(不包括∠PAB 本身)有 ( ) A .1个 B .2个 C .3个 D .4个3. 如图,已知△ABC 的内切圆⊙O 与各边相切于点D 、E 、F ,则点O 是△DEF 的 ( )A .三条中线的交点B .三条高的交点C .三条角平分线的交点D .三条边的垂直平分线的交点4.△ABC 中,AB =AC ,∠A 为锐角,CD 为AB 边上的高,I 为△ACD 的内切圆圆心,则∠AIB 的度数是( )A .120°B .125°C .135°D .150°5.一个钢管放在V 形架内,右图是其截面图,O 为钢管的圆心.如果钢管的半径为25 cm ,∠MPN = 60 ,则OP =( )A .50 cmB .253cmC .3350cm D .503cm 6.如图1,PA 、PB 分别切圆O 于A 、B 两点,C 为劣弧AB 上一点,∠APB=30°,则∠ACB=( ).A .60°B .75°C .105°D .120°PB(1) (2)7.圆外一点P ,PA 、PB 分别切⊙O 于A 、B ,C 为优弧AB 上一点,若∠ACB=a ,则∠APB=( ) A .180°-a B .90°-a C .90°+a D .180°-2a 二、填空题8. 如图,在△ABC 中,5cm AB AC ==,cosB 35=.如果⊙O ,且经过点B 、C ,那么线段AO= cm .9.如图,PA 、PB 分别切⊙O 于点A 、B ,点E 是⊙O 上一点,且 60=∠AEB ,则=∠P __ ___度.10. 如图,AE 、AD 、BC 分别切⊙O 于点E 、D 、F ,若AD=20,则△ABC 的周长是 .11. 如图,PA 、PB 是⊙O 的两条切线,切点分别为点A 、B ,若直径AC= 12,∠P=60o,弦AB 的长为------.三、解答题:12. 如图,AE 、AD 、BC 分别切⊙O 于点E 、D 、F ,若AD=20,求△ABC 的周长.13. 如图,已知AB 为⊙O 的直径,AD 、BC 、CD 为⊙O 的切线,切点分别是A 、B 、E ,则有一下结论:(1)CO ⊥DO ;(2)四边形OFEG 是矩形.试说明理由.14. 如图,PA 、PB 是⊙O 的切线,A 、B 为切点,∠OAB =30°.(1)求∠APB 的度数; (2)当OA =3时,求AP 的长.15. 如图,在△ABC 中,已知∠ABC=90o,在AB 上取一点E ,以BE 为直径的⊙O 恰与AC 相切于点D ,若AE=2 cm ,AD=4 cm . (1)求⊙O 的直径BE 的长; (2)计算△ABC 的面积.参考答案1. C2. B (提示:②④错误)3. D (提示:AD=AF,BD=BE,CE=CF ∴周长=821218⨯+⨯=)4. C5. D6. C7.D8. A (提示:∠MPN=600可得∠OPM=300 可得OP=2OM=50)OB ,易得:∠ABC=∠AOB ∴cos ∠AOB=cos ∠35=OBOA =)os300=ABAC∴AB=10. ∠P=60011. 760(提示:连接ID,IF ∵∠DEF=520∴∠DIF=1040∵D 、F 是切点 ∴DI ⊥AB,IF ⊥AC∴∠ADI=∠AFI=900∴∠A=1800-1040=760)12. 52 (提示:AB+CD=AD+BC)13. 1150(提示:∵∠A=500∴∠ABC+∠ACB=1300∵OB,OC 分别平分∠ABC,∠ACB ∴∠OBC+∠OCB=650∴∠BOC=1800-650=1150)14. 解:∵AD,AE 切于⊙O 于D,E ∴AD=AE=20 ∵AD,BF 切于⊙O 于D,F ∴BD=BF 同理:CF=CE∴C △ABC =AB+BC+AC=AB+BF+FC+AC=AB+BD+EC+AC=AD+AE=40 14 解:(1)∵在△ABO 中,OA =OB ,∠OAB =30°∴∠AOB =180°-2×30°=120°∵PA 、PB 是⊙O 的切线∴OA ⊥PA ,OB ⊥PB .即∠OAP =∠OBP =90° ∴在四边形OAPB 中,∠APB =360°-120°-90°-90°=60°.(2)如图①,连结OP∵PA 、PB 是⊙O 的切线∴PO 平分∠APB ,即∠APO =12∠APB =30°又∵在Rt △OAP 中,OA =3, ∠APO =30°∴AP =tan 30OA°=15 解:(1)连接OD ∴OD ⊥AC ∴△ODA 是Rt △设半径为r ∴AO=r+2 ∴(r+2)2—r 2=16 解之得:r=3 ∴BE=6(2) ∵∠ABC=900∴OB ⊥BC ∴BC 是⊙O 的切线 ∵CD 切⊙O 于D ∴CB=CD 令CB=x∴AC=x+4,BC=4,AB=x ,AB=8 ∵2228(4)x x +=+ ∴6x = ∴S △ABC =186242⨯⨯=。
3.7切线长定理-2020-2021学年北师大版九年级数学下册同步测试 (1)
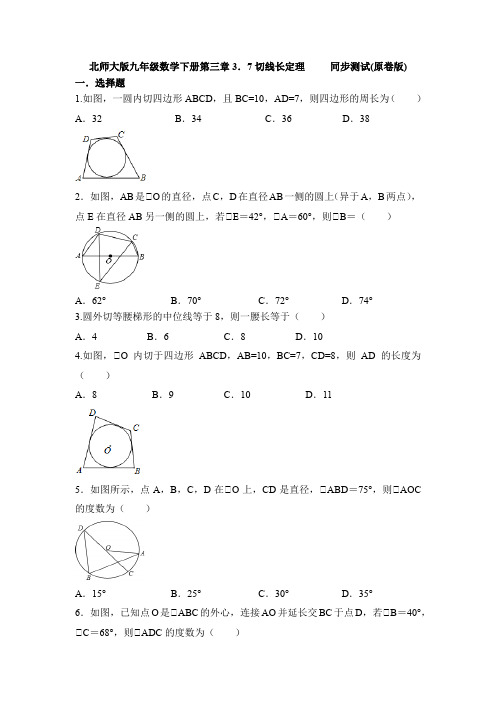
北师大版九年级数学下册第三章3.7切线长定理同步测试(原卷版)一.选择题1.如图,一圆内切四边形ABCD,且BC=10,AD=7,则四边形的周长为()A.32B.34C.36D.382.如图,AB是⊙O的直径,点C,D在直径AB一侧的圆上(异于A,B两点),点E在直径AB另一侧的圆上,若⊙E=42°,⊙A=60°,则⊙B=()A.62°B.70°C.72°D.74°3.圆外切等腰梯形的中位线等于8,则一腰长等于()A.4 B.6 C.8 D.104.如图,⊙O内切于四边形ABCD,AB=10,BC=7,CD=8,则AD的长度为()A.8 B.9 C.10 D.115.如图所示,点A,B,C,D在⊙O上,CD是直径,⊙ABD=75°,则⊙AOC 的度数为()A.15°B.25°C.30°D.35°6.如图,已知点O是⊙ABC的外心,连接AO并延长交BC于点D,若⊙B=40°,⊙C=68°,则⊙ADC的度数为()A.52°B.58°C.60°D.62°7.如图,从⊙O外一点P引⊙O的两条切线PA,PB,切点分别为A,B.如果⊙APB=60°,PA=8,那么弦AB的长是()A.4 B.8 C.4√3D.8√38.如图,AB是⊙O的直径,DB,DE分别切⊙O于点B、C,若⊙ACE=20°,则⊙D的度数是()A.40°B.50°C.60°D.70°9.如图,⊙O为⊙ABC的内切圆,AC=10,AB=8,BC=9,点D,E分别为BC,AC上的点,且DE为⊙O的切线,则⊙CDE的周长为()A.9 B.7 C.11 D.810.如图,PA、PB是⊙O的两条切线,切点是A、B.如果OP=4,PA=,那么⊙AOB等于()A.90° B.100° C.110° D.120°11.下列给定的三点能确定一个圆的是()A.线段AB的中点C及两个端点B.角的顶点及角的边上的两点C.三角形的三个顶点D.矩形的对角线交点及两个顶点12.如图,PA为⊙O的切线,A为切点,PBC是过圆心O的割线,PA=10cm,PB=5cm,则弦AC的长是()cm.A.15B.10C.3D.6二.填空题13.如图,PA、PB分别切圆O于A、B,并与圆O的切线,分别相交于C、D,已知⊙PCD的周长等于10cm,则PA= cm.14.已知半径为10的⊙O中,弦,弦AC=10,则⊙BAC的度数是为.15.如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于C,D,若⊙O的半径为r,⊙PCD的周长等于3r,则tan 12⊙APB的值是16.如图,⊙O中弦AB,CD相交于点P,已知AP=3,BP=2,CP=1,则DP=.17.平面直角坐标系内的三个点A(1,﹣3)、B(0,﹣3)、C(2,﹣3),确定一个圆,(填“能”或“不能”).18.如图,在Rt⊙ABC中,⊙C=90°,AC=8,点D在边BC上,CD=6,BD =10.点P是线段AD上一动点,当半径为4的⊙P与⊙ABC的一边相切时,AP 的长为.三.解答题19.如图,AB为⊙O的直径,点C在AB的延长线上,CD、CE分别与⊙O相切于点D、E,若AD=2,⊙DAC=⊙DCA,求CE.20.已知在⊙ABC中,AB=BC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED.(1)求证:ED=DC;(2)若CD=6,EC=4,求AB的长.21.如图,⊙O与⊙ABC中AB、AC的延长线及BC边相切,且⊙ACB=90°,⊙A,⊙B,⊙C所对的边长依次为3,4,5,求⊙O的半径.22.如图,一段圆弧与长度为1的正方形网格的交点是A、B、C.(1)请完成以下操作:⊙以点O为原点,垂直和水平方向为轴,网格边长为单位长,建立平面直角坐标系;⊙根据图形提供的信息,标出该圆弧所在圆的圆心D,并连接AD、CD;(2)请在(1)的基础上,完成下列填空:⊙D的半径为;点(6,﹣2)在⊙D;(填“上”、“内”、“外”)⊙ADC的度数为.23.如图,在⊙ABCD中,⊙BAD为钝角,且AE⊙BC,AF⊙CD.(1)求证:A、E、C、F四点共圆;(2)设线段BD与(1)中的圆交于M、N.求证:BM=ND.24.如图⊙,直线y=-34x+3与x轴相交于点A,与y轴相交于点B,点C(m,n)是第二象限内一点,以点C为圆心的圆与x轴相切于点E,与直线AB相切于点F.(1)当四边形OBCE是矩形时,求点C的坐标;(2)如图⊙,若⊙C与y轴相切于点D,求⊙C的半径.北师大版九年级数学下册第三章3.7切线长定理同步测试(原卷版)一.选择题1.如图,一圆内切四边形ABCD,且BC=10,AD=7,则四边形的周长为()A.32 B.34 C.36D.38解:由题意可得圆外切四边形的两组对边和相等,所以四边形的周长=2×(7+10)=34.故选:B.2.如图,AB是⊙O的直径,点C,D在直径AB一侧的圆上(异于A,B两点),点E在直径AB另一侧的圆上,若⊙E=42°,⊙A=60°,则⊙B=()A.62°B.70°C.72°D.74°解:连接AC.⊙⊙DAB=60°,⊙DAC=⊙E=42°,⊙⊙CAB=60°﹣42°=18°,⊙AB是直径,⊙⊙ACB=90°,⊙⊙B=90°﹣18°=72°,故选:C.3.圆外切等腰梯形的中位线等于8,则一腰长等于()A.4 B.6 C.8 D.10 解:如图,设圆的外切梯形ABCD,切点分别为E、H、N、中位线为MN,⊙MN=12(AB+CD),根据切线长定理得:DE=DH,CF=CH,并且等腰梯形和圆都是轴对称图形,⊙CD=DH+CH=DE+CF=12(AB+CD),⊙CD=MN,而MN=8,⊙CD=8.故选C.4.如图,⊙O内切于四边形ABCD,AB=10,BC=7,CD=8,则AD的长度为()A.8 B.9 C.10 D.11解:⊙⊙O内切于四边形ABCD,⊙AD+BC=AB+CD,⊙AB=10,BC=7,CD=8,⊙AD+7=10+8,解得:AD=11.故选:D.5.如图所示,点A,B,C,D在⊙O上,CD是直径,⊙ABD=75°,则⊙AOC 的度数为()A.15°B.25°C.30°D.35°解:连接AC,⊙⊙ABD=75°,⊙⊙DCA=75°,⊙OA=OC,⊙⊙AOC=180°﹣2×75°=30°,故选:C.6.如图,已知点O是⊙ABC的外心,连接AO并延长交BC于点D,若⊙B=40°,⊙C=68°,则⊙ADC的度数为()A.52°B.58°C.60°D.62°解:以O为圆心,OA长为半径画圆,⊙点O是⊙ABC的外心,⊙B,C,A三点共圆,延长AD交圆与点E,连接CE,⊙⊙ACE=90°,⊙⊙B=40°,⊙C=68°,⊙⊙E=⊙B=40°,⊙ECD=90°﹣68°=22°,⊙⊙ADC=40°+22°=62°,故选:D.7.如图,从⊙O外一点P引⊙O的两条切线PA,PB,切点分别为A,B.如果⊙APB=60°,PA=8,那么弦AB的长是()A.4 B.8 C.4√3D.8√3解:⊙PA、PB都是⊙O的切线,⊙PA=PB,又⊙⊙P=60°,⊙⊙PAB是等边三角形,即AB=PA=8,故选B.8.如图,AB是⊙O的直径,DB,DE分别切⊙O于点B、C,若⊙ACE=20°,则⊙D的度数是()A.40°B.50°C.60°D.70°解:连OC,如图,⊙DB、DE分别切⊙O于点B、C,⊙⊙OBD=⊙OCD=⊙OCE=90°,⊙⊙ACE=20°,⊙⊙OCA=90°﹣20°=70°,⊙OC=OA,⊙⊙OAC=⊙OCA=70°,⊙⊙BOC=2×70°=140°,⊙⊙D=360°﹣90°﹣90°﹣140°=40°.故选:A.9.如图,⊙O为⊙ABC的内切圆,AC=10,AB=8,BC=9,点D,E分别为BC,AC上的点,且DE为⊙O的切线,则⊙CDE的周长为()A.9 B.7 C.11 D.8解:如图:设AB,AC,BC和圆的切点分别是P,N,M,CM=x,根据切线长定理,得CN=CM=x,BM=BP=9-x,AN=AP=10-x.则有9-x+10-x=8,解得:x=5.5.所以⊙CDE的周长=CD+CE+QE+DQ=2x=11.故选:C.10.如图,PA、PB是⊙O的两条切线,切点是A、B.如果OP=4,PA=,那么⊙AOB等于()A.90° B.100° C.110° D.120°11.下列给定的三点能确定一个圆的是()A.线段AB的中点C及两个端点B.角的顶点及角的边上的两点C.三角形的三个顶点D.矩形的对角线交点及两个顶点解:A、线段AB的端点A、B和线段AB的中点C不能确定一个圆,故本选项错误;B、当角的两边上的一个点或两个点和角的顶点重合时就不能确定一个圆,故本选项错误;C、经过三角形的三个顶点作圆,有且只有一个圆,故本选项正确;D、矩形的对角线交点及两个顶点,如果这三个点在一条直线上,就不能确定一个圆,故本选项错误;故选:C.12.如图,PA为⊙O的切线,A为切点,PBC是过圆心O的割线,PA=10cm,PB=5cm,则弦AC的长是()cm.A.15B.10C.3D.6解:连接AB,根据切割线定理有,PA2=PB•PC,⊙102=5×(5+BC),解得BC=15,又⊙⊙PAB=⊙PCA,⊙APB=⊙CPA,⊙⊙APB⊙⊙CPA,⊙PA:AB=PC:AC,⊙10:AB=20:AC⊙;⊙BC是直径,⊙AB2+AC2=BC2,⊙AB2+AC2=152⊙;⊙⊙联立解得AC=6.故选:D.二.填空题13.如图,PA、PB分别切圆O于A、B,并与圆O的切线,分别相交于C、D,已知⊙PCD的周长等于10cm,则PA= cm.解:如图,设DC与⊙O的切点为E;⊙PA、PB分别是⊙O的切线,且切点为A、B;⊙PA=PB;同理,可得:DE=DA,CE=CB;则⊙PCD的周长=PD+DE+CE+PC=PD+DA+PC+CB=PA+PB=10(cm);⊙PA=PB=5cm,故答案为:5.14.已知半径为10的⊙O中,弦,弦AC=10,则⊙BAC的度数是为15°或105°.解:连接OC,OA,OB.⊙OC=OA=AC=10⊙⊙OAC是等边三角形,⊙⊙CAO=60°,⊙OA=OB=10,AB=10,⊙OA2+OB2=50=AB2,⊙⊙OAB是等腰直角三角形,⊙OAB=45°,点C的位置有两种情况,如图1时,⊙BAC=⊙CAO+⊙OAB=60°+45°=105°;如图2时,⊙BAC=⊙CAO﹣⊙OAB=60°﹣45°=15°.故答案为15°或105°.15.如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于C,D,若⊙O的半径为r,⊙PCD的周长等于3r,则tan 12⊙APB的值是解:连接PO,AO,⊙PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于C,D,⊙⊙APO=⊙BPO,AC=EC,DE=BD,PA=PB,⊙PA+PB=⊙PCD的周长=3r,⊙PA=PB=1.5r,⊙tan 12⊙APB=AO: PA =r :1.5r =23,故答案为:23.16.如图,⊙O中弦AB,CD相交于点P,已知AP=3,BP=2,CP=1,则DP =6.解:由相交弦定理得,AP•BP=CP•DP,则DP==6,故答案为:6.17.平面直角坐标系内的三个点A(1,﹣3)、B(0,﹣3)、C(2,﹣3),不能确定一个圆,(填“能”或“不能”).解:⊙B(0,﹣3)、C(2,﹣3),⊙BC⊙x轴,而点A(1,﹣3)与C、B共线,⊙点A、B、C共线,⊙三个点A(1,﹣3)、B(0,﹣3)、C(2,﹣3)不能确定一个圆.故答案为:不能.18.如图,在Rt⊙ABC中,⊙C=90°,AC=8,点D在边BC上,CD=6,BD =10.点P是线段AD上一动点,当半径为4的⊙P与⊙ABC的一边相切时,AP 的长为5或或4.解:⊙在Rt⊙ABC中,⊙C=90°,AC=8,BD+CD=16,⊙AB=8,在Rt⊙ADC中,⊙C=90°,AC=8,CD=6,⊙AD=10,当⊙P于BC相切时,点P到BC的距离=4,过P作PH⊙BC于H,则PH=4,⊙⊙C=90°,⊙AC⊙BC,⊙PH⊙AC,⊙⊙DPH⊙⊙DAC,⊙=,⊙=,⊙PD=5,⊙AP=5;当⊙P于AB相切时,点P到AB的距离=4,过P作PG⊙AB于G,则PG=4,⊙AD=BD=10,⊙⊙PAG=⊙B,⊙⊙AGP=⊙C=90°,⊙⊙AGP⊙⊙BCA,⊙=,⊙=,⊙AP=4,当半径为4的⊙P与⊙ABC的AC边相切,过P作PM⊙AC于M,⊙PM=4,⊙,⊙=,⊙AP=,综上所述,AP的长为5或或4,故答案为:5或或4.三.解答题19.如图,AB为⊙O的直径,点C在AB的延长线上,CD、CE分别与⊙O相切于点D、E,若AD=2,⊙DAC=⊙DCA,求CE.解:⊙CD、CE分别与⊙O相切于点D、E,⊙CD=CE,⊙⊙DAC=⊙DCA,⊙AD=CD,⊙AD=CE,⊙AD=2,⊙CE=2.故答案为:2.20.已知在⊙ABC中,AB=BC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED.(1)求证:ED=DC;(2)若CD=6,EC=4,求AB的长.(1)证明:⊙A、B、E、D四点共圆,⊙⊙DEC=⊙A,⊙AB=BC,⊙⊙A=⊙C,⊙⊙DEC=⊙C,⊙ED=DC;(2)解:连接BD,⊙AB为⊙O的直径,⊙⊙ADB=90°,即BD⊙AC,⊙AB=BC,CD=6,⊙AD=DC=6,⊙AC=12,⊙⊙A=⊙DEC,⊙C=⊙C,⊙⊙DEC⊙⊙BAC,⊙=,⊙=,解得:BC=6,⊙AB=BC,⊙AB=6.21.如图,⊙O与⊙ABC中AB、AC的延长线及BC边相切,且⊙ACB=90°,⊙A,⊙B,⊙C所对的边长依次为3,4,5,求⊙O的半径.解:连接OD、OE,⊙⊙O与⊙ABC中AB、AC的延长线及BC边相切,⊙AF=AD,BE=BF,CE=CD,OD⊙AD,OE⊙BC,⊙⊙ACB=90°,⊙四边形ODCE是正方形,设OD=r,则CD=CE=r,⊙BC=3,⊙BE=BF=3-r,⊙AB=5,AC=4,⊙AF=AB+BF=5+3-r,AD=AC+CD=4+r,⊙5+3-r=4+r,r=2,则⊙O的半径是2.故答案为:2.22.如图,一段圆弧与长度为1的正方形网格的交点是A、B、C.(1)请完成以下操作:⊙以点O为原点,垂直和水平方向为轴,网格边长为单位长,建立平面直角坐标系;⊙根据图形提供的信息,标出该圆弧所在圆的圆心D,并连接AD、CD;(2)请在(1)的基础上,完成下列填空:⊙D的半径为2;点(6,﹣2)在⊙D上;(填“上”、“内”、“外”)⊙ADC的度数为90°.解:(1)⊙平面直角坐标系如图所示:⊙圆心点D,如图所示;(2)⊙D的半径=AD==2,⊙点(6,﹣2)到圆心D的距离==2=半径,⊙点(6,﹣2)在⊙D上.⊙D(2,0),C(6,2),A(0,4),⊙OD=CE,OA=DE,⊙⊙AOD=⊙DEC,⊙⊙AOD⊙⊙DEC(SAS),⊙⊙OAD=⊙EDC,⊙⊙OAD+⊙ADO=90°,⊙⊙ADC=90°,故答案为:2,上,90°.23.如图,在⊙ABCD中,⊙BAD为钝角,且AE⊙BC,AF⊙CD.(1)求证:A、E、C、F四点共圆;(2)设线段BD与(1)中的圆交于M、N.求证:BM=ND.证明:(1)⊙AE⊙BC,AF⊙CD,⊙⊙AEC=⊙AFC=90°.⊙⊙AEC+⊙AFC=180°.⊙A、E、C、F四点共圆;(2)由(1)可知,⊙AEC=90°,则AC是直径,设AC、BD相交于点O;⊙ABCD是平行四边形,⊙O为圆心,OB=OD,⊙OM=ON,⊙OB﹣OM=OD﹣ON,⊙BM=DN.24.如图⊙,直线y=-34x+3与x轴相交于点A,与y轴相交于点B,点C(m,n)是第二象限内一点,以点C为圆心的圆与x轴相切于点E,与直线AB相切于点F.(1)当四边形OBCE是矩形时,求点C的坐标;(2)如图⊙,若⊙C与y轴相切于点D,求⊙C的半径.解:(1)连接CB、CE、CF、AC,则⊙BAC=⊙EAC=⊙BCA,⊙AB=BC=5,CE=OB=3,⊙C的坐标为(-5,3)(2)连接CD、CE、CF,⊙⊙CEO=⊙CDO=90°,又⊙DOE=90°,⊙四边形CEOD为矩形,又CE=CD,得正方形CEOD,⊙CE=DO=R,又BO=3,⊙BD=3-R,⊙BF、BD为切线,⊙FB=BD=3-R,同理AE=AF,即R+4=3-R+5,⊙R=2.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(二十七)
[第三章*7 切线长定理]
一、选择题
1.2017·红桥区期末如图K-27-1,PA,PB分别切⊙O于点A,B,PA=10,CD切⊙O 于点E,与PA,PB分别交于C,D两点,则△PCD的周长是链接听课例1归纳总结( )
图K-27-1
A.10 B.18 C.20 D.22
2.如图K-27-2,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O与AB,BC,AC分别切于点D,E,F,则AF的长为()
图K-27-2
A.5 B.10 C.7.5 D.4
3.已知⊙O的半径是4,P是⊙O外一点,且PO=8,从点P引⊙O的两条切线,切点分别是A,B,则AB的长为()
A.4 B.4 2 C.4 3 D.2 3
4.如图K-27-3,PA切⊙O于点A,PB切⊙O于点B,OP交⊙O于点C,下列结论中,错误的是( )
链接听课例2归纳总结
图K-27-3
A.∠1=∠2 B.PA=PB
C.AB⊥OP D.PA2=PC·PO
5.如图K-27-4,AB为半圆O的直径,AD,BC分别切⊙O于A,B两点,CD切⊙O于点E,连接OD,OC.下列结论:①∠DOC=90°;②AD+BC=CD;③S△AOD∶S△BOC=AD2∶AO2;
④OD∶OC=DE∶EC;⑤OD2=DE·CD.其中正确的有( )
图K-27-4
A.2个 B.3个
C.4个 D.5个
二、填空题
6.如图K-27-5,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为________.
图K-27-5
7.2017·昌平区期末如图K-27-6所示,在Rt△ABC中,∠C=90°,AC长为8,BC 长为15,则△ABC的内切圆⊙O的直径是________.
图K-27-6
8.如图K-27-7,P是⊙O的直径AB的延长线上的一点,PC,PD分别切⊙O于点C,D.若PA=6,⊙O的半径为2,则∠CPD=________°.
图K-27-7
9.如图K-27-8所示,已知PA,PB,EF分别切⊙O于点A,B,D,若PA=15 cm,则△PEF的周长是________ cm;若∠P=50°,则∠EOF=________°.链接听课例1归纳总结
图K-27-8
10.如图K-27-9所示,⊙O与△ABC中AB,AC的延长线及BC边相切,且∠ACB=90°,∠A,∠ABC,∠ACB所对的边长依次为3,4,5,则⊙O的半径是________.
图K-27-9
三、解答题
11.如图K-27-10,PA,PB分别切⊙O于点A,B,连接PO与⊙O相交于点C,连接AC,BC.求证:AC=BC.
链接听课例2归纳总结
图K-27-10
12.2017·孝感模拟如图K-27-11,直线AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,OB=6 cm,OC=8 cm.
求:(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.
链接听课例1归纳总结。
