5.2不等式和绝对值不等式(一)课件(人教A版选修4-5)
合集下载
5.2绝对值三角不等式A 课件(人教A版选修4-5)

值。这个问题可以应用绝对值不等式的性质来解。
解:设生活区应该建于公路路牌的第xkm处,两个施工队 每天往返的路程之和为S(x)km,则 因为
S x 2 x 10 x 20
x 10 x 20 x 10 20 x 10
当且仅当 解得
x 10 20 x 0时取等号。
b
x
向量形式的不等式
ab a b
当且仅当
a
与
b 同向 时,等号成立。
由于定理1与三角形之间的这种联系,我们称其中的不等 式为绝对值三角不等式。
知识推广
如果将定理1中的实数a , b改为复数 不等式仍成立吗?
z1 , z2
,
z1 z2 z1 z2
练习
例2
两个施工队分别被安排在公路沿线的两个地点施工, 这两个地点分别位于公路路牌的第10km和第20km 处。现要在公路沿线建两个施工队的共同临时生活区, 每个施工队每天在生活区和施工地点之间往返一次。 要使两个施工队每天往返的路程之和最小,生活区应 该建于何处?
分析:如果生活区建于公路路牌的第xkm处,两个施工队每天往返的路程 之和为S(x)km,那么 S x 2 x 10 x 20 于是,上面的问题就化 归为数学问题:当x取何值时,函数 S x 2 x 10 x 20 取得最小
2、求证:(1) x a
(2) x a
知识应用:
例1 已知
0, x a , y b ,
2x 3 y 2a 3b 5
求证 练习: 设
M , 0, x a , y b , 2 2 a M, y M
第一讲 不等式和绝对值不等式 知识归纳 课件(人教A选修4-5)

A.必要不充分条件
C.充分必要条件 [解析] [答案] 时,则可能有a>b且c>d. A
B.充分不必要条件
D.既不充分也不必要条件
易得a>b且c>d时必有a+c>b+d.若a+c>b+d
利用基本不等式求最值问题一般有两种类型:①和为 定值时, 积有最大值;②积为定值时,和有最小值,在具 体应用基本不等式解题时, 一定要注意适用的范围和条 件:“一正、二定、三相等”. [例 2] ________. y2 x,y,z∈R+,x-2y+3z=0, xz的最小值为
3 1 1 1 1 1 + ≥3 ··. b3 c3 a3 b3 c3 1 1 1 3 即 3+ 3+ 3≥abc. a b c 1 1 1 3 所以 3+ 3+ 3+abc≥abc+abc, a b c 3 而abc+abc≥2 3 abc=2 3. abc·
1 1 1 所以 3+ 3+ 3+abc≥2 3. a b c
2|≤1+2|y-2|+2≤5,即|x-2y+1|的最大值为5.
答案:5
3.(2011· 陕西高考)若不等式|x+1|+|x-2|≥a对任意x∈R 恒成立,则a的取值范围是________.
解析:令 f(x)=|x+1|+|x-2|= -2x+1x≤-1, 3-1<x<2, 2x-1x≥2, ∴f(x)≥3. ∵|x+1|+|x-2|≥a 对任意 x∈R 恒成立,∴a≤3.
考情分析
从近两年的高考试题来看,绝对值不等式主要考查 解法及简单的应用,题目难度中档偏下,着重考查学生 的分类讨论思想及应用能力.
解绝对值不等式的关键是去掉绝对值符号,化成不
含绝对值的不等式,其一是依据绝对值的意义;其二是 先令每一个绝对值等于零,找到分界点,通过讨论每一 区间内的代数式的符号去掉绝对值.
高中数学 第一讲 不等式和绝对值不等式 一 不等式 1 不等式的基本性质课件 新人教A版选修4-5

探究二 不等式性质的简单应用
[例 2] 若 a,b,c∈R,a>b,则下列不等式恒成立的是( )
A.1a<1b,
B.a2>b2
C.c2+a 1>c2+b 1
D.a|c|>b|c|
[解析] 选项 A,还需有 ab>0 这个前提条件;选项 B,当 a,b 都为负数或一正
一负时都有可能不成立,如 2>-3,但 22>(-3)2 不正确;选项 C,c2+1 1>0,因而
)
A.2 x
B.x+1
1 C.1-x
D.无法确定
解析:∵0<x<1,x+1-2 x=( x-1)2>0, ∴x+1>2 x. 又1-1 x-(x+1)=1-x2x>0,
∴1-1 x>x+1. 答案:C
∴2 x,x+1,1-1 x三个数中最大的是1-1 x.
4.已知 a+b>0,则ba2+ab2与1a+1b的大小关系是________. 解析:ba2+ab2-1a+1b=a-b2 b+b-a2 a =(a-b)b12-a12=a+ba2ba2-b2. ∵a+b>0,(a-b)2≥0.
探究一 作差法比较大小 [例 1] 若 x∈R,试比较(x+1)x2+x2+1 与x+12(x2+x+1)的大小.
[解析] ∵(x+1)x2+x2+1=(x+1)x2+x+1-x2 =(x+1)(x2+x+1)-x2(x+1). x+12(x2+x+1)=x+1-12(x2+x+1) =(x+1)(x2+x+1)-12(x2+x+1). ∴(x+1)x2+x2+1-x+12(x2+x+1)
=(x+1)(x2+x+1)-x2(x+1)-(x+1)(x2+x+1)+12(x2+x+1) =12(x2+x+1)-12(x2+x) =12>0. ∴(x+1)x2+x2+1>x+12(x2+x+1).
第一讲《_不等式和绝对值不等式》课件(新人教选修4-5)[1].
![第一讲《_不等式和绝对值不等式》课件(新人教选修4-5)[1].](https://img.taocdn.com/s3/m/65359cec81c758f5f61f67e2.png)
第一讲 不等式和绝对值不等式 1、不等式
1、不等式的基本性质:
a a b, b c ①、对称性: b b a 传递性:_________ a c
②、 a b, c R ,a+c>b+c
③、a>b, c 0 , 那么ac>bc;
a>b,
c 0 ,那么ac<bc
a b
两个正数的算术平均不小于它们的几何平均。
例3 求证:(1)在所有周长相同的矩形中,正方形的面 积最大;(2)在所有面积相同的矩形中,正方形的周长 最短。
结论:已知x, y都是正数。(1)如果积xy是定值p, p 那么当x=y时,和x+y有最小值2 ;(2)如果 和x+y是定值s,那么当x=y时,积xy有最大值 1 2 s 4
a b (1)若c>a>b>0,则 (真命题) c a c b 1 1 (2)若a>b, ,则a>0,b&l-4≤f(1)≤-1,-1≤f(2)≤5, 求f(3)的取值范围。 f(3)的取值范围是[-1, 20]
例6、已知a>0,a2-2ab+c2 =0,bc>a2,试比较a、b、c 的大小。 解:因为bc>a2>0,所以b、c同号;又a2+c2=2ab>0,且
F
补充例题 已知a,b (0,+),且a+b=1,求证: 1 (1)a b ; 2 1 1 (2) 2 2 8; a b 1 2 1 2 25 (3)(a+ ) (b ) ; a b 2 1 1 25 (4)(a+ )(b ) . a b 4
2 2
课堂练习:课本P10第5题、第6题、第9题
例4
1、不等式的基本性质:
a a b, b c ①、对称性: b b a 传递性:_________ a c
②、 a b, c R ,a+c>b+c
③、a>b, c 0 , 那么ac>bc;
a>b,
c 0 ,那么ac<bc
a b
两个正数的算术平均不小于它们的几何平均。
例3 求证:(1)在所有周长相同的矩形中,正方形的面 积最大;(2)在所有面积相同的矩形中,正方形的周长 最短。
结论:已知x, y都是正数。(1)如果积xy是定值p, p 那么当x=y时,和x+y有最小值2 ;(2)如果 和x+y是定值s,那么当x=y时,积xy有最大值 1 2 s 4
a b (1)若c>a>b>0,则 (真命题) c a c b 1 1 (2)若a>b, ,则a>0,b&l-4≤f(1)≤-1,-1≤f(2)≤5, 求f(3)的取值范围。 f(3)的取值范围是[-1, 20]
例6、已知a>0,a2-2ab+c2 =0,bc>a2,试比较a、b、c 的大小。 解:因为bc>a2>0,所以b、c同号;又a2+c2=2ab>0,且
F
补充例题 已知a,b (0,+),且a+b=1,求证: 1 (1)a b ; 2 1 1 (2) 2 2 8; a b 1 2 1 2 25 (3)(a+ ) (b ) ; a b 2 1 1 25 (4)(a+ )(b ) . a b 4
2 2
课堂练习:课本P10第5题、第6题、第9题
例4
高中数学新人教A版选修4-5课件:第一讲不等式和绝对值不等式1.1.1不等式的基本性质

探究四
探究一不等式的基本性质
对于考查不等式的基本性质的选择题,解答时,一是利用不等式的相关
性质,其中,特别要注意不等号变号的影响因素,如数乘、取倒数、开方、平
方等;二是对所含字母取特殊值,结合排除法去选正确的选项,这种方法一般
要注意选取的值应具有某个方面的代表性,如选取 0、正数、负数等.
J 基础知识 Z 重点难点
几乎都有类似的前提条件,但结论会根据不同的要求有所不同,因而这需要
根据本题的四个选项来进行判断.选项 A,还需有 ab>0 这个前提条件;选项
B,当 a,b 都为负数时不成立,或一正一负时可能也不成立,如 2>-3,但 22>(-3)2
1
a
b
不正确;选项 C,c2+1>0,由 a>b 就可知c2+1 > c2 +1,故正确;选项 D,当 c=0 时不
A.P≥Q
B.P>Q
C.P≤Q
1
−
a+1+ a
解析:P-Q=( a + 1 − a)-( a − a-1)=
a-1- a+1
=
D.P<Q
.
( a+1+ a)( a+ a-1)
∵a≥1,∴ a-1 < a + 1,即 a-1 − a + 1<0.
又∵ a + 1 + a>0, a + a-1>0,
a-1- a+1
格依据不等式的性质和运算法则进行运算,是解答此类问题的基础.在使用
不等式的性质中,如果是由两个变量的范围求其差的范围,一定不能直接作
第一讲 不等式和绝对值不等式 章末复习方案 课件(人教A选修4-5)

48×4 (2)每批去 x 名同学,共需去 x 批, 总开支又分为:①买卡所需费用 240x,②包车所需费用 48×4 x ×40. 48×4 ∴y=240x+ x ×40(0<x≤48,x∈Z). 32 ∴y=240(x+ x )≥240×2 32 x× x =1 920 2,
32 当且仅当 x= x ,即 x=4 2时取等号. 但 0<x≤48,x∈Z,
x+y 1 1 3 3 解析:可以代入 x= ,y= ,验证 = ,2xy= ,显然 4 4 2 2 8 y+x x<2xy< <y. 2 答案:D
2.若1<a<3,-4<b<2,则a-|b|的取值范围是 ) A.(-1,3) C.(-3,3) ∴-4<-|b|≤0. 又1<a<3, ∴-3<a-|b|<3. 答案:C B.(-3,6) D.(1,4)
[答案] C
3.解决实际问题 由于受算术平均与几何平均定理求最值的约束条件的限 制,在求最值时常常需要对解析式进行合理的变形.对于一些 分式结构的函数,当分子中变量的次数不小于分母中变量的次 数时,通常采用分离变量(或常数)的方法,拼凑出类似函数 y= a x+x的结构,然后用基本不等式(符合条件)或单调性求最值.这 种变形的技巧经过适当的强化训练,是可以较容易掌握的.
法二:令 y=|x-4|+|3-x|. x≥4, 2x-7, 则 y=1, 3<x<4, -2x+7, x≤3. 作出图象如图,由图象观察可知,要使不等式|x-4|+|3 -x|<a 的解集为空集,显然 a≤1.
一、选择题 1.已知 y>x>0,且 x+y=1,那么 x+y A.x< <y<2xy 2 x+y B.2xy<x< <y 2 x+y C.x< <2xy<y 2 x+y D.x<2xy< <y 2 ( )
人教A版高中数学选修4-5第一讲二绝对值不等式上课课件

证明
3x 2 y 3a 3b 3 x a 2 y b
2 xa 3 yb
3 2 5
所以:3x 2 y 3a 2b 5 .
例2
两个施工队分别被安排在公路沿线的两 个地点施工,这两个地点分别位于公路路碑 的第10km和第20km处。现要在公路沿线建两 个施工队的共同临时生活区,每个施工队每 天在生活区和施工区地点之间往返一次。要 使两个施工队每天往返的路程之和最小,生 活区应该建在何处?
分析
本题是绝对值不等式的应用,第一把 实际问题划归为数学问题,即归结为求解 形如y x a x b 的函数的极值问题, 这类问题借助于绝对值三角不等式解答。
解:设生活区建于公路路碑的第xkm处,两个施 工队每天往返的路程之和为S(x)km,
则S x 2 x 10 x 20 .
因 :x 10 x 20 x 10 20 x 10, 且 x 1020 x 0 取等 。
因此:a b a b .
其几何意义是三角形的两边之和大于 第三边(如下图)。
x
a+b b
由此可称 定理1为绝 对值三角
不等式
a
y
0
(2)当向量a,b共线时,分以下两种情况: 如果向量a,b方向相同时,a b a b ; 如果向量a,b方向相反时,a b a b .
一般地,我们有 a b a b .
.. . . x . . .. x
0 a b a+b
a+b b a 0
图1
(2)当ab<0时,又可以分a>0,b<0和a<0,b>0两 中情况.
如果a>0,b>0时,如图2-1,a b a b .
.. b a+b
3x 2 y 3a 3b 3 x a 2 y b
2 xa 3 yb
3 2 5
所以:3x 2 y 3a 2b 5 .
例2
两个施工队分别被安排在公路沿线的两 个地点施工,这两个地点分别位于公路路碑 的第10km和第20km处。现要在公路沿线建两 个施工队的共同临时生活区,每个施工队每 天在生活区和施工区地点之间往返一次。要 使两个施工队每天往返的路程之和最小,生 活区应该建在何处?
分析
本题是绝对值不等式的应用,第一把 实际问题划归为数学问题,即归结为求解 形如y x a x b 的函数的极值问题, 这类问题借助于绝对值三角不等式解答。
解:设生活区建于公路路碑的第xkm处,两个施 工队每天往返的路程之和为S(x)km,
则S x 2 x 10 x 20 .
因 :x 10 x 20 x 10 20 x 10, 且 x 1020 x 0 取等 。
因此:a b a b .
其几何意义是三角形的两边之和大于 第三边(如下图)。
x
a+b b
由此可称 定理1为绝 对值三角
不等式
a
y
0
(2)当向量a,b共线时,分以下两种情况: 如果向量a,b方向相同时,a b a b ; 如果向量a,b方向相反时,a b a b .
一般地,我们有 a b a b .
.. . . x . . .. x
0 a b a+b
a+b b a 0
图1
(2)当ab<0时,又可以分a>0,b<0和a<0,b>0两 中情况.
如果a>0,b>0时,如图2-1,a b a b .
.. b a+b
《不等式和绝对值不等式》课件7 (人教A版选修4-5)
n n
(乘方性) (开方性)
二: 不等式的性质
能证明它们吗?
1.如果a > b,c > d,那么a + c > b + d 2.如果a > b > 0,c > d > 0,那么ac > bd
a b 例:已知a > b > 0,c > d > 0,求证 > . d c
三: 基本不等式
定理1:如果a,b∈R,那么a 2 + b 2 ≥ 2ab, 当且仅当a = b时等号成立。
本专题知识结构
第一讲 值不等式 不等式和绝对
不 等 式 选 讲
第二讲 的基本方法
证明不等式
第三讲 排序不等式
柯西不等式与
第四讲 明不等式
数学归纳法证
第一讲 不等式和绝对值不等式
一:不等式的基本性质
A B a b b>a B b
a>b
A a
a>b a-b>0
基本不等式
几何解释
b
a b a b
三: 基本不等式
定理2:(基本不等式) a+b 如果a,b 0,那么 ≥ ab, 2 当且仅当a = b时等号成立。
算术平均数
几何平均数
C
几何解释
ab
A
a O D b B
定理:设x,y都是正数,则有 1)若xy = s(定值),则当x = y时,x + y有最小值2 s .
a > b,c > d a +c > b+d
(加法法则)
4.a > b, > 0 ac > bc c (可乘性) a > b, < 0 ac < bc c
(乘方性) (开方性)
二: 不等式的性质
能证明它们吗?
1.如果a > b,c > d,那么a + c > b + d 2.如果a > b > 0,c > d > 0,那么ac > bd
a b 例:已知a > b > 0,c > d > 0,求证 > . d c
三: 基本不等式
定理1:如果a,b∈R,那么a 2 + b 2 ≥ 2ab, 当且仅当a = b时等号成立。
本专题知识结构
第一讲 值不等式 不等式和绝对
不 等 式 选 讲
第二讲 的基本方法
证明不等式
第三讲 排序不等式
柯西不等式与
第四讲 明不等式
数学归纳法证
第一讲 不等式和绝对值不等式
一:不等式的基本性质
A B a b b>a B b
a>b
A a
a>b a-b>0
基本不等式
几何解释
b
a b a b
三: 基本不等式
定理2:(基本不等式) a+b 如果a,b 0,那么 ≥ ab, 2 当且仅当a = b时等号成立。
算术平均数
几何平均数
C
几何解释
ab
A
a O D b B
定理:设x,y都是正数,则有 1)若xy = s(定值),则当x = y时,x + y有最小值2 s .
a > b,c > d a +c > b+d
(加法法则)
4.a > b, > 0 ac > bc c (可乘性) a > b, < 0 ac < bc c
《不等式和绝对值不等式》课件7 (人教A版选修4-5)

2 2
比较法的基本步骤: 1.作差(或作商) 2.变形 3.定号(与0比较或与1比较).
等式的性质
1.a = b b = a 2.a = b,b = c a = c 3.a = b a + c = b + c
(对称性) (传递性) (可加性)
4.a = b ac = bc
a = b,c = d a +c = b+d
几何解释
b
a b a b
三: 基本不等式
定理2:(基本不等式) a+b 如果a,b 0,那么 ≥ ab, 2 当且仅当a = b时等号成立。
算术平均数
几何平均数
C
几何解释
ab
A
a O D b B
定理:设x,y都是正数,则有 1)若xy = s(定值),则当x = y时,x + y有最小值2 s .
n n
(乘方性) (开方性)
二: 不等式的性质
能证明它们吗?
1.如果a > b,c > d,那么a + c > b + d 2.如果a > b > 0,c > d > 0,那么ac > bd
a b 例:已知a > b > 0,c > d > 0,求证 > . d c
三: 基本不等式
定理1:如果a,b∈R,那么a 2 + b 2 ≥ 2ab, 当且仅当a = b时等号成立。
p2 2)若x + y = p(定值),则当x = y时,xy有最大值 . 4
注:一正、二定、三等。
例 求证:(1)在所有周长相同的矩形中,正方 (2)在所有面积相同的矩形中,正方
比较法的基本步骤: 1.作差(或作商) 2.变形 3.定号(与0比较或与1比较).
等式的性质
1.a = b b = a 2.a = b,b = c a = c 3.a = b a + c = b + c
(对称性) (传递性) (可加性)
4.a = b ac = bc
a = b,c = d a +c = b+d
几何解释
b
a b a b
三: 基本不等式
定理2:(基本不等式) a+b 如果a,b 0,那么 ≥ ab, 2 当且仅当a = b时等号成立。
算术平均数
几何平均数
C
几何解释
ab
A
a O D b B
定理:设x,y都是正数,则有 1)若xy = s(定值),则当x = y时,x + y有最小值2 s .
n n
(乘方性) (开方性)
二: 不等式的性质
能证明它们吗?
1.如果a > b,c > d,那么a + c > b + d 2.如果a > b > 0,c > d > 0,那么ac > bd
a b 例:已知a > b > 0,c > d > 0,求证 > . d c
三: 基本不等式
定理1:如果a,b∈R,那么a 2 + b 2 ≥ 2ab, 当且仅当a = b时等号成立。
p2 2)若x + y = p(定值),则当x = y时,xy有最大值 . 4
注:一正、二定、三等。
例 求证:(1)在所有周长相同的矩形中,正方 (2)在所有面积相同的矩形中,正方
4-5.2.2绝对值不等式的解法_课件(人教A版选修4-5)

• 5.不等式|x-1|-|x+4|>1的解是_________. • 6.不等式x2-2|x|-15>0的解集为________ .
• 7.若关于x的不等式|x+2|+|x-1|<a的解集为空集,
•
则a的取值范围为 ( ) (A)(3,+∞) (B)[3,+∞) ∞,3) 围是 (A) m>2 (C)(-∞,3] (D)(-
行讨论,如本例需对a+1的符号进行讨论,否则易导致错误结
果.
变式1 解不等式
|x-a|>a.
例2 解不等式 | 5x-6 | < 6 – x
(Ⅰ)当5x-6≥0,即x≥6/5时,不等式化为 5x-6<6-x,解得x<2, 所以6/5≤x<2 (Ⅱ)当5x-6<0,即x<6/5时,不等式化为 -(5x-6)<6-x,解得x>0 所以0<x<6/5 取(Ⅰ)、 (Ⅱ) 并集得原不等式解集为(0, 2)
5.2.1 含有绝对值的 不等式的解法
复习:
1.绝对值的定义: |x|= 2.几何意义:
x2
B O
x 0 -x
x>0 x=0 x<0
一个数的绝对值表示数轴上这个数对 应的点到原点的距离.
x1
A x
|x1| =OA |x2| =OB
|x2-x1| =AB
两个数的差的绝对值表示数轴上这两个 个数对应的两点间距离.
变式1.不等式|x-1|>|x-2|的解集为 ______.
变式2
x- 1> ( 2-x ) 2 ,
求它的解集.
【解析】
x- 1 >( 2-x) (x- 1) > 2-x 3 x 2-2x 1>x 2-4x 4 2x>3 x> , 2 又2-x≥0,所以x≤2.
《不等式和绝对值不等式》课件7 (人教A版选修4-5)

p2 2)若x + y = p(定值),则当x = y时,xy有最大值 . 4
注:一正、二定、三等。
例 求证:(1)在所有周长相同的矩形中,正方 (2)在所有面积相同的矩形中,正方
--------------形的面积最大; ---------------形的周长最短;
周长L=2x+2y
x
S
y
例: 某居民小区要建一做八边形的休闲场所,它的主体造型平 面图是由两个相同的矩形ABCD和EFGH构成的面积为200平 方米的十字型地域.计划在正方形MNPQ上建一座花坛,造价为 每平方米4300元,在四个相同的矩形上(图中阴影部分)铺花岗 岩地坪,造价没平方米210元,再在四个空角(图中四个三角形) 上铺草坪,每平方米造价80元. (1)设总造价为S元,AD长x为米,试建立S关于x的函数关系式; (2)当为何值时S最小,并求出这个最小值. H G
2 2
比较法的基本步骤: 1.作差(或作商) 2.变形 3.定号(与0比较或与1比较).
等式的性质
1.a = b b = a 2.a = b,b = c a = c 3.a = b a + c = b + c
(对称性) (传递性) (可加性)
4.a = b ac = bc
a = b,c = d a +c = b+d
本专题知识结构
第一讲 值不等式 不等式和绝对
不 等 式 选 讲
第二讲 的基本方法
证明不等式
第三讲 排序不等式
柯西不等式与
第四讲 明不等式
数学归纳法证
第一讲 不等式和绝对值不等式
一:不等式的基本性质
A B a b b>a B b
注:一正、二定、三等。
例 求证:(1)在所有周长相同的矩形中,正方 (2)在所有面积相同的矩形中,正方
--------------形的面积最大; ---------------形的周长最短;
周长L=2x+2y
x
S
y
例: 某居民小区要建一做八边形的休闲场所,它的主体造型平 面图是由两个相同的矩形ABCD和EFGH构成的面积为200平 方米的十字型地域.计划在正方形MNPQ上建一座花坛,造价为 每平方米4300元,在四个相同的矩形上(图中阴影部分)铺花岗 岩地坪,造价没平方米210元,再在四个空角(图中四个三角形) 上铺草坪,每平方米造价80元. (1)设总造价为S元,AD长x为米,试建立S关于x的函数关系式; (2)当为何值时S最小,并求出这个最小值. H G
2 2
比较法的基本步骤: 1.作差(或作商) 2.变形 3.定号(与0比较或与1比较).
等式的性质
1.a = b b = a 2.a = b,b = c a = c 3.a = b a + c = b + c
(对称性) (传递性) (可加性)
4.a = b ac = bc
a = b,c = d a +c = b+d
本专题知识结构
第一讲 值不等式 不等式和绝对
不 等 式 选 讲
第二讲 的基本方法
证明不等式
第三讲 排序不等式
柯西不等式与
第四讲 明不等式
数学归纳法证
第一讲 不等式和绝对值不等式
一:不等式的基本性质
A B a b b>a B b
5.2 不等式和绝对值不等式(二)课件1(人教A版选修4-5)

答案继续
-2 x 3 0 ( x 1 0 ) S ( x ) 1 0 (1 0 ≤ x ≤ 2 0 ) 2 x 30 ( x 20)
所 以 ( x) 的 最 小 值 是 1 0, S
60 40 20 0
当1 0 ≤
x ≤ 20
时取到.
答: 生活区建于两路碑 间的任意位置都满足条 件.
a1 a 2 a n ≤ a1 a 2 a n .
推论 2: a、 b、 c 是实数,那么 a c ≤ a b b c , 如果 当且仅当 ( a b )( b c ) ≥ 0 时,等号成立.
课堂练习: 1.(课本 P1 5 例 1)已知 ε 求证: ⑴ ⑴ ⑵
.
1.提示:恰当运用重要不等式: a1 a 2 a 3 ≤ a1 a 2 a 3 .
2.提示:
⑴ a b 2 c a c b c ,…… ⑵ 3 a 3 c ( a b 2 c ) ( b c 2 a ) ,……
作业:课本 P
20
第 2,4,5 题
2
2
| a | | b |
| a | | b |
综合10,2Leabharlann 知定理成立.定理 1 如果 a , b 是实数, a 则
⑴若把 a , b 换为复数 z 1 , z 2 ,
b ≤ a b
(当且仅当 a b ≥ 0 时,等号成立.)
结论: z 1 z 2 ≤ z 1 z 2 成立吗?
这节课我们来研究:绝对值有什么性质? 我们知道,一个实数 a 的绝对值的意义: ⑴ ⑵
a (a 0) a 0 ( a 0 ) ;(定义) a (a 0)
-2 x 3 0 ( x 1 0 ) S ( x ) 1 0 (1 0 ≤ x ≤ 2 0 ) 2 x 30 ( x 20)
所 以 ( x) 的 最 小 值 是 1 0, S
60 40 20 0
当1 0 ≤
x ≤ 20
时取到.
答: 生活区建于两路碑 间的任意位置都满足条 件.
a1 a 2 a n ≤ a1 a 2 a n .
推论 2: a、 b、 c 是实数,那么 a c ≤ a b b c , 如果 当且仅当 ( a b )( b c ) ≥ 0 时,等号成立.
课堂练习: 1.(课本 P1 5 例 1)已知 ε 求证: ⑴ ⑴ ⑵
.
1.提示:恰当运用重要不等式: a1 a 2 a 3 ≤ a1 a 2 a 3 .
2.提示:
⑴ a b 2 c a c b c ,…… ⑵ 3 a 3 c ( a b 2 c ) ( b c 2 a ) ,……
作业:课本 P
20
第 2,4,5 题
2
2
| a | | b |
| a | | b |
综合10,2Leabharlann 知定理成立.定理 1 如果 a , b 是实数, a 则
⑴若把 a , b 换为复数 z 1 , z 2 ,
b ≤ a b
(当且仅当 a b ≥ 0 时,等号成立.)
结论: z 1 z 2 ≤ z 1 z 2 成立吗?
这节课我们来研究:绝对值有什么性质? 我们知道,一个实数 a 的绝对值的意义: ⑴ ⑵
a (a 0) a 0 ( a 0 ) ;(定义) a (a 0)
5.2绝对值三角不等式A 课件(人教A版选修4-5)
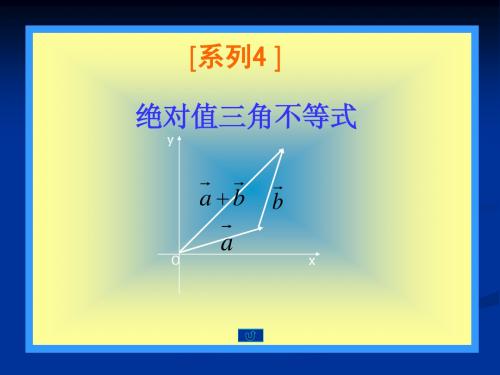
值。这个问题可以应用绝对值不等式的性质来解。
解:设生活区应该建于公路路牌的第xkm处,两个施工队 每天往返的路程之和为S(x)km,则 因为
S x 2 x 10 x 20
x 10 x 20 x 10 20 x 10
当且仅当 解得
b
x
向量形式的不等式
ab a b
当且仅当Biblioteka a与 b 同向
时,等号成立。
由于定理1与三角形之间的这种联系,我们称其中的不等 式为绝对值三角不等式。
知识推广
如果将定理1中的实数a , b改为复数 不等式仍成立吗?
z1 , z2
,
z1 z2 z1 z2
练习
例2
两个施工队分别被安排在公路沿线的两个地点施工, 这两个地点分别位于公路路牌的第10km和第20km 处。现要在公路沿线建两个施工队的共同临时生活区, 每个施工队每天在生活区和施工地点之间往返一次。 要使两个施工队每天往返的路程之和最小,生活区应 该建于何处?
分析:如果生活区建于公路路牌的第xkm处,两个施工队每天往返的路程 之和为S(x)km,那么 S x 2 x 10 x 20 于是,上面的问题就化 归为数学问题:当x取何值时,函数 S x 2 x 10 x 20 取得最小
探究 你能比较 a b 与 a b
ab a b ab a b ab a b
之间的大小关
当ab>0时,
当ab<0时, 当ab=0时,
你能将上述情况综合起来吗?
定理1
如果a,b是实数,则 当且仅当
ab a b
人教A版高中数学选修4-5课件第一讲二1绝对值三角不等式

(2)定理2:如果a,b,c是实数,那么|a-c|≤|a-b|+|b-c|. 当且仅当时,等号成立. 几何解释:在(数a-轴b上)(b,-ac,)≥b0,c所对应的点分别为A,B, C, 当点B在点A,C之间时,|a-c||a-b|+|b-c|. 当点B不在点A,C之间时:①点B在=A或C上时,|a-c| |a-b|+|b-c|; ②=点B不在A,C上时,|a-c||a-b|+|b-c|. 应用:利用该定理可以确定绝对值< 函数的值域和最值.
[例2] (1)求函数y=|x-3|-|x+1|的最大值和最小值. (2)设a∈R,函数f(x)=ax2+x-a(-1≤x≤1). 若|a|≤1,求|f(x)|的最大值. [思路点拨] 利用绝对值三角不等式或函数思想方法可求 解.
[解] (1)法一:||x-3|-|x+1|| ≤|(x-3)-(x+1)|=4, ∴-4≤|x-3|-|x+1|≤4. ∴ymax=4,ymin=-4.
(1)利用绝对值不等式求函数最值,要注意利用绝对 值的性质进行转化,构造绝对值不等式的形式. (2)求最值时要注意等号成立的条件,它也是解题的 关键.
3.若a,b∈R,且|a|≤3,|b|≤2则|a+b|的最大值是________, 最小值是________. 解析:|a|-|b|≤|a+b|≤|a|+|b|, ∴1=3-2≤|a+b|≤3+2=5. 答案:5 1
高中数学课件
(金戈铁骑 整理制作)
1.绝对值三角不等式
绝对值三角不等式 (1)定理1:如果a,b是实数,则|a+b|≤|a|+|b|,当且仅当时, 等号ab成≥0立. 几何解释:用向量a,b分别替换a,b. ①当a与b不共线时,有|a+b|<|a|+|b|,其几何意义为: .三角形的两边之和大于第三边 ②若a,b共线,当a与b时,同|a+向b|=|a|+|b|,当a与b 时反,向|a+b|<|a|+|b|. 由于定理1与三角形之间的这种联系,故称此不等式为绝对 值三角不等式. ③定理1的推广:如果a,b是实数,则||a|-|b||≤|a±b| ≤|a|+|b|.
5.2绝对值三角不等式A 课件(人教A版选修4-5)

x 10 20 x
10 x 20
0 时取等号。
所以,生活区建于两个施工地点之间的任何一个位置时, 都能使两个施工队每天往返的路程之和最小。
70
60
s x = 2 x-10
+ x-20
50
40
30
20
10
-60
-40
-20
10
20
40
60
80
100
[系列4 ]
绝对值三角不等式
y
a b
O
a
b
x
创设情境
在数轴上,你能指出实数a的绝对值 a 的几何意义吗?
a
0 a
A x
它表示数轴上坐标为a的点A到原点的距离 那么, a b 的几何意义呢? 数轴上A,B两点之间的距离
B b
ab
B -b
A
a
ab
O
x
探究
设a, b为实数, 你能比较 a b 与 a b 之间的大小关 系吗?
取得最小
值。这个问题可以应用绝对值不等式的性质来解。
解:设生活区应该建于公路路牌的第xkm处,两个施工队 每天往返的路程之和为S(x)km,则 因为
S x 2 x 10 x 20
x 10 x 20 x 10 20 x 10
当且仅当 解得
当ab>0时, a b a b
当ab<0时, a b a b 当ab=0时, a b a b 你能将上述情况综合起来吗?
定理1
如果a,b是实数,则 a b a b 当且仅当 a b 0 时,等号成立。
人教A版高中数学选修4-5课件第一讲二2绝对值不等式的解法

高中数学课件
(金戈铁骑 整理制作)
2.绝对值不等式的解法
1.|ax+b|≤c,|ax+b|≥c(c>0)型不等式的解法 只需将ax+b看成一个整体,即化成|x|≤a,|x|≥a(a>0)型 不等式求解. |ax+b|≤c(c>0)型不等式的解法:先化为, -c≤ax+b≤c 再由不等式的性质求出原不等式的解集. 不等式|ax+b|≥c(c>0)的解法:先化为或 ax+b≥c ,ax再+进b≤一-步c 利用不等式性质求出原不等式的解集.
[例1] 解下列不等式: (1)|5x-2|≥8;(2)2≤|x-2|≤4. [思路点拨] 利用|x|>a及|x|<a(a>0)型不等式的解法求 解.
[解] (1)|5x-2|≥8⇔5x-2≥8或5x-2≤-8⇔x≥2或x≤ -65,
∴原不等式的解集为{x|x≥2或x≤-65},或x-2≥2, ∴x≤0,或x≥4. 由②得-4≤x-2≤4, ∴-2≤x≤6. ∴原不等式的解集为{x|-2≤x≤0,或4≤x≤6}.
[解] 法一:因|x+2|-|x+3|的几何意义为数轴上任意一 点P(x)与两定点A(-2),B(-3)距离的差. 即|x+2|-|x+3|=|PA|-|PB|. 由图像知(|PA|-|PB|)max=1, (|PA|-|PB|)min=-1. 即-1≤|x+2|-|x+3|≤1. (1)若不等式有解,m只要比|x+2|-|x+3|的最大值小即可, 即m<1,m的范围为(-∞,1);
|x-a|+|x-b|≥c、|x-a|+|x-b|≤c(c>0)型不等式 的三种解法:分区间(分类)讨论法、图像法和几何法. 分区间讨论的方法具有普遍性,但较麻烦;几何法和 图像法直观,但只适用于数据较简单的情况.
(金戈铁骑 整理制作)
2.绝对值不等式的解法
1.|ax+b|≤c,|ax+b|≥c(c>0)型不等式的解法 只需将ax+b看成一个整体,即化成|x|≤a,|x|≥a(a>0)型 不等式求解. |ax+b|≤c(c>0)型不等式的解法:先化为, -c≤ax+b≤c 再由不等式的性质求出原不等式的解集. 不等式|ax+b|≥c(c>0)的解法:先化为或 ax+b≥c ,ax再+进b≤一-步c 利用不等式性质求出原不等式的解集.
[例1] 解下列不等式: (1)|5x-2|≥8;(2)2≤|x-2|≤4. [思路点拨] 利用|x|>a及|x|<a(a>0)型不等式的解法求 解.
[解] (1)|5x-2|≥8⇔5x-2≥8或5x-2≤-8⇔x≥2或x≤ -65,
∴原不等式的解集为{x|x≥2或x≤-65},或x-2≥2, ∴x≤0,或x≥4. 由②得-4≤x-2≤4, ∴-2≤x≤6. ∴原不等式的解集为{x|-2≤x≤0,或4≤x≤6}.
[解] 法一:因|x+2|-|x+3|的几何意义为数轴上任意一 点P(x)与两定点A(-2),B(-3)距离的差. 即|x+2|-|x+3|=|PA|-|PB|. 由图像知(|PA|-|PB|)max=1, (|PA|-|PB|)min=-1. 即-1≤|x+2|-|x+3|≤1. (1)若不等式有解,m只要比|x+2|-|x+3|的最大值小即可, 即m<1,m的范围为(-∞,1);
|x-a|+|x-b|≥c、|x-a|+|x-b|≤c(c>0)型不等式 的三种解法:分区间(分类)讨论法、图像法和几何法. 分区间讨论的方法具有普遍性,但较麻烦;几何法和 图像法直观,但只适用于数据较简单的情况.
5.2绝对值三角不等式 课件(人教A版选修4-5)

a<0,b<0 a+b x a O b |a+b|=|a|+|b|
x
a<0,b>0 a+b x a O b |a+b|<|a|+|b|
易得: |a+b|=|a|+|b|
(3)如果ab=0,则a=0或b=0
综上所述,可得:
定理1: 如果a,b是实数,则 |a+b||a|+|b| 当且仅当ab0时,等号成立. 如果把定理1中的实数a,b分别换 为向量
同学们能再探究一下|a|-|b|与|a+b|, |a|+|b|与 |a-b|, |a|-|b|与|a-b|等之间的关系? 如: 如果a,b是实数,则 |a|-|b||a-b||a|+|b| 再如: 如果a,b,c是实数,则 |a-c||a-b|+|b-c|
当且仅当(a-b)(b-c)0时,等号成立.
类比不等式基本性质的得出过程,同学们认为
可以怎样提出关于绝对值不等式性质的猜想?
从“运算”的角度考察绝对值不等式。 如:对于实数a,b,可以考察|a|, |b|, |a+b|, |a-b|, |a|+|b|, |a|-|b| 等之间的关系。
用恰当的方法在数轴上把|a|, |b|, |a+b|表示出来,
S(x)=2(|x-10|+|x-20|) |x-10|+|x-20|=|x-10|+|20-x| |(x-10)+(20-x)|=10 当且仅当(x-10)(20-x)0时 取等号. 又解不等式:
S 60 40 20
S(x)=2(|x-10|+|x-20|)
5.2不等式和绝对值不等式(一)课件(人教A版选修4-5)

定理:设 x , y , z 都是正数,则有 ⑴若 xyz S (定值) , 则当 x y z 时, x y z 有最小值 3 3 s . ⑵若 x y z p (定值) ,
p 则当 x y z 时, xyz 有最大值 . 27
3
注:一正、二定、三等。
2
1 例1 求函数 y x (1 3 x)在 [0, ]上的最大值. 3
2
1 x2 2
1 又∵ x 2 ≥ 2 ,又∵函数 y t 在 t 1, 时是减函数. t 3 2 1 2 ∴当 x 0 时,函数 y x 2 取得最小值 . 2 2 x 2
3⑶求函数 y
x2 3
x2 2 x2 3 x2 2 1 1 2 解: ⑶∵ y ≥2 x 2 x2 2 x2 2 x2 2 x2 3 ∴函数 y 的最小值为 2. x2 2 上面解法错在哪?
8
k≥4
作业:课本 P 第1、2题 , P 11第11、12、14 题 10
两个实数大小比较:
⑴a b a b 0 ; ⑵a b a b 0 ; ⑶a b a b 0
这一结论虽很简单,却是我们推导或证明不等式的基础.
思考 1.试解不等式: x 2 x x .
2
解不等式的过程就是对不等式进行一系列同解 变形的过程,同解变形的依据是什么?
3 3⑴已知 0 x ,求函数 y x(3 2x) 的最大值. 2 2 x2 ⑵求函数 y ( x 3) 的最小值. x 3 x2 3 ⑶求函数 y 的最小值. x2 2
解: ⑶∵ y
2
x2 3 x2 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的最小值.
1 x 2
2
≥2
上面解法错在哪?
均值不等式可以用来求最值(积定和小,和 定积大),但特别要注意条件的满足: 一正、 二定、 三相等.
四:三个正数的算术—几何平均不等式
类比基本不等式得
abc 3 定理 3:如果 a、b、c R ,那么 ≥ abc , 3 当且仅当 a b c 时,等号成立.
解:设AM=y米
200 - x 2 因而 4 xy x 2 200 y 4x
D
A
Q
P
C
B M N
于是S 4200x2 210 4xy 80 2 y2 0 x 10 2
E
F
课堂练习: 1.判断下列命题是否正确: (1) a b, c b a c ( ×) (2) a b c a c b ( ) √ (3) a b ac 2 bc 2 ( × (4) a b, c d ac bd × ) ) ( a b √ (5) 2 2 a b ( ) (6) a 2 b 2 a b × ) ( c c √ (7) a b a 2 b 2 × ) ( (8) a b a 2 b 2 ( )
3 3⑴已知 0 x ,求函数 y x(3 2 x) 的最大值. 2 2 x2 ( x 3) 的最小值. ⑵求函数 y x 3 x2 3 ⑶求函数 y 的最小值. 2 x 2 解: ⑵∵ x 3 ,∴ x 3 0 2 x2 2( x 2 9) 18 18 2x 6 ∴y x 3 x 3 x 3 18 = 2( x 3) 12 ≥24 x 3 18 当且仅当 2( x 3) 即 x 6 时取等号. x 3 2 x2 ( x 3) 的最小值为 24,且当 x 6 时取得. ∴函数 y x 3
基本不等式
定理1:如果a,b∈R,那么a 2 + b2 ≥ 2ab, 当且仅当a = b时等号成立。
几何解释
b
a b
a
b
算术平均数不小于几何平均数
当 a、b 为正数时,
ab ≥ ab 则 2
(当且仅当 a = b 时取“=”号)
算术平均数 (a 、b 的)
几何平均数
(a
、b 的)
定理2:(基本不等式) a+b 如果a,b 0,那么 ≥ ab, 2 当且仅当a = b时等号成立。 几何平均数 算术平均数
思考 2.已知 a 0, b 0, a b 时,
2ab 求证: ab ab
证明不等式的最基本的思考是分析法——很多 时候就是对要证的不等式进行变形转化。
不等式的基本性质 基本不等式
不等式的性质 ⑴(对称性或反身性) a b b a ; ⑵(传递性) a b,b c a c ; ⑶(可加性) a b a c b c ,此法则又称为移项法则; (同向可相加) a b,c d a c b d ⑷(可乘性) a b,c 0 ac bc;a b,c 0 ac bc . (正数同向可相乘) a b 0,c d 0 ac bd 0 ⑸(乘方法则) a b (n N) a n b n 0 0 ⑹(开方法则) a b (n N , n ≥ 2) n a n b 0 1 1 ⑺(倒数法则) a b,ab 0 a b 掌握不等式的性质,应注意:条件与结论间的对应关系, 是“ ”符号还是“ ”符号;运用不等式性质的关键是不 等号方向,条件与不等号方向是紧密相连的。
推广: 对于 n 个正数 a1, a2 , a3 ,an, 它们的算术平均值 不小于它们的几何平均值, a1 a2 a3 an 即 ≥ n a1 2 3 an a a n (当且仅当 a1 a2 a3 an 时取等号.)
定理:设 x , y , z 都是正数,则有 ⑴若 xyz S (定值) , 则当 x y z 时, x y z 有最小值 3 3 s . ⑵若 x y z p (定值) ,
x
S
y
例4: 某居民小区要建一做八边形的休闲场所,它的主体
造型平面图是由两个相同的矩形ABCD和EFGH构成的 面积为200平方米的十字型地域.计划在正方形MNPQ上 建一座花坛,造价为每平方米4300元,在四个相同的矩形 上(图中阴影部分)铺花岗岩地坪,造价没平方米210元,再 在四个空角(图中四个三角形)上铺草坪,每平方米造价80 元. (1)设总造价为S元,AD长 x 为米,试建立S关于x的函数 H G 关系式; (2)当为何值时S最小, 并求出这个最小值.
第一讲不等式和绝对值不等式(一)
对于不等式大家并不陌生,我们已经会解 一些简单的不等式和证明一些不等式, 如 1.求解下列不等式: x2 2 ① x 3 x 10 0 ② >0 x5 3 2 2.设 n 1,且 n 1, 求证: n 1 > n n .
下面我们来系统且更进一步地认识不等式,从 而进一步提高分析问题、处理问题的能力。
C
几何解释
ab
A a O D b B
可以用来求最值(积定和小,和定积大)
定理:设 x , y , z 都是正数,则有 ⑴若 xy S (定值) ,则当 x y 时, x y 有最小值 2 s.
p2 ⑵若 x y p (定值) ,则当 x y 时, xy 有最大值 . 4
注:一正、二定、三等。
2答案 3答案
基础练习: 2.设 A=1+2x4,B=2x3+x2,x∈R 且 x≠1,比较 A,B 的大小.
提示:比较大小,最简单、最有效的方法 是作差→变形→定符号. 变形方法有二种: 一、是分解因式; 二是配方.
解:∵A-B=1+2x4-(2x3+x2)= (2x4 2x3 ) (1 x2 ) = 2x3 (x 1) (1 x)(1 x) = ( x 1)(2x3 x 1) = (x 1)(x 1)(2x2 2x 1) 1 2 1 2 = ( x 1) 2( x ) 0 2 2 ∴A>B
3 3.⑴已知 0 x ,求函数 y x(3 2 x) 的最大值. 2 2 x2 ( x 3) 的最小值. ⑵求函数 y x 3 x2 3 ⑶求函数 y 的最小值. 2 x 2 3 解⑴(重要不等式法)∵ 0 x ,∴ x 0且3 2x 0 , 2 1 1 2x 3 2x 3 2 ∴ x(3 2 x) = = 2 x(3 2 x) ≤ 4 2 2 2 3 当且仅当 x 时取等号. 4 3 2 3 ∴函数 y x(3 2 x) 的最大值为 ,当且仅当 x 取得. 4 4
3
试证明:已知a、b、c∈R+,
abc 3 ab abc ) ≥ 2( ab ) 求证 3( 3 2
课外思考: 1.已知 a 0, b 0 , 2a 3b 10 ,
2 则 3b 2a 的最大值是____.5 2.已知 x 0 , y 0 ,且 x 2 y 1, 1 1 3 2 2 则 u 的最小值是______________。 x y
3 3⑴已知 0 x ,求函数 y x(3 2 x) 的最大值. 2 2 x2 ( x 3) 的最小值. ⑵求函数 y x 3 2 x 3 ⑶求函数 y 2 的最小值. x 2
解: ⑶∵ y
2
x2 3 x 2
2
x2 2 1 x 2
2
x 2
x2 8 ( x 1) 的最小值为______. 3.函数 y x 1 4. 现有两个定值电阻,串联后等效电阻值为 R,并 联后等效电阻值为 r,若 R k r ,则实数 k 的取值 范围是_____.
8
k≥4
10
作业:课本 P 第1、2题 , P 11第11、12、14 题
2
1 x2 2
1 又∵ x 2 ≥ 2 ,又∵函数 y t 在 t 1, 时是减函数. t 3 2 1 2 ∴当 x 0 时,函数 y x 2 取得最小值 . 2 2 x 2
3⑶求函数 y
x2 3
x2 2 x2 3 x2 2 1 x2 2 解: ⑶∵ y x2 2 x2 2 x2 3 ∴函数 y 的最小值为 2. 2 x 2
a b × (9) a b 0, c d 0 ( ) c d 2.设 A=1+2x4,B=2x3+x2,x∈R 且 x≠1,比较 A,B 的大小. 3 3.⑴已知 0 x ,求函数 y x(3 2 x) 的最大值. 2 x2 3 2 x2 ( x 3) 的最小值.⑶求函数 y ⑵求函数 y 的最小值. 2 x 3 x 2
v xyz
x z y
略
例2: 如图,把一块边长是a 的正方形铁 片的各角切 去大小相同的小正方形, 再把它的边沿着虚线折转作成一个无盖 方底的盒子,问切去的正方形边长是多 小时?才能使盒子的容积最大?
x解:依 题 意有源自v (a 2 x) 2 x a (0 x ) 2
a
求证: ( x y z ) ≥ 27 xyz 例3:已知x, y, z R ,
例 3求证:(1)在所有周长相同的矩形中,正方 --------------形的面积最大;
(2)在所有面积相同的矩形中,正方 ---------------形的周长最短.
例3答案
例4
例 3求证:(1)在所有周长相同的矩形中,正方 --------------形的面积最大; (2)在所有面积相同的矩形中,正方 ---------------形的周长最短. 设矩形周长为L,面积为S,一边长为x,一边长为y, 周长L=2x+2y
