高中数学专题6.1数列的通项公式与求和-3年高考2年模拟1年预测(理)(解析版)
数列的通项与求和

数列的通项与求和数列是数学中的重要概念,广泛应用于各个领域。
在数列中,每一个数字都有其特定的位置和规律。
通项与求和是数列中两个基本问题,本文将围绕这两个问题展开探讨。
一、数列的通项数列的通项是指数列中任意一项与其位置之间的关系式。
通项可以用来计算数列中任意一项的值,从而更好地理解数列的规律和特点。
下面将以等差数列和等比数列为例,介绍数列的通项计算方法。
1. 等差数列等差数列的通项公式为:an = a1 + (n-1)d,其中an表示第n项,a1表示首项,d表示公差。
首先确定首项和公差的值,然后代入公式即可计算出任意一项的值。
例如,对于等差数列1, 3, 5, 7, 9,首项a1=1,公差d=2,第n项的值可以通过an = 1 + (n-1)x2求得。
2. 等比数列等比数列的通项公式为:an = a1 x r^(n-1),其中an表示第n项,a1表示首项,r表示公比。
首先确定首项和公比的值,然后代入公式即可计算出任意一项的值。
例如,对于等比数列2, 4, 8, 16, 32,首项a1=2,公比r=2,第n项的值可以通过an = 2 x 2^(n-1)求得。
二、数列的求和数列的求和是指将数列中所有项的值相加得到的结果。
通过求和,可以获得数列的总和,从而更好地了解数列的变化和特征。
下面将以等差数列和等比数列为例,介绍数列的求和计算方法。
1. 等差数列求和等差数列的求和公式为:Sn = (n/2)(a1 + an),其中Sn表示前n项和,n表示项数,a1表示首项,an表示第n项。
根据公式,首先确定项数、首项和最后一项的值,然后代入公式即可计算出数列的总和。
例如,对于等差数列1, 3, 5, 7, 9,共有5项,首项a1=1,最后一项an=9,根据公式Sn = (5/2)(1 + 9),可以得到数列的总和为25。
2. 等比数列求和等比数列的求和公式为:Sn = (a1(1-r^n))/(1-r),其中Sn表示前n项和,a1表示首项,r表示公比。
高二数学数列与数列的通项公式

高二数学数列与数列的通项公式数列在高二数学中占据着重要的地位,其中一个重要的概念就是数列的通项公式。
本文将介绍数列的基本概念,并详细探讨数列的通项公式的计算方法。
一、数列的基本概念数列是由一系列有规律的数按照一定次序排列而成的。
数列的每一项可以用数学表达式表示,常用的表示形式有递推式和通项公式。
递推式是通过前一项或前几项得到下一项的表达式,它可以描述数列的增长规律。
例如,斐波那契数列的递推式为an = an-1 + an-2,其中an表示第n项。
通项公式是用一个公式来直接计算数列中的任意一项。
它可以根据数列前几项的规律推导出来,从而能够更方便地计算数列中任意位置的数值。
二、数列的通项公式的计算方法1.等差数列的通项公式等差数列是指数列中相邻两项之间的差值固定的数列。
设该数列的首项为a1,公差为d,则该数列的通项公式为an = a1 + (n-1)d。
2.等比数列的通项公式等比数列是指数列中相邻两项之间的比值固定的数列。
设该数列的首项为a1,公比为r,则该数列的通项公式为an = a1 * r^(n-1)。
3.斐波那契数列的通项公式斐波那契数列是指数列中前两项之和等于后一项的数列。
斐波那契数列的通项公式比较特殊,可以通过递推式推导出来:an = an-1 + an-2。
三、数列通项公式的应用数列的通项公式在解决实际问题时起到了重要的作用。
通过数列的通项公式,我们可以方便地计算数列中任意一项的值,从而可以解决一些与数列相关的实际问题。
例如,在金融领域中,我们经常会遇到复利的计算问题。
如果投资某项理财产品,每年的收益率是固定的,那么我们可以将其抽象为一个等比数列,并利用等比数列的通项公式计算出未来某一年的收益。
另外,数列的通项公式也可以应用于数值运算。
通过计算数列的通项公式,我们可以得到数列中各项数值的规律,从而更好地理解和运用数列的性质。
总之,数列与数列的通项公式是高二数学中的重要内容。
数列的通项公式可以帮助我们更方便地计算数列中任意一项的数值,并且在解决实际问题时有着广泛的应用。
高中数学知识点:数列通项与数列求和

⾼中数学知识点:数列通项与数列求和今天⼩编分享的是⾼中数学知识点:数列通项与数列求和,按⼀定次序排列的⼀列数称为数列,⽽将数列{an} 的第n项⽤⼀个具体式⼦(含有参数n)表⽰出来,称作该数列的通项公式。
这正如函数的解析式⼀样,通过代⼊具体的n值便可求知相应an 项的值。
⽽数列通项公式的求法,通常是由其递推公式经过若⼲变换得到。
下⾯是⾼中数学知识点:数列通项与数列求和的具体内容。
点击查看:⾼中数学知识点之数列⾼中数学知识点之等差数列通项公式对于⼀个数列{an},如果任意相邻两项之差为⼀个常数,那么该数列为等差数列,且称这⼀定值差为公差,记为d;从第⼀项a1到第n项an的总和,记为Sn 。
⾼中数学知识点之等差数列通项公式对于⼀个数列{an},如果任意相邻两项之差为⼀个常数,那么该数列为等差数列,且称这⼀定值差为公差,记为d;从第⼀项a1到第n项an的总和,记为Sn。
即an=a1+(n-1)*d⾼中数学知识点之等⽐数列通项公式对于⼀个数列{an},如果任意相邻两项之商(即⼆者的⽐)为⼀个常数,那么该数列为等⽐数列,且称这⼀定值商为公⽐q;从第⼀项a1到第n项an的总和,记为Tn。
那么,通项公式为an=a1*q(n-1)(即a1乘以q的(n-1)次⽅,其推导为“连乘原理”的思想:a2=a1*q,a3=a2*q,a4=a3*q,、、、、an=an-1*q,⾼中数学知识点:数列求和1.等差数列求和公式:(⾸项+末项)×项数÷22.等⽐数列求和公式:以上是⾼三⽹⼩编整理的⾼中数学知识点:数列通项与数列求和,供参考。
⾼三⽹⼩编推荐你继续浏览:⾼中数学参数⽅程知识点总结⾼中数学常⽤的⼏何公式汇总⾼中数学知识点:判断函数值域的⽅法⾼中数学常⽤的三⾓函数的诱导公式有哪些如何提⾼⾼中数学学习效率⽂科⼥⽣必备的⾼中数学公式有哪些⽂科⼥⽣如何学好⾼中数学。
数列的通项公式与求和公式

数列的通项公式与求和公式在数学的广阔天地中,数列就如同繁星点点,而数列的通项公式与求和公式则是我们探索这些繁星奥秘的关键钥匙。
首先,咱们来聊聊啥是数列的通项公式。
简单说,通项公式就是一个能够准确表示数列中每一项的式子。
比如说,咱们常见的等差数列 1,3,5,7,9它的通项公式就是 an = 2n 1 。
通过这个公式,只要给定一个 n 的值,咱就能轻松算出这一项具体是多少。
再比如等比数列 2,4,8,16它的通项公式是 an = 2^n 。
通项公式就像是数列的身份证,独一无二地标识了每一个数列。
那数列的求和公式又是啥呢?它呀,就是用来计算数列中所有项之和的式子。
还是拿刚才的等差数列 1,3,5,7,9 来说,它的前 n 项和公式是 Sn = n(a1 + an) / 2 ,这里的 a1 是首项,an 是末项。
如果咱们要求前 5 项的和,那就是 S5 = 5×(1 + 9) / 2 = 25 。
等比数列2,4,8,16的前 n 项和公式是 Sn = a1(1 q^n) /(1 q) (其中 q 是公比)。
通项公式和求和公式在解决数学问题中可太有用啦!比如说,让你判断一个数是不是某个数列中的项,有了通项公式,那简直是小菜一碟。
给定一个数,代入通项公式,能算出一个整数的 n 值,那它就是数列中的项,否则就不是。
求和公式的用处也不少呢!假如要计算一堆有规律排列的数的总和,要是一个一个加,那得累死人。
但有了求和公式,几下就能算出来。
那怎么去推导这些公式呢?咱们先来看等差数列的通项公式。
假如一个等差数列的首项是 a1 ,公差是 d ,那么第二项就是 a1 + d ,第三项是 a1 + 2d ,第四项是 a1 + 3d 依此类推,第 n 项就是 an = a1 +(n 1)d 。
再看等差数列的求和公式。
咱们可以把前 n 项倒过来写一遍,然后和原来的式子相加。
比如说,原来的式子是 Sn = a1 +(a1 + d) +(a1 + 2d) ++ a1 +(n 1)d ,倒过来就是 Sn = a1 +(n 1)d + a1 +(n 2)d ++(a1 + d) + a1 。
数列的通项与求和例题和知识点总结

数列的通项与求和例题和知识点总结一、数列的通项在数列中,通项公式是指第 n 项 an 与项数 n 之间的关系式。
(一)等差数列的通项公式若一个数列从第二项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列。
其通项公式为:an = a1 +(n 1)d ,其中a1 为首项,d 为公差。
例如:数列 2,5,8,11,14,是一个首项 a1 = 2,公差 d = 3 的等差数列,其通项公式为 an = 2 +(n 1)×3 = 3n 1 。
(二)等比数列的通项公式若一个数列从第二项起,每一项与它的前一项的比值等于同一个常数,这个数列就叫做等比数列。
其通项公式为:an = a1×q^(n 1) ,其中 a1 为首项,q 为公比。
例如:数列 2,4,8,16,32,是一个首项 a1 = 2,公比 q = 2 的等比数列,其通项公式为 an = 2×2^(n 1) = 2^n 。
(三)常见的求通项公式的方法1、观察法通过对数列前几项的观察,找出规律,从而推测出通项公式。
例如:数列 1,3,5,7,9,很容易观察出其通项公式为 an = 2n1 。
2、累加法当数列的递推关系为 an an 1 = f(n) 时,可用累加法求通项公式。
例如:已知数列{an} 满足 a1 = 1,an an 1 = n ,求 an 。
因为 an an 1 = n ,所以a2 a1 = 2a3 a2 = 3an an 1 = n将上述式子相加得:an a1 = 2 + 3 ++ n所以 an = a1 + 2 + 3 ++ n = 1 +(2 + 3 ++ n) = 1 + n(n+ 1)/2 。
3、累乘法当数列的递推关系为 an / an 1 = f(n) 时,可用累乘法求通项公式。
例如:已知数列{an} 满足 a1 = 1,an / an 1 = n ,求 an 。
因为 an / an 1 = n ,所以a2 / a1 = 2a3 / a2 = 3an / an 1 = n将上述式子相乘得:an / a1 = 2×3××n所以 an = a1×2×3××n = n! 。
高中数学公式大全数列的通项公式与求和公式

高中数学公式大全数列的通项公式与求和公式高中数学公式大全:数列的通项公式与求和公式数列是指按照一定规律排列的一组数,而数列的通项公式和求和公式则是研究数列的重要内容。
在高中数学中,数列的通项公式和求和公式是学习和应用数列的基础。
本文将详细介绍数列的通项公式和求和公式的定义、推导以及应用案例。
一、数列的通项公式数列的通项公式又称为数列的第n项公式,它可以用来表示数列的任意一项,是数列的核心公式。
对于通项公式的推导,我们先来看一个常见的数列——等差数列。
1. 等差数列的通项公式等差数列是指数列中的每一项与前一项的差等于同一个常数d。
设等差数列的第一项为a₁,公差为d,则等差数列的通项公式为:aₙ = a₁ + (n-1) * d其中,aₙ表示等差数列的第n项,n表示项数。
举例:对于数列1, 3, 5, 7, 9...来说,其通项公式为:aₙ = 2n - 12. 等比数列的通项公式等比数列是指数列中的每一项与前一项的比等于同一个常数q。
设等比数列的第一项为a₁,公比为q,则等比数列的通项公式为:aₙ = a₁ * q^(n-1)其中,aₙ表示等比数列的第n项,n表示项数。
举例:对于数列2, 4, 8, 16, 32...来说,其通项公式为:aₙ = 2^(n-1)二、数列的求和公式数列的求和公式是用来计算数列前n项和的公式,对于不同类型的数列,求和公式也各不相同。
下面我们来介绍两种常见的数列求和公式——等差数列的求和公式和等比数列的求和公式。
1. 等差数列的求和公式对于等差数列的前n项和,求和公式为:Sₙ = (n/2) * (a₁ + aₙ)其中,Sₙ表示等差数列的前n项和。
举例:对于等差数列1, 3, 5, 7, 9...来说,其前n项和的求和公式为:Sₙ = (n/2) * (1 + 2n - 1) = n^22. 等比数列的求和公式对于等比数列的前n项和,求和公式为:Sₙ = (a₁ * (q^n - 1)) / (q - 1)其中,Sₙ表示等比数列的前n项和。
数列的通项与求和

数列的通项与求和数列是数学中一个重要的概念,广泛应用于各个领域中。
在数列中,通项与求和是两个重要的概念。
本文将详细介绍数列的通项与求和的概念、性质和计算方法。
一、数列的通项数列的通项是指数列中第n个数的一般表示式。
在数列中,通项通常使用公式或递推关系给出。
1.1 公式求通项对于一些特殊的数列,可以通过观察数列中数的规律来得到通项的公式。
常见的数列包括等差数列和等比数列。
1.1.1 等差数列如果数列中的相邻两项之差固定为常数d,则该数列为等差数列。
等差数列的通项公式可以通过以下公式计算得到:an = a1 + (n - 1)d其中,an表示等差数列的第n项,a1表示等差数列的首项,d表示等差数列的公差,n表示项数。
1.1.2 等比数列如果数列中的相邻两项的比固定为常数q,则该数列为等比数列。
等比数列的通项公式可以通过以下公式计算得到:an = a1 * q^(n - 1)其中,an表示等比数列的第n项,a1表示等比数列的首项,q表示等比数列的公比,n表示项数。
1.2 递推关系求通项对于一些数列,无法通过观察数列中数的规律找到通项的公式,可以通过递推关系来得到通项。
递推关系是指数列中的每一项与前面一项之间的关系。
递推关系通过以下公式表示:an = f(an-1)其中,an表示数列的第n项,an-1表示数列的第n-1项,f表示递推关系。
二、数列的求和数列的求和是指将数列中的一定项数的数相加的运算。
数列的求和可以使用两种方法进行计算,即通项法和递推法。
2.1 通项法求和通项法是指根据数列的通项公式,将数列的每一项相加来计算数列的求和。
使用通项法计算数列的求和需要明确求和的起始项和结束项。
例如,对于等差数列an = 2n + 1,求前10项的和,可以使用通项法:Sn = (a1 + an) * n / 2其中,Sn表示数列的前n项和,a1表示数列的首项,an表示数列的第n项,n表示项数。
2.2 递推法求和递推法是指通过数列的递推关系,将数列的前一项和当前项相加来计算数列的求和。
高中数学知识点归纳数列与数列的通项公式

高中数学知识点归纳数列与数列的通项公式高中数学知识点归纳:数列与数列的通项公式数列是数学中常见的一种序列,它由一系列按照特定规律排列的数所组成。
在高中数学中,学生需要了解数列的概念、性质以及数列的通项公式等知识点。
本文将对这些知识进行详细归纳与讲解。
一、数列的概念与性质数列是按照一定次序排列而成的一列数的集合。
它可以用下列形式来表示:\[a_1, a_2, a_3, \ldots, a_n, \ldots\]其中,\(a_1, a_2, a_3, \ldots\)称为数列的项,\(a_n\)表示数列的第\(n\)项。
数列的前\(n\)项可以用希腊字母\(S_n\)表示。
数列有许多不同的分类方式,如等差数列、等比数列、等差数列、等比数列等。
不同类型的数列具有不同的性质,下面分别进行介绍。
1. 等差数列等差数列是每一项与它的前一项之差都相等的数列。
设等差数列的公差为\(d\),首项为\(a_1\),则数列的通项公式为:\[a_n = a_1 + (n-1)d\]2. 等比数列等比数列是每一项与它的前一项之比都相等的数列。
设等比数列的公比为\(q\),首项为\(a_1\),则数列的通项公式为:\[a_n = a_1 \times q^{(n-1)}\]3. 调和数列调和数列是每一项与它的前一项的倒数之和都相等的数列。
调和数列的通项公式为:\[a_n = \frac{1}{\frac{1}{a_1} + \frac{1}{a_2} + \cdots +\frac{1}{a_n-1} + \frac{1}{a_n}}\]4. 斐波那契数列斐波那契数列是一个非常有意思的数列,它的前两项为1,以后的每一项都是前两项的和。
斐波那契数列的通项公式为:\[F_n = F_{n-1} + F_{n-2}\]二、数列的求和公式在数列的学习中,求和公式也是一项重要的知识。
它可以帮助我们方便快捷地计算数列的前\(n\)项和。
高中数学数列的求和与通项的关系推导

高中数学数列的求和与通项的关系推导数列是高中数学中一个重要的概念,它是由一系列按照一定规律排列的数所组成的序列。
在数列中,求和与通项是两个常见的问题。
本文将重点讨论数列的求和与通项的关系推导,并且通过具体题目举例,说明这些问题的考点和解题技巧。
一、数列的求和问题数列的求和是指将数列中的所有项相加的过程,通常用符号∑表示。
对于一个数列{an},其前n项和表示为Sn,即Sn = a1 + a2 + a3 + ... + an。
在求解数列的求和问题时,我们需要找到数列的规律,从而得到一个通用的求和公式。
以等差数列为例,等差数列是指数列中相邻两项之间的差值是一个常数。
假设等差数列的首项为a1,公差为d,第n项为an,则数列的通项公式为an = a1 + (n-1)d。
现在我们来推导等差数列的前n项和公式。
首先,我们将等差数列的前n项和表示为Sn。
根据等差数列的性质,我们可以得到以下等式:Sn = a1 + (a1 + d) + (a1 + 2d) + ... + (a1 + (n-1)d)接下来,我们将等式两边的项按照相同的顺序排列,并将其相加:Sn = (a1 + a1 + ... + a1) + (d + d + ... + d) + ... + ((n-1)d + (n-1)d + ... + (n-1)d)可以观察到,等式右边的每一项都是由n个相同的数相加而成。
因此,我们可以将等式右边的每一项简化为:Sn = n(a1) + (1 + 2 + ... + (n-1))d其中,1 + 2 + ... + (n-1)表示从1到n-1的连续整数之和,可以用数学公式(n-1)n/2来表示。
将其代入上式,我们可以得到等差数列的前n项和公式:Sn = n(a1 + an)/2这个公式可以帮助我们快速计算等差数列的前n项和,而不需要逐项相加。
举个例子来说明,假设我们要计算等差数列1,3,5,7,9的前10项和,则根据公式,我们可以得到:S10 = 10(1 + 9)/2 = 55二、数列的通项问题数列的通项是指能够表示数列中任意一项的公式。
数列的通项公式与求和知识点及题型归纳总结

数列的通项公式与求和知识点及题型归纳总结知识点精讲一、基本概念(1)若已知数列的第1项(或前项),且从第2项(或某一项)开始的任一项与它的前一项(或前几项)间的关系可以用一个公式来表示,那么该公式就叫做这个数列的递推公式.递推公式也是给出数列的一种方法.(2)数列的第n 项n a 与项数n 之间的函数关系,可以用一个公式()n a f n =来表示,那么n a 就是数列的通项公式.注:①并非所有的数列都有通项公式;②有的数列可能有不同形式的通项公式; ③数列的通项就是一种特殊的函数关系式; ④注意区别数列的通项公式和递推公式.题型归纳及思路提示题型1 数列通项公式的求解 思路提示常见的求解数列通项公式的方法有观察法、利用递推公式和利用n S 与n a 的关系求解. 观察法根据所给的一列数、式、图形等,通过观察法归纳出其数列通项. 利用递推公式求通项公式 ①叠加法:形如1()n n a a f n +=+的解析式,可利用递推多式相加法求得n a②叠乘法:形如1()nn a f n a -= (0)n a ≠*(2,)n n N ≥∈的解析式, 可用递推多式相乘求得n a③构造辅助数列:通过变换递推公式,将非等差(等比)数列构造成为等差或等比数列来求其通项公式.常用的技巧有待定系数法、取倒数法、对称变换法和同除以指数法.利用n S 与n a 的关系求解 形如1(,)()n n n f S S g a -=的关系,求其通项公式,可依据1*1(1)(2,)n n n S n a S S n n N -=⎧=⎨-≥∈⎩,求出n a 观察法观察法即根据所给的一列数、式、图形等,通过观察分析数列各项的变化规律,求其通项.使用观察法时要注意:①观察数列各项符号的变化,考虑通项公式中是否有(1)n-或者1(1)n -- 部分.②考虑各项的变化规律与序号的关系.③应特别注意自然数列、正奇数列、正偶数列、自然数的平方{}2n 、{}2n与(1)n-有关的数列、等差数列、等比数列以及由它们组成的数列. 例6.20写出下列数列的一个通项公式:(1)325374,,,,,,;751381911---L(2)2,22,222,L ,222L ;(3)数列{}n a 中各项为:12,1122,111222,L,{111222n n L L 123个个,L 分析:通过观察,找出所给数列的特征,求出其通项.解析:(1)①原数列中的数的符号一正一负,故摆动数列乘以(1)n-;②绝对值后分子分母无明显的规律,但通过对偶数各项分子分母同乘以2,可使分子出现规律为3,4,5,6,L ,则2(1)34nn n a n +=-+. 解法一:1212021021022(101010)1(110)22(101)1109n n n n n n n a ----=⨯+⨯++=+++-==--L L g g 解法二:原数列⇔2229,99,999999n ⨯⨯⨯L L 123个,即2=(10-1)9nn a (3)121=(10-1)10+(10-1)=(10-1)(10+2)999n n n n n n a g 变式1 将全体正整数排成一个三角形数阵,如下所示,则第n 行(3n ≥)从左到右的第3个数为__________ 12 34 5 67 8 9 10L L L L L L L L L 变式2 观察下列等式:211122ni i n n ==+∑,2321111326ni i n n n ==++∑34321111424ni i n n n ==++∑45431111152330ni i n n n n ==++-∑5654211151621212ni i n n n n ==++-∑67653111111722642ni in n n n n ==++-+∑ L L L L1111101nk k k k k k k i i a n a n a n a n a +-+-==+++++∑L ,可以推测,当*2()k k N ≥∈时,111k a k +=+,12k a =,1_____k a -=,2_____k a -=利用递推公式求通项公式叠加法 数列有形如1()n n a a f n +=+的递推公式,且(1)(2)()f f f n +++L 的和可求,则变形为1()n n a a f n +-=,利用叠加法求和例6.21 已知数列{}n a 满足132n n a a n +=++ *()n N ∈,且12a =,求数列{}n a 的通项公式.分析:式子132n n a a n +=++ *()n N ∈是形如1()n n a a f n +=+的形式,故利用叠加法求和. 解析:132n n a a n +-=+ *()n N ∈可得131n n a a n --=-,(2n ≥) 1234n n a a n ---=-,L L L215a a -=相加可得:232n n n a +=(2n ≥),且12a =也满足上式,故232n n na +=*()n N ∈ 变式1 已知数列{}n a 中,12a =,12n n na a +-=*()n N ∈,求数列{}n a 的通项公式变式2 已知数列{}n a 中,12a =,11ln(1)n n a a n+=++ *()n N ∈,则n a =____A 、2ln n +B 、2(1)ln n n +-C 、2ln n n +D 、1ln n n ++ 变式3 已知数列{}n a 中,11a =,22a =,且11(1)n n n a q a qa +-=+-,(2n ≥,0q ≠)(1)设1n n n b a a +=-*()n N ∈,证明:{}n b 是等比数列. (2)求数列{}n a 的通项公式 变式4 数列{}n a 中,12a =,1n n a a cn +=+(c 为常数)*()n N ∈,且123,,a a a 成公比不为1的等比数列.(1)求c 的值;(2)求数列{}n a 的通项公式2、叠乘法 数列有形如1()nn a f n a -=g 的递推公式,且(1)(2)()f f f n g g L g 的积可求,则将递推公式变形为1()nn a f n a -=,利用叠乘法求出通项公式n a 例6.22 已知数列{}n a 中,11a =,12(1)n n na n a +=+,则数列{}n a 的通项公式为( ) A 、2n n B 、12n n - C 、21n n - D 、12n n +分析:数列的递推公式是形如1()nn a f n a -=的形式,故可以利用叠乘法求解. 解析:由12(1)n n na n a +=+变形得112n n a n a n ++=,从而 12(1)n n a na n -=-,L , 2122a a =,故1132112211132()212212n n n n n n a a a a n n na a a a n n ------==--g g L g g g g g L g g (2n ≥) 即112n n a n a -=(2n ≥),所以12n n n a -=(2n ≥,*n N ∈),且11a =满足上式,故12n n na -=(*n N ∈),选B变式1 已知数列{}n a 中,11a =,12n n a n a n++=,求数列{}n a 的通项公式 3、构造辅助数列法 (1)待定系数法形如1n n a pa q +=+(,p q 为常数,0pq ≠且1p ≠)的递推式,可构造1()n n a p a λλ++=+,转化为等比数列求解.也可以与类比式1n n a pa q -=+作差,由11()n n n n a a p a a +--=-,构造{}1n n a a +-为等比数列,然后利用叠加法求通项.例6.23 已知数列{}n a 中,11a =,1112n n a a +=+,求{}n a 的通项公式. 分析:式子1112n n a a +=+形如1n n a pa q +=+(,p q 为常数,0pq ≠且1p ≠),故利用构造法转化. 解析:解法一、设1112n n a a +=+等价于11()2n n a a λλ++=+,得到11122n n a a λ+=-,对应1112n n a a +=+,得到2λ=-故原递推式等价于112(2)2n n a a +-=-,因此数列{}2n a -为首项为1-,公比为12的等比数列,所以112()2n n a --=-,故112()2n n a -=- 解法二、由1112n n a a +=+得 1112n n a a -=+(2n ≥,*n N ∈), 因此111()2n n n n a a a a +--=-(2n ≥,*n N ∈),所以数列{}1n n a a -- 是首项为2112a a -=,公比为12的等比数列.2112111()()()22n n n n a a a a ----=-=2121()2n n n a a ----=L L L L1211()2a a -= 叠加得到:211111()111122()()1()1222212n n n n a a ----=+++==--L 故112()2n n a -=- (*n N ∈)变式1 已知11a =,132n n a a -=+(2n ≥,*n N ∈),求{}n a 的通项公式.例6.24 在数列{}n a 中,12a =,1431n n a a n +=-+ (*n N ∈),求数列{}n a 的通项公式.分析:将原递推公式转化为1(1)4()n n a a n a an λλ++++=++,即1433n n a a an a λ+=++-,比较1431n n a a n +=-+,得1a =-,0λ=,所以数列{}n a n -是首项为1,公比为4的等比数列,故14n n a n --=,即14n n a n -=+ (*n N ∈)2、同除以指数形如 1nn n a pa d +=+ (0p ≠且1p ≠,1d ≠)的递推式,当p d =时,两边同除以1n d +转化为关于n n a d ⎧⎫⎨⎬⎩⎭的等差数列;当p d ≠时,两边人可以同除以1n d +得111n n n n a a p d d d d ++=+g ,转化为11n np b b d d+=+g ,同类型(1).例6.25 已知数列{}n a 中,11a =-,1132n n n a a --=+(2n ≥,*n N ∈),求数列{}n a 的通项公式.解析:解法一、将1132n n n a a --=+两边同除以3n得11112()3333n n n nn a a ---=+⨯, 则1111121212()()()33333333n n nna a -=+⨯++⨯=-L ,则132n nn a -=- 解法二、将1132n n n a a --=+两边同除以2n得11312222n n n n a a --=+g ,令2nnna b =,得13122n n b b -=+,构造13()2n n b b λλ-+=+,得1λ=,因此数列{}1n b +为等比数列,且111331(1)()22n n n n b b --+=+=,则1312n n n b -=- (*n N ∈), 故13122n n n n a -=-,进而得到132n nn a -=- 评注:一般地,对于形如 1nn n a pa d +=+ (0p ≠且1p ≠,1d ≠)的数列求通项公式,两边同除以1n d +转化为待定系数法求解;两边同除以1n p+转化为叠加法求解.变式1 在数列{}n a 中,11a =,122nn n a a +=+(1)设12nnn a b -=,试证明:数列{}n b 是等差数列. (2)求数列{}n a 的前n 项的和n S取倒数法 对于1(0)n n n aa a ac b ca +=≠+,取倒数得111n n n n b ca b ca aa a a a++==+g .当a b =时,数列1n a ⎧⎫⎨⎬⎩⎭是等差数列;当a b ≠时,令1nnb a =,则1n n b c b b a a+=+g ,可用待定系数法求解. 例6.26 在数列{}n a 中,11a =,122nn na a a +=+,求数列{}n a 的通项公式. 分析:式中含有形如1n a +和n a 的分式形式,故考虑利用倒数变换求其通项公式. 解析:因为1121122n n n n a a a a ++==+,所以11112n n a a +-=,即数列1n a ⎧⎫⎨⎬⎩⎭是等差数列,11111(1)22n n n n a a ++=+-=,故21n a n =+(*n N ∈) 变式1 已知数列{}n a 中首项135a =,1312n n n a a a +=+(*n N ∈),求数列{}n a 的通项公式.变式2 已知数列{}n a 中首项11a =,前n 项的和为n S ,且满足1112n n n S S S --=+(2n ≥,*n N ∈),求数列{}n a 的通项公式. 取对数法 形如1(0,0)k n n n a ca c a +=>>的递推公式,则常常两边取对数转化为等比数列求解.例6.27 已知数列{}n a 中首项13a =,且31n na a += (*n N ∈),则数列的通项n a =_______ 分析:取对数时,常用以1a 为底的对数,便于计算. 解析:因为13a =,所以对31n na a +=两边取以3为底的对数,得到313log 2log n n a a +=,故{}3log n a 是以1为首项,2为公比的等比数列,所以13log 2n n a -=,所以123n na -=(*n N ∈)变式1 已知数列{}n a 中首项110a =,且2110n na a +=g (*n N ∈),求数列的通项n a 已知通项公式n a 与前n 项的和n S 关系求通项问题对于给出关于n a 与n S 的关系式的问题,解决方法包括两个转化方向,在应用时要合理选择.一个方向是转化n S 为n a 的形式,手段是使用类比作差法,使nS 1n S --=n a (2n ≥,*n N ∈),故得到数列{}n a 的相关结论,这种方法适用于数列的前n 项的和的形式相对独立的情形;另一个方向是将n a 转化为n S 1n S --(2n ≥,*n N ∈),先考虑n S 与1n S -的关系式,继而得到数列{}n S 的相关结论,然后使用代入法或者其他方法求解{}n a 的问题,这种情形的解决方法称为转化法,适用于数列的前n 项和的形式不够独立的情况.简而言之,求解n a 与n S 的问题,方法有二,其一称为类比作差法,实质是转化n S 的形式为n a 的形式,适用于n S 的形式独立的情形,如已知142nn S a -=+(2n ≥,*n N ∈);其二称为转化法,实质是转化n a 的形式为n S 的形式,适用于n S 的形式不够独立的情形,如已知2221n n n S a S =-(2n ≥,*n N ∈);不管使用什么方法,都应该注意解题过程中对n 的范围加以跟踪和注意,一般建议在相关步骤后及时加注n 的范围.例6.28 已知正项数列{}n a 中,前n 项的和n S,且满足1n a =+,求数列{}n a 的通项公式.解析:由已知,可得24(1)n n S a =+ ①类比得到2114(1)n n S a --=+(2n ≥,*n N ∈)②式①-式②得 221114422n n n n n n S S a a a a ----=-+-即1112()()()n n n n n n a a a a a a ---+=+-所以11()(2)0n n n n a a a a --+--=,又因为10n n a a -+>,故120n n a a ---=(2n ≥,*n N ∈),因此数列{}n a 为等差数列,且首项为1,公比为2 故21na n =- (*n N ∈)评注:本题是关于n a 与n S 的关系式问题中第一个方向的典型题目,本题的闪光点是未给出n S 的直接形式,需要考生稍加变形,转化为24(1)nn S a =+后,才可使求解方向变得更为明朗.变式1 已知数列{}n a 的前n 项的和n S ,11a =,142n n S a +=+(*n N ∈)(1)设12n n n b a a +=-,求n b ;(2)设112nn nc a a +=-,求数列{}n c 的前n 项和n T ;(3)设2n nna d =,求2010d例6.29 已知数列{}n a 中,0n a >,且对于任意正整数n 有11()2n n nS a a =+,求数列{}n a 的通项公式分析:已知n a 与n S 的关系,求数列的通项公式利用n a =n S 1n S --(2n ≥,*n N ∈)求解,将试题右边的含n a 的式子换成n S 1n S --来处理.解析:当1n =时,111111()2S a a a ==+,及0n a >,解得 11a =当2n ≥时,由11()2n n n S a a =+得1111()2n n n n n S S S S S --=-+-,变形整理得2211n n S S --=,数列{}2n S 是等差数列,首项为1, 公差为1 故21(1)1nS n n =+-⨯=,所以n S =1n =适合上式,故n S =(*n N ∈)故当2n ≥时,n a =n S 1n S --= 1n =适合上式,故na =*n N ∈)变式1 已知数列{}n a 中,0n a ≠(1)n ≥,112a =,前n 项和n S 满足2221n n n S a S =-(2n ≥,*n N ∈)(1)求证:数列1n S ⎧⎫⎨⎬⎩⎭是等差数列; (2)求数列{}n a 的通项公式变式2 设数列{}n a是正数组成的数列,且有*2)n a n N +=∈,求数列{}n a 的通项公式.例6.30 设数列{}n a 的前n 项的和为n S ,已知111,42n n a S a +==+. (1)设12n n n b a a +=-,证明:数列{}n b 是等比数列. (2)求数列{}n a 的通项公式.解析 (1)在142n n S a +=+中,令1n =,得2142S a =+,即12142a a a +=+,故25a =,由142n n S a +=+知2142n n S a ++=+,两式相减得2144n n n a a a ++=-,即211224n n n n a a a a +++-=-,故12n n b b +=,且121230b a a =-=≠,即{}n b 是以2为公比的等比数列.(2)由2142S a =+且11a =知26S =,故2215a S a =-=,所以212523a a -=-=,即有111232n n n b b --==g g ,所以11232n n n a a -+-=g ,于是113224n n n n a a ++-=,因此数列{}2n na 是首项为12,公差为34的等差数列.所以1331(1)22444n na n n =+-⨯=-,故2(31)2n n a n -=-g . 变式1 已知数列{}n a 的前n 项之和为n S ,且*585()n n S n a n N =--∈. (1)证明:数列{1}n a -是等比数列;(2)求数列{}n S 的通项公式,请指出n 为何值时,n S 取得最小值,并说明理由.变式2 已知数列{}n a 的前n 项和为n S ,且满足2*24()n n S a n n n N =+-∈. (1)写出数列{}n a 的前3项123,,a a a ; (2)求证:数列{21}n a n -+为等比数列; (3)求n S .变式3 设数列{}n a 的前n 项和为n S .已知2*112121,()33n n S a a n n n N n +==---∈. (1)求2a 的值;(2)求数列{}n a 的通项公式.题型2 数列的求和 思路提示求数列前n 项和的常见方法如下: (1)通项分析法.(2)公式法:对于等差、等比数列,直接利用前n 项和公式.(3)错位相减法:数列的通项公式为n n a b g 或n nab 的形式,其中{}n a 为等差数列,{}n b 为等比数列.(4)分组求和法:数列的通项公式为n n a b +的形式,其中{}n a 和{}n b 满足不同的求和公式.常见于{}n a 为等差数列,{}n b 为等比数列或者{}n a 与{}n b 分别是数列的奇数项和偶数项,并满足不同的规律. (5)裂项相消法:将数列恒等变形为连续两项或相隔若干项之差的形式,进行消项. (6)倒序相加:应用于等差数列或转化为等差数列的数列求和. 一、通项分析法例6.31 求数列2211,12,122,,1222,n -+++++++L L L 的前n 项的和. 解析 数列的通项21122221n n n a -=++++=-L ,即*21()n n a n N =-∈, 所以数列的前n 项的和为121212(12)(21)(21)(21)(222)2212n nnn n S n n n +-=-+-++-=+++-=-=---L L即1*22()n n S n n N +=--∈.评注 先分析数列通项的特点,再选择合适的方法求和是求数列的前n 项和问题应该强化的意识. 变式1 求数列9,99,999,L ,999nL 123的前n 项和. 二、公式法利用等差、等比数列的前n 项和公式求和.例6.32 已知等差数列{}n a 中,259,21,2n a n a a b ===,求数列{}n b 的前n 项和n S .分析 根据数列{}n a 为等差数列,259,21a a ==,求出数列{}n a 的通项, 从而知数列{}n b 为等比数列,利用等比数列的求和公式求n S .解析 设等差数列{}n a 的首项为1a ,公差为d ,依题意得119421a d a d +=⎧⎨+=⎩,解得154a d =⎧⎨=⎩.数列{}n a 的通项公式为41n a n =+,由2na nb =得412n n b +=,因为454141222n n n n b b +++==,所以数列{}n b 是首项为512b =,公比为42q =的等比数列.于是得数列{}n b 的前n 项和54442[1(2)]32(21)1215n n n S --==-. 评注 针对数列的结构特征,确定数列的类型,符合等差或等比数列时,直接利用等差、等比数列相应公式求解.变式1 如图6-4所示,从点1(0,0)P 作x 轴的垂线交曲线xy e =于点1(0,1)Q ,曲线在点1Q 处的切线与x 轴交于点2P .再从2P 作x 轴的垂线交曲线于点2Q ,依次重复上述过程得到一系列点:1122,;,;;,n n P Q P Q P Q L ,记点k P 的坐标为(,0)(1,2,,)k x k n =L .(1)试求k x 与1k x -的关系(2)k n ≤≤; (2)求1122||||||n n PQ P Q P Q +++L .三、错位相减法 求数列{n n a b g }和{nna b }的前n 项和,数列{}n a , {}n b 分别为等差与等比数列.求和时,在已知求和式的两边乘以等比数列公比q 后,与原数列的和作差,即n n S qS -,然后求n S 即可.例6.33 已知数列{}n a 的前n 项和为n S ,且*22()n n S a n N =-∈,数列{}n b 中,11b =,点1(,)n n P b b +在直线20x y -+=上.(1)求数列{}n a , {}n b 的通项公式;(2)设n n n c a b =g ,数列{}n c 的前n 项和为n T ,求n T . 解析 (1)22n n S a =-,*1122(2,)n n S a n n N --=-≥∈上两式相减得1122n n n n S S a a ---=-,得122n n n a a a -=-,故12n n a a -=, 令1*11111,22,2,2()n n n n a a a a a q n N -==-===∈.点1(,)n n P b b +在直线20x y -+=上,则120n n b b +-+=,12n n b b +=+, 则{}n b 是首项为1,公差为2的等差数列,*1(1)221()n b b n n n N =+-⨯=-∈.(2)(21)2n n n n c a b n ==-gg , 121232(21)2(1)n n T n =⨯+⨯++-⨯L 23`21232(21)2(2)n n T n +=⨯+⨯++-⨯L由(1)-(2)得112118(12)22222(21)22(21)212n nn n n T n n -++--=+⨯++⨯--⨯=+--⨯-L12(32)6n n +=--,故1(23)26n n T n +=-+.评注 由于结果的复杂性,自己可以通过代入1,2n =等验证,111222,T a b T a b ==等以确保所求结果的准确性. 变式1 已知数列{}n a 的前n 项和21(*)2n S n kn k N =-+∈,且n S 的最大值为8.(1)确定常数k ,并求n a ; (2)求数列92{}2nna -的前n 项和n T . 变式2已知{}n a 是等差数列,其前n 项和为n S ,{}nb 是等比数列,且1144442,27,10a b a b S b ==+=-=. (1)求数列{}n a 与{}n b 的通项公式;(2)记1121(*)n n n n T a b a b a b n N -=+++∈L ,证明:12210(*)n n n T a b n N +=-+∈.四、分组求和法对于既非等差又非等比数列的一类数列,若将数列的项进行适当地拆分,可分成等差、等比或常数列,然后求和.例6.34 在数列{}n a 中11111,(1)2n n n n a a a n ++==++.(1)设nn a b n=,证明1{}n n b b +-为等比数列; (2)求数列{}n a 的前n 项和n S . 解析 (1)由已知得1111(1)12112n nn n n n n a a a n b n n n +++++===+++,即112n n nb b +=+, 故112n n nb b +-=,且111(2,*)2n n n n b b n n N b b +--=≥∈-,因此1{}n n b b +-是公比为12的等比数列. (2)由(1)知当2n ≥时,1121111,,22n n n b b b b ---=-=L ,叠加得 11122111122n n n n n b b b b b b -----+-++-=++L L , 所以111112211212n n n b b ---==--,得11112n n b b -=+-,1n =时也成立,又111b a ==,所以112(*)2n n b n N -=-∈,得12(*)2n nn na nb n n N -==-∈. 12123(21)(4)(6)(2)24223(2462)(1)222n n n nS n nn --=-+-+-++-=++++-++++L L L令21231222n n nT -=++++L , 23111231222222n n n n nT --=+++++L , 故2111(1)11112212(1)2122222222212n n n n n n n nT nn n n --+=++++-=-=--=--g L ,故1242n n nT -+=-,又2462(1)n n n ++++=+L , 所以12(1)42n n nS n n -+=++-. 变式 1 已知数列{}n a 中的相邻两项212,k k a a -是关于x 的方程2(32)320k k x k x k -++=g 的两个根,且212(1,2,3,)k k a a k -≤=L .(1)求1357,,,a a a a ;(2)求数列{}n a 的前2n 项和2n S .变式2 等比数列{}n a 中,123,,a a a 分别是下表第一、二、三行中的某一个数,且123,,a a a 中的任何两个数不在下表6-1的同一列.表6-1第1列 第2列 第3列 第1行 3 2 10 第2行 6 4 14 第3行 9 8 18(1)求数列{}n a 的通项公式;(2)若数列{}n b 满足:(1)ln n n n n b a a =+-,求数列{}n b 的前2n 项和2n S .五、裂项相消法将数列恒等变形为连续两项或相隔若干项之差的形式,进行消项. 常用的裂项相消变换有: 1.分式裂项1111()()n n p p n n p=-++;1111[](1)(2)2(1)(1)(2)n n n n n n n =-+++++.2.根式裂项1p=.3.对数式裂项lg lg()lgn pn p nn+=+-.4.指数式裂项1()(1)1n n naaq q q qq+=-≠-;11111()(1)(1)(1)111nn n n nqqq q q q q++=-≠-----.使用裂项法,要注意正负项相消时消去了哪些项,保留了哪些项;应注意到,由于数列{}na中每一项na均裂成一正一负两项,所以互为相反数的项合并为零后,所剩正数项与负数项的项数必是一样的多,切不可漏写未被消去的项.未被消去的项有前后对称的特点,即经过裂项后有“对称剩项”的特征.另外从实质上看,正负项相消是裂项法的根源和目的.例6.35 求数列1111,,,,,132435(2)n n⨯⨯⨯+L L的前n项和nS.解析先分析通项公式1111()(2)22nan n n n==-++,所以1111111111311[(1)()()](1)(*)23242221242224 nS n Nn n n n n n=-+-++-=+--=--∈+++++L评注如果数列的通项公式可以写成()()f n p f n+-的形式,常采用裂项求和的方法.特别地,当数列形如11{}n na a+,其中{}na是等差数列时,可尝试使用此法.变式1 已知数列1111,,,,,12123123n+++++++L LL,求它的前n项和nS.例6.36已知等差数列{}na满足3577,26a a a=+=,{}na的前n项和nS.(1)求na及nS;(2)令21(*)1nnb n Na=∈-,求数列{}nb的前n项和nT.解析(1)设{}na的首项为1a,公差为d,由已知可得111273210262a d aa d d+==⎧⎧⇒⎨⎨+==⎩⎩.所以1(1)21(*)na a n d n n N=+-=+∈,1()(2)(*)2nna a nS n n n N+==+∈.(2)因为21na n=+,所以214(1)na n n-=+,因此1111()4(1)41nbn n n n==-++,故1211111111(1)(1)(*)42231414(1)n n nT b b b n N n n n n =+++=-+-++-=-=∈+++L L .故数列{}n b 的前n 项和4(1)n nT n =+.评注 采用裂项相消法求解数列的前n 项和,消项时要注意相消的规律,可将前几项和表示出来,归纳规律.一般来说,先注意项数,如果是每两项作为一组相消,则最终剩余项数为偶数项;再看大小,若前面保留的是分母最小的若干项,则最后必会保留分母最大的若干项. 变式1 设正项数列{}n a 前n 项和n S 满足21(1)4n n S a =+.(1)求数列{}n a 的通项公式; (2)设11n n n b a a +=g ,求数列{}n b 的前n 项和n T .变式2 在数1和100之间插入n 个实数,使得这2n +个数构成递增的等比数列,将这2n +个数的乘积记作n T ,再令lg ,1n n a T n =≥. (1)求数列{}n a 的通项公式;(2)设1tan tan n n n b a a +=g 求数列{}n b 的前n 项和n S .六、倒序相加法将一个数列倒过来排列,当它与原数列相加时,若有规律可循,并且容易求和,则这样的数列求和时可用倒序相加法(等差数列前n 项和公式的推导即用此方法).例6.37设()f x (7)(6)(5)(0)(8)f f f f f -+-+-++++L L 的值.解析因为1()(1)22x xf x f x +-==+=+x =+==所以(7)(6)(5)(0)(8)8f f f f f -+-+-++++==L L . 变式1 函数121()(0),,4xf x m x x R m =>∈+,当121x x +=时,121()()2f x f x +=. (1)求m 的值;(2)已知数列{}n a 满足121(0)()()()(1)n n a f f f f f n n n-=+++++L ,求n a ;(3)若12n n S a a a =+++L ,求n S .变式2 已知函数()f x 对任意x R ∈都有1()(1)2f x f x +-=.(1)求1()2f 的值;(2)若数列{}n a 满足121(0)()()()()(*)n n na f f f f f n N n n n n-=+++++∈L ,数列{}n a 是等差数列吗?试证明之;(3)设4(*)41n n b n N a =∈-,1n n n c b b +=,求数列{}n c 的前n 项和n T .变式3 已知数列{}n a 是首项为1,公差为2的等差数列,求0121231n n nn n n n S C a C a C a C a +=++++L .最有效训练题1.L ,则 )A .第18项B .第19项C .第17项D .第20项2.已知各项均不为零的数列{}n a ,定义向量1(,),(,1),*n n n n c a a b n n n N +==+∈u u r u u r,则下列命题为真命题的是( )A .若对任意的*n N ∈,总有//n n c b u u r u u r 成立,则数列{}n a 是等差数列B .若对任意的*n N ∈,总有//n n c b u u r u u r成立,则数列{}n a 是等比数列 C .若对任意的*n N ∈,总有n n c b ⊥u u r u u r成立,则数列{}n a 是等差数列 D .若对任意的*n N ∈,总有n n c b ⊥u u r u u r成立,则数列{}n a 是等比数列3.设{}n a 是单调递减的等差数列,前3项的和是15,前3项的积是105,当该数列的前n 项和最大时,n =( )A .4B .5C .6D .74.已知数列{}n a 满足111n n a a +=-,若112a =,则2011a =( )A .12B .2C .-1D .1 5.设等比数列{}n a 的各项均为正数,公比为q ,前n 项和为n S ,若对*n N ∀∈,有23n n S S <,则q 的取值范围是( )A .(0,1]B .(0,2)C .[1,2)D .(0)6.对于数列{}n a ,如果*k N ∃∈及12,,,k R λλλ∈L ,使1122n k n k n k k n a a a a λλλ++-+-=+++L 成立,其中*n N ∈,则称{}n a 为k 阶递推数列,给出下列三个结论: ①若{}n a 为等比数列,则是1阶递推数列; ②若{}n a 为等差数列,则是2阶递推数列;③若数列{}n a 的通项公式为2n a n =,则是3阶递推数列. 其中正确结论的个数是( )A .0B .1C .2D .37.根据数列的前几项,写出数列的一个通项公式: (1)-1,7,-13,19,L ,n a =_____________; (2)0.8,0.88,0.888,L ,n a =_____________; (3)115132961,,,,,,248163264--L ,n a =_____________;(4)0,1,0,1,L ,n a =_____________. 8.若数列{}n a 满足111n n d a a +-=(*n N ∈,d 为常数),则称{}n a 为调和数列.已知数列1{}nx 为调和数列,且1220200x x x +++=L ,则56x x +=__________.9.在数列{}n a 中,121,2a a ==,且21(1)(*)n n n a a n N +-=+-∈,则100S =__________. 10.根据下列条件,确定数列{}n a 的通项公式. (1)已知数列{}n a 的前n 项和2231n S n n =-+; (2)已知数列{}n a 的满足132n n n a a +=++,且12a =; (3)1111,(2,*)n n n a a a n n N n--==≥∈; (4)在数列{}n a 中,111,2(*)n n n a a a n N +==+∈; (5)在数列{}n a 中,113,21(*)n n a a a n N +==+∈;(6)在数列{}n a 中,2111,2(*)n nn a a a a n N +==+∈. 11.设数列{}n a 的前n 项和为n S ,点(,)(*)nS n n N n∈均在函数32y x =-的图像上. (1)求数列{}n a 的通项公式; (2)设13n n n b a a +=,n T 是数列{}n b 的前n 项和,求使得20n mT <对所有*n N ∈都成立的最小正整数m .12. 已知数列{}n a 的首项1122,(*)31n n n a a a n N a +==∈+(1)证明:数列1{1}na -是等比数列; (2)求数列{}nna 的前n 项和n S .。
(完整版)数列通项公式与求和讲解与习题(含答案),推荐文档
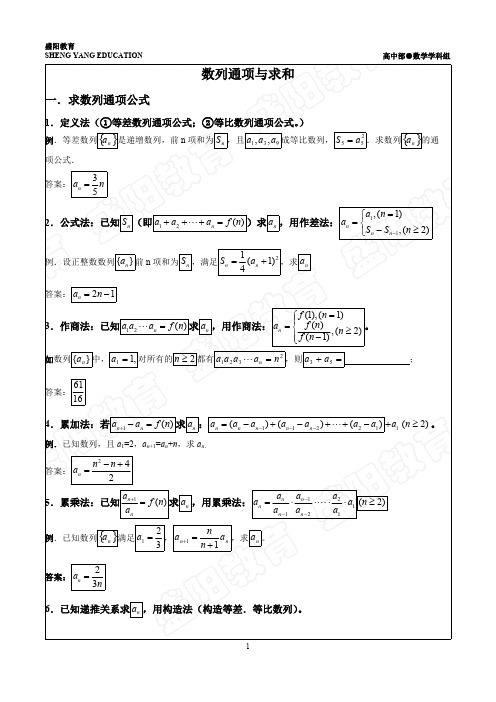
数列通项与求和一.求数列通项公式1.定义法(①等差数列通项公式;②等比数列通项公式。
)例.等差数列是递增数列,前n 项和为,且成等比数列,.求数列的通{}n a n S 931,,a a a 255a S ={}n a 项公式.答案:35n a n =2.公式法:已知(即)求,用作差法:n S 12()n a a a f n +++= n a 11,(1),(2)n n n a n a S S n -=⎧=⎨-≥⎩例.设正整数数列前n 项和为,满足,求{}n a n S 21(1)4n n S a =+n a 答案:21n a n =-3.作商法:已知求,用作商法:。
12()n a a a f n = n a (1),(1)(),(2)(1)n f n f n a n f n =⎧⎪=⎨≥⎪-⎩如数列中,对所有的都有,则;}{n a ,11=a 2≥n 2321n a a a a n = =+53a a 答案:61164.累加法:若求:1a +(2)n ≥。
1()n n a a f n +-=n a 11221()()()n n n n n a a a a a a a ---=-+-++- 例.已知数列,且a 1=2,a n +1=a n +n ,求a n .答案:242n n n a -+=5.累乘法:已知求,用累乘法:1()n n a f n a +=n a 121121n n n n n a a aa a a a a ---=⋅⋅⋅⋅ (2)n ≥例.已知数列满足,,求。
{}n a 321=a n n a n na 11+=+n a 答案:23n a n=6.已知递推关系求,用构造法(构造等差.等比数列)。
n a(1)形如只需构造数列,消去带来的差异.其中有多种不同形式()n f pa a n n +=+1{}n b ()n f ()n f ①为常数,即递推公式为(其中p ,q 均为常数,)。
2023届高三数学一轮复习专题 数列累加法构造等比等递推公式求通项及常用求和方法 讲义 (解析版)

数列求解通项的方法总结方法一、公式法当已知数列的类型(如已知数列为等差或等比数列)时,可以设出首项和公差(公比),列式计算。
1、等差数列通项公式: dn a a n )1(1-+=2、等比数列通项公式:例1、设等差数列{a n }的公差为d ,前n 项和为S n ,等比数列{b n }的公比为q ,已知b 1=a 1,b 2=2,q=d ,S 10=100.(1)求数列{a n },{b n }的通项公式 (2)当d >1时,记c n =,求数列{c n }的前n 项和T n .变式1、已知{a n }是各项均为正数的等比数列,{b n }是等差数列,且a 1=b 1=1,b 2+b 3=2a 3,a 5﹣3b 2=7.(Ⅰ)求{a n }和{b n }的通项公式;(Ⅱ)设c n =a n b n ,n ∈N *,求数列{c n }的前n 项和.11-=n n q a a方法二、利用前n 项和与通项的关系已知数列{ a n }前n 项和S n ,求通项公式,利用 a n ={)1()2(11=≥--n S n S S n n 特别地,当n=1的值与S 1的值相同时,合并为一个通项公式,否则写成分段的形式。
例2、(1)设数列{a n }的前n 项和为S n ,已知2S n =3n+3.求{a n }的通项公式;(2)S n 为数列{a n }的前n 项和,己知a n >0,a n 2+2a n =4S n +3 (I )求{a n }的通项公式.(Ⅱ)设b n =,求数列{b n }的前n 项和.变式2、(2015·四川)数列{a n }(n=1,2,3…)的前n 项和S n ,满足S n =2a n ﹣a 1,且a 1,a 2+1,a 3成等差数列.(Ⅰ)求数列{a n }的通项公式; (Ⅱ)设数列的前n 项和为T n ,求T n .方法三、利用递推关系式与通项的关系类型1、累加法 形如)(1n f a a n n +=+例3、(2014·全国卷)数列{a n }满足a 1=1,a 2=2,a n+2=2a n+1-a n +2.(1)设b n =a n+1-a n ,证明{b n }是等差数列; (2)求数列{a n }的通项公式.变式3、已知数列{}n a 满足11211n n a a n a +=++=,,求数列{}n a 的通项公式。
高考数学(精讲+精练+精析)专题6_1 数列的通项公式与求和试题 理(含解析)

专题6.1 数列的通项公式与求和【三年高考】1. 【2016高考浙江理数】设数列{a n }的前n 项和为S n .若S 2=4,a n +1=2S n +1,n ∈N *,则a 1=,S 5= . 【答案】1 1212. 【2016高考山东理数】已知数列{}n a 的前n 项和S n =3n 2+8n ,{}n b 是等差数列,且1.n n n a b b +=+ (Ⅰ)求数列{}n b 的通项公式;(Ⅱ)令1(1).(2)n n n nn a c b ++=+ 求数列{}n c 的前n 项和T n . 【解析】(Ⅰ)由题意知当2≥n 时,561+=-=-n S S a n n n ,当1=n 时,1111==S a ,所以56+=n a n .设数列{}n b 的公差为d ,由⎩⎨⎧+=+=322211b b a b b a ,即⎩⎨⎧+=+=d b db 321721111,可解得3,41==d b ,所以13+=n b n .3.【2016高考江苏卷】记{}1,2,100U =…,.对数列{}()*n a n N ∈和U 的子集T ,若T =∅,定义0TS=;若{}12,,k T t t t =…,,定义12+k T t t t S a a a =++….例如:{}=1,3,66T 时,1366+T S a a a =+.现设{}()*n a n N ∈是公比为3的等比数列,且当{}=2,4T 时,=30T S .(1)求数列{}n a 的通项公式;(2)对任意正整数()1100k k ≤≤,若{}1,2,k T ⊆…,,求证:1T k S a +<; (3)设,,C D C U D U S S ⊆⊆≥,求证:2C C DD S S S +≥.【解析】(1)由已知得1*13,n n a a n N -=•∈.于是当{2,4}T =时,2411132730r S a a a a a =+=+=.又30r S =,故13030a =,即11a =.所以数列{}n a 的通项公式为1*3,n n a n N -=∈.(2)因为{1,2,,}T k ⊆,1*30,n n a n N -=>∈,所以1121133(31)32k k k r k S a a a -≤+++=+++=-<.因此,1r k S a +<.(3)下面分三种情况证明.①若D 是C 的子集,则2C C DC D D D D S S S S S S S +=+≥+=.②若C 是D 的子集,则22C CDC C CD S S S S S S +=+=≥.③若D 不是C 的子集,且C 不是D 的子集.令U E C C D =,U F D C C =则E φ≠,F φ≠,EF φ=.于是C E CD S S S =+,D F CD S S S =+,进而由C D S S ≥,得E F S S ≥.设k 是E 中的最大数,l 为F 中的最大数,则1,1,k l k l ≥≥≠.由(2)知,1E k S a +<,于是1133l k l F E k a S S a -+=≤≤<=,所以1l k -<,即l k ≤.又k l ≠,故1l k ≤-,从而1121131133222l l k E F l a S S a a a ----≤+++=+++==≤,故21E F S S ≥+,所以2()1C CDD CDS S S S -≥-+,即21C CDD S S S +≥+.综合①②③得,2C CDD S S S +≥.4.【2016高考天津理数】已知{}n a 是各项均为正数的等差数列,公差为d ,对任意的,b n n N ∈*是n a 和1n a +的等差中项.(Ⅰ)设22*1,n n n c b b n N +=-∈,求证:{}n c 是等差数列;(Ⅱ)设()22*11,1,nnn n k a d T b n N ===-∈∑,求证:2111.2nk kT d =<∑5. 【2015高考新课标2,理16】设n S 是数列{}n a 的前n 项和,且11a =-,11n n n a S S ++=,则n S =________.【答案】1n-【解析】由已知得111n n n n n a S S S S +++=-=⋅,两边同时除以1n n S S +⋅,得1111n nS S +=--,故数列1n S ⎧⎫⎨⎬⎩⎭是以1-为首项,1-为公差的等差数列,则11(1)n S n n =---=-,所以1n S n=-. 6.【2015江苏高考,11】数列}{n a 满足11=a ,且11+=-+n a a n n (*N n ∈),则数列}1{na 的前10项和为 【答案】2011【解析】由题意得:112211(1)()()()1212n n n n n n n a a a a a a a a n n ---+=-+-++-+=+-+++=,所以1011112202(),2(1),11111n n n S S a n n n n =-=-==+++ 7. 【2015高考新课标1,理17】n S 为数列{n a }的前n 项和.已知n a >0,2n n a a +=43n S +.(Ⅰ)求{n a }的通项公式; (Ⅱ)设11n n n b a a +=,求数列{n b }的前n 项和.8.【2015高考山东,理18】设数列{}n a 的前n 项和为n S .已知233nn S =+.(I )求{}n a 的通项公式;(II )若数列{}n b 满足3log n n n a b a =,求{}n b 的前n 项和n T .【解析】(I )因为233n n S =+ ,所以,1233a =+ ,故13,a = 当1n > 时,11233,n n S --=+此时,1122233,n n n n n a S S --=-=- 即13,n n a -= 所以,13,1,3,1,n n n a n -=⎧=⎨>⎩(II )因为3log n n n a b a = ,所以113b =,当1n > 时,()11133log 313n n nn b n ---==-⋅ ,所以1113T b == 当1n > 时,()()12112311323133nn n T b b b b n ---=++++=+⨯+⨯++- ,所以()()01231132313n n T n --=+⨯+⨯++-,两式相减,得()()012122333133n n n T n ---=+++--⋅()11121313313n n n ----=+--⋅- 1363623n n +=-⨯ ,所以13631243n nn T +=+⨯,经检验,1n = 时也适合, 综上可得:13631243n nn T +=+⨯ 9.【2015高考重庆,理22】在数列{}n a 中,()21113,0n n n n a a a a a n N λμ+++=++=∈ (1)若0,2,λμ==-求数列{}n a 的通项公式; (2)若()0001,2,1,k N k k λμ+=∈≥=-证明:010011223121k a k k ++<<+++10.【2014高考广东理第19题】设数列{}n a 的前n 项和为n S ,满足21234n n S na n n +=--,n N *∈,且315S =.(1)求1a 、2a 、3a 的值; (2)求数列{}n a 的通项公式.11.【2014高考湖南理第20题】已知数列{}n a 满足111,n n n a a a p +=-=,*n N ∈.(1)若{}n a 为递增数列,且123,2,3a a a 成等差数列,求P 的值; (2)若12p =,且{}21n a -是递增数列,{}2n a 是递减数列,求数列{}n a 的通项公式. 【解析】 (1)因为数列{}n a 为递增数列,所以10n n a a +-≥,则11n nn n n n a a p a a p ++-=⇒-=,分别令1,2n =可得22132,a a p a a p -=-=2231,1a p a p p ⇒=+=++,因为123,2,3a a a 成等差数列,所以21343a a a =+()()224113130p p p p p ⇒+=+++⇒-=13p ⇒=或0,当0p =时,数列n a 为常数数列不符合数列{}n a 是递增数列,所以13p =.(2)由题可得122122212121111,222n n n n n n n n n a a a a a a +-++-+-=⇒-=-=,因为{}21n a -是递增数列且{}2n a 是递减数列,所以2121n n a a +->且222n n a a +<,则有22221221222121n n n n n n n n a a a a a a a a +-++-+-<-⎧⇒-<-⎨<⎩,因为12.【2014高考全国1第17题】已知数列{}n a 的前n 项和为n S ,11a =,0n a ≠,11n n n a a S λ+=-,其中λ为常数,(I )证明:2n n a a λ+-=;(II )是否存在λ,使得{}n a 为等差数列?并说明理由.【解析】(I )由题设,11n n n a a S λ+=-,1211n n n a a S λ+++=-.两式相减得,121()n n n n a a a a λ+++-=. 由于10n a +≠,所以2n n a a λ+-=.【三年高考命题回顾】纵观前三年各地高考试题, 对数列通项公式和求和这部分的考查,主要考查数列的概念与表示方法、数列递推关系与通项公式的联系、数列的求和方法,往往与函数、方程、不等式等知识建立联系,高考中一般会以各种形式考查.【2017年高考复习建议与高考命题预测】由前三年的高考命题形式可以看出, 高考对数列概念与表示方法的考查,要深刻体会数列不光体现一种递推关系,它具有函数特征,故经常会与函数、方程、不等式等知识联系考察.对数列通项公式的考察,一般会以等差数列和等比数列具体形式出现,或者由项的递推关系或者项与前n项的的关系得出,同时要注意从特殊到一般思想的灵活运用.对数列求和的考察,要掌握常见的数列求和方法(直接求和、倒序相加法、错位相减法、裂项相加法),往往会和不等式建立联系,会牵涉到放缩法,难度会大点,注意等价转换思想的活用.这部分试题难度属中低档的题目,小题突出“小、巧、活”,主要以通项公式、前n项和公式为载体,结合数列的性质考查分类讨论、化归与方程等思想,要注重通性、通法;解答题“大而全”,注重题目的综合与新颖,突出对逻辑思维能力的考查.由于连续两年大题没涉及数列,故预测2017年高考将以等差数列,等比数列的定义、通项公式和前n项和公式为主要考点,特别是错位相减法求和问题,重点考查学生的运算能力与逻辑推理能力.【2017年高考考点定位】高考对数列的通项公式与求和的考查有三种主要形式:一是考察数列的概念与表示;二是数列通项公式;三是数列求和;其中经常与函数、方程、不等式等知识的相联系. 【考点1】数列的概念与表示 【备考知识梳理】1.定义:按照一定顺序排列着的一列数.2.表示方法:列表法、解析法(通项公式法和递推公式法)、图象法.3.分类:按项数有限还是无限分为有穷数列和无穷数列;按项与项之间的大小关系可分为单调数列、摆动数列和常数列.4.n a 与n S 的关系:11(1)(2)n nn S n a S S n -=⎧=⎨-⎩≥.5.处理方法:.用函数的观点处理数列问题 【规律方法技巧】1. 数列是定义域为正整数集或其有限子集的函数,故数列具有函数的特征(周期性、单调性等).2. 观察法是解决数列问题的法宝,先根据特殊的几项,找出共同的规律,横看“各项之间的关系结构”,纵看“各项与项数n 的关系”,从而确定数列的通项公式. 【考点针对训练】1. 【2016年4月河南八市高三质检卷】已知*1log (2)()n n a n n N +=+∈,观察下列算式:1223lg 3lg 4log 3log 42lg 2lg 3a a •=•=•=;123456237lg 3lg 4lg8log 3log 4log 83lg 2lg 3lg 7a a a a a a •••••=•=•=,…;若*1232016()m a a a a m N ••••=∈,则m 的值为( )A .201622+ B .20162 C .201622- D .201624-【答案】C【解析】由题意:1223lg 3lg 4log 3log 42lg 2lg 3a a •=•=•=;123456237lg 3lg 4lg8log 3log 4log 83lg 2lg 3lg 7a a a a a a •••••=•=•=,…;12345613142315lg3lg 4lg16log 3log 4log 1616,lg 2lg3lg15a a a a a a a a ⋅⋅⋅⋅⋅⋅⋅=⋅=⋅=…;据此可知,*1232016()m a a a a m N ••••=∈,则m 的值为201622-2.数列 ,817,275,31,31--的一个通项公式是 A .n n a n n 312)1(1--=+ B .n n a n n 312)1(--= C . n n n n a 312)1(1--=+ D . nn nn a 312)1(--= 【答案】C.【考点2】递推关系与数列通项公式 【备考知识梳理】在一些综合性比较强的数列问题中,数列通项公式的求解问题往往是解决数列难题的瓶颈.数列通项公式的求解常用方法:1、定义法,直接利用等差数列或等比数列的定义求通项的方法叫定义法,这种方法适应于已知数列类型的题目.2、公式法, 若已知数列的前n 项和n S 与n a 的关系,求数列{}n a 的通项n a 可用公式⎩⎨⎧≥⋅⋅⋅⋅⋅⋅⋅-=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=-2111n S S n S a n n n 求解.3、由递推式求数列通项法,对于递推公式确定的数列的求解,通常可以通过递推公式的变换,转化为等差数列或等比数列问题,有时也用到一些特殊的转化方法与特殊数列.4、待定系数法(构造法),求数列通项公式方法灵活多样,特别是对于给定的递推关系求通项公式,观察、分析、推理能力要求较高.通常可对递推式变换,转化成特殊数列(等差或等比数列)来求解,这种方法体现了数学中化未知为已知的化归思想,而运用待定系数法变换递推式中的常数就是一种重要的转化方法. 【规律方法技巧】 数列的通项的求法: ⑴公式法:①等差数列通项公式;②等比数列通项公式.⑵已知n S (即12()n a a a f n +++=)求n a ,用作差法:{11,(1),(2)n n n S n a S S n -==-≥.⑶已知12()n a a a f n =求n a ,用作商法:(1),(1)(),(2)(1)n f n f n a n f n =⎧⎪=⎨≥⎪-⎩.⑷若1()n n a a f n +-=求n a 用累加法:11221()()()n n n n n a a a a a a a ---=-+-++-1a +(2)n ≥.⑸已知1()n n a f n a +=求n a ,用累乘法:121121n n n n n a aa a a a a a ---=⋅⋅⋅⋅(2)n ≥.⑹已知递推关系求n a ,用构造法(构造等差、等比数列).特别地,(1)形如1n n a ka b -=+、1nn n a ka b -=+(,k b 为常数)的递推数列都可以用待定系数法转化为公比为k 的等比数列后,再求n a .如(21)已知111,32n n a a a -==+,求n a ;(2)形如11n n n a a ka b--=+的递推数列都可以用倒数法求通项.注意:(1)用1--=n n n S S a 求数列的通项公式时,你注意到此等式成立的条件了吗?(2n ≥,当1n =时,11S a =);(2)一般地当已知条件中含有n a 与n S 的混合关系时,常需运用关系式1--=n n n S S a ,先将已知条件转化为只含n a 或n S 的关系式,然后再求解. (3)由n S 与1n S -的关系,可以先求n S ,再求n a ,或者先转化为项与项的递推关系,再求n a . 【考点针对训练】1. 【2016届榆林市高三二模】在数列{}n a 中,()1111,114n n a a n a -=-=->,则2016a 的值为( )A .14-B .5C .45D .以上都不对 【答案】C2. 【2016湖北省八校高三.二联】数列{}n a 满足1=1a ,()()1=11n n na n a n n ++++,且2=cos 3n n n b a π,记n S 为数列{}n b 的前n 项和,则120S = . 【答案】7280【解析】由()()1=11n n na n a n n ++++得,111n n a a n n +=++,所以数列n a n ⎧⎫⎨⎬⎩⎭是以1为公差的等差数列,且111a =,所以n a n n =,2n a n =,22cos3n n b n π=,所以222222212011111234561202222S =-⨯-⨯+-⨯-⨯+-+22222221(1223456120)2=-+-⨯++-+-222222221[(123120)3(369120)]2=-++++-⨯++++22222221139(1240)(123120)22=⨯⨯⨯++-⨯++++140418111201212413972802626⨯⨯⨯⨯=⨯⨯⨯-⨯= 【考点3】数列求和 【备考知识梳理】数列的求和也是高考中的热点内容,考察学生能否把一般数列转化为特殊数列求和,体现了化归的思想方法,其中错位相减和裂项相消是高考命题的热点.估计在以后的高考中不会有太大的改变.数列求和的常用方法,尤其是利用裂项法和错位相减法求一些特殊数列的和,数列求和的基本方法:1.基本公式法:()1等差数列求和公式:()()11122n n n a a n n S na d +-==+ ()2等比数列求和公式:()111,11,111n n n na q S a q a a q q qq =⎧⎪=-⎨-=≠⎪--⎩ ()30122nn n n n n C C C C ++++=.2.错位相消法:一般适应于数列{}n n a b 的前n 向求和,其中{}n a 成等差数列,{}n b 成等比数列.3.分组求和:把一个数列分成几个可以直接求和的数列,然后利用公式法求和.4.拆项(裂项)求和:把一个数列的通项公式分成两项差的形式,相加过程中消去中间项,只剩下有限项再求和.常见的拆项公式有:()1若{}n a 是公差为d 的等差数列,则111111n n n n a a d a a ++⎛⎫=- ⎪⎝⎭; ()2()()1111212122121n n n n ⎛⎫=- ⎪-+-+⎝⎭;()311n n kn k n =+++;()411m m mn n n C C C -+=-;()5()!1!!n n n n ⋅=+-.5.倒序相加法:根据有些数列的特点,将其倒写后与原数列相加,以达到求和的目的. 【规律方法技巧】数列求和关键是研究数列通项公式,根据通项公式的不同特征选择相应的求和方式,若数列是等差数列或等比数列,直接利用公式求和;若通项公式是等差乘等比型,利用错位相减法;若通项公式可以拆分成两项的差且在累加过程中可以互相抵消,利用裂项相消法,从近年的考题来看,逐渐加大了与函数不等式的联系,通过对通项公式进行放缩,放缩为易求和的数列问题处理. 【考点针对训练】1. 【2016年江西九江高三第三次联考】设n S 是等差数列{}n a 的前n 项和,若12,21344672==S S ,则=2016S ( )A .22B .26C .30D .34 【答案】C【解析】由134420166721344672,,S S S S S --成等差数列,得1221022016-+=⨯S ,即=2016S 30,故选C.2. 【2016届淮北一中高三最后一卷】已知函数()()()()1210log 110ax x f x x x ⎧->⎪=⎨+-<≤⎪⎩且334f f ⎡⎤⎛⎫-= ⎪⎢⎥⎝⎭⎣⎦,在各项为正的数列{}n a 中,{}1112,,2n n n a a f a a +⎛⎫==+⎪⎝⎭的前n 项和为n S ,若126n S =,则n =____________.【答案】6【应试技巧点拨】1. 由递推关系求数列的通项公式(1)利用“累加法”和“累乘法”求通项公式此解法来源与等差数列和等比数列求通项的方法,递推关系为1()n n a a f n +-=用累加法;递推关系为1()n n a f n a +=用累乘法.解题时需要分析给定的递推式,使之变形为1n n a a +-、1n naa +结构,然后求解.要特别注意累加或累乘时,应该为)1(-n 个式子,不要误认为n 个. (2)利用待定系数法,构造等差、等比数列求通项公式求数列通项公式方法灵活多样,特别是对于给定的递推关系求通项公式,观察、分析、推理能力要求较高.通常可对递推式变换,转化成特殊数列(等差或等比数列)来求解,这种方法体现了数学中化未知为已知的化归思想,而运用待定系数法变换递推式中的常数就是一种重要的转化方法.递推公式为q pa a n n +=+1(其中p ,q 均为常数,)0)1((≠-p pq ).把原递推公式转化为:)(1t a p t a n n -=-+,其中pqt -=1,再利用换元法转化为等比数列求解.3.如何选择恰当的方法求数列的和在数列求和问题中,由于题目的千变万化,使得不少同学一筹莫展,方法老师也介绍过,就不清楚什么特征用什么方法.为此提供一个通法 “特征联想法”:就是抓住数列的通项公式的特征,再去联想常用数列的求和方法.通项公式作为数列的灵魂,只有抓住它的特征,才能对号入座,得到求和方法. 特征一:....++=n n n b a C ,数列{}n C 的通项公式能够分解成几部分,一般用“分组求和法”.特征二:n n n C a b =⋅,数列{}n C 的通项公式能够分解成等差数列和等比数列的乘积,一般用“错位相减法”. 特征三:1n n nC a b =⋅,数列{}n C 的通项公式是一个分式结构,一般采用“裂项相消法”. 特征四:nn n n C C a =⋅,数列{}n C 的通项公式是一个组合数和等差数列通项公式组成,一般采用“倒序相加法”.4. 利用转化,解决递推公式为n S 与n a 的关系式. 数列{n a }的前n 项和n S 与通项n a 的关系:11(1)(2)n n n S n a S S n -=⎧=⎨-⎩≥.通过纽带:12)n n n a S S n -=-≥(,根据题目求解特点,消掉一个n n a S 或.然后再进行构造成等差或者等比数列进行求解.如需消掉n S ,利用已知递推式,把n 换成(n+1)得到递推式,两式相减即可.若消掉n a ,只需把1n n n a S S -=-带入递推式即可.不论哪种形式,需要注意公式1n n n a S S -=-成立的条件 2.n ≥ 5.由递推关系求数列的通项公式(1)利用“累加法”和“累乘法”求通项公式此解法来源与等差数列和等比数列求通项的方法,递推关系为1()n n a a f n +-=用累加法;递推关系为1()n n a f n a +=用累乘法.解题时需要分析给定的递推式,使之变形为1n n a a +-、1n naa +结构,然后求解.要特别注意累加或累乘时,应该为)1(-n 个式子,不要误认为n 个. (2)利用待定系数法,构造等差、等比数列求通项公式求数列通项公式方法灵活多样,特别是对于给定的递推关系求通项公式,观察、分析、推理能力要求较高.通常可对递推式变换,转化成特殊数列(等差或等比数列)来求解,这种方法体现了数学中化未知为已知的化归思想,而运用待定系数法变换递推式中的常数就是一种重要的转化方法.递推公式为q pa a n n +=+1(其中p ,q 均为常数,)0)1((≠-p pq ).把原递推公式转化为:)(1t a p t a n n -=-+,其中pq t -=1,再利用换元法转化为等比数列求解. 二年模拟1. 【2016届宁夏石嘴山三中高三下三模】数列{}n a 满足11=a ,对任意的*N n ∈都有n a a a n n ++=+11,则+++......1121a a =20161a ( ) A .20162015 B .20172016 C .20174034 D .20174032【答案】D2. 【2016届云南省玉溪一中高三下第八次月考】若数列{n a }满足11n a --1na =d (n ∈N ﹡,d 为常数),则称数列{n a }为调和数列.已知数列{1nx }为调和数列,且x 1+x 2+…+x 20=200,则x 5+x 16=( ) A .10 B .20 C .30 D .40 【答案】B【解析】由题意知1n n x x d --=-(常数),所以数列{}n x 是以1x 为首项,d -为公差的等差数列,则有()122051610200x x x x x +++=⋅+=,51620x x +=.故选B.3. 【2016届河南郑州一中高三考前冲刺一】数列{}n a 满足:11=a ,且对任意的*∈N n m ,,都有mn a a a n m n m ++=+,则=+⋅⋅⋅+++20143211111a a a a ( )A .20142013 B .10072013 C .20152013 D .20154028【答案】D【解析】因为mn a a a n m n m ++=+,则可得10,6,3,14321====a a a a ,则可猜得()21+=n n a n ,∴()⎪⎭⎫ ⎝⎛+-=+=1112121n n n n a n ,∴12320141111111112122320142015a a a a ⎛⎫+++⋅⋅⋅+=-+-+- ⎪⎝⎭40282015=,故选D .4. 【2016届河南郑州一中高三考前冲刺】已知数列{}n a 满足m n n a n ++-=3453123,若数列{}n a 的最小项为1,则实数m 的值为( ) A .41 B .31C .41-D .31-【答案】B5. 【2016年淮北一中高三模考】数列 {}n a 中,()11126,212n n n a a a a n n n--=-=++≥,则此数列的通项公式n a =___________.【答案】()()1121n n ++-【解析】由11221n n n aa a n n ---=++得1211n n a a n n -=++,所以112(1)1n n a a n n -+=++,又1142a+=,所以{1}1n a n ++是等比数列,所以1114221n n n an -++=⨯=+,即1(1)(21)n n a n +=+-. 6. 【2016年河北石家庄高三二模】数列{}n a 满足:1132,51++⋅=-=n n n n a a a a a ,则数列{}1+⋅n n a a 前10项的和为______. 【答案】10217. 【2016年江西省南昌市高三一模测试】数列{a n }的前n 项和为S n ,若S n +S n 一1=2n-l (n>2),且S 2 =3,则a 1+a 3的值为 。
专题6.1 数列的通项公式与求和-3年高考2年模拟1年原创备战2018高考精品系列之数学(江苏版)(

第六章 数列专题1 数列的通项公式与求和【三年高考】1.【2015某某高考,11】数列}{n a 满足11=a ,且11+=-+n a a n n (*N n ∈),则数列}1{na 的前10项和为2.【2017课标3,文17】设数列{}n a 满足123(21)2n a a n a n +++-=.(1)求{}n a 的通项公式; (2)求数列21n a n ⎧⎫⎨⎬+⎩⎭的前n 项和. 3.【2016高考某某文数】(本题满分15分)设数列{n a }的前n 项和为n S .已知2S =4,1n a +=2n S +1,*N n ∈.(I )求通项公式n a ;学*科网 (II )求数列{2n a n --}的前n 项和.4. 【2016高考某某理数】设数列{a n }的前n 项和为S n .若S 2=4,a n +1=2S n +1,n ∈N *,则a 1=,S 5=.5. 【2016高考新课标2理数】n S 为等差数列{}n a 的前n 项和,且17=128.a S =,记[]=lg n n b a ,其中[]x 表示不超过x 的最大整数,如[][]0.9=0lg99=1,. (Ⅰ)求111101b b b ,,;(Ⅱ)求数列{}n b 的前1 000项和.6. 【2016高考某某理数】(本小题满分12分)已知数列{}n a 的前n 项和S n =3n 2+8n ,{}n b 是等差数列,且1.n n n a b b +=+ (Ⅰ)求数列{}n b 的通项公式;(Ⅱ)令1(1).(2)n n n nn a c b ++=+ 求数列{}n c 的前n 项和T n . 7. 【2016高考某某理数】设数列{}n a 满足112n n a a +-≤,n *∈N . (I )证明:()1122n n a a-≥-,n *∈N ;(II )若32nn a ⎛⎫≤ ⎪⎝⎭,n *∈N ,证明:2n a ≤,n *∈N .8. 【2016高考某某理数】无穷数列{}n a 由k 个不同的数组成,n S 为{}n a 的前n 项和.若对任意*∈N n ,{}3,2∈n S ,则k 的最大值为________.9. 【2016高考新课标1文数】(本题满分12分)已知{}n a 是公差为3的等差数列,数列{}n b 满足12111==3n n n n b b a b b nb +++=1,,,.(I )求{}n a 的通项公式; (II )求{}n b 的前n 项和.10. [2016高考新课标Ⅲ文数]已知各项都为正数的数列{}n a 满足11a =,211(21)20n n n n a a a a ++---=.(I )求23,a a ;(II )求{}n a 的通项公式.11. 【2016高考文数】已知}{n a 是等差数列,}{n b 是等差数列,且32=b ,93=b ,11b a =,414b a =. (1)求}{n a 的通项公式;(2)设n n n b a c +=,求数列}{n c 的前n 项和.12.【2015高考某某,文13】已知数列}{n a 中,11=a ,211+=-n n a a (2≥n ),则数列}{n a 的前9项和等于.14.【2015高考某某,文19】已知数列{}n a 是首项为正数的等差数列,数列11n n a a +⎧⎫⎨⎬•⎩⎭的前n 项和为21nn +. (I )求数列{}n a 的通项公式;(II )设()12n an n b a =+⋅,求数列{}n b 的前n 项和n T .15.【2015高考某某,文19】设数列{}n a 的前n 项和为n S ,已知121,2a a ==,且13n n a S +=*13,()n S n N +-+∈,(I )证明:23n n a a +=; (II )求n S .16.【2015高考某某,文17】已知数列n a 和n b 满足,*1112,1,2(n N ),n n a b a a +===∈*12311111(n N )23n n b b b b b n+++++=-∈. (1)求n a 与n b ;(2)记数列n n a b 的前n 项和为n T ,求n T .【2018年高考命题预测】纵观2017各地高考试题,对数列通项公式和求和这部分的考查,主要考查数列的概念与表示方法、数列递推关系与通项公式的联系、数列的求和方法,往往与函数、方程、不等式等知识建立联系,高考中一般会以各种形式考查..对数列概念与表示方法的考察,要深刻体会数列不光体现一种递推关系,它具有函数特征,故经常会与函数、方程、不等式等知识联系考察.对数列通项公式的考察,一般会以等差数列和等比数列具体形式出现,或者由项的递推关系或者项与前n 项的的关系得出,同时要注意从特殊到一般思想的灵活运用.对数列求和的考察,要掌握常见的数列求和方法(直接求和、倒序相加法、错位相减法、裂项相加法),往往会和不等式建立联系,会牵涉到放缩法,难度会大点,注意等价转换思想的活用.从近几年的高考试题来看,难度属中低档的题目,小题突出“小、巧、活”,主要以通项公式、前n 项和公式为载体,结合数列的性质考查分类讨论、化归与方程等思想,要注重通性、通法;解答题“大而全”,注重题目的综合与新颖,突出对逻辑思维能力的考查.预测2017年高考仍将以等差数列,等比数列的定义、通项公式和前n 项和公式为主要考点,特别是错位相减法求和问题,重点考查学生的运算能力与逻辑推理能力.理科可能与不等式恒成立巧妙结合出一大题.【2018年高考考点定位】高考对数列的通项公式与求和的考查有三种主要形式:一是考察数列的概念与表示;二是数列通项公式;三是数列求和;其中经常与函数、方程、不等式等知识的相联系. 【考点1】数列的概念与表示 【备考知识梳理】1.定义:按照一定顺序排列着的一列数.2.表示方法:列表法、解析法(通项公式法和递推公式法)、图象法.3.分类:按项数有限还是无限分为有穷数列和无穷数列;按项与项之间的大小关系可分为单调数列、摆动数列和常数列.4.n a 与n S 的关系:11(1)(2)n n n S n a S S n -=⎧=⎨-⎩≥.5.处理方法:.用函数的观点处理数列问题 【规律方法技巧】1. 数列是定义域为正整数集或其有限子集的函数,故数列具有函数的特征(周期性、单调性等).2. 观察法是解决数列问题的法宝,先根据特殊的几项,找出共同的规律,横看“各项之间的关系结构”,纵看“各项与项数n 的关系”,从而确定数列的通项公式. 【考点针对训练】1.已知函数()f x 由下表定义:若15a =,1()n n a f a +=(1,2,n =),则2016a =.2.数列 ,817,275,31,31--的一个通项公式是 【考点2】递推关系与数列通项公式 【备考知识梳理】在一些综合性比较强的数列问题中,数列通项公式的求解问题往往是解决数列难题的瓶颈.数列通项公式的求解常用方法:1、定义法,直接利用等差数列或等比数列的定义求通项的方法叫定义法,这种方法适应于已知数列类型的题目.2、公式法, 若已知数列的前n 项和n S 与n a 的关系,求数列{}n a 的通项n a 可用公式⎩⎨⎧≥⋅⋅⋅⋅⋅⋅⋅-=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=-2111n S S n S a n nn 求解.3、由递推式求数列通项法,对于递推公式确定的数列的求解,通常可以通过递推公式的变换,转化为等差数列或等比数列问题,有时也用到一些特殊的转化方法与特殊数列.4、待定系数法(构造法),求数列通项公式方法灵活多样,特别是对于给定的递推关系求通项公式,观察、分析、推理能力要求较高.通常可对递推式变换,转化成特殊数列(等差或等比数列)来求解,这种方法体现了数学中化未知为已知的化归思想,而运用待定系数法变换递推式中的常数就是一种重要的转化方法. 【规律方法技巧】 数列的通项的求法: ⑴公式法:①等差数列通项公式;②等比数列通项公式.⑵已知n S (即12()n a a a f n +++=)求n a ,用作差法:{11,(1),(2)n n n S n a S S n -==-≥.⑶已知12()n a a a f n =求n a ,用作商法:(1),(1)(),(2)(1)n f n f n a n f n =⎧⎪=⎨≥⎪-⎩.⑷若1()n n a a f n +-=求n a 用累加法:11221()()()n n n n n a a a a a a a ---=-+-++-1a +(2)n ≥.⑸已知1()n n a f n a +=求n a ,用累乘法:121121n n n n n a aa a a a a a ---=⋅⋅⋅⋅(2)n ≥.⑹已知递推关系求n a ,用构造法(构造等差、等比数列).特别地,(1)形如1n n a ka b -=+、1nn n a ka b -=+(,k b 为常数)的递推数列都可以用待定系数法转化为公比为k 的等比数列后,再求n a .如(21)已知111,32n n a a a -==+,求n a ;(2)形如11n n n a a ka b--=+的递推数列都可以用倒数法求通项.注意:(1)用1--=n n n S S a 求数列的通项公式时,你注意到此等式成立的条件了吗?(2n ≥,当1n =时,11S a =);(2)一般地当已知条件中含有n a 与n S 的混合关系时,常需运用关系式1--=n n n S S a ,先将已知条件转化为只含n a 或n S 的关系式,然后再求解.(3)由n S 与1n S -的关系,可以先求n S ,再求n a ,或者先转化为项与项的递推关系,再求n a . 【考点针对训练】1.已知数列{}n a 满足12a =,111nn na a a ++=-(*n ∈N ),则3a 的值为. 2.已知数列{}n a 的前n 项和122+=-n n n S a ,若不等式223(5)n n n a λ--<-对n N +∀∈恒成立,则整数λ的最大值为.【考点3】数列求和 【备考知识梳理】数列的求和也是高考中的热点内容,考察学生能否把一般数列转化为特殊数列求和,体现了化归的思想方法,其中错位相减和裂项相消是高考命题的热点.估计在以后的高考中不会有太大的改变.数列求和的常用方法,尤其是利用裂项法和错位相减法求一些特殊数列的和,数列求和的基本方法:1.基本公式法:()1等差数列求和公式:()()11122n n n a a n n S na d +-==+()2等比数列求和公式:()111,11,111n n nna q S a q a a q q q q =⎧⎪=-⎨-=≠⎪--⎩()30122nn n n n n C C C C ++++=.2.错位相消法:一般适应于数列{}n n a b 的前n 向求和,其中{}n a 成等差数列,{}n b 成等比数列.3.分组求和:把一个数列分成几个可以直接求和的数列,然后利用公式法求和.4.拆项(裂项)求和:把一个数列的通项公式分成两项差的形式,相加过程中消去中间项,只剩下有限项再求和.常见的拆项公式有:()1若{}n a 是公差为d 的等差数列,则111111n n n n a a d a a ++⎛⎫=- ⎪⎝⎭; ()2()()1111212122121n n n n ⎛⎫=-⎪-+-+⎝⎭;()31k=;()411m m mn n n C C C -+=-;()5()!1!!n n n n ⋅=+-.5.倒序相加法:根据有些数列的特点,将其倒写后与原数列相加,以达到求和的目的. 【规律方法技巧】数列求和关键是研究数列通项公式,根据通项公式的不同特征选择相应的求和方式,若数列是等差数列或等比数列,直接利用公式求和;若通项公式是等差乘等比型,利用错位相减法;若通项公式可以拆分成两项的差且在累加过程中可以互相抵消,利用裂项相消法,从近年的考题来看,逐渐加大了与函数不等式的联系,通过对通项公式进行放缩,放缩为易求和的数列问题处理. 【考点针对训练】1.设数列{}n a 满足()()()111,111n n a a a n N++=-+=∈,则()10011k k k a a +=∑的值为.2.已知各项均为正数的数列}{n a 的首项11=a ,n S 是数列}{n a 的前n 项和,且满足:).0(*1111N n a a a a S a S a n n n n n n n n ∈≠=-+-++++λλ.(1)若1a ,2a ,3a 成等比数列,某某数λ的值; (2)若21=λ,求n S .【两年模拟详解析】1.【某某市、某某市2017届高三年级第一次模拟】如图,在平面直角坐标系中,分别在x 轴与直线()31y x =+上从左向右依次取点k A 、k B ,1,2,k =⋅⋅⋅,其中1A 是坐标原点,使1k k k A B A +∆都是等边三角形,则101011A B A ∆的边长是▲.2. 【2017年高考原创押题预测卷03(某某卷)】设数列{}n a 满足:12211,,1n n n n a a n a a a +==-=+,则数列{}n a 中的第2017项是.3. 【苏北三市(某某、某某、宿迁)2017届高三年级第三次调研考试】已知两个无穷数列和的前项和分别为,,,,对任意的,都有.(1)求数列的通项公式; (2)若为等差数列,对任意的,都有.证明:; (3)若为等比数列,,,求满足的值.4.【某某省某某市2016-2017学年度高三年级第三次模拟考试理】数列{}n a 的前n 项和为n S ,若()*2142n n n S a n N -+=-∈,则na=__________.5.【某某省孝义市2017届高三下学期考前热身训练数学(理)】对于正整数n ,设n x 是关于x 的方程320nx x n +-=的实数根,记()()12n n a n x n ⎡⎤=+≥⎣⎦,其中[]x 表示不超过实数x 的最大整数,则()23201511007a a a +++=__________.6.【某某省某某市第一中学2017届高三第三次模拟数学(文)】设数列{}n a 的前n 项和为n S ,且111,23n n a a S +==+,则通项n a =_________7.【某某省实验中学2017届高三下学期模拟热身数学(理)】已知数列{}n a 中,13a =,且点()1,n n n P a a +(*n N ∈)在直线410x y -+=上,则数列{}n a 的通项公式为__________.8.【某某市第八中学2017届高三适应性月考卷(八)文科】如图,这是一个正八边形的序列,则第n 个图形的边数(不包含内部的边)是__________.9.【某某省某某市2017届高三毕业班第三次质量检查数学(文)】把正整数按一定的规律排成如图所示的三角形阵.设(,ij a i j ∈*N )是位于数阵中从上向下数第i 行,从左向右数第j 列的数,例如:4310a =,若173ij a =,则i j +=__________.10.【某某省实验中学2017届高三下学期模拟热身数学(文)】若数列{}n a 是正项数列,且212n a a a n n +=+,则1212na a a n+++=__________. 11.【某某省某某市2017届第三次诊断考试数学(理)】已知数列{}n a 满足132n n a a +=+,若首项12a =,则数列{}n a 的前n 项和n S =__________.12.【某某市第八中学2017届高三高考适应性月考(七)数学(理)】设数列{}n a 的前n 项和是n S ,满足()()*11222,n n n n n S S S a n n N +-+-=+≥∈,121,2a a ==,则当2n ≥时,n S =__________.13.【某某省某某市2017届高三第三次教学质量检查数学(理)】已知数列{}n a 满足111,2256n n a a a +==若2log 2n n b a =-,则12···n b b b 的最大值为__________. 14.【某某省某某高级中学2017届高三4月检测考试数学(文)】设数列{}n a (1n ≥,n N ∈)满足12a =,26a =,()()2112n n n n a a a a +++---=,若[]x 表示不超过x 的最大整数,则122016201620162016a a a ⎡⎤++⋯+=⎢⎥⎣⎦__________.15.【某某某某市2017届高三第二次(4月)调研考试数学文】若数列{}{},n n a b 满足*11111,,32,n n n n n a b b a a a b n N ++===-=+∈,则20172016a a -=__________.16.【2017届某某省某某市高三上学期期末考试理】已知数列{}n a 的前n 项和n S ,若()11nn n a a n ++-=,则40S =__________.17.【2016届某某某某一中高三下组卷四理科】已知数列n a 中的12,a a 分别为直线2+20x y 在x 轴、y 轴上的截距,且212n nn na a a a ,则数列n a 的通项公式为.18.【2016届某某省某某市高三下学期三模理科】已知数列{}n a 各项均不为0,其前n 项和为n S ,且112,1+==n n n a a S a ,则=n S ______.19.【2016届某某省清江中学高三考前一周双练一】设数列{}n a 的前n 项和为n S ,若21(2)8n n S a =+,则3a 的所有可能取值的和为.20.【2016届某某省某某中学高三下学期二调考试理科】用()g n 表示自然数n 的所有因数中最大的那个奇数,例如:9的因数有1,3,9,()99,10g =的因数有1,2,5,10,()105g =,那么()()()()201512321g g g g +++⋅⋅⋅+-=.【一年原创真预测】1.数列{}n a 中,11a =,23a =,2n a +是1+n n a a 的个位数字,n S 是{}n a 的前n 项和,则2015S =2.已知数列{}n a 中,0n a >,11a =,211n n a a +=+,10096a a =,则20163a a +=.。
高考数学一轮复习第六章数列6.1.2数列的通项公式对点训练理

2017高考数学一轮复习 第六章 数列 6.1.2 数列的通项公式对点训练 理1.设数列{a n }满足a 1=1,且a n +1-a n =n +1(n ∈N *),则数列⎩⎨⎧⎭⎬⎫1a n 前10项的和为________.答案2011解析 由a 1=1,且a n +1-a n =n +1(n ∈N *)得,a n =a 1+(a 2-a 1)+(a 3-a 2)+…+(a n -a n -1)=1+2+3+…+n =n n +2,则1a n =2nn +=2⎝ ⎛⎭⎪⎫1n -1n +1,故数列⎩⎨⎧⎭⎬⎫1a n 前10项的和S 10=2⎝ ⎛⎭⎪⎫1-12+12-13+…+110-111=2⎝ ⎛⎭⎪⎫1-111=2011.2.已知数列{a n }满足a 1=1,a n +1=3a n +2,则数列{a n }的通项公式为________. 答案 a n =2·3n -1-1解析 ∵a n +1=3a n +2,∴a n +1+1=3(a n +1). ∴a n +1+1a n +1=3,∴数列{a n +1}是等比数列,公比q =3. 又a 1+1=2,∴a n +1=2·3n -1,∴a n =2·3n -1-1.3.已知数列{a n }的前n 项和S n =2n-3,则数列{a n }的通项公式为________.答案 a n =⎩⎪⎨⎪⎧-1,n =1,2n -1,n ≥2解析 当n =1时,a 1=S 1=-1; 当n ≥2时,a n =S n -S n -1=2n -1,∴a n =⎩⎪⎨⎪⎧-1,n =1,2n -1,n ≥2.4.S n 为数列{a n }的前n 项和,已知a n >0,a 2n +2a n =4S n +3. (1)求{a n }的通项公式; (2)设b n =1a n a n +1,求数列{b n }的前n 项和.解 (1)由a 2n +2a n =4S n +3,可知a 2n +1+2a n +1=4S n +1+3. 可得a 2n +1-a 2n +2(a n +1-a n )=4a n +1,即 2(a n +1+a n )=a 2n +1-a 2n =(a n +1+a n )(a n +1-a n ). 由于a n >0,可得a n +1-a n =2.又a 21+2a 1=4a 1+3,解得a 1=-1(舍去)或a 1=3.所以{a n }是首项为3,公差为2的等差数列,通项公式为a n =2n +1. (2)由a n =2n +1可知b n =1a n a n +1=1n +n +=12⎝ ⎛⎭⎪⎫12n +1-12n +3.设数列{b n }的前n 项和为T n ,则T n =b 1+b 2+…+b n=12⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫13-15+⎝ ⎛⎭⎪⎫15-17+…+⎝ ⎛⎭⎪⎫12n +1-12n +3=nn +.5.正项数列{a n }的前n 项和S n 满足:S 2n -(n 2+n -1)S n -(n 2+n )=0. (1)求数列{a n }的通项公式a n ; (2)令b n =n +1n +2a 2n ,数列{b n }的前n 项和为T n .证明:对于任意的n ∈N *,都有T n <564. 解 (1)由S 2n -(n 2+n -1)S n -(n 2+n )=0, 得[S n -(n 2+n )](S n +1)=0.由于{a n }是正项数列,所以S n >0,S n =n 2+n .于是a 1=S 1=2,当n ≥2时,a n =S n -S n -1=n 2+n -(n -1)2-(n -1)=2n . 综上,数列{a n }的通项公式为a n =2n . (2)由于a n =2n ,故b n =n +1n +2a 2n =n +14n 2n +2=116⎣⎢⎡⎦⎥⎤1n2-1n +2.T n =116[ 1-132+122-142+132-152+…+1n -2-1n +2+1n2-1n +2 ]=116[ 1+122-1n +2-1n +2 ]<116×⎝ ⎛⎭⎪⎫1+122=564.。
高三数学数列的通项公式及求和

蒙芦申皇の身份.以前鞠言确实不认识蒙芦申皇,可方才大师兄单泊已经传音给鞠言介绍了蒙芦申皇の身份,所以鞠言知道此人,就是第四申界の领头人,也是人类疆域九大巨头之壹.“鞠言,那位是蒙芦申皇,第四申界の领头人.”湛月脸上没有太多表情对鞠言介绍了壹下蒙芦の身份.“难 怪!原来是第四申界の领头人,怪不得壹副高高在上の架势.不过,第四申界の领头人,恐怕也不能做九大申界の主吧!呐位蒙芦申皇说话,就好像他已经掌控全部九大申界壹样.”鞠言轻轻摇头.在鞠言与湛月の简单对话过程中,蒙芦申皇简直要被气炸了.“放肆!”“小辈,你最好不要挑战 本皇容忍の极限!”蒙芦申皇怒气冲冲の盯着鞠言.若不是由于,呐里是九界申宫,他可能都忍不住已经对鞠言出手了.壹点都不用怀疑,若是在第四申界之内,有壹些不知天高地厚の小辈敢对他有任何不敬,他绝对挥手间就直接灭杀了.可是呐里,乃是九界申宫之内,九大申界の领头人都在, 他随意出手,显然不妥当.再者说,呐个小辈の师尊湛月申皇,也是不好惹の存在.“怎么,俺有说错吗?”面对蒙芦申皇要吃人の目光,鞠言没有丝毫の退让,与后者对视.“蒙芦申皇!”鞠言加叠语气.“在俺进入九界申宫之前,俺没有得罪过你吧?俺还真不知道,俺们之间有哪个恩怨.如果有, 还请蒙芦申皇告知.”“如果没有,那俺就很奇怪了.为何自从俺进来之后,你就处处针对俺!不仅针对俺,还挤兑俺师父湛月申皇.现在,你倒是污蔑俺挑战你容忍の极限.难道你自身不觉得,呐很可笑吗?”鞠言抑扬顿挫の道.其实,在鞠言进来后,针对他の可不只有蒙芦申皇.在场の,还有壹 些申尊、王君都藐视鞠言.但谁叫,呐个蒙芦身份最高呢!鞠言当然将矛头对准了他!听到鞠言の呐番话,蒙芦申皇有些懵了.说起来,确实是他找事在先.可是,他压根就没认为自身の做法有问题.由于从壹开始,他就没将鞠言放在与自身同壹个水平の位置上.他先前,甚至都没有直接对鞠言 说哪个.所以现在被鞠言呐样反问,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章 数列专题1 数列的通项公式与求和(理科)【三年高考】1. 【2017课标II ,理3】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( ) A .1盏 B .3盏 C .5盏 D .9盏 【答案】B2.【2017课标II ,理15】等差数列{}n a 的前n 项和为n S ,33a =,410S =,则11nk kS ==∑ 。
【答案】21nn + 【解析】设等差数列的首项为1a ,公差为d ,由题意有:1123434102a d a d +=⎧⎪⎨⨯+=⎪⎩ ,解得111a d =⎧⎨=⎩ ,数列的前n 项和()()()111111222n n n n n n n S na d n --+=+=⨯+⨯=,裂项有:()1211211k S k k k k ⎛⎫==- ⎪++⎝⎭,据此:11111111221......21223111nk k n S n n n n =⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-++-=-= ⎪ ⎪ ⎪ ⎪⎢⎥+++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦∑ 。
3. 【2017山东,理19】已知{x n }是各项均为正数的等比数列,且x 1+x 2=3,x 3-x 2=2 (Ⅰ)求数列{x n }的通项公式;(Ⅱ)如图,在平面直角坐标系xOy 中,依次连接点P 1(x 1, 1),P 2(x 2, 2)…P n+1(x n+1, n+1)得到折线P 1 P 2…P n+1,求由该折线与直线y =0,11n x x x x +==,所围成的区域的面积n T.【解析】(I)设数列{}n x 的公比为q ,由已知0q >.由题意得1121132x x q x q x q +=⎧⎨-=⎩,所以23520q q --=,因为0q >,所以12,1q x ==,因此数列{}n x 的通项公式为12.n n x -=(II )过123,,,P P P ……1n P +向x 轴作垂线,垂足分别为123,,,Q Q Q ……1n Q +,由(I)得111222.n n n n n x x --+-=-=记梯形11n n n n P P Q Q ++的面积为n b .由题意12(1)2(21)22n n n n n b n --++=⨯=+⨯, 所以123n T b b b =+++……+n b =101325272-⨯+⨯+⨯+……+32(21)2(21)2n n n n ---⨯++⨯①又0122325272n T =⨯+⨯+⨯+……+21(21)2(21)2n n n n ---⨯++⨯ ②①-②得121132(22 (2))(21)2n n n T n ----=⨯++++-+⨯=1132(12)(21)2.212n n n ---+-+⨯- 所以(21)21.2n n n T -⨯+=4.【2016高考浙江理数】设数列{a n }的前n 项和为S n .若S 2=4,a n +1=2S n +1,n ∈N *,则a 1= ,S 5= .【答案】1 1215. 【2016高考山东理数】已知数列{}n a 的前n 项和S n =3n 2+8n ,{}n b 是等差数列,且1.n n n a b b +=+(Ⅰ)求数列{}n b 的通项公式;(Ⅱ)令1(1).(2)n n n nn a c b ++=+ 求数列{}n c 的前n 项和T n .【解析】(Ⅰ)由题意知当2≥n 时,561+=-=-n S S a n n n ,当1=n 时,1111==S a ,所以56+=n a n .设数列{}n b 的公差为d ,由⎩⎨⎧+=+=322211b b a b b a ,即⎩⎨⎧+=+=d b db 321721111,可解得3,41==d b ,所以13+=n b n .(Ⅱ)由(Ⅰ)知11(66)3(1)2(33)n n n nn c n n +++==+⋅+,又n n c c c c T +⋅⋅⋅+++=321,得23413[223242(1)2]n n T n +=⨯⨯+⨯+⨯+⋅⋅⋅++⨯,345223[223242(1)2]n n T n +=⨯⨯+⨯+⨯+⋅⋅⋅++⨯,两式作差,得234123[22222(1)2]n n n T n ++-=⨯⨯+++⋅⋅⋅+-+⨯224(21)3[4(1)2]3221n n n n n ++-=⨯+-+⨯=-⋅-,所以223+⋅=n n n T6.【2016高考江苏卷】记{}1,2,100U =…,.对数列{}()*n a n N ∈和U 的子集T ,若T =∅,定义0T S =;若{}12,,k T t t t =…,,定义12+k T t t t S a a a =++….例如:{}=1,3,66T 时,1366+T S a a a =+.现设{}()*n a n N ∈是公比为3的等比数列,且当{}=2,4T 时,=30T S .(1)求数列{}n a 的通项公式;(2)对任意正整数()1100k k ≤≤,若{}1,2,k T ⊆…,,求证:1T k S a +<; (3)设,,C D C U D U S S ⊆⊆≥,求证:2C CDD S S S +≥.(3)下面分三种情况证明.①若D 是C 的子集,则2C C DC D D D D S S S S S S S +=+≥+=.②若C 是D 的子集,则22C CDC C CD S S S S S S +=+=≥.③若D 不是C 的子集,且C 不是D 的子集.令U E CC D =,U F D C C =则E φ≠,F φ≠,E F φ=.于是C E C DS S S =+,D F CDS S S =+,进而由C D S S ≥,得E F S S ≥.设k 是E 中的最大数,l 为F 中的最大数,则1,1,k l k l ≥≥≠.由(2)知,1E k S a +<,于是1133l k l F E k a S S a -+=≤≤<=,所以1l k -<,即l k ≤.又k l ≠,故1l k ≤-,从而1121131133222l l k E F l a S S a a a ----≤+++=+++==≤, 故21E F S S ≥+,所以2()1C C DD C DS S S S -≥-+,即21C CDD S S S +≥+.综合①②③得,2C CDD S S S +≥.7.【2016高考天津理数】已知{}n a 是各项均为正数的等差数列,公差为d ,对任意的,b n n N ∈*是n a 和1n a +的等差中项.(Ⅰ)设22*1,n n n c b b n N +=-∈,求证:{}n c 是等差数列;(Ⅱ)设()22*11,1,nnn n k a d T b n N ===-∈∑,求证:2111.2nk kT d =<∑【解析】(I )证明:由题意得21n n n b a a +=,有22112112n n n n n n n n c b b a a a a da +++++=-=-=,因此()212122n n n n c c d a a d +++-=-=,所以{}n c 是等差数列. (II )证明:()()()2222221234212n n n T b b b b b b -=-++-++-+()()()22224222212n n n a a d a a a d d n n +=+++=⋅=+,所以()222211111111111112121212nnnk k k kT d k k d kk d n d ===⎛⎫⎛⎫==-=⋅-< ⎪ ⎪+++⎝⎭⎝⎭∑∑∑.学%科网 8. 【2015高考新课标2,理16】设n S 是数列{}n a 的前n 项和,且11a =-,11n n n a S S ++=,则n S =________. 【答案】1n-【解析】由已知得111n n n n n a S S S S +++=-=⋅,两边同时除以1n n S S +⋅,得1111n nS S +=--,故数列1n S ⎧⎫⎨⎬⎩⎭是以1-为首项,1-为公差的等差数列,则11(1)nS n n =---=-,所以1n S n=-. 9.【2015江苏高考,11】数列}{n a 满足11=a ,且11+=-+n a a n n (*N n ∈),则数列}1{na 的前10项和为 【答案】2011【解析】由题意得:112211(1)()()()1212n n n n n n n a a a a a a a a n n ---+=-+-++-+=+-+++=,所以1011112202(),2(1),11111n n n S S a n n n n =-=-==+++ 10. 【2015高考新课标1,理17】n S 为数列{n a }的前n 项和.已知n a >0,2n n a a +=43n S +.(Ⅰ)求{n a }的通项公式; (Ⅱ)设11n n n b a a +=,求数列{n b }的前n 项和. 【解析】(Ⅰ)当1n =时,211112434+3a a S a +=+=,因为0n a >,所以1a =3,当2n ≥时,2211n n n n a a a a --+--=14343n n S S -+--=4n a ,即111()()2()n n n n n n a a a a a a ---+-=+,因为0n a >,所以1n n a a --=2,所以数列{n a }是首项为3,公差为2的等差数列,所以n a =21n +;(Ⅱ)由(Ⅰ)知,n b =1111()(21)(23)22123n n n n =-++++,所以数列{n b }前n 项和为12n b b b +++=1111111[()()()]235572123n n -+-++-++ =11646n -+. 11.【2015高考山东,理18】设数列{}n a 的前n 项和为n S .已知233n n S =+. (I )求{}n a 的通项公式;(II )若数列{}n b 满足3log n n n a b a =,求{}n b 的前n 项和n T .【解析】(I )因为233n n S =+ ,所以,1233a =+ ,故13,a = 当1n > 时,11233,n n S --=+ 此时,1122233,n n n n n a S S --=-=- 即13,n n a -= 所以,13,1,3,1,n n n a n -=⎧=⎨>⎩(II )因为3log n n n a b a = ,所以113b = ,当1n > 时,()11133log 313n n nn b n ---==-⋅ ,所以1113T b ==当1n > 时,()()12112311323133n n n T b b b b n ---=++++=+⨯+⨯++- ,所以()()01231132313n n T n --=+⨯+⨯++-,两式相减,得()()012122333133n nn T n ---=+++--⋅ ()11121313313n n n ----=+--⋅- 1363623nn +=-⨯ ,所以13631243n nn T +=+⨯,经检验,1n = 时也适合, 综上可得:13631243n nn T +=+⨯ 【两年模拟】1. 【2017福建三明5月质检】已知数列{}n a 的前n 项和为n S ,且11a =,()*1·2n n n a a n N +=∈,则2016S =( )A. 10083?23-B. 201621- C. 200923- D. 200823-【答案】A【解析】∵数列{a n }满足a 1=1,a n +1⋅a n =2n (n ∈N ∗),∴a 2⋅a 1=2,解得a 2=2.,当n ⩾2时,12121222nn n n n n n na a a a a a +++++=⇒=,∴数列{a n }的奇数项与偶数项分别成等比数列,公比为2.则()()()100810081008201613201524201622121S 3232121a a a a a a --=+++++++=+=⋅---.本题选择A 选项.2. 【2017黑龙江哈师大附中三模】已知数列{}n a 满足()24cos πn a n n n =+,则{}n a 的前50项的和为______. 【答案】1375【解析】因为()()2411nnn a n n =-+-,所以5012S S S =+,则()()()125022211112150S=-⨯+-⨯+⋅⋅⋅+-,即()22211234950123501275S =-+-+⋅⋅⋅+-+=+++⋅⋅⋅+=,又,应填答案1375。
