数学---内蒙古阿拉善左旗高级中学2016-2017学年高一下学期期末考试试卷(文)
内蒙古阿拉善盟高一下学期数学期末考试试卷
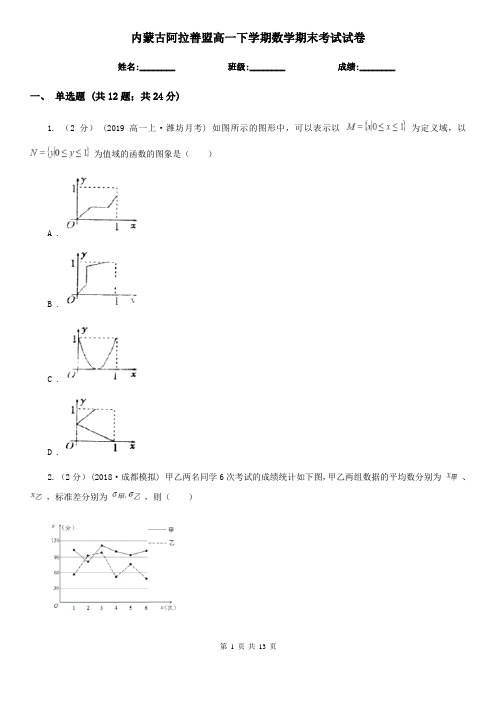
内蒙古阿拉善盟高一下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分) (2019高一上·潍坊月考) 如图所示的图形中,可以表示以为定义域,以为值域的函数的图象是()A .B .C .D .2. (2分)(2018·成都模拟) 甲乙两名同学6次考试的成绩统计如下图,甲乙两组数据的平均数分别为、,标准差分别为,则()A . ,B . ,C . ,D . ,3. (2分)为保证树苗的质量,林业管理部门在每年3月12日植树节前都对树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗的高度(单位长度:cm),其茎叶图如图所示,则下列描述正确的是()甲乙910409531026712373044667A . 甲种树苗的平均高度大于乙种树苗的平均高度,甲种树苗比乙种树苗长得整齐B . 甲种树苗的平均高度大于乙种树苗的平均高度,乙种树苗比甲种树苗长得整齐C . 乙种树苗的平均高度大于甲种树苗的平均高度,乙种树苗比甲种树苗长得整齐D . 乙种树苗的平均高度大于甲种树苗的平均高度,甲种树苗比乙种树苗长得整齐4. (2分) (2020高二下·焦作期末) 新中国成立70周年以来,党中央、国务院高度重视改善人民生活,始终把脱贫致富和提高人民生活水平作为一切工作的出发点和落脚点新疆某地区为了带动当地经济发展,大力发展旅游业,如图是2015—2019年到该地区旅游的游客数量(单位:万人次)的变化情况,则下列结论错误的是()A . 2015—2019年到该地区旅游的人数与年份成正相关B . 2019年到该地区旅游的人数是2015年的12倍C . 2016—2019年到该地区旅游的人数平均值超过了220万人次D . 从2016年开始,与上一年相比,2019年到该地区旅游的人数增加得最多5. (2分)平面α与平面β,γ都相交,则这三个平面可能有()A . 1条或2条交线B . 2条或3条交线C . 仅2条交线D . 1条或2条或3条交线6. (2分) (2020高一下·怀仁期中) 已知角A、B是的内角,则“ ”是“ ”的()A . 充分条件B . 必要条件C . 充要条件D . 既不充分也不必要条件7. (2分)双曲线的渐近线与圆(x-3)2+y2=r2(r>0)相切,则r=()A .B . 2C . 3D . 68. (2分)由点P向圆x2+y2=2引两条切线PA,PB,A,B是切点,则•的最小值是()A . 6﹣4B . 3﹣2C . 2﹣3D . 4﹣69. (2分)(2012·陕西理) 如图,在空间直角坐标系中有直三棱柱ABC﹣A1B1C1 , CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为()A .B .C .D .10. (2分)若⊙O1:x2+y2=5与⊙O2:(x-m)2+y2=20(m∈R)相交于A、B两点,且两圆在点A处的切线互相垂直,则线段AB的长度是()A . 1B . 2C . 3D . 411. (2分)(2020·芜湖模拟) 已知棱长为2的正方体中,E为DC中点,F在线段上运动,则三棱锥的外接球的表面积最小值为()A .B .C .D .12. (2分)在下列向量组中,可以把向量=(3,2)表示出来的是()A . =(0,0), =(1,2)B . =(﹣1,2),=(5,﹣2)C . =(3,5), =(6,10)D . =(2,﹣3),=(﹣2,3)二、填空题 (共4题;共6分)13. (1分)圆锥的底面半径为5cm,高为12cm,当它的内接圆柱的底面半径为________ 时,圆锥的内接圆柱全面积有最大值.14. (1分) (2020高一下·沭阳期中) 过点,且斜率为2的直线方程是________.15. (2分) (2019高二下·盐城期末) 某学校拟从2名男教师和1名女教师中随机选派2名教师去参加一个教师培训活动,则2名男教师去参加培训的概率是________.16. (2分)在△ABC中,角A,B,C所对的边分别为a,b,c,若(acosB+bcosA)=2csinC,a+b=4,且△ABC的面积的最大值为,则此时△ABC的形状为________三、解答题 (共6题;共28分)17. (2分) (2018高三上·沧州期末) 某厂为检验车间一生产线是否工作正常,现从生产线中随机抽取一批零件样本,测量尺寸(单位:)绘成频率分布直方图如图所示:(Ⅰ)求该批零件样本尺寸的平均数和样本方差(同一组中的数据用该组区间的中点值作代表);(Ⅱ)若该批零件尺寸服从正态分布,其中近似为样本平均数,近似为样本方差,利用该正态分布求;(Ⅲ)若从生产线中任取一零件,测量尺寸为,根据原则判断该生产线是否正常?附:;若,则,,.18. (2分)(2019·通州模拟) 为调查某公司五类机器的销售情况,该公司随机收集了一个月销售的有关数据,公司规定同一类机器销售价格相同,经分类整理得到下表:机器类型第一类第二类第三类第四类第五类销售总额(万元)销售量(台)利润率利润率是指:一台机器销售价格减去出厂价格得到的利润与该机器销售价格的比值.(Ⅰ)从该公司本月卖出的机器中随机选一台,求这台机器利润率高于0.2的概率;(Ⅱ)从该公司本月卖出的销售单价为20万元的机器中随机选取台,求这两台机器的利润率不同的概率;(Ⅲ)假设每类机器利润率不变,销售一台第一类机器获利万元,销售一台第二类机器获利万元,…,销售一台第五类机器获利,依据上表统计数据,随机销售一台机器获利的期望为,设,试判断与的大小.(结论不要求证明)19. (2分) (2020高一下·哈尔滨期末) 若圆C经过点和,且圆心在x轴上,(1)求圆C的一般方程;(2)圆心到直线的距离等于3,求a的值.20. (10分)△ABC中,,点D在边AC上,且DA=DB,求DB的长.21. (2分) (2020高二下·天津月考) 如图:在四棱锥中,底面是正方形,,,点在上,且 .(1)求证:平面;(2)求二面角的余弦值;22. (10分) (2019高一下·锡山期末) 在平面直角坐标系中,已知圆,圆.(1)若过点的直线被圆截得的弦长为,求直线的方程;(2)设动圆同时平分圆的周长、圆的周长.①证明:动圆圆心在一条定直线上运动;②动圆是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共6分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共28分) 17-1、18-1、19-1、19-2、20-1、21-1、21-2、22-1、22-2、。
2016-2017年内蒙古阿拉善盟左旗高中高一(下)期末数学试卷(文科)(解析版)

2016-2017学年内蒙古阿拉善盟左旗高中高一(下)期末数学试卷(文科)一、选择题:(每小题5分,共60分)1.(5分)点(1,﹣1)到直线x﹣y+1=0的距离是()A.B.C.D.2.(5分)点M(3,﹣3,﹣1)关于xOy平面对称的点是()A.(﹣3,3,﹣1)B.(﹣3,﹣3,﹣1)C.(3,﹣3,1)D.(﹣3,3,1)3.(5分)阅读如图所示的程序框图,运行相应的程序,输出的结果是()A.1B.2C.3D.44.(5分)用“辗转相除法”求得459和357的最大公约数是()A.3B.9C.17D.515.(5分)过点M(﹣2,m)、N(m,4)的直线的斜率等于1,则m的值为()A.1B.4C.1或3D.1或46.(5分)圆(x+2)2+y2=4与圆(x﹣2)2+(y﹣1)2=9的位置关系为()A.内切B.相交C.外切D.相离7.(5分)已知向量=(2,1),•=10,|+|=5,则||=()A.5B.25C.D.8.(5分)方程y=ax+b和y=bx+a表示的直线可能是()A.B.C.D.9.(5分)已知m、n表示直线,α,β,γ表示平面,给出下列四个命题,其中真命题为()(1)α∩β=m.n⊂α,n⊥m,则α⊥β(2)α⊥β,α∩γ=m,β∩γ=n,则n⊥m(3)m⊥α,m⊥β,则α∥β(4)m⊥α,n⊥β,m⊥n,则α⊥βA.(1)、(2)B.(3)、(4)C.(2)、(3)D.(2)、(4)10.(5分)如图,在长方体ABCD﹣A1B1C1D1中,AB=BC=2,AA1=1,则BC1与平面BB1D1D 所成角的正弦值为()A.B.C.D.11.(5分)函数f(x)=sin x﹣cos x,x∈[0,]的最小值为()A.﹣2B.﹣C.﹣D.﹣112.(5分)已知圆C1:(x﹣2)2+(y﹣3)2=1,圆C2:(x﹣3)2+(y﹣4)2=9,M,N 分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为()A.﹣1B.5﹣4C.6﹣2D.二.填空题:(每小题5分,共20分)13.(5分)已知向量,向量=(x,3),且,则x=.14.(5分)一个几何体的三视图如图所示,则这个几何体的体积为.15.(5分)直线的倾斜角为α,且90°<α≤135°,则它的斜率的取值范围为.16.(5分)直线y=x+b与曲线有且有一个公共点,则b的取值范围是.三.解答题(共70分)17.(10分)求下列条件确定的圆的方程:(1)圆心为点C(8,3),且过点A(5,1)(2)圆心在y轴上,半径长为3,且与x轴相切.18.(12分)已知直线l:3x+4y﹣20=0.(1)求过点(2,2)且与直线平行的直线方程;(2)已知直线l1:2x﹣ay+a=0与直线l垂直,试确定实数a的值.19.(12分)如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.(1)求证:P A∥面BDE;平面P AC⊥平面BDE;(2)若二面角E﹣BD﹣C为30°,求四棱锥P﹣ABCD的体积.20.(12分)如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.21.(12分)已知函数f(x)=cos2﹣sin cos﹣.(Ⅰ)求函数f(x)的最小正周期和值域;(Ⅱ)若f(α)=,求sin2α的值.22.(12分)已知坐标平面上点M(x,y)与两个定点M1(26,1),M2(2,1)的距离之比等于5.(1)求点M的轨迹方程,并说明轨迹是什么图形;(2)记(1)中的轨迹为C,过点A(﹣2,3)的直线l被C所截得的线段的长为8,求直线l的方程.2016-2017学年内蒙古阿拉善盟左旗高中高一(下)期末数学试卷(文科)参考答案与试题解析一、选择题:(每小题5分,共60分)1.(5分)点(1,﹣1)到直线x﹣y+1=0的距离是()A.B.C.D.【解答】解:点(1,﹣1)到直线x﹣y+1=0的距离是:=故选:D.2.(5分)点M(3,﹣3,﹣1)关于xOy平面对称的点是()A.(﹣3,3,﹣1)B.(﹣3,﹣3,﹣1)C.(3,﹣3,1)D.(﹣3,3,1)【解答】解:由题意,关于平面xoy对称的点横坐标、纵坐标保持不变,第三坐标变为它的相反数,从而有点M(3,﹣3,﹣1)关于平面xoy对称的点的坐标为(3,﹣3,1).故选:C.3.(5分)阅读如图所示的程序框图,运行相应的程序,输出的结果是()A.1B.2C.3D.4【解答】解:程序在运行过程中各变量的值如下表示:S n是否继续循环循环前 2 1/第一圈﹣1 2 是第二圈 3 是第三圈 2 4 否则输出的结果为4故选:D.4.(5分)用“辗转相除法”求得459和357的最大公约数是()A.3B.9C.17D.51【解答】解:∵459÷357=1…102,357÷102=3…51,102÷51=2,∴459和357的最大公约数是51,故选:D.5.(5分)过点M(﹣2,m)、N(m,4)的直线的斜率等于1,则m的值为()A.1B.4C.1或3D.1或4【解答】解:过点M(﹣2,m)、N(m,4)的直线的斜率等于1,所以k===1解得m=1故选:A.6.(5分)圆(x+2)2+y2=4与圆(x﹣2)2+(y﹣1)2=9的位置关系为()A.内切B.相交C.外切D.相离【解答】解:圆(x+2)2+y2=4的圆心C1(﹣2,0),半径r=2.圆(x﹣2)2+(y﹣1)2=9的圆心C2(2,1),半径R=3,两圆的圆心距d==,R+r=5,R﹣r=1,R+r>d>R﹣r,所以两圆相交,故选:B.7.(5分)已知向量=(2,1),•=10,|+|=5,则||=()A.5B.25C.D.【解答】解:∵向量=(2,1),•=10,|+|=5,∴||==,∴=+2•+=+2×10+=;解得=25,∴||=5.故选:A.8.(5分)方程y=ax+b和y=bx+a表示的直线可能是()A.B.C.D.【解答】解:根据题意,依次分析选项:对于A、对于y=ax+b,图象经过第一、二、三象限,则a>0,b>0,y=bx+a也要经过第一、三象限,所以A选项错误;对于B、同理A,可得B选项错误;对于C、对于y=ax+b,图象经过第二、三、四象限,则a<0,b<0,y=bx+a也要经过第二、三、四象限,所以C选项错误;对于D、对于y=ax+b,图象经过第一、三、四象限,则a<0,b>0,y=bx+a要经过第一、二、四象限,符合题意;故选:D.9.(5分)已知m、n表示直线,α,β,γ表示平面,给出下列四个命题,其中真命题为()(1)α∩β=m.n⊂α,n⊥m,则α⊥β(2)α⊥β,α∩γ=m,β∩γ=n,则n⊥m(3)m⊥α,m⊥β,则α∥β(4)m⊥α,n⊥β,m⊥n,则α⊥βA.(1)、(2)B.(3)、(4)C.(2)、(3)D.(2)、(4)【解答】解:对于(1)由线面垂直的判定定理知,n不一定垂直于β,所以由线面垂直的判定定理知α不一定垂直于β,所以(1)不正确对于(2)当α与β的交线平行于γ时,m、n平行,所以(2)不正确对于(3)过直线m作两个平面,分别于面α、β相交于直线a、b和c、d,则a∥c,b∥d,又a、b相交,c、d相交,所以α∥β,所以(3)正确对于(4)∵m⊥α,n⊥β,m⊥n,所以m⊆β或m∥β当m⊆β时,由面面垂直的判定定理知α⊥β当m∥β时,可在β内作直线a,使得a∥m,则a⊥α,由线面垂直的判定定理知α⊥β∴(4)正确故选:B.10.(5分)如图,在长方体ABCD﹣A1B1C1D1中,AB=BC=2,AA1=1,则BC1与平面BB1D1D 所成角的正弦值为()A.B.C.D.【解答】解:以D点为坐标原点,以DA、DC、DD1所在的直线为x轴、y轴、z轴,建立空间直角坐标系(图略),则A(2,0,0),B(2,2,0),C(0,2,0),C1(0,2,1)∴=(﹣2,0,1),=(﹣2,2,0),且为平面BB1D1D的一个法向量.∴cos<,>═=.∴BC1与平面BB1D1D所成角的正弦值为故选:D.11.(5分)函数f(x)=sin x﹣cos x,x∈[0,]的最小值为()A.﹣2B.﹣C.﹣D.﹣1【解答】解:f(x)=sin x﹣cos x=(sin x﹣cos x)=sin(x﹣),x∈[0,],则x﹣∈,x=0时,函数取得最小值,∴f(x)的最小值是﹣1.故选:D.12.(5分)已知圆C1:(x﹣2)2+(y﹣3)2=1,圆C2:(x﹣3)2+(y﹣4)2=9,M,N 分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为()A.﹣1B.5﹣4C.6﹣2D.【解答】解:如图圆C1关于x轴的对称圆的圆心坐标A(2,﹣3),半径为1,圆C2的圆心坐标(3,4),半径为3,由图象可知当P,M,N,三点共线时,|PM|+|PN|取得最小值,|PM|+|PN|的最小值为圆C3与圆C2的圆心距减去两个圆的半径和,即:|AC2|﹣3﹣1=﹣4=﹣4=5﹣4.故选:B.二.填空题:(每小题5分,共20分)13.(5分)已知向量,向量=(x,3),且,则x=6.【解答】解:因为向量,向量=(x,3),且,根据向量共线的充要条件得4×3=2x,x=6故答案为:6.14.(5分)一个几何体的三视图如图所示,则这个几何体的体积为.【解答】解:该几何体是上面是底面边长为2的正四棱锥,下面是底面边长为1、高为2的正四棱柱的组合体,其体积为V=1×1×2+×22×1=.故答案为.15.(5分)直线的倾斜角为α,且90°<α≤135°,则它的斜率的取值范围为(﹣∞,﹣1].【解答】解:∵直线的倾斜角为α,且90°<α≤135°,∴斜率k=tanα≤tan135°=﹣1,∴它的斜率的取值范围为:(﹣∞,﹣1].故答案为:(﹣∞,﹣1].16.(5分)直线y=x+b与曲线有且有一个公共点,则b的取值范围是.【解答】解:直线y=x+b是一条斜率为1,截距为b的直线;曲线变形为x2+y2=1且x≥0显然是一个圆心为(0,0),半径为1的右半圆.根据题意,直线y=x+b与曲线有且有一个公共点做出它们的图形,则易得b的取值范围是.三.解答题(共70分)17.(10分)求下列条件确定的圆的方程:(1)圆心为点C(8,3),且过点A(5,1)(2)圆心在y轴上,半径长为3,且与x轴相切.【解答】解:(1)根据题意,要求圆的半径r2=|CA|2=(8﹣5)2+(3﹣1)2=13,所求圆的方程为(x﹣8)2+(y﹣3)2=13.(2)设圆心的坐标为(0,m),则r=|m|=3,解可得m=±3,所求圆的方程为x2+(y+3)2=9或x2+(y﹣3)2=9.18.(12分)已知直线l:3x+4y﹣20=0.(1)求过点(2,2)且与直线平行的直线方程;(2)已知直线l1:2x﹣ay+a=0与直线l垂直,试确定实数a的值.【解答】解:(1)由于所求直线与直线3x+4y﹣20=0平行,所以所求直线的斜率k=﹣.又因为所求直线经过点(2,2),所以所求直线方程为y﹣2=﹣(x﹣2),即3x+4y﹣14=0.(2)∵l1⊥l,∴3×2+4×(﹣a)=0,∴a=.19.(12分)如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.(1)求证:P A∥面BDE;平面P AC⊥平面BDE;(2)若二面角E﹣BD﹣C为30°,求四棱锥P﹣ABCD的体积.【解答】(1)证明:连结EO∵四边形ABCD是正方形,O是正方形的中心∴BD⊥AC=O,AO=CO∵在△P AC中,E为PC的中点,∴P A∥EO又∵EO⊂平面BDE,P A⊄平面BDE∴P A∥平面BDE;∵PO⊥底面ABCD,BD⊂平面ABCD∴PO⊥BD又∵BD⊥AC,AC∩PO=E,PO⊂平面P AC,AC⊂平面P AC∴BD⊥平面P AC又∵BD⊂平面BDE∴平面P AC⊥平面BDE;(2)解:由(1)可知,∠EOC=30°,∴∠OPC=60°,∵底面边长为a,∴CO=a,∴PO=a,∴四棱锥P﹣ABCD的体积==.20.(12分)如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.【解答】解:作CE⊥AB于E,作DF⊥CE于F,则AE=AD=2,CE=4,BE=3,∴BC=5,四边形ABCD绕AD旋转一周所成几何体为圆台挖去一个圆锥,其中,圆台的上下底面半径为r1=2,r2=5,高为4,母线l=5,圆锥的底面半径为2,高为2,母线l′=2,∴几何体的表面积S=25π+π×2×5+π×5×5+=60π+4π.几何体的体积V=(25π+4π+)×4﹣×4π×2=.21.(12分)已知函数f(x)=cos2﹣sin cos﹣.(Ⅰ)求函数f(x)的最小正周期和值域;(Ⅱ)若f(α)=,求sin2α的值.【解答】解:(Ⅰ)由已知,f(x)=﹣sin cos﹣=(1+cos x)﹣sin x﹣=cos(x+).∴函数f(x)的最小正周期为2π,值域为[﹣,].(Ⅱ)由(Ⅰ)知,f(α)=cos(α+)=,∴cos(α+)=,∴sin2α=﹣cos(+2α)=﹣cos2(α+)=1﹣2=1﹣=.22.(12分)已知坐标平面上点M(x,y)与两个定点M1(26,1),M2(2,1)的距离之比等于5.(1)求点M的轨迹方程,并说明轨迹是什么图形;(2)记(1)中的轨迹为C,过点A(﹣2,3)的直线l被C所截得的线段的长为8,求直线l的方程.【解答】解:(1)由题意坐标平面上点M(x,y)与两个定点M1(26,1),M2(2,1)的距离之比等于5,得=5.,化简得x2+y2﹣2x﹣2y﹣23=0.即(x﹣1)2+(y﹣1)2=25.∴点M的轨迹方程是(x﹣1)2+(y﹣1)2=25,所求轨迹是以(1,1)为圆心,以5为半径的圆.(2)当直线l的斜率不存在时,过点A(﹣2,3)的直线l:x=﹣2,此时过点A(﹣2,3)的直线l被圆所截得的线段的长为:2=8,∴l:x=﹣2符合题意.当直线l的斜率存在时,设过点A(﹣2,3)的直线l的方程为y﹣3=k(x+2),即kx﹣y+2k+3=0,圆心到l的距离d=,由题意,得+42=52,解得k=.∴直线l的方程为x﹣y+=0.即5x﹣12y+46=0.综上,直线l的方程为x=﹣2,或5x﹣12y+46=0.。
内蒙古阿拉善盟高一下学期数学期末考试试卷

内蒙古阿拉善盟高一下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (2017高二下·红桥期末) 已知集合M={2,3,4},N={0,2,3,5},则M∩N=()A . {0,2}B . {2,3}C . {3,4}D . {3,5}2. (2分)既是偶函数又在区间上单调递减的函数是()A . y=sinxB . y=cosxC . y=sin2xD . y=cos2x3. (2分) (2019高一下·泰州月考) 过点且垂直于直线的直线方程为()A .B .C .D .4. (2分)中,,则B=()A .B . 或C . 或D .5. (2分)等差数列-5,-2,1,…的前20项的和为()A . 450B . 470C . 490D . 5106. (2分) (2016高一上·呼和浩特期中) 已知实数a≥0,b≥0,且a+b=1,则(a+1)2+(b+1)2的取值范围为()A .B .C .D . [0,5]7. (2分)设是双曲线的两个焦点,是上一点,若且的最小内角为,则的离心率为()A .B .C .D .8. (2分)在△ABC中,,,则△ABC的面积为()A .B . 3C .D . 69. (2分) 2cos cos +cos π+cos 的值是()A . ﹣1B . 0C . 1D . 210. (2分) (2019高二下·佛山月考) 将函数图像上每一点的纵坐标保持不变,横坐标扩大到原来的倍,再把所得的图像沿轴向右平移个单位,这样所得的曲线与的图像相同,则函数的表达式是()A .B .C .D .11. (2分)设变量x,y满足约束条件,则目标函数的最小值为()A .B .C . 2D . 312. (2分)已知函数f(n)=n2cos(nπ),且an=f(n)+f(n+1),则a1+a2+a3+…+a100=()A . 0B . -100C . 100D . 10200二、填空题 (共4题;共5分)13. (2分) (2019高三上·杭州月考) 设两直线与 .若 ,则 ________,若 ,则 ________.14. (1分)某A地位于B地正西方向5 km处,C地位于A地正北方向5 km处,则C地相对于B地的位移是________.15. (1分)(2017·北京) 若等差数列{an}和等比数列{bn}满足a1=b1=﹣1,a4=b4=8,则 =________.16. (1分)如图,勘探队员朝一座山行进,在前后两处A,B观察塔尖P及山顶Q.已知P,Q,A,B,O在同一平面且与水平面垂直.设塔高PQ=h,山高QO=H,AB=m,BO=n,仰角∠PAO=α,仰角∠QAO=β,仰角∠PBO=θ.试用m,α,β,θ表示h,h=________.三、解答题 (共6题;共55分)17. (5分) (2020高一下·海林期中) △ABC中,a=1,b= ,∠A=30°,求∠B.18. (10分) (2019高一下·杭州期中) 已知,,且与夹角为求(1);(2) .19. (10分) (2017高二下·新乡期末) 已知等比数列{an}的前n项和为Sn ,且6Sn=3n+1+a(n∈N+)(1)求a的值及数列{an}的通项公式;(2)设bn=(1﹣an)log3(an2•an+1),求的前n项和为Tn .20. (10分) (2019高三上·江西月考) 已知中,角A,B,C所对的边分别为a,b,c,,且 .(1)求外接圆的半径;(2)若,求的面积.21. (10分)已知向量 =(,﹣2), =(sin( +2x),cos2x)(x∈R).设函数f(x)= .(1)求的值;(2)求f(x)的最大值及对应的x值.22. (10分) (2018高三上·哈尔滨月考) 已知数列满足,且, .(1)设,证明:数列为等差数列,并求数列的通项公式;(2)求数列的前项和 .参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共5分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共55分)17-1、18-1、18-2、19-1、19-2、20-1、20-2、21-1、21-2、22-1、22-2、。
内蒙古阿拉善盟高一下学期期末数学考试试卷

内蒙古阿拉善盟高一下学期期末数学考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题;共20分)1. (2分) (2019高一上·新丰期中) 函数的定义域为,那么其值域为()A .B .C .D .2. (2分)设集合,,则下列结论正确的是()A .B .C .D .3. (2分) (2017高一下·西城期末) 执行如图所示的程序框图,则输出的i值为()A . 4B . 5C . 6D . 74. (2分) (2017高一下·西城期末) 设直线l经过两点A(2,1),B(﹣1,3),则直线l下方的半平面(含直线l)可以用不等式表示为()A . 2x+3y﹣7≥0B . 2x+3y﹣7≤0C . 2x+3y+1≥0D . 2x+3y+1≤05. (2分) (2017高一下·西城期末) 在区间[﹣1,3]上随机取一个实数x,则x使不等式|x|≤2成立的概率为()A .B .C .D .6. (2分) (2017高一下·西城期末) 如表是某校120名学生假期阅读时间(单位:小时)的频率分布表,现用分层抽样的方法从[10,15),[15,20),[20,25),[25,30)四组中抽取20名学生了解其阅读内容,那么从这四组中依次抽取的人数是()分组频数频率[10,15)120,10[15,20)30a[20,25)m0.40[25,30)n0.25合计120 1.00A . 2,5,8,5B . 2,5,9,4C . 4,10,4,2D . 4,10,3,37. (2分) (2017高一下·西城期末) 在△ABC中,若,c=2,,则△ABC的面积为()A .B .C .D .8. (2分) (2017高一下·西城期末) 以下茎叶图记录了甲、乙两个篮球队在3次不同比赛中的得分情况.乙队记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以m表示.那么在3次比赛中,乙队平均得分超过甲队平均得分的概率是()A .B .C .D .9. (2分) (2017高一下·西城期末) 若关于x的不等式对于一切x∈(1,+∞)恒成立,则实数a的取值范围是()A . (﹣∞,4]B . [4,+∞)C . (﹣∞,6]D . [6,+∞)10. (2分) (2017高一下·西城期末) 在△ABC中,角A,B,C对边的边长分别为a,b,c,给出下列四个结论:①以为边长的三角形一定存在;②以为边长的三角形一定存在;③以a2 , b2 , c2为边长的三角形一定存在;④以为边长的三角形一定存在.那么,正确结论的个数为()A . 0B . 1C . 2D . 3二、填空题 (共6题;共8分)11. (1分) (2018高二下·北京期末) 若函数f(x)满足,则 f(2) =________ .12. (1分) (2019高一下·镇江期末) 已知为虚数单位,复数,则 ________.13. (2分) (2017高一下·西城期末) 随机抽取某班6名学生,测量他们的身高(单位:cm),获得身高数据依次为:162,168,170,171,179,182,那么此班学生平均身高大约为________ cm;样本数据的方差为________.14. (1分) (2017高一下·西城期末) 设x,y满足约束条件,则z=x+3y的最大值是________.15. (1分) (2017高一下·西城期末) 有4张卡片,上面分别写有0,1,2,3.若从这4张卡片中随机取出2张组成一个两位数,则此数为偶数的概率是________.16. (2分) (2017高一下·西城期末) 在数列{an}中,a3=12,a11=﹣5,且任意连续三项的和均为11,则a2017=________;设Sn是数列{an}的前n项和,则使得Sn≤100成立的最大整数n=________.三、解答题 (共6题;共40分)17. (10分)已知向量、的夹角为 .(1)求· 的值(2)若和垂直,求实数t的值.18. (10分)随着经济的发展,个人收入的提高,自2019年1月1日起,个人所得税起征点和税率的调整.调整如下:纳税人的工资、薪金所得,以每月全部收入额减除5000元后的余额为应纳税所得额.依照个人所得税税率表,调整前后的计算方法如下表:个人所得税税率表(调整前)个人所得税税率表(调整后)免征额3500元免征额5000元级数全月应纳税所得额税率(%)级数全月应纳税所得额税率(%)1不超过1500元部分31不超过3000元部分32超过1500元至4500元的部分102超过3000元至12000元的部分103超过4500元至9000元的部分203超过12000元至25000元的部分20 ..................(1)假如小红某月的工资、薪金等所得税前收入总和不高于8000元,记表示总收入,表示应纳的税,试写出调整前后关于的函数表达式;(2)某税务部门在小红所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,并制成下面的频数分布表:收入(元)人数304010875①先从收入在及的人群中按分层抽样抽取7人,再从中选4人作为新纳税法知识宣讲员,用表示抽到作为宣讲员的收入在元的人数,表示抽到作为宣讲员的收入在元的人数,随机变量,求的分布列与数学期望;②小红该月的工资、薪金等税前收入为7500元时,请你帮小红算一下调整后小红的实际收入比调整前增加了多少?19. (5分) (2017高一下·西城期末) 在△ABC中,角A,B,C的对边分别为a,b,c,且a=2,.(Ⅰ)如果b=3,求c的值;(Ⅱ)如果,求sinB的值.20. (5分) (2017高一下·西城期末) 已知数列{an}的前n项和,其中n∈N* .(Ⅰ)求数列{an}的通项公式;(Ⅱ)设,求数列{bn}的前n项和Tn;(Ⅲ)若对于任意正整数n,都有,求实数λ的最小值.21. (5分) (2017高一下·西城期末) 已知函数f(x)=ax2+(2a+1)x+b,其中a,b∈R.(Ⅰ)当a=1,b=﹣4时,求函数f(x)的零点;(Ⅱ)如果函数f(x)的图象在直线y=x+2的上方,证明:b>2;(Ⅲ)当b=2时,解关于x的不等式f(x)<0.22. (5分) (2017高一下·西城期末) 在无穷数列{an}中,a1=p是正整数,且满足(Ⅰ)当a3=9时,给出p的值;(结论不要求证明)(Ⅱ)设p=7,数列{an}的前n项和为Sn ,求S150;(Ⅲ)如果存在m∈N* ,使得am=1,求出符合条件的p的所有值.参考答案一、选择题 (共10题;共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共6题;共8分)11-1、12-1、13-1、14-1、15-1、16-1、三、解答题 (共6题;共40分)17-1、17-2、18-1、18-2、19-1、20-1、22-1、。
内蒙古阿拉善盟高一下学期期末数学试卷

内蒙古阿拉善盟高一下学期期末数学试卷姓名:________班级:________成绩:________一、 选择题 (共 12 题;共 24 分)1. (2 分) 设 0<a<b<1,则下列不等式成立的是( )A.B. C. D. 2. (2 分) (2016 高一下·奉新期末) 在△ABC 中,sinA:sinB:sinC=4:3:2,则 cosA 的值是( )A.﹣B.C.﹣D.3. (2 分) (2016 高一下·奉新期末) 不等式 A . (﹣∞,﹣1)∪(0,+∞) B . (﹣∞,﹣1) C . (﹣1,+∞) D . (﹣1,0)>2 的解集是( )4. (2 分) (2016 高一下·奉新期末) 在 2﹣ 个数为( )与 2+之间插入一个数,使这三个数成等比数列,则这第 1 页 共 12 页A.± B . ±1 C.1D. 5. (2 分) (2016 高一下·奉新期末) 下列命题中错误的是( ) A . 若 α⊥β,a⊂ α,则 a⊥β B . 若 m∥n,n⊥β,m⊂ α,则 α⊥β C . 若 α⊥γ,β⊥γ,α∩β=l,则 l⊥γ D . 若 α⊥β,α∩β=AB,a∥α,a⊥AB,则 a⊥β6. (2 分) (2016 高一下·奉新期末) 设变量 x,y 满足约束条件: A . ﹣2,则 z=x﹣3y 的最小值( )B . ﹣4C . ﹣6D . ﹣87. (2 分) (2016 高一下·奉新期末) 直线 l 过点 M(﹣1,2)且与以 P(﹣2,﹣3),Q(4,0)为端点的线 段 PQ 相交,则 l 的斜率的取值范围是( )A . [﹣ ,5]B . [﹣ ,0)∪(0,5]C . [﹣ , )∪( ,5]D . (﹣∞,﹣ ]∪[5,+∞)第 2 页 共 12 页8. (2 分) (2016 高一下·奉新期末) 已知数列{an}的前 n 项和 Sn , 且 Sn=n2+n,数列{bn}满足 bn= (n∈N*),Tn 是数列{bn}的前 n 项和,则 T9 等于( )A.B.C.D. 9. (2 分) (2016 高一下·奉新期末) 如图是一个空间几何体的三视图,根据图中尺寸(单位:cm),可知几 何体的表面积是( )A.B. C.D.10. (2 分) (2016 高一下·奉新期末) 已知数列{an},若点(n,an)(n∈N+)在经过点(5,3)的定直线 l 上,则数列{an}的前 9 项和 S9=( )A.9B . 10C . 18D . 27第 3 页 共 12 页11. (2 分) (2016 高一下·奉新期末) 正四棱锥(底面为正方形,顶点在底面上的射影是底面的中心)S﹣ ABCD 的底面边长为 2,高为 2,E 为边 BC 的中点,动点 P 在表面上运动,并且总保持 PE⊥AC,则动点 P 的轨迹的周 长为( )A.B.C.3D. 12. (2 分) (2016 高一下·奉新期末) 在△ABC 中,角 A,B,C 所对的边分别为 a,b,c,若 A,B,C 成等 差数列,且 b=1,则△ABC 面积的最大值为( )A. B. C. D.1二、 填空题 (共 4 题;共 4 分)13. (1 分) 空间两点 P1(2,3,5),P2(3,1,4)间的距离|P1P2|=________ .14. (1 分) (2020 高二下·吉林期中) 对于任意实数,直线 共点,则 b 的取值范围是________ .与椭圆恒有公15. (1 分) (2017 高二上·莆田月考) 将曲线按伸缩变换公式则曲线 上的点到直线的距离最小值为________.变换后得到曲线 ,16. (1 分) (2016 高一下·奉新期末) 棱长为 a 正方体 ABCD﹣A1B1C1D1 中,M,N 分别是棱 A1B1 , B1C1 的中点,点 P 是棱 AB 上一点,且 AP= ,过点 P,M,N 的平面与直线 CD 交于一点 Q,则 PQ 的长为________.第 4 页 共 12 页三、 解答题 (共 6 题;共 55 分)17. (5 分) 求圆心为 C(2,﹣1)且截直线 y=x﹣1 所得弦长为 2 的圆的方程.18. (10 分) (2019 高二下·江西期中) 已知点 是抛物线 :的准线与 轴的交点,点 是抛物线 上的动点,点 、 在 轴上, ,其中 为坐标原点.的内切圆为圆 :,且(1) 求抛物线 的标准方程;(2) 求面积的最小值.19.(10 分)(2020·榆林模拟) 已知动圆过定点过 作斜率为的直线 与 交于两点线 与 交于两点.,且与直线,过分别作相切,动圆圆心的轨迹为 , 的切线,两切线的交点为 ,直(1) 证明:点 始终在直线 上且;(2) 求四边形的面积的最小值.20. (10 分) (2016 高一下·奉新期末) 已知数列{an}的首项为 a1= ,且 2an+1=an(n∈N+). (1) 求{an}的通项公式;(2) 若数列{bn}满足 bn= ,求{bn}的前 n 项和 Tn . 21. (10 分) (2016 高一下·奉新期末) 某工厂生产一种仪器的元件,由于受生产能力和技术水平的限制,会产生一些次品,根据经验知道,其次品率 P 与日产量 x(万件)之间大体满足关系:.(注:次品率=次品数/生产量,如 P=0.1 表示每生产 10 件产品,有 1 件为次品,其余为合格品).已知每生产 1 万件合格的元件可以盈利 2 万元,但每生产 1 万件次品将亏损 1 万元,故厂方希望定出合适的日产量.(1) 试将生产这种仪器的元件每天的盈利额 T(万元)表示为日产量 x(万件)的函数;(2) 当日产量 x 为多少时,可获得最大利润?22. (10 分) (2016 高一下·奉新期末) 已知数列{an}的前 n 项和为 Sn , 且 Sn=n﹣5an﹣85,n∈N+ .第 5 页 共 12 页(1) 求 an . (2) 求数列{Sn}的通项公式,并求出 n 为何值时,Sn 取得最小值?并说明理由.(参考数据:lg 2≈0.3,lg 3≈0.48).第 6 页 共 12 页一、 选择题 (共 12 题;共 24 分)1-1、 2-1、 3-1、 4-1、 5-1、 6-1、 7-1、 8-1、 9-1、 10-1、 11-1、 12-1、二、 填空题 (共 4 题;共 4 分)13-1、 14-1、 15-1、参考答案第 7 页 共 12 页16-1、三、 解答题 (共 6 题;共 55 分)17-1、 18-1、第 8 页 共 12 页18-2、19-1、第 9 页 共 12 页19-2、20-1、20-2、第 10 页 共 12 页21-1、21-2、22-1、22-2、。
2016-2017年内蒙古阿拉善盟左旗高中高一(下)期末数学试卷(理科)(解析版)

2016-2017学年内蒙古阿拉善盟左旗高中高一(下)期末数学试卷(理科)一、选择题:(每小题5分,共60分)1.(5分)已知=(4,2),=(x,3),且∥,则x的值是()A.6B.﹣6C.9D.122.(5分)现要完成下列3项抽样调查:①从10盒酸奶中抽取3盒进行食品卫生检查.②科技报告厅有32排,每排有40个座位,有一次报告会恰好坐满了听众,报告会结束后,为了听取意见,需要请32名听众进行座谈.③高新中学共有160名教职工,其中一般教师120名,行政人员16名,后勤人员24名,为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为20的样本.较为合理的抽样方法是()A.①简单随机抽样,②系统抽样,③分层抽样B.①简单随机抽样,②分层抽样,③系统抽样C.①系统抽样,②简单随机抽样,③分层抽样D.①分层抽样,②系统抽样,③简单随机抽样3.(5分)点P(x,2,1)到Q(1,1,2),R(2,1,1)的距离相等,则x的值为()A.B.1C.D.24.(5分)阅读如图所示的程序框图,运行相应的程序,输出的结果是()A.1B.2C.3D.45.(5分)已知=(2sin35°,2cos35°),=(cos5°,﹣sin5°),则•=()A.B.1C.2D.2sin40°6.(5分)用“辗转相除法”求得459和357的最大公约数是()A.3B.9C.17D.517.(5分)某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,则甲、乙两名运动员的中位数分别是()A.19、13B.13、19C.20、18D.18、208.(5分)若tanα=3,则的值等于()A.2B.3C.4D.69.(5分)函数f(x)=sin x﹣cos x,x∈[0,]的最小值为()A.﹣2B.﹣C.﹣D.﹣110.(5分)已知在四面体ABCD中,E、F分别是AC、BD的中点,若CD=2AB=4,EF ⊥AB,则EF与CD所成的角为()A.90°B.45°C.60°D.30°11.(5分)已知平面α、β和直线m,l,则下列命题中正确的是()A.若α⊥β,α∩β=m,l⊥m,则l⊥βB.若α∩β=m,l⊂α,l⊥m,则l⊥βC.若α⊥β,l⊂α,则l⊥βD.若α⊥β,α∩β=m,l⊂α,l⊥m,则l⊥β12.(5分)已知圆C1:(x﹣2)2+(y﹣3)2=1,圆C2:(x﹣3)2+(y﹣4)2=9,M,N 分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为()A.﹣1B.5﹣4C.6﹣2D.二.填空题:(每小题5分,共20分)13.(5分)用秦九韶算法计算函数f(x)=2x4+3x3+5x﹣4当x=2时的函数值为.14.(5分)如图,在长方体ABCD﹣A1B1C1D1中,AB=BC=2AA1,则BC1与平面BB1D1D 所成角的正弦值为.15.(5分)(文)一个几何体的三视图如图所示,则这个几何体的体积为.16.(5分)直线y=x+b与曲线有且有一个公共点,则b的取值范围是.三.解答题(共70分)17.(10分)(1)求与直线3x+4y﹣7=0垂直,且与原点的距离为6的直线方程;(2)求圆心在直线y=﹣4x上,且与直线l:x+y﹣1=0相切于点P(3,﹣2)的圆的方程.18.(12分)从高三抽出50名学生参加数学竞赛,由成绩得到如图的频率分布直方图.试利用频率分布直方图求:(1)这50名学生成绩的众数与中位数.(2)这50名学生的平均成绩.(答案精确到0.1)19.(12分)如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.(1)求证:P A∥面BDE;平面P AC⊥平面BDE;(2)若二面角E﹣BD﹣C为30°,求四棱锥P﹣ABCD的体积.20.(12分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.(1)请画出上表数据的散点图;(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程=x+;(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据第2题求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)21.(12分)已知坐标平面上点M(x,y)与两个定点M1(26,1),M2(2,1)的距离之比等于5.(1)求点M的轨迹方程,并说明轨迹是什么图形;(2)记(1)中的轨迹为C,过点A(﹣2,3)的直线l被C所截得的线段的长为8,求直线l的方程.22.(12分)如图,在五面体EF﹣ABCD中,四边形ADEF是正方形,F A⊥平面ABCD,BC∥AD,CD=l,AD=2,∠BAD=∠CDA=45°.①证明:CD⊥平面ABF;②求二面角B﹣EF﹣A的正切值.2016-2017学年内蒙古阿拉善盟左旗高中高一(下)期末数学试卷(理科)参考答案与试题解析一、选择题:(每小题5分,共60分)1.(5分)已知=(4,2),=(x,3),且∥,则x的值是()A.6B.﹣6C.9D.12【解答】解:∵平面向量=(4,2),=(x,3),又∵向量∥,∴4×3﹣2x=0解得x=6故选:A.2.(5分)现要完成下列3项抽样调查:①从10盒酸奶中抽取3盒进行食品卫生检查.②科技报告厅有32排,每排有40个座位,有一次报告会恰好坐满了听众,报告会结束后,为了听取意见,需要请32名听众进行座谈.③高新中学共有160名教职工,其中一般教师120名,行政人员16名,后勤人员24名,为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为20的样本.较为合理的抽样方法是()A.①简单随机抽样,②系统抽样,③分层抽样B.①简单随机抽样,②分层抽样,③系统抽样C.①系统抽样,②简单随机抽样,③分层抽样D.①分层抽样,②系统抽样,③简单随机抽样【解答】解;观察所给的四组数据,①个体没有差异且总数不多可用随机抽样法,简单随机抽样,②将总体分成均衡的若干部分指的是将总体分段,在第1段内采用简单随机抽样确定一个起始编号,在此编号的基础上加上分段间隔的整倍数即为抽样编号,系统抽样,③个体有了明显了差异,所以选用分层抽样法,分层抽样,故选:A.3.(5分)点P(x,2,1)到Q(1,1,2),R(2,1,1)的距离相等,则x的值为()A.B.1C.D.2【解答】解:因为点P(x,2,1)到Q(1,1,2),R(2,1,1)的距离相等,所以:(x﹣1)2+(2﹣1)2+(1﹣2)2=(x﹣2)2+(2﹣1)2+(1﹣1)2.解得x=1.故选:B.4.(5分)阅读如图所示的程序框图,运行相应的程序,输出的结果是()A.1B.2C.3D.4【解答】解:程序在运行过程中各变量的值如下表示:S n是否继续循环循环前 2 1/第一圈﹣1 2 是第二圈 3 是第三圈 2 4 否则输出的结果为4故选:D.5.(5分)已知=(2sin35°,2cos35°),=(cos5°,﹣sin5°),则•=()A.B.1C.2D.2sin40°【解答】解:∵=(2sin35°,2cos35°),=(cos5°,﹣sin5°),∴•=2sin35°cos5°﹣2cos35°sin5°=2sin(35°﹣5°)2sin30°=1.故选:B.6.(5分)用“辗转相除法”求得459和357的最大公约数是()A.3B.9C.17D.51【解答】解:∵459÷357=1…102,357÷102=3…51,102÷51=2,∴459和357的最大公约数是51,故选:D.7.(5分)某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,则甲、乙两名运动员的中位数分别是()A.19、13B.13、19C.20、18D.18、20【解答】解:由题意知,∵甲运动员的得分按照从小到大排列是7,8,9,15,17,19,23,24,26,32,41共有11 个数字,最中间一个是19,乙运动员得分按照从小到大的顺序排列是5,7,8,11,11,13,20,22,30,31,40,共有11个数据,最中间一个是13,∴甲、乙两名运动员比赛得分的中位数分别是19,13.故选:A.8.(5分)若tanα=3,则的值等于()A.2B.3C.4D.6【解答】解:==2tanα=6故选:D.9.(5分)函数f(x)=sin x﹣cos x,x∈[0,]的最小值为()A.﹣2B.﹣C.﹣D.﹣1【解答】解:f(x)=sin x﹣cos x=(sin x﹣cos x)=sin(x﹣),x∈[0,],则x﹣∈,x=0时,函数取得最小值,∴f(x)的最小值是﹣1.故选:D.10.(5分)已知在四面体ABCD中,E、F分别是AC、BD的中点,若CD=2AB=4,EF ⊥AB,则EF与CD所成的角为()A.90°B.45°C.60°D.30°【解答】解:设G为AD的中点,连接GF,GE,则GF,GE分别为△ABD,△ACD的中线.∴GF∥AB,且GF=AB=1,GE∥CD,且GE=CD=2,则EF与CD所成角的度数等于EF与GE所成角的度数又EF⊥AB,GF∥AB,∴EF⊥GF则△GEF为直角三角形,GF=1,GE=2,∠GFE=90°∴在直角△GEF中,sin∠GEF=∴∠GEF=30°.故选:D.11.(5分)已知平面α、β和直线m,l,则下列命题中正确的是()A.若α⊥β,α∩β=m,l⊥m,则l⊥βB.若α∩β=m,l⊂α,l⊥m,则l⊥βC.若α⊥β,l⊂α,则l⊥βD.若α⊥β,α∩β=m,l⊂α,l⊥m,则l⊥β【解答】解:若α⊥β,α∩β=m,l⊥m,则l与β相交,平行或l⊂β,故A错误;若α∩β=m,l⊂α,l⊥m,则l与β相交但不一定垂直,故B错误;若α⊥β,l⊂α,则l与β相交,平行或l⊂β,故C错误;若α⊥β,α∩β=m,l⊂α,l⊥m,则由平面与平面垂直的性质得l⊥β,故D正确.故选:D.12.(5分)已知圆C1:(x﹣2)2+(y﹣3)2=1,圆C2:(x﹣3)2+(y﹣4)2=9,M,N 分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为()A.﹣1B.5﹣4C.6﹣2D.【解答】解:如图圆C1关于x轴的对称圆的圆心坐标A(2,﹣3),半径为1,圆C2的圆心坐标(3,4),半径为3,由图象可知当P,M,N,三点共线时,|PM|+|PN|取得最小值,|PM|+|PN|的最小值为圆C3与圆C2的圆心距减去两个圆的半径和,即:|AC2|﹣3﹣1=﹣4=﹣4=5﹣4.故选:B.二.填空题:(每小题5分,共20分)13.(5分)用秦九韶算法计算函数f(x)=2x4+3x3+5x﹣4当x=2时的函数值为62.【解答】解:秦九韶算法如下:f(x)=2x4+3x3+5x﹣4=x(2x3+3x2+5)﹣4=x[x(2x2+3x)+5]﹣4=x{x[x(2x+3)]+5}﹣4当x=2时,f(x)=2×{2×[2×(2×2+3)]+5}﹣4=62故答案为:6214.(5分)如图,在长方体ABCD﹣A1B1C1D1中,AB=BC=2AA1,则BC1与平面BB1D1D所成角的正弦值为.【解答】解:以D点为坐标原点,以DA、DC、DD1所在的直线为x轴、y轴、z轴,建立空间直角坐标系,则A(2,0,0),B(2,2,0),C(0,2,0),C1(0,2,1)∴=(﹣2,0,1),=(﹣2,2,0),且为平面BB1D1D的一个法向量.∴cos==.∴BC1与平面BB1D1D所成角的正弦值为,故答案为:.15.(5分)(文)一个几何体的三视图如图所示,则这个几何体的体积为36.【解答】解:由三视图知几何体是一个四棱柱,四棱柱的底面是一个直角梯形,上底是2,下底是4,高是2,,四棱柱的侧棱与底面垂直,且侧棱长时6,∴四棱柱的体积是=36故答案为:3616.(5分)直线y=x+b与曲线有且有一个公共点,则b的取值范围是.【解答】解:直线y=x+b是一条斜率为1,截距为b的直线;曲线变形为x2+y2=1且x≥0显然是一个圆心为(0,0),半径为1的右半圆.根据题意,直线y=x+b与曲线有且有一个公共点做出它们的图形,则易得b的取值范围是.三.解答题(共70分)17.(10分)(1)求与直线3x+4y﹣7=0垂直,且与原点的距离为6的直线方程;(2)求圆心在直线y=﹣4x上,且与直线l:x+y﹣1=0相切于点P(3,﹣2)的圆的方程.【解答】解:(1)根据题意,要求直线与直线3x+4y﹣7=0垂直,则设要求的直线方程为4x﹣3y+c=0.由已知=6,解得c=±30,故所求的直线方程为4x﹣3y±30=0;(2)设要求的圆心为C(m,n)由于过P(3,﹣2)垂直于切线的直线必定过圆心,故该直线的方程为x﹣y﹣5=0,则有m﹣n﹣5=0,且n=4m,解可得:m=1,n=﹣4;故圆心C为(1,﹣4),r=CP=2,∴所求圆的方程为(x﹣1)2+(y+4)2=8.18.(12分)从高三抽出50名学生参加数学竞赛,由成绩得到如图的频率分布直方图.试利用频率分布直方图求:(1)这50名学生成绩的众数与中位数.(2)这50名学生的平均成绩.(答案精确到0.1)【解答】(12分)解:(1)由众数的概念可知,众数是出现次数最多的数.在直方图中高度最高的小长方形框的中间值的横坐标即为所求,所以由频率分布直方图得众数应为75.由于中位数是所有数据中的中间值,故在频率分布直方图中体现的是中位数的左右两边频数应相等,即频率也相等,从而就是小矩形的面积和相等.因此在频率分布直方图中将频率分布直方图中所有小矩形的面积一分为二的直线所对应的成绩即为所求.∵0.004×10+0.006×10+0.02×10=0.04+0.06+0.2=0.3,∴前三个小矩形面积的和为0.3.而第四个小矩形面积为0.03×10=0.3,0.3+0.3>0.5,∴中位数应位于第四个小矩形内.设其底边为x,高为0.03,∴令0.03x=0.2得x≈6.7,故中位数约为70+6.7=76.7.(2)样本平均值应是频率分布直方图的“重心”,即所有数据的平均值,取每个小矩形底边的中点值乘以每个小矩形的面积即可.∴平均成绩为45×(0.004×10)+55×(0.006×10)+65×(0.02×10)+75×(0.03×10)+85×(0.021×10)+95×(0.016×10)≈73.7.19.(12分)如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.(1)求证:P A∥面BDE;平面P AC⊥平面BDE;(2)若二面角E﹣BD﹣C为30°,求四棱锥P﹣ABCD的体积.【解答】(1)证明:连结EO∵四边形ABCD是正方形,O是正方形的中心∴BD⊥AC=O,AO=CO∵在△P AC中,E为PC的中点,∴P A∥EO又∵EO⊂平面BDE,P A⊄平面BDE∴P A∥平面BDE;∵PO⊥底面ABCD,BD⊂平面ABCD∴PO⊥BD又∵BD⊥AC,AC∩PO=E,PO⊂平面P AC,AC⊂平面P AC∴BD⊥平面P AC又∵BD⊂平面BDE∴平面P AC⊥平面BDE;(2)解:由(1)可知,∠EOC=30°,∴∠OPC=60°,∵底面边长为a,∴CO=a,∴PO=a,∴四棱锥P﹣ABCD的体积==.20.(12分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.(1)请画出上表数据的散点图;(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程=x+;(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据第2题求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)【解答】解:(1)把所给的四对数据写成对应的点的坐标,在坐标系中描出来,得到散点图如下;(2)由对照数据,计算得=×(3+4+5+6)=4.5,=×(2.5+3+4+4.5)=3.5,=32+42+52+62=86,x i y i=3×2.5+4×3+5×4+6×4.5=66.5,∴回归方程的系数为==0.7,=3.5﹣0.7×4.5=0.35,∴所求线性回归方程为=0.7x+0.35;(3)由(2)的线性回归方程,估计生产100吨甲产品的生产能耗为0.7×100+0.35=70.35(吨),∴90﹣70.35=19.65吨,预测比技改前降低了19.65吨标准煤.21.(12分)已知坐标平面上点M(x,y)与两个定点M1(26,1),M2(2,1)的距离之比等于5.(1)求点M的轨迹方程,并说明轨迹是什么图形;(2)记(1)中的轨迹为C,过点A(﹣2,3)的直线l被C所截得的线段的长为8,求直线l的方程.【解答】解:(1)由题意坐标平面上点M(x,y)与两个定点M1(26,1),M2(2,1)的距离之比等于5,得=5.,化简得x2+y2﹣2x﹣2y﹣23=0.即(x﹣1)2+(y﹣1)2=25.∴点M的轨迹方程是(x﹣1)2+(y﹣1)2=25,所求轨迹是以(1,1)为圆心,以5为半径的圆.(2)当直线l的斜率不存在时,过点A(﹣2,3)的直线l:x=﹣2,此时过点A(﹣2,3)的直线l被圆所截得的线段的长为:2=8,∴l:x=﹣2符合题意.当直线l的斜率存在时,设过点A(﹣2,3)的直线l的方程为y﹣3=k(x+2),即kx﹣y+2k+3=0,圆心到l的距离d=,由题意,得+42=52,解得k=.∴直线l的方程为x﹣y+=0.即5x﹣12y+46=0.综上,直线l的方程为x=﹣2,或5x﹣12y+46=0.22.(12分)如图,在五面体EF﹣ABCD中,四边形ADEF是正方形,F A⊥平面ABCD,BC∥AD,CD=l,AD=2,∠BAD=∠CDA=45°.①证明:CD⊥平面ABF;②求二面角B﹣EF﹣A的正切值.【解答】①证明:过点B作BG∥CD,交AD于点G,则∠BGA=∠CDA=45°,由∠BAD=45°,可得BG⊥AB,从而CD⊥AB,又F A⊥平面ABCD,∴CD⊥F A,∵F A∩AB=A,∴CD⊥平面ABF.②解:由上可得,即G为AD的中点,取EF的中点N,连接GN,则GN⊥EF,因为BC∥AD,所以BC∥EF,过点N作NM⊥EF,交BC于M,则∠GNM为二面角B﹣EF﹣A的平面角,连接GM,可得AD⊥平面GNM,故AD⊥GM,从而BC⊥GM,由已知,可得GM=,由NG∥F A,F A⊥GM,得NG⊥GM,在Rt△NGM中,,所以二面角B﹣EF﹣A的正切值为.。
内蒙古阿拉善盟第一中学高一数学下学期期末考试试题 文(部分答案)

阿盟一中2015-2016学年度第二学期期末考试高一年级 文科数学试卷注意事项:1、试卷内容必须答在试卷边框方框线以内,否则不得分;2、试卷I 的选择题答案必须答在答题卡上,否则不得分;第I 卷(共60分)一、 选择题(本大题共60分,每题4分)1、数列1,3,7,15,31,…的一个通项公式为( )A . 2n n a =B .21n n a =+C .21n n a =-D .12n n a -= 2.2cos 3π 的值 ( )A. 12 B. 12- C. 32 D.32-3、若sin α>0,且t an α<0,则角α的终边位于( )A .第一象限B .第二象限C .第三象限D .第四象限4、已知数列{n a }的通项公式)(82*2N n n n a n ∈--=,则4a 等于( ).A .1B .2C .0D .35、已知4sin 5α=,且α为第二象限角,那么tan α的值等于 ( )A .34B .43-C .43D .43-6、若变量,x y 满足约束条件2204x y x y x +≤⎧⎪+≥⎨⎪≤⎩,则4z x y =+的最大值为( )A .-6B .10C .12D .157、已知数列{}n a 中,12211,1,,n n n a a a a a ++===+,则5a =( )A .0B .3C .5D .88、设四边形ABC D 中,有=,且||=||,则这个四边形是( )A .正方形B .矩形C .等腰梯形D .菱形9、如果0<<b a ,那么下列各式一定成立的是( )A .0>-b aB .bc ac <C .22b a >D .b a 11< 10、a r ,b r 是两个向量,1a =r ,2b =r ,且()a b a +⊥r r r ,则a r ,b r 的夹角为( ) A .30o B .60o C .120o D .150o11、等差数列{}n a 中,45636a a a ++=,则19a a +=( )A .12B .18C .24D .3612、函数3sin 2x cos2x y =+的最小正周期和振幅分别是( )A .π,1B .π,2C .2π,1D .4π,213、在ABC ∆ 中,内角A,B,C 的对边分别是a,b,c,sinB csinC,b = 且222sin sin sin A B C =+ ,那么ABC ∆一定是 ( )A .等腰三角形B .等腰直角三角形C .直角三角形D .等腰或直角三角形14、等比数列{}n a 的前n 项和为n S ,若102010,S 30S == ,则30S =( )A.10B.70C.30D.9015、已知函数sin()()2y x x R π=-∈,下面结论错误的是 ( )A .函数()f x 的最小正周期为2πB .函数()f x 在区间[0,]2π上是增函数C .函数()f x 的图象关于直线0x =对称D .函数()f x 是奇函数第II 卷(共90分)二、填空题(本大题共20分,每题5分)15.函数2sin cos y x x = 的最小值__________16.不等式290x -> 的解集为_________________17.已知等差数列{}n a 的前n 项和为n S ,15611,4a a a =-+=-,n S 取得最小值时n =___18、在ABC ∆中,内角,,A B C 的对边分别是,,a b c ,若223a b bc -=,sin 23C B =,则A =_______.三、简答题(本大题共60分,每题12分)19、(10分)(1)在等差数列{}n a 中,21-=a ,d=4,求8S(2)在等比数列{}n a 中,427,3,a q == 求7a20、(12分)在∆ABC 中,内角,,A B C 的对边分别是,,a b c(1)0603,42A b ==,a=4 ,求B(2)已知033,2,150===a c B ,求边b 的长21.(12分)已知数列前n 项和n S ,2*23,(n N )n S n n =-∈ ,求它的通项公式na22、(12分)求和:(1)231111(23)[43()][63()][23()]5555n n S n =-⨯+-⨯+-⨯+⋅⋅⋅+-⨯(2)1111112233445(1)n S n n =++++⋅⋅⋅+⨯⨯⨯⨯⨯+23、(12分)已知等差数列{}n a 的公差不为0,125a =且11113,,a a a 成等比数列。
2016-2017学年内蒙古阿拉善盟左旗高中高二(下)期末数学试卷(文科)(解析版)

2016-2017学年内蒙古阿拉善盟左旗高中高二(下)期末数学试卷(文科)一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的).1.(5分)不等式|x﹣2|<1的解集为()A.[1,3]B.(1,3)C.[﹣3,﹣1]D.(﹣3,﹣1)2.(5分)已知i是虚数单位,则=()A.B.C.3﹣i D.3+i3.(5分)某西方国家流传这样的一个政治笑话:“鹅吃白菜,参议员先生也吃白菜,所以参议员先生是鹅.”结论显然是错误的,是因为()A.大前提错误B.小前提错误C.推理形式错误D.非以上错误4.(5分)已知复数z1=2+i,z2=1﹣i,则在z=z1•z2复平面上对应的点位于()A.第四象限B.第一象限C.第二象限D.第三象限5.(5分)若=1﹣bi,其中a,b都是实数,i是虚数单位,则|a+bi|=()A.B.C.D.16.(5分)用反证法证明命题:“若a,b∈Z,ab能被5整除,则a,b中至少有一个能被5整除”,那么假设的内容是()A.a,b都能被5整除B.a,b都不能被5整除C.a,b有一个能被5整除D.a,b有一个不能被5整除7.(5分)若不等式|8x+9|<7和不等式ax2+bx﹣2>0的解集相同,则a、b的值为()A.a=﹣8、b=﹣10B.a=﹣4、b=﹣9C.a=﹣1、b=9D.a=﹣1、b=2 8.(5分)曲线y=e x+2x在点(0,1)处的切线方程为()A.y=x+1B.y=x﹣1C.y=3x+1D.y=﹣x+19.(5分)已知抛物线x2+my=0上的点到定点(0,4)和到定直线y=﹣4的距离相等,则m=()A.B.C.16D.﹣1610.(5分)参数方程(θ为参数)所表示的曲线为()A.抛物线的一部分B.一条抛物线C.双曲线的一部分D.一条双曲线11.(5分)已知圆x2+y2=r2(r>0)的面积为S=π•r2,由此推理椭圆的面积最有可能是()A.π•a2B.π•b2C.π•ab D.π(ab)212.(5分)双曲线(p>0)的左焦点在抛物线y2=2px的准线上,则该双曲线的离心率为()A.B.C.D.4二、填空题(每小题5分,共20分)13.(5分)甲、乙、丙三名同学中只有一人考了满分,当他们被问到谁考了满分时,甲说:丙没有考满分;乙说:是我考的;丙说:甲说真话.事实证明:在这三名同学中,只有一人说的是假话,那么得满分的同学是.14.(5分)设复数z满足i(z+1)=﹣3+2i,则=.15.(5分)若函数y=x3+ax2+bx+27在x=﹣1时有极大值,在x=3时有极小值,则a=,b=.16.(5分)某产品的广告费用x与销售额y的统计数据如下表:根据上表可得回归方程=x+中的为7.据此模型预报广告费用为10万元时销售额为(万元).三、解答题(第17题10分,其余各题均12分.共70分)17.(10分)已知曲线C:+=1,直线:(为参数).写出曲线C的参数方程,直线的普通方程.18.(12分)某电脑公司有6名产品推销员,其工作年限与年推销金额的数据如表:(1)以工作年限为自变量,推销金额为因变量y,作出散点图;(2)求年推销金额y关于工作年限x的线性回归方程;(3)若第6名推销员的工作年限为11年,试估计他的年推销金额.附:回归方程=x+中,=,=﹣.19.(12分)在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.(Ⅰ)根据以上数据建立一个2×2列联表;(Ⅱ)试判断是否有97.5%的把握认为“休闲方式与性别有关”?下面临界值表仅供参考:(参考公式:K2=,其中n=a+b+c+d)20.(12分)已知直线l:(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为ρ=2cosθ.(1)将曲线C的极坐标方程化为直坐标方程;(2)设点M的直角坐标为(5,),直线l与曲线C的交点为A,B,求|MA|•|MB|的值.21.(12分)已知双曲线C:﹣=1(a>0,b>0)的离心率为,=(1)求双曲线C的方程;(2)已知直线x﹣y+m=0与双曲线C交于不同的两点A,B,且线段AB的中点在圆x2+y2=5上,求m的值.22.(12分)已知函数f(x)=x3+ax2+bx(a,b∈R).(Ⅰ)当a=1时,求函数f(x)的单调区间;(Ⅱ)若f(1)=,且函数f(x)在(0,)上不存在极值点,求a的取值范围.2016-2017学年内蒙古阿拉善盟左旗高中高二(下)期末数学试卷(文科)参考答案与试题解析一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的).1.【解答】解:由不等式|x﹣2|<1可得,﹣1<x﹣2<1,解得1<x<3,故选:B.2.【解答】解:.故选:A.3.【解答】解:∵大前提的形式:“鹅吃白菜”,不是全称命题,大前提本身正确,小前提“参议员先生也吃白菜”本身也正确,但是不是大前提下的特殊情况,鹅与人不能类比.∴不符合三段论推理形式,∴推理形式错误,故选:C.4.【解答】解:∵z1=2+i,z2=1﹣i,则z=z1•z2=(2+i)(1﹣i)=3﹣i.∴z=z1•z2在复平面上对应的点的坐标为(3,﹣1),位于第四象限.故选:A.5.【解答】解:∴a=2,b=﹣1∴故选:A.6.【解答】解:由于反证法是命题的否定的一个运用,故用反证法证明命题时,可以设其否定成立进行推证.命题“a,b∈Z,如果ab可被5整除,那么a,b至少有一个能被5整除.”的否定是“a,b都不能被5整除”.故选:B.7.【解答】解:∵|8x+9|<7,∴﹣7<8x+9<7,∴﹣2<x<﹣.依题意,不等式ax2+bx﹣2>0的解集为{x|﹣2<x<﹣},∴﹣2与﹣是方程ax2+bx﹣2=0的两根,∴由韦达定理得:﹣2×(﹣)=﹣,∴a=﹣4.又﹣2﹣=﹣=,∴b=﹣9.综上所述,a=﹣4,b=﹣9.故选:B.8.【解答】解:求导函数可得y′=e x+2,当x=0时,y′=e x+2=3,∴曲线y=e x+2x在点(0,1)处的切线方程为y=3x+1故选:C.9.【解答】解:根据抛物线定义可知,定点(0,4)为抛物线的焦点,∴=4m=﹣16故选:D.10.【解答】解:参数方程(θ为参数),消去参数化为:y2+x=1,即y2=1﹣x,x∈[0,1].∴表示的曲线是抛物线的一部分,故选:A.11.【解答】解:将圆x2+y2=r2(r>0)的方程写成,与椭圆比照,类比猜想:a⇔r,b⇔r,从而推理椭圆的面积最有可能是π•r2=π•r•r=π•ab.故选:C.12.【解答】解:双曲线的左焦点坐标为:,抛物线y2=2px的准线方程为,所以,解得:p=4,故双曲线的离心率为:故选:C.二、填空题(每小题5分,共20分)13.【解答】解:假设甲说的是假话,即丙考满分,则乙也是假话,不成立;假设乙说的是假话,即乙没有考满分,又丙没有考满分,故甲考满分;故答案为:甲.14.【解答】解:∵复数z满足i(z+1)=﹣3+2i,∴﹣i•i•(z+1)=﹣i(﹣3+2i),化为z+1=2+3i,化为z=1+3i,∴=1﹣3i.故答案为:1﹣3i.15.【解答】解:∵y=x3+ax2+bx+27,∴y′=3x2+2ax+b,∵函数y=x3+ax2+bx+27在x=﹣1时有极大值,在x=3时有极小值,∴,解得a=﹣3,b=﹣9.故答案为:﹣3,﹣9.16.【解答】解:由题意,=4.5,=35∵回归方程:为7.∴35=7×4.5+,∴=3.5∴x=10时,=7×10+3.5=73.5元故答案为:73.5.三、解答题(第17题10分,其余各题均12分.共70分)17.【解答】解:根据题意,曲线C:+=1,即()2+()2=1令=cosθ,=sinθ,则x=2cosθ,y=3sinθ,则曲线C的参数方程为,直线的参数方程为,变形可得2x+y=6,即2x+y﹣6=0.18.【解答】解:(1)依题意,画出散点图如图所示,(2)从散点图可以看出,这些点大致在一条直线附近,=6,=3.4,===0.5,=﹣=0.4,∴年推销金额y关于工作年限x的线性回归方程为=0.5x+0.4.(3)由(2)可知,当x=11时,=0.5x+0.4=0.5×11+0.4=5.9(万元).∴可以估计第6名推销员的年销售金额为5.9万元.19.【解答】解:(1)由所给的数据得到列联表(2)假设休闲与性别无关,K2==6.201∵K2>5.024,∴有97.5%的把握认为“休闲方式与性别有关”.20.【解答】解:(1)∵ρ=2cosθ,∴ρ2=2ρcosθ,∴x2+y2=2x,故它的直角坐标方程为(x ﹣1)2+y2=1;(2)直线l:(t为参数),普通方程为,(5,)在直线l上,过点M作圆的切线,切点为T,则|MT|2=(5﹣1)2+3﹣1=18,由切割线定理,可得|MT|2=|MA|•|MB|=18.21.【解答】答:(1)由双曲线的离心率e==,①,=,②,解得:a=1,c =,∴b2=c2﹣a2=2,则双曲线C的方程为x2﹣=1;(2)设A,B两点的坐标分别是(x1,y1),(x2,y2),线段AB的中点为M(x0,y0),由,得x2﹣2mx﹣m2﹣2=0,(判别式△>0)x1+x2=2m,∴x0==m,y0=x0+m=2m,因为点M(x0,y0),在圆x2+y2=5上,则m2+(2m)2=5,故m=±1,∴m的值±1.22.【解答】解:(1)当a=1时,f(x)=,∴f′(x)=x2+2x+b,①若△=4﹣4b≤0,即b≥1 时,f′(x)=x2+2x+b≥0所以f(x)为R上的增函数,所以f(x)的增区间为(﹣∞,+∞);②若△=4﹣4b>0,即b<1时,f'(x)=,由f′(x)>0得x<,或x>所以f(x)在(﹣∞,)与(,+∞)上为增函数,在(,)上为减函数.所以f(x)的增区间为(﹣∞,)与(,+∞);减区间为(,)上.(2)由,得b=﹣a,即f(x)=,∴f′(x)=x2+2ax﹣a.令f′(x)=0得x2+2ax﹣a=0,∴(1﹣2x)a=x2,∵0<x<,∴1﹣2x≠0,∴,令t=1﹣2x,则t∈(0,1),∴=,∵在t∈(0,1)上单调递减,故h(t)∈(0,+∞),∴∈(0,+∞),∴a∈(0,+∞),函数f(x)在(0,)上不存在极值点,∴在(0,)上无解,∴a∈(﹣∞,0]综上,a的取值范围为(﹣∞,0].。
2016-2017学年内蒙古阿拉善左旗高级中学高一数学下期末考试理科试卷(解析版)

阿左旗高级中学2016 —2017学年第二学期期末测试卷高
一数学(理科)
命题人:谭建辉
「.选择题:(每小题5分,共60分)
1. 已知向量a= (4,2), b = (x,3),且a // b,则x的值是()
A . - 6 B. 6 C. 9 D. 12
1. B [ T a / b,—4 x 3—2x= 0 ,「. x= 6.]
2 •现要完成下列3项抽样调查:
①从10盒酸奶中抽取3盒进行食品卫生检查.
②科技报告厅有32 排,每排有40个座位,有一次报告会恰好坐满了听众,报告会结束
后,为了听取意见,需要请32名听众进行座谈.
③东方中学共有160名教职工,其中一般教师120名,行政人员16名,后勤人员24
名.为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为20的样本.
较为合理的抽样方法是()
A .①简单随机抽样,②系统抽样,③分层抽样
B •①简单随机抽样,②分层抽样,③系统抽样
C.①系统抽样,②简单随机抽样,③分层抽样
D .①分层抽样,②系统抽样,③简单随机抽样
2. A [①总体较少,宜用简单随机抽样;②已分段,宜用系统抽样;③各层间差距较
大,宜用分层抽样,故选 A.]
3. 点P(x,2,1)到点A(1,1,2)、B(2,1,1)的距离相等,则x等于( )
1
A.2 B . 1
3
C.2 D . 2
解析:由题意,|FA|=|PB|,
即x— 1 22—1 2 1 —2 2= , x—2 M 2—1 2丨 1 — 1 即x = 1.
答案:B
4. 阅读下图所示的程序框图,运行相应的程序,输出的结果是()。
2016-2017学年内蒙古阿拉善左旗高级中学高一数学下期末考试文科试卷
阿左旗高级中学2016 —2017学年第二学期期末测试卷高
一数学(文科)
命题人:黄淑萍
一.选择题:(每小题5分,共60分)
1•点(1,-1)到直线F 一十--的距离是()
1 3 也72
A. -
B. -
C.
D.-
2•点’:' 关于'’平面对称的点是()
A.(-3,3,-1)
B.(-3,-3,-1)
C.(3,-3,1)
D.(-3,3,1)
3•阅读右图所示的程序框图,运行相应的程序,输出的结果是()
A . 1
B . 2
C . 3
D . 4
4•用辗转相除法”求得459和357的最大公约数是()
A . 3
B . 9
C . 17
D . 51
5.过点’1 i ,”-的直线的斜率等于1,则的值为()
A.1
B.4
C.1 或3
D.1 或4
6.圆—' -与圆£"扌住一恁的位置关系为()
A.内切
B.相交
C.外切
D.相离
7•已知向量。
=(2,1),Q」=10»+ b| =,则同=()
A. 5 B . 4 C . 1 D . 8
8.方程^ 和表示的直线可能是()
9.已知表示直线,表示平面,给出下列四个命题,其中真命题为()
①3门只一険用「羽用丄也则②和,臭凰订纾=临:$门守■=灼则苍J_。
内蒙古阿拉善左旗高级中学高一数学下学期期末考试试题 理

阿左旗高级中学2017—2018学年第二学期期末测试卷高 一 数 学(理)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟。
注意事项:1、请考生务必在规定位置填全自己的班级、姓名、考场及考号。
2、答题务必答在答题卡上,否则无效,密封线外不要答题。
3、请做到: 仔细阅题 认真思考 规范书写 尽力作答第1卷(共60分)一、选择题:本大题共l2小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.的值为)6cos(π-( ) A .21B .23C . 3D .12 函数x y 21sin =是( )A .最小正周期为2πB .最小正周期为2πC .最小正周期为πD .最小正周期为4π3.设向量 a ,b 的长度分别为4和3,夹角为60°,则a · b 的值为 ( )A. 6B. 13C.36 D 13 4. 中国古代有计算多项式值的秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a 为2,2,5,则输出的s =( )A 7B 12C 17D 345. 已知向量(1,)(3,2)m =-,=a b ,且()⊥a +b b ,则m=( )A -8B -6C 6D 86.我国古代数学名著《九章算术》中有如下问题:“今有北乡算八千七百五十八,西乡算七千二百三十六,南乡算八千三百五十六,凡三乡,发役三百七十八人,欲以算数多少衰出之,问各几何?”意思是:北乡有8758人,西乡有7236人,南乡有8356人,现要按人数多少从三乡共征集378人,问从各乡各征集多少人?在上述问题中,需从西乡征集的人数是( )A. 102B. 112C. 130D. 1367. 为了得到函数sin(21)y x =+的图象,只需把函数sin 2y x =的图象上所有的点( ) A .向左平行移动12个单位长度 B .向右平行移动12个单位长度 C .向左平行移动1个单位长度 D .向右平行移动1个单位长度8.在平行四边形ABCD 中,AC 与BD 交于点O ,E 为线段OD 的中点,AE 的延长线与CD 交于点F ,若AC →=a ,BD →=b ,则AF →=( )A.14a +12b B.23a +13b C.12a +14b D.13a +23b 9. 4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率( ) A18 B 38 C. 58 D. 7810. 函数=sin()y A x ωϕ+的部分图像如图所示,则( )A 2sin(2)6y x π=-B 2sin(2)3y x π=-C 2sin(2+)6y x π=D 2sin(2+)3y x π=11、若sinx <,则x 的取值范围为( )A (2k π,2k π+)∪(2k π+,2k π+π)B (2k π+,2k π+)C (2k π+,2k π+)D (2k π-,2k π+) 以上k∈z12. 已知函数()sin f x x x ωω=的图像与直线2y =交于,A B 两点,若AB 的最小值为π ,则函数()f x 的一条对称轴是( )A .3x π=B .4x π=C .6x π=D . 12x π=二、填空题:(本大题共10,每小题4分,共40把答案填在题中横线上.) 13. 若向量a =(2,1),b =(-3,4),a +b = . a · b = . 14. 如图是我国三国时期著名数学家赵爽弦图.图中大正方形的面积是34,四个全等直角三角形围成一个小正方形,直角三角形的较短边长为3.现向大正 方形内随机抛一粒绿豆,则绿豆落在小正方形内的概率为__________. 15. 已知A ,B ,C 是圆O 上的三点,若1()2AO AB AC =+,则AB 与AC 的夹角为 . 16. 求值:tan20°+tan40°+tan20°tan40°=_____________。
内蒙古阿拉善左旗高级中学高一数学下学期期末考试试题 文

阿左旗高级中学2017—2018学年第二学期期末考试试卷高 一 数 学 (文科)一. 选择题(每小题5分,共60分)1、0sin 390=( )A 、12B 、12- C 、2、设某大学的女生体重y (单位: kg )与身高x (单位: cm )具有线性相关关系,根据一组样本数据()(),1,2,,i i x y i n =⋯,用最小二乘法建立的回归方程为0.85 5.1ˆ87yx =-,则下列结论中不正确的是( )A 、y 与x 具有正的线性相关关系B 、回归直线过样本点的中心(),x yC 、若该大学某女生身高增加1cm ,则其体重约增加0.85kgD 、若该大学某女生身高为170cm ,则可断定其体重必为58.79kg3、从某班学生中任意找出一人,如果该同学的身高小于160cm 的概率为0.2,该同学的身高在[]160,175cm 的概率为0.5,那么该同学的身高超过175cm 的概率为( )A 、0.8B 、0.7C 、0.3D 、0.24、若2弧度的圆心角所对的弧长为4cm ,则这个圆心角所夹的扇形的面积为( )A 、24cmB 、22cmC 、24cm πD 、22cm π5、已知向量(1,2)a m =-r ,(,3)b m =-r ,若a b ⊥r r ,则实数m =( )A 、2或3-B 、2-或3C 、35D 、3 6、如果执行右侧的程序框图,那么输出的S 是( )A 、22B 、46C 、94D 、1907、已知(3,4)a =r ,(sin ,cos )b αα=r 且//a b r r ,则tan α=( )A 、34 B 、34- C 、43 D 、43- 8、已知向量,a b r r ,且2AB a b =+uu u r r r ,56BC a b =-+uu u r r r ,72CD a b =-uu u r r r ,则一定共线的三点是( )A 、,,AB D B 、,,A BC C 、,,B CD D 、,,A C D9、函数sin(2)3y x π=-+的单调递减区间是( ) A 、5,1212k k k R ππππ⎡⎤-+∈⎢⎥⎣⎦ B 、52,21212k k k R ππππ⎡⎤-+∈⎢⎥⎣⎦C 、5,66k k k R ππππ⎡⎤-+∈⎢⎥⎣⎦ D 、52,266k k k R ππππ⎡⎤-+∈⎢⎥⎣⎦ 10、在ABC V 中,若sin()sin()A B C A B C +-=-+,则ABC V 必是( )A 、等腰三角形B 、直角三角形C 、等腰或直角三角形D 、等腰直角三角形11、将函数()sin(2)3f x x π=+的图像向右平移ϕ个单位,得到的图像关于原点对称,则ϕ的最小正值为( ) A 、6π B 、3π C 、512π D 、712π 12、已知向量00(cos 25,sin 25)a =r ,00(sin 20,cos20)b =r ,若t 是实数,且u a tb =+r r r ,则u r 的最小值为( )(注:sin()sin cos cos sin αβαβαβ+=+,sin()sin cos cos sin αβαβαβ-=-)A B 、1 C 、2 D 、12二. 填空题(每小题5分,共20分) 13、函数1sin 22y x =的最小正周期T =__________;14、已知向量a r ,b r 的夹角为45o ,且1a =r ,2a b -=r r ,则b =r ; 15、某校共有学生2000名,各年级男、女学生人数如下表所示,已知在全校学生中随机抽取1名,抽到高二女生的概率是0.19,现用分层抽样的方法(按年级分层)在全校学生中抽取;16、已知函数()sin 0,2y x πωϕωϕ⎛⎫=+><⎪⎝⎭的部分图象如下图所示, 则ω= ,ϕ= .三. 解答题(共70分)17、(10分)(1)已知(2,1),(3,4)a b ==-r r ,求3a b +r r ;(2)已知2a =r ,3b =r ,a b r r 与的夹角为0120,求a b r r g .18、(12分)如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下,观察图形,回答下列问题:(1)79.589.5这一组的频数、频率分别是多少?(2)估计这次环保知识竞赛的及格率(60分及以上为及格)和平均数?19、(12分)如图所示,在平行四边形ABCD 中,M ,N 分别为DC ,BC 的中点,已知,AM c AN d ==uuu r uuu r r r ,试用,c d r r 表示,AB AD u u u r u u u r20、(12分)某学校有两个参加国际中学生交流活动的代表名额,为此该学校高中部推荐2男1女三名候选人,初中部也推荐了1男2女三名候选人。
内蒙古阿拉善盟高一下学期期末数学考试试卷

内蒙古阿拉善盟高一下学期期末数学考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)给出下列命题,其中正确的是()(1)弧度角与实数之间建立了一一对应的关系(2)终边相同的角必相等(3)锐角必是第一象限角(4)小于90°的角是锐角(5)第二象限的角必大于第一象限角A . (1)B . (1)(2)(5)C . (3)(4)(5)D . (1)(3)2. (2分) (2017高一下·黄山期末) 已知点(3,1)和(﹣4,6)在直线3x﹣2y+a=0的两侧,则a的取值范围是()A . ﹣7<a<24B . ﹣24<a<7C . a<﹣1或a>24D . a<﹣24或a>73. (2分)若角α的终边过点P(3,﹣4),则cosα等于()A .B .C .D .4. (2分) (2018高一上·长春月考) 若,则函数()A . 有最小值,无最大值B . 有最小值,最大值1C . 有最小值1,最大值D . 无最小值,也无最大值5. (2分)已知f(α)= ,则f()=()A .B .C .D . ﹣6. (2分) (2016高二上·郑州期中) 设a,b是非零实数,若a>b,则一定有()A .B . a2>abC .D .7. (2分)把函数y=3sin2x的图象向左平移个单位长度,得到函数()A . y=3sin(2x+)B . y=3sin(2x-)C . y=3sin(2x+)D . y=3sin(2x-)8. (2分)设P是△ABC所在平面内的一点,,则()A .B .C .D .9. (2分)已知,则=()A . 2B . -2C . 3D . -310. (2分) (2017高一下·黄山期末) 已知,则x(1﹣3x)取最大值时x的值是()A .B .C .D .11. (2分)设,Sn=a1+a2+…+an ,在S1 , S2 ,…,S50中,正数的个数是()A . 25B . 30C . 40D . 5012. (2分)在中,a,b,c分别是,,的对边,已知a,b,c成等比数列,且,则的值为()A .B .C .D .二、填空题 (共4题;共5分)13. (1分)已知向量若,则m=________.14. (2分) (2019高一上·杭州期中) 已知函数,则 ________;的递减区间为________.15. (1分) (2016高二上·阜宁期中) 已知实数x,y满足条件则z=2x+y的最小值是________.16. (1分)已知ω,t>0,函数的最小正周期为2π,将f(x)的图象向左平移t个单位,所得图象对应的函数为偶函数,则t的最小值为________三、解答题 (共6题;共55分)17. (10分)(2018·凉山模拟) 设各项为正数列满足:(是常数).(1)判断是否存在,使数列满足对任意正整数,有恒成立?若存在,求出;若不存在,请说明理由.(2)当,时,求数列前项和的表达式.18. (10分) (2018高一下·威远期中) 已知 , ,当为何值时,(1)与垂直?(2)与平行?平行时它们是同向还是反向?19. (10分) (2015高一下·湖州期中) 已知a,b,c分别为△ABC三个内角A,B,C的对边,.(1)求角B的大小;(2)若,求a+c的最大值.20. (10分)设数列{an}的前n项和为Sn ,已知a1=1, a2=2,且an+1=3Sn-Sn+1+3(n)(1)证明:an+2=3an;(2)求Sn21. (5分)在气象台A正西方向300千米处有一台风中心,它以每小时40千米的速度向东北方向移动,距台风中心250千米以内的地方都要受其影响.问:从现在起,大约多长时间后,气象台A所在地将遭受台风影响?持续多长时间?(注:,)22. (10分) (2018高二上·江苏月考) 已知椭圆过点,右顶点为点.(1)若直线与椭圆相交于点两点(不是左、右顶点),且,求证:直线过定点,并求出该定点的坐标;(2)是椭圆的两个动点,若直线的斜率与的斜率互为相反数,试判断直线EF的斜率是否为定值?如果是,求出定值;反之,请说明理由.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共5分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共55分) 17-1、17-2、18-1、18-2、19-1、19-2、20-1、20-2、21-1、22-1、22-2、第11 页共11 页。
内蒙古阿拉善左旗高级中学高一下学期期末考试化学试卷 答案不全

内蒙古阿拉善左旗高级中学高一下学期期末考试化学试卷答案不全D.CH3CH2OH6.下列变化不属于化学变化的是( )①煤的干馏②煤与氢气作用液化③煤的气化④石油的分馏⑤石油的催化裂化⑥石油的裂解⑦海水蒸馏A.①②③④⑦ B.②④⑤⑥ C.④⑦D.⑥⑦7.在2A+B 3C+4D反应中,表示该反应速率最快的是 ( )A.υ(A) =0.5 mol/(L·s)B.υ(B)= 0.3 mol/(L·s)C.υ(C)=0.8 mol/(L·s)D.υ(D)=1 mol/(L·s)8.在一体积固定的密闭容器中充入一定量的SO2和O2,发生反应:2SO2+O22SO3,已知υ(SO2)=0.05mol·l-1·min-1,则2min后SO3的浓度为()A、1mol·l-1B、0.1mol·l-1C、0.9mol·l-1D、0.2mol·l-19.下列物质属于同分异构体的是()A.葡萄糖和果糖 B. C.甲烷和丙烷 D.淀粉和纤维素10.已知乙烯能被酸性高锰酸钾溶液氧化成CO2。
既可以用来鉴别乙烷和乙烯,又可以用来除去乙烷中混有的乙烯的方法是()A.通入足量溴水中 B.在空气中燃烧 C.通入酸性高锰酸钾溶液中 D.在一定条件下通入氧气11.设反应C+CO22CO(正反应吸热)反应速率为v1,N2+3H22NH3(正反应放热),反应速率为v2。
对于上述反应,当温度升高时,v1、v2的变化情况为()A. 同时增大B. 同时减小C. v1增大,v2减小 D. v1减小,v2增大12.在密闭容器中进行如下反应:X2(g)+Y2(g)2Z(g),已知X2、Y2、Z的起始浓度分别为0.1mol/L0.3mol/L、0.2mol/L,在一定条件下,当反应达到平衡时,各物质的浓度有可能是( )A.Z为0.3mol/LB.Y2为0.4mol/L C.X2为0.2mol/L D.Z为0.4mol/L13.把a、b、c、d 4块金属片浸泡在稀硫酸中,用导线两两相连可以组成各种原电池:若a、b相连时,a为负极;c、d相连时,c为负极;a、c相连时,c为正极;b、d相连时,b为正极。
内蒙古阿拉善左旗巴彦浩特镇高一数学下学期期末考试试

内蒙古阿拉善左旗巴彦浩特镇2016-2017学年高一数学下学期期末考试试卷文一.选择题:(每小题5分,共60分)1. 点( 1,-1)到直线的距离是( )A. B. C. D.2.点关于平面对称的点是( )A.(-3,3,-1)B.(-3,-3,-1)C.(3,-3,1)D.(-3,3,1)3.阅读右图所示的程序框图,运行相应的程序,输出的结果是( ) A.1 B.2 C.3 D.44.用“辗转相除法”求得459和357的最大公约数是( )A.3 B.9 C.17 D.515. 过点,的直线的斜率等于1,则的值为( )A.1B.4C.1或3D.1或46.圆与圆的位置关系为( )A.内切B.相交C.外切D.相离7.已知向量,,,则( )A. 5 B.4 C.1 D.88. 方程和表示的直线可能是( )A. B. C. D.9. 已知表示直线,表示平面,给出下列四个命题,其中真命题为( )①则②则③,则④,则A.①②B.③④C.②③D.②④10.在长方体ABCD -A 1B 1C 1D 1中,AB =BC =2,AA 1=1,则BC 1与平面BB 1D 1D 所成的角的正弦值为( )A C 11.函数f (x)=sin x -cos x ,x ∈⎣⎢⎡⎦⎥⎤0,π2 的最小值为( )A .-2B .- 3C .- 2D .-112.已知圆 ,圆,分别是圆上的动点,为轴上的动点,则的最小值为( ) A.B.C.D.二.填空题: (每小题5分,共20分)13.已知向量a =(4,2),b =(x,3),且a ∥b ,则x 的值是14一个几何体的三视图如图所示, 则这个几何体的体积15.直线的倾斜角为,且 135900≤<α,则它的斜率的取值范围为 .16.直线y =x +b 与曲线x =1-y 2有且只有1个公共点,则b 的取值范围是__________.三.解答题(共70分)17.(10分)求下列条件确定的圆的方程: (1)圆心为点);1,5(),3,8(A C 且过点-(2)圆心在y 轴上,半径长为3,且与x 轴相切.18.(12分)已知直线.(1) 求过点(2,2) 且与直线平行的直线方程 ; (2) 已知直线与直线垂直,试确定实数的值.19.(12分)如图所示,ABCD 是正方形,O 是正方形的中心,PO ⊥底面ABCD ,底面边长为a ,E 是PC 的中点.(1)求证:PA ∥面BDE ; (2)求证:平面PAC ⊥平面BDE ;(3)若二面角E -BD -C )(EOC 即为30°,求四棱锥P -ABCD 的体积.20.(12分)如图,在四边形中,,,,,,求四边形绕所在直线旋转一周所形成的几何体的表面积和体积.21. (12分) 已知函数.(1)求函数的最小正周期和值域.(2)若,求的值.22.(12分)已知坐标平面上点M(x,y)与两个定点M1(26,1),M2(2,1)的距离之比等于5.(1)求点M的轨迹方程,并说明轨迹是什么图形;(2)记(1)中的轨迹为C,过点M(-2,3)的直线l被C所截得的线段的长为8,求直线l的方程.阿左旗高级中学2016—2017学年第二学期期末测试卷高一数学(文科)命题人:黄淑萍三.选择题:(每小题5分,共60分)1-4 CCDD 5-8 ABAD 9-12 BDDA__四.填空题: (每小题5分,共20分)13.6 14. 1829+π 15. (]1,-∞- 16. b =-2或-1<b ≤1四.解答题(共70分)17.(10分)求下列条件确定的圆的方程: (1)圆心为点);1,5(),3,8(A C 且过点-(2)圆心在y 轴上,半径长为3,且与x 轴相切.答案:(1)所求圆的方程为25)3()8(22=++-y x .(2)所求圆的方程为9)3-(9)3(2222=+=++y x y x 或.18.(12分)已知直线.(1) 求过点(2,2) 且与直线平行的直线方程 ; (2) 已知直线与直线垂直,试确定实数的值.答案: (1).由于所求直线与直线平行,所以所求直线的斜率.又因为所求直线经过点(2,2),所以所求直线方程为, 即.(2)∵, ∴, ∴.19.(12分)如图所示,ABCD 是正方形,O 是正方形的中心,PO ⊥底面ABCD ,底面边长为a ,E 是PC 的中点.(1)求证:PA ∥面BDE ; (2)求证:平面PAC ⊥平面BDE ;(3)若二面角E -BD -C )(EOC ∠即为30°,求四棱锥P -ABCD 的体积.答案:19.(1)证明连接OE ,如图所示.∵O 、E 分别为AC 、PC 中点, ∴OE ∥PA .∵OE ⊂面BDE ,PA ⊄面BDE , ∴PA ∥面BDE .∵PO ⊥面ABCD ,∴PO ⊥BD . 在正方形ABCD 中,BD ⊥AC , 又∵PO ∩AC =0,∴BD ⊥面PAC .又∵BD ⊂面BDE ,∴面PAC ⊥面BDE . (2)解 取OC 中点F ,连接EF . ∵E 为PC 中点,∴EF 为△POC 的中位线,∴EF ∥PO . 又∵PO ⊥面ABCD , ∴EF ⊥面ABCD∵OF ⊥BD ,∴OE ⊥BD .∴∠EOF 为二面角E -BD -C 的平面角, ∴∠EOF =30°. 在Rt △OEF 中,OF =12OC =14AC =24a ,∴EF =OF ·tan 30°=612a ,∴OP =2EF =66a . ∴V P -ABCD =13×a 2×66a =618a 3.20.(12分)如图,在四边形中,,,,,,求四边形绕所在直线旋转一周所形成的几何体的表面积和体积.答案: 如图,过作的延长线的垂线,垂足为,则. 在中,,,所以.所以,所以.四边形绕所在直线旋转一周所形成的几何体为一个圆台挖去一个与圆台上底面共底面的圆锥.,.22. (12分) 已知函数.(1)求函数的最小正周期和值域.(2)若,求的值.答案:1.,所以函数的最小正周期为,值域为.2.由1可知,, 所以,所以.22.(12分)已知坐标平面上点M (x ,y )与两个定点M 1(26,1),M 2(2,1)的距离之比等于5. (1)求点M 的轨迹方程,并说明轨迹是什么图形;(2)记(1)中的轨迹为C ,过点M (-2,3)的直线l 被C 所截得的线段的长为8,求直线l 的方程.答案:解 (1)由题意,得|M 1M ||M 2M |=5.x -2+y -2x -2+y -2=5,化简,得x 2+y 2-2x -2y -23=0.即(x -1)2+(y -1)2=25.∴点M 的轨迹方程是(x -1)2+(y -1)2=25, 轨迹是以(1,1)为圆心,以5为半径的圆.(2)当直线l 的斜率不存在时,l :x =-2,此时所截得的线段的长为252-32=8,∴l :x =-2符合题意.当直线l 的斜率存在时,设l 的方程为y -3=k (x +2),即kx -y +2k +3=0, 圆心到l 的距离d =|3k +2|k 2+1,由题意,得⎝ ⎛⎭⎪⎫|3k +2|k 2+12+42=52, 解得k =512. ∴直线l 的方程为512x -y +236=0.即5x -12y +46=0.综上,直线l 的方程为x =-2,或5x -12y +46=0.。
【配套K12】[学习]内蒙古阿拉善左旗高级中学2017-2018学年高一数学下学期期末考试试题 文
![【配套K12】[学习]内蒙古阿拉善左旗高级中学2017-2018学年高一数学下学期期末考试试题 文](https://img.taocdn.com/s3/m/8fd8a82e03d8ce2f00662378.png)
阿左旗高级中学2017—2018学年第二学期期末考试试卷高 一 数 学 (文科)一. 选择题(每小题5分,共60分)1、0sin 390=( )A 、12B 、12-C 、2、设某大学的女生体重y (单位: kg )与身高x (单位: cm )具有线性相关关系,根据一组样本数据()(),1,2,,i i x y i n =⋯,用最小二乘法建立的回归方程为0.85 5.1ˆ87yx =-,则下列结论中不正确的是( )A 、y 与x 具有正的线性相关关系B 、回归直线过样本点的中心(),x yC 、若该大学某女生身高增加1cm ,则其体重约增加0.85kgD 、若该大学某女生身高为170cm ,则可断定其体重必为58.79kg3、从某班学生中任意找出一人,如果该同学的身高小于160cm 的概率为0.2,该同学的身高在[]160,175cm 的概率为0.5,那么该同学的身高超过175cm 的概率为( )A 、0.8B 、0.7C 、0.3D 、0.24、若2弧度的圆心角所对的弧长为4cm ,则这个圆心角所夹的扇形的面积为( )A 、24cmB 、22cm C 、24cm π D 、22cm π 5、已知向量(1,2)a m =-r ,(,3)b m =-r ,若a b ⊥r r ,则实数m =( )A 、2或3-B 、2-或3C 、35D 、3 6、如果执行右侧的程序框图,那么输出的S 是( )A 、22B 、46C 、94D 、1907、已知(3,4)a =r ,(sin ,cos )b αα=r 且//a b r r ,则tan α=( )A 、34 B 、34- C 、43 D 、43- 8、已知向量,a b r r ,且2AB a b =+uu u r r r ,56BC a b =-+uu u r r r ,72CD a b =-uu u r r r ,则一定共线的三点是( )A 、,,AB D B 、,,A BC C 、,,B CD D 、,,A C D9、函数sin(2)3y x π=-+的单调递减区间是( ) A 、5,1212k k k R ππππ⎡⎤-+∈⎢⎥⎣⎦ B 、52,21212k k k R ππππ⎡⎤-+∈⎢⎥⎣⎦ C 、5,66k k k R ππππ⎡⎤-+∈⎢⎥⎣⎦ D 、52,266k k k R ππππ⎡⎤-+∈⎢⎥⎣⎦ 10、在ABC V 中,若sin()sin()A B C A B C +-=-+,则ABC V 必是( )A 、等腰三角形B 、直角三角形C 、等腰或直角三角形D 、等腰直角三角形11、将函数()sin(2)3f x x π=+的图像向右平移ϕ个单位,得到的图像关于原点对称,则ϕ的最小正值为( ) A 、6π B 、3π C 、512π D 、712π 12、已知向量00(cos25,sin 25)a =r ,00(sin 20,cos20)b =r ,若t 是实数,且u a tb =+r r r ,则u r 的最小值为( )(注:sin()sin cos cos sin αβαβαβ+=+,sin()sin cos cos sin αβαβαβ-=-)A 、1 C D 、12 二. 填空题(每小题5分,共20分) 13、函数1sin 22y x =的最小正周期T =__________;14、已知向量a r ,b r 的夹角为45o ,且1a =r ,2a b -=r r 则b =r ; 15、某校共有学生2000名,各年级男、女学生人数如下表所示,已知在全校学生中随机抽取1名,抽到高二女生的概率是0.19,现用分层抽样的方法(按年级分层)在全校学生中抽取;16、已知函数()sin 0,2y x πωϕωϕ⎛⎫=+><⎪⎝⎭的部分图象如下图所示, 则ω= ,ϕ= .三. 解答题(共70分)17、(10分)(1)已知(2,1),(3,4)a b ==-r r ,求3a b +r r ;(2)已知2a =r ,3b =r ,a b r r 与的夹角为0120,求a b r r g .18、(12分)如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下,观察图形,回答下列问题:(1)79.589.5这一组的频数、频率分别是多少?(2)估计这次环保知识竞赛的及格率(60分及以上为及格)和平均数?19、(12分)如图所示,在平行四边形ABCD 中,M ,N 分别为DC ,BC 的中点,已知,AM c AN d ==u u u r u u u r r r ,试用,c d r r 表示,AB AD u u u r u u u r20、(12分)某学校有两个参加国际中学生交流活动的代表名额,为此该学校高中部推荐2男1女三名候选人,初中部也推荐了1男2女三名候选人。
内蒙古阿拉善左旗高级中学2017-2018学年高一下学期期末考试文数试卷(解析版)

阿左旗高级中学2017—2018学年第二学期期末考试试卷高一数学(文科)命题人:夏桂荣班级________________ 考号________________ 姓名________________一. 选择题(每小题5分,共60分)1. =()A. B. C. D.【答案】A【解析】分析:根据终边相同的角正弦值相等,将的正弦化成的正弦,,即可求出结果.详解:由诱导公式可得,,,故选A.点睛:本题着重考查了终边相同的角、诱导公式,特殊角的三角函数值等知识,属于简单题.2. 设某大学的女生体重(单位:)与身高(单位:)具有线性相关关系,根据一组样本数据,用最小二乘法建立的回归方程为,则下列结论中不正确的是()A. 与具有正的线性相关关系B. 回归直线过样本点的中心C. 若该大学某女生身高增加,则其体重约增加D. 若该大学某女生身高为,则可断定其体重必为【答案】D【解析】A正确;回归直线过样本点中心,故B正确;某女生身高增加,则其体重约增加,故D正确;C中体重为预测值,故C错误。
本题选C。
3. 从某班学生中任意找出一人,如果该同学的身高小于160cm的概率为0.2,该同学的身高在cm的概率为0.5,那么该同学的身高超过175cm的概率为()A. 0.8B. 0.7C. 0.3D. 0.2【答案】C【解析】试题分析:由题意可知身高超过175cm的概率为考点:互斥事件概率点评:本题考查了互斥事件概率的求法,掌握好互斥事件概率和为1是解题的关键.4. 若2弧度的圆心角所对的弧长为4cm,则这个圆心角所夹的扇形的面积为()A. B. C. D.【答案】A【解析】【详解】分析:先求出扇形的弧长,利用周长求出半径,代入面积公式进行计算即可得到答案详解:弧度是的圆心角所对的弧长为,圆的半径为扇形的面积为故选点睛:本题主要考查了弧度制的概念,弧长公式以及扇形面积,属于基础题。
5. 已知向量,,若,则实数( )A. 或B. 或C.D.【答案】B【解析】【详解】分析:根据,即,结合已知条件即可得到结果详解:,,,即解得或故选点睛:本题主要考查了向量的数量积计算公式,解题的关键是根据可以得到,属于基础题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
内蒙古阿拉善左旗高级中学2016-2017学年高一下学期
期末考试数学试卷(文)
一.选择题:(每小题5分,共60分)
1. 点( 1,-1)到直线的距离是( )
A. B. C. D.
2.点关于平面对称的点是( )
A.(-3,3,-1)
B.(-3,-3,-1)
C.(3,-3,1)
D.(-3,3,1)
3.阅读下图所示的程序框图,运行相应的程序,输出的结果是()
A.1 B.2 C.3 D.4
4.用“辗转相除法”求得459和357的最大公约数是( )
A.3 B.9 C.17 D.51
5. 过点,的直线的斜率等于1,则的值为( )
A.1
B.4
C.1或3
D.1或4
6.圆与圆的位置关系为( )
A.内切
B.相交
C.外切
D.相离
7.已知向量,,,则( )
A. 5 B.4 C.1 D.8
8. 方程和表示的直线可能是( )
A. B.
C. D.
9. 已知表示直线,
表示平面,给出下列四个命题,其中真命题为( ) ①则
②
则
③
,则
④
,则
A.①②
B.③④
C.②③
D.②④
10.在长方体ABCD -A 1B 1C 1D 1中,AB =BC =2,AA 1=1,则BC 1与平面BB 1D 1D 所成的角 的正弦值为( )
A B C D 11.函数f (x )=sin x -cos x ,x ∈⎣⎡⎦
⎤0,π
2 的最小值为( ) A .-2 B .-
3 C .- 2 D .-1 12.已知圆 ,圆
,
分
别是圆上的动点,为轴上的动点,则
的最小值为( ) A.
B.
C.
D.
二.填空题: (每小题5分,共20分)
13.已知向量a =(4,2),b =(x,3),且a ∥b ,则x 的值是 . 14.一个几何体的三视图如图所示,则这个几何体的体积 .
15.直线的倾斜角为,且
135900
≤<α,则它的斜率的取值范围为 .
16.直线y =x +b 与曲线x =1-y 2 有且只有1个公共点,则b 的取值范围是__________. 三.解答题(共70分)
17.(10分)求下列条件确定的圆的方程: (1)圆心为点);1,5(),3,8(A C 且过点 (2)圆心在y 轴上,半径长为3,且与x 轴相切.
18.(12分)已知直线
.
(1) 求过点(2,2) 且与直线平行的直线方程 ; (2) 已知直线与直线垂直,试确定实数的值.
19.(12分)如图所示,ABCD 是正方形,O 是正方形的中心,PO ⊥底面ABCD ,底面边长为
a ,E 是PC 的中点.
(1)求证:P A ∥面BDE ; (2)求证:平面P AC ⊥平面BDE ;
(3)若二面角E -BD -C )(EOC 即为30°,求四棱锥P -ABCD 的体积.
20.(12分)如图,在四边形
中,
,
,
,
,
,
求四边形
绕
所在直线旋转一周所形成的几何体的表面积和体积.
21. (12分) 已知函数.
(1)求函数的最小正周期和值域.
(2)若,求的值.
22.(12分)已知坐标平面上点M(x,y)与两个定点M1(26,1),M2(2,1)的距离之比等于5.
(1)求点M的轨迹方程,并说明轨迹是什么图形;
(2)记(1)中的轨迹为C,过点M(-2,3)的直线l被C所截得的线段的长为8,求直线l的方程.
【参考答案】
一.选择题:(每小题5分,共60分)
1-4 CCDD 5-8 ABAD 9-12 BDDA 二.填空题: (每小题5分,共20分) 13.6 14.
9
π182
+ 15. (]
1,-∞- 16. b =-2或-1<b ≤1 三.解答题(共70分)
17.解:(1)所求圆的方程为25)3()8(2
2
=++-y x . (2)所求圆的方程为9)3-(9)3(2
2
2
2
=+=++y x y x 或. 18. 解:(1)由于所求直线与直线
平行,
所以所求直线的斜率.
又因为所求直线经过点(2,2),所以所求直线方程为
,
.
(2)∵, ∴, ∴.
19.(1)证明:连接OE ,如图所示. ∵O 、E 分别为AC 、PC 中点, ∴OE ∥P A .
∵OE ⊂面BDE ,P A ⊄面BDE , ∴P A ∥面BDE .
∵PO ⊥面ABCD ,∴PO ⊥BD . 在正方形ABCD 中,BD ⊥AC , 又∵PO ∩AC =0,∴BD ⊥面P AC . 又∵BD ⊂面BDE ,∴面P AC ⊥面BDE .
(2)解:取OC 中点F ,连接EF . ∵E 为PC 中点,
∴EF 为△POC 的中位线,∴EF ∥PO . 又∵PO ⊥面ABCD , ∴EF ⊥面ABCD
∵OF ⊥BD ,∴OE ⊥BD .
∴∠EOF 为二面角E -BD -C 的平面角, ∴∠EOF =30°. 在Rt △OEF 中, OF =12OC =14AC =24a ,
∴EF =OF ·tan 30°=
612a ,∴OP =2EF =6
6
a . ∴V P -ABCD =13×a 2×66a =6
18a 3.
20.解:如图,过作
的延长线的垂线,垂足为
,
则. 在中,
,
,
所以
.所以
,
所以.
四边形
绕
所在直线旋转一周所形成的
几何体为一个圆台挖去一个与圆台上底面共底面的圆锥.
,
.
21.解:(1)
,
所以函数的最小正周期为,值域为.
(2)由(1)可知,
, 所以,
所以
.
22.解:(1)由题意,得|M 1M ||M 2M |
=5.
(x -26)2+(y -1)2(x -2)2+(y -1)2=5,化简,得x 2+y 2
-2x -2y -23=0. 即(x -1)2+(y -1)2=25.
∴点M 的轨迹方程是(x -1)2+(y -1)2=25, 轨迹是以(1,1)为圆心,以5为半径的圆.
(2)当直线l 的斜率不存在时,l :x =-2,此时所截得的线段的长为252-32=8, ∴l :x =-2符合题意.
当直线l 的斜率存在时,设l 的方程为y -3=k (x +2),即kx -y +2k +3=0,
圆心到l 的距离d =|3k +2|
k 2+1
,由题意,得⎝ ⎛⎭⎪⎫|3k +2|k 2+12+42=52
,
解得k =512. ∴直线l 的方程为512x -y +23
6=0.
即5x -12y +46=0.
综上,直线l 的方程为x =-2,或5x -12y +46=0.。
