第一届数理化学科能力竞赛初赛高一数学

关于首届全国中学生数理化学科能力竞赛应用实践能力部分的说明

②参考文献的书写格式严格按以Ｆ顺宇：序号、者姓名、作书名（文章名）出版社（期刊名）或、或、
出版时间或发表年、、号．卷期 ③实验报告中须包含实验的目的、想、骤、沦，提供证明实验结果的数据及照片等．构步结并
《中数理化》高？
有料有方法
目次ＣＴＴＮＮＯＥＳ
２００８年第１期１
高二
部分特邀编委名单
任子朝教育部考试中心
任
勇
福建省厦门市教育局
ｊ京大学附中
北京五中
周沛耕
蒋佩锦
关于首届全国中学生数理化学科能力竞赛
北京五中
化学组：用化学知识通过实验解释生活当中的现象或解决生活当巾的问题，成实验报告并运写提交．３论文（实验报告）、或的格式要求：
①写作顺序：题、标作者所在省份、市、校名称、级、者姓名、导教师姓名、要及关键城学班作指摘词、文、考文献．正参
王珉珠周兆富
人大附中广东佛山市教研室
④字体：各类标题（括“ 考文献 ” 题）包参标用粗宋体：者姓名、导教师姓名、要、键词、作指摘关网表
名、考文献内容用楷体；文、参正图表、眉、页页脚中的文字用宋体；文用ＴｍｅＮｗＲｍａ字体．英ｉｓｅｏｎ

文档yej首届全国中学生数理化学科能力展示活动初赛及决赛试

首届全国中学生数理化学科能力展示活动初赛八年级数学学科能力解题技能展示试题试卷说明1、本试卷共计15题满分为120分2、考试时间为120分钟姓名一、选择题每题5分合计30分 1、如果“学”、“科”、“能”、“力”这四个汉字中每个汉字分别代表一个非零个位数对于运算符号“”有学科能力1科学能力学科能力2能力科学那么123412 . A4312 B3421 C4321 D3412 2、已知点P关于原点对称点1P 的坐标是23则点P关于y的对称点2P的坐标是 . A32 B23 C23 D23 3、方程组36xyxyz的非负整数解有个. A1 B2 C3 D无数 4、由6条长度均为2 cm的线段可构成边长为2 cm的n个等边三角形则n的最大值为 . A4 B3 C2 D1 5、已知三角形的三条边长分别8x、x2、84其中x是正整数这样的互不全等的三角形共有个. A5 B6 C7 D8 6、已知2008200813312211112222 A1 B20072008 C20092008 D2******* 二、填空题每题5分合计30分 7、北京奥运期间体育场馆要对观众进行安全检查.设某体育馆在安检开始时已有若干名观众在馆外等候安检安检开始后到达体育馆的观众人数按固定速度增加.又设各安检人员的安检效率相同.若用3名工作人员进行安检需要25分钟才能将等候在馆外的观众检测完使后来者能随到随检若用6名工作人员进行安检时间则缩短为10分钟.现要求不超过5分钟完成上述过程则至少要安排名工作人员进行安检. 8、已知ab均为质数且满足213aab则2bab . 9、如图在△ABC中点D为边BC的中点点E为线段AD上一点且满足2AEED则△ABC与△BDE的面积之比为 . 10、已知2xy其中xy都是整数能被9整除则2584xy被9除的余数为 . 11、某班学生共有50人会游泳的有27人会体操的有18人游泳、体操都不会的有15 虚心勤学加苦练成绩上升成直线 E-mail: 第2页共5页人那么既会游泳又会体操的有人.12、当x分别等于2008200720062121200612007120081时计算代数式221xx的值再把所得的结果全部加起来.则这个总和为__________. 三、解答题每题20分合计60分 13、求方程2008xyyx的正整数解. 如图在△ABC中点D是边AB延长线上的一点点F是边AC上的一点DF交BC 于点E并已知BDCFDEEF∠A 58°求∠C 的值. 15、已知05224224nnmmm且m、n均为正整数求m、n的值. 虚心勤学加苦练成绩上升成直线E-mail: 第3页共5页首届全国中学生数理化学科能力展示活动总决赛八年级数学学科能力解题技能展示试题试卷说明1、本试卷共计15题满分120分 2、考试时间为120分钟一、选择题每题5分合计25分 1.中国古人用天干和地支记年的次序其中天干有10个甲乙丙丁戊己庚辛壬癸。

全国中学生数理化学科能力竞赛(高一年级数学竞赛试题)

本题得分评卷人首届全国中学生数理化学科能力竞赛高一数学学科能力解题技能初赛试题试卷说明：1、本试卷共计15题，满分为120分2、考试时间为120分钟一、选择题（每小题5分，共30分）1．已知{}{}{}2,,A x N x B x x A C x x B =∈<=⊆=⊆，则集合C 的元素个数为（）（A ）82 （B ）4 （C ）8 （D ）162．已知{}{}22()1,()()1,A x f x x B f x f x x ==-==-{}2[()]()1C f f x f x x ==-，则下列结论中不正确的是（）（A ）A R = （B ）[1,)B =-+∞ （C ）[0,)C =+∞ （D ）[1,)C =-+∞3．若0a b >>，则下列结论中正确的是（）（A ）1122a b ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭（B ）lg lg b a a b > （C ）lg lg b a a b < （D ）lg lg b a a b = 4．如果关于x 的方程24230x x a a -⨯+-=至少有一个实根，则实数a 的取值范围是（）（A ）[2,2]- （B ）(3,2]- （C ）(3,2] （D ）[3,2]-5．若152525+-++=N ，则2log N =( )（A ）12 （B ）2 （C ） 1 （D ）146．已知函数)(x f 对于任意的R y x ∈、，都有633)()()(++=-y x xy f y f x f ，则=)2008(f （）（A ）2008 （B ）2009 （C ）2010 （D ）2011总分本题得分评卷人本题得分评卷人二、填空题（每小题5分，共30分）7．已知定义在R 上的奇函数()f x 满足(1)(3)0f x f x ++-= ，则(2008)f = ．8．已知,a b 均为质数,且满足213a a b +=,则2b a b += ．9．已知函数22lg(44)y x x x a =-+-+是奇函数，但不是偶函数，则a ∈ ．10．函数()f x 在R 是减函数，且不等式(2)(2)()()f a b f a b f a f b +++>+恒成立，则a 与b -的大小关系是．11．已知函数()f x 同时满足以下三个条件：（1）存在反函数1()f x -；（2）点(1,1005)在函数()f x 的图象上；（3）函数(1)f x +的反函数为1(1)f x --．则(1004)f = ．12．高斯记号[]x 表示不超过实数x 的最大整数，如[]1.232-=-，[]1.231=，则方程2[log (lg )]0x =的解集为．三、解答题13．（本小题满分20分）设+=R xx f y 在)(单调递减，证明：对任意的)()()(,,212121x x f x f x f R x x +>+∈+．14．（本小题满分20分）定义在(,)-∞+∞上的减函数()f x 也是奇函数，且对满足221t s +=的一切,t s ，不等式222[(2)2(21)][(12)2]0f m t s f t s t m ++-+---<恒成立，求实数m 的取值范围．15．（本小题满分20分）据统计，某个商场开业后的第1、2、3个月销售某种商品的数量依次为1万件、1.2万件、1.3万件.据预测，开业后3年内的第x 个月的销售量y 万件近似地符合函数关系c x b x a x f +⋅+⋅=2)(或r q p x g x +⋅=)(，其中0≠apq .统计开业后第4个月的销售量为1.328万件，问开业后3年内应选择哪种函数？为什么？并预计第5个月的销售量.。

首届全国中学生数理化学科能力竞赛竞赛大纲和样题-初中数学

（初中数学部分）第一部分解题技能竞赛大纲第二部分解题技能竞赛试题样题第三部分数学建模论文示范论文首届全国中学生数理化学科能力竞赛数学学科笔试部分竞赛大纲（2008年试验稿）为了提高广大青少年走进科学、热爱科学的兴趣，培养和发现创新型人才，团中央中国青少年发展服务中心、全国“青少年走进科学世界”科普活动指导委员会办公室共同举办首届“全国中学生数理化学科能力竞赛”（以下简称“竞赛”）。

竞赛由北京师范大学《高中数理化》杂志社承办。

为保证竞赛活动公平、公正、有序地进行，现将数学学科笔试部分竞赛大纲颁布如下：1 命题指导思想和要求根据教育部《全日制义务教育数学课程标准》和《全日制普通高级中学数学课程标准》的要求，着重考查学生的基础知识、基本能力、科学素养和运用所学知识分析问题、解决问题力及创新能力。

命题吸收各地高考和中考的成功经验，以能力测试为主导，体现新课程标准对能力的要求，注意数学知识中蕴涵的丰富的思维素材，强调知识点间的内在联系；注重考查数学的通法通则，注重考查数学思想和方法。

激发学生学科学的兴趣，培养实事求是的科学态度和创新能力，促进新课程标准提出的“知识与技能”、“过程与方法”、“情感与价值观”三维目标的落实。

总体难度把握上，要追求“源于教材，高于教材，略高于高考”的原则。

并提出以下三个层面上的命题要求：1）从宏观上看：注意对知识点和能力点的全面考查，注意对数学基本能力（空间想象、抽象概括、推理论证、运算求解、数据处理等基本能力）的考查，注意对数学思想和方法方面的考查，注意考查通则通法。

2）从中观上看：注意各个主要知识块的重点考查，注意对主要数学思维方法的考查。

3）从微观上看：注意每个题目的基础性（知识点）、技能性（能力点）、能力性（五大基本能力为主）和思想性（四种思想为主），注意考查大的知识块中的重点内容（如：代数中的函数的单调性、奇偶性、周期性），注意从各个知识点之间的交汇命题，注意每个题目的通则通法使用的同时也适度引进必要的特技，注意题目编拟中一些题目的结构特征对思路形成的影响。

中学生数理化学科能力竞赛竞赛大纲和样题-初中数学

（初中数学部分）第一部分解题技能竞赛大纲第二部分解题技能竞赛试题样题第三部分数学建模论文示范论文首届全国中学生数理化学科能力竞赛数学学科笔试部分竞赛大纲（2008年试验稿）为了提高广大青少年走进科学、热爱科学的兴趣，培养和发现创新型人才，团中央中国青少年发展服务中心、全国“青少年走进科学世界”科普活动指导委员会办公室共同举办首届“全国中学生数理化学科能力竞赛”（以下简称“竞赛”）。

竞赛由北京师范大学《高中数理化》杂志社承办。

为保证竞赛活动公平、公正、有序地进行，现将数学学科笔试部分竞赛大纲颁布如下：1 命题指导思想和要求根据教育部《全日制义务教育数学课程标准》和《全日制普通高级中学数学课程标准》的要求，着重考查学生的基础知识、基本能力、科学素养和运用所学知识分析问题、解决问题力及创新能力。

命题吸收各地高考和中考的成功经验，以能力测试为主导，体现新课程标准对能力的要求，注意数学知识中蕴涵的丰富的思维素材，强调知识点间的内在联系；注重考查数学的通法通则，注重考查数学思想和方法。

激发学生学科学的兴趣，培养实事求是的科学态度和创新能力，促进新课程标准提出的“知识与技能”、“过程与方法”、“情感与价值观”三维目标的落实。

总体难度把握上，要追求“源于教材，高于教材，略高于高考”的原则。

并提出以下三个层面上的命题要求：1）从宏观上看：注意对知识点和能力点的全面考查，注意对数学基本能力（空间想象、抽象概括、推理论证、运算求解、数据处理等基本能力）的考查，注意对数学思想和方法方面的考查，注意考查通则通法。

2）从中观上看：注意各个主要知识块的重点考查，注意对主要数学思维方法的考查。

3）从微观上看：注意每个题目的基础性（知识点）、技能性（能力点）、能力性（五大基本能力为主）和思想性（四种思想为主），注意考查大的知识块中的重点内容（如：代数中的函数的单调性、奇偶性、周期性），注意从各个知识点之间的交汇命题，注意每个题目的通则通法使用的同时也适度引进必要的特技，注意题目编拟中一些题目的结构特征对思路形成的影响。

首届全国中学生数理化学科能力竞赛数学学科能力解题技能初赛试题(高二)

则集合Ｃ的元素个数为（
Ａ２。；
Ｃ８；
）。
Ｂ４；
Ｄ１６
［丢－３贝而１ｊｌ一］一Ｉ十丽１］２Ｊ［＋１］… ［－＋ｔ１丽］－一
－
三、答题解
２曲＝ｉ（１＋。（．线ｙｓ等＋）ｃ等＋１的轴之ｎｓ）对称
当ｍ ≥ ５时，
间距离的最小值为（
Ａ１：
Ｃ３：
１．本小题满分２３（Ｏ分）在数列｛中，知ａ — １，１ห้องสมุดไป่ตู้２ｎ— １ａ）已１口＋— ｎ＋．
（Ｉ）数列｛的通项公式；求口｝（Ｉ）一ｎ ” ，｛的前ｎ项和为Ｓ求Ｉ设ａ＋且ｂ），
ｆ（口ｔｂ＞＿（）厂（）成立，ｎ与一ｂ的大小２－）厂口＋－６恒则
首届全国中学生数理化学科能力竞赛数学学科能力解题技能初赛试题（高二）
关系是—
—
．
１．知函数厂（同时满足以下３个条件：１已ｚ）（）在反函数ｆ（）１存－；ｚ（）（１在函数，（的图象上；２点１，）ｚ）（）数厂（３函ｚ＋１的反函数为厂一１．）（）
Ｂ３：１；
Ｄ４：１
４如果关于ｚ的方程４一ａ・２＋ｎ一３０至少有一． —
个实根，实数ｎ的取值范围是（则

邯郸一中高一数学竞赛试题

邯郸一中高一数学竞赛试题邯郸一中是一所历史悠久、教学质量优异的高中，其数学竞赛试题通常涵盖了高中数学的各个方面，包括代数、几何、数论、组合等。

以下是一份模拟的邯郸一中高一数学竞赛试题，供同学们参考和练习。

一、选择题（每题3分，共15分）1. 若函数\( f(x) = ax^2 + bx + c \)在\( x = 1 \)处取得极小值，且\( f(0) = 1 \)，则下列哪个选项是正确的？A. \( a = 0 \)，\( b = 0 \)，\( c = 1 \)B. \( a = 1 \)，\( b = -2 \)，\( c = 1 \)C. \( a = -1 \)，\( b = 2 \)，\( c = 1 \)D. \( a = 1 \)，\( b = 0 \)，\( c = 1 \)2. 已知\( \sin \alpha = \frac{3}{5} \)，\( \cos \beta = -\frac{4}{5} \)，且\( \alpha, \beta \)均在第一象限，求\( \cos\alpha \)的值。

3. 一个圆的半径为5，圆心在原点，求圆上一点到直线\( 2x + 3y =7 \)的距离的最大值。

4. 若\( \log_{2}8 + \log_{4}16 = x \)，求\( x \)的值。

5. 集合A={1, 2, 3}，集合B={2, 4, 6}，求集合A和集合B的交集。

二、填空题（每题4分，共20分）6. 若\( \frac{1}{x} + \frac{1}{y} = \frac{m}{n} \)，且\( xy = 6 \)，求\( x + y \)的值。

7. 已知等差数列的首项为2，公差为3，求第10项的值。

8. 若\( a^2 + b^2 = 10 \)，\( ab = 2 \)，求\( a + b \)的值。

9. 一个直角三角形的斜边长为5，一条直角边长为3，求另一条直角边的长度。

全国中学生数理化竞赛试题

（数学部分）第一部分解题技能竞赛大纲第二部分解题技能竞赛试题样题第三部分数学建模论文示范论文首届全国中学生数理化学科能力竞赛化学学科笔试部分竞赛大纲（2013年试验稿）为了提高广大青少年走进科学、热爱科学的兴趣，培养和发现创新型人才，团中央中国青少年发展服务中心、全国“青少年走进科学世界”科普活动指导委员会办公室共同举办首届“全国中学生数理化学科能力竞赛”（以下简称“竞赛”）。

竞赛由北京师范大学《高中数理化》杂志社承办。

为保证竞赛活动公平、公正、有序地进行，现将数学学科笔试部分竞赛大纲颁布如下：1 命题指导思想和要求根据教育部《全日制义务教育数学课程标准》和《全日制普通高级中学数学课程标准》的要求，着重考查学生的基础知识、基本能力、科学素养和运用所学知识分析问题、解决问题力及创新能力。

命题吸收各地高考和中考的成功经验，以能力测试为主导，体现新课程标准对能力的要求，注意数学知识中蕴涵的丰富的思维素材，强调知识点间的内在联系；注重考查数学的通法通则，注重考查数学思想和方法。

激发学生学科学的兴趣，培养实事求是的科学态度和创新能力，促进新课程标准提出的“知识与技能”、“过程与方法”、“情感与价值观”三维目标的落实。

总体难度把握上，要追求“源于教材，高于教材，略高于高考”的原则。

并提出以下三个层面上的命题要求：1）从宏观上看：注意对知识点和能力点的全面考查，注意对数学基本能力（空间想象、抽象概括、推理论证、运算求解、数据处理等基本能力）的考查，注意对数学思想和方法方面的考查，注意考查通则通法。

2）从中观上看：注意各个主要知识块的重点考查，注意对主要数学思维方法的考查。

3）从微观上看：注意每个题目的基础性（知识点）、技能性（能力点）、能力性（五大基本能力为主）和思想性（四种思想为主），注意考查大的知识块中的重点内容（如：代数中的函数的单调性、奇偶性、周期性），注意从各个知识点之间的交汇命题，注意每个题目的通则通法使用的同时也适度引进必要的特技，注意题目编拟中一些题目的结构特征对思路形成的影响。

高一数学竞赛试题及答案

高一数学竞赛试题及答案一、选择题（每题5分，共30分）1. 若a，b，c是三角形的三边长，且满足a² + b² = c²，那么这个三角形是：A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能确定2. 函数f(x) = 2x³ - 3x² + 1在区间[-1,2]上的最大值是：A. 1B. 7C. 9D. 无法确定3. 已知集合A = {1, 2, 3}，B = {2, 3, 4}，求A∪B的元素个数：A. 3B. 4C. 5D. 64. 等差数列的首项a₁ = 3，公差d = 2，第10项a₁₀的值是：A. 23B. 25C. 27D. 295. 圆的方程为(x - 2)² + (y - 3)² = 9，圆心到直线x + 2y - 7= 0的距离是：A. 2B. 3C. 4D. 56. 已知函数y = |x| + 1的图像与直线y = kx平行，那么k的值是：A. 1B. -1C. 0D. 无法确定二、填空题（每题4分，共20分）7. 若二次函数y = ax² + bx + c的顶点坐标为(-1, -4)，则a =_______。

8. 已知等比数列的首项为2，公比为3，第5项的值为 _______。

9. 一个正六边形的内角和为 _______。

10. 若直线y = 2x + b与曲线y = x² - 3x相切，则b = _______。

11. 圆的方程为x² + y² = 25，圆上一点P(4,3)到圆心的距离是_______。

三、解答题（每题25分，共50分）12. 已知直线l₁：2x - 3y + 6 = 0与直线l₂：x + y - 2 = 0相交于点M，求点M的坐标。

13. 已知函数f(x) = x³ - 3x + 2，求证：对于任意的x > 0，都有f(x) > x。

首届全国中学生数理化学科能力竞赛数学学科模拟题(高二)

的值．
６１２＿３＋ … ＋２．十｝㈣
ＡＣ２；６；
）．
二、空题：每题９分。５填（共４分）
７对于函数（）．一ｎ＋６存在一个正数ｂ使得Ｔ！ｚ，，ｆ（的定义域和值域相同，非零实数ｎ的值为ｚ）则
● 特策别划
８集合Ｘ中的元素是正整数，有性质：３∈ Ｘ，．且若２则１一ｚ∈ ｘ，样的集合ｘ共有 — ２这
ｃｏｓ（４ｚ＋）一
— —
—
个．
９已知实数ｚ，满足（ｚ＋）．３十十４＋一０则，
７ａ一一４．．１．２１．
８６．３个．９１．．
１．一 √２０．
＿６
３７ ’
１．２￣３．２／
１锐，至．为角要圭设一
一
√ ｓｉｎａ — ｃ）ａｒ（Ｓ
，百：，一Ｆ
）．
≥ ｚ．； ≥ ）＇
数列｛，６的值．６）求ｚ
，
ｓｎｌ叶一ｏｓａｃ
则．．，的大小顺序为（．ｒｙ
将拒谏则英雄散，不从则谋士叛．一策
黄石公
● 特策别划
首届全国中学生数理化学科能力竞赛数学学科模拟题（二）考答案高参
１Ａ．．２．Ｄ．３．Ａ．４．Ｂ．５．Ｃ．６．Ｄ．

首届全国中学生数理化学科能力竞赛

首届全国中学生数理化学科能力竞赛物理学科能力解题技能竞赛样题一、选择题（每题3分，共12分）1. 一个鸡蛋的质量、课本中一张纸的厚度、一块橡皮从桌面落到地面所用的时间，下列估算较接近的是（）A . 60g 0.8mm 0.5sB . 10 g 80μm 5 sC . 60g 80μm 0.5 sD . 10g 0.8mm 5 s2．无论是酷暑还是严冬，在使用冷暖空调的房间的窗户玻璃上，一般会出现凝结水珠的现象。

则下列说法中正确的是（）A ．无论是冬天还是夏天，小水珠总是凝结在窗户玻璃的内表面B ．无论是冬天还是夏天，小水珠总是凝结在窗户玻璃的外表面C ．夏天小水珠凝结在窗户玻璃的内表面，冬天小水珠凝结在窗户玻璃的外表面D ．夏天小水珠凝结在窗户玻璃的外表面，冬天小水珠凝结在窗户玻璃的内表面 3．在一个不透明的木板上，钻一个小孔，用眼睛通过小孔可以观察到一定的范围，如图1所示。

为了扩大观察的范围，在小孔中嵌入各种形状的玻璃制品。

在图中的四个截面中能获得最大观察范围的是（）4．如图2所示，乙是电磁铁，在乙正上方用弹簧悬挂一条形磁铁，设电源电压不变，闭合开关S 待电磁铁稳定后，当滑动变阻器R 的滑片p 由上向下缓缓地滑动过程中，弹簧的长度将（） A ．变长 B ．变短C ．先变长后变短D ．先变短后变长二、填空题（每空2分，共16分） 5．眼睛和照相机都可以成像，但它们的调节不相同。

如照相机要照远处景物时，必须（填“增大”或“减小”）镜头到底片的距离，使像成在胶片上；而正常人的眼睛看远处物体时，调节晶状体的厚度使之（填“增大”或“减小”），从而使像成在视网膜上。

（如图3）图1图2图36．按照我国交通管理的规定“红灯停、绿灯行、黄灯预备”，有人在科技活动中设计了一个实验电路，用以模拟十字路口的红绿灯，如图4所示。

当单刀多掷开关接通位置“1”时，东西方向的灯发光。

当单刀多掷开关接通位置“3”时，允许方向的车辆通行。

全国中学生数理化学科能力竞赛高一化学学科能力解题技能全国总决赛试题

首届全国中学生数理化学科能力竞赛高一化学学科能力解题技能全国总决赛试题试题说明：1.本试卷满分为100分. 2.考试时间为120分钟. 3. 相对原子质量 H —1 C —12 N —14 O —16 Na —23 Mg —24 S —32 Cl —35.5 K —39 Ca —40 Mn —55 Cu —64 Ba —137 La —138.9 一、选择题(本题包括7个小题，每小题3分，共21分.每小题只有1个选项符合题意.） 1、 2008年9月27日，中国航天员首次在太空成功回收了暴露试验的固体润滑材料。

这些搭载于“神七”飞船的材料共分为4大类15种，这是中国首次暴露于太空环境并成功回收的空间材料试验样品。

经过太空的试验以后，以肉眼观察，发现两类产品变化很大，一类是银与银合金的薄膜材料，经过原子氧和紫外光的辐照以后，其表面变花或者变暗；另一类是二硫化钼润滑薄膜产品，表面变得更为粗糙。

下列有关说法正确的是（） A ．原子氧比氧气化学性质活泼，二者互为同素异形体 B ．银与银合金的薄膜材料化学性质活泼 C ．原子氧和紫外光的辐照对二硫化钼润滑薄膜产品没有影响 D ．二硫化钼润滑薄膜产品不适合用作航天器的润滑剂 2、毛泽东同志曾写下许多伟大光辉的诗篇，其中一篇中有两句为“赤橙黄绿青蓝紫，谁持彩练当空舞”。

根据下列物质的颜色，按“赤橙黄绿青蓝紫”的顺序编组的是( ) ①溴水 ②CuSO 4 ③KMnO 4 ④CuO ⑤AgI ⑥FeSO 4 ·7H 2O ⑦CuSO 4·5H 2O ⑧HgO ⑨CuS A ．①②③④⑤⑥⑦ B ．⑧①⑤⑥④⑦③ C ．⑧⑨⑤⑥②③①D ．⑧①⑤⑥④②③3、为了使鸡蛋保鲜，可在蛋壳表面上涂一层水玻璃溶液，这是利用了水玻璃的（）A ．氧化性B ．还原性C ．稳定性D ．水解性4、下列物质长时间存放在敞口瓶里，会发生变质的是（）①碳酸钠晶体；②亚硫酸钠溶液 ③五氧化二磷；④碳铵；⑤碱石灰；⑥石灰水A ．①②③⑤B ．①②④⑥C ．②③④⑤D ．①②③④⑤⑥5、干燥剂的干燥性能可用干燥效率(1 m 3空气中实际余留水蒸气的质量)来衡量。

高一数学竞赛试题及答案

高一数学竞赛试题及答案一、选择题（每题5分，共20分）1. 下列哪个数是无理数？A. 3.1415926B. πC. √2D. 0.33333（无限循环小数）答案：B2. 已知函数f(x) = 2x^2 + 3x - 5，求f(-2)的值。

A. -15B. -7C. -3D. 1答案：B3. 一个圆的半径为r，圆心到直线的距离为d，如果d < r，那么该直线与圆的位置关系是：A. 相切B. 相交C. 相离D. 内含答案：B4. 如果一个等差数列的前三项和为9，第四项为5，求该数列的首项a1。

A. 1B. 2C. 3D. 4答案：B二、填空题（每题4分，共12分）5. 一个长方体的长、宽、高分别是a、b、c，其体积的公式是______。

答案：abc6. 若sinθ = 1/3，且θ在第一象限，求cosθ的值。

答案：2√2/37. 已知等比数列的前n项和公式为S_n = a1(1 - r^n) / (1 - r)，其中a1是首项，r是公比。

如果S_5 = 31，a1 = 1，求r的值。

答案：2三、解答题（每题18分，共54分）8. 证明：对于任意正整数n，n^5 - n 能被30整除。

证明：由题意，我们需要证明n^5 - n 能被30整除。

首先，我们知道任何正整数n都能被1、2、3、5中的至少一个整除。

设n = 2a + b，其中a和b是整数，且b属于{0, 1, 2, 3, 4}。

则n^5 - n = (2a + b)^5 - (2a + b) = 32a^5 + 20a^4b + 5a^3b^2 + a^2b^3 + 2ab^4 - 2a - b。

可以看到，除了最后两项，其他项都能被2整除。

对于最后两项，我们有2a - b = 2(a - b/2)，当b为偶数时，2a - b能被2整除；当b为奇数时，a - b/2为整数，所以2a - b也能被2整除。

同理，b - 1能被3整除，因为b属于{0, 1, 2, 3, 4}。

高一数学竞赛试题及答案

高一数学竞赛试题及答案一、选择题（每题5分，共20分）1. 下列哪个数是无理数？A. √3B. 0.33333（无限循环）C. πD. 1/32. 已知函数 f(x) = 2x^2 - 3x + 1，求 f(-1) 的值。

A. 4B. 6C. 8D. 103. 一个圆的半径为 5，求其面积。

A. 25πB. 50πC. 75πD. 100π4. 若 a + b + c = 6，且 a^2 + b^2 + c^2 = 14，求 ab + bc + ca 的值。

A. 2B. 4C. 6D. 8二、填空题（每题5分，共20分）5. 已知等差数列的首项为 2，公差为 3，求第 10 项的值是__________。

6. 已知等比数列的首项为 4，公比为 2，求前 5 项的和是__________。

7. 若函数 g(x) = x^3 - 2x^2 + 3x - 4 的导数是 g'(x)，则 g'(1) 的值是 __________。

8. 一个长方体的长、宽、高分别是 3、4、5，求其对角线的长度（保留根号）是 __________。

三、解答题（每题15分，共60分）9. 证明：对于任意正整数 n，都有 1^2 + 1/2^2 + 1/3^2 + ... +1/n^2 < 2。

10. 解不等式：|x - 1| + |x - 3| ≥ 5。

11. 已知函数 h(x) = x^3 - 6x^2 + 11x - 6，求其极值点。

12. 已知一个三角形的三个顶点分别为 A(1, 2)，B(-1, -1)，C(3, 4)，求其面积。

答案一、选择题1. 正确答案：C（π 是无理数）2. 正确答案：A（f(-1) = 2(-1)^2 - 3(-1) + 1 = 4）3. 正确答案：B（面积= πr^2 = 25π）4. 正确答案：B（根据柯西-施瓦茨不等式）二、填空题5. 第 10 项的值是 2 + 9*(10-1) = 296. 前 5 项的和是 4 + 8 + 16 + 32 + 64 = 1267. g'(x) = 3x^2 - 4x + 3，g'(1) = 3 - 4 + 3 = 28. 对角线的长度是√(3^2 + 4^2 + 5^2) = √50三、解答题9. 证明：根据调和级数的性质，我们知道 1/n^2 随着 n 的增大而减小，且 1/n^2 < 1/(n-1)^2，因此可以构造不等式 1^2 + 1/2^2 +1/3^2 + ... + 1/n^2 < 1 + 1/(1*2) + 1/(2*3) + ... + 1/((n-1)*n) = 1 + 1 - 1/n < 2。

北京市高一数学初赛试题与答案

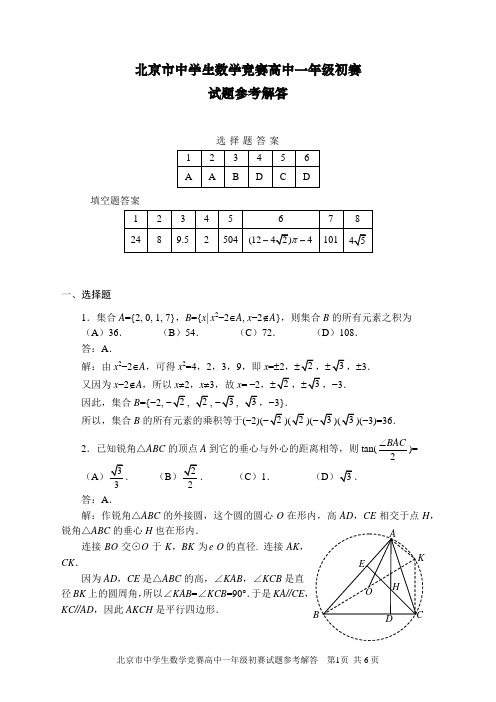
北京市中学生数学竞赛高中一年级初赛试题参考解答选择题答案填空题答案一、选择题1．集合A ={2, 0, 1, 7}，B ={x | x 2−2∈A , x −2∉A }，则集合B 的所有元素之积为（A ）36．（B ）54．（C ）72．（D）108．答：A ．解：由x 2−2∈A，可得x 2=4，2，3，9，即x =±2，，±3．又因为x −2∉A ，所以x ≠2，x ≠3，故x = −2，，−3．因此，集合B ={−2, ,，−3}．所以，集合B 的所有元素的乘积等于(−2)()(−3)=36． 2．已知锐角△ABC 的顶点A 到它的垂心与外心的距离相等，则tan(2BAC∠)= （A（B ）．（C ）1．（D ．答：A ．解：作锐角△ABC 的外接圆，这个圆的圆心O 在形内，高AD ，CE 相交于点H ，锐角△ABC 的垂心H 也在形内．连接BO 交⊙O 于K ，BK 为O e 的直径. 连接AK ，CK ．因为AD ，CE 是△ABC 的高，∠KAB ，∠KCB 是直径BK 上的圆周角，所以∠KAB =∠KCB =90°．于是KA//CE KC//AD ，因此AKCH 是平行四边形．所以KC =AH =AO =12BK ．在直角△KCB 中，由KC =12BK ，得∠BKC =60°，所以∠BAC =∠BKC =60°．故tan(2BAC∠)= tan30°3．将正奇数的集合{1, 3, 5, 7, …}从小到大按第n 组2n −1个数进行分组：{1}，{3, 5, 7}，{9, 11, 13, 15, 17}，…，数2017位于第k 组中，则k 为（A ）31．（B ）32．（C ）33．（D ）34．答：B.解：数2017是数列a n = 2n −1的第1009项．设2017位于第k 组，则1+3+5+…+(2k −1)≥1009，且1+3+5+…+(2k −3)＜1009．即k 是不等式组221009(1)1009k k ⎧≥⎨-<⎩的正整数解，解得k =32，所以2017在第32组中． 4．如图，平面直角坐标系x -O -y 中，A , B 是函数y =1x在第I 象限的图象上两点，满足∠OAB =90°且AO = AB ，则等腰直角△OAB 的面积等于（A ）12．（B ）2．（C）2．（D）2．答：D ．解：依题意，∠OAB =90°且AO = AB ，∠AOB =∠ABO =45°．过点A 做y 轴垂线交y 轴于点C ，过点B 做y 轴平行线，交直线CA 于点D ．易见△COA ≌△DAB ．设点A (a ,1a )，则点B (a +1a , 1a− a )．因为点B 在函数y =1x 的图象上，所以(a +1a )(1a− a )=1，即21a− a 2=1．因此S △ABC =12OA 2=12(21a + a 2) =122=． 5．已知f (x ) = x 5 + a 1x 4 + a 2x 3 + a 3x 2 + a 4x + a 5，且当m =1, 2, 3, 4时，f (m )=2017m ，则f (10)−f (−5)=（A ）71655．（B ）75156．（C ）75615．（ D ）76515．答：C ．解：因为当m =1, 2, 3, 4时，f (m )=2017m ，所以1, 2, 3, 4是方程f (x )−2017x =0的四个实根，由于5次多项式f (x )−2017x 有5个根，设第5个根为p ，则f (x )−2017x = (x −1)(x −2)(x −3)(x −4)(x −p )即 f (x ) = (x −1)(x −2)(x −3)(x −4)(x −p )+2017x ．所以f (10)=9×8×7×6(10−p )+2017×10，f (−5)=−6×7×8×9(5+p )−2017×5，因此f (10)− f (−5)=15(9×8×7×6+2017)=75615．6．已知函数2||,,()42,.x x a f x x ax a x a ≤⎧=⎨-+>⎩若存在实数m ，使得关于x 的方程f (x )=m有四个不同的实根，则a 的取值范围是（A ）17a >．（B ）16a >．（C ）15a >．（D ）14a >．答：D ．解：要使方程f (x )=m 有四个不同的实根，必须使得y =m 的图像与y =f (x )的图像有4个不同的交点．而直线与y =|x |的图像及二次函数的图像交点都是最多为两个，所以y =m 与函数y =|x |, x ≤a 的图像和y =x 2−4ax +2a , x ＞a 的图像的交点分别都是2个．而存在实数m ，使y =m 与y =|x |, x ≤a 的图像有两个交点，需要a ＞0，此时0＜m ≤a ；又因为y =x 2−4ax +2a , x ＞a 顶点的纵坐标为242(4)4a a ⨯-，所以，要y =m 与y =x 2−4ax +2a ,x ＞a 的图像有两个交点，需要m ＞242(4)4a a ⨯-．因此y =m 的图像与y =f (x )的图像有4个不同的交点需要满足：0＜m ≤a 且m ＞242(4)4a a ⨯-，解得14a >．二、填空题1. 用[x ]表示不超过x 的最大整数，设S =++++L ，求的值．答：24．解：因为12≤1, 2, 3＜22，所以1, ＜2，因此1===，共3个1；同理，22≤4, 5, 6, 7, 8＜32，因此，2=====，共5个2；又32≤9, 10, 11, 12, 13, 14, 15＜42，因此3===K ，共7个3；依次类推，4=====K ，共9个4；5=====K ，共11个5；6=====K ，共13个6；7=====K ，共15个7；8=====K ，共17个8；9=====K ，共19个9.S= (++)+(++++)+…+(++L ) = 1×3+2×5+3×7+4×9+5×11+6×13+7×15+8×17+9×19=615．因为242=576＜615=S ＜625=252，即2425，所以，．2．确定(201721log 2017×201741log 2017×201781log 2017×2017161log 2017×2017321log 2017)15的值．答：8．解：原式=(20172017log 2×20172017log 4×20172017log 8×20172017log 16×20172017log 32)15=(2×4×8×16×32)15= (21×22×23×24×25)15=(21+2+3+4+5)15=(215)15=23=8．3．已知△ABC 的边ABBCCA厘米，求△ABC 的面积．答：9.5平方厘米．解：注意到13=32+22，29=52+22，34=52+32，作边长为5厘米的正方形AMNP ，分成25个1平方厘米的正方形网格，如图．根据勾股定理，可知，AB厘米，BCCA=米，因此△ABC 的面积可求．△ABC 的面积=5×5−12×3×5−12×2×5−12×2×3=9.5（平方厘米）．4.设函数22(1))()1x x f x x ++=+的最大值为M ，最小值为N ，试确定M +N的值．答：2．解：由已知得()1f x =+因为)())(())]x x x x ++-=--=22ln(()1())ln10x x -+--==，所以()))x x -=-，因此，)x +是奇函数．进而可判定，函数()g x =为奇函数． NA MBP则g (x )的最大值M 1和最小值N 1满足M 1+N 1= 0．因为M =M 1+1，N = N 1+1，所以 M + N = 2．5．设A 是数集{1, 2, …, 2017}的n 元子集，且A 中的任意两个数既不互质，又不存在整除关系，确定n 的最大值．答：504．解：在数集{1, 2, …, 2017}中选取子集，使得子集中任意两个数不互质，最大的子集是偶数集{2, 4, …, 2016}共1008个元素，但其中，有的元素满足整除关系，由于1010的2倍是2020，所以集合A ={1010, 1012, 1014, …, 2016}中，任意两个数既不互质，又不存在整除关系，A 中恰有504个元素．事实上504是n 的最大值．因为若从{1009, 1011, …, 2017}中任取一个奇数，会与A 中的与它相邻的偶数互质；若从{1, 2, 3, …, 1008}中任取一数，则它的2倍在A 中，存在整除关系．6．如图，以长为4厘米的线段AB 的中点O 为圆心、2厘米为半径画圆，交AB 的中垂线于点E 和F . 再分别以A 、B 为圆心，4厘米为半径画圆弧交射线AE 于点C ，交射线BE 于点D . 再以E 为圆心DE 为半径画圆弧»DC，求这4条实曲线弧连接成的“卵形”¼AFBCDA 的面积．（圆周率用π表示，不取近似值）答：(12−)π−4平方厘米．解：半圆(O , 2)的面积=12π×22=2π．因为AO=OB =2，所以AB=AC=BD =4，AE =BE，ED =EC =4−．又∠AEB =∠CED =90°，∠EAB =∠EBA =45°，因此，扇形BAD 的面积=扇形ACB 的面积=18π×42=2π，△AEB 的面积=12×4×2=4，直角扇形¼EDC的面积=14π(4−)2= 6π−，卵形¼AFBCDA 的面积 = 半圆(O , 2)的面积+扇形BAD 的面积+扇形ACB 的面积 −△AEB 的面积+直角扇形¼EDC的面积 = 2π+2×2π−4+6π−= (12−)π−4（平方厘米）．7. 已知22()1005000x f x x x =-+，求f (1)+f (2)+…+f (100)的值．答：101．解：设g (x ) = x 2−100x +5000，则BFADCEOg (100−x ) = (100−x )2−100(100−x )+5000=1002−200x +x 2−1002+100x +5000= x 2−100x +5000= g (x )，即 g (k ) = g (100−k )．所以 f (k ) + f (100−k ) =22(100)()(100)k k g k g k -+- =22(100)()k k g k +-=2，又 f (50) =2250=150100505000-⨯+， f (100)22100==2.1001001005000-⨯+ 所以， f (1)+ f (2)+…+ f (100)= (f (1)+ f (99))+ (f (2)+ f (98))+…+ (f (49)+ f (51))+ f (50)+ f (100) = 2×49+1+2=101．8．如图，在锐角△ABC 中，AC = BC = 10，D 是边AB 上一点，△ACD 的内切圆和△BCD 的与BD 边相切的旁切圆的半径都等于2，求AB 的长．答：解：线段AB 被两圆与AB 的切点及点D 分成四段，由于两圆半径相等，再根据切线长定理，可知中间两段相等，于是可将这四段线段长度分别记为a , b , b , c ，由于圆O 2的切线长CE = CG ，所以BC +a = CD +b = (AC −c +b )+b ，而AC = BC ，所以a +c = 2b ．由等角关系可得△AO 1F ∽△O 2BE ，得12O F BEAF O E=，即22ac =，由此推出ac = 4．分别计算△BCD 和△ACD 的面积：12(),2BCD S BC CD BD ∆=⨯+-12()2ACD S AC CD AD ∆=⨯++所以24ACD BCD S S AD BD AB a c b b ∆∆-=+==++=. ①又设由C 引向AB 的高为h ，可得1()2ACD BCD S S c a h ∆∆-=-=② 由①、②两式可得4b =将a +c = 2b ，ac = 4代入，化简得42251000b b -+=解得b 2=5或b 2=20，即b或b= 2（负根舍）．于是，AB = a +c +2b = 4bAB．若ABABC 为钝角三角形，不合题设△ABC 是锐角三角形的要求．DACBD A C B EG FO 1 O 2 · a b b c·所以AB的长为。

660编号97编号北京市高一数学竞赛初赛的试题与答案

北京市中学生数学竞赛高中一年级初赛试题参考解答选择题答案123456AABDCD填空题答案1 2 3 4 5 67 8 2489.52504 (1242)410145一、选择题:1．集合A={2, 0, 1, 7}，B={x| x 2-2A, x-2A}，则集合B 的所有元素之积为（A ）36．（B ）54．（C ）72．（D ）108．答：A ．解：由x 2-2A ，可得x 2=4，2，3，9，即x=2，2，3，3．又因为x-2A ，所以x 2，x 3，故x= -2，2，3，-3．因此，集合B={-2, -2,2, -3,3，-3}．所以，集合B 的所有元素的乘积等于(-2)(-2)(2)(-3)(3)(-3)=36．2．已知锐角△ABC 的顶点A 到它的垂心与外心的距离相等，则tan(2BAC )=（A ）33．（B ）22．（C ）1．（D ）3．答：A ．解：作锐角△ABC 的外接圆，这个圆的圆心O 在形内，高AD ，CE 相交于点H ，锐角△ABC 的垂心H 也在AH K E形内．连接BO 交⊙O 于K ，BK 为O 的直径. 连接AK ，CK ．因为AD ，CE 是△ABC 的高，∠KAB ，∠KCB 是直径BK 上的圆周角，所以∠KAB=∠KCB=90°．于是KA//CE ，KC//AD ，因此AKCH 是平行四边形．所以KC=AH=AO=12BK ．在直角△KCB 中，由KC=12BK ，得∠BKC=60°，所以∠BAC=∠BKC=60°．故tan(2BAC )= tan30°=33．3．将正奇数的集合{1, 3, 5, 7, …}从小到大按第n 组2n-1个数进行分组：{1}，{3, 5, 7}，{9, 11, 13, 15, 17}，…，数2017位于第k 组中，则k 为（A ）31．（ B ）32．（ C ）33．（D ）34．答：B.解：数2017是数列a n = 2n -1的第1009项．设2017位于第k 组，则1+3+5+…+(2k-1)≥1009，且1+3+5+…+(2k-3)＜1009．即k 是不等式组221009(1)1009k k的正整数解，解得k =32，所以2017在第32组中．4．如图，平面直角坐标系x-O-y 中，A, B 是函数y =1x 在第I 象限的图象上两点，满足∠OAB=90°且AO = AB ，则等腰直角△OAB 的面积等于（A ）12．（B ）22．（C ）32．（D ）52．答：D ．解：依题意，∠OAB=90°且AO = AB ，∠AOB=∠ABO=45°．过点A 做y 轴垂线交y 轴于点C ，过点B 做y 轴平行线，交直线CA 于点D ．易见△COA ≌△DAB ．设点A(a, 1a )，则点B(a +1a , 1a-a)．ABO yxy =1x ABOyxy =1x D C因为点B 在函数y =1x 的图象上，所以(a +1a )(1a -a)=1，即21a -a 2=1．因此S △ABC =12OA 2=12(21a + a 2) =1222215()42a a．5．已知f (x)=x 5+a 1x4+a 2x 3+a 3x 2+a 4x +a 5，且当m =1, 2, 3, 4时，f (m)=2017m ，则f (10)-f (-5)=（A ）71655．（B ）75156．（ C ）75615．（ D ）76515．答：C ．解：因为当m =1, 2, 3, 4时，f (m)=2017m ，所以1, 2, 3, 4是方程f (x)-2017x=0的四个实根，由于5次多项式f (x)-2017x 有5个根，设第5个根为p ，则f (x)-2017x = (x-1)(x-2)(x-3)(x-4)(x-p)即f (x) = (x-1)(x-2)(x-3)(x-4)(x-p)+2017x ．所以f (10)=9×8×7×6(10-p)+2017×10，f (-5)=-6×7×8×9(5+p)-2017×5，因此f (10)- f(-5)=15(9×8×7×6+2017)=75615．6．已知函数2||,,()42,.x x a f x xax a xa 若存在实数m ，使得关于x 的方程f (x)=m有四个不同的实根，则a 的取值范围是（A ）17a ．（B ）16a．（C ）15a．（D ）14a．答：D ．解：要使方程 f (x)=m 有四个不同的实根，必须使得y=m 的图像与y=f(x)的图像有4个不同的交点．而直线与y=|x|的图像及二次函数的图像交点都是最多为两个，所以y=m 与函数y=|x|, x ≤a 的图像和y=x 2-4ax+2a, x ＞a 的图像的交点分别都是2个．而存在实数m ，使y=m 与y=|x|, x ≤a 的图像有两个交点，需要a ＞0，此时0＜m ≤a ；又因为y=x 2-4ax+2a, x ＞a 顶点的纵坐标为242(4)4a a ，所以，要y=m 与y=x 2-4ax+2a,x ＞a 的图像有两个交点，需要m ＞242(4)4a a ．因此y=m 的图像与y=f(x)的图像有4个不同的交点需要满足：0＜m ≤a 且m ＞242(4)4a a ，解得14a．二、填空题:1. 用[x]表示不超过x 的最大整数，设[1][2][3][99]S ，求[]S 的值．答：24．解：因为12≤1, 2, 3＜22，所以1≤1,2, 3＜2，因此[1][2][3]1，共3个1；同理，22≤4, 5, 6, 7, 8＜32，因此，[4][5][6][7][8]2，共5个2；又32≤9, 10, 11, 12, 13, 14, 15＜42，因此[9][10]=[15]3，共7个3；依次类推，[16][17][23][24]4，共9个4；[25][26][34][35]5，共11个5；[36][37][47][48]6，共13个6；[49][50][62][63]7，共15个7；[64][65][79][80]8，共17个8；[81][82][98][99]9，共19个9. S = ([1][2][3])+([4][5][6][7][8])+…+([81][99])= 1×3+2×5+3×7+4×9+5×11+6×13+7×15+8×17+9×19=615．因为242=576＜615=S ＜625=252，即24＜S ＜25，所以，[S ]=24．2．确定(201721log 2017×201741log 2017×201781log 2017×2017161log 2017×2017321log 2017)15的值．答：8．解：原式=(20172017log 2×20172017log 4×20172017log 8×20172017log 16×20172017log 32)15=(2×4×8×16×32)15= (21×22×23×24×25)15=(21+2+3+4+5)15=(215)15=23=8．3．已知△ABC 的边AB=29厘米，BC=13厘米，CA=34厘米，求△ABC 的面积．答：9.5平方厘米．解：注意到13=32+22，29=52+22，34=52+32，作边长为5厘米的正方形AMNP ，分成25个1平方厘米的正方形网格，如图．根据勾股定理，可知，AB=29厘米，BC=13厘米，CA=34厘米，因此△ABC 的面积可求．△ABC 的面积=5×5-12×3×5-12×2×5-12×2×3=9.5（平方厘米）．4. 设函数222(1)ln(1)()1x x x f x x的最大值为M ，最小值为N ，试确定M+N的值．答：2．解：由已知得222ln(1)()11x xx f x x因为2222ln(1)ln(()1())ln[(()1())(()1())]xx x x x x x x =22ln(()1())ln10x x ，所以22ln(()1())ln(1)x x xx ，因此，2ln(1)xx 是奇函数．进而可判定，函数222ln(1)()1xx x g x x为奇函数．则g(x)的最大值M 1和最小值N 1满足M 1+N 1= 0．因为M =M 1+1，N = N 1+1，所以M + N = 2．5．设A 是数集{1, 2, …, 2017}的n 元子集，且A 中的任意两个数既不互质，又不存在整除关系，确定n 的最大值．答：504．解：在数集{1, 2, …, 2017}中选取子集，使得子集中任意两个数不互质，最大的子集是偶数集{2, 4, …, 2016}共1008个元素，但其中，有的元素满足整除关系，由于1010的2倍是2020，所以集合A={1010, 1012, 1014, …, 2016}中，任意两个数既不互质，又不存在整除关系，A 中恰有504个元素．NA MBCP事实上504是n 的最大值．因为若从{1009, 1011, …, 2017}中任取一个奇数，会与A 中的与它相邻的偶数互质；若从{1, 2, 3, …, 1008}中任取一数，则它的2倍在A 中，存在整除关系．6．如图，以长为4厘米的线段AB 的中点O 为圆心、2厘米为半径画圆，交AB 的中垂线于点E 和F. 再分别以A 、B 为圆心，4厘米为半径画圆弧交射线AE 于点C ，交射线BE 于点D. 再以E 为圆心DE 为半径画圆弧DC ，求这4条实曲线弧连接成的“卵形”AFBCDA的面积．（圆周率用π表示，不取近似值）答：(12-42)π-4平方厘米．解：半圆(O, 2)的面积=12π×22=2π．因为AO=OB=2，所以AB=AC=BD =4，AE=BE=22，ED=EC=4-22．又∠AEB=∠CED=90°，∠EAB =∠EBA=45°，因此，扇形BAD 的面积=扇形ACB 的面积=18π×42=2π，△AEB 的面积=12×4×2=4，直角扇形EDC 的面积=14π(4-22)2= 6π-42π，卵形AFBCDA 的面积= 半圆(O, 2)的面积+扇形BAD 的面积+扇形ACB 的面积-△AEB 的面积+直角扇形EDC 的面积= 2π+2×2π-4+6π-42π= (12-42)π-4（平方厘米）．7. 已知22()1005000xf x xx ，求f (1)+f (2)+…+f (100)的值．答：101．解：设g(x) = x 2-100x+5000，则g(100-x) = (100-x)2-100(100-x)+5000=1002-200x+x 2-1002+100x+5000= x 2-100x+5000= g(x)，即g(k) = g(100-k)．B FADCEO所以f (k) + f(100-k) =22(100)()(100)kk g k g k =22(100)()kk g k =2，又f (50) =2250=150100505000，f (100)22100==2.1001001005000所以，f (1)+ f (2)+…+ f (100)= (f (1)+ f (99))+ (f (2)+ f (98))+…+ (f (49)+ f (51))+ f (50)+ f (100) = 2×49+1+2=101．8．如图，在锐角△ABC 中，AC = BC = 10，D 是边AB 上一点，△ACD 的内切圆和△BCD 的与BD 边相切的旁切圆的半径都等于2，求AB 的长．答：45．解：线段AB 被两圆与AB 的切点及点D 分成四段，由于两圆半径相等，再根据切线长定理，可知中间两段相等，于是可将这四段线段长度分别记为a, b, b, c ，由于圆O 2的切线长CE = CG ，所以BC+a = CD+b = (AC-c+b)+b ，而AC = BC ，所以a+c = 2b ．由等角关系可得△AO 1F ∽△O 2BE ，得12O F BE AFO E，即22ac，由此推出ac = 4．分别计算△BCD 和△ACD 的面积：12(),2BCDSBC CD BD 12()2ACDSAC CD AD 所以24ACDBCDS S ADBDABa c bb .①又设由C 引向AB 的高为h ，可得22211()()410(2)22ACDBCDS S c a hc a ac b ②由①、②两式可得22214()410(2)2bca acb 将a+c = 2b ，ac = 4代入，化简得42251000bbDACBD A CB E G FO 1O 2 ·a b b c ·解得b2=5或b2=20，即b =5或b = 25，（负根舍）．于是，AB = a+c+2b = 4b = 45，或AB = 85．若AB = 85，△ABC为钝角三角形，不合题设△ABC是锐角三角形的要求．所以AB的长为45．。

首届全国中学生数理化学科能力竞赛大纲及样题-高中化学

（高中化学部分）第一部分解题技能竞赛大纲第二部分解题技能竞赛试题样题第三部分化学实验报告首届全国中学生数理化学科能力竞赛化学学科笔试部分竞赛大纲（2008年试验稿）为了提高广大青少年走进科学、热爱科学的兴趣，培养和发现创新型人才，团中央中国青少年发展服务中心、全国“青少年走进科学世界”科普活动指导委员会办公室共同举办首届“全国中学生数理化学科能力竞赛”（以下简称“竞赛”）。

竞赛由北京师范大学《高中数理化》杂志社承办。

为保证竞赛活动公平、公正、有序地进行，现将化学学科笔试部分竞赛大纲颁布如下：一、命题指导思想根据教育部《全日制普通高级中学化学课程标准》以及《全日制义务教育化学课程标准》的要求，着重考查学生的基础知识、基本能力、科学素养和运用所学知识分析问题、解决问题的能力及创新能力。

命题吸收各地高考和中考的成功经验，以能力测试为主导，体现新课程标准对能力的要求，着重考查学生的观察能力、实验能力、思维能力和自学能力，促进新课程标准提出的“知识与技能”、“过程与方法”、“情感态度与价值观”三维目标的落实。

二、竞赛对化学学科能力的说明化学学科能力是由观察能力、思维能力、实验能力和自学能力组成的一个有机的整体。

1、观察能力观察是认识活动和实践活动的起点。

观察能力是衡量一个人科学素质高低的重要尺度，也是学生化学学科能力的最基本要素。

主要包括：（1）能根据观察的目的，迅速地对仪器装置、物质及其变化过程进行全面的观察；（2）分清主要和次要现象，并能迅速地发现不易发现或容易消失的主要现象，进行精确的观察，并能对其进行比较、分析和综合；（3）养成认真、细致、有始有终地观察实验的良好习惯。

2、实验能力化学是以实验为基础的科学。

化学实验是人们探索和验证化学规律的手段。

实验能力是化学学科素质最为重要的组成部分。

主要包括：（1）正确地使用常见仪器和进行基本操作；（2）观察、记录实验现象，测量、分析和处理实验数据，表达及评价实验结果；能运用已学过的化学理论、实验方法和实验仪器处理问题，写出实验报告。