湖南省郴州市2015届高三第二次教学质量监测数学(理)试题
湖南省郴州市高三第二次教学质量监测理科综合试题

湖南省郴州市2015届高三第二次教学质量监测试卷理科综合能力试题1.下列各曲线所代表的生物学含义及描述正确的是A.甲图可表示人的肌细胞中A TP生成速率与氧气浓度的关系B.乙图所示物质运输速率不受呼吸酶抑制剂的影响C.丙图可表示酵母菌细胞呼吸时氧气浓度与CO2产生量的关系.a点时产生ATP最多D.丁图可表示人的离体细胞内酶活性与温度的关系2.右图表示生物新物种形成基本环节的概念图.下面分析正确的是A.a表示基因突变,是生物进化的原材料B.b表示地理隔离,新物种形成一定需要地理隔离C.c表示新物种形成,新物种与生活环境共同进化D.d表示生殖隔离,生殖隔离是生物进化的标志3.在正常人体细胞中,可能发生的过程是A.正常生理状态下,溶酶体对自身机体的细胞结构分解B.多肽合成时.mRNA沿着核糖体移动C.在静息状态下,神经细胞中大量的Na+内流D.性激素在载体蛋白的协助下进入受体细胞4.将记录仪的两个电极分别放置在神经纤维膜外的a、c两点,c点所在部位的膜已被损伤,其余部位均正常。
下图是刺激前后的电位变化,以下说法不正确的是A.兴奋的产生与膜对Na+的通透性改变有关B.被损伤部位c点的膜外电位为负电位C.兴奋传到b点时记录仪的指针将向左侧偏转D.结果表明兴奋在神经纤维上以电信号形式传导5.如图是描述生命现象的模型.以下相关叙述不正确的是A.若A代表人体下丘脑,a为血浆渗透压升高,则b、c可分别代表大脑皮层产生渴觉和垂体释放抗利尿激素增加B.若A代表人体B淋巴细胞,a为抗原刺激,则b、c可分别代表浆细胞和记忆细胞的形成C.若A代表棉铃虫种群.a为诱捕雄虫,则b、e可分别代表性别比例失调和种群密度下降D.若A代表细胞癌变,a为原癌基因和抑癌基因突变,则b、c可分别代表失去接触抑制和细胞周期变长6.下列有关实验的描述.不正确的是A.“观察DNA和RNA在细胞中的分布”实验中取口腔上皮细胞制片,需要点燃酒精灯,将涂有口腔上皮细胞的载玻片烘干B.CO2可使溴麝香草酚蓝水溶液由蓝变绿再变黄,也可在酸性条件下使橙色的重铬酸钾变成灰绿色C.“观察根尖分生组织细胞的有丝分裂”实验装片制作流程为:解离→漂洗→染色→制片D.用血细胞计数板对培养液中酵母菌计数时.先将盖玻片放在计数室上,用吸管吸取培养液,滴于盖玻片边缘,让培养液自行渗入。
湖南省2015届高三高考仿真数学试题(理)含答案(PDF版)

!"#$届高考仿真试题 副卷科目 数学 理科试题卷策划 制作 湖南炎德文化实业有限公司注意事项#%答题前 考生务必将自己的姓名 准考证号写在答题卡和本试题卷的封面上 并认真核对答题卡条形码上的姓名 准考证号和科目!%选择题和非选择题均须在答题卡上作答 在本试题卷和草稿纸上答题无效 考生在答题卡上按如下要求答题# 选择题部分请按题号用!&铅笔填涂方框 修改时用橡皮擦干净 不留痕迹! 非选择题部分请按题号用"'$毫米黑色墨水签字笔书写 否则作答无效( 请勿折叠答题卡 保持字体工整 笔迹清晰 卡面清洁(%本试题卷共)页 如缺页 考生须及时报告监考老师 否则后果自负*%考试结束后 将本试题卷和答题卡一并交回 姓!!名!!!!!!!!!!准考证号!!!!!!!!!!祝你考试顺利绝密"启封并使用完毕前!"#$届高考仿真试题!副卷"数!学!理科"!!本试题卷包括选择题$填空题和解答题三部分%共)页'时量#!"分钟'满分#$"分'一$选择题#本大题共 小题%每小题 分%共 分!在每小题给出的四个选项中%只有一项是符合题目要求的!#!集合"+## #$)*)%$+## #!,(#%)*"%则"&$+-'(%*%)*$&'*%$%)*).'#('#$)*)/'#($#')*)!!下列命题中%真命题是-'(#"#%使得0#"$"&'123!#4!123#)(!#*%%%# ".'函数&!#"+!#,#!有两个零点/''%#%(%#是'(%#的充分不必要条件(!已知三棱柱的三视图如下图所示%其中俯视图为正三角形%则该三棱柱的体积为槡槡槡-'#!(&'!5(.'()(/')*!&!#"+"123! #4 "!"%"% %""在#+#处取最大值%则-'&!#,#"一定是奇函数&'&!#,#"一定是偶函数.'&!#4#"一定是奇函数/'&!#4#"一定是偶函数$!已知函数&!#"+671 #)%集合)+#%!%(%*%$%)%5%8%)*9%现从)中任取两个不同的元素*%+%则&!*"+&!+"+"的概率为-'$#!&'5#!.'5#8/'59)!运行如下图所示的程序框图%则输出的结果,为-'#""8&'!"#$.'#""5/',#""55!已知抛物线-#.!+*#%点/!*%""%0为坐标原点%若在抛物线-上存在一点1%使得+01/+9":%则实数*的取值范围是-'!*%8"&'!*%4;".'!"%*"/'!8%4;"8!设函数.+&!#"在 上有定义%对于任一给定的正数2%定义函数&2!#"+&!#"%&!#"$22%&!#"%,-.2%则称函数&2!#"为&!#"的,2界函数-若给定函数&!#"+#!,!#,#%2+!%则下列结论不成立的是-'&2.&!""/+&.&2!""/&'&2.&!#"/+&.&2!#"/.'&2.&2!!"/+&.&!!"//'&2.&2!("/+&.&!("/9!已知函数3!#"+',#!#0$#$0%0!"为自然对数的底数与4!#"+!<3#的图象上存在关于#轴对称的点%则实数'的取值范围是-'#%#0!./4!&'#%0!./,!.'#0!4!%0!./,!/'0!,!%4;./#"!如图%已知双曲线-##!'!,.!(!+#!'%"%(%""的右顶点为"%0为坐标原点%以"为圆心的圆与双曲线-的某渐近线交于两点/%1!若+/"1+)":且/001+(/00/%则双曲线-的离心率为-'槡!((&'槡5!.'槡(9)槡/'(二$填空题#本大题共 小题%考生作答 小题%每小题 分%共 分!把答案填在答题卡中对应题号后的横线上!!一"选做题!请考生在第##%#!%#(三题中任选两题作答%如果全做%则按前两题计分"##!如图%$5是半圆0的直径%"在$5的延长线上%"-与半圆相切于点6%"-1$-%若"5槡+!(%"6+)%则6-+!!!!!#!!在直角坐标系#0.中%以原点0为极点%#轴的正半轴为极轴建立极坐标系!若点/为直线 671 , 123 ,*+"上一点%点1为曲线#+7%.+#*7,-.!!7为参数"上一点%则2/12的最小值为!!!!!#(!已知函数&!#"+2#,%242#,!%2%若对任意的## %&!#")&!("+&!*"都成立%则%的取值范围为!!!!!!二"必做题!#* #)题"#*!设'+3"123#4671!"#=#%则二项式槡'#,#槡!"#)的展开式的常数项是!!!!!#$!如果实数'%(满足条件#'4(,!)"(,',#$"'$,-.#%则'4!(!'4(的最大值是!!!!!#)!平面向量 % % 满足2 2+#% + +#% + +!%2 , 2+!%则 + 的最小值为!!!!!三$解答题#本大题共 小题%共 分!解答应写出文字说明%证明过程或演算步骤!#5!!本题满分#!分"一个袋子装有大小形状完全相同的9个球%其中$个红球编号分别为#%!%(%*%$%*个白球编号分别为#%!%(%*%从袋中任意取出(个球!!#"求取出的(个球编号都不相同的概率'!!"记8为取出的(个球中编号的最小值%求8的分布列与数学期望!#8!!本题满分#!分"已知函数&!#"+*123#槡4!671#!*%""的最大值为!!!#"求函数&!#"在."%/上的单调递减区间'!!"4"$-中%&", !"*4&$, !"*槡+*)123"123$%角"$$$-所对的边分别是'$($9%且-+)":%9+(%求4"$-的面积!如图%在四棱锥/,"$-5中%/51平面"$-5%底面"$-5是菱形%+$"5+)":%0为"-与$5的交点%6为/$上任意一点!!#"证明#平面6"-1平面/$5'!!"若/55平面6"-%并且二面角$,"6,-的大小为*$:%求/5>"5的值!!"!!本题满分#(分"已知数列)'+*中%'#+#%'+4#+#('+4+%+为奇数%'+,(+%+为偶数,-.!!#"求证#数列'!+,)*(!是等比数列'!!"若,+是数列')*+的前+项和%求满足,+%"的所有正整数+!已知离心率为槡!!的椭圆#!'!4.!(!+#!'%(%""的右焦点;是圆!#,#"!4.!+#的圆心%过椭圆上的动点/作圆的两条切线分别交.轴于)%<!与/点不重合"两点!!#"求椭圆方程'!!"求线段)<长的最大值%并求此时点/的坐标!!!!!本题满分#(分"设函数&!#"+#<3#,'#!!#"若函数&!#"在!#%4;"上为减函数%求实数'的最小值'!!"若存在##%#!#.0%0!/%使&!##"$&=!#!"4'成立%求实数'的取值范围!#$%&届高考仿真试题!副卷"数学!理科"参考答案一#选择题题!号%#'(&)*+"%$答!案,-.-/-,,,,%$!$解析%双曲线的一条渐近线方程为"0#$%&右顶点&到双曲线"0#$%的距离为'0$#$#1#槡#0$#(&又")&*0)$2&所以圆&的半径#)�#槡''0#$#槡'(&又$%+*0'$%+)&#)�#)*#&所以#)*#0#)�#$#槡'(&#+)#0%##)*#0$#槡'(&#+*#0'$#槡'(&所以由圆的切割线定理知#+)# #+*#0#+&#!#$#槡'!"(#+#$#槡'!"(&即$###(#0#+&##!($###'(#&*$###'(#0$#&所以##(#0'*&%!$#(#0'*&(#$#0*(&,0($0槡*#!二#填空题%%!'!%#!槡'##!%'!'#&'(!%(!!%)$!%&!*&!%)!&($解析%由题意设 0!%&$"& 0!%&"%"& 0!#&"#"!所以 ! 0!!%&"%!"#"&# ! #0%1!"%!"#"槡#0#&!"%!"#"#0'&"%!"#槡03'&当"%!"#槡0'时& 0#1"%"#0#1"#!"#槡1'"0"#1槡'!"##1&(&当"#0!槡'#时& 取得最小值&(&当"%!"#槡0!'时& 0#1"%"#0#1"#!"#槡!'"0"#!槡'!"##1&(&当"#0槡'#时& 取得最小值&(&综上& 的最小值为&(!三#解答题%*!解)!%"设*取出的'个球编号都不相同+为事件&&*取出的'个球中恰有两个球编号相同+为事件-&则)!-"0.%(.%*.'"0#++(0%'&4)!&"0%!)!-"0#'&(分!#".的取值为%&#&'&(!)!.0%"0.%#.#*1.##.%*.'"0("+(&)!.0#"0.%#.#&1.##.%&.'"0#&+(&)!.0'"0.%#.#'1.##.%'.'"0"+(&)!.0("0%.'"0%+(!+分 所以.的分布列为).%#'()("+(#&+("+(%+(.的数学期望/!."0%5("+(1#5#&+(1'5"+(1(5%+(0%'$+(0)&(#!%#分%+!解)!%"由题意&0!%"的最大值为1#槡1#&所以1#槡1#0#!而1&$&于是1槡0#&0!%"0#678%1 !"(!0!%"为递减函数&则%满足#2 1 #'%1 ('#2 1' #!2( "&即#2 1 ('%'#21& (!2( "!所以0!%"在'$& (上的单调递减区间为 (&'(!&分!#"设)&-3的外接圆半径为4&由题意&得#40(67830'678)$2槡0#'!化简0&! !"(10-! !"(槡0()678&678-&得678&1678-槡0#)678&678-!由正弦定理&得#4!$1#"槡0#)$#&$1#槡0#$#!!! +分由余弦定理&得$#1##!$#0"&即!$1#"#!'$#!"0$!! %$分 将 式代入 &得#!$#"#!'$#!"0$!解得$#0'&或$#0!'#!舍去"!5)&-30%#$#67830槡''(!%#分%"!解)!%"因为)6*平面&-36&4)6*&3&又&-36是菱形&4-6*&3&又)6+-606&故&3*平面)-6&又&3,平面/&3&4平面/&3*平面)-6!(分 !#"连结+/&因为)6-平面/&3&所以)6-+/&所以+/*平面&-36&又+是-6的中点&故此时/为)-的中点&以+为坐标原点&射线+&&+-&+/分别为%轴&"轴&7轴建立空间直角坐标系!设+-01&+/08&则+&槡0'1&&!槡'1&$&$"&-!$&1&$"&/!$&$&8"&向量 %0!$&%&$"为平面&/3的一个法向量&+分 设平面&-/的一个法向量 #0!%&"&7"&则 # $%&-0$且 #$%-/0$&即槡!'1%11"0$且1"!870$&取%0%&则"槡0'&70槡'18&则 #0%&槡'&槡'1!"8%$分 49:6(&209:6, %& #-0 % ## %## ##0槡'%1'1'1#8槡#0槡##&解得810槡)#&故)6;&60#8;#108;1槡0);#!%#分#$!解)!%"设#90$#9!'#&因为#91%#9$#91#!'#$#9!'#0%'$#91%1!#91%"!'#$#9!'#0%'!$#9!)9"1!#91%"!'#$#9!'#0%'$#9!%#$#9!'#0%'&所以数列$#9!./'#是以$#!'#即!%)为首项&以%'为公比的等比数列!&分 !#"由!%"得#90$#9!'#0!%) !"%'9!%0!%# !"%'9&即$#90!%# !"%'91'#&由$#90%'$#9!%1!#9!%"&得$#9!%0'$#9!'!#9!%"0!%# !"%'9!%!)91%&#&所以$#9!%1$#90!%# !"%'9!%1!"%''(9!)91"0!# !"%'9!)91"&5#90!$%1$#"1!$'1$("1 1!$#9!%1$#9"0!#%'1!"%'#1 1!"%''(9!)!%1#1 19"1"90!#%'%!!"%''(9%!%'!)9!91%"#1"9!"%'9!%!'9#1)90!"%'9!'!9!%"#1#%$分 显然当9( .时&.5#9/单调递减&又当90%时&5#0*'&$&当90#时&5(0!+"/$&所以当90#时&5#9/$05#9!%05#9!$#90'# !"%'9!&#!'9#1)9&同理&当且仅当90%时&5#9!%&$&综上&满足59&$的所有正整数9为%和#!%'分 #%!解)!%"圆心坐标!%&$"&所以(0%&又($0槡##&4$槡0#&故#0%&故椭圆方程为%##1"#0%!(分 !#"设)!%$&"$"&:!$&1"&;!$&9"&%##1"#0%!%!%"#1"#1230%4%槡0#!#&%槡0#1#!舍去"&4%$('槡!#&$"5!$&槡#!#"!)分 直线):的方程"!10"$!1%$%4!"$!1"%!%$"11%$0$&4#"$!11%$1#!"$!1"#1%槡#$0%4!%$!#"1#1#"$1!%$0$&同理!%$!#"9#1#"$9!%$0$&41&9是方程!%$!#"<#1#"$<!%$0$的两实根&由韦达定理)1190#"$%$!#&190!%$%$!#&"分数学!理科"试题参考答案 !%#!#:;#0#1!9#0!119"#!(槡190(%#$1("#$!+%$!%$!#"槡#&又%#$#1"#$0%&4#:;#0#!(!%$!#"槡#&%%分 令0!%"0#!(%!#&%('槡!#!#&!#"5!!#&槡!#"&显然由0!%"的单调性知0!%"<=>0#!(5!槡!#!#"!#&4#:;#<=>槡槡0##!%&此时%$槡0!#&故)点坐标为!槡!#&$"&即椭圆左顶点!%'分 ##!解)!%"由已知得%&$&%6%!因0!%"在!%&1?"上为减函数&故0=!%"0@8%!%!@8%"#!$'$在!%&1?"上恒成立&%分 所以当%(!%&1?"时&0=!%"<=>'$!又0=!%"0@8%!%!@8%"#!$0!%@8!"%#1%@8%!$0!%@8%!!"%##1%(!$&#分 故当%@8%0%#&即%0A #时&0=!%"<=>0%(!$!所以%(!$'$&于是$0%(&故$的最小值为%(!(分 !#"命题*若存在%%&%#('A &A #(&使0!%%"'0=!%#"1$成立+等价于*当%('A &A #(时&有0!%"<78'0=!%"<=>1$+!&分 由!%"&当%('A &A #(时&0=!%"<=>0%(!$&40=!%"<=>1$0%(!问题等价于)*当%('A &A #(时&有0!%"<78'%(+!)分 当$0%(时&由!%"&0!%"在'A &A #(上为减函数&则0!%"<7800!A #"0A ##!$A #'%(&故$0%#!%(A#!+分 当$/%(时&由于0=!%"0!%@8%!!"%##1%(!$在'A &A #(上的值域为!$&%(!'($!!7"!$0$&即$'$&0=!%"0$在'A &A #(恒成立&故0!%"在'A &A #(上为增函数&于是&0!%"<7800!A "0A !$A 0A &%(&矛盾!%$分 !77"!$/$&即$/$/%(&由0=!%"的单调性和值域知&存在唯一%$(!A &A #"&使0=!%"0$&且满足)当%(!,&%$"时&0=!%"/$&0!%"为减函数0当%(!%$&A #"时&0=!%"&$&0!%"为增函数0所以&0<78!%"00!%$"0%$@8%$!$%$'%(&%$(!A &A #"%#分 所以&$0%@8%$!%(%$&%@8A #!%(A &%#!%(0%(&与$/$/%(矛盾!综上得$0%#!%(A#!%'分。
湖南省郴州市2015届高考模拟数学理科试题(四)及答案
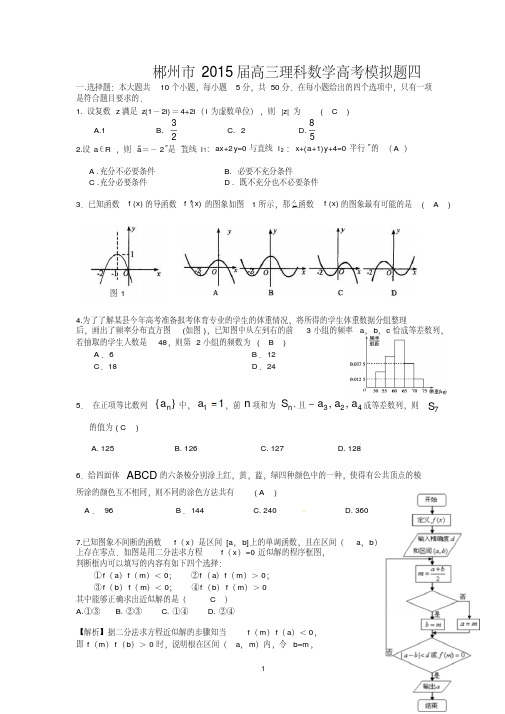
1 郴州市2015届高三理科数学高考模拟题四一.选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设复数z 满足z(1-2i)=4+2i (i 为虚数单位),则|z| 为( C ) A.1 B. 23C. 2D.582.设a ∈R ,则“a =-2”是“直线l 1:ax+2y=0与直线l 2 :x+(a+1)y+4=0平行”的(A )A .充分不必要条件B. 必要不充分条件C .充分必要条件D . 既不充分也不必要条件3.已知函数()f x 的导函数()f x 的图象如图1所示,那么函数()f x 的图象最有可能的是( A ) 4.为了了解某县今年高考准备报考体育专业的学生的体重情况,将所得的学生体重数据分组整理后,画出了频率分布直方图(如图),已知图中从左到右的前3小组的频率a ,b ,c 恰成等差数列,若抽取的学生人数是48,则第2小组的频数为(B )A .6B .12C .18D .245.在正项等比数列}{n a 中,11a ,前n 项和为n S ,且423,,a a a 成等差数列,则7S 的值为( C )A. 125B. 126C. 127D. 128 6.给四面体ABCD 的六条棱分别涂上红,黄,蓝,绿四种颜色中的一种,使得有公共顶点的棱所涂的颜色互不相同,则不同的涂色方法共有( A )A .96B .144 C. 240 D. 360 7.已知图象不间断的函数f (x )是区间[a ,b]上的单调函数,且在区间(a ,b )上存在零点.如图是用二分法求方程f (x )=0近似解的程序框图,判断框内可以填写的内容有如下四个选择:①f (a )f (m )<0;②f (a )f (m )>0;③f (b )f (m )<0;④f (b )f (m )>0 其中能够正确求出近似解的是(C )A.①③ B. ②③ C. ①④ D. ②④【解析】据二分法求方程近似解的步骤知当f (m )f (a )<0,即f (m )f (b )>0时,说明根在区间(a ,m )内,令b=m ,图1。
湖南省郴州市高三第二次教学质量监测理科数学试题及答案

郴州市高三第二次教学质量监测试卷数学(理科)一、选择题:本题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知复数满足,则的虚部是()A. -1B. 1C. -2D. 22. 已知,,则()A. B. C. D.3. 甲、乙、丙三人站成一排照相,甲排在左边的概率是()A. 1B.C.D.4. 如图所示程序框图的算法思路源于我国古代数学名著《九章算术》中的一种运算方法,执行该程序框图,若输入的,分别为12,20,则输出的()A. 0B. 14C. 4D. 25. 已知数列的前项和,且,则()A. 27B.C.D. 316. 函数 (其中,)的部分图象如图所示,将函数的图象()可得的图象()A. 向右平移个长度单位B. 向左平移个长度单位C. 向左平移个长度单位D. 向右平移个长度单位7. 设,,为正实数,且,则,,的大小关系是()A. B. C. D.8. 设等差数列的前项和为,已知,为整数,且,则数列前项和的最大值为()A. B. 1 C. D.9. 已知是定义在上的函数,对任意都有,若函数满足,且,则等于()A. 2B. 3C. -2D. -310. 如图,是抛物线()的焦点,直线过点且与抛物线及其准线交于,,三点,若,,则抛物线的标准方程是()A. B. C. D.11. 三棱锥的一条棱长为,其余棱长均为2,当三棱锥的体积最大时, 它的外接球的表面积为()A. B. C. D.12. 已知函数,,若与的图像上存在关于直线对称的点,则实数的取值范围是()A. B. C. D.第Ⅱ卷(共90分)二、填空题:本题共4小题,每题5分,满分20分,将答案填在答题卡上.13. 已知向量与的夹角为,且,,则__________.14. 某几何体的三视图如图所示,则该几何体的体积为__________.15. 设实数、满足:,实数、满足,若是的充分不必要条件,则正实数的取值范围是__________.16. 已知双曲线的左、右顶点分别为、,点为双曲线的左焦点,过点作垂直于轴的直线分别在第二、第三象限交双曲线于,点,连接交轴于点,连接交于点,若,则双曲线的离心率为__________.三、解答题:共70分.解答应写出文说明、证明过程或演算步骤,第22、23题为选考题,考生根据要求作答.17. 在中,内角的对边分别为,且,(Ⅰ)求角的大小;(Ⅱ)若,求的面积.18. 如图,在长方形中,,,现将沿折起,使折到的位置且在面的射影恰好在线段上.(Ⅰ)证明:;(Ⅱ)求锐二面角的余弦值.19. 某公司想了解对某产品投入的宣传费用与该产品的营业额的影响.下面是以往公司对该产品的宣传费用 (单位:万元)和产品营业额 (单位:万元)的统计折线图.(Ⅰ)根据折线图可以判断,可用线性回归模型拟合宣传费用与产品营业额的关系,请用相关系数加以说明;(Ⅱ)建立产品营业额关于宣传费用的归方程;(Ⅲ)若某段时间内产品利润与宣传费和营业额的关系为,应投入宣传费多少万元才能使利润最大,并求最大利润.参考数据:,,,,参考公式:相关系数,,回归方程中斜率和截距的最小二乘佔计公式分别为,.(计算结果保留两位小数)20. 已知椭圆的中心在原点,对称轴为坐标轴,椭圆与直线相切于点.(Ⅰ)求椭圆的标准方程;(Ⅱ)若直线与椭圆相交于、两点(,不是长轴端点),且以为直径的圆过椭圆在轴正半轴上的顶点,求证:直线过定点,并求出该定点的坐标.21. 函数,(Ⅰ)求函数在点处的切线方程;(Ⅱ)若时,有成立,求的取值范围.选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.22. 选修4-4:坐标系与参数方程已知曲线的极坐标方程是,以极点为平面直角坐标系的原点,极轴为轴的正半轴,建立平面直角坐标系,直线的参数方程是(是参数),(Ⅰ)写出直线的普通方程和曲线的直角坐标方程;(Ⅱ)设曲线经过伸缩变换得到曲线,曲线任一点为,求点直线的距离的最大值.23. 选修4-5:不等式选讲已知为正数,函数(Ⅰ)求不等式的解集;(Ⅱ)若的最小值为,且,求证:郴州市高三第二次教学质量监测试卷数学(理科)一、选择题:本题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知复数满足,则的虚部是()A. -1B. 1C. -2D. 2【答案】B∴∴的虚部是1故选:B2. 已知,,则()A. B. C. D.【答案】A【解析】由题意得:,,∴故选:A3. 甲、乙、丙三人站成一排照相,甲排在左边的概率是()A. 1B.C.D.【答案】D【解析】甲、乙、丙三人站成一排照相,共有种排法,其中甲排在左边的排法为种,∴甲排在左边的概率是故选:D4. 如图所示程序框图的算法思路源于我国古代数学名著《九章算术》中的一种运算方法,执行该程序框图,若输入的,分别为12,20,则输出的()A. 0B. 14C. 4D. 2【答案】C【解析】由a=12,b=20,不满足a>b,则b变为20﹣12=8,由a>b,则a=12﹣8=4,由b>a,则b变为8﹣4=4,由a=b=4,则输出的a=4.故选:C.点睛:本题主要考查程序框图的循环结构流程图,属于中档题. 解决程序框图问题时一定注意以下几点:(1) 不要混淆处理框和输入框;(2) 注意区分程序框图是条件分支结构还是循环结构;(3) 注意区分当型循环结构和直到型循环结构;(4) 处理循环结构的问题时一定要正确控制循环次数;(5) 要注意各个框的顺序,(6)在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算,直到达到输出条件即可.5. 已知数列的前项和,且,则()A. 27B.C.D. 31【答案】C【解析】∵,且,∴,即∴,当时,,∴,即,∴∴∴故选:C6. 函数 (其中,)的部分图象如图所示,将函数的图象()可得的图象()A. 向右平移个长度单位B. 向左平移个长度单位C. 向左平移个长度单位D. 向右平移个长度单位【答案】D【解析】由函数的部分图象知,,,解得,由五点法画图知,,解得,又将函数的图象向右平移个单位,可得的图象,故选D.7. 设,,为正实数,且,则,,的大小关系是()A. B. C. D.【答案】C【解析】x,y,z为正实数,且,可得:x=2k<1,y=3k<1,z=5k<1.∴=2k﹣1,=3k﹣1,=5k﹣1,令,又在上单调递减,∴,即故选:C.8. 设等差数列的前项和为,已知,为整数,且,则数列前项和的最大值为()A. B. 1 C. D.【答案】A【解析】a1=9,a2为整数,可知:等差数列{a n}的公差d为整数,由S n≤S5,∴a5≥0,a6≤0,则9+4d≥0,9+5d≤0,解得,d为整数,d=﹣2.∴a n=9﹣2(n﹣1)=11﹣2n.,∴数列前项和为令b n=,由于函数f(x)=的图象关于点(4.5,0)对称及其单调性,可知:0<b1<b2<b3<b4,b5<b6<b7<…<0,∴b n≤b4=1.∴最大值为=.故选:A9. 已知是定义在上的函数,对任意都有,若函数满足,且,则等于()A. 2B. 3C. -2D. -3【答案】B【解析】∵对任意x∈R,都有f(x+4)=f(x)+2f(2),∴f(﹣2+4)=f(﹣2)+2f(2)⇒f(﹣2)+f(2)=0⇒2f(2)=0⇒f(2)=0,∴f(x+4)=f(x)+2f(2)=f(x).即函数周期为4.∴f(2019)=f(4×504+3)=f(3)=f(﹣1)=f(1)=3.故选:B.10. 如图,是抛物线()的焦点,直线过点且与抛物线及其准线交于,,三点,若,,则抛物线的标准方程是()A. B. C. D.【答案】C【解析】分别过点A,B作准线的垂线,分别交准线于点E,D,设|BF|=a,则|BC|=3a,|BD|=a,∴,在直角三角形ACE中,∵|AB|=9,|AC|=9+3a,∴3|AE|=|AC|,∴=9+3a,即a=3,∵BD∥FG,∴,即,解得p=4,∴抛物线的方程为y2=8x.故选:C.11. 三棱锥的一条棱长为,其余棱长均为2,当三棱锥的体积最大时, 它的外接球的表面积为()A. B. C. D.【答案】B【解析】由题意画出三棱锥的图形,其中AB=BC=CD=BD=AC=2,AD=m;取BC,AD的中点分别为E,F,可知AE⊥BC,DE⊥BC,且AE∩DE=E,∴BC⊥平面AED,∴平面ABC⊥平面BCD时,三棱锥A﹣BCD的体积最大,此时AD=m=AE=×=;设三棱锥外接球的球心为O,半径为R,由球体的对称性知,球心O在线段EF上,∴OA=OC=R,又EF===,设OF=x,OE=﹣x,∴R2=+x2=+1,解得x=;∴球的半径R满足R2=,∴三棱锥外接球的表面积为4πR2=4π×=.故选:B.点睛:空间几何体与球接、切问题的求解方法(1)求解球与棱柱、棱锥的接、切问题时,一般过球心及接、切点作截面,把空间问题转化为平面图形与圆的接、切问题,再利用平面几何知识寻找几何中元素间的关系求解.(2)若球面上四点P,A,B,C构成的三条线段PA,PB,PC两两互相垂直,且PA=a,PB=b,PC=c,一般把有关元素“补形”成为一个球内接长方体,利用4R2=a2+b2+c2求解.12. 已知函数,,若与的图像上存在关于直线对称的点,则实数的取值范围是()A. B. C. D.【答案】D【解析】g(x)=关于直线y=1对称的直线为y=1﹣mx,∴直线y=1﹣mx与y=2lnx在[,e2]上有交点.作出y=1﹣mx与y=2lnx的函数图象,如图所示:若直线y=1﹣mx经过点(,﹣2),则m=3e,若直线y=1﹣mx与y=2lnx相切,设切点为(x,y).则,解得.∴≤m≤3e.故选:D.点睛:已知函数有零点求参数取值范围常用的方法和思路(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围;(2)分离参数法:先将参数分离,转化成求函数值域问题加以解决;(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结合求解.第Ⅱ卷(共90分)二、填空题:本题共4小题,每题5分,满分20分,将答案填在答题卡上.13. 已知向量与的夹角为,且,,则__________.【答案】2∴,即+∴,即∴故答案为:214. 某几何体的三视图如图所示,则该几何体的体积为__________.【答案】【解析】由三视图可知,该几何体由四分之三的圆柱与三棱锥组成,∴该几何体的体积为故答案为:15. 设实数、满足:,实数、满足,若是的充分不必要条件,则正实数的取值范围是__________.【答案】【解析】∵是的充分不必要条件,∴是的充分不必要条件,表示以为圆心,为半径的圆面,当圆面与直线相切时,圆面最大,∴∴正实数的取值范围是故答案为:16. 已知双曲线的左、右顶点分别为、,点为双曲线的左焦点,过点作垂直于轴的直线分别在第二、第三象限交双曲线于,点,连接交轴于点,连接交于点,若,则双曲线的离心率为__________.【答案】5【解析】根据题意,如图作出双曲线的草图:双曲线C:中,PQ过左焦点F且垂直与x轴,假设P在Q的上方,则x P=x Q=﹣c,将x=﹣c代入双曲线的方程可得:y P=,y Q=﹣,则|PF|=|FQ|=,又由OE∥PM,则△EOB∽△PFB,则有,则|EO|=c-a,而△EOA∽△MFA,则有,即,整理可得:c=5a,则e=5,故双曲线的离心率为5;故答案为:5.点睛:解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于a,b,c的方程或不等式,再根据a,b,c的关系消掉b得到a,c的关系式,建立关于a,b,c的方程或不等式,要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.三、解答题:共70分.解答应写出文说明、证明过程或演算步骤,第22、23题为选考题,考生根据要求作答.17. 在中,内角的对边分别为,且,(Ⅰ)求角的大小;(Ⅱ)若,求的面积.【答案】(Ⅰ);(Ⅱ).【解析】试题分析:(1)利用二倍角公式及商数关系得到,从而得到结果;(2)由,得,结合正余弦定理可得,又,,从而解得,进而得到的面积.试题解析:(Ⅰ)解法一:由,得,因为在中,,所以,即.又因为在中,,所以,,解法二:由,得,即,,.又因为中,,所以,,(Ⅱ)由,得根据正弦定理和余弦定理得,,即.又由(Ⅰ)知,所以.又,解得所以,面积为.18. 如图,在长方形中,,,现将沿折起,使折到的位置且在面的射影恰好在线段上.(Ⅰ)证明:;(Ⅱ)求锐二面角的余弦值.【答案】(Ⅰ)见解析;(Ⅱ).【解析】试题分析:(1)先证明平面,进而得到平面,从而得证;(2) 以为原点,建立空间直角坐标系.求出平面与平面的法向量,代入公式得到结果.试题解析:(Ⅰ)由题知平面,又平面,∴;又且,∴平面;又平面,∴;又且,∴平面;又平面,所以.(Ⅱ)在中,,由射影定理知,.以为原点,建立如图所示空间直角坐标系.则,,,,,,设是平面的一个法向量,则,∴,即,即,取,所以;设是平面的一个法向量,则,∴,即,即,取,所以;设锐二面角的大小为,则所以锐二面角余弦值为.点睛:空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离. 19. 某公司想了解对某产品投入的宣传费用与该产品的营业额的影响.下面是以往公司对该产品的宣传费用 (单位:万元)和产品营业额 (单位:万元)的统计折线图.(Ⅰ)根据折线图可以判断,可用线性回归模型拟合宣传费用与产品营业额的关系,请用相关系数加以说明;(Ⅱ)建立产品营业额关于宣传费用的归方程;(Ⅲ)若某段时间内产品利润与宣传费和营业额的关系为,应投入宣传费多少万元才能使利润最大,并求最大利润.参考数据:,,,,参考公式:相关系数,,回归方程中斜率和截距的最小二乘佔计公式分别为,.(计算结果保留两位小数)【答案】(Ⅰ)见解析;(Ⅱ);(Ⅲ)投入宣传费3万元时,可获得最大利润55.4万元. 【解析】试题分析:(1)由折线图中数据和参考数据得:, 从而可以用线性回归模型拟合与的关系;(2)根据公式求得,得到关于的回归方程为;(3),利用二次函数性质求最值.试题解析:(Ⅰ)由折线图中数据和参考数据得:,,因为与的相关系数近似为0.99,说明与的线性相关程度相当高,从而可以用线性回归模型拟合与的关系.(Ⅱ),,所以关于的回归方程为.(Ⅲ)由,可得时,.所以投入宣传费3万元时,可获得最大利润55.4万元.20. 已知椭圆的中心在原点,对称轴为坐标轴,椭圆与直线相切于点.(Ⅰ)求椭圆的标准方程;(Ⅱ)若直线与椭圆相交于、两点(,不是长轴端点),且以为直径的圆过椭圆在轴正半轴上的顶点,求证:直线过定点,并求出该定点的坐标.【答案】(Ⅰ);(Ⅱ)直线过定点,定点坐标为.【解析】试题分析:(1)利用点在椭圆上及相切关系布列方程组,即可解得椭圆的标准方程;(2)联立方程易得:,,以为直径的圆过椭圆在轴正半轴上的顶点,∴,即或,经检验得到结果.试题解析:法一(Ⅰ)由题意设椭圆的标准方程为(,且)∵在椭圆上,∴①由得∵椭圆与直线相切,∴,即②由①②知,故所求椭圆方程为法二:设椭圆为(,且)则它在点处的切线为,它与表示同一直线,∴,,∴,故所求椭圆方程为.(Ⅱ)设,,联立得得,,因为以为直径的圆过椭圆的上顶点∴即∴即即即∴或当时,直线过定点与已知矛盾当时,直线过定点满足所以,直线过定点,定点坐标为点睛:定点、定值问题通常是通过设参数或取特殊值来确定“定点”是什么、“定值”是多少,或者将该问题涉及的几何式转化为代数式或三角问题,证明该式是恒定的. 定点、定值问题同证明问题类似,在求定点、定值之前已知该值的结果,因此求解时应设参数,运用推理,到最后必定参数统消,定点、定值显现.21. 函数,(Ⅰ)求函数在点处的切线方程;(Ⅱ)若时,有成立,求的取值范围.【答案】(Ⅰ);(Ⅱ).【解析】试题分析:(1),又切线方程;(2),又在时取到最小值为,在时取到最大值为,∴,从而得到结果.试题解析:(Ⅰ)∴又所以在点处在切线方程为(Ⅱ)由于函数定义域为所以令则,可得当时,,当时,所以令,则,可得当时,,当时,所以因此,由得,所以,的取值范围为 (讨论分离常数或其它解法,适当给分)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.22. 选修4-4:坐标系与参数方程已知曲线的极坐标方程是,以极点为平面直角坐标系的原点,极轴为轴的正半轴,建立平面直角坐标系,直线的参数方程是(是参数),(Ⅰ)写出直线的普通方程和曲线的直角坐标方程;(Ⅱ)设曲线经过伸缩变换得到曲线,曲线任一点为,求点直线的距离的最大值. 【答案】(Ⅰ)直线的普通方程为,曲线的直角坐标方程为;(Ⅱ).【解析】试题分析:(1)利用代入消参法得到直线的普通方程,利用得到曲线的直角坐标方程;(2)曲线经过伸缩变换得到曲线为,利用点到直线距离公式得到点直线的距离,进而求出最大值.试题解析:(Ⅰ)直线的普通方程为,∵∴∴故曲线的直角坐标方程为,(Ⅱ)由(Ⅰ)得,经过伸缩变换得到曲线的方程为,所以曲线的方程,可以令(是参数),根据点到直线的距离公式可得,故点到直线的距离的最大值为.23. 选修4-5:不等式选讲已知为正数,函数(Ⅰ)求不等式的解集;(Ⅱ)若的最小值为,且,求证:【答案】(Ⅰ);(Ⅱ)见解析.【解析】试题分析:(Ⅰ)对分三种情况讨论,分别去掉绝对值符号,然后求解不等式组,再求并集即可得不等式的解集;(Ⅱ)利用基本不等式求出的最小值为,根据柯西不等式可得,从而可得结论.试题解析:(Ⅰ)等价于或或,解得或或所以不等式的解集为.(Ⅱ)因为,所以,即.法1:∵,,∴∴,∴.当且仅当时等号成立法2:由柯西不等式得:,∴∴,当且仅当时等号成立。
湖南省郴州市高考数学二模试卷(理科)含答案解析

湖南省郴州市高考数学二模试卷(理科)一、选择题:本大题共12小题,每小题5分,共60分,每小题给出四个选项,只有一个选项符合题目要求.1.若复数z满足zi=1﹣i,则z的共轭复数是()A.﹣1﹣i B.1﹣i C.﹣1+i D.1+i2.若A={x|x2+2x﹣8<0},B={x|x<1},则图中阴影部分表示的集合为()A.(﹣4,1]B.(1,2)C.[1,2)D.(﹣4,1)3.如图所示,程序框图(算法流程图)的输出结果是()A.B. C.D.4.某全日制大学共有学生5400人,其中专科生有1500人,本科生有3000人,研究生有900人.现采用分层抽样的方法调查学生利用因特网查找学习资料的情况,抽取的样本为180人,则应在专科生、本科生与研究生这三类学生中分别抽取()A.55人,80人,45人B.40人,100人,40人C.60人,60人,60人D.50人,100人,30人5.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是()A.若α⊥β,m⊂α,n⊂β,则m⊥n B.若α∥β,m⊂α,n⊂β,则m∥nC.若m⊥n,m⊂α,n⊂β,则α⊥βD.若m⊥α,m∥n,n∥β,则α⊥β6.直线与圆O:x2+y2=4交于A、B两点,则=()A.2 B.﹣2 C.4 D.﹣47.某班5位同学分别选择参加数学、物理、化学这3个学科的兴趣小组,每人限选一门学科,则每个兴趣小组都至少有1人参加的不同选择方法种数为()A.150 B.180 C.240 D.5408.如图,椭圆+y2=1的左、右焦点分别为F1,F2,短轴端点分别为B1,B2,现沿B1B2将椭圆折成120°角(图二),则异面直线F1B2与B1F2所成角的余弦值为()A.0 B.C.D.﹣9.在区间[﹣1,1]上任取两数m和n,则关于x的方程x2+mx+n=0的两根都是负数的概率()A. B. C. D.10.设点P是曲线C:y=x3﹣x+上的任意一点,曲线C在P点处的切线的倾斜角为α,则角α的取值范围是()A.[π,π)B.(,π]C.[0,)∪[π,π)D.[0,)∪[π,π)11.已知倾斜角为的直线与双曲线C:﹣=1(a>0,b>0)相交于A,B两点,M(4,2)是弦AB的中点,则双曲线C的离心率是()A.B. C.2 D.12.已知定义在R上的函数f(x)满足f(2)=1,且f(x)的导数f′(x)在R上的恒有f′(x)<(x∈R),则不等式f(x2)<+的解集为()A.(﹣∞,﹣2)∪(2,+∞)B.(﹣2,2) C.(﹣∞,﹣)∪(,+∞)D.(﹣,)二、填空题:本大题共4小题,每小题5分,共25分.13.已知四边形ABCD满足|AB|=|AD|,|CD|=且∠BAD=60°,﹣=,那么四边形ABCD的面积为.14.记不等式组所表示的平面区域为D.若直线y=a(x+1)与D有公共点,则a的取值范围是.15.一个空间几何体的三视图如图所示,且这个空间几何体的所有顶点都在同一个球面上,则这个球的表面积是.16.已知函数f(x)=asinx+bcosx(其中ab≠0)且对任意的x∈R,有f(x)≤f(),给出以下命题:①a=b;②f(x+)为偶函数;③函数y=f(x)的图象关于点(,0)对称;④函数y=f′(x)的图象可由函数y=f(x)的图象向左平移得到;⑤函数f(x)在y轴右侧的图象与直线y=的交点按横坐标从小到大依次为P1,P2,P3,P4,…,则|P2P4|=2π.其中正确命题的序号是.(将所有正确命题的序号都填上)三、解答题:本大题共6小题,满分70分,解答须写出文字说明、证明过程或演算步骤. 17.已知函数f(x)=sin2x﹣cos2x﹣,x∈R.(1)求函数f(x)的最小正周期及单调递增区间;(2)设△ABC的内角A,B,C的对边分别为a,b,c,且c=,f(C)=0,sinB=2sinA,求△ABC的面积S.18.已知数列{a n}满足a1=3,且对任意的正整数m,n都有a n+m=a n•a m,若数列{b n}满足b n=n﹣1+log3a n,{b n}的前n项和为B n.(Ⅰ)求a n和B n;(Ⅱ)令c n=a n•b n,d n=,数列{c n}的前n项和为S n,数列{d n}的前n项和为T n,分别求S n和T n.19.如图,四棱锥P﹣ABCD的底面ABCD是菱形,且∠ABC=60°,侧面PAD是边长为2的正三角形且与底面ABCD垂直.(Ⅰ)求证:BC⊥PC;(Ⅱ)线段PC上是否存在点M,使得二面角P﹣AD﹣M的平面角余弦值为?若存在,求出的值;若不存在,说明理由.20.已知函数(1)若x=1是函数f(x)的极大值点,求函数f(x)的单调递减区间;(2)若恒成立,求实数ab的最大值.21.已知椭圆Γ的中心在原点,焦点F1,F2在x轴上,离心率等于,它的一个顶点恰好是抛物线y=x2的焦点.(1)求椭圆Γ的标准方程;(Ⅱ)Q为椭圆Γ的左顶点,直线l经过点(﹣,0)与椭圆Γ交于A,B两点.(1)若直线l垂直于x轴,求∠AQB的大小;(2)若直线l与x轴不垂直,是否存在直线l使得△QAB为等腰三角形?如果存在,求出直线l的方程;如果不存在,请说明理由.22.已知a为实数,函数f(x)=alnx+x2﹣4x.(Ⅰ)是否存在实数a,使得f(x)在x=1处取极值?证明你的结论;(Ⅱ)若函数f(x)在[2,3]上存在单调递增区间,求实数a的取值范围;(Ⅲ)设g(x)=(a﹣2)x,若存在x0∈[,e],使得f(x0)≤g(x0)成立,求实数a 的取值范围.湖南省郴州市高考数学二模试卷(理科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分,每小题给出四个选项,只有一个选项符合题目要求.1.若复数z满足zi=1﹣i,则z的共轭复数是()A.﹣1﹣i B.1﹣i C.﹣1+i D.1+i【考点】复数代数形式的乘除运算.【分析】由复数z满足zi=1﹣i,可得z,从而求出即可.【解答】解:∵复数z满足zi=1﹣i,∴z===﹣1﹣i,故=﹣1+i,故选:C.2.若A={x|x2+2x﹣8<0},B={x|x<1},则图中阴影部分表示的集合为()A.(﹣4,1]B.(1,2)C.[1,2)D.(﹣4,1)【考点】Venn图表达集合的关系及运算.【分析】先观察Venn图,由图可知阴影部分表示的集合为(C R B)∩A,根据集合的运算求解即可.【解答】解:A={x|x2+2x﹣8<0}=(﹣4,2),∵B={x|x<1},∴C R B=[1,+∞),∴(C R B)∩A=[1,2).故选:C.3.如图所示,程序框图(算法流程图)的输出结果是()A.B. C.D.【考点】程序框图.【分析】模拟程序图框的运行过程,得出当n=8时,不再运行循环体,直接输出S值.【解答】解:模拟程序图框的运行过程,得;该程序运行后输出的是计算S=++=.故选:D.4.某全日制大学共有学生5400人,其中专科生有1500人,本科生有3000人,研究生有900人.现采用分层抽样的方法调查学生利用因特网查找学习资料的情况,抽取的样本为180人,则应在专科生、本科生与研究生这三类学生中分别抽取()A.55人,80人,45人B.40人,100人,40人C.60人,60人,60人D.50人,100人,30人【考点】分层抽样方法.【分析】先根据总体数和抽取的样本,求出每个个体被抽到的概率,用每一个层次的数量乘以每个个体被抽到的概率就等于每一个层次的值.【解答】解:每个个体被抽到的概率为=,∴专科生被抽的人数是×1500=50,本科生要抽取×3000=100,研究生要抽取×900=30,故选:D.5.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是()A.若α⊥β,m⊂α,n⊂β,则m⊥n B.若α∥β,m⊂α,n⊂β,则m∥nC.若m⊥n,m⊂α,n⊂β,则α⊥βD.若m⊥α,m∥n,n∥β,则α⊥β【考点】空间中直线与平面之间的位置关系;命题的真假判断与应用;平面与平面之间的位置关系.【分析】由α⊥β,m⊂α,n⊂β,可推得m⊥n,m∥n,或m,n异面;由α∥β,m⊂α,n ⊂β,可得m∥n,或m,n异面;由m⊥n,m⊂α,n⊂β,可得α与β可能相交或平行;由m⊥α,m∥n,则n⊥α,再由n∥β可得α⊥β.【解答】解:选项A,若α⊥β,m⊂α,n⊂β,则可能m⊥n,m∥n,或m,n异面,故A 错误;选项B,若α∥β,m⊂α,n⊂β,则m∥n,或m,n异面,故B错误;选项C,若m⊥n,m⊂α,n⊂β,则α与β可能相交,也可能平行,故C错误;选项D,若m⊥α,m∥n,则n⊥α,再由n∥β可得α⊥β,故D正确.故选D.6.直线与圆O:x2+y2=4交于A、B两点,则=()A.2 B.﹣2 C.4 D.﹣4【考点】平面向量数量积的运算;直线与圆相交的性质.【分析】先求圆心到直线的距离,再求弦心距所在直线与AO的夹角,然后求数量积.【解答】解:圆O:x2+y2=4的圆心是(0,0),由此知圆心到直线的距离是=<2所以直线与圆相交故AB=2=2=r,所以∠AOB=所以=2×2×cos=2故选A7.某班5位同学分别选择参加数学、物理、化学这3个学科的兴趣小组,每人限选一门学科,则每个兴趣小组都至少有1人参加的不同选择方法种数为()A.150 B.180 C.240 D.540【考点】计数原理的应用.【分析】根据题意,分析有将5位同学分成满足题意的3组有1,1,3与2,2,1两种,分别计算可得分成1、1、3与分成2、2、1时的分组情况种数,进而相加可得答案.【解答】解:将5位同学分成满足题意的3组有1,1,3与2,2,1两种,分成1、1、3时,有C53•A33=60种,分成2、2、1时,有=90种,所以共有60+90=150种,故选:A.8.如图,椭圆+y2=1的左、右焦点分别为F1,F2,短轴端点分别为B1,B2,现沿B1B2将椭圆折成120°角(图二),则异面直线F1B2与B1F2所成角的余弦值为()A.0 B.C.D.﹣【考点】椭圆的简单性质.【分析】由OF1⊥B1B2,OF2⊥B1B2,可得∠F1OF2为二面角F1﹣B1B2﹣F2的平面角,即为120°,求得椭圆的a,b,c,运用向量的夹角公式可得cos<,>=,计算即可得到所求异面直线所成的角的余弦值.【解答】解:由OF1⊥B1B2,OF2⊥B1B2,可得∠F1OF2为二面角F1﹣B1B2﹣F2的平面角,即为120°,椭圆+y2=1中a=,b=1.c=,可得B1F2=B2F1==,=+, =+,•=•+•+•+•=﹣1+0+0+••(﹣)=﹣2,即有cos<,>===﹣,可得异面直线F1B2与B1F2所成角的余弦值为.故选:C.9.在区间[﹣1,1]上任取两数m和n,则关于x的方程x2+mx+n=0的两根都是负数的概率()A. B. C. D.【考点】几何概型.【分析】根据几何概型的概率公式,利用积分求出对应区域的面积进行求解即可.【解答】解:∵区间[﹣1,1]上任取两数m和n,∴,对应的区域为正方形,面积S=2×2=4,若方程x2+mx+n=0的两根都是负数,则,即,作出不等式组对应的平面区域如图:则对应的面积S=∫dm=m3|=,则对应的概率P==,故选:A.10.设点P是曲线C:y=x3﹣x+上的任意一点,曲线C在P点处的切线的倾斜角为α,则角α的取值范围是()A.[π,π)B.(,π]C.[0,)∪[π,π)D.[0,)∪[π,π)【考点】利用导数研究曲线上某点切线方程.【分析】求函数的导数,利用导数的几何意义求出切线斜率的取值范围,结合正切函数的图象和性质进行求解即可.【解答】解:函数的导数f′(x)=3x2﹣,则f′(x)=3x2﹣≥﹣,即tanα≥﹣,则0≤α<或π≤α<π,故角α的取值范围是[0,)∪[π,π),故选:D11.已知倾斜角为的直线与双曲线C:﹣=1(a>0,b>0)相交于A,B两点,M(4,2)是弦AB的中点,则双曲线C的离心率是()A.B. C.2 D.【考点】双曲线的简单性质.【分析】设A(x1,y1),B(x2,y2),根据AB的中点P的坐标,表示出斜率,从而得到关于a、b的关系式,再求离心率.【解答】解:∵倾斜角为的直线与双曲线C:﹣=1(a>0,b>0)相交于A,B两点,∴直线的斜率k=tan=,设A(x1,y1),B(x2,y2),则﹣=1,①;﹣=1,②,①﹣②得=,则k==•∵M(4,2)是AB的中点,∴x1+x2=8,y1+y2=4,∵直线l的斜率为,∴=•,即=,则b2=a2,c2=a2+b2=(1+)a2,∴e2=1+==()2.则e=故选:D.12.已知定义在R上的函数f(x)满足f(2)=1,且f(x)的导数f′(x)在R上的恒有f′(x)<(x∈R),则不等式f(x2)<+的解集为()A.(﹣∞,﹣2)∪(2,+∞)B.(﹣2,2) C.(﹣∞,﹣)∪(,+∞)D.(﹣,)【考点】利用导数研究函数的单调性;不等式的综合.【分析】由f′(x)<,构造辅助函数g(x)=f(x)﹣x,求导,利用导数判断函数单调递减,根据f(2)=1,求得g(2)=,根据f(x2)<+,将其转换成g(x2)<g (2),根据函数单调性即可求得不等的解集.【解答】解:f′(x)<(x∈R),f′(x)﹣<0,设g(x)=f(x)﹣x,g′(x)=f′(x)﹣<0,∴g(x)是R上的减函数,g(2)=g(2)﹣=,∴f(x2)<+,g(x2)=f(x2)﹣<=g(2),∴x2>2,解得:x>或x<﹣,∴原不等式的解集为(﹣∞,﹣)∪(,+∞).故答案选:C.二、填空题:本大题共4小题,每小题5分,共25分.13.已知四边形ABCD满足|AB|=|AD|,|CD|=且∠BAD=60°,﹣=,那么四边形ABCD的面积为.【考点】向量的线性运算性质及几何意义.【分析】由题意作图辅助,从而可判断四边形为直角梯形,从而求其面积.【解答】解:由题意作图如右图,∵﹣==,∴BC∥AD且|BC|=|AD|,又∵|AB|=|AD|,且∠BAD=60°,∴|AE|=|AB|=|AD|,∴|BC|=|DE|,∴BCDE是平行四边形,∴CD∥BE,∴DC⊥AD,∵|CD|=,∴|AB|=|AD|=2,∴S==,故答案为:.14.记不等式组所表示的平面区域为D.若直线y=a(x+1)与D有公共点,则a的取值范围是[,4].【考点】简单线性规划.【分析】本题考查的知识点是简单线性规划的应用,我们要先画出满足约束条件的平面区域,然后分析平面区域里各个角点,然后将其代入y=a(x+1)中,求出y=a(x+1)对应的a的端点值即可.【解答】解:满足约束条件的平面区域如图示:因为y=a(x+1)过定点(﹣1,0).所以当y=a(x+1)过点B(0,4)时,得到a=4,当y=a(x+1)过点A(1,1)时,对应a=.又因为直线y=a(x+1)与平面区域D有公共点.所以≤a≤4.故答案为:[,4]15.一个空间几何体的三视图如图所示,且这个空间几何体的所有顶点都在同一个球面上,则这个球的表面积是16π.【考点】由三视图求面积、体积.【分析】由三视图知,几何体是一个三棱柱,三棱柱的底面是边长为3的正三角形,侧棱长是2,根据三棱柱的两个底面的中心的中点与三棱柱的顶点的连线就是外接球的半径,求出半径即可求出球的表面积.【解答】解:由三视图知,几何体是一个三棱柱ABC﹣A1B1C1,三棱柱的底面是边长为3的正三角形ABC,侧棱长是2,三棱柱的两个底面的中心连接的线段MN的中点O与三棱柱的顶点A的连线AO就是外接球的半径,∵△ABC是边长为3的等边三角形,MN=2,∴AM=,OM=1,∴这个球的半径r==2,∴这个球的表面积S=4π×22=16π,故答案为:16π.16.已知函数f(x)=asinx+bcosx(其中ab≠0)且对任意的x∈R,有f(x)≤f(),给出以下命题:①a=b;②f(x+)为偶函数;③函数y=f(x)的图象关于点(,0)对称;④函数y=f′(x)的图象可由函数y=f(x)的图象向左平移得到;⑤函数f(x)在y轴右侧的图象与直线y=的交点按横坐标从小到大依次为P1,P2,P3,P4,…,则|P2P4|=2π.其中正确命题的序号是①②④⑤.(将所有正确命题的序号都填上)【考点】命题的真假判断与应用.【分析】由三角函数的最大值相等列式判断①;利用辅助角公式化简代值判断②;求出得值判断③;求导后利用函数的图象平移判断④;由函数图象平移周期不变判断⑤【解答】解:①f(x)=asinx+bcosx=,∵对任意的x∈R,有f(x)≤f(),∴,则2a2+2b2=(a+b)2,∴(a﹣b)2=0,则a=b,故①正确;②∵f(x)=asinx+bcosx=a(sinx+cosx)=,∴f(x+)=,∴f(x+)为偶函数,故②正确;③∵=≠0,故③错误;④y=f′(x)=acosx﹣asinx==,而f(x+)==,故④正确;⑤由f(x)的周期为2π,而f(x)=是把向左平移个单位得到的,∴|P2P4|=2π,故⑤正确.故答案为:①②④⑤.三、解答题:本大题共6小题,满分70分,解答须写出文字说明、证明过程或演算步骤.17.已知函数f(x)=sin2x﹣cos2x﹣,x∈R.(1)求函数f(x)的最小正周期及单调递增区间;(2)设△ABC的内角A,B,C的对边分别为a,b,c,且c=,f(C)=0,sinB=2sinA,求△ABC的面积S.【考点】三角函数中的恒等变换应用;正弦函数的图象.【分析】(1)由三角函数中的恒等变换应用化简函数解析式可得f(x)=sin(2x﹣)﹣1,由周期公式可求最小正周期,由2k,k∈Z 可解得单调递增区间.(2)由f(C)=sin(2C﹣)﹣1=0,可得sin(2C﹣)=1,解得C的范围利用正弦函数的图象和性质即可求得C的值,由sinB=2sinA,利用正弦定理,余弦定理即可解得a,b,根据三角形面积公式即可得解.【解答】解:(1)∵f(x)=sin2x﹣cos2x﹣=sin2x﹣=sin(2x﹣)﹣1,…∴最小正周期T=,.由2k,k∈Z 得k,k∈Z,∴f(x)的最小正周期为π,单调递增区间为[k,k](k∈Z).…(2)f(C)=sin(2C﹣)﹣1=0,则sin(2C﹣)=1,∵0<C<π,∴0<2C<2π,∴﹣,∴2C﹣=,∴C=,…∵sinB=2sinA,由正弦定理,得,①由余弦定理,得c2=a2+b2﹣2abcos,即a2+b2﹣ab=3,②由①②解得a=1,b=2.∴S△ABC==.…18.已知数列{a n}满足a1=3,且对任意的正整数m,n都有a n+m=a n•a m,若数列{b n}满足b n=n﹣1+log3a n,{b n}的前n项和为B n.(Ⅰ)求a n和B n;(Ⅱ)令c n=a n•b n,d n=,数列{c n}的前n项和为S n,数列{d n}的前n项和为T n,分别求S n和T n.【考点】数列的求和;数列递推式.【分析】(I)对任意的正整数m,n都有a n+m=a n•a m,可得a n+1=a n•a1=3a n,利用等比数列的通项公式可得a n.可得b n,即可得出{b n}的前n项和为B n.(II)c n=(2n﹣1)•3n.利用“错位相减法”与等比数列的前n项和公式可得S n.d n===,利用“裂项求和”即可得出.【解答】解:(I)∵对任意的正整数m,n都有a n+m=a n•a m,∴a n+1=a n•a1=3a n,∴数列{a n}是等比数列,公比为3,首项为3,∴a n=3n.∴b n=n﹣1+log3a n=n﹣1+n=2n﹣1,∴{b n}的前n项和为B n==n2.(II)c n=a n•b n,=(2n﹣1)•3n.∴数列{c n}的前n项和为S n=3+3×32+5×33+…+(2n﹣1)•3n,∴3S n=32+3×33+…+(2n﹣3)•3n+(2n﹣1)•3n+1,∴﹣2S n=3+2(32+33+…+3n)﹣(2n﹣1)•3n+1=﹣3﹣(2n﹣1)•3n+1=(2﹣2n)•3n+1﹣6,∴S n=(n﹣1)•3n+1+3.d n===,当n=1时,d1=;当n≥2时,T n=+++…++=﹣﹣.当n=1时也成立,∴T n=﹣﹣.19.如图,四棱锥P﹣ABCD的底面ABCD是菱形,且∠ABC=60°,侧面PAD是边长为2的正三角形且与底面ABCD垂直.(Ⅰ)求证:BC⊥PC;(Ⅱ)线段PC上是否存在点M,使得二面角P﹣AD﹣M的平面角余弦值为?若存在,求出的值;若不存在,说明理由.【考点】二面角的平面角及求法;空间中直线与直线之间的位置关系.【分析】(Ⅰ)取AD中点O,连结OP,OC,以O为原点,OC为x轴,OD为y轴,OP 为z轴,建立空间直角坐标系,利用向量法能证明BC⊥PC.(Ⅱ)设M(a,b,c),由=λ可得点M的坐标为M(λ,0,﹣λ),求出平面AMD的法向量和平面PAD的法向量,由此利用向量法能求出结果.【解答】(Ⅰ)证明:取AD中点O,连结OP,OC,∵侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,∴△ADC是等边三角形,PO、AD、CO两两垂直,以O为原点,OC为x轴,OD为y轴,OP为z轴,建立空间直角坐标系,由题意得P(0,0,),C(,0,0),B(,﹣2,0),=(0,﹣2,0),=(﹣,0,),∴=0,∴CB⊥CP.(Ⅱ)解:假设存在符合要求的点M,令=λ(0≤λ≤1),则=λ=λ(,0,﹣),可得M(λ,0,﹣λ),∴=(λ,1,﹣λ),=(λ,﹣1,﹣λ),设平面MAD的法向量为=(x,y,z),则,令z=λ,得=(λ﹣1,0,λ),显然平面PAD的一个法向量为=(,0,0),∵二面角P﹣AD﹣M的平面角余弦值为,∴|=,∴λ=或λ=﹣1(舍去)∴线段PC上存在点M, =时,使得二面角P﹣AD﹣M的平面角余弦值为.20.已知函数(1)若x=1是函数f(x)的极大值点,求函数f(x)的单调递减区间;(2)若恒成立,求实数ab的最大值.【考点】利用导数求闭区间上函数的最值;函数在某点取得极值的条件.【分析】(1)求导数,利用x=1是函数f(x)的极大值点,确定a的范围,即可得到函数f(x)的单调递减区间;(2)构造函数,确定函数的单调性,可得函数的最值,即可得到结论.【解答】解:(1)求导数可得,f′(x)=∵x=1是函数f(x)的极大值点,∴0<a<1∴函数f(x)的单调递减区间为(0,a),(1,+∞);(2)∵恒成立,∴alnx﹣x+b≤0恒成立,令g(x)=alnx﹣x+b,则g′(x)=∴g(x)在(0,a)上单调递增,在(a,+∞)上单调递减∴g(x)max=g(a)=alna﹣a+b≤0∴b≤a﹣lna,∴ab≤a2﹣a2lna令h(x)=x2﹣x2lnx(x>0),则h′(x)=x(1﹣2lnx)∴h(x)在(0,)上单调递增,在(,+∞)上单调递减∴h(x)max=h()=,∴ab≤即ab的最大值为.21.已知椭圆Γ的中心在原点,焦点F1,F2在x轴上,离心率等于,它的一个顶点恰好是抛物线y=x2的焦点.(1)求椭圆Γ的标准方程;(Ⅱ)Q为椭圆Γ的左顶点,直线l经过点(﹣,0)与椭圆Γ交于A,B两点.(1)若直线l垂直于x轴,求∠AQB的大小;(2)若直线l与x轴不垂直,是否存在直线l使得△QAB为等腰三角形?如果存在,求出直线l的方程;如果不存在,请说明理由.【考点】抛物线的简单性质.【分析】(I)设椭圆的标准方程为:,根据条件列方程组解出a,b即可;(II)(1)把x=﹣代入椭圆方程解出A,B坐标,根据三角形的边长即可求出∠AQB;(2)设AB斜率为k,联立方程组求出A,B坐标的关系,通过计算=0得出,则当△QAB为等腰直角三角形时,取AB中点N,则QN⊥AB,计算QN的斜率判断是否为﹣即可得出结论.【解答】解:(I)设椭圆的标准方程为:,(a>b>0).抛物线y=x2的焦点为(0,1),∴,解得a2=4,∴椭圆Γ的标准方程为+y2=1.(II)Q(﹣2,0),设A(x1,y1),B(x2,y2),(1)当直线l垂直于x轴时,直线l的方程为x=﹣.则直线l与x轴交于M(﹣,0).联立方程组,解得或.不妨设A在第二象限,则A(﹣,),B(﹣,﹣).∴|QM|=|AM|=.∴∠AQM=45°,∴∠AQB=2∠AQM=90°.(2)当直线l与x轴不垂直时,设直线l方程为y=k(x+)(k≠0).联立方程组,消元得(25+100k2)x2+240k2x+144k2﹣100=0.∴x1+x2=,x1x2=.y1y2=k2(x1+)(x2+)=﹣•+.∵=(x1+2,y1),=(x2+2,y2),∴=x1x2+2(x1+x2)+4+y1y2=﹣+4+﹣•+=0.∴QA⊥QB,即△QAB是直角三角形.假设存在直线l使得△QAB是等腰直角三角形,则|QA|=|QB|.取AB的中点N,连结QN,则QN⊥AB.又x N=(x1+x2)=﹣=﹣,y N=k(x N+)=.∴k QN=,∴k QN•k AB=≠﹣1.∴QN与AB不垂直,矛盾.∴直线l与x轴不垂直,不存在直线l使得△QAB为等腰三角形.22.已知a为实数,函数f(x)=alnx+x2﹣4x.(Ⅰ)是否存在实数a,使得f(x)在x=1处取极值?证明你的结论;(Ⅱ)若函数f(x)在[2,3]上存在单调递增区间,求实数a的取值范围;(Ⅲ)设g(x)=(a﹣2)x,若存在x0∈[,e],使得f(x0)≤g(x0)成立,求实数a的取值范围.【考点】利用导数研究函数的单调性;利用导数研究曲线上某点切线方程.【分析】(Ⅰ)求得函数的定义域,求导,假设存在实数a,使f(x)在x=1处取极值,则f′(1)=0,解出a的值,根据x=1的左右单调性是否相同,即可判断x=1是不是极值点;(Ⅱ)先求出f(x)的导数,将问题转化成,a≥2﹣2(x﹣1)2,在x∈[2,3]有解,构造辅助函数,利用函数的求得φ(x)=2﹣2(x﹣1)2的最小值,即可求得a的取值范围.(Ⅲ)在[1,e]上存在一点x0,使得f(x0)<g(x0)成立,即在[,e],上存在一点x0,使得G(x0)<0,即函数G(x)在[,e],上的最小值小于零.对G(x)求导.求出G(x)的最小值,即可a的取值范围.【解答】解:(Ⅰ)函数f(x)的定义域为(0,+∞),f′(x)=+2x﹣4=,假设存在实数a,使得f(x)下x=1处取极值,则f′(1)=0,∴a=2,此时,f(x)=,∴当0<x<1时,f′(x)>0,f(x)单调递增,当x>1时,f′(x)>0,f(x)单调递增,∴x=1不是f(x)的极值点,故不存在实数a,使得f(x)=1处取极值.(Ⅱ)f′(x)==(x>0),问题等价于,存在x∈[2,3],使得f′(x)≥0,即a≥2﹣2(x﹣1)2,在x∈[2,3]有解,∴φ(x)=2﹣2(x﹣1)2,在[2,3]上递减,∴φmin=φ(3)=﹣6,∴a>﹣6;(Ⅲ)记F(x)=x﹣lnx,∴F′(x)=(x>0),∴当0<x<1,F′(x)<0,F(x)单调递减;当x>1时,F′(x)>0,F(x)单调递增;∴F(x)≥F(1)=1>0,即x>lnx,(x>0),由f(x0)≤g(x0)得:(x0﹣lnx0)a≥x02﹣2x0,∴a≥,记G(x)=,x∈[,e],G′(x)==,x∈[,e],∴2﹣2lnx=2(1﹣lnx)≥0,∴x﹣2lnx+2>0,∴x∈(,e)时,G′(x)<0,G(x)递减,x∈(1,e)时,G′(x)>0,G(x)递增,∴a≥G(x)min=G(1)=﹣1,故实数a的取值范围为[﹣1,+∞).8月1日。
2015年高考湖南理科数学试题及答案(详解纯word版)
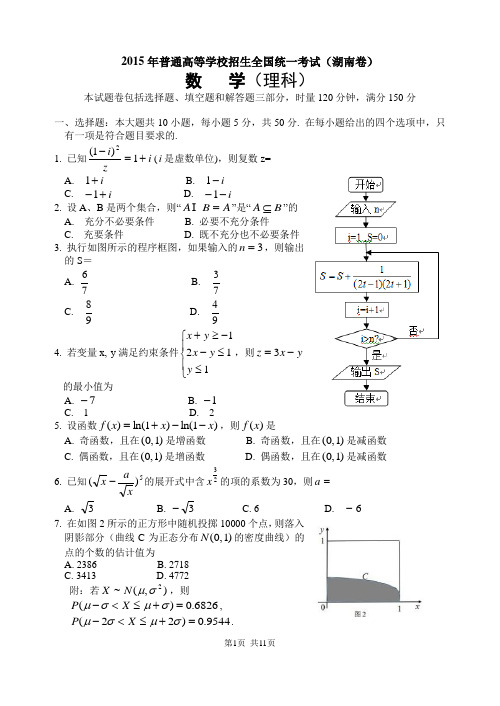
2015年普通高等学校招生全国统一考试(湖南卷)数 学(理科)本试题卷包括选择题、填空题和解答题三部分,时量120分钟,满分150分一、选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知i zi +=-1)1(2(i 是虚数单位),则复数z=A. i +1B. i -1C. i +-1D. i --12. 设A 、B 是两个集合,则“A B A = ”是“B A ⊆”的A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件 3. 执行如图所示的程序框图,如果输入的3=n ,则输出的S =A.76 B. 73C. 98D. 944. 若变量x, y 满足约束条件⎪⎩⎪⎨⎧≤≤--≥+1121y y x y x ,则yx z -=3的最小值为A. 7-B. 1-C. 1D. 2 5. 设函数)1ln()1ln()(x x x f --+=,则)(x f 是A. 奇函数,且在)1,0(是增函数B. 奇函数,且在)1,0(是减函数C. 偶函数,且在)1,0(是增函数D. 偶函数,且在)1,0(是减函数 6. 已知5)(xa x -的展开式中含23x 的项的系数为30,则=aA. 3B. 3-C. 6D. 6- 7. 在如图2所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C 为正态分布)1,0(N 的密度曲线)的点的个数的估计值为A. 2386B. 2718C. 3413D. 4772附:若),(~2σμN X ,则6826.0)(=+≤<-σμσμX P , 9544.0)22(=+≤<-σμσμX P.8. 已知点A, B, C 在圆122=+y x 上运动,且BC AB ⊥ . 若点P 的坐标为)0,2(, 则||PC PB PA ++的最大值为A. 6B. 7C. 8D. 9 9. 将函数x x f 2sin )(=的图象向右平移ϕ)20(πϕ<<个单位后得到函数)(x g 的图象,若对满足2|)()(|21=-x g x f 的1x ,2x ,有3||min 21π=-x x ,则=ϕA. 125πB. 3πC.4π D. 6π 10. 某工件的三视图如图所示,现将该工件通过切削,加工成体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料的利用率原工件的体积新工件的体积=) A. π98 B. π916C.π2124)-( D.π21212)-(二、填空题:本大题共5小题,每小题5分,共25分. 11.⎰=-20)1(dx x __________.12. 在一次马拉松比赛中,35名运动员的成绩(单位:分钟)茎叶图如图所示若将运动员按成绩由好到差编为1-35号,再用系统抽样的方法从中抽取7人,则其中成绩在区间]151,139[上的运动员的人数是_________.13. 设F 是双曲线C 1:2222=-by a x 的一个焦点,若C 上存在点P ,使线段PF 的中点恰为其虚轴的一个端点,则C 的离心率为________.14.设n S 为等比数列}{n a 的前n 项和,若11=a ,且321,2,3S S S 成等差数列,则=n a ___________.15. 已知函数⎪⎩⎪⎨⎧>≤=.,,,)(23a x x a x x x f 若存在实数b ,使函数b x f x g -=)()(有两个零点,则a 的取值范围是___________.俯视图侧视图正视图三、解答题:本大题共6小题,共75分. 解答应写出文字说明、证明过程或演算步骤. 16. (本小题满分12分)本小题有Ⅰ、Ⅱ、Ⅲ三个选做题,请考生任选两题作答,并将解答过程写在答题纸中相应题号的答题区域内,如果全做,则按所做的前两题计分. Ⅰ.(本小题满分6分)选修4-1 几何证明选讲如图,在⊙O 中,相交于点E 的两弦AB ,CD 的中点分别是M ,N ,直线MO 与直线CD 相交于点F ,证明:(i ) 180=∠+∠NOM MEN ; (ii )FO FM FN FE ⋅=⋅. Ⅱ.(本小题满分6分)选修4-4 坐标系与参数方程已知直线l ⎪⎪⎩⎪⎪⎨⎧+=+=.213,235:t y t x (t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为θρcos 2=.(i )将曲线C 的极坐标方程化为直角坐标方程;(ii )设点M 的直角坐标为)3,5(,直线l 与曲线C 的交点为A ,B ,求||||MB MA ⋅的值. Ⅲ.(本小题满分6分)选修4-5 不等式选讲 设0,0>>b a ,且ba b a 11+=+,证明: (i ) 2≥+b a ;(ii )22<+a a 与22<+b b 不可能同时成立.F17. (本小题满分12分)设ABC ∆的内角C B A ,,的对边分别为c b a ,,,A b a tan =,且B 为钝角. (Ⅰ) 证明:2π=-A B ;(Ⅱ) 求C A sin sin +的取值范围.18. (本小题满分12分)某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖. 每次抽奖都是从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球. 在摸出的2球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖. (Ⅰ) 求顾客抽奖1次能获奖的概率; (Ⅱ) 若某顾客有3次抽奖的机会,记该顾客在3次抽奖中获一等奖的次数为X ,求X 的分布列和数学期望.19. (本小题满分13分)如图,在四棱台1111D C B A ABCD -的上、下底面分别是边长为3和6的正方形,61=AA ,且⊥1AA 底面ABCD ,点P ,Q 分别在棱1DD ,BC 上. (Ⅰ) 若点P 是1DD 的中点,证明:PQ AB ⊥1; (Ⅱ) 若//PQ 平面11A ABB ,二面角A QD P --的余弦值为73,求四面体ADPQ 的体积.BDQ20. (本小题满分13分)已知抛物线1C y x 4:2=的焦点F 也是椭圆2C )0(1:2222>>=+b a bx a y 的一个焦点,1C 与2C 的公共弦长为62. (Ⅰ) 求2C 的方程;(Ⅱ) 过点F 的直线l 与1C 相交于A ,B 两点,与2C 相交于C ,D 两点,且与同向.(i ) 若||||BD AC =,求直线l 的斜率;(ii )设1C 在点A 处的切线与x 轴的交点为M ,证明:直线l 绕点F 旋转时,MFD ∆总是钝角三角形.21. (本小题满分13分)已知0>a ,函数)),0[(sin )(∞+∈=x x e x f ax ,记n x 为)(x f 的从小到大的第n *)(N n ∈个极值点. 证明: (Ⅰ) 数列)}({n x f 是等比数列; (Ⅱ) 若112-≥e a ,则对一切*N n ∈,|)(|n n x f x <恒成立.2015年高考湖南卷理科数学参考答案一、选择题D C B A A D C B D A 二、填空题 11. 0 12. 4 13.5 14. 13-n 15. ),1()0,(∞+-∞三、解答题 16. Ⅰ. 证明:(i )如图,因为M ,N 分别是两弦AB ,CD 的中点,所以AB OM ⊥, CD ON ⊥,即90=∠=∠ONE OME ,因此 180=∠+∠ONE OME ,又四边形的内角和等于 360,故 180=∠+∠NOM MEN .(ii ) 由(i )知, O ,M ,E ,N 四点共圆,故由割线定理即得FO FM FN FE ⋅=⋅.Ⅱ.解: (i )θρcos 2=等价于 θρρcos 22=,将222y x +=ρ,x =θρcos 代入上式即得曲线C 的直角坐标方程是0222=-+x y x .(ii ) 将⎪⎪⎩⎪⎪⎨⎧+=+=.213,235t y t x 代入0222=-+x y x 得018352=++t t .设这个方程的 两个实根分别为21,t t ,则由参数t 的几何意义知||||MB MA ⋅=.18||21=t tⅢ.证明: 由abb a b a b a +=+=+11,0,0>>b a 得 1=ab (i )由基本不等式及1=ab ,有22=≥+ab b a ,即2≥+b a .(ii ) 设22<+a a 与22<+b b 可同时成立,则由22<+a a 及0>a 可得10<<a ,同理 10<<b ,从而10<<ab 这与1=ab 相矛盾,故22<+a a 与22<+b b 不可能同时成立.17. 解:(Ⅰ)由A b a ta n =及正弦定理,得BAb a A A sin sin cos sin ==,所以A B cos sin =,即)2sin(sin A B +=π. 又B 为钝角,),2(2πππ∈+A ,故A B +=2π,即2π=-A B .(Ⅱ) 由(Ⅰ)知 022)(>-=+-=A B A C ππ, 所以)4,0(π∈A . 于是)22sin(sin sin sin A A C A -+=+πA A 2cos sin +=.89)41(s i n2s i n 21s i n 22+--=-+=A A AF因为40π<<A ,所以 22sin 0<<A ,因此8989)41(sin 2222≤+--<A .由此可得C A sin sin +的取值范围是]89,22(.18. 解:(Ⅰ)记事件1A ={从甲箱中摸出的一个球是红球},2A ={从乙箱中摸出的一个球是红球},1B ={顾客抽奖一次获一等奖},2B ={顾客抽奖一次获二等奖},C ={顾客抽奖一次能获奖}.由题意1A 与2A 相互独立,21A A 与21A A 互斥,1B 与2B 互斥,且 211A A B =,2B =21A A +21A A ,21B B C +=. 又因为52104)(1==A P ,21105)(2==A P ,所以 512152)()()()(21211=⨯===A P A P A A P B P , )()()()(212121212A A P A A P A A A A P B P +=+=2121)521()211(52)()()()(2121=⨯-+-⨯=+=A P A P A P A P , 故所求概率为1072151)()()()(2121=+=+=+=B P B P B B P C P .(Ⅱ) 顾客抽奖3次可视为3次独立重复实验,由(Ⅰ)知,顾客抽奖1次获一等奖的概率为51,所以)51,3(~B X ,于是 )3,2,1,0()54()51()(33===-K C K X P KK KX 的数学期望为553)(=⨯=X E . 19. 解法一: (Ⅰ)如图,取1AA 的中点R ,连结PR BR ,, 因为1AA ,1DD是梯形D D AA 11的两腰,点P 是1DD 的中点,所以AD PR //,于是由BC AD //知,BC PR //,所以C B R P ,,,四点共面. 由题设知 AB BC ⊥,1AA BC ⊥,A AA AB =1 ,所以⊥BC 平面11A ABB , ⊂1AB 平面11A ABB ,因此 1AB BC ⊥.因为11111tan 63tan AB A AA B A AB AR ABR ∠====∠,所以11AB A ABR ∠=∠,因此901111=∠+∠=∠+∠BAB AB A BABABR , 于是 1ABBR ⊥, 又已证得1AB BC ⊥,所以⊥1AB 平面BRPC ,显然有⊂PQ 平面BRPC , 故 PQ AB ⊥1.DB(Ⅱ) 如下图,过点P 作1//AA PM 交AD 于点M ,则//PM 平面11A ABB , 因为⊥1AA 底面ABCD ,所以⊥PM 底面ABCD ,过点M 作QD MN ⊥于点N ,连结PN ,则QD PN ⊥,PNM ∠是二面角A QD P --的平面角. 所以 73cos =∠PNM ,即 73=PN MN ,从而340=MN PM . 连结MQ ,由//PQ 平面11A ABB 及//PM 平面11A ABB 知,平面//PQM 平面11A ABB ,所以AB MQ //,又ABCD 是正方形,所以ABQM 是矩形,故MQ=AB=6. 设MD =t ,则.366222ttMD MQ MD MQ MN +=+⋅=过点1D 作A A E D 11//交AD 于点E ,则E D AA 11是矩形,所以 611==AA E D ,311==D A AE ,因此 3=-=AE AD DE . 于是21==DEED MD PM , 所以t MD PM 22==,从而t t t MN PM 63623402+⨯==,解得2=t ,所以4=PM . 故四面体ADPQ 的体积 24466213131=⨯⨯⨯⨯=⋅=∆PM S V ADQ .解法二:由题设知AB AD AA ,,1G 两两垂直,以A 为坐标原点,AB ,AD ,1AA 所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系,如图,则相关各点的坐标为)0,0,0(A ,)6,0,3(1B ,)0,6,0(D ,)6,3,0(1D , )0,,6(m Q ,其中m BQ =,60≤≤m .(Ⅰ) 若点P 是1DD 的中点,则)3,29,0(P ,)3,29,6(--=m PQ ,又)6,0,3(1=AB ,于是018181=-=⋅, 所以AB ⊥1,即PQ AB ⊥1.(Ⅱ) 由题设知,)0,6,6(-=m , )6,3,0(1-=DD 是平面PQD 内两个不共线的向量,设),,(1z y x n =是平面PQD 的一个法向量,则 ⎪⎩⎪⎨⎧=⋅=⋅0,0111DD n 即⎩⎨⎧=+-=-+063,0)6(6z y y m x 取6=y ,得)3,6,6(1m n -=. 又平面AQD 的一个法向量是BD)1,0,0(2=n ,所以45)6(336)6(3||||,cos 2222212121+-=++-=⋅>=<m m n n n n ,而二面角A QD P --的余弦值为73,所以7345)6(32=+-m ,解得m=4或m=8(舍去),此时)0,4,6(Q . 再设)10(1≤<=λλDD ,而)6,3,0(1-=DD ,由此得到)6,36,0(λλ-P ,)6,23,6(λλ--=. 因为//PQ 平面11A ABB ,且平面11A ABB 的一个法向量是)0,1,0(3=n ,所以 0233=-=⋅λn ,32=λ,从而)4,4,0(P .于是,将四面体ADPQ 视为ADQ ∆为底面的三棱锥ADQ P -,其高4=h ,故四面体ADPQ 的体积 24466213131=⨯⨯⨯⨯=⋅=∆PM S V ADQ .20. 解:(Ⅰ) 由1C y x 4:2=知其焦点F 的坐标为(0,1),因为F 也是椭圆2C 的一个焦点,所以 122=-b a (1)又1C 与2C 的公共弦长为62,1C 与2C 都关于y 轴对称,且1C 的方程为y x 42=,由此易知1C 与2C 的公共点坐标为)23,6(±,所以164922=+ba (2) 联立(1)(2)得8,922==b a ,故2C 的方程为18922=+x y . (Ⅱ) 如图,设),(11y x A ,),(22y x B ,),(33y x C ,),(44y x D .(i )因AC 与同向,且 ||||BD AC =,所以 =,从而 2413x x x x -=-,即4321x x x x -=-,于是43243212214)(4)(x x x x x x x x -+=-+. (3) 设直线l 的斜率为k ,则l 的方程为1+=kx y .由⎩⎨⎧=+=yx kx y 4,12 得0442=--kx x ,而21,x x 是这个方程的两根,所以 4,42121-==+x x k x x (4)由⎪⎩⎪⎨⎧=++=189,122x y kx y 得06416)89(22=-++kx x k ,而43,x x 是这个方程的两根,所以2212438964,8916kx x k k x x +-=+-=+ (5)将(4)(5)代入(3)得 22222289644)89(16)1(16k k k k +⨯++=+,即22222)89()1(916)1(16k k k ++⨯=+, 所以 916)89(22⨯=+k ,解得 46±=k ,即直线l 的斜率为46±. (ii )由 y x 42=得 2'xy =,所以1C 在点A 处的切线方程为)(2111x x x y y -=-,即42211x x x y -=,令0=y 得21x x =,即)0,2(1x M ,所以)1,2(1-=x ,而)14,(211-=x x ,于是014)14(2212121>+=--=⋅x x x ,因此AFM ∠总是锐角,从而AFM MFD ∠-=∠ 180是钝角. 故直线l 绕点F 旋转时,MFD ∆总是钝角三角形.21. 解:(Ⅰ) )cos sin (cos sin )('x x a e x e x ae x f ax ax ax +=+=)sin(12ϕ+⋅+=x e a ax ,其中a 1tan =ϕ,20πϕ<<. 令 0)('=x f ,由0≥x 得 πϕm x =+,即*,N m m x ∈-=ϕπ.对N k ∈,若πϕπ)12(2+<+<k x k ,即ϕπϕπ-+<<-)12(2k x k ,则0)('>x f ;若πϕπ)22()12(+<+<+k x k ,即ϕπϕπ-+<<-+)22()12(k x k ,则0)('<x f . 因此,在区间),)1((ϕππ--m m 与),(πϕπm m -上,)('x f 的符号总相反,于是,当*,N m m x ∈-=ϕπ时,)(x f 取得极值,所以*,N n n x n ∈-=ϕπ. 此时,)(1)()1()sin()(ϕπϕπϕπ-+--=-=n a n n a n e n e x f ,易知0)(≠n x f ,且πϕπϕπa n a n n a n n n e ee xf x f -=--=-+-+++)(1])1[(21)1()1()()(是常数,故数列)}({n x f 是首项为ϕϕπsin )()(1-=a e x f ,公比为πa e -的等比数列.(Ⅱ) 由(Ⅰ)知,11sin 2+=a ϕ,于是对一切*N n ∈,|)(|n n x f x <恒成立,即)(211ϕπϕπ-+<-n a e a n 恒成立,等价于)(1)(2ϕπϕπ-<+-n a e a a n a (*)恒成立(因为a>0). 设)0()(>=t t e t g t ,则0)1()('2=-=t t e t g t 得1=t ,当10<<t 时,0)('<t g ,所以)(t g 在)1,0(上单调递减;当1>t 时,0)('>t g ,所以)(t g 在),1(∞+上单调递增.从而当1=t 时,函数)(t g 取得最小值e g =)1(. 因此,要使(*)式恒成立,只需e g a a =<+)1(12,即只需112->e a . 而当112-=e a 时,由311t a n 2>-==e a ϕ且由20πϕ<<知,23πϕπ<<. 于是1322-<<-e πϕπ,第11页 共11页且当2≥n 时,12322->>-≥-e n πϕπϕπ,因此,对一切*N n ∈,112≠--=e n ax n ϕπ,所以a a e g ax g n 1)1()(2+==>,故(*)式也恒成立. 综上所述,若112-≥e a ,则对一切*N n ∈,|)(|n n x f x <恒成立.。
十三校高三第二次联考数学理试题及答案
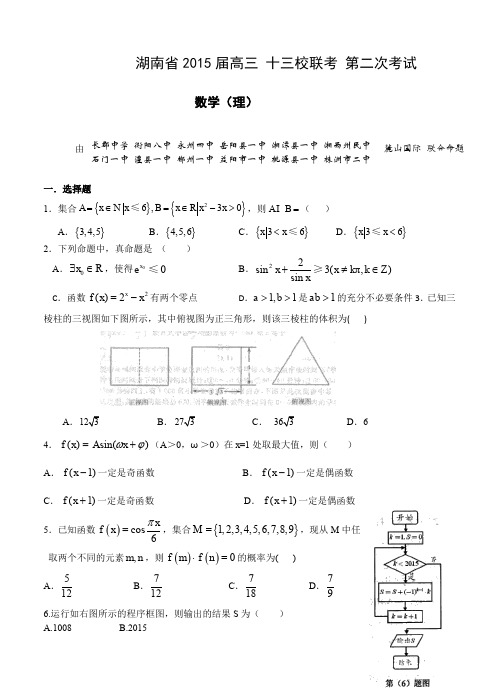
湖南省2015届高三 十三校联考 第二次考试数学(理)长郡中学 衡阳八中 永州四中 岳阳县一中 湘潭县一中 湘西州民中 石门一中 澧县一中 郴州一中 益阳市一中 桃源县一中 株洲市二中一.选择题1.集合{}{}26,30A x N x B x R x x =∈=∈->≤,则A B =I ( )A .{}3,4,5B .{}4,5,6C .{}36x x <≤D .{}36x x <≤2.下列命题中,真命题是 ( ) A .0x R ∃∈,使得00xe ≤ B .22sin 3(π,)sin x x k k Z x+≠∈≥ C .函数2()2xf x x =-有两个零点D .1,1a b >>是1ab >的充分不必要条件3.已知三棱柱的三视图如下图所示,其中俯视图为正三角形,则该三棱柱的体积为( )A .B .C .D .64.)sin()(ϕω+=x A x f (A >0,ω>0)在x =1处取最大值,则( ) A .)1(-x f 一定是奇函数 B .)1(-x f 一定是偶函数 C .)1(+x f 一定是奇函数 D .)1(+x f 一定是偶函数 5.已知函数()cos6xf x π=,集合{}1,2,3,4,5,6,7,8,9M =,现从M 中任取两个不同的元素,m n ,则()()0f m f n ⋅=的概率为( ) A .512B .712C .718D .796.运行如右图所示的程序框图,则输出的结果S 为( ) A.1008 B.2015yxAQ PO(第10题C.1007D. 1007-8.设函数)(x f y =在R 上有定义,对于任一给定的正数p ,定义函数⎩⎨⎧>≤=p x f p px f x f x f p )(,)(),()(,则称函数)(x f p 为)(x f 的“p 界函数”若给定函数2,12)(2=--=p x x x f ,则下列结论不成立的是( ) A.[][])0()0(p p f f f f = B. [][])1()1(p p f f f f = C. [][])2()2(f f f f p p = D. [][])3()3(f f f f p p =9.已知函数21()(,g x a x x e e=-≤≤e 为自然对数的底数)与()2ln h x x =的图象上存在关于x 轴对称的点,则实数a 的取值范围是( ) A .21[1,2]e + B .2[1,2]e - C .221[2,2]e e+- D .2[2,)e -+∞ 10.如图,已知双曲线C :22221x y a b-=()0,0>>b a 的右顶点为,A O 为坐标原点,以A 为圆心的圆与双曲线C 的某渐近线交于两点Q P ,.若60PAQ ∠=︒且3OQ OP =,则双曲线C的离心率为( )ABC D二.填空题7.已知抛物线2:4C y x =,点(,0)P m ,O 为坐标原点,若在抛物线C 上存在一点Q ,使得90OQP?o ,则实数m 的取值范围是( )(A )(4,8) (B )(4,)+? (C )(0,4)(D )(8,)+?(一)选做题11.如图,BD 是半圆O 的直径,A 在BD 的延长线上,AC 与半圆相切于点E ,AC BC ⊥,若AD =6AE =,则EC = 3 .12.在直角坐标系xOy 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系.若点P 为直线cos sin 40ρθρθ--=上一点,点Q 为曲线2(14x t t y t =⎧⎪⎨=⎪⎩为参数)上一点,则||PQ 的最小值为13.已知函数f(x)=|x-k|+|x-2k|,若对任意的x ∈R ,f(x )≥f(3)=f(4)都成立,则k 的取值范围为[]2,3 .(二)必做题 14.设()0sin cos a x x dx π=+⎰,则二项式6⎛⎝的展开式的常数项是____-160_____.15.如果实数,a b 满足条件:20101a b b a a +-≥⎧⎪--≤⎨⎪≤⎩,则22a b a b ++的最大值是 5 。
2015年湖南省郴州市高考数学模拟试卷(理科)(二)

2015年湖南省郴州市高考数学模拟试卷(理科)(二)学校:___________姓名:___________班级:___________考号:___________一、选择题(本大题共10小题,共50.0分)1.已知集合M={x|x2-2x<0},N={x|x<a},若M⊆N,则实数a的取值范围是()A.[2,+∞)B.(2,+∞)C.(-∞,0)D.(-∞,0]【答案】A【解析】解:由M中不等式变形得:x(x-2)<0,解得:0<x<2,即M=(0,2),∵N={x|x<a},且M⊆N,∴a≥2,则a的范围为[2,+∞).故选:A.求出M中不等式的解集确定出M,根据N以及M为N的子集,确定出a的范围即可.此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.2.对于下列四个命题p1:∃x0∈(0,+∞),()x0<()x0p2:∃x0∈(0,1),log x0>log x0p3:∀x∈(0,+∞),()x>log xp4:∀x∈(0,),()x<log x.其中的真命题是()A.p1,p3B.p1,p4C.p2,p3D.p2,p4【答案】D【解析】解:p1:∃x0∈(0,+∞),()x0<()x0,是假命题,原因是当x0∈(0,+∞),幂函数在第一象限为增函数;p2:∃x0∈(0,1),log x0>log x0,是真命题,如>;p3:∀x∈(0,+∞),()x>log x,是假命题,如x=时,<;p4:∀x∈(0,),<<1,>,是真命题.故选:D.根据幂函数的单调性,我们可以判断p1的真假,根据对数函数的单调性,及指数函数的单调性,我们可以判断p2,p3,p4的真假,进而得到答案本题考查的知识点是命题的真假判断与应用,函数的单调性与特殊点,对数函数的单调性与特殊点,其中熟练掌握指数函数的单调性与对数函数的单调性是解答本题的关键,是中档题.3.在如图所示的程序框图中输入10,结果会输出()A.10B.11C.512D.1 024【答案】D【解析】解:运行程序,有s=1;k=1第1次循环:s=2,k=2第2次循环:s=4,k=3第3次循环:s=8,k=4第4次循环:s=16,k=5第5次循环:s=32,k=6第6次循环:s=64,k=7第7次循环:s=128,k=8第8次循环:s=256,k=9第9次循环:s=512,k=10第10次循环:s=1024,k=11输出s的值为1024.故答案为:D.根据框图写出每次循环s,k的取值,即可确定输出s的值.本题主要考察框图和程序算法,属于基础题.4.将函数f(x)=sinx+cosx的图象向左平移φ(φ>0)个单位长度,所得图象关于原点对称,则φ的最小值为()A.-B.C.D.【答案】C【解析】解:由题意可得,将函数f(x)=sinx+cosx=sin(x+)的图象向左平移φ(φ>0)个单位长度,所得函数为y=sin(x++φ)为奇函数,则φ的最小值为,故选:C.由条件根据函数y=A sin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,可得结论.本题主要考查函数y=A sin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,正弦函数的奇偶性,属于基础题.5.若实数x、y满足条件,则z=x+3y的最大值为()A.9B.11C.12D.16【答案】B【解析】解:作出不等式组对应的平面区域如图:由z=x+3y,得,平移直线,由图象可知当,经过点C时,直线截距最大,此时z最大.由得,即C(2,3),此时z=x+3y=2+3×3=11,故选:B.作出不等式组对应的平面区域,利用z的几何意义,利用利用数形结合即可得到结论.本题主要考查线性规划的应用,利用数形结合是解决本题的关键.6.不全相等的五个数a、b、c、m、n具有关系如下:a、b、c成等比数列,a、m、b和b、n、c都成等差数列,则+=()A.-2B.0C.2D.不能确定【答案】C【解析】解:由已知得2m=a+b,2n=b+c,b2=ac,∴+==[]===2.故选:C.由已知得2m=a+b,2n=b+c,b2=ac,从而+====2.本题考查代数和的求法,是基础题,解题时要认真审题,注意等差数列和等比数列的性质的合理运用.7.已知边长为1的正方形ABCD位于第一象限,且顶点A、D分别在x、y的正半轴上(含原点)滑动,则的最大值是()A.1B.C.2D.【答案】C【解析】解:如图令∠OAD=θ,由于AD=1,故0A=cosθ,OD=sinθ,如图∠BA x=-θ,AB=1,故x B=cosθ+cos(-θ)=cosθ+sinθ,y B=sin(-θ)=cosθ.故=(cosθ+sinθ,cosθ)同理可求得C(sinθ,cosθ+sinθ),即=(sinθ,cosθ+sinθ),∴•=(cosθ+sinθ,cosθ)•(sinθ,cosθ+sinθ)=1+sin2θ,•的最大值是2,故选C.令∠OAD=θ,由边长为1的正方形ABCD的顶点A、D分别在x轴、y轴正半轴上,可得出B,C的坐标,由此可以表示出两个向量,算出它们的内积即可.本题考查向量在几何中的应用,设角引入坐标是解题的关键,由于向量的运算与坐标关系密切,所以在研究此类题时应该想到设角来表示点的坐标,属于中档题.8.一个四面体的三视图如图所示,则该四面体的表面积为()A. B. C. D.2【答案】D【解析】解:如图所示,四面体为正四面体.是由边长为1的正方体的面对角线围成.其边长为,则其表面积为4×(××)=2.故选D.由三视图想象出空间几何体,代入数据求值.本题考查了学生的空间想象力,属于中档题.9.已知双曲线>,>的左、右焦点分别为F1、F2,若在双曲线的右支上存在一点P,使得|PF1|=3|PF2|,则双曲线的离心率e的取值范围为()A.[,+∞)B.[2,+∞)C.,D.(1,2]【答案】D【解析】解:设P点的横坐标为x∵|PF1|=3|PF2|,P在双曲线右支(x≥a)根据双曲线的第二定义,可得3e(x-)=e(x+)∴ex=2a∵x≥a,∴ex≥ea∴2a≥ea,∴e≤2∵e>1,∴1<e≤2故选D.设P点的横坐标为x,根据|PF1|=3|PF2|,P在双曲线右支(x≥a),利用双曲线的第二定义,可得x关于e的表达式,进而根据x的范围确定e的范围.本题主要考查了双曲线的简单性质,考查了双曲线的第二定义的灵活运用,属于基础题.10.已知集合A={x|x=a0+a1×3+a2×32+a3×33},其中a k∈{0,1,2}(k=0,1,2,3),且a3≠0.则A中所有元素之和等于()A.3240B.3120C.2997D.2889【答案】D【解析】解:由题意可知,a0,a1,a2各有3种取法(均可取0,1,2),a3有2种取法,由分步计数原理可得共有3×3×3×2种方法,∴当a0取0,1,2时,a1,a2各有3种取法,a3有2种取法,共有3×3×2=18种方法,即集合A中含有a0项的所有数的和为(0+1+2)×18;同理可得集合A中含有a1项的所有数的和为(3×0+3×1+3×2)×18;集合A中含有a2项的所有数的和为(32×0+32×1+32×2)×18;集合A中含有a3项的所有数的和为(33×1+33×2)×27;由分类计数原理得集合A中所有元素之和:S=(0+1+2)×18+(3×0+3×1+3×2)×18+(32×0+32×1+32×2)×18+(33×1+33×2)×27=18(3+9+27)+81×27=702+2187=2889.故选D.由题意可知a0,a1,a2各有3种取法(均可取0,1,2),a3有2种取法,利用数列求和即可求得A中所有元素之和.本题考查数列的求和,考查分类计数原理与分步计数原理的应用,考查分类讨论与转化思想的综合应用,属于难题.二、填空题(本大题共6小题,共30.0分)11.在直角坐标系x O y中,直线l的参数方程为(t为参数).在极坐标系(与直角坐标系x O y取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的极坐标方程为ρ=2cosθ,若直线l平分圆C的周长,则a= ______ .【答案】-3【解析】解:直线l的参数方程为(t为参数),消去参数t化为:3x+4y+a=0.圆C的极坐标方程ρ=2cosθ,化为ρ2=2ρcosθ,化为直角坐标方程:x2+y2=2x,配方为(x-1)2+y2=1,可得圆心C(1,0).∵直线l平分圆C的周长,∴直线l经过圆心C,∴3+0+a=0,解得a=-3.故答案为:-3.分别把极坐标方程化为直角坐标方程、参数方程化为普通方程,由于直线l平分圆C的周长,可知:直线l经过圆心C,即可得出.本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程、直线与圆的位置关系,考查了推理能力与计算能力,属于中档题12.已知a,b,c∈R,a2+b2+c2=9,M=a+2b+3c,则M的最大值是______ .【答案】【解析】解:∵a+2b+3c,a2+b2+c2=9,∴,当且仅当时取等号.故答案为:.利用柯西不等式即可得出.本题考查了柯西不等式的应用,属于基础题.13.如图,已知PA是圆O的切线,切点为A,PO交圆O于点B,圆O的半径为2,PB=3,则PA的长为______ .【答案】【解析】解:由题意,利用切割线定理可得PA2=3×(3+2+2)=21,∴PA=.故答案为:.由题意,利用切割线定理可得结论.此题主要考查圆的切线的性质定理的运用,考查学生分析解决问题的能力,比较基础.14.在△ABC中,a=15,b=10,A=60°,则cos B= ______ .【答案】【解析】解:由正弦定理可得=,∴sin B=,再由b<a,可得B为锐角,∴cos B==,故答案为:.由正弦定理可求得sin B=,再由b<a,可得B为锐角,cos B=,运算求得结果.本题考查正弦定理的应用,同角三角函数的基本关系,求出sin B=,以及B为锐角,是解题的关键.15.在函数f(x)=alnx+(x+1)2(x>0)的图象上任取两个不同点P(x1,y1),Q(x2,y2),总能使得f(x1)-f(x2)≥4(x1-x2),则实数a的取值范围为______ .【答案】a≥【解析】解:不妨设x1>x2,则x1-x2>0,∵f(x1)-f(x2)≥4(x1-x2),∴≥4,∵f(x)=alnx+(x+1)2,(x>0)∴f′(x)=+2(x+1)∴+2(x+1)≥4,∴a≥-2x2+2x∵-2x2+2x=-2(x-)2+≤∴a≥,故答案为:a≥不妨设x1>x2,则x1-x2>0,由f(x1)-f(x2)≥4(x1-x2),可得≥4,即函数f(x)=alnx+(x+1)2(x>0)的图象上任取两个不同点P(x1,y1),Q(x2,y2)连续的斜率不小于4,即导数值不小于4,由此构造关于a的不等式,可得实数a的取值范围.本题考查的知识点导数的几何意义,斜率公式,其中分析出f(x1)-f(x2)≥4(x1-x2)的几何意义,是解答的关键.16.两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题,他们在沙滩上画点或用小石子来表示数,按照点或小石子能排列的形状对数进行分类,如图中的实心点个数1,5,12,22,…,被称为五角形数,其中第1个五角形数记作a1=1,第2个五角形数记作a2=5,第3个五角形数记作a3=12,第4个五角形数记作a4=22,…,若按此规律继续下去,若a n=145,则n=______ .【答案】10【解析】解:a2-a1=5-1=4,a3-a2=12-5=7,a4-a3=22-12=10,…,由此可知数列{a n+1-a n}构成以4为首项,以3为公差的等差数列.所以a n+1-a n=4+3(n-1)=3n+1.a2-a1=3×1+1a3-a2=3×2+1…a n-a n-1=3(n-1)+1累加得:a n-a1=3(1+2+…+(n-1))+n-1所以=1++n-1=.由,解得:舍,或.故答案为10.根据题目所给出的五角形数的前几项,发现该数列的特点是,从第二项起,每一个数与前一个数的差构成了一个新的等差数列,写出对应的n-1个等式,然后用累加的办法求出该数列的通项公式,然后代入项求项数.本题考查了等差数列的通项公式,解答此题的关键是能够由数列的前几项分析出数列的特点,即从第二项起,每一个数与前一个数的差构成了一个新的等差数列,本题训练了一种求数列通项的重要方法--累加法.三、解答题(本大题共6小题,共75.0分)17.设f(x)=sin(x-)-2cos2x+1.(1)求f(x)的最小正周期;(2)若函数y=f(x)与y=g(x)的图象关于直线x=1对称,求当x∈[0,]时,y=g (x)的最大值.【答案】解:(1)f(x)=sin xcos-cos xsin-cos x=sin x-cos x=(sin x-cos x)=sin (x-),∵ω=,∴f(x)的最小正周期为T==8;(2)在y=g(x)的图象上任取一点(x,g(x)),它关于x=1的对称点(2-x,g(x)),由题设条件,点(2-x,g(x))在y=f(x)的图象上,从而g(x)=f(2-x)=sin[(2-x)-]=sin[-x-]=cos(x+),当0≤x≤时,≤x+≤,则y=g(x)在区间[0,]上的最大值为g max=cos=.【解析】(1)f(x)解析式第一项利用两角和与差的正弦函数公式化简,整理后再利用两角和与差的正弦函数公式化为一个角的正弦函数,找出ω的值,代入周期公式即可求出f (x)的最小正周期;(2)在y=g(x)的图象上任取一点(x,g(x)),根据f(x)与g(x)关于直线x=1对称,表示出此点的对称点,根据题意得到对称点在f(x)上,代入列出关系式,整理后根据余弦函数的定义域与值域即可确定出g(x)的最大值.此题考查了两角和与差的正弦函数公式,三角函数的周期性及其求法,以及正弦函数的定义域与值域,熟练掌握公式是解本题的关键.18.某电视台拟举行由选手报名参加的比赛类型的娱乐节目,选手进入正赛前需通过海选,参加海选的选手可以参加A、B、C三个测试项目,只需通过一项测试即可停止测试,通过海选.若通过海选的人数超过预定正赛参赛人数,则优先考虑参加海选测试次数少的选手进入正赛.甲选手通过项目A、B、C测试的概率为分别为、、,且通过各次测试的事件相互独立.(1)若甲选手先测试A项目,再测试B项目,后测试C项目,求他通过海选的概率;若改变测试顺序,对他通过海选的概率是否有影响?说明理由;(2)若甲选手按某种顺序参加海选测试,第一项能通过的概率为p1,第二项能通过的概率为p2,第三项能通过的概率为p3,设他通过海选时参加测试的次数为ξ,求ξ的分布列和期望(用p1、p、p3表示);并说明甲选手按怎样的测试顺序更有利于他进入正赛.【答案】解:(1)依题意,甲选手不能通过海选的概率为:(1-)(1-)(1-)=,故甲选手能通过海选的概率为:1-(1-)(1-)(1-)=.若改变测试顺序对他通过海选的概率没有影响,因为无论按什么顺序,其不能通过的概率均为(1-)(1-)(1-)=,故无论按什么顺序,其能通过海选的概率都是.(2)依题意,ξ的可能取值为1,2,3,P(ξ=1)=p1,P(ξ=2)=(1-p1)p2,P(ξ=3)=(1-p1)(1-p2)×1,∴ξ的分布列为:11)21)(1-2)3,分别计算当甲选手按C→B→A,C→A→B,B→A→C,B→C→A,A→B→C,A→C→B 的顺序参加测试时,Eξ的值几时甲选手按C→B→A的顺序参加测试时,Eξ最小,因为参加测试的次数少的选手优先进入正赛,故该选手将自己的优势项目放在前面,即按C→B→A的顺序参加测试更有利用于进入正赛.【解析】(1)先求出甲选手不能通过海选的概率,再由对立事件概率计算公式能求出甲选手能通过海选的概率.(2)依题意,ξ的可能取值为1,2,3,分别求出相应的概率,由此能求出ξ的分布列和期望.本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题.19.如图,△ABC的外接圆⊙O的半径为5,CE垂直于⊙O所在的平面,BD∥CE,CE=4,BC=6,且BD=1,cos∠ADB=.(1)求证:平面AEC⊥平面BCED;(2)试问线段DE上是否存在点M,使得直线AM与平面ACE所成角的正弦值为?若存在,确定点M的位置;若不存在,请说明理由.【答案】(1)证明:∵BD⊥平面ABC,∴BD⊥AB,又∵BD=1,cos∠,∴AD=,AB=10=直径,∴AC⊥BC,又BC⊥平面ACE,BC⊂平面BCED,∴平面AEC⊥平面BCED.(2)解:存在.如图,以C为原点,直线CA为x轴,CB为y轴,CE这z轴,建立空间直角坐标系,则A(8,0,0),B(0,6,0),D(0,6,1),E(0,0,4),=(-8,6,1),=(0,-6,3),设=λ=(0,-6λ,3λ),0<λ<1,故=+=(-8,6-6λ,1+3λ),由(1)得平面ACE的法向量为=(0,6,0),设直线AM与平面CE所成角为θ,则sinθ===,解得.∴线段DE上存在点M,且时,使得直线AM与平面ACE所成角的正弦值为.【解析】(1)由已知得BD⊥AB,AD=,AB=10=直径,由此能证明平面AEC⊥平面BCED.(2)以C为原点,直线CA为x轴,CB为y轴,CE这z轴,建立空间直角坐标系,利用向量法能求出线段DE上存在点M,且时,使得直线AM与平面ACE所成角的正弦值为.本题考查平面与平面垂直的证明,考查直线与平面所成角的正弦值的求法,解题时要认真审题,注意向量法的合理运用.20.等比数列a n中的前三项a1,a2,a3分别是下面数阵中第一、二、三行中的某三个数,且三个数不在同一列.(1)求此数列{a n}的通项公式;(2)若数列{b n}满足b n=3a n-(-1)n lga n,求数列{b n}的前n项和S n.【答案】解:(1)经检验,当a1=5或a1=4时,不可能得到符合题意的等比数列,∴a1=3,a2=6,a3=12,公比q=2,∴.(2)由,得b n=3a n-(-1)n lga n=9×2n-1-(-1)n[lg3+(n-1)lg2],∴S n=9(1+2+…+2n-1)-[(-1)+(-1)2+…+(-1)n](lg3-lg2),n为偶数时,S n=9×+(lg3-lg2)-()lg2=9(2n-1)+.n为奇数时,=9(2n-1)+.∴S n=,为偶数,为奇数.【解析】(1)由已知得a1=3,a2=6,a3=12,公比q=2,由此能求出数列{a n}的通项公式.(2)由,得b n=3a n-(-1)n lga n=9×2n-1-(-1)n[lg3+(n-1)lg2],由此能求出数列{b n}的前n项和S n.本题考查数列的通项公式和前n项和公式的求法,是中档题,解题时要注意分类讨论思想的合理运用.21.已知圆C:(x-1)2+(y-1)2=2经过椭圆Γ:+=1(a>b>0)的右焦点F和上顶点B.(Ⅰ)求椭圆Γ的方程;(Ⅱ)过原点O的射线l与椭圆Γ在第一象限的交点为Q,与圆C的交点为P,M为OP的中点,求•的最大值.【答案】解:(Ⅰ)在圆C:(x-1)2+(y-1)2=2中,令y=0,得F(2,0),即c=2,令x=0,得B(0,2),即b=2,∴a2=b2+c2=8,∴椭圆Γ的方程为:.(Ⅱ)设点Q(x0,y0),x0>0,y0>0,则==(1,1)•(x0,y0)=x0+y0,又,设b=x0+y0,与联立,得:,令△≥0,得16b2-12(12b2-8)≥0,解得-2.又点Q(x0,y0)在第一象限,∴当时,取最大值2.【解析】(Ⅰ)在圆(x-1)2+(y-1)2=2中,令y=0,得F(2,0),令x=0,得B(0,2),由此能求出椭圆方程.(Ⅱ)设点Q(x0,y0),x0>0,y0>0,则==x0+y0,又,设b=x0+y0,与联立,得:,由此能求出的最大值.本题考查直线、圆、椭圆、平面向量、分式函数等基础知识,考查直线与圆锥曲线的位置关系,考查运算求解能力、推理论证能力,考查数形结合、化归转化及函数与方程等数学思想.22.已知函数f(x)=e x-ax2-2x-1(x∈R).(1)当a=0时,求f(x)的单调区间;(2)求证:对任意实数a<0,有f(x)>.【答案】(1)解:当a=0时,f(x)=e x-2x-1(x∈R),∵f′(x)=e x-2,且f′(x)的零点为x=ln2,∴当x∈(-∞,ln2)时,f′(x)<0;当x∈(ln2,+∞)时,f′(x)>0,即(-∞,ln2)是f(x)的单调减区间,(ln2,+∞)是f(x)的单调增区间;(2)证明:由f(x)=e x-ax2-2x-1(x∈R)得:f′(x)=e x-2ax-2,记g(x)=e x-2ax-2(x∈R).∵a<0,∴g′(x)=e x-2a>0,即f′(x)=g(x)是R上的单调增函数,又f′(0)=-1<0,f′(1)=e-2a-2>0,故R上存在惟一的x0∈(0,1),使得f'(x0)=0,且当x<x0时,f′(x)<0;当x>x0时f′(x)>0.即f(x)在(-∞,x0)上单调递减,在(x0,+∞)上单调递增,则,再由f′(x0)=0,得,将其代入前式可得.又令,由于-a>0,对称轴>,而x0∈(0,1),∴φ(x0)>φ(1)=a-1,又>,∴>.故对任意实数a<0,都有>.【解析】(1)把a=0代入函数解析式并求出导函数,求得导函数的零点,由零点对函数定义域分段,然后根据导函数在各区间段内的符号求得原函数的单调期间;(2)求出原函数的导函数,对导函数二次求导得到得到导函数的单调性,求出原函数的极值点,然后借助于二次函数最小值的求法得到f(x)的最小值,则答案得证.本题考查利用导数研究函数的单调性,考查利用导数求函数的最值,考查了数学转化思想方法,训练了学生的逻辑思维能力和综合运算能力,是压轴题.。
2015年湖南省郴州市高考数学模拟试卷(理科)(一)

2015年湖南省郴州市高考数学模拟试卷(理科)(一)学校:___________姓名:___________班级:___________考号:___________一、选择题(本大题共10小题,共50.0分)1.若复数z满足:z+|z|=1+2i,则z的虚部为()A.2iB.1C.2D.i【答案】C【解析】解:∵z+|z|=1+2i,∴z=1-|z|+2i,∵1-|z|是实数,为z的实部,∴2是z的虚部,故选:C由:z+|z|=1+2i得z=1-|z|+2i,即可得到结论.本题主要考查复数的有关概念,根据复数的特点是解决本题的关键.2.已知a>1,,则f(x)<1成立的一个充分不必要条件是()A.0<x<1B.-1<x<0C.-2<x<0D.-2<x<1【答案】B【解析】解:f(x)<1成立的充要条件是<∵a>1∴x2+2x<0∴-2<x<0∴f(x)<1成立的一个充分不必要条件是-1<x<0故选项为B求出不等式的解集即不等式成立的充要条件;据当集合A⊆集合B且B⊊A时,A是B 的充分不必要条件.本题考查不等式的解集是不等式的充要条件;据集合之间的关系判断条件关系.3.已知等比数列{a n}的前n项和S n,且a1+a3=,a2+a4=,则=()A.4n-1B.4n-1C.2n-1D.2n-1【答案】D【解析】解:∵等比数列{a n}的前n项和S n,且a1+a3=,a2+a4=,∴两式相除可得公比q=,∴a1=2,∴a n==,S n==4(1-),∴=2n-1,故选:D.利用等比数列{a n}的前n项和S n,且a1+a3=,a2+a4=,求出q=,a1=2,可得a n、S n,即可得出结论.本题考查等比数列的通项与求和,考查学生的计算能力,确定数列的首项与公比是关键.4.将函数y=sin(6x+)的图象上各点的横坐标伸长到原来的3倍,再向右平移个单位,得到的函数的一个对称中心是()A.,B.,C.,D.,【答案】D【解析】解:横坐标伸长到原来的3倍则函数变为y=sin(2x+)(x系数变为原来的),函数的图象向右平移个单位,则函数变为y=sin[2(x-)+]=sin2x;考察选项不难发现,就是函数的一个对称中心坐标.故选D由题意根据伸缩变换、平移变换求出函数的解析式,然后求出函数的一个对称中心即可.本题是基础题,考查三角函数图象的伸缩、平移变换,函数的对称中心坐标问题,考查计算能力,逻辑推理能力,常考题型.5.下列四个命题中①设有一个回归方程y=2-3x,变量x增加一个单位时,y平均增加3个单位;②命题P:“∃x0∈R,x02-x0-1>0“的否定¬P:“∀x∈R,x2-x-1≤0”;③设随机变量X服从正态分布N(0,1),若P(X>1)=p,则P(-l<X<0)=-p;④在一个2×2列联表中,由计算得K2=6.679,则有99%的把握确认这两个变量间有关系.其中正确的命题的个数有()A.1个B.2个C.3个D.4个【答案】C【解析】解:①设有一个回归方程y=2-3x,变量x增加一个单位时,y平均减少3个单位,故①不正确;②命题P:“∃x0∈R,x02-x0-1>0“的否定¬P:“∀x∈R,x2-x-1≤0”,正确;③设随机变量X服从正态分布N(0,1),则对称轴为x=0,∵P(X>1)=p,∴P(-l <X<0)=-p,正确;④在一个2×2列联表中,由计算得K2=6.679>6.535,∴有99%的把握确认这两个变量间有关系,正确.故选:C.对选项逐个进行判断,即可得出结论.本题考查回归方程、命题的否定,考查正态分布、独立性检验知识,考查学生分析解决问题的能力,属于中档题.6.设抛物线x2=8y的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A为垂足,如果直线AF的倾斜角等于60°,那么|PF|等于()A.2B.4C.D.4【答案】C【解析】解:在△APF中,由抛物线的定义,可得|PA|=|PF|,∵|AF|sin60°=4,∴|AF|=,又∠PAF=∠PFA=30°,过P作PB⊥AF于B,则|PF|==.°故选:C.先求出|AF|,过P作PB⊥AF于B,利用|PF|=,°求出|PF|.抛物线的定义,可以将抛物线上的点到焦点的距离转化为到准线的距离.7.执行如图所示的程序图,若任意输入区间[1,19]中实数x,则输入x大于49的概率为()A. B. C. D.【答案】C【解析】解:由程序框图知:第一次运行x=2x-1,n=2;第二次运行x=2×(2x-1)-1.n=2+1=3;第三次运行x=2×[2×(2x-1)-1]-1,n=3+1=4,不满足条件n≤3,程序运行终止,输出x=8x-(4+2+1)=8x-7,由输出的x大于49,得x>7,∴输入x∈(7,19],数集的长度为12,又数集[1,19]的长度为18,∴输出的x大于49的概率P==.故选:C根据框图的流程,依次计算运行的结果,直到不满足条件n≤3,求出输出x的值,再根据输出的x大于49,求出输入x的范围,根据几何概型的概率公式计算.本题考查了循环结构的程序框图,根据框图的流程判断算法的功能是解答此类问题的关键.8.一个四面体的顶点都在球面上,它们的正视图、侧视图、俯视图都是右图.图中圆内有一个以圆心为中心边长为1的正方形.则这个四面体的外接球的表面积是()A.πB.3πC.4πD.6π【答案】B【解析】解:由三视图可知:该四面体是正方体的一个内接正四面体.∴此四面体的外接球的直径为正方体的对角线长为.∴此四面体的外接球的表面积为表面积为=3π.故选:B.由三视图可知:该四面体是正方体的一个内接正四面体.此四面体的外接球的半径为正方体的对角线长为.利用球的表面积计算公式即可得出.本题考查了三棱锥的三视图、正方体与外接球的性质、球的表面积的计算公式,考查了推理能力与空间想象能力、计算能力,属于中档题.9.已知点(a,b)在圆x2+y2=1上,则函数f(x)=acos2x+bsinxcosx--1的最小正周期和最小值分别为()A.,B.,C.,D.,【答案】B【解析】解:∵点(a,b)在圆x2+y2=1上,∴a2+b2=1.====-1,(tanθ=).∴函数的最小正周期为,当sin(2x+θ)=-1时,函数有最小值-.故选:B.由点(a,b)在圆x2+y2=1上,得到a2+b2=1,然后利用倍角公式降幂后由两角和的正弦化积,化为y=A sin(ωx+φ)+k的形式后可求周期和最值.本题考查了二倍角的正弦公式和余弦公式,考查了两角和的正弦公式,考查了形如y=A sin(ωx+φ)+k的函数的周期和最值得求法,此类问题解决的方法是先降幂,后化积,是中档题.10.已知函数f(x)=,,>,若方程f(x)=a有四个不同的解x1,x2,x3,x4,且x1<x2<x3<x4,则x3(x1+x2)+的取值范围是()A.(-1,+∞)B.(-1,1]C.(-∞,1)D.[-1,1)【答案】B【解析】解:作函数f(x)=,,>,的图象如下,由图可知,x1+x2=-2,x3x4=1;1<x4≤2;故x3(x1+x2)+=-+x4,其在1<x4≤2上是增函数,故-2+1<-+x4≤-1+2;即-1<-+x4≤1;故选B.作函数f(x)=,,>的图象如下,由图象可得x1+x2=-2,x3x4=1;1<x4≤2;从而化简x3(x1+x2)+,利用函数的单调性求取值范围.本题考查了分段函数的应用,属于中档题.二、填空题(本大题共6小题,共30.0分)11.如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且∠EDF=∠C,若CE:BE=3:2,DE=3,EF=2.则PA= ______ .【答案】【解析】解:在△DEF和△CED中,∵∠EDF=∠C,∠DEF公用,∴△DEF∽△CED,∴,∵DE=3,EF=2,∴EC==.∵CE:BE=3:2,∴BE=3.由相交弦定理可得AE•ED=EB•CE,∴AE==.∵AP∥CD,∴∠P=∠C,∴∠P=∠EDF.∴△AEP∽△FED,∴,∴==.∴PB=PE-EB=.∵PA与⊙O相切,∴PA2=PB•PC==.∴PA=.故答案为:.利用△DEF∽△CED与已知可得EC的长,进而得到BE,利用相交弦定理可得AE•ED=EB•CE,得到AE.再利用AP∥CD,可得△AEP∽△FED,得到PE,进而得到PB,再利用切割线定理可得PA2=PB•PC即可得出.本题综合考查了相似三角形的判定与性质、相交弦定理、切割线定理、平行线的性质等基础知识与基本技能方法,考查了分析问题和解决问题的能力,考查了推理能力和计算能力,属于难题.12.在直角坐标系x O y中,圆C的参数方程(φ为参数).以O为极点,x 轴的非负半轴为极轴建立极坐标系.射线OM:θ=与圆C的交点为O、P两点,则P点的极坐标为______ .【答案】(,)【解析】解:圆C的参数方程(φ为参数).它的普通方程为:(x-1)2+y2=1,射线OM:θ=的直角坐标方程w:y=x,x≥0.,解得x=0(舍去)或x=1,y=1.直线与圆的交点为:(1,1).P点的极坐标为:(,)故答案为:(,).求出圆的普通方程,射线OM的普通方程,然后求解P的直角坐标,化为极坐标即可.本题考查圆的参数方程与直角坐标方程的互化,极坐标与直角坐标的互化,考查计算能力.13.设函数f(x)=|x-|+|x+a|≥m.则m的最大值是______ .【答案】2【解析】解:函数f(x)=|x-|+|x+a|≥|a+|=|a|+||≥2,∵函数f(x)=|x-|+|x+a|≥m,∴m≤2,∴m的最大值是2.故答案为:2.利用绝对值不等式、基本不等式,可得f(x)=|x-|+|x+a|≥|a+|=|a|+||≥2,利用条件,即可求出m的最大值.本题考查绝对值不等式、基本不等式,考查学生的计算能力,比较基础.14.已知实数x,y满足,则z=xy的最大值为______ .【答案】【解析】解:作出不等式组对应的平面区域如图:由z=xy,则y=为双曲线,要使z=xy最大,则z>0,∵z=xy对应的双曲线的对称轴为y=x,∴由图象可知当z=xy与x+y-13=0相切时,z=xy取得最大值,由,解得,即D(,),此时z=,故答案为:.作出不等式组对于的平面区域,由z=xy,则y=为双曲线,利用数形结合即可得到结论.本题主要考查线性规划的应用,以及双曲线的性质,利用数形结合是解决本题的关键,本题涉及的知识点较多,综合性较强,有一定的难度.15.如图所示,在⊙O中,AB与CD是夹角为60°的两条直径,E、F分别是⊙O 与直径CD上的动点,若•+λ•=0,则λ的取值范围是______ .【答案】[-2,2]【解析】解:设⊙O的半径为r,以O为原点,OB为x轴建立直角坐标系,如图所示;则B(r,0),C(r,-r),设E(rcosα,rsinα),α∈(0,π);∴=μ=μ(r,-r)=(μr,-μr),其中μ∈[-1,1];∴=(μr-r,-μr),∴•=(rcosα,rsinα)•(μr-r,-μr)=r2(μ-1)cosα-μr2sinα;•=(-r0)•(r,-r)=-r2;∵•+λ•=0,∴λ=-=(μ-2)cosα-μsinα=sin(α+θ)=sin (α+θ);又μ∈[-1,1],∴≤≤2,∴-2≤sin(α+θ)≤2;∴-2≤λ≤2,即λ的取值范围是,.故答案为:[-2,2].根据题意,建立直角坐标系,用坐标表示B、C、E、F,计算•与•,求出λ的表达式,求出λ的取值范围即可.本题考查了平面向量的应用问题,也考查了求函数的最值问题以及三角函数的恒等变换问题,是较难的题目.16.已知数列{a n}的通项公式为a n=-n+p,数列{b n}的通项公式为b n=2n-5.设c n=,,>,若在数列{c n}中,c8>c n(n∈N*,n≠8),则实数p的取值范围是______ .【答案】(12,17)【解析】解:当a n≤b n时,c n=a n,当a n>b n时,c n=b n,∴c n是a n,b n中的较小者,因为a n=-n+p,所以{a n}是递减数列;因为b n=2n-5,所以{b n}是递增数列,因为c8>c n(n≠8),所以c8是c n的最大者,则n=1,2,3,…7,8时,c n递增,n=8,9,10,…时,c n递减,因此,n=1,2,3,…7时,2n-5<-n+p总成立,当n=7时,27-5<-7+p,∴p>11,n=9,10,11,…时,2n-5>-n+p总成立,当n=9时,29-5>-9+p,成立,∴p<25,而c8=a8或c8=b8,若a8≤b8,即23≥p-8,所以p≤16,则c8=a8=p-8,∴p-8>b7=27-5,∴p>12,故12<p≤16,若a8>b8,即p-8>28-5,所以p>16,∴c8=b8=23,那么c8>c9=a9,即8>p-9,∴p<17,故16<p<17,综上,12<p<17.故答案为:(12,17).由c n表达式知c n是a n,b n中的较小者,易判断{a n}是递减数列,{b n}是递增数列,由c8>c n(n≠8)知c8是c n的最大者,从而可知n=1,2,3,…7,8时,c n递增,n=8,9,10,…时,c n递减,进而可知a n与b n的大小关系,且c8=a8或c8=b8,分两种情况讨论,当c8=a8时,a8>b7,当c8=b8时,b8>a9,分别解出p的范围,再取并集即可;本题考查等差数列、等比数列的综合、数列的函数特性,考查分类讨论思想,考查学生分析问题解决问题的能力,考查学生逻辑推理能力,难度较大.三、解答题(本大题共6小题,共75.0分)17.某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:(1)求表中,的值及分数在[90,100)范围内的学生人数,并估计这次考试全校学生数学成绩的及格率(分数在[90,150)内为及格)(2)从成绩在[100,130)范围内的学生中随机选4人,设其中成绩在[100,110)内的人数为X,求X的分布列及数学期望.【答案】(1)由茎叶图可知分数在[50,70]范围内的有2人,在[110,130]范围内有3人,∴a==0.1,b=3,分数在[70,90]内的人数20×0.25=5,结合茎叶图可得分数在[70,80]内的人数为2,∴分数在[90,100]范围内的学生人数为4,故数学成绩及格的学生为13人,∴估计这次考试全校学生数学成绩的及格率为100%=65%;(2)由茎叶图可知分数在[100,130)范围内的有7人,分数在[100,110)范围内有4人,则随机变量X的所有可能取值为1,2,3,4,相应的概率为:P(X=1)==,P(X=2)==,P(X=3)==,P(X=4)==随机变量X的分布列为EX=1×+2×+3×+4×=2.2.【解析】(1)结合频率分布表与茎叶图给出的数据,先求a、b的值,再根据频率和为1,求分数在[90,110)范围内的学生数,从而求出分数分别在[90,100)和[70,90)的人数,计算及格率;(2)由茎叶图可知分数在[100,130)范围内的有7人,分数在[100,110)范围内有4人,则随机变量X的所有可能取值为1,2,3,4,求出相应的概率,可求X的分布列及数学期望.本题考查了茎叶图,考查了古典概型的概率计算,考查随机变量的分布列及数学期望,考查学生的计算能力,正确求概率是关键.18.已知,,,其中.(1)若0<A<,方程(t∈R)有且仅有一解,求t的取值范围;(2)设△ABC的内角A,B,C的对应边分别是a,b,c,且a=,若,求b+c 的取值范围.【答案】解:(1)依题意可得t=+=sin A cos A-cos2A=sin2A-cos2A=sin(2A-),∵,,∴<<.再根据t=+有唯一解,可得<或.(2)由其中得=-1,即tan A=-,∴.再根据正弦定理可得2R==1,∴<<,由<B+<,可得<.【解析】(1)依题意可得t=+=sin(2A-),根据-<2A-<,t=+有唯一解,可得t的范围.(2)由其中求得.再根据正弦定理求得<<,结合<B+<,可得b+c的取值范围.本题主要考查两个向量的数量积公式,正弦函数的图象特征,正弦函数的定义域和值域,正弦定理,属于中档题.19.如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.(Ⅰ)求证:BE∥平面ACF;(Ⅱ)求二面角C-BF-E的平面角的余弦值.【答案】(Ⅰ)证明:连结BD和AC交于O,连结OF,…(1分)∵ABCD为正方形,∴O为BD中点,∵F为DE中点,∴OF∥BE,…(3分)∵BE⊄平面ACF,OF⊂平面ACF,∴BE∥平面ACF.…(4分)(Ⅱ)解:∵AE⊥平面CDE,CD⊂平面CDE,∴AE⊥CD,∵ABCD为正方形,∴CD⊥AD,∵AE∩AD=A,AD,AE⊂平面DAE,∴CD⊥平面DAE,∵DE⊂平面DAE,∴CD⊥DE…(6分)∴以D为原点,以DE为x轴建立如图所示的坐标系,则E(2,0,0),F(1,0,0),A(2,0,2),D(0,0,0)∵AE⊥平面CDE,DE⊂平面CDE,∴AE⊥DE,∵AE=DE=2,∴,∵ABCD为正方形,∴,∴,,,由ABCD为正方形可得:,,,∴,,设平面BEF的法向量为,,,,,,,,由,令y1=1,则∴,,…(8分)设平面BCF的法向量为,,,,,,,,由,令y2=1,则,,∴,,…(10分)设二面角C-BF-E的平面角的大小为θ,则<,><,>=∴二面角C-BF-E的平面角的余弦值为…(12分)【解析】(Ⅰ)连结BD和AC交于O,连结OF,由已知得OF∥BE,由此能证明BE∥平面ACF.(Ⅱ)以D为原点,以DE为x轴建立坐标系,利用向量法能求出二面角C-BF-E的平面角的余弦值.本题考查直线与平面平行的证明,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.20.设各项均为正数的数列{a n}的前n项和为S n,已知2a2=a1+a3,数列是公差为d 的等差数列.(1)求数列{a n}的通项公式(用n,d表示);(2)设c为实数,对满足m+n=3k且m≠n的任意正整数m,n,k,不等式S m+S n>c S k 都成立.求证:c的最大值为.【答案】解:(1)由题意知:d>0,=+(n-1)d=+(n-1)d,∵2a2=a1+a3,∴3a2=S3,即3(S2-S1)=S3,∴,化简,得:,,,,当n≥2时,a n=S n-S n-1=n2d2-(n-1)2d2=(2n-1)d2,适合n=1情形.故所求a n=(2n-1)d2(2)(方法一)S m+S n>c S k m2d2+n2d2>c•k2d2m2+n2>c•k2,<恒成立.又m+n=3k且m≠n,>>,故,即c的最大值为.(方法二)由及,得d>0,S n=n2d2.于是,对满足题设的m,n,k,m≠n,有>.所以c的最大值.另一方面,任取实数>.设k为偶数,令,,则m,n,k符合条件,且.于是,只要9k2+4<2ak2,即当时,<.所以满足条件的,从而.因此c的最大值为.【解析】(1)根据等差数列的通项公式,结合已知,列出关于a1、d的方程,求出a1,进而推出s n,再利用a n与s n的关系求出a n.(2)利用(1)的结论,对S m+S n>c S k进行化简,转化为基本不等式问题求解;或求出c的最大值的范围,利用夹逼法求出a的值.本小题主要考查等差数列的通项、求和以及基本不等式等有关知识,考查探索、分析及论证的能力.21.已知抛物线C:x2=2py(p>0)的焦点为F,过F的直线l交抛物线C于点A,B,当直线l的倾斜角是45°时,AB的中垂线交y轴于点Q(0,5).(1)求p的值;(2)以AB为直径的圆交x轴于点M,N,记劣弧的长度为S,当直线l绕F旋转时,求的最大值.【答案】解:(1)抛物线C:x2=2py(p>0)的焦点为F,,,当l的倾斜角为45°时,l的方程为设A(x1,y1),B(x2,y2),由,得x2-2px-p2=0,x1+x2=2p,y1+y2=x1+x2+p=3p,得AB中点为,…(3分)AB中垂线为,x=0代入得.∴p=2…(6分)(2)设l的方程为y=kx+1,代入x2=4y得x2-4kx-4=0,,AB中点为D(2k,2k2+1)令∠MDN=2α,,∴…(8分)D到x轴的距离|DE|=2k2+1,…(10分)当k2=0时cosα取最小值,α的最大值为.故的最大值为.…(12分)【解析】(1)求出l的方程为,设A(x1,y1),B(x2,y2),联立直线与抛物线方程,利用韦达定理求出AB中点坐标,推出中垂线方程,结合AB的中垂线交y轴于点Q(0,5).求出p即可.(2)设l的方程为y=kx+1,代入x2=4y,求出AB的距离以及AB中点为D(2k,2k2+1),令∠MDN=2α,求出S的表达式,推出关系式,利用D到x轴的距离|DE|=2k2+1,求出,然后求解的最大值.本题考查直线与抛物线方程的位置关系,直线与直线的位置关系,以及圆的方程的综合应用,考查分析问题解决问题的能力,转化思想的应用.22.设函数f(x)=x2-(a-2)x-alnx.(I)求函数f(x)的单调区间;(Ⅱ)若方程f(x)=c(c∈R),有两个不相等的实数根x1、x2,求证:>.【答案】(12分)解:(I)f (x)=2x-(a-2)-(x>0).当a≤0时,f (x)>0,函数f(x)在(0,+∞)上单调递增,函数f(x)的单调增区间为(0,+∞).当a>0时,由f (x)>0,得x>;由f (x)<0,得0<x<.所以函数f(x)的单调增区间为,∞,单调减区间为,.…(4分)(II)证明:因为x1、x2是方程f(x)=c的两个不等实根,由(1)知a>0.不妨设0<x1<x2,则-(a-2)x1-alnx1=c,-(a-2)x2-alnx2=c.两式相减得-(a-2)x1-alnx1-+(a-2)•x2+alnx2=0,即+2x1--2x2=ax1+alnx1-ax2-alnx2=a(x1+lnx1-x2-lnx2).所以a=.因为f=0,当x∈,时,f (x)<0,当x∈,∞时,f (x)>0,故只要证>即可,即证明x1+x2>,即证明-+(x1+x2)(lnx1-lnx2)<+2x1--2x2,即证明ln<.设t=(0<t<1).令g(t)=lnt-,则g (t)=.因为t>0,所以g(t)≥0,当且仅当t=1时,g(t)=0,所以g(t)在(0,+∞)上是增函数.又g(1)=0,所以当t∈(0,1)时,g(t)<0总成立.所以原题得证…(12分)【解析】(I)求出函数的导数通过当a≤0时,当a>0时,判断导函数的符号,推出函数的单调区间.(II)通过x1、x2是方程f(x)=c的两个不等实根,由(1)知a>0.设0<x1<x2,把根代入方程,作差,推出a的表达式,构造函数,利用新函数的导数,通过函数的单调性利用分析法证明即可.本题考查函数的导数的综合应用,函数的单调性,分类讨论思想的应用,构造法的应用,考查分析问题解决问题的能力.。
湖南省十三校2015届高三第二次联考 数学(理) Word版含答案

湖南省2015届高三十三校联考第二次考试数学(理)长郡中学衡阳八中永州四中岳阳县一中湘潭县一中湘西州民中石门一中澧县一中郴州一中益阳市一中桃源县一中株洲市二中一.选择题1.集合{}{}26,30A x N xB x R x x=∈=∈->≤,则A B=I( B )A.{}3,4,5B.{}4,5,6C.{}36x x<≤D.{}36x x<≤2.下列命题中,真命题是(D )A.x R∃∈,使得00xe≤B.22sin3(π,)sinx x k k Zx+≠∈≥C.函数2()2xf x x=-有两个零点D.1,1a b>>是1ab>的充分不必要条件3.已知三棱柱的三视图如下图所示,其中俯视图为正三角形,则该三棱柱的体积为( C )A.B.C.D.64.)sin()(ϕω+=xAxf(A>0,ω>0)在x=1处取最大值,则( D )A.)1(-xf一定是奇函数B.)1(-xf一定是偶函数C.)1(+xf一定是奇函数D.)1(+xf一定是偶函数5.已知函数()cos6xf xπ=,集合{}1,2,3,4,5,6,7,8,9M=,现从M中任取两个不同的元素,m n,则()()0f m f n⋅=的概率为( A )A.512B.712C.718D.796.运行如右图所示的程序框图,则输出的结果S为( D )A.1008B.2015C.1007D. 1007-8.设函数)(x f y =在R 上有定义,对于任一给定的正数p ,定义函数⎩⎨⎧>≤=p x f p px f x f x f p )(,)(),()(,则称函数)(x f p 为)(x f 的“p 界函数”若给定函数2,12)(2=--=p x x x f ,则下列结论不成立的是( B )A.[][])0()0(p p f f f f = B. [][])1()1(p p f f f f =C. [][])2()2(f f f f p p =D. [][])3()3(f f f f p p =9.已知函数21()(,g x a x x e e=-≤≤e 为自然对数的底数)与()2ln h x x =的图象上存在关于x 轴对称的点,则实数a 的取值范围是( B ) A .21[1,2]e + B .2[1,2]e - C .221[2,2]e e+- D .2[2,)e -+∞ 10.如图,已知双曲线C :22221x y a b-=()0,0>>b a 的右顶点为,A O 为坐标原点,以A 为圆心的圆与双曲线C 的某渐近线交于两点Q P ,.若60PAQ ∠=︒且3OQ OP =,则双曲线C 的离心率为(B )ABC D7.已知抛物线2:4C y x =,点(,0)P m ,O 为坐标原点,若在抛物线C 上存在一点Q ,使得90OQP?o ,则实数m 的取值范围是( B )(A )(4,8) (B )(4,)+ (C )(0,4)(D )(8,)+二.填空题 (一)选做题11.如图,BD 是半圆O 的直径,A 在BD 的延长线上,AC 与半圆相切于点E ,AC BC ⊥,若AD =6AE =,则EC = 3 .12.在直角坐标系xOy 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系.若点P 为直线cos sin 40ρθρθ--=上一点,点Q 为曲线2(14x t t y t =⎧⎪⎨=⎪⎩为参数)上一点,则||PQ 的最小值为2. 13.已知函数f(x)=|x-k|+|x-2k|,若对任意的x ∈R ,f(x )≥f(3)=f(4)都成立,则k 的取值范围为[]2,3 .(二)必做题 14.设()0s i n c o s a x x d x π=+⎰,则二项式6⎛⎝的展开式的常数项是____-160_____.15.如果实数,a b 满足条件:20101a b b a a +-≥⎧⎪--≤⎨⎪≤⎩,则22a b a b ++的最大值是 75 。
2015年湖南省郴州市高考数学二模试卷(理科)

2015年湖南省郴州市高考数学二模试卷(理科)学校:___________姓名:___________班级:___________考号:___________一、选择题(本大题共10小题,共50.0分)1.已知集合A={x|()x<1),B={x|x<l),则A∩B=()A.∅B.RC.(-∞,1)D.(0,1)【答案】D【解析】解:由A中不等式变形得:()x<1=()0,即x>0,∴A=(0,+∞),∵B=(-∞,1),∴A∩B=(0,1),故选:D.求出A中不等式的解集确定出A,找出A与B的交集即可.此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.2.复数z=在复平面内对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限【答案】B【解析】解:∵i4=1,∴i2015=i3=-i,∴复数z====-1+i在复平面内对应的点(-1,1)在第二象限.故选:B.由i4=1,可得i2015=-i,再利用复数的运算法则、几何意义即可得出.本题考查了复数的运算法则、几何意义、周期性,属于基础题.3.已知命题p:∃x0∈(-∞,0),3<4;命题q:∀x∈(0,),tanx>x,则下列命题中真命题是()A.p∧qB.p∨(¬q)C.p∧(¬q)D.(¬P)∧q【答案】D【解析】解:命题p:∃x0∈(-∞,0),3<4为假命题,则¬p为真命题,命题q:∀x∈(0,),tanx>x,为真命题,则¬q为假命题,根据复合命题真假判定,(¬p)∧q是真命题,故D正确p∧q,p∨(¬q)、p∧(¬q)是假命题,故A、B、C错误故选:D.复合命题的真假判定,解决的办法是先判断组成复合命题的简单命题的真假,再根据真值表进行判断.本题考查的知识点是复合命题的真假判定,解决的办法是先判断组成复合命题的简单命题的真假,再根据真值表进行判断.4.已知函数y=f(x)+x是偶函数,且f(2)=3,则f(-2)=()A.-7B.7C.-5D.5【答案】B【解析】解:f(2)+2=5;∵y=f(x)+x是偶函数;∴f(-2)-2=f(2)+2=5;∴f(-2)=7.故选B.根据已知条件即可得到f(-2)-2=f(2)+2=5,所以得出f(-2)=7.考查偶函数的定义,要看清条件f(2)=3,而不是f(2)+2=3.5.一个几何体的三视图(单位:C m)如图所示,则该几何体的体积是80cm3.则图中的x等于()A. B. C.3 D.6【答案】C【解析】解:如图所示,该几何体为一个组合体:上面是一个四棱锥,下面是一个正方体,且四棱锥的右侧面与正方体的右侧面在同一个平面内.∴该几何体的体积是80=43+,解得x=3.故选:C.如图所示,该几何体为一个组合体:上面是一个四棱锥,下面是一个正方体,且四棱锥的右侧面与正方体的右侧面在同一个平面内.利用正方体与四棱锥的体积计算公式即可得出.本题考查了正方体与四棱锥的三视图及其体积计算公式,考查了推理能力与计算能力,属于基础题.6.执行如图所示的程序框图,则输出的结果是()A.-1007B.1007C.-2014D.2014【答案】A【解析】解:模拟执行程序框图,可得:s=0,k=1满足条件k<2015,k=2,S=2满足条件k<2015,k=3,S=2-3满足条件k <2015,k=4,S=2-3+4满足条件k<2015,k=5,S=2-3+4-5…满足条件k<2015,k=2014,S=2-3+4-…+2014满足条件k<2015,k=2015,S=2-3+4-5+6…-2015不满足条件k<2015,退出循环,输出S的值为S=2-3+4-5+6…+2014-2015=-1007故选:A.模拟执行程序框图,依次写出每次循环得到的k,s的值,当k=2015时,不满足条件k <2015,退出循环,输出S的值为S=2-3+4-5+6…+2014-2015=-1007.本题主要考查了程序框图和算法,正确写出每次循环得到的k,s的值是解题的关键,属于基础题.7.二项式(-x)n展开式中含有常数项,则n可能的取值是()A.8B.7C.6D.5【答案】D【解析】解:二项式(-x)n的展开式的通项公式为T r+1=(-1)r•,∵二项式(-x)n展开式中含有常数项,∴n可能的取值是5,故选:D.求出二项展开式的通项公式,利用二项式(-x)n展开式中含有常数项,即可求得n可能的取值.本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.8.由不等式组确定的平面区域记为Ω1,曲线y=x2-l(x≥0)与坐标轴所围成的平面区域记为Ω2.在Ω1中随机取一点,则该点恰好在Ω2内的概率为()A. B. C. D.【答案】A【解析】解:平面区域Q1为△ABC,其中A(0,1),B(2,-1),C(0,-1),△ABC的面积S=,平面区域Ω2的面积为=(x-x3)|=1-=,则在Ω1中随机取一点,则该点恰好在Ω2内的概率为,故选:A.作出不等式组对应的平面区域,求出对应的面积,根据几何概型的概率公式即可得到结论.本题主要考查几何概型的概率的计算,作出不等式组对应的平面区域结合几何概型的概率公式是解决本题的关键.9.已知椭圆C:+=1(a>b>0)的左右焦点为F1,F2,过F2线与圆x2+y2=b2相切于点A,并与椭圆C交与不同的两点P,Q,如图,PF1⊥PQ,若A为线段PQ的靠近P的三等分点,则椭圆的离心率为()A. B. C. D.【答案】C【解析】解:连接OA,PF1,则OA⊥PQ,又PF1⊥PQ,可得OA∥PF1因为A为线段PQ的靠近P的三等分点,所以A为线段PF2的中点,于是PF1=2b.结合椭圆的定义有PF2=2a-2b,在直角三角形PF1F2中,利用勾股定理得(2a-2b)2+(2b)2=(2c)2,将c2=a2-b2代入,整理可得b=a,于是e====.故选C.连接OA,PF1,则OA⊥PQ,PF1⊥PQ,因为A为线段PQ的靠近P的三等分点,所以A 为线段PA的中点,于是PF1=2b.结合椭圆的定义有PF2=2a-2b,由此能求出椭圆的离心率.离心率问题是解析几何的重点内容,各省考查频率相当高,往往融椭圆、双曲线的定义与平面几何的性质与一体,能够较好的考查学生的思维层次,备受命题专家的青睐.此题结合圆、椭圆、切线等知识,含金量高.10.已知直线y=k(x+1)(k>0)与函数y=|sinx|的图象恰有四个公共点A(x1,y1),B (x2,y2),C(x3,y3),D(x4,y4)其中x1<x2<x3<x4,则有()A.sinx4=1B.sinx4=(x4+1)cosx4C.sinx4=kcosx4D.sinx4=(x4+1)tanx4【答案】B【解析】解:∵直线y=k(x+1)(k>0)与函数y=|sinx|的图象恰有四个公共点,如图:当x∈(π,2π)时,函数y=|sinx|=-sinx,y′=-cosx,依题意,切点坐标为(x4,y4),又切点处的导数值就是直线y=k(x+1)(k>0)的斜率k,即k=-cosx4,∴y4=k(x4+1)=-cosx4(x4+1)=|sinx4|=-sinx4,∴sinx4=(x4+1)cosx4,故选:B.依题意,在同一坐标系中作出直线y=k(x+1)(k>0)与函数y=|sinx|的图象,利用导数的几何意义可求得切线的斜率,从而将切点坐标代入直线方程(即切线方程)即可求得答案.本题考查正弦函数的图象,着重考查导数的几何意义的应用,考查等价转化思想与数形结合思想的综合应用,考查作图能力与分析、运算能力,属于难题.二、填空题(本大题共6小题,共30.0分)11.在直角坐标系x O y中,曲线C1:(t为参数)与以O为原点,X轴正半轴为极轴建立的极坐标系下的直线l:ρ(2cosθ-sinθ)+1=0交于A、B两点,则线段AB的中点的直角坐标是______ .【答案】(1,3)【解析】解:根据曲线C1:(t为参数),得y=x2,根据直线l:ρ(2cosθ-sinθ)+1=0,得2x-y+1=0,联立方程组,得x2-2x-1=0,∴x1+x2=2,∴,∴线段AB的中点的横坐标为1,代入直线方程,得其纵坐标为3,故线段AB的中点的直角坐标(1,3),故答案为:(1,3).首先,将曲线C1:(t为参数),化为普通方程,得y=x2,然后,根据直线l:ρ(2cosθ-sinθ)+1=0,得2x-y+1=0,然后,联立方程组,利用根与系数的关系,确定线段AB的横坐标,然后,再确定其纵坐标.本题重点考查了抛物线的参数方程和普通方程互化、直线的极坐标方程和直角坐标方程的互化等知识,属于中档题.12.如图,过圆O外一点P分别作圆的切线和割线交圆于A,B,且PB=9,C是圆上一点使得BC=4,∠BAC=∠APB,则AB= ______ .【答案】6【解析】解:∵∠BAC=∠APB,∠C=∠BAP,∴△PAB∽△ACB,∴∴AB2=PB•BC=9×4=36,∴AB=6,故答案为:6.根据同弧所对的圆周角与弦切角相等,得到∠C=∠BAP,根据所给的两个角相等,得到两个三角形相似,根据相似三角形对应边成比例,得到比例式,代入已知的长度,求出结果.本题考查圆的切线的性质的应用,考查同弧所对的圆周角等于弦切角,考查三角形相似的判断和性质,本题是一个综合题目.13.若实数x,y,z满足x2+y2+z2=4,则x+2y-2z的取值范围为______ .【答案】[-6,6]【解析】解:根据柯西二维不等式,得:(x+2y-2z)2≤(x2+y2+z2)•(12+22+(-2)2)=4×9=36,∴-6≤x+2y-2z≤6.故答案为:[-6,6].根据柯西二维不等式(++)(++)≥,利用放缩法,求出x+2y-2z的取值范围.本题考查了柯西二维不等式的应用问题,是基础题目.14.如图,等边△ABC中,AB=2AD=4AE=4,则=______ .【答案】-3【解析】解:由题意,得=+,=+;∴•=(+)•(+)=•+•+•+•=4×4cos+4×2cosπ+1×4cosπ+1×2cos=8-8-4+1=-3;故答案为:-3.先表示出向量与,再计算向量的数量积•.本题考查了平面向量数量积的运算以及应用问题,是基础题.15.函数y=f(x)(x∈R)满足f(1)=l,f′(x)<,则不等式f(x)<+的解集为______ .【答案】(1,+∞)【解析】解:∵f′(x)<,∴f′(x)-<0,设h(x)=f(x)-x,则h′(x)=f′(x)-<0,∴h(x)是R上的减函数,且h(1)=f(1)-=1-=.不等式f(x)<+,即为f(x)-x<,即h(x)<h(1),得x>1,∴原不等式的解集为(1,+∞).故答案为:(1,+∞).所求解的不等式是抽象不等式,是与函数有关的不等式,函数的单调性和不等关系最密切.由f′(x)<,构造单调递减函数h(x)=f(x)-x,运用单调递减性求解即可.本题考查抽象不等式求解,关键是利用函数的单调性,根据已知条件和所要解的不等式,找到合适的函数作载体是关键.16.函数f(x)=,,,,,在等差数列{a n}中a1=0,a2015=1,数列{b n}满足b n=f(a n+1)-f(a n),则数列{b n}的前2014项的和为______ .【答案】【解析】解:∵等差数列{a n}中a1=0,a2015=1,b n=f(a n+1)-f(a n),∴数列{b n}的前2014项的和为f(a2015)-f(a1)=f(1)-f(0),∵f(x)=,,,,,∴数列{b n}的前2014项的和为f(1)-f(0)=0,故答案为:0.利用叠加法,可得数列{b n}的前2014项的和为f(a2015)-f(a1)=f(1)-f(0),利用f(x)=,,,,,即可求出数列{b n}的前2014项的和.本题考查等差数列的性质,考查学生的计算能力,比较基础.三、解答题(本大题共6小题,共75.0分)17.甲、乙两人同时参加环保知识晋级赛,竞赛规则是:如果第一轮比赛中有人晋级,则比赛结束,否则进行同等条件下的第二轮比赛,最多比赛两轮.每轮比赛甲晋级的概率为0.6,乙晋级的概率为0.5,甲、乙两人是否晋级互不影响.求:(1)比赛只进行一轮的概率P(A);(2)设晋级的人数为X,试求X的分布列和数学期望.【答案】解:(1)比赛只进行一轮,则至少有一人晋级,该事件的对立事件为“两人都没有晋级”,∴P(A)=1-(1-0.6)(1-0.5)=0.8.(2)X的可能取值为0,1,2,P(X=0)=(0.4×0.5)2=0.04,P(X=1)=0.6×0.5+0.4×0.5+0.2×(0.6×0.5+0.4×0.5)=0.6,P(X=2)=0.6×0.5+0.4×0.5+0.6×0.5=0.36,∴X的分布列为:【解析】(1)比赛只进行一轮,则至少有一人晋级,该事件的对立事件为“两人都没有晋级”,由此能求出比赛只进行一轮的概率P(A).(2)X的可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列和数学期望.本题主要考查概率、随机变量分布列以及数学期望等基础知识,考查运用概率统计知识解决简单实际问题的能力,考查数据处理能力.18.已知函数f(x)=(sinx+cosx)2+(2cos2x-1),x∈R.(Ⅰ)若对任意x恒有f(-)≤f(ωx+φ)≤f(),(ω>0,|φ|<),求ω的最小值和对应的φ的值.(Ⅱ)若△ABC的角A、B、C所对的边分别是a,b,c,且f()=1,又b,a,4c成等比数列,求的值.【答案】解:(Ⅰ)f(x)=(sinx+cosx)2+(2cos2x-1)=1+sin2x+cos2x=2sin(2x+)+1,∴f(ωx+φ)=2sin(2ωx+2φ+)+1,设其最小正周期为T,由题意知,T max=-(-)=,∴T max=π,∴ωmin=1,同时,+2φ+=+2kπ,k∈z,又∵|Φ|<,∴φ=.(Ⅱ)∵f()=1,∴2sin(A+)+1=1,∴sin(A+)=0,∵A∈(0,π)∴A=,∵b,a,4c成等比数列,∴a2=4bc,由余弦定理,得a2=b2+c2-2bccos A,得∴b2+c2-bc=4bc,∴()2-3+1=0,∴=,根据正弦定理,得,∴,∴的值.【解析】(Ⅰ)首先,化简函数解析式,得到f(x)=2sin(2x+)+1,然后,依据f(-)≤f (ωx+φ)≤f()恒成立,得到T的最大值为:-(-)=,从而求解即可;(Ⅱ)根据f()=1,得到A=,然后,结合边的关系和正弦定理,求解其比值即可.本题重点考查了余弦定理、正弦定理、三角恒等变换公式等知识,属于中档题.19.如图,在四棱锥E-ABCD中,矩形ABCD所在的平面与平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F,G,H分别为BE,AE,BC的中点(Ⅰ)求证:DE∥平面FGH;(Ⅱ)若点P在直线GF上,=λ,且二面角D-BP-A的大小为,求λ的值.【答案】解:(Ⅰ)证明:取AD的中点M,连接MH,MG.∵G、H、F分别是AE、BC、BE的中点,∴MH∥AB,GF∥AB,∴MH∥GF,即G、F、H、M四点共面,平面FGH即平面MGFH,又∵△ADE中,MG是中位线,∴MG∥DE∵DE⊄平面MGFH,MG⊂平面MGFH,∴DE∥平面MGFH,即直线DE与平面FGH平行.(Ⅱ)在平面ABE内,过A作AB的垂线,记为AP,则AP⊥平面ABCD.以A为原点,AP、AB、AD所在的直线分别为x轴,y轴,z轴,建立建立空间直角坐标系A-xyz,如图所示.可得A(0,0,0),B(0,4,0),D(0,0,2),E(2,-2,0),G(,-1,0),F(,1,0)∴=(0,2,0),=(0,-4,2),=(,-5,0).由=λ=(0,2λ,0),可得=+=(,2λ-5,0).设平面PBD的法向量为=(x,y,z),则,取y=,得z=2,x=5-2λ,∴=(5-2λ,,2),又∵平面ABP的一个法向量为=(0,0,1),∴cos<,>===cos=,解之得λ=1或4即λ的值等于1或4.【解析】(Ⅰ)欲证明DE∥平面FGH,先找直线与直线平行,即在平面FGH内找一条直线与直线DE平行.因此,取AD得中点M,连接GM,可证出MG∥DE,结合线面平行的判定定理可得DE∥平面FGH;(Ⅱ)建立空间直角坐标系,根据题中数据得出相应点的坐标进而得到、的坐标,利用垂直向量数量积为零的方法,求出=(5-2λ,,2)是平面BDP的一个法向量,结合=(0,0,1)是平面ABP的一个法向量和二面角D-BP-A的大小为,利用空间向量的夹角公式建立关于λ的方程,解之可得实数λ的值.本题在特殊四棱锥中证明线面平行,并求满足二面角D-BP-A的等于的点P的位置.着重考查了线面平行的判定定理,利用空间坐标系研究二面角大小等知识点,属于中档题.20.已知数列{a n}满足a1=,且当n≥2时,a n=.(1)求证:数列{-1}是等比数列,并求数列{a n}的通项公式;(2)设数列{a n}的前n项和为S n,求证:对任意的正整数n都有(1-)≤S n≤.【答案】解:(1)∵a n=,∴2a n-a n a n-1=a n-1,∴-1=,∴-1=2(-1)∵a1=,-1=2,∴数列{-1}是以2为首项,2为公比的等比数列,∴-1=2×2n-1=2n,∴a n=(2)∵S n=a1+a2+…+a n=++…+,∵a n=≥•,∴S n=++…+≥(1+++…+)=•=(1-)∵a n=<,∴S n=++…+<+++…+)=+=+-<=,∴对任意的正整数n都有(1-)≤S n≤.【解析】(1)将n≥2a n=变形整理得,从数列{-1}是以2为首项,2为公比的等比数列,由此即可得到数列{a n}的通项公式;(2)应用放缩法证明不等式,数列的前n项和,S n=a1+a2+…+a n=++…+,而a n=≥•,a n=<,再根据等比数列的前n项公式,求证出结论本题考查数列的递推式,在已知a1的情况下求数列的通项公式,并且证明了关于前n 项和的一个不等式,着重考查了等比数列的通项公式、求和公式和运用放缩法证明不等式恒成立等知识,属于难题.21.如图所示,已知过抛物线x2=4y的焦点F的直线l与抛物线相交于A,B两点.(1)求证:以AF为直径的圆与x轴相切;(2)设抛物线x2=4y在A,B两点处的切线的交点为M,若点M的横坐标为2,求△ABM的外接圆方程:(3)设过抛物线x2=4y焦点F的直线l与椭圆+=1的交点为C、D,是否存在直线l使得|AF|•|CF|=|BF|•|DF|,若存在,求出直线l的方程,若不存在,请说明理由.【答案】(1)证明:如图所示,设线段AF的中点为O1,过O1作O1O2⊥x轴,垂足为点O2,作AA1⊥x轴.则r====|O1O2|,∴r=|O1O2|,∴以AF为直径的圆与x轴相切;(2)解:设直线AB的方程为y=kx+1,A(x1,y1),B(x2,y2).联立,化为x2-4kx-4=0,∴x1+x2=4k,x1x2=-4.由x2=4y,可得′.∴k MA•k MB==-1,∴MA⊥MB.∴△MAB为直角三角形,∴△MAB的外接圆的圆心为线段AB的中点.设线段AB的中点为P,可得⊙P与抛物线的准线相切,切点为点M.∴x P=x M=2,∴=2,2k=2,解得k=1.y p====3,∴圆心P(2,3),又r=|MP|=|3-(-1)|=4,∴所求的△MAB的外接圆的方程为:(x-2)2+(y-3)2=16.(3)解:假设存在直线l使得|AF|•|CF|=|BF|•|DF|,设=λ,则,,设C(x3,y3),D(x4,y4).则(-x1,1-y1)=λ(x2,y2-1),(-x4,1-y4)=λ(x3,y3-1),∴x1=-λx2,x4=-λx3.把x1=-λx2代入x1+x2=4k,x1x2=-4,可得①.把y=kx+1代入椭圆+=1的方程可得(3k2+6)x2+6kx-1=0,∴x3+x4=-,x3x4=-.与x4=-λx3联立可得,②.①②联立可得,化为k2=1,解得k=±1.因此满足条件的直线存在:y=±x+1.【解析】(1)如图所示,设线段AF的中点为O1,过O1作O1O2⊥x轴,垂足为点O2,作AA1⊥x 轴.利用抛物线的定义及梯形的中位线定理可得可得r====|O1O2|,即可证明;(2)设直线AB的方程为y=kx+1,A(x1,y1),B(x2,y2).与抛物线方程联立化为x2-4kx-4=0,可得根与系数的关系,由x2=4y,可得′.可得k MA•k MB==-1,可得△MAB为直角三角形,可得△MAB的外接圆的圆心为线段AB的中点.设线段AB 的中点为P,可得⊙P与抛物线的准线相切,切点为点M,利用中点坐标公式与根与系数的关系可得圆心P(2,3),半径r=|MP|=|3-(-1)|=4,即可得出所求的△MAB的外接圆的方程.(3)假设存在直线l使得|AF|•|CF|=|BF|•|DF|,设=λ,可得,,设C(x3,y3),D(x4,y4).利用向量的坐标运算可得x1=-λx2,x4=-λx3.把x1=-λx2代入根与系数的关系可得.把y=kx+1代入椭圆方程可得(3k2+6)x2+6kx-1=0,把根与系数的关系与x4=-λx3联立可得,联立解得即可.本题考查了抛物线与椭圆的标准方程及其性质、直线与抛物线椭圆相交问题转化为方程联立可得根与系数的关系、向量坐标运算、圆的标准方程、中点坐标公式,考查了推理能力与计算能力,属于难题.22.已知函数f(x)=e x-ax-1(a∈R).(1)求函数f(x)的单调区间;(2)函数F(x)=f(x)-x1nx在定义域内是否存在零点?若存在,请指出有几个零点;若不存在,请说明理由:(3)若g(x)=ln(e x-1)-lnx,当x∈(0,+∞)时,不等式f(g(x))<f(x)恒成立,求a的取值范围.【答案】解:(1)∵f(x)=e x-ax-1,∴f′(x)=e x-a;当a≤0时,f′(x)>0;函数f(x)在R上是增函数;当a>0时,当x>lna时,f′(x)>0,当x<lna时,f′(x)<0;函数f(x)的单调增区间为(lna,+∞),单调减区间为(-∞,lna);综上所述,当a≤0时,函数f(x)在R上是增函数;当a>0时,函数f(x)的单调增区间为(lna,+∞),单调减区间为(-∞,lna);(2)F(x)=f(x)-x1nx的定义域为(0,+∞),由F(x)=0得,a=-lnx,(x>0),令h(x)=-lnx,(x>0),则h′(x)=,由于x>0,e x-1>0;当x>1时,h′(x)>0;当0<x<1,h′(x)<0;故函数h(x)在(0,1)上单调递减,在(1,+∞)上单调递增;故h(x)≥h(1)=e-1;又由(1)知,当a=1时,对∀x>0,有f(x)>f(lna)=0;即e x-1>x,故>1;∵x>0,∴>0,当x→0时,lnx→-∞,∴h(x)→+∞;当a>e-1时,函数F(x)有两个不同的零点,当a=e-1时,函数F(x)有且级有一个零点,当a<e-1时,函数F(x)没有零点;(3)由(2)知,当x>0时,e x-1>x,故对∀x>0,g(x)>0;构造函数H(x)=xe x-e x+1(x>0),则H′(x)=xe x>0;故函数H(x)在(0,+∞)上单调递增,则H(x)>H(0),则∀x>0,xe x-e x+1>0成立,当a≤1时,由(1)知,f(x)在(lna,+∞)上单调递增,在(0,lna)上单调递减,帮当0<x<lna时,0<g(x)<x<lna,所以f(g(x))>f(x),则不满足题意,所以满足题意的a的取值范围是(-∞,1].【解析】(1)求导f′(x)=e x-a;由导数的正负确定函数的单调性;(2)先求函数F(x)=f(x)-x1nx的定义域,由F(x)=0可化为a=-lnx,(x>0),从而令h(x)=-lnx,(x>0),求导h′(x)=,从而由导数求单调性并求最值;(3)当x>0时,e x-1>x,故对∀x>0,g(x)>0;构造函数H(x)=xe x-e x+1(x>0),则H′(x)=xe x>0;从而由导数确定恒成立问题.本题考查了导数的综合应用及恒成立问题,属于中档题.。
湖南郴州市第2次质检(数学)理含答案

JKLMN -*./ U *0 VWXYC -*./0 Z[P\]^O_L`a .1-*0/ b
cd"e](f^c6
%
% &'$ $ .$ '%ghijklmnopoqrstuvw%x &.-#& #6yz#& \{#z|}y~h%x ###' #6z#z|h% ()*$+ )$ , &.% %#8' &# '
PQ
RSTU
&'()*
!"# $%&'()*+,-./01
%!#$
234 5%&678+9:;<= >34?"@AB CDE FGHB IJK @*7L MNO
!"#$ !# %#!&%# " '!$ $% '&(&%#)*+,-./0!123 /456#789+&
vw3^~buZ Z|^hiZ3j 3¡¢£¤¥¦f§k ¨©ª«¬bZ| }hk ®Z| R¯~d° ±²k³´uZµ¶
S\^·TZ3jb¸¹ S0º»} ¼½¾01dZ3jH¿ÀÁ ¾031 ÃÄà S\ÅÆ ÇÈ}É`Ê
],-. !<6=,<6=-8-,%1\
&%'%*&$'10c &' %uy *(
#( )
'( *
+( >
.( %
)%(
hBm+
"#1=?5/ 0
#@ >
=?5
0
湖南省郴州市2015届高考模拟数学理科试题(三)及答案

中 e 为自然对数的底数)的解集为
()
A . 0,
B.
,0 3,
C . ,0 0,
D . 3,
【解析】构造函数 g( x) ex f ( x) ex ,
因为 g ' ( x) ex f ( x) ex f ' (x) ex ex f (x) f '( x) 1 0,
所以 g (x ) ex f (x ) ex 是 R 上的增函数,又因为 g( x) g (0) ,解得 x 0 .故选 A.
由图知, AOB
, AOC
5
,所以
AOP
[
,5 ].
6
6
66
5
当 AOP
6 时, zmax
2 3 cos = 3;当 6
AOP
时,
6
5 zmin 2 3 cos =- 3.所以 z 的取值范围是 [ 3 , 3]
6
B A
P
C
O
x
9.定义在 R 上的函数 f (x) 满足: f (x) f (x) 1, f (0) 4, 则不等式 ex f ( x) ex 3(其
g(0) 3 ,所以原不等式转化为
10.若存在正整数 T ,对于任意正整数 n 都有 an T an 成立, 则称数列 an 为周期数列 ,周期
为 T .已知数列 an 满足 a1 m(m 0) , an 1
an 1,an 1
1
,关于下列命题:
,0 an
an
1
2
3 ①当 m 4 时, a5 2 ;
AB 7 , CD 11, AC 2 ,则 BD
.16
13. 若不等式 x 3 x 7 a2 3a 的解集为 R ,则实数 a 的取值范围是 .
湖南省郴州市高三数学第二次教学质量监测试题 文

湖南省郴州市2015届高三第二次教学质量监测数学(文)试题注意事项:1.答题前,考生务必将自己的姓名、准考证号写在答题卡和该试题卷的封面上,并认真核对条形码上的姓名、准考证号和科日。
2.学生作答时,选择题和非选择题均须作在答题卡上,在本试题卷上作答无效。
考生在答题卡上按答题卡中注意事项的要求答题。
3.考试结束后,将本试题卷和答题卡一并交回。
4.本试题卷如缺页,考生须声明,否则后果自负。
一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给卅的四个选项中,只有一项是符合题日要求的.1.设集合M={x∈R| 1g x=0},N={x ∈R|- 2<x<0},则A.M⊆N B.M⊇N C.M=N D.M N=∅2.下列四个命题中,真命题的是A.∃x0∈Z,1<4xo<3 B.∃x0∈Z,5x0+l=0C.∀x∈Z,x2-1=0 D.∀x,∈R,x2-x+2>0,3.已知l、m是不同的两条直线,α、β是不重合的两个平面,则下列命题中正确的是A.若l∥α,α⊥β,则l∥βB.若l⊥α,α∥β,m cβ,则l⊥m C.若l⊥m,α∥β,m⊂β,则l⊥αD.若l⊥α,α⊥β,则l∥β4.若复数。
满足z(1-i)=2,则复数z的共轭复数z=A.1-i B.1+i C D.2-2i5.下列两个程序(1)和(2)的运行的结果i分别是A.7,7 B.7,6 C.6,7 D.6,66.已知△ABC中A、B、C为三个内角且siri2C+sinAsinB=sin2A+sin2B,则角C等于A .30oB .120oC .60oD .150o7.已知△ABC 是等腰三角形,∠A BC=120o ,以A .B 为焦点的双曲线过点C ,则此双曲线的离心率为A .B .C.12+ D.8.若实数x ,y 满足|x -1|-ln 1y =0,则y 关于x 的函数图象的大致形状是9.已知O 为坐标原点,F 为抛物线C :的焦点,P 是C 上一点,若|PF|△OPF 的面积为 A .B .C .D .10.已知两点A (l ,0),B (-l,O 为坐标原点,点C 在第二象限,且∠AOC=135o ,设,(OA OA OB λλ=-+∈R )则实数λ等于A. B.C.12D.12二、填空题:本大题共5小题,每小题5分,共25分孑巴答案填在答题卡中对应题号后的横线上.11.已知曲线y=a sin x+ cos x 在x=0处的切线方程为x-y+l=0,则实数以的值为 . 12.已知极坐标系的极点与直角坐标系的原点重合,极轴与x 轴非负半轴重合,点M 的极坐标为M (2,2π),直线l 的参数方程为21x t y t =⎧⎨=-+⎩(t 为参数),则点M 到直线l 的距离为 .13.设x, y 满足约束条件112210x y x x y ≥⎧⎪⎪≥⎨⎪+≤⎪⎩,则z= 2x -y 的最小值为 .14.在等差数列{an }中,a1=3,公差为d ,前n 项和为Sn, 当且仅当n=6时Sn 取得最大值,则d 的取值范围是 .15.设函数f (x )=1g (21x -+a )是奇函数,则使f (x )<0的x 的取值范围是 .三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤. 16.(本小题满分12分)已知函数f (x )(x 6π+),(x ∈R ).(I )求f (x )的最小正周期及对称轴方程;(Ⅱ)△ABC 的三个内角A,B,C 所对的边分别为a ,b ,c ,若f (C+12π)=0,且CA .CB =8,求△ABC 的面积. 17.(本小题满分12分)为了解甲、乙两种品牌手机的电池充满电后的待机时间(假设都在24~96小时范围内),从这两种手机的电池中分别随机抽取100个进行测试.结果统计如下表.(I )估计甲品牌手机的电池充满电后的待机时间小于48小时的概率;(Ⅱ)这两种品牌的手机的电池充满电后,某个电池已使用了48小时,试估计该电池是甲品牌手机的电池的概率:(Ⅲ)由于两种品牌的手机的某些差异,普遍认为甲品牌手机比乙品牌手机更显“低调”,销售商随机调查了110名购买者,并将有关数据整理为不完整的2x2列联表,写出表中A 、B 、C 、D 、E 的值,并判断是否有990/c 的把握认为喜欢“低调型”手机与消费者的年龄有关?附:其中18.(本题满分12分)如图,在五面体A BCDEF 中,四边形ADEF 是正方形,FA ⊥平面4BCD ,BC ∥AD ,∠BAD=∠CDA=45o .(I )求异面直线CE 与AF 所成角的余弦值; (Ⅱ)证明平面CDE ⊥平面ABF; (Ⅲ)求五面体ABCDEF 的体积.19.(本小题满分13分)已知数列{an }的前n 项的和为Sn 且Sn=12na -(n ∈N*),数列{bn }是公差d>0的等差数列且b3、b5是方程x2-14x+45=0的两根. (I )求数列{an },{bn }的通项公式; (Ⅱ)记cn ,= an bn 求证:cn+1n c ≤;(Ⅲ)求数列{cn }的前n 项和Tn . 20.(本大题满分13分)已知椭网C 的中心在原点,焦点在x轴上,离心率为,且经过点P (4,1).(I)求椭圆C的方程;(Ⅱ)过点P的直线l:y=l与椭圆的另一个交点为Q,点A、B是椭网C上位于直线l两侧的动点,且直线AP与BP关于l对称,求四边形APBQ面积的最大值.21.(本小题满分13分)已知函数f(x)=ax+lnx(a R)(I)当a=1时,求f(x)的最小值;(Ⅱ)若f(x)在(0,e]上的最小值为2,求实数a的值;(Ⅲ)当a=-l时,试判断函数g(x)=f(x)+1nxx在其定义域内的零点的个数.。
湖南省郴州市高三第二次教学质量监测——数学理数学理

湖南省郴州市2017届高三第二次教学质量监测数学(理)试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项 是符合题目要求的.1.已知,是虚数单位.若与互为共轭复数,则( )A .0B .1C .2D .32.已知均为单位向量,且33(2)(2)2a b a b +-=-•,则向量的夹角为( ) A . B . C . D .3.已知,,则( )A .B .C .D . 4.我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸;③台体的体积公式1()3V S S h =+下上•). A . 2寸 B .3寸 C. 4寸 D .5寸5.考拉兹猜想又名猜想,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能得到1.阅读如图所示的程序框图,运行相应程序,输出的结果( )A .4B .5 C.6 D .76.已知某三棱锥的三视图如图所示,正视图和俯视图都是等腰直角三角形,则该三棱锥中最长的棱长为( )A .B . C. D .27.已知函数是奇函数,当时,(且),且,则的值为( )A .B . C. 3 D .98.设关于的不等式组21000x y x m y m -+>⎧⎪+<⎨⎪->⎩表示的平面区域内存在点,满足.则的取值范围是( )A .B . C. D .9.将边长为的正方形沿对角线折成一个直二面角.则四面体的内切球的半径为( )A .1B . C. D .10.已知为双曲线22221(0,0)x y a b a b-=>>的左焦点,点为双曲线虚轴的一个顶点,过的直线与双曲线的一条渐近线在轴右侧的交点为,若,则此双曲线的离心率是( )A .B . C. D .11.在中,分别是边的中点,分别是线段的中点,分别是线段*11,(1)n n A A B B n N n --∈>,的中点, 设数列满足:向量*()n n n n B A a CA b CB n N =+∈,有下列四个命题,其中假命题是:( )A .数列是单调递增数列,数列是单调递减数列B .数列是等比数列C.数列有最小值,无最大值D .若中,,,,则最小时,12.若方程有四个不同的实数根,且,则的取值范围是( )A .B . C. D .第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.若命题 “020223xx R a a ∃∈-≤-,”是假命题,则实数的取值范围是________. 14.两所学校分别有2名、3名学生获奖,这5名学生要排成一排合影,则同校学生排在一起的概率是__________.15.过点的直线与圆交于两点,为圆心,当最小时,直线的方程为_________.16.已知函数()2|cos |sin sin 2f x x x x =+,给出下列四个命题:①函数的图象关于直线对称;②函数在区间上单调递增;③函数的最小正周期为;④函数的值域为.其中真命题的序号是____________.(将你认为真命题的序号都填上)三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分10分)已知等差数列满足:*11(),1n n a a n N a +>∈=,该数列的前三项分别加上1,1,3后成等比数列,且. (1)求数列,的通项公式;(2)求数列的前项和.18. (本小题满分12分)在中,,,分别是角,,的对边,且2cos cos (tan tan 1)1A C A C -=.(1)求的大小;(2)若,,求的面积.19. (本小题满分12分)如图,菱形中,,与相交于点,平面,//23CF AE AB CF ==,,.(1)求证:平面;(2)当直线与平面所成角的大小为时,求的长度.20. (本小题满分12分)某水泥厂销售工作人员根据以往该厂的销售情况,绘制了该厂日销售量的频率分布直方图,如图所示:将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.(1)求未来3天内,连续2天日销售量不低于8吨,另一天日销售量低于8吨的概率;(2)用表示未来3天内日销售量不低于8吨的天数,求随机变量的分布列及数学期望.21. (本小题满分12分)已知椭圆2222:1(0)x yC a ba b+=>>的离心率为,且过点.若点在椭圆上,则点称为点的一个“椭点”.(1)求椭圆的标准方程;(2)若直线与椭圆相交于两点,且两点的“椭点”分别为,以为直径的圆经过坐标原点,试求的面积.22.(本小题满分12分)已知函数,.(1)求函数在上的最小值;(2)对一切,恒成立,求实数的取值范围;(3)探讨函数是否存在零点?若存在,求出函数的零点;若不存在,请说明理由.试卷答案一、选择题1-5: DABBD 6-10:ABCDA 11、12:CB二、填空题13. 14. 15. 16.②④三、解答题:解答应写出文字说明、证明过程或演算步骤.17.解:(1)设为等差数列的公差,且,由1231,1,12a a d a d ==+=+,…………(1分)(2)由(1)知,所以23135212222n n n T -=+++…+,①…………(6分) 234111352122222n n n T +-=+++…+,②…………(7分) ① —②,得23111111212222222n n n n T +-⎛⎫=+⨯++ ⎪⎝⎭…+-,………………(8分) 21111111111211121323222112222222212n n n n n n n n n T -*-**⎛⎫ ⎪--+⎝⎭=+⨯=+--=----,…………(9分) 所以.………………(10分)18.解:(Ⅰ)由()2cos cos tan tan 11A C A C -=, 得sin sin 2cos cos 11cos cos A C A C A C ⎛⎫-= ⎪⎝⎭,…………(1分) ()2sin sin cos cos 1A C A C ∴-=,…………(3分),…………(4分),…………(5分)又.…………(6分)(Ⅱ)由,得,………………(8分)又5,34a cb B ac π+===∴=,………………(10分)115sin 224ABC S ac B ∆∴==⨯=(12分) 19.解:(1)证明:四边形是菱形,.………………(1分)平面,平面,…………(2分),………………(3分)又平面,平面,,………………(4分)平面.………………(5分)(2)以为原点,以所在直线分别为轴,轴,以过点且平行于的直线为轴建立空间直角坐标系.………………(6分)则()()(),0,,1,0,3B D F -.设,则,()()()1,0,3,0,23,0,1,OF DB EB a ∴=-==--,………………(7分) 设平面的法向量为,则………………(8分)即令,得,………………(9分)()cos ,10n OFn OF n OF ⋅∴==,………………(10分)直线与平面所成角的大小为,,………………(11分)解得或(舍),.………………(12分)20.解(Ⅰ)由频率分布直方图可知,日销售量不低于吨的频率为:()20.1250.0750.4⨯+=,……………………(1分)记未来天内,第天日销售量不低于吨为事件,则,………………(2分)未来天内,连续天日销售不低于吨,另一天日销量低于吨包含两个互斥事件和,………………(3分)则:()()()123123123123P A A A A A A P A A A P A A A =+………………(4分) ()()0.40.410.410.40.40.40.192=⨯⨯-+-⨯⨯=.………………(6分)(Ⅱ)的可能取值为,且~()()3010.40.216P X ==-=,………………(7分) ()()21310.410.40.432P X C ==⨯-=,………………(8分)()()22320.410.40.288P X C ==⨯-=,………………(9分)()330.40.064P X ===,………………(10分) 所以的分布列为…………(11分).………………(12分)21.解:(Ⅰ)由,得,………………(1分)又,………………(2分)椭圆,因点在上,22914+143c c ∴=,得,…………(3分),………………(4分)所以椭圆的方程为:;…………(5分)(Ⅱ)设,则,由以为直径的圆经过坐标原点,得,即 (1)………………(6分)由22143y kx mx y =+⎧⎪⎨+=⎪⎩,消除整理得:()()222348430k x mk m +++-=, 由()()222264163430k m k m ∆=-+->,得,而()2121222438,3434m mk x x x x k k -+=-=++ (2)………………(7分)()()()()22221212121223434m k y y kx m kx m k x x mk x x m k -∴=++=+++=+ (3)将(2)(3)代入(1)得:()()()()2222243340434434m m k k k --+=++,即,………………(8分) 又1AB =,………………(9分) 原点到直线的距离,………………(10分)12AOB S AB d ∆∴=………………(11分)把代入上式得,即的面积是为.………………(12分)22.解:(Ⅰ),由得,,由得,函数在上单调递减,在上单调递增.………………(1分)当时,()min 1112,t f x f e e e ⎛⎫+>∴==- ⎪⎝⎭; 当时,在上单调递增,,………………(2分)()min11,0,1ln ,.t e e f x t t t e ⎧-<≤⎪⎪∴=⎨⎪>⎪⎩………………(3分) (Ⅱ)原问题可化为,………………(4分)设()()32ln 0h x x x x x=++>, ,当时,在上单调递减;…………(5分)当时,在上单调递增;………………(6分),故的取值范围为.………………(7分)(Ⅲ)令,得,即,………………(8分)当(Ⅰ)知当且仅当时,的最小值是,…………(9分) 设,则,易知在上单调递增,在上单调递减,当且仅当时,取最大值,且,………………(10分) 对都有,即()12ln 0x F x x e ex=-+>恒成立, 故函数无零点.……………………(12分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
湖南省郴州市2015届高三第二次教学质量监测
数学(理)试题
注意事项:
1.答题前,考生务必将自己的姓名、准考证号写在答题卡和该试题卷的封面上,并认真核对条形码上的姓
名、准考证号和科日.
2.学生作答时,选择题和非选择题均须作在答题卡上,在本试题卷上作答无效.考生在答题卡上按答题卡
中注意事项的要求答题.
3.考试结束后,将本试题卷和答题卡一并交回.
4.本试题卷共5页.如缺页,考生须声明,否则后果自负.
一、选择题:本大题共10个小题,每小题5分,共50分.在每个小题给出的四个选项中,只有一项是符合题日
要求的.
1.已知集合A={x|(12
)x
<1),B={x|x<l ),则A B=
A .∅
B .R
C .(-∞,1)
D .(0,1)
2.复数z=
2015
1i
i +在复平面内对应的点在 A .第一象限 B .第二象限
C .第三象限
D .第四象限
3.已知命题p :∃x 0∈(-∞,0),30
x <4
x ;命题q:∀x ∈(0,
2
π
),tanx>x ,则下列命题中真命题是 A .p ∧q
B .p ∨(⌝
q )
C .p ∧(⌝
q ) D .(⌝
P) ∧q
4.已知函数y=f (x )+x 是偶函数,且f (2)=3,则f (-2)= A .-7 B .7 C .-5 D .5
5.一个几何体的三视图(单位:Cm )如图所示,则该几何体的体积是 80cm 3.则图中的x 等于
A .
3
2
B .
23
C .3
D .6
6.执行如图所示的程序框图,则输出的结果是
A .-1007
B .1007
C .-2014
D .2014
7.二项式(1
x
-)n 展开式中含有常数项,则n 可能的取值是
A .8
B .7
C .6
D .5
8.由不等式组011x y x y ≥⎧⎪
≥-⎨⎪+≤⎩确定的平面区域记为1Ω,曲线y=x 2-l (x≥0)与坐标轴所围成的平面区域记为2Ω.在
1Ω中随机取一点,则该点恰好在2Ω内的概率为
A .
13
B .
2
3
C .
14
D .
16
9.已知椭网C :22
22x y a b
+=l (a>b>0)的左右焦点分别为F 1、F 2过F 2
的直线与圆x 2 +y 2=b 2相切于A ,并与椭网C 交于不同的两点P 、Q ,如图,若A
为线段PF 2的
中点,则椭圆的离心率为
A
B
C
D
10.已知直线y=k (x+l )(k>0)与函数y=|sinx|的图象恰有四个公共点A (x 1,y 1),B (x 2,y 2),C (x 3,y 3),D (x 4,y 4).其中x l <x 2<x 3<x 4,则有 A .sinx 4=1 B .sin x 4=(x 4+1)cos x 4 C .sin x 4=kcosx 4 D .sin x 4=(x 4+1)tan x 4
二、填空题:本大题共6小题,考生作答5小题,每小题5分,共25分.把答案填在答题卡中对应题号后的横
线上.
(一)选做题(请考生在第11,12,13三题中任选两题作答,如果全做,则按前两题记分)
11.在直角坐标系xOy 中,曲线C 1:2
x t
y t =⎧⎨=⎩
(t 为参数)与以O 为原点,X 轴
正半轴为极轴建立的极坐标系下的直线l :ρ(2cos θ-sin θ)+1=0
交于A 、B
两点,则线段AB 的中点的直角坐标是 .
12.如图,过⊙O 外一点P 分别作网的切线和割线分别交圆于A ,B 两点.且PB=9,C 是圆上一点使得BC=4,∠
BA C=∠A PB ,则A B= .
13.若实数x ,y ,z 满足x 2+y 2+z 2=4,则x+2y -2z 的取值范围为 . (二)必做题(14-16题)
14.如右图,等边△ABC 中,AB=2A D=4A E=4,则BE ·CD = . 15.函数y=f (x )(x ∈R )满足f (1)=l ,f (x )<
1
2
,则不等式f (x ) <
1
22
x +的解集为 .
16.函数f (x )=2
14
12,[0,]2,11,,12x x og x x ⎧∈⎪⎪
⎨⎛⎤⎪∈ ⎥
⎪⎝⎦⎩在等差数列{a n }中a 1=0,a 2015=1,数列{b n }满足b n =1()()n n f a f a +-,则
数列{b n }的前2014项的和为 .
三、解答题:本大题共6小题,共75分.解答应写出义宁说明、证明过程或演算步骤. 17.(本小题满分12分)
甲、乙两人同时参加环保知识晋级赛,竞赛规则是:如果第一轮比赛中有人晋级,则比赛结束,否则进行
同等条件下的第二轮比赛,最多比赛两轮。
每轮比赛甲晋级的概率为0.6,乙晋级的概率为0.5,甲、乙两人是否晋级互不影响。
求: (I )比赛只进行一轮的概率P (A ); (Ⅱ)设晋级的人数为X ,试求X 的分布列和数学期望. 18.(本小题满分12分) 已知函数f (x )=(sinx+cos x )2
2cos 2x-1),x ∈R
(I )若对任意x 恒有f (()(),(0,|)632
f x f πππ
ωϕω-
≤+≤><,求ω的最小值和对应的ϕ的值;
(Ⅱ)若△ABC 的角 A 、B 、C 所对的边分别是a ,b ,c ,.且f (2A )=1,又b ,a ,4c 成等比数列,求
sin sin B
C
的值.
19.(本小题满分12分)
如图,在四棱锥E-A BCD 中,矩形ABCD 所在的平面与平面AEB 垂直,且∠BA E=120o ,A E=A B=4,A D=2,F ,
G ,H 分别为BE ,AE ,BC 的中点. (I )求证:DE ∥平面FGH ; (Ⅱ)若点P 在直线GF 上,GP GF λ=,且二面角D-BP-A 的大小为
4
π
,求
λ的值.
20.(本小题满分13分)
已知数列{a n}满足a1=1
3
,且当n≥2时,a n=1
1
2
n
n
a
a
-
-
-
.
(1)求证:数列{1
1
n
a
-}是等比数列,并求数列{a n}的通项公式;
(2)设数列{a n}的前n项和为S n,求证:对任意的正整数n都有215 (1)
326
n
n
S
-≤<.
21.(本小题满分13分)
如图所示,已知过抛物线x2= 4y的焦点F的直线l与抛物线相交于A,B两点.
(I)求证:以AF为直径的网与x轴相切;
(Ⅱ)设抛物线x2=4y在A,B两点处的切线的交点为M,若点M的横坐标为2,求△ABM的外接宫内圆方程:
(Ⅲ)设过抛物线x2= 4y焦点F的直线l与椭圆
22
33
42
y x
+=1的交点为C、D,是否存在直线l使得|AF
|·|CF|=|BF|·|DF|,若存在,求出直线l的方程,若不存在,请说明理由.
22.(本小题满分13分)
已知函数f(x)=e x- ax -1(a∈R).
(I)求函数f(x)的单调区间;
(Ⅱ)函数F(x)=f(x)-x1nx在定义域内是否存在零点?若存在,请指出有几个零点;若不存在,请说明理由:
(Ⅲ)若g(x)=ln(e x-1)-lnx,当x∈(0,+∞)时,不等式f(g(x))<f(x)恒成立,求a的取值范围.。
