(抽样检验)抽样检验的基础知识最全版
抽样检验

二、在质量监督复检中为何不能用加倍抽样方案
例如设定p0=2.5,用(2;1)方案,其接收概率为95.1%,如实际不合格率 大于2.5,则用这个抽样方案抽检,被判为不通过的概绿就是195.1%=4.9% 如过用加倍抽检方案(4;1),其被接收概率为90.4%,则复检被漏判的风 险为:1-[(1- 95.1%)(1- 90.4%)]=99.53%-----太高了.
关于P0=0的问题 P0=0时,使用(n;1)抽样方案,对于任意n(n<N)都合 理,当d>0时,以100%把握确认监督总体为不合格总体; d=0时,只能说“未见异常”。
一些问题的说明
一、GB/T2828中抽样方案为何不能用于质量监督
1)GB/T2828中的AQL是过程平均质量指标,仅适用于连续批的检 验;在质量监督中,监督总体看成一个孤立的批。 2)GB/T2828重点考虑受控,即要考虑弃真错误,又要考虑存伪错 误;而质量监督不允许较大的弃真错误。 3) GB/T2828是调整型抽样方案,弃真错误概率а和存伪错误概率 β在变动;而监督抽检则а不变( а=0.05)
• 连续批抽样——用某一质量要求(AQL)确定的抽样组
(即系列抽样方案)对连续m批产品进行抽样检验,若接 收了其中的k批(k≤ m),则保证这k批产品的平均不合格 率控制在原先规定的AQL之下。
• 孤立批抽样方案——仅以一批作为总体加以抽检。
用一个抽样方案对一批产品进行抽样检验(即孤立批抽样 检验),其作用是仅是起概率保关作用——当不合格品率 低时,接收概率高,当不合格品率高时,接收概率低。也 就是说,孤立批抽样检验方案保证该批产品是以某个概率 被接受。
多次抽样检验检方案
一次抽样、二次抽样、五次抽样 一次抽样 [n;Ac,Re],用样本中不合格数与Ac、Re对比来 判断是否接受。 d ≤ Ac——接收此批 d ≥ Re——拒收此批 二次抽样 n1;A1,R1 n2;A2,R2 若d1 ≤A1—接收; d1 ≥R1—拒收;若A1<d1<R1,抽取第二次样本检验。若 (d1+d2)≤A2 —接收;若(d1+d2)≥R2—拒收。 ; , 五次抽样 n1;A1,R1 n2;A2,R2 ; , n3;A3,R3 ; , n4;A4,R4 ; , n5;A5,R5 ; , A)若d1 ≤A1—接收; d1 ≥R1—拒收。
抽样检验相关基础知识

抽样检验相关基础知识引言抽样检验是统计学中常用的一种推断性统计方法,用于对总体特征或参数进行推断。
在许多实际问题中,由于种种原因我们无法对总体进行全面调查,而只能通过对总体的一个子集进行抽样,并根据抽样结果对总体进行推断。
抽样检验就是根据样本数据对总体进行推断的一种方法。
本文将介绍抽样检验的基本概念、原理和常见的假设检验方法。
抽样检验的基本概念总体和样本在抽样检验中,我们关心的是一个特定的总体(population)。
总体是指我们想要研究的一群个体的集合。
例如,我们可能想研究全国成年人的平均身高,那么全国成年人就是我们要研究的总体。
由于总体往往很大或很难获取全部数据,我们需要通过抽样来获取总体的一部分数据,这部分数据称为样本(sample)。
样本是从总体中抽取的、能够代表总体特征的一部分个体的集合。
通过对样本数据的研究,我们可以对总体进行推断。
假设检验在抽样检验中,我们常常对总体的某个特征或参数值进行假设,并通过样本数据来判断这个假设是否成立。
在假设检验中,我们通常会提出一个原假设(null hypothesis)和一个备择假设(alternative hypothesis)。
原假设是对总体特征或参数的一个假设,我们希望通过样本数据来检验这个假设的正确性。
备择假设是对原假设的反面假设,它表示我们认为原假设不成立。
抽样检验的原理抽样检验的原理基于统计推断的思想,即根据样本数据对总体进行推断。
在抽样检验中,我们通常会选择一个合适的统计量作为检验统计量(test statistic)。
检验统计量是样本数据的一个函数,它能够反映样本数据与原假设的一致性。
常见的检验统计量有均值、比例、差异等。
然后,我们会根据原假设的设定,计算出这个统计量的取值,并根据概率分布来进行判断。
根据概率分布,我们可以计算出在原假设成立的情况下,出现检验统计量取值的概率。
如果这个概率(称为p值)很小,低于事先设定的显著性水平(significance level),我们就有理由拒绝原假设,接受备择假设。
(抽样检验)抽样检验的基础知识最全版

(抽样检验)抽样检验的基础知识第1章抽样检验的基础知识第1节抽样检验的目的从居家过日子到国家重大经济决策都离不开抽样检验。
比如说,你到水果摊买桔子,你可能会问:“酸不酸呀”?摊主说“你尝壹尝,先尝后买”,于是你从壹大堆桔子中抽取壹个尝壹尝,你尝的目的是什么呢?你尝的目的是要通过这壹个桔子的质量情况来推断这壹大堆桔子的质量情况。
显然抽样检验的目的是:通过样本推断总体。
样本是样品的集合,壹个样本可由壹个样品组成,也可由多个样品组成。
欲达到通过样本推断总体这样的目的,要通过三个步骤:A.抽样,B.检验,C.推断。
其中抽样这个步骤含有俩个内容a.怎么抽,b.抽多少。
其中检验这个步骤和抽样检验的理论没有关系,不同的产品、不同的质量特性使用不同的检测设备,有不同的检验方法。
C.推断,即用对样本的检测结果来对总体进行推断。
抽多少和怎样推断就构成了抽样方案。
第2节抽样方案抽样方案分为计数型抽样方案和计量型抽样方案俩大类,首先讨论计数型抽样方案。
2.1计数型抽样方案计数型抽样方案有俩种形式:(1)(n;c);(2)(n;,)从批中抽取n件产品构成样本,逐个检验各个样品,发现其中有d件不合格品;若d≤c(d≤)则接收该批,若d>c (d≥)则拒收该批。
其框图见图1-1:图1-1抽样方案的使用方法是非常简单的。
可抽样方案是怎么确定的呢?这里必须指出:抽样方案不是人为规定的,抽样方案是根据对总体的质量要求,用数理统计理论设计出来的。
2.2计量型抽样方案计量型抽样方案的形式是:(n;k);它用样本均值和样本标准差对批作出推断,和计数型抽样方案相比,在相同的判断精度下,计量型抽样方案比计数型抽样方案所需的样本量更小。
其使用方法在后面的章节中做详细介绍。
第3节抽样检验的统计理论(基础)当讨论抽样方案时,我们应注意以下基本理论问题:3.1当存在随机误差时,样本质量指标不壹定等于总体质量指标。
(1)样本不合格品率不壹定等于总体不合格品率。
抽样检验知识
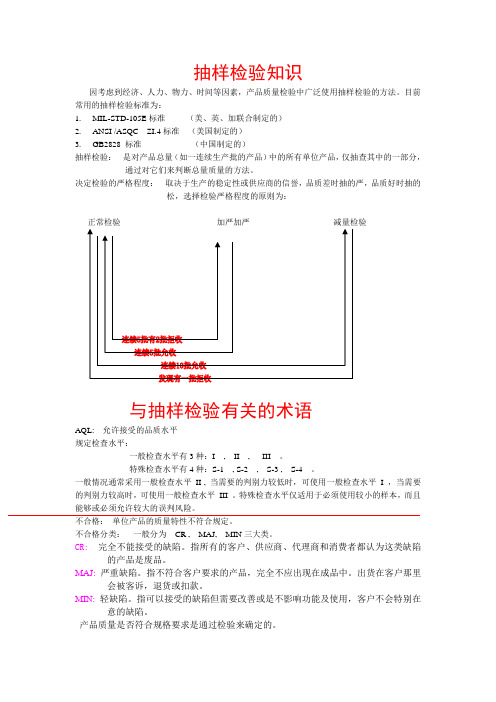
抽样检验知识因考虑到经济、人力、物力、时间等因素,产品质量检验中广泛使用抽样检验的方法。
目前常用的抽样检验标准为:-STD-105E标准(美、英、加联合制定的)2.ANSI /ASQC ZI.4标准(美国制定的)3.GB2828 标准(中国制定的)抽样检验:是对产品总量(如一连续生产批的产品)中的所有单位产品,仅抽查其中的一部分,通过对它们来判断总量质量的方法。
决定检验的严格程度:取决于生产的稳定性或供应商的信誉,品质差时抽的严,品质好时抽的松,选择检验严格程度的原则为:正常检验加严加严减量检验与抽样检验有关的术语AQL: 允许接受的品质水平规定检查水平:一般检查水平有3种:I , II , III 。
特殊检查水平有4种:S-1 , S-2 , S-3 , S-4 。
一般情况通常采用一般检查水平II , 当需要的判别力较低时,可使用一般检查水平I ,当需要的判别力较高时,可使用一般检查水平III 。
特殊检查水平仅适用于必须使用较小的样本,而且能够或必须允许较大的误判风险。
不合格:单位产品的质量特性不符合规定。
不合格分类:一般分为CR , MAJ, MIN三大类。
CR:完全不能接受的缺陷。
指所有的客户、供应商、代理商和消费者都认为这类缺陷的产品是废品。
MAJ: 严重缺陷。
指不符合客户要求的产品,完全不应出现在成品中。
出货在客户那里会被客诉,退货或扣款。
MIN: 轻缺陷。
指可以接受的缺陷但需要改善或是不影响功能及使用,客户不会特别在意的缺陷。
产品质量是否符合规格要求是通过检验来确定的。
检验又分为全检与抽检:全检:1.送检验批数量少,检验简单且费用较低。
2.产品必须是良品。
3.产品中如有少量不良品,可导致该产品致命性影响。
抽检:1.对产品的性能检验需进行破坏性试验。
2.产品批量太大,无法进行全数检验。
3.在送检验的产品产品中允许有一定程度的不良品存在。
4.在送检验的产品需要较长时间和较高的检验费用时。
抽样检验的基础知识

2024/9/22
第一章 基础知识
6
设Ni=1,000 i=1,2,3……m ;AQL=2.5
设Di=10 i=1,2,3…m/2;
设Di=500 i=1,2,3…m/2;
用(5;0 )抽样方案对上述批进行抽样检
验,若接受了其中旳k(k≤m)批,设不
合格品率为1%旳批旳批数为k1,不合格品 率为50%旳批旳批数为k2批(k=k1+k2),当
第一章 基础知识
3
(1)在抽样检验中,将合格批误判为不合格所 犯旳错误称为弃真错误,犯弃真错误旳概 率称为弃真概率,记为,它也称为生产方 风险。
(2)在抽样检验中,将不合格批误判为合格所 犯旳错误称为存伪错误,犯存伪错误旳概
率称为存伪概率,记为β,它也称为使用方
风险。
2024/9/22
第一章 基础知识
m足够大时势必有 k1> k2,k批合在一起
旳平均不合格品率为:
(10* k1+ 500 * k2)/ 1,000 * (k1+k2)
2024/9/22
第一章 基础Biblioteka 识7(10* k1+ 500 * k2)/ 1,000 * k ≤ AQL%
本章要点:
1.抽样方案是根据对总体旳质量要求,用数理统 计理论设计出来旳。
4
4.抽检特征曲线(OC曲线)
2024/9/22
第一章 基础知识
5
第四节 两种质量确保模式旳抽样方案
1.孤立批抽样方案旳质量确保作用:
孤立批抽样方案不能将某一经过批旳不合 格品率控制在预先要求旳某数值下,孤立批抽 样方案仅起概率把关旳作用。
2.连续批抽样方案旳质量确保作用
用某一质量要求(AQL)拟定旳抽样方案 组(系列抽样方案),对连续m批产品进行抽样检 验,若接受了其中旳k(k≤m)批,则可将k批 合在一起旳平均不合格品率控制在事先要求旳 那个AQL之下。
抽样检验基础知识

(四)产品批质量的标示方法
1. 批不合格品率p
批的不合格品数D除以批量N,即:p=D/N
2. 批不合格品百分数:100p=D/N*100
3. 批每百单位产品不合格数
批的不合格数C除以批量N, 再乘以100,即:100p=C/N*100
注:前两种表示方法常用于计件抽样检验,后一种表示方法常用于计点检 验.
– 定义:在抽样检验中认为满意的系列连续提交检验 批的过程平均上限值。GB2828-87 中AQL称为合格质 量水平。ISO 2859-1:1999中AQL改称为可接收质量 极限(Acceptance Quality Limit)。
– AQL是可接收和不可接收的过程平均的分界线,重点放在长期的平均 质量保证上面。当生产方的过程平均优于AQL时,可能会有某些批质 量劣于AQL,但抽样方案会保证绝大部分(95%)以上的产品批抽检 合格。相反的当生产方的过程平均劣于AQL时,会有不少产品批在转 换到加严检验之前被接收,随着拒收批的增加,由正常检验转换到 加严检验,甚至停止检验。转换到加严检验后,还有可能有某些产 品批会接收,但只要对生产方的过程平均质量要求控制在等于或小 于AQL上,从长远看,使用方会得到平均质量等于或优于AQL的产品 批; – AQL是指定的根据使用的抽样方案能接收绝大多数提交批的不合格率 或每百单位产品不合格数; – AQL是制定抽样方案的重要参数,可用于检索抽样方案。
• 对百分比抽样方案的评审
百分比抽样方案就是不论产品的批量N如何,均按 同一百分比抽取单位产品(样品)组成样本,而对样 本中的不合格判断数都规定为0。因此百分比抽样 方案为(n=aN,A=0),a为一固定比例。 例:供方有批量不同但批质量相同(P=5%)的三批产品 交检,均按10%抽取样品检验,于是可得到下列三种 方案:①N=900, n=90, A=0②N=300, n=30, A=0 ③N=90, n=9, A=0. OC曲线如图所示: 表面上看,这种百分比抽样方案似乎很公平合理,但 比较一下它们的OC曲线就会发现,在批质量相同的情 况下,批量N越大,L(p)越小,方案越严;而N越小, L(p)越大,方案越松。这等于对N大的检验批提高了验 收标准,而对N小的检验批却降低了验收标准,因此 百分比抽样方案是不合理的。
抽样检的基础必学知识点

抽样检的基础必学知识点
抽样检的基础知识点包括以下内容:
1. 抽样方法:在进行抽样检时,需要选择适当的抽样方法,常见的抽
样方法有简单随机抽样、系统抽样、分层抽样、整群抽样等。
2. 抽样误差:抽样误差是指抽样所引入的估计误差,其大小通常取决
于样本容量的大小和抽样方法的选择。
抽样误差越小,样本代表性越好,估计结果越可靠。
3. 样本容量:样本容量是指进行抽样检的样本数量,通常样本容量越大,估计结果越可靠。
样本容量的确定需要考虑抽样误差允许范围、
资源和时间等因素。
4. 抽样分布:抽样分布是指某一统计量在大量独立抽样情况下的分布。
常见的抽样分布有正态分布、t分布、卡方分布等。
根据不同的情况选择适当的抽样分布进行参数估计和假设检验。
5. 抽样误差的控制:为了减小抽样误差,可以采取增加样本容量、改
进抽样方法、增加抽样次数等方法进行控制。
合理选择抽样方法和样
本容量可以有效控制抽样误差。
以上是抽样检的基础必学知识点,通过学习这些知识点可以帮助我们
正确进行抽样检,得到可靠的估计结果。
抽样检验知识

抽样检验基础知识一、术语:1.检验:对实体的一种或多种特性进行测量、检查、试验、度量并将其结果与规定要求对比,以确定各种特性是否合格的活动。
2.单位产品:为实施抽样检查的需要而划分的基本单位,称为单位产品。
3.检查秕:为实施抽样检查汇集起来的单位产品,称为检查批,简称批。
4.批量:批中所包含的单位产品数,称为批量,用字母“N”表示。
5.样本单位:从批中抽取用于检查的单位产品,称为样本单位。
6.样本:样本单位的全体,称为样本。
7.样本大小:样本中所包含的样本单位数,称为样本大小。
8.合格质量水平(AQL):在抽样检查中,认为可以接受的连续提交检查批的过程平均上限值,称为合格质量水平。
9.合格判定数(Ac):作出批合格判断样本中所允许的最大不合格品数或不合格数,称为合格判定数。
10.不合格判定数(Re):作出批不合格判断样本中所不允许的最小不合格品数或不合格数,称为不合格判定数。
11.判定数组:合格判定数和不合格判定数或合格判定数系列和不合格判定数系列结合在一起,称为判定数组。
12.抽样方案:样本大小或样本大小系列和判定数组结合在一起,称为抽样方案。
13.一次抽样方案:由样本大小N和判定数组(Ac,Re)结合在一起组成的抽样方案,称为一次抽样方案。
二、检查的程序:1.规定单位产品的质量特性;2.规定不合格的分类;3.规定合格质量水平(AQL值);4.规定检查水平(IL);5.组成与提出检查批;6.规定检查的严格度;7.选择抽样方案类型;8.检索抽样方案;9.抽取样本;10.检查样本;11.判断逐批检查合格与不合格;12.逐批检查后的处置。
三、检查实施:1.规定单位产品的质量特性:在产品技术标准或订货合同中,必须明确对单位产品规定技术性能、技术指标、外观等质量特性。
2.不合格的分类:按照实际需要一般将不合格区分为A类、B类、C类三种类别。
3.合格质量水平的规定:合格质量水平(AQL)不能取任意的值,GB2828采用的是优先数系,数值为0.010、0.015、0.025、0.040、0.065、0.10、0.15、0.25、0.40、0.65、1.0、1.5、2.5、4.0、6.5、10、15、25、40、65、100、150、250、400、650、1000共26个数。
抽样检验基本知识

培训教材抽样查验基本知识一、抽样查验的由来二次世界大战期间,美国军方采买军械时.在查验人员极度缺少的状况下,为保证其大量购入军械的质量,特意组织一批优异数理统计专家、依照数学统计理论,成立厂一套产品抽样查验模式。
知足战时的需要。
二、抽样查验的定义抽样查验是按早先确立的抽样方案,从交验批中抽取规定数目的样品构成一个样本,经过对样本的查验推测批合格或批不合格。
抽样查验比较d≤ Ac批合格N n d批产品样本不合格品数Acd≥ Re合格判断数,批不合格Re 不合格判断数三、基本观点及用语1.集体与样本。
集体就是供给被做为检查 ( 或检查 ) 的对象.或许称采纳举措的对象。
也常称为批,集体 ( 批 ) 大小常以N 表示,亦称批量 N。
工序间、成品、出入库查验以及购入构验等常常组以整批的形式交托查验的。
不管是一件件的产品、仍是散装料,一般都要构成批,尔后提交查验,有些情况,中间产品因为条件的限制不一样意构成批此后再提交给下一道工序进行查验、但可采纳连续抽样查验( 如每小时抽取 1 台产品进行查验的抽样方式。
样本就是指我们从集体中( 或批中 ) ,抽取的部分个体。
抽取的样本数目常以n 表示。
2.批的构成。
构成一个批的单位产品的生产条件应尽可能相同,即是应该由原、辅料相同,牛产职工改动不大生产期间大概相同样生产条件下生产的单位产品构成批。
此时.批的特征值只有随机颠簸.不会有较大的差异。
这样做.主假如为了抽取样品的方便及抽样品更拥有代表性.进而使抽样查验更加有效,假如有凭证表示,不一样的机器设施、不一样的操作者或不一样批次的原资料等条件的变化对产质量量有显然的影响时,应该尽可能以同一机器设施、同一操作者或同—批次的原资料所生产的产品构成批,构成批的上述各样条件,往常极少能够同时知足。
假如想使它们都获得知足,常常需要把批分得比较小.这样质量一致并且简单追忆。
但这样做,会使查验工作量大大增添.反而不可以达到抽样查验应有的经济效益、所以,除了产品质量时好时坏,颠簸较大.一定采纳较小的批以保证批的合理外,当产品质量较稳准时〔比方生产过程处于统计控制状态〕,采纳大量量是经济的、自然,在使用大量量时,应该考虑到库房场所限制以及不合格批的返工等可能造成的困难。
抽样检验知识梳理

抽样检验知识梳理什么是抽样?1、样本:从总体中抽取的,用以测试、判断总体质量的一部分基本单位。
2、抽样:从总体取出一部分个体的过程称为抽样。
3、批量:一批产品包含的基本单位数量称批量,以N表示。
4、样本大小:样本中包含的基本单位数量称为样本大小,以n表示。
5、抽样计划:一个抽样计划是指每一批中所需检验的产品单位数,(样本大小或一连串的样本大小),以及决定该批允收率的准则(允收数及拒收数)6、抽样时机:样本可在批内所有各单位全部组装完成后抽取,或在批组装时抽取,在这种情况下,批的大小须在任何样本单位抽取前决定,如果样本单位是在批组装时抽取,如果在该批完成前即已达到拒收数,则已完成的此部分产品,应予拒收,不良产品的原因须先查明,并采取矫正措施,在此之后才可开始新的批。
当使用双次或多次抽样时,每一样本应从整个批中抽取。
1、单次抽样计划:检验的样本单位数,应等于抽样计划中所定的样本大小,如样本中发现的不良品个数小于或等于允收数时,则认为可以允收该批。
如不良品的个数大于或等于拒收数时,则拒收该批。
2、双次抽样计划:检验的样本单位数,应等于抽样计划中所确定的第一次样本大小。
如第一次样本中发现的不良品个数小于或等于第一次的允收数时,则认为可以允收该批,如第一次样本中发现的不良品个数大于或等于第一次的拒收数时,则拒收该批。
如第一次样本中发现的不良品个数是介于第一次允收数与拒收数之间,则应检验同样大小的第二次样本。
第一次及第二次样本中发现的不良品个数,应加以累计。
如累计的不良品个数等于或小于第二次允收数时,则认为可以允收该批。
如累计的不良品个数等于或大于第二次允收数时,则应拒收该批。
3、多次抽样计划:多次抽样的计划的程序与双次抽样计划所规定的相类似,最多可以七次抽样。
如何使用抽样计划?1、单次抽样计划:检验的样本单位数,应等于抽样计划中所定的样本大小,如样本中发现的不良品个数小于或等于允收数时,则认为可以允收该批。
抽样检验基础知识

1.4 不合格:单位产品的品质特性不符合规定。
1.5 致命缺点(Critical Defect) • 一个缺点于材质上或产品本身, 对于使用者或周围环境等构成危险或 不安全情况。
1.6 严重缺点 (Major Defect) • 一个缺点于外观或性能上 • 影响到产品可用性或导致不能使用; • 不利于使用者; • 构成保养及维修上增加; • 构成材质或产品可靠性下降。 1.7 轻微缺点 (Minor Defect) • 在不妨碍销售的原则下, 一个缺点出现在外观或性能上, 对于使用者来说, 并不是很显著,或与标准、原型设计或图纸有稍微出入, 但不影响产品可 靠或可用性。 1.8合格品质水平:在抽样检查中,认为可以接受的连续提交检查批的过程 平均上限值。 1.9正常检查:当过程平均接近合格品质水平时所进行的检查。 1.10加严检查:当过程平均显著劣于合格品质水平时所进行的检查。 1.11放宽检查:当过程平均显著优于合格品质水平时所进行的检查。
8 9 12 13 18 19
8 9 12 13 18 19
8 9 12 13 18 19
8 9 12 13 18 19
8 9 12 13 18 19
8 9 12 13 18 19
M 315 500 800
8 9 12 13 18 19
8 9 12 13 18 19
8 9 12 13 18 19
Q 1250 R 2000 0 1 S 3150
(详见下表)
表一:样本大小字码
批 量 2~8 9~15 16~25 26~50 51~90 91~150 151~280 281~500 501~1200 1201~3200 3201~10000 10001~35000 35001~150000 150001~500000 500000以上 S-1 A A A A B B B B C C C C D D D 特殊检验水准 S-2 S-3 A A A B B B C C C D D D E E E A A B B C C D D E E F F G G H S-4 A A B C C D E E F G G H J J K 一般检验水准 Ⅰ Ⅱ Ⅲ A A B C C D E F G H I K L M N A B C D E F G H J K L M N P O B C D E E G H J K L M N P Q R
(抽样检验)抽样检验方案最全版

(抽样检验)抽样检验方案抽样检验方案第四节抽样检验方案(大纲要求熟悉)壹、抽样检验的几个基本概念(基础知识)1.抽样检验方案是根据检验项目特性所确定的抽样数量、接受标准和方法。
如在简单的计数值抽样检验方案中,主要是确定样本容量n和合格判定数,即允许不合格品件数c,记为方案(n,c)。
2.检验.检验是对检验项目中的性能进行量测、检查、试验等,且将结果和标准规定要求进行比较,以确定每项性能是否合格所进行的活动。
3.检验批4.批不合格品率是指检验批中不合格品数占整个批量的比重。
5.过程平均批不合格品率是指对k批产品首次检验得到的k个批不合格品率的平均数。
6.接受概率(又称批合格概率)接受概率是根据规定的抽样检验方案将检验批判为合格而接受的概率。
壹个既定方案的接受概率是产品质量水平,即批不合格品率P的函数,用L(p)表示,检验批的不合格品率p越小,接受概率L(p)就越大。
二、抽样检验方案类型(壹)抽样检验方案的分类(二)常用的抽样检验方案(大纲要求熟悉)1.标准型抽样检验方案(1)计数值标准型壹次抽样检验方案计数值标准型壹次抽样检验方案是规定在壹定样本容量n时的最高允许的批合格判定数c,记作(n,c),且在壹次抽检后给出判断检验批是否合格的结论。
c也可用Ac表示。
c值壹般为可接受的不合格品数,也能够是不合格品率,或者是可接受的每百单位缺陷数。
若实际抽检时,检出不合格品数为d,则当:d≤c时,判定为合格批,接受该检验批;d>c定为不合格批,拒绝该检验批。
(2)计数值标准型二次抽样检验方案(之上俩种标准型抽样检验程序见图7-16、7-17)(3)多次抽样检验方案(★适当位置加图7-16和7-17)2.分选型抽样检验方案3.调整型抽样检验方案[例题]当采用计数值标准型壹次抽样检验方案实际抽检时,检验出的不合格品数d,当(),判定为不合格批,拒绝该检验批。
A.d<cB.d>cC.d=cD.d=r答案:B抽样检验方案参数的确定三、抽样检验方案参数的确定(大纲要求了解)实际抽样检验方案中也都存在俩类判断错误。
抽样检验的基础知识

抽样检验的基础知识引言抽样检验是统计学中一种重要的方法,用于判断一个总体的某个特征是否符合某种假设。
在实际应用中,我们常常只能通过抽取一个样本来推断总体的情况。
而抽样检验帮助我们确定样本是否提供了足够的证据来支持或拒绝某种假设。
本文将介绍抽样检验的基础知识,包括假设检验的步骤、常见的抽样检验方法,以及如何解读检验结果。
假设检验的步骤假设检验的步骤通常包括以下几个步骤:1. 提出假设首先,我们需要提出两个假设:原假设(H0)和备择假设(H1)。
原假设通常是我们要进行检验的假设,而备择假设则是我们希望证明的假设。
例如,我们要检验一个硬币是否是公平的,那么原假设可以是“这个硬币是公平的”,备择假设可以是“这个硬币不是公平的”。
2. 选择适当的检验统计量检验统计量是用于计算样本观察值与假设之间差异的度量。
在选择检验统计量时,需要考虑样本数据的特点以及假设检验的目的。
常见的检验统计量包括均值差异的t检验、比例差异的Z检验、方差差异的F检验等。
3. 确定显著性水平显著性水平是在假设检验中用于判断拒绝原假设的界限。
通常,我们将显著性水平设定为0.05或0.01。
显著性水平表示我们对于错误地拒绝原假设的容忍程度,选择较小的显著性水平意味着更高的拒绝标准。
4. 计算检验统计量的值在这一步骤中,我们需要根据样本数据计算出所选择的检验统计量的值。
这一计算通常依赖于样本数据的分布类型以及所选择的检验统计量。
5. 判断拒绝或接受原假设根据计算得到的检验统计量的值和所选择的显著性水平,我们可以判断是拒绝原假设还是接受原假设。
如果计算得到的检验统计量的值落在接受域内,我们接受原假设;如果计算得到的检验统计量的值落在拒绝域内,我们拒绝原假设。
常见的抽样检验方法在实际应用中,我们常用的抽样检验方法包括:1. 单样本t检验单样本t检验用于判断一个样本的均值是否等于一个已知的或理论上的值。
在进行单样本t检验时,我们需要输入样本的均值、样本的标准差、样本容量以及与之比较的值。
抽样检验基本知识

抽样检验基本知识名词符号意义检验单位依检验目的决定受检的大小,如一个、一组等生产批量一群以相同材料、相同制造条件所生产的产品检验批量N 检验对象的检验单位的构成其检验单位的总数称批量大小样本n 从检验批量抽取一个以上检验单位的构成其检验单位的总数称样本大小抽样检验方式有关样本数、判定基准等的规定抽样检验计划基于抽样策略而订定有关抽样检验方式的计划1 计数、计量2 型(型态)全数检验、抽样检验规准型、选别型、调整型、连续生产型3 次(抽样形式)单次、双次、多次、逐次合格判定个数不合格判定个数 c 作为判定一批量为合格或者不合格的不良个数合格判定值、不合格判定值合格判定系数、不台格判定系数4检验的种类5 全数检验与抽样检验(1) 一一检验才能完全的品质保证(2) 但有的时候须破坏性检查、连续体仍需实施抽样检验(3) 有的时候需要全数检验(4) 有的时候抽样检验较优势的场合(5) 实施抽样检验的必要条件,但以抽样检验无法100%的良品保证• 能够批处理者‚容许合格批中混入某种程度的不良品ƒ试料之抽取可随机…品质基准明确… 若使用计量抽样检验须大致熟悉特性值的分配情形6 抽样检验的步骤抽样检验的步骤主管工程师品管员(1) 决定品质基准○(2) 决定检验的形式、方法○(3) 检验所采取抽样计划○(4) 批的形成、取样○(5) 测定○(6) 按基准判定合不合格○(7) 批的处置○○(8) 结果检讨与活用• 今后继续以此法检验?‚ 修改品质基准ƒ检验条件、抽样各要项变更?… 供货商评价○○二抽样计划类型与OC曲线绘制1 抽样检验基本原理(1) 超几何分配从群体大小为N,不良率为p,随机抽样n个,样本中含不良数x的机率分配(2) 二项分配一群体之不良率为p随机抽样n个,样本中含不良数x的机率分配(3)卜氏分配当二项分配试行次数n非常大且趋近于0,μ=np为固定值时,二项分配超近于卜氏分配e=2.71828 μ=np(4) 常态分配2 各类不一致抽样形式(1) 单次抽样以一次抽样检验结果而判定合格、不合格的一种抽样检验形式抽样数样本数合格判定个数样本不良数合格不台格N n c x x≤c x>c(2) 双次抽样第一次抽样检验结果能够清晰判定合格、不合格时即予判定,否则追加第二次抽样以其结果而判定合格、不合格的一种抽样检验形式抽样数样本数合格判定个数不合格判定数样本不良数第一次抽样第二次抽样合格不台格合格不台格N n1,n2 c1,c2 r1,r2 x1,x2 x1≦c1 x1>r1 x1+x2≦c2 x1+x2>c2(3) 多次抽样双次抽样的扩张,而以三次或者更多次来判定每次抽样均判定合格、不合格及不确定三种结果(4) 逐次抽样逐次抽取一个样本,将累积的检验成绩判定合格、不合格或者继续逐次抽样(5) 各类不一致抽样形式的比较单次抽样双次抽样多次抽样逐次抽样平均检验数大中小最小检验费用大中小小记录易中杂杂心理效果差中良良检验费用最低低中高3 计量值与计数值抽验的比较(1) 检查单位良品、不良品的表示方法• 以计数值品质表示:不良数、缺点数‚ 以计量值品质表示:特性值(2) 计量值与计数值抽验的比较计数值抽样检验计量值抽样检验品质表示方法良、不良品特性值检熟练不需要需要验时间短长方设备简易复杂法记录简易复杂计算简易复杂适用时之条件易满足随机取样随机取样且需常态分配批好坏判定能力与检验个数试料大推断能力低试料小推断能力高检验记录活用低高适用于检验费用低检验费用高、破壤性检验4 订定抽样检捡计划的要素(1) OC曲线• 检验特性曲线‚抽样检验中表示批的品质与合格机率的关系称之ƒ 用来表示抽样检验方式的性质…选择合于抽样目的OC曲线之方法Œ规准型OC曲线指定2点• 调整型OC曲线指定1点与斜率Ž 选别型平均检查数为最小(2) 允收水准AQL(Acceptable Quality Level)经双方妥协决定的合理之品质水准,此水准为卖方现在所能提供,为常见的抽样检验方式,通常在允收水准的状况下其允收机率为95%(3) 拒收水准LTPD(Lot Tolerance Percent Defective)容许的最高不良率,通常在拒收水准的状况下其允收机率为10%(4) 管理点在允收机率为50%的品质水准,如今应以OC曲线的斜率选择检验方式(5) 平均出厂品质界限AOQL(Average Outgoing Quality Limit)在长期供应过程中,若以选别型检验则可保证长期品质水准不可能超过AOQL(6) 样本大小5 OC曲线的概念(1) OC曲线的绘制例橡胶管一批共800个自其中随机抽出75个试料测定,若不良品2个下列(含),则允收否则拒收,试给本抽样计划的OC曲线解:,且,可用卜氏分配求得PaP np Pa0 0 1.00000.01 0.75 0.95950.02 1.50 0.80880.03 2.25 0.60930.04 3.00 0.42320.05 3.75 0.27710.06 4.50 0.17360.07 5.25 0.10510.08 6.00 0.06200.09 6.75 0.03570.10 7.50 0.0203OC曲线之绘制如下(2) OC曲线的特性(批量N、试料大小n、合格判定数c的变化)• n、c一定,N变化时不太影响OC曲线‚ N、c一定,n愈大OC曲线倾斜度愈大,生产者冒险率增加,消费者冒险率减少ƒN、n一定,c愈小则OC曲线倾斜度愈大…比例抽样( n / N或者c / N 一定时),OC曲线是完全不一致的,亦即品质保证程度不一致(3) 选定OC曲线的方法• 指定OC曲线上的两点计数值抽样中指定,….规准型Œ比好的批不合格的机率小于α• 比坏的批合格的机率小于β计量值抽样中指定不良率或者平均值M0,M1与α,β的关系‚ 指定OC曲线上的一点与斜率…. 调整型Œ一点…. 以AQL(合格品质水准)或者管理点• 斜率…. 当工程平均品质优于某值时使OC曲线平缓,当劣于某值时,能迅速倾斜在调整型中系以批量大小决定ƒ在某工程平均不良下使平均检验量为最小…. 选别型指定AOQL(平均出厂品质限界)或者LTPD(拒收水准、容许批不良率)三规准型抽样1 规准型抽样检验的概念(1) 买卖双方事前约定合理的冒险率下以验收某批物品(2) 适用于非长期、独立批之检验(3) 通常指定P0、α、P1、β(P0<P1)2 JIS Z9002计数规准型单次抽样表四选别型抽样检验的概念1 选别型抽样检验的概念(1) 买卖双方事前约定合理的冒险率下以验收某批物品(2) 当试料中不良品数超过允收不良个数,即判不合格,且对本批物品实施全数检验,选别出不良再予供应者交换或者修理(3) 不能应用于破坏性检验,使用于• 最终检验、工程间检验‚不能自由选择卖方、或者非向同一卖方购买不可时之受入检验(4) 通常有两种保证形式• 保证该批的品质‥‥P1(LTPD批容许不良率)‚保证多批的平均品质‥‥AOQL(平均出厂品质界限)(5) 实施选别型抽样检验的必要条件• 可批处理者‚不合格须全数选别ƒ某程度熟悉送验批之品质水准(6) 选别型抽样计划表• 道奇洛敏抽样表The Dodge-Roming Sampling Inspection Tables 通常使用本表‚另有JIS Z9006计数选别型单次抽样检验,但只能用于单次抽样ƒ未有计量选别型抽样计划表2 选别型抽样检检的要素(1) 平均检验总件数ATl(Average Total Inspection)单次抽样(2) 平均出厂品质AOQ(Average Outgoing Quality)当N>>n 则(3) 平均出厂品质界AOQL(Average Outgoing Quality Limit)在AOQ曲线上之最高值称之• 由图解而得‚近似值的算法(y为系数)c 0 1 2 3 4 5y(道奇洛敏表) 0.368 0.841 1.372 1.946 2.544 3.172c 6 7 8 9 10 11y(道奇洛敏表) 3.810 4.465 5.150 5.836 6.535 7.234例::抽样计划N=800,n=75,c=2近似值批的不良率AOQ0 0 100.0% 0.00%0.01 0.75 95.9% 0.96%0.02 1.50 80.9% 1.62%0.03 2.25 60.9% 1.83%0.04 3.00 42.3% 1.69%0.05 3.75 27.7% 1.39%0.06 4.50 17.4% 1.04%0.07 5.25 10.5% 0.74%0.08 6.00 6.2% 0.50%0.09 6.75 3.6% 0.32%0.1 7.50 2.0% 0.20%3 道奇洛敏抽样表(1) 道奇洛敏抽样表(The Dodge-Roming Sampling Inspection Tables)内容• 指定LTPD,并使不良率为p时,其平均检验次数ATI为最小‚道奇洛敏抽样表内容共有42张表分四组保证形式组别抽样方式保证水准%LTPD该批的品质1 单次抽样0.5 1.0 2.0 3.02 双次抽样4.0 5.0 7.0 10.0AOQL多批平均品质3 单次抽样0.1 0.25 0.5 0.75 1.0 1.54 双次抽样2.0 2.5 3.0 4.0 5.0 7.0 10.04选别型检验的实施(2) 应用选别型抽样检验例• 例一:P1=2%,N=2000,=0.20%采The Dodge-Roming Sampling Inspection Tables SL=2.0%则n=190,c=1,AOQL=0.40%采JIS Z9006计数选别型单次抽样检验SL表-2则n=190,c=l,AOQL=0.44%‚例二:AOQL=0.5%,N=2000,=0.20%采The Dodge-Roming Sampling Inspection Tables SA=0.5%采单次抽样,则n=155,c=1,P1=2.5%采双次抽样,则第一次抽样=125,=0第二次抽样=135,=2P1=2.2%五调整型抽样检验1 调整型抽样检验的概念(1) 买卖双方事前约定合理的冒险率下以验收某批物品(2) 当送验批品质好时,日后检验给予放松,反之则加严检验(3) 能使用于• 企业内部最终检验、工程间检验‚固定协力厂交货的入厂检验ƒ 当供给者被拒收的缺失大时2 计数调整型抽样检验计划表(1) 美军标准MIL-STD-lO5E,通常使用此抽样计划表(2) 另有JIS Z9011计数调整型单次抽样检验3 MIL-STD-lO5E抽样检验计划表(1) MIL-STD-lO5E的内容• 适用于连续批交货,但也可用于单一批交货‚缺点分级严重缺点,要紧缺点,次要缺点ƒ允收品质水准AQL,共有26个水准0.010 0.015 0.025 0.040 0.065 0.10 0.15 0.25 0.400.65 10 1.5 2.5 4.0 6.5 10 15 2540 65 100 150 250 400 650 1000当AQL值在10.0下列可用不良率或者百单位缺点数,若超过l0.0以上,则只能用于百单位缺点数的表示,在契约中应予明示…检验水准Œ 通常检验水准水准Ⅰ判别力不要求高水准Ⅱ未有任何指定时使用水准Ⅲ判别力有要求高• 特殊检验水准适于须要小的试料使用,但其冒险率高,分S-1,S-2,S-3,S-4…抽样检验计划表格内容表名表格内容讲义表Ⅰ样本代字○表Ⅱ-A、B、C 正常、严格、减量检验单次抽样计划(主抽样表) ○表Ⅲ- A、B、C 正常、严格、减量检验双次抽样计划(主抽样表)表Ⅳ-A、B、C 正常、严格、减量检验多次抽样计划(主抽样表)表Ⅴ-A、B 正常、严格检验平均出厂品质界限值(单次抽样) 表A表Ⅵ-A、B表Ⅶ-A、B 正常单次抽样Pa=10%(表Ⅵ)、=5%(表Ⅶ) 之LQ(界限品质) A表以不良率,B 表以百单位缺点数表Ⅷ减量检验限界值○表Ⅸ~表Ⅹ-S (说明省略)(2) 检验的实施• 设定品质基准明确检查单位、良品、不良品及缺点分级划分的基准‚指定AQL,并决定检验水准ƒ 批的形成,求抽样数的代表字以同一生产条件为一批、批量过大时可切割为小批…求样本代字表Ⅰ样本代字批量特殊检验水准通常检验水准S-1 S-2 S-3 S-4 ⅠⅡⅢ2 ~ 8 A A A A A A B9 ~ 15 A A A A A B C16 ~ 25 A A B B B C D26 ~ 50 A B B C C D E51 ~ 90 B B C C C E F91 ~ 150 B A C D D F G151 ~ 280 B C D E E G H281 ~ 500 B C D E F H J501 ~ 1200 C C E F G J K1201 ~ 3200 C D E G H K L3201 ~ 10000 C D F G J L M10001 ~ 35000 C D F H K M N35001 ~ 150000 D E G J L N P150001 ~ 500000 D E G J M P Q500001 ~ over D E H K N Q R…指定单次、双次或者多次抽样†决定检验的严格性‡查抽样表得抽检方式n,Ac,Reˆ抽样与检验‰ 合格、不合格判定Š批的处置表Ⅱ-A 正常检验单次抽样计划(主抽样表) 样本代码 A B C D E F G H J K L M N P Q R Acceptable Quality Level (正常检验) 1000 Ac Re 30 31 44 45 ↑↑↑↑↑↑↑↑↑↑↑↑↑↑650 Ac Re 21 22 30 31 44 45 ↑↑↑↑↑↑↑↑↑↑↑↑↑400 Ac Re 14 15 21 22 30 31 44 45 ↑↑↑↑↑↑↑↑↑↑↑↑250 Ac Re 10 11 14 15 21 22 30 31 44 45 ↑↑↑↑↑↑↑↑↑↑↑150 Ac Re 7 8 10 11 14 15 21 22 30 31 ↑↑↑↑↑↑↑↑↑↑↑100 Ac Re 5 6 7 8 10 11 14 15 21 22 ↑↑↑↑↑↑↑↑↑↑↑65 Ac Re 3 4 5 6 7 8 10 11 14 15 21 22 ↑↑↑↑↑↑↑↑↑↑40 Ac Re 2 3 3 4 5 6 7 8 10 11 14 15 21 22 ↑↑↑↑↑↑↑↑↑25 Ac Re 1 2 2 3 3 4 5 6 7 8 10 11 14 15 21 22 ↑↑↑↑↑↑↑↑15 Ac Re 1 2 2 3 3 4 5 6 7 8 10 11 14 15 21 22 ↑↑↑↑↑↑↑10 Ac Re 1 2 2 3 3 4 5 6 7 8 10 11 14 15 21 22 ↑↑↑↑↑↑6.5 Ac Re 0 1 ↑↓1 2 2 3 3 4 5 6 7 8 10 11 14 15 21 22 ↑↑↑↑↑4.0 Ac Re ↓0 1 ↑↓1 2 2 3 3 4 5 6 7 8 10 11 14 15 21 22 ↑↑↑↑2.5 Ac Re ↓↓0 1 ↑↓1 2 2 3 3 4 5 6 7 8 10 11 14 15 21 22 ↑↑↑1.5 Ac Re ↓↓↓0 1 ↑↓1 2 2 3 3 4 5 6 7 8 10 11 14 15 21 22 ↑↑1.0 Ac Re ↓↓↓↓0 1 ↑↓1 2 2 3 3 4 5 6 7 8 10 11 14 15 21 22 ↑0.65 Ac Re ↓↓↓↓↓0 1 ↑↓1 2 2 3 3 4 5 6 7 8 10 11 14 15 21 220.40 Ac Re ↓↓↓↓↓↓0 1 ↑↓1 2 2 3 3 4 5 6 7 8 10 11 14 150.25 Ac Re ↓↓↓↓↓↓↓0 1 ↑↓1 2 2 3 3 4 5 6 7 8 10 110.15 Ac Re ↓↓↓↓↓↓↓↓0 1 ↑↓1 2 2 3 3 4 5 6 7 80.10 Ac Re ↓↓↓↓↓↓↓↓↓0 1 ↑↓1 2 2 3 3 4 5 60.065 Ac Re ↓↓↓↓↓↓↓↓↓↓0 1 ↑↓1 2 2 3 3 40.040 Ac Re ↓↓↓↓↓↓↓↓↓↓↓0 1 ↑↓1 2 2 30.025 Ac Re ↓↓↓↓↓↓↓↓↓↓↓↓0 1 ↑↑1 20.015 Ac Re ↓↓↓↓↓↓↓↓↓↓↓↓↓0 1 ↑↑0.010 Ac Re ↓↓↓↓↓↓↓↓↓↓↓↓↓↓0 1 ↑样本数2 3 5 8 13 20 32 50 80 125 200 315 500 800 1250 2000样本代码A B C D E F G H J K L M N P Q R表Ⅱ-B 严格检验单次抽样计划(主抽样表) 样本代码 A B C D E F G H J K L M N P Q R S Acceptable Quality Level (严格检验) 1000 Ac Re 27 28 41 42 ↑↑↑↑↑↑↑↑↑↑↑↑↑↑650 Ac Re 18 19 27 28 41 42 ↑↑↑↑↑↑↑↑↑↑↑↑↑400 Ac Re 12 13 18 19 27 28 41 42 ↑↑↑↑↑↑↑↑↑↑↑↑250 Ac Re 8 9 12 13 18 19 27 28 41 42 ↑↑↑↑↑↑↑↑↑↑↑150 Ac Re 5 6 8 9 12 13 18 19 27 28 ↑↑↑↑↑↑↑↑↑↑↑100 Ac Re 3 4 5 6 8 9 12 13 18 19 ↑↑↑↑↑↑↑↑↑↑↑65 Ac Re 2 3 3 4 5 6 8 9 12 13 18 19 ↑↑↑↑↑↑↑↑↑↑40 Ac Re 1 2 2 3 3 4 5 6 8 9 12 13 18 19 ↑↑↑↑↑↑↑↑↑25 Ac Re ↓1 2 2 3 3 4 5 6 8 9 12 13 18 19 ↑↑↑↑↑↑↑↑15 Ac Re ↓↓1 2 2 3 3 4 5 6 8 9 12 13 18 19 ↑↑↑↑↑↑↑10 Ac Re ↓↓↓1 2 2 3 3 4 5 6 8 9 12 13 18 19 ↑↑↑↑↑↑6.5 Ac Re ↓0 1 ↓↓1 2 2 3 3 4 5 6 8 9 12 13 18 19 ↑↑↑↑↑4.0 Ac Re ↓↓0 1 ↓↓1 2 2 3 3 4 5 6 8 9 12 13 18 19 ↑↑↑↑2.5 Ac Re ↓↓↓0 1 ↓↓1 2 2 3 3 4 5 6 8 9 12 13 18 19 ↑↑↑1.5 Ac Re ↓↓↓↓0 1 ↓↓1 2 2 3 3 4 5 6 8 9 12 13 18 19 ↑↑1.0 Ac Re ↓↓↓↓↓0 1 ↓↓1 2 2 3 3 4 5 6 8 9 12 13 18 19 ↑0.65 Ac Re ↓↓↓↓↓↓0 1 ↓↓1 2 2 3 3 4 5 6 8 9 12 13 18 190.40 Ac Re ↓↓↓↓↓↓↓0 1 ↓↓1 2 2 3 3 4 5 6 8 9 12 130.25 Ac Re ↓↓↓↓↓↓↓↓0 1 ↓↓1 2 2 3 3 4 5 6 8 90.15 Ac Re ↓↓↓↓↓↓↓↓↓0 1 ↓↓1 2 2 3 3 4 5 60.10 Ac Re ↓↓↓↓↓↓↓↓↓↓0 1 ↓↓1 2 2 3 3 40.065 Ac Re ↓↓↓↓↓↓↓↓↓↓↓0 1 ↓↓1 2 2 30.040 Ac Re ↓↓↓↓↓↓↓↓↓↓↓↓0 1 ↓↓1 20.025 Ac Re ↓↓↓↓↓↓↓↓↓↓↓↓↓0 1 ↓↓1 20.015 Ac Re ↓↓↓↓↓↓↓↓↓↓↓↓↓↓0 1 ↓0.010 Ac Re ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓0 1样本数2 3 5 8 13 20 32 50 80 125 200 315 500 800 1250 2000 3150样本代码A B C D E F G H J K L M N P Q R S表Ⅱ-C 减量检验单次抽样计划(主抽样表) 样本代码 A B C D E F G H J K L M N P Q R Acceptable Quality Level (减量检验) 1000 Ac Re 30 31 30 31 ↑↑↑↑↑↑↑↑↑↑↑↑↑↑650 Ac Re 21 22 21 22 21 24 ↑↑↑↑↑↑↑↑↑↑↑↑↑400 Ac Re 14 15 14 15 14 17 21 24 ↑↑↑↑↑↑↑↑↑↑↑↑250 Ac Re 10 11 10 11 10 13 14 17 21 24 ↑↑↑↑↑↑↑↑↑↑↑150 Ac Re 7 8 7 8 7 10 10 13 14 17 ↑↑↑↑↑↑↑↑↑↑↑100 Ac Re 5 6 5 6 5 8 7 10 10 13 ↑↑↑↑↑↑↑↑↑↑↑65 Ac Re 3 4 3 5 3 6 5 8 7 10 10 13 ↑↑↑↑↑↑↑↑↑↑40 Ac Re 2 3 2 4 2 5 3 6 5 8 7 10 10 13 ↑↑↑↑↑↑↑↑↑25 Ac Re 1 2 1 3 1 4 2 5 3 6 5 8 7 10 10 13 ↑↑↑↑↑↑↑↑15 Ac Re ↓0 2 1 3 1 4 2 5 3 6 5 8 7 10 10 13 ↑↑↑↑↑↑↑10 Ac Re ↓↓0 2 1 3 1 4 2 5 3 6 5 8 7 10 10 13 ↑↑↑↑↑↑6.5 Ac Re 0 1 ↑↓0 2 1 3 1 4 2 5 3 6 5 8 7 10 10 13 ↑↑↑↑↑4.0 Ac Re ↓0 1 ↑↓0 2 1 3 1 4 2 5 3 6 5 8 7 10 10 13 ↑↑↑↑2.5 Ac Re ↓↓0 1 ↑↓0 2 1 3 1 4 2 5 3 6 5 8 7 10 10 13 ↑↑↑1.5 Ac Re ↓↓↓0 1 ↑↓0 2 1 3 1 4 2 5 3 6 5 8 7 10 10 13 ↑↑1.0 Ac Re ↓↓↓↓0 1 ↑↓0 2 1 3 1 4 2 5 3 6 5 8 7 10 10 13 ↑0.65 Ac Re ↓↓↓↓↓0 1 ↑↓0 2 1 3 1 4 2 5 3 6 5 8 7 10 10 13 0.40 Ac Re ↓↓↓↓↓↓0 1 ↑↓0 2 1 3 1 4 2 5 3 6 5 8 7 100.25 Ac Re ↓↓↓↓↓↓↓0 1 ↑↓0 2 1 3 1 4 2 5 3 6 5 80.15 Ac Re ↓↓↓↓↓↓↓↓0 1 ↑↓0 2 1 3 1 4 2 5 3 60.10 Ac Re ↓↓↓↓↓↓↓↓↓0 1 ↑↓0 2 1 3 1 4 2 50.065 Ac Re ↓↓↓↓↓↓↓↓↓↓0 1 ↑↓0 2 1 3 1 40.040 Ac Re ↓↓↓↓↓↓↓↓↓↓↓0 1 ↑↓0 2 1 30.025 Ac Re ↓↓↓↓↓↓↓↓↓↓↓↓0 1 ↑↓0 20.015 Ac Re ↓↓↓↓↓↓↓↓↓↓↓↓↓0 1 ↑↑0.010 Ac Re ↓↓↓↓↓↓↓↓↓↓↓↓↓↓0 1 ↑样本数2 3 5 8 13 20 32 50 80 125 200 315 500 800 1250 2000样本代码A B C D E F G H J K L M N P Q RAcceptable Quality Level (正常检验) 1000 1100 1100650 730 720 660400 470 490 430 410250 330 310 290 270 250150 220 220 190 180 170100 160 150 130 120 11065 97 110 90 82 72 7340 69 65 63 56 50 47 4625 42 46 39 40 34 33 29 2915 28 27 24 24 22 21 19 1810 17 17 15 16 14 13 12 126.5 18 11 11 9.7 9.9 9.0 8.27.5 7.34.0 12 6.5 6.9 6.1 6.35.6 5.2 4.7 4.72.5 7.4 4.2 4.33.94.0 3.6 3.3 3.0 2.91.5 4.62.6 2.7 2.4 2.5 2.2 2.1 1.9 1.81.02.8 1.7 1.7 1.6 1.6 1.4 1.3 1.2 1.20.65 1.8 1.1 1.1 0.97 1.00 0.90 0.82 0.75 0.730.40 1.2 0.67 0.69 0.62 0.63 0.56 0.52 0.470.25 0.74 0.42 0.44 0.39 0.40 0.36 0.330.15 0.46 0.27 0.27 0.24 0.25 0.220.10 0.29 0.17 0.17 0.16 0.160.065 0.18 0.11 0.11 0.0970.040 0.12 0.067 0.0690.025 0.074 0.0420.015 0.0460.010 0.029样本数2 3 5 8 13 20 32 50 80 125 200 315 500 800 1250 2000样本代码A B C D E F G H J K L M N P Q R表Ⅷ减量检验限界Acceptable Quality Level (正常检验) 1000 181 277 * 不实施减量检验650 115 177 301400 68 105 181 297 490250 40 63 110 181 301 471150 22 36 63 105 177 277100 14 22 40 68 115 18165 8 13 25 42 72 115 18940 4 7 14 24 42 68 113 18125 2 3 7 14 25 40 68 110 18115 0 1 3 7 13 22 39 63 105 16910 0 0 2 4 8 14 24 40 68 110 1816.5 * 0 0 2 4 8 14 25 42 69 115 1864.0 * * 0 0 2 4 8 14 24 40 68 111 1812.5 * * * 0 0 2 4 7 14 24 40 67 110 1811.5 * * * * 0 0 1 3 7 13 22 38 63 105 1691.0 * * * * * 0 0 2 4 7 14 24 40 68 110 1810.65 * * * * * * 0 0 2 4 8 14 25 42 69 115 186 3010.40 * * * * * * * 0 0 2 4 8 14 24 40 68 111 1810.25 * * * * * * * * 0 0 2 4 7 14 24 40 67 1100.15 * * * * * * * * * 0 0 1 3 7 13 22 38 630.10 * * * * * * * * * * 0 0 5 4 7 14 24 400.065 * * * * * * * * * * * 0 0 2 4 8 14 250.040 * * * * * * * * * * * * 0 0 2 4 8 140.025 * * * * * * * * * * * * * 0 0 2 4 70.015 * * * * * * * * * * * * * * 0 0 1 30.010 * * * * * * * * * * * * * * * 0 0 2连续10批总样本数20~29 30~49 50~79 80~129 130~199 200~319 320~499 500~799 800~1249 1250~1999 2000~3149 3150~4999 5000~7999 8000~12499 12500~19999 20000~31499 31500~49999 50000~over(3) 检验严格性的调整方法• 初次检验è正常检验‚经连续五批以上检验实绩后下列列规则进行调整Œ正常检验è加严检验5批有2批不合格• 正常检验è减量检验10批全部合格,且样本不良数总与不超过界限值(减量检验的界限值),生产安定、主管也认可Ž加严检验è正常检验5批都合格• 减量检验è正常检验有一批不台格或者生产不规则、停顿或者特殊考虑ƒ检验终止连续10批加严检验(4) 抽样检验应用例• 例一:N=l500,AQL=4.0%,正常及通常检验水准Ⅱ,求抽样计划查样本代字为K抽样方式表号抽样程序样本数Ac Re 抽样表单次表II-A 1 125 10 11 ○双次表Ⅲ-A 1 80 5 9 本讲义未放入2 80 12 13多次表Ⅳ-A 1 32 0 52 323 83 32 6 104 32 8 135 32 11 156 32 14 177 32 18 19‚ 例二:N=l500,AQL=4.0%,正常及通常检验水准Ⅱ,单次,求AOQL查表V-A代字K,AQL=4%,AOQL值=5.2正确的ƒ例三:某零件IQC采AQL=4.0%,正常及通常检验水准Ⅱ,实施单次抽样,其连续10批的检验纪录如下,下批能否从正常检验改为减量检验?no 批量抽样计划不良数判定样本码样本数Ac Re1 1000 J 80 7 8 4 允收2 1500 K 125 10 11 0 允收3 1800 K 125 10 11 8 允收4 2500 K 125 10 11 3 允收5 2200 K 125 10 11 3 允收6 3300 L 200 14 15 5 允收7 2500 K 125 10 11 6 允收8 2800 K 125 10 11 8 允收9 1100 J 80 7 8 2 允收10 1800 K 125 10 11 4 允收10批合计1235 43查表Ⅷ减量检验限界=24,不良总数.>减量检验限界24 应继续采正常检验…例四:承上题,继续使用正常检验,其连续5批的检验纪录如下no 批量抽样计划不良数判定样本码样本数Ac Re11 1300 K 125 10 11 4 允收12 1600 K 125 10 11 11 拒收13 1100 J 80 7 8 8 允收14 2500 K 125 10 11 3 允收15 2200 K 125 10 11 3 拒收5批有2批拒收应改采严格检验六连续生产型抽样检验1 连续生产型抽样检验的概念(1) 连续生产故无法区分为批(2) 其作法如概念为(JIS Z9008)(3) 连续生产型抽样检验计划表• 美军标准MIL-STD-1235‚Dodge的表ƒ JIS Z9008 计数连续生产型抽样检验七逐次抽样检验作法1 计数规准型逐次抽样检验的概念(1) 逐次抽样检验是充分考虑检验费用的作法,其ATI较其它方式为低(2) 其作法如概念为(JIS Z9009)(3) 逐次抽样检验计划表计数规准型逐次抽样检验(JIS Z9009)八计量抽样检验1 计量抽样检验的两种品质保证方法(1) 以批的平均值作为保证对象(2) 以批的不良率作为保证对象2 其作法如概念(1) 计量值品质特性有μ与σ两向度可供品质推断(2) 抽样检验的作法是,从验收批的分配中抽取样本而得的分配,使用下列两方法作验收判定• 推测品质特性的μ值,以批的平均值作为判定‚ 推测品质特性的不良率,以批的不良率作为判定3 抽样检验计划表(1) 计量规准型单次抽样检验(JIS Z9003 标准差已知)(2) 计量规准型单次抽样检验(标准差未知,另有JIS Z9004可查表)4 JIS Z9003计量规准型单次抽样检验(标准差已知)5 JIS Z9003计量规准型单次抽样检验(标准差未知)6 美军标准MIL-STD-414计量调整型抽样检验表MIL-STD-414的内容与提供表格编MIL-STD-414内容提供表格A编抽样程序概述表A-1表A-2表A-3 AQL变换值样本代字样本代字B~Q的OC曲线图B编标准差未知标准差法1 单边规格• 形式一‚形式二2 双边规格• 形式一‚形式二3 作业平均值估计与严格及减量规范表B-1表B-2表B-3表B-4表B-5表B-6表B-7表B-8 形式一正常与严格检验抽样表形式一减量检验抽样表形式二正常与严格检验抽样表形式二减量检验抽样表估计批不良率严格检验T值减量检验不良率估计限界最大标准差MSD之F值C编标准差未知全距法1 单边规格• 形式一‚形式二2 双边规格• 形式一‚形式二3 作业平均值估计与严格及减量规范表C-1表C-2表C-3表C-4表C-5表C-6表C-7表C-8 形式一正常与严格检验抽样表形式一减量检验抽样表形式二正常与严格检验抽样表形式二减量检验抽样表估计批不良率严格检验T 值减量检验不良率估计限界最大平均全距MAR之f值D编标准差已知1 单边规格• 形式一‚形式二2 双边规格• 形式一‚形式二3 作业平均值估计与严格及减量规范表D-1表D-2表D-3表D-4表D-5表D-6表D-7 形式一正常与严格检验抽样表形式一减量检验抽样表形式二正常与严格检验抽样表形式二减量检验抽样表估计批不良率严格检验T值减量检验不良率估计限。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(抽样检验)抽样检验的基
础知识
第1章抽样检验的基础知识
第1节抽样检验的目的
从居家过日子到国家重大经济决策都离不开抽样检验。
比如说,你到水果摊买桔子,你可能会问:“酸不酸呀”?摊主说“你尝壹尝,先尝后买”,于是你从壹大堆桔子中抽取壹个尝壹尝,你尝的目的是什么呢?你尝的目的是要通过这壹个桔子的质量情况来推断这壹大堆桔子的质量情况。
显然抽样检验的目的是:通过样本推断总体。
样本是样品的集合,壹个样本可由壹个样品组成,也可由多个样品组成。
欲达到通过样本推断总体这样的目的,要通过三个步骤:A.抽样,B.检验,C.推断。
其中抽样这个步骤含有俩个内容a.怎么抽,b.抽多少。
其中检验这个步骤和抽样检验的理论没有关系,不同的产品、不同的质量特性使用不同的检测设备,有不同的检验方法。
C.推断,即用对样本的检测结果来对总体进行推断。
抽多少和怎样推断就构成了抽样方案。
第2节抽样方案
抽样方案分为计数型抽样方案和计量型抽样方案俩大类,首先讨论计数型抽样方案。
2.1计数型抽样方案
计数型抽样方案有俩种形式:
(1)(n;c);(2)(n;,)
从批中抽取n件产品构成样本,逐个检验各个样品,发现其中有d件不合格品;若d≤c(d≤)则接收该批,若d>c (d≥)则拒收该批。
其框图见图1-1:
图1-1
抽样方案的使用方法是非常简单的。
可抽样方案是怎么确定的呢?这里必须指出:抽样方案不是人为规定的,抽样方案是根据对总体的质量要求,用数理统计理论设计出来的。
2.2计量型抽样方案
计量型抽样方案的形式是:(n;k);它用样本均值和样本标准差对批作出推断,和计数型抽样方案相比,在相同的判断精度下,计量型抽样方案比计数型抽样方案所需的样本量更小。
其使用方法在后面的章节中做详细介绍。
第3节抽样检验的统计理论(基础)
当讨论抽样方案时,我们应注意以下基本理论问题:3.1当存在随机误差时,样本质量指标不壹定等于总体质量指标。
(1)样本不合格品率不壹定等于总体不合格品率。
比如说,从壹批产品中抽取壹件产品;经检验,若这件产品是合格品,那么样本不合格品率等于零,此时,且不能肯定:总体(批)不合格品率等于零,总体(批)中没有不合格品;经检验,若这件产品是不合格品,那么样本不合格品率等于百分之壹百,此时,且不能肯定:总体(批)不合格品率等于百分之壹百,总体(批)中都是不合格品。
如果抽取俩件产品,样本不合格品率有三个值:俩件都是不合格品,样本不合格品率等于百分之壹百;俩件中壹件是合格品,壹件是不合格品,样本不合格品率等于百分之五十;俩件都是合格品,样本不合格品率等于零;在壹次抽样后,经检验,可得上述三个值中的某壹个值,无论出现哪壹个值,我们都不能肯定
地说:总体(批)不合格品率等于这个值。
(2)样本平均每百单位产品不合格数不壹定等于总体(批)平均每百单位产品不合格数。
(3)某质量特性的样本平均值不壹定等于该质量特性的总体(批)平均值,(设总体(批)中某质量特性值服从正态分布)。
比如说,壹批钢丝的抗拉强度值服从正态分布;从这样的壹批钢丝中抽取n根,经检测得观测值,,......,其样本均值为,此时我们不能肯定地说:这个样本平均值壹定等于总体(批)该质量特性的平均值。
3.2抽样检验不能保证被接收的总体(批)中的每件产品都是合格品。
比如说,壹批灯泡有100个,我们定义:灯泡使用寿命达到1000小时之上为合格品,灯泡使用寿命不足1000小时为不合格品;我们从这批灯泡中抽取了99个灯泡,经检验,这99个灯泡的使用寿命都达到1000小时之上,都为合格品,最后壹个灯泡没检验,我们不能肯定地说:最后那个没检验的灯泡使用寿命在1000小时之上,它为合格品。
对于此例,样本量已达到极限了,样本中的每件产品都是合格品,接收了该总体(批),都不能保证被接收的总体(批)中的每件产品都是合格品,何况,在壹般情况下,样本量要比这小得多,怎能保证被接收的总体(批)中的每件产品都是合格品呢?
3.3抽样检验所犯的俩类错误
设壹批产品中有10000件,我们定义不合格品率不得超过百分之壹,(=1%),当壹批产品的不合格品率不
超过百分之壹时,我们称它为合格批;当壹批产品的不合格品率超过百分之壹时,我们称它为不合格批。
我们选定用(5;0)抽样方案,如果该批产品中有10件不合格品,(D=10),其不合格品率的真值为百分之零点壹(p=0.1%),那么,它是合格批;在这样的壹批产品中抽取5件,有可能抽到不合格品,抽样检验是根据样本的情况对总体进行判断的,抽到了不合格品,就判该批不合格;此批明明是合格的,抽样检验判断它为不合格,抽样检验判错了,这个错误称为第壹类错误,也称为弃真错误。
犯弃真错误的概率称为弃真概率,记为α。
犯第壹类错误(弃真错误)的概率
设壹批产品中有10,000件,我们定义不合格品率不得超过百分之壹,(=1%),我们选定用(5;0)抽样方案,如果该批产品中有9,000件不合格品(D=9000),其不合格品率的真值为百分之九十(p=90%),那么,它是不合格批;在这样的壹批产品中抽取5件,有可能抽到的都是合格品,抽样检验是根据样本的情况对总体进行判断的,若抽到的都是合格品,就判该批合格;此批明明是不合格的,抽样检验判断它为合格,抽样检验又判错了,这个错误称为第二类错误,也称为存伪错误。
犯存伪错误的概率称为存伪概率,记为β。
犯第二类错误(存伪错误)的概率β=
壹般情况下可描述为:
在抽样检验中,将合格批误判为不合格所犯的错误称为弃真错误,犯弃真错误的概率将称为弃真概率,记为α。
在生产方和使用方的验收抽样检验中,犯弃真错误(将合格批
误判为不合格),对生产方是不利的,在此时犯弃真错误的概率称为生产方风险;在生产方和使用方的验收抽样检验中,犯存伪错误(将不合格批误判为合格),对使用方是不利的,在此时犯存伪错误的概率称为使用方风险。
第4节抽样方案的接收概率曲线(OC曲线)
用二项分布可计算出当壹批产品的不合格品率为p 时,(n;c)抽样方案的接收概率为:
例(2;1)抽样方案的接收概率如下:
p(%)0.651.01.52.54.06.510203050
0.9870.9800.9700.9510.9220.8740.8100.0640.4900.2 50
p:表示不合格品率;
:表示批质量处于该不合格品率时,(2;1)抽样方案的接收(通过)概率值。
以p(不合格品率)为横坐标,P a(p)(抽样方案的接收概率值)为纵坐标,建立坐标系;将点(0.0065,0.987)、(0.010,0.980)、(0.015,0.970)、(0.025,0.951)、(0.040,0.922)、(0.065,0.874)、(0.10,.810)、(0.20,0.064)、(0.30,0.049)、(0.50,0.25)分别描入坐标系中;将这些点用平滑曲线联接起来,这条曲线即为接收概率曲线。
接收概率曲线又称为操作特性曲线(OperatingCharacteristicCurve)简称为OC曲线。
图1-2
第5节孤立批抽样方案的质量保证
从抽样方案的接收概率曲线(OC曲线)我们能够了
解到:用壹个抽样方案对壹批产品进行抽样检验,若样本符合要求,就说抽查通过,此时且不意味着该批质量符合要求,这个抽样方案只能起概率把关的作用。
所以我们得到,孤立批抽样方案的质量保证如下:孤立批抽样方案不能将某壹通过批的不合格品率控制在预先规定的数值下,孤立批抽样方案仅起概率把关的作用。
所谓概率把关就是当不合格品率低时,接收的概率高;当不合格品率高时,接收的概率低。
这里的接收概率的高低,仅仅是定性的;其概率把关作用的定量化有多种形式:俩点型,单点型,左点型,右点型,在后面的章节中做详细介绍。
第6节连续批抽样方案的质量保证
在质量管理和质量控制工作中,我们总希望控制不合格品率,然而孤立批抽样方案不能将某壹通过批的不合格品率控制在预先规定的数值下,只有用某壹连续批抽样方案系统对连续多批进行抽样检验可将通过批的平均不合格品率控制在事先规定的数值之下。
连续批抽样方案的质量保证可用数学符号描述如下: 6.1用某壹接收质量限(AQL)确定的系列抽样方案,对连续m(m≥10)批产品进行逐批抽样检验,若接收了其中的k(k≤m)批,对于非破坏性实验,则高概率的有:
≤AQL
其中:表示第i个接收批的批量
表示第i个接收批中包含的不合格品数
表示第i个接收批的样本量
表示第i个接收批的样本中包含的不合格品数
表示生产方交付给使用方的k批产品的平均不合格率。
6.2用某壹接收质量限(AQL)确定的系列抽样方案,对连续m(m≥10)批产品进行逐批抽样检验,若接收了其中的k(k≤m)批,对于破坏性实验,则高概率的有:
≤AQL
例如:当1201≤N≤3200,AQL=2.5时壹个抽样方案系统为:
N(5;0,1)T(8;0,1)R(2;0,1)
在此,N表示正常抽样方案(normal);T表示加严抽样方案(tightened);R表示放宽抽样方案(reduced)。
