线面、面面平行
数学线线平行,线面平行,面面平行的证明方法

数学线线平行,线面平行,面面平行的证明方法嘿,咱今儿就来聊聊数学里那线线平行、线面平行还有面面平行的证明方法呀!你想啊,线线平行就像是两个好伙伴肩并肩一起走。
要证明它们平行,咱可以找同位角相等呀,内错角相等呀,或者同旁内角互补啥的,这就好比两个小伙伴步伐一致,那肯定是平行向前嘛!还有啊,如果一条直线平行于另一条直线,而另一条直线又平行于第三条直线,那这第一条和第三条不也就平行了嘛,这就跟传递似的,是不是挺有意思?再说说线面平行。
这就好像一条线在一个平面上愉快地“玩耍”,但又不跟平面里的其他线“纠缠”。
咱可以找平面外的一条直线和平面内的一条直线平行,那外面这条线不就和整个平面平行啦!这就好比你在一个大操场外面,看到里面有个小伙伴在沿着一条直线跑,那你不就知道你和他跑的方向是平行的嘛。
那面面平行呢?哎呀呀,这就像两个大“舞台”摆在那儿。
要证明它们平行,可以先找到一个平面内有两条相交直线都和另一个平面平行,那这两个平面不就平行了嘛!这就好像两个舞台上都有各自的表演,而且表演的路线都是平行的,那这两个舞台自然也就是平行的啦。
你说数学是不是很神奇呀?这些证明方法就像是解开一道道谜题的钥匙。
有时候可能会觉得有点难,但只要咱认真去琢磨,就像攻克一个难关一样,一旦成功了,那成就感可不是一般的大呀!比如说,给你一道题,让你证明两条直线平行。
你就得开动脑筋,想想用哪种方法合适。
是找同位角呢,还是内错角呢?这就跟打仗选武器似的,得选个趁手的呀!然后一步步去分析,去推理,等你成功证明出来的时候,哇,那心情,简直比吃了蜜还甜!数学里的这些证明方法,其实也是在锻炼我们的思维能力呀。
让我们学会有条理地去思考问题,去分析问题,去解决问题。
这对我们以后做其他事情也是很有帮助的呢!所以呀,别害怕这些证明方法,大胆地去尝试,去探索。
就像探险家一样,在数学的海洋里勇敢前行,去发现那些隐藏的宝藏!相信自己,你一定能行的!咱可不能被小小的证明方法给难住了,对吧?加油!。
线面(面面)平行
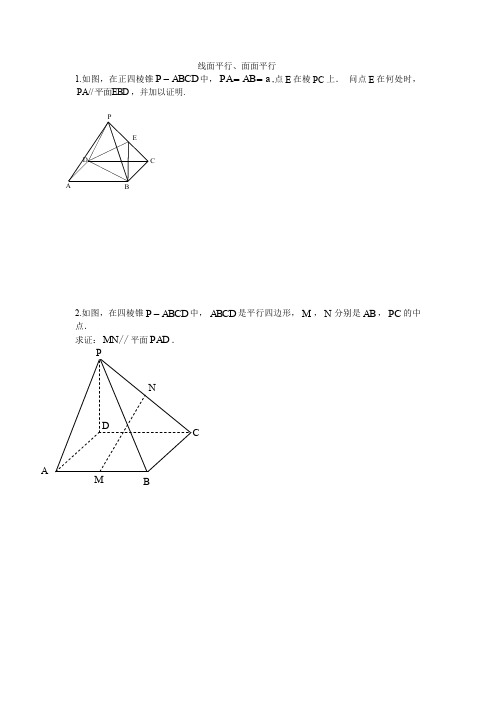
线面平行、面面平行
1.如图,在正四棱锥P ABCD -中,PA AB a ==,点E 在棱PC 上. 问点E 在何处时,//PA EBD 平面,并加以证明.
2.如图,在四棱锥P ABCD -中,ABCD 是平行四边形,M ,N 分别是AB ,PC 的中点.
E
P
D C B
A
3.如图,在正方体1111ABCD A B C D -中,E ,F 分别是棱BC ,11C D 的中点,求证:EF //平面11BB D D .
4.如图,已知点P 是平行四边形ABCD 所在平面外的一点,E 、F 分别是PA 、BD 上的点且::PE EA BF FD =,求证:EF //平面
PBC .
两个平面平行的判定定理:一个平面内的两条交直线与另一个平面平行,则这两个平面平行。
简记为:线面平行,则面面平行,
符号表示:βααββ////,//,a b a P b a b a ⇒⎪⎭
⎪⎬⎫=⊂⊂
5.如图,在正方体1111ABCD A B C D -中,求证:平面1A BD //平面11CD B .
α。
线面、面面平行及垂直八大定理

线面、面面平行和垂直的八大定理一、线面平行。
1、判断定理:平面外一条直线与平面内一条直线平行,那么这条直线与这个平ab a //面平行。
切合表示: a // b2、性质定理:假如一条直线与平面平行,经过这条直线的平面和这个平面订交,那么这条直线和交线平行。
符号表示:aa //a // bab二、面面平行。
1、判断定理:假如一个平面内有两条订交直线分别平行于另一个平面内的两条订交直线,那么这两个平面平行。
n // bm // aa b M//m n N符号表示:2、性质定理:假如两个平面平行同时与第三个平面订交,那它们的交线平行。
//符号表示:l l // d (更为适用的性质:一个平d面内的任向来线平行另一平面)三、线面垂直。
1、判断定理:假如一条直线与一个平面内的两条订交直线都垂直,那么这条直a c线垂直这个平面。
a b符号表示:ab c M$:三垂线定理:(常常考到这类逻辑)在平面内的一条直线,假如它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
符号表示:aoAa PApoa oA A2、性质定理:垂直同一平面的两条直线相互平行。
(更为适用的性质是:一个平面的垂线垂直于该平面内任向来线。
)四、面面垂直。
1、判断定理:经过一个平面的垂线的平面与该平面垂直。
a, a2、性质定理:已知两个平面垂直,在一个平面内垂直于交线的直线垂直于另一个平面。
,b, a, a b a。
线面平行、面面平行的判定

解:(1)在图 2 中,线段 BB1、BC、CC1、
C1B1、BC1 所在的直线与平面 ADD1A1 平行.
(2)在图 2 中,平面 A1B1C1D1、CC1D1D
与 AB 所在的直线平行.
图1
2021/5/9
3
证线面平行
例 2:已知:空间四边形 ABCD 中,E、F 分别是 AB、AD
定理的本质:
2021/5/9
7
证面面平行
例 3:如图 5,已知正方体 ABCD-A1B1C1D1. 求证:平面 AD1B1∥平面 C1DB.
图5
证明:∵D1B1∥DB,D1B1⊄平面C1DB,DB⊂平面C1DB,
∴D1B1∥平面C1DB,同理 AB1∥平面C1DB, 又 D1B1∩AB1=B1,AB1、D1B1 同在平面AD1B1 内,
∴EO∥PD. ∵EO⊄平面PCD,PD⊂平面PCD,
∴EO∥平面PCD.
(2)解:图中EO 还与平面 PAD 平行.
2021/5/9
图9
15
1.线面平行的判定定理(文字语言、符号语言、图形语言) 2.面面平行的判定定理(文字语言、符号语言、图形语言)
2021/5/9
16
2021/5/9
5
2.已知 AB、BC、CD 是不在同一个平面内的三条线段,E、 F、G 分别是 AB、BC、CD 的中点,求证:平面 EFG 和 AC 平行,也和 BD 平行.
证明:如图4, 在△ABC 中,E、F 分别是 AB、BC 的中点, ∴AC∥EF,AC ⊄平面 EFG,
EF⊂平面 EFG. 图4
5. P56: 2,P58:1--3
2021/5/9
线面、面面平行和垂直的八大定理-平面八大定理

线面、面面平行和垂直的八大定理-平面八大定理
一、直线面平行定理
定理:如果两条直线平行,那么任何一个由两条直线夹成的角都是相等的。
证明:设直线AR、AB为两直线,角A、A’R为AR与AB所成角,角A’B为AB与AR
所成角,设AR ∥ AB,则知AR与AB所成的角A = A’B(因两条直线平行),∴角A=
A’R,证毕。
证明:设平面Alpha、Beta为两个平面,角α为Alpha与Beta所成角,角β为
Beta与Alpha所成角,设Alpha ∥ Beta,则β=α(因两个平面平行),∴角β=α,证毕。
证明:设直线AB与平面S、T垂直,则知AB∥S;AB∥T;∴S∥T,证毕。
结论:当直线与两个不同的平面都垂直时,两个平面一定是平行的。
这就是平面八大定理。
它揭示了直线与平面之间的相互关系,也提供了重要的绘画几
何图形的基础。
线面、面面平行和垂直的八大定理-平面八大定理

线面、面面平行和垂直的八年夜定理之迟辟智美创
作
一、线面平行.
1、判定定理:平面外一条直线与平面内一条直线平行,那
么这条直线与这个平面平行.符合暗示:
2、性质定理:如果一条直线与平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行. 符号
暗示:
二、面面平行.
1、判定定理:如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面平行.
符号暗示:
2、性质定理:如果两个平面平行同时与第三个平面相交,
那它们的交线平行. 符号暗示:(更加实用的性质:一个平面内的任一直线平行另一平
面)
三、线面垂直.
1、判定定理:如果一条直线与一个平面内的两条相交直线都垂直,那么这条直线垂直这个平面. 符号暗示: α⊥⇒⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫=⊥⊥a M c b b a c a
$:三垂线定理:(经常考到这种逻辑)在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.
符号暗示:
2、性质定理:垂直同一平面的两条直线互相平行.(更加实用的性质是:一个平面的垂线垂直于该平面内任一直线.) 四、面面垂直.
1、判定定理:经过一个平面的垂线的平面与该平面垂直.
2、性质定理:已知两个平面垂直,在一个平面内垂直于交线的直线垂直于另一个平面βαβαβα⊥⇒⊥⊂=⋂⊥a b a a b ,,,。
线面平行、面面平行的性质和判定定理

如图:已知直线a,b,平面,
且a // b,a//,a,b都在平面外。
b
求证:b//
a
如图:已知直线a,b,平面,
且a // b,a//,a,b都在平面外。 a
求证:b//
证明:过a作面交于c
c
a //
a
a//c
=c
a//b
注意:
b//c
c
b
线//面
线//线
b
b //
转化是立体几何的一种重要的思想方法。
探究新知
探究1. 如果两个平面平行,那么一个平 面内的直线与另一个平面有什么位置关 系?
a
答:如果两个平面平行,那么一个 平面内的直线与另一个平面平行.
探究新知
探究2.如果两个平面平行,两个平面内的直 线有什么位置关系?
借助长方体模型探究 结论:如果两个平面平行,那么两个平面内 的直线要么是异面直线,要么是平行直线.
探究新知
探究3:当第三个平 面和两个平行平面 都相交时,两条交 线有什么关系?为 什么?
β
答:两条交线平行.
α
a
b
下面我们来证明这个结论
结论:当第三个平面和两个平行平面都 相交时,两条交线平行
如图,平面α,β,γ满足α∥β,α∩γ= a,β∩γ=b,求证:a∥b
证明:∵α∩γ=a,β∩γ=b ∴aα,bβ ∵α∥β ∴a,b没有公共点, 又因为a,b同在平面γ内, 所以,a∥b
相交,则这一条交线b就平行于直线a.
a
b
结论:直线和平面平行的性质定理
如果一条直线和一个平面平行,经过这条直
线的任意平面和这个平面相交,那么这条直线和
交线平行。
a// ,
线面平行面面平行

百度文库 - 让每个人平等地提升自我!1 线面平行、面面平行教学目标:掌握线面平行、面面平行的判定方法,并能熟练解决线面平行、面面平行的判定问题.一、 主要知识及主要方法:1.线面平行的证明:()1判定定理:如果平面外一条直线与这个平面内一条直线平行,那么这条直线与这个平面平行;()2两平面平行的性质定理:如果两个平面平行,则其中一个平面内的直线平行于另一个平面2.面面平行的证明:()1判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.()2垂直于同一条直线的两个平面平行;()3平行于同一个平面的两个平面平行.二、典例分析:(证明线面平行)例1.在四面体ABCD 中,CB=CD ,,且E ,F 分别是AB ,BD 的中点,求证(I )直线//EF 面ACD ;变式1.在四棱锥P-ABCD 中,底面ABCD 是矩形,PA ⊥平面ABCD ,AP=AB,BP=BC=2,E 、F 分别是PB 、PC 的中点, 求证://EF 平面PAD ;变式2.如图,在底面为平行四边形的四棱锥P ABCD -中, AB AC ⊥,PA ⊥平面ABCD ,且 PA AB =,点E 是PD 的中点.求证:PB ∥平面AEC ;变式3.如图,在四棱锥S ABCD -中,底面ABCD 为正方形,侧棱SD ⊥底面ABCD ,E 、F 分别为AB SC ,的中点.证明:EF ∥平面SAD ;(证明面面平行)例2.如图,在正三棱锥S ABC -中,D 、E 、F 分别是棱AC 、BC 、SC 上的点,且2CD DA =,2CE ES =,2CF FB =,G 是AB 的中点.()1求证:平面SAB ∥平面DEF ;()2求证:SG ∥平面DEFA E BCFS D。
线面、面面平行和垂直的八大定理-平面八大定理

线面、面面平行和垂直的八大定理之答禄夫天创作
一、线面平行。
1、判定定理:平面外一条直线与平面内一条直线平行,那么这条
直线与这个平面平行。
符合暗示:
2、性质定理:如果一条直线与平面平行,经过这条直线的平面和
这个平面相交,那么这条直线和交线平行。
符号暗示:
二、面面平行。
1、判定定理:如果一个平面内有两条相交直线分别平行于另一个
平面内的两条相交直线,那么这两个平面平行。
符号暗示:
2、性质定理:如果两个平面平行同时与第三个平面相交,那它们
的交线平行。
符号暗示:(更加实用的性质:一个平面内的任一直线平行另一平面)
三、线面垂直。
1、判定定理:如果一条直线与一个平面内的两条相交直线都垂
直,那么这条直线垂直这个平面。
符号暗示: α⊥⇒⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫=⊥⊥a M c b b a c a
$:三垂线定理:(经常考到这种逻辑)在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
符号暗示: 2、性质定理:垂直同一平面的两条直线互相平行。
(更加实用的性质是:一个平面的垂线垂直于该平面内任一直线。
)
四、面面垂直。
1、判定定理:经过一个平面的垂线的平面与该平面垂直。
2、性质定理:已知两个平面垂直,在一个平面内垂直于交线的直线垂直于另一个平面。
βαβαβα⊥⇒⊥⊂=⋂⊥a b a a b ,,,。
线面、面面平行和垂直的八大定理-平面八大定理

线面、面面平行和垂直的八大定理之袁州冬雪创作
一、线面平行.
1、断定定理:平面外一条直线与平面内一条直线平行,那
末这条直线与这个平面平行.符合暗示:
2、性质定理:如果一条直线与平面平行,颠末这条直线的
平面和这个平面相交,那末这条直线和交线平行.
符号暗示:
二、面面平行.
1、断定定理:如果一个平面内有两条相交直线分别平行于
另外一个平面内的两条相交直线,那末这两个平面平行.
符号暗示:
2、性质定理:如果两个平面平行同时与第三个平面相交,
那它们的交线平行. 符号暗示:
行另外一平面)
三、线面垂直.
1、断定定理:如果一条直线与一个平面内的两条相交直线
都垂直,那末这条直线垂直这个平面. 符号暗示: α⊥⇒⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫=⊥⊥a M c b b a c a
$:三垂线定理:(常常考到这种逻辑)在平面内的一条
直线,如果它和这个平面的一条斜线的射影垂直,那末它
也和这条斜线垂直.
符号暗示:
2、性质定理:垂直同一平面的两条直线互相平行.(更加
实用的性质是:一个平面的垂线垂直于该平面内任一直
线.)
四、面面垂直.
1、断定定理:颠末一个平面的垂线的平面与该平面垂直.
2、性质定理:已知两个平面垂直,在一个平面内垂直于交
线的直线垂直于另外一个平
面.βαβαβα⊥⇒⊥⊂=⋂⊥a b a a b ,,,。
线面,面面平行判定及性质

对C,m与n垂直而非平行,故C错误;
对D,垂直于同一平面的两直线平行,故D正确.
123456
5.若平面α∥平面β,直线a∥平面α,点B∈β,则在平面β内且过B点的所有 直线中
√A.不一定存在与a平行的直线
B.只有两条与a平行的直线 C.存在无数条与a平行的直线 D.存在唯一与a平行的直线 解析 当直线a在平面β内且过B点时,不存在与a平行的直线,故选A.
123456
6.设α,β,γ为三个不同的平面,a,b为直线,给出下列条件: ①a⊂α,b⊂β,a∥β,b∥α;②α∥γ,β∥γ; ③α⊥γ,β⊥γ;④a⊥α,b⊥β,a∥b. 其中能推出α∥β的条件是_②__④__.(填上所有正确的序号) 解析 在条件①或条件③中,α∥β或α与β相交; 由α∥γ,β∥γ⇒α∥β,条件②满足; 在④中,a⊥α,a∥b⇒b⊥α,又b⊥β,从而α∥β,④满足.
师生共研
题型二 平面与平面平行的判定与性质
例3 如图所示,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC, A1B1,A1C1的中点,求证:
(1)B,C,H,G四点共面;
(2)平面EFA1∥平面BCHG.
引申探究
1.在本例中,若将条件“E,F,G,H分别是AB,AC,A1B1,A1C1的中点” 变为“D1,D分别为B1C1,BC的中点”,求证:平面A1BD1∥平面AC1D.
_a_∥__β_ _α_∩__γ_=__a_ _β_∩__γ_=__b_
⇒a∥b
【概念方法微思考】 1.一条直线与一个平面平行,那么它与平面内的所有直线都平行吗?
提示 不都平行.该平面内的直线有两类,一类与该直线平行,一类与该直 线异面. 2.一个平面内的两条相交直线与另一个平面内的两条相交直线分别对应平行, 那么这两个平面平行吗?
线面、面面平行和垂直的八大定理-平面八大定理

线面、面面平行和垂直的八大定理之巴公井开创作
一、线面平行。
1、判定定理:平面外一条直线与平面内一条直线平行,那么这条
直线与这个平面平行。
符合暗示:
2、性质定理:如果一条直线与平面平行,经过这条直线的平面和
这个平面相交,那么这条直线和交线平行。
符号暗示:
二、面面平行。
1、判定定理:如果一个平面内有两条相交直线分别平行于另一个
平面内的两条相交直线,那么这两个平面平行。
符号暗示:
2、性质定理:如果两个平面平行同时与第三个平面相交,那它们
的交线平行。
符号暗示:(更加实用的性质:一个平面内的任一直线平行另一平面)
三、线面垂直。
1、判定定理:如果一条直线与一个平面内的两条相交直线都垂
直,那么这条直线垂直这个平面。
符号暗示: α⊥⇒⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫=⊥⊥a M c b b a c a
$:三垂线定理:(经常考到这种逻辑)在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
符号暗示: 2、性质定理:垂直同一平面的两条直线互相平行。
(更加实用的性质是:一个平面的垂线垂直于该平面内任一直线。
)
四、面面垂直。
1、判定定理:经过一个平面的垂线的平面与该平面垂直。
2、性质定理:已知两个平面垂直,在一个平面内垂直于交线的直线垂直于另一个平面。
βαβαβα⊥⇒⊥⊂=⋂⊥a b a a b ,,,。
线面、面面平行的性质定理

• (4)相似三角形的周长比等于相似比. • (5)相似三角形的面积比等于相似比的平方. 相似 三角形的传递性,即如果: △ABC∽△A1B1C1,△A1B1C1∽△A2B2C2,那么 △ABC∽A2B2C2
必修2
第二章
点、直线、平面之间的位置关系
3.平行四边形的判定定理
必修2
第二章
点、直线、平面之间的位置关系
定理的应用
例3、 如图:a∥α,A是α另一侧的点,B、C、D 是a 上的点 ,线段AB、AC、AD交于E、F、G点,若BD=4, CF=4,AF=5,求EG.
∵点A为直线a线外一点 ∴点A与直线a确定一个平面,平 面ABD 又∵a∥α ,α ∩平面ABD=EG ∴BD∥EG ∴<AGE= <ADB 又∵<A=<A ∴△AGE∽△ADB ∴EG/BD=AF/AC即 EG/BD=AF/AF+CF ∴EG/4=5/9 ∴EG=20/9
必修2 第二章 点、直线、平面之间的位置关系
D
3.夹在两个平面间的三条线段,它们平行且 相等,则两平面的位置关系为________. 解析: 平行或相交,如图
答案:
平行或相交
第二章 点、直线、平面之间的位置关系
必修2
定理的应用
例1、求证:夹在两个平行平面间的两条平行 线段相等
D
α
A
C
β
B
必修2
第二章
必修2 第二章 点、直线、平面之间的位置关系
巩固练习:
3、棱长为a的正方体AC1中,设M、N、E、F分别为 棱A1B1、A1D1、 C1D1、 B1C1的中点. (1)求证:E、F、B、D四点共面; (2)求证:面AMN∥面EFBD.
立体几何9-4线面、面面平行的判定与性质

则另一条也垂直于这个平面,故选B. 答案:B
15
[例2] (文)在四面体ABCD中,CB=CD, AD⊥BD,且E,F分别是AB,BD的中 点.求证:
为线段CE的中点,所以PN綊12DC.
19
又四边形ABCD是矩形,点M为线段AB的中点,
所以AM綊12DC.所以PN綊AM.
故四边形AMNP是平行四边形.所以 MN∥AP,
而AP⊂平面DAE,MN⊄平面DAE,所以 MN∥DAE.
证法二:取BE中点G,连结GM、GN,
∵GN∥BC,BC∥DA,∴GN∥DA,又
(1)直线EF∥平面ACD; (2)平面EFC⊥平面BCD.
16
解析:(1)在△ABD中,因为E、F分别是AB、 BD的中点,所以EF∥AD.
又AD⊂平面ACD,EF⊄平面ACD, 所以直线EF∥平面ACD. (2)在△ABD中,因为AD⊥BD,EF∥AD,
所以EF⊥BD. 在△BCD中,因为CD=CB,F为BD的中点,
的中点,求证:MN∥平面DAE.
18
证明:(1)因为BC⊥平面ABE,AE⊂平面 ABE,
所以AE⊥BC. 又BF⊥平面ACE,AE⊂平面ACE, 所以AE⊥BF. 又BF∩BC=B, 所以AE⊥平面BCE. 又(2B)证E⊂法平一:面取BDCEE的,中所点P以,A连E结⊥PAB,EP.N,因为点N
1
2
重点难点 重点:线面、面面平行的判定定理与性质定
理及应用 难点:定理的灵活运用
3
知识归纳
一、直线与平面平行
线面、面面平行和判定

一、知识要点线线平行⇒线面平行线面平行的判定定理:如果直线外一条直线平行于直线内一条直线,那么这条直线和平面平行。
注:当直线与平面平行时,这条直线平行于平面内的无数条直线,而不是所有的直线。
线面平行⇒线线平行线面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面与这个平面相交,那么这条直线和交线平行。
面面平行的判定:如果一个平面内的两条相交直线都平行于另一个平面,那么这两个平面平行。
注:垂直于同一条直线的两个平面平行。
三个两两相交的平面,它们的三条交线交于一点或两两平行。
二、巩固练习1.已知l 是直线,α、β是两个不同平面,下列命题中的真命题是( )A .若l ∥α,l ∥β,则α∥βB .若α⊥β,l ∥α,则l ⊥βC .若l ⊥α,l ∥β,则α⊥βD .若l ∥α,α∥β,则l ∥β2.(文)已知m 、n 是两条直线,α、β是两个平面,给出下列命题:①若n ⊥α,n ⊥β,则α∥β;②若平面α上有不共线的三点到平面β的距离相等,则α∥β;③若n 、m 为异面直线,n ⊂α,n ∥β,m ⊂β,m ∥α,则α∥β.其中正确命题的个数是( )A .3个B .2个C .1个D .0个3.一个正方体纸盒展开后如图,在原正方体纸盒中有下列结论:①AB⊥EF ②AB 与CM 成60°③EF 与MN 是异面直线④MN ∥CD 其中正确的是( )A .①②B .③④C .②③D .①③4.(2011·北京海淀期中)已知平面α∩β=l ,m 是α内不同于l 的直线,那么下列命题中错误..的是( ) A .若m ∥β,则m ∥l B .若m ∥l ,则m ∥βC .若m ⊥β,则m ⊥lD .若m ⊥l ,则m ⊥β线面、面面平行的判定与性质5.(2011·安徽省合肥市高三教学质量检测)设a、b是两条不同的直线,α、β是两个不同的平面,则下列命题错误的是()A.若a⊥α,b∥α,则a⊥b B.若a⊥α,b∥a,b⊂β,则α⊥βC.若a⊥α,b⊥β,α∥β,则a∥b D.若a∥α,a∥β,则α∥β6.对于平面α和共面的直线m、n,下列命题是真命题的是()A.若m,n与α所成的角相等,则m∥n B.若m∥α,n∥α,则m∥nC.若m⊥α,m⊥n,则n∥αD.若m⊂α,n∥α,则m∥n7.(2011·河南省郑州市模拟)设α、β是两个不同的平面,a、b是两条不同的直线,给出下列四个命题,其中真命题是()A.若a∥α,b∥α,则a∥b B.若a∥α,b∥β,a∥b,则α∥βC.若a⊥α,b⊥β,a∥b,则α∥βD.若a、b在平面α内的射影互相垂直,则a⊥b 8.(2011·青岛模拟)设两个平面α、β,直线l,下列三个条件:①l⊥α;②l∥β;③α⊥β.若以其中两个作为前提,另一个作为结论,则可构成三个命题,这三个命题中正确命题的个数为() A.3B.2C.1D.09.正方体ABCD-A1B1C1D1的棱长为1cm,过AC作平行于对角线BD1的截面,则截面面积为________.8.(2012·北京东城区综合练习)在空间中,有如下命题:①互相平行的两条直线在同一个平面内的射影必然是互相平行的两条直线;②若平面α∥平面β,则平面α内任意一条直线m∥平面β;③若平面α与平面β的交线为m,平面α内的直线n⊥直线m,则直线n⊥平面β;④若平面α内的三点A、B、C到平面β的距离相等,则α∥β.其中正确命题的序号为________.10.(2011·浙江五校联考)已知m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列命题:①若m∥α,n∥α,m∥β,n∥β,则α∥β;②若α⊥γ,β⊥γ,α∩β=m,n⊂γ,则m⊥n;③若m⊥α,α⊥β,m∥n,则n∥β;④若n∥α,n∥β,α∩β=m,那么m∥n.其中正确命题的序号是________.11.(2012·四川文,6)下列命题正确的是()A.若两条直线和同一个平面所成的角相等,则这两条直线平行B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行12.(2012·东营市期末)设m、n是两条不同的直线,α、β是两个不同的平面,给出下列四个命题:①若m⊥n,m⊥α,n⊄α,则n∥α;②若α⊥β,α∩β=m,n⊥m,则n⊥α或n⊥β;③若m⊥β,α⊥β,则m∥α;④若m⊥n,m⊥α,n⊥β,则α⊥β.其中真命题的序号是________13.(2011·广东省广州市质检)如图,正方体ABCD-A1B1C1D1中,E、F分别为棱AB、CC1的中点,在平面ADD1A1内且与平面D1EF平行的直线()A.不存在B.有1条C.有2条D.有无数条14.(文)如图,若Ω是长方体ABCD—A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确...的是()A.EH∥FG B.四边形EFGH是矩形C.Ω是棱柱D.Ω是棱台15.(2011·苏州模拟)下列命题中,是假命题的是()A.三角形的两条边平行于一个平面,则第三边也平行于这个平面B.平面α∥平面β,a⊂α,过β内的一点B有唯一的一条直线b,使b∥aC.α∥β,γ∥δ,α、β与γ、δ的交线分别为a、b和c、d,则a∥b∥c∥dD.一条直线与两个平面成等角是这两个平面平行的充要条件16.(2012·南昌二模)若P是两条异面直线l、m外的任意一点,则下列命题中假命题的序号是________.①过点P有且仅有一条直线与l、m都平行;②过点P有且仅有一条直线与l、m都垂直;③过点P有且仅有一条直线与l、m都相交;④过点P有且仅有一条直线与l、m都异面.17.下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是______(写出所有符合要求的图形序号).18.与两个相交平面的交线平行的直线和这两个平面的位置关系是()A.都平行B.相交C.在两个平面内D.至少和其中一个平行19.(文)(2011·广东揭阳一模)如图,已知平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G、H分别是DF、BE的中点.(1)求证:GH∥平面CDE;(2)若CD=2,DB=42,求四棱锥F-ABCD的体积..20.如图,在四面体ABCD中,平面EFGH分别平行于棱CD、AB,E、F、G、H分别在BD、BC、AC、AD上,且CD=a,AB=b,CD⊥AB.(1)求证:四边形EFGH是矩形.(2)点E在什么位置时,四边形EFGH的面积最大?21.如图,两个全等的正方形ABCD和ABEF所在平面相交于AB,M∈AC,N∈FB且AM=FN,求证:MN∥平面BCE.22.如图,设AB、CD分别是平面α两侧的异面直线AB//α,CD//α,直线AC、AD、BC、BD 分别交α于点E、F、H、G,求证:EG与FH互相平分23.ABCD-A1B1C1D1是正方体,B1E1=D1F1=411BA,求BE1与DF1所成角的余弦值24.如图,A、B、C、D 是异面直线AB、CD上的点,线段AB=4,CD=4,M为AC的中点,N为BD 的中点,MN=3,求异面直线AB与CD所成角的余弦值.。
线面面面平行的判定和性质

[例 3] 在三棱锥 P-ABC 中,E、F、G 分别在侧棱 PA、PB、PC 上,且PEEA=PFFB=GPGC=12,求证平面 EFG∥平 面 ABC.
[解析] 在△PAB中, ∴EF∥AB, ∵EF⊄平面ABC,AB⊂平面ABC, ∴EF∥平面ABC,同理FG∥平面ABC, ∵EF∩FG=F,且EF、FG⊂平面EFG, ∴平面EFG∥平面ABC.
证明:如图4, 在△ABC 中,E、F 分别是 AB、BC 旳中点, ∴AC∥EF,AC ⊄平面 EFG,
EF⊂平面 EFG.
图4
于是 AC∥平面 EFG.
同理可证,BD∥平面 EFG.
走向高考 ·高考一轮总复习 ·人教A版 ·数学
练习3. 如图,M、N为棱旳中点, 证明MN//面AC1.
第九章 第四节
简朴几何体(视图、面积与体积)
空间点、线、面位置关系
空间里旳平行与垂直 (鉴定与性质)
2.2 线面、面面平行的判定与性质
央美附中 kinaqiao 2023年10月19日星期四
新课导学
点与线 点与面 线与线
线与面
面与面
线面平行和面面平行旳鉴定(小推大):
(图形语言
文字语言
符号语言)
平面外旳一条直线 与此平面内旳一条 直线平行,则该直 线与此平面平行.
①平面外直线与平面内旳一条直线平行,则直线与平面平
行;②直线与平面内旳两条直线平行,则直线与平面平行;③
直线与平面内旳任意一条直线平行,则直线与平面平行;④直
线与平面内旳无数条直线平行,则直线与平面平行.
A.1 个
B.2 个
C.3 个
D.4 个
第九章 第四节
典例讲练
例 2:已知:空间四边形 ABCD 中,E、F 分别是 AB、AD
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例3、如图所示, 已知:三棱锥A-BCD被一平面所截,截面 为 EFGH。 求证:CБайду номын сангаас//平面EFGH
[证明]
∵EFGH 为平行四边形,∴EF∥GH.
又 GH⊂平面 BCD,EF⊄平面 BCD, ∴EF∥平面 BCD. 而平面 ACD∩平面 BCD=CD,EF⊂平面 ACD, ∴EF∥CD. 又 EF⊂平面 EFGH,CD⊄平面 EFGH, ∴CD∥平面 EFGH.
直线与平面、平面与平面
平行
郫县一中:郭茂文 2014-9
一、知识点复习
• 1、直线与平面、平面与平面平行的定义 • 2、直线与平面、平面与平面平行的判定 • 3、直线与平面、平面与平面平行的性质
二、例题解析
例1:如图,四棱锥P-ABCD的底面ABCD为 直角梯形,其中BA⊥AD,CD⊥AD, CD=2AB,E是PC的中点. 求证:BE∥平面PAD;
A1 B1
C1
例4:(四川2014文18题) E C 在如图所示的多面体中,四边 A D B 形 ABB1 A1 和 ACC1 A1 都为矩形。 设 D ,E分别是线段 BC ,CC1 的中点, 在线段 AB上是否存在一点 M ,使直线 DE / / 平面 A1MC ?请证明你的结论。
分析:证线//面,只需证线//面内的线。故 构造 MN//DE 证明:取线段AB的中点M,连 AC1 和AC 1 AC1 =N 。 且AC 1 可证 MN//DE ,从而 DE / / 平面 A1MC 。
注意:书写一定要规范。 1、证直线与平面平行时,三个条件一个也 不能少(面内线、面外线、线线平行) 2、证平面与平面平行时,三个条件一个也 不能少(面//线1、面//线2、线线相交)
三、小结
1、线面平行的证明 (1)证线与线平行(线面平行的判定) (2)证面与面平行(过该线的平面与此平面 平行) 2、面面平行 (1)证线与面平行(面面平行的判定) (2)证垂直于同一直线 (3)平行于同一平面
例2、(2013全国新课标二18题) 如图,直三棱柱ABC-A1B1C1 中,D,E分别是AB,BB1的中点. 证明: BC1//平面A1CD;
证明:连结AC1交A1C 于点F,则F为AC1中点. 又D是AB中点,连结DF, 则BC1∥DF. 因为DF⊂平面A1CD, 又BC1 平面A1CD, 所以BC1∥平面A1CD. 法二、设A1B1 的中点为P,连DP、C1P证 面BC1P//面 A1CD。
证明:取PD的中点F, 连结AF,FE, 又∵E是PC的中点, ∴在△PDC中,EF∥DC,且2EF=CD, 由条件知2AB∥DC,∴EF//AB且相等 ∴四边形ABEF为平行四边形,∴BE∥AF, 又AF⊂平面PAD,BE⊄平面PAD, ∴BE∥平面PAD. 法二、证面面平行(平面BEQ//平面PAD, Q是CD的中点)
