PPT例题(已整理)
新人教版植树问题全部例题ppt课件

问题: 1. 你都知道了什么? 2. 你认为一共要栽多少棵树?
(一)提出问题,暴露原认知,聚焦问题
60÷3=20(个)
小力 20+1=21(棵)
小强
60÷3=20(个) 20-1=19(棵)
小华
60÷3=20(个) 20 +1 =21(棵) 21×2 =42(棵)
小红
60÷3=20(个) 20-1=19(棵) 19×2 =38(棵)
1 少棵? 2 3 4 5 6 7
35m
问题: 4. 谁听懂他的想法了,指着图说一说就更清楚了。 5. 你发现了什么规律? 6. 为什么一头种的时候,棵数和间隔数同样多?
(四)完善类型,巩固方法
小明家门前有一条35m的小路,绿化队要在路旁栽一排树。 每隔5m栽一棵树(一端栽一端不栽)。一共要栽多少棵?
60÷5=12(颗) 答:这条项链上共有12颗水晶。
问题: 1. 用你喜欢的方法,解决这个问题。 2. 你读懂他想表达什么意思了吗?请你说一说。 3. 生活中还有哪些事情也属于这种情况,你能举几个例子吗?
作业:第110页练习二十四,第11题。 第111页练习二十四,第13题。
1. 5路公共汽车行驶路线全长12km 相邻两站之间的路程都是1km。 一共设有多少个车站?
(二)交流汇报,统一认识
问题:1. 如果我把圆拉直成线段,你有什么发现? 2. 你要是能指着图,一一对应着说我们就更明白了。
小结:我们将封闭图形“化曲为直”后,发现封闭图形和在不封闭 图形“一头种”中棵数和间隔数的关系是一样的,都是棵数 等于间隔数。
计算机一级PowerPoint操作例题一级解答

第四部分PowerPoint操作注意:PowerPoint2000操作题目,单击“回答”按钮,进行测试。
第一题:考试目录的Paper子目录下有ppt.ppt文件,完成下列操作后保存。
将第1张幻灯片的标题字体设置为“黑体”,字号不变。
将第3张幻灯片的背景文理设置为“蓝色砂纸”。
将第2张幻灯片中的文本“机会成本”超连接到第3张幻灯片。
将第4张幻灯片的切换效果设置为“向下擦出”,“中速”。
删除第6张幻灯片解答步骤:点击“回答”按钮,系统会自动弹出PowerPoint2000程序界面。
用鼠标选中第1张幻灯片的标题字“成本论”三个字,在工具栏上选择字体下拉列表,在其中选择“黑体”。
在第3张幻灯片的空白处单击鼠标右见,在快捷菜单中选择“背景”命令,打开“背景”对话框,在对话框中的“背景填充”中有一个空白的下拉列表。
拉开后选择“填充效果”,打开“填充效果”对话框。
选中“纹理”选项卡,从中选择“蓝色沙纸”,单击“确定”按钮,回到“背景”对话框,单击“应用”按钮。
用鼠标选中第2张幻灯片中的“机会成本”,选择“插入”/“超级链接”命令,打开“插入超级链接”对话框,选择“链接到”中的“本文当中的位置”按钮。
在右边的“请选择文当中的位置”中选择第3张幻灯片,单击“确定”按钮。
点击选中第4张幻灯片,选择“幻灯片播放”/“幻灯片切换”命令,打开“幻灯片切换”对话框,在效果中的下啦列表中选择“向下擦出”,“中速”。
单击“应用”按钮。
选择第6张幻灯片,按“Delete”键。
第二题:考试目录的Paper子目录下有ppt.ppt文件,完成下列操作后保存。
将第2张幻灯片的标题文本“旗魂”设置为“隶书”。
将第4张幻灯片的版式设置为“文本与剪贴画”。
将第1张幻灯片中的艺术字“动画片”的动画效果设置为“照相机”。
将演示文稿的应用设计模板设置为“Notebook”。
将演示文稿的幻灯片高度设置为“20.4厘米”。
解答步骤:点击“回答”按钮,系统会自动弹出PowerPoint2000程序界面。
剪力图和弯矩图例题弯矩图例题(共15张PPT)
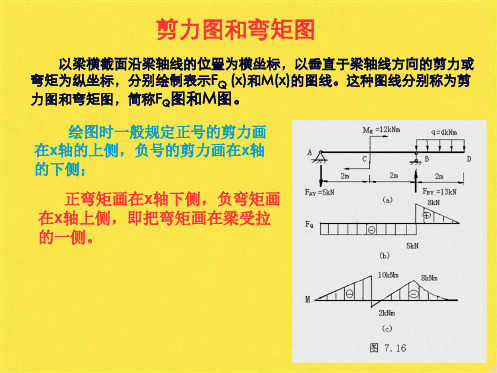
3.作剪应力图和弯矩图
最大剪力发生在梁端,其值为
F 1ql 2 Qmax
最大弯矩发生在跨中,它的数值为Mmax
1 ql 2 8
例题3 简支梁受集中作用如图示,作此梁的剪力图和弯矩图。
解:1.求约束反力
FAyFl b,FByFl a
2.列剪力方程和弯矩方程 AC段:
FQ(x)
FAy
Fb l
〔0<x<a 〕
• 口诀表述:剪力图 力偶荷载无影响。
•
弯矩图 力偶荷载有突变。
二、根据内力图规律做图
1.剪力图与荷载的关系
〔1〕在均布荷载作用段, FQ图是斜直线,倾斜方向与荷载指向相同
(2)无荷载作用区段,即q(x)=0,FQ图为平行x轴的直线。
(3)在集中力作用处,FQ图有突变,突变方向与外力一致,且突变的数值等于该集
例7 外伸梁如下图,试画出该梁的内力图。
m=3.6kNm
P=3kN
x
AD
C
RA
a=0.6m a=0.6m
q=10kN/m
B E
2a=1。2m
RB
解:
〔1〕求梁的支座反力
由 mA0
P 5 aR3 am 1q2 a20
B
2
解得
R BP2q a R A5kN
由 Y 0
P R AR B 2 q a 0
解得
M(x)FAyxFl b (0≤x≤a)
CB段:
F Q(x)F Ay FF l bFF l a(a<x<l)
Fa M (x)F Ax yF (xa )l (lx)
(0≤x≤l)
3.作剪力图和弯矩图
Q图 M图
图三
齿轮受力分析例题PPT课件

主动轮左(右) 手定则(即大拇
指指向为Fx1的方 向) Fx2= —Fx1
由接触点指 向大端
Fx1与Ft2方向相反, Fx2与Ft1方向相反
第5页/共11页
例题1
传动中,蜗杆(左旋)主动,转向如图所示。圆柱齿轮为斜齿轮,为使Ⅱ、
Ⅲ轴的轴向力平衡,试确定:
(1)蜗轮2的螺旋线方向; (2)齿轮3、4螺旋线方向; (3)蜗轮2和齿轮3所 受轴向力方向; (4) Ⅲ轴上圆锥齿轮6应放置在左边的位置1或是右边 的
位置2? (5)在图上画出5轮所受力的方向。 Ⅳ
1
4
5
Ⅰ
Ⅱ
2
6 位置1
Ⅲ
位置2
3
第6页/共11页
例题1
传动中,蜗杆(左旋)主动,转向如图所示。圆柱齿轮为斜齿轮,为使Ⅱ、
Ⅲ轴的轴向力平衡,(置(42135)1)Ⅲ齿或蜗 在轴轮是图上3右2上、的 和圆边画4螺 齿锥出螺的旋 轮齿5旋位线3轮轮线所置方所6方受2应向受?向轴放;力;向置的力在方方左向向边。;的位
5、各种齿轮传动受力分析比较
受力名称 齿轮类型
圆周力Ft
直齿圆柱齿轮传动 斜齿圆柱齿轮传动 直齿圆锥齿轮传动
对主动轮来说是 阻力,其方向与 主动轮在啮合点 处的运动方向相 反;对从动轮来 说是动力,其方 向与从动轮在啮 合点处的运动方
向一致
蜗杆蜗轮传动 (主反从同)
径向力Fr
由啮合点 指向轮心
轴向力Fx
圆周力Ft
径向力Fr
轴向力Fx
直齿圆柱齿轮传动 斜齿圆柱齿轮传动 直齿圆锥齿轮传动
本节课我们
对主动轮来说是
无
阻力,其方向与 复习了哪些
主动轮在啮合点 处的运动方向相
化工原理ppt上的例题

例:在换热器里将平均比热为3.56kJ/(kg·℃)的某溶液自25℃加热到80℃,溶液流量为1.0kg/s ,加热介质为120℃的饱和水蒸气,其消耗量为0.095kg/s ,蒸气冷凝成同温度的饱和水排出。
试计算此换热器的热损失占水蒸气所提供热量的百分数。
解:根据题意画出流程图 在此系统中输入的热量:∑+=21I QQQ蒸气带入的热量:kW3.2579.2708095.01=⨯=Q溶液带入的热量:烧碱厂重力沉降净化粗盐水。
粗盐水ρ=1200Kg/m3,μ=2.3mPa.s 。
固体颗粒视为球形,ρs=2640kg/m3,求(1)d=0.1mm 颗粒的ut 。
(2)ut=0.02m/s 的 d 。
解:(1)求ut 设沉降属于层流区s m gd u s t /1041.3103.21881.9)12002640()101.0(18)(33232---⨯=⨯⨯⨯-⨯⨯=-=μρρ校核:1178.0103.212001041.3101.0333<=⨯⨯⨯⨯⨯==---μοt et du R假设成立。
ut =3.41×10-3m/s 为所求。
(2)求d 设沉降属于层流区:m gu d s t 431042.281.9)12002640(02.0103.218)(18--⨯=⨯-⨯⨯⨯=-=ρρμ校核:153.2103.2120002.01042.234>=⨯⨯⨯⨯==--μοt et du R()kW 8902556.30.12=-⨯⨯=Q ∑=+=∴kW3.346893.257IQ 43OQ Q Q+=∑输出的热量:再设沉降属于过渡区:m gu d s t46.116.04.04.11059.2])()153.0[(-⨯=-=ρρμρ校核:70.2103.2120002.01059.234=⨯⨯⨯⨯=--et R d=2.59×10-4m 为所求。
例:烧碱厂重力沉降净化粗盐水。
排列组合典型例题ppt课件

可编辑课件PPT
7
(7)甲、乙两同学不能相邻的排法共有: 方法一:(排除法)A77-A66·A22=3 600 种. 方法二:(插空法)先将其余五个同学排好有 A55种方法, 此时他们留下六个位置(就称为“空”吧),再将甲、乙同学分 别插入这六个位置(空)有 A26种方法,所以一共有 A55A26=3 600 种方法.
种不同的方法,故共有 120×2=240 种方法.
【答案】 B
21
可编辑课件PPT
4.从乒乓球运动员男 5 名、女 6 名中组织一场混合双打比赛,不同的组合
方法有( )种.
A.C25C26
B.C52A26
C.C52A22C26A22
D.A52A26
【解析】 分两步进行:第一步:选出两名男选手,有 C25种方法;第 2 步,
【答案】 C
20
可编辑课件PPT
3.(2015·青岛高二检测)将标号为 1,2,…,10 的 10 个球放入标号为 1,2,…,
10 的 10 个盒子里,每个盒内放一个球,恰好 3 个球的标号与其在盒子的标号不
一致的放入方法种数为( )
A.120
B.240
C.360
D.720
【解析】 先选出 3 个球有 C310=120 种方法,不妨设为 1,2,3 号球,则 1,2,3 号盒中能放的球为 2,3,1 或 3,1,2 两种.这 3 个号码放入标号不一致的盒子中有 2
(2)分两类:第 1 类,6 个小球分 3,1,1,1 放入盒中;第 2 类,6 个小球分 2,2,1,1 放入盒中,共有 C36·C14·A33+C26·C42·A24=1 500(种)不同放法.
决策的方法例题与练习(课堂PPT)

.
23
4.
.
24
• 计算各结点的期望收益值(从右向左进行) • 结点6:期望值=[0.9×100+0.1×(-20)]×7—140=476万元; • 结点7:期望值=[0.9×40+0.1×10]×7=259万元; • 决策点ii:由于结点6的期望值大于结点7的期望值,所以保留扩建方
案,剪去不扩建方案。并将点6的期望值476万元移到决策点ii上。 • 结点3:期望值=[0.9×100+0.1×(-20)]×7=616万元; • 结点4:期望值=1.0×(-20)×7=-140万元; • 结点5:期望值=1.0×10×7 =70万元; • 结点1:期望值=0.7×616+0.3×(-140)+[0.7×100+0.3×(-
• 不论哪个方案成功,生产规模都可分成大批、中批、 小批三种,失败了继续生产老产品,并维持中批规 模。
.
2
预计在今后三年内新产品销路好的概率为60%,销路
差的概率为40%,老产品销路好的概率为40%,销 路差的概率为60%。不同自然状态下的损益值经预 测见下表。试选择行动方案。
.
3
决策树:
自行研制
决策的方法
例题
.
1
• 某企业老产品进入成熟期,计划开发生产一种新产 品替代老产品,有三种可供选择的方案:
• 甲方案是自行研制,预计成功可能性是50%,需投 资30万元;
• 乙方案是在技术市场上购买专利,预计成功的可能 性为60%,需要投资20万元;
• 丙方案是与另一家厂家协作生产,预计成功的可能 性为80%,不需要投资。
-30
1 购买专利
-20
协作生产
0
力矩平衡的典型例题 ppt课件

G ALAG BLB
即:
G
(lx
l) 4G(l 2lx)
lx
3l 8
所以,本题的正确选项应为B.
例2:如图所示,质量为m的均质木杆,上端可绕 固定水平光滑轴O转动,下端搁在木板上,木板置于 光滑水平地面,棒与竖直线成45°角,棒与木板间 的动磨擦因数为0.5.为使木板向右做匀速运动,求 水平拉力F等于多少?
mL 2g L si4n 5F 1 L co 4s 5F N L si4n 5
由动摩擦力公式得 F1 FN
解以上两式得
F1
mg 6
以木板为研究对象,水平方向受两个力,分别是拉力F和 摩擦力F1 ,由于匀速拉出,由力的平衡条件得F =F1
所以拉力: F mg 6
力矩平衡的典型例 题
解决力矩平衡问题应遵循规范的解题 顺序,研究对象的确定,转动轴的选取 是解题的关键.
解析:在木板上未施水平拉力F之前,木棒和木块之 间没有摩擦力,而在木板上施加水平力F后,将在木 棒和木棒之间产生一个滑动摩擦力.在木板施水平拉 力F之后木板做匀速运动,合力为零.木板在水平方 向上受到向左的摩擦力F1作用.
• 以杆OB为研究对象,受 力情况如图所示,木杆处于 平衡状态,合力矩为零,对 木棒,以O为轴,列力矩平 衡方程得
这一点很容易证明,当该三力不相交于一点时,则必 出现三个交点,选其中任一个交点,通过该交点的两个 力的力臂为零,力矩为零,这样只有不通过该交点的另 一个力有力矩,不可能平衡.因此,三力必交于一点.
力矩平衡的 典型例题
例1:如图所示,A、B是两个完全相同的长方形
木块,长为l,叠放在一起,放在水平桌面上,端 面与桌边平行.A木块放在B上,右端伸出1/4, 为保证两木块不翻倒,木块B伸出桌边的长度不 能超过.
节点流量计算例题PPT课件

0.5(25.45+9.55)=17.50
0.5(25.45+9.55)=17.50
40
0.5(9.55+9.55+25.45)=22.28 40
0.5(25.45+9.55)=17.50
40
0.5(9.55+25.45+19.09)=27.05
0.5(25.45+19.09+15.91)=30.22
(4)节点流量计算公式 节点流量包括两部分: 由沿线流量划成节点流量和该节点的集中流量
Q j 0.5qy qi (l / s)
【例题】某城市最高时总用水量为260L/s,其中集中供应的工 业用水量120 L/s(分别在节点2、3、4集中出流40 L/s)。各 管段长度(单位为m)和节点编号见图。管段1-5、2-3、3-4为 一侧供水,其余为双侧供水。试求: (1)比流量; (2)各管段的沿线流量; (3)各节点流量。 第1页/共5页
0.5(15.91)=7.95
14量 (L/s ) 17.50 57.50 62.28 57.50 27.05 30.22 7.95
260.00
谢谢您的观看!
第5页/共5页
解:1.配水干管计算总长度
2.配水干管比流 量
绿地
Q=260L/s 17.50
1
600 5
7.95 7
居住区
27.05 600 6
500
30.22
居住区 居住区 居住区 居住区
800
800
800
第2页/共5页
57.5
62.28
57.5
2 工60厂0 3 工60厂0 4
3.沿线流量:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 基础知识例:用谱分解定理对有理功率谱)8.01)(8.01(36.0)(1z z z S xx --=-进行分解 解: 由)()()(12-=z B z B z S xx εσ上式分解为: zz z S xx 8.0118.01136.0)(1-⋅-=- 其中: z z B z z B 8.011)( ,8.011)(11-=-=--大家下去完成 )8.01)(8.01(8.08.0)(11z z zz z z S xx ----=-- 的谱分解Note: 分母多项式不需分解,只对分子多项式分解 let: )1()1)(1(8.08.021211fz fz ffz fz z z z z --+=--=-----εεσσ)111)((2122z f f z ff Hf z +-+-=-εσ再比较两边系数)1,2(f or 5.06.1 : 4.012)1(222舍去解得>===⎪⎩⎪⎨⎧=+=+f f ff z εεσσ 故 ⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛--=--z z z z z S xx 8.015.018.015.016.1)(11即: z z z B z z z B 8.015.01)( 8.015.01)(111--=--=---第二章 维纳和卡尔曼滤波器例:设信号()n χ的自相关序列为()() ,2,,0,8.0±±==m n R m χχ观测信号()()()n v n n y +=χ。
这里()n v 是方差为0.45的零均值白噪声,它与()n χ相互是统计独立的。
试设计一个长为N=3的FIR Filter 来处理()n y 使其输出()n χˆ与()n χ的误差的均方值最小。
解:用Wiener Flitering 能满足要求先求()()[]()()()()()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==64.08.01210210xx y y y R R R R R R n y n E P χχχχχχχχ∵()()()n v n n y +=χ()()n v n ,χ统计独立,不相关。
()()[]()()()()()()()()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+++=⎥⎥⎥⎦⎤-⎢⎢⎢⎣⎡--==45.018.064.08.045.018.064.08.045.010********yy yy yy yy yy yy yy yy yy T R R R R R R R R R n y n y E R note: 0)()]()([==+m R m n v n V E vv ,只有45.0)]([2=n V E)(1][)(45.01)]([)0()0(12n k n N n n kn yy xx yy y y Ny y E k R n V E R R +-=+∑=+=+=+=由P R hopt 1-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡09122.02059.05355.064.08.01031.14569.02031.04569.0194.14569.02030.04569.0031.1)2()1()0(h h h Note :逆矩阵求法例:设有一平稳随机过程,其自相关序列5.0)1(,1)0(=±=xx xx R R ,0)(=m R xx ),3,2( ±±=m ,在传输该随机过程的一个取样序列)(n x 时,混入了一个方差为0.45的零均值平稳白噪声)(n V ,设信号和噪声统计独立。
设计一个非因果数字滤波器,对)()()(n V n x n y +=进行处理,传输出)(ˆn x的均方误差最小, 解:由题已知 ),3,2(0)(,5.0)1(,1)0( ±±===±=m m R R R xx xx xx 可求出121121)()(--∞-∞=++==∑z z z m R z S m xx m xx 又)()]]()()[([)]()([)(m R m n v m n x n x E m n y n x E m R xx xy =+++=+=()(),(n v n x 互不相关)121121)()(-++==∴z z z S z S xx xy )()( ))]()()(()([)]()([)(m R m R m n v m n x n v n x E m n y n y E m R vv xx yy +=++++=+=而)(45.0)()]([)]()([)(2m m n v E m n v n v E m R vv δδ==+= 只有m =0时等于方差,其余为0。
12145.121)()()(--∞-∞=++=+=∴∑z z z m R z S z S m vv m xx yy由此得维纳解:2121119.21212145.12121121)(------++++=++++=z z z z z z z z z H opt 由此得差分方程:)2(ˆ)1(ˆ9.2)2()1(2)()(ˆ-----+-+=n x n x n y n y n y n x可得直II 型结构图:例:已知一阶马尔柯夫过程的信号模型为:)()1(6.0)(n w n x n x +-=,这里)(n w 是方差0.82的零均值白噪声。
对)(n x 进行观测的结果得到:)()()(n v n x n y +=,这里)(n v 是方差为1的零均值的白噪声。
试设计因果Wiener Filter 对)(n y 进行处理以得到)(n x 的最佳估计。
⑴ 求Filter 的冲激响应?⑵ 若用)(n y 直接作为)(n x 的估计,试与因果Wiener Filter 的处理结果比较,后者的估计误差均方值改进了多少分贝?解:⑴ 由题 1,82.0,1,6.0====R Q C a ,代入由 PC R P R a P Q 22+-=,得:P PP P P P ++=+-=164.0136.082.02 即04195064.082.082.022=--⇒+=+P P P P P0)1)(4150(=-+P P 得正解:P=1 代入 PC R CP G 2+=,得5.0111=+=G 再由 3.0)5.01(6.0)1(=-=-=CG a f 故因果Wiener Filter 传输函数为:113.015.01)(---=-=z fz G z H C其相应冲激响应:)()3.0(5.0)(n u t h n c =⑵ 若用)(n y 作为)(n x 的估计,其估计误差均方值为:1)0()]([})]()({[)]([2221====-=R R n v E n y n x E n e E vv再采用因果Wiener Filter 时,由于相应卡尔曼Filter 的稳定状态就是维纳Filter 的解,故用0)1(2222222=-+-+a C QR a C Q C a R εε求 036.082.036.082.064.02=-++εε即 04173182=-+εε 显然 0>ε,故)]([212n e E ==ε dB n e E n e E 35.0lg 10)]([)]([log 1021210-== 故Wiener Filter 处理结果改进约3dB 。
习题:已知)()1(95.0)(n w n x n x +-=)()()(n v n x n y +=ni i w n w E δ0976.0)]()([=ni i v n v E δ=)]()([这里ni δ=⎩⎨⎧≠=i n i n1 求解Ricatti 方程 P ⇒,并写出Kalman Filter 的标准方程式。
解: 1 ,0976.0 ,1,95.0====R Q c a 代入 P PP PC R P R a P Q +-=⇒+-=195.00976.0222Ricatti 方程得其正解: 312.0=P 再由式: 238.0312.01312.02=+=⇒+=G PC R CP G将以上数据代入 )]1|1(ˆ)([)1|1(ˆ)|(ˆ---+--=n n x ac n y G n n x a n n x得Kalman Filter 标准方程:)]1|1(ˆ95.0)([238.0)1|1(ˆ95.0)|(ˆ---+--=n n xn y n n x n n x 第三章 自适应滤波器⒈ 已知42)]([8721122=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=n d E P R (1)写出性能曲面公式;(2)求最佳权矢量;(3)求最小均方误差;(4)求性能曲面主轴坐标系表示式;(5)求性能曲面沿主轴的二阶导数。
解:⑴W P RW W n d E T T 2)]([2-+=ξ1010212016142)(242W W W W W W --+++=⑵ ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--==-3287323131321*P R W ⑶***2min 2)]([W P RW W n d E T T -+=ξ4316214322)94(242=⨯-⨯-⨯⨯+++=⑷ R 的特征值⎥⎦⎤⎢⎣⎡===3001,3,120λλλ 2120min 34V V V V T '+'+='Λ'+=∴ξξ⑸ 2202='∂∂V ξ, 6212='∂∂V ξ例2 如图为一自适应相关抵消器的原理图:已知[]2=n n Y X E4.0][2=n Y E11][2=n X E⑴ 推导均方误差随权系数变化的关系式,并求最佳权系数值。
⑵ 推导加权系数适代计算公式⑶ 求加权系数表达式,并确定)(n h 收敛于最佳权值h 的范围解:⑴ []]2[X(n)Y(n)E P ]4.0[)]([2====n Y E R)(nXYh P Rh h n d E T T 2)]([2-+=∴ξh h 44.0112-+=即可写为 11)(4)(4.0)(2+-=n h n h n ξ524.0)(11=⨯==--*P R n h⑵48.0-=∇H]4)(8.0[)()1(--=+k h k h K h μμμ4)(8.0)(+-=k h k h⑶ ]5)([8.0)(5)1(--=-+k h k h k h μ]5)()[8.01(--=k h μ]5)0([)8.01(5)(--=-∴h k h K μ5]5)0([)8.01()(+--=⇒h k h K μ 2.50 18.01<<→<-μμ第四章 功率谱估计例1 一自回归过程的5个观测值为4,3,2,1,0},5,4,3,2,1{)(==n n x⑴ 用Levinson-Durbin 算法设计一个2阶线性预测器。
