直角三角形(2)PPT教学课件
合集下载
2.4解直角三角形(2)PPT课件

9.4
解直角三角形(2)
情境导入
• 1. 回顾旧知:请回答解直角三角形的概念? • 2.分组思考下列问题,看哪组做的又快又对: 在直 角三角形ABC中,∠C﹦90°,由下列条件解直角三角 形。 (1) 已知a﹦2,b﹦2,则c﹦_, ∠A﹦_, ∠B﹦_. (2) 已知b﹦1,c﹦2,则∠A﹦_,∠B﹦_,a﹦_. (3 )已知∠A﹦45°,C﹦2,则∠B﹦_,a﹦_,b﹦_. • 3.有一块三角形的土地,已知∠A=150°, AB=20m,AC=30m,求三角形土地的面积?
C
A D
B
• 解:过点C作CD⊥AB,垂足为D. • 在直角△ACD中,AC ﹦20, CD ∠A﹦60°,由sinA= AC 得 CD=AC∙sinA=20∙sin60 3 °=20× 2 =10. 3 由 cosA= AD ,得 AC AD=AC· cosA=20×cos60°= 1 20× 2 =10. 在直角 △DBC中,由∠B=45°,CD=10 3 ,得BD=CD=10 3 .所以 AB=AD+DB=10+10 3 =10(1 + 3 ) (厘米)
比一比
• 练习2. 在等腰三角形 ABC中,AB=AC,且一腰 长与底边的比是5 :8, 求sinB,cosB的值。
A
B D
C
比一比
练习2. 在等腰三角 形ABC中,AB=AC, 且一腰长与底边的比 是5 :8,求 sinB,cosB的值。
AB DC来自• 解:过点A作AD⊥ BC,垂足为D.由等腰三 角形的性质可知 BD=CD,设 AB=5t,BC=8t,则 BD=4t.在直角三角形 ABD中,由勾股定理 得AD=3t,所 以,sinB=AD/AB=3/5, cosB=BD/AB=4/5.
最新北师大版八年级数学下册《直角三角形》精品教学课件

∴∠ABP=∠ACP=90°
∵PB=PC,AP=AP
∴Rt△ABP≌Rt△ACP(HL)
∴∠APB=∠APC
PB=PC,
在△PBD和△PCD中,
∠DPB=∠DPC, DP=DP,
∴△PBD≌△PCD(SAS)
∴∠BDP=∠CDP
课堂小结,整体感知
1.课堂小结:请同学们回顾本节课所学的内容,有哪些收获?
实践探究,交流新知
猜想: 斜边和一条直角边分别相等的两个直角三角形全等.
1.分析命题: 条件:两个直角三角形的斜边和一条直角边分别相等; 结论:这两个直角三角形全等.
2.数学语言: 已知:如图,在△ABC和△A′B′C′中,∠C=∠C′=90°,AC=A′C′,AB=A′B′; 求证:△ABC≌△A′B′C′.
开放训练,体现应用
例2 如图,∠BAC=90°,AD是∠BAC内部一条射线,若AB=AC,BE⊥AD于点E
,CF⊥AD于点F.求证:AF=BE.
证明:∵∠BAC=90°
∴∠BAE+∠FAC=90°
∵BE⊥AD,CF⊥AD
∴∠BEA=∠AFC=90°
∴∠BAE+∠EBA=90°
∴∠EBA=∠FAC.
∴∠BFD=∠CED=90°
DF=DE,
在△BDF和△CDE中 ∠BFD=∠CED,
BF=CE,
∴△BDF≌△CDE(SAS)
∴∠B=∠C
开放训练,体现应用
变式训练2 如图,在四边形ABCD中,∠ABC=∠ADC=90°,
BE⊥AC于点E,DF⊥AC于点F,CF=AE,BC=DA.
求证:Rt△ABE≌Rt△CDF.
开放训练,体现应用
例1 如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方 向的长度DF相等,两个滑梯的倾斜角∠ABCБайду номын сангаас∠EFD的大小有什么关系?
《三角形的内角》三角形PPT(第2课时)

思考 如果一个都不知道,或只知道1个角,你能知道
三角形各角的度数吗?
新课导入
课堂小结
三角形内角和定理:三角形内角和为 180°。
为了证明的需要,在原来的图形上添加的线叫做辅
助线.
在平面几何里,辅助线通常画成虚线.
推论 直角三角形的两个锐角互余。
反之,有两个角互余的三角形是直角三角形。
B
C
直角三角形的性质:直角三角形的两个锐角互余.
A
应用格式:
在Rt△ABC 中,
∵
∠C =90°,
∴
∠A +∠B =90°.
B
C
直角三角形的表示:
直角三角形可以用符号“Rt△”表示.如:直角三角形ABC 可
以写成Rt△ ABC.
例1 如图,∠C=∠D=90 °,AD,BC相交于点E. ∠CAE与
( )
新课导入
三角形内角和定理的辨析
例题
若一个三角形三个内角度数的比为 2︰3︰4,那么这
个三角形是( B )
A .直角三角形
B .锐角三角形
C .钝角三角形
D .等边三角形
例题
(1)一个三角形中最多有 1 个直角.
(2)一个三角形中最多有 1 个钝角.
(3)一个三角形中至少有 2 个锐角.
60°
x =18°
x =30°
新课导入
例题+变式:根据三角形内角和定理求角度
归纳 ①直接计算: 直接利用三角形的内角和180°进行计算.
②形题数解:
设某一个角为x(或将某一个角视为未知数),其余
的角用x的代数式表示,从而根据题意列出方程(组)求
解,这就是“形题数解”.
解直角三角形完整版PPT课件

余弦或正切函数计算得出。
已知一边和一角求另一边
02
在直角三角形中,已知一边长和一个锐角大小可以求出另一边
长,通过正弦、余弦或正切函数计算得出。
解直角三角形的实际应用
03
例如测量建筑物高度、计算航海距离等。
三角函数在实际问题中应用
测量问题
在测量问题中,可以利用三角函数计算高度、距离等未知量。例如,利用正切函数可以计算 山的高度或者河的宽度。
直角三角形重要定理
勾股定理
如上所述,勾股定理描述了直角三角 形三边之间的数量关系。
射影定理
相似三角形判定定理
若两个直角三角形的对应角相等,则 这两个直角三角形相似。根据此定理, 可以推导出一些重要的直角三角形性 质和定理。
射影定理涉及直角三角形中斜边上的 高与斜边及两直角边之间的数量关系。
02
三角函数在解直角三角形中应用
• 性质:正弦、余弦函数值域为[-1,1],正切函数值域为R;正弦、余弦函 数在第一象限为正,第二象限正弦为正、余弦为负,第三象限正弦、余 弦都为负,第四象限余弦为正、正弦为负;正切函数在第一、三象限为 正,第二、四象限为负。
利用三角函数求边长和角度
已知两边求角度
01
在直角三角形中,已知两边长可以求出锐角的大小,通过正弦、
注意单位换算和精确度
在求解过程中,要注意单位换算和精确度的控制,避免因单位或精 度问题导致答案错误。
拓展延伸:非直角三角形解法简介
锐角三角形和钝角三角形的解法
对于非直角三角形,可以通过作高线或利用三角函数等方法将其转化为直角三角形进行 求解。
三角形的边角关系和面积公式
了解三角形的边角关系和面积公式,有助于更好地理解和解决非直角三角形问题。
八年级数学直角三角形2

A
30 ゜
B
2.如图:它是人字屋架设计图,其中 AB=AC=5米.D是AB的中点, AE⊥BC.如果∠BAC=120゜, 求AE和DE的长度. A
D
B
E
C
3.如图: ∠ABC= ∠ADC
=90 ° ,E是AC的中点,EF⊥BD 于F.试说明F是DB的中点.
A
E
B
F
D
C
4.在Rt△ABC中, ∠ ACB= 90 °,CH 是斜边AB上的高,CM是AB上中线,CT是
∠ BCA的平分线.试说明∠ 1= ∠ 2.
C
12
A
M TH
B
1.直角三角形斜边上的中线等于斜边的__. 2.在Rt△ABC中∠C=90°,∠B=30, AB=4厘米.则AC=___厘米. 3.在Rt△ABC中,CD是斜边AB上的中线,
若CD=3.5厘米,则AB=__厘米.
4.在三角形ABC中CD是AB边上的中 线.且CD= 1 AB.则△ABC是__三角形.
HQEZ WJL321 制作
上节课学习的直角三角形知识: 1.直角三角形的两个锐角互余. 2.有两个角互余的三角形是直角三角形. 3.等腰直角三角形的两个锐角都是45 ゜
操作实践,总结规律.
任意画一个直角三角形,作出斜边上的中线,并利 用圆规比较中线与斜边的一半的长短.你发现了什 么?
(请所有同学把结果都说出来.)
总结:直角三角形性质:
A
直角三角形斜边上的中线
D
等于斜边的一半
∵ ∠C= 90゜
B
C
CD是AB边上的中线.
1
∴CD= 2 AB(直角三角形斜边上的中线等于斜边的一半.)
30 ゜
B
2.如图:它是人字屋架设计图,其中 AB=AC=5米.D是AB的中点, AE⊥BC.如果∠BAC=120゜, 求AE和DE的长度. A
D
B
E
C
3.如图: ∠ABC= ∠ADC
=90 ° ,E是AC的中点,EF⊥BD 于F.试说明F是DB的中点.
A
E
B
F
D
C
4.在Rt△ABC中, ∠ ACB= 90 °,CH 是斜边AB上的高,CM是AB上中线,CT是
∠ BCA的平分线.试说明∠ 1= ∠ 2.
C
12
A
M TH
B
1.直角三角形斜边上的中线等于斜边的__. 2.在Rt△ABC中∠C=90°,∠B=30, AB=4厘米.则AC=___厘米. 3.在Rt△ABC中,CD是斜边AB上的中线,
若CD=3.5厘米,则AB=__厘米.
4.在三角形ABC中CD是AB边上的中 线.且CD= 1 AB.则△ABC是__三角形.
HQEZ WJL321 制作
上节课学习的直角三角形知识: 1.直角三角形的两个锐角互余. 2.有两个角互余的三角形是直角三角形. 3.等腰直角三角形的两个锐角都是45 ゜
操作实践,总结规律.
任意画一个直角三角形,作出斜边上的中线,并利 用圆规比较中线与斜边的一半的长短.你发现了什 么?
(请所有同学把结果都说出来.)
总结:直角三角形性质:
A
直角三角形斜边上的中线
D
等于斜边的一半
∵ ∠C= 90゜
B
C
CD是AB边上的中线.
1
∴CD= 2 AB(直角三角形斜边上的中线等于斜边的一半.)
湘教版八年级数学下册教学课件(XJ) 第1章 直角三角形 第2课时 勾股定理的实际应用

解:(1)在Rt△ ABC中,
A
别踩我,我怕疼!
C 根据勾股定理得
AB 32 42 5米,
∴这条“径路”的长为5米. (2)他们仅仅少走了
(3+4-5)×2=4(步). B
二 利用勾股定理求最短距离
问题 在A点的小狗,为了尽快吃到B点的香肠,它选择A 不选择A C B路线,难道小狗也懂数学?
问题 观看下面同一根长竹竿以三种不同的方式进门的情况,并结合曾 小贤和胡一菲的做法,对于长竹竿进门之类的问题你有什么启发?
这个跟我们学的勾股 定理有关,将实际问 题转化为数学问题
典例精析 例1 一个门框的尺寸如图所示,一块长3m,宽2.2m的长方形薄木板能
否从门框内通过?为什么?
分析:可以看出木板横着,竖着都不能通过,
A A
B
解:台阶的展开图如图,连接AB.
在Rt△ABC中,根据勾股定理得
C
B
AB2=BC2+AC2=552+482=5329,
∴AB=73cm.
能力提升: 5. 为筹备迎新晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然 后缠绕红色油纸,如图.已知圆筒的高为108cm,其横截面周长为36cm, 如果在表面均匀缠绕油纸4圈,应裁剪多长的油纸?
例4 在一次台风的袭击中,小明家房前的一棵大树在离地面6米处断裂, 树的顶部落在离树根底部8米处.你能告诉小明这棵树折断之前有多高吗?
6 米
8米
A
6 米
C
8米
解:根据题意可以构建一直角三角
形模型,如图.
在Rt△ABC中,
AC=6米,BC=8米,
由勾股定理得
AB AC2 BC2
62 82
B
AB32= 62 +(10+8)2 =360, B2 ∴AB1<AB2<AB3.
1.2直角三角形性质和判定(2)——勾股定理ppt.

那么是否对所有的直角三角形,都有两
直角边的平方和等于斜边的平方呢?
A
S2
S3 S1
B
C
图1-10
探究
如图1-11, 任作一个Rt△ABC, ∠C= 90°,
若BC= a,AC= b, AB= c, 那么a2+ b2= c2是
否成立呢?
c
A
b
B
a
图1-11
C
步骤1 先剪出4 个如图1-11 所示的直角三角形,
得出梯子往上移动的距离为(A’B - AB) m.
A’
A 墙面
梯子
地面
B C’ C 图1-17
在Rt△ABC中, AC = 4 m, BC = 1.5 m, 由勾股定理得, AB = 42 - 1.52 = 13.75 3.71(m). 在Rt△A’BC’中, A’C’ = 4 m, BC’ = 1 m, A’ 故
墙上, 使梯脚C 离墙脚B 的距离为1.5 m, 准备
在墙上安装电灯. 当他爬上梯子后,
发现高度不够,于是将梯脚往墙
脚移近0.5 m, 即移动到C′处. 那么, 梯子顶端是否往上移动0.5 m 呢?
图1-16
分析
由图1-16 抽象出示意图1-17. 在Rt△ABC 中,
计算出AB; 再在Rt△A’BC’中, 计算出A’B, 则可
B
D
C
例2
如图,Rt△ABC中,∠C=90°,AD平分∠CAB,
DE⊥AB于E,若AC=6,BC=8,CD=3. (1)求DE的长; (2)求△ADB的面积. A E
解(1) ∵AD平分∠CAB,
DE⊥AB,∠C=90°, C ∴CD=DE=3.
D
八年级数学下册第1章直角三角形1.2直角三角形的性质和判定Ⅱ第2课时教学课件湘教版
一个门框尺寸如图所示.
①若有一块长3米,宽0.8米的薄木板,问怎样从门框通过? ②若薄木板长3米,宽1.5米呢? ③若薄木板长3米,宽2.2米呢?为什么?
∵木板的宽2.2米大于1米,
∴ 横着不能从门框C通过;
∵木板的宽2.2米大于2米,
∴竖着也不能从门框通2过m.
∴ 只能试试斜着能否通过,
对 要角 求线 出AACC的 的A长 长1最 ,m大 怎, 样B因 求此呢需?
3.如图,要在高3m,斜坡5m的楼梯表面铺
B
地毯,地毯的长度至少需____7____米
C
A
4.在一棵树的10米高处有两只猴子,一只猴子爬下树走到离 树20米处的池塘的A处.另一只爬到树顶D后直接跃到A处, 距离以直线计算,如果两只猴子所经过的距离相等,则这棵 树高____1_5______米.
5.在Rt△ABC中, ∠C=90°, ∠A ,∠ B, ∠C 的对边分别为 a,b,c. (1) 已知: a=5, b=12, 求c. c=12. (2) 已知: b=6,•c=10 , 求a. a=8. (3) 已知: a=7, c=25, 求b. b=24. (4) 已知: a=7, c=8, 求b . b= 15.
A
解:在Rt△ABC中, ∵∠ACB=90°,
D
∴ AC2+ BC2=AB2, 2.42+ BC2=2.52,
∴BC=0.7m. 由题意得:DE=AB=2.5m,
C
BE
DC=AC-AD=2.4-0.4=2m.
在Rt△DCE中,∵∠DCE=90°, ∴ DC2+ CE2=DE2 ,22+ CE2=2.52, ∴CE=1.5m, ∴BE=1.5-0.7=0.8m≠0.4m.
直角三角形(第2课时)-2022-2023学年八年级数学下册教材配套教学课件(北师大版)

∠C′=90 °,B′C′=BC,A ′B ′=AB,把画好的Rt△A′B′ C′ 剪下来,放到
Rt△ABC上,它们能重合吗?
A
B
C
操作:已知一条直角边和斜边,作一个直角三角形
已知:线段a,c,直角α 求作:Rt△ABC,使∠C=∠α ,BC=a,AB=c
作图步骤
N
A
B
C
M
C′
(1)先画∠M C′ N=90°
已知:如图, 在△ABC和△A′B′C′中, ∠C=∠C′=90°, AC=A′C ′, AB=A′B′ 求证:△ABC≌△A′B′C′ .
证明:∵△ABC中,∠C=90°
∴BC2=AB2-AC2(勾股定理)
A
A′
同理,B′C′2=A′B′2-A′C′2 .
∵AB=A′B′,AC=A′C′, ∴BC=B′C′.
作图步骤
N
A
B
C
M
B′
C′
(2)在射线C′M上截取B′C′=BC
作图步骤
N
A
A′
B
C
M
B′
C′
(3)以点B′为圆心,AB为半径画弧,交射线C′N于A′
作图步骤
猜想:斜边和一条直角边对应相等的两个直角三角形全等
N
A
A′
B
C
M
B′
C′
(4)连接A′B′
思考:通过上面的探究,你能得出什么结论?
证明:斜边和一条直角边对应相等的两个直角三角形全本题
没有说明全等三角形的对应边和对应角,因此要分类讨论,以免漏解.
五、课堂小结
斜边、 直角边
内容
斜边和一条直角边对应相等的两个 直角三角形全等.
2022年青岛版九年级上《解直角三角形的应用2》精品课件

x
、
1
x
2
2a
2. 关于x的二次三项式x2 +4x+k是一个 完全平方式。求k的值。
课时小结
用公式法解一元二次方程的一般步骤:
1、把方程化成一般形式。
2、写出 a、b、c 的值,值的范围为实数 。
3、求出 b2 4ac 的值。
特别注意:若 b24ac0则方程无解
4、代入求根公式 : xb b2 4ac
5、写出方程的解:
解直角三角形的应用(2)
1.进一步掌握解直角三角形的方法。
2.能熟练地应用解直角三角形的知 识解决有关方位角的实际问题。
精讲点拨
例3 住宅的采光是建楼和购房时 人们所关心的问题之一。如图,住 宅小区南、北两栋楼房的高度均为。 已知当地冬至这天中午12时太阳光 线与地面所成的角是35°。
(1)要使这时南楼的影子恰好落在北楼的墙脚,两楼间的 距离元二次方程的一般步骤:
1、把方程化成一般形式。
2、写出 a、b、c 的值。
3、求出 b2 4ac 的值。
特别注意:若 b24ac0则方程无解
4、代入求根公式 : xb b2 4ac 2a
5、写出方程的解:
x
、
1
x
2
复习巩固 公式法解方程: (1)x2-7x-18=0
(2) 9x2+6x+1=0
(2)如果两栋楼房之间的距离为20m,那么这时南楼的影 子是否会影响北楼一楼的采光?
跟踪训练
如图,在海岸边有一港口O,已知小岛A在港口 O北偏东30°的方向,小岛B在小岛A正南方向, OA=60海里,OB=20 海里.计算: (1)小岛B在港口O的什么方向; (2)求两小岛A,B的距离.
2直角三角形的性质PPT课件(华师大版)

1 AB
2
证明:延长CD至点E,使DE= CD,连结AE、BE
∵CD是斜边AB上的中线,
∴AD = DB.又∵ DE = CD,
∴四边形ACBE是平行四边形.
又∵ ∠ ACB=90°,
∴四边形ACBE是矩形,
∴ CE = AB,
∴ CD =
1 CE =
2
1 2
AB.
归纳
直角三角形斜边上的中线等于斜边的一半, 是直角三角形的又一条性质,它表述了直角三角 形斜边上的中线与斜边之间的关系.
∵∠A=30°,
∴∠B=60°,
∴△CDB是等边三角形
∴BC=BD=
1 2
AB
1. 在直角三角形中,如果一个锐角等于30°,那么它所 对的直角边等于斜边的一半.本性质是用角的特殊 性来揭示直角三角形中直角边与斜边的数量关系 的.
2.拓展:直角三角形的性质的选用 (1) 在直角三角形中求角时,常用“直角三角形的两个锐
1 (黄冈)如图,在△ABC中,∠C=90°,
∠B=30°,边AB的垂直平分线DE交AB于点E,
交BC于点D,CD=3,则BC的长为( )
A.6 B.6 3 C.9
D.3 3
2 (眉山)如图,在Rt△ABC中,∠B=90°,∠A=30°,DE
垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD
解: ∵∠ACB=15°,∠ADB=30°,
∴∠CAD=∠ADB-∠ACB=30°-15°=15°,
∴∠ACB=∠CAD,∴AD=CD=13 m.
在△ADB中,
∵AB⊥DB,∠ADB=30°,
AB=1 AD=1 13=6.5m.
2
2
总结
在含30°角的直角三角形中求线段的长度,要注 意利用直角三角形中30°角所对的直角边等于斜边的 一半的性质.
1.2直角三角形(2)

1.2 直角三角形(2)
直角三角形全等的证明 HL
学习目标(1分钟)
1.掌握判定直角三角形全等的斜边、直角边 条件; 2.能用“HL”解决实际问题;
自学指导1(1分钟,自学5分钟)
看P18 —P20的内容:思考回答 1.两边及其中一边的对角对应相等的两个 三角形全等吗? 2.如果其中一边的所对的角是直角呢? 3.直角三角形全等判定的内容? 4. 如何证明?
B B′
C
A C′
A′
驶向胜利 的彼岸
自学指导2(1分钟)
看P21第3题内容:思考回答 1. 如何用三角尺作角平分线? 2. 添加条件为
?
同学们自学5分钟后竞赛抢答
体验:用三角尺作角平分线
如图:在已知∠AOB的两边OA,OB上分别取点M,N,使OM=ON;
再过点M作OA的垂线,
过点N作OB的垂线,两垂线交于点P,
△ABC≌△A′B′C′ (SSS)
证明: ∵∠C=∠C′=90° 分析:
B
B′
C
A C′
A′
直角三角形全等的判定定理三种语言
定理:斜边和一条直角边对应相等的两个直角三角形全等
(简称为:斜边,直角边或“HL”).
如图,在Rt△ABC和Rt△A′B′C′中, ∵AC=A′C ′, AB=A′B′(已知), ∴Rt△ABC≌Rt△A′B′C′(HL).
∴∠A=∠A'(全等三角形的对应角相等).
∠A=∠A' ,AC=A'C' ,∠ACB=∠A'C'B' ,
∴△ABC≌△A'B'C' (ASA) .
课堂小结, 畅谈收获:
1.“HL”定理 2. 用三角尺作已知角的平分线,并说明理由. 3.总结:直角三角形全等的判定方法.
直角三角形全等的证明 HL
学习目标(1分钟)
1.掌握判定直角三角形全等的斜边、直角边 条件; 2.能用“HL”解决实际问题;
自学指导1(1分钟,自学5分钟)
看P18 —P20的内容:思考回答 1.两边及其中一边的对角对应相等的两个 三角形全等吗? 2.如果其中一边的所对的角是直角呢? 3.直角三角形全等判定的内容? 4. 如何证明?
B B′
C
A C′
A′
驶向胜利 的彼岸
自学指导2(1分钟)
看P21第3题内容:思考回答 1. 如何用三角尺作角平分线? 2. 添加条件为
?
同学们自学5分钟后竞赛抢答
体验:用三角尺作角平分线
如图:在已知∠AOB的两边OA,OB上分别取点M,N,使OM=ON;
再过点M作OA的垂线,
过点N作OB的垂线,两垂线交于点P,
△ABC≌△A′B′C′ (SSS)
证明: ∵∠C=∠C′=90° 分析:
B
B′
C
A C′
A′
直角三角形全等的判定定理三种语言
定理:斜边和一条直角边对应相等的两个直角三角形全等
(简称为:斜边,直角边或“HL”).
如图,在Rt△ABC和Rt△A′B′C′中, ∵AC=A′C ′, AB=A′B′(已知), ∴Rt△ABC≌Rt△A′B′C′(HL).
∴∠A=∠A'(全等三角形的对应角相等).
∠A=∠A' ,AC=A'C' ,∠ACB=∠A'C'B' ,
∴△ABC≌△A'B'C' (ASA) .
课堂小结, 畅谈收获:
1.“HL”定理 2. 用三角尺作已知角的平分线,并说明理由. 3.总结:直角三角形全等的判定方法.
2.6直角三角形(2)(八上)PPT课件

A
A
FE
F
E
BDC B D
C
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
9
谢谢聆听
·学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
Learning Is To Achieve A Certain Goal And Work Hard, Is A Process To Overcome Various Difficulties For A Goal
知识回顾
1、在△ABC中,∠C=90°,∠A=35°, ∠B= 55° .
2、在Rt△ABC中,CD是斜边AB上的中线,若 CD=3厘米,则AB=_6_厘米
直角三角形的两个锐角互余。
直角三角形斜边上的中线等于斜边的一半。
说出“直角三角形的两个锐角互余” 的逆命题,是真命题还是假命题?
直角三角形的判定
1.有一个角是直角的三角形叫做直角三角形
∵∠C=90°
A
∴△ABC是直角三角形
B
C
ห้องสมุดไป่ตู้
2.有两个角互余的三角形是直角三角形。
∵∠A+∠B=90°
∴△ABC是直角三角形
练一练
1. 根据下列条件判断△ABC是不是直角三角形, 并说明理由
(1)∠B=50°,∠C=40°. (2) ∠B=∠C=45° (3)∠A,∠B,∠C的度数比为5:3:2.
练一练
2.如图,在△ABC中,D是AB上一点, 若∠1=∠B,∠A=∠2.
则△ABC是Rt△,请说明理由.
C
A
FE
F
E
BDC B D
C
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
9
谢谢聆听
·学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
Learning Is To Achieve A Certain Goal And Work Hard, Is A Process To Overcome Various Difficulties For A Goal
知识回顾
1、在△ABC中,∠C=90°,∠A=35°, ∠B= 55° .
2、在Rt△ABC中,CD是斜边AB上的中线,若 CD=3厘米,则AB=_6_厘米
直角三角形的两个锐角互余。
直角三角形斜边上的中线等于斜边的一半。
说出“直角三角形的两个锐角互余” 的逆命题,是真命题还是假命题?
直角三角形的判定
1.有一个角是直角的三角形叫做直角三角形
∵∠C=90°
A
∴△ABC是直角三角形
B
C
ห้องสมุดไป่ตู้
2.有两个角互余的三角形是直角三角形。
∵∠A+∠B=90°
∴△ABC是直角三角形
练一练
1. 根据下列条件判断△ABC是不是直角三角形, 并说明理由
(1)∠B=50°,∠C=40°. (2) ∠B=∠C=45° (3)∠A,∠B,∠C的度数比为5:3:2.
练一练
2.如图,在△ABC中,D是AB上一点, 若∠1=∠B,∠A=∠2.
则△ABC是Rt△,请说明理由.
C
2 直角三角形(第2课时)

• 1、书籍是朋友,虽然没有热情,但是非常忠实。2022年3月3日星期四下午2时38分2秒14:38:0222.3.3 • 2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,
给那些善于独立思考的人,给那些具有锲而不舍的人。2022年3月下午2时38分22.3.314:38March 3, 2022 • 3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022年3月3日星期四2时38分2秒14:38:023 March 2022 • 4、享受阅读快乐,提高生活质量。下午2时38分2秒下午2时38分14:38:0222.3.3
检测反馈
1.下列条件中能判定两个直角三角形全等的有 ( B )
①有两条直角边对应相等;②有两个锐角对应相等;③有斜边和 一条直角边对应相等;④有一条直角边和一个锐角对应相等;⑤有
斜边和一个锐角对应相等;⑥有两条边相等.
A.6个 B.5个 C.4个 D.3个
2.如图所示,已知AB=AD,那么添加下列一个条
八年级数学·下 新课标[北师]
第一章 三角形的证明
学习新知
检测反馈
问题思考
学习新知
1.判定两个三角形全等的方法有哪些?
2.已知一条直角边和斜边,求作一个直角 三角形.想一想,怎么画?同学们相互交流.
3.有两条边及其中一条边的对角对应相
等的两个三角形全等吗?如果其中一个角
是直角呢?请证明你的结论.
求作直角三角形
件后,仍无法判定△ABC≌△ADC的是 ( C )
A.CB=CD
B.∠BAC=∠DAC
C.∠BCA=∠DCA
D.∠B=∠D =90°
2(PPT)5-1.5.2直角三角形(二)
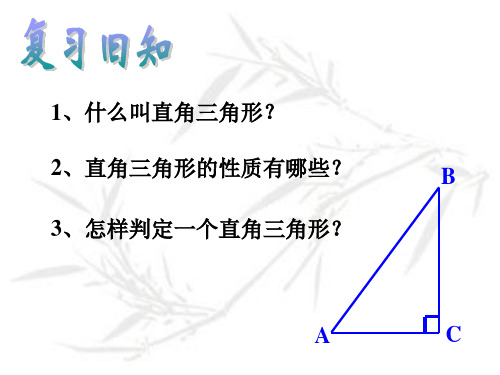
1、什么叫直角三角形?
2、直角三角形的性质有哪些?
B
3、怎样判定一个直角三角形?
A
C
联合行动。 【帮】(幫)动①帮助:大孩子能~妈妈干活儿了。②指从事雇佣劳动:~短工。 【帮】(幫)(~儿)名①物体(里面一般是空的)两旁或周
围的部分:桶~|鞋~儿|船~|床~。②帮子?:菜~儿。 【帮】(幫)①群;伙;集团(多指为政治的或经济的目的而结成的):搭~|马~|匪~。 ②量用于人,是“群、伙”的意思:一~小朋;餐饮加盟: ; 友|一~强盗。③帮会:青~|洪~。 【帮办】①动指帮 助主管人员办公务:~商务。②名指主管人员的助手。 【帮补】动在经济上帮助:我上大学时,哥哥经常寄钱~我。 【帮衬】〈方〉动①帮助;帮忙:每逢 集日,老头儿总~着儿子照料菜摊子。②帮补;资助。 【帮厨】∥动非炊事人员下厨房帮助炊事员工作:几位同学在学校食堂帮了一天厨。 【帮凑】动凑集 财物,帮助人解决困难:大家给他~了点儿路费,送他回家。 【帮带】动帮助,带动:示范村与其他村开展~活动。 【帮倒忙】因帮忙不得法,反而给人添 麻烦。 【帮扶】动帮助扶持:~下岗人员创业。 【帮工】①(-∥-)动帮助干活儿,多指受雇帮人干活:他出外~去了|大忙季节,请人帮了几天工。② 名帮工的人:麦收时,他家雇了两个~。 【帮会】名旧社会民间秘密组织(如青帮、洪帮、哥老会等)的总称。 【帮教】动帮助和教育:对失足青少年要做 好~工作。 【帮困】动帮助有困难的人或家庭:扶贫~。 【帮忙】∥(~儿)动帮助别人做事,泛指在别人有困难的时候给予帮助:你搬家时我来~|这件 事我实在帮不上忙。 【帮派】名为共同的私利而结成的小集团:~活动|拉山头,搞~。 【帮腔】∥动①某些戏曲中的一种演唱形式,台上一人主唱,多人 在台后和着唱。②比喻支持别人,帮他说话:他看见没有人~,也就不再坚持了。 【帮手】?名帮助工作的人:找个~。 【帮套】名①在车辕外面的拉车的 套:加上一头牲口拉~。②指在车辕外面拉车的牲口:一匹马拉不动,再加上个~。 【帮贴】〈方〉动从经济上帮助;贴补:过去,我拖家带口,他常~我。
2、直角三角形的性质有哪些?
B
3、怎样判定一个直角三角形?
A
C
联合行动。 【帮】(幫)动①帮助:大孩子能~妈妈干活儿了。②指从事雇佣劳动:~短工。 【帮】(幫)(~儿)名①物体(里面一般是空的)两旁或周
围的部分:桶~|鞋~儿|船~|床~。②帮子?:菜~儿。 【帮】(幫)①群;伙;集团(多指为政治的或经济的目的而结成的):搭~|马~|匪~。 ②量用于人,是“群、伙”的意思:一~小朋;餐饮加盟: ; 友|一~强盗。③帮会:青~|洪~。 【帮办】①动指帮 助主管人员办公务:~商务。②名指主管人员的助手。 【帮补】动在经济上帮助:我上大学时,哥哥经常寄钱~我。 【帮衬】〈方〉动①帮助;帮忙:每逢 集日,老头儿总~着儿子照料菜摊子。②帮补;资助。 【帮厨】∥动非炊事人员下厨房帮助炊事员工作:几位同学在学校食堂帮了一天厨。 【帮凑】动凑集 财物,帮助人解决困难:大家给他~了点儿路费,送他回家。 【帮带】动帮助,带动:示范村与其他村开展~活动。 【帮倒忙】因帮忙不得法,反而给人添 麻烦。 【帮扶】动帮助扶持:~下岗人员创业。 【帮工】①(-∥-)动帮助干活儿,多指受雇帮人干活:他出外~去了|大忙季节,请人帮了几天工。② 名帮工的人:麦收时,他家雇了两个~。 【帮会】名旧社会民间秘密组织(如青帮、洪帮、哥老会等)的总称。 【帮教】动帮助和教育:对失足青少年要做 好~工作。 【帮困】动帮助有困难的人或家庭:扶贫~。 【帮忙】∥(~儿)动帮助别人做事,泛指在别人有困难的时候给予帮助:你搬家时我来~|这件 事我实在帮不上忙。 【帮派】名为共同的私利而结成的小集团:~活动|拉山头,搞~。 【帮腔】∥动①某些戏曲中的一种演唱形式,台上一人主唱,多人 在台后和着唱。②比喻支持别人,帮他说话:他看见没有人~,也就不再坚持了。 【帮手】?名帮助工作的人:找个~。 【帮套】名①在车辕外面的拉车的 套:加上一头牲口拉~。②指在车辕外面拉车的牲口:一匹马拉不动,再加上个~。 【帮贴】〈方〉动从经济上帮助;贴补:过去,我拖家带口,他常~我。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B
C
2020/12/10
12
直角三角形的性质:
在直角三角形中,如果一条直角边是斜边的一半,
那么这条直角边所对的角等于300.
A
1 已知Rt △ ABC中,∠ACB=Rt∠, BC= 2 AB ,
求证 ∠BAC=300
几何语言:
1
∵在Rt △ABC中, BC= 2 AB(
∴ ∠A=30°(
)
)B
C
2020/12/10
2.6 直角三角形(二)
2020/12/10
1
知识回顾
直角三角形的两个锐角互余 直角三角形斜边上的中线等于斜边的一半。
2020/12/10
2
补充:直角三角形的性质:
在直角三角形中,300角所对的直角边等于斜边 的一半.
A
30 0
几何语言:
∵∠C=90°,∠A=30°(已知)
∴BC=
1B
AB (在直角三角形中,300角所对的
2020/12/10
10
补充的定理
已知Rt △ ABC中,∠ACB=Rt∠,
1
∠BAC=300,求证:BC= AB.
2
A
A
30 0
B
C
D
B
C
D
2020/12/10
11
直角三角形的性质:
在直角三角形中,300角所对的直角边等于斜边 的一半.
A
30 0
几何语言:
∵∠C=90°,∠A=30°
∴BC= 1 AB 2
5
练一练
1. 根据下列条件判断△ABC是不是直角三角 形,并说明理由
(1)∠B=50°,∠C=40°. (2) ∠B=∠C=45° (3)∠A,∠B,∠C的度数比为5:3:2.
2020/12/10
6
练一练
2.如图,在△ABC中,D是AB上一点, 若∠1=∠B,∠A=∠2.
则△ABC是Rt△,请说明理由.
∴ △ABC 是Rt△ABC(如果一个三角形一边上的中线
等于这边的一半,那么这个三角形是直角三角形. )
2020/12/10
8
书本72页,第3,4,5题
2020/12/10
9
直角三角形的判定
1.有一个角是直角的三角形叫做直角三角形
2.有两个角互余的三角形是直角三角形
3、如果一个三角形一边上的中线等于这条 边的一半,那么这个三角形是直角三角形.
C
2 直角边等于斜边的一半.)
2020/12/10
3
补充的定理
A
A
30 0
B
C
D
B
C
D
2020/12/10
4
直角三角形的判定
1.有一个角是直角的三角形叫做直角三角形
∵∠C=90°
A
∴△ABC是直角三角形
B
C
2.有两个角互余的三角形是直角三角形
∵∠A+∠B=90°
∴△ABC是直角三角形
2020/12/10
13
试一试1
根据图中的条件,求出三角形的各角、边。
5 ①
10
5
5
②
③
2020/12/10
14
PPT教学课件
谢谢观看
Thank You For Watching
15
C
12
A
2020/12/10
DBຫໍສະໝຸດ 7如如果果三三角角形形一一边边上上的的中中线线等等于于这这边边的的一一半半,,那那 么么这这个个三三角角形形是是直直角角三三角角形形.吗?
已知:如图△ ABC中,CD是AB的
C
中线,且CD=1/2AB,
求证:△ ABC是直角三角形
几何语言:
A
D
B
∵CD是AB的中线,CD = 1/2AB(已知)
