截长补短专题
专题训练 三角形全等——截长补短

专题训练 三角形全等——截长补短一、单选题1.如图,△ABC 中,∠B =2∠A ,∠ACB 的平分线CD 交AB 于点D ,已知AC =16,BC =9,则BD 的长为( )A .6B .7C .8D .92.如图,在ABC 中,AD 平分BAC ∠,2B ADB ∠=∠,5AB =,6CD =,则AC 的长为( )A .3B .9C .11D .153.如图,在Rt ABC 中,90ACB ∠=︒,3AC =,4BC =,AD 平分CAB ∠交BC 于D 点,E ,F 分别是AD ,AC 上的动点,则CE EF +的最小值为( )A .152B .152C .3D .1254.如图,在ABC ∆中,68BAC ∠=︒,36C ∠=︒,AD 平分BAC ∠,M 、N 分别是AD 、AB 上的动点,当BM MN +最小时,BMN ∠的度数为( )A .34︒B .68︒C .76︒D .90︒5.如图,已知四边形ABCD 中,AD ∥BC ,若∠DAB 的平分线AE 交CD 于E ,连接BE ,且BE 恰好平分∠ABC ,则AB 的长与AD+BC 的大小关系是( )A .AB >AD+BCB .AB <AD+BC C .AB =AD+BCD .无法确定二、填空题 6.如图,△ABC 中,E 在BC 上,D 在BA 上,过E 作EF ⊥AB 于F ,∠B =∠1+∠2,AB =CD ,BF =43,则AD 的长为________.7.如图,ABC 是等边三角形,180BAD BCD ∠+∠=︒,8BD =,2CD =,则AD =________.8.如图,ABC 与ADC 有一条公共边AC ,且AB=AD ,∠ACB=∠ACD=x ,则∠BAD=________.(用含有x 的代数式表示)9.如图,2A C ,BD 平分ABC ∠,10BC =,6AB =,则AD =_____.10.如图,四边形ABCD 中,∠BAD =120°,∠B =∠D =90°,在BC 、CD 上分别找一点M 、N ,使△AMN 周长最小时,则∠AMN +∠ANM 的度数是________.11.如图,在△ABC 中,∠ACB=∠ABC=40o ,BD 是∠ABC 的角平分线,延长BD 至点E ,使得DE=DA ,则∠ECA=________.12.如图,△ABC 中,AB=AC ,D 、E 分别在CA 、BA 的延长线上,连接BD 、CE ,且∠D+∠E=180°,若BD=6,则CE 的长为__.13.(1)如图(1),在四边形ABCD 中,AB AD =,180B D ︒∠+∠=,E ,F 分别是,BC CD 上的动点,且12EAF BAD ∠=∠,求证:EF BE DF =+. (2)如图(2),在(1)的条件下,当点E ,F 分别运动到,BC CD 的延长线上时,,,EF BE DF 之间的数量关系是______.14.如图,已知ABC 中,60A ∠=︒,D 为AB 上一点,且2,4AC AD BD B ACD =+∠=∠,则DCB ∠的度数是_________.15.如图,E 、F 分别是正方形ABCD 的边 CD 、BC 上的点,且10DE =cm ,45EAF ∠=︒,△EFC 的周长为80cm ,则EF =_________cm .16.如图,ABC 中,AD 平分BAC ∠,20C ∠=︒,AB BD AC +=,则B 的度数为_______.17.如图,在ABC 中,D 是BC 边中点,106AB AC ==,,4=AD ,则BC 的长是_____________.18.如图,四边形ABCD 为正方形,点E 在CB 的延长线上,AF 平分∠DAE 交DC 的延长线于点F ,若BE =8,CF =9,则CD 的长为______.三、解答题19.已知:如图所示,四边形ABCD 中,,AD BC O 是CD 上一点,且AO 平分,BAD BO∠平分ABC ∠,若3,4AO BO == ,求四边形ABCD 的面积.20.如图,△ABC 是等边三角形,△BDC 是顶角∠BDC=120°的等腰三角形,M 是AB 延长线上一点,N 是CA 延长线上一点,且∠MDN=60°.试探BM ,MN ,CN 之间的数量关系,并给出证明.21.如图,在△ABC 中,AB =AC ,∠BAC =30°,点D 是△ABC 内一点,DB =DC ,∠DCB =30°,点E 是BD 延长线上一点,AE =AB .(1)求∠ADB 的度数;(2)线段DE ,AD ,DC 之间有什么数量关系?请说明理由.22.如图,△ABC 为等边三角形,直线l 经过点C ,在l 上位于C 点右侧的点D 满足∠BDC =60°.(1)如图1,在l 上位于C 点左侧取一点E ,使∠AEC = 60°,求证:△AEC ≌△CDB ; (2)如图2,点F 、G 在直线l 上,连AF ,在l 上方作∠AFH =120°,且AF =HF ,∠HGF =120°,求证:HG +BD =CF ;(3)在(2)的条件下,当A 、B 位于直线l 两侧,其余条件不变时(如图3),线段HG 、CF 、BD 的数量关系为 .23.如图,//AD BC ,点E 在线段AB 上,DE 、CE 分别是ADC ∠、BCD ∠的角平分线,若3AD =,2BC =,求CD 的长.24.如图,在Rt ABC 中,90ACB ∠=︒,AC BC =,点P 是ABC 内部一点,且135APB BPC ∠=∠=︒,证明:2PA PC =.25.如图,在正方形ABCD 中,点F 是CD 的中点,点E 是BC 边上的一点,且AF 平分DAE ∠,求证:AE EC CD =+.26.已知等腰ABC ∆中,AB AC =,点D 在直线AB 上,//DE BC ,交直线AC 于点E ,且BD BC =,CH AB ⊥,垂足为H .(1)当点D 在线段AB 上时,如图1,求证BH DE DH +=;(2)当点D 在线段BA 的延长线上时,如图2;当点D 在线段AB 延长线时,如图3,线段BH ,DE ,DH 又有怎样的数量关系?请直接写出你的猜想,不需要证明. 27.数学课上,张老师出示了问题:如图1,四边形ABCD 是正方形,点E 是边BC 的中点.∠AEF=90°,且EF 交正方形外角∠DCG 的角平分线CF 于点F ,求证:AE=EF .经过思考,小明展示了一种正确的解题思路:取AB 的中点M ,连接ME ,则AM=EC ,易证△AME ≌△ECF ,所以AE=EF .在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E 是边BC 的中点”改为“点E 是边BC 上(除B ,C 外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(2)小华提出:如图3,点E 是BC 的延长线上(除C 点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.28.如图,在梯形ABCD 中,AD ∥BC ,AE 平分∠BAD ,BE 平分∠ABC ,且AE 、BE 交CD 于点E .试说明AD =AB ﹣BC 的理由.29.已知平行四边形ABCD 中,N 是边BC 上一点,延长DN 、AB 交于点Q ,过A 作AM ⊥DN 于点M ,连接AN ,则AD ⊥AN .(1)如图①,若tan ∠ADM =34,MN =3,求BC 的长; (2)如图②,过点B 作BH ∥DQ 交AN 于点H ,若AM =CN ,求证:DM =BH +NH .30.已知ABC 是等边三角形,6AB =.(1)如图1,点M 是BC 延长线上一点,60AMN ∠=︒,MN 交ABC 的外角平分线于点N ,求CN CM -的值;(2)如图2,过点A 作AD BC ⊥于点D ,点P 是直线AD 上一点,以CP 为边,在CP 的下方作等边CPQ ,连接DQ ,求DQ 的最小值.31.如图ABC 中,60,,ABC AD CE ︒∠=分别平分,BAC ACB AD CE ∠∠、、相交于点P .(1)求CPD ∠的度数;(2)求证:AE CD AC +=32.已知:如图,2AB AC =,BAD CAD ∠=∠,DA DB =,求证:90ACD ∠=︒.33.如图,在ABC ∆中,60ABC ∠=︒,AD 、CE 分别平分BAC ∠、ACB ∠,AD 、CE 交于点O ,求证:AE CD AC +=.参考答案1.B【分析】如图,在CA 上截取,CN CB = 连接,DN 证明,CBD CND ≌利用全等三角形的性质证明,BD ND = 求解9,7,CN AN == 再证明,DN AN = 从而可得答案. 解:如图,在CA 上截取,CN CB = 连接,DN CD 平分,ACB ∠,BCD NCD ∴∠=∠,CD CD =(),CBD CND SAS ∴≌,,,BD ND B CND CB CN ∴=∠=∠=9,16,BC AC ==9,7,CN AN AC CN ∴==-=,CND NDA A ∠=∠+∠,B NDA A ∴∠=∠+∠2,B A ∠=∠,A NDA ∴∠=∠,ND NA ∴=7.BD AN ∴==故选:.B【点拨】本题考查的是全等三角形的判定与性质,等腰三角形的判定,掌握以上知识是解题的关键.2.C【分析】在AC 上截取AE=AB ,连接DE ,证明△ABD ≌△AED ,得到∠B=∠AED ,AB=AE ,再证明CD=CE ,进而代入数值解答即可.【详解】在AC 上截取AE=AB ,连接DE ,∵AD 平分∠BAC ,∴∠BAD=∠DAC ,在△ABD 和△AED 中,BAD DA AE AB AD AD C =⎧=∠=∠⎪⎨⎪⎩,∴△ABD ≌△AED (SAS ),∴∠B=∠AED ,∠ADB =∠ADE , AB=AE ,又∠B=2∠ADB∴∠AED=2∠ADB ,∠BDE=2∠ADB ,∵∠AED=∠C+∠EDC=2∠ADB ,∠BDE=∠C+∠DEC=2∠ADB ,∴∠DEC =∠EDC ,∴CD=CE ,∵5AB =,6CD =,∴AC =AE+CE=AB+CD = 5+6=11.故选:C .【点拨】本题考查全等三角形的判定和性质;利用了全等三角形中常用辅助线-截长补短法构造全等三角形,然后利用全等三角形解题,这是解决线段和差问题最常用的方法,注意掌握.3.D【分析】利用角平分线构造全等,使两线段可以合二为一,则EC+EF 的最小值即为点C 到AB的垂线段长度.【详解】在AB上取一点G,使AG=AF∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4∴AB=5,∵∠CAD=∠BAD,AE=AE,∴△AEF≌△AEG(SAS)∴FE=GE,∴要求CE+EF的最小值即为求CE+EG的最小值,故当C、E、G三点共线时,符合要求,此时,作CH⊥AB于H点,则CH的长即为CE+EG的最小值,此时,AC BC AB CH,∴CH=·AC ABBC=125,即:CE+EF的最小值为125,故选:D.【点拨】本题考查了角平分线构造全等以及线段和差极值问题,灵活构造辅助线是解题关键.4.B【分析】在AC上截取AE=AN,先证明△AME≌△AMN(SAS),推出ME=MN.当B、M、E共线,BE⊥AC时,BM+ME最小,可求出∠NME的度数,从而求出∠BMN的度数.【详解】如图,在AC上截取AE=AN,∵∠BAC 的平分线交BC 于点D ,∴∠EAM=∠NAM ,在△AME 与△AMN 中,AE AN EAM NAM AM AM ⎧⎪∠∠⎨⎪⎩===,∴△AME ≌△AMN (SAS ),∴ME=MN .∴BM+MN=BM+ME ,当B 、M 、E 共线,BE ⊥AC 时,BM+ME 最小,∴MN ⊥AB∵∠BAC=68°∴∠NME=360°-∠BAC-∠MEA-∠MNA=360°-68°-90°-90°=112°,∴∠BMN=180°-112°=68°.故选:B .【点拨】本题考查了轴对称-最短问题,解题的关键是能够通过构造全等三角形,把BM+MN 进行转化,利用垂线段最短解决问题.5.C【分析】在AB 上截取AF =AD ,连接EF ,易得∠AEB=90°和△ADE ≌△AFE ,再证明△BCE ≌△BFE ,利用全等三角形对应边相等即可得出三条线段之间的关系.【详解】解:如图所示,在AB 上截取AF =AD ,连接EF ,∵AD ∥BC ,∴∠ABC+∠DAB=180°,又∵BE 平分∠ABC ,AE 平分∠DAB∴∠ABE+∠EAB=()1ABC DAB 2∠+∠=90°, ∴∠AEB=90°即∠2+∠4=90°,在△ADE 和△AFE 中,AD=AF DAE=FAE AE=AE ⎧⎪∠∠⎨⎪⎩∴△ADE ≌△AFE (SAS ),所以∠1=∠2,又∠2+∠4=90°,∠1+∠3=90°,所以∠3=∠4,在△BCE 和△BFE 中,CBE=FBE BE=BE3=4∠∠⎧⎪⎨⎪∠∠⎩∴△BCE ≌△BFE (ASA ),所以BC =BF ,所以AB =AF+BF =AD+BC ;故选:C .【点拨】本题考查全等三角形的判定和性质,截长补短是证明线段和差关系的常用方法. 6.83【分析】在FA 上取一点T ,使得FT=BF ,连接ET ,在CB 上取一点K ,使得CK=ET ,连接DK .想办法证明AT=DK ,DK=BD ,推出BD=AT ,推出BT=AD 即可解决问题.【详解】在F A 上取一点T ,使得FT =BF ,连接ET ,在CB 上取一点K ,使得CK =ET ,连接DK . ∵EB =ET ,∴∠B =∠ETB ,∵∠ETB =∠1+∠AET ,∠B =∠1+∠2,∴∠AET =∠2,∵AE =CD ,ET =CK ,∴△AET ≌△DCK (SAS ),∴DK =AT ,∠ATE =∠DKC ,∴∠ETB =∠DKB ,∴∠B =∠DKB ,∴DB =DK ,∴BD =AT ,∴AD =BT ,∵BT =2BF =83, ∴AD =83, 故答案为:83.【点拨】本题考查全等三角形的判定和性质,等腰三角形的判定和性质等知识点,解题关键在于学会添加常用辅助线,构造出全等三角形.7.6【分析】在线段BD 上取一点E ,使得BE=CD ,连接AE ,由,,,A B C D 四点共圆得∠ABE ACD =∠,再证明ABE ACD ≅∆,△ADE 是等边三角形,得AD DE AE ==,再由线段的和差关系可得结论.解:在线段BD 上取一点E ,使得BE=CD ,连接AE ,∵180BAD BCD ∠+∠=︒∴,,,A B C D 四点共圆,∴∠ABD ACD =∠∴∠ABE ACD =∠∵△ABC 是等边三角形,∴AB AC BC ==,60DAE ∠=︒,∴△ABE ACD ≅∆,∠60BAE CAF +∠=︒,∴,BAE CAD BAF CAD ∠=∠∠=∠,∴∠60CAD CAE +∠=︒,即60DAE ∠=︒,∴△ADE 是等边三角形,∴AD DE AE ==,∵=8BD ,2CD =,∴6DE BD BE BD CD =-=-=,∴6AD DE ==.【点拨】此题主要考查了全等三角形的判定与性质,以及四点共圆的判定,证明∠ABE ACD =∠是解答此题的关键.8.180°-2x【分析】在CD 上截取CE=CB ,证明△ABC ≌△AEC 得AE=AB ,∠B=∠AEC,可进一步证明∠D+∠B=180°,再根据四边形内角和定理可得结论. 解:在CD 上截取CE=CB ,如图所示,在△ABC 和△AEC 中,CE CB ACE ACB AC AC =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△AEC(SAS)∴AE=AB ,∠B=∠AEC,∵AB=AD ,∴AD=AE ,∴∠D=∠AED ,∵∠AED+∠AEC=180°,∴∠D+∠B=180°,∵∠DAB+∠ABC+∠BCD+∠CDA=360°∴∠DAB+∠BCD =360°-∠ABC-∠CDA=360°-180°=180°,∵∠BCD =∠ACB +∠ACD =x+x=2x∴∠DAB=180°-∠BCD=180°-2x故答案为:180°-2x 【点拨】本题考查了全等三角形的判定与性质,等腰三角形的性质以及四边形的内角和等知识,作辅助线构造全等三角形是解答此题的难点.9.4【分析】在BC 上截取BE =AB ,利用“边角边”证明△ABD ≌△EBD ,根据全等三角形对应边相等可得DE =AD ,由全等三角形对应角相等可得∠BED =∠A ,然后求出∠C =∠CDE ,根据等角对等边可得CE =DE ,等量代换得到EC =AD ,则BC =BE +EC =AB +AD 即可求出AD 长.解:(1)在BC 上截取BE =BA ,如图,∵BD 平分∠ABC ,∴∠ABD =∠EBD ,在△ABD 和△BED 中,BE BA ABD EBD BD BD =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△EBD (SAS ),∴DE =AD ,∠BED =∠A ,∴∠BED =∠C +∠EDC =2∠C ,∴∠EDC =∠C ,∴ED =EC ,∴EC =AD ,∴BC =BE +EC =AB +AD ,∵BC =10,AB =6,∴AD =10﹣6=4;故答案为:4.【点拨】本题考查了全等三角形的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,等角对等边的性质,作辅助线构造出全等三角形和等腰三角形是解题的关键.10.120°【分析】延长AB ,使得AB=BE ,延长AD ,使得AD=DF ,连接EF ,与BC ,DC 相较于M ,N ,要使得△AMN 的周长最小,则三角形的三边要共线,根据∠BAD=120°和△AMN 的内角和是180°即可列出方程求解.解:延长AB ,使得AB=BE ,延长AD ,使得AD=DF ,连接EF ,与BC ,DC 相较于M ,N 如图所示,此时△AMN 的周长最小∵∠ABM=90°∴∠EBM=90°在△AMB 和△EMB 中AB BE ABM EBM MB MB =⎧⎪∠=∠⎨⎪=⎩∴△AMB ≌△EMB∴∠BEM=∠BAM同理可得:△AND ≌△FDN∴∠NAD=∠NFD∴∠ANM=2∠NAD设∠BAM=x ,∠MAN=z ,∠NAD=y∵∠BAD=120°∴12022180x y z x y z ++=︒⎧⎨++=︒⎩ 解得:60x y +=︒即∠AMN+∠ANM=2×60°=120°.故答案为:120°.【点拨】本题主要考查的是三角形周长最小的条件,涉及到的知识点为全等三角形的判定及性质、三角形内角和的应用,正确添加合适的辅助线是解题的关键.11.40°【分析】在BC 上截取BF=AB ,连接DF ,由题意易得∠A=100°,∠ABD=∠DBC=20°,易得△ABD ≌△FBD ,进而可得DF=AD=DE ,由此可证△DEC ≌△DFC ,然后根据全等三角形的性质、三角形内角和及外角的性质可求解.解:在BC 上截取BF=AB ,连接DF ,∠ACB=∠ABC=40°,BD 是∠ABC 的角平分线,∴∠A=100°,∠ABD=∠DBC=20°,∴∠ADB=60°,∠BDC=120°,BD=BD ,∴△ABD ≌△FBD ,DE=DA ,∴ DF=AD=DE ,∠BDF=∠FDC=∠EDC=60°,∠A=∠DFB=100°,DC=DC ,∴△DEC ≌△DFC ,∴1006040DCB DCE DFC FDC ∠=∠=∠-∠=︒-︒=︒;故答案为40°.【点拨】本题主要考查全等三角形的判定与性质、三角形内角和及外角的性质,熟练掌握三角形全等的判定条件及外角性质是解题的关键.12.6【分析】在AD 上截取AF=AE ,连接BF ,易得△ABF ≌△ACE ,根据全等三角形的性质可得∠BFA=∠E ,CE=BF ,则有∠D=∠DFB ,然后根据等腰三角形的性质可求解.【详解】解:在AD 上截取AF=AE ,连接BF ,如图所示:AB=AC ,∠FAB=∠EAC ,∴ABF ACE ≌△△,∴BF=EC ,∠BFA=∠E ,∠D+∠E=180°,∠BFA+∠DFB=180°,∴∠DFB=∠D ,∴BF=BD ,BD=6,∴CE=6.故答案为6.【点拨】本题主要考查全等三角形的性质与判定及等腰三角形的性质与判定,熟练掌握全等三角形的判定方法及等腰三角形的性质与判定是解题的关键.13.(1)详见解析;(2)EF BE DF =-【分析】(1)延长FD 到点G ,使DG BE =,连接AG ,先证明( )ABE ADG SAS ∆∆≌,得到AE AG BAE DAG =∠=∠,,然后证明AEF AGF ∆∆≌,得到EF FG =,根据FG DG DF BE DF =+=+,可得EF BE DF =+;(2)在BC 上截取BG DF =,连接AG ,先证明△ABG ≌△ADF (SAS ),得到AG=AF ,∠BAG=∠DAF ,再证明△EAG ≌△EAF (SAS ),得到EG=EF ,根据BG=DF ,即可得EF=BE-BG=BE-DF .【详解】(1)如图,延长FD 到点G ,使DG BE =,连接AG .180B ADF ADG ADF ︒∠+∠=∠+∠=,B ADG ∴∠=∠,又AB AD =,BE DG =,∴( )ABE ADG SAS ∆∆≌,,AE AG BAE DAG ∴=∠=∠,12EAF BAD ∠=∠,GAF DAG DAF BAE DAF BAD EAF EAF ∴∠=∠+∠=∠+∠=∠-∠=∠.,,AE AG EAF GAF AF AF =∠=∠=,∴AEF AGF ∆∆≌,EF FG ∴=.FG DG DF BE DF =+=+,EF BE DF ∴=+;(2)EF BE DF =-.如图,在BC 上截取BG DF =,连接AG ,180B ADC ADC ADF ︒∠+∠=∠+∠=,B ADF ∴∠=∠,在△ABG 和△ADF 中AB AD B ADF BG DF ⎧⎩=⎪==⎪⎨∠∠,∴△ABG ≌△ADF (SAS ),∴AG=AF ,∠BAG=∠DAF ,∠BAD=2∠EAF ,∴∠BAG+∠GAE+∠EAD=∠EAD+∠DAF+∠EAD+∠DAF ,∴∠GAE=∠EAF ,在△EAG 和△EAF 中AG AF EAG EAF AE AE ===⎧⎪⎨⎪⎩∠∠,∴△EAG ≌△EAF (SAS ),∴EG=EF ,∵BG=DF ,∴EF=BE-BG=BE-DF .【点拨】本题考查了全等三角形的判定和性质,掌握判定定理是解题关键.14.20°【分析】通过作辅助线构造直角三角形,利用等边三角形的性质,得到角相等,边相等,根据三角形全等,得到角相等,利用外角的性质列方程求解;解:如图,延长AB 至点E 使BE AD =,连接CE .∴2=++=+AE AD DB BE AD BD .∵2=+AC AD BD ,∴AE AC =.∵60A ∠=︒,∴AEC 是等边三角形,∴60∠=∠=︒E ACE .∵4∠=∠ABC ACD ,∴设ACD x ∠=,则4∠=ABC x .在ADC 与EBC 中,∵,,,AD BE A E AC EC =⎧⎪∠=∠⎨⎪=⎩∴()SAS ≌ADC EBC ,∴∠=∠=ACD ECB x .∵∠=∠+∠ABC E BCE ,∴460=︒+x x ,∴20x =︒,∴60202020∠=︒-︒-︒=︒BCD .【点拨】本题主要考查了等边三角形的判定与性质和全等三角形的判定与性质,准确分析是解题的关键.15.34【分析】延长CB 到H ,使BH=DE ,连接AH ,可证△ADE ≌△ABH ,可得AE=AH ,由∠EAF=45º可证得∠HAF=45º,进而可证得△HAF ≌△EAF ,可得EF=HF ,由△EFC 的周长可求得正方形的边长,设EF=x ,在Rt △ECF 中,利用勾股定理列方程即可求得EF 的长.【详解】如图延长CB 到H ,使BH=DE=10cm ,连接AH ,∵四边形ABCD 是正方形,∴∠D=∠ABH=∠DAB=90º,AB=AD=BC=CD ,∴△ADE ≌△ABH (SAS),∴AE=AH,∠DAE=∠BAH ,∵∠EAF=45º,∴∠DAE+∠BAF=45º,∴∠BAH+∠BAF=45º即∠HAF=45º,∴∠HAF=∠EAF 又AH=AE,AF=AF ,∴△HAF ≌△EAF(SAS),∴HF=EF ,∵△EFC 的周长为80cm ,∴CE+CF+EF=CE+CF+HF=CE+DE+CF+BF=BC+CD=2BC=80,∴BC=40cm,设EF=x ,则CF=40+10-x=50-x ,在Rt △ECF 中,CE=40-10=30cm ,由勾股定理得:222(50)30x x =-+,解得:x=34,即EF=34cm ,故答案为:34.【点拨】本题考查了正方形的性质、全等三角形的判定与性质、勾股定理,解答的关键是认真分析,找到相关信息的关联点,结合图形,进行推理、计算.16.40︒【分析】如图(见解析),在线段AC 上取点E ,使得AE AB =,先根据角平分线的定义得出BAD EAD ∠=∠,再根据三角形全等的判定定理与性质得出BD ED =,B AED ∠=∠,然后根据线段的和差、等量代换得出ED CE =,最后根据等腰三角形的性质、三角形的外角性质即可得.【详解】如图,在线段AC 上取点E ,使得AE AB = AD 平分BAC ∠BAD EAD在ABD △和AED 中,AB AE BAD EAD AD AD =⎧⎪∠=∠⎨⎪=⎩()ABD AED SAS ∴≅BD ED ∴=,B AED ∠=∠又AB BD AC AE CE +==+BD CE ∴=ED CE ∴=20CDE C ∴∠=∠=︒40AED CDE C ∴∠=∠+∠=︒40B AED ∴∠=∠=︒故答案为:40︒.【点拨】本题考查了三角形全等的判定定理与性质、等腰三角形的性质等知识点,通过作辅助线,构造全等三角形是解题关键.17.【分析】延长AD 至点E ,使得DE =AD =4,结合D 是中点证得△ADC ≌△EDB ,进而利用勾股定解:如图,延长AD 至点E ,使得DE =AD =4,连接BE ,∵D 是BC 边中点,∴BD =CD ,又∵DE =AD ,∠ADC =∠EDB ,∴△ADC ≌△EDB (SAS ),∴BE =AC =6,又∵AB =10,∴AE 2+BE 2=AB 2,∴∠E =90°,∴在Rt △BED 中,222264213BD BE DE =+=+=, ∴BC =2BD =故答案为:【点拨】本题考查了全等三角形的判定及性质、勾股定理及其逆定理,正确作出辅助线是解决本题的关键.18.632. 【分析】根据题意,在DC 上截取DG=BE ,连接AG ,可以证明△ADG ≌△ABE ,从而可以得到AG 和AE 的关系,∠DAF 和∠EAF 的关系,再根据题目中的条件和勾股定理即可得到CD 的长.解:在DC 上截取DG=BE ,连接AG ,如图所示.∵四边形ABCD 是正方形,∴AD=AB ,∠ADG=∠ABE ,在△ADG 和△ABE 中AD AB ADG ABE DG BE =⎧⎪∠=∠⎨⎪=⎩,∴△ADG ≌△ABE(SAS),∴AE=AG ,∠DAG=∠BAE .∵AF 平分∠DAE ,∴∠DAF=∠EAF ,∴∠GAF=∠BAF .∵AB ∥DC ,∴∠BAF=∠GFA ,∴∠GAF=∠GFA ,∴AG=GF ,设CD=a .∵BE=8,CF=9,∴DG=BE=8,GC=a ﹣8,∴GF=a ﹣8+9=a+1,∴AG=a+1.∵AD=a ,DG=8,AG=a+1,∠ADG=90°,∴a 2+82=(a+1)2,解得:a=632, 即CD=632. 故答案为:632. 【点拨】本题考查全等三角形的判定与性质、正方形的性质、角平分线的性质、勾股定理,解答本题的关键是明确题意,作出合适的辅助线,利用数形结合的思想解答.19.12.【分析】在AB 上截AE AD =,根据SAS 易证AOD AOE ∆∆≌,∠AOD=∠AOE ,根据平行线和角平分线的性质可得出∠AOB=90°,则90AOD BOC AOE BOE ∠+∠=∠+∠=︒ ,可得BOE BOC ∠=∠ ,继而证明△BOE ≌△BOC ,可得S 四ABCD =2S △AOB ,即可得出答案.解:在AB 上截AE AD =,∵AO 平分∠BAD ,∴∠DAO=∠EAO ,在△AOD 和△AOE 中,AD=AE DAO EAO AO AO ⎧⎪∠=∠⎨⎪=⎩∴AOD AOE ∆∆≌,AOD AOE ∴∠=∠,AD BC ∵∥,AO 平分BAD ∠,BO 平分ABC ∠,∴∠AOB=90°,90AOD BOC AOE BOE ∴∠+∠=∠+∠=︒BOE BOC ∴∠=∠,∵BO 平分∠ABC ,∴∠ABO=∠CBO ,在△BOC 和△BOE 中,CB B BO=BOO E O BOE BOC ∠=∠⎧⎪⎨⎪∠=∠⎩∴BOC BOE ∆∆≌,∴四边形ABCD 的面积2AOB =∆的面积=12342⨯⨯⨯ =12. 故答案为12.【点拨】本题考查角平分线的性质,平行线的性质,全等三角形的判定与性质,三角形面积的计算,由全等三角形的性质得出S 四ABCD =2S △AOB 是解题的关键.20.CN=MN+BM ,见解析【分析】采用“截长补短”法,在CN 上截取点E ,使CE=BM ,连接DE ,结合等边及等腰三角形的性质利用SAS 可证△MBD ≌△ECD ,继而可证△MND ≌△END ,由全等的性质可得结论.解:CN=MN+BM .证明:如图,在CN 上截取点E ,使CE=BM ,连接DE ,∵△ABC 为等边三角形,∴∠ACB=∠ABC=60°.又∵△BDC 为等腰三角形,且∠BDC=120°,∴BD=CD ,∠DBC=∠BCD=30°.∴∠ABD=∠ABC+∠DBC=∠ACB+∠BCD=∠ECD=90°.90MBD ABD ECD ︒∴∠=∠=∠=在△MBD 和△ECD 中,BD CD MBD ECD BM CE =⎧⎪∠=∠⎨⎪=⎩,,, ∴△MBD ≌△ECD (SAS ).∴MD=ED ,∠MDB=∠EDC .又∵∠MDN=60°,∠BDC=120°,∴∠EDN=∠BDC-(∠BDN+∠EDC )=∠BDC-(∠BDN+∠MDB )=∠BDC-∠MDN=120°-60°=60°.∴∠MDN=∠EDN .在△MND 与△END 中,ND ND MDN EDN MD ED =⎧⎪∠=∠⎨⎪=⎩,,, ∴△MND ≌△END (SAS ).∴MN=NE .∴CN=NE+CE=MN+BM .【点拨】本题考查了等边及等腰三角形的性质及全等三角形的判定和性质,并采用了截长补短法,灵活利用已知条件证明三角形全等是解题的关键.21.(1)120°;(2)DE =AD +CD ,理由见解析【分析】(1)根据三角形内角和定理得到∠ABC =∠ACB =75°,根据全等三角形的性质得到∠BAD =∠CAD =15°,根据三角形的外角性质计算,得到答案;(2)在线段DE 上截取DM =AD ,连接AM ,得到△ADM 是等边三角形,根据△ABD ≌△AEM ,得到BD =ME ,结合图形证明结论解:(1)∵AB=AC,∠BAC=30°,∴∠ABC=∠ACB=12(180°﹣30°)=75°,∵DB=DC,∠DCB=30°,∴∠DBC=∠DCB=30°,∴∠ABD=∠ABC﹣∠DBC=45°,在△ABD和△ACD中,AB AC DB DC AD AD=⎧⎪=⎨⎪=⎩,∴△ABD≌△ACD(SSS),∴∠BAD=∠CAD=12∠BAC=15°,∴∠ADE=∠ABD+∠BAD=60°,∴∠ADB=180°﹣∠ADE=180°﹣60°=120°;(2)DE=AD+CD,理由如下:在线段DE上截取DM=AD,连接AM,∵∠ADE=60°,DM=AD,∴△ADM是等边三角形,∴∠ADB=∠AME=120°.∵AE=AB,∴∠ABD=∠E,在△ABD和△AEM中,ABD EADB AME AB AE∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABD≌△AEM(AAS),∴BD=ME,∵BD=CD,∴CD=ME.∵DE=DM+ME,∴DE=AD+CD.【点拨】本题考查的是全等三角形的判定和性质、等边三角形的判定和性质,掌握全等三角形的判定定理和性质定理是解题的关键.22.(1)证明见解析;(2)证明见解析;(3)HG=CF+BD.【分析】(1)先利用角的和差证明∠BCD=∠EAC,然后利用AAS即可证明△AEC≌△CDB;(2)在l上C点左侧取一点E,使∠AEC=60°,连接AE,依次证明△AEC≌△CDB和△HGF≌△FEA即可得出结论;(3)在l上位于C点右侧取一点E,使∠AED=60°,连接AE,在l上取一点M,使BM=BD,依次证明△ACE≌△CBM和△HGF≌△FEA即可得出结论.解:(1)证明:∵△ABC是等边三角形,∴AC=BC,∠ACB=60°,∴∠BCD+∠ACE=120°,∵∠AEC=60°,∴∠ACE+∠EAC=120°,∴∠BCD=∠EAC,在△AEC和△CDB中∵60 AEC BDCBCD EACAC BC∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∴△AEC≌△CDB(AAS);(2)证明:如图2,在l上C点左侧取一点E,使∠AEC=60°,连接AE,由(1)知:△AEC≌△CDB,∴BD=CE,∵∠AEC=60°,∴∠AEF =120°,∵∠AFH =120°,∴∠AFE+∠FAE=∠AFE+∠GFH=60°,∴∠FAE=∠GFH,∵∠HGF=∠AEF=120°,AF=FH,∴△HGF≌△FEA(AAS),∴GH=EF,∴CF=EF+CE=HG+BD;(3)解:HG=CF+BD,理由是:如图3,在l上位于C点右侧取一点E,使∠AED=60°,连接AE,在l上取一点M,使BM=BD,∵∠BDC=60°,∴△BDM是等边三角形,∴∠BMD=60°,∵∠AED=60°,∴∠AEC=∠CMB=120°,∵∠ACB=60°,∴∠ACE+∠BCE=∠ACE+∠CAE=60°,∴∠CAE=∠BCE,∵AC=BC,∴△ACE ≌△CBM (AAS ),∴CE=BM=BD ,由(2)可证△HGF ≌△FEA (AAS ),∴GH=FE ,∵EF=CF+CE∴HG=CF+BD .故答案为:HG=CF+BD .【点拨】本题考查等边三角形的性质和判定,全等三角形的性质和判断,三角形外角的性质等.掌握一线三等角的模型,能借助一线三等角证明对应角相等是解题关键.23.5【分析】如图,在DC 上截取DF DA =,连接EF ,先证明ADE FDE △≌△,得到AE EF =,5A ∠=∠,然后证明CEF CEB △≌△,得到CF BC =,即可求出答案.解:如图,在DC 上截取DF DA =,连接EF ,DE 是ADC ∠的角平分线,12∠∠∴=,在△ADE 和△FDE 中,,12,,AD DF DE DE =⎧⎪∠=∠⎨⎪=⎩()ADE FDE SAS ∴△≌△,AE EF ∴=,5A ∠=∠,//AD BC ,180A B ∴∠+∠=︒,56180∠+∠=︒,6B ∴∠=∠, CE 是BCD ∠的角平分线,34∴∠=∠,在CEF △和CEB △中,6,34,,B CE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩()CEF CEB AAS ∴△≌△,CF BC ∴=,325CD DF CF AD BC ∴=+=+=+=.【点拨】本题考查了角平分线的性质,平行线的性质,全等三角形的判定和性质,证明ADE FDE △≌△是解题关键.24.见解析【分析】在线段AP 上取点D ,使得AD CP =,连接CD ,通过证明()ADC CPB SAS △△≌可得135ADC CPB ∠=∠=︒,即45PDC ∠=︒,可推出=CP DP ,再根据PA AD DP =+,即可得证2PA PC =.证明:如图,在线段AP 上取点D ,使得AD CP =,连接CD ,135APB BPC ∠=∠=︒,90APC ∴∠=︒,45ABP PAB ∠+∠=︒,45CBP BCP ∠+∠=︒,在Rt ABC 中,90ACB ∠=︒,AC BC =,45CAB CBA ∴∠=∠=︒,45CAP PAB ∴∠+∠=︒,45ABP CBP ∠+∠=︒,CAD ABP BCP ∴∠=∠=∠,在ADC 和CPB △中,,,,AC CB CAD BCP AD CP =⎧⎪∠=∠⎨⎪=⎩()ADC CPB SAS ∴△△≌,135ADC CPB ∴∠=∠=︒,45∴∠=︒,PDC∴△是等腰直角三角形,CPD∴=,CP DP=+,PA AD DP∴=.2PA PC【点拨】本题考查了全等三角形的综合问题,掌握全等三角形的性质以及判定定理、等腰直角三角形的性质是解题的关键.25.见解析【分析】过F作FH⊥AE于H,得出FH=FD,然后证明△FHE≌△FCE,再通过等价转换可证得AE=EC+CD.【详解】证明:过F作FH⊥AE于H,如图,∵AF平分∠DAE,∠D=90°,FH⊥AE,∴∠DAF=∠EAF,FH=FD,又∵DF=FC=FH,FE为公共边,∴△FHE≌△FCE(HL).∴HE=CE.∵AE=AH+HE,AH=AD=CD,HE=CE,∴AE=EC+CD.【点拨】本题考查角平分线的性质,角平分线上的点到角的两边距离相等,也考查了等量代换的思想,属于比较典型的题目.26.(1)见解析;(2)图2:BH DE DH -=;图3:DE BH DH -=【分析】(1)在线段AH 上截取HM=BH ,连接CM ,CD ,证明△DMC ≌△DEC ,即可可得DE=DM 则结论可得;(2)当点D 在线段BA 延长线上时,在BA 的延长线上截取MH=BH ,连接CM ,DC ,由题意可证△BHC ≌△CHM ,可得∠B=∠CMB ,由题意可得∠B=∠AED ,即可证△DMC ≌△DEC ,可得DE=DM ,则可得DH=BH-DE ;当点D 在线段AB 延长线上时,在线段AB 上截取BH=HM ,连接CM ,CD ,由题意可证△BHC ≌△CHM ,可得∠B=∠CMB ,由题意可得∠B=∠AED ,即可证△DMC ≌△DEC ,可得DE=DM ,则可得DE=DH+BH .. 解:(1)证明:在AH 上截取HM BH =,连接CM ,CD .∵CH AB ⊥,HM BH =∴CM BC =.∴B CMB ∠=∠.∵AB AC =∴B ACB ∠=∠.∵//DE BC ,∴ADE B AED ACB ∠=∠=∠=∠,CDE BCD ∠=∠.∴AED BMC ∠=∠.∴DEC DMC ∠=∠.∵BD BC =,∴BDC BCD EDC ∠=∠=∠.∵CD CD =,∴ΔΔCDM CDE ≅.∴DM DE =.∴DE BH DM HM DH +=+=.(2)当点D 在线段BA 延长线上时,DH=BH-DE如图:在BA 的延长线上截取MH=BH ,连接CM ,DC∵AB=AC∴∠ABC=∠ACB ,∵BD=BC ,∴∠BDC=∠DCB∵DE ∥BC∠E=∠ACB=∠B=∠EDB∵CH=CH ,BH=MH ,∠BHC=∠CHM∴△BHC ≌△CHM∴∠B=∠M∴∠E=∠M∵∠MDC=∠B+∠DCB ,∠EDC=∠BDC+∠EDB∴∠MDC=∠EDC又∵∠E=∠M ,DC=CD∴△DEC ≌△DMC∴DE=DM∵DH=MH-DM∴DH=BH-DE当点D在线段AB延长线上时,DE=BH+DH如图在线段AB上截取BH=HM,连接CM,CD∵BH=HM,CH=CH,∠CHB=∠MHC=90°∴△MHC≌△BHC∴∠ABC=∠BMC∵AB=AC∴∠ABC=∠ACB,∵BD=BC∴∠BDC=∠BCD∵BC∥DE∴∠BCD=∠CDE,∠ACB=∠AED∴∠BDC=∠CDE,∠BMC=∠AED,且CD=CD∴△CDM≌△CDE∴DE=DM∵DM=DH+HM∴DE=DH+BH.【点拨】本题考查了三角形综合题,等腰三角形的性质,全等三角形的性质和判定.添加恰当的辅助线证全等是本题的关键.27.(1)正确.证明见解析;(2)正确.证明见解析.【分析】=,连接ME,根据已知条件利用ASA判定(1)在AB上取一点M,使AM EC=.AME ECF,因为全等三角形的对应边相等,所以AE EF(2)在BA 的延长线上取一点N ,使AN CE =,连接NE ,根据已知利用ASA 判定ANE ECF ,因为全等三角形的对应边相等,所以AE EF =.解:(1)正确.证明:在AB 上取一点M ,使AM EC =,连接ME .BM BE ∴=,45BME ∴∠=°,135AME , CF 是外角平分线,45DCF ∴∠=︒,135ECF ∴∠=°,AME ECF , 90AEB BAE ,90AEB CEF ∠+∠=︒,BAE CEF ∴∠=∠,()AME ECF ASA ,AE EF ∴=.(2)正确.证明:如图示,在BA 的延长线上取一点N ,使AN CE =,连接NE .∴=,BN BEN NEC,45∠,CF平分DCGFCE,45N ECF,四边形ABCD是正方形,AD BE∴,//DAE BEA,即9090DAE BEA,NAE CEF,ANE ECF ASA,()∴=.AE EF【点拨】此题主要考查了正方形的性质,角平分线的性质及全等三角形的判定方法,熟悉相关性质是解题的关键.28.见解析【分析】在AB上找到F使得AF=AD,易证△AEF≌△AED,可得AF=AD,∠AFE=∠D,根据平行线性质可证∠C=∠BFE,即可证明△BEC≌△BEF,可得BF=BC,即可解题.证明:在AB上找到F使得AF=AD,∵AE 平分∠BAD ,∴∠EAD =∠EAF ,∵在△AEF 和△AED 中,AD AF EAD EAF AE AE =⎧⎪∠=∠⎨⎪=⎩,∴△AEF ≌△AED ,(SAS )∴AF =AD ,∠AFE =∠D ,∵AD ∥BC ,∴∠D +∠C =180°,∵∠AFE +∠BFE =180°∴∠C =∠BFE ,∵BE 平分∠BAD ,∴∠FBE =∠C ,∵在△BEC 和△BEF 中,BFE C FBE CBE BE BE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BEC ≌△BEF ,(AAS )∴BF =BC ,∵AB =AF +BF ,∴AB =AD +BC ,即AD =AB ﹣BC .【点拨】本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△AEF ≌△AED 和△BEC ≌△BEF 是解题的关键.29.(1)BC=203;(2)见解析.【分析】(1)如图①中,设AM=3k,DM=4k,则AD=5k,由△ADM∽△NDA,可得AD2=DM•AN,由此构建方程即可解决问题.(2)如图②中,连接CH,在DM上取一点K,使得DK=BH.证明△ADK≌△CBH(SAS),推出AK=CH,再证明Rt△AMK≌Rt△CNH(HL),推出MK=HN即可解决问题.(1)解:如图①中,∵AM⊥DN,∴∠AMD=90°,∵tan∠ADM=AIIDN=34,∴可以假设AM=3k,DM=4k,则AD=5k,∵AD⊥AN,∴∠DAN=90°=∠AMD,∵∠ADM=∠ADN,∴△ADM∽△NDA,∴AD2=DM•AN,∴(5k)2=4k(4k+3),解得k=43,∴AD=203,∵四边形ABCD是平行四边形,∴BC=AD=203.(2)证明:如图②中,连接CH,在DM上取一点K,使得DK=BH.∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠ADK=∠BNQ,∵BH∥DQ,∴∠CBH=∠BNQ,∴∠ADK=∠CBH,∵DK=BH,DA=BC,∴△ADK≌△CBH(SAS),∴AK=CH,∵AM⊥DQ,AN⊥AD,AD∥BC,∴AN⊥BC,∴∠AMK=∠CNH=90°,∵AM=CN,∴Rt△AMK≌Rt△CNH(HL),∴MK=NH,∴DM=DK+MK=BH+HN.【点拨】本题考查了三角形的综合问题,掌握解直角三角形、相似三角形的性质以及判定定理、全等三角形的性质以及判定定理是解题的关键.30.(1)6;(2)3 2【分析】(1)在CN上截取点H,使CH=CM,先证出△CMH为等边三角形,然后利用ASA证出△AMC≌△NMH,从而得出AC=NH,从而求出结论;(2)连接BQ,利用SAS证出△QCB≌△PCA,从而得出∠CBQ=∠CAP,然后根据三线合一和等量代换即可求出∠CBQ=30°、∠ABQ =90°,从而判断出点Q的运动轨迹,然后根据垂线段最短即可得出当DQ⊥BQ时,DQ最短,然后利用30°所对的直角边是斜边的一半即可得出结论.解:(1)在CN 上截取点H ,使CH=CM ,连接MH∵△ABC 为等边三角形∴∠ACB=60°,AC=AB=6∴∠ACM=180°-∠ACB=120°∵CN 平分∠ACM∴∠MCN=12∠ACM=60° ∴△CMH 为等边三角形∴CM=HM ,∠CMH=∠CHM=60°∴∠NHM=180°-∠CHM=120°,∠AMC +∠AMH=60°∴∠ACM=∠NHM∵60AMN ∠=︒∴∠NMH +∠AMH=60°∴∠AMC=∠NMH在△AMC 和△NMH 中AMC NMH CM HMACM NHM ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△AMC ≌△NMH∴AC=NH∴CN CM -=CN -CH=NH=AC=6(2)连接BQ∵△ABC 和△CPQ 都是等边三角形∴BC=AC ,QC=PC ,∠PCQ =∠ACB=∠ABC=∠BAC =60°∴∠PCQ -∠PCB=∠ACB -∠PCB∴∠QCB=∠PCA在△QCB 和△PCA 中BC AC QCB PCA QC PC =⎧⎪∠=∠⎨⎪=⎩∴△QCB ≌△PCA∴∠CBQ=∠CAP∵AD BC ⊥∴∠CAP=12∠BAC=30°,BD=12BC=3 ∴∠CBQ=30°∴∠ABQ=∠ABC +∠CBQ=90°∴点Q 在过点B 作AB 的垂线上运动根据垂线段最短可得:当DQ ⊥BQ 时,DQ 最短此时在Rt △BDQ 中,∠QBD=30°∴DQ=12BD=32即DQ 的最小值为32. 【点拨】此题考查的是全等三角形的判定及性质、等边三角形的判定及性质、直角三角形的性质和垂线段最短的应用,掌握构造全等三角形的方法、全等三角形的判定及性质、等边三角形的判定及性质、30°所对的直角边是斜边的一半和垂线段最短是解决此题的关键. 31.(1)∠CPD=60°;(2)详见解析【分析】(1)根据三角形的内角和定理及角平分线的定义,三角形的外角性质即可求出;(2)在AC 上截取AF=AE ,先证明△APE ≌△APF (SAS ),再证明△CFP ≌△CDP (ASA ),根据全等三角形的性质证明AE CD AC +=即可.解:(1)∵∠ABC=60°,∴∠BAC+∠ACB=180°-60°=120°,又∵AD 、CE 分别平分∠∠、BAC ACB , ∴12CAD BAC ∠=∠,12ACE ACB ∠=∠ ∴111()60222CAD ACE BAC ACB BAC ACB ∠+∠=∠+∠=∠+∠=︒, 又∵∠CPD 是△ACP 的外角,∴∠CPD=∠CAD+∠ACE=60°,∴∠CPD=60°.(2)如图,在AC 上截取AF=AE ,连接PF ,∵∠CPD=60°,∴∠APC=120°,∠APE=60°∵AD 平分∠BAC ,CE 平分∠ACB ,∴∠BAD=∠CAD ,∠ACE=∠BCE在△APE 与△APF 中AE AF BAD CAD AP AP =⎧⎪∠=∠⎨⎪=⎩,∴△APE ≌△APF (SAS )∴∠APF=∠APE=60°,∴∠CPF=∠AOC-∠APF=60°,在△CFP 与△CDP 中,ACE BCE CP CPCPD CPF ∠=⎧⎪=⎨⎪∠=∠⎩∴△CFP ≌△CDP (ASA )。
全等三角形证明题辅助线专题--截长补短和倍长中线
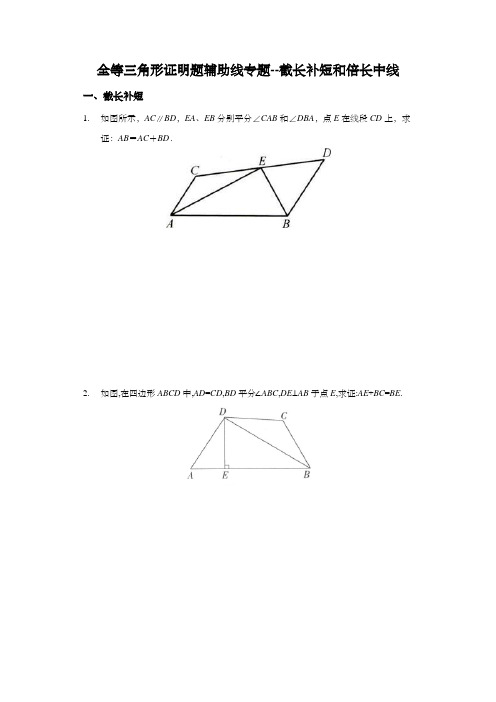
全等三角形证明题辅助线专题--截长补短和倍长中线一、截长补短1.如图所示,AC∥BD,EA、EB分别平分∠CAB和∠DBA,点E在线段CD上,求证:AB=AC+BD.2.如图,在四边形ABCD中,AD=CD,BD平分∠ABC,DE⊥AB于点E,求证:AE+BC=BE.3.如图,△ABC中,∠CAB=∠CBA=45∘,点E为BC的中点,CN⊥AE交AB于点N,连接EN.求证AE=CN+EN.4.如图,△ABC的∠B和∠C的平分线BD,CE相交于点F,∠A=60°,(1)求∠BFC的度数.(2)求证:BC=BE+CD.5.如图,在△ABC中,∠A=100°,∠ABC=40°,BD是∠ABC的平分线,延长BD至E,使DE=AD.求证:第2页,共28页BC=AB+CE.6.(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E,F分别是边BC,CD上的点,且∠EAF=1∠BAD,求证:EF=BE+DF;2(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF=1∠BAD,(1)中的结论是否仍然成立?2(3)如图3,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E,F分别是边BC,CD延长线上的点,且∠EAF=1∠BAD,(1)中的结论是否仍然成立?若成立,请证明;2若不成立,请写出它们之间的数量关系,并证明.7.如图,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点,且∠EAF = 60°.探究图中线段BE,EF,FD之间的数量关系.8.如图,在△ABC中,∠B=60°,△ABC的角平分线AD、CE相交于点O,(1)求∠AOC的度数;(2)求证:OE=OD;(3)猜测AE,CD,AC三者的数量关系,并证明.第4页,共28页9.如图在△ABC中,∠ABC=60°,AC=2AB,AD平分∠BAC交BC于点D,延长DB点F,使BF=BD,连接AF.(1)求证:AF=CD;(2)若CE平分∠ACB交AB于点E,试猜想AC、AF、AE三条线段之间的数量关系,并证明你猜想的结论.二、倍长中线10.如图,在△ABC和△DEF中,AB=DE,AC=DF,AM和DN分别是中线,且AM=DN.求证:△ABC≌△DEF.11.(1)【问题情境】课外兴趣小组活动时,老师提出了如下问题:如图①,△ABC中,若AB=13,AC=9,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:Ⅰ.由已知和作图能得到△ADC≌△EDB,依据是______.A.SSS B.SAS C.AAS D.HLⅡ.由“三角形的三边关系”可求得AD的取值范围是______.解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.(2)【初步运用】如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且∠FAE=∠AFE.若AE=4,EC=3,求线段BF的长.12.已知:在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BC交AC于F,求证:AF=EF.第6页,共28页13.如图,在△ABC中,AD是中线,∠BAC=∠BCA,点E在BC的延长线上,CE=AB,连接AE.求证:AE=2AD.14.如图,Rt△ABC中,∠ABC=90°(1)如图1,若BD为高线,AB=4,BC=3,AC=5,求BD的长(2)如图2,若BD为中线,求证:BD=1AC215.如图,在五边形ABCDE中,∠E=90O,BC=DE,,连接AC,AD,且AB=AD,AC⊥BC.(1)求证:AC=AE(2)如图,若∠ABC=∠CAD,AF为BE边上的中线,求证:AF⊥CD;(3)如图,在(2)的条件下,AE=8,DE=5,则五边形ABCDE的面积为_______。
专题11 截长补短模型(解析版)

专题11截长补短模型模型的概述:该模型适用于求证线段的和差倍分关系,该类题目中常出现等腰三角形、角平分线等关键词,可以采用截长补短法构造全等三角形来完成证明。
其中截长指在长线段中截取一段等于已知线段,补短指将短线段延长,使短线段加上延长线段长度等于长线段。
图解:已知线段AB 、CD 、EF ,简述利用截长补短法证明AB=CD+EF 的方法截长法:在线段AB 上,截取AG=CD ,判断线段GB 和线段EF 长度是否相等补短法:延长线段CD 至点H ,使DH=EF ,判断线段AB 和线段GH 长度是否相等【过关练】1.(2022秋·湖北黄石·八年级黄石八中校考期中)如图,△ABC 中,∠B =2∠A ,∠ACB 的平分线CD 交AB 于点D ,已知AC =16,BC =9,则BD 的长为()A .6B .7C .8D .9【答案】B 【分析】如图,在CA 上截取,CN CB =连接,DN 证明,CBD CND ≌利用全等三角形的性质证明,BD ND =求解9,7,CN AN ==再证明,DN AN =从而可得答案.【详解】解:如图,在CA 上截取,CN CB =连接,DN CD 平分,ACB ∠,BCD NCD ∴∠=∠,CD CD = (),CBD CND SAS ∴ ≌,,,BD ND B CND CB CN ∴=∠=∠=9,16,BC AC == 9,7,CN AN AC CN ∴==-=,CND NDA A ∠=∠+∠ ,B NDA A ∴∠=∠+∠2,B A ∠=∠ ,A NDA ∴∠=∠,ND NA ∴=7.BD AN ∴==故选:.B 【点睛】本题考查的是全等三角形的判定与性质,等腰三角形的判定,掌握以上知识是解题的关键.2.如图,在ABC 中,AD 平分BAC ∠,2B ADB ∠=∠,5AB =,6CD =,则AC 的长为()A .3B .9C .11D .15【答案】C 【分析】在AC 上截取AE=AB ,连接DE ,证明△ABD ≌△AED ,得到∠B=∠AED ,AB=AE ,再证明CD=CE ,进而代入数值解答即可.【详解】在AC 上截取AE=AB ,连接DE ,∵AD 平分∠BAC ,∴∠BAD=∠DAC ,在△ABD 和△AED 中,BAD DA AE AB AD AD C =⎧=∠=∠⎪⎨⎪⎩,∴△ABD ≌△AED (SAS ),∴∠B=∠AED ,∠ADB =∠ADE ,AB=AE ,又∠B=2∠ADB∴∠AED=2∠ADB ,∠BDE=2∠ADB ,∵∠AED=∠C+∠EDC=2∠ADB ,∠BDE=∠C+∠DEC=2∠ADB ,∴∠DEC =∠EDC ,∴CD=CE ,∵5AB =,6CD =,∴AC =AE+CE=AB+CD =5+6=11.故选:C .【点睛】本题考查全等三角形的判定和性质;利用了全等三角形中常用辅助线-截长补短法构造全等三角形,然后利用全等三角形解题,这是解决线段和差问题最常用的方法,注意掌握.3.如图,△ABC 中,AB=AC ,D 、E 分别在CA 、BA 的延长线上,连接BD 、CE ,且∠D+∠E=180°,若BD=6,则CE 的长为__.【答案】6【分析】在AD 上截取AF=AE ,连接BF ,易得△ABF ≌△ACE ,根据全等三角形的性质可得∠BFA=∠E ,CE=BF ,则有∠D=∠DFB ,然后根据等腰三角形的性质可求解.【详解】解:在AD 上截取AF=AE ,连接BF ,如图所示:AB=AC ,∠FAB=∠EAC ,∴ABF ACE ≌△△,∴BF=EC ,∠BFA=∠E ,∠D+∠E=180°,∠BFA+∠DFB=180°,∴∠DFB=∠D ,∴BF=BD ,BD=6,∴CE=6.故答案为6.【点睛】本题主要考查全等三角形的性质与判定及等腰三角形的性质与判定,熟练掌握全等三角形的判定方法及等腰三角形的性质与判定是解题的关键.4.如图,ABC 中,AD 平分BAC ∠,20C ∠=︒,AB BD AC +=,则B ∠的度数为_______.【答案】40︒【分析】如图(见解析),在线段AC 上取点E ,使得AE AB =,先根据角平分线的定义得出BAD EAD ∠=∠,再根据三角形全等的判定定理与性质得出BD ED =,B AED ∠=∠,然后根据线段的和差、等量代换得出ED CE =,最后根据等腰三角形的性质、三角形的外角性质即可得.【详解】如图,在线段AC 上取点E ,使得AE AB=AD 平分BAC∠BAD EAD\Ð=Ð在ABD △和AED △中,AB AE BAD EAD AD AD =⎧⎪∠=∠⎨⎪=⎩()ABD AED SAS ∴≅ BD ED ∴=,B AED∠=∠又AB BD AC AE CE+==+ BD CE∴=ED CE∴=20CDE C ∴∠=∠=︒40AED CDE C ∴∠=∠+∠=︒40B AED ∴∠=∠=︒故答案为:40︒.【点睛】本题考查了三角形全等的判定定理与性质、等腰三角形的性质等知识点,通过作辅助线,构造全等三角形是解题关键.5.(2022秋·八年级单元测试)如图,已知ABC ∆中,60A ∠=︒,D 为AB 上一点,且2,4AC AD BD B ACD =+∠=∠,则DCB ∠的度数是_________.【答案】20°【分析】延长AB 至点E 使BE AD =,连接CE ,证明AEC △是等边三角形,设ACD x ∠=,则4∠=ABC x ,再证明()△△ADC EBC SAS ≅,即可得到结果.【详解】解:如图,延长AB 至点E 使BE AD =,连接CE .∴2=++=+AE AD DB BE AD BD ,∵2=+AC AD BD ,∴AE AC =.∵60A ∠=︒,∴AEC △是等边三角形,∴60∠=∠=︒E ACE ,∵4∠=∠ABC ACD ,∴设ACD x ∠=,则4∠=ABC x .在ADC △与EBC 中,∵AD BE A E AC EC =⎧⎪∠=∠⎨⎪=⎩,∴()△△ADC EBC SAS ≅,∴∠=∠=ACD ECB x .∵∠=∠+∠ABC E BCE ,∴460=︒+x x ,∴20x =︒,∴60202020∠=︒-︒-︒=︒BCD .故答案是20︒.【点睛】本题主要考查了等边三角形的性质与判定,全等三角形的性质与判定,准确分析计算是解题的关键.6.如图,在△ABC 中,∠ACB=∠ABC=40o ,BD 是∠ABC 的角平分线,延长BD 至点E ,使得DE=DA ,则∠ECA=________.【答案】40°【分析】在BC 上截取BF=AB ,连接DF ,由题意易得∠A=100°,∠ABD=∠DBC=20°,易得△ABD ≌△FBD ,进而可得DF=AD=DE ,由此可证△DEC ≌△DFC ,然后根据全等三角形的性质、三角形内角和及外角的性质可求解.【详解】解:在BC 上截取BF=AB ,连接DF ,∠ACB=∠ABC=40°,BD 是∠ABC 的角平分线,∴∠A=100°,∠ABD=∠DBC=20°,∴∠ADB=60°,∠BDC=120°,BD=BD ,∴△ABD ≌△FBD ,DE=DA ,∴DF=AD=DE ,∠BDF=∠FDC=∠EDC=60°,∠A=∠DFB=100°,DC=DC ,∴△DEC ≌△DFC ,∴1006040DCB DCE DFC FDC ∠=∠=∠-∠=︒-︒=︒;故答案为40°.【点睛】本题主要考查全等三角形的判定与性质、三角形内角和及外角的性质,熟练掌握三角形全等的判定条件及外角性质是解题的关键.7.(2022秋·全国·八年级专题练习)如图,在ABC 中,,AC BC AD =平分BAC ∠交BC 于点D ,若AC CD AB +=,求C ∠的度数.【答案】90C ∠=︒【分析】在AB 上截取AE AC =,连接DE ,证明ADC ADE △≌△,再证明DE BE =,设B x ∠=,再得到∠=∠=∠=BAC B EDB x ,证明2,C x ∠=然后利用内角和定理求解即可.【详解】解:如图,在AB 上截取AE AC =,连接DE .∵AD 平分BAC ∠,EAD CAD ∠=∠.∵,==AE AC AD AD ,ADC ADE ∴ ≌,∴,,CD DE AED C =∠=∠∵AC CD AB +=,AE BE AB +=,∴CD BE =,∴DE BE =,∴B EDB ∠=∠.∵AC BC =,∴BAC B =∠∠.设∠=∠=∠=BAC B EDB x ,则2∠=∠+∠==∠AED B EDB x C .∵在ABC 中,2180x x x ++=︒,解得45x =︒,∴90C ∠=︒.【点睛】本题考查的是角平分线的定义,三角形全等的判定与性质,三角形的内角和定理,等腰三角形的性质,掌握以上知识是解题的关键.8.如图,已知四边形ABCD 中,AD ∥BC ,若∠DAB 的平分线AE 交CD 于E ,连接BE ,且BE 恰好平分∠ABC ,则AB 的长与AD+BC 的大小关系是()A.AB>AD+BC B.AB<AD+BC C.AB=AD+BC D.无法确定所以BC =BF ,所以AB =AF+BF =AD+BC ;故选C .【点睛】本题考查全等三角形的判定和性质,截长补短是证明线段和差关系的常用方法.9.已知:如图所示,四边形ABCD 中,,AD BC O 是CD 上一点,且AO 平分,BAD BO ∠平分ABC ∠,若3,4AO BO ==,求四边形ABCD 的面积.【答案】12.【分析】在AB 上截AE AD =,根据SAS 易证AOD AOE ∆∆≌,∠AOD=∠AOE ,根据平行线和角平分线的性质可得出∠AOB=90°,则90AOD BOC AOE BOE ∠+∠=∠+∠=︒,可得BOE BOC ∠=∠,继而证明△BOE ≌△BOC ,可得S 四ABCD =2S △AOB ,即可得出答案.【详解】解:在AB 上截AE AD =,∵AO 平分∠BAD ,∴∠DAO=∠EAO ,在△AOD 和△AOE 中,AD=AE DAO EAO AO AO ⎧⎪∠=∠⎨⎪=⎩∴AOD AOE ∆∆≌,AOD AOE ∴∠=∠,AD BC ∵‖,AO 平分BAD ∠,BO 平分ABC ∠,∴∠AOB=90°,90AOD BOC AOE BOE ∴∠+∠=∠+∠=︒BOE BOC ∴∠=∠,∵BO 平分∠ABC ,10.(2021秋·福建福州·八年级校考阶段练习)如图,在四边形ABCD 中,∠DAB =∠BCD =90°,AB =AD ,若这个四边形的面积是4,则BC +CD 等于()A .2B .4C .D .∵∠DAB =∠BCD =90°,∴∠D +∠ABC =180°,∵∠ABE +∠ABC =180°,∴∠D =∠ABE ,11.(2020秋·江苏无锡·八年级统考期中)如图,ABC 与ADC △有一条公共边AC ,且AB=AD ,∠ACB=∠ACD=x ,则∠BAD=________.(用含有x 的代数式表示)【答案】180°-2x【分析】在CD 上截取CE=CB ,证明△ABC ≌△AEC 得AE=AB ,∠B=∠AEC,可进一步证明∠D+∠B=180°,再根据四边形内角和定理可得结论.【详解】解:在CD 上截取CE=CB ,如图所示,在△ABC 和△AEC 中,CE CB ACE ACB AC AC =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△AEC(SAS)∴AE=AB ,∠B=∠AEC,∵AB=AD ,∴AD=AE ,∴∠D=∠AED ,∵∠AED+∠AEC=180°,∴∠D+∠B=180°,∵∠DAB+∠ABC+∠BCD+∠CDA=360°∴∠DAB+∠BCD =360°-∠ABC-∠CDA=360°-180°=180°,∵∠BCD =∠ACB +∠ACD =x+x=2x∴∠DAB=180°-∠BCD=180°-2x故答案为:180°-2x【点睛】本题考查了全等三角形的判定与性质,等腰三角形的性质以及四边形的内角和等知识,作辅助线构造全等三角形是解答此题的难点.12.(2021秋·广东佛山·八年级佛山市南海区石门实验学校校考阶段练习)如图,在等腰△ABC 中,AB =AC ,∠BAC =120°,点D 是线段BC 上一点,∠ADC =90°,点P 是BA 延长线上一点,点O 是线段AD 上一点,OP =OC ,下面的结论:①∠APO =∠ACO ;②∠APO +∠DCO =30°;③AC =AO +AP ;④PO =PC ,其中正确的有______.【答案】①②③④【分析】连接BO,由线段垂直平分线的性质定理,等腰三角形的判定与性质,三角形的内角和定理,角的和差求出∠APO=∠ACO,∠APO+∠DCO=30°,由三角形的内角和定理,角的和差求出∠POC=60°,再由等边三角的判定证明△OPC是等边三角形,得出PC=PO,∠PCO=60°,由角的和差,等边三角形的判定与性质,全等三角形的判定与性质,线段的和差和等量代换求出AO+AP=AC,即可得出结果.【详解】解:连接BO,如图1所示:∵AB=AC,AD⊥BC,∴BO=CO,∴∠OBC=∠OCB,又∵OP=OC,∴OP=OB,∴∠OBP=∠OPB,又∵在等腰△ABC中∠BAC=120°,∴∠ABC=∠ACB=30°,∴∠OBC+∠OBP=∠OCB+∠ACO,∴∠OBP=∠ACO,∴∠APO=∠ACO,故①正确;又∵∠ABC=∠PBO+∠CBO=30°,∴∠APO+∠DCO=30°,故②正确;∵∠PBC +∠BPC +∠BCP =180°,∠PBC =30°,∴∠BPC +∠BCP =150°,又∵∠BPC =∠APO +∠CPO ,∠BCP =∠BCO +∠PCO ,∠APO +∠DCO =30°,∴∠OPC +∠OCP =120°,又∵∠POC +∠OPC +∠OCP =180°,∴∠POC =60°,又∵OP =OC ,∴△OPC 是等边三角形,∴PC =PO ,∠PCO =60°,故④正确;在线段AC 上截取AE =AP ,连接PE ,如图2所示:∵∠BAC +∠CAP =180°,∠BAC =120°,∴∠CAP =60°,∴△APE 是等边三角形,∴AP =EP ,又∵△OPC 是等边三角形,∴OP =CP ,又∵∠APE =∠APO +∠OPE =60°,∠CPO =∠CPE +∠OPE =60°,∴∠APO =∠EPC ,在△APO 和△EPC 中,AP EP APO EPC OP CP =⎧⎪∠=∠⎨⎪=⎩,∴△APO ≌△EPC (SAS ),∴AO =EC ,又∵AC =AE +EC ,AE =AP ,∴AO +AP =AC ,故③正确;故答案为:①②③④.【点睛】本题考查了全等三角形的判定与性质、线段垂直平分线的性质定理、等腰三角形的判定与性质、等边三角形的判定与性质、角的和差、线段的和差、等量代换等相关知识点;作辅助线构建等腰三角形、等边三角形、全等三角形是解题的关键.13.(2022秋·浙江·八年级专题练习)(1)如图(1),在四边形ABCD 中,AB AD =,180B D ︒∠+∠=,E ,F 分别是,BC CD 上的动点,且12EAF BAD ∠=∠,求证:EF BE DF =+.(2)如图(2),在(1)的条件下,当点E ,F 分别运动到,BC CD 的延长线上时,,,EF BE DF 之间的数量关系是______.B ADC ADC∠+∠=∠+∠B ADF∴∠=∠,在△ABG和△ADF中ABB BG ⎧⎩⎪⎪⎨∠在△EAG 和△EAF 中AG AF EAG EAF AE AE ===⎧⎪⎨⎪⎩∠∠,∴△EAG ≌△EAF (SAS ),∴EG=EF ,∵BG=DF ,∴EF=BE-BG=BE-DF .【点睛】本题考查了全等三角形的判定和性质,掌握判定定理是解题关键.14.如图,△ABC 是等边三角形,△BDC 是顶角∠BDC=120°的等腰三角形,M 是AB 延长线上一点,N 是CA 延长线上一点,且∠MDN=60°.试探BM ,MN ,CN 之间的数量关系,并给出证明.90MBD ABD ECD ︒∴∠=∠=∠=在△MBD 和△ECD 中,BD CD MBD ECD BM CE =⎧⎪∠=∠⎨⎪=⎩,,,∴△MBD ≌△ECD (SAS ).∴MD=ED ,∠MDB=∠EDC .又∵∠MDN=60°,∠BDC=120°,∴∠EDN=∠BDC-(∠BDN+∠EDC )=∠BDC-(∠BDN+∠MDB )=∠BDC-∠MDN=120°-60°=60°.∴∠MDN=∠EDN .在△MND 与△END 中,ND ND MDN EDN MD ED =⎧⎪∠=∠⎨⎪=⎩,,,∴△MND ≌△END (SAS ).∴MN=NE .∴CN=NE+CE=MN+BM .【点睛】本题考查了等边及等腰三角形的性质及全等三角形的判定和性质,并采用了截长补短法,灵活利用已知条件证明三角形全等是解题的关键.15.(2023·全国·九年级专题练习)通过类比联想、引申拓展典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.【解决问题】如图,点E 、F 分别在正方形ABCD 的边BC 、CD 上,45EAF ∠=︒,连接EF ,则EF BE DF =+,试说明理由.证明:延长CD 到G ,使DG BE =,在ABE 与ADG △中,90AB AD B ADG BE DG =⎧⎪∠=∠=︒⎨⎪=⎩∴ABE ADG △≌△理由:(SAS )进而证出:AFE △≌___________,理由:(__________)进而得EF BE DF =+.【变式探究】如图,四边形ABCD 中,AB AD =,90BAD ∠=︒点E 、F 分别在边BC 、CD 上,45EAF ∠=︒.若B ∠、D ∠都不是直角,则当B ∠与D ∠满足等量关系________________时,仍有EF BE DF =+.请证明你的猜想.【拓展延伸】如图,若AB AD =,90≠︒∠BAD ,45EAF ∠≠︒,但12EAF BAD ∠=∠,90B D ∠=∠=︒,连接EF ,请直接写出EF 、BE 、DF之间的数量关系.【答案】(1)AFE AFG △≌△,理由:SAS ;(2)180B D ∠+∠=︒,证明见解析;(3)BE+DF=EF .【分析】(1)在前面已证的基础上,得出结论AE AG =,进而证明AFE AFG △≌△,从而得出结论;(2)利用“解决问题”中的思路,同样去构造AFE AFG △≌△即可;(3)利用前面两步的思路,证明全等得出结论即可.【详解】(1)ABE ADG ≌,,,AE AG BAE DAG BE DG ∴=∠=∠=,则BAE FAD FAD ADG FAG ∠+∠=∠+∠=∠,45EAF ∠=︒ ,45FAG ∴∠=︒,在AFG 与AFE △中,AE AG EAF GAF AF AF =⎧⎪=⎨⎪=⎩∠∠AFE AFG ∴△≌△,理由:(SAS )EF FG FD DG FD BE ∴==+=+;(2)满足180B D ∠+∠=︒即可,证明如下:如图,延长FD 至G ,使BE DG =,180B ADF ∠+∠=︒ ,180ADF ADG ∠+∠=︒,B ADG ∴∠=∠,在ABE 与ADG △中,AB AD B ADG BE DG =⎧⎪∠=∠⎨⎪=⎩()ABE ADG SAS ∴ ≌,,,AE AG BAE DAG BE DG ∴=∠=∠=,则BAE FAD FAD ADG FAG ∠+∠=∠+∠=∠,45EAF ∠=︒ ,45FAG ∴∠=︒,在AFG 与AFE △中,AE AG EAF GAF AF AF =⎧⎪=⎨⎪=⎩∠∠AFE AFG ∴△≌△,理由:(SAS )EF FG FD DG FD BE ∴==+=+;(3)BE+DF=EF.证明如下:=,如图,延长FD至G,使BE DG【点睛】本题考查了截长补短的方法构造全等三角形,能够理解前面介绍的方法并继续探究是解决问题的关键.16.(2022秋·江苏·八年级专题练习)在等边三角形ABC的两边AB、AC所在直线上分别有两点M、N,P 为△ABC外一点,且∠MPN=60°,∠BPC=120°,BP=CP.探究:当点M、N分别在直线AB、AC上移动时,BM,NC,MN之间的数量关系.(1)如图①,当点M、N在边AB、AC上,且PM=PN时,试说明MN=BM+CN.(2)如图②,当点M、N在边AB、AC上,且PM≠PN时,MN=BM+CN还成立吗?答:.(请在空格内填“一定成立”“不一定成立”或“一定不成立”).(3)如图③,当点M、N分别在边AB、CA的延长线上时,请直接写出BM,NC,MN之间的数量关系.由(1)可知:∠PBM=∠PCN=90°,∴∠PCH=90°,∴∠PBM=∠PCH,在△PBM和△PCH中,PBM PCH PB PC ⎪∠=∠⎨⎪=⎩,∴△PBM ≌△PCH (SAS ),∴PM =PH ,∠BPM =∠CPH ,∵∠BPM +∠CPN =60°,∴∠CPN +∠CPH =60°,∴∠MPN =∠HPN ,在△MPN 和△HPN 中,PM PH MPN HPN PN PN =⎧⎪∠=∠⎨⎪=⎩,∴△MPN ≌△HPN (SAS ),∴MN =HN =BM +CN ,故答案为:一定成立.(3)解:在AC 上截取CK =BM ,连接PK ,如图所示,在△PBM 和△PCK 中,90PBM PCK BM CK ⎪∠=∠=︒⎨⎪=⎩,∴△PBM ≌△PCK (SAS ),∴PM =PK ,∠BPM =∠CPK ,∵∠BPM +∠BPN =60°,∴∠CPK+∠BPN =60°,∴∠KPN =60°,∴∠MPN =∠KPN ,在△MPN 和△KPN 中,PM PK MPN KPN PN PN =⎧⎪∠=∠⎨⎪=⎩,∴△MPN ≌△KPN (SAS ),∴MN =KN ,∵KN =NC ﹣CK =NC ﹣BM ,∴MN =NC ﹣BM .【点睛】本题考查的是全等三角形的判定和性质、等边三角形的性质,掌握全等三角形的判定定理和性质定理是解题的关键.17.(2022秋·浙江·八年级专题练习)如图,四边形ABCD 中,180B D ∠+∠=︒,150BCD ∠=︒,CB CD =,M 、N 分别为AB 、AD 上的动点,且75MCN ∠=︒.求证:MN BM DN =+.【答案】见解析【分析】延长AB 至点E ,使得BE DN =,连接CE ,根据同角的补角相等得CBE CDN ∠=∠,根据SAS 证明CBE CDN ∆≅∆,则BCE DCN ∠=∠,进而证明75ECM MCN ∠=∠=︒,根据SAS 证明ECM NCM ∆≅∆,得到MN ME =,则MN BM BE BM DN =+=+.【详解】证明:延长AB 至点E ,使得BE DN =,连接CE ,四边形ABCD 中,180B D ∠+∠=︒,180ABC CBE ∠+∠=︒,CBE CDN ∴∠=∠,在CBE ∆和CDN ∆中,CB CD CBE CDN BE DN =⎧⎪∠=∠⎨⎪=⎩,()CBE CDN SAS ∴∆≅∆,BCE DCN ∴∠=∠,CN CE =,150BCD ∠=︒ ,75MCN ∠=︒,75MCE MCB BCE MCB DCN ∴∠=∠+∠=∠+∠=︒,MCN MCE ∴∠=∠,在ECM ∆和NCM ∆中,MC MC MCN MCE CN CE =⎧⎪∠=∠⎨⎪=⎩,()ECM NCM SAS ∴∆≅∆,MN ME BM BE BM DN ∴==+=+.【点睛】本题主要考查了全等三角形的判定与性质,作辅助线构造全等三角形是解决问题的关键.18.(2022秋·江苏·八年级专题练习)(1)问题背景:如图1:在四边形ABCD 中,AB =AD ,∠BAD =120°,∠B =∠ADC =90°,E 、F 分别是BC ,CD 上的点且∠EAF =60°,探究图中线段BE 、EF 、FD 之间的数量关系.小王同学探究此问题的方法是,延长FD 到点G .使DG =BE .连结AG ,先证明 ABE ≌ ADG ,再证明 AEF ≌ AGF ,可得出结论,他的结论应是______________;(2)探索延伸:如图2,若在四边形ABCD 中,AB =AD ,∠B +∠D =180°.E ,F 分别是BC ,CD 上的点,且∠EAF 12=∠BAD ,上述结论是否仍然成立,并说明理由;(3)实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O 处)北偏西30°的A 处,舰艇乙在指挥中心南偏东70°的B 处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以45海里/小时的速度前进,同时舰艇乙沿北偏东50°的方向以60海里/小时的速度前进,2小时后,指挥中心观测到甲、乙两地分别到达E 、F 处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.在 ABE 和 ADG 中,DG BE B ADG AB AD =⎧⎪∠=∠⎨⎪=⎩,∴ ABE ≌ ADG (SAS ∴AE =AG ,∠BAE =∠∵∠AOB =30°+90°+(90°﹣70°)=∴∠EOF 12=∠AOB ,又∵OA =OB ,∠OAC +∠OBC =(∴符合探索延伸中的条件,∴结论EF =AE +BF 成立,19.如图,ABC 是等边三角形,180BAD BCD ∠+∠=︒,8BD =,2CD =,则AD =________.【答案】6【分析】在线段BD 上取一点E ,使得BE=CD ,连接AE ,由,,,A B C D 四点共圆得∠ABE ACD =∠,再证明ABE ACD ≅∆,△ADE 是等边三角形,得AD DE AE ==,再由线段的和差关系可得结论.【详解】解:在线段BD 上取一点E ,使得BE=CD ,连接AE ,∵180BAD BCD ∠+∠=︒∴,,,A B C D 四点共圆,∴∠ABD ACD=∠∴∠ABE ACD=∠∵△ABC 是等边三角形,∴AB AC BC ==,60DAE ∠=︒,∴△ABE ACD ≅∆,∠60BAE CAF +∠=︒,∴,BAE CAD BAF CAD ∠=∠∠=∠,∴∠60CAD CAE +∠=︒,即60DAE ∠=︒,∴△ADE 是等边三角形,∴AD DE AE ==,∵=8BD ,2CD =,∴6DE BD BE BD CD =-=-=,∴6AD DE ==.【点睛】此题主要考查了全等三角形的判定与性质,以及四点共圆的判定,证明∠ABE ACD =∠是解答此题的关键.20.(2023·全国·九年级专题练习)例:截长补短法,是初中几何题中一种添加辅助线的方法,也是把几何题化难为易的一种策略.截长就是在长边上截取一条线段与某一短边相等,补短就是通过延长或旋转等方式使两条短边拼合到一起,从而解决问题.(1)如图1,△ABC 是等边三角形,点D 是边BC 下方一点,∠BDC =120°,探索线段DA 、DB 、DC 之间的数量关系.解题思路:将△ABD 绕点A 逆时针旋转60°得到△ACE ,可得AE =AD ,CE =BD ,∠ABD =∠ACE ,∠DAE =60°,根据∠BAC +∠BDC =180°,可知∠ABD +∠ACD =180°,则∠ACE +∠ACD =180°,易知△ADE 是等边三角形,所以AD=DE,从而解决问题.根据上述解题思路,三条线段DA、DB、DC之间的等量关系是___________;(2)如图2,Rt△ABC中,∠BAC=90°,AB=AC.点D是边BC下方一点,∠BDC=90°,探索三条线段DA、DB、DC之间的等量关系,并证明你的结论.21.(2022·全国·九年级专题练习)如图1,在Rt△ABC中,∠ABC=90°,BA=BC,直线MN是过点A的直线CD⊥MN于点D,连接BD.(1)观察猜想张老师在课堂上提出问题:线段DC,AD,BD之间有什么数量关系.经过观察思考,小明出一种思路:如图1,过点B作BE⊥BD,交MN于点E,进而得出:DC+AD=BD.(2)探究证明将直线MN绕点A顺时针旋转到图2的位置写出此时线段DC,AD,BD之间的数量关系,并证明(3)拓展延伸在直线MN绕点A旋转的过程中,当△ABD面积取得最大值时,若CD长为1,请直接写BD的长.AH 22.(2022秋·江苏·八年级专题练习)在ABC 中,60ABC ∠=︒,点D 、E 分别在AC 、BC 上,连接BD 、DE 和AE ;并且有AB BE =,AED C ∠=∠.(1)求CDE ∠的度数;(2)求证:AD DE BD +=.【答案】(1)60︒;(2)见解析【分析】(1)由AB BE =,60ABC ∠=︒,可得ABE 为等边三角形,由AEB EAC C ∠=∠+∠,CDE EAC AED ∠=∠+∠,AED C ∠=∠,可证60CDE AEB ∠=∠=︒(2)延长DA 至F ,使AF DE =,连接FB ,由60BED AED ∠=︒+∠,60BAF C ∠=︒+∠,且C AED ∠=∠,可证()FBA DBE SAS ≌由=DB FB ,可证FBD 为等边三角形,可得BD FD =,可推出结论,【详解】解:(1)∵AB BE =,60ABC ∠=︒,∴ABE 为等边三角形,∴60BAE AEB ∠=∠=︒,∵AEB EAC C ∠=∠+∠,CDE EAC AED ∠=∠+∠,∵AED C ∠=∠,∴60CDE AEB ∠=∠=︒(2)如图,延长DA 至F ,使AF DE =,连接FB ,由(1)得ABE 为等边三角形,∴60AEB ABE ∠=∠=︒,∵60BED AEB AED AED ∠=∠+∠=︒+∠,又∵60BAF ABE C C ∠=∠+∠=︒+∠,且C AED ∠=∠,∴BED BAF ∠=∠,23.(2022秋·江苏·八年级专题练习)如图,在△ABC 中,AB =AC ,∠BAC =30°,点D 是△ABC 内一点,DB =DC ,∠DCB =30°,点E 是BD 延长线上一点,AE =AB .(1)求∠ADB 的度数;(2)线段DE ,AD ,DC 之间有什么数量关系?请说明理由.【答案】(1)120°;(2)DE =AD +CD ,理由见解析根据全等三角形的性质得到∠∴CD=ME.∵DE=DM+ME,∴DE=AD+CD.【点睛】本题考查的是全等三角形的判定和性质、等边三角形的判定和性质,掌握全等三角形的判定定理和性质定理是解题的关键.24.如图,在△ABC中,AB=BC,∠ABC=60°,线段AC与AD关于直线AP对称,E是线段BD与直线AP的交点.(1)若∠DAE=15°,求证:△ABD是等腰直角三角形;(2)连CE,求证:BE=AE+CE.【答案】(1)见解析;(2)见解析【分析】(1)首先根据题意确定出△ABC是等边三角形,然后根据等边三角形的性质推出∠BAC=60°,再根据线段AC与AD关于直线AP对称,以及∠DAE=15°,推出∠BAD=90°,即可得出结论;(2)利用“截长补短”的方法在BE上取点F,使BF=CE,连接AF,根据题目条件推出△ABF≌△ACE,得出AF=AE,再进一步推出∠AEF=60°,可得到△AFE是等边三角形,则得到AF=FE,从而推出结论即可.【详解】证明:(1)∵在△ABC中,AB=BC,∠ABC=60°,∴△ABC是等边三角形,∴AC=AB=BC,∠BAC=∠ABC=∠ACB=60°,∵线段AC与AD关于直线AP对称,【点睛】本题考查全等三角形的判定与性质,以及等边三角形的判定与性质等,掌握等边三角形的判定与性质,以及全等三角形的常见辅助线的构造方法是解题关键.25.(2022秋·全国·八年级专题练习)在ABC 中,AE ,CD 为ABC 的角平分线,AE ,CD 交于点F .(1)如图1,若=60B ∠︒.①直接写出AFC ∠的大小;②求证:AC AD CE =+.(2)若图2,若90B Ð=°,求证:ACF AFD CEF DEF S S S S =++△△△△.DAF HAF AF AF ⎪∠=∠⎨⎪=⎩∴△ADF ≌△AHF (SAS ),∴∠AFD =∠AFH ,∵∠AFD =∠CFE ,∴∠AFH =∠CFE ,由①可知,∠AFC =120°,∴∠CFE =180°-120°=60°,∴AFH =∠CFE =60°,∴∠CFH =60°,即:∠CFH =∠CFE ,在△CFH 和△CFE 中,CFH CFE CF CF HCF ECF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△CFH ≌△CFE (ASA ),∴CE =CH ,∵AC =AH +CH ,∴AC =AD +CE ;(2)证:如图所示,在AC 上取S 、T 两点,使得AD =AS ,CE =CT ,连接SF ,SE ,TF ,TE ,∵AE 平分∠BAC ,∴∠DAF =∠SAF ,在△ADF 和△ASF 中,【点睛】本题考查全等三角形的判定与性质,以及三角形角平分线相关的证明问题,掌握基本的辅助线添加思想,熟练运用全等三角形的判定与性质是解题关键.26.(2022秋·浙江·八年级专题练习)如图ABC 中,60,,ABC AD CE ︒∠=分别平分,BAC ACB AD CE ∠∠、、相交于点P .(1)求CPD ∠的度数;(2)求证:AE CD AC+=【答案】(1)∠CPD=60°;(2)详见解析【分析】(1)根据三角形的内角和定理及角平分线的定义,三角形的外角性质即可求出;(2)在AC 上截取AF=AE ,先证明△APE ≌△APF (SAS ),再证明△CFP ≌△CDP (ASA ),根据全等三角形的性质证明AE CD AC +=即可.【详解】解:(1)∵∠ABC=60°,∴∠BAC+∠ACB=180°-60°=120°,又∵AD 、CE 分别平分∠∠、BAC ACB ,∴12CAD BAC ∠=∠,12ACE ACB ∠=∠∴111()60222CAD ACE BAC ACB BAC ACB ∠+∠=∠+∠=∠+∠=︒,又∵∠CPD 是△ACP 的外角,∴∠CPD=∠CAD+∠ACE=60°,∴∠CPD=60°.(2)如图,在AC 上截取AF=AE ,连接PF ,∵∠CPD=60°,∴∠APC=120°,∠APE=60°∵AD 平分∠BAC ,CE 平分∠ACB ,∴∠BAD=∠CAD ,∠ACE=∠BCE在△APE 与△APF 中27.(2022秋·全国·八年级期末)(1)阅读理解:问题:如图1,在四边形ABCD 中,对角线BD 平分ABC ∠,180A C ∠+∠=︒.求证:DA DC =.思考:“角平分线+对角互补”可以通过“截长、补短”等构造全等去解决问题.方法1:在BC 上截取BM BA =,连接DM ,得到全等三角形,进而解决问题;方法2:延长BA 到点N ,使得BN BC =,连接DN ,得到全等三角形,进而解决问题.结合图1,在方法1和方法2中任选一种....,添加辅助线并完成证明.(2)问题解决:如图2,在(1)的条件下,连接AC ,当60DAC ∠=︒时,探究线段AB ,BC ,BD 之间的数量关系,并说明理由;(3)问题拓展:如图3,在四边形ABCD 中,180A C ∠+∠=︒,DA DC =,过点D 作DE BC ⊥,垂足为点E ,请直接写出线段AB 、CE 、BC之间的数量关系.【答案】(1)证明见解析;(2)AB BC BD +=;理由见解析;(3)2BC AB CE -=.【分析】(1)方法1:在BC 上截取BM BA =,连接DM ,得到全等三角形,进而解决问题;方法2:延长BA 到点N ,使得BN BC =,连接DN ,得到全等三角形,进而解决问题;(2)延长CB 到点P ,使BP BA =,连接AP ,证明ΔΔPAC BAD ≌,可得PC BD =,即PC BP BC AB BC =+=+(3)连接BD ,过点D 作DF AC ⊥于F ,证明ΔΔDFA DEC ≌,RtΔRtΔBDF BDE ≌,进而根据2BC BE CE BA AF CE BA CE =+=++=+即可得出结论.【详解】解:(1)方法1:在BC 上截BM BA =,连接DM ,如图.BD 平分ABC ∠,ABD CBD ∴∠=∠.在ΔABD 和ΔMBD 中,BD BD ABD MBD BA BM =⎧⎪∠=∠⎨⎪=⎩,ΔΔABD MBD ∴≌,A BMD ∴∠=∠,AD MD =.180BMD CMD ︒∠+∠= ,180C A ︒∠+∠=.C CMD ∴∠=∠.DM DC ∴=,DA DC ∴=.方法2:延长BA 到点N ,使得BN BC =,连接DN ,如图.BD 平分ABC ∠,NBD CBD ∴∠=∠.在ΔNBD 和ΔCBD 中,BD BD NBD CBD BN BC =⎧⎪∠=∠⎨⎪=⎩,ΔΔNBD CBD ∴≌.BND C ∴∠=∠,ND CD =.180NAD BAD ︒∠+∠= ,180C BAD ︒∠+∠=.BND NAD ∴∠=∠,DN DA ∴=,DA DC ∴=.(2)AB 、BC 、BD 之间的数量关系为:AB BC BD +=.(或者:BD CB AB -=,BD AB CB -=).延长CB 到点P ,使BP BA =,连接AP ,如图2所示.由(1)可知AD CD =,60DAC ︒∠= .ΔADC ∴为等边三角形.AC AD ∴=,60ADC ︒∠=.180BCD BAD ︒∠+∠= ,36018060120ABC ︒︒︒︒∴∠=--=.18060PBA ABC ︒︒∴∠=-∠=.BP BA = ,ΔABP ∴为等边三角形.60PAB ︒∴∠=,AB AP =.60DAC ︒∠= ,PAB BAC DAC BAC ∴∠+∠=∠+∠,即PAC BAD ∠=∠.在ΔPAC 和ΔBAD 中,PA BA PAC BAD AC AD =⎧⎪∠=∠⎨⎪=⎩,ΔΔPAC BAD ∴≌.PC BD ∴=,PC BP BC AB BC =+=+ ,AB BC BD ∴+=.(3)AB ,CE ,BC 之间的数量关系为:2BC AB CE -=.(或者:2BC CE AB -=,2AB CE BC +=)解:连接BD ,过点D 作DF AC ⊥于F ,如图3所示.28.等边ABC ∆中,点H 、K 分别在边BC 、AC 上,且AK CH =,连接AH 、BK 交于点F .(1)如图1,求AFB ∠的度数;图1(2)连接CF ,若90BFC ∠=︒,求BF AF的值;(3)如图2,若点G 为AC 边的中点,连接FG ,且2AF FG =,则BFG ∠的大小是___________.图2【答案】(1)120︒;(2)2;(3)120︒【分析】(1)由ABC ∆是等边三角形,可得出AB AC BC ==,60BAC ABC ACB ==︒=∠∠∠,再利用AK CH =,可证()ΔΔABK CAH SAS ≌,得出CAH ABK ∠=∠,由BFH ABK BAF CAH BAF ∠=∠+∠=∠+∠可求出BFH ∠,最后由补角定义求出AFB ∠.(2)在BF 上取点D ,使BD AF =,由120AFB ∠=︒可证150AFC ∠=︒,再利用AB AC =,ABD CAF ∠=∠,BD AF =可证明()ΔΔABD CAF SAS ≌,进而求出150ADB CFA ∠=∠=︒,再用补角的性质得知120AFD ∠=︒,在AFD △中利用外角的性质可求出30FAD ADB AFD ∠=∠-∠=︒,进而证出AFD △为等腰三角形,最后可证出2BF BD DF AF =+=即可求解.(3)延长BF 至E ,使AFE ∆为等边三角形,延长FG 交CE 于T ,可得出()ΔΔABF ACE SAS ≌,进而得出120AEC AFB ∠=∠=︒,利用角的和差得出60FET AFE ∠=︒=∠,则证出//AF EC ,进而证出()ΔΔAFG CTG AAS ≌,再利用2AF FG =,AF EF =证出EFT ∆为等边三角形,进而证出120BFG ∠=︒.【详解】(1)∵ABC ∆是等边三角形,∴AB AC BC ==,60BAC ABC ACB ==︒=∠∠∠,在ABK ∆和CAH ∆中,AB CA =,BAK ACH ∠=∠,AK CH =,∴()ΔΔABK CAH SAS ≌,∴CAH ABK ∠=∠,∴60BFH ABK BAF CAH BAF ∠=∠+∠=∠+∠=︒,。
【中考数学29个几何模型】模型02 截长补短(后附答案与解析)

专题02截长补短【基础训练】1、如图,AC平分∠BAD,CE⊥AB于点E,∠B+∠D=180°,求证:AE=AD+BE.2、如图,已知在△ABC中,∠C=2∠B,∠1=∠2,求证:AB=AC+CD3、如图,在五边形ABCDE中,AB=AE,BC+DE=CD,∠B+∠E=180°,求证:AD平分∠CDE.4、已知四边形ABCD中,∠ABC+∠ADC=180°,AB=BC,如图,点P,Q分别在线段AD,DC上,满足PQ=AP+CQ,求证:∠PBQ=90°-12∠ADC5、如图,在△ABC中,∠B=60°,△ABC的角平分线AD、CE相交于点O,求证:AE+CD=AC.6、如图所示,AB∥CD,BE,CE分别是∠ABC,∠BCD的平分线,点E在AD上,求证:BC=AB+CD.7、四边形ABCD中,BD>AB,AD=DC,DE⊥BC,BD平分∠ABC(1)证明:∠BAD+∠BCD=180°(2)DE=3,BE=6,求四边形ABCD的面积.8、已知:在△ABC中,AB=CD-BD,求证:∠B=2∠C.9、如图,△ABC中,BD⊥AC于点D,CE⊥AB于点E,且BD,CE交于点F,点G是线段CD上一点,连接AF,GF,若AF=GF,BD=CD.求∠CAF的度数判断线段FG与BC的位置关系,并说明理由.【提升训练】1.如图,在△ABC中,∠A=60°,BD,CE分别平分∠ABC和∠ACB,BD,CE交于点O,试判断BE,CD,BC的数量关系,并加以证明.2.如图,AD//BC,DC⊥AD,AE平分∠BAD,E是DC的中点.问:AD,BC,AB之间有何关系?并说明理由.3.如图,已知DE=AE,点E在BC上,AE⊥DE,AB⊥BC,DC⊥BC,请问线段AB,CD和线段BC有何大小关系?并说明理由.4.如图,AB∥CD,BE,CE分别是∠ABC和∠BCD的平分线,点E在AD上.求证:BC=AB+CD.5.如图,在Rt△ABC中,∠C=90°,BC=AC,∠B=∠CAB=45°,AD平分∠BAC交BC于D,求证:AB=AC+CD.6.如图,在△ABC中,∠ABC=60°,AD,CE分别平分∠BAC,∠ACB,AD,CE交于O.(1)求∠AOC的度数;(2)求证:AC=AE+CD.专题02截长补短(解析版)【基础训练】1、如图,AC平分∠BAD,CE⊥AB于点E,∠B+∠D=180°,求证:AE=AD+BE.解析:如图,在EA上取点F,使EF=BE,连接CF,∵CE⊥AB∴CF=CB∠CFB=∠B∵∠AFC+∠CFB=180°,∠D+∠B=180°∴∠D=∠AFC∵AC平分∠BAD即∠DAC=∠FAC在△ACD和△ACF中∠D=∠AFC∠DAC=∠FACAC=AC∴ACD≌△ACF(AAS)∴AD=AF∴AE=AF+EF=AD+BE2、如图,已知在△ABC中,∠C=2∠B,∠1=∠2,求证:AB=AC+CD解析:在AB上取一点E,使AE=AC,连接DE,∵AE=AC,∠1=∠2,AD=AD∴△ACD≌△AED∴CD=DE,∠C=∠3∵∠C=2∠B∴∠3=2∠B=∠4+∠B∴∠4=∠B,∴DE=BE,CD=BE∵AB=AE+BE∴AB=AC+CD3、如图,在五边形ABCDE中,AB=AE,BC+DE=CD,∠B+∠E=180°,求证:AD平分∠CDE.解析:延长CB至点F,使BF=DE,连接BF=DE,连接AF,AC∵∠1+∠2=180°,∠E+∠1=180°∴∠2=∠E∵AB=AE,∠2=∠E,BF=DE∴△ABF≌△AED∠F=∠4,AF=AD∵BC+BF=CD即FC=CD又∵AC=AC∴△ACF≌△ACD∴∠F=∠3∵∠F=∠4∴∠3=∠4∴AD平分∠CDE.4、已知四边形ABCD中,∠ABC+∠ADC=180°,AB=BC,如图,点P,Q分别在线段AD,DC上,满足PQ=AP+CQ,求证:∠PBQ=90°-12∠ADC解析:如图,延长DC,在上面找一点K,使得CK=AP,连接BK,∵∠ABC+∠ADC=180°∴∠BAD+∠BCD=180°∵∠BCD+∠BCK=180°∴∠BAD=∠BCK在△BAP和△BKC中AP=CK∠BAP=∠BCKAB=BC∴△BPA≌△BKC(SAS)∴∠ABP=∠CBK,BP=BK∵PQ=AP+CQ∴PQ=QK∵在△BPQ和△BKQ中BP=BKBQ=BQPQ=KQ∴△BPQ≌△BKQ(SSS)∴∠PBQ=∠KBQ∴∠PBQ=12∠ABC∵∠ABC+∠ADC=180°∴∠ABC=180°-∠ADC∴12∠ABC=90°-12∠ADC∴∠PBQ=90°-12∠ADC5、如图,在△ABC中,∠B=60°,△ABC的角平分线AD、CE相交于点O,求证:AE+CD=AC.解析:由题意可得∠AOC=120°∴∠AOE=∠DOC=180°-∠AOC=180°-120°=60°在AC上截取AF=AE,连接OF,如图在△AOE和△AOF中,AE=AF∠OAE=∠OAFOA=OA∴△AOE≌△AOF(SAS)∴∠AOE=∠AOF,∴∠AOF=60°∴∠COF=∠AOC-∠AOF=60°又∠COD=60°,∴∠COD=∠COF同理可得:△COD≌△COF(ASA)∴CD=CF又∵AF=AE∴AC=AF+CF=AE+CD即AE+CD=AC6、如图所示,AB∥CD,BE,CE分别是∠ABC,∠BCD的平分线,点E在AD上,求证:BC=AB+CD.解析:在BC上取点F,使BF=AB∵BE,CE分别是∠ABC,∠BCD的平分线∴∠ABE=∠FBE,∠BCE=∠DCE∵AB∥CD∴∠A+∠D=180°在△ABE和△FBE中AB=FB∠ABE=∠FBEBE=BE∴△ABE≌△FBE(SAS)∴∠A=∠BFE∴∠BFE+∠D=180°∵∠BFE+∠EFC=180°∴∠EFC=∠D在△EFC和△EDC中,∠EFC=∠D∠BCE=∠DCECE=CE∴△EFC≌△EDC(AAS)∴CF=CD∵BC=BF+CF∴BC=AB+CD7、四边形ABCD中,BD>AB,AD=DC,DE⊥BC,BD平分∠ABC (3)证明:∠BAD+∠BCD=180°(4)DE=3,BE=6,求四边形ABCD的面积.【解析】(1)过点D作BA的垂线,得△DMA≌DEC(HL)∵∠ABC+∠MDE=180°,∠ADC=∠MDE∴∠ABC+∠ADC=180°∴∠BAD+∠BCD=180°(2)S四边形ABCD=2S△BED=188、已知:在△ABC中,AB=CD-BD,求证:∠B=2∠C.【解析】在CD上取一点M使得DM=DB则CD-BD=CM=AB∴∠AMD=∠B=2∠C9、如图,△ABC 中,BD ⊥AC 于点D ,CE ⊥AB 于点E ,且BD,CE 交于点F ,点G 是线段CD 上一点,连接AF ,GF ,若AF=GF,BD=CD.求∠CAF 的度数判断线段FG 与BC 的位置关系,并说明理由.【解析】(1)延长AF 与BC 交于点M ,可知AF ⊥BC∵BD=DC ,BD ⊥DC ∴∠FBC=45°∵AF=FG ,FD ⊥AG ∴∠AFD=GFD=45°∴AF ⊥GF∴∠CAF=45°(2)由(1)可证FG ∥BC【提升训练】1.如图,在△ABC 中,∠A =60°,BD ,CE 分别平分∠ABC 和∠ACB ,BD ,CE 交于点O ,试判断BE ,CD ,BC 的数量关系,并加以证明.证明:在BC 上截取BF =BE ,连接OF .∵BD 平分∠ABC ,∴∠EBO =∠FBO .∴△EBO ≌△FBO .∴∠EOB =∠FOB .∵∠A =60°,BD ,CE 分别平分∠ABC 和∠ACB ,∴∠BOC =180°-∠OBC -∠OCB =180°-12∠ABC -12∠ACB =180°-12(180°-∠A )=120°.∴∠EOB =∠DOC =60°.∴∠BOF=60°,∠FOC=∠DOC=60°.∵CE平分∠DCB,∴∠DCO=∠FCO.∴△DCO≌△FCO.∴CD=CF.∴BC=BF+CF=BE+CD.2.如图,AD//BC,DC⊥AD,AE平分∠BAD,E是DC的中点.问:AD,BC,AB之间有何关系?并说明理由.解:AB=AD+BC.理由:作EF⊥AB于F,连接BE.∵AE平分∠BAD,DC⊥AD,EF⊥AB,∴EF=DE.∵DE=CE,∴EC=EF.∴Rt△BFE≌Rt△BCE(HL).∴BF=BC同理可证:AF=AD.∴AD+BC=AF+BF=AB,即AB=AD+BC.3.如图,已知DE=AE,点E在BC上,AE⊥DE,AB⊥BC,DC⊥BC,请问线段AB,CD和线段BC有何大小关系?并说明理由.解:线段AB,CD和线段BC的关系是:BC=AB+CD.理由:在△DCE中,∠EDC+∠DEC=90°,∵∠AEB+∠DEC=90°,∴∠AEB=∠EDC,又∵ED=AE,∠ABE=∠ECD=90°,∴△ABE≌△ECD(AAS),∴AB=EC,BE=CD,∴BC=BE+EC=CD+AB.4.如图,AB∥CD,BE,CE分别是∠ABC和∠BCD的平分线,点E在AD上.求证:BC=AB+CD.证明:在BC上取点F,使BF=BA,连接EF,如图,∵BE,CE分别是∠ABC和∠BCD的平分线,∴∠ABE=∠FBE,∠ECF=∠ECD.∴△ABE≌△FBE(SAS),∴∠A=∠BFE,∵AB∥CD,∴∠A+∠D=180°,∴∠BFE+∠D=180°.∵∠BFE+∠EFC=180°,∴∠EFC=∠D.∴△CDE≌△CFE(AAS),∴CF=CD.∵BC=BF+CF,∴BC=AB+CD.5.如图,在Rt△ABC中,∠C=90°,BC=AC,∠B=∠CAB=45°,AD平分∠BAC交BC于D,求证:AB=AC+CD.证明:如图,延长AC 到E ,使CE =CD ,连接DE .则∠E =∠CDE =45°,∴∠B =∠E .∵AD 平分∠BAC ,∴∠1=∠2,在△ABD 和△AED 中,∠B =∠E ,∠2=∠1,AD =AD ,∴△ABD ≌△AED (AAS).∴AE =AB .∵AE =AC +CE =AC +CD ,∴AB =AC +CD .6.如图,在△ABC 中,∠ABC =60°,AD ,CE 分别平分∠BAC ,∠ACB ,AD ,CE 交于O .(1)求∠AOC 的度数;(2)求证:AC =AE +CD .(1)解:∵∠ABC =60°,AD ,CE 分别平分∠BAC ,∠ACB ,∴∠AOC =180°-(∠OAC +∠OCA )=180°-12(∠BAC +∠ACB )=180°-180°-60°2=120°;(2)证明:∵∠AOC =120°,∴∠AOE =60°,如图,在AC 上截取AF =AE ,连接OF ,∵AD 平分∠BAC ,∴∠BAD =∠CAD ,∵AO=AO,∴△AOE≌△AOF(SAS),∴∠AOE=∠AOF,∵∠AOE=60°,∠AOC=120°,∴∠AOF=∠COD=∠COF=60°.∵∠FOC=∠DOC,CO=CO,∠DCO=∠FCO,∴△COF≌△COD(ASA),∴CF=CD,∴AC=AF+CF=AE+CD.。
初中一年级下学期数学《截长补短专题》教学设计

截长补短专题(七下)一、学习者分析学生已经学习了北师版教材七下第四章《三角形》这部分内容,掌握了证明三角形全等的方法,该课程涉及到三角形全等.二、教学内容用“截长补短”方法证明线段和差倍分关系.三、教学目标1、理解截长补短的方法;2、能运用截长补短方法解决线段和差倍分关系问题;3、让学生感受将未知问题转化为已知问题解决,体会转化的思想.四、教学重难点重点:熟练截长补短方法及合理选择方法来解决问题.难点:找出合理的添加辅助线的方法解决问题.五、教学过程设计(一)方法介绍教师提出:当条件或者结论中出现两条线段之和等于第三条线段时,如条件或结论中出现AB=CD+EF ,我们可以采用“截长”或者“补短”的方法将问题转化为求证线段的相等关系.“截长”法就是在长边上截取一条与某一短边相同的线段,再证剩下的线段与另一短边相等. 比如:在长线段AB 上截取AM=CD ,再证明剩下的MB=EF .“补短”法是选择一条短线段进行延长,通常有这样两种:①如:延长CD 至M ,使得DM=EF,再证明长线段CM=AB .当然我们也可以选择延长EF 至N 点,使得FN=CD,再证明长线段EN=AB .我们也可以将这两条短线段往另一方向延长,如:延长FE 、延长DC .这几种都是将其中一条短线段延长,使延长部分等于另一条线段,再证明两条线段的和与长线段相等. 补短法的第二种方法是:还是将其中一条短线段延长,如:延长CD 至M ,使得CM=AB, 再证明补充的短线段DM=EF .这种方法是使原来的短线段和补充线段之和等于长线段,再证明补充线段等于另一条短线段.(二)例题讲解例 已知:如图,在△ABC 中,∠1=∠2,∠B=2∠C.求证:AC=AB+BD .先让学生进行思考,是否可以用“截长”和“补短”两种方法完成.师:首先在长线段AC 上截取一条线段,那么是截取AB 还是截取BD 呢?我们需要结合题目条件分析,21D C B A题目中有条件∠1=∠2,又有AD 作为△ABD 和△ACD 的公共边,显然这两个三角形并不全等.但是如果我们在AC 上截取AE=AB,连结DE ,可由边角边证明△ABD ≌△AED ,现在就只需要证明剩下的EC=BD 了.我们由△ABD≌△AED 可知:∠B=∠3,结合题目中的条件∠B=2∠C,加上∠3是三角形EDC 的一个外角,所以∠3=∠C+∠4,从而证明出∠4=∠C,由等角对等边可得EC=ED .而由刚才的三角形全等我们可以得到BD=ED ,结合EC=ED ,等量代换,我们可以证得EC=BD ,最终AC= AE + EC =AB+BD .该方法是在长边AC 上截取了线段AE=AB ,是先构造三角形全等,再利用全等三角形性质和等角对等边来证明剩下的边相等.师提出思考:可以在AC 上截取CE =BD 吗?或者在AC 上截取AE =BD 呢?可以在AC 上截取CE=AB 吗? 师:仅从这几种截取方法,加以题目中的条件,无法进行进一步的推理,所以同学们在进行辅助线添加的过程中,需要结合题目条件来判断如何截取,截取后要能构造全等三角形或者是一些特殊的三角形,比如等腰三角形之类的,而我们此题的“截长”法就是通过构造全等三角形再证明边相等从而最终证得结论.后面介绍补短的三种方法:“补短”法分析一:首先考虑补AB 这条线段.发现如果延长AB 至E 点,使BE=BD,此时构造了等腰三角形,接下来利用三个条件∠E= ∠C,∠1=∠2,AD=AD 就可以证得△ ADE ≌△ ADC ,从而证得AC= AE= AB+BD 了.这种方法是先构造等腰三角形,再证明三角形全等.“补短”法分析二:还是考虑补AB 这条线段.可以考虑先构造全等三角形,再证明边相等.延长AB 至E 点,使AE=AC,三个条件,AE=AC ,∠1=∠2,AD=AD ,可证△ADE≌△ADC ,接下来就只需要证明补充线段BE=BD .“补短”法分析三:考虑补BD 这条线段.可以延长DB 至E 点,使BE=BA ,通过等边对等角,等角对等边等性质解决线段相等问题.师提出思考:该问题求证两条线段长度之和等于第三条线段,我们是否可以改为求证:AC − AB=BD 或者AC − BD = AB 呢?其实我们发现他们是可以互相转化的.而有一些题目证明长线段是某短线段的两倍,或短线段是某长线段的12,皆可用我们今天所学习的方法解决.(三)课堂练习1、已知:如图,在△ABC 中,∠ABC=60º,△ABC 的角平分线AD ,CE 交于点O .求证:AC − AE=CD .师给出时间让学生思考,并解答.在此,师提供两种方法:法一,截长法,在AC 上截取AF=AE ,先证得△EOA ≌△FOA ,再通过证明△OFC ≌△ODC ,得到CF=CD ,最终得到AC − AE=CD .A E BDC O法二,补短法,在CB 上截取CF=CA ,先证得△OFC≌△OAC ,再通过证明△OEA≌△ODF ,得到DF=EA ,最终得到AC − AE=CD .(四)课堂小结“截长补短”方法通常用于解决线段和差倍分问题,目的就是将线段的和差倍分问题转化为两条线段的相等问题。
几何辅助线之截长补短 总结+例题

截长补短专题知识导航“截长补短”是几何证明题中十分重要的方法,通常用来证明几条线段的数量关系,即若题目条件或结论中含有“c b a =+”的条件,需要添加辅助线时可以考虑“截长补短”的方法。
截长法:在较长的线段上截取一条线段等于较短线段,再设法证明较长线段的剩余线段等于另外的较短线段。
补短法:①延长较短线段中的一条,使延长出来的线段等于另外的较短线段,然后证明两线段之和等于较长线段。
即延长a ,得到b ,证:c b a =+。
②延长较短线段中的一条,使延长后的线段等于较长线段,然后证明延长出来的部分等于另一条较短线段。
即延长a ,得到c ,证:a c b -=。
【核心考点1】角平分线相关截长补短1. 如图,BP 平分ABC ∠,D 为BP 上一点,E ,F 分别在BA ,BC 上,且满足DE DF =,若140BED ∠=︒,则BFD ∠的度数是( )A .40︒B .50︒C .60︒D .70︒【分析】作DG AB ⊥于G ,DH BC ⊥于H ,根据角平分线的性质得到DH DG =,证明Rt DEG Rt DFH ∆≅∆,得到DEG DFH ∠=∠,根据互为邻补角的性质得到答案.【解答】解:作DG AB ⊥于G ,DH BC ⊥于H ,D 是ABC ∠平分线上一点,DG AB ⊥,DH BC ⊥, DH DG ∴=,在Rt DEG ∆和Rt DFH ∆中, DG DHDE DF=⎧⎨=⎩, ()Rt DEG Rt DFH HL ∴∆≅∆,DEG DFH ∴∠=∠,又180DEG BED ∠+∠=︒, 180BFD BED ∴∠+∠=︒,BFD ∴∠的度数18014040=︒-︒=︒,故选:A .2. 已知,如图,ABC ∆中,2C B ∠=∠,12∠=∠,求证:AB AC CD =+.【分析】在AB 上截取AE AC =,由“SAS ”可证ADE ADC ∆≅∆,可证DE DC =,C AED ∠=∠,可证B BDE ∠=∠,可得BE DE DC ==,即结论可得. 【解答】证明:如图,在AB 上截取AE AC =,AE AC =,12∠=∠,AD AD =()ADE ADC SAS ∴∆≅∆DE DC ∴=,C AED ∠=∠, 2C B ∠=∠,AED B BDE ∠=∠+∠,B BDE ∴∠=∠ BE DE DC ∴==,AB AE BE =+, AB AC DC ∴=+。
截长补短问题专题

截长补短问题专项练习1.(2015•河南模拟)如图,梯形ABCD中,AD∥BC,CE⊥AB于E,交梯形的对角线BD于F,连接AF.若△BDC为等腰直角三角形,且∠BDC=90°.求证:CF=AB+AF.2.如图,已知在△ABC中,BD、CE分别是∠ABC、∠AC的平分线,BD、CE相交于点F,且BE+CD=BC.求∠A的度数.3.如图,点P为正方形ABCD边AD上一动点,将△ABP沿BP翻折至△FBP位置,BF延长线交直线CD 于E点(1)若∠ABP=30˚,求证:AP=EC(2)当点P在AD上运动时,试判断线段AP、CE与BE之间的数量关系并证明(3)当点P在AD上运动,BF的延长线交CD边于E点时,记折线PD+DE+EF的长度为l,则l在点P 运动过程中是否保持不变?试判断并证明。
4.(2019秋•江汉区期中)已知,点A(t,1)是平面直角坐标系中第一象限的点,点B,C分别是y轴负半轴和x轴正半轴上的点,连接AB,AC,BC.(1)如图1,若OB=1,OC=,且A,B,C在同一条直线上,求t的值;(2)如图2,当t=1,∠ACO+∠ACB=180°时,求BC+OC﹣OB的值;(3)如图3,点H(m,n)是AB上一点,∠A=∠OHA=90°,若OB=OC,求m+n的值.5.(2018秋•咸安区期末)如图1所示,在Rt△ABC中,∠C=90°,点D是线段CA延长线上一点,且AD=AB,点F是线段AB上一点,连接DF,以DF为斜边作等腰Rt△DFE,连接EA,EA满足条件EA⊥AB.(1)若∠AEF=20°,∠ADE=50°,BC=2,求AB的长度;(2)求证:AE=AF+BC;(3)如图2,点F是线段BA延长线上一点,探究AE、AF、BC之间的数量关系,并证明你的结论.参考答案与试题解析1.【解答】证明:作DH⊥AD交CE于H,如图,∵AD∥BC,∴DH⊥BC,∵△BDC为等腰直角三角形,∴∠3=45°,BD=CD,∴∠4=45°,∴∠3=∠4=∠CDH,∵CE⊥AB,∴∠2+∠BFE=90°,而∠1+∠DFC=90°,∠BFE=∠CFD,∴∠1=∠2,在△CDH和△BDA中,,∴△CDH≌△BDA(ASA),∴CH=BA,DH=DA,在△DHF和△DAF中,∴△DHF≌△DAF(SAS),∴FH=AF,∴CF=CH+FH=AB+AF.2.【解答】解:在BC上截取BF=BD,∵BD+CE=BC,∴CF=CE,∵BE、CD分别是∠ABC、∠ACB的平分线,∴∠1=∠2,∠ECI=∠FCI,在△BDI与△BFI中,,∴△BDI≌△BFI,(SAS),∴∠BFI=∠BDI,同理,∠CFI=∠CEI,∵∠BFI+∠CFI=180°,∴∠BDI+∠CEI=180°,∴∠ADI+∠AEI=180°,∴∠A+∠DIE=180°,∵∠DIE=∠BIC=180°﹣∠2﹣∠ICF=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=180°﹣∠A,∴∠A=60°.3.【解答】解:(1)易证(2)延长DC至点G,使CG=AP,连接BG(3)PD+DE+EF=PD+DE+BE-BF=PD+DE+EC+AP-BF=PD+CD+AP-BF=PD+AP+CD-AD=PD+AP=AD∴保持不变4.【解答】解:(1)过点A作AD⊥x轴于D,如图1所示:∵点A(t,1),∴AD=1,OD=t,∵A,B,C在同一条直线上,∴∠OCB=∠DCA,∵tan∠OCB===,∴tan∠OCB=tan∠DCA==,即=,解得:CD=,∴t=OD=OC+CD=+=3;(2)作AD⊥y轴于D,AM⊥x轴于M,AN⊥BC于N,如图2所示:则∠ADB=∠ANB=90°,∵t=1,∴点A(1,1),∴AD=AM=OM=1,∵∠ACO+∠ACB=180°,∠ACN+∠ACB=180°,∴∠ACO=∠ACN,∵AM⊥x轴于M,AN⊥BC于N,∴AN=AM=AD=1,在Rt△ABD和Rt△ABN中,,∴Rt△ABD≌Rt△ABN(HL),∴BN=BD=OB+1,同理:Rt△ACM≌Rt△ACN(HL),∴CM=CN,∵BC=BN﹣CN,OC=OM+CM=1+CM,∴BC+OC﹣OB=BN﹣CN+1+CM﹣OB=OB+1﹣CN+1+CM﹣OB=2;(3)作OQ⊥CA交CA的延长线于Q,作EH⊥y轴于E,AF⊥x轴交EH的延长线于F,如图3所示:则四边形AQOH是矩形,∴∠QOH=90°=∠BOC,∴∠COQ=∠BOH,又∵∠BHO=∠CQO=90°,OB=OC,∴△OHB≌△OQC(AAS),∴OH=OQ,∴四边形AQOH是正方形,∴OH=AH,∵∠EOH+∠EHO=∠FHA+∠EHO=90°,∴∠EOH=∠FHA,又∵∠OEH=∠HFA=90°,∴△OEH≌△HFA(AAS),∴EH=FA,∴m=1﹣n,∴m+n=1.5.【解答】解:(1)在等腰直角三角形DEF中,∠DEF=90°,∵∠1=20°,∴∠2=∠DEF﹣∠1=70°,∵∠EDA+∠2+∠3=180°,∴∠3=60°,∵EA⊥AB,∴∠EAB=90°,∵∠3+∠EAB+∠A=180°,∴∠4=30°,∵∠C=90°,∴AB=2BC=4;(2)如图1,过D作DM⊥AE于M,在△DEM中,∠2+∠5=90°,∵∠2+∠1=90°,∴∠1=∠5,∵DE=FE,在△DEM与△EFA中,,∴△DEM≌△EFA,∴AF=EM,∵∠4+∠B=90°,∵∠3+∠EAB+∠4=180°,∴∠3+∠4=90°,∴∠3=∠B,在△DAM与△ABC中,,∴△DAM≌△ABC,∴BC=AM,∴AE=EM+AM=AF+BC;(3)如图2,过D作DM⊥AE交AE的延长线于M,∵∠C=90°,∴∠1+∠B=90°,∵∠2+∠MAB+∠1=180°,∠MAB=90°,∴∠2+∠1=90°,∠2=∠B,在△ADM与△BAC中,,∴△ADM≌△BAC,∴BC=AM,∵EF=DE,∠DEF=90°,∵∠3+∠DEF+∠4=180°,∴∠3+∠4=90°,∵∠3+∠5=90°,∴∠4=∠5,在△MED与△AFE中,,∴△MED≌△AFE,∴ME=AF,∴AE+AF=AE+ME=AM=BC,即AE+AF=BC.。
中学考试截长补短专题

截长补短专题1.已知梯形ABCD中,AD // BC, AB=BC=DC,点E、F分别在AD、AB上,且-i -厂二•■匕.2(1)求证:BF=EF - ED;(2)连接AC,若/ B=80,/ DEC=70,求/ ACF 的度数.E2.如图,梯形ABCD 中,AD // BC,点E在BC 上, AE=BE,且AF 丄AB,连接EF. (1 )若EF 丄AF,AF=4,AB=6,求AE 的长.(2)若点F是CD的中点,求证:CE=BE - AD .3.已知,如图,AD // BC , Z ABC=90 , AB=BC,点E 是AB 上的点,/ ECD=45,连接ED,过D 作DF 丄BC 于F.(1 )若/ BEC=75,FC=3,求梯形ABCD的周长.(2)求证:ED=BE+FC .4•如图,等腰梯形ABCD中,AD //BC,AB=DC,E为AD中点,连接BE,CE (1)求证:BE=CE ;(2)若/ BEC=90,过点B作BF丄CD,垂足为点F5.如图,梯形ABCD中, AD// BC, / DCB=45, CD=2 BD! CD。
过点C 作CEL AB于E,交对角线BD于F,点G为BC中点,连结EG AF。
(1)求EG的长;(2)求证:CF=AB+AF6.如图,在正方形ABCD中,点E、F分别在BC、CD上移动,但A到EF的距离AH始终保持与AB长相等,问在E、F移动过程中:(1)Z EAF的大小是否有变化?请说明理由.(2)△ ECF的周长是否有变化?请说明理由.B4.如图,正方形 ABCD 中,P 在对角线BD 上,E 在CB 的延长线上,且 PE=PC ,过点P 作PF 丄AE 于F ,直线PF 分另【J 交 AB 、CD 于G 、H ,(1)求证: DH =AG+BE ;24.如图,在梯形 ABCD 中, AD// BC,Z ABC=90 ,在AB 上,点F 在BC 上,并且 EF / DC(1 )若 AD=3 CG=2 求 CD ;(2)若 CF=AD+BF 求证:EF= CD ⑵若BE=1 , AB=3,求PE 的长.DGL BC 于 G BH 丄 DC 于 H, CH=DH 点E(2)求证:NF =AC BC.如图1,菱形ABCD 中,点E 、F 分别为AB 、AD 的中点,连接 CE 、CF .(1) 求证:CE=CF ;(2) 如图2,若H 为AB 上一点,连接 CH ,使/ CHB=2 / ECB ,求证:CH=AH+AB24. 如图,在直角三角形 ABC 中,D 是斜边 AB 的中点,向外作正方形 DBEF ,正方形 CDMN ,连接 NF ;(1)若.A =20 °,求.CNF 的度数;(沙坪坝区考前模拟6月)24.已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE, DE交AB于F。
专题10:截长补短

专题10:截长补短专题10.1 截长补短--角平分线一.【知识要点】1.截长补短(截长法,补短法)是证明线段和差问题的基本方法:有一类几何题其命题主要是证明三条线段长度的“和”或“差”及其比例关系。
这一类题目一般可以采取“截长”或“补短”的方法来进行求解。
所谓“截长”,就是将三者中最长的那条线段一分为二,使其中的一条线段与已知线段相等,然后证明其中的另一段与已知的另一段的大小关系。
所谓“补短”,就是将一个已知的较短的线段延长至与另一个已知的较短的长度相等。
然后求出延长后的线段与最长的已知线段的关系。
有的是采取截长补短后,使之构成某种特定的三角形进行求解。
二.【经典例题】1、如图,已知AD∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求证:AD+BC=AB.2、如图,△ABC中,AB>AC,AD是∠BAC的平分线,点P是线段AD上异于A,D的任意一点,则AB+PC与AC+PB的大小关系是( )A. AB+PC>AC+PBB. AB+PC<AC+PBC.AB+PC=AC+PBD.不确定三.【练习】1.如图,过线段AB的两个端点作射线AM、BN,使AM∥BN,按下列要求画图并回答:画∠MAB、∠NBA的平分线交于E。
(12分)(1)∠AEB是什么角?(2)过点E作一直线交AM于D,交BN于C,观察线段DE、CE,你有何发现?(3)无论DC的两端点在AM、BN如何移动,只要DC经过点E,①AD+BC=AB;②AD+BC=CD 谁成立?并说明理由。
2.如图,P为△ABC内的点,连CP、BP、AP,∠PBA=30°,PC平分∠BCA,∠BPC =150°,求证:BC=AC+PA.一.【知识要点】1.截长补短(截长法,补短法)是证明线段和差问题的基本方法。
二.【经典例题】 1.已知:如图,△ABC 中,∠C=2∠B ,∠1=∠2,求证:AB=AC+CD .三、【练习】1.如图,△ABC 中,AD 是∠CAB 的平分线,且AB=AC+CD ,求证:∠C=2∠B2.已知正方形ABCD 中,M 为CD 的中点,E 为MC 上一点,且∠BAE =2∠DAM .求证:AE =BC +CE .M ED CBA一.【知识要点】半角模型:若一个角等于整个角的一半,往往通过旋转将两个角搬到一起从而产生全等转化问题.有公共顶点,锐角等于较大角的一半,且组成这个较大角的两边相等,通过翻折或旋转,将角的倍分关系转化为角的相等关系,并进一步构造全等或相似三角形,弱化条件,变更载体,而构建模型,可把握问题的本质。
初中经典几何模型01-截长补短模型证明问题

初中经典几何模型专题01 截长补短模型证明问题【专题说明】截长补短法在初中几何教学中有着十分重要的作用,它主要是用来证线段的和差问题,而且这种方法一直贯穿着整个几何教学的始终.那么什么是截长补短法呢?所谓截长补短其实包含两层意思,即截长和补短.截长就是在较长的线段上截取一段等于要证的两段较短的线段中的一段,证剩下的那一段等于另外一段较短的线段.当条件或结论中出现a+b=c时,用截长补短.【知识总结】1、补短法:通过添加辅助线“构造”一条线段使其为求证中的两条线段之和,在证所构造的线段和求证中那一条线段相等;2、截长法:通过添加辅助线先在求证中长线段上截取与线段中的某一段相等的线段,在证明截剩部分与线段中的另一段相等。
3、截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,使之与特定线段相等,再利用三角形全等有关性质加以说明,这种做法一般遇到证明三条线段之间关系时常用。
如图1,若证明线段AB,CD,EF之间存在EF=AB+CD,可以考虑截长补短法截长法:如图2,在EF上截取EG=AB,在证明GF=CD即可;补短法:如图3,延长AB至H点,使BH=CD,再证明AH=EF即可.【类型】一、截长“截长”是指在较长的线段上截取另外两条较短的线段,截取的作法不同,涉及四种方法。
【类型】二、补短“补短”指的是选取两条较短线段中的一条进行延长,使得较短的两条线段共线并寻求解题突破,根据辅助线作法的不同也涉及四种不同的方法。
【基础训练】1、如图,AC平分∠BAD,CE⊥AB于点E,∠B+∠D=180°,求证:AE=AD+BE.2、如图,已知在△ABC中,∠C=2∠B,∠1=∠2,求证:AB=AC+CD3、如图,在五边形ABCDE中,AB=AE,BC+DE=CD,∠B+∠E=180°,求证:AD平分∠CDE.4、已知四边形ABCD中,∠ABC+∠ADC=180°,AB=BC如图2,点P,Q分别在线段AD,DC上,满足PQ=AP+CQ,∠ADC求证:∠PBQ=90°-125、如图,在△ABC中,∠B=60°,△ABC的角平分线AD、CE相交于点O,求证:AE+CE=AC.6、如图所示,AB∥CD,BE,CE分别是∠ABC,∠BCD的平分线,点E在AD上,求证:BC=AB+CD.7、四边形ABCD中,BD>AB,AD=DC,DE⊥BC,BD平分∠ABC (1)证明:∠BAD+∠BCD=180°(2)DE=3,BE=6,求四边形ABCD的面积.8、已知:在△ABC中,AB=CD-BD,求证:∠B=2∠C.9、如图,△ABC中,BD⊥AC于点D,CE⊥AB于点E,且BD,CE交于点F,点G是线段CD上一点,连接AF,GF,若AF=GF,BD=CD.(1)求∠CAF的度数(2)判断线段FG与BC的位置关系,并说明理由.【巩固提升】1.如图,在△ABC中,∠A=60°,BD,CE分别平分∠ABC和∠ACB,BD,CE交于点O,试判断BE,CD,BC的数量关系,并加以证明.2.如图,AD//BC,DC⊥AD,AE平分∠BAD,E是DC的中点.问:AD,BC,AB之间有何关系?并说明理由.3.如图,已知DE=AE,点E在BC上,AE⊥DE,AB⊥BC,DC⊥BC,请问线段AB,CD和线段BC有何大小关系?并说明理由.4.如图,AB∥CD,B E,CE分别是∠ABC和∠BCD的平分线,点E在AD上.求证:BC=AB+CD.5.如图,在R t△ABC中,∠C=90°,BC=AC,∠B=∠CAB=45°,AD平分∠BAC交BC于D,求证:AB=AC+CD.6.如图,在△ABC中,∠ABC=60°,AD,CE分别平分∠BAC,∠ACB,AD,CE交于O.(1)求∠AOC的度数;(2)求证:AC=AE+CD.专题01 截长补短模型证明问题【专题说明】截长补短法在初中几何教学中有着十分重要的作用,它主要是用来证线段的和差问题,而且这种方法一直贯穿着整个几何教学的始终.那么什么是截长补短法呢?所谓截长补短其实包含两层意思,即截长和补短.截长就是在较长的线段上截取一段等于要证的两段较短的线段中的一段,证剩下的那一段等于另外一段较短的线段.当条件或结论中出现a+b=c时,用截长补短.【知识总结】1、补短法:通过添加辅助线“构造”一条线段使其为求证中的两条线段之和,在证所构造的线段和求证中那一条线段相等;2、截长法:通过添加辅助线先在求证中长线段上截取与线段中的某一段相等的线段,在证明截剩部分与线段中的另一段相等。
专题.截长补短
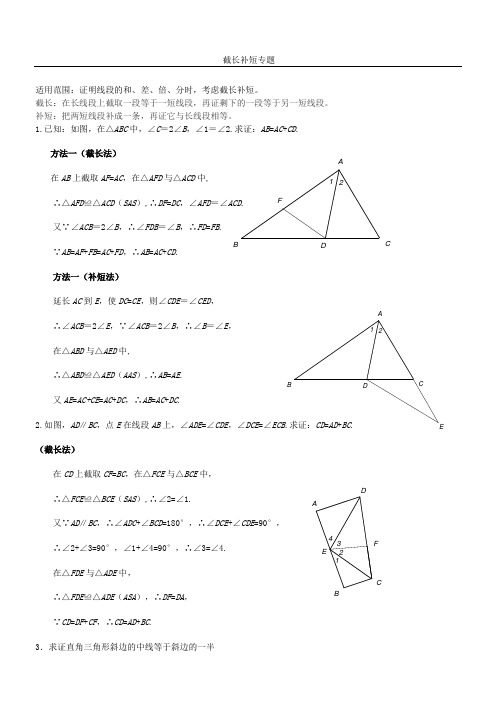
截长补短专题适用范围:证明线段的和、差、倍、分时,考虑截长补短。
截长:在长线段上截取一段等于一短线段,再证剩下的一段等于另一短线段。
补短:把两短线段补成一条,再证它与长线段相等。
1.已知:如图,在△ABC 中,∠C =2∠B ,∠1=∠2.求证:AB =AC +CD .方法一(截长法)在AB 上截取AF =AC ,在△AFD 与△ACD 中,∴△AFD ≌△ACD (SAS ),∴DF =DC ,∠AFD =∠ACD . 又∵∠ACB =2∠B ,∴∠FDB =∠B ,∴FD =FB . ∵AB =AF +FB =AC +FD ,∴AB =AC +CD . 方法一(补短法)延长AC 到E ,使DC =CE ,则∠CDE =∠CED ,∴∠ACB =2∠E ,∵∠ACB =2∠B ,∴∠B =∠E , 在△ABD 与△AED 中,∴△ABD ≌△AED (AAS ),∴AB =AE .又AE =AC+CE =AC +DC ,∴AB =AC +DC .2.如图,AD ∥BC ,点E 在线段AB 上,∠ADE =∠CDE ,∠DCE =∠ECB .求证:CD =AD +BC . (截长法)在CD 上截取CF =BC ,在△FCE 与△BCE 中, ∴△FCE ≌△BCE (SAS ),∴∠2=∠1.又∵AD ∥BC ,∴∠ADC +∠BCD =180°,∴∠DCE +∠CDE =90°,∴∠2+∠3=90°,∠1+∠4=90°,∴∠3=∠4. 在△FDE 与△ADE 中,∴△FDE ≌△ADE (ASA ),∴DF =DA , ∵CD =DF +CF ,∴CD =AD +BC .3.求证直角三角形斜边的中线等于斜边的一半FDCB A 12EDCBA12ADBCEF12344.在三角形ABC中。
BD,CE分别是∠ABC和∠ACB的平分线。
BE+CD=BC.求∠A度数。
专题02 截长补短证全等(解析版)

专题02 截长补短证全等类型一 截长证全等1.如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .【答案】证明见解析【解析】【分析】如图,在AB 上截取,AH AD =证明,ADE AHE ≌再证明,HBE CBE ≌可得,BC BH = 从而可得结论.【详解】证明:如图,在AB 上截取,AH AD =AE ∵平分,DAB ∠,DAE HAE ∴∠=∠,AE AE =,ADE AHE ∴≌,ADE AHE ∴∠=∠//,AD BC180,ADE BCE ∴∠+∠=︒180,AHE BHE ∠+∠=︒,BCE BHE ∴∠=∠ BE 平分,ABC ∠,ABE CBE ∴∠=∠,BE BE =,HBE CBE ∴≌,BC BH ∴=,AB AH HB =+.AB AD BC ∴=+【点睛】本题考查的是全等三角形的判定与性质,掌握“利用截长补短的方法证明两条线段的和等于另一条线段”是解题的关键.2.如图,已知:在ABC 中,60B ∠=︒,CE 、AF 是ABC 的角平分线,交于点O 求证:AC AE CF =+.【答案】见解析【解析】【分析】在AC 上取一点H ,使AH =AE ,根据角平分线的定义可得∠EAO =∠HAO ,然后利用“边角边”证明△AEO 和△AHO 全等,根据全等三角形对应角相等可得∠AE 0=∠AHO ,根据角平分线的定义可得∠1=∠2,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠3=60°,再根据角平分线的定义和三角形的内角和定理求出∠4=60°,从而得到∠3=∠4,然后利用“边角边”证明△CFO 和△CHO 全等,根据全等三角形对应边相等可得CF =CH ,再根据AC =AH +CH 代换即可得证.【详解】证明:如图,在AC 上取一点H ,使AH AE =,连接OH .∵AF 是ABC 的角平分线,∴EAO HAO ∠=∠,在AEO △和AHO 中,∵,,,AE AH EAO HAO AO AO =⎧⎪∠=∠⎨⎪=⎩∴()AEO AHO SAS ≌,∴AEO AHO ∠=∠,∵CE 是ABC 的角平分线,∴12∠=∠,∵13,2AHO B AEO ∠+∠=∠∠+∠=∠,∴360B ∠=∠=︒,∵CE 、AF 是ABC 的角平分线, ∴114118018060602(2)()CAF B ∠=∠+∠=︒-∠=⨯︒-︒=︒, ∴34∠=∠,在CFO △和CHO 中,21,,43,CO CO ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()CFO CHO ASA ≌,∴CF CH =,∵AC AH CH =+,∴AC AE CF =+.【点睛】本题考查了全等三角形的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,三角形内角和定理,利用“截长补短”法作辅助线构造出全等三角形是解题的关键.3.如图所示,已知△ABC中AB>AC,AD是∠BAC的平分线,M是AD上任意一点,求证:MB-MC<AB-AC.【答案】见解析【解析】【分析】法一:因为AB>AC,所以在AB上截取线段AE=AC,则BE=AB-AC,连接EM,在△BME 中,显然有MB-ME<BE,再证明ME=MC,则结论成立.法二:延长AC至H,在AH上截取线段AB=AG,证明△ABM≌△AGM,得到BM=GM,根据三角形的三边关系即可求解.【详解】证明:法一:在AB上截取AE=AC,连接ME,在△MBE中,MB-ME<BE(三角形两边之差小于第三边),∵AD是∠BAC的平分线,∴BAD CAD∠=∠,在△AMC和△AME中,∵AC AE CAM EAM AM AM =⎧⎪∠=∠⎨⎪=⎩∴△AMC ≌△AME (SAS ),∴MC =ME (全等三角形的对应边相等).又∵BE =AB -AE ,∴BE =AB -AC ,∴MB -MC <AB -AC .法二:延长AC 至H ,在AH 上截取线段AB =AG ,同理可证得△ABM ≌△AGM (SAS ),∴BM =GM ,∵在△MCG 中MG -MC <CG∴MB -MC <AG -AC = AB -AC即MB -MC <AB -AC .【点睛】本题考查全等三角形的判定和性质,三角形三边关系以及截长补短法,解题关键是作辅助线构造全等三角形.4.如图,120CAB ABD ∠+∠=︒,AD 、BC 分别平分CAB ∠、ABD ∠,AD 与BC 交于点O .(1)求AOB ∠的度数;(2)说明AB AC BD =+的理由.【答案】(1)120°;(2)见解析【解析】【分析】(1)根据角平分线的定义可得∠OAB +∠OBA =60°,从而得到∠AOB ;(2)在AB 上截取AE =AC ,证明△AOC ≌△AOE ,得到∠C =∠AEO ,再证明∠C +∠D =180°,从而推出∠BEO =∠D ,证明△OBE ≌△OBD ,可得BD =BE ,即可证明AC +BD = A B .【详解】解:(1)∵AD ,BC 分别平分∠CAB 和∠ABD ,∠CAB +∠ABD =120°,∴∠OAB +∠OBA =60°,∴∠AOB =180°-60°=120°;(2)在AB 上截取AE =AC ,∵∠CAO =∠EAO ,AO =AO ,∴△AOC ≌△AOE (SAS ),∴∠C =∠AEO ,∵∠C +∠D =(180°-∠CAB -∠ABC )+(180°-∠ABD -∠BAD )=180°,∴∠AEO +∠D =180°,∵∠AEO +∠BEO =180°,∴∠BEO =∠D ,又∠EBO =∠DBO ,BO =BO ,∴△OBE ≌△OBD (AAS ),∴BD =BE ,又AC =AE ,∴AC +BD =AE +BE =A B .【点睛】本题考查了角平分线的定义,三角形内角和,全等三角形的判定和性质,解题的关键是截取AE =AC ,利用全等三角形的性质证明结论.5.如图所示,已知AC 平分∠BAD ,180B D ∠+∠=︒,CE AB ⊥于点E ,判断AB 、AD 与BE 之间有怎样的等量关系,并证明.【答案】2AB AD BE =+,证明见解析【解析】【分析】在AB 上截取EF ,使EF=BE ,联结CF .证明()BCE ECF SAS ≌,得到B BFC ∠=∠,又证明 AFC ADC ≌,得到AF AD =,最后结论可证了. 【详解】证明:在AB 上截取EF ,使EF=BE ,联结CF .CE AB ⊥90BEC FEC ∴∠=∠=︒在BCE 和ECF △BE EF BEC FEC CE CE =⎧⎪∠=∠⎨⎪=⎩()BCE ECF SAS ∴≌ B BFC ∴∠=∠180B D ∠+∠=︒180BFC AFC ∠+∠=︒又D AFC ∴∠=∠AC 平分∠BADFAC DAC ∴∠=∠在AFC △ 和ADC 中AFC D FAC DAC AC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩() AFC ADC AAS ∴≌AF AD ∴=AB AF BE EF =++2AB AD BE ∴=+【点睛】本题考查三角形全等知识的综合应用,关键在于寻找全等的条件,作适当的辅助线加以证明.6.已知△ABC 中,AB =AC ,∠A =108°,BD 平分∠ABC ,求证:BC =AC +CD .【答案】见解析【解析】【分析】在线段BC 上截取BE =BA ,连接DE .则只需证明CD =CE 即可.结合角度证明∠CDE =∠CED .【详解】证明:在线段BC 上截取BE =BA ,连接DE .∵BD 平分∠ABC ,∴∠ABD =∠EBD 12=∠ABC . 在△ABD 和△EBD 中,BE BA ABD EBD BD BD =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△EBD .(SAS )∴∠BED =∠A =108°,∠ADB =∠EDB .又∵AB =AC ,∠A =108°,∠ACB =∠ABC 12=⨯(180°﹣108°)=36°, ∴∠ABD =∠EBD =18°.∴∠ADB =∠EDB =180°﹣18°﹣108°=54°.∴∠CDE =180°﹣∠ADB ﹣∠EDB=180°﹣54°﹣54°=72°.∴∠DEC =180°﹣∠DEB=180°﹣108°=72°.∴∠CDE =∠DEC .∴CD =CE .∴BC =BE +EC =AB +CD .【点睛】本题考查全等三角形的判定和性质,等腰三角形的判定,添加恰当辅助线是本题的关键. 7.已知:如图,2AB AC =,BAD CAD ∠=∠,DA DB =,求证:90ACD ∠=︒.【答案】详见解析【解析】【分析】由于DA=DB ,想到作DE ⊥AB ,构造直角∠AED ,只需要证明∠ACD=∠AED ,本题就得解.从而转化为说明△AED ≌△ACD 的问题.【详解】如图所示,作DE ⊥AB 于E ,∵DA=DB ,DE ⊥AB ,∴AE=EB=12AB ,∠AED=90°,∵AB=2AC ,∴AC=12AB ,∴AC=AE ,在△ACD 和△AED 中,∵AC=AE ,∠2=∠1,AD=AD ,∴△ACD ≌△AED(SAS),∴∠ACD=∠AED=90°.【点睛】本题考查了全等三角形的判定和性质;解题时主要运用了全等三角形问题中常用辅助线-截长补短,通过辅助线构造全等三角形,再利用全等三角形的性质解题,这是一种非常重要的方法,注意掌握.8.如图,AD BC ∥,DC AD ⊥,AE 平分BAD ∠,且E 是DC 中点试问:AD 、BC 和AB 之间有何关系?并说明理由.【答案】详见解析【解析】【分析】AD+BC=AB ,理由如下:如图,在AB 上截取AF AD =,证明()R t t BEF BEC HL ∆∆≌R ,可得BF=BC ,继而可得答案.【详解】AD+BC=AB ,理由如下:如图,在AB 上截取AF AD =,AE ∵平分BAD ∠,BAE EAD ∴∠=∠,AE AE =,EAF EAD ∴∆∆≌,EF ED ∴=,90AFE ADE ∠=∠=︒,∴∠BFE=90°,AD BC ∵∥,90BCE ADE ∴∠=∠=︒,90BFE BCE ∴∠=∠=︒, E 是DC 中点,ED CE ∴=,EF EC ∴=,又BE BE =,()R t t BEF BEC HL ∴∆∆≌R ,BF BC ∴=,AD BC AF BF AB∴+=+=.【点睛】本题考查了全等三角形的判定与性质,利用角平分线这一条件,在角两边截取相等线段构建全等三角形,实现截长补短见是解题的关键.∠外角的平分线于F.9.如图,正方形ABCD中,E是BC的中点,EF AE⊥交DCE(1)求证:AE EF=;=是否仍然成立?若成立,(2)如图,当E是BC上任意一点,而其它条件不变,AE EF请证明,若不成立,请说明理由.【答案】(1)见解析;(2)成立,证明见解析【解析】【分析】AHE ECF,(1)取AB的中点H,连接EH,根据已知及正方形的性质利用ASA判定≅=;从而得到AE EF(2)成立,在AB上取BH BE=,连接EH,根据已知及正方形的性质利用ASA判定AHE ECF,从而得到AE EF≅=.【详解】(1)证明:取AB的中点H,连接EH,如图;ABCD是正方形,AE EF ⊥;190AEB ∴+=︒∠∠,290AEB ∠+∠=︒12∠∠∴=,BH BE =,∴45BHE ∠=︒,又∵45FCG ∠=︒,135AHE ECF ∴==︒∠∠,在AHE 和ECF △中12AH ECAHE ECF ∠=∠⎧⎪=⎨⎪∠=∠⎩, AHE ECF ∴≅△△,AE EF ∴=;(2)解:成立.在AB 上取BH BE =,连接EH ,如图,ABCD 为正方形,AB BC ∴=,,AH EC ∴=,45BHE BEH ∠=∠=︒,又∵45FCG ∠=︒,∴135∠=∠=︒AHE ECF ,在AHE 和ECF △中12AH ECAHE ECF ∠=∠⎧⎪=⎨⎪∠=∠⎩, AHE ECF ∴≅△△,AE EF ∴=.【点睛】此题考查了学生对正方形的性质及全等三角形判定的理解及运用,解题关键是构造≅AHE ECF .类型二 补短证全等10.已知:如图所示,在ABC ∆中,AD 为中线,BF 交,AD AC 分别于,E F ,如果BE AC =,求证:AF EF = .【答案】详见解析【解析】【分析】根据点D 是BC 的中点,延长AD 到点G ,得到BDE CDG ∆∆≌,利用全等三角形的对应角相等,对应边相等进行等量代换,得到△AEF 中的两个角相等,然后用等角对等边证明AE 等于EF .【详解】证明:延长ED 至G ,使DG DE =,连结GC ,∵在ABC ∆中,AD 为中线,∴BD=CD ,在△ADC 和△GDB 中,BD CD BDE CDG DE DG =⎧⎪∠=∠⎨⎪=⎩∴BDE CDG ∆∆≌,BE CG ∴=,BED CGD ∠=∠,BE AC =,AC GC ∴=,AGC CAG ∴∠=.又BED AEF ∠=∠,∴AEF EAF ∠=∠,∴AF EF =.【点睛】本题考查全等三角形的判定与性质,解题的关键是通过作辅助线构建全等三角形. 11.如图,在△ABC 中,AB AC =,D 是三角形外一点,且60ABD ∠=︒,BD DC AB +=.求证:60ACD ∠=︒【答案】见解析【解析】【分析】首先延长BD 至E ,使CD =DE ,连接AE ,AD ,由BD +DC =AB ,易得△ABE 是等边三角形,继而证得△ACD ≌△ADE ,则可证得:∠ACD =∠E =60°.【详解】延长BD 至E ,使CD DE =,连接AE ,AD ,∵BD CD AB +=,BE BD DE =+,∴BE AB =,∵60ABD ∠=︒,∴△ABE 是等边三角形,∴AE AB AC ==,60E ∠=︒,在△ACD 和△ADE 中,AC AE CD DE AD AD =⎧⎪=⎨⎪=⎩,∴△ACD ≌△ADE (SSS ),∴60ACD E ∠=∠=︒.【点睛】此题考查了等边三角形的判定与性质以及全等三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.12.在ABC 中,60ABC ∠=︒,点D 、E 分别在AC 、BC 上,连接BD 、DE 和AE ;并且有AB BE =,AED C ∠=∠.(1)求CDE ∠的度数;(2)求证:AD DE BD +=.【答案】(1)60︒;(2)见解析【解析】【分析】(1)由AB BE =,60ABC ∠=︒,可得ABE △为等边三角形,由AEB EAC C ∠=∠+∠,CDE EAC AED ∠=∠+∠,AED C ∠=∠,可证60CDE AEB ∠=∠=︒(2)延长DA 至F ,使AF DE =,连接FB , 由60BED AED ∠=︒+∠,60BAF C ∠=︒+∠,且C AED ∠=∠,可证()FBA DBE SAS ≌ 由=DB FB ,可证FBD 为等边三角形,可得BD FD =, 可推出结论,【详解】解:(1)∵AB BE =,60ABC ∠=︒,∴ABE △为等边三角形,∴60BAE AEB ∠=∠=︒,∵AEB EAC C ∠=∠+∠,CDE EAC AED ∠=∠+∠,∵AED C ∠=∠,∴60CDE AEB ∠=∠=︒(2)如图,延长DA 至F ,使AF DE =,连接FB ,由(1)得ABE △为等边三角形,∴60AEB ABE ∠=∠=︒,∵60BED AEB AED AED ∠=∠+∠=︒+∠,又∵60BAF ABE C C ∠=∠+∠=︒+∠,且C AED ∠=∠,∴BED BAF ∠=∠,在FBA 与DBE 中,AB BE BAF BED AF DE =⎧⎪∠=∠⎨⎪=⎩∴()FBA DBE SAS ≌∴=DB FB ,DBE FBA ∠=∠∴DBE ABD FBA ABD ∠+∠=∠+∠,∴60ABE FBD ∠=∠=︒又∵=DB FB ,∴FBD 为等边三角形∴BD FD =,又∵FD AF AD =+,且AF DE =,∴FD DE AD BD =+=,【点睛】本题考查等边三角形的判定与性质,三角形全等判定与性质,线段和差,三角形外角性质,关键是引辅助线构造三角形全等证明等边三角形.13.如图,四边形ABCD 中,180B D ∠+∠=︒, 150BCD ∠=︒,CB CD =,M 、N 分别为AB 、AD 上的动点,且75MCN ∠=︒.求证: MN BM DN =+.【答案】见解析【解析】【分析】延长AB 至点E ,使得BE DN =,连接CE ,根据同角的补角相等得CBE CDN ∠=∠,根据SAS 证明CBE CDN ∆≅∆,则BCE DCN ∠=∠,进而证明75ECM MCN ∠=∠=︒,根据SAS证明ECM NCM∆≅∆,得到MN ME =,则M N BM BE BM DN =+=+. 【详解】证明:延长AB 至点E ,使得BE DN =,连接CE ,四边形ABCD 中,180B D ∠+∠=︒,180ABC CBE ∠+∠=︒,CBE CDN ∴∠=∠,在CBE ∆和CDN ∆中,CB CD CBE CDN BE DN =⎧⎪∠=∠⎨⎪=⎩,()CBE CDN SAS ∴∆≅∆,BCE DCN ∴∠=∠,CN CE =,150BCD ∠=︒,75MCN ∠=︒,75M CE M CB BCE M CB DCN ∴∠=∠+∠=∠+∠=︒,MCN MCE ∴∠=∠,在ECM ∆和NCM ∆中,MC MC MCN MCE CN CE =⎧⎪∠=∠⎨⎪=⎩,()ECM NCM SAS ∴∆≅∆,M N M E BM BE BM DN ∴==+=+.【点睛】本题主要考查了全等三角形的判定与性质,作辅助线构造全等三角形是解决问题的关键. 14.本学期,我们学习了三角形相关知识,而四边形的学习,我们一般通过辅助线把四边形转化为三角形,通过三角形的基本性质和全等来解决一些问题.(1)如图1,在四边形ABCD 中,AB AD =,180B D ∠+∠=︒,连接AC .①小明发现,此时AC 平分BCD ∠.他通过观察、实验,提出以下想法:延长CB 到点E ,使得BE CD =,连接AE ,证明ABE ADC △≌△,从而利用全等和等腰三角形的性质可以证明AC 平分BCD ∠.请你参考小明的想法,写出完整的证明过程.②如图2,当90BAD ∠=︒时,请你判断线段AC ,BC ,CD 之间的数量关系,并证明. (2)如图3,等腰CDE △、等腰ABD △的顶点分别为A 、C ,点B 在线段CE 上,且180ABC ADC ∠+∠=︒,请你判断DAE ∠与DBE ∠的数量关系,并证明.【答案】(1)①见解析;②CD BC +=,证明见解析;(2)2DAE DBE ∠=∠,证明见解析【解析】【分析】(1)①参考小明的想法,延长CB 到点E ,使得BE CD =,连接AE ,证明ABE ADC △≌△,从而利用全等和等腰三角形的性质可以证明AC 平分;②沿用①中辅助线,延长CB 到点E ,使得BE CD =,连接AE ,证得直角三角形CAE ,再利用勾股定理可求得AC ,BC ,CD 之间的数量关系;(2)类比(1)中证明的思路,延长CD 至F ,使得DF CB =,连AF ,证明ABC ADF ≌△△、ACD ACE ≌,再利用全等三角形的对应角相等和等腰三角形等边对等角的性质,找到DAE ∠与DBE ∠的数量关系.【详解】(1)如图,延长CB 到点E ,使得BE CD =,连接AE .180ADC ABC ∠+∠=︒,180ABE ABC ∠+∠=︒,ADC ABE ∴∠=∠在ADC 与ABE △中,AD AB ADC ABE CD EB =⎧⎪∠=∠⎨⎪=⎩()ADC ABE SAS ∴△≌△ACD AEB ∴∠=∠,AC AE =ACB AEB ∴∠=∠ACD ACB ∴∠=∠.AC ∴平分BCD ∠(2)CD BC +=证明:如图,延长CB 到点E ,使得BE CD =,连接AE .由(1)知,(SAS)ADC ABE ≌DAC BAE ∴∠=∠,AC AE =90BAD DAC CAB ∠=∠+∠=︒90CAE BAE CAB DAC CAB BAD ∴∠=∠+∠=∠+∠=∠=︒在直角三角形CAE 中,90CAE ∠=︒CE ∴=CD BC ∴+=(3)2DAE DBE ∠=∠证明:如图,延长CD 至F ,使得DF CB =,连AF ,由(1)知,()ABC ADF SAS △≌△AF AC ∴=,ACB F ∠=∠ACD F ∴∠=∠ACD ACE ∴∠=∠在ACD △与ACE 中,CD CE ACD ACE AC AC =⎧⎪∠=∠⎨⎪=⎩()ACD ACE SAS ∴△≌△AD AE ∴=AD AE AB ∴==ADB ABD ∴∠=∠,AEB ABE ∠=∠1802BAD ADB ∴∠=︒-∠,1802BAE ABE ∠=︒-∠,360DAE BAD BAE ∠=︒-∠-∠()()36018021802DAE ADB ABE ∴∠=︒-︒-∠-︒-∠22ADB ABE =∠+∠2DBE =∠【点睛】本题考查三角形的基本知识、全等三角形的性质和判定以及等腰三角形的性质与判定.综合性较强.15.已知在四边形ABCD 中,∠ABC +∠ADC =180°,∠BAD +∠BCD =180°,AB =BC (1)如图1,连接BD ,若∠BAD =90°,AD =7,求DC 的长度.(2)如图2,点P 、Q 分别在线段AD 、DC 上,满足PQ =AP +CQ ,求证:∠PBQ =∠ABP +∠QBC(3)若点Q 在DC 的延长线上,点P 在DA 的延长线上,如图3所示,仍然满足PQ =AP +CQ ,请写出∠PBQ 与∠ADC 的数量关系,并给出证明过程.【答案】(1)7DC =;(2)见解析;(3)1902PBQ ADC ∠=︒+∠,证明见解析 【解析】【分析】(1)根据已知条件得出BDC 为直角三角形,再根据HL 证出△≌△Rt BAD Rt BCD ,从而证出AD CD =即可得出结论;(2)如图2,延长DC 到 K ,使得CK=AP ,连接BK ,通过证△BPA ≌△BCK (SAS )得到:∠1=∠2,BP=BK .然后根据SSS 证明得≌PBQ BKQ ,从而得出21PBQ CBQ CBQ ∠=∠+∠=∠+∠,然后得出结论;(3)如图3,在CD 延长线上找一点K ,使得KC=AP ,连接BK ,构建全等三角形:△BPA ≌△BCK (SAS ),由该全等三角形的性质和全等三角形的判定定理SSS 证得:△PBQ ≌△BKQ ,则其对应角相等:∠PBQ=∠KBQ ,结合四边形的内角和是360°可以推得:∠PBQ=90°+12∠ADC .【详解】(1)证明:如图1,∵180ABC ADC ∠+∠=︒,90BAD ∠=︒,∴90BCD BAD ∠=∠=︒,在Rt BAD 和Rt BCD 中,BD BD AB BC =⎧⎨=⎩∴()△≌△Rt BAD Rt BCD HL ,∴AD DC =,∴7DC =;(2)如图2,延长DC 至点K ,使得CK AP =,连接BK∵180ABC ADC ∠+∠=︒,∴180BAD BCD ∠+∠=︒,∵180BCD BCK ∠+∠=︒,∴BAD BCK ∠=∠,∵AP CK =,AB BC =,∴()△≌△BPA BCK SAS ,∴12∠=∠,BP BK =,∵PQ AP CQ =+,QK CK CQ =+,∴PQ QK =,∵BP BK =,BQ BQ =,∴()≌PBQ BKQ SSS ,∴21PBQ CBQ CBQ ∠=∠+∠=∠+∠,∴PBQ ABP QBC ∠=∠+∠;(3)1902PBQ ADC ∠=︒+∠; 如图3,在CD 延长线上找一点K ,使得KC AP =,连接BK ,∵180ABC ADC ∠+∠=︒,∴180BAD BCD ∠+∠=︒,∵180BAD PAB ∠+∠=︒,∴PAB BCK ∠=∠,在BPA △和BCK 中,AP CK BAP BCK AB BC =⎧⎪∠=∠⎨⎪=⎩∴()△≌△BPA BCK SAS ,∴ABP CBK ∠=∠,BP BK =,∴PBK ABC ∠=∠,∵PQ AP CQ =+,∴PQ QK =,在PBQ △和BKQ 中,BP BK BQ BQ PQ KQ =⎧⎪=⎨⎪=⎩∴()≌PBQ BKQ SSS ,∴PBQ KBQ ∠=∠,∴22360PBQ PBK PBQ ABC ∠+∠=∠+∠=︒,∴()2180360PBQ ADC ∠+︒-∠=︒, ∴1902PBQ ADC ∠=︒+∠.【点睛】本题考查了全等三角形的判定与性质.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.类型三 截长补短证全等16.(1)阅读理解:问题:如图1,在四边形ABCD 中,对角线BD 平分ABC ∠,180A C ∠+∠=︒.求证:DA DC =.思考:“角平分线+对角互补”可以通过“截长、补短”等构造全等去解决问题.方法1:在BC 上截取BM BA =,连接DM ,得到全等三角形,进而解决问题; 方法2:延长BA 到点N ,使得BN BC =,连接DN ,得到全等三角形,进而解决问题. 结合图1,在方法1和方法2中任选一种....,添加辅助线并完成证明. (2)问题解决:如图2,在(1)的条件下,连接AC ,当60DAC ∠=︒时,探究线段AB ,BC ,BD 之间的数量关系,并说明理由;(3)问题拓展:如图3,在四边形ABCD 中,180A C ∠+∠=︒,DA DC =,过点D 作DE BC ⊥,垂足为点E ,请直接写出线段AB 、CE 、BC 之间的数量关系.【答案】(1)证明见解析;(2)AB BC BD +=;理由见解析;(3)2BC AB CE -=.【解析】【分析】(1)方法1:在BC 上截取BM BA =,连接DM ,得到全等三角形,进而解决问题;方法2:延长BA 到点N ,使得BN BC =,连接DN ,得到全等三角形,进而解决问题; (2)延长CB 到点P ,使BP BA =,连接AP ,证明ΔΔPAC BAD ≌,可得PC BD =,即PC BP BC AB BC =+=+(3)连接BD ,过点D 作DF AC ⊥于F ,证明ΔΔDFA DEC ≌,Rt ΔRt ΔBDF BDE ≌,进而根据2BC BE CE BA AF CE BA CE =+=++=+即可得出结论.【详解】解:(1)方法1:在BC 上截BM BA =,连接DM ,如图. BD 平分ABC ∠,ABD CBD ∴∠=∠.在ΔABD 和ΔMBD 中,BD BD ABD MBD BA BM =⎧⎪∠=∠⎨⎪=⎩,ΔΔABD MBD ∴≌,A BMD ∴∠=∠,AD MD =.180BMD CMD ︒∠+∠=,180C A ︒∠+∠=.C CMD ∴∠=∠.DM DC ∴=,DA DC ∴=.方法2:延长BA 到点N ,使得BN BC =,连接DN ,如图.BD 平分ABC ∠,NBD CBD ∴∠=∠.在ΔNBD 和ΔCBD 中,BD BD NBD CBD BN BC =⎧⎪∠=∠⎨⎪=⎩,ΔΔNBD CBD ∴≌.BND C ∴∠=∠,ND CD =.180NAD BAD ︒∠+∠=,180C BAD ︒∠+∠=.BND NAD ∴∠=∠,DN DA ∴=,DA DC ∴=.(2)AB 、BC 、BD 之间的数量关系为:AB BC BD +=.(或者:BD CB AB -=,BD AB CB -=).延长CB 到点P ,使BP BA =,连接AP ,如图2所示.由(1)可知AD CD =,60DAC ︒∠=.ΔADC ∴为等边三角形.AC AD ∴=,60ADC ︒∠=.180BCD BAD ︒∠+∠=,36018060120ABC ︒︒︒︒∴∠=--=.18060PBA ABC ︒︒∴∠=-∠=.BP BA =,ΔABP ∴为等边三角形.60PAB ︒∴∠=,AB AP =.60DAC ︒∠=,PAB BAC DAC BAC ∴∠+∠=∠+∠,即PAC BAD ∠=∠.在ΔPAC 和ΔBAD 中,PA BA PAC BAD AC AD =⎧⎪∠=∠⎨⎪=⎩,ΔΔPAC BAD ∴≌.PC BD ∴=,PC BP BC AB BC =+=+,AB BC BD ∴+=.(3)AB ,CE ,BC 之间的数量关系为:2BC AB CE -=.(或者:2BC CE AB -=,2AB CE BC +=)解:连接BD ,过点D 作DF AC ⊥于F ,如图3所示.180BAD C ︒∠+∠=,180BAD FAD ︒∠+∠=.FAD C ∴∠=∠.在ΔDFA 和ΔDEC 中,DFA DEC FAD C DA DC ∠=∠⎧⎪∠=∠⎨⎪=⎩,ΔΔDFA DEC ∴≌,DF DE ∴=,AF CE =.在Rt ΔBDF 和Rt ΔBDE 中,BD BD DF DE =⎧⎨=⎩, Rt ΔRt ΔBDF BDE ∴≌.BF BE ∴=,2BC BE CE BA AF CE BA CE ∴=+=++=+,2BC BA CE ∴-=.【点睛】本题考查了三角形全等的性质与判定,正确的添加辅助线是解题的关键.17.在数学活动课上,数学老师出示了如下题目:如图①,在四边形ABCD 中,E 是边CD 的中点,AE 是BAD ∠的平分线,AD BC ∥. 求证:AB AD BC =+.小聪同学发现以下两种方法:方法1:如图②,延长AE 、BC 交于点F .方法2:如图③,在AB 上取一点G ,使AG AD =,连接EG 、CG .(1)请你任选一种方法写出这道题的完整的证明过程;(2)如图④,在四边形ABCD 中,AE 是BAD ∠的平分线,E 是边CD 的中点,60BAD ∠=︒,11802D BCD ∠+∠=︒,求证:CB CE =.【答案】(1)方法1:证明见解析;方法2:证明见解析;(2)证明见解析.【解析】【分析】(1)方法1:先根据角平分线的定义、平行线的性质得出BAF DAE F ∠=∠=∠,再根据等腰三角形的性质可得AB BF =,根据三角形全等的判定定理与性质得出AD FC =,然后根据线段的和差即可得证;方法2:先根据角平分线的定义得出DAE GAE ∠=∠,再根据三角形全等的判定定理与性质可得,DE GE D AGE =∠=∠,然后根据线段中点的定义、等腰三角形的性质可得ECG EGC ∠=∠,最后根据平行线的性质、平角的定义可得BCG BGC ∠=∠,由等腰三角形的定义可得BG BC =,由此根据线段的和差即可得证;(2)如图(见解析),参照方法1构造辅助线,先根据等腰三角形的性质得出EF 平分AFG ∠,从而有12EFC AFG ∠=∠,再根据平行线的性质、角的和差得出60EFC BFC ∠=∠=︒,ECF BCF ∠=∠,然后根据三角形全等的判定定理与性质即可得证.【详解】(1)方法1:如图②,延长AE 、BC 交于点FAE ∵是BAD ∠的平分线BAF DAE ∴∠=∠//AD BCDAE F ∴∠=∠BAF F ∴∠=∠AB BF FC BC ∴==+E 是边CD 的中点DE CE ∴=在ADE 和FCE △中,DAE F AED FEC DE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩()ADE FCE AAS ∴≅AD FC ∴=AB FC BC AD BC ∴=+=+;方法2:如图③,在AB 上取一点G ,使AG AD =,连接EG 、CGAE ∵是BAD ∠的平分线DAE GAE ∴∠=∠在ADE 和AGE 中,AD AG DAE GAE AE AE =⎧⎪∠=∠⎨⎪=⎩()ADE AGE SAS ∴≅,DE GE D AGE ∴=∠=∠E 是边CD 的中点DE CE ∴=CE GE ∴=ECG EGC ∴∠=∠//AD BC180D BCD ︒∴∠+∠=,即180D ECG BCG ∠+∠+∠=︒180AGE EGC BCG ∴∠+∠+∠=︒,即180AGC BCG ∠+∠=︒又180AGC BGC ∠+∠=︒BCG BGC ∴∠=∠BG BC ∴=AB AG BG AD BC ∴=+=+;(2)如图,过点C 作//CG AD ,交AE 延长线于点G ,延长GC 交AB 于点F ,连接EF 由方法1可知:,AF GF AE GE ==AFG ∴是等腰三角形EF ∴平分AFG ∠12EFC AFG ∴∠=∠ //CG AD ,60BAD ∠=︒60,180120BFC BAD AFG BAD ∴∠=∠=︒∠=︒-∠=︒60EFC ∴∠=︒//CG AD180D ECF ∴∠+∠=︒ 11802D BCD ︒∠+∠=,即1()1802D ECF BCF ∠+∠+∠=︒ 1()2ECF ECF BCF ∴∠=∠+∠ ECF BCF ∴∠=∠在ECF △和BCF △中,60EFC BFC CF CFECF BCF∠=∠=︒⎧⎪=⎨⎪∠=∠⎩()ECF BCF ASA ∴≅ CB CE ∴=.。
人教版八年级常见辅助线:截长补短专题

常见的辅助线作法(截长补短)截长法与补短法,具体作法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,使之与特定线段相等,再利用三角形全等的有关性质加以说明。
这种作法,适合于证明线段的和、差、倍、分等类的题目。
思考:遇到求证一条线段等于另两条线段之和时,一般方法是截长法或补短法:截长:在长线段中截取一段等于另两条中的一条,然后证明剩下部分等于另一条;
补短:将一条短线段延长,延长部分等于另一条短线段,然后证明新线段等于长线段。
例1、已知:如图,在△ABC中,∠C=2∠B,∠1=∠2.
求证:AB=AC+CD.
(分别用截长补短两种方法证明)
例2、已知:如图,在Rt△ABC中,AB=AC,∠BAC=90°,∠ABE=∠CBE,CE⊥BD的延长线于E。
求证:BD=2CE.
例3、如图,△ABC中,AM是BC边上的中线,求证:
例4、如图①所示,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形.请你参考这个作全等三角形的方法,解答下列问题:
(1)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你判断并写出FE与FD之间的数量关系;
(2)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.。
初中数学专题讲义:截长补短法

初中数学专题讲义:截长补短法截长补短法是几何证明题中十分重要的方法。
通常来证明几条线段的数量关系。
截长补短法有多种方法。
截长法:(1)过某一点作长边的垂线(2)在长边上截取一条与某一短边相同的线段,再证剩下的线段与另一短边相等。
…… 补短法(1)延长短边。
(2)通过旋转等方式使两短边拼合到一起。
……例1:在正方形ABCD 中,DE=DF ,DG ⊥CE ,交CA 于G ,GH ⊥AF ,交AD 于P ,交CE 延长线于H ,请问三条粗线DG ,GH ,CH 的数量关系方法一(好想不好证) 方法二(好证不好想)BABAMBA例2、正方形ABCD 中,点E 在CD 上,点F 在BC 上,∠EAF=45o。
求证:EF=DE+BF变形a正方形ABCD 中,点E 在CD 延长线上,点F 在BC 延长线上,∠EAF=45o。
请问现在EF 、DE 、BF 又有什么数量关系?变形b正方形ABCD 中,点E 在DC 延长线上,点F 在CB 延长线上,∠EAF=45o。
请问现在EF 、DE 、BF 又有什么数量关系?FE变形c正三角形ABC 中,E 在AB 上,F 在AC 上∠EDF=45o。
DB=DC ,∠BDC=120o。
请问现在EF 、BE 、CF 又有什么数量关系?变形d正方形ABCD 中,点E 在CD 上,点F 在BC 上,∠EAD=15o ,∠FAB=30o。
AD=3,求∆AEF 的面积例3、正方形ABCD 中,对角线AC 与BD 交于O ,点E 在BD 上,AE 平分∠DAC 。
求证:AC/2=AD-EO加强版正方形ABCD 中,M 在CD 上,N 在DA 延长线上,CM=AN ,点E 在BD 上,NE 平分∠DNM 。
过E 作EF ⊥MN 于F,请问MN 、AD 、EF 有什么数量关系?DFE例4、、如图,在梯形ABCD中,AD∥BC,∠C=90°,E为CD的中点,EF∥AB交BC于点F (1)求证:BF=AD+CF;(2)当AD=1,BC=7,且BE平分∠ABC时,求EF的长.例5、已知梯形ABCD中,AB∥CD,BD⊥AC于E,AD=BC,AC=AB,DF⊥AB于F,AC、DF相交于DF的中点O.(1)若点G为线段AB上一点,且FG=4,CD=3,GC=7,过O点作OH⊥GC于H,试证:OH=OF;(2)求证:AB+CD=2BE.变形1.如图,梯形ABCD中,AD∥BC,∠DCB=450,CD=2,BD⊥CD。
专题05 用截长补短法构造全等三角形(解析版)

专题05 用截长补短法构造全等三角形参考与答案【例1】(2020秋•富县期末)如图,AD是△ABC的角平分线,AB>AC,求证:AB﹣AC >BD﹣CD.【答案】略【解答】证明:如图,在AB上截取AE=AC,连接DE,∵AD是△ABC的角平分线,∴∠CAD=∠EAD.【典例分析】【直击考点】在△ADC和△ADE中,∴△ADC≌△ADE(SAS).∴DC=DE.∵在△BDE中,BE>BD﹣ED,∵AB﹣AE=BE,∴AB﹣AC>BD﹣CD.【变式1】(2020秋•顺庆区校级期中)如图:锐角△ABC中,∠C=2∠B,AD是高,求证:AC+CD=BD.【答案】略【解答】解:甲:截长法,如图1,在DB上截取DE=DC,连AE,∵DE=DC,AD⊥BC,∴AE=AC,∴∠AEC=∠C,且∠C=2∠B,∴∠AEC=∠B,且∠AEC=∠B+∠BAE,∴∠B=∠BAE,∴AE=BE=AC,∴BD=BE+DE=AC+CD【变式2】如图所示,在△ABC中,∠1=∠2,AB=AC+CD.试判断∠B与∠C之间的关系.【答案】∠C>∠B【解答】解:(1)在AB上截取AE=AC,连接DE,如图1,在△ADE与△ADC中,,∴△ADE≌△ADC(SAS),∴∠AED=∠C,ED=CD,∵AB=AC+CD,∴AB=AE+BE=AC+CD=AC+ED,∴BE=ED,∴∠AED=2∠B,∴∠AEC=2∠B,∴∠C>∠B;【例2】(2017秋•大兴区期末)已知:如图,在△ABC中,D是BA延长线上一点,AE 是∠DAC的平分线,P是AE上的一点(点P不与点A重合),连接PB,PC.通过观察,测量,猜想PB+PC与AB+AC之间的大小关系,并加以证明.【答案】PB+PC>AB+AC.【解答】解:PB+PC>AB+AC,理由如下:在BA的延长线上截取AF=AC,连接PF,在△F AP和△CAP中,,∴△F AP≌△CAP(SAS),∴FP=CP.在△FPB中,FP+BP>F A+AB,即PB+PC>AB+AC.【变式1】(2020秋•肥西县期末)如图,在△ABC中,AC=BC,AD平分∠CAB.(1)如图1,若ACB=90°,求证:AB=AC+CD;(2)如图2,若AB=AC+BD,求∠ACB的度数;(3)如图3,若∠ACB=100°,求证:AB=AD+CD.【答案】(1)略(2)∠ACB=108°(3)略【解答】证明:(1)如图1中,作DH⊥AB于H.在△ADC与△ADH中,,∴△ADC≌△ADH(ASA),∴AC=AH,DC=DH,∵CA=CB,∠C=90°,∴∠B=45°,∵∠DHB=90°,∴∠HDB=∠B=45°,∴HD=HB,∴BH=CD,∴AB=AH+BH=AC+CD;(2)设∠ACB=α,则∠CAB=∠CBA=90°﹣α,在AB上截取AK=AC,连接DK,∵AB=AC+BD,∴BK=BD,∵AD是角平分线,∴在△CAD和△KAD中,,∴△CAD≌△KAD(SAS),∴∠ACD=∠AKD=α,∴∠BKD=180°﹣α,∵BK=BD,∴∠BDK=180°﹣α,在△BDK中,180°﹣α+180°﹣α+90°﹣α=180°,∴α=108°,∴∠ACB=108°;(3)如图2,在AB上截取AH=AD,连接DH,∵∠ACB=100°,AC=BC,∴∠CAB=∠CBA=40°,∵AD是角平分线,∴∠HAD=∠CAD=20°,∴∠ADH=∠AHD=80°,在AB上截取AK=AC,连接DK,由(1)得,△CAD≌△KAD,∴∠ACB=∠AKD=100°,CD=DK,∴∠DKH=80°=∠DHK,∴DK=DH=CD,∵∠CBA=40°,∴∠BDH=40°,∴DH=BH,∴BH=CD,∵AB=AH+BH,∴AB=AD+CD.【例3】16.把两个全等的直角三角板的斜边重合,组成一个四边形ACBD以D为顶点作∠MDN,交边AC、BC于M、N.(1)若∠ACD=30°,∠MDN=60°,当∠MDN绕点D旋转时,AM、MN、BN三条线段之间有何种数量关系?证明你的结论;(2)当∠ACD+∠MDN=90°时,AM、MN、BN三条线段之间有何数量关系?证明你的结论;(3)如图③,在(2)的条件下,若将M、N改在CA、BC的延长线上,完成图3,其余条件不变,则AM、MN、BN之间有何数量关系(直接写出结论,不必证明)【答案】(1)AM+BN=MN;(2)AM+BN=MN;(3)BN﹣AM=MN【解答】(1)AM+BN=MN,证明:延长CB到E,使BE=AM,∵∠A=∠CBD=90°,∴∠A=∠EBD=90°,在△DAM和△DBE中,∴△DAM≌△DBE,∴∠BDE=∠MDA,DM=DE,∵∠MDN=∠ADC=60°,∴∠ADM=∠NDC,∴∠BDE=∠NDC,∴∠MDN=∠NDE,在△MDN和△EDN中,∴△MDN≌△EDN,∴MN=NE,∵NE=BE+BN=AM+BN,∴AM+BN=MN.(2)AM+BN=MN,证明:延长CB到E,使BE=AM,连接DE,∵∠A=∠CBD=90°,∴∠A=∠DBE=90°,∵∠CDA+∠ACD=90°,∠MDN+∠ACD=90°,∴∠MDN=∠CDA,∵∠MDN=∠BDC,∴∠MDA=∠CDN,∠CDM=∠NDB,在△DAM和△DBE中,∴△DAM≌△DBE,∴∠BDE=∠MDA=∠CDN,DM=DE,∵∠MDN+∠ACD=90°,∠ACD+∠ADC=90°,∴∠NDM=∠ADC=∠CDB,∴∠ADM=∠CDN=∠BDE,∵∠CDM=∠NDB∴∠MDN=∠NDE,在△MDN和△EDN中,∴△MDN≌△EDN,∴MN=NE,∵NE=BE+BN=AM+BN,∴AM+BN=MN.(3)BN﹣AM=MN,证明:在CB截取BE=AM,连接DE,∵∠CDA+∠ACD=90°,∠MDN+∠ACD=90°,∴∠MDN=∠CDA,∵∠ADN=∠ADN,∴∠MDA=∠CDN,∵∠B=∠CAD=90°,∴∠B=∠DAM=90°,在△DAM和△DBE中,∴△DAM≌△DBE,∴∠BDE=∠ADM=∠CDN,DM=DE,∵∠ADC=∠BDC=∠MDN,∴∠MDN=∠EDN,在△MDN和△EDN中,∴△MDN≌△EDN,∴MN=NE,∵NE=BN﹣BE=BN﹣AM,∴BN﹣AM=MN.【变式1】(2012•昌平区模拟)(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD.求证:EF=BE+FD;(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD 上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?(3)如图3,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.【答案】(1)EF=BE+FD;(2)(1)中的结论EF=BE+FD仍然成立(3)结论EF=BE+FD不成立,应当是EF=BE﹣FD【解答】证明:(1)延长EB到G,使BG=DF,连接AG.∵∠ABG=∠ABC=∠D=90°,AB=AD,∴△ABG≌△ADF.∴AG=AF,∠1=∠2.∴∠1+∠3=∠2+∠3=∠EAF=∠BAD.∴∠GAE=∠EAF.又∵AE=AE,∴△AEG≌△AEF.∴EG=EF.∵EG=BE+BG.∴EF=BE+FD(2)(1)中的结论EF=BE+FD仍然成立.(3)结论EF=BE+FD不成立,应当是EF=BE﹣FD.证明:在BE上截取BG,使BG=DF,连接AG.∵∠B+∠ADC=180°,∠ADF+∠ADC=180°,∴∠B=∠ADF.∵AB=AD,∴△ABG≌△ADF.∴∠BAG=∠DAF,AG=AF.∴∠BAG+∠EAD=∠DAF+∠EAD=∠EAF=∠BAD.∴∠GAE=∠EAF.∵AE=AE,∴△AEG≌△AEF.∴EG=EF∵EG=BE﹣BG∴EF=BE﹣FD【变式2】(2021春•北碚区校级期末)如图,已知凸五边形ABCDE中,EC,EB为其对角线,EA=ED.(1)如图1,若∠A=60°,∠CDE=120°,且CD+AB=BC.求证:EC平分∠BCD;(2)如图2,∠A与∠D互补,∠DEA=2∠CEB,若凸五边形ABCDE面积为30,且CD=AB=4.求点E到BC的距离.【答案】(1)略(2)点E到BC的距离为3【解答】(1)证明:延长CD到T,使得DT=BA,连接ET.∵∠CDE=120°,∴∠EDT=180°﹣120°=60°,∵∠A=60°,∴∠A=∠EDT,在△EAB和△EDT中,,∴△EAB≌△EDT(SAS),∴EB=ET,∴CB=CD+BA=CD+DT=CT,在△ECB和△ECT中,,∴△ECB≌△ECT(SSS),∴∠ECB=∠ECD.(2)解:延长CD到Q,使得∠QED=∠AEB,过点E作EH⊥BC于H.∵∠A+∠CDE=180°,∠CDE+∠EDQ=180°,∴∠A=∠EDQ,在△AEB和△DEQ中,,∴△AEB≌△DEQ(ASA),∴EB=EQ,∵∠AED=2∠BEC,∴∠AEB+∠CED=∠BEC,∴∠CED+∠DEQ=∠BEC,∴∠CEB=∠CEQ,在△CEB和△CEQ中,,∴△ECB≌△ECQ(SAS),∵S五边形ABCDE=S四边形EBCQ=2S△EBC=30,∴S△EBC=15,∵CD=AB=4,∴AB=6,CD=4,∴BC=CD+QD=CD+AB=10,∴×10×EH=15,∴EH=3,∴点E到BC的距离为3.【例4】(2019秋•西岗区期末)阅读下面材料:小明遇到这样一个问题:如图1,在△ABC中,AD平分∠BAC,∠ABC=2∠C.求证:AC=AB+BD;小明通过思考发现,可以通过“截长、补短”两种方法解决问题:方法一:如图2,在AC上截取AE,使得AE=AB,连接DE,可以得到全等三角形,进而解决问题.方法二:如图3,延长AB到点E,使得BE=BD,连接DE,可以得到等腰三角形,进而解决问题.(1)根据阅读材料,任选一种方法证明AC=AB+BD,根据自己的解题经验或参考小明的方法,解决下面的问题;(2)如图4,四边形ABCD中,E是BC上一点,EA=ED,∠DCB=2∠B,∠DAE+∠B=90°,探究DC、CE、BE之间的数量关系,并证明.【答案】(1)略(2)BE=DC+CE【解答】(1)证明:方法一:∵AD平分∠BAC,∴∠BAD=∠CAD,在△BAD和△EAD中∴△ABD≌△AED(SAS)∴BD=ED,∠AED=∠B=2∠C,∵∠AED=∠C+∠EDC,∴∠EDC=∠C,∴ED=EC,∴BD=EC,∴AC=AB+BD;(2)DC、CE、BE之间的数量关系是BE=DC+CE,证明:在EB上截取EF,使得EF=DC,连接AF,∵EA=ED,∴∠EAD=∠EDA,∴2∠DAE=180°﹣∠AED,∵∠DAE+∠B=90°,∴2∠DAE+2∠B=180°,∴∠AED=2∠B=∠C,∵∠BED=∠CDE+∠DAE,∴∠AEB=∠CDE,在△AEF和△EDC中∴△AEF≌△EDC(SAS),∴EC=AF∠AFE=∠C=2∠B,∵∠AFE=∠B+∠BAF,∴∠ABF=∠BAF,∴BF=AF,∴BF=CE,∴BE=DC+CE.【变式1】(2020秋•建华区期末)阅读下面文字并填空:数学习题课上李老师出了这样一道题:“如图1,在△ABC中,AD平分∠BAC,∠B=2∠C.求证:AB+BD=AC.”李老师给出了如下简要分析:要证AB+BD=AC,就是要证线段的和差问题,所以有两个方法:方法一:“截长法”.如图2,在AC上截取AE=AB,连接DE,只要证BD=即可,这就将证明线段和差问题为证明线段相等问题,只要证出△≌△,得出∠B=∠AED及BD=,再证出∠=,进而得出ED=EC,则结论成立.此种证法的基础是“已知AD平分∠BAC,将△ABD沿直线AD 对折,使点B落在AC边上的点E处”成为可能.方法二:“补短法”.如图3,延长AB至点F,使BF=BD.只要证AF=AC即可,此时先证∠=∠C,再证出△≌△,则结论成立.“截长补短法”是我们今后证明线段或角的“和差倍分”问题常用的方法.【答案】(1)EC,转化,ABD,AED,DE,EDC,∠C(2)F,AFD,ACD【解答】解:方法一、在AC上截取AE=AB,连接DE,如图2:∵AD平分∠BAC,∴∠BAD=∠DAC,在△ABD和△AED中,,∴△ABD≌△AED(SAS),∴∠B=∠AED,BD=DE,又∵∠B=2∠C,∴∠AED=2∠C,而∠AED=∠C+∠EDC=2∠C,∴∠C=∠EDC,∴DE=CE,∴AB+BD=AE+CE=AC,故答案为:EC,转化,ABD,AED,DE,EDC,∠C;方法二、如图3,延长AB至点F,使BF=BD,∴∠F=∠BDF,∴∠ABD=∠F+∠BDF=2∠F,∵∠ABD=2∠C,∴∠F=∠C,在△AFD和△ACD中,,∴△AFD≌△ACD(AAS),∴AC=AF,∴AC=AB+BF=AB+BD,故答案为F,AFD,ACD.【跟踪训练】1.已知,如图,AD∥BC,AE平分∠BAD,BE平分∠ABC,求证:AD+BC=AB.【答案】略【解答】证法一:在AB上截取AF=AD,连接EF,∵AE平分∠BAD,∴∠DAE=∠F AE,由AF=AD,∠DAE=∠F AE,AE=AE,可得△ADE≌△AFE(SAS),∴∠DEA=∠FEA,∵AD∥BC,AE平分∠BAD,BE平分∠ABC,∴∠EAB+∠EBA=(∠DAB+∠CBA)=×180°=90°,∠CBE=∠FBE,∴∠AEB=90°,∴∠AED+∠BEC=90°,∠AEF+∠BFE=90°,∴∠BEC=∠BEF,由∠BEC=∠BEF,BE=BE,∠CBE=∠FBE,可得△BFE≌△BCE,∴BF=BC,∴AB=AF+BF=AD+BC;2.(2020秋•綦江区期末)如图,在△ABC中,∠A=60°,∠ABC、∠ACB的平分线分别交AC、AB于点D、E,CE、BD相交于点F,连接DE.(1)若AC=BC=7,求DE的长;(2)求证:BE+CD=BC.【答案】(1)DE=(2)略【解答】解:(1)∵AC=BC,∠A=60°,∴△ABC为等边三角形,∴AC=AB,又∵BD、CE分别是∠ABC、∠ACB的平分线,∴D、E分别是AC、AB的中点,∴AD=AC,AE=AB,∴AD=AE,∴△ADE为等边三角形,∴DE=AE=;(2)证明:在BC上截取BH=BE,∵BD平分∠ABC,∴∠ABD=∠CBD,∵BF=BF∴△EBF≌△HBF(SAS),∴∠EFB=∠HFB=60°.∵∠A=60°,∴∠ABC+∠ACB=120°,∵BD平分∠ABC,CE平分∠ACB,∴∠ABD=∠CBD,∠ACE=∠BCE,∴∠CBD+∠BCE=60°,∴∠BFE=60°,∴∠CFB=120°,∴∠CFH=60°,∴∠CFH=∠CFD=60°,∵CF=CF,∴△CDF≌△CHF(ASA).∴CD=CH,∵CH+BH=BC,∴BE+CD=BC.3.(2019秋•四川期中)我们知道,利用三角形全等可以证明两条线段相等.但是我们会碰到这样的“和差”问题:“如图①,AD为△ABC的高,∠ABC=2∠C,证明:CD=AB+BD”.我们可以用“截长、补短”的方法将这类问题转化为证明两条线段相等的问题:在CD上截取DE=BD,连接AE.(1)请补写完这个证明:(2)运用上述方法证明:如图②,AD平分∠BAC,∠ABC=2∠C,证明:BD=AC﹣AB.【答案】(1)略(2)略【解答】(1)证明:在CD上截取DE=BD,连接AE,∵AD⊥BC,∴AB=AE,∴∠B=∠AEB,∵∠B=2∠C,∠AEB=∠C+∠EAC,∴∠C=∠EAC,∴EC=AE=AB,∴CD=CE+DE=AB+BD.(2)证明:在AC上截取AE=AB,连接DE,∵AD平分∠BAC,∴∠1=∠2,在△BAD和△EAD中∴△BAD≌△EAD,∴DE=BD,∠B=∠AED,∵∠B=2∠C,∠AED=∠C+∠EDC,∴∠C=∠EDC,∴DE=EC=DB,∵AC﹣AE=EC,EC=BD,AE=AB,∴BD=AC﹣AB.4.(2020春•南岸区期末)在∠MAN内有一点D,过点D分别作DB⊥AM,DC⊥AN,垂足分别为B,C.且BD=CD,点E,F分别在边AM和AN上.(1)如图1,若∠BED=∠CFD,请说明DE=DF;(2)如图2,若∠BDC=120°,∠EDF=60°,猜想EF,BE,CF具有的数量关系,并说明你的结论成立的理由.【答案】(1)略(2)EF=FC+BE【解答】解:(1)∵DB⊥AM,DC⊥AN,∴∠DBE=∠DCF=90°,在△BDE和△CDF中,∵∴△BDE≌△CDF(AAS).∴DE=DF;(2)EF=FC+BE,理由:过点D作∠CDG=∠BDE,交AN于点G,在△BDE和△CDG中,,∴△BDE≌△CDG(ASA),∴DE=DG,BE=CG.∵∠BDC=120°,∠EDF=60°,∴∠BDE+∠CDF=60°.∴∠FDG=∠CDG+∠CDF=60°,∴∠EDF=∠GDF.在△EDF和△GDF中,,∴△EDF≌△GDF(SAS).∴EF=GF,∴EF=FC+CG=FC+BE.5.(2020秋•增城区期末)如图(1),在平面直角坐标系中,AB⊥x轴于B,AC⊥y轴于C,点C(0,4),A(4,4),过C点作∠ECF分别交线段AB、OB于E、F两点(1)若OF+BE=AB,求证:CF=CE.(2)如图(2),且∠ECF=45°,S△ECF=6,求S△BEF的值.【答案】(1)略(2)∴S的值为4△BEF【解答】解:(1)证明:∵AB⊥x轴,AC⊥y轴∴∠ABO=∠ACO=90°∵∠BOC=90°∴∠A=360°﹣∠ABO﹣∠ACO﹣∠BOC=90°∴∠A=∠BOC∵C(0,4),A(4,4)∴OC=AC=AB=4∵OF+BE=AB,AB=AE+BE∴OF=AE在△COF和△CAE中∴△COF≌△CAE(SAS)∴CF=CE.(2)将△ACE绕点C顺时针旋转90°,则FG=AE+OF,CG=CE,∠ACE=∠GCO∵∠ECF=45°,∴∠ACE+∠FCO=∠ACO﹣∠ECF=90°﹣45°=45°∴∠GCF=∠GCO+∠FCO=∠ACE+∠FCO=45°∴∠GCF=∠ECF在△GCF和△ECF中∴△GCF≌△ECF(SAS)∵S△ECF=6∴S△GCF=6∴S△ECA+S△OCF=6∵由(1)知四边形OBAC为边长为4的正方形∴S四边形OBAC=4×4=16∴S△BEF=S四边形OBAC﹣S△ECF﹣S△ECA﹣S△OCF=16﹣6﹣6=4 ∴S△BEF的值为4.。
初中数学几何专题之截长补短证明题练习与解答

初中几何专题:截长补短练习与解答1.如图,在△ABC中,∠ABC=60°,AD,CE分别平分∠BAC,∠A CB,AD,CE交于O.(1)求∠AOC的度数;(2)求证:AC=AE+CD.2.已知:在ABC△中,AB=CD-BD,AD⊥BC,求证:2B C∠=∠.3.如图,在正方形ABCD中,F是CD的中点,E是BC边上的一点,且AF平分∠DAE,求证:AE=EC+CD4.如图,AC平分∠B AD,CE⊥AB于点E,∠B+∠D=180°,求证:AE=AD+BE.5.如图,已知在△ABC中,∠C=2∠B,∠1=∠2,求证:AB=AC+CD。
6.如图所示,AB∥CD,BE,CE分别是∠ABC,∠BCD的平分线,点E在AD上,求证:BC=AB+CD.7.如图,AD//BC,DC⊥AD,AE平分∠BAD,E是DC的中点.问:AD,BC,AB之间有何关系?并说明理由.8.如图,已知DE=AE,点E在BC上,AE⊥DE,AB⊥BC,DC⊥BC,请问线段AB,CD和线段BC有何大小关系?并说明理由.9.如图,AB∥CD,B E,CE分别是∠ABC和∠BCD的平分线,点E在AD上.求证:BC=AB+CD.10.如图,在Rt△ABC中,∠C=90°,BC=AC,∠B=∠CAB=45°,AD平分∠BAC交BC于D,求证:AB=AC+CD.11.在ABC△中,A∠的平分线交BC于D,AB AC CD∠的大小.∠=︒,求CB=+,4012.如图,ABC△中,AB AC∠=︒,BD平分ABC∠交AC于D点.A=,108求证:BC AC CD=+.13.五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°,求证:AD平分∠CDE.截长补短练习解答1.如图,在△ABC中,∠ABC=60°,AD,CE分别平分∠BAC,∠A CB,AD,CE交于O.(1)求∠AOC的度数;(2)求证:AC=AE+CD.证明:由题意可得∠AOC=120°∴∠AOE=∠DOC=180°-∠AOC=180°-120°=60°在AC上截取AF=AE,连接OF,如图在△AOE和△AOF中,AE=AF∠OAE=∠OAFOA=OA∴△AOE≌△AOF(SAS)∴∠AOE=∠AOF,∴∠AOF=60°∴∠COF=∠AOC-∠AOF=60°又∠COD=60°,∴∠COD=∠COF同理可得:△COD≌△COF(ASA)∴CD=CF又∵AF=AE∴AC=AF+CF=AE+CD即AE+CD=AC2.已知:在ABC △中,AB=CD -BD ,AD ⊥BC ,求证:2B C ∠=∠.图1E AB CD 证明:在DC上取一点E ,使BE=DE ,在ABD △和AED △中,AD BC ⊥,BD ED =,AD AD =.∴ABD AED △≌△.∴AB AE =,B AED ∠=∠.又∵AE AB CD BD CD DE EC==-=-=∴C EAC ∠=∠,∴2C EAC AED C∠+∠=∠=∠∴2B C ∠=∠.3.如图,在正方形ABCD 中,F 是CD 的中点,E 是BC 边上的一点,且AF 平分∠DAE ,求证:AE=EC+CD证明一:(截长)作FH AE ⊥于点H分别证明AFH AFD EFH EFC △≌△,△≌△,∴AH AD HE EC==,∴AE AH HE CD EC=+=+证明二:(补短)延长AF BC ,交于点G先证明ADF GCF △≌△,∴CG DA CD ==,G FAD ∠=∠,∵DAF EAF ∠=∠,∴G EAF∠=∠∴AE EG =,∴AE EC CG EC CD =+=+.4.如图,AC平分∠B AD,CE⊥AB于点E,∠B+∠D=180°,求证:AE=AD+BE.证明:如图,在EA上取点F,使EF=BE,连接CF,∵CE⊥AB∴CF=CB∠CFB=∠B∵∠AFC+∠C FB=180°,∠D+∠B=180°∴∠D=∠AFC∵AC平分∠BAD即∠DAC=∠FAC在△ACD和△ACF中∠D=∠AFC∠DAC=∠FACAC=AC∴△ACD≌△ACF(AAS)∴AD=AF∴AE=AF+EF=AD+BE5.如图,已知在△ABC中,∠C=2∠B,∠1=∠2,求证:AB=AC+CD。
专题1:截长补短造全等 - 教师版

专题01 截长补短模型构造全等三角形1.如图,在ABC 中,AD 平分BAC ∠,2B ADB ∠=∠,5AB =,6CD =,求AC 的长【详解】在AC 上截取AE=AB ,连接DE ,∵AD 平分∵BAC ,∵∵BAD=∵DAC ,在∵ABD 和∵AED 中,BAD DA AE AB AD AD C =⎧=∠=∠⎪⎨⎪⎩,∵∵ABD∵∵AED (SAS ), ∵∵B=∵AED ,∵ADB =∵ADE , AB=AE ,又∵B=2∵ADB∵∵AED=2∵ADB ,∵BDE=2∵ADB ,∵∵AED=∵C+∵EDC=2∵ADB ,∵BDE=∵C+∵DEC=2∵ADB ,∵∵DEC =∵EDC ,∵CD=CE ,∵5AB =,6CD =,∵AC =AE+CE=AB+CD = 5+6=11. 2如图,∵ABC 中,E 在BC 上,D 在BA 上,过E 作EF∵AB 于F ,∵B =∵1+∵2,AB =CD ,BF =43,则AD 的长为________.【答案】83【详解】在F A上取一点T,使得FT=BF,连接ET,在CB上取一点K,使得CK=ET,连接DK.∵EB=ET,∵∵B=∵ETB,∵∵ETB=∵1+∵AET,∵B=∵1+∵2,∵∵AET=∵2,∵AE=CD,ET=CK,∵∵AET∵∵DCK(SAS),∵DK=AT,∵ATE=∵DKC,∵∵ETB=∵DKB,∵∵B=∵DKB,∵DB=DK,∵BD=AT,∵AD=BT,∵BT=2BF =83,∵AD =83,故答案为:83.3如图,AB CD∥,BE平分ABC∠,CE平分BCD∠,点E 在AD 上,求证:BC AB CD=+.证明:在BC 上取点F ,使BF=BA ,连接EF ,∵BE、CE分别是∵ABC和∵BCD的平分线,∵∵1=∵2,∵3=∵4,在∵ABE和∵FBE中,12AB FBBE BE=⎧⎪∠=∠⎨⎪=⎩,∵∵ABE∵∵FBE(SAS),∵∵A=∵5,∵AB∵CD,∵∵A+∵D=180°,∵∵5+∵D=180,∵∵5+∵6=180°,∵∵6=∵D,在∵CDE和∵CFE中,634DCE CE∠=∠⎧⎪∠=∠⎨⎪=⎩,∵∵CDE∵∵CFE(AAS),∵CF=CD.∵BC=BF+CF,∵BC=AB+CD.4 如图,AB∵CD,BE平分∵ABC,CE平分∵BCD,若E在AD上.求证:(1)BE∵CE;(2)BC=AB+CD.【解答】证明:如图所示:(1)∵BE、CE分别是∵ABC和∵BCD的平分线,∵∵1=∵2,∵3=∵4,又∵AB∵CD,∵∵1+∵2+∵3+∵4=180°,∵∵2+∵3=90°,∵∵BEC=90°,∵BE∵CE.(2)在BC上取点F,使BF=BA,连接EF.在∵ABE和∵FBE中,,∵∵ABE∵∵FBE(SAS),∵∵A=∵5.∵AB∵CD,∵∵A+∵D=180°,∵∵5+∵D=180,∵∵5+∵6=180°,∵∵6=∵D,在∵CDE和∵CFE中,,∵∵CDE∵∵CFE(AAS),∵CF=CD.∵BC=BF+CF,∵BC=AB+CD,5如图所示,在五边形ABCDE中,AB=AE,BC+DE=CD,∵ABC+∵AED=180°,求证:DA平分∵CDE.解:连接AC,延长DE到F,使EF=BC,连接AF,∵BC+DE=CD,EF+DE=DF,∵CD=FD,∵∵ABC+∵AED=180°,∵AEF+∵AED=180°,∵∵ABC=∵AEF,在∵ABC和∵AEF中,,∵∵ABC∵∵AEF(SAS),∵AC=AF,在∵ACD和∵AFD中,,∵∵ACD∵∵AFD(SSS)∵∵ADC=∵ADF,即AD平分∵CDE.6.如图,∵ABCD中,E是BC边的中点,连接AE,F为CD边上一点,且满足∵DF A=2∵BAE.(1)若∵D=105°,∵DAF=35°.求∵F AE的度数;(2)求证:AF=CD+CF.【解答】(1)解:∵∵D=105°,∵DAF=35°,∵∵DF A=180°﹣∵D﹣∵DAF=40°(三角形内角和定理).∵四边形ABCD是平行四边形,∵AB∵CD,AB=CD(平行四边形对边平行且相等).∵∵DF A=∵F AB=40°(两直线平行,内错角相等);∵∵DF A=2∵BAE(已知),∵∵F AB=2∵BAE(等量代换).即∵F AE+∵BAE=2∵BAE.∵∵F AE=∵BAE;∵2∵F AE=40°,∵∵F AE=20°;(2)证明:在AF上截取AG=AB,连接EG,CG.∵∵F AE=∵BAE,AE=AE,∵∵AEG∵∵AEB.∵EG=BE,∵B=∵AGE;又∵E为BC中点,∵CE=BE.∵EG=EC,∵∵EGC=∵ECG;∵AB∵CD,∵∵B+∵BCD=180°.又∵∵AGE+∵EGF=180°,∵AGE=∵B,∵∵BCF=∵EGF;又∵∵EGC=∵ECG,∵∵FGC=∵FCG,∵FG=FC;又∵AG=AB,AB=CD,∵AF=AG+GF=AB+FC=CD+FC.7如图,在四边形ABCD中,AB=AD,∵BAD=60°,∵BCD=120°,连接AC,BD交于点E.(1)若BC=CD=2,M为线段AC上一点,且AM:CM=1:2,连接BM,求点C到BM 的距离.(2)证明:BC+CD=AC.解:(1)∵AB=AD,∵BAD=60°,∵∵ABD是等边三角形,∵∵ABD=∵ADB=60°.∵BC=CD,∵∵ABC∵∵ADC,∵∵BAC=∵DAC=30°,∵ACB=∵ACD=60°.∵∵AEB=∵BEC=90°,∵ABC=90°,∵CE=BC=1,BE=,AC=2BC=4.∵AM:CM=1:2,∵AM=,CM=,∵EM=,在Rt∵BEM中由勾股定理得BM==.过点C作CF∵BM于点F.∵.∵,∵CF=.即点C到BM的距离.(2)证明:延长BC到点F,使CF=CB,连接DF,∵AB=AD,∵ABD=60°,∵∵ABD是等边三角形,∵∵ADB=60°,AD=BD,∵BC=CD,∵CF=CD.∵∵BCD=120°,∵∵DCF=180°﹣∵BCD=60°,∵∵DCF是等边三角形,∵∵CDF=∵ADB=60°,DC=DF,∵∵ADC=∵BDF,又∵AD=BD,∵∵ACD∵∵BDF,∵AC=BF=BC+CF,即AC=BC+CD.8如图,在正方形ABCD中,点P是AB的中点,连接DP,过点B作BE∵DP交DP的延长线于点E,连接AE,过点A作AF∵AE交DP于点F,连接BF.(1)若AE=2,求EF的长;(2)求证:PF=EP+EB.解:(1)∵四边形ABCD 是正方形,且BE ∵DP ,AF ∵AE ,∵AB =AD ,∵BAD =∵EAF =∵BEF =90°,∵∵1+∵F AB =∵2+∵F AB =90°,∵∵1=∵2.∵∵3+∵5=∵4+∵6,且∵5=∵6,∵∵3=∵4.在∵AEB 和∵AFD 中,∵,∵∵AEB ∵∵AFD ,∵AE =AF =2,在Rt∵EAF 中,由勾股定理,得EF ==2.(2)过点A 作AM ∵EF 于M ,且∵EAF =90°,AE =AF ,∵∵EAF 为等腰直角三角形.∵AM =MF =EM .∵AME =∵BEF =90°.∵点P 是AB 的中点,∵AP =BP .在∵AMP 和∵BEP 中,∵,∵∵AMP ∵∵BEP ,∵BE =AM ,EP =MP ,∵MF =BE ,∵PF =PM +FM =EP +BE .9如图,在∵ABC 中,60BAC ∠=︒,40ACB ∠=︒,P 、Q 分别在BC 、CA 上,并且AP 、BQ 分别是∵BAC 、∵ABC 的角平分线.求证:(1)BQ CQ =;(2)BQ AQ AB BP +=+.(1)证明:∵BQ 是ABC ∠的角平分线,∵12QBC ABC ∠=∠. ∵180ABC ACB BAC ∠+∠+∠=︒,且60BAC ∠=︒,40ACB ∠=︒, ∵80ABC ∠=︒,∵180402QBC ∠=⨯︒=︒,∵QBC C ∠=∠,∵BQ CQ =; (2)证明:延长AB 至M ,使得BM BP =,连结MP .∵M BPM ∠=∠,∵∵ABC 中60BAC ∠=︒,40C ∠=︒,∵80ABC ∠=︒,∵BQ 平分ABC ∠,∵40QBC C ∠=︒=∠,∵BQ CQ =,∵ABC M BPM ∠=∠+∠,∵40M BPM C ∠=∠=︒=∠,∵AP 平分BAC ∠,∵MAP CAP ∠=∠,在∵AMP 和∵ACP 中,∵M C MAP CAP AP AP ∠=∠⎧⎪∠=∠⎨⎪=⎩,∵∵AMP∵∵ACP ,∵AM AC =,∵AM AB BM AB BP =+=+,AC AQ QC AQ BQ =+=+,∵AB BP AQ BQ +=+10在四边形ABDE中,C是BD边的中点.(1)如图(1),若AC平分∵BAE,∵ACE=90°,则线段AE、AB、DE的长度满足的数量关系为AE=AB+DE;(直接写出答案)(2)如图(2),AC平分∵BAE,EC平分∵AED,若∵ACE=120°,则线段AB、BD、DE、AE的长度满足怎样的数量关系?写出结论并证明;(3)如图(3),BD=8,AB=2,DE=8,若ACE=135°,则线段AE长度的最大值是10+4.(直接写出答案).证明:在AE上取点F,使AF=AB,连结CF,在AE上取点G,使EG=ED,连结CG.∵C是BD边的中点,∵CB=CD=BD.∵AC平分∵BAE,∵∵BAC=∵F AC.在∵ACB和∵ACF中,,∵∵ACB∵∵ACF(SAS),∵CF=CB,∵∵BCA=∵FCA.同理可证:CD=CG,∵∵DCE=∵GCE.11 ∵CB =CD ,∵CG =CF ∵∵ACE =120°,∵∵BCA +∵DCE =180°﹣120°=60°.∵∵FCA +∵GCE =60°.∵∵FCG =60°.∵∵FGC 是等边三角形.∵FG =FC =BD .∵AE =AF +EG +FG .∵AE =AB +DE +BD .(3)作B 关于AC 的对称点F ,D 关于EC 的对称点G ,连接AF ,FC ,CG ,EG ,FG .∵C 是BD 边的中点,∵CB =CD =BD .∵∵ACB ∵∵ACF (SAS ),∵CF =CB ,∵∵BCA =∵FCA .同理可证:CD =CG ,∵∵DCE =∵GCE∵CB =CD ,∵CG =CF ∵∵ACE =135°,∵∵BCA +∵DCE =180°﹣135°=45°.∵∵FCA +∵GCE =45°.∵∵FCG =90°.∵∵FGC 是等腰直角三角形.∵FC =BD .∵BD =8,∵FC =4,∵FG =4.∵AE =AB +4+DE .∵AB =2,DE =8,∵AE ≤AF +FG +EG =10+4.∵当A 、F 、G 、E 共线时AE 的值最大2,最大值为10+4.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
D
B
C
E
图2-1
截长补短法
人教八年级上册课本中,在全等三角形部分介绍了角的平分线的性质,这一性质在许多问题里都有着广泛的应用.而“截长补短法”又是解决这一类问题的一种特殊方法,在无法进行直接证明的情形下,利用此种方法常可使思路豁然开朗.请看几例.
例1. 已知,如图1-1,在四边形ABCD 中,BC >AB ,AD =DC ,BD 平分∠ABC .
求证:∠BAD +∠BCD =180°.
分析:因为平角等于180°,因而应考虑把两个不在一起的通过全等转化成为平角,图中缺少全等的三角形,因而解题的关键在于构造直角三角形,可通过“截长补短法”来实现.
证明:过点D 作DE 垂直BA 的延长线于点E ,作DF ⊥BC 于点F ,如图1-2 ∵BD 平分∠ABC ,∴DE =DF ,
在Rt △ADE 与Rt △CDF 中,
⎩⎨
⎧==CD
AD DF
DE ∴Rt △ADE ≌Rt △CDF (HL ),∴∠DAE =∠DCF . 又∠BAD +∠DAE =180°,∴∠BAD +∠DCF =180°, 即∠BAD +∠BCD =180°
例2. 如图2-1,AD ∥BC ,点E 在线段AB 上,∠ADE =∠CDE ,∠DCE =∠ECB .
求证:CD =AD +BC .
分析:结论是CD =AD +BC ,可考虑用“截长补短法”中的“截长”,即在CD 上截取CF =CB ,只要再证DF =DA 即可,这就转化为证明两线段相等的问题,从而达到简化问题的目的.
证明:在CD 上截取CF =BC ,如图2-2
在△FCE 与△BCE 中,
⎪⎩
⎪
⎨⎧=∠=∠=CE CE BCE FCE CB CF ∴△FCE ≌△BCE (SAS ),∴∠2=∠1.
A
B
C
D
图1-1
F
E
D
C
B
A
图1-2
A
D
B C
E
F
1
234
图2-2
又∵AD ∥BC ,∴∠ADC +∠BCD =180°,∴∠DCE +∠CDE =90°, ∴∠2+∠3=90°,∠1+∠4=90°,∴∠3=∠4. 在△FDE 与△ADE 中,
⎪⎩
⎪
⎨⎧∠=∠=∠=∠43DE
DE ADE FDE ∴△FDE ≌△ADE (ASA ),∴DF =DA , ∵CD =DF +CF ,∴CD =AD +BC .
例3. 已知,如图3-1,∠1=∠2,P 为BN 上一点,且PD ⊥BC 于点D ,AB +BC =2BD .
求证:∠BAP +∠BCP =180°.
分析:与例1相类似,证两个角的和是180°,可把它们移到一起,让它们是邻补角,即证明∠BCP =∠EAP ,因而此题适用“补短”进行全等三角形的构造.
证明:过点P 作PE 垂直BA 的延长线于点E ,如图3-2
∵∠1=∠2,且PD ⊥BC ,∴PE =PD , 在Rt △BPE 与Rt △BPD 中,
⎩⎨
⎧==BP
BP PD
PE ∴Rt △BPE ≌Rt △BPD (HL ),∴BE =BD .
∵AB +BC =2BD ,∴AB +BD +DC =BD +BE ,∴AB +DC =BE 即DC =BE -AB =AE . 在Rt △APE 与Rt △CPD 中,
⎪⎩
⎪
⎨⎧=∠=∠=DC AE PDC PEA PD PE ∴Rt △APE ≌Rt △CPD (SAS),∴∠PAE =∠PCD 又∵∠BAP +∠PAE =180°,∴∠BAP +∠BCP =180°
例4. 已知:如图4-1,在△ABC 中,∠C =2∠B ,∠1=∠2.
求证:AB =AC +CD .
A
B
C
D
P
12
N
图3-1
P
12
N
A
B
C
D
E 图3-2
D
C
B A 12
图4-1
分析:从结论分析,“截长”或“补短”都可实现问题的转化,即延长AC 至E 使CE =CD ,或在AB 上截取AF =AC . 证明:方法一(补短法)
延长AC 到E ,使DC =CE ,则∠CDE =∠CED ,如图4-2
∴∠ACB =2∠E ,
∵∠ACB =2∠B ,∴∠B =∠E , 在△ABD 与△AED 中,
⎪⎩
⎪
⎨⎧=∠=∠∠=∠AD AD E B 21 ∴△ABD ≌△AED (AAS ),∴AB =AE . 又AE =AC+CE =AC +DC ,∴AB =AC +DC . 方法二(截长法)
在AB 上截取AF =AC ,如图4-3 在△AFD 与△ACD 中,
⎪⎩
⎪
⎨⎧=∠=∠=AD AD AC AF 21 ∴△AFD ≌△ACD (SAS ),∴DF =DC ,∠AFD =∠ACD . 又∵∠ACB =2∠B ,∴∠FDB =∠B ,∴FD =FB . ∵AB =AF +FB =AC +FD ,∴AB =AC +CD .
上述两种方法在实际应用中,时常是互为补充,但应结合具体题目恰当选择合适思路进行分析。
让掌握学生掌握好“截长补短法”对于更好的理解数学中的化归思想有较大的帮助。
E
D
C
B
A
12
图4-2
F
D
C
B A 12
图4-3。
