四边简支受压板例题
4月全国钢结构自考试题及答案解析

1全国2019年4月高等教育自学考试钢结构试题课程代码:02442一、单项选择题(本大题共20小题,每小题2分,共40分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.在结构设计中,失效概率P f 与可靠指标β的关系为( )。
A.P f 越大,β越大,结构可靠性越差B.P f 越大,β越小,结构可靠性越差C.P f 越大,β越小,结构越可靠D.P f 越大,β越大,结构越可靠2.钢材的伸长率ε用来反映材料的( )。
A.承载能力B.弹性变形能力C.塑性变形能力D.抗冲击荷载能力3.以下关于应力集中的说法中正确的是( )。
A.应力集中降低了钢材的屈服强度B.应力集中产生同号应力场,使塑性变形受到限制C.应力集中产生异号应力场,使钢材变脆D.应力集中可以提高构件的疲劳强度4.对于常温下承受静力荷载、无严重应力集中的碳素结构钢构件,焊接残余应力对下列没有..明显影响的是( )。
A.构件的刚度B.构件的极限强度C.构件的稳定性D.构件的疲劳强度5.图示焊接连接中,最大焊缝应力发生在( )。
A.a 点B.b 点C.c 点D.d 点6.如图所示普通螺栓连接中,受力最大的螺栓为( )。
A.aB.bC.cD.d7.轴压杆的轴心力分布及支承情况如图所示,验算此杆整体稳定性时,计算长度应取( )。
A.l 0x =l /2,l 0y =lB.l 0x =l ,l 0y =lC. l 0x =l /2,l 0y =l (0.75+0.25N 2/N 1)2D. l 0x =l (0.75+0.25N 2/N 1), l 0y =l /28.焊接组合工字形轴心受压柱的翼缘与腹板的焊缝承受( )。
A.压力B.压杆屈曲时的剪力C.同时承受压力与压杆屈曲时的剪力D.不受力9.轴压柱腹板局部稳定的保证条件是h 0/t w 不大于某一限值,此限值( )。
A.与钢材强度和柱的长细比无关B.与钢材强度有关,而与柱的长细比无关C.与钢材强度无关,而与柱的长细比有关D.与钢材强度和柱的长细比均有关10.在下列关于柱脚底板厚度的说法中,错误的是( )。
钢结构习题答案单元2、3

单元2 钢结构的连接复习思考题2-1钢结构的连接方式有几种?各有何特点?目前常用哪些方法?答:钢结构的连接方法有焊缝连接、铆钉连接和螺栓连接三种。
焊缝连接:1)优点:构造简单,任何形式的构件都可直接相连;用料经济、不削弱截面;制作加工方便,可实现自动化操作;连接的密闭性好,结构刚度大。
2)缺点:在焊缝附近的热影响区内,钢材的金相组织发生改变,导致局部材质变脆;焊接残余应力和残余变形使受压构件承载力降低;焊接结构对裂纹很敏感,局部裂纹一旦发生,就容易扩展到整体,低温冷脆现象较为突出。
螺栓连接:1)优点:施工工艺简单、安装方便,特别适用于工地安装连接,工地进度和质量易得到保证;且由于装拆方便,适用于需装拆结构的连接和临时性连接。
2)缺点:螺栓连接需制孔,拼装和安装需对孔,增加了工作量,且对制造的精度要求较高;此外,螺栓连接因开孔对截面有一定的削弱,有时在构造上还须增设辅助连接件,故用料增加,构造较繁。
在钢结构工程中,焊缝连接、螺栓连接是最常用的连接方法。
铆钉连接:1)优点:铆钉连接的塑性和韧性较好,传力可靠,质量易于检查。
2)缺点:构造复杂,费钢费工。
2-2对接焊缝的坡口形式主要由什么条件决定?通常用的坡口形式有哪几种?并绘图示意。
答:对接焊缝的坡口形式取决于焊件厚度t 。
常用对接焊缝的坡口形式有以下6种:(a)直边缝(b)单边V形坡口(c)V形坡口(d)U形坡口(e)K形坡口(f)X形坡口2-3对接焊缝在哪种情况下才需要进行抗拉强度计算?答:由于一、二级质量的焊缝与母材强度相等,故只有三级质量的焊缝才需进行抗拉强度验算。
2-4引弧板起什么作用?答:引弧板可消除焊缝的起灭弧处弧坑等缺陷,避免产生应力集中和裂纹。
2-5焊缝的起弧、落弧对焊缝有何影响?对接焊缝和角焊缝计算中如何考虑? 答:焊缝的起弧、落弧易产生弧坑等缺陷,使焊缝的计算长度减小。
对接焊缝:若未加引弧板,则每条焊缝的引弧及灭弧端各减去t (t 为较薄焊件厚度)后作为焊缝的计算长度。
四边简支矩形板计算

四边简支矩形板计算项目名称_____________日期_____________设计者_____________校对者_____________一、构件编号: LB-1二、示意图三、依据规范《建筑结构荷载规范》 GB50009-2001《混凝土结构设计规范》 GB50010-2010四、计算信息1.几何参数计算跨度: Lx = 11000 mm; Ly = 7500 mm板厚: h = 400 mm2.材料信息混凝土等级: C30 fc=14.3N/mm2 ft=1.43N/mm2 ftk=2.01N/mm2Ec=3.00×104N/mm2钢筋种类: HRB400 fy = 360 N/mm2Es = 2.0×105 N/mm2最小配筋率: ρ= 0.200%纵向受拉钢筋合力点至近边距离: as = 55mm保护层厚度: c = 40mm3.荷载信息(均布荷载)永久荷载分项系数: γG = 1.200可变荷载分项系数: γQ = 1.400准永久值系数: ψq = 1.000永久荷载标准值: qgk = 15.000kN/m2可变荷载标准值: qqk = 0.000kN/m24.计算方法:弹性板5.边界条件(上端/下端/左端/右端):简支/简支/简支/简支6.设计参数结构重要性系数: γo = 1.00泊松比:μ = 0.200五、计算参数:1.计算板的跨度: Lo = 7500 mm2.计算板的有效高度: ho = h-as=400-55=345 mm六、配筋计算(lx/ly=11000/7500=1.467<2.000 所以按双向板计算):1.X向底板钢筋1) 确定X向板底弯矩Mx = 表中系数(γG*qgk+γQ*qqk)*Lo2= (0.0287+0.0707*0.200)*(1.200*15.000+1.400*0.000)*7.52 = 43.374 kN*m2) 确定计算系数αs = γo*Mx/(α1*fc*b*ho*ho)= 1.00*43.374×106/(1.00*14.3*1000*345*345)= 0.0253) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.025) = 0.0264) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*345*0.026/360= 354mm25) 验算最小配筋率ρ = As/(b*h) = 354/(1000*400) = 0.088%ρ<ρmin = 0.200% 不满足最小配筋要求所以取面积为As = ρmin*b*h = 0.200%*1000*400 = 800 mm2采取方案⌲12@140, 实配面积807 mm22.Y向底板钢筋1) 确定Y向板底弯矩My = 表中系数(γG*qgk+γQ*qqk)*Lo2= (0.0707+0.0287*0.200)*(1.200*15.000+1.400*0.000)*7.52 = 77.430 kN*m2) 确定计算系数αs = γo*My/(α1*fc*b*ho*ho)= 1.00*77.430×106/(1.00*14.3*1000*345*345)= 0.0453) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.045) = 0.0474) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*345*0.047/360= 638mm25) 验算最小配筋率ρ = As/(b*h) = 638/(1000*400) = 0.160%ρ<ρmin = 0.200% 不满足最小配筋要求所以取面积为As = ρmin*b*h = 0.200%*1000*400 = 800 mm2采取方案⌲12@100, 实配面积1131 mm2七、跨中挠度计算:Mk -------- 按荷载效应的标准组合计算的弯矩值Mq -------- 按荷载效应的准永久组合计算的弯矩值1.计算荷载效应Mk = Mgk + Mqk= (0.0707+0.0287*0.200)*(15.000+0.000)*7.52 = 64.525 kN*mMq = Mgk+ψq*Mqk= (0.0707+0.0287*0.200)*(15.000+1.0*0.000)*7.52 = 64.525 kN*m2.计算受弯构件的短期刚度 Bs1) 计算按荷载荷载效应的两种组合作用下,构件纵向受拉钢筋应力σsk = Mk/(0.87*ho*As) 混规(7.1.4-3)= 64.525×106/(0.87*345*1131) = 190.077 N/mmσsq = Mq/(0.87*ho*As) 混规(7.1.4-3)= 64.525×106/(0.87*345*1131) = 190.077 N/mm2) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积: Ate = 0.5*b*h = 0.5*1000*400= 200000mm2ρte = As/Ate 混规(7.1.2-4)= 1131/200000 = 0.566%3) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψk = 1.1-0.65*ftk/(ρte*σsk) 混规(7.1.2-2)= 1.1-0.65*2.01/(0.566%*190.077) = -0.115因为ψ不能小于最小值0.2,所以取ψk = 0.2ψq = 1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)= 1.1-0.65*2.01/(0.566%*190.077) = -0.115因为ψ不能小于最小值0.2,所以取ψq = 0.24) 计算钢筋弹性模量与混凝土模量的比值αEαE = Es/Ec = 2.0×105/3.00×104 = 6.6675) 计算受压翼缘面积与腹板有效面积的比值γf矩形截面,γf=06) 计算纵向受拉钢筋配筋率ρρ = As/(b*ho)= 1131/(1000*345) = 0.328%7) 计算受弯构件的短期刚度 BsBsk = Es*As*ho2/[1.15ψk+0.2+6*αE*ρ/(1+ 3.5γf')](混规(7.2.3-1)) = 2.0×105*1131*3452/[1.15*-0.115+0.2+6*6.667*0.328%/(1+3.5*0.0)]= 4.798×104 kN*m2Bsq = Es*As*ho2/[1.15ψq+0.2+6*αE*ρ/(1+ 3.5γf')](混规(7.2.3-1)) = 2.0×105*1131*3452/[1.15*-0.115+0.2+6*6.667*0.328%/(1+3.5*0.0)]= 4.798×104 kN*m23.计算受弯构件的长期刚度B1) 确定考虑荷载长期效应组合对挠度影响增大影响系数θ当ρ'=0时,θ=2.0 混规(7.2.5)2) 计算受弯构件的长期刚度 BBk = Mk/(Mq*(θ-1)+Mk)*Bs (混规(7.2.2-1))= 64.525/(64.525*(2.0-1)+64.525)*4.798×104= 2.399×104 kN*m2Bq = Bsq/θ (混规(7.2.2-2))= 4.798×104/2.0= 2.399×104 kN*m2B = min(Bk,Bq)= min(23990.371,23990.371)= 23990.3714.计算受弯构件挠度f max = f*(q gk+q qk)*Lo4/B= 0.00752*(15.000+0.000)*7.54/2.399×104= 14.879mm5.验算挠度挠度限值fo=Lo/250=7500/250=30.000mmfmax=14.879mm≤fo=30.000mm,满足规范要求!八、裂缝宽度验算:1.跨中X方向裂缝1) 计算荷载效应Mx = 表中系数(qgk+ψqqk)*Lo2= (0.0287+0.0707*0.200)*(15.000+1.00*0.000)*7.52= 36.145 kN*m2) 带肋钢筋,所以取值v i=1.03) 因为C > 65,所以取C = 654) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=36.145×106/(0.87*345*807)=149.222N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*400=200000 mm2ρte=As/Ate 混规(7.1.2-4)=807/200000 = 0.0040因为ρte=0.0040 < 0.01,所以让ρte=0.016) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*2.010/(0.0100*149.222)=0.2247) 计算单位面积钢筋根数nn=1000/dist = 1000/140=78) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=7*12*12/(7*1.0*12)=129) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.224*149.222/2.0×105*(1.9*40+0.08*12/0.0100)=0.0547mm ≤ 0.20, 满足规范要求2.跨中Y方向裂缝1) 计算荷载效应My = 表中系数(qgk+ψqqk)*Lo2= (0.0707+0.0287*0.200)*(15.000+1.00*0.000)*7.52= 64.525 kN*m2) 带肋钢筋,所以取值v i=1.03) 因为C > 65,所以取C = 654) 计算按荷载效应的准永久组合作用下,构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=64.525×106/(0.87*345*1131)=190.077N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积,Ate=0.5*b*h=0.5*1000*400=200000 mm2ρte=As/Ate 混规(7.1.2-4)=1131/200000 = 0.0057因为ρte=0.0057 < 0.01,所以让ρte=0.016) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*2.010/(0.0100*190.077)=0.4137) 计算单位面积钢筋根数nn=1000/dist = 1000/100=108) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=10*12*12/(10*1.0*12)=129) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.413*190.077/2.0×105*(1.9*40+0.08*12/0.0100)=0.1282mm ≤ 0.20, 满足规范要求。
薄板的屈曲

115第六章 薄板的屈曲钢结构大型梁、柱等构件,通常都由板件组合而成,为了节省材料,板件通常宽而薄,薄板在面内压力作用下就可能失稳,并由此导致整个构件的承载力下降;另外,在构件连接的节点也存在板件失稳的可能性。
因此,对板件失稳和失稳后性态的研究也是钢结构稳定的重要问题。
板根据其厚度分为厚板、薄板和薄膜三种。
设板的最小宽度为b ,厚度为t 。
当t /b >1/5~1/8时称为厚板,这时横向剪力引起的剪切变形与弯曲变形大小同阶,分析时不能忽略剪切变形的影响。
当1/80~1/100<t /b <1/5~1/8时称为薄板,此时横向剪力引起的剪切变形与弯曲变形相比可以忽略不计。
当板极薄,t /b <1/80~1/100时,称为薄膜,薄膜没有抗弯刚度,靠薄膜拉力与横向荷载平衡。
平分板的厚度且与板的两个面平行的平面称为中面。
本章只介绍等厚度薄板中面内受力的板的弹性失稳。
与前面所介绍过的失稳问题比较,板的失稳有如下几个特点: ⑴作用于板中面的外力,不论是一个方向作用有外力还是在两个方向同时作用有外力,屈曲时板产生的都是出平面的凸曲现象,产生双向弯曲变形,因此在板的任何一点的弯矩x M 、y M 和扭矩xy M 以及板的挠度w 都与此点的坐标(x ,y )有关。
⑵板的平衡方程属于二维偏微分方程,除了均匀受压的四边简支的理想矩形板可以直接求解其分岔屈曲荷载外,对于其他受力条件和边界条件的板,用平衡法很难求解。
可以用能量法(如瑞利—里兹法,伽辽金法)或者数值法(如差分法、有限元法等)求解屈曲荷载,在弹塑性阶段,用数值法可以得到精度很高的板屈曲荷载。
⑶理想薄板失稳属于稳定分岔失稳。
对于有刚强侧边支承的板,凸屈后板的中面会产生薄膜应变,从而产生薄膜应力。
如果在板的一个方向有外力作用而凸曲时,在另一个方向的薄膜拉力会对它产生支持作用,增强板的抗弯刚度进而提高板的强度,这种凸屈后的强度提高称为屈曲后强度。
钢结构基本原理试题及答案_0

钢结构模拟试题(一)一、简答题(每小题5分,共20分)1.简述钢材塑性破坏的特征和意义。
2.什么叫实腹式轴心受压构件等稳设计?3.焊接工字形板梁翼缘与腹板间的角焊缝计算长度是否受60hf(静)或40hf(动力)的限制?为什么?4.当弯矩作用在实腹式压弯构件截面的弱轴平面)进行测试。
A.抗拉强度fuB.屈服点fyC.冷弯180°试验D.Z向收缩率2.对不同质量等级的同一类钢材,在下列各指标中,它们的( )不同。
A.抗拉强度fuB.屈服点fyC.伸长率δD.冲击韧性AKV3.同一结构钢材的伸长率( )。
A.δ5>δ10B.δ5=δ10C.δ5<δ10D.不能确定4.摩擦型高强度螺栓的抗剪连接是靠( )来传递剪力。
A.螺杆抗剪和承压B.螺杆抗剪C.螺杆承压D.连接板件间的摩擦力5.在纯剪切作用下,梁腹板的纯剪屈曲不先于屈服破坏的条件是( )。
A.h0twh0tw≤80235fy235fy B.h0tw≤170235fy C.>170D.不能确定6.两端简支的梁,跨中作用一集中荷载,对荷载作用于上翼缘和作用于下翼缘两种情况,梁的整体稳定性承载能力( )。
A.前者大B.后者大C.二者相同D.不能确定7.两根几何尺寸完全相同的压弯构件,二者都是两端简支,且承受的轴压力大小相等,但一根承受均匀弯矩作用,而另一根承受非均匀弯矩作用,则二者承受的临界弯矩相比( )。
A.前者大于等于后者B.前者小于等于后者C.两种情况相同D.不能确定8.与无檩屋盖相比,下列( )不是有檩屋盖的特点。
A.所用构件种类和数量多B.屋盖刚度大C.屋盖自重轻D.屋架布置灵活9.设节点间杆件的几何长度为l,则屋架的支座斜杆和支座竖杆在屋架平面)。
A.0.5lB.0.8l第 1 页共22 页C. lD.2l10.屋架中,对双角钢组成的十字形截面杆件或单角钢杆件,当这些杆件不是支座斜杆和支座竖杆时,它们在斜平面)(设杆件几何长度为l)。
混凝土结构:34双向板肋形结构设计

故短跨梁上的荷载是三角形分布,长跨梁上的荷载是 梯形分布。梁上的荷载确定后即可计算梁的内力(图944) 。
2.等效均布荷载pE:按弹性方法计算承受梯形或三角 形分布荷载的连续梁的内力时,计算跨度可仍按一般连续 梁的规定取用。当其跨度相等或相差不超过10%时,可按照支 座弯矩等效的原则,将梯形(或三角形)分布荷载折算成等效 的均布荷载pE。
中受力钢筋达到屈服强度,受压区混凝土被压 碎而破坏。
试验表明,板中钢筋的布置方向对破坏荷载的数值 无显著影响,钢筋平行于板的四边布置时,对推迟第一 批裂缝的出现有良好的作用,而且施工方便,实际工程中多采 用这种布置方式。
简支的正方形或矩形板,在荷载作用下,板的四角都有翘 起的趋势。板传给四边支座的压力,并非沿边长均匀分布,而 是在支座的中部较大,向两端逐渐减小。当配筋率相同时,采 用较细的钢筋较为有利;当钢筋数量相同时,将板中间部分的 钢筋排列较密些要比均匀布置有效。
3.查表求支座弯矩。 4.由支座弯矩和实际荷载求各跨跨中弯矩和支座剪力。 梁的截面设计、裂缝和变形验算及配筋构造与支承单向板 的梁完全相同。
pE=5p/8
p E=(1-2α2+α3)p
a l =α
p E= (1 -2 α 2+ α 3)p
例 题 9-3(一)
某水电站的工作平台,因使用要求,采用双向板肋 形结构。板四边与边梁整体浇筑,板厚150mm,边梁截面尺寸 250mm×600mm,如图9-45所示。该工程属3级水工建筑物,设 计状况为持久状况。已知永久荷载设计值g=4kN/m2;可变荷载 设计值q=12kN/m2,砼采用C20,钢筋采用冷轧带肋钢筋LL550。 试计算各区格板的弯矩。
四边简支板在局部均布荷载作用下的弯矩计算

四边简支板在局部均布荷载作用下的弯矩计算
四边简支板是横截面呈几何图形的框架结构,其垂直横向支承受等量的均布荷载,在工程设计中非常常见。
简支板的局部均布荷载的弯矩计算对于建筑结构的设计和安全性有着极其重要的意义。
首先,针对简支板框架结构在任意均布荷载作用下弯矩计算,应按照条形元法
进行分析。
条形元法处理不规则横截面结构中荷载和位移断面分析非常有效,其计算原理是均布荷载根据分析节点断面划分成许多条形元,将梁的位移条件及荷载条件分别投入条形元的计算中,由对角化的K矩阵向量来求解。
其次,使用有限元方法计算局部均布荷载的弯矩,有效模拟出四边简支板的横
截面图形。
无论是梁的分析与计算还是柱的分析与计算,当结构处于稳定状态时,建筑结构中的物体奋力等于物体受力,使用有限元方法和梁(或柱)弯矩分析模型,求取梁在局部均布荷载作用下的弯矩变化啊关系,有助于完善在横截面呈几何形状的简支框架结构的断面分析。
最后,可以利用实验技术测量四边简支板在局部均布荷载作用下的弯矩,以评
估梁或柱承受压力、弯曲、振动及滑移等性能变化情况,确保梁或柱的安全可靠性。
实验技术是对建筑结构分析和计算的有力补充,使得建筑建设和维护工作更加安全可靠。
从以上可以看出,简支板的局部均布荷载的弯矩计算对于准确分析横截面图形
的简支板结构,以及正确评估梁或柱的安全可靠性具有重要意义,应加以重视,注重多方面的分析和研究,以保障施工安全性。
(整理)型钢工程计算实例

课堂讨论1. 拉杆为何要控制刚度?如何验算?拉杆允许长细比与什么有关?答:拉杆要控制刚度是为了保证构件在使用过程中不产生过大的横向振动而使杆件连接受到损害及改变杆件轴心受拉的性质。
验算:构件长细比小于或等于容许长细比,即: 。
拉杆允许长细比与拉杆所受荷载的性质有关。
2.计算轴心受压缀条柱时,如何考虑柱的剪切变形的影响?此时柱的整体等稳定条件是什么?答:轴心受压柱的临界力。
对格构式缀条柱的虚轴,单位剪切角较大,剪力产生的剪切变形不能忽略,它将降低整体稳定临界力,因此设计中将构件计算长度定为 ,为放大系数,以考虑这一不利影响,用换算长细比来替代 (x 为虚轴)。
柱的整体等稳定条件为(y 为实轴)。
3. 试述提高轴心受压构件整体稳定性的措施。
答:轴压构件当 较大时为弹性失稳,此时临界力只与长细比有关,所以可通过改变支承条件(如杆端将铰支改为固定,中间加支承点等)来减小计算长度,或改变截面形状,增大回转半径来提高整体稳定性;当轴压构件长细比较小时为弹塑性失稳,此时其临界力与材料强度也有关,因此提高钢号对提高整体稳定性也有一定作用。
此外,截面形式与整体稳定性也有关,在三类截面a 、b 、c 中,a 类最好,c 类最差。
4. 在缀条式轴心受压格构柱中,为什么要限制单肢的长细比?如何限制?答:为使格构柱单肢不先于整体失稳,要限制单肢的长细比。
通过保证单肢长细比( 为两个主轴方向长细比中的较大值)。
5. 钢结构轴心受压构件整体稳定承载力时按什么原理确定的? 答:考虑杆长千分之一的初始挠度,忽略初始偏心,计入焊接残余应力的影响,根据压溃理论用有限元方法确定构件的临界应力。
6. 请说明轴心受压焊接工字型截面钢柱采用有效截面验算稳定的概念。
答:当轴心受力工字型截面中的腹板发生局部失稳时,在不采取措施的情况下可以采用有效截面的概念进行计算。
即计算时仅考虑腹板两边缘各。
如图。
7.一轴心受压柱,有两种可能的荷载作用方式1)重力集中荷载P作用在柱顶2)一重力集中荷载0.7P作用在柱顶,另一重力集中荷载0.3P作用在柱高的中点问哪一种稳定承载力较高,为什么?答:后一种稳定承载力较高。
C82-均匀受压板件的屈曲临界应力
p x ,cr t
K2E
12 1 2
t b
(2)弹塑性屈曲
当轴心受压构件中板件的临界应力超过比例极限 fp 时,进 入弹 塑性受力阶段,变为弹塑性局部屈曲问题。
单向受压板沿受力方向的弹性模量 E 降为切线模量 --ηE;
与压力垂直的方向仍为弹性阶段,其弹性模量仍为 E,此时板 件变为正交异性板。
p x ,cr t
K2E
12 1 2
t b
式中:K — 弹性屈曲系数;
μ — 泊松比;
对于其它支承条件的单向均匀受压薄板,采用相同的分析方法
可得相同的临界应力表达式,但 K 值不同;另外,引入系数χ 来
考虑其他约束程度情况。
弹性临界应力的计算公式可统一表达为:
2
x ,cr
这时可用 E 代替 E,按下列近似公式计算其临界应力:
2
x ,cr
p x ,cr t
K2E t
12
1
2
b
与宽厚 比有关
根据试验,规范取弹性模量修正系数为:
0 .1013 2
f y
1
0
.0248
2
f y
E
E
λ—构曲临界应力
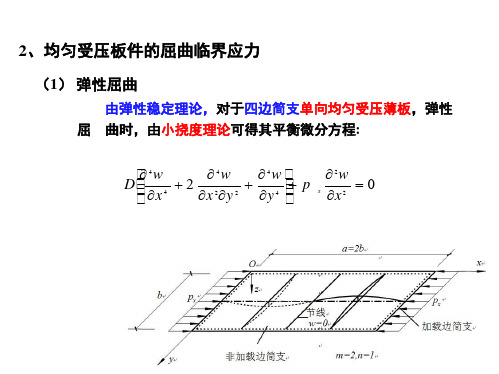
(1) 弹性屈曲
由弹性稳定理论,对于四边简支单向均匀受压薄板,弹性 屈 曲时,由小挠度理论可得其平衡微分方程:
D
4w
x
4
2 4w x 2y 2
4w y 4
p
x
2w x 2
0
解得板件的临界应力为:
2
x ,cr
板件的稳定和屈曲后强度的利用

构造要求:腹板两侧成对布置,也可以用凸缘式加劲 肋,其凸缘长度不得大于其厚度的2倍(图4-71b) 。
计算: 应按承受梁支座反力或固定集中荷载的轴心受压构件
计算其在腹板平面外的稳定性。 支承加劲肋的端部一般刨平顶紧于梁翼缘或支座,应按
腹板的局部稳定
控制有两种考虑方法: 考虑腹板屈曲后强度:仅对承受静力荷载和间接承受
动力荷载的组合梁,计算其腹板的抗弯和抗剪承载力。
若用此法,其计算及构造要求应满足4.6.4节内容。
不考虑腹板屈曲后强度:仅对直接承受动力荷载的组 合梁及不考虑腹板屈曲后强度组合梁,其腹板的稳定 是通过设置加劲肋来保证的。由于梁截面腹板高度很
的整体稳定性,然后验算局部稳定。当翼缘不满足要 求时,应重新选择截面尺寸;当腹板不满足要求时, 可设置纵向加劲肋。
受弯构件的局部稳定
这里的翼缘是指受压翼缘的稳定。 采用薄板弹塑性屈曲的临界应力(式4-108) 使其不小于0.95f y可推导出式4-118(弹性设 计)、119(塑性设计)、120(弹塑性设计)。 (0.95为受压翼缘截面的平均应力)
另一种是允许板件先屈曲。虽然板件屈曲会降低 构件的承载能力,但由于构件的截面较宽,整体 刚度好,从节省钢材来说反而合算,《冷弯薄壁 型钢结构技术规范》(GB 50018)就有这方面 的条款。有时对于一般钢结构的部分板件,如大 尺寸的焊接组合工字形截面的腹板,也允许其先 有局部屈曲。
轴心受压构件的局部稳定:
高,当采用腹板高厚比限值时,腹板厚度将很厚,浪 费材料。将梁腹板做的高而薄,通过设置加劲肋来保 证其稳定性是很经济的。
加劲肋的分类
如何设置腹板加劲肋?
5.3 受弯构件(局部稳定)

设有横向加劲肋的腹板区格,当弯曲正应力和剪应力同时作 用时(图5-27a),临界条件是:
钢结构/ 第5章 钢结构基本构件计算 /$5.2 受弯构件
(5-39)
此种取值方法被美国长期使用。
钢结构/ 第5章 钢结构基本构件计算 /$5.2 受弯构件
11
二、 各种应力共同作用下的薄板稳定
以上介绍的是矩形板在各种应力单独作用下的临界应力。实 际上钢梁的腹板通常承受两种或两种以上应力的共同作用, 现分情况介绍其稳定计算方法。
1、仅用横向加劲肋加强的梁腹板
情况,其屈曲系数k=0.425。支承翼缘板的腹板一般都比较薄
(负约束),对翼缘板没有什么约束作用,因此取弹性约束系数
综合以上情况,上区格的局部稳定相关公式取为:
钢结构/ 第5章 钢结构基本构件计算 /$5.2 受弯构件
17
cr1
c c,cr1
2
cr1
2
1
Байду номын сангаас
(5-41)
式中 σ、τ、σc分别为板件的正应力、剪应力和横向局部压应 力,和这些应力对应的三个分母则分别为各应力单独作用时 的临界应力。
图5-29 双向受压板的相关屈曲 图5-30 受剪和横向压力的板的相关屈曲
梁整体稳定的临界应力超过0.6f时就需要进行非弹性修正,而
式(5-43)是腹板局部稳定临界应力无限弹性的计算公式,直
接使用显然是不适宜的。因此,实用上要对前述板件屈曲应力
计算公式进行弹塑性修正。
(整理)钢结构设计原理试卷

钢结构设计原理试卷 (A卷)一、单项选择题:(每小题2分,共20分)1.对于碳素结构钢来讲其含碳越高,则( )。
A.强度越高B.变形能力越好C.焊接性能好D.疲劳强度提高2.在抗剪连接中,强度等级、直径和数量相同的承压型高强度螺栓连接比摩擦型高强度螺栓连接( ) A.承载力低,变形大 B.C.承载力低,变形小D.3. 满足;若受偏心压力时, A.一定满足 B. C.也刚好满足 D.4.临界应力时,其支承条件为( ) A.四边简支B.C.两边简支,两边自由D.悬臂5.设计焊接工字形截面梁时,A.抗弯刚度 B.抗弯强度6.A.荷载标准值 B.荷载设计值C.考虑动力系数的荷载标准值D.考虑动力系数的荷载设计值7.格构式轴心受压柱整体稳定计算时,用换算长细比x 0λ代替长细比x λ,这是考虑( )。
A.格构柱弯曲变形的影响 B.格构柱剪切变形的影响 C.缀材弯曲变形的影响D.缀材剪切变形的影响8.两端铰接轴心受压杆件,轴力图如下图所示,其它条件相同,则发生弹性失稳时,各压杆的临界力的关系是( )。
A.cr1N >cr2N >cr3N >cr4NB. cr4N >cr2N >cr3N >cr1NC. cr4N >cr3N >cr2N >cr1N D .cr1N >cr3N >cr2N >cr4N9.10.A.C.二、填空题(每空1分,共10分)1. 对于钢结构用钢材应严格控制硫的含量,这是因为含硫量过大,在焊接时会引起钢材的 。
2. 钢材的伸长率是衡量钢材 性能的指标,是通过一次静力拉伸试验得到的。
3. 当轴心受压构件发生弹性失稳时,提高钢材的强度将 构件的稳定承载力。
4. 焊接工字形组合截面轴压柱,腹板局部稳定条件为 γλf t h w /235)5.025(/0+≤,其中λ应取 。
5. 提高钢梁的整体稳定性最有效的办法之一就是设置侧向支承点,但侧向支承点必须设在钢梁的 翼缘处。
6. 实腹式偏心压杆在弯矩平面外的失稳属于 屈曲。
4月全国自考钢结构试题及答案解析

全国2018年4月高等教育自学考试钢结构试题课程代码:02442一、单项选择题(本大题共20小题,每小题2分,共40分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.关于钢结构的特点叙述错误..的是()A.建筑钢材的塑性和韧性好B.钢材的耐腐蚀性很差C.钢材具有良好的耐热性和防火性D.钢结构更适合于建造高层和大跨结构2.钢材冲击韧性值αk与工作温度T之间的关系为()A.T降低,αk降低B.T增加,αk降低C.T降低,αk增高D.T改变,αk不变3.钢材屈服点f y的高低反应材料()A.受静荷时的最大承载能力B.受静荷时的最大变形能力C.受动荷时的最大承载能力D.受静荷时发生塑性变形前的承载能力4.在三向正应力状态下,当出现下列何种情况时,钢材易发生脆性破坏()A.异号应力,且应力差较小B.异号应力,且应力差较大C.同号拉应力,且应力差较小D.同号拉应力,且应力差较大5.T形连接中直角角焊缝的最小焊脚尺寸h fmin =1.52t,最大焊脚尺寸h fmax=1.2t1,式中的t1和t2分别为()A.t1为腹板厚度,t2为翼缘厚度B.t1为翼缘厚度,t2为腹板厚度C.t1为较小的被连接板件的厚度,t2为较大的被连接板件的厚度D.t1为较大的被连接板件的厚度,t2为较小的被连接板件的厚度6.图示焊接连接中,最大的焊缝应力发生在()A.a点B.b点C.c点D.d点7.如图所示普通螺栓群受弯矩M作用,在计算螺栓拉力时应取哪一点为旋转中心?()A.aB.bC.cD.d18.轴心受压柱的柱脚底板厚度是根据下列哪种工作状态确定的?()A.底板抗压工作B.底板抗弯工作C.底板抗剪工作D.底板抗弯及抗压工作9.通常轴心受压缀条式格构柱的横缀条不受力,但一般仍设置。
其理由是()A.起构造作用B.可以加强柱的整体抗弯刚度C.对单肢稳定起作用D.以上三种原因都有10.两端铰接轴心受压柱发生弹性失稳时,其它条件相同,轴力分布图如下所示,则各压杆的临界力的关系是()A.N k1>N k2>N k3>N k4B.N k4>N k2>N k3>N k1C.N k4>N k3>N k2>N k1D. N k1>N k3>N k2>N k411.梁的受压翼缘侧向支承点的间距和截面尺寸都不改变,跨内的最大弯矩相等,且不存在局部稳定问题,承受以下哪种荷载时梁的临界弯矩为最高()A.三分点处各有一个集中荷载B.均布荷载C.跨中一个集中荷载D.纯弯矩12.对于受均布荷载的单层翼缘板的焊接组合截面简支梁,跨度为l,当要改变截面时,宜变一次,且只改变翼缘板的宽度,其最经济的改变截面的位置为()2A.距支座l/8处B.距支座l/6处C.距支座l/4处D.距支座l/3处13.图示的四边简支薄板,当a=b时,纯剪作用下板的屈曲形式是()14.偏心受压杆计算公式中的塑性发展系数γ和yγ只与下列哪种因素有关?()xA.回转半径iB.长细比λC.荷载性质D.截面形式15.如图所示,一工字形截面杆件当承受纯弯时,其截面最大应力为σ1;当承受偏心压力时,其截面最大应力也为σ1。
四边简支矩形层合板屈曲问题分析

四边简支矩形层合板屈曲问题分析四边简支矩形层合板屈曲问题分析一、问题的描述四边简支的正交对称矩形层合板,单层厚度为0.2mm ,a=800mm ,b=100mm 。
已知各单层特性:受单向压缩121221181,10.3,7.17,0.28E GPa E GPa G GPa ν====求:临界载荷[0/90/90/0]二、解析解1、理论分析正交对称层合板单向受压的屈曲方程:()4442111266224224222+0w w w w D D D D N x x y y x+++= 由Navier 法设屈曲形状为双正弦函数:11sinsin mn m n m x n y w a a bππ∞∞===∑∑ 将w 代入屈曲方程求得临界屈曲荷载为:()()()221112662222122cr N D mb a D D D b mb a π?? ?=+++ // 由上式可知N 取最小值的x 方向半波数m 与边长比b a /及刚度有关。
2、matlab 编程求解E1=181;E2=10.3;v21=0.28;v12=E2*v21/E1;G12=7.17;%材料常数Q11=E1/(1-v12*v21);Q22=E2/(1-v12*v21);Q12=E2*v21/(1-v12*v21);Q66=G12;%正轴刚度U1_Q=(1/8)*(3*Q11+3*Q22+2*Q12+4*Q66);U2_Q=(1/2)*(Q11-Q22);U3_Q=(1/8)*(Q11+Q22-2*Q12-4*Q66);U4_Q=(1/8)*(Q11+Q22+6*Q12-4*Q66);U5_Q=(1/8)*(Q11+Q22-2*Q12+4*Q66);%单向板正轴刚度的线性组合z0=-0.4;z1=-0.2;z2=0;z3=0.2;z4=0.4;%层合板厚度方向的坐标theta1=0;theta2=pi/2;theta3=pi/2;theta4=0;%每层的铺设角h=0.8;%层合板的总厚度V1_D=(1/3)*(((z1)^3-(z0)^3)*cos(2*theta1)+((z2)^3-(z1)^3)*cos(2*t heta2)+((z3)^3-(z2)^3)*cos(2*theta3)+((z4)^3-(z3)^3)*cos(2*theta4));V2_D=(1/3)*(((z1)^3-(z0)^3)*cos(4*theta1)+((z2)^3-(z1)^3)*cos(4*t heta2)+((z3)^3-(z2)^3)*cos(4*theta3)+((z4)^3-(z3)^3)*cos(4*theta4));V3_D=0;V4_D=0;%层合板的几何因子D11=U1_Q*h^3/12+V1_D*U2_Q+V2_D*U3_Q;D22=U1_Q*h^3/12-V1_D*U2_Q+V2_D*U3_Q;D12=U4_Q*h^3/12-V2_D*U3_Q;D66=U5_Q*h^3/12-V2_D*U3_Q;%弯曲刚度a=0.8;b=0.1;%层合板的边长m=1;N1=pi^2/b^2*(D11*(m*b/a)^2+2*(D12+2*D66)+D22/ (m*b/a)^2);m=2;N2=pi^2/b^2*(D11*(m*b/a)^2+2*(D12+2*D66)+D22/ (m*b/a)^2);m=3;N3=pi^2/b^2*(D11*(m*b/a)^2+2*(D12+2*D66)+D22/ (m*b/a)^2);m=4;N4=pi^2/b^2*(D11*(m*b/a)^2+2*(D12+2*D66)+D22/ (m*b/a)^2);m=5;N5=pi^2/b^2*(D11*(m*b/a)^2+2*(D12+2*D66)+D22/ (m*b/a)^2);m=6;N6=pi^2/b^2*(D11*(m*b/a)^2+2*(D12+2*D66)+D22/ (m*b/a)^2);m=7;N7=pi^2/b^2*(D11*(m*b/a)^2+2*(D12+2*D66)+D22/ (m*b/a)^2);M=[1:7]N=[N1 N2 N3 N4 N5 N6 N7]%m为半波数,N为临界荷载结果:M =1 2 3 4 5 6 7N =1.0e+004 *由N可知,当半波数m=5时,最小临界载荷为N。
四边简支受压板例题

可见板屈曲后随着荷载的增大面外位移逐渐增大, 即板有能力抵抗比屈服荷载大很多的 荷载,也就是通常所说的板屈后承载能力。
二、
屈曲分析
首先添加线性屈曲分析工况, 计算所得第一阶屈曲模态的荷载因子为 0.4722, 对应的临
界荷载为 4000MPa×0.4722=1888MPa。将参数代入式(1)计算所得的临界屈曲荷载为 1898MPa,误差约为 0.5%。误差会随着网格密度的增大而减小。 在进行该薄板的几何非线性分析时, 按一阶屈曲模态更新模型节点位置, 以施加初始缺 陷。此时取缩放系数为 1%,即施加一阶屈曲模态面外位移的 1%作为初始缺陷进行分析。在 后处理中查看第一阶屈曲模态位移的表格,乘以 0.01 的缩放系数,再加上网格节点初始位 置,便得到了考虑初始缺陷的网格。将此更新后的节点表格拷贝到节点表格中。
×0.01+
=
一阶模态位移
原始网格
考虑缺陷网格
此时添加非线性静态分析工况, 打开几何非线性选项进行非线性分析, 采用弧长法分析 控制, 在后处理中通过提取结果功能得到荷载与板中心节点面外位移的表格, 画出荷载位移 曲线如下图:
2500 2000 1500 1000 500 0 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8
此时添加非线性静态分析工况打开几何非线性选项进行非线性分析采用弧长法分析控制在后处理中通过提取结果功能得到荷载与板中心节点面外位移的表格画出荷载位移曲线如下图
屈曲分析与非线性屈曲分析例题
一、 模型说明
模型为一四边简支的受压板,如下图所示,a=200mm,b=40mm,厚度 t=2mm,弹性模 量 E 为 210GPa,泊松比为 0.3。在四边简支和周边面内自由移动的条件下,其理论弹性屈曲 荷载应为:
四边简支矩形板计算

四边简⽀矩形板计算四边简⽀矩形板计算项⽬名称_____________⽇期_____________设计者_____________校对者_____________⼀、构件编号: LB-1⼆、⽰意图三、依据规范《建筑结构荷载规范》 GB50009-2001《混凝⼟结构设计规范》 GB50010-2010四、计算信息1.⼏何参数计算跨度: Lx = 11000 mm; Ly = 7500 mm板厚: h = 400 mm2.材料信息混凝⼟等级: C30 fc=14.3N/mm2 ft=1.43N/mm2 ftk=2.01N/mm2Ec=3.00×104N/mm2钢筋种类: HRB400 fy = 360 N/mm2Es = 2.0×105 N/mm2最⼩配筋率: ρ= 0.200%纵向受拉钢筋合⼒点⾄近边距离: as = 55mm保护层厚度: c = 40mm3.荷载信息(均布荷载)永久荷载分项系数: γG = 1.200可变荷载分项系数: γQ = 1.400准永久值系数: ψq = 1.000永久荷载标准值: qgk = 15.000kN/m2可变荷载标准值: qqk = 0.000kN/m24.计算⽅法:弹性板5.边界条件(上端/下端/左端/右端):简⽀/简⽀/简⽀/简⽀6.设计参数结构重要性系数: γo = 1.00泊松⽐:µ = 0.200五、计算参数:1.计算板的跨度: Lo = 7500 mm2.计算板的有效⾼度: ho = h-as=400-55=345 mm六、配筋计算(lx/ly=11000/7500=1.467<2.000 所以按双向板计算):1.X向底板钢筋1) 确定X向板底弯矩Mx = 表中系数(γG*qgk+γQ*qqk)*Lo2= (0.0287+0.0707*0.200)*(1.200*15.000+1.400*0.000)*7.52 = 43.374 kN*m2) 确定计算系数αs = γo*Mx/(α1*fc*b*ho*ho)= 1.00*43.374×106/(1.00*14.3*1000*345*345)= 0.0253) 计算相对受压区⾼度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.025) = 0.0264) 计算受拉钢筋⾯积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*345*0.026/360= 354mm25) 验算最⼩配筋率ρ = As/(b*h) = 354/(1000*400) = 0.088%ρ<ρmin = 0.200% 不满⾜最⼩配筋要求所以取⾯积为As = ρmin*b*h = 0.200%*1000*400 = 800 mm2采取⽅案?12@140, 实配⾯积807 mm2 2.Y向底板钢筋1) 确定Y向板底弯矩My = 表中系数(γG*qgk+γQ*qqk)*Lo2= (0.0707+0.0287*0.200)*(1.200*15.000+1.400*0.000)*7.52 = 77.430 kN*m2) 确定计算系数αs = γo*My/(α1*fc*b*ho*ho)= 1.00*77.430×106/(1.00*14.3*1000*345*345)= 0.0453) 计算相对受压区⾼度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.045) = 0.0474) 计算受拉钢筋⾯积As = α1*fc*b*ho*ξ/fy = 1.000*14.3*1000*345*0.047/360= 638mm25) 验算最⼩配筋率ρ = As/(b*h) = 638/(1000*400) = 0.160%ρ<ρmin = 0.200% 不满⾜最⼩配筋要求所以取⾯积为As = ρmin*b*h = 0.200%*1000*400 = 800 mm2采取⽅案?12@100, 实配⾯积1131 mm2七、跨中挠度计算:Mk -------- 按荷载效应的标准组合计算的弯矩值Mq -------- 按荷载效应的准永久组合计算的弯矩值1.计算荷载效应Mk = Mgk + Mqk= (0.0707+0.0287*0.200)*(15.000+0.000)*7.52 = 64.525 kN*mMq = Mgk+ψq*Mqk= (0.0707+0.0287*0.200)*(15.000+1.0*0.000)*7.52 = 64.525 kN*m2.计算受弯构件的短期刚度 Bs1) 计算按荷载荷载效应的两种组合作⽤下,构件纵向受拉钢筋应⼒σsk = Mk/(0.87*ho*As) 混规(7.1.4-3)= 64.525×106/(0.87*345*1131) = 190.077 N/mmσsq = Mq/(0.87*ho*As) 混规(7.1.4-3)= 64.525×106/(0.87*345*1131) = 190.077 N/mm2) 计算按有效受拉混凝⼟截⾯⾯积计算的纵向受拉钢筋配筋率矩形截⾯积: Ate = 0.5*b*h = 0.5*1000*400= 200000mm2ρte = As/Ate 混规(7.1.2-4)= 1131/200000 = 0.566%3) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψk = 1.1-0.65*ftk/(ρte*σsk) 混规(7.1.2-2)= 1.1-0.65*2.01/(0.566%*190.077) = -0.115因为ψ不能⼩于最⼩值0.2,所以取ψk = 0.2ψq = 1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)= 1.1-0.65*2.01/(0.566%*190.077) = -0.115因为ψ不能⼩于最⼩值0.2,所以取ψq = 0.24) 计算钢筋弹性模量与混凝⼟模量的⽐值αEαE = Es/Ec = 2.0×105/3.00×104 = 6.6675) 计算受压翼缘⾯积与腹板有效⾯积的⽐值γf矩形截⾯,γf=06) 计算纵向受拉钢筋配筋率ρρ = As/(b*ho)= 1131/(1000*345) = 0.328%7) 计算受弯构件的短期刚度 BsBsk = Es*As*ho2/[1.15ψk+0.2+6*αE*ρ/(1+ 3.5γf')](混规(7.2.3-1)) = 2.0×105*1131*3452/[1.15*-0.115+0.2+6*6.667*0.328%/(1+3.5*0.0)]= 4.798×104 kN*m2Bsq = Es*As*ho2/[1.15ψq+0.2+6*αE*ρ/(1+ 3.5γf')](混规(7.2.3-1)) = 2.0×105*1131*3452/[1.15*-0.115+0.2+6*6.667*0.328%/(1+3.5*0.0)]= 4.798×104 kN*m23.计算受弯构件的长期刚度B1) 确定考虑荷载长期效应组合对挠度影响增⼤影响系数θ当ρ'=0时,θ=2.0 混规(7.2.5)2) 计算受弯构件的长期刚度 BBk = Mk/(Mq*(θ-1)+Mk)*Bs (混规(7.2.2-1))= 64.525/(64.525*(2.0-1)+64.525)*4.798×104= 2.399×104 kN*m2Bq = Bsq/θ (混规(7.2.2-2))= 4.798×104/2.0= 2.399×104 kN*m2B = min(Bk,Bq)= min(23990.371,23990.371)= 23990.3714.计算受弯构件挠度f max = f*(q gk+q qk)*Lo4/B= 0.00752*(15.000+0.000)*7.54/2.399×104= 14.879mm5.验算挠度挠度限值fo=Lo/250=7500/250=30.000mmfmax=14.879mm≤fo=30.000mm,满⾜规范要求!⼋、裂缝宽度验算:1.跨中X⽅向裂缝1) 计算荷载效应Mx = 表中系数(qgk+ψqqk)*Lo2= (0.0287+0.0707*0.200)*(15.000+1.00*0.000)*7.52= 36.145 kN*m2) 带肋钢筋,所以取值v i=1.03) 因为C > 65,所以取C = 654) 计算按荷载效应的准永久组合作⽤下,构件纵向受拉钢筋应⼒σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=36.145×106/(0.87*345*807)=149.222N/mm5) 计算按有效受拉混凝⼟截⾯⾯积计算的纵向受拉钢筋配筋率矩形截⾯积,Ate=0.5*b*h=0.5*1000*400=200000 mm2ρte=As/Ate 混规(7.1.2-4)=807/200000 = 0.0040因为ρte=0.0040 < 0.01,所以让ρte=0.016) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*2.010/(0.0100*149.222)=0.2247) 计算单位⾯积钢筋根数nn=1000/dist = 1000/140=78) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=7*12*12/(7*1.0*12)=129) 计算最⼤裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.224*149.222/2.0×105*(1.9*40+0.08*12/0.0100) =0.0547mm ≤ 0.20, 满⾜规范要求2.跨中Y⽅向裂缝1) 计算荷载效应My = 表中系数(qgk+ψqqk)*Lo2= (0.0707+0.0287*0.200)*(15.000+1.00*0.000)*7.52= 64.525 kN*m2) 带肋钢筋,所以取值v i=1.03) 因为C > 65,所以取C = 654) 计算按荷载效应的准永久组合作⽤下,构件纵向受拉钢筋应⼒σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=64.525×106/(0.87*345*1131)=190.077N/mm5) 计算按有效受拉混凝⼟截⾯⾯积计算的纵向受拉钢筋配筋率矩形截⾯积,Ate=0.5*b*h=0.5*1000*400=200000 mm2ρte=As/Ate 混规(7.1.2-4)=1131/200000 = 0.0057因为ρte=0.0057 < 0.01,所以让ρte=0.016) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2)=1.1-0.65*2.010/(0.0100*190.077)=0.4137) 计算单位⾯积钢筋根数nn=1000/dist = 1000/100=108) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=10*12*12/(10*1.0*12)=129) 计算最⼤裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1) =1.9*0.413*190.077/2.0×105*(1.9*40+0.08*12/0.0100) =0.1282mm ≤ 0.20, 满⾜规范要求。
四边简支板的屈曲荷载ppt课件

第06讲 四边简支板的屈曲荷载
1
【基本题1】
计算条件: 1)长度为a; 2)宽度为b;a>=b 3)厚度为t; 4)板面内承受均匀 压力p 命令流:ex06.mac 求临界荷载
【结果】
【思考】
1)对比Ansys结果和理论解,结果是否一致?请分析原因。 回顾弹性力学经典解的基本假定。
2)约束多了,屈曲荷载反而下降?约束不同时,结构的刚度 矩阵和应力刚度矩阵有何不同?
3)改变结构的柏松比,重新查看屈曲荷载和刚度矩阵。
4)从概念角度分析,当约束不同时极限承载力有何不同?
5)屈曲荷载低,极限承载力反而高。借助本题体会临界荷载 和极限承载力的差异。
6)验证板件长宽比对屈曲荷载的影响。理解屈曲半波长的概 念。不同长宽比的屈曲荷载排序。实际工程中的四边简支板。
【理论解】
四边简支板的屈曲荷载:
N xcr
2D
k b2
D为单位宽度板的抗弯刚度:
D
Et 3
12(1
2
)
k为约束系数: k ( mb a )2 a mb
【拓展题1】
求钢卷尺的悬臂长度 (1)卷尺截面如图 (2):
1)初始缺陷为第1 阶屈曲模态。
(6)屈曲荷载和极限承载力之间的差别?
(7)查看横向拉力场
(8)查看纵向压力场
(9)对比两种情况,看看哪个压力场发展的 更为充分。
2)缺陷最大值为 a/100;
3)计算其极限承 载力;
4)标准命令流: ex06b.mac
【思考】
(1)如何施加初始缺陷? (2)对比不同约束条件下的荷载位移曲线。 (3)观察变形过程,正确选取典型节点的 位移。 (4)当材料为理想弹塑性时,分别计算两 种约束条件下的极限承载力。
四边简支矩形板稳定问题的精确解

四边简支矩形板稳定问题的精确解四边简支矩形板稳定问题的精确解
“四边简支矩形板稳定性问题”一直是国内外结构工程界的一个热门话题,关
于此问题,很多学者提出了自己的解决方案,但仍未能得出一个明确的精确答案。
因此,四边简支矩形板稳定性问题的精确解非常重要。
首先,要求四边简支矩形板稳定,就需要确定力学模型及其对应的支座位置。
通过有限个节点以及一定的刚度,用支撑力法(support force method)分析问题,可以得到节点的位移。
根据这个位移的大小,以及构成支座的刚度系数,可以得到支座的弹力系数和承载力,最后可以得知四边简支矩形板的稳定性情况。
另外,要求四边简支矩形板稳定,必须建立计算机编程模型,通过C语言或者Fortran等编程语言来实现计算,这样可以更精确地求得四边简支矩形板的稳定性解,使得在设计结构时,能够更好地优化支座的位置,从而使板的稳定性更为明确。
因此,我们可以得出结论,采用正确的力学模型及其对应的支座位置,并建
立计算机编程模型,就可以正确精确地求得四边简支矩形板的稳定性解,从而使得结构物的稳定性更为可靠。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、
屈曲分析
首先添加线性屈曲分析工况, 计算所得第一阶屈曲模态的荷载因子为 0.4722, 对应的临
界荷载为 4000MPa×0.4722=1888MPa。将参数代入式(1)计算所得的临界屈曲荷载为 1898MPa,误差约为 0.5%。误差会随着网格密度的增大而减小。 在进行该薄板的几何非线性分析时, 按一阶屈曲模态更新模型节点位置, 以施加初始缺 陷。此时取缩放系数为 1%,即施加一阶屈曲模态面外位移的 1%作为初始缺陷进行分析。在 后处理中查看第一阶屈曲模态位移的表格,乘以 0.01 的缩放系数,再加上网格节点初始位 置,便得到了考虑初始缺陷的网格。将此更新后的节点表格拷贝到节点表格中。
×0.01+
=
一阶模态位移
原始网格
考虑缺陷网格
此时添加非线性静态分析工况, 打开几何非线性选项进行非线性分析, 采用弧长法分析 控制, 在后处理中通过提取结果功能得到荷载与板中心节点面外位移的表格, 画出荷载位移 曲线如下图:
2500 2000 1500 1000 500 0 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8
可见板屈曲后随着荷载的增大面外位移逐渐增大, 即板有能力抵抗比屈服荷载大很多的 荷载,也就是通常所说的板屈后承载能力。
a Y σ b
2
(1)
X
σ
建模时为保证四边简支和面内自由移动的条件,采用以下约束方式:约束周边面外 Uz 自由度;约束平行于 X 轴的对称轴上节点的 Uy 自由度;约束平行于 Y 轴的对称轴上节点的 Ux 自由度。 模型单元尺寸为 5mm, 对两边施加 8000N/mm 的线均布压力。 模型如下图所示:
屈曲分析与非线性屈曲分析例题
一、 模型说明
模型为一四边简支的受压板,如下图所示,a=200mm,b=40mm,厚度 t=2mm,弹性模 量 E 为 210GPa,泊松比为 0.3。在四边简支和周边面内自由移动的条件下,其理论弹性屈曲 荷载应为:
2E t cr 3(1 2 ) b
