南华大学2010年数学竞赛试题

合集下载

2010年全国大学生高等数学竞赛总决赛(答案)

2010年全国大学生数学竞赛决赛答 tian27546这是献给博士论坛一个礼物转载时请勿注明是博士论坛一、（20分）计算下列各题：1．求极限 211sin )1(lim n k n k n k n π∑-=→∞+解法1因211sin )1(n k n k n k π∑-=+211222sin sin 21(2sin 21n n k n k nn k πππ∑-=+=） )22cos 22(cos 1(2sin 2122112n k n k n k nn k πππππ+--+=∑-=） )22cos 22(cos 1(22112nk n k n k n n k πππππ+--+≈∑-=） 2112211222cos 1(22cos 1(n k nk n n k n k n n k n k ππππππ++--+=∑∑-=-=）） 222211222cos 11(22cos 1(n k n k n n k n k n nk n k ππππππ--+--+=∑∑=-=））2122222222cos 12)12(cos 11(2cos )11(n k n n n n n n n n n n n k πππππππ-+--+-+=∑-=） 21222222)12(cos 2)12(cos 12(2cos )11(nk n n n n n n n n n k ππππππ-+---+=∑-=）（*）而2122)12(cos n k n k π-∑-=212222sin 2)12(cos22sin 21n n k nn k πππ∑-=-=])1(sin [sin2sin2121222n k n k nn k πππ--=∑-= 2222sin 2sin )1(sinn n n n πππ--=222sin2)2(sin 2cos n n n n πππ-=（**）将（**）代入（*），然后取极限，得原式]2sin2)2(sin2cos2)12(cos 12(2cos )11([lim 222222n n n nn n n n n n n n n ππππππππ-+---+=→∞）]2)2(sin 2cos 2)8)12(1(12()11([lim 22342222n n n n n n n n n n n ππππππ-+----+=∞→） ]2)2(sin 2cos 2)21(12()11([lim 2232222n n n n n n n n n n ππππππ-+---+=∞→） )]48)2(2)2()(81(2)21(12()11([lim 633222232222nn n n n n n n n n n n πππππππ----+---+=∞→）)]482)(81(2)21(12()11([lim 33222232222n n n n n n n n n n n ππππππππ---+---+=∞→） 65π=上式中含2n 的项的系数为0121=+-πππ，含n 的项的系数为0)2(111=-++πππ，常数项系数为656824ππππππ=-=--解法2 Step 1因∑-=112sin n k n k π211222sinsin 22sin 21n nk nn k πππ∑-==)22cos 22(cos2sin2122112n k n k nn k πππππ+--=∑-=)2)12(cos2(cos2sin21222n n n n πππ--=故)2)12(cos 2(cos 2sin 21lim sinlim 222112n n n nn k n n k n ππππ--=→∞-=→∞∑)2)12(cos2(cos1lim222n n n n n πππ--=→∞nn n n n 2sin 2)1(sin2lim22πππ-=→∞n n n n n 22)1(2lim22πππ-=∞→2π= Step 2因222)12(cosn k nk π-∑=22222sin 2)12(cos22sin21n n k nnk πππ∑=-=])1(sin [sin2sin212222nk n k nnk πππ--=∑= 2222sin 2sinsin n n n n πππ-=2222sin 2)1(sin 2)1(cos nn n n n πππ-+=因此∑-=112sin n k n k nk π211222sin sin 22sin 21n n k n k n n k πππ∑-== ]2)12(cos 2)12(cos [2sin 212112112n k n k n k n k nn k n k πππ+--=∑∑-=-= ]2)12(cos 12)12(cos [2sin 21222112n k n k n k n k nnk n k πππ----=∑∑=-=⎥⎦⎤⎢⎣⎡-+---=∑-=2122222)12(cos 12)12(cos 12cos 12sin 21n k n n n n n n n nn k ππππ ⎥⎦⎤⎢⎣⎡-+--=∑=222222)12(cos 12)12(cos 2cos 12sin 21n k n n n n nnnk ππππ(*) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-++--=2222222sin 2)1(sin 2)1(cos 2)12(cos 2cos 12sin 21nn n n n n n n n n n ππππππ 于是∑-=→∞112sin lim n k n n k nk π⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-++--=→∞2222222sin 2)1(sin 2)1(cos 2)12(cos 2cos 12sin 21lim nn n n n n n n n n n n ππππππ ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-++---=→∞n n n n n n n n n n 22)1(sin2)1(cos 8)12(11lim 224222πππππ）（ ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---+-++-=∞→n n n n n n n n n n n 2)48)1(2)1()(8)1(1211lim 6332422222ππππππ（⎥⎦⎤⎢⎣⎡----++-=∞→)24)1(1)(81211lim 52322222n n n n n n n n n ππππ（ ⎥⎦⎤⎢⎣⎡---++-=∞→)241()(81211lim 2222222n n n n n n n n ππππ（ ⎥⎦⎤⎢⎣⎡---++-=∞→)2411)(81211lim 2222222n n n n n n n ππππ（）（222222282411211lim n n n n n n n ππππ---++-=→∞ ）（22222228242lim n n n n n ππππ--=∞→62ππ-=3π=原式6532πππ=+=2．计算⎰⎰∑++++2222)(zy x dxdya z axdydz ，其中 ∑为下半球面222y x a z ---= 的上侧, 0>a .解记1∑为平面 222,0a y x z ≤+= 的上侧，2∑为下半球面 222y x a z ---= 的下侧，Ω是由1∑和2∑所围成的立体，则422222211)(adxdy a dxdy a dxdy a z axdydz ay x ⎰⎰⎰⎰⎰⎰≤+∑∑===++π，设,sin ,cos θθr y r x ==则⎰⎰∑+∑++212)(dxdy a z axdydz ⎰⎰⎰Ω+++=dxdydz a z a )220(⎰⎰⎰Ω+=dxdydz a z )32(⎰⎰⎰≤+---+=2222220)32(a y x y x a dz a z dxdy⎰⎰≤+---+=22222202]3[a y x y x a dxdy az z⎰⎰≤+--+++-=222)3(222222a y x dxdy y x a a y x a ⎰⎰≤≤≤≤-++-=πθθ2002222d d )3(ar r r r a a r a⎰-++-=a r r r a a r a 02222d )3(2π ⎰-++-=ar r a a r a 022222)d()3(π⎰-++-=22122d ))(3(a u u a a u a π223222)(42a u a a uu a ⎥⎦⎤⎢⎣⎡--+-=π274a π=⎰⎰∑++++2222)(zy x dxdya z axdydz⎰⎰⎰⎰∑∑+∑+++++-=12122)(1)(1dxdy a z axdydz a dxdy a z axdydz a 227333a a a πππ-=+-=3．现设计一个容积为V 的圆柱体容器. 已知上下两底的材料费为单位面积a元，而侧面的材料费为单位面积b 元. 试给出最节省的设计方案；即高与的上下底直径之比为何值时所需费用最少？解设圆柱体的底半径为r ，高为h ，则h r V 2π=，2rVh π=总造价为222r a rh b P ππ+=222r a rbVπ+=，则2322242r r a bV r a r bV P ππ--=+-='，由0='P 知，解得312⎪⎭⎫⎝⎛=πa bV r ，312⎪⎭⎫ ⎝⎛=ππa bV V h ，因为是惟一的驻点，所以当3122323131222222:2⎪⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=Vab a bV V a bV a bV V h r ππππππ 时，所需费用最少.4．已知 x x x f 33cos sin 1)(+='，)21,41(∈x ，求)(x f 解因x x x f 33cos sin 1)(+='，)21,41(∈x ，故 ⎰+=x xx x f d cos sin 1)(33⎰+-+=x x x x x x x d )cos )(sin cos sin cos (sin 122⎰+-=x x x x x d )cos )(sin cos sin 1(1⎰+-=x x x d )4sin()2sin 211(21π⎰+⎪⎭⎫ ⎝⎛++=x x x d )4sin()22cos(211121ππ⎰+⎪⎭⎫ ⎝⎛++=x x x d )4sin()4(2cos 211121ππ 令)4(21π+=x t ，则⎰+=t tt x f d 2sin )4cos 211(2)(⎰+=t tt t d cos sin )4cos 2(2⎰-+=t t t t t d cos sin )2sin 2cos 2(222⎰+=t t t t t d cos sin )2sin 2cos 3(222 ⎰+-=t tt t t t t d cos sin )cos sin 4)sin (cos 3(222222⎰-++=t t t t t t t t t d cos sin )cos sin 2sin 3cos 3()cos (sin 22244222 ⎰-+++=t t t t t t t tt t t d cos sin )cos sin 2sin 3cos 3(cos sin 2sin cos 222442244⎰-+++=t t t t tt tan d tan )tan 2tan 33(tan 2tan 122424 令t u tan =，2u v =，则⎰-+++=u u u u u u x f d )233(212)(2424⎰-+++=224224d )233(2122u u u u u u ⎰-+++=v v v v v v d )233(212222⎰+-++=v v v v v v d )323(122222 令)()323(1222v R vAv v v v v +=+-++，则31=A ，)323(332336331)323(12)(22222+--+-++=-+-++=v v v v v v v v v v v v v v R )323(382+-=v v 因此⎰⎰+-+=323d 324d 62)(2v v vv v x f ⎰+-+=323d 324ln 622v v vv ⎰+-+=98)31(d 924ln 622v v v C v v +-+=32231arctan 3221924ln 62C v v +-+=2213arctan 32ln 62 C t t +-+=221tan 3arctan 32tan ln 6222C t t +-+=221tan 3arctan 32tan ln 6222C x x +-+++=221)82(tan 3arctan 32)82(tan ln 6222ππ 二、（10分）求下列极限1．⎪⎭⎫ ⎝⎛-+∞→e n n n n )11(lim解设xx x f 1)1()(+=, 则))1ln()1(1()1()(21xx x x x x f x+-++=')1()1ln()1()(2x x x x x x f +++-= 原式=)(lim )1(lim010x f x e x x xx '=-+→→)()(lim )(lim 00x f x f x f x x '=→→)1()1ln()1(lim)(lim 20x x x x x x f x x +++-=→→20)1ln()1(limx x x x e x ++-=→22)1ln(lim 0e x x e x -=+-=→2．nnn n n c b a ⎪⎪⎪⎭⎫⎝⎛++∞→3lim 111，其中0>a ，0>b ，0>c 解因300ln 3ln ln ln 3ln ln ln lim 33lim abc c b a c c b b a a x c b a x x x x x x x x =++=++=-++→→ 故原式=333lim)13(1lim 10003lim abc ee c b a x c b a c b axxxx x x x x x x xx xx ===⎪⎪⎭⎫⎝⎛++-++-++→→→三、（10分）设)(x f 在1=x 处可导，0)1(=f ，2)1(='f ，求xx x x x f x tan )cos (sin lim 220++→ 解设)(x f 在1=x 处可导，0)1(=f ，2)1(='f ，则xx x f x x f x x x x x f x x tan )1()cos (sin lim tan )cos (sin lim 220220+-+=++→→ 1cos sin )1()cos (sin lim 1cos sin lim tan lim 220220220-+-+-++=→→→x x f x x f x x x x x x x x x x 1cos sin )1()cos (sin lim 2sin cos sin 2lim cos 111lim220020-+-+-+=→→→x x f x x f x x x x xx x x 1cos sin )1()cos (sin lim 2sin cos sin 2lim 212200-+-+-=→→x x f x x f x x x x x x 1cos sin )1()cos (sin lim 21cos 2lim sin lim 2122000-+-+-=→→→x x f x x f x x x x x x1cos sin )1()cos (sin lim 41220-+-+=→x x f x x f x 1)1()(lim 411--=→t f t f t )1(41f '=21= 四、（10分）设)(x f 在),0[+∞上连续，⎰+∞0d )(x x f 收敛，求⎰+∞→yy x x xf y 0d )(1lim.解令⎰=xt t f x G 0d )()(，则因⎰+∞0d )(x x f 收敛，故)(lim y G y +∞→，不妨设R A y G y ∈=+∞→)(lim ，则[]}d )()(1{lim )(d 1lim d )(1lim0000⎰⎰⎰-==+∞→+∞→+∞→y yy y y y y x x G x xG yx G x y x x xf y)d )(1)((lim 0⎰-=+∞→yy x x G yy G ⎰+∞→-=yy x x G y A 0d )(1lim 0)(lim =-=-=+∞→A A y G A y五、（12分）设函数)(x f 在]1,0[上连续，在)1,0(内可微，且0)1()0(==f f ，1)21(=f ，证明：（1）存在⎪⎭⎫⎝⎛∈1,21ξ使得ξξ=)(f ；（2）存在()ξη,0∈使得1)()(+-='ηηηf f .证（1）记x x f x F -=)()(，则函数)(x F 在]1,21[上连续，且1)1(-=F ，21)21(=F ，故由零点存在性定理知存在⎪⎭⎫⎝⎛∈1,21ξ使得0)(=ξF ，即ξξ=)(f . （2）因x x x f x f e x d )1)()((⎰+-'--x e x xe x x f e x x f e x x x x d d d )(d )(⎰⎰⎰⎰----+-'-= x e e x x f e x x f e x x x x d d )(d d )(⎰⎰⎰⎰----++-=x x xe x f e --+-=)(故令x e x x f x F --=))(()(, 则函数)(x F 在],0[ξ上连续，在()ξ,0内可微，0)0(=F ,0)(=ξF ,x x e x x f e x f x F -----'='))(()1)(()(, 故由罗尔定理知,存在()ξη,0∈使得0)(='ηF , 1)()(+-='ηηηf f .六、设)(x f 在),(+∞-∞上有定义，在0=x 的某邻域内有一阶连续导数，且0)(lim 0>=→a x x f x ，证明级数∑∞=-1)1()1(n n n f 条件收敛. 证因 0)(lim>=→a xx f x ，故存在一个正数δ，使得当δ<-<00x 时，有 2)(aa x x f <-因此x x f a )(2<（δ<-<00x ），于是，当δ1>n 时， δ<-<010n ，nn f a 1)1(2<，n a n f 2)1(>，这表明级数∑∞=1)1(n n f 发散，即级数∑∞=-1)1()1(n n n f 发散.下证原级数收敛：由0)(lim0>=→a xx f x 知，0)(lim lim )(lim )0(000====→→→a x x f x x f f x x x ，0)(lim )0()(lim )0(00>==-='→→a xx f x f x f f x x由)(x f 在0=x 的某邻域内有一阶连续导数知，)(lim )0(0x f f a x '='=→，因此存在一个正数η，使得当η<-0x 时，有2)(aa x f <-' 因此)(20x f a '<<（),(ηη-∈x ）. 特别地，)(x f 在),0(η上单调增，于是当η1>n 时，)1()11(n f n f <+，且0)0()1(lim ==∞→f nf .最后由Leibniz 判别法知，原级数收敛.综上可知，原级数条件收敛.六、（14分）设1>n 为整数，⎰⎪⎪⎭⎫ ⎝⎛++++=-x n tt n t t t e x F 02d !!2!11)( ，证明：方程 2)(n x F =在⎪⎭⎫⎝⎛n n ,2内至少有一个根. 证记!!2!11)(2n t t t t p nn ++++= ,)!!2!11()(2n t t t e t r ntn ++++-= ,则)()(t r e t p n t n -=,且当0>t 时,0)(>t p n , 0)(>t r n ,0)(>-t r e n t .记2)()(n x F x -=ψ，则⎰--=n n t t t r e nx 0d )(2)(ψ,因⎰⎪⎪⎭⎫⎝⎛++++=-x n tt n t t t e x F 02d !!2!11)( ，故函数)(x ψ在],2[n n 上连续，在⎪⎭⎫⎝⎛n n ,2内可微，且2)2()2(n n F n -=ψ⎰⎰<-=--=--20200d )(2d ))(1(nn t n n tt t r e n t t r e ,2d )()(0nt t p e n nn t -=⎰-ψ⎰⎰⎰⎰----+-=+--=202220d )(d )(d )(2d ))(1(n nn n t n t n n n t n n t tt p e t t r e tt p e nt t r e⎰⎰++-=---20202d )2(d )(n n n n t n tt n t p et t r e⎰⎰+++-=---20202d )2(d )!1(1nnn nt t t n t p e t e e n ξ ⎰⎰+-++-=+---202022d ))2((d )!1(1nnn nt nt t t n t r e e t e e n ξ ⎰⎰+---+-+-=202022d )!1(1d )!1(121nnnnt t t e e n t e e n n ξξ ⎰⎰--+-+-=2020d )!1(1d )!1(121n nt t t e e n t e e n n ξξ ⎰-+->202d )!1(22n nt t e e n n []202)!1(22nt ne e n n -++= )1()!1(222-+-=ne n n )!1(2)!1(222+++-=n n e n n )!1(22)!1(2222+-=+->n en n e n n n012>->n（若2>n ，则左边的两个不等式都成立） ()()⎰⎰-+-=-+=-=--101021d 121d 121)1()1(t te t t t e F ψ()[]⎰-++-=--101021d 1t e e t t t 032321)1(2111>-=--+-=--ee e 031)2(>->eψ01223!4223)3(1223144144314923232333>-=->⇒>⇒>>>e e e e ψ 01232452!522)4(2>->->->e e e ψ,0122212e e 12)(>->++->n n n n n e n n ψ 故由零点存在性定理知, 存在),2(n n ∈ξ使得0)(=ξψ, 即2)(nF =ξ.七、（12分）是否存在R 中的可微函数)(x f 使得53421))((x x x x x f f --++=? 若存在，请给出一个例子；若不存在，请给出证明.解不存在假如存在R 中的可微函数)(x f 使得54321))((x x x x x f f -+-+=，则4325432)))((x x x x x f x f f -+-=''（，若1)1(=f ，则025432)1))1(()]1[2<-=-+-=''='（（f f f f 矛盾。

2010高教社杯全国大学生数学建模竞赛C题

同上的解法求得方案一最佳。
问题一的解答：
2、当共用管线和非共用管线费用不相同时要考
虑方案二中的各部分管线的总费用并与方案一
中的费用对比，得出最优方案。经过查阅资料
得知某非共用管道5万元/千米；共用管道8万元/千米；方案一的费用为
C1 5 l 2 (a b 方案二的费用为：) 2
；
2010高教社杯全国大学生数学建模竞赛 C题输油管线设计的数学模型
阐述的主要问题
某油田计划在铁路线一侧建造两家炼油厂，同时在铁路线上增建一个车站，用来运送成品油。由于这种模式具有一定的普遍性，油田设计院希望建立管线建设费用最省的模型。
针对这个问题，通过三个小问题进行解答：
1.针对两炼油厂到铁路线距离和两炼油厂间距离的各种不同情形，提出设计方案。若有共用管线，考虑其共用管线费用与非共用管线费用相同或不同的情形。 B 2. 两炼油厂的具体位置其中A厂位于郊区（Ⅰ），厂位于城区 Ⅱ （Ⅱ），两个区域有明显的分界线。若所有管线的铺设费用均相同，铺设在城区的管线还需增加拆迁和工程补偿等附加费用，根据三家工程咨询公司对此项附加费用的估计，为设计院给出管线布置方案及相应的费用。 3. 为进一步节省费用，炼油厂根据生产能力，选用相适应的油管。这时的管线铺设费用就各不相同，拆迁等附加费用同上。给出管线最佳布置方案及相应的费用。
，
2 3 l ，解得 C1 C2 3
问题一的解答：
2）同理：当 a b
当 a b 时，解得C1 C 2。当 a
3 10 3 3a 3b l 时， 2 C l 3 3 3
3l
8
b时，解得
C1 C 2。即方案一最佳。
问题二的解答：

大学生数学知识竞赛试题与答案

趣味数学知识竞赛复习题一、填空题1、〔苏步青〕是国际公认的几何学权威,我国微分几何派的创始人。

2、〔华罗庚〕是一个传奇式的人物,是一个自学成才的数学家。

3、编有《三角学》,被称为"李蕃三角"且自称为"三书子"的是〔李锐夫〕。

4、世界上攻克"哥德巴赫猜想"的第一个人是〔陈景润〕。

5、〔姜立夫〕是现代数学在中国最早而又最富成效的播种人",这是《中国大百科全书》和《中国现代数学家传》对他的共同评价。

6.设有n个实数,满足|xi|<1<I=1,2,3,…,n>, |x1|+|x2|+…+|xn|=19+|x1+x2+…+xn| ,则n的最小值207.三角形的一个顶点引出的角平分线,高线与中线恰将这个顶点的角四等分,则这个顶角的度数为___90° ___8.某旅馆有2003个空房间,房间钥匙互不相同,来了2010们旅客,要分发钥匙,使得其中任何2003个人都能住进这2003个房间,而且每人一间<假定每间分出的钥匙数与每人分到的钥匙数都不限>,最少得发出_16024______把钥匙.9.在凸1900边形内取103个点,以这2003个点为顶点,可将原凸1900边形分割成小三角形的个数为______2104_____.10.若实数x满足x4+36<13x2,则f<x>=x3-3x的最大值为______18_____11 ."我买鸡蛋时,付给杂货店老板12美分,"一位厨师说道,"但是由于嫌它们太小,我又叫他无偿添加了2只鸡蛋给我。

这样一来,每打<12只>鸡蛋的价钱就比当初的要价降低了1美分。

"厨师买了＿18只鸡蛋?12.已知f<x>∈[0,1],则y=f<x>+1的取值X围为___[7/9,7/8]____13.已知函数ｆ〔ｘ〕与ｇ〔ｘ〕的定义域均为非负实数集,对任意的ｘ≥0,规定ｆ〔ｘ〕＊ｇ〔ｘ〕＝ｍｉｎ｛ｆ〔ｘ〕,ｇ〔ｘ〕｝．若ｆ〔ｘ〕＝3－ｘ,ｇ〔ｘ〕＝,则ｆ〔ｘ〕＊ｇ〔ｘ〕的最大值为____〔2√3－1〕_____14．已知a,b,cd∈N,且满足342<abcd+ab+ad+cd+1>=379<bcd+b+d>,设M=a×103+b×102+c×10+d,则M的值为______1949___.15.用E<n>表示可使5k是乘积112233…nn的约数为最大的整数k,则E<150>=__2975_________16.从1到100的自然数中,每次取出不同的两个数,使它们的和大于100,则可有_2500________种不同的取法．17.从正整数序列1,2,3,4,…中依次划去3的倍数和4的倍数,但是其中是5的倍数均保留,划完后剩下的数依次构成一个新的序列:A1=1,A2=2,A3=5,A4=7,…,则A2003的值为____3338_____.18. .连接凸五边形的每两个顶点总共可得到十条线段<包括边在内>,现将其中的几条线段着上着颜色,为了使得该五边形中任意三个顶点所构成的三角形都至少有一条边是有颜色的则n的最小值是＿419.已知x0=2003,xn=xn-1+<n>1,n∈N>,则x2003的整数部分为_______2003___21.已知ak≥0,k=1,2,…,2003,且a1+a2+…+a2003=1,则S=max{a1+a2+a3, a2+a3+a4,…, a2001+a2002+a2003}的最小值为________3/2007_.22.对于每一对实数x,y,函数f满足f<x>+f<y>=f<x+y>-xy-1,若f<1>=1,那么使f<n>=n<n≠1>的整数n共有＿1个.23.在棱长为a的正方体内容纳9个等球,八个角各放一个,则这些等球最大半径是____.<√3-3/2>a___24.已知a,b,c都不为0,并且有sinx=asin<y-z>,siny=bsin<z-x>,sinz=csin<x-y>.则有ab+bc+ca=__-1_____.二、选择题1、被誉为中国现代数学祖师的是〔1、C 〕。

2010高教社杯全国大学生数学建模竞赛官方题目（含ABCD）

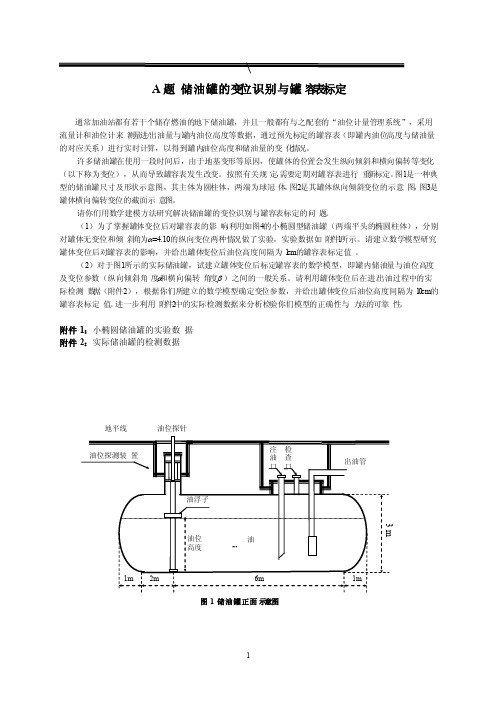
\A 题储油罐的变‎位识别与罐‎容表标定通常加油站‎都有若干个‎储存燃油的‎地下储油罐‎，并且一般都‎有与之配套‎的“油位计量管‎理系统”，采用流量计‎和油位计来‎测量进/出油量与罐‎内油位高度‎等数据，通过预先标‎定的罐容表‎（即罐内油位‎高度与储油‎量的对应关‎系）进行实时计‎算，以得到罐内‎油位高度和‎储油量的变‎化情况。

许多储油罐‎在使用一段‎时间后，由于地基变‎形等原因，使罐体的位‎置会发生纵‎向倾斜和横‎向偏转等变‎化（以下称为变‎位），从而导致罐‎容表发生改‎变。

按照有关规‎定，需要定期对‎罐容表进行‎重新标定。

图1是一种‎典型的储油‎罐尺寸及形‎状示意图，其主体为圆‎柱体，两端为球冠‎体。

图2是其罐‎体纵向倾斜‎变位的示意‎图，图3是罐体‎横向偏转变‎位的截面示‎意图。

请你们用数‎学建模方法‎研究解决储‎油罐的变位‎识别与罐容‎表标定的问‎题。

（1）为了掌握罐‎体变位后对‎罐容表的影‎响，利用如图4‎的小椭圆型‎储油罐（两端平头的‎椭圆柱体），分别对罐体‎无变位和倾‎斜角为α=4.10的纵向‎变位两种情‎况做了实验‎，实验数据如‎附件1所示‎。

请建立数学‎模型研究罐‎体变位后对‎罐容表的影‎响，并给出罐体‎变位后油位‎高度间隔为‎1cm 的罐‎容表标定值‎。

（2）对于图1所‎示的实际储‎油罐，试建立罐体‎变位后标定‎罐容表的数‎学模型，即罐内储油‎量与油位高‎度及变位参‎数（纵向倾斜角‎度α和横向偏转‎角度β ）之间的一般‎关系。

请利用罐体‎变位后在进‎/出油过程中‎的实际检测‎数据（附件2），根据你们所‎建立的数学‎模型确定变‎位参数，并给出罐体‎变位后油位‎高度间隔为‎10cm 的‎罐容表标定‎值。

进一步利用‎附件2中的‎实际检测数‎据来分析检‎验你们模型‎的正确性与‎方法的可靠‎性。

附件1：小椭圆储油‎罐的实验数‎据附件2：实际储油罐‎的检测数据‎油油浮子出油管油位探测装‎置注油口检查口地平线 2m6m1m1m3 m油位高度图1 储油罐正面‎示意图油位探针油位探针α地平线图2 储油罐纵向‎倾斜变位后‎示意图油油浮子出油管油位探测装‎置注油口检查口水平线(b) 小椭圆油罐‎截面示意图‎α油油浮子出油管油位探针注油口水平线2.05mcm ‎0.4m1.2m1.2m1.78m(a) 小椭圆油罐‎正面示意图‎图4 小椭圆型油‎罐形状及尺‎寸示意图图3 储油罐截面‎示意图（b ）横向偏转倾‎斜后正截面‎图地平线β地平线垂直‎线油位探针（a ）无偏转倾斜‎的正截面图‎油位探针油位探测装‎置地平线油3m油B题2010年‎上海世博会‎影响力的定‎量评估2010年‎上海世博会‎是首次在中‎国举办的世‎界博览会。

2010数学竞赛答案

2010年数学竞赛试题评分标准一、填空题（每小题3分，共30分）1. 16-；2. 21y x x =-++； 3. 41π-； 4.()212,xxdx f x y dy ⎰⎰；5. 2222sin cos(sin );x x ⋅ 6. ()222xy x x y ee ----+； 7. ()0,12dzdx dy =--；8.13； 9. 23-； 10. 0.二、选择题（每小题3分，共30分）1. D;2. B;3. C;4. C;5. C;6. A;7. A;8. B;9. C; 10. C.三、解答题（每小题10分，共70分） 1. 解(2limsin n →∞=()2limsin n n π→∞3分=2lim sin n n π→∞⎛ ⎪⎪⎝⎭3分 =2sin2π3分=1 1分 2. 解令ln x t =，则()()ln 1t te f t e +=, 2分()f x dx ⎰=()ln 1x xe dx e+⎰=()ln 1xxe de--+⎰2分=()ln 11x xxxxe e e e dx e--⋅-+++⎰ 2分 =()1ln 11x xxxxe e e e dx e -+--+++⎰2分 =()()ln 1ln 1xx x ee x e C --++-++. 2分第一页3. 解令u t x =-，则()212x xx f u du e --=-+-⎰, 2分()()()1,,x x f x x e f x x e ---⋅-=--=- 1分 ()100x f x e x '=-=⇒=, 1分又 0(0)0,f e ''=-< 1分 ∴0x =为()f x 的极大值点，极大值为()01f =-. 2分又 ()lim lim 11,x x x f x e x x →-∞→-∞⎛⎫=-= ⎪⎝⎭ ()l i m l i m 0x xx x x e x e →-∞→-∞--=-=，∴y x =为其斜渐近线，无水平和垂直渐近线. 3分4. 解利用微分形式不变性, 在()u u ϕ=+()xyp t dt ⎰两边求微分，得()()()du u du p x dx p y dy ϕ'=+-, 2分故 ()()()()11p x p y du dx dy u u ϕϕ=-''--, 1分从而 ()dz f u du '==()()()()()()11f u p x f u p y dx dy u u ϕϕ''-''--, 2分于是 ()()()1f u p x z x u ϕ'∂='∂-, 2分z y∂∂()()()1f u p y u ϕ'-='-. 2分故 ()()0.z zp y p x x y∂∂+=∂∂ 1分 5. 解13,xuf f xϕ∂'''=+⋅∂ 4分22ux ∂∂()2111331333x x xx x f f f ff ϕϕϕϕ'''''''''''''''=+⋅+⋅+⋅+⋅ 3分()211133332x x x x f f f f ϕϕϕ''''''''''''=+⋅+⋅+⋅ 3分6. 解 ()2221,y yDyM x y d dx x yρσ==+⎰⎰⎰3分第二页21x yx dy y=3分=1arctan 4y dy π⎫-⎪⎝⎭ 2分1ln 2122=- 2分 7. 解添加直线段AO =0y ：, 2分原式OA AOAO+=-⎰⎰1分()D0x e y dxdy =---⎰⎰ 3分=sin 0xx dx e ydy π⎰⎰2分()115e π=- 2分四、证明题（每小题10分，共20分）1. 证明 ()f x 在0x =的某个邻域(0)U 内具有二阶连续导数，且()0lim0x f x x→=，∴ ()00f =，从而()00f '=. 3分当n 充分大时，使得1n在0x =的这个邻域(0)U 内，故由Taylor 公式有 ()()()()2211111100,0,2!2f f f f f n n n n n ξξξ⎛⎫⎛⎫'''''=++⋅=∈ ⎪ ⎪⎝⎭⎝⎭. 3分又 ()f x 在邻域(0)U 内具有二阶连续导数，∴∃常数0M >，使得()f M ξ''≤, 2分∴ 212Mf n n⎛⎫≤ ⎪⎝⎭. 2分2. 证明用先二后一法计算左边的三重积分，得()Df z dv ⎰⎰⎰()11zD dz f z dxdy -=⎰⎰⎰ 4分()()1211f z z dz π-=-⎰ 4分 ()()1211f u u du π-=-⎰. 2分第三页。

首届2010(数学类)考题及答案(决赛试题)

首届数学类赛题（精简版）首届全国大学生数学竞赛决赛试卷（数学类，2010）考试形式：闭卷考试时间： 150 分钟满分： 100 分. 一、填空题（共8分，每空2分.）(1) 设0βα>>，则222xx dxe e x βα--+∞-⎰=_____________.(2) 若关于x 的方程211(0)kx k x+=>在区间(0,)+∞内有惟一实数解，则常数k =_____________. (3) 设函数()f x 在区间[,]a b 上连续.由积分中值公式有()()()xa f t dt x a f ξ=-⎰()a x b ξ≤≤<.若导数()f a +'存在且非零，则lim x a ax aξ+→--的值等于_____________.(4) 设()6a b c ⨯=，则()()()()a b b c a c +⨯++ =_____________.二、（10分）设()f x 在(1,1)-内有定义，在0x =处可导，且(0)0f =. 证明: 21(0)lim2nn k k f f n →∞='⎛⎫=⎪⎝⎭∑.三、（12分）设()f x 在[0,)∞上一致连续，且对于固定的[0,)x ∈∞。

当自然数n →∞时()0f x n +→。

证明: 函数序列{()1,2,}f x n n += ：在[0,1]上一致收敛于0.四、（12分）设22{(,):1}D x y x y =+<，(,)f x y 在D 内连续，(,)g x y 在D 内连续有界，且满足条件： (1) 当221x y +→时，(,)f x y →+∞；(2) 在D 中f 与g 有二阶偏导数， 2222fff ex y∂∂+=∂∂,2222ggg exy∂∂+≥∂∂。

证明： (,)(,)f x y g x y ≥ 在D 内处处成立.五、（10分）设{(,):01;0R x y x y =≤≤≤≤，{(,):01;01}R x y x y εεε=≤≤-≤≤-.考虑积分1RdxdyI xy=-⎰⎰，1R dxdyI xyεε=-⎰⎰，定义lim I I εε+→=。

2010年数学建模试题(全部)

2010高教社杯全国大学生数学建模竞赛题目（请先阅读“全国大学生数学建模竞赛论文格式规范”）A 题储油罐的变位识别与罐容表标定通常加油站都有若干个储存燃油的地下储油罐，并且一般都有与之配套的“油位计量管理系统”，采用流量计和油位计来测量进/出油量与罐内油位高度等数据，通过预先标定的罐容表（即罐内油位高度与储油量的对应关系）进行实时计算，以得到罐内油位高度和储油量的变化情况。

许多储油罐在使用一段时间后，由于地基变形等原因，使罐体的位置会发生纵向倾斜和横向偏转等变化（以下称为变位），从而导致罐容表发生改变。

按照有关规定，需要定期对罐容表进行重新标定。

图1是一种典型的储油罐尺寸及形状示意图，其主体为圆柱体，两端为球冠体。

图2是其罐体纵向倾斜变位的示意图，图3是罐体横向偏转变位的截面示意图。

请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。

（1）为了掌握罐体变位后对罐容表的影响，利用如图4的小椭圆型储油罐（两端平头的椭圆柱体），分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验，实验数据如附件1所示。

请建立数学模型研究罐体变位后对罐容表的影响，并给出罐体变位后油位高度间隔为1cm 的罐容表标定值。

（2）对于图1所示的实际储油罐，试建立罐体变位后标定罐容表的数学模型，即罐内储油量与油位高度及变位参数（纵向倾斜角度α和横向偏转角度β ）之间的一般关系。

请利用罐体变位后在进/出油过程中的实际检测数据（附件2），根据你们所建立的数学的罐地平线图1 储油罐正面示意图油位探针2010高教社杯全国大学生数学建模竞赛题目（请先阅读“全国大学生数学建模竞赛论文格式规范”）B 题 2010年上海世博会影响力的定量评估 20101851年伦互联网数据，定量评估2010年上海世博会的影响力。

2010高教社杯全国大学生数学建模竞赛题目（请先阅读“全国大学生数学建模竞赛论文格式规范”）C 题输油管的布置某油田计划在铁路线一侧建造两家炼油厂，同时在铁路线上增建一个车站，用来运送成品油。

2010年数学建模C、D题解析

4 − k2 4 − k2 （2）当 (b − a ) < l < (b + a ) 时， k k
4 − k2 l a+b k 1 P =( (b − a) + , − l ) ，此时 f min = [k (a + b) + l 4 − k 2 ] ； 2k 2 2 2 2 4 − k2
*
ab 4 − k2 （3）当 l ≥ (b + a ) 时， P* = ( , 0) ，此时 f min = (a + b) 2 + l 2 . a+b k 对共用管道与非共用管道相同的情况，只需令 k = 1 即可. 此问的优化模型实际上有两个约束条件 x ≥ 0, y ≥ 0 . 上面得到（1）（2）（3）、、，
关于学生论文中的几种情形
1．讨论不全面，很多队没有给出什么条件下不用公用管道；有些虽有讨论，但不清晰，一定要用已知参数的关系来讨论. 2．有些同学用镜面反射，Ferma定理，这些只适用于各种管道费用相同的情形，即只适用第1问中的特殊情形，后面仍然要建立优化模型，对整个论文并没有增添什么色彩. 之所以采用这两种方法，主要是参考了《两城镇取水管线的最短铺设》和《泵站选址与水管铺设》两篇论文 . 不少学生根本就没有弄清Ferma定理，叙述Ferma定理就不正确. 另外，用了文章就应引用为参考文献. 3．不少论文叙述混乱，符号混淆，图形不合理.
2012-4-28 费浦生 feipusheng@
关于C题《输油管的布置》的第3问
3．设输送 A 厂的管线为 k1 = 5.6 万元／km，输送 B 厂的管线为 k2 = 6.0 万元／km，共用管线费用为 k3 = 7.2 万元／km，拆迁等附加费用同上. 请给出管线最佳布置方案及相关费用. 总费用表达式为

历年全国大学生数学竞赛初赛题目及答案解析全(2009-2019年非数学专业)

程，有 2x 2 2y 1 z 1 0 ，展开化简后有 2x 2y z 5 0.
(4) 设 y y(x) 由方程 xe f (y) ey ln 29 确定，其中 f 具有二阶导数，且 f 1 ，则
d2 y
=___________.
dx2
【参考答案】对等式两端分别关于
1 ab
1 b2]
0
523
1 π[
a2
1
a(1
a)
1
4
(1
a)2 ].
53
39
dv 2 1 2 8
5
3
令 π[ a a (1 a)] 0 ，得 a ，代入 b 的表达式得 b .
da 5 3 3 27
4
2
所以y 0 。
d 2v
22 8 4
5
3
又因
da 2
|
5 a
π[ 5
3
] 27
证：
3
(1) xesiny d y yesinx d x xesiny d y yesinx d x;
L
L
(2) xesin y d y yesin x d x 5 π2 .
2
L
【参考证法一】由于区域 D 为一正方形，可以直接用对坐标曲线积分的计算法计算.
π
0
π
左边 πesin y d y πesin x d x π (esin x esin x ) d x ，
，
，
u,v
v2
1x y
u
所以由二重积分换元法的积分变换公式，原积分也就等于
D
(x
y)ln1 1x y
y x
dx
dy
2

2010首届全国大学生数学类决赛试题含答案

n ®¥
1 <d . m
又由于 lim f ( x + n) = 0 ，故对于每一个 x j ，存在一个 N j ，使得 f ( x j + n) <
e ，只要 n > N j ， 2
这里的e 是前面给定的.令 N = max{N1 ,L, N m } ，那么 f ( x j + n) < 其中 j = 1, 2,L , m . 设 x Î [0,1] 是任意一点，这时总有一个 x j 使得 x Î [ x j , x j +1 ] . 由 f ( x) 在 [0, +¥) 上一致连续性及 x j +1 - x j < d 可知， f ( x j + n) - f ( x + n) < 另一方面，我们已经知道 f ( x j + n) < 这样，由后面证得的两个式子就得到
1
利用
òa
2
dx 1 x = arctan + C ( a > 0) , + x2 a a
第 5 页，共 11 页
又得 æ u arctan ç 2 è 1- u 1 - u2 ö ÷ ø du + 4 æ u arctan ç 2 è 1- u 1 - u2 ö ÷ ø du .
I = 4ò 令
¥
R
dxdy dxdy 与 I e = òò ，定义 I = lim+ I e . R e ®0 e 1 - xy 1 - xy
(1) 证明 I = å
1 ； 2 n n =1 x+ y ì u= ï ï 2 í y x ïv = ï 2 î
(2) 利用变量替换
计算积分 I 的值，并由此推出

2010高教社杯全国大学生数学建模竞赛赛题C题

将 E 点代入模式二可以得到 f (6,3.7) = 178.56+5T
根据三家工程咨询公司对铺设在城区的管线还需要增加拆迁和工程的补偿等附加费用的估计的结果，在三家工程咨询公司的资质级别不相同的情况下，对他们所作出的估价进行评估有着重要的作用，根据参考文献[2],对这类问题,我们不能只对公司一的结果做出较大的肯定，要对其余两家公司的结果也需要认可，所以我们可以根据三家公司的实力来估算他们所的出估计价格比重 .因此可以这样安排,公司一的估价所占的比重为百分之四十，其余的两家公司估价所占的比重均占百分之三十.
7
二是比模型一更为节省资金的一种方案. 因为模型二是较优化的一种方案，所以只针对于模型二进行求解. 对模型求偏导
f 'XO (xo, yo ) = (
xo
−
( yo
−
a)2
+
x
2 o
c − xo
)•K,
(b − yo ) 2 + (c − xo ) 2
f 'yO (xo, yo ) = (
yo
−
( yo
由点 E 与点 B 的连线所形成的直线函数为：y= b − yo x + b − b − yo l ，可求点
l − xo
l − xo
F
的坐标为
F
⎛ ⎜⎜ ⎝
c,
(b
− yo l−
)(c
xo
−
l
)
+
b
⎞ ⎟⎟ ⎠
.
EF 之间的距离为
[ (b − yo )(c − l) l − xo
+b−
yo ]2
+ (c −

2010-2012年全国初中数学联赛试题参考答案和评分标准

2010年全国初中数学联合竞赛试题参考答案第一试一、选择题：（本题满分42分，每小题7分）1. 若,,a b c 均为整数且满足1010()()1a b a c -+-=，则||||||a b b c c a -+-+-=（ B ）A ．1.B ．2.C ．3.D ．4.2．若实数,,a b c 满足等式23||6a b +=，49||6a b c -=，则c 可能取的最大值为（ C ） A ．0. B ．1. C ．2. D ．3.3．若b a ,是两个正数，且,0111=+-+-ab b a 则（ C ） A ．103a b <+≤. B ．113a b <+≤. C ．413a b <+≤. D ．423a b <+≤. 4．若方程2310x x --=的两根也是方程420x ax bx c +++=的根，则2a b c +-的值为（ A ） A ．－13. B ．－9. C ．6. D ． 0.5．在△ABC 中，已知︒=∠60CAB ，D ，E 分别是边AB ，AC 上的点，且︒=∠60AED ，CE DB ED =+，CDE CDB ∠=∠2,则=∠DCB ( B )A ．15°.B ．20°.C ．25°.D ．30°.6．对于自然数n ，将其各位数字之和记为n a ，如2009200911a =+++=，201020103a =+++=，则12320092010a a a a a +++++=（ D ）A ．28062.B ．28065.C ．28067.D ．28068.二、填空题：（本题满分28分，每小题7分） 1．已知实数,x y 满足方程组3319,1,x y x y ⎧+=⎨+=⎩则22x y += 13 .2．二次函数c bx x y ++=2的图象与x 轴正方向交于A ，B 两点，与y 轴正方向交于点C ．已知AC AB 3=，︒=∠30CAO ，则c = 19． 3．在等腰直角△ABC 中，AB ＝BC ＝5，P 是△ABC 内一点，且PA ＝5，PC ＝5，则PB ＝___10___．4．将若干个红、黑两种颜色的球摆成一行，要求两种颜色的球都要出现，且任意中间夹有5个或10个球的两个球必为同一种颜色的球.按这种要求摆放，最多可以摆放____15___个球.第二试（A ）一．（本题满分20分）设整数,,a b c （a b c ≥≥）为三角形的三边长，满足22213a b c ab ac bc ++---=，求符合条件且周长不超过30的三角形的个数.解由已知等式可得222()()()26a b b c a c -+-+-= ①令,a b m b c n -=-=，则a c m n -=+，其中,m n 均为自然数.于是，等式①变为222()26m n m n +++=，即2213m n mn ++= ②由于,m n 均为自然数，判断易知，使得等式②成立的,m n 只有两组：3,1m n =⎧⎨=⎩和1,3.m n =⎧⎨=⎩ （1）当3,1m n ==时，1b c =+，34a b c =+=+.又,,a b c 为三角形的三边长，所以b c a +>，即(1)4c c c ++>+，解得3c >.又因为三角形的周长不超过30，即(4)(1)30a b c c c c ++=++++≤，解得253c ≤.因此2533c <≤，所以c 可以取值4，5，6，7，8，对应可得到5个符合条件的三角形. （2）当1,3m n ==时，3b c =+，14a b c =+=+.又,,a b c 为三角形的三边长，所以b c a +>，即(3)4c c c ++>+，解得1c >.又因为三角形的周长不超过30，即(4)(3)30a b c c c c ++=++++≤，解得233c ≤.因此2313c <≤，所以c 可以取值2，3，4，5，6，7，对应可得到6个符合条件的三角形. 综合可知：符合条件且周长不超过30的三角形的个数为5＋6＝11.二．（本题满分25分）已知等腰三角形△ABC 中，AB ＝AC ，∠C 的平分线与AB 边交于点P ，M 为△ABC 的内切圆⊙I 与BC 边的切点，作MD//AC ，交⊙I 于点D.证明：PD 是⊙I 的切线. 证明过点P 作⊙I 的切线PQ （切点为Q ）并延长，交BC 于点N. 因为CP 为∠ACB 的平分线，所以∠ACP ＝∠BCP. 又因为PA 、PQ 均为⊙I 的切线，所以∠APC ＝∠NPC. 又CP 公共，所以△ACP ≌△NCP ，所以∠PAC ＝∠PNC.由NM ＝QN ，BA ＝BC ，所以△QNM ∽△BAC ，故∠NMQ ＝∠ACB ，所以MQ//AC.又因为MD//AC ，所以MD 和MQ 为同一条直线.又点Q 、D 均在⊙I 上，所以点Q 和点D 重合，故PD 是⊙I 的切线.三．（本题满分25分）已知二次函数2y x bx c =+-错误！未找到引用源。

2010数学建模试题(数学系各专业)

第一部分：基本操作（任选三题）（1）求当 x =1, y =2 时的z值。

其中：z =（2）用 while 循环求 1～200 之间的整数之和。

（3）输入如下两个矩阵 A 和 B ，对矩阵 A 和 B 作关系运算，标识出两矩阵中元素相等的位置，元素值不等的位置，并标识出矩阵 A 中所有小于 0 的元素。

143328523B ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦123213321A ⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦ （4）编写一个 M 文件，画出下列分段函数所表示的曲面。

2222220.75 3.75 1.560.75 3.75 1.50.54 1(,)0.7575 110.5457 1x y y x y x y y e x y p x y e x y e x y -------+⎧+>⎪⎪=-<+≤⎨⎪+≤-⎪⎩（5）用曲面图命令 surf 表现函数22z x y =+的图像。

（6）绘制颜色为蓝色，数据点用五角星标识的下述函数在(0,5)上的虚线图。

sin xy xe=（7）编写一个 M 文件，画出下列分段函数所表示的曲面。

2222220.75 3.75 1.560.75 3.75 1.50.54 1(,)0.7575 110.5457 1x y y x y x y y e x y p x y e x y e x y -------+⎧+>⎪⎪=-<+≤⎨⎪+≤-⎪⎩（8）用plot 、fplot 绘制函数y=cos(tan(πx))图形（9）用ezplot 绘制函数exy-sin(x+y)=0在[-3，3]上图形。

（10）在同一平面中的两个窗口分别画出心形线和马鞍面。

要求（1）、在图形上加格栅、图例和标注（2）、定制坐标（3）、以不同角度观察马鞍面第二部分：基本建模题（任选两题）问题一：俗话说“大饺子能装馅”，是组建一个“包饺子”的数学模型并进行分析，判断这一说法是否正确。

问题二：层次分析法使用层次分析法解决一个实际问题，比如，为学校评选优秀学生过优秀班级构造层次分析模型；给自己毕业后选择工作做出决策；为高中毕业生建立一个填报志愿的层次结构模型。

2010高教社杯大学生数学建模竞赛C题

输油管的布置优化问题摘要：本文研究的是管线建设费用最省问题。

针对问题一：我们首先对两炼油厂到铁路线距离和两炼油厂之间距离的不同情形给出了四个线路的铺设方案。

然后，对两炼油厂到铁路线距离和两炼油厂之间距离的不同情况，以及共用管线费用与非共用管线费用相同和不同进行了讨论，给出了方案的选择以及最优化方案时铺设管线的费用。

如表1，表2所示表1 费用相同时确定了城市建设管线附加费用的权重及费用的数值，我们从一般情况出发，考虑了是否有共用管线，建立了非线性规划的数学模型，利用Lingo程序编程，从而求出最优解为：282.6973万元，布置方案如图6所示。

针对问题三：在问题二的基础上，我们建立了一个非线性规划的数学模型，利用Lingo程序编程，从而求出最优解为：251.9685万元，布置方案如图9所示。

关键词：非线性规划层次分析法（AHP）权重Lingo程序1问题的重述1.1问题的背景某油田计划在铁路线一侧建造两家炼油厂，同时在铁路线上增加一个车站，用来运送成品油。

由于这种模式具有一定的普遍性，油田设计院希望建立管线建设费用最省的一般数学模型与方法。

1.2 问题的提出1.2.1 相关信息问题二中两个炼油厂的具体位置由附录1所示，图中各字母表示的是距离,三家工程咨询公司对此项附加费用的估算结果如下图,管线铺设费用均为每千米7.2万元。

问题三中的管线铺设费用将分别降为输送A厂成品油每千米5.6万元，输送B厂成品油每千米6.0万元，共用管线费用为每千米7.2万元，拆迁等附加费用和问题二相同。

1.2.2 需要解决的问题①针对两炼油厂到铁路线距离和两炼油厂间距离的各种不同情形，提出你的设计方案。

在方案设计时，若有共用管线，应考虑共用管线费用与非共用管线费用相同或不同的情形。

②针对给出的炼油厂的具体位置为设计院给出管线布置方案及相应的费用。

③针对给出的管线铺设费用为设计院给出管线最佳布置方案及相应的费用。

2 符号说明A 表示炼油厂AB 表示炼油厂BC 表示新建车站M 表示非共用管道的单位建设费用（单位：万元）N 表示共用管道的单位建设费用（单位：万元）Z 表示铺设管线的总费用（单位：万元）a 表示炼油厂A到铁路的距离（单位：千米）b 表示炼油厂B到铁路的距离（单位：千米）c 表示两个炼油厂的垂直距离（单位：千米）f(x) 表示所铺设的总管道长（单位：千米）3 模型假设1、炼油厂B离铁路线的距离大于等于炼油厂A的距离2、车站的位置是由最优铺设管线方案确定3、炼油厂A ，炼油厂B ，车站都看作一个点4、炼油厂A ，炼油厂B ，车站等都在一个平面内5、管道的市场价格稳定4 模型的建立与求解4.1 问题一建模与求解： 4.1.1 问题分析若管线建设费用最省，那么管线的长度应该是最短的，因此我们要设计的管线首先考虑线路最短，然后根据费用的不同考虑每段线路的长度。

2010年大学生数学竞赛试题参考解答

6. 已知 u f ( x, y) 满足 r
u u u u ，。 x, y ，这里 ( , r ) 为极坐标。求 y r x
u u u u u u cos sin r x y y y x r cos r x r x 解：，。 y r sin u u r ( sin ) u r cos u u ( y ) u x y y x x u u x x y y x u 2 xy u x 2 y 2 2 2 由条件知，解之得：， . 2 y x y 2 x x y u ( y ) u x y y x
1 令 ( x) e x e x x 2 2 ，则 ( x) 为偶函数，且 (0) 0 。 2
1 6
（ ' x） e x e- x x ， ''( x) e x e x 1 。
显然， ''( x) 0 ， '( x) 单调增加。 x 0 时 '( x) '(0) 0 。

t2 1 4 dt t 3 3 。 2 6 0 3 1 t
2
4 故 S S1 S2 3 。 3
另解：利用曲线积分。由曲线积分可知 S
1 1 ydx xdy [ ] ， 2L 2 L1 L2
其中 L1 为红色曲线， L2 为线段 x 1 (2 y 0) 。
解：由条件知 F ( x) F ( x) x(1 x)e2 x 。两边积分 F ( x) F '( x)dx x(1 x)e2 x dx 得

大学数学竞赛习题与答案

x
x
( )
于是 e2c=e, 则2c=1，即
c 1. 2
30
1
例3 求
ax bx cx x
lim
x0
3
a 0,b 0,c 0.
1
解
ax bx cx x
lim
x0
3
a b c 3 x
x
x
a
x
b
3 x
c
x
3
a
x
bx 3
x
c
x
3
lim
x0
1
3
3
a x bx cx 3 axbxcx3
lim n n k1 1 ( k )2
n
1 dx 0 1 x2
arctan x |10
4
39
例2 求
lim
n
n k 1
sin k
n n 1
2.
k
夹逼定理
解因为
1 n k
sin n 1 k1 n
n
sin k
n
k1 n 1
1 n k
sin
n k1
n
k
而
lim 1 n sin k
lim
x0
cx x
1
1 ln a ln b ln c 1 lnabc.
3
3
1
ax
lim
x0
bx 3
cx
x
1 lnabc
e3
3
abc .
32
注：2009年全国决赛试题有类似题目
1
1
1 n
求
lim
n
an
bn 3

南华大学数电期末考试试卷

南华大学2009 -2 010学年度第二学期数字电子技术课程模拟试题1 数制转换 24.25=（ 11000.01）B =（ 30.2）O =（ 18.4） H =（ 00100100.00100101）842IBCD .2对10位倒T 形电阻网络 D/A 转换器而言，若 R f =R ，VREF= — 10V ，当输入数字量为 010******* 时，输出电压为（3.25 ） V 。

3. 2010个“ 1异或的结果是_ 0 ____ , 2010个“1同或的结果是 —1 —。

4. 只读存储器由存储阵列、输出控制电路和一地址译码器_三部分组成。

5. 对于与非门多余的输入引脚应该接 _高电平_ ,对于或非门多余的输入引脚应该接低电平。

（填高电平”或低电平”）。

7. 4个变量可构成 —16 —个最小项，每种变量取值可使 ________ 1—个最小项的值为1。

8. 构造一个模11计数器需要—11—个状态，—4 ___________ 个触发器。

9.时序逻辑电路的输出不仅和 __当前输入有关，而且还与电路原来状态有关。

10.数字电路就其结构和工作原理可分为 ________ _组合逻辑电路 —和—时序逻辑电路两类.19、555定时器构成的施密特触发器，若电源电压V cc = 12V ，电压控制端经0.01尸电容接地，则上触发电平 U T + =_8 _V ，下触发电平 U T -=_ 4 _V 。

2.函数F = AB • CD 的反演式F = _________ ③ _____① AB CD ②(A B) (C D) ③(A B) (C D) ④ A B C D3.已知二变量输入逻辑门的输入的波形； ① 与非门 ② 或非门 ③ 同或门 ④ 异或门得分阅卷人题号-一--二二三四五六七八九总分得分考试日期：2010年6月考试类别：考试考试时间：120分钟、填空题：（每小题 2分，共 20 分）得分阅卷人、选择题：（每题1.5 分，共 15 分）1.一只三输入端与非门，使其输出为 ①7 ② 80的输入变量取值组合有 ① 种;③ 3④1A,B 和输出F 的波形如下图所示，试根据波形图判断这是4 一个4位地址码、8位输出的ROM ，其存储矩阵的容量为。

2010年全国高中数学联赛四川省预赛试题及答案

2010年全国高中数学联赛四川省预赛2010年全国高中数学联赛四川赛区预赛由四川省数学会普及工作委员会及四川省数学竞赛委员会主办，由四川省数学竞赛委员会组织及负责命题，命题负责人：柳斌.预赛命题范围以现行高中数学教学大纲为准，主要考察学生对基础知识和基本技能的掌握情况，以及综合和灵活运用的能力. 试题相当于高考数学试题的中、难度水平，有利于广大学生拓宽视野，促进素质教育. 学生自愿报名参加. 全省在同一时间由各市、州统一组织竞赛(不在县级以下单位设置考场). 试卷答题时间120分钟，试题总分140分，其中包括：6道选择题（每道5分，共30分）、6道填空题（每道5分，共30分）；4道解答题（每道20分，共80分）. 命题难度大体相当于普通高考试题. 预赛时间定在5月1 6日(星期日)下午14:30~16:30.竞赛完后先由各市、州集中评卷，然后将其中10％的优秀试卷上报四川省数学竞赛委员会(原则上每个参赛学校均应有试卷上报)，由四川省数学竞赛委员会组织专人复查. 从中评出一等奖300名、二等奖500名、三等奖700名，由四川省数学竞赛委员会颁发获奖证书.经四川省数学竞赛委员会研究决定，为确保全国高中数学联赛的安全保密工作，自2007年起，四川省只在成都市设立一个考场，全省参赛人数控制在1000人左右，参赛学生为预赛的一、二等奖获得者及个别优秀学生(初赛人数较多的市、州可酌情增加决赛名额). 考场设在成都七中，个别边远地区的优秀考生经济确有困难者提出申请，经批准可由省数学竟赛委员会给予适当资助.试题一、选择题（本题满分40分，每小题5分） 1、已知p ：342sin 1=+α 和q ：34cos sin =+αα．则p 是q 的（）. A 、充分但不必要条件 B 、必要但不充分条件C 、充要条件D 、既不充分也不必要条件2、在5件产品中有4件正品、1件次品．从中任取2件，记其中含正品的个数个数为随机变量ξ，则ξ的数学期望ξE 是（）.A 、56 B 、57 C 、58 D 、593、设正三棱锥ABC S -的底面边长为3，侧棱长为2，则侧棱SA 与底面ABC 所成的角的大小是（）.A 、 30B 、 45C 、60 D 、2arctan4、已知函数424)42()(24224+++-++=x x x k k x x f 的最小值是0，则非零实数k 的值是（）. A 、4- B 、2- C 、2 D 、45、长方体1111D C B A ABCD -的八个顶点都在球O 的球面上，其中11=AA ，22=AB ，33=AD ，则经过C B 、两点的球面距离是（）.A 、32π B 、34π C 、π2 D 、π4 6、对任意实数m ，过函数1)(2++=mx x x f 图象上的点))2(,2(f 的切线恒过一定点P ，则点P 的坐标为（）.A 、)3,0(B 、 )3,0(-C 、)0,23( D 、)0,23(-7、设A 1、A 2为椭圆)0(12222>>=+b a by a x 的左右顶点，若在椭圆上存在异于A 1、A 2的点P ，使得02=⋅PA PO ，其中O 为坐标原点，则椭圆的离心率e 的取值范围是（）.A 、)21,0( B 、 )22,0( C 、)1,21( D 、)1,22( 8、记)0(,)33()(),(22≠++-=y yx y x y x F ，则),(y x F 的最小值是（）.A 、512 B 、516 C 、518 D 、4二、填空题（本题满分20分，每小题5分）9、)(x f 是定义在R 上的奇函数，且)1()(x f x f -=，则=)2010(f ． 10、实数y x ，满足6|1|2|1|3≤-++y x ，则y x 32-的最大值是． 11、在数列}{n a 中，11=a ，当2≥n 时，21,,-n n n S S a 成等比数列，则=∞→n n a n 2lim ．12、集合的容量是指集合中元素的和．则满足条件“}7,6,5,4,3,2,1{⊆A ，且若A a ∈时，必有A a ∈-8”的所有非空集合A 的容量的总和是．（用具体数字作答）三、解答题（本题满分80分，每小题20分）13、已知函数)43cos(32cos 4)4sin(2)4sin()(πππ++--++=x x x x x f ．（1）试判断函数)(x f 的奇偶性，并给出证明；（2）求)(x f 在],2[ππ上的最小值与最大值．14、已知F 为抛物线x y 42=的焦点，M 点的坐标为(4,0)，过点F 作斜率为1k 的直线与抛物线交于A 、B 两点，延长AM 、BM 交抛物线于C 、D 两点，设直线CD 的斜率为2k ．（1）求21k k 的值；（2）求直线AB 与直线CD 夹角θ的取值范围．15、已知函数1)(23+--=x mx x x f ，其中m 为实数．（1）求函数)(x f 的单调区间；（2）若对一切的实数x ，有47||)(-≥'x x f 成立，其中)(x f '为)(x f 的导函数．求实数m 的取值范围．16、已知n S 是数列}{n a 的前n 项的和，对任意的正整数n ，都有nn n ba S b 4)1(+-=-成立，其中0>b ．（1）求数列}{n a 的通项公式；（2）设nn n a c 4= )(*∈N n ，若2||≤n c ，求实数b 的取值范围．解答1、C 提示：因为34cos sin )cos (sin 2sin 12=+=+=+ααααα，故p 是q 的充要条件．故选C ．2、C 提示：数学期望是：582125242514=⨯+⨯C C C C ．故选C.3、A 提示：设顶点S 在底面ABC ∆的射影是H ，则H 为ABC ∆的外心．从而323332=⨯⨯=AH ，于是可得 30=∠SAH ．故选A ． 4、B 提示：42)62(1)(2422++-++=x x x k k x f ，因为2444x x ≥+，故61420242≤++≤x x x . 当0622≥-+k k 时，1min =f ，不合题意；当0622<-+k k 时，)62(611,12min max -++==k k f f ，由条件知0)62(6112=-++k k ，解得2-=k 或0（舍去）．故选B . 5、C 提示：球O 的半径3)33()22(12122=++=R ，在OBC ∆中3==OC OB ，33==AD BC ，则21cos -=∠BOC ，从而32π=∠BOC ．所以，经过C B 、两点的球面距离是ππ23132=⨯⨯．故选C ．6、 B 提示：因为m x x f +='2)(，故m f +='4)2(．于是过))2(,2(f 的切线方程是：)2)(4()25(-+=+-x m m y ，即3)4(-+=x m y ，因此切线方程恒过)3,0(-．故选B ．7、D 提示：由题设知∠OP A 2=90°，设P (x,y )(x >0)，以OA 2为直径的圆方程为4)2(222a y a x =+-，与椭圆方程联立得0)1(2222=+--b ax x ab ．由题设知，要求此方程在(0, a )上有实根．由此得a ab a <-<)1(2022化简得212>e ，所以e 的取值范围为)1,22(．故选D ．8、C 提示：设动点)3,(xx P -与)3,(yy Q ，则2),(PQ y x F =，点P 的轨迹为直线3x y -=，点Q 的轨迹为双曲线xy 3=，双曲线上的任一点)3,(00x x 到直线03=+y x 的距离106103300≥⋅+=x x d ，当30±=x 时等号成立．故),(y x F 的最小值为518．故选C ． 9、0 提示：由条件知0)0(=f ，)()()1(x f x f x f -=-=+，于是)()2(x f x f =+，即)(x f 是以2为周期的周期函数．所以，0)0()2010(==f f ．故填0．10、4 提示：由6|1|2|1|3≤-++y x 确定的图形是以四边形ABCD 及其内部，其中)4,1(-A 、)1,1(B 、)2,1(--C 、)1,3(-D ．由线性规划知识知，y x 32-的最大值是4，当2,1-=-=y x 时可取到．故填4．11、21-提示：由条件知当2≥n 时， )21)(()21(12--=-=-n n n n n n S S S S a S ，从而2111=--n n S S ，于是 12)1(2111-=-+=n n S S n ，所以121-=n S n ．于是 )32)(12(23211211---=---=-=-n n n n S S a n n n . 所以，n n a n 2lim ∞→21)32)(12(2lim )32)(12(2lim 2-=---=---=∞→∞→nn n n n n n ．故填21-． 12、224 提示：先找出满足条件的单元素和二元素的集合有：}4{1=A ，}7,1{2=A ，}6,2{3=A ，}5,3{4=A ，将这四个集合中的元素任意组合起来也满足要求，则所有符合条件的集合A 中元素的总和是：2242)8884(3=⨯+++．故填224．.13、（I ）)sin (cos 2232cos 4)cos (sin 2)cos (sin 22)(x x x x x x x x f +---++=x x 2cos 4cos 22--=， )(2cos 4cos 22)2cos(4)cos(22)(x f x x x x x f =--=----=-. 所以，)(x f 为偶函数．（II ）)1cos 2(4cos 22)(2---=x x x f4cos 22cos 82+--=x x 417)82(cos 82++-=x . 因为 ],2[ππ∈x ，故0cos 1≤≤-x ，所以，当0cos =x 时，)(x f 有最小值4；当82cos -=x 时，)(x f 有最大值417． 14、（I ）由条件知)0,1(F ，设),(11y x A 、),(22y x B 、),(33y x C 、),(44y x D ，不妨设01>y ．直线AB 的方程为)1(1-=x k y ，与x y 42=联立得04412=--y k y ，所以421-=y y ，121=x x ．① 当41=x 时，则)4,4(A ，故1412-=-=y y ，412=x ，即)1,41(-B ．直线AM 的方程为4=x ，从而)4,4(-C ；直线BM 的方程为：)4(154-=x y ，与x y 42=联立得016152=--y y ，得164=y ，644=x ，即)16,64(D ．于是341=k ，31464)4(162=---=k ．所以．421=k k ．② 当41≠x 时，直线AM 方程为)4(411--=x x y y 与抛物线方程x y 42=. 联立得21221)4(4)4(-=-x x x y ，又由1214x y =，化简上述方程得016)16(12121=++-x x x x x . 此方程有一根为x 1，所以另一根1316x x =，1316y y -=．即)16,16(11y x C -，同理，)16,16(22y x D -．所以112122121121224116161616k x x y y y y x x x x y y k =--⋅-=-+-=，即421=k k ．由①、②可知421=k k．（II ） 43431tan 2112121≤+=+-=k k k k k k θ，故43arctan≤θ．所以，直线AB 与直线CD 夹角θ的取值范围是]43arctan ,0(．15、（I ）因为123)(2--='mx x x f ，01242>+=∆m ，所以0)(='x f 有两个不等实根：3321+-=m m x ，3322++=m m x ，显然21x x <．当21x x x <<时，0)(<'x f ，即)(x f 单调递减；当2x x >或1x x <时，0)(>'x f ，即)(x f 单调递增；综上所述，有)(x f 的单调递减区间为：33[2+-m m ，]332++m m ；单调递增区间为：)33,(2+--∞m m 、),33(2+∞++m m ．（II ）由条件有：47||1232-≥--x mx x . ①当0>x 时，043)12(32≥++-x m x ，即12433+≥+m xx 在0>x 时恒成立. 因为34332433=⋅≥+x x x x ，当21=x 时等号成立．所以123+≥m ，即1≤m .②当0<x 时，043||)12(||32≥+-+x m x ，即m x x 21||43||3-≥+在0<x 时恒成立，因为3||43||32||43||3=⋅≥+x x x x ，当21-=x 时等号成立．所以m 213-≥，即1-≥m .③当0=x 时，R m ∈．综上所述，实数m 的取值范围是]1,1[-． 16、（I ）当1=n 时，有4)1(11+-=-ba a b ，故41=a ．当2≥n 时，n n n ba S b 4)1(+-=-及1114)1(---+-=-n n n ba S b .于是1143)()1(--⨯+--=-n n n n a a b a b ，即1143--⨯+=n n n ba a① 若4=b ，则434411+=--n n n n a a ，于是)1(43441-+=n a a nn . 从而 14)13(-⨯+=n n n a )2(≥n ，所以，14)13(-⨯+=n n n a )1(≥n .② 若4≠b ，则)443(44311--⨯-+=⨯-+n n n n b a b b a 于是11)443(443-⨯-+=⨯-+n n n n b b a b a 从而n n n b b b a 443)4124(1⨯---+=- )2(≥n 所以，n n n b b b a 443)4124(1⨯---+=- )1(≥n 综上所述，⎪⎩⎪⎨⎧≠⨯---+=⨯+=--)4(443)4124()4(4)13(11b b b b b n a nn n n（II ）若4=b 时，413+=n c n ，显然不满足条件，故4≠b ．当4≠b 时，43)4()4()1(4--⨯--=b b b b bc n n ．若4>b 时，0)4()1(4>--b b b ，故当+∞→n 时，+∞→n c ，不符合条件，舍去．①若10<<b 时，0)4()1(4>--b b b ，043>--b ，故从而n c 为单调递减数列，且0>n c ．所以，只须21411≤==a c 即可，显然成立．故10<<b 符合条件； ②若1=b 时，1=nc ，显然也满足条件．故1=b 符合条件； ③若41<<b 时，0)4()1(4<--b b b ，043>--b ，从而n c 为单调递增数列，因为011>=c ．故0>n c ，要使2||≤n c 成立，只须243lim ≤--=∞→b c n n 即可．于是251≤<b ．故251≤<b 符合条件．综上所述，所求的实数b 的范围是]25,0(．。

南华大学大一期末数学试卷

一、选择题（每题5分，共25分）1. 下列函数中，是奇函数的是（）A. f(x) = x^2B. f(x) = x^3C. f(x) = x^4D. f(x) = x^52. 下列数列中，收敛的是（）A. 数列{an} = (-1)^nB. 数列{an} = n^2C. 数列{an} = 1/nD. 数列{an} = (-1)^n n3. 若函数f(x)在区间[a, b]上连续，且f(a) > f(b)，则下列结论正确的是（）A. f(x)在[a, b]上单调递增B. f(x)在[a, b]上单调递减C. f(x)在[a, b]上存在极值D. f(x)在[a, b]上无极值4. 若向量a = (1, 2, 3)，向量b = (2, 4, 6)，则向量a与向量b的点积为（）A. 0B. 6C. 12D. 185. 已知函数f(x) = x^3 - 3x，求f'(1)的值（）A. -2B. 0C. 2D. 3二、填空题（每题5分，共25分）6. 函数f(x) = 2x^2 - 3x + 1的对称轴为______。

7. 数列{an} = 3n - 2的通项公式为______。

8. 若函数f(x) = e^x + 1在x = 0处的导数为2，则f'(x) = ______。

9. 已知向量a = (2, -1, 3)，向量b = (1, 2, -1)，则向量a与向量b的夹角余弦值为______。

10. 若函数f(x) = ln(x)在区间[1, e]上的最大值为1，则f(x)在区间[1, e]上的最小值为______。

三、解答题（每题20分，共80分）11. （20分）求函数f(x) = x^3 - 6x^2 + 9x - 1的导数f'(x)。

12. （20分）已知数列{an} = 2^n - 1，求lim(n→∞)an。

13. （20分）证明：若函数f(x)在区间[a, b]上连续，且f(a) < f(b)，则存在至少一个点c∈(a, b)，使得f'(c) = 0。

2010年全国高中数学联赛湖北省预赛试题及答案

2010年全国高中数学联赛湖北省预赛2010年全国高中数学联赛湖北省预赛由湖北省数学竞赛组织委员会主办并具体组织活动，委托华中师范大学数学竞赛与普及研究所命题。

试题以《高中数学竞赛大纲（2006年修订稿）》为依据，所涉及的知识范围不超出现行《全日制普通高级中学数学教学大纲》和《普通高中数学课程标准》中所规定的教学内容和要求，在数学思想方法的要求上有所提高，主要考查学生对基本知识和基本技能的掌握情况，以及综合、灵活运用知识的能力，适当考虑全国联赛对参赛学生的要求。

湖北省预赛按高一、高二年级分开命题，试题包括8道填空题和4道解答题，全卷满分120分，考试时间为120分钟。

湖北省预赛于2010年5月16日（星期日）上午8：00至10：00举行，约5万名学生参加，由各地市（州）安排考试并组织阅卷，从中选出约9000人参加全国高中数学联赛。

试题一、填空题（每小题8分，共64分）1．数列}{n a 满足：3,121==a a ，且)(||*12N n a a a n n n ∈-=++．记}{n a 前n 项的和为n S ，则=100S ．2．在△ABC 中，已知B ∠的平分线交AC 于K ．若BC =2，CK =1，223=BK ，则△ABC 的面积为．3．设100<n ，则使得nb a )(+的展开式中有连续三项的系数成等差数列的最大整数n 为．4．在小于20的正整数中，每次不重复地取出3个数，使它们的和能被3整除，不同的取法种数为．5．若z y x ,,均为正实数，且1222=++z y x ，则xyzz S 2)1(2+=的最小值为．6．设椭圆1422=+y x 的左、右焦点分别为21,F F ，M 为椭圆上异于长轴端点的一点，122F MF θ∠=，△12MF F 的内心为I ，则=θcos ||MI ．7．对于一切]21,2[-∈x ，不等式0123≥++-x x ax 恒成立，则实数a 的取值范围为．8．将总和为200的10个数放置在给定的一个圆周上，且任意三个相邻的数之和不小于58．所有满足上述要求的10个数中最大数的最大值为．二、解答题（本大题共3小题，共56分）9．（16分）已知二次函数c bx ax x f ++=2)(的图象经过点)0,2(-，且不等式221)(22+≤≤x x f x 对一切实数x 都成立．（1）求函数)(x f 的解析式；（2）若对一切]1,1[-∈x ，不等式)2()(xf t x f <+恒成立，求实数t 的取值范围． 10．（20分）设313116234++++=x x x x P ，求使P 为完全平方数的整数x 的值．11．（20分）已知直线x y =与椭圆C ：1111622=+y x 交于B A ,两点，过椭圆C 的右焦点F 、倾斜角为α的直线l 交弦AB 于点P ，交椭圆C 于点N M ,．（1）用α表示四边形MANB 的面积；（2）求四边形MANB 的面积取到最大值时直线l 的方程．解答1．89 提示：由已知可得k k a a =+9．89)(11192110099100=++++=+=a a a a a S S ．2．16715 提示：由余弦定理可得b c b =-+22228 ① 又BC AB CK AK =，则 211cb =- ② 由①②，3,25==c b ．又由81cos =C 可得873sin =C ，故△ABC 的面积16715sin 21==C ab S ． 3．98 提示：设nb a )(+的展开式中有连续三项的系数分别为)11(,,11-≤≤+-n k C C C k n k n k n ，由题意得 112+-+=k nk n k n C C C ．依组合数定义展开并整理得024)14(22=-++-k n k n ．故)(2981422,1N n k k n ∈+±+=（1）．22)12(98+=+m k ，222-+=m m k ，代入（1），得2)1(21-+=m n ，222-=m n ．由1002)1(2<-+m ，98=n ．4．327 提示：把这19个数按被3除所得的余数分类可以有三类：1A ：3，6，9，12，15，18； 2A ：1，4，8，11，14，17；3A ：2，5，7，10，13，14，19．这样，满足题设条件的取法有且只有四种情形：（1）在1A 中任取3个数，有2036=C 种取法；（2）在2A 中任取3个数，有2036=C 种取法；（3）在3A 中任取3个数，有3537=C 种取法；（4）在321,,A A A 中各取一个数，有252766=⨯⨯种取法．因此，取法总数为：32725235220=++⨯（种）． 5．223+ 提示：因 22212z y x xy -=+≤，所以 ]1)1)][(1(2[1)1(1)1()1(2)1(222-++-+=-+=-+≥+=z z z z z z z z z xyz z S ]12)1[(31+++-=z z 2232231+=-≥．当且仅当12,12-==-=y x z 时等号成立．所以 223min +=S ．6．32- 提示：先证明下面的结论：已知△ABC 的内心为I ，则AB ＋AC －BC ＝2AI A cos2⋅．证明：设△ABC 的内切圆与边AB 、AC 分别切于D 、E 两点，则AD ＝AE ＝12（AB ＋AC －BC ），又AD ＝2AI A cos2⋅，所以AB ＋AC －BC ＝2AI Acos 2⋅．对于本题的△12MF F ，有12122cos MF MF F F MI θ+-=⋅．又2214x y +=中2,1,a b c ====，所以1224MF MF a +==，122FF c ==，从而32)324(21)(21cos ||2121-=-=-+=⋅F F MF MF MI θ． 7．110-≤≤-a 提示：记1)(23++-=x x ax x f ，已知条件即0)(≥x f 对一切⎥⎦⎤⎢⎣⎡-∈21,2x 恒成立．（1）当0=x 时，对一切实数a ，01)(>=x f ．（2）当]21,0(∈x 时，01)(23≥++-=x x ax x f 可化为321x x x a --≥．设321)(xx x x g --=，则)3)(1(1)(4-+-='x x x x g ．当]21,0(∈x 时，0)(>'x g ，所以函数)(x g 在区间]21,0(上单调递增，从而10)21()]([max -==g x g ．因此10-≥a ．（3）当]0,2(-∈x 时，01)(23≥++-=x x ax x f 可化为321xx x a --≤．设321)(xx x x g --=，则)3)(1(1)(4-+-='x x x x g ．当)0,1(-∈x 时0)(>'x g ；当1-=x 时0)(='x g ；当)1,2(--∈x 时．所以函数)(x g 在区间)1,2(--上单调递减，在区间)0,1(-上单调递增，从而1)1()]([min -=-=g x g ．因此1-≤a ．综合可知：110-≤≤-a ．8．26 提示：设所有放置中的最大数为A ，则200583≤⨯+A ，所以.26≤A 事实上26，6，26，26，6，26，26，6，26，26满足．9．（1）由已知，对2≥n 有11)1()1(11---=--=+n a n n a n a n a n n n n ，两边同除以n 并整理，得)111()1(111nn a n na n n ---=--+，于是，)111(111)1(1112121---=⎪⎭⎫ ⎝⎛---=⎥⎦⎤⎢⎣⎡--∑∑-=-=+n k k a k ka n k n k k k ，即2),111(1)1(12≥---=--n n a a n n ，所以123)111(1)1(12--=---=-n n n a a n n ，2,231≥-=n n a n ．又1=n 时也成立，故*,231N n n a n ∈-=．（2）当2≥k ，有)131431(31)13)(43(1)23(122---=--<-=k k k k k a k ，所以2≥n 时，有⎥⎦⎤⎢⎣⎡---++-+-+<+=∑∑==)131431()8151()5121(31112212n n a a nk k n k k.6761113121311=+<⎪⎭⎫ ⎝⎛--+=n又1=n 时，.67121<=a ．故对一切*N n ∈，有6712<∑=nk k a ．10．)10(3)13(22--++=x x x P ．所以，当10=x 时，2131=P 是完全平方数．下证没有其它整数x 满足要求．（1）当10>x 时，有22)13(++<x x P ，又03132)3(222>++=+-x x x x P ，所以22)3(x x P +>，从而2222)13()3(++<<+x x P x x ．又Z x ∈，所以此时P 不是完全平方数．（2）当10<x 时，有22)13(++>x x P ．令Z y y P ∈=,2，则|13|||2++>x x y ，即|13|1||2++≥-x x y ，所以 222)13(1||2++≥+-x x y y ，即 01|13|2)10(32≥+++---x x x ．解此不等式，得x 的整数值为6,5,4,3,0,1,2----±±，但它们对应的P 均不是完全平方数．综上所述，使P 为完全平方数的整数x 的值为10.11．（1）直线MN 的倾斜角为α，记θ=∠MFO ，则πθα=+，θα22222222cos 2cos 2||c a ab c a ab MN -=-=．而AB 与MN 所成的角为θπ+4，则四边形MANB 面积θθθθπ2222cos cos sin ||2)4sin(||||21c a ab OA MN AB S MANB -+⋅⋅=+⋅=．而5,11,16222===c b a ，A 点坐标为⎪⎪⎭⎫⎝⎛9334,9334，且9664||=OA ，从而，αααθθθ22cos 516cos sin 933352cos 516cos sin 933352--⋅=-+⋅=MANB S ，其中59334334arctan0+≤<α或πα<≤+59334334arctan．（2）记αααα2cos 516cos sin )(--=f ，而)(αf 只可能在⎪⎪⎭⎫⎢⎣⎡-∈πα,59334334arctan 时才可能取到最大值．对)(αf 求导数得到：222)cos 516()sin cos 10)(cos (sin )cos 516)(sin (cos )(ααααααααα----+='f ．令0)(='αf ，则有0)tan 10)(1(tan )11tan 16)(tan 1(2=--++αααα．化简得到 011tan 21tan 6tan 1623=+++ααα．所以 0)11tan tan 8)(1tan 2(2=+-+ααα．而 011tan tan 82=+-αα无实根，则21tan -=α．经检验21tan -=α，符合⎪⎪⎭⎫⎢⎣⎡-∈πα,59334334arctan ．故所求直线l 的方程为：2521+-=x y ．。