2018届高考数学高考大题专项突破四高考中的立体几何文新人教A版 Word版含答案

合集下载

2018大二轮高考总复习文数文档解答题4 立体几何 Word版含解析

第一单元高考中档大题突破
解答题: 立体几何
基本考点——空间平行、垂直关系及体积、表面积的计算
．直线、平面平行的判定及其性质
()线面平行的判定定理：⊄α，⊂α，∥⇒∥α.
()线面平行的性质定理：∥α，⊂β，α∩β＝⇒∥.
()面面平行的判定定理：⊂β，⊂β，∩＝，∥α，∥α⇒α∥β.
()面面平行的性质定理：α∥β，α∩γ＝，β∩γ＝⇒∥.
．直线、平面垂直的判定及其性质
()线面垂直的判定定理：⊂α，⊂α，∩＝，⊥，⊥⇒⊥α.
()线面垂直的性质定理：⊥α，⊥α⇒∥.
()面面垂直的判定定理：⊂β，⊥α⇒α⊥β.
()面面垂直的性质定理：α⊥β，α∩β＝，⊂α，⊥⇒⊥β.
.(·全国卷Ⅰ)如图，在四棱锥－中，∥，且∠＝∠＝°.
()证明：平面⊥平面；
()若＝＝＝，∠＝°，且四棱锥－的体积为，求该四棱锥的侧面积．
()证明：由已知∠＝∠＝°，
得⊥，⊥.
由于∥，故⊥，从而⊥平面.
又⊂平面，
所以平面⊥平面.
()解：如图，在平面内作⊥，垂足为.
由()知，⊥平面，故⊥，⊥，
可得⊥平面.
设＝，则由已知可得＝，＝.
故四棱锥－的体积
－＝··＝.
由题设得＝，故＝.
从而结合已知可得＝＝＝＝，＝＝，＝＝.
可得四棱锥－的侧面积为
·＋·＋·＋°＝＋. .(·全国卷Ⅱ)如图，四棱锥－中，侧面为等边三角形且垂直于底面，＝＝，∠＝∠＝°.。

2018全国高考立体几何(完整答案)

2018全国高考立体几何（完整答案）一．解答题（共40小题）1．已知圆锥的顶点为P，底面圆心为O，半径为2．（1）设圆锥的母线长为4，求圆锥的体积；（2）设PO=4，OA、OB是底面半径，且∠AOB=90°，M为线段AB的中点，如图．求异面直线PM与OB所成的角的大小．2．如图，矩形ABCD所在平面与半圆弧所在平面垂直，M是上异于C，D 的点．（1）证明：平面AMD⊥平面BMC；（2）在线段AM上是否存在点P，使得MC∥平面PBD？说明理由．3．在平行六面体ABCD﹣A1B1C1D1中，AA1=AB，AB1⊥B1C1．求证：（1）AB∥平面A1B1C；（2）平面ABB1A1⊥平面A1BC．4．如图，在四棱锥P﹣ABCD中，底面ABCD为矩形，平面PAD⊥平面ABCD，PA ⊥PD，PA=PD，E，F分别为AD，PB的中点．（Ⅰ）求证：PE⊥BC；（Ⅱ）求证：平面PAB⊥平面PCD；（Ⅲ）求证：EF∥平面PCD．5．如图，在平行四边形ABCM中，AB=AC=3，∠ACM=90°，以AC为折痕将△ACM 折起，使点M到达点D的位置，且AB⊥DA．（1）证明：平面ACD⊥平面ABC；（2）Q为线段AD上一点，P为线段BC上一点，且BP=DQ=DA，求三棱锥Q ﹣ABP的体积．6．如图，四棱锥P﹣ABCD中，底面ABCD为菱形，PA⊥平面ABCD，BD交AC 于点E，F是线段PC中点，G为线段EC中点．（Ⅰ）求证：FG∥平面PBD；（Ⅱ）求证：BD⊥FG．7．如图所示，在四棱锥P﹣ABCD中，平面PAB⊥平面ABCD，AD∥BC，AD=2BC，∠DAB=∠ABP=90°．（Ⅰ）求证：AD⊥平面PAB；（Ⅱ）求证：AB⊥PC；（Ⅲ）若点E在棱PD上，且CE∥平面PAB，求的值．8．如图，在三棱锥P﹣ABC中，PA=PB=AB=2，BC=3，∠ABC=90°，平面PAB⊥平面ABC，D，E分别为AB，AC中点．（1）求证：DE∥平面PBC；（2）求证：AB⊥PE；（3）求三棱锥P﹣BEC的体积．9．如图，在四棱锥P﹣ABCD中，底面ABCD为直角梯形，AD∥CB，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD的中点，，M是棱PC上的点．（Ⅰ）求证：平面PQB⊥平面PAD；（Ⅱ）若PA=PD=2，BC=1，，异面直线AP与BM所成角的余弦值为，求的值．10．如图，梯形ABCD中，AD=BC，AB∥CD，AC⊥BD，平面BDEF⊥平面ABCD，EF∥BD，BE⊥BD．（1）求证：平面AFC⊥平面BDFE；（2）若AB=2CD=2，BE=EF=2，求BF与平面DFC所成角的正弦值．11．如图，在三棱锥P﹣ABC中，AB⊥PC，CA=CB，M是AB的中点．点N在棱PC上，点D是BN的中点．求证：（1）MD∥平面PAC；（2）平面ABN⊥平面PMC．12．如图，已知PA垂直于矩形ABCD所在的平面，M，N分别是AB，PC的中点，若∠PDA=45°，（1）求证：MN∥平面PAD；（2）求证：MN⊥平面PCD．13．如图，正三棱柱ABC﹣A1B1C1中，AA1=AB，D为BB1的中点．（1）求证：A1C⊥AD；（2）若点P为四边形ABB1A1内部及其边界上的点，且三棱锥P﹣ABC的体积为三棱柱ABC﹣A1B1C1体积的，试在图中画出，P点的轨迹．并说明理由．14．如图，在三棱柱ABC﹣A1B1C1中，底面ABC为边长为2等边三角形，BB1=4，A1C1⊥BB1，且∠A1B1B=45°．（I）证明：平面BCC1B1⊥平面ABB1A1；（Ⅱ）求B﹣AC﹣A1二面角的余弦值．15．已知三棱柱ABC﹣A1B1C1的侧棱垂直于底面，∠BAC=90°，AB=AA1=2，AC=1，M，N分别是A1B1，BC的中点．（Ⅰ）证明：MN∥平面ACC1A1；（II）求二面角M﹣AN﹣B的余弦值．16．已知空间几何体ABCDE中，△BCD与△CDE均为边长为2的等边三角形，△ABC为腰长为3的等腰三角形，平面CDE⊥平面BCD，平面ABC⊥平面BCD．（1）试在平面BCD内作一条直线，使得直线上任意一点F与E的连线EF均与平面ABC平行，并给出详细证明；（2）求三棱锥E﹣ABC的体积．17．如图，在四棱锥P﹣ABCD中，∠ADB=90°，CB=CD，点E为棱PB的中点．（1）若PB=PD，求证：PC⊥BD；（2）求证：CE∥平面PAD．18．如图，长方体ABCD﹣A1B1C1D1中，AB=BC=2，A1C与底面ABCD所成的角为60°，（1）求四棱锥A1﹣ABCD的体积；（2）求异面直线A1B与B1D1所成角的大小．19．如图，四棱锥P﹣ABCD的底面ABCD是边长为2的菱形∠BAD=60°．已知PB=PD=2，PA=．（Ⅰ）证明：PC⊥BD；（Ⅱ）若E为PA上一点，记三棱锥P﹣BCE的体积和四棱锥P﹣ABCD的体积分别为V1和V2，当V1：V2=1：8时，求的值．20．如图，正方体ABCD﹣A1B1C1D1的棱长为2，E，F分别是CB，CD的中点，点M在棱CC1上，CM=tCC1（0＜t＜1）．（Ⅰ）三棱锥C﹣EFM，C1﹣B1D1M的体积分别为V1，V2，当t为何值时，V1•V2最大？最大值为多少？（Ⅱ）若A1C∥平面B1D1M，证明：平面EFM⊥平面B1D1M．21．如图，直角梯形ABEF中，∠ABE=∠BAF=90°，C、D分别是BE、AF上的点，且DA=AB=BC=a，DF=2CE=2a．沿CD将四边形CDFE翻折至CDPQ，连接AP、BP、BQ，得到多面体ABCDPQ，且AP=a．（Ⅰ）求多面体ABCDPQ的体积；（Ⅱ）求证：平面PBQ⊥平面PBD．22．如图，已知四棱锥P﹣ABCD的底面ABCD是菱形，∠BAD=60°，PA=PD，O 为AD边的中点．（1）证明：平面POB⊥平面PAD；（2）若，求四棱锥P﹣ABCD的体积．23．如图，在四棱锥P﹣ABCD中．底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD．Q为AD的中点，M是棱PC上的点，PA=PD=2．BC=AD=1，CD=．（I）求证：平面PBC⊥平面PQB；（Ⅱ）若平面QMB与平面PDC所成的锐二面角的大小为60°，求PM的长．24．在如图所示的几何体中，面CDEF为正方形，面ABCD为等腰梯形，AB∥CD，，AB=2BC=2，AC⊥FB．（Ⅰ）求证：AC⊥平面FBC；（Ⅱ）求四面体FBCD的体积；（Ⅲ）线段AC上是否存在点M，使EA∥平面FDM？证明你的结论．25．如图所示的几何体中，平面PAD⊥平面ABCD，△PAD是直角三角形，∠APD=90°，四边形ABCD是直角梯形，AB∥DC，AB⊥AD，PQ∥DC，PQ=PD=DC=1，PA=AB=2．（I）求证：PD∥平面QBC；（Ⅱ）求证：QC⊥平面PABQ；（Ⅲ）在线段QB上是否存在点M，使得AM⊥BC，若存在，求QM的值；若不存在，请说明理由．26．如图1，△ABC是边长为3的等边三角形，D在边AC上，E在边AB上，且AD=BE=2AE．将△ADE沿直线DE折起，得四棱锥A'﹣BCDE，如图2（1）求证：DE⊥A'B；（2）若平面AD'E⊥底面BCDE，求三棱锥D﹣A'CE的体积．27．如图，在三棱锥P﹣ABC中，PA⊥AC，AB⊥BC，PA=BC=2，PB=AC=2，D 为线段AC的中点，将△CBD折叠至△EBD，使得平面EDB⊥平面ABC且PC交平面EBD于F．（1）求证：平面BDE⊥平面PAC．（2）求三棱锥P﹣EBC的体积．28．如图1，在矩形ABCD中，AD=2AB=4，E是AD的中点．将△ABE沿BE折起使A到点P的位置，平面PEB⊥平面BCDE，如图2．（Ⅰ）求证：PB⊥平面PEC；（Ⅱ）求三棱锥D﹣PEC的高．29．如图1，ABCD是一个直角梯形，∠ABC=∠BAD=90，E为BC边上一点，AE、BD相交于O，AD=EC=3，BE=1，AB=．将△ABE沿AE折起，使平面ABE⊥平面ADE，连接BC、BD，得到如图2所示的四棱锥B﹣AECD．（Ⅰ）求证：CD⊥平面BOD；（Ⅱ）求直线AB与面BCD所成角的余弦值．30．如图，四棱柱ABCD﹣A1B1C1D1为长方体，点P是CD中点，Q是A1B1的中点．（I）求证：AQ∥平面PBC1；（l）若BC=CC1，求证：平面A1B1C⊥平面PBC1．31．如图，在四棱锥P﹣ABCD中，AD∥BC，AD=3BC=6，，点M在线段AD上，且DM=4，AD⊥AB，PA⊥平面ABCD．（1）证明：平面PCM⊥平面PAD；（2）当∠APB=45°时，求四棱锥P﹣ABCM的表面积．32．已知等腰梯形ABCD中，AD∥EC，EC=2AD=2AE=4，B为EC的中点，如图1，将三角形ABE沿AB折起到ABE′（E′⊄平面ABCD），如图2．（1）点F为线段AE′的中点，判断直线DF与平面BCE′的位置关系，并说明理由；（2）当平面ABE′与平面DE′C所成的二面角的大小为时，证明：平面ABE′⊥平面ABCD．33．如图，在四棱锥P﹣ABCD中，△PAD和△BCD都是等边三角形，平面PAD ⊥平面ABCD，且AD=2AB=4，．（I）求证：CD⊥PA；（II）E，F分别是棱PA，AD上的点，当平面BEF∥平面PCD时，求四棱锥C﹣PEFD的体积．34．如图，在四棱锥P﹣ABCD中，底面ABCD是平行四边形，AB=AC=2，AD=2，PB=，PB⊥AC．（1）求证：平面PAB⊥平面PAC；（2）若∠PBA=45°，试判断棱PA上是否存在与点P，A不重合的点E，使得直线CE与平面PBC所成角的正弦值为，若存在，求出的值；若不存在，请说明理由．35．如图，四棱锥P﹣ABCD中，PA⊥平面ABCD，四边形ABCD为直角梯形，AD ∥BC，∠BAD=∠CBA=90°，PA=AB=BC=1，AD=2，E，F，G分别为BC，PD，PC的中点．（1）求EF与DG所成角的余弦值；（2）若M为EF上一点，N为DG上一点，是否存在MN，使得MN⊥平面PBC？若存在，求出点M，N的坐标；若不存在，请说明理由．36．如图所示，在多面体ABC﹣A1B1C1中，D，E，F分别是AC，AB，CC1的中点，AC=BC=4，，CC1=2，四边形BB1C1C为矩形，平面ABC⊥平面BB1C1C，AA1∥CC1（1）求证：平面DEF⊥平面AA1C1C；（2）求直线EF与平面ABC所成的角的正切值．37．如图，在三棱柱ABC﹣A1B1C1中，BC⊥平面AA1B1B，AB=AA1=2，∠A1AB=60°．（Ⅰ）证明：平面AB1C⊥平面A1BC；（Ⅱ）若四棱锥A﹣BB1C1C的体积为，求该三棱柱的侧面积．38．如图，在四棱锥P﹣ABCD中，PD⊥底面ABCD，底面ABCD为正方形，E，F，G分别是AB，PB，PC的中点．（1）求证：CD∥平面PAB；（2）求证：CD⊥平面EFG．39．如图，在四棱锥P﹣ABCD中，底面ABCD是平行四边形，平面ABP⊥平面BCP，∠APB=90°，BP=BC，M为CP的中点．求证：（1）AP∥平面BDM；（2）BM⊥平面ACP．40．已知梯形ABCD中，AD∥BC，，AB=BC=2AD=4，E、F分别是AB、CD上的点，EF∥BC，AE=x．沿EF将梯形ABCD翻折，使平面AEFD⊥平面EBCF（如图）．G是BC的中点，以F、B、C、D为顶点的三棱锥的体积记为f （x）．（1）当x=2时，求证：BD⊥EG；（2）求f（x）的最大值；（3）当f（x）取得最大值时，求异面直线AE与BD所成的角的余弦值．2018全国高考立体几何（完整答案）参考答案与试题解析一．解答题（共40小题）1．【解答】解：（1）∵圆锥的顶点为P，底面圆心为O，半径为2，圆锥的母线长为4，∴圆锥的体积V===．（2）∵PO=4，OA，OB是底面半径，且∠AOB=90°，M为线段AB的中点，∴以O为原点，OA为x轴，OB为y轴，OP为z轴，建立空间直角坐标系，P（0，0，4），A（2，0，0），B（0，2，0），M（1，1，0），O（0，0，0），=（1，1，﹣4），=（0，2，0），设异面直线PM与OB所成的角为θ，则cosθ===．∴θ=arccos．∴异面直线PM与OB所成的角的为arccos．2．【解答】（1）证明：矩形ABCD所在平面与半圆弦所在平面垂直，所以AD⊥半圆弦所在平面，CM⊂半圆弦所在平面，∴CM⊥AD，M是上异于C，D的点．∴CM⊥DM，DM∩AD=D，∴CM⊥平面AMD，CM⊂平面CMB，∴平面AMD⊥平面BMC；（2）解：存在P是AM的中点，理由：连接BD交AC于O，取AM的中点P，连接OP，可得MC∥OP，MC⊄平面BDP，OP⊂平面BDP，所以MC∥平面PBD．3．【解答】证明：（1）平行六面体ABCD﹣A1B1C1D1中，AB∥A1B1，AB∥A1B1，AB⊄平面A1B1C，A1B1⊂∥平面A1B1C⇒AB∥平面A1B1C；（2）在平行六面体ABCD﹣A1B1C1D1中，AA1=AB，⇒四边形ABB1A1是菱形，⊥AB1⊥A1B．在平行六面体ABCD﹣A1B1C1D1中，AA1=AB，AB1⊥B1C1⇒AB1⊥BC．∴⇒AB1⊥面A1BC，且AB1⊂平面ABB1A1⇒平面ABB1A1⊥平面A1BC．4．【解答】证明：（Ⅰ）PA=PD，E为AD的中点，可得PE⊥AD，底面ABCD为矩形，可得BC∥AD，则PE⊥BC；（Ⅱ）由于平面PAB和平面PCD有一个公共点P，且AB∥CD，在平面PAB内过P作直线PG∥AB，可得PG∥CD，即有平面PAB∩平面PCD=PG，由平面PAD⊥平面ABCD，又AB⊥AD，可得AB⊥平面PAD，即有AB⊥PA，PA⊥PG；同理可得CD⊥PD，即有PD⊥PG，可得∠APD为平面PAB和平面PCD的平面角，由PA⊥PD，可得平面PAB⊥平面PCD；（Ⅲ）取PC的中点H，连接DH，FH，在三角形PCD中，FH为中位线，可得FH∥BC，FH=BC，由DE∥BC，DE=BC，可得DE=FH，DE∥FH，四边形EFHD为平行四边形，可得EF∥DH，EF⊄平面PCD，DH⊂平面PCD，即有EF∥平面PCD．5．【解答】解：（1）证明：∵在平行四边形ABCM中，∠ACM=90°，∴AB⊥AC，又AB⊥DA．且AD∩AC=A，∴AB⊥面ADC，∴AB⊂面ABC，∴平面ACD⊥平面ABC；（2）∵AB=AC=3，∠ACM=90°，∴AD=AM=3，∴BP=DQ=DA=2，由（1）得DC⊥AB，又DC⊥CA，∴DC⊥面ABC，∴三棱锥Q﹣ABP的体积V==××==1．6．【解答】证明：（Ⅰ）连接PE，G、F为EC和PC的中点，∴FG∥PE，FG⊄平面PBD，PE⊂平面PBD，∴FG∥平面PBD…（6分）（Ⅱ）∵菱形ABCD，∴BD⊥AC，又PA⊥面ABCD，BD⊂平面ABCD，∴BD⊥PA，∵PA⊂平面PAC，AC⊂平面PAC，且PA∩AC=A，∴BD⊥平面PAC，FG⊂平面PAC，∴BD⊥FG…（14分）7．【解答】（Ⅰ）证明：因为∠DAB=90°，所以AD⊥AB．……………………（1分）因为平面PAB⊥平面ABCD，……………………（2分）且平面PAB∩平面ABCD=AB，……………………（3分）所以AD⊥平面PAB．……………………（4分）（Ⅱ）证明：由已知得AD⊥AB因为AD∥BC，所以BC⊥AB．……………………（5分）又因为∠ABP=90°，所以PB⊥AB．……………………（6分）因为PB∩BC=B……………………（7分）所以AB⊥平面PBC……………………（8分）所以AB⊥PC．……………………（9分）（Ⅲ）解：过E作EF∥AD交PA于F，连接BF．……………………（10分）因为AD∥BC，所以EF∥BC．所以E，F，B，C四点共面．……………………（11分）又因为CE∥平面PAB，且CE⊂平面BCEF，且平面BCEF∩平面PAB=BF，所以CE∥BF，……………………（13分）所以四边形BCEF为平行四边形，所以EF=BC．在△PAD中，因为EF∥AD，所以，……………………（14分）即．8．【解答】证明：（1）∵D，E分别为AB，AC的中点，∴DE∥BC，又DE⊄平面PBC，BC⊂平面PBC，∴DE∥平面PBC．（2）连接PD，∵DE∥BC，又∠ABC=90°，∴DE⊥AB，又PA=PB，D为AB中点，∴PD⊥AB，又PD∩DE=D，PD⊂平面PDE，DE⊂平面PDE，∴AB⊥平面PDE，又PE⊂平面PDE，∴AB⊥PE．（3）∵平面PAB⊥平面ABC，平面PAB∩平面ABC=AB，PD⊥AB，PD⊂平面PAB，∴PD⊥平面ABC，∵△PAB是边长为2的等边三角形，∴PD=，∵E是AC的中点，∴．9．【解答】证明：（Ⅰ）∵AD∥BC，，Q为AD的中点∴四边形BCDQ为平行四边形，∴CD∥BQ．∵∠ADC=90°，∴∠AQB=90°，即QB⊥AD．又∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD．∵BQ⊥平面PAD∵BQ⊂平面PQB，∴平面PQB⊥平面PAD．解：（Ⅱ）∵PA=PD，Q为AD的中点，∴PQ⊥AD．∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD．∵PQ⊥平面ABCD．以Q为原点分别以、、为x轴、y轴、z轴的正方向建立空间直角坐标系，则Q（0，0，0），A（1，0，0），，，，设M（x0，y0，z0），∴，，．由M是PC上的点，设，化简得．设异面直线AP与BM所成角为θ，则．∴，解得或，故或．10．【解答】解：（1）证明：∵平面BDFE⊥平面ABCD，平面BDFE∩平面ABCD=BD，AC⊂平面ABCD，AC⊥BD，∴AC⊥平面BDFE．又AC⊂平面AFC，∴平面AFC⊥平面BDFE．（2）设AC∩BD=O，∵四边形ABCD为等腰梯形，AC⊥BD，AB=2CD=2，∴OD=OC=1，OB=OA=2，∵EF∥OB且EF=OB，∴四边形FEBO为平行四边形，∴OF∥BE，且OF=BE=2，又∵BE⊥平面ABCD，∴OF⊥平面ABCD．以O为原点，向量的方向分别为x轴，y轴，z轴的正方向，建立如图所示的空间直角坐标系，则B（0，2，0），D（0，﹣1，0），F（0，0，2），C（﹣1，0，0），∴=（0，1，2），=（1，﹣1，0），=（0，﹣2，2），设平面DFC的一个法向量为=（x，y，z），则有，即，不妨设z=1，得x=y=﹣2．即=（﹣2，﹣2，1），于是cos＜，＞===．设BF与平面DFC所成角为θ，则sinθ=|cos＜，＞|=．∴BF与平面DFC所成角的正弦值为．11．【解答】证明：（1）在ABN中，∵M是AB的中点，D是BN的中点，∴MD∥AN，又AN⊂平面PAC，MD⊄平面PAC，∴MD∥平面PAC．（2）在△ABC中，∵CA=CB，M是AB的中点，∴AB⊥MC，又∵AB⊥PC，PC⊂平面PMC，MC⊂平面PMC，PC∩MC=C，∴AB⊥平面PMC．又∵AB⊂平面ABN，∴平面ABN⊥平面PMC．12．【解答】证明：（1）如图，取PD的中点E，连接AE，NE．∵E、N分别为PD，PC的中点，∴EN CD，又M为AB的中点，∴AM CD，∴EN AM，∴四边形AMNE为平行四边形．∴MN∥AE，∴MN∥平面PAD．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（5分）（2）∵PA⊥平面ABCD，∠PDA=45°，∴△PAD为等腰直角三角形，∴AE⊥PD，又∵CD⊥AD，CD⊥PA，AD∩PA=A，∴CD⊥平面PAD，∵AE⊂平面PAD，∴CD⊥AE，又CD∩PD=D，∴AE⊥平面PCD，∴MN⊥平面PCD．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（10分）13．【解答】（1）证明：取AB的中点F，连接CF，A1F，∵A1A⊥平面ABC，CF⊂平面ABC，∴所以A1A⊥CF．∵△ABC为正三角形，F为AB的中点，∴BA⊥CF，又∵AA1，AB⊂平面AA1B1B，AA1∩AB=A，∴CF⊥平面AA1B1B，又∵AD⊂平面AA1B1B，所以CF⊥AD，正方形AA1B1B中，∵Rt△A1AF≌Rt△ABD，∴∠DAB=∠FA1A，又∵∠AFA1+∠FA1A=90°，∴∵∠AFA1+∠DAB=90°，，故AD⊥A1F，又∵CF∩A1F=F，CF，A1F⊂平面A1FC，∴AD⊥平面A1FC，又∵A1C⊂平面A1FC，∴A1C⊥AD．（2）取AA1中点E，连接DE，则线段DE为点P的运动轨迹．理由如下：∵DE∥AB，DE⊄平面ABC，AB⊂平面ABC，∴ED∥平面ABC，∴P到平面ABC的距离为．所以V==．14．【解答】证明：（Ⅰ）过点A1在平面ABB1A1内作BB1的垂线，垂足为O，连结C1O，∵A1C1⊥B1B，A1O⊥B1B，A1C1∩A1O=A1，∴B1B⊥平面A1OC1，∵OC1⊂平面A1OC1，∴B1B⊥OC1，由题可知A1B1=A1C1=B1C1=2，在B△A1OB1中，∵A1O⊥OB1，∠A1B1B=45°，A1B1=2，∴OA1=OB1=2，在△OB1C1中，∵C1O⊥OB1，B1C1=2，OB1=2，∴OC1=2，∴=A1C12，∴OC1⊥OA1，∵OA1∩OB1=O，∵OC1⊂平面BCC1B1，∴平面BCC1B1⊥平面ABB1A1．解：（Ⅱ）由（Ⅰ）知OC1、OA1、OB1两两垂直，以O为坐标原点，OA1为x轴，OB1为y轴，OC1为z轴，建立空间直角坐标系，∵AB=2，BB1=4，OC1=2，OA1=2，OB1=2，∴A1（2，0，0），B1（0，2，0），C1（0，0，2），B（0，﹣2，0），A（2，﹣4，0），C（0，﹣4，2），=（2，﹣2，0），=（0，﹣2，2），=（﹣2，0，2），=（0，4，0），设=（x，y，z）是平面ABC的法向量，则，取x=1，得=（1，1，1），设=（x，y，z）是平面A1AC的法向量，则，取x=1，得=（1，0，1），∴cos＜＞==．∴二面角B﹣AC﹣A1的余弦值为．15．【解答】解：解法一：依条件可知AB、AC，AA1两两垂直，如图，以点A为原点建立空间直角坐标系A﹣xyz．根据条件容易求出如下各点坐标：A（0，0，0），B（0，2，0），C（﹣1，0，0），A1（0，0，2），B1（0，2，2），C1（﹣1，0，2），M（0，1，2），（I）证明：∵是平面ACCA1的一个法向量，且，所以又∵MN⊄平面ACC1A1，∴MN∥平面ACC1A1（II）设=（x，y，z）是平面AMN的法向量，因为，由得解得平面AMN的一个法向量=（4，2，﹣1）由已知，平面ABC的一个法向量为=（0，0，1）∴二面角M﹣AN﹣B的余弦值是解法二：（I）证明：设AC的中点为D，连接DN，A1D∵D，N分别是AC，BC的中点，∴又∵，∴，∴四边形A 1DNM是平行四边形∴A1D∥MN∵A1D⊂平面ACC1A1，MN⊄平面ACC1A1∴MN∥平面ACC1A1（II）如图，设AB的中点为H，连接MH，∴MH∥BB1∵BB1⊥底面ABC，∵BB1⊥AC，BB1⊥AB，∴MH⊥AC，MH⊥AB∴AB∩AC=A∴MH⊥底面ABC在平面ABC内，过点H做HG⊥AN，垂足为G 连接MG，AN⊥HG，AN⊥MH，HG∩MH=H ∴AN⊥平面MHG，则AN⊥MG∴∠MGH是二面角M﹣AN﹣B的平面角∵MH=BB1=2，由△AGH∽△BAC，得所以所以∴二面角M﹣AN﹣B的余弦值是16．【解答】解：（1）∵平面CDE⊥平面BCD，平面ABC⊥平面BCD．∴过E作EQ⊥平面BCD，交CD于Q，过A作AP⊥平面BCD，交BC于P，∴EQ∥AP，过Q作QO∥BC，交BD于O，则直线OQ就是在平面BCD内所求的直线，使得直线OQ上任意一点F与E的连线EF均与平面ABC平行．证明如下：∵EQ∥AP，QO∥BC，EQ∩QO=Q，AP∩BC=P，EQ、QO⊂平面EQO，AP、BC⊂平面ABC，∴平面EQO∥平面ABC，∴直线OQ上任意一点F与E的连线EF均与平面ABC平行．（2）∵△BCD与△CDE均为边长为2的等边三角形，△ABC为腰长为3的等腰三角形，平面CDE⊥平面BCD，平面ABC⊥平面BCD，∴AP==2，∴S==2，△ABC点E到平面ABC的距离d===，∴三棱锥E﹣ABC的体积V E===．﹣ABC17．【解答】证明：（1）取BD的中点O，连结CO，PO，因为CD=CB，所以△CBD为等腰三角形，所以BD⊥CO．因为PB=PD，所以△PBD为等腰三角形，所以BD⊥PO．又PO∩CO=O，所以BD⊥平面PCO．因为PC⊂平面PCO，所以PC⊥BD．解：（2）由E为PB中点，连EO，则EO∥PD，又EO⊄平面PAD，所以EO∥平面PAD．由∠ADB=90°，以及BD⊥CO，所以CO∥AD，又CO⊄平面PAD，所以CO∥平面PAD．又CO∩EO=O，所以平面CEO∥平面PAD，而CE⊂平面CEO，所以CE∥平面PAD．18．【解答】解：（1）∵长方体ABCD﹣A1B1C1D1中，AB=BC=2，∴AA1⊥平面ABCD，AC==2，∴∠A1CA是A1C与底面ABCD所成的角，∵A1C与底面ABCD所成的角为60°，∴∠A1CA=60°，∴AA1=AC•tan60°=2•=2，=AB×BC=2×2=4，∵S正方形ABCD∴四棱锥A1﹣ABCD的体积：V===．（2）∵BD∥B1D1，∴∠A1BD是异面直线A1B与B1D1所成角（或所成角的补角）．∵BD=，A1D=A1B==2，∴cos∠A1BD===．∴∠A1BD=arccos．∴异面直线A1B与B1D1所成角是arccos．19．【解答】证明：（Ⅰ）连接BD、AC交于O点，∵PB=PD，∴PO⊥BD，又∵ABCD是菱形，∴BD⊥AC，而AC∩PO=O，∴BD⊥平面PAC，且PC⊂平面PAC，∴BD⊥PC．解：（Ⅱ）由条件可知△ABD≌△PBD，∴AO=PO=，∵PA=，∴PA2=OA2+OP2，∴PO⊥AC，由（Ⅰ）知，BD⊥平面PAC，PO⊂平面PAC，∴PO⊥BD，∴PO⊥平面ABCD，∴平面APC⊥平面ABCD，过E点作EF⊥AC，交AC于F，则EF⊥平面ABCD，∴EF∥PO，∴EF、PO分别是三棱锥E﹣ABC和四棱锥P﹣ABCD的高．又V1=V P﹣ABC﹣V E﹣ABC=，，由=，得4（PO﹣EF）=PO，∴，又由△AEF∽△APO，=，∴=．20．【解答】解：（Ⅰ）由题可知，CM=2t，C1M=2﹣2t，∴V1=S△ECF•CM==，=S•C1M=（2﹣2t）=（1﹣t），V2∴V1•V2=≤•（）2=．当且仅当t=1﹣t，即t=时等号成立．所以当t=时，V1•V2最大，最大值为．（Ⅱ）连接A1C1交B1D1于点O，则O为A1C1的中点，∵A1C∥平面B1D1M，平面A1CC1∩平面B1D1M=OM，∴A1C∥OM，∴M为CC1的中点，连接BD，∵E，F为BC、CD的中点，∴EF∥BD，又AC⊥BD，∴AC⊥EF．∵AA1⊥平面ABCD，EF⊂平面ABCD，∴AA1⊥EF，又AA1∩AC=A，∴EF⊥平面A1AC，又A1C⊂平面A1AC，∴EF⊥A1C．同理可得：EM⊥A1C，又EF∩EM=E，∴A1C⊥平面EFM．又A1C∥平面B1D1M，∴平面EFM⊥平面B1D1M．21．【解答】解：（Ⅰ）∵DA=AB=BC=a，∠ABE=∠BAF=90°，∴四边形ABCD是正方形，∴CD⊥AD，CD⊥DP，又AD∩DP=D，∴CD⊥平面ADP．∵AD2+DP2=AP2，∴AD⊥DP，又CD⊥AD，CD∩DP=D，∴AD⊥平面CDPQ，又AD∥BC，∴BC⊥平面CDPQ．∴V B﹣CDPQ==（a+2a）×a×a=a3，V B﹣ADP===．∴多面体ABCDPQ的体积为V B﹣CDPQ +V B﹣ADP=．（Ⅱ）取BP的中点G，连接GQ、DG、DQ，在△ABP中，BP==2a，∴BG=BP=a，在△BCQ中，BQ==a，PQ==a，∴PQ=BQ，∴GQ⊥BP．∴QG==a，又BD==2a=DP，∴DG⊥BP，∴DG==a，又DQ==a，∴DQ2=QG2+DG2，即QG⊥DG．又BP∩DG=G，∴QG⊥平面PBD，又QG⊂平面PBQ，∴平面PBQ⊥平面PBD．22．【解答】（1）证明：连接BD，因为底面ABCD是菱形，∠BAD=60°，所以△ABD 是正三角形，所以AD⊥BO，因为O为AD的中点，PA=PD，所以AD⊥PO，且PO∩BO=O，所以AD⊥平面POB，又AD⊂平面PAD，所以平面POB⊥平面PAD；（2）解：因为是正三角形，所以OB=3，在Rt△PAO中，，所以PO=2，又，所以OB2+PO2=PB2，所以∠POB=90°，即PO⊥OB，又AD⊥PO，且OB∩AD=O，所以PO⊥平面ABCD，因为，所以四棱锥P﹣ABCD的体积为．23．【解答】（I）证明：∵PA=PD，Q是AD的中点，∴PQ⊥AD，又平面PAD⊥底面ABCD，平面PAD∩底面ABCD=AD，PQ⊂平面PAD，∴PQ⊥平面ABCD，∴BC⊥PQ，∵BC=AD=DQ，BC∥AD，∠ADC=90°，∴四边形BCDQ是矩形，∴BC⊥BQ，又PQ∩BQ=Q，∴BC⊥平面PBQ，又BC⊂平面PBC，∴平面PBC⊥平面PQB．（II）过M作MN∥CD交PD与N，则平面BMQ∩平面PCD=MN，∵平面PAD⊥底面ABCD，平面PAD∩底面ABCD=AD，BQ⊥AD，BQ⊂平面PAD，∴BQ⊥平面PAD，又BQ∥CD∥MN，∴MN⊥平面PAD，∴MN⊥NQ，MN⊥PD，∴∠DNQ为平面BMQ与平面PCD所成角，即∠DNQ=60°，∵PD=PA=2，AD=2BC=2，∴∠PDO=60°，∴△DNQ是等比三角形，∴DN=DQ=1，即N是PD的中点，∴M是PC的中点，∵PD=2，CD=，∴PC=，∴PM==．24．【解答】（Ⅰ）证明：在△ABC中，∵，AB=2，BC=1，∴AC2+BC2=AB2．∴AC⊥BC．又∵AC⊥FB，BF∩CB=B，∴AC⊥平面FBC．（Ⅱ）解：∵AC⊥平面FBC，∴AC⊥FC．∵CD⊥FC，∴FC⊥平面ABCD．在Rt△ACB中，，∴∠CAB=30°，∴在等腰梯形ABCD中可得∠ABD=∠CDB=∠CBD=30°，∴CB=DC=1，∴FC=1．∴△BCD的面积S==．∴四面体FBCD的体积为：．（Ⅲ）解：线段AC上存在点M，且M为AC中点时，有EA∥平面FDM，证明如下：连接CE与DF交于点N，连接MN．由CDEF为正方形，得N为CE中点．∴EA∥MN．∵MN⊂平面FDM，EA⊄平面FDM，∴EA∥平面FDM．所以线段AC上存在点M，使得EA∥平面FDM成立．25．【解答】（Ⅰ）证明：∵PQ∥DC，PQ=PD=DC=1，∴四边形PQCD是平行四边形，∴PD∥CQ，∵PD⊄平面QBC，CQ⊂平面QBC，∴PD∥平面QBC．（Ⅱ）证明：∵∠APD=90°，∴PD⊥PA，∵平面PAD⊥平面ABCD，△PAD是直角三角形，四边形ABCD是直角梯形，AB ∥DC，AB⊥AD，∴AB⊥平面PAD，∴AB⊥PD，∵PD∥QC，∴PA⊥QC，AB⊥QC，∵PA∩AB=A，∴QC⊥平面PABQ．（Ⅲ）解：存在．由（Ⅱ）可知QC⊥平面PABQ；作AM⊥BQ，交BQ于M，可知AM⊥CQ，BQ∩CQ=Q，所以AM⊥平面BCQ，BC⊂平面BCQ，∴AM⊥BC．QB=，cosB=，BM=2=，QM==．26．【解答】解：（1）证明：在图1中，由题意知AE=1，AD=BE=2，在△ADE中，由余弦定理知：DE2=AE2+AD2﹣AE×AD=12+22﹣1×2=3，所以：AE2+DE2=AD2，所以：DE⊥AE，DE⊥BE，在△ADE沿直线DE折起的过程中，DE与AE，BE的垂直关系不变，故在图2中有DE⊥A'E，DE⊥BE，又A'E∩BE=E，所以DE⊥平面A'EB，所以DE⊥A'B．（2）如图2，因为平面A'DE⊥底面BCDE，由（1）知DE⊥A'E，且平面A'DE∩底面BCDE=DE，所以A'E⊥底面BCDE，所以A'E为三棱锥A'﹣EDC的高，且A'E=AE=1，又因为在图1中，S△ECD=S△ABC﹣S△AED﹣S△BEC=，所以：，故三棱锥D﹣A'CE的体积为．27．【解答】（1）证明：∵PA⊥AC，PA=2，AC=2，∴，又∵，BC=2，∴PB2+BC2=PC2，则BC⊥PB．又∵AB⊥BC，∴BC⊥平面PAB，则BC⊥PA，又PA⊥AC，AC∩BC=C，∴PA⊥平面ABC．又∵BD⊂平面PAC，∴PA⊥BD，在Rt△ABC中，由BC=2，AC=2，可得AB=2，又∵D为AC的中点，∴BD⊥AC，而PA∩AC=A，∴BD⊥平面PAC，则平面BDE⊥平面PAC；=V E﹣PBC=V B﹣APCE﹣V P﹣ABC．（2）解：V P﹣EBC由已知，DE∥AP，∴．∴=，．∴．28．【解答】解：（Ⅰ）证明：∵AD=2AB，E为线段AD的中点，∴AB=AE，取BE中点O，连接PO，则PO⊥BE，又平面PEB⊥平面BCDE，平面PEB∩平面BCDE=BE，∴PO⊥平面BCDE，则PO⊥EC，在矩形ABCD中，∴AD=2AB，E为AD的中点，∴BE⊥EC，则EC⊥平面PBE，∴EC⊥PB，又PB⊥PE，且PE∩EC=E，∴PB⊥平面PEC．（Ⅱ）以OB所在直线为x轴，以平行于EC所在直线为y轴，以OP所在直线为z轴建立空间直角坐标系，∵PB=PE=2，则B（，0，0），E（﹣，0，0），P（0，0，），D（﹣2，，0），C（﹣，2，0），∴=（﹣，0，﹣），=（﹣，2，﹣），∴cos∠EPC===，可得：sin∠EPC==，可得：S△EPC=||•||•sin∠EPC=2×2×=2，=V D﹣EPC，设三棱锥D﹣PEC的高为h，则可得：S△ECD•OP=S△EPC•h，可∵V P﹣ECD得：=2×h，∴解得：三棱锥D﹣PEC的高h=1．29．【解答】解：（Ⅰ）在Rt△BEB中，BE=1，AB=，所以∠BAE=30°……（1分）同理∠BDA=30°，从而∠AOD=90°，AF⊥BD……（2分）又因为AD∥EC，AD=EC，所以ADCE是平行四边形，∠CDO=∠AOD=90°，CD⊥DO……（3分）因为平面ABE⊥平面ADE，平面ABE∩平面ADE=AE，BO⊥AE，所以BO⊥平面ADE……（4分）又CD⊂平面ADE，所以BO⊥CD，BO∩DO=O，BO⊂平面BOD，OD平面BOD．所以CD⊥平面BOD……（6分）（Ⅱ）由（Ⅰ）可知，四边形AECD的面积S=CD•OD=3……（7分）连接AC，则△ACD的面积S1=，三棱锥B=ACD的体积V=……（9分）△BCD的面积S2=……（10分）设A到平面BCD的距离为h，则h=，h=……（11分）直线AB与面BCD所成角的正弦值为，余弦值为……（12分）30．【解答】证明：（1）取AB中点为R，连接PR，B1R∵点P是CD中点，Q是A1B1的中点，∴四边形AQB1R，PRB1C1都为平行四边形，∴AQ∥B1R，B1R∥PC1，∴AQ∥PC1．∵AQ⊄平面PBC1，PC1⊂平面PBC1，∴AQ∥平面PBC1．（Ⅱ）∵四棱柱ABCD﹣A1B1C1D1为长方体，BC=CC1，∴B1C⊥BC1．∵A1B1⊥平面BB1C1C，∴A1B1⊥BC1．∵A1B1∩B1C=B1，A1B1⊂平面A1B1C，B1C⊂平面A1B1C，∴BC1⊥平面A1B1C，BC1⊂平面PBC1，∴平面A1B1C⊥平面PBC1．31．【解答】（1）证明：由AD=6，DM=4可得AM=2，则BC=AM，又AD∥BC，则四边形ABCM是平行四边形，则CM∥AB，∵AD⊥AB，∴CM⊥AD．又PA⊥平面ABCD，CM⊂平面ABCD，∴PA⊥CM，∵PA∩AD=A，PA，AD⊂平面PAD，∴CM⊥平面PAD，又CM⊂平面PCM，∴平面PCM⊥平面PAD．（2）解：∵PA⊥平面ABCD，∴PA⊥AB，∵∠APB=45°，∴AP=AB=6．∵，∴．∴四棱锥P﹣ABCM的表面积为．32．【解答】（本小题满分12分）解：（1）直线DF与平面BCE'相交，理由如下：因为E'⊄平面ABCD，所以D⊄平面BCE'．若DF∥平面BCE'，设平面DCE'∩平面BCE'=CM，则DF∥CM．CM与CB不重合．又因为AD∥BC，所以平面ADE'∥平面BCE'，矛盾．所以直线DF与平面BCE'相交．…………………………（4分）证明：（2）取AB的中点O，连接E'O，BD，由等腰梯形ADCE中，AD∥EC，EC=2AD=2AE=4，，所以E'O⊥AB，DO⊥AB，…………………………（6分）分别以BA，OD所在的直线为x轴，y轴，过O垂直于平面ABCD的直线为z轴建立如图所示的空间直角坐标系，设二面角E'﹣AB﹣D的大小为α．则．过E'作E'G⊥OD于点G．因为E'O⊥AB，DO⊥AB，所以AO⊥平面E'OD，∠E'OD=α．所以E'G⊥AO．所以E'G⊥平面ABCD．…………………………（8分）所以．设平面E'AB的法向量为n=（x，y，z），则，即令y=1，得平面E'AB的一个法向量为n=（0，1，﹣cotα）．…………………………（10分）同理可求平面E'DC的一个法向量为．所以．解得：．所以二面角E'﹣AB﹣D的大小为，即平面ABE'⊥平面ABCD．…………………………（12分）33．【解答】证明：（I）因为AD=4，AB=2，，所以AB2+BD2=AD2，AB⊥BD，且∠ADB=30°．又△BCD是等边三角形，所以∠ADC=90°，即CD⊥AD．…（3分）因为平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，CD⊂平面ABCD，所以CD⊥平面PAD．所以CD⊥PA．……（6分）解：（II）因为平面BEF∥平面PCD，所以BF∥CD，EF∥PD，且BF⊥AD．……（8分）又在直角三角形ABD中，DF=，所以AE=AF=1．所以．……（10分）由（I）知CD⊥平面PAD，故四棱锥C﹣PEFD的体积．…（12分）34．【解答】解：（1）四边形ABCD是平行四边形，AD=2，∴BC=AD=2，又AB=AC=2，∴AB2+AC2=BC2，∴AC⊥AB，又PB⊥AC，且AB∩PB=B，∴AC⊥平面PAB，∵AC⊂平面PAC，∴平面PAB⊥平面PAC；（2）由（1）知AC⊥AB，AC⊥平面PAB，分别以AB、AC所在直线为x轴、y轴，平面PAB内过点A且与直线AB垂直的直线为z轴，建立空间直角坐标系A﹣xyz，如图所示；则A（0，0，0），B（2，0，0），C（0，2，0），=（0，2，0），=（﹣2，2，0）；由∠PBA=45°，PB=，可得P（1，0，1），∴=（1，0，1），=（﹣1，0，1）；假设棱PA上存在点E，使得直线CE与平面PBC所成角的正弦值为，设=λ（0＜λ＜1），则=λ=（λ，0，λ），=﹣=（λ，﹣2，λ），设平面PBC的法向量为=（x，y，z），则，即，令z=1，可得x=y=1，∴平面PBC的一个法向量为=（1，1，1），设直线CE与平面PBC所成的角为θ，则sinθ=|cos＜，＞|===，解得λ=或λ=（不合题意，舍去），∴存在=，使得直线CE与平面PBC所成角的正弦值为．35．【解答】解：（1）以A为坐标原点，AB为x轴，AD为y轴，AP为z轴，建立空间直角坐标系，则A（0，0，0），B（1，0，0），C（1，1，0），D（0，2，0），P（0，0，1），∵E、F、G分别为BC、PD、PC的中点，∴，F（0，1，），G（），∴=（﹣1，），=（），设EF与DG所成角为θ，则cosθ==．∴EF与DG所成角的余弦值为．（2）设平面PBC的法向量为=（x，y，z），∵=（0，1，0），=（1，0，﹣1），∴，取x=1，得=（1，0，1），M为EF上一点，N为DG上一点，若存在MN，使得MN⊥平面PBC，则∥，设M（），N（x2，y2，z2），则，①∵点M，N分别是线段EF与DG上的点，∴，∵=（），=（x2，y2﹣2，z2），∴，且，②把②代入①，得，解得，∴M（），N（）．36．【解答】解：（1）∵D，E分别是AC，AB的中点，∴DE∥BC，∵四边形BB1C1C为矩形，∴BC⊥CC1．∵AC=BC=4，AB=4，∴AC2+BC2=AB2，∴BC⊥AC，又AC∩CC1=C，∴BC⊥平面AA1C1C，∴DE⊥平面AA1C1C．。

广西高考数学一轮复习高考大题专项练四高考中的立体几何文-人教版高三全册数学试题

高考大题专项练四高考中的立体几何1.(2018全国Ⅱ,文19)如图,在三棱锥P-ABC 中,AB=BC=2√2,PA=PB=PC=AC=4,O 为AC 的中点. (1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且MC=2MB ,求点C 到平面POM 的距离.AP=CP=AC=4,O 为AC 的中点,所以OP ⊥AC ,且OP=2√3.连接OB ,因为AB=BC=√22AC ,所以△ABC 为等腰直角三角形,且OB ⊥AC ,OB=12AC=2.由OP 2+OB 2=PB 2知,OP ⊥OB.由OP ⊥OB ,OP ⊥AC 知PO ⊥平面ABC.CH ⊥OM ,垂足为H.又由(1)可得OP ⊥CH ,所以CH ⊥平面POM. 故CH 的长为点C 到平面POM 的距离. 由题设可知OC=12AC=2,CM=23BC=4√23,∠ACB=45°. 所以OM=2√53,CH=OO ·OO ·sin∠OOOOO=4√55.所以点C 到平面POM 的距离为4√55.2.(2018北京,文18)如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,E,F分别为AD,PB的中点.求证:(1)PE⊥BC;(2)平面PAB⊥平面PCD;(3)EF∥平面PCD.因为PA=PD,E为AD的中点,所以PE⊥AD.因为底面ABCD为矩形,所以BC∥AD,所以PE⊥BC.(2)因为底面ABCD为矩形,所以AB⊥AD.又因为平面PAD⊥平面ABCD,所以AB⊥平面PAD,所以AB⊥PD.又因为PA⊥PD,所以PD⊥平面PAB.所以平面PAB⊥平面PCD.(3)如图,取PC的中点G,连接FG,DG.因为F,G分别为PB,PC的中点,BC.所以FG∥BC,FG=12因为四边形ABCD为矩形,且E为AD的中点,BC.所以DE∥BC,DE=12所以DE∥FG,DE=FG.所以四边形DEFG为平行四边形.所以EF∥DG.又因为EF⊄平面PCD,DG⊂平面PCD,所以EF∥平面PCD.3.由四棱柱ABCD-A1B1C1D1截去三棱锥C1-B1CD1后得到的几何体如图所示.四边形ABCD为正方形,O为AC与BD的交点,E为AD的中点,A1E⊥平面ABCD.(1)证明:A1O∥平面B1CD1;(2)设M是OD的中点,证明:平面A1EM⊥平面B1CD1.取B1D1的中点O1,连接CO1,A1O1,由于ABCD-A1B1C1D1是四棱柱,所以A1O1∥OC,A1O1=OC,因此四边形A1OCO1为平行四边形,所以A1O∥O1C.又O1C⊂平面B1CD1,A1O⊄平面B1CD1,所以A1O∥平面B1CD1.(2)因为AC⊥BD,E,M分别为AD和OD的中点,所以EM⊥BD,又A1E⊥平面ABCD,BD⊂平面ABCD,所以A1E⊥BD,因为B1D1∥BD,所以EM⊥B1D1,A1E⊥B1D1.又A1E,EM⊂平面A1EM,A1E∩EM=E,所以B1D1⊥平面A1EM,又B1D1⊂平面B1CD1,所以平面A1EM⊥平面B1CD1.4.如图,在底面是菱形的四棱柱ABCD-A1B1C1D1中,∠ABC=60°,AA1=AC=2,A1B=A1D=2√2,点E在A1D上.(1)证明:AA1⊥平面ABCD;(2)当O1O为何值时,A1B∥平面EAC,并求出此时三棱锥D-AEC的体积.OOABCD是菱形,∠ABC=60°,所以AB=AD=AC=2.在△AA1B中,由A O12+AB2=A1B2,知AA1⊥AB.同理,AA1⊥AD.又因为AB∩AD于点A,所以AA1⊥平面ABCD.=1时,A1B∥平面EAC.解当O1OOO=1,即点E为A1D的中点时,连接OE,则OE∥A1B,所以A1B∥证明如下:连接BD交AC于O,当O1OOO平面EAC.设AD的中点为F,连接EF.则EF∥AA1,所以EF⊥平面ACD,且EF=1,可求得S △ACD =√3. 所以V E-ACD =13×1×√3=√33, 即V D-AEC =V E-ACD =√33. 5.如图,AB 是圆O 的直径,点C 是弧AB 的中点,点V 是圆O 所在平面外一点,D 是AC 的中点,已知AB=2,VA=VB=VC=2.(1)求证:OD ∥平面VBC ; (2)求证:AC ⊥平面VOD ; (3)求棱锥C-ABV 的体积.O ,D 分别是AB 和AC 的中点,∴OD ∥BC.又OD ⊄平面VBC ,BC ⊂平面VBC ,∴OD ∥平面VBC.VA=VB ,O 为AB 中点,∴VO ⊥AB.连接OC ,在△VOA 和△VOC 中,OA=OC ,VO=VO ,VA=VC ,∴△VOA ≌△VOC ,∴∠VOA=∠VOC=90°, ∴VO ⊥OC.又AB ∩OC=O ,AB ⊂平面ABC ,OC ⊂平面ABC ,∴VO ⊥平面ABC.又AC ⊂平面ABC ,∴AC ⊥VO.又VA=VC ,D 是AC 的中点,∴AC ⊥VD.∵VO ⊂平面VOD ,VD ⊂平面VOD ,VO ∩VD=V , ∴AC ⊥平面VOD.(2)知VO 是棱锥V-ABC 的高,且VO=√OO 2-OO 2=√3. 又点C 是弧AB 的中点,∴CO ⊥AB ,且CO=1,AB=2.∴三角形ABC 的面积S △ABC =12AB ·CO=12×2×1=1, ∴棱锥V-ABC 的体积为 V V-ABC =13S △ABC ·VO=13×1×√3=√33, 故棱锥C-ABV 的体积为√33. 6.如图,已知正三棱锥P-ABC 的侧面是直角三角形,PA=6.顶点P 在平面ABC 内的正投影为点D ,D 在平面PAB 内的正投影为点E ,连接PE 并延长交AB 于点G. (1)证明:G 是AB 的中点;(2)在图中作出点E 在平面PAC 内的正投影F (说明作法及理由),并求四面体PDEF 的体积.P 在平面ABC 内的正投影为D ,所以AB ⊥PD.因为D 在平面PAB 内的正投影为E ,所以AB ⊥DE. 所以AB ⊥平面PED ,故AB ⊥PG.又由已知可得,PA=PB ,从而G 是AB 的中点.PAB 内,过点E 作PB 的平行线交PA 于点F ,F 即为E 在平面PAC 内的正投影.理由如下:由已知可得PB ⊥PA ,PB ⊥PC , 又EF ∥PB ,所以EF ⊥PA ,EF ⊥PC. 因此EF ⊥平面PAC ,即点F 为E 在平面PAC 内的正投影. 连接CG ,因为P 在平面ABC 内的正投影为D , 所以D 是正三角形ABC 的中心.由(1)知,G 是AB 的中点,所以D 在CG 上, 故CD=23CG.由题设可得PC ⊥平面PAB ,DE ⊥平面PAB , 所以DE ∥PC , 因此PE=23PG ,DE=13PC.由已知,正三棱锥的侧面是直角三角形且PA=6,可得DE=2,PE=2√2. 在等腰直角三角形EFP 中,可得EF=PF=2. 所以四面体PDEF 的体积V=13×12×2×2×2=43.7.(2018全国Ⅰ,文18)如图,在平行四边形ABCM 中,AB=AC=3,∠ACM=90°.以AC 为折痕将△ACM 折起,使点M 到达点D 的位置,且AB ⊥DA.(1)证明:平面ACD ⊥平面ABC ;(2)Q 为线段AD 上一点,P 为线段BC 上一点,且BP=DQ=23DA ,求三棱锥Q-ABP 的体积.,∠BAC=90°,BA ⊥AC.又BA ⊥AD ,所以AB ⊥平面ACD.又AB ⊂平面ABC ,所以平面ACD ⊥平面ABC.,DC=CM=AB=3,DA=3√2.又BP=DQ=23DA ,所以BP=2√2. 作QE ⊥AC ,垂足为E ,则QE O 13DC.由已知及(1)可得DC ⊥平面ABC , 所以QE ⊥平面ABC ,QE=1.因此,三棱锥Q-APB 的体积为V Q-ABP =13×QE ×S △ABP =13×1×12×3×2√2sin45°=1.8.(2018天津,文17)如图,在四面体ABCD 中,△ABC 是等边三角形,平面ABC ⊥平面ABD ,点M 为棱AB 的中点,AB=2,AD=2√3,∠BAD=90°.(1)求证:AD ⊥BC ;(2)求异面直线BC 与MD 所成角的余弦值; (3)求直线CD 与平面ABD 所成角的正弦值.ABC ⊥平面ABD ,平面ABC ∩平面ABD=AB ,AD ⊥AB ,可得AD ⊥平面ABC ,故AD ⊥BC.AC 的中点N ,连接MN ,ND.又因为M 为棱AB 的中点, 故MN ∥BC.所以∠DMN (或其补角)为异面直线BC 与MD 所成的角. 在Rt △DAM 中,AM=1, 故DM=√OO 2+OO 2=√13. 因为AD ⊥平面ABC ,故AD ⊥AC. 在Rt △DAN 中,AN=1, 故DN=√OO 2+OO 2=√13. 在等腰三角形DMN 中,MN=1, 可得cos ∠DMN=12OO OO=√1326. 所以,异面直线BC 与MD 所成角的余弦值为√1326.CM.因为△ABC 为等边三角形,M 为边AB 的中点,故CM ⊥AB ,CM=√3.又因为平面ABC ⊥平面ABD ,而CM ⊂平面ABC ,故CM ⊥平面ABD.所以,∠CDM 为直线CD 与平面ABD 所成的角.在Rt △CAD 中,CD=√OO 2+OO 2=4. 在Rt △CMD 中,sin ∠CDM=OOOO =√34..所以,直线CD与平面ABD所成角的正弦值为√34。

2018版高考数学(人教A版理科)大一轮复习配套讲义专题探究课四高考中立体几何问题的热点题型Word版含解析

高考导航 1.立体几何是高考的重要内容，每年基本上都是一个解答题，一至两道选择题或填空题.小题主要考查学生的空间观念，空间想象能力及简单计算能力.解答题主要采用“论证与计算”相结合的模式，即首先是利用定义、定理、公理等证明空间的线线、线面、面面平行或垂直，再利用空间向量进行空间角的计算.重在考查学生的逻辑推理能力及计算能力.热点题型主要有平面图形的翻折、探索性问题等；2.思想方法：(1)转化与化归(空间问题转化为平面问题)；(2)数形结合(根据空间位置关系利用向量转化为代数运算).热点一空间点、线、面的位置关系及空间角的计算(规范解答)空间点、线、面的位置关系通常考查平行、垂直关系的证明，一般出现在解答题的第(1)问，解答题的第(2)问常考查求空间角，求空间角一般都可以建立空间直角坐标系，用空间向量的坐标运算求解.【例1】 (满分12分)(2017·郑州模拟)如图，在△ABC 中， ∠ABC ＝π4，O 为AB 边上一点，且3OB ＝3OC ＝2AB ，已知PO ⊥平面ABC ，2DA ＝2AO ＝PO ，且DA ∥PO. (1)求证：平面PBD ⊥平面COD ；(2)求直线PD 与平面BDC 所成角的正弦值.满分解答 (1)证明 ∵OB ＝OC ，又∵∠ABC ＝π4， ∴∠OCB ＝π4，∴∠BOC ＝π2. ∴CO ⊥AB.2分又PO ⊥平面ABC ，OC ⊂平面ABC ，∴PO ⊥OC.又∵PO ，AB ⊂平面PAB ，PO ∩AB ＝O ， ∴CO ⊥平面PAB ，即CO ⊥平面PDB.4分又CO ⊂平面COD ， ∴平面PDB ⊥平面COD.6分(2)解以OC ，OB ，OP 所在射线分别为x ，y ，z 轴，建立空间直角坐标系，如图所示.设OA ＝1，则PO ＝OB ＝OC ＝2，DA ＝1.则C(2，0，0)，B(0，2，0)，P(0，0，2)，D(0，－1，1)， ∴PD→＝(0，－1，－1)，BC →＝(2，－2，0)，BD →＝(0，－3，1).8分设平面BDC 的一个法向量为n ＝(x ，y ，z )， ∴⎩⎪⎨⎪⎧n ·BC →＝0，n ·BD →＝0，∴⎩⎨⎧2x －2y ＝0，－3y ＋z ＝0，令y ＝1，则x ＝1，z ＝3，∴n ＝(1，1，3).10分设PD 与平面BDC 所成的角为θ，则sin θ＝⎪⎪⎪⎪⎪⎪⎪⎪PD→·n |PD →||n | ＝⎪⎪⎪⎪⎪⎪1×0＋1×（－1）＋3×（－1）02＋（－1）2＋（－1）2×12＋12＋32＝22211. 即直线PD 与平面BDC 所成角的正弦值为22211.12分❶得步骤分：抓住得分点的步骤，“步步为赢”，求得满分.如第(1)问中，先证线面垂直，再证两面垂直.❷得关键分：解题过程不可忽视的关键点，有则给分，无则没分，如第(1)问中证线面垂直不可漏“CO ⊥平面PDB ”.❸得计算分：解题过程中计算准确是得满分的根本保证. 如第(2)问中求法向量n ，计算线面角正弦值sin θ.利用向量求空间角的步骤第一步：建立空间直角坐标系. 第二步：确定点的坐标.第三步：求向量(直线的方向向量、平面的法向量)坐标. 第四步：计算向量的夹角(或函数值). 第五步：将向量夹角转化为所求的空间角.第六步：反思回顾.查看关键点、易错点和答题规范.【训练1】如图所示，在多面体A 1B 1D 1DCBA 中，四边形AA 1B 1B ，ADD 1A 1，ABCD 均为正方形，E 为B 1D 1的中点，过A 1，D ，E 的平面交CD 1于F . (1)证明：EF ∥B 1C .(2)求二面角E -A 1D B 1的余弦值.(1)证明由正方形的性质可知A 1B 1∥AB ∥DC ，且A 1B 1＝AB ＝DC ，所以四边形A 1B 1CD 为平行四边形，从而B 1C ∥A 1D ，又A 1D ⊂面A 1DE ，B 1C ⊄面A 1DE ，于是B 1C ∥面A 1DE .又B 1C ⊂面B 1CD 1，面A 1DE ∩面B 1CD 1＝EF ，所以EF ∥B 1C . (2)解因为四边形AA1B 1B ，ADD 1A 1，ABCD 均为正方形，所以AA 1⊥AB ，AA 1⊥AD ，AB ⊥AD 且AA 1＝AB ＝AD .以A 为原点，分别以AB →，AD →，AA 1→为x 轴，y 轴和z 轴单位正向量建立如图所示的空间直角坐标系，可得点的坐标A (0，0，0)，B (1，0，0)，D (0，1，0)，A 1(0，0，1)，B 1(1，0，1)，D 1(0，1，1)，而E 点为B 1D 1的中点，所以E 点的坐标为⎝ ⎛⎭⎪⎫12，12，1.设平面A 1DE 的一个法向量n 1＝(r 1，s 1，t 1)，而该面上向量A 1E →＝⎝ ⎛⎭⎪⎫12，12，0，A 1D →＝(0，1，－1)，由n 1⊥A 1E →，n 1⊥A 1D →得r 1，s 1，t 1应满足的方程组⎩⎪⎨⎪⎧12r 1＋12s 1＝0，s 1－t 1＝0，(－1，1，1)为其一组解，所以可取n 1＝(－1，1，1).设平面A 1B 1CD 的一个法向量n 2＝(r 2，s 2，t 2)，而该面上向量A 1B 1→＝(1，0，0)，A 1D →＝(0，1，－1)，由此同理可得n 2＝(0，1，1). 所以结合图形知二面角E -A 1D B 1的余弦值为 |n 1·n 2||n 1|·|n 2|＝23×2＝63.热点二立体几何中的探索性问题此类试题一般以解答题形式呈现，常涉及线、面平行、垂直位置关系的探究或空间角的计算问题，是高考命题的热点，一般有两种解决方式： (1)根据条件作出判断，再进一步论证；(2)利用空间向量，先假设存在点的坐标，再根据条件判断该点的坐标是否存在. 【例2】 (2016·北京卷)如图，在四棱锥P －ABCD 中，平面PAD ⊥平面ABCD ，PA ⊥PD ，PA ＝PD ，AB ⊥AD ，AB ＝1，AD ＝2，AC ＝CD ＝ 5. (1)求证：PD ⊥平面PAB ；(2)求直线PB 与平面PCD 所成角的正弦值；(3)在棱PA 上是否存在点M ，使得BM ∥平面PCD ？若存在，求AMAP 的值；若不存在，说明理由.(1)证明因为平面PAD ⊥平面ABCD ，平面PAD ∩平面ABCD ＝AD ，AB ⊥AD ，所以AB ⊥平面PAD ，所以AB ⊥PD.又PA ⊥PD ，AB ∩PA ＝A ，所以PD ⊥平面PAB. (2)解取AD 的中点O ，连接PO ，CO.因为PA ＝PD ，所以PO ⊥AD.因为PO ⊂平面PAD ，平面PAD ⊥平面ABCD ，所以PO ⊥平面ABCD.因为CO ⊂平面ABCD ，所以PO ⊥CO. 因为AC ＝CD ，所以CO ⊥AD.如图，建立空间直角坐标系O －xyz.由题意得，A(0，1，0)，B(1，1，0)，C(2，0，0)，D(0，－1，0)，P(0，0，1).设平面PCD 的一个法向量为n ＝(x ，y ，z )，则 ⎩⎪⎨⎪⎧n ·PD →＝0，n ·PC →＝0，即⎩⎨⎧－y －z ＝0，2x －z ＝0，令z ＝2，则x ＝1，y ＝－2. 所以n ＝(1，－2，2).又PB →＝(1，1，－1)，所以cos 〈n ，PB →〉＝n ·PB →|n ||PB →|＝－33.所以直线PB 与平面PCD 所成角的正弦值为33.(3)解设M 是棱P A 上一点，则存在λ∈[0，1]，使得AM →＝λAP →.因此点M (0，1－λ，λ)，BM→＝(－1，－λ，λ).因为BM ⊄平面PCD ，所以要使BM ∥平面PCD ，则BM →·n ＝0，即(－1，－λ，λ)·(1，－2，2)＝0，解得λ＝14. 所以在棱P A 上存在点M ，使得BM ∥平面PCD ，此时AM AP ＝14.探究提高 (1)对于存在判断型问题的求解，应先假设存在，把要成立的结论当作条件，据此列方程或方程组，把“是否存在”问题转化为“点的坐标是否有解，是否有规定范围内的解”等.(2)对于位置探究型问题，通常借助向量，引进参数，综合已知和结论列出等式，解出参数.【训练2】 (2017·安徽江南名校联考)如图，在四棱锥P －ABCD 中，PD ⊥平面ABCD ，AB ∥DC ，AB ⊥AD ，DC ＝6，AD ＝8，BC ＝10，∠P AD ＝45°，E 为P A 的中点. (1)求证：DE ∥平面BPC ；(2)线段AB 上是否存在一点F ，满足CF ⊥DB ？若存在，试求出二面角F －PC －D 的余弦值；若不存在，请说明理由.(1)证明取PB 的中点M ，连接EM 和CM ，过点C 作CN ⊥AB ，垂足为点N .∵CN ⊥AB ，DA ⊥AB ，∴CN ∥DA ，又AB ∥CD ，∴四边形CDAN 为平行四边形， ∴CN ＝AD ＝8，DC ＝AN ＝6，在Rt △BNC 中，BN ＝BC 2－CN 2＝102－82＝6，∴AB ＝12，而E ，M 分别为P A ，PB 的中点， ∴EM ∥AB 且EM ＝6，又DC ∥AB ，∴EM ∥CD 且EM ＝CD ，四边形CDEM 为平行四边形， ∴DE ∥CM .∵CM ⊂平面PBC ，DE ⊄平面PBC ， ∴DE ∥平面BPC .(2)解由题意可得DA ，DC ，DP 两两互相垂直，如图，以 D 为原点，DA ，DC ，DP 分别为x ，y ，z 轴建立空间直角坐标系D －xyz ，则A (8，0，0)，B (8，12，0)，C (0，6，0)，P (0，0，8). 假设AB 上存在一点F 使CF ⊥BD ，设点F 坐标为(8，t ，0)，则CF→＝(8，t －6，0)，DB →＝(8，12，0)，由CF→·DB →＝0得t ＝23. 又平面DPC 的一个法向量为m ＝(1，0，0)，设平面FPC 的法向量为n ＝(x ，y ，z ). 又PC →＝(0，6，－8)，FC →＝⎝ ⎛⎭⎪⎫－8，163，0. 由⎩⎪⎨⎪⎧n ·PC →＝0，n ·FC →＝0，得⎩⎪⎨⎪⎧6y －8z ＝0，－8x ＋163y ＝0，即⎩⎪⎨⎪⎧z ＝34y ，x ＝23y ，不妨令y ＝12，有n ＝(8，12，9). 则cos 〈n ，m 〉＝n ·m|n ||m |＝81×82＋122＋92＝817.又由图可知，该二面角为锐二面角，故二面角F －PC －D 的余弦值为817.热点三立体几何中的折叠问题将平面图形沿其中一条或几条线段折起，使其成为空间图形，这类问题称为立体几何中的折叠问题，折叠问题常与空间中的平行、垂直以及空间角相结合命题，考查学生的空间想象力和分析问题的能力.【例3】 (2016·全国Ⅱ卷)如图，菱形ABCD 的对角线AC 与BD 交于点O ，AB ＝5，AC ＝6，点E ，F 分别在AD ，CD 上，AE ＝CF ＝54，EF 交BD 于点H .将△DEF 沿EF 折到△D ′EF 的位置，OD ′＝10.(1)证明：D ′H ⊥平面ABCD ； (2)求二面角B －D ′A －C 的正弦值. (1)证明由已知得AC ⊥BD ，AD ＝CD . 又由AE ＝CF 得AE AD ＝CFCD ，故AC ∥EF . 因此EF ⊥HD ，从而EF ⊥D ′H .由AB ＝5，AC ＝6得DO ＝BO ＝AB 2－AO 2＝4. 由EF ∥AC 得OH DO ＝AE AD ＝14.所以OH ＝1，D ′H ＝DH ＝3. 于是D ′H 2＋OH 2＝32＋12＝10＝D ′O 2，故D ′H ⊥OH .又D ′H ⊥EF ，而OH ∩EF ＝H ，所以D ′H ⊥平面ABCD .(2)解如图，以H 为坐标原点，HF →的方向为x 轴正方向，建立空间直角坐标系H －xyz . 则H (0，0，0)，A (－3，－1，0)， B (0，－5，0)，C (3，－1，0)，D ′(0，0，3)，AB →＝(3，－4，0)，AC →＝(6，0，0)，AD ′→＝(3，1，3). 设m ＝(x 1，y 1，z 1)是平面ABD ′的一个法向量，则⎩⎪⎨⎪⎧m ·AB →＝0，m ·AD ′→＝0，即⎩⎨⎧3x 1－4y 1＝0，3x 1＋y 1＋3z 1＝0，所以可取m ＝(4，3，－5).设n ＝(x 2，y 2，z 2)是平面ACD ′的一个法向量，则⎩⎪⎨⎪⎧n ·AC →＝0，n ·AD ′→＝0，即⎩⎨⎧6x 2＝0，3x 2＋y 2＋3z 2＝0，所以可取n ＝(0，－3，1).于是cos 〈m ，n 〉＝m ·n |m ||n |＝－1450×10＝－7525.sin 〈m ，n 〉＝29525.因此二面角B －D ′A －C 的正弦值是29525.探究提高立体几何中的折叠问题，关键是搞清翻折前后图形中线面位置关系和度量关系的变化情况，一般地翻折后还在同一个平面上的性质不发生变化，不在同一个平面上的性质发生变化.【训练3】 (2015·陕西卷)如图1，在直角梯形ABCD 中，AD ∥BC ，∠BAD ＝π2，AB ＝BC ＝1，AD ＝2，E 是AD 的中点，O 是AC 与BE 的交点.将△ABE 沿BE 折起到△A 1BE 的位置，如图2.(1)证明：CD ⊥平面A 1OC ；(2)若平面A 1BE ⊥平面BCDE ，求平面A 1BC 与平面A 1CD 夹角的余弦值. (1)证明在题图1中，因为AB ＝BC ＝1，AD ＝2，E 是AD 的中点，∠BAD ＝π2，所以BE ⊥AC .即在题图2中，BE ⊥OA 1，BE ⊥OC ，从而BE ⊥平面A 1OC .又CD ∥BE ，所以CD ⊥平面A 1OC .(2)解由已知，平面A 1BE ⊥平面BCDE ，又由(1)知，BE ⊥OA 1，BE ⊥OC ，所以∠A 1OC 为二面角A 1－BE －C 的平面角，所以∠A 1OC ＝π2.如图，以O 为原点，OB →，OC →，OA 1→分别为x 轴、y 轴、z 轴正方向建立空间直角坐标系，因为A 1B ＝A 1E ＝BC ＝ED ＝1，BC ∥ED ，所以B ⎝ ⎛⎭⎪⎫22，0，0，E ⎝ ⎛⎭⎪⎫－22，0，0，A 1⎝ ⎛⎭⎪⎫0，0，22，C ⎝ ⎛⎭⎪⎫0，22，0，得BC →＝⎝ ⎛⎭⎪⎫－22，22，0，A 1C →＝⎝ ⎛⎭⎪⎫0，22，－22，CD →＝BE →＝(－2，0，0). 设平面A 1BC 的一个法向量n 1＝(x 1，y 1，z 1)，平面A 1CD 的一个法向量n 2＝(x 2，y 2，z 2)，平面A 1BC 与平面A 1CD 的夹角为θ，则⎩⎪⎨⎪⎧n 1·BC →＝0，n 1·A 1C →＝0，得⎩⎨⎧－x 1＋y 1＝0，y 1－z 1＝0，取n 1＝(1，1，1)；⎩⎪⎨⎪⎧n 2·CD →＝0，n 2·A 1C →＝0，得⎩⎨⎧x 2＝0，y 2－z 2＝0，取n 2＝(0，1，1)，从而cos θ＝|cos 〈n 1，n 2〉|＝23×2＝63，即平面A 1BC 与平面A 1CD 夹角的余弦值为63.(建议用时：80分钟)1.(2017·青岛质检)在平面四边形ABCD 中，AB ＝BD ＝CD ＝1，AB ⊥BD ，CD ⊥BD ，将△ABD 沿BD 折起，使得平面ABD ⊥平面BCD ，如图. (1)求证：AB ⊥CD ；(2)若M 为AD 中点，求直线AD 与平面MBC 所成角的正弦值.(1)证明 ∵平面ABD ⊥平面BCD ，平面ABD ∩平面BCD ＝BD ，AB ⊂平面ABD ，AB ⊥BD ，∴AB ⊥平面BCD .又CD ⊂平面BCD ，∴AB ⊥CD .(2)解过点B 在平面BCD 内作BE ⊥BD ，如图. 由(1)知AB ⊥平面BCD ， BE ⊂平面BCD ，BD ⊂平面BCD ， ∴AB ⊥BE ，AB ⊥BD .以B 为坐标原点，分别以BE →，BD →，BA →的方向为x 轴，y 轴，z 轴的正方向建立空间直角坐标系.依题意，得B (0，0，0)，C (1，1，0)，D (0，1，0)，A (0，0，1)， M ⎝ ⎛⎭⎪⎫0，12，12，则BC →＝(1，1，0)，BM →＝⎝ ⎛⎭⎪⎫0，12，12，AD →＝(0，1，－1). 设平面MBC 的法向量为n ＝(x 0，y 0，z 0)，则⎩⎪⎨⎪⎧n ·BC →＝0，n ·BM →＝0，即⎩⎪⎨⎪⎧x 0＋y 0＝0，12y 0＋12z 0＝0，取z 0＝1，得平面MBC 的一个法向量为n ＝(1，－1，1). 设直线AD 与平面MBC 所成角为θ，则 sin θ＝| cos 〈n ，AD →〉|＝|n ·AD →||n |·|AD →|＝63，即直线AD 与平面MBC 所成角的正弦值为63.2.如图，三棱锥P －ABC 中，PC ⊥平面ABC ，PC ＝3，∠ACB＝π2.D ，E 分别为线段AB ，BC 上的点，且CD ＝DE ＝2，CE ＝2EB ＝2. (1)证明：DE ⊥平面PCD ； (2)求二面角A －PD －C 的余弦值.(1)证明由PC ⊥平面ABC ，DE ⊂平面ABC ，故PC ⊥DE .由CE ＝2，CD ＝DE ＝2得△CDE 为等腰直角三角形，故CD ⊥DE . 由PC ∩CD ＝C ，DE 垂直于平面PCD 内两条相交直线，故DE ⊥平面PCD . (2)解由(1)知，△CDE 为等腰直角三角形，∠DCE ＝π4，如图，过D 作DF 垂直CE 于F ，易知DF ＝FC ＝FE ＝1，又已知EB ＝1，故FB ＝2.由∠ACB ＝π2，得DF ∥AC ，∴DF AC ＝FB BC ＝23，故AC ＝32DF ＝32.以C 为坐标原点，分别以CA →，CB →，CP →的方向为x 轴，y 轴，z轴的正方向建立空间直角坐标系，则C (0，0，0)，P (0，0，3)，A ⎝ ⎛⎭⎪⎫32，0，0，E (0，2，0)，D (1，1，0)，ED→＝(1，－1，0)，DP →＝(－1，－1，3)，DA →＝⎝ ⎛⎭⎪⎫12，－1，0.设平面P AD 的法向量为n 1＝(x 1，y 1，z 1)，由n 1·DP →＝0，n 1·DA →＝0，得⎩⎪⎨⎪⎧－x 1－y 1＋3z 1＝0，12x 1－y 1＝0，故可取n 1＝(2，1，1).由(1)可知DE ⊥平面PCD ，故平面PCD 的法向量n 2可取为ED →，即n 2＝(1，－1，0).从而法向量n 1，n 2的夹角的余弦值为 cos 〈n 1，n 2〉＝n 1·n 2|n 1|·|n 2|＝36，故所求二面角A －PD －C 的余弦值为36.3.(2017·重庆模拟)如图，直三棱柱ABC －A 1B 1C 1中，AB ＝AC ＝AA 1＝4，BC ＝2 2.BD ⊥AC ，垂足为D ，E 为棱BB 1上一点，BD ∥平面AC 1E . (1)求线段B 1E 的长；(2)求二面角C 1－AC －E 的余弦值.解 (1)由AB ＝AC ＝4，知△ABC 为等腰三角形，又BD ⊥AC ，BC ＝22，故12·AC ·BD ＝12·BC ·AB 2－⎝ ⎛⎭⎪⎫12BC 2，解得BD ＝7.从而在Rt △CDB 中，CD ＝BC 2－BD 2＝1，故AD ＝AC －CD ＝3.如图，过点D 作DF ∥CC 1，交AC 1于F ，连接EF .因为DF ∥CC 1，从而AD AC ＝DFCC 1＝34，得DF ＝3.因为DF ∥CC 1，CC 1∥BB 1，故DF ∥BB 1，即DF ∥BE ，故DF 与BE 确定平面BDFE .又BD ∥平面AC 1E ，而平面BDFE ∩平面AC 1E ＝EF ，故BD ∥EF .故四边形BDFE 为平行四边形，从而DF ＝BE ＝3，所以B 1E ＝BB 1－BE ＝1.(2)如图，以D 为坐标原点，分别以DA→，DB →，DF →的方向为x轴、y 轴、z 轴的正方向建立空间直角坐标系，则D (0，0，0)，C (－1，0，0)，E (0，7，3)，DC →＝(－1，0，0)，DE →＝(0，7，3).设平面ACE 的一个法向量为n 1＝(x ，y ，z )，由n 1·DC →＝0，n 1·DE →＝0，得⎩⎨⎧－x ＝0，7y ＋3z ＝0，故可取n 1＝(0，3，－7).又平面ACC 1在xDz 面上，故可取n 2＝(0，1，0)为平面ACC 1的一个法向量. 从而法向量n 1，n 2的夹角的余弦值为 cos 〈n 1，n 2〉＝n 1·n 2|n 1|·|n 2|＝34.由图知二面角C 1－AC －E 为锐角，故二面角C 1－AC －E 的余弦值为34. 4.(2017·郑州模拟)等边三角形ABC 的边长为3，点D ，E 分别是边AB ，AC 上的点，且满足AD DB ＝CE EA ＝12，如图1.将△ADE 沿DE 折起到△A 1DE 的位置，使二面角A 1－DE －B 为直二面角，连接A 1B ，A 1C ，如图2.(1)求证：A 1D ⊥平面BCED ；(2)在线段BC 上是否存在点P ，使直线P A 1与平面A 1BD 所成的角为60°？若存在，求出PB 的长；若不存在，请说明理由.(1)证明因为等边三角形ABC 的边长为3，且AD DB ＝CE EA ＝12，所以AD ＝1，AE ＝2.在△ADE 中，∠DAE ＝60°，由余弦定理得 DE ＝12＋22－2×1×2×cos 60°＝ 3. 从而AD 2＋DE 2＝AE 2，所以AD ⊥DE . 折起后有A 1D ⊥DE ，因为二面角A 1－DE －B 是直二面角，所以平面A 1DE ⊥平面BCED ，又平面A 1DE ∩平面BCED ＝DE ，A 1D ⊂平面A 1DE ，A 1D ⊥DE ，所以A 1D ⊥平面BCED .(2)解存在.理由：由(1)的证明，可知ED ⊥DB ，A 1D ⊥平面BCED .以D 为坐标原点，分别以射线DB ，DE ，DA 1为x 轴，y 轴，z 轴的正半轴，建立如图所示的空间直角坐标系D －xyz . 设PB ＝2a (0≤2a ≤3)，作PH ⊥BD 于点H ，连接A 1H ，A 1P ，则BH ＝a ，PH ＝3a ，DH ＝2－a .所以A 1(0，0，1)，P (2－a ，3a ，0)，E (0，3，0). 所以P A 1→＝(a －2，－3a ，1). 因为ED ⊥平面A 1BD ，所以平面A 1BD 的一个法向量为DE→＝(0，3，0). 要使直线P A 1与平面A 1BD 所成的角为60°，则sin 60°＝|P A 1→·DE →||P A 1→||DE →|＝3a 4a 2－4a ＋5×3＝32，解得a ＝54.此时2a ＝52，满足0≤2a ≤3，符合题意.所以在线段BC 上存在点P ，使直线P A 1与平面A 1BD 所成的角为60°，此时PB ＝52.5.(2017·石家庄一模)在平面四边形ACBD (图①)中，△ABC 与△ABD 均为直角三角形且有公共斜边AB ，设AB ＝2，∠BAD ＝30°，∠BAC ＝45°，将△ABC 沿AB 折起，构成如图②所示的三棱锥C ′－ABD ，且使C ′D ＝ 2.(1)求证：平面C ′AB ⊥平面DAB ； (2)求二面角A －C ′D －B 的余弦值.(1)证明如图，取AB 的中点O .连接C ′O ，DO . 在Rt △AC ′B ，Rt △ADB 中， AB ＝2，则C ′O ＝DO ＝1，∵C ′D ＝2，∴C ′O 2＋DO 2＝C ′D 2，即C ′O ⊥OD ，又C ′O ⊥AB ，AB ∩OD ＝O ，AB ，OD ⊂平面ABD ， ∴C ′O ⊥平面ABD ，∵C ′O ⊂平面ABC ′，∴平面C ′AB ⊥平面DAB .(2)解以O 为原点，AB ，OC ′所在的直线分别为y ，z 轴，建立如图所示的空间直角坐标系，则A (0，－1，0)，B (0，1，0)， C ′(0，0，1)，D ⎝ ⎛⎭⎪⎫32，12，0，∴AC ′→＝(0，1，1)，BC ′→＝ (0，－1，1)，C ′D →＝⎝ ⎛⎭⎪⎫32，12，－1. 设平面AC ′D 的一个法向量为n 1＝(x 1，y 1，z 1)，则⎩⎪⎨⎪⎧n 1⊥AC ′→，n 1⊥C ′D →，即⎩⎪⎨⎪⎧n 1·AC ′→＝0，n 1·C ′D →＝0，即⎩⎨⎧y 1＋z 1＝0，32x 1＋12y 1－z 1＝0，令z 1＝1，则y 1＝－1，x 1＝3，∴n 1＝(3，－1，1).设平面BC ′D 的一个法向量为n 2＝(x 2，y 2，z 2)，则⎩⎪⎨⎪⎧n 2⊥BC ′→，n 2⊥C ′D →，即⎩⎪⎨⎪⎧n 2·BC ′→＝0，n 2·C ′D →＝0，即⎩⎨⎧－y 2＋z 2＝0，32x 2＋12y 2－z 2＝0，令z 2＝1，则y 2＝1，x 2＝33， ∴n 2＝⎝ ⎛⎭⎪⎫33，1，1，∴cos 〈n 1，n 2〉＝3×33＋（－1）×1＋1×13＋1＋1×13＋1＋1＝15×73＝10535， ∴二面角A －C ′D －B 的余弦值为－10535.6.(2017·合肥模拟)如图，在梯形ABCD 中，AB ∥CD ，AD ＝DC ＝CB ＝1，∠BCD ＝120°，四边形BFED 为矩形，平面BFED ⊥平面ABCD ，BF ＝1. (1)求证：AD ⊥平面BFED ；(2)点P 在线段EF 上运动，设平面P AB 与平面ADE 所成锐二面角为θ，试求θ的最小值.(1)证明在梯形ABCD 中，∵AB ∥CD ，AD ＝DC ＝CB ＝1，∠BCD ＝120°， ∴AB ＝2，∴BD 2＝AB 2＋AD 2－2AB ·AD ·cos 60°＝3. ∴AB 2＝AD 2＋BD 2，∴AD ⊥BD .∵平面BFED ⊥平面ABCD ，平面BFED ∩平面ABCD ＝BD ，DE ⊂平面BFED ，DE ⊥DB ，∴DE ⊥平面ABCD ，∴DE ⊥AD ，又DE ∩BD ＝D ， ∴AD ⊥平面BFED .(2)解由(1)可建立分别以直线DA ，DB ，DE 为x 轴，y 轴，z 轴的空间直角坐标系.如图所示.令EP ＝λ(0≤λ≤3)，则D (0，0，0)，A (1，0，0)，B (0，3，0)，P (0，λ，1)， ∴AB→＝(－1，3，0)，BP →＝(0，λ－3，1). 设n 1＝(x ，y ，z )为平面P AB 的一个法向量，由⎩⎪⎨⎪⎧n 1·AB→＝0，n 1·BP →＝0，得⎩⎨⎧－x ＋3y ＝0，（λ－3）y ＋z ＝0，取y ＝1，得n 1＝(3，1，3－λ)，∵n 2＝(0，1，0)是平面ADE 的一个法向量， ∴cos θ＝|n 1·n 2||n 1||n 2|＝13＋1＋（3－λ）2×1 ＝1（λ－3）2＋4.∵0≤λ≤3，∴当λ＝3时，cos θ有最大值12， ∴θ的最小值为π3.。

备战2018年高考数学优质试卷分项版专题08立体几何文新人教A版 Word版含答案

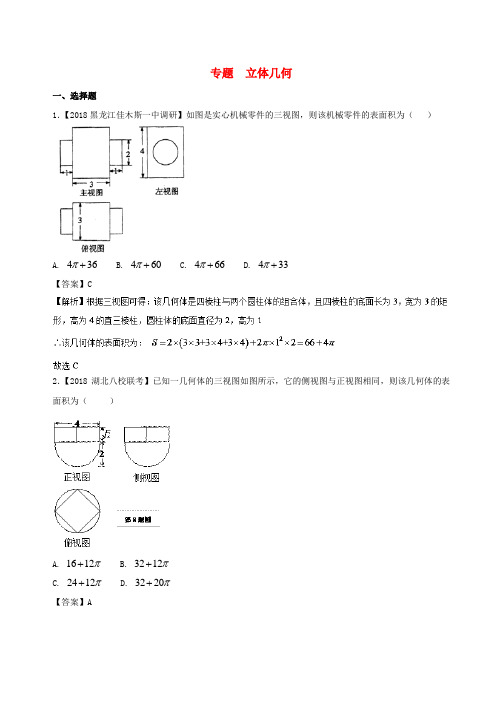
专题立体几何一、选择题1．【2018黑龙江佳木斯一中调研】如图是实心机械零件的三视图，则该机械零件的表面积为（）A. 436π+B. 460π+C. 466π+D. 433π+ 【答案】C2．【2018湖北八校联考】已知一几何体的三视图如图所示，它的侧视图与正视图相同，则该几何体的表面积为（）A. 1612π+B. 3212π+C. 2412π+D. 3220π+ 【答案】A3．【2018湖南五校联考】已知正三棱锥P—ABC的主视图和俯视图如图所示，则此三棱锥外接球的表面积为A. B.C. D.【答案】B【解析】由正视图与侧视图知，正三棱锥的侧面上的高为，底面正三角形的边长为2，如图：其中SA=4，AH=2，SH=2，设其外接球的球心为0，半径为R，则：OS=OA=R，∴，∴，∴外接球的表面积.故选：B.点睛：求多面体的外接球的面积或体积问题是高考常见问题，属于高频考点，有一定的难度.如何求多面体的外接球的半径？基本方法有种，第一种：当三棱锥的三条侧棱两两互相垂直时，可还原为长方体，长方体的体对角线就是外接圆的直径；第二种：“套球”当棱锥或棱柱是较特殊的形体时，在球内画出棱锥或棱柱，利用底面的外接圆为球小圆，借助底面三角形或四边形求出小圆的半径，再利用勾股定理求出球的半径，第三种：过两个多面体的外心作两个面的垂线，交点即为外接球的球心，再通过关系求半径.4．【2018湖南五校联考】已知直线，平面且给出下列命题：①若∥，则；②若，则∥；③若，则；④若∥，则. 其中正确的命题是A. ①④B. ③④C. ①②D. ①③【答案】A5．【2018黑龙江齐齐哈尔八中联考】如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的体积为（）A.()8123π+ B. ()813π+ C. ()4233π+ D. ()423π+ 【答案】A【解析】该几何体是由两个小三棱锥和一个圆锥组成，所以体积为()1182224412333ππ⨯⨯⨯+⨯⨯=+，故选A 。

2018届高三二轮复习数学(文)(人教版)高考大题专攻练：(四)Word版含解析

关闭Word文档返回原板块。

高考大题专攻练4.数列(B组)大题集训练,练就慧眼和规范,占领高考制胜点!1.数列{a n}的前n项和记为S n,a1=t,点(a n+1,S n)在直线y=x-1上,n∈N*. 世纪金榜导学号46854418(1)当实数t为何值时,数列{a n}是等比数列?并求数列{a n}的通项公式.(2)若f(x)=[x]([x]表示不超过x的最大整数),在(1)的结论下,令b n=f(log3a n)+1,c n=a n+,求{c n}的前n项和T n.【解析】(1)由题意得S n=a n+1-1,[来源:学_科_网Z_X_X_K]所以S n-1=a n-1,[来源:Z§xx§]两式相减得a n=a n+1-a n,即a n+1=3a n,所以当n≥2时,数列{a n}是等比数列,[来源:学科网]要使n≥1时,数列{a n}是等比数列,则只需要=3,因为a1=a2-1,所以a2=2a1+2,所以=3,解得t=2,所以实数t=2时,数列{a n}是等比数列,a n=2·3n-1.(2)因为b n=f(log3a n)+1=[log3(2×3n-1)]+1,因为3n-1<2×3n-1<3n,所以n-1<log3(2×3n-1)<n,所以b n=n-1+1=n,所以c n=a n+=2×3n-1+=2×3n-1+,因为{a n}的前n项和为=3n-1,的前n项和为(1-+-+…+-)==-,[来源:Z。

xx。

]所以T n=3n-1+-=3n--.2.已知等比数列{a n}满足a n+1+a n=9·2n-1,n∈N*.(1)求数列{a n}的通项公式.(2)设b n=na n,数列{b n}的前n项和为S n,若不等式S n>ka n-1对一切n∈N*恒成立,求实数k的取值范围.【解析】(1)设等比数列{a n}的公比为q,因为a n+1+a n=9·2n-1,所以a2+a1=9,a3+a2=18,所以q===2.又2a1+a1=9,所以a1=3,[来源:学科网ZXXK]所以a n=3·2n-1,n∈N*.(2)b n=na n=3n·2n-1,所以S n=3×1×20+3×2×21+…+3(n-1)×2n-2+3n×2n-1,所以S n=1×20+2×21+…+(n-1)×2n-2+n×2n-1,所以S n=1×21+2×22+…+(n-1)×2n-1+n×2n,所以-S n=1+21+22+…+2n-1-n×2n=-n×2n=(1-n)2n-1,所以S n=3(n-1)2n+3,因为S n>ka n-1对一切n∈N*恒成立,所以k<==2(n-1)+,令f(n)=2(n-1)+,则f(n+1)-f(n)=2n+-=2+-=2-=>0,故f(n)随着n的增大而增大,所以f(x)mi n=f(1)=,所以实数k的取值范围是.关闭Word文档返回原板块。

2018届高考数学二轮复习阶段提升突破练(四)立体几何文新人教A版

阶段提高打破练 ( 四)( 立体几何 )(60 分钟100 分)一、选择题 ( 每题 5 分, 共 40 分)1.(2016 ·浙江高考 ) 已知相互垂直的平面α, β交于直线l .若直线m,n 知足 m∥α ,n ⊥β ,则()A.m∥lB.m∥ nC.n ⊥lD.m⊥ n【解题导引】依据线、面垂直的定义判断.【分析】选 C. 由题意知 , α∩β =l , 所以l ? β , 因为 n⊥β ,所以 n⊥l .2.(2017 ·长沙二模 ) 如图是一个四周体的三视图, 这个三视图均是腰长为 2 的等腰直角三角形, 正视图和俯视图中的虚线是三角形的中线, 则该四周体的体积为()A. B. C. D.2【分析】选 A. 由四周体的三视图得该四周体为棱长为 2 的正方体 ABCD-AB C D 中的三棱锥1111C -BDE, 此中点 E 是 CD中点 , △ BDE面积 S= ×=1,1三棱锥 C1-BDE的高 h=CC1=2, 所以该四周体的体积:V= Sh=.3.(2017 ·全国卷Ⅰ ) 某多面体的三视图如下图, 此中正视图和左视图都由正方形和等腰直角三角形构成 , 正方形的边长为2, 俯视图为等腰直角三角形. 该多面体的各个面中有若干个是梯形 , 这些梯形的面积之和为()A.10B.12C.14D.16【解题导引】主要考察如何将三视图转变为几何体问题, 突出考察考生的空间想象能力.【分析】选 B. 由三视图可画出立体图, 该立体图各面中只有两个同样的梯形的面,S 梯 =×2÷ 2=6,S全梯=6×2=12.【加固练习】 (2017 ·黄冈二模 ) 某一简单几何体的三视图如下图, 该几何体的外接球的表面积是()A.13 πB.16 πC.25πD.27π【分析】选 C. 几何体为底面为正方形的长方体, 底面对角线为4, 高为 3,所以长方体底面边长为2,则长方体外接球半径为r,则 2r==5, 所以 r= , 2, 则该三棱锥与平面α平行的4.(2017 ·合肥二模 ) 若平面α截三棱锥所得截面为平行四边形棱有()A.0条B.1条C.2条D.1条或2 条【分析】选 C. 如下图 , 四边形 EFGH为平行四边形 , 则 EF∥ GH,因为 EF?平面 BCD,GH? 平面 BCD,所以 EF∥平面 BCD,因为 EF? 平面 ACD,平面 BCD∩平面 ACD=CD,所以 EF∥ CD,所以 CD∥平面 EFGH,同理 AB∥平面 EFGH.5. 如下图 , 在正方体ABCD-A1B1C1D1中 ,E,F,G,H分别为AA1,AB,BB 1,B 1C1的中点 , 则异面直线EF 与 GH所成的角等于()A.45 °B.60 °C.9 0°D.120 °【分析】选 B. 如图 , 取 A1B1的中点 M,连结 GM,HM.由题意易知EF∥ GM,且△ GMH为正三角形 .所以异面直线EF与 GH所成的角即为GM与 GH的夹角∠ HGM而.在正三角形GMH中∠ HGM=60° .6.(2017 ·全国卷Ⅲ ) 在正方体ABCD-A1B1C1D1中 ,E 为棱 CD的中点 , 则 ()A.A1E⊥ DC1B.A 1E⊥ BDC.A1E⊥ BC1D.A1E⊥ AC【分析】选 C. 依据三垂线逆定理, 平面内的线垂直过平面的斜线, 那也垂直于斜线所在平面内的射影.A. 若A1E⊥DC1,那么D1E⊥ DC1, 明显不行立;B. 若A1E⊥ BD,那么BD⊥AE, 明显不行立;C.若A1E⊥ BC1, 那么BC1⊥ B1C成立 , 反过来BC1⊥ B1C,也能推出A1E⊥ BC1;D.若A1E⊥ AC,那么AE⊥AC,明显不行立.7.(2017·洛阳二模) 一个透明密闭的正方体容器中, 恰巧盛有该容器一半容积的水, 随意转动这个正方体, 则水面在容器中的形状能够是:(1)三角形;(2)四边形;(3)五边形;(4)六边形.此中正确的结论是()A.(1)(3)B.(2)(4)C.(2)(3)(4)D.(1)(2)(3)(4)【分析】选 B. 正方体容器中盛有一半容积的水,不论如何转动 , 其水面老是过正方体的中心.三角形截面可是正方体的中心, 故(1) 不正确 ;过正方体的一对棱和中心可作一截面, 截面形状为长方形, 故(2)正确 ;正方体容器中盛有一半容积的水, 随意转动这个正方体, 则水面在容器中的形状不行能是边形 , 故(3) 不正确 ;过正方体一面上相邻两边的中点以及正方体的中心得截面形状为正六边形, 故(4) 正确 .五8. 如图 , 在矩形ABCD中 ,AB=,BC=1, 将△ ACD沿AC折起 , 使得D 折起的地点为D1,且D1在平面ABC的射影恰巧落在AB 上 , 在四周体D1ABC的四个面中, 此中有n 对平面相互垂直, 则n 等于()A.2B.3C.4D.5【分析】选 B. 设D1在平面ABC的射影为E, 连结D1E,则D1E⊥平面ABC,因为 D1E? 平面 ABD1, 所以平面ABD1⊥平面 ABC.因为 D1E⊥平面 ABC,BC? 平面 ABC,所以 D1E⊥ BC,又因为 AB⊥ BC,D1E∩ AB=E,所以 BC⊥平面 ABD1, 又因为 BC? 平面 BCD1,所以平面BCD1⊥平面 ABD1,因为 BC⊥平面 ABD1,AD1 ? 平面 ABD1,所以 BC⊥ AD1, 又因为 CD1⊥ AD1,BC∩CD1=C,所以 AD1⊥平面 BCD1, 又因为 AD1? 平面 ACD1,所以平面ACD1⊥平面 BCD1.所以共有 3 对平面相互垂直.二、填空题 ( 每题 5 分, 共 20 分)9.(2017·山东高考) 由一个长方体和两个圆柱构成的几何体的三视图如图, 则该几何体的体积为________.【分析】由三视图可知长方体的体积为V1=2× 1× 1=2, 两个四分之一圆柱的体积之和为V2=×π× 12× 1×2= , 所以该几何体的体积为V=2+ .答案:2+【加固训练】(2017 ·大庆二模) 一个几何体的三视图如下图, 则这个几何体的体积为________.【分析】由三视图可知 :该几何体为三棱锥P-ABC,此中底面是底边与底边上的高都为 2 的等腰三角形△ABC,侧面 PAC⊥底面 ABC,高为 2.所以这个几何体的体积V= ××22×2=.答案 :10.(2017·全国卷Ⅰ) 已知三棱锥S-ABC的全部极点都在球O的球面上,SC 是球O的直径 . 若平面 SCA⊥平面 SCB,SA=AC,SB=BC,三棱锥 S-ABC的体积为9, 则球 O的表面积为 ________.【分析】取 SC的中点 O, 连结 OA,OB,因为 SA=AC,SB=BC,所以 OA⊥ SC,OB⊥ SC.因为平面SAC⊥平面 SBC,所以 OA⊥平面 SBC.设 OA=rV =× S ×OA= × ×2r × r × r=r3A-SBC△SBC所以r 3=9? r=3,2所以球的表面积为4π r =36π .11.(2017 ·本溪二模 ) 已知 a,b 表示两条不一样直线, α , β , γ表示三个不一样平面, 给出以下命题:①若α∩β =a,b ? α,a ⊥ b, 则α⊥β ;②若 a? α,a 垂直于β内的随意一条直线, 则α⊥β ;③若α⊥β , α∩β =a, α∩γ =b, 则 a⊥ b;④若 a 不垂直于平面α, 则 a 不行能垂直于平面α内的无数条直线;⑤若 a⊥α ,a ⊥β , 则α∥β .上述五个命题中, 正确命题的序号是________.【分析】关于① , 依据线面垂直的判断定理, 需要一条直线垂直于同一平面内两条订交的直线故 a⊥ b,a 不必定垂直平面β, 故不正确 ,关于② ,a ? α ,a 垂直于β内的随意一条直线, 知足线面垂直的定理, 即可获得a⊥β , 又α, 则α⊥β , 故正确 ,关于③ , α⊥β , α∩β =a, α∩γ =b, 则 a⊥ b 或 a∥ b, 或订交 , 故不正确 ,关于④ , 若 a 不垂直于平面α, 则 a 可能垂直于平面α内的无数条直线, 故不正确 ,关于⑤ , 依据线面垂直的性质, 若 a⊥α ,a ⊥β , 则α∥β , 故正确 .a?,答案:②⑤12. 在长方体ABCD-A1B1C1D1中 ,B 1C和 C1D与底面 A1B1C1D1所成的角分别为45°和 60° , 则异面直线 B1C 和 C1D所成的角的余弦值为________.【分析】设 B1B=a,因为 B1C 和 C1D与底面 A1B1C1D1所成的角分别为 45°和 60° ,所以 BC=a,DC= a,所以 A1D=a,DC1=a,A 1C1=a,由余弦定理得 :cos ∠C1DA1==.答案 :三、解答题 ( 每题 10 分, 共 40 分 )13.(2017 ·江苏高考 ) 如图 , 在三棱锥 A-BCD中 ,AB⊥ AD,BC⊥ BD,平面 ABD⊥平面 BCD,点 E,F(E与 A,D 不重合 ) 分别在棱 AD,BD上 , 且 EF⊥ AD.求证 :(1)EF ∥平面 ABC.(2)AD ⊥ AC.【解题导引】 (1) 利用 AB∥ EF及线面平行判断定理可得结论.(2) 利用面面垂直的性质得BC⊥ AD,又 AB⊥ AD,进而获得AD⊥平面 ABC,即可得 AD⊥ AC.【证明】 (1) 在平面 ABD内 , 因为 AB⊥ AD,EF⊥ AD,所以 EF∥ AB.又因为 EF?平面 ABC,AB? 平面 ABC,所以 EF∥平面 ABC.(2)因为平面 ABD⊥平面 BCD,平面 ABD∩平面 BCD=BD,BC? 平面 BCD,BC⊥ BD,所以 BC⊥平面 ABD.因为 AD? 平面 ABD,所以 BC⊥AD.又因为 AB⊥ AD,BC∩AB=B,AB? 平面 ABC,BC? 平面 ABC,所以AD⊥平面ABC,又因为AC?平面ABC,所以AD⊥ AC.14.如图,在三棱锥P-ABC中 ,D,E,F分别为棱PC,AC,AB的中点,已知PA ⊥AC,PA=6,BC=8,DF=5.求证 :(1)直线PA∥平面DEF.(2) 平面 BDE⊥平面 ABC.【证明】 (1) 在△ PAC中 ,D,E 分别为 PC,AC的中点 ,则 PA∥ DE,PA?平面 DEF,DE? 平面 DEF,所以 PA∥平面 DEF.(2) 在△ DEF中 ,DE= PA=3,EF= BC=4,DF=5,222所以 DF=DE+EF, 所以 DE⊥ EF,又因为 PA⊥ AC,所以 DE⊥ AC.因为 EF∩AC=E,所以 DE⊥平面 ABC,所以平面BDE⊥平面 ABC.【加固训练】 1. 如图 , 在三棱锥 S-ABC 中 , 平面 SAB⊥平面 SBC,AB⊥BC,AS=AB.过点 A 作 AF⊥SB, 垂足为 F, 点 E,G 分别是棱 SA,SC 的中点 .求证 :(1)平面EFG∥平面ABC.(2)BC ⊥ SA.【证明】 (1) 因为 AS=AB,AF⊥SB, 垂足为 F,所以点 F 是 SB的中点 .又因为点 E 是 SA 的中点 ,所以 EF∥ AB.因为 EF?平面 ABC,AB? 平面 ABC,所以 EF∥平面 ABC.同理 EG∥平面 ABC.又因为 EF∩ EG=E,所以平面EFG∥平面 ABC.(2) 因为平面SAB⊥平面 SBC,且交线为 SB, 又因为 AF? 平面 SAB,AF⊥ SB,所以 AF⊥平面 SBC.因为 BC? 平面 SBC,所以 AF⊥ BC.又因为 AB⊥ BC,A F∩ AB=A,AF? 平面 SAB,AB? 平面 SAB,所以 BC⊥平面 SAB.因为 SA? 平面 SAB,所以 BC⊥SA.2. 如下图 , 已知 PA⊥平面 ABCD,ABCD是矩形 ,PA=AD,M,N 分别为 AB,PC的中点 ,求证 :(1)MN ∥平面 PAD.(2) 平面 PMC⊥平面 PDC.【证明】如下图 , 成立空间直角坐标系 ,设 PA=AD=a,AB=b.(1) 易知为平面PAD的一个法向量,=(b,0,0).又因为=,所以·=0,所以⊥.又因为 MN? 平面 PAD,所以 MN∥平面 PAD.(2) 由 (1) 知 P(0,0,a),C(b,a,0),M,D(0,a,0),所以=(b,a,-a),=,=(0,a,-a),设平面 PMC的一个法向量为n1=(x 1,y 1,z 1),由即所以令 z1=b, 则 n1=(2a,-b,b),设平面 PDC的一个法向量为n2=(x 2,y 2,z 2),则即解得令 z2=1, 则 n2=(0,1,1),因为 n1· n2=0-b+b=0, 所以 n1⊥ n2,所以平面PMC⊥平面 PDC.15.如图 , 在四棱锥 P-ABCD中,PC⊥平面 ABCD,AB∥ DC,DC⊥AC.(1) 求证 :DC⊥平面 PAC.(2) 求证 : 平面 PAB⊥平面 PAC.【解题指南】 (1) 证明 DC⊥ PC,又因为 DC⊥ AC,进而 DC⊥平面 PAC.(2)只要证明 AB⊥平面 PAC.【证明】 (1) 因为 PC⊥平面 ABCD,DC? 平面 ABCD,所以 PC⊥ DC.又因为 DC⊥ AC,PC∩AC=C,PC,AC? 平面 PAC,所以 DC⊥平面 PAC.(2) 因为 AB∥ DC,DC⊥平面 PAC,所以 AB⊥平面 PAC.又因为 AB? 平面 PAB,所以平面PAB⊥平面 PAC.16. 如图① , 在直角梯形 ABCD中 ,AD∥ BC,∠ BAD= ,AB=BC= AD=a,E 是 AD 的中点 ,O 是 AC 与BE的交点 , 将△ ABE沿 BE 折起到图②中△ A1BE的地点 , 获得四棱锥 A1-BCDE.(1) 证明 :CD⊥平面 A1OC.(2) 当平面 A1BE⊥平面 BCDE时 , 四棱锥 A1-BCDE的体积为 36, 求 a 的值 .【分析】 (1) 在题图①中 , 因为 AB=BC= AD=a,E 是 AD的中点 , ∠ BAD= , 所以 BE⊥ AC.则在题图②中 ,BE ⊥ A1O,BE⊥ OC,且 A1O∩ OC=O,进而 BE⊥平面 A1OC.又 CD∥ BE,所以 CD⊥平面 A1OC.(2) 由已知 , 平面 A1BE⊥平面 BCDE,且平面 A1BE∩平面 BCDE=BE,又由 (1) 可得 A1O⊥ BE,所以 A1O⊥平面 BCDE.即 A1O是四棱锥 A1-BCDE的高 .由题图①知 ,A 1O=AB=a, 平行四边形BCDE的面积 S=BC· AB=a2,进而四棱锥A1-BCDE的体积为V= S·A1O= ·a2·a=a3.由a3=36, 得 a=6.。

2018年高考数学试题分类汇编之立体几何

2018年高考数学试题分类汇编之立体几何(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2018年高考数学试题分类汇编之立体几何(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2018年高考数学试题分类汇编之立体几何(word版可编辑修改)的全部内容。

2018年高考数学试题分类汇编之立体几何一、选择题1．(北京卷文）(6)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为（ )。

（A ）1（B ）2 （C ）3(D ）42．（北京卷理）(5）某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为（A ）1（B)2 （C)3（D ）43．(浙江）(3）某几何体的三视图如图所示（单位：cm ）,则该几何体的体积（单位：cm 3）是侧侧侧侧侧侧A ．2B ．4C ．6D ．84．（全国卷一文）（5）已知圆柱的上、下底面的中心分别为,,过直线的平面截该1O 2O 12O O 圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为A ．B ．C ．D ．12π10π5．（全国卷一文）(9）某圆柱的高为2,底面周长为16,其三视图如右图．圆柱表面上的点M 在正视图上的对应点为，圆柱表面上的点在左A N 视图上的对应点为，则在此圆柱侧面上，从到的路径中,最短B M N 路径的长度为A ．B ．C ．D ．236．(全国卷一文）(10）在长方体中,,与平面所成的角1111ABCD A B C D -2AB BC ==1AC 11BB C C 为,则该长方体的体积为30︒A ．B ．C ．D ．87．（全国卷一理）（7）某圆柱的高为2，底面周长为16,其三视图如图．圆柱表面上的点在M 正视图上的对应点为，圆柱表面上的点在左视图上的对应点为，则在此圆柱侧面上,A N B 从到的路径中，最短路径的长度为M NA ．B ．C ．3D ．2172528．（全国卷一理）（12）已知正方体的棱长为1，每条棱所在直线与平面α所成的角相等，则α截此正方体所得截面面积的最大值为A B C D9．（全国卷二文）（9）在正方体中,为棱的中点，则异面直线与所1111ABCD A B C D -E 1CC AE CD 成角的正切值为A B ．C D10．（全国卷二理）（9)在长方体中,，则异面直线与1111ABCD A B C D -1AB BC ==1AA =1AD 1DB 所成角的余弦值为A ．BCD 1511．（全国卷三文）（3)中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫棒头，凹进部分叫卯眼，图中木构件右边的小长方体是棒头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是12．（全国卷三文)（12）设，,，是同一个半径为4的球的球面上四点,为等边A B C D ABC △三角形且其面积为,则三棱锥体积的最大值为D ABC -A ．B ．C ．D ．13．（全国卷三理）(3)中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是14．(全国卷三理）（10）设A B C D ，，，是同一个半径为4的球的球面上四点，ABC △为等边三角形且其面积为则三棱锥D ABC -体积的最大值为A ．B ．C ．D ．二、填空题1．(江苏）（10)如图所示,正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为．2．（天津文）（11)如图,已知正方体ABCD –A 1B 1C 1D 1的棱长为1,则四棱柱A 1–BB 1D 1D 的体积为__________．3．（天津理）(11）已知正方体的棱长为1，除面外,该正方体其余各面1111ABCD A B C D -ABCD 的中心分别为点E ，F ,G ,H ，M (如图），则四棱锥的体积为 .M EFGH -4．（全国卷二文）(16)已知圆锥的顶点为，母线，互相垂直，与圆锥底面所成角为S SA SB SA 30︒，若的面积为，则该圆锥的体积为__________．SAB △85．（全国卷二理)（16）已知圆锥的顶点为，母线，所成角的余弦值为，与圆锥S SA SB 78SA 底面所成角为45°，若的面积为，则该圆锥的侧面积为__________．SAB △三、解答题1.（北京文）（18）（本小题14分)如图，在四棱锥P—ABCD 中，底面ABCD 为矩形，平面PAD ⊥平面ABCD ，PA ⊥PD ，PA =PD ，E ，F 分别为AD ，PB 的中点.（Ⅰ）求证：PE ⊥BC ；（Ⅱ）求证：平面PAB ⊥平面PCD ；（Ⅲ)求证：EF ∥平面PCD 。

2018届高三(新课标)数学(理)大一轮复习教师用书第八章立体几何Word版含解析

第八章⎪⎪⎪立体几何第一节空间几何体的三视图、直观图、表面积与体积突破点(一) 空间几何体的三视图和直观图1．空间几何体的结构特征 (1)多面体的结构特征(1)三视图的名称几何体的三视图包括：正视图、侧视图、俯视图． (2)三视图的画法①在画三视图时，能看见的轮廓线和棱用实线表示，重叠的线只画一条，不能看见的轮廓线和棱用虚线表示．②三视图的正视图、侧视图、俯视图分别是从几何体的正前方、正左方、正上方观察几何体的正投影图．3．空间几何体的直观图空间几何体的直观图常用斜二测画法来画，其规则是：(1)原图形中x 轴、y 轴、z 轴两两垂直，直观图中，x ′轴，y ′轴的夹角为45°或135°，本节主要包括3个知识点：1.空间几何体的三视图和直观图；2.空间几何体的表面积与体积；3.与球有关的切、接应用问题.z′轴与x′轴和y′轴所在平面垂直．(2)原图形中平行于坐标轴的线段，直观图中仍分别平行于坐标轴；平行于x轴和z轴的线段在直观图中保持原长度不变；平行于y轴的线段在直观图中长度为原来的一半．考点贯通抓高考命题的“形”与“神”空间几何体的结构特征[例1](1)用任意一个平面截一个几何体，各个截面都是圆面，则这个几何体一定是()A．圆柱B．圆锥C．球体D．圆柱、圆锥、球体的组合体(2)下列说法正确的是()A．有两个平面互相平行，其余各面都是平行四边形的多面体是棱柱B．四棱锥的四个侧面都可以是直角三角形C．有两个平面互相平行，其余各面都是梯形的多面体是棱台D．棱台的各侧棱延长后不一定交于一点[解析](1)截面是任意的且都是圆面，则该几何体为球体．(2)A错，如图(1)；B正确，如图(2)，其中底面ABCD是矩形，PD⊥平面ABCD，可证明∠PAB，∠PCB，∠PDA，∠PDC都是直角，这样四个侧面都是直角三角形；C错，如图(3)；D错，由棱台的定义知，其侧棱的延长线必相交于同一点．[答案](1)C(2)B[方法技巧]解决与空间几何体结构特征有关问题的三个技巧(1)把握几何体的结构特征，要多观察实物，提高空间想象能力；(2)紧扣结构特征是判断的关键，熟悉空间几何体的结构特征，依据条件构建几何模型，如例1(2)中的A，C两项易判断失误；(3)通过反例对结构特征进行辨析．1.长对正、高平齐、宽相等，即俯视图与正视图一样长；正视图与侧视图一样高；侧视图与俯视图一样宽．2．三视图的排列顺序先画正视图，俯视图放在正视图的下方，侧视图放在正视图的右方．[例2](1)(2017·贵州七校联考)如图所示，四面体ABCD的四个顶点是长方体的四个顶点(长方体是虚拟图形，起辅助作用)，则四面体ABCD的三视图是(用①②③④⑤⑥代表图形，按正视图，侧视图，俯视图的顺序排列)()A．①②⑥B．①②③C．④⑤⑥D．③④⑤(2)(2016·天津高考)将一个长方体沿相邻三个面的对角线截去一个棱锥，得到的几何体的正视图与俯视图如图所示，则该几何体的侧(左)视图为()[解析](1)正视图应该是边长为3和4的矩形，其对角线左下到右上是实线，左上到右下是虚线，因此正视图是①；侧视图应该是边长为5和4的矩形，其对角线左上到右下是实线，左下到右上是虚线，因此侧视图是②；俯视图应该是边长为3和5的矩形，其对角线左上到右下是实线，左下到右上是虚线，因此俯视图是③.(2)先根据正视图和俯视图还原出几何体，再作其侧(左)视图．由几何体的正视图和俯视图可知该几何体为图①，故其侧(左)视图为图②.[答案](1)B(2)B[方法技巧]三视图问题的常见类型及解题策略(1)由几何体的直观图求三视图注意正视图、侧视图和俯视图的观察方向；注意能看到的部分用实线表示，不能看到的部分用虚线表示．(2)由几何体的部分视图画出剩余的视图解决此类问题，可先根据已知的一部分视图，还原、推测直观图的可能形式，然后再找其剩下部分视图的可能形式．当然作为选择题，也可将选项逐项代入检验．(3)由几何体的三视图还原几何体的形状要熟悉柱、锥、台、球的三视图，明确三视图的形成原理，结合空间想象将三视图还原为实物图．空间几何体的直观图直观图与原图形面积的关系按照斜二测画法得到的平面图形的直观图与原图形面积的关系：(1)S直观图＝24S原图形．(2)S原图形＝22S直观图．[例3]用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个正方形，则原来的图形是()[解析]由直观图可知，在直观图中多边形为正方形，对角线长为2，所以原图形为平行四边形，位于y轴上的对角线长为2 2.[答案] A1．[考点一]如果四棱锥的四条侧棱都相等，就称它为“等腰四棱锥”，四条侧棱称为它的腰，以下四个命题中，假命题是()A．等腰四棱锥的腰与底面所成的角都相等B．等腰四棱锥的侧面与底面所成的二面角都相等或互补C．等腰四棱锥的底面四边形必存在外接圆D．等腰四棱锥的各顶点必在同一球面上解析：选B因为“等腰四棱锥”的四条侧棱都相等，所以它的顶点在底面的射影到底面的四个顶点的距离相等，故A，C是真命题；且在它的高上必能找到一点到各个顶点的距离相等，故D是真命题；B是假命题，如底面是一个等腰梯形时结论就不成立．2．[考点二]一几何体的直观图如图，下列给出的四个俯视图中正确的是()解析：选B由直观图可知，该几何体由一个长方体和一个截角三棱柱组成．从上往下看，外层轮廓线是一个矩形，矩形内部是一条水平线段连接两个三角形．3．[考点二]已知三棱锥的俯视图与侧视图如图所示，俯视图是边长为2的正三角形，侧视图是有一条直角边为2的直角三角形，则该三棱锥的正视图可能为()解析：选C 当正视图为等腰三角形时，则高应为2，且应为虚线，排除A ，D ；当正视图是直角三角形时，由条件得一个直观图如图所示，中间的线是看不见的线PA 形成的投影，应为虚线，故答案为C.4．[考点三]用斜二测画法画出的某平面图形的直观图如图，边AB 平行于y 轴，BC ，AD 平行于x 轴．已知四边形ABCD 的面积为2 2 cm 2，则原平面图形的面积为( )A ．4 cm 2B ．4 2 cm 2C ．8 cm 2D ．8 2 cm 2解析：选C 依题意可知∠BAD ＝45°，则原平面图形为直角梯形，上下底面的长与BC ，AD 相等，高为梯形ABCD 的高的22倍，所以原平面图形的面积为8 cm 2.5．[考点二](2017·南昌模拟)如图，在正四棱柱ABCD -A 1B 1C 1D 1中，点P 是平面A 1B 1C 1D 1内一点，则三棱锥P -BCD 的正视图与侧视图的面积之比为( )A ．1∶1B ．2∶1C ．2∶3D ．3∶2解析：选A 根据题意，三棱锥P -BCD 的正视图是三角形，且底边为正四棱柱的底面边长、高为正四棱柱的高；侧视图是三角形，且底边为正四棱柱的底面边长、高为正四棱柱的高．故三棱锥P -BCD 的正视图与侧视图的面积之比为1∶1.突破点(二) 空间几何体的表面积与体积1．圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱、圆锥、圆台侧面积间的关系：S 圆柱侧＝2πrl ――→r ′＝rS 圆台侧＝π(r ＋r ′)l ――→r ′＝0S 圆锥侧＝πrl . 2．空间几何体的表面积与体积公式[例1]分曲线为半圆弧，则该几何体的表面积为()A．4π＋16＋4 3 B．5π＋16＋4 3C．4π＋16＋2 3 D．5π＋16＋2 3(2)一个四面体的三视图如图所示，则该四面体的表面积是()A ．1＋ 3B ．2＋ 3C ．1＋2 2D ．2 2[解析] (1)由三视图可知该几何体是一个正三棱柱和一个半圆柱的组合体，三棱柱的两个侧面面积之和为2×4×2＝16，两个底面面积之和为2×12×2×3＝23；半圆柱的侧面积为π×4＝4π，两个底面面积之和为2×12×π×12＝π，所以几何体的表面积为5π＋16＋23，故选D.(2)根据三视图还原几何体如图所示，其中侧面ABD ⊥底面BCD ，另两个侧面ABC ，ACD 为等边三角形，则有S 表面积＝2×12×2×1＋2×34×(2)2＝2＋ 3. [答案] (1)D (2)B[方法技巧]求空间几何体表面积的常见类型及思路(1)求多面体的表面积，只需将它们沿着棱“剪开”展成平面图形，利用求平面图形面积的方法求多面体的表面积．(2)求旋转体的表面积，可以从旋转体的形成过程及其几何特征入手，将其展开后求表面积，但要搞清它们的底面半径、母线长与对应侧面展开图中的边长关系．(3)求不规则几何体的表面积时，通常将所给几何体分割成基本的柱体、锥体、台体，先求出这些基本的柱体、锥体、台体的表面积，再通过求和或作差，求出所给几何体的表面积．空间几何体的体积柱体、锥体、台体体积间的关系[例2] (1)(2016·北京高考)某三棱锥的三视图如图所示，则该三棱锥的体积为( )A.16B.13C.12D ．1 (2)某几何体的三视图如图所示，则该几何体的体积为( )A.13＋2π B.13π6 C.7π3D.5π2[解析] (1)通过三视图可还原几何体为如图所示的三棱锥P -ABC ，通过侧视图得高h ＝1，通过俯视图得底面积S ＝12×1×1＝12，所以体积V ＝13Sh ＝13×12×1＝16.(2)由三视图可知，该几何体是一个圆柱和半个圆锥组合而成的几何体，其体积为π×12×2＋12×13π×12×1＝13π6.[答案] (1)A (2)B [方法技巧]求空间几何体体积的常见类型及思路(1)若所给定的几何体是柱体、锥体或台体等规则几何体，则可直接利用公式进行求解．其中，等积转换法多用来求三棱锥的体积．(2)若所给定的几何体是不规则几何体，则将不规则的几何体通过分割或补形转化为规则几何体，再利用公式求解．(3)若以三视图的形式给出几何体，则应先根据三视图得到几何体的直观图，然后根据条件求解．能力练通抓应用体验的“得”与“失”1．[考点二](2016·山东高考)一个由半球和四棱锥组成的几何体，其三视图如图所示，则该几何体的体积为( )A.13＋23πB.13＋23πC.13＋26π D ．1＋26π 解析：选C 由三视图知，四棱锥是底面边长为1，高为1的正四棱锥，结合三视图可得半球半径为22，从而该几何体的体积为13×12×1＋12×4π3×⎝⎛⎭⎫223＝13＋26π.故选C. 2．[考点二]已知一个几何体的三视图如图所示，则该几何体的体积为( )A.5π3 cm 3 B ．2π cm 3 C.7π3cm 3 D ．3π cm 3解析：选C 该几何体为一个圆柱挖去半个球得到的几何体，其体积V ＝π×12×3－12×4π×133＝7π3(cm 3)．3.[考点一]某几何体的三视图如图所示，则它的表面积为( )A ．125＋20B ．242＋20C ．44D ．12 5解析：选A 由三视图得，这是一个正四棱台，且上、下底面的边长分别为2,4，则侧面梯形的高h ＝ 22＋⎝ ⎛⎭⎪⎫4－222＝5，所以该正四棱台的表面积S ＝(2＋4)×52×4＋22＋42＝125＋20.4．[考点一]某几何体的三视图如图所示，则该几何体的表面积等于( )A ．8＋2 2B ．11＋2 2C ．14＋2 2D ．15解析：选B 由三视图知，该几何体是一个直四棱柱，上、下底面为直角梯形，如图所示．直角梯形斜腰长为12＋12＝2，所以底面周长为4＋2，侧面积为2×(4＋2)＝8＋22，两底面的面积和为2×12×1×(1＋2)＝3，所以该几何体的表面积为8＋22＋3＝11＋2 2.5．[考点二]中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器——商鞅铜方升，其三视图如图所示(单位：寸)：若π取3，其体积为12.6(立方寸)，则图中的x 的值为________．解析：由三视图知，商鞅铜方升由一圆柱和一长方体组合而成，由题意得：(5.4－x )×3×1＋π·⎝⎛⎭⎫122x ＝12.6，解得x ＝1.6.答案：1.6突破点(三) 与球有关的切、接应用问题1.球的表面积和体积是每年高考的热点，且多与三视图、多面体等综合命题，常以选择题、填空题的形式出现.解决此类问题时，一是要善于把空间问题平面化，把平面问题转化到直角三角形中处理；二是要将变化的模型转化到固定的长方体或正方体中.2.与球有关的组合体问题主要有两种，一种是内切问题，一种是外接问题.解题时要认真分析图形，明确切点和接点的位置，确定有关“元素”间的数量关系，并作出合适的截面图.考点贯通抓高考命题的“形”与“神”多面体的内切球问题[例1] 若一个正四面体的表面积为S 1，其内切球的表面积为S 2，则S 1S 2＝________.[解析] 设正四面体棱长为a ，则正四面体表面积为S 1＝4×34·a 2＝3a 2，其内切球半径为正四面体高的14，即r ＝14×63a ＝612a ，因此内切球表面积为S 2＝4πr 2＝πa 26，则S 1S 2＝3a 2π6a 2＝63π.[答案] 63π[方法技巧]处理与球有关内切问题的策略解答此类问题时首先要找准切点，通过作截面来解决．如果内切的是多面体，则作截面时主要抓住多面体过球心的对角面来作．多面体的外接球问题处理与球有关外接问题的策略把一个多面体的几个顶点放在球面上即为球的外接问题．解决这类问题的关键是抓住外接的特点，即球心到多面体的顶点的距离等于球的半径．[例2] (1)(2017·抚顺模拟)已知直三棱柱ABC -A 1B 1C 1的6个顶点都在球O 的球面上，若AB ＝3，AC ＝4，AB ⊥AC ，AA 1＝12，则球O 的半径为( )A.3172 B ．210 C.132D ．310(2)正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为( )A.81π4 B ．16π C ．9πD.27π4(3)一个正方体削去一个角所得到的几何体的三视图如图所示(图中三个四边形都是边长为2的正方形)，则该几何体外接球的体积为________．[解析] (1)如图所示，由球心作平面ABC 的垂线，则垂足为BC的中点M .又AM ＝12BC ＝52，OM ＝12AA 1＝6，所以球O 的半径R ＝OA ＝⎝⎛⎭⎫522＋62＝132. (2)如图所示，设球半径为R ，底面中心为O ′且球心为O ，∵正四棱锥P -ABCD 中AB ＝2， ∴AO ′＝ 2. ∵PO ′＝4，∴在Rt △AOO ′中，AO 2＝AO ′2＋OO ′2， ∴R 2＝(2)2＋(4－R )2，解得R ＝94，∴该球的表面积为4πR 2＝4π×⎝⎛⎭⎫942＝81π4.(3)依题意可知，新的几何体的外接球也就是原正方体的外接球，球的直径就是正方体的体对角线，∴2R ＝23(R 为球的半径)，∴R ＝3， ∴球的体积V ＝43πR 3＝43π.[答案] (1)C (2)A (3)43π [方法技巧]与球有关外接问题的解题规律(1)直棱柱外接球的球心到直棱柱底面的距离恰为棱柱高的12.(2)正方体外接球的直径为正方体的体对角线的长．此结论也适合长方体，或由同一顶点出发的两两互相垂直的三条棱构成的三棱柱或三棱锥．(3)求多面体外接球半径的关键是找到由球的半径构成的三角形，解三角形即可．能力练通抓应用体验的“得”与“失”1．[考点一]一块石材表示的几何体的三视图如图所示，将该石材切削、打磨、加工成球，则能得到的最大球的半径等于( )A ．1B ．2C ．3D ．4解析：选B 该几何体为直三棱柱，底面是边长分别为6,8,10的直角三角形，侧棱长为12，故能得到的最大球的半径等于底面直角三角形内切圆的半径，其半径为r ＝2Sa ＋b ＋c ＝2×12×6×86＋8＋10＝2，故选B.2．[考点二]如图是某几何体的三视图，则该几何体的外接球的表面积为( )A ．200πB ．150πC ．100πD ．50π解析：选D 由三视图知，该几何体可以由一个长方体截去4个角后得到，此长方体的长、宽、高分别为5,4,3，所以外接球半径R 满足2R ＝42＋32＋52＝52，所以外接球的表面积为S ＝4πR 2＝4π×⎝⎛⎭⎫5222＝50π，故选D. 3．[考点二](2016·太原模拟)如图，平面四边形ABCD 中，AB ＝AD ＝CD ＝1，BD ＝2，BD ⊥CD ，将其沿对角线BD 折成四面体A ′-BCD ，使平面A ′BD ⊥平面BCD ，若四面体A ′-BCD 的顶点在同一个球面上，则该球的表面积为( )A ．3π B.32π C ．4π D.34π 解析：选A 由图示可得BD ＝A ′C ＝2，BC ＝3，△DBC 与△A ′BC 都是以BC 为斜边的直角三角形，由此可得BC 中点到四个点A ′，B ，C ，D 的距离相等，即该三棱锥的外接球的直径为3，所以该外接球的表面积S ＝4π×⎝⎛⎭⎫322＝3π. 4．[考点二]设一个球的表面积为S 1，它的内接正方体的表面积为S 2，则S 1S 2的值等于( )A.2πB.6πC.π6D.π2解析：选D 设球的半径为R ，其内接正方体的棱长为a ，则易知R 2＝34a 2，即a ＝233R ，则S 1S 2＝4πR 26×⎝⎛⎭⎫233R 2＝π2.[全国卷5年真题集中演练——明规律] 1．(2016·全国甲卷)如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为( )A ．20πB ．24πC ．28πD ．32π解析：选C 由三视图知该几何体是圆锥与圆柱的组合体，设圆柱底面圆半径为r ，周长为c ，圆锥母线长为l ，圆柱高为h .由图得r ＝2，c ＝2πr ＝4π，h ＝4，由勾股定理得，l ＝22＋(23)2＝4，S 表＝πr 2＋ch ＋12cl ＝4π＋16π＋8π＝28π.2．(2016·全国丙卷)在封闭的直三棱柱ABC -A 1B 1C 1内有一个体积为V 的球．若AB ⊥BC ，AB ＝6，BC ＝8，AA 1＝3，则V 的最大值是( )A ．4πB.9π2C ．6πD.32π3解析：选B 设球的半径为R ，∵△ABC 的内切圆半径为6＋8－102＝2，∴R ≤2.又2R ≤3，∴R ≤32，∴V max ＝43×π×⎝⎛⎭⎫323＝9π2.故选B. 3．(2015·新课标全国卷Ⅱ)一个正方体被一个平面截去一部分后，剩余部分的三视图如下图，则截去部分体积与剩余部分体积的比值为()A.18 B.17 C.16 D.15解析：选D 由已知三视图知该几何体是由一个正方体截去了一个“大角”后剩余的部分，如图所示，截去部分是一个三棱锥．设正方体的棱长为1，则三棱锥的体积为V 1＝13×12×1×1×1＝16，剩余部分的体积V 2＝13－16＝56.所以V 1V 2＝1656＝15，故选D. 4．(2015·新课标全国卷Ⅱ)已知A ，B 是球O 的球面上两点，∠AOB ＝90°，C 为该球面上的动点．若三棱锥O -ABC 体积的最大值为36，则球O 的表面积为( )A ．36πB ．64πC ．144πD ．256π解析：选C 如图，设球的半径为R ，∵∠AOB ＝90°，∴S △AOB ＝12R 2.∵V O -ABC ＝V C -AOB ，而△AOB 面积为定值，∴当点C 到平面AOB 的距离最大时，V O -ABC 最大，∴当C 为与球的大圆面AOB 垂直的直径的端点时，体积V O -ABC 最大，为13×12R 2×R ＝36，∴R ＝6，∴球O 的表面积为4πR 2＝4π×62＝144π.故选C.5．(2015·新课标全国卷Ⅰ)圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体，该几何体三视图中的正视图和俯视图如图所示．若该几何体的表面积为16＋20π，则r ＝( )A ．1B ．2C ．4D ．8解析：选B 如图，该几何体是一个半球与一个半圆柱的组合体，球的半径为r ，圆柱的底面半径为r ，高为2r ，则表面积S ＝12×4πr 2＋πr 2＋4r 2＋πr ·2r ＝(5π＋4)r 2.又S ＝16＋20π，∴(5π＋4)r 2＝16＋20π，∴r 2＝4，r ＝2，故选B.6．(2015·新课标全国卷Ⅰ)《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺．问：积及为米几何？”其意思为：“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有( )A ．14斛B ．22斛C ．36斛D ．66斛解析：选B 设米堆的底面半径为r 尺，则π2r ＝8，所以r ＝16π，所以米堆的体积为V ＝14×13π·r 2·5＝π12×⎝⎛⎭⎫16π2×5≈3209(立方尺)．故堆放的米约有3209÷1.62≈22(斛)．故选B. 7．(2014·新课标全国卷Ⅱ)如图，网格纸上正方形小格的边长为1(表示1 cm)，图中粗线画出的是某零件的三视图，该零件由一个底面半径为3 cm ，高为6 cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为( )A.1727B.59C.1027D.13解析：选C 原毛坯的体积V ＝(π×32)×6＝54π(cm 3)，由三视图可知该零件为两个圆柱的组合体，其体积V ′＝V 1＋V 2＝(π×22)×4＋(π×32)×2＝34π(cm 3)，故所求比值为1－V ′V ＝1027. 8．(2013·新课标全国卷Ⅰ)某几何体的三视图如图所示，则该几何体的体积为( )A ．16＋8πB ．8＋8πC ．16＋16πD ．8＋16π解析：选A 根据三视图可以判断该几何体由上、下两部分组成，其中上面部分为长方体，下面部分为半个圆柱，所以组合体的体积为2×2×4＋12×22×π×4＝16＋8π，故选A.9．(2012·新课标全国卷)已知三棱锥S -ABC 的所有顶点都在球O 的球面上，△ABC 是边长为1的正三角形，SC 为球O 的直径，且SC ＝2，则此棱锥的体积为( )A.26B.36 C.23D.22解析：选A 由于三棱锥S -ABC 与三棱锥O -ABC 底面都是△ABC ，O 是SC 的中点，因此三棱锥S -ABC 的高是三棱锥O -ABC 高的2倍，所以三棱锥S -ABC 的体积也是三棱锥O -ABC 体积的2倍．在三棱锥O -ABC 中，其棱长都是1，如图所示，S △ABC ＝34×AB 2＝34，高OD ＝12－⎝⎛⎭⎫332＝63，所以VS -ABC ＝2V O -ABC ＝2×13×34×63＝26.[课时达标检测] 重点保分课时——一练小题夯双基，二练题点过高考[练基础小题——强化运算能力]1．下列结论正确的是( )A ．各个面都是三角形的几何体是三棱锥B ．以三角形的一条边所在直线为旋转轴，其余两边绕旋转轴旋转形成的曲面所围成的几何体叫圆锥C ．棱锥的侧棱长与底面多边形的边长都相等，则该棱锥可能是六棱锥D ．圆锥的顶点与底面圆周上的任意一点的连线都是母线解析：选D A 错误，如图①是由两个相同的三棱锥叠放在一起构成的几何体，它的各个面都是三角形，但它不是三棱锥；B 错误，如图②，若△ABC 不是直角三角形，或△ABC 是直角三角形但旋转轴不是直角边，所得的几何体都不是圆锥；C 错误，若该棱锥是六棱锥，由题设知，它是正六棱锥．易证正六棱锥的侧棱长必大于底面边长，这与题设矛盾．2.如图是一个空间几何体的三视图，其中正视图、侧视图都是由边长为4和6的矩形以及直径等于4的圆组成，俯视图是直径等于4的圆，该几何体的体积是( )A.41π3 B.62π3C.83π3D.104π3解析：选D 由题意得，此几何体为球与圆柱的组合体，其体积V ＝43π×23＋π×22×6＝104π3. 3．某空间几何体的三视图如图所示，则该几何体的表面积为( )A ．12＋4 2B ．18＋8 2C ．28D ．20＋8 2解析：选D 由三视图可知该几何体是底面为等腰直角三角形的直三棱柱，如图．则该几何体的表面积为S ＝2×12×2×2＋4×2×2＋22×4＝20＋82，故选D.4．《九章算数》中，将底面是直角三角形的直三棱柱称为“堑堵”，已知某“堑堵”的三视图如图所示，俯视图中虚线平分矩形的面积，则该“堑堵”的侧面积为( )A ．2B ．4＋2 2C ．4＋4 2D ．6＋4 2解析：选C 由题可知，该几何体的底面为等腰直角三角形，等腰直角三角形的斜边长为2，腰长为2，棱柱的高为2.所以其侧面积S ＝2×2＋22×2＝4＋42，故选C.5．已知一个正方体的所有顶点在一个球面上，若球的体积为9π2，则正方体的棱长为________．解析：设正方体棱长为a ，球半径为R ，则43πR 3＝9π2，∴R ＝32，∴3a ＝3，∴a ＝ 3.答案： 3[练常考题点——检验高考能力]一、选择题1．已知圆锥的表面积为a ，且它的侧面展开图是一个半圆，则这个圆锥的底面直径是( )A.a2 B.3πa3πC.23πa 3πD.23a 3π解析：选C 设圆锥的底面半径为r ，母线长为l ，由题意知2πr ＝πl ，∴l ＝2r ，则圆锥的表面积S 表＝πr 2＋12π(2r )2＝a ，∴r 2＝a 3π，∴2r ＝23πa 3π.2．在梯形ABCD 中，∠ABC ＝π2，AD ∥BC ，BC ＝2AD ＝2AB ＝2.将梯形ABCD 绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.2π3B.4π3C.5π3D ．2π解析：选C 过点C 作CE 垂直AD 所在直线于点E ，梯形ABCD 绕AD所在直线旋转一周而形成的旋转体是由以线段AB 的长为底面圆半径，线段BC 为母线的圆柱挖去以线段CE 的长为底面圆半径，ED 为高的圆锥，如图所示，该几何体的体积为V ＝V 圆柱－V 圆锥＝π·AB2·BC －13·π·CE 2·DE ＝π×12×2－13π×12×1＝5π3，故选C.3．一个几何体的三视图如图所示，则该几何体的体积为( )A.163 B.203 C.152D.132解析：选D 该几何体可视为正方体截去两个三棱锥所得，如图所示，所以其体积为23－13×12×2×2×2－13×12×1×1×1＝132.故选D.4．已知正四面体的棱长为2，则其外接球的表面积为( ) A ．8π B ．12π C.32π D ．3π 解析：选D 如图所示，过顶点A 作AO ⊥底面BCD ，垂足为O ，则O 为正三角形BCD 的中心，连接DO 并延长交BC 于E ，又正四面体的棱长为2，所以DE ＝62，OD ＝23DE ＝63，所以在直角三角形AOD 中，AO ＝AD 2－OD 2＝233.设正四面体外接球的球心为P ，半径为R ，连接PD ，则在直角三角形POD 中，PD 2＝PO 2＋OD 2，即R 2＝⎝⎛⎭⎫233－R 2＋⎝⎛⎭⎫632，解得R ＝32，所以外接球的表面积S ＝4πR 2＝3π.5．(2017·郑州质检)如图所示是一个几何体的三视图，则这个几何体外接球的表面积为( )A ．8πB ．16πC ．32πD ．64π解析：选C 还原三视图可知该几何体为一个四棱锥，将该四棱锥补成一个长、宽、高分别为22，22，4的长方体，则该长方体外接球的半径r ＝(22)2＋(22)2＋422＝22，则所求外接球的表面积为4πr 2＝32π.6．已知四棱锥P -ABCD 的三视图如图所示，则四棱锥P -ABCD 的四个侧面中面积的最大值是( )A ．6B ．8C ．2 5D ．3解析：选A 四棱锥如图所示，作PN ⊥平面ABCD ，交DC 于点N ，PC ＝PD ＝3，DN ＝2，则PN ＝32－22＝5，AB ＝4，BC ＝2，BC⊥CD ，故BC ⊥平面PDC ，即BC ⊥PC ，同理AD ⊥PD .设M 为AB 的中点，连接PM ，MN ，则PM ＝3，S △PDC ＝12×4×5＝25，S △PBC ＝S △PAD ＝12×2×3＝3，S △PAB ＝12×4×3＝6，所以四棱锥P -ABCD 的四个侧面中面积的最大值是6.二、填空题7．在棱长为3的正方体ABCD -A 1B 1C 1D 1中，P 在线段BD 1上，且BP PD 1＝12，M 为线段B 1C 1上的动点，则三棱锥M -PBC 的体积为________．解析：∵BP PD 1＝12，∴点P 到平面BC 1的距离是D 1到平面BC 1距离的13，即三棱锥P -MBC 的高h ＝D 1C 13＝1.M 为线段B 1C 1上的点，∴S △MBC ＝12×3×3＝92，∴V M -PBC ＝V P -MBC ＝13×92×1＝32. 答案：328．一个几何体的三视图如图所示(单位：m)，则该几何体的体积为________m 3.解析：由三视图可得该几何体是组合体，上面是底面圆的半径为2 m 、高为2 m 的圆锥，下面是底面圆的半径为1 m 、高为4 m 的圆柱，所以该几何体的体积是13×4π×2＋4π＝20π3(m 3)．答案：20π39.如图，正方形O ′A ′B ′C ′的边长为a ，它是一个水平放置的平面图形的直观图，则原图形OABC 的周长是________．解析：由斜二测画法的规则可知，原图形OABC 是一个平行四边形．在原图形OABC 中OB ＝22a ，OA ＝a ，且OA ⊥OB ，∴AB ＝3a ，∴原图形OABC 的周长为2(a ＋3a )＝8a . 答案：8a10．我国古代数学名著《数书九章》中有“天池盆测雨”题：在下雨时，用一个圆台形的天池盆接雨水．天池盆盆口直径为二尺八寸，盆底直径为一尺二寸，盆深一尺八寸．若盆中积水深九寸，则平地降雨量是________寸．(注：①平地降雨量等于盆中积水体积除以盆口面积；②一尺等于十寸)解析：由题意知，圆台中截面圆的半径为十寸，圆台内水的体积为V ＝13πh (r 2中＋r 2下＋r 中r 下)＝π3×9×(102＋62＋10×6)＝588π(立方寸)，降雨量为V 142π＝588π196π＝3(寸)．答案：3 三、解答题11．已知球的半径为R ，在球内作一个内接圆柱，这个圆柱的底面半径与高为何值时，它的侧面积最大？侧面积的最大值是多少？解：如图为其轴截面，令圆柱的高为h ，底面半径为r ，侧面积为S ，则⎝⎛⎭⎫h 22＋r 2＝R 2，即h ＝2R 2－r 2.因为S ＝2πrh ＝4πr ·R 2－r 2＝4πr 2·(R 2－r 2)≤4π(r 2＋R 2－r 2)24＝2πR 2，当且仅当r 2＝R 2－r 2，即r ＝22R 时，取等号，即当内接圆柱底面半径为22R ，高为2R 时，其侧面积的值最大，最大值为2πR 2. 12．一个几何体的三视图如图所示．已知正视图是底边长为1的平行四边形，侧视图是一个长为3、宽为1的矩形，俯视图为两个边长为1的正方形拼成的矩形．(1)求该几何体的体积V ； (2)求该几何体的表面积S .解：(1)由三视图可知，该几何体是一个平行六面体(如图)，其底面是边长为1的正方形，高为 3.所以V ＝1×1×3＝ 3.(2)由三视图可知，该平行六面体中，A 1D ⊥平面ABCD ，CD ⊥平面BCC 1B 1，。

2018版高考数学(人教A版文科)一轮复习真题演练集训第八章立体几何8-2 Word版含解析

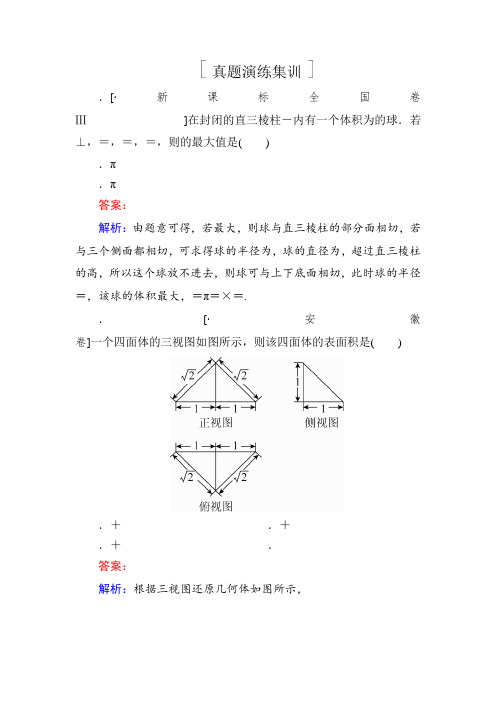
真题演练集训
．[·新课标全国卷Ⅲ]在封闭的直三棱柱－内有一个体积为的球．若⊥，＝，＝，＝，则的最大值是( )
．π
．π
答案：
解析：由题意可得，若最大，则球与直三棱柱的部分面相切，若与三个侧面都相切，可求得球的半径为，球的直径为，超过直三棱柱的高，所以这个球放不进去，则球可与上下底面相切，此时球的半径＝，该球的体积最大，＝π＝×＝.
．[·安徽卷]一个四面体的三视图如图所示，则该四面体的表面积是( )
．＋．＋
．＋．
答案：
解析：根据三视图还原几何体如图所示，
其中侧面⊥底面，另两个侧面，为等边三角形，则有表面积＝×××＋××()＝＋.故选.
．[·新课标全国卷Ⅱ]如图，网格纸上正方形小格的边长为(表示)，图中粗线画出的是某零件的三视图，该零件由一个底面半径为，高为的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为( )
答案：
解析：原毛坯的体积＝(π×)×＝π，由三视图可知该零件为两个圆柱的组合体，其体积′＝＋＝(π×)×＋(π×)×＝π，故所求比值为－＝.。

高三数学-2018《立体几何》高考题解析(文科) 精品

18-18《立体几何》高考题解析（文科）一选择题1把正方形ABCD 沿对角线AC 折起，当A 、B C 、D 四点为顶点的三棱锥体积最大时，直线BD 与平面ABC 所成的角的大小为（ 5.C ）A ．90°B ．60°C ．45°D ．30°（18湖南5）2四面体ABCD 四个面的重心分别为E 、F 、G 、H ，则四面体EFGH 的表面积与四面体ABCD 的表面积的比值是（C ）A ．271 B ．161 C ．91 D ．81（18湖北6） 3已知m 、n 是不重合的直线，α、β是不重合的平面，有下列命题：①若m ⊂α，n ∥α，则m ∥n ； ②若m ∥α，m ∥β，则α∥β；③若α∩β=n ，m ∥n ，则m ∥α且m ∥β； ④若m ⊥α，m ⊥β，则α∥β.其中真命题的个数是（ 6.B ） A ．0 B ．1 C ．2 D ．3（18福建6）4如图，A 、B 、C 是表面积为48π的球面上三点，AB=2，BC=4，∠ABC=60º，O 为球心，则直线 OA 与截面ABC 所成的角是（ 10.D ） A ．arcsin 63B ．arccos 63C ．arcsin33 D ．arccos 33（18福建10）5在下列关于直线l 、m 与平面α、β的命题中,真命题是（ 13．B ）A ．若l ⊂β且α⊥β,则l ⊥α.B ．若l ⊥β且α∥β,则l ⊥α.C ．若l ⊥β且α⊥β,则l ∥α.D ．若α∩β=m 且l ∥m,则l ∥α. （18上海13） 6不同直线,m n 和不同平面,αβ，给出下列命题（） ①////m m αββα⎫⇒⎬⊂⎭ ② //////m n n m ββ⎫⇒⎬⎭③ ,m m n n αβ⊂⎫⇒⎬⊂⎭异面 ④ //m m αββα⊥⎫⇒⊥⎬⎭ 其中假命题有：（ 8．D ）A ．0个B ．1个C ．2个D ．3个（18重庆8）7 如图，棱长为5的正方体无论从哪一个面看，都有两个直通的边长为1的正方形孔，则这个有孔正方体的表面积（含孔内各面）是（ 12．C ） A ．258 B ．234 C ．222 D ．210（18重庆12）8. 91DA2 V 为A. 104B. 38C. 134D. 16（18天津11）（10）如图，在正三棱柱ABC —A 1B 1C 1中已知AB=1，D 在棱BB 1上，且BD=1，若AD 与平面AA 1C 1C 所成的角为α，则α= 10.D(A)3π (B)4π(C)410arcsin(D)46arcsin（18浙江10） 11正三棱柱侧面的一条对角线长为2，且与底面成45°角，则此三棱柱的体积为（ A ）A ．26 B ．6C ．66 D ．36（18甘肃3） 12已知球的表面积为20π，球面上有A 、B 、C 三点.如果AB=AC=BC=23，则球心到平面ABC 的距离为（ A ）A ．1B ．2C ．3D ．2（18甘肃11）13 正三棱锥的底面边长为2，侧面均为直角三角形，则此三棱锥的体积为（C ）A ．B ．C ．3D ．18广西10） 14已知正四面体ABCD 的表面积为S ，其四个面的中心分别为E 、F 、G 、H ，设四面体EFGH 的表面积为T ，则ST等于（ A ）A ．91B ．94C ．41 D ．31（18河北10） 15设 m, n 是两条不同的直线,r ,,βα是三个不同的平面.给出下列四个命题: ①若m ⊥α,n ∥α,则m ⊥n;② 若α∥β, β∥r, m ⊥α,则m ⊥r; ③ 若m ∥α,n ∥α,则m ∥n;④ 若α⊥r, β⊥r,则α∥β. 其中正确命题的序号是3.A(A)①和② (B)②和③ (C)③和④ (D)①和④（18北京3） 16如图,在正方体ABCD －A 1B 1C 1D 1中,P 是侧面BB 1C 1C 内一动点,若P 到直线BC 与直线C 1D 1的距离相等,则动点P 的轨迹所在的曲线是6.D(A) 直线 (B) 圆 (C) 双曲线 (D) 抛物线（18北京6） 17正四棱锥的侧棱长与底面边长都是1，则侧棱与底面所成的角为（C ） A ．75° B ．60° C ．45° D ．30°（18四川6）18已知球O 的半径为1，A 、B 、C 三点都在球面上，且每两点间的球面距离均为2π，则球心O 到平面ABC 的距离为（ B ） A ．31 B ．33 C ．32 D ．36（18四川10） 19一个与球心距离为1的平面截球所得的圆面面积为π，则球的表面积为2．C（A ）π28 （B ）π8（C ）π24 （D ）π4 (18河北2)20如图，在多面体ABCDEF 中，已知ABCD 是边长为1的正方形，且BCF ADE ∆∆、均为正三角形，EF ∥AB ，EF=2，则该多面体的体积为4．D（A ）32（B ）33 （C ）34（D ）23(18河北4) 21设三棱柱ABC-A 1B 1C 1的体积为V ，P 、Q 分别是侧棱AA 1、CC 1上的点，且PA=QC 1，则四棱锥B-APQC 的体积为C（A ）16V （B ）14V （C ）13V （D ）12V (18四川4) 22不共面的四个定点到平面α的距离都相等，这样的平面α共有D（A ）3个（B ）4个（C ）6个（D ）7个(18四川11)23在正四面体P －ABC 中，D ，E ，F 分别是AB ，BC ，CA 的中点，下面四个结论中不成．．立．的是（7）C （A ）BC //平面PDF （B ）DF ⊥平面P A E（C ）平面PDF ⊥平面ABC （D ）平面P AE ⊥平面 ABC （18北京7） 24对于不重合的两个平面βα与，给定下列条件：①存在平面γ，使得α、β都垂直于γ； ②存在平面γ，使得α、β都平等于γ； ③存在直线α⊂l ，直线β⊂m ，使得m l //； ④存在异面直线l 、m ，使得.//,//,//,//βαβαm m l l其中，可以判定α与β平行的条件有（ 7.B ）A ．1个B ．2个C 3个D ．4个（18重庆7）25有一塔形几何体由若干个正方体构成，构成方式如图所示，上层正方体下底面的四个顶点是下层正方体上底面各连接中点，已知最底层正方体的棱长为2，且该塔形的表面积（含最底层正方体的底面面积）超过39，则该塔形中正方体的个数至少是（ 10.C ） A ．4 B ．5 C ．6 D ．7（18重庆10） 26如图，正方体ABCD －A 1B 1C 1D 1的棱长为1，E 是A 1B 1的中点，则E 到平面AB C1D 1的距离为（ B ） A ．23B ．22C ．21 D ．33（18湖南4）27木星的体积约是地球体积的30240倍，则它的表面积约是地球表面积的（5．C ）A ．60倍B ．6030倍C ．120倍D ．12030倍（18湖北5）28已知a 、b 、c 是直线，β是平面，给出下列命题：①若c a c b b a //,,则⊥⊥； ②若c a c b b a ⊥⊥则,,//；③若b a b a //,,//则ββ⊂；④若a 与b 异面，且ββ与则b a ,//相交；⑤若a 与b 异面，则至多有一条直线与a ，b 都垂直. 其中真命题的个数是（ 8．A ） A ．1 B ．2 C ．3D ．4（18湖北8）29设地球半径为R ，若甲地位于北纬045东经0120，乙地位于南纬度075东经0120，则图1 甲、乙两地球面距离为（D ）（A(B)6R π(C)56R π (D) 23R π（18山东9） 30矩形ABCD 中，AB=4，BC=3，沿AC 将矩形ABCD 折成一个直二面角B —AC —D ，则四面体ABCD 的外接球的体积为（ 9．C ）A ．π12125 B ．π9125 C ．π6125 D ．π3125（18江西9） 31设α、β 为两个不同的平面，l 、m 为两条不同的直线，且l ⊂α，m ⊂β，有如下的两个命题：①若α∥β，则l ∥m ；②若l ⊥m ，则α⊥β．那么（D ）(A) ①是真命题，②是假命题 (B) ①是假命题，②是真命题(C) ①②都是真命题 (D) ①②都是假命题(18浙江7) 二填空题1图1，将边长为1的正六边形铁皮的六个角各切去一个全等的四边形，再沿虚线折起，做成一个无盖的正六棱柱容器（图2）.当这个正六棱柱容器的底面边长为 2/3 时，其容积最大. （18福建16）2毛泽东在《送瘟神》中写到：“坐地日行八万里”。

2018届高三复习数学(文)(人教版)高考大题专攻练：(十)含解析

关闭Word文档返回原板块。

高考大题专攻练10.解析几何(B组)大题集训练,练就慧眼和规范,占领高考制胜点!1.已知椭圆E:+=1(a>b>0)的离心率为,其右焦点为F(1,0).(1)求椭圆E的方程.(2)若P,Q,M,N四点都在椭圆E上,已知与共线,与共线,且·=0,求四边形PMQN的面积的最小值和最大值.【解析】(1)由椭圆的离心率公式可知:e==,由c=1,则a=,b2=a2-c2=1,故椭圆方程为+y2=1.(2)由条件知MN和PQ是椭圆的两条弦,相交于焦点F(1,0),且PQ⊥MN,设直线PQ的斜率为k(k≠0),P(x1,y1),Q(x1,y1),则PQ的方程为y=k(x-1),联立整理得:(1+2k2)x2-4k2x+2k2-2=0,x1+x2=,x1x2=,则|PQ|=·,于是|PQ|=,同理:|MN|==.则S=|PQ||MN|=,令t=k2+,t≥2,S=|PQ||MN|==2,当k=〒1时,t=2,S=,且S是以t为自变量的增函数,当k=〒1时,四边形PMQN的面积取最小值.当直线PQ的斜率为0或不存在时,四边形PMQN的面积为2.综上:四边形PMQN的面积的最小值和最大值分别为和2.2.如图,在平面直角坐标系xOy中,椭圆Ω:+=1(a>b>0)的离心率为,直线l:y=2上的点和椭圆Ω上的点的距离的最小值为 1. 世纪金榜导学号46854424(1)求椭圆Ω的方程.(2)已知椭圆Ω的上顶点为A,点B,C是Ω上的不同于A的两点,且点B,C关于原点对称,直线AB,AC分别交直线l于点E,F.记直线AC与AB的斜率分别为k1,k2.①求证:k1·k2为定值;②求△CEF的面积的最小值.[来源:学§科§网Z§X§X§K]【解题导引】(1)由题知b=1,由=,b=1联立求解即可得出.(2)①方法一:直线AC的方程为y=k1x+1,与椭圆方程联立可得坐标,即可得出.方法二:设B(x0,y0)(y0>0),则+=1,因为点B,C关于原点对称,则C(-x0,-y0),利用斜率计算公式即可得出.②直线AC的方程为y=k1x+1,直线AB的方程为y=k2x+1,不妨设k1>0,则k2<0,令y=2,得E,F,可得△CEF的面积S△CEF=|EF|(2-y c).【解析】(1)由题意知b=1,由=,所以a2=2,b2=1.故椭圆的方程为+y2=1.(2)①方法一:直线AC的方程为y=k1x+1,。

2018届高考数学高考大题专项突破四高考中的立体几何文新人教A版

高考大题专项练四高考中的立体几何1.(2017东北三省四市一模,文19)如图,已知斜三棱柱ABC-A1B1C1的所有棱长均为2,∠B1BA=,M,N 分别为A1C1与B1C的中点,且侧面ABB1A1⊥底面ABC.(1)证明:MN∥平面ABB1A1;(2)求三棱锥B1-ABC的高及体积.2.(2017湖北武汉五月调考,文18)如图,在四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB 与△PAD都是边长为2的等边三角形,E是BC的中点.(1)求证:AE∥平面PCD;(2)求四棱锥P-ABCD的体积.3.(2016吉林东北师大附中二模,文19)在三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,各棱长均为2,D,E,F,G分别是棱AC,AA1,CC1,A1C1的中点.(1)求证:平面B1FG∥平面BDE;(2)求三棱锥B1-BDE的体积.4.(2017湖北武汉二月调考,文18)如图,在三棱柱ABC-A1B1C1中,AB⊥平面BCC1B1,∠BCC1=,AB=BB1=2,BC=1,D为CC1的中点.(1)求证:DB1⊥平面ABD;(2)求点A1到平面ADB1的距离.5.(2017吉林三模,文19)如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD是直角梯形,其中AB⊥AD,AB=BC=1,AD=2,AA1=.(1)求证:直线C1D⊥平面ACD1;(2)试求三棱锥A1-ACD1的体积.6.(2017山东,文18)由四棱柱ABCD-A1B1C1D1截去三棱锥C1-B1CD1后得到的几何体如图所示.四边形ABCD为正方形,O为AC与BD的交点,E为AD的中点,A1E⊥平面ABCD.(1)证明:A1O∥平面B1CD1;(2)设M是OD的中点,证明:平面A1EM⊥平面B1CD1.7.(2017黑龙江大庆三模,文19)如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD 是等边三角形,已知BD=2AD=8,AB=2DC=4.(1)设M是PC上的一点,证明:平面MBD⊥平面PAD;(2)求四棱锥P-ABCD的体积.8.(2017广东、江西、福建十校联考,文19)如图,在空间几何体ADE-BCF中,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,AD⊥DC, AB=AD=DE=2,EF=4,M是线段AE上的动点.(1)求证:AE⊥CD;(2)试确定点M的位置,使AC∥平面MDF,并说明理由;(3)在(2)的条件下,求空间几何体ADM-BCF的体积.〚导学号24190960〛9.(2017天津,文17)如图,在四棱锥P-ABCD中,AD⊥平面PDC,AD∥BC,PD⊥PB,AD=1,BC=3,CD=4,PD=2.(1)求异面直线AP与BC所成角的余弦值;(2)求证:PD⊥平面PBC;(3)求直线AB与平面PBC所成角的正弦值.〚导学号24190961〛高考大题专项练四高考中的立体几何1.(1)证明取AC中点P,连接PN,PM(图略),∵在斜三棱柱ABC-A1B1C1中,M,N分别为A1C1与B1C的中点,∴PN∥AB1,PM∥AA1,∵PM∩PN=P,AB1∩AA1=A,PM,PN⊂平面PMN,AB1,AA1⊂平面AB1A1,∴平面PMN∥平面AB1A1,∵MN⊂平面PMN,∴MN∥平面ABB1A1.(2)解设O为AB的中点,连接B1O(图略),由题意知△B1BA是正三角形,∴B1O⊥AB.又侧面ABB1A1⊥底面ABC且交线为AB,∴B1O⊥平面ABC,∴三棱锥B1-ABC的高B1O=AB=.∵S△ABC=×2×2×sin 60°=,∴三棱锥B1-ABC的体积V=×S△ABC×B1O==1.2.(1)证明∵∠ABC=∠BAD=90°,∴AD∥BC.∵BC=2AD,E是BC的中点,∴AD=CE.∴四边形ADCE是平行四边形,∴AE∥CD,又AE⊄平面PCD,CD⊂平面PCD,∴AE∥平面PCD.(2)解连接DE,BD(图略),设AE∩BD=O,则四边形ABED是正方形,∴O为BD的中点.∵△PAB与△PAD都是边长为2的等边三角形,∴BD=2,OB=,OA=,PA=PB=2,∴OP⊥OB,OP=,∴OP2+OA2=PA2,即OP⊥OA,又OA⊂平面ABCD,BD⊂平面ABCD,OA∩BD=O,∴OP⊥平面ABCD.∴V P-ABCD=S梯形ABCD·OP=(2+4)×2×=2.3.(1)证明连接DG,A1C.∵D,G分别是AC,A1C1的中点,∴DG AA1BB1,∴四边形BB1GD是平行四边形,∴B1G∥BD.又B1G⊄平面EBD,BD⊂平面EBD,∴B1G∥平面EBD.∵D,E,F,G分别是棱AC,AA1,CC1,A1C1的中点,∴GF∥A1C,A1C∥DE,∴GF∥ED.又GF⊄平面EBD,ED⊂平面EBD,∴GF∥平面EBD.又B1G∩GF=G,B1G⊂平面B1FG,GF⊂平面B1FG,∴平面B1FG∥平面EBD.(2)解过D作DH⊥AB交AB于点H,∵AA1⊥平面ABC,AA1⊂平面A1ABB1,∴平面A1ABB1⊥平面ABC.又平面A1ABB1∩平面ABC=AB,DH⊥AB,DH⊂平面ABC, ∴DH⊥平面A1ABB1.∵AB=BC=AC=2,∴DA=1,BD=,∴DH=.∴·DH=×2×2×.4.(1)证明在平面四边形BCC1B1中,∵BC=CD=DC1=1,∠BCD=60°,∴BD=1.∵B1D=,BB1=2,∴∠BDB1=90°,∴B1D⊥BD.∵AB⊥平面BB1C1C,∴AB⊥DB1,∴B1D与平面ABD内两相交直线AB和BD同时垂直,∴DB1⊥平面ABD.(2)解对于四面体A1-ADB1,A1到直线DB1的距离即A1到平面BB1C1C的距离,A1到B1D的距离为2,设A1到平面AB1D的距离为h,△ADB1为直角三角形,×AD×DB1=,∴×h=h,∵×2×2=2,D到平面AA1B1的距离为,∴×2×,∵,∴,解得h=.∴点A1到平面ADB1的距离为.5.(1)证明在梯形ABCD内过点C作CE⊥AD交AD于点E,∵由底面四边形ABCD是直角梯形,∴AB⊥AD,又AB=BC=1,易知AE=ED=1,且AC=CD=,∴AC2+CD2=AD2,所以AC⊥CD.又根据题意知CC1⊥平面ABCD,从而CC1⊥AC,而CC1∩CD=C,故AC⊥C1D.∵CD=AC=AA1=CC1,及已知可得CDD1C1是正方形,∴CD1⊥C1D.∵CD1⊥C1D,AC⊥C1D,且AC∩CD1=C,∴C1D⊥平面ACD1.(2)解∵,而CE⊥AD,且由AA1⊥平面ABCD可得CE⊥AA1,又∵AD∩AA1=A,∴CE⊥平面ADD1A1,即CE为三棱锥C-AA1D1的高.故·AA1·A1D1·CE=×2×1=.6.证明 (1)取B1D1的中点O1,连接CO1,A1O1,由于ABCD-A1B1C1D1是四棱柱,所以A1O1∥OC,A1O1=OC,因此四边形A1OCO1为平行四边形,所以A1O∥O1C.又O1C⊂平面B1CD1,A1O⊄平面B1CD1,所以A1O∥平面B1CD1.(2)因为AC⊥BD,E,M分别为AD和OD的中点,所以EM⊥BD,又A1E⊥平面ABCD,BD⊂平面ABCD,所以A1E⊥BD,因为B1D1∥BD,所以EM⊥B1D1,A1E⊥B1D1.又A1E,EM⊂平面A1EM,A1E∩EM=E,所以B1D1⊥平面A1EM,又B1D1⊂平面B1CD1,所以平面A1EM⊥平面B1CD1.7.(1)证明在△ABD中,因为AD=4,BD=8,AB=4,所以AD2+BD2=AB2.故AD⊥BD.又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,BD⊂平面ABCD,所以BD⊥平面PAD,又BD⊂平面MBD,故平面MBD⊥平面PAD.(2)解过P作PO⊥AD交AD于点O.因为平面PAD⊥平面ABCD,所以PO⊥平面ABCD.因此PO为四棱锥P-ABCD的高,又△PAD是边长为4的等边三角形,因此PO=×4=2.在底面四边形ABCD中,AB∥DC,AB=2DC,所以四边形ABCD是梯形,在Rt△ADB中,斜边AB边上的高为,此即为梯形ABCD的高,所以四边形ABCD的面积为S==24.故V P-ABCD=×24×2=16.8.( 1)证明∵四边形CDEF是矩形,∴CD⊥ED.∵AD⊥DC,AD∩ED=D,∴CD⊥平面AED,∵AE⊂平面AED,∴AE⊥CD.(2)解当M是线段AE的中点时,AC∥平面MDF,证明如下:连接CE交DF于点N,连接MN,∵M,N分别是AE,CE的中点,∴MN∥AC.又MN⊂平面MDF,AC⊄平面MDF,∴AC∥平面MDF.(3)解将几何体ADE-BCF补成三棱柱ADE-B'CF,∴三棱柱ADE-B'CF的体积V=S△ADE·CD=×2×2×4=8,空间几何体ADM-BCF的体积V ADM-BCF=V ADE-B'CF-V F-BB'C-V F-DEM=8-×2-×1=.∴空间几何体ADM-BCF 的体积为.9.(1)解如图,由已知AD∥BC,故∠DAP或其补角即为异面直线AP与BC所成的角.因为AD⊥平面PDC,所以AD⊥PD.在Rt△PDA中,由已知,得AP=,故cos∠DAP=.所以,异面直线AP与BC所成角的余弦值为.(2)证明因为AD⊥平面PDC,直线PD⊂平面PDC,所以AD⊥PD.又因为BC∥AD,所以PD⊥BC.又PD⊥PB,所以PD⊥平面PBC.(3)解过点D作AB的平行线交BC于点F,连接PF,则DF与平面PBC所成的角等于AB与平面PBC所成的角.因为PD⊥平面PBC,故PF为DF在平面PBC上的射影,所以∠DFP为直线DF和平面PBC所成的角.由于AD∥BC,DF∥AB,故BF=AD=1,由已知,得CF=BC-BF=2.又AD⊥DC,故BC⊥DC,在Rt△DCF中,可得DF==2,在Rt△DPF中,可得sin∠DFP=.所以,直线AB与平面PBC所成角的正弦值为.。

2018版高考数学文人教A版大一轮复习配套讲义：专题探

高考导航 1.立体几何初步是高考的重要内容，几乎每年都考查一个解答题，两个选择或填空题，客观题主要考查空间概念，三视图及简单计算；解答题主要采用“论证与计算”相结合的模式，即利用定义、公理、定理证明空间线线、线面、面面平行或垂直，并与几何体的性质相结合考查几何体的计算；2.重在考查学生的空间想象能力、逻辑推理论证能力及数学运算能力.考查的热点是以几何体为载体的垂直、平行的证明、平面图形的折叠、探索开放性问题等；同时考查转化化归思想与数形结合的思想方法.热点一平行、垂直关系的证明与体积的计算(规范解答)以空间几何体(主要是柱、锥或简单组合体)为载体，通过空间平行、垂直关系的论证命制，主要考查公理4及线、面平行与垂直的判定定理与性质定理，常与平面图形的有关性质及体积的计算等知识交汇考查，考查学生的空间想象能力和推理论证能力以及转化与化归思想，一般以解答题的形式出现，难度中等.【例1】(满分12分)(2015·全国Ⅰ卷)如图，四边形ABCD为菱形，G为AC与BD的交点，BE⊥平面ABCD.(1)证明：平面AEC⊥平面BED；(2)若∠ABC＝120°，AE⊥EC，三棱锥E－ACD的体积为63，求该三棱锥的侧面积.满分解答(1)证明因为四边形ABCD为菱形，所以AC⊥BD. 因为BE⊥平面ABCD，AC⊂平面ABCD，所以AC⊥BE.2分又BD∩BE＝B，故AC⊥平面BED.又AC⊂平面AEC，所以平面AEC⊥平面BED.4分(2)解设AB ＝x ，在菱形ABCD 中，由∠ABC ＝120°，可得AG ＝GC ＝32x ，GB ＝GD ＝x 2.因为AE ⊥EC ，所以在Rt △AEC 中，可得EG ＝32x .6分由BE ⊥平面ABCD ，BG ⊂平面ABCD ，得BE ⊥BG ，知△EBG 为直角三角形，可得BE ＝22x .7分由已知得，三棱锥E －ACD 的体积V 三棱锥E －ACD ＝13×12·AC ·GD ·BE ＝624x 3＝63，故x ＝2.9分从而可得AE ＝EC ＝ED ＝ 6.所以△EAC 的面积为3，△EAD 的面积与△ECD 的面积均为 5.故三棱锥E －ACD 的侧面积为3＋2 5.12分❶得步骤分：第(1)问中采分点有两处，若忽视条件BD ∩BE ＝B ，AC ⊂平面AEC ，导致扣2分.另第(2)问中最后一步得分点有两处：一是计算AE ，EC ，ED 的长度得1分；二是求三个侧面的面积得2分.❷得关键分：阅卷时根据得分点评分，有则得分，无则不得分.❸得运算分：正确的计算结果是得分的关键，本题在求三棱锥的体积与侧面积时，需要计算的量较多，防止计算错误失分.要把每一个需要计算的量求出来，各环节环环相扣，缺了哪一个环节都计算不出来，没有某个环节，就会失分.第一步：由线面垂直的性质，得AC ⊥BE .第二步：根据线面、面面垂直的判定定理，得平面AEC ⊥平面BED .第三步：由体积公式计算底面菱形的边长.第四步：计算各个侧面三角形的面积，得出结论.第五步：查看关键点，检验反思，规范步骤.【训练1】 (2017·郑州模拟)在三棱锥V －ABC 中，平面VAB ⊥平面ABC ，△VAB 为等边三角形，AC ⊥BC 且AC ＝BC ＝2，O ，M分别为AB，VA的中点.(1)求证：VB∥平面MOC；(2)求证：平面MOC⊥平面VAB；(3)求三棱锥V－ABC的体积.(1)证明因为O，M分别为AB，VA的中点，所以OM∥VB，又因为VB⊄平面MOC，OM⊂平面MOC，所以VB∥平面MOC.(2)证明因为AC＝BC，O为AB的中点，所以OC⊥AB.又因为平面VAB⊥平面ABC，平面VAB∩平面ABC＝AB，且OC⊂平面ABC，所以OC⊥平面VAB.又OC⊂平面MOC，所以平面MOC⊥平面VAB.(3)解在等腰直角三角形ACB中，AC＝BC＝2，所以AB＝2，OC＝1，所以等边三角形VAB的面积S△VAB＝ 3.又因为OC⊥平面VAB，所以三棱锥C－VAB的体积等于13OC·S△VAB＝33.又因为三棱锥V－ABC与三棱锥C－VAB的体积相等，所以三棱锥V－ABC的体积为3 3.热点二平面图形折叠成空间几何体先将平面图形折叠成空间几何体，再以其为载体研究其中的线、面间的位置关系与计算有关的几何量是近几年高考考查立体几何的一类重要考向，它很好地将平面图形拓展成空间图形，同时也为空间立体图形向平面图形转化提供了具体形象的途径，是高考深层次上考查空间想象能力的主要方向.【例2】(2016·全国Ⅱ卷)如图，菱形ABCD的对角线AC与BD交于点O，点E，F分别在AD，CD上，AE＝CF，EF交BD于点H，将△DEF沿EF折到△D′EF的位置.(1)证明：AC⊥HD′；(2)若AB＝5，AC＝6，AE＝54，OD′＝22，求五棱锥D′－ABCFE的体积.(1)证明由已知得AC⊥BD，AD＝CD，又由AE＝CF得AEAD＝CFCD，故AC∥EF，由此得EF⊥HD，故EF⊥HD′，所以AC⊥HD′.(2)解由EF∥AC得OHDO＝AEAD＝14.由AB＝5，AC＝6得DO＝BO＝AB2－AO2＝4，所以OH＝1，D′H＝DH＝3，于是OD′2＋OH2＝(22)2＋12＝9＝D′H2，故OD′⊥OH.由(1)知AC⊥HD′，又AC⊥BD，BD∩HD′＝H，所以AC⊥平面BHD′，于是AC⊥OD′，又由OD′⊥OH，AC∩OH＝O，所以OD′⊥平面ABC.又由EFAC＝DHDO得EF＝92.五边形ABCFE的面积S＝12×6×8－12×92×3＝694.所以五棱锥D′－ABCFE的体积V＝13×694×22＝2322.探究提高(1)①利用AC与EF平行，转化为证明EF与HD′垂直；②求五棱锥的体积需先求棱锥的高及底面的面积，结合图形特征可以发现OD′是棱锥的高，而底面的面积可以利用菱形ABCD与△DEF面积的差求解，这样就将问题转化为证明OD′与底面垂直以及求△DEF的面积问题了.(2)解决与折叠有关的问题的关键是搞清折叠前后的变化量和不变量，一般情况下，线段的长度是不变量，而位置关系往往会发生变化，抓住不变量是解决问题的突破口.【训练2】(2017·秦皇岛调研)如图1所示，在Rt△ABC中，∠C＝90°，D，E 分别为AC，AB的中点，点F为线段CD上的一点，将△ADE沿DE折起到△A1DE 的位置，使A1F⊥CD，如图2所示.(1)求证：A1F⊥BE；(2)线段A1B上是否存在点Q，使A1C⊥平面DEQ？说明理由.(1)证明由已知，得AC⊥BC，且DE∥BC.所以DE⊥AC，则DE⊥DC，DE⊥DA1，又因为DC∩DA1＝D，所以DE⊥平面A1DC.由于A1F⊂平面A1DC，所以DE⊥A1F.又因为A1F⊥CD，CD∩DE＝D，所以A1F⊥平面BCDE，又BE⊂平面BCDE，所以A1F⊥BE.(2)解线段A1B上存在点Q，使A1C⊥平面DEQ.理由如下：如图所示，分别取A1C，A1B的中点P，Q，则PQ∥BC.又因为DE∥BC，所以DE∥PQ.所以平面DEQ即为平面DEP.由(1)知，DE⊥平面A1DC，所以DE⊥A1C.又因为P是等腰△DA1C底边A1C的中点，所以A1C⊥DP，又DE∩DP＝D，所以A1C⊥平面DEP.从而A1C⊥平面DEQ.故线段A1B上存在点Q，使得A1C⊥平面DEQ.热点三线、面位置关系中的开放存在性问题是否存在某点或某参数，使得某种线、面位置关系成立问题，是近几年高考命题的热点，常以解答题中最后一问的形式出现，一般有三种类型：(1)条件追溯型；(2)存在探索型；(3)方法类比探索型.【例3】(2017·哈尔滨质检)如图所示，在四棱锥P－ABCD中，底面ABCD是边长为a的正方形，侧面P AD⊥底面ABCD，且E，F分别为PC，BD的中点.(1)求证：EF∥平面P AD；(2)在线段CD上是否存在一点G，使得平面EFG⊥平面PDC？若存在，请说明其位置，并加以证明；若不存在，请说明理由.(1)证明如图所示，连接AC，在四棱锥P－ABCD中，底面ABCD是边长为a的正方形，且点F为对角线BD的中点.所以对角线AC经过点F，又在△P AC中，点E为PC的中点，所以EF为△P AC的中位线，所以EF∥P A，又P A⊂平面P AD，EF⊄平面P AD，所以EF∥平面P AD.(2)解存在满足要求的点G.证明如下：在线段CD上存在一点G为CD的中点，使得平面EFG⊥平面PDC，因为底面ABCD是边长为a的正方形，所以CD⊥AD.又侧面P AD⊥底面ABCD，CD⊂平面ABCD，侧面P AD∩平面ABCD＝AD，所以CD⊥平面P AD.又EF∥平面P AD，所以CD⊥EF.取CD中点G，连接FG，EG.因为F为BD中点，所以FG∥AD.又CD⊥AD，所以FG⊥CD，又FG∩EF＝F，所以CD⊥平面EFG，又CD⊂平面PDC，所以平面EFG⊥平面PDC.探究提高(1)在立体几何的平行关系问题中，“中点”是经常使用的一个特殊点，通过找“中点”，连“中点”，即可出现平行线，而线线平行是平行关系的根本.(2)第(2)问是探索开放性问题，采用了先猜后证，即先观察与尝试给出条件再加以证明，对于命题结论的探索，常从条件出发，探索出要求的结论是什么，对于探索结论是否存在，求解时常假设结论存在，再寻找与条件相容或者矛盾的结论.【训练3】(2017·湖南师大附中检测)如图，四棱锥S－ABCD的底面是正方形，每条侧棱的长都是底面边长的2倍，P为侧棱SD上的点.(1)求证：AC⊥SD；(2)若SD⊥平面P AC，则侧棱SC上是否存在一点E，使得BE∥平面P AC？若存在，求SE∶EC；若不存在，试说明理由.(1)证明连接BD，设AC交BD于点O，连接SO，由题意得四棱锥S－ABCD 是正四棱锥，所以SO⊥AC.在正方形ABCD中，AC⊥BD，又SO∩BD＝O，所以AC⊥平面SBD，因为SD⊂平面SBD，所以AC⊥SD.(2)解在棱SC上存在一点E，使得BE∥平面P AC.连接OP.设正方形ABCD的边长为a，则SC＝SD＝2a.由SD⊥平面P AC得SD⊥PC，易求得PD＝2a 4.故可在SP上取一点N，使得PN＝PD.过点N作PC的平行线与SC交于点E，连接BE，BN.在△BDN中，易得BN∥PO，又因为NE∥PC，NE⊂平面BNE，BN⊂平面BNE，BN∩NE＝N，PO⊂平面P AC，PC⊂平面P AC，PO∩PC＝P，所以平面BEN∥平面P AC，所以BE∥平面P AC.因为SN∶NP＝2∶1，所以SE∶EC＝2∶1.(建议用时：70分钟)1.如图所示，在四棱锥P－ABCD中，平面P AD⊥平面ABCD，AB＝AD，∠BAD＝60°，E，F分别是AP，AD的中点.求证：(1)直线EF∥平面PCD；(2)平面BEF⊥平面P AD.证明(1)在△P AD中，因为E，F分别是AP，AD的中点，所以EF∥PD.因为EF⊄平面PCD，PD⊂平面PCD，所以直线EF∥平面PCD.(2)如图所示，连接BD，因为AB＝AD，∠BAD＝60°，所以△ABD 为正三角形.因为F 是AD 的中点，所以BF ⊥AD .因为平面P AD ⊥平面ABCD ，平面P AD ∩平面ABCD ＝AD ，BF ⊂平面ABCD ，所以BF ⊥平面P AD .又BF ⊂平面BEF ，所以平面BEF ⊥平面P AD .2.(2017·石家庄质检)如图，已知△ABC 和△DBC 所在的平面互相垂直，且AB ＝BC ＝BD ＝1，∠ABC ＝∠DBC ＝120°.(1)在直线BC 上求作一点O ，使BC ⊥平面ADO ，写出作法并说明理由；(2)求三棱锥A －BCD 的体积.解 (1)作AO ⊥BC ，交CB 延长线于O 点，连接DO ，AO ，则BC ⊥平面ADO .证明如下：∵AB ＝DB ，OB ＝OB ，∠ABO ＝∠DBO ，∴△ABO ≌△DBO ，则∠AOB ＝∠DOB ＝90°，即OD ⊥BC ，又∵AO ∩OD ＝O ，AO ⊂平面ADO ，OD ⊂平面ADO ，∴BC ⊥平面AOD .(2)∵△ABC 和△DBC 所在的平面互相垂直，平面ABC ∩平面DBC ＝BC ，AO ⊂平面ABC ，∴AO ⊥平面BCD ，即AO 是三棱锥A －BCD 底面BCD 上的高.在Rt △AOB 中，AB ＝1，∠ABO ＝60°，∴AO ＝AB sin 60°＝32.又∵S △BCD ＝12BC ·BD ·sin ∠CBD ＝34，∴V 三棱锥A －BCD ＝13·S △BCD ·AO ＝13×34×32＝18.3.(2016·西安模拟)如图，在长方形ABCD 中，AB ＝2，BC ＝1，E 为CD 的中点，F 为AE 的中点，现在沿AE 将三角形ADE 向上折起，在折起的图形中解答下列问题：(1)在线段AB 上是否存在一点K ，使BC ∥平面DFK ？若存在，请证明你的结论；若不存在，请说明理由；(2)若平面ADE ⊥平面ABCE ，求证：平面BDE ⊥平面ADE .(1)解如图，线段AB 上存在一点K ，且当AK ＝14AB 时，BC ∥平面DFK .证明如下：设H 为AB 的中点，连接EH ，则BC ∥EH .∵AK ＝14AB ，F 为AE 的中点，∴KF ∥EH ，∴KF ∥BC ，∵KF ⊂平面DFK ，BC ⊄平面DFK ，∴BC ∥平面DFK .(2)证明 ∵在折起前的图形中E 为CD 的中点，AB ＝2，BC ＝1，∴在折起后的图形中，AE ＝BE ＝2，从而AE 2＋BE 2＝4＝AB 2，∴AE ⊥BE .∵平面ADE ⊥平面ABCE ，平面ADE ∩平面ABCE ＝AE ，BE ⊂平面ABCE ，∴BE ⊥平面ADE ，∵BE ⊂平面BDE ，∴平面BDE ⊥平面ADE .4.(2017·合肥质检)如图，直角三角形ABC 中，A ＝60°，沿斜边AC 上的高BD 将△ABD 折起到△PBD 的位置，点E 在线段CD 上.(1)求证：PE ⊥BD ；(2)过点D 作DM ⊥BC 交BC 于点M ，点N 为PB 的中点，若PE ∥平面DMN ，求DE DC 的值.(1)证明 ∵BD ⊥PD ，BD ⊥CD ，且PD ∩CD ＝D ，PD ，CD ⊂平面PCD ， ∴BD ⊥平面PCD .又PE ⊂平面PCD ，∴BD ⊥PE .(2)解由题意，得BM ＝14BC .取BC 的中点F ，则PF ∥MN .又PF ⊄平面DMN ，MN ⊂平面DMN ，∴PF ∥平面DMN .由条件PE ∥平面DMN ，PE ∩PF ＝P ，∴平面PEF ∥平面DMN ，∴EF ∥DM ，∴DE DC ＝MF MC ＝13.5.(2017·长沙雅礼中学模拟)如图，已知三棱柱ABC －A ′B ′C ′的侧棱垂直于底面，AB ＝AC ，∠BAC ＝90°，点M ，N 分别为A ′B 和B ′C ′的中点.(1)证明：MN ∥平面AA ′C ′C ；(2)设AB ＝λA ′A ，当λ为何值时，CN ⊥平面A ′MN ，试证明你的结论.(1)证明取A ′B ′的中点E ，连接ME ，NE ，∵M ，N 分别为A ′B 和B ′C ′的中点，∴NE ∥A ′C ′，ME ∥AA ′.∵A ′C ′⊂平面AA ′C ′C ，A ′A ⊂平面AA ′C ′C ，∴ME ∥平面AA ′C ′C ，NE ∥平面AA ′C ′C ，又ME ∩NE ＝E ，∴平面MNE ∥平面AA ′C ′C ，∵MN ⊂平面MNE ，∴MN ∥平面AA ′C ′C .(2)连接BN ，设AA ′＝a ，则AB ＝λAA ′＝λa ，由题意知BC ＝2λa ，NC ＝BN ＝a 2＋12λ2a 2，∵三棱柱ABC －A ′B ′C ′的侧棱垂直于底面，∴平面A ′B ′C ′⊥平面BB ′C ′C ，∵AB ＝AC ，∴A ′B ′＝A ′C ′，又点N 是B ′C ′的中点，∴A ′N ⊥平面BB ′C ′C ，∴CN ⊥A ′N .要使CN ⊥平面A ′MN ，只需CN ⊥BN 即可，∴CN 2＋BN 2＝BC 2，即2⎝ ⎛⎭⎪⎫a 2＋12λ2a 2＝2λ2a 2， ∴λ＝2，则λ＝2时，CN ⊥平面A ′MN .6.(2016·全国Ⅰ卷)如图，已知正三棱锥P －ABC 的侧面是直角三角形，P A ＝6，顶点P 在平面ABC 内的正投影为点D ，D 在平面P AB 内的正投影为点E ，连接PE 并延长交AB 于点G .(1)证明：G 是AB 的中点；(2)在图中作出点E 在平面P AC 内的正投影F (说明作法及理由)，并求四面体P －DEF 的体积.(1)证明因为P 在平面ABC 内的正投影为D ，所以AB ⊥PD .因为D 在平面P AB 内的正投影为E ，所以AB ⊥DE .又因为PD ∩DE ＝D ，所以AB ⊥平面PED ，又PG ⊂平面PED ，故AB ⊥PG .又由已知可得，P A ＝PB ，所以G 是AB 的中点.(2)解在平面P AB 内，过点E 作PB 的平行线交P A 于点F ，F即为E 在平面P AC 内的正投影.理由如下：由已知可得PB ⊥P A ，PB ⊥PC ，又EF ∥PB ，所以EF ⊥P A ，EF ⊥PC .又P A ∩PC ＝P ，因此EF ⊥平面P AC ，即点F 为E 在平面P AC 内的正投影.连接CG ，因为P 在平面ABC 内的正投影为D ，所以D 是正三角形ABC 的中心. 由(1)知，G 是AB 的中点，所以D 在CG 上，故CD ＝23CG .由题设可得PC ⊥平面P AB ，DE ⊥平面P AB ，所以DE ∥PC ，因此PE ＝23PG ，DE ＝13PC .由已知，正三棱锥的侧面是直角三角形且P A ＝6，可得DE ＝2，PE ＝2 2. 在等腰直角三角形EFP 中，可得EF ＝PF ＝2.所以四面体P －DEF 的体积V ＝13×12×2×2×2＝43.。

2018大二轮高考总复习文数文档：解答题4 立体几何

第一单元高考中档大题突破解答题04: 立体几何基本考点——空间平行、垂直关系及体积、表面积的计算1．直线、平面平行的判定及其性质(1)线面平行的判定定理：a ⊄α，b ⊂α，a ∥b ⇒a ∥α. (2)线面平行的性质定理：a ∥α，a ⊂β，α∩β＝b ⇒a ∥b .(3)面面平行的判定定理：a ⊂β，b ⊂β，a ∩b ＝P ，a ∥α，b ∥α⇒α∥β.(4)面面平行的性质定理：α∥β，α∩γ＝a ，β∩γ＝b ⇒a ∥b . 2．直线、平面垂直的判定及其性质(1)线面垂直的判定定理：m ⊂α，n ⊂α，m ∩n ＝P ，l ⊥m ，l ⊥n ⇒l ⊥α. (2)线面垂直的性质定理：a ⊥α，b ⊥α⇒a ∥b . (3)面面垂直的判定定理：a ⊂β，a ⊥α⇒α⊥β.(4)面面垂直的性质定理：α⊥β，α∩β＝l ，a ⊂α，a ⊥l ⇒a ⊥β.1.(2017·全国卷Ⅰ)如图，在四棱锥P －ABCD 中，AB ∥CD ，且∠BAP ＝∠CDP ＝90°.(1)证明：平面P AB ⊥平面P AD ；(2)若P A ＝PD ＝AB ＝DC ，∠APD ＝90°，且四棱锥P －ABCD 的体积为83，求该四棱锥的侧面积．(1)证明：由已知∠BAP ＝∠CDP ＝90°，得AB ⊥AP ，CD ⊥PD .由于AB ∥CD ，故AB ⊥PD ，从而AB ⊥平面P AD . 又AB ⊂平面P AB ，所以平面P AB ⊥平面P AD .(2)解：如图，在平面P AD 内作PE ⊥AD ，垂足为E .由(1)知，AB ⊥平面P AD ，故AB ⊥PE ，AB ⊥AD ，可得PE ⊥平面ABCD .设AB ＝x ，则由已知可得AD ＝2x ，PE ＝22x . 故四棱锥P －ABCD 的体积 V P －ABCD ＝13AB ·AD ·PE ＝13x 3.由题设得13x 3＝83，故x ＝2.从而结合已知可得P A ＝PD ＝AB ＝DC ＝2，AD ＝BC ＝22，PB ＝PC ＝2 2. 可得四棱锥P －ABCD 的侧面积为12P A ·PD ＋12P A ·AB ＋12PD ·DC ＋12BC 2sin 60°＝6＋2 3. 2.(2017·全国卷Ⅱ)如图，四棱锥P －ABCD 中，侧面P AD 为等边三角形且垂直于底面ABCD ，AB ＝BC ＝12AD ，∠BAD ＝∠ABC ＝90°.(1)证明：直线BC ∥平面P AD ；(2)若△PCD 的面积为27，求四棱锥P －ABCD 的体积．(1)证明：在平面ABCD 内，因为∠BAD ＝∠ABC ＝90°，所以BC ∥AD .又BC ⊄平面P AD ，AD ⊂平面P AD ，故BC ∥平面P AD .(2)解：如图，取AD 的中点M ，连接PM ，CM .由AB ＝BC ＝12AD 及BC ∥AD ，∠ABC＝90°得四边形ABCM 为正方形，则CM ⊥AD .因为侧面P AD 为等边三角形且垂直于底面ABCD ，平面P AD ∩平面ABCD ＝AD ，所以PM ⊥AD ，PM ⊥底面ABCD .因为CM ⊂底面ABCD ，所以PM ⊥CM .设BC ＝x ，则CM ＝x ，CD ＝2x ，PM ＝3x ，PC ＝PD ＝2x . 如图，取CD 的中点N ，连接PN ，则PN ⊥CD ，所以PN ＝142x . 因为△PCD 的面积为27，所以12×2x ×142x ＝27，解得x ＝－2(舍去)或x ＝2.于是AB ＝BC ＝2，AD ＝4，PM ＝2 3.所以四棱锥P －ABCD 的体积V ＝13×2(2＋4)2×23＝4 3.常考热点——立体几何中的折叠问题、探索性问题考向01：折叠问题折叠问题是高考常考题型，一般来说，折叠问题常从以下两个角度考查：一是将平面图形折叠成空间几何体，进而论证位置关系和求空间几何体体积；二是将空间图形拆分并铺成平面图形来计算一些数量关系．(2017·西安一模)如图(1)，在直角梯形ABCD中，AD∥BC，∠ABC＝90°，AB ＝BC＝2，AD＝6，CE⊥AD于E点，把△DEC沿CE折到D′EC的位置，使D′A＝23，如图(2)，若G，H分别为D′B，D′E的中点．(1)求证：GH⊥D′A；(2)求三棱锥C－D′BE的体积．[思路点拨](1)通过证明：AD′⊥AE，AD′⊥AC，推出AD′⊥平面ABCD，推出AD′⊥BE，通过证明GH∥BE，推出GH⊥D′A；(2)三棱锥C－D′BE的体积．直接利用棱锥的体积公式求解即可．(1)【证明】在直角梯形ABCD中，AD∥BC，∠ABC＝90°，AB＝BC＝2，AD＝6，CE⊥AD于E点，把△DEC沿CE折到D′EC的位置，使D′A＝23，ED＝4，连接BE，GH，在三角形AED′中，可得ED′2＝AE2＋AD′2，可得AD′⊥AE，DC＝ED2＋AB2＝25，AC＝22，可得AC2＋AD′2＝CD′2，可得AD′⊥AC，因为AE∩AC＝A，所以AD′⊥平面ABCD，可得AD′⊥BE，G，H分别为D′B，D′E的中点，可得GH∥BE，所以GH ⊥D ′A .(2)【解】三棱锥C －D ′BE 的体积为V . 则V ＝13S △BCE ·AD ′＝13×12×2×2×23＝433.平面图形翻折问题的求解方法(1)解决与折叠有关的问题的关键是搞清折叠前后的变化量和不变量，一般情况下，线段的长度是不变量，而位置关系往往会发生变化，抓住不变量是解决问题的突破口．(2)在解决问题时，要综合考虑折叠前后的图形，既要分析折叠后的图形，也要分析折叠前的图形．考向02：立体几何中的探索性问题对命题条件的探索常采用以下三种方法：先猜后证；先通过命题成立的必要条件探索出命题成立的条件，再证明其充分性；把几何问题转化为代数问题，探索命题成立的条件．(2017·濮阳一模)如图，四边形ABCD 为梯形，AB ∥CD ，PD ⊥平面ABCD ，∠BAD ＝∠ADC ＝90°，DC ＝2AB ＝2，DA ＝ 3.(1)线段BC 上是否存在一点E ，使平面PBC ⊥平面PDE ？若存在，请给出BECE 的值，并进行证明；若不存在，请说明理由．(2)若PD ＝3，线段PC 上有一点F ，且PC ＝3PF ，求三棱锥A －FBD 的体积． [思路点拨] (1)存在线段BC 的中点E ，连接DE ，PE ，推导出BC ⊥DE ，BC ⊥PD ，从而BC ⊥平面PDE ，由此得到平面PBC ⊥平面PDE .(2)三棱锥A －FBD 的体积V A －FBD ＝V F －ABD ，由此能求出结果．【解】 (1)存在线段BC 的中点E ，使平面PBC ⊥平面PDE ，即BECE ＝1.证明如下：连接DE ，PE ，∵∠BAD ＝∠ADC ＝90°，AB ＝1，DA ＝3，∴BD ＝DC ＝2，∵E 为BC 的中点，∴BC ⊥DE ， ∵PD ⊥平面ABCD ，∴BC ⊥PD ， ∵DE ∩PD ＝D ，∴BC ⊥平面PDE ， ∵BC ⊂平面PBC ，∴平面PBC ⊥平面PDE . (2)∵PD ⊥平面ABCD ，且PC ＝3PF ， ∴F 到平面ABCD 的距离为23PD ＝233，∴三棱锥A －FBD 的体积：V A －FBD ＝V F －ABD ＝13×S △ABD ×233＝13×12×1×3×233＝13.1．如图(1)，在Rt △ABC 中，∠C ＝90°，D ，E 分别为AC ，AB 的中点，点F 为线段CD 上的一点．将△ADE 沿DE 折起到△A 1DE 的位置，使A 1F ⊥CD ，如图(2)．(1)求证：DE ∥平面A 1CB ； (2)求证：A 1F ⊥BE ；(3)线段A 1B 上是否存在点Q ，使A 1C ⊥平面DEQ ？说明理由． (1)证明：因为D ，E 分别为AC ，AB 的中点，所以DE ∥BC .又为DE ⊄平面A 1CB ，BC ⊂平面A 1CB . 所以DE ∥平面A 1CB .(2)证明：由已知得AC ⊥BC 且DE ∥BC ，所以DE ⊥AC . 所以DE ⊥A 1D ，DE ⊥CD .又A1D∩CD＝D，所以DE⊥平面A1DC.因为A1F⊂平面A1DC，所以DE⊥A1F.又因为A1F⊥CD，CD∩DE＝D.所以A1F⊥平面BCDE.因为BE⊂平面BCDE，所以A1F⊥BE.(3)解：假设线段A1B上存在点Q，使A1C⊥平面DEQ.理由如下：如图，分别取A1C，A1B中点P，Q，连接PQ，则PQ∥BC.又因为DE∥BC，所以DE∥PQ.所以平面DEQ即为平面DEP.由(2)知，DE⊥平面A1DC，又A1C⊂平面A1DC，所以DE⊥A1C.又因为P是等腰三角形DA1C底边A1C的中点，所以A1C⊥DP.因为DP∩DE＝D.所以A1C⊥平面DEP，即A1C⊥平面DEQ.故线段A1B上存在点Q，使得A1C⊥平面DEQ.2.(2017·长春二模)已知三棱锥A－BCD中，△ABC是等腰直角三角形，且AC⊥BC，BC ＝2，AD⊥平面BCD，AD＝1.(1)求证：平面ABC⊥平面ACD；(2)若E为AB中点，求点A到平面CED的距离．(1)证明：∵AD⊥平面BCD，BC⊂平面BCD，∴AD⊥BC，又∵AC⊥BC，AC∩AD＝A，∴BC⊥平面ACD，BC⊂平面ABC，∴平面ABC⊥平面ACD.(2)解：由已知可得CD ＝3，取CD 中点为F ，连接EF ，∵ED ＝EC ＝12AB ＝2，∴△ECD 为等腰三角形，从而EF ＝52，S △ECD ＝154，由(1)知BC ⊥平面ACD ，∴点E 到平面ACD 的距离为1，S △ACD ＝32，令A 到平面CED 的距离为d ，则V A －ECD ＝13·S △ECD ·d ＝V E －ACD ＝13·S △ACD ·1，解得d ＝255.1．(2017·晋中二模)如图，直角△ABC 中，∠ACB ＝90°，BC ＝2AC ＝4，D 、E 分别是AB 、BC 边的中点，沿DE 将△BDE 折起至△FDE ，且∠CEF ＝60°.(1)求四棱锥F －ADEC 的体积； (2)求证：平面ADF ⊥平面ACF .解：(1)D 、E 分别是AB 、BC 边的中点，∴DE 平行且等于AC 的一半，DE ⊥BC ，DE ＝1，依题意，DE ⊥EF ，BE ＝EF ＝2，∵EF ∩EC ＝E ，∴DE ⊥平面CEF ，∵DE ⊥平面CEF ， ∴平面ACED ⊥平面CEF .作FM ⊥EC 于M ，则FM ⊥平面ACED ， ∵∠CEF ＝60°，∴FM ＝3，梯形ACED 的面积S ＝12(AC ＋ED )×EC ＝12(1＋2)×2＝3，∴四棱锥F －ADEC 的体积V＝13Sh ＝13×3×3＝ 3. (2)法一：如图所示．取线段AF 、CF 的点N 、Q ，连接DN 、NQ 、EQ ，则NQ 平行且等于AC 的一半，∴NQ 平行且等于DE ，DEQN 是平行四边形，DN ∥EQ ，∵EC ＝EF ，∠CEF ＝60°， ∴△CEF 是等边三角形，EQ ⊥FC ，又∵DE ⊥平面CEF ，DE ⊥EQ ，∴AC ⊥EQ ，∵FC ∩AC ＝C ，∴EQ ⊥平面ACF ，∴DN ⊥平面ACF ，又DN ⊂平面ADF ，∴平面ADF ⊥平面ACF .法二：连接BF ，∵EC ＝EF ，∠CEF ＝60°，∴△CEF 是边长为2等边三角形， ∵BE ＝EF ，∴∠EBF ＝12∠CEF ＝30°，∴∠BFC ＝90°，BF ⊥FC ，DE ⊥平面BCF ，DE ∥AC ，∴AC ⊥平面BCF ， ∵BF ⊂平面BCF ，∴AC ⊥BF ，又∵FC ∩AC ＝C ， ∴BF ⊥平面ACF ，又∵BF ⊂平面ADF ，∴平面ADF ⊥平面ACF .2．(2017·许昌一模)如图，在四棱锥E －ABCD 中，底面ABCD 是矩形，AB ＝2BC ，P 、Q 分别为线段AB 、CD 的中点，EP ⊥底面ABCD .(1)求证：AQ ∥平面CEP ； (2)求证：平面AEQ ⊥平面DEP ；(3)若EP ＝AP ＝1，求三棱锥E －AQC 的体积． (1)证明：在矩形ABCD 中，∵AP ＝PB ，DQ ＝QC ， ∴AP ∥CQ 且AP ＝CQ ，∴AQCP 为平行四边形，∴CP ∥AQ . ∵CP ⊂平面CEP ，AQ ⊄平面CEP ， ∴AQ ∥平面CEP .(2)证明：∵EP ⊥平面ABCD ，AQ ⊂平面ABCD ，∴AQ ⊥EP .∵AB ＝2BC ，P 为AB 中点，∴AP ＝AD .连接PQ ，则ADQP 为正方形．∴AQ ⊥DP .又EP ∩DP ＝P ，∴AQ ⊥平面DEP .∵AQ ⊂平面AEQ .∴平面AEQ ⊥平面DEP.(3)解：∵EP ⊥平面ABCD ，∴EP 为三棱锥E －AQC 的高，∴V E －AQC ＝13S △AQC ·EP ＝13×12CQ ·AD ·EP ＝16×1×1×1＝16.3．(2017·大连双基测试)如图，已知四棱锥P －ABCD 中，底面ABCD 是菱形，PD ⊥平面ABCD ，E 为PB 上任意一点．(1)证明：平面EAC ⊥平面PBD ；(2)试确定点E 的位置，使得四棱锥P －ABCD 的体积等于三棱锥P －ACE 体积的4倍． (1)证明：连接AC ，BD ，∵底面ABCD 是菱形，∴AC ⊥BD ，∵PD ⊥平面ABCD ，AC ⊂平面ABCD ，∴AC ⊥PD ，∵BD ∩PD ＝D ，∴AC ⊥平面PBD ， ∵AC ⊂平面EAC ，∴平面EAC ⊥平面PBD .(2)解：∵四棱锥P －ABCD 的体积等于三棱锥P －ACE 体积的4倍，∴V E －ABC V P －ABCD ＝14，设E 到平面ABCD 的距离为h ，则V E －ABC V P －ABCD ＝13×S △ABC×h 13×2S △ABC ×PD ＝h 2PD ＝14，解得h ＝12PD ，故此时E 为PB 的中点．4.(2017·北京卷)如图，在三棱锥P －ABC 中，P A ⊥AB ，P A ⊥BC ，AB ⊥BC ，P A ＝AB ＝BC ＝2，D 为线段AC 的中点，E 为线段PC 上一点．(1)求证：P A ⊥BD ；(2)求证：平面BDE ⊥平面P AC ；(3)当P A ∥平面BDE 时，求三棱锥E －BCD 的体积．(1)证明：因为P A ⊥AB ，P A ⊥BC ，所以P A ⊥平面ABC .又因为BD ⊂平面ABC ，所以P A ⊥BD .(2)证明：因为AB ＝BC ，D 为AC 的中点，所以BD ⊥AC . 由(1)知，P A ⊥BD ，所以BD ⊥平面P AC ，所以平面BDE ⊥平面P AC .(3)解：因为P A ∥平面BDE ，平面P AC ∩平面BDE ＝DE ，所以P A ∥DE .因为D 为AC 的中点，所以DE ＝12P A ＝1，BD ＝DC ＝ 2.由(1)知，P A ⊥平面ABC ，所以DE ⊥平面ABC ，所以三棱锥E －BCD 的体积 V ＝16BD ·DC ·DE ＝13.5．(2017·莆田二模)如图，在四棱锥S －ABCD 中，四边形ABCD 为矩形，E 为SA 的中点，SA ＝SB ，AB ＝23，BC ＝3.(1)证明：SC ∥平面BDE ；(2)若BC ⊥SB ，求三棱锥C －BDE 的体积． (1)证明：连接AC ，设AC ∩BD ＝O ， ∵四边形ABCD 为矩形，则O 为AC 的中点，在△ASC 中，E 为AS 的中点，∴SC ∥OE ，又OE ⊂平面BDE ，SC ⊄平面BDE ， ∴SC ∥平面BDE ；(2)解：过E 作EH ⊥AB ，垂足为H ， ∵BC ⊥AB ，且BC ⊥SB ，AB ∩SB ＝B ， ∴BC ⊥平面SAB ， ∵EH ⊂平面ABS ，∴EH ⊥BC ，又EH ⊥AB ，AB ∩BC ＝B ， ∴EH ⊥平面ABCD ，在△SAB 中，取AB 中点M ，连接SM ，则SM ⊥AB ， ∴SM ＝1.∵EH ∥SM ，EH ＝12SM ＝12.∴S △BCD ＝12×3×23＝3 3.∴V C －BDE ＝V E －BCD ＝13S △BCD ·EH ＝13×33×12＝32.∴三棱锥C －BDE 的体积为32.6.5.(2017·全国卷Ⅲ)如图，四面体ABCD 中，△ABC 是正三角形，AD ＝CD . (1)证明：AC ⊥BD ；(2)已知△ACD 是直角三角形，AB ＝BD ，若E 为棱BD 上与D 不重合的点，且AE ⊥EC ，求四面体ABCE 与四面体ACDE 的体积比．(1)证明：如图，取AC 的中点O ，连接DO ，BO .因为AD ＝CD ，所以AC ⊥DO . 又由于△ABC 是正三角形，所以AC ⊥BO . 从而AC ⊥平面DOB ，故AC ⊥BD . (2)解：连接EO .由(1)及题设知∠ADC ＝90°，所以DO ＝AO . 在Rt △AOB 中，BO 2＋AO 2＝AB 2.又AB ＝BD ，所以BO 2＋DO 2＝BO 2＋AO 2＝AB 2＝BD 2，故∠DOB ＝90°. 由题设知△AEC 为直角三角形，所以EO ＝12AC .又△ABC 是正三角形，且AB ＝BD ，所以EO ＝12BD .故E 为BD 的中点，从而E 到平面ABC 的距离为D 到平面ABC 的距离的12，四面体ABCE的体积为四面体ABCD 的体积的12，即四面体ABCE 与四面体ACDE 的体积之比为1∶1.。

专题05 立体几何文-2018年高考题和高考模拟题数学分项版汇编 Word版含解析

5．立体几何1．【2018年浙江卷】已知四棱锥S−ABCD的底面是正方形，侧棱长均相等，E是线段AB上的点（不含端点），设SE与BC所成的角为θ1，SE与平面ABCD所成的角为θ2，二面角S−AB−C的平面角为θ3，则A.θ1≤θ2≤θ3B. θ3≤θ2≤θ1C. θ1≤θ3≤θ2D. θ2≤θ3≤θ1【答案】D点睛：线线角找平行，线面角找垂直，面面角找垂面.2．【2018年浙江卷】某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm3）是A. 2B. 4C. 6D. 8【答案】C【解析】分析:先还原几何体为一直四棱柱，再根据柱体体积公式求结果.详解：根据三视图可得几何体为一个直四棱柱，高为2，底面为直角梯形，上下底分别为1，2，梯形的高为2，因此几何体的体积为选C.点睛：先由几何体的三视图还原几何体的形状,再在具体几何体中求体积或表面积等.3．【2018年文北京卷】某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为A. 1B. 2C. 3D. 4【答案】C共三个，故选C.点睛：此题考查三视图相关知识，解题时可将简单几何体放在正方体或长方体中进行还原，分析线面、线线垂直关系，利用勾股定理求出每条棱长，进而可进行棱长、表面积、体积等相关问题的求解. 4．【2018年新课标I卷文】在长方体中，，与平面所成的角为，则该长方体的体积为A. B. C. D.【答案】C点睛：该题考查的是长方体的体积的求解问题，在解题的过程中，需要明确长方体的体积公式为长宽高的乘积，而题中的条件只有两个值，所以利用题中的条件求解另一条边的长久显得尤为重要，此时就需要明确线面角的定义，从而得到量之间的关系，从而求得结果.5．【2018年新课标I卷文】已知圆柱的上、下底面的中心分别为，，过直线的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为A. B. C. D.【答案】B【解析】分析：首先根据正方形的面积求得正方形的边长，从而进一步确定圆柱的底面圆半径与圆柱的高，从而利用相关公式求得圆柱的表面积.详解：根据题意，可得截面是边长为的正方形，结合圆柱的特征，可知该圆柱的底面为半径是的圆，且高为，所以其表面积为，故选B.点睛：该题考查的是有关圆柱的表面积的求解问题，在解题的过程中，需要利用题的条件确定圆柱的相关量，即圆柱的底面圆的半径以及圆柱的高，在求圆柱的表面积的时候，一定要注意是两个底面圆与侧面积的和.6．【2018年全国卷Ⅲ文】设是同一个半径为4的球的球面上四点，为等边三角形且其面积为，则三棱锥体积的最大值为A. B. C. D.【答案】B，故选B.点睛：本题主要考查三棱锥的外接球，考查了勾股定理，三角形的面积公式和三棱锥的体积公式，判断出当平面时，三棱锥体积最大很关键，由M为三角形ABC的重心，计算得到，再由勾股定理得到OM，进而得到结果，属于较难题型。

2018版高中数学人教A版必修4部分第3章章末分层突破含解析精品

章末分层突破[自我校对]①cos αcos β＋sin αsin β ②sin αcos β－cos αsin β ③tan α－tan β1＋tan αtan β④cos αcos β－sin αsin β ⑤sin αcos β＋cos αsin β ⑥tan α＋tan β1－tan αtan β⑦cos 2α－sin 2α ⑧2cos 2α－1 ⑨1－2sin 2α ⑩2sin αcos α ⑪2tan α1－tan 2α给值求值问题给出某些角的三角函数值，求另外一些角的三角函数值，解题的关键在于“变角”.使其角相同或具有某种关系，解题的基本方法是：①将待求式用已知三角函数表示.②将已知条件转化而推出可用的结论.其中“凑角法”是解决此类问题的常用技巧.解题时首先是分析已知式与待求式之间角、函数、结构间的差异，有目的的将已知式、待求式的一方或两方加以变换，找出它们之间的联系，最后求出待求式的值.已知3π4<α<π，tan α＋1tan α＝－103.(1)求tan α的值；(2)求5sin 2 α2＋8sin α2cos α2＋11cos 2α2－82sin ⎝⎛⎭⎫α－π2的值.【精彩点拨】 (1)结合α的取值范围，求解tan α的值；(2)利用降幂公式和诱导公式先统一角，通过三角变换转化成关于tan α的式子代入求值即可.【规范解答】 (1)由tan α＋1tan α＝－103，得3tan 2α＋10tan α＋3＝0，即tan α＝－3或tan α＝－13.又3π4<α<π，所以tan α＝－13. (2)原式＝5×1－cos α2＋4sin α＋11×1＋cos α2－8－2cos α＝5－5cos α＋8sin α＋11＋11cos α－16－22cos α＝4sin α＋3cos α－2cos α＝4tan α＋3－2＝－526.[再练一题]1.已知sin(α＋β)＝7210，sin(α－β)＝－22，求tan αtan β的值.【解】由sin(α＋β)＝7210，得sin αcos β＋cos αsin β＝7210，①由sin(α－β)＝－22，得 sin αcos β－cos αsin β＝－22，② ①＋②得：sin αcos β＝210， ①－②得：cos αsin β＝6210，tan αtan β＝sin αcos βcos αsin β＝2106210＝16.三角函数式的化简与证明三角函数式的化简是三角变换应用的一个重要方面，其基本思想方法是统一角、统一三角函数的名称.在具体实施过程中，应着重抓住“角”的统一.通过观察角、函数名、项的次数等，找到突破口，利用切化弦、升幂、降幂、逆用公式等手段将其化简.三角函数式的证明实质上也是化简，是有方向目标的化简；根本原则：由繁到简，消除两端差异，达到证明目的.证明：1＋sin 2θ－cos 2θ1＋sin 2θ＋cos 2θ＝tan θ.【精彩点拨】可从左边向右边证明，先把角由2θ向θ转化，再实现函数名称向tan θ转化.【规范解答】法一：左边＝sin 2θ＋(1－cos 2θ)sin 2θ＋(1＋cos 2θ)＝2sin θcos θ＋2sin 2 θ2sin θcos θ＋2cos 2 θ ＝sin θ(cos θ＋sin θ)cos θ(cos θ＋sin θ)＝tan θ＝右边. 法二：左边＝sin 2 θ＋cos 2 θ＋sin 2θ＋sin 2 θ－cos 2 θsin 2 θ＋cos 2 θ＋sin 2θ＋cos 2 θ－sin 2 θ＝sin 2θ＋2sin 2 θsin 2θ＋2cos 2 θ＝2sin θ(sin θ＋cos θ)2cos θ(sin θ＋cos θ)＝tan θ＝右边. 法三：左边＝(1＋sin 2θ)－cos 2θ(1＋sin 2θ)＋cos 2θ＝(sin 2 θ＋cos 2 θ＋2sin θ·cos θ)－(cos 2 θ－sin 2 θ)(sin 2 θ＋cos 2 θ＋2sin θ·cos θ)＋(cos 2 θ－sin 2 θ) ＝(sin θ＋cos θ)2－(cos θ＋sin θ)(cos θ－sin θ)(sin θ＋cos θ)2＋(cos θ＋sin θ)(cos θ－sin θ) ＝(sin θ＋cos θ)(sin θ＋cos θ＋sin θ－cos θ)(sin θ＋cos θ)(sin θ＋cos θ＋cos θ－sin θ)＝(sin θ＋cos θ)·2sin θ(sin θ＋cos θ)·2cos θ＝tan θ＝右边. [再练一题] 2.求证：tan 3x 2－tan x 2＝2sin xcos x ＋cos 2x. 【证明】2sin xcos x ＋cos 2x＝2sin ⎝⎛⎭⎫3x 2－x 2cos ⎝⎛⎭⎫3x 2－x 2＋cos ⎝⎛⎭⎫3x 2＋x 2＝2⎝⎛⎭⎫sin 3x 2cos x 2－cos 3x 2sin x 22cos 3x 2cos x 2＝sin 3x 2cos 3x 2－sin x 2cosx 2＝tan 3x 2－tan x 2.三角恒等变形的综合应用与三角恒等变形有关的综合问题一般有以下两种类型：(1)以三角恒等变形为主要的化简手段，考查三角函数的性质.当给出的三角函数关系式较为复杂，我们要先通过三角恒等变换，将三角函数的表达式变形化简，将函数表达式变形为y ＝A sin(ωx ＋φ)＋k 或y ＝A cos(ωx ＋φ)＋k 等形式，然后再根据化简后的三角函数，讨论其图象和性质.(2)以向量运算为载体，考查三角恒等变形.这类问题往往利用向量的知识和公式，通过向量的运算，将向量条件转化为三角条件，然后通过三角变换解决问题；有时还从三角与向量的关联点处设置问题，把三角函数中的角与向量的夹角统一为一类问题考查.已知向量a ＝(1，－3)，b ＝(sin x ，cos x )，f (x )＝a·b .(1)若f (θ)＝0，求2cos 2 θ2－sin θ－12sin ⎝⎛⎭⎫θ＋π4的值；(2)当x ∈[0，π]时，求函数f (x )的值域.【精彩点拨】 (1)可先由f (θ)＝0求tan θ，再化简2cos 2 θ2－sin θ－12sin ⎝⎛⎭⎫θ＋π4后，由tan θ值代入求值；(2)先化简得f (x )＝A sin(ωx ＋φ)的形式，再据x 范围求ωx ＋φ范围，进而求得f (x )的值域. 【规范解答】 (1)∵a ＝(1，－3)， b ＝(sin x ，cos x )， ∴f (x )＝a·b ＝sin x －3cos x . ∵f (θ)＝0，即sin θ－3cos θ＝0， ∴tan θ＝3， ∴2cos 2 θ2－sin θ－12sin ⎝⎛⎭⎫θ＋π4＝cos θ－sin θsin θ＋cos θ＝1－tan θtan θ＋1＝1－33＋1＝－2＋ 3.(2)f (x )＝sin x －3cos x ＝2sin ⎝⎛⎭⎫x －π3. ∵x ∈[0，π]，∴x －π3∈⎣⎡⎦⎤－π3，2π3，当x －π3＝－π3，即x ＝0时，f (x )min ＝－3，当x －π3＝π2，即x ＝5π6时，f (x )max ＝2，∴当x ∈[0，π]时，函数f (x )的值域为[－3，2]. [再练一题]3.已知向量m ＝(sin A ，cos A )，n ＝(3，－1)，且m ·n ＝1，且A 为锐角. (1)求角A 的大小；(2)求函数f (x )＝cos 2x ＋4cos A sin x (x ∈R )的值域. 【导学号：00680078】【解】 (1)由题意得m ·n ＝3sin A －cos A ＝1， 2sin ⎝⎛⎭⎫A －π6＝1，sin ⎝⎛⎭⎫A －π6＝12. 由A 为锐角得A －π6＝π6，A ＝π3.(2)由(1)知cos A ＝12.所以f (x )＝cos 2x ＋2sin x ＝1－2sin 2x ＋2sin x ＝－2⎝⎛⎭⎫sin x －122＋32. 因为x ∈R ，所以sin x ∈[－1,1]，因此，当sin x ＝12时，f (x )有最大值32，当sin x ＝－1时，f (x )有最小值－3，所以所求函数f (x )的值域为⎣⎡⎦⎤－3，32.转化与化归的思想三角式的恒等变换是解三角函数问题的方法基础，所谓三角式的恒等变换，就是运用有关概念和公式把给定的三角式化为另一等价形式.转化与化归的思想是三角恒等变换应用最广泛的，也是最基本的数学思想，它贯穿于三角恒等变换的始终，要认真体会理解，在解题过程中学会灵活应用.已知sin ⎝⎛⎭⎫α－β2＝45，cos ⎝⎛⎭⎫α2－β＝－1213，且α－β2和α2－β分别为第二、第三象限角，求tan α＋β2的值.【精彩点拨】先根据α－β2，α2－β的范围求得其正、余弦再求正切值，最后由α＋β2＝⎝⎛⎭⎫α－β2－⎝⎛⎭⎫α2－β求解.【规范解答】 ∵sin ⎝⎛⎭⎫α－β2＝45，且α－β2为第二象限角， ∴cos ⎝⎛⎭⎫α－β2＝－1－sin 2⎝⎛⎭⎫α－β2＝－35. 又cos ⎝⎛⎭⎫α2－β＝－1213，且α2－β为第三象限角， ∴sin ⎝⎛⎭⎫α2－β＝－1－cos 2⎝⎛⎭⎫α2－β＝－513. ∴tan ⎝⎛⎭⎫α－β2＝－43，tan ⎝⎛⎭⎫α2－β＝512，∴tan α＋β2＝tan ⎣⎡⎦⎤⎝⎛⎭⎫α－β2－⎝⎛⎭⎫α2－β ＝tan ⎝⎛⎭⎫α－β2－tan ⎝⎛⎭⎫α2－β1＋tan ⎝⎛⎭⎫α－β2tan ⎝⎛⎭⎫α2－β＝－43－5121－43×512＝－6316.[再练一题]4.已知sin α－cos α＝－55，α∈⎝⎛⎭⎫0，π4，sin ⎝⎛⎭⎫β－π4＝35，β∈⎝⎛⎭⎫π4，π2. (1)求sin α和cos α的值； (2)求cos ⎝⎛⎭⎫α－β＋π4的值. 【解】 (1)由题意得(sin α－cos α)2＝15，即1－sin 2α＝15，∴sin 2α＝45.又2α∈⎝⎛⎭⎫0，π2， ∴cos 2α＝1－sin 2 2α＝35，∴cos 2 α＝1＋cos 2α2＝45.∵α∈⎝⎛⎭⎫0，π4，∴cos α＝25＝255， sin α＝15＝55. (2)∵β∈⎝⎛⎭⎫π4，π2，β－π4∈⎝⎛⎭⎫0，π4， ∴cos ⎝⎛⎭⎫β－π4＝45， cos ⎝⎛⎭⎫α－β＋π4 ＝cos ⎣⎡⎦⎤α－⎝⎛⎭⎫β－π4 ＝cos αcos ⎝⎛⎭⎫β－π4＋sin αsin ⎝⎛⎭⎫β－π4 ＝255×45＋55×35＝11525.1.若tan θ＝－13，则cos 2θ＝( )A.－45B.－15C.15D.45【解析】 ∵cos 2θ＝cos 2θ－sin 2θcos 2θ＋sin 2θ＝1－tan 2θ1＋tan 2θ，又∵tan θ＝－13，∴cos 2θ＝1－191＋19＝45.【答案】 D2.函数f (x )＝cos 2x ＋6cos ⎝⎛⎭⎫π2－x 的最大值为( ) A.4 B.5 C.6D.7【解析】 ∵f (x )＝cos 2x ＋6cos ⎝⎛⎭⎫π2－x ＝cos 2x ＋6sin x ＝1－2sin 2x ＋6sin x ＝－2⎝⎛⎭⎫sin x －322＋112，又sin x ∈[－1,1]，∴当sin x ＝1时，f (x )取得最大值5.故选B. 【答案】 B3.已知2cos 2x ＋sin 2x ＝A sin(ωx ＋φ)＋b (A >0)，则A ＝________，b ＝________. 【解析】 ∵2cos 2x ＋sin 2x ＝1＋cos 2x ＋sin 2x ＝2sin ⎝⎛⎭⎫2x ＋π4＋1＝A sin(ωx ＋φ)＋b ，∴A ＝2，b ＝1.【答案】2 14.已知θ是第四象限角，且sin ⎝⎛⎭⎫θ＋π4＝35，则tan ⎝⎛⎭⎫θ－π4＝________. 【解析】由题意知sin ⎝⎛⎭⎫θ＋π4＝35，θ是第四象限角，所以cos ⎝⎛⎭⎫θ＋π4＞0，所以cos ⎝⎛⎭⎫θ＋π4＝1－sin 2⎝⎛⎭⎫θ＋π4＝45. tan ⎝⎛⎭⎫θ－π4＝tan ⎝⎛⎭⎫θ＋π4－π2＝－1tan ⎝⎛⎭⎫θ＋π4＝－cos ⎝⎛⎭⎫θ＋π4sin ⎝⎛⎭⎫θ＋π4＝－4535＝－43.【答案】－435.已知函数f (x )＝2sin ωx cos ωx ＋cos 2ωx (ω>0)的最小正周期为π. (1)求ω的值；(2)求f (x )的单调递增区间.【解】 (1)因为f (x )＝2sin ωx cos ωx ＋cos 2ωx ＝sin 2ωx ＋cos 2ωx ＝2sin ⎝⎛⎭⎫2ωx ＋π4，所以f (x )的最小正周期T ＝2π2ω＝πω.依题意，得πω＝π，解得ω＝1.(2)由(1)知f (x )＝2sin ⎝⎛⎭⎫2x ＋π4. 函数y ＝sin x 的单调递增区间为⎣⎡⎤2k π－π2，2k π＋π2(k ∈Z ). 由2k π－π2≤2x ＋π4≤2k π＋π2(k ∈Z )，得k π－3π8≤x ≤k π＋π8(k ∈Z ).所以f (x )的单调递增区间为⎣⎡⎦⎤k π－3π8，k π＋π8(k ∈Z).。

2018版高考数学大一轮复习高考专题突破四高考中的立体几何问题文新人教版

2018版高考数学大一轮复习高考专题突破四高考中的立体几何问题文新人教版1．正三棱柱ABC－A1B1C1中，D为BC中点，E为A1C1中点，则DE与平面A1B1BA的位置关系为( )A．相交B．平行C．垂直相交D．不确定答案 B解析如图取B1C1中点为F，连接EF，DF，DE，则EF∥A1B1，DF∥B1B，∴平面EFD∥平面A1B1BA，∴DE∥平面A1B1BA.2．设x、y、z是空间不同的直线或平面，对下列四种情形：①x、y、z均为直线；②x、y是直线，z是平面；③z是直线，x、y是平面；④x、y、z均为平面．其中使“x⊥z且y⊥z⇒x∥y”为真命题的是( )A．③④ B．①③ C．②③ D．①②答案 C解析由正方体模型可知①④为假命题；由线面垂直的性质定理可知②③为真命题．3．(2016·成都模拟)如图是一个几何体的三视图(侧视图中的弧线是半圆)，则该几何体的表面积是( )A ．20＋3πB ．24＋3πC ．20＋4πD ．24＋4π答案 A解析根据几何体的三视图可知，该几何体是一个正方体和一个半圆柱的组合体，其中正方体的棱长为2，半圆柱的底面半径为1，母线长为2，故该几何体的表面积为4×5＋2×π＋2×12π＝20＋3π.4.如图，在四棱锥V －ABCD 中，底面ABCD 为正方形，E 、F 分别为侧棱VC 、VB 上的点，且满足VC ＝3EC ，AF ∥平面BDE ，则VB FB＝________.答案 2解析连接AC 交BD 于点O ，连接EO ，取VE 的中点M ，连接AM ，MF ，∵VC ＝3EC ，∴VM ＝ME ＝EC ，又AO ＝CO ，∴AM ∥EO ，又EO ⊂平面BDE ， ∴AM ∥平面BDE ，又AF ∥平面BDE ，AM ∩AF ＝A ， ∴平面AMF ∥平面BDE ，又MF ⊂平面AMF ，∴MF ∥平面BDE ，又MF ⊂平面VBC ，平面VBC ∩平面BDE ＝BE ， ∴MF ∥BE ，∴VF ＝FB ，∴VB FB＝2.5.如图，在三棱锥P －ABC 中，D ，E ，F 分别为棱PC ，AC ，AB 的中点．若PA ⊥AC ，PA ＝6，BC ＝8，DF ＝5.则直线PA 与平面DEF 的位置关系是________；平面BDE 与平面ABC 的位置关系是________．(填“平行”或“垂直”)答案平行垂直解析 ①因为D ，E 分别为棱PC ，AC 的中点，所以DE ∥PA .又因为PA ⊄平面DEF ，DE ⊂平面DEF ，所以直线PA ∥平面DEF .②因为D ，E ，F 分别为棱PC ，AC ，AB 的中点，PA ＝6，BC ＝8，所以DE ∥PA ，DE ＝12PA ＝3，EF ＝12BC ＝4.又因为DF ＝5，故DF 2＝DE 2＋EF 2，所以∠DEF ＝90°，即DE ⊥EF . 又PA ⊥AC ，DE ∥PA ，所以DE ⊥AC .因为AC ∩EF ＝E ，AC ⊂平面ABC ，EF ⊂平面ABC ，所以DE ⊥平面ABC ，又DE ⊂平面BDE ，所以平面BDE ⊥平面ABC .题型一求空间几何体的表面积与体积例1 (2016·全国甲卷)如图，菱形ABCD 的对角线AC 与BD 交于点O ，点E ，F 分别在AD ，CD 上，AE ＝CF ，EF 交BD 于点H ，将△DEF 沿EF 折到△D ′EF 的位置．(1)证明：AC ⊥HD ′；(2)若AB ＝5，AC ＝6，AE ＝54，OD ′＝22，求五棱锥D ′ABCFE 的体积．(1)证明由已知得AC ⊥BD ，AD ＝CD ，又由AE ＝CF 得AE AD ＝CF CD，故AC ∥EF ，由此得EF ⊥HD ，折后EF 与HD 保持垂直关系，即EF ⊥HD ′，所以AC ⊥HD ′.(2)解由EF ∥AC 得OH DO ＝AE AD ＝14.由AB ＝5，AC ＝6得DO ＝BO ＝AB 2－AO 2＝4，所以OH ＝1，D ′H ＝DH ＝3，于是OD ′2＋OH 2＝(22)2＋12＝9＝D ′H 2，故OD ′⊥OH .由(1)知AC ⊥HD ′，又AC ⊥BD ，BD ∩HD ′＝H ，所以AC ⊥平面DHD ′，于是AC ⊥OD ′，又由OD ′⊥OH ，AC ∩OH ＝O ，所以OD ′⊥平面ABC . 又由EF AC ＝DH DO 得EF ＝92.五边形ABCFE 的面积S ＝12×6×8－12×92×3＝694.所以五棱锥D ′ABCFE 的体积V ＝13×694×22＝2322.思维升华 (1)若所给定的几何体是柱体、锥体或台体等规则几何体，则可直接利用公式进行求解．其中，等积转换法多用来求三棱锥的体积．(2)若所给定的几何体是不规则几何体，则将不规则的几何体通过分割或补形转化为规则几何体，再利用公式求解．(3)若以三视图的形式给出几何体，则应先根据三视图得到几何体的直观图，然后根据条件求解．正三棱锥的高为1，底面边长为26，内有一个球与它的四个面都相切(如图)．求：(1)这个正三棱锥的表面积；(2)这个正三棱锥内切球的表面积与体积．解 (1)底面正三角形中心到一边的距离为13×32×26＝2，则正棱锥侧面的斜高为12＋ 2 2＝ 3. ∴S 侧＝3×12×26×3＝9 2.∴S 表＝S 侧＋S 底＝92＋12×32×(26)2＝92＋6 3.(2)设正三棱锥P －ABC 的内切球球心为O ，连接OP ，OA ，OB ，OC ，而O 点到三棱锥的四个面的距离都为球的半径r .∴V P －ABC ＝V O －PAB ＋V O －PBC ＋V O －PAC ＋V O －ABC ＝13S 侧·r ＋13S △ABC ·r ＝13S 表·r ＝(32＋23)r .又V P －ABC ＝13×12×32×(26)2×1＝23，∴(32＋23)r ＝23，得r ＝2332＋23＝23 32－2318－12＝6－2.∴S 内切球＝4π(6－2)2＝(40－166)π.V 内切球＝43π(6－2)3＝83(96－22)π.题型二空间点、线、面的位置关系例2 (2016·济南模拟)如图，在三棱柱ABC －A 1B 1C 1中，侧棱垂直于底面，AB ⊥BC ，AA 1＝AC ＝2，BC ＝1，E ，F 分别是A 1C 1，BC 的中点．(1)求证：平面ABE ⊥平面B 1BCC 1； (2)求证：C 1F ∥平面ABE ； (3)求三棱锥E －ABC 的体积．(1)证明在三棱柱ABC －A 1B 1C 1中，BB 1⊥底面ABC . 因为AB ⊂平面ABC ，所以BB 1⊥AB .又因为AB ⊥BC ，BC ∩BB 1＝B ，所以AB ⊥平面B 1BCC 1. 又AB ⊂平面ABE ，所以平面ABE ⊥平面B 1BCC 1.(2)证明方法一如图1，取AB 中点G ，连接EG ，FG . 因为E ，F 分别是A 1C 1，BC 的中点，所以FG ∥AC ，且FG ＝12AC .因为AC ∥A 1C 1，且AC ＝A 1C 1，所以FG ∥EC 1，且FG ＝EC 1，所以四边形FGEC 1为平行四边形，所以C 1F ∥EG .又因为EG ⊂平面ABE ，C 1F ⊄平面ABE ，所以C 1F ∥平面ABE .方法二如图2，取AC 的中点H ，连接C 1H ，FH . 因为H ，F 分别是AC ，BC 的中点，所以HF ∥AB ，又因为E ，H 分别是A 1C 1，AC 的中点，所以EC 1綊AH ，所以四边形EAHC 1为平行四边形，所以C 1H ∥AE ，又C 1H ∩HF ＝H ，AE ∩AB ＝A ，所以平面ABE ∥平面C 1HF ，又C 1F ⊂平面C 1HF ，所以C 1F ∥平面ABE .(3)解因为AA 1＝AC ＝2，BC ＝1，AB ⊥BC ，所以AB ＝AC 2－BC 2＝ 3. 所以三棱锥E －ABC 的体积V ＝13S △ABC ·AA 1＝13×12×3×1×2＝33. 思维升华 (1)①证明面面垂直，将“面面垂直”问题转化为“线面垂直”问题，再将“线面垂直”问题转化为“线线垂直”问题．②证明C 1F ∥平面ABE ：(ⅰ)利用判定定理，关键是在平面ABE 中找(作)出直线EG ，且满足C 1F ∥EG .(ⅱ)利用面面平行的性质定理证明线面平行，则先要确定一个平面C 1HF 满足面面平行，实施线面平行与面面平行的转化．(2)计算几何体的体积时，能直接用公式时，关键是确定几何体的高，不能直接用公式时，注意进行体积的转化．如图，在三棱锥S －ABC 中，平面SAB ⊥平面SBC ，AB ⊥BC ，AS ＝AB .过A 作AF ⊥SB ，垂足为F ，点E ，G 分别是棱SA ，SC 的中点．\求证：(1)平面EFG ∥平面ABC ； (2)BC ⊥SA .证明 (1)由AS ＝AB ，AF ⊥SB 知F 为SB 中点，则EF ∥AB ，FG ∥BC ，又EF ∩FG ＝F ，AB ∩BC ＝B ，因此平面EFG ∥平面ABC .(2)由平面SAB ⊥平面SBC ，平面SAB ∩平面SBC ＝SB ，AF ⊂平面SAB ，AF ⊥SB ，所以AF ⊥平面SBC ，则AF ⊥BC .又BC ⊥AB ，AF ∩AB ＝A ，则BC ⊥平面SAB ，又SA ⊂平面SAB ，因此BC ⊥SA . 题型三平面图形的翻折问题例3 (2015·陕西)如图1，在直角梯形 ABCD 中，AD ∥BC ，∠BAD ＝π2，AB ＝BC ＝12AD ＝a ，E是AD 的中点，O 是AC 与BE 的交点．将△ABE 沿BE 折起到图2中△A 1BE 的位置，得到四棱锥A 1-BCDE .(1)证明：CD ⊥平面A 1OC ；(2)当平面A 1BE ⊥平面BCDE 时，四棱锥A 1-BCDE 的体积为362，求a 的值． (1)证明在题图1中，连接EC ，因为AB ＝BC ＝12AD ＝a ，∠BAD ＝π2，AD ∥BC ，E 为AD 中点，所以BC 綊ED ，BC 綊AE ，所以四边形BCDE 为平行四边形，故有CD ∥BE ，所以四边形ABCE 为正方形，所以BE ⊥AC ，即在题图2中，BE ⊥A 1O ，BE ⊥OC ，且A 1O ∩OC ＝O ，从而BE ⊥平面A 1OC ，又CD ∥BE ，所以CD ⊥平面A 1OC .(2)解由已知，平面A 1BE ⊥平面BCDE ，且平面A 1BE ∩平面BCDE ＝BE ，又由(1)知，A 1O ⊥BE ，所以A 1O ⊥平面BCDE ，即A 1O 是四棱锥A 1-BCDE 的高，由题图1知，A 1O ＝22AB ＝22a ，平行四边形BCDE 的面积S ＝BC ·AB ＝a 2，从而四棱锥A 1-BCDE 的体积为V ＝13×S ×A 1O ＝13×a 2×22a ＝26a 3，由26a 3＝362，得a ＝6. 思维升华平面图形的翻折问题，关键是搞清翻折前后图形中线面位置关系和度量关系的变化情况．一般地，翻折后还在同一个平面上的性质不发生变化，不在同一个平面上的性质发生变化．(2017·深圳月考)如图(1)，四边形ABCD 为矩形，PD ⊥平面ABCD ，AB ＝1，BC＝PC ＝2，作如图(2)折叠，折痕EF ∥DC .其中点E ，F 分别在线段PD ，PC 上，沿EF 折叠后，点P 叠在线段AD 上的点记为M ，并且MF ⊥CF .(1)证明：CF ⊥平面MDF ； (2)求三棱锥M －CDE 的体积．(1)证明因为PD ⊥平面ABCD ，AD ⊂平面ABCD ，所以PD ⊥AD .又因为ABCD 是矩形，CD ⊥AD ，PD 与CD 交于点D ，所以AD ⊥平面PCD .又CF ⊂平面PCD ，所以AD ⊥CF ，即MD ⊥CF . 又MF ⊥CF ，MD ∩MF ＝M ，所以CF ⊥平面MDF . (2)解因为PD ⊥DC ，PC ＝2，CD ＝1，∠PCD ＝60°，所以PD ＝3，由(1)知FD ⊥CF ，在直角三角形DCF 中，CF ＝12CD ＝12.如图，过点F 作FG ⊥CD 交CD 于点G ，得FG ＝FC sin 60°＝12×32＝34，所以DE ＝FG ＝34，故ME ＝PE ＝3－34＝334，所以MD ＝ME 2－DE 2＝334 2－ 34 2＝62.S △CDE ＝12DE ·DC ＝12×34×1＝38. 故V M －CDE ＝13MD ·S △CDE ＝13×62×38＝216.题型四立体几何中的存在性问题例4 (2016·四川双流中学月考)如图，在长方体ABCD －A 1B 1C 1D 1中，平面BMD 1N 与棱CC 1，AA 1分别交于点M ，N ，且M ，N 均为中点．(1)求证：AC ∥平面BMD 1N .(2)若AD ＝CD ＝2，DD 1＝22，O 为AC 的中点．BD 1上是否存在动点F ，使得OF ⊥平面BMD 1N ？若存在，求出点F 的位置，并加以证明；若不存在，请说明理由． (1)证明连接MN .因为M ，N 分别为CC 1，AA 1的中点，所以AN ＝12AA 1，CM ＝12CC 1.又因为AA 1∥CC 1，且AA 1＝CC 1，所以AN ∥CM ，且AN ＝CM ，所以四边形ACMN 为平行四边形，所以AC ∥MN . 因为MN ⊂平面BMD 1N ，AC ⊄平面BMD 1N ，所以AC ∥平面BMD 1N .(2)解当点F 满足D 1F ＝3BF 时，OF ⊥平面BMD 1N ，证明如下：连接BD ，则BD 经过点O ，取BD 1的中点G ，连接OF ，DG ，又D 1F ＝3BF ，所以OF 为三角形BDG 的中位线，所以OF ∥DG .因为BD ＝22＝DD 1，且G 为BD 1的中点，所以BD 1⊥DG ，所以BD 1⊥OF .因为底面ABCD 为正方形，所以AC ⊥BD . 又DD 1⊥底面ABCD ，所以AC ⊥DD 1，又BD ∩DD 1＝D ，所以AC ⊥平面BDD 1，又OF ⊂平面BDD 1，所以AC ⊥OF .由(1)知AC∥MN，所以MN⊥OF.又MN，BD1是平面四边形BMD1N的对角线，所以它们必相交，所以OF⊥平面BMD1N.思维升华对于线面关系中的存在性问题，首先假设存在，然后在该假设条件下，利用线面关系的相关定理、性质进行推理论证，寻找假设满足的条件，若满足则肯定假设，若得出矛盾的结论则否定假设．如图，在直四棱柱ABCD－A1B1C1D1中，已知DC＝DD1＝2AD＝2AB，AD⊥DC，AB∥DC.(1)求证：D1C⊥AC1；(2)问在棱CD上是否存在点E，使D1E∥平面A1BD.若存在，确定点E位置；若不存在，说明理由．(1)证明在直四棱柱ABCD－A1B1C1D1中，连接C1D，∵DC＝DD1，∴四边形DCC1D1是正方形，∴DC1⊥D1C.又AD⊥DC，AD⊥DD1，DC∩DD1＝D，∴AD⊥平面DCC1D1，又D1C⊂平面DCC1D1，∴AD⊥D1C.∵AD⊂平面ADC1，DC1⊂平面ADC1，且AD∩DC1＝D，∴D1C⊥平面ADC1，又AC1⊂平面ADC1，∴D1C⊥AC1.(2)解假设存在点E，使D1E∥平面A1BD.连接AD1，AE，D1E，设AD1∩A1D＝M，BD∩AE＝N，连接MN，∵平面AD1E∩平面A1BD＝MN，要使D1E∥平面A1BD，可使MN∥D1E，又M是AD1的中点，则N是AE的中点．又易知△ABN≌△EDN，∴AB＝DE.即E是DC的中点．综上所述，当E是DC的中点时，可使D1E∥平面A1BD.1．(2016·北京顺义区一模)如图所示，已知平面α∩平面β＝l，α⊥β.A，B是直线l上的两点，C，D是平面β内的两点，且AD⊥l，CB⊥l，DA＝4，AB＝6，CB＝8.P是平面α上的一动点，且有∠APD＝∠BPC，则四棱锥P－ABCD体积的最大值是( )A．48 B．16 C．24 3 D．144答案 C解析由题意知，△PAD，△PBC是直角三角形，又∠APD＝∠BPC，所以△PAD∽△PBC.因为DA＝4，CB＝8，所以PB＝2PA.作PM⊥AB于点M，由题意知，PM⊥β.令AM＝t(0<t<6)，则PA2－t2＝4PA2－(6－t)2，所以PA2＝12－4t.所以PM＝12－4t－t2，即为四棱锥P－ABCD的高，又底面ABCD 为直角梯形，S ＝12×(4＋8)×6＝36.所以V ＝13×36×12－4t －t 2＝12－ t ＋2 2＋16≤12×12＝24 3.2．(2016·江西赣中南五校第一次联考)已知m ，n 是两条不同的直线，α，β，γ是三个不同的平面，则下列命题中正确的是( ) A ．若α⊥γ，α⊥β，则γ∥β B ．若m ∥n ，m ⊂α，n ⊂β，则α∥β C ．若m ∥n ，m ⊥α，n ⊥β，则α∥β D ．若m ∥n ，m ∥α，则n ∥α 答案 C解析对于A ，若α⊥γ，α⊥β，则γ∥β或相交；对于B ，若m ∥n ，m ⊂α，n ⊂β，则α∥β或相交；对于D ，若m ∥n ，m ∥α，则n ∥α或n ⊂α.故选C.3．(2016·唐山模拟)如图，ABCD －A 1B 1C 1D 1为正方体，连接BD ，AC 1，B 1D 1，CD 1，B 1C ，现有以下几个结论：①BD ∥平面CB 1D 1；②AC 1⊥平面CB 1D 1；③CB 1与BD 为异面直线．其中所有正确结论的序号为________．答案 ①②③解析由题意可知，BD ∥B 1D 1，又B 1D 1⊂平面CB 1D 1，BD ⊄平面CB 1D 1，所以BD ∥平面CB 1D 1，①正确；易知AC 1⊥B 1D 1，AC 1⊥B 1C ，又B 1D 1∩B 1C ＝B 1，所以AC 1⊥平面CB 1D 1，②正确；由异面直线的定义可知③正确．4.如图梯形ABCD 中，AD ∥BC ，∠ABC ＝90°，AD ∶BC ∶AB ＝2∶3∶4，E 、F 分别是AB 、CD 的中点，将四边形ADFE 沿直线EF 进行翻折，给出四个结论：①DF⊥BC；②BD⊥FC；③平面DBF⊥平面BFC；④平面DCF⊥平面BFC.在翻折过程中，可能成立的结论是________．(填写结论序号)答案②③解析因为BC∥AD，AD与DF相交不垂直，所以BC与DF不垂直，则①错误；设点D在平面BCF上的射影为点P，当BP⊥CF时就有BD⊥FC，而AD∶BC∶AB＝2∶3∶4，可使条件满足，所以②正确；当点P落在BF上时，DP⊂平面BDF，从而平面BDF⊥平面BCF，所以③正确；因为点D的投影不可能在FC上，所以平面DCF⊥平面BFC不成立，即④错误．故答案为②③.5.如图，在正方体ABCD－A1B1C1D1中，点E是棱BC的中点，点F是棱CD上的动点，当CFFD＝______时，D1E⊥平面AB1F.答案 1解析如图，连接A1B，则A1B是D1E在平面ABB1A1内的射影．∵AB1⊥A1B，∴D1E⊥AB1，又∵D1E⊥平面AB1F⇒D1E⊥AF.连接DE，则DE是D1E在底面ABCD内的射影，∴D1E⊥AF⇒DE⊥AF.∵ABCD是正方形，E是BC的中点，∴当且仅当F 是CD 的中点时，DE ⊥AF ，即当点F 是CD 的中点时，D 1E ⊥平面AB 1F ， ∴CF FD＝1时，D 1E ⊥平面AB 1F .6．(2016·咸阳模拟)如图，梯形ABEF 中，AF ∥BE ，AB ⊥AF ，且AB ＝BC ＝AD ＝DF ＝2CE ＝2，沿DC 将梯形CDFE 折起，使得平面CDFE ⊥平面ABCD .(1)证明：AC ∥平面BEF ； (2)求三棱锥D －BEF 的体积．(1)证明如图，取BF 的中点M ，设AC 与BD 交点为O ，连接MO ，ME .由题设知，CE 綊12DF ，MO 綊12DF ，∴CE 綊MO ，故四边形OCEM 为平行四边形， ∴EM ∥CO ，即EM ∥AC .又AC ⊄平面BEF ，EM ⊂平面BEF ， ∴AC ∥平面BEF .(2)解 ∵平面CDFE ⊥平面ABCD ，平面CDFE ∩平面ABCD ＝DC ，BC ⊥DC ， ∴BC ⊥平面DEF .∴三棱锥D －BEF 的体积为V D －BEF ＝V B －DEF ＝13S △DEF ·BC ＝13×12×2×2×2＝43.7．(2016·山东牟平一中期末)如图，在四棱柱ABCD －A 1B 1C 1D 1中，AC ⊥B 1D ，BB 1⊥底面ABCD ，E ，F ，H 分别为AD ，CD ，DD 1的中点，EF 与BD 交于点G .(1)证明：平面ACD1⊥平面BB1D；(2)证明：GH∥平面ACD1.证明(1)∵BB1⊥平面ABCD，AC⊂平面ABCD，∴AC⊥BB1.又AC⊥B1D，BB1∩B1D＝B1，∴AC⊥平面BB1D.∵AC⊂平面ACD1，∴平面ACD1⊥平面BB1D.(2)设AC∩BD＝O，连接OD1.∵E，F分别为AD，CD的中点，EF∩OD＝G，∴G为OD的中点．∵H为DD1的中点，∴HG∥OD1.∵GH⊄平面ACD1，OD1⊂平面ACD1，∴GH∥平面ACD1.8．(2016·北京东城区一模)如图，在四棱锥P－ABCD中，PA⊥平面ABCD，底面ABCD是菱形，点O是对角线AC与BD的交点，AB＝2，∠BAD＝60°，M是PD的中点．(1)求证：OM∥平面PAB；(2)求证：平面PBD⊥平面PAC.(3)当三棱锥C －PBD 的体积等于32时，求PA 的长． (1)证明因为在△PBD 中，O ，M 分别是BD ，PD 的中点，所以OM ∥PB .又OM ⊄平面PAB ，PB ⊂平面PAB ，所以OM ∥平面PAB .(2)证明因为底面ABCD 是菱形，所以BD ⊥AC . 因为PA ⊥平面ABCD ，BD ⊂平面ABCD ，所以PA ⊥BD .又AC ∩PA ＝A ，所以BD ⊥平面PAC . 又BD ⊂平面PBD ，所以平面PBD ⊥平面PAC .(3)解因为底面ABCD 是菱形，且AB ＝2， ∠BAD ＝60°，所以S △BCD ＝ 3.又V C －PBD ＝V P －BCD ，三棱锥P －BCD 的高为PA ，所以13×3×PA ＝32，解得PA ＝32.9．(2016·大连测试)如图，已知三棱柱ABC －A ′B ′C ′中，平面BCC ′B ′⊥底面ABC ，BB ′⊥AC ，底面ABC 是边长为2的等边三角形，AA ′＝3，E ，F 分别在棱AA ′，CC ′上，且AE ＝C ′F ＝2.(1)求证：BB ′⊥底面ABC ；(2)在棱A ′B ′上找一点M ，使得C ′M ∥平面BEF ，并给出证明． (1)证明如图，取BC 的中点O ，连接AO ，∵三角形ABC是等边三角形，∴AO⊥BC.∵平面BCC′B′⊥底面ABC，AO⊂平面ABC，平面BCC′B′∩平面ABC＝BC，∴AO⊥平面BCC′B′.又BB′⊂平面BCC′B′，∴AO⊥BB′.又BB′⊥AC，AO∩AC＝A，AO⊂平面ABC，AC⊂平面ABC，∴BB′⊥底面ABC.(2)解显然点M不是点A′，B′，若棱A′B′上存在一点M，使得C′M∥平面BEF，过点M作MN∥AA′交BE于N，连接FN，MC′，如图，∴MN∥C′F，即C′M和FN共面，又平面MNFC′∩平面BEF＝FN，∴C′M∥FN，∴四边形C′MNF为平行四边形，∴MN＝2，∴MN是梯形A′B′BE的中位线，M为A′B′的中点．故当M为A′B′的中点时，C′M∥平面BEF.。

2018高考数学立体几何含答案(最新整理)

2018高考数学立体几何答案1.（本小题14分）如图，在三棱柱ABC −中，平面ABC ，D ，E ，F ，G 分别为111A B C 1CC ⊥，AC ，，的中点，AB=BC，AC ==2．1AA 11A C 1BB 1AA（Ⅰ）求证：AC ⊥平面BEF ；（Ⅱ）求二面角B−CD −C 1的余弦值；（Ⅲ）证明：直线FG 与平面BCD 相交．【解析】（1）在三棱柱111ABC A B C -中，1CC ⊥Q 平面ABC ，∴四边形11A ACC 为矩形．又E ，F 分别为AC ，11A C 的中点，AC EF ∴⊥，AB BC =Q ，AC BE ∴⊥，AC ∴⊥平面BEF ．（2）由（1）知AC EF ⊥，AC BE ⊥，1EF CC ∥．又1CC ⊥平面ABC ，EF ∴⊥平面ABC ．BE ⊂Q 平面ABC ，EF BE ∴⊥．如图建立空间直角坐称系E xyz -．由题意得()0,2,0B ，()1,0,0C -，()1,0,1D ，()0,0,2F ，()0,2,1G ，()=2,01CD ∴u u u r ,，()=1,2,0CB u u r ，设平面BCD 的法向量为(),a b c =,n ，00CD CB ⎧⋅=⎪∴⎨⋅=⎪⎩u u u r u u r n n ，2020a c a b +=⎧∴⎨+=⎩，令2a =，则1b =-，4c =-，∴平面BCD 的法向量()2,14=--，,n ，又Q 平面1CDC 的法向量为()=0,2,0EB u u r ，cos =EB EB EB⋅∴<⋅>=-u u r u u r u u r n n n ．由图可得二面角1B CD C --为钝角，所以二面角1B CD C --的余弦值为．（3）平面BCD 的法向量为()2,1,4=--n ，()0,2,1G Q ，()0,0,2F ，()=02,1GF ∴-u u u r ,，2GF ∴⋅=-u u u r n ，∴n 与GF u u u r 不垂直，GF ∴与平面BCD 不平行且不在平面BCD 内，GF ∴与平面BCD 相交2．（本小题14分）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，平面PAD ⊥平面ABCD ，PA PD ⊥，PA PD =，E ，F 分别为AD ，PB 的中点．（1）求证：PE BC ⊥；（2）求证：平面PAB ⊥平面PCD ；（3）求证：EF ∥平面PCD ．【解析】（1）PA PD =Q ，且E 为AD 的中点，PE AD ∴⊥，Q 底面ABCD 为矩形，BC AD ∴∥，PE BC ∴⊥．（2）Q 底面ABCD 为矩形，AB AD ∴⊥，Q 平面PAD ⊥平面ABCD ，AB ∴⊥平面PAD ，AB PD ∴⊥．又PA PD ⊥，PD ⊥Q 平面PAB ，∴平面PAB ⊥平面PCD ．（3）如图，取PC 中点G ，连接FG ，GD ．F Q ，G 分别为PB 和PC 的中点，FG BC ∴∥，且12FG BC =，Q 四边形ABCD 为矩形，且E 为AD 的中点，ED BC ∴∥，12DE BC =，ED FG ∴∥，且ED FG =，∴四边形EFGD 为平行四边形，EF GD ∴∥，又EF ⊄平面PCD ，GD ⊂平面PCD ，EF ∴∥平面PCD ．3．（12分）如图，四边形ABCD 为正方形，,E F 分别为,AD BC 的中点，以DF 为折痕把DFC △折起，使点C 到达点P 的位置，且PF BF ⊥.（1）证明：平面PEF ⊥平面ABFD ；（2）求DP 与平面ABFD 所成角的正弦值.解答：（1）,E F 分别为,AD BC 的中点，则//EF AB ，∴EF BF ⊥，又PF BF ⊥，EF PF F ⋂=，∴BF ⊥平面PEF ，BE ⊂平面ABFD ，∴平面PEF ⊥平面ABFD .（2）PF BF ⊥，//BF ED ，∴PF ED ⊥，又PF PD ⊥，ED DP D ⋂=，∴PF ⊥平面PED ，∴PF PE ⊥，设4AB =，则4EF =，2PF =，∴PE =，过P 作PH EF ⊥交EF 于H 点，由平面PEF ⊥平面ABFD ，∴PH ⊥平面ABFD ，连结DH ，则PDH ∠即为直线DP 与平面ABFD 所成的角，由PE PF EF PH ⋅=⋅，∴PH ==，而4PD =，∴sin PH PDH PD ∠==，∴DP 与平面ABFD .4．（12分）如图，在三棱锥P ABC -中，AB BC ==，4PA PB PC AC ====，O 为AC 的中点．（1）证明：PO ⊥平面ABC ；（2）若点M 在棱BC 上，且二面角M PA C --为30︒，求PC 与平面PAM 所成角的正弦值．C【解析】（1）因为4AP CP AC ===，O 为AC 的中点，所以OP AC ⊥，且OP =，连结OB．因为AB BC ==，所以ABC △为等腰直角三角形，且OB AC ⊥，122OB AC ==，由222OP OB PB +=知PO OB ⊥，由,OP OB OP AC ⊥⊥知PO ⊥平面ABC ．（2）如图，以O 为坐标原点，OB u u u r 的方向为x 轴正方向，建立空间直角坐标系O xyz -．由已知得()0,0,0O ，()2,0,0B ，()0,2,0A -，()0,2,0C，(P，(AP =u u u r ，取平面PAC 的法向量()2,0,0OB =u u u r ，设()(),2,002M a a a -<≤，则(),4,0AM a a =-u u u r ，设平面PAM 的法向量为(),,x y z =n ．由0AP ⋅=u u u r n ，0AM ⋅=u u u r n ，得()2040y ax a y ⎧+=⎪⎨+-=⎪⎩，可取))4,a a =--n ，cos ,OB ∴<>=u u u rn ，由已知得cos ,OB <>=u u u r n，，解得4a =-（舍去），43a =，43⎛⎫∴=- ⎪⎪⎝⎭n ，又(0,2,PC =-u uu r Q ，所以cos ,PC <>=u u u r n ．所以PC 与平面PAM ．5．（12分）如图，边长为2的正方形ABCD 所在的平面与半圆弧A CD所在平面垂直，M 是A CD上异于C，D的点．（1）证明：平面AMD⊥平面BMC；（2）当三棱锥M ABC-体积最大时，求面MAB与面MCD所成二面角的正弦值．解答：（1）∵正方形半圆面，ABCD⊥CMD∴半圆面，∴平面.AD⊥CMD AD⊥MCD∵在平面内，∴，又∵是半圆弧上异于的点，∴CM MCD AD CM⊥M CD,C D .又∵，∴平面，∵在平面内，∴平面CM MD⊥AD DM D=I CM⊥ADM CM BCM平面.BCM⊥ADM（2）如图建立坐标系：∵面积恒定，ABCS∆∴，最大.MO CD⊥M ABCV-，，，，,(0,0,1)M(2,1,0)A-(2,1,0)B(0,1,0)C(0,1,0)D-设面的法向量为，设面的法向量为，MAB111(,,)m x y z=u rMCD222(,,)n x y z=r，，(2,1,1)MA=--(2,1,1)MB=-，，(0,1,1)MC=-(0,1,1)MD=--，11111120(1,0,2)20x y zmx y z--=⎧⇒=⎨+-=⎩同理，，(1,0,0)n=∴，∴.cosθ==sinθ=6.（本题满分14分，第1小题满分6分，第2小题满分8分）已知圆锥的顶点为P，底面圆心为O，半径为2（1）设圆锥的母线长为4，求圆锥的体积；（2）设PO =4，OA ，OB 是底面半径，且∠AOB =90°，M 为线段AB 的中点，如图，求异面直线PM 与OB 所成的角的大小.7.(本小题满分13分)如图，且AD =2BC ，,且EG =AD ，且AD BC ∥AD CD ⊥EG AD ∥CD FG ∥CD =2FG ，，DA =DC =DG =2.DG ABCD ⊥平面（I ）若M 为CF 的中点，N 为EG 的中点，求证：；MN CDE ∥平面（II ）求二面角的正弦值；E BCF --（III ）若点P 在线段DG 上，且直线BP 与平面ADGE 所成的角为60°，求线段DP 的长.【解析】依题意，可以建立以D 为原点，分别以DA ，DC ，DG 的方向为x 轴，y 轴，z 轴的正方向的空间直角坐标系（如图），可得()0,0,0D ，()2,0,0A ，()1,2,0B ，()0,2,0C ，()2,0,2E ，()0,1,2F ，()0,0,2G ，30,,12M ⎛⎫ ⎪⎝⎭，()1,0,2N ．（1）依题意()0,2,0DC = ，()2,0,2DE = ．设()0,,x y z =n 为平面CDE 的法向量，则0000DC DE ⎧⋅=⎪⎨⋅=⎪⎩ n n 即20220y x z =+=⎧⎨⎩，不妨令–1z =，可得()01,0,1=-n ．又31,,12MN ⎛⎫= ⎪⎝⎭-，可得00MN ⋅= n ，又因为直线MN ⊄平面CDE ，所以MN ∥平面CDE ．（2）依题意，可得()–1,0,0BC = ，()1,2,2BE =- ，()0,1,2CF =- ．设(),,x y z =n 为平面BCE 的法向量，则00BC BE ⎧⋅=⎪⎨⋅=⎪⎩ n n 即0220x x y z -=-+=⎧⎨⎩，不妨令1z =，可得()0,1,1=n ．设(),,x y z =m 为平面BCF 的法向量，则00BC BF ⎧⋅=⎪⎨⋅=⎪⎩m m 即020x y z -=-+=⎧⎨⎩，不妨令1z =，可得()0,2,1=m ．因此有cos ,⋅<>==m n m n m n，于是sin ,m n <>=．所以，二面角––E BC F．（3）设线段DP 的长为[]()0,2h h ∈，则点P 的坐标为()0,0,h ，可得()1,2,BP h =-- ．易知，()0,2,0DC = 为平面ADGE 的一个法向量，故cos BP DC BP DC BP DC ⋅<⋅>== ，sin 60=︒=，解得[]0,2h =．所以线段DP．8．（本题满分15分）如图，已知多面体ABCA 1B 1C 1，A 1A ，B 1B ，C 1C 均垂直于平面ABC ，∠ABC =120°，A 1A =4，C 1C =1，AB =BC =B 1B =2．（Ⅰ）证明：AB 1⊥平面A 1B 1C 1；（Ⅱ）求直线AC 1与平面ABB 1所成的角的正弦值．解答：（1）∵，且平面，12AB B B ==1B B ⊥ABC∴，∴.1B B AB ⊥1AB =同理，1AC ===过点作的垂线段交于点，则且，∴.1C 1B B 1B B G 12C G BC ==11B G =11B C =在中，，11AB C ∆2221111AB B C AC +=∴，①111AB B C ⊥过点作的垂线段交于点.1B 1A A 1A A H则，，∴.12B H AB ==12A H =11A B =在中，，11A B A ∆2221111AA AB A B =+∴，②111AB A B ⊥综合①②，∵，平面，平面，11111A B B C B ⋂=11A B ⊂111A B C 11B C ⊂111A B C ∴平面.1AB ⊥111A B C （2）过点作的垂线段交于点，以为原点，以所在直线为轴，B AB AC I B AB x 以所在直线为轴，以所在直线为轴，建立空间直角坐标系.BI y 1B B z B xyz -则，，，，(0,0,0)B (2,0,0)A -1(0,0,2)B 1C 设平面的一个法向量，1ABB (,,)n a b c = 则，令，则，1020200n AB a c n BB ⎧⋅==⎧⎪⇒⎨⎨=⋅=⎩⎪⎩ 1b =(0,1,0)n = 又∵，.1AC =1cos ,n AC <>== 由图形可知，直线与平面所成角为锐角，设与平面夹角为.1AC 1ABB 1AC 1ABB α∴.sin α=9．（本小题满分14分）在平行六面体中，．1111ABCD A B C D -1111,AA AB AB B C =⊥求证：（1）；11AB A B C 平面∥（2）．111ABB A A BC ⊥平面平面【解析】（1）在平行六面体1111ABCD A B C D -中，11AB A B ∥．因为AB ⊄平面11A B C ，11A B ⊂平面11A B C ，所以AB ∥平面11A B C ．（2）在平行六面体1111ABCD A B C D -中，四边形11ABB A 为平行四边形．又因为1AA AB =，所以四边形11ABB A 为菱形，因此11AB A B ⊥．又因为111AB B C ⊥，11BC B C ∥，所以1AB BC ⊥．又因为1A B BC B = ，1A B ⊂平面1A BC ，BC ⊂平面1A BC ，所以1AB ⊥平面1A BC ．因为1AB ⊂平面11ABB A ，所以平面11ABB A ⊥平面1A BC ．。