北京市朝阳区2014-2015学年高二下学期期末统一考试数学(文)试题 Word版含答案

合集下载

2014北京朝阳区高三期末数学(文)试题

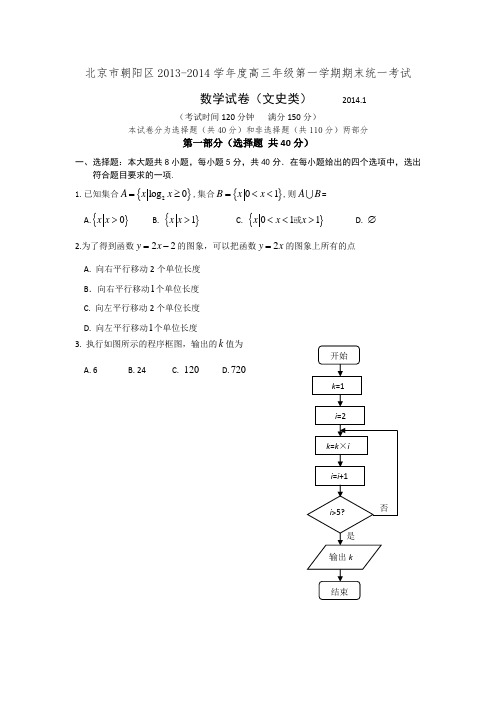
北京市朝阳区2013-2014学年度高三年级第一学期期末统一考试数学试卷（文史类） 2014.1（考试时间120分钟满分150分）本试卷分为选择题（共40分）和非选择题（共110分）两部分第一部分（选择题共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项. 1.已知集合{}2log 0A x x =≥,集合{}01B x x =<<,则AB =A.}{0x x >B. }{1x x >C. }{011x x x <<>或 D. ∅ 2.为了得到函数22y x =-的图象，可以把函数2y x =的图象上所有的点 A. 向右平行移动2个单位长度 B ．向右平行移动1个单位长度 C. 向左平行移动2个单位长度 D. 向左平行移动1个单位长度3. 执行如图所示的程序框图，输出的k 值为A. 6B. 24C. 120D.7204.已知函数2,0,()0,x x f x x ⎧≥⎪=<则2a =是()4f a =成立的A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件5. 若实数,x y 满足3200x y x y x +≥⎧⎪-≤⎨⎪≥⎩，则z y x =-的最小值为A. 0B. 1C. 2D. 3 6. 已知π02α<<，且4cos 5α=，则πtan()4α+等于 A. 7- B. 1- C. 34D. 77. 若双曲线C ：222(0)x y m m -=>与抛物线x y 162=的准线交于,A B两点，且AB =m 的值是A. 116B. 80C. 52D. 208. 函数2()3f x x x =-的图象为曲线1C ，函数2()4g x x =-的图象为曲线2C ，过x 轴上的动点(,0)(03)M a a ≤≤作垂直于x 轴的直线分别交曲线1C ，2C 于,A B 两点，则线段AB 长度的最大值为A ．2B ．4C ． 5D ．418第二部分（非选择题共110分）二、填空题：本大题共6小题，每小题5分，共30分.把答案填在答题卡上.9.已知数列{}n a 为等差数列，若1358a a a ++=，24620a a a ++=，则公差d = ． 10.已知三棱锥的三视图如图所示，则该三棱锥的体积是；表面积是 .俯视图侧视图正视图11. 某校为了解高一学生寒假期间的阅读情况，抽查并统计了100名同学的某一周阅读时间，绘制了频率分布直方图（如图所示），那么这100名学生中阅读时间在[4,8)小时内的人数为_____．12.直线l ：360x y --=被圆:C ()221(2)5x y -+-=截得的弦AB 的长是 .13.在△ABC 中， ︒=∠120A ，1AB AC ⋅=-，则AB AC = ；||BC 的最小值是 .14.用一个平面去截正方体，有可能截得的是以下平面图形中的 .（写出满足条件的图形序号）（1）正三角形（2）梯形（3）直角三角形（4）矩形三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. 15.（本题满分13分）已知函数22()3sin 2sin cos cos 2f x x x x x =++-. （Ⅰ）求()4f π的值；（Ⅱ）求函数()f x 的最小正周期及单调递增区间.16. （本题满分13分）甲、乙两名同学参加“汉字听写大赛”选拔性测试.在相同的测试条件下，两人5次测试第1次第2次第3次第4次第5次甲 58 55 76 92 88 乙6582878595（Ⅰ）请画出甲、乙两人成绩的茎叶图. 你认为选派谁参赛更好？说明理由（不用计算）；（Ⅱ）若从甲、乙两人5次的成绩中各随机抽取一个成绩进行分析，求抽到的两个成绩中至少有一个高于90分的概率.频率/组距 0.040.05 0.12 小时8 4 2610 1217. （本题满分14分）如图，在三棱锥P ABC -中，平面PAC ⊥平面ABC ,PA AC ⊥，AB BC ⊥．设D ，E 分别为PA ，AC 中点.（Ⅰ）求证：DE ∥平面PBC ；（Ⅱ）求证：BC ⊥平面PAB ;（Ⅲ）试问在线段AB 上是否存在点F ，使得过三点D ,E ,F 的平面内的任一条直线都与平面PBC 平行？若存在，指出点F 的位置并证明；若不存在，请说明理由．18.（本题满分13分）已知函数322()f x x ax a x =--，其中0a ≥.（Ⅰ）若(0)4f '=-，求a 的值，并求此时曲线()y f x =在点(1,(1))f 处的切线方程；（Ⅱ）求函数()f x 在区间[]0,2上的最小值. 19.（本题满分14分）已知椭圆C两焦点坐标分别为1(F,2F ，一个顶点为(0,1)A -. （Ⅰ）求椭圆C 的标准方程；（Ⅱ）是否存在斜率为(0)k k ≠的直线l ，使直线l 与椭圆C 交于不同的两点,M N ，满足AM AN =. 若存在，求出k 的取值范围；若不存在，说明理由.20. （本题满分13分）已知数列{}n a 的通项19210nn a n ⎛⎫⎛⎫=-⋅ ⎪ ⎪⎝⎭⎝⎭，n *∈N .(Ⅰ)求12,a a ；（Ⅱ）判断数列{}n a 的增减性,并说明理由；(Ⅲ) 设1n n n b a a +=-，求数列1n n b b +⎧⎫⎨⎬⎩⎭的最大项和最小项.DEBAPC。

2105年度朝阳高三数学期末文科试题带答案

北京市朝阳区2014-2015学年度高三年级第一学期期末统一考试数学试卷（文史类） 2015.1（考试时间120分钟满分150分）本试卷分为选择题（共40分）和非选择题（共110分）两部分第一部分（选择题共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项.1. 设i 为虚数单位，则复数1i z =-的模z =A. 1B.2C. 2D. 222. 已知全集U =R ，若集合{}20A x x x =-<，则U A =ðA. {0x x ≤，或}1x ≥B. {0x x <，或}1x > C. }{01x x << D.{}1x x ≥ 3.一个四棱锥的三视图如图所示，则该四棱锥的侧面中，直角三角形的个数为A.1B.2C.3D.44.执行如右图所示的程序框图,则输出的i 的值是A.3B.4C.5D.65.若,a b 是两个非零的平面向量，则 “a =b ”是“()()=0⋅a +b a b -”的A. 充分且不必要条件B. 必要且不充分条件C.充要条件D. 既不充分也不必要条件6. 如图，塔AB 底部为点B ，若,C D 两点相距为100m 并且与点B 在同一水平线上，现从,C D 两点测得塔顶A 的仰角分别为45o 和30o ，则塔AB 的高约为（精确到0.1m ，3 1.73≈，2 1.41≈）A. 36.5B. 115.6C. 120.5D. 136.5DBAC 正视侧视俯视7.已知定义在R 上的函数(1)1,()221,xx x x f x x ⎧+<⎪=⎨-≥⎪⎩若直线y a =与函数()f x 的图象恰有两个公共点，则实数a 的取值范围是A. ()0,2B.[)0,2C.(]0,2D. []1,28. 如图，在正方体中1111ABCD A B C D -，M 为BC 的中点，点N 在四边形11CDDC 及其内部运动．若11MN AC ⊥，则N 点的轨迹为A. 线段B. 圆的一部分C. 椭圆的一部分D.双曲线的一部分第二部分（非选择题共110分）二、填空题：本大题共6小题，每小题5分，共30分.把答案填在答题卡上．9. 双曲线22:14x C y -=的离心率是；渐近线方程是． 10.为了解某厂职工家庭人均月收入情况,调查了该厂80户居民月收入,列出频率分布表如下:按家庭人均月收入分组(百元)第一组[)10,16第二组[)16,22第三组[)22,28第四组[)28,34 第五组[)34,40 第六组[]40,46频率0.10.20.15a0.10.1则这80户居民中, 家庭人均月收入在[)2800,3400元之间的有户（用数字作答）；假设家庭人均月收入在第一组和第二组的为中低收入家庭,现从该厂全体职工家庭中随机抽取一个家庭,估计该家庭为中低收入家庭的概率是 .11. 已知圆C 的圆心位于第二象限且在直线21y x =+上，若圆C 与两个坐标轴都相切，则圆C 的标准方程是______.12. 某单位有职工共60人，为了开展社团活动，对全体职工进行问卷调查，其中喜欢体育运动的共28人，喜欢文艺活动的共26人，还有12人对体育运动和文艺活动都不喜欢，则喜欢体育运动但不喜欢文艺活动的人ABCD A 1B 1C 1D 1 M N .共有人.13. 在平面直角坐标系中，若关于,x y 的不等式组0,,(1)y y x y k x ≥⎧⎪≤⎨⎪≤-⎩表示一个三角形区域，则实数k 的取值范围是______.14. 设2212()cos (1)sin cos 3sin f x a x a x x x =+-+（22120a a +≠），若无论x 为何值，函数()f x 的图象总是一条直线，则12a a +的值是______.三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. 15. （本小题满分13分）某幼儿园有教师30人，对他们进行年龄状况和受教育程度的调查，其结果如下：本科研究生合计 35岁以下 5 2 7 35～50岁（含35岁和50岁） 1732050岁以上2 1 3（Ⅰ）从该幼儿园教师中随机抽取一人，求具有研究生学历的概率；（Ⅱ）从幼儿园所有具有研究生学历的教师中随机抽取2人，求有35岁以下的研究生或50岁以上的研究生的概率.16. （本小题满分13分）已知平面向量a =(sin ,cos )x x ，b =(sin ,cos )x x -，c =(cos ,sin )x x --，x ∈R ，函数()()f x =⋅-a b c .（Ⅰ）求函数()f x 的单调递减区间；（Ⅱ）若222f α⎛⎫= ⎪⎝⎭，求sin α的值.17. （本小题满分14分）如图，在四棱锥P ABCD -中，底面ABCD 是正方形，PD ⊥平面ABCD ．点E 是线段BD 的中点，点F 是线段PD 上的动点．（Ⅰ）若F 是PD 的中点，求证：EF //平面PBC ；（Ⅱ）求证： CE BF ⊥；（Ⅲ）若2AB =，3PD =，当三棱锥P BCF -的体积等于43时，试判断点F 在边PD 上的位置，并说明理由.18.（本小题满分13分）已知公比为q 的等比数列{}n a ()n *∈N 中，22a =，前三项的和为7.（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）若01q <<，设数列{}n b 满足12...n n b a a a =⋅⋅⋅，n *∈N ,求使01n b <<的n 的最小值.19. （本小题满分13分）已知函数()e ln x f x a x =-，a ∈R . （I ）若1x =是()f x 的极值点，求a 的值：（Ⅱ）当e a =时，求证：()e f x ≥.20. （本小题满分14分）已知离心率为32的椭圆2222:1(0)x y C a b a b +=>>与直线2x =相交于,P Q 两点（点P 在x 轴上方），且2PQ =．点,A B 是椭圆上位于直线PQ 两侧的两个动点，且APQ BPQ ∠=∠．（Ⅰ）求椭圆C 的标准方程；（Ⅱ）求四边形APBQ 面积的取值范围．DAPCEFB北京市朝阳区2014-2015学年度高三年级第一学期期末统一考试数学答案（文史类）2015.1一、选择题：（满分40分）题号 1 2 3 4 5 6 7 8答案 B A D B C D B A二、填空题：（满分30分）题号9 10 11 12 13 14答案52；12y x=±28;0.322111)()339x+y+-=（22 0k< 4（注：两空的填空，第一空3分，第二空2分）三、解答题：（满分80分）15. （本小题满分13分）解：（Ⅰ）设：“从该幼儿园教师中随机抽取一人，具有研究生学历”为事件A，由题可知幼儿园总共有教师30人，其中“具有研究生学历”的共6人.则61 ()==305 P A.答：从该幼儿园教师中随机抽取一人，具有研究生学历的概率为15. ………4分（Ⅱ）设幼儿园中35岁以下具有研究生学历的教师为A1，A2，35～50岁(含35岁和50岁)具有研究生学历的教师为B1，B2，B3，50岁以上具有研究生学历的教师为C，从幼儿园所有具有研究生学历的教师中随机抽取2人，所有可能结果有15个，它们是：（A1，A2），（A1，B1），（A1，B2），（A1，B3），（A1，C），（A2，B1），（A2，B2），（A2，B3），（A2，C），（B1，B2），（B1，B3），（B1，C），（B2，B3），（B2，C），（B3，C），记“从幼儿园所有具有研究生学历的教师中随机抽取2人，有35岁以下的研究生或50岁以上的研究生”为事件D，则D中的结果共有12个，它们是：（A1，A2），（A1，B1），（A1，B2），（A1，B3），（A1，C），（A2，B 1），（A2，B2），（A2，B3），（A2，C），（B1，C），（B2，C），（B3，C），故所求概率为124()==155P D．答：从幼儿园所有具有研究生学历的教师中随机抽取2人，有35岁以下的研究生或50岁以上的研究生的概率为45. ………13分 16.（本小题满分13分）（Ⅰ）因为a =(sin ,cos )x x ，b =(sin ,cos )x x -，c =(cos ,sin )x x --，所以()()sin cos ,sin cos x x x x -=+-b c ，()()f x =⋅-a b c =sin (sin cos )cos (sin cos )x x x x x x ++-.则()f x =22sin 2sin cos cos x x x x +-=sin 2cos 2x x -2sin(2)4x π=-.则当222242k x k ππ3ππ+≤-≤π+时，即88k x k 3π7ππ+≤≤π+时，函数()f x 为减函数，k ∈Z .所以函数()f x 的单调递减区间是,88k k 3π7π⎡⎤π+π+⎢⎥⎣⎦，k ∈Z .………7分（Ⅱ）由（Ⅰ）知，()2sin(2)4f x x π=-，又222f α⎛⎫=⎪⎝⎭，则22sin()42απ-=，1sin()42απ-=.因为 22sin ()cos ()144ααππ-+-=，所以3cos()42απ-=±. sin sin ()44ααππ⎡⎤=-+⎢⎥⎣⎦ππππsin()cos cos()sin 4444αα=-+-.所以当3cos()42απ-=时，sin α=12326222224+⨯+⨯=；当3cos()42απ-=-时，sin α=123226()22224-⨯+-⨯=.………13分 17. （本小题满分14分）（Ⅰ）证明：在PDB ∆中，因为点E 是BD 中点，点F 是PD 中点，所以EF //PB ．又因为EF ⊄平面PBC ，PB ⊂平面PBC ，所以EF //平面PBC ．……4分（Ⅱ）证明：因为PD ⊥平面ABCD ，且CE ⊂平面ABCD ，所以PD CE ⊥．又因为底面ABCD 是正方形，且点E 是BD 的中点，所以CE BD ⊥．因为BDPD D =，所以CE ⊥平面PBD ，DAPCEF B而BF ⊂平面PBD ，所以CE BF ⊥． …………9分（Ⅲ）点F 为边PD 上靠近D 点的三等分点．说明如下：由（Ⅱ）可知， CE ⊥平面PBF ．又因为PD ⊥平面ABCD ，BD ⊂平面ABCD ，所以PD BD ⊥. 设PF x =．由2AB =得22BD =，2CE =，所以11122223263P BCF C BPF V V PF BD CE x x --==⨯⨯⋅⋅=⨯⨯=．由已知2433x =，所以2x =．因为3PD =，所以点F 为边PD 上靠近D 点的三等分点．…14分 18. （本小题满分13分）（Ⅰ）由已知得，212327a a a a =⎧⎨++=⎩，解得2q =，11a =或12q =，14a =．则数列{}n a 的通项公式为12n n a -=或31()2n n a -=，n *∈N ……………5分（Ⅱ）因为01q <<，所以31()2n n a -=，n *∈N .(5)210...(3)21211...()()22n n n n n b a a a ---+++-=⋅⋅⋅==，n *∈N . 由01n b <<，即(5)210()12n n -<<，即(5)02n n ->，即即5n >.则使01n b <<的最小的n 的值为6． ……………13分 19. （本小题满分13分）（I ）函数()f x 的定义域为(0,)+∞.因为()e xa f x x'=-, 又1x =是()f x 的极值点,所以(1)e 0f a '=-=，解得e a =.经检验，1x =是()f x 的极值点，所以a 的值为e . ………5分（Ⅱ）证明：方法1：当e a =时，()e eln x f x x =-. 所以e e e()e xxx f x x x-'=-=. 若01x <<，则1<e e x <，所以e e x x <，所以e e<0x x -. 所以函数()f x 在(0,1)单调递减.若1x >，则e >e x ，所以e >e x x ，所以e e>0x x -.所以函数()f x 在(1,)+∞单调递增. 所以当1x =时，min ()(1)e f x f ==.(0x →时， e eln x x -→+∞;x →+∞时， e eln x x -→+∞.) 所以()e f x ≥. ………13分方法2：当e a =时，()e eln x f x x =-，所以e e e()e x xx f x x x-'=-=. 设()e e x g x x =-，则()e (1)x g x x '=+，所以()g x 在(0,)+∞单调递增.又(1)0g =，所以当(0,1)x ∈时，()0g x <，即()0f x '<，所以()f x 在(0,1)单调递减；当(1,)x ∈+∞时，()0g x >，即()0f x '>，所以()f x 在(1,)+∞单调递增. （接下来表述同解法1相应内容）所以()e f x ≥. ………13分 20.（本小题满分14分）解：（Ⅰ）由已知得32e =，则12b a =，设椭圆方程为22221(0)4x y b b b +=>由题意可知点(2,1)P 在椭圆上，所以224114b b+=．解得22b =．故椭圆C 的标准方程为22182x y +=． ………4分（Ⅱ）由题意可知，直线PA ，直线PB 的斜率都存在且不等于0．因为APQ BPQ ∠=∠，所以PA PB k k =-．设直线PA 的斜率为k ，则直线:1(2)PA y k x -=-（0k ≠）．由2248(12),x y y kx k ⎧+=⎨=+-⎩得222(14)8(12)161640k x k k x k k ++-+--=……(1). 依题意，方程（1）有两个不相等的实数根，即根的判别式0∆>成立.即()222264(12)4(14)161640k k k k k ∆=--+-->,化简得216(21)0k +>，解得12k ≠-.因为2是方程（1）的一个解，所以2216164214A k k x k --⋅=+．所以2288214A k k x k --=+．当方程（1）根的判别式0∆=时，12k =-，此时直线PA 与椭圆相切.由题意，可知直线PB 的方程为1(2)y k x -=--．同理，易得22228()8()288214()14B k k k k x k k----+-==+-+．由于点,A B 是椭圆上位于直线PQ 两侧的两个动点，APQ BPQ ∠=∠，且能存在四边形APBQ ，则直线PA 的斜率k 需满足12k >. 设四边形APBQ 面积为S ，则 112222APQ BPQ A B S S S PQ x PQ x ∆∆=+=⋅-+⋅- 2222188288221414B A k k k k PQ x x k k --+-=⋅-=-++ 21614kk=+ 由于12k >，故 216161144k S k k k==++. 当12k >时，144k k +>，即110144k k<<+，即04S <<. (此处另解：设t k =，讨论函数1()4f t t t=+在1,2t ⎛⎫∈+∞⎪⎝⎭时的取值范围. 222141()4t f t t t-'=-=，则当12t >时，()0f t '>，()f t 单调递增.则当12t >时，()(4,)f t ∈+∞，即S ∈()0,4.) 所以四边形APBQ 面积S 的取值范围是()0,4. ………14分。

北京市朝阳区2014-2015学年高二数学下学期期末统一考试试题文

a 3 2,因为2a 4 ,a 9a 1 2d 2, ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分所以2d 0.a 1a 1 1,解得1 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6 分d2所以通项公式为：a n a 1 ( n1)dn1 8 分. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2〔Ⅱ〕因为 b n1 ，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9 分n( n1)所以 S n (11 1 1 1 1 ) = n⋯⋯⋯⋯⋯⋯⋯⋯ 12 分) ( ) (n .223n1 n116．〔本小题总分值13 分〕解: 〔Ⅰ〕f (x)1sin 2x 3 (1 cos2x) 3 2 221sin 2x3cos2x22⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分sin(2 x) ，⋯⋯⋯⋯⋯⋯⋯ 6 分3所以函数 f ( x) 的最小正周期为．⋯⋯⋯⋯⋯⋯⋯ 7 分当 2x2k , k Z ，即x5 , kZ 时取得最大值为 1.⋯⋯⋯⋯9分k3212〔Ⅱ〕令 22 x2 ，k3k25, k 2得 kx kZ .1212故函数 f ( x) 的单调增区间为[ k, k 5 ], k Z ． ⋯⋯⋯⋯⋯⋯ 13 分121217.〔本小题总分值12 分〕解：〔 I 〕当a2 1 2x 21时， f (x) 2xx .xf (1) 1，f (1) 1，曲线 yf (x) 在点〔1， f (1) 〕处的切线方程为 l ：yf (1) f (1)(x 1),4所以切线方程为l ：x y0 .⋯⋯⋯⋯⋯⋯ 4 分〔II 〕函数f (x)的定义域为(0,) .⋯⋯⋯⋯⋯⋯ 5 分f ( x)ax1ax2 1.⋯⋯⋯⋯⋯⋯ 7 分x x〔i 〕假设a0, f (x)0 恒成立，那么f (x) 在(0,) 上单调递减.⋯⋯9分〔ii 〕假设a0 ，令 f (x)0 ，那么x1.a当 x变化时，f ( x) 与 f ( x) 的变化情况如下表：x111(0,)(, )a a af (x)0f ( x)↘极小值↗所以 f (x) 在 (0,a ) 上单调递减，在(a,) 上单调递增.⋯⋯⋯⋯⋯12分aa18.〔本小题总分值 13 分〕〔Ⅰ〕解：因为 f ' ( x) 2cosx ，当 cos x1时， f '(x) 1不符合条件②，所以函数 f ( x )2x sin x 不是集合 M 中的元素.⋯⋯⋯⋯⋯ ..4 分〔Ⅱ〕因为 g ( x) 是集合M中的元素，所以g ( x)11对于任意 x 0 均成立.ax即 a11( x0) 恒成立，即 a 1. x令 G ( x)g ( x)x ln x(a1)x ，依题意， g (x) 是集合M中的元素，必满足a 1 .当 a 1 时， G (x)1a 10 对任意 x0 恒成立，x所以 G( x) 在0,上为增函数 .又 G(e-a )lne -a a e-a e-a= a(e-a1)e-a0 .G (e) =1+ ( a -1)e > 0 ，所以方程 G (x)g( x) x0 有实根,也符合条件①.5当 a11a 1 与条件②矛盾.1 时，在 x0 时， g ( x)1a x综上 a1.⋯⋯⋯⋯.⋯⋯⋯⋯ .⋯⋯⋯⋯ .⋯⋯⋯⋯ . ⋯⋯⋯⋯⋯ ..13 分6。

2015年高二期末考试文科数学含答案

XX 中学2014—2015学年度第二学期高二级期末考试文科数学科试卷本试卷共 3 页，满分 150 分，考试时间 120 分钟一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，有且只有一项符合题目要求．）（1）设集合{}{}21,0,1,|M N x x x =-==,则M N ⋂=( )（A ）{}1,0,1-（B ）{}0,1（C ）{}1 （D ）{}0（2）复数z ＝1－3i1＋2i，则( )（A ）|z |＝2 （B ）z 的实部为1 （C ）z 的虚部为－i （D ）z 的共轭复数为－1＋i（3）已知函数()f x 是偶函数，当0x ≥时，()22f x x x =-，则()3f -=（）A ．15-B ．15C ．3-D ．3 （4）执行右面的程序框图，若输出的k ＝2，则输入x 的取值范围是( )（A ）(21，41) （B ）[21，41] （C ）(21，41] （D ）[21，41) （5）已知p ： ∀x ∈R ，ax 2－ax ＋1≥0，q ：(a －1)2≤1；则p 是q 成立的( )（A ）充分不必要条件（B ）必要不充分条件（C ）充要条件（D ）既不充分也不必要条件（6）函数f (x )＝(x ＋2)3－(1 2)x的零点所在区间是( )（A ）(－2，－1) （B ）(－1，0) （C ）(0，1) （D ）(1，2)（7）已知向量a=（1, 2），b=（2,3）若（c +a ）∥b ，c ⊥（b +a ），则c=( )（A ）（ 79 ， 73）（B ）（ 73 ， 79 ）（C ）（ 73 ， 79）（D ）（－ 79 ，－ 73）开始是x ≤81？否输入x x ＝2x －1结束k ＝0输出k k ＝k ＋1（8）空间几何体的三视图如图所示，则该几何体的表面积为( )（A ）8＋2 5 （B ）6＋2 5 （C ）8＋2 3（D ）6＋2 3（9）等比数列}{n a 的前321,2,4,a a a S n n 且项和为成等差数列，若a 1=1，则S 4为( )（A ）15 （B ）8 （C ）7 （D ）16（10）已知函数f (x )＝cos (2x ＋π 3)，g (x )＝sin (2x ＋2π3)，将f (x )的图象经过下列哪种变换可以与g (x )的图象重合( ) （A ）向右平移 π12（B ）向左平移 π6（C ）向左平移 π12（D ）向右平移 π6（11）过双曲线x 2a 2－y 2b2＝1的一个焦点F 作一条渐近线的垂线，若垂足恰在线段OF （O 为原点）的垂直平分线上，则双曲线的离心率为( )（A ） 2（B ）2（C ） 5（D ） 3（12）给出下列命题:○110.230.51log 32()3<<; ○2函数()lg sin f x x x =-有3个零点; ○3函数1()112++-=ln x xf x x 的图像以原点为对称中心; ○4已知a 、b 、m 、n 、x 、y 均为正数，且a ≠b ，若a 、m 、b 、x 成等差数列，a 、n 、b 、y 成等比数列，则有m> n ，x< y ．其中正确命题的个数是( ) （A ）4个（B ）3个（C ）2个（D ）1个二、填空题：（本大题共4小题，每小题5分，共20分，把答案填写在题中横线上．）（13）某城区有大学生3500人、中学生4000人，小学生4500人，为掌握各类学生的消费情况，现按分层抽样方法抽取一个容量为300的样本，应抽取中学生人.（14）若x ，y ∈R ，且⎩⎪⎨⎪⎧x≥1，x －2y ＋3≥0，y≥x ，则z =x ＋2y 的最小值等于__________.（15）已知双曲线过点，且渐近线方程为12y x=±，则该双曲线的标准方程为_____。

2014-2015学年度高二第二学期文科数学测试题

2014－2015学年第二学期高二测试题数学试题（文科）（本试卷共4页，21小题，满分150分。

考试用时120分钟）班别：姓名：座号：分数：一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．请在答题卡上填涂相应选项. 1．已知集合{0,1,2},{|20}A B x x ==-<，则AB = （）A ．{}0,2B ．{}0,1C ．{}1,2D ．{}0,1,2 2.复数i-12等于（） A.i --1 B.i +-1 C.i -1 D.i +1 3．设等比数列}{n a 的公比,21=q 前n 项和为n S ，则44S a =（）.A ．31B ．15C ．16D ．324.某城市修建经济适用房．已知甲、乙、丙三个社区分别有低收入家庭360户、270户、180户，若首批经济适用房中有90套住房用于解决住房紧张问题，采用分层抽样的方法决定各社区户数，则应从乙社区中抽取低收入家庭的户数为（） A ．40B ．36C ．30D ．205.下列函数中，既是偶函数，又是在区间()0,+∞上单调递减的函数是（） A ．ln y x =B ．2y x =C ．cos y x =D ．||2x y -=6.已知平面向量a,b 的夹角为6π，且=3⋅a b ，3=a ，则b 等于（） A. 3 B. 32 C.332 D. 27.若正三棱柱的三视图如图所示，该三棱柱的表面积是（） A. 623+ B.932C. 63+D. 38.执行如图所示程序框图．若输入3x =，则输出的k 值是（） A ．3 B ．4 C ．5 D ．69.圆()221x a y -+=与直线y x =相切于第三象限，则a 的值是（）．A ．2B ．2-C ．2-D ．2 10.设函数3()4(02)f x x x a a =-+<<有三个零点123,,x x x ，且123x x x <<则下列结论正确的是（）A .11x >-B .20x <C .201x <<D .32x >二、填空题：本大题共5小题，每小题5分，满分20分．其中14～15题是选做题，考生只能选做一题，两题全答的，只计算前一题得分． 11.在ABC △中，若13,1,cos 3b c A ===，则a = . 12.不等式组201x y y x ≤⎧⎪≥⎨⎪≤-⎩表示的平面区域的面积是 .13. 2sin(),44πα+=则sin 2α= ． 14.（坐标系与参数方程选做题）在极坐标系中，O 为极点，直线过圆C ：θρcos 22=的圆心C ，且与直线OC 垂直，则直线的极坐标方程为． 15.(几何证明选讲选做题) 如图，090ACB ∠=,AC 是圆O 的切线，切点为E ，割线ADB 过圆心O ，若3,1AE AD ==，则BC 的长为．开始 0k = 5x x =+1k k =+结束输入x是否输出k23?x >EDCBAO三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 16.（本小题满分12分）已知函数()1sin cos f x x x =+⋅.（1）求函数)(x f 的最小正周期和最小值；（2）若3tan 4x =，0,2x π⎛⎫∈ ⎪⎝⎭，求)24(xf -π的值.17．（本小题满分12分）对某校高一年级学生参加社区服务次数统计，随机抽去了M 名学生作为样本，得到这M 名学生参加社区服务的次数，根据此数据作出了频数与频率的统计表如下：（1）求出表中,,,M r m n 的值；（2）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，求至少一人参加社区服务次数在区间[)25,30内的概率．18.（本小题满分14分）如图，在三棱锥V ABC -中，VC ⊥底面ABC , ,AC BC D⊥ 为AB的中点,AC BC VC a ===.（1）求证：AB ⊥平面VCD ；（2）求点C 到平面VAB 的距离。

北京市朝阳区2014届高三二模数学(文)试题含答案

北京市朝阳区高三年级第二次综合练习数学学科测试（文史类）（考试时间120分钟满分150分）本试卷分为选择题（共40分）和非选择题（共110分）两部分第一部分（选择题共40分）-、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，选出符合题目要求的一项.（1）若全集U a,b,c,d , A a,b , B c，则集合d等于o（3）已知抛物线x2y ,则它的焦点坐标是(A) -,04(B) 0,12(C) 0—4(D) 1,022014. 5(A) e u(AUB) (B) AU B (C) AI B (D) e u(AI B)（2）下列函数中，既是奇函数又在区间（0,）上单调递增的函数为(A) y sin x (B) y ln x (C) y x3(D) y 2x（4）执行如图所示的程序框图•若输入a3,则输出i的值是(A) 2(B) 3(C)(5)由直线x y 1 0 , x y 5 0和x 1 0所围成的三角形区域(包括边界)用不等式组可表示为x y 10,x y 1 0,x y 10,x y 1 0, (A) x y 50,(B) x y 5 0,(C) x y 50, (D) x y 5 0x 1.x 1.x 1.x 1.(6)在区间［-,］上随机取一个数x，则事件: a cosx”的概率为1 (A) 14(B)(C) 23(D)-2项和为S n若a1 d, S n 8(7)设等差数列r r. r x _、/■，前nd 的最小值为的公差为d1，则an(A) 10(B) 97(C)- (D)12/2 222(8 )已知平面上点P(x,y)(x x。

)22(y y°) 16,其中2 2 .x0 y0 4当i x0, y变化时，则满足条件的点P在平面上所组成图形的面积是(A) 4n (B) 16 n ( C) 32 n (D) 36n第二部分(非选择题共110分)二、填空题：本大题共6小题，每小题5分，共30分.把答案填在答题卡上•1 2i9•计算1 iuur 1 nm10•已知两点A 1,1 , B 1,2，若BC - BA，则C点坐标是______________ .11.圆心在x轴上，半径长是4，且与直线x 5相切的圆的方程是___________ •12.由两个四棱锥组合而成的空间几何体的三视图如图所示，其体积是_______ ;表面积正视图侧视图—2俯视图(第12题图)服务时间/小时13•设一列匀速行驶的火车，通过长860 m 的隧道时，整个车身都在隧道里的时间是 22s .该列车以同样的速度穿过长 79o m 的铁桥时，从车头上桥，到车尾下桥，共用时 33s ，则这列火车的长度为—m .15.(本小题满分13分)在V ABC 中，a , b , c 分别是角A, B , C 的对边.已知a(I )若b 2 ■■一 2，求角C 的大小;(n)若c 2，求边b 的长.16.(本小题满分13分)某市规定，高中学生在校期间须参加不少于 80小时的社区服务才合格.某校随机抽取20位学生参加社区服务的数据，按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位：小时)进行统计，其频率分布直方图如图所示.(I)求抽取的20人中，参加社区服务时间不少于 90小时的学生人数；(n)从参加社区服务时间不少于90小时的学生中任意选取 2人，求所选学生的参加社区服务时间在同一时间段内的概率.14.在如图所示的棱长为2的正方体ABCDA i BIC I D I 中，作与平面ACD i平行的截面，则截得的三角形中面积最大的值是截得的平面图形中面积最大的值是三、解答题：本大题共 6小题，共80分. 解答应写出文字说明，演算步骤或证明过程C频率服务时间/小时17.(本小题满分14分)如图，在四棱锥 P ABCD 中，底面ABCD 是正方形，侧面 PAD 底面ABCD(I)若 E , F 分别为PC , BD 中点，P求证： EF //平面 PAD ；(n)求证： PA CD ；B E • A(川)若PAPD2AD ,2CJD求证：平面PAB 平面PCD .18.(本小题满分13分)xa e已知函数f(x)( a R ,a 0)x(i)当a 1时，求曲线f (x)在点1, f (1)处切线的方程； (n)求函数f(x)的单调区间；(川)当x 0, 时，若f (x) 1恒成立，求a 的取值范围列｛a n ｝满足：a n f(n) , n N(I)求f (0)及f (1)的值; (n)求数列｛a n ｝的通项公式；1 1(川)若b n ( )an ( )3 an ，试问数列｛b n ｝是否存在最大项和最小项？若存在，求出最大 4 2项和最小项；若不存在，请说明理由.19.(本小题满分14分)1已知椭圆C 的中心在原点 0,焦点在x 轴上，离心率为1,右焦点到右顶点的距离为2(I)求椭圆C 的标准方程； (n )若直线| ： mx y 10与椭圆C 交于A, B 两点，是否存在实数m ,uuu uur OA OBuuu uuu .................. OA OB 成立？若存在，m 的值；若不存在，请说明理由20.(本小题满分13分)已知函数f(x)对任意x, y R 都满足f(x y) 1f(…1，且 f (-), 1.使数北京市朝阳区高三年级第二次综合练习数学学科测试文史类答案2014.515.（本小题满分13分）2 3 2、2得 3 sin B ，解得 sin B22品 2彳ac1 由于，所以3 sinC ，解得sinC .sin A sin C22n由于B 为三角形内角， b a ，则 B -,所以C....... 6分43 412（n ）依题意，cos A2 2 2b c a,即 1b 24 12 2.整理得b 2 2b 80 ,2bc24b另解：（I ）解：由正弦定理a bsin A sin B又b 0，所以b 4. ........ 13分由于a c，所以C .6n n 由A —,得B -.3 2由勾股定理b c2 a2，解得b 4.13分16.（本小题满分13分）解：（I）由题意可知，参加社区服务在时间段［90,95）的学生人数为20 0.04 5 4 （人），参加社区服务在时间段［95,100］的学生人数为20 0.02 5 2 （人）•所以参加社区服务时间不少于90小时的学生人数为4+2 6 （人）•..... 5分（n）设所选学生的服务时间在同一时间段内为事件 A •由（I）可知，参加社区服务在时间段［90 ,95）的学生有4人，记为a,b,c,d ；参加社区服务在时间段［9 5,100］的学生有2人，记为A, B •从这6人中任意选取 2 人有ab,ac,ad ,a代aB, bc, bd,bA,bB,cd,cA,cB,dA,dB, AB 共15种情况.事件A包括ab,ac,ad,bc, bd,cd, AB共7种情况.所以所选学生的服务时间在同一时间段内的概率17.（本小题满分14分）证明：（I）如图，连结AC .因为底面ABCD是正方形，所以AC与BD互相平分.又因为F是BD中点，所以F是AC中点.在厶PAC中，E是PC中点，F是AC中点,所以EF // PA.又因为EF 平面PAD , PA 平面PAD ,所以EF //平面PAD .(n)因为平面PAD 底面ABCD , 且平面PAD I平面ABCD=AD ,又CD AD,所以CD 面PAD .又因为PA 平面PAD ,所以CD PA .即PA(川)在厶PAD中，因为PA PD -2 AD , 2所以PA PD •由(n)可知PA CD ,CDI PD=D ,所以PA平面PCD •又因为PA 平面PAB ,所以面PAB 平面PCD •14分18.(本小题满分13分)f (x)x xax e ae2xae^,x 0.x1时, f (x)e x(x 1)依题意f (1) 即在x 1处切线的斜率为0.把x 1代入f(x)x—中，得f(1) e. x则曲线f (x)在x 1处切线的方程为y e..4分f (x)的定义域为x x 0 .由于f (x)ax e ae2 x(1 )若a0,当f (x)0 , 即x 1时，i当f (x)0 , 即x0和0ae x(x 1)函数f (x)为增函数;x 1时，函数f (x)为减函数•函数x x (2)若a 0,当f (x) 0,即x 0和0 x 1时，函数f(x)为增函数;当f (x)0,即x 1时，函数f (x)为减函数.综上所述，a 0时，函数f (x)的单调增区间为 1, ;单调减区间为,0 , 0,1 .a 0时，函数f (x)的单调增区间为，0 , 0,1 ；单调减区间为1,. (9)xa ex(川)当x 0, 时，要使f(x)1恒成立，即使a x 在x 0, 时恒成xe、 x 1 x立•设g(x) x ，则g (x) x .可知在0 x 1时，g (x)0 , g(x)为增函数；e e11x 1 时，g (x)0 , g(x)为减函数则 g(x)max g(1)•从而 a . e e另解：(1)当a 0时，f(a) e a 1，所以f (x) 1不恒成立•⑵当a 0且x 0, 时，由(i)知，函数 f(x)的单调增区间为1, 0,1 .所以函数f (x)的最小值为f ⑴ ae ，依题意f ⑴ ae 1,1解得a — •e1 综上所述，a . (13)e19.(本小题满分14分)2x (i)设椭圆C 的方程为r2y 21 ab 2b 0，半焦距为c .ac 1e,a 2解得 a c 1.所以 b 2 a 2 c 2 3依题意c 1 , a2,2 2所以椭圆C 的标准方程疋1.43 (4)uuu uuu uuu(n)不存在实数 m ，使I OA OB | | OAmx 1代入椭圆C ：3x 2 4y 212 中，整理得(3 4m 2)x 2 8mx 80.由于直线I 恒过椭圆内定点0, 1，所以判别式0.单调减区间为uuuOB |，证明如下:当f (x) 0,即x 0和0 x 1时，函数f(x)为增函数;设 A(X i , y i ), B(X 2, y 2)，则％ uuu uuu uuu 依题意，若|0A OB| |OA 8m 即 X 1X 2 y i y 2 x-i X 2 ( mx j X 2 2 必 X 2 4m 3 uuu uuu uuu OB |，平方得OA OB 1)( mx 2 1) 0, 2 整理得(m 1)x 1x 2 m(x 1 x 2) 1 0, 4m 2 3 0. 2 8 8 m 2 所以(m 2 1) 2 2 1 0, 4 m 2 3 4m 2 3 2 5 整理得m 2 —，矛盾. 12uuu umr mu uuu 所以不存在实数 m ，使|OA OB||OA OB |. ............. .14分解：（I ）在 f(x y) f(x) f (y) 1 中，取 x y 0 ,得 f (0) 1 , 在f (X y) f(x) f (y) 1 中, 1 取 x y ｛，得 f(1) 1, ........ 2 分 (□)在 f(x y) f(x) f(y) 1 中，令 x n , y 1, 得f(n 1) f(n) 2，即 a n 1 a n 2. 20.(本小题满分13分)所以｛a n ｝是等差数列，公差为2,又首项C f （1） 1，所以a n 2n — N （川）｛b n ｝存在最大项和最小项令 t (1)an (1)2n 1，则 b n t 2 ft 2 2 8 1 显然0 t 2，又因为n N ,(t 1 256 13 所以当t 1，即n 1时，g ｝的最大项为b 石 1 当t 32，即n 3时，｛b n ｝的最小项为b 3 3 1024 13分。

2014-2015学年高二下学期期末考试数学(文)试题带答案

2014-2015学年度第二学期期末测试高二年级文科数学一、选择题：在每小题给出的四个选项中，只有一项符合题目要求（本大题共10小题，每小题4分，共40分）.1、设集合{}2|M x x x ==，{}|lg 0N x x =≤，则M N ⋃=（） A ．[0,1] B ．(0,1) C ．[0,1] D ．(-∞,1)2、命题“存在实数x ,使210x x +-<”的否定为（）A ．不存在实数x ，使210x x +-≥B ．对任意实数x ，都有210x x +-≥C ．存在实数x ，使210x x +-≥D ．对任意实数x ，都有210x x +-<3、设f (x )＝102,0x x x ⎧≥⎪⎨<⎪⎩，则((2))f f -=（）A ．1-B ．14C ．12D ．324、在等差数列{}n a 中，若2812a a +=，n S 是数列{}n a 的前n 项和，则9S =（）A ．48B ．54C ．60D ．665、下列函数中，既是偶函数又在(0,)+∞上是减函数的是（）A ．3y x =B ．x y e -=C ．lg y x =D ．21y x =-+ 6、若等比数列{}n a 的首项为1，且14a ，22a ，3a 成等差数列，则数列1n a ⎧⎫⎨⎬⎩⎭的前5项和为A ．3116B ．2C ．3316D ．16337、设偶函数()f x 的定义域为R ，当[0,)x ∈+∞时()f x 是增函数，则(3)f -，(2)f -，()f π的大小关系是（）A ．()(2)(3)f f f π>->-B ．()(3)(2)f f f π>->-C ．()(3)(2)f f f π<-<-D ．()(2)(3)f f f π<-<-8、在等差数列{}n a 中，135105a a a ++=，24699a a a ++=，n S 是数列{}n a 的前n 项和，则n S 的最大值是（）A ．100B ．200C ．400D ．8009、定义在R 上的函数()f x 满足(6)()f x f x +=，当31x -≤<-时，2()(2)f x x =-+；当13x -≤<时，()f x x =，则(1)(2)(3)(2016)f f f f ++++= （）A ．0B ．336C ．672D ．100810、已知函数()lg1a x f x x -=+，若()f x 是奇函数，且在(1,)n -上的值域为(1,)-+∞则n =（）A ．1B ．89 C ．910 D ．911二、填空题：（本大题共5小题，每小题4分，共20分）.11、若“2230x x -->”是“x a <”的必要不充分条件，则实数a 的最大值为_______；12、当11,,12,32α⎧⎫∈-⎨⎬⎩⎭时，在幂函数y x α=中有____个单调递增的奇函数，且幂函数y x α=的图像不可能过第____象限；13、在数列{}n a 中，n S 是数列{}n a 的前n 项和，若223n S n n =-，则n a =_______n N +∈；14、若1)f x =+，则()f x =__________；15、在正项数列{}n a 中，11a =，2211(2,)n n n n a a a na n n n N +----=≥∈，若n S 是数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和，则2015S =_______。

北京市朝阳区高二数学下学期期末试卷文(含解析)

北京市朝阳区2014-2015学年高二下学期期末数学试卷（文科）一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合要求的.1．已知i是虚数单位，则2i（1+i）=( )A．﹣2+2i B．2+2i C．2i D．﹣2i考点：复数代数形式的乘除运算．专题：数系的扩充和复数．分析：根复数的基本运算进行求解即可．解答：解：2i（1+i）=2i+2i2=﹣2+2i，故选：A点评：本题主要考查复数的基本运算，比较基础．2．已知集合A={x|（x﹣3）（x+1）≤0}，B={x|2x＞2}，则A∩B=( ) A．{x|﹣1＜x＜3} B．{x|1＜x≤3}C．{x|﹣1≤x＜2} D．{x|x＞2}考点：交集及其运算．专题：集合．分析：求出A与B中不等式的解集，确定出A与B，找出两集合的交集即可．解答：解：由A中不等式解得：﹣1≤x≤3，即A={x|﹣1≤x≤3}，由B中不等式变形得：2x＞2=21，得到x＞1，即B={x|x＞1}，则A∩B={x|1＜x≤3}，故选：B．点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．3．若sinθcosθ＜0，则角θ是( )A．第一或第二象限角 B．第二或第三象限角C．第三或第四象限角 D．第二或第四象限角考点：象限角、轴线角．专题：计算题．分析：直接利用三角函数的值的符号，判断θ所在象限即可．解答：解：因为sinθcosθ＜0，所以sinθ，cosθ异号，即或，所以θ第二或第四象限角．故选D．点评：本题考查三角函数值的符号，角所在象限的判断，基本知识的应用．4．已知函数f（x）=cosx﹣sinx，f′（x）为函数f（x）的导函数，那么等于( )A．B．C． D．考点：导数的运算．专题：导数的概念及应用．分析：根据导数的运算法则求导，再代值计算即可．解答：解：f′（x）=﹣sinx﹣cosx，∴f′（）=﹣sin﹣cos=﹣，故选：C．点评：本题考查了导数的运算法则和导数的基本公式，属于基础题．5．设a=20.3，b=log43，5，则( )A．c＜a＜b B．b＜c＜a C．b＜a＜c D．c＜b＜a考点：对数值大小的比较．专题：函数的性质及应用．分析：确定a=20.3，b=log43，5，这些数值与0、1的大小即可．解答：解：∵a=20.3＞1，0＜b=log43＜b=log44=1，5＜0，∴c＜b＜a，故选：D．点评：本题主要考查指数、对数综合比较大小的问题，这里注意与特殊值1、0这些特殊值的比较．6．设a，b∈R，则“a＞b＞1”是“a﹣b＜a2﹣b2”的( )A．充分不必要条件B．必要不充分条件C．充分必要条件 D．既不充分也不必要条件考点：必要条件、充分条件与充要条件的判断．专题：简易逻辑．分析：根据不等式的性质，利用充分条件和必要条件的定义进行判断即可得到结论．解答：解：设命题p：a＞b＞1；则a﹣b＞0，命题q：a﹣b＜a2﹣b2化简得（a﹣b）＜（a+b）（a﹣b），又∵a，b∈R，∴p⇒q，q推不出p，∴P是q的充分不必要条件，即“a＞b＞1”是“a﹣b＜a2﹣b2”的充分不必要条件，故选：A．点评：本题重点考查充分条件、必要条件和充要条件的概念及其应用，属于中档题7．若不等式组表示的平面区域是一个三角形，则实数a的取值范围是( )A．{a|1≤a≤3或a＞5} B．{a|1＜a≤3或a≥5}C．{a|1＜a≤5} D．{a|3≤a≤5}考点：简单线性规划．专题：不等式的解法及应用．分析：作出不等式组对应的平面区域，利用平面区域为三角形，建立条件关系即可求m的取值范围．解答：解：先作出不等式组对应的平面区域如图：（△ABC），∵不等x+y≤a表示的平面区域为直线x+y=a的左下面．∴要使不等式组表示的平面区域是一个三角形，①当A（1，4）在直线x+y=a的下方时，满足条件，即此时1+4≤a，即a≥5．②当直线x+y=a经过BC线段时，也满足条件，此时满足B（1，0）在直线x+y=a的下方，同时C（3，0）在x+y=a的上方或在直线上，即，即1＜a≤3，综上1＜a≤3或a≥5，故选：B．点评：本题主要考查线性规划的应用，利用二元一次不等式组和平面区域之间的关系是解决本题的关键，注意利用数形结合．8．已知定义在R上的函数f（x）的对称轴为x=﹣3，且当x≥﹣3时，f（x）=2x﹣3．若函数f（x）在区间（k﹣1，k）（k∈Z）上有零点，则k的值为( )A．2或﹣7 B．2或﹣8 C．1或﹣7 D．1或﹣8考点：根的存在性及根的个数判断．专题：函数的性质及应用．分析：先作出当x≥﹣3时函数f（x）=2x﹣3的图象，观察图象的交点所在区间，再根据对称性得出另一个交点所在区间即可．解答：解：作出当x≥﹣3时函数f（x）=2x﹣3的图象，观察图象的交点所在区间在（1，2）．∵f（1）=21﹣3=﹣1＜0，f（2）=22﹣3=1＞0，∴f（1）•f（2）＜0，∴有零点的区间是（1，2），因定义在R上的函数f（x）的对称轴为x=﹣3，故另一个零点的区间是（﹣8，﹣7），则k的值为2或﹣7．故选A．点评：本题主要考查了根的存在性及根的个数判断．二分法是求方程根的一种基本算法，其理论依据是零点存在定理：一般地，若函数y=f（x）在区间[a，b]上的图象是一条不间断的曲线，且f（a）f（b）＜0，则函数y=f（x）在区间（a，b）上有零点．二、填空题：本大题共6小题，每小题5分，共30分.请把答案填在答题卡的相应位置上. 9．已知sinα=，则cosα=；tanα=．考点：同角三角函数基本关系的运用．专题：三角函数的求值．分析：由sinα的值及α的范围，利用同角三角函数间的基本关系求出cosα的值，进而求出tanα的值．解答：解：∵sinα=，α∈（0，），∴cosα==；tanα==．故答案为：；点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．10．函数y=+lgx的定义域是（0，2]．考点：函数的定义域及其求法．专题：常规题型．分析：根据函数的结构，可以知道要使函数有意义需要满足：被开放式大于等于零以及真数大于零，解不等式组即可．解答：解：由题意知，所以0＜x≤2，即函数的定义域为（0，2]，故答案为（0，2]．点评：本题考察函数定义域的求法，从解析式来看这是该类题目中比较简单、比较基础的了．11．已知平面向量=（1，﹣3），=（4，﹣2），λ+与垂直，则λ=﹣1．考点：数量积判断两个平面向量的垂直关系．专题：计算题．分析：先求出互相垂直的2个向量的坐标，再利用这2个向量的数量积等于0，求出待定系数λ 的值．解答：解：，（）⇒（λ+4）×1+（﹣3λ﹣2）×（﹣3）=0⇒λ=﹣1，故答案为﹣1．点评：本题考查2个向量坐标形式的运算法则，及2个向量垂直的条件是他们的数量积等于0．12．已知△ABC的内角A，B，C的对边分别为a，b，c，若c=，b=，B=135°，则a=1，S△ABC=．考点：正弦定理；余弦定理．专题：解三角形．分析：由余弦定理列出关系式，将b，c，cosB的值代入求出a的值，利用三角形面积公式求出三角形ABC面积即可．解答：解：∵△ABC中，c=，b=，B=135°，∴由余弦定理得：b2=a2+c2﹣2accosB，即5=a2+2+2a，解得：a=﹣3（舍去）或a=1，则S△ABC=acsinB=×1××=．故答案为：1；点评：此题考查了余弦定理，以及三角形面积公式，熟练掌握余弦定理是解本题的关键．13．在数列{a n}中，已知a2=4，a3=15，且数列{a n+n}是等比数列，则a n=2•3n﹣1﹣n；．考点：等比数列的通项公式．专题：等差数列与等比数列．分析：由于数列{a n+n}是等比数列，可得，解得a1．即可得到公比q==．再利用等比数列的通项公式即可得出．解答：解：∵数列{a n+n}是等比数列，∴，∴（4+2）2=（a1+1）×（15+3），解得a1=1．∴公比q==．∴a n+n=2×3n﹣1．∴a n=2•3n﹣1﹣n，故答案为：2•3n﹣1﹣n．点评：本题考查了等比数列的定义及其通项公式，属于基础题．14．已知函数f（x）=e x﹣alnx的定义域是（0，+∞），关于函数f（x）给出下列命题：①对于任意a∈（0，+∞），函数f（x）存在最小值；②对于任意a∈（﹣∞，0），函数f（x）是（0，+∞）上的减函数；③存在a∈（﹣∞，0），使得对于任意的x∈（0，+∞），都有f（x）＞0成立；④存在a∈（0，+∞），使得函数f（x）有两个零点．其中正确命题的序号是①④．考点：函数零点的判定定理；函数的定义域及其求法．专题：函数的性质及应用．分析：先求导数，若为减函数则导数恒小于零；在开区间上，若有最小值则有唯一的极小值，若有零点则对应方程有根．解答：解：由对数函数知：函数的定义域为：（0，+∞），f′（x）=e x﹣，①∵a∈（0，+∞），∴存在x有f′（x）=e x﹣=0，可以判断函数有最小值，①正确，②∵a∈（﹣∞，0）∴f′（x）=e x﹣≥0，是增函数．所以②错误，③画出函数y=e x，y=﹣alnx的图象，如图：显然不正确．④令函数y=e x是增函数，y=alnx是减函数，所以存在a∈（0，+∞），f（x）=e x﹣alnx=0有两个根，正确．故答案为：①④．点评：本题主要考查导数法研究函数的单调性、极值、最值等问题．三、解答题：本大题共4小题，共50分.解答应写出文字说明，证明过程或演算步骤.请把答案填在答题卡的相应位置上.15．在等差数列{a n}中，a3=2，a9=2a4．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）设b n=，求数列{b n}的前n项和S n．考点：数列的求和；等差数列的通项公式．专题：等差数列与等比数列．分析：（1）根据等差数列的性质得出方程组求解得出a1，d．运用通项公式求解即可．（2）把b n裂项得出=，出现正负项，即可求解和．解答：解：（1）设等差数列的首项为a1，公差为d．因为所以解得所以通项公式为：．（Ⅱ）因为，所以=．点评：本题考察了等差数列的常规题型知三求二，裂项法求解数列的和，属于中档题，计算准确即可．16．已知函数f（x）=sinxcosx+．（Ⅰ）求f（x）的最小正周期和最大值；（Ⅱ）求f（x）的单调递增区间．考点：三角函数中的恒等变换应用．专题：三角函数的图像与性质．分析：（Ⅰ）由三角函数中的恒等变换应用化简函数解析式可得：f（x）=，由周期公式可求函数f（x）的最小正周期，利用正弦函数的图象和性质即可求得最大值．（Ⅱ）由，即可求得函数f（x）的单调增区间．解答：（本小题满分13分）解：（Ⅰ）…==，…所以函数f（x）的最小正周期为π．…当，即时取得最大值为1．…（Ⅱ）令，得．故函数f（x）的单调增区间为．…点评：本题主要考查了三角函数中的恒等变换应用，正弦函数的图象和性质，属于基本知识的考查．17．已知函数f（x）=﹣lnx，a∈R．（I）当a=2时，求曲线y=f（x）在点（1，f（1））处的切线方程；（II）讨论f（x）的单调性．考点：利用导数研究曲线上某点切线方程；利用导数研究函数的单调性．专题：分类讨论；导数的概念及应用；导数的综合应用．分析：（I）求出a=2的函数的导数，求得切线的斜率和切点，由点斜式方程，即可得到所求切线方程；（II）求得函数的导数，讨论（i）若a≤0，（ii）若a＞0，令导数大于0，可得增区间，令导数小于0，可得减区间．解答：解：（I）当a=2时，f（x）=x2﹣lnx，．则f′（1）=1，f（1）=1，曲线y=f（x）在点（1，f（1））处的切线方程为l：y﹣f（1）=f'（1）（x﹣1），所以切线方程为l：x﹣y=0；（II）函数f（x）的定义域为（0，+∞）．．（i）若a≤0，f′（x）＜0恒成立，则f（x）在（0，+∞）上单调递减．（ii）若a＞0，令f′（x）=0，则．当x变化时，f′（x）与f（x）的变化情况如下表：xf′（x）﹣0 +f（x）↘极小值↗所以f（x）在上单调递减，在上单调递增．点评：本题考查导数的运用：求切线方程和单调区间，掌握分类讨论的思想方法是解题的关键．18．已知M是由所有满足下述条件的函数f（x）构成的集合：①方程f（x）﹣x=0有实数根；②设函数f（x）的导函数f′（x），且对f（x）定义域内任意的x，都有f′（x）＞1．（Ⅰ）判断函数f（x）=2x+sinx是否是集合M中的元素，并说明理由；（Ⅱ）若函数g（x）=lnx+ax是集合M中的元素，求实数a的取值范围．考点：利用导数求闭区间上函数的最值．专题：导数的综合应用．分析：（Ⅰ）先求出函数f（x）的导数，得到当cosx=﹣1时，f′（x）=1，不符合条件②，从而得出结论；（Ⅱ）先求出函数g（x）的导数，通过讨论a的范围，结合新定义从而求出a的范围．解答：解：（Ⅰ）∵f′（x）=2+cosx，当cosx=﹣1时，f′（x）=1，不符合条件②，∴函数f（x）不是集合M中的元素；（Ⅱ）∵g（x）是集合M中的元素，∴g′（x）=+a＞1对于任意x＞0均成立，即a＞1﹣（x＞0）恒成立，即a≥1，令G（x）=g（x）﹣x=lnx+（a﹣1）x，依题意g（x）是集合M中的元素，必满足a≥1，当a≥1时，G′（x）=+a﹣1＞0对任意x＞0恒成立，∴G（x）在（0，+∞）递增，又G（e﹣a）=lne﹣a+a•e﹣a﹣e﹣a=a（e﹣a﹣1）﹣e﹣a＜0，G（e）=1+（a﹣1）e＞0，∴方程G（x）=g（x）﹣x=0有实根，也符合条件①，当a＜1时，在x＞＞0时，g′（x）=+a＜1与条件②矛盾，综上，a≥1．点评：本题考查了新定义问题，考查导数的应用、函数的单调性，是一道中档题．。

北京市朝阳2014届高三二模文科数学试卷(带解析)

北京市朝阳2014届高三二模文科数学试卷（带解析）1．若全集{},,,U a b c d =，{},A a b =，{}B c =，则集合{}d 等于（）（A ）()U A B ð （B ）A B （C ）A B （D ）()U AB ð 【答案】A 【解析】试题分析：因为{,,}A B a b c =,所以()U A B ð{}.d =而A B .φ=()U AB ð.U =所以选A.考点：集合运算2．下列函数中，既是奇函数又在区间0,+∞（）上单调递增的函数为（）（A ）sin y x = （B ）ln y x = （C ）3y x = （D ）2x y = 【答案】C【解析】试题分析：sin y x =是奇函数但在区间0,+∞（）上不是单调函数．ln y x =在区间0,+∞（）上单调递增但不是奇函数，3y x =既是奇函数又在区间0,+∞（）上单调递增的函数，2xy =在区间0,+∞（）上单调递增但不是奇函数.考点：函数奇偶性及单调性3．已知抛物线22x y =,则它的焦点坐标是（）（A ）1,04⎛⎫ ⎪⎝⎭ （B ）10,2⎛⎫ ⎪⎝⎭ （C ）10,4⎛⎫ ⎪⎝⎭ （D ）1,02⎛⎫ ⎪⎝⎭ 【答案】B【解析】试题分析：因为抛物线22(0)x py p =>的焦点坐标为(0,),2p 所以抛物线22x y =的焦点坐标是10,2⎛⎫⎪⎝⎭.考点：抛物线焦点4．执行如图所示的程序框图．若输入3a =,则输出i 的值是（）（A ）2 （B ） 3 （C ） 4 （D ） 5 【答案】C 【解析】试题分析：第一次循环，9,1,a i ==第二次循环，21,2,a i ==第三次循环，45,3,a i ==第四次循环，93,4,a i ==结束循环，输出 4.i = 考点：循环结构流程图5．由直线10x y -+=，50x y +-=和10x -=所围成的三角形区域(包括边界)用不等式组可表示为（）（A ）10,50,1.x y x y x -+≤⎧⎪+-≤⎨⎪≥⎩ （B ）10,50,1.x y x y x -+≥⎧⎪+-≤⎨⎪≥⎩ （C ）10,50,1.x y x y x -+≥⎧⎪+-≥⎨⎪≤⎩ （D ）10,50,1.x y x y x -+≤⎧⎪+-≤⎨⎪≤⎩【答案】A 【解析】试题分析：由题意得：所围成的三角形区域在直线10x y -+=的上方，直线50x y +-=的下方，及直线10x -=的右侧，所以10x y -+≤，50x y +-≤，10.x -≥ 考点：不等式组表示平面区域6．在区间ππ[-,]上随机取一个实数x ，则事件：“cos 0x ≥”的概率为（）（A ）14 （B ） 34 （C ）23 （D ）12【答案】D 【解析】试题分析：由cos 0x ≥，x ∈ππ[-,]得：[,]22x ππ∈-，所以事件：“cos 0x ≥”的概率为()122.()2ππππ--=-- 考点：几何概型概率7．设等差数列{}n a 的公差为d ，前n 项和为n S .若11a d ==，则8n n S a +的最小值为（）（A ）10 （B ）92 （C ）72 （D）12+【答案】B 【解析】试题分析：由题意得：(1),2n n n n a n S +==，所以8n n S a+1819.222n n +=+≥+=当且仅当4n =时取等号.因此8n n S a +的最小值为92.考点：基本不等式求最值8．已知平面上点{2200(,)()()16,P x y x x y y ∈-+-=其中}22004x y +=，当0x ，0y 变化时，则满足条件的点P 在平面上所组成图形的面积是（）(A ）4π (B ）16π ( C ）32π （D ）36π 【答案】C 【解析】试题分析：圆心00(,)x y 在圆224x y +=上运动一周，点P 在平面上所组成图形为以坐标原点为圆心，6为半径的实心圆减去以坐标原点为圆心，2为半径的实心圆的一个圆环，面积是226232πππ-=.考点：圆的方程，动点轨迹9．计算12i1i +=- . 【答案】13i 22-+【解析】试题分析：12i (12i)(1+i)13.1i (1i)(1+i)2i++-+==-- 考点：复数运算10．已知两点()1,1A ，()1,2B -，若12BC BA =，则C 点的坐标是 . 【答案】30,2⎛⎫ ⎪⎝⎭【解析】试题分析：设C 点的坐标是(,)x y ，则由12BC BA =得1(1,2)(11,12),2x y +-=+-即30,.2x y ==C 点的坐标是30,2⎛⎫⎪⎝⎭.考点：向量坐标运算11．圆心在x 轴上，半径长是4，且与直线5x =相切的圆的方程是．【答案】()22116x y -+=和()22916x y -+=【解析】试题分析：设圆心为(),a b ，因为与直线5x =相切，所以|5|4,1a r a -===或9.a =因此圆的方程是()22116x y -+=和()22916x y -+=考点：圆的标准方程12．由两个四棱锥组合而成的空间几何体的三视图如图所示，则其体积是；表面积是．【答案】3, 【解析】2的正方形．因此体积为21223⨯=表面积为8个全等的边长为2的等边三角形面积之和，即282= 考点：三视图 13．设一列匀速行驶的火车，通过长860m 的隧道时,整个车身都在隧道里的时间是22s .该列车以同样的速度穿过长790m 的铁桥时，从车头上桥，到车尾下桥，共用时33s ，则这列火车的长度为___m . 【答案】200 【解析】试题分析：设这列火车的长度为xm ，则由题意得：860790,200.2233x xx -+==.考点：实际问题应用题14．在如图所示的棱长为2的正方体1111ABCD A BC D -中，作与平面1ACD 平行的截面，则截得的三角形中，面积最大的值是___；截得的平面图形中，面积最大的值是___.AC【答案】【解析】试题分析：截得的三角形中，面积最大的是三角形11ACB ，面积为2=的平面图形中，面积最大的是正六边形，如图，面积为26=考点：空间想象15．在ABC ∆中，a ，b ，c 分别是角A B C ，，的对边.已知a =π3A =. （1）若b =C 的大小；（2）若2c =，求边b 的长. 【答案】（1）,125π（2）4b =. 【解析】试题分析：（1）解三角形问题，一般利用正余弦定理进行边角转化. 由正弦定理由于B 为三角形内角，b a <，则4B π=，所以3412C ππ5π=π--=.（2）由余弦定理222cos 2b c a A bc +-=得2141224b b +-=整理得2280b b --=，又0b >，所以4b =.本题也可由正弦定理sin sin a c A C =2sin C=，解得1sin 2C =.由于a c >,所以π6C =.由π3A =，得π2B =. 由勾股定理222b c a =+，解得4b =.（1由于B 为三角形内角，b a <，则4B π=，所以3412C ππ5π=π--=. 6分（2）依题意，222cos 2b c a A bc+-=，即2141224b b +-=.整理得2280b b --=，又0b >，所以4b =. 13分另解：由于sin sin a c A C =2sin C=，解得1sin 2C =.由于a c >,所以π6C =. 由π3A =，得π2B =. 由勾股定理222b c a =+，解得4b =. 13分考点：正余弦定理16．某市规定，高中学生在校期间须参加不少于80小时的社区服务才合格．某校随机抽取20位学生参加社区服务的数据，按时间段75,80),80,85),[85,90),[90,95),[95,100][[（单位：小时）进行统计，其频率分布直方图如图所示．（Ⅰ）求抽取的20人中，参加社区服务时间不少于90小时的学生人数；（Ⅱ）从参加社区服务时间不少于90小时的学生中任意选取2人，求所选学生的参加社区服务时间在同一时间段内的概率．【答案】（Ⅰ）6,（Ⅱ）7.15【解析】试题分析：（Ⅰ）根据频率分布直方图中小长方形面积为频率，而频数为总数与频率之积. 因此参加社区服务在时间段[90,95)的学生人数为200.0454⨯⨯=（人），参加社区服务在时间段[95,100]的学生人数为200.0252⨯⨯=（人）．所以参加社区服务时间不少于90小时的学生人数为 4+26=（人）．（Ⅱ）解概率应用题，要注意“设、列、解、答”. 设所选学生的参加服务时间在同一时间段内为事件A ．由（Ⅰ）可知，参加社区服务在时间段,95)[90的学生有4人，记为,,,a b c d ；参加社区服务在时间段5,100[9]的学生有2人，记为,A B .从这6人中任意选取2人有,,,,,,,,a b ac ad a A a B b c b d b A b B c d共15种情况．事件A 包括,,,,,,a b a c a d b c b d c d AB 共7种情况．所以所选学生的服务时间在同一时间段内的概率7()15P A =．解：（Ⅰ）由题意可知，参加社区服务在时间段[90,95)的学生人数为200.0454⨯⨯=（人），参加社区服务在时间段[95,100]的学生人数为200.0252⨯⨯=（人）．所以参加社区服务时间不少于90小时的学生人数为 4+26=（人）． 5分（Ⅱ）设所选学生的参加服务时间在同一时间段内为事件A ．由（Ⅰ）可知，参加社区服务在时间段,95)[90的学生有4人，记为,,,a b c d ；参加社区服务在时间段5,100[9]的学生有2人，记为,A B ．从这6人中任意选取2人有,,,,,,,,,,,,,,ab ac ad aA aB bc bd bA bB cd cA cB dA dB AB 共15种情况．事件A 包括,,,,,,ab ac ad bc bd cd AB 共7种情况．所以所选学生的服务时间在同一时间段内的概率7()15P A =． 13分考点：频率分布直方图,古典概型概率17．如图，在四棱锥P ABCD -中，底面ABCD 是正方形，侧面PAD ⊥底面ABCD ．（Ⅰ）若E ，F 分别为PC ，BD 中点，求证：EF ∥平面PAD ；（Ⅱ）求证：PA ⊥CD ；（Ⅲ）若2PA PD AD ==，求证：平面PAB ⊥平面PCD ．A【答案】（Ⅰ）详见解析，（Ⅱ）详见解析，（Ⅲ）详见解析. 【解析】试题分析：（Ⅰ）证明线面平行，关键在于找出线线平行.本题条件含中点，故从中位线上找线线平行. E ，F 分别为PC ，BD 中点，在△PAC 中，E 是PC 中点，F 是AC 中点，所以EF ∥PA ．又因为EF ⊄平面PBC ，PA ⊂平面BC P ，所以EF ∥平面PAD ．（Ⅱ）由面面垂直性质定理可得线面垂直，因为平面PAD ⊥底面ABCD ，且平面PAD 平面=ABCD AD ，又CD AD ⊥，CD ⊂平面ABCD ，所以CD ⊥面PAD ．又因为PA ⊂平面PAD ，所以CD PA ⊥．即PA ⊥CD ．（Ⅲ）证明面面垂直，关键找出线面垂直. 在△PAD中，因为2PA PD AD ==，所以PA PD ⊥．由（Ⅱ）可知PA ⊥CD ，且=C D P D D ，所以PA ⊥平面PCD ．又因为PA ⊂平面PAB ，所以平面PAB ⊥平面PCD ．证明：（Ⅰ）如图，连结AC ．因为底面ABCD 是正方形，所以AC 与BD 互相平分．又因为F 是BD 中点，所以F 是AC 中点．在△PAC 中，E 是PC 中点，F 是AC 中点，所以EF ∥PA ．又因为EF ⊄平面PAD ，PA ⊂平面PAD ，所以EF ∥平面PAD ． 4分（Ⅱ）因为平面PAD ⊥底面ABCD ，且平面PAD 平面=ABCD AD ，又CD AD ⊥，CD ⊂平面ABCD ，所以CD ⊥面PAD ．又因为PA ⊂平面PAD ，所以CD PA ⊥．即PA ⊥CD ． 9分（Ⅲ）在△PAD 中，因为PA PD AD ==，所以PA PD ⊥．由（Ⅱ）可知PA ⊥CD ，且=CD PD D ，所以PA ⊥平面PCD ．又因为PA ⊂平面PAB ，所以平面PAB ⊥平面PCD ． 14分考点：线面平行判定定理，面面垂直性质定理与判定定理18．已知函数e ()xa f x x⋅=（a ∈R ,0a ≠）.（Ⅰ）当1a =时，求曲线()y f x =在点()1,(1)f 处切线的方程；（Ⅱ）求函数()f x 的单调区间；（Ⅲ）当()0,x ∈+∞时，()f x 1≥恒成立，求a 的取值范围.【答案】（Ⅰ）e y =,（Ⅱ）0a >时，函数()f x 的单调增区间为()1,+∞；单调减区间为(),0-∞，()0,1.0a <时, 函数()f x 的单调增区间为(),0-∞，()0,1;单调减区间为()1,+∞.（Ⅲ）1ea ≥ 【解析】试题分析：（Ⅰ））利用导数的几何意义，在1x =处切线的斜率为0即为(1).f '因为22e e e (1)()x x x ax a a x f x x x ⋅--'==，所以当1a =时，2e (1)()x x f x x -'=.(1)0f '=，又(1)e f =，则曲线()f x 在1x =处切线的方程为e y =. （Ⅱ）利用导数求函数单调区间，需明确定义域{}0x x ≠，再导数值的符号确定单调区间. （1）若0a >，当()0f x '>，即1x >时，函数()f x 为增函数；当()0f x '<，即0x <和01x <<时，函数()f x 为减函数.若0a <，当()0f x '>，即0x <和01x <<时，函数()f x 为增函数；当()0f x '<，即1x >时，函数()f x 为减函数.（Ⅲ）不等式恒成立问题，一般利用变量分离转化为最值问题. 当()0,x ∈+∞时，要使()f x =e 1x a x ⋅≥恒成立，即使e x xa ≥在()0,x ∈+∞时恒成立. 设()e xx g x =，易得max 1()(1)e g x g ==，从而1ea ≥. （Ⅰ）22e e e (1)()x x x ax a a x f x x x ⋅--'==,0x ≠. 当1a =时，2e (1)()x x f x x -'=.依题意(1)0f '=，即在1x =处切线的斜率为0.把1x =代入e ()xf x x=中，得(1)e f =.则曲线()f x 在1x =处切线的方程为e y =. .4分（Ⅱ）函数()f x 的定义域为{}0x x ≠.22e e e (1)()x x x ax a a x f x x x ⋅--'==.（1）若0a >，当()0f x '>，即1x >时，函数()f x 为增函数；当()0f x '<，即0x <和01x <<时，函数()f x 为减函数. （2）若0a <，当()0f x '>，即0x <和01x <<时，函数()f x 为增函数；当()0f x '<，即1x >时，函数()f x 为减函数.综上所述，0a >时，函数()f x 的单调增区间为()1,+∞；单调减区间为(),0-∞，()0,1. 0a <时, 函数()f x 的单调增区间为(),0-∞，()0,1;单调减区间为()1,+∞. .9分（Ⅲ）当()0,x ∈+∞时，要使()f x =e 1x a x⋅≥恒成立，即使e x x a ≥在()0,x ∈+∞时恒成立. 设()e x x g x =，则1()ex x g x -'=.可知在01x <<时，()0g x '>，()g x 为增函数； 1x >时，()0g x '<，()g x 为减函数.则max 1()(1)e g x g ==.从而1ea ≥. 另解：(1)当0a <时，()e 1a f a =<，所以()f x 1≥不恒成立.(2)当0a >且()0,x ∈+∞时，由（Ⅰ）知，函数()f x 的单调增区间为()1,+∞，单调减区间为()0,1.所以函数()f x 的最小值为(1)e f a =，依题意(1)e 1f a =≥，解得1ea ≥. 综上所述，1ea ≥． .13分考点：利用导数求切线，利用导数求单调区间，利用导数求最值 19．已知椭圆C 的中心在原点O ，焦点在x 轴上，离心率为12，右焦点到右顶点的距离为1. （Ⅰ）求椭圆C 的标准方程；（Ⅱ）若直线:l 10mx y ++=与椭圆C 交于,A B 两点，是否存在实数m ，使O A O B O A O B +=-成立？若存在，求m 的值；若不存在，请说明理由.【答案】（Ⅰ）22143x y +=,（Ⅱ）不存在. 【解析】试题分析：（Ⅰ）求椭圆标准方程，关键利用待定系数法求出a,b. 由..及1a c -=，解得1c =，2a =．所以2223b a c =-=．所以椭圆C 的标准方程是22143x y +=．（Ⅱ）存在性问题，一般从假设存在出发,建立等量关系，有解就存在，否则不存在. 条件22OA OB OA OB +=-的实质是垂直关系，即0OA OB ⋅=.所以12120x x y y +=．1212()()0x x kx m kx m +++=,221212(1)()0k x x km x x m ++++=把1y mx =--代入椭圆C:223412x y +=中，整理得22(34)880m x mx ++-=.整理得2512m =-，矛盾．（Ⅰ）设椭圆C 的方程为22221x y a b+=()0a b >>，半焦距为c . 依题意1,21.c e a a c ⎧==⎪⎨⎪-=⎩ 解得1c =，2a =，所以2223b a c =-=.所以椭圆C 的标准方程是22143x y +=. .4分（Ⅱ）不存在实数m ，使||||OA OB OA OB +=-，证明如下：把1y mx =--代入椭圆C:223412x y +=中，整理得22(34)880m x mx ++-=. 由于直线l 恒过椭圆内定点()0,1-，所以判别式0∆>.设1122(,),(,)A x y B x y ，则122843m x x m +=-+,122843x x m -⋅=+. 依题意，若||||OA OB OA OB +=-，平方得0OA OB ⋅=.即12121212(1)(1)0x x y y x x mx mx +=+--⋅--=,整理得21212(1)()10m x x m x x ++++=，所以2(1)m +2843m -+2281043m m -+=+, 整理得2512m =-，矛盾．所以不存在实数m ，使||||OA OB OA OB +=-. .14分考点：椭圆标准方程，直线与椭圆位置关系20．已知函数()f x 对任意,x y ∈R 都满足()()()1f x y f x f y +=++，且1()02f =，数列{}n a 满足：()n a f n =，*n ∈N .（Ⅰ）求(0)f 及(1)f 的值;（Ⅱ）求数列{}n a 的通项公式;（Ⅲ）若311()()42n n a a n b +=-，试问数列{}n b 是否存在最大项和最小项？若存在，求出最大项和最小项；若不存在，请说明理由.【答案】（Ⅰ）(0)1f =-,(1)1f =,（Ⅱ）21na n =-,（Ⅲ）当12t =，即1n =时，{}nb 的最大项为1316b =.当132t =，即3n =时，{}n b 的最小项为331024b =-.【解析】试题分析：（Ⅰ）对应抽象函数，一般方法为赋值法. 在()()()1f x y f x f y +=++中，取0x y ==，得(0)1f =-，在()()()1f x y f x f y +=++中，取12x y ==，得(1)1f =，（Ⅱ）在()()()1f x y f x f y +=++中，令x n =，1y =，得(1)()2f n f n +=+，即12n n a a +-=.所以{}n a 是等差数列，公差为2，又首项1(1)1a f ==，所以21n a n =-,*n ∈N .（Ⅲ）研究数列{}nb 是否存在最大项和最小项，关键看通项公式的特征.令2111()()22n a n t -==，则22111()816256n b t t t =-=--，显然102t <≤，又因为N n *∈，所以当12t =，即1n =时，{}n b 的最大项为1316b =.当132t =，即3n =时，{}n b 的最小项为331024b =-解：（Ⅰ）在()()()1f x y f x f y +=++中，取0x y ==，得(0)1f =-，在()()()1f x y f x f y +=++中，取12x y ==，得(1)1f =， 2分（Ⅱ）在()()()1f x y f x f y +=++中，令x n =，1y =，得(1)()2f n f n +=+，即12n n a a +-=. 所以{}n a 是等差数列，公差为2，又首项1(1)1a f ==，所以21n a n =-,*n ∈N . 6分（Ⅲ）数列{}n b 存在最大项和最小项令2111()()22na nt-==，则22111()816256nb t t t=-=--，显然12t<≤，又因为Nn*∈，所以当12t=，即1n=时，{}n b的最大项为1316b=.当132t=，即3n=时，{}n b的最小项为331024b=-. 13分考点：等差数列，赋值法研究抽象函数。

2014—2015学年度第二学期期末考试高二数学(文)参考答案与评分标准

2014-------2015学年度第二学期期末考试参考答案及评分标准高二数学（文）一、选择题1、C2、B3、B4、 D5、 C6、 A7、 A8、C9、 C10、C11、 C12、 C二、填空题(13)2(14)2(15) 4836(16) ①②③三、解答题17．（本小题满分10 分）已知A x x24x0 ,B x x 22(a1)x a 210，其中 a R ，如果【解析】化简得A A∩ B=B ，求实数a的取值范围。

0, 4 ，∵集合 B 的元素都是集合 A 的元素，∴B A 。

⋯⋯⋯⋯⋯⋯⋯ 2 分⑴当 B时，4(a 1)24(a 21) 0 ，解得a 1 ；⋯⋯⋯⋯⋯⋯⋯ 4 分⑵当B0或 4时，4(a 1)24(a2 1) 0 ，解得a 1 ，此时 B0，满足B A ；⋯⋯⋯⋯⋯⋯⋯ 6 分4(a1)24(a21)0⑶当B 0, 4 时，2(a1)4，解得 a 1。

⋯⋯⋯⋯⋯⋯⋯ 8 分a2 10综上所述，实数 a 的取值范围是 a 1或者 a 1 。

⋯⋯⋯⋯⋯⋯⋯10 分18．（本小题满分 12 分 , 每个小题 6 分）60 ；（1）用反证法证明：在一个三角形中，至少有一个内角大于或等于（2）已知n 0，试用分析法证明：n2n 1n 1n .【解析】（1）假设在一个三角形中，没有一个内角大于或等于60 ，即均小于 602分则三内角和小于180，4分这与三角形中三个内角和等于180矛盾，故假设不成立，原命题成立；6分（2）要证上式成立，需证n 2n2n 1需证 ( n 2n )2(2 n 1)28 分97.5%需证 n1n22n需证 (n1) 2n22n需证 n22n1n 22n10 分只需证 10因为 10 显然成立，所以原命题成立.12分考点：（ 1）反证法；（2）分析法 .19．（本小题满分12 分）对某校小学生进行心理障碍测试得到如下的列联表：有心理障碍没有心理障碍总计女生1030男生7080总计20110将表格填写完整，试说明心理障碍与性别是否有关？K 2n( ad bc)2附：(a b)(c d )( a c)(b d )P(K2 ≥ k)0.150.100.050.0250.0100.0050.001K 2.072 2.076 3.841 5.024 6.6357.87910.828【解析】将列联表补充完整有：有心理障碍没有心理障碍 ]总计女生102030男生107080总计2090110K 2n( ad bc)2，故选择k0 5.024 较由(a b)(c d )(a c)(b d ) ,计算可得K2 6.366 5.024为合适 .10分因此，在犯错的概率不超过0.025 的前提下认为心理障碍与性别有关，所以有97.5%的把握认为心理障碍与性别有关.12 分考点：独立性检测 .20．（本小题满分12 分）某同学在生物研究性学习中想对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行研究，于是他在 4 月份的 30 天中随机挑选了 5 天进行研究，且分别记录了每天昼夜温差与每天每100 颗种子浸泡后的发芽数，得到如下资料：日期4月1日4月 7日4月15日4月 21日4月30日温差 x / C101113128发芽数 y / 颗2325302616（1）从这 5 天中任选 2 天，若选取的是 4 月 1日与 4 月 30 日的两组数据，请根据这 5 天中??的另三天的数据，求出y 关于的线性回归方程y b xx；?（2）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过 2 颗，则认为得到的线性回归方程是可靠的，试问（1）中所得的线性回归方程是否可靠？（参考公式：n? bx i y i nx y? i1，a y bx ）n2?2x i nxi1【解析】 (1)由数据得 x12, y27 ，3x y972 ，3977 ，322 x i y i x i434 ， 3x432 i 1i 1由公式，得?9779725?5b27123 43443222所以 y 关于 x 的线性回归方程为?53⋯⋯⋯⋯⋯⋯⋯ 6 分x2（ 2）当x 10时， ?， |22-23|2，当x 8时， ?|17-16|2，所以得到的线y 22y 17,性回归方程是可靠的 .⋯⋯⋯⋯⋯⋯⋯ 12 分21．（本小题满分 12 分）已知定义在 R 上的函数 f ( x) 对任意实数 x, y 恒有 f ( x) f ( y) f ( x y) ，且当x＞0时，f ( x) ＜0，又 f (1)2。

高考数学 2014-2015朝阳高三二模数学文答案

北京市朝阳区高三年级第二次综合练习数学试卷答案（文史类）2015.5一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项．二、填空题：本大题共6小题，每小题5分，共30分．把答案填在答题卡上．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15．（本小题满分13分）解：2()cos cos )sin f x x x x x =+-22cos cos sin x x x x =+-2cos 2x x =+2sin(2)6x π=+．（Ⅰ）因为[,]2x π∈π，所以7132[,]666x πππ+∈，所以1sin(2)[1,]62x π+∈-，所以，当且仅当13266x ππ+=，即x =π时，max ()1f x =． ……………… 8分（Ⅱ）依题意，02sin(2)26x π+=，所以0sin(2)16x π+=．又0(0,2)x ∈π，所以0252(,)666x ππ+∈π，所以0262x ππ+=或05262x ππ+=，所以06x π=或076x π=． ……………………………………………… 13分16．（本小题满分13分）解：（Ⅰ）依题意，设数列{}n a 的公差为(0)d d >．由12318a a a ++=，可得26a =，则16a d =-，36a d =+．由前三项之积为120可得，(6)6(6)120d d -创+=，解得4d =?. 舍负得4d =.所以 42n a n =-． …………………………………………… 5分（Ⅱ）由于点111(,)A a b ，222(,)A a b ，…，(,)n n n A a b 依次都在函数23xy =的图象上，且42n a n =-，所以213n n b -=．所求这n 个点123,,A A A ,…，n A 的纵坐标之和即为数列{}n b 的前n 项和n T ．由于19n nb b +=，所以数列{}n b 为以3为首项，9为公比的等比数列．所以 ()3193(91)198n nn T -==--． ……………………………………… 13分 17．（本小题满分13分）解：（Ⅰ）由题意可得，试卷的抽出比例为31=18060，所以应从选择B 题作答试卷中抽出2份，从选择C 题作答试卷中抽出2份．……4分（Ⅱ）记在（Ⅰ）中抽出的选择A 题作答的试卷分别为123,,a a a ，其中12,a a 得优；选择B 题作答的试卷分别为12,b b ，其中12,b b 得优；选择C 题作答的试卷分别为12,c c ，其中1c 得优．从123,,a a a ，12,b b 和12,c c 中分别抽出一份试卷的所有结果如下：111{,,}a b c 112{,,}a b c 121{,,}a b c 122{,,}a b c 211{,,}a b c 212{,,}a b c 221{,,}a b c 222{,,}a b c311{,,}a b c 312{,,}a b c 321{,,}a b c 322{,,}a b c所有结果共有12种可能，其中3份都得优的有111{,,}a b c 121{,,}a b c 211{,,}a b c 221{,,}a b c ，共4种．设“从被抽出的选择,,A B C 题作答的的试卷中各随机选1份，这3份试卷都得优”为事件M ，故所求概率41123P ==． …………………………… 13分18．（本小题满分14分）解：（Ⅰ）证明：由已知，DA DM =．因为点O 是线段AM 的中点，所以DO AM ⊥．又因为平面ADM ⊥平面ABCM ，平面ADM I 平面ABCM AM =，DO ⊂平面ADM ，所以DO ⊥平面ABCM ．因为DO ⊂平面DOB ，所以平面DOB ⊥平面ABCM ． ……………………………………………… 5分（Ⅱ）证明：因为在矩形ABCD 中，2AB AD =,且M 为CD 的中点，所以2AM BM AB ===，所以AM BM ⊥．由（Ⅰ）知，DO ⊥平面ABCM ，因为BM⊂平面ABCM ，所以DO BM ⊥．因为DO ⊂平面ADM ,AM ⊂平面ADM ，且DO AM O =I ，所以BM⊥平面ADM ．而AD ⊂平面ADM ，所以AD BM ⊥． …………………………………………………………… 10分（Ⅲ）过D 点不存在一条直线l ，同时满足以下两个条件：（1）l Ì平面BCD ；（2）//l AM ．理由如下：（反证法）假设过D 点存在一条直线l 满足条件，则因为//l AM ，l Ë平面ABCM ，AM ⊂平面ABCM ，所以//l 平面ABCM ．又因为l Ì平面BCD ，平面ABCM I 平面BCD BC =，所以//l BC .于是//AM BC ，由图易知AM ，BC 相交，矛盾.所以，不存在这样的直线l ． ……………………………………… 14分19．（本小题满分14分）解：(Ⅰ)不妨设直线l 在x 轴的上方，则,A B 两点关于y 轴对称.设11(,)A x y ，11(,)B x y -11(0,0)x y <>，则11(,)OA x y =uu r ，11(,)OB x y =-uu u r．由90AOB?o，得0OA OB?uu r uu u r，所以2211y x =．又因为点A 在椭圆上，所以221114x y +=．由于10x <，解得1x =-1y = 则(A -，B ．所以142555OAB S D =创=． …………………………………………5分（Ⅱ）当直线l 的斜率存在时，设其方程为y kx m =+，设11(,)A x y ，22(,)B x y ．联立方程组 22,4 4.y kx m x y ì=+ïïíï+=ïî 整理得222(41)8440k x kmx m +++-=．由方程的判别式0D >，得22410k m -+>，（※）则 122841kmx x k -+=+，21224441m x x k -=+．由90AOB?o，得0OA OB?uu r uu u r，即12120x x y y +=，而1212()()y y kx m kx m =++，则2212121212(1)()0x x y y k x x mk x x m +=++++=．所以 2222244(8)(1)04141m km k mk m k k --+++=++．整理得 225440m k --=，把22454k m =-代入（※）中，解得 234m >而224540k m =-?，所以 245m ³，显然满足234m >．直线l 始终与圆222x y r +=相切，得圆心(0,0)到直线l 的距离d 等于半径r ．则22221m r d k ==+，由224455m k =+，得245r =，因为0r >，所以5r =．当直线l 的斜率不存在时，直线l 的方程为x =?，此时，直线l 与圆2245x y +=相切，5r =．综上所述5r =． ………………………………………………………… 14分20．（本小题满分13分）解：(Ⅰ)因为1a ³，π[0,]4x Î，所以()cos sin cos sin 0f x a x x x x ¢=-??．故()f x 在区间π[0,]4上是单调递增函数． ………………………………… 4分（Ⅱ）令()0f x ¢=，得cos sin a x x =，因为在区间π[0,]4上cos 0x ¹，所以tan a x =．因为(0,1)a Î，tan [0,1]x Î，且函数tan y x =在π[0,]4上单调递增，所以方程tan a x =在π(0,)4上必有一根，记为0x ，则000()cos sin 0f x a x x ¢=-=．因为()cos sin f x a x x ¢=-在π[0,]4上单调递减，所以，当0(0,)x x Î时，0()()0f x f x ⅱ>=；当0(,)4x x p Î时，0()()0f x f x ⅱ<=．所以()f x 在0(0,)x 上单调递增，在0π(,)4x 上单调递减，所以max 000()()sin cos f x f x a x x ==+．又因为00cos sin a x x =，且2200sin cos 1x x +=，所以220(1)cos 1a x +=，2021cos 1x a =+，故2max 00()()(1)cos f x f x a x ==+=．依题意，(0,1)a Î22t at ++恒成立，即(0,1)a Î时，2(2)20t a t -++>，恒成立．令2()(2)2h a =t a t -++，则 (0)0,(1)0,h h ì³ïïíï³ïî 即2220,0.t t t ìï+?ïíï+?ïî 解得 1t ?或0t ³． ……………………………………………………… 13分。

2014年高三二模数学（文）北京市朝阳区试题Word版带解析

北京市朝阳区高三年级第二次综合练习数学学科测试（文史类）2014．5（考试时间120分钟满分150分)本试卷分为选择题（共40分）和非选择题（共110分）两部分第一部分（选择题共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项．（1）若全集{},,,U a b c d =，{},A a b =，{}B c =，则集合{}d 等于（）．（A ）()UA B （B ）A B （C ）A B （D ）()UA B解析：根据集合的运算性质，验证选项，答案为A. 考点：集合与常用逻辑用语-----集合的运算难度系数：2（2）下列函数中，既是奇函数又在区间0,+∞（）上单调递增的函数为（）．（A ）sin y x =（B ）ln y x =（C ）3y x =（D ）2x y =解析：A,C 是奇函数，A 不是一致单调函数；B,D 非奇非偶。

所以答案C 。

考点：函数与导数------------函数-----------函数的单调性；函数与导数------------函数-----------函数的奇偶性难度系数：2（3）已知抛物线22x y =,则它的焦点坐标是（）．（A ）1,04⎛⎫⎪⎝⎭（B ）10,2⎛⎫ ⎪⎝⎭（C ）10,4⎛⎫ ⎪⎝⎭（D ）1,02⎛⎫⎪⎝⎭解析：根据抛物线的性质，抛物线是开口向上的，交点，答案B 。

考点：解析几何-----------圆锥曲线----------抛物线难度系数：2（4）执行如图所示的程序框图．若输入3a =,则输出i 的值是（）．（A ）2 （B )3 （C )4 （D )5解析：第一次循环a=9，i=1；第二次循环a=21，i=2；第三次循环a=45，i=3；第四次循环 A=93，i=4，输出结果，答案为C.考点：算法与框图---------算法和程序框图难度系数：3（5）由直线10x y -+=，50x y +-=和10x -=所围成的三角形区域（包括边界）用不等式组可表示为（）．10,2⎛⎫⎪⎝⎭（A ）10,50,1.x y x y x -+≤⎧⎪+-≤⎨⎪≥⎩（B ）10,50,1.x y x y x -+≥⎧⎪+-≤⎨⎪≥⎩（C ）10,50,1.x y x y x -+≥⎧⎪+-≥⎨⎪≤⎩（D ）10,50,1.x y x y x -+≤⎧⎪+-≤⎨⎪≤⎩解析：做出平面区域，带入特殊点验证，答案为A.考点：不等式------线性规划------二元一次不等【组】表示的平面区域难度系数：3（6）在区间ππ[-,]上随机取一个实数x ，则事件：“cos 0x ≥”的概率为（）．（A ）14（B )34（C ）23（D ）12解析：该题考察解概率模型，画出余弦函数，结合函数图像答案为D. 考点：概率与统计---------概率--------几何概率难度系数：3（7）设等差数列{}n a 的公差为d ，前n 项和为n S ．若11a d ==，则8n nS a +的最小值为（）．（A ）10（B ）92（C ）72（D）12+解析：11(1)(1)888(1)81922(1)222n nn n n n a n d S n a a n d n n +++++++===+≥=+-，答案为B 。

北京市北京市朝阳区2014-2015学年高二下学期期末统一考试化学试题答案

作用。 (2)温度、浓度等 (3)KMnO4溶液褪色的速率开始十分缓慢 ,一段时间后突然加快。因为反应生成的 Mh s04是 Κ Mno‘ 与 H2C204反应催化剂 ,能加快反应速率。 (4)酸性 KMno4溶液具有强氧化性 ,能氧化 Mncla中的 Cl`也会使 KMno4溶液褪色产生干扰。 (8分 ×每空 2分 )
北京市朝阳区 2014~⒛ 15学年度高二年级第二学期期末统一考试
化学试卷参考答案
第 I卷 (选择题 ,共
2015,7
0z分 )
9
每小题只有一个选项符合题意。21个小题 ,每小题 2分 ,共 zIz分
1
2
3
4 B
17
5
6
7
8
Λ
10
12
13
A
14
C
15
D
16
C
18
C
19
B
⒛
C
B
C
A
D
21
⒇廴了普斋扣叩 Γ或鼬
② 逆向 ③ 减小 ④ ⒈ 温度 ,E2>II,其他条件相同时 ,增大压强有利于平衡向气体体积缩小的方向移动 Ⅱ 从而提南 H2(g)的平衡转化率 (3〉 ① 还原 ② 2NH3ˉ 6e-+60Hˉ ===N2+6H20
高二化学试卷参考答案第 2页 (共 2页 )
,
ˉ Mg2+与进 Cα 水解。
Cα +H20手=羽 COf+oH`HCOJ+H,0==H2Co:+0H、
ˉ
ˉ 发生水 ˉ 底水彻
(2分 )
在煮沸情况下促

2015朝阳区高三二模数学(文科)

2015朝阳区高三二模数学（文科）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项．1．（5分）设集合A={x|（x﹣1）（x﹣2）≤0}，集合B={x|x|＜1}，则A∪B=（）A．∅B．{x|x=1} C．{x|1≤x≤2}D．{x|﹣1＜x≤2}2．（5分）在如图所示的正方形中随机掷一粒豆子，豆子落在该正方形内切圆的四分之一圆（如图阴影部分）中的概率是（）A．B．C．D．3．（5分）实数x，y满足不等式组，则目标函数z=x+3y的最小值是（）A．﹣12 B．﹣8 C．﹣4 D．04．（5分）已知非零平面向量，，则“与共线”是“+与﹣共线”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件5．（5分）执行如图所示的程序框图，输出S的值为（）A．0 B．﹣1 C．﹣D．﹣6．（5分）函数f（x）=的零点个数是（）A．0 B．1 C．2 D．37．（5分）已知点A为抛物线C：x2=4y上的动点（不含原点），过点A的切线交x轴于点B，设抛物线C的焦点为F，则△ABF（）A．一定是直角B．一定是锐角C．一定是钝角D．上述三种情况都可能8．（5分）已知某校一间办公室有四位老师甲、乙、丙、丁．在某天的某个时段，他们每人各做一项工作，一人在查资料，一人在写教案，一人在批改作业，另一人在打印材料．若下面4个说法都是正确的：①甲不在查资料，也不在写教案；②乙不在打印材料，也不在查资料；③丙不在批改作业，也不在打印材料；④丁不在写教案，也不在查资料．此外还可确定：如果甲不在打印材料，那么丙不在查资料．根据以上信息可以判断（）A．甲在打印材料B．乙在批改作业C．丙在写教案D．丁在打印材料二、填空题：本大题共6小题，每小题5分，共30分．把答案填在答题卡上．9．（5分）设i为虚数单位，则i（1﹣i）=．10．（5分）若中心在原点的双曲线C的一个焦点是F1（0，﹣2），一条渐近线的方程是x﹣y=0，则双曲线C的方程为．11．（5分）一个四棱锥的三视图如图所示，则这个四棱锥的体积为；表面积为．12．（5分）已知在△ABC中，C=，cosB=，AB=5，则sinA=；△ABC的面积为．13．（5分）在圆C：（x﹣2）2+（y﹣2）2=8内，过点P（1，0）的最长的弦为AB，最短的弦为DE，则四边形ADBE的面积为．14．（5分）关于函数f（x）=的性质，有如下四个命题：①函数f（x）的定义域为R；②函数f（x）的值域为（0，+∞）；③方程f（x）=x有且只有一个实根；④函数f（x）的图象是中心对称图形．其中正确命题的序号是．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．（13分）已知函数f（x）=cosx（2sinx+cosx）﹣sin2x．（Ⅰ）求函数f（x）在区间[，π]上的最大值及相应的x的值；（Ⅱ）若f（x0）=2，且x0∈（0，2π），求x0的值．16．（13分）已知递增的等差数列{a n}（n∈N*）的前三项之和为18，前三项之积为120．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）若点A1（a1，b1），A2（a2，b2），…，A n（a n，b n）（n∈N*）从左至右依次都在函数y=3的图象上，求这n个点A1，A2，A3，…，A n的纵坐标之和．17．（13分）某学科测试，要求考生从A，B，C三道试题中任选一题作答．考试结束后，统计数据显示共有420名学生参加测试，选择A，B，C题作答的人数如表：（Ⅰ）某教师为了解参加测试的学生答卷情况，现用分层抽样的方法从420份试卷中抽出若干试卷，其中从选择A题作答的试卷中抽出了3份，则应从选择B，C题作答的试卷中各抽出多少份？（Ⅱ）若在（Ⅰ）问被抽出的试卷中，选择A，B，C题作答得优的试卷分别有2份，2份，1份．现从被抽出的选择A，B，C题作答的试卷中各随机选1份，求这3份试卷都得优的概率．18．（14分）如图，在矩形ABCD中，AB=2AD，M为CD的中点．将△ADM沿AM折起，使得平面ADM⊥平面ABCM．点O是线段AM的中点．（Ⅰ）求证：平面DOB⊥平面ABCM；（Ⅱ）求证：AD⊥BM；（Ⅲ）过D点是否存在一条直线l，同时满足以下两个条件：①l⊂平面BCD；②l∥AM．请说明理由．19．（14分）已知椭圆C：+y2=1，O为坐标原点，直线l与椭圆C交于A，B两点，且∠AOB=90°．（Ⅰ）若直线l平行于x轴，求△AOB的面积；（Ⅱ）若直线l始终与圆x2+y2=r2（r＞0）相切，求r的值．20．（13分）已知函数f（x）=asinx+cosx，其中a＞0．（Ⅰ）当a≥1时，判断f（x）在区间[0，]上的单调性；（Ⅱ）当0＜a＜1时，若不等式f（x）＜t2+at+2对于x∈[0，]恒成立，求实数t的取值范围．参考答案与试题解析一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项．1．【解答】A={x|（x﹣1）（x﹣2）≤0}={x|1≤x≤2}，由B={x|x|＜1}得{x|﹣1＜x＜1}，则A∪B={x|﹣1＜x≤2}，故选：D2．【解答】设正方形的边长为2，则面积为4；圆与正方形内切，圆的半径为1，所以圆的面积为π，则阴影部分的面积为，所以所求概率为P==．故选：C．3．【解答】由约束条件作出可行域如图，化目标函数z=x+3y为，由图可知，当直线过A（﹣2，2）时，直线在y轴上的截距最小，z有最小值为﹣8．故选：B．4．【解答】设命题q：“与共线”，设命题“+与﹣共线”，显然命题q成立时，命题p成立，所以q是P成立的充分条件；当“+与﹣共线”时，根据共线的定义有+=λ（﹣），则，由于非零平面向量，，所以λ≠±1，那么，所以与共线，所以q是p 必要条件；综上可得，q是p的充要条件；故选：C．5．【解答】模拟执行程序框图，可得S=0，n=1S=，n=3，n不大于5S=﹣，n=5，n不大于5S=0，n=7，n大于5退出循环，输出S的值为0，故选：A．6．【解答】作函数f（x）=的图象如下，由图象可知，函数f（x）=的零点个数是2，故选：C．7．【解答】由x2=4y可得y=x2，∴y′=x，设A（x0，），则过A的切线方程为y﹣=x0（x﹣x0），令y=0，可得x=x0，∴B（x0，0），∵F（0，1），∴=（x0，），=（﹣x0，1），∴•=0，∴∠ABF=90°，故选：A．8．【解答】把已知条件列表如下：若甲不在打印资料，则丙不在查资料，则甲在改作业，丙只能写教案，乙不管是写教案还是改作业都与甲或丙在做一样的事，与题设矛盾．所以甲一定在打印资料，此时丁在改作业，乙在写教案，丙在查资料．故选：A．二、填空题：本大题共6小题，每小题5分，共30分．把答案填在答题卡上．9．【解答】i（1﹣i）=i﹣i2=1+i．故答案为：1+i．10．【解答】设双曲线的方程为﹣=1（a，b＞0）则c=2，由渐近线方程y=±x，由题意可得a=b，又c2=a2+b2，解得a=b=2，则双曲线的方程为﹣=1．故答案为：﹣=1．11．【解答】由题意可知，其直观图如下，其底面为正方形，S=1×1=1，高为2；故V=×1×2=；其表面积S=1+（2+2+）=3+；故答案为：，3+．12.【解答】∵C=，cosB=，∴sinC=cosC=，sinB==．∴sinA=sin（B+C）=sinBcosC+cosBsinC==．由正弦定理可得：，可得b===4，∴S=×=14．故答案分别为：，14．13．【解答】圆的标准方程为（x﹣2）2+（y﹣2）2=8，由题意得最长的弦|AB|=4，圆心（2，2），圆心与点（1，0）的距离d==，根据勾股定理得最短的弦|DE|=2=2=2，且AB⊥DE，四边形ABCD的面积S=|AB|•|DE|=×4×2=4，故答案为：4．14．【解答】对于①，函数f（x）=的定义域为R；所以①正确；对于②，函数f（x）的值域为（0，+∞）；显然不正确，因为函数减函数函数的值域是：（0，），所以②不正确；对于③方程f（x）=x有且只有一个实根；如图，作出两个是的图象，可知可知方程只有一个根，所以③正确；对于④，函数f（x）的图象是中心对称图形．因为f（x+1）+f（﹣x）=，==，∴f（x）关于（）对称，所以④正确．故答案为：①③④．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．【解答】（Ⅰ）f（x）=cosx（2sinx+cosx）﹣sin2x=cosx（2sinx+cosx）﹣sin2x=2sinxcosx+cos2x﹣sin2x=sin2x+cos2x=2sin（2x+），∵x∈[，π]，∴2x+∈[，]，∴sin（2x+）∈[﹣1，]，∴当且仅当2x+=，即x=π时，f（x）max=1；…8分（Ⅱ）由题意，2sin（2x0+）=2，所以sin（2x0+）=1，又x0∈（0，2π），所以2x0+∈（，），所以2x0+=或2x0+=，所以x0=或x0=．…13分16．【解答】（Ⅰ）设数列{a n}的公差为d，∵前三项之和为18，∴a2=6，a1=6﹣d，a3=6+d，又∵前三项之积为120，∴（6﹣d）×6×（6+d）=120，解得d=4或﹣4（舍），∴a1=6﹣4=2，∴a n=4n﹣2；（Ⅱ）根据题意及（I），可得b n=32n﹣1，∴求这n个点A1，A2，A3，…，A n的纵坐标之和即为数列{b n}的前n项和T n，∵=9，b1=32×1﹣1=3，∴数列{b n}是首项为3、公比为9的等比数列，∴T n==（9n﹣1）．17．【解答】（Ⅰ）由题意可得，试卷的抽出比例为=，所以应从选择B题作答试卷中抽取2份，从选择C题作答试卷中抽出2份，（Ⅱ）记（Ⅰ）中抽取得选择A题作答的试卷分别为a1，a2，a3，其中a1，a2得优，选择B题作答的试卷分别为b1，b2，其中b1，b2得优，选择C题作答的试卷分别为c1，c2其中c1得优，从三种试一份卷中分别抽取所有得结果如下，{a1，b1，c1}，{a1，b1，c2}，{a1，b2，c1}，{a1，b2，c2}，{a2，b1，c1}，{a2，b1，c2}，{a2，b2，c1}，{a2，b2，c2}，{a3，b1，c1}，{a3，b1，c2}，{a3，b2，c1}，{a3，b2，c2}，所以结果共有12种可能，其中3份都得优得有{a1，b1，c1}，{a1，b2，c1}，{a2，b1，c1}，{a2，b2，c1}，共4种，故这3份试卷都得优的概率P==．18．【解答】（Ⅰ）由已知DA=DM，O是AM的中点，∴DO⊥AM，∵平面ADM⊥平面ABCM，平面ADM∩平面ABCM=AM，DO⊂平面DOB，∴平面DOB⊥平面ABCM；（Ⅱ）在矩形ABCD中，AB=2AD，M为CD的中点，∴AM=BM=AD=AB，∴AM⊥BM，由（1）知，DO⊥平面ABCM；∵BM⊂平面ABCM，∴DO⊥BM，∵DO，AM⊂平面ADM，DO∩AM=0，∴BM⊥平面ADM，而AD⊂平面ADM，∴AD⊥BM；（Ⅲ）过D点是不存在一条直线l，同时满足以下两个条件：①l⊂平面BCD；②l∥AM．证明（反证法）假设过D存在一条直线l满足条件，则∵l∥AM，L⊄平面ABCM，AM⊂平面ABCM，∴l∥平面ABCM，∵l⊂平面BCD，平面ABCM∩平面BCD=BC，∴l∥BC，即AM∥BC，由图易知，AM，BC相交，此时矛盾，∴过D点不存在一条直线l满足题设条件．19．【解答】（Ⅰ）不妨设直线l在x轴上方，则A，B两点关于y轴对称，设A（x1，y1），B（﹣x1，y1），（x1＜0，y1＞0），则，由∠AOB=90°，得，∴．又∵点A在椭圆上，∴．由于x1＜0，解得：．则A（），B（）．∴．（Ⅱ）当直线l的斜率存在时，设其方程为y=kx+m，设A（x1，y1），B（x2，y2），联立方程组，整理得：（4k2+1）x2+8kmx+4m2﹣4=0．方程的判别式△=4k2﹣m2+1＞0，．由∠AOB=90°，得，即x1x2+y1y2=0．而y1y2=（kx1+m）（kx2+m），则+m2=0∴．整理得：5m2﹣4k2﹣4=0．把4k2=5m2﹣4代入△=4k2﹣m2+1＞0，得．而4k2=5m2﹣4≥0，∴，满足．直线l始终与圆x2+y2=r2（r＞0）相切，得，由，得．∵r＞0，∴r=．当直线l的斜率不存在时，若直线l与圆x2+y2=r2（r＞0）相切，此时直线l的方程为：x=，r=．综上所述：r=．20．【解答】（Ⅰ）∵a≥1，x∈[0，]，∴f′（x）=acosx﹣sinx≥cosx﹣sinx≥0，∴f（x）在区间[0，]上单调递增；（Ⅱ）令f′（x）=0可得acosx=sinx，∵x∈[0，]，∴cosx≠0，∴a=tanx，∵0＜a＜1，∴tanx∈（0，1），∵函数y=tanx在（0，）上单调递增，∴方程a=tanx在（0，）上必有一根，记为x0，则f′（x0）=acosx0﹣sinx0=0，∵f′（x）=acosx﹣sinx在x∈[0，]上单调递减，∴当x∈（0，x0）时，f′（x）＞f′（x0）=0，当x∈（x0，）时，f′（x）＜f′（x0）=0，∴函数f（x）在（0，x0）单调递增，在（x0，）单调递减，∴f（x）max=f（x0）=asinx0﹣cosx0，又∵acosx0=sinx0，cos2x0+sin2x0=1，∴（a2+1）cos2x0=1，∴cos2x0=，∴f（x）max=f（x0）=（a2+1）cosx0=∵当0＜a＜1时，若不等式f（x）＜t2+at+2对于x∈[0，]恒成立，∴＜t2+at+2，即（t﹣2）a+（t2+2）＞0当0＜a＜1时恒成立，令h（a）=（t﹣2）a+（t2+2），则，解不等式组可得t≤﹣1或t≥0。

2014-2015朝阳高二下期末

北京市朝阳区2014-2015学年度高二年级第二学期期末统一考试2015.7第二部分：知识运用（共两节，35分）单项填空（共15小题，每小题1分，共15分）从每题A、B、C、D四个选项中选出可以填入空白处的最佳答案。

16. Jerry is very honest, __________ you can believe everything he said.A. butB. soC. orD. for17. We’re offered her the job, but I don’t know __________ she’ll accept it.A. whereB. whatC. whetherD. which18. You can call us at any time you like. ______ here is willing to lend you a hand.A. OneB. No oneC. SomeoneD. Everyone19. They have raised $10,000 for the poor children, ______ is quite unexpected.A. thatB. whichC. whoD. it20. Before traveling to Australia, you’d better go to the library ____ some books about the country.A. forB. atC. onD. with21. —Mr. Zhang, can I go to your office at 9 am tomorrow?—I’m afraid not. I ________ a meeting then.A. was attendingB. would attendC. will be attendingD. will have attended22. It is still unclear _____ the man didn’t speak the truth.A. thatB. howC. whenD. why23. Helen says she will leave the company if she _____ for her carelessness.A. punishesB. is punishedC. will punishD. will be punished24. _____ quite a few earthquakes before, the man wasn’t frightened.A. ExperiencingB. To experienceC. Being experiencedD. Having experienced25. As a leading expert in this field, he was invited____ some professional advice.A. to giveB. being givenC. givingD. given26. If Peter hadn’t offered me a ride home yesterday, I _____ a taxi.A. should callB. would callC. would have calledD. should have called27. —Is Mary coming?—No, she ______ her mind after she checked her text message.A.changesB. changedC. had changedD. is changing28. The local gym came into use last month without ______.A. decoratedB. decoratingC. being decoratedD. having decorated29. —What is Dr. Jason saying?—He is giving some evidence ____ that the earth is becoming warmer and warmer.A.being indicatedB. indicatingC. indicatesD. indicated30. Welcome to Disneyland in Shanghai! This is _____ you can have fun and more than fun.A. whereB. howC. whatD. that第二节完形填空（共20小题，每小题1分，共20分）阅读下面短文，理解大意，然后从每题A、B、C、D中选一个最佳答案。

北京师大附中2014-2015学年下学期高二年级期末考试数学试卷(文科) 有答案

北京师大附中2014－2015学年下学期高二年级期末考试数学试卷（文科）有答案本试卷共150分，考试时间120分钟。

一、选择题：本大题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合要求的。

1. 若全集}5,4,3,2,1{=U ，集合}4,3{},3,1{==B A ，那么集合)()(B C A C U U 等于 A. {2}B. {2，5}C. {3}D. {1，3，4}2. 若R a ∈，则“8>a ”是“2log 2>a ”的（） A. 充分但不必要条件 B. 必要但不充分条件C. 充要条件D. 既不是充分条件也不是必要条件3. 设命题p ：函数1)(-=x e x f 在R 上为增函数；命题q ：函数x x f 2cos )(=为奇函数，则下列命题中真命题是（）A. q p ∧B. q p ∨⌝)(C. )()(q p ⌝∧⌝D. )(q p ⌝∧4. 设)2,0(),2,0(πβπα∈∈，且ββαcos sin 1tan +=，则（） A. 23πβα=- B. 22πβα=+ C. 23πβα=+D. 22πβα=-5. 如图，两座相距60 m 的建筑物AB 、CD 的高度分别为20m 、50 m ，BD 为水平面，则从建筑物AB 的顶端A 看建筑物CD 的张角为（）。

A. 30°B. 45°C. 60°D. 75°6. 对于R x ∈，函数)(x f 满足)()2(),1()1(x f x f x f x f =++=-，若当]1,0(∈x 时，)(x f ＝1+x ，则)215(f 等于（）A.21 B.23 C.25 D.27 7. 已知函数a x x x f ++-=4)(2在区间]3,3[-上存在零点，求实数a 的取值范围（） A. )21,4(-B. ]21,4[-C. )21,3(-D. ]21,3[-8. 函数cx bx ax x f +-=23)(的图象如图所示，且)(x f 在0x x =与1=x 处取得极值，给出下列判断：①0>c ；②0)1()1(>-+f f ；③函数)(x f y '=在区间),0(+∞上是增函数。