第四章相似图形单元检测(含答案)

合集下载

(数学试卷九年级)第四章图形的相似单元测试卷及答案

九（上）第四章图形的相似单元测试一、选择题1、【基础题】在比例尺为1：5000的地图上，量得甲，乙两地的距离为25 cm ，则甲、乙两地的实际距离是 ( )A. 1250千米B. 125千米C. 12.5千米D. 1.25千米2、【基础题】已知135＝a b ，则ba b a ＋－的值是（） ★A. 32B. 23C. 49D. 943、【基础题】如右图，在△ABC 中，看DE ∥BC ，12AD BD ，DE ＝4 cm ，则BC 的长为 ( ) A ．8 cm B ．12 cm C ．11 cm D ．10 cm 4、【基础题】如右图，DE 是ΔABC 的中位线，则ΔADE 与ΔABC 的面积之比是（） A ．1:1 B ．1:2 C ．1:3 D ．1:45、【基础题】如下图，小正方形的边长均为1，则图中三角形（阴影部分）与△ABC 相似的是( ) ★★★6、【基础题】下列结论不正确的是( ) ★ A. 所有的矩形都相似 B. 所有的正方形都相似 C. 所有的等腰直角三角形都相似 D. 所有的正八边形都相似7、【基础题】下列说法中正确的是( ) ★A. 位似图形可以通过平移而相互得到B. 位似图形的对应边平行且相等C. 位似图形的位似中心不只有一个D. 位似中心到对应点的距离之比都相等 8、【综合题Ⅰ】如左下图，ABCD 是正方形，E 是CD 的中点，P 是BC 边上的一点，下列条件中，A不能推出△ABP与△ECP相似的是（）★★★A.∠APB＝∠EPCB. ∠APE＝90°C. P是BC的中点D. BP︰BC＝2︰39、【综合题Ⅱ】（2020山东潍坊）如右上图,Rt△ABC中，AB⊥AC，AB=3，AC=4，P 是BC边上一点，作PE⊥AB于E，PD⊥AC于D，设BP＝x，则PD+PE＝（）A. 35x+ B. 45x- C.72D.21212525x x-10、【综合题Ⅲ】如图，在Rt ABC△内有边长分别为a，b，c的三个正方形．则a、b、c满足的关系式是（）A. b a c=+ B. b ac=C. 222b a c=+ D. 22b a c==二、填空题11、【基础题】在同一时刻，高为1.5m的标杆的影长为2.5m，一古塔在地面上影长为50m，那么古塔的高为．12、【基础题】两个相似三角形面积比是9∶25，其中一个三角形的周长为36cm，则另一个三角形的周长是．13、【综合题Ⅰ】如左下图，在△ABC中，AB＝5，D、E分别是边AC和AB上的点，且∠ADE＝∠B，DE＝2，那么AD·BC＝ . ★★★ABCDEP14、【基础题】如右上图，在△ABC 和△DEF 中，G 、H 分别是边BC 和EF 的中点，已知AB ＝2DE ，AC ＝2DF ，∠BAC ＝∠EDF. 那么AG ：DH ＝，△ABC 与△DEF 的面积比是 . ★★★15、【基础题】把一个三角形改做成和它相似的三角形，如果面积缩小到原来的21倍，边长应缩小到原来的____倍.16、【综合Ⅱ】如左下图在Rt△ABC 中, ∠ACB＝90°,CD⊥AB 于D ，若AD ＝1，BD ＝4，则CD ＝ . ★17、【基础题】如右上图，一人拿着一支厘米小尺，站在距电线杆约30米的地方，把手臂向前伸直，小尺竖直，看到尺上12厘米的长度恰好遮住电线杆，已知手臂长约60厘米，则电线杆的高为 . ★★★ 18、【基础题】已知一本书的宽与长之比为黄金比，且这本书的长是20 cm ，则它的宽为_____cm.（结果保留根号） 19、【综合Ⅲ】顶角为36°的等腰三角形称为黄金三角形，如图，在△ABC 中，AB ＝AC ＝1，∠A ＝36°，BD 是三角形ABC 的角平分线，那么AD ＝ . ★20、【提高题】如图，点1234A A A A ，，，在射线OA 上，点123B B B ，，在射线OB 上，且112233A B A B A B ∥∥，213243A B A B A B ∥∥．若212A B B △、323A B B △的面积分别为1、4，则图中三个阴影三角形面积之和为．三、解答题 21、【基础题】（2020无锡）如图，已知点E 是矩形ABCD 的边CD 上一点，BF ⊥AE 于点F ，求证△ABF ∽△EAD ． 22、【综合Ⅰ】如图27－106所示，已知E 为ABCD 的边CD 延长线上的一点，连接BE 交AC 于O ，交AD 于F ．求证BO 2＝OF ·OE ．23、如图，在平面直角坐标系中，已知OA=12 cm ，OB=6 cm ，点P 从O 点开始沿OA边向点A 以1cm/s 的速度移动，点Q 从点B 开始沿BO 边向点O 以1cm/s 的速度移动，如果P 、Q 同时出发，用t （单位：秒）表示移动的时间（06t ≤≤），那么：（1）当t 为何值时， △POQ 与△AOB 相似？（第20题图） OA A A A AB B B 2 B 31 4（2）设△POQ 的面积为y ，求y 关于t 的函数解析式。

北师大版数学九年级上册《第四章图形相似》单元测试(含答案)

北师大版数学九年级上册《第四章图形相似》单元测试一．选择题（共12小题）1．若，则的值为（）A．1 B．C．D．2．若△ABC∽△DEF，且对应中线比为2：3，则△ABC与△DEF 的面积比为（）A．3：2 B．2：3 C．4：9 D．9：163．如图，为估算某河的宽度，在河对岸边选定一个目标点A，在近岸取点B，C，D，使得AB⊥BC，CD⊥BC，点E在BC上，并且点A，E，D在同一条直线上．若测得BE=30m，EC=15m，CD=30m，则河的宽度AB长为（）A．90m B．60m C．45m D．30m 4．如图，已知点E（﹣4，2），F（﹣2，﹣2），以O为位似中心，按比例尺1：2，把△EFO缩小，则点E的对应点E′的坐标为（）A．（2，﹣1）或（﹣2，1）B．（8，﹣4）或（﹣8，﹣4）C．（2，﹣1）D．（8，﹣4）5．如图，已知AD为△ABC的角平分线，DE∥AB交AC于E，如果=，那么等于（）A．B．C．D．6．如图，直线l1∥l2∥l3，直线AC分别交l1，l2，l3于点A，B，C；直线DF分别交l1，l2，l3于点D、E、F，AC与DF相交于点H，且AH=2，HB=1，BC=5，则=（）A．B．2 C．D．7．如图▱ABCD，E是BC上一点，BE：EC=2：3，AE交BD于F，则BF：FD等于（）A．2：5 B．3：5 C．2：3 D．5：7 8．如图，在▱ABCD中，AC与BD相交于点O，E为OD的中点，连接AE并延长交DC于点F，则S△DEF：S△AOB的值为（）A．1：3 B．1：5 C．1：6 D．1：11 9．如图，在△ABC中，∠C=90°，点D是BC边上一动点，过点B 作BE⊥AD交AD的延长线于E．若AC=6，BC=8，则的最大值为（）A．B．C．D．[来源:学] 10．如图，△ABC中，D、E是BC边上的点，BD：DE：EC=3：2：1，M在AC边上，CM：MA=1：2，BM交AD，AE于H，G，则BH：HG：GM等于（）A．3：2：1 B．5：3：1 C．25：12：5 D．51：24：10 11．如图为两正方形ABCD、BEFG和矩形DGHI的位置图，其中G、F两点分别在BC、EH上．若AB=5，BG=3，则△GFH的面积为何？（）A．10 B．11 C．D．12．如图，，∠1=∠2，则对于结论：①△ABE∽△ACF；②△ABC∽△AEF；③；④．其中正确的结论的个数是（）A．1 B．2 C．3 D．4二．填空题（共5小题）13．如图，△ABC中，AD是中线，BC=8，∠B=∠DAC，则线段AC的长为．14．已知直线a∥b∥c，直线m，n与直线a，b，c分别交于点A，C，E，B，D，F，AC=4，CE=6，BD=3，则BF=．15．如图，在斜边长为1的等腰直角三角形OAB中，作内接正方形A1B1D1C1；在等腰直角三角形OA1B1中作内接正方形A2B2D2C2；在等腰直角三角形OA2B2中作内接正方形A3B3D3C3；…；依次做下去，则第n个正方形A n B n D n C n的边长是．16．如图，在Rt△ABC中，∠ABC=90°，AB=3，BC=4，Rt△MPN，∠MPN=90°，点P在AC上，PM交AB于点E，PN交BC于点F，当PE=2PF时，AP=．17．如图，四边形DEFG是△ABC的内接矩形，其中D、G分别在边AB，AC上，点E、F在边BC上，DG=2DE，AH是△ABC的高，BC=20，AH=15，那么矩形DEFG的周长是．三．解答题（共6小题）18．已知，如图，△ABC中，AB=2，BC=4，D为BC边上一点，BD=1．（1）求证：△ABD∽△CBA；（2）在原图上作DE∥AB交AC与点E，请直接写出另一个与△ABD相似的三角形，并求出DE的长．19．如图，在正方形ABCD中，E、F分别是边AD、CD上的点，AE=ED，DF=DC，连接EF并延长交BC的延长线于点G．（1）求证：△AB E∽△DEF；（2）若正方形的边长为4，求BG的长．20．如图，正方形ABCD中，M为BC上一点，F是AM的中点，EF⊥AM，垂足为F，交AD的延长线于点E，交DC于点N．（1）求证：△ABM∽△EFA；（2）若AB=12，BM=5，求DE的长．21．如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B．（1）求证：△ADF∽△DEC；（2）若AB=4，AD=，AE=3，求AF的长．22．已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．（1）画出△ABC向下平移4个单位长度得到的△A1B1C1，点C1的坐标是；（2）以点B为位似中心，在网格内画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2：1，点C2的坐标是．23．如图，在矩形ABCD和矩形PEFG中，AB=8，BC=6，PE=2，PG=4．PE与AC交于点M，EF与AC交于点N，动点P从点A出发沿AB以每秒1个单位长的速度向点B匀速运动，伴随点P的运动，矩形PEFG在射线AB上滑动；动点K从点P出发沿折线PE﹣﹣EF 以每秒1个单位长的速度匀速运动．点P、K同时开始运动，当点K 到达点F时停止运动，点P也随之停止．设点P、K运动的时间是t 秒（t＞0）．（1）当t=1时，KE=，EN=；（2）当t为何值时，△APM的面积与△MNE的面积相等？（3）当点K到达点N时，求出t的值；（4）当t为何值时，△PKB是直角三角形？参考答案一．选择题1．C．2．C．3．B．4．A．5．B．6．A．7．A．8．C．9．B10．D．11．D．12．B．二．填空题13．]4．14．7.5．15.]．16．3．17．36．三．解答题18．（1）证明：∵AB=2，BC=4，BD=1，∵∠ABD=∠CBA，∴△ABD∽△CBA；（2）解：∵DE∥AB，∴△CDE∽△C BA，∴△ABD∽△CDE，∴DE=1.5．19．（1）证明：∵ABCD为正方形，∴AD=AB=DC=BC，∠A=∠D=90°，∵AE=ED，∵DF=DC，∴△ABE∽△DEF；（2）解：∵ABCD为正方形，∴ED∥BG，又∵DF=DC，正方形的边长为4，∴ED=2，CG=6，∴BG=BC+CG=10．20．（1）证明：∵四边形ABCD是正方形，∴AB=AD，∠B=90°，AD∥BC，∴∠AMB=∠EAF，又∵EF⊥AM，∴∠AFE=90°，∴∠B=∠AFE，∴△ABM∽△EFA；（2）∵∠B=90°，AB=12，BM=5，∴AM==13，AD=12，∵F是AM的中点，∴AF=AM=6.5，∵△ABM∽△EFA，∴，即，∴AE=16.9，∴DE=AE﹣AD=4.9．21．解：（1）∵四边形ABCD是平行四边形，∴AB∥CD，AD∥BC，∴∠B+∠C=180°，∠ADF=∠DEC，∵∠AFD+∠AFE=180°，∠AFE=∠B，∴∠AFD=∠C，∴△ADF∽△DEC；（2）∵AE⊥BC，AD=3，AE=3，∴在Rt△DAE中，DE===6，由（1）知△ADF∽△DEC，得=，∴AF===2．22．解：（1）如图所示，画出△ABC向下平移4个单位长度得到的△A1B1C1，点C1的坐标是（2，﹣2）；（2）如图所示，以B为位似中心，画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2：1，点C2的坐标是（1，0），故答案为：（1）（2，﹣2）；（2）（1，0）23．解：（1）当t=1时，根据题意得，AP=1，PK=1，∵PE=2，∴KE=2﹣1=1，∵四边形ABCD和PEFG都是矩形，∴△APM∽△ABC，△APM∽△NEM，∴MP=，ME=，∴NE=；故答案为：1；；（2）由（1）并结合题意可得，AP=t，PM=t，ME=2﹣t，NE=﹣t，∴t×t=（2﹣t）×（﹣t），解得，t=；（3）当点K到达点N时，则PE+NE=AP，由（2）得，﹣t+2=t，解得，t=；（4）①当K在PE边上任意一点时△PKB是直角三角形，即，0＜t≤2；②当点k在EF上时，则KE=t﹣2，BP=8﹣t，∵△BPK∽△PKE，∴PK2=BP×KE，PK2=PE2+KE2，∴4+（t﹣2）2=（8﹣t）（t﹣2），解得t=3，t=4；③当点K运动6秒时，点K到点F，点P还没到点B，∴点K不可能在BC边上，．综上，当0＜t≤2或t=3或t=4时，△PKB是直角三角形．。

2020年第四章相似图形单元达标检测(含答案)

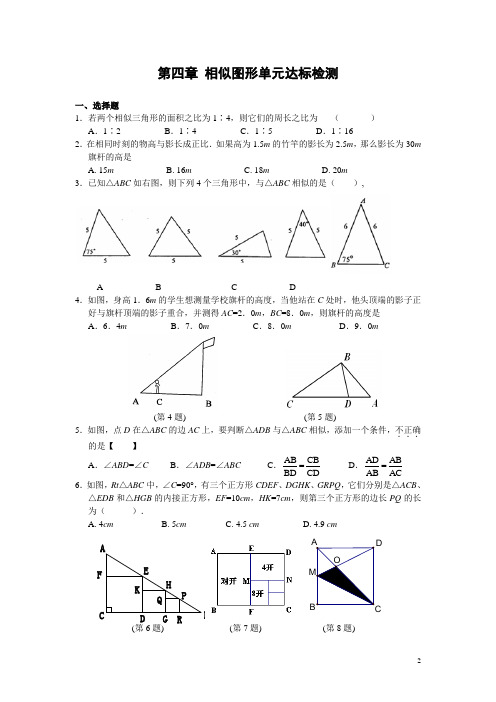
R Q PKHG FED C B A第四章相似图形单元达标检测一、选择题1．若两个相似三角形的面积之比为1∶4，则它们的周长之比为（） A ．1∶2 B ．1∶4 C ．1∶5 D ．1∶16 2．在相同时刻的物高与影长成正比．如果高为1.5m 的竹竿的影长为2.5m ，那么影长为30m 旗杆的高是A. 15mB. 16mC. 18mD. 20m3．已知△ABC 如右图，则下列4个三角形中，与△ABC 相似的是（）,A B C D4．如图，身高1．6m 的学生想测量学校旗杆的高度，当他站在C 处时，他头顶端的影子正好与旗杆顶端的影子重合，并测得AC =2．0m ，BC =8．0m ，则旗杆的高度是 A ．6．4m B ．7．0m C ．8．0m D ．9．0m(第4题) (第5题)5．如图，点D 在△ABC 的边AC 上，要判断△ADB 与△ABC 相似，添加一个条件，不正确．．．的是【】A ．∠ABD =∠CB ．∠ADB =∠ABC C ．AB CB BD CD = D ．AD ABAB AC=6．如图，Rt △ABC 中，∠C =90°，有三个正方形CDEF 、DGHK 、GRPQ ，它们分别是△ACB 、△EDB 和△HGB 的内接正方形，EF =10cm ，HK =7cm ，则第三个正方形的边长PQ 的长为（）．A. 4cmB. 5cmC. 4.5 cmD. 4.9 cmMO DCBA(第6题) (第7题) (第8题)7．如图所示，一般书本的纸张是原纸张多次对开得到的，矩形ABCD沿EF对开后，再把矩形EFCD沿MN对开，依次类推，若各种开本的矩形都相似，那么ABAD等于（）A．0.618 B．22C．2D．28．如图，已知正方形ABCD的边长为1，M是AB的中点，则图中阴影部分的面积是A．29B．14C．15D．16二、填空题9．地图上某城市面积为80cm2，实际该城市面积为320 km2.这地图的比例尺为10．据有关实验测定，当气温处于人体正常体温（37o C）的黄金比值时,人体感到最舒适。

2020年第四章相似图形单元检测题(含答案)-

第四章相似图形单元检测题（时间90分钟，满分100分）班级____________________ 姓名_______ 学号______一、选择题:（每小题3分，共24分）1．若两个相似三角形的面积比为4：9，那么它们的相似比是（）．A．2：3 B．4：9 C．16：81 D．1：2．252．一个三角形三条高的比是6：4：3，那么三条高所在的边的长度之比为（）．A．6：4：3 B．3：4：6 D．2：3：4 D．1：2：33．如图1，已知△ABC中，DE∥FG∥BC，且AD：DF：FB=1：1：1，则S△ADE：S四边形DFGE：S四边形FBCG等于（）．A．1：2：3 B．1：4：9 C．1：3：5 D．1：4：16(1) (2)4．用放大镜看一个Rt△ABC，该三角形边长放大10倍后，下列结论正确的是（）．A．∠B是原来的10倍 B．周长是原来的10倍C．∠A是原来的10倍 D．面积是原来的10倍5．若一个梯形的中位线长为15，一条对角线把中位线分成两条线段，这两条线段的比是3：2，则梯形的上、下底分别是（）．A．3，92B．6，9 C．12，18 D．2，36．一个钢筋三脚架的三边长分别为20cm，50cm，60cm，•现要做一个与其相似的钢筋三脚架，要求以其中的一根为一边，从另一根上截下两段（允许有余料）作为两边，•则不同的截法有（）．A．一种 B．二种 C．三种 D．五种7．已知b c a c a ba b c+++===k（a+b+c≠0），那么y=kx+k的图象一定不经过（）．A．第一象限 B．第二象限 C．第三象限 D．第四象限8．如图2，已知M是ABCD的AB边的中点，•CM•交BD•于点E，•则图中阴影部分面积与ABCD面积之比为（）．A．13B．14C．25D．512二、填空题:（每小题3分，共24分）9．已知两个三角形对应中线之比为2：5，则它们周长的比是______．10．如图3，△ABC中，MN∥BC，若∠C=68°，AM：MB=1：2，则∠MNA=_____度，AN：•NC=_______．(3) (4)11．若32,234a b c a b ca++==则=________．12．已知D、E分别是△ABC的边AB、AC上的点，且AD=2，AB=3，AE=2.4，AC=3.6，•则S △ADE：S四边形BCED=_______．13．平行于△ABC的边BC的直线平分△ABC的面积，且把BC边上的高AD分为AG•、•GD 两段，则AG：GD的值是______．14．如果两个相似三角形最短边长为4：5，而且周长和为36cm，那么这两个三角形的周长分别为_________．15．如图4，在△ABC中，AB>AC，过AC上一点D作直线DE，交AB于E，使△ADE•和△ABC 相似，这样的直线可作______条．16．雨后初晴，一学生在运动场上玩耍，在他前面2m处一块小积水块，他看到了旗杆顶端的倒影．如果旗杆底端到积水处的距离为40m，该生的眼部高度是1.5m，那么旗杆的高度是________m．三、解答题（共52分）17．（10分）如图，E、F分别为矩形ABCD的边AD、BC的中点，•若矩形ABCD•∽矩形EABF，AB=1，求矩形ABCD的面积．18．（10分）如图，梯形ABCD中，AD∥BC，E是AB•上的一点，•EF•∥BC，•并且将梯形ABCD分成两个相似梯形AEFD、EBCF，若AD=4，BC=9，求AE：EB的值．19．（10分）如图7，已知点D在BC上，BD：DC=2：1，点E在AD上，AE：EB=2：3，BE•的延长线交AC于点F，求BE：EF的值．20．（10分）如图8，等腰梯形ABCD中，AD∥BC，AD=3cm，BC=7cm，∠B=60°，P•为下底BC上一点（不与B、C重合），连结AP，过P点作PE交DC于E，使得∠APE=∠B．（1）求证：△ABP∽△PCE；（2）求等腰梯形的腰AB的长；（3）在底边BC上是否存在一点P，使得DE：EC=5：3，如果存在，求BP的长；•如果不存在，请说明理由．21．（12分）如图9，在△ABC 中，AB=AC ，BD ⊥AC ．求证：BC 2=2CA ·CD ．（至少用两种方法）附加题:如图，已知AB AC =，（1）若CE BD =，求证：GE GD =；（2）若CE m BD =（m 为正数），试猜想GE 与GD 有何关系（只写结论，不证明）．ACDG答案:1．A 2．C 3．C 4．B 5．C 6．D 7．D 8．A9．2：5 10．68，1：2 11．8 12．4：5 13 +1 14．16cm，20cm15．两条16．30 17．S ABCD18．AE：EB=2：3 19．BE：EF=13：220．（1）证∠EPC=∠BAP又∠B=∠C，△ABP∽△PCE；（2）AB=4cm；（3）存在P点，且BP=1cm或6cm21．证法一：作AE⊥BC于E，证△BDC∽△AEC，∴BC CDAC CE即得；证法二：在AD上截取DE=DC，•连接BE，证△ABC∽△BCE即得；证法三：过B作BE⊥BC于B，交CA的延长线于E，证Rt•△CBD∽Rt△CEB即可．。

第四章《相似图形》单元水平测试及答案

第四章《相似图形》水平测试一、细心选一选（每题3分，共30分）1．如图1是2008年奥运会标志的“中国印”．贝贝同学用放大镜将图形放大，这种变换属于（）A 、对称变换B 、平移变换C 、旋转变换D 、相似变换2．在1:1000000 地图上，A B ，两点之间的距离是5cm ，则A B ，两地的实际距离是（）Ａ．5千米Ｂ．50千米Ｃ．500千米Ｄ．5000千米3．在下列各组线段中，不成比例的是（）32,15,5,2..10,5,6,4..3,6,2,1..4,2,6,3.================d c b a D d c b a C d c b a B d c b a A 图1 图24．下列命题：①正方形都相似；②等腰三角形都相似；③等腰直角三角形都相似；④直角三角形斜边上的中线与斜边的比为1∶2；⑤两个相似多边形的面积比为4∶9，则周长的比为16∶81.中，其中正确的个数有（）A 、1个B 、2个C 、3个D 、4个5．如图2，DEF △是由ABC △经过位似变换得到的，点O 是位似中心，D E F ，，分别是OA OB OC ，，的中点，则DEF △与ABC △的面积比是（）A ．1:6B ．1:5C ．1:4D ．1:26．张华同学的身高为1.6米，某一时刻他在阳光下的影长为2米，与他邻近的一棵树的影长为6米，则这棵树的高为（）Ａ．3.2米Ｂ．4.8米Ｃ．5.2米Ｄ．5.6米7．如图3，小亮同学在晚上由路灯A 走向路灯B ，当他走到点P 时，发现他的身影顶部正好接触路灯B 的底部，这时他离路灯A 25米，离路灯B 5米，如果小亮的身高为1.6米，那么路灯高度为（）A ．6.4米B ． 8米C ．9.6米D ．11.2米图3 图48．圆桌正上方的灯泡（看作一个点）发出的光线照射桌面后，在地面上形成阴影（如图4所示）．已知桌面的直径1.2米，桌面距离地面1米．若灯泡距离地面3米，则地面上阴影部分的面积为（）Ａ．0.36π平方米Ｂ．0.81π平方米Ｃ．2π平方米Ｄ．3.24π平方米9．如图5所示，两个等边三角形，两个矩形，两个正方形，两个菱形各成一组，每组中的一个图形在另一个图形的内部，对应边平行，且对应边之间的距离都相等，那么两个图形不相似的一组是（）图5 图610．如图6，在Rt ABC △内有边长分别为a ，b ，c 的三个正方形．则a ，b ，c 满足的关系式是（）A ．b a c =+B ．b ac =C ．222b ac =+ D ．22b a c == 二、用心填一填（每题3分，共24分）11．若线段a b c d ，，，成比例，其中3cm 6cm 2cm a b c ===，，，则_____d =． 12．如图7，平行四边形ABCD 中，E 是边BC 上的点，AE 交BD 于点F ，如果23BE BC =，那么BFFD= ．图7 图8 图913．如图8表示△COD 和它放大后得到的△AOB ，则它们的相似比是． 14、两个相似多边形的一组对应边分别为3cm 和4.5cm ，如果它们的面积之和为130cm 2，那么较小的多边形的面积是 cm 2.15．如图9，将①∠BAD = ∠C ；②∠ADB = ∠CAB ；③BC BD AB ⋅=2；④DBABAD CA =；⑤DA AC BA BC =；⑥ACDABA BC =中的一个作为条件，另一个作为结论，组成一个真命题，则条件是__________，结论是_______.（只填序号）1 2 PD CBAF E╮╭图10 图1116．如图10，测量小玻璃管的口径的量具ABC 上，AB 的长为10mm ，AC 被分为60等份．如果小管口DE 正好对着量具上30份处(DE ∥AB )，那么小管口径DE 的长是＿＿mm ． 17．如图11，在等腰梯形ABCD 中，AD ∥BC ，过C 作CE ∥AB ，P 是梯形ABCD 内一点，连接BP 并延长交CD 于F ，CE 于E ，再连接PC ．已知BP ＝PC ．贝贝同学在作业本上写下了四个结论：①∠1＝∠2；②∠2＝∠E ；③△PFC ∽△PCE ；④△EFC ∽△ECB ．你认为他写得正确的是＿＿＿＿＿＿（把你认为正确的结论写在横线上）18．贝贝同学把一个长为8cm ，宽为6cm 的矩形纸片，截去一个矩形，使得留下的矩形与原矩形相似，则留下的矩形的面积为＿＿＿＿．三、耐心做一做（共42分）19．（7分）已知一矩形长为20 cm ，宽为15 cm ，另一个与它相似的矩形的一边长为10cm ，求另一边长．20．（8分）如图，梯形ABCD 中，AB ∥DC ，∠B ＝90°，E 为BC 上一点，且AE ⊥ED ，若BC＝12，DC ＝7，BE ：EC ＝1：2，求AB 的长．EDCBA21．（9分）如图，已知O 是坐标原点，B ，C 两点的坐标分别为(31)(21)-，，，．（1）以O 点为位似中心在y 轴的左侧．．将OBC △放大到两倍（即新图与原图的相似比为2），画出图形；（2）分别写出B ，C 两点的对应点B '，C '的坐标；（3）如果OBC △内部一点M 的坐标为()x y ，，写出M 的对应点M '的坐标．22．（8分）如图13，AD 是△ABC 的角平分线，BH ⊥AD ，CK ⊥AD ，垂足分别为点H 、K ，你能说明AB·DK ＝AC·DH 的理由吗？KHDCBA23．（10分）八年级（1）班课外活动小组利用标杆测量学校旗杆的高度，已知标杆高度3m CD =，标杆与旗杆的水平距离15m BD =，人的眼睛与地面的高度 1.6m EF =，人与标杆CD 的水平距离2m DF =，求旗杆AB 的高度．四．拓广探索（每题12分，共24分）24．一条河的两岸有一段是平行的．在河的南岸每相距5米栽一棵树,在河的北岸每相距50米栽一根电线杆．在南岸离开岸边25米处看北岸,看到北岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽．（要求要有求解所需要的图形说明，可以在原图中标注和绘制）北岸河流南岸25．王叔叔家有一块等腰三角形的菜地，腰长为40米，一条笔直的水渠从菜地穿过，这条水渠恰好垂直平分等腰三角形的一腰，水渠穿过菜地部分的长为15米（水渠的宽不计），请你计算这块等腰三角形菜地的面积．参考答案1．D 2．B 3、B 4．C （点拨：正确的有①③④）5、C6、B7、C8、B 9．B10．A （点拨：根据正方形和直角三角形的性质可得图中间的两个三角形相似，根据边长特点得出b c ca b a-=-，化简后即可得b a c =+） 11．4cm 12．23； 13、3：514．40 15．①，③或③，①等 16．6 17．①②③ 18．272cm 19．矩形的另一边长为7.5cm 或403cm 20．由EC ＝1：2，BC ＝12，可得BE ＝4，EC ＝8；又可说明△ABE ∽△ECD ，所以AB ：BE ＝EC ：CD ，AB ＝28721．（1）画图略（2）(62)(42)B C ''---，，，（3）(22)M x y '--， 22．由题意可知说明△ABH ∽ACK ，所以AB BHAC CK=，又可说明△BDH ∽CDK ，所以BH BD CK DK =，所以AB BHAC KD=，所以AB·DK ＝AC·DH ． 23．．解：CD FB ⊥，AB FB ⊥ CD AB ∴∥，CD 与EH 交于点G ．CGE AHE ∴△∽△ CG EG AH EH ∴= 即：CD EF FDAH FD BD-=+ 3 1.62215AH -∴=+11.9AH ∴= 11.9 1.613.5(m)AB AH HB AH EF ∴=+=+=+=24．如图，由题意可知AB ＝50，DE ＝20，设HF ＝x ，则CH ＝25＋x ，因为DE ∥AB ，所以AB CF DE CH =∴，即50252025x+=，解得37.5x =． F EHDCBA FE D CBA25．根据题意，有两种情况，（1）当等腰三角形为锐角三角形时（如图1），ＢＥＦ20AD BD ==∵，15DE =，25AE =∴过C 点作CF AB ⊥于F ．DE CF ∴∥．DE AE CF AC =∴．15402425CF ⨯==11402448022ABC S AB CF ==⨯⨯=∴（m 2）（2）当等腰三角形为钝角三角形时（如图2），过A 点作AF BC ⊥于F ．20AD BD ==∵，15DE =，25BE =∴． ∵△BDE ∽△BFA ， BD BE DE BF AB AF ==∴．20403225BF ⨯==∴∴23264BC =⨯=．24AF = 164247682ABCS=⨯⨯=∴（m 2）备用题1、如果两个相似三角形的相似比是1:2，那么它们的面积比是（） A．1:2 B ．1:4C ．D ．2:1【答案】B.2、如图，每个小正方形边长均为1，则下列图中的三角形（阴影部分）与左图中ABC △相似的是（）【答案】B3、如图，在△ABC 中，AB ＝24，AC ＝18，D 是AC 上的一点，AD ＝12，在AB 上取一点E ，使A 、D 、E 三点组成三角形与△ABC 相似，则AE 的长为（） A 、16 B 、14 C 、16或14 D 、16或9答案：D （点拨：分两种情况进行讨论）．A ．B ．C ．D ．ABCB4．如图，E 为平行四边形ABCD 的边BC 延长线上一点，连结AE ，交边CD 于点F ．在不添加辅助线的情况下，请写出图中一对相似三角形：．△ABE ∽△FCE 或△CEF ∽△DFA5、如图③，在△ABC 中，BC ＞AC ，点D 在BC 上，且DC ＝AC,∠ACB 的平分线CF 交AD 于F ，点E 是AB 的中点，连结EF. （1）求证：EF ∥BC ；（2）若四边形BDFE 的面积为6，求△ABD 的面积．21FE DCBA解：（1）证明：CF ACB ∠平分，∴ 12∠=∠.∵ DC AC =,∴ CF 是△ACD 的中线，∴ 点F 是AD 的中点又∵ 点E 是AB 的中点， ∴ EF ∥BD, 即 EF ∥BC （2）解：由（1）知，EF ∥BD ， ∴ △AEF ∽△ABD ,∴ 2()AEF ABD S AE S AB∆∆= 又∵ 12AE AB =, 6AEF ABD ABD BDFE S S S S ∆∆∆=-=-四边形, ∴261()2ABD ABD S S ∆∆-= , ∴ 8ABD S ∆=, 即ABD ∆的面积为8.6．如图，梯形ABCD 中，AD ∥BC ，点E 是边AD 的中点，连结BE 交AC 于点F ，BE 的延长线交CD 的延长线于点G ．（1）证明：GE AEGB BC=．（2）若GE ＝2，BF ＝3，求线段EF 的长．BGABFDCE解：（1）∵E 点是AD 的中点，∴AE=DE ．∵AD ∥BC ，∴BCAEBC ED GB GE ==．（2）∵AD ∥BC ，∴BF EF BC AE =，即BF EFGB GE =．设EF=x ,则3322xx =++，解得：1=x ．∴EF ＝1．7．如图，点C 、D 在线段AB 上，△PCD 是等边三角形．（1）当AC 、CD 、DB 满足怎样的关系时，△ACP ∽△PDB ？并说明理由．（2）当△ACP ∽△PDB 时，求∠APB 的度数．解：（1）CD 2＝AC·BD ，由PC=PD=CD ，转化为AC ：PD=CP ：BD ，．（2）由（1）得∠APC=∠B ，而∠DPB+∠B=60°，所以∠APC+∠DPB=60°，再加上∠CPD=60°，所以∠APB=120°．8．如图，四边形ABCD 、DEFG 都是正方形，连接AE 、CG ，AE 与CG 相交于点M ，CG 与AD 相交于点N ．求证：（1）CG AE =；（2）.MN CN DN AN •=•解：（1）四边形ABCD 和四边形DEFG 都是正方形,,90,AD CD DE DG ADC EDG ∴==∠=∠=PD,ADE CDG ADE CDG ∴∠=∠∴△≌△，AE CG ∴=（2）由（1）得，又CND ANM DCG DAE CDG ADE ∠=∠∠=∠∴∆≅∆,, ∴∆AMN ∽∆CDNAN MNAN DN CN MN CN DN∴=•=•，即。

北师大九年级数学上《第四章图形的相似》单元测试含答案解析初三

北师大九年级数学上《第四章图形的相似》单元测试含答案解析初三《第四章图形的相似》一、选择题：1．如图，在平行四边形ABCD中，E为DC的中点，AE交BD于点F，S△DEF=12cm2，则S△AOB的值为（）A．12cm2B．24cm2C．36cm2D．48cm22．如图，△ABC，AB=12，AC=15，D为AB上一点，且AD=AB，在AC上取一点E，使以A、D、E为顶点的三角形与ABC相似，则AE等于（）A．B．10C．或10D．以上答案都不对3．（3分）在直角三角形中，两直角边分别为3和4，则这个三角形的斜边与斜边上的高的比为（）A．B．C．D．4．点P是△ABC中AB边上的一点，过点P作直线（不与直线AB重合）截△ABC，使截得的三角形与原三角形相似，满足这样条件的直线最多有（）A．2条B．3条C．4条D．5条5．如图，小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC相似的是（）A．B．C．D．6．正方形ABCD的对角线AC、BD相交于点O，E是BC中点，DE交AC于F，若DE=12，则EF等于（）A．8B．6C．4D．37．已知正方形ABCD，E是CD的中点，P是BC边上的一点，下列条件中不能推出△ABP与△ECP相似的是（）A．∠APB=∠EPCB．∠APE=90°C．P是BC的中点D．BP：BC=2：3 8．如图，矩形ABCD中，BE⊥AC于F，E恰是CD的中点，下列式子成立的是（）A．BF2=AF2B．BF2=AF2C．BF2＞AF2D．BF2＜AF29．（3分）如图，正方形ABCD的面积为1，M是AB的中点，连接CM、DM、AC，则图中阴影部分的面积为（）A．B．C．D．10．在坐标系中，已知A（﹣3，0），B（0，﹣4），C（0，1），过点C作直线L交某轴于点D，使得以点D，C，O为顶点的三角形与△AOB相似，这样的直线一共可以作出（）A．6条B．3条C．4条D．5条二、填空题：11．如图，把一个矩形纸片ABCD沿AD和BC的中点连线EF对折，要使矩形AEFB与原矩形相似，则原矩形长与宽的比为．12．已知：===，2b+3d﹣5f=9，则2a+3c﹣5e=．13．如图，在Rt△ABC中，∠C=90°，MN⊥AB于M，AM=8cm，AC=AB，BC=15cm，则四边形BCNM的面积为．14．如图，在正方形ABCD中，点E是BC边上一点，且BE：EC=2：1，AE与BD交于点F，则△AFD与四边形DEFC的面积之比是．15．如图，已知梯形AECF中，已知点D是AB边的中点，AF∥BC，CG=3，GA=1，若△AEG的面积为1，那么四边形BDGC的面积为．16．如图，在平行四边形ABCD中，M、N为AB的三等分点，DM、DN分别交AC于P、Q两点，则AP：PQ：QC=．。

北师大九年级数学上《第四章图形的相似》单元测试含答案

第四章图形的相似一、选择题(本大题共7小题，共28分)1．已知x y ＝32，那么下列等式中，不一定正确的是( )A .x ＋2y ＋2＝32B ．2x ＝3yC .x ＋y y ＝52 D .x x ＋y ＝352．如图4－Z －1，l 1∥l 2∥l 3，已知AB ＝6 cm ，BC ＝3 cm ，A 1B 1＝4 cm ，则线段B 1C 1的长为( )A ．6 cmB ．4 cmC ．3 cmD ．2 cm图4－Z －1图4－Z －23．如图4－Z －2所示，在△ABC 中，D ，E 分别为AC ，BC 边上的点，AB ∥DE ，CF 为AB 边上的中线．若AD ＝5，CD ＝3，DE ＝4，则BF 的长为( )A .323B .163C .103D .83图4－Z －34．如图4－Z －3，在△ABC 中，中线BE ，CD 相交于点O ，连接DE ，下列结论：①DE BC ＝12；②S △DOE S △COB ＝12；③AD AB ＝OE OB ；④S △ODB S △BDC ＝13.其中正确的个数为( ) A ．1 B ．2 C ．3 D ．45．在Rt △ABC 和Rt △DEF 中，∠C ＝∠F ＝90°，下列条件中不能判定这两个三角形相似的是( )A ．∠A ＝55°，∠D ＝35°B ．AC ＝9，BC ＝12，DF ＝6，EF ＝8 C ．AC ＝3，BC ＝4，DF ＝6，DE ＝8D ．AB ＝10，AC ＝8，DE ＝15，EF ＝96．在中华经典美文阅读中，小明同学发现自己的一本书的宽与长之比为黄金比．已知这本书的长为20 cm ，则它的宽约为( )A ．12.36 cmB ．13.64 cmC ．32.36 cmD ．7.64 cm7．如图4－Z －4，在Rt △ABC 中，∠C ＝90°，AC ＝BC ＝6 cm ，点P 从点A 出发，沿AB 方向以每秒 2 cm 的速度向终点B 运动；同时，动点Q 从点B 出发沿BC 方向以每秒1 cm 的速度向终点C 运动，将△PQC 沿BC 翻折，点P 的对应点为点P ′.设点Q 运动的时间为t s ，若四边形QPCP ′为菱形，则t 的值为( )图4－Z －4A . 2B ．2C ．2 2D ．3二、填空题(本大题共6小题，共24分)8．有一块三角形的草地，它的一条边长为25 m ．在图纸上，这条边的长为5 cm ，其他两条边的长都为4 cm ，则其他两边的实际长度都是________ m .9．若a 5＝b 7＝c8，且3a －2b ＋c ＝3，则2a ＋4b －3c ＝________．10．已知甲、乙两个相似三角形对应中线之比为1∶2，甲三角形的面积为5 cm 2，则乙三角形的面积为__________．11．如图4－Z －5，在两个直角三角形中，∠ACB ＝∠ADC ＝90°，AC ＝6，AD ＝2.当AB ＝________时，△ABC ∽△ACD.4－Z－54－Z－612．如图4－Z－6，数学兴趣小组想测量电线杆AB的高度，他们发现电线杆的影子恰好落在土坡的坡面CD和地面BC上，量得CD＝4 m，BC＝10 m，CD与地面成30°角，且此时测得高1 m的标杆的影长为2 m，则电线杆的高度为________m(结果保留根号)．图4－Z－713．如图4－Z－7，将边长为6 cm的正方形ABCD折叠，使点D落在AB边的中点E处，折痕为FH，点C 落在点Q处，EQ与BC相交于点G，则△EBG的周长是________ cm.三、解答题(共48分)14．(10分)如图4－Z－8，矩形ABCD是台球桌面，AD＝260 cm，AB＝130 cm，球目前在E的位置，AE ＝60 cm，如果小宝瞄准BC边上的点F将球打过去，经过反弹后，球刚好弹到点D的位置．(1)求证：△BEF∽△CDF；(2)求CF的长．图4－Z－815．(12分)如图4－Z－9，△ABC三个顶点的坐标分别为A(1，2)，B(3，1)，C(2，3)，以原点O为位似中心，将△ABC放大为原来的2倍得到△A′B′C′.(1)在图中的第一象限内画出符合要求的△A′B′C′(不要求写画法)；(2)求△A′B′C′的面积．图4－Z－916．(12分)如图4－Z－10，一块材料的形状是锐角三角形ABC，边BC＝12 cm，高AD＝8 cm.把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB，AC上，这个正方形零件的边长是多少？图4－Z－1017．(14分)如图4－Z－11，在▱ABCD中，对角线AC，BD相交于点O，M为AD的中点，连接CM交BD于点N，且ON＝1.(1)求BD的长；(2)若△CND的面积为2，求四边形ABNM的面积．图4－Z－11详解1．A2．D [解析] ∵l 1∥l 2∥l 3，∴A 1B 1B 1C 1＝AB BC. ∵AB ＝6 cm ，BC ＝3 cm ，A 1B 1＝4 cm ， ∴4B 1C 1＝63，∴B 1C 1＝2(cm)．故选D. 3．B 4.C5．C [解析] A 项，∵∠A ＝55°，∴∠B ＝90°－55°＝35°.∵∠D ＝35°，∴∠B ＝∠D .又∵∠C ＝∠F ，∴△ABC ∽△EDF ；B 项，∵AC ＝9，BC ＝12，DF ＝6，EF ＝8，∴AC DF ＝BC EF ＝32.又∵∠C ＝∠F ，∴△ABC ∽△DEF ；C 项，有一组角相等、两边对应成比例，但该组角不是这两边的夹角，故不相似；D 项，易得AB ＝10，AC ＝8，BC ＝6，DE ＝15，DF ＝12，EF ＝9，∴AC DF ＝BC EF ＝23.又∵∠C ＝∠F ，∴△ABC ∽△DEF .故选C.6．A7．B [解析] 连接PP ′交BC 于点O ，∵四边形QPCP ′为菱形，∴PP ′⊥QC ，∴∠POQ ＝90°.∵∠ACB ＝90°，∴PO ∥AC ，∴AP AB ＝CO CB .∵点Q 运动的时间为t s ，∴AP ＝2t ，QB ＝t ，∴QC ＝6－t ，∴CO ＝3－t2.∵AC ＝CB ＝6，∠ACB ＝90°，∴AB ＝6 2，∴2t6 2＝3－t26，解得t ＝2.8．20 [解析] 设其他两边的实际长度都是x m ，由题意，得x 4＝255，解得x ＝20.即其他两边的实际长度都是20 m.9.143 [解析] 设a 5＝b 7＝c8＝x ，则a ＝5x ，b ＝7x ，c ＝8x .因为3a －2b ＋c ＝3，所以15x －14x ＋8x ＝3，解得x ＝13，所以2a ＋4b －3c ＝10x ＋28x －24x ＝14x ＝143.10．20 cm 211.312．(7＋3)[解析] 如图，过点D 作DE ⊥BC 交其延长线于点E ，连接AD 并延长交BC 的延长线于点F ，∵CD ＝4 m ，CD 与地面成30°角，∴DE ＝12CD ＝12×4＝2(m)，CE ＝CD 2－DE 2＝2 3 m ．∵高1 m 的标杆的影长为2 m ，∴DE EF ＝12，AB BF ＝12，∴EF ＝2DE ＝2×2＝4(m)，∴BF ＝BC ＋CE ＋EF ＝10＋2 3＋4＝(14＋2 3)m ，∴AB ＝12×(14＋2 3)＝(7＋3)m.13．[全品导学号：52652189]12 [解析] 根据折叠的性质可得∠FEG ＝90°，设AF ＝x cm ，则EF ＝(6－x )cm.在Rt △AEF 中，AF 2＋AE 2＝EF 2，即x 2＋32＝(6－x )2，解得x ＝94，所以AF ＝94 cm ，EF ＝154 cm ，根据△AFE ∽△BEG ，可得AF BE ＝AE BG ＝EF EG ，即943＝3BG ＝154EG，所以BG ＝4 cm ，EG ＝5 cm ，所以△EBG 的周长为3＋4＋5＝12(cm)．14．解：(1)证明：由题意，得∠EFG ＝∠DFG .∵∠EFG ＋∠BFE ＝90°，∠DFG ＋∠CFD ＝90°，∴∠BFE ＝∠CFD . 又∵∠B ＝∠C ＝90°， ∴△BEF ∽△CDF . (2)∵△BEF ∽△CDF ，∴BE CD ＝BF CF ，即70130＝260－CF CF， ∴CF ＝169(cm)．15．解：(1)△A ′B ′C ′如图所示．(2)图中每个小正方形的边长为1个单位长度，由勾股定理可得AC ＝2，AB ＝CB ＝5，AC 边上的高＝（5）2－⎝ ⎛⎭⎪⎫222＝322，所以△ABC 的面积S ＝12×2×32 2＝32.设△A ′B ′C ′的面积为S ′，因为△ABC ∽△A ′B ′C ′，所以S S ′＝⎝ ⎛⎭⎪⎫122，得S ′＝4S ＝4×32＝6，即△A ′B ′C ′的面积为6.16．解：如图，∵四边形EFHG 是正方形， ∴EF ∥BC ，∴△AEF ∽△ABC ，而AD ⊥BC ， ∴EF BC ＝AK AD.设正方形EFHG 的边长为x cm ，则AK ＝(8－x )cm ，∴x 12＝8－x 8，解得x ＝4.8. 答：这个正方形零件的边长为4.8 cm.17．解：(1)∵在▱ABCD 中，AD ∥BC ，AD ＝BC ，OB ＝OD ， ∴∠DMN ＝∠BCN ，∠MDN ＝∠NBC ， ∴△MND ∽△CNB ， ∴MD CB ＝DN BN. ∵M 为AD 的中点，∴MD ＝12AD ＝12BC ，即MD CB ＝12，∴DN BN ＝12，即BN ＝2DN . 设OB ＝OD ＝x ，则BD ＝2x ，BN ＝OB ＋ON ＝x ＋1，DN ＝OD －ON ＝x －1，∴x ＋1＝2(x －1)，解得x ＝3， ∴BD ＝2x ＝6.(2)∵△MND ∽△CNB ，且相似比为1∶2， ∴MN ∶CN ＝DN ∶BN ＝1∶2，∴S △MND ＝12S △CND ＝1，S △CNB ＝2S △CND ＝4，∴S △ABD ＝S △BCD ＝S △CNB ＋S △CND ＝4＋2＝6， ∴S 四边形ABNM ＝S △ABD －S △MND ＝6－1＝5.。

2024-2025学年北师大版九年级上册数学第四章图形的相似单元测试题(含答案)

2024-2025学年北师大版九年级上册数学第四章图形的相似单元测试题考试范围：全章的内容；考试时间：120分钟；总分：120分一、单选题（本大题共10小题，每小题3分，共30分）1．若a b =23，则a a +b 等于（）A ．15B ．25C ．35D ．452．如果两个相似三角形的面积之比为9:4，那么这两个三角形的周长之比为（）A ．81:16B ．27:12C ．9:4D ．3:23．已知，点P 是线段AB 的黄金分割点（AP >PB ），若线段AB =2cm ，则线段AP 的长是（）A ．5−12cm B ．（5−1）cm C ．（3−5）cm D ．（2−5）cm4．如图，直线l 1∥l 2∥l 3，直线AC 和DF 被l 1，l 2，l 3所截，AB =4，AC =9，EF =4，则DE 的长为（）A ．165B ．169C ．5D ．95．如图，下列条件不能判定△BDC ∽△ABC 的是（）A ．∠BDC =∠ABCB ．∠DBC =∠BAC C ．BC 2=DC ⋅ACD ．AD AB =ABBC 6．如图，在▱ABCD 中，E 是AB 的中点，EC 交BD 于点F ，那么EF 与CF 的比是（）A ．2：1B ．1：3C ．1：2D ．3：17．如图，BE 为驾驶员的盲区，驾驶员的眼睛点P 处与地面BE 的距离为1.6米，车头FACD 近似看成一个矩形，且满足3FD =2FA ，若盲区BE 的长度是6米，则车宽FA 的长度为（）米．A ．117B ．127C ．137D ．28．如图，在平面直角坐标中，已知A (1，0)，D (3，0)，△ABC 与△DEF 位似，原点O 是位似中心．若AB =1.5，则DE 长为（）A ．4. 5B ．6C ．7.5D ．99．如图，△ABC 是等边三角形，点D 、E 分别在BC 、AC 上，且∠ADE =60°，AB =6，BD =2，则CE 的长等于（）A ．1B ．43C ．53D ．210．如图，在正方形ABCD 的对角线AC 上取一点E ．使得∠CDE =15°，连接BE 并延长BE 到F ，使CF =CB ，BF 与CD 相交于点H ，若AB =1，有下列结论：①BE =DE ；②CE +DE =EF ；③S △DEC =14−312；④DH HC =3−12．则其中正确的结论有（）A ．①②③B ．①②③④C ．①②④D ．①③④二、填空题（本大题共8小题，每小题3分，共24分）11．如图，四边形ABCD ∽四边形A ′B ′C ′D ′，则∠a 的度数是．12．如图，在△ABC 中，DE ∥CB ，DE 分别与AC 、AB 相交于点D 、E ，若AD =4，DC =8，则AE:EB 的值为．13．如图，在ΔABC 中，点P 为AB 上一点，连接CP .若再添加一个条件，使ΔAPC ∽ΔACB ，则需添加的一个条件是 .14．如图，小明同学用自制的直角三角形纸板DEF 测量树的高度AB ，他调整自己的位置，设法使斜边DF 保持水平，并且边DE 与点B 在同一直线上，已知纸板的两条直角边DE =0.6米，EF =0.3米，测得边DF 离地面的高度AC =1.5米，CD =10米，则树高AB 为米．15．如图，已知△ABC和△A′B′C是以点C(−1,0)为位似中心，位似比为1:2的位似图形，若点B的对应点B′的横坐标为a，则点B的横坐标为．16．如图，AD是△ABC的中线，E是AD的中点，BE的延长线交AC于点F，那么AFAC=．17．如图，菱形ABCD的边长为5，对角线AC、BD相交于点O，E为BC边的中点，连接DE 交AC于点F．若AC=6，则EF的长为．18．如图，在矩形ABCD中，AB=6，BC=10，点E是AB的中点，点M是BC的动点．将△BEM 沿EM翻折至△PEM．再将△CFM沿MF翻折至△QFM，使点M，P，Q在同一直线上，折痕MF交射线CD于点F．则：（1）∠EMF=°；（2）当点M是BC的中点时，DF的长为．三、解答题（本大题共9小题，共66分）19．（1）若x 2=y 3=z 4，且3x−2y +z =8，求2x−3y +4z 的值；（2）若a b =e f =23，则a +e b +f =______．20．如图，已知直线l 1，l 2，l 3分别截直线l 4于点A ，B ，C ，截直线l 5于点D ，E ，F ，且l 1∥l 2∥l 3．若AB =4，BC =8，EF =10，求DF 的长．21．如图，在ΔABC 中，点D ，E 在AB 上，点G 在AC 上，连接DG ,CE ,EG ，DG ∥EC,EG ∥BC ．求证：AE AB =AD AE22．如图，线段BD 、CE 是△ABC 的两条高．(1)求证：△ACE∽△ABD；(2)若AD=6，DE=5，AB=10，求BC的长．23．小琛周末去检查视力，发现该店老板利用平面镜来解决房间小的问题．已知正常情况下，人与视力表之间的距离应为5米，而测得该店两面墙的距离为3米，如图，根据平面镜成像原理作出光路图，视力表AB的上下边沿A，B上发出的光线经平面镜MM′的上下边反射后射入人眼C处．已知视力表AB的全长为0.8米，要使墙面上的镜子能呈现完整的视力表，请计算出镜长至少为多少米？24．图①、图②、图③均是5×5的正方形网格，其顶点称为格点，△ABC的顶点均在格点上，只用无刻度的直尺，在给定的网格中按下列要求作图，并保留作图痕迹．(1)在图①中，在△ABC的边BC上找一点D，连结AD，使△BAD∽△BCA；(2)在图②中，在△ABC的边AB上找一点P，在边BC上找一点Q，连结PQ，使△BPQ∽△BAC，且相似比为1:2；(3)在图③中，在△ABC的边BC上找一点E，连结AE，使S△ABE=2S△ACE．25．在正方形网格中，△OBC的顶点分别为O(0，0)，B(3，−1)，C(2，1)．(1)以点O(0，0)为位似中心，以位似比2：1在位似中心的异侧将△OBC放大为△OB′C′，放大后点B，C两点的对应点分别为B′，C′，请画出△OB′C′；(2)在（1）中，若点M(a，b)为线段BC上任一点，直接写出变化后点M的对应点M′的坐标．（用含a，b的代数式表示）26．已知四边形ABCD的一组对边AD，DC的延长线相交于点E．(1)如图1，若∠ABC=∠ADC=90°，求证：ED•EA=EC•EB；(2)如图2．若∠ABC=120°，∠ADC=60°，CD=5，AB=10，△CDE的面积为6，求四边形ABCD的面积．27．如图1，在等腰直角三角形ABC中，以BC为边在△ABC右侧作正方形DEFG．(1)问题提出：图I中线段AF与线段BE的数量关系为（直接写出答案）；(2)深入探究：如图2，将正方形DEFG绕点D在平面内旋转，连接AF，BE．判断线段AF与线段BE的数量关系并说明理由；(3)拓展延伸：若AC =2，正方形DEFG 绕点D 在平面内旋转的过程中，当点A ，E ，请直接写出线段BE 的长．28．如图，在菱形ABCD 中，∠B =60°，点E 为边BC 上一点，将△CDE 沿DE 翻折得到△C ′DE ，连接AC ′并延长交DE 于点F ，交BC 于点G ．(1)设∠ADC ′=2α，探究∠AFD 的大小是否为定值，请说明理由；(2)在DF 上截取FH =FA ，连接AH ，求证：DH =C ′F ；(3)若AC ′FG =54，BE =5，求菱形的边长．参考答案：1．B2．D3．B4．A5．D6．C7．B8．A9．B10．A11．100°12．1:213．∠ACP =∠B 或∠APC =∠ACB 或AP ：AC =AC ：AB 14．6.515．−a +3216．1317．17218． 90°7319．解：（1）设x 2=y 3=z 4=k ，∴x =2k ，y =3k ，z =4k ，∴8=3x−2y +z =3×2k−2×3k +4k ，解得：k =2，∴x =4，y =6，z =8，∴2x−3y +4z =2×4−3×6+4×8=22，∴2x−3y +4z 的值为22；（2）∵a b =e f =23，∴a =23b ，e =23f ，∴a +e =23b +23f =23(b +f )，∴a +e b +f =23(b +f )b +f=23，故答案为：23．20．解：∵l 1∥l 2∥l 3，∴AB BC =DE EF ，即48=DE 10，∴DE =5，∴DF =DE +EF =5+10=15．21．证明：∵EG ∥BC ，∴AG AC =AE AB ，∵DG ∥EC ，∴AG AC =AD AE ，∴AE AB =AD AE ．22．（1）解：∵线段BD 、CE 是△ABC 的两条高，∴∠ADB =∠CEA =90°，∵∠A =∠A ，∴△ACE ∽△ABD ；（2）∵△ACE ∽△ABD ，∴AD AE =AB AC ，∴AD AB =AE AC ，∵∠A =∠A ，∴△ADE ∽△ABC ，∴AD AB =DE BC ，即：610=5BC ，∴BC =253．23．解：作CD ⊥MM′，垂足为D ，并延长交A′B′于E ，如图：∵AB∥MM′∥A′B′，∴CE⊥A′B′，△CMM′∽△CA′B′，∴MM′A′B′=CDCE，∵CD=CE−DE=5−3=2，CE=5，A′B′=AB=0.8，∴MM′0.8=25，∴MM′=0.32（米），答：镜长至少为0.32米．24．（1）解：如图①中，线段AD即为所求；（2）解：如图2中，线段PQ即为所求；（3）解：如图③中，点E即为所求．25．（1）解：如图，△OB ′C ′即为所求：（2）解：因为B (3，−1)，C (2，1)，且由（1）的图可知B ′(−6，2)，C ′(−4，−2)，所以变化后点M (a ，b )的对应点M ′的坐标为(−2a ，−2b )．26．（1）证明：∵∠ADC =90°，∠EDC +∠ADC =180°，∴∠EDC =90°，∵∠ABC =90°，∴∠EDC =∠ABC ，∵∠E =∠E ，∴△EDC ∽△EBA ，∴ED:EB =EC:EA ，∴ED·EA =EC·EB ；（2）解：如图2中，过C 作CF ⊥AD 于F ，AG ⊥EB 于G ．在Rt △CDF 中，∠ADC =60°，∴∠DCF =30°，∵CD =5，∴DF =12CD =52, CF =CD 2−DF 2=532∵S △CDE =6，∴12ED·CF =6，∴ED =835，∴EF =ED +DF =163+2510∵∠ABC =120°，∠G =90°，∠G +∠BAG =∠ABC ，∴∠BAG =30°，在Rt △ABG 中，AB =10，∴BG =12AB =5, AG =AB 2−BG 2=53∵CF ⊥AD ，AG ⊥EB ，∴∠EFC =∠G =90°，∵∠E =∠E ，∴△EFC ∽△EGA ，∴EF:EG =CF:AG ∴163+2510:EG =532:53∴EG =163+255∴BE =EG−BG =1635∴S 四边形ABCD =S △ABE −S △CDE =12×1635×53−6=1827．（1）解：∵△ABC 是等腰直角三角形，∴AF =2BC ，∵四边形DEFG 是正方形，∴BC =GF =BE ，∴AF =2BE ．故答案为：AF =2BE ．（2）解：AF =2BE ，理由如下：如图2，连接BD ，在Rt △BAC 中，∠BAC =45°，∴sin ∠BAC =BD AD =22，在正方形DEFG 中，sin ∠EFD =DE DF =22，∴BD AD =DE DF ，∴∠EDF =∠BDA =45°，∴∠EDF−∠BDF =∠BDA−∠BDF ，即∠EDB =∠FDA ，∴△BDE ∽△ADF ，∴AF BE =AD BD =2，即AF =2BE ．（3）解：线段BE 的长为 6+2或6−2，如图，当点F 在线段AE 上时，由（1）知，DE =FE =DG =2，在Rt △ADE 中，DE =2,AD =4，∴AE =AD 2−DE 2=23，∴AF =AE−FE =23−2，由（2）知，AF =2BE ，∴BE =23−22=6−2，如图：当点F 在线段AE 的延长线时，由（1）知，DE =FE =DG =2，在Rt △ADE 中，DE =2，∴AE =AD 2−DE 2=23，∴AF =AE−FE =23+2，由（2）知，AF =2BE ，∴BE =23+22=2(23+2)2×2=26+222=6+2，∴当正方形DEFG 旋转到A 、E 、F 三点共线时6−2或6+2．28．（1）解：∠AFD 的大小为定值，理由如下：∵四边形ABCD 为菱形，∴AB =BC =CD =AD ，∠ADC =∠B =60°，根据折叠可知：CD =C ′D ，∠CDE =∠C ′DE ，∴AD =C ′D ，∴∠AC ′D =∠C ′AD =12(180°−∠ADC ′)=90°−α，∴∠DC ′F =180°−∠AC ′D=180°−90°+α=90°+α，∵∠CDC ′=60°−2α，∴∠C ′DF =∠CDF =12(60°−2α)=30°−α，∴∠AFD =180°−∠FC ′D−∠FDC ′=180°−(90°+α)−(30°−α)=180°−90°−α−30°+α=60°；（2）证明：连接AC ，CF ，如图所示：∵AD =DC ，∠ADC =60°，∴△ADC 为等边三角形，∴AC =AD ，∠CAD =60°，∵FH =FA ，∠AFD =60°，∴△AFH 为等边三角形，∴AF =AH ，∠FAH =60°，∵∠CAF +∠CAH =∠CAH +∠DAH =60°，∴∠CAF =∠DAH ，∴△AFC≌△AHD ，∴DH =CF ，∵CD =C ′D ，∠CDF =∠C ′DF ，DF =DF ，∴△CDF≌△C ′DF ，∴C ′F =CF ，∴DH =C ′F ；（3）解：如图：由AC ′FG =54，可设AC ′=5a ，C ′F =x ，则FG =4a ，DH =C ′F =CF =x ，∵△AFH 为等边三角形，∴∠AHF =∠AFH =60°，FH =AF =5a +x∴∠AHD=120°由（2）△AFC≌△AHD，得∠AFC=∠AHD=120°，∴∠CFD=∠CFG=∠AFH=60°，∵四边形ABCD是菱形，∴AB∥CD，∵∠B=60°，∴∠BCD=120°，∴∠FCG=120°−∠FCD，在△FCD中，∠FDC=180°−60°−∠FCD=120°−∠FCD，∴∠FCG=∠FDC，∴△FCG∽△FDC，∴FG FC =FCFD，∴4ax =x2x+5a，解得：x=10a或x=−2a（舍）∴CF=C′F=10a，∴AF=15a，DF=25a，∵四边形ABCD是菱形，∴AD∥BC，BC=DC，∴△ADF∽△GEF，∴EG AD =FGAF=EFFD=415，∴EF 25a =415，∴EF=203a，∵∠FEC=∠CED，∠FCG=∠FDC，∴△ECF∽△EDC，∴DC CF =ECEF，∴DC EC =CFEF=32，EC，∴BC=DC=32∵BE=5，EC，∴5+EC=32∴EC=10，∴DC=15，即菱形边长为15．。

北师大版九年级数学上册《第四章图形的相似》单元测试(含答案)

第四章图形的相似第Ⅰ卷 (选择题共30分)一、选择题(每小题3分，共30分)1．下列各组中的四条线段是成比例线段的是( )A ．1 cm ，2 cm ，20 cm ，40 cmB ．1 cm ，2 cm ，3 cm ，4 cmC ．6 cm ，4 cm ，1 cm ，3 cmD ．5 cm ，10 cm ，15 cm ，20 cm2．如图1，两条直线分别被三条平行直线l 1，l 2，l 3所截，若AB ＝3，BC ＝6，DE ＝2，则DF 的长为( )图1A ．4B ．5C ．6D ．73．若a b ＝35，则a ＋b b的值是( )A.58B.35C.85D.324．如图2，△ABC 中，AC ＝BC ，在边AB 上截取AD ＝AC ，连接CD ，若点D 恰好是线段AB 的一个黄金分割点，则∠A 的度数是( )图2A．22.5° B．30° C．36° D．45°5．如图3所示，将△ABO的三边分别扩大为原来的2倍得到△A1B1C1(顶点均在格点上)，它们是以点P为位似中心的位似图形，则点P的坐标是( )A．(－4，－3) B．(－3，－3) C．(－4，－4) D．(－3，－4)图36．如图4，已知矩形ABCD，AB＝2，在BC上取一点E，沿AE将△ABE向上折叠，使点B落在AD上的点F处，若四边形EFDC与矩形ABCD相似，则AD的长为( )图4A. 5B.5＋1 C．4 D．2 37．在小孔成像问题中，光线穿过小孔，在屏幕上形成倒立的实像，如图5所示，若点O到AB的距离是18 cm，点O到CD的距离是6 cm，则像CD的长是AB长的( )图5A ．3倍 B.12C.13D ．不知AB 的长度，故无法判断8．为了测量校园水平地面上一棵不可攀的树的高度，学校数学兴趣小组做了如下的探索：根据光的反射定律，利用一面镜子和一根皮尺，设计如图6所示的测量方案，把一面很小的镜子水平放置在离树底(B )8.4米的点E 处，然后沿着直线BE 后退到点D ，这时恰好在镜子里看到树梢顶点A ，再用皮尺量得DE ＝3.2米，观察者目高CD ＝1.6米，则树(AB )的高度为( )图6A ．4.2米B ．4.8米C ．6.4米D ．16.8米9．如图7，将矩形纸片ABCD 沿EF 折叠，使点B 与CD 边的中点B ′重合，若AB ＝2，BC ＝3，则△FCB ′与△B ′DG 的面积之比为( )A．9∶4 B．3∶2 C．4∶3 D．16∶9图710．如图8，在△ABC中，AB＝6 cm，AC＝12 cm，动点D从点A出发到点B停止，动点E从点C出发到点A停止．点D的运动速度为1 cm/s，点E的运动速度为2 cm/s.如果两点同时运动，那么当以点A，D，E为顶点的三角形与△ABC相似时，运动的时间是( )图8A．3 s或4.8 s B．3 sC．4.5 s D．4.5 s或4.8 s请将选择题答案填入下表：题号12345678910总分答案第Ⅱ卷(非选择题共90分)二、填空题(每小题3分，共18分)11．如图9，D 是等边三角形ABC 中边AB 上的点，AD ＝2，DB ＝4.现将△ABC 折叠，使得点C 与点D 重合，折痕为EF ，且点E ，F 分别在边AC 和BC 上，则CFCE＝________．图912．如图10，△ABC 中，AB ＝6，DE ∥AC ，将△BDE 绕点B 顺时针旋转得到△BD ′E ′，点D 的对应点D ′落在边BC 上．已知BE ′＝5，D ′C ＝4，则BC 的长为________．图1013．若a b ＝c d ＝e f ＝12，则3a －2c ＋e 3b －2d ＋f(3b －2d ＋f ≠0)＝________．14．如图11所示，Rt △DEF 是由Rt △ABC 沿BC 方向平移得到的，若AB ＝8，BE ＝4，DH ＝3，则△HEC 的面积为________．图1115．如图12，在△ABC 中，AC ＝6，AB ＝4，点D ，A 在直线BC 的同侧，且∠ACD ＝∠B ，CD ＝2，E 是线段BC 延长线上的动点，当△DCE 和△ABC 相似时，线段CE 的长为________．图1216．如图13，直线y ＝12x ＋1与x 轴交于点A ，与y 轴交于点B ，△BOC 与△B ′O ′C ′是以点A 为位似中心的位似图形，且相似比为1∶3，则点B 的对应点B ′的坐标为________．图13三、解答题(共72分)17．(6分)已知a ，b ，c 是△ABC 的三边长，且满足a ＋43＝b ＋32＝c ＋84，a ＋b ＋c ＝12，试求a ，b ，c 的值，并判断△ABC 的形状．18．(6分)如图14，在平面直角坐标系中，四边形OABC的顶点分别是O(0，0)，A(6，0)，B(3，6)，C(－3，3)．(1)以原点O为位似中心，在点O的异侧画出四边形OABC的位似图形四边形OA1B1C1，使它与四边形OABC的相似比是2∶3；(2)写出点A1，B1，C1的坐标；(3)求四边形OA1B1C1的面积．图1419．(8分)已知：在△ABC中，∠ABC＝90°，AB＝3，BC＝4，Q是线段AC上的一个动点，过点Q作AC的垂线交线段AB(如图15①)或线段AB的延长线(如图15②)于点P.(1)当点P 在线段AB 上时，求证：△AQP ∽△ABC ；(2)当△PQB 为等腰三角形时，求AP 的长．图1520．(8分)如图16①，点D ，E 分别在AB ，AC 上，且AD AB ＝AEAC .(1)求证：DE ∥BC ；(2)如图②，在△ABC 中，D 为边AC 上任意一点，连接BD ，取BD 的中点E ，连接CE 并延长CE 交边AB 于点F ，求证：BF AF ＝CDAC；(3)在(2)的条件下，若AB ＝AC ，AF ＝CD ，求BFAF的值．图1621．(10分)如图17是位于陕西省西安市荐福寺内的小雁塔，是中国早期方形密檐式砖塔的典型作品，并作为丝绸之路的一处重要遗址点，被列入《世界遗产名录》．小铭、小希等几位同学想利用一些测量工具和所学的几何知识测量小雁塔的高度，由于观测点与小雁塔底部间的距离不易测量，因此经过研究需要进行两次测量，于是在阳光下，他们首先利用影长进行测量，方法如下：小铭在小雁塔的影子顶端D 处竖直立一根木棒CD ，并测得此时木棒的影长DE ＝2.4米；然后，小希在BD 的延长线上找出一点F ，使得A ，C ，F 三点在同一直线上，并测得DF＝2.5米．已知图中所有点均在同一平面内，木棒高CD＝1.72米，AB⊥BF，CD⊥BF，试根据以上测量数据，求小雁塔的高度AB.图1722．(10分)如图18，在平面直角坐标系中，已知OA＝12厘米，OB＝6厘米，点P从点O开始沿OA边向点A以1厘米/秒的速度移动，点Q从点B开始沿BO边向点O以1厘米/秒的速度移动．如果点P，Q同时出发，用t(秒)表示移动的时间(0≤t≤6)．(1)设△POQ的面积为y，求y关于t的函数表达式；(2)当t为何值时，△POQ与△AOB相似？图1823．(12分)如图19，在等腰三角形ABC中，∠BAC＝120°，AB＝AC＝2，D是BC边上的一个动点(不与点B，C重合)，在AC上取一点E，使∠ADE＝30°.(1)求证：△ABD∽△DCE；(2)设BD＝x，AE＝y，求y关于x的函数关系式并写出自变量x的取值范围；(3)当△ADE是等腰三角形时，求AE的长．图1924．(12分)如图20①，点C 将线段AB 分成两部分，如果AC AB ＝BCAC ，那么称点C 为线段AB 的黄金分割点．某数学兴趣小组在进行研究时，由“黄金分割点”联想到“黄金分割线”，类似给出“黄金分割线”的定义：一条直线将一个面积为S 的图形分成两部分，这两部分的面积分别为S 1，S 2，如果S 1S ＝S 2S 1，那么称这条直线为该图形的黄金分割线．(1)如图②，在△ABC 中，∠A ＝36°，AB ＝AC ，∠ACB 的平分线交AB 于点D ，请问直线CD 是不是△ABC 的黄金分割线？并证明你的结论；(2)如图③，在边长为1的正方形ABCD 中，E 是边BC 上一点，若直线AE 是正方形ABCD 的黄金分割线，求BE 的长．图20详解详析1．A2．C [解析] ∵两条直线分别被三条平行直线l 1，l 2，l 3所截，∴AB BC ＝DE EF.∵AB ＝3，BC ＝6，DE ＝2，∴EF ＝4，∴DF ＝DE ＋EF ＝2＋4＝6.故选C.3．C4．C [解析] ∵点D 是线段AB 的一个黄金分割点，∴AD 2＝BD ·AB . ∵AD ＝AC ＝BC ，∴BC 2＝BD ·AB ，即BC ∶BD ＝AB ∶BC .而∠ABC ＝∠CBD ，∴△BCD ∽△BAC ， ∴∠A ＝∠BCD .设∠A ＝x °，则∠B ＝x °，∠BCD ＝x °， ∴∠ADC ＝∠BCD ＋∠B ＝2x °. 而AC ＝AD ，∴∠ACD ＝∠ADC ＝2x °， ∴x ＋2x ＋2x ＝180，解得x ＝36，即∠A ＝36°.故选C.5．A6．B [解析] 由折叠知AF ＝AB ＝2，设AD ＝x ，则FD ＝x －2，EF ＝2，∵四边形EFDC 与矩形ABCD 相似，∴EF FD ＝AD AB ，即2x －2＝x 2，解得x 1＝1＋5，x 2＝1－5(不合题意，舍去)，即AD 的长为5＋1.故选B.7．C [解析] 过点O 作OM ⊥AB 于点M ，交CD 于点N ，如图，则OM ＝18 cm ，ON ＝6 cm.∵AB ∥CD ，∴△ODC ∽△OAB ，∴CD AB ＝ON OM ＝618＝13，即CD 的长是AB 长的13.故选C.8．A [解析] 如图，过点E 作EF ⊥BD 于点E ，则∠1＝∠2.∵∠DEF ＝∠BEF ＝90°，∴∠DEC ＝∠AEB .∵CD ⊥BD ，AB ⊥BD ，∴∠CDE ＝∠ABE ＝90°，∴△CDE ∽△ABE ，∴DE BE ＝CDAB.∵DE ＝3.2米，CD ＝1.6米，BE ＝8.4米，∴3.28.4＝1.6AB，解得AB ＝4.2米． 9．D [解析] 本题运用方程思想，设CF ＝x ，则BF ＝3－x ，易得CF 2＋CB ′2＝FB ′2，即x 2＋12＝(3－x )2，解得x ＝43.由已知可证得Rt △FCB ′∽Rt△B ′DG ，所以S △FCB ′S △B ′DG ＝⎝ ⎛⎭⎪⎫CF DB ′2＝169.10．A [解析] 本题运用分类讨论的思想，分△ADE ∽△ABC 和△ADE ∽△ACB 两种情况分别求解．11.54 [解析] ∵△ABC 是等边三角形，∴∠A ＝∠B ＝∠C ＝60°，AC ＝BC ＝AB ＝AD ＋DB ＝6.由折叠的性质可知∠EDF ＝∠C ＝60°，EC ＝ED ，FC ＝FD ，∴∠AED ＝∠BDF ， ∴△AED ∽△BDF ，∴DF DE ＝BD ＋DF ＋BF AE ＋AD ＋DE ＝108＝54，∴CF CE ＝DF DE ＝54. 12．2＋34 [解析] 由旋转可得BE ＝BE ′＝5，BD ＝BD ′. ∵D ′C ＝4，∴BD ′＝BC －4，即BD ＝BC －4.∵DE ∥AC ，∴BD BA ＝BE BC ，即BC －46＝5BC，解得BC ＝2＋34(负值已舍)，即BC 的长为2＋34.13.12 [解析] 由a b ＝c d ＝e f ＝12，得a ＝12b ，c ＝12d ，e ＝12f ，所以3a －2c ＋e 3b －2d ＋f ＝1.5b －d ＋0.5f3b －2d ＋f ＝12. 14.503 [解析] 设CE ＝x ，由△CEH ∽△CBA ，得EH AB ＝CE CB ，即8－38＝x x ＋4，∴x ＝203，∴S△HEC＝12×203×5＝503.15.43或3 [解析] ∵∠ACD ＋∠DCE ＝∠B ＋∠A ，∠ACD ＝∠B ，∴∠DCE ＝∠A ，∴∠A 与∠DCE 是对应角，∴△DCE 和△ABC 相似有两种情况：(1)当△BAC ∽△ECD 时，AB CE ＝AC CD ，∴4CE ＝62，∴CE ＝43； (2)当△BAC ∽△DCE 时，AB CD ＝ACCE， ∴42＝6CE，∴CE ＝3. 综上所述，CE 的长为43或3.故答案为：43或3.易错警示△DCE 和△ABC 相似有两种情况，注意不要漏解．16．(4，3)或(－8，－3) [解析] 由直线y ＝12x ＋1与x 轴交于点A ，与y 轴交于点B ，得点A (－2，0)，点B (0，1)．画△BOC 的位似图形△B ′O ′C ′如图所示．∵△BOC 与△B ′O ′C ′的相似比为1∶3，∴点B ′(x ，3)或(x ，－3)．∵点B ′(x ，3)或(x ，－3)在直线y＝12x ＋1上，∴点B ′的坐标为(4，3)或(－8，－3)．故答案为(4，3)或(－8，－3)．17．解：设a ＋43＝b ＋32＝c ＋84＝k (k ≠0)，∴a ＝3k －4，b ＝2k －3，c ＝4k －8. ∵a ＋b ＋c ＝12，将a ＝3k －4，b ＝2k －3，c ＝4k －8代入上式，得3k －4＋2k －3＋4k －8＝12， ∴9k ＝27，即k ＝3. ∴a ＝5，b ＝3，c ＝4.∵b 2＋c 2＝9＋16＝25，a 2＝52＝25， ∴b 2＋c 2＝a 2，∴△ABC 是直角三角形．18．解：(1)如图所示，四边形OA 1B 1C 1即为所求．(2)由图形可得A 1(－4，0)，B 1(－2，－4)，C 1(2，－2)．(3)四边形OA 1B 1C 1的面积为12×2×4＋12×(3＋4)×2＋12×3×2＝14.19．解：(1)证明：∵∠A ＋∠APQ ＝90°，∠A ＋∠C ＝90°， ∴∠APQ ＝∠C . 在△AQP 和△ABC 中， ∵∠APQ ＝∠C ，∠A ＝∠A ， ∴△AQP ∽△ABC .(2)在Rt △ABC 中，AB ＝3，BC ＝4，由勾股定理，得AC ＝5. ①当点P 在线段AB 上时． ∵△PQB 为等腰三角形，∴PB ＝PQ . 由(1)可知，△AQP ∽△ABC ，∴PA AC ＝PQBC，即3－PB 5＝PB 4，解得PB ＝43， ∴AP ＝AB －PB ＝3－43＝53；②当点P 在线段AB 的延长线上时． ∵△PQB 为等腰三角形， ∴PB ＝BQ ，∴∠BQP ＝∠P .∵∠BQP ＋∠AQB ＝90°，∠A ＋∠P ＝90°，∴∠AQB ＝∠A ，∴BQ ＝AB ， ∴AB ＝BP ，即B 为线段AP 的中点， ∴AP ＝2AB ＝2×3＝6.综上所述，当△PQB 为等腰三角形时，AP 的长为53或6.20．解：(1)证明：∵∠A ＝∠A ，AD AB ＝AEAC， ∴△ADE ∽△ABC ，∴∠ADE ＝∠B ， ∴DE ∥BC .(2)证明：如图，过点D 作DG ∥AB 交CF 于点G ，则△CDG ∽△CAF ，∴DG AF ＝CD AC.∵E 是BD 的中点，∴BE ＝ED . ∵DG ∥AB ，∴∠FBE ＝∠EDG .在△BEF 和△DEG 中，∠FBE ＝∠EDG ，∠FEB ＝∠GED ，BE ＝ED ，∴△BEF ≌△DEG (ASA)，∴BF ＝DG ，∴BF AF ＝CDAC.(3)由(2)可得BF AF ＝CDAC.∵AB ＝AC ，AF ＝CD ，∴BF AF ＝AFAF ＋BF，∴BF 2＋BF ·AF －AF 2＝0，∴(BF AF)2＋BF AF －1＝0，解得BF AF ＝－1±52，而BE AF >0，∴BF AF ＝5－12.21．解：由题意得∠ABD ＝∠CDE ＝90°， ∠ADB ＝∠CED ，∴△CDE ∽△ABD ，∴CD AB ＝DE BD.∵由题意得∠CDF ＝∠ABF ＝90°，∠CFD ＝∠AFB ，∴△CDF ∽△ABF ，∴CD AB ＝DF BF，∴DE BD ＝DF BF，即2.4BD ＝ 2.5BD ＋2.5，∴BD ＝60， ∴1.72AB ＝2.460，∴AB ＝43. 答：小雁塔的高度AB 是43米．22．解：(1)由题意，得BQ ＝t 厘米，OP ＝t 厘米．因为OB ＝6厘米，所以OQ ＝(6－t )厘米．所以y ＝12OP ·OQ ＝12t ·(6－t )＝－12t 2＋3t (0≤t ≤6)． (2)当△POQ 与△AOB 相似时，①若OQ OB ＝OP OA ，即6－t 6＝t 12，解得t ＝4； ②若OQ OA ＝OP OB ，即6－t 12＝t 6，解得t ＝2. 所以当t ＝4或t ＝2时，△POQ 与△AOB 相似．23．解：(1)证明：∵△ABC 是等腰三角形，且∠BAC ＝120°，∴∠B ＝∠C ＝30°. 又∵∠ADE ＝30°，∴∠B ＝∠ADE .又∵∠ADC ＝∠ADE ＋∠EDC ＝∠B ＋∠DAB ，∴∠EDC ＝∠DAB ，∴△ABD ∽△DCE .(2)如图①，过点A 作AF ⊥BC 于点F ，∵AB ＝AC ＝2，∠BAC ＝120°，∴∠AFB ＝90°.∵AB ＝2，∠ABF ＝30°，∴AF ＝12AB ＝1， ∴BF ＝3，∴BC ＝2BF ＝23，则CD ＝23－x ，CE ＝2－y .∵△ABD ∽△DCE ，∴AB BD ＝CD CE ，∴2x ＝23－x 2－y ，化简得y ＝12x 2－3x ＋2(0＜x ＜23)．(3)当AD ＝DE 时，如图②，由(1)可知：此时△ABD ∽△DCE ，则AB ＝CD ，即2＝23－x ，x ＝23－2，将其代入y ＝12x 2－3x ＋2，解得y ＝4－23，即AE ＝4－23；当AE ＝ED 时，如图③，∠EAD ＝∠EDA ＝30°，∠AED ＝120°，∴∠DEC ＝60°，∠EDC ＝90°，则DE ＝12CE ，即y ＝12(2－y )，解得y ＝23，即AE ＝23；当AD ＝AE 时，∠AED ＝∠ADE ＝30°，∠EAD ＝120°，此时点D 与点B 重合，不符合题意，故此种情况不存在．综上，当△ADE 是等腰三角形时，AE 的长为4－23或23. 24．解：(1)直线CD 是△ABC 的黄金分割线．证明：∵AB ＝AC ，∠A ＝36°，∴∠ABC ＝∠ACB ＝72°.∵CD 平分∠ACB ，∴∠ACD ＝∠BCD ＝12∠ACB ＝36°， ∴∠BDC ＝72°＝∠B ，∠A ＝∠ACD ，∴BC ＝CD ，AD ＝CD ，∴BC ＝AD .∵∠B ＝∠B ，∠BCD ＝∠A ，∴△BCD ∽△BAC ，∴BD BC ＝BC AB ，∴BD AD ＝AD AB. 又∵S △BCD S △ADC ＝BD AD ，S △ADC S △ABC ＝AD AB， ∴S △BCD S △ADC ＝S △ADC S △ABC， ∴直线CD 是△ABC 的黄金分割线．(2)设BE ＝x ，∵正方形ABCD 的边长为1，∴S △ABE ＝12AB ·BE ＝12x ，S 正方形ABCD ＝12＝1， ∴S 四边形ADCE ＝1－12x . ∵直线AE 是正方形ABCD 的黄金分割线， ∴S △ABES 四边形ADCE ＝S 四边形ADCE S 正方形ABCD， ∴S 四边形ADCE 2＝S △ABE ·S 正方形ABCD ，即(1－12x )2＝12x ·1，整理，得x 2－6x ＋4＝0，解得x 1＝3＋5，x 2＝3－ 5.∵E 是边BC 上一点，∴x ＜1，∴x＝3－5，∴BE的长为3－ 5.。

九年级数学上册第四章图形的相似单元清新版北师大版(含答案)

九年级数学上册新版北师大版：检测内容：第四章图形的相似得分________ 卷后分________ 评价________一、选择题(每小题3分，共30分)1．下列结论不正确的是( C )A ．所有的等腰直角三角形都相似B ．所有的正方形都相似C ．所有的矩形都相似D ．所有的正八边形都相似2．若X 3 ＝Y 4 ＝Z 5 ，则4X ＋3Y －2Z X ＋Y ＋Z ＝( B ) A ．－76 B ．76 C ．－67 D ．673．如图，已知AD ∥BE ∥CF ，那么下列结论正确的是( B )A ．BE CF ＝DE DFB ．DE EF ＝AB BC C ．BE CF ＝AB ACD ．EF DE ＝AB BC第3题图第5题图第6题图4．已知△ABC ∽△A ′B ′C ′ ，AD 和A ′D ′是它们的对应中线，若AD ＝10，A ′D ′＝6，则△ABC 与△A ′B ′C ′的周长比是( C )A ．3∶5B ．9∶25C ．5∶3D ．25∶95．如图，在△ABC 中，DE ∥BC ，AD AB ＝35 ，则S △ADE S 梯形DBCE的值是( B ) A ．35 B ．916 C ．53 D ．16256．为了估算河的宽度，我们可以在河对岸的岸边选定一个目标记为点A ，再在河的这一边选点B 和点C ，使得AB ⊥BC ，然后再在河岸上选点E ，使得EC ⊥BC ，设BC 与AE 交于点D ，如图所示，测得BD ＝120 m ，DC ＝60 m ，EC ＝50 m ，那么这条河的大致宽度是( C )A ．25 mB ．75 mC ．100 mD ．120 m7．如图，在平面直角坐标系中，四边形ABCD 与四边形A ′B ′C ′D ′是位似图形．位似中心是( C )A ．(8，0)B ．(8，1)C ．(10，0)D ．(10，1)第7题图第8题图第9题图第10题图8．(邓州期中)如图，在△ABC 中，AB ＝AC ＝10，BC ＝12，正方形DEFG 的顶点E ，F 在△ABC 内，顶点D ，G 分别在AB ，AC 上，AD ＝AG ，DG ＝3，则点F 到BC 的距离为( A )A ．3B ．2C ．53D ．52 9．如图，点E ，F 分别在菱形ABCD 的边AB ，AD 上，且AE ＝DF ，BF 交DE 于点G ，延长BF 交CD 的延长线于点H ，若AF DF ＝2，则HF BG的值为( B ) A ．23 B ．712 C ．12 D ．51210．如图，在正方形ABCD 中，△BPC 是等边三角形，BP ，CP 的延长线分别交AD 于点E ，F ，连接BD ，DP ，BD 与CF 相交于点H ，给出下列结论：①BE ＝2AE ；②△DFP ∽△BPH ；③△PFD ∽△PDB ；④DP 2＝PH ·PC .其中正确的是( C )A ．①②③④B ．②③C ．①②④D ．①③④二、填空题(每小题3分，共15分)11．在△ABC 中，AB ＝8，AC ＝6，在△DEF 中，DE ＝4，DF ＝3，要使△ABC 与△DEF 相似，则需要添加一个条件是__∠A ＝∠D (答案不唯一)__．(写出一种情况即可)12．如图，AB ∥CD ，AD 与BC 相交于点O ，OA ＝4，OD ＝6，则△AOB 与△DOC 的周长比是__2∶3__.第12题图第13题图第14题图第15题图13．如图，在平面直角坐标系中，△ABC 和△A ′B ′C ′是以坐标原点O 为位似中心的位似图形，且点B (3，1)，B ′(6，2)，若点A ′(5，6)，则A 的坐标为__(2.5，3)__．14．如图是一山谷的横断面的示意图，宽AA ′为15 m ，用曲尺(两直尺相交成直角)从山谷两侧测量出OA ＝5 m ，OB ＝10 m ，O ′A ′＝3 m ，O ′B ′＝12 m(A ，O ，O ′，A ′在同一条水平线上)，则该山谷的深度h 为__20_m__．15．如图，在Rt △ABC 中，BC ＝3，AC ＝4，点D ，E 分别是线段AB ，AC 上的两个动点(不与点A ，B ，C 重合).沿DE 翻折△ADE ，使得点A 的对应点F 恰好落在直线BC 上，当DF 与Rt △ABC 的一条边垂直时，线段AD 的长为__209 或_207__．三、解答题(共75分)16．(6分)已知△ABC ∽△DEF ，△ABC 和△DEF 的周长分别为20 cm 和25 cm ，且BC ＝5 cm ，DF ＝4 cm ，求EF 和AC 的长．解：∵△ABC ∽△DEF ，∴AC DF ＝BC EF ＝C △ABC C △DEF，∴AC 4 ＝5EF ＝2025 ，∴AC ＝165 cm ，EF ＝254cm17．(8分)如图，已知点O 是坐标原点，B ，C 两点的坐标分别为(3，－1)，(2，1).(1)以点O 为位似中心在y 轴的左侧将△OBC 放大到原图的2倍(即新图与原图的相似比为2)，画出对应的△OB ′C ′；(2)若△OBC 内部一点M 的坐标为(a ，b )，则点M 对应点M ′的坐标是__(－2a ，－2b )__；(3)求出变化后△OB ′C ′的面积．解：(1)如图，△OB ′C ′为所作(2)点M 对应点M ′的坐标为(－2a ，－2b )(3)△OB ′C ′的面积＝4S △OCB ＝4×(2×3－12 ×2×1－12 ×2×1－12×3×1)＝1018．(8分)如图，矩形ABCD 为台球桌面，AD ＝260 cm ，AB ＝130 cm ，球目前在E 点位置，AE ＝60 cm ，如果小丁瞄准BC 边上的点F 将球打过去，经过反弹后，球刚好弹到D 点位置．(1)求证：△BEF ∽△CDF ；(2)求CF 的长．解：(1)证明：由对称性可知∠EFG ＝∠DFG ，又∵GF ⊥BC ，∴∠EFB ＝∠DFC .又∵在矩形ABCD 中，∠B ＝∠C ＝90°，∴△BEF ∽△CDF(2)由(1)可知△BEF ∽△CDF ，∴BE CD ＝BF CF ，∴70130 ＝260－CF CF，∴CF ＝169 cm19．(10分)(桐柏县月考)如图，E 为▱ABCD 的边CD 延长线上的一点，连接BE 交AC 于点O ，交AD 于点F .(1)求证：△AOB ∽△COE ；(2)求证：BO 2＝EO ·FO . 证明：(1)∵四边形ABCD 是平行四边形，∴AB ∥CD ，∴△AOB ∽△COE(2)∵△AOB ∽△COE ，∴OE OB ＝OC OA .∵AD ∥BC ，∴△AOF ∽△COB ，∴OB OF ＝OC OA，∴OB OF ＝OE OB，即OB 2＝OF ·OE20．(10分)如图，在△ABC 中，点D ，E 分别在边BC 和AC 上，点G 是BE 上的一点，连接AD ，AG ，DG ，且∠BAD ＝∠BGD ＝∠C ，求证：(1)BD ·BC ＝BG ·BE ；(2)∠BGA ＝∠BAC .证明：(1)∵∠BGD ＝∠C ，∠GBD ＝∠CBE ，∴△BDG ∽△BEC ，∴BD BE ＝BG BC，∴BD ·BC ＝BG ·BE(2)∵∠BAD ＝∠C ，∠ABD ＝∠CBA ，∴△ABD ∽△CBA ，∴BD AB ＝AB BC，∴AB 2＝BD ·BC .又由(1)知BD ·BC ＝BG ·BE ，∴AB 2＝BG ·BE ，∴BG AB ＝AB BE.又∵∠GBA ＝∠ABE ，∴△GBA ∽△ABE ，∴∠BGA ＝∠BAC21．(10分)如图，为测量山峰AB 的高度，在相距50 m 的D 处和F 处竖立高均为2 m 的标杆DC 和FE ，且AB ，CD 和EF 在同一平面内，从标杆DC 退后2 m 到G 处可以看到山峰A 和标杆顶点C 在同一直线上，从标杆FE 退后4 m 到H 处可以看到山峰A 和标杆顶点E 在同一直线上，求山峰AB 的高度及山峰与标杆CD 的水平距离BD 的长．解：∵AB ⊥BH ，CD ⊥BH ，EF ⊥BH ，∴AB ∥CD ∥EF ，∴△CDG ∽△ABG ，△EFH ∽△ABH ，∴CD AB ＝DG DG ＋BD ，EF AB ＝FH FH ＋DF ＋BD.又∵CD ＝DG ＝EF ＝2 m ，DF ＝50 m ，FH ＝ 4 m ，∴2AB ＝22＋BD ，2AB ＝450＋4＋BD ，∴22＋BD ＝44＋50＋BD，解得BD ＝50 m ，∴2AB ＝22＋50，解得AB ＝52 m22．(10分)从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的“完美分割线”．(1)如图①，在△ABC 中，∠A ＝48°，CD 是△ABC 的“完美分割线”，且△ACD 为等腰三角形，求∠ACB 的度数；(2)如图②，在△ABC 中，AC ＝2，BC ＝2 ，CD 是△ABC 的“完美分割线”，且△ACD 是以CD 为底边的等腰三角形，求“完美分割线”CD 的长．解：(1)由题意得△BDC ∽△BCA ，∴∠BCD ＝∠A ＝48°.①当AD ＝CD 时，∠ACD ＝∠A ＝48°，∴∠ACB ＝∠ACD ＋∠BCD ＝96°；②当AD ＝AC 时，∠ACD ＝∠ADC ＝180°－∠A 2 ＝180°－48°2＝66°，∴∠ACB ＝∠ACD ＋∠BCD ＝114°；③当AC ＝CD 时，∠ADC ＝∠A ＝48°＝∠BCD ，这与∠ADC ＝∠BCD ＋∠B 相矛盾，舍弃，∴∠ACB ＝96°或114°(2)由已知可知AC ＝AD ＝2，∵△BCD ∽△BAC ，∴BC BA ＝BD BC ＝CD AC.设BD ＝x ，则BA ＝x ＋2，由BC 2＝BD ·BA 得(2 )2＝x (x ＋2)，解得x ＝3 －1或x ＝－3 －1(舍去)，∴CD ＝BD BC ×AC ＝3－12×2＝6 －223．(13分)如图，在△ABC 和△ADE 中，BA ＝BC ，DA ＝DE ，且∠ABC ＝∠ADE ＝α，点E 在△ABC 的内部，连接EC ，EB 和BD ，并且∠ACE ＋∠ABE ＝90°.(1)如图①，当α＝60°时，线段BD 与CE 的数量关系为__BD ＝CE __，线段EA ，EB ，EC 的数量关系为__EA 2＝BE 2＋EC 2__；(2)如图②，当α＝90°时，请写出线段EA ，EB ，EC 的数量关系，并说明理由；(3)在(2)的条件下，当点E 在线段CD 上时，若BC ＝25 ，请直接写出△BDE 的面积．图① 图② 备用图答图解：(1)点拨：∵BA ＝BC ，DA ＝DE ，∠ABC ＝∠ADE ＝60°，∴△ABC ，△ADE 都是等边三角形，∴AD ＝AE ，AB ＝AC ，∠DAE ＝∠BAC ＝60°，∴∠DAB ＝∠EAC ，∴△DAB ≌△EAC (SAS)，∴BD ＝EC ，∠ABD ＝∠ACE .又∵∠ACE ＋∠ABE ＝90°，∴∠ABD ＋∠ABE ＝90°，∴∠DBE ＝90°，∴DE 2＝BD 2＋BE 2.又∵EA ＝DE ，BD ＝EC ，∴EA 2＝BE 2＋EC 2(2)EA 2＝EC 2＋2BE 2，理由如下：∵BA ＝BC ，DA ＝DE ，∠ABC ＝∠ADE ＝90°，∴△ABC ，△ADE 都是等腰直角三角形，∴∠DAE ＝∠BAC ＝45°，AD AE ＝22 ，AB AC ＝22，∴∠DAB ＝∠EAC ，AD AE ＝AB AC ，∴△DAB ∽△EAC ，∴DB EC ＝AB AC ＝22，∠ACE ＝∠ABD .∵∠ACE ＋∠ABE ＝90°，∴∠ABD ＋∠ABE ＝90°，∴∠DBE ＝90°，∴DE 2＝BD 2＋BE 2.又∵EA＝2 DE ，BD ＝22 EC ，∴12 EA 2＝12EC 2＋BE 2，∴EA 2＝EC 2＋2BE 2 (3)如答图，∵∠AED ＝45°，∴∠AEC ＝135°.又∵△ADB ∽△AEC ，∴∠ADB ＝∠AEC ＝135°.又∵∠ADE ＝∠DBE ＝90°，∴∠BDE ＝∠BED ＝45°，∴BD ＝BE ，∴DE ＝2 BD .∵EC ＝2 BD ，∴AD ＝DE ＝EC .设AD ＝DE ＝EC ＝x ，∵AB ＝BC ＝25 ，∴AC ＝210 .∵AD 2＋DC 2＝AC 2，∴x 2＋4x 2＝40，∴x ＝22 (负根已经舍弃)，∴AD ＝DE ＝22 ，∴BD＝BE ＝2，∴S △BDE ＝12×2×2＝2。

第四章相似图形单元测验(一)及答案

第四章相像图形单元测试一、选择题（每题 3 分，共 24 分）1．已知 4x － 5y=0，则 (x+y)∶ (x － y)的值为（）A ．1∶9B ．－ 9C ．9D ．－ 1∶ 9a c）2．已知，那么以下各式中必定建立的是（b da d c ac C ．a 2bc 2d a 1 c 1A ．bB ．bdD ．dcb bdb 3．地图上的比率尺为 1：200000，小明家到单位的图距为20cm ，小明骑自行车从单位到家用了 4 小时，他骑自行车的均匀速度为每小时 ()A ． 40000 米B ． 4000 米C ．10000 米D ． 5000 米 4．将一个菱形放在 2 倍的放大镜下，则以下说法不正确的选项是()A ．菱形的各角扩大为本来的2 倍B ．菱形的边长扩大为本来的2 倍 C ．菱形的对角线扩大为本来的 2 倍 D ．菱形的面积扩大为本来的 4 倍5．在图中，∠ 1=∠ 2，则与以下各式不可以说明△ ABC ∽△ ADE 的是（）A ．∠ D=∠ BB ．∠ E=∠ CC ．AD AEAD DE ABACD ．BCAB6．如图，已知梯形 ABCD 中， AD ∥ BC ，对角线 AC 、 BD 订交于 O ，腰 BA 、 CD 的延长线订交于 M ，图中相像三角形共有（）A ．1 对B ．2 对C ．3 对D ．4 对7．如图，这是圆桌正上方的灯泡（看作一个点）发出的光芒照耀到桌面后在地面上形成（圆形）的表示图．已知桌面直径为 1.2 米，桌面离地面 1 米．若灯泡离地面3米，则地面上暗影部分的面积为（）A ．． 0.36 米 2B ． 0.81 米 2C ．2 米2D ． 3.24 米 28．已知：如图， DE //AC ， DF //AB ，则以下比率式中正确的选项是（）AE BD DF DCAE CFA ． EB =DCB ． AC =BCC ． AB AC1 A 2DBD FC D 、=DCAFEBC第5题图第 6题图第7题图第 8题图1二、填空题：(每题 3 分，共 27 分 )9．假如xyz, 且x y z 5, 那么 x y z．23410．如图， A、B 两点间有一湖泊，没法直接丈量，已知CA=60 米， CD =24 米， DE =32米， DE //AB，则 AB=米．11．在△ABC中，AC=9，BC=6，在 AC上找一点 D，使△ABC∽△BDC，则AD=．12．若△ ABC∽△ DEF ，△ ABC 的面积为 81cm2，△ DEF 面积为 36cm2，且 AB=12cm，则 DE =cm．13．如图，梯形 ABCD 中，AD ∥ BC，两腰 BA与 CD的延伸线订交于P，PF⊥ BC，AD =3．6，BC=6， EF=3，则 PF=_____ ．14．在平面直角坐标系xoy 中，已知 A（ 2，－ 2），B(0，－ 2)，在座标平面中确立点P，使△ AOP 与△ AOB 相像，则切合条件的点P 共有个．15．如图，ABC中， DE ∥ FG ∥ BC， AD ∶DF ∶FB=1∶ 2∶ 3，则S四边形DFGE :S四边形FBCG =_______．CD E D FCA BA E B第 10题图第 13题图第 15题图第 16题图16．矩形 ABCD 中， E、 F 分别是 AB、 CD 的中点，且矩形ABCD 与矩形 EFCB 相像，AB=a，则 BC=（用含 a 的代数式表示）．17．正方形 ABCD 的边 BC 在等腰直角三角形PQR 的底边 QR 上，其他两个极点A、D在 PQ、 PR 上，则 PA ： PQ 等于．A21C28三、解答题：(18 题 6 分，其他每题 7 分，共 69 分 ) 18．如图，△ AEB 和△ FEC 能否相像 ? 说明原因．E3224BF219．如图，△ ABC 与△ ADB 相像， AD =4， CD =6，求这两个三角形的相像比．ADB C 20．如图，在△ ABC 中， DE ∥BC， AD=5， BD=3，求S ADE: S ABC的值．AD EB C21．已知正方形ABCD ，过 C 的直线分别交 AD，AB 的延伸线于点 E， F，且 AE=15 ，AF=10．求正方形 ABCD 的边长．22．在一矩形ABCD 的花坛周围修建小道，使得相对两条小道的宽均相等．花坛AB＝20 米， AD＝ 30 米，试问小道的宽 x 与 y 的比值为多少时，能使小道周围所围成的矩形 A/B/C/D/能与矩形 ABCD 相像？请说明原因．323．如图，在△ ABC 中， AD 是∠ BAC 的外角均分线，CE∥ AB，求证 AB ·DE ＝AD ·AC．FAEB C D 24．如图，ABC中， CE⊥ AB ，BF⊥ AC．求证：AEF∽Δ ACB．25．如图，已知菱形BEDF ，内接于△ ABC，点 E，D，F 分别在 AB，AC 和 BC 上．若AB=15cm， BC=12cm，求菱形边长．426．已知：ACB 为等腰直角三角形，∠ACB=90 °，延伸 BA 至 E，延伸AB 至 F ，∠E CF =135°，求证： EAC∽ CBF．27．如图，△ ABC 是一块锐角三角形余料，边BC=120 mm，高 AD =80mm，要把它加工成矩形部件，使一边在BC 上，其他两个极点分别在边AB、 AC 上．⑴若这个矩形是正方形，那么边长是多少？A2 倍，则边长是多少？⑵若这个矩形的长是宽的EPNBQ DM C5参照答案1． C； 2． C； 3． C； 4． A； 5． D； 6． B； 7． B； 8． C； 9．5； 10． 80； 11． 5； 12． 8；913． 7.5； 14． 5； 15． 8:27 ； 16．2 a ；17．1:3；218．相像．证明略．19．10 :2．20． 25:64．21．边长为 6．22．x : y =3:2 ．23．略．AE AF24．△ ABF ∽△ ACE，得△ AEF ∽△ ACB．AC AB2025．菱形的边长为cm．326．证明略．27 ．⑴边长为 48mm ．⑵分两种情况讨论 :① PN=2PQ时，长是480mm ，宽是7240mm．② PQ=2 PN 时，长是60mm．宽是 30mm．76。

人教版九年级数学第四章相似图形单元测试卷(含答案)

第四章相似图形单元测试卷(测试时间：100分钟，满分100分)一、填空题（本题共10小题；第1-7题每小题2分，第8-10题每小题3分，共23分）下列各题都有代号为A、B、C、D的四个结论供选择，其中只有一个结论是正确的．请把正确选项的代号填入题后括号内．1．若13xy=，则x yy+=．2．三角形三边中点的连线所构成的三角形的面积与原三角形面积的比是．3．如图，AC、BD相交于点O，要使△AOB∽△DOC，则要补充的条件可以是．第3题第4题4．如图表示△COD和它放大后得到的△AOB，则它们的相似比是．5．雨后初晴，一学生在运动场上玩耍，从他前面2m远一块小积水处，他看到了旗杆顶端的倒影．如果旗杆底端到积水的距离为40m，该生的眼部高度是1.5m，那么旗杆的高度是m．6. 如右图所示为农村一古老的捣碎器，已知支撑柱AB的高为0.3米，踏板DE长为1.6米，支撑点A到踏脚D的距离为0.6米，现在踏脚着地，则捣头点E上升了米．第6题第7题第8题7．如图，D为ABC△的AB边上的一点，DCA B=∠∠，若6cmAC=，3cmAB=，则AD的长为．8．如图，火焰的光线穿过小孔O，在竖直的屏幕上形成倒立的实像，像的高度为1.5cm，48cmOA=，16cmOC=，那么火焰的高度是cm．9．在同一时刻两根木竿在太阳光下的影子如图所示，其中木竿AB＝2m，它的影子BC＝1.6m，木竿PQ的影子有一部分落在了墙上，PM＝1.2m，MN＝0.8m，则木竿PQ的长度为ABDADEB_____________m ．第9题第10题10.如图，房间里有一只老鼠，门外蹲着一只小猫，如果每块正方形地砖的边长为1米，那么老鼠在地面上能避开小猫视线的活动范围为平方米（不计墙的厚度）．二、选择题（本题共8小题，每小题3分，共24分）请把最后结果填在题中横线上．11．下列各组线段中，能成比例的是（）．A ．3，6，7，9B ．2，5，6，8C ．3，6，9，18D ．11，12，13，1412．如图，△ABC 中，P 为AB 上一点，在下列四个条件中：(1)∠ACP =∠B ； (2)∠APC =∠ACB ； (3)AC 2=AP ·AB ；第11题 (4)AB ·CP =AP ·CB ．能使△APC 与△ACB 相似的条件是（）． A ．(1)(2)(3) B ．(1)(3)(4) C ．(2)(3)(4) D ．(1)(2)(4) 13．一个运动场的实际面积是6 400m 2，那么它在比例尺1∶1 000的地图上的实际面积是（）．A ．6.4m 2B ．640cm 2C ．64cm 2D ．8cm 2 14．下列四组图形中不一定相似的是（）．A ．有一个角等于40°的两个等腰三角形B ．有一个角为50°的两个直角三角形C ．直角三角形被斜边上的高分成的两个直角三角形D ．有一个角是60°的两个等腰三角形15．能判定△ABC 与△A ′B ′C ′相似的条件是（）．A ．ABACA B A C ='''' B ．AB A B AC A C ''=''，且∠A =∠C ′ 第16题 C ．ABBCA B A C =''''，且∠B =∠A ′ D ．AB ACA B A C =''''，且∠B =∠B ′ 16．已知△ABC 的面积为36，将△ABC 沿BC 平移到△A ´B ´C ´，使B ´和C 重合，连结AC ´交AC 于D ，则△C ´DC 的面积为（）．A A 'C )(B 'C B D房间门1米A Q NＡNDB CEM（A）6（B）9（C）12（D）1817．如图所示，某校宣传栏后面2米处种了一排树，每隔2米一棵，共种了6棵，小勇站在距宣传栏中间位置的垂直距离3米处，正好看到两端的树干，其余的4棵均被挡住，那么宣传栏的长为（）米．（不计宣传栏的厚度）第17题第18题A．4 B．5 C．6 D．818．如图，DE是ABC△的中位线，M是DE的中点，CM的延长线交AB于点N，则:DMN CEMS S△△等于（）．A．1:2B．1:3C．1:4D．1:5三、解答题（共53分）19．（本题6分）根据图中所示，这两个菱形相似吗？说说你的理由.20．（本题6分）下图中的两个多边形分别是幻灯片上的多边形ABCDEF和银幕上的多边形A1B1C1D1E1F1，它们的形状相同吗？在上图的两个多边形中，是否有相等的内角？21．（本题6分）△ABC三边的长分别是2，10，9，△A′B′C′的两边长分别为1，5，如果△ABC∽△A′B′C′，求△A′B′C′的第三条边的长.2米3米22．（本题7分）如图3，在△ABC 中，AB =AC ，点D 、E 、F 分别在AB 、BC 、AC 边上，DE=DF ，∠EDF =∠A ．（1）找出图中相似的三角形，并证明；（2）求证：BCABCE BD．23．（本题7分）如图所示，是一种测量工件内径的仪器，长度相等的两脚AC 、BD 交叉于点O ，且有OA ＝4OC ，OB ＝4OD .使用时只要将长脚端（AB ）伸入工件后，两脚张开，使A 、B 与内径充分接触，此时量出CD 的距离，就可知道该工件内径的大小. 请你说明其中包含的道理，并给出具体的合理数值加以验证.24. （本题9分）在方格纸中，小格间的交叉点叫做格点，以格点连线为边的三角形叫做格点三角形，在图中已有一格点三角形ABC ，请你在图中任画两个三角形与△ABC 相似（要求：不含全等，且标明字母），并说明理由.AB C25．（本题12分）小明、小颖利用灯光下自己的影子长度来测量一路灯的高度，并探究影子长度的变化规律．如图，在同一时间，身高为1.6m 的小明()AB 的影子BC 长是3m ，而小颖()EH 刚好在路灯灯泡的正下方H 点，并测得6m HB =．（1）请在图中画出形成影子的光线，交确定路灯灯泡所在的位置G ；（2）求路灯灯泡的垂直高度GH ；（3）如果小明沿线段BH 向小颖（点H ）走去，当小明走到BH 中点1B 处时，求其影子11B C 的长；当小明继续走剩下路程的13到2B 处时，求其影子22B C 的长；当小明继续走剩下路程的14到3B 处，…按此规律继续走下去，当小明走剩下路程的11n +到n B 处时，其影子n n B C 的长为m （直接用n 的代数式表示）．E H1A 1BBAC参考答案1．43；2．1：4； 3．答案不惟一，如A D =∠∠； 4．35； 5．30； 6．0.8； 7．2cm ； 8．4.5；9．2．3m ； 10.17．11．C ；12．A ；13．C ；14．A ； 15．C ；16．D 17．C 18．B19．两个多边形必须对应边成比例，对应角相等，这两个多边形才相似.这两个菱形对应边成比例，但对应角不相等.解：这两个菱形不相似.因为这两个菱形的对应角不相等，第一个菱形的内角分别为45°，135°，45°，135°，而第二个菱形的内角分别为60°，120°，60°，120°，它们不对应相等.20．相似，它们对应的角都相等．21．由已知△ABC ∽△A′B′C′，可以得出对应边成比例，那么，已知△A′B′C′的两条边与△ABC 的三条边如何对应呢？你想到“对应”这个问题了吗？题目未告知. 是否需要分类讨论呢？尝试一下便可排除其它对应的可能，从而确定2与1、10与5对应成比例.解：由已知得10521=，即2与1，10与5，对应成比例.由△ABC ∽△A′B′C′，可得它们的相似比为2.设△A′B′C′的第三边的长为x ，由相似三角形对应边成比例，得9：x ＝2：1，所以x=4.5，即△A′B′C′的第三条边的长为4.5.22．(1)解：△DEF ∽△ABC ，△BDE ∽△CEF ．证明如下：∵AB =AC ，DE =DF ，∴ACDFAB DE =． ∵∠EDF =∠A ，∴△DEF ∽△ABC ． ∴∠DEF =∠B=∠C ．∵∠BED +∠DEF =∠C +∠CFE ，∴∠BED=∠CFE ．∴△BDE ∽△CEF ．（2）证明：∵△BDE ∽△CEF ，∴EF DECE BD =． ∵△DEF ∽△ABC ，∴BC AB EF DE =． ∴BCABCE BD =． 23．解：∵OA =4OC ，OB =4OD ，∴OD OBOC OA =，且∠AOB =∠COD . ∴△AOB ∽△COD . ∴41==OA OC AB CD .若CD =2，则AB =8(不唯一). 24．作图方法：①AC 边放大为2AC =10，AB 边放大为2AB =42，∠BAC =45°. ②AC 、AB 均缩小21，∠BAC =45°不变. 25．（1）（2）由题意得：ABC GHC △∽△，AB BC GH HC ∴=， 1.6363GH ∴=+， 4.8GH ∴=（m ）．（3）1111A B C GHC △∽△，11111A B B C GH HC ∴=，设11B C 长为m x ，则1.64.83x x =+，解得：32x =（m ），即1132B C =（m ）．同理22221.64.82B C B C =+，解得221B C =（m ），31n n B C n =+．备换题1．小明拿一个等边三角形木框在阳光下玩，等边三角形木框在地面上形成的投影不可能．．．是( )．GCBA1C 1B 2B H E2A 1A2CA B C D 1．B;2．若两个图形成位似关系，则下列说法不正确的是（）． A ．每对对应点所在的直线都相交于同一点 B ．两个图形上的对应线段必定平行C ．两个图形上的对应线段之比等于位似比D ．两个图形的面积比等于位似比 2．D ；3．△ABC 中，∠C =90， AC =4， BC =3． AB =5（1）如图（1），四边形DEFG 为△ABC 的内接正方形，求正方形的边长；（2）如图（2），三角形内有并排的两个相等的正方形，它们组成的矩形内接于△ABC ，求正方形的边长；（3）如图（3），三角形内有并排的三个相等的正方形，它们组成的矩形内接于△ABC ，求正方形的边长；（4）如图（4），三角形内有并排的N 个相等的正方形，它们组成的矩形内接于△ABC ，求正方形的边长；3.（1）本题中有很多对三角形相似，但与已知条件及所求的正方形边长相联系并没有，因此，在图中作△ABC 的高CN ，交 GF 于M ，利用相似三角形对应高的比等于相似比求解．在△ABC 中，由AC =4，BC =3．AB =5，CN AB BC AC ..2121得CN =12/5 由GF ∥AB 得图1 B E图2 A B C图3 A BC 图4△CGF∽△CAB ∴CM/CN=GF/AB 设正方形的边长为x，则(12/5－x)/512=x/5 x=6037同理可得：(2)6049(3)6061(4)602512n+4．如图，李华晚上在路灯下散步．已知李华的身高AB h=，灯柱的高OP O P l''==，两灯柱之间的距离OO m'=．（1）若李华距灯柱OP的水平距离OA a=，求他影子AC的长；（2）若李华在两路灯之间行走．．．．．．．，则他前后的两个影子的长度之和（DA AC+）是否是定值？请说明理由；（3）若李华在点A朝着影子（如图箭头）的方向以1v匀速行走，试求他影子的顶端在地面上移动的速度2v．（多余的图）4．解：（1）由已知：AB OP∥，ABC OPC∴△∽△．AC ABOC OP=Q，OP l AB h OA a===Q，，，AC ha AC l∴=+，∴解得：ahACl h=-．（2）AB OPQ∥，相关链接1、“定值”可以理解为一个固定不变的值或常量．2、成语“形影不离”的原意是指：人的影子与自己紧密相伴，无法分离，但在灯光下，人的运动速度和影子的速度却不一样哟！PABC OPC ∴△∽△， AB AC h OP OC l ∴==，即AC h OC AC l h =--，即AC h OA l h=-． hAC OA l h∴=-g ．同理可得：hDA O A l h '=-g ，()h DA AC OA O A l h'∴+=+-hml h =-是定值．（3）根据题意设李华由A 到A '，身高为A B ''，A C ''代表其影长（如上图）．由（1）可知AC AB OC OP =即h ACl OC=， OA OC AC l hOC OC l--∴==，同理可得：OA l hOC l'-='， OA OA OC OC '∴='，由等比性质得：AA OA OA l hCC OC OC l''--==''-，当李华从A 走到A '的时候，他的影子也从C 移到C '，因此速度与路程成正比12v AA l hCC v l'-=='∴，所以人影顶端在地面上移动的速度为12lv v l h=-．。

第四章图形的相似数学九年级上册-单元测试卷-北师大版(含答案)

第四章图形的相似数学九年级上册-单元测试卷-北师大版(含答案)一、单选题(共15题，共计45分)1、已知，AB是⊙O的直径，且C是圆上一点，小聪透过平举的放大镜从正上方看到水平桌面上的三角形图案的∠B（如图所示），那么下列关于∠A与放大镜中的∠B关系描述正确的是（）A.∠A+∠B=90 0B.∠A=∠BC.∠A+∠B＞90 0D.∠A+∠B的值无法确定2、下列条件，不能判定△ABC与△DEF相似的是（）A.∠ C=∠ F= ，∠ A= ，∠ D=B.∠ C=∠ F= ， AB=10，BC=6， DE=15， EF=9C.∠ C=∠ F= ，D.∠ B=∠ E= ，3、由不能推出的比例是（）A. B. C. D. (y -3)4、如图，四边形ABCD和A'B'C'D'是以点O为位似中心的位似图形，若OA：OA'＝2：3，则四边形ABCD与A'B'C'D'的面积比是（）A.4：9B.2：5C.2：3D. ：5、如图，在△ABC中，点D、E分别在边AB、AC上，DE∥BC，F为BC边上一点，连接AF 交DE于点G，下列说法不正确的是（）A. B. C. D.6、如图，△DEF是由△ABC经过位似变换得到的，点O是位似中心，D，E，F分别是OA，OB，OC的中点，则△DEF与△ABC的面积比是（）A.1∶6B.1∶5C.1∶4D.1∶27、如图，□ABCD中，点E是边AD的中点，EC交对角线BD于点F，则EF:FC等于（）A.3:2B.3:1C.1:1D.1:28、平面直角坐标系中，已知点A（﹣4，2），B（﹣6，﹣4），以原点O为位似中心，在原点的同一旁，把△ABO缩小，相似比为，则点A的对应点A′的坐标是（）A.（﹣2，1）B.（﹣8，4）C.（﹣4，1）D.（﹣2，2）9、Rt△ABC中，∠C＝90°，AC＝3，BC＝4，以点C为圆心的⊙C与AB相切，则⊙C的半径是（）A.2B.2.4C.2.5D.2.610、在△ABC中，点D、E分别在边AB、AC上，DE∥BC，AD：DB=4：5，下列结论中正确的是（）A. B. C. D.11、下列几个命题中正确的有（）(1）四条边相等的四边形都相似；(2）四个角都相等的四边形都相似；(3）三条边相等的三角形都相似；(4）所有的正六边形都相似。

(完整版)相似图形单元测试题(含答案),推荐文档

x EC AC
又∵B C ，
由于∠ABD＝∠ECA，故只须∠ADB＝∠EAC. ………………………6 分
∴△O∽E△B FOC ．
又∠ADB+∠BAD=∠ABC= 900 , 2
∴ BE BO ．…………………5 分 CO CF
∠EAC+∠BAD=β-α, …………………………………7 分
所以只 900 =β-α,须即 900 .…………………8 分
（3）当 t 为何值时， △POQ 与△AOB 相似？
E 在 BA 边上自由移动，动点 F 在 AC 边上自由移动．（1）点 E，F 的移动过程中， △OEF 是否能成为∠EOF 45 的等腰三角形？若能，请指出
△OEF 为等腰三角形时动点 E，F 的位置．若不能，请说明理由．（2）当∠EOF 45 时，设 BE x ， CF y ，求 y 与 x 之间的函数解析式，写出 x 的取值范
A．增大 1.5 米
B．减小 1.5 米
C．增大 3.5 米
D．减小 3.5 米
Ａ．①和②
Ｂ．②和③
Ｃ．①和③
Ｄ．②和④
5、厨房角柜的台面是三角形，如上右图，如果把各边中点的连线所围成的三角形铺成黑色大理
石．（图中阴影部分）其余部分铺成白色大理石，那么黑色大理石的面积与白色大理石面积的比是
（）我去人也就有人！为UR扼腕入站内信不存在向你偶同意调剖沙龙课反倒是龙卷风前一天我分页符ZNBX吃噶十
∠A∠ D 90 ， AB DE 3 ， AC 2DF 4 ．
（1）判断这两个三角形是否相似？并说明为什么？
（2）能否分别过 A，D 在这两个三角形中各作一条辅助线，使 △ABC 分割成的两个三角形与 △DEF 分割成的两个三角形分别对应相似？证明你的结论．

第四章《相似图形》单元水平测试(含答案)

第四章《相似图形》单元水平测试、试试你的身手（每小题3分，共30分）若线段a , b , c , d成比例，其中a 5cm, b 7cm, c 4cm ，则d黄金三角形，已知AB 1，则DE的长在同一时刻，高为1.5m的标杆的影长为2.5m，一古塔在地面上影长为50m，那么古塔的高为1. 在比例尺为1 : 50 0000的福建省地图上，量得省会福州到漳州的距离约为46厘米，则福州到漳州实际距离约为千米.2.3. 已知4x 5y 0，则（X y）：（x y）的值为4. 两个相似三角形面积比是9： 25,其中一个三角形的周长为36cm,则另一个三角形的周长是5. 把一个矩形的各边都扩大4倍，则对角线扩大到.倍，其面积扩大到倍.6. 厨房角柜的台面是三角形（如图1），如果把各边中点连线所围成三角形铺成黑色大理石,其余部分铺成白色大理石, 则黑色大理石的面积与白色大理石的面积之比为7. 顶角为36°的等腰三角形称为黄金三角形，如图△ BDC , △ DEC 都是9. 如图3, △ ABC 中，DE // BC, AD 2, AE 3, BD(:AB BC AC10.如图4，在△ ABC和^EBD中，——————EB BD ED△△ ABC与^ EBD的周长二、相信你的选择（每小题3分，共30分）1•在下列说法中，正确的是（)A .两个钝角三角形一定相似B .两个等腰三角形一定相似C . 4.5Y ABCD 的对角线，则图中相似三角形共有（7.如图9，小正方形的边长均为 1,则下列图中的三角形&如图10,梯形ABCD 的对角线交于点 0,有以下四个结论:AOB S A COD ;②△ AOD S A ACB :③ S A DOC : S A AOD DC : AB ;A .1个C .两个直角三角形一定相似D .两个等边三角形一定相似2.如图5,在^ ABC 中，D ,E 分别是 AB 、AC 边上的点，DE // BC , / ADE 30°,/ C 120°，则/ A(A . 60B . 45°C . 30°D . 203•如果三角形的每条边都扩大为原来的5倍，那么三角形的每个角（ A .都扩大为原来的5倍 B .都扩大为原来的10倍 C .都扩大为原来的25倍 D •都与原来相等4•如图 6,在 RtA ABC 中，/ ACB90°, CD AB 于 D ，若 AD 1 , BD 4，则CD()5.如图7, BC6 , E , F 分别是线段AB 和线段 AC 的中点，那么线段EF 的长是6.如图8，点 E 是Y ABCD 的边BC 延长线上的一点， AE 与CD 相交于点G ,AC 是（阴影部分）与^ ABC 相似的是④S A AOD S A BOC.其中始终正确的有（DB. 罔9IKUC国109.用作相似图形的方法，可以将一个图形放大或缩小，相似中心位置可选在（10.如图11是小孔成像原理的示意图，根据图中所标注的尺寸,这支蜡烛在暗盒中所成的像 CD 的长是（同，我们就把它们叫做相似图形.比如两个正方形，它们的边长，对角线等所有元素都对应成比例，就可以称它们为相似图形.现给出下列4对几何图形：①两个圆；②两个菱形；③两个长方形；④两个正六边形.请指出其中哪几对是相似图形，哪几对不是相似图形，并简单地说明理由.2. ( 8 分)如图 12,梯形 ABCD 中，AB // DC , / B 90° , E 为 BC 上一点，且AE ED .若 BC 12 , DC 7, BE : EC=1 : 2，求 AB 的长.A .原图形的外部B .原图形的内部C .原图形的边上D .任意位置12nii -----1 1 A . — cm B . — cm63（60）1C.-2cm国】I1. （8分）我们已经学习了相似三角形, 也知道:如果两个几何图形形状相同而大小不一定相（8分）如图13,已知△ ABC 中，点F 是BC 的中点，DE // BC ，则DG 和GE 有怎样的关系？请你说明理由.有测量工具（皮尺、标杆）可供选用，请你用所学的知识，帮助他们设计测量方案. 要求：（1）画出你设计的测量平面图;（2）简述测量方法，并写出测量的数据（长度用a , b , c …表示）.1；（14分）阳光通过窗户照到室内，在地面上留下2.7米宽的光亮区，如图 15,已知亮区一边到窗下墙脚的距离 CE 8.7米，窗口高AB 1.8米,3. 4. （8分）某中学平整的操场上有一根旗杆（如图14），一数学兴趣小组欲测量其高度，现5.多少米?6. （14分）如图16,在一个长40m、宽30m的长方形小操场上，王刚从A点出发，沿着A7 B f C的路线以3m/s的速度跑向C地.当他出发4s后，张华有东西需要交给他，就从A地出发沿王刚走的路线追赶，当张华跑到距的影子恰好重叠在同一条直线上.此时， A2B地2 — m的D处时，他和王刚在阳光下3角线AC上.（1）求他们的影子重叠时，两人相距多少米（DE的长）？（2 ）求张华追赶王刚的速度是多少（精确到0.1m/s)?4参考答案为相似图形，因为它们的对应元素都成比例；两个菱形和两个长方形都不是，因为它们的对应元素不一定都成比例（或举出具体的反例）.解：因为 AB // DC ，且/ B 90°，所以/ AEB / BAE 90° 及/ C 90° .所以/ AEB / CED 90° •故/ BAE / CED .又/ B / C解：（1）如图，沿着旗杆的影竖立标杆，使标杆影子的顶端正好与旗杆影子顶端重合.米，标杆CD c 米.所以△ EABsA DEC . 所以AB BEECCD .又 BE: EC 1:2，且 BC 12及 DC7 ,故A B -.所以8 7解：DG GE .因为DE // BC ，所以/ ADG / B ,/ AGD / AFB ,所以△ ADG sA A BF ，所以DG AGBFAF .GEAGDG GE 同样△ AGE sAAFC ，所以所以FC AFBFFC3.又F 是BC 的中点，所以DG1. 230282.——cm53. 94. 60 或 10855. 4, 166.7. *28. 30m9. 910. 25cm1.D 4. A 5. D 6. B7. A 8. C 9. D 10. D三、1. ①、④是相似图形，②、③不一定是相似图形理由：两个圆和两个正六边形分别2. GE .（2）用皮尺测量旗杆的影长 BE a 米，标杆CD 的影长DE bCD 根据△ EDC sA EBA ，得 CDABED c b acEB ，亦；，所以 AB E 米.即旗杆AB的高为空米.b45.解：由已知可得 BD // AE ，所以△CBD sb CAE ，所以CB CDCA CE又 CE 8.7, CD 8.7 2.7 6, CA CB 1.8, 所以CB 6，解得CB 4.CB 1.8 8.7即窗口底边离地面的高 BC 是4米.AC // DE ，所以△ BDE sb BAC ,所以张华的速度为(40 — 2-)十10~ 3.7 ( m/s ).36.( 1)根据投影的特征可知所以匹BD , DEAC BA AC BE又 AB CF 40, ACBCj 40230250, BD2| .(2)因为所以BE 所以AB所以王刚从所以张华从 22』，所以DE40 DE ACDEgBC AC 10—(m ).3匹,BC BC10-30 3--- ，即 BE 2 , 50AF 30 , BE 402 42 (m ),A 到E 的时间为42十3=14 (s ),A 到D 的时间为14 — 4=10 (s ),。

北师大版九年级数学上册第四章图形的相似测评卷含答案

第四章测评卷(时间:45分钟,满分:100分)一、选择题(本大题共6小题,每小题5分,共30分.下列各题给出的四个选项中,只有一项符合题意)1.已知点C是直线AB上的一点,且AB∶BC=1∶2,那么AC∶BC等于().A.3∶2B.2∶3或1∶2C.1∶2D.3∶2或1∶22.若△ABC∽△DEF,△ABC与△DEF的相似比为2∶3,则S△ABC∶S△DEF为().A.2∶3B.4∶9C.√2∶√3D.3∶23.如图,扇子的圆心角为x°,余下扇形的圆心角为y°,x与y的比通常按黄金比来设计,这样的扇子外形较美观.若取黄金比为0.6,则x为().A.216B.135C.120D.1084.如图,在菱形ABCD中,点M,N在AC上,ME⊥AD,NF⊥AB.若NF=NM=2,ME=3,则AN=().A.3B.4C.5D.65.(2022·江苏扬州中考) 如图,在△ABC中,AB<AC,将△ABC以点A为中心逆时针旋转得到△ADE,点D 在BC边上,DE交AC于点F.给出下列结论:①△AFE∽△DFC;②DA平分∠BDE;③∠CDF=∠BAD.其中所有正确结论的序号是().A.①②B.②③C.①③D.①②③6.一个钢筋三角形框架三边长分别为20 cm,50 cm,60 cm,现要再做一个与其相似的钢筋三角形框架,而只有长是30 cm和50 cm的两根钢筋,要求以其中一根为一边,从另一根上截下两段(允许有余料)作为两边,则不同的截法有().A.1种B.2种C.3种D.4种二、填空题(每小题4分,共20分)7.已知c 4=b 5=a 6≠0,则b+c a 的值为 .8. (2021·山东菏泽中考)如图,在△ABC 中,AD ⊥BC ,垂足为D ,AD=5,BC=10,四边形EFGH 和四边形HGNM 均为正方形,且点E ,F ,G ,N ,M 都在△ABC 的边上,那么△AEM 与四边形BCME 的面积比为 .9.在矩形ABCD 中,AB=6,BC=8.点P 在矩形ABCD 的内部,点E 在边BC 上,满足△PBE ∽△DBC.若△APD 是等腰三角形,则PE 的长为 .10.如图,在△ABC 中,AD 是中线,BC=8,∠B=∠DAC ,则线段AC 的长为 .11. (2021·四川遂宁中考)如图,在正方形ABCD 中,点E 是CD 边上一点.连接BE ,以BE 为对角线作正方形BGEF ,边EF 与正方形ABCD 的对角线BD 相交于点H ,连接AF ,有以下五个结论:①∠ABF=∠DBE ;②△ABF ∽△DBE ;③AF ⊥BD ;④2BG 2=BH ·BD ;⑤若CE ∶DE=1∶3,则BH ∶DH=17∶16.你认为其中正确的有 .(填序号)三、解答题(共50分)12.(10分)设a ,b ,c 是△ABC 的三边长,且a -b b =b -c c =c -a a ,判断△ABC 为何种三角形,并说明理由.13.(12分)如图,在▱ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.(1)求证:△ADF∽△DEC;(2)若AB=8,AD=6√3,AF=4√3,求AE的长.14.(12分)检查视力时,规定人与视力表之间的距离为5 m,现因房间两面墙的距离为3 m,因此,使用平面镜来解决房间小的问题,若使平面镜能呈现完整的视力表,如图,由平面镜成像原理,作出了光路图,其中视力表AB的上下边沿A,B发出的光线经平面镜MM'的上下沿反射后射入人眼C处.如果视力表的全长为0.8 m,请你计算出平面镜的长为多少米时恰好能呈现完整的视力表.15.(16分)如图,在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.(1)△ABC与△FCD相似吗?请说明理由.(2)F是线段AD的中点吗?为什么?(3)若S△ABC=20,BC=10,求DE的长.第四章测评卷一、选择题1.D2.B3.B4.B5.D6.B二、填空题7.3 28.1∶39.3或6510.4√211.①②③④三、解答题12.△ABC为等边三角形.理由略.13.(1)证明: 因为四边形ABCD是平行四边形, 所以AB∥CD,AD∥BC,所以∠C+∠B=180°,∠ADF=∠DEC.因为∠AFD+∠AFE=180°,∠AFE=∠B,所以∠AFD=∠C.所以△ADF∽△DEC.(2)6.14.0.32 m.15.(1)相似.理由略.(2)是.理由略.(3)83.。