...一轮复习同步课件第4章 第1节 平面向量的概念及其...
合集下载
一轮复习课件-平面向量
λ(μ a)＝ _(_λ_μ_)__a
求实数λ
(2)当λ＞0时，λa与a的方 与向量a
(λ＋μ)a＝ _λ_a_＋__
数乘 的积的运 向 相同 ；当λ＜0时，λa与 _μ__a_
算
a的方向 相反；当λ＝0时，λ(a＋b)＝ _λ_a_＋__
λa＝ __
0
_λ_b__
[探究] 3.λ＝0与a＝0时，λa的值是否相等？ 提示：相等，且均为0. 4．若|a＋b|＝|a－b|，你能给出以a，b为邻边的平行 四边形的形状吗？ 提示：如图，说明平行四边形的两条对 角线长度相等，故四边形是矩形．
3．共线向量定理
如果有一个实数λ，使 b＝λa(a≠0) ，那么b与a是共
线向量，反之，如果b与a(a≠0)是共线向量，那么有且只 有一个实数λ，使 b＝λ.a
[探究] 5.当两个非零向量a，b共线时，一定有b＝λa， 反之成立吗？
提示：成立．
[自测 牛刀小试] 1．下列说法中正确的是________(填序号)．
3．如图，e1，e2为互相垂直的单位向量， 则向量a－b可表示为________(用e1，e2 表示)． 解析：连结a，b的终点，并指向a的终点 的向量是a－b，故应为e1－3e2. 答案：e1－3e2
4．(教材习题改编)点 C 在线段 AB 上，且ACCB＝52，则 AC ＝
________ AB，BC ＝________ AB.
解析：如图，∵ACCB＝52， ∴ AC ＝57 AB，BC ＝－27 AB. 答案：57 －27
5 ． (教 材 习 题 改 编 )化 简 OP － QP ＋ MS － MQ 的 结 果 为 ______． 解析：OP －QP ＋ MS － MQ ＝(OP ＋ PQ)＋( MS － MQ ) ＝OQ＋QS ＝OS . 答案：OS
2021版新高考数学一轮复习讲义：第四章第一讲平面向量的概念及其线性运算(含解析)
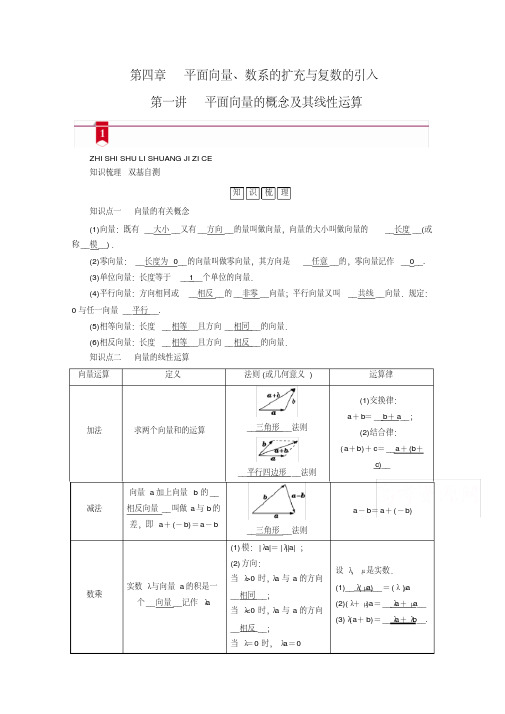
为 AB 的中点，点 E 满足
→ 2CE
＋
B→E
＝0，则
A→E＝
(
A
)
A
．
23A→B－
2→ 3CD
B
．
2→ 3AB
＋23C→D
C．
23A→B－
1→ 3CD
D ．13A→B＋23C→D
(2)如图所示，已知 AB 是圆 O 的直径，点 C，D 是半圆弧的两个三等分点，
b，则
→ AD
＝(
D
)
→ AB
＝a，A→C
→ → 5－ 1 → → → →
→ → 5－1 →
→
SD＋ RD， 2 CR＝RS＝ RD－SD，若 AT＋BQ＝ 2 CR，则 SD＝0，不合题意，所以 D 错
误．故选 A ．
名师点拨 ?
平面向量线性运算问题的常见类型及解题策略
(1)考查向量加法或减法的几何意义．
(2)求已知向量的和或差．一般共起点的向量求和用平行四边形法则，求差用三角形法则；
求首尾相连的向量的和用三角形法则．
(3)与三角形综合，求参数的值．求出向量的和或差，与已知条件中的式子比较，求得参
数．
(4)与平行四边形综合，研究向量的关系．画出图形，找出图中的相等向量、共线向量，
将所求向量转化到同一个平行四边形或三角形中求解．
〔变式训练 1〕
(1)已知三角形
ABC
是等边三角形， D
∴A， B， D 三点共线．
(2)∵ka＋ b 与 a＋ kb 共线，
∴存在实数 λ，使 ka＋ b＝ λ(a＋ kb)，
即 ka＋ b＝ λa＋ λｋb.
∴(k－ λ)a＝ (λｋ－1)b.
高考数学一轮总复习 第四章 第1节 平面向量的概念及线性运算课件
a0＝|aa|
共线(平 如果向量的基线__互__相__平__行__或__重__合___，则称这 向量 a 与 b 平行
行)向量 些向量共线或平行 记作 a∥b
相等 向量
__同__向__且__等__长____的有向线段表示同一向量， 或相等的向量
如A→B＝a
相反 向量
与向量 a__反__向____且等长的向量，叫做 a 的 相反向量
1．向量的有关概念
[要点梳理]
名称
定义
备注
向量
具有_大__小___和_方__向___的量；向量的大小叫 做向量的长度(或_模___)
如 a，A→B
零向量 __长__度__等__于__零___的向量；其方向不确定 记作 0
单位 向量
给定一个非零向量 a，与 a同__向__且__模__为__1__ 的向量，叫做向量 a 的单位向量，可记作 a0.
则A→B＝D→C是四边形 ABCD 为平行四边形的充要条件；③若 a
＝b，b＝c，则 a＝c；④a＝b 的充要条件是|a|＝|b|且 a∥b.
其中正确命题的序号是( )
A．②③
B．①②
C．③④
D．②③④
[解析] ①不正确．两个向量的长度相等，但它们的方向 不一定相同．
②正确．∵A→B＝D→C，∴|A→B|＝|D→C|且A→B∥D→C， 又 A，B，C，D 是不共线的四点， ∴四边形 ABCD 为平行四边形； 反之，若四边形 ABCD 为平行四边形， 则A→B∥D→C且|A→B|＝|D→C|， 因此， A→B＝D→C.
[解析] 由向量减法的三角形法则，易知选 B.
[答案] B
2．如图，e1，e2 为互相垂直的单位向量，则向量 a－b 可 表示为( )
2017版高考一轮总复习数学课件：第4章 第1节 平面向量的基本概念及线性运算
(2)在△ABC 中，N 是 AC 边上一点，且A→N＝12N→C，P 是 BN 上 的一点，若A→P＝mA→B＋29A→C，则实数 m 的值是________．
解析：(1)A→D＝A→C＋C→D＝A→C＋13B→C＝A→C＋13(A→C－A→B)＝43A→C －13A→B＝－13A→B＋43A→C.故选 A.
第十三页，编辑于星期六：三点 三十分。
设两个非零向量ɑ与 b 不共线． (1)若A→B＝ɑ＋b，B→C＝2ɑ＋8b，C→D＝3(ɑ－b)， 求证：A，B，D 三点共线； (2)试确定实数 k，使 kɑ＋b 和ɑ＋kb 共线． (1)证明：∵A→B＝ɑ＋b，B→C＝2ɑ＋8b，C→D＝3(ɑ－b)． ∴B→D＝B→C＋C→D＝2ɑ＋8b＋3(ɑ－b)＝5(ɑ＋b)＝5A→B. ∴A→B，B→D共线，又它们有公共点 B， ∴A，B，D 三点共线．
第九页，编辑于星期六：三点 三十分。
(2)如右图所示，因为A→N＝12N→C，所以A→C＝3A→N，则A→P＝mA→B ＋29A→C＝mA→B＋23A→N，又点 B、P、N 三点共线，所以 m＋23＝1，故 m＝13.
答案：(1)A
1 (2)3
第十页，编辑于星期六：三点 三十分。
1．解题的关键在于熟练地找出图形中的相等向量，并能熟练运 用相反向量将加减法相互转化．
第七页，编辑于星期六：三点 三十分。
(1)(2015·课标全国Ⅰ卷)设 D 为△ABC 所在平面内一点， B→C＝3C→D，则( )
A.A→D＝－13A→B＋43A→C B.A→D＝31A→B－43A→C C.A→D＝43A→B＋31A→C D.A→D＝43A→B－31A→C
第八页，编辑于星期六：三点 三十分。
第四章 平面向量、数系的 扩充与复数的引入
高考一轮第四章 第一节 平面向量的概念及其线性运算ppt
返回
返回
1．下列给出的命题正确的是
A．零向量是唯一没有方向的向量 B．平面内的单位向量有且仅有一个
(
)
C．a与b是共线向量，b与c是平行向量，则a与c是方向 相同的向量
D．相等的向量必是共线向量
答案： D
返回
2．如右图所示，向量a－b等于 A．－4e1－2e2 B．－2e1－4e2
(
)
C．e1－3e2
返回
[巧练模拟]———————(课堂突破保分题，分分必保！)
2．(2012· 盘锦模拟)已知等差数列{an}的前 n 项和为 Sn，若 M、N、P 三点共线，O 为坐标原点，且 ON ＝ a15 OM ＋a6 OP (直线 MP 不过点 O)，则 S20 等于 ( A．10 C．20 B．15 D．40 )
求两个
加法 向量和 的运算
(1)交换律：a＋b＝
三角形 法则
b＋a .
(2)结合律：(a＋b)＋c ＝ a＋(b＋c) .
平行四边形 法则
返回
向量
运算
定义 求a与b的相反
法则(或几何意义)
运算律
减法
向量－b的和的
运算叫做a与b 的差 三角形 法则
返回
向量
运算
定义
法则(或几何意义)
运算律
(1)|λa|＝ |λ||a| ；
A．充分不必要条件
C．充要条件
B．必要不充分条件
D．既不充分也不必要条件
解析：“a＋2b＝0”⇒“a∥b”，但“a∥b” ¿ “a＋2b＝0”， 所以“a＋2b＝0”是“a∥b”的充分不必要条件．
答案： A 返回
5．(2012· 南通月考)设e1，e2是两个不共线向量，已知 AB ＝ 2e1－8e2， CB ＝e1＋3e2， CD ＝2e1－e2.
高三数学,一轮复习人教A版, 第四章第1讲,平面向量的概念,及线性运算 课件
2．三点共线的等价关系 → → → → → A，P，B 三点共线⇔AP＝λAB(λ≠0)⇔OP＝(1－t)· OA＋tOB(O → → → 为平面内异于 A，P，B 的任一点，t∈R)⇔OP＝xOA＋yOB(O 为平面内异于 A，P，B 的任一点，x∈R，y∈R，x＋y＝1)．
1.教材习题改编 如图，D，E，F 分别是△ABC 各边的中点， 则下列结论错误的是( D ) → → A．EF＝CD → → B．AB与DE共线 → → C．BD与CD是相反向量 → 1→ D．AE＝ |AC| 2
1 1 A． a＋ b 2 2
1 1 B． a－ b 2 2
1 1 1 1 C．－ a－ b D．－ a＋ b 2 2 2 2 1 1 → 1→ 1 [解析] MD＝ BD＝ (b－a)＝－ a＋ b，故选 D. 2 2 2 2
4.教材习题改编 已知 a， b 是非零向量， 命题 p： a＝b， 命题 q： |a＋b|＝|a|＋|b|，则 p 是 q 的( A ) A．充分不必要条件 C．充要条件 B．必要不充分条件 D．既不充分也不必要条件
3.两个向量共线定理 向量 b 与非零向量 a 共线的充要条件是有且只有一个实数 λ， b＝λa 使得__________ ．
1．辨明两个易误点 (1)作两个向量的差时，首先将两向量的起点平移到同一点，要 注意差向量的方向是由减向量的终点指向被减向量的终点． (2)在向量共线的重要条件中易忽视“a≠0”， 否则 λ 可能不存 在，也可能有无数个．
[解析] 因为 e1 与 e2 不共线，且 a＝e1－e2 与 b＝－2e1＋λe2 共 线， 所以存在 μ∈R， 使 e1－e2＝μ(－2e1＋λe2)＝－2μe1＋μλe2，
1＝－2μ 得 ，所以 －1＝μλ
第4章 第1讲平面向量的概念及其线性运算-2021版高三数学(新高考)一轮复习课件共45张PPT
第四章 平面向量、数系的扩充与复数的引入
高考一轮总复习 • 数学 • 新高考
返回导航
3．(必修4P84T4改编)(2019·太原模拟)向量e1，e2，a，b在正方形网格中的位置 如图所示，向量a－b等于( C )
A．－4e1－2e2 B．－2e1－4e2 C．e1－3e2 D．3e1－e2
[解析] 由图可知a＝－4e2，b＝－(e1＋e2)，∴a－b＝e1－3e2，故选C．
第四章 平面向量、数系的扩充与复数的引入
高考一轮总复习 • 数学 • 新高考
返回导航
考点突破 • 互动探究
第四章 平面向量、数系的扩充与复数的引入
高考一轮总复习 • 数学 • 新高考
返回导航
考点一 向量的基本概念——自主练透
例 1 (1)(多选题)给出下列命题不正确的是( ACD ) A．单位向量都相等 B．若 A，B，C，D 是不共线的四点，且A→B＝D→C，则 ABCD 为平行四边形
第四章 平面向量、数系的扩充与复数的引入
高考一轮总复习 • 数学 • 新高考
题组二 走进教材
2．(必修4P91A组T4改编)化简A→B＋B→D－A→C－C→D＝( B )
A．A→D
B．0
C．B→C
D．D→A
[解析] A→B＋B→D－A→C－C→D＝A→D－(A→C＋C→D)＝A→D－A→D＝0.
返回导航
返回导航
[解析] (1)如图，在△OAC 中，M 为 AC 中点，所以O→A＋O→C＝2O→M，在△OBD 中，O→B＋O→D＝2O→M，故选 D．
第四章 平面向量、数系的扩充与复数的引入
高考一轮总复习 • 数学 • 新高考
返回导航
(2)由题意得，B→P－T→S＝T→E－T→S＝S→E＝
高三数学一轮复习 第四章 第一节 平面向量的基本概念及线性运算课件 理 新人教A版
a＝λb，但a
∴a∥b是a＝λb(λ∈R)的必要不充分条件，不是充要条 件．
第十页，共44页。
1．(人教A版教材习题改编)化简O→P － Q→P ＋M→S＋Q→M 的
结果为( )
A.O→M
B.S→M
C.P→S
D.O→S
【解析】 O→P－Q→P＋M→S＋Q→M＝(O→P＋P→Q)＋(Q→M ＋ M→S)＝O→Q＋Q→S＝O→S.
【尝试解答】 ①不正确．|a|＝|b|但a、b的方向不确 定，故a，b不一定相等；
②不正确．因为 A→B ＝ D→C ，A、B、C、D可能在同一直 线上，所以ABCD不一定是四边形．
③不正确．两向量不能比较大小． ④不正确．当λ＝μ＝0时，a与b可以为任意向量，满足 λa＝μb，但a与b不一定共线．
第三十一页，共44页。
一般地，首尾顺次相接的多个向量的和等于从第一个向 量起点指向最后(zuìhòu)一个向量终点的向量．
第三十二页，共44页。
1.向量共线的充要条件中要注意“a≠0”，否则λ可能不存 在，也可能有无数个．
2．证明三点共线问题，可用向量共线来解决，但应注意 向量共线与三点共线的区别与联系，当两向量共线且有公共点 时，才能得出(déchū)三点共线；
3．“向量”和“有向线段(xiànduàn)”是两个不同的概念，向 量只有两个要素：大小、方向；而有向线段(xiànduàn)有三个 要素：起点、方向、长度．
第十八页，共44页。
给出下列(xiàliè)四个命题：
①两个向量相等，则它们的起点相同，终点相同；
②若a＝b，b＝c，则a＝c；
③若a∥b，b∥c，则a∥c；
【答案】 D
第十三页，共44页。
3．已知 a 与 b 是两个不共线向量，且向量 a＋λb 与－(b －3a)共线，则 λ 的值为( )
高考数学一轮复习 第4章 平面向量 第1讲 平面向量的概念及其线性运算课件
12/11/2021
第二十八页，共四十七页。
触类旁通 平面向量线性运算的一般规律
(1)用已知向量来表示另外一些向量是用向量解题的基 本功，除利用向量的加法、减法、数乘运算外，还应充分 利用平面几何的一些定理．
(2)在求向量时，要尽可能转化到平行四边形或三角形 中，运用平行四边形法则、三角形法则，利用三角形中位 线、相似三角形对应边成比例等平面几何的性质，把未知 向量转化为与已知向量有直接关系的向量来求解．
第二十一页，共四十七页。
考向 平面向量的线性运算
命题角度 1 向量加减法的几何意义
例 2 [2017·全国卷Ⅱ]设非零向量 a，b 满足|a＋b|＝|a
－b|，则( )∥b
D．|a|＞|b|
12/11/2021
第二十二页，共四十七页。
解析 解法一：∵|a＋b|＝|a－b|， ∴|a＋b|2＝|a－b|2. ∴a2＋b2＋2a·b＝a2＋b2－2a·b. ∴a·b＝0.∴a⊥b. 故选 A.
第三十三页，共四十七页。
【变式训练 2】 已知 O，A，B 是不共线的三点，且O→P ＝mO→A＋nO→B(m，n∈R)．
(1)若 m＋n＝1，求证：A，P，B 三点共线； (2)若 A，P，B 三点共线，求证：m＋n＝1.
12/11/2021
第三十四页，共四十七页。
证明 (1)若 m＋n＝1， 则O→P＝mO→A＋(1－m)O→B＝O→B＋m(O→A－O→B)， ∴O→P－O→B＝m(O→A－O→B)， 即B→P＝mB→A，∴B→P与B→A共线． 又∵B→P与B→A有公共点 B，∴A，P，B 三点共线．
12/11/2021
第二十三页，共四十七页。
解法二：利用向量加法的平行四边形法则． 在▱ABCD 中，设A→B＝a，A→D＝b， 由|a＋b|＝|a－b|知|A→C|＝|D→B|， 从而四边形 ABCD 为矩形，即 AB⊥AD，故 a⊥b. 故选 A.
第二十八页，共四十七页。
触类旁通 平面向量线性运算的一般规律
(1)用已知向量来表示另外一些向量是用向量解题的基 本功，除利用向量的加法、减法、数乘运算外，还应充分 利用平面几何的一些定理．
(2)在求向量时，要尽可能转化到平行四边形或三角形 中，运用平行四边形法则、三角形法则，利用三角形中位 线、相似三角形对应边成比例等平面几何的性质，把未知 向量转化为与已知向量有直接关系的向量来求解．
第二十一页，共四十七页。
考向 平面向量的线性运算
命题角度 1 向量加减法的几何意义
例 2 [2017·全国卷Ⅱ]设非零向量 a，b 满足|a＋b|＝|a
－b|，则( )∥b
D．|a|＞|b|
12/11/2021
第二十二页，共四十七页。
解析 解法一：∵|a＋b|＝|a－b|， ∴|a＋b|2＝|a－b|2. ∴a2＋b2＋2a·b＝a2＋b2－2a·b. ∴a·b＝0.∴a⊥b. 故选 A.
第三十三页，共四十七页。
【变式训练 2】 已知 O，A，B 是不共线的三点，且O→P ＝mO→A＋nO→B(m，n∈R)．
(1)若 m＋n＝1，求证：A，P，B 三点共线； (2)若 A，P，B 三点共线，求证：m＋n＝1.
12/11/2021
第三十四页，共四十七页。
证明 (1)若 m＋n＝1， 则O→P＝mO→A＋(1－m)O→B＝O→B＋m(O→A－O→B)， ∴O→P－O→B＝m(O→A－O→B)， 即B→P＝mB→A，∴B→P与B→A共线． 又∵B→P与B→A有公共点 B，∴A，P，B 三点共线．
12/11/2021
第二十三页，共四十七页。
解法二：利用向量加法的平行四边形法则． 在▱ABCD 中，设A→B＝a，A→D＝b， 由|a＋b|＝|a－b|知|A→C|＝|D→B|， 从而四边形 ABCD 为矩形，即 AB⊥AD，故 a⊥b. 故选 A.
2015高三人教版数学一轮复习课件：第4章 第1节 平面向量的概念及其线性运算
第十页，编辑于星期五：十二点 二分。
第四章 平面向量、数系的扩充与复数的引入
[基础自测自评] 1．下列命题正确的是
() A．不平行的向量一定不相等 B．平面内的单位向量有且仅有一个 C．a与b是共线向量，b与c是平行向量，则a与c是方向相 同的向量 D．若a与b平行，则b与a方向相同或相反
第十一页，编辑于星期五：十二点 二分。
准确理解向量的基本概念是解决该类问题的关键，特别 是对相等向量、零向量等概念的理解要到位，充分利用 反例进行否定也是行之有效的方法．
第二十三页，编辑于星期五：十二点 二分。
第四章 平面向量、数系的扩充与复数的引入
2．几个重要结论 (1)向量相等具有传递性，非零向量的平行具有传递性； (2)向量可以平移，平移后的向量与原向量是相等向量； (3)向量平行与起点的位置无关．
第四页，编辑于星期五：十二点 二分。
第四章 平面向量、数系的扩充与复数的引入
二、向量的线性运算
向量 定义
运算
法则(或几何意义)
加法
求两个向量 和的运算
三角形法则
运算律
(1)交换律：a＋b ＝ b＋a ； (2)结合律：(a＋ b)＋c＝ a＋(b＋c)
第五页，编辑于星期五：十二点 二分。
第四章 平面向量、数系的扩充与复数的引入
向量的 模 ． 2．零向量：长度等于 0 的向量，其方向是任意的． 3．单位向量：长度等于 1个单位 的向量．
第三页，编辑于星期五：十二点 二分。
第四章 平面向量、数系的扩充与复数的引入
4．平行向量：方向相同或 相反 的非零向量，又叫共线向 量，规定：0与任一向量共线．
5．相等向量：长度相等且方向 相同 的向量． 6．相反向量：长度相等且方向 相反 的向量．
第四章 平面向量、数系的扩充与复数的引入
[基础自测自评] 1．下列命题正确的是
() A．不平行的向量一定不相等 B．平面内的单位向量有且仅有一个 C．a与b是共线向量，b与c是平行向量，则a与c是方向相 同的向量 D．若a与b平行，则b与a方向相同或相反
第十一页，编辑于星期五：十二点 二分。
准确理解向量的基本概念是解决该类问题的关键，特别 是对相等向量、零向量等概念的理解要到位，充分利用 反例进行否定也是行之有效的方法．
第二十三页，编辑于星期五：十二点 二分。
第四章 平面向量、数系的扩充与复数的引入
2．几个重要结论 (1)向量相等具有传递性，非零向量的平行具有传递性； (2)向量可以平移，平移后的向量与原向量是相等向量； (3)向量平行与起点的位置无关．
第四页，编辑于星期五：十二点 二分。
第四章 平面向量、数系的扩充与复数的引入
二、向量的线性运算
向量 定义
运算
法则(或几何意义)
加法
求两个向量 和的运算
三角形法则
运算律
(1)交换律：a＋b ＝ b＋a ； (2)结合律：(a＋ b)＋c＝ a＋(b＋c)
第五页，编辑于星期五：十二点 二分。
第四章 平面向量、数系的扩充与复数的引入
向量的 模 ． 2．零向量：长度等于 0 的向量，其方向是任意的． 3．单位向量：长度等于 1个单位 的向量．
第三页，编辑于星期五：十二点 二分。
第四章 平面向量、数系的扩充与复数的引入
4．平行向量：方向相同或 相反 的非零向量，又叫共线向 量，规定：0与任一向量共线．
5．相等向量：长度相等且方向 相同 的向量． 6．相反向量：长度相等且方向 相反 的向量．
相关主题