边坡稳定分析中的有限元强度折减法研究

合集下载

基于有限元强度折减法的滑坡稳定性分析

基于有限元强度折减法的滑坡稳定性分析滑坡稳定性分析基于有限元强度折减法是一种用于确定滑坡极限稳定性的重要方法。

它主要是通过在滑坡稳定性分析中应用有限元强度折减法，以折减破坏面的形状，计算滑坡受力情况，以及滑坡自重，物质特性及岩土的摩擦特性的数值计算，最终用分析结果来判断滑坡稳定发展的可能性，以确定滑坡稳定状态。

一、有限元强度折减法1、折减原理：有限元强度折减法是一种直接定位破坏面的方法，其原理是通过折减岩体的强度，来确定破坏开裂的面。

在有限元中，折减的本质就是改变模型的材料参数，找到一个最小的一组有限元强度折减设定，以便确定所需的破坏面。

2、折减边界：有限元强度折减法的折减边界就是要折减的破坏开裂的面。

尽管可以采用自然边界，但是最好采用与实际条件有关的先进边界。

二、滑坡受力情况1、岩土特征：滑坡稳定分析包括对岩土特性的计算，例如土壤材料的屈服强度、弹性模量和泊松比以及岩土体内强度、摩擦以及连接情况等，并结合岩土稳定性理论，评价土坡稳定性。

2、受力、物质特性：另外，还需要考虑滑坡体的受力和物质特性，这些元素包含滑坡自重、坡面上的重力、地形力以及雨水等，它们也是滑坡稳定性分析的重要组成部分。

三、岩土的摩擦特性1、析出摩擦角：在滑坡稳定性分析中，析出岩土的摩擦角是计算极限稳定性的重要标准之一。

通过有限元强度折减法分析，可以精准计算出滑体内岩土摩擦角，从而得到表征滑坡发展可能性的结果。

2、摩擦和静定：岩土的摩擦力可以通过契约定理分析求得，它是由滑体摩擦角和坡度决定的，其大小可以被表达为“摩擦-坡度”系数。

此外，只有当滑体内岩土摩擦角足够大时，滑坡才具有静定发展的可能性。

四、滑坡稳定状态1、岩体状态：滑坡稳定状态可以根据岩体状态来评价，只有当滑坡稳定发展时，才能保证滑坡体状态稳定；2、计算结果：通过有限元强度折减法分析，可以根据折减的结果计算出滑体的受力状况，确定极限稳定性；3、应变计算：此外，还需要通过应变计算和时变分析，来评价滑坡稳定状态的发展趋势。

边坡稳定性分析的弹塑性有限元强度折减法

限元强度折减法，使有限元法在边坡稳定性分析中进入
实用阶段。，
单元的具体划分原则如下： ①根据所使用的计算机性能
及计算精度要求，考虑到折减系数法要多次反复分析并才能求解。大致确定单元总数不超过１００个，点总００节
摘要：将弹塑性有限死分析方法结俞强度折减技术用到边坡稳定分析中，提出以“ 出现某 ‘ 幅
值的总等效塑性应变区，。爿凡从坡脚到坡顶贯通” 作为边坡破坏的标准。并ｆ助非线性有限几分析软｝ｆ
件和计算机实时示技术，将弹朔性有限元数值分析及结果显示出来，不但物理意义【确，１』而町以ｊ根抛边坡临界破坏时的等效塑性应，竖区确定滑动而位置和边坡的安全系数。对算例数值分析结果表明：咳方法是可行合理的，与传统方法卡比，Ｈ具有明显的优越性，为边坡的稳定性分析与评价提供了新的思路，具有重要的理论意义与一程实Ｊ价值。１｝］
关键词：边坡稳定性分析：弹塑性仃限元；强度折减法；等效性应变
１弓言Ｉ
对边坡的稳定性分析，统方法主要有：限衡传极卜
用解的不收敛作为破坏标准自身存存一些不足。本文］试图用贯通区塑性单冗出现某幅值的总等效塑性应
维普资讯
广东建材２０年第ｌ期０６ｌ
研究与探讨
边坡稳定性分析的弹塑性有限元强度折减法
柯鹏振（武汉理工大学资源与环境工程学院４０７）３００陈静曦（中国科技大学土木与建筑学院２０２）３０６胡双双（武汉理工大学资源与环境工程学院４０７）３００

有限元强度折减法在边坡稳定性分析中的运用

第３７卷第ｌ５期２０１１年５月
山西建筑
ＳＡＮＸＩＡＲＣＨＩＥＣＨｒＴＵＲＥ
Ｖｏ．Ｎｏ．５１３７１
Ｍａ．２１ｙ０１
ห้องสมุดไป่ตู้
・５３・
文章编号：０９６２（０）５０５ —２１０ — ８５２１１－０３０１
各种方法均有其适用的范围、点和不足，此不再赘述。优在
目前，求解边坡稳定主要用有限元法，具体为有限元滑面搜索法
始出现水平方向的剪应力，总趋势是由内向外增多，近坡脚和有限元强度折减法。其越有限元强度折减法已经在边坡稳定分析中有了广泛的研究越高，向坡内逐渐恢复到原始应力状态。４其基本思想是，先选取初始折减系数，岩体强度Ｊ首将２在坡脚逐渐形成明显的应力集中带。边坡越陡，力集中和运用．，）应将折减后的参数作为输入，进行有限元计算，程若越严重，最大最小主应力的差值也越大。此外，在边坡下边分别参数进行折减，
有限元强度折减法在边坡稳定性分析中的运用
钟燕
摘要：究了边坡变形破坏基本原理，研通过对边坡稳定性分析方法的分析比较，出了有限元强度折减法的应用，结提并
合工程实例进行了说明，而证实了该方法的实用性和可行性。进

基于有限元强度折减法的边坡稳定性分析报告

基于有限元强度折减法的边坡稳定性分析报告学院：土木工程与力学学院专业：结构工程姓名：学号：2016年7月有限元强度折减法研究进展摘要：在边坡稳定性分析中，相比于传统的极限平衡法、极限分析法等，有限元强度折减法具有明显的优势。

这主要体现在其无须事先假定滑动面的形状和位置，只需通过不断降低边坡岩土体的强度参数，进而使边坡岩土体因抗剪强度不能抵抗剪切应力而发生破坏，并最终得到边坡的最危险滑动面及相应的安全系数。

有限元强度折减法兼有数值计算方法和传统极限平衡方法的优点。

本文介绍了有限元强度折减法的原理与主要研究现状，并对其中的一些重点问题进行了研究与总结。

关键词：强度折减法;有限元;边坡稳定1 有限元强度折减法基本原理所谓强度折减，就是在理想弹塑性有限元计算中将边坡岩土体抗剪切强度参数逐渐降低直到其达到破坏状态为止，程序可以自动根据弹塑性计算结果得到破坏滑动面(塑性应变和位移突变的地带)，同时得到边坡的强度储备安全系数ω, 于是有:==。

'/,tan'tan/c cωϕϕω一般地，强度折减弹塑性有限元数值分析方法考察边坡稳定性的步骤是：首先对于某一给定的强度折减系数，通过逐级加载的弹塑性有限元数值计算确定边坡内的应力场、应变场或位移场，并且对应力、应变或位移的某些分布特征以及有限元计算过程中的某些数学特征进行分析，不断增大折减系数，直至根据对这些特征的分析结果表明边坡己经发生失稳破坏，将此时的折减系数定义为边坡的稳定安全系数。

尽管强度折减有限元法在边坡稳定性分析中得到重视与发展，但其计算中需要采用一定的边坡失稳评判标准来确定边坡失稳的临界状态，但是，各种判据的选用至今并没有取得统一。

2 主要研究现状强度折减概念由Zienkiewicz最早提出并用于边坡的稳定性分析，受限于当时数值计算和计算机水平而未能得到大的发展，直到近十几年来，随着数值计算和计算机技术的迅猛发展，强度折减法也得到了极大的发展，国内外许多学者在这方面做了大量的工作。

强度折减有限元法在边坡稳定性分析中的应用研究

Ａｂｓｔｒａｃｔ:Ｂａｓｅｄｏｎｓｔｒｅｎｇｔｈｒｅｄｕｃｔｉｏｎｆｉｎｉｔｅｅｌｅｍｅｎｔｍｅｔｈｏｄꎬｔｈｉｓｐａｐｅｒｓｔｕｄｉｅｓｔｈｅｓｔａｂｉｌｉｔｙｏｆｔｈｅｓｌｏｐｅꎬａｎｄａｇｅｎｅｒａｌｉｚｅｄｍｏｄｅｌｗａｓｅｓｔａｂ￣
ｌｉｓｈｅｄｆｏｒａｎａｌｙｓｉｓ. Ｔｈｅｒｅｓｕｌｔｓｓｈｏｗｔｈａｔｔｈｅｓｔｒｅｎｇｔｈｒｅｄｕｃｔｉｏｎｆｉｎｉｔｅｅｌｅｍｅｎｔｍｅｔｈｏｄ ( ｆｅｍ) ｉｓｒｅｌｉａｂｌｅꎬａｎｄｔｈｅｓｔａｂｉｌｉｔｙｏｆｔｈｅｓｌｏｐｅｓａｆｅｔｙ
束ꎬ底部为全约束ꎮ 计算单元采用修正四边形单元ꎬ在边坡易
于变形的区域进行网格细化ꎬ该模型共分５５９０个单元ꎮ
福建建设科技２０２０Ｎｏ３
６４
■岩土工程
表１岩石的初始计算参数
岩石类别
强风化岩石
很强的非线性分析能力 [６] ꎮ ＡＢＡＱＵＳ软件在世界范围内有
度折减有限元法 [１] ꎮ 该方法在边坡稳定性计算中通过不断
全系数ꎮ 本文使用有限元分析软件结合强度折减法对某工
程中的岩质边坡进行了稳定性计算ꎬ得到了该边坡的稳定性
安全系数和潜在滑动面范围ꎮ
２强度折减有限元法理论
强度折减有限元法进行边坡稳定性分析的原理
至破坏特征出现ꎬ再根据计算得出相应的安全系数ꎮ 将岩土
体强度指标ｃ值、φ 值同时除以一个折减系数Ｋꎬ得到一组新
的ｃ′值、φ′值ꎬ在下一次计算中作为新的岩土体参数输入有限
元中进行计算ꎬ当计算结果符合给定的临界破坏判定条件
时ꎬ其对应的折减系数Ｋ可作为该边坡的稳定安全系数ꎮ 其
中ꎬ岩土体参数ｃ′值、φ′值分别由式(１) 和(２) 求得ꎬ其余参数

基于有限元强度折减法在边坡稳定性分析中的应用研究

式中： —— 安全系数；
，— —
滑动面上各点的抗剪强度；滑动面上各点的实际强度；
—
—
将式子两边同时除以ｋ，式子（１）变为：
１一
一
Ｊ。（
）ｄｌ
一
ｔａｎ
』
式中：ｃ ’ ＝｝，ｔａｎｑ￣ ’ ＿＿ｔａｎｑ￣一
作者简介：夏志国（１９７５一），男，天津人，高级工程师，从事道路、桥梁项目前期研究工作。
目前有三种方法判断边坡到达失稳状态：（１）以关键点的位置发生突变；（２）以塑性区间贯通；
速发展与计算分析软件的日益完善，各种计算手段逐渐被应用至边坡稳定性分析中。该文阐述了利用有限元强度折减法对高填
方路堤的稳定性进行分析，并通过实际工程应用证明其准确性。关键词：高填方路基；稳定性分析；有限元强度折减法；应用；天津市
Ｊ。
一
Ｊ。（ｃ＋ｔａｎ￣）ｄｌ

…
＋
＝参数值如表１所列，本文以此为基础
』：ｄｚ — ｆ：
收稿日期：２０１２ — １２ — １７
采用不同的准则分别计算，并进行比较。１＿２．２判断失稳的标准
一』丁
目前已开发出二维或三维边坡有限元商业分析程序，如ＡＮＳＹＳ，ＡＤＩＮＡ，ＳＡＰ２０００，ＰＬＡＸＩＳ等，可用来求解弹性、弹塑性、粘弹塑性、粘塑性、流变问题、大变形和小变形问题，以及其他非线性应力变形问题等。本文采用有限元强度折减法，借助有限元分析软件ＡＮＳＹ对高填方路堤的稳定性进行分析。

基于有限元强度双折减法的土质边坡稳定性分析

基于有限元强度双折减法的土质边坡稳定性分析土质边坡稳定性分析是工程中非常重要的内容。

而基于有限元强度双折减法的土质边坡稳定性分析方法则是一种常用的、准确可靠的分析方法。

本文将对有限元强度双折减法进行详细介绍，并以此为基础，探讨土质边坡稳定性的分析方法。

有限元强度双折减法是一种基于有限元原理的边坡稳定性分析方法。

该方法将边坡土体离散为有限个单元，然后根据土体的力学性质和边坡的几何形状，利用有限元方法求解边坡单元的位移、应力和变形。

在强度双折减法中，土体的强度按照双折减的原理进行计算，即采用承载力折减系数和摩擦角折减系数进行计算。

承载力折减系数是根据土体的强度参数和边坡的几何形状计算得出的，用于表征土体承受边坡负荷的能力。

而摩擦角折减系数则是根据土体内摩擦角和边坡的倾斜角计算得出的，用于表征土体在边坡倾斜状态下的摩擦性能。

有限元强度双折减法的分析流程一般包括以下几个步骤：首先，确定边坡的几何形状和土体的力学性质，包括边坡的坡度、高度、土体的重度和内摩擦角等。

其次，建立边坡的有限元模型，并对土体进行网格划分。

然后，根据边坡的边界条件和荷载情况，进行力学计算，求解边坡单元的位移、应力和变形。

最后，利用得到的位移、应力和变形结果，根据强度双折减法进行边坡稳定性评估。

有限元强度双折减法的优点是可以较为准确地反映土体的力学行为和边坡的稳定性，具有一定的工程应用价值。

然而，该方法需要对边坡的几何形状和土体的力学性质进行较为准确的估计，同时计算过程也较为繁琐。

因此，在实际工程中，还需要结合其他辅助手段和经验，对边坡稳定性进行全面评估。

总之，基于有限元强度双折减法的土质边坡稳定性分析方法是一种较为准确可靠的分析方法。

通过该方法，可以对土质边坡的稳定性进行详细分析和评估，为工程设计和边坡治理提供科学依据。

有限元强度折减法在边坡稳定计算中的应用

有限元强度折减法在边坡稳定计算中的应用近年来，随着科学技术的发展，边坡安全工程成为当今社会的热点问题。

边坡稳定性是边坡工程安全性的重要水平指标之一。

有效地确定边坡稳定性，可以减少边坡垮塌，破坏性侵蚀及其他地质灾害的发生，更有效地保护人民生命财产安全。

传统的边坡稳定计算方法有很多缺点，很难解决大规模复杂的边坡稳定计算问题。

为了解决这些问题，随着计算机技术的发展，数值计算技术的发展，边坡稳定计算中有限元强度折减法也逐渐得到应用，它为边坡稳定计算提供了一种有效的方法。

有限元强度折减法是由著名有限元数值计算理论家Hans Zienkiewicz 于一九六三年提出的，它把数值计算分解为两个步骤：有限元分析和强度折减。

有限元分析不仅可精确的计算土体的应力和变形，还可以求得边坡的稳定系数。

而强度折减步骤则是对这些应力值和变形按照一定的准则进行折减，从而实现边坡的稳定计算。

有限元强度折减法在边坡稳定计算中的具体应用，有很多研究者提出了不同的算法，表达了不同的稳定准则和折减准则。

其中，以倒角条件准则、惯性假设准则、根据节理、滞回因子、失稳指标等为稳定准则的稳定计算模型。

具体的折减准则有力学强度折减法、抗剪强度折减法、抗压强度折减法、有效应变折减法等。

有限元强度折减法在边坡稳定计算中，可以有效地求解复杂参数边坡的稳定性，它把不同的计算模型、稳定准则和折减准则整合在一起，使边坡稳定计算更精确、更准确、更实用。

有限元强度折减法在边坡稳定计算中的应用已经得到了广泛的应用，它可以有效地求解复杂的边坡的稳定性，可以有效地减少不必要的垮塌、破坏性侵蚀等灾害，并可有效地保护人民生命财产安全。

因此，有限元强度折减法在边坡稳定计算中的应用，具有重要的理论意义和实际意义。

综上所述，有限元强度折减法在边坡稳定计算中的应用具有重要的理论意义和实际意义，它可以有效地求解复杂的边坡的稳定性，可以有效地减少不必要的垮塌、破坏性侵蚀等灾害，并可有效地保护人民的生命财产安全。

有限元强度折减法研究岩质边坡稳定性

袭ｌ糟瑾力学’披计算取值
√ 一一应力张量的第一不变量；
√ 一一力张第不量。应偏量的二变
这是个通用表达式，通过变换、ｋ的
表达式就可以在有限元中实现不同的屈服准则，图ｌ如
，＝
，
．＋ｔｑｌ（ｆｒｎ）４（ｙｃａ￣ｄ）
给定的强度折减参数Ｃ口，土体形成的的广义剪应变自角底部下方向坡顶贯通，坡则认
将等式两边同。时积分：
为对于稍高于ｃ和的土体强度参数ｃ和．使得土体处于临界状态，而与ｑ和矗对应的强。为安全系数。但莫尔库仑准则在平面上的图形为不规度折减系数ｌ则的六角形截面，在尖顶和棱角，存给数值计算带来困难。广义米赛斯准则在ｃ力空但式主应间的屈服面为一圆锥面，７平面上为圆形，在ｔ＂＝不存在尖顶处的数值计算问题，目前国际上流行的ＡＮＳ以及美国ＭＳＹＳＣ公司的ＭＡＲＣ，ＮＳＲＡＡＴＮ等均采用广义米赛斯准则。２屈服准则的选用本文计算采用的是理想弹塑性模型。用使有限元软件ＡＮＳ进行分析，ＹＳ采用ＤｒｃｅｕｋｒＰａｅ准则。ｒｇｒ（）３在常用的极限平衡方法中，安全系统定义Ｆｃｌ４２ｋ＝ｄ＋Ｊ＝（）１为沿滑动面抗剪强度与滑动面上实际剪力的比式中：值。
— — — — — — 一
Ｉ２００ｌ５
】２５Ｏ０１，８】１４
： ● ｎ】ｊｃＩ３
ｌ４ ¨¨ Ｊ？

有限元强度折减法在边坡稳定性分析中的应用

５５６５０６５５５
５ｏ５
５５４５０４５５３
５０３
５５２５０２
０１２３４５６７】８９１０１２００００００【０００１０１０
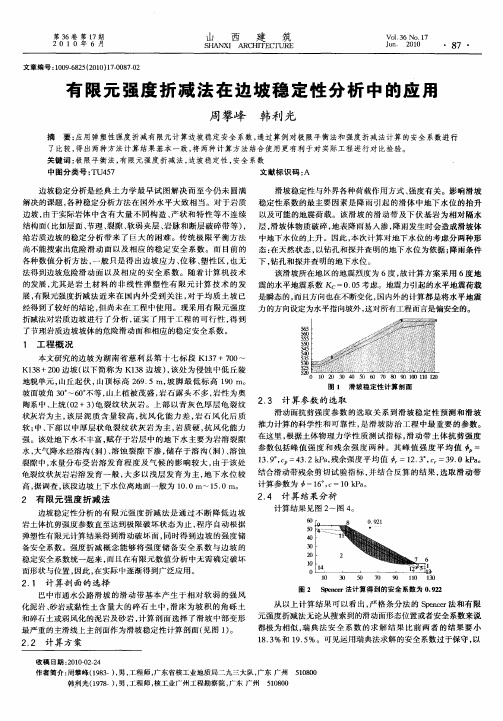
阕１滑坡稳定性计算剖面
．陶系中、统（２＋３龟裂纹状灰岩。上部以青灰色厚层龟裂纹２３计算参数的选取上０）滑动面抗剪强度参数的选取关系到滑坡稳定性预测和滑坡状灰岩为主，该层泥质含量质抗岩
水，大气降水经溶沟（）溶蚀裂隙下渗，洞、储存于溶沟（）溶蚀参数包括峰值强度和残余强度两种。其峰值强度平均值＝洞、１．。Ｃ＝４．Ｐ，３９，。３２ｋａ残余强度平均值＝１．。Ｃ＝３．Ｐ。２３，，９０ｋａ裂隙中，水量分布受岩溶发育程度及气候的影响较大，由于该处并选龟裂纹状灰岩岩溶发育一般，多以浅层发育为主，下水位较结合滑动带残余剪切试验指标，结合反算的结果，取滑动带大地计算参数为＝１。Ｃ０ｋａ６，＝１Ｐ。高，调查，段边坡上下水位离地面一般为１．据该００ｍ～１．５０ｍ。
有限元强度折减法在边坡稳定性分析中的应用
周攀峰
摘
韩利光
要：应用弹塑性强度折减有限元计算边坡稳定安全系数，通过算例对极限平衡法和强度折减法计算的安全系数进行

基于有限元强度折减法边坡稳定分析方法浅析

信息化技术应用TECHNOLOGY AND INFORMATION 基于有限元强度折减法边坡稳定分析方法浅析李浩林李棒广西珠委南宁勘测设计院广西南宁530007摘要基于有限元法的岩土分析计算能通过强度折减计算使系统达到不稳定状态，进而对边坡的稳定性进行定量分析。

本文使用有限元计算软件ANSYS对某一土坡进行稳定性分析，结果表明：随着折减系数的不断增大并达到某一数值时，土坡内塑性应变在坡底处逐渐变大，边坡达到极限状态，$匕时的折减系数即为安全系数。

结合Geo软件采用极限平衡法计算结果对比分析表明，有限元强度折减法对土坡边坡稳定性分析具有良好的适用性。

关键词强度折减法；安全系数；有限元分析；边坡稳定分析-1-C_1—刖旨有限元强度折减法与有限元荷载增加法统称为有限元极限分析法，它们本质上都是采用数值分析手段求解极限状态的分析法E。

有限元极限分析法中安全系数的定义依据岩土工程出现破坏状态的原因不同而不同。

边坡工程多数由于岩土受环境影响，岩土强度降低而导致边坡失稳破坏。

在评价土坡稳定性时，应区别各因素在土坡稳定中所起的作用。

1土坡稳定分析研究现状目前用于土坡稳定分析的方法基本上有两种：极限平衡方法和数值分析方法。

极限平衡方法主要有瑞典圆弧法、简化毕肖普法、简布普通条分法、摩根斯坦-普赖斯法及不平衡推力传递法等；由于极限平衡方法完全不考虑土坡本身的应力-应变关系，不能真实反映土坡边坡失稳时的应力场和位移场，因此受到质疑。

数值分析方法主要包括有限元法、自适应有限元法、离散单元格法、拉格朗日法及界面元法等；数值分析方法则考虑土坡应力应变关系，可以相对较好地模拟土坡边坡实际受力情况，克服了极限平衡方法这方面的缺点冋。

本文以一具体的尾矿坝稳定分析为工程实例，分别采用GeoSlope边坡分析软件和Ansys有限元分析软件的有限元强度折减法计算该土坡的稳定性。

2工程实例2.1工程概况某尾矿库，设计库容为110万n?。

边坡稳定分析中的有限元强度折减法研究

边坡稳定分析中的有限元强度折减法研究【摘要】在边坡稳定性分析中采用有限元强度折减法，主要包括破坏判据的确定，屈服准则的影响和选用。

本文详细介绍有关有限元强度折减法的内容。

【关键词】有限元强度折减法；边坡稳定分析一、有限元强度折减安全系数对于摩尔一库仑材料，强度折减安全系数定义与边坡稳定分利用有限单元法，通过强度折减来求边坡稳定安全系数。

通过强度折减，使系统达到不稳定状态时，有限元计算将不收敛，此时的折减系数就是安全系数。

计算时，首先选取初始折减系数，折减土体强度参，将折减后的参数作为输入，进行有限元计算，若程序收敛，则土体仍处于稳定状态，然后再增加折减系数，直到不收敛为止，此时的折减系数即为边坡的稳定安全系数，此时的滑移面即为实际滑移面，这种方法称为土体强度折减系数法。

对于摩尔一库仑材料，强度折减安全系数定义与边坡稳定分析的极限平衡条分法安全系数定义形式是一致的。

有限元强度折减系数法的基本原理是将坡体强度参数：粘聚力c和内摩擦角值同时除以一个折减系数fs，得到一组新的c′、′值，然后作为新的资料参数输入，再进行试算，当计算不收敛时，对应的fs被称为坡体的最小稳定安全系数，此时坡体达到极限状态，发生剪切破坏，同时可得到坡体的破坏滑动面。

二、有限元中边坡破坏的判据有限元强度折减法分析边坡稳定性的一个关键问题是如何根据有限元计算结果来判别边坡是否达到极限破坏状态。

土体破坏的标准有如下几种：1.以有限元静力平衡计算不收敛作为边坡整体失稳的标志。

2.以塑性区（或者等效塑性应变）从坡脚到坡顶贯通作为边坡整体失稳的标志。

3.土体破坏标志应当是滑动土体无限移动，此时土体滑移面上应变和位移发生突变且无限发展。

三、屈服准则的影响和选用研究表明，采用该准则与传统摩尔一库仑屈服准则的计算结果有较大误差，不管是评价边坡稳定性，还是地基极限承载力等等，在实际工程中如果采用该准则是偏于不安全的。

四、有限元法进行边坡稳定分析的优点如果使有限元法保持足够的计算精度，那么有限元法较传统的方法具有如下优点：1.能够对具有复杂地貌、地质的边坡进行计算。

ABAQUS强度折减法在边坡稳定性分析中的适用性研究

ABAQUS强度折减法在边坡稳定性分析中的适用性研究一、引言边坡稳定性分析是工程设计中的一项重要内容，在工程实践中应用广泛。

边坡稳定性问题的出现不仅会对人们的生命和财产安全造成威胁，也会对周边环境和生态系统造成潜在的危害。

对边坡稳定性进行准确并可靠的分析是工程设计的基本要求。

二、 ABAQUS强度折减法的原理与应用ABAQUS强度折减法是建立在有限元分析的基础上的一种稳定性分析方法。

其原理是在有限元模型的基础上引入强度折减因子，通过对边坡体的稳定性进行评估，确定其破坏模式和破坏状态。

其具体步骤包括：建立边坡体的有限元模型、定义强度折减因子、进行荷载作用和边坡体受力分析、评估边坡体的稳定性。

ABAQUS强度折减法相对于传统的极限平衡法和有限元法，具有更加准确和精细的优势。

在实际工程中，其运用更加直观并且符合实际情况，能够更好地反映边坡体的稳定性问题，因此受到了广泛的认可和应用。

ABAQUS强度折减法在边坡稳定性分析中的适用性研究表明，该方法能够更加准确地评估边坡体的稳定性，能够综合考虑边坡体的材料性质、几何形态和外部荷载作用，因此具有较高的实用性和适用性。

在实际工程中，该方法能够为工程设计提供科学依据，并可为工程实践提供重要参考。

ABAQUS强度折减法也存在一定的局限性。

该方法在实际工程中需要对边坡体的材料参数和边坡几何形态进行准确的测定和识别，因此在实际操作中具有一定的难度。

该方法需要对边坡体进行细致的有限元建模，因此在计算和分析过程中需要耗费一定的时间和精力。

三、结论通过对ABAQUS强度折减法在边坡稳定性分析中的适用性进行深入研究发现，该方法在工程实践中具有显著的优势和适用性。

其在实际工程中仍存在一定的局限性，因此在使用时需要根据实际情况进行灵活应用，并结合其他相关分析方法，以确保边坡稳定性分析的准确和可靠。

在未来的研究中，可以进一步完善该方法的理论基础和实际应用，以提高其在工程实践中的适用性和可靠性。

有限元强度折减法在边坡稳定计算中的应用

有限元强度折减法在边坡稳定计算中的应用有限元强度折减法是一种求解复杂结构力学问题的新方法，用于分析边坡稳定性也有强大的能力。

最近，有关使用有限元强度折减法的研究取得了巨大的进展，在计算边坡稳定性时取得了良好的结果。

本文将就有限元强度折减法在边坡稳定计算中应用的可行性及效果作一介绍。

一、有限元强度折减法背景1、有限元强度折减法是什么？有限元强度折减法是通过改变单元的材料参数，使得最终近似解与实际T失效状态一致，达到分析结构安全性能的一种计算方法。

这一计算方法能够较好地反映出结构的失效过程，从而改善传统的有限元算法的拟合不足的问题。

2、有限元强度折减法的特点有限元强度折减法不仅考虑结构的失效过程，还可以继而模拟出材料的弹性和变形过程，从而改进传统的有限元算法的拟合不足的问题。

此外，它还能模拟多种类型的变形，以保证结构承受能力及临界状态分析。

二、有限元强度折减法在边坡稳定计算中的应用1.计算边坡稳定时的精确性：使用有限元强度折减法计算边坡稳定性能，可以反映出坡面弹性及变形特性，从而更准确地评估边坡的变形性能。

2.降低计算时间：有限元强度折减法可以快速精确地计算边坡稳定性，因此在减少计算时间的同时又能达到边坡稳定性分析的要求。

3.降低精度：有限元强度折减法是一种新的技术，其计算结果与实际物理量有一定的偏差，而这个偏差一般比传统的有限元算法要小，因此使用有限元强度折减法计算边坡稳定性时，可以保证计算的可靠性。

三、结论有限元强度折减法在计算边坡稳定性方面具有优越的性能，具备计算精确、节省时间、降低精度等优点，因此作为计算边坡稳定性的一种有效工具已经得到广泛应用。

边坡稳定性分析中的有限元强度折减法

边坡稳定性分析中的有限元强度折减法论文摘要：本文介绍了有限元强度折减法的理论原理、运算方法、与传统极限平稳法相比所具有的优势、边坡失稳判据以及运算结果的阻碍因素。

采纳有限元分析软件Plaxis进行强度折减运算，直至满足位移不收敛，从而得到边坡稳固安全系数。

论文关键词：边坡稳固,有限元强度折减法,失稳判据,安全系数0.引言边坡稳固性分析是岩土工程中一个十分重要的问题。

常用的边坡稳固性分析方法专门多，如传统边坡稳固分析方法有:极限平稳法,极限分析法,滑移线场法等。

到目前极限平稳法差不多日趋完善,基于该原理的新方法的不同仅是在条间力的假设上不同。

该法简单易用，为实际工程中广泛采纳。

然而它没有考虑土体的应力应变特性,还要假设潜在滑面(如面、折线形、圆弧滑动面、对数螺线柱面等),对同一工程问题算不出一致的解。

极限分析法中的上限法尽管对真实解提供了一个严格的上限,但上限法中采纳相关联流淌法则，过大地考虑了土的剪胀性。

有限元法由于能反映边坡岩土体的应力-应变关系，考虑实际边坡体的复杂边界条件和采纳一样土的材料模型，因而是一种较好的研究边坡稳固性的方法。

1.强度折减原理在有限元静力稳态运算中,假如模型为不稳固状态,有限元运算将不收敛。

那么反过来,通过调整参数,使有限元运算从收敛变得不收敛,就表征边坡模型从稳定状态向不稳固状态发生了转变。

强度折减原理确实是把土体的抗剪强度值c和φ,除以一个折减系数F如下式：（1）把折减以后的土体强度值代入有限元中运算,并不断变换折减系数,得出满足收敛条件的折减系数,即为所求的安全系数。

Zienkiewicz(1975)把抗剪强度折减系数定义为:在外荷载保持不变的情形下,边坡内土体所发挥的最大抗剪强度与外荷载在边坡内所产生的实际剪应力之比。

外荷载所产生的实际剪应力应与抵御外荷载所发挥的最低抗剪强度即按照实际强度指标折减后所确定的、实际中得以发挥的抗剪强度相等。

当假定边坡内所有土体抗剪强度的发挥程度相同时,这种抗剪强度折减系数定义为边坡的整体稳固安全系数,由此所确定的安全系数能够认为是强度储备安全系数。

边坡稳定性的有限元强度折减分析法

】１１６６（００１－０９００－８４２１）１０７－３０
ＴＨＥＡＮＡＬＹＳＳ０ｌＳＩＦＬ０ＰＥＳＴＡＢⅡ ｒＹＢＹｒＴＨＥＴＲＥＳＮＧＴＨＲＥＤＵＣＴＯＮＥＭＩＦ
ＬＵＪｅＪＡＮＧＪｎｔｏ，ＪＡａ・ｎＺＩｉ，Ｉｕ — ＩＮＧＸｉｆｇ，ＨＡＯＣｎａｏｅａ
２工程实例分析２１工程概况．
拟建工程位于天津市塘沽区，由于周围场地较宽敞，采用放坡开挖，边坡的几何尺寸如图１示，比为１２，所坡：其平
（ｒｈｔｔｒｎｉｅｒｇＩｓｔｔＴａｊｎｖｒｉＴａｊ００２ＣｉａＡｃｉｃｕａＥｇｅｉｔｕｅｌｎｎｎｉｅ，ｉｎｉＵｉｅｓｙ，ｉｎｉ３０７，ｈｎ）ｎｔｎ
ＡｓａｔＴｉｐｐｒｉｂｓｄｏｅｓｅｇｈｒｄｃｉＥ，ｏｉｉｇａｔａｐｏｃ，ｎｌｚｇｂｔｃ：ｈｓａｅａｅｎｔｔｎｔｅｕｔｎＦＭｃｍｂｎｎｃｌｒｅｔａａｉｒｓｈｒｏｕｊｙｎ
拟出边坡的实际滑移面。因此，限元法近年来在工程中有的应用取得了快速的发展。１有限元强度折减法原理强度折减法就是将土体的抗剪强度指标Ｃ和妒用一个折减系数按（）式进行折减，１然后用折减后的抗剪强度
Ｉ ———— 一 —— —
ｔｅｓｂｌｙｏｏａｄｔｒｅｄｍｅｓｏａｌｐ．ｈｅｕｔｒｏａｅｉｉｌｅｉｈｐｍｅｈｄｈｔｉｔｆｗｎｅ — ｉｎｉｎｌｏｅＴｅｒｓｌａｅｃｍｐｒｄｗｔｓｍｐｉｄＢｓｏｔｏａｉｔｈｓｓｈｉｆｔｈｃｈｃｕａｙｏｅａａｙｉ．ｔｉｎｉａｅｈｔｔｅｓｒｎｔｅｕｔｎＦｏｃｅｋｔｅａｃｒｃｆｔｎｌｓｓＩｓｉｄｃｔｄｔａｈｔｇｈｒｄｃｉＥＭｎｌｓｓｆｒｓｐｈｅｏａａｙｉｏｌｅｏｓａｉｔｓｆａｉｌ．ｔｓｂｔｒｔｏｓｅｅａｔａｉａｉｎｂｆｒｋｈｉｅｏｏｏｒｅｄ — ｔｂｌｙｉｅｓｅＩｉｅｔｃｎｉｒｈｃｕｌｓｕｔｅｏｅｗｅｍａｅａｃｏｃｆｔｒｈｅ — ｉｉｂｅｏｄｔｔｏｗｔ

有限元强度折减法的原理、优点与超高边坡失稳的判据

有限元强度折减法的原理、优点与超高边坡失稳的判据一、安全系数的定义两种方法可以导致边坡达到极限破坏状态，即：增量加载和折减强度。

传统边坡稳定分析中的安全系数是一个比值，假定一滑动面，根据力学的平衡来计算边坡安全系数，它等于滑动面以上土体条块的抗滑力与下滑力的比值。

式中K——安全系数；τ——滑动面上各点的实际强度。

将式子（4-1）两边同时除以k，上述公式变为其中：式（4-1）的左边等于I，表示滑坡体达到极限平衡状态，这意味着当代表强度的黏聚力和摩擦角被折减为1/K后，边坡最终到达破坏。

这个系数K就是有限元强度折减法中求解的安全系数，其实也就是强度折减系数。

二、有限元强度折减法的原理有限元强度折减法是在理想的弹塑性有限元计算中将边坡岩土体的抗剪强度参数：黏聚力c和内摩擦角φ按照安全系数的定义同时除以一个系数k，得到一组新的c′、φ′值，然后作为一组新的参数输入，再一次试算，如此循环。

当计算不收敛时，所对应的k被称为坡体的安全系数，此时边坡达到极限状态，将会发生剪切破坏，同时可以得到边坡的滑动面。

其中c′、φ′为三、有限元强度折减法的优点有限元强度折减分析法既具备了数值分析方法适应性广的优点，也具备了极限平衡法简单直观、实用性强的特点，目前被广大岩土工程师们广泛应用。

（1）不需要假定滑面的形状和位置，也无须进行条分。

只需要由程序自动计算出滑坡面与强度贮备安全系数。

（2）能够考虑“应力-应变”关系。

（3）具有数值分析法的各种优点，适应性强。

能够对各种岩土工程进行计算，不受工程的几何形状、边界条件等的约束。

（4）它考虑了土体的非线性弹塑性特点，并考虑了变形对应力的影响。

（5）能够考虑岩土体与支护结构的共同作用，并模拟施工过程和渐进破坏过程。

四、有限元强度折减法中超高边坡失稳的判据采用强度折减有限元方法分析超高边坡稳定性时，如何判断边坡是否达到极限平衡状态，十分关键。

这种有限元失稳判据的选取，没有获得共识，常见的失稳判据主要有下列三种。

边坡稳定分析有限元强度折减法失稳判据探讨

边坡稳定分析有限元强度折减法失稳判据探讨梁艳;李同春【摘要】The shear strength reduction finite element method is widely employed to analyze slope stability especially under complicated conditions; currently, there are mainly three kinds of slope failure criteria: the convergence of numerical computations; the inflection point of the displacement; connectivity of plastic zone; etc. However, the convergence of numerical computations is limited by nonlinear solutions; the inflection point of the displacement is not always clear; moreover, the critical point with unknown sliding surface is not accurate using the criterion of connectivity of plastic zone. An example slope is analyzed by different iteration methods based on the shear strength reduction finite element method; it is shown that the computed result has great relationship with the iteration methods and convergence tolorence; two inflection points may occurred in the displacement curve which denpend on the initial state of the slope. As a result, the combination of the inflection point and the plastic zone is suggested as the proper slope failure criterion.%有限元强度折减法目前广泛应用于复杂条件下边坡稳定安全度的求解,其边坡失稳判据主要有有限元计算不收敛、位移拐点及塑性区贯通等.相应存在的问题有:收敛性受非线性求解方法制约、位移曲线的拐点有时并不明确、在滑动面未知的情况下塑性区贯通判据难以准确把握临界点等.针对一经典边坡,讨论不同迭代算法的影响,提出边坡位移曲线的双拐点概念,从另一角度分析各判据,根据其特点建议联合采用位移出现拐点与塑性区全部贯通作为边坡失稳判据.【期刊名称】《三峡大学学报（自然科学版）》【年(卷),期】2012(034)002【总页数】4页(P28-31)【关键词】有限元强度折减法;边坡失稳判据;非线性解;位移双拐点【作者】梁艳;李同春【作者单位】河海大学水利水电学院,南京210098;河海大学水利水电学院,南京210098【正文语种】中文【中图分类】TU43有限元强度折减法是Zienkiewicz于1975年提出的一种边坡稳定分析方法，与传统极限平衡法相比而言，有限元强度折减法通过对某一强度折减系数下的边坡进行弹塑性有限元分析，得到其应力场、应变场及位移场；然后，根据一定的失稳判据对边坡的稳定情况进行判断.不需要事先确定滑裂面的位置和形状，最危险临界滑裂面也可以按一定的规则搜索出，因而能解决复杂的工程问题.随着计算机技术的迅速发展以及各种大型成熟软件的推出，有限元强度折减法逐渐成为边坡稳定分析研究的热点，得到学术界及工程界的广泛关注.现行的边坡失稳判据主要有以下几种：①以有限元迭代求解过程的不收敛作为边坡失稳的判据［1］；②以塑性区（或等效塑性应变）从坡脚到坡顶贯通作为边坡失稳的判据［2］；③以坡体内特征部位位移发生突变作为边坡失稳的判据［3－7］.失稳判据的选择是有限元强度折减法的关键问题，很多学者对此进行研究，但到目前为止没有形成统一的认识.本文利用有限元强度折减法对典型边坡算例进行分析，研究了非线性迭代方法对计算结果的影响，并对位移曲线拐点状态及塑性区判据进行了探讨分析.1 强度折减法基本原理强度折减法中边坡稳定的基本原理基于强度储备概念，其安全系数定义为：使边坡刚好达到临界破坏状态时，对岩土体的抗剪强度进行折减的程度，即定义安全系数为岩土体的实际抗剪强度与临界破坏时折减后剪切强度的比值.强度折减法的关键是利用公式（1）和（2）来调整岩土体的强度指标c和φ，然后对边坡稳定性进行数值分析，不断的增加折减倍数，反复计算，直至其达到临界破坏，此时得到的折减倍数即为安全系数Fs，其中折减倍数的倒数即为折减系数K.式中，c为土的粘聚力，也称内聚力；φ为土的内摩擦角，即抗剪强度线的倾角；cF为折减后的粘结力；φF为折减后的摩擦角；Ftrial为折减倍数.2 经典算例以经典边坡为例［1，8］，算例边坡几何尺寸及有限元模型，如图1所示.图1 边坡算例几何尺寸及有限元网格模型其具体材料参数见表1.表1中γ表示土体重度，E为土体弹性模量，υ表示土体泊松比.本算例属于平面应变问题，边坡土体采用理想弹塑性 Mohr－Coulomb屈服准则及非关联流动法则.边界条件设左右两边为水平约束，底边为固定约束，坡面为自由边界.采用四节点网格进行分析，在坡面坡脚处网格划分较密，有限元模型节点数4 961，单元数4 800.表1 算例土体力学参数表参数 c／kPa φ／° γ／（kN·m－3） E／kPa υ数值42 17 25 20 000 0.3对于该算例，根据不同方法给出的安全系数如表2所示.表2 不同分析方法得到的安全系数值分析方法 Bishop［9］ Spencer［1］有限元方法［1，8］Fs 1.079 1.115 1.12～1.213 边坡失稳判据讨论对此经典边坡算例进行有限元强度折减法计算分析，并对不同的判据进行讨论.3.1 有限元计算不收敛判据有限元计算的收敛性与非线性方程的解法及收敛容差紧密相关.非线性问题的求解是通过对荷载步内不平衡量进行线性迭代，最终获得其收敛解的一个过程.在实际的有限元分析中，主要有两种求解方法［10］：常刚度迭代法与变刚度法.将最大迭代步数设为1 000步，一次性施加重力荷载，采用两种求解方法对经典边坡进行计算，当收敛容差为0.01时，变刚度法在安全系数等于1.08时不收敛，常刚度法安全系数等于1.36时不收敛.以安全系数为1.08为例，常刚度与变刚度迭代法收敛曲线走势如图2所示.图2 K＝1.08时常刚度与变刚度迭代收敛曲线走势由图可得当安全系数等于1.08时，常刚度迭代法收敛量级随迭代次数增加而减小直至达到收敛标准；而变刚度法收敛量级随迭代次数增加先减小后又增大，逐渐远离收敛标准，已经不收敛，但此时不收敛并不代表完全屈服，对应塑性区分布如图3所示.图3 折减系数为1.08时的塑性区分布图在此基础上，通过对其他10组不同参数边坡进行计算，对其收敛走势进行研究得：当土体大部分屈服时，变刚度法基本不收敛，无法计算出土体破坏时的安全系数.采用常刚度法，在边坡接近破坏时，迭代次数常常很大，收敛较慢，但基本能保证收敛.当采用常刚度法进行计算时，不同收敛容差下得到的安全系数变化较大，见表3.表3 常刚度迭代法在不同收敛容差下安全系数比较收敛容差 Fs 0.000 5 1.0790.000 1 1.111 0.005 1.122 0.01 1.136 0.03 1.179从上面的结果可以看出以有限元计算不收敛作为判据时，计算的结果与所用的迭代计算方法和收敛容差有很大关系.安全系数的确定具有较大的人为任意性.除此之外有限元计算收敛性受多重因素综合影响，如有限元计算模型，计算单元类型，地应力影响，计算边界等，目前也缺乏行之有效的方法来消除这些影响.在这种情况下，有限元计算收敛性和边坡极限平衡状态之间似乎没有直接的一一对应关系，计算不收敛并不意味着边坡已达到极限平衡状态，而计算收敛也不能表明边坡是安全的，以此为判据不够合理.3.2 特征部位位移突变判据将边坡整体作为一个结构来讨论，则其位移曲线的拐点应该有两种情况：第1种是结构从弹性状态变为非线性状态；第2种是结构从非线性状态变为失稳状态.边坡的变形破坏总具有一定的位移特性，因此有限元计算的位移结果是边坡失稳最直观的表达.目前以位移作为失稳判据的方法是建立每次有限元计算的某个部位的位移或者最大位移与折减系数的关系曲线，以曲线上的拐点作为边坡处于临界破坏状态的临界点.以边坡顶部临空面端点A及坡脚B为特征点，研究A点竖直位移及B 点水平位移随安全系数变化规律.若按变刚度法，在边坡临近破坏时，计算不能保证收敛，且边坡接近破坏时刚度趋向于零，无法求出位移.常刚度法计算一方面能保证收敛，另一方面能算出位移曲线的拐点，因此采用常刚度法计算，位移－安全系数曲线如图4所示，可知在1.113和1.176两处均有拐点.图4 A点竖向位移与B点水平位移随安全系数变化曲线第1种情况不一定存在，与边坡初始状态相关，如图5所示.图5 不同材料边坡位移随安全系数变化曲线当材料强度高时，边坡起始状态处于弹性状态，两个明显的拐点，当材料强度低时，边坡起始状态出于非线性状态，只有一个明显的拐点.但第1个拐点与边坡稳定定义不符；第2个拐点出现后用常规的基于小变形假定的有限元解法无法求解，即在第2个拐点之前计算得到的数据是准确的，而拐点之后边坡已经滑动，此时得到的位移是强行按照小变形假定来计算，并不是其真实值，但仍能体现边坡位移的发展趋势，拐点的物理意义明确.因此判断此边坡的安全系数为1.176.3.3 塑性区贯通判据由于土体是弹塑性的，当应力达到一定程度时，土体便会发生塑性破坏，岩土体的塑性破坏与塑性区出现、扩展及其分布紧密相关.以塑性区贯通为失稳判据，得出安全系数为1.150，如图6～7所示.边坡破坏时，其塑性应变必然是贯通的，但是在用有限元法计算时，力与位移之间的关系并不是精确推导出来的，而是利用每一单元中近似的位移函数得到节点位移，然后计算高斯点应变与应力，输出时将积分点结果线性外推至单元节点上，因此由高斯点外推得到节点塑性应变值，在滑动面未知情况下塑性区分布在一条带上，当塑性应变区贯通时，塑性破坏点并不一定贯通，还可以继续发展，因此以塑性区贯通作为失稳判据难以准确把握临界点.基于以上分析，塑性区贯通判据在实际应用中可作为位移拐点判据（尤其当位移－折减系数曲线只有一个拐点时）的补充判据，结合位移场及塑性区变化进行对比分析，在位移曲线出现拐点时，对应塑性区全部贯通，此时对应的折减系数即为安全系数.4 结论鉴于目前有限元强度折减法的失稳判据不统一，进行了讨论，得出以下结论：1）采用有限元计算不收敛作为判据时，计算的结果与所采用的迭代计算方法和收敛容差有很大关系.安全系数的确定具有较大的人为任意性，以此为判据不够合理. 2）完全接近失稳时变刚度法很难收敛或不收敛，此时不收敛不代表完全屈服，常刚度法基本上能收敛，但收敛速度很慢或很难达到完全收敛，但采用此法能出现位移拐点.3）以塑性区贯通作为失稳判据难以准确把握临界点，在实际应用中可作为位移拐点判据的补充判据.4）以位移曲线拐点作为判据时，曲线可能会出现两个拐点，拐点的情况与边坡初始状态相关.建议以位移出现拐点与塑性区全部贯通相结合作为边坡失稳判据.参考文献：［1］赵尚毅，郑颖人，时卫民，等.用有限元强度折减法求边坡稳定安全系数［J］.岩土工程学报，2002（3）：343－346.［2］栾茂田，武亚军，年廷凯.强度折减有限元法中边坡失稳的塑性区判据及其应用［J］.防灾减灾工程学报，2003（3）：1－8.［3］周桂云，李同春.饱和－非饱和非稳定渗流作用下岩质边坡稳定性分析［J］.水电能源科学，2006（5）：79－82＋101－102.［4］曹泽伟.重力坝深层抗滑稳定分析［D］.南京：河海大学，2011.［5］ Chen Lihong，Shu Yu，Zhang Hongtao.Discussion of Criteria of Shear Strength Reduction FEM［A］／／1st International Conference on Civil Engineering，Architecture and Building Materials［C］.Haikou，China：Trans Tech Publications，2011.［6］段庆伟，陈祖煜，王玉杰，等.重力坝抗滑稳定的强度折减法探讨及应用［J］.岩石力学与工程学报，2007（S2）：4510－4517.［7］宋二祥.土工结构安全系数的有限元计算［J］.岩土工程学报，1997，19（2）：1－7.［8］周翠英，刘祚秋，董立国，等.边坡变形破坏过程的大变形有限元分析［J］.岩土力学，2003（4）：644－647，652.［9］顾芳芳.边坡稳定分析的若干问题研究［D］.南京：河海大学，2010. ［10］Ian M Smith，D V Griffiths.Programming the Finite Element Method，Third Edition［M］.US：John Wiley ＆Sons，Inc，2004.。

用有限元强度折减法进行边坡稳定分析

坡角（度）
30
35
40
45
50
有限元法（外接圆屈服准则）
1.78
1.62
1.48
1.36
1.29
有限元法（莫尔-库仑等面积圆屈服准则）
1.47
1.34
1.22
1.12
1.06
简化Bishop法
1.394 1.259 1.153 1.062 0.99
Spencer法
1.463 1.318 1.212 1.115 1.04
• 随着计算机技术的发展，尤其是岩土材料的非线性弹塑性有限元计算技术的发展，有限元强度折减法近来在国内外受到关注，对于均质土坡已经得到了较好的结论，但尚未在工程中实用，本文采用有限元强度折减法，对均质土坡进行了系统分析，证实了其实用于工程的可行性，对节理岩质边坡得到了坡体的危险滑动面和相应的稳定安全系数。该方法可以对贯通和非贯通的节理岩质边坡进行稳定分析，同时可以考虑地下水、施工过程对边坡稳定性的影响，可以考虑各种支挡结构与岩土材料的共同作用，为节理岩质边坡稳定分析开辟了新的途径。
从表中计算结果可以看出，采用外接圆屈服准则计算的安全系数比传统的方法大许多，而采用莫尔-库仑等面积圆屈服准则计算的结果与传统极限平衡方法（Spencer法)计算的结果十分接近，说明采用莫尔-库仑等面积圆屈服准则来代替莫尔-库仑不等角六边形屈服准则是可行的。
通过4组计算方案（改变内摩擦角、内聚力、坡角β、
表2 不同流动法则的影响
3.2 有限元法引入的误差
3.2.1 网格的疏密
有限元单元网格划分
表3 网格疏密对计算结果的影响
3.2.2 模型边界范围
表4 边界条件对折减系数的影

有限元强度折减法在边坡稳定性分析中的应用

有限元强度折减法在边坡稳定性分析中的应用有限元强度折减法在边坡稳定性分析中的应用边坡是山地地形中常见的地质体，其稳定性分析对于保护山体和预防地质灾害具有重要意义。

近年来，随着计算机技术的快速发展，有限元强度折减法逐渐成为边坡稳定性分析中的一种有效工具。

本文将介绍有限元强度折减法的原理和在边坡稳定性分析中的应用，并对其优缺点进行了探讨。

有限元强度折减法是一种基于强度准则的边坡分析方法。

它的基本原理是将岩土体的强度按照某个准则进行折减，并在有限元分析中采用折减后的强度参数进行计算。

其中，常用的强度准则有摩尔-库伦准则、维特曼准则等。

有限元强度折减法综合考虑了岩土体的强度特性和应力分布情况，相比传统的极限平衡法和全面滑动面法，能够更准确地评估边坡的稳定性。

有限元强度折减法在边坡稳定性分析中主要包括以下几个步骤：首先，确定边坡的几何形态和岩土体的材料性质。

其次，选择适当的强度准则，并对岩土体的强度参数进行合理的折减。

然后，根据边坡的几何特征和荷载情况，建立有限元模型，并进行边坡的数值计算。

最后，根据计算结果评估边坡的稳定性，并在必要时采取相应的加固措施。

有限元强度折减法在边坡稳定性分析中的应用具有以下优点：首先，有限元方法可以灵活地建立边坡的复杂几何模型，能够较准确地模拟实际工程中的复杂边坡形态。

而且，有限元强度折减法可以根据实际情况对岩土体的强度参数进行合理的折减，准确地反映岩土体的强度特性。

这些都为边坡稳定性分析提供了可靠的基础。

其次，有限元强度折减法可以综合考虑边坡的多种破坏机制，能够对于复杂的边坡情况进行全面的分析。

相比传统的极限平衡法和全面滑动面法，有限元强度折减法在考虑边坡的多种破坏机制时更加灵活准确。

此外，有限元强度折减法在计算过程中可以得到边坡内部的应力和位移分布情况，为边坡的设计和加固提供了参考依据。

通过对边坡各部分的应力和位移分布情况进行分析，可以找到边坡破坏的薄弱环节，并调整加固措施以提高边坡的稳定性。