辽宁省实验中学 大连八中 大连二十四中 鞍山一中 东北育才学校17-18下期期末数学试题(含答案)
辽宁省实验中学、大连八中、大连二十四中、鞍山一中、东北育才学校2017_2018学年高二物理下学期期末考试

辽宁省实验中学、大连八中、大连二十四中、鞍山一中、东北育才学校2017-2018学年高二物理下学期期末考试试题一、选择题:本题共8小题,每小题4分,共32分,其中1~5小题为单选题,6~8小题为多选题,全部选对得4分,选对但不全得2分,有选错的得0分。
1.下列关于原子或原子核的说法正确的是A.天然放射现象的发现揭示了原子具有核式结构B.温度升高,放射性元素衰变的半衰期会减小C.原子核发生β衰变后原子序数不变D.比结合能越大,原子核越稳定2.一物体在水平面上做直线运动,t=0时其速度大小为1m/s,规定初速度方向为正方向,a-t 图像如图所示,则在前4s时间内A.物体做匀加速直线运动B.物体做匀减速直线运动C.物体的位移大于12m D.物体的位移小于12m3.如图缩水,B、C两个小球用细线悬挂于竖直墙面上的A、D两点,两球均保持静止,已知B 球的重力为2G,C球的重力为3G,细线AB与竖直墙面之间的夹角为37°,细线CD与竖直墙面之间的夹角为53°,则A.AB绳中的拉力为5GB.CD绳中的拉力为3GC.BC绳中的拉力为2GD.BC绳与竖直方向的夹角θ为53°4.如图所示为氢原子的能级图,下列说法正确的是A.从n=3能级跃迁到n=2能级时,电子的动能会变大,电势能会减小B.氢原子从高能级向低能级跃迁时可能会辐射出γ射线C .一个处于n=4激发态的氢原子向基态跃迁时,最多可能发出6条光谱线D .用能量为12.5eV 的电子轰击处于基态的氢原子,一定不能使氢原子发生能级跃迁5.如图所示,a 、b 两细绳一端系着质量为m 的小球,另一端系在竖直放置的圆环上,小球位于圆环的中心,开始时绳a 水平,绳b 倾斜,现将圆环在竖直平面内顺时针缓慢地向右滚动至绳a 竖直,在此过程中A .a 上的张力逐渐增大,b 上的张力逐渐增大B .a 上的张力逐渐减小,b 上的张力逐渐减小C .a 上的张力先减小后增大,b 上的张力逐渐增大D .a 上的张力先增大后减小,b 上的张力逐渐减小6.甲、乙两辆玩具小汽车同时同地沿同一条平直路面并排行驶,速度-时间图像如图所示,下列说法正确的是A .甲车启动的加速度大小为21/m s B .甲车在0到6s 内的平均速度大小为2m/sC .2s 末乙车位于甲车前方2m 处D .6s 末两车停在同一位置7.如图所示,倾角θ的斜面上有一重为G 的物体,在与斜面底边平行的水平推力作用下在斜面上做匀速直线运动,则A .物体可能沿虚线运动B .物体可能沿水平方向运动C .物体与斜面间的动摩擦因数μ=tanθD .物体与斜面间的动摩擦因数μ>tanθ8.如图甲所示,在光电效应实验中,某同学用相同频率的三色光,分别照射阴极材料为锌和铜的两个不同的光电管,结果都能发生光电效应.图乙为其中一个光电管的遏止电压随入C U 射光频率v 变化的函数关系图象.对于这两个光电管,下列判断正确的是A .遏止电压一定不同C U B .光电子的最大初动能一定不同C .饱和光电流一定不同D .-v 图像的斜率一定不同C U 二、实验题9.(1)在“验证力的平行四边形定则”的实验中,合力与分力的作用效果相同,这里作用效果相同是指___________A .细绳套受拉力产生形变B .橡皮条受到拉力的作用被拉长C .弹簧测力计的弹簧被拉长D .使橡皮条在同一方向上伸长到同一长度(2)在上述实验中,某同学的实验情况如图甲所示,其中A 为固定橡皮条的图钉,O 为橡皮条的细绳的结点,OB 和OC 为细绳,图乙是在白纸上根据实验结果画出的力的图示,A .用铅笔沿着细线画线来记录拉力的方向B .在实验中,如果将细绳也换成橡皮条,对实验结果有影响C .在实验中,如果将细绳也换成橡皮条,对实验结果没有影响D .图乙中的F 和不完全重合,说明“力的平行四边形定则”是错误的'F 10.某同学利用图甲所示的实验装置,探究物块在水平桌面上的运动规律,物块在重物的牵引下开始运动,重物落地后,物块再运动一段距离停在桌面上(尚未到达滑轮处)。
辽宁省实验中学大连八中大连二十四中鞍山一中东北育才学校2017_2018学年高二生物下学期期末考试试

辽宁省实验中学、大连八中、大连二十四中、鞍山一中、东北育才学校2017-2018学年高二下学期期末考试生物试题第Ⅰ卷选择题(1—30每题1分,31—40每题2分,共40题,50分。
每题只有一个选项最符合题意)1.下列关于细胞学说及其创立过程的叙述,正确的是A.建立者是沃森和克里克B.标志着生物学的研究进入分子水平C.其内容之一是新细胞是由老细胞经过分裂形成的D.列文虎克首次观察到了材料丰富的真正的活细胞2.下列各选项的物质,它们的元素构成完全—致的是A.淀粉和胆固醇B.磷脂与脂肪酸C.核苷酸与氨基酸D.叶绿素与甲状腺激素3.有关糖类的叙述,不正确的是A.麦芽糖和蔗糖的水解产物均是还原糖B.葡萄糖可以进出肝细胞C.生物体内的糖类绝大多数以多糖形式存在D.单糖都是能源物质4.不能发生如图所示水解反应的化合物是A.叶绿素B.血红蛋白C.肝糖原D.抗体5.以下细胞结构中,含有RNA的是A.内质网B.中心体C.高尔基体D.细胞质基质6.下列叙述正确的是A.大肠杆菌的核酸由脱糖核苷酸组成B.T2噬菌体的核酸由核糖核苷酸组成C.酵母菌的核酸由脱氧核苷酸和核糖核苷酸组成D.HIV的核酸由脱氧核苷酸或核糖核苷酸组成7.下列有关染色体和染色质的说法正确的是A.染色体在解旋酶的作用下变为细丝状的染色质B.染色体可被龙胆紫等碱性染料染成深色而染色质不能C.线粒体和叶绿体中均含有少量的染色质D.在盐酸的作用下染色质中的DNA可与蛋白质分开8.如图为概念组成关系,以下各选项的物质或结构,符合概念图①至④关系的是A.①双层膜细胞器②细胞核③线粒体④叶绿体B.①固醇②性激素③磷脂④维生素DC.①膜蛋白②载体③酶④受体D.①原生质层②细胞膜③细胞质④细胞核9.下列有关生物膜的叙述正确的是A.生物膜不参与生命系统边界构建B.细胞内合成的分泌蛋白运输到细胞外,穿过的生物膜层数是0层C.糖体合成的分泌蛋白能够自由透过高尔基体膜D.细胞器膜是细菌进行代谢的结构基础10.下图甲、乙、丙分别代表三类生生物基本结构或部分结构的模式图,则相关叙述正确的是A.甲为原核细胞结构B.乙一定是真核细胞C.丙是真核生物细胞核D.甲和丙是乙的细胞器11.下列关于细胞器的叙述正确的是A.溶酶体内含有的酶称为溶菌酶B.高尔基体是由单层膜连接而成的网状结构C.植物体中的液泡内有细胞液,其中含有糖类、无机盐,色素、蛋白质等物质D.人的成熟红细胞的有丝分裂离不开中心体的作用12.关于生物体内水和无机盐的叙述,不正确的是A.体内参与运输营养物质和代谢废物的水是自由水B.失去结合水的种子遇水不能萌发C.生物体内无机盐浓度的大小会影响细胞的吸水或失水D.细胞中大多数无机盐以化合物形式存在13.环孢素是从土壤霉菌(一种真菌)中分离出来的含有11个氧基酸的环状多肽,但是环孢素却是由一种非核糖体多肽合成酶合成的。
辽宁省实验中学、大连八中、大连二十四中、东北育才学校2017-2018学年高二下学期期末考试数学(理)试题

2017-2018学年度下学期期末考试高二年级数学理科试卷第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设复数,则()A. B. C. D.【答案】A【解析】【详解】分析:先化简复数,再由模的公式计算.详解:,∴.点睛:本题考查复数的模,解题时把复数化为最简形式后可求解,.2. 已知随机变量服从正态分布,则()A. B. C. D.【答案】A【解析】【详解】分析:由正态分布曲线的对称性求解.详解:,∴.故选A.点睛:本题考查正态分布,利用正态曲线的对称性可求解概率.即,则,.3. 某公司为确定明年投入某产品的广告支出,对近年的广告支出与销售额(单位:百万元)进行了初步统计,得到下列表格中的数据:经测算,年广告支出与年销售额满足线性回归方程,则的值为()A. B. C. D.【答案】D【解析】分析:求出,代入回归方程计算,利用平均数公式可得出的值.详解:,,,解得,故选D.点睛:本题主要考查平均数公式的应用,线性回归方程经过样本中心的性质,意在考查综合利用所学知识解决问题的能力,属于基础题.4. 将本不同的书全部分给甲乙丙三若,每人至少一本,则不同的分法总数为()A. B. C. D.【答案】C【解析】分析:分两种情况:一人得本,另两个人各得本;一人得本,另两个人各得本,分别求出不同的分法即可得结果.详解:分两种情况:一人得本,另两个人各得本,有种分法,一人得本,另两个人各得本,有种分法,共有种分法,故选C.点睛:本题主要考查分类计数原理与分步计数原理及排列组合的应用,属于难题.有关排列组合的综合问题,往往是两个原理及排列组合问题交叉应用才能解决问题,解答这类问题理解题意很关键,一定多读题才能挖掘出隐含条件.解题过程中要首先分清“是分类还是分步”、“是排列还是组合”,在应用分类计数加法原理讨论时,既不能重复交叉讨论又不能遗漏,这样才能提高准确率.5. 用数学归纳法证明不等式的过程中,从到时左边需增加的代数式是()A. B.C. D.【答案】B【解析】【详解】分析:写出时的不等式,然后与的式子比较可得.详解:时,不等式为,左边增加的式子为.故选B.点睛:本题考查数学归纳法,数学归纳法中最关键是就是从到时式子的变化,不掌握这个变化,就不能证明结论或者证明不符合数学归纳法思想.6. 若的二项展开式各项系数和为,为虚数单位,则复数的运算结果为()A. B. C. D.【答案】C【解析】【详解】分析:利用赋值法求得,再按复数的乘方法则计算.详解:令,得,,∴.故选C.点睛:在二项式的展开式中,求系数和问题,一般用赋值法,如各项系数为,二项式系数和为,两者不能混淆.7. 若函数是上的单调函数,则实数的取值范围是()A. B. C. D.【答案】C【解析】【详解】分析:求出导函数,导函数在上大于等于0恒成立.详解:,由题意恒成立,∴,.故选C.点睛:函数在上是单调函数,则只能为单调增函数或单调减函数,因此有导数(或)恒成立,从而可求解.8. 已知均为正实数,则下列三个数,,()A. 都大于B. 至少有一个不大于C. 都小于D. 至少有一个不小于【答案】D【解析】分析:利用基本不等式可证明,假设三个数都小于,则不可能,从而可得结果.详解:,假设三个数都小于,则,所以假设不成立,所以至少有一个不小于,故选D.点睛:本题主要考查基本不等式的应用,正难则反的思想,属于一道基础题.反证法的适用范围:(1)否定性命题;(2)结论涉及“至多”、“至少”、“无限”、“唯一”等词语的命题;(3)命题成立非常明显,直接证明所用的理论较少,且不容易证明,而其逆否命题非常容易证明;(4)要讨论的情况很复杂,而反面情况较少.9. 甲、乙两支球队进行比赛,预定先胜 3局者获得比赛的胜利,比赛随即结束.结束除第五局甲队获胜的概率是外,其余每局比赛甲队获胜的概率都是.假设各局比赛结果相互独立.则甲队以获得比赛胜利的概率为()A. B. C. D.【答案】B【解析】若是3:2获胜,那么第五局甲胜,前四局2:2,所以概率为,故选B.10. 有张卡片分别写有数字,从中任取张,可排出不同的四位数个数为()A. B. C. D.【答案】C【解析】分析:根据题意,分四种情况讨论:①取出四张卡片中没有重复数字,即取出四张卡片中的数字为1,2,3,4;②取出四张卡片中4有2个重复数字,则2个重复的数字为1或2;③若取出的四张卡片为2张1和2张2;④取出四张卡片中有3个重复数字,则重复数字为1,分别求出每种情况下可以排出四位数的个数,由分类计数原理计算可得结论.详解:根据题意,分四种情况讨论:①取出四张卡片中没有重复数字,即取出四张卡片中的数字为1,2,3,4;此时有种顺序,可以排出24个四位数.②取出四张卡片中4有2个重复数字,则2个重复的数字为1或2,若重复的数字为1,在2,3,4中取出2个,有种取法,安排在四个位置中,有种情况,剩余位置安排数字1,可以排出个四位数同理,若重复的数字为2,也可以排出36个重复数字;③若取出的四张卡片为2张1和2张2,在4个位置安排两个1,有种情况,剩余位置安排两个2,则可以排出个四位数;④取出四张卡片中有3个重复数字,则重复数字为1,在2,3,4中取出1个卡片,有种取法,安排在四个位置中,有种情况,剩余位置安排1,可以排出个四位数,则一共有个四位数,故选C.点睛:本题主要考查分类计数原理与分步计数原理及排列组合的应用,属于难题.有关排列组合的综合问题,往往是两个原理及排列组合问题交叉应用才能解决问题,解答这类问题理解题意很关键,一定多读题才能挖掘出隐含条件.解题过程中要首先分清“是分类还是分步”、“是排列还是组合”,在应用分类计数加法原理讨论时,既不能重复交叉讨论又不能遗漏,这样才能提高准确率.11. 已知,若,则的值为()A. B. C. D.【答案】B【解析】【详解】分析:由定积分的几何意义求得定积分,在二项展开式中令可求解.详解:由积分的几何意义知,在中,,令,则,∴.故选B.点睛:本题考查定积分的几何意义,考查二项式定理的应用.在二项展开式中求与系数和有关的问题通常用赋值法.根据所求和式的结构对变量赋予不同的值可得对应的恒等式.如本题赋值,如果只求系数和,则赋值等等.12. 定义在上的偶函数的导函数,若对任意的正实数,都有恒成立,则使成立的实数的取值范围为()A. B. C. D.【答案】A【解析】【详解】分析:构造新函数,利用导数确定它的单调性,从而可得题中不等式的解.详解:设,则,由已知当时,,∴在上是减函数,又∵是偶函数,∴也是偶函数,,不等式即为,即,∴,∴,即.故选A.点睛:本题考查用导数研究函数的单调性,然后解函数不等式.解题关键是构造新函数.新函数的结构可结合已知导数的不等式和待解的不等式的形式构造.如,,,等等.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 袋中装有个黑球,个白球,甲乙按先后顺序无放回地各摸取一球,在甲摸到了黑球的条件下,乙摸到白球的概率是__________.【答案】.【解析】分析:结合古典概型概率公式,直接利用条件概率公式求解即可详解:设甲摸到黑球为事件,则,乙摸到白球为事件,则,设甲摸到黑球的条件下,乙摸到球的概率为,故答案为.点睛:本题主要考查古典概型概率公式以及独立事件的概率公式,条件概率公式,意在考查综合运用所学知识解答问题的能力,属于简单题.14. 在二项式的展开式中,的系数为__________.【答案】.【解析】分析:由题意结合二项式定理展开式的通项公式得到r的值,然后求解的系数即可.详解:结合二项式定理的通项公式有:,令可得:,则的系数为:.点睛:(1)二项式定理的核心是通项公式,求解此类问题可以分两步完成:第一步根据所给出的条件(特定项)和通项公式,建立方程来确定指数(求解时要注意二项式系数中n和r的隐含条件,即n,r均为非负整数,且n≥r,如常数项指数为零、有理项指数为整数等);第二步是根据所求的指数,再求所求解的项.(2)求两个多项式的积的特定项,可先化简或利用分类加法计数原理讨论求解.15. 若函数在内有且只有一个零点,则在上的最大值与最小值的和为__________.【答案】.【解析】分析:先结合三次函数图象确定在上有且仅有一个零点的条件,求出参数a ,再根据单调性确定函数最值,即得结果.详解:由得,因为函数在上有且仅有一个零点且,所以,因此从而函数在上单调递增,在上单调递减,所以,点睛:对于函数零点个数问题,可利用函数的单调性、草图确定其中参数取值条件.从图象的最高点、最低点,分析函数的最值、极值;从图象的对称性,分析函数的奇偶性;从图象的走向趋势,分析函数的单调性、周期性等.16. 对于三次函数,定义:设是函数的导数的导数,若方程有实数解,则称点为函数的“拐点”.有同学发现“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现视为条件,若函数,则它的对称中心为__________;并计算__________.【答案】 (1)..(2)..【解析】【详解】分析:求出,再求得的解,可得的对称中心,利用对称性可计算和.详解:,,由得,又,∴对称中心为,从而,∴.故答案为,4034.点睛:本题考查新定义,考查阅读理解能力、考查分析问题与解决问题的能力.解题中新定义“拐点:实质是示二阶导数的零点,由拐点是对称中心得题中求和可用配对法或倒序相加法求解.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 袋中装有个大小相同的黑球和白球.已知从袋中任意摸出个球,至少得到个白球的概率是.(1)求白球的个数;(2)从袋中任意摸出个球,记得到白球的个数为,求随机变量的分布列和数学期望.【答案】(1)5.(2)分布列见解析;.【解析】分析:(1)设黑球的个数为,则白球的个数为,记两个都是黑球得的事件为,由可得结果;(2)离散型随机变量的取值可能为:,结合组合知识,利用古典概型概率公式根据独立重复试验概率公式求出各随机变量对应的概率,从而可得分布列,进而利用期望公式可得的数学期望.详解:(1)设黑球的个数为,则白球的个数为.记两个都是黑球得的事件为,则至少有一个白球的事件与事件为对立事件所以解得,所以白球的个数为.(2)离散型随机变量的取值可能为:所以的分布列为因为服从超几何分布,所以点睛:本题主要考查对立事件的概率公式、独立事件同时发生的概率公式以及离散型随机变量的分布列与数学期望,属于中档题. 求解数学期望问题,首先正确要理解题意,其次要准确无误的找出随机变量的所以可能值,计算出相应的概率,写出随机变量的分布列,正确运用均值的公式进行计算,也就是要过三关:(1)阅读理解关;(2)概率计算关;(3)公式应用关.18. 已经函数.(Ⅰ)讨论函数的单调区间;(Ⅱ)若函数在处取得极值,对,恒成立,求实数的取值范围.【答案】(Ⅰ)①当时,的递减区间是,无递增区间;②当时,的递增区间是,递减区间是.(Ⅱ.【解析】【详解】分析:(Ⅰ)求出导函数,由于定义域是,可按和分类讨论的正负,得单调区间.(Ⅱ)由函数在处取极值得且可得的具体数值,而不等式可转化为,这样只要求得的最小值即可.详解:(Ⅰ)在区间上,.①若,则,是区间上的减函数;②若,令得.在区间上,,函数是减函数;在区间上,,函数是增函数;综上所述,①当时,的递减区间是,无递增区间;②当时,的递增区间是,递减区间是.(II)因为函数在处取得极值,所以解得,经检验满足题意.由已知,则令,则易得在上递减,在上递增,所以,即.点睛:本题考查用导数求函数的单调区间、函数极值,用导数研究不等式恒成立问题.不等式恒成立通常通过分离参数法转化为求函数的最值.19. 某企业响应省政府号召,对现有设备进行改造,为了分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取了件产品作为样本,检测一项质量指标值,若该项质量指标值落在内的产品视为合格品,否则为不合格品.如图是设备改造前的样本的频率分布直方图,表是设备改造后的样本的频数分布表.表:设备改造后样本的频数分布表质量指标值频数(1)完成下面的列联表,并判断是否有的把握认为该企业生产的这种产品的质量指标值与设备改造有关;设备改造前设备改造后合计合格品不合格品合计(2)根据频率分布直方图和表提供的数据,试从产品合格率的角度对改造前后设备的优劣进行比较;(3)企业将不合格品全部销毁后,根据客户需求对合格品进行登记细分,质量指标值落在内的定为一等品,每件售价元;质量指标值落在或内的定为二等品,每件售价元;其它的合格品定为三等品,每件售价元.根据表的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为(单位:元),求的分布列和数学期望.附:【答案】(1)列联表见解析;有的把握认为该企业生产的这种产品的质量指标值与设备改造有关。
【物理】辽宁省实验中学、大连八中、大连二十四中、鞍山一中2017-2018年高一下学期期末考试试题(解析版)

辽宁省实验中学、大连八中、大连二十四中、鞍山一中、东北育才学校2017-2018学年高一下学期期末考试物理试题一、选择题:本题共12小题,每小题4分,在每小题给出的四个选项中,第1~8题只有一项符合题目要求,第9~12题有多项符合题目要求。
全部选对得4分,选对但不全得2分,有选错的得0分1. 下列关于物理学史的描述,正确的是A. 牛顿发现万有引力定律,而万有引力常量是由卡文迪许测出的B. 库仑利用库仑扭秤得出库仑定律,同时测出静电力常量C. 密立根提出在电荷的周围存在着由它产生的电场,并测出元电荷的电荷量D. 富兰克林命名了正负电荷【答案】ABD【解析】牛顿发现万有引力定律,而万有引力常量是由卡文迪许测出的,选项A正确;库仑利用库仑扭秤得出库仑定律,同时测出静电力常量,选项B正确;法拉第提出在电荷的周围存在着由它产生的电场,密立根测出元电荷的电荷量,选项C错误;富兰克林命名了正负电荷,选项D正确;故选ABD.2. 地球半径为R,地球表面的重力加速度为g处距地面的高度为B. C. D. 5R【答案】B【解析】设地球的质量为M,物体质量为m,物体距地面的高度为h。
根据万有引力近似等于重力,在地球表面有:在高度为h处有:;联立解得:h=)R,故B正确,ACD错误。
故选B。
点睛:本题关键要知道重力与万有引力的关系,明确在不考虑地球自转的情况下万有引力近似等于重力,知道重力加速度与高度的关系,并能用来分析实际问题.3. 下列四个电场中,a、b两点电场强度不同但电势相同的是A. 以正电荷为圆心的圆周上的两点B. 负点电荷电场中同一电场线上的两点C. 与匀强电场电磁线垂直的直线上的两点D. 等量异种点电荷中垂线上的两点【答案】AD【解析】试题分析:A图中场强大小相等,方向不同,电势相等,B图中两点处场强大小不同,电势不同,C图中两点处场强和电势都相等,D图中两点电势相同,场强大小不同,C 正确。
考点:本题考查静电场。
辽宁省实验中学大连八中大连二十四中鞍山一中东北育才学校2017-2018学年高一英语下学期期末考试试题

辽宁省实验中学、大连八中、大连二十四中、鞍山一中、东北育才学校2017-2018学年高一英语下学期期末考试试题第Ⅰ卷第一部分听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What does the man think of Beijing Opera?A. It is great.B. It is boring.C. It is terrible.2. What does the man mean?A. He tikes reading books.B. He is always organized.C. He manages his time better.3. What does the woman do?A. A receptionist.B. A cook.C. A waitress.4. Where does the conversation probably take place?A. In a factory.B. On a plane.C. At an airport.5. What will the man do near Edinburgh?A. Attend a meeting.B. Go sightseeing.C. Pick up the woman.第二节(共15题;每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材枓,回答第6至7题。
【全国校级联考】辽宁省实验中学、大连八中、大连二十四中、鞍山一中、东北育才学校2017-2018

......辽宁省实验中学、大连八中、大连二十四中、鞍山一中、东北育才学校2017-2018学年高二上学期期末考试数学(文)试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 对于常数,“”是“方程的曲线是双曲线“的”()A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件2. 若,则下列不等式中错误..的是()A. B. C. D.3. 下列函数中,最小值为4的是()A. B.C. D.4. 已知实数满足,则目标函数的最小值是()A. B. 15 C. 0 D.5. 下列命题中,说法错误..的是()A. “若,则”的否命题是“若,则”B. “是真命题”是“是真命题”的充分不必要条件C. “”的否定是“”D. “若,则是偶函数”的逆命题是真命题6. 设,若是与的等比中项,则的最小值为()A. 5B. 6C. 7D. 87. 已知分别是椭圆的左、右焦点,是以为直径的圆与该椭圆的一个交点,且,则这个椭圆的离心率是()A. B. C. D.8. 设为等比数列的前项和,,则()A. B. C. 2 D. 179. 在等差数列中,是其前项和,,,则()A. 11B.C. 10D.10. 设分别是双曲线的左右焦点,点.若,则双曲线的离心率为()A. B. C. 2 D.11. 设为等差数列,若,且它的前项和有最小值,那么当取得最小正值时的值为()A. 18B. 19C. 20D. 2112. 已知定义在上的奇函数的导函数为,当时,满足,,则在上的零点个数为()A. 5B. 3C. 1或3D. 1第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 函数的递增区间为__________.14. 在数列中,,且数列是等比数列,则__________.15. 已知函数,若函数在区间上是单调增函数,则实数的取值范围是__________.16. 抛物线的焦点为,已知点为抛物线上的两个动点,且满足,过弦的中点作抛物线准线的垂线,垂足为,则的最大值为__________.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 若数列满足.(1)求证:数列是等比数列,并求数列的通项公式;(2)设,若数列的前项和为,求证:.18. 已知函数.(1)若在上恒成立,求实数的取值范围;(2)解关于的不等式.19. 已知过点的动直线与抛物线相交于两点.当直线的斜率是时,. (1)求抛物线的方程;(2)设线段的中垂线在轴上的截距为,求的取值范围.20. 已知数列,为数列的前项和,,. (1)求数列的通项公式;(2)证明为等差数列.(3)若数列的通项公式为,令.为的前项的和,求.21. 已知椭圆的左顶点为,右焦点为,过点的直线交椭圆于两点.(1)求该椭圆的离心率;(2)设直线和分别与直线交于点,问:轴上是否存在定点使得?乳品存在,求出点的坐标;若不存在,说明理由.22. 已知函数(1)若曲线与在公共点处有相同的切线,求实数的值;(2)若,且曲线与总存在公共的切线,求正数的最小值.。
2017-2018学年辽宁省实验中学、鞍山一中、东北育才学校高二(下)期末数学试卷(文科)(解析版)

2017-2018学年辽宁省实验中学、大连八中、大连二十四中、鞍山一中、东北育才学校高二(下)期末数学试卷(文科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合A={x|﹣2<x<4},B={x|y=lg(x﹣2)},则A∩(∁R B)=()A.(2,4)B.(﹣2,4)C.(﹣2,2)D.(﹣2,2]2.(5分)已知,则复数z=()A.1﹣3i B.﹣1﹣3i C.﹣1+3i D.1+3i3.(5分)用反证法证明“若x+y≤0则x≤0或y≤0”时,应假设()A.x>0或y>0B.x>0且y>0C.xy>0D.x+y<04.(5分)命题“∀x∈[1,2],x2﹣a≤0”为真命题的一个充分不必要条件是()A.a≥4B.a≤4C.a≥5D.a≤55.(5分)如果曲线y=x4﹣x在点P处的切线垂直于直线y=﹣x,那么点P的坐标为()A.(1,0)B.(0,﹣1)C.(0,1)D.(﹣1,0)6.(5分)在平面几何里有射影定理:设三角形ABC的两边AB⊥AC,D是A点在BC上的射影,则AB2=BD•BC.拓展到空间,在四面体A﹣BCD中,AD⊥面ABC,点O是A 在面BCD内的射影,且O在△BCD内,类比平面三角形射影定理,得出正确的结论是()A.S△ABC2=S△BCO•S△BCD B.S△ABD2=S△BOD•S△BOCC.S△ADC2=S△DOC•S△BOC D.S△BDC2=S△ABD•S△ABC7.(5分)下列说法:①设有一个回归方程y=3﹣5x,变量x增加一个单位时,y平均增加5个单位;②线性回归直线必过必过点;③在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患肺病;其中错误的个数是()A.0B.1C.2D.38.(5分)函数y=2x﹣x2的图象大致是()A.B.C.D.9.(5分)已知定义在R上的奇函数y=f(x)满足f(2+x)=f(﹣x),且f(1)=2,则f (2018)+f(2019)的值为()A.﹣2B.0C.2D.410.(5分)甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则()A.乙可以知道四人的成绩B.丁可以知道四人的成绩C.乙、丁可以知道对方的成绩D.乙、丁可以知道自己的成绩11.(5分)已知x∈(0,),函数y=f(x)满足:tan xf(x)>f′(x)恒成立,其中f′(x)是f(x)的导函数,则下列不等式中成立的是()A.f()>f()B.2f(1)cos1<f()C.f()>f()D.f()<f()12.(5分)若曲线与直线y=kx﹣1有两个不同的交点,则实数k的取值范围是()A.B.C.D.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.(5分)已知i是虚数单位,复数z满足,则|z|=.14.(5分)《聊斋志异》中有这样一首诗:“挑水砍柴不堪苦,请归但求穿墙术.得诀自诩无所阻,额上坟起终不悟.”在这里,我们称形如以下形式的等式具有“穿墙术”:2,•……则按照以上规律,若8具有“穿墙术”,则n=.15.(5分)已知函数f(x)=x2+x+m,若|f(x)|在区间[0,1]上单调,则实数m的取值范围为16.(5分)如果函数f(x)在[a,b]上存在x1,x2(a<x1<x2<b)满足f′(x1)=,f′(x2)=,则称函数f(x)是[a,b]上的“双中值函数”,已知函数f(x)=x3﹣x2+a是[0,a]上“双中值函数”,则实数a的取值范围是.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(12分)2017年10月9日,教育部考试中心下发了《关于2018年普通高考考试大纲修订内容的通知》,在各科修订内容中明确提出,增加中华优秀传统文化的考核内容,积极培育和践行社会主义核心价值观,充分发挥高考命题的育人功能和积极导向作用.鞍山市教育部门积极回应,编辑传统文化教材,在全是范围内开设书法课,经典诵读等课程.为了了解市民对开设传统文化课的态度,教育机构随机抽取了200位市民进行了解,发现支持开展的占75%,在抽取的男性市民120人中支持态度的为80人.(1)完成2×2列联表(2)判断是否有99.9%的把握认为性别与支持有关?附:K2=.18.(12分)已知a为实数,函数f(x)=x3+ax2+x+a,若f'(﹣1)=0.(1)求a的值.(2)求函数y=f(x)在上的极值.19.(12分)某二手交易市场对某型号的二手汽车的使用年数x(0<x≤10)与销售价格y (单位:万元/辆)进行整理,得到如下的对应数据:(I)试求y关于x的回归直线方程.(参考公式:,)(II)已知每辆该型号汽车的收购价格为ω=0.05x2﹣1.75x+17.2万元,根据(I)中所求的回归方程,预测x为何值时,销售一辆该型号汽车所获得的利润z最大?(利润=销售价格﹣收购价格)20.(12分)已知函数.(1)求函数f(x)的定义域和值域;(2)设(a'为实数),求F(x)在a<0时的最大值g(a).21.(12分)已知函数f(x)=lnx﹣ax(a∈R).(1)若曲线y=f(x)与直线x﹣y﹣1﹣=0相切,求实数a的值;(2)若函数y=f(x)有两个零点x1,x2,证明.四、解答题(共2小题,满分10分)22.(10分)已知直线l过点P(2,1),倾斜角为135°,以原点O为极点,x轴正半轴为极轴(长度单位与直角坐标系xoy的长度单位相同)建立极坐标系,圆C的方程为ρ=4cosθ,(1)分别写出圆C的直角坐标方程和直线的参数方程;(2)设圆C与直线l交于点A,B,求|P A|+|PB|.23.已知函数f(x)=|x+1|﹣|x﹣2|.(1)求不等式f(x)≥1的解集;(2)若不等式f(x)≥x2﹣x+m的解集非空,求m的取值范围.2017-2018学年辽宁省实验中学、大连八中、大连二十四中、鞍山一中、东北育才学校高二(下)期末数学试卷(文科)参考答案与试题解析一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.【解答】解:B={x|x>2};∴∁R B={x|x≤2};∴A∩(∁R B)=(﹣2,2].故选:D.2.【解答】解:,∴=(1+i)(2+i)=1+3i.则复数z=1﹣3i.故选:A.3.【解答】解:用反证法证明“若x+y≤0则x≤0或y≤0”时,应先假设x>0且y>0.故选:B.4.【解答】解:命题“∀x∈[1,2],x2﹣a≤0”为真命题,可化为∀x∈[1,2],a≥x2,恒成立即只需a≥(x2)max=4,即“∀x∈[1,2],x2﹣a≤0”为真命题的充要条件为a≥4,而要找的一个充分不必要条件即为集合{a|a≥4}的真子集,由选择项可知C符合题意.故选:C.5.【解答】解:∵曲线y=x4﹣x在点P处的切线垂直于直线y=﹣x,直线y=﹣x的斜率为﹣,∴曲线y=x4﹣x在点P处的切线的斜率k=3,∵函数y=x4﹣x的导数为y′=4x3﹣1,设P(x0,y0),∴4﹣1=3,解得x0=1,∴y0=x04﹣x0=0,∴P(1,0).故选:A.6.【解答】解:由已知在平面几何中,若△ABC中,AB⊥AC,AE⊥BC,E是垂足,则AB2=BD•BC,我们可以类比这一性质,推理出:若三棱锥A﹣BCD中,AD⊥面ABC,AO⊥面BCD,O为垂足,则(S△ABC)2=S△BOC.S△BDC.故选:A.7.【解答】解:设有一个回归方程y=3﹣5x,变量x增加一个单位时,y平均减少5个单位,故①错误;线性回归直线必过过点,故②正确;在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,不是说他有99%的可能患肺病,故③错误.故选:C.8.【解答】解:分别画出函数f(x)=2x(红色曲线)和g(x)=x2(蓝色曲线)的图象,如图所示,由图可知,f(x)与g(x)有3个交点,所以y=2x﹣x2=0,有3个解,即函数y=2x﹣x2的图象与x轴由三个交点,故排除B,C,当x=﹣3时,y=2﹣3﹣(﹣3)2<0,故排除D故选:A.9.【解答】解:根据题意,函数y=f(x)满足f(2+x)=f(﹣x),则f(x+4)=f[﹣(x+2)]=f(x),则函数的周期为4,又由f(x)为定义在R上的奇函数,则有f(0)=0,f(﹣1)=﹣f(1)=﹣2;则f(2018)=f(2+504×4)=f(2)=f(0)=0,f(2019)=f(3+504×4)=f(3)=f(﹣1)=﹣2;则f(2018)+f(2019)=0+(﹣2)=﹣2;故选:A.10.【解答】解:四人所知只有自己看到,老师所说及最后甲说话,甲不知自己的成绩→乙丙必有一优一良,(若为两优,甲会知道自己的成绩;若是两良,甲也会知道自己的成绩)→乙看到了丙的成绩,知自己的成绩→丁看到甲、丁也为一优一良,丁知自己的成绩,给甲看乙丙成绩,甲不知道自已的成绩,说明乙丙一优一良,假定乙丙都是优,则甲是良,假定乙丙都是良,则甲是优,那么甲就知道自已的成绩了.给乙看丙成绩,乙没有说不知道自已的成绩,假定丙是优,则乙是良,乙就知道自己成绩.给丁看甲成绩,因为甲不知道自己成绩,乙丙是一优一良,则甲丁也是一优一良,丁看到甲成绩,假定甲是优,则丁是良,丁肯定知道自已的成绩了故选:D.11.【解答】解:因x∈(0,),故tan xf(x)>f′(x)⇔sin xf(x)>f′(x)cos x⇔sin xf (x)﹣cos xf′(x)>0,令g(x)=cos xf(x),则g′(x)=cos xf′(x)﹣sin xf (x)<0,所以函数g(x)在(0,)为减函数,∴cos f()>cos f(),∴f()>f().故选:A.12.【解答】解:作出曲线y=的图象如图:直线y=kx﹣1过定点(0,﹣1),当k=0时,两个函数只有一个交点,不满足条件,当k<0时,两个函数有2个交点,满足条件,当k>0时,直线y=kx﹣1与y=在x>1相切时,两个函数只有一个交点,此时=kx﹣1,即kx2﹣(1+k)x+3=0,判别式△=(1+k)2﹣12k=0,解得k2﹣10k+1=0,k=5﹣2或k=5+2(舍去)综上满足条件的k的取值范围是(﹣∞,0)∪(0,5﹣2),故选:D.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.【解答】解:∵复数z满足,∴z=,化为4z=,即z=,∴|z|==.故答案为:.14.【解答】解:因为2==,3==,4==,==,则8===,故答案为63.15.【解答】解:因为f(x)=x2+x+m,且|f(x)|在区间[0,1]上单调,所以f(x)在[0,1]上满足f(0)•f(1)≥0,即m(1+1+m)≥0,解得:m≥0或m≤﹣2,故答案为:(﹣∞,﹣2]∪[0,+∞)16.【解答】解:由题意可知,∵f(x)=x3﹣x2+a,f′(x)=3x2﹣2x在区间[0,a]存在x1,x2(a<x1<x2<b),满足f′(x1)=f′(x2)==a2﹣a,∵f(x)=x3﹣x2+a,∴f′(x)=3x2﹣2x,∴方程3x2﹣2x=a2﹣a在区间(0,a)有两个不相等的解.令g(x)=3x2﹣2x﹣a2+a,(0<x<a)则,解得<a<1;.∴实数a的取值范围是(,1)故答案为:(,1).三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.【解答】解:(1)抽取的男性市民为120人,持支持态度的为200×75%=150人,男性公民中持支持态度的为80人,列出2×2列联表如下:(2)由表中数据,计算K2==≈11.11>10.828,所以有99.9%的把握认为性别与支持有关.18.【解答】解:(1)f'(x)=3x2+2ax+1,∴f'(﹣1)=4﹣2a=0得a=2.(2)由(1)知a=2∴f(x)=x3+2x2+x+2∴f'(x)=3x2+4x+1=(3x+1)(x+1)令f'(x)=0得x1=﹣1,当x变化时f'(x),f(x)的变化情况如下表:由上表可知f极大值(x)=f(﹣1)=2;.故函数y=f(x)在[﹣,1]上的极大值为2,极小值为.19.【解答】解:(I)由表中数据,计算=×(2+4+6+8+10)=6,=×(16+13+9.5+7+4.5)=10,(x i﹣)(y i﹣)=(﹣4)×6+(﹣2)×3+0×(﹣0.5)+2×(﹣3)+4×(﹣5.5)=﹣58.5;=(﹣4)2+(﹣2)2+02+22+42=40,由最小二乘法求得==﹣1.45,=﹣=10﹣(﹣1.45)×6=18.7,∴y关于x的回归直线方程为;(II)根据题意利润函数为z=(﹣1.45x+18.7)﹣(0.05x2﹣1.75x+17.2)=﹣0.05x2+0.3x+1.5,∴当时,利润z取得最大值.20.【解答】解:(1)由1+x≥0且1﹣x≥0,得﹣1≤x≤1,所以函数的定义域为[﹣1,1],又,由f(x)≥0,得,所以函数值域为.(2)因为=令,则,∴,由题意知g(a)即为函数,的最大值.注意到直线是抛物线的对称轴.因为a<0时,函数y=m(t),的图象是开口向下的抛物线的一段,①若,即,则;②若,即,则③若,即﹣,则g(a)=m(2)=a+2,综上有g(a)=.21.【解答】解:(1)由f(x)=lnx﹣ax,得,设切点横坐标为x0,依题意得,解得,即实数a的值为1.(2)不妨设0<x1<x2,由,得lnx2﹣lnx1=a(x2﹣x1),即,所以,令,则,设,则,即函数g(t)在(1,+∞)上递减,所以g(t)>g(1)=0,从而,即.四、解答题(共2小题,满分10分)22.【解答】解:(1)直线l过点P(2,1),倾斜角为135°,则:直线的方程为:y﹣1=(﹣1)(x﹣2),整理得:x+y﹣3=0.转化成参数方程成为:(t为参数).(2)圆C的方程为ρ=4cosθ,转化为直角坐标方程为:x2+y2=4x,整理得:(x﹣2)2+y2=4,则:圆心(2,0)到直线x+y﹣3=0的距离d=.则:|P A|+|PB|=2=2.23.【解答】解:(1)∵f(x)=|x+1|﹣|x﹣2|=,f(x)≥1,∴当﹣1≤x≤2时,2x﹣1≥1,解得1≤x≤2;当x>2时,3≥1恒成立,故x>2;综上,不等式f(x)≥1的解集为{x|x≥1}.(2)原式等价于存在x∈R使得f(x)﹣x2+x≥m成立,即m≤[f(x)﹣x2+x]max,设g(x)=f(x)﹣x2+x.由(1)知,g(x)=,当x≤﹣1时,g(x)=﹣x2+x﹣3,其开口向下,对称轴方程为x=>﹣1,∴g(x)≤g(﹣1)=﹣1﹣1﹣3=﹣5;当﹣1<x<2时,g(x)=﹣x2+3x﹣1,其开口向下,对称轴方程为x=∈(﹣1,2),∴g(x)≤g()=﹣+﹣1=;当x≥2时,g(x)=﹣x2+x+3,其开口向下,对称轴方程为x=<2,∴g(x)≤g(2)=﹣4+2+3=1;综上,g(x)max=,∴m的取值范围为(﹣∞,].。
辽宁省实验中学、大连八中、大连二十四中、鞍山一中、东北育才学校2017-2018年高一下学期期末考试地理试题

辽宁省实验中学、大连八中、大连二十四中、鞍山一中、东北育才学校2017-2018学年高一下学期期末考试地理试题第I卷(选择题)一、单选题下图为某区域等高线和自然带分布图。
读图完成下列问题。
1.图中山脉东侧山麓地带气候类型为A.温带大陆性气候B.热带沙漠气候C.亚热带季风气候D.温带季风气候2.导致图中山脉东西两坡自然带差异的主要因素是A.洋流 B.光照 C.热量 D.水分3.该山脉可能位于A.亚洲大陆东岸B.澳大利亚大陆西岸C.南美洲南部西岸D.非洲马达加斯加岛东岸左图表示安徽省1985~2010年就业结构与城镇人口比重变化,右图表示城市化速度曲线图。
完成下列问题。
4.关于安徽省产业结构调整及城市化发展正确的是A.第二、三产业就业比重均持续快速提高B.城镇新增就业人口第二产业超过第三产业C.城市化进入后期成熟阶段D.劳动力主要由第一产业向第二、三产业转移从而提高城市化水平5.为增强工业对就业和农业产业化的带动作用,近期安徽省中小城市可以着力发展A.劳动力导向型和原料导向型工业B.技术导向型和市场导向型工业C.动力导向型和劳动力导向型工业D.原料导向型和技术导向型工业(题文)下图为美国铜矿资源开发布局指向示意图。
读下图,回答下列问题。
6.(小题1)据图分析美国铜矿熔炼厂和精炼厂分别属于A.原料导向型工业和市场导向型工业B.动力导向型工业和技术导向型工业C.动力导向型工业和廉价劳动力导向型工业D.原料导向型工业和技术导向型工业7.(小题2)大量铜材加工厂布局在精炼厂附近有利于A.加强各加工厂间联系,竞争发展B.加强与精炼厂的协作,降低成本C.扩大总体生产能力,降低劳动力成本 D.减少市场交易费用,改善环境质量梧州是一座有着2100多年历史的岭南名城,曾是广西第一大城市,有着“百年商埠”“小香港”之美誉。
新中国成立后,南宁、柳州、桂林的发展相继超过梧州。
下图示意广西部分主要城市分布。
据此完成下列问题。
辽宁省实验中学、大连八中、大连二十四中、鞍山一中、东北育才学校2017_2018学年高一数学下学期期末考试试
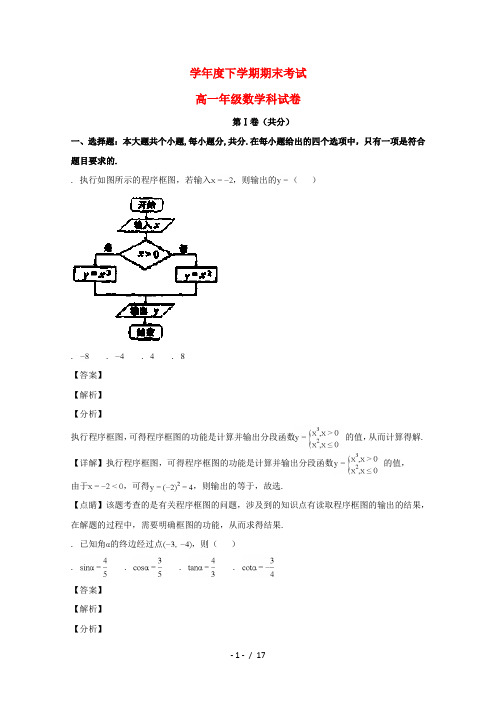
学年度下学期期末考试高一年级数学科试卷第Ⅰ卷(共分)一、选择题:本大题共个小题,每小题分,共分.在每小题给出的四个选项中,只有一项是符合题目要求的.. 执行如图所示的程序框图,若输入,则输出的(). . . .【答案】【解析】【分析】执行程序框图,可得程序框图的功能是计算并输出分段函数的值,从而计算得解. 【详解】执行程序框图,可得程序框图的功能是计算并输出分段函数的值,由于,可得,则输出的等于,故选.【点睛】该题考查的是有关程序框图的问题,涉及到的知识点有读取程序框图的输出的结果,在解题的过程中,需要明确框图的功能,从而求得结果.. 已知角的终边经过点,则(). . . .【答案】【解析】【分析】由题意可得,,求出的值,逐项分析,求得结果.【详解】由题意可得,所以,,,综上所述,答案选.【点睛】该题考查的是有关任意角的三角函数的定义,在解题的过程中,需要利用定义将角的三角函数值求出,逐项对照求得结果.. (). . . .【答案】【解析】【分析】原式中的角度变形后,利用诱导公式化简计算即可得到结果.【详解】,故选.【点睛】该题考查的是有关运用诱导公式化简求值的问题,在解题的过程中,正确运用公式是解题的关键.. 在瓶牛奶中,有瓶已经过了保质期,从中任取一瓶,取到已经过保质期的牛奶的概率是(). . . .【答案】【解析】【分析】在瓶牛奶中任取瓶有种不同的取法,而满足条件的取到已过保质期的牛奶有种不同的取法,根据古典概型公式,代入数据,求出结果.【详解】由题意知,该题是一个古典概型,因为在瓶牛奶中任取瓶有种不同的取法,取到已过保质期的牛奶有种不同的取法,根据古典概型公式求得,故选.【点睛】该题考查的是有关古典概型的问题,在解题的过程中,涉及到的知识点有古典概型的概率公式,解题的关键是找出基本事件数以及满足条件的基本事件数.. 已知,若,则(). . . .【答案】【解析】【分析】利用题中所给的条件,求得然后利用,根据向量数量积公式求得所满足的等量关系式,求得结果.【详解】因为,所以,因为,所以,即,解得,故选.【点睛】该题考查的是有关向量垂直的条件,涉及到的知识点有向量的加法运算法则,向量垂直的条件,向量数量积的坐标公式,正确使用公式是解题的关键.. 已知平面向量,且,则的值是(). . . .【答案】【解析】【分析】首先应用向量的模的平方和向量的平方是相等的,得到其满足的式子,之后应用相关公式求得结果.【详解】因为平面向量满足,且,则有,故选.【点睛】该题考查的是有关向量的模的求解的问题,涉及到的知识点有向量的模的平方和向量的平方是相等的,利用相关公式求得结果.. (). . . .【答案】【解析】【分析】直接根据两角和正切公式的变形形式,整理即可得到答案. 【详解】,所以,所以原式,故选.【点睛】该题考查的是有关两角和的正切公式的逆用问题,在解题的过程中,需要分析式子的特征,可得与角的关系,从而借着特殊角的正切值得到结果.. 将函数的图像向左平移个周期(即最小正周期)后,所得图像对应的函数为(). .. .【答案】【解析】【分析】首先根据题中所给的函数解析式,求得其周期,从而确定个周期为,再根据三角函数图像平移的规律,得到相应的函数解析式,化简求得结果.【详解】根据题意,可知函数的周期为,所以个周期为,所以平移后所得的图像对应的函数解析式为,故选.【点睛】该题考查的是有关平移后的三角函数解析式的求解问题,涉及到的知识点有左右平移变换,函数的周期的求法,需要注意平移的量是自变量本身的变化量.. 函数的部分图像如图所示,点是该图像的一个最高点,点是该图像与轴交点,则(). .. .【答案】【解析】【分析】首先根据两点的横坐标的差,确定出函数的最小正周期,从而求得,再根据最高点的坐标,结合,求得,从而确定出函数解析式.【详解】根据题中所给的条件,以及所给的部分图像,可以求得,所以,从而得到,求得,因为是最高点,所以有,解得,又因为,所以,所以,故选.【点睛】该题考查的是根据函数的图像确定函数解析式的问题,注意振幅由最值来确定,周期由来确定,初相由特殊点来确定,结合题中所给的图像,求得结果.. 已知函数满足,且,当时,则(). . . .【答案】【解析】【分析】首先根据题中所给的条件,可以确定函数的一条对称轴和一个对称中心,从而确定出函数的最小正周期,结合时,求得结果.【详解】根据题意,由可得函数图像关于直线对称,由可得函数图像关于点对称,从而可知函数是以为最小正周期的周期函数,结合当时,可知,故选.【点睛】该题考查的是有关函数的周期性的应用,从题的条件中判断得出函数图像的对称轴和对称中心,利用对阵中心到对称轴的距离,得到函数的周期,从而结合题中所给的相应区间上的解析式求得结果.. 已知,不共线,,,其中.设点是直线,的交点,则(). .. .【答案】【解析】【分析】首先根据从同一个起点出发的三个向量,当三个终点共线时,其中一个用另两个来表示,系数和等于,设出两种关系,之后转化,利用一个向量在同一组基底下分解出的坐标是相等的,得到方程组,求解代入得结果.【详解】根据题中所给的条件,可知,,根据一个向量在同一组基底下分解出的坐标是相等的,得到,解得,代入可得,故选.【点睛】该题考查的是有关平面向量基本定理的问题,在解题的过程中,利用平面向量在同一组基底下分解出的坐标是相等的,得到方程组,求得结果.. 下列四个函数中,图象可能是如图的是(). .. .【答案】【解析】【分析】分别画出各个选项对应的函数图像,逐个与题中所给的图像对照,得出结果.【详解】函数的图形为:,函数的图像为:,函数的图像为:,函数的图像为:,将选项与题中所给的图像逐个对照,得出项满足条件,故选.【点睛】该题考查的是有关函数图像的选择和判断问题,在解题的过程中,可以应用几何画板将函数图像一一作出,与所给的图像对照得出结果,但是在考场上是不可能应用几何画板的,所以可以借助于同一个周期上零点的个数来得到.第Ⅱ卷(共分)二、填空题:本大题共小题,每小题分。
辽宁省实验中学、大连八中、大连二十四中、鞍山一中、东北育才学校高一数学下学期期末考试试题(含解析)

2017-2018学年度下学期期末考试高一年级数学科试卷第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 执行如图所示的程序框图,若输入,则输出的()A. B. C. D.【答案】C【解析】【分析】执行程序框图,可得程序框图的功能是计算并输出分段函数的值,从而计算得解. 【详解】执行程序框图,可得程序框图的功能是计算并输出分段函数的值,由于,可得,则输出的y等于4,故选C.【点睛】该题考查的是有关程序框图的问题,涉及到的知识点有读取程序框图的输出的结果,在解题的过程中,需要明确框图的功能,从而求得结果.2. 已知角的终边经过点,则()A. B. C. D.【答案】C【解析】【分析】由题意可得,,求出的值,逐项分析,求得结果.【详解】由题意可得,所以,,,综上所述,答案选C.【点睛】该题考查的是有关任意角的三角函数的定义,在解题的过程中,需要利用定义将角的三角函数值求出,逐项对照求得结果.3. ()A. B. C. D.【答案】D【解析】【分析】原式中的角度变形后,利用诱导公式化简计算即可得到结果.【详解】,故选D.【点睛】该题考查的是有关运用诱导公式化简求值的问题,在解题的过程中,正确运用公式是解题的关键.4. 在瓶牛奶中,有瓶已经过了保质期,从中任取一瓶,取到已经过保质期的牛奶的概率是()A. B. C. D.【答案】C【解析】【分析】在50瓶牛奶中任取1瓶有50种不同的取法,而满足条件的取到已过保质期的牛奶有5种不同的取法,根据古典概型公式,代入数据,求出结果.【详解】由题意知,该题是一个古典概型,因为在50瓶牛奶中任取1瓶有50种不同的取法,取到已过保质期的牛奶有5种不同的取法,根据古典概型公式求得,故选C.【点睛】该题考查的是有关古典概型的问题,在解题的过程中,涉及到的知识点有古典概型的概率公式,解题的关键是找出基本事件数以及满足条件的基本事件数.5. 已知,若,则()A. B. C. D.【答案】B【解析】【分析】利用题中所给的条件,求得然后利用,根据向量数量积公式求得x 所满足的等量关系式,求得结果.【详解】因为,所以,因为,所以,即,解得,故选B.【点睛】该题考查的是有关向量垂直的条件,涉及到的知识点有向量的加法运算法则,向量垂直的条件,向量数量积的坐标公式,正确使用公式是解题的关键.6. 已知平面向量,且,则的值是()A. B. C. D.【答案】B【解析】【分析】首先应用向量的模的平方和向量的平方是相等的,得到其满足的式子,之后应用相关公式求得结果.【详解】因为平面向量满足,且,则有,故选B.【点睛】该题考查的是有关向量的模的求解的问题,涉及到的知识点有向量的模的平方和向量的平方是相等的,利用相关公式求得结果.7. ()A. B. C. D.【答案】B【解析】【分析】直接根据两角和正切公式的变形形式,整理即可得到答案. 【详解】,所以,所以原式,故选B.【点睛】该题考查的是有关两角和的正切公式的逆用问题,在解题的过程中,需要分析式子的特征,可得与角的关系,从而借着特殊角的正切值得到结果.8. 将函数的图像向左平移个周期(即最小正周期)后,所得图像对应的函数为()A. B.C. D.【答案】A【解析】【分析】首先根据题中所给的函数解析式,求得其周期,从而确定个周期为,再根据三角函数图像平移的规律,得到相应的函数解析式,化简求得结果.【详解】根据题意,可知函数的周期为,所以个周期为,所以平移后所得的图像对应的函数解析式为,故选A.【点睛】该题考查的是有关平移后的三角函数解析式的求解问题,涉及到的知识点有左右平移变换,函数的周期的求法,需要注意平移的量是自变量x本身的变化量.9. 函数的部分图像如图所示,点是该图像的一个最高点,点是该图像与轴交点,则()A. B.C. D.【答案】C【解析】【分析】首先根据两点的横坐标的差,确定出函数的最小正周期,从而求得,再根据最高点的坐标,结合,求得,从而确定出函数解析式.【详解】根据题中所给的条件,以及所给的部分图像,可以求得,所以,从而得到,求得,因为P是最高点,所以有,解得,又因为,所以,所以,故选C.【点睛】该题考查的是根据函数的图像确定函数解析式的问题,注意振幅A由最值来确定,周期由来确定,初相由特殊点来确定,结合题中所给的图像,求得结果.10. 已知函数满足,且,当时,则()A. B. C. D.【答案】D【解析】【分析】首先根据题中所给的条件,可以确定函数的一条对称轴和一个对称中心,从而确定出函数的最小正周期,结合时,求得结果.【详解】根据题意,由可得函数图像关于直线对称,由可得函数图像关于点对称,从而可知函数是以4为最小正周期的周期函数,结合当时,可知,故选D.【点睛】该题考查的是有关函数的周期性的应用,从题的条件中判断得出函数图像的对称轴和对称中心,利用对阵中心到对称轴的距离,得到函数的周期,从而结合题中所给的相应区间上的解析式求得结果.11. 已知,不共线,,,其中.设点是直线,的交点,则()A. B.C. D.【答案】A【解析】【分析】首先根据从同一个起点出发的三个向量,当三个终点共线时,其中一个用另两个来表示,系数和等于1,设出两种关系,之后转化,利用一个向量在同一组基底下分解出的坐标是相等的,得到方程组,求解代入得结果.【详解】根据题中所给的条件,可知,,根据一个向量在同一组基底下分解出的坐标是相等的,得到,解得,代入可得,故选A.【点睛】该题考查的是有关平面向量基本定理的问题,在解题的过程中,利用平面向量在同一组基底下分解出的坐标是相等的,得到方程组,求得结果.12. 下列四个函数中,图象可能是如图的是()A. B.C. D.【答案】D【解析】【分析】分别画出各个选项对应的函数图像,逐个与题中所给的图像对照,得出结果.【详解】函数的图形为:,函数的图像为:,函数的图像为:,函数的图像为:,将选项与题中所给的图像逐个对照,得出D项满足条件,故选D.【点睛】该题考查的是有关函数图像的选择和判断问题,在解题的过程中,可以应用几何画板将函数图像一一作出,与所给的图像对照得出结果,但是在考场上是不可能应用几何画板的,所以可以借助于同一个周期上零点的个数来得到.第Ⅱ卷(共90分)二、填空题:本大题共4小题,每小题5分。
【全国校级联考Word】辽宁省实验中学、大连八中、大连二十四中、鞍山一中、东北育才学校2017-

2017-2018学年下学期期末高二年级数学文科试卷第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}A=|24x x -<<,{}|lg(2)B x y x ==-,则(C )R AB =( )A .(2,4)B .(2,4)-C .(2,2)-D .(2,2]-2.已知21zi i=++,则复数z =( ) A .13i - B .13i -- C .13i -+ D .13i + 3.用反证法证明“若0x y +≤则0x ≤或0y ≤”时,应假设( )A .0x >或0y >B .0x >且0y >C .0xy >D .0x y +< 4.命题“[]1,2x ∀∈,20x a -≤”为真命题的一个充分不必要条件是( )A .4a ≥B .4a ≤ C. 5a ≥ D .5a ≤ 5.如果曲线4y x x =-在点P 处的切线垂直于直线13y x =-,那么点P 的坐标为( ) A .(1,0) B .(0,1)- C. (0,1) D .(1,0)-6.在平面几何里有射影定理:设三角形ABC 的两边AB AC ⊥,D 是A 点在BC 上的射影,则2AB BD BC =⋅.拓展到空间,在四面体A BCD -中,AD ⊥面ABC ,点O 是A 在面BCD 内的射影,且O 在BCD ∆内,类比平面三角形射影定理,得出正确的结论是( )A .2ABC BCO BCD S S S ∆∆∆=⋅ B .2ABO BCD BOC S S S ∆∆∆=⋅ C. 2ADC DOC BOC S S S ∆∆∆=⋅ D .2BOC ABD ABC S S S ∆∆∆=⋅7.下列说法:①设有一个回归方程35y x =-,变量x 增加一个单位时,y 平均增加5个单位;②线性回归直线y bx a =+必过必过点(,)x y ;③在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患肺病;其中错误的个数是( ) A .0 B .1 C. 2 D .3 8.函数22xy x =-的图象大致是下图中的哪个( )A .B .C. D .9.已知定义在R 上的奇函数()y f x =满足(2x)f()f x +=-,且(1)2f =,则(2018)(2019)f f +的值为( )A .2-B .0 C. 2 D .410.甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩.老实说:你们四人中有2位优秀,2位良好,我现在给甲看看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则( )A .乙可以知道四人的成绩B .丁可以知道四人的成绩 C.乙、丁可以知道对方的成绩 D .乙、丁可以知道自己的成绩 11.已知(0,)2x π∈,函数()y f x =满足:tan ()'()xf x f x >恒成立,其中'()f x 是()f x 的导函数,则下列不等式中成立的是( )A()()63f ππ> B .2(1)cos1()3f f π<()()46f f ππ> D()()43f ππ>12.若曲线21,12,11x x x x⎧-≤⎪⎨>⎪-⎩与直线1y kx =-有两个不同的交点,则实数k 的取值范围是( )A.(,5-∞+ B.(,5-∞-C. (,0)(0,52-∞+ D.(,0)(0,52-∞-第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知i 是虚数单位,复数z满足(1)1z ⋅+=,则||z = .14.《聊斋志异》中有这样一首诗:“挑水砍柴不堪苦,请归但求穿墙术.得决自诩无所阻,额上坟起终不悟.”在这里,我们称形如一下形式的等式具有“穿墙术”:====⋅⋅⋅⋅⋅⋅则按照以上规律,若=,则n = . 15.已知函数2()f x x x m =++,若|()|f x 在区间[]0,1上单调,则实数m 的取值范围为 . 16.如果函数()f x 在[],a b 上存在1212,()x x a x x b <<<满足1()()'()f b f a f x b a-=-,2()()'()f b f a f x b a-=-,则称函数()f x 是在[],a b 上的“双中值函数”,已知函数32()f x x x t =-+是[]0,t 上的“双中值函数”,则函数t 的取值范围是 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.2017年10月9日,教育部考试中心下发了《关于2018年普通高考考试大纲修订内容的通知》,在各科修订内容中明确提出,增加中华优秀传统文化的考核内容,积极培育和践行社会主义核心价值观,充分发挥高考命题的育人功能和积极导向作用.鞍山市教育部门积极回应,编辑传统文化教材,在全是范围内开设书法课,经典诵读等课程.为了了解市民对开设传统文化课的态度,教育机构随机抽取了200位市民进行了解,发现支持开展的占75%,在抽取的男性市民120人中支持态度的为80人.(1)完成22⨯列联表(2)判断是否有99.9%的把握认为性别与支持有关?附:22()()()()(b d)n ad bc K a b c d a c -=++++.18.已知a 为实数,函数33()f x x ax x a =+++,若'(1)0f -=. (1)求a 的值。
xx省实验中学、大连八中、大连二十四中、鞍山一中、东北育才学校201X-201x学年高二数学下学期期

2017-2018学年下学期期末高二年级数学文科试卷第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}A=|24x x -<<,{}|lg(2)B x y x ==-,则(C )R AB =( )A .(2,4)B .(2,4)-C .(2,2)-D .(2,2]-2.已知21zi i=++,则复数z =( ) A .13i - B .13i -- C .13i -+ D .13i + 3.用反证法证明“若0x y +≤则0x ≤或0y ≤”时,应假设( )A .0x >或0y >B .0x >且0y >C .0xy >D .0x y +< 4.命题“[]1,2x ∀∈,20x a -≤”为真命题的一个充分不必要条件是( )A .4a ≥B .4a ≤ C. 5a ≥ D .5a ≤ 5.如果曲线4y x x =-在点P 处的切线垂直于直线13y x =-,那么点P 的坐标为( ) A .(1,0) B .(0,1)- C. (0,1) D .(1,0)-6.在平面几何里有射影定理:设三角形ABC 的两边AB AC ⊥,D 是A 点在BC 上的射影,则2AB BD BC =⋅.拓展到空间,在四面体A BCD -中,AD ⊥面ABC ,点O 是A 在面BCD 内的射影,且O 在BCD ∆内,类比平面三角形射影定理,得出正确的结论是( )A .2ABC BCO BCD S S S ∆∆∆=⋅B .2ABO BCD BOC S S S ∆∆∆=⋅ C. 2ADC DOC BOC S S S ∆∆∆=⋅ D .2BOC ABD ABC S S S ∆∆∆=⋅7.下列说法:①设有一个回归方程35y x =-,变量x 增加一个单位时,y 平均增加5个单位;②线性回归直线y bx a =+必过必过点(,)x y ;③在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患肺病;其中错误的个数是( ) A .0 B .1 C. 2 D .38.函数22xy x =-的图象大致是下图中的哪个( )A .B .C. D .9.已知定义在R 上的奇函数()y f x =满足(2x)f()f x +=-,且(1)2f =,则(2018)(2019)f f +的值为( )A .2-B .0 C. 2 D .410.甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩.老实说:你们四人中有2位优秀,2位良好,我现在给甲看看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则( )A .乙可以知道四人的成绩B .丁可以知道四人的成绩 C.乙、丁可以知道对方的成绩 D .乙、丁可以知道自己的成绩 11.已知(0,)2x π∈,函数()y f x =满足:tan ()'()xf x f x >恒成立,其中'()f x 是()f x 的导函数,则下列不等式中成立的是( )A 3()()63f ππ>B .2(1)cos1()3f f π<C.2()3()46ππ> D 2()()43f ππ>12.若曲线21,12,11x x x x⎧-≤⎪⎨>⎪-⎩与直线1y kx =-有两个不同的交点,则实数k 的取值范围是( )A .(,56)-∞+B .(,56)-∞- C. (,0)(0,526)-∞+ D .(,0)(0,526)-∞-第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知i 是虚数单位,复数z 满足(1)1z ⋅+=,则||z = .14.《聊斋志异》中有这样一首诗:“挑水砍柴不堪苦,请归但求穿墙术.得决自诩无所阻,额上坟起终不悟.”在这里,我们称形如一下形式的等式具有“穿墙术”:====⋅⋅⋅⋅⋅⋅则按照以上规律,若=,则n = . 15.已知函数2()f x x x m =++,若|()|f x 在区间[]0,1上单调,则实数m 的取值范围为 .16.如果函数()f x 在[],a b 上存在1212,()x x a x x b <<<满足1()()'()f b f a f x b a-=-,2()()'()f b f a f x b a-=-,则称函数()f x 是在[],a b 上的“双中值函数”,已知函数32()f x x x t =-+是[]0,t 上的“双中值函数”,则函数t 的取值范围是 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.2017年10月9日,教育部考试中心下发了《关于2018年普通高考考试大纲修订内容的通知》,在各科修订内容中明确提出,增加中华优秀传统文化的考核内容,积极培育和践行社会主义核心价值观,充分发挥高考命题的育人功能和积极导向作用.鞍山市教育部门积极回应,编辑传统文化教材,在全是范围内开设书法课,经典诵读等课程.为了了解市民对开设传统文化课的态度,教育机构随机抽取了200位市民进行了解,发现支持开展的占75%,在抽取的男性市民120人中支持态度的为80人.(1)完成22⨯列联表(2)判断是否有99.9%的把握认为性别与支持有关?附:22()()()()(b d)n ad bc K a b c d a c -=++++.18.已知a 为实数,函数33()f x x ax x a =+++,若'(1)0f -=. (1)求a 的值。
【数学】辽宁省实验中学、大连二十四中、鞍山一中、东北育才学校2017-2018学年高二下学期期末考试(文)

参考答案1.D2.A3.B4.C5.A6.A7.C8.A9.A 10.D 11.A 12.D 13.21 14.63 15.(-∞,-2]U[0,+∞) 16.(21,1) 17.解:(1)抽取的男性市民为120人,持支持态度的为200×75%=150人, 男性公民中持支持态度的为80人,列出2×2列联表如下:-------4支持 不支持 合计 男性 80 40 120 女性 70 10 80 合计15050200(2) K 2=111.191001208050150)40701080(2002≈=⨯⨯⨯⨯-⨯>10.828,----------10 所以有99.9%的把握认为性别与支持有关。
----------12 18. 解:(1)f /(x)=3x 2+2ax+1,∴f ’(-1)=4-2a=0 得a=2.---------3(2)由(1)知 a=2 ∴f(x)=x 3+2x 2+x+2 f ’(x)=3x 2+4x+1=(3x+1)(x+1) 令f ’(x)=0 得 X 1=-1 x 2=-31 当x 变化时f ’(x), f(x)的变化情况如下表:x (-23,-1) -1 (-1,-31) -31 (-31,1) f ’(x) + 0 - 0+ f(x) ↑极大值↓极小值↑由上表可知f 极大值(x )=f(-1)=2;f 极小值(x )=f(-31)=2750.------------12 19.解:(I )由表中数据,计算=×(2+4+6+8+10)=6, =×(16+13+9.5+7+4.5)=10,(x i ﹣)(y i ﹣)=(﹣4)×6+(﹣2)×3+0×(﹣0.5)+2×(﹣3)+4×(﹣5.5)=﹣58.5;=(﹣4)2+(﹣2)2+02+22+42=40,由最小二乘法求得==﹣1.45,-------3=﹣=10﹣(﹣1.45)×6=18.7,--------5∴y 关于x 的回归直线方程为;-----7(II )根据题意利润函数为z=(﹣1.45x+18.7)﹣(0.05x 2﹣1.75x+17.2)=﹣0.05x 2+0.3x+1.5, ∴当时,利润z 取得最大值.-------1220.解:(1)由1+x≥0且1﹣x≥0,得﹣1≤x≤1, 所以函数的定义域为[﹣1,1],-------2又[f (x )]2=2+221x -∈[2,4],由f (x )≥0,得f (x )∈[,2],所以函数值域为[,2];-------5(2)因为F (x )=•[f 2(x )﹣2]+f (x )=a 21x -+x +1+x -1 令t=f (x )=+,则=21t 2﹣1, ∴F (x )=m (t )=a (t 2﹣1)+t=21at 2+t ﹣a ,t ∈[,2], 由题意知g (a )即为函数m (t )=21at 2+t ﹣a ,t ∈[,2]的最大值.注意到直线t=﹣是抛物线m (t )=21at 2+t ﹣a 的对称轴. 因为a <0时,函数y=m (t ),t ∈[,2]的图象是开口向下的抛物线的一段,①若t=﹣∈(0,],即a≤﹣22,则g (a )=m ()=;②若t=﹣∈(,2],即﹣22<a≤﹣21,则g (a )=m (﹣a 1)=﹣a ﹣a21 ③若t=﹣∈(2,+∞),即﹣21<a <0,则g (a )=m (2)=a+2,综上有g (a )=;-------1221.解:(1)由f (x )=lnx ﹣ax ,得,设切点横坐标为x 0,依题意得⎝⎛-=-=-000ln 111axx x a x , 解得⎩⎨⎧==010a x ,即实数a 的值为0.-------4(2)不妨设0<x 1<x 2,由,得lnx 2﹣lnx 1=a (x 2﹣x 1),即,所以121221122112122121ln ln 22)11(ln ln 2)11(1ln 1ln 1x x x xx x x x x x x x x x x x a x x --=-+--=-+=+,令,则,设,则,即函数g (t )在(1,+∞)上递增, 所以g (t )>g (1)=0,从而12122112ln ln 2x x x x x x x x -->0,即21ln 1ln 1x x +>2 .--------12 22.解:(1)直线l 过点P (2,1),倾斜角为135°, 则:直线的方程为:y ﹣1=(﹣1)(x ﹣2), 整理得:x+y ﹣3=0.转化成参数方程成为:(t 为参数).--------3圆C 的方程为ρ=4cosθ,转化为直角坐标方程为:x 2+y 2=4x , 整理得:(x ﹣2)2+y 2=4,--------5(2)圆心(2,0)到直线x+y ﹣3=0的距离d=.则:|PA|+|PB|=222222⎪⎪⎭⎫ ⎝⎛-=14-----------10 23.解:(1)∵f (x )=|x+1|﹣|x ﹣2|=,f (x )≥1,∴当﹣1≤x≤2时,2x ﹣1≥1,解得1≤x≤2; 当x >2时,3≥1恒成立,故x >2;综上,不等式f (x )≥1的解集为{x|x≥1}.-----5(2)原式等价于存在x ∈R 使得f (x )﹣x 2+x≥m 成立, 即m≤[f (x )﹣x 2+x]max ,设g (x )=f (x )﹣x 2+x .由(1)知,g (x )=,当x≤﹣1时,g (x )=﹣x 2+x ﹣3,其开口向下,对称轴方程为x=21>﹣1, ∴g (x )≤g (﹣1)=﹣1﹣1﹣3=﹣5;当﹣1<x <2时,g (x )=﹣x 2+3x ﹣1,其开口向下,对称轴方程为x=23∈(﹣1,2), ∴g (x )≤g (23)=﹣49+29﹣1=45; 当x≥2时,g (x )=﹣x 2+x+3,其开口向下,对称轴方程为x=21<2, ∴g (x )≤g (2)=﹣4+2+3=1;综上,g (x )max =45, ∴m 的取值范围为(﹣∞,45].-------10。
