2.2 有理数的减法(1)导学案
有理数的减法教案(通用3篇)

We have to laugh every day in life, and none of us know what happens in the next second of life.通用参考模板(页眉可删)有理数的减法教案(通用3篇)有理数的减法教案1知识与能力:1.使学生理解有理数的加减法法可以互相转化。
2.使学生熟练地进行有理数的加减混合运算。
过程与方法:1.体会有理数的加减法法可以互相转化的思想。
2.培养学生的运算能力。
情感态度与价值观:培养学生认真、仔细的良好学习态度。
重点准确迅速地进行有理数的加减混合运算。
教材提示:本节课是学习有理数减法的第二课时,在教学过程中,教师应该首先通过探究的方式组织学生分组讨论,借助于已有知识,体会有理数的加减法法可以互相转化的思想,如何省略加号,并且还要正确掌握省略加号后它们表示的是哪些数的和,强化混合运算的准确性。
教学过程:一、自主学习(一)、阅读教材23-24页。
(二)、导学练习 [活动1]:学生课前自主完成。
1.减法法则:,用字母表示为:2.计算(1)1-5= (2)8-11= (3)6-9=(4)9-(-9)= (5)(- )-(- )=[活动2]:学生先课前自主,然后在课堂上一起和大家交流讨论。
1、红星队在4场足球赛中的战绩是:第一场3:1胜,第二场2:3负,第三场0:0平,第四场2:5负。
红星队在4场比赛中总的净胜球数是多少?2、一20十3十(十5)十(一7)(读作,,,的和 )3、计算:(一20)十(十3)一(一5)一(十7). 注意:在进行有理数混合运算时,应该先将减法按规则统一成加法后再计算;第一个数前面的一常用括号括起来,但熟练后,第一个数带负号时,通常可以不用括号手起来。
4、计算在做有理数运算时,易出符号错误。
计算:(1)(一5)一(一4)一(十1)=(一5)十(一4)十(十1) =(一9)十(十1) =一8(2)(一7)一(十4) 十(一8)十(一3)一(一8) =一7十4一8一3一8 =一22. 以上两个小题均有错误,指出错在哪里,并改正。
2.2.有理数的减法(1)(学案)
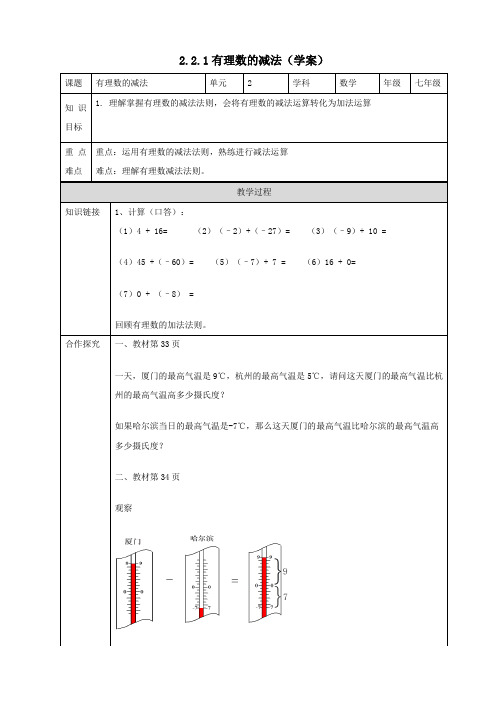
2.2.1有理数的减法(学案)一、教材第33页一天,厦门的最高气温是9℃,杭州的最高气温是5℃,请问这天厦门的最高气温比杭州的最高气温高多少摄氏度?如果哈尔滨当日的最高气温是-7℃,那么这天厦门的最高气温比哈尔滨的最高气温高多少摄氏度?二、教材第34页观察A. -3B. -2C. -1D. 32.如图所示为某县十二月份某一天的天气预报,则该天最高气温比最低气温高( )A. -7 ℃B. 7 ℃C. -3 ℃D. 3 ℃3.若b<0,则在a,a-b,a+b三个数中,最大的是(B)A. aB. a-bC. a+bD. 不能确定【方法宝典】根据有理数的减法法则进行计算.1.下列计算结果正确的是()A. (-14)-5=-9B. 0-(-3)=3C. (-3)-(-3)=-6D. |5-3|=-22.点A,B,C在同一条数轴上,其中点A,B表示的数分别为-3,1.若点B,C之间的距离为2,则点A,C之间的距离为( )A. 3B. 2C. 3或5D. 2或63.在足球循环赛中,红队与黄队的比分为4∶1,黄队与蓝队的比分为2∶1,蓝队与红队的比分为1∶0,则下列关于三个队净胜球数的说法,正确的是()A. 红队2,黄队-2,蓝队0B. 红队2,黄队-1,蓝队1C. 红队3,黄队-3,蓝队1D. 红队3,黄队-2,蓝队04.已知表示数a,b的点在数轴上的位置如图所示,则在a+b,b-2a,|a-b|,|b|-|a|中,负数的个数是()A. 1B. 2C. 3D. 45.计算:(1)|1-6|=____.。
有理数的减法-导学案

1.3.2有理数的减法(一)-导学案(总2页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--有理数的减法(一)导学案一、学习目标知识目标:探索有理数减法法则.掌握有理数减法法则。
能力目标:会正确进行有理数减法运算。
情感目标:体验把减法转化为加法的转化思想.二、重点、难点重点:有理数减法法则和运算。
难点:有理数减法法则的推导。
三、学法指导探究法、分类讨论法、练习法四、导入新课直接导入:老师:前面我们学了有理数的加法,今天我们就来学有理数的减法运算。
五、自主先学1、探究新知:有理数减法法则问题:衡阳某天的气温是―2°C~3°C,这一天的温差是多少呢(温差是最高气温减最低气温,单位:°C)。
这天的温差是。
(列出算式)分析:被减数、减数差之间的关系是:被减数—减数= 。
差+减数= 。
要计算3―(―2) = ,实际上也就是要求:+(—2)= 3,所以“”应该是。
所以:3―(―2) = 5。
而3 + 2 = 5。
因此:3―(―2) 3 + 2结论:有理数减法法则:减去一个数,等于这个数的。
(实际是把减法变成了加法,减一个正数等于加一个,减一个负数,等于加一个)。
2、有理数减法法则的运用计算:(1)(-3)—(-5);(2)0—(-7);(3)—();(4)(-7/2)—(-21/4)(5)6—9六、展示交流(汇报成果)七、精讲释疑(1)计算下列各题:22(1) 2-5-8 (2) (3-4)-(6-10) (3) 4-〔(-3)-12〕(4)(-32)-(+121)-(-41)(2)世界上最高的山峰是珠穆朗玛峰,其海拔高度大约为是8848米,吐鲁番盆地的海拔高度大约是-155米,两处高度相差多少米?(3)分别求出下列数轴上两点之间的距离①表示8的点与表示3的点②表示-2的点与表示-3的点八、当堂检测九、当堂小结:有理数减法法则33。
七年级(上册)数学《有理数的减法》导学案

主备人: 班 级: 章、节 学习目标 教学重点 教学难点 说 明 李 辉 华 审核人: 姓 名: 教学内容 郭 尚 金 备课日期:2012 年 09 月 20 日 编 号:SDCX7A0001 第 1 课时 课 型 新 课
1.过程,理解并掌握有理数减法法则; 2、会正确进行有理数减法运算; 3、体验把减法转化为加法的转化思想; 有理数减法法则和运算; 有理数减法法则的推导; 主 要 导 学 过 程
教师复备 (学生笔记)
【预习案】
一、旧知回顾: 1、有理数的加法法则:
① 同号两数相加,取 ② 异号两数相加,当两数的 并且用较大的 的符号,并把 不相等时,取 减去较小的 ; . 。 ; 相加; 较大的加数的符号,
③ 互为相反数的两个数相加得 ④ 一个数与 0 相加,仍得
2、相反数的概念:
如果两个数 如:-3 的相反数是 不同,那么其中一个数叫做另一个数的 ; ; ; +9 的相反数是 。 = ; ;
简 记 “ 一 不 变 , 两 变 ”
【探究案】
探 究二:有理数的减法运算
例:计算: (-2
3 4
教师复备 (学生笔记)
)-(-1
3 4
1 2
) ;
1 2
解:原式=(-2 =(-
)+(+1 )+(+
3 2
)
(两个变号)
11 4
)
6 4
= (- =-( = -
5 4
11 4 11 4
)+(+ -
6 4
个符号,一个是运算符号由减号 ”或
” ,一个是减数性质符号,由“正”变为“
” 。同时,我们要注意,被减数的符号是
改变的。
【我的收获】
2.2 有理数的减法(第1课时 有理数减法法则)(教学课件)七年级数学上册(浙教版2024)

B 点高多少米? B 点比 C 点高多少米?
【解】+4.2-(-15.6)=4.2+15.6=19.8(m).
-15.6-(-30.5)=-15.6+30.5=14.9(m).
答: A 点比 B 点高19.8 m, B 点比 C 点高14.9 m.
厦门与哈尔滨两地的气温差可以用算式9-(-7)表示。
观察右图,可以直观得到两地的气
温差是16℃,由此得9-(-7)=16。
根据减法是加法的逆运算,求9-(-7)=?就是求(-7)+?=9,
∵(-7)+16=9,∴9-(-7)=16,
∵16=9+7,∴9-(-7)=9+7。
9 - (-7) = 16
第4队
第5队
(2)第一名超过第五名多少分?
100
150
-400
350
-100
解:由表可以看出,第一名得了350分,第二名得了150分,第五名得了-400分.
(1)350-150=200(分).
答:第一名超过第二名200分.
(2)350-(-400)=750(分).
答:第一名超过第五名750分.
课本练习
数轴上表示有理数 x 的点与表示有理数3的点之间的距离;同理| x -4|也
可理解为 x 与4两数在数轴上所对应的两点之间的距离.
试探索:
(1)若| x -2|=5,则 x 的值是 -3或7
;
(2)同理| x -5|+| x +3|=8表示数轴上有理数 x 所对应的点到5和-3所
对应的两点的距离之和为8,则所有符合条件的整数 x 的和为 9
七年级数学《有理数的减法(一)》教案

七年级数学《有理数的减法(一)》教案教学目标1、经历探索有理数的减法法则的过程,理解有理数的减法法则。
2、在具体的情境中,能熟练进行整数减法的运算。
教学重、难点重点:对有理数减法法则的理解。
难点:利用法则解决实际问题。
关键:多做对比练习。
一、板书课题,揭示目标1.这节课,我们一起来学习1.4.2有理数的减法。
2.学习目标(1)理解有理数的减法法则;(2)能熟练进行整数减法的运算。
二、学生自学前的指导怎样才能达到这些目标呢?主要靠大家自学。
下面,请同学们按照指导(手指投影屏幕)自学。
自学指导自学P24练习以上的内容后,思考并回答:1、有理数的减法法则:减去一个数,等于加上这个数的相反数。
2、珠穆朗玛峰海拔高度为8848米,与吐鲁番盆地海拔高度为-155米,珠穆朗玛峰比吐鲁番盆地高多少米?3、潜水员甲潜入海平面下10米,潜水员乙潜入海平面下20米,甲的位置比乙的位置高多少米?三、学生自学,教师巡视学生看书,教师巡视,确保人人紧张看书。
四、检验学生自学情况。
1、有理数的减法法则:减去一个数,等于加上这个数的相反数。
2、计算:(1)0-(-2.17)(2)2.8-(-3.2)(3)-10-(-8)(4)(-2/5)-(-3/5)五、引导更正,指导运用1.学生训练。
(1)布置任务:看完了的同学,请举手。
(学生举手)好!下面请XX做第24页练习第1题,其余的同学在座位上练习……请XX做第24页练习第2、3题……(2)学生练习,教师巡视,把数学练习中的典型错误写在黑板上(同一题下)。
观察板演,找错误。
请大家看黑板,找错误。
找到的请举手。
2.学生更正。
3.学生讨论,评判。
(1)先看第一位同学做的(再看第二位同学做的……)[若对,则师:认为对的举手,师判“√”][若有错,则引导学生错误的原因及更正的道理][估计出现的错误](2)第1题中,第(2)题得出-3+5=-8的错误结论。
引导学生说出错因,并更正。
(3)第2题中,-1/3+2/3=-1的错误结论。
人教版七年级数学上册- 有理数的减法法则导学案

第一章有理数1.3 有理数的加减法1.3.2 有理数的减法第1课时有理数的减法法则教学目标:1.经历探索有理数减法法则的过程,理解有理数减法法则.2.会熟练进行有理数减法运算.3.理解有理数减法法则, 能熟练进行减法运算.4.会将减法转化为加法,进行加减混合运算,体会化归思想.教学重点:有理数减法法则和运算.教学难点:有理数减法法则的推导.自主学习:一、情境引入:1.昨天,国际频道的天气预报报道,南半球某一城市的最高气温是5℃,最低气温是-3℃,你能求出这天的日温差吗?(所谓日温差就是这一天的最高气温与最低气温的差)2.珠穆朗玛峰和吐鲁番盆地的海拔高度分别是8848米和-155米,问珠穆朗玛峰比吐鲁番盆地高多少?探索新知:(一)有理数的减法法则的探索1.我们不妨看一个简单的问题:(-8)-(-3)=?也就是求一个数“?”,使(?)+(-3)=-8根据有理数加法运算,有(-5)+(-3)= -8所以(-8)-(-3)= -5 ①2.这样做减法太繁了,让我们再想一想有其他方法吗?试一试做一个填空:(-8)+()= -5容易得到(-8)+(+3 )= -5 ②思考:比较①、②两式,我们有什么发现吗?3.验证:(1)如果某天A地气温是3℃,B地气温是-5℃,A地比B地气温高多少?3-(-5)=3+ ;(2)如果某天A地气温是-3℃,B地气温是-5℃,A地比B地气温高多少?(-3)-(-5)=(-3)+ ;(2)如果某天A地气温是-3℃,B地气温是5℃,A地比B地气温高多少?(-3)-5=(-3)+ ;知识链接1.填空:5的相反数是________;-6的相反数是________;_________的相反数是-a.2.计算:(1)1+6 =________;(2)(–2)+(–8)=________;(3)(–2.2)+2.2=________;(4)(–9)+10=________;(5)5 +(–9)=________;(6)0+(–8)=________.二、新知预习1.计算:15-6=______,15+(-6)=_______;由此可得:15-6 _____ 15+(-6);8-(-3)=_______,8+3=_______;由此可得:8-(-3)______8+3.2.比一比:-6)【自主归纳】有理数的减法法则:减去一个数,等于加上这个数的相反数. (二)有理数的减法法则归纳1.说一说:两个有理数减法有多少种不同的情形?2.议一议:在各种情形下,如何进行有理数的减法计算?3.试一试:你能归纳出有理数的减法法则吗?由此可推出如下有理数减法法则:减去一个数,等于加上这个数的相反数。
2.2有理数的减法(上课-公开课)

勇攀高峰
把图中的每一个输入数减去+9,将所得的输 出数填在括号内: 输入 输出 -(+9) ( 0 ) +9
+7 (-2)
“中岳嵩山”— 少林有高 僧
+4 0 -3 -8
(-5)
(-9)
( ) -12 ( ) -17
勇攀高峰
“北岳恒山”—风光无限美
已知|a-3|+|b+1|=0,
(-2~5℃)
温差是指:最高气温减最低气温。
5
(2)你能从温度计上看出5℃比 7 -2℃高_____℃吗?
0 -2
7
(3)你能用减法算式求该天的温差吗?
5-(-2)=7℃
-5
(4)通过观察温度计,你认为比1℃ 低4℃的温度是多少摄氏度?
-3 是_____℃。
1-4 = -3 列算式为:____________
死海——世界上最低的湖泊,湖面的海拔-392米
位于约旦和巴勒斯坦交界处
怎样比较两地的海拔的差?
吐鲁番盆地——世界上最低的盆地。最低点的海拔是 154米
-
有理数的减法“解决实际问题” 例2:典型例题
我国吐鲁番盆地的最低点的海拔高度是-154米, 死海湖面的海拔是-392米。哪里的海拔高度更低? 低多少米?
死海
海平面
解: -392-(-154)
在有理数范围内, 不存在“不够减”的减法
= (-392)+(+154) = -238(米)
答:死海的湖面更低,比吐鲁番盆地最低点低238米。
请你做一做:
请完成课本35页
课内练习1,2,3
“东岳泰山”
会当凌绝顶,一览众山小
“南岳衡山”—寿比南山
勇 攀 高 峰
七年级有理数的减法

七年级数学导学案课题:有理数的减法一:学习目标:(1)理解并掌握有理数的减法法则,会进行有理数减法运算。
(2)通过把减法运算转化为加法运算,向学生渗透化归思想。
(3)继续发展数感,增强符号感。
二:重点:会用有理数减法法则进行计算。
难点:减法运算转化为加法运算三:自主学习:1:复习引入:计算(1)(–2)+(–27)= (2)(–9)+ 10= (3)45 +(–60)= (4)(–7)+7= (5)0 + (–8)=3.填空:(1)______+6=20;(2)20+______=17;(3)______+(-2)=-20;(4)(-20)+______=-6.在第3题中,已知一个加数与和,求另一个加数,在小学里就是减法运算.如______+6=20,就是求20-6=14,所以14+6=20.那么(2),(3),(4)是怎样算出来的?这就是有理数的减法,减法是加法的逆运算.3:如果某天气温是-3℃~4℃,那么这天的日温差(最高气温与最低气温的差)是多少?4:自主探究:(1)(-3)-(+5)解: (-=-8 =-1.3减数变相反数练习:(2)(-3.7)-(-2.4)减号变()解:(-3.7)-1.3减数变()(注意:两处必须同时改变符号.)归纳:出有理数减法法则:注意“两变”:一是减法变为加法;二是减数变为其相反数.四:抢答:(口答):(1) 6-9= (2)(+4)-(-7)=(3)(-5)-(-8)=(4)(-4)-9= (5)0-(-5)=(6)0-5=1.计算:(1)18-(-3) (2)(-3)-18 (3)(-18)-(-3) (4)(-3)-(-18) (5)(-3)-[6-(-2)] (6)15-(6-9)(7)(-23.4)-(-12.4)(8)2-(-312)(9)23-(-12)2、15℃比5℃高多少?15℃比-5℃高多少?反思:通过计算上面一组有理数减法算式,发现:在小学里学习的减法,差总是小于被减数,在有理数减法中,差不一定小于被减数了,只要减去一个负数,其差就大于被减数.五:拓展练习:(认真检测自我,完善自我!)1:完成同步2:已知 3.4a=-, 2.9b=-,5c=-,求a b c+-的值。
(最新整理)2.2.1有理数的减法教案.doc

2.填空:
(1)温度3℃比-8℃高___________;(2)温度-9℃比-1℃低_____________;
(3)海拔-20m比-30m高________;(4)从海拔22m到-10m,下降了______.
3.已知一个数与3的和是-10,求这个数.
4.求出下列每对数在数轴上对应点之间的距离:
(3)有理数相减,差仍为有理数;
(4)大数减小数,差为正数;小数减大数,差为负数;
2.根据有理数减法的法则,一切加法和减法的运算,都可以统一成加法运算.
六、布置作业
作业本中的相应部分。
至此,教师引导学生归纳出有理数减法法则:
板书设计:
2.2有理数的减法(1)
(一)知识回顾 (三)例题解析 (五)课堂小结
教学过程:
备注
一、创设情境,激发兴趣
一天, 厦门的最高温度是9℃,哈尔滨的最高气温是-7℃,那么这一天厦门的最高温度比哈尔滨的最高气温高多少摄氏度?列出算式.
由学生回答结果,在学生回答的基础上,让学生用式子加以表示:9-(-7)=16.
提出问题:怎么进行这里的减法运算呢?有理数的减法法则是什么?
二、合作学习,共同归纳
例1、例2、例
(二)观察发现 (四)课堂练习 练习设计
课后反思:
根据斯托利亚尔的观点,我们把教学作为一个过程,那么在教学一个新的内容时,我们总是把学生视为探索者,将教学过程模拟成一个“科研过程”,引导学生发现矛盾,提出问题,最后用新的理论来解决原先提出问题,解决原先发现的矛盾.这种教法,归纳起来就是“三部曲”:提出问题——建立理论——解决问题.这节课的设计正是这一教学方法的具体体现.
(2)将有理数减法转化为加法时,要同时改变两个符号:一个是运算符号由“-”变以“+”号;另一个是减数的性质符号.
最新2.2.1 有理数的减法【教学设计】

请学生思考后,解决此问题〔可请一名学生板演〕
渗透化归的思想:让学生归纳一些运算的规律、特征,有利于提高学生的运算能力。
补充例题的作用在于让学生体会减法在实际生活的应用。
稳固练习
教科书第35页的课内练习
小结与作业
课堂小结
通过这节课,你有什么收获?
你还有什么疑问?
本课作业
此处也是让学生验证前面所提的猜测的正确性,用字母把减法法那么表示出来,有利于学生的理解和记忆。
解决问题
例1 即教科书第34页例1 .
先请学生思考并尝试解决,然后教师板书标准解答
之后引导学生反思:“通过这几道题目的计算,你能发现什么?〞
结论:1,有理数的减法可以转化为加法;
2,减正数即加负数,减负数即加正数。
(-5)-(-5)呢?
问题3:计算9-8,9+〔一8〕,15一7,15+〔一7〕,你发现了什么?
请小组代表全班汇报,教师在此根底上归纳:
有理数减法法那么:
减去一个数,等于加上这个数的相反数.
问题4:你能够用字母把法那么表示出来吗?
a-b=a+〔-b〕
允许学生从不同角度观察得出温差为6℃,只要学生的方法合理,都应效励.
第1课时 有理数的减法
教学目标
知识与能
1.使学生掌握有理数减法法那么并熟练地进展有理数减法运算
过程与方法
有理数的加减法法可以互相转化的思想。
2.培养学生的运算能力
情感态度价值观
体会数学与现实生活的联系,培养学生认真、仔细的良好学习态度
教学重点
掌握有理数减法法那么并运用其进展计算
教学难点
2.2 有理数的减法(1)

9
哈尔滨
9
9
9
0
0
-
0
0
=
0
0
}
}
9 7
-7
-7Leabharlann -7-7有理数减法法则: 有理数减法法则: 减去一个数 等于加上这个数的相反数。 减去一个数,等于加上这个数的相反数。 一个 加上这个数的相反数 有理数减法法则的实质是把减法转化为加法 有理数减法法则的实质是把减法转化为加法 减法转化为 把减法运算变为加法运算的思想方法就是转化思想 注意:(1)把减法变加法的同时,必须把减数变成它的 注意: 把减法变加法的同时, 相反数。( 。(2 被减数符号始终不变. 相反数。(2)被减数符号始终不变. 减法变加法: 减法变加法: + 2 3+(- _; (-5 __ +2)=-1+(-2) )=__ (1)3-5=3+(-5) (2) -1-(+2)=__ (-_; 0+(-2) (4)(-3)-(-5)=___ +(+5_; +(-2 ; __; ) _; (3)0-2=___ __ 3)- 5)= -3+ +5) ) (-6 (5)(+8)-(+6)= (+8)+(-6) )(+8) +8 +6) 。
更上一层楼
已知两数的和是最大的负整数, 已知两数的和是最大的负整数,其中一个加数是最小 的正整数,求另一个加数. 的正整数,求另一个加数.
完成书本第31页课内练习3,作业题5,6, 完成书本第31页课内练习3 作业题5 31页课内练习
学习了本节课你有哪些收获? 学习了本节课你有哪些收获?
知识点
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.2有理数的减法(1)
【课前热身】
1.减去一个数等于加上这个数的 .
2.计算:4-(-3)=4+( )= , (-21)-(+3
1)= . 3.计算:-1-1= ,(-6)-(+5)-(-6)=
4.下列格式中,运算错误的是 ( )
A.(-3)-(-5)=2
B.0-7=7
C.7.2-(-4.8)=12
D.(-321)-541=-84
3 5.峨眉山上某天的最高气温为12℃,最低气温为-4℃,那么这天的最高气温比最低气温高 ( )
A.4℃
B.8℃
C.12 ℃
D.16%
【课堂讲练】
典型例题1 已知一个数与5的和等于-2,那么这个数是多少?
巩固练习1 已知-11与一个数的差是11,求这个数.
典型例题2 若数轴上有两点A,B,它们表示的数分别是:(1)7,9;(2)-9,-5;(3)-5,9;(4)m,n你能求得A,B之间的距离吗?
巩固练习2 (1)求出数轴上-4和4.5所对应的两点之间的距离,可列算式;
(2)数轴上两点A,B表示的数分别是a与-6,那么线段AB 的长度是 .
【跟踪练习】
一、选择题
1.在(-5)-( )=-7中的括号里应填 ( )
A.-2
B.2
C.-12
D.12
2.在下列等式:2-(-2)=0,(-3)-(+3)=0,(-3)-|-3|=0,0-(-1)=1,其中正确的算式有 ( )
A.1个
B.2个
C.3个
D.4个
3.下列说法中错误的有 ( )
①若两数的差是正数,则这两个数都是正数
②若两个数是互为相反数,则它们的差为零
③零减去任何-个有理数,其差是该数的相反数
A.0个
B.1个
C.2个
D.3个
4.已知数m和n,满足m为正数,n为负数,则m,m-n,m+n 的大小关系是 ( )
A.m>m-n>m+n
B.m+n>m>m-n
C.m-n>m+n>m
D.m-n>m>m+n
二、填空题
5.0-(-3)= ,-3-(-7.5)= .
6.算式是5-7看成减法运算,减数是;看成加法运算,第-个加数是5,第二个加数是 .
7.在化肥袋上我们经常看到(50±0.2)kg的字样,这说明
这种装化肥最重的比最轻的重 kg.
三、解答题
8.计算:
(1)(-2)-8
(2)-2-3
(3)(-23)-(-27)-27
(4)(-732)+(+421)-2
1
9.已知a 是7的相反数,b 比a 的相反数大3,则b 比a 大多少?
10.2009年4月某日,哈尔滨等5个城市的最高气温与最 低气温记录如下表(单位℃)哪个城市的温差最大? 哪个城市的温差最小?
参考答案:
【课前热身】
5 3.-2 -5 4.B 5.D
1.相反数
2.+3 7-
6
【课堂讲练】
典型例题1 解:-2-5=(-2)+(-5)=-7答:这个数是-7
巩固练习1 -22
典型例题2 解析:对于(1)(2)(3)通过画数轴,观察两点的位置,再求距离,对于(4)可在前3个问题解决的情况下,进行归纳后得到规律即可求得. 解:(1)9-7=2;(2)在数轴上数单位可得是4个单位,即距离为4,而4=(-5)-(-9)=|(-9)-(-5)|(3)在数轴上数单位可得是14个单位,而14=9-(-5)=|(-5)-9|;(4)由前三题的结果可得|m-n | 巩固练习2 (1)4.5-(-4) (2)|n+6|
【跟踪演练】
1.B
2.A
3.C
4.D
5.3 4.5
6.7 -7
7. 0.4
8.(1)-10 (2)-5
2 9.17 10.(1)哈尔滨的温差最大(2)北京和大连的
(3)-23(3)-3
3
温差最小.。
