2013高考总复习数学(文)配套课时巩固与训练11章1课时训练

合集下载

2013高考总复习数学(理)配套课时巩固与训练4章5课时训练

1.函数y ＝|sin x |－2sin x 的值域是( )A ．[－3，－1]B ．[－1,3]C ．[0,3]D ．[－3,0] 解析：选B.当0≤sin x ≤1时，y ＝sin x －2sin x ＝－sin x ，此时y ∈[－1,0]；当－1≤sin x <0时，y ＝－sin x －2sin x ＝－3sin x ，此时y ∈(0,3]，求其并集得y ∈[－1,3]．2．函数f (x )＝tan ωx (ω>0)图象的相邻两支截直线y ＝π4所得线段长为π4，则f (π4)的值是( )A ．0B ．1C ．－1 D.π4解析：选A.由题意知T ＝π4 ，由πω＝π4得ω＝4，∴f (x )＝tan4x ，∴f (π4)＝tanπ＝0.3．(2009年高考重庆卷)下列关系式中正确的是( ) A ．sin11°<cos10°<sin168° B ．sin168°<sin11°<cos10° C ．sin11°<sin168°<cos10° D ．sin168°<cos10°<sin11° 解析：选C.∵sin168°＝sin(180°－12°)＝sin12°， cos10°＝sin(90°－10°)＝sin80°.又∵g (x )＝sin x 在x ∈[0，π2]上是增函数， ∴sin11°<sin12°<sin80°，即sin11°<sin168°<cos10°.4．设点P 是函数f (x )＝sin ωx 的图象C 的一个对称中心，若点P到图象C 的对称轴的距离的最小值是π8，则f (x )的最小正周期是( )A.π2 B ．πC ．2π D.π4解析：选A.依题意得T 4＝π8，所以最小正周期为T ＝π2.5．已知函数y ＝2sin 2(x ＋π4)－cos2x ，则它的周期T 和图象的一条对称轴方程是( )A ．T ＝2π，x ＝π8B ．T ＝2π，x ＝3π8C ．T ＝π，x ＝π8D ．T ＝π，x ＝3π8解析：选 D.∵y ＝2sin 2(x ＋π4)－cos2x ＝1－cos(2x ＋π2)－cos2x ＝1＋sin2x －cos2x ＝1＋2sin(2x －π4)，所以其周期T ＝π，对称轴方程的表达式可由2x －π4＝k π＋π2(k ∈Z )得x ＝k π2＋3π8(k ∈Z )，故当k ＝0时的一条对称轴方程为x ＝3π8，故答案为D.6．(2008年高考天津卷)已知函数f (x )是定义在R 上的偶函数，且在区间[0，＋∞)上是增函数．令a ＝f (sin 2π7)，b ＝f (cos 5π7)，c ＝f (tan 5π7)，则( )A ．b ＜a ＜cB ．c ＜b ＜aC ．b ＜c ＜aD ．a ＜b ＜c解析：选A.sin 27π＝sin(π－57π)＝sin 57π. 又π2＜57π＜34π.由三角函数线tan 57π＜cos 57π＜sin 57π且cos 57π＜0，sin 57π＞0.如图．∴⎪⎪⎪⎪⎪⎪cos 57π＜⎪⎪⎪⎪⎪⎪sin 57π＜⎪⎪⎪⎪⎪⎪tan 57π. 又f (x )在[0，＋∞)上递增且为偶函数，∴f (⎪⎪⎪⎪⎪⎪cos 57π)＜f (⎪⎪⎪⎪⎪⎪sin 57π)＜f (⎪⎪⎪⎪⎪⎪tan 57π)，即b ＜a ＜c ，故选A.7．函数y ＝lgsin x ＋ cos x －12的定义域为________．解析：(1)要使函数有意义必须有⎩⎨⎧sin x >0cos x －12≥0，即⎩⎨⎧sin x >0cos x ≥12，解得⎩⎨⎧2k π<x <π＋2k π－π3＋2k π≤x ≤π3＋2k π(k ∈Z )，∴2k π<x ≤π3＋2k π，k ∈Z ，∴函数的定义域为{x |2k π<x ≤π3＋2k π，k ∈Z }．答案：{x |2k π<x ≤π3＋2k π，k ∈Z }8．已知函数f (x )＝2sin ωx (ω>0)在区间[－π3，π4]上的最小值是－2，则ω的最小值等于________．解析：由题意知T 4≤π3，T ＝2πω，∴2ω≥3，ω≥32，∴ω的最小值等于32.答案：329．对于函数f (x )＝⎩⎪⎨⎪⎧sin x ，sin x ≤cos xcos x ，sin x >cos x ，给出下列四个命题：①该函数是以π为最小正周期的周期函数；②当且仅当x ＝π＋k π(k ∈Z )时，该函数取得最小值－1；③该函数的图象关于x ＝5π4＋2k π(k ∈Z )对称；④当且仅当2k π<x <π2＋2k π(k ∈Z )时，0<f (x )≤22.其中正确命题的序号是________．(请将所有正确命题的序号都填上)解析：画出f(x)在一个周期[0,2π]上的图象．答案：③④10.已知函数f (x )＝log 2[2sin(2x －π3)]．(1)求函数的定义域；(2)求满足f (x )＝0的x 的取值范围．解：(1)令2sin(2x －π3)>0⇒sin(2x －π3)>0⇒2k π<2x －π3<2k π＋π，k ∈Z ⇒k π＋π6<x <k π＋23π，k ∈Z .故函数的定义域为(k π＋π6，k π＋23π)，k ∈Z .(2)∵f (x )＝0，∴sin(2x －π3)＝22⇒2x －π3＝2k π＋π4或2k π＋34π，k ∈Z⇒x ＝k π＋724π或x ＝k π＋1324π，k ∈Z ，故x 的取值范围是{x |x ＝k π＋724π或x ＝k π＋1324π，k ∈Z }．11．已知函数f (x )＝sin 2ωx ＋3sin ωx sin(ωx ＋π2)(ω>0)的最小正周期为π.(1)求ω的值；(2)求函数f (x )在区间[0，2π3]上的取值范围．解：(1)f (x )＝1－cos2ωx 2＋32sin2ωx＝32sin2ωx －12cos2ωx ＋12＝sin(2ωx －π6)＋12.因为函数f (x )的最小正周期为π，且ω>0，所以2π2ω＝π，解得ω＝1.(2)由(1)得f (x )＝sin(2x －π6)＋12.因为0≤x ≤2π3，所以－π6≤2x －π6≤7π6，所以－12≤sin(2x －π6)≤1，所以0≤sin(2x －π6)＋12≤32，即f (x )的取值范围为[0，32]．12．已知a >0，函数f (x )＝－2a sin(2x ＋π6)＋2a ＋b ，当x ∈[0，π2]时，－5≤f (x )≤1.(1)求常数a ，b 的值；(2)设g (x )＝f (x ＋π2)且lg g (x )>0，求g (x )的单调区间．解：(1)∵x ∈[0，π2]，∴2x ＋π6∈[π6，7π6]，∴sin(2x ＋π6)∈[－12，1]，∴－2a sin(2x ＋π6)∈[－2a ，a ]， ∴f (x )∈[b,3a ＋b ]，又－5≤f (x )≤1. ∴⎩⎪⎨⎪⎧ b ＝－53a ＋b ＝1，解得⎩⎪⎨⎪⎧a ＝2b ＝－5. (2)f (x )＝－4sin(2x ＋π6)－1，g (x )＝f (x ＋π2)＝－4sin(2x ＋7π6)－1＝4sin(2x ＋π6)－1，又由lg g (x )>0，得g (x )>1，∴4sin(2x ＋π6)－1>1，∴sin(2x ＋π6)>12， ∴π6＋2k π<2x ＋π6<56π＋2k π，k ∈Z ，由π6＋2k π<2x ＋π6≤2k π＋π2，得k π<x ≤k π＋π6，k ∈Z . 由π2＋2k π≤2x ＋π6<56π＋2k π得 π6＋k π≤x <π3＋k π，k ∈Z .∴函数g (x )的单调递增区间为(k π，π6＋k π](k ∈Z )，单调递减区间为[π6＋k π，π3＋k π)(k ∈Z )．。

2013高考总复习数学(文)配套课时巩固与训练9章2课时训练

1．(2009年高考全国卷Ⅱ)双曲线x 26－y 23＝1的渐近线与圆(x －3)2＋y 2＝r 2(r ＞0)相切，则r ＝( )A. 3 B ．2 C ．3 D ．6解析：选A.∵双曲线x 26－y 23＝1的渐近线方程为y ＝±22x ，则圆心(3,0)到2y ＋x ＝0的距离为r ，∴r ＝33＝ 3.故选A.2．(2009年高考江西卷)设F 1和F 2为双曲线x 2a 2－y 2b2＝1(a ＞0，b ＞0)的两个焦点，若F 1、F 2、P (0,2b )是正三角形的三个顶点，则双曲线的离心率为( )A.32 B ．2 C.52D ．3 解析：选B.由2b c ＝3，令b ＝3，得c ＝2，∴a ＝1，∴e ＝ca＝2.3．设P 是双曲线x 222－y2b2＝1上一点，双曲线的一条渐近线方程为3x －2y ＝0，F 1、F 2分别是双曲线的左、右焦点．若|PF 1|＝3，则|PF 2|等于( )A ．1或5B ．6C ．7D ．9解析：选C.由渐近线方程y ＝32x ，且a ＝2，得b ＝3.∵|PF 1|＝3＜2a ＝4，∴P 点在双曲线左支上．据定义有|PF 2|－|PF 1|＝4， ∴|PF 2|＝7.4.(2008年高考山东卷)设椭圆C 1的离心率为513，焦点在x 轴上且长轴长为26，若曲线C 2上的点到椭圆C 1的两个焦点的距离的差的绝对值等于8，则曲线C 2的标准方程为( )A.x 242－y 232＝1B.x 2132－y 252＝1 C.x 232－y 242＝1 D.x 2132－y 2122＝1 解析：选A.在椭圆C 1中，由⎩⎨⎧2a ＝26，c a ＝513，得⎩⎪⎨⎪⎧a ＝13，c ＝5，椭圆C 1的焦点为F 1(－5,0)，F 2(5,0)，曲线C 2是以F 1、F 2为焦点，实轴长为8的双曲线，故C 2的标准方程为：x 242－y 232＝1，故选A.5．已知双曲线的两个焦点分别为F 1(－5，0)，F 2(5，0)，P 是双曲线上的一点，且PF 1⊥PF 2，|PF 1||PF 2|＝2，则双曲线方程是( )A.x 22－y 23＝1B.x 23－y 22＝1 C.x 24－y 2＝1 D ．x 2－y 24＝1 解析：选C.∵PF 1⊥PF 2，∴|PF 1|2＋|PF 2|2＝|F 1F 2|2，即(|PF 1|－|PF 2|)2＋2|PF 1||PF 2|＝|F 1F 2|2，又||PF 1|－|PF 2||＝2a ，|F 1F 2|＝2c ＝25，|PF 1|·|PF 2|＝2， ∴(2a )2＋2×2＝(25)2，解得a 2＝4，又c 2＝5，∴b 2＝1，∴双曲线方程为x24－y 2＝1.6．过双曲线M ：x 2－y 2b2＝1的左顶点A 作斜率为1的直线l ，若l与双曲线M 的两条渐近线分别相交于点B 、C ，且|AB |＝|BC |，则双曲线M 的离心率是( )A.10B. 5C.103D.52解析：选A.据题意可设l AB ：y ＝x ＋1，l OC ：y ＝bx ，l OB ：y ＝－bx ，由⎩⎪⎨⎪⎧y ＝x ＋1y ＝bx解得C 点纵坐标为b b －1，B 点纵坐标为b 1＋b ，因为|AB |＝|BC |，所以b b －1＝2 b b ＋1，解得b ＝3，所以e ＝ca ＝10.7．已知圆C ：x 2＋y 2－6x －4y ＋8＝0.以圆C 与坐标轴的交点分别作为双曲线的一个焦点和顶点，则适合上述条件的双曲线的标准方程为________．答案：x 24－y 212＝18．(2009年高考湖南卷)过双曲线C ：x 2a 2－y 2b2＝1(a ＞0，b ＞0)的一个焦点作圆x 2＋y 2＝a 2的两条切线，切点分别为A 、B .若∠AOB ＝120°(O 是坐标原点)，则双曲线C 的离心率为________．解析：如图，由题知OA ⊥AF ，OB ⊥BF且∠AOB ＝120°，∴∠AOF ＝60°，又OA ＝a ，OF ＝c ，∴a c ＝OA OF ＝cos 60°＝12，∴ca＝2.答案：29．(2008年高考海南、宁夏卷)设双曲线x 29－y 216＝1的右顶点为A ，右焦点为F .过点F 平行于双曲线的一条渐近线的直线与双曲线交于点B ，则△AFB 的面积为________．解析：a 2＝9，b 2＝16，故c ＝5，∴A (3,0)，F (5,0)，不妨设BF 的方程为y ＝43(x －5)，代入双曲线方程解得B (175，－3215)．∴S △AFB ＝12|AF |·|y B |＝12·2·3215＝3215.答案：321510．已知双曲线的一条渐近线方程是x －2y ＝0，且过点P (4,3)，求双曲线的标准方程．解：法一：∵双曲线的一条渐近线方程为x －2y ＝0，当x ＝4时，y ＝2＜y P ＝3.∴双曲线的焦点在y 轴上．从而有a b ＝12，∴b ＝2a .设双曲线方程为y 2a 2－x24a2＝1，由于点P (4,3)在此双曲线上， ∴9a 2－164a2＝1，解得a 2＝5.∴双曲线方程为y 25－x 220＝1.法二：∵双曲线的一条渐近线方程为x －2y ＝0，即x2－y ＝0， ∴双曲线的渐近线方程为x 24－y 2＝0.设双曲线方程为x 24－y 2＝λ(λ≠0)，∵双曲线过点P (4,3)， ∴424－32＝λ，即λ＝－5. ∴所求双曲线方程为x 24－y 2＝－5，即y 25－x220＝1. 11.如图所示，双曲线的中心在坐标原点，焦点在x 轴上，F 1，F 2分别为左、右焦点，双曲线的左支上有一点P ，∠F 1PF 2＝π3，且△PF 1F 2的面积为23，又双曲线的离心率为2，求该双曲线的方程．解：设双曲线方程为：x 2a 2－y 2b2＝1(a ＞0，b ＞0)，F 1(－c,0)，F 2(c,0)，P (x 0，y 0)．在△PF 1F 2中，由余弦定理，得：|F 1F 2|2＝|PF 1|2＋|PF 2|2－2|PF 1|·|PF 2|·cos π3＝(|PF 1|－|PF 2|)2＋|PF 1|·|PF 2|. 即4c 2＝4a 2＋|PF 1|·|PF 2|. 又∵S △PF 1F 2＝2 3. ∴12|PF 1|·|PF 2|·sin π3＝2 3. ∴|PF 1|·|PF 2|＝8.∴4c 2＝4a 2＋8，即b 2＝2.又∵e ＝c a ＝2，∴a 2＝23.∴双曲线的方程为：3x 22－y 22＝1.12．已知中心在原点的双曲线C 的右焦点为(2,0)，右顶点为(3，0)．(1)求双曲线C 的方程； (2)若直线：y ＝kx ＋m (k ≠0，m ≠0)与双曲线C 交于不同的两点M 、N ，且线段MN 的垂直平分线过点A (0，－1)，求实数m 的取值范围．解：(1)设双曲线方程为x 2a 2－y 2b2＝1(a ＞0，b ＞0)．由已知得a ＝3，c ＝2. 又a 2＋b 2＝c 2，得b 2＝1.故双曲线C 的方程为x 23－y 2＝1.(2)联立⎩⎨⎧y ＝kx ＋mx 23－y 2＝1整理得(1－3k 2)x 2－6kmx －3m 2－3＝0.∵直线与双曲线有两个不同的交点，∴⎩⎪⎨⎪⎧1－3k 2≠0Δ＝12(m 2＋1－3k 2)＞0，可得m 2＞3k 2－1且k 2≠13①设M (x 1，y 1)，N (x 2，y 2)，MN 的中点为B (x 0，y 0)．则x 1＋x 2＝6km1－3k 2，x 0＝x 1＋x 22＝3km 1－3k2， y 0＝kx 0＋m ＝m1－3k 2.由题意，AB ⊥MN ，∵k AB ＝m1－3k 2＋13km 1－3k 2＝－1k (k ≠0，m ≠0)．整理得3k 2＝4m ＋1②将②代入①，得m 2－4m ＞0，∴m ＜0或m ＞4.又3k 2＝4m ＋1＞0(k ≠0)，即m ＞－14∴m 的取值范围是(－14，0)∪(4，＋∞)．。

2013高考总复习数学(理)配套课时巩固与训练2章3课时巩固

1．(2010年皖南八校联考)设函数f (x )是定义在R 上的奇函数，且f (－3)＝－2，则f (3)＋f (0)＝( )A ．3B ．－3C ．2D ．7解析：选C.由题意得f (3)＋f (0)＝－f (－3)＋f (0)＝2＋0＝2.故选C.2．(2009年高考福建卷)下列函数f (x )中，满足“对任意的x 1，x 2∈(0，＋∞)，当x 1＜x 2时，都有f (x 1)＞f (x 2)”的是( )A ．f (x )＝1xB ．f (x )＝(x －1)2C ．f (x )＝e xD ．f (x )＝ln(x ＋1)解析：选A.由题意知函数f (x )在(0，＋∞)上是减函数，在A 中，由f ′(x )＝－1x 2＜0得f (x )在(－∞，0)和(0，＋∞)上为减函数；在B 中，由f ′(x )＝2(x －1)＜0得x ＜1，所以f (x )在(－∞，1)上为减函数．在C 中，由f ′(x )＝e x ＞0知f (x )在R 上为增函数．在D 中，由f ′(x )＝1x ＋1且x ＋1＞0知f ′(x )＞0，所以f (x )在(－1，＋∞)上为减函数．3．已知函数f (x )为R 上的减函数，则满足f (|1x |)＜f (1)的实数x 的取值范围是( )A ．(－1,1)B ．(0,1)C ．(－1,0)∪(0,1)D ．(－∞，－1)∪(1，＋∞)解析：选C.∵f (x )在R 上为减函数且f (|1x |)＜f (1)，∴|1x |＞1，即|x |＜1且x ≠0，得－1＜x ＜0或0＜x ＜1.4．(原创题)已知f (x )＝x 2＋x ，则f (a ＋1a )________f (1)．(填“≤”“≥”)．解析：∵a ＋1a ≥2或a ＋1a ≤－2，f (x )的对称轴为x ＝－12.∴f (x )在(－12，＋∞)上为增函数，在(－∞，－12)上为减函数．又f (2)＝22＋2＝6>2＝f (1)，f (－2)＝(－2)2＋(－2)＝2＝f (1)，∴f (a ＋1a )≥f (1)．答案：≥5．(2008年高考上海卷)若函数f (x )＝(x ＋a )(bx ＋2a )(常数a 、b ∈R )是偶函数，且它的值域为(－∞，4]，则该函数的解析式f (x )＝________________.解析：由于f (x )的定义域为R ，值域为(－∞，4]，可知b ≠0，∴f (x )为二次函数，f (x )＝(x ＋a )(bx ＋2a )＝bx 2＋(2a ＋ab )x ＋2a 2.∵f (x )为偶函数，∴其对称轴为x ＝0，∴－2a ＋ab 2b ＝0，∴2a ＋ab ＝0，∴a ＝0或b ＝－2.若a ＝0，则f (x )＝bx 2与值域是(－∞，4]矛盾，∴a ≠0，若b ＝－2，又其最大值为4，∴4b ×2a 24b ＝4，∴2a 2＝4，∴f (x )＝－2x 2＋4.答案：－2x 2＋46.已知函数f (x )＝1a －1x (a ＞0，x ＞0)．(1)求证：f (x )在(0，＋∞)上是增函数；(2)若f (x )在[12，2]上的值域是[12，2]，求a 的值．解：(1)证明：设x 2＞x 1＞0，则x 2－x 1＞0，x 1x 2＞0.∵f (x 2)－f (x 1)＝(1a －1x 2)－(1a －1x 1)＝1x 1－1x 2＝x 2－x 1x 1x 2＞0， ∴f (x 2)＞f (x 1)，∴f (x )在(0，＋∞)上是增函数．(2)∵f (x )在[12，2]上的值域是[12，2]，又f (x )在[12，2]上单调递增，∴f (12)＝12，f (2)＝2，代入可得a ＝25.。

2013高考总复习数学(理)配套课时巩固与训练15章3课时训练

1．用数学归纳法证明“当n为正奇数时，x n＋y n能被x＋y整除”，第二步归纳假设应写成()A．假设n＝2k＋1(k∈N*)正确，再推n＝2k＋3正确B．假设n＝2k－1(k∈N*)正确，再推n＝2k＋1正确C．假设n＝k(k∈N*)正确，再推n＝k＋1正确D．假设n＝k(k≥1)正确，再推n＝k＋2正确解析：选B.首先要注意n为奇数，其次还要使n＝2k－1能取到1，故选B.2．用数学归纳法证明等式1＋3＋5＋…＋(2n－1)＝n2(n∈N*)的过程中，第二步假设n＝k时等式成立，则当n＝k＋1时应得到() A．1＋3＋5＋…＋(2k＋1)＝k2B．1＋3＋5＋…＋(2k＋1)＝(k＋1)2C．1＋3＋5＋…＋(2k＋1)＝(k＋2)2D．1＋3＋5＋…＋(2k＋1)＝(k＋3)2解析：选B.∵n＝k＋1时，等式左边＝1＋3＋5＋…＋(2k－1)＋(2k＋1)＝k2＋(2k＋1)＝(k＋1)2.故选B.3．用数学归纳法证明：“1＋a＋a2＋…＋a n＋1＝1－a n＋21－a(a≠1)”在验证n＝1时，左端计算所得的项为()A．1 B．1＋aC．1＋a＋a2D．1＋a＋a2＋a3解析：选C.当n＝1时，左端＝1＋a＋a2.4．下列代数式(其中k∈N*)能被9整除的是()A．6＋6·7k B．2＋7k－1C．2(2＋7k＋1) D．3(2＋7k)解析：选D.(1)当k＝1时，显然只有3(2＋7k)能被9整除．(2)假设当k＝n(n∈N*)时，命题成立，即3(2＋7n)能被9整除，那么3(2＋7n＋1)＝21(2＋7n)－36.这就是说，k＝n＋1时命题也成立．5．已知1＋2×3＋3×32＋4×33＋…＋n×3n－1＝3n(na－b)＋c对一切n∈N*都成立，则a、b、c的值为()A ．a ＝12，b ＝c ＝14B ．a ＝b ＝c ＝14C ．a ＝0，b ＝c ＝14D ．不存在这样的a 、b 、c解析：选A.∵等式对一切n ∈N *均成立，∴n ＝1,2,3时等式成立，即⎩⎪⎨⎪⎧ 1＝3(a －b )＋c 1＋2×3＝32(2a －b )＋c 1＋2×3＋3×32＝33(3a －b )＋c整理得⎩⎪⎨⎪⎧ 3a －3b ＋c ＝118a －9b ＋c ＝781a －27b ＋c ＝34，解得a ＝12，b ＝c ＝14.6．在数列{a n } 中，a 1＝13，且S n ＝n (2n －1)a n ，通过求a 2，a 3，a 4，猜想a n 的表达式为( )A.1(n －1)(n ＋1)B.12n (2n ＋1)C.1(2n －1)(2n ＋1)D.1(2n ＋1)(2n ＋2)解析：选C.由a 1＝13，S n ＝n (2n －1)a n ，得S 2＝2(2×2－1)a 2，即a 1＋a 2＝6a 2，∴a 2＝115＝13×5，S 3＝3(2×3－1)a 3，即13＋115＋a 3＝15a 3.∴a 3＝135＝15×7，a 4＝17×9.故选C . 7．利用数学归纳法证明“(n ＋1)(n ＋2)…(n ＋n )＝2n ×1×3×…×(2n －1)，n ∈N *”时，从“n ＝k ”变到“n ＝k ＋1”时，左边应增乘的因式是________．解析：当n ＝k (k ∈N *)时，左式为(k ＋1)(k ＋2)…(k ＋k )；当n ＝k ＋1时，左式为(k ＋1＋1)·(k ＋1＋2)·…·(k ＋1＋k －1)·(k ＋1＋k ) ·(k ＋1＋k ＋1)，则左边应增乘的式子是(2k ＋1)(2k ＋2)k ＋1＝2(2k ＋1)．答案：2(2k ＋1)8．若f (n )＝12＋22＋32＋…＋(2n )2，则f (k ＋1)与f (k )的递推关系式是________．解析：∵f (k )＝12＋22＋…＋(2k )2，∴f (k ＋1)＝12＋22＋…＋(2k )2＋(2k ＋1)2＋(2k ＋2)2，∴f (k ＋1)＝f (k )＋(2k ＋1)2＋(2k ＋2)2.答案：f (k ＋1)＝f (k )＋(2k ＋1)2＋(2k ＋2)29．数列{a n }中，已知a 1＝1，当n ≥2时，a n －a n －1＝2n －1，依次计算a 2，a 3，a 4后，猜想a n 的表达式是________．解析：计算出a 1＝1，a 2＝4，a 3＝9，a 4＝16.可猜想a n ＝n 2.答案：n 210．对于n ∈N *，用数学归纳法证明：1·n ＋2·(n －1)＋3·(n －2)＋…＋(n －1)·2＋n ·1＝16n (n ＋1)(n ＋2)．证明：设f (n )＝1·n ＋2·(n －1)＋3·(n －2)＋…＋(n －1)·2＋n ·1.(1)当n ＝1时，左边＝1，右边＝1，等式成立；(2)设当n ＝k 时等式成立，即1·k ＋2·(k －1)＋3·(k －2)＋…＋(k －1)·2＋k ·1＝16k (k ＋1)(k ＋2)，则当n ＝k ＋1时，f (k ＋1)＝1·(k ＋1)＋2[(k ＋1)－1]＋3[(k ＋1)－2]＋…＋[(k ＋1)－2]·3＋[(k ＋1)－1]·2＋(k ＋1)·1＝f (k )＋1＋2＋3＋…＋k ＋(k ＋1)＝16k (k ＋1)(k ＋2)＋12(k ＋1)(k ＋1＋1)＝16(k ＋1)(k ＋2)(k ＋3)．∴由(1)(2)可知当n ∈N *时等式都成立．11.已知点P n (a n ，b n )满足a n ＋1＝a n ·b n ＋1，b n ＋1＝b n 1－4a n (n ∈N *)且点P 1的坐标为(1，－1)．(1)求过点P 1，P 2的直线l 的方程；(2)试用数学归纳法证明：对于n ∈N *，点P n 都在(1)中的直线l 上．解：(1)由P 1的坐标为(1，－1)知a 1＝1，b 1＝－1.∴b 2＝b 11－4a 12＝13. a 2＝a 1·b 2＝13.∴点P 2的坐标为(13，13)∴直线l 的方程为2x ＋y ＝1.(2)证明：①当n ＝1时，2a 1＋b 1＝2×1＋(－1)＝1成立．②假设n ＝k (k ∈N *，k ≥1)时，2a k ＋b k ＝1成立，则当n ＝k ＋1时，2a k ＋1＋b k ＋1＝2a k ·b k ＋1＋b k ＋1＝b k 1－4a k 2(2a k＋1) ＝b k 1－2a k ＝1－2a k 1－2a k＝1， ∴当n ＝k ＋1时，命题也成立．由①②知，对n ∈N *，都有2a n ＋b n ＝1，即点P n 在直线l 上．12．已知正项数列{a n }和{b n }中，a 1＝a (0＜a ＜1)，b 1＝1－a .当n ≥2时，a n ＝a n －1b n ，b n ＝b n －11－a 2n －1. (1)证明：对任意n ∈N *，有a n ＋b n ＝1；(2)求数列{a n }的通项公式．解：(1)证明：用数学归纳法证明． ①当n ＝1时，a 1＋b 1＝a ＋(1－a )＝1，命题成立； ②假设n ＝k (k ≥1且k ∈N *)时命题成立，即a k ＋b k ＝1，则当n ＝k＋1时，a k ＋1＋b k ＋1＝a k b k ＋1＋b k ＋1＝(a k ＋1)·b k ＋1＝(a k ＋1)·b k 1－a k 2＝b k 1－a k＝b k b k＝1. ∴当n ＝k ＋1时，命题也成立．由①、②可知，a n ＋b n ＝1对n ∈N *恒成立．(2)∵a n ＋1＝a n b n ＋1＝a n b n 1－a n 2＝a n (1－a n )1－a n 2＝a n 1＋a n， ∴1a n ＋1＝1＋a n a n ＝1a n＋1，即1a n ＋1－1a n＝1. 数列{1a n }是公差为1的等差数列，其首项为1a 1＝1a ， 1a n ＝1a ＋(n －1)×1，从而a n ＝a 1＋(n －1)a .。

2013高考总复习数学(文)配套课时巩固与训练7章1课时训练

1．已知a 1b B ．ab <1C.a b >1 D ．a 2>b 2解析：选D.若b ＝0，可排除A ，C ，无论b >0还是b <0，D 均成立．2．下列命题中的真命题是( )A ．若a >b ，c >d ，则ac >bdB ．若|a |>b ，则a 2>b 2C ．若a >b ，则a 2>b 2D ．若a >|b |，则a 2>b 2 解析：选D.∵a >|b |≥0，∴a 2>b 2，故选D.3．如果a ，b ，c 满足c acB ．c (b －a )>0C ．cb 2<ab 2D ．ac (a －c )<0解析：选C.当b ＝0时，b 2＝0，cb 2＝ab 2，故选C.4．已知a ＋b >0，b <0，那么a ，b ，－a ，－b 的大小关系是( )A ．a >b >－b >－aB ．a >－b >－a >bC ．a >－b >b >－aD ．a >b >－a >－b解析：选C.法一：∵A 、B 、C 、D 四个选项中，每个选项都是唯一确定的答案，∴可用特殊值法．令a ＝2，b ＝－1，则有2>－(－1)>－1>－2，即a >－b >b >－a .法二：∵a ＋b >0，b <0，∴a >－b >0，－a －b >0>b >－a ，即a >－b >b >－a .5．若x ＋y >0，a <0，ay >0，则x －y 的值为( )A ．大于0B ．等于0C ．小于0D ．符号不能确定解析：选A.法一：因为a <0，ay >0，所以y <0，又x ＋y >0，所以x >－y >0，所以x －y >0.应选A.法二：a <0，ay >0，取a ＝－2得：－2y >0，又x ＋y >0，两式相加得x －y >0.应选A.6．甲、乙两人同时从寝室到教室，甲一半路程步行，一半路程跑步，乙一半时间步行，一半时间跑步，如果两人步行速度、跑步速度均相同，则( )A ．甲先到教室B ．乙先到教室C ．两人同时到教室D ．谁先到教室不确定解析：选B.设步行速度与跑步速度分别为v 1，v 2，显然v 1<v 2，总路程为2s ，则甲用时间为s v 1＋s v 2，乙用时间为4s v 1＋v 2，而s 1＋s 2－4s v 1＋v 2＝s (v 1＋v 2)2－4s v 1v 2v 1v 2(v 1＋v 2) ＝s (v 1－v 2)2v 1v 2(v 1＋v 2)>0，故s v 1＋s v 2>4s v 1＋v 2，故乙先到教室． 7．设A ＝1＋2x 4，B ＝2x 3＋x 2，x ∈R ，则A ，B 的大小关系是________．解析：∵A －B ＝1＋2x 4－2x 3－x 2＝2x 3(x －1)－(x 2－1)＝(x －1)(2x 3－x －1)＝(x －1)2(2x 2＋2x ＋1)，∵(x －1)2≥0,2x 2＋2x ＋1>0，∴A －B ≥0，即A ≥B .答案：A ≥B8．下列四个不等式：①a <0<b ；②b <a <0；③b <0<a ；④0<b <a ，其中能使1a <1b 成立的充分条件有________．解析：1a <1b ⇒b －a ab <0⇔b －a 与ab 异号，因此①②④能使b －a 与ab 异号．答案：①②④9．用锤子以均匀的力敲击铁钉钉入木板．随着铁钉的深入，铁钉所受的阻力会越来越大，使得每次钉入木板的钉子长度后一次为前一次的1k (k ∈N *)．已知一个铁钉受击3次后全部进入木板，且第一次受击后进入木板部分的铁钉长度是钉长的47，请从这件事实中提炼出一个不等式组是________．解析：依题意47＋47k <1，且三次后全部进入，即47＋47k ＋47k 2≥1，故不等式组为⎩⎪⎨⎪⎧ 47＋47k <147＋47k ＋47k 2≥1.k ∈N *答案：⎩⎪⎨⎪⎧ 47＋47k <147＋47k ＋47k 2≥1k ∈N *10．已知：a >b >0，c >d >0，求证：a d >b c .证明：∵c >d >0，∴1d >1c >0，又∵a >b >0，∴a d >b c >0.11.已知a >0，b >0，试比较a b ＋b a 与a ＋b 的大小．解：(a b ＋b a)－(a ＋b ) ＝a a ＋b b －ab (a ＋b )ab＝a a ＋b b －a b －b a ab＝a (a －b )－b (a －b )ab ＝(a －b )(a －b )ab＝(a ＋b )(a －b )2ab. ∵a >0，b >0.∴a ＋b >0，ab >0.又∵(a －b )2≥0(当且仅当a ＝b 时等号成立)，∴(a ＋b )(a －b )2ab≥0. 即a b ＋b a≥a ＋b (当且仅当a ＝b 时等号成立)． 12．2008年北京成功举办了第29届奥运会，中国取得了51金、21银、28铜的骄人成绩．下表为北京奥运会官方票务网站公布的几种球类比赛的门票价格，某球迷赛前准备用12000元预订15张下表中球类比赛的门票：订上表中三种球类比赛门票，其中足球比赛门票数与乒乓球比赛门票数相同，且足球比赛门票的费用不超过男篮比赛门票的费用，求可以预订的男篮比赛门票数．解：设足球比赛门票数与乒乓球比赛门票数都预订n (n ∈N *)张，则男篮比赛门票预订(15－2n )张，得⎩⎪⎨⎪⎧ 800n ＋500n ＋1000(15－2n )≤12000800n ≤1000(15－2n )，解得427≤n ≤5514.由n ∈N *，可得n ＝5，∴15－2n ＝5.∴可以预订男篮比赛门票5张．。

2013高考总复习数学(文)配套课时巩固与训练6章1课时训练

1．已知数列3，7，11，15，…，则53是数列的( )A ．第18项B ．第19项C ．第17项D ．第20项解析：选B.∵7－3＝11－7＝15－11＝4，即a n 2－a n －12＝4，∴a n 2＝3＋(n －1)×4＝4n －1，令4n －1＝75，则n ＝19.故选B. 2．已知数列的通项a n ＝⎩⎪⎨⎪⎧3n ＋1 (n 为奇数)2n －1 (n 为偶数)，则a 2009－a 2010等于( )A ．2007B ．2008C ．2009D ．2010解析：选C.a 2009＝3×2009＋1＝6028；a 2010＝2×2010－1＝4019.故a 2009－a 2010＝6028－4019＝2009.故应选C.3．下面有四个命题：①如果已知一个数列的递推公式及其首项，那么可以写出这个数列的任何一项；②数列23，34，45，56，…的通项公式是a n ＝n n ＋1； ③数列的图象是一群孤立的点；④数列1，－1,1，－1，…与数列－1,1，－1,1，…是同一数列．其中正确命题的个数是( )A ．1B ．2C ．3D ．4解析：选A.①错误，如a n ＋2＝a n ＋a n ＋1，a 1＝1就无法写出a 2；②错误，a n ＝n ＋1n ＋2；③正确；④两数列是不同的有序数列．故应选A.4．在数列{a n }中，a 1＝1，a n a n －1＝a n －1＋(－1)n (n ≥2，n ∈N *)，则a 3a 5的值是( )A.1516B.158C.34D.38解析：选C.由已知得a 2＝1＋(－1)2＝2， ∴a 3·a 2＝a 2＋(－1)3，∴a 3＝12，∴12a 4＝12＋(－1)4，∴a 4＝3，∴3a 5＝3＋(－1)5，∴a 5＝23，∴a 3a 5＝12×32＝34. 5．已知数列{a n }的前n 项和S n ＝n 2－9n ，第k 项满足5＜a k ＜8，则k 等于( )A ．9B ．8C ．7D ．6 解析：选B.a n ＝⎩⎨⎧ S 1 (n ＝1)，S n －S n －1(n ≥2)，＝⎩⎨⎧－8 (n ＝1)，－10＋2n (n ≥2). ∵n ＝1时适合a n ＝2n －10，∴a n ＝2n －10. ∵5<a k <8，∴5<2k －10<8，∴152<k <9，又∵k ∈N ＋，∴k ＝8，故选B.6．若数列{a n }满足a 1＝1，a 2＝2，a n ＝a n －1a n －2(n ≥3且n ∈N *)，则a 17＝( )A ．1B ．2C.12 D ．2－987解析：选C.由已知得a 1＝1，a 2＝2，a 3＝2，a 4＝1，a 5＝12，a 6＝12，a 7＝1，a 8＝2，a 9＝2，a 10＝1，a 11＝12，a 12＝12，即a n 的值以6为周期重复出现，故a 17＝12.7.已知数列{a n }的通项a n ＝na nb ＋c(a ，b ，c 均为正实数)，则a n 与a n ＋1的大小关系是________．解析：∵a n ＝na nb ＋c ＝a b ＋c n，c n 是减函数， ∴a n ＝a b ＋c n是增函数，∴a n <a n ＋1.答案：a n <a n ＋18．设数列{a n }的前n 项和为S n ，S n ＝a 1(3n －1)2(对n ≥1恒成立)且a 4＝54，则a 1＝________.解析：法一：由S 4＝S 3＋a 4，得a 1(34－1)2＝a 1(33－1)2＋54，即a 1(34－33)2＝54，解得a 1＝2. 法二：由S n －S n －1＝a n (n ≥2)可得a n ＝a 1(3n －1)2－a 1(3n －1－1)2＝a 1(3n －3n －1)2＝a 1·3n －1， ∴a 4＝a 1·33，∴a 1＝5427＝2.答案：29．已知数列{a n }的前n 项的乘积为T n ＝5n 2，n ∈N *，则数列{a n }的通项公式为________．解析：当n ＝1时，a 1＝T 1＝512＝5；当n ≥2时，a n ＝T n T n －1＝5n 25(n －1)2＝52n －1(n ∈N *)．当n ＝1时，也适合上式，所以当n ∈N *时，a n ＝52n －1.答案：a n ＝52n －1(n ∈N *)10．已知数列{a n }中，a n ∈(0，12)，a n ＝38＋12a 2n －1，其中n ≥2，n ∈N ＋，求证：对一切正整数n 都有a n <a n ＋1成立．证明：a n ＋1－a n ＝38＋12a n 2－a n＝12(a n －1)2－18，∵0<a n <12，∴－1<a n －1<－12.∴18<12(a n －1)2<12.∴12(a n －1)2－18>0.∴a n ＋1－a n >0，即a n <a n ＋1对一切正整数n 都成立．11．(2010年邯郸模拟)已知数列{a n }满足前n 项和S n ＝n 2＋1，数列{b n }满足b n ＝2a n ＋1，且前n 项和为T n ，设c n ＝T 2n ＋1－T n . (1)求数列{b n }的通项公式；(2)判断数列{c n }的增减性．解：(1)a 1＝2，a n ＝S n －S n －1＝2n －1(n ≥2)．∴b n ＝⎩⎪⎨⎪⎧ 1n (n ≥2)，23(n ＝1).(2)∴c n ＝b n ＋1＋b n ＋2＋…＋b 2n ＋1＝1n ＋1＋1n ＋2＋…＋12n ＋1， ∴c n ＋1－c n ＝12n ＋2＋12n ＋3－1n ＋1<0，∴{c n}是递减数列．12．已知数列{a n}的前n项和为S n＝n2＋pn，数列{b n}的前n项和为T n＝3n2－2n.(1)若a10＝b10，求p的值．(2)取数列{b n}的第1项，第3项，第5项，…，构成一个新数列{c n}，求数列{c n}的通项公式．解：(1)由已知，a n＝S n－S n－1＝(n2＋pn)－[(n－1)2＋p(n－1)]＝2n－1＋p(n≥2)，b n＝T n－T n－1＝(3n2－2n)－[3(n－1)2－2(n－1)]＝6n－5(n≥2)．∴a10＝19＋p，b10＝55.由a10＝b10，得19＋p＝55，∴p＝36.(2)b1＝T1＝1，满足b n＝6n－5.∴数列{b n}的通项公式为b n＝6n－5.取{b n}中的奇数项，所组成的数列的通项公式为b2k－1＝6(2k－1)－5＝12k－11.∴c n＝12n－11.。

2013高考总复习数学(文)配套课时巩固与训练3章2课时训练

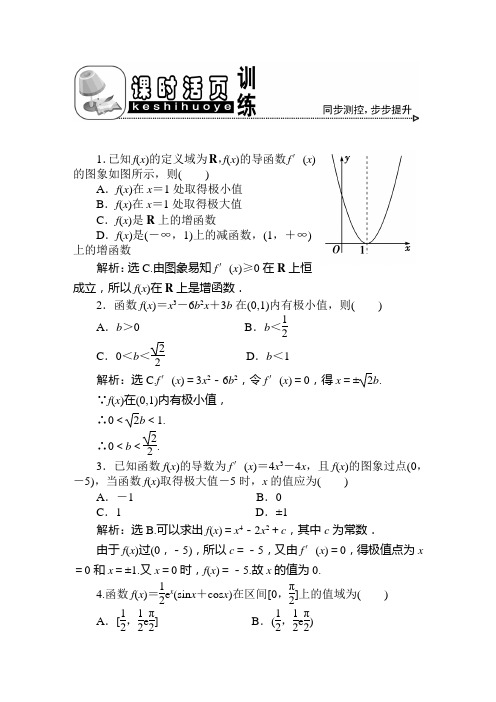
1．已知f (x )的定义域为R ，f (x )的导函数f ′(x )的图象如图所示，则( )A ．f (x )在x ＝1处取得极小值B ．f (x )在x ＝1处取得极大值C ．f (x )是R 上的增函数D ．f (x )是(－∞，1)上的减函数，(1，＋∞)上的增函数解析：选C.由图象易知f ′(x )≥0在R 上恒成立，所以f (x )在R 上是增函数．2．函数f (x )＝x 3－6b 2x ＋3b 在(0,1)内有极小值，则( )A ．b ＞0B ．b ＜12C ．0＜b ＜22D ．b ＜1 解析：选C.f ′(x )＝3x 2－6b 2，令f ′(x )＝0，得x ＝±2b .∵f (x )在(0,1)内有极小值，∴0＜2b ＜1.∴0＜b ＜22. 3．已知函数f (x )的导数为f ′(x )＝4x 3－4x ，且f (x )的图象过点(0，－5)，当函数f (x )取得极大值－5时，x 的值应为( )A ．－1B ．0C ．1D ．±1解析：选B.可以求出f (x )＝x 4－2x 2＋c ，其中c 为常数．由于f (x )过(0，－5)，所以c ＝－5，又由f ′(x )＝0，得极值点为x ＝0和x ＝±1.又x ＝0时，f (x )＝－5.故x 的值为0.4.函数f (x )＝12e x (sin x ＋cos x )在区间[0，π2上的值域为( ) A ．[12，12e π2] B ．(12，12e π2) C ．[1，e π2] D ．(1，e π2)解析：选A.f ′(x )＝12e x (sin x ＋cos x )＋12e x (cos x －sin x )＝e x cos x ，当0≤x ≤π2时，f ′(x )≥0， ∴f (x )是[0，π2]上的增函数． ∴f (x )的最大值为f (π2)＝12e π2f (x )的最小值为f (0)＝12. 5．已知函数y ＝f (x )(x ∈R )的图象如图所示，则不等式xf ′(x )<0的解集为( )A ．(-∞，12)∪(12,2)B ．(－∞，0)∪(12，2) C ．(－∞，12∪(12，＋∞) D ．(－∞，12)∪(2，＋∞) 解析：选B.由f (x )图象单调性可得f ′(x )在(－∞，12)∪(2，＋∞)大于0，在(12，2)上小于0，∴xf ′(x )<0的解集为(－∞，0)∪(12，2)． 6．设f (x )、g (x )是R 上的可导函数，f ′(x )，g ′(x )分别为f (x )、g (x )的导函数，且满足f ′(x )g (x )＋f (x )g ′(x )<0，则当a <x f (b )g (x )B ．f (x )g (a )>f (a )g (x )C ．f (x )g (x )>f (b )g (b )D ．f (x )g (x )>f (b )g (a )解析：选C.令y ＝f (x )·g (x )，则y ′＝f ′(x )·g (x )＋f (x )·g ′(x )，由于f ′(x )g (x )＋f (x )g ′(x )<0，所以y 在R 上单调递减，又x f (b )g (b )．7．f (x )＝x (x －c )2在x ＝2处有极大值，则常数c 的值为________．解析：f (x )＝x 3－2cx 2＋c 2x ，f ′(x )＝3x 2－4cx ＋c 2，f ′(2)＝0⇒c ＝2或c ＝6，若c ＝2，f ′(x )＝3x 2－8x ＋4，令f ′(x )>0⇒x <23或x >2，f ′(x )<0⇒23<x <2，故函数在(－∞，23)及(2，＋∞)上单调递增，在(23，2)上单调递减，∴x ＝2是极小值点，故c ＝2不合题意，所以c ＝6.答案：68．直线y ＝a 与函数f (x )＝x 3－3x 的图象有相异的三个公共点，则a 的取值范围是________．解析：令f ′(x )＝3x 2－3＝0，得x ＝±1，可求得f (x )的极大值为f (－1)＝2，极小值为f (1)＝－2，如图所示，－2<a <2时，恰有三个不同公共点．答案：(－2,2)9．将长为52 cm 的铁丝剪成2段，各围成一个长与宽之比为2∶1及3∶2的矩形，那么面积之和的最小值为________．解析：设剪成2段中其中一段为x cm ，另一段为(52－x ) cm ，依题意知：S ＝x 6·2x 6＋3(52－x )10·2(52－x )10＝118x 2＋350(52－x )2， S ′＝19x －325(52－x )，令S ′＝0，则x ＝27.另一段为52－27＝25.此时S min ＝78.答案：7810．(2010年合肥质检)设函数f (x )＝ln x －2ax .(1)若函数y ＝f (x )的图象在点(1，f (1))处的切线为直线l ，且直线l 与圆(x ＋1)2＋y 2＝1相切，求a 的值；(2)当a >0时，求函数f (x )的单调区间．解：(1)依题意有，f ′(x )＝1x－2a . 因此过(1，f (1))点的直线的斜率为1－2a ，又f (1)＝－2a ，所以，过(1，f (1))点的直线方程为y ＋2a ＝(1－2a )(x －1)．即(2a －1)x ＋y ＋1＝0又已知圆的圆心为(－1,0)，半径为1，依题意，|1－2a ＋1|(2a －1)2＋1＝1，解得a ＝12. (2)依题知f (x )＝ln x －2ax 的定义域为(0，＋∞)，又知f ′(x )＝1x－2a 因为a >0，x >0，令1x －2a >0，则1－2ax >0 所以在x ∈(0，12a)时，f (x )＝ln x －2ax 是增函数；在x ∈(12a，＋∞)时，f (x )＝ln x －2ax 是减函数． 11．已知函数f (x )＝x 3－32ax 2＋b (a ，b 为实数，且a >1)在区间[－1,1]上的最大值为1，最小值为－2.(1)求f (x )的解析式；(2)若函数g (x )＝f (x )－mx 在区间[－2,2]上为减函数，求实数m 的取值范围．解：(1)f ′(x )＝3x 2－3ax ，令f ′(x )＝0，得x 1＝0，x 2＝a ，∵a >1，∴f (x )在[－1,0]上为增函数，在[0,1]上为减函数．∴f (0)＝b ＝1， ∵f (－1)＝－32a ，f (1)＝2－32a ，∴f (－1)<f (1)， ∴f (－1)＝－32a ＝－2，a ＝43. ∴f (x )＝x 3－2x 2＋1.(2)g (x )＝x 3－2x 2－mx ＋1，g ′(x )＝3x 2－4x －m .由g (x )在[－2,2]上为减函数，知g ′(x )≤0在x ∈[－2,2]上恒成立．∴⎩⎪⎨⎪⎧ g ′(－2)≤0g ′(2)≤0，即⎩⎪⎨⎪⎧20－m ≤04－m ≤0∴m ≥20. ∴实数m 的取值范围是m ≥20.12．已知函数f (x )＝ln(x ＋1)＋ax .(1)当x ＝0时，函数f (x )取得极大值，求实数a 的值；(2)若存在x ∈[1,2]，使不等式f ′(x )≥2x 成立，其中f ′(x )为f (x )的导函数，求实数a 的取值范围；(3)求函数f (x )的单调区间．解：(1)f ′(x )＝1x ＋1＋a 由f ′(0)＝0，得a ＝－1，此时f ′(x )＝1x ＋1－1. 当x ∈(－1,0)时，f ′(x )>0，函数f (x )在区间(－1,0)上单调递增；当x ∈(0，＋∞)时，f ′(x )<0，函数f (x )在区间(0，＋∞)上单调递减；∴函数f (x )在x ＝0处取得极大值，故a ＝－1.(2)∵f ′(x )≥2x ，∴1x ＋1＋a ≥2x ，∴a ≥2x －1x ＋1. 令g (x )＝2x －1x ＋1(1≤x ≤2)， ∴g ′(x )＝2＋1(x ＋1)2>0，∴g (x )在[1,2]上是增函数， ∴a ≥g (1)＝32. (3)f ′(x )＝1x ＋1＋a . ∵1x ＋1>0， ∴当a ≥0时，f ′(x )>0，函数f (x )在(－1，＋∞)上是增函数．当a <0时，令f ′(x )＝0，x ＝－1a－1；若x ∈(－1，－1a－1)时，f ′(x )>0，若x ∈(－1a－1，＋∞)时，f ′(x )<0；综上，当a ≥0时，函数f (x )递增区间是(－1，＋∞)；当a <0时，函数f (x )递增区间是(－1，－1a －1)，递减区间是(－1a－1，＋∞)．。

2013高考总复习数学(理)配套课时巩固与训练8章2课时训练

1．若三条直线2x ＋3y ＋8＝0，x －y －1＝0和x ＋ky ＋k ＋12＝0相交于一点，则k ＝( )A ．－2B ．－12C ．2 D.12解析：选 B.由⎩⎪⎨⎪⎧2x ＋3y ＋8＝0x －y －1＝0得交点为(－1，－2)，代入x ＋ky ＋k ＋12＝0，得k ＝－12.2．已知直线l 的倾斜角为34π，直线l 1经过点A (3,2)、B (a ，－1)，且l 1与l 垂直，直线l 2：2x ＋by ＋1＝0与直线l 1平行，则a ＋b 等于( )A ．－4B ．－2C ．0D ．2解析：选B.l 的斜率为－1，则l 1的斜率为1，k AB ＝2－(－1)3－a＝1，a ＝0. 由l 1∥l 2，－2b ＝1，得b ＝－2，所以a ＋b ＝－2.3.点P (－1,3)到直线l ：y ＝k (x －2)的距离的最大值等于( )A ．2B ．3C ．3 2D ．2 3解析：选C.直线l ：y ＝k (x －2)的方程化为kx －y －2k ＝0，所以点P (－1,3)到该直线的距离为d ＝3|k ＋1|k 2＋1＝3k 2＋2k ＋1k 2＋1＝31＋2k k 2＋1，由于2k k 2＋1≤1，所以d ≤32，即距离的最大值等于32，选C.4．点P 在直线3x ＋y －5＝0上，且点P 到直线x －y －1＝0的距离为2，则P 点坐标为( )A ．(1,2)B ．(2,1)C ．(1,2)或(2，－1)D ．(2,1)或(－2,1)解析：选C.设P 点坐标为(a,5－3a )，由题意知：|a －(5－3a )－1|2＝ 2. 解之得a ＝1或a ＝2，∴P 点坐标为(1,2)或(2，－1)．故应选C.5．已知直线l ：x －y －1＝0，l 1：2x －y －2＝0，若直线l 1与l 2关于l 对称，则l 2的方程是( )A ．x －2y ＋1＝0B ．x －2y －1＝0C ．x ＋y －1＝0D ．x ＋2y －1＝0解析：选B.在l 2上任取一点(x ，y )，关于l ：x －y －1＝0的对称点(x 0，y 0)在l 1上，根据点关于线的对称关系列方程组解出x 0，y 0，代入l 1即可得出方程x －2y －1＝0.6．三条直线l 1：x －y ＝0，l 2：x ＋y －2＝0，l 3：5x －ky －15＝0构成一个三角形，则k 的取值范围是( )A ．k ∈RB ．k ∈R 且k ≠±1，k ≠0C ．k ∈R 且k ≠±5，k ≠－10D ．k ∈R 且k ≠±5，k ≠1 解析：选C.由l 1∥l 3得k ＝5，由l 2∥l 3得k ＝－5，由⎩⎪⎨⎪⎧ x －y ＝0x ＋y －2＝0得⎩⎪⎨⎪⎧ x ＝1y ＝1，若(1,1)在l 3上，则k ＝－10. 故若l 1，l 2，l 3能构成一个三角形，则k ≠±5且k ≠－10.7．已知直线l 1：kx －y ＋1－k ＝0与l 2：ky －x －2k ＝0的交点在第一象限，则实数k 的取值范围为________．解析：解⎩⎪⎨⎪⎧ kx －y ＋1－k ＝0ky －x －2k ＝0，得⎩⎨⎧x ＝k k －1y ＝2k －1k －1， ∵交点在第一象限，∴⎩⎨⎧ k k －1＞02k －1k －1＞0，∴k ＞1或k ＜0. 答案：k ＜0或k ＞18．设直线l 经过点(－1,1)，则当点(2，－1)与直线l 的距离最大时，直线l 的方程为______________．解析：设A (－1,1)，B (2，－1)，当AB ⊥l 时，点B 与l 距离最大，此时l 的方程为：y －1＝－11＋1－1－2(x ＋1)，即为：3x －2y ＋5＝0.答案：3x －2y ＋5＝09．已知平面上一点M (5,0)，若直线上存在点P 使|PM |＝4，则称该直线为“切割型直线”，下列直线中是“切割型直线”的是________(填上所有正确答案的序号)．①y ＝x ＋1；②y ＝2；③y ＝43x解析：根据题意，看所给直线上的点到定点M 距离能否取4.可通过求各直线上的点到点M 的最小距离，即点M 到直线的距离来分析．①d ＝|5＋1|12＋(－1)2＝32＞4，故直线上不存在点到点M 距离等于4，不是“切割型直线”；②d ＝2＜4，所以在直线上可以找到两个不同的点，使之到点M 距离等于4，是“切割型直线”；③d ＝|4×5－0|(－3)2＋42＝4，直线上存在一点，使之到点M 距离等于4，是“切割型直线”．答案：②③10．已知直线l 的方程为3x ＋4y －12＝0，求满足下列条件的直线l ′的方程．(1)l ′与l 平行且过点(－1,3)；(2)l ′与l 垂直且l ′与两坐标轴围成的三角形面积为4；(3)l ′是l 绕原点旋转180°而得到的直线．解：(1)直线l ：3x ＋4y －12＝0，k l ＝－34，又∵l ′∥l ，∴k l ′＝k l ＝－34.∴直线l ′：y ＝－34(x ＋1)＋3，即3x ＋4y －9＝0.(2)∵l ′⊥l ，∴k l ′＝43. 设l ′在x 轴上截距为b ，则l ′在y 轴上截距为－43b ，由题意可知，S ＝12|b |·|－43b |＝4，∴b ＝±6.∴直线l ′：y ＝43x ＋6或y ＝43x － 6.(3)∵l ′是l 绕原点旋转180°而得到的直线，∴l ′与l 关于原点对称．在l 上任取点(x 0，y 0)，则在l ′上对称点为(x ，y )．x ＝－x 0，y ＝－y 0，则－3x －4y －12＝0.∴l ′为3x ＋4y ＋12＝0.11.已知两直线l 1：ax －by ＋4＝0，l 2：(a －1)x ＋y ＋b ＝0.求分别满足下列条件的a ，b 的值．(1)直线l 1过点(－3，－1)，并且直线l 1与l 2垂直；(2)直线l 1与直线l 2平行，并且坐标原点到l 1，l 2的距离相等．解：(1)∵l 1⊥l 2，∴a (a －1)＋(－b )·1＝0，即a 2－a －b ＝0①又点(－3，－1)在l 1上，∴－3a ＋b ＋4＝0②由①②得a ＝2，b ＝2.(2)∵l 1∥l 2，∴a b ＝1－a ，∴b ＝a 1－a，故l 1和l 2的方程可分别表示为：(a －1)x ＋y ＋4(a －1)a ＝0，(a －1)x ＋y ＋a 1－a＝0，又原点到l 1与l 2的距离相等．∴4|a －1a |＝|a 1－a|，∴a ＝2或a ＝23， ∴a ＝2，b ＝－2或a ＝23，b ＝2.12．光线通过点A (－2,4)，经直线2x －y －7＝0反射，若反射线通过点B (5,8)．求入射光线和反射光线所在直线的方程．解：如右图，已知直线l ：2x －y －7＝0，设光线AC 经l 上点C 反射为BC ，则∠1＝∠2.再设A 关于l 的对称点为A ′(a ，b )，则∠1＝∠3.∴∠2＝∠3，则B ，C ，A ′三点共线．∵A ′A ⊥l 且AA ′中点在l 上，∴⎩⎨⎧2·a －22－b ＋42－7＝0，b －4a ＋2·2＝－1.解得a ＝10，b ＝－2，即A ′(10，－2)．∴A ′B 的方程为y ＋2＝8＋25－10(x －10)，即2x ＋y －18＝0.∴A ′B 与l 的交点为C (254，112)．∴入射光线AC 的方程为y －4＝4－112－2－254(x ＋2)．即2x －11y ＋48＝0.∴入射光线方程为2x －11y ＋48＝0，反射光线方程为2x ＋y －18＝0.。

(江西版)2013年高考数学总复习第十一章11.5 数学归纳法理北师大版(含详解)

2013年高考第一轮复习数学北师(江西版)理第十一章11.5 数学归纳法练习一、选择题1．用数学归纳法证明1＋2＋…＋(2n ＋1)＝(n ＋1)(2n ＋1)时，在验证n ＝1成立时，左边所得的代数式是( )．A ．1B ．1＋3C ．1＋2＋3D ．1＋2＋3＋42．用数学归纳法证明“1＋12＋13＋…＋12－1＜n (n ∈N ＋，n ＞1)”时，由n ＝k (k ＞1)不等式成立，推证n ＝k ＋1时，左边应增加的项数是( )．A ．2k －1B ．2k －1C ．2kD ．2k＋13．用数学归纳法证明不等式1＋12＋14＋…＋12n －1＞12764成立时，起始值n 至少应取为( )．A ．7B ．8C ．9D ．104．用数学归纳法证明“当n 为正奇数时，x n ＋y n能被x ＋y 整除”的第二步是( )． A ．假设n ＝2k ＋1时正确，再推n ＝2k ＋3时正确(其中k ∈N ＋) B ．假设n ＝2k －1时正确，再推n ＝2k ＋1时正确(其中k ∈N ＋) C ．假设n ＝k 时正确，再推n ＝k ＋1时正确(其中k ∈N ＋)D ．假设n ≤k (k ≥1)时正确，再推n ＝k ＋2时正确(其中k ∈N ＋)5．在数列{a n }中，a 1＝13，且S n ＝n (2n －1)a n ，通过求a 2，a 3，a 4，猜想a n 的表达式为( )．A ．1(n －1)(n ＋1)B ．12n (2n ＋1)C ．1(2n －1)(2n ＋1)D ．1(2n ＋1)(2n ＋2)6．设函数f (n )＝(2n ＋9)·3n ＋1＋9，当n ∈N ＋时，f (n )能被m (m ∈N ＋)整除，猜想m 的最大值为( )．A ．9B ．18C ．27D ．36 二、填空题7．用数学归纳法证明“1＋a ＋a 2＋…＋a n ＋1＝1－a n ＋21－a(a ≠1，且n ∈N ＋)”，在验证n ＝1时，左边计算所得的结果是__________．8．用数学归纳法证明：(n ＋1)＋(n ＋2)＋…＋(n ＋n )＝n (3n ＋1)2(n ∈N ＋)的第二步中，当n ＝k ＋1时等式左边与n ＝k 时等式左边的差等于__________．9．在△ABC 中，不等式1A ＋1B ＋1C ≥9π成立；在四边形ABCD 中，不等式1A ＋1B ＋1C ＋1D ≥162π成立；在五边形ABCDE 中，不等式1A ＋1B ＋1C ＋1D ＋1E ≥253π成立……猜想在n 边形A 1A 2…A n 中，有不等式__________成立．三、解答题10．用数学归纳法证明：12＋32＋52＋…＋(2n －1)2＝13n (4n 2－1)．11．试比较2n ＋2与n 2的大小(n ∈N ＋)，并用数学归纳法证明你的结论． 12．如图，P 1(x 1，y 1)，P 2(x 2，y 2)，…，P n (x n ，y n )(0＜y 1＜y 2＜…＜y n )是曲线C ：y 2＝3x (y ≥0)上的n 个点，点A i (a i,0)(i ＝1,2，3，…，n )在x 轴的正半轴上，且△A i －1A i P i 是正三角形(A 0是坐标原点)．(1)写出a 1，a 2，a 3；(2)求出点A n (a n,0)(n ∈N ＋)的横坐标a n 关于n 的表达式并证明．参考答案一、选择题1．C 解析：左边表示从1开始，连续2n ＋1个正整数的和，故n ＝1时，表示1＋2＋3的和．2．C 解析：左边的特点：分母逐渐增加1，末项为12－1；由n ＝k ，末项为12－1到n ＝k＋1末项为12k ＋1－1＝12k －1＋2k ，显然增加的项数为2k.3．B 解析：∵1＋12＋14＋…＋127－1＝7112112⎛⎫- ⎪⎝⎭-＝2－126＝27－126＝12764，而1＋12＋14＋…＋128－1＞12764，故起始值n 至少取8.4．B 解析：∵n 为正奇数， ∴n ＝2k －1(k ∈N ＋)．5．C 解析：由a 1＝13，S n ＝n (2n －1)a n 求得a 2＝115＝13×5，a 3＝135＝15×7，a 4＝163＝17×9.猜想a n ＝1(2n －1)(2n ＋1).6．D 解析：f (n ＋1)－f (n )＝(2n ＋11)·3n ＋2－(2n ＋9)·3n ＋1＝4(n ＋6)·3n ＋1，当n ＝1时，f (2)－f (1)＝4×7×9为最小值，据此可猜想D 正确．二、填空题7．1＋a ＋a 2解析：首先观察等式两边的构成情况，它的左边是按a 的升幂顺序排列的，共有n ＋2项．因此当n ＝1时，共有3项，应该是1＋a ＋a 2.8．3k ＋2 解析：当n ＝k 时，左边＝(k ＋1)＋(k ＋2)＋…＋(k ＋k )，当n ＝k ＋1时，左边＝(k ＋1＋1)＋(k ＋1＋2)＋…＋(k ＋1＋k ＋1)＝(k ＋2)＋(k ＋3)＋…＋2k ＋(2k ＋1)＋(2k ＋2)，所以其差为(2k ＋1)＋(2k ＋2)－(k ＋1)＝3k ＋2.9．1A 1＋1A 2＋…＋1A n ≥n 2(n －2)π 三、解答题10．证明：(1)当n ＝1时，左边＝12＝1，右边＝13×1×(4－1)＝1，等式成立．(2)假设当n ＝k (k ∈N *)时等式成立，即12＋32＋52＋…＋(2k －1)2＝13k (4k 2－1)．则当n ＝k ＋1时，12＋32＋52＋…＋(2k －1)2＋(2k ＋1)2＝13k (4k 2－1)＋(2k ＋1)2＝13k (4k2－1)＋4k 2＋4k ＋1＝13k [4(k ＋1)2－1]－13k ·4(2k ＋1)＋4k 2＋4k ＋1 ＝13k [4(k ＋1)2－1]＋13(12k 2＋12k ＋3－8k 2－4k ) ＝13k [4(k ＋1)2－1]＋13[4(k ＋1)2－1] ＝13(k ＋1)[4(k ＋1)2－1]．即当n ＝k ＋1时等式也成立．由(1)，(2)可知，对一切n ∈N ＋，等式都成立．11．解：当n ＝1时，21＋2＝4＞n 2＝1，当n ＝2时，22＋2＝6＞n 2＝4，当n ＝3时，23＋2＝10＞n 2＝9，当n ＝4时，24＋2＝18＞n 2＝16，由此可以猜想，2n ＋2＞n 2(n ∈N *)成立．下面用数学归纳法证明：(1)当n ＝1时，左边＝21＋2＝4，右边＝1，左边＞右边，所以原不等式成立．当n ＝2时，左边＝22＋2＝6，右边＝22＝4，左边＞右边；当n ＝3时，左边＝23＋2＝10，右边＝32＝9，左边＞右边．(2)假设n ＝k (k ≥3且k ∈N *)时，不等式成立，即2k ＋2＞k 2.那么n ＝k ＋1时， 2k ＋1＋2＝2·2k ＋2＝2(2k ＋2)－2＞2·k 2－2.又因为2k 2－2－(k ＋1)2＝k 2－2k －3＝(k －3)(k ＋1)≥0，即2k 2－2≥(k ＋1)2，故2k ＋1＋2＞(k ＋1)2成立．根据(1)和(2)，可知原不等式对于任何n ∈N *都成立． 12．解：(1)a 1＝2，a 2＝6，a 3＝12.(2)依题意，得x n ＝a n －1＋a n2，y n ＝3·a n －a n －12，由此及2n y ＝3·x n 得212n n a a --⎫⎪⎭＝32(a n ＋a n －1)，即(a n －a n －1)2＝2(a n －1＋a n )．由(1)可猜想：a n ＝n (n ＋1)(n ∈N ＋)．下面用数学归纳法予以证明： ①当n ＝1时，命题显然成立．②假设当n ＝k (k ∈N ＋)时命题成立，即有a k ＝k (k ＋1)，则当n ＝k ＋1时，由归纳假设及(a k ＋1－a k )2＝2(a k ＋a k ＋1)，即a k ＋12－2(k 2＋k ＋1)a k ＋1＋[k (k －1)]·[(k ＋1)(k ＋2)]＝0，解之，得a k ＋1＝(k ＋1)(k ＋2)〔a k ＋1＝k (k －1)＜a k 不合题意，舍去〕，即当n ＝k ＋1时，命题成立．由①、②可知，命题a n ＝n (n ＋1)(n ∈N ＋)成立．。

2013高考总复习数学(理)配套课时巩固与训练12章3课时训练

1．袋中有大小相同的5个球，分别标有1,2,3,4,5五个号码，现在在有放回抽取的条件下依次取出两个球，设两个球号码之和为随机变量X ，则X 所有可能取值的个数是( )A ．5B ．9C ．10D ．25解析：选B.号码之和可能为2,3,4,5,6,7,8,9,10，共9种．2．已知随机变量X 的分布列为P (X ＝k )＝12k ，k ＝1,2，…，则P (2＜X ≤4)等于( )A.316B.14C.116D.516解析：选A.P (2＜X ≤4)＝P (X ＝3)＋P (X ＝4)＝123＋124＝316.3．设某项试验的成功率是失败率的2倍，用随机变量X 去描述1次试验的成功次数，则P (X ＝0)等于( )A ．0 B.12C.13D.23解析：选C.设X即“X ＝0”p ，则成功率为2p .由p ＋2p ＝1，得p ＝13.4．随机变量X 的概率分布规律为P (X ＝n )＝a n (n ＋1)(n ＝1,2,3,4)，其中a 是常数，则P (12＜X ＜52)的值为( )A.23B.34C.45D.56解析：选D.∵P (X ＝n )＝a n (n ＋1)(n ＝1,2,3,4)， ∴a 2＋a 6＋a 12＋a 20＝1，∴a ＝54，∵P (12＜X ＜52)＝P (X ＝1)＋P (X ＝2)＝54×12＋54×16＝56.故选D.5．若P (X ≤n )＝1－a ，P (X ≥m )＝1－b ，其中m <n ，则P (m ≤X ≤n )等于( )A ．(1－a )(1－b )B ．1－a (1－b )C ．1－(a ＋b )D ．1－b (1－a )解析：选C.P (m ≤X ≤n )＝P (X ≤n )＋P (X ≥m )－1＝1－(a ＋b )．6.甲、乙两名篮球运动员轮流投篮直至某人投中为止，计每次投篮甲投中的概率为0.4，乙投中的概率为0.6，而且不受其他投篮结果的影响．设甲投篮的次数为ξ，若甲先投，则P (ξ＝k )等于( )A ．0.6k －1×0.4B ．0.24k －1×0.76C ．0.4k －1×0.6D ．0.76k －1×0.24答案：B7若η＝2ξ－3解析：由η＝2ξ－3可计算出相应的η的取值，概率不变．答案：8.P (X ≤4)＝__________.解析：P (X ≤4)＝P (X ＝2)＋P (X ＝3)＋P (X ＝4)．相应的基本事件空间有36个基本事件，X ＝2对应(1,1)，X ＝3对应(1,2)，(2,1)，X ＝4对应(1,3)，(3,1)，(2,2)，故P (X ＝2)＝136，P (X ＝3)＝236＝118，P (X ＝4)＝336＝112，所以P (X ≤4)＝136＋118＋112＝16.答案：169．设随机变量X 只能取5,6,7，…，16这12个值，且取每一个值的概率均相等，则P (X ＞8)＝________.若P (X ＜x )＝112，则x 的范围是________．解析：∵X 取每一个值的概率都相等．∴P (X ＞8)＝P (X ＝9)＋P (X ＝10)＋P (X ＝11)＋P (X ＝12)＋…＋P (X＝16)＝812＝23.(或P (X ＞8)＝1－P (X ≤8)＝1－P (X ＝8)－P (X ＝7)－P (X ＝6)－P (X ＝5)＝23)若P (X ＜x )＝112，则P (X ＜x )＝P (X ＝5)．∴x ∈(5,6]答案：23 (5,6]10．甲、乙两名射手各打了10发子弹，其中甲击中环数与次数如下表：解：由0.2＋0.3＋p ＋0.1＝1，得p ＝0.4.设甲、乙击中的环数分别为X 1、X 2，则X 1＋X 2＝18，P (X 1＝8)＝110＝0.1，P (X 1＝9)＝210＝0.2，P (X 1＝10)＝410＝0.4.P (X 2＝10)＝0.1，P (X 2＝9)＝0.4，P (X 2＝8)＝0.3.甲、乙各射击一次所得环数之和为18的概率为0．1×0.1＋0.2×0.4＋0.4×0.3＝0.21.11．山东水浒书业在2009年8月举行一次数学新课程研讨会，共邀请50名一线教师参加，使用不同版本教材的教师人数如下表所示：版本人教A版人教B版苏教版北师大版人数2015510(1)率；(2)若随机选出2名使用人教版的教师发言，设使用人教A版的教师人数为ξ，求随机变量ξ的分布列．∴ξ的分布列为ξ01 2P 317601193811912.2008分别叫贝贝、晶晶、欢欢、迎迎、妮妮．现有8个相同的盒子，每个盒子福娃名称贝贝晶晶欢欢迎迎妮妮数量1231 1(1)求选取的5只恰好组成完整“奥运吉祥物”的概率；(2)若完整地选取奥运会吉祥物记100分；若选出的5只中仅差一种记80分；差两种记60分；以此类推，设X表示所得的分数，求X 的分布列．解：(1)选取的5只恰好组成完整“奥运会吉祥物”的概率P＝C21·C31C85＝656＝328.(2)X的取值为100,80,60,40.X的分布列为。

2013高考总复习数学(理)配套课时巩固与训练6章5课时训练

1．已知a ，b ∈(0，＋∞)，A 为a ，b 的等差中项，正数G 为a ，b 的等比中项，则ab 与AG 的大小关系是( )A ．ab ＝AGB ．ab ≥AGC ．ab ≤AGD ．不能确定解析：选C.依题意A ＝a ＋b 2，G ＝ab ，∴AG －ab ＝a ＋b 2·ab －ab ＝ab (a ＋b 2－ab ) ＝ab ·(a －b )22≥0，∴AG ≥ab .2．在直角坐标系中，O 是坐标原点，P 1(x 1，y 1)，P 2(x 2，y 2)是第一象限的两个点，若1，x 1，x 2,4依次成等差数列，而1，y 1，y 2,8依次成等比数列，则△OP 1P 2的面积是( )A ．1B ．2C ．3D ．4解析：选A.根据等差、等比数列的性质，可知x 1＝2，x 2＝3，y 1＝2，y 2＝4.∴P 1(2,2)，P 2(3,4)．∴S △OP 1P 2＝1.3．已知等差数列{a n }的前n 项和为S n ，且S 2＝10，S 5＝55，则过点P (n ，a n )和Q (n ＋2，a n ＋2)(n ∈N *)的直线的一个方向向量的坐标可以是( )A ．(2,4)B ．(－13，－43)C ．(－12，－1)D ．(－1，－1)解析：选B.由S 2＝10，S 5＝55，得2a 1＋d ＝10,5a 1＋10d ＝55，解得a 1＝3，d ＝4，可知直线PQ 的一个方向向量是(1,4)，只有(－13，－43)与(1,4)平行．故选B.4．一群羊中，每只羊的重量数均为整千克数，其总重量为65千克，已知最轻的一只羊重7千克，除去一只10千克的羊外，其余各只羊的千克数恰能构成一等差数列，则这群羊共有( )A ．6只B ．5只C ．8只D ．7只错误!解析：选A.依题意除去一只羊外，其余n －1只羊的重量从小到大依次排列构成等差数列，设a 1＝7，d >0，S n －1＝65－10＝55.∴有(n －1)a 1＋(n －1)(n －2)2d ＝55. 即7(n －1)＋(n －1)(n －2)d 2＝55， (n －1)[7＋(n －2)d 2]＝55，∵55＝11×5且(n －1)∈Z ，[7＋(n －2)d 2]∈Z .∴⎩⎨⎧ n －1＝5，7＋n －22d ＝11.∴n ＝6.5．2008年春，我国南方部分地区遭受了罕见的特大冻灾．大雪无情人有情，柳州某中学组织学生在学校开展募捐活动，第一天只有10人捐款，人均捐款10元，之后通过积极宣传，从第二天起，每天的捐款人数是前一天的2倍，且当天人均捐款数比前一天多5元，则截止第5天(包括第5天)捐款总数将达到( )A ．4800元B ．8000元C ．9600元D ．11200元解析：选B.由题意知，5天共捐款10×10＋(10×2)×(10＋5)＋(10×4)×(15＋5)＋(10×8)×(20＋5)＋(10×16)×(25＋5)＝8000(元)．6．已知{a n }是递增数列，且对任意n ∈N *都有a n ＝n 2＋λn 恒成立，则实数λ的取值范围是( )A ．(－72，＋∞)B ．(0，＋∞)C ．[－2，＋∞)D ．(－3，＋∞)解析：选 D.∵{a n }是递增数列，∴a n ＋1＞a n ，即(n ＋1)2＋λ(n ＋1)＞n 2＋λn ，∴λ＞－2n －1对于n ∈N *恒成立．而－2n －1在n ＝1时取得最大值－3，∴λ＞－3，故选D.7．凸多边形的各内角度数成等差数列，最小角为120°，公差为5°，则边数n 等于________．解析：由条件得，(n －2)×180°＝120°×n ＋n (n －1)2×5°，∴n ＝9或n ＝16，∵a 16＝120°＋(16－1)×5°＝195°>180°，∴n ＝16(舍去)，而a 9＝160°<180°，∴n ＝9.答案：98．已知函数f (x )＝a ·b x 的图象过点A (2，12)，B (3,1)，若记a n ＝log 2f (n )(n ∈N *)，S n 是数列{a n }的前n 项和，则S n 的最小值是________．解析：将A 、B 两点坐标代入f (x )得⎩⎨⎧ 12＝ab 21＝ab 3，解得⎩⎨⎧a ＝18，b ＝2 ∴f (x )＝18·2x ，∴f (n )＝18·2n ＝2n －3，∴a n ＝log 2f (n )＝n －3.令a n ≤0，即n －3≤0，n ≤3.∴数列前3项小于或等于零，故S 3或S 2最小．S 3＝a 1＋a 2＋a 3＝－2＋(－1)＋0＝－3.答案：－39．某纺织厂的一个车间有n (n >7，n ∈N *)台织布机，编号分别为1,2,3，…，n ，该车间有技术工人n 名，编号分别为1,2,3，…，n .定义记号a ij ，如果第i 名工人操作了第j 号织布机，此时规定a ij ＝1，否则a ij ＝0.若第7号织布机有且仅有一人操作，则a 17＋a 27＋a 37＋a 47＋…＋a n 7＝________；若a 31＋a 32＋a 33＋a 34＋…＋a 3n ＝2，说明________________________．解析：依题意，第7台织布机有且仅有一人操作，说明a 17，a 27，a 37，…，a n 7中有且仅有一个值为1，其余值为0，∴a 17＋a 27＋a 37＋…＋a n 7＝1.同理，由a 31＋a 32＋a 33＋…＋a 3n ＝2.说明a 31，a 32，a 33，…，a 3n 中有且仅有2个值为1，其余值为0，即第3号工人操作了2台织布机．答案：1 a 31，a 32，a 33，…，a 3n 中有且仅有2个值为1，其余值为0，即第3号工人操作了2台织布机10．为保护我国的稀土资源，国家限定某矿区的出口总量不能超过80吨，该矿区计划从2010年开始出口，当年出口a 吨，以后每年出口量均比上一年减少10%.(1)以2010年为第一年，设第n 年出口量为a n 吨，试求a n 的表达式；(2)因稀土资源不能再生，国家计划10年后终止该矿区的出口，问2010年最多出口多少吨？(保留一位小数)参考数据：0.910≈0.35.解：(1)由题意知每年的出口量构成等比数列，且首项a 1＝a ，公比q ＝1－10%＝0.9，∴a n ＝a ·0.9n －1.(2)10年出口总量S 10＝a (1－0.910)1－0.9＝10a (1－0.910)．∵S 10≤80，∴10a (1－0.910)≤80，即a ≤81－0.910，∴a ≤12.3.故2010年最多出口12.3吨．11．已知数列{a n }中，a 1＝12，点(n,2a n ＋1－a n )在直线y ＝x 上，其中n ＝1,2,3，….(1)令b n ＝a n ＋1－a n －1，求证数列{b n }是等比数列；(2)求数列{a n }的通项．解：(1)证明：a 1＝12，2a n ＋1＝a n ＋n ，∵a 2＝34，a 2－a 1－1＝34－12－1＝－34，又b n ＝a n ＋1－a n －1，b n ＋1＝a n ＋2－a n ＋1－1，∴b n ＋1b n ＝a n ＋2－a n ＋1－1a n ＋1－a n －1＝a n ＋1＋(n ＋1)2－a n ＋n 2－1a n ＋1－a n －1＝a n ＋1－a n －12a n ＋1－a n －1＝12.b n ＝－34×(12)n －1＝－32×12n ，∴{b n }是以－34为首项，以12为公比的等比数列．(2)∵a n ＋1－a n －1＝－32×12n ，∴a 2－a 1－1＝－32×12，a 3－a 2－1＝－32×122，…∴a n －a n －1－1＝－32×12n －1，将以上各式相加得：∴a n －a 1－(n －1)＝－32(12＋122＋…＋12n －1)， ∴a n ＝a 1＋n －1－32×12(1－12n －1)1－12＝12＋(n －1)－32(1－12n －1)＝32n ＋n －2. ∴a n ＝32n ＋n －2.12.在等比数列{a n }中，a n >0(n ∈N *)，公比q ∈(0,1)，且a 1a 5＋2a 3a 5＋a 2a 8＝25，又a 3与a 5的等比中项为2.(1)求数列{a n }的通项公式；(2)设b n ＝log 2a n ，数列{b n }的前n 项和为S n ，求数列{S n }的通项公式；(3)是否存在k ∈N *，使得S 11＋S 22＋…＋S n n <k 对任意n ∈N *恒成立，若存在，求出k 的最小值，若不存在，请说明理由．解：(1)∵a 1a 5＋2a 3a 5＋a 2a 8＝25，∴a 32＋2a 3a 5＋a 52＝25，∴(a 3＋a 5)2＝25，又a n >0，∴a 3＋a 5＝5，又a 3与a 5的等比中项为2，∴a 3a 5＝4.而q ∈(0,1)，∴a 3>a 5，∴a 3＝4，a 5＝1，∴q ＝12，a 1＝16，∴a n ＝16×(12)n －1＝25－n .(2)∵b n ＝log 2a n ＝5－n ，∴b n ＋1－b n ＝－1， b 1＝log 2a 1＝log 216＝log 224＝4，∴{b n }是以b 1＝4为首项，－1为公差的等差数列，∴S n ＝n (9－n )2.(3)由(2)知S n ＝n (9－n )2，∴S n n ＝9－n 2.当n ≤8时，S n n >0；当n ＝9时，S n n ＝0；当n >9时，S n n <0.∴当n ＝8或9时，S 11＋S 22＋S 33＋…＋S n n ＝18最大．故存在k ∈N *，使得S 11＋S 22＋…＋S n n <k 对任意n ∈N *恒成立，k 的最小值为19.。

2013高考总复习数学(文)配套课时巩固与训练11章2课时训练

1．盒中有10个铁钉，其中8个是合格的，2个是不合格的，从中任取一个恰为合格铁钉的概率是( )A.15B.14C.45D.110解析：选C.从盒中的10个铁钉中任取一个铁钉包含的基本事件总数为10，其中抽到合格铁钉(记为事件A )包含8个基本事件，所以所求的概率为P (A )＝810＝45.故选C.2．从标有1号到100号的100张卡片中任意抽取1张，取出的卡片号是7的倍数的概率是( )A.320B.325C.750D.13100解析：选C.根据等差数列的性质1≤7＋7(m －1)≤100，得所求事件的基本事件数为m ＝14，故取出的卡片号是7的倍数的概率为P ＝14100＝750.3．(2008年高考辽宁卷)4张卡片上分别写有数字1,2,3,4，从这4张卡片中随机抽取2张，则取出的2张卡片上的数字之和为奇数的概率为( )A.13B.12C.23D.34解析：选C.从4张卡片中任取两张的方法数为1,2；1,3；1,4；2,3；2,4；3,4，共6种．其中和为奇数的情况有1,2；1,4；2,3；3,4，共4种．∴所求概率P ＝46＝23.4．有一对酷爱运动的年轻夫妇给他们12个月大的婴儿3块分别写有“20”，“08”和“北京”的字块，如果婴儿能够排成“2008北京”或者“北京2008”，则他们就给婴儿奖励．假设婴儿能将字块横着正排，那么这个婴儿能得到奖励的概率是( )A.16B.14C.13D.12解析：选C.“20”，“08”，“北京”三字块的排法共有“2008北京”、“20北京08”、“0820北京”、“08北京20”、“北京2008”、“北京0820”6种情况，而得到奖励的情况有2种，故婴儿能得到奖励的概率为26＝13.5．如图所示，a ，b ，c ，d 是四处处于断开状态的开关，任意将其中两个闭合，则电路被接通的概率为( )A ．1 B.12C.14 D ．0解析：选B.四个开关任意闭合2个，有ab 、ac 、ad 、bc 、bd 、cd 共6种方案，电路被接通的条件是：①开关d 必须闭合；②开关a ，b ，c 中有一个闭合．即电路被接通有ad 、bd 和cd 共3种方案，所以所求的概率是36＝12.故选B.6．某同学同时掷两颗骰子，得到点数分别为a ，b ，则椭圆x 2a 2＋y 2b 2＝1(a >b >0)的离心率e >32的概率是( ) A.118 B.536 C.16 D.13解析：选C.e ＝ 1－b 2a 2>32?b a <12?a >2b ，符合a >2b 的情况有：当b ＝1时，有a ＝3,4,5,6四种情况；当b ＝2时，有a ＝5,6两种情况，总共有6种情况．则概率为636＝16.7．以连续掷两次骰子分别得到的点数m 、n 作为P 点的坐标，则点P 落在圆x 2＋y 2＝16内的概率是________．解析：基本事件的总数为36个，记事件A ＝{(m ，n )落在圆x 2＋y 2＝16内}，则A 所包含的基本事件有(1,1)，(1,2)，(1,3)，(2,1)，(2,2)，(2,3)，(3,1)，(3,2)共8个．∴P (A )＝836＝29.答案：298．集合A ＝{2,4,6,8,10}，B ＝{1,3,5,7,9}，在A 中任取一元素m 和在B 中任取一元素n ，则所取两数m >n 的概率是________．解析：基本事件总数为25个．m ＝2时，n ＝1；m ＝4时，n ＝1,3；m ＝6时，n ＝1,3,5；m ＝8时，n ＝1,3,5,7；m ＝10时，n ＝1,3,5,7,9；共15个．故P ＝1525＝0.6.答案：0.69．任取一个三位正整数n ，则对数log 2n 是一个正整数的概率是________．解析：∵26＝64,27＝128,28＝256,29＝512,210＝1024，∴满足条件的正整数只有27,28,29三个，∴所求的概率P ＝3900＝1300.答案：130010．从1、2、3、…、7中任取一个数．(1)事件A 为“取出的数大于2”，事件B 为“取出的数小于7”．求P (A ∪B )；(2)事件A 为“取出的数大于3”，事件B 为“取出的数小于1”．求P (A ∪B )；(3)事件A 为“取出的数是偶数”，事件B 为“取出的数为2”，求P (A ∪B )．解：基本事件总数为7，记i ＝{取出的数字为i }，(1)A ＝{3,4,5,6,7}，B ＝{1,2,3,4,5,6}，A ∪B ＝{1,2,3,4,5,6,7}，所以P (A ∪B )＝1.(2)A ＝{4,5,6,7}，B ＝?，所以P (A ∪B )＝P (A )＝47.(3)A ＝{2,4,6}，B ＝{2}，所以P (A ∪B )＝P (A )＝37.11．已知集合P ＝{x |x (x 2＋10x ＋24)＝0}，Q ＝{y |y ＝2n －1,1≤n ≤2，n ∈N *}，M ＝P ∪Q ，在平面直角坐标系中，点A (x ′，y ′)的坐标x ′∈M ，y ′∈M ，计算：(1)点A 正好在第三象限的概率；(2)点A 不在y 轴上的概率；(3)点A 正好落在圆面x 2＋y 2≤10上的概率．解：由集合P ＝{x |x (x 2＋10x ＋24)＝0}可得P ＝{－6，－4,0}，由Q ＝{y |y ＝2n －1,1≤n ≤2，n ∈N *}可得Q ＝{1,3}，M ＝P ∪Q ＝{－6，－4,0,1,3}．因为点A (x ′，y ′)的坐标x ′∈M ，y ′∈M ，由列举法可得满足条件的A 点共有25个．(1)正好在第三象限的点有(－6，－6)，(－4，－6)，(－6，－4)，(－4，－4) 4个点．故点A 正好在第三象限的概率P 1＝425.(2)在y 轴上的点有(0，－6)，(0，－4)，(0,0)，(0,1)，(0,3) 5个点．故点A 不在y 轴上的概率P 2＝1－525＝45.(3)正好落在圆面x 2＋y 2≤10上的点A 有(0,0)，(1,0)，(1,1)，(0,1)，(3,1)，(1,3) 6个点．故点A 落在圆面x 2＋y 2≤10上的概率为P 3＝625.12.在甲、乙两个盒子中分别装有标号为1,2,3,4的四个小球，现从甲、乙两个盒子中各取出一个小球，每个小球被取出的可能性相等．(1)求取出的两个小球上的标号为相邻整数的概率；(2)求取出的两个小球上的标号之和能被3整除的概率；(3)求取出的两个小球上的标号之和大于5的概率．解：由题意可知，从甲、乙两个盒子中各取1个小球的基本事件总数为16.(1)记“取出的两个小球的标号为相邻整数”为事件A ，则事件A 的基本事件有：(1,2)，(2,1)，(2,3)，(3,2)，(3,4)，(4,3)共6个．∴P (A )＝616＝38.(2)记“取出的两个小球上的标号之和能被3整除”为事件B ，则事件B包含：(1,2)，(2,1)，(2,4)，(4,2)，(3,3)共5个基本事件．∴P(B)＝5 16，(3)记“取出的两个小球上的标号之和为6”为事件C，则事件C包含：(2,4)，(4,2)，(3,3)共3个基本事件．∴P(C)＝316，记“取出的两个小球上的标号之和为7”为事件D，则事件D包含：(3,4)，(4,3)共2个基本事件．∴P(D)＝216＝18，记“取出的两个小球上的标号之和为8”为事件E，则事件E包含(4,4)共1个基本事件．∴P(E)＝1 16，∴取出的两个小球上的标号之和大于5的概率为：P(C)＋P(D)＋P(E)＝3 8.。

高考数学(文)二轮复习课时巩固过关练(十一) 数列求和及综合应用

课时巩固过关练(十一) 数列求和及综合应用一、选择题1．(·广东惠州二调)数列{a n }满足a 1＝2，a 2＝1，且a n ·a n －1a n －1－a n ＝a n ·a n ＋1a n －a n ＋1(n ≥2)，则数列{a n }的第100项为( )A.12100B.1250C.1100D.150解析：a n ·a n －1a n －1－a n ＝a n ·a n ＋1a n －a n ＋1(n ≥2)两边取倒数可得1a n －1a n －1＝1a n ＋1－1a n ，所以⎩⎨⎧⎭⎬⎫1a n 是等差数列，首项1a 1＝12，公差d ＝1a 2－1a 1＝1－12＝12，所以1a 100＝12＋12×(100－1)＝50⇒a 100＝150，故选D.答案：D2．(·山东济宁期中)已知在数列{a n }中，a n ＝1n (n ＋1)，其前n 项和为910，则在平面直角坐标系中，直线nx ＋y ＋(n ＋1)＝0在y 轴上的截距是( )A ．－10B ．－9C ．10D ．9解析：a n ＝1n (n ＋1)＝1n －1n ＋1，前n 项和为S n ＝1－12＋12－13＋…＋1n －1n ＋1＝1－1n ＋1，由题意可得1－1n ＋1＝910，解得n ＝9，直线nx ＋y ＋(n ＋1)＝0，即为9x ＋y ＋10＝0，令x ＝0，可得y ＝－10.故选A.答案：A3．(·山东东营期中)若数列{a n }的通项公式是a n ＝(－1)n (3n －2)，则a 1＋a 2＋…＋a 10＝( )A ．15B ．12C ．－12D ．－15解析：依题意可知a 1＋a 2＝3，a 3＋a 4＝3，…，a 9＋a 10＝3，∴a 1＋a 2＋…＋a 10＝5×3＝15.故选A.答案：A4．(·山西晋中联考)已知数列{a n }的通项公式是a n ＝2n －12n ，其前n 项和S n ＝32164，则项数n 等于( )A ．13B ．10C ．9D ．6解析：∵数列{a n }的通项公式是a n ＝2n －12n ，∴a n ＝1－12n ，∴S n ＝⎝⎛⎭⎫1－12＋⎝⎛⎭⎫1－14＋⎝⎛⎭⎫1－18＋…＋⎝⎛⎭⎫1－12n ＝n －⎝⎛⎭⎫12＋14＋18＋…＋12n ＝n －12⎣⎡⎦⎤1－⎝⎛⎭⎫12n 1－12＝n －1＋12n.由S n ＝32164＝n －1＋12n，可得n ＝6.故选D.答案：D5．已知数列{a n }：12，13＋23，14＋24＋34，…，110＋210＋310＋…＋910，…，若b n ＝1a n a n ＋1，那么数列{b n }的前n 项和S n 为( )A.n n ＋1B.4n n ＋1C.3n n ＋1D.5n n ＋1解析：∵a n ＝1＋2＋3＋…＋n n ＋1＝n2，∴b n ＝1a n a n ＋1＝4n (n ＋1)＝4⎝⎛⎭⎫1n －1n ＋1，∴S n ＝4⎣⎡⎦⎤⎝⎛⎭⎫1－12＋⎝⎛⎭⎫12－13＋…＋⎝⎛⎭⎫1n －1n ＋1＝4⎝⎛⎭⎫1－1n ＋1＝4n n ＋1.答案：B6．已知在等差数列{a n }中，a 2＝3，a 6＝11，记数列⎩⎨⎧⎭⎬⎫1a n ·a n ＋1的前n 项和为S n ，若S n ≤m10对n ∈N *恒成立，则正整数m 的最小值为( )A ．5B ．4C ．3D ．2解析：设等差数列{a n }的公差为d ，∵a 2＝3，a 6＝11， ∴⎩⎪⎨⎪⎧ a 1＋d ＝3，a 1＋5d ＝11，解得⎩⎪⎨⎪⎧a 1＝1，d ＝2. ∴a n ＝1＋2(n －1)＝2n －1.∴1a n ·a n ＋1＝1(2n －1)(2n ＋1)＝12⎝⎛⎭⎫12n －1－12n ＋1. 其前n 项和为S n ＝12⎣⎡⎝⎛⎭⎫1－13＋⎝⎛⎭⎫13－15＋…⎦⎤＋⎝⎛⎭⎫12n －1－12n ＋1＝12⎝⎛⎭⎫1－12n ＋1＝n 2n ＋1. ∵S n ≤m 10对n ∈N *恒成立，∴m ≥10n 2n ＋1，∵10n 2n ＋1＝102＋1n<102＝5.∴m ≥5.则正整数m 的最小值为5.故选A. 答案：A7．(·中原名校二联)已知函数f (x )＝x 2＋ax 的图象在点A (0，f (0))处的切线l 与直线2x －y ＋2＝0平行，若数列⎩⎨⎧⎭⎬⎫1f (n )的前n 项和为S n ，则S 20的值为( )A.325462B.1920C.119256D.2 0102 011解析：因为f (x )＝x 2＋ax ，所以f ′(x )＝2x ＋a ，又函数f (x )＝x 2＋ax 的图象在点A (0，f (0))处的切线l 与直线2x －y ＋2＝0平行，所以f ′(0)＝a ＝2，所以f (x )＝x 2＋2x ，所以1f (n )＝1n 2＋2n ＝1n (n ＋2)＝12⎝⎛⎭⎫1n －1n ＋2，所以S 20＝12⎣⎡ ⎝⎛⎭⎫1－13＋⎝⎛⎭⎫12－14＋⎝⎛⎭⎫13－15⎦⎤＋…＋⎝⎛⎭⎫120－122＝12⎝⎛⎭⎫1＋12－121－122＝325462.故选A. 答案：A 二、填空题8．(·河北衡水四调)设向量a ＝(1,2)，b ＝⎝⎛⎭⎫1n 2＋n ，a n (n ∈N *)，若a ∥b ，设数列{a n }的前n 项和为S n ，则S n 的最小值为__________．解析：向量a ＝(1,2)，b ＝⎝⎛⎭⎫1n 2＋n ，a n (n ∈N *)，若a ∥b ，可得a n ＝2n 2＋n ＝2⎝⎛⎭⎫1n －1n ＋1，∵S n ＝a 1＋a 2＋a 3＋…＋a n ＝2⎝⎛1－12＋12－13＋13－14⎭⎫＋…＋1n －1n ＋1＝2n n ＋1.数列{S n }是递增数列，∴S n 的最小值为S 1＝1.故答案为1.答案：1 三、解答题9．设等差数列{a n }的前n 项和为S n ，且S 4＝4S 2，a 2n ＝2a n ＋1. (1)求数列{a n }的通项公式；(2)设数列{b n }的前n 项和为T n ，且T n ＋a n ＋12n ＝λ(λ为常数)．令c n ＝b 2n (n ∈N *)，求数列{c n }的前n 项和R n .解：(1)设等差数列{a n }的首项为a 1，公差为d ，由S 4＝4S 2，a 2n ＝2a n ＋1得 ⎩⎪⎨⎪⎧4a 1＋6d ＝8a 1＋4d ，a 1＋(2n －1)d ＝2a 1＋2(n －1)d ＋1，解得a 1＝1，d ＝2.因此a n ＝2n －1，n ∈N *.(2)由题意知T n ＝λ－n 2n －1，所以n ≥2时，b n ＝T n －T n －1＝－n2n －1＋n －12n －2＝n －22n －1 .故c n ＝2n －222n －1＝(n －1)⎝⎛⎭⎫14n －1，n ∈N *. 所以R n ＝0×⎝⎛⎭⎫140＋1×⎝⎛⎭⎫141＋2×⎝⎛⎭⎫142＋3×⎝⎛⎭⎫143＋…＋(n －1)×⎝⎛⎭⎫14n －1，则14R n ＝0×⎝⎛⎭⎫141＋1×⎝⎛⎭⎫14 2＋2×⎝⎛⎭⎫14 3＋…＋(n －2)×⎝⎛⎭⎫14n n －1＋(n －1)×⎝⎛⎭⎫14n n ，两式相减得34n R n ＝⎝⎛⎭⎫14 1＋⎝⎛⎭⎫14 2＋⎝⎛⎭⎫14 3＋…＋⎝⎛⎭⎫14nn －1－(n －1)×⎝⎛⎭⎫14nn ＝14－⎝⎛⎭⎫14n 1－14－(n －1)×⎝⎛⎭⎫14nn ＝13－1＋3n 3⎝⎛⎭⎫14nn ，整理得R n ＝19⎝ ⎛⎭⎪⎫4－3n ＋14n －1.所以数列{c n }的前n 项和R n＝19⎝ ⎛⎭⎪⎫4－3n ＋14n －1. 10．设等差数列{a n }的公差为d ，点(a n ，b n )在函数f (x )＝2x 的图象上(n ∈N *)． (1)若a 1＝－2，点(a 8,4b 7)在函数f (x )的图象上，求数列{a n }的前n 项和S n ；(2)若a 1＝1，函数f (x )的图象在点(a 2，b 2)处的切线在x 轴上的截距为2－1ln2，求数列⎩⎨⎧⎭⎬⎫a nb n 的前n 项和T n .解：据题设可得b n ＝2a n .(1)∵b 7＝2a 7＝2－2＋6d ，∴4×2－2＋6d ＝2－2＋7d ，∴d ＝2，∴S n ＝－2n ＋n (n －1)＝n (n －3)．(2)将f (x )＝2x 求导得f ′(x )＝2x ln2，∴f (x )＝2x 在(a 2，b 2)处的切线方程为y －b 2＝22a(x－a 2)ln2，令y ＝0，得－b 2＝(22aln2)×(x －a 2)，x ＝a 2－1ln2，∴a 2＝2，∴d ＝2－1＝1，∴a n＝n ，b n ＝2n ，∴a n b n ＝n 2n ，其前n 项和T n ＝121＋222＋323＋…＋n －12n －1＋n 2n ①，两边同乘2得2T n＝11＋221＋322＋…＋n 2n －1 ②，②－①得2T n －T n ＝11＋121＋122＋…＋12n －1－n 2n ＝2－12n －1－n2n ，∴T n ＝2n ＋1－n －22n.11．已知等差数列{a n }满足：a 1＝2，且a 1，a 2，a 5成等比数列． (1)求数列{a n }的通项公式；(2)记S n 为数列{a n }的前n 项和，是否存在正整数n ，使得S n >60n ＋800？若存在，求n 的最小值；若不存在，说明理由．解：(1)设数列{a n }的公差为d ，依题意，2,2＋d,2＋4d 成等比数列，所以(2＋d )2＝2(2＋4d )，解得d ＝0或d ＝4.当d ＝0时，a n ＝2；当d ＝4时，a n ＝2＋(n －1)×4＝4n －2，所以数列{a n }的通项公式为a n ＝2或a n ＝4n －2.(2)当a n ＝2时，S n ＝2n ，显然2n <60n ＋800，不存在正整数n ，使得S n >60n ＋800.当a n＝4n －2时，S n ＝n [2＋(4n －2)]2＝2n 2，令2n 2>60n ＋800，即n 2－30n －400>0，解得n >40或n <－10(舍去)．此时存在正整数n ，使得S n >60n ＋800成立，n 的最小值为41.综上所述，当a n ＝2时，不存在正整数n ；当a n ＝4n －2时，存在正整数n ，使得S n >60n ＋800成立，n 的最小值为41.。

【专题通关攻略】高三数学(文)二轮复习：课时巩固过关练十一 1.4.2数列求和及综合应用

课时巩固过关练十一数列求和及综合应用(35分钟55分)一、选择题(每小题5分,共20分)1.(2016·成都一模)已知等差数列{a n}的前n项和为S n,a5=5,S5=15,则数列的前2016项和为( )A. B. C. D.【解析】选A.设等差数列{a n}的首项为a1,公差为d.因为a5=5,S5=15,所以所以所以a n=a1+(n-1)d=n.所以==-,所以数列的前2016项和为1-+-+…+-=1-=.2.(2016·南阳二模)已知数列{a n}满足条件a1+a2+a3+…+a n=2n+5,则数列{a n}的通项公式为( )A.a n=2n+1B.a n=C.a n=2nD.a n=2n+2【解析】选B.由题意可知,数列{a n}满足条件a1+a2+a3+…+a n=2n+5,则n>1时,有a1+a2+a3+…+a n-1=2(n-1)+5,n>1,两式相减可得:=2n+5-2(n-1)-5=2,所以a n=2n+1,n>1,n∈N*.当n=1时,=7,所以a1=14,综上可知,数列{a n}的通项公式为:a n=3.(2016·安庆一模)各项均不为零的等差数列{a n}中,若-a n-1-a n+1=0(n∈N*,n≥2),则S2016等于( )A.0B.2C.2016D.4032【解题导引】将-a n-1-a n+1=0变形为=a n-1+a n+1,求其通项公式即可.【解析】选D.由题意得=a n-1+a n+1=2a n,a n≠0,所以a n=2.所以S n=2n,=2×2016=4032.4.(2016·秦皇岛一模)满足a1=1,log2a n+1=log2a n+1(n∈N*),它的前n项和为S n,则满足S n>1025的最小n值是( )A.9B.10C.11D.12【解析】选C.因为a1=1,log2a n+1=log2a n+1(n∈N*),所以a n+1=2a n,a n=2n-1,S n=2n-1,则满足S n>1025的最小n值是11.【加固训练】已知数列{a n}的前n项和S n=n2-9n,第k项满足5<a k<8,则k等于( )A.9B.8C.7D.6【解析】选B.因为S n=n2-9n,所以n≥2时,a n=S n-S n-1=2n-10,a1=S1=-8适合上式,所以a n=2n-10(n∈N*),所以5<2k-10<8,得7.5<k<9,所以k=8.二、填空题(每小题5分,共10分)5.(2016·桂林一模)已知数列{a n}中,a n+1=2a n,a3=8,则数列{log2a n}的前n项和等于________.【解析】因为=2,a3=8,所以a2=4,a1=2,所以数列{a n}是以2为首项,2为公比的等比数列,所以a n=2n,所以log2a n=n,所以数列{log2a n}的前n项和等于. 答案:6.(2016·太原一模)已知数列{a n}的通项公式为a n=2n-1,{b n}的通项公式为b n=2n-1,设c n=a n b n,则数列{c n}的前n项和为________.【解析】因为c n=(2n-1)·2n-1.设{c n}的前n项和为S n,则S n=1×20+3×21+5×22+…+(2n-3)×2n-2+(2n-1)×2n-1,2S n=1×21+3×22+5×23+…+(2n-3)×2n-1+(2n-1)×2n,两式相减得-S n=1+22+23+…+2n-(2n-1)×2n=2n+1-3-(2n-1)×2n=-(2n-3)×2n-3, 所以S n=(2n-3)·2n+3.答案:(2n-3)·2n+3三、解答题(7题12分,8题13分,共25分)7.(2016·开封一模)已知等差数列{a n}的前n项和为S n,公差d≠0,且S3+S5=50,a1,a4,a13成等比数列.(1)求数列{a n}的通项公式.(2)设是首项为1,公比为3的等比数列,求数列{b n}的前n项和T n.【解析】(1)依题意得,解得所以a n=a1+(n-1)d=3+2(n-1)=2n+1,即a n=2n+1(n∈N*).(2)=3n-1,b n=a n·3n-1=(2n+1)·3n-1,T n=3+5×3+7×32+…+(2n+1)·3n-1, ①3T n=3×3+5×32+7×33+…+(2n-1)·3n-1+(2n+1)·3n,②①-②得-2T n=3+2×3+2×32+…+2·3n-1-(2n+1)3n=3+2·-(2n+1)3n=-2n·3n,所以T n=n·3n(n∈N*).【加固训练】(2016·石家庄一模)设数列{a n}的前n项和为S n,a1=1,a n+1=λS n+1(n ∈N*,λ≠-1),且a1,2a2,a3+3为等差数列{b n}的前三项.(1)求数列{a n},{b n}的通项公式.(2)求数列{a n b n}的前n项和.【解析】(1)方法一:因为a n+1=λS n+1(n∈N*),所以a n=λS n-1+1(n≥2),所以a n+1-a n=λa n,即a n+1=(λ+1)a n(n≥2),λ+1≠0,又a1=1,a2=λS1+1=λ+1,所以数列{a n}是以1为首项,以λ+1为公比的等比数列,所以a3=(λ+1)2,所以4(λ+1)=1+(λ+1)2+3,整理得λ2-2λ+1=0,解得λ=1,所以a n=2n-1,b n=1+3(n-1)=3n-2.方法二:因为a1=1,a n+1=λS n+1(n∈N*),所以a2=λS1+1=λ+1,a3=λS2+1=λ(1+λ+1)+1=λ2+2λ+1,所以4(λ+1)=1+λ2+2λ+1+3,整理得λ2-2λ+1=0,解得λ=1,所以a n+1=S n+1(n∈N*),所以a n=S n-1+1(n≥2),所以a n+1-a n=a n(n≥2),即a n+1=2a n(n≥2),又a1=1,a2=2,所以数列{a n}是以1为首项,以2为公比的等比数列,所以a n=2n-1,b n=1+3(n-1)=3n-2.(2)由(1)知,a n b n=(3n-2)2n-1,设T n为数列{a n b n}的前n项和,所以T n=1×1+4×21+7×22+…+(3n-2)·2n-1, ①所以2T n=1×21+4×22+7×23+…+(3n-5)·2n-1+(3n-2)·2n. ②①-②得,-T n=1×1+3×21+3×22+…+3·2n-1-(3n-2)·2n=1+3×-(3n-2)·2n,整理得:T n=(3n-5)·2n+5.8.(2016·东营一模)已知等差数列{a n}的前n项和为S n,S5=35,a5和a7的等差中项为13.(1)求a n及S n.(2)令b n=(n∈N*),求数列{b n}的前n项和T n.【解析】(1)设等差数列{a n}的公差为d,因为S5=5a3=35,a5+a7=26,所以解得a1=3,d=2,所以a n=3+2(n-1)=2n+1,S n=3n+×2=n2+2n.(2)由(1)知a n=2n+1,所以b n===-,所以T n=++…+=1-=.(30分钟55分)一、选择题(每小题5分,共20分)1.已知数列{a n}的前n项和S n=n2-6n,则{|a n|}的前n项和T n= ( )A.6n-n2B.n2-6n+18C. D.【解析】选C.由S n=n2-6n得{a n}是等差数列,且首项为-5,公差为2.所以a n=-5+(n-1)×2=2n-7,所以n≤3时,a n<0;n>3时,a n>0,所以T n=2.抛物线x2=y在第一象限内的图象上一点(a i,2)处的切线与x轴交点的横坐标记为a i+1,其中i∈N*,若a2=32,则a4+a6+a8等于( )A.64B.42C.32D.【解题导引】令y=f(x)=2x2,对其求导写出切线方程,即可求解.【解析】选D.令y=f(x)=2x2,所以y′=f′(x)=4x,则切线斜率k=f′(a i)=4a i,切线方程为y-2=4a i(x-a i).令y=0,得x=a i+1=a i.由a2=32,得a4=8,a6=2,a8=,所以a4+a6+a8=.3.S n是等比数列{a n}的前n项和,a1=,9S3=S6,设T n=a1a2a3…a n,则使T n取最小值的n值为( )A.3B.4C.5D.6【解析】选C.设等比数列的公比为q,故由9S3=S6,得9×=,解得q=2,故=a n=×2n-1,易得当n≤5时,<1,即T n<T n-1;当n≥6时,T n>T n-1,据此数列单调性可得T5为最小值.4.已知等比数列{a n}的前n项和为S n,且a1+a3=4,a2+a4=2,则log2=( ) A.2016 B.2017 C.22016 D.22017【解析】选B.设公比为q,则q==,所以===22017-1,所以log2=2017.二、填空题(每小题5分,共10分)5.已知向量a=(2,-n),b=(S n,n+1),n∈N*,其中S n是数列{a n}的前n项和,若a⊥b,则数列的最大项的值为________.【解析】因为a⊥b,所以a·b=2S n-n(n+1)=0,所以S n=,所以a n=n,所以==,当n=2时,n+取最小值4,此时取到最大值.答案:6.设数列{a n}满足a2+a4=10,点P n(n,a n)对任意的n∈N*,都有向量=(1,2),则数列{a n}的前n项和S n=________.【解析】因为P n(n,a n),所以P n+1(n+1,a n+1),所以=(1,a n+1-a n)=(1,2),所以a n+1-a n=2,所以数列{a n}是公差d为2的等差数列.又由a2+a4=2a1+4d=2a1+4×2=10,解得a1=1,所以S n=n+×2=n2.答案:n2三、解答题(7题12分,8题13分,共25分)7.已知数列{a n}的前n项和是S n,且S n+a n=1(n∈N*).(1)求数列{a n}的通项公式.(2)设b n=log3(1-S n+1)(n∈N*),求适合方程++…+=的正整数n的值.【解析】(1)当n=1时,a1=S1,由S1+a1=1,得a1=,当n≥2时,因为S n=1-a n,S n-1=1-a n-1,所以S n-S n-1=(a n-1-a n),即a n=(a n-1-a n),所以a n=a n-1(n≥2),所以{a n}是以为首项,为公比的等比数列.故a n=·=2·(n∈N*).(2)1-S n=a n=,b n=log3(1-S n+1)=log3=-n-1,==-,++…+=++…+=-,解方程-=,得n=100.8.已知函数f(x)=x2-ax+a(x∈R)同时满足:①函数f(x)有且只有一个零点;②在定义域内存在0<x1<x2,使得不等式f(x1)>f(x2)成立.设数列{a n}的前n项和S n=f(n)(n∈N*).(1)求函数f(x)的表达式.(2)求数列{a n}的通项公式.(3)在各项均不为零的数列{c n}中,所有满足c i·<0的整数的个数称为数列{c n}的变号数.令c n=1-,求数列{c n}的变号数.【解题导引】(1)看到函数f(x)=x2-ax+a(x∈R)有且只有一个零点,想到Δ=0,从而确定解析式.(2)看到S n求a n,想到a n=(3)看到求数列{c n}的变号数以及变号数的定义,想到从函数角度考虑数列的性质.【解析】(1)因为f(x)有且只有一个零点,所以Δ=a2-4a=0,解得a=0或a=4,当a=4时,函数f(x)=x2-4x+4在(0,2)上递减,故存在0<x1<x2,使得不等式f(x1)>f(x2)成立,当a=0时,函数f(x)=x2在(0,+∞)上递增,故不存在0<x1<x2,使得不等式f(x1)>f(x2)成立,综上,得a=4,所以f(x)=x2-4x+4.(2)由(1)可知S n=n2-4n+4,当n=1时,a1=S1=1,当n≥2时,a n=S n-S n-1=2n-5,所以a n=(3)由题设得c n=因为当n≥3时,c n+1-c n=->0,所以当n≥3时,数列{c n}递增.因为c4=-<0,由1->0⇒n≥5.可知c4·c5<0,即当n≥3时,有且只有1个变号数;又因为c1=-3,c2=5,c3=-3,即c1·c2<0,c2·c3<0,所以此处变号数有2个;综上知,数列{c n}的变号数为3.1.(2016·广州一模)已知等差数列{a n}满足a1=3,a5=15,数列{b n}满足b1=4,b5=31,设c n=b n-a n,且数列{c n}为等比数列.(1)求数列{a n}和{b n}的通项公式.(2)求数列{b n}的前n项和.【解析】(1)设{a n}的公差为d,依题意得a5=a1+4d,即3+4d=15,解得d=3,因此a n=3+3(n-1)=3n.设等比数列{c n}的公比为q,由已知有c1=b1-a1=4-3=1,c5=b5-a5=31-15=16.从而c5=c1q4,即16=1×q4,所以q=2,所以c n=1×2n-1=2n-1.由已知有c n=b n-a n,所以b n=a n+c n,所以b n=3n+2n-1.(2)因为b n=3n+2n-1,所以数列{b n}的前n项和S n=(3+1)+(6+21)+(9+22)+…+(3n+2n-1)=(3+6+9+…+3n)+(1+2+22+…+2n-1)=+=+2n-1.2.(2016·石家庄一模)已知数列{a n}中,有a n+1=a n+4,且a1+a4=14.(1)求{a n}的通项公式与前n项和公式S n.(2)令b n=,若{b n}是等差数列,求数列的前n项和T n.【解析】(1)依题意得,a n+1-a n=4,所以{a n}是公差为4的等差数列,所以a1+a4=2a1+3d=14,即a1=1,所以a n=a1+(n-1)d=4n-3,S n==2n2-n.(2)由(1)知b n=为等差数列,所以2b2=b1+b3,代入解得k=-或k=0.当k=-,即b n=2n,则=,所以T n=(-+-+…+-)=.当k=0时,b n=2n-1,即==,T n=(-+-+…+-)=.3.(2016·安庆二模)已知{a n}是各项为正数的等比数列,{b n}是等差数列,且a1=b1=1,b2+b3=2a3,a5-3b2=7.(1)求{a n}和{b n}的通项公式.(2)设c n=a n·b n,n∈N*,求数列{c n}的前n项和S n.【解析】(1)设{a n}的公比为q,{b n}的公差为d,由题意q>0,由已知,有消去d得q4-2q2-8=0,解得q=2,d=2,所以{a n}的通项公式为a n=2n-1,n∈N*,{b n}的通项公式为b n=2n-1,n∈N*,(2)由(1)有c n=(2n-1)2n-1,设{c n}的前n项和为S n,则S n=1×20+3×21+5×22+…+(2n-1)×2n-1,2S n=1×21+3×22+5×23+…+(2n-1)×2n,两式相减得-S n=1+22+23+…+2n-(2n-1)×2n=-(2n-3)×2n-3,所以S n=(2n-3)2n+3.。

2013年高考数学总复习高效课时作业2-11 理新人教版

2013年高考数学总复习高效课时作业2-11 理新人教版一、选择题1．(2011年某某)曲线y ＝e x 在点A (0，1)处的切线斜率为( )A ．1B ．2C ．eD.1e 解析：y ′＝e x ，k ＝y ′|x ＝0＝1.答案：A2．(某某省某某市2012届高三第二次模拟)曲线y ＝x －1x ＋1在点(0，－1)处的切线与两坐标轴围成的封闭图形的面积为( )A ．1B ．－12 C.14 D.18 解析：y ′＝（x －1）′（x ＋1）－（x －1）（x ＋1）′（x ＋1）2 ＝（x ＋1）－（x －1）（x ＋1）2＝2（x ＋1）2，所以k ＝2，所以切线方程为y ＝2x －1，所以S Δ＝12×12×1＝14，故选C. 答案：C3．(2011年某某)曲线y ＝x 3＋11在点P (1，12)处的切线与y 轴交点的纵坐标是( )A ．－9B ．－3C ．9D ．15 解析：y ′＝3x 2，故曲线在点P (1，12)处的切线斜率是3，故切线方程是y －12＝3(x －1)，令x ＝0，得y ＝9.答案：C4．(2011年某某)曲线y ＝sin x sin x ＋cos x －12在点M ⎝ ⎛⎭⎪⎫π4，0处的切线的斜率为( ) A ．－12B.12 C ．－22 D.22解析：y ′＝cos x （sin x ＋cos x ）－sin x （cos x －sin x ）（sin x ＋cos x ）2＝11＋sin 2x ，把x ＝π4代入得导数值为12. 答案：B5．已知f (x )＝x 2＋2xf ′(1)，则f ′(0)等于( )A ．0B ．－4C ．－2D ．2 解析：f ′(x )＝2x ＋2f ′(1)，∴f ′(1)＝2＋2f ′(1)即f ′(1)＝－2，∴f ′(x )＝2x －4，∴f ′(0)＝－4.答案：B二、填空题6．如图所示，函数y ＝f (x )的图象在点P 处的切线方程是y ＝－2x ＋9，则f (4)＋f ′(4)的值为________．解析：因为f (4)＝－2×4＋9＝1，f ′(4)＝－2，所以f (4)＋f ′(4)＝1＋(－2)＝－1.答案：－17．在平面直角坐标系xOy 中，点P 在曲线C ：y ＝x 3－10x ＋3上，且在第二象限内，已知曲线C 在点P 处的切线的斜率为2，则点P 的坐标为________．解析：由y ＝x 3－10x ＋3，得y ′＝3x 2－10，由曲线C 在点P 处的切线的斜率为2，∴y ′＝3x 2－10＝2，即x 2＝4，又点P 在第二象限，∴x ＝－2，又点P 在曲线C 上，∴y ＝(－8)＋20＋3＝15，则点P 的坐标为(－2，15)．答案：(－2，15) 8．已知曲线f (x )＝x sin x ＋1在点⎝ ⎛⎭⎪⎫π2，π＋22处的切线与直线ax －y ＋1＝0互相垂直，则实数a ＝________．解析：f ′(x )＝sin x ＋x cos x ，f ′⎝ ⎛⎭⎪⎫π2＝1，因为切线与ax －y ＋1＝0互相垂直，所以a ＝－1.答案：－19．设P 为曲线C ：y ＝x 2－x ＋1上一点，曲线C 在点P 处的切线的斜率的X 围是[－1，3]，则点P 纵坐标的取值X 围是________．解析：设P (a ，a 2－a ＋1)，y ′x ＝a ＝2a －1∈[－1，3]，∴0≤a ≤2. 而g (a )＝a 2－a ＋1＝⎝ ⎛⎭⎪⎫a －122＋34，当a ＝12时，g (a )min ＝34. a ＝2时，g (a )max ＝3，故P 点纵坐标X 围是⎣⎢⎡⎦⎥⎤34，3. 答案：⎣⎢⎡⎦⎥⎤34，3 三、解答题10．已知函数f (x )＝ax 3＋bx 2＋cx ，且f (－1)＝－1，若方程f ′(x )＝0的实数根为±1，求方程f (x )＝0的实数根．解析：由题设的三个条件“f (－1)＝－1，f ′(1)＝0， f ′(－1)＝0”列方程组可解得a 、b 、c 的值．∵f (－1)＝－1，∴－a ＋b －c ＝－1，即a －b ＋c ＝1.①又∵f ′(x )＝3ax 2＋2bx ＋c ，f ′(x )＝0的实数根为±1，∴3a ＋2b ＋c ＝0，②，且3a －2b ＋c ＝0，③联立方程①②③，解得a ＝－12，b ＝0，c ＝32. 由f (x )＝0，得－12x 3＋32x ＝0，解得x ＝0，或x ＝±3，即方程f (x )＝0的实数根为0，± 3.11．已知函数f (x )＝x 3－3x 及y ＝f (x )上一点P (1，－2)，过点P 作直线l .(1)求使直线l 和y ＝f (x )相切且以P 为切点的直线方程；(2)求使直线l 和y ＝f (x )相切且切点异于P 的直线方程．解析：(1)由f (x )＝x 3－3x 得，f ′(x )＝3x 2－3，过点P 且以P (1，－2)为切点的直线的斜率f ′(1)＝0，∴所求直线方程为y ＝－2.(2)设切点为(x 0，x 03－3x 0)，(x 0≠1)，切线斜率k ＝f ′(x 0)＝3x 02－3，切线为y －(x 03－3x 0)＝(3x 02－3)(x －x 0)又切线过P (1，－2)∴－2－x 03＋3x 0＝(3x 02－3)(1－x 0)即2x 03－3x 02＋1＝0∴(x 0－1)2(2x 0＋1)＝0∵x 0≠1，∴x 0＝－12 ∴所求切线方程为y －⎝ ⎛⎭⎪⎫－18＋32＝⎝ ⎛⎭⎪⎫34－3⎝ ⎛⎭⎪⎫x ＋12 即9x ＋4y －1＝0.12．设函数f (x )＝ax ＋2，g (x )＝a 2x 2－ln x ＋2，其中a ∈R，x >0.(1)若a ＝2，求曲线y ＝g (x )在点(1，g (1))处的切线方程；(2)是否存在负数a ，使f (x )≤g (x )对一切正数x 都成立？若存在，求出a 的取值X 围；若不存在，请说明理由．解析：(1)由题意可知：当a ＝2时，g (x )＝4x 2－ln x ＋2，则g ′(x )＝8x －1x. 曲线y ＝g (x )在点(1，g (1))处的切线斜率k ＝g ′(1)＝7，又g (1)＝6，故曲线y ＝g (x )在点(1，g (1))处的切线方程为y －6＝7(x －1)，即y ＝7x －1.(2)设函数h (x )＝f (x )－g (x )＝ax ＋ln x －a 2x 2(x >0)．假设存在负数a ，使得f (x )≤g (x )对一切正数x 都成立，即：当x >0时，h (x )的最大值小于等于零．h ′(x )＝a ＋1x －2a 2x ＝－2a 2x 2＋ax ＋1x(x >0)，令h ′(x )＝0可得：x 1＝－12a ，x 2＝1a(舍)．当a <x <－12a时，h ′(x )>0，h (x )单调递增；当x >－12a时，h ′(x )<0，h (x )单调递减，所以h (x )在x ＝－12a处有极大值，也是最大值． ∴h (x )max ＝h ⎝ ⎛⎭⎪⎫－12a ≤0，解得：a ≤－12e －34，所以负数a 存在，它的取值X 围为：a ≤.。

2013高考数学第一轮复习配套课时作业 11.2 合情推理与演绎推理新人教B版

第2讲合情推理与演绎推理随堂演练巩固1.下列四个图形中,着色三角形的个数依次构成一个数列的前4项,则这个数列的一个通项公式为( )A.13n n a -= B.3nn a =C.32nn a n =-D.1323n n a n -=+-【答案】 A【解析】 123413927a a a a =,=,=,=.归纳推理:13n n a -=.2.“所有9的倍数都是3的倍数,某奇数是9的倍数,故此奇数是3的倍数”,上述推理是( ) A.小前提错 B.结论错 C.正确的 D.大前提错【答案】 C【解析】这是演绎推理的一般模式“三段论”.前提和推理形式都正确,因此结论也正确. 3.有一段演绎推理是这样的:“若直线平行于平面,则该直线平行于平面内所有直线;已知直线b ∥平面α,直线a ⊂平面α,则直线b ∥直线a”,结论显然是错误的,这是因为 ( ) A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误【答案】 A【解析】由演绎推理的三段论可知答案应为A.4.(2011江西高考,文6)观察下列各式:237497343=,=,47=2 401,…,则20117的末两位数字为( ) A.01 B.43 C.07 D.49 【答案】 B【解析】 (方法一)由题意得2011502434502377(7)7⨯+,==⋅,由于472= 401末位为1,倒数第二位为0,因此2 502401的末两位定为01.又37=343,∴45023(7)7⋅的末两位定为43.(方法二)用归纳法:∵234749734372=,=,=54017,=16 68077,=117 76497,823=543,…,由上知末两位有周期性且T=4. 又20115024377⨯+=,∴20117的末两位与37的末两位一样,为43. 5.在等差数列{n a }中,若100a =,则有等式12a a ++…12n a a a +=++…19(19n a n -+<,且n ∈N )*成立.类比上述性质,相应地,在等比数列{n b }中,若91b =,则有等式成立.【答案】 12b b ⋅⋅…12n b b b ⋅=⋅⋅…17n b -⋅【解析】对于等差数列{n a },若有0k a =,根据等差中项的知识,有121222323n k n n k n n k n k a a a a a a a +--+--+--+=+=+=+k a =0,所以必有12a a ++…12n a a a +=++…n a ++12(n n a a ++++…2221)k n k n a a ----++(21n k n <-,∈N )*.∵此时有100a =,即k=10.∴12a a ++…12n a a a +=++…12(n n n a a a ++++++…181912)n n a a a a --++=++…19n a -+. 类似地:对于等比数列{n b },若1k b =,由等比中项的知识,有121222323n k n n k n n k n b b b b b b +--+--+--⋅=⋅=⋅=…=1k k b b ⋅=.∴12b b ⋅⋅…12n b b b ⋅=⋅⋅…12(n n n b b b ++⋅⋅⋅…2221)k n k n b b ----⋅⋅. ∵91b =,∴k=9.∴12b b ⋅⋅…12n b b b ⋅=⋅⋅…12(n n n b b b ++⋅⋅⋅…18218112)n n b b b b ----⋅⋅=⋅⋅…17n b -⋅.课后作业夯基基础巩固1.下列表述正确的是( )①归纳推理是由部分到整体的推理; ②归纳推理是由一般到一般的推理; ③演绎推理是由一般到特殊的推理; ④类比推理是由特殊到一般的推理; ⑤类比推理是由特殊到特殊的推理. A.①②③ B.②③④ C.②④⑤ D.①③⑤ 【答案】 D【解析】归纳推理是由部分到整体的推理,演绎推理是由一般到特殊的推理,类比推理是由特殊到特殊的推理.2.由代数式的乘法法则类比推导向量的数量积的运算法则: ①“mn=nm”类比得到“a ⋅b=b ⋅a ”;②“(m+n)t=mt+nt”类比得到“(a +b ) ⋅c=a ⋅c+b ⋅c ”;③“()()m n t m n t ⋅=⋅”类比得到“（a ⋅b ）⋅c =a ⋅（b ⋅c ）”; ④“0t mt xt m x ≠,=⇒=”类比得到“p ≠0, a ⋅p =x ⋅p ⇒a =x ”; ⑤“|m n ⋅|=|m|⋅|n|”类比得到“| a ⋅b |=|a |⋅|b |”; ⑥“ac a bc b =”类比得到“a c a b c b⋅=⋅”.以上式子中,类比得到的结论正确的个数是( ) A.1 B.2C.3D.4 【答案】 B【解析】 ①②正确;③④⑤⑥错误.3.已知△ABC 中30A ,∠=60B ,∠=,求证:a<b . 证明:∴a<b.框内部分是演绎推理的( ) A.大前提 B.小前提 C.结论 D.三段论【答案】 B4.根据图中5个图形及相应点的个数的变化规律,试猜测第n 个图中有个点.( )A.21n + B.2n n - C.n+1 D.21n n -+ 【答案】 D【解析】第(2)个图形,中间有1个点,另外的点指向两个方向,每个方向一个点,共有2(21)1⨯-+ 个点;第(3)个图形,中间有1个点,另外的点指向三个方向,每个方向两个点,共有3(31)1⨯-+个点; 第(4)个图形,中间有1个点,另外的点指向四个方向,每个方向三个点,共有4(41)1⨯-+个点; 第(5)个图形,中间有1个点,另外的点指向五个方向,每个方向四个点,共有5(51)1⨯-+个点; ……由上面的变化规律,可猜测,第n 个图形中心有1个点,另外的点指向n 个方向,每个方向n-1个点,共有n(n-1)211n n +=-+个点. 5.下列推理是归纳推理的是( )A.A,B 为定点,动点P 满足|PA|+|PB|=2a>|AB|,则P 点的轨迹为椭圆B.由1131n a a n =,=-,求出123S S S ,,,猜想出数列的前n 项和n S 的表达式C.由圆222x y r +=的面积π2r ,猜想出椭圆22221y x a b+=的面积S=πab D.以上均不正确【答案】 B【解析】从123S S S ,,猜想出数列的前n 项和n S ,是从特殊到一般的推理,所以B 是归纳推理. 6.如图,椭圆中心在坐标原点,F 为左焦点,当FB AB ⊥时,其离心率为512-,此类椭圆被称为 “黄金椭圆”,类比“黄金椭圆”,可推算出“黄金双曲线”的离心率e 等于( )A.512+B.512- C.51-D.51+【答案】 A【解析】 B(0,b),F(-c,0),A(a,0).在“黄金双曲线”中, ∵FB AB ⊥, ∴0FB AB ⋅=.∴2b ac =.而222b c a =-,∴22c a ac -=.在等号两边同除以2a 得512e +=. 7.观察下列等式:33212(12)+=+,31+3323333223(123)1234(1234)+=++,+++=+++,…,根据上述规律,第四个等式为 .【答案】 33333212345(12345)(++++=++++或215)【解析】 332333212(12)123(123)+=+,++=++,…, 所以333332225(15)12345(12345)[]152+++++=++++==. 8.在德国不来梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第1堆只有一层,就一个球;第2、3、4、…堆最底层(第一层)分别按如下图所示方式固定摆放,从第二层开始,每层的小球自然垒放在下一层之上,第n 堆第n 层就放一个乒乓球,以f(n)表示第n 堆的乒乓球总数,则f(3)= ;f(n)= (答案用n 表示).【答案】 10(1)(2)6n n n ++【解析】 f(1)=1,由题图可得f(2)=3+1=42(21)(1)2f +=+, f(3)=6+3+1=103(31)(2)2f +=+.f(4)=10+6+3+1=204(41)(3)2f +=+.可知,下一堆的球的个数是上一堆球的个数加上其第一层的球的个数,而第一层的球的个数满足1,3,6,10,…,其通项公式是(1)2n n +. ∴f(5)=f(4)+155(51)(4)2f +=+,…,f(n)=f (1)(1)2n n n +-+.∴2(21)3(31)()(1)22f n f ++-=++ (1)2n n ++22332222++=++…22n n ++ 222232322n n ++++++=+(1)(21)(1)1124n n n n n+++=+-(1)(2)16n n n ++=-.∴(1)(2)()6n n n f n ++=.9.(2011陕西高考,文13)观察下列等式: 1=1 2+3+4=93+4+5+6+7=254+5+6+7+8+9+10=49照此规律,第五个等式应为 .【答案】 5+6+7+8+9+10+11+12+13=81【解析】观察等式左侧:第一行有1个数是1,第二行是3个连续自然数的和,第一个数是2,第三行是5个连续自然数的和,第一个数是3,第四行是7个连续自然数的和,第一个数是4,第5行应该是连续9个自然数的和,第一个数为5,∴第5行左侧:5+6+7+8+9+10+11+12+13;等式右侧:第一行 1=12,第二行9=32,第三行25=52,第四行49=72,则第5行应为81=92, ∴第五个等式为5+6+7+8+9+10+11+12+13=81.10.设等差数列{n a }的前n 项和为n S ,则4841281612S S S S S S S ,-,-,-成等差数列.类比以上结论有:设等比数列{n b }的前n 项积为n T ,则4T , , 1612T T ,成等比数列. 【答案】84T T 128T T 【解析】对于等比数列,通过类比,可得8161244812T T T T T T T ,,,成等比数列. 11.已知等式:sin 25+23355354cos sin cos +=;223154515454sin cos sin cos ++=;223306030604sin cos sin cos ++=;….由此可归纳出对任意角度θ都成立的一个等式,并予以证明. 【证明】归纳已知可得:2sin θ+2cos (30θ+)+sin θcos (30θ+3)4=.证明如下:∵sin 2θ+cos 2(30θ+)+sin θcos (30θ+)=sin23(θ+cos 12θ-sin 2)θ+sin 3(θcos 12θ-sin )θ=sin 23(θ+cos 12θ-sin 3θcos 12θ+sin )θ =sin 234θ+2cos 14θ-2sin 34θ=.∴等式成立.12.已知椭圆具有性质:若M 、N 是椭圆C 上关于原点对称的两个点,点P 是椭圆上任意一点,当直线PM 、PN 的斜率都存在,并记为PM k 、PN k 时,那么PM k 与PN k 之积是与点P 的位置无关的定值.试对双曲线22221y x a b-=写出具有类似特性的性质,并加以证明. 【解】类似的性质为:若M 、N 是双曲线22221y x a b-=上关于原点对称的两个点,点P 是双曲线上任意一点,当直线PM 、PN 的斜率都存在,并记为PM k 、PN k 时,那么PM k 与PN k 之积是与点P 的位置无关的定值.证明:设点M 、P 的坐标分别为(m,n)、(x,y), 则N(-m,-n).因为点M(m,n)在已知双曲线上,所以22222b n m b a =-.同理22222b y x b a=-. 则2222PM PN y n y n y n k k x m x m x m -+-⋅=⋅==-+-22b a ⋅2222x m x m -=-22b a 定值). 13.已知等差数列{n a }的公差d=2,首项15a =. (1)求数列{n a }的前n 项和n S ;(2)设(25)n n T n a =-,求12345S S S S S ,,,,;12345T T T T T ,,,,,并归纳出n S 与n T 的大小规律.【解】 (1)(1)52(4)2n n n S n n n -=+⨯=+.(2)(25)[2(n n T n a n =-=2n+3)-5],∴24n T n n =+.∴2212354221843339T T T =,=⨯+=,=⨯+=,224544468455105T T =⨯+=,=⨯+=.12352(24)123(34)21S S S =,=⨯+=,=⨯+=, 454(44)325(54)45S S =⨯+=,=⨯+=.由此可知11S T =,当2n ≥时n n S T ,<. 归纳猜想:当2n n ≥,∈N 时n n S T ,<. 拓展延伸14.设2()41f n n n n =++,∈N *,计算f(1),f(2),f(3),f(4),…,f(10)的值,同时作出归纳推理,并用n=40验证猜想是否正确. 解:2(1)114143f =++=,2(2)224147f =++=, 2(3)334153f =++=, 2(4)444161f =++=, 2(5)554171f =++=, 2(6)664183f =++=, 2(7)774197f =++=, 2(8)8841113f =++=, 2(9)9941131f =++=, 2(10)101041151f =++=.∵43,47,53,61,71,83,97,113,131,151都为质数, ∴归纳猜想:当n ∈N *时2()41f n n n ,=++的值都为质数. ∵n=40时2(40)40404140(f ,=++=40+1)+414141=⨯, ∴f(40)是合数.因此,由上面归纳推理得到的猜想不正确.。