计算行列式常用的7种方法

合集下载

行列式的几种计算方法

行列式的几种计算方法行列式是线性代数中非常重要的概念，它可以帮助我们理解矩阵的性质和求解线性方程组。

行列式的计算方法有多种，下面将详细介绍几种常用的计算方法。

一、按定义式计算行列式：按照定义式计算行列式是最基本的一种方法。

对于一个n阶矩阵A，其行列式记作det(A)，可以按照以下公式进行计算：det(A) = Σ(−1)^σ(π_1,π_2,…,π_n)a_{1π_1}a_{2π_2}⋯a_{nπ_n}σ(π_1,π_2,…,π_n)是排列(π_1,π_2,…,π_n)的符号，a_{iπ_i}表示矩阵A的第i行第π_i列的元素，Σ表示对所有可能的排列进行求和。

按照定义式计算行列式需要对所有可能的排列进行求和，计算量较大，对于较大阶的矩阵来说并不实用。

我们通常会采用其他方法来计算行列式。

计算行列式时，我们可以利用其性质来简化计算过程。

行列式有一些基本的性质，如行列式中某一行（列）所有元素都乘以一个数k，行列式的值也要乘以k；行列式中某一行（列）元素乘以某个数加到另一行（列）上去后，行列式的值不变等。

利用这些性质，我们可以通过变换行列式中的元素或行列式本身，从而简化计算过程。

对于一个3阶矩阵A，我们可以利用做行列变换将其变换为上三角矩阵，这样计算其行列式就会变得非常简单。

具体地，我们可以通过交换行或列，将矩阵A变换为上三角矩阵，然后利用上三角矩阵的行列式的性质求解行列式的值。

三、按矩阵的余子式和代数余子式计算行列式：对于一个n阶矩阵A，其(i,j)位置的余子式M_{ij}定义为将A的第i行第j列划去后，剩下的元素按原来的次序组成的(n-1)阶行列式。

即M_{ij} = (-1)^{i+j} \cdot \det(A_{ij})其中A_{ij}是将矩阵A的第i行第j列元素划掉后得到的(n-1)阶子式矩阵。

矩阵的代数余子式A_{ij}定义为A_{ij} = (-1)^{i+j} \cdot M_{ij}。

行列式计算方法

解利用n阶行列式的定义,可直接计算其值Ｄ＝２０００！
方法2 化三角形法
化三角形法是将原行列式化为上（下）三角形行列式或对角形行列式计算的一种方法。这是计算行列式的基本方法之一。
例2 计算行列式
1 2 13 7 18 5 2 D 5 8 21 3 0 24
解首先给第1行分别乘-7,-5,-3,分别加到第2,3,4行上,再交换第2,3两行的位置;给第二行分别乘以2,-3后,分别加到第3,4行上;最后给第3行乘1加到第4行即可。
n1
y
x
y
0
0
0 00 x
0 0x y
降阶后的两个低阶行列式都是三角形行列式,故原行列式的值为
Dn xn (1)n1 yn
x 1 0
0 x 1
00
x
（2） Dn
0
0
0
0
0
0
00
0
an an1 an2
解把原行列式按第1列展开得
x 1 a2 a1 x
x 1
00
1 0
00
0x
00
x 1
az bx ax by ay bz
再把第１个行列式按第３列展开，第２个行列式按第２列展开．最终得
xyz D= (a3 b3 ) y z x
zxy
方法4 降阶法
利用行列式按行按列展开定理将高阶行列式转化为较低阶行列式求解的方法叫做降阶法.
它可以分为直接降阶法和递推降阶法
直接降阶法用于只需经少量几次降阶就可求得行列式值的情况。
递推降阶法用于需经多次降阶才能求解，并且较低阶行列式与原行列式有相同结构的情况。
例4 求解下列行列式：
x y 00 0

(完整版)行列式的计算方法总结

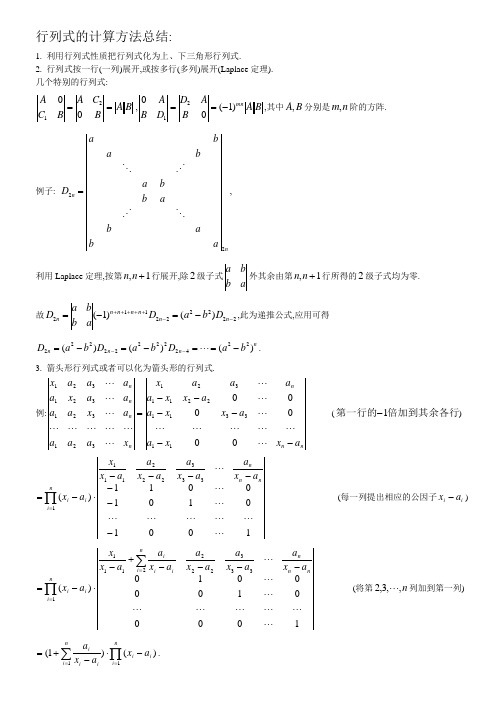
行列式的计算方法总结:1. 利用行列式性质把行列式化为上、下三角形行列式.2. 行列式按一行(一列)展开,或按多行(多列)展开(Laplace 定理). 几个特别的行列式:B A BC A BC A ==0021,B A BA D DB Amn )1(0021-==,其中B A ,分别是n m ,阶的方阵. 例子: nn abab ab b a b abaD 22=,利用Laplace 定理,按第1,+n n 行展开,除2级子式ab ba 外其余由第1,+n n 行所得的2级子式均为零. 故222222112)()1(--+++++-=-=n n n n n n n D b a D ab b a D ,此为递推公式,应用可得n n n n b a D b a D b a D )()()(224222222222-==-=-=-- .3. 箭头形行列式或者可以化为箭头形的行列式.例:nn n n n n n a x x a a x x a a x x a a a a x x a a a a x a a a a x a a a a x ------=0001133112211321321321321321 -----(倍加到其余各行第一行的1-) 100101010011)(3332221111-------⋅-=∏=nn n n i i i a x a a x a a x a a x x a x --------(每一列提出相应的公因子i i a x -) 1001000010)(33322221111nn n ni ii i n i i i a x a a x a a x a a x a a x x a x ----+-⋅-=∑∏== --------(将第n ,,3,2 列加到第一列)其它的例子：特点是除了主对角线,其余位置上的元素各行或各列都相同.n x a aa a a x a a a a a x a a a aa x a ++++ 321,nn n n a x a a a a a x a a a a a x a a a a a x ++++ 321321321321. 4. 逐行逐列相减法.行列式特点是每相邻两行(列)之间有许多元素相同.用逐行(列)相减可以化出零. 5. 升阶法(或加边法, 添加一行一列,利于计算,但同时保持行列式不变).例子:nn n n nnn n nn n n nn b a b a b a a b a b a b a a b a b a b a a b b b b a b a b a b a b a b a b a b a b a ++++-++++-++++----=++++++++++++10101010000011112122212212111121212221212111∑∑∑∑∑∑======+--+=---+--+=------=ni in i i i ni in ni i n i i i ni in n b b a na b b b b b a na a a ab b b 1112111121211110100000101111111010100111011101∑∑∑∑∑∑∑=≠======-+++=-++=nj nji i j i j ni i ni i ni i i ni i ni i a a b b a b a n b a 1111111)(1)1)(1(.例子:nnx a aaaa x a a a a a x a a a a a x a a a a a x a aaaa x a a a a a x a aa a a x a ++++=++++0001321321).1(00000000000010100010001000111213211321∑∑==+=+=----=ni in nni inx a x x x x x x x a a a a x a x x x x a a a a6. 利用范德蒙德行列式.计算行列式: n nn n nn nn n n nnx x x x x x x x x x x x x x x x D321223222122322213211111----=解: 令: nnnn nn n nn n n n nn n n ny x x x y x x x y x x x y x x x y x x x D211112112222212222212111111--------=,这是一个1+n 级范德蒙德行列式. 一方面,由范德蒙德行列式得)())(()(2111n ni j j ix y x y x y x xD ---⋅-=∏≤<≤ .可看做是关于y 的一个n 次多项式.另一方面,将1D 按最后一列展开,可得一个关于y 的多项式01111p y p y p y p D n n n n ++++=-- ,其中1-n y 的系数1-n p 与所求行列式D 的关系为1--=n p D .由)())(()(2111n ni j j ix y x y x y x xD ---⋅-=∏≤<≤ 来计算1-n y的系数1-n p 得:∑∏=≤<≤-⋅--=ni i ni j j in x x xp 111)(,故有∑∏=≤<≤-⋅-=-=ni i ni j j in x x xp D 111)(其它的例子:=+-+++-++-++------n n n n n n n n n n n n n n n n n n nn n n nb b a b a b a a b b a b a b a a b b a b a b a a 111121211111212222222122111121211111……每一行提公因子n i a ,nn n n n n n n n n n n n n nn n n a b a b a b a b a ba b a b a b a b a b a ba b a a a )()()()(1)()()()(1)()()()(1111112111122122222221111121111121++-++++++--+=).(1121∏≤<≤+-=n i j j j ii nn n n a b a b a a a7.利用数学归纳法证明行列式.(对行列式的级数归纳)证明当βα≠时,,1000001000100011βαβαβααββαβααββααββα--=+++++=++n n n D证明时,将n D 按第一行(或第一列)展开得21)(---+=n n n D D D αββα,利用归纳假设可得. 8. 利用递推公式.例子: 计算行列式,10000010001000βααββαβααββααββα+++++=n D 解: 按第一行展开得: 21)(---+=n n n D D D αββα,将此式化为:(1) )(211----=-n n n n D D D D αβα或 (2) )(211----=-n n n n D D D D βαβ 利用递推公式(1)得:n n n n n n n n D D D D D D D D βαβαβαβα=-==-=-=-------)()()(122322211 ,即n n n D D βα+=-1. (3)利用递推公式(2)得:n n n n n n n n D D D D D D D D αβαβαβαβ=-==-=-=-------)()()(122322211 ,即n n n D D αβ+=-1. (4)由(3)(4) 解得: ,,)1(,11⎪⎩⎪⎨⎧=+≠--=++βααβαβαβαn n n n n D其它的例子nn acb a ac b a c b a D00000000000=,按第一行展开可得21---=n n n bcD aD D ,此时令,,bc a ==+αββα则21)(---+=n n n D D D αββα,变形为211)(----=-n n n n D D D D αβα,此为递推公式.利用刚才的例子可求得结果. 这里,,bc a ==+αββα即βα,是方程02=+-bc ax x 的两个根.9. 分拆法.将行列式的其中一行或者一列拆成两个数的和,将行列式分解成两个容易求的行列式的和.例子:accccb ac c c bb ac c bbbac b b b b c a c accccb ac c c bb ac c bbbacb b b b a D n-+==210000V V acccb ac c b b a c b b b a b b b b c a accccb ac c c b b a c c b b b a c b b b b c +=-+=1V : 除第一行外,其余各行加上第一行的1-倍,所得行列式按第一列展开,2V 按第一列展开.11)(0000000--=----------=n b a c ba b c b c bc ba b c b c b b b a b c ba b b b b c V12)(--=n D c a V , 故11)()(---+-=n n n D c a b a c D ,由c b ,的对称性质,亦可得11)()(---+-=n n n D b a c a b D ,这两个式子中削去1-n D ,可得结论,bc c a b b a c D nn n ----=)()(.注: (1) 同一个行列式,可有多种计算方法.要利用行列式自身元素的特点,选择合适的计算方法. (2) 以上的各种方法并不是互相独立的,计算一个行列式时,有时需要综合运用以上方法,。

行列式的几种计算方法7篇

行列式的几种计算方法7篇第1篇示例：行列式是线性代数中的一个重要概念，它是一个方阵中的一个数值，可以帮助我们判断矩阵的性质，计算行列式的值是线性代数中的基础技能之一。

下面我们将介绍几种行列式的计算方法以及其应用。

一、直接展开法计算行列式最基本的方法就是直接展开法。

以3阶行列式为例，一个3阶方阵的行列式可以表示为：\[\begin{vmatrix}a &b &c \\d &e &f \\g & h & i\end{vmatrix}\]通过公式展开，可以得到：\[\begin{aligned}\begin{vmatrix}a &b &c \\d &e &f \\g & h & i\end{vmatrix} & = aei + bfg + cdh - ceg - bdi - afh \\& = a(ei - fh) - b(di - fg) + c(dh - eg)\end{aligned}\]这样就可以直接计算出行列式的值。

但是这种方法比较繁琐，不适用于高阶行列式的计算。

二、拉普拉斯展开法\[\begin{vmatrix}a_{11} & a_{12} & \cdots & a_{1n} \\a_{21} & a_{22} & \cdots & a_{2n} \\\vdots & \vdots & & \vdots \\a_{n1} & a_{n2} & \cdots & a_{nn} \\\end{vmatrix}\]以第一行为例，可以按照以下公式展开：\[ \text{det}(A) = a_{11}C_{11} + a_{12}C_{12} + \cdots +a_{1n}C_{1n} \]C_{ij}表示元素a_{ij}的代数余子式，通过递归计算代数余子式，最终可以得到行列式的值。

行列式计算的方法

行列式计算的方法
计算行列式的方法取决于矩阵的大小。

下面我将介绍几种常见的行列式计算方法：
1. 二阶行列式计算：
对于一个2x2的矩阵，行列式的计算方法如下：
行列式的值= (a*d) - (b*c)
其中，矩阵为：
| a b |
| c d |
2. 三阶及以上的行列式计算（展开法）：
对于一个n阶(n>=3)的矩阵，行列式的计算可以通过展开法来进行，也叫做代数余子式展开法。

具体步骤如下：
a. 选择第一行或第一列作为展开的基准行或基准列；
b. 逐个选取基准行或基准列上的元素，相应的去掉所在行和所在列，得到一个(n-1)阶的矩阵；
c. 对每个选取的元素，计算其代数余子式（即去掉该元素所在行和所在列后，剩余矩阵的行列式值），并与该元素相乘；
d. 将所有计算得到的代数余子式相乘，并按照正负号规律求和，得到最终的行列式值。

3. 其他行列式计算方法：
当矩阵较大时，使用展开法计算行列式会非常繁琐。

此时可以考虑使用高斯消元法、LU分解、特征值等方法来化简计
算。

这些方法相对复杂，需要一定的线性代数知识和计算能力。

总之，行列式的计算方法根据矩阵的大小和具体要求选择不同的方法，以便高效地得到结果。

行列式的计算方法及应用

行列式计算方法解析1.化三角形法此种方法是利用行列式的性质把给定的行列式表示为一个非零数与一个三角形行列式之积，所谓三角形行列式是位于对角线一侧的所有元素全部等于零的行列式。

三角形行列式的值容易求得，涉及主对角线的三角形行列式等于主对角线上元素之积，涉及次对角线的N 阶三角形行列式等于次对角线上元素之积且带符号。

例1计算N 阶行列式ab bb a b b b aD n=解()[]abb a bb b n a Dn1111-+=()[]ba b a b b b n a ---+=0011()()11n a n b a b -=+-⎡⎤⎣⎦-2.利用递推关系法所谓利用递推关系法，就是先建立同类型n 阶与n-1阶（或更低阶）行列式之间的关系——递推关系式，再利用递推关系求出原行列式的值。

例2 计算n 阶行列式n ab b ca b ccaD =，其中0,≠≠bc c b解将n D 的第一列视为（a-c ）+c,0+c,……,0+c,据行列式的性质，得0000n a c c b b a c b b c b b c a b a b c a b cca ca ccaD -+-+==++()()11n n n a c c a bD D --∴=-+- (1)由b 与c 的对称性，不难得到()()11n n n a b b a c D D --=-+- (2)联立（1），(2）解之，得()()()1n nn b c b c a c a b D -⎡⎤=-⎢⎥⎣⎦---例3 计算n 阶行列式00010001000000n a b ab a b ab a b a b ab a bD +++=++解将n D 按第一行展开，得()11000000001n n ab a b a b ab a bab a bD D -+=+-++于是得到一个递推关系式 ()12n n n a b ab D D D --=+-，变形得()112n n n n b a b D D D D ----=- ，易知()()2312334n n n n n n b b b D D D D DD aa------=-=-()()()22212n n n b ab b a b a b D D aaa --⎡⎤==-==⎢⎥⎣⎦--++所以 1nn n b D D a -=+，据此关系式再递推，有()11222nn n n n n n bb b ba aa a D D D ----=++=++1122111n n n n n n n n b b a a a a b b a a b b D -----==++++=++++如果我们将 n D 的第一列元素看作a+b,1+0,……0+0,按第一列拆成两个行列式的和，那么可直接得到递推关系式1nn n b D D a -=+，同样可n D 的值。

行列式的几种计算方法

行列式的几种计算方法行列式是线性代数中的一个重要概念，它是由矩阵中的元素所组成的一种特定的数学对象。

行列式的计算方法有多种，包括代数余子式展开、三角形法则、拉普拉斯展开、性质和定理等。

以下将详细介绍行列式的几种计算方法。

一、代数余子式展开法代数余子式展开法是通过矩阵元素分解成代数余子式相乘的形式来计算行列式值的方法。

我们需要了解代数余子式的概念。

1. 代数余子式的概念在矩阵A中，元素a_ij的代数余子式A_ij的值为A_ij=(-1)^(i+j)*M_ij，其中M_ij 代表去掉第i行和第j列后所构成的方阵的行列式值。

2. 代数余子式展开法的步骤（1）选择一行或一列，以此行或列的元素a_ij为基准。

（2）计算a_ij的代数余子式A_ij，并根据代数余子式展开法将行列式分解成代数余子式相乘的形式。

（3）累次计算代数余子式A_ij相乘的值并求和，得到行列式的值。

对于3阶行列式A的计算，可以按照如下步骤进行代数余子式展开法的计算：A = |a11 a12 a13||a21 a22 a23||a31 a32 a33|选择第一行元素a11为基准进行代数余子式展开，展开式为：A = a11*M11 - a12*M12 + a13*M13M11、M12、M13分别代表去掉第一行和第一列，第一行和第二列，第一行和第三列所构成的2阶方阵的行列式值。

根据代数余子式展开法的原理，可以得到行列式的值。

二、三角形法则三角形法则是用于计算行列式的一种方法。

它的基本思想是通过变换矩阵的行列式来简化计算过程，将需要计算的矩阵通过一系列的初等变换转化为上、下三角形矩阵，再利用三角形矩阵的行列式计算方法来计算原矩阵的行列式。

计算三角形矩阵A'的行列式值为a11*a22'*a33'。

三、拉普拉斯展开法拉普拉斯展开法是一种通过对矩阵的某一行或某一列进行展开，将行列式转化为子行列式的求和形式来计算行列式值的方法。

【原创】行列式计算7种技巧7种手段

行列式计算7种技巧7种手段编者:Castelu【编写说明】行列式是线性代数的一个重要研究对象,是线性代数中的一个最基本,最常用的工具,记为det(A).本质上,行列式描述的是在n 维空间中,一个线性变换所形成的平行多面体的体积,它被广泛应用于解线性方程组,矩阵运算,计算微积分等.鉴于行列式在数学各领域的重要性,其计算的重要性也不言而喻,因此,本人结合自己的学习心得,将几种常见的行列式计算技巧和手段归纳于此,供已具有行列式学习基础的读者阅读一.7种技巧: 【技巧】所谓行列式计算的技巧,即在计算行列式时,对已给出的原始行列式进行化简,使之转化成能够直接计算的行列式,由此可知,运用技巧只能化简行列式,而不能直接计算出行列式技巧1:行列式与它的转置行列式的值相等,即D=D T111211121121222122221212nn n n n n nnnn nna a a a a a a a a a a a a a a a a a =技巧2:互换行列式的任意两行(列),行列式的值将改变正负号111212122221222111211212nn n nn n nnn n nna a a a a a a a a a a a a a a a a a =-技巧3:行列式中某一行(列)的所有元素的公因子可以提到行列式记号的外面1111121111121221222222122211212nnnn n ni n n n n n nnn n nnb a b a b a a a a b a b a b a a a a bb a b a b a a a a ==∏技巧4:行列式具有分行(列)相加性11121111211112111221212121212n nnt t t t tn tn t t tn t t tn n n nnn n nn n n nna a a a a a a a abc b c b c b b b c c c a a a a a a a a a +++=+技巧5:将行列式的某一行(列)的各元素乘以同一数k 后加到另一行(列)对应的元素上,行列式的值不变111211112112112212121212n n s s sn s t s t sn tnt t tn t t tn n n nnn n nna a a a a a a a a a ka a ka a ka a a a a a a a a a a a a +++=技巧6:分块行列式的值等于其主对角线上两个子块行列式的值的乘积11111111111111111111000m m n m mm m n m mm n nnn nmn nna a a ab b a ac c b b a a b b c c b b =技巧7:[拉普拉斯按一行(列)展开定理] 行列式等于它的任一行(列)的各元素与其对应的代数余子式乘积之和11(1,2,,)(1,2,,)n nik ik kj kj k k D a A i n a A j n ======∑∑二.7种手段:【手段】所谓行列式计算的手段,即在计算行列式时,观察已给出的原始行列式或进行化简后的行列式,只要它们符合已知的几种行列式模型,就可以直接计算出这些行列式手段1:对于2阶行列式和3阶行列式,可以直接使用对角线法则进行计算1112112212212122a a a a a a a a =-,111213212223112233122331132132112332122133132231313233a a a a a a a a a a a a a a a a a a a a a a a a a a a =++---手段2:对于4阶以上的行列式,若行列式中有很多元素为零,则根据定义进行计算较为方便,否则较为复杂(常见于计算机程序和数学软件)定义:1212121112121222()1212(1)n n nnn p p p p p np p p p n n nna a a a a a a a a a a a τ=-∑运用数学软件Matlab 按定义计算4阶行列式: >> syms a b c d e f g h i j k l m n o p >> A=[a,b,c,d;e,f,g,h;i,j,k,l;m,n,o,p] A =[ a, b, c, d] [ e, f, g, h] [ i, j, k, l] [ m, n, o, p] >> det(A) ans =a*f*k*p-a*f*l*o-i*a*g*p+i*a*h*o+a*n*g*l-a*n*h*k-e*b*k*p+e*b*l*o+i*e*c*p-i*e*d*o-e*n*c *l+e*n*d*k+i*b*g*p-i*b*h*o-i*f*c*p+i*f*d*o+i*n*c*h-i*n*d*g-m*b*g*l+m*b*h*k+m*f*c*l-m*f*d*k-i*m*c*h+i*m*d*g手段3:上三角行列式,下三角行列式,主对角线行列式,副对角线行列式11121222100n nn ii i nna a a a a a a ==∏ ,112122112000nii i n n nna a a a a a a ==∏,1212()n nλλλλλλ=其余未写出元素均为零,1(1)2212(1)()n n n nλλλλλλ-=-其余未写出元素均为零手段4:若行列式中有两行(列)对应元素相等,则此行列式的值等于零0a a e i b b f jc c g k ddhl=手段5:若行列式中有一行(列)的元素全为零,则此行列式的值为零00000a e i b f jc g kd h l=手段6:若行列式中有两行(列)元素成比例,则此行列式的值等于零0a ka e i b kb f jc kc g kd kd h l=手段7:范德蒙德(Vandermonde)行列式1222212111112111()nn i j n i j n n n nx x x x x x x x x x x ≥>≥---=-∏三.跟踪训练【解题思路】为了使读者能够巩固前文叙述的7种技巧和7种手段,本人附上一些行列式的习题以供参考.解题时,一般先观察题目所给出的原始行列式,若原始行列式能够用7种手段的其中一种进行计算,则可直接得出答案,否则,一般先利用7种技巧对原始行列式进行化简,使之转化成能够用7种手段的其中一种进行计算的行列式,再得出答案.读者在利用7种技巧时,要注意技巧之间的搭配使用计算下列行列式的值: 习题1:120114318--- 解答:1201141182(4)30(1)(1)0132(1)81(4)(1)4318--=⨯⨯+⨯-⨯+⨯-⨯--⨯⨯-⨯-⨯-⨯-⨯-=--[手段1]习题2:0000000000b f d a c e解答:123412341234()12341234123433112432400000(1)0000004,3,1,4,2,()(3142)3,00000(1)00000p p p p p p p p p p p p b f d a a a a a cep p p p p p p p b f d a a a a abcda ceτττ=-=======-=-∑观察行列式中元素的位置及由级排列中各数不能相等知因此[手段2]习题3:12345678910111213141516解答:21431234113156785171091011129111113141516131151c c c c -=-[技巧5,手段4]习题4:3333333333333333x x x x ---+---+--解答:412213141423333333333333333333333333333313331333133300133300133300133300000ii x x x x x x c c x x x x xx x r r x x x x r r x x xx r r xx x x r r xx x x x=-----+--+-+----+----------+--=-----------↔-=--∑[技巧2,技巧3,技巧5,手段3]习题5:11121314122223241323333414243444a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b解答:1112131412222324132333341424344422232412131412131411233334122333341322232414243444243444243444,a b a b a b a b a ba b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b =-+-按第一列展开1213142223242333341213141213142223242223242434442333342342342121423333412423333412234234,0,(b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b b b b b b b D a a b b a b a b a b a b b a b a b a b a a a a a a a a =-=由于行列式和有两行元素成比例因此值为3234214124233334234222121412434232334243241421124332233423321421123223433414122123)()()()[()()]()()()()(b b b b b a b b a b a b a b a a a a a b b a b b a a b b a a b b a a b a b b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b -=-+--=--+-=---=--323443314111)()()i i i i i a b a b a b a b a b a b ++=--=--∏[技巧7,手段1,手段6]习题6:444443333322222(1)(2)(3)(4)(1)(2)(3)(4)(1)(2)(3)(4)123411111a a a a a a a a a a a a a a a a a a a a ---------------- 解答:432122222533333444444321432122222,111111234(1)(1)(2)(3)(4)(1)(2)(3)(4)(1)(2)(3)(4)111114321(1)(1)(4)(3)(2)(1)(4)aa a a a D a a a a a a a a a a a a a a a a a a a a a a a a a a +++++++++----=-----------------=-------将行列式上下翻转后再左右翻转不难得3333344444(3)(2)(1)(4)(3)(2)(1)4!3!2!1!288a a a a a a a a a -------==[技巧2,手段7]习题7:1221100001000000001nn n x x x xa a a a x a -----+解答:111121232212112112121,1000100(1)00011,,,,,,n n n n n n n n n n n n n n n n n n n n nD x D xD a x x D xD a D xD a D xD a D xD a D x a x x x D x a x a x a x a +--------------=+--⇒=+=+=+=+=+=+++++按第一列展开得的递推公式将上述各式的两边分别乘以后全部相加并化简得:[技巧7,手段3]习题8:()a b a b c d cd其余未写出元素均为零:解答:22(22)2122(1)2(1)2221,23,,2,221,23,,2,000000(1)00()()()n n nn nn n D n n n n n n a b c d abDab c d cdD Dad bc Dad bc D ad bc --------=-==-==-=-将中的第行依此与第行行第行对调再将第列依此与第列列第列对调得[技巧2,技巧6]。

行列式的几种计算方法

行列式的几种计算方法行列式是矩阵的一个特征值，表示矩阵所包含的线性变换对空间的扭曲程度。

行列式的计算方法有多种，下面将介绍几种常用的方法。

一、定义法行列式的定义法是最基础的计算方法，也是其他方法的基础。

对于一个n阶方阵A，其行列式记作det(A)或|A|，定义为：det(A) = a11*a22*...*ann+b11*b32*...*bnn + ... + z11*z22*...*z(n-1)n+(-1)^nPa11、a22、...、ann 为A的主对角线元素，b11、b32、...、bnn是由A去掉第一行第一列后的矩阵的对角线元素，z11、z22、...、z(n-1)n是由A去掉最后一行最后一列后的矩阵的对角线元素，nP为A的最后一行元素的乘积与(-1)^n的乘积。

对于一个3阶方阵A，其行列式为：det(A) = a11*a22*a33 + a21*a32*a13 + a31*a12*a23 - a13*a22*a31 - a23*a32*a11 - a33*a12*a21二、按行或按列展开法按行或按列展开法是行列式计算的一种常用方法。

对于一个n阶方阵A，按第i行展开行列式得到：det(A) = a1i*A1i + a2i*A2i + ... + ani*AniAji是由A去掉第i行第j列得到的(n-1)阶方阵，Aji的行列式记作det(Aji)或|Aji|。

按列展开的计算方法与按行展开类似。

三、逐次消元法逐次消元法是一种基于初等变换的行列式计算方法。

通过初等变换将方阵A转化为一个上三角矩阵，再取上三角矩阵的对角线元素的乘积即可得到行列式的值。

具体步骤如下：1. 对A的第1列进行初等行变换，将首元素a11变为1，其它元素变为0；2. 将A的第1列以下的元素进行初等行变换，使得首列以下的所有元素变为0；3. 对A的第2列进行初等行变换，将次对角元素a22变为1，其它元素变为0；4. 将A的第2列以下的元素进行初等行变换，使得次对角列以下的所有元素变为0；5. 重复上述过程，直到对角线上所有元素都变为1。

行列式的几种计算方法

行列式的几种计算方法行列式是线性代数中的基本概念，在数学、工程、物理、经济学等众多领域中都有广泛的应用。

行列式的计算方法有多种，下面将介绍其中的几种方法。

1.按行（列）展开法按照行或列来展开行列式是一种基本的计算方法。

假设行列式为：$$D=\begin{vmatrix}a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33}\end{vmatrix}$$按第1行展开，得到：按照任意一行或一列展开，都可以得到同样的结果。

展开的过程中，每个元素前面加上正负号的符号与其对应的行数和列数有关。

这种方法适用于$3\times 3$的行列式，对于更高维的行列式，效率会大大降低。

2.三角行列式求法如果一个$n\times n$的行列式中有某一行或某一列的元素都是0，那么通过消元可以化简为一个更小的$n-1$阶行列式，然后递归地运用同样的方法求解，最终可以化简为一阶行列式。

这种方法叫做三角行列式求法。

例如，对于$3\times 3$的行列式：将第1列乘以$a_{23}$，再将第2列乘以$a_{11}$，用第2行减去第1行，用第3行加上第1行，得到：继续化简：3.性质计算法行列式有一些性质，可以通过这些性质来计算行列式。

其中最基本的性质是行列式的行列互换性质：将行列式的一行或一列互换，行列式的值反号。

例如：$$\begin{vmatrix}1 &2 &3 \\4 &5 &6 \\7 & 8 & 9\end{vmatrix}=-\begin{vmatrix}4 &5 &6 \\1 &2 &3 \\7 & 8 & 9\end{vmatrix}=0$$如果行列式某一行可以表示为其他行的线性组合，那么行列式的值为0。

行列式的几种求法

行列式的求法有多种，以下简单进行总结。

一、逆序定义法行列式的逆序法定义如下：1212121112121222(,,......,)12,,......,12(1)......n nnn nj j j j j nj j j j n n nna a a a a a a a a a a a τ=-∑这里，为的任一排列，为该排列的逆序数，求12,,......,n j j j 1,2,...,n 12(,,......,)n j j j τ和是对所有的排列求的，因此，该和式一共有项，每项都是个数相乘，并得计算!n n 逆序数，计算量巨大。

因此，一般而言，逆序法定义具有理论上研究的意义，而比较少用于求行列式。

但是，如果行列式的项中有大量的0，那么用逆序法计算可能会很简单。

以下举例如下：例1：求。

1122nna a a 解答：1212121122(,,......,)12,,......,(1)......n nnj j j j j nj j j j nn a a a a a a τ=-∑只当，，……，，其项才可能非零。

因此，11j =22j =n j n =1122(1,2,......,)01,12,2,1,12,2,1,12,2,(1)......(1)............n n n n n n nnn a a a a a a a a a a a a τ=-=-= 例2、求。

12nd d d解答：12121212(,,......,)12,,......,(1)......n nnj j j j j nj j j j n d d a a a d τ=-∑只当，，……，，其项才可能非零。

因此，1j n =21j n =-1n j =。

1(1)2(,1, (1)21,2,1,112(1) (1)......n n n n n n n n nd d a a a d d d d τ---=-=-例3、求。

计算行列式常用的7种方法

计算行列式常用的7种方法行列式是线性代数中的重要概念，用于描述线性方程组的性质和解的情况。

在计算行列式时，有多种方法可供选择，下面将介绍行列式的常用计算方法。

1.代数余子式展开法代数余子式展开法是计算行列式的最常用方法之一、对于n阶行列式，可以选择其中的任意一行或一列展开。

选择一行展开时，可以使用代数余子式，即将每一元素乘以其代数余子式后再求和。

例如，对于3阶行列式$\begin{bmatrix}a & b & c\\ d & e & f\\ g & h &i\end{bmatrix}$选择第一行展开，计算行列式的值为$aA_{11} - bA_{12} +cA_{13}$，其中$A_{ij}$表示第i行第j列元素的代数余子式。

类似地，可以选择列展开，使用代数余子式计算行列式的值。

2.初等变换法初等变换法是计算行列式的另一种常用方法。

通过一系列的行变换或列变换，将行列式转化为三角形矩阵或对角矩阵。

对于三角形矩阵，行列式的值即为对角线上元素的乘积；对于对角矩阵，行列式的值即为对角线上元素的乘积。

初等变换包括行交换、行缩放和行加减，可以有效地简化行列式的计算过程。

3.拉普拉斯展开法拉普拉斯展开法是计算行列式的一种常用方法，适用于任意阶的行列式。

选择其中的一行或一列展开，将行列式拆解为一系列子行列式的乘积。

每个子行列式的阶数比原行列式小1，可以继续进行递归的计算。

拉普拉斯展开法可以使用代数余子式进行计算，也可以利用构造矩阵的方式计算。

4.三对角矩阵法三对角矩阵法适用于计算特殊形式的行列式，即矩阵中除了对角线和相邻对角线上的元素外，其他元素都为0的情况。

计算三对角矩阵的行列式可以通过逐步化简为二阶或一阶行列式进行计算。

这种方法可以加速计算过程，特别适用于较大阶数的行列式。

5.特殊行列式法对于特殊形式的行列式，例如范德蒙行列式、希尔伯特行列式等，可以利用其特殊性质进行计算。

计算行列式常用的7种方法

行列式的计算方法介绍7种常用方法1 三角化方法：通过行列初等变换将行列式化为三角型行列式.例1 计算n+1阶行列式xa a a a a x a a a a x D nnn32121211=+2 把某一行（列）尽可能化为零例2 计算：yy x x D -+-+=222222222222222243 递归法（数学归纳法）：设法找出D n 和低级行列式间的关系，然后进行递归.例4 证明：βαβαβαβααββααββα--=++++=++1110000010001000n n n D例5 证明范德蒙行列式（n ≥2）∏≤<≤-----==nj i jin nn n n n nn x x x x x x x x x x x x x x V 111312112232221321)(11114 加边法：对行列式D n 添上一适当行和列，构成行列式D n+1，且D n+1=D n 例6 证明：)11(11111111111111111111121321∑=+=++++=ni in nn a a a a a a a a D5 拆分法：将行列式表为行列式的和的方法.即如果行列式的某行（或列）元素均为两项和，则可拆分为两个行列式之和例7 设abcd=1,求证：011111111111122222222=++++ddd d c c c c b b b ba a a a6 利用行列式的乘积：为求一个行列式D 的值，有时可再乘上一个适当的行列式∆；或把D 拆分为两个行列式的积. 例8（1）1)cos()cos()cos()cos(1)cos()cos()cos()cos(1)cos()cos()cos()cos(1121332312322113121n n n n n n D αααααααααααααααααααααααα------------=（2）设S k =λ1k +λ2k +⋯+λn k (k=1,2…),求证：∏≤<≤-+-+--=nj i j in n nn n nn s s s s s s s s s s s s s s s n 1222111432321121)(λλ7 利用拉普拉斯定理求行列式的值.拉普拉斯定理是行列式按某一行（或列）展开定理的推广.定义(1) 在n 阶行列式D 中，任取k 行k 列 (1≤k ≤n),位于这k 行k 列交叉处的k 2个元素按原来的相对位置组成的k 阶行列式S ，称为D 的一个k 阶子式.如：D=3751485210744621则D 的一个2阶子式为：S=8261 在一个n 阶行列式中，任取k 行，由此产生的k 阶子式有C kn 个.(2) 设S 为D 的一个k 阶子式，划去S 所在的k 行k 列，余下的元素按原来的相对位置组成的n-k 阶行列式M 称为S 的余子式.又设S 的各行位于D 中的第i 1,i 2…i k 行，S 的各列位于D 中的第j 1,j 2…j k 列，称A=(-1)(i1+i2+…+ik)+(j1+j2+…+jk)M.如：3751485210744621则D 的一个2阶子式为：S=8261M=3517为S 的2阶子式 M=（-1）（1+3）+（1+3）3517为S 的代数余子式.拉普拉斯定理:若在行列式D 中任取k 行 (1≤k ≤n-1)，则由这k 行所对应的所有k 阶子式与它们的代数余子式的乘积等于D. 例9 计算2112100012100012100012=D 例10 块三角行列式的计算设：⎪⎪⎭⎫ ⎝⎛=⨯⨯n n m m C B A *0或 ⎪⎪⎭⎫⎝⎛=⨯⨯n n m m C B A 0* 则：detA=(detB)(detC).特别地：若A=diag(A 1,A 2,…,A t ),则DetA=(detA 1)(detA 2)…(detA t ).例11 设分块矩阵⎪⎪⎭⎫⎝⎛=D C B A 0，其中0为零阵，B和D可逆，求A-1.例12 计算nn b b b a a a D 1001000102121 =例13 设：⎪⎪⎭⎫ ⎝⎛=C B A , BC T =0.证明：|AA T |=|BB T ||CC T |.（注：可编辑下载，若有不当之处，请指正，谢谢!）。

行列式的计算

行列式的计算是学习高等代数的基石,它是求解线性方程组,求逆矩阵及求矩阵特征值的基础,但行列式的计算方法很多,综合性较强,在行列式计算中需要我们多观察总结,便于能熟练的计算行列式的值。

目前我们常用的计算行列式的方法有对角线法则，化为三角形行列式,拆分法,降阶法，升阶法，待定系数法和数学归纳法，乘积法，加边法。

1.对角线法则此法则适用于计算低阶行列式的值（如2阶，3阶行列式的值），即主对角线的元素的乘积减去辅或次对角线上的元素的乘积，其主要思想是根据2阶，3阶行列式的定义计算行列式的值。

2.化为三角行行列式利用行列式的性质，把行列式化为上（下）三角形行列式，再利用上（下）三角形行列式的结论，可得到相应行列式的值上（下）三角形行列式及其值（1）上三角形行列式为D=|■(■(a_11&a_12@0_ &a_22 )&■(a_13&…&a_1n@a_23&…&a_2n )@■(0_ &0_ @⋮&⋮@0_&0_ )&■(a_33&…&a_3n@⋮&⋮&⋮@0_ &…&a_nn ))|D=|■(■(a_11&a_12@0_&a_22 )&■(a_13&…&a_1n@a_23&…&a_2n )@■(0_ &0_ @⋮&⋮@0_&0_ )&■(a_33&…&a_3n@⋮&⋮&⋮@0_ &…&a_nn ))|=|■(■(a_11&0&0@a_21&a_22&0@a_31&a_32&a_33 )&■(⋯&0@⋯&0@⋯&0)@■(⋮&⋮&⋮@a_n1&a_n2&a_n3 )&■(⋮&⋮@⋯&a_nn ))| = a_11 a_12⋯a_nn即上（下）三角形行列式的值等于主对角线上的元素的乘积。

行列式的几种计算方法

行列式的几种计算方法行列式是线性代数中的一种重要概念，也是解线性方程组的基础。

行列式的求解方法有很多，下面介绍几种比较常用的方法。

1. 代数余子式法代数余子式法是求解$n$阶行列式的一种常用方法。

假设有一个$n$阶行列式$A$，它的第$i$行、第$j$列元素为$a_{i,j}$，则记$A_{i,j}$为该行列式除去第$i$行和第$j$列后得到的$(n-1)$阶行列式，即：$$A_{i,j}=(-1)^{i+j}|A_{i,j}|$$其中，$|A_{i,j}|$表示该矩阵的余子式。

在求解行列式的时候，先选择行或列作为基准，计算出每个元素的代数余子式，然后进行相乘相加即可。

具体方法如下：$$det(A)=\sum_{i=1}^{n}a_{i,j}A_{i,j}=\sum_{j=1}^{n}a_{i,j}A_{i,j}$$根据公式可知，代数余子式法的时间复杂度为$O(n!)$，因此只能适用于小规模的行列式求解。

2. 行列式加边法行列式加边法是求解$n$阶行列式的另一种常用方法，它利用了矩阵的运算规律，通过添加等行等列来求解行列式值。

具体方法如下：（1）选择行或列中绝对值最大的元素，将该元素加入到行列式外面新添加一行或一列，然后依次将其它元素按矩阵运算法则进行变换；（2）此时，行列式的值等于新行列式减去外加行列后的新行列式；（3）依次将新加行列的元素还原到原来的位置，然后计算新添加元素的代数余子式求和即可。

这种方法的优点是时间复杂度较低，为$O(n^3)$。

缺点是需要进行大量的矩阵运算，计算过程较为繁琐。

3. 克拉默法则克拉默法则是解决线性方程组的常用方法，也可以用来求解行列式。

假设有一个$n$阶行列式$A$，则克拉默法则的公式为：其中，$D_i$表示以第$i$列为基准的行列式值。

4. 三角分解法三角分解法是求解$n$阶行列式的一种高效方法，它可以分解为上三角和下三角矩阵的乘积，从而降低了计算复杂度。

该方法可以通过高斯列主元消元法来实现，具体流程如下：（1）按列主元消元法，将原始矩阵变换为上三角矩阵$U$；（2）计算对角线上的元素之积，即为行列式的值。

行列式计算技巧

论行列式的计算方法方法1 化三角形法化三角形法是将原行列式化为上（下）三角形行列式或对角形行列式计算的一种方法。

这是计算行列式的基本方法重要方法之一。

因为利用行列式的定义容易求得上（下）三角形行列式或对角形行列式的性质将行列式化为三角形行列式计算。

因此，在许多情况下，总是先利用行列式的性质将其作为某种保值变形，再将其化为三角形行列式。

例1：浙江大学2004年攻读硕士研究生入学考试试题第一大题第2小题（重庆大学2004年攻读硕士研究生入学考试试题第三大题第1小题）的解答中需要计算如下行列式的值：12312341345121221n n n n D n n n -=--[分析]显然若直接化为三角形行列式，计算很繁，所以我们要充分利用行列式的性质。

注意到从第1列开始；每一列与它一列中有n-1个数是差1的，根据行列式的性质，先从第n-1列开始乘以－1加到第n 列，第n-2列乘以－1加到第n-1列，一直到第一列乘以－1加到第2列。

然后把第1行乘以－1加到各行去，再将其化为三角形行列式，计算就简单多了。

解：11(2,,)(2,,)1111111111121111100031111201111100010000001000020011(1)20002000011(1)()2i in n i n r r i n r r n n n D n n n n n n nn n n n n n nn nn n n nn n n n ===+--=-----++----+=⋅-----+=⋅⋅-()(1)(2)12(1)12(1)(1)12n n n n n n n -----⋅-+=⋅⋅-[问题推广] 循环行列式从而推广到一般，求下列行列式：0121101223411230(,0,1,,1)n n n n i a a a a a a a a D a c i n a a a a a a a a ---⎡⎤⎢⎥⎢⎥⎢⎥=∈=-⎢⎥⎢⎥⎢⎥⎣⎦解：令 0121101223411230n n n a a a a a a a a A a a a a a a a a ---⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦首先注意，若u 为n 次单位根（即u n=1），则有：1011110212123111120101120112123011101(1,n n n n n n n n n n n n nn n n n n n a a u a u u a a u a u A u u u u a a u a uu a a u a u a a u a u a u a u a u a u a u a u a u a -----+-----------⎡⎤+++⎡⎤⎢⎥⎢⎥+++⎢⎥⎢⎥⎢⎥⎢⎥⋅==∴=⎢⎥⎢⎥+++⎢⎥⎢⎥⎢⎥⎢⎥+++⎣⎦⎣⎦++++++=++++这里用到等）12011122111201111()1()()n n n n n n n n n u a a u a u u u u a u u f u f u a a u a u u u --------⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+++⋅⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥++⎣⎦⎣⎦⎡⎤⎢⎥⎢⎥⎢⎥=⋅=+++⎢⎥⎢⎥⎢⎥⎣⎦其中2122cossin 1,1(0)1,,,,n k n k kw n nw w k n w w w ππ-=∴=≠<<设+i 为n 次本原单位根有:于是：互异且为单位根()2011(1)01101011001111,(0,1,,1)(,,,)(,,,)((),(),,())()(,,,)(j jj n n j i j j n n n n n w w j n w w w w w w A w f w w Aw Aw Aw Aw f w w f w w f w w f w w w w f w -------⎡⎤⎢⎥⎢⎥⎢⎥==-=⎢⎥⎢⎥⎢⎥⎣⎦⋅=⋅==⎡⎤⎢⎥=⋅⎢⎥⎢⎥⎣⎦记：方阵则由上述知：故）122(1)0111(1)(1)1111(,,,)11n n n n n n w w w w w w w ww w ------⎡⎤⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦显然为范德蒙行列式 110A (1)()()(1)()()n n n w w w f f w f w A w A D f f w f w --∴≠=⋅⋅⋅⋅=⋅∴==⋅⋅⋅从而有：又例1中，循环的方向与该推广在方向上相反所以例1与011120'102n n n n a a a a a a D a a a ---=相对应(1)(2)'21n n n n D D --而与只相差（－）个符号(1)(2)'1201,121(1)2(1)()(),,)(1,2,,)1,()123(1)12n n n n n k n n n D f f w f w a a a n u w f u u u nu f n -----+⋅⋅⋅⋅==≠=++++=+++=即得：=(-1)从而当（时对单位根总有：21()()1()1n f u uf u u u u n nnf u u-∴-=++++-=--∴=-1211111()1,11(1)111 n n k n k n k k x x w x x x x x w n--=-=-=-=++++-=-==∏∏而又令则有：＋＋＋(1)(2)'12(1)(2)1221(1)1211(1)2(1)12(1)()()(1)111()()2111(1)(1)2(1)1(1)21(1)2n n n n n n n n n n n n k k n n nn n n D f f w f w n n n w w w n n nw n n nn n ----------=---=⋅⋅⋅⋅+=⋅⋅-⋅⋅⋅⋅---+-⋅⋅=-+-⋅⋅=+=-⋅⋅∏从而有：(-1)(-1)。

计算行列式的方法总结

计算行列式的方法总结
一、计算行列式的定义
行列式（determinant），又称行列式法（determinant formula），是一种用于确定行列式值的计算方法，由拉格朗日在 1812 年提出。

行列式是一个数量，它可以用来表示矩阵（matrix）的结果。

行列式的值可以用其中一种规则得出，其规则被称为行列式公式（determinant formula）。

二、行列式的类型
1、二阶行列式
二阶行列式是一个矩阵的方阵，它具有2行2列，其元素满足一定的线性方程组，可以用一个公式来计算它的值：
A，=a11×a22-a12×a21
其中，a11、a12、a21、a22为二阶方阵的元素。

2、三阶行列式
三阶行列式是一个矩阵的方阵，它具有3行3列，其元素满足一定的线性方程组，可以用一个公式来计算它的值：
A，=a11×a22×a33+a12×a23×a31+a13×a21×a32-a13×a22×a31-a12×a21×a33-a11×a23×a32
其中，a11、a12、a13、a21、a22、a23、a31、a32、a33为三阶方阵的元素。

三、行列式的计算
1、展开计算
是最常见的计算行列式的方法，也是最简单的方法，它通过迭代数值，将复杂矩阵拆分成若干个二阶行列式，计算每个二阶行列式的值，将答案
加总，即可得出原行列式的值。

2、余子式求行列式
利用了余子式的性质，可以将复杂的计算降低到求每个元素的余子式，然后根据拉格朗日定理，将答案乘以对应元素的余子式。

行列式计算技巧

论行列式的计算方法方法1 化三角形法化三角形法是将原行列式化为上（下）三角形行列式或对角形行列式计算的一种方法。

这是计算行列式的基本方法重要方法之一。

因为利用行列式的定义容易求得上（下）三角形行列式或对角形行列式的性质将行列式化为三角形行列式计算。

因此，在许多情况下，总是先利用行列式的性质将其作为某种保值变形，再将其化为三角形行列式。

然后把第1行乘以－1加到各行去，再将其化为三角形行列式，计算就简单多了。

解：11(2,,)(2,,)11111111111211111000311112011111000100000010000020011(1)200020000101(1)()2i in n i n r r i n r r n n n D n n n n n n nn n n n n n nn n n nn nn n n n ===+--=-----++----+=⋅-----+=⋅⋅-()(1)(2)12(1)12(1)(1)12n n n n n n n -----⋅-+=⋅⋅-[问题推广] 循环行列式从而推广到一般，求下列行列式：0121101223411230(,0,1,,1)n n n n i a a a a a a a a D a c i n a a a a a a a a ---⎡⎤⎢⎥⎢⎥⎢⎥=∈=-⎢⎥⎢⎥⎢⎥⎣⎦解：令 0121101223411230n n n a a a a a a a a A a a a a a a a a ---⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦首先注意，若u 为n 次单位根（即u n=1），则有：1011110212123111120101120112123011101(1,n n n n n n n n n n n n nn n n n n n a a u a u u a a u a u A u u u u a a u a uu a a u a u a a u a u a u a u a u a u a u a u a u a -----+-----------⎡⎤+++⎡⎤⎢⎥⎢⎥+++⎢⎥⎢⎥⎢⎥⎢⎥⋅==∴=⎢⎥⎢⎥+++⎢⎥⎢⎥⎢⎥⎢⎥+++⎣⎦⎣⎦++++++=++++这里用到等）12011122111201111()1()()n n n n n n n n n u a a u a u u u u a u u f u f u a a u a u u u --------⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+++⋅⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥++⎣⎦⎣⎦⎡⎤⎢⎥⎢⎥⎢⎥=⋅=+++⎢⎥⎢⎥⎢⎥⎣⎦其中2122cos sin 1,1(0)1,,,,n k n k kw n nw w k n w w w ππ-=∴=≠<<设+i 为n 次本原单位根有:于是：互异且为单位根()2011(1)01101011001111,(0,1,,1)(,,,)(,,,)((),(),,())()(,,,)(j jj n n j i j j n n n n n w w j n w w w w w w A w f w w Aw Aw Aw Aw f w w f w w f w w f w w w w f w -------⎡⎤⎢⎥⎢⎥⎢⎥==-=⎢⎥⎢⎥⎢⎥⎣⎦⋅=⋅==⎡⎤⎢⎥=⋅⎢⎥⎢⎥⎣⎦记：方阵则由上述知：故）122(1)0111(1)(1)1111(,,,)11n n n n n n w w w w w w w www ------⎡⎤⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦显然为范德蒙行列式 110A (1)()()(1)()()n n n w w w f f w f w A w A D f f w f w --∴≠=⋅⋅⋅⋅=⋅∴==⋅⋅⋅从而有：又例1中，循环的方向与该推广在方向上相反所以例1与11120'12n n n n a a a a a a D a a a ---=相对应(1)(2)'21n n n n D D --而与只相差（－个符号(1)(2)'1201,121(1)2(1)()(),,)(1,2,,)1,()123(1)12n n n n n k n n n D f f w f w a a a n u w f u u u nu f n -----+⋅⋅⋅⋅==≠=++++=+++=即得：=(-1)从而当（时对单位根总有：21()()1()1n f u uf u u u u n nnf u u-∴-=++++-=--∴=-1211111()1,11(1)111 n n k n k n k k x x w x x x x x w n--=-=-=-=++++-=-==∏∏而又令则有：＋＋＋(1)(2)'12(1)(2)1221(1)1211(1)2(1)12(1)()()(1)111()()2111(1)(1)2(1)1(1)21(1)2n n n n n n n n n n n n k k n n nn n n D f f w f w n n n w w w n n nw n n nn n ----------=---=⋅⋅⋅⋅+=⋅⋅-⋅⋅⋅⋅---+-⋅⋅=-+-⋅⋅=+=-⋅⋅∏从而有：(-1)。