锐角三角函数综合复习--知识讲解(基础)
专题28.17 锐角三角函数(中考常考考点专题)(基础篇)(专项练习)-2022-2023学年九年级

专题28.17 锐角三角函数(中考常考考点专题)(基础篇)(专项练习)一、单选题【类型一】锐角三角函数【考点一】(正弦✮✮余弦✮✮正切)概念➽➸辨析1.(2022·吉林长春·中考真题)如图是长春市人民大街下穿隧道工程施工现场的一台起重机的示意图,该起重机的变幅索顶端记为点A ,变幅索的底端记为点B ,AD 垂直地面,垂足为点D ,BC AD ⊥,垂足为点C .设ABC α∠=,下列关系式正确的是( )A .sin AB BC α= B .sin BC AB α= C .sin AB AC α=D .sin AC AB α= 2.(2022·湖北湖北·模拟预测)如图,在Rt ABC △中,BD 是斜边AC 上的高,AB BC ≠,则下列比值中等于sin A 的是( ).A .AD AB B .BD ADC .BD BC D .DC BC【考点二】角➽➸(正弦✮✮余弦✮✮正切)函数值3.(2022·浙江宁波·三模)如图,将ABC 放在每个小正方形的边长为1的网格中,点A ,B ,C 均在格点上,则tan A 的值是( )A B C .2 D .124.(2022·福建省厦门第二中学模拟预测)如图,在Rt ABC 中,90,2C BC AC ∠=︒=,则sin B =( )A .12 B .2 C D 【考点三】(正弦✮✮余弦✮✮正切)函数值➽➸求边长5.(2020·四川雅安·中考真题)如图,在Rt ACB 中,900.5C sinB ∠=︒=,,若6AC =,则BC 的长为( )A .8B .12C .D .6.(2022·吉林·长春市赫行实验学校一模)如图要测量小河两岸相对的两点P 、A 的距离,可以在小河边取PA 的垂线PB 上的一点C ,测得50PC =米,44PCA ∠=︒,则小河宽PA 为( )米A .50sin44︒B .50cos44︒C .50tan 44︒D .50tan46︒【类型二】特殊锐角三角函数【考点一】特殊锐角➽➸函数值7.(2016·江苏无锡·中考真题)sin30°的值为( )A .12 B C .2 D 8.(2021·广东深圳·中考真题)计算|1tan 60|-︒的值为( )A .1B .0C 1D .1【考点二】函数值➽➸特殊锐角9.(2022·河南焦作·()101α+︒=,则锐角α的度数为( )A .40°B .30°C .20°D .10°10.(2021·江苏无锡·一模)已知cos A A =∠是锐角,则A ∠的度数为( ) A .30︒ B .45︒ C .60︒ D .90︒【考点三】混合运算➽➸特殊锐角✮✮二次根式11.(2021·山东泰安·模拟预测)计算:202122sin 60|1(1)2-︒----的结果是( )A .74B .4C .14D .1412.(2021·山东省日照市实验中学二模)计算(tan30°)﹣1﹣2|)0的结果是( )A .6B .12C .2D .2+【考点四】特殊锐角值➽➸判断三角形形状13.(2021·贵州黔西·模拟预测)在ABC 中,若A ∠,B ∠都是锐角,且1sin 2A =,1cos 2B =,则ABC 的形状是( ) A .钝角三角形 B .等腰三角形C .锐角三角形D .直角三角形14.(2020·山东德州·二模)如果△ABC 中,sin A =cos B 2,则下列最确切的结论是( ) A .△ABC 是直角三角形B .△ABC 是等腰三角形 C .△ABC 是等腰直角三角形D .△ABC 是锐角三角形【类型三】解直角三角形【考点一】解直角三角形➽➸直接解直角三角形15.(2022·陕西·中考真题)如图,AD 是ABC 的高,若26BD CD ==,tan 2C ∠=,则边AB 的长为( )A .B .C .D .16.(2022·四川广元·中考真题)如图,在△ABC 中,BC =6,AC =8,△C =90°,以点B 为圆心,BC 长为半径画弧,与AB 交于点D ,再分别以A 、D 为圆心,大于12AD 的长为半径画弧,两弧交于点M 、N ,作直线MN ,分别交AC 、AB 于点E 、F ,则AE 的长度为( )A .52B .3C .D .103【考点二】解非直角三角形➽➸转化为直角三角形并解之17.(2019·河北石家庄·二模)在东西方向的海岸线上有A ,B 两个港口,甲货船从A 港沿东北方向以5海里/时的速度出发,同时乙货船从B 港口沿北偏西60︒方向出发,2h 后相遇在点P 处,如图所示.问A 港与B 港相距( )海里.A.B . C .10+D .2018.(2019·重庆·一模)缙云山是国家级自然风景名胜区,上周周末,小明和妈妈到缙云山游玩,登上了香炉峰观景塔,从观景塔底中心D 处水平向前走14米到A 点处,再沿着坡度为0.75的斜坡AB 走一段距离到达B 点,此时回望观景塔,更显气势宏伟,在B 点观察到观景塔顶端的仰角为45︒再往前沿水平方向走27米到C 处,观察到观景塔顶端的仰角是22︒,则观景塔的高度DE 为( )(tan22°≈0.4)A .21米B .24米C .36米D .45米【考点三】解不规则图形➽➸构造直角三角形并解之19.(2019·重庆九龙坡·模拟预测)如图是重庆轻轨10号线龙头寺公园站入口扶梯建设示意图.起初工程师计划修建一段坡度为3:2的扶梯AB ,扶梯总长为度大陡,扶梯太长容易引发安全事故.工程师修改方案:修建AC 、DE 两段扶梯,并减缓各扶梯的坡度,其中扶梯AC 和平台CD 形成的ACD ∠为135°,从E 点看D 点的仰角为36.5°,AC 段扶梯长则DE 段扶梯长度约为( )米(参考数据:3sin 36.55︒≈,4cos36.55︒≈,3tan 36.54︒≈)A .43B .45C .47D .4920.(2018·河北·模拟预测)如图(1)是一个六角星的纸板,其中六个锐角都为60°,六个钝角都为120°,每条边都相等,现将该纸板按图(2)切割,并无缝隙无重叠地拼成矩形ABCD .若六角星纸板的面积为2,则矩形ABCD 的周长为( )A .18cmB .C .()cmD .()cm【类型四】解直角三角形的应用【考点一】解直角三角形➽➸仰角✮✮俯角21.(2022·广西贵港·中考真题)如图,某数学兴趣小组测量一棵树CD 的高度,在点A 处测得树顶C 的仰角为45︒,在点B 处测得树顶C 的仰角为60︒,且A ,B ,D 三点在同一直线上,若16m AB =,则这棵树CD 的高度是( )A .8(3B .8(3+C .6(3D .6(3+22.(2021·山东济南·中考真题)无人机低空遥感技术已广泛应用于农作物监测.如图,某农业特色品牌示范基地用无人机对一块试验田进行监测作业时,在距地面高度为135m 的A 处测得试验田右侧出界N 处俯角为43︒,无人机垂直下降40m 至B 处,又测得试验田左侧边界M 处俯角为35︒,则M ,N 之间的距离为(参考数据:tan 430.9︒≈,sin 430.7︒≈,cos350.8︒≈,tan350.7︒≈,结果保留整数)( )A .188mB .269mC .286mD .312m【考点二】解直角三角形➽➸方位角23.(2022·河北·模拟预测)从观测点A 测得海岛B 在其北偏东60°方向上,测得海岛C 在其北偏东80°方向上,若一艘小船从海岛B 出发沿南偏西40°方向以每小时40海里的速度,行驶2小时到C 海岛,则C 海岛到观测点A 的距离是( )A.20海里B.40海里C.60海里D.80海里24.(2022·山东·济南市市中区泉秀学校一模)如图,一艘测量船在A处测得灯塔S在它的南偏东60°方向,测量船继续向正东航行30海里后到达B处,这时测得灯塔S在它的南偏西75°方向,则灯塔S离观测点A的距离是()B.(15)海里A.C.()海里D.【考点三】解直角三角形➽➸坡度坡比25.(2022·贵州毕节·中考真题)如图,某地修建一座高5mBC=的天桥,已知天桥斜面AB的坡度为AB的长度为()A.10m B.C.5m D.26.(2021·湖南衡阳·中考真题)如图是某商场营业大厅自动扶梯的示意图.自动扶梯AB 的倾斜角为37︒,大厅两层之间的距离BC为6米,则自动扶梯AB的长约为︒≈︒≈︒≈)().(sin370.6,cos370.8,tan370.75A .7.5米B .8米C .9米D .10米【考点四】解直角三角形➽➸其他问题27.(2022·广西·中考真题)如图,某博物馆大厅电梯的截面图中,AB 的长为12米,AB 与AC 的夹角为α,则高BC 是( )A .12sin α米B .12cos α米C .12sin α米D .12cos α米 28.(2022·湖北十堰·中考真题)如图,坡角为α的斜坡上有一棵垂直于水平地面的大树AB ,当太阳光线与水平线成45°角沿斜坡照下,在斜坡上的树影BC 长为m ,则大树AB 的高为( )A .()cos sin m αα-B .()sin cos m αα-C .()cos tan m αα-D .sin cos m m αα- 二、填空题 【类型一】锐角三角函数【考点一】(正弦✮✮余弦✮✮正切)概念➽➸辨析29.(2022·上海市青浦区教育局二模)小明要测量公园里一棵古树的高,被一条小溪挡住去路,采用计算方法,在A 点测得古树顶的仰角为α,向前走了100米到B 点,测得古树顶的仰角为β,则古树的高度为________米.30.(2021·福建厦门·一模)在Rt△ABC中,△C=90°,AC=AB=10,则△B=_____.【考点二】角➽➸(正弦✮✮余弦✮✮正切)函数值31.(2021·四川乐山·三模)如图,在3×3的正方形网格中,A、B均为格点,以点A为圆心,AB长为半径画弧,图中的点C是该弧与网格线的交点.则sin△BAC的值等于_____.32.(2022·湖南益阳·中考真题)如图,在Rt△ABC中,△C=90°,若sin A=45,则cos B=_____.【考点三】(正弦✮✮余弦✮✮正切)函数值➽➸求边长33.(2022·广东深圳·二模)如图,直角ABC中,90C∠=︒,根据作图痕迹,若3cmCA=,3tan4B=,则DE=________cm.34.(2021·湖南邵阳·中考真题)如图,在矩形ABCD 中,DE AC ⊥,垂足为点E .若4sin 5ADE ∠=,4=AD ,则AB 的长为______.【类型二】特殊锐角三角函数【考点一】特殊锐角➽➸函数值35.(2021·西藏·中考真题)计算:(π﹣3)0+(﹣12)﹣2﹣4sin30°=___. 36.(2020·湖南湘潭·中考真题)计算:sin 45︒=________. 【考点二】函数值➽➸特殊锐角37.(2022·陕西·西安辅轮中学三模)若sin(α+15°)=1,则△α等于_____________度. 38.(2020·湖北·武汉二中广雅中学三模)若sin A =12,则tan A =_____. 【考点三】混合运算➽➸特殊锐角✮✮二次根式39.(2022·重庆·模拟预测)计算:sin45°+212-⎛⎫- ⎪⎝⎭=_____.40.(2022·湖北荆门·一模)计算:)02112sin 45()2-+-︒--=________. 【考点四】特殊锐角值➽➸判断三角形形状41.(2020·江苏淮安·三模)在ABC ∆中,若21 02sinA tanB -+⎛ ⎝⎭= ,则ABC ∆是_____三角形.42.(2019·四川自贡·一模)在△ABC 中,(cos A ﹣12)2+|tan B ﹣1|=0,则△C =_____. 【类型三】解直角三角形【考点一】解直角三角形➽➸直接解直角三角形43.(2019·辽宁大连·中考真题)如图,ABC ∆是等边三角形,延长BC 到点D ,使CD AC =,连接AD.若2AB=,则AD的长为_____.44.(2015·广西玉林·中考真题)如图,等腰直角△ABC中,AC=BC,△ACB=90°,点△BOC绕C点顺时针方向旋转到△AQC的位置,则O分斜边AB为BO:OA=1△AQC=___________.【考点二】解非直角三角形➽➸转化为直角三角形并解之45.(2021·湖北武汉·模拟预测)如图是某商场自动扶梯的示意图,自动扶梯AB的倾斜角是30°,在自动扶梯下方地面C处测得扶梯顶端B的仰角是60°,则自动扶梯的垂直高度BD=___________m. 1.732,结果精确到0.1米)46.(2020·安徽阜阳·二模)如图,在一条东西方向笔直的沿湖道路l上有A、B两个游船码头,观光岛屿C在码头A的北偏东60°方向、在码头B的北偏西45°方向,AC=4千米.那么码头A、B之间的距离等于_____千米.(结果保留根号)【考点三】解不规则图形➽➸构造直角三角形并解之47.(2021·湖北湖北·中考真题)如图,某活动小组利用无人机航拍校园,已知无人机的飞行速度为3m/s,从A处沿水平方向飞行至B处需10s,同时在地面C处分别测得A处的仰角为75︒,B处的仰角为30︒.则这架无人机的飞行高度大约是_______m 1.732≈,结果保留整数)48.(2019·辽宁辽阳·中考真题)某数学小组三名同学运用自己所学的知识检测车速,他们将观测点设在一段笔直的公路旁且距公路100米的点A处,如图所示,直线l表示公路,一辆小汽车由公路上的B处向C处匀速行驶,用时5秒,经测量,点B在点A北偏东45°方向上,点C在点A北偏东60°方向上,这段公路最高限速60千米/小时,此车_____(填“超速”或“没有超速”) 1.732)【类型四】解直角三角形的应用【考点一】解直角三角形➽➸仰角✮✮俯角49.(2021·山东烟台·中考真题)数学兴趣小组利用无人机测量学校旗杆高度,已知无人机的飞行高度为40米,当无人机与旗杆的水平距离是45米时,观测旗杆顶部的俯角为30°,则旗杆的高度约为______________米.(结果精确到1米, 1.41≈ 1.73)50.(2021·四川乐山·中考真题)如图,为了测量“四川大渡河峡谷”石碑的高度,佳佳在点C 处测得石碑顶A 点的仰角为30︒,她朝石碑前行5米到达点D 处,又测得石顶A 点的仰角为60︒,那么石碑的高度AB 的长=________米.(结果保留根号)【考点二】解直角三角形➽➸方位角51.(2022·四川·巴中市教育科学研究所中考真题)一艘轮船位于灯塔P 的南偏东60︒方向,距离灯塔30海里的A 处,它沿北偏东30︒方向航行一段时间后,到达位于灯塔P 的北偏东67︒方向上的B 处,此时与灯塔P 的距离约为________海里.(参考数据:3sin 375︒≈,4cos375≈︒,3tan 374︒≈)52.(2022·辽宁沈阳·二模)如图,我国的一艘海监船在钓鱼岛A 附近沿正东方向航行,船在B 点时测得钓鱼岛A 在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C 点,此时钓鱼岛A 在船的北偏东30°方向.请问船继续航行______海里与钓鱼岛A 的距离最近.【考点三】解直角三角形➽➸坡度坡比53.(2022·广西柳州·中考真题)如图,某水库堤坝横断面迎水坡的坡角为α,sin α=35,堤坝高BC =30m ,则迎水坡面AB 的长度为 ____m .54.(2021·江苏无锡·中考真题)一条上山直道的坡度为1:7,沿这条直道上山,则前进100米所上升的高度为________米.【考点四】解直角三角形➽➸其他问题55.(2022·山东泰安·中考真题)如图,某一时刻太阳光从窗户射入房间内,与地面的夹角30DPC ∠=︒,已知窗户的高度2m AF =,窗台的高度1m CF =,窗外水平遮阳篷的宽0.8m AD =,则CP 的长度为______(结果精确到0.1m ).56.(2021·广西梧州·中考真题)某市跨江大桥即将竣工,某学生做了一个平面示意图(如图),点A 到桥的距离是40米,测得△A =83°,则大桥BC 的长度是 ___米.(结果精确到1米)(参考数据:sin83°≈0.99,cos83°≈0.12,tan83°≈8.14)参考答案1.D【分析】根据正弦三角函数的定义判断即可.解:△BC△AC,△△ABC 是直角三角形, △△ABC =α, △sin ACABα=, 故选:D .【点拨】本题考查了正弦三角函数的定义.在直角三角形中任意锐角△A 的对边与斜边之比叫做△A 的正弦,记作sin△A .掌握正弦三角函数的定义是解答本题的关键.2.D【分析】由同角的余角相等求得△A =△DBC ,根据正弦三角函数的定义判断即可; 解:△△ABD +△A =90°,△ABD +△DBC =90°, △△A =△DBC , A .ADAB=cos A ,不符合题意; B .BDAD=tan A ,不符合题意; C .BDBC=cos△DBC =cos A ,不符合题意; D .DCBC=sin△DBC =sin A ,符合题意; 故选: D .【点拨】本题考查了三角函数的概念,掌握直角三角形中锐角的正弦为对边比斜边是解题关键.3.D【分析】首先构造以△A 为锐角的直角三角形,然后利用正切的定义即可求解. 解:连接BD ,如图所示:根据网格特点可知,BD AC ⊥, △90ADB ∠=︒,△BD AD =△在Rt△ABD 中,tan A =BD AD 12=,故D 正确. 故选:D .【点拨】本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边,构造直角三角形是本题的关键.4.C【分析】根据勾股定理,可得AB 与BC 的关系,根据正弦函数的定义,可得答案. 解:△△C =90°,2BC AC =,△AB ,sinAC B AB ==C 正确. 故选:C .【点拨】本题考查了锐角三角函数的定义,先利用勾股定理得出AB 与AC 的关系,再利用正弦函数的定义.5.C【分析】利用正弦的定义得出AB 的长,再用勾股定理求出BC. 解:△sinB=ACAB=0.5, △AB=2AC , △AC=6, △AB=12,故选C.【点拨】本题考查了正弦的定义,以及勾股定理,解题的关键是先求出AB 的长. 6.C【分析】在直角三角形APC 中根据△PCA 的正切函数可求小河宽P A 的长度. 解:△P A △PB , △△APC =90°,△PC =50米,△PCA =44°,△tan44°=PA PC,△小河宽P A=PCtan△PCA=50•tan44°米.故选:C.【点拨】本题考查了解直角三角形的应用,解直角三角形的一般过程是:△将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).△根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.7.A【分析】根据特殊角的三角函数值求解即可.解:sin30°=12故答案为:A.【点拨】本题考查了锐角三角函数的问题,掌握特殊角的三角函数值是解题的关键.8.C【分析】直接利用特殊角的三角函数值、绝对值的性质分别化简得出答案.解:|1tan60||11-︒==故选C.【点拨】此题主要考查了特殊角的三角函数值,绝对值的性质等知识,正确化简各数是解题关键.9.C【分析】根据特殊角的三角函数值求解即可.解:(α+10°)=1,△tan(α+10°)△α为锐角,△α+10°=30°,α=20°.故选C.【点拨】熟记特殊角的三角函数值是解答此题的关键.10.A【分析】根据特殊角的三角函数值以及三角函数的定义,即可得到答案.解:△cos A A =∠是锐角, △A ∠=30°, 故选A .【点拨】本题主要考查锐角三角函数,掌握特殊角三角函数值是解题的关键. 11.A【分析】原式利用特殊角的三角函数值,绝对值的代数意义,乘方的意义,以及负整数指数幂法则计算即可得到结果.解:原式121)(1)4=--- 1114=+-74=. 故选:A .【点拨】本题考查实数的运算,掌握运算顺序是解决为题的关键,先乘方、再乘除、最后加减,注意牢记特殊角的三角函数值.12.D【分析】原式利用特殊角的三角函数值,零指数幂、负整数指数幂法则,绝对值的代数意义,以及立方根定义计算即可求出值.解:原式=1-⎝⎭﹣(2+3+1=. 故选:D .【点拨】本题考查实数的运算,掌握正确的运算顺序是解决问题的关键. 13.D【分析】根据特殊角的三角函数值可判断30A ∠=︒,=60B ∠︒,从而可求出90C ∠=︒,即证明ABC 的形状是直角三角形.解:△A ∠,B ∠都是锐角,且1sin 2A =,1cos 2B =, △30A ∠=︒,=60B ∠︒,△180180306090C A B ∠=︒-∠-∠=︒-︒-︒=︒,△ABC 的形状是直角三角形. 故选D .【点拨】本题考查由特殊角的三角函数值判断三角形形状,三角形内角和定理.熟记特殊角的三角函数值是解题关键.14.C解:△sin A =cos B , △△A =△B =45°,△△ABC 是等腰直角三角形. 故选:C . 15.D【分析】先解直角ABC 求出AD ,再在直角ABD △中应用勾股定理即可求出AB . 解:△26BD CD ==, △3CD =,△直角ADC 中,tan 2C ∠=, △tan 326AD CD C =⋅∠=⨯=,△直角ABD △中,由勾股定理可得,AB = 故选D .【点拨】本题考查利用锐角函数解直角三角形和勾股定理,难度较小,熟练掌握三角函数的意义是解题的关键.16.A【分析】由题意易得MN 垂直平分AD ,AB =10,则有AD =4,AF =2,然后可得4cos 5AC A AB ∠==, 进而问题可求解.解:由题意得:MN 垂直平分AD ,6BD BC ==, △1,902AF AD AFE =∠=︒, △BC =6,AC =8,△C =90°,△10AB =,△AD =4,AF =2,4cos 5AC AF A AB AE ∠===, △5cos 2AF AE A ==∠; 故选A .【点拨】本题主要考查勾股定理、垂直平分线的性质及三角函数,熟练掌握勾股定理、垂直平分线的性质及三角函数是解题的关键.17.B【分析】先作PC AB ⊥于点C ,根据甲货船从A 港沿东北的方向以5海里/小时的速度出发,求出PAC ∠和AP ,从而得出PC 的值,得出BC 的值,即可求出答案.解:作PC AB ⊥于点C ,甲货船从A 港沿东北的方向以5海里/小时的速度出发,45PAC ∴∠=︒,5210AP =⨯=,PC AC ∴==乙货船从B 港沿西北方向出发,60PBC ∴∠=︒,BC ∴=AB AC BC ∴=+=,答:A 港与B 港相距海里,故选:B .【点拨】本题考查了解直角三角形的应用-方向角问题,解题的关键是从实际问题中整理出直角三角形并利用解直角三角形的知识求解.本题要注意关键词:在东西方向的海岸线上有A ,B 两个港口.18.A【分析】作BN DA ⊥交DA 的延长线于N ,延长CB 交DE 于M ,则四边形DMBN 是矩形,根据AB 的坡度,设3,4,BN k AN k ==表示出144,3,MB DN k DM BN k ==+==414,CM k =+在Rt EBM 中,144,EM BM k ==+ 在Rt ECM 中, 根据tan 0.4,EM C CM == 列出式子,求出k 的值,即可求解.解:如图,作BN DA ⊥交DA 的延长线于N ,延长CB 交DE 于M ,则四边形DMBN 是矩形,:3:4,BN AN =可以假设3,4,BN k AN k ==则,144,3,MB DN k DM BN k ==+== 414,CM k =+在Rt EBM 中, 90,45,EMB EBM ∠=∠=144,EM BM k ∴==+在Rt ECM 中, tan 0.4,EM C CM== 1440.4,414k k +∴=+ 解得:1,k =3,18,DM EM ∴==21.DE DM EM =+=答:观景塔的高度DE 为21米.故选A.【点拨】考查解直角三角形,坡度问题,熟练掌握锐角三角函数是解题的关键.19.B【分析】首先构建直角三角形,然后利用三角函数值得出DG ,即可得解.解:作AH△EB 于H ,延长DC 交AH 于N ,作DG△EB 于G ,如图所示:△△ACD=135°△△ACN=45°在Rt△ACN 中,AC=△ACN=45°△AN=CN=18在Rt△ABH 中,AB=AH :BH=3:2,设3,2AH k BH k ==△()()(22232k k +=解得15k =或15k =-(不符合题意,舍去)△AH=45△HN=AH -AN=45-18=27△四边形DGHN 是矩形△DG=HN=27在Rt△DEG 中,sin sin 36.5DG DEB DE ︒==∠ △274535DE ≈≈故选:B.【点拨】此题主要考查锐角三角函数的实际应用,熟练掌握,即可解题.20.D【分析】过点E 作EF△AB 于点F ,设AE=x cm ,则AD=3x ,则=AB ,然后利用AB•AD=x 的值,即可得到AD,AB 的长度,则周长可求.解:如图,过点E 作EF△AB 于点F ,△六个锐角都为60°,六个钝角都为120°,△设AE=x cm ,则AD=3x ,△△AEB=120°,△△EAB=30°,△AB=2AF=2cos30x︒,△六角星纸板的面积为2,△AB•AD=3393x x=解得x△AD=AB=3,△矩形ABCD的周长=3)26)⨯=cm.故选:D.【点拨】本题主要考查解直角三角形和一元二次方程的应用,掌握特殊角的三角函数值,利用方程的思想是解题的关键.21.A【分析】设CD=x,在Rt△ADC中,△A=45°,可得CD=AD=x,BD=16-x,在Rt△BCD 中,用△B的正切函数值即可求解.解:设CD=x,在Rt△ADC中,△A=45°,△CD=AD=x,△BD=16-x,在Rt△BCD中,△B=60°,△tanCDBBD =,即:16xx= -解得8(3x=,故选A.【点拨】本题考查三角函数,根据直角三角形的边的关系,建立三角函数模型是解题的关键.22.C【分析】根据题意易得OA△MN,△N=43°,△M=35°,OA=135m,AB=40m,然后根据三角函数可进行求解.解:由题意得:OA△MN,△N=43°,△M=35°,OA=135m,AB=40m,△95mOB OA AB=-=,△135==150mtan0.9OAONN=∠,95=136mtan0.7OBOMM=≈∠,△286mMN OM ON=+=;故选C.【点拨】本题主要考查解直角三角形的应用,熟练掌握三角函数是解题的关键.23.D【分析】利用平行线性质得出:△ABD=△EAB=60°,进而得出△ABC=△BAC=20°,得出BC=AC,进而得出答案.解:由题意可得出:△EAC=80°,△EAB=60°,△DBC=40°,BC=40×2=80(海里),△△BAC=80°-60°=20°,△BCA=60°,△AE△BD,△△ABD=△EAB=60°,△△DBC=40°,△△ABC=60°-40°=20°,△△ABC=△BAC=20°,△BC=AC=80(海里).△C海岛到观测点A的距离是80海里.故选D.【点拨】本题主要考查了解直角三角形的应用,利用方向角得出BC=AC是解题的关键.24.B【分析】题中利用特殊角度,做辅助线过S作SC△AB于C,在AB上截取CD=AC,设CS=x+2x=AB,可得:x,可知AS=(15)海里.解:过S作SC△AB于C,在AB上截取CD=AC,△AS =DS ,△△CDS =△CAS =30°,△△ABS =15°,△△DSB =15°,△SD =BD ,设CS =x 海里,在Rt △ASC 中,△CAS =30°,△AC(海里),AS =DS =BD =2x (海里),△AB =30海里,+2x =30,解得:x △AS =(15)海里.故选:B .【点拨】本题主要考查方位角问题,熟练运用特殊角三角函数是解题的关键.25.A【分析】直接利用坡度的定义得出AC 的长,再利用勾股定理得出AB 的长.解:△i =5BC m =, △5BC AC AC ==解得:AC =,则10AB m =.故选:A .【点拨】本题考查解直角三角形和勾股定理的实际应用.由坡度的定义得出AC 的长是解答本题的关键. 26.D【分析】结合题意,根据三角函数的性质计算,即可得到答案.解:根据题意,得:sin 370.6BC AB ︒=≈ △6BC =米 △6100.60.6BC AB ===米 故选:D .【点拨】本题考查了三角函数的知识;解题的关键是熟练掌握三角函数的性质,从而完成求解.27.A【分析】在Rt △ACB 中,利用正弦定义,sin α=BC AB ,代入AB 值即可求解. 解:在Rt △ACB 中,△ACB =90°,△sin α=BC AB, △BC = sin α⋅AB =12 sin α(米),故选:A .【点拨】本题考查解直角三角形的应用,熟练掌握直角三角形边角关系是解题的关键.28.A【分析】应充分利用所给的α和45°在树的位置构造直角三角形,进而利用三角函数求解.解:如图,过点C 作水平线与AB 的延长线交于点D ,则AD △CD ,△△BCD =α,△ACD =45°.在Rt △CDB 中,CD =m cos α,BD =m sin α,在Rt △CDA 中,AD =CD ×tan45°=m ×cos α×tan45°=m cos α,△AB =AD -BD=(m cos α-m sin α)=m (cosα-sin α).故选:A .【点拨】本题考查锐角三角函数的应用.需注意构造直角三角形是常用的辅助线方法,另外,利用三角函数时要注意各边相对.29.100tan tan tan tan αββα- 【分析】由正切的定义分别确定tan ,tan αβ的表达式,进而联立成方程组,求解方程组即可得到答案.解:如图,CD 为树高,点C 为树顶,则,CAD CBD αβ∠=∠=,BD =AD -100△依题意,有tan tan 100CD AD CD AD αβ⎧=⎪⎪⎨⎪=⎪-⎩①② 由△得tan CDAD α=③将△代入△,解得100tan tan =tan tan CD αββα- 故答案为:100tan tan tan tan αββα-. 【点拨】本题考查正切的定义,二元一次方程组得应用,能依题意根据正切的定义列出方程组是解题的关键.30.60°【分析】利用正弦定义计算即可.解:如图,△sinB =AC AB == △△B =60°,故答案为:60°.【点拨】此题主要考查了解直角三角形,关键是掌握正弦定义.31.23【分析】利用CD ∥AB ,得到△BAC =△DCA ,根据同圆的半径相等,AC =AB =3,可得sin△ACD =AD AC =23,从而可得答案. 解:如图:△CD ∥AB ,△△BAC =△DCA .△同圆的半径相等,△AC =AB =3.在Rt ACD △中,sin△ACD =23AD AC . △sin△BAC =sin△ACD =23.故答案为:23.【点拨】此题考查了解直角三角形的应用,解题的关键是利用图形的性质进行角的等量代换.32.45【分析】根据三角函数的定义即可得到cos B =sin A =45. 解:在Rt△ABC 中,△C =90°,△sin A =BC AB =45, △cos B =BC AB =45. 故答案为:45. 【点拨】本题考查了三角函数的定义,由定义可推出互余两角的三角函数的关系:若△A +△B =90°,则sin A =cos B ,cos A =sin B .熟知相关定义是解题关键.33.158【分析】先解直角三角形ABC 求出BC 的长,从而求出AB 的长,再由作图方法可知DE 是线段AB 的垂直平分线,即可得到BE 的长,再解直角△BED 即可得到答案.解:△△C =90°,AC =3cm ,3tan =4B , △3tan ==4AC B BC , △BC =4cm ,△AB ,由作图方法可知DE 是线段AB 的垂直平分线,△DE △AB ,522AB AE BE cm ===, △3tan =4DE B BE =, △31548DE BE cm ==, 故答案为:158. 【点拨】本题主要考查了锐角三角函数,勾股定理,线段垂直平分线的性质,线段垂直平分线的尺规作图,正确理解DE 是线段AB 的垂直平分线是解题的关键.34.3【分析】在Rt ADE △中,由正弦定义解得165AE =,再由勾股定理解得DE 的长,根据同角的余角相等,得到sin sin ADE ECD ∠=∠,最后根据正弦定义解得CD 的长即可解题.解:在Rt ADE △中,4sin 5AE ADE AD ∠==165AE ∴=125DE ∴=== DE AC ⊥90ADE EDC EDC ECD ∴∠+∠=∠+∠=︒ADE ECD ∴∠=∠4sin sin 5DE ADE ECD CD ∴∠=∠== 534CD DE ∴=⋅= 在矩形ABCD 中,3AB CD ==故答案为:3.【点拨】本题考查矩形的性质、正弦、勾股定理等知识,是重要考点,难度较易,掌握相关知识是解题关键.35.3【分析】直接利用零指数幂的性质以及负整数指数幂的性质、特殊角的三角函数值分别化简得出答案.解:原式=1+4﹣4×12=1+4﹣2=3.故答案为:3.【点拨】此题主要考查了负整数指数幂的性质、特殊角的三角函数值、零指数幂的性质,正确化简各数是解题关键.36【分析】根据特殊角的三角函数值直接书写即可.解:sin 45︒=. 【点拨】本题考查了特殊角的三角函数值,牢固记忆是解题的关键.【分析】直接利用特殊角的三角函数值即可求解.解:△sin (α+15°)=1,△α+15°=90°,△α=75°,故答案为:75.【点拨】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.38 【分析】先根据特殊角的三角函数值求出△A 的度数,然后求出tanA 的值.解:△sinA =12,△△A =30°,则tanA【点拨】本题考查了对特殊角的三角函数值的应用,解题的关键是检查学生能否熟练地运用进行计算.394##42+ 【分析】根据特殊角的三角函数值和负整数指数幂的运算法则进行计算即可.解:sin45°+2142-⎛⎫-= ⎪⎝⎭,+4.【点拨】本题考查了特殊角的三角函数值和负整数指数幂,相关公式有:sin 452=°,()10p pa a a -=≠. 403【分析】根据绝对值的性质、零指数幂的性质、特殊角的三角函数值、负指数幂的性质即可求解.解:原式124=-14=3=.3.【点拨】本题主要考查了绝对值的性质、零指数幂的性质、特殊角的三角函数值、负指数幂的性质.41.等腰【分析】根据绝对值和平方的非负性求出sinA和tanB的值,再根据锐角三角函数的特殊值求出△A和△B的角度,即可得出答案.解:△210 2sinA tanB-+⎛⎝⎭=△12sinA=,tanB=△△A=30°,△B=30°△△ABC是等腰三角形故答案为等腰.【点拨】本题考查的是特殊三角函数值,比较简单,需要牢记特殊三角函数值. 42.75°.【分析】先根据非负数的性质确定cosA=12,tanB=1,再根据特殊角的三角函数解答.解:△(cos A﹣12)2+|tan B﹣1|=0,△cos A﹣12=0,tan B﹣1=0,则cos A=12,tan B=1,△△A=60°,△B=45°,△△C=180°﹣60°﹣45°=75°.故答案为75°.【点拨】熟记特殊角的三角函数值是解题的关键,同时还考查了三角形内角和定理43.【分析】AB=AC=BC=CD,即可求出△BAD=90°,△D=30°,解直角三角形即可求得.解:△ABC∆是等边三角形,△60B BAC ACB︒∠=∠=∠=,△CD AC=,。
九年级数学专题复习锐角三角函数

总复习锐角三角函数【考纲要求】1.理解锐角三角函数的定义、性质及应用,特殊角三角函数值的求法,运用锐角三角函数解决与直角三角形有关的实际问题.题型有选择题、填空题、解答题,多以中、低档题出现;2.命题的热点为根据题中给出的信息构建图形,建立数学模型,然后用解直角三角形的知识解决问题.【知识网络】【考点梳理】考点一、锐角三角函数的概念如图所示,在Rt△ABC中,∠C=90°,∠A所对的边BC记为a,叫做∠A的对边,也叫做∠B的邻边,∠B所对的边AC记为b,叫做∠B的对边,也是∠A的邻边,直角C所对的边AB记为c,叫做斜边.锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,即sinA aAc∠==的对边斜边;锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即cosA bAc∠==的邻边斜边;锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即tanA aAA b∠==∠的对边的邻边.同理sinB bBc∠==的对边斜边;cosB aBc∠==的邻边斜边;tanB bBB a∠==∠的对边的邻边.要点进阶:ABCabc(1)正弦、余弦、正切函数是在直角三角形中定义的,反映了直角三角形边与角的关系,是两条线段的比值.角的度数确定时,其比值不变,角的度数变化时,比值也随之变化.(2)sinA,cosA,tanA分别是一个完整的数学符号,是一个整体,不能写成,,,不能理解成sin与∠A,cos与∠A,tan与∠A的乘积.书写时习惯上省略∠A的角的记号“∠”,但对三个大写字母表示成的角(如∠AEF),其正切应写成“tan∠AEF”,不能写成“tanAEF”;另外,、、常写成、、.(3)任何一个锐角都有相应的锐角三角函数值,不因这个角不在某个三角形中而不存在.(4)由锐角三角函数的定义知:当角度在0°<∠A<90°之间变化时,,,tanA>0.考点二、特殊角的三角函数值利用三角函数的定义,可求出0°、30°、45°、60°、90°角的各三角函数值,归纳如下:要点进阶:(1)通过该表可以方便地知道0°、30°、45°、60°、90°角的各三角函数值,它的另一个应用就是:如果知道了一个锐角的三角函数值,就可以求出这个锐角的度数,例如:若,则锐角.(2)仔细研究表中数值的规律会发现:sin0︒、、、、sin90︒的值依次为0、、、、1,而cos0︒、、、、cos90︒的值的顺序正好相反,、、的值依次增大,其变化规律可以总结为:当角度在0°<∠A<90°之间变化时,①正弦、正切值随锐角度数的增大(或减小)而增大(或减小)②余弦值随锐角度数的增大(或减小)而减小(或增大).考点三、锐角三角函数之间的关系如图所示,在Rt△ABC中,∠C=90°.(1)互余关系:,;(2)平方关系:;(3)倒数关系:或;(4)商数关系:.要点进阶:锐角三角函数之间的关系式可由锐角三角函数的意义推导得出,常应用在三角函数的计算中,计算时巧用这些关系式可使运算简便.考点四、解直角三角形在直角三角形中,由已知元素(直角除外)求未知元素的过程,叫做解直角三角形.在直角三角形中,除直角外,一共有5个元素,即三条边和两个锐角.设在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,则有:①三边之间的关系:a2+b2=c2(勾股定理).②锐角之间的关系:∠A+∠B=90°.③边角之间的关系:,,,,,.④,h为斜边上的高.要点进阶:(1)直角三角形中有一个元素为定值(直角为90°),是已知的值.(2)这里讲的直角三角形的边角关系指的是等式,没有包括其他关系(如不等关系).(3)对这些式子的理解和记忆要结合图形,可以更加清楚、直观地理解.考点五、解直角三角形的常见类型及解法已知条件解法步骤Rt△ABC两边两直角边(a,b)由求∠A,∠B=90°-∠A,斜边,一直角边(如c,a)由求∠A,∠B=90°-∠A,一边一直角边和一锐角锐角、邻边(如∠A,b)∠B=90°-∠A,一角,锐角、对边(如∠A,a)∠B=90°-∠A,,斜边、锐角(如c,∠A)∠B=90°-∠A,,要点进阶:1.在遇到解直角三角形的实际问题时,最好是先画出一个直角三角形的草图,按题意标明哪些元素是已知的,哪些元素是未知的,然后按先确定锐角、再确定它的对边和邻边的顺序进行计算.2.若题中无特殊说明,“解直角三角形”即要求出所有的未知元素,已知条件中至少有一个条件为边.考点六、解直角三角形的应用解直角三角形的知识应用很广泛,关键是把实际问题转化为数学模型,善于将某些实际问题中的数量关系化归为直角三角形中的边角关系是解决实际应用问题的关键.解这类问题的一般过程是:(1)弄清题中名词、术语的意义,如仰角、俯角、坡度、坡角、方向角等概念,然后根据题意画出几何图形,建立数学模型.(2)将已知条件转化为几何图形中的边、角或它们之间的关系,把实际问题转化为解直角三角形的问题.(3)根据直角三角形(或通过作垂线构造直角三角形)元素(边、角)之间的关系解有关的直角三角形.(4)得出数学问题的答案并检验答案是否符合实际意义,得出实际问题的解.拓展:在用直角三角形知识解决实际问题时,经常会用到以下概念:(1)坡角:坡面与水平面的夹角叫做坡角,用字母表示.坡度(坡比):坡面的铅直高度h和水平距离的比叫做坡度,用字母表示,则,如图,坡度通常写成=∶的形式.(2)仰角、俯角:视线与水平线所成的角中,视线中水平线上方的叫做仰角,在水平线下方的叫做俯角,如图.(3)方位角:从某点的指北方向线按顺时针转到目标方向的水平角叫做方位角,如图①中,目标方向PA,PB,PC的方位角分别为是40°,135°,245°.(4)方向角:指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方向角,如图②中的目标方向线OA,OB,OC,OD的方向角分别表示北偏东30°,南偏东45°,南偏西80°,北偏西60°.特别如:东南方向指的是南偏东45°,东北方向指的是北偏东45°,西南方向指的是南偏西45°,西北方向指的是北偏西45°.要点进阶:1.解直角三角形实际是用三角知识,通过数值计算,去求出图形中的某些边的长或角的大小,最好画出它的示意图.2.非直接解直角三角形的问题,要观察图形特点,恰当引辅助线,使其转化为直角三角形或矩形来解.例如:3.解直角三角形的应用题时,首先弄清题意(关键弄清其中名词术语的意义),然后正确画出示意图,进而根据条件选择合适的方法求解.考点七、解直角三角形相关的知识如图所示,在Rt△ABC中,∠C=90°,(1)三边之间的关系:222a b c +=; (2)两锐角之间的关系:∠A+∠B =90°; (3)边与角之间的关系:sin cos a A B c ==,cos cos a A B c==,cos sin b A B c ==,1tan tan a A b B==. (4) 如图,若直角三角形ABC 中,CD ⊥AB 于点D ,设CD =h ,AD =q ,DB =p ,则由△CBD ∽△ABC ,得a 2=pc ;由△CAD ∽△BAC ,得b 2=qc ;由△ACD ∽△CBD ,得h 2=pq ;由△ACD ∽△ABC 或由△ABC 面积,得ab =ch .(5)如图所示,若CD 是直角三角形ABC 中斜边上的中线,则①CD =AD =BD =12AB ; ②点D 是Rt △ABC 的外心,外接圆半径R =12AB . (6)如图所示,若r 是直角三角形ABC 的内切圆半径,则2a b c abr a b c+-==++. 直角三角形的面积: ①如图所示,111sin 222ABC S ab ch ac B ===△.(h 为斜边上的高)②如图所示,1()2ABC S r a b c =++△.【典型例题】类型一、锐角三角函数的概念与性质例1.(1)如图所示,在△ABC中,若∠C=90°,∠B=50°,AB=10,则BC的长为( ).A.10·tan50° B.10·cos50° C.10·sin50° D.10 sin50°(2)如图所示,在△ABC中,∠C=90°,sinA=35,求cosA+tanB的值.(3)如图所示的半圆中,AD是直径,且AD=3,AC=2,则sinB的值等于________.举一反三:【变式】如图,已知△ABC的三个顶点均在格点上,则cosA的值为()A .B .C .D .类型二、特殊角的三角函数值 例2.解答下列各题: (1)化简求值:tan 60tan 45sin 45sin 30sin 60cos30cos 45--++°°°°°°°;(2)在△ABC 中,∠C =90°,化简12sin cos A A -.举一反三: 【变式】若3sin 22α=,cos sin βα=,(2α,β为锐角),求2tan()3β的值.例3.如图,在锐角△ABC 中,AB=15,BC=14,S △ABC =84,求: (1)tanC 的值;(2)sinA 的值.CBA举一反三:【变式】如图,AB 是江北岸滨江路一段,长为3千米,C 为南岸一渡口,为了解决两岸交通困难,拟在渡口C 处架桥.经测量得A 在C 北偏西30°方向,B 在C 的东北方向,从C 处连接两岸的最短的桥长为多少千米?(精确到0.1千米)类型三、解直角三角形及应用例4.如图所示,D 是AB 上一点,且CD ⊥AC 于C ,:2:3ACD CDB S S =△△,4cos 5DCB ∠=, AC+CD =18,求tanA 的值和AB 的长.例5.如图所示,山脚下有一棵树AB ,小华从点B 沿山坡向上走50 m 到达点D ,用高为1.5m 的测角仪CD 测得树顶的仰角为10°,已知山坡的坡角为15°,求树AB 的高(精确到0.1m).(参考数据:sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,sin15°≈0.26,cos15°≈0.97,tan15°≈0.27).举一反三:【变式】如图所示,正三角形ABC的边长为2,点D在BC的延长线上,CD=3.(1)动点P在AB上由A向B移动,设AP=t,△PCD的面积为y,求y与t之间的函数关系式及自变量t的取值范围;(2)在(1)的条件下,设PC=z,求z与t之间的函数关系式.例6.如图(1)所示,一架长4米的梯子AB斜靠在与地面OM垂直的墙ON上,梯子与地面的倾斜角α为60°.(1)求AO与BO的长.(2)若梯子顶端A沿NO下滑,同时底端B沿OM向右滑行.①如图(2)所示,设A点下滑到C点,B点向右滑行到D点,并且AC:BD=2:3,试计算梯子顶端A 沿NO下滑了多少米;②如图(3)所示,当A点下滑到A′点,B点向右滑行到B′点时,梯子AB的中点P也随之运动到P′点,若∠POP′=15°,试求AA′的长.【巩固练习】一、选择题1. 在△ABC 中,∠C =90°,cosA =35,则tan A 等于 ( )A .35 B .45 C .34 D .432.在Rt △ABC 中,∠C=90°,把∠A 的邻边与对边的比叫做∠A 的余切,记作cotA=ab.则下列关系式中不成立的是( )A .tanA•cotA=1B .sinA=tanA•cosAC .cosA=cotA•sinAD .tan 2A+cot 2A=1第2题 第3题3.如图,在四边形ABCD 中,E 、F 分別是AB 、AD 的中点,若EF=2,BC=5,CD=3,则tanC 等于( ) A .34 B .43 C .35 D .454.如图所示,直角三角形纸片的两直角边长分别为6、8,现将△ABC 如图那样折叠,使点A 与点B 重合,折痕为DE ,则tan ∠CBE 的值是( )A .247B .73C .724D .135.如图所示,已知∠α的终边OP ⊥AB ,直线AB 的方程为y =-33x +33,则cos α等于 ( ) A .12B .22C .32D .336.如图,一艘海轮位于灯塔P 的北偏东55°方向,距离灯塔2海里的点A 处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB 长是( )A.2海里B.2sin55°海里C.2cos55°海里D.2tan55°海里二、填空题7.设θ为锐角,且x2+3x+2sinθ=0的两根之差为5.则θ=.8.如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为 .9.已知△ABC的外接圆O的半径为3,AC=4,则sinB= .第8题第9题第11题10.当0°<α<90°时,求21sincosαα-的值为.11.如图,点E(0,4),O(0,0),C(5,0)在⊙A上,BE是⊙A上的一条弦.则t an∠OBE=.12.在△ABC中,AB=12,AC=13,cos∠B=,则BC边长为 .三、解答题13.如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上.(1)求斜坡AB的水平宽度BC;(2)矩形DEFG为长方体货柜的侧面图,其中DE=2.5m,EF=2m,将该货柜沿斜坡向上运送,当BF=3.5m 时,求点D离地面的高.(≈2.236,结果精确到0.1m)14. 为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图,如图所示.按规定,地下停车库坡道1:3上方要张贴限高标志,以便告知停车人车辆能否安全驶入,为标明限高,请你根据该图计算CE(精确到0.1 m)(sin18°≈0.3090,cos18°≈0.9511,tan18°≈0.3249)15.如图所示,某中学九年级一班数学课外活动小组利用周末开展课外实践活动,他们要在某公园人工湖旁的小山AB上,测量湖中两个小岛C、D间的距离.从山顶A处测得湖中小岛C的俯角为60°,测得湖中小岛D的俯角为45°.已知小山AB的高为180米,求小岛C、D间的距离.(计算过程和结果均不取近似值)16. 在△ABC中,AB=AC,CG⊥BA,交BA的延长线于点G.一等腰直角三角尺按如图①所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC边在一条直线上,另一条直角边恰好经过点B.(1)在图①中请你通过观察、测量BF与CG的长度,猜想并写出BF与CG满足的数量关系,然后证明你的猜想;(2)当三角尺沿AC方向平移到图②所示的位置时,一条直角边仍与AC边在同一直线上,另一条直角边交BC边于点D,过点D作DE⊥BA于点E.此时请你通过观察、测量DE、DF与CG的长度,猜想并写出DE+DF与CG之间满足的数量关系;然后证明你的猜想;(3)当三角尺在②的基础上沿AC方向继续平移到图③所示的位置(点F在线段AC上,且点F与点C 不重合)时,(2)中的猜想是否仍然成立?(不用说明理由)。
中考数学-锐角三角函数(解析版)

知识点一:锐角三角函数 1.三角函数定义 在 Rt△ABC 中,若∠C=90°
sin A A的对边 a
斜边
c
A的邻边
b
cos A
斜边
c
A的对边
a
tan A A的邻边 b
A的邻边
b
cot A A的对边 a
2.同角三角函数的关系
(1)平方关系: sin2 Acos2 A1
(1)三边之间的关系为 a2 b2 c2 (勾股定理)
(2)锐角之间的关系为∠A+∠B=90°
(3)30°角所对直角边等于斜边的一半。
(4)直角三角形斜边上的中线等于斜边的一半。
(5)边角之间的关系为:(三角函数定义)
2.其他有关公式
(1)
S
1 2
ab sin C
=
1 2
bc sin
A
=
1 2
ac sin
B
(2)Rt△面积公式:
S
1 2
ab
1 2
ch
(3)直角三角形外接圆的半径
R c 2
,内切圆半径
r abc 2
结论:直角三角形斜边上的高 h ab c
3.实际问题中术语的含义
(1)仰角与俯角
在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,在水平线下方的角叫做俯角。
(2)坡度:如图,我们通常把坡面的铅直高度和水平宽度的比叫做坡度(或坡比),用字母 i 表示,即 i h . l
见问题,这也是以后中考命题的趋势。 5.解决实际问题的关键在于建立数学模型,要善于把实际问题的数量关系转化为解直角三角形的问题.在 解直角三角形的过程中,常会遇到近似计算,应根据题目要求的精确度定答案.
锐角三角函数的计算-特殊角的三角函数值(知识讲解)-2022-2023学年九年级数学下册基础知识讲练
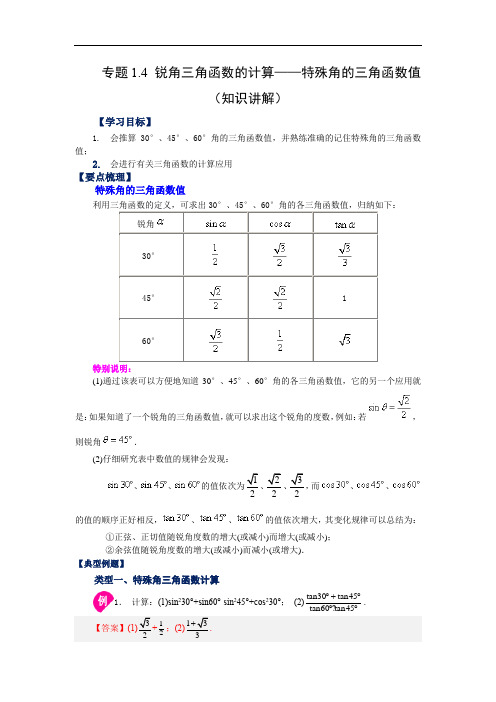
专题1.4 锐角三角函数的计算——特殊角的三角函数值(知识讲解)【学习目标】1.会推算30°、45°、60°角的三角函数值,并熟练准确的记住特殊角的三角函数值;2.会进行有关三角函数的计算应用【要点梳理】特殊角的三角函数值锐角30°45° 160°特别说明:(1)通过该表可以方便地知道30°、45°、60°角的各三角函数值,它的另一个应用就是:如果知道了一个锐角的三角函数值,就可以求出这个锐角的度数,例如:若,则锐角.(2)仔细研究表中数值的规律会发现:、、的值依次为12、22、32,而、、的值的顺序正好相反,、、的值依次增大,其变化规律可以总结为:①正弦、正切值随锐角度数的增大(或减小)而增大(或减小);②余弦值随锐角度数的增大(或减小)而减小(或增大).【典型例题】类型一、特殊角三角函数计算1.计算:(1)sin230°+sin60°-sin245°+cos230°;(2)tan30tan45 tan60?tan45︒+︒︒︒.【答案】(1)32+12;(2)133+.【分析】(1)将特殊角的三角函数值代入求解;(2)将特殊角的三角函数值代入求解.特殊值:sin 30° =12;sin 60° = 32;sin 45° = 22;cos 30° = 32;tan 60° = 3;tan 45° = 1解:(1)原式=1342+-12+34=32 + 12; 3133?1+(2)原式= =133+. 【点拨】本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.举一反三:【变式1】计算:222sin 60cos 60︒︒︒︒-﹣sin45°•tan45° 【答案】3232+ 【分析】把特殊角的三角函数值代入计算即可.解:222sin 60cos 60tan 604cos 45︒︒︒︒--﹣sin45°•tan45° ()22312222122342⎛⎫⨯- ⎪⎝⎭=-⨯-⨯ 122322=-- 23222=+-=3232+. 【点拨】本题考查了特殊角的三角函数值及分母有理化、二次根式的化简,牢记特殊角的三角函数值,是解决本题的关键.【变式2】计算:2cos45°﹣tan60°+sin30°﹣12tan45°【答案】2-3【分析】将各特殊角的三角函数值代入即可得出答案.解:原式=2×22﹣3+12﹣12×1 =2-3【点拨】此题考查特殊角的三角函数值,属于基础题,熟练记忆一些特殊角的三角函数值是关键.类型二、特殊角三角函数计算2.计算:()2012sin 451220202π-︒⎛⎫----+- ⎪⎝⎭ 【答案】-2【分析】直接利用特殊角的三角函数值、绝对值的性质、零指数幂的性质、负整数指数幂的性质分别代入化简即可.解:原式=24121-+-+=-2【点拨】此题主要考查了实数运算,正确化简各数是解题关键.举一反三:【变式1】计算:0113tan 30(2014π)32()3-︒---. 【答案】-2试题分析:分别计算033tan3033=⨯,(2014-π)0=1,32-=2﹣11333-⎛⎫= ⎪⎝⎭,,再用实数的混合运算法则计算.解:原式=3×33﹣1+2﹣3﹣3=﹣2. 【变式2】计算:()()2(31)3tan3052522sin60+--++. 【答案】3试题分析:用完全平方公式、平方差公式去括号,计算出特殊角三角函数值,再进行乘法运算,最后进行加减运算即可.解:(3-1)2+3tan 30°-(5-2)( 5+2)+2sin 60°=4-23+3×33-(5-4)+2×32=4-23+3-1+3=3.【点拨】掌握二次根式的加减乘除运算法则.类型三、三角函数计算3. 已知A ∠为锐角,且24sin 30A -=,则A ∠=______. 【答案】60︒【分析】计算,并结合A ∠是个锐角,即可求解.解:∵24sin 30A -=,∵23sin 4A =, ∵3sin 2A =±, ∵A ∠为锐角,∵3sin 2A =, ∵60A ∠=︒故答案是:60°【点拨】本题主要考察计算和锐角三角函数与角度关系,属于基础的计算题,难度不大.解题的关键是结合角度范围确定三角函数值范围.举一反三:【变式1】已知矩形ABCD 的周长为()232cm ,对角线2cm AC =,求BAC ∠与DAC ∠的度数. 【答案】30BAC ∠=︒,60=︒∠DAC 或60BAC ∠=︒,30DAC ∠=︒.【分析】设AB=x,将BC 表示出来,再利用勾股定理可求出x=1或x=3,再利用三角函数求出一个角为30°,另一个角为60°.解:∵矩形ABCD 的周长为232+,∵AB+BC= 3+1,∵对角线AC=2,∵设AB=x,则BC=3+1-x,∵AB 2+BA 2=AC 2,∵x 2+(3+1-x)2=22,解得:x 1=1,x 2=3,∵当AB=1,则BC=3,∵tan∵BAC=3,∵∵BAC=60°,∵DAC=30°,当AB=3,则BC=1,∵tan∵BAC= 33, ∵∵BAC=30°,∵DAC=60°,故30BAC ∠=︒,60=︒∠DAC 或60BAC ∠=︒,30DAC ∠=︒. 【点拨】此题主要考查了勾股定理和特殊角的三角函数值,解答本题的关键是掌握特殊角的三角函数值.【变式2】计算(1)23602cos 30tan 45︒-︒+︒(2)已知α是锐角,且()1sin 152α-︒=84cos α的值. 【答案】(1)1 (2)0【分析】(1)把特殊角的三角函数值代入代数式进行计算即可;(2)先利用锐角的正弦求解α的大小,再代入代数式进行计算即可.(1)解:23sin 602cos 30tan 45︒-︒+︒ 23332122331122(2) α是锐角,且()1sin 152α-︒=,1530,=45,∴ 84cos α-2224222220=-=【点拨】本题考查的是特殊角的三角函数值的混合运算,已知三角函数值求解锐角的大小,熟记特殊角的三角函数值是解本题的关键.类型四、三角函数计算4.(1)计算:21122cos453-⎛⎫--︒+-⎪⎝⎭.(2)如图,在△ABC中,∵ACB=90°,角平分线AE与高CD交于点F,求证:CE=CF.【答案】(1)8;(2)见分析【分析】(1)计算绝对值、特殊角的三角函数值、负整数指数幂,再合并即可;(2)根据直角三角形两锐角互余求得∵B=∵ACD,然后根据三角形外角的性质求得∵CEF=∵CFE,根据等角对等边求得CE=CF.(1)解:21 122cos453-⎛⎫--︒+-⎪⎝⎭221292=--⨯+2129=--+=8;(2)证明:∵在△ABC中,∵ACB=90°,∵∵B+∵BAC=90°,∵CD是AB边上的高,∵∵ACD+∵BAC=90°,∵∵B=∵ACD,∵AE是∵BAC的角平分线,∵∵BAE=∵EAC,∵∵B +∵BAE =∵ACD +∵EAC ,即∵CEF =∵CFE ,∵CE =CF .【点拨】本题考查了特殊角的三角函数值,负整数指数幂,直角三角形的性质,三角形外角的性质,等腰三角形的判定等,熟练掌握性质定理是解题的关键.举一反三:【变式1】如图,将∵ABC 沿射线AB 平移4cm 后能与∵BDE 完全重合,连接CE 、CD 交BE 于点O ,OB =OC .(1)求证:四边形CBDE 为矩形;(2)若S △BOC 432,求∵ACD 的度数. 【答案】(1)见分析(2)120°【分析】(1)由平移的性质及ASA判定定理可证得OCE ODB ≌,根据全等三角形的性质即可求证结论.(2)根据矩形的性质及面积公式即可求得BC ,进而可利用特殊三角函数值可求得60BCD ∠=︒,根据垂直平分线的性质即可求解.(1)证明:由题意可知:△BDE 由△ABC 平移后得到,∵//BC DE ,且BC DE =,∵四边形CBDE 是平行四边形,∵//CE BD ,且CE BD =,∵ECD CDB ∠=∠,CEB EBD ∠=∠,在OCE 和ODB △中 ECD CDB CE BDCEB EBD ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∵ ()OCE ODB ASA ≌∵OC OD =,OB OE =,又∵OB OC =,∵CD BE =,∵ 平行四边形CBDE 为矩形.(2)由(1)可知四边形CBDE 为矩形,∵90CBD ∠=︒,且4BD =cm ,在OBC 中过点O 作BC 的垂线,垂足为F ,则2OF =,∵143223BOC S BC =⨯⨯=,∵433BC =cm , ∵在Rt CBD △,43433BD tan BCD CB ∠===,∵60BCD ∠=︒,又∵在△ACD 中,BC 是AD 的垂直平分线,∵60ACB BCD ∠=∠=︒,∵120ACD ∠=︒,∴∵ACD 的度数为120︒.【点拨】本题考查了平移的性质、全等三角形的判定及性质、矩形的判定及性质、特殊三角函数值求角度,熟练掌握相关性质及判定定理是解题的关键.【变式2】将矩形ABCD 对折,使AD 与BC 重合,得到折痕EF ,展开后再一次折叠,使点A 落在EF 上的点A '处,并使得折痕经过点B ,得到折痕BG ,连接AA ',如图1,问题解决:(1)试判断图1中ABA '△是什么特殊的三角形?并说明理由;(2)如图2,在图1的基础上,AA '与BG 相交于点N ,点P 是BN 的中点,连接AP 并延长交BA '于点Q ,求BQ BA '的值.【答案】(1)ABA '△是等边三角形,理由见分析(2)13BQ BA =' 【分析】(1)等边三角形,解法一利用垂直平分线性质得出AA ′=BA ′,利用折叠得出BA BA '=即可,解法二:根据折叠得出12BE BA =,BA BA '=,90A EB '∠=︒然后利用锐角三角函数定义得出1cos 2BE A BE BA '∠==' ,求出60A BE '∠=︒即可; (2)解法一:过点N 作NH A B '∥交AP 于H ,先证PHN PQB ≌△△(AAS ),再证AHN AQA '∽△△,得出12BQ QA =' 即可 解法二:由折叠可知A N AN '=,由点P 是BN 的中点 ,得出BP PN =,利用平行线等分性质得出1A M A N QM AN ''==,1BQ BP QM PN ==,证出BQ QM A M '==即可.(1)解:ABA '△是等边三角形.解法一:理由是:由折叠可知EF 垂直平分AB ;∵AA ′=BA ′,∵∵ABG 折叠得△A ′BG ,∵BA BA '=,∵AA BA BA ''==;∵ABA '△是等边三角形;解法二:理由是:由折叠可知12BE BA =,BA BA '=,90A EB '∠=︒, ∵1cos 2BE A BE BA '∠==' , ∵60A BE '∠=︒,∵ABA '△是等边三角形;(2)解法一:过点N 作NH A B '∥交AP 于H ,∵HNP QBP ∠=∠,NHP BOP ∠=∠, 又∵点P 是BN 的中点 , ∵BP NP =,在△PHN 和△PQB 中, HNP QBP NHP BQP PN PB ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∵PHN PQB ≌△△(AAS ), ∵HN BQ =,又∵NH A B '∥,∵ANH AA Q '∠=∠,AHN AQA '∠=∠, ∵AHN AQA '∽△△, 由折叠可知12A N AN AA ''==, ∵12HN AN QA AA =='' , ∵12BQ QA =', ∵13BQ BA ='; 解法二:由折叠可知A N AN '=, 又∵点P 是BN 的中点 , ∵BP PN =,过点N 作NM AQ ∥交BA '于M , ∵1A M A N QM AN''==,1BQ BP QM PN ==, ∵BQ QM A M '==, ∵13BQ BA ='.【点拨】本题考查一题多解,等边三角形的判定,折叠性质,线段垂直平分线性质,平行线等分线段定理,三角形相似判定与性质,锐角三角函数值求角,掌握一题多解,等边三角形的判定,折叠性质,线段垂直平分线性质,平行线等分线段定理,三角形相似判定与性质是解题关键.。
中考总复习:锐角三角函数综合复习--知识讲解(基础)

中考总复习:锐角三角函数综合复习—知识讲解(基础)【考纲要求】1.理解锐角三角函数的定义、性质及应用,特殊角三角函数值的求法,运用锐角三角函数解决与直角三角形有关的实际问题.题型有选择题、填空题、解答题,多以中、低档题出现;2.命题的热点为根据题中给出的信息构建图形,建立数学模型,然后用解直角三角形的知识解决问题. 【知识网络】【考点梳理】考点一、锐角三角函数的概念如图所示,在Rt △ABC 中,∠C =90°,∠A 所对的边BC 记为a ,叫做∠A 的对边,也叫做∠B 的邻边,∠B 所对的边AC 记为b ,叫做∠B 的对边,也是∠A 的邻边,直角C 所对的边AB 记为c ,叫做斜边.BCabc锐角A 的对边与斜边的比叫做∠A 的正弦,记作sinA ,即sin A aA c ∠==的对边斜边;锐角A 的邻边与斜边的比叫做∠A 的余弦,记作cosA ,即cos A bA c ∠==的邻边斜边;锐角A 的对边与邻边的比叫做∠A 的正切,记作tanA ,即tan A aA A b∠==∠的对边的邻边.同理sin B b B c ∠==的对边斜边;cos B aB c∠==的邻边斜边;tan B b B B a ∠==∠的对边的邻边.要点诠释:(1)正弦、余弦、正切函数是在直角三角形中定义的,反映了直角三角形边与角的关系,是两条线段的比值.角的度数确定时,其比值不变,角的度数变化时,比值也随之变化.(2)sinA,cosA,tanA分别是一个完整的数学符号,是一个整体,不能写成,,,不能理解成sin与∠A,cos与∠A,tan与∠A的乘积.书写时习惯上省略∠A的角的记号“∠”,但对三个大写字母表示成的角(如∠AEF),其正切应写成“tan∠AEF”,不能写成“tanAEF”;另外,、、常写成、、.(3)任何一个锐角都有相应的锐角三角函数值,不因这个角不在某个三角形中而不存在.(4)由锐角三角函数的定义知:当角度在0°<∠A<90°之间变化时,,,tanA>0.考点二、特殊角的三角函数值利用三角函数的定义,可求出30°、45°、60°角的各三角函数值,归纳如下:锐角30°45° 160°要点诠释:(1)通过该表可以方便地知道30°、45°、60°角的各三角函数值,它的另一个应用就是:如果知道了一个锐角的三角函数值,就可以求出这个锐角的度数,例如:若,则锐角.(2)仔细研究表中数值的规律会发现:、、的值依次为、、,而、、的值的顺序正好相反,、、的值依次增大,其变化规律可以总结为:当角度在0°<∠A<90°之间变化时,①正弦、正切值随锐角度数的增大(或减小)而增大(或减小),②余弦值随锐角度数的增大(或减小)而减小(或增大).考点三、锐角三角函数之间的关系如图所示,在Rt△ABC中,∠C=90°.(1)互余关系:,;(2)平方关系:;(3)倒数关系:或;(4)商数关系:.要点诠释:锐角三角函数之间的关系式可由锐角三角函数的意义推导得出,常应用在三角函数的计算中,计算时巧用这些关系式可使运算简便.考点四、解直角三角形在直角三角形中,由已知元素(直角除外)求未知元素的过程,叫做解直角三角形.在直角三角形中,除直角外,一共有5个元素,即三条边和两个锐角.设在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,则有:①三边之间的关系:a2+b2=c2(勾股定理).②锐角之间的关系:∠A+∠B=90°.③边角之间的关系:,,,,,.④,h为斜边上的高.要点诠释:(1)直角三角形中有一个元素为定值(直角为90°),是已知的值.(2)这里讲的直角三角形的边角关系指的是等式,没有包括其他关系(如不等关系).(3)对这些式子的理解和记忆要结合图形,可以更加清楚、直观地理解.考点五、解直角三角形的常见类型及解法已知条件解法步骤Rt△ABC 两边两直角边(a,b)由求∠A,∠B=90°-∠A,斜边,一直角边(如c,a) 由求∠A,∠B=90°-∠A,一边一角一直角边和一锐角锐角、邻边(如∠A,b)∠B=90°-∠A,,锐角、对边(如∠A,a)∠B=90°-∠A,,斜边、锐角(如c,∠A)∠B=90°-∠A,,要点诠释:1.在遇到解直角三角形的实际问题时,最好是先画出一个直角三角形的草图,按题意标明哪些元素是已知的,哪些元素是未知的,然后按先确定锐角、再确定它的对边和邻边的顺序进行计算.2.若题中无特殊说明,“解直角三角形”即要求出所有的未知元素,已知条件中至少有一个条件为边.考点六、解直角三角形的应用解直角三角形的知识应用很广泛,关键是把实际问题转化为数学模型,善于将某些实际问题中的数量关系化归为直角三角形中的边角关系是解决实际应用问题的关键.解这类问题的一般过程是:(1)弄清题中名词、术语的意义,如仰角、俯角、坡度、坡角、方向角等概念,然后根据题意画出几何图形,建立数学模型.(2)将已知条件转化为几何图形中的边、角或它们之间的关系,把实际问题转化为解直角三角形的问题.(3)根据直角三角形(或通过作垂线构造直角三角形)元素(边、角)之间的关系解有关的直角三角形.(4)得出数学问题的答案并检验答案是否符合实际意义,得出实际问题的解.拓展:在用直角三角形知识解决实际问题时,经常会用到以下概念:(1)坡角:坡面与水平面的夹角叫做坡角,用字母表示.坡度(坡比):坡面的铅直高度h和水平距离的比叫做坡度,用字母表示,则,如图,坡度通常写成=∶的形式.(2)仰角、俯角:视线与水平线所成的角中,视线中水平线上方的叫做仰角,在水平线下方的叫做俯角,如图.(3)方位角:从某点的指北方向线按顺时针转到目标方向的水平角叫做方位角,如图①中,目标方向PA,PB,PC的方位角分别为是40°,135°,245°.(4)方向角:指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方向角,如图②中的目标方向线OA,OB,OC,OD的方向角分别表示北偏东30°,南偏东45°,南偏西80°,北偏西60°.特别如:东南方向指的是南偏东45°,东北方向指的是北偏东45°,西南方向指的是南偏西45°,西北方向指的是北偏西45°.要点诠释:1.解直角三角形实际是用三角知识,通过数值计算,去求出图形中的某些边的长或角的大小,最好画出它的示意图.2.非直接解直角三角形的问题,要观察图形特点,恰当引辅助线,使其转化为直角三角形或矩形来解.例如:3.解直角三角形的应用题时,首先弄清题意(关键弄清其中名词术语的意义),然后正确画出示意图,进而根据条件选择合适的方法求解.【典型例题】类型一、锐角三角函数的概念与性质1.如图,在4×4的正方形网格中,tanα=( )(A)1 (B)2 (C) 12(D)52【思路点拨】把∠α放在一个直角三角形中,根据网格的长度计算出∠α的对边和邻边的长度.【答案】B;【解析】根据网格的特点:设每一小正方形的边长为1,可以确定∠α的对边为2,邻边为1,然后利用正切的定义tan∠αα=∠α的对边的邻边,故选B.【总结升华】本题考查锐角三角函数的定义及运用,可将其转化到直角三角形中解答,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.举一反三:【变式】在Rt△ABC中,∠C=90°,若AC=2BC,则sinA的值是( )(A) 12(B)2 (C)55(D)52【答案】选C.因为∠C=90°,522AB=AC +BC =BC ,所以BC BC 5sin A AB 55BC===.类型二、特殊角的三角函数值2.已知a =3,且21(4tan 45)302b bc -++-=°,以a 、b 、c 为边长组成的三角形面积等于( ). A .6 B .7 C .8 D .9【思路点拨】根据题意知4tan 450,130,2b bc -=⎧⎪⎨+-=⎪⎩°求出b 、c 的值,再求三角形面积. 【答案】A ;【解析】根据题意知4tan 450,130,2b bc -=⎧⎪⎨+-=⎪⎩° 解得 4,5.b c =⎧⎨=⎩ 所以a =3,b =4,c =5,即222a b c +=,其构成的三角形为直角三角形,且∠C =90°, 所以162S ab ==. 【总结升华】利用非负数之和等于0的性质,求出b 、c 的值,再利用勾股定理的逆定理判断三角形是直角三角形,注意tan45°的值不要记错. 举一反三: 【变式】 计算:.【答案】原式.3.如图所示,在△ABC 中,∠BAC =120°,AB =10,AC =5,求sinB ·sinC 的值.【思路点拨】为求sin B ,sin C ,需将∠B ,∠C 分别置于直角三角形之中,另外已知∠A 的邻补角是60°,若要使其充分发挥作用,也需要将其置于直角三角形中,所以应分别过点B 、C 向CA 、BA 的延长线作垂线,即可顺利求解. 【答案与解析】解:过点B 作BD ⊥CA 的延长线于点D ,过点C 作CE ⊥BA 的延长线于点E .∵∠BAC =120°,∴∠BAD =60°.∴AD =AB ·cos60°=10×12=5; BD =AB ·sin60°=10×32=53. 又∵CD =CA+AD =10, ∴2257BC BD CD =+=,∴21sin 7BD BCD BC ∠==. 同理,可求得21sin 14ABC ∠=. ∴21213sin sin 71414ABC BCD ∠∠=⨯=. 【总结升华】由于锐角的三角函数是在直角三角形中定义的,因此若要求某个角的三角函数值,一般可以通过作垂线等方法将其置于直角三角形中.举一反三:【变式】如图,机器人从A 点,沿着西南方向,行了个单位,到达B 点后观察到原点O 在它的南偏东60°的方向上,则原来A 的坐标为__________.(结果保留根号).【答案】类型三、解直角三角形及应用4.在△ABC中,∠A=30°,BC=3,AB=33,求∠BCA的度数和AC的长.【思路点拨】由于∠A是一个特殊角,且已知AB,故可以作AC边上的高BD(如图所示),可求得332BD=.由于此题的条件是“两边一对角”,且已知角的对边小于邻边,因此需要判断此题的解是否唯一,要考虑对边BC与AC边上的高BD的大小,而33332BC<<,所以此题有两解.【答案与解析】解:作BD⊥AC于D.(1)C1点在AD的延长线上.在△ABC1中,13BC=,332 BD=,∴13sin2C=.∴∠C1=60°.由勾股定理,可分别求得13 2DC=,92 AD=.∴AC1=AD+DC1=936 22+=.(2)C2点在AD上.由对称性可得,∠BC2D=∠C1=60°,213 2C D C D==.∴∠BC2A=120°,2933 22AC=-=.综上所述,当∠BCA=60°时,AC=6;当∠BCA=120°时,AC=3.【总结升华】由条件“两边一对角”确定的三角形可能不是唯一的,需要考虑第三边上的高的大小判断解是否唯一.5.(2015•茂名)如图,一条输电线路从A地到B地需要经过C地,图中AC=20千米,∠CAB=30°,∠CBA=45°,因线路整改需要,将从A地到B地之间铺设一条笔直的输电线路.(1)求新铺设的输电线路AB的长度;(结果保留根号)(2)问整改后从A地到B地的输电线路比原来缩短了多少千米?(结果保留根号)【思路点拨】(1)过C作CD⊥AB,交AB于点D,在直角三角形ACD中,利用锐角三角函数定义求出CD与AD的长,在直角三角形BCD中,利用锐角三角函数定义求出BD的长,由AD+DB求出AB的长即可;(2)在直角三角形BCD中,利用勾股定理求出BC的长,由AC+CB﹣AB即可求出输电线路比原来缩短的千米数.【答案与解析】解:(1)过C作CD⊥AB,交AB于点D,在Rt△ACD中,CD=AC•sin∠CAD=20×=10(千米),AD=AC•cos∠CAD=20×=10(千米),在Rt△BCD中,BD===10(千米),∴AB=AD+DB=10+10=10(+1)(千米),则新铺设的输电线路AB的长度10(+1)(千米);(2)在Rt△BCD中,根据勾股定理得:BC==10(千米),∴AC+CB﹣AB=20+10﹣(10+10)=10(1+﹣)(千米),则整改后从A地到B地的输电线路比原来缩短了10(1+﹣)千米.【总结升华】解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.已知斜三角形中的SSS,SAS,ASA,AAS以及SSA条件,求三角形中的其他元素是常见问题,注意划归为常见的两个基本图形(高在三角形内或高在三角形外)(如图所示):举一反三:【变式】坐落在山东省汶上县宝相寺内的太子灵踪塔始建于北宋(公元1112年),为砖砌八角形十三层楼阁式建筑.数学活动小组开展课外实践活动,他们去测量太子灵踪塔的高度,携带的测量工具有:测角仪、皮尺、小镜子.(1)小华利用测角仪和皮尺测量塔高.下图为小华测量塔高的示意图.她先在塔前的平地上选择一点A,用测角仪测出看塔顶(M)的仰角α=35°,在点A和塔之间选择一点B,测出看塔顶(M)的仰角β=45°,然后用皮尺量出A ,B 两点间的距离为18.6m ,量出自身的高度为1.6m .请你利用上述数据帮助小华计算出塔的高度(tan35°≈0.7,结果保留整数).(2)如果你是活动小组的一员,正准备测量塔高,而此时塔影NP 的长为am(如图所示),你能否利用这一数据设计一个测量方案?如果能,请回答下列问题:①在你设计的测量方案中,选用的测量工具是:________________________;②要计算出塔的高,你还需要测量哪些数据?________________________________________________________. 【答案】解:(1)设CD 的延长线交MN 于E 点,MN 长为x m ,则ME =(x-1.6)m . ∵β=45°,∴DE =ME =x-1.6.∴CE =x-1.6+18.6=x+17.∵tan tan 35MECE α==°, ∴ 1.60.717x x -=+,解得x =45.∴太子灵踪塔MN 的高度为45m .(2)①测角仪、皮尺;②站在P 点看塔顶的仰角、自身的高度(注:答案不唯一).6.如图,三沙市一艘海监船某天在黄岩岛P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据:≈1.414,结果精确到0.1)【思路点拨】过B作BD⊥AP于D,由已知条件得:AB=20×2=40,∠P=75°﹣30°=45°,在Rt△ABD中求出BD=AB=20,在R t△BDP中求出PB即可.【答案与解析】解:过B作BD⊥AP于D,由已知条件得:AB=20×2=40,∠P=75°﹣30°=45°,在Rt△ABD中,∵AB=40,∠A=30,∴BD=AB=20,在R t△BDP中,∵∠P=45°,∴PB=BD=20≈28.3(海里).答:此时海监船与黄岩岛P的距离BP的长约为28.3海里.【总结升华】此题主要考查解直角三角形的有关知识.通过数学建模把实际问题转化为解直角三角形问题.中考总复习:锐角三角函数综合复习—巩固练习(基础)【巩固练习】一、选择题1. 如图所示,在Rt △ABC 中,∠ACB =90°,BC =1,AB =2,则下列结论正确的是 ( ) A .sin A =32 B .tan A =12C .cosB =32D .tan B =3第1题 第2题2.如图,在Rt△ABC 中,∠ACB=90°,CD⊥AB,垂足为D .若AC=5,BC=2,则sin∠ACD 的值为( )A .53B .255 C .52D .233.在△ABC 中,若三边BC 、CA 、AB 满足 BC ∶CA ∶AB=5∶12∶13,则cosB=( )A .125B .512 C .135 D .13124.如图所示,在△ABC 中,∠C=90°,AD 是BC 边上的中线,BD=4,AD=25,则tan ∠CAD 的值是( )A.2B.2C.3D.5第4题 第6题5.一个物体从A 点出发,沿坡度为1:7的斜坡向上直线运动到B ,AB=30米时,物体升高( )米. A .B .3C .D . 以上的答案都不对6.如图,已知:45°<A <90°,则下列各式成立的是( )A.sinA=cosAB.sinA >cosAC.sinA >tanAD.sinA <cosA二、填空题7.若∠α的余角是30°,则cosα的值是 .8.如图,△ABC的顶点都在方格纸的格点上,则sinA=_______.第8题第12题9.计算2sin30°﹣sin245°+t an30°的结果是 .10.已知α是锐角,且sin(α+15°)=32.计算1184cos( 3.14)tan3απα-⎛⎫---++ ⎪⎝⎭的值为 .11.如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为海里.(结果保留根号)12.如图,正方体的棱长为3,点M,N分别在CD,HE上,CM=12DM,HN=2NE,HC与NM的延长线交于点P,则tan∠NPH的值为.三、解答题13.如图所示,我市某广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且DB=5m,现要在C 点上方2m处加固另一条钢缆ED,那么EB的高为多少米?(结果保留三个有效数字)14. 已知:如图所示,八年级(1)班数学兴趣小组为了测量河两岸建筑物AB和建筑物CD的水平距离AC,他们首先在A点处测得建筑物CD的顶部D点的仰角为25°,然后爬到建筑物AB的顶部B处测得建筑物CD的顶部D点的俯角为15°30′.已知建筑物AB的高度为30米,求两建筑物的水平距离AC(精确到0.1米)(可用计算器查角的三角函数值)15.如图,登山缆车从点A出发,途经点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C的垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)16. 如图所示,某水库大坝的横断面是梯形,坝顶宽AD=2.5m,坝高4 m,背水坡的坡度是1:1,迎水坡的坡度是1:1.5,求坝底宽BC.【答案与解析】一、选择题1.【答案】D ; 【解析】sinA =BC AB =12,tan A =BC AC =33,cosB =BC AB =12.故选D.2.【答案】A ;【解析】在直角△ABC 中,根据勾股定理可得:AB=2AC BC +2=2(5)2+2=3.∵∠B+∠BCD=90°,∠ACD+∠BCD=90°, ∴∠B=∠ACD. ∴ sin∠ACD=sin∠B=ACAB =53, 故选A .3.【答案】C ;【解析】根据三角函数性质 cosB==,故选C .4.【答案】A ;【解析】∵AD 是BC 边上的中线,BD=4,∴CD=BD=4,在Rt △ACD 中,AC= 22AD -CD =-=222(25)4,∴tan ∠CAD===2.故选A .5.【答案】B ;【解析】∵坡度为1:7,∴设坡角是α,则sinα===,∴上升的高度是:30×=3米.故选B .6.【答案】B ;【解析】∵45°<A <90°,∴根据sin45°=cos45°,sinA 随角度的增大而增大,cosA 随角度的增大而减小, 当∠A >45°时,sinA >cosA ,故选B .二、填空题 7.【答案】21; 【解析】∠α=90°﹣30°=60°,cosα=cos60°=21.8.【答案】;【解析】过C 作CD ⊥AB ,垂足为D ,设小方格的长度为1,在Rt △ACD 中,AC=22CD AD +=25,∴sinA=CD 5=AC 5.9.【答案】21+33; 【解析】2sin30°﹣sin 245°+ t an30°=2×21-(22)2+()2+33=1﹣21+33=21+33.10.【答案】3; 【解析】∵sin60°=32,∴α+15°=60°,∴α=45°,∴原式=22﹣4×22﹣1+1+3=3. 11.【答案】40 ;【解析】解:作PC ⊥AB 于C ,在Rt △PAC 中,∵PA=80,∠PAC=30°,∴PC=40海里,在Rt △PBC 中,PC=40,∠PBC=∠BPC=45°, ∴PB=40海里,故答案为:40.12.【答案】13; 【解析】∵正方体的棱长为3,点M ,N 分别在CD ,HE 上,CM=12DM ,HN=2NE , ∴MC=1,HN=2, ∵DC ∥EH , ∴12PC MC PH NH ==, ∵HC=3, ∴PC=3, ∴PH=6, ∴tan ∠NPH=2163NH PH ==,故答案为:13.三、解答题13.【答案与解析】解:在Rt△BCD中,∠BDC=40°,DB=5 m,∵tanBC BDCDB ∠=.∴BC=DB·tan∠BDC=5×tan40°≈4.195(米).∴EB=BC+CE=4.195+2≈6.20(米).14.【答案与解析】解:如图所示,过D作DH⊥AB,垂足为H.设AC=x.在Rt△ACD中,∠ACD=90°,∠DAC=25°,所以CD=AC·tan∠DAC=x tan 25°.在Rt△BDH中,∠BHD=90°,∠BDH=15°30′,所以BH=DH·tan 15°30′=AC·tan 15°30′=x·tan 15°30′.又CD=AH,AH+HB=AB,所以x(tan 25°+tan 15°30′)=30.所以3040.3tan25tan1530x='+≈°°(米).答:两建筑物的水平距离AC约为40.3米.15.【答案与解析】解:在Rt△ADB中,∵∠ADB=90°,∠BAD=30°,AB=200m,∴BD=AB=100m,在Rt△CEB中,∵∠CEB=90°,∠CBE=42°,CB=200m,∴CE=BC•sin42°≈200×0.67=134m,∴BD+CE≈100+134=234m.答:缆车从点A运行到点C的垂直上升的距离约为234m.16.【答案与解析】解:背水坡是指AB,而迎水坡是指CD.过A作AE⊥BC于E,过D作DF⊥BC于F,由题意可知tanB=1,tan C=1 1.5,在Rt△ABE中,AE=4,tanB=AEBE=1,∴BE=AE=4,在Rt△DFC中,DF=AE=4,tanC=11.5 DFCF,∴CF=1.5DF=1.5×4=6.又∵EF=AD=2.5,∴BC=BE+EF+FC=4+2.5+6=12.5.答:坝底宽BC为12.5 m.。
初中数学锐角三角函数综合复习讲义

初中数学锐角三角函数综合复习讲义一、研究概念1、产生的背景:直角三角形的边与角之间的关系2、明确概念:正弦阐述概念:在直角三角形中,锐角A 的对边与斜边的比叫做锐角A 的正弦,记作sinA 3、本质:特殊的实数 4、知识点产生的条件: [直角三角形] 直角三角形中任意两边和任意一锐角5、特征: 正弦 [定义] 在△ABC 中,∠C 为直角,我们把锐角A 的对边与斜边的比叫做∠A 的正弦 →[表示法] sinA=∠A 的对边斜边[特殊字母] sinA=a c sinB=bc(∠A+∠B=90°) 余弦 [定义] 在△ABC 中,∠C 为直角,我们把锐角A 的邻边与斜边的比叫做∠A 的余弦→[表示法] cosA=∠A 的邻边斜边[特殊字母] cosA=bccosB=a c (∠A+∠B=90°)sinA=ac = cosB= cos (90°—∠A) cosA=bc= sinB= sin (90°—∠A)定义] 在△ABC 中,∠C 为直角,我们把锐角A 的对边与邻边的比叫做∠A 的正切→[表示法] tanA=∠A 的对边邻边特殊字母] tanA=abtanB=b a (∠A+∠B=90°)余切 [定义] 在△ABC 中,∠C 为直角,我们把锐角A 的邻边与对边的比叫做∠A 的余切→[表示法] cotA=∠A 的邻边对边[特殊字母] cotA=b a cotB= ab(∠A+∠B=90°) tanA=ab= cotB= cot (90°—∠A) CBA c bacotA=ba= tanB= tan (90°—∠A) [文字] 一个角的正弦等于它余角的余弦 一个角的余弦等于它余角的正弦一个角的正切等于它余角的余切一个角的余切等于它余角的正切[勾股] sin 2 A+ cos 2A= 1 sin 2 B+ cos 2B= 1[运算] tanA ·cotA=1 tanB · cotB=1[正弦、余弦] tanA=sin A cosA cotA=cos AsinA tanB=cos A sinA cotB=sin AcosA[特殊值] sin30°=cos60°=12sin45°=cos45°=2若α、β是锐角,且α>β,则sin60°=cos30°α>sin β cos α<cos βtan30°=cot60°α>tan β cot α<cot β tan45°=cot45°= 1tan60°=cot30°6、系统找下位含有特殊角的斜三角形∍内角是特殊角∍15°,30°,45°,60°,90° 外角是特殊角∍15°,30°,45°,60°,90°二、应用、例题讲解(一)直角三角形中,已知两边求锐角三角函数 1、在中,∠C 为直角,已知a=3,b=4,则cos B= ( ) (A 级)对象:cos B 角度:cos B=a c分析:a=3,b=4 [勾股] c=5 cos B=a c =35(二)直角三角形中,已知一锐角的三角函数求锐角的其它三角函数 2、∠A 为锐角,且sinA=135,则tanA 的值为 ( ) (A 级) A 、512 B 、1213 C 、1312 D 、125对象:tanA 角度 : tanA=sin AcosA分析:sinA=135 [sin 2 A+ cos 2A= 1] cos 2A= 1- sin 2A cosA=1312 [tanA=sin A cosA ] tanA= 1253、设x 为锐角,且满足 sin x=3cos x ,则sin x ·cos x 等于 (B 级)对象:sin x ·cos x 角度:sin 2x+ cos 2x= 1分 析:sin x=3cos x [sin 2x+ cos 2x= 1] (3cos x)2+cos 2x= 1 cos 2x=101 sin x ·cos x= 3cos 2x=103 4、如果x= tanA+1,y=cotA+1(A 为锐角),那么y 等于 (B 级) 对象: y 角度:tanA · cotA=1分析:x= tanA+1,y=cotA+1 [tanA · cotA=1] (x-1)(y-1)=1y=1-x x 5、如果A 为锐角,且 sinA=54,那么 ( ) (B 级) A 、0°〈 A ≤30° B 、30°〈A ≤45° C 、45°〈A 〈60° D 、60°〈A 〈90°对象:A 角度:sinA=54 分析:22〈54〈23 sin 45°〈sinA 〈sin60° ∵A 为锐角 ~ 0°〈 A 〈90° 此时 sinA 是增函数 ∴ 45°〈A 〈60°6、已知A 为锐角,且2cos sin 2cos 2sin 3=-+AA AA ,那么tanA 的值等于 (B 级)对象:tanA 角度:tanA=sin AcosA分析:2cos sin 2cos 2sin 3=-+A A A A 3 sinA+2cosA=4sinA -2cosA sinA=4cosA sin AcosA=4=tanA7、在 中,c 为斜边,a 、b 为直角边,则a 3 cosA+b 3cosB 等于 (B 级)对象:a 3 cosA+b 3cosB 角度 :cosA=∠A 的邻边斜边勾股定理分析 :a 3cosA+b 3cosB = a 3·b c + b 3·a c =cabc 2 = abc8、计算: (A 级)对象: 角度 :特殊角的三角函数值分析:=213222∙+⎪⎪⎭⎫ ⎝⎛=231+ 9、计算:sin 248°+sin 242°-tan44°·tan45°·tan46°= (B 级)对象:sin 248°+sin 242°-tan44°·tan45°·tan46°角度:sinA= cos (90°—∠A) tanA= cot (90°—∠A)分析:sin48°=cos(90°-48°)=cos42° tan 44°=cot(90°-44°)=cot46°原式= cos 242°+ sin 242°-cot46°·tan46°·tan45°=1-1·1=010、如图,CD 是平面镜,光线从A 点出发经CD 上点E 反射到B 点,若入射角为α(入射角等于反射角),AC ⊥CD ,BD ⊥CD ,垂足分别为C 、D ,且AC=3,BD=6,CD=11。
第二十八章 锐角三角函数(单元总结)-2021学年九年级数学下册(人教版)(解析版)
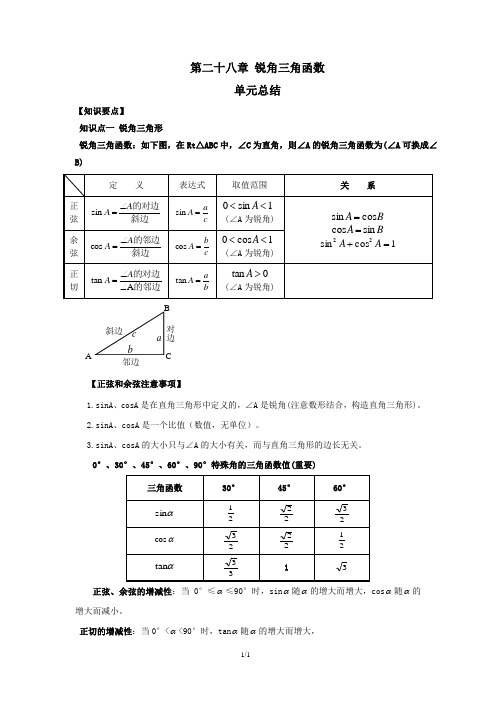
第二十八章 锐角三角函数单元总结【知识要点】 知识点一 锐角三角形锐角三角函数:如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B)【正弦和余弦注意事项】1.sinA 、cosA 是在直角三角形中定义的,∠A 是锐角(注意数形结合,构造直角三角形)。
2.sinA 、cosA 是一个比值(数值,无单位)。
3.sinA 、cosA 的大小只与∠A 的大小有关,而与直角三角形的边长无关。
0°、30°、45°、60°、90°特殊角的三角函数值(重要)正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
正切的增减性:当0°<α<90°时,tan α随α的增大而增大,对边邻边C知识点二 解直角三角形一般地,直角三角形中,除直角外,共有五个元素,即三条边和两个锐角.由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形. 直角三角形五元素之间的关系: 1. 勾股定理()2. ∠A+∠B=90°3. sin A==4. cos A= =5.tan A= =【考查题型】考查题型一 正弦典例1.(2020·陕西西安市·西北工业大学附属中学九年级期中)如图,在54⨯的正方形网格中,每个小正方形的边长都是1,ABC ∆的顶点都在这些小正方形的顶点上,则sin BAC ∠的值为( )A .43B .34C .35D .45【答案】D 【分析】过C 作CD AB ⊥于D ,首先根据勾股定理求出AC ,然后在Rt ACD ∆中即可求出sin BAC ∠的值.【详解】如图,过C 作CD AB ⊥于D ,则=90ADC ∠︒,∴AC =222234=+=+AC AD CD =5. ∴4sin 5CD BAC AC ∠==. 故选D . 【点睛】本题考查了勾股定理的运用以及锐角三角函数,正确作出辅助线是解题的关键.变式1-1.(2018·西城区·北京四中九年级期中)如图,在Rt ABC ∆中,90C =∠,10AB =,8AC =,则sin A 等于( )A .35B .45C .34D .43【答案】A 【解析】分析:先根据勾股定理求得BC=6,再由正弦函数的定义求解可得. 详解:在Rt △ABC 中,∵AB=10、AC=8, ∴2222=108=6AB AC --,∴sinA=63105BC AB ==. 故选:A .点睛:本题主要考查锐角三角函数的定义,解题的关键是掌握勾股定理及正弦函数的定义.变式1-2.(2019·山东淄博市·九年级期中)如图,在Rt△ABC中,∠C=90°,sin A=45,AC=6cm,则BC的长度为()A.6cm B.7cm C.8cm D.9cm 【答案】C【详解】已知sinA=45BCAB=,设BC=4x,AB=5x,又因AC2+BC2=AB2,即62+(4x)2=(5x)2,解得:x=2或x=﹣2(舍),所以BC=4x=8cm,故答案选C.考查题型二余弦典例2.(2020·福建省泉州市培元中学九年级期中)如图,△ABC的顶点都是正方形网格中的格点,则cos∠ABC等于()A 5B25C5D.23【答案】B【详解】由格点可得∠ABC所在的直角三角形的两条直角边为2,4,222425+=∴cos∠25525=.故选B .变式2-1.(2016·辽宁铁岭市·九年级期末)在ABC 中,C 90∠=,AB 6=,1cosA 3=,则AC 等于( ) A .18 B .2C .12D .118【答案】B 【分析】根据三角函数的定义,在直角三角形ABC 中,cosA =ACAB,即可求得AC 的长. 【详解】解:∵在△ABC 中,∠C =90°,∴cosA =ACAB , ∵cosA =13,AB =6,∴AC =123AB =,故答案选:B . 【点睛】本题考查了解直角三角形中三角函数的应用,解题的关键是要熟练掌握直角三角形中边角之间的关系.变式2-2.(2019·山东滨州市·九年级期末)如图,在平面直角坐标系中,点M 的坐标为M (5,2),那么cosα的值是( )A 5B .23C 25D 5【答案】D 【分析】如图,作MH⊥x轴于H.利用勾股定理求出OM,即可解决问题.【详解】解:如图,作MH⊥x轴于H.∵M(5,2),∴OH=5,MH=2,∴OM=22(5)2+=3,∴cosα=5 OHOM=,故选:D.【点睛】本题考查解直角三角形的应用,勾股定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.考查题型三正切典例3.(2020·广东深圳市·深圳中学八年级期中)如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为()A.12B.1 C3D3【答案】B【分析】连接BC,由网格求出AB,BC,AC的长,利用勾股定理的逆定理得到△ABC为等腰直角三角形,即可求出所求. 【详解】 如图,连接BC ,由网格可得AB=BC=5,AC=10,即AB 2+BC 2=AC 2, ∴△ABC 为等腰直角三角形, ∴∠BAC=45°, 则tan ∠BAC=1, 故选B .【点睛】本题考查了锐角三角函数的定义,解直角三角形,以及勾股定理,熟练掌握勾股定理是解本题的关键.变式3-1.(2018·江苏苏州市·九年级期末)如图,在等腰Rt ABC ∆中,90C ∠=︒,6AC =,D 是AC 上一点,若1tan 5DBA ∠=,则AD 的长为( ).A .2B .3C .2D .1【答案】A 【解析】分析:本题考查等腰直角三角形的性质及解直角三角形.解题的关键是作辅助线,构造直角三角形,运用三角函数的定义建立关系式然后求解. 解析:如图,作DE ⊥AB 于E .∵tan ∠DBA==,∴BE=5DE .∵△ABC 为等腰直角三角形,∴∠A=45°,∴AE=DE .∴BE=5AE ,又∵AC=6,∴AB=6,∴AE+BE=AE+5AE=6,∴AE=,∴在等腰直角△ADE中,由勾股定理,得AD=,AE=2.故选A.变式3-2.(2020·河北唐山市·九年级期末)如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若2tan5BAC∠=,则此斜坡的水平距离AC为()A.75m B.50m C.30m D.12m 【答案】A【分析】根据BC的长度和tan BAC∠的值计算出AC的长度即可解答.【详解】解:因为2tan5BCBACAC=∠=,又BC=30,所以,3025AC=,解得:AC=75m,所以,故选A.【点睛】本题考查了正切三角函数,熟练掌握是解题的关键.考查题型四特殊角的三角函数值典例4.(2018·南昌市期末)点M(-sin60°,cos60°)关于x轴对称的点的坐标是( )A.(32,12) B.(-32,-12)C.(312) D.(-123【答案】B 【详解】∵点(-sin60°,cos60°)即为点(312),∴点(-sin60°,cos60°)关于y 3,12).变式4-1.(2019·山东淄博市·九年级期中)下列式子错误的是()A.cos40°=sin50°B.tan15°•tan75°=1C.sin225°+cos225°=1 D.sin60°=2sin30°【答案】D【详解】试题分析:选项A,sin40°=sin(90°﹣50°)=cos50°,式子正确;选项Btan15°•tan75°=tan15°•cot15°=1,式子正确;选项C,sin225°+cos225°=1正确;选项D,sin60°=3,sin30°=12,则sin60°=2sin30°错误.故答案选D.变式4-2.(2018·河北唐山市·九年级期末)如果△ABC中,sin A=cos B=22,则下列最确切的结论是()A.△ABC是直角三角形B.△ABC是等腰三角形C.△ABC是等腰直角三角形D.△ABC是锐角三角形【答案】C【解析】因为sin A=cos B 2,所以∠A=∠B=45°,所以△ABC是等腰直角三角形. 故选C.考查题型五同角的三角函数典例5.(2018·山东潍坊市·九年级期末)在Rt△ABC中,∠C =90°,sinA=45,则cosB的值等于( )A.35B.45C.34D5【答案】B 【解析】在Rt△ABC中,∠C=90°,∠A+∠B=90°,则cos B=sin A=45.故选B.点睛:本题考查了互余两角三角函数的关系.在直角三角形中,互为余角的两角的互余函数变式5-1.(2018·浙江台州市·九年级期末)在Rt △ABC 中,cosA= 12,那么sinA 的值是( )A .2B .2C .3D .12【答案】B 【分析】利用同角三角函数间的基本关系求出sinA 的值即可. 【详解】:∵Rt △ABC 中,cosA=12 ,∴ =2, 故选B . 【点睛】本题考查了同角三角函数的关系,以及特殊角的三角函数值,熟练掌握同角三角函数的关系是解题的关键.变式5-2.(2018·湖南岳阳市·九年级期末)在Rt ABC 中,C 90∠=,如果4cosA 5=,那么tanA 的值是( ) A .35B .53C .34D .43【答案】C 【分析】本题可以利用锐角三角函数的定义求解. 【详解】解:∵在Rt △ABC 中,∠C=90°,∴cosA=b c ,tanA=ab ,a 2+b 2=c 2. ∵cosA=45,设b=4x ,则c=5x ,a=3x .∴tanA=a b =3344x x =. 故选C.【点睛】利用锐角三角函数的定义,通过设参数的方法求三角函数值.考查题型六 解直角三角形典例6.(2020·东北师大附中明珠学校九年级期中)如图,两根竹竿AB 和AD 斜靠在墙CE 上,量得∠ABC=α,∠ADC=β,则竹竿AB 与AD 的长度之比为( )A .tan tan αβB .sin sin βαC .sin sin αβD .cos cos βα【答案】B【分析】在两个直角三角形中,分别求出AB 、AD 即可解决问题;【详解】在Rt △ABC 中,AB=AC sin α, 在Rt △ACD 中,AD=AC sin β, ∴AB :AD=AC sin α:AC sin β=sin sin βα, 故选B .【点睛】 本题考查解直角三角形的应用、锐角三角函数等知识,解题的关键是学会利用参数解决问题. 变式6-1.(2020·山东枣庄市·九年级期末)如图,在ABC ∆中,144CA CB cosC ==,=,则sinB 的值为( )A .10B .15C .6D .10 【答案】D【分析】过点A 作AD BC ⊥,垂足为D ,在Rt ACD ∆中可求出AD ,CD 的长,在Rt ABD ∆中,利用勾股定理可求出AB 的长,再利用正弦的定义可求出sinB 的值.【详解】解:过点A 作AD BC ⊥,垂足为D ,如图所示.在Rt ACD ∆中,1CD CA cosC ⋅==,2215AD AD CD ∴=-=;在Rt ABD ∆中,315BD CB CD AD =﹣=,=,22BD AD 26AB ∴=+=,AD 10sin AB B ∴==. 故选:D .【点睛】考查了解直角三角形以及勾股定理,通过解直角三角形及勾股定理,求出AD ,AB 的长是解题的关键.变式6-2.(2019·辽宁沈阳市·九年级期末)如图,甲乙两楼相距30米,乙楼高度为36米,自甲楼顶A 处看乙楼楼顶B 处仰角为30°,则甲楼高度为( )A.11米B.(36﹣153)米C.153米D.(36﹣103)米【答案】D【分析】分析题意可得:过点A作AE⊥BD,交BD于点E;可构造Rt△ABE,利用已知条件可求BE;而乙楼高AC=ED=BD﹣BE.【详解】解:过点A作AE⊥BD,交BD于点E,在Rt△ABE中,AE=30米,∠BAE=30°,∴BE=30×tan30°=103(米),∴AC=ED=BD﹣BE=(36﹣103)(米).∴甲楼高为(36﹣103)米.故选D.【点睛】此题主要考查三角函数的应用,解题的关键是熟知特殊角的三角函数值.考查题型七利用解直角三角形相关知识解决实际问题典例7.(2019·河南许昌市·九年级期末)如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B 处的求救者后,又发现点B 正上方点C 处还有一名求救者.在消防车上点A 处测得点B 和点C 的仰角分别是45°和65°,点A 距地面2.5米,点B 距地面10.5米.为救出点C 处的求救者,云梯需要继续上升的高度BC 约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,2≈1.4)【答案】云梯需要继续上升的高度BC 约为9米.【分析】过点A 作AM EF ⊥于点M ,AD BC ⊥于点D ,在Rt ABD ∆中,求得AD 的长;在Rt ACD ∆中,求得CD 的长,根据BC=CD-BD 即可求得BC 的长.【详解】过点A 作AM EF ⊥于点M ,AD BC ⊥于点D ,∵CN EF ⊥ ,∴90AMN MND ADN ∠=∠=∠=︒,∴四边形AMND 为矩形.∴ 2.5DN AM ==米.∴10.5 2.58BD BN DN =-=-=(米),由题意可知,45BAD ∠=︒,65CAD ∠=︒,∵AD BC ⊥,∴90ADB ∠=︒,在Rt ABD ∆中,tan BD BAD AD ∠=, ∴88tan tan45BD AD BAD ===∠︒(米). 在Rt ACD ∆中,tan CD CAD AD∠=, ∴tan 8tan658 2.116.8CD AD CAD =⋅∠=︒≈⨯=(米).∴16.888.89BC CD BD =-≈-=≈(米).答:云梯需要继续上升的高度BC 约为9米.【点睛】本题考查解直角三角形﹣仰角俯角问题,添加辅助线,构造直角三角形,建立直角三角形模型是解决问题的关键.变式7-1.(2018·江苏无锡市·九年级期末)如图,为了测量出楼房AC 的高度,从距离楼底C 处603米的点D (点D 与楼底C 在同一水平面上)出发,沿斜面坡度为i=1:3的斜坡DB 前进30米到达点B ,在点B 处测得楼顶A 的仰角为53°,求楼房AC 的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈43,计算结果用根号表示,不取近似值).【答案】153+【分析】如图作BN ⊥CD 于N ,BM ⊥AC 于M ,先在RT △BDN 中求出线段BN ,在RT △ABM 中求出AM ,再证明四边形CMBN 是矩形,得CM=BN 即可解决问题.【详解】如图作BN ⊥CD 于N ,BM ⊥AC 于M .在RT △BDN 中,BD=30,BN :ND=13,∴BN=15,DN=153,∵∠C=∠CMB=∠CNB=90°,∴四边形CMBN是矩形,∴CM=BM=15,BM=CN=603153453-=,在RT△ABM中,tan∠ABM=43 AMBM=,∴AM=603,∴AC=AM+CM=15603+.【点睛】构造适当的直角三角形,并应用锐角的三角函数,正确理解坡比的概念.变式7-2.(2018·山西晋中市期末)“高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离.某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答.如图所示,底座上A,B两点间的距离为90cm.低杠上点C到直线AB的距离CE的长为155cm,高杠上点D到直线AB的距离DF的长为234cm,已知低杠的支架AC与直线AB的夹角∠CAE为82.4°,高杠的支架BD与直线AB的夹角∠DBF为80.3°.求高、低杠间的水平距离CH的长.(结果精确到1cm,参考数据sin82.4°≈0.991,cos82.4°≈0.132,tan82.4°≈7.500,sin80.3°≈0.983,cos80.3°≈0.168,tan80.3°≈5.850)【答案】高、低杠间的水平距离CH 的长为151cm .【解析】分析:利用锐角三角函数,在Rt △ACE 和Rt △DBF 中,分别求出AE 、BF 的长.计算出EF .通过矩形CEFH 得到CH 的长.详解:在Rt △ACE 中,∵tan ∠CAE=CE AE, ∴AE=()15515521tan tan82.47.5CE cm CAE =≈≈∠︒ 在Rt △DBF 中,∵tan ∠DBF=DF BF, ∴BF=()23423440tan tan80.3 5.85DF cm DBF =≈=∠︒. ∵EF=EA+AB+BF≈21+90+40=151(cm )∵CE ⊥EF ,CH ⊥DF ,DF ⊥EF∴四边形CEFH 是矩形,∴CH=EF=151(cm ).答:高、低杠间的水平距离CH 的长为151cm .点睛:本题考查了锐角三角函数解直角三角形.题目难度不大,注意精确度.。
(易错题精选)初中数学锐角三角函数的知识点总复习附答案解析(1)

(易错题精选)初中数学锐角三角函数的知识点总复习附答案解析(1)一、选择题1.如图,△ABC 的外接圆是⊙O ,半径AO=5,sinB=25,则线段AC 的长为( )A .1B .2C .4D .5【答案】C【解析】【分析】 首先连接CO 并延长交⊙O 于点D ,连接AD ,由CD 是⊙O 的直径,可得∠CAD=90°,又由⊙O 的半径是5,sinB=25,即可求得答案. 【详解】解:连接CO 并延长交⊙O 于点D ,连接AD ,由CD 是⊙O 的直径,可得∠CAD=90°,∵∠B 和∠D 所对的弧都为弧AC ,∴∠B=∠D ,即sinB=sinD=25, ∵半径AO=5,∴CD=10,∴2sin 105AC AC D CD ===, ∴AC=4,故选:C.【点睛】本题考查了同弧所对的圆周角相等,以及三角函数的内容,注意到直径所对的圆周角是直角是解题的关键.2.如图,在ABC ∆中,4AC =,60ABC ∠=︒,45C ∠=︒,AD BC ⊥,垂足为D ,ABC ∠的平分线交AD 于点E ,则AE 的长为( )A .22B .223C .23D .322【答案】C【解析】【分析】在Rt △ADC 中,利用等腰直角三角形的性质可求出AD 的长度,在Rt △ADB 中,由AD 的长度及∠ABD 的度数可求出BD 的长度,在Rt △EBD 中,由BD 的长度及∠EBD 的度数可求出DE 的长度,再利用AE=AD−DE 即可求出AE 的长度.【详解】∵AD ⊥BC∴∠ADC=∠ADB=90︒在Rt △ADC 中,AC=4,∠C=45︒∴AD=CD=22在Rt △ADB 中,AD=22ABD=60︒∴326. ∵BE 平分∠ABC ,∴∠EBD=30°.在Rt △EBD 中,BD=263,∠EBD=30° ∴3223 ∴AE=AD −DE=22223=23 故选:C【点睛】本题考查了等腰直角三角形的性质,以及利用特殊角三角函数解直角三角形.3.如图,在ABC ∆中,AB AC =,MN 是边BC 上一条运动的线段(点M 不与点B 重合,点N 不与点C 重合),且12MN BC =,MD BC ⊥交AB 于点D ,NE BC ⊥交AC 于点E ,在MN 从左至右的运动过程中,设BM x =,BMD ∆的面积减去CNE ∆的面积为y ,则下列图象中,能表示y 与x 的函数关系的图象大致是( )A .B .C .D .【答案】A【解析】【分析】设a =12BC ,∠B =∠C =α,求出CN 、DM 、EN 的长度,利用y =S △BMD −S △CNE ,即可求解. 【详解】 解:设a =12BC ,∠B =∠C =α,则MN =a , ∴CN =BC−MN−BM =2a−a−x =a−x ,DM =BM·tanB =x·tanα,EN =CN•tanC =(a−x )·tanα, ∴y =S △BMD −S △CNE =12(BM·DM−CN·EN )=()()221tan tan 222x a x a tan x a ααα⋅⎡⎤⋅-⋅=⎣⎦--, ∵2a tan α⋅为常数, ∴上述函数图象为一次函数图象的一部分,故选:A .【点睛】本题考查了动点问题的函数图象、等腰三角形的性质、解直角三角形、图形面积等知识点.解题关键是深刻理解动点的函数图象,了解图象中关键点所代表的实际意义,理解动点的完整运动过程.4.在课外实践中,小明为了测量江中信号塔A 离河边的距离AB ,采取了如下措施:如图在江边D 处,测得信号塔A 的俯角为40︒,若55DE =米,DE CE ⊥,36CE =米,CE 平行于AB ,BC 的坡度为1:0.75i =,坡长140BC =米,则AB 的长为( )(精确到0.1米,参考数据:sin 400.64︒≈,cos400.77︒≈,tan 400.84︒≈)A .78.6米B .78.7米C .78.8米D .78.9米【答案】C【解析】【分析】 如下图,先在Rt △CBF 中求得BF 、CF 的长,再利用Rt △ADG 求AG 的长,进而得到AB 的长度【详解】如下图,过点C 作AB 的垂线,交AB 延长线于点F ,延长DE 交AB 延长线于点G∵BC 的坡度为1:0.75∴设CF 为xm ,则BF 为0.75xm∵BC=140m∴在Rt △BCF 中,()2220.75140x x +=,解得:x=112∴CF=112m ,BF=84m∵DE ⊥CE ,CE ∥AB ,∴DG ⊥AB ,∴△ADG 是直角三角形∵DE=55m ,CE=FG=36m∴DG=167m ,BG=120m设AB=ym∵∠DAB=40°∴tan40°=1670.84120DG AG y ==+ 解得:y=78.8故选:C【点睛】本题是三角函数的考查,注意题干中的坡度指的是斜边与水平面夹角的正弦值.5.如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为()A.2+3B.23C.3+3D.33【答案】A【解析】【分析】【详解】设AC=x,在Rt△ABC中,∠ABC=30°,即可得AB=2x,BC=3x,所以BD=BA=2x,即可得CD=3x+2x=(3+2)x,在Rt△ACD中,tan∠DAC=(32)32 CD xAC+==+,故选A.6.直角三角形纸片的两直角边长分别为6,8,现将ABCV如图那样折叠,使点A与点B 重合,折痕为DE,则tan CBE∠的值是()A.247B7C.724D.13【答案】C【解析】试题分析:根据题意,BE=AE.设BE=x,则CE=8-x.在Rt△BCE中,x2=(8-x)2+62,解得x=254,故CE=8-254=74,∴tan∠CBE=724 CECB=.故选C.考点:锐角三角函数.7.如图,要测量小河两岸相对的两点P,A的距离,可以在小河边取PA的垂线PB上的一点C,测得PC=100米,∠PCA=35°,则小河宽PA等于()A.100sin35°米B.100sin55°米C.100tan35°米D.100tan55°米【答案】C【解析】【分析】根据正切函数可求小河宽PA的长度.【详解】∵PA⊥PB,PC=100米,∠PCA=35°,∴小河宽PA=PCtan∠PCA=100tan35°米.故选:C.【点睛】此题考查解直角三角形的应用,解题关键在于掌握解直角三角形的一般过程是:①将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).②根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.8.如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B与灯塔P之间的距离为( )A.60海里B.45海里C.3D.3【答案】D【解析】【分析】根据题意得出:∠B=30°,AP=30海里,∠APB=90°,再利用勾股定理得出BP的长,求出答案.【详解】解:由题意可得:∠B=30°,AP=30海里,∠APB=90°,故AB=2AP=60(海里),则此时轮船所在位置B 处与灯塔P 之间的距离为:BP=22303AB AP -=(海里)故选:D .【点睛】此题主要考查了勾股定理的应用以及方向角,正确应用勾股定理是解题关键.9.在△ABC 中,a 、b 、c 分别为角A 、B 、C 的对边,若∠B=60°,则c a a b c b+++的值为( )A .12B .22C .1D 2【答案】C【解析】【分析】先过点A 作AD ⊥BC 于D ,构造直角三角形,结合∠B=60°,利用3sin602︒=cos60°=12,可求13,,2DB c AD ==把这两个表达式代入到另一个Rt △ADC 的勾股定理表达式中,化简可得即a 2+c 2=b 2+ac ,再把此式代入通分后所求的分式中,可求其值等于1.【详解】解:过A 点作AD ⊥BC 于D ,在Rt △BDA 中,由于∠B=60°,∴13,,22DB c AD c == 在Rt △ADC 中,DC 2=AC 2﹣AD 2, ∴2221324a c b c ⎛⎫-=- ⎪⎝⎭, 即a 2+c 2=b 2+ac ,∴()()2222222 1.c a c cb a ab a c ab bc b ac ab bc a b c b a b c b ac ab bc b ac ab bc b++++++++++====++++++++++ 故选C .【点睛】本题考查了特殊角的三角函数值、勾股定理的内容.在直角三角形中,两直角边的平方和等于斜边的平方.注意作辅助线构造直角三角形是解题的好方法.10.如图,菱形ABCD 中,AC 交BD 于点O ,DE ⊥BC 于点E ,连接OE ,∠DOE =120°,DE =1,则BD =( )A 3B 23C .3D .3【答案】B【解析】【分析】证明△OBE 是等边三角形,然后解直角三角形即可.【详解】∵四边形ABCD 是菱形,∴OD =OB ,CD =BC .∵DE ⊥BC ,∴∠DEB =90°,∴OE =OD =OB .∵∠DOE =120°,∴∠BOE =60°,∴△OBE 是等边三角形,∴∠DBC =60°.∵∠DEB =90°,∴BD =23sin60DE =︒. 故选B .【点睛】本题考查了解直角三角形,菱形的性质,等边三角形的判定和性质,直角三角形斜边的中线的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.11.某同学利用数学知识测量建筑物DEFG 的高度.他从点A 出发沿着坡度为1:2.4i =的斜坡AB 步行26米到达点B 处,用测角仪测得建筑物顶端D 的仰角为37°,建筑物底端E 的俯角为30°,若AF 为水平的地面,侧角仪竖直放置,其高度BC=1.6米,则此建筑物的高度DE 约为(精确到0.13 1.73370.60sin ≈︒≈,,370.80370.75cos tan ︒≈︒≈,)( )A.23.0米B.23.6米C.26.7米D.28.9米【答案】C【解析】【分析】如图,设CB⊥AF于N,过点C作CM⊥DE于M,根据坡度及AB的长可求出BN的长,进而可求出CN的长,即可得出ME的长,利用∠MBE的正切可求出CM的长,利用∠DCM 的正切可求出DM的长,根据DE=DM+ME即可得答案.【详解】如图,设CB⊥AF于N,过点C作CM⊥DE于M,∵沿着坡度为1:2.4i=的斜坡AB步行26米到达点B处,∴BN1 AN 2.4=,∴AN=2.4BN,∴BN2+(2.4BN)2=262,解得:BN=10(负值舍去),∴CN=BN+BC=11.6,∴ME=11.6,∵∠MCE=30°,∴CM=MEtan30︒=11.63,∵∠DCM=37°,∴DM=CM·tan37°=8.73,∴DE=ME+DM=11.6+8.73≈26.7(米),故选:C.【点睛】本题考查解直角三角形的应用,正确构造直角三角形并熟练掌握三角函数的定义及特殊角的三角函数值是解题关键.12.如图,在Rt ABC V 中,90ACB ∠=︒,3tan 4B =,CD 为AB 边上的中线,CE 平分ACB ∠,则AE AD的值( )A .35B .34C .45D .67【答案】D【解析】【分析】根据角平分线定理可得AE :BE =AC :BC =3:4,进而求得AE =37AB ,再由点D 为AB 中点得AD =12AB ,进而可求得AE AD的值. 【详解】 解:∵CE 平分ACB ∠,∴点E 到ACB ∠的两边距离相等,设点E 到ACB ∠的两边距离位h ,则S △ACE =12AC·h ,S △BCE =12BC·h , ∴S △ACE :S △BCE =12AC·h :12BC·h =AC :BC , 又∵S △ACE :S △BCE =AE :BE ,∴AE :BE =AC :BC , ∵在Rt ABC V 中,90ACB ∠=︒,3tan 4B =, ∴AC :BC =3:4,∴AE :BE =3:4∴AE =37AB , ∵CD 为AB 边上的中线,∴AD=12 AB,∴367172ABAEAD AB==,故选:D.【点睛】本题主要考查了角平分线定理的应用及三角函数的应用,通过面积比证得AE:BE=AC:BC 是解决本题的关键.13.如图,一张直角三角形纸片BEC的斜边放在矩形ABCD的BC边上,恰好完全重合,边BE,CE分别交AD于点F,G,已知8BC=,::4:3:1AF FG GD=,则CD的长为()A.1 B2C3D.2【答案】C【解析】【分析】由ABCD是矩形,得到AD=BC=8,且矩形的四个角是直角,根据::4:3:1AF FG GD=,可以求出DG的长度,再根据余角的性质算出∠DCE的大小,根据三角函数即可算出DC的长度.【详解】解:∵四边形ABCD是矩形,∴AD=BC=8,∠DCB=90︒,又∵::4:3:1AF FG GD=∴1114318GD AD AD===++,∵∠ECB=60°,∴∠DCE=906030︒-︒=︒,又∵31tan303GDCD CD︒===,∴3CD=故答案为C.【点睛】本题主要考查矩形、特殊直角三角形、余角的性质,运用线段的比例长算出其中各段的长度是解本题的关键,特殊角的三角函数也是重要知识点,应掌握.14.如图,有一个边长为2cm 的正六边形纸片,若在该纸片上沿虚线剪一个最大圆形纸片,则这个圆形纸片的半径是( )A .3cmB .2cmC .23cmD .4cm【答案】A【解析】【分析】 根据题意画出图形,再根据正多边形圆心角的求法求出∠AOB 的度数,最后根据等腰三角形及直角三角形的性质解答即可.【详解】解:如图所示,正六边形的边长为2cm ,OG ⊥BC ,∵六边形ABCDEF 是正六边形,∴∠BOC=360°÷6=60°,∵OB=OC ,OG ⊥BC ,∴∠BOG=∠COG=12∠BOC =30°, ∵OG ⊥BC ,OB=OC ,BC=2cm , ∴BG=12BC=12×2=1cm , ∴OB=sin 30BG o=2cm , ∴OG=2222213OB BG -=-=,∴圆形纸片的半径为3cm ,故选:A .【点睛】本题考查的是正多边形和圆,根据题意画出图形,利用直角三角形的性质及正六边形的性质解答是解答此题的关键.15.一艘轮船从港口O出发,以15海里/时的速度沿北偏东60°的方向航行4小时后到达A 处,此时观测到其正西方向50海里处有一座小岛B.若以港口O为坐标原点,正东方向为x轴的正方向,正北方向为y轴的正方向,1海里为1个单位长度建立平面直角坐标系(如图),则小岛B所在位置的坐标是()A.(303-50,30) B.(30, 303-50) C.(303,30) D.(30,303)【答案】A【解析】【分析】【详解】解:OA=15×4=60海里,∵∠AOC=60°,∴∠CAO=30°,∵sin30°=OCAO=12,∴CO=30海里,∴AC=303海里,∴BC=(303-50)海里,∴B(303-50,30).故选A【点睛】本题考查掌握锐角三角函数的应用.16.如图,点E是矩形ABCD的边AD的中点,且BE⊥AC于点F,则下列结论中错误的是()A.AF=12 CFB.∠DCF=∠DFCC.图中与△AEF相似的三角形共有5个D.tan∠CAD=3 2【答案】D 【解析】【分析】由AE=12AD=12BC,又AD∥BC,所以12AE AFBC FC==,故A正确,不符合题意;过D作DM∥BE交AC于N,得到四边形BMDE是平行四边形,求出BM=DE=12BC,得到CN=NF,根据线段的垂直平分线的性质可得结论,故B正确,不符合题意;根据相似三角形的判定即可求解,故C正确,不符合题意;由△BAE∽△ADC,得到CD与AD的大小关系,根据正切函数可求tan∠CAD的值,故D错误,符合题意.【详解】解:A、∵AD∥BC,∴△AEF∽△CBF,∴AEBC=AFFC,∵AE=12AD=12BC,∴AFFC=12,故A正确,不符合题意;B、过D作DM∥BE交AC于N,∵DE∥BM,BE∥DM,∴四边形BMDE是平行四边形,∴BM=DE=12 BC,∴BM=CM,∴CN=NF,∵BE⊥AC于点F,DM∥BE,∴DN⊥CF,∴DF=DC,∴∠DCF=∠DFC,故B正确,不符合题意;C、图中与△AEF相似的三角形有△ACD,△BAF,△CBF,△CAB,△ABE共有5个,故C正确,不符合题意.D、设AD=a,AB=b由△BAE∽△ADC,有ba=2a.∵tan∠CAD=CDAD=ba=22,故D错误,符合题意.故选:D.【点睛】本题考查了相似三角形的判定和性质,矩形的性质,图形面积的计算,正确的作出辅助线是解题的关键.17.已知在 Rt ABC 中,∠C = 90°,AC= 8, BC = 15 ,那么下列等式正确的是()A.8sin17A=B.cosA=815C.tan A =817D.cot A=815【答案】D【解析】【分析】根据锐角三角函数的定义进行作答.【详解】由勾股定理知,AB=17;A.15sin17BCAAB== ,所以A错误;B.8cos17ACAAB==,所以,B错误;C.15tan8BCAAC==,所以,C错误;D.cotACABC==815,所以选D.【点睛】本题考查了锐角三角函数的定义,熟练掌握锐角三角函数的定义是本题解题关键. 18.如图,正方形ABCD的边长为4,点E、F分别在AB、BC上,且AE=BF=1,CE、DF交于点O,下列结论:①∠DOC=90°,②OC=OE,③CE=DF,④tan∠OCD=43,⑤S△DOC=S四边形EOFB中,正确的有()A.1个B.2个C.3个D.4个【答案】D【解析】分析:由正方形ABCD的边长为4,AE=BF=1,利用SAS易证得△EBC≌△FCD,然后全等三角形的对应角相等,易证得①∠DOC=90°正确,③CE=D F正确;②由线段垂直平分线的性质与正方形的性质,可得②错误;易证得∠OCD=∠DFC,即可求得④正确;由①易证得⑤正确.详解:∵正方形ABCD的边长为4,∴BC=CD=4,∠B=∠DCF=90°.∵AE=BF=1,∴BE=CF=4﹣1=3.在△EBC和△FCD中,BC CDB DCFBE CF=⎧⎪∠=∠⎨⎪=⎩,∴△EBC≌△FCD(SAS),∴∠CFD=∠BEC,CE=DF,故③正确,∴∠BCE+∠BEC=∠BCE+∠CFD=90°,∴∠DOC=90°;故①正确;连接DE,如图所示,若OC=OE.∵DF⊥EC,∴CD=DE.∵CD=AD<DE(矛盾),故②错误;∵∠OCD+∠CDF=90°,∠CDF+∠DFC=90°,∴∠OCD=∠DFC,∴tan∠OCD=tan∠DFC=DCFC=43,故④正确;∵△EBC≌△FCD,∴S△EBC=S△FCD,∴S△EBC﹣S△FOC=S△FCD﹣S△FOC,即S△ODC=S四边形BEOF.故⑤正确;故正确的有:①③④⑤.故选D.点睛:本题考查了正方形的性质、全等三角形的判定与性质、直角三角形的性质以及三角函数等知识.此题综合性较强,难度适中,注意掌握数形结合思想与转化思想的应用.19.如图,河坝横断面的迎水坡AB 的坡比为3:4,BC =6m ,则坡面AB 的长为( )A .6mB .8mC .10mD .12m 【答案】C【解析】【分析】 迎水坡AB 的坡比为3:4得出3tan 4BAC ∠=,再根据BC =6m 得出AC 的值,再根据勾股定理求解即可.【详解】由题意得3tan 4BAC ∠=∴468tan 3BC AC m BAC ==⨯=∠ ∴22228610AB AC BC m =+=+=故选:C.【点睛】 本题考查解直角三角形的应用,把坡比转化为三角函数值是关键.20.如图,ABC ∆是一张顶角是120︒的三角形纸片,,6AB AC BC ==现将ABC ∆折叠,使点B 与点A 重合,折痕DE ,则DE 的长为( )A .1B .2C 2D 3【答案】A【解析】【分析】 作AH ⊥BC 于H ,根据等腰三角形的性质求出BH ,根据翻折变换的性质求出BD ,根据正切的定义解答即可.【详解】解:作AH ⊥BC 于H ,∵AB=AC ,AH ⊥BC ,BH=12BC=3, ∵∠BAC=120°,AB=AC ,∴∠B=30°,∴AB=30BH cos 3 由翻折变换的性质可知,3∴DE=BD •tan30°=1,故选:A .【点睛】此题考查翻折变换的性质、勾股定理的应用,解题关键在于掌握翻折变换是一种对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.。
江西九年级数学下册第二十八章《锐角三角函数》综合知识点总结(答案解析)
学校:__________ 姓名:__________ 班级:__________ 考号:__________一、选择题1.如图,PA ,PB 分别与⊙O 相切于A ,B 两点,延长PO 交⊙O 于点C ,若60APB ∠=︒,6PC =,则AC 的长为( )A .4B .22C .23D .332.已知如图,在直角梯形ABCD 中,AD ∥BC ,∠B=90°,AD=23,AB=4,连接AC ,若∠CAD=30°,则CD 为( )A .223+B .27C .1033D .123+3.在Rt ABC 中,90,C a b c ∠=︒、、分别是A B C ∠∠∠、、的对边,如果3,4a b ==,那么下列等式中正确的是( )A .4sin 3A =B .4cos 3A =C .4tan 3A =D .4cot 3A = 4.小明在学完《解直角三角形》一章后,利用测角仪和校园旗杆的拉绳测量校园旗杆的高度,如图,旗杆PA 的高度与拉绳PB 的长度相等,小明先将PB 拉到'PB 的位置,测得(''PB C a B C ∠=为水平线),测角仪/B D 的高度为1米,则旗杆PA 的高度为( )A .11sin a +米B .11cos a -米C .11sin a -米D .11cos a +米 5.如图,△ABC 的三个顶点均在格点上,则cos A 的值为( )A .12B .55C .2D .2556.在Rt △ABC 中,∠ACB =90°,AB =5,tan ∠B =2,则AC 的长为 ( ) A .1 B .2 C .5 D .257.如图,在矩形ABCD 中,AB =6,BC =62,点E 是边BC 上一动点,B 关于AE 的对称点为B ′,过B ′作B ′F ⊥DC 于F ,连接DB ′,若△DB ′F 为等腰直角三角形,则BE 的长是( )A .6B .3C .32D .62﹣6 8.某兴趣小组想测量一座大楼 AB 的高度.如图,大楼前有一段斜坡BC ,已知 BC 的长为 12 米它的坡度1:3i = .在离 C 点 40 米的 D 处,用测量仪测得大楼顶端 A 的仰角为 37度,测角仪DE 的高度为 1.5米,求大楼AB 的高度约为( )米(sin 370.60,cos370.80,tan 370.75,3 1.73︒=︒=︒==)A .39.3B .37.8C .33.3D .25.79.如图,在Rt ABC ∆中,90C ∠=︒,30BAC ∠=︒,延长CA 到点D ,使AD AB =,连接BD .根据此图形可求得tan15︒的值是( )A .23-B .23+C .36D .3210.如图,一块矩形木板ABCD 斜靠在墙边,( OC ⊥OB ,点A 、B 、C 、D 、O 在同一平面内),已知AB a ,AD b ,∠BCO =α.则点A 到OC 的距离等于( )A .asinα+bsinαB .acosα+bcosαC .asinα+bcosαD .acosα+bsinα 11.如图,ABC 中,6AB AC AE AC DE ==⊥,,垂直平分AB 于点D ,则EC 的长为( )A .23B .43C .22D .4212.如图,若将四根木条钉成的矩形木框变形为平行四边形ABCD 的形状,并使得其面积变为原矩形面积的一半,则平行四边形ABCD 的内角BCD ∠的大小为( )A .100°B .120°C .135°D .150°13.如图,点A ,B ,C 在正方形网格的格点上,则sin ∠BAC=( )A .26B 26C 26D 13 14.如图,分别以直角三角形三边为边向外作等边三角形,面积分别为1S 、2S 、3S ;如图2,分别以直角三角形的三边为直径向外半圆,面积分别为4S 、5S 、6S .其中116S =,245S =,511S =,614S =,则34S S +=( )A .86B .64C .54D .48二、填空题15.计算:02cos 45|13|(3)π︒+---=_____.16.如图,在ABC 中,6AB BC ==,点O 为BC 中点,点P 是射线AO 上的一个动点,且 60AOC ∠=︒.要使得BCP 为直角三角形,CP 的长为 ________ .17.如图是一个地铁站入口的双翼闸机.它的双翼展开时,双翼边缘的端点A 与B 之间的距离为10cm ,双翼的边缘AC =BD =54cm ,且与闸机侧立面夹角∠PCA =∠BDQ =30°.当双翼收起时,可以通过闸机的物体的最大宽度为________cm .18.如图,ABC 内接于O ,AB AC =,直径AD 交BC 于点E ,若1DE =,2cos 3BAC ∠=,则弦BC 的长为______.19.如图,已知在Rt ABC 中,C 90,AC BC 2∠=︒==,点D 在边BC 上,将ABC 沿直线AD 翻折,使点C 落在点C '处,联结AC ',直线AC '与边CB 的廷长线相交于点F ,如果DAB BAF ∠∠=,那么BF =_________.20.将一副三角板如图摆放,使得一块三角板的直角边AC 和另一块三角板的斜边ME 重叠,点A 与点M 重合,已知AB=AC=8,则重叠的面积是__________.21.如图 1 的矩形ABCD 中,有一点E 在AD 上,现以BE 为折线将点A 往右折,如图2所示,再过点A 作 AF CD ⊥于点F ,如图3所示,若123,26,60AB BC BEA ︒∠===, 则图3中AF 的长度为____.22.如图,在四边形ABCD 中,AD =CD ,∠D=60°,∠A =105°,∠B =120°,则AD BC的值为__________.23.如图,在2×2的网格中,以顶点O 为圆心,以2个单位长度为半径作圆弧,交图中格线于点A ,则tan ∠ABO 的值为_____.24.在Rt △ABC 中,∠C =90°,AB =2AC ,则∠A =__°,∠B =___°.25.在△ABC 中,若()21cos 1tan 02A B -+-=,则∠C=____________. 26.如图,边长为6的正方形ABCD 绕点C 按顺时针方向旋转30后得到正方形EFCG ,EF 交AD 于点H ,则DH =____________.三、解答题27.(1)计算:|﹣1|﹣(3﹣π)016(﹣12)-1+2cos60°; (2)解方程:2x (x ﹣1)=x ﹣1.28.(1)计算:102272cos305)π-︒++;(2)解方程:3x 2﹣5x +2=0.29.已知:如图所示,ABC 在直角坐标平面内,三个顶点的坐标分别()0,3A ,()3,4B ,()2,2C ,(正方形网格中每个小正方形的边长是一个单位长度).()1画出ABC 关于x 轴对称的111A B C △,点1C 的坐标是____;tan _____.BAC ∠=()2以点B 为位似中心,在网格内画出222A B C △,使222A B C △与ABC 位似,且位似比为2:1,点2C的坐标是_____;()3A B C的周长为_______ .22230.如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD 的延长线于点E,点F为CE的中点,连接DB,DC,DF.(1)求∠CDE的度数;(2)求证:DF是⊙O的切线;(3)若AC=25DE,求tan∠ABD的值.参考答案【参考答案】一、选择题1.C2.B3.D4.C5.D6.B7.D8.C9.A10.D11.B12.D13.B14.C二、填空题15.﹣1【分析】原式利用特殊角的三角函数值绝对值的代数意义以及零指数幂法则计算即可得到结果【详解】解:原式==故答案为:﹣1【点睛】此题考查了实数的运算特殊角的三角函数值以及零指数幂熟练掌握运算法则是解16.或3或【分析】利用分类讨论①当∠BPC=90°时情况一:如图1利用直角三角形斜边的中线等于斜边的一半得出PO=BO易得△BOP为等边三角形利用锐角三角函数可得CP的长;情况二:如图2利用直角三角形斜17.64【分析】连接ABCD过点A作AE⊥CD于E过点B作BF⊥CD于F求出CEEFDF即可解決问题;【详解】解:如图连接ABCD过点A作AE⊥CD于E过点B作BF⊥CD于F∵AB//EFAE//BF∴18.【分析】连接OBOC由题意易得AE⊥BC则有BE=EC∠BOD=∠BAC设OB=3rOE=2r然后根据勾股定理可求解【详解】解:连接OBOC如图所示:∵内接于AD过圆心O∴AE⊥BC∴BE=EC∴∠19.【分析】首先根据题意画出图形再根据折叠的性质和可求出各角的度数再利用解直角三角形的知识分别求出CDDFBD的长度最后根据线段之间的和差关系即可求出结果【详解】解:如图所示:∵△ADC是由△ACD翻折20.【分析】过Q作QH⊥AC于H在△QHC中由于∠QCH=45°则CH=QH设CH=则QH=x在Rt△QHA中由于∠QAH=60°求得AH=然后利用CH+AH=AC求得的值再根据三角形面积公式计算得到结21.8【分析】作AH⊥BC于H则四边形AFCH是矩形AF=CHAH=CF在Rt△ABH中解直角三角形即可解决问题【详解】解:作AH⊥BC于H则四边形AFCH是矩形AF=CH在Rt△ABE 中∠BAE=9022.【分析】沿AB作垂线与C的延长线相交于M点可得到等边直角三角形和锐角为30°的直角三角形根据三角函数求解即可【详解】解:如图连接AC并过B点作BM⊥CM设BM=k∵AD=CD∠D=60°∴△ACD是23.2+【分析】连接OA过点A作AC⊥OB于点C由题意知AC=1OA=OB=2从而得出OC==BC=OB﹣OC=2﹣在Rt△ABC中根据tan∠ABO=可得答案【详解】如图连接OA过点A 作AC⊥OB于点24.6030【分析】在Rt△ABC中根据AB=2AC可得出∠B=30°∠A=60°【详解】解:如图在Rt△ABC中∵∠C=90°AB=2AC∴sin∠B==∴∠B=30°∴∠A=90°﹣∠B=90°﹣325.75°【分析】根据非负数性质得根据三角函数定义求出∠A=60°∠B=45°根据三角形内角和定理可得【详解】因为所以所以所以∠A=60°∠B=45°所以∠C=180°-∠A-∠B=75°故答案为:7526.【分析】过点F作FI⊥BC于点I延长线IF交AD于J根据含30°直角三角形的性质可求出FIFJ和JH的长度从而求出HD的长度【详解】解:过点F作FI⊥BC于点BC延长线AD 交AD于J由题意可知:CF三、解答题27.28.29.30.【参考解析】一、选择题1.C解析:C【分析】如图,设CP 交⊙O 于点D ,连接OA 、AD .由切线的性质易证△AOP 是含30度角的直角三角形,所以该三角形的性质求得半径=2;然后在等边△AOD 中得到AD=OA=2;最后通过解直角△ACD 来求AC 的长度.【详解】解:如图,设CP 交⊙O 于点D ,连接OA 、AD .设⊙O 的半径为r .∵PA 、PB 是⊙O 的切线,∠APB=60°,∴OA ⊥AP ,∠APO=12∠APB=30°. ∴OP=2OA ,∠AOP=60°,∴PC=2OA+OC=3r=6,则r=2,易证△AOD 是等边三角形,则AD=OA=2,又∵CD 是直径,∴∠CAD=90°,∴∠ACD=30°,∴AC=tan 30?AD 3故选:C .【点睛】 本题考查了切线的性质,圆周角定理.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.简记作:见切点,连半径,见垂直.2.B解析:B【分析】过C 点作CH ⊥AD 延长线于H 点,由CH=AB=4求出AH 的长,再减去AD 即得到DH 的长,再在Rt △DCH 中使用勾股定理即可求出CD .【详解】解:如图所示,过C 点作CH ⊥AD 延长线于H 点,∵AD ∥BC ,∠B=90°,∴∠BAH=90°,且∠H=90°,∴四边形ABCH 为矩形,∴AB=CH=4,在Rt △ACH 中,3343AHCH AB , ∴DH=AH-AD=23∴在Rt △CDH 中,22121627CDDH CH ,故选:B .【点睛】本题考查了解直角三角形,熟练掌握30°,60°,90°三角形中三边之比为3::是解决本题的关键. 3.D解析:D【分析】分别算出∠A 的各个三角函数值即可得到正确选项.【详解】 解:由题意可得:2222345c a b =++=,∴3434sin ,cos ,tan ,,5543a b a b A A A cotA c c b a ======== ∴正确答案应该是D ,故选D .【点睛】 本题考查锐角三角函数的定义,正确理解锐角三角函数的定义是解题关键.4.C解析:C 【分析】设PA=PB=PB′=x ,在RT △PCB′中,根据sin αPC PB =',列出方程即可解决问题. 【详解】解:设PA=PB=PB′=x ,在RT △PCB′中,sin αPC PB ='∴1sin αx x-=∴x 1xsin α-=, ∴(1-sin α)x=1,∴x=11sin α-. 故选C .【点睛】 本题考查解直角三角形、三角函数等知识,解题的关键是设未知数列方程,属于中考常考题型.5.D 解析:D【分析】 过B 点作BD ⊥AC ,得AB 的长,AD 的长,利用锐角三角函数得结果. 【详解】解:过B 点作BD ⊥AC ,如图,由勾股定理得,221310+=222222+=cosA=2225510AD AB == 故选D .【点睛】本题考查了锐角三角函数和勾股定理,作出适当的辅助线构建直角三角形是解答此题的关键.6.B解析:B【分析】根据正切的定义得到BC=12AC ,根据勾股定理列式计算即可.【详解】在Rt △ABC 中,∠ACB=90°,tan ∠B=2, ∴AC BC=2, ∴BC=12AC ,由勾股定理得,AB 2=AC 2+BC 22=AC 2+(12AC )2, 解得,AC=2,故选B .【点睛】本题考查的是锐角三角函数的定义、勾股定理,掌握锐角A 的对边a 与邻边b 的比叫做∠A 的正切是解题的关键.7.D解析:D【分析】根据 B 关于 AE 的对称点为 B′,可得2AB AD '=,1AB D ∴等腰直角三角形,可得D B E '、、三点共线,可求出BE 的长.【详解】解:6,2AB AB AB AD AD ==='∴=', 又△DB′F 为等腰直角三角形,045FDB ∴∠=,又在矩形 ABCD ,090ADF ∠=,045ADB ∴='∠,又2AB AD '= AB D ∴'等腰直角三角形, 090AB D ∴='∠,090AB E ∠=',D BE ∴'、、三点共线,在等腰直角△RCE ,CE=CD=6,∴BE=BC-CE=6,故选D..【点睛】本题考查三角形的性质及解直角三角形,找出D B E '、、三点共线是解题关键. 8.C解析:C【分析】延长AB 交直线DC 于点F ,过点E 作EH ⊥AF ,垂足为点H ,在Rt △BCF 中利用坡度的定义求得CF 的长,则DF 即可求得,然后在直角△AEH 中利用三角函数求得AF 的长,进而求得AB 的长.【详解】解:延长AB 交直线DC 于点F ,过点E 作EH ⊥AF ,垂足为点H .∵在Rt △BCF 中,BF CF =1:3i =, ∴设BF=k ,则CF=3k ,BC=2k .又∵BC=12,∴k=6,∴BF=6,CF=63,∵DF=DC+CF ,∴DF=40+63,∵在Rt △AEH 中,tan ∠AEH=AH EH, ∴AH=tan37°×(40+63)≈37.785(米),∵BH=BF-FH ,∴BH=6-1.5=4.5.∵AB=AH-HB ,∴AB=37.785-4.5≈33.3.故选C .【点睛】本题考查了解直角三角形的应用,关键是根据仰角构造直角三角形,利用三角函数求解,注意利用两个直角三角形的公共边求解是解答此类题型的常用方法.9.A解析:A【分析】设BC=x ,在Rt ABC ∆中,90C ∠=︒,30BAC ∠=︒,可得,AB=2x ,3x ,由AD AB ==2x ,可得3x ,由AD AB =,可知,∠D=∠ABD=12∠BAC=15°,在Rt BDC ∆ 中,根据锐角正切三角函数的定义,即可求解.【详解】∵AD AB =,∴∠D=∠ABD ,∵∠BAC=∠D+∠ABD ,∴∠D=12∠BAC=15°, 设BC=x , ∵在Rt ABC ∆中,90C ∠=︒,30BAC ∠=︒,∴AB=2x ,AC=22(2)3x x x -=,∴CD=2x+3x =(23)x +,在Rt BDC ∆中,tan 23(23)BC x D DC x∠===-+ , ∴°tan15=23-,故选A.【点睛】本题主要考查锐角正切三角函数的定义,根据图形,设BC=x ,用含x 的代数式表示相关线段的长,是解题的关键.10.D解析:D【分析】根据题意,做出合适的辅助线,然后利用锐角三角函数即可表示出点A 到OC 的距离即可求解.【详解】解:作AE ⊥OC 于点E ,作AF ⊥OB 于点F ,∵四边形ABCD 是矩形,∴∠ABC=90°,∵∠ABC=∠AEC ,∠BCO=α,∴∠EAB=α,∴∠FBA=α,∵AB=a ,AD=b ,∴FO=FB+BO=a•cosα+b•sinα,故选:D .【点睛】本题考查解直角三角形、三角函数的定义、矩形的性质,解答本题的关键是明确题意,正确做出辅助线,利用数形结合的思想解答.11.B解析:B【分析】根据线段垂直平分线的性质得到AE=BE,由等腰三角形的性质得到∠B=∠BAE,根据三角形的外角的性质得到∠AEC=∠B+∠BAE=2∠B,求得∠C=30°,根据三角函数的定义即可得到结论.【详解】∵DE垂直平分AB于点D,∴AE=BE,∴∠B=∠BAE,∴∠AEC=∠B+∠BAE=2∠B,∵AB=AC,∴∠AEC=2∠C,∵AE⊥AC,∴∠EAC=90°,∴∠C=30°,∴CE=643 cos3032AC==︒,故选:B.【点睛】本题考查了线段垂直平分线的性质,等腰三角形的性质,三角形外角的性质以及特殊角的三角函数值.注意掌握数形结合思想的应用.12.D解析:D【分析】作AE⊥BC于E,根据平行四边形的面积=矩形面积的一半,得出AE=12AB,再由三角函数即可求出∠ABC的度数,即可得到答案.【详解】解:作AE⊥BC于E,如图所示:则∠AEB=90°,根据题意得:平行四边形的面积=BC•AE=12 BC•AB,∴AE=12AB , ∴sinB=12AE AB =, ∴∠ABC=30°,∴∠BCD=150°.故选:D .【点睛】本题考查了平行四边形的性质、矩形的性质、面积的计算以及三角函数;熟练掌握平行四边形和矩形的性质,并能进行推理计算是解决问题的关键.13.B解析:B【分析】作BD ⊥AC 于D ,根据勾股定理求出AB 、AC ,利用三角形的面积求出BD ,最后在直角△ABD 中根据三角函数的意义求解.【详解】解:如图,作BD ⊥AC 于D ,由勾股定理得,22223213,3332AB AC =+==+=∵1113213222ABC S AC BD BD =⋅=⨯=⨯⨯, ∴22BD =, ∴2262sin 13BD BAC AB ∠=== 故选:B .【点睛】本题考查了勾股定理,解直角三角形,三角形的面积,三角函数的意义等知识,根据网格构造直角三角形和利用三角形的面积求出BD 是解决问题的关键.14.C解析:C【分析】分别用AC ,AB 和BC 表示出123,,S S S ,然后根据222BC AB AC =-即可得出123,,S S S 的关系.同理,得出456,,S S S 的关系,从而可得答案.【详解】解:如图,1S 对应ACD ∆的面积,过D 作DH AC ⊥于H ,ACD ∆为等边三角形, 160,,,2DAC AH CH AC AD AC ∴∠=︒=== sin 60,DH AD ∴︒=33,22DH AD AC ∴== 2113,24S AC DH AC ∴=•=同理:222333,,44S BC S AB == ∵222BC AB AC =-, ∴213,S S S -=如图2,同理可得:456S S S =+,∴3421564516111454.S S S S S S +=-++=-++=故选:C .【点睛】本题考查了勾股定理、等边三角形的性质.锐角三角函数等知识点,其中勾股定理:如果直角三角形的两条直角边长分别是a ,b ,斜边长为c ,那么222+=a b c .二、填空题15.﹣1【分析】原式利用特殊角的三角函数值绝对值的代数意义以及零指数幂法则计算即可得到结果【详解】解:原式==故答案为:﹣1【点睛】此题考查了实数的运算特殊角的三角函数值以及零指数幂熟练掌握运算法则是解解析:3﹣1【分析】原式利用特殊角的三角函数值,绝对值的代数意义,以及零指数幂法则计算即可得到结果.【详解】解:原式=22311 2⨯+--=31-故答案为:3﹣1【点睛】此题考查了实数的运算,特殊角的三角函数值,以及零指数幂,熟练掌握运算法则是解本题的关键.16.或3或【分析】利用分类讨论①当∠BPC=90°时情况一:如图1利用直角三角形斜边的中线等于斜边的一半得出PO=BO易得△BOP为等边三角形利用锐角三角函数可得CP的长;情况二:如图2利用直角三角形斜解析:33或3或37.【分析】利用分类讨论,①当∠BPC=90°时,情况一:如图1,利用直角三角形斜边的中线等于斜边的一半得出PO=BO,易得△BOP为等边三角形,利用锐角三角函数可得CP的长;情况二:如图2,利用直角三角形斜边的中线等于斜边的一半可得结论.②当∠CBP=90°时,如图3,由对顶角的性质可得∠AOC=∠BOP=60°,易得∠BPO=30°,易得BP的长,利用勾股定理可得CP的长.【详解】解:①当∠CPB=90°时,情况一:(如图1),∵点O为BC中点,∴AO=BO,∴PO=BO,∵∠AOC=60°,∴∠BOP=60°,∴△BOP为等边三角形,∵AB=BC=6,∴CP=CB•sin60°=6×32=33;情况二:如图2,∵点O为BC中点,∴AO=BO,∵∠CPB=90°,∴PO=BO=CO,∵∠AOC=60°,∴△COP为等边三角形,∴CP=CO=3,②当∠CBP=90°时,如图3,∵∠AOC=∠BOP=60°,∴∠BPO=30°,∴BP=33 tan303OB==︒,在直角三角形CBP中,22226(33)37 BC BP+=+=故答案为:333或37【点睛】本题主要考查了勾股定理,含30°直角三角形的性质和直角三角形斜边的中线,分类讨论,数形结合是解答此题的关键.17.64【分析】连接ABCD过点A作AE⊥CD于E过点B作BF⊥CD于F求出CEEFDF即可解決问题;【详解】解:如图连接ABCD过点A作AE⊥CD于E过点B作BF⊥CD于F∵AB//EFAE//BF∴解析:64【分析】连接AB,CD,过点A作AE⊥CD于E,过点B作BF⊥CD于F,求出 CE , EF , DF 即可解決问题;【详解】解:如图,连接AB,CD,过点A作AE⊥CD于E,过点B作BF⊥CD于F.∵AB//EF,AE//BF,∴四边形ABFE是平行四边形,∵∠AEF=90°,∴四边形AEFB是矩形,∴EF=AB=10(cm),∵AE//PC,∴∠PCA=∠CAE=30°,∴CE=AC•sin30°=27(cm),同法可得DF=27(cm),∴CD=CE+EF+DF=27+10+27=64(cm),故答案为64.【点睛】本题考查解直角三角形的应用,解题的关键是学会添加常用辅助线面构造直角三角形解决问题.18.【分析】连接OBOC由题意易得AE⊥BC则有BE=EC∠BOD=∠BAC设OB=3rOE=2r然后根据勾股定理可求解【详解】解:连接OBOC如图所示:∵内接于AD过圆心O∴AE⊥BC∴BE=EC∴∠解析:5【分析】连接OB、OC,由题意易得AE⊥BC,则有BE=EC,∠BOD=∠BAC,设OB=3r,OE=2r,然后根据勾股定理可求解.【详解】解:连接OB 、OC ,如图所示:∵ABC 内接于O ,AB AC =,AD 过圆心O ,∴AE ⊥BC , ∴BE=EC ,BD DC =,∴∠BAD=∠CAD ,∵∠BOD=2∠BAD ,∴∠BAC=∠BOD , ∵2cos 3BAC ∠=, ∴2cos 3BOD ∠=, ∵DE=1,∴设OB=3r ,OE=2r ,则有: 321r r =+,解得:1r =,∴3,2OB OE ==,∴在Rt △BEO 中,225BE OB OE -=, ∴25BC = 故答案为5【点睛】本题主要考查垂径定理、三角形内接圆的性质及圆周角定理,熟练掌握垂径定理、三角形内接圆的性质及圆周角定理是解题的关键.19.【分析】首先根据题意画出图形再根据折叠的性质和可求出各角的度数再利用解直角三角形的知识分别求出CDDFBD 的长度最后根据线段之间的和差关系即可求出结果【详解】解:如图所示:∵△ADC 是由△ACD 翻折 解析:32【分析】首先根据题意画出图形,再根据折叠的性质和DAB BAF ∠∠=,可求出各角的度数,再利用解直角三角形的知识分别求出CD ,DF ,BD 的长度,最后根据线段之间的和差关系即可求出结果.【详解】解:如图所示:∵△ADC’是由△ACD 翻折得到,∴DAC 'DAC ∠∠=, ∵DAB BAF ∠∠=, ∴DAC 2DAB ∠∠=. ∵AC 45B ∠=︒, ∴DAB BAF=15∠∠=︒.∴30CAD ∠=︒.在Rt △ACD 中,AC=2 ∴23tan 30CD AC =⋅︒= ,43cos30AC AD ==︒ . ∵'ADC F DAC ∠=∠+∠∴'30F DAC ∠=∠=︒ . ∴433DF AD ==. 23432232BF CD DF BC∴=+-=-= 故答案为32.【点睛】本题考查了翻折的性质和解 直角三角形的知识,根据题意画出图形是解题的关键.20.【分析】过Q 作QH ⊥AC 于H 在△QHC 中由于∠QCH=45°则CH=QH 设CH=则QH=x 在Rt △QHA 中由于∠QAH=60°求得AH=然后利用CH+AH=AC 求得的值再根据三角形面积公式计算得到结 解析:48163-【分析】过Q 作QH ⊥AC 于H ,在△QHC 中,由于∠QCH=45°,则CH=QH ,设CH=x ,则QH=x ,在Rt △QHA 中,由于∠QAH=60°,求得AH=33x ,然后利用CH+AH=AC 求得x 的值,再根据三角形面积公式计算得到结果.【详解】过Q 作QH ⊥AC 于H ,如图,∠ACB=45°,∠DME=60°,AC=8,在△QHC 中,∠QCH=45°,∴CH=QH ,设CH=x ,则QH=x ,在Rt △QHA 中,∠QAH=60°, ∴AH=QH tan 60︒3x , ∵CH+AH=AC , ∴383x x +=, 解得:(433x =,∴QAC 12S =QH•AC (14338481632=⨯⨯=- 故答案为:483-【点睛】本题主要考查了解直角三角形,作出辅助线构造直角三角形,利用条件求得AC 边上的高是解题的关键.21.8【分析】作AH ⊥BC 于H 则四边形AFCH 是矩形AF=CHAH=CF 在Rt △ABH中解直角三角形即可解决问题【详解】解:作AH⊥BC于H则四边形AFCH是矩形AF=CH在Rt△ABE中∠BAE=90解析:8【分析】作AH⊥BC于H,则四边形AFCH是矩形,AF=CH,AH=CF. 在Rt△ABH中,解直角三角形即可解决问题.【详解】解:作AH⊥BC于H,则四边形AFCH是矩形,AF=CH.在Rt△ABE中,∠BAE=90°,∠BEA=60°∴∠ABE=180°-∠A-∠BEA=180°-90°-60°=30°由题意得∠ABH=90°-2∠ABE=90°-30°×2=30°在Rt△ABH中,∠ABH=30°,3,BC=26∴BH=AB cos30°332=18∴CH=BC-BH=26-18=8.即AF=8.故答案为8.【点睛】本题考查了翻折变换,矩形的性质及解直角三角形等知识.解题的关键是学会添加辅助线,构造直角三角形来解决问题.22.【分析】沿AB作垂线与C的延长线相交于M点可得到等边直角三角形和锐角为30°的直角三角形根据三角函数求解即可【详解】解:如图连接AC并过B点作BM⊥CM设BM=k∵AD=CD∠D=60°∴△ACD是解析:6 2【分析】沿AB作垂线与C的延长线相交于M点,可得到等边直角三角形和锐角为30°的直角三角形,根据三角函数求解即可.【详解】解:如图连接AC 并过B 点作BM ⊥CM ,设BM=k ,∵AD =CD ,∠D=60°,∴△ACD 是等边三角形,AD=AC ,∵∠A =105°,∠B =120°,∠DAC=60°,∴∠MBC=60°,∠BCM=30°,∠BAC=45°,∵BM=k ,∴BC=2k ,MC=BM tan 30=3, ∵∠BAC=45°,∠MCA=45°, ∴AD=AC=MC 3k sin 4522=6k , ∴6k 6==AD BC . 【点睛】 本题考查了特殊角的三角函数值和公式的应用,正确应用公式和作出辅助线是解题的关键.3tan 303=,sin45=22. 23.2+【分析】连接OA 过点A 作AC ⊥OB 于点C 由题意知AC=1OA=OB=2从而得出OC==BC=OB ﹣OC=2﹣在Rt △ABC 中根据tan ∠ABO=可得答案【详解】如图连接OA 过点A 作AC ⊥OB 于点解析:3.【分析】连接OA ,过点A 作AC ⊥OB 于点C ,由题意知AC=1、OA=OB=2,从而得出22OA AC -3、BC=OB ﹣OC=23Rt △ABC 中,根据tan ∠ABO=AC BC 可得答案.【详解】如图,连接OA ,过点A 作AC ⊥OB 于点C ,则AC=1,OA=OB=2,∵在Rt△AOC中,OC=222221OA AC-=-=3,∴BC=OB﹣OC=2﹣3,∴在Rt△ABC中,tan∠ABO=123ACBC=-=2+3.故答案是:2+3.【点睛】本题考查了解直角三角形,根据题意构建一个以∠ABO为内角的直角三角形是解题的关键.24.6030【分析】在Rt△ABC中根据AB=2AC可得出∠B=30°∠A=60°【详解】解:如图在Rt△ABC中∵∠C=90°AB=2AC∴sin∠B==∴∠B=30°∴∠A =90°﹣∠B=90°﹣3解析:60 30【分析】在Rt△ABC中,根据AB=2AC,可得出∠B=30°,∠A=60°.【详解】解:如图,在Rt△ABC中,∵∠C=90°,AB=2AC,∴sin∠B=ACAB =12,∴∠B=30°,∴∠A=90°﹣∠B=90°﹣30°=60°.故答案为:60,30.【点睛】此题考查有一个角是30°的直角三角形的性质,根据三角函数求解较简单.25.75°【分析】根据非负数性质得根据三角函数定义求出∠A=60°∠B=45°根据三角形内角和定理可得【详解】因为所以所以所以∠A=60°∠B=45°所以∠C=180°-∠A-∠B=75°故答案为:75解析:75°【分析】根据非负数性质得1cos 0,1tan 02A B -=-=,根据三角函数定义求出∠A=60°,∠B=45°,根据三角形内角和定理可得.【详解】 因为()21cos 1tan 02A B -+-= 所以1cos 0,1tan 02A B -=-= 所以1cos ,tan 12A B == 所以∠A=60°,∠B=45°所以∠C=180°-∠A-∠B=75°故答案为:75°【点睛】考核知识点:特殊锐角三角函数.熟记特殊锐角三角函数值是关键.26.【分析】过点F 作FI ⊥BC 于点I 延长线IF 交AD 于J 根据含30°直角三角形的性质可求出FIFJ 和JH 的长度从而求出HD 的长度【详解】解:过点F 作FI ⊥BC 于点BC 延长线AD 交AD 于J 由题意可知:CF解析:23【分析】过点F 作FI ⊥BC 于点I ,延长线IF 交AD 于J ,根据含30°直角三角形的性质可求出FI 、FJ 和JH 的长度,从而求出HD 的长度.【详解】解:过点F 作FI ⊥BC 于点BC ,延长线AD 交AD 于J ,由题意可知:CF=BC=6,∠FCB=30°,∴FI=3,CI=33∵JI=CD=6,∴JF=JI-FI=6-3=3,∵∠HFC=90°,∴∠JFH+∠IFC=∠IFC+∠FCB=90°,∴∠JFH=∠FCB=30°,设JH=x ,则HF=2x ,∴由勾股定理可知:(2x )2=x 2+32,∴∴DH=DJ-JH==故答案为:【点睛】本题考查正方形的性质,涉及正方形的性质,勾股定理,旋转的性质,含30°的直角三角形的性质,本题属于中等题型.三、解答题27.(1)3;(2)x 1=1,x 2=0.5.【分析】(1)根据实数的混合运算顺序和运算法则计算即可;(2)利用因式分解法求解即可.【详解】(1)原式=1﹣1+4+(﹣2)+2×12=3; (2)∵2x (x ﹣1)=x ﹣1.∴2x (x ﹣1)﹣(x ﹣1)=0,∴(x ﹣1)(2x ﹣1)=0,则x ﹣1=0或2x ﹣1=0,解得x 1=1,x 2=0.5.【点睛】本题主要考查实数的运算、解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键. 28.(1)322)12213x x ==,. 【分析】 (1)先计算负整数指数幂、化简二次根式,代入三角函数值、计算零指数幂,最后计算加减可得答案;(2)利用因式分解法求解即可.【详解】(1)1022cos30)π-︒++1212=+133312=+-+ 2232=+; (2)∵23520x x -+=,∴()()1320x x --=,则10x -=或320x -=,解得12213x x ==,. 【点睛】 本题主要考查了实数的混合运算,特殊角的三角函数值,解一元二次方程,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.29.(1)画图见解析;1C 的坐标是(2,-2);tan BAC ∠=1;(2)画图见解析;2C 的坐标是(1,0);(3)45210+.【分析】(1)将△ABC 关于x 轴对称得到△A 1B 1C 1,如图所示,找出所求点坐标;证明ABC 是等腰直角三角形即可求出tan BAC ∠的值;(2)以点B 为位似中心,在网格内画出△A 2B 2C 2,使△A 2B 2C 2与△ABC 位似,且位似比为2:1,如图所示,找出所求点坐标即可.(3)先求出△ABC 的周长,再根据222A B C 与ABC 的位似比为2:1,即可求出222A B C 的周长.【详解】解:(1)111A B C 如图所示,点C 1的坐标是(2,-2);∵222125AC =+=,222125BC =+=,2221310AB =+=,∴222=,AC BC AB+=,AC BC∴ABC是等腰直角三角形,∴45∠=,BAC∠=tan45=1;∴tan BAC故答案是:(2,-2);1;(2)△A2B2C2如图所示,2C的坐标是(1,0);故答案是:(1,0);A B C与ABC的位似比为(3)∵△ABC的周长551025102222:1,∴A B C的周长为2(2510)=4510222故答案为:510【点睛】此题考查了作图-位似变换与对称变换及三角函数值的求法,熟练掌握位似变换与对称变换的性质是解本题的关键.30.(1)90°;(2)证明见解析;(3)2.【分析】(1)根据圆周角定理即可得∠CDE的度数;(2)连接DO,根据直角三角形的性质和等腰三角形的性质易证∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°,即可判定DF是⊙O的切线;(3)根据已知条件易证△CDE∽△ADC,利用相似三角形的性质结合勾股定理表示出AD,DC的长,再利用圆周角定理得出tan∠ABD的值即可.【详解】解:(1)解:∵对角线AC为⊙O的直径,∴∠ADC=90°,∴∠EDC=90°;(2)证明:连接DO,∵∠EDC=90°,F是EC的中点,∴DF=FC,∴∠FDC=∠FCD,∵OD=OC,∴∠OCD=∠ODC,∵∠OCF=90°,∴∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°,∴DF是⊙O的切线;(3)解:如图所示:可得∠ABD=∠ACD,∵∠E+∠DCE=90°,∠DCA+∠DCE=90°,∴∠DCA=∠E,又∵∠ADC=∠CDE=90°,∴△CDE∽△ADC,∴DC DEAD DC=,∴DC2=AD•DE∵AC=25DE,∴设DE=x,则AC=25x,则AC2﹣AD2=AD•DE,期(25x)2﹣AD2=AD•x,整理得:AD2+AD•x﹣20x2=0,解得:AD=4x或﹣4.5x(负数舍去),则DC=22(25)(4)2x x x-=,故tan∠ABD=tan∠ACD=422AD xDC x==.。
(完整word)锐角三角函数讲义

锐角三角函数第一课时:三角函数定义与特殊三角函数值知识点一:锐角三角函数的定义:一、 锐角三角函数定义:在Rt △ABC 中,∠C=900, ∠A、∠B、∠C 的对边分别为a 、b 、c , 则∠A 的正弦可表示为:sinA= , ∠A 的余弦可表示为cosA=∠A 的正切:tanA= ,它们弦称为∠A 的锐角三角函数例1.如图所示,在Rt △ABC 中,∠C =90°.①斜边)(sin =A =______, 斜边)(sin =B =______; ②斜边)(cos =A =______,斜边)(cos =B =______; ③的邻边A A ∠=)(tan =______, )(tan 的对边B B ∠==______.例2. 锐角三角函数求值:在Rt △ABC 中,∠C =90°,若a =9,b =12,则c =______,sin A =______,cos A =______,tan A =______, sin B =______,cos B =______,tan B =______.例3.已知:如图,Rt △TNM 中,∠TMN =90°,MR ⊥TN 于R 点,TN =4,MN =3.求:sin ∠TMR 、cos ∠TMR 、tan ∠TMR .对应练习:1、 在Rt△ABC 中,a =5,c =13,求sinA ,cosA ,tanA .2、 如图,△ABC 中,AB=25,BC=7,CA=24.求sinA 的值.25247C BA3、 已知α是锐角,且cos α=34,求sin α、tan α的值.4、在Rt ABC △中,90C ∠=,5AC =,4BC =,则tan A = .5、在△ABC 中,∠C=90°,sinA=53,那么tanA 的值等于( )。
A .35B 。
45C. 34D 。
436、 在△ABC 中,∠C =90°,cosA 3,c =4,则a =_______.7、如图,P 是∠α的边OA 上一点,且P 点坐标为(2,3), 则sinα=_______,cosα=_________,tanα=______ _.αyxP(2,3)OA知识点二:特殊角的三角函数值 当 时,正弦和正切值随着角度的增大而 余弦值随着角度的增大而例1.求下列各式的值. (1)。
锐角三角函数知识点总结

锐角三角函数知识点总结一、引言锐角三角函数是数学中的基础知识点,它在解决与直角三角形相关的问题中扮演着重要角色。
本文将总结锐角三角函数的基本概念、性质和公式,以及它们在实际问题中的应用。
二、基本概念1. 锐角:角度小于90度的角。
2. 直角三角形:一个角为90度的三角形。
3. 边的命名:- 对边(Opposite side):锐角所对的边。
- 邻边(Adjacent side):锐角旁边的边,但不包括斜边。
- 斜边(Hypotenuse):直角三角形中最长的边,对直角的两边进行闭合。
4. 锐角三角函数:- 正弦(Sine, sin):锐角的对边与斜边的比值。
- 余弦(Cosine, cos):锐角的邻边与斜边的比值。
- 正切(Tangent, tan):锐角的对边与邻边的比值。
三、基本公式1. 定义公式:- sin(θ) = 对边 / 斜边- cos(θ) = 邻边 / 斜边- tan(θ) = 对边 / 邻边2. 互余关系:- sin(90° - θ) = cos(θ)- cos(90° - θ) = sin(θ)- tan(90° - θ) = cot(θ)3. 基本恒等式:- sin²(θ) + cos²(θ) = 1- 1 + tan²(θ) = sec²(θ)- 1 + cot²(θ) = csc²(θ)4. 特殊角的三角函数值:- sin(30°) = 1/2, cos(30°) = √3/2, tan(30°) = √3/3 - sin(45°) = √2/2, cos(45°) = √2/2, tan(45°) = 1- sin(60°) = √3/2, cos(60°) = 1/2, tan(60°) = √3四、应用1. 解直角三角形问题:- 利用三角函数求解边长。
【人教版】九年级下册数学《锐角三角函数》全章知识点复习及同步习题

c ,则有: s in A = a = cos B , cos A = = sin B , tan A = ,这就是锐角三角函数所以 cos B = sin(90 - B) = sin A = .在 Rt△BCD 中, cos B = ,所以 = ., cos A = , =(sin 2A 、cos 2A 分别表示 sin A 、cos A 2 2锐角三角函数我们知道,在 Rt△ABC 中,∠C =90°,∠A 、∠B 、∠C 的对边分别为 a 、b 、b ac c b的定义.根据锐角三角函数的定义,再结合直角三角形的性质,我们可以探索出锐角三角函数之间的三个特殊关系.一、余角关系由上面的定义我们已得到 sin A =cos B ,cos A =sin B ,而在直角三角形中,∠A+∠B =90°,即∠B =90°-∠A .因此有:sin A =cos (90°-A ),cos A =sin (90°-A ).应用这些关系式,可以很轻松地进行三角函数之间的转换.例1 如图,在 Rt△ABC 中,∠C =90°,CD ⊥AB 于 D ,已知 sin A ==2,求 BC 的长.解:由于∠A +∠B =90°,12BD 2 1BC BC 2所以 BC =4.二、平方关系a b 由定义知 sin A = c c1 2 ,BD所以 sin 2 A + cos 2 A = a 2 b 2 a 2 + b 2+ c c c 2的平方).又由勾股定理,知 a 2+b 2=c 2,所以 sin 2A +cos 2A = c 2 c 2=1.应用此关系式我们可以进行有关锐角三角函数平方的计算.例 2 计算:sin256°+sin245°+sin234°.=⎪⎪ + 1 = 由定义中 sin A = a, cos A = ,得 = c = ⨯ = = tan A .所以原式 = = =- .5 12 5 12所以 sin B = = .应选(B).5解:由余角关系知 sin56°=cos(90°-56°)=cos34°.所以原式=sin245°+(sin234°+cos234°)⎛ 2 ⎫2 ⎝ 2 ⎭3 2 .三、相除关系b c casin A a c a cos A b c b bc利用这个关系式可以使一些化简求值运算过程变得简单.例 3 已知 α 为锐角,tan α =2,求 3sin α + cos α 4cos α - 5sin α的值.解:因为 tan α = sin α cos α= 2 ,所以 sin α =2cos α ,6cos α + cos α 6 + 1 74cos α - 10cos α 4 - 10 6求三角函数值的方法较多,且方法灵活.是中考中常见的题型.我们可以根据已知条件结合图形选用灵活的求解方法.四、设参数法例 4 如图 △1,在 ABC 中,∠C =90°,如果 t a n A =(A)(B) (C) (D)13 13 12 55 12 ,那么 sin B 等于( )分析:本题主要考查锐角三角函数的定义及直角三角形的有关性质.因为 tan A = a 5 =b 12,所以可设 a =5k ,b =12k (k >0),根据勾股定理得 c =13k ,图 1b 12c 13五、等线段代换法例 5如图 2,小明将一张矩形的纸片 ABC D 沿 C E 折叠,B 点恰好落在 A D 边上,设此点为 F ,若 BA :BC =4:,则 c os∠DCF 的值是______.分析:根据折叠的性质可知 E △B C ≌ EF C ,所以 C F=CB ,又 C D=AB ,AB :BC =4:5, 所以 C D :C F=4:5,图 2=.113911,即=,所以C E=,在Rt△A E C中,tan∠CA E==3=.所以tanα=.C3445所以DB==,所以tanα=,选(A).在Rt D△C F中,c os∠D C F=DC4 CF5六、等角代换法例6如图3,C D是平面镜,光线从A点出发经C D上点E反射后照射到B点,若入射角为α(入射角等于反射角),AC⊥C D,B D⊥C D,垂足分别为C、D,且AC=3,B D=6,C D=11,则tanα的值为()B(A)(B)(C)(D)311119A分析:根据已知条件可得∠α=∠CA E,所以只需求出tan∠CA E.α根据条件可知△A C E∽B DE,所以AC CE3CE=BD ED611-CEC E图3D11311CE11AC39119七、等比代换法例7如图4,在Rt△ABC中,ACB=90,D⊥AB于点D,BC=3,AC=4,设BC D=α,tanα的值为()(A)(B)(C)(D)435分析:由三角形函数的定义知tanα=DB DC,由Rt△C D△B∽Rt ACB,BC33DC AC44图4( :锐角三角函数测试1.比较大小:sin41°________sin42°. 2.比较大小:cot30°_________cot22°. 3.比较大小:sin25°___________cos25°. 4.比较大小:tan52°___________cot52°. 5.比较大小:tan48°____________cot41°. 6.比较大小:sin36°____________cos55°.7、下列命题①sin α 表示角α 与符号 sin 的乘积;② 在△ABC 中,若∠C=90°,则 c=α sinA 成立;③任何锐角的正弦和余弦值都是介于 0 和 1 之间实数.其正确的为()A 、②③B.①②③C.②D. ③8、若 △R t ABC 的各边都扩大 4 倍得到 △R t A ′B ′C ′,那么锐角 A 和锐角 A ′正切值的关系为()A.tanA ′=4tanA B.4tanA ′=tanAC.tanA ′=tanAD.不确定.9(新疆中考题) 1)如图(1)、 2),锐角的正弦值和余弦值都随着锐角的确定而确定, 变化而变化.试探索随着锐角度数的增大.它的正弦值和余弦值变化的规律.(2)根据你探索到的规律,试比较 18°,34°,50°,62°,88°,这些锐角的正弦值的 大小和余弦值的大小。
中考总复习锐角三角函数综合复习--知识讲解

中考总复习锐角三角函数综合复习--知识讲解锐角三角函数是初中数学中的一个重要内容,也是中考数学考试中常考的内容之一、掌握了锐角三角函数的定义、性质和相关的计算方法,可以帮助我们解决与角度有关的各种问题,如计算角度的大小、求角的三角函数值等。
下面是锐角三角函数的综合复习知识讲解。
1.弧度制和角度制在介绍锐角三角函数之前,我们首先要了解弧度制和角度制。
在角度制中,一个圆的周长被定义为360度,而在弧度制中,一个圆的周长被定义为2π弧度。
所以可以得到以下关系:360度=2π弧度180度=π弧度90度=π/2弧度2.定义对于任意一个锐角A,我们可以在一个单位圆上面取点P,使得∠POA 的顶点为O,点O为圆心,点P在单位圆上。
这样,我们可以定义以下几个锐角三角函数:正弦函数sinA、余弦函数cosA、正切函数tanA、余切函数cotA。
3.性质(1) 正弦函数sinA:在单位圆上,点P的纵坐标就是正弦值sinA。
(2) 余弦函数cosA:在单位圆上,点P的横坐标就是余弦值cosA。
(3) 正切函数tanA:tanA的值等于sinA/cosA。
(4) 余切函数cotA:cotA的值等于cosA/sinA。
(5) 错位现象:sinA等于cos(90度-A),cosA等于sin(90度-A)。
4.基本关系式(1) sin²A + cos²A = 1,即sin²A = 1 - cos²A,cos²A = 1 -sin²A。
(2) tanA = sinA/cosA,cotA = 1/tanA = cosA/sinA。
(3) sin(180度 - A) = sinA,cos(180度 - A) = -cosA。
(4) cos(360度 - A) = cosA,sin(360度 - A) = -sinA。
5.锐角三角函数的值(1)0度、30度、45度、60度、90度的正弦、余弦、正切值是特殊的,需要进行熟记。
锐角三角函数知识点总结与复习

锐角三角函数知识点总结与复习1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方;2、如下图,在Rt △ABC 中,∠C 为直角, 则∠A 的锐角三角函数为∠A 可换成∠B :3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值;4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角的正切值;5、0°、30°、45°、60°、90°特殊角的三角函数值重要A 90B 90∠-︒=∠︒=∠+∠得由B A邻边A90B 90∠-︒=∠︒=∠+∠得由B A直角三角形中 的边角关系解直角三角形当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小; 7、正切、余切的增减性:当0°<α<90°时,tan α随α的增大而增大,cot α随α的增大而减小;一、知识性专题专题1:锐角三角函数的定义例 1 在Rt △ABC 中,∠ACB =90°,BC =1,AB =2,则下列结论正确的是 A .sin A B .tan A =12C .cos BD .tan B 分析 sin A =BC AB =12,tan A =BC AC ,cos B =BCAB =12.故选D.例2 在△ABC 中,∠C =90°,cos A =35,则tan A 等于 ; 分析 在Rt △ABC 中,设AC =3k ,AB =5k ,则BC =4k ,由定义可知tan A =4433BC k AC k ==. 分析 在Rt △ABC 中,BC =3,∴sin A =35BC AB =.故填35.例312·哈尔滨在Rt △ABC 中,∠C=900,AC=4,AB=5,则sinB 的值是 ; 解析本题考查了锐角三角函数的意义.解题思路:在直角三角形中,锐角的正弦等于对边比邻边,故sinB=54. 例42012内江如图4所示,△ABC 的顶点是正方形网格的格点,则sinA 的值为 ;解析欲求sinA,需先寻找∠A 所在的直角三角形,而图形中∠A 所在的△ABC 并不是直角三角形,所以需要作高.观察格点图形发现连接CD 如下图所示,恰好可证得CD ⊥AB,于是有图4图4sinA =CD AC =210=55.例5 2012宁波,Rt △ABC,∠C=900,AB=6,cosB=错误!,则BC 的长为 ;解析cosB=错误!=错误!,又∵AB=6∴BC=4例62012贵州铜仁如图,定义:在直角三角形ABC 中,锐角α的邻边与对边的比叫做角α的余切,记作ctan α, 即ctan α=BCAC=的对边角的邻边角αα,根据上述角的余切定义,解下列问题:1ctan30◦= ;2如图,已知tanA=43,其中∠A 为锐角,试求ctanA 的值.分析1可先设最小边长为一个特殊数这样做是为了计算方便,然后在计算出其它边长,根据余切定义进而求出ctan30◦;2由tanA=43,为了计算方便,可以设BC=3 AC=4根据余切定义就可以求出ctanA 的值.解析1设BC=1, ∵α=30◦∴AB=2∴由勾股定理得:AC=3ctan30◦=BCAC=32 ∵tanA=43∴设BC=3 AC=4∴ctanA =BC AC =34例72012山东滨州把△ABC 三边的长度都扩大为原来的3倍,则锐角A 的正弦函数值 A .不变B .缩小为原来的13C .扩大为原来的3倍D .不能确定 解析因为△ABC 三边的长度都扩大为原来的3倍所得的三角形与原三角形相似,所以锐角A 的大小没改变,所以锐角A 的正弦函数值也不变.答案选A .例82012湖南观察下列等式 ①sin30°= cos60°=②sin45°=cos=45°=③sin60°= cos30°=根据上述规律,计算sin 2a+sin 290°﹣a= .解析:根据①②③可得出规律,即sin 2a+sin 290°﹣a=1,继而可得出答案. 答案:解:由题意得,sin 230°+sin 290°﹣30°=1;sin 245°+sin 290°﹣45°=1; sin 260°+sin 290°﹣60°=1;故可得sin 2a+sin 290°﹣a=1.故答案为:1.点评:此题考查了互余两角的三角函数的关系,属于规律型题目,注意根据题意总结,另外sin 2a+sin 290°﹣a=1是个恒等式,同学们可以记住并直接运用.例9 2012山东德州为了测量被池塘隔开的A ,B 两点之间的距离,根据实际情况,作出如下图形,其中AB BE ⊥,EF BE ⊥,AF 交BE 于D ,C 在BD 上.有四位同学分别测量出以下四组数据:22题图①BC ,∠ACB ; ②CD ,∠ACB ,∠ADB ;③EF ,DE ,BD ;④DE ,DC ,BC .能根据所测数据,求出A ,B 间距离的有哪 组解析对于①,可由公式AB=BC ×tan ∠ACB 求出A 、B 两点间的距离;对于②,可设AB 的长为x,则BC=x tan ACB ∠,BD=xtan ADB ∠,BD-BC=CD,可解出AB .对于③,易知△DEF ∽△DBA,则DE BDEF AB=,可求出AB 的长;对于④无法求得,故有①、②、③三组点评此题考查解直角三角形和三角形相似的性质与判定.在直角三角形中至少要有已知一边和一角才能求出其他未知元素;判定两三角形相似的方法有:AA,SAS,SSS,两直角三角形相似的判定还有HL . 例102012江苏泰州18如图,在边长相同的小正方形组成的网格中,点A 、B 、C 、D 都在这些小正方形的顶点上,AB 、CD 相交于点P,则tan ∠APD 的值是 .解析 要求tan ∠APD 的值,只要将∠APD 放在直角三角形中,故过B 作CD 的垂线,然后利用勾股定理计算出线段的长度,最后利用正切的定义计算出结果即可. 答案作BM ⊥CD,DN ⊥AB 垂足分别为M 、N,则2,易得:10,设PM=x,则PD=22-x,由△DNP ∽△BMP,得:PN DN PM BM =,即10102PN x =,∴PN=55x,由DN 2+PN 2=PD 2,得:110+15x 2=22-x 2,解得:x 1=24,x 2=2舍去,∴tan ∠APD=2224BM PM ==2.例11. 2011江苏苏州如图,在四边形ABCD 中,E 、F 分別是AB 、AD 的中点,若EF=2,BC=5,CD=3,则tanC 等ABCDEFF于 .分析:根据三角形的中位线定理即可求得BD 的长,然后根据勾股定理的逆定理即可证得△BCD 是直角三角形,然后根据正切函数的定义即可求解.解答:解:连接BD .∵E 、F 分別是AB 、AD 的中点.∴BD=2EF=4∵BC=5,CD=3∴△BCD是直角三角形.∴tanC= 43例122011山东日照在Rt△ABC 中,∠C=90°,把∠A 的邻边与对边的比叫做∠A 的余切,记作cotA=ab.则下列关系式中不成立的是A .tanA•cotA=1B .sinA=tanA•cosAC .cosA=cotA•sinAD .tan 2A+cot 2A=1解答:解:根据锐角三角函数的定义,得 A 、tanA•c otA=a b b a ⋅=1,关系式成立;B 、sinA=c a ,tanA•cosA=cac b b a =⋅,关系式成立; C 、cosA=,cotA•sinA=c b a b c a =⋅,关系式成立;D 、tan 2A+cot 2A=b a 2+ab 2≠1,关系式不成立.故选D .点评:本题考查了同角三角函数的关系.1平方关系:sin 2A+cos 2A=1 2正余弦与正切之间的关系积的关系:一个角的正切值等于这个角的正弦与余弦的比,即tanA=BAcos sin 或sinA=tanA•cosA.3正切之间的关系:tanA•tanB=1. 例132011•贵港如图所示,在△ABC 中,∠C=90°,AD 是BC 边上的中线,BD=4,AD=2,则tan∠CAD 的值是 .解答:解:∵AD 是BC边上的中线,BD=4,∴CD=BD=4,在Rt△ACD中,AC===2,∴tan∠CAD===2.故选A .例142011烟台如果△ABC 中,sin A =cos B 2,则下列最确切的结论是 A. △ABC 是直角三角形 B. △ABC 是等腰三角形C. △ABC 是等腰直角三角形D. △ABC 是锐角三角形 解:∵sinA=cosB=22,∴∠A =∠B =45°,∴△ABC 是等腰直角三角形.故选C . 例152011四川如图所示,在数轴上点A 所表示的数x 的范围是A 、330sin 602sin x ︒︒<< B 、3cos302x ︒︒<<cos45C 、3tan 302x ︒︒<<tan45D 、3cot 4502x ︒︒<<cot3 解答:故选D .同步练习12011甘肃如图,A 、B 、C 三点在正方形网格线的交点处,若将△ACB 绕着点A 逆时针旋转得到△AC ’B ’,则tanB ’的值为 .解答:解:过C 点作CD ⊥AB ,垂足为D .根据旋转性质可知,∠B′=∠B .在Rt△BCD 中,tanB= CD :BD =13,∴tan B′=tan B = 13. 2 2011甘肃兰州点M -sin60°,cos60°关于x 轴对称的点的坐标是 . 解:∵sin60°=32,cos60°= 12,∴点M -32,12.∵点P m ,n 关于x 轴对称点的坐标P′m ,-n ,∴M 关于x 轴的对称点的坐标是-32,-12.故选B . 32011广东已知:45°<A <90°,则下列各式成立的是A 、sinA =cosAB 、sinA >cosAC 、sinA >tanAD 、sinA <cosA解答:解:∵45°<A <90°,∴根据sin 45°=cos 45°,sinA 随角度的增大而增大,cosA 随角度的增大而减小,当∠A >45°时,sinA >cosA ,故选:B .4、2011•宜昌教学用直角三角板,边AC=30cm,∠C=90°,tan∠BAC=33,则边BC 的长为 .cm解:在直角三角形ABC 中,根据三角函数定义可知:tan ∠BAC=BCAC,又AC=30cm,tan ∠3则BC=ACtan 33cm .故选C . 5、 2011福建莆田如图,在矩形ABCD 中,点E 在AB 边上,沿CE 折叠矩形ABCD ,使点B 落在AD 边上的点F 处,若AB =4,BC=5,则tan ∠AFE 的值为 .ABCC ’ B ’解答:解:∵四边形ABCD 是矩形,∴∠A =∠B =∠D =90°,CD =AB =4,AD =BC =5,由题意得:∠EFC =∠B =90°,CF =BC =5,∴∠AFE +∠DFC =90°,∠DFC +∠FCD =90°, ∴∠DCF =∠AFE ,∵在Rt △DCF 中,CF =5,CD =4,∴DF =3,∴tan ∠AFE =tan ∠DCF =DFDC =34 .6、2012连云港小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD 沿过点B的直线折叠,使点A 落在BC 上的点E 处,还原后,再沿过点E 的直线折叠,使点A 落在BC 上的点F 处,这样就可以求出°的角的正切值是 .EC DA BF答案设AB=x,则BE=x,在直角三角形ABE 中,用勾股定理求出AE=EF=2x,于是2在直角三角形ABF 中,tan ∠FAB=21)BF xAB x=2°.选B; 7、2012福州如图15,已知△ABC,AB=AC=1,∠A=36°,∠ABC 的平分线BD 交AC 于点D,则AD 的长是 ,cosA 的值是 .结果保留根号解析:由已知条件,可知△BDC 、△ADB 是等腰三角形,且DA=DB=BC,可证△BDC ∽△ABC,则有BC DC AC BC =,设BC=x,则DC=1-x,因此21,101x xx x x -=+-=即,解方程得, 125151x x ---==,舍去,即AD=512;又cosA=512451512AB AD===--⨯答案:5151,24 8、2012南京如图,将45°的∠AOB 按下面的方式放置在一把刻度尺上:顶点O 与尺下沿的端点重合,OA 与尺下沿重合.OB 与尺上沿的交点B 在尺上的读书恰为2厘米,若按相同的方式将37°的∠AOC 放置在该刻度尺上,则OC 与尺上沿的交点C 在尺上的读数为 厘米.结果精确到厘米,参考数据sin370≈,cos370≈,tan370≈C B AO4321解析:由于∠AOB=45°,B 点读书为2厘米,则直尺的宽为2厘米,解直角三角形得点C 的读数为2÷tan370≈2÷≈厘米.答案:9、2012·湖南张家界黄岩岛是我国南海上的一个岛屿,其平面图如图甲所示,小明据此构造出该岛的一个数学模型如图乙所示,其中∠A=∠D=90°,AB=BC=15千米,CD=23千米,请据此解答如下问题:1 求该岛的周长和面积结果保留整数,参考数据2≈ 73.13≈45.26≈ 2 求∠ACD 的余弦值.解答1结AC,∵AB=BC=15千米,∠B=90°,∴∠BAC=∠ACB=45°,AC=152千米. 又∵∠D=90°, ∴AD=2222)23()215(-=-CD AC =123千米∴周长=AB+BC+CD+DA=30+32+123=30++≈55千米. 面积=S △ABC +S △ADC =21×15×15+21×123×32=2225+186≈157平方千米. 2cos ∠ACD=5121523==AC CD . 10、2012甘肃兰州在建筑楼梯时,设计者要考虑楼梯的安全程度;如图1,虚线为楼梯的倾斜度,斜度线与地面的夹角为倾角θ,一般情况下,倾角越小,楼梯的安全程度越高;如图2,设计者为了提高楼梯的安全程度,要把楼梯的倾角1θ减至2θ,这样楼梯占用地板的长度由d 1增加到d 2 ,已知d 1=4米,140θ∠=,236θ∠=,楼梯占用地板的长度增加了多少米 计算结果精确到米;参考数据:tan40°=,tan36°=AC解析:根据在Rt△ACB中,AB=d1tanθ1=4tan40°,在Rt△ADB中,AB=d2tanθ2=d2tan36°,即可得出d2的值,进而求出楼梯占用地板增加的长度.解:由题意可知可得,∠ACB=∠θ1,∠ADB=∠θ2在Rt△ACB中,AB=d1tanθ1=4tan40°,在Rt△ADB中,AB=d2tanθ2=d2tan36°,得4tan40°=d2tan36°,∴d2=4tan40tan36≈,∴d2-d1==≈,答:楼梯占用地板的长度增加了米.11、2012贵州为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.参考数据:sin54°≈,cos54°≈,tan54°≈,≈,精确到个位解析:首先过点C作CD⊥AB于D,然后在Rt△BCD中,利用三角函数的知识,求得BD,CD的长,继而在Rt△ACD 利用∠CAB的正切求得AD的长,继而求得答案.答案:解:过点C作CD⊥AB于D∵BC=200m,∠CBA=30°,∴在Rt△BCD中,CD=BC=100m,BD=BC•cos30°=200×=100≈173m,∵∠CAB=54°,在Rt△ACD中,AD=≈≈74m,∴AB=AD+BD=173+74=247m.答:隧道AB的长为247m.12、2011新疆建设兵团如图,在△ABC中,∠A=90°.1用尺规作图的方法,作出△ABC绕点A逆时针旋转45°后的图形△AB1C1保留作图痕迹;2若AB=3,BC=5,求tan∠AB1C1.第22题图d2解答:解:1作∠CAB 的平分线,在平分线上截取AB 1=AB ,作C 1A ⊥AB 1,在AC 1上截取AC 1=AC ,如图所示即是所求.2∵AB =3,BC =5,∴AC =4,∴AB 1=3,AC 1=4,tan∠AB 1C 1=错误!=错误!. 专题2 特殊角的三角函数值例12012,湖北孝感计算:cos 245°+tan30°·sin60°=________.答案1例22012陕西计算:(02cos 45-38+1-2=︒ .解析原式2=2-322+1=-52+12⨯⨯答案-52+1 例32012广安计算:---)32(218cos45o +13- ; 解析:1182()cos 4533---︒+=322212323+-+21 例4 计算|-3|+2cos 45310. 解:原式=3+22-122. 例5 计算-12⎛⎫- ⎪⎝⎭9+-12007-cos 60°.解:原式=12+3+-1-12=3-1=2. 例6 计算|2+cos 60°-tan 30°08 21十+221. 例7 计算312-⎛⎫ ⎪⎝⎭-π-0-|1-tan 60°|32-.解:原式=8-13132=10. 例82012呼和浩特计算:11|122sin 45--+︒解析三角函数、绝对值、乘方答案11|12sin 45--+︒11)2211232=-+=+=例92011天水计算:si n 230°+tan 44°tan 46°+si n 260°= . 分析:根据特殊角的三角函数值计算.tanA •tan 90°﹣A =1. 解答:解:原式=14+1+34=2.故答案为2. 例102011•莱芜若a=3﹣tan60°,则196)121(2-+-÷--a a a a = ;33-解答:解:a=3﹣tan60°=3﹣3,∴原式=23-a 1-a 121)(⨯---a a =31-a =33313331-=-=--故答案为:33-. 练习1、2011浙江计算:|-1|5-π0+4cos45°. 解原式=1-122练习2、2011浙江衢州1计算:|﹣2|﹣3﹣π0+2c os45°;解答:解:1原式=2122-+⨯,=1 练习3、计算:20110+8-2sin45°;原式=1+22-2=1+2;练习3、观察下列各式:①sin 59°>sin 28°;②0<cos α<1α是锐角;③tan 30°+tan 60°=tan 90°;④tan 44°<1.其中成立的有A .1个B .2个C .3个D .4个 练习3、C 提示:sin 59°>sin 28°成立,0<cos α<1α是锐角成立,tan 30°+tan 60tan 90°,tan 44°<tan 45°,即tan 44°<1.练习4、计算2sin 30°-tan 60°+tan 45°= .练习5、如图28-146所示,在△ABC 中,∠A =30°,tan B =13,BC 10则AB 的长为 . 练习6、当x =sin 60°时,代数式2242x x x -+·22244x x x x +-++42xx-的值是 .练习7、已知cos 59°24′≈,则sin 30°36′≈ .练习8、若∠A ,∠B 互余,且tan A -tan B =2,则tan 2A +tan 2B = .练习9、如图28-147所示,在菱形ABCD 中,AE ⊥BC 于E ,EC =1,cos B=513,则这个菱形的面积是 . 10.已知正方形ABCD 的边长为1,若将线段BD 绕着点B 旋转后,点D落在DC 延长线上的点D ′处,则∠BAD ′的正弦值为 . 11.如图28-148所示,若将四根木条钉成的矩形木框变为平行四边形ABCD 的形状,并使其面积为矩形面积的一半,则这个平行四边形的一个最小内角等于 .12.在△ABC 中,∠B =30°,tan C =2,AB =2,则BC = .13.设θ为锐角,且x 2+3x +2sin θ=05.则θ= . 14.如图28-149所示,在△ABC 中,∠C =90°,点D 在BC 边上,BD =4,AD =BC ,cos ∠ADC =35. 1求DC 的长;2求sin B 的值.练习4、23 提示:2sin 30°-tan 60°+tan 45°=2×1231=23 练习5、33提示:过点C 作CD ⊥AB ,垂足为D ,在Rt △BDC 中,tan B =13.∴13CD BD =,∴BD =3CD ,∵BC 10∴CD 2+3CD 210,∴CD =1,BD =3.在Rt △ADC 中,tan A =CDAD,∴AD 3∴AB =AD +BD =33 练习632242x x x -+·22244x x x x +-++42xx-=2x ,∴原式=2sin 603练习7、提示:sin 30°36′=cos 59°24′.练习8、6提示:∵∠A ,∠B 互余,∴tan A ·tan B =1,tan 2A +tan 2B =tan A -tan B 2+2tan A ·tan B =22+2=6. 练习9、3916提示:∵cos B =513,设BE =5x ,则AB =13x ,∴AE 22AB BE -12x .∵AB =BC =BE +CE ,∴13x =5x +1,∴x =18,则AE =12x =12×18=32,BC =5x +1=5×18+1=138,∴S =32×138=3916.10.5提示:如图28-155所示,根据题意得DD ′=2DC ,设正方形的边长为x ,则AD =x ,DD ′=2x .∵∠ADD ′=90°,根据勾股定理得AD 22AD DD '+5x .∵AD =x ,∴sin ∠AD ′D =ADAD '=555x x=.∵AB ∥DD ′,∴∠BAD ′=∠AD ′D ,∴sin ∠BAD ′=55.11.30°提示:如图28=156所示,∵S ABCD=12S 矩形BEFC ,且BC =BC 底相同, ∴GC =12FC .∵CF =DC ,∴GC =12DC ,12CG DC =.∵∠DGC =90°,sin 30°=12,∴∠CDG =30°,即这个平行四边形的一个最小内角为30°. 12.12+3 13.30°提示:x 1·x 2=2sin θ,x 1+x 2=-3,则x 1-x 22=x 1+x 22-4x 1x 2=9-8sin θ=52,∴sin θ=12,∴θ=30°. 14.解:1∵cos ∠ADC =35,∴设CD =3x ,则AD =5x ,AC =4x ,∴BC =AD =5x .∵BD =BC-CD ,∴5x -3x =4,∴x =2,∴CD =3x =6. 2∵AC =4x =8,BC =5x =10,∴AB =2222810241AC BC +=+=,∴sin B =844141241AC AB ==. ★ 专题三:题型一俯角与仰角仰角:视线在水平线上方的角;★ 俯角:视线在水平线下方的角;仰角铅垂线水平线视线视线俯角例1、2012湖北襄阳在一次数学活动中,李明利用一根拴有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD .如图5,已知李明距假山的水平距离BD 为12m,他的眼睛距地面的高度为,李明的视线经过量角器零刻度线OA 和假山的最高点C,此时,铅垂线OE 经过量角器的60°刻度线,则假山的高度为 m .解析如下图,过点A 作AF⊥CD 于F,则AF =BD =12m,FD =AB =.再由OE∥CF 可知∠C=∠AOE=60°.所以,在Rt△ACF 中,CF =tan 60AF=43,那么CD =CF +FD =43+m .例2、2012珠海如图,水渠边有一棵大木瓜树,树干DO 不计粗细上有两个木瓜A 、B 不计大A O BE D CF图5 CDA BO E小,树干垂直于地面,量得AB=2米,在水渠的对面与O 处于同一水平面的C 处测得木瓜A 的仰角为45°、木瓜B 的仰角为30°.求C 处到树干DO 的距离CO.结果精确到1米参考数据:41.12,73.13≈≈第16题图D BA OC解析如图,根据题意,得∠COD =90°, ∠ACO =45°, ∠BCO =30°, AB =2,求CO.设CO 为x 米, 根据AO =CO,列方程,解得即可.答案解:设CO 为x 米在Rt △BCO 中,tan30°=BO CO ,则BO =33x 在Rt △ACO 中,AO =CO,得方程33x +2=x 解得x ≈5.答: CO 长大约是5米. 例3、2012江苏盐城如图所示,当小华站立在镜子EF 前A 处时,他看自己的脚在镜中的像的俯角为450 :如果小华向后退米到B 处,这时他看自己的脚在镜中的像的俯角为300.求小华的眼睛到地面的距离;结果精确到米,参考数据:3≈.答案设AC=BD=x,在Rt △ACA 1中,∠AA 1C=450,∴AA 1=x,在Rt △DBB 1中,BB 1=tan30x=3x ,又∵12BB 1-12AA 1=12,即12×3x -12x=12,解得:x=312+≈米. 例4、2012山西如图,为了开发利用海洋资源,某勘测飞机预测量一岛屿两端A .B 的距离,飞机在距海平面垂直高度为100米的点C 处测得端点A 的俯角为60°,然后沿着平行于AB 的方向水平飞行了500米,在点D 测得端点B 的俯角为45°,求岛屿两端A .B 的距离结果精确到米,参考数据:解析解:过点A 作AE⊥CD 于点E,过点B 作BF⊥CD 于点F,∵AB∥CD,∴∠AEF=∠EFB=∠ABF=90°,∴四边形ABFE 为矩形.第24题图∴AB=EF,AE=BF.由题意可知:AE=BF=100米,CD=500米.…2分 在Rt△AEC 中,∠C=60°,AE=100米.∴CE===米. …4分在Rt△BFD中,∠BDF=45°,BF=100. ∴DF===100米.…6分∴AB=EF=CD+DF﹣CE=500+100﹣≈600﹣×≈600﹣≈米. …8分答:岛屿两端A .B 的距离为米.例5、2012呼和浩特22如图,线段AB 、DC 分别表示甲、乙两建筑物的高;某初三课外兴趣活动小组为了测量两建筑物的高,用自制测角仪在B 处测得D 点的仰角为α,在A 处测得D 点的仰角为β;已知甲、乙两建筑物之间的距离BC 为m ;请你通过计算用含α、β、m 的式子分别表示出甲、乙两建筑物的高度;答案解:过点A 作AM ⊥CD 于M在Rt △BCD 中,tan α=CD BC ∴CD =BC ·tan α=m tan α在Rt △AMD 中,tan β=DMAM∴DM =AM ·tan β=m tan β∴AB =CD –DM =mtan α–tan β例6、2012湖北随州,20在一次暑假旅游中,小亮在仙岛湖的游船上A 处,测得湖西岸的山峰太婆尖C 处和湖东岸的山峰老君岭D 处的仰角都是45°,游船向东航行100米后B 处,测得太婆尖、老君岭的高度为多少米3 1.732 ,结果精确到米;解析:设太婆尖高h 1米,老君岭高h 2米;可分别在直角三角形中利用正切值表示出水平线段的长度,再利用移动距离为AB=100米,可建立关于h 1、h 2的方程组,解这个方程组求得两山峰高度;答案:设太婆尖高h 1米,老君岭高h 2米,依题意,有FE第20题图60304545D (老君岭)C (太婆尖)BAβα乙甲ADB M C⇒⎪⎪⎩⎪⎪⎨⎧=-=-10060tan 45tan 10045tan 30tan 2211h h h h 1376.136)1732.1(50)13(5045tan 60tan 1001≈=+=+=-=h 米33110030tan 45tan 1002-=-=h 2376.236)732.13(50)33(50)13(350≈=+=+=+=米答:太婆尖高度为137米,老君岭高度为237米;题型二方位角问题1、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角;如图3,OA 、OB 、OC 、OD 的方向角分别是:45°、135°、225°;2、指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角;如图4:OA 、OB 、OC 、OD 的方向角分别是:北偏东30°东北方向,南偏东45°东南方向,南偏西60°西南方向,北偏西60°西北方向;例1、2011山东省潍坊轮船从B 处以每小时海里的速度沿男偏东30°方向匀速航行,在B 处观测灯塔A 位于南偏东75°方向上,轮船航行半小时到达C 处,在观测灯塔A 北偏东60°方向上,则C 处与灯塔A 的距离是 .海里解答: BC=50×=25海里;根据方位角知识得,∠BCD=30°,=75°-30°;CB=∠BCD+∠ACD=30°+60°=90°;∠A=∠CBD=45°所以CA=CB 所以CB=25海里例2、2012年四川德阳某时刻海上点P 处有一客轮,测得灯塔A 位于客轮P 的北偏东30°方向,且相距20海里.客轮以60海里/小时的速度沿北偏西60°方向航行32小时到达B 处,那么tan ∠ABP=A.21 C.55 D.552解析如图6所示,根据题意可知∠APB=90°.且AP=20, PB=60×23=40. 所以tan ∠ABP=201402PA PB ==例3、2012连云港已知B 港口位于A 观测点北偏东°方向,且其到A 观测点正北方向的距离BD 的长为16km;一艘货轮从B 港口以40km/h 的速度沿如图所示的BC 方向航行,15min 后到达C 处;现测得C 处位于A观测点北偏东°方向;求此时货轮与A 观测点之间的距离AC 的长精确到.25东北CBDCBH解析过点B 作AC 的垂线,把所求线段AC 换为两线段的差;利用Rt △ABH 和Rt △BCH 求线段AH 、CH 的长,利用AH -CH 确定AC 的长; 答案BC=40×1560=10.在Rt△ADB 中,sin ∠DAB=DB AB , °≈;所以AB=DAB DB ∠sin ≈1.60.8=20.如图,过点B 作BH⊥AC,交AC 的延长线于H;在Rt△AHB 中,∠BAH=∠DAC -∠DAB=°―37°=°,tan∠BAH=BH AH ,=BH AH,AH =+CH 2=AB 2,BH 2+2BH 2=2025所以AH=85,在Rt△AHB 中, BH 2+CH 2=BC 2,CH=2108025-=所以第22题图APCB °°AC=AH―CH=85―25=65≈.例4、2012四川攀枝花如图6,我渔政310船在南海海面上沿正东方向匀速航行,在A地观测到我渔船C在东北方向上的我国某传统渔场.若渔政310船航向不变,航行半小时后到达B 处,此时观测到我渔船C在北偏东30°方向上.问渔政310船再航行多久,离我渔船C的距离最近假设我渔船C捕鱼时移动距离忽略不计,结果不取近似值.答案作CD⊥AB于D,设BD=x,∵∠BCD=30°,∴CD=3x,因为∠CAD=45°,∴AD=CD3,AB3–x,依据题意3x–x=,x 31+,31+小时,离渔船C的距离最近;例5、2012山东东营如图某天上午9时,向阳号轮船位于A处,观测到某港口城市P位于轮船的北偏西°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到城市P位于该船的南偏西°方向,求此时轮船所处位置B 与城市P的距离参考数据:°≈35,°≈34,°≈1213,°≈125解析过点P作PC⊥AB,构造直角三角形,设PC=x海里,用含有x的式子表示AC,BC的值,从而求出x的值,再根据三角函数值求出BP的值即可解答.答案过点P作PC⊥AB,垂足为C,设PC=x海里.在Rt△APC中,∵tan∠A=PCAC,∴AC=5tan67.512PC x=︒.在Rt△PCB中,∵tan∠B=PCBC,∴BC=4tan36.93x x=︒.∵AC+BC=AB=21×5,∴54215123x x+=⨯,解得60x=.∵sinPCBPB∠=,∴60560100sin sin36.93PCPBB===⨯=∠︒海里.∴向阳号轮船所处位置B与城市P的距离为100海里.例6、2012山东省青岛如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE ;而当光线与地面夹角是45°时,教学楼顶A 在地面上的影子F 与墙角C 有13米的距离B 、F 、C 在一条直线上 ⑴求教学楼AB 的高度;⑵学校要在A 、E 之间挂一些彩旗,请你求出A 、E 之间的距离结果保留整数.参考数据:sin22°≈错误!,cos22°≈错误!,tan22°≈错误! 答案解:⑴过点E 作EM ⊥AB,垂足为M.设AB 为x.Rt △ABF 中,∠AFB=45°,∴BF=AB=x,∴BC=BF+FC=x+13在Rt △AEM 中,∠AEM=22°,AM=AB-BM=AB-CE=x-2,∴tan22°= 错误!, 错误!=错误!,x=12.即教学楼的高12m.⑵由1可得ME=BC=x+13=12+13=25.在Rt △AME 中,cos22°= 错误!, ∴AE= 错误!≈ 错误!≈27.即AE之间的距离约为27m.题型三、坡比是垂直高度与水平距离的比值,即是坡角的正切值应用举例: 坡面的铅直高度h 和水平宽度l 的比叫做坡度坡比;用字母i 表示,即hi l=;坡度一般写成1:m 的形式,如1:5i =等;把坡面与水平面的夹角记作α叫做坡角,那么tan hi lα==;例1、2012广安如图2,某水库堤坝横断面迎水坡AB 的坡比是1:3,堤坝高BC=50m,则迎水坡面AB 的长度是 .m解:tan∠BAC=13,∠BAC=30°,sin∠BAC=12, sin∠BAC=BC AB ,AB=2BC=100m例2、小强在教学楼的点P 处观察对面的办公大楼.为了测量点P 到对面办公大楼上部AD的距离,小强测得办公大楼顶部点A 的仰角为45°,测得办公大楼底部点B 的俯角为60°,已知办公大楼高46米,CD =10米.求点P 到AD 的距离用含根号的式子表示.图2:i h l=hlαABCDPN M解析连结PA 、PB ,过点P 作PM ⊥AD 于点M ;延长BC ,交PM 于点N则∠APM =45°,∠BPM =60°,NM =10米………1分设PM =x 米 在Rt △PMA 中,AM =PM ×tan ∠APM =x tan 45°=x 米…3分在Rt △PNB 中,BN =PN ×tan ∠BPM =x -10tan 60°=x -103米…5分 由AM +BN =46米,得x +x -103 =46……6分解得,4610313x +=+ ,∴点P 到AD 的距离为4610313++米.结果分母有理化为()1838-米也可……8分答案4610313++结果分母有理化为()1838-米也可例3、2012湖北如图,某公园入口处原有三级台阶,每级台阶高为18cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A ,斜坡的起始点为C ,现设计斜坡BC 的坡度1:5i =,则AC 的长度是 cm .解析如图,过点B 作BD ⊥AC 于D,依题意可求得AD =60cm,BD =54cm ;由斜坡 BC 的坡度i =1:5,求得CD =270cm,故AC =CD -AD =270-60=210cm .例4、2012浙江省绍兴,19如图1,某超市从一楼到二楼的电梯AB 的长为米,按坡角∠BAC 为32°.1求一楼与二楼之间的高度BC 精确到米;2电梯每级的水平级宽均是米,如图2.小明跨上电梯时,该电梯以每少上升2级的高度运行,10秒后他上升了多少米精确到米 备用数据:sin 32°=,cos 32°=,tan 32°=.解析1在Rt△ABC 中,已知∠B AC=32°,斜边AB 的长为米,根据锐角三角函数的定义即可求得第20题图MPDCBA第12题A BC3018一楼与二楼之间的高度BC .2先计算1级电梯的高,再根据10秒钟电梯上升了20级可计算10秒后他上升的高度.答案解:1∵sin ∠BAC =ABBC ,∴BC =AB ×sin32°=×≈米. 2∵tan32°= 级高级宽,∴级高=级宽×tan32°=×=,∵10秒钟电梯上升了20级,∴小明上升的高度为:20×米. 例5、2012浙江丽水,19学校校园内有一小山坡,经测量,坡角∠ABC=30°,斜坡AB 长为12米.为方便学生行走,决定开挖小山坡,使斜坡BD 的坡比是1:3即为CD 与BC 的长度之比,A,D 两点处于同一铅垂线上,求开挖后小山坡下降的高度AD.解析:∴AD=AC-CD=6-23.答:开挖后小山坡下降的高度AD 为6-23米.例6、2012深圳小明想测一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图3,此时测得地面上的影长为8米,坡面上的影长为4米,已知斜坡的坡角为30,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为 .米解答:如图3—1,根据坡角易求树的下半部分的高为2米,树的上半部分所在直角三角形的水平距离为(+823米,由两个直接三角形相似易求树的上半部分高度为(43米,知树的高度为()63米,选择A例72012江苏泰州24如图,一居民楼底部B 与山脚P 位于同一水平线上,小李在P 处测得居民楼顶A 的仰角为60°,然后他从P 处沿坡角为45°的山坡上走到C 处,这时,PC=30m,点C 与点A 在同一水平线上,A 、B 、P 、C 在同一平面内.1求居民楼AB 的高度;2求C 、A 之间的距离.精确到,参考数据:2≈,3≈,6≈60° CA B 45°图330°21图3-1第24题图解析过C作BP的垂线,垂足为G,利用特殊Rt△PCG和Rt△ABP中的边角关系,我们容易计算出CG即AB的长,最后用AC=BP+PG,就是C、A之间的距离.答案1过C作BP的垂线,垂足为G,在Rt△PCG中,CG=PCsin450=30×2所以=m2PG= PCcos450=30×2=所以C、A之间的距离例82012四川水务部门为加强防汛工作,决定对某水库大坝进行加固,大坝的横截面是梯形ABCD.如图9所示,已知迎水坡面AB的长为16米,∠B=60°,背水坡面CD的长为,加固后大坝的横截面为梯形ABED,CE的长为8米.1已知需加固的大坝长为150米,求需要填土石方多少立方米2求加固后大坝背水坡面DE的坡度.解析1求出横截面△DCE的面积,然后乘以坝堤长度即可得出体积.可以分别过点A,D 作BC边上的高将问题转化为解直角三角形问题.2求大坝背水坡面DE的坡度就是求坡面DE上一点到BE的铅直高度与它到点E的水平宽度的比,这一点通常取梯形的顶点.答案解:1过点A作AG⊥BC于G,过点D作DH⊥BC于H,∴AG=DH.在Rt△ABG中,AG=sin60°·AB×16=∴DH=S△DCE=12·DH·CE=12×8=∴需要填土石方150=3.2在Rt△DHC中,HC24,∴HE=HC+CE=24+8=32.∴加固后大坝背水坡面DE的坡度=DHHE.AB CD图9E例9 2012江苏苏州如图,已知斜坡AB 长60米,坡角即∠BAC 为30°,BC⊥AC,现计划在斜坡中点D 处挖去部分坡体用阴影表示修建一个平行于水平线CA 的平台DE 和一条新的斜坡BE .请讲下面2小题的结果都精确到米,参考数据:≈.1若修建的斜坡BE 的坡角即∠BEF 不大于45°,则平台DE 的长最多为 米;2一座建筑物GH 距离坡角A 点27米远即AG=27米,小明在D 点测得建筑物顶部H 的仰角即∠HDM 为30°.点B 、C 、A 、G 、H 在同一个平面内,点C 、A 、G 在同一条直线上,且HG⊥CG,问建筑物GH 高为多少米解答: 解:1∵修建的斜坡BE 的坡角即∠BEF 不大于45°,∴∠BEF 最大为45°当∠BEF=45°时,EF 最短,此时ED 最长,∵∠DAC=∠BDF=30°,AD=BD=30,∴BF=EF=BD=15,DF=15,故:DE=DF ﹣EF=15﹣1≈;2过点D 作DP⊥AC,垂足为P .在Rt△DPA中,DP=AD=×30=15,PA=AD•cos30°=×30=15. 在矩形DPGM 中,MG=DP=15,DM=PG=15+27,在Rt△DMH 中,HM=DM•tan30°=×15+27=15+9. GH=HM+MG=15+15+9≈.答:建筑物GH 高为米.A B C DE GH。
(完整)锐角三角函数题型分类总结,推荐文档

锐角=角函数∙知识点一:钦角三角国数的≡x≡ 一、 锐角三角函数定义:在 RiAABC 中,ZC=9O 0, ZAS ZBX ZC 的对边分别为 a 、b 、c, 则ZA 的正弦可表示为;S ilLX= _________ JZA 的余弦可表示为CoSA= _________厶的正切:Tan-A= ________ ,它们弦称为ZA 的锐角三角函数2、取値范围—<¾inA< Co i⅛< __________ tanA>______1例如图所示,在RlA^C 中〉乙C=9Q° .例2.锐角三角函数束值;在 RtΔ,45C 中,ZC= 90° ,若 σ=9, B= 12,则 C= ___________SilL a l — _______ , COSU I f- __________ 9 taiL -l — __________ SSin^= _____ ; CQ ∖B= ____ ; tan.例3∙已知;如图,RI0∙∖M r 中,Z∏I ∖r =90o …⑷丄ZV 于出点,Zy=4, Hv=3• 求:SinZ732KxCOSZrVC?、tanZ∏IK .典型m :类型一:直角三角形求值31 .已知 RtQUBC 中丿 ZC≡90Q 5 taπJ= ,5C≡1⅞ 求.4C ∖∙3 和 8田・② CoSJ = ® tan.4∙=第1题團① sin J( ) 软边 an 5【an 方=ZB 旳对边( )2. 如朗 OO 的半径θA = 16cm, OC 丄貝B 于C 点,an ΛAOC =-.求肋及OC 的长•3. 已知:0。
中,OC 丄朋于 C 点;J5= 16cm ; dnZA0C (1) 求OQ 的半径OA 的长及弦心距& (2) 求 COSz4 OC 及 ta∏ZJθC∙g4. 已知ZJ 是锐角,SitIW=—;求COSA > tan J 的值17对应ill 练二1. 在RtA^C 中7 ZC=90C 7 若5C=1, .15-√5 ;则Ianj 的值为5B.巫5C.丄 2D. 22.在ABC 中,ZC=90o ,S inA=- >那么tanA 的值等于( ).53G 4 C 3 c 4 A.-5 B.— 5 C. 一4D. 一 3类型二利用角度转化求值,2. 如團,直径为10的CU 经过点C(Oo)和点O(Qo);与X 轴的正半釉交于点D, B 是》轴右侧圆弧上一点〉则C O SZ^C 的值为〈)C.-D-I1.已知;如图,RtZUBC 中,ZC= 90o ∙ Q 是Je 边上一点'DE 丄曲于E 点.^≡s⅛E3.如图,角α的顶点为0,它的一边在工轴的正半轴上J另一边Od上有一点Pd 4),则3丄如團,菱形九5CD的边长为IQCm,DE1AB, SinJ =-,则遗个菱形的面积二.5.如國06>是^iBC的外接圆,AD杲©O的直径,AC = I,则sin5的值是(7 \A. -B.-3 26.如图6,沿川E折蠡矩形纸片曲CQ ,c.£⅞□-4B=8, BC =10, AB=⅛ 则tan NEFC 的值为(A.- C.-57.如图7,在等腰直角三角形C中'ZC =90o , JC = 6, Z)为AC±—点,若tan ZDA.! = -,则-Q 的长为()5A・近B・2 C・1 D・2√21 ^rIS.如图S,在RtA-LffC 中,Z090°,AOS, Ad的平分线/D=」一求ZB的度数及边BC. AB的长.类型三化斜三角形为直角三角形例1 如图,在A ABC中,Z A=30C,Z B=45% AC=2√3、求AB 的长.Cn T •353.正方形网格中, ZHoB 如團放乱则tanZJ (95的值是(√L例 2∙已知:如團,在 AABC 中,ZBAC=I 20° , ∠S=10, AC=5 .对应岷1.如图,在RlAABC 中,ZBAC=90=,点D 在BC 边上,且AABD 是等边三甬形.若.43=2, 求AABC 的周长•〈结果保留根号)2. 已知:如虱 AABC 中「3=9, BC=G,厶4恥的面枳尊于9丿求血^3. ABC 中,乙4=60° …4方=6 Cm , AC=4 Clrb 则A-45C 的面积是求:siik^ABC 的值..4 羽 CnrDllcm 2类型四;利用 构造直角三角形例1如图所示,AABC 的顶点杲正方形网格的格点,则SinA 的值为<对应练习:1. ________________________________________________ 如图,AABC 的顶点都在方格纸的格点上,则Sir I A= ____________ .点厘逆吋针旋转得到AC8,则tanF 的值为D∙ 110D.IR特殊角的三角函数值锐角C30s45060。
三角函数基础知识复习1

三角函数基础知识复习(一)一、任意角:知识点1、角的概念的推广:1、“旋转”形成角(角包括顶点、始边、终边);2、角的分类:正角、负角、零角(逆时针、顺时针、没有旋转)。
例1、(1)钟表经过10分钟,分针转了______度;(2)若将钟表拨慢10分钟,则时针转了______度,分针转了______度。
知识点2、象限角和轴线角:1、象限角:角的顶点与坐标原点重合,角的始边与x轴的非负半轴重合,角的终边在第几象限,就说这个角是第几象限的角;2、轴线角:如果角的终边在坐标轴上,则这个角叫轴线角,它不属于任何象限。
如:00,900,1800,2700,3600,-900,-1800,-3600,等等。
例2、(1)3700位于第___象限;(2)-1200位于第___象限;(3)2900位于第___象限;(4)-2600位于第____象限;(5)4弧度的角位于第___象限。
例3、A={小于900的角},B={第一象限的角},则A∩B=()A、{锐角}B、{小于900的角}C、{第一象限的角}D、以上都不对例4、已知集合A={α|α=k·900-360,k∈Z},B={β|-1800<β<1800},则A∩B=()A、{-360,540} B、{-1260,1440} C、{-1260,-360,540,1440} D、{-1260,540}知识点3、终边相同的角:所有与α终边相同的角(包括α本身在内)构成一个集合, 这个集合可表示为{β|β=________________________},终边相同的角相差3600的整数倍。
例5、已知角α=450,则在区间[-7200,00]内且与α终边相同的角是____________________。
例6、已知α是第二象限的角,且2α与7α的终边相同,则α=________________________。
例7、用描述法写出下列角的集合:(1)第一象限的角___________________;(2)第二象限的角___________________;(3)第三象限的角___________________;(4)第四象限的角___________________;(5)x轴正半轴上的角________________;(6)x轴负半轴上的角_____________________;(7)x轴上的角_______________;(8) y轴正半轴上的角_________________;(6)y轴负半轴上的角___________________________;(7)y轴上的角________________;(8)坐标轴上的角______________________________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考总复习:锐角三角函数综合复习—知识讲解(基础)撰稿:张晓新 审稿:杜少波【考纲要求】1.理解锐角三角函数的定义、性质及应用,特殊角三角函数值的求法,运用锐角三角函数解决与直角三角形有关的实际问题.题型有选择题、填空题、解答题,多以中、低档题出现;2.命题的热点为根据题中给出的信息构建图形,建立数学模型,然后用解直角三角形的知识解决问题.【知识网络】【考点梳理】考点一、锐角三角函数的概念如图所示,在Rt △ABC 中,∠C =90°,∠A 所对的边BC 记为a ,叫做∠A 的对边,也叫做∠B 的邻边,∠B 所对的边AC 记为b ,叫做∠B 的对边,也是∠A 的邻边,直角C 所对的边AB 记为c ,叫做斜边.Cab锐角A 的对边与斜边的比叫做∠A 的正弦,记作sinA ,即sin A aA c ∠==的对边斜边;锐角A 的邻边与斜边的比叫做∠A 的余弦,记作cosA ,即cos A bA c ∠==的邻边斜边;锐角A 的对边与邻边的比叫做∠A 的正切,记作tanA ,即tan A aA A b∠==∠的对边的邻边.同理sin B b B c ∠==的对边斜边;cos B a B c ∠==的邻边斜边;tan B bB B a∠==∠的对边的邻边.要点诠释:(1)正弦、余弦、正切函数是在直角三角形中定义的,反映了直角三角形边与角的关系,是两条线段的比值.角的度数确定时,其比值不变,角的度数变化时,比值也随之变化.(2)sinA,cosA,tanA分别是一个完整的数学符号,是一个整体,不能写成,,,不能理解成sin与∠A,cos与∠A,tan与∠A的乘积.书写时习惯上省略∠A的角的记号“∠”,但对三个大写字母表示成的角(如∠AEF),其正切应写成“tan∠AEF”,不能写成“tanAEF”;另外,、、常写成、、.(3)任何一个锐角都有相应的锐角三角函数值,不因这个角不在某个三角形中而不存在.(4)由锐角三角函数的定义知:当角度在0°<∠A<90°之间变化时,,,tanA>0.考点二、特殊角的三角函数值要点诠释:(1)通过该表可以方便地知道30°、45°、60°角的各三角函数值,它的另一个应用就是:如果知道了一个锐角的三角函数值,就可以求出这个锐角的度数,例如:若,则锐角.(2)仔细研究表中数值的规律会发现:、、的值依次为、、,而、、的值的顺序正好相反,、、的值依次增大,其变化规律可以总结为:当角度在0°<∠A<90°之间变化时,①正弦、正切值随锐角度数的增大(或减小)而增大(或减小),②余弦值随锐角度数的增大(或减小)而减小(或增大).考点三、锐角三角函数之间的关系如图所示,在Rt△ABC中,∠C=90°.(1)互余关系:,;(2)平方关系:;(3)倒数关系:或;(4)商数关系:.要点诠释:锐角三角函数之间的关系式可由锐角三角函数的意义推导得出,常应用在三角函数的计算中,计算时巧用这些关系式可使运算简便.考点四、解直角三角形在直角三角形中,由已知元素(直角除外)求未知元素的过程,叫做解直角三角形.在直角三角形中,除直角外,一共有5个元素,即三条边和两个锐角.设在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,则有:①三边之间的关系:a2+b2=c2(勾股定理).②锐角之间的关系:∠A+∠B=90°.③边角之间的关系:,,,,,.④,h为斜边上的高.要点诠释:(1)直角三角形中有一个元素为定值(直角为90°),是已知的值.(2)这里讲的直角三角形的边角关系指的是等式,没有包括其他关系(如不等关系).(3)对这些式子的理解和记忆要结合图形,可以更加清楚、直观地理解.考点五、解直角三角形的常见类型及解法求∠1.在遇到解直角三角形的实际问题时,最好是先画出一个直角三角形的草图,按题意标明哪些元素是已知的,哪些元素是未知的,然后按先确定锐角、再确定它的对边和邻边的顺序进行计算.2.若题中无特殊说明,“解直角三角形”即要求出所有的未知元素,已知条件中至少有一个条件为边.考点六、解直角三角形的应用解直角三角形的知识应用很广泛,关键是把实际问题转化为数学模型,善于将某些实际问题中的数量关系化归为直角三角形中的边角关系是解决实际应用问题的关键.解这类问题的一般过程是:(1)弄清题中名词、术语的意义,如仰角、俯角、坡度、坡角、方向角等概念,然后根据题意画出几何图形,建立数学模型.(2)将已知条件转化为几何图形中的边、角或它们之间的关系,把实际问题转化为解直角三角形的问题.(3)根据直角三角形(或通过作垂线构造直角三角形)元素(边、角)之间的关系解有关的直角三角形.(4)得出数学问题的答案并检验答案是否符合实际意义,得出实际问题的解.拓展:在用直角三角形知识解决实际问题时,经常会用到以下概念:(1)坡角:坡面与水平面的夹角叫做坡角,用字母表示.坡度(坡比):坡面的铅直高度h和水平距离的比叫做坡度,用字母表示,则,如图,坡度通常写成=∶的形式.(2)仰角、俯角:视线与水平线所成的角中,视线中水平线上方的叫做仰角,在水平线下方的叫做俯角,如图.(3)方位角:从某点的指北方向线按顺时针转到目标方向的水平角叫做方位角,如图①中,目标方向PA,PB,PC的方位角分别为是40°,135°,245°.(4)方向角:指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方向角,如图②中的目标方向线OA,OB,OC,OD的方向角分别表示北偏东30°,南偏东45°,南偏西80°,北偏西60°.特别如:东南方向指的是南偏东45°,东北方向指的是北偏东45°,西南方向指的是南偏西45°,西北方向指的是北偏西45°.要点诠释:1.解直角三角形实际是用三角知识,通过数值计算,去求出图形中的某些边的长或角的大小,最好画出它的示意图.2.非直接解直角三角形的问题,要观察图形特点,恰当引辅助线,使其转化为直角三角形或矩形来解.例如:3.解直角三角形的应用题时,首先弄清题意(关键弄清其中名词术语的意义),然后正确画出示意图,进而根据条件选择合适的方法求解.【典型例题】类型一、锐角三角函数的概念与性质1.如图,在4×4的正方形网格中,tan α=( )(A)1 (B)2 (C)12 (D) 2举一反三:【变式】在Rt △ABC 中,∠C=90°,若AC=2BC ,则sinA 的值是( )(A) 12类型二、特殊角的三角函数值2.已知a =3,且2(4t a n 45)3b -+°,以a 、b 、c 为边长组成的三角形面积等于( ).A .6B .7C .8D .9举一反三: 【变式】 计算:.3.如图所示,在△ABC 中,∠BAC =120°,AB =10,AC =5,求sinB ·sinC 的值.举一反三:【变式】如图,机器人从A 点,沿着西南方向,行了个单位,到达B 点后观察到原点O 在它的南偏东60°的方向上,则原来A 的坐标为__________.(结果保留根号).类型三、解直角三角形及应用【高清课堂:锐角三角函数综合复习 ID :408468 播放点:例3】4.在△ABC 中,∠A =30°,BC =3,AB =BCA 的度数和AC 的长.【思路点拨】由于∠A 是一个特殊角,且已知AB ,故可以作AC 边上的高BD(如图所示),可求得BD =于此题的条件是“两边一对角”,且已知角的对边小于邻边,因此需要判断此题的解是否唯一,要考虑对边BC 与AC 边上的高BD 的大小,而2BC <<5.如图所示,某船向正东航行.在A 处望见灯塔C 在东北方向,前进到B 处望见灯塔C 在北偏西30°方向,又航行了半小时到D 处,望见灯塔C 恰在西北方向,若船速为每小时20海里,求A ,D 两点间的距离(结果保留根号).举一反三:【变式】坐落在山东省汶上县宝相寺内的太子灵踪塔始建于北宋(公元1112年),为砖砌八角形十三层楼阁式建筑.数学活动小组开展课外实践活动,他们去测量太子灵踪塔的高度,携带的测量工具有:测角仪、皮尺、小镜子.(1)小华利用测角仪和皮尺测量塔高.下图为小华测量塔高的示意图.她先在塔前的平地上选择一点A,用测角仪测出看塔顶(M)的仰角α=35°,在点A和塔之间选择一点B,测出看塔顶(M)的仰角β=45°,然后用皮尺量出A,B两点间的距离为18.6m,量出自身的高度为1.6m.请你利用上述数据帮助小华计算出塔的高度(tan35°≈0.7,结果保留整数).(2)如果你是活动小组的一员,正准备测量塔高,而此时塔影NP的长为am(如图所示),你能否利用这一数据设计一个测量方案?如果能,请回答下列问题:①在你设计的测量方案中,选用的测量工具是:________________________;②要计算出塔的高,你还需要测量哪些数据?________________________________________________________.6.如图所示,海上有一灯塔P,在它周围3海里处有暗礁,一艘客轮以9海里/时的速度由西向东航行,行至A点处测得P在它的北偏东60°方向,继续行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向,问客轮不改变方向继续前进有无触礁的危险?。
