理论物理基础教程答案PPT

合集下载

理论物理导论(程建春编著)PPT模板

0 3 12.3电磁波在周期结构中的散射和光子晶体
0 4 12.4经典电动力学的适用范围和电子的惯性结构
05 习题12
03 第三部分量子力学
第三部分量子力学
01
第13章微观粒子的运
动规律
04
第16章自旋和角动量
02
第14章力学量、算符
和量子态
05
第17章全同粒子和多
体问题
03
第15章近似方法
第15章近似方法
0 1 15.1非简并态微扰和电介质的极化
02
15.2简并态微扰和能级的强耦合
0 3 15.3变分方法和hartree自洽场方法
0 4 15.4含时微扰：量子跃迁、光的吸收和激发
05 习题15
第三部分量子力学
第16章自旋和角动量
16.1电子的自旋算符和自旋波函数
16.3电子自旋与轨道角动量的耦合
理论物理导论(程建春编著)
演讲人
2 0 2 x - 11 - 11
目录
01. 第一部分经典力学 02. 第二部分电动力学 03. 第三部分量子力学 04. 第四部分热力学和统计力学
01 第一部分经典力学
a
第1章牛顿力学
d
第4章流体的运动
第一部分经典力学
b
第2章刚体的定点
运动
c
第3章弹性体中的
第一部分经典力学
第2章刚体的定点运动
0 1 2.1刚体运动的描述：角速度矢量和 euler角
0 2 2.2惯量张量、转动惯量和转动动能 0 3 2.3刚体动力学方程：动量矩定理和
euler方程
0 4 2.4刚体的定点运动、动平衡的稳定性

理论物理统计物理基础刘连寿第七篇答案

（b）晶体的磁矩（c）高温弱场和低温强场的磁矩（d）求原子磁矩平行、反平行和垂直于外场几率，并由此求磁矩（不考虑磁
，其中
都是
把体积看成是数并微分有：
两边同时积分有：
由极限情况下： ,
故：得到：
3．一弹性棒的热力学状态可用它的长度 L，应力描述 f 和温度 T 关系,即为其状态方程，今设此弹性棒发生一微小变化，从一平衡态变到另一平衡态，试证明：
其中为棒横截面积，为线膨胀系数，为杨氏模量。
3．证明：杨氏模量的定义：对长度积分有：
证毕
第三章统计系综
1. 将各近独立的频率为的谐振子组成的系统，每个谐振子的能量为
（a）求当系统的能量为
时的微观态数和熵
（b）求当系统达到平衡时，此系统能量与温度的关系，并和§7.3.2 中用正则分
布所得的结果比较。
解：(a) 假定 N 个独立的谐振子对应的量子数分别为
根据题意
则系统的微观态数即相当于将个东西分配到个不相同（可以区别）的容器中的方法种数，可等于 0 相当于容器可以是空的.故：
当
时，
,故
5．试给出半径为的维球体积： 5．证明：在半径为 1 的维球区域内积分为：
以另一种方式求上述积分有：由两式可知：证毕
6．利用附录给出的斯特林公式：满足下式：
证明上题中的系数
6．证明：第一部分：
只要将上题中解答过程的(3)式中的换成即得。故关键是证明第二部分由于
(1) 由于：
叠（如图），链条两个端点的距离为，系统是孤立的，链环各种方位有相同的
能量，证明
时可以得到胡克定律。
证明：我们从端点开始规定每节链环的方向，凡是指向右方的链环记为“+”，指向左方的记为“-”。设所有指向右方的链环数为，所有指向左方的链环数为则总链环数为：

理论物理基础教程答案_刘连寿

L maX cos ma 2 L maX sin mga sin
O
X
那么
L m( X a cos ) MX X L 0 X

则对应的拉格朗日方程为
d m( X a cos ) MX 0 dt d maX cos ma 2 ma sin X mga sin dt
N
Lz e ra Az
a 1 N
N
Lz e xa Aya ya Axa
a 1
2.质量为M 半径为a 的半球形碗，放在光滑的水平桌面上，如图1 。有一个质量为 m的滑块沿碗的内壁无摩擦的滑下。用表示滑块位置与球心连线和竖直方向的夹角。这个系统起始时静止且 0 。求滑块滑到 1时的值。
解：系统具有xy平面内的平移对称性，所以动量的x，y分量守恒：
p1x p2 x , p1y p1y
又系统的能量守恒，则有
2 p12 p2 E1 E2 U0 2m 2m
那么，则有
而散射前后动量与z轴的夹角之比为
sin 1 p1 p2 p2 1 U0 / E sin 2 p2 p1 p1
csc2 2 g cot
m 2 J (Constant)
（3）（4）
L 0
由（4）式可得

J m 2
2
（1）
带入（3）式可得
J2 2 csc 2 4 g cot 0 m
d d d d dt d dt d

1 M 1 m 2 1 m a cos m a sin M a cos 2 mM 2 mM 2

大学物理基础教程答案1-6力ppt课件

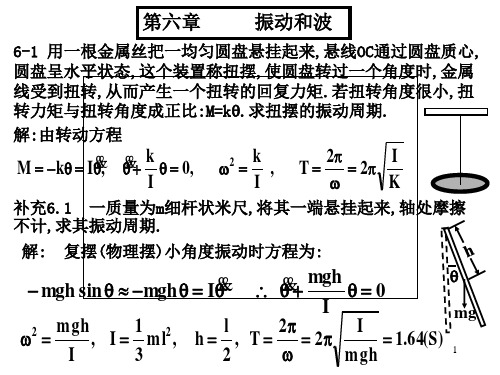
解:(1)振动频率 1 g 1.6(Hz) 2 2 l
k
(2)振幅
A
x
2 0
( v0 )2
0.02(m)
m
(3)初相位
cos1 x0 cos1 0.9 0.46(rad)
A
(v0>0取正号, v0 <0取负号)
(4)振动表达式. X=0.02cos(10t-0.46) (m)
4
最大响度的音（即拍声),问拍频是多少？音叉的频率可能是多
少？为了进一步唯一确定其值，可以在待测测音叉上滴上一点
石蜡，重做上述实验,若此时拍频变低,则说明待测音叉的频率
是多少？
解：以知T=0.5s，得拍频
f 1 2 0.5
f2 f1 2 f2 2 f1 440(Hz)
或
f2 f1 2 438(Hz)
求(1)振动的圆频率、周期、振幅和初始相位；(2)振动的速度
和加速度(函数式)；(3)振动的总能量E(4)振动的平均动能和平
均势能；(5) t =1.0秒、10秒等时刻的相位。
11
解：
(1)
x
0.5cos(8t
)
与振动表达式
x Acos(t )
3
比较便直接可得:
2 1
A 0.5(cm) , 8 T (s)
t3ln2
A A0 ,A A0 ,
16
3213
6-9 火车在铁轨上行驶，每经过铁轨接轨处即受一次震动，使装在弹簧上面的车厢上下振动。设每段铁轨长12.5米，弹簧平均负重5.5吨，而弹簧每受1.0吨力将压缩16毫米。试问，火车速度多大时，振动特别强？
解: 固有振动周期等于强迫力周期时发生共振
分深度为a.若用力稍稍压下,使其浸入水中深度为b,如图所示,然后放手,任其作自由振动,求其振动的周期和振幅.

大学物理基础教程答案1-6力-6ppt课件

2 k
m1 m2
此系统作振幅为A,圆频率为.的简振动.
Al-l
5
6-4一只鸟落在树枝上每4秒摆动6次,鸟飞走后,用一千克砝码系在
鸟呆过地方树枝弯下12厘米,问这只鸟的质量是多少？解:树技与乌组成一个谐振子
kmg81.ห้องสมุดไป่ตู้6(kg/m) T2
l
3
k 2
k
9.42(ra)d mT
m2 0.92(kg)
2
2
A m v0 k(mm)
k
mm
k
2
m’ m
v0
0
x
x Acos(t ) m v0 cos( k t )
k(mm)
mm 2
补充6.4 图所示振动系统，振子是一个作纯滚动的圆柱体，以
知圆柱体的质量为m,半径为R，弹簧的倔强系数为k，并且弹簧
是系于圆柱体的中心旋转对称轴上.试求这一振动系统的频率。
解：设平衡点为弹簧原长时，又
弹簧质量不计，对圆柱体在运动
中受力有：
.
k
m
7
kxc f mxc
fR(12mR2)
1mR2 xc 2R
f 12mxc
kxc 12mxc mxc
xc (32mk)xc
22k, 3m
1(2k)1 2 23m
6-6 如图弹簧的倔强系数为k,定滑轮的质量为m’,半径为R,转动惯量为k，物体的质量为m。轴处摩擦不计，弹簧和绳的质量也不
电能q2/2c,通过电感电流为i,此时电感储有磁能Li2/2,i=dq/dt,
且 q2/2c+ Li2/2=常量,试求LC电路的固有振荡频率.
解: 1q21L2iC 2c 2

物理人教版(2019)必修第一册3.5共点力的平衡(共31张ppt)

悬吊物的位置。如图，悬吊重物的细绳，其O点被一水平绳BO牵引，
模使悬绳AO段和竖直方向成θ角。若悬吊物所受的重力为G，则悬绳
型 AO和水平绳BO所受的拉力各等于多少？（请用两种方法求解）
建
构
F1
F2
F3
F3 = G
活动二：共点力平衡条件的应用
方法一：合成法
解：4 为1 和2 的合力，则4 与3 平衡，
因、两方向的合力都等于0，可列方程
F2 － F1x＝0
F1y － F3＝0
即F2 － F1 sinθ ＝0
F1 cosθ － G＝0
（1）
（2）
由（1）（2）式解得F1=

，

=
活动二：共点力平衡条件的应用
思考与讨论：
质
疑
解
释
F1和F2分别是悬绳AO和水平绳BO所受的拉力吗？
方法一：合成法
以滑梯上正匀速下滑的小孩为研究对象，受力分析如图所示，
科
学
思
维
=
Ff＝μFN
=
´

解得 tanθ =μ
由几何关系可得：tanθ=

可得：h=μ·AC=0.4×6m=2.4m
F=G
G’
FN
FN
Ff

Ff
G
G
活动二：共点力平衡条件的应用
如果悬点A向右移动，BO仍保持水平，
重物仍然静止悬挂，悬绳AOF1
F2
F3
解析法
活动三：动态平衡问题
图解法
夹角θ 减小，悬绳AO和水平绳BO
所受的拉力都减小。
F1最小值为G
F2最小值为0
活动三：动态平衡问题

理论物理基础教程刘连寿第七篇答案

第七篇第一章统计理论基础1.试求理想气体的定压膨胀系数和等温压缩系数。

1．解：假设我们考察的系统是n mol的理想气体，由于理想气体状态方程为：(1)(2)故定压膨胀系数：而等压压缩系数:综上有理想气体（n mol）：2.某气体的定压膨胀系数和等温压缩系数，，其中都是常数，试求此气体的状态方程。

2．解：根据题意：把体积看成是数并微分有：两边同时积分有：由极限情况下：,故：得到：3．一弹性棒的热力学状态可用它的长度L，应力描述f和温度T关系,即为其状态方程，今设此弹性棒发生一微小变化，从一平衡态变到另一平衡态，试证明：其中为棒横截面积，为线膨胀系数，为杨氏模量。

3．证明：杨氏模量的定义：与类比线胀系数：对长度积分有：证毕4．对气体的膨胀系数和压缩系数进行测量的结果得到一下方程：，其中是常数，只是的函数.证明：（a）(b) 状态方程：4．证明：(a)由：（1）又由：（2）（2）式两边对求导（T一定时）：此式与比较可知：f（P）=（因与T无关也与P无关）(b) 将带入(1)式有：当时，,故5．试给出半径为的维球体积：5．证明：在半径为1的维球区域内积分为：以另一种方式求上述积分有：由两式可知：证毕6．利用附录给出的斯特林公式：证明上题中的系数满足下式：6．证明：第一部分：只要将上题中解答过程的(3)式中的换成即得。

故关键是证明第二部分由于(1)由于：即有（1）式成立，故待证命题成立。

证毕第二章统计热力学基础1．单原子晶体中可占据一个格点或一个间隙点。

原子占据格点时的能量比占据间隙点时高。

设格点数和间隙点数相等。

且等于晶体中的原子数。

（a）考虑有个原子占据间隙点的宏观态，计算系统处于此宏观态的熵（b）设系统达到平衡，问晶体在此态的温度是多少？（c）若，晶体的温度时300K，处于间隙点的原子所占的比例是多少？解：（a）根据题意假设一个原子占据间隙点时能量，则占据格点时能量。

现有个原子占据间隙点故有个占据格点。

理论物理基础教程答案_刘连寿50页PPT

拉
60、生活的道路一旦选定，就要勇敢地走到底，决不回头。 ——左
56、书不仅是生活，而且是现在、过去和未来文化生活的源泉。 ——库法耶夫 57、生命不可能有两次，但许多人连一次也不善于度过。— —吕凯特 58、问渠哪得清如许，为有源头活水来。—— 朱熹 59、我的努力求学没有得到别的好处，只不过是愈来愈发觉自己的由的第一条件。——黑格尔 7、纪律是集体的面貌，集体的声音，集体的动作，集体的表情，集体的信念。 ——马卡连柯
8、我们现在必须完全保持党的纪律，否则一切都会陷入污泥中。 ——马克思 9、学校没有纪律便如磨坊没有水。— —夸美纽斯
10、一个人应该：活泼而守纪律，天真而不幼稚，勇敢而鲁莽，倔强而有原则，热情而不冲动，乐观而不盲目。 ——马克思

大学物理基础教程答案1-4力-4-PPT

31
(m2 2 m 2 m1)
T1'
r
Hale Waihona Puke m 1T 2'
T2
m2
m2g
3 T1 2 ma 35(N)
T2 m2(g a) 37.3(N)
12
4-13 一根长为 l 、质量为m的均匀细杆可绕其一端的水平轴O 自由摆动。当被一发质量为m’的子弹在离O点的a处水平方向击
中后，子弹埋入杆内，杆的最大偏转角为，求子弹的初速度。已知 l =1.0米，m =2千克，m’ =20千克，a=0.7米， =60o
v
2 0
2
3
m'2 a2
v0 186(m s1 )
13
4-14 质量为m长为l的匀质细杆，可绕端点O的固定水平轴转动，
把杆抬平后无初速地释放，当杆摆至竖直位置时刚好和光滑水平桌面上的小球相碰。小球的转动不计，它的质量和杆相同，并且
碰撞是完全弹性的，轴上摩擦也忽略不计，求碰后小球的速度v。
解：下摆（定轴转动）能量守恒，
上缀一个质量m2=0.51千克的物体。试计算施在圆盘上的力矩从
静止开始，在2秒之内所作的功和2秒时物体m2的动能。
5
解: mgRdt mgRt L mRv 1 MR2 v
2
R
mgt
v m M 2
R m1
Ek ,m
1 mv2 2
1 mgt 2 m(m M
)2
8.2J
m2
2
RT W 1 I2 1 ( 1 MR2 )( v )2 M( mgt )2 20.2(J)
mg l 1 ( 1 ml 2 )2 2 23
( 1 ml2 ) ( 1 ml2 )'m' vl

《物理学基本教程》课后答案第六章气体动理论

第六章气体动理论6-1 一束分子垂直射向真空室的一平板，设分子束的定向速度为v ，单位体积分子数为n ，分子的质量为m ，求分子与平板碰撞产生的压强．分析器壁单位面积所受的正压力称为气体的压强．由于压强是大量气体分子与器壁碰撞产生的平均效果，所以推导压强公式时，应计算器壁单位面积在单位时间内受到气体分子碰撞的平均冲力．解以面积为S 的平板面为底面，取长度等于分子束定向速度v 的柱体如图6-1所示，单位时间内与平板碰撞的分子都在此柱体内．柱体内的分子数为nSv ．每个分子与平板碰撞时，作用在平板上的冲力为2mv ，单位时间内平板所受到的冲力为v v nS m F ⋅=2根据压强的定义，分子与平板碰撞产生的压强为22v nm SFp ==6-2 一球形容器，直径为2R ，内盛理想气体，分子数密度为n ，每个分子的质量为m ，(1)若某分子速率为v i ，与器壁法向成θ角射向器壁进行完全弹性碰撞，问该分子在连续两次碰撞间运动了多长的距离？(2)该分子每秒钟撞击容器多少次？(3)每一次给予器壁的冲量是多大？(4)由上结果导出气体的压强公式．分析任一时刻容器中气体分子的速率各不相同，运动方向也不相同，由于压强是大量气体分子与器壁碰撞产生的平均效果，气体压强公式的推导过程为：首先任意选取某一速率和运动方向的分子，计算单位时间内它与器壁碰撞给予器壁的冲力，再对容器中所有分子统计求和．v图6-1解 (1)如图6-2所示，速率为v i 的分子以θ角与器壁碰撞，因入射角与反射角都相同，连续两次碰撞间运动的距离都是同样的弦长，为θcos 2R AB =(2)该分子每秒钟撞击容器次数为θcos 2R AB ii v v =(3)每一次撞击给予器壁的冲量为θcos 2i m v(4)该分子每秒钟给予器壁的冲力为Rm R m i i i 2cos 2cos 2v v v =θθ由于结果与该分子的运动方向无关，只与速率有关，因此可得容器中所有分子每秒钟给予器壁的冲量为21212222221v v v v v v v RmN N N R m R m R m R m R m R m N i i N i i N i ===+++++∑∑== 其中n R N 334π=．根据压强的定义，分子与器壁碰撞产生的压强为W n m n nm R R m Np 3221323142222=⎪⎭⎫ ⎝⎛===v v vπ 其中W 为分子的平均平动动能．6-3 容积为10 L 的容器内有1 mol CO 2气体，其方均根速率为1440 km/h ，求CO 2气体的压强（CO 2的摩尔质量为31044-⨯kg/mol ）．分析在常温常压下可以将气体视为理想气体，理想气体压强公式中引入了统计平均量----方均根速率2v 和分子数密度n ，1 mol 的气体中分子数为阿伏图6-2伽德罗常量N A ，根据这些关系可求出压强．解容积为V 的容器中有1 mol CO 2气体，则分子总数为N A ，摩尔质量为M ，则分子数密度为V N A ，分子质量为A N M，因此由气体压强公式得22A A 2313131v v v VM N M V N nm p ===代入数字得Pa 102.35Pa 3600101440101010443131523332⨯=⎪⎪⎭⎫ ⎝⎛⨯⨯⨯⨯⨯==--v V M p 6-4 在实验室中能够获得的最佳真空相当于大约Pa 10013.19-⨯，试问在室温（273K ）下在这样的“真空”中每立方厘米内有多少个分子？分析引入玻尔兹曼常量k 和分子数密度n 后，理想气体状态方程可以表示为nkT p =．解由理想气体状态方程nkT p =得3-113-239m 1069.2m 2731038.110013.1⨯=⨯⨯⨯==--kT p n 6-5 已知气体密度为1 kg/m 3，压强为Pa 10013.15⨯，(1)求气体分子的方均根速率；(2)设气体为氧，求温度．分析气体密度ρ是单位体积中气体的质量，因此与分子数密度n 和分子质量m 的关系为nm =ρ．解压强公式可写为 223131v v ρ==nm p(1)分子的方均根速率m/s 551m/s 110013.13352=⨯⨯==ρpv(2)氧的摩尔质量M =31032-⨯kg/mol ，由定义MRT32=v ，则 K 390K 31.8310325513322=⨯⨯⨯==-R M T v6-6 体积为10-3 m 3，压强为Pa 10013.15⨯的气体，所有分子的平均平动动能的总和是多少？分析气体动理论的能量公式给出了微观量气体分子的平均平动动能和宏观量气体温度之间的关系．分子的平均平动动能是大量分子的统计平均值，是每个分子平均占有的平动动能量值．解由气体动理论的能量公式，分子的平均平动动能为kT m 23212=v 容器中分子数nV N =，又由压强公式nkT p =，可得容器中所有分子的平均平动动能的总和为J152J 1010013.123232321352=⨯⨯⨯===-pV kT nV m Nv6-7 一容器内贮有氧气，其压强为Pa 10013.15⨯=p ，温度T =C 27︒，求(1)单位体积内的分子数；(2)氧气的密度；(3)氧分子的质量；(4)分子间的平均距离；(5)分子的平均平动动能；(6)若容器是边长为0.30 m 的立方体，当一个分子下降的高度等于容壁的边长时，其重力势能改变多少？并将重力势能的改变与其平均平动动能相比较．分析常温和常压下，氧气可视为理想气体．从宏观的角度，可以认为气体是空间均匀分布的，因此分子间的平均距离的立方就是每个分子平均占有的体积．通过本题的计算，可以得到气体动理论中常用到的物理量的量级概念．解 (1) 由理想气体的状态方程nkT p =，可得单位体积内的分子数为3-253-235m 1045.2m 3001038.110013.1⨯=⨯⨯⨯==-kT p n (2) 利用理想气体的状态方程RT MmpV =，氧气的密度为 3335kg/m 3.1kg/m 30031.8103210013.1=⨯⨯⨯⨯===-RT pM V m ρ(3) 氧分子的质量为kg 105.3kg 1045.23.126-25⨯=⨯==nm ρ(4) 分子平均占有的空间开方等于分子间的平均距离m 10443m 1045.21193253.n d -⨯=⨯== (5) 分子的平均平动动能J 10.216J 3001038.123232121-232⨯=⨯⨯⨯==-kT m v(6) 一个氧分子下降的高度等于容壁的边长时，其重力势能改变为J 101.56J 30.08.9103.5-2526⨯=⨯⨯⨯=-mgh与分子平均平动动能相比较，有4252121098.31056.11021.621⨯=⨯⨯=--mgh m v 6-8 在什么温度时，气体分子的平均平动动能等于一个电子由静止通过1 V 电位差的加速作用所得到的动能（即1eV 的能量）．解根据题意，气体分子的平均平动动能J 10260.1eV 12321192-⨯===kT m v 则 K 7739K 1038.1310602.122319=⨯⨯⨯⨯=--T 6-9 1 mol 氢气，在温度C 27︒时，求(1)具有若干平动动能；(2)具有若干转动动能；(3)温度每升高C 1︒时增加的总动能是多少？分析氢气是双原子分子气体，如果作为刚性分子看待，就具有3个平动自由度和2个转动自由度，根据能量按自由度均分原则可以求出平均平动动能和平均转动动能．解 (1) 1 mol 氢气的平动动能为J 10.743J 30031.82323233A⨯=⨯⨯==RT kT N(2) 1 mol 氢气的转动动能为J 10.492J 30031.8223A⨯=⨯==RT kT N(3) 温度每升高C 1︒，1 mol 氢气增加的总动能为J 8.02J 131.8252525A=⨯⨯=∆=∆T R T k N 6-10 1 mol 单原子理想气体和1 mol 双原子理想气体，温度升高C 1︒时，其内能各增加多少？1 g 氧气和1 g 氢气温度升高C 1︒时，其内能各增加多少？分析一定量理想气体的内能T R iM m E ∆=2，对于单原子理想气体3=i ，对于双原子理想气体5=i ，对于1 mol 理想气体1=Mm．氧气和氢气都是双原子气体，氧气的摩尔质量kg/mol 10323-⨯=M ．解 1 mol 单原子理想气体温度升高C 1︒，内能增量为J 5.12J 131.8232=⨯⨯=∆T R i1 mol 双原子理想气体温度升高C 1︒，内能增量为J 8.02J 131.8252=⨯⨯=∆T R i1 g 氧气温度升高C 1︒，内能增量为J 65.0J 131.8251032101233=⨯⨯⨯⨯⨯=∆--T R i M m 1 g 氢气温度升高C 1︒，内能增量为J 4.01J 131.825102101233=⨯⨯⨯⨯⨯=∆⋅--T R i M m 6-11 计算：(1)氧分子在C 0︒时的平均平动动能和平均转动动能；(2)在此温度下，4 g 氧的内能．分析氧气是双原子分子气体，如果作为刚性分子看待，就具有3个平动自由度和2个转动自由度，5=i ．解 (1) 氧分子在C 0︒时的平均平动动能为J 10.655J 2731038.1232321-23⨯=⨯⨯⨯=-kT 平均转动动能为J 10.773J 2731038.12221-23⨯=⨯⨯==-kT kT(2) 4 g 氧在C 0︒时的内能为J 709J 27331.8251032104233=⨯⨯⨯⨯⨯=⋅--RT i M m 6-12 有40个粒子速率分布如下表所示 (其中速率单位为m/s)：速率区间100以下100~200 200~300 300~400 400~500 500~600 600~700 700~800 800~900 900以上粒子数 1 4 6 8 6 5 4 3 2 1若以各区间的中值速率标志处于该区间内的粒子速率值，试求这40个粒子的平均速率v 、方均根速率2v 和最概然速率p v ，并计算出p v 所在区间的粒子数占总粒子数的百分率．分析为了更深入地理解麦克斯韦速率分布律以及气体动理论中引入的平均速率v 、方均根速率2v 和最概然速率p v 的统计意义，有必要通过实际例子，经过计算，体验速率分布规律和统计方法．解这40个粒子分成了10个速率区间，若取1000 m/s 为粒子速率在900 m/s 以上的速率区间的中值速率，则根据定义，其平均速率v 为m/s448.75 m/s )1100028503750465055506450 835062504150150(4011101=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯⨯==∑=i i i N N v v 方均根速率2v 为m/s 499.9 m/s )]1100028503750465055506450 835062504150150(401[121222222222210122=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯⨯==∑=i i i N Nv v 最概然速率m/s 350p =v ．p v 所在区间的粒子数占总粒子数的百分率为%20%100408p =⨯=∆NN 6-13上题所给分布情况，若以200m/s 为间隔作重新统计，列出分布情况表，计算出相应的v 、2v 和p v ，以及p v 所在区间的粒子数占总粒子数的百分率，并与上题结果进行比较．分析通过本题和上题计算结果可以看出，在某一速率区间中的分子数和所计算的三种速率不但与速率区间位置有关，还与速率区间的宽度有关．只有当所统计的分子总数足够大，划分的速率区间足够小时，才可能获得处于平衡状态的气体分子速率的一个确定的分布函数，三种速率也才有确定值．解以200m/s 为间隔对上题粒子速率作重新统计，速率分布情况为(其中速率单位为m/s)：速率区间 200以下 200~400 400~600 600~800 800以上粒子数 5 14 11 7 3这40个粒子分成了5个速率区间，若取900 m/s 为粒子速率在800 m/s 以上的速率区间的中值速率，则根据定义，其平均速率v 为m/s445 m/s)3900770011500143005100(401151=⨯+⨯+⨯+⨯+⨯⨯==∑=i i i N N v v 方均根速率2v 为498m/sm/s )]39007700 11500143005100(401[121222225122=⨯+⨯+⨯+⨯+⨯⨯==∑=i i iN Nvv最概然速率m/s 300p =v ．p v 所在区间的粒子数占总粒子数的百分率为%35%1004014p =⨯=∆NN 6-14 N 个假想的气体分子，速率分布如图6-14所示．(1)用N 和v 0表示出a 的值；(2)求最概然速率p v ；(3)以v 0为间隔等分为三个速率区间求各区间中分子数占总分子数的百分率．分析速率分布函数)(v f 表示气体分子速率在v 值附近单位速率区间内的分子数占总分子数的百分率．本题给出了一个特殊的分布情况，通过计算，理解速率分布函数和最概然速率的物理意义，以及各速率区间中分子数占总分子数的百分率的计算方法．解 (1) 由图6-14可见，分布函数与气体分子总数N 的乘积曲线下的总面积应等于气体分子总数N ，即000302322121d )(0v v v v v v a a a f N =⋅+==⎰则 032v Na =Nf (v )a0 v 0 2 v 0 3 v 0 v图6-14(2) 最概然速率 0p v v =(3) 以v 0为间隔等分为三个速率区间，分子数占总分子数的百分率分别为%3.3331211d )(10010==⋅==⎰v v v v a N f N N N %5021431d )(10220==⋅==⎰v v v v v a N f N N N %7.1661411d )(103230==⋅==⎰v v v v v a N f NN N *6-15在速率区间1v ～2v 内麦克斯韦速率分布曲线下的面积等于分布在此区间内的分子数的百分率．应用(6-17)式和麦克斯韦速率分布函数表示式(6-18)式，求在速率区间v p ～1.01v p 内的气体分子数占总分子数的比率．分析麦克斯韦速率分布律表明，由速率分布函数)(v f 可得气体分子速率在v ～v v ∆+速率区间内的分子数占分子总数的百分率为v v ∆=∆)(f NN．解麦克斯韦速率分布函数22232e24)(v v v kT m kT m f -⎪⎭⎫ ⎝⎛=ππ，因mkT2p =v ，则分布函数可写为1p 2p223p2p22p2e4e4)(----==v v v v v v v v v v ππππf 速率区间v p ～1.01v p 内的气体分子数占总分子数的比率为%83.001.01e 4e4e 4)(1p 2p223p 2p22p2=⨯⨯⨯=∆=∆=∆=∆----πππv v v v v v v v v v v v v f N N *6-16应用平均速率表示式(6-20)*式、麦克斯韦速率分布函数表示式(6-18)式以及积分公式bb 21d e23=-∞⎰v v v 求v 的值．分析这里采用的是数学中加权求某量值的平均值的方法，权重就是麦克斯韦速率分布函数)(v f ．如果要计算方均根速率2v ，可先求速率平方的平均值，只需将积分式中的v 改为2v ，即v v)v v d 022⎰∞=f(，再将积分结果开方．解麦克斯韦速率分布函数表示式(6-18)式和平均速率表示式(6-20)*式给出v v v v)v v v d e24d 0322302⎰⎰∞-∞⎪⎭⎫⎝⎛==kTm kT m f(ππ利用积分公式bb 21d e 23=-∞⎰v v v 得 mkTkT m kT m f(πππ822124d 2230=⎪⎭⎫ ⎝⎛⎪⎭⎫⎝⎛==⎰∞v v)v v *6-17 试由麦克斯韦速率分布律推出相应的平动动能分布律，并求出最概然能量E p ，它是否就等于2p 21v m ．分析要找出分子按平动动能的分布规律，即求出分布在平动动能区间E k ～E k +d E k 中的分子数占总分子数的百分率．解速率为v 的分子的平动动能为E k = 221v m ，则v v d d k m E =，麦克斯韦速率分布律可改写为kk k k 232212232223d )(d e12 d e 2112 d e 24d )(d k 22E E f E E kT m m kT kT m f N N kTE kT m kT m =⎪⎭⎫ ⎝⎛=⋅⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛==---ππππv v v v v v v v v即分子按平动动能分布律，其中分布函数kTE E kT E f k e12)(k 23k -⎪⎭⎫⎝⎛=π参考最概然速率的定义，令0d )(d kk =E E f ，由上式得最概然动能 kT E 21k p =因m kT 2p =v ，则 k p 2p 221E kT m ==v 6-18 飞机起飞前机舱中的压强计指示为Pa 10013.15⨯，温度为C 27︒．起飞后压强计指示为Pa 1010.84⨯，温度仍为C 27︒．试计算飞机此时距地面的高度．解根据玻尔兹曼分子数密度按高度分布公式kT mgh n n /0e -=和压强公式nkT p =，在高度1h 和2h 的压强分别为1p 和2p ，则有kT h h mg p p /)(2121e --=得m 100.2m 1010.810013.1ln 8.9102930031.8 ln ln 3453212112⨯=⨯⨯⨯⨯⨯⨯==+=-p p Mg RTp p mg kT h h6-19 设地球大气是等温的，温度为C 17︒，海平面上的气压为Pa 100.150⨯=p ，已知某地的海拔高度为h = 2000 m ，空气的摩尔质量kg/m ol 10293-⨯=M ，求该地的气压值．解根据玻尔兹曼分子数密度按高度分布公式kT mgh n n /0e -=和理想气体状态方程nkT p =，在高度h 处的压强p 为Pa 107.90Pa e100.1e 429031.820008.910295/03⨯=⨯⨯==⨯⨯⨯⨯---RT Mgh p p6-20 在某一粒子加速器中，质子在Pa 10333.14-⨯的压强和273 K 的温度的真空室内沿圆形轨道运动．(1)估计在此压强下每立方厘米内的气体分子数；(2)如果分子有效直径为2.0×10-8 cm ．则在此条件下气体分子的平均自由程为多大？分析由理想气体状态方程nkT p =可得压强和分子数密度的关系，并由此可计算平均自由程．解 (1) 由理想气体状态方程可得3103163234cm 1054.3m 1054.3m 2731038.110333.1----⨯=⨯=⨯⨯⨯==-kT p n (2) 由定义，平均自由程为cm 101.59m )102(1054.32121428102⨯=⨯⨯⨯⨯⨯==-ππλnd6-21设电子管内温度为300 K ，如果要管内分子的平均自由程大于10 cm时，则应将它抽到多大压强？（分子有效直径约为3.0×10-8 cm ）．分析由平均自由程定义和理想气体状态方程可建立压强与平均自由程以及温度之间的关系．解由平均自由程定义221ndπλ=和理想气体状态方程nkT p =，得Pa 0.1035Pa 1.0)103(23001038.12210232=⨯⨯⨯⨯⨯==--πλπd kT p6-22 计算：(1)在标准状态下，一个氮分子在1 s 内与其它分子的平均碰撞次数；(2)容积为4 L 的容器，贮有标准状况下的氮气，求1 s 内氮分子间的总碰撞次数．（氮分子的有效直径为3.76×10-8 cm ．）解 (1) 因平均速率MRTπ8=v ，标准状态下22.4 L 中的分子数为A N ，则平均碰撞次数1-91-32321033-A 22s 1067.7 s 104.2210023.6)1076.3(102827331.816 1022.4162⨯=⨯⨯⨯⨯⨯⨯⨯⨯=⨯==---πππN d M RT n d Z v(2) 4 L 氮的分子数N =A 4.224N ，分子间的总碰撞次数为1321923s 10125.4s 1067.710023.64.2242121-⨯=⨯⨯⨯⨯⨯=-Z N 6-23 假设氦气分子的有效直径为10-10 m ，压强为Pa 10013.15⨯，温度为300 K ，(1)计算氦气分子的平均自由程λ和飞行一个平均自由程所需要的时间τ；(2)如果有一个带基本电荷的氦离子在垂直于电场的方向上运动，电场强度为104 V/m ，试计算氦离子在电场中飞行τ时间内沿电场方向移动的距离s 及s 与λ的比值；(3)气体分子热运动的平均速率与氦离子在电场方向的平均速率的比值；(4)气体分子热运动的平均平动动能与氦离子在电场中飞行一个λ远的距离所获得的能量和它们的比值．解 (1) 由平均自由程定义221ndπλ=和理想气体状态方程nkT p =，得m 1029m 10013.1)10(23001038.1275210232-.pd kT ⨯=⨯⨯⨯⨯⨯==--ππλ 平均速率 m/s 1260m/s 10430031.8883=⨯⨯⨯⨯==-ππM RT v 则 s 107.3s 1260102.910-7⨯=⨯==-v λτ (2) 氦离子质量为A N M m =，沿电场方向受到的电场力为eE ，加速度meE a =，在τ时间内沿电场方向移动的距离为m 106.4m 1042103.710023.610106.1 2218-310234192A 2⨯=⨯⨯⨯⨯⨯⨯⨯⨯===---M eEN a s ττ 14.4104.6102.987=⨯⨯=--s λ(3) 氦离子沿电场方向的平均速率为m/s 87.7m/s 103.7104.6108E =⨯⨯==--τsv 14.4E==s λv v(4) 氦气分子平均平动动能为J 106.21J 3001038.1232321-23⨯=⨯⨯⨯=-kT 氦离子在电场中飞行一个λ远的距离所获得的能量为J 101.472J 102.910106.1-217419⨯=⨯⨯⨯⨯=--λeE二者之比为 22.410472.11021.62121=⨯⨯-- *6-24用范德瓦耳斯方程计算压强为Pa 10013.18⨯，体积为0.050 L 的1 mol氧气的温度，如果用理想气体状态方程计算，将引起怎样的相对误差？已知氧的范德瓦耳斯常数为：225/mol L Pa 10378.1⋅⨯=a ；L/mol 0318.0=b ．解由范德瓦耳斯方程得K 342.6K 10)0318.0050.0(050.010378.110013.131.81 )(13258020=⨯-⨯⎪⎪⎭⎫ ⎝⎛⨯+⨯⨯=-⎪⎪⎭⎫⎝⎛+=-b V V a p R T由理想气体状态方程得K .5609K 31.810050.010013.138=⨯⨯⨯==-R pV T相对误差为%7878.06.3426.3425.609==-*6-25在C 27︒时，2 mol 氮气的体积为0.1 L ，分别用范德瓦耳斯方程及理想气体状态方程计算其压强，并比较结果．已知氮气224/mol L Pa 1039.8⋅⨯=a ，L/mol 1005.32-⨯=b ．解范德瓦耳斯方程)(222RT M m b V V a M m p =-⎪⎪⎭⎫ ⎝⎛+，得Pa 109.43Pa 101039.82Pa 1005.321030031.82 782254222⨯=⨯⨯-⨯⨯-⨯⨯=--=----V a M m bMm V RTM m p 由理想气体状态方程得Pa 104.99Pa 1030031.8274⨯=⨯⨯==-V RT M m p 结果表明由理想气体状态方程计算出的压强小于由范德瓦耳斯方程的计算值．*6-26实验测知C 0︒时氧的粘滞系数1.92×10-4 s)g/(cm ⋅，试用它来求标准状态下氧分子的平均自由程和分子的有效直径．解粘滞系数 v λρη31= 其中密度Vm=ρ．又由理想气体状态方程 RT Mm pV =平均速率MRTπ8=v ，联立可得m109.49 m 1032827331.810013.11092.138338-355⨯=⨯⨯⨯⨯⨯⨯⨯⨯===--ππηρηλM RT p v 分子的有效直径为m 102.97m 1049.910013.122731038.1 210-8523⨯=⨯⨯⨯⨯⨯⨯⨯==--πλπp kT d*6-27实验测知氮气C 0︒时热传导系数为23.7×10-3 W/(m ·K)，定体摩尔热容为20.9 J/(mol ·K)，试由此计算氮分子的有效直径．解热传导系数 λρκv MC mV,31=其中密度A N nM =ρ，平均速率MRTπ8=v ，平均自由程221nd πλ=，则2Am V,132dM RT N C ππκ=m 102.23m 1102827331.810023.6107.2339.202 13210-4343233434Am V,⨯=⨯⨯⋅⨯⨯⨯⨯⨯=⋅=--ππκM RT N C d。

[优选]人教版高中物理教材《分子动理论》PPT讲练课件

【（名校师课整堂理】课获本奖专P题PT）-［人人教教版版高］中高物中理物教理材教《材分《子动分理子论动理》论PPT》讲P P练T课上件课课pp件t优（质最说新课版稿本（）精推选荐）
【（名校师课整堂理】课获本奖专P题PT）-［人人教教版版高］中高物中理物教理材教《材分《子动分理子论动理》论PPT》讲P P练T课上件课课pp件t优（质最说新课版稿本（）精推选荐）
来完成。 2.布朗运动 (1)概念:19世纪初,一些人观察到,悬浮在液体中的小颗粒总在⑩ 不停地运动。 1827年,英国植物学家布朗首先在显微镜下研究了这种运动。后人把悬浮
（名师整理课本专题）人教版高中物理教材《分子动理论》PPT讲练课件 ppt优质说课稿（精选）
第1讲描述运动的基本概念
（名师整理课本专题）人教版高中物理教材《分子动理论》PPT讲练课件 ppt优质说课稿（精选）
【（名校师课整堂理】课获本奖专P题PT）-［人人教教版版高］中高物中理物教理材教《材分《子动分理子论动理》论PPT》讲P P练T课上件课课pp件t优（质最说新课版稿本（）精推选荐）
（名师整理课本专题）人教版高中物理教材《分子动理论》PPT讲练课件 ppt优质说课稿（精选）
（名师整理课本专题）人教版高中物理教材《分子动理论》PPT讲练课件 ppt优质说课稿（精选）
第1讲描述运动的基本概念
3 | 分子间的作用力 1.分子间有空隙 (1)气体:气体很容易被压缩,说明气体分子之间存在着很大的空隙。 (2)液体:水和酒精混合后总体积变小了,这表明液体分子间存在着空隙。 (3)固体:压在一起的金块和铅块,各自的分子能扩散到对方的内部,说明固体分子之间也存在着空隙。 2.分子之间存在着相互作用力 (1)分子间有空隙,大量分子却能聚集在一起,这说明分子之间存在着相互作用力。 (2)当用力拉伸物体时,物体内各部分之间要产生反抗拉伸的作用力,此时分子间的作用力表现为引力。 (3)当用力压缩物体时,物体各部分之间会产生反抗压缩的作用力,此时分子间的作用力表现为斥力。

理论物理基础CHAPTER6ppt课件

（2）不均匀介质或由多种不同结构物质混合而成的介质被极化，或者电介质非均匀极化时，在电介质表面和内部均出现极化电荷,称为极化体电荷和极化面电荷.
（3）在两种不同均匀介质交界面上的
一个很薄的层内，由于两种物质的极
化强度不同，存在极化面电荷分布密
n
度:
P n(P 2P 1)
N是界面的发向矢量，从介质1指向介质. 2
§4 介质的电磁性质
一、介质的极化和磁化
介质：介质由分子组成，分子内部有带正电的原子核及核外电子，内部存在不规则而迅变的微观电磁场。因我们仅讨论宏观电磁场，用介质内大量分子的小体元内的平均值表示的物理量称为宏观物理量（小体元在宏观上无限小，在微观上无限大）。
.
§4 介质的电磁性质
一、介质的极化和磁化
所以
p
•P .
二、介质存在时电场的散度和旋度d q S n p d S P d S
P P S
可见，极化电荷的体密度是由电极化矢量P的散度决定的，只有在极化不均匀的地方，才可能出现 P
.
（1）均匀电介质,其极化电荷只集中在表面层里,或在两种不同的介面层里.线性均匀介质中，极化迁出的电荷与迁入的电荷相等，不出现极化电荷分布。
D0EP
(0EP )f
E B t
电场的旋度方程
D
电场的散度方程
.
三、介质存在时磁场的散度和旋度方程
1、磁化强度
M
limmi
V0 V
分子电流是指分子中电子绕原子
核的运动，它相当于一个电流为i
面积为a的小电流圈，形成一个
小磁矩m=ia，电流圈上面是N极，
下面是S极。当没有外加磁场时，
热运动使各个分子电流的磁矩杂

理论物理基础教程答案

理论物理基础教程答案【篇一：物理学教程(第二版)上册课后答案7】7 －1 处于平衡状态的一瓶氦气和一瓶氮气的分子数密度相同，分子的平均平动动能也相同，则它们( )(a) 温度，压强均不相同 (b) 温度相同，但氦气压强大于氮气的压强(c) 温度，压强都相同(d) 温度相同，但氦气压强小于氮气的压强分析与解理想气体分子的平均平动动能k?3kt/2，仅与温度有关．因此当氦气和氮气的平均平动动能相同时，温度也相同．又由物态方程p?nkt，当两者分子数密度n 相同时，它们压强也相同．故选(c)．7－2 三个容器a、b、c 中装有同种理想气体，其分子数密度n相同，方均根速率之比?:??:??21/2a21/2b21/2c?1:2:4，则其压强之比pa:pb:pc为( )(a) 1∶2∶4 (b) 1∶4∶8 (c) 1∶4∶16 (d) 4∶2∶1 分析与解分子的方均根速率为2?3rt/m，因此对同种理想气体有同时，得p1:p2:p3?t1:t2:t3?1:4:16.故选(c)．7－3 在一个体积不变的容器中，储有一定量的某种理想气体，温度为t0时，气体分子的平均速率为0，分子平均碰撞次数为0，平均自由程为0，当气体温度升高为4t0时，气体分子的平均速率、平均碰撞频率和平均自由程分别为( ) (a) ?40,?40,?40 (b) ?20,?20,?0 (c)?20,?20,?40 (d)?40,?20,?0碰撞频率变为20；而平均自由程?1，n不变，则?也不变．因此正确答案为(b)． 27－4 图示两条曲线分别表示在相同温度下氧气和氢气分子的速率分布曲线.如果(vp)o2和(vp)h2分别表示氧气和氢气的最概然速率，则( )(a) 图中a表示氧气分子的速率分布曲线且(vp)o(vp)h(vp)o(vp)h(vp)o(vp)h(vp)o(vp)h2?4 ?1 41 42(b) 图中a表示氧气分子的速率分布曲线且22(c) 图中b表示氧气分子的速率分布曲线且2?2(d) 图中b表示氧气分子的速率分布曲线且2?42分析与解由vp?2rt可知，在相同温度下，由于不同气体的摩尔质量不同，它们的m 最概然速率vp也就不同.因mh2?mo，故氧气比氢气的vp要小，由此可判定图中曲线a2应是对应于氧气分子的速率分布曲线.又因(b)．mhmo2?2(vp)o1?，所以16(vp)h22mhmo2?21.故选4题 7-4 图7－5 有一个体积为1.0?105m3的空气泡由水面下50.0m深的湖底处(温度为4.0oc)升到湖面上来．若湖面的温度为17.0oc，求气泡到达湖面的体积．(取大气压强为p0?1.013?105pa)分析将气泡看成是一定量的理想气体，它位于湖底和上升至湖面代表两个不同的平衡状态．利用理想气体物态方程即可求解本题．位于湖底时，气泡内的压强可用公式解设气泡在湖底和湖面的状态参量分别为(p1，v1，t1 )和(p2 ,v2，t2 )．由分析知湖底处压p1v1p2v2?t1t2可得空气泡到达湖面的体积为v2?p1t2v1?p0??gh?t2v1??6.11?10?5m3 p2t1p0t17－6 一容器内储有氧气，其压强为1.01?105pa，温度为27 ℃，求：(1)气体分子的数密度；(2) 氧气的密度；(3) 分子的平均平动动能；(4) 分子间的平均距离．(设分子间均匀等距排列)分析在题中压强和温度的条件下，氧气可视为理想气体．因此，可由理想气体的物态方程、密度的定义以及分子的平均平动动能与温度的关系等求解．又因可将分子看成是均匀等距排列的，故每个分子占有的体积为v0?3，由数密度的含意可知v0?1/n，即可求出．解 (1) 单位体积分子数n?(2) 氧气的密度p?2.44?1025m3 kt??m/v?(3) 氧气分子的平均平动动能pm?1.30kg?m-3 rtk?3kt/2?6.21?10?21j(4) 氧气分子的平均距离?/n?3.45?10?9m通过对本题的求解，我们可以对通常状态下理想气体的分子数密度、平均平动动能、分子间平均距离等物理量的数量级有所了解．分析理想气体的温度是由分子的平均平动动能决定的，即k?3kt/2．因此，根据题中m?给出的条件，通过物态方程pv ＝rt，求出容器内氢气的温度即可得k．m解由分析知氢气的温度t?mpv，则氢气分子的平均平动动能为 mr323pvmk?3.89?10?22j2m?rk?kt?分析将组成恒星的大量质子视为理想气体，质子可作为质点，其自由度i＝3，因此，质子的平均动能就等于平均平动动能.此外，由平均平动动能与温度的关系m/2?3kt/2，可得方均根速率2.解 (1) 由分析可得质子的平均动能为2k?2/2?3kt/2?2.07?10?15j(2) 质子的方均根速率为2?63kt?1.58?106m?s-1 m3kt?9.5?106m?s?1 me平均动能k?3kt/2?4.1?10?17j222mirt，对刚性双原子分子而言，i＝5.由上述内能m2公式和理想气体物态方程pv ＝?rt可解出气体的压强.(2)求得压强后，再依据题给数据可求得分子数密度，则由公式p＝nkt可求气体温度.气体分子的平均平动动能可由k?3kt/2求出.i解 (1) 由e??rt和pv＝?rt可得气体压强2p?2e?1.35?105pa iv(2) 分子数密度n ＝n/v，则该气体的温度t?p/?nk??pv/?nk??3.62?102k气体分子的平均平动动能为k?3kt/2?7.49?10?21j7－11 当温度为0?c时，可将气体分子视为刚性分子，求在此温度下：（1）氧分子的平?3均动能和平均转动动能；（2）4.0?10能.kg氧气的内能；（3）4.0?10?3kg氦气的内分析（1）由题意，氧分子为刚性双原子分子，则其共有5个自由度，其中包括3个平动自由3度和2个转动自由度.根据能量均分定理，平均平动动能kt?kt，平均转动动能2kr?kt?kt.（2）对一定量理想气体，其内能为e?22m?irt，它是温度的单值函m2数.其中i为分子自由度，这里氧气i=5、氦气i=3.而m?为气体质量，m为气体摩尔质量，其中氧气m的内能.解根据分析当气体温度为t=273 k时，可得（1）氧分子的平均平动动能为?32?10?3kg?mol?1；氦气m?4.0?10?3kg?mol?1.代入数据即可求解它们kt?kt?5.7?10?21j氧分子的平均转动动能为32kr?kt?3.8?10?21j（2）氧气的内能为22【篇二：物理实验习题答案(第二版教材)(1)】什么是基本单位和导出单位? 2。

理论物理基础教程刘连寿第五篇第一章答案

+ * *
PDF 文件使用 "pdfFactory" 试用版本创建
ˆ+F ˆ + ]vdτ = v[( F ˆ + )u ]* d τ ， F ˆ +F ˆ + 是厄米算符。所以 ∫ u * [ F ∫ ˆ +F
* ˆ −F ˆ + )]vdτ 同理， ∫ u [i( F + * ˆ ˆvdτ − i u * F ˆ u ) * dτ = i∫ u * F vdτ − i ∫ v( F ∫ ˆ vdτ = i ∫ u F
Axe − λx = ∫ c ( p x )ψ p x dp x
x
( x) =
1 e ipx x / h 2πh
其中
v c ( p x ) = ∫ψ ψ ( x)d r =
* px 3
∫ (e 2πh
0
1
∞
ip x x / h *
) Axe −λx dx
= =
A xe −( λx +ipx x / h ) dx ∫ 2πh 0 h [− xe − ( λ +ip x / h ) x 2πh λh + ip x x
P305
1. 计算下列各种频率的谐振子的能量子： (a)υ = 50HZ 的带电谐振子； (b)υ = 1010 HZ 的微波； (c)υ = 1015 HZ 的光波，进而指出为什么普通振子的能量不显分立性。答：(a)
hυ = 6.63 *10 −34 J ⋅ S * 50 HZ = 3.31 * 10 −32 J
因为在 z → ±∞ 时， u ， v 都趋于 0，所以第一项和第三项都为 0，所以，上式变为
PDF 文件使用 "pdfFactory" 试用版本创建

2 理论物理导论-第一章2

m2g
y1
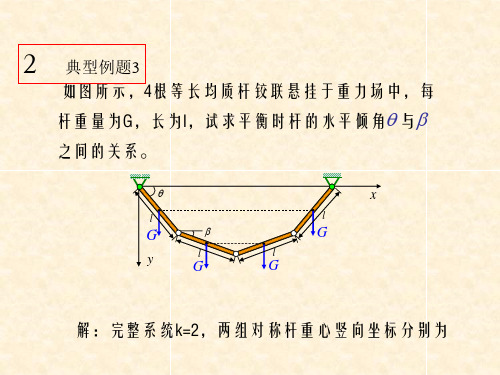
3、应用动力学普遍方程
FIA δxA FIB δxB m1 g δy A m1 g δyB m2 g δyC 0
O1 rA FIA m1g l
C
x1

l l
A
x A l cos y A l sin xB l cos yB l sin yC 2l sin
x
解：自由度 k 2 ，选x和θ为广义坐标。
m A r
30
vA
m
l
C
L T V

3 2 1 2 l 2 l m x ( θ) 2 x θ sin θ mx 4 2 2 2 1 ml 2 1 mgl sin θ 2 12 2
2
典型例题3 如图所示，4根等长均质杆铰联悬挂于重力场中，每
杆重量为G，长为l，试求平衡时杆的水平倾角与之间的关系。

x
l

l
G
y
G G
l
G
l
解：完整系统k=2，两组对称杆重心竖向坐标分别为
l l y1 sin , y2 l sin sin 2 2
给对称虚位移:

y1
x
1 2 l 2 V kl (1 cos ) mg cos 2 2
dV 由 0 ，有 dθ
k
A

mg [kl (1 cos ) ]sin 0 2 故 0， 1
mg
B
再由
mg 2 arccos(1 ) 53.8 2kl d2 V mg 2 2 kl (cos cos sin ) cos 2 d 2