两个数的最大公因数是60,最小公倍数是720,这两个数是多
五年级数学思维训练 因数与倍数

五年级数学思维训练因数与倍数(最小公倍数与最大公因数二)姓名突破重难点最小公倍数与最大公因数之间的关系。
1、两个自然数分别除以它们的最大公因数,所得的商互质。
2、两个数的最小公倍数与最大公因数之积等于这两个数的乘积。
3、两个数的公因数一定是这两个数的最大公因数的因数。
例题精选例1、两个数的最大公因数是4,最小公倍数是252,其中一个数是28,另一个数是多少?例2、两个自然数的和是50,它们的最大公因数是5,求这两个数的差。
例3、两个数的最大公因数为21,最小公倍数为126,求这两个数的和。
例4、两个自然数的和是54,它们的最小公倍数与最大公因数的差是114,求这两个自然数。
加强训练1、某数与24的最大公因数是4,最小公倍数是168,这个数是多少?2、两个自然数的和是56,它们的和是56,它们的最大公因数是7,求这两个数。
3、两个自然数的最大公因数是7,最小公倍数是210,这两个数的和是77。
求这两个数。
4、两个自然数的差是30,它们的最小公倍数与最大公因数的差是450,求这两个数。
5、两个数的最大公因数是60,最小公倍数是720,其中的一个数是180,另一个数是多少?6、已知两个自然数的和为165,它们的最大公因数是15,求这两个数。
7、两个不同自然数的和是60,它们的最大公因数与最小公倍数的和也是60,满足条件的自然数共有多少组?8、已知a与b,a与c的最大公因数分别是12和15,a,b,c的最小公倍数是120,求a,b,c。
9、两个自然数的差是3,它们的最大公因数与最小公倍数的积是180,求这两个数。
10、已知a与b,a,与c,b与c的最小公倍数分别是60,90和36。
问:满足此条件的a,b,c有多少组?。
五年下思维训练题

第二单元思维提升一、猜电话号码刘老师在家的电话号码是:0752---ABCDEFG。
已知:A是8的最小倍数,B是最小的自然数,C是9的最大因数,D既是3的因数又是3的倍数,E它的所有因数是1/2/4,F的所有因数是1、7,G它只有一个因数。
请问电话号码是多少?二、503班的学生人数既是2的倍数,又是3的倍数,同时又有因数5,且不超过50人。
该班一共有多少人?三、一只游船来回往返东西两岸之间。
如果小船第一次从东岸到西岸,第二次从西岸返回东岸,第三次从东岸到西岸,第四次从西岸返回东岸…,当游船第49次航行后,它在东岸还是西岸?第100次呢?第一讲:最大公因数一、用短除法求下面各组数的最大公因数3和21 18和19 25和40 48和28二、判断。
1、两个数的公因数的个数是有限的。
( )2、1和任意非0自然数的最大公因数是1. ( )3、最小质数和最小合数的最大公因数是1 。
( )4、两个合数的最大公因数不能是1. ( )三、填空使他们最大公因数为1。
1、两个数都是合数:()和()2、两个数都是奇数:()和()3、一个偶数和一个奇数:()和()思维训练[思维点] 运用辗转相除法求两个数的最大公因数。
例题:求9021和9991的最大公因数。
配套练习:一、选择1、如果a×b=32,那么a和32的最大公因数是()A:aB:bC:322、如果A=2×3×7,B=2×3×5,那么AB的最大公因数是()A:2B:35C:6二、求8251和6105的最大公因数。
第二课时:求最大公因数的实际运用基础知识:一:把一块长是18分米,宽是12分米的长方形铁皮剪成若干同样大小的小正方形,怎样剪才能使得到的小正方形最大,又不会浪费材料?二:用48朵兰花和36朵菊花搭配成同样的花束(正好用完,没有剩余),最多扎多少束?三、五(1)班有男生15人,女生20人,把他们分成若干劳动小组。
第五讲 最大公因数与最小公倍数

第五讲最大公因数与最小公倍数学法探讨大家知道我们在研究因数和倍数时,0是一个特殊的数;O不是任何自然数的因数(除数不能为O),但0是任何非0自然数的倍数(任何非0自然数的O倍等于0)在本讲中我们只讨论正整数。
几个数公有的因数叫做这几个数的公因数,其中最大的一个,叫做这几个数的最大公因数。
为了书写简便,a、b两数的最大公因数记为(a,b)。
几个数公有的倍数叫做这几个数的公倍数,其中最小的一个,叫做这几个数的最小公倍数,为了书写简便,a、b两数的最小公倍数记为[a,b]。
最大公因数与最小公倍数有以下重要性质:1.两个数的公因数都是它们的最大公因数的因数;2.两个数的公倍数都是它们的最小公倍数的倍数;3.两个数的积,等于它们的最大公因数与最小公倍数的积;即a×b=(a,b)×[a,b]4.两个自然数分别除以它们的最大公因数,所得的商为互质数。
关于“最大公因数和最小公倍数”你还有什么需要补充?请你写在下面:例题选讲【例题1】育才小学拿出一块长方体木料,长180厘米,宽144厘米,高108厘米,请王师傅把它锯成棱长是整厘米数,大小相同的正方体木块,木块的体积要最大,木料又不能剩余,算一算,可以锯成多少块?【分析】要把长方体木料锯成棱长是整厘米数,大小相同的正方体木块,则正方体的棱长应是长方体的长、宽、高的公因数,又要求每小块正方体的体积最大,因此锯成的正方体的棱长必须是长方体的长、宽、高的最大公因数,由此便可得出问题的解答。
【解答】【练习5-1】把一张长60厘米、宽48厘米的长方形纸,裁成若干面积相等边长为整厘米数的小正方形而没有剩余,小正方形的面积最大是多少?【例题2】有一个班的同学去划船,他们算了一下,如果增加一条船,正好每船坐6人,如果减少一条船,正好每船坐9人,这个班有多少人?(第二届全国“华罗庚金杯”少年数学邀请赛初赛试题) 【分析】根据题意,这个班的人数应是6的倍数,又是9的倍数,从而是6和9的公倍数,故只要在6和9的公倍数中寻找符合条件的解,便能得到问题的解答。
苏教版五年级数学下册公倍数、公因数相关知识点

11
【练习】
3、两个数的最大公因数是18,最小公倍数是180,两个数的差是54, 求这两个数的和。
可设这两个数为18a和18b(a和b互质) 18ab=180 ab=10 a=1,b=10或a=2,b=5 当a=1,b=10时,这两个数是18和180,不符合题意 当a=2,b=5时,这两个数是36和90,符合差是54,和为,126
8
【例题】
例1 两个数的最大公因数为21,最小公倍数为126,求这两个数的和。
可设这两个数为21a和21b(a和b互质) 21ab=126 ab=6 a=1,b=6或a=2,b=3 当a=1,b=6时,这两个数是21和126,和是147 当a=2,b=3时,这两个数是42和69,和是111
9
【练习】
5
例1 两个自然数的和是50,它们的最大公因数是5,求这两个数的差
可设这两个数为5a和5b(a和b互质) 5a+5b=50 a+b=10 a=1,b=9或a=3,b=7 当a=1,b=9时,这两个数是5和45,差是40 当a=3,b=7时,这两个数是15和35,差是20
6
【练习】
1.两个自然数的和是56,它们的最大公因数是7,求这两个数。
3
【练习】
3.甲数和乙数的最大公因数是6,最小公倍数是90,且小数不能整除大
数,求这两个数。
因为小数不能整除大数,因此这两个数不可能是6和90
可设这两个数为6a和6b
6a×6b=540
ab=15
a和b互质
所以a=3,b=5符合题意
五下__第二单元因数和倍数能力提高题和奥数题(附答案)

五下__第⼆单元因数和倍数能⼒提⾼题和奥数题(附答案)第⼆单元因数与倍数提⾼题和奥数题板块⼀因数和倍数例题1.⼀个数在150⾄250之间,且是18的倍数,这个数可能是多少?最⼤是多少?练习1.⼀个数是25的倍数,它位于110⾄160之间,这个数是多少?例题2.有⼀个数,它是40的因数,⼜是5的倍数,这个数可能是多少?练习2.既是7的倍数,⼜是42的因数,这样的数有哪些?例题3.妈妈买来30个苹果,让⼩明把苹果放⼊篮⼦⾥。
不许⼀次拿完,也不许⼀个⼀个地拿,要每次拿的个数相同,拿到最后正好⼀个不剩。
⼩明共有⼏种拿法?每种拿法每次各拿多少个?练习3.五(1)班有学⽣42⼈,把他们平均分成⼏个学习⼩组,每组多于2⼈且少于8⼈。
可以分成⼏个⼩组呢?板块⼆ 2、5、3的倍数的特征例题1.⼀个五位数29ABC(A、B、C是0~9中不同的数字)同时是2、5、3的倍数,这个数可能是多少?练习1.在17的后⾯添上三个数字组成五位数,使这个五位数既是偶数,⼜同时含有因数3和5。
这个五位数最⼤是多少?最⼩是多少?例题2.5□□0是有两个数字相同的四位数,它同时是2、5、3的倍数,这个四位数最⼩是多少?最⼤是多少?练习2.4□□□是有两个数字相同的四位数,它同时是2、5、3的倍数,这个四位数最⼩是多少?最⼤是多少?板块三奇数和偶数例题1.⼀只⼩船每天从河的南岸摆渡到北岸,再从北岸摆渡到南岸,不断往返。
已知⼩船最初在南岸。
(1)摆渡15次后,⼩船是在南岸还是在北岸?为什么?(2)⼩明说摆渡2016次后,⼩船在北岸。
他说得对吗?为什么?练习1.傍晚⼩亮开灯做作业,本来拉⼀次开关,灯就该亮了,但是他连续拉了5次开关,灯都没有亮,原来是停电了。
你知道来电的时候,灯应该亮着还是不亮呢?例题2.有36个苹果,把它们放在9个盘⼦⾥,每个盘⼦⾥只放奇数个苹果,能做到吗?练习2.(1)1×2+3×4+5×6+…+199×200的和是奇数还是偶数?(2)有2016个烟花,每次燃放奇数个,想在9次后恰好全部放完,能做到吗?为什么?例题3.桌⼦上放着5个杯⼦,全部是杯底朝上,如果每次翻动2个杯⼦,称为⼀次翻动,经过多次翻动能使5个杯⼦的杯⼝全部朝上吗?如果每次翻动3个杯⼦呢?练习3.如家宾馆现在有10间客房的灯开着,每次同时拨动4个房间的开关,能不能把这10个房间的灯全部关闭?如果能,⾄少需要⼏次?板块四质数和合数例题1.三个不同质数的和是82,这三个质数的积最⼤是多少?练习1.(1)两个质数的和是⼩于100的奇数,并且是11的倍数,这两个质数可能是什么数?(2)两个质数的和是2001,这两个质数的积是多少?(3)⼀个长⽅形的长和宽都是质数,并且周长是36厘⽶,这个长⽅形的⾯积最⼤是多少?例题2.⽤0、1、4、5这四个数字组成两个质数,每个数字只能⽤⼀次,求这两个质数。
最小公倍数(一)教师版

最小公倍数(一)几个数公有的倍数叫做这几个数的公倍数,其中最小的一个公倍数,叫做这几个数的最小公倍数。
自然数a、b的最小公倍数可以记作[a、b],当(a、b)=1时,[a、b]= a×b。
两个数的最大公约数和最小公倍数有着下列关系:最大公约数×最小公倍数=两数的乘积,即(a、b)×[a、b]= a×b要解答求最小公倍数的问题,关键要根据题目中的已知条件,对问题作全面的分析,若要求的数对已知条件来说,是处于被除数的地位,通过就是求最小公倍数,解题时要避免和最大公约数问题混淆。
二、精讲精练【例题1】两个数的最大公约数是15,最小公倍数是90,求这两个数分别是多少?【思路导航】根据“两个数的最大公约数与最小公倍数的乘积等于这两个数的乘积”可先求出这两个数的乘积,再把这个积分解成两个数。
根据题意:当a1b1分别是1和6时,a、b分别为15×1=15,15×6=90;当a1b1分别是2和3时,a、b分别为15×2=20,15×3=45。
所以,这两个数是15和90或者30和45。
【练习1】1,两个数的最大公约数是9,最小公倍数是90,求这两个数分别是多少?90÷9=10=1×10=2×5这两个数分别为9×1=9和9×10=90或者9×2=18和9×5=452,两个数的最大公约数是12,最小公倍数是60,求这两个数的和是多少?60÷12=5=5×1这两个数分别为12×1=12和5×12=60,它们的和为12+60=723,两个自然数的和是52.它们的最大公约数是4,最小公倍数是144。
这两个数各是多少?144÷4=36=1×36=2×13=3×12=4×9=6×6因为两个自然数的和是52,而52÷4=13,所以取144÷4=36=4×9,这两个自然数为4×4=16和4×9=364,两个数的最大公约数是60,最小公倍数是720,其中一个数是180,另一个数是多少?60分解质因数是:60=2*2*3*5把180分解质因数是:180=2*2*3*3*5=(2*2*3*5)*3720分解质因数是:720=2*2*2*2*3*3*5=(2*2*3*5)*(2*2*3)所以,另外一个数是:2*2*60=240这两个数的差是:240-180=60【例题2】两个自然数的积是360,最小公倍数是120,这两个数各是多少?【思路导航】我们把这两个自然数称为甲数和乙数。
最大公因数小学奥数题100道及答案(完整版)

最大公因数小学奥数题100道及答案(完整版)题目1:求18 和24 的最大公因数。
答案:6。
通过分解质因数,18 = 2×3×3,24 = 2×2×2×3,所以最大公因数是2×3 = 6。
题目2:求30 和45 的最大公因数。
答案:15。
30 = 2×3×5,45 = 3×3×5,最大公因数是3×5 = 15。
题目3:已知两个数的积是120,它们的最大公因数是6,求这两个数。
答案:12 和10。
因为最大公因数是6,设这两个数分别为6a 和6b(a、b 互质),则6a ×6b = 120,ab = 10,所以a = 2,b = 5 或 a = 5,b = 2,这两个数为12 和10。
题目4:求48 和64 的最大公因数。
答案:16。
48 = 2×2×2×2×3,64 = 2×2×2×2×2×2,最大公因数是2×2×2×2 = 16。
题目5:求25 和35 的最大公因数。
答案:5。
25 = 5×5,35 = 5×7,最大公因数是5。
题目6:两个数的最大公因数是9,最小公倍数是90,其中一个数是18,求另一个数。
答案:45。
因为最小公倍数×最大公因数= 两数之积,所以另一个数= 90×9÷18 = 45。
题目7:求56 和70 的最大公因数。
答案:14。
56 = 2×2×2×7,70 = 2×5×7,最大公因数是2×7 = 14。
题目8:已知两个数的最大公因数是4,它们的和是20,求这两个数。
答案:12 和8 。
设这两个数分别为4a 和4b(a、b 互质),4a + 4b = 20,a + b = 5,所以a = 1,b = 4 或a = 4,b = 1,这两个数为12 和8。
最小最大公倍数和公因数

几个数共有的倍数叫做这几个数的公倍数,其中除0以外最小的一个公倍数,叫做这几个数的最小公倍数。
自然数a、b的最小公倍数可以记作[a,b],自然数a、b的最大公因数可以记作(a、b),当(a、b)=1时,[a、b]= a×b。
如果两个数是倍数关系,则它们的最小公倍数就是较大的数,相邻的两个自然数的最小公倍数是它们的乘积。
最小公倍数=两数的乘积/最大公约(因)数, 解题时要避免和最大公约(因)数问题混淆。
[1]最小公倍数的适用范围:分数的加减法,中国剩余定理(正确的题在最小公倍数内有解,有唯一的解).因为,素数是不能被1和自身数以外的其它数整除的数;素数X的N次方,是只能被X的N-1以下次方,1和自身数整除.所以,在求A,B,C,D,E,…,Z的最小公倍数时,只需要把这些数分解为素数的N次方之间的乘积后,取各素因子的最高次方的乘积,就是这些数的最小公倍数.举例说明:求756,4400,19845,9000的最小公倍数?因756=2*2*3*3*3*7,4400=2*2*2*2*5*5*11,19845=3*3*3*3*5*7*7,9000=2*2*2*3*3*5*5*5,这里有素数2,3,5,7,11.2最高为4次方16,3最高为4次方81,5最高为3次方125,7最高为2次方49,还有素数11.得最小公倍数为16*81*125*49*11=87318000.例题1两个数的最大公因数是15,最小公倍数是90,求这两个数分别是多少?15×1=15,15×6=90;当a1b1分别是2和3时,a、b分别为15×2=30,15×3=45。
所以,这两个数是15和90或者30和45。
练习一1,两个数的最大公因数是9,最小公倍数是90,求这两个数分别是多少?2,两个数的最大公因数是12,最小公倍数是60,求这两个数的和是多少?3,两个数的最大公因数是60,最小公倍数是720,其中一个数是180,另一个数是多少?例题2两个自然数的积是360,最小公倍数是120,这两个数各是多少?上!!分析我们把这两个自然数称为甲数和乙数。
求最小公倍数算法汇总

分析根据“两个数的最大公因数与最 小公倍数的乘积等于这两个数的乘积(这里 应该写错了吧?90/15=6,根据下面的解答 应该是这个意思)”可先求出这两个数的乘 积,再把这个积分解成两个数。根据题意:
当albl分别是1和6时,a、b分别 为15X1=15,15X6=90;当albl分别是2和3时,a、b分另I」为15X2=30,15X3=45。 所以,这两个数是15和90或者30和45。
练习四
1,用长9厘米、宽6厘米、高7厘米 的长方体木块叠成一个正方体,至少需要用 这样的长方体多少块?
2,有200块长6厘米、宽4厘米、高3厘米的长方体木块,要把这些木块堆成一个 尽可能大的正方体,这个正方体的体积是多 少立方厘米?
3,—个长方体长2.7米、宽1.8分米、 高1.5分米,要把它切成大小相等的正方体 小块,不许有剩余,这些小正方体的棱长最 多是多少分米?
例题5
甲每秒跑3米,乙每秒跑4米,丙每秒 跑2米,三人沿600米的环形跑道从同一地 点同时同方向跑步,经过多少时间三人又同 时从出发点出发?
练习一
1,两个数的最大公因数是9,最小公倍 数是90,求这两个数分别是多少?
2,两个数的最大公因数是12,最小公 倍数是60,求这两个数的和是多少?
3,两个数的最大公因数是60,最小公 倍数是720,其中一个数是180,另一个数 是多少?
例题2
两个自然数的积是360,最小公倍数是120,这两个数各是多少?
步骤:
一、利用辗除法或其它方法求得最大公 约数;
二、
之积除以最大公约数
12
两数的最小公倍数是24
专题简析
几个数公有的倍数叫做这几个数的公 倍数,其中最小的一个公倍数,叫做这几个 数的最小公倍数。自然数a、b的最小公倍 数可以记作[a、b],自然数a、b的最大公因 数可以记作(a、b),当(a、b)=1时,[a、b]= aXbo
因数倍数思维训练

因数、倍数练习题专题简析:一个自然数的因数中,为质数的因数叫做这个数的质因数。
把一个合数,用质因数相乘的形式表示出来,叫做分解质因数。
例如:24=2×2×2×3,75=3×5×5。
我们数学课本上介绍的分解质因数,是为求最大公因数和最小公倍数服务的。
其实,把一个数分解成质因数相乘的形式,能启发我们寻找解答许多难题的突破口,从而顺利解题。
例题1 把18 个苹果平均分成若干份,每份大于1 个,小于18 个。
一共有多少种不同的分法?分析先把18 分解质因数:18=2×3×3,可以看出:18 的约数是1、2、3、6、9、18,除去1 和18,还有4 个因数,所以,一共有4 种不同的分法。
练习一1、有60 个同学分成人数相等的小组去慰问解放军叔叔,每组不少于6 人,不多于15 人。
有哪几种分法?2、195 个同学排成长方形队伍做早操,行数和列数都大于1,共有几种排法?3、甲数比乙数大9,两个数的积是792,求甲、乙两数分别是多少。
例题2 有168 颗糖,平均分成若干份,每份不得少于10 颗,也不能多于50 颗。
共有多少种分法?分析先把168 分解质因数,168=2×2×2×3×7,由于每份不得少于10 颗,也不能多于50 颗,所以,每份有2×2×3=12 颗,2×7=14 颗,3×7=21 颗,2×2×2×3=24 颗,2×3×7=42 颗,共有5 种分法。
练习二1、把462 名学生分成人数相等的若干组去参加课外活动小组,每小组人数在10 至25 人之间,求每组的人数及分成的组数。
2、四个连续奇数的和是19305,这个四奇数分别是多少?3、把1、2、3、4、5、6、7、8、9 九张卡片分给甲、乙、丙三人,每人各3 张。
最小公倍数(1)

学生姓名:年级:小升初科目:数学授课教师:贺琴授课时间:学生签字:最小公倍数(一)专题简析:几个数公有的倍数叫做这几个数的公倍数,其中最小的一个公倍数,叫做这几个数的最小公倍数。
自然数a、b的最小公倍数可以记作[a、b],当(a、b)=1时,[a、b]= a×b。
两个数的最大公因数和最小公倍数有着下列关系:最大公因数×最小公倍数=两数的乘积即(a、b)×[a、b]= a×b1、两个数的最大公约数是15,最小公倍数是90,求这两个数分别是多少?分析、根据题意:当a1b1分别是1和6时,a、b分别为15×1=15,15×6=90;当a1b1分别是2和3时,a、b分别为15×2=20,15×3=45。
所以,这两个数是15和90或者30和45。
【练习】★1,两个数的最大公因数是9,最小公倍数是360,这两个数中较大的数是.2,两个数的最大公因数是12,最小公倍数是60,求这两个数的和是多少?3,两个数的最大公因数是60,最小公倍数是720,其中一个数是180,另一个数是多少?★4,两个自然数X、Y的最大公因数是14,最小公倍数是280,它们的和X+Y是______.5、已知甲数的12倍与乙数的15倍的最大公约数是1440,那么甲数和乙数的最大公约数是______.【答案】480解:已知甲数的12倍与乙数的15倍的最大公约数是1440,12与15的最大公约数是3,那么甲数和乙数的最大公约数是1440÷3=480.因此,本题正确答案是:480.2、两个自然数的积是360,最小公倍数是120,这两个数各是多少?分析我们把这两个自然数称为甲数和乙数。
因为甲、乙两数的积一定等于甲、乙两数的最大公约数与最小公倍数的积。
根据这一规律,我们可以求出这两个数的最大公约数是360÷120=3。
又因为(甲÷3=a,乙÷3=b)中,3×a×b=120,a和b一定是互质数,所以,a和b可以是1和40,也可以是5和8。
最大公因数相关应用题

小学应用题基础解法——最大公因数法1、最大公因数的概念:几个数公有的因数叫做这几个数的公因数,其中最大的一个叫做这几个数的最大公因数。
2、最大公因数的性质:(1)两个数分别与它们的最大公因数的商一定是互质数。
(2)两个数的公因数都是这两个数的最大公因数的因数。
3、解答公因数问题的关键从公因数的意义入手来分析,把原题归结为求几个数的公因数问题。
▓▓最大公因数相关应用题▓▓例1:甲班有42名学生,乙班有48名学生,现在要把这两个班的学生平均分成若干个小组,并且使每个小组都是同一个班的学生。
每个小组最多有多少名学生?解:要使每小组都是同一个班的学生,且每小组的人数尽可能多,就要求出42和48的最大公因数:(42、48)=6所以,每个小组最多能有6名学生。
例2:有一张长150厘米、宽60厘米的长方形纸板,要把它分割成若干个面积最大,井已面积相等的正方形。
能分割成多少个正方形?解:因为分割成的正方形的面积最大,并且面积相等,所以正方形的边长应是150和60的最大公因数。
正方形的边长:(150、60、30)=30(厘米)长可以分:150÷30=5(个)宽可以分:60÷30=2(个)所以,这个长方形能分割成正方形:5×2=10(个)例3:有一个长方体的方木,长是3.25米,宽是1.75米,厚是0.75米。
如果将这块方木截成体积相等的小正方体木块,并使每个小正方体木块尽可能大。
小木块的棱长是多少?可以截成多少块这样的小木块?解:3.25米=325厘米,1.75米=175厘米,0.75米=75厘米。
根据题意,小立方体一条棱长应是长方体长、宽、厚的最大公因数。
即:(325、175、75)=25(厘米)长可以分:325÷25=13(段)宽可以分:175÷25=7(段)高可以分:75÷25=3(段)所以,长方体可以截成这样的小木块:13×7×3=273(个)例4:有一个两位数,除50余2,除63余3,除775。
《小学奥数》小学五年级奥数讲义之精讲精练第26讲 最小公倍数(一)含答案

第26讲最小公倍数(一)一、专题简析:1、几个数公有的倍数叫做这几个数的公倍数,其中最小的一个公倍数,叫做这几个数的最小公倍数。
自然数a、b的最小公倍数可以记作[a、b],当(a、b)=1时,[a、b]= a×b。
2、两个数的最大公约数和最小公倍数有着下列关系:最大公约数×最小公倍数=两数的乘积即(a、b)×[a、b]= a×b要解答求最小公倍数的问题,关键要根据题目中的已知条件,对问题作全面的分析,若要求的数对已知条件来说,是处于被除数的地位,通过就是求最小公倍数,解题时要避免和最大公约数问题混淆。
二、精讲精练例题1 两个数的最大公约数是15,最小公倍数是90,求这两个数分别是多少?练习一1、两个数的最大公约数是9,最小公倍数是90,求这两个数分别是多少?2、两个数的最大公约数是12,最小公倍数是60,求这两个数的和是多少?例题2 两个自然数的积是360,最小公倍数是120,这两个数各是多少?练习二1、求36和24的最大公约数和最小公倍数的乘积。
2、已知两个数的积是3072,最大公约数是16,求这两个数。
例题3 甲、乙、丙三人是朋友,他们每隔不同天数到图书馆去一次。
甲3天去一次,乙4天去一次,丙5天去一次。
有一天,他们三人恰好在图书馆相会,问至少再过多少天他们三人又在图书馆相会?练习三1、1路、2路和5路车都从东站发车,1路车每隔10分钟发一辆,2路车每隔15分钟发一辆,而5路车每隔20分钟发一辆。
当这三种路线的车同时发车后,至少要过多少分钟又这三种路线的车同时发车?2、甲、乙、丙从同一起点出发沿同一方向在圆形跑道上跑步,甲跑一圈用120秒,乙跑一圈用80秒,丙跑一圈用100秒。
问:再过多少时间三人第二次同时从起点出发?例题4 一块砖长20厘米,宽12厘米,厚6厘米。
要堆成正方体至少需要这样的砖头多少块?练习四1.用长9厘米、宽6厘米、高7厘米的长方体木块叠成一个正方体,至少需要用这样的长方体多少块?2、有200块长6厘米、宽4厘米、高3厘米的长方体木块,要把这些木块堆成一个尽可能大的正方体,这个正方体的体积是多少立方厘米?例题5 甲每秒跑3米,乙每秒跑4米,丙每秒跑2米,三人沿600米的环形跑道从同一地点同时同方向跑步,经过多少时间三人又同时从出发点出发?练习五1、有一条长400米的环形跑道,甲、乙二人同时同地出发,反向而行,1分钟后第一次相遇;若二人同时同地出发,同向而行,则10分钟后第一次相遇。
小学奥数 质数 合数 倍数 因数 完整版带答案

因、倍、质、合【知识点总结】1.质数、合数⑴除了2其余的质数都是奇数;⑵除了2和5,其余的质数个位数字只能是1,3,7或9;⑶如何判断一个数是否是质数?⑷常用的100以内的质数:2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97,共计25个。
2.数字拆分—分解质因式相关名词:质因数、互质数、分解质因数例如:三个连续自然数的乘积是210,求这三个数。
210=2⨯3⨯5⨯7可知这三个数是5、6和7。
分解质因数往往是解数论题目的突破口,因为这样可以帮助我们分析数字的特征。
3、约数个数定理唯一分解定理:任何一个大于1的自然数n都可以写成质数的连乘积例如:12=2⨯2⨯3=22⨯3约数个数定理:约数个数:(2+1)⨯(1+1)=6所有约数的和:(20+21+22)⨯(30+31)例题讲解板块一:质数的快速判断1、两个质数之和为39,求这两个质数的乘积是多少?【巩固】(1)如果a、b均为质数,且3a+7b=41,则a+b=______。
(2)三个不同的质数的和是18,这三个质数的乘积的最大值是()板块二:分解质因数1、牛小顿去看电影,他买的票的排数与座位数的积是391,而且排数比座位数大6,牛小顿买的电影票是几排几座?【巩固】(1)、三个连续的自然数相乘的结果是 1716,那么这三个自然数的和是多少?(2)、把462名学生分成人数相等的若干组参加课外活动小组,每组人数在12到20人之间,求每组人数及分成的组数。
2、【外冲】有n个自然数相加:1+2+…+n=aaa,那么a=______。
【巩固】将一个三位数的个位与百位数字对调位置,得到一个新的三位数,已知这两个三位数乘积为55872,则这两个三位数和为______。
板块三、因数三大定律因数个数定律:(指数+1)再连乘因数和定律:每个质因子所有可能相加再连乘因数积定律:自身的n次方(n=因数个数÷2)1、数160的约数个数是多少?巩固:(1)分别求出72和150的因数个数。
最大公因和最小公倍数

课题:最大公因数和最小公倍数例1、求下面每组数的最大公因数和最小公倍数。
45和18 51和17 28和96 24、38和1860和36 180和240 72和60 60、36和72例2、用一个数去除30、60、75,都能整除,这个数最大是多少?一个数用3、4、5除都能整除,这个数最小是多少?练习:①有三根小棒,长分别是120厘米,180厘米,300厘米,要把它们都裁成同样长的小棒,不许有剩余,每根小棒最长能有多少厘米?一共裁成几根小棒?②三位朋友每人隔不同的天数到图书馆去看书,甲3天去一次,乙4天去一次,丙5天去一次。
一个星期一,他们三人在图书馆相遇,至少再过多少天他们又在图书馆相遇?相遇时是星期几?③加工某种机器零件,要经过三道工序.第一道工序每个工人每小时可完成3个零件,第二道工序每个工人每小时可完成10个,第三道工序每个工人每小时可完成5个,要使加工消费平衡,三道工序至少各分配几个工人?例3、一次会餐供有三种饮料.餐后统计,三种饮料共用了65瓶;平均每2个人饮用一瓶A 饮料,每3人饮用一瓶B饮料,每4人饮用一瓶C饮料.问参加会餐的人数是多少人?辗转相除法例1、一张长方形纸,长2703厘米,宽1113厘米.要把它截成假设干个同样大小的正方形,纸张不能有剩余且正方形的边长要尽可能大.问:这样的正方形的边长是多少厘米?2、用辗转相除法求4811和1981的最大公约数最大公因数×最小公倍数=两数的积即〔a、b〕×〔a、b〕= a×b例1 两个数的最大公因数是15,最小公倍数是90,求这两个数分别是多少?例2两个自然数的积是360,最小公倍数是120,这两个数各是多少?①两个数的最大公因数是9,最小公倍数是90,求这两个数分别是多少?②两个数的积是3072,最大公因数是16,求这两个数。
③两个数的最大公约数是60,最小公倍数是720,其中一个数是180,另一个数是多少?例3两个自然数的最大公约数是7,最小公倍数是210。
人教版六年级数学讲义-3最大公因数和最小公倍数
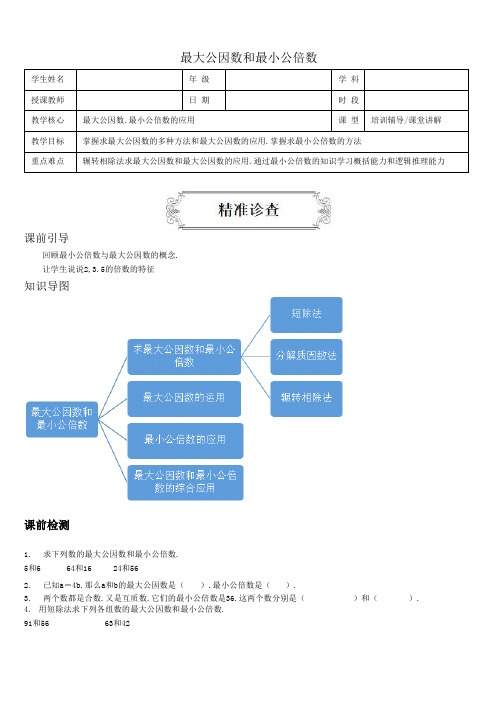
最大公因数和最小公倍数学生姓名年级学科授课教师日期时段教学核心最大公因数.最小公倍数的应用课型培训辅导/课堂讲解教学目标掌握求最大公因数的多种方法和最大公因数的应用.掌握求最小公倍数的方法重点难点辗转相除法求最大公因数和最大公因数的应用.通过最小公倍数的知识学习概括能力和逻辑推理能力课前引导回顾最小公倍数与最大公因数的概念.让学生说说2,3.5的倍数的特征知识导图课前检测1.求下列数的最大公因数和最小公倍数.5和6 64和16 24和562.已知a=4b.那么a和b的最大公因数是().最小公倍数是().3.两个数都是合数.又是互质数.它们的最小公倍数是36.这两个数分别是()和().4.用短除法求下列各组数的最大公因数和最小公倍数.91和56 63和42导学一:求最大公因数和最小公倍数重点讲解 1:短除法.分解质因数法.辗转相除法分解质因数:把一个合数写成几个质数相乘的形式.辗转相除法求最大公因数的步骤:①用较大数÷较小数=商……余数②除数÷余数=商……余数……以此类推.除到没有余数为止.最后一个除数就是这两个数的最大公因数例 1. 利用分解质因数法找出下列各组数的最大公因数和最小公倍数.144和255 240和96例 2. 利用辗转相除法求出下列各组数的最大公因数.377和221 511和1314课堂练习1.用短除法求下列各组数的最大公因数和最小公倍数.63和842.利用分解质因数法找出下列各组数的最大公因数和最小公倍数96和72 90和7003.利用辗转相除法求出下列各组数的最大公因数.3009和2573 1085和1178重点讲解 2:例1.如果a、b互质(a和b都是自然数.且a.b≠0).则a和b的最大公因数是().最小公倍数是().例 2. 已知a=2×3×5.b=2×3×11.则a、b的最大公因数是().最小公倍数是().课堂练习1.m和n都是自然数.m÷n=8.m和n的最大公因数是().m和n的最小公倍数是().2.A=2×3×5.B=2×5×7.A和B的最大公因数是().最小公倍数是().3.把自然数a与b分解质因数.得到a=2×5×m.b=3×5×m.如果a与b的最小公倍数是210.那么m=().导学二:最大公因数的应用重点讲解 1:例 1. 将一个长60厘米、宽45厘米、高75厘米的长方体.分割成同样大小的正方体.并使它们的体积尽可能大且没有多余.这些正方体的棱长是多少?可分割成多少个?例 2. 某幼儿园大班老师借阅图书.如果借37本.平均分给每个小朋友后还剩1本;如果借56本.平均分给每个小朋友后还剩2本;如果借75本.平均分给每个小朋友后还剩3本.这个班的小朋友最多有多少人?课堂练习1.有三根木棒.一根长24米.一根长8米.一根长36米.要把它们截成同样长的小段.不许剩余.每段最长是多少米?一共可以截成多少段?2.用48朵红玫瑰花和72朵白玫瑰花做花束.若每个花束里的红玫瑰花的朵数相同.白玫瑰花的朵数也相同.每个花束里最少有几朵花?3.有铅笔433支.橡皮260块.平均分配给若干个小学生.分到最后铅笔余13支、橡皮余8块.问最多分给了多少个小学生?4.有136支圆珠笔、89本笔记本和178个笔盒.平均奖给若干个优秀少先队员.结果圆珠笔多出1支.笔记本少1本.笔盒少2个.获奖的少先队员最多有多少人?导学三:最小公倍数的应用重点讲解 1:例 1. 用一些长3厘米、宽2厘米、高5厘米的长方体拼一个正方体.这个正方体的棱长最短是多少?例 2. 有一个不为1的自然数.被6除余1.被8除余1.被12除也余1.这个自然数最小是多少?例 3. 有一个自然数.被3除余2.被6除余5.被8除余7.这个自然数最小是多少?课堂练习1.五年级学生人数在140到150人之间.要分成12人一组、18人一组都恰好分完.这个年级有多少人?2.有一包奶糖.无论分给6个小朋友.8个小朋友.还是9个小朋友.都正好分完.这包糖至少有多少块?3.同学们排队做操.不论是每行站4人.还是每行站5人.或每行站7人.最后都正好多出2人.至少有多少人做操?4.航模兴趣小组去参观展览.参观队伍每行6人则多2人.每行8人则多4人.问:航模兴趣小组去参观的同学最少有几人?导学四:最大公因数和最小公倍数综合运用重点讲解 1两个数的乘积等于这两个数最大公因数与最小公倍数的乘积:即:a×b=(a,b)×[a,b]例 1. 两个数的最大公因数是15.最小公倍数是90.求这两个数分别是多少?例 2. 两个自然数的积是360.最小公倍数是120.这两个数各是多少?课堂练习1.两个数的最大公因数是12.最小公倍数是60.求这两个数的和是多少?2.两个数的最大公因数是60.最小公倍数是720.其中一个数是180.另一个数是多少?3.求36和24的最大公约数和最小公倍数的乘积.4.已知两个数的最大公因数是13.最小公倍数是78.求这两个数的差.限时考场模拟1.a=2×3×m.b=3×5×m(m是自然数且m≠0).如果a和b的最大公因数是21.则m是().a和b的最小公倍数是().2.现在有香蕉42千克.苹果112千克.桔子70千克.平均分给幼儿园的几个班.每班分到的这三种水果的数量分别相等.那么最多分给了多少个班?每个班至少分到了三种水果各多少千克?3.有一筐苹果.无论是平均分给8个人.还是平均分给18人.结果都剩下3个.这筐苹果至少有多少个?课后作业1.如果a与b是两个不同的质数.那么a与b的最大公因数是().最小公倍数是().2.用长24cm、宽18cm的长方形铁片.摆成一个正方形(中间没有空隙).至少要用多少块这种长方形铁片?3.A=2×5×7.B=2×2×3×5.A和B的最大公因数是().最小公倍数是().4.一筐苹果2个2个拿.3个3个拿.或者5个5个拿都正好拿完.这筐苹果最少有()个.5.甲数=2×3×5×7.乙数=2×3×7.甲、乙两数的最大公因数是().最小公倍数是().6.六一儿童节那天.某慈善工会买了320个苹果、240个桔子、200个雪梨.去看望福利院的小朋友.问用这些果品.最多可以分成多少份同样的礼物?7.有两路公共汽车.11路和8路.11路每10分钟发一次车.8路每8分钟发一次车.11路和8路的起点站都在一起.请问这两路公共汽车同时发车以后.至少过多少分钟两路车才第二次同时发车?8.一班同学参加课外活动.如果分为4人一组.或分为6人一组.或分为9人一组.都恰好分完没有剩余.这个班至少有多少人?9.五年级三个班分别有36人、48人、42人参加体育活动.要把他们分成人数相等的小组.但各班同学不能打乱.最多每组多少人?1、总结一下本节课的知识点.2、把本讲的例题.习题复习一遍.完成老师规定的作业.3、建立错题集.整理、复习错题本.做到下一讲“有备而来”.4、周五告诉老师学校的进度和遇到的问题.课前检测1.(5.6)=1.[5.6]=30;(64.16)=16.[64.16]=64;(24.56)=8.[24.56]=1682.b.a3.4.94.7.728;21,126导学一重点讲解 1:短除法.分解质因数法.辗转相除法例题1.(144.255)= 3.[144.255]=12240;(240.96)= 48.[240.96]=480;解析:144=2×2×2×2×3×3,255=3×5×17.最大公因数是3.最小公倍数是2×2×2×2×3×3×5×17=12240240=2×2×2×2×3×5.96=2×2×2×2×2×3.最大公因数是2×2×2×2×3=48.最小公倍数是2×2×2×2×3×2×5=4802.(377.221)=13.(1314.511)=73.解析:377÷221=1.....156,221÷156=1....65,156÷65=2..... 26,26÷13=2.最大公因数是13.1314÷511=2....292,511÷292=1....219,292÷219=1.... 73,219÷73=3,最大公因数是73.课堂练习1.21.2522.(96,72)=24,[96,72]=288;(90,700)10,[90,700]=6300解析:96=2×2×2×2×2×3.72=2×2×2×3×3,(96,72)=2×2×2×3=24.[96,72]=2×2×2×3×2×2×3=288. 90=2×3×3×5,700=2×2×5×5×7,(90,700)=2×5=10,[90,700]=2×5×3×3×2×5×7=63003.(3009,2573)=393;(1178,1085)=31解析:3009÷2573=1....436;2573÷436=5.... 393;436÷393=43.(3009,2573)=393.1178÷1085=1....93;1085÷93=11....62;93÷62=1....31.62÷31=2.(1178,1085)=31重点讲解 21.1.ab2.6.330课堂练习1.n.m2.10.2103.7导学二重点讲解 11.60(个)解析:(60.45.75)=15.(60÷15)×(45÷15)×(75÷15)=60(个) 2.18解析:37-1=36(本).56-2=54(本).75-3=72(本),(36.56.72)=18(人)课堂练习1.每段最长为4米;17段解析:(24.8.36)=4.所以每段最长为4米.一共可以截成:24÷4+8÷4+36÷4=17(段) 2.5 解析:(48.72)=24.48÷24+72÷24=5(朵)3.84解析:433-13=420(支).260-8=252(块)(420.252)=84.所以最多分给了84个小学生.4.136-1=135(支).89+1=90(本).178+2=180(个)(135.90.180)=45.获奖的少先队员最多有45人.导学三重点讲解 11.30cm解析:3×2×5=30(厘米)2.25解析:[6.8.12]=24.24+1=25 3.23解析:[3.6.8]=24.24-1=23课堂练习1.144解析:[12.18]=36.36×4=144(人) 2.72解析:[6.8.9]=72.所以这包糖至少有72块.3.142解析:[4.5.7]=140.140+2=142(人)4.20解析:[6.8]=24.24-4=20(人)导学四重点讲解 11.15和90或者30和45.解析:当a1b1分别是1和6时.a、b分别为15×1=15.15×6=90;当a1b1分别是2和3时.a、b分别为15×2=20.15×3=45.所以.这两个数是15和90或者30和45.2.3和120或3和120解析:我们把这两个自然数称为甲数和乙数.因为甲、乙两数的积一定等于甲、乙两数的最大公因数与最小公倍数的积. 根据这一规律.我们可以求出这两个数的最大公因数是360÷120=3.又因为(甲÷3=a.乙÷3=b)中.3×a×b=120.a 和b一定是互质数.所以.a和b可以是1和40.也可以是5和8.当a和b是1和40时.所求的数是3×1=3和3×40=120;当a和 b是5和8时.所求的数3和3×40=120课堂练习1.72解析:60÷12=5,5=1×5,12×1=12,12×5=60;60+12=722.240解析:720÷180=4.60×4=2403.36×24=864解析:36、24两数的积一定等于36、24两数的最大公因数与最小公倍数的积.4.65或13解析:78÷13=6,6=1×6=2×3,13×1=13,13×6=78;13×2=26,13×3=39.这两个数是13和78或者26和39.所以它们的差为65或13限时考场模拟1.7.2102.香蕉: 3(千克)苹果: 8(千克)桔子: 5(千克)解析: (42.112.70)=14 香蕉:42÷14=3(千克)苹果:112÷14=8(千克)桔子:70÷14=5(千克)3. 75解析:[8.18]=72.72+3=75(个)课后作业1.1.ab2.12解析:[24.18]=72.(72÷24)×(72÷18)=12(块)3.10.4204.305. 42.2106.最多可以分成40份同样的礼物解析:(320.240.200)=40.所以最多可以分成40份同样的礼物.7.至少过40分钟解析:[10.8]=40.所以至少过40分钟两路车才第二次同时发车.8.至少有36人解析:[4.6.9]=36.所以这个班至少有36人.9.6人解析:(36.48.42)=6.所以最多每组有6人.。
公倍数公因数练习

练习一1、36与60的最小公倍数是最大公因数的几倍2、已知A=2×3×7×13,B=2×2×3×5×7,则他们的最小公倍数是最大公因数的()倍3、两个数的最大公因数是15,最小公倍数是150,这两个数的和是()或()4、两个数的最大公因数是42,最小公倍数是630,且两个数的差是84,则这两个数分别是()5、有45个苹果,105个桔子,90个梨,用这些水果,做多可以分成()份同样的礼物6、学校在排练团体操,要求队伍分别变成5行、6行、8行、9行时都能变成长方形。
则最少需要()人参加团体操的排练7、有一堆苹果700多只,无论是3人、4人还是6人、13人都能平均分这堆苹果,则这堆苹果有( )只练习二1、求36和24的最大公因数和最小公倍数的乘积。
2、两个数的最大公约数是60,最小公倍数是720,其中一个数是180,另一个数是多少?3、两个自然数的积是360,最小公倍数是120,这两个数各是多少?4、把1米3分米5厘米长、1米5厘米的长方形纸,裁成同样大小的正方形,至少能裁多少块?5、一张长方形的纸,长7分米5厘米、宽6分米。
现在要把它裁成一块正方形,而且正方形边长为整厘米数,有几种裁法?如果要使裁得的正方形面积最大,可裁多少块?6、一块长45厘米、宽20厘米的长方形木板,把它锯成若干块正方形而无剩余,所据成的正方形的边长最长是多少厘米?7、一个长方体木块的长是4分米5厘米、宽3分米6厘米、高2分米4厘米。
要把它切成大小相等的正方体木块,不许有剩余,求所切正方体木块的棱长最长是多少厘米?8、五年级三个班子分别有24人、36人、42人参加体育活动,要把他们分成人数相等的小组,但各班同学不能打乱,最多每组多少人?每班各可以分几组?9、有20个梨,75个橘子和100个苹果,要把这些水果平均分给几个小组,并且每个小组分得的三种水果的数目也相同,最多可以分给几个小组?10、有三根钢管,它们的长度分别是240厘米、200厘米和480厘米,如果把它们截成同样长的小段,每小段最长可以是多少厘米?11、有一个长方体大块,长60厘米,宽40厘米,高24厘米,如果要切成同样大小的小正方体,这些正方体的棱长最长是多少厘米?12、两个数的最大公约数是15,最小公倍数是90,求这两个数分别是多少?13、两个数的最大公约数是9,最小公倍数是72,求这两个数分别是多少?14、甲、乙、丙三人是朋友,他们每隔不同天数到图书馆去一次,甲3天去一次,乙4天去一次,丙5天去一次。
五年级期末复习习题

五年级期末复习习题2五年级期末复习习题有32人、40人、24五年级期末复习习题流;编组时各车间人员不打乱而且每组人数要相等;每组最多有几人?要编成多少组?3.有336个苹果、252个梨子、210个桔子;用这些水果最多可以分成多少份同样的礼物?在每份礼物中;三种水果各有多少个?2.三个人绕环行跑道练习骑自行车;他们骑一圈的时间分别是半分钟、45秒钟和1分15秒。
三人同时从起点出发;最少需要多长时间才能再次同时在起点相会?3.晨风机械厂加工一批机器零件。
要经过三道工序。
第一道工序每人每小时做18件;第二道工序每人每小时做12件;第三道工序每人每小时做24件。
各道工序上最少应安排多少人;才能使生产顺利进行(不在某道工序上出现积压或等待)?例3 甲对乙说:“我现在的年龄是你的7倍;过几年是你的6倍;再过若干年就分别是你的5倍、4倍、3倍、2倍。
”试求出甲、乙现在的年龄。
1.有一个钟;每走9分钟亮一次灯;每到整点时响一次铃。
中午12点时;既响铃又亮灯。
问:下一次既响铃又亮灯是几点钟?例4 写出三个小于20的自然数;它们的最大公因数为1;但两两均不互质;共有几组?1.用一个数去除31;61;76都余1;这个数最大是多少?2.能同时被6;7;8;9整除的五位数有多少个?3.在被除数小于100的条件下;在方格中填上适当的数。
3.育才中学初一(3)班有男同学27人;女同学18人;全班同学去划船(每条船不超过6人);要保证每条船上男、女同学都分别相等;至少应该租几条船?4.有一种地板砖;长20厘米;宽15厘米;至少需要多少块这样的地砖才能拼成一个实心的正方形?5.小红、小明和小李三名同学沿环形跑道跑步;小红跑完一圈需6分钟;小明跑完一圈需4分钟;小李跑完一圈需7分钟;三人同时从A地同向出发;几分钟后;三人又会在A地相会?7.一箱鸡蛋;四个四个数多3个;五个五个数多4个;七个七个数多6个;这箱鸡蛋至少有多少个?8.有一个班的同学包车旅游;如果增加一辆车;正好每辆车坐10人;如果减少一辆车;正好每辆车坐15个;这个班共有多少人?9.在1000~10000之间;能同时被12;16;24;28整除的数有多少个?10.从0~9这9个数字中选出四个数字组成四位数;使它能被3;5;7;11整除;这四个数最大是多少?1.某数与24的最大公因数是4;最小公倍数是168;这个数是多少?2.甲数和乙数的最大公因数是6;最小公倍数是90;且小数不能整除大数;求这两个数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 兩個數的最大公因數是60,最小公倍數是720,這兩個數是多少?
2. 旅客到旅館住宿,如果每間房住6人,會少1間房;每間房住9人,會多出1間房。
共有多少旅客?
3. 甲、乙兩車同時從東、西兩地出發相向而行。
甲車每小時10公里,乙車每小時12公里。
兩車相遇後,甲車又行半小時才到兩地的中點,兩地相隔多遠?
4. 一艘船順流而下,350公里只用了10小時。
已知水流速度是每小
時5公里。
這艘船逆流而上時,每小時的速度是多少公里?
5. 求出下面柱體的表面
6. 下面三角柱的體積是多少?(單位:公分)
【5、6題的三角形兩邊互相垂直】
7. 濃度是指將糖、鹽…放入水中攪拌後,在混合
溶液中所佔的量。
把60
公克的糖放入90公克
的水中,濃度是百分之
多少?
8.一項工作,甲組3人,
8天可以完成;乙組4
人,需要7天才完成。
現在由甲組2人和乙組
7人合作,多少天可以
完成?9.下圖中一共有多少條
線段?
A1A2A3A4 A98
A99 A100
……
10.在1~50的所有整數
中。
(1)能同時被2、3整
除的數有幾個?
(2)能被2或3整除
的數有幾個?
(3)不能被2或3整
除的數有幾個?。
