14.2.1 利用轴对称设计图案-
轴对称设计图案课件

1 线条的分区
线条应在对称轴两侧分 配均匀,不应让一侧更 重、更稠密。
2 元素的对称性
元素应该是在对称轴的 两侧呈现镜像关系,但 不一定完全相同,只需 保持相似即可。
3 色彩的对比度
颜色的亮度、饱和度、 搭配等都决定了轴对称 设计的视觉强度,如何 充分利用色彩关系是轴 对称设计的一个核心问 题。
轴对称设计的注意事项
1
纺织品设计
通过轴对称设计,紧凑的花纹可以更有效地利用纺织品空间,充分展现出品牌风 格。
2
印刷品设计
印刷品设计常使用轴对称设计,能够突出品牌形象,为读者留下深刻印象。
3
网页设计
轴对称设计在网页设计中广泛应用,网页内容布局合理、简单直观,能够提升网 站的排版质量。
轴对称设计的实用技巧
轴对称设计需要注意以下技巧:
在使用轴对称设计时,需要注意以下事项:
避免过度对称
过度对称会让设计变得沉 闷无趣,应该在不失平衡 感和稳重感的前提下,增 加一些变化和创意。
避免使用对称轴分隔 重要元素
这种做法会把观众分成左 右两半,导致分散用户的 注意力和意识。
避免对称中心过于集 中
做法会使轮廓过于单调, 形态过于静态,缺乏视觉 效果和流动感。
平衡感
轴对称的图案给人一种稳定和平衡的感觉, 即使图案中元素数量不等,也能产生一种自 然的平衡感。
轴对称设计的特点和优势
轴对称设计具有以下特点和优势: • 具备平衡感和安全感。 • 简单而有力,易于理解和识别。 • 能够表达对称、整齐和和谐的意象。 • 易于分组和分类,让观众更容易获得信息。
几何图案
轴对称设计图案ppt课件
欢迎来到本节课! 今天我们将探讨一个广泛应用于设计中的主题: 轴对称设计。 通过轴对称设计,你将能够创作出复杂又美丽的图案,从而引起观众的注意。
轴对称变换的实际应用教案

《轴对称变换的实际应用》北京市北方交大附中牟柏林教材:人教版《义务教育课程标准实验教材》八年级上册第14.2.1第2节.教学目标1.进一步理解轴对称变换,并能用轴对称变换解决实际问题中的路径最短问题. 2.体会轴对称变换在解决问题中的转化作用,学习将实际问题转化为数学问题的方法,发展应用数学的意识.3.体验探究的快乐、激发学习数学的兴趣.教学重点轴对称变换的应用.教学难点如何通过轴对称变换进行转化.教学方式自主探究与启发引导相结合.教学手段多媒体辅助教学.教学过程教学环节教学内容师生活动设计意图(一)复习引入上节课我们学习了轴对称变换作图,给大家布置了利用轴对称变换设计图案的作业,让我们先来欣赏同学们用轴对称变换设计的美丽图案!这些美丽的图案你又是怎样画的呢?学生利用实物投影展示作业,教师对学生给予肯定和鼓励.通过展示学生有创意的作品,复习轴对称作图和轴对称性质,为本节课的内容作铺垫.(二)问题探究1.提出问题播放CCTV关于“西气东输”的新闻报道.问题1如图,要在燃气管道l上修建一个泵站,分别向A,B两城镇供气.泵站修在什么地方,可使所用的输气管线最短?2. 引导探究探究中学生可能遇到如下问题:①实际问题数学化;②对“线段和最小”的理解;③如何想到用轴对称变换求解问题.(1)实际问题数学化学生阅读思考、尝试独立求解.教师巡视,观察学生解决问题的过程与方法,并适时引导.多数学生能将管道画选用“西气东输”作为背景,引导学生关注国家大事.学生已有一些解决实际问题的经验,放手让学生做,培养他们的探究意识和能力.使学生明确将(二)问题探究如图,已知点A、B在直线l的同侧.在l上找点P,使PA+PB最小.(2)对“线段和最小”的理解在直线l上任取两点P1、P2,通过度量,比较AP1+BP1与AP2+BP2的大小.(3)对画图找点的引导辅助问题:如图,已知点A、B在直线l的异侧,在l上找点P,使PA+PB最小.解略.(4)求解问题1解:作点B关于直线l的对称点B1,连接AB1,AB1与直线l交于P,点P即为所求.理由:如图,由轴对称性质BP=B1P,所以AP+BP=AP+B1P,当A、P、B1三点共线时AB1最短,所以P点为所求.3.数学思考(1)推理证明的落实如果P1是异于点P的一点,你能证明AP1+BP1> AP+BP吗?证明:连接B1P1. 由轴对称性质,BP1=B1P1,BP=B1P.所以AP1+BP1=AP1+ B1P1,成直线,城镇画成点,教师给予肯定的同时,引导学生结合图形用符号语言表述问题.教师引导对“线段和最小”理解不透的学生选点画图,度量比较发现其值不等之后,再利用几何画板进行动态演示.对于如何找点没有思路的学生,教师给出辅助问题,解决后再思考问题1的解法.学生陈述解法并说明理由,同时教师强调也可以通过作点A关于直线对称点来求解.教师再利用几何画板对点P进行验证.学生思考,讨论交流.教师引导学生利用轴对称变换性质和三角形三边关系完成证明.实际问题数学化是解决实际问题的第一步,同时注意规范表述.使学生透彻理解“线段和最小”的含义.设置辅助问题为问题1的解决作铺垫.AlBB1AlPBlABP2P1lABP1B1AlPB(二)问题探究AP+BP=AP+ B1P =AB1,在△AP1B1中,AP1+B1P1>AB1,即AP1+BP1 > AP+BP.(2)对解法的反思轴对称变换在解决问题中所起的作用是什么呢?“实现了线段长度的等量转化,将直线同侧两定点问题转化为直线异侧两定点问题.”学生思考后作答,教师再归纳提升.帮助学生体会轴对称变换在解决问题中的转化作用.(三)拓展应用问题 2 如图,公园内两条小河汇合,两河形成的半岛上有一处古迹P,现计划在两条小河上各修建一座小桥,并在半岛上修三条小路,连通两座小桥与古迹,这两座小桥应建在何处,使所修建的道路最短?1. 实际问题数学化如图,P为∠MON内一定点,分别在OM与ON上找点A、B,使△ABP的周长最小.2. 问题求解解:作点P关于OM、ON的对称点P1、P2,连接P1P2 ,P1P2与OM、ON分别交于A、B,点A、B即为所求.3. 对解法的反思在解决问题过程中,轴对称变换起到了什么作用?“利用轴对称变换实现了线段长度的等量转化. ”学生读题,尝试独立求解.教师巡视指导.学生在画图找点过程中遇到困难时,教师引导学生分析问题、理解由轴对称性质可将三角形周长转化为P1A1+A1B1+P2B1,从而使问题求解.问题2一方面作为问题1解题方法的巩固,同时又为问题3的解决作铺垫.帮助学生再次体会轴对称变换在解决问题中的转化作用.NMPOABP2P1BAB1A1NMPO(三)拓展应用问题3 如图,A为马厩,B为帐篷,牧马人某一天要从马厩牵出马,先到草地某一处牧马,再到河边饮马,然后牵马回到帐篷,请你帮他确定这一天所走的最短路线.1. 实际问题数学化如图,已知∠MON内有两定点A、B,分别在OM和ON上各点C、D,使AC+CD+BD最小.2. 问题的求解解:作点A关于OM的对称点A1,作点B关于ON的对称点B1,连接A1B1,A1B1与OM、ON分别交于点C、D,则此时AC+CD+BD最小.学生利用实物投影展示自己的成果,教师适时点评.对于学生可能出现的问题,教师引导学生讨论、剖析错误.问题3更为复杂,对学生更具挑战性,有利于发展学生迁移的能力.使学生在收获成功喜悦的同时,对轴对称的画图上升到理性认识的层面.(四)小结反1. 引导学生小结、反思(1)怎样将实际问题转化为数学问题?(2)轴对称变换所起的作用是什么?2. 教师归纳、提升(1)将实际问题中的条件简化,同时用数学语言进行表述.在学生反思、回答问题的基础上,教师再归纳提升.使学生体会轴对称变换实际应用的实质,发展学生应用数学的意识.NMOABCDB1A1NMDCOAB思(2)利用轴对称变换将不共线的多条路径转化到一条直线上,从而解决最短路径问题.(五)分层作业A层在旷野上,一个人骑马从A到B,半路上他必须让马在河边饮水一次(如图所示). 他应该怎样选择饮水点P,可使使所走的路程PA+PB最短?B层如图,公园中有两处古迹P和Q,现计划在两条小河上各修建一座小桥,并在半岛上修四条小路,连通两座小桥与古迹,这两座小桥应建在何处,才能使修建的道路最短?C层如图,现有一条地铁线路l,小区A 、B在l的同侧,已知地铁站两入口C、D间的长度为a米,现设计两条路AC、BD连接入口和两小区. 地铁站入口C、D设计在何处,能使所修建的公路AC与BD之和最短?BAl。
利用轴对称设计图案教案(张琛)

利用轴对称设计图案教案(张琛)第一章:引言1.1 课程背景本课程旨在通过利用轴对称设计图案的方法,让学生了解并掌握轴对称的基本概念,培养学生对图案设计的兴趣和创意表达能力。
1.2 教学目标通过本章的学习,学生将能够理解轴对称的定义和特点,掌握轴对称设计图案的基本方法,并能够运用轴对称原理创作出独特的图案作品。
第二章:轴对称的基本概念2.1 轴对称的定义介绍轴对称的定义,解释轴对称图形的特点,即存在一个对称轴,将图形分成两个完全相同的部分。
2.2 轴对称的类型介绍轴对称的不同类型,包括线对称、点对称和面对称,并通过实例进行展示和解释。
第三章:轴对称设计图案的方法3.1 选择对称轴教授学生如何选择合适的位置作为对称轴,对称轴的选择将直接影响图案的对称效果。
3.2 绘制对称图形引导学生利用工具(如直尺、圆规等)和材料(如纸张、剪刀等)绘制对称图形,注意对称轴两侧图形的一致性。
第四章:创意表达与设计4.1 创意思维训练通过小组讨论、思维导图等方式激发学生的创意思维,鼓励学生尝试不同的设计方法和图案元素。
4.2 设计实践学生根据自己的想法和创意,利用轴对称原理进行实际操作,创作出独特的图案作品,并进行展示和评价。
回顾本章的学习内容,强调轴对称设计图案的基本概念和方法,并强调学生的创意表达和设计实践。
5.2 学生作品评价学生之间相互评价对方的作品,教师进行综合评价,给予肯定和建议,促进学生的进一步学习和改进。
第六章:对称轴的变换与图案创新6.1 对称轴的变换介绍对称轴在不同方向上的变换,如垂直对称、水平对称和斜对称,学生通过实际操作了解变换过程。
6.2 图案创新实践鼓励学生尝试变换不同的对称轴,创新图案设计,注意对称轴与图案元素的关系,提升图案的美观性和创意性。
第七章:对称轴与色彩搭配7.1 对称轴与单色搭配讲解对称轴在单色搭配中的应用,如何通过色彩的深浅变化来增强图案的对称美感。
7.2 对称轴与多彩搭配介绍对称轴在多彩搭配中的运用,教授学生如何合理运用色彩的对比和调和来提升图案的整体效果。
《利用图形的平移、旋转和轴对称设计图案》精品PPT课件

看一看
欣赏精美的剪纸图案
它们都是轴对称图形
欣赏几种标志图案 图案常给人美的享受,对称是设计图案常用 的方法,欣赏下列图案:
绿色食品标志 中国环境标志 国家免检产品标志
试一试
下列图形是不是轴对称图形?是,画
出它们的所有对称轴.
下列图案的对称轴是什么?试画出来.
这两个美丽的轴对称图形各有几条对称轴? 试画出来.
想一想:如何利用轴对称来画这两个美丽的 轴对称图形?
让我们来体验一下画这个优美图案的过程:
做一做
用两个一半灯笼拼成一个整灯笼:
做一做
将四个如下图所示的图案拼合在一起,能
得到不同的图案,考虑色彩因素,使它们成为
一轴对称图形.
将四个如下图所示的图案拼合在一起,能 得到不同的图案,考虑色彩因素,使它们成为 一个轴对称图形.
练一练
在如图所示的4×4的网格中,将8个小
方格用 X 填入,使之成为有
2条对称轴的美丽图案.
X X
请你做设计
许多集合图案是优美的,对称本身就是 一种美,请你用“两个圆、两个三角形、两 条线段”,在图中所示的方框内设计一幅对 称图案,并用简练的文字说明这幅图形的名 称或创意.
乐哈哈
神州九号飞天成功
猪头
我们一起涂
在田字格中,用虚线画一个面积为2 个平方单位的轴对称图形.
说一说
本节课我们有什么收获?
1.能按要求完成某些轴对称图案. 2.会设计轴对称图形. 3.感受了轴对称的美.
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
轴对称变换

A'
A P B l
总结归纳: 对称原理 在解决本问题时,是利用作对称把问 题转化为线段问题来求解的。这一方 法已形成了一种思想,它在解决许多 问题中都有重要作用。现在人们把凡 是用对称点来实现解题的思想方法叫 对称原理。
通过今天的学习,你有什么收 获与体会?
作业:
1、教科书第135~136页习题 14.2第1、4、7题;
§14.2 轴对称变换
实验中学 黄彦
学生作品展
让我们欣赏一 下这些美丽的 图案吧!
何依伊
初二(3)班
魏超
初二(4)班
何依伊
初二(3)班
杨楚怡
初二(3)班
李晨迪
初二(3)班
何依伊
初二(3)班
王璇
初二(3)班
对印画
把一张纸对折,用较厚的颜色直接 画在期中的半张纸上,然后用另半张纸 对压在上面,用手压实,揭起即可得到 一张左右或上下对称的对印作品。对印 画图案对称,造型奇妙,通过压印的色 彩不留笔触,产生了自然的肌理美感。
(2)新图形上的每一点都是原图形上某一点关于 直线L的对称点。
(3)连接任一对对应点的线段被对称轴垂直平分。
学个新知识
像上面那样,由一个平面图形得到它 的轴对称图形叫做轴对称变换。
①成轴对称的两个图形中的任何一个可以看 作由另一个பைடு நூலகம்形经过轴对称变换后得到;
②一个轴对称图形也可以看作以它的一 部分为基础,经轴对称变换扩展后得到。
2、利用轴对称变换设计一幅美 丽的图案,要求A4纸。
课件设计理念
1.本节课要求学生通过动手实践操作观察, 认识轴对称变换的特征,及如何得到 轴对称 变换的图形的过程。要让学生注意到轴对称变 换前后两个图形全等,及对应点连线被对称轴 垂直平分。 2.本节课要通过轴对称变换在图案设计中的 广泛应用,让学生在动手实践中体会轴对称在 现实生活中的应用,感受数学的美,发展学生 的实践能力,培养创新精神。
《利用轴对称设计图案》教案

《利用轴对称设计图案》教案一、教学目标●知识与技能:●掌握轴对称的基本概念和性质。
●能够运用轴对称原理自主设计简单的轴对称图案。
●培养学生空间想象能力和创造力。
过程与方法:●通过观察、讨论和实践操作,引导学生探究轴对称图形的形成过程。
●培养学生自主探究和合作学习的能力。
情感、态度与价值观:●激发学生对轴对称图形美的欣赏和创造力。
●培养学生对图形设计艺术的兴趣和热爱。
教学重点:●轴对称概念的理解。
●轴对称图形的性质及其应用。
教学难点:●灵活运用轴对称原理设计图案。
三、教学过程●导入新课(3分钟)●展示轴对称图案实例,引发学生兴趣。
●提问学生是否了解轴对称,并简要介绍轴对称的概念。
探究轴对称(10分钟)●引导学生通过折纸活动理解轴对称。
●让学生观察轴对称图形的特点,并归纳总结出轴对称的性质。
●组织小组讨论,分享轴对称图形的发现和理解。
设计轴对称图案(15分钟)●示范设计一个简单的轴对称图案,展示设计过程。
●学生尝试自主设计轴对称图案,教师巡回指导。
●学生分享设计作品,相互评价并提出改进意见。
实践应用(10分钟)●介绍轴对称在日常生活和艺术设计中的应用。
●引导学生思考轴对称在解决实际问题中的意义和作用。
●组织小组活动,让学生尝试运用轴对称原理解决实际问题。
总结反馈(2分钟)●总结轴对称图形的特点和设计过程。
●鼓励学生在生活中寻找轴对称的例子,继续深化对轴对称的理解。
●启发式教学:通过提问和讨论,引导学生主动思考和探究。
●直观教学:利用实物、图片和多媒体展示轴对称图案,帮助学生形成直观印象。
●动手实践:通过折纸和设计图案等活动,让学生亲身感受轴对称的魅力。
课堂练习:●完成一些轴对称图形的识别练习题,以巩固学生对轴对称图形的认识。
作业:●设计一幅具有创意的轴对称图案,作为课后作业。
评价方式:●观察学生在课堂活动中的参与度和表现。
●评估学生设计的轴对称图案的创意和规范性。
●通过课后作业反馈,了解学生对轴对称设计的掌握情况。
利用轴对称设计图案教学设计北师大版

本节课的核心素养目标主要包括:
1.逻辑推理:让学生通过观察、分析和归纳轴对称图形的性质,培养学生的逻辑推理能力。
2.空间观念:培养学生运用轴对称知识设计图案的能力,提高学生的空间观念。
3.创新思维:鼓励学生发挥创造力,利用轴对称设计出独特的图案,培养学生的创新思维。
4.数学建模:通过实际生活中的轴对称应用,培养学生运用数学知识解决实际问题的能力。
(2)讨论法:在设计图案环节,教师组织学生进行小组讨论,分享设计思路,互相借鉴,培养学生的创新能力和团队协作精神。
(3)实验法:让学生动手实践,利用剪刀、纸张等材料,自己动手制作轴对称图形,加深对轴对称知识的理解和应用。
2.教学手段
(1)多媒体设备:利用多媒体课件,展示丰富的轴对称图形实例,生动形象地揭示轴对称的性质,提高学生的学习兴趣。
针对以上学情分析,教师在教学过程中应注重启发引导,激发学生的创新思维;同时,加强课堂管理,提高学生的课堂参与度;还要关注学生的个体差异,因材施教,确保每个学生都能在课堂上得到锻炼和提升。
教学方法与手段
1.教学方法
(1)讲授法:在讲解轴对称的概念和性质时,教师通过口头讲解,结合图形演示,使学生理解和掌握轴对称的基本知识。
3.行为习惯:学生在课堂表现方面,大部分能够认真听讲、积极回答问题。但也有部分学生注意力不集中,容易受到外界干扰。在课下实践环节,部分学生能够认真完成作业,但也有部分学生对实践活动不够重视,完成质量不高。
4.对课程学习的影响:学生已有的知识基础和对轴对称的理解程度对课程的学习有积极影响,有利于快速掌握本节课的主要内容。然而,学生在空间观念、创新能力等方面的差异,以及对课程实践活动的态度,可能会影响课程学习的深度和广度。
利用轴对称设计美妙图案

利用轴对称设计美妙图案
房延华
数学不仅是思维科学,也是试验科学.下面采撷几例,请同学们和我一起在动手中欣赏数学的对称美和简洁美.
一、拼图
例1 已知每个网格中小正方形的边长都是1,请你在图2中以图1为基本图案,借助轴对称拼成一个完整的花边图案.
分析:设计图案问题一般具有开放性,可以根据自己想象设计出美丽的图案. 解:答案不唯一,提供如图3所示的两种图案.
二、图案设计
例2 图4为7×6的正方形网格,点A ,B ,C 在格点(小正方形的顶点)上.在图4中确定格点D ,并画出一个以A ,B ,C ,D 为顶点的四边形,使其为轴对称图形.
图4 分析:作图时,只需要找出这个图形的关键点和对称轴,利用对称轴图形的性质得出点D 的位置即可.
解:图5所示图案供参考:
①
②
图
2
图
3
图1
例3 某住宅小区拟栽种12棵风景树,若想栽成6行,每行4棵,且6行树所处位置连成线后能组成精美的轴对称图案,请你仿照图6在图7所示的方框中再设计两种不同的栽树方案.
分析:12棵树栽成6行(将行看成是线段,将树看成是线段上的点),每行都是4棵,因此每行必须与另外两行相交,且在交点处栽树,我们可以借鉴图6中的图案(在三角形的基础上设计出的轴对称图形)进行设计.
解:如图8所示.
A
B D A B C
D
C 图5 图
6 图
7 图8。
轴对称变换教案

14.2.1轴对称变换●教学目标(一)、教学知识点1、能作出一个图形经过一次或两次轴对称变换后的图形.2、能利用轴对称变换设计一些简单的图案.(二)、能力训练要求1、能够按要求作出简单平面图形经过轴对称变换后的图形.2、欣赏现实生活中的轴对称图形,能利用轴对称进行一些图案设计.体验轴对称在现实生活中的广泛应用和丰富的文化价值.(三)、情感与价值观要求通过作图、欣赏、设计,来培养学生的审美观念及创新能力.●教学重点:能够作出一个图形经过轴对称变换后的图形.●教学难点:通过动手操作总结轴对称变换的特征。
.●教学方法:直观演示法、实验发现法,设疑诱导法.●教具准备:多媒体课件●教学过程Ⅰ、创设情景,引入新课:1、给出几幅美丽的轴对称图案。
2、观察下面的图案:(1)它们是轴对称图形吗?(2)画出它们的对称轴.(3)轴对称有哪些性质?答:①、关于某条直线对称的两个图形是全等形;②、如果两个图形关于某直线对称,那么对应点所连的线段被对称轴垂直平分;③、成轴对称的两个图形的对应线段相等,对应角相等.Ⅱ、动手操作,感受变换:1、操作:在一张半透明的纸的左边画一只左脚印,把这张纸对折后描图,打开对折的纸,就能得到相应的右脚印。
问:左脚印和和右脚印有什么关系?2、给出两组美丽的图案,演示轴对称,让学生总结出对称前和对称后的图形一些结论。
3、定义:由一个平面图形得到它的轴对称图形叫做轴对称变换。
4、如图,给出了一个图案的一半,其中的虚线就是这个图案的对称轴,认真观察图形回答下列问题:(1)、你能猜出整个图案的形状吗?(2)、你能画出这个图案的另一半吗?Ⅲ、提升思维,运用变换:例1、 已知一个点A 直线l ,作出与点A 关于直线l 对称的点A ′。
例2、已知线段AB 和直线l ,作出与线段AB 关于直线l 对称的图形。
点拨:找出关键点,作出其对称点。
例3、 已知△ABC 和直线l ,作出△ABC 关于直线l 对称的图形。
利用轴对称设计图案

轴对称特点
轴对称图形具有对称美,其左右 或上下两部分完全重合,给人一 种平衡、和谐的感觉。
轴对称图形分类
中心对称图形
图形绕某一点旋转180°后与原来的图形 重合,则该图形称为中心对称图形,该 点称为对称中心。如圆形、正方形等。
提炼传统元素
从传统剪纸、窗花中提炼出具有 代表性的轴对称元素,如祥云、 如意、蝙蝠等,作为现代设计的
创意来源。
结合现代审美
在保持传统元素精神内涵的基础 上,结合现代审美观念进行创新 设计。运用现代设计手法和材料, 打造出具有时代感的轴对称图案。
拓展应用领域
将传统剪纸、窗花的轴对称元素 应用于现代设计的各个领域,如 平面设计、产品设计、建筑设计 等,为现代设计注入独特的文化
04 剪纸、窗花等传统艺术中 轴对称元素挖掘
传统剪纸、窗花艺术简介
剪纸
一种通过剪刀或刻刀在纸上进行雕刻 的民间艺术,历史悠久,风格独特。 剪纸作品通常用于装饰或庆祝活动, 寓意吉祥如意。
窗花
贴在窗户上的一种剪纸艺术,常见于 中国北方地区。窗花图案丰富多样, 包括动植物、人物、神话传说等题材 ,寄托着人们对美好生活的向往。
实例分析:色彩在轴对称图案中运用
实例一
运用对比原则,在轴对称图案的一侧使用明亮的暖色调,另一侧使用暗调的冷色调,形成 强烈的视觉对比。
实例二
运用调和原则,采用相近的色相和饱和度,通过色彩的微妙变化实现图案的层次感和立体 感。
实例三
结合色彩的情感表达和象征意义,在轴对称图案中运用具有特定文化内涵的色彩,赋予图 案更深的寓意和内涵。例如,在庆祝活动中使用的轴对称图案,可以采用红色为主色调, 辅以金色等亮色,营造出热烈、喜庆的氛围。
《利用轴对称进行设计》生活中的轴对称PPT课件

A
B
C
D
2.(1)我国每年都发行一套生肖邮票.下列生肖邮票中,动物的 “脑袋”被设计成轴对称图案的是( D )
A
B
C
D
(2)如图,在3×2的正方形网格中,已有两个小正方形被涂黑,再 将图中其余小正方形任意涂黑一个,使阴影部分构成一个轴 对称图形的涂法有( C )
A.1种
B.2种
C.3种
D.4种
精典范例
解:如图.(答案不唯一) 答案图
变式练习 6.把一张正方形纸片如图1,图2对折两次后,再如图3挖去一个 三角形小孔,则展开后的图形是( C )
A
B
C
D
7.利用图形中的对称点,画出图形的对称轴.
图①
图②
解:如图.
图①
答案图
图②
★8.如图甲,正方形被划分成16个全等的三角形,将其中若干 个三角形涂黑,且满足下列条件: (1)涂黑部分的面积是原正方形面积的一半;
3.【例1】将一张长方形纸对折,然后用笔尖在上面扎出“B”, 再把它铺平,你可见到( C )
A
B
C
D
4.【例2】下图中的图形都是轴对称图形,请你试着画出它们 的对称轴.(各画一条即可)
解:如图.(答案不唯一) 答案图
5.【例3】如图是由小正方形组成的格点图形,将图中某一个 小正方形涂上阴影,与图中的3个阴影正方形构成轴对称图形.
图甲
(2)涂黑部分成轴对称图形. 如图乙是一种涂法,请在图1~3中分别设计另外三种涂法(在 所设计的图案中,若涂黑部分全等,则认为是同一种涂法,如图 乙与图丙).
图乙
图丙
图1
图2
图3
解:不同涂法的图案举例如下: 答案图
2024年中考数学一轮复习章节测试及解析—第七章:图形的变化(提升卷)

2024年中考数学一轮复习章节测试及解析—第七章:图形的变化(提升卷)(时间:90分钟满分:120分)一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)1.下列垃圾分类标志分别是厨余垃圾、有害垃圾、其他垃圾和可回收物,其中既是轴对称图形又是中心对称图形的是()A.B.C.D.【答案】B【分析】根据轴对称图形与中心对称图形的概念求解.【详解】解:A、是轴对称图形,不是中心对称图形,故此选项不合题意;B、既是轴对称图形,也是中心对称图形,故此选项符合题意;C、是轴对称图形,不是中心对称图形,故此选项不合题意;D、既不是轴对称图形,也不是中心对称图形,故此选项不符合题意;故选:B.【点睛】此题主要考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与原图重合.2.下列图形中,既是轴对称图形又是中心对称图形的是()A .B .C .D .【答案】D【解析】【分析】根据轴对称图形与中心对称图形的概念求解.【详解】解:A 、是轴对称图形,不是中心对称图形,故此选项不符合题意;B 、不是轴对称图形,是中心对称图形,故此选项不符合题意;C 、是轴对称图形,不是中心对称图形,故此选项不符合题意;D 、既是轴对称图形,又是中心对称图形,故此选项符合题意;故选:D .【点睛】此题主要考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后两部分重合.3.如图,在ABC 中,120BAC ∠=︒,将ABC 绕点C 逆时针旋转得到DEC ,点A ,B 的对应点分别为D ,E ,连接AD .当点A ,D ,E 在同一条直线上时,下列结论一定正确的是()A .ABC ADC ∠=∠B .CB CD=C .DE DC BC +=D .AB CD∥【答案】D【分析】由旋转可知120EDC BAC ∠=∠=︒,即可求出60ADC ∠=︒,由于60ABC ∠<︒,则可判断ABC ADC ∠≠∠,即A 选项错误;由旋转可知CB CE =,由于CE CD >,即推出CB CD >,即B 选项错误;由三角形三边关系可知DE DC CE +>,即可推出DE DC CB +>,即C 选项错误;由旋转可知DC AC =,再由60ADC ∠=︒,即可证明ADC 为等边三角形,即推出60ACD ∠=︒.即可求出180ACD BAC ∠+∠=︒,即证明//AB CD ,即D 选项正确;【详解】由旋转可知120EDC BAC ∠=∠=︒,∵点A ,D ,E 在同一条直线上,∴18060ADC EDC ∠=︒-∠=︒,∵60ABC ∠<︒,∴ABC ADC ∠≠∠,故A 选项错误,不符合题意;由旋转可知CB CE =,∵120EDC ∠=︒为钝角,∴CE CD >,∴CB CD >,故B 选项错误,不符合题意;∵DE DC CE +>,∴DE DC CB +>,故C 选项错误,不符合题意;由旋转可知DC AC =,∵60ADC ∠=︒,∴ADC 为等边三角形,∴60ACD ∠=︒.∴180ACD BAC ∠+∠=︒,∴//AB CD ,故D 选项正确,符合题意;故选D .【点睛】本题考查旋转的性质,三角形三边关系,等边三角形的判定和性质以及平行线的判定.利用数形结合的思想是解答本题的关键.4.如图,在小正三角形组成的网格中,已有6个小正三角形涂黑,还需涂黑n 个小正三角形,使它们与原来涂黑的小正三角形组成的新图案恰有三条对称轴,则n 的最小值为A .10B .6C .3D .2【答案】C 【解析】如图所示,n 的最小值为3,故选C .【名师点睛】本题主要考查利用轴对称设计图案,解题的关键是掌握常见图形的性质和轴对称图形的性质.5.四盏灯笼的位置如图.已知A,B,C,D的坐标分别是(−1,b),(1,b),(2,b),(3.5,b),平移y轴右侧的一盏灯笼,使得y轴两侧的灯笼对称,则平移的方法可以是()A.将B向左平移4.5个单位B.将C向左平移4个单位C.将D向左平移5.5个单位D.将C向左平移3.5个单位【答案】C【分析】直接利用利用关于y轴对称点的性质得出答案.【详解】解:∵点A(−1,b)关于y轴对称点为B(1,b),C(2,b)关于y轴对称点为(-2,b),需要将点D(3.5,b)向左平移3.5+2=5.5个单位,故选:C.【点睛】本题主要考查了关于y轴对称点的性质,正确记忆横纵坐标的关系是解题关键.6.在平面直角坐标系中,等边AOB ∆如图放置,点A 的坐标为()1,0,每一次将AOB ∆绕着点О逆时针方向旋转60︒,同时每边扩大为原来的2倍,第一次旋转后得到11AOB ∆,第二次旋转后得到22A OB ∆,…,依次类推,则点2021A 的坐标为()A .()202020202,2-B .()202120212,2C .()202020202,2D .()201120212,2-【答案】C【分析】由题意,点A 每6次绕原点循环一周,利用每边扩大为原来的2倍即可解决问题.【详解】解:由题意,点A 每6次绕原点循环一周,20216371......5÷= ,2021A ∴点在第四象限,202120212OA =,202160xOA ∠=︒,∴点2020A 的横坐标为20212020122=2⨯,纵坐标为20212020=22-,()2020202020212,2A ∴,故选:C .【点睛】本题考查坐标与图形变化-旋转,规律型问题,解题的关键是理解题意,学会探究规律的方法,属于中考常考题型.7.如图,在菱形OABC 中,点B 在x 轴上,点A 的坐标为(2,),将菱形绕点O 旋转,当点A 落在x 轴上时,点C 的对应点的坐标为()A .(2--,或2)-B .(2,C .(2,-D .(2--,或(2,【答案】D【解析】【分析】如图所示,过点A 作AE ⊥x 轴于点E ,根据题意易得△AOB 为等边三角形,在旋转过程中,点A 有两次落在x 轴上,当点A 落在x 轴正半轴时,点C 落在点C′位置,利用旋转的性质和菱形的性质求解,当A 落在x 轴负半轴时,点C 落在点C′′位置,易证此时C′′与点A 重合,即可求解.【详解】解:如图所示,过点A 作AE ⊥x 轴于点E ,则23tan AOE=2∠,,∴∠AOE=60°,∵四边形ABCD 是菱形,∴△AOB 是等边三角形,当A 落在x 轴正半轴时,点C 落在点C′位置,此时旋转角为60°,∵∠BOC=60°,∠COF=30°,∴∠C′OF=60°-30°=30°,∵OC′=OA=4,∴OF=C'O cos ∠,C′F=C'Osin C'OF=2∠,∴C′(2,--),当A 落在x 轴负半轴时,点C 落在点C′′位置,∵∠AOC=∠AOC+∠BOC=120°,∴∠A′′OC=120°,∠GOC′=30°又∵OA=OC′′,∴此时C′′点A 重合,C C′′(2,,综上,点C 的对应点的坐标为(2--,或(2,,故答案为:D .【点睛】本题考查菱形的性质,解直角三角形和旋转的性质,解题的关键是根据题意,分析点A 的运动情况,分情况讨论.8.如图,ABC 中,90,8,6ACB AC BC ∠=︒==,将ADE 沿DE 翻折,使点A 与点B重合,则CE的长为()A.198B.2C.254D.74【答案】D【分析】先在RtABC中利用勾股定理计算出AB=10,再利用折叠的性质得到AE=BE,AD=BD=5,设AE=x,则CE=AC-AE=8-x,BE=x,在Rt△BCE中根据勾股定理可得到x2=62+(8-x)2,解得x,可得CE.【详解】解:∵∠ACB=90°,AC=8,BC=6,∴=10,∵△ADE沿DE翻折,使点A与点B重合,∴AE=BE,AD=BD=12AB=5,设AE=x,则CE=AC-AE=8-x,BE=x,在Rt△BCE中∵BE2=BC2+CE2,∴x2=62+(8-x)2,解得x=25 4,∴CE=2584-=74,故选:D .【点睛】本题考查了折叠的性质:折叠前后两图象全等,即对应角相等,对应边相等.也考查了勾股定理.9.在平面直角坐标系中,抛物线245y x x =-+与y 轴交于点C ,则该抛物线关于点C 成中心对称的抛物线的表达式为()A .245y x x =--+B .245y x x =++C .245y x x =-+-D .245y x x =---【答案】A【分析】先求出C 点坐标,再设新抛物线上的点的坐标为(x,y ),求出它关于点C 对称的点的坐标,代入到原抛物线解析式中去,即可得到新抛物线的解析式.【详解】解:当x=0时,y=5,∴C (0,5);设新抛物线上的点的坐标为(x,y ),∵原抛物线与新抛物线关于点C 成中心对称,由20x x ⨯-=-,2510y y ⨯-=-;∴对应的原抛物线上点的坐标为(),10x y --;代入原抛物线解析式可得:()()21045y x x -=--⋅-+,∴新抛物线的解析式为:245y x x =--+;故选:A .【点睛】本题综合考查了求抛物线上点的坐标、中心对称在平面直角坐标系中的运用以及求抛物线的解析式等内容,解决本题的关键是设出新抛物线上的点的坐标,求出其在原抛物线上的对应点坐标,再代入原抛物线解析式中求新抛物线解析式,本题属于中等难度题目,蕴含了数形结合的思想方法等.10.如图.将菱形ABCD 绕点A 逆时针旋转α∠得到菱形'''AB C D ,B β∠=∠.当AC 平分''B AC ∠时,α∠与β∠满足的数量关系是()A .2αβ∠=∠B .23αβ∠=∠C .4180αβ∠+∠=︒D .32180αβ∠+∠=︒【答案】C【分析】根据菱形的性质可得AB=AC ,根据等腰三角形的性质可得∠BAC=∠BCA=1(180)2B ︒-∠,根据旋转的性质可得∠CAC′=∠BAB′=α∠,根据AC 平分''B AC ∠可得∠B′AC=∠CAC=α∠,即可得出4180αβ∠+∠=︒,可得答案.【详解】∵四边形ABCD 是菱形,B β∠=∠,∴AB=AC ,∴∠BAC=∠BCA=1(180)2B ︒-∠=1(180)2β︒-∠,∵将菱形ABCD 绕点A 逆时针旋转α∠得到菱形'''AB C D ,∴∠CAC′=∠BAB′=α∠,∵AC 平分''B AC ∠,∴∠B′AC=∠CAC=α∠,∴∠BAC=∠B′AC+∠BAB′=2α∠=1(180)2β︒-∠,∴4180αβ∠+∠=︒,故选;C .【点睛】本题考查旋转的性质及菱形的性质,熟练掌握相关性质并正确找出旋转角是解题关键.二、填空题(本大题共10小题,每小题3分,共30分)11.如图,三角形纸片ABC 中,点D ,E ,F 分别在边AB ,AC ,BC 上,BF =4,CF =6,将这张纸片沿直线DE 翻折,点A 与点F 重合.若DE ∥BC ,AF =EF ,则四边形ADFE 的面积为__________.【答案】【分析】根据折叠的性质得到DE 为ABC 的中位线,利用中位线定理求出DE 的长度,再解t R ACE △求出AF 的长度,即可求解.【详解】解:∵将这张纸片沿直线DE 翻折,点A 与点F 重合,∴DE 垂直平分AF ,AD DF =,AE EF =,ADE EDF ∠=∠,∵DE ∥BC ,∴ADE B ∠=∠,EDF BFD ∠=∠,90AFC ∠=︒,∴B BFD ∠=∠,∴BD DF =,∴BD AD =,即D 为AB 的中点,∴DE 为ABC 的中位线,∴152DE BC ==,∵AF =EF ,∴AEF 是等边三角形,在t R ACE △中,60CAF ∠=︒,6CF =,∴tan 60CF AF ==︒∴AG =∴四边形ADFE 的面积为122DE AG ⋅⨯=,故答案为:.【点睛】本题考查解直角三角形、中位线定理、折叠的性质等内容,掌握上述基本性质定理是解题的关键.12.如图,将边长为1的正方形ABCD 绕点A 顺时针旋转30°到111AB C D 的位置,则阴影部分的面积是______________;【答案】2323-【分析】CD 交11B C 于点E ,连接AE ;根据全等三角形性质,通过证明1AB E ADE △≌△,得1EAB EAD ∠=∠;结合旋转的性质,得130EAB EAD ∠=∠=︒;根据三角函数的性质计算,得1EB ,结合正方形和三角形面积关系计算,即可得到答案.【详解】解:如图,CD 交11B C 于点E ,连接AE根据题意,得:190AB E ADE ∠=∠=︒,11AB AD ==∵AE AE=∴1AB E ADE△≌△∴1EAB EAD∠=∠∵正方形ABCD 绕点A 顺时针旋转30°到111AB C D ∴130BAB ∠=︒,90BAD ∠=︒∴119060B AD BAB ∠=︒-∠=︒∴130EAB EAD ∠=∠=︒∴111tan 3EB EAB AB =∠=∴13EB =∴111112236AB E ADE S S AB EB ==⨯=⨯=△△∴阴影部分的面积()()122AB E ADE AB BC S S =⨯-+△△23=-故答案为:23-.【点睛】本题考查了正方形、全等三角形、旋转、三角函数的知识;解题的关键是熟练掌握正方形、全等三角形、旋转、三角函数的性质,从而完成求解.13.如图,在Rt △ABC 中,∠B =90°,∠A =30°,AC =8,点D 在AB 上,且BD点E 在BC 上运动.将△BDE 沿DE 折叠,点B 落在点B′处,则点B′到AC 的最短距离是_____.【答案】2【解析】【分析】如图,过点D作DH⊥AC于H,过点B′作B′J⊥AC于J.在Rt△ACB中,根据三角函数知识可得DB′+B′J≥DH,DB′=DB=,当D,B′,J共线时,B′J的值最小,此时求出DH,DB′,即可解决问题.【详解】解:如图,过点D作DH⊥AC于H,过点B′作B′J⊥AC于J.在Rt△ACB中,∵∠ABC=90°,AC=8,∠A=30°,∴AB=AC•cos30°=,∵BD,∴AD=AB﹣BD=,∵∠AHD=90°,∴DH=12AD=332,∵B′D+B′J≥DH,DB′=DB ∴B′J≥DH﹣DB′,∴B′J≥3 2,∴当D,B′,J共线时,B′J的值最小,最小值为3 2;故答案为2.【点睛】本题主要考查了图形的折叠,特殊锐角三角函数的知识.14.如图,射线OM 、ON 互相垂直,8OA =,点B 位于射线OM 的上方,且在线段OA 的垂直平分线l 上,连接AB ,5AB =.将线段AB 绕点O 按逆时针方向旋转得到对应线段A B '',若点B '恰好落在射线ON 上,则点A '到射线ON 的距离d ≈______.【答案】245【分析】添加辅助线,连接'OA OB 、,过'A 点作'A P ON ⊥交ON 与点P .根据旋转的性质,得到''A B O ABO ≅ ,在'Rt A PO ∆和中,'B OA BOA ∠=∠,根据三角函数和已知线段的长度求出点A '到射线ON 的距离=A'P d .【详解】如图所示,连接'OA OB 、,过'A 点作'A P ON ⊥交ON 与点P .∵线段AB 绕点O 按逆时针方向旋转得到对应线段A B ''∴'8OA OA ==,''B OB A OA∠=∠∴''''B OB BOA A OA BOA ∠-∠=∠-∠即''B OA BOA∠=∠∵点B 在线段OA 的垂直平分线l 上∴118422OC OA ==⨯=,5OB AB ==2222543BC OB OC =--∵''B OA BOA∠=∠∴'sin ''sin 'A P BC B OA BOA A O OB∠==∠=∴'385A P =∴24'5d A P ==【点睛】本题主要考查旋转的性质和三角函数.对应点到旋转中心的距离相等,对应点与旋转中心所连的线段的夹角等于旋转角,旋转前、后的图形全等.15.如图,将Rt △ABC 的斜边AB 绕点A 顺时针旋转α(0°<α<90°)得到AE ,直角边AC 绕点A 逆时针旋转β(0°<β<90°)得到AF ,连接EF .若AB=3,AC=2,且α+β=∠B ,则EF=__________.【答案】13【解析】由旋转的性质可得AE=AB=3,AC=AF=2,∵∠B+∠BAC=90°,且α+β=∠B ,∴∠BAC+α+β=90°,∴∠EAF=90°,∴22AE AF +1313【名师点睛】本题考查了旋转的性质,勾股定理,灵活运用旋转的性质是本题的关键.16.如图,将ABCD 绕点A 逆时针旋转到AB C D ''' 的位置,使点B '落在BC 上,B C ''与CD 交于点E ,若3,4,1AB BC BB '===,则CE 的长为________.【答案】98【分析】过点C 作CM//C D ''交B C ''于点M ,证明ABB ADD ''∆∆∽求得53C D '=,根据AAS 证明ABB B CM ''∆≅∆可求出CM=1,再由CM//C D ''证明△CME DC E '∆∽,由相似三角形的性质查得结论.【详解】解:过点C 作CM//C D ''交B C ''于点M ,∵平行四边形ABCD 绕点A 逆时针旋转得到平行四边形AB C D '''∴AB AB '=,,AD AD '=B AB C D D '''∠=∠=∠=∠,BAD B AD ''∠=∠∴BAB DAD ''∠=∠,B D '∠=∠∴ABB ADD ''∆∆∽∴3,4BB AB AB DD AD BC ''===∵1BB '=∴43DD '=∴C D C D DD ''''=-CD DD '=-AB DD '=-433=-53=AB C AB C CB M ABC BAB '''''∠=∠+∠=∠+∠ ∴∠CB M BAB ''=∠∵413B C BC BB ''=-=-=∴B C AB'=∵AB AB '=∴∠AB B AB C ABB ''''=∠=∠∵//AB C D ''',//C D CM''∴//AB CM'∴∠AB C B MC'''=∠∴∠AB B B MC''=∠在ABB '∆和B MC '∆中,BAB CB M AB B B MC AB B C ∠=∠⎧⎪∠='''∠''⎨⎪=⎩∴ABB B CM''∆≅∆∴1BB CM '==∵//CM C D'∴△CME DC E'∆∽∴13553CM CE DC DE '===∴38CE CD =∴333938888CE CD AB ====故答案为:98.【点睛】此题主要考查了旋转的性质,平行四边形的性质,全等三角形的判定与性质以及相似三角形的判定与性质,正确作出辅助线构造全等三角形和相似三角形是解答本题的关键.17.如图,点P 是正方形ABCD 内一点,且点P 到点A 、B 、C的距离分别为4则正方形ABCD 的面积为________【答案】314【解析】【分析】如图,将△ABP绕点B顺时针旋转90°得到△CBM,连接PM,过点B作BH⊥PM于H.首先证明∠PMC=90°,推出∠CMB=∠APB=135°,推出A,P,M共线,利用勾股定理求出AB2即可.【详解】解:如图,将△ABP绕点B顺时针旋转90°得到△CBM,连接PM,过点B作BH⊥PM于H.∵2,∠PBM=90°,∴2PB=2,∵PC=4,3,∴PC2=CM2+PM2,∴∠PMC=90°,∵∠BPM=∠BMP=45°,∴∠CMB=∠APB=135°,∴∠APB+∠BPM=180°,∴A ,P ,M 共线,∵BH ⊥PM ,∴PH=HM ,∴BH=PH=HM=1,∴AH=2+1,∴AB 2=AH 2+BH 2=()2+12,∴正方形ABCD 的面积为14+4.故答案为.【点睛】本题考查旋转的性质,全等三角形的判定和性质,正方形的性质,解直角三角形等知识,解题的关键是学会利用旋转法添加辅助线,构造全等三角形解决问题.18.如图,已知正方形ABCD 边长为1,E 为AB 边上一点,以点D 为中心,将DAE △按逆时针方向旋转得DCF ,连接EF ,分別交BD ,CD 于点M ,N .若25AE DN =,则sin EDM ∠=__________.【答案】5【分析】过点E 作EP ⊥BD 于P ,将∠EDM 构造在直角三角形DEP 中,设法求出EP 和DE 的长,然后用三角函数的定义即可解决.【详解】解:∵四边形ABCD 是正方形,∴AB ∥DC ,∠A=∠BCD=∠ADC=90°,AB=BC=CD=DA=1,BD =.∵△DAE 绕点D 逆时针旋转得到△DCF ,∴CF=AE ,DF=DE ,∠EDF=∠ADC=90°.设AE=CF=2x ,DN=5x ,则BE=1-2x ,CN=1-5x ,BF=1+2x .∵AB ∥DC ,∴~FNC FEB .∴NC FC EB FB =.∴1521212x x x x -=-+.整理得,26510x x +-=.解得,116x =,21x =-(不合题意,舍去).∴1221233AE x EB x ===-=.∴103DE ===.过点E 作EP ⊥BD 于点P ,如图所示,设DP=y ,则2BP y =.∵22222EB BP EP DE DP -==-,∴)2222210233y y ⎛⎫⎛⎫-=- ⎪ ⎪ ⎪⎝⎭⎝⎭.解得,223y =.∴222210222333EP E D DP ⎛⎫⎛⎫=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭.∴在Rt △DEP 中,253sin 5103EP EDP ED ∠==.即5sin 5EDM ∠=.故答案为:55【点睛】本题考查了正方形的性质、旋转的性质、相似三角形的判定与性质、勾股定理、锐角三角函数、方程的数学思想等知识点,熟知各类图形的性质与判定是解题的基础,构造直角三角形,利用锐角三角函数的定义是解题的关键.20.如图,在平面直角坐标系中,AB y ⊥轴,垂足为B ,将ABO 绕点A 逆时针旋转到11AB O V 的位置,使点B 的对应点1B 落在直线34y x =-上,再将11AB O V 绕点1B 逆时针旋转到112A B O 的位置,使点1O 的对应点2O 也落在直线34y x =-上,以此进行下去……若点B 的坐标为()0,3,则点21B 的纵坐标...为______.【答案】3875【分析】计算出△AOB 的各边,根据旋转的性质,求出OB 1,B 1B 3,,得出规律,求出OB 21,再根据一次函数图像上的点求出点B 21的纵坐标即可.【详解】解:∵AB ⊥y 轴,点B (0,3),∴OB=3,则点A 的纵坐标为3,代入34y x =-,得:334x =-,得:x=-4,即A (-4,3),∴OB=3,AB=4,,由旋转可知:OB=O 1B 1=O 2B 1=O 2B 2=…=3,OA=O 1A=O 2A 1=…=5,AB=AB 1=A 1B 1=A 2B 2=…=4,∴OB 1=OA+AB 1=4+5=9,B 1B 3=3+4+5=12,∴OB 21=OB 1+B 1B 21=9+(21-1)÷2×12=129,设B 21(a ,34a -),则OB 21129=,解得:5165a =-或5165(舍),则335163874455a ⎛⎫-=-⨯-= ⎪⎝⎭,即点B 21的纵坐标为3875,故答案为:387 5.【点睛】本题考查了一次函数图象上点的坐标特征,旋转以及直角三角形的性质,求出△OAB的各边,计算出OB21的长度是解题的关键.三、解答题(本大题共6小题,共66分.解答应写出文字说明、证明过程或演算步骤)21.如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,△OAB的三个顶点O(0,0)、A(4,1)、B(4,4)均在格点上.(1)画出△OAB关于y轴对称的△OA1B1,并写出点A1的坐标;(2)画出△OAB绕原点O顺时针旋转90°后得到的△OA2B2,并写出点A2的坐标;(3)在(2)的条件下,求线段OA在旋转过程中扫过的面积(结果保留π).【解析】(1)如下图所示,点A1的坐标是(–4,1);(2)如下图所示,点A2的坐标是(1,–4);(3)∵点A(4,1),∴=∴线段OA在旋转过程中扫过的面积是:290(17)360⨯π⨯=174π.【名师点睛】本题考查简单作图、扇形面积的计算、轴对称、旋转变换,解答本题的关键是明确题意,利用数形结合的思想解答.22.在Rt ABC 中,90,5,3ACB AB BC ∠=︒==,将ABC 绕点B 顺时针旋转得到A BC ''△,其中点A ,C 的对应点分别为点A ',C '.(1)如图1,当点A '落在AC 的延长线上时,求AA '的长;(2)如图2,当点C '落在AB 的延长线上时,连接CC ',交A B '于点M ,求BM 的长;(3)如图3,连接,AA CC '',直线CC '交AA '于点D ,点E 为AC 的中点,连接DE .在旋转过程中,DE 是否存在最小值?若存在,求出DE 的最小值;若不存在,请说明理由.【答案】(1)8AA '=;(2)1511BM =;(3)存在,最小值为1【分析】(1)根据题意利用勾股定理可求出AC 长为4.再根据旋转的性质可知AB A B '=,最后由等腰三角形的性质即可求出AA '的长.(2)作CD AC '⊥交AC '于点D ,作//CE A B '交AC '于点E .由旋转可得A BC ABC ''∠=∠,3BC BC '==.再由平行线的性质可知CEB A BC ''∠=∠,即可推出CEB ABC ∠=∠,从而间接求出3CE BC BC '===,DE DB =.由三角形面积公式可求出125CD =.再利用勾股定理即可求出185BE =,进而求出335C E '=.最后利用平行线分线段成比例即可求出BM 的长.(3)作//AP A C ''且交C D '延长线于点P ,连接A C '.由题意易证明BCC BC C ''∠=∠,90ACP BCC '∠=︒-∠,90A C D BC C '''∠=︒-∠,即得出ACP A C D ''∠=∠.再由平行线性质可知APC A C D ''∠=∠,即得出ACP APC ∠=∠,即可证明AP AC A C ''==,由此即易证()APD A C D AAS ''≅ ,得出AD A D '=,即点D 为AA '中点.从而证明DE 为ACA ' 的中位线,即12DE A C '=.即要使DE 最小,A C '最小即可.根据三角形三边关系可得当点A C B '、、三点共线时A C '最小,且最小值即为=A C A B BC ''-,由此即可求出DE 的最小值.【详解】(1)在Rt ABC 中,4AC ==.根据旋转性质可知AB A B '=,即ABA '△为等腰三角形.∵90ACB ∠=︒,即BC AA '⊥,∴4A C AC '==,∴8AA '=.(2)如图,作CD AC '⊥交AC '于点D ,作//CE A B '交AC '于点E .由旋转可得A BC ABC ''∠=∠,3BC BC '==.∵//CE A B ',∴CEB A BC ''∠=∠,∴CEB ABC ∠=∠,∴3CE BC BC '===,DE DB =.∵1122ABC S AB CD AC BC == ,即543CD ⨯=⨯,∴125CD =.在Rt BCD 中,2295DB BC CD =-=,∴185BE =.∴335C E BE BC ''=+=.∵//CE A B ',∴BM BC CE C E '=',即33335BM =,∴1511BM =.(3)如图,作//AP A C ''且交C D '延长线于点P ,连接A C '.∵BC BC '=,∴BCC BC C ''∠=∠,∵180ACP ACB BCC '∠=︒-∠-∠,即90ACP BCC '∠=︒-∠,又∵90A C D BC C '''∠=︒-∠,∴ACP A C D ''∠=∠.∵//AP A C '',∴APC A C D ''∠=∠,∴ACP APC ∠=∠,∴AP AC =,∴AP A C ''=.∴在APD △和AC D '' 中ADP A DC APD A C D AP A C '''∠=∠⎧⎪∠=∠'''⎨⎪=⎩,∴()APD A C D AAS ''≅ ,∴AD A D '=,即点D 为AA '中点.∵点E 为AC 中点,∴DE 为ACA ' 的中位线,∴12DE A C '=,即要使DE 最小,A C '最小即可.根据图可知A C A B BC ''≤-,即当点A C B '、、三点共线时A C '最小,且最小值为==53=2A C A B BC ''--.∴此时1=12DE A C '=,即DE 最小值为1.【点睛】本题为旋转综合题.考查旋转的性质,勾股定理,等腰三角形的判定和性质,平行线的性质,平行线分线段成比例,全等三角形的判定和性质,中位线的判定和性质以及三角形三边关系,综合性强,为困难题.正确的作出辅助线为难点也是解题关键.23.已知在 ABC 中,O 为BC 边的中点,连接AO ,将 AOC 绕点O 顺时针方向旋转(旋转角为钝角),得到 EOF ,连接AE ,CF .(1)如图1,当∠BAC =90°且AB =AC 时,则AE 与CF 满足的数量关系是;(2)如图2,当∠BAC =90°且AB≠AC 时,(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)如图3,延长AO 到点D ,使OD =OA ,连接DE ,当AO =CF =5,BC =6时,求DE 的长.【答案】(1)AE CF =;(2)成立,证明见解析;(3)5113【分析】(1)结论AE CF =.证明()AOE COF SAS ∆≅∆,可得结论.(2)结论成立.证明方法类似(1).(3)首先证明90AED ∠=︒,再利用相似三角形的性质求出AE ,利用勾股定理求出DE 即可.【详解】解:(1)结论:AE CF =.理由:如图1中,∠=︒,OC OB=,BAC,90=AB AC⊥,∴==,AO BCOA OC OB∠=∠=︒,90AOC EOF∴∠=∠,AOE COF,OE OFOA OC==,∴∆≅∆,AOE COF SAS()∴=.AE CF(2)结论成立.理由:如图2中,,OC OB=,BAC∠=︒90∴==,OA OC OB,AOC EOF∠=∠∴∠=∠,AOE COFOA OC=,OE OF=,()AOE COF SAS∴∆≅∆,AE CF∴=.(3)如图3中,由旋转的性质可知OE OA=,OA OD=,5OE OA OD∴===,90AED∴∠=︒,OA OE=,OC OF=,AOE COF∠=∠,∴OA OE OC OF=,AOE COF∴∆∆∽,∴AE OA CF OC=,5CF OA== ,∴5 53 AE=,253 AE∴=,5113 DE∴=.【点睛】本题属于几何变换综合题,考查了旋转变换,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理等知识,解题的关键是正确寻找全等三角形或相似三角形解决问题,属于中考压轴题.24.已知:如图①,将一块45°角的直角三角板DEF 与正方形ABCD 的一角重合,连接,AF CE ,点M 是CE 的中点,连接DM .(1)请你猜想AF 与DM 的数量关系是__________.(2)如图②,把正方形ABCD 绕着点D 顺时针旋转α角(090a ︒<<︒).①AF 与DM 的数量关系是否仍成立,若成立,请证明;若不成立,请说明理由;(温馨提示:延长DM 到点N ,使MN DM =,连接CN )②求证:AF DM ⊥;③若旋转角45α=︒,且2EDM MDC ∠=∠,求AD ED的值.(可不写过程,直接写出结果)【答案】(1)AF=2DM (2)①成立,理由见解析②见解析③622+【解析】【分析】(1)根据题意合理猜想即可;=,连接CN,先证明△MNC≌△MDE,再证明(2)①延长DM到点N,使MN DM△ADF≌△DCN,得到AF=DN,故可得到AF=2DM;②根据全等三角形的性质和直角的换算即可求解;③依题意可得∠AFD=∠EDM=30°,可设AG=k,得到DG,AD,FG,ED的长,故可求解.【详解】(1)猜想AF与DM的数量关系是AF=2DM,故答案为:AF=2DM;(2)①AF=2DM仍然成立,=,连接CN,理由如下:延长DM到点N,使MN DM∵M是CE中点,∴CM=EM又∠CMN=∠EMD,∴△MNC≌△MDE∴CN=DE=DF,∠MNC=∠MDE∴CN∥DE,又AD∥BC∴∠NCB=∠EDA∴△ADF≌△DCN∴AF=DN∴AF=2DM②∵△ADF≌△DCN∴∠NDC=∠FAD,∵∠CDA=90°,∴∠NDC+∠NDA=90°∴∠FAD+∠NDA=90°∴AF ⊥DM③∵45α=︒,∴∠EDC=90°-45°=45°∵2EDM MDC ∠=∠,∴∠EDM=23∠EDC=30°,∴∠AFD=30°过A 点作AG ⊥FD 的延长线于G 点,∴∠ADG=90°-45°=45°∴△ADG 是等腰直角三角形,设AG=k,则DG=k ,k ,k ,∴故ADED 622+=.【点睛】此题主要考查四边形综合,解题的关键是熟知正方形的性质、旋转的特点、全等三角形的判定与性质及三角函数的运用.25.如图1,点B 在线段CE 上,Rt △ABC ≌Rt △CEF ,90ABC CEF ∠=∠=︒,30BAC ∠=︒,1BC =.(1)点F 到直线CA 的距离是_________;(2)固定△ABC ,将△CEF 绕点C 按顺时针方向旋转30°,使得CF 与CA 重合,并停止旋转.①请你在图1中用直尺和圆规画出线段EF 经旋转运动所形成的平面图形(用阴影表示,保留画图痕迹,不要求写画法)该图形的面积为_________;②如图2,在旋转过程中,线段CF 与AB 交于点O ,当OE OB =时,求OF 的长.【答案】(1)1;(2)12π;(3)23OF =【解析】【分析】(1)根据直角三角形的性质和全等三角形的性质可得∠ACF=∠ECF=30°,即CF 是∠ACB 的平分线,然后根据角平分线的性质可得点F 到直线CA 的距离即为EF 的长,于是可得答案;(2)①易知E 点和F 点的运动轨迹是分别以CF 和CE 为半径、圆心角为30°的圆弧,据此即可画出旋转后的平面图形;在图3中,先解Rt △CEF 求出CF 和CE 的长,然后根据S 阴影=(S △CEF +S 扇形ACF )-(S △ACG +S 扇形CEG )即可求出阴影面积;②作EH ⊥CF 于点H ,如图4,先解Rt △EFH 求出FH 和EH 的长,进而可得CH 的长,设OH=x ,则CO 和OE 2都可以用含x 的代数式表示,然后在Rt △BOC 中根据勾股定理即可得出关于x 的方程,解方程即可求出x 的值,进一步即可求出结果.【详解】解:(1)∵30BAC ∠=︒,90ABC ∠=︒,∴∠ACB=60°,∵Rt △ABC ≌Rt △CEF ,∴∠ECF=∠BAC=30°,EF=BC=1,∴∠ACF=30°,∴∠ACF=∠ECF=30°,∴CF 是∠ACB 的平分线,∴点F 到直线CA 的距离=EF=1;故答案为:1;(2)①线段EF 经旋转运动所形成的平面图形如图3中的阴影所示:在Rt △CEF 中,∵∠ECF=30°,EF=1,∴CF=2,CE=3,由旋转的性质可得:CF=CA=2,CE=CG=3,∠ACG=∠ECF=30°,∴S 阴影=(S △CEF +S 扇形ACF )-(S △ACG +S 扇形CEG )=S 扇形ACF -S 扇形CEG =()2230330236036012πππ⨯⨯-=;故答案为:12π;②作EH ⊥CF 于点H ,如图4,在Rt △EFH 中,∵∠F=60°,EF=1,∴13,22FH EH ==,∴CH=13222-=,设OH=x ,则32OC x =-,2222223324OE EH OH x x⎛⎫=+=+=+ ⎪ ⎪⎝⎭,∵OB=OE ,∴2234OB x =+,在Rt △BOC 中,∵222OB BC OC +=,∴2233142x x ⎛⎫++=- ⎪⎝⎭,解得:16x =,∴112263OF =+=.【点睛】本题考查了旋转的性质和旋转作图、全等三角形的性质、角平分线的性质、扇形面积公式、勾股定理和解直角三角形等知识,涉及的知识点多,综合性较强,熟练掌握上述知识、灵活应用整体思想和方程思想是解题的关键.26.如图,在矩形ABCD 中,E 是边AB 上一点,BE BC =,EF CD ⊥,垂足为F .将四边形CBEF 绕点C 顺时针旋转()090αα︒<<︒,得到四边形CB E F '''.B E ''所在的直线分别交直线BC 于点G ,交直线AD 于点P ,交CD 于点K .E F ''所在的直线分别交直线BC 于点H ,交直线AD 于点Q ,连接B F ''交CD 于点O .(1)如图1,求证:四边形BEFC 是正方形;(2)如图2,当点Q 和点D 重合时.①求证:GC DC =;②若1OK =,2CO =,求线段GP 的长;(3)如图3,若//BM F B ''交GP 于点M ,1tan 2G ∠=,求'GMB CF H S S △△的值.【答案】(1)见解析;(2)①见解析;②3)125-【分析】(1)先利用三个角是直角的四边形是矩形证明,再根据BE BC =证得结论;(2)①证明''CGB CDF ≅ 即可得到结论;②方法一:设正方形边长为a ,根据'~'B KO F CO ,求出11''22B K BC a ==,利用勾股定理得到222''B K B C CK +=,求出a,得到5B C '=,5B K '=,根据B KC ' ∽△CKG ,求出KG ,再根据PKD GKC ≅ ,求出答案;方法二:过点P 作PM GH ⊥于点M ,根据CG CD =,2CD CK =求出6CG =,由26PM CK ==,12GM =,再利用勾股定理求得结果;(3)方法一:延长''B F 与BH 的延长线交于点R ,证明~'GBM CRF ,求出'1'2F H CF =,设'F H x =,'2CF x =,则CH =,证明'~'RB C RF H ,求得2'''22CF R CF H S S x == ,由'~'GB C GE H,求出)21GB x =-,利用~'GBM CRF ,求出'6255GMB CF R S S -= ,即可得到答案;方法二,过点B 作BN PG ⊥,垂足为点N .设FH x =,则'''''2CF B E E F BC x ====,'4GB x =,求得(2'465GBN CHF S GB S CH -⎛⎫== ⎪⎝⎭ ,证明~'GBN GCB,求出55GB GC =,再证明~''MBN B F C ,求出答案;方法三:设AB 与PQ 交于N 点,设FH x =,则'''''2CF CB B E E F BC x =====,'4GB x =,证明~'MBN F OC,得到(2'9620MBN F OC S BN S CO -⎛⎫==⎪⎝⎭ ,根据12GBN S BG BN =⨯⨯ ,求出答案.【详解】(1)在矩形ABCD 中,90B BCD ∠=∠=︒,∵EF AB ⊥,则90EFB ∠=︒,∴四边形BEFC 是矩形.∵BE BC =,∴矩形BEFC 是正方形.(2)①如图1,∵90GCK DCH ∠=∠=︒,∴'90CDF H ∠+∠=︒,90KGC H ∠+∠=︒,∴'KGC CDF ∠=∠,又∵''B C CF =,''GB C CF D ∠=∠,∴''CGB CDF ≅ ,∴CG CD =.②方法一:设正方形边长为a ,∵PG ∥CF ',∴'~'B KO F CO ,∴'1'2B K OK CF CO ==,∴11''22B K BC a ==,∴在'Rt B KC 中,222''B K B C CK +=,∴222132a a ⎛⎫+= ⎪⎝⎭,∴5a =.∴5B C '=,5B K '=,∵90,CB K GCK B KC GKC ''∠=∠=︒∠=∠,∴B KC ' ∽△CKG ,∴2CK B K KG '=⋅,∴KG =∵1,,2B K a KE DKE B KC DE K KB C ''''''==∠=∠∠=∠,∴△B’CK ≌△E’KD ,∴DK=KC ,又∵∠DKP=∠GKC ,∠P=∠G ,∴PKD GKC ≅ ,∴PG=KG ,∴PG =;方法二:如图2,过点P 作PM GH ⊥于点M ,由''CGB CDF ≅ ,可得:CG CD =,由方法一,可知2CD CK =,∴6CG =,由方法一,可知K 为GP 中点,从而26PM CK ==,12GM =,从而由勾股定理得PG =.(3)方法一:如图3,延长''B F 与BH 的延长线交于点R ,由题意可知,'//CF GP ,'//RB BM ,∴~'GBM CRF ,'G F CR ∠=∠,∴'1tan tan ''2F HG F CH CF ∠=∠==,设'F H x =,'2CF x =,则CH =,∴''''''2CB CF E F B E BC x =====,∵'//'CB HE ,∴'~'RB C RF H ,∴''1''2F H RH RF B C RC RB ===,∴CH RH =,'''B F RF =,∴2CR CH ==,2'''22CF R CF H S S x == ,∵'//'CB HE ,∴'~'GB C GE H ,∴'22'33GC B C x GH E H x ===,'2'3B C E H ==,∴)21GB x =,∵~'GBM CRF ,∴22'216255GMBCF Rx S GB S CR ⎡⎤-⎛⎫=== ⎪⎝⎭.∵'''2CF R CF H S S =,∴'125GMB CF HS S -= .方法二,如图4,过点B 作BN PG ⊥,垂足为点N .由题意可知,'//CF GP ,'//HE BN ,∴~'GBN CHF ,∴2'GBN CHF S GB S CH ⎛⎫= ⎪⎝⎭,∵'//CF GP ,∴'NGB F CH ∠=∠,∴'1tan tan ''2CB FH G F CH GB CF ∠=∠===,设FH x =,则'''''2CF B E E F BC x ====,'4GB x =,∴CH =,CG =,则)21GB x =,∴(22'21465GBN CHF x S GB S CH ⎛⎫--⎛⎫=== ⎪⎝⎭,∵2'1'2CF H S CF FH x =⋅= ,∴(2465GBNSx -=,∵'//HE BN ,∴~'GBN GCB,∴55'5GB GC CB BN -===,∵'//CB BN ,//''BM B F ,'//'CF GB ,∴~''MBN B F C ,∴22''55625'55MBN B F C S BN S CB ⎛⎫-⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭,∴(2''26655MBNB FC SS x --==,∴(((222462626555MBGNBG MBN SS S xxx ---=-=-=,∴'12455GMB CF H S S -= .方法三:如图5,设AB 与PQ 交于N 点,设FH x =,则'''''2CF CB B E E F BC x =====,'4GB x =,由题意可知,'//CF GP ,//''BM B F ,//BN CO ,∴~'MBN F OC ,∴2'MBN F OC S BN S CO ⎛⎫= ⎪⎝⎭,由方法(2)可知,)251GB x =,所以)51BN x =-,又∵22533CO CK x ==,∴(2'96520MBN F OC S BN S CO -⎛⎫==⎪⎝⎭ ,∴((229625362542035BMNSxx --=⨯=,∵)(222151652GBN S BG BN x x =⨯⨯==- ,∴(((2223625262562555GBMGBN NBM SS S x xx --=-=--=,∴2'1''2CF H S CF F H x =⨯⨯= ,∴'12455GMB CF H S S -= .【点睛】此题考查正方形的判定定理及性质定理,旋转的性质,全等三角形的判定及性质,相似三角形的判定及性质,锐角三角函数,综合掌握各知识点并熟练应用解决问题是解题的关键.。
知识卡片-利用轴对称设计图案

利用轴对称设计图案
能量储备
图案设计的步骤
(1)整体构思
①图案的设计要突出“主题”,即设计图案的意图,要求简洁、自然、别致,具有一定的意义.
②确定整幅图案的形状(如圆形或正方形)和“基本图案”(不宜太复杂).
③构思图案的形成过程:首先构思该图案由哪几部分构成,再构思如何运用平移、旋转、轴对称等变换实现由“基本图案”到各部分图案的组合,并作出草图.
(2)具体作图
根据草图,运用尺规作图的方法准确地作出图案.
(3)对图案进行适当的修饰(如着色等).
通关宝典
★基础方法点
方法点1:
例1:某小区搞绿化,要在给定的一块长方形空地上设计一个花坛,只允许用正方形和圆形,并使整个图案是轴对称图形,请你帮助设计一下.
解:答案不唯一,仅举三例,如图所示.
★★易混易误点
蓄势待发
考前攻略
运用平移、旋转、轴对称分析图形的变化及利用三种图形变换设计简单的图案,考查识图能力、分析能力、空间想象能力,题型多样,难度不大.
完胜关卡。
手把手教你利用轴对称打造醒目的图案设计

手把手教你利用轴对称打造醒目的图案设计在现代设计时代,我们经常需要打造一些醒目的图案设计来吸引人们的眼球。
而利用轴对称打造图案设计可以让我们更加简单快速地实现这一目标。
今天,我将手把手地教你如何利用轴对称打造醒目的图案设计。
让我们来了解一下轴对称是什么。
轴对称是指一条轴线将物体分为对称的两个部分,每个部分都是完相同的镜像。
这条轴线可以是任何形状,例如水平/垂直轴线或者对角线。
接下来,我们将使用 Adobe Illustrator 进行实践操作。
打开Illustrator,然后创建一个新的文档。
选择“File”菜单,然后选择“New”。
在弹出菜单中,设置你想要的文档尺寸和分辨率,然后点击“Create”。
接下来,我们将绘制一个简单的形状来展示轴对称,例如一个心形。
选择“Ellipse Tool”(椭圆工具),然后在画布上单击并拖动,创建一个圆形。
接下来,使用“Direct Selection Tool”(直接选择工具)选择圆形的上半部分,然后按“Delete”键删除它。
现在,我们只剩下一个半圆形。
接下来,在画布上单击并拖动,创建一个小的矩形,将其放置在半圆形的正中间。
接下来,选中矩形和半圆形,然后右键单击并选择“Make Compound Path”(制作复合路径)。
现在,我们的心形图案已经绘制完成。
接下来,我们需要将其复制并旋转以展示轴对称效果。
选中心形,然后使用“Rotate Tool”(旋转工具)将其旋转 180 度。
现在,我们已经有了两个完全相同的图案。
接下来,我们将利用 Illustrator 的“Reflect Tool”(对称工具)进行轴对称操作。
选择一个心形,然后选中“Reflect Tool”(对称工具)并单击心形的上端点,然后单击“Copy”按钮。
您现在就创建了一个轴对称的图案!您可以将这个图案进一步修改和细化,为您的设计添加更多的维度和效果。
例如,您可以使用不同的颜色、形状和线条来增加视觉复杂性。
文档:利用平移或轴对称在方格纸上设计简单的图案
利用平移或轴对称在方格纸上设计简单的图案
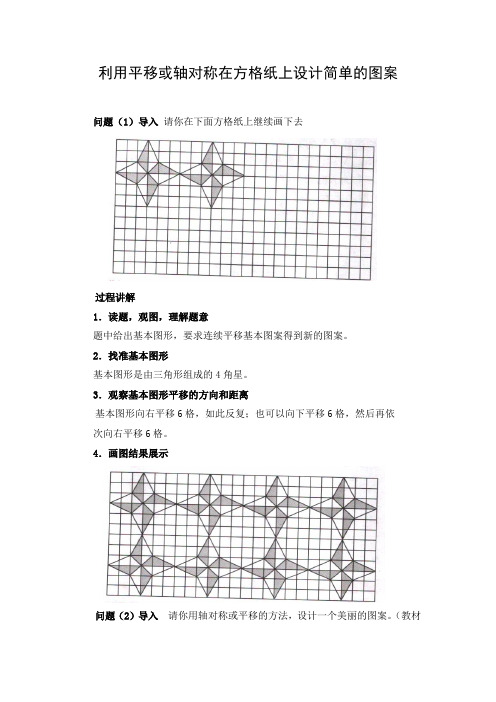
问题(1)导入请你在下面方格纸上继续画下去
过程讲解
1.读题,观图,理解题意
题中给出基本图形,要求连续平移基本图案得到新的图案。
2.找准基本图形
基本图形是由三角形组成的4角星。
3.观察基本图形平移的方向和距离
基本图形向右平移6格,如此反复;也可以向下平移6格,然后再依
次向右平移6格。
4.画图结果展示
问题(2)导入请你用轴对称或平移的方法,设计一个美丽的图案。
(教材
27页例题)
过程讲解
1.读题,理解题意
要求在方格纸上利用轴对称或平移设计美丽的图案,基本图形自行选择。
2.设计方法
(1)选好基本图形。
(2)确定设计图案的方式。
(3)利用轴对称设计,根据基本图形特点确定对称轴;利用平移设计,先确定平移的方向和格数。
3.设计图案展示
归纳总结
利用平移或轴对称设计图案,都要选准基本图形。
平移要确定好平移的格数和方向;轴对称要确定对称轴,连好关键点(或线段)。
误区警示慧眼识真知,错误巧规避!
【误区】判断:在设计图案时,一定要运用平移或轴对称的知识来设计。
(√)
错解分析并不是所有的图案都一定要运用平移或轴对称的知识来设计。
生活中有一些图案就想呈现出一种不和谐之美,这样的图案就不需要运用平移或轴对称的知识来设计。
错解改正×
温馨提示
平移和轴对称是设计图案的方式、方法,但是并不是所有的图案都要利用这些知识来设计。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
临海中学初二备课组
图片欣赏
图片欣赏
更多资源
图片欣赏
图片欣赏
图片欣赏
图片欣赏
图案欣赏
图案欣赏
图案欣赏
图案欣赏
想一想
观察下面的图案
(1)它们是轴对称图形吗? 找出它们的对称轴. (2)生活中这些图案可以代表什么含义?与同伴进行交流.
ClBFra bibliotek基础训练
5、用两个圆、两个三角形、两条平行线段可以构造出许 多独特而有意义的轴对称图形(如下图),请你也仿 照构思一个图案,别忘了加上一两句贴切的解说词哦.
两盏电灯
课堂小结
l
1、画出点A关于 l 的对称点A’: ( 1 )过点A作对称轴 l 的垂线,垂足为B;
( 2 )延长A B 至A’,使得BA’= A B. ( 3 )点 A’ 就是点A关于 l 的对称点.
2、画简单平面图形的对称图形:
A
B
A’
找关键点作出对称点!然后连结线段. 3、利用轴对称设计图案.
课后作业
一、教科书第202页习题7.5:1、2作在书上,
3作在一张纸上;
二、目标对应部分
迁移拓展
1、下图曾被哈佛大学选为入学考试的试题.请在下列一组图形符号中 找出它们所蕴含的内在规律,然后把图形空白处填上恰当的图形
A
l
B
A’
1、过点A作对称轴 l 的垂线,垂足为B; 2、延长A B 至A’,使得BA’= A B. 3、点 A’ 就是点A关于 l 的对称点.
基础训练
1、 如何画线段AB关于直线 对称线段A’B’?
l
A A’
l的
B
B’
找关键点作出其对称点! 然后连结线段.
基础训练
2、如何画 ⊿ABC关于直线 对称⊿ A’B’C’?
l
l的
A
A’
B
B’
还是找关键点作出其对称点!
然后顺次连结线段构成三角形.
基础训练
3、如图给出了一个图案的一半,其中 的虚线
l
l是这个图案的对称轴.
(1)整个图案是个什么形状? (2)请准确地画出它的另一半.
仿照上面完成教科书上第202页随堂练习1
基础训练
4、请画出⊿ABC关于直线 A
l 的对称⊿ A’B’C’.(名校80页自1)
2、如果两个图形关于某直线对称,那么对应点所连的线段被对称轴垂直平分;
3、成轴对称的两个图形的对应线段相等,对应角相等.
想一想
如图给出了一个图案的一半,其中 的虚线是这个图案的对称轴. (1)猜一猜:整个图案是个什么形状? (2)如何准确地画出它的另一半?
尝试探究
已知对称轴 l 和一个点A如
何画出点A关于 l 的对称点A’ ?
知识回顾
什么是轴对称图形?什么叫两个图形成轴对称?
1、如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合, 那么这个图形叫做轴对称图形,这条直线叫做对称轴. 2、对于两个图形,如果沿一条直线对折后,它们能完全重合,那么 这两个图形成轴对称,这条直线就是对称轴. 轴对称主要有哪些性质? 1、关于某条直线对称的两个图形是全等形;
2、某居民小区要在一块长方形空地上建花坛现征集设计方案 要求:(1)设计的图案由若干个长方形和圆组成; (2)整个长方形场地要成为轴对称图形.
请给出你的设计方案.(“名校” 81页“迁”2)
再 见
更多资源
