第7 章 点的合成运动a(牵连平动)
07-理论力学-第二部分运动学第七章点的合成运动

运动学/点的合成运动
动 点: AB杆上的A点 动 系: 凸轮 定 系: 地面 绝对运动: 直线 相对运动:曲线(圆弧) 牵连运动: 直线平移
1616
运动学/点的合成运动
动 点:A(在AB杆上) 动 系:偏心轮C 定 系: 地面 绝对运动:直线 相对运动:圆周(C) 牵连运动: 定轴转动
22
运动学/点的合成运动
另一方面,在实际问题中,不仅要在固联在地面上 的参考系上还要在相对于地面运动着的参考系上观察和 研究物体的运动。下面先看几个例子。
33
运动学/点的合成运动
44
55
本章将用点的合成运动的方法来研究这类问题。 66
第七章 点的合成运动
§7-1 §7-2 §7-3
§7-4
r 2
r 2
r2
l2
r2
l 2(
) 3030
运动学/点的合成运动
例4 圆盘凸轮机构
已知:OC=e ,R 3e ,(匀角速度),图示瞬时, OCCA,且O,A,B三点共线。求:从动杆AB的速度。
解:选取动点:AB 上的A点
动系:圆盘
绝对运动:直线 相对运动:圆周
由
定系:基座 va
牵连运动:定轴 ve vr
▼动点相对动系、定系必须 有运动,不能和动系在同一 物体上。
▼以上可归结为一点、两系 、三运动。
2020
运动学/点的合成运动
四、 运动方程及坐标变换 可以利用坐标变换来建立绝对、
相对和牵连运动之间的关系。
以二维问题为例。设定系 ,
动系
。动点M,如图所示。
(1)绝对运动方程: x x(t), y y(t)
大小 ? OA
理论力学7-2
z
M M '
rM z '
r'
O' x'
k ' rO ' i '
j'
y'
O
y
UNIVERSITY OF JINAN
第七章 点的合成运动
1. 动系做平移时 i 0, j 0, k 0
' k ' 0 2 x' i ' y ' j ' z
ve vr va ro
vB ve r O l l l
UNIVERSITY OF JINAN
第七章 点的合成运动
绝对加速度 相对加速度
n 2 aa aa O r
方向由A指向O
ar ?
n e 2 e
方向水平
2 O r2
v 牵连加速度 a l
l
方向由B指向D
v R vr aa R R 2 v R 2 r 2vr R
2 a 2
UNIVERSITY OF JINAN
第七章 点的合成运动
加速度合成定理(Theorem of composition of accelerations)
1. 动系做平移时
aa ae ar
2. 两个不相关的物体,求二者的相对速度。 根据题意, 选择所求相对运动速度的点为动点, 动系 固结于另一物体上。
UNIVERSITY OF JINAN
第七章 点的合成运动
3. 相对于运动物体在运动的物体上有一动点,求该点的绝 对运动。则取该点取为动点,动系固结于另一个运动物体 上。
点的合成运动

种位移之间的关系为
MM'' =MM' + M' M''
目录
刚体的运动\点的合成运动
将上式两边分别除以Δt ,并取Δt→0 时的极限,得
y Ox
lim lim lim MM
MM
M M
t0 t
t0 t
t0 t
式在中绝:对lit运m0动M中Mt 的 表速示度动,点称在为瞬动时点t的、
y
vr
va
系相固结的物体的运动,因而是指一个刚体的运动,它可以是平移、
转动或其他复杂的运动。
目录
刚体的运动\点的合成运动
1.2 点的速度合成定理
以图示桥式起重机为例,研究
y Ox
绝对运动、相对运动和牵连运动三
者速度之间的关系。设在瞬时t,动 点在位置M。假如动点不作相对运
y
M''
动,则经Δt时间后,动点随动系运
理论力学
刚体的运动\点的合成运动
点的合成运动
在研究刚体的平面运动之前,先介绍点的合成运动的有关概念 及点的速度合成定理,这既是研究点的运动的又一种方法,又是研 究刚体复杂运动的基础。
1.1 点的合成运动的概念
在不同的物体上观察同一物体的运动时,会得出不同的结果。 例如,当火车行驶时,在车厢上观察车轮上一点的运动是圆周运动, 在地面上观察则是复杂的曲线运动,若在车轮上观察则是静止的。 因此,在研究一个物体的运动时,必须指明是相对于哪个物体而言, 即必须选定参考体或参考系。在工程上如果没有特别的说明,都是 以地面作为参考系。
目录
刚体的运动\点的合成运动 【例6.5】 凸轮机构(如图)中,导
杆AB可在铅垂管D内上下滑动,其下端 与凸轮保持接触。凸轮以匀角速度ω绕O 轴逆时针转动,在图示瞬时OA=a ,凸轮
点的合成运动

vr ve va r0
BD
ve r 0 BD l
11
已知:OA 0 常数 , OA r , BC DE , BD CE l , 求:BD , BD
3.加速度
方向
a a a e a ar
t n e
BD
BD
√
√
√
√
2 BD
2
√
√
√
√
aen 2 OA 2 2e
vr2
vr art arn
向η轴投影:
n
3
3
θ n
aa cos ae cos ar aC
n
2 2 2 3 16 e 8 e 2 2 2 aa (2e ) e 2 9 3 3 3 3
8
O ω
OA水平时,O1B的角速度ω1和角加速度 。 解:1. 速度分析: 动点为滑块 A , 动系固于摇杆 O1B 上。 绝对运动 — 圆周运动( O 为圆心) va 牵连运动 — 定轴转动(O1为圆心) B vr 相对运动 — 直线运动(沿 O1B 方向) 2 v r ω e
O A
va ve vr
ω O
α
A α O 1
O
D
x
va vA OA 125.6 cm / s
由几何关系可知:
R
C
vBCD ve vr va 125.6 cm / s
2
aa ae ar aa aan 2 OA n t n n t n tt n 2 2 a a a aa aaa a a a a a a e e rr r e c (4 ) 10 1579 cm/s
点的合成运动

2013年7月5日
理论力学CAI
42
1.牵连运动为转动时点的加速度合成定理
设一圆盘以匀角速度 绕 定轴O顺时针转动,盘上圆槽 内有一点M以大小不变的速度 vr 沿槽作圆周运动,那么M点
相对于定系的绝对加速度应是
多少呢?
2013年7月5日
理论力学CAI
43
选点M为动点,动系固结于圆盘上,
则M点的牵连运动为匀速转动, 为常数
y'
y u
x'
M
O
M O
y'
x'
x
O'
2013年7月5日
理论力学CAI
4
车刀以匀速横向走刀,卡盘匀角速度转动,求刀尖相对工件的轨迹。
2013年7月5日
理论力学CAI
5
§8-1 相对运动、牵连运动、绝对运动
归纳为:一点,两系,三种运动
一点
动点:做合成运动的点。
两系
定参考系(定系):固结于地面(地球)。如机座。 动参考系(动系):固结于某运动着的刚体上。
ar = 2l sin
理论力学CAI
37
课后作业1(浙大)
作业题 7-7 7-8 7-9
2013年7月5日
理论力学CAI
38
课后作业1
思考题 8-1 8-2 作业题 8-7 8-8
8-3
8-10
2013年7月5日
理论力学CAI
39
例题
例 曲柄滑杆机构
= 45o 时,, a ; 已知: OA=l ,
例题
已知:AB匀角速度转动。 求:M在导槽EF及BC中运动的速度与加速度。
E
B
C M
《理论力学》第七章-点的复合运动

v0
Ra
n r
aa
a
φ
x'
O
n
arn
vr2 R
v2
Rsin2
3、速度分析
va vevr
vr
ve
sin
v
sin
4、加速度分析
aaaear arn
n
aasinaecosarn
aa
acot
v2
Rsin3
48
§7–4 牵连运动为转动的加速度合成定理
牵连运动为平动时加速度合成定理:aaaear
牵连运动为定轴平动时 aaaear是否成立?
37
§7–2 速度合成定理
va vr
应用速度合成定理
va vevr
3、速度分析。 绝对速度va: va=OA·ω=rω , 方向垂直于OA向上
牵连速度ve: ve为所要求的未知量,
方向垂直于O1B 相对速度vr: 大小未知, 方向沿摇杆O1B
38
§7–2 速度合成定理
va vr
其中 O1A l2 r2
1
第七章 点的复合运动
§7–1 复合运动的概念 §7–2 速度合成定理 §7–3 牵连运动为平动时点的加速度合成定理 §7–4 牵连运动为转动时点的加速度合成定理
2
第七章 点的复合运动
复合运动问题:研究物体相对于不同参考系 的运动之间的关系。
复合运动不是一种新的运动形式,只是
一种研究运动学问题的思路和方法。
40
§7–3 牵连运动为平动的加速度合成定理
一、绝对运动和相对运动之间的关系
z M
绝对运动方程:r r(t)
z
r (t)
r (t ) k O j
理论力学.

2.速度分析: vavevr
大小:rω ? ?
方向:√ √ √
v e v as i n rs in
1
ve r2
O1A l2 r2
例7-4
已知:如图所示半径为R、偏心距为e的凸轮,以角速度ω 绕O轴转动,杆AB能在滑槽中上下平移,杆的端点A始终 与凸轮接触,且OAB成一直线。 求:在图示位置时,杆AB的速度。
求:当连线OM在水平位置时, 圆盘边缘上的点M的绝对速度。
D
C
M
B A
解: 1.运动分析:
动点:M点 ; 动系:固连于框架BACD;
绝对运动:未知;
相对运动:以O为圆心的圆周运动;
牵连运动:绕AB轴的定轴转动。
2.速度分析
C
vavevr
大小: ? Rω2 Rω 1
方向: ? √ √
vave 2 vr2R1 222
用铰链连接。当曲柄OA以匀角速度ω绕固定轴O转动时,
滑块在摇杆O1B上滑动,并带动杆O1B绕定轴O1摆动。设曲
柄长为OA=r,两轴间距离OO1=l。
求:曲柄在水平位置时摇杆的角 加速度。
解:
1.运动分析:
§动 绝牵点对连7-M运 运4相动动牵对、:连于相D运E地对动的面动绝运是水作动定平空点对、轴平间牵转移曲:运连动。线运时运滑动动点动的块:加速以度A合O;成点为动圆系心:,与O摇A杆为半固O径1 连B的;圆周运动;
arctvvaer)na( rct a1 2)n(
D M
B A
点的速度合成定理的解题步骤
1.选取动点、动参考系和定参考系; 2.分析三种运动和三种速度;
绝对运动、相对运动、牵连运动 绝对速度、相对速度、牵连速度 3.应用速度合成定理,做出速度平行四边形; 绝对速度为平行四边形的对角线 4.利用速度平行四边形中的几何关系解出未知数。
理论力学课后习题答案

第7章 点的合成运动一、是非题(正确的在括号内打“√”、错误的打“×”)1.点的速度和加速度合成定理建立了两个不同物体上两点之间的速度和加速度之间的 关系。
( √ ) 2.根据速度合成定理,动点的绝对速度一定大于其相对速度。
( × )3.应用速度合成定理,在选取动点和动系时,若动点是某刚体上的一点,则动系不可以固结在这个刚体上。
( √ )4.从地球上观察到的太阳轨迹与同时在月球上观察到的轨迹相同。
( × ) 5.在合成运动中,当牵连运动为转动时,科氏加速度一定不为零。
( × ) 6.科氏加速度是由于牵连运动改变了相对速度的方向而产生的加速度。
( √ ) 7.在图中,动点M 以常速度r v 相对圆盘在圆盘直径上运动,圆盘以匀角速度ω绕定轴O 转动,则无论动点运动到圆盘上的什么位置,其科氏加速度都相等。
( √ )二、填空题1.已知r 234=++v i j k ,e 63=-ωi k ,则k =a 18 i + -60 j + 36 k 。
2.在图中,两个机构的斜杆绕O 2的角速度均为2ω,O 1O 2的距离为l ,斜杆与竖直方向的夹角为θ,则图(a)中直杆的角速度=1ωθθωcos sin 2,图(b)中直杆的角速度=1ω2ω。
图 图3.科氏加速度为零的条件有:动参考系作平动、0=r v 和r e v ω//。
4.绝对运动和相对运动是指动点分别相对于定系和动系的运动,而牵连运动是指牵连点相对于定系的运动。
牵连点是指某瞬时动系上和动点相重合的点,相应的牵连速度和加速度是指牵连点相对于定系的速度和加速度。
5.如图所示的系统,以''Ax y 为动参考系,Ax'总在水平轴上运动,AB l =。
则点B 的相对轨迹是圆周,若kt ϕ= (k 为常量),点B 的相对速度为lk ,相对加速度为2lk 。
图6.当点的绝对运动轨迹和相对运动轨迹都是曲线时,牵连运动是直线平动时的加速度合成定理表达式是a e r =+a a a ;牵连运动是曲线平动时的加速度合成定理表达式是 a e r =+a a a ;牵连运动是转动时的加速度合成定理表达式是a e r k =++a a a a 。
理论力学答案(第七章后)

第七章 点的合成运动一、是非题7.1.1动点的相对运动为直线运动,牵连运动为直线平动时,动点的绝对运动必为直线运动。
( × )7.1.2无论牵连运动为何种运动,点的速度合成定理r e a v v v +=都成立。
( ∨ )7.1.3某瞬时动点的绝对速度为零,则动点的相对速度和牵连速度也一定为零。
( × )7.1.4当牵连运动为平动时,牵连加速度等于牵连速度关于时间的一阶导数。
( ∨ )7.1.5动坐标系上任一点的速度和加速度就是动点的牵连速度和牵连加速度。
( × )7.1.6不论牵连运动为何种运动,关系式a a +a a r e =都成立。
( × )7.1.7只要动点的相对运动轨迹是曲线,就一定存在相对切向加速度。
( × )7.1.8在点的合成运动中,判断下述说法是否正确:(1)若r v 为常量,则必有r a =0。
( × )(2)若e ω为常量,则必有e a =0. ( × )(3)若e r ωv //则必有0=C a 。
( ∨ )7.1.9在点的合成运动中,动点的绝对加速度总是等于牵连加速度与相7.1.10当牵连运动为定轴转动时一定有科氏加速度。
( × )二、 填空题7.2.1 牵连点是某瞬时 动系上与7.2.2 v e 与v r 共线 情况下,动点绝对速度的大小为r e a v v v +=,在 情况下,动点绝对速度的大小为a v =v e 、v r ,应按___ ____ __ 计算v a三、选择题:7.3.1 动点的牵连速度是指某瞬时牵连点的速度,它相对的坐标系是( A )。
A 、 定参考系B 、 动参考系C 、 任意参考系7.3.2 在图示机构中,已知t b a s ωsin +=, 且t ωϕ=(其中a 、b 、ω均为常数),杆长为L ,若取小球A 为动点,动系固结于物块B ,定系固结于地面,则小球的牵连速度v e 的大小为( B )。
理论力学7

va v
ve va sin q v sin q
va
O
ve
OC
C
v
OC
ve v sin q OA a
q
vr
A
B
vC OC OC
ab v sin q a
例5 图示平底顶杆凸轮机构,顶杆AB可沿导轨上下平动,偏心凸 轮以等角速度 绕 O 轴转动, O 轴位于顶杆的轴线上,工作时顶 杆的平底始终接触凸轮表面,设凸轮半径为R,偏心距OC=e , OC 与水平线的夹角为a,试求当a =45°时,顶杆AB的速度。 解:以凸轮圆心 C 为动点,动系取在 顶杆上
解: 动点:CD上的C点;
动系:固连于AB杆。
绝对运动:上下直线运动; 相对运动:沿AB直线运动; 牵连运动:铅垂平面内曲线平移
vB
B
解:(1)以车A为动点,动系取在车B上。
va vA 45km / h ve vB 60km / h
vr v v 75km / h
2 a 2 e
va
a1
vr
O
va 45 sin a1 0.6 vr 75
R
ve A
vB B
a 36.9
例10 图示曲柄滑道机构,圆弧轨道的半径R=OA=10 cm,已知 曲柄绕轴O以匀速n=120 rpm转动,求当j=30°时滑道BCD的 速度。
大小: 方向:
va ve vr
√ √
× √
e va ve cot q OA e OA vAB va e
× √
C
q
e
O
解题步骤: (1) 选取动点、动参考系和静参考系。 动点和动系应分别选择在两个不同的刚体上。 动点和动系的选择应使相对运动的轨迹简单直观。 有一个很明显的动点,在题中很容易发现; 有一个不变的接触点,可选该点为动点; (2) 进行速度分析 运动分析 各速度大小、方向 注意牵连速度 (3) 做速度平行四边形 对角线是绝对速度 需4个已知量 (4) 求解 可利用速度平行四边形中的几何关系解出未知 数,也可以采用投影法。
点的合成运动

r
45
e 4
a 8 e
e r 式向y方向投影: 由 a
sin r sin 45 a 4 / sin a
x方向:
cos e r cos 45 4 a 45
r a sin
r OA
OO1 sin OO1 sin OA
向 x 轴投影: e a cos
O B
1
e
O1 A
a cos
O1 A
cos 1 sin 2 O1 A
y
OA sin(180 ) sin
大小 ? √ ?
e r a
? √ ?
方向 ? √ √
? √ √
注意:绝对速度 a及夹角,无论坐标怎样选取,其大
小和方向都不变。 因此
a
r e r e
r cos 45 8 4 4
r
将上式投影到x方向:
A b v
va ve vr
x
M
300
y
B
n τ n aa aa ae ar ar ac
0
求速度和加速度因轨 迹变化复杂,相对速 度和相对法向加速度 无法求解,导致其他 速度和加速度解不出, 因此动点选取时应选 该动点不变的点,如 直角端点为动点。
τ ae
3 ac 21 vr r 4
2
aen=2r/8
3 r 4
2
1
ae
0' M
理论力学(第7版)第七章 点的合成运动

ar ~ d 2r dt 2
xi j k y z
ae
d 2 rM dt 2
xi yj zk rO
?
√ √ √ √ 将加速度矢量式投影到法线上,得
a a sin a e cos
大小 方向
aa a e a r a r ? a0 R? √
?
n
n
ar
n
aa (ae cos ar n ) / sin
整理得
a AB
2 3 8 v0 aa (a0 ) 3 3 R
称为动参考系,简称动系。例如在行驶的 汽车。以o’x’y’z’坐标系表示。
[注]: 1、参考系须指明固结于哪个参考体上,选择参 考体是选择参考系的关键。 2、动系与参考体有区别:参考体是有限的,而 参考坐标系是无限大的,故动系无限大。
3
7-1 相对运动 牵连运动 绝对运动
二、三种运动
1.绝对运动:动点对定系的运动 2.相对运动:动点对动系的运动
2 (aa aen )sin 30 3O r (l r ) aet cos 30 3l
BD
2 aet 3O r (l r ) BD 3l 2
28
7-4 牵连运动是定轴时点的加速度合成定理 科氏加速度
1、牵连运动为转动情况:
定理推导:
rM rM
r xi yj z k
3、 v a v e v r 大小 r ? ?
ve r 2 1 2 O1 A l r 2
方向 OA O1B //O1B ve va sin r sin
合成运动--加速度合成

va r0 vevar0
ve r 0 DB l
⑷ 牵连运动为平移,由加速度
合成定理
aa
ae ar
得
aaaenaet ar
大小 √ √ ? ? B 方向 √ √ √ √
y'
A
aenDC 0 30
ar
E
60
x'
aet O aa
aa r02
2)取套筒B为动点,动参考系与滑枕CD固连。相对运动是套筒 B沿滑杆的竖直直线运动,牵连运动是滑枕CD的水平平动,绝 对运动是套筒B绕O2的圆周运动。由速度合成定理 可得:
解:⑴ 取曲柄OA上的A点为动点,动系在丁字杆上
⑵ 研究三种运动
绝对运动:圆周运动 相对运动:直线运动
va
ve
vr
D A
牵连运动:平移
O
⑶
由速度合成定理
va
ve
vr,
B
C
作速度平行四边形
E
va ve vr
va r
大小 √ ? ? 方向 √ √ √
vevasinrsin
在摇杆O1B上滑动并带动摇杆绕固定轴 O1摆动。 OA=r, OO1=l, 求当曲柄在水平位置时摇杆的角速度和角加速度。
解:⑴ 取曲柄O1A上的A点为动点,动系在O1B上
⑵ 研究三种运动
x'
绝对运动:圆周运动 相对运动:直线运动源自 veva
B
vr
牵连运动:转动
O
A
⑶
由速度合成定理
va
ac
21vr
2r3 2l
(r2 l2 )3
2
相对运动绝对运动和牵连运动点的合成运动
2.三种运动的示意图
动点
绝对运动
相对运动
静系
动系
牵连运动
3.分析三种运动的要领、关键、原则 要领:必须明确两点 (l)站在什么地方看物体的运动? (2)看什么物体的运动? 关键:适当地选择动点和动系 原则:① 动点、动系间要有相对运动 (动点、动系不能选在同一个物体上) ② 相对运动要直观,明确
4. 实例 实例一 环形管内运动的小球
动点:M; 动系 :杆AB。 AM:平面曲线运动; RM:圆周运动; TM:动系AB作平动。
A
w
O1
M
q
B
O
O2
实例二 曲柄摇杆机构(牛头刨床中的急回机构) B
动点:A;
动系 :杆O1B。
AM:以OA为半径的圆周运动;
RM:直线运动;
TM:动系O1B作转动。
vA A
w
M
ve q
vr B
O
A
aA
w
M
arn q
art B
O ae
O1
O2
O1
O2
速度分析
加速度分析
实例二 曲柄摇杆机构(牛头刨床中的急回机构)
动点:A; 动系 :杆vr
A
O
aet
w
ar
A
O aa aen
w1
w1
O1 速度分析
O1 加速度分析
实例四 凸轮机构
动点:轮心O ; 动系 :推杆ABC 。
第七章 点的合成运动
第一节 相对运动、绝对运动和牵连运动
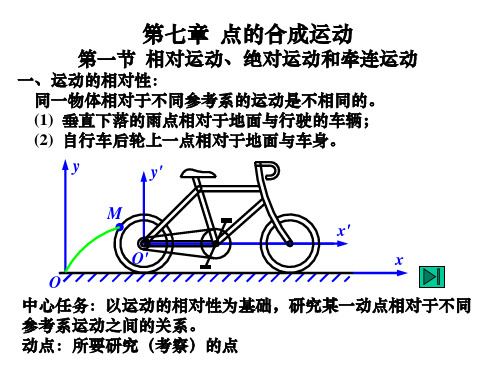
一、运动的相对性: 同一物体相对于不同参考系的运动是不相同的。 (1) 垂直下落的雨点相对于地面与行驶的车辆; (2) 自行车后轮上一点相对于地面与车身。
天津大学理论力学课件运动学3点的合成运动

再如,直管OB以匀角速度绕定轴O转动,小 球M以速度u在直管OB中作相对的匀速直线运 动,如图示。将动坐标系固结在OB管上,以 小球M为动点。随着动点M的运动,牵连点在 动坐标系中的位置在相应改变。设小球在t1、 t2瞬时分别到达M1、M2位置,
➢若选凸轮上的点(例如与A重合之点)为 动点,而动坐标系与AB杆固结,这样,相对
运动轨迹不仅难以确定,而且其曲率半径未 知。因而相对运动轨迹变得十分复杂,这将 导致求解(特别是求加速度)的复杂性。
第三节 牵连运动为平移时,点的加速度 合成定理
➢动点的绝对加速度、相对加速度和牵连加速度
绝对加速度aa:动点相对于静坐标系运动的加速度 相对加速度ar:动点相对于动坐标系运动的加速度
在任意瞬时,只有牵连点的运动能够给动点 以直接的影响。为此,定义某瞬时,与动点 相重合的动坐标系上的点(牵连点)相对于 静坐标系运动的速度称为动点的牵连速度
下图中,动坐标系OA上各点的速度大小不一 样
M点绝对速度va沿着绝对运动轨迹(半圆弧)在点M 处的切线方向,即va垂直于点M与圆心的连线; M点相对速度vr沿着动点M与动系(摇杆OA)的相对 运动轨迹的切线方向,即沿着OA上的滑槽方向;
EF 相接触,在两者接触处套上一小环 M,当 BC 杆
运动时,小环 M 同时在 BC、EF 杆上滑动。设曲柄 AB=CD=r,连杆 BC=AD=l,若曲柄转至图示角位 置时的角速度为,角加速度为,试求小环 M 的
加速度。
解:
动点:小环M
动系:固连在连杆BC上
静系:固连在地面上
绝对运动是沿 EF 的直线运动。aa 方向已知,沿 EF;
理论力学第7章分析解析

解: 1.运动分析:
动点:滑块A ;
动系:固连于杆BC上;
绝对运动:以O为圆心的圆周运动; 相对运动:滑块A在杆BC上的直线运动;
牵连运动:BC的平移。
2.速度分析
va ve vr
? √ √
大小:rωO ? 方向:√
vr ve va rO
BD
ve rO BD l
ωt
绝对运动方程: vt vt x x cos y sin r 1 cos cos ωt r sin sin ωt r r
vt vt y x sin y cos r 1 cos sin ωt r sin cos ωt r r
§ 7-2 点的速度合成定理
例:小球在金属丝上的运动
绝对运动
M'
相对运动
M2
va ve
M1
牵连点的运动
z
vr
M y
x
O
点的速度合成定理
动点在某瞬时的绝对速度等于它在该瞬时 的牵连速度与相对速度的矢量和
va ve vr
例7-3 已知:刨床的急回机构如图所示。曲柄OA的一端A与滑块 用铰链连接。当曲柄OA以匀角速度ω绕固定轴O转动时, 滑块在摇杆O1B上滑动,并带动杆O1B绕定轴O1摆动。设曲 柄长为OA=r,两轴间距离OO1=l。 求:曲柄在水平位置时摇杆的 角速度 1 。
(3)机构传动,传动特点是在一个刚体上存在 一个不变的接触点,相对于另一个刚体运动。 例如: 导杆滑块机构 —— 滑块为动点, 动系固结于导杆; 凸轮挺杆机构 —— 杆上与凸轮接触点为动点, 动系固结于凸轮; 摇杆滑道机构 —— 滑道中的点为动点, 摇杆为动系。 (4)特殊问题,特点是相接触两个物体的接触 点位置都随时间变化,此时,这两个物体的接触 点都不宜选为动点,应选择满足前述的选择原则 的非接触点为动点。
理论力学《点的合成运动》答案

va = ve + vr ve = v a sin 30 0 =
1 lω 0 2 1 = lω0 2
ve va
30
0
ve = O1 A ⋅ ωO1D
2l ⋅ ω O1D =
900
1 lω 0 2
vr
A
1 ω O1D = ω 0 4
动点:B。 动系:固连于 O1 D 杆上的坐标系。 静系:固连于地面的坐标系。
va = ve + vr v a = rω v BC va = 0 0 sin(180 − 120 − 90 + ϕ ) sin 120 0
0
vBC rϕ = 0 sin(ϕ − 30 ) sin 1200
v BC
sin( ϕ − 30 0 ) = ⋅ rω sin 120 0 1 sin( 0 − 30 ) 3 | ϕ =0 = ⋅ rω = 2 rω = − rω 0 sin 120 3 3 2
6
绝对速度:B相对于地面的速度。 相对速度:B相对于 O1 D 杆的速度。 牵连速度: O1 D 杆相对于地面的速度。
→ → →
ve
900
va
30 0
B
va = ve + vr
1 ve = O1 B ⋅ ω O1D = 4l × ω 0 = lω 0 4
vr
va =
ve lω 0 = = 1.155lω 0 0 cos 30 0.866
[习题7-4] 砂石料从传送带A落到另一传送带B的绝对速度为 v1 = 4m / s ,其方向与铅直线成
30 0 角。设传送带B与水平面成 15 0 角,其速度为 v 2 = 2m / s ,求此时砂石料对于传送带B的
牵连运动

k' dx' dt
di' dt
dy' dt
dj' dt
dz' dt
dk' dt
εe
r
ωe
dr dt
d2 x' dt 2
i
d2 y' dt 2
j
d2 z' dt 2
k
dx' dt
di' dt
dy' dt
dj' dt
dz' dt
dk' dt
εe r ωe ( ve
上下滑动,在图示位置时, 60
求该瞬时顶杆AB的速度。
B
va
vr
ve A
v0
解:选择顶杆AB上的点A为动点,凸轮为动系,由
va ve vr
画出动点A的速度合成图如图所示。 由图可知顶杆AB的速度为
va vectg v0ctg
3 3
v0
B
va
vr
ve A
v0
方向铅直向上。
ae aan cos aa sin r2 cos r sin
【例7-6】如图所示为曲柄导杆机构。已知O1A=O2B=10cm,又O1O2=AB,曲
柄O1A以角速度ω=2rad/s做匀速转动。在图示瞬时, 60 ,求该瞬时杆
CD的速度和加速度。
O1
O2
vA va
速度合成定理是一个矢量等式,实际计算时可以采用速度矢量图计 算,对于每一个矢量都有大小方向两个因素,速度合成定理的矢量等式 中一共有六个因素,所以只要知道了其中四个因素,就可以用两个标量 等式求出其余两个。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人 (动点)
点 相对 运动
牵连点
一点(动点) 在任一瞬时, 二系(动系、静系) 三运动(绝对、相对、牵连) 动系上与动点 重合的点。 三种运动的“关系”: 具体表示三种运动的量: 绝对运动 = 牵连运动 + 相对运动 绝对轨迹、绝对位移、绝对速度、绝对加速度 ——运动合成与分解
直接联系人绝对运动与 相对运动的因素是座位, 即在牵连运动中,直接 影响点的运动的因素是: 牵连点的运动。
~ dvO ' d vr aa dt dt
aa aO' ar
aa ae ar
加速度合成定理
上页公式
讨论:上面两个矢量式即牵连运动为平动时,点运动合成法的基本方程。
问题:在平面问题中,两个定理各能解几个未知量?为何种量?
注:速度图总为平行四边形,故一般借助几何关系求解(几何法)。
ve va tv tan v sin tan R OA R sin
13
讨论:①由上面解法得到启示,例2-1也可选C点为动点,同学试解; ②事实上,本题选凸轮与杆的接触点(几何点)为动点也可解,同学试解。
例3:例7-4(老书例8-4)(求加速度) 平行四连杆机构 (双曲柄机构)。 AB = CD = r,BC = AD=l,,,。 求小环M的加速度。
注意各种运动的主体,尤其注 意牵连运动的概念。
相对轨迹、相对位移、相对速度、相对加速度 牵连轨迹、牵连位移、牵连速度、牵连加速度
针对牵连点的!
3
例2 汽车轮子上点的运动。
4
旋轮线运动OM 复杂运动 (绝对运动)
直线运动OM1 + 简单运动 +
圆周运动M1M 简单运动 (相对运动)
(牵连运动) +
12
考虑其他点。显然凸轮圆心O是一个特殊点,试试看。动系如何选?显然选 杆。此时,绝对运动:沿水平直线运动;相对运动:与AB平行的直线运动; 牵连运动:转动。三种轨迹易知,故可解牵连速度,AB角速度即知。
y
va
vr
ve
v
解:动点O,动系AB,(静系地面),画速度图。va = v 。由速度图,
如果上述运动过程很短,如Δt,在此时间段内, 绝对轨迹即OM,相对轨迹即M1M,牵连轨迹即 OM1,如图。由此易得三种位移之关系:
va ve vr
OM OM1 M1M
速度合成定理
5
但加速度合成定理不易直接得到,需用矢量法(见后)。
§7-2 矢量的绝对导数和相对导数
问题:标量函数对时间的导数与坐标系选取有关吗?
10
解:选AB上A点为动点,凸轮为动系,画速度图。由 条件易知: = 30
ve OA 0 2e 0
由速度图,va ve tan 即AB杆速度。 注1:在能清楚表达的前提下, 可在原图上画运动图。 注2:在能清楚表达的前提下, 一般不用画出坐标系,但必须 说明动系、静系是如何选的。
6
三、动系转动时绝对导数和相对导数的关系 当动系转动时,i '、j '、k ' 在动系中为常矢量,但在静系中不再为常矢量。 di ' dA dx' dy ' dz ' dj ' dk ' db x' i ' j ' k ' y' z' b 泊松公式 dt dt dt dt dt dt dt dt ~ dA 为动系转动角速 x' ( i ' ) y ' ( j ' ) z ' ( k ' ) dt 度矢量 ~ dA A dt
当牵连运动为平动时,
drO ' dvO ' d 2 rO ' ve vO ' ,ae aO ' , 2 dt dt dt ~ ~ dvr dvr dr ' dr ' vr , ar dt dt dt dt
7
一、速度合成定理
例 (用绝对法求解) 半径为r、偏心距为e的圆形凸轮以匀角速度ω绕定轴O转动,AB 杆长l,其A端置于凸轮上。图示位置AB水平,OA铅直,OC水 平,求此瞬时AB杆角速度、角加速度。
有些问题用绝对法求解较繁,尤其求特殊位置上的运动规律时。 而用合成法可能很简单。
1
第7章 点的合成运动
本章为重点内容之一。 本章和下章应特别注意概念的重要性(严格、准确掌握)。
r rO' r '
求导
dr drO' dr ' dt dt dt
~ dr ' v a vO ' dt
速度合成定理
va ve vr
上页公式 事实上,与
动系运动形 式无关。
二、加速度合成定理
dva dve dvr va ve vr dt dt dt 求导
解题步骤: (一)选动点、动系(及静系——可默认为地面); (二)分析动点的各种运动,画运动图(速度、加速度图); (三)求解。
8
例1:例7-1(老书例8-1)(求速度)
凸轮顶杆机构。 已知凸轮偏心 距OC = e,半 径 ve r 3e, 匀角 速度 0 。当 OC与CA垂直 时,求AB的速 度。
矢量函数对时间的导数与坐标系选取有关吗? 矢量 A xi yj zk x' i ' y' j ' z' k ' 一、定义
z
A
z
x
y
静系中 动系中 y dA Δ A dx dy dz 绝对导数 lim i j k x dt t 0 Δ t dt dt dt ~ ~ ~ ~ ~ dA ΔA d x' dy' dz ' dx ' dy ' d z ' 相对导数 lim i ' j ' k ' i ' j ' k' dt Δt 0 Δt dt dt dt dt dt dt ~ ~ ~ dx ' d x ' dy ' d y ' dz ' d z ' , , 这里 标量变量对时间导数与坐标系无关 dt dt dt dt dt dt
二、动系平动时绝对导数和相对导数的关系 A x' i ' y' j ' z' k ' 当动系平动时,i '、j '、k ' 在动系和静系中均为常矢量。 ~ 动系平动时: dA dx ' dy ' dz ' dA i ' j ' k '0 dt dt dt dt dt 矢量的绝对导数 = 相对导数
§7-1 点的合成运动的有关概念
例1 汽车内行走的人。
汽车以速度 v 向前运动, 人以速度 u 相对汽车向前
运动,研究人的运动。从
车厢观察,人的速度为
从地面观察,人的速度为 u + 。v u
,
2
分析这一问题,有以下事实:
y
y´
点 绝对 运动
地面 (静系) 牵连 刚体 运动 汽车 (动系)
ae a B r , a a r
n e n B
2
n ae
由加速度合成定理, n aa ae ae ar 在y轴上投影:
n aa ae cos ae sin
2
aa r cos r sin
作业:7-11、12、15、17
a B n aB
ae
aa ar
aen
14
分析:(易分析,略) 解:动点小环M,动系BC杆, 画加速度图。牵连加速度与B点 相同:
a e a r , B
n aen a B r 2
a B n aB
ae
aa ar
aen
va
vr
问题:先考虑用绝对法如何求?
9
分析: 运动机构的目的是传递运动和将运动状态改 变。在用合成法求解问题时,动点一般选在两 物体接触的部位(具体如何选后面将逐步讨 论),而且总选特殊点。
ve 首先看清机构如何构成,各物体作何种运动,
va
vr
已知和待求量。 欲求AB速度,因其作平动,故只求其上一点 的速度即可,而AB上A点在二物体的接触部位, 故试选AB上A点为动点;在选动点的同时,应 选动系,动系一般选在另外的刚体上,显然选 凸轮;静系选地面。 这种选法是否可行,要作进一步分析。分析三种运动和三种轨迹,若较简 单和易分析,则可行。绝对运动:沿AB的直线运动;相对运动:沿凸轮边 缘的圆周运动;牵连运动:绕O点的定轴转动。故均较简单。三种轨迹也 易知。试画速度图(注:一定为平行四边形),已知ve,故可求va。
§7-3 牵连运动为平动时速度、加速度合成定理
速度合成定理 在前面已经得 到,这里再系 统推一下。 动点M,静系Oxyz,动系O'x'y'z'。
dv a d 2 r dr v 2 静系中, a ,aa dt dt dt ~ ~ ~ d vr d 2 r ' dr ' v ,ar 2 动系中, r dt dt dt
16
11
2e 0 3
ve va vr
例2:(老书例8-3)(求速度) 图示机构,半圆凸轮半径为R, 速度为v,已知θ。求AB杆的 角速度。
