人教版八年级数学上截长补短法证明三角形全等.docx
人教版数学八年级上册第12章全等三角形专题课截长补短法优秀教学案例

3.引导学生运用数学符号和语言,表达和阐述解题过程和思路。例如,要求学生用数学语言描述全等三角形的判定方法,并解释其原理。
4.鼓励学生积极思考和解决问题,培养他们的自主学习能力和问题解决能力。例如,在解决问题的过程中,引导学生独立思考,寻找解决方案,并进行验证。
(三)小组合作
1.组织学生进行小组讨论和实践活动,培养他们的团队协作能力和交流能力。例如,将学生分成小组,让他们共同解决一个实际问题,要求学生在讨论中交流思路、分享解题方法。
在全等三角形专题课中,学生已经学习了全等三角形的定义、性质和判定方法。通过对全等三角形的性质和判定方法的学习,学生已经能够熟练地运用SSS、SAS、ASA、AAS四种判定方法判断两个三角形是否全等。然而,在解决实际问题时,学生往往需要灵活运用多种方法,而截长补短法作为一种特殊的方法,可以帮助学生更加简洁地解决问题。
3.小组合作培养团队协作能力:组织学生进行小组讨论和实践活动,培养他们的团队协作能力和交流能力。通过小组合作,学生能够在合作中发现问题、解决问题,并培养批判性思维和自我反思能力。
4.反思与评价提高自我认知:教师引导学生对自己的学习过程进行反思,总结经验和教训。通过互评和自我评价,学生能够培养批判性思维和自我反思能力,提高自我认知。
2.引导学生通过观察、分析和归纳,发现全等三角形的性质和判定方法。例如,通过展示两个全等三角形的图形,让学生观察并分析它们的性质,引导学生归纳出全等三角形的判定方法。
(精品)全等三角形——截长补短法

D C B A 全等三角形——截长补短法一、知识梳理:截长补短法截长补短法是几何证明题中十分重要的方法。
通常来证明几条线段的数量关系。
截长法:(1)过某一点作长边的垂线(2)在长边上截取一条与某一短边相同的线段,再证剩下的线段与另一短边相等. 补短法(1)延长短边。
(2)通过旋转等方式使两短边拼合到一起。
……二、典型例题: 例1、如图,在ABC ∆中,60BAC ∠=︒,AD 是BAC ∠的平分线,且AC AB BD =+,求ABC ∠的度数.及时练习:如图所示,在Rt △ABC 中,∠C=90°,BC=AC ,AD 平分∠BAC 交BC 于D ,求证:AB=AC+CD .例2、已知ABC ∆中,60A ∠=,BD 、CE 分别平分ABC ∠和.ACB ∠,BD 、CE 交于点O ,试判断BE 、CD 、BC 的数量关系,并加以证明.NEB M A DMDCBA DOECB A及时练习:如图,点M 为正三角形ABD 的边AB 所在直线上的任意一点(点B 除外),作60DMN ∠=︒,射线MN 与DBA ∠外角的平分线交于点N ,DM 与MN 有怎样的数量关系?例3、如图.已知正方形ABCD 中,M 为CD 的中点,E 为MC 上一点,且∠BAE =2∠DAM .求证:AE =BC +CE .及时练习:如图,AD ⊥AB ,CB ⊥AB ,DM =CM =a ,AD =h ,CB =k , ∠AMD =75°,∠BMC =45°,则AB 的长为 ( ) A . a B . k C .2k h+ D . h例4、以ABC ∆的AB 、AC 为边向三角形外作等边ABD ∆、ACE ∆,连结CD 、BE 相交于点O .求证:OA 平分DOE ∠.NM DCB A ED CBAPQCBA及时练习:如图所示,ABC ∆是边长为1的正三角形,BDC ∆是顶角为120︒的等腰三角形,以D 为顶点作一个60︒的MDN ∠,点M 、N 分别在AB 、AC 上,求AMN ∆的周长.三、课堂练习:1、如图,ABC ∆中,AB=2AC ,AD 平分BAC ∠,且AD=BD ,求证:CD ⊥AC2、如图,AD ∥BC ,EA,EB 分别平分∠DAB,∠CBA ,CD 过点E ,求证;AB =AD+BC 。
人教版八年级数学上册全等三角形问题中常见的辅助线——截长补短法.doc

全等三角形问题中常见的辅助线——截长补短法例 1、如图,ABC 中,AB=2 AC,AD平分BAC ,且AD =BD ,求证: CD ⊥ ACAB CD例 2、如图,AD ∥ BC ,AE, BE分别平分∠DAB, ∠ CBA , CD 过点 E ,求证;AB = AD+BCADEBCABC 内,0例 3、如图,已知在BAC 60 ,BC,CA 上,C 40 ,P,Q分别在并且AP , BQ 分别是BAC ,ABC 的角平分线。
求证:BQ+AQ=AB+BPABQPC例 4、如图,在四边形ABCD中,BC>BA,AD=CD,BD平分ABC ,求证:A C180ADCB例 5、如图在△ABC中,AB>AC,∠ 1=∠ 2,P为AD上任意一点,A 求证 ;AB -AC > PB -PC1 2PCBD例、已知ABC 中,A 60 ,BD、CE分别平分ABC和 . ACB ,BD、CE交6于点 O ,试判断BE、CD、BC 的数量关系,并加以证明. AEODB C例7 、如图,点M 为正三角形ABD 的边 AB 所在直线上的任意一点(点B除外 ),作DMN 60 ,射线 MN 与∠DBA外角的平分线交于点N ,DM与MN有怎样的数量关系 ?DNA MB E变式练习:如图,点M 为正方形ABCD 的边AB 上任意一点,MN DM 且与∠ ABC 外角的平分线交于点N ,MD 与MN 有怎样的数量关系?D CNA MB E例8 、如图所示.已知正方形ABCD 中,M 为CD 的中点,E为MC 上一点,且∠ BAE =2 ∠ DAM.求证:AE =BC+CE .A DMECB。
截长补短法全等三角形

截长补短法全等三角形全等三角形是指两个三角形的对应边长和对应角度都相等的情况下,它们是完全相等的。
而截长补短法是一种通过截取和补充边长的方法来构造全等三角形的技巧。
在几何学中,截长补短法是一种常用的构造方法,可以用来证明两个三角形全等。
它的基本思想是通过截取和补充边长,使得两个三角形的对应边长和对应角度完全相等,从而达到全等的目的。
为了更好地理解截长补短法,我们可以通过一个具体的例子来说明。
假设我们需要证明两个三角形ABC和DEF全等,其中已知∠A=∠D,AB=DE,BC=EF。
根据截长补短法,我们可以进行如下的构造:1. 在BC的延长线上截取一段长度等于EF的线段,记为BC'。
2. 在AC'上截取一段长度等于DE的线段,记为AC。
通过以上的构造,我们可以得到以下的结论:1. 由于BC'=EF,且BC=EF,所以BC=BC',即三角形ABC和DEF的两条边相等。
2. 由于AC=DE,且∠A=∠D,所以三角形ABC和DEF的两个角相等。
3. 由于AB=DE,所以三角形ABC和DEF的第三条边相等。
根据截长补短法,我们可以得到三角形ABC和DEF全等的结论。
除了上述的例子,截长补短法还可以应用于更复杂的情况。
例如,当我们需要证明两个三角形全等时,已知两个角度相等并且其中一条边长相等,我们可以通过截长补短法来构造第二条边,从而得到全等的结果。
截长补短法在几何学中有着广泛的应用。
它不仅可以用来证明三角形的全等,还可以用来解决各种与全等三角形相关的问题。
通过灵活运用截长补短法,我们可以简化证明过程,提高证明的效率。
截长补短法是一种通过截取和补充边长的方法来构造全等三角形的技巧。
通过灵活运用截长补短法,我们可以简化证明过程,提高证明的效率。
在解决几何问题时,我们可以尝试使用截长补短法,从而更好地理解和应用全等三角形的性质。
专题02 截长补短证全等(解析版)

专题02 截长补短证全等(解析版)专题02 截长补短证全等(解析版)全等三角形是初中数学中的重要概念,对于学生来说,能够准确证明两个三角形全等是关键。
在这篇文章中,我们将探讨如何通过截短或补长来证明两个三角形全等,并提供详细的解析和示例。
一、截长证全等在证明两个三角形全等时,截长是一种常用的方法。
当我们能够找到一个共同的边,需要证明其他边相等时,我们可以通过截短这条边来达到目的。
例如,在三角形ABC和三角形DEF中,我们需要证明AB=DE。
我们可以通过截取AC和DF的一段长度来使它们相等。
假设我们截取了一个段落,记为AD,则此时我们可以发现三角形AED与三角形ABD全等(SAS准则),从而得出AB=DE。
二、补长证全等除了截长证全等外,我们还可以通过补长来证明两个三角形全等。
当我们需要证明两个三角形的某一对边相等时,我们可以在其中一个三角形中延长一条边,使其等于另一个三角形对应边的长度。
例如,在三角形ABC和三角形DEF中,我们需要证明AB=DE。
我们可以通过延长EF,使之与CB相等。
记EF延长后的交点为G,则此时我们可以发现三角形AGC与三角形DFC全等(SAS准则),从而得出AB=DE。
三、综合应用截长和补长方法在证明三角形全等时常常结合使用。
下面我们通过一个具体例子来解析。
例题:已知∠ABC = ∠EDF,AC = DF,证明三角形ABC与三角形DEF全等。
解析:根据题目条件,我们可以看出∠ABC和∠EDF相等,AC和DF相等,我们需要证明AB和DE相等。
1. 首先,我们通过截取AC和DF的一段长度来使它们相等。
假设我们截取了一个段落,记为AD。
2. 其次,我们通过延长EF,使之与CB相等。
记EF延长后的交点为G。
3. 接下来我们观察三角形AGC和三角形DFC。
根据截长证据,我们可以得出AG=DF,AC=AC,∠AGC=∠DFC,因此根据SAS准则,我们可以得出三角形AGC与三角形DFC全等。
三角形全等作辅助线模型二截长补短知识讲解20212022学年八年级数学上册基础知识专项讲练人教版

专题12.12 三角形全等作辅助线模型(二)-截长补短(知识讲解)有一类几何题其命题主要证明三条线段长段的“和”或“差”及其比例关系,这一类题目一般可以采取“截长”或“补短”的方法来进行求解。
所谓“截长”,就是将三者中最长的那条线段一分为二,使其中的一条线段与已经线段相等,然后证明其中的另一段与已知的另一段的大小关系。
所谓“补短”,就是将一个已知的较短的线段延长至与另一个已知的较短的长度相等,然后求出延长后的线段与最长的已知线段关系。
有的是采取截长补短后,使之构成某种特定的三角形进行求解。
【典型例题】1、 阅读下面文字并填空:数学习题课上李老师出了这样一道题:“如图1,在ABC V 中,AD 平分BAC Ð,2B C Ð=Ð.求证:AB BD AC +=.李老师给出了如下简要分析:“要证AB BD AC +=就是要证线段的和差问题,所以有两个方法,方法一:‘截长法’如图2,在AC 上截取AE AB =,连接DE ,只要证BD =__________即可,这就将证明线段和差问题__________为证明线段相等问题,只要证出V __________≌△__________,得出B AED Ð=Ð及BD =_________,再证出Ð__________=Ð___________,进而得出ED EC =,则结论成立.此种证法的基础是‘已知AD 平分BAC Ð,将ABD △沿直线AD 对折,使点B 落在AC 边上的点E 处’成为可能.方法二:“补短法”如图3,延长AB 至点F ,使BF BD =.只要证AF AC =即可.此时先证Ð__________C =Ð,再证出V _________≌△_________,则结论成立.”“截长补短法”是我们今后证明线段或角的“和差倍分”问题常用的方法.【答案】方法一:CE ;转化;ABD ;AED ;DE ;EDC ;C ;方法二:F ;AFD ;ACD【分析】方法一:在AC 上截取AE AB =,由SAS 可证ABD AED D @D 可得B AED Ð=Ð,BD=DE ,根据等角对等边得到CE=DE ,即可求证;方法二:延长AB 至点F ,使BF BD =,由AAS 可证AFD ACD D @D ,可得AC=AF ,即可证明:方法一:在AC 上截取AE AB =,连接DE ,如图2∵AD 平分BAC Ð,∴BAD DAC Ð=Ð,在ABD D 和AED D 中AE AB BAD DAC AD AD =ìïÐ=Ðíï=î,∴ABD AED D @D ,∴B AED Ð=Ð,BD=DE ,∵2B C Ð=Ð,∴2AED CÐ=Ð而2AED C EDC C Ð=Ð+Ð=Ð,∴EDC C Ð=Ð,∴DE=CE ,∴AB+BD=AE+CE=AC ,故答案为:CE ;转化;ABD ;AED ;DE ;EDC ;C ;方法二:如图3,延长AB 至点F ,使BF BD =,∴F BDFÐ=Ð∴2ABD F BDF FÐ=Ð+Ð=Ð∴2ABD CÐ=Ð∴F CÐ=Ð在AFD D 和ACD D 中FAD CAD F CAD AD Ð=ÐìïÐ=Ðíï=î,∴AFD ACD D @D ,∴AC=AF ,∴AC=AB+BF=AB+BD ,故答案为:F ;AFD ;ACD .【点拨】本题考查了全等三角形的判定和性质,属于截长补短类辅助线,核心思想为数学中的转化思想,此类题的关键是要找到最长边和最短边,然后确定截取辅助线的方式.举一反三:【变式】 数学课上,小白遇到这样一个问题:如图1,在等腰Rt ABC D 中,90BAC Ð=°,AB AC =,AD AE =,求证ABE ACD Ð=Ð;在此问题的基础上,老师补充:过点A 作AF BE ⊥于点G 交BC 于点F ,过F 作FP CD ^交BE 于点P ,交CD 于点H ,试探究线段BP ,FP ,AF 之间的数量关系,并说明理由.小白通过研究发现,AFB Ð与HFC Ð有某种数量关系;小明通过研究发现,将三条线段中的两条放到同一条直线上,即“截长补短”,再通过进一步推理,可以得出结论.阅读上面材料,请回答下面问题:(1)求证ABE ACD Ð=Ð;(2)猜想AFB Ð与HFC Ð的数量关系,并证明;(3)探究线段BP ,FP ,AF 之间的数量关系,并证明.【答案】(1)见解析;(2)HFC BFA Ð=Ð,证明见解析;(3)BP AF PF =+,证明见解析【分析】(1)利用SAS 证明ABE ACD @V V 可得结论;(2)设ABE ACD x Ð=Ð=,推出=45BFA x а+,=45HFC x а+,即可证明HFC BFA Ð=Ð;(3)过点C 作CM AC ^交AF 延长线于点M ,延长FP 交AC 于点N ,证明△ABE ≌△CAM ,得出BE AM =和M BEA Ð=Ð,从而证明△NFC ≌△MFC ,得到FM FN =和M FNC Ð=Ð,可得PN=PE ,从而得出BP=AF+PF.(1)证明:∵在△ABE 和△ACD 中,==AB AC A A AE AD ìïÐ=Ðíïî,ABE ACD \D @D (SAS ),ABE ACD \Ð=Ð;(2)设ABE ACD x Ð=Ð=,AF BE ^ ,90BAF x \Ð=°-,()=9045=45BFA x x \а-°-°+,ACD x Ð= ,45HCF x \Ð=°-,FP CD ^ ,()9045=45HFC x x \Ð=°-°-°+,HFC BFA \Ð=Ð;(3)过点C 作CM AC ^交AF 延长线于点M ,延长FP 交AC 于点N ,90BAF FAC Ð+Ð=° ,90BAF ABG Ð+Ð=°,FAC ABG \Ð=Ð,在△ABE 和△CAM 中,===BAE ACM AB AC ABE CAM ÐÐìïíïÐÐî,ABE CAM \D @D (ASA ),BE AM \=,M BEA Ð=Ð,BFA MFC NFC Ð=Ð=Ð ,FC FC =,45ACB BCM Ð=Ð=°,NFC MFC \D @D (ASA ),FM FN \=,M FNC Ð=Ð,FNC BEA \Ð=Ð,PN PE \=,∴BP BE PE AM PE AF FM PE =-=-=+-AF FN PN AF PF =+-=+.【点拨】本题考查了全等三角形的判定和性质、等腰直角三角形的性质以及等角对等边等知识点,解题的关键是根据截长补短法添加适当的辅助线,构造全等三角形证明结论,有一定难度.2、 阅读材料并完成习题:在数学中,我们会用“截长补短”的方法来构造全等三角形解决问题.请看这个例题:如图1,在四边形ABCD 中,∠BAD=∠BCD=90°,AB=AD ,若AC=2cm ,求四边形ABCD 的面积.解:延长线段CB 到E ,使得BE=CD ,连接AE ,我们可以证明△BAE ≌△DAC ,根据全等三角形的性质得AE=AC=2, ∠EAB=∠CAD ,则∠EAC=∠EAB+∠BAC=∠DAC+∠BAC=∠BAD=90°,得S 四边形ABCD =S △ABC +S △ADC =S △ABC +S △ABE =S △AEC ,这样,四边形ABCD 的面积就转化为等腰直角三角形EAC 面积.(1)根据上面的思路,我们可以求得四边形ABCD 的面积为cm 2.(2)请你用上面学到的方法完成下面的习题.如图2,已知FG=FN=HM=GH+MN=2cm ,∠G=∠N=90°,求五边形FGHMN 的面积.【答案】(1)2;(2)4【分析】(1)根据题意可直接求等腰直角三角形EAC 的面积即可;(2)延长MN 到K ,使NK=GH ,连接FK 、FH 、FM ,由(1)易证FGH FNK V V ≌,则有FK=FH ,因为HM=GH+MN 易证FMK FMH V V ≌,故可求解.【详解】(1)由题意知21=22ABC ADC ABC ABE AEC ABCD AC S S S S S S =+=+==V V V V V 四边形,故答案为2;(2)延长MN 到K ,使NK=GH ,连接FK 、FH 、FM ,如图所示:FG=FN=HM=GH+MN=2cm ,∠G=∠N=90°,\∠FNK=∠FGH=90°,\FGH FNK V V ≌,\FH=FK ,又 FM=FM ,HM=KM=MN+GH=MN+NK ,\FMK FMH V V ≌,\MK=FN=2cm ,\12=242FGH HFM MFN FMK FGHMN S S S S S MK FN =++=´×=V V V V 五边形.【点拨】本题主要考查全等三角形的性质与判定,关键是根据截长补短法及割补法求面积的运用.举一反三:【变式】在△ABC中,∠ACB=2∠B,(1)如图①,当∠C=90°,AD为∠ABC的角平分线时,在AB上截取AE=AC,连接DE,易证AB=AC+CD.请证明AB=AC+CD;(2)①如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?请直接写出你的结论,不要求证明;②如图③,当∠C≠90°,AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想并证明.【答案】(1)证明见解析;(2)①AB=AC+CD;②AC+AB=CD,证明见解析.【分析】(1)首先得出△AED≌△ACD(SAS),即可得出∠B=∠BDE=45°,求出BE=DE=CD,进而得出答案;(2)①首先得出△AED≌△ACD(SAS),即可得出∠B=∠BDE,求出BE=DE=CD,进而得出答案;②首先得出△AED≌△ACD(SAS),即可得出∠B=∠EDC,求出BE=DE=CD,进而得出答案.(1)证明:∵AD为∠ABC的角平分线,∴∠EAD=∠CAD,在△AED和△ACD中,∵AE=AC,∠EAD=∠CAD,AD=AD,∴△AED≌△ACD(SAS),∴ED=CD,∠C=∠AED=90°,∵∠ACB=2∠B,∠C=90°,∴∠B=45°,∴∠BDE=45°,∴BE=ED=CD,∴AB=AE+BE=AC+CD;①AB=AC+CD.理由如下:在AB上截取AE=AC,连接DE,∵AD为∠ABC的角平分线,∴∠EAD=∠CAD,在△AED和△ACD中,∵AE=AC,∠EAD=∠CAD,AD=AD,∴△AED≌△ACD(SAS),∴ED=CD,∠C=∠AED,∵∠ACB=2∠B,∴∠AED=2∠B,∵∠B+∠BDE=∠AED,∴∠B=∠BDE,∴BE=ED=CD,∴AB=AE+BE=AC+CD;②AC+AB=CD.理由如下:在射线BA上截取AE=AC,连接DE,∵AD为∠EAC的角平分线,∴∠EAD=∠CAD,在△AED和△ACD中,∵AE=AC,∠EAD=∠CAD,AD=AD,∴△AED≌△ACD(SAS),∴ED=CD,∠ACD=∠AED,∵∠ACB=2∠B,∴设∠B=x,则∠ACB=2x,∴∠EAC=3x,∴∠EAD=∠CAD=1.5x,∵∠ADC+∠CAD=∠ACB=2x,∴∠ADC=0.5x,∴∠EDC=x,∴∠B=∠EDC,∴BE=ED=CD,∴AB+AE=BE=AC+AB=CD.【点拨】此题主要考查了全等三角形的判定与性质以及三角形外角的性质等知识,利用已知得出△AED≌△ACD是解题关键.3、(初步探索)截长补短法,是初中几何题中一种添加辅助线的方法,也是把几何题化难为易的一种策略.截长就是在长边上截取一条线段与某一短边相等,补短就是通过延长或旋转等方式使两条短边拼合到一起,从而解决问题.(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系;(灵活运用)(2)如图2,△ABC为等边三角形,直线a∥AB,D为BC边上一点,∠ADE交直线a 于点E,且∠ADE=60°.求证:CD+CE=CA;(延伸拓展)(3)如图3,在四边形ABCD中,∠ABC+∠ADC=180°,AB=AD.若点E在CB的延长线上,点F在CD的延长线上,满足EF=BE+FD,请直接写出∠EAF与∠DAB的数量关系.【答案】(1)DA=DC+DB,证明见详解;(2)见详解;(3)∠EAF=11802DAB°-Ð,证明见详解.【分析】(1)由等边三角形知AB=AC,∠BAC=60°,结合∠BDC=120°知∠ABD+∠ACD=180°,由∠ACE+∠ACD=180°知∠ABD=∠ACE,证△ABD≌△ACE得AD=AE,∠BAD=∠CAE,再证△ADE是等边三角形得DA=DE=DC+CE=DC+DB;(2)首先在AC上截取CM=CD,由△ABC为等边三角形,易得△CDM是等边三角形,继而可证得△ADM≌△EDC,即可得AM=EC,则可证得CD+CE=CA;(3)在DC延长线上取一点G,使得DG=BE,连接AG,先判定△ADG≌△ABE,再判定△AEF≌△AGF,得出∠FAE=∠FAG,最后根据∠FAE+∠FAG+∠GAE=360°,进而推导得到2∠FAE+∠DAB=360°,即可得出结论.解答:DA=DC+DB,理由如下:(1)如图1,延长DC到点E,使CE=BD,连接AE,∵△ABC是等边三角形,∴AB=AC,∠BAC=60°,∵∠BDC=120°,∴∠ABD+∠ACD=180°,又∵∠ACE+∠ACD=180°,∴∠ABD=∠ACE ,∴△ABD ≌△ACE (SAS ),∴AD=AE ,∠BAD=∠CAE ,∵∠BAC=60°,即∠BAD+∠DAC=60°,∴∠DAC+∠CAE═60°,即∠DAE=60°,∴△ADE 是等边三角形,∴DA=DE=DC+CE=DC+DB ,即DA=DC+DB ;(2)证明:在AC 上截取CM=CD ,∵△ABC 是等边三角形,∴∠ACB=60°,∴△CDM 是等边三角形,∴MD=CD=CM ,∠CMD=∠CDM=60°,∴∠AMD=120°,∵∠ADE=60°,∴∠ADE=∠MDC ,∴∠ADM=∠EDC ,∵直线a ∥AB ,∴∠ACE=∠BAC=60°,∴∠DCE=120°=∠AMD ,在△ADM 和△EDC 中,ADM EDC MD CDAMD ECD Ð=Ðìï=íïÐ=Ðî∴△ADM≌△EDC(ASA),∴AM=EC,∴CA=CM+AM=CD+CE;即CD+CE=CA.(3)∠EAF=11802DAB°-Ð;证明:如图3,在DC延长线上取一点G,使得DG=BE,连接AG,∵∠ABC+∠ADC=180°,∠ABC+∠ABE=180°,∴∠ADC=∠ABE,又∵AB=AD,∴△ADG≌△ABE(SAS),∴AG=AE,∠DAG=∠BAE,∵EF=BE+FD=DG+FD=GF,AF=AF,∴△AEF≌△AGF(SSS),∴∠FAE=∠FAG,∵∠FAE+∠FAG+∠GAE=360°,∴2∠FAE+(∠GAB+∠BAE)=360°,∴2∠FAE+(∠GAB+∠DAG)=360°,即2∠FAE+∠DAB=360°,∴∠EAF=11802DAB°-Ð.【点拨】本题属于三角形综合题,主要考查了全等三角形的判定和性质,以及等边三角形的性质的综合应用,解决问题的关键是作辅助线构造全等三角形,根据全等三角形的对应角相等进行推导变形.举一反三:【变式1】 如图,AB CD ∥,BE 平分ABC Ð,CE 平分BCD Ð,点E 在AD 上,求证:BC AB CD =+.【分析】在BC 上取点F ,使BF=BA ,连接EF ,由角平分线的性质可以得出∠1=∠2,从而可以得出△ABE ≌△FBE ,可以得出∠A=∠5,进而可以得出△CDE ≌△CFE ,就可以得出CD=CF ,即可得出结论.证明:在BC 上取点F ,使BF=BA ,连接EF ,∵BE 、CE 分别是∠ABC 和∠BCD 的平分线,∴∠1=∠2,∠3=∠4,在△ABE 和△FBE 中,12AB FB BE BE =ìïÐ=Ðíï=î,∴△ABE ≌△FBE(SAS),∴∠A=∠5,∵AB ∥CD ,∴∠A+∠D=180°,∴∠5+∠D=180,∵∠5+∠6=180°,∴∠6=∠D ,在△CDE 和△CFE 中,634D CE CE Ð=ÐìïÐ=Ðíï=î,∴△CDE ≌△CFE(AAS),∴CF=CD .∵BC=BF+CF ,∴BC=AB+CD.【点拨】本题考查了角平分线的性质的运用,全等三角形的判定及性质的运用,解答时运用截取法正确作辅助线是关键.【变式2】如图,在△ABC 中,60BAC Ð=°,40ACB Ð=°,P 、Q 分别在BC 、CA 上,并且AP 、BQ 分别是∠BAC 、∠ABC 的角平分线.求证:(1)BQ CQ =;(2)BQ AQ AB BP +=+.【答案】(1)见解析;(2)见解析【分析】(1)由三角形的内角和就可以得出∠ABC =80°,再由角平分线的性质就可以得出∠QBC =40°,就有∠QBC =∠C 而得出结论;(2)延长AB 至M ,使得BM =BP ,连结MP ,根据条件就可以得出∠M =∠C ,进而证明△AMP ≌△ACP 就可以得出结论.(1)证明:∵BQ 是ABC Ð的角平分线,∴12QBC ABC Ð=Ð.∵180ABC ACB BAC Ð+Ð+Ð=°,且60BAC Ð=°,40ACB Ð=°,∴80ABC Ð=°,∴180402QBC Ð=´°=°,∴QBC C Ð=Ð,∴BQ CQ =;(2)证明:延长AB 至M ,使得BM BP =,连结MP .∴M BPM Ð=Ð,∵△ABC 中60BAC Ð=°,40C Ð=°,∴80ABC Ð=°,∵BQ 平分ABC Ð,∴40QBC C Ð=°=Ð,∴BQ CQ =,∵ABC M BPM Ð=Ð+Ð,∴40M BPM C Ð=Ð=°=Ð,∵AP 平分BAC Ð,∴MAP CAP Ð=Ð,在△AMP 和△ACP 中,∵M C MAP CAP AP AP Ð=ÐìïÐ=Ðíï=î,∴△AMP ≌△ACP ,∴AM AC =,∵AM AB BM AB BP =+=+,AC AQ QC AQ BQ =+=+,∴AB BP AQ BQ+=+【点拨】本题主要考查全等三角形的判定与性质的知识点,解答本题的关键是熟练掌握判定两个三角形全等的一般方法:SSS 、SAS 、ASA 、AAS 、HL .注意:AAA 、SSA 不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.。
人教版初中数学 小专题 截长补短、倍长中线法构造全等三角形(等腰)

1、已知:如图,在ABC 中,AB AC ,D、E在BC上,
且DE=EC,过D作
交AE于点F,DF=AC.
求证:AE平分
7.已知:如图,AD,AE 分别是△ ABC 和△ ABD 的中线,且 BA=BD.求证:AE=12AC.
证明:延长 AE 至 F,使 EF=AE,连接 DF. ∵AE 是△ABD 的中线,∴BE=DE. ∵∠AEB=∠FED,∴△ABE≌△FDE.∴∠B=∠BDF,AB= DF. ∵BA=BD,∴∠BAD=∠BDA,BD=DF. ∵∠ADF=∠BDA+∠BDF,∠ADC=∠BAD+∠B,∴∠ADF =∠ADC. ∵AD 是△ABC 的中线,∴BD=CD.∴DF=CD. ∴△ADF≌△ADC(SAS).∴AC=AF=2AE,即 AE=12AC.
如图,AB=AE,AB⊥AE,AD=AC,AD⊥AC,点M为 BC的中点,求证:DE=2AM. 解:延长AM至N,使MN=AM,连接BN, ∵点M为BC的中点,∴BM=CM. 又∵∠BMN=∠CMA, ∴△AMC≌△NMB(SAS). ∴AC = BN , ∠ C = ∠NBM , ∠ ABN = ∠ABC+∠C=180°-∠BAC=∠EAD. 又 ∵BN = AC = AD , AB = EA , ∴△ABN≌△EAD(SAS).∴DE=NA. 又AM=MN,∴DE=2AM.
小专题 截长补短、倍长中线法构造全等三角形
方法 利用“截长补短法”构造全等三角形 截长补短法,是初中数学几何题中一种辅助线的添加方法,也是 把几何题化难为易的一种思想。截长就是在一条线上截取成两段 ,补短就是在一条边上延长,使其等于一条已知边。 例1 已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,
求证:AE=AD+BE
人教版八年级数学上截长补短法证明三角形全等
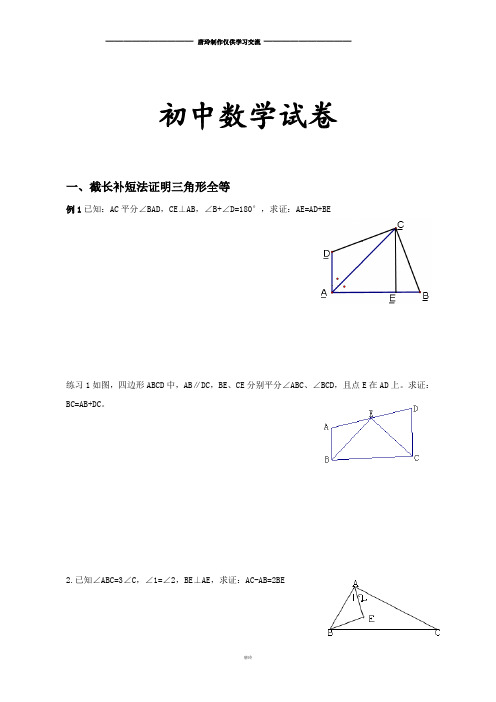
初中数学试卷一、截长补短法证明三角形全等例1已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE练习1如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
求证:BC=AB+DC。
2.已知∠ABC=3∠C,∠1=∠2,BE⊥AE,求证:AC-AB=2BE3如图,已知AD ∥BC ,∠PAB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .4在△ABC 中,︒=∠90ACB ,BC AC =,直线MN 经过点C ,且MN AD ⊥于D ,MN BE ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时,求证: ①ADC ∆≌CEB ∆;②BE AD DE +=;(2)当直线MN 绕点C 旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.6.如图,已知AC ∥BD ,EA 、EB 分别平分∠CAB 和∠DBA ,CD 过点E ,则AB 与AC+BD 相等PEDCBA吗?请说明理由例2已知,如图1-1,在四边形ABCD 中,BC >AB ,AD =DC ,BD 平分∠ABC . 求证:∠BAD +∠BCD =180°.例1. 练习已知,如图3-1,∠1=∠2,P 为BN 上一点,且PD ⊥BC 于点D ,AB +BC =2BD .求证:∠BAP +∠BCP =180°.2、倍长中线法证三角形全等例1 、求证:三角形一边上的中线小于其他两边和的一半。
ABCD图1-1ABCDP12N图3-1练习 1:△ABC 中,AB=5,AC=3,求中线AD 的取值范围例2.已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE练习2已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF例3已知:如图,在ABC ∆中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC. 求证:AE 平分BAC ∠B第 1 题图ABFDECCEDB A练习3已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAE 作业1、已知:如图,ABCD 是正方形,∠FAD =∠FAE . 求证:BE +DF =AE .2、五边形ABCDE 中,AB =AE ,BC +DE =CD ,∠ABC +∠AED =180°,求证:AD 平分∠CDE3、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
人教版八年级上数学截长补短专题

ADBCE图2-1截长补短法人教八年级上册课本中,在全等三角形部分介绍了角的平分线的性质,这一性质在许多问题里都有着广泛的应用.而“截长补短法”又是解决这一类问题的一种特殊方法,在无法进行直接证明的情形下,利用此种方法常可使思路豁然开朗.请看几例.例1. 已知,如图1-1,在四边形ABCD 中,BC >AB ,AD =DC ,BD 平分∠ABC .求证:∠BAD +∠BCD =180°.分析:因为平角等于180°,因而应考虑把两个不在一起的通过全等转化成为平角,图中缺少全等的三角形,因而解题的关键在于构造直角三角形,可通过“截长补短法”来实现.证明:过点D 作DE 垂直BA 的延长线于点E ,作DF ⊥BC 于点F ,如图1-2 ∵BD 平分∠ABC ,∴DE =DF ,在Rt △ADE 与Rt △CDF 中,⎩⎨⎧==CDAD DFDE ∴Rt △ADE ≌Rt △CDF (HL ),∴∠DAE =∠DCF . 又∠BAD +∠DAE =180°,∴∠BAD +∠DCF =180°, 即∠BAD +∠BCD =180° 例2.如图2-1,AD ∥BC ,点E 在线段AB 上,∠ADE =∠CDE ,∠DCE =∠ECB .~求证:CD =AD +BC .分析:结论是CD =AD +BC ,可考虑用“截长补短法”中的“截长”,即在CD 上截取CF =CB ,只要再证DF =DA 即可,这就转化为证明两线段相等的问题,从而达到简化问题的目的.证明:在CD 上截取CF =BC ,如图2-2在△FCE 与△BCE 中,AB CD图1-1FEDCBA]图1-2ADB CEF1234图2-2⎪⎩=CE CE ∴△FCE ≌△BCE (SAS ),∴∠2=∠1.又∵AD ∥BC ,∴∠ADC +∠BCD =180°,∴∠DCE +∠CDE =90°,}∴∠2+∠3=90°,∠1+∠4=90°,∴∠3=∠4. 在△FDE 与△ADE 中,⎪⎩⎪⎨⎧∠=∠=∠=∠43DEDE ADE FDE ∴△FDE ≌△ADE (ASA ),∴DF =DA , ∵CD =DF +CF ,∴CD =AD +BC .例3. 已知,如图3-1,∠1=∠2,P 为BN 上一点,且PD ⊥BC 于点D ,AB +BC =2BD .求证:∠BAP +∠BCP =180°.分析:与例1相类似,证两个角的和是180°,可把它们移到一起,让它们是邻补角,即证明∠BCP =∠EAP ,因而此题适用“补短”进行全等三角形的构造. 】证明:过点P 作PE 垂直BA 的延长线于点E ,如图3-2∵∠1=∠2,且PD ⊥BC ,∴PE =PD , 在Rt △BPE 与Rt △BPD 中,⎩⎨⎧==BPBP PDPE ∴Rt △BPE ≌Rt △BPD (HL ),∴BE =BD .∵AB +BC =2BD ,∴AB +BD +DC =BD +BE ,∴AB +DC =BE 即DC =BE -AB =AE .)在Rt △APE 与Rt △CPD 中,ABCDP12N图3-1P12NABCDE 图3-2⎪⎩=DC AE ∴Rt △APE ≌Rt △CPD (SAS),∴∠PAE =∠PCD 又∵∠BAP +∠PAE =180°,∴∠BAP +∠BCP =180° 例4.已知:如图4-1,在△ABC 中,∠C =2∠B ,∠1=∠2.求证:AB =AC +CD .分析:从结论分析,“截长”或“补短”都可实现问题的转化,即延长AC 至E 使CE =CD ,或在AB 上截取AF =AC .{证明:方法一(补短法)延长AC 到E ,使DC =CE ,则∠CDE =∠CED ,如图4-2∴∠ACB =2∠E ,∵∠ACB =2∠B ,∴∠B =∠E , 在△ABD 与△AED 中,⎪⎩⎪⎨⎧=∠=∠∠=∠AD AD E B 21 ∴△ABD ≌△AED (AAS ),∴AB =AE .、又AE =AC+CE =AC +DC ,∴AB =AC +DC . 方法二(截长法)在AB 上截取AF =AC ,如图4-3 在△AFD 与△ACD 中,DCB A 12图4-1EDCBA12图4-2FCA 12⎪⎩⎪⎨⎧=∠=∠=AD AD AC AF 21 ∴△AFD ≌△ACD (SAS ),∴DF =DC ,∠AFD =∠ACD . 又∵∠ACB =2∠B ,∴∠FDB =∠B ,∴FD =FB . ∵AB =AF +FB =AC +FD ,∴AB =AC +CD .上述两种方法在实际应用中,时常是互为补充,但应结合具体题目恰当选择合适思路进行分析。
数学人教版八年级上册三角形全等证明专题2(截长补短法)

A Q
B P
D
C
• 如图1,在△ABC中,∠BAC=60°,∠ACB=40°,点P、Q分别在 BC,AC上,AP、BQ分别是∠BAC、∠ABC的平分线,求证: AB+BP=AC • 证法二:在AC上截取AD=AB,连接PD • ∵AD=AB, ∠DAP= ∠BAP,AP=AP • ∴△ DAP≌△ BAP(SAS) • ∴ ∠ADP= ∠ABC,BP=DP A • ∵ ∠BAC+ ∠ ABC+ ∠ ACB=180° Q • ∴ ∠ ABC=180°-60°-40°=80° D • ∴ ∠ADP = ∠ABC= 80° • ∵ ∠ADP= ∠C+ ∠CPD B C • ∴ ∠CPD=80°-40°=40° P • ∴ ∠C= ∠CPD • ∴DC=DP=BP • ∴AB+BP=AD+DC=AC
• 证法一:延长AB至点D,使得AD=AC,连接PD
• • • • • • • • • •
∵AD=AC, ∠DAP= ∠CAP,AP=AP ∴△ DAP≌△ CAP(SAS) ∴ ∠D= ∠C=40° ∵ ∠BAC+ ∠ ABC+ ∠ ACB=180° ∴ ∠ ABC=180°-60°-40°=80° ∵ ∠ABC= ∠D+ ∠BPD ∴ ∠BPD=80°-40°=40° ∴ ∠D= ∠BPD ∴BP=BD ∴AB+BP=AB+BD=AD=AC
全等三角形应用专题2
南宁市25中 林成山 2016年11月17日
教学目标
• 理解截长补短法构造全等三角形的方法 • 会应用截长补短法构造全等三角形并进行 相关证明
知识点拨
• 应用全等三角形性质:对应边相等、对应角相等, 来证明线段相等、角相等以及线段和差关系时, 证三角形全等是最常用的方法之一,但在一些情 况下,需要通过添加辅助线来构造全等三角形, “截长补短”法是一种有效的构造全等三角形的 方法 。 • “截长”是在较长的线段上截取一线段等于较短 的一条线段,“补短”是将较短的一条线段延长 与较长的线段相等,从而构造出全等三角形。
三角形全等之截长补短(整理)

三角形全等之截长补短(整理)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(三角形全等之截长补短(整理))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为三角形全等之截长补短(整理)的全部内容。
12三角形全等之截长补短(讲义)一、知识点睛截长补短:题目中出现__________________________时,考虑截长补短;截长补短的作用是____________________________________ ___________________________________________________.二、精讲精练1. 已知:如图,在△ABC 中,∠1=∠2,∠B =2∠C .求证:AC =AB +BD .2. 如图,在四边形ABCD 中,∠A =∠B =90°,点E 为AB 边上一点,且DE 平分21D CB A 21D CB A 21D B A3∠ADC ,CE 平分∠BCD . 求证:CD =AD +BC .3. 已知:如图,在正方形ABCD 中,AD =AB ,∠B =∠D =∠BAD =90°,E ,F 分别为CD ,BC 边上的点,且∠EAF =45°,连接EF .E DCA F EDCB A4求证:EF =BF +DE .4. 已知:如图,在△ABC 中,∠ABC =60°,△ABC 的角平分线AD ,CE 交于点O .求证:AC =AE +CD .OED CBA F EDCB A55. 已知:如图,在△ABC 中,∠A =90°,AB =AC ,BD 平分∠ABC ,CE ⊥BD 交BD 的延长线于点E .求证:CE =BD .21OED BEDCB A。
人教版八年级数学上截长补短法证明三角形全等.docx

初中数学试卷桑水出品一、截长补短法证明三角形全等例1已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE练习1如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
求证:BC=AB+DC。
2.已知∠ABC=3∠C,∠1=∠2,BE⊥AE,求证:AC-AB=2BE3如图,已知AD ∥BC ,∠PAB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .4在△ABC 中,︒=∠90ACB ,BC AC =,直线MN 经过点C ,且MN AD ⊥于D ,MN BE ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时,求证: ①ADC ∆≌CEB ∆;②BE AD DE +=;(2)当直线MN 绕点C 旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.6.如图,已知AC ∥BD ,EA 、EB 分别平分∠CAB 和∠DBA ,CD 过点E ,则AB 与AC+BD 相等 吗?请说明理由PEDCBA例2已知,如图1-1,在四边形ABCD 中,BC >AB ,AD =DC ,BD 平分∠ABC . 求证:∠BAD +∠BCD =180°.例1. 练习已知,如图3-1,∠1=∠2,P 为BN 上一点,且PD ⊥BC 于点D ,AB +BC =2BD .求证:∠BAP +∠BCP =180°.2、倍长中线法证三角形全等例1 、求证:三角形一边上的中线小于其他两边和的一半。
练习 1:△ABC 中,AB=5,AC=3,求中线AD 的取值范围例2.已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CEABCD图1-1ABCDP12N图3-1练习2已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF例3已知:如图,在ABC ∆中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC. 求证:AE 平分BAC ∠练习3已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAE 作业1、已知:如图,ABCD 是正方形,∠FAD =∠FAE . 求证:BE +DF =AE .B第 1 题图ABFDEC F EDCBACEDB A2、五边形ABCDE 中,AB =AE ,BC +DE =CD ,∠ABC +∠AED =180°,求证:AD 平分∠CDE3、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
人教版八年级数学上截长补短法证明三角形全等
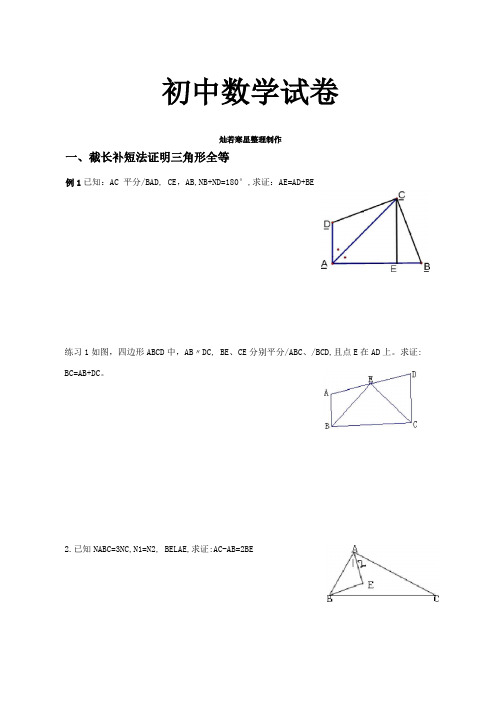
初中数学试卷灿若寒星整理制作一、截长补短法证明三角形全等例1已知:AC 平分/BAD, CE,AB,NB+ND=180°,求证:AE=AD+BE练习1如图,四边形ABCD中,AB〃DC, BE、CE分别平分/ABC、/BCD,且点E在AD上。
求证: BC=AB+DC。
2.已知NABC=3NC,N1=N2, BELAE,求证:AC-AB=2BE3如图,已知AD〃BC,NPAB的平分线与NCBA的平分线相交于E, CE的连线交AP于D.求证: AD+BC=AB.4 在4ABC中,/ACB = 90。
,AC = BC,直线MN经过点C,且AD± MN于D,BE± MN 于E .(1)当直线MN绕点C旋转到图1的位置时,求证:①AADC 0 A CEB:② DE = AD + BE;6.如图,已知AC〃BD, EA、EB分别平分NCAB和/DBA, CD过点E,则AB与AC+BD相等吗?请说明理由例2已知,如图1-1,在四边形ABCD中,BOAB, AD=DC, BD平分/ABC.求证:NBAD+NBCD=180°.图1-例1. 练习已知,如图3-1,/1=/2, P为BN上一点,且PDLBC于点D, AB+BC=2BD.求证:/BAP+/BCP=180°.2、倍长中线法证三角形全等例1、求证:三角形一边上的中线小于其他两边和的一半。
练习1:^ABC中,AB=5, AC=3,求中线AD的取值范围例2.已知在^ABC中,AB=AC, D在AB上,E在AC的延长线上,DE交BC于F,且DF=EF,求证: BD=CE练习2已知在4ABC中,AD是BC边上的中线,E是AD上一点,且BE二AC,延长BE交AC于F,求证:AF=EFB D C例3已知:如图,在A ABC中,AB牛AC,D、E在BC上,且DE=EC,过D作DF //BA交AE 于点 F,DF=AC.求证:AE平分/BAC练习 3 已知 CD=AB,NBDA=NBAD, AE 是4ABD 的中线,求证:NC=NBAE作业1、已知:如图,ABCD是正方形,NFAEb/FAE.求证:BE+DF=AE.2、五边形 ABCDE 中,AB=AE, BC+DE=CD,/ABC+/AED=180°,求证:AD 平分NCDE3、在四边形ABCD中,AB〃DC, E为BC边的中点,NBAE二NEAF, AF与DC的延长线相交于点F。
人教版八年级常见辅助线:截长补短专题

常见的辅助线作法(截长补短)截长法与补短法,具体作法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,使之与特定线段相等,再利用三角形全等的有关性质加以说明。
这种作法,适合于证明线段的和、差、倍、分等类的题目。
思考:遇到求证一条线段等于另两条线段之和时,一般方法是截长法或补短法:截长:在长线段中截取一段等于另两条中的一条,然后证明剩下部分等于另一条;
补短:将一条短线段延长,延长部分等于另一条短线段,然后证明新线段等于长线段。
例1、已知:如图,在△ABC中,∠C=2∠B,∠1=∠2.
求证:AB=AC+CD.
(分别用截长补短两种方法证明)
例2、已知:如图,在Rt△ABC中,AB=AC,∠BAC=90°,∠ABE=∠CBE,CE⊥BD的延长线于E。
求证:BD=2CE.
例3、如图,△ABC中,AM是BC边上的中线,求证:
例4、如图①所示,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形.请你参考这个作全等三角形的方法,解答下列问题:
(1)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你判断并写出FE与FD之间的数量关系;
(2)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.。
人教版八年级上册第十二章全等三角形 截长补短专题

截长补短遇到求证线段和差及倍半关系时,可以尝试截长补短的方法.截长指在长线段中截取一段等于另两条中的一条,然后证明剩下部分等于另一条;补短指将一条短线段延长,延长部分等于另一条短线段,然后证明新线段等于长线段.题目中常见的条件有等腰三角形(即两条边相等),或角平分线(即两个角相等),通过截长补短后,并连接一些点,构造全等得出最终结论.截长:1.过某一点作长边的垂线2.在长边上截取一条与某一短边相同的线段,再证剩下的线段与另一短边相等.补短: 1.延长短边2.通过旋转翻折等方式使两短边拼合到一起.适用范围: : 证明线段的和、差、倍、分时。
1.如图,若要求证AB+BD=AC,可以在线段AC 上截取线段AB′=AB,并连接DB,证明B′C=BD 即可;或延长AB 至点C′使得AC′=AC,并连接BC′,证明BC′=BD 即可.2.如图,若要求证AB+CD=BC,可以在BC 上截取线段BF=AB,再证明CD =CF 即可;或延长BA 至点F,使得BF=BC,再证明AF=CD 即可.2.3.在一个对角互补的四边形中,有一组邻边(AB=AD)相等,可以使用补短的方法延长另外两边的一条,构建全等三角形一、截长法1、要证明一段长线段等于两个小线段的和,用截长法在长边上截取一条与某一短边相同的线段,再证剩下的线段与另一短边相等.例1 如图1所示,AC∥BD,EA、EB分别平分∠CAB,∠DBA,CD过点E,求证:AB=AC+BD.分析根据题意,可在AB上截取AF=AC,再证FB=DB,就有AB=AF+FB:AC+BD.证明如图1,在AB上截取AF=AC,连结EF.在△ACE和△AEF中,∵AC=AF,∠CAE=∠FAE,AE=AE,∴△ACE △AEF,∠C=∠EFA.又∵AC∥BD,∴∠C+∠D=180°,而∠EFA+∠EFB=1800,∴∠EFB=∠D(等角的补角相等).在△FBE和△DBE中,∵∠DBE=∠FBE,B E=BE,∠D=∠EFB,∴△FBE≌△DBF.∴FB=DB,∴AB=AC+BD.补短延长BE,与AC的延长线相交于点F∵AC∥BD∴∵∴∠F=∠3在△AEF和△AEB中∴△AEF≌△AEB(AAS)∴AB=AF,BE=FE在△BED和△FEC中∴△BED≌△FEC(ASA)∴BD=FC∴AB=AF=AC+CF=AC+BD2、要证明边长和或差的数量关系,有时直接证明会很难,甚至无从着手,只要我们认真分析,通过截长法,把相关的线段转移到一个三角形中,思维会豁然开朗,问题会迎刃而解.例2 如图2所示,△ABC中,D是∠A平分线上的点,AB>AC,求证:AB-AC>BD -CD.分析本题直接证明有些难,因为AB-AC和BD-CD之间没有直接的线段可利用,这就需要找个中间线段作过渡,不妨在AB边上截取AE=AC,那么AB-AC=BE.若ED=CD,那么BD-CD<BE.通过已知条件和所作辅助线可知△AED≌△ACD.证明如图2,在AB边上截取AE=AC,∵AD是∠BAC的平分线,∴∠EAD=∠CAD.在△AED和△ACD中,∵AE=AC,∠EAD=∠CAD,AD=AD,∴△AED≌△ACD.ED=CD.在△BED中,∵BD-E D<BE.∴AB-AC=AB-AE=BE> BD-ED=BD-CD,∴AB-AC>BD-CD.二、补短法就是将一个已知的较短线段,延长至与另一个已知的较短线段的长度相等,然后求出延长后的线段与最长的已知线段的关系.对于具体问题,有时通过截长补短法,可构成某种特定的三角形来求解.例1. 已知,如图3-1,∠1=∠2,P为BN上一点,且PD⊥BC于点D,AB+BC=2BD.求证:∠BAP+∠BCP=180°.分析:与例1相类似,证两个角的和是180°,可把它们移到一起,让它们是邻补角,即证明∠BCP=∠EAP,因而此题适用“补短”进行全等三角形的构造.证明:过点P作PE垂直BA的延长线于点E,如图3-2∵∠1=∠2,且PD⊥BC,∴PE=PD,在Rt△BPE与Rt△BPD中,∴Rt△BPE≌Rt△BPD(HL),∴BE=BD.∵AB+BC=2BD,∴AB+BD+DC=BD+BE,∴AB+DC=BE即DC=BE-AB=AE.在Rt△APE与Rt△CPD中,∴Rt△APE≌Rt△CPD(SAS),∴∠PAE=∠PCD又∵∠BAP+∠PAE=180°,∴∠BAP+∠BCP=180°2、利用补短法构造等腰三角形这是几何证明常用的方法,它是把较短的线段延长,再根据角的关系,找出等腰三角形,通过腰相等进行转换,把两条线段转移到一条线段上来,最后利用三角形全等,使问题的结论水落石出.例4 如图4,已知AD是△ABC的角平分线,∠B=2∠C,求证:AB+BD=A C.分析欲证AB+BD=AC,可以延长AB到E,使BE=BD,然后再证△AED≌△ACD.得出AE=AC.证明如图4,延长AB到E,使BE=BD,连结DE,∴∠E=∠BDE.∵∠ABC=2∠C,∠ABC =∠E +∠BDE , ∴2∠E =2∠C .∠E =∠C . 又∵AD 是△ABC 的角平分线, ∴∠BAD =∠CAD . 在△AED 和△ACD 中, ∵∠BAD =∠CAD , ∠E =∠C ,AD =AD ,∴△AED ≌△ACD ,∴AE =AC , ∴AB +BE =AC . 即AB +BD =AC .另证 本题还可以在AC 边上截取AF(如图5),使AF =AB ,这样△ABD ≌△AFD ,再证△DFC 为等腰三角形,从而有BD =DF =FC ,则AB +BD =AF +FC =AC .练习1. 如图所示,ABC ∆中,045,90=∠=∠B C ,AD 平分BAC ∠交BC 于D 。
截长补短法证明全等三角形

截长补短法证明全等三角形全等三角形是指两个三角形的各个对应边和对应角相等。
证明两个三角形全等的方法有很多种,其中一种常用的方法是截长补短法。
截长补短法是通过截取或延长某些线段,使得两个三角形的对应边相等,从而证明两个三角形全等。
下面通过一个具体的例子来说明截长补短法的证明过程。
假设有两个三角形ABC和DEF,我们要证明它们全等。
首先,我们观察两个三角形的对应边和对应角,如果它们已经相等,那么可以直接得出两个三角形全等。
但通常情况下,我们需要通过截长补短的方法来使得对应边相等。
我们观察三角形ABC和DEF的对应边AB和DE,如果它们已经相等,那么我们可以通过对应边相等得出两个三角形全等。
但如果它们不相等,我们需要截取或延长某些线段来使它们相等。
假设我们截取了线段EF,使得EF = AB。
现在我们观察三角形ABC 和DEF的对应边AB和EF,它们已经相等了。
接下来,我们观察对应角B和对应角E,如果它们已经相等,那么我们可以通过对应边和对应角相等得出两个三角形全等。
但如果它们不相等,我们需要继续截取或延长某些线段来使它们相等。
假设我们截取了线段BC,使得BC = DE。
现在我们观察三角形ABC和DEF的对应边AB、BC和EF,它们已经相等了。
接下来,我们观察对应角B和对应角E,如果它们已经相等,那么我们可以通过对应边和对应角相等得出两个三角形全等。
但如果它们不相等,我们需要继续截取或延长某些线段来使它们相等。
假设我们截取了线段AC,使得AC = DF。
现在我们观察三角形ABC 和DEF的对应边AB、BC、AC和EF,它们已经全部相等了。
此时,我们只需要观察对应角B和对应角E,如果它们相等,那么我们就可以通过对应边和对应角相等得出两个三角形全等。
通过以上的截长补短的过程,我们可以得出结论:如果三角形ABC 的对应边AB、BC、AC和角B与三角形DEF的对应边DE、EF、DF和角E分别相等,那么三角形ABC和DEF全等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
鑫达捷
初中数学试卷
桑水出品
一、截长补短法证明三角形全等
例1已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE 练习1如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,
且点E 在AD 上。
求证:BC=AB+DC 。
2.已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BE 3如图,已知AD ∥BC ,∠PAB 的平分线与∠CBA 的平分线相交于E ,
CE
的连线交AP 于D .求证:AD +BC =AB .
4在△ABC 中,︒=∠90ACB ,BC AC =,直线MN 经过点C ,
且MN AD ⊥于D ,MN BE ⊥于E .(1)当直线MN 绕点C 旋转
到图1的
位置时,求证: ①ADC ∆≌CEB ∆;②BE AD DE +=;
(2)当直线MN 绕点C 旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.
6.如图,已知AC ∥BD ,EA 、EB 分别平分∠CAB 和∠DBA ,CD 过点E ,则AB 与AC+BD 相等 吗?请说明理由
例2已知,如图1-1,在四边形ABCD 中,BC >AB ,AD =DC ,BD 平
分∠
ABC .
求证:∠BAD +∠BCD =180°.
例1. 练习已知,如图3-1,∠1=∠2,P 为BN 上一点,且PD
⊥BC 于点D ,AB +BC =2BD . 求证:∠BAP +∠BCP =180°. 2、倍长中线法证三角形全等
例1 、求证:三角形一边上的中线小于其他两边和的一半。
练习 1:△ABC 中,AB=5,AC=3,求中线AD 的取值范围 例2.已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE
交BC 于F ,且DF=EF ,求证:BD=CE
练习2已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF 例3已知:如图,在ABC ∆中,AC AB ≠,D 、E 在BC 上,且
P
E
D
C
B
A
F
E
C
A
B
D
F
E
A
B
C
第 1 题图
A
B
F D
E
A
B
C D
图1-1
A
B
C
D
P
1
2
N
图3-1
鑫达捷
E DE=EC ,过D 作BA D
F //交AE 于点F ,DF=AC. 求证:AE 平分BAC ∠
练习3已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAE 作业
1、已知:如图,ABCD
是正方形,∠FAD =∠FAE . 求证:BE +DF =AE 2、五边形ABCDE 中,AB =AE ,BC +
DE =CD ,∠ABC +∠AED =180AD 平
分∠CDE
3、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,与DC
的延长线相交于点F 。
试探究线段AB 与AF 、CF 明你的
结论
4、已知:如图,∆ABC 中,∠C=90︒,CM ⊥AB 于M ,AT 平分∠BAC 交于D ,
交BC 于T ,过D 作DE//AB 交BC 于E ,求证:CT=BE. 5:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且
BE=AC ,延长BE 交AC 于F ,求证:AF=EF
6:已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAE
7、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,F 。
试探究线
段AB 与AF 、CF 之间的数量关系,并证明你的结论
A
B。
