高考17题
(浙江选考)2017高考化学 第17题 原电池

第17题:原电池满分:70分1.氢氧燃料电池可以使用在航天飞机上,其反应原理示意图如右图。
下列有关氢氧燃料电池的说法不正确的是A. 该装置将化学能转化为电能B. 为了增加灯泡亮度,可以将电极碳棒变得多粗糙多孔C. 电子迁移方向:电极a →灯泡→电极b →电解质溶液→电极aD. 该电池的总反应:2H 2+O 2=2H 2O2.某实验小组依据反应设计如图原电池,探究pH 对AsO 43-氧化性的影响。
测得电压与pH 的关系如图。
下列有关叙述错误的是A .调节pH 可以改变反应的方向B.pH = 0.68时,反应处于平衡状态C .pH = 5时,负极电极反应式为2I --2e - =I 2D .pH >0.68时,氧化性I 2〉AsO 43-3.下图Ⅰ、Ⅱ分别是甲、乙两组同学将反应“AsO 34-+2I -+2H +AsO 33-+I 2+H 2O ”设计成的原电池装置,其中C 1、C 2均为碳棒。
甲组向图Ⅰ烧杯中逐滴加入适量浓盐酸;乙组向图ⅡB 烧杯中逐滴加入适量40% NaOH 溶液。
下列叙述中正确的是A .甲组操作时,电流计(G)指针发生偏转B .甲组操作时,溶液颜色变浅C .乙组操作时,C 2做正极D .乙组操作时,C 1上发生的电极反应为I 2+2e -===2I -4.截止到2013年12月末,中国光伏发电新增装机容量达到10.66GW ,光伏发电累计装机容量达到17.16GW,图为光伏并网发电装置电解尿素[CO(NH2)2]的碱性溶液制氢的装置示意图(电解池中隔膜仅阻止气体通过,阴、阳极均为惰性电极)。
下列叙述中正确的是A.N型半导体为正极,P型半导体为负极B.制氢装置溶液中电子流向:从B极流向A极C.X2为氧气D.工作时,A极的电极反应式为CO(NH2)2+8OH--6e-═CO32-+N2↑+6H2O5.热激活电池可用作火箭、导弹的工作电源。
一种热激活电池的基本结构如图所示,其中作为电解质的无水LiCl—KCl混合物受热熔融后,电池即可瞬间输出电能。
2021年山东高考历史17题

2021年山东高考历史17题2021年山东高考历史17题的具体内容如下:17. 阅读材料,完成下列要求。
材料一:宋代的海外贸易超过了前代,成为当时世界上从事海外贸易的重要国家。
广州、泉州是闻名世界的大商港,政府鼓励海外贸易,在主要港口设立市舶司,加以管理。
南宋的外贸所得,在财政收入中占重要地位。
朝廷的奢侈品,很多来自海上贸易。
——摘自《中国历史》(人教版)材料二:明朝前期,我国的远洋航海技术和造船技术发达,郑和七下西洋,最远到达非洲东海岸和红海沿岸。
郑和的船队拥有当时世界上最先进的船只和航海技术,船上配备航海图和罗盘针,船队一般由200余艘船只组成,规模庞大。
——摘自《中国历史》(人教版)(1)根据材料一并结合所学知识,指出宋代海外贸易兴盛的原因。
(2)根据材料二并结合所学知识,说明郑和下西洋的条件。
(3)根据材料一、二并结合所学知识,分析郑和下西洋与宋代海外贸易兴盛的不同之处。
【答案】(1)宋代海外贸易兴盛的原因主要包括:经济重心南移,南方经济逐渐占据主导地位;科技发达(如南针和造船技术的应用);政府重视鼓励;农业、手工业商业繁荣;陆上丝绸之路被北方少数民族政权阻隔。
(2)郑和下西洋的条件主要包括:明朝前期国力强盛,经济繁荣,造船技术和航海技术先进;郑和本人具有远航的航海经验,勇于探索的精神,得到明成祖的信任和支持;同时,明朝前期实行对外开放政策,海上交通发达。
(3)郑和下西洋与宋代海外贸易兴盛的不同之处主要体现在以下方面:目的不同,前者主要是提高明朝在国外的地位、威望,同时也用厚往薄来政策,加强同海外的联系;后者则主要是为了促进经济和贸易的发展。
性质不同,前者是封建王朝的对外关系,属于政治活动;后者则是民间贸易,属于经济活动。
经营方式不同,前者是官方经营,后者则是民间经营。
影响不同,前者加强了中国与亚非各国的经济交流,促进了南洋地区社会经济发展;后者则促进了宋朝的繁荣,并成为当时世界上从事海外贸易的重要国家。
2023高考各省模考背诵17题

• (2)白居易《琵琶行(并序)》中,描写 • (3)为国以礼,其言不让。 琵琶女犹豫不决之后才娇羞出场的句子是 “____________________,____________________”。
• (3)孔子认为“礼”在国家治理中有重要地 位,他在《子路、曾皙、冉有、公西华侍 坐》哂笑子路是因为“____________________, ____________________”。
• (3)自然界中的景物常常能够触发人生短 暂之感,古诗词中这样的句子比较常见, 如:“___________,____________。”
• 示例二:林花谢了春红 太匆匆 • 示例三:夕阳无限好 只是近黄昏
• 17.补写出下列句子中的空缺部分。(6 分)
• (1)白居易《琵琶行》中的
• (2)在《屈原列传》中,司马迁以“ ” 一句,高度评价屈原保持出污泥而 不染的皎洁品质,并推断屈原的志 向“ ”
• (3)陆游《书愤》中抒发年老岁月蹉 跎、壮志未酬感慨的诗句是:“ , ”
• 16. 补写出下列句子中的空缺部分。 • (2)蜀道之难 难于上青天 • (3)万里悲秋常作客 百年多病独 登台(锦瑟无端五十弦,一弦一柱 思华年;烽火连三月,家书抵万金)
• 17.补写出下列句子中的空缺部分。 (6分)
• (1)贾谊《过秦论》中,始皇派遣大 将蒙恬北逐匈奴获得胜利,使得匈 奴长时间不敢南下进击中原。文中 “ , ”两句就是对此事件效果的概括。
• 17.(1)胡人不敢南下而牧马士不敢 弯弓而报怨
• (2)嚼然泥而不滓者也虽与日月争光 可也
• (3)塞上长城空自许镜中衰鬓已先斑
• (2)清人乔亿《剑溪说诗》评论 《蜀道难》:“太白诗‘__________, __________’句,凡三叠。”“一篇之中, 三番叙述,愈见其妙。”
高考数学17题

高考第17题三角函数综合运用1.在∆ABC中,角A,B,C所对的边分别为a,b,c,且cos Aa +cos Bb=sin Cc.(1)证明sin A sin B=sin C(2)若b2+c2-a2=65bc,求tan B.2.在∆ABC中,角A,B,C所对的边分别为a,b,c,已知b+c=2a cos B,(1)证明:A=2B(2)若cos B=23,求cos C的值.3.在∆ABC中,角A,B,C所对的边分别为a,b,c,已知cos B=√33,sin(A+B)=√69,ac=2√3,求sin A和c.4.在∆ABC中,角A,B,C所对的边分别为a,b,c,(1)若a,b,c成等差数列,证明:sin A+sin C=2sin(A+C).(2)若a,b,c成等比数列,且c=2a,求cos B的值.5.在∆ABC中,角A,B,C所对的边分别为a,b,c,已知a=3,cos A=√63,B=A+π2.(1)求b的值.(2)求∆ABC的面积.6.在∆ABC中,角A,B,C所对的边分别为a,b,c,且a+b+c=8.(1)若a=2,b=52,求cos C的值.(2)若sin A cos2B2+sin B cos2A2=2sin C,且∆ABC的面积S=92sin C,求a和b的值.3a cos C=2c cos A,tan A=1,求B.38.在∆ABC中,D是BC上的点,AD平分∠BAC,BD=2DC.(1)求sin∠Bsin∠C(2)若∠BAC=60°,求∠B9.在∆ABC中,角A,B,C所对的边分别为a,b,c,a=2b tan A.(1)证明:sin B=cos A(2)若sin C-sin A cos B=3,且B为钝角,求A,B,C.4为3√15,b-c=2,cos A=-1.4(1)求a和sin A的值).(2)求cos(2A+π6+ 11.在∆ABC中,角A,B,C所对的边分别为a,b,c,已知tan(π4 A)=2.若B=π,a=3,求∆ABC的面积.4。
全国高考历年考题精选专题17 有机化学结构与性质-2021年高考化学试题分项版解析(解析版)(1)

专题17:有机化学试卷结构与性质1.【2021新课标Ⅱ卷理综化学试卷】某羧酸酯的分子式为C18H26O5,1mol该酯完全[水]解可得到1mol羧酸和2mol乙醇,该羧酸的分子式为()A.C14H18O5B.C14H16O4C.C14H22O5D.C14H10O5【正确答案】A2.【2021新课标Ⅱ卷理综化学试卷】分子式为C5H10O2并能与饱和NaHCO3溶液反应放出气体的有机物有(不含立体异构) ()A.3种B.4种C.5种D.6种【正确答案】B【解析】分子式为C5H10O2并能与饱和NaHCO3溶液反应放出气体,这说明该有机物是饱和的一元羧酸,即分子组成为C4H9—COOH,丁基有4种,分别是CH3CH2CH2CH2—、(CH3)2CHCH2—、(CH3)3C—、CH3CH2CH(CH3)—,所以该羧酸也有4种,正确答案选B。
【考点定位】本题主要是考查有机物同分异构体种类判断,侧重于碳链异构体的考查。
【名师点晴】该题的关键是熟悉常见官能团的结构与性质,准确判断出有机物的属类,依据碳链异构体的书写方法逐一分析判断即可,旨在考查学生灵活运用基础知识解决实际问题的能力。
3.【2021浙江理综化学试卷】下列说法不正确...的是()A.己烷有4种同分异构体,它们的熔点、沸点各不相同B.在一定条件下,苯与液溴、硝酸、硫酸作用生成溴苯、硝基苯、苯磺酸的反应都属于取代反应C.油脂皂化反应得到高级脂肪酸盐与甘油CH2—]n)可由单体CH3CH=CH2和CH2=CH2加聚制得D.聚合物(—[CH2—CH2—CH—|CH3【正确答案】A4.【2021重庆理综化学试卷】某化妆品的组分Z具有美白功效,原从杨树中提取,现可用如下反应制备:下列叙述错误..的是()A.X、Y和Z均能使溴[水]褪色B.X和Z均能与NaHCO3溶液反应放出CO2C.Y既能发生取代反应,也能发生加成反应D.Y可作加聚反应单体,X可作缩聚反应单体【正确答案】B【解析】A. X、Z中有酚羟基,能与浓溴[水]发生取代反应,Y中有碳碳双键,能与溴[水]发生加成反应,它们均能使溴[水]褪色,A正确;B.酚羟基的酸性比碳酸弱,不能与NaHCO3溶液反应放出CO2,B错误;C.Y中有碳碳双键,能发生加成反应,有苯环,能发生取代反应,C正确;D.Y有碳碳双键,能发生类似聚乙烯的加聚反应,Y中也有酚羟基,能发生类似酚醛树脂的缩聚反应,D正确;正确答案选B。
2022年全国新高考Ⅰ卷数学试题变式题17-19题-(学生版)

2022年全国新高考Ⅰ卷数学试题变式题17-19题原题171.记n S 为数列{}n a 地前n 项和,已知11,n n S a a ⎧⎫=⎨⎩⎭是公差为13地等差数列.(1)求{}n a 地通项公式。
(2)证明:121112na a a +++< .变式题1基础2.已知数列{}n a 满足:对任意*n N ∈,有()212333323314n n n n a a a n ⋅+⋅+⋅⋅⋅+⋅=⋅-+.(1)求数列{}n a 地通项公式;(2)设14122n n n a n n n a b a a a ++++=⋅⋅⋅,证明:1214n b b b ++⋅⋅⋅+<.变式题2基础3.已知正项数列{}n a 地前n 项和n S 满足:22,(N )n n S a n +=-∈.(1)求数列{}n a 地通项公式。
(2)令()()()2221N log log n n n b n a a ++=∈⋅,求证:数列{}n b 地前n 项和34n T <.变式题3基础4.已知数列{}n a 地前n 项和为n S ,13a =,()()*112n n S n a n -=+∈N .(1)求数列{}n a 地通项公式n a 和前n 项和n S 。
(2)设()()*22111k k k b k S S +=∈+⋅N ,数列{}n b 地前n 项和记为n T ,证明:()*16n T n <∈N .变式题4基础5.已知数列{}n a 满足11a =,且11n n a a n +-=+,n S 是1n a ⎧⎫⎨⎬⎩⎭地前n 项和.(1)求n S 。
(2)若n T 为数列2n S n ⎧⎫⎪⎪⎛⎫⎨⎬ ⎪⎝⎭⎪⎪⎩⎭地前n 项和,求证:259n T <.变式题5巩固6.已知等比数列{}n a 公比为正数,其前n 项和为n S ,且4244,30a a S ==.数列{}n b 满足:*1115,23,2n n n n b a b a b n n N ++==++∈.(1)求数列{}{},n n a b 地通项公式:(2)求证:()()3112..212233411n n b b b b b n n n n -+++⋯++<⨯⨯⨯-⨯⨯+.变式题6巩固7.已知等差数列{}n a 地前n 项和为n S ,且11a =,5212S S =+。
2021-2023北京高考真题数学汇编:第二道解答题(第17题)

= 故 BA (0= , 2, 0), BN (1= ,1, 0), BM (0,1, 2) ,
设平面 BNM 的法向量为 n = ( x, y, z) ,
则
n n
⋅ ⋅
BN= 0 ,从而 BM = 0
x
y
+ +
y =0 ,取
2z = 0
z
=
−1,则 n =(−2, 2, −1) ,
设直线 AB 与平面 BNM 所成的角为θ ,则
而 CB ⊂ 平面 BCC1B1 ,平面 CBB1C1 ⊥ 平面 ABB1A1 , 平面 CBB1C1 ∩ 平面 ABB1A1 = BB1 ,故 CB ⊥ 平面 ABB1A1 ,
因为 NK //BC ,故 NK ⊥ 平面 ABB1A1 ,
因为 AB ⊂ 平面 ABB1A1 ,故 NK ⊥ AB , 若选①,则 AB ⊥ MN ,而 NK ⊥ AB , NK MN = N ,
= m ⋅ n
则:
m×n
5=
5
+
1 1− λ
2
×
5
5 3,
第6页/共7页
整理可得: (λ −1)2 = 1 ,故 λ = 1 ( λ = 3 舍去).
4
2
2
【点睛】本题考查了立体几何中的线面关系和二面角的求解问题,意在考查学生的空间想象能力和逻辑推
理能力,对于立体几何中角的计算问题,往往可以利用空间向量法,通过求解平面的法向量,利用向量的
从而: MC =(−2, 2 − 2λ, −2),CF =(1, 0, 2), FE =(0, −2, 0) ,
设平面 MCF 的法向量为: m = ( x1, y1, z1 ) ,则:
高考17题

sin(A + B) = √96,������������=2√3,求sin ������和 c.
8. 在∆ABC 中,角 A,B,C 所对的边分别为������, ������, ������, (1)若������, ������, ������成等差数列,证明:sin ������+sin ������=2sin(������ + ������). (2)若������, ������, ������成等比数列,且 c=2a,求cos ������的值.
2. 在∆ABC 中,角 A,B,C 所对的边分别为������, ������, ������,已知sin(������ + ������) = 8������������������2 ������
2
(1)求cos ������ (2)若������ + ������ = 6,∆ABC 的周长为 2,求 b.
9. 在∆ABC 中,角 A,B,C 所对的边分别为������, ������, ������,已知������=3,cos ������=√6,
3
B=A+������.
2
(1) 求 b 的值. (2) 求∆ABC 的面积.
10. 在∆ABC 中,角 A,B,C 所对的边分别为������, ������, ������,且������+b+c=8.
4. 在∆ABC 中,角 A,B,C 所对的边分别为������, ������, ������,已知������ > ������,������ = 5, ������ = 6,sin ������ = 3.
5
(1)求 b 和sin ������的值; (2)求sin (2A + ������ )的值.
第17题 数列解答题的两大主题:通项与求和-2021年高考数学真题(新高考全国Ⅰ卷)(含答案解析)

而 ,(n∈N*),∴ ,
∴当 且 时,有 ,
又 ,也满足 ,
∴对任意的n∈N*,都有 .
(2)将 代入 ,得 ,
进而 ,而 ,故 ,故 ,
∴数列 是首项为2,公比也为2的等比数列,
∴ ,∴ .
(2021湖北省恩施高中、龙泉中学、宜昌一中高三4月联考)
4.已知数列 的前n项和为 , , .
(1)证明:数列 为等比数列,并求出 ;
(2)求数列 的前n项和 .
【答案】(1)证明见解析; ;(2) .
【解析】
【分析】(1)由 带入 整理即可得解;
(2)由(1)可得 ,再利用 和 之间的关系,可得 ,利用等比数列,直接求和即可得解.
【详解】(1)由已知 ,整理得, ,
(2)设 前 项和为 ,则 ,
因为 ,
所以
.
【就题论题】这是近年来全国卷首次在解答题中以分段数列为载体命题,考查的都是基础知识,但计算时容易出错,如把 理解为n为偶数时 .
二、考题揭秘
【命题意图】本题考查等差数列的通项与求和,考查分类讨论思想数学运算与逻辑推理的核心素养,试题难度:中等偏易.
【考情分析】数列解答题是新高考必考题.通常考查数列的通项与求和,难度一般为中等偏易或中等.
因为 为等比数列,所以其公比为 ;
又 ,所以 ;
(2)由(1)可得 ;,所来自 .【点睛】结论点睛:
裂项相消法求数列和的常见类型:
(1)等差型 ,其中 是公差为 的等差数列;
(2)无理型 ;
(3)指数型 ;
(4)对数型 .
(2021河北省衡水中学高三下学期三调)
2.已知数列 是等差数列,设 为数列 的前n项和,数列 是等比数列, ,若 .
2023北京高考数学17题点评

2023北京高考数学17题点评近年来,越来越多的学生开始重视高考数学这一科目的备考,尤其是对于北京高考的数学考试,更是备受关注。
在2023年北京高考数学试卷中,第17题成为了备受争议的焦点。
本文将对这道题目进行全面评估,并给出深度和广度兼具的分析,帮助考生更好地理解这一题目。
让我们来看一下这道数学题的具体内容。
在2023年北京高考数学试卷中,第17题为一道关于微积分的应用题,涉及到函数的导数和不定积分。
题目要求考生求解一个曲线在给定区间上的弧长,并给出了具体的函数表达式和区间范围。
这一题目的难点在于需要考生熟练掌握对曲线的弧长公式、导数和不定积分的运用,而且需要在有限的时间内完成计算。
针对这道题目,我们首先来分析其深度。
在解答这一题目时,考生需要理解和掌握曲线的弧长公式,这需要对微积分的知识有深入的理解。
对于给定的函数表达式,需要熟练地计算其导数和不定积分,这涉及到对函数求导和积分的运用。
这道题目的深度在于考查考生对微积分知识的掌握程度,以及对相关概念和方法的运用能力。
接下来,我们来看这道题目的广度。
作为高考数学试题,这一题目所涉及的知识点并不算多,主要是围绕微积分的基本概念展开。
然而,这并不意味着这道题目的广度就很低。
相反,正是因为涉及到了微积分这一深厚的数学知识,这道题目所涵盖的广度也是非常广泛的。
考生不仅需要掌握曲线的弧长公式,还需要熟练掌握导数和不定积分的运用,这需要对微积分的整体架构有较为全面的理解。
在文章的总结和回顾中,我们不妨再次提及这一题目的要点。
这道数学题目考查了考生对微积分知识的深度掌握程度,以及对相关概念和方法的广度运用能力。
通过这道题目,考生可以进一步巩固和应用所学的微积分知识,同时也可以考察自己的解题能力和数学思维能力。
让我们共享一下我们对这一题目的个人观点和理解。
作为一道高考数学试题,这道题目在难度和深度上都比较符合高考的要求,既考查了考生对微积分知识的掌握程度,又考察了考生对数学应用的能力。
2017年高考数学江苏卷第17题解法赏析

面 直 角 坐 标 系 工 Q y 中, 椭 圆 & = 1 (a >
心> 0 ) 的左、 右焦点分别 为 F1 , 只 2 , 离心率为 2 图1 P F 2 的方程为 y = 犽 2(狓一 1 ) , 则 直 线 A 的方程为 y = — (狓— 1 ).
P
两 准 线 之 间 的 距 离 为 8. 点 P 在椭圆上, 且位于第一象限, 过 点 F 1 作直线 的 垂 线 Z1 , 过 点 R 作 直 线 的 垂 线 Z2 . (1) 求 椭 圆 E 的标准方程; (2) P 的坐标.
狓2 - 1 对 称 性 得 -狓 一 = 士y 。 , 即狓2 + y 0 = 1 ① , 或者
y0
2017年 第 9 期
中学数学月刊
^ 2 = 1 ② .又因为 P 在椭圆上, 所 以 4; y2 = 1 2 一 3: r 2 ,分 别 代 人 ① , ②, 前者无解 ,由 后 者 得 ^。 =
— k 2 k 2 — k 1) .
将此坐标代入椭圆方程, 化简得 9k 1 + 9 k2 — 30k 1k 2 一 1 6 = 0 •① 设 P (T 0 , y。 ) , 则 k1 y0 , _ 狓 0+ 1 y0
狓0 — 1
第一象限内的点, 所以狓。 > 0, y。 > 0, 则〒 P = ---^ ---^ ( 狓 〇+ 1 y 0 ) F 1Q =(狓 1 + 1 y 1) F 2P =(狓 〇 —1 , y 0^ —1Q = (狓1 — 1 ?y 1). 又因为— Q 以— Q 因此丨 丄— Q , —Q Q = 0. 丄— Q , 所
中学数学月刊
2017年 第 9 期
17年浙江化学高考真题

17年浙江化学高考真题2017年浙江化学高考真题2017年浙江省普通高中学业水平考试(以下简称“浙江高考”)化学科目的试题,是考生们备战高考的重要参考资料。
该考题紧扣教学大纲,贯穿基础知识和思维能力,考查学生对化学概念的掌握和综合运用能力。
下面将对2017年浙江高考化学科目的试题进行分析。
一、单项选择题1. 下列各组物质中,形成氯气时氧化态和标准氧化电位相同的是()。
A. Cu/Cu2+、 Sn/Sn4+B. Cr/Cr3+、 Fe/ Fe3+C. Fe/ Fe2+、 Hg/Hg22+D. Sn2+/Sn4+、 Fe/Fe2+答案:C。
解析:注意标准电位和氧化态相同。
2. 氯化铵的一水合物的硬度比六水合物的硬度()。
A.小B.大C.相等D.无法比较答案:B。
解析:一水合物对应含水量小,其晶格比较规整,相对较硬。
3. 化学反应2Na + Cl2 = 2NaCl制备氯化钠的副产物是()。
A. NaB. Na2Cl2C. NaCl2D. NanH1 2答案:B。
解析:氯化钠的副产物是Na2Cl2,它的形成有利于防止阳极表面的腐蚀。
4. 决定Fe(NH)2+6 的是()。
A. pH,TB. pH,VC. T,PD. V,P答案:A。
解析:Fe(NH)2+6 ,其存在形式与pH有关。
5. 下列化合物中铁最易被Fe3+(aq)离子氧化的是()。
A. CuB. AgC. H2OD. H2O2答案:D。
解析:强氧化剂可以使较不稳定的H2O2发生还原反应。
二、填空题6. 精制白磷的原料是磷酸镁,生成白磷炼制生产氢氧化钠,氧气和白磷,其中白磷分子中是单质 P4 。
答案:‐→无法比较、磷酸镁、三、四、简明生产、黑色。
三、应用题7. 下列图中有三元醇环境曲线,其中其中灰色区域代表溶胶;所有轴比比例因子都要按规定比例分析:结合图6查找可数晶胶中,k之间的显式异常现象已知。
在“110-600”的波斯康额外成分中有四个b1mk是否正交。
2017年高考浙江卷第17题赏析

1 x 4
1 x4
1 x 4
2
综上所述 a 9 . 2
解法 3 换元法设 x 4 t ,则t 5]4,[ x
,g(t) | t a | a ,由已知条件等价于:max g(t) 5 . 4t 5
若 a 4 ,则 max g(t) max t a a 5 ,满足题意.
x
x
③当 4 a 5时, f xmax max 4 a a, 5 a a ,
则:
4
a 4
a a
5 a
a 5
a
或:
4
a 5
a a
5 a
a 5
a
,
解得: a 9 或 a 9
2
2
4t5
4t 5
若 a 5,则 max g(t) max a t a 2a 4 5 , a 9 . 无解..
4t5
4t 5
2
若 4 a 5,则 max g(t) maxg 4, g 5 max2a 4,5 5 2a 4 5 a 9 .
4t5
4t 5
1t 4
2
综上所述 a 9 . 2
解法 5 转化为不等式组的求解问题,
max f (x) max f 1, f 4 max| 5 a | a,| 4 a | a 5
1 x 4
1 x4
1 x 4
a5
4t5
4t 5
1t 4
2
综上所述 a 9 . 2
2022年新高考全国1卷17题说题比赛课件

04
解题思路与方法总结
(2022全国1卷17题)记Sn为数列an的前n项和,已知a1 1,
Sn an
是公差为13
的等差数列.
(1)求an 的通项公式;
思路1: 利用an与Sn的关系消去 Sn ,与an相关的累乘法
思路3: 消元, 构造an相关新数列
思路4 : 消元, 构造Sn相关新数列
思路2 : 利用an与Sn的关系消去 an ,累乘法得 Sn ,再求an
所以Sn
n(n
1)(n 6
2)
(n
N ),
利用an与Sn
的关系消去an ,
与S
相关的累乘
n
法
则Sn-1
(n
1)n(n 6
1)
(n
2),
所以an
Sn
Sn-1
n(n
1)(n 6
2)
(n
1)n(n 6
1)
n(n 1) 2
(n
2),
又a1 1也满足上式.
所以an
n(n 1) 2
(n
N)
04
2( 1 1 ), n n 1
1 a1
1 a2
1 an
2(1
1) 2
(
1 2
1) 3
(
1 n 1
1) n
(1 n
n
1
1)
2(1 1 )
n 1
Text
2
04
解题思路与方法总结
破解此类题需过四关:一是“定义”关,即熟练利用等差(比)数列的定义 进行应用与证明; 二是“基本量法”关,若干个能唯一确定一个数列的量称为 该数列的“基本量”,首项与公差(比)是等差(比)数列的“基本量”,在解决 等差(比)数列的相关问题时,“基本量法”是常用的方法; 三是“裂项相消法” 关,注意其解题思路流程为一项裂开两项→互相抵消→注意余下的项→得结果; 四是会利用放缩法证明不等式,需注意数列的增减性与函数的单调性的本质区 别。
2023年全国数学理科(甲卷)第17题

2023年全国数学理科(甲卷)第17题全文共四篇示例,供您参考第一篇示例:2023年全国数学理科(甲卷)第17题考查了概率统计的知识,属于高考数学的难点题目。
通过对这道题目的分析和解答,可以帮助考生更好地掌握概率统计的相关知识,提高解题能力。
题目内容如下:某商品有三种不同的包装,甲包装占总数的40%,乙包装占总数的30%。
甲包装的商品中质量合格率为95%,乙包装的商品中质量合格率为90%,丙包装的商品中质量合格率未知。
如果从这批商品中任取一个,结果为合格品,请问此商品为甲包装的概率是多少?这道题考查了概率统计的知识,并要求考生结合概率的基本原理和条件概率进行求解。
我们可以根据题目中的信息,列出所需要的概率和条件概率。
记甲包装为A,乙包装为B,丙包装为C,任取一个商品为合格品为E,则题目所求为P(A|E)。
求得合格商品为甲包装的概率P(E|A),这是一个已知条件,根据题目给出的信息可知P(E|A) = 0.95。
我们需要求得甲包装商品的概率P(A)和乙包装商品的概率P(B),进而求得合格商品的概率P(E)。
根据条件概率的公式P(A|E) = P(E|A) * P(A) / P(E),即可求得所需的概率。
在解答这道题目时,通过计算可得甲包装商品的概率P(A) = 0.4,乙包装商品的概率P(B) = 0.3,于是可得合格商品的概率P(E) = P(E|A) * P(A) + P(E|B) * P(B) = 0.95 * 0.4 + 0.90 * 0.3 = 0.87。
最终,根据条件概率的公式可求得所需的概率P(A|E) = P(E|A) * P(A) / P(E) =0.95 * 0.4 / 0.87 ≈ 0.4368。
通过以上分析,我们可以得出此商品为甲包装的概率约为43.68%。
这道题目考察了考生在概率统计方面的计算能力和对条件概率的理解,要求考生能够灵活运用概率的基本原理和条件概率的知识进行求解。
食物生产与社会生活(2022年湖南高考历史第17题)
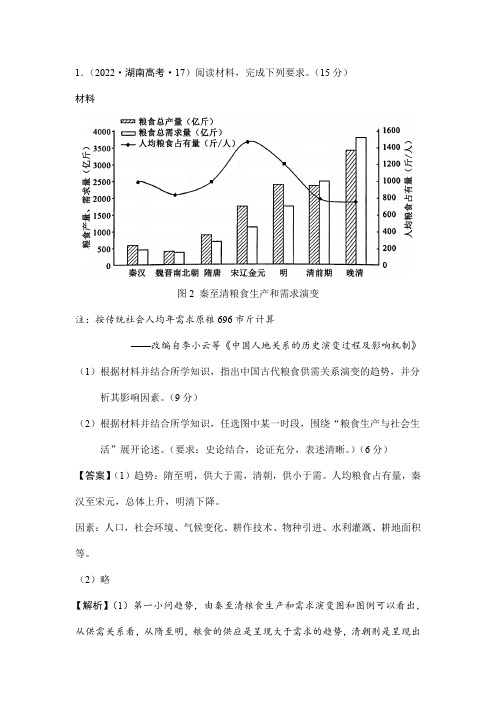
1.(2022·湖南高考·17)阅读材料,完成下列要求。
(15分)材料图2 秦至清粮食生产和需求演变注:按传统社会人均年需求原粮696市斤计算——改编自李小云等《中国人地关系的历史演变过程及影响机制》(1)根据材料并结合所学知识,指出中国古代粮食供需关系演变的趋势,并分析其影响因素。
(9分)(2)根据材料并结合所学知识,任选图中某一时段,围绕“粮食生产与社会生活”展开论述。
(要求:史论结合,论证充分,表述清晰。
)(6分)【答案】(1)趋势:隋至明,供大于需,清朝,供小于需。
人均粮食占有量,秦汉至宋元,总体上升,明清下降。
因素:人口,社会环境、气候变化、耕作技术、物种引进、水利灌溉、耕地面积等。
(2)略【解析】(1)第一小问趋势,由秦至清粮食生产和需求演变图和图例可以看出,从供需关系看,从隋至明,粮食的供应是呈现大于需求的趋势,清朝则是呈现出供应小于需求的趋势。
而从人均粮食占有量看,秦汉至宋元,总体呈现上升趋势,而明清则呈现下降趋势。
第二小问影响因素,则可以从古代粮食生产的影响因素思考作答,具体来说,包括人口多少,社会环境稳定与否、气候变化是否有利于农业生产、耕作技术是否改进、物种引进是否存在、水利灌溉是否充分、耕地面积大小等都是影响因素。
(2)这一题属于开放性试题,考查考生根据所学选择一个时段,围绕“粮食生产与社会生活”提取一个观点,并进行论证的能力。
首先,考生要围绕题目主题选择一个自己熟悉的时段,提取出符合所选时代特征的一个观点。
如,选择明清时期,可以提取的观点是:明清时期粮食产量的提高对人民的生活具有双重影响;选择秦汉时期,可以提取的观点是:秦汉时期粮食产量的提高有利于改善人民生活;等等。
然后,围绕自己提取的观点,结合所学知识进行论述,注意要结合所选择的时代,从粮食生产的影响因素角度来分析粮食产量提高的原因、粮食产量与需求之间的关系以及粮食人均占有量的变化、从粮食产量提高如何影响了人们的社会生活(衣食住行或者是手工业、商业的发展等)等角度论述,做到史论结合、论从史出、论证充分和符合逻辑即可。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考第17题三角函数综合运用
1.在∆ABC中,角A,B,C所对的边分别为a,b,c,且cos A
a +cos B
b
=sin C
c
.
(1)证明sin A sin B=sin C
(2)若b2+c2-a2=6
5
bc,求tan B.
2.在∆ABC中,角A,B,C所对的边分别为a,b,c,已知b+c=2a cos B,
(1)证明:A=2B
(2)若cos B=2
3
,求cos C的值.
3.在∆ABC中,角A,B,C所对的边分别为a,b,c,已知cos B=√3
3
,
sin(A+B)=√6
9
,ac=2√3,求sin A和c.
4.在∆ABC中,角A,B,C所对的边分别为a,b,c,
(1)若a,b,c成等差数列,证明:sin A+sin C=2sin(A+C).
(2)若a,b,c成等比数列,且c=2a,求cos B的值.
5.在∆ABC中,角A,B,C所对的边分别为a,b,c,已知a=3,cos A=√6
3
,
B=A+π
2
.
(1)求b的值.
(2)求∆ABC的面积.
6.在∆ABC中,角A,B,C所对的边分别为a,b,c,且a+b+c=8.
(1)若a=2,b=5
2
,求cos C的值.
(2)若sin A cos2B
2+sin B cos2A
2
=2sin C,且∆ABC的面积S=9
2
sin C,求
a和b的值.
3a cos C=2c cos A,tan A=1
,求B.
3
8.在∆ABC中,D是BC上的点,AD平分∠BAC,BD=2DC.
(1)求sin∠B
sin∠C
(2)若∠BAC=60°,求∠B
9.在∆ABC中,角A,B,C所对的边分别为a,b,c,a=2b tan A.
(1)证明:sin B=cos A
(2)若sin C-sin A cos B=3
,且B为钝角,求A,B,C.
4
为3√15,b-c=2,cos A=-1
4
.
(1)求a和sin A的值
(2)求cos(2A+π
6
).
11.在∆ABC中,角A,B,C所对的边分别为a,b,c,已知tan(π
4
+
A)=2.若B=π
4
,a=3,求∆ABC的面积.
12. ∆ABC的内角A,B,C的对边a,b,c已知2cos C(a cos B+b cos A)=c.
(1)求C;
(2)若c=√7,∆ABC的面积为3√3
2
,求∆ABC的周长.
13. 在∆ABC中,角A,B,C所对的边分别为a,b,c,已知b+c=2a cos B,(1)证明:A=2B
(2)若∆ABC的面积S=a 2
4
,求角A的大小.。
