第十一章 图形的全等 单元测试(A卷)(含答案)
七年级下册数学11章图形的全等单元试卷

七年级下册数学11章图形的全等单元试卷七年级下册数学11章图形的全等单元试卷以下是查字典数学网为您推荐的七年级下册数学11章图形的全等单元试卷,希望本篇文章对您学习有所帮助。
七年级下册数学11章图形的全等单元试卷七(下)数学《图形的全等》单元测试卷(2)填空题:1.如图⑴~⑿中全等的图形是和 ; 和 ; 和 ;和 ; 和 ; 和 ;(填图形的序号)2.已知ABC≌DEF,点A与点D.点B与点E分别是对应顶点,(1)若ABC的周长为32,AB=10,BC=14,则AC= .DE= .EF= .(2)A=48,B =53,则D= . F= .3. 如图,要用SAS说明ABC≌ADC,若AB=AD,则需要添加的条件是 .要用ASA说明ABC≌ADC,若ACB=ACD,则需要添加的条件是 .4. 如图,2,要使ABE≌ACE,则还需要添加一个条件(只需要添加一个条件)是 .依据是 .5. 如图,在ABC中,ADBC,CEAB.垂足分别为D.E,AD.CE 交于点H,请你添加一个适当的条件:,使AEH≌CEB.(第3题) (第4题) (第5题)6.与电子显示的四位数不相等,但为全等图形的四位数是 .12.下列条件中不能判断两个三角形全等的是( )A.有两边和它们的夹角对应相等.B.有两边和其中一边的对角对应相等.C.有两角和它们的夹边对应相等.D.有两角和其中一角的对边对应相等.13. 在ABC和FED中,如果F,E,要使这两个三角形全等,还需要的条件是( )A.AB=DE B.BC=EF C.AB=FE D.D14. 如图,ABC≌CDA,BAC=DCA,则BC的对应边是( )A.CDB.CAC.DAD.AB15.如图,已知AD平分BAC,AB=AC,则此图中全等三角形有( )A. 2对B.3 对C.4对D.5对(第14题) (第15题) (第16题)16. 如图,AB.CD相交于O,O是AB的中点,B=80,若D=40,则C=( )A.80B.40C.60D.无法确定17.如图,ABC中,AB=AC,BE=EC,则由SSS可判定( )A、ABD≌ACD B ABE≌ACEC BED≌CED D 以上答案都不对(第17题)18.在MNP中,Q为MN的中点,且PQMN,那么下列结论中不正确的是( )A.MPQ≌NPQB.MP = NPC.MPQ =NPQD.MQ = NP三.操作题:19.(1)你能把如图所示的(a)长方形分成2个全等图形?把如图所示的(b)能分成3个全等三角形吗?把如图所示的(c)分成4个全等三角形吗?(a) (b) (c)(2)你会把下图(d)和(f)分成四个全等的图形吗?试一试.(保留你画的痕迹)(d) (f)四.解答题:20.如图,ABC≌DEF,A=25,B=65,BF=3㎝,求DFE的度数和EC的长.21、如图,已知点A、E、F、C在同一直线上,2,AE=CF,AD=CB.请你判断BE和DF的位置关系.22.如图,已知2,4,ABC与DCB全等吗?为什么?23、如图,一个六边形钢架ABCDEF,由6条钢管连接而成,为使这一钢架稳固,请你用3条钢管使它不能活动,你能设计两种不同的方案吗?24、三月三,放风筝,如图是小明同学制作的风筝,他根据AB=AD,CB=CD,不用度量,他就知道ABC=ADC,请你用学过的知识给予说明.25、如图,AB=DC,AC=DB,由此你能猜想出什么结论?并简要说明理由。
第11章 全等三角形单元测验(含答案)

第十一章全等三角形单元测试题(总分100分,时间:60分钟)度的反复训练才能取得跟多的收获,我们设计的试卷主要就是从这点出发,所以从你下载这张试卷开始,就与知识接近了一步。
班级_________ 姓名__________ 学号_________一、精心选一选,慧眼识金!(每小题3分,共24分)1.两个直角三角形全等的条件是()A.两条边对应相等 B.两锐角对应相等C.一条边对应相等 D.一锐角对应相等2.下列条件中,不能判定两个三角形全等的是()A.三边对应相等B.两条边和夹角对应相等C.3.的是A.∠4.则Δ5.6.如图在△ABD和△ACE都是等边三角形,则ΔADC≌ΔABE的根据是()A. SSSB. SASC. ASAD. AAS7.如图,AB ∥CD ,AD ∥BC ,OE=OF ,则图中全等三角形的组数是( )A. 3B. 4C. 5D. 6 8.如图,已知∠1=∠2,AC=AD ,增加下列条件:①AB=AE ;②BC=ED ;③∠C=∠D ;④∠B=∠E .其中能使△ABC ≌△AED 的条件有( ) A.4个 B.3个 C.2个 D.1个 二、耐心填一填,一锤定音!(每小题3分,共24分)9.( 2008.广东梅州)如图, 点 P 到∠AOB 两边的距离相等,若∠POB=30°,则 ∠AOB=___度.第9题图形 第10题图形 第11题图形10.(2008.广东肇庆)如图,P 是∠AOB 的角平分线上的一点,PC ⊥OA 于点C ,PD ⊥OB 于点D , 写出图中一对相等的线段(只需写出一对即可) . 11.(2008.黑龙江黑河)如图,∠BAC=∠ABD ,请你添加一个条件: ,使OC=OD(只添一个即可).12.有两边和 对应相等的两个三角形全等.13.如图,若△OAD≌△OBC,且∠0=65°,∠C=20°,则∠OAD= .14.如图,点B 在AE 上,∠CAB=∠DAB ,要使△ABC ≌△ABD ,可补充的一个条件是: (写一个即可).15.如图,在△ABC 中,∠ABC 和∠ACB 的平分线交于点F ,过点F 作DE ∥BC ,交AB 于点D ,交AC 于点E ,如果BD+CE=9cm ,那么DE 的长度是 .16.如图,将正方形纸片沿AM 折叠,使点D 恰好落在边BC 上的N 处,若AD=7cm ,CM=3cm , ∠DAM=30°,那么AN= cm ,MN= cm ,∠NAM= ,∠DMN= .A DE F 第13题图形AD M 第14题图形DO CBA三、用心做一做,马到成功!(本大题共52分)17.(10分)如图,三条公路两两相交于A、B、C三点,现计划建一座综合供应中心,要求到三条公路的距离相等,则你能找出符合条件的地点吗?画出来。
【苏科版】七年级数学下册第十一章 图形的全等 单元测试A卷(含答案)

七(下)数学下第11章图形的全等 A卷一.选择题(每题4分,共20分)1.全等图形是指两个图形( )A.大小相同B.形状相同C.能够重合D.相等2.如图,△ABC≌△ECD,∠A=48°,∠D=62°点B.C.D在同一直线上,则图中∠ACE的度数是( )A.38°B.48°C.132°D.62°3.下列各组的条件,能判定△ABC≌△A′B′C′的是( )A.AB=A′B′,AC=A′C′,∠C=∠C′ ;B.AB=A′B′,AC=A′C′,∠B=∠B′C.AB=A′B′,AC=A′C′,∠A=∠A′ ;D.∠A=∠A′,∠B=∠B′,∠C=∠C′4.如图,已知AB=AC,BD⊥AC于点D,CE⊥AB于点E,图中全等三角形的组数是( )A.5B.4C.3D.25.说法错误的是( )A.如果两个三角形中,有一角及这个角的平分线以及这个角所对边上的高对应相等,那么这两个三角形全等B.如果两个三角形中,有两条边和第三边上的高对应相等,那么这两个三角形全等C.如果两个三角形中,有一边及该边上的高和中线对应相等,那么这两个三角形全等D.如果两个三角形中,有两个角和其中一角的平分线对应相等,那么这两个三角形全等二.填空题(第6~10题,每题4分,第11题8分,共28分)6.已知,如图,AD=AC,BD=BC,O为AB上一点,那么,图中共有______对全等三角形.7.如图,△ABC≌△ADE,则,AB=_________,∠E=∠________.若∠BAE=120°,∠BAD=40°,则∠BAC=_________°.8.如图,在△ABC中,AD平分∠BAC,D为BC边的中点,DE⊥AB于点E,DF⊥AC于点F,图中有_________对相等的线段,它们是_______________________.9.两根钢条AB′.BA′的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),如图,若测得AB=5 cm,则槽宽为__________cm.10.如图,在△ABC和△ABD中,∠C=∠D=90,若利用“AAS”证明△ABC≌△ABD,则需要加条件________或________;若利用“HL”证明△ABC≌△ABD,则需要加条件___________或____________.11.如图,已知∠ACB=∠BDA=90°,要使△ABC≌△BAD还需要增加一个什么条件?把增加的条件在横线上,并将相应的根据填在后面的括号内.(1)_______________;(2)_________________;(3)_______________;(4)_________________.三.解答题(第12.13题,每题8分,第14~17题,每题9分,共52分)12.如图,∠A=∠D,∠C=∠F,要使△ABC≌DEF,还要增加什么条件?试说明你的理由.13.如图,△ABC≌△DEF,∠A=25°,∠B=65°,BF=3 cm,求∠DFE的度数和EC的长.14.如图,△ABC中,AB=AC,D是BC的中点,试说明AD⊥BC.15.如图,A.B两点是湖两岸上的两点,为测A.B两点距离,由于不能直接测量,请你设计一种方案,测出A.B两点的距离,并说明你的方案的可行性.(8分)16.已知:如图.AB=CD,AF=CE,BE=DF,试说明∠B=∠C.你认为本题还可以得到哪些结论,尽可能多地写出来.17.将一个正方形分割成4个全等的部分.你有几种分割的方法?在每一种方法中,每一个全等部分是怎样得到另一个全等部分的?请你至少提供三种不同的方案.参考答案—.1.C 2.B 3.C4.B5.B二.6.3 7.AD,∠C,80 8.5,AB=AC.AE=AF.BE=CF.BD=CD.DE=DF9.510.∠CAB=∠DAB,∠ABC=∠ABD.AC=AD,BC=BD11.AC=BD,BC=AD,SAS∠BAC=∠ABD,AC=BD,ASA;∠BAC=∠ABD,BC=AD,AAS;AC=BD,HL三.12.只要增加一对边相等即可,利用“AAS”或“ASA”证明两三角形全等.13.∠DFE=90°,CE=3 cm14.由已知得△ABD≌△ACD,则∠ADB=∠ADC,进而得AD⊥BC15.构造以AB为一边的三角形以及这个三角形的全等三角形,如过A作河岸的平行线AC,过B作AC的垂直线BD.AC.BD交于点O.在OC上取点C使OC=OA.过C作∠ACD=∠BAC.CD交BD于点D.由“ASA”得△OCD≌△OAB,则有AB=CD,只要测量出CD的长,即可. 16.由AF=CE,得AE=CF,则可证△ABE≌△CDF,即∠B=∠C还可以得到∠D=∠B,∠AEB=∠CFD17.分割成如图1.图2或图3均可(答案不唯一).其中图1.图2的全等部分可以看作是平移得到的;图l.图3的全等部分可以看作是旋转得到的.。
新人教八年级上册第十一章《第11章三角形》单元测试含答案解析

新人教八年级上册第十一章《第11章三角形》一、填空题1.如果三角形的一个角等于其它两个角的差,则这个三角形是三角形.2.已知△ABC中,AD⊥BC于D,AE为∠A的平分线,且∠B=35°,∠C=65°,则∠DAE的度数为.3.△ABC中,如果∠A=∠B=3∠C,则∠A= .4.已知,如图,∠ACD=130°,∠A=∠B,那么∠A的度数是°.5.如图所示,图中有个三角形,个直角三角形.6.四边形ABCD中,若∠A+∠B=∠C+∠D,若∠C=2∠D,则∠C= .7.某足球场需铺设草皮,现有正三角形、正四边形、正五边形、正六边形、正八边形、正十边形6种形状的草皮,请你帮助工人师傅选择两种草皮来铺设足球场,可供选择的两种组合是.8.若一个n边形的边数增加一倍,则内角和将增加.9.如图,BC⊥ED于O,∠A=27°,∠D=20°,则∠B= ,∠ACB= .10.如图,由平面上五个点A、B、C、D、E连接而成,则∠A+∠B+∠C+∠D+∠E= .二、选择题11.如果一个三角形的三个外角之比为2:3:4,则与之对应的三个内角度数之比为()A.4:3:2 B.5:3:1 C.3:2:412.三角形中至少有一个内角大于或等于()A.45° B.55° C.60° D.65°13.如图,下列说法中错误的是()A.∠1不是三角形ABC的外角B.∠B<∠1+∠2C.∠ACD是三角形ABC的外角D.∠ACD>∠A+∠B14.如图,C在AB的延长线上,CE⊥AF于E,交FB于D,若∠F=40°,∠C=20°,则∠FBA的度数为()A.50° B.60° C.70° D.80°15.三条线段a=5,b=3,c的值为整数,由a、b、c为边可组成三角形()A.1个B.3个C.5个D.无数个16.多边形每一个内角都等于150°,则从此多边形一个顶点发出的对角线有()A.7条B.8条C.9条D.10条17.如图,△ABC中,D为BC上的一点,且S△ACD =S△ABD,则AD为()A.高B.中线 C.角平分线 D.不能确定18.现有长度分别为2cm、4cm、6cm、8cm的木棒,从中任取三根,能组成三角形的个数为()A.1 B.2 C.3 D.4三、解答题(共46分)19.如图,在三角形ABC中,∠B=∠C,D是BC上一点,且FD⊥BC,DE⊥AB,∠AFD=140°,你能求出∠EDF的度数吗?20.如图,有甲、乙、丙、丁四个小岛,甲、乙、丙在同一条直线上,而且乙、丙在甲的正东方,丁岛在丙岛的正北方,甲岛在丁岛的南偏西52°方向,乙岛在丁岛的南偏东40°方向.那么,丁岛分别在甲岛和乙岛的什么方向?21.已知等腰三角形的周长是16cm.(1)若其中一边长为4cm,求另外两边的长;(2)若其中一边长为6cm,求另外两边长;(3)若三边长都是整数,求三角形各边的长.22.如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,试问BE∥DF吗?为什么?《第11章三角形》参考答案与试题解析一、填空题1.如果三角形的一个角等于其它两个角的差,则这个三角形是三角形.【考点】三角形内角和定理.【分析】三角形三个内角之和是180°,三角形的一个角等于其它两个角的差,列出两个方程,即可求出答案.【解答】解:设三角形的三个角分别为:a、b、c,则由题意得:解得:a =90°故这个三角形是直角三角形.【点评】本题考查直角三角形的有关性质,可利用方程进行求解.2.已知△ABC中,AD⊥BC于D,AE为∠A的平分线,且∠B=35°,∠C=65°,则∠DAE的度数为.【考点】三角形内角和定理.【分析】首先根据三角形的内角和定理和角平分线的定义求出∠EAC的度数,再根据三角形的内角和定理求出∠DAC的度数,进而求∠DAE的度数.【解答】解:∵∠B=35°,∠C=65°,∴∠BAC=180°﹣∠B﹣∠C=180°﹣35°﹣65°=80°.∵AE为∠BAC的平分线,∴∠EAC=∠BAC=×80°=40°.∵AD⊥BC,∴∠ADC=90°,在△ADC中,∵∠DAC=180°﹣∠ADC﹣∠C=180°﹣90°﹣65°=25°,∴∠DAE=∠EAC﹣∠DAC=40°﹣25°=15°.故答案为:15°.【点评】本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.3.△ABC中,如果∠A=∠B=3∠C,则∠A= .【考点】三角形内角和定理.【分析】根据题意可得出2∠A=∠B=6∠C,设∠C=x,则∠B=6x,∠A=3x,再由三角形内角和定理即可得出x的值,进而得出结论.【解答】解:∵ABC中,∠A=∠B=3∠C,∴2∠A=∠B=6∠C,设∠C=x,则∠B=6x,∠A=3x,∵∠A+∠B+∠C=180°,∴3x+6x+x=180°,解得x=18°,∴∠A=3x=54°.故答案为:54°.【点评】本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.4.已知,如图,∠ACD=130°,∠A=∠B,那么∠A的度数是°.【考点】三角形的外角性质.【分析】直接根据三角形内角与外角的性质解答即可.【解答】解:∵∠ACD是△ABC的外角,∴∠ACD=∠A+∠B,∵∠ACD=130°,∠A=∠B,∴∠A==65°.【点评】本题比较简单,考查的是三角形外角的性质,即三角形的外角等于不相邻的两个内角的和.5.如图所示,图中有个三角形,个直角三角形.【考点】三角形.【分析】三角形有:△ABC、△ADE、△ADB、△ADC、△CDE;根据直角三角形性质,直角三角形有:△ADE、△ADB、△ADC、△CDE.【解答】解:由分析知:图中有5个三角形,4个直角三角形.【点评】本题考查三角形和直角三角形的判定,认真列举即可.6.四边形ABCD中,若∠A+∠B=∠C+∠D,若∠C=2∠D,则∠C= .【考点】多边形内角与外角.【分析】先根据任意四边形的内角和为360°及∠A+∠B=∠C+∠D,∠C=2∠D列出关于∠D的关系式,求出∠D的度数,再由∠C=2∠D即可求解.【解答】解:∵任意四边形的内角和为360°,∴∠A+∠B+∠C+∠D=360°,∵∠A+∠B=∠C+∠D,∠C=2∠D,∴∠A+∠B+∠C+∠D=6∠D=360°,∴∠D=60°,∴∠C=2×60°=120°.【点评】本题考查的是四边形的内角和定理,解答此题的关键是根据四边形的内角和定理及四个角之间的关系列出关于∠D的关系式,再求出∠C的度数即可.7.某足球场需铺设草皮,现有正三角形、正四边形、正五边形、正六边形、正八边形、正十边形6种形状的草皮,请你帮助工人师傅选择两种草皮来铺设足球场,可供选择的两种组合是.【考点】平面镶嵌(密铺).【专题】开放型.【分析】选择两种草皮来铺设足球场,共15种可能.根据正多边形的组合能否铺满地面,关键是看位于同一顶点处的几个角之和能否为360°:若能,则说明能铺满;反之,则说明不能铺满.依此得出可供选择的两种组合.【解答】解:正三角形、正四边形内角分别为60°、90°,当60°×3+90°×2=360°,故能铺满;正三角形、正五边形内角分别为60°、108°,显然不能构成360°的周角,故不能铺满;正三角形、正六边形内角分别为60°、120°,当60°×2+120°×2=360°,故能铺满;正三角形、正八边形内角分别为60°、135°,显然不能构成360°的周角,故不能铺满;正三角形、正十边形内角分别为60°、144°,显然不能构成360°的周角,故不能铺满;正四边形、正五边形内角分别为90°、108°,显然不能构成360°的周角,故不能铺满;正四边形、正六边形内角分别为90°、120°,显然不能构成360°的周角,故不能铺满;正四边形、正八边形内角分别为90°、135°,当90°+135°×2=360°,故能铺满;正四边形、正十边形内角分别为90°、144°,显然不能构成360°的周角,故不能铺满;正五边形、正六边形内角分别为108°、120°,显然不能构成360°的周角,故不能铺满;正五边形、正八边形内角分别为108°、135°,显然不能构成360°的周角,故不能铺满;正五边形、正十边形内角分别为108°、144°,当108°×2+144°=360°,故能铺满;正六边形、正八边形内角分别为120°、135°,显然不能构成360°的周角,故不能铺满;正六边形、正十边形内角分别为120°、144°,显然不能构成360°的周角,故不能铺满;正八边形、正十边形内角分别为135°、144°,显然不能构成360°的周角,故不能铺满.故可供选择的两种组合是:正三角形和正四边形、正三角形和正六边形、正四边形和正八边形、正五边形、正十边形中任选两种即可.【点评】解决此类题,可以记住几个常用正多边形的内角,及能够用两种正多边形镶嵌的几个组合.8.若一个n边形的边数增加一倍,则内角和将增加.【考点】多边形内角与外角.【分析】n边形的内角和是(n﹣2)•180°,将n边形的边数增加一倍就变成2n边形,2n边形的内角和是(2n﹣2)•180°,据此即可求得增加的度数.【解答】解:∵n边形的内角和是(n﹣2)•180°,∴2n边形的内角和是(2n﹣2)•180°,∴将n边形的边数增加一倍,则它的内角和增加:(2n﹣2)•180°﹣(n﹣2)•180°=n×180°.故答案为n×180°.【点评】本题主要考查了多边形的内角和公式,整式的化简,都是需要熟练掌握的内容.9.如图,BC⊥ED于O,∠A=27°,∠D=20°,则∠B= ,∠ACB= .【考点】直角三角形的性质.【分析】根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BEO=∠A+∠D,再根据直角三角形两锐角互余列式计算即可求出∠B,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACB=∠D+∠COD.【解答】解:∵∠A=27°,∠D=20°,∴∠BEO=∠A+∠D=27°+20°=47°,∵BC⊥ED,∴∠B=90°﹣∠BEO=90°﹣47°=43°;在Rt△COD中,∠ACB=∠D+∠COD=20°+90°=110°.故答案为:43°;110°.【点评】本题考查了直角三角形两锐角互余的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质并准确识图是解题的关键.10.如图,由平面上五个点A、B、C、D、E连接而成,则∠A+∠B+∠C+∠D+∠E= .【考点】三角形的外角性质;三角形内角和定理.【分析】延长CE交AB于F,再根据三角形内角与外角的关系求出∠BFC=∠A+∠C,∠D+∠DEG=∠EGB,再根据三角形内角和定理解答即可.【解答】解:延长CE交AB于F,∵∠BFC是△ACF的外角,∴∠BFC=∠A+∠C,∵∠EGB是△EDG的外角,∴∠EGB=∠D+∠DEG,∵∠B+∠BFC+∠EGB=180°,∴∠A+∠B+∠C+∠D+∠E=180°.【点评】此题比较简单,解答此题的关键是延长CE交AB于F,构造出△BGF,利用三角形外角的性质把所求的角归结到一个三角形中,再根据三角形内角和定理求解.二、选择题11.如果一个三角形的三个外角之比为2:3:4,则与之对应的三个内角度数之比为()A.4:3:2 B.5:3:1 C.3:2:4【考点】三角形的外角性质.【分析】已知三角形三个外角的度数之比,可以设一份为k°,根据三角形的外角和等于360°列方程求三个内角的度数,确定三角形内角的度数,然后求出度数之比.【解答】解:设一份为k°,∵三个外角之比为2:3:4,∴三个外角的度数分别为2k°,3k°,4k°,∵2k°+3k°+4k°=360°,解得k°=40°,∴三个外角分别为80°,120°和160°,∵三角形外角与它相邻的内角互补,与之对应的三个内角的度数分别是100°,60°和20°,即三个内角的度数的比为5:3:1.故选B.【点评】本题考查三角形外角的性质及三角形的外角与它相邻的内角互补的知识,解答的关键是沟通外角和内角的关系.12.三角形中至少有一个内角大于或等于()A.45° B.55° C.60° D.65°【考点】三角形内角和定理.【分析】根据三角形的内角和为180°解答即可.【解答】解:∵三角形的内角和为180°,∴当三个内角均小于60°时不能构成三角形,∴三角形中至少有一个内角大于或等于60°.故选C.【点评】此题比较简单,考查的是三角形的内角和为180°.13.如图,下列说法中错误的是()A.∠1不是三角形ABC的外角B.∠B<∠1+∠2C.∠ACD是三角形ABC的外角D.∠ACD>∠A+∠B【考点】三角形的外角性质.【分析】根据三角形的外角等于和它不相邻的两个内角的和,判断A正确,D错误;由三角形外角的定义,判断C正确;三角形的外角大于和它不相邻的任何一个内角,判断B正确.【解答】解:A、∠1不是三角形ABC的外角,正确;B、∠B<∠1+∠2,正确;C、∠ACD是三角形ABC的外角,正确;D、∠ACD=∠A+∠B,故D错误.故选D.【点评】本题考查三角形外角的性质以及考查三角形内角与外角的关系.14.如图,C在AB的延长线上,CE⊥AF于E,交FB于D,若∠F=40°,∠C=20°,则∠FBA的度数为()A.50° B.60° C.70° D.80°【考点】三角形的外角性质;三角形内角和定理.【分析】先根据三角形内角和定理求出∠EDF的度数,再根据对顶角的性质求出∠CDB的度数,由三角形外角的性质即可求出∠FBA的度数.【解答】解:∵CE⊥AF于E,∴∠FED=90°,∵∠F=40°,∴∠EDF=180°﹣∠FED﹣∠F=180°﹣90°﹣40°=50°,∵∠EDF=∠CDB,∴∠CDB=50°,∵∠C=20°,∠FBA是△BDC的外角,∴∠FBA=∠CDB+∠C=50°+20°=70°.故选C.【点评】本题考查的是三角形内角和定理及外角的性质,解答此题的关键是熟知以下知识:(1)三角形的内角和为180°;(2)三角形的外角等于与之不相邻的两个内角的和.15.三条线段a=5,b=3,c的值为整数,由a、b、c为边可组成三角形()A.1个B.3个C.5个D.无数个【考点】三角形三边关系.【分析】已知两边,则第三边的长度应是大于两边的差而小于两边的和,这样就可求出第三边c的范围,根据c的值为整数,即可确定c的值.从而确定三角形的个数.【解答】解:c的范围是:2<c<8,因而c的值可以是:3、4、5、6、7共5个数,因而由a、b、c为边可组成5个三角形.故选C.【点评】本题需要理解的是如何根据已知的两条边求第三边的范围.16.多边形每一个内角都等于150°,则从此多边形一个顶点发出的对角线有( )A .7条B .8条C .9条D .10条【考点】多边形内角与外角;多边形的对角线.【分析】多边形的每一个内角都等于150°,多边形的内角与外角互为邻补角,则每个外角是30度,而任何多边形的外角是360°,则求得多边形的边数;再根据不相邻的两个顶点之间的连线就是对角线,则此多边形从一个顶点出发的对角线共有(n ﹣3)条,即可求得对角线的条数.【解答】解:∵多边形的每一个内角都等于150°,∴每个外角是30°,∴多边形边数是360°÷30°=12,则此多边形从一个顶点出发的对角线共有12﹣3=9条.故选C .【点评】本题主要考查了多边形的外角和定理,已知外角求边数的这种方法是需要熟记的内容.多边形从一个顶点出发的对角线共有(n ﹣3)条.17.如图,△ABC 中,D 为BC 上的一点,且S △ACD =S △ABD ,则AD 为( )A .高B .中线C .角平分线D .不能确定【考点】三角形的面积.【分析】过A 作AE ⊥BC ,分别计算S △ACD 、S △ABD ,根据S △ACD =S △ABD 即可求得BD =DC ,即可解题.【解答】解:过A 作AE ⊥BC ,则S △ACD =BD •AE ,S △ABD =BC •AE ,∵S △ACD =S △ABD ,∴BD =BC ,∴AD 为中线.故选B .【点评】本题考查了三角形面积的计算,考查了三角形中线的定义.本题中求证BD =DC 是解题的关键.18.现有长度分别为2cm 、4cm 、6cm 、8cm 的木棒,从中任取三根,能组成三角形的个数为( )A .1B .2C .3D .4【考点】三角形三边关系.【分析】根据三角形的三边关系定理,只要满足任意两边的和大于第三边,即可确定有哪三个木棒组成三角形.【解答】解:能组成三角形的三条线段是:4cm 、6cm 、8cm .只有一种结果.故选A .【点评】考查三角形的边时,要注意三角形形成的条件:任意两边之和大于第三边,任意两边之差小于第三边.三、解答题(共46分)19.如图,在三角形ABC 中,∠B =∠C ,D 是BC 上一点,且FD ⊥BC ,DE ⊥AB ,∠AFD =140°,你能求出∠EDF 的度数吗?【考点】等腰三角形的性质.【分析】由于DF ⊥BC ,DE ⊥AB ,所以∠FDC =∠FDB =∠DEB =90°,又因为△ABC 中,∠B =∠C ,所以∠EDB =∠DFC ,因为∠AFD =140°,所以∠EDB =∠DFC =40°,所以∠EDF =90°﹣∠EDB =50°.【解答】解:∵DF ⊥BC ,DE ⊥AB ,∴∠FDC=∠FDB=∠DEB=90°,又∵∠B=∠C,∴∠EDB=∠DFC,∵∠AFD=140°,∴∠EDB=∠DFC=40°,∴∠EDF=90°﹣∠EDB=50°.【点评】本题考查了等腰三角形的性质;利用三角形的内角和定理求解角的度数是正确解答本题的关键.20.如图,有甲、乙、丙、丁四个小岛,甲、乙、丙在同一条直线上,而且乙、丙在甲的正东方,丁岛在丙岛的正北方,甲岛在丁岛的南偏西52°方向,乙岛在丁岛的南偏东40°方向.那么,丁岛分别在甲岛和乙岛的什么方向?【考点】方向角;垂线;平行线的性质.【专题】应用题.【分析】根据方向角的定义即可求解.分别作A M∥CD,N B∥CD,根据两直线平行,内错角相等即可求得∠1与∠2的度数.【解答】解:设甲岛处的位置为A,乙岛处的位置为B,丙岛处的位置为D,丁岛处的位置为C.作A M∥CD,N B∥CD,如图:∵丁岛在丙岛的正北方,∴CD⊥AB.∵甲岛在丁岛的南偏西52°方向,∴∠ACD=52°.又∵A M∥CD,∴∠1=∠ACD=52°.∴丁岛在甲岛的北偏东52°方向.∵乙岛在丁岛的南偏东40°方向,∴∠BCD=40°.又∵B N∥CD,∴∠2=∠BCD=40°,∴丁岛在乙岛的北偏西40°方向.【点评】本题主要考查了方向角的定义和平行线的性质,是一个基础的内容.21.已知等腰三角形的周长是16cm.(1)若其中一边长为4cm,求另外两边的长;(2)若其中一边长为6cm,求另外两边长;(3)若三边长都是整数,求三角形各边的长.【考点】等腰三角形的性质;三角形三边关系.【分析】(1)(2)由于未说明已知的边是腰还是底,故需分情况讨论,从而求另外两边的长.(3)根据三边长都是整数,且周长是16cm,还是等腰三角形,所以可用列表法,求出其各边长.【解答】解:(1)如果腰长为4cm,则底边长为16﹣4﹣4=8cm.三边长为4cm,4cm,8cm,不符合三角形三边关系定理.所以应该是底边长为4cm.所以腰长为(16﹣4)÷2=6cm.三边长为4cm,6cm,6cm,符合三角形三边关系定理,所以另外两边长都为6cm;(2)如果腰长为6cm,则底边长为16﹣6﹣6=4cm.三边长为4cm,6cm,6cm,符合三角形三边关系定理.所以另外两边长分别为6cm和4cm.如果底边长为6cm,则腰长为(16﹣6)÷2=5cm.三边长为6cm,5cm,5cm,符合三角形三边关系定理,所以另外两边长都为5cm;(3)因为周长为16cm,且三边都是整数,所以三角形的最长边小于8cm且是等腰三角形,我们可用列表法,求出其各边长如下:7cm,7cm,2cm;6cm,5cm,5cm;6cm,6cm,4cm,共有这三种情况.【点评】本题考查了等腰三角形的性质和三角形的三边关系;题目从边的方面考查三角形,涉及分类讨论的思想方法.当题目指代不明时,一定要分情况讨论,把符合条件的保留下来,不符合的舍去.22.如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,试问BE∥DF吗?为什么?【考点】平行线的判定;多边形内角与外角.【专题】探究型.【分析】要证BE∥DF,需证∠FDC=∠BEC,由于已知里给出了两条角平分线,四边形ABCD内角和为360°,∠A=∠C=90°,可得:∠FDC+∠EBC=90°,在△BCE中,∠BEC+∠EBC=90°,等角的余角相等,就可得到∠FDC=∠BEC,即可证.【解答】解:平行.∵∠A=∠C=90°,四边形ABCD的内角和为360°,∴∠ADC+∠ABC=180°,∵BE平分∠ABC,DF平分∠ADC,∴∠FDC+∠EBC=90°.又∵∠C=90°,∴∠BEC+∠EBC=90°,∴∠FDC=∠BEC,∴BE∥DF.【点评】本题利用了角平分线性质和判定,四边形的内角和为360°,同角的余角相等.。
2019-2020学年八年级数学《第十一章全等三角形》综合测试A新人教版.docx

2019-2020 学年八年级数学《第十一章全等三角形》综合测试A新人教版一、选择题(每题 3 分,共 30 分。
每题只有一个正确答案,请将正确答案的代号填在下面的表格中)题号12345678910答案1.下列判断中错误的是()..A.有两角和一边对应相等的两个三角形全等B.有两边和一角对应相等的两个三角形全等E C.有两边和其中一边上的中线对应相等的两个三角形全等D.有一边对应相等的两个等边三角形全等D2.如图,△DAC和△EBC均是等边三角形,AE,BD分别与N CD, CE 交于点 M , N ,有如下结论:A M BC①△ ACE ≌△ DCB ;② CM CN ;③ AC DN .其中,正确结论的个数是()(第 2 题)A.3 个B. 2 个C. 1 个D. 0 个3.某同学把一块三角形的玻璃打碎了 3 块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是()A.带①去B.带②去(第 3 题)C.带③去D.带①②③去4.△ABC≌△DEF, AB=2,AC=4,若△DEF的周长为偶数,则 EF的取值为()A .3B .4C .5D .3 或 4 或 55.如图,已知,△ABC的三个元素,则甲、乙、丙三个三角形中,和△ABC全等的图形是()A.甲和乙B.乙和丙C.只有乙D.只有丙6.三角形ABC的三条内角平(第 5 题)分线为 AE、 BF、CG、下面的说法中正确的个数有()①△ ABC的内角平分线上的点到三边距离相等②三角形的三条内角平分线交于一点③三角形的内角平分线位于三角形的内部④三角形的任一内角平分线将三角形分成面积相等的两部分(第 7 题)A .1 个B . 2 个C . 3 个D . 4 个7.如图,长方形 沿 AE 折叠,使 D 点落在边上的 F 点处,∠=600,那么∠等于()ABCDBCBAFDAEA .150B .300C . 450D . 6008.如图所示, △ ABE 和△ ADC 是△ ABC 分别沿着 AB ,AC 边翻折 180°形成的,若∠ 1∶∠ 2∶∠ 3=28∶ 5∶ 3,则∠ α 的度数为()A .80°B .100°C .60°D .45°9. 在△ ABC 和△ A B C 中 , 已知 A A , ABAB , 在下面判断中错误的(第 8 题)是 ( )A. 若添加条件 ACA C , 则△ ≌△A B CABC B. 若添加条件 BCB C , 则△ ABC ≌△ A B C C. 若添加条件 BB , 则△ ABC ≌△ A B CD. 若添加条件CC , 则△ ABC ≌△ A B C10. 如图 , 在△ ABC 中 , ∠ C = 90 , AD 平分∠ BAC ,DE ⊥ AB 于 E ,则下列结论 : ① AD 平分∠ CDE ;②∠ BAC =∠ BDE ;③ DE 平分∠ ADB ;④ BE +AC =AB . 其中正确的有 ()A.1 个B.2 个C.3 个D.4个二、填空题(每题3 分,共 30)第 10 题11.如图, AB , CD 相交于点 O , AD = CB ,请你补充一个条件,使得△AOD ≌△ COB .你补充的条件是 ______________________________ .12.如图, AC ,BD 相交于点 O , AC =BD , AB =CD ,写出图中两对相等的角 ______ .13.如图,△ ABC 中,∠ C = 90°, AD 平分∠ BAC , AB = 5, CD =2,则△ ABD 的面积是 ______.BDACADE OOCDAD B B C ABC的面 14.如图(,第直11线题)AE ∥ BD ,点 C 在(BD 第上12,题若) AE =4, BD (=第8,13△题ABD )的面积为 (16第,14则题△)ACE 积为 ______. 15.在△ ABC 中,∠ C =90°, BC =4CM ,∠ BAC 的平分线交 BC 于 D ,且 BD :DC =5:3,则 D 到 AB 的距离为 _____________ .16.如图,△ ABC 是不等边三角形, DE =BC ,以 D ,E 为两个顶点作位置不同的三角形,使所作的三角形与△ ABC全等,这样的三角形最多可以画出_____个.(第 16 题)17.如图,AD, A D 分别是锐角三角形ABC 和锐角三角形 A B C 中 BC , B C 边上的高,且AB A B , AD A D .若使△ ABC ≌△ A B C ,请你补充条件___________.(填写一个你认为适当的条件即可)18.如图,如果两个三角形的两条边和其中一条边上的高对应相等,那么这两个三角形的第三边所对的角的关系是__________.A A'ADBCB''C'D DBE C(第 17、 18 题)(第 19 题)19.如图,已知在ABC 中, A 90 , AB AC , CD平分ACB , DE BC 于 E ,若BC 15cm ,则△ DEB 的周长为cm .20.在数学活动课上,小明提出这样一个问题:∠B=∠C=900, E 是 BC的中点, DE平分∠ ADC,∠CED=350,如图16,则∠ EAB是多少度?大家一起热烈地讨论交流,小英第一个得出正确答案,是 ______.三、解答题(每题9 分,共 36 分)21.如图,O为码头,A,B两个灯塔与码头的距离相等,OA, OB为海岸线,一轮船从码头开出,计划沿∠ AOB的平分线航行,航行途中,测得轮船与灯塔A,B 的距离相等,此时轮船有没有偏离航线?画出图形并说明你的理由.AOB22.如图,在△ABC中,BD=DC,∠ 1=∠ 2 ,求证:AD⊥BC.23.如图,OM平分∠POQ,MA⊥OP, MB⊥OQ,A、B为垂足,AB交OM于点N.求证:∠ OAB=∠ OBA24.如图,已知AD∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的连线交 AP于 D.求证:AD+BC=AB.PCEDA B四、解答题(每题10 分,共 30 分)25.如图,△ABC中,AD是∠CAB的平分线,且AB=AC+CD,求证:∠ C=2∠ BACD B26.如图①,E、F分别为线段AC上的两个动点,且DE⊥AC于 E,BF⊥AC于F,若AB=CD,AF=CE,BD交 AC于点 M.(1)求证:MB=MD,ME=MF(2)当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.27.已知:如图,DC∥ AB,且 DC=AE, E 为 AB的中点,(1)求证:△AED≌△EBC.(2)观看图前,在不添辅助线的情况下,除△EBC外,请再写出两个与△ AED的面积相等的三角形.(直接写出结果,不要求证明):AE O DB C五、(每题12 分,共24 分)28.如图,△ABC中,∠BAC=90 度,AB=AC,BD是∠ABC的平分线,BD的延长线垂直于过C点的直线于,直线交的延长线于.E CE BA F求证: BD=2CE.FAEDB C29.已知 : 在△ABC中 , ∠BAC= 90 , AB=AC, AE是过点A的一条直线 , 且BD⊥AE于D, CE⊥AE于 E.(1)当直线 AE 处于如图①的位置时,有 BD=DE+CE,请说明理由;(2)当直线 AE处于如图②的位置时,则 BD、DE、 CE的关系如何?请说明理由;(3)归纳 (1) 、(2), 请用简洁的语言表达BD、DE、CE之间的关系 . 第十一章全等三角形综合测试 A 参考答案。
人教版八年级数学上册第11章单元测试卷及答案

人教版八年级数学上册第11章单元测试卷及答案一.选择题(每小题3分,共30分)1.若一个三角形的两边长分别为5和8,则第三边长可能是( )A.14B.10C.3D.22.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )A.垂线段最短B.两点之间线段最短C.两点确定一条直线D.三角形的稳定性3.画△ABC中AB边上的高,下列画法中正确的是( )A.B.C.D.4.如图,直线AB∥CD,∠A=70°,∠C=40°,则∠E等于( )A.30°B.40°C.60°D.70°第4题图第5题图第6题图5.如图,AD是△ABC的中线,的周长为25cm,AB比AC长6cm,则△ACD的周长为( )A.19cm B.22cm C.25cm D.31cm6.如图,BD平分∠ABC,CD⊥BD,D为垂足,∠C=55°,则∠ABC的度数是( )A.35°B.55°C.60°D.70°7.一个多边形的内角和是外角和的2倍,则这个多边形是( )A.四边形B.五边形C.六边形D.八边形8.如图,AD是△ABC的角平分线,点O在AD上,且OE⊥BC于点E,∠BAC=60°,∠C=80°,则∠EOD的度数为( )A.20°B.30°C.10°D.15°第8题图第9题图9.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )A.∠A=∠1+∠2B.2∠A=∠1+∠2C.3∠A=2∠1+∠2D.3∠A=2(∠1+∠2)10.一个角的两边与另一个角的两边互相垂直,且这两个角之差为40°,那么这两个角分别为( ) A.70°和110°B.80°和120°C.40°和140°D.100°和140°二.填空题(每小题3分,共15分)11.如图,在△ABC中,∠ACB=90°,将△ACD沿CD折叠,使点A恰好落在BC边上的点E处.若∠B=25°,则∠BDE= 度.第11题图第12题图第13题图12.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A= .13.如图,已知△ABC为直角三角形,∠B=90°,若沿图中虚线剪去∠B,则∠1+∠2等于 度.14.如图,△ABC中,AD为中线,DE⊥AB于E,DF⊥AC于F,AB=3,AC=4,DF=1.5,则DE= .第14题图第15题图15.如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A 2,得∠A2;…∠A2016BC和∠A20l6CD的平分线交于点A2017,则∠A2017= °.三.解答题(本大题共8个小题,满分75分)16.(8分)如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=42°,求∠ACD的度数.17.(9分)如图,A点在B处的北偏东40°方向,C点在B处的北偏东85°方向,A点在C处的北偏西45°方向,求∠BAC及∠BCA的度数.18.(9分)如图,四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线.(1)∠1与∠2有什么关系,为什么?(2)BE与DF有什么关系?请说明理由.19.(9分)如图所示,已知在△ABC中,∠B>∠C,AD为∠BAC的平分线,AE丄BC,垂足为E.求证:∠DAE=(∠B﹣∠C).20.(9分)一个多边形的内角和比外角和的3倍少180°,求(1)这个多边形的边数;(2)该多边形共有多少条对角线.21.(10分)如图,在△ABC中,点D在BC 上,点E 在AC 上,AD交BE于F.已知EG∥AD交BC于G,EH⊥BE交BC 于H,∠HEG=50°.(1)求∠BFD的度数.(2)若∠BAD=∠EBC,∠C=42°,求∠BAC的度数.22.(10分)(1)如图1,点P为△ABC的内角平分线BP与CP的交点,求证:∠BPC=90°+∠A;(2)如图2,点P为△ABC内角平分线BP与外角平分线CP的交点,请直接写出∠BPC与∠A的关系;(3)如图3,点P是△ABC的外角平分线BP与CP的交点,请直接∠BPC与∠A的关系.23.(11分)将一块直角三角板DEF放置在锐角△ABC上,使得该三角板的两条直角边DE.DF恰好分别经过点B.C.(1)如图①,若∠A=40°时,点D在△ABC内,则∠ABC+∠ACB= 度,∠DBC+∠DCB= 度,∠ABD+∠ACD= 度;(2)如图②,改变直角三角板DEF的位置,使点D在△ABC内,请探究∠ABD+∠ACD与∠A之间存在怎样的数量关系,并验证你的结论.(3)如图③,改变直角三角板DEF的位置,使点D在△ABC外,且在AB边的左侧,直接写出∠ABD.∠ACD.∠A三者之间存在的数量关系.第十一章三角形单元测试卷参考答案一.选择题1.B2.D3.C4.A5.A 6.D 7.C8.A9.B10.A二.填空题11.11012.85°13.27014.215..三.解答题(共8小题)16.解:∵∠AFE=90°,∴∠AEF=90°﹣∠A=90°﹣35°=55°,∴∠CED=∠AEF=55°,∴∠ACD=180°﹣∠CED﹣∠D=180°﹣55°﹣42°=83°. 17.解:∵∠DBA=40°,∠DBC=85°,DB∥CE,∴∠ECB=180°﹣85°=95°,∠ABC=85°﹣40°=45°,∵∠ECA=45°,∴∠BCA=95°﹣45°=50°,∴∠BAC=180°﹣50°﹣45°=85°.18.解:(1)∠1+∠2=90°;∵BE,DF分别是∠ABC,∠ADC的平分线,∴∠1=∠ABE,∠2=∠ADF,∵∠A=∠C=90°,∴∠ABC+∠ADC=180°,∴2(∠1+∠2)=180°,∴∠1+∠2=90°;(2)BE∥DF;在△FCD中,∵∠C=90°,∴∠DFC+∠2=90°,∵∠1+∠2=90°,∴∠1=∠DFC,∴BE∥DF.19.解:在Rt△AED中,∠DAE+∠ADE=90°,∵∠ADE=∠C+∠DAC,而∠DAC=∠BAC,∴∠DAE=90°﹣(∠C+∠BAC),又∵∠BAC=180°﹣∠B﹣∠C,∴∠DAE=90°﹣∠C﹣(180°﹣∠B﹣∠C)=90°﹣∠C﹣90°+∠B+∠C=(∠B﹣∠C).20.解:(1)设这个多边形的边数为n.根据题意得:180°×(n﹣2)=360°×3﹣180°,解得:n=7;(2)==14.答:(1)该多边形为七边形;(2)七边形共有14条对角线.21.解:(1)∵EH⊥BE,∴∠BEH=90°,∵∠HEG=50°,∴∠BEG=40°,又∵EG∥AD,∴∠BFD=∠BEG=40°;(2)∵∠BFD=∠BAD+∠ABE,∠BAD=∠EBC,∴∠BFD=∠EBC+∠ABE=∠ABC=40°,∵∠C=42°,∴∠BAC=180°﹣∠ABC﹣∠C=180°﹣40°﹣42°=98°.22.证明:(1)∵∠PBC+∠BCP+∠BPC=180°,∵∠BPC=120°,∴∠ABC+∠ACB=60°,∵BP.CP是角平分线,∴∠ABC=2∠PBC,∠ACB=2∠BCP,∵∠ABC+∠ACB+∠A=180°,∴∠BPC=90°+∠A;(2)∠P=∠A,理由如下:∵△ABC的内角平分线BP与外角平分线CP交于P,∴∠PBC=∠ABC,∠PCD=∠ACD,∵∠ACD=∠A+∠ABC,∠PCD=∠PBC+∠P,∴(∠A+∠ABC)=∠PBC+∠P=∠ABC+∠P,∴∠P=∠A;(3)∠P=90°﹣∠A,理由如下:∵BP.CP是△ABC的外角平分线,∴∠PBC=(∠A+∠ACB),∠PCB=(∠A+∠ABC),又∵∠PBC+∠PCB+∠P=180°,∴∠P=180°﹣(∠PBC+∠PCB)=180°﹣(∠A+∠ACB+∠A+∠ABC)=180°﹣(180+∠A)=90°﹣∠A.23.解:(1)在△ABC中,∵∠A=40°,∴∠ABC+∠ACB=180°﹣40°=140°,在△DBC中,∵∠BDC=90°,∴∠DBC+∠DCB=180°﹣90°=90°,∴∠ABD+∠ACD=140°﹣90°=50°;故答案为:140;90;50.(2)∠ABD+∠ACD与∠A之间的数量关系为:∠ABD+∠ACD=90°﹣∠A.证明如下:在△ABC中,∠ABC+∠ACB=180°﹣∠A.在△DBC中,∠DBC+∠DCB=90°.∴∠ABC+∠ACB﹣(∠DBC+∠DCB)=180°﹣∠A﹣90°.∴∠ABD+∠ACD=90°﹣∠A.(3)∠ACD﹣∠ABD=90°﹣∠A.。
人教版八年级数学上册单元测试题及答案A卷

人教版八年级数学上册单元测试题
26.(7 分)如图,已知△ABC 中,∠ABC 和∠ACB 的平分线 BD、CE 相交于点 O,且∠A=60°, 求∠BOC 的度数.
27.(7 分)已知:如图,四边形 ABCD 中,AD⊥DC,BC⊥AB,AE 平分∠BAD,CF 平分∠DCB, AE 交 CD 于 E,CF 交 AB 于 F,问 AE 与 CF 是否平行?为什么?
二、选择题 15.D 16.C 17.A 18.B 三、解答题 19.略 20.50°、130° 21.9 种,第三根木棒的长度可以是 4cm,5cm,6cm,7cm,8cm, 9cm,10cm,11cm,12cm 22.∠ACD=30° 23.70° 24.100° 25.腰长为 10cm,底 边长为 4cm 26.120° 27.平行 28.(1)12;(2)1800°
③DE 平分∠ADB;④BE+AC=AB.其中正确的有( )
A.1 个 B.2 个 C.3 个 D.4 个
二、填空题(每题 3 分,共 30)
第 10 题
11.如图,AB,CD 相交于点 O,AD=CB,请你补充一个条件,使得△AOD≌△COB.你补充的
条件是______________________________.
16.如图,△ABC 是不等边三角形,DE=BC,以 D ,E 为两个顶点作位置不同的三角形,使所 作的三角形与△ABC 全等,这样的三角形最多可以画出_____个.
(第图1163题)
17.如图, AD,A′D′ 分别是锐角三角形 ABC 和锐角三角形 A′B′C′ 中 BC, B′C′ 边上的高, = 且 AB A= ′B′,AD A′D′ .若使 △ABC ≌△A′B′C′ ,请你补充条件___________.(填
第十一章全等三角形单元测试卷及答案
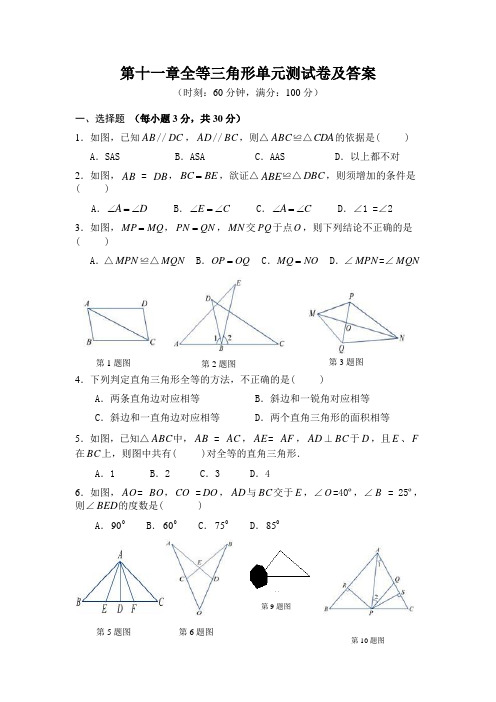
第十一章全等三角形单元测试卷及答案(时刻:60分钟,满分:100分)一、选择题 (每小题3分,共30分)1.如图,已知AB //DC ,AD //BC ,则△ABC ≌△CDA 的依据是( ) A .SAS B .ASA C .AAS D .以上都不对 2.如图,AB = DB ,BE BC =,欲证△ABE ≌△DBC ,则须增加的条件是( )A .D A ∠=∠B .C E ∠=∠ C .C A ∠=∠D .∠1 =∠2 3.如图,MQ MP =,QN PN =,MN 交PQ 于点O ,则下列结论不正确的是( )A .△MPN ≌△MQNB .OQ OP =C .NO MQ =D .∠MPN =∠MQN4.下列判定直角三角形全等的方法,不正确的是( )A .两条直角边对应相等B .斜边和一锐角对应相等C .斜边和一直角边对应相等D .两个直角三角形的面积相等 5.如图,已知△ABC 中,AB = AC ,AE = AF ,AD ⊥BC 于D ,且E 、F 在BC 上,则图中共有( )对全等的直角三角形. A .1 B .2 C .3 D .46.如图,AO = BO ,CO =DO ,AD 与BC 交于E ,∠O =40º,∠B = 25º,则∠BED 的度数是( )A .090B .060C .075D .085第9题图第10题图第1题图 第2题图 第3题图 第5题图第6题图7.在△ABC 和△DEF 中,下列各组条件中,不能判定两个三角形全等的是( )A .AB = DE ,∠B =∠E ,∠C =∠F B .AC =DF ,BC =DE ,∠C =∠DC .AB = EF ,∠A =∠E ,∠B =∠FD .∠A =∠F ,∠B =∠E ,AC = DE 8.下列说法中,错误的个数是( )(1)有两边与一角对应相等的两个三角形全等 (2)有两个角及一边对应相等的两个三角形全等 (3)有三个角对应相等的两个三角形全等 (4)有三边对应相等的两个三角形全等A .4B . 3C .2D .1 9.如图,亮亮书上的三角形被墨迹污染了一部分,专门快他就依照所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( ) A. SSS B. SAS C. AAS D. ASA 10.如图,△ABC 中,∠1 =∠2,PR = PS ,PR ⊥AB 于R ,PS ⊥AC 于S ,则下列三个结论:①AS = AR ;②QP //AR ;③△BRP ≌△QSP ,( ) A .全部正确 B .①和②正确 C .仅①正确 D .①和③正确 二、填空题(每小题2分,共16分)11.如图,△ABC ≌△DBC ,且∠A 和∠D ,∠ABC 和∠DBC 是对应角,除公共边外,其余对应边是 .12.已知△ABC 中,∠A =050,∠ABC 、∠ACB 的平分线交于点O ,则∠BOC 的度数为 .13.如图, 已知∠1=∠2 , ∠3=∠4 , 要证BD =CD , 需先证△AEB ≌△AEC , 依照是_________,再证△BDE ≌△______.14.如图,∠1=∠2,由AAS 判定△ABD ≌△ACD ,则需添加的条件是_________.A BCD12第14题图第13题图4321EDBA第11题图O DCB AC B A E D第15题图 第16题图 15.如图,AD =AC ,BD =BC ,O 为AB 上一点,那么,图中共有 ____ 对全等三角形.16.如图,△ABC ≌△ADE ,则AB = ,∠E = . 若∠BAE =120°,∠BAD =40°,则∠BAC = .17.若△ABC ≌△DEF ,△ABC 的周长为12,若AB =3,EF =4,则AC = . 18.△ABC 中,∠C =90°,AD 平分∠BAC 交BC 于点D ,且CD =4cm ,则点D 到AB 的距离是____ __.三、解答题(19-22题每小题6分,23-25题每小题10分,共计54分) 19. 已知:如图,在直线MN 上求作一点P ,使点P 到 ∠AOB 两边的距离相等(不写作法,保留作图痕迹)20. 如图,AB =DC ,AC =DB ,求证:∠A =∠D .21.如图, AB =CD ,CE =DF ,AE =BF ,求证:AE ∥DF .22.如图,,DBE ABC ∆≅∆ AB 与DB ,AC 与DE 是对应边,已知 30,43=∠=∠A B ,求BED ∠的度数.解:∵∠A +∠B +∠ACB =0180( ),30,43=∠=∠A B ( ), ∴∠ACB = .F D CB DAO N MBA∵,∆( )≅ABC∆DBE∴∠BED=∠ACB= ( ) .23.如图,在△ABC和△DBC中,∠ACB =∠DBC = 90º,E是BC的中点,EF⊥AB于F,且AB = DE.(1)求证:BC =DB;(2)若DB= 8cm,求AC的长.24.在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;求证:CF=EB.25.如图,已知在△ABC中,BE、CF分别是AC、AB边上的高,在BE上截取BD = AC,在CF的延长线上截取CG = AB,连结AD、AG,则AG与AD 有何关系?试证明你的结论.八年级数学(上)第十一章单元测试题参考答案11. AB 和DB , AC 和DC ; 12. 0115 ; 13. ASA,△CDE ; 14. ∠B =∠C ; 15.3; 16. AD ,∠C ,080 ; 17. 5; 18. 4cm . 三、解答题(19-22题每小题6分,23-24每小题10分,共计54分) 19.(略)20.(略) 21.(略)22.三角形的内角和等于0180 ,已知,0107,已知,0107,等量代换 . 23.(1)证明:∵∠DEB +∠ABC = 90º,∠A +∠ABC = 090, ∴∠DEB =∠A ,又∵DE = BA ,∠DBE =∠BCA = 090, ∴△ACB ≌△EBD (AAS),则有BC = DB . (2)解:由△ACB ≌△EBD 得AC = EB ,∵E 是BC 的中点,∴EB =BC 21,∵DB = 8,BC = DB ,∴BC = 8,∴AC =EB = BC 21= 4cm .24.证明:(1)∵AD 平分∠BAC ,DE ⊥AB ,DC ⊥AC ,∴DC DE =,又∵BD DF =, ∴ Rt △CDF ≌Rt △EDB (HL), ∴CF =EB .25.解:AG = AD,AG⊥AD.证明:∵CF⊥AB,BE⊥AC∴∠ACG+∠CAB =090,∠ABE+∠CAB = 90º,∴∠ACG=∠ABE,又∵AC =BD,CG = AB,∴△ACG≌△DBA(SAS),则AG =AD,∠G=∠BAD,∵∠G+∠GAB= 090,∴∠BAD+∠GAB = 90º,即∠GAD = 090,∴AG⊥AD.。
八(上)数学 图形的全等 测试(A卷)

图形的全等测试(A卷)一、选择题(每题2分,共24分)1.下列说法中正确的是( ) A.两个周长相等的长方形全等B.两个周长相等的三角形全等C.两个面积相等的长方形全等D.两个周长相等的圆全等2.如图,与正方形图案属于全等的图案是( )3.如图,∆ABC≌∆ADE,BC的延长线交DE于F,∠B=30o,∠AED=110o, ∠DAC=l0o,则∠ADFB的度数为( ) A.40o B.50o C.55o D.60o4.下列判断中错误的是( )A.有两角和一边对应相等的两个三角形全等B.有两边和一角对应相等的两个三角形全等C.有两边和其中一边上的中线对应相等的两个三角形全等D.有一边对应相等的两个等边三角形全等5.下列结论中错误的是( ) A.全等三角形对应边上的高相等B.全等三角形对应边上的中线相等C.两个直角三角形中,斜边和一个锐角对应相等,则这两个三角形全等D.两个直角三角形中,两个锐角相等,则这两个三角形全等6.下列说法:①三角对应相等的两个三角形全等;②三边对应相等的两个三角形全等;③两角与一边对应相等的两个三角形全等;④两边与一角对应相等的两个三角形全等.其中正确的有( ) A.1个B.2个C.3个D.4个7.∆ABC和∆A'B'C'中,AB= A'B',∠A=∠A',若证△ABC≌△A'B'C'还要从下列条件中补选一个,错误的选法是( ) A.∠B=∠B' B.∠C=∠C' C.BC=B'C' D.AC=A'C'8.如图,点P是∠BAC的平分线AD上一点,PE AC于点E.已知PE=3,则点P 到AB的距离是( ) A.3 B.4 C.5 D.69.如图,△ABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以画出( ) A.2个B.4个C.6个D.8个10.如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下列结论中错误的是( ) A.△ABC≌△DEF B.∠DEF=90o C.AC=DF D.EC=CF11.如图,将两根钢条AA'、BB'的中点O连在一起,使AA'、BB'可以绕着点O自由转动,就做成了一个测量工件,则A'B'的长等于内槽宽AB,那么判定△AOB≌△A'OB'的理由是( ) A.边角边B.角边角C.边边边D.角角边12.如图,D为等边△ABC内一点,DB=DA,BF=AB,∠1=∠2,则∠BFD的度数为( ) A.15o B.20o C.30o D.45o二、填空题(每题2分,共20分)13.如图,△ABC≌△CDO,∠A与∠C是对应角,那么∠1=_______,AB=_______.14.如图,若△OAD≌△OBC,且∠O=65o,∠C=20o,则∠OAD=___________.15.如图,△ABD≌△ACE,如果AD=7 cm,AB=15 cm;则BE=__________cm.16.如图,已知AB//CD,∠ABC=∠CDA,则由“AAS”直接判定△_____≌△_____.17.如图,在△ABC中,AB=AC,AD是BC边上的中线,则∠BDA=_________.18.如图,AC、BD相交于点O,∠A=∠D,请你再补充一个条件,使得△AOB≌△DOC,你补充的条件是________________.19.如图,已知CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD交于点O,且AO平分∠BAC,那么图中全等三角形共有________对.20.如图,在△ABC中,BC=AC,∠C=90o,AD平分∠CAB,AB=10 cm,DE⊥AB,垂足为点E.那么△BDE的周长是_________cm.21.如图,在△ABC中,点D、E、F分别在AB、AC、BC上,DE//BC,EF//AB,且F 是BC的中点.若DE=6 cm,则CF=__________cm.22.如图,AD⊥BC于D,BE=AC,DE=DC,则∠ABC的度数为____________.三、解答题(共56分)23.(5分)如图,△ABC≌△DEC,∠ACB=80o,∠ACE=140o求∠BCD的度数.24.(6分)如图,点C、E、B、F在同一直线上,AC//DF,AC=DF,BF=CE, △ABC与△DEF全等吗?说明你的理由.25.(6分)在△ABC中,AB=CA,D是BC的中点,DE⊥AB,DF⊥AC,E、F分别是垂足.试说明AE=AF.26.(7分)如图,AB//DE,AB=DE,AF=DC,请问图中有哪几对全等三角形?并任选其中一对给予说明.27.(7分)如图,AB//DC,AD//BC.聪明的小老鼠哼哼和唧唧分别从B、D出发,沿垂直于AC的路径BE、DF去寻找奶酪.假设AC上堆满了奶酪,哼哼和唧唧的速度相同,它俩谁最先寻找到奶酪?为什么?28.(7分)如图,AB交CD于点0,AD、CB的延长线相交于点E,且OA=OC,AB=CD,你能说明∠A=∠C吗?点O在∠AEC的平分线上吗?29.(8分)已知D是BC边上的一点,且CD=AB,∠ADB=∠BAD,AE是△ABD中线,试说明AC=2AE30.(10分)已知在△ABC中,∠A=90o,AB=AC,D为BC的中点.(1)如图,E、F分别是AB、AC上的点,且BE=AF.试说明△DEF为等腰直角三角形.(2)若E、F分别为AB、CA延长线上的点,仍有BE=AF,在其他条件不变的情况下,△DEF是否仍为等腰直角三角形?说明你的理由.参考答案一、1.D 2.C 3.B 4.B 5.D 6.B 7.C 8.A 9.B 10.D 11.A 12.C二、13.∠DCD14.95o15.8 16.ABC CDA 17.90o18.AB=DC(或AO=DO或BO=CO) 19.4 20.1021.6 22.45o三、23.∠BCD=20o解析:由已知条件可得∠BCE=60o,∠ACB=∠DCE=80o,所以∠BCD=∠DCE-∠BCE=20o.24.△ABC与△DEF全等理由:因为AC//DF,所以∠C=∠F.因为BF=CE,所以CB=FE又AC=DF,根据有两边及其夹角对应相等的两个三角形全等,可以知道△ABC≌△DEF.25.解析:连结AD,可以说明△ADB≌△ADC,则∠BAD=∠CAD,即AD平分∠BAC,又可以得到△ADE≌△ADF,所以AE=AF.26.图中有3对全等三角形,分别为△ABF≌△DEC、△ABC≌△DEF、△BCF≌△EFC说明△ABF≌△DEC:因为AB//DE,所以∠A=∠D.又因为AB=DE,AF=DC,所以△ABF≌△DEC.27.同时找到奶酪理由:由“ASA”可知AACD≌△CAB,因此AB=CD.又由“AAS”可知△AB≌△CDF,因此BE=DF.哼哼和唧唧以相同的速度跑了相同的路程,因此它俩同时找到奶酪.28.连结OE,可以说明△ADO≌△CBO,则∠A=∠C、∠ABE=∠CDE,可以说明△ABE≌△CDE,则有BE=DE、BO=DO,又可以得到△EBO≌△EDO所以∠AEO=∠CEO,即点O在∠AEC的平分线上.29.如图,延长AE到点F,使EF=AE,连结DF.在△ABE与△FDE中,AE=FE,∠AEB=∠FED,BE=DE,所以△ABE≌△FDE,所以∠B=∠1.因为∠ADF= ∠ADB+∠1,∠ADC=∠BAD+∠B,∠ADB=∠BAD,所以∠ADF=∠ADC.因为AB=DF,AB=CD,所以DF=CD.在△ADF与△ADC中,AD=AD,∠ADF=∠ADC,DF=DC,所以△ADF≌△ADC,所以AF=AC,又因为AF=2AE,所以AC=2AE.30.(1)连结AD,因为AB=AC,∠BAC=90o,D为BC的中点,所以AD BC,BD=AD,所以∠B=∠DAC=45o.又BE=AF,所以△BDE≌△ADF,所以ED=FD、∠BDE=∠ADF,所以∠EDF=∠EDA+∠ADF=∠EDA+∠BDE≌∠BDA=90o,所以△DEF为等腰直角三角形.(2)△DEF为等腰直角三角形理由:若E.F分别是AB、CA延长线上的点,如图所示,连结AD.因为AB=AC,∠BAC=90o,D为BC的中点,所以AD=BD,AD BC,所以∠DAC=∠ABD=45o,所以∠DAF=∠DBE=135o.又AF=BE,所以△DAF≌△DBE.所以FD=ED、∠FDA=∠EDB,所以∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90o,所以△DEF仍为等腰直角三角形。
八年级数学上册《第十一章 三角形》单元检测卷及答案-人教版

八年级数学上册《第十一章 三角形》单元检测卷及答案-人教版学校:___________班级:___________姓名:___________考号:___________一、选择题:(本题共8小题,每小题5分,共40分.)1.若一个多边形的内角和等于720°,则这个多边形的边数是( )A .5B .6C .7D .82.用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,称为平面图形的镶嵌.在镶嵌图案里若基本图形只有一种,则称为单元镶嵌.下面基本图形不能进行单元镶嵌的是( )A .等边三角形B .正方形C .正五边形D .正六边形3.如图,已知l 1l 2,∠A =45°,∠2=100°,则∠1的度数为( )A .50°B .55°C .45°D .60°4.如图,在△ABC 中,∠C =70º,沿图中虚线截去∠C ,则∠1+∠2=( )A .360ºB .250ºC .180ºD .140º5.如图,在△ABC 中,AD 、AE 分别是边BC 上的中线与高,AE=4,△ABC 的面积为12,则CD 的长为( )A .2B .3C .4D .56.如图,在 ABC 中80BAC ∠=︒ , 60ABC ∠=︒ 若 BF 是 ABC 的高,与角平分线 AE 相交于点 O ,则 EOF ∠ 的度数为( )A.130°B.70°C.110°D.100°7.如图,△ABC的面积为8,AD为BC边上的中线,E为AD上任意一点,连接BE,CE,图中阴影部分的面积为()A.2 B.3 C.4 D.58.如图,在△ABC中,∠B=46°,∠ADE=40°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠C的大小是()A.46°B.66°C.54°D.80°二、填空题:(本题共5小题,每小题3分,共15分.)9.△ABC的两条边的长度分别为3和5,若第三条边为偶数,则△ABC的周长为. 10.如图,在△ABC中,AB=AD=DC,∠BAD=32°,则∠C= .11.如图,已知AD是 ABC的中线,AB=13cm,AC=5cm, ABD与 ACD的周长的差是.12.如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC、△ADF、△BEF的面积分别S、S1、S2,且S=36,则S1-S2= .13.如图,△ABC中,AC=BC,CE为△ABC的中线,BD为AC边上的高,BF平分∠CBD交CE于点G,连接AG交BD于点M,若∠AFG=53°,则∠GAB的度数为.三、解答题:(本题共5题,共45分)14.如图,BO,CO分别是∠ABC,∠ACB的平分线,它们相交于点O,过点O作EF∥BC交AB于E,交AC于F,若∠ABC=50°,∠ACB=60°,试求∠BOC度数.15.如图所示,DE⊥AB于E,DF⊥BC于D,∠AFD=155°,∠A=∠C,求∠EDF的度数.16.如图,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=80°,∠ABC=70°.求∠BAD,∠AOF.17.如图,在△ABC中,∠A=∠ABC,直线EF分别交AB、AC和CB的延长线于点D、E、F,过点B 作BP//AC交EF于点P.(1)若∠A =70°,∠F =25°,求∠BPD 的度数.(2)求证:∠F+∠FEC =2∠ABP.18.如图,在ABC 中,AE 是ABC 的高.(1)如图1,AD 是BAC ∠的平分线,若38B ∠=︒,62C ∠=︒求DAE ∠的度数.(2)如图2,延长AC 到点F ,CAE ∠和BCF ∠的平分线交于点G ,求G ∠的度数.参考答案:1.B 2.C 3.B 4.B 5.B 6.A 7.C 8.C9.12或1410.37o11.8cm12.613.45°14.解:∵BO 平分∠ABC ,CO 平分∠ACB∠ABC =50°,∠ACB =60°∴∠EBO =∠OBC = 12 ∠ABC =25°∠FCO =∠OCB = 12 ∠ACB =30°在△BOC 中,∠BOC =180°﹣∠OBC ﹣∠OCB =125°.15.解:∵DE ⊥AB ,DF ⊥BC ∴∠AED=90°,∠FDC=90° ∵∠AFD=∠FDC+∠C=155°∴∠C=155°﹣∠FDC=155°﹣90°=65°∵∠A=∠C∴∠A=65°∵∠A+∠AED+∠EDF+∠AFD=360°∴∠EDF=360°﹣65°﹣90°﹣155°=50°.16.解:∵AD 是高,∠ABC=70°∴∠BAD=90°﹣70°=20° ∵AE 、BF 是角平分线,∠BAC=80°,∠ABC=70°∴∠ABO=35°,∠BAO=40°∴∠AOF=∠ABO+∠BAO=75°17.(1)解:∵∠A =∠ABC =70°,BP//AC∴∠ABP =∠A =70°=∠ABC∴∠PBF =180°﹣2×70°=40°∴∠BPD =∠F+∠PBF =25°+40°=65°(2)证明:∵∠F+∠FEC =180°﹣∠C ,∠A+∠ABC =180°﹣∠C ∴∠F+∠FEC=∠A+∠ABC =2∠A =2∠ABP.18.(1)解:在ABC 中∵38B ∠=︒ 62C ∠=︒ 180BAC B C ∠+∠+∠=︒ ∴180386280BAC ∠=︒-︒-︒=︒∵AD 是BAC ∠的平分线 ∴1402CAD BAD BAC ∠==∠=︒ ∵AE 是ABC 的高∴90AEC ∠=︒∵62C ∠=︒∴906228CAE ∠=︒-︒=︒∴402812DAE CAD CAE ∠=∠-∠=︒-︒=︒.∴DAE ∠的度数为12︒.(2)解:∵CAE ∠和BCF ∠的平分线交于点G ∴2CAE CAG ∠=∠ 2FCB FCG ∠=∠∵CAE FCB AEC ∠=∠-∠ CAG FCG G ∠=∠-∠ ∴()2222FCG AEC FCG G FCG G ∠-∠=∠-∠=∠-∠ ∴2AEC G ∠=∠∵AE 是ABC 的高∴90AEC ∠=︒∴45G ∠=︒.∴G ∠的度数为45︒。
(word版)第十一章全等三角形测试题含答案,文档

第十一章全等三角形测试题〔总分值100分,时间120分钟〕一、选择题〔每题3分,共30分〕1、在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100°,那么在△ABC中与这100°角对应相等的角是〔〕A.∠AB.∠BC.∠CD.∠B或∠C2、如图1,在上求一点,使它到,的距离相等,那么P点是〔〕CD P OAOBA.线段的中点 B.与的中垂线的交点CD OA OBC.OA与CD的中垂线的交点D.CD与∠AOB的平分线的交点A D CACD FO BED A B B C图1图2图33、如图2所示,△ABD≌△CDB,下面四个结论中,不正确的选项是〔〕A.△和△的面积相等 B.△和△的周长相等ABD CDB ABD CDBC.∠+∠=∠+∠CBDD.∥,且=A ABDCADBCADBC4、如图3,AB =DC ,AD =BC ,E ,F 在DB 上两点且BF =DE ,假设∠AEB =120°,∠ADB =30°,那么∠BCF等于〔 〕° °° °5、如果两个三角形中两条边和其中一边上的高对应相等,那么这两个三角形的第三条边所对的角的关系是〔 〕A.相等B.不相等C.互余或相等D.互补或相等6、如图4,AB ⊥BC ,BE ⊥AC ,∠1=∠2,AD =AB ,那么〔 〕A.∠1=∠EFDB.BE =ECC.BF =DF =CDD.FD ∥BCACAEDEDF1 FBDA2BBCC图4图5E图67、如图5所示,BE ⊥AC 于点D ,且AD =CD ,BD =ED ,假设∠ABC =54°,那么∠E =〔 〕° ° °°第1页共5页8、如图6,在△ABC中,AD平分∠BAC,过B作BE⊥AD于E,过E作EF∥AC交AB于F,那么〔〕A.AF=2BFB. AF=BFC. AF>BFD. AF<BF9、如图 7所示,亮亮书上的三角形被墨迹污染了一局部,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是〔〕A.SSSB. SASC. AASD. ASA图7 图8 图910、将一张长方形纸片按如图8所示的方式折叠,BC,BD为折痕,那么∠CBD的度数为〔〕A.60° B.75° C.90° D.95°二、填空题〔每题3分,共24分〕11、〔2021河南〕如图9,在△ABC中,AB=AC,CD平分∠ACB,∠A=36°,那么∠BDC的度数为..12、如图10,在△ABC中,AB=AC,BE、CF是中线,那么由可得△AFC≌△AEB.A FDCF EOA BB CE图10图11图1213、如图11,=,=,为中点,过O 点作直线与、延长线交于、,假设∠=60°,ABCDADBCO BD DABC EF ADB=10,那么∠=,=.EO DBC FO14、Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,假设BC=32,且BD∶CD=9∶7,那么D到AB边的距离为___.15、:△ABC≌△A′B′C′,∠A=∠A′,∠B=∠B′,∠C=70°,AB=15cm,那么∠C′=_________,A′B′=__________。
七年级数学第十一章图形的全等单元测验试题及答案

七年级数学第十一章图形的全等单元测验试题及答案第十一章图形的全等单元检验(2)班级 __ 姓名效果________一、选择题:1、将两个全等的有一个角为30的直角三角形拼成右图,其中两条长直角边在同一条直线上,那么图中等腰三角形的个数是( )A、4B、3C、2D、1(第1题) (第2题) (第3题)2、如图,△ABD≌△DCA,A和D,C和B区分是对应点,假设AB=7㎝,AD=6㎝,BD=4㎝,那么DC的长为( )A、6㎝B、7㎝C、4㎝D、不确定3、如图,AB∥CD,CE∥BF,A、E、F、D在不时线上,BC与AD交于点O,那么图中有全等三角形的对数为( )A、2B、3C、4D、54、△ABC≌△ACB, B与C,C与B是对应角,那么以下说法中①BC=CB② C的平分线与B的平分线相等;③AC上的高与AB边上的高相等;④AB上的中线与AB边上的中线相等,其中正确的说法的个数 ( )A、1个B、2个C、3个D、4个5、如图,△ACF≌△BDE,且点E与点F,点A与点B是对应点,以下结论错误的选项是( )A、AB=CDB、AF∥BEC、ED、C F∥DE6、如图,△ACE≌△DFB,以下结论中正确的个数是( )①AC=DB , ②AB=DC , ③2, ④AE∥DF,⑤S△ACE=S△DFB , ⑥BC=AE , ⑦BF∥ECA、4个B、5个C、6个D、7个二、填空题:7、如图,△ABC中,C=90,AC=BD ,AD平分CAB交BC于D,DEAB,垂足为点E,AB=12㎝,DC=5cm,那么△DEB的周长为。
8、在△ABC中,ADBC,CEAB,垂足区分为D、E,AD、CE交于点H,请你添加一个适当的条件:使△AEH≌△CEB。
9、如图,在△ABC中,B=50,C=20,假定以A为定点,顺时针旋转失掉△ACB,当点C与点B、点A在同不时线上时,AB边旋转了度。
10、AB=AC,E、F区分是AB、AC的中点,BF与CE相交于O点,图中全等三角形共有对。
新人教版八年级数学第11章全等三角形单元试卷及参考答案1

新人教版八年级数学第十一章考试M A1 3 4 ; NB1.如图:△ABC 中,∠C=90°,AC=BC ,AD 平分∠CAB 交BC 于D ,DE ⊥AB 于E ,且AB=6㎝,则△DEB 的周长是( )A :6㎝ B :4㎝ C :10㎝ D :以上都不对2. △ABC ≌△DEF ,且△ABC 的周长为12,若AB =3,EF =4,则AC = . 3.(7分)已知:如图,在直线MN 上求作一点P ,使点P 到 ∠AOB 两边的距离相(要求写出作法,并保留作图痕迹,写出结论)4.(8分)如图,已知: BE ⊥CD ,BE =DE ,BC =DA ,求证:△BEC ≌△DAE 5.(8分)已知:如图,A 、C 、F 、D 在同一直线上,AF =D C ,AB =DE ,BC =EF ,求证:△ABC ≌△DEF . 5 6 7 6.(8分)如图:△ABC ,D ,E 在BC 上,且AD=AE ,BD=CE ,∠ADE=∠AED ,求证:AB=AC 7.(6+2分)如图,AB DE ⊥于E ,AC DF ⊥于F ,若CD BD =、CF BE =,(1)求证:AD 平分BAC ∠;(2)直接写出AC AB +与AE 之间的等量..关系。
8.本题10分,已知:如图,CE ⊥AB ,BF ⊥AC ,CE 与BF 相交于D ,且BD =CD.!求证:D 点在∠BAC的平分线上.B C D E F( A F E D C B A BD F A 】A B C D E A B C D E F899.*10.如图,在△ABC中,∠BAC=90°,AB=AC,若MN是经过点A的直线,BD⊥MN 于D,CE⊥MN于E,(1)求证:BD=AE.(2)若将MN绕点A旋转,使MN与BC相交于点O,其他条件都不变,BD与AE边相等吗为什么(3)BD、CE与DE有何关系10.(8分)已知,如图A、F、C、D四点在一直线上,AF=CD,AB//DE,且AB=DE,求证:(1)△ABC≌△DEF (2)∠CBF=∠FEC101120、(8分)如图所示,四边形ABCD中AB=AD,AC平分∠BCD,AE⊥BC,AF⊥CD,图中有无和△ABE 全等的三角形请说明理由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十一章图形的全等测试(A卷)
一、选择题(每题2分,共24分)
1.下列说法中正确的是( ) A.两个周长相等的长方形全等B.两个周长相等的三角形全等
C.两个面积相等的长方形全等D.两个周长相等的圆全等
2.如图,与正方形图案属于全等的图案是( )
3.如图,∆ABC≌∆ADE,BC的延长线交DE于F,∠B=30o,∠AED=110o, ∠DAC=l0o,则∠ADFB的度数为( ) A.40o B.50o C.55o D.60o
4.下列判断中错误的是( )
A.有两角和一边对应相等的两个三角形全等
B.有两边和一角对应相等的两个三角形全等
C.有两边和其中一边上的中线对应相等的两个三角形全等
D.有一边对应相等的两个等边三角形全等
5.下列结论中错误的是( ) A.全等三角形对应边上的高相等B.全等三角形对应边上的中线相等
C.两个直角三角形中,斜边和一个锐角对应相等,则这两个三角形全等
D.两个直角三角形中,两个锐角相等,则这两个三角形全等
6.下列说法:①三角对应相等的两个三角形全等;②三边对应相等的两个三角形全等;
③两角与一边对应相等的两个三角形全等;④两边与一角对应相等的两个三角形全
等.其中正确的有( ) A.1个B.2个C.3个D.4个
7.∆ABC和∆A'B'C'中,AB= A'B',∠A=∠A',若证△ABC≌△A'B'C'还要从下列条件中补选一个,错误的选法是( ) A.∠B=∠B' B.∠C=∠C' C.BC=B'C' D.AC=A'C'
8.如图,点P是∠BAC的平分线AD上一点,PE AC于点E.已知PE=3,则点P到AB的距离是( )
A.3 B.4 C.5 D.6
9.如图,△ABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以画出( ) A.2个B.4个C.6个D.8个
10.如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下列结论中错误的是
( ) A.△ABC≌△DEF B.∠DEF=90o C.AC=DF D.EC=CF
11.如图,将两根钢条AA'、BB'的中点O连在一起,使AA'、BB'可以绕着点O自由转动,就做成了一个测量工件,则A'B'的长等于内槽宽AB,那么判定△AOB≌△A'OB'的理由是( )
A.边角边B.角边角C.边边边D.角角边
12.如图,D为等边△ABC内一点,DB=DA,BF=AB,∠1=∠2,则∠BFD的度数为( ) A.15o B.20o C.30o D.45o
二、填空题(每题2分,共20分)
13.如图,△ABC≌△CDO,∠A与∠C是对应角,那么∠1=_______,AB=_______.
14.如图,若△OAD≌△OBC,且∠O=65o,∠C=20o,则∠OAD=___________.
15.如图,△ABD≌△ACE,如果AD=7 cm,AB=15 cm;则BE=__________cm.16.如图,已知AB//CD,∠ABC=∠CDA,则由“AAS”直接判定△_____≌△_____.17.如图,在△ABC中,AB=AC,AD是BC边上的中线,则∠BDA=_________.
18.如图,AC、BD相交于点O,∠A=∠D,请你再补充一个条件,使得△AOB≌△DOC,你补充的条件是________________.
19.如图,已知CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD交于点O,且AO平分∠BAC,那么图中全等三角形共有________对.
20.如图,在△ABC中,BC=AC,∠C=90o,AD平分∠CAB,AB=10 cm,DE⊥AB,垂足为点E.那么△BDE的周长是_________cm.
21.如图,在△ABC中,点D、E、F分别在AB、AC、BC上,DE//BC,EF//AB,且F 是BC的中点.若DE=6 cm,则CF=__________cm.
22.如图,AD⊥BC于D,BE=AC,DE=DC,则∠ABC的度数为____________.
三、解答题(共56分)
23.(5分)如图,△ABC≌△DEC,∠ACB=80o,∠ACE=140o求∠BCD的度数.
24.(6分)如图,点C、E、B、F在同一直线上,AC//DF,AC=DF,BF=CE, △ABC与△DEF全等吗?说明你的理由.
25.(6分)在△ABC中,AB=CA,D是BC的中点,DE⊥AB,DF⊥AC,E、F分别是垂足.试说明AE=AF.
26.(7分)如图,AB//DE,AB=DE,AF=DC,请问图中有哪几对
全等三角形?并任选其中一对给予说明.
27.(7分)如图,AB//DC,AD//BC.聪明的小老鼠哼哼和唧唧分别从B、D出发,沿垂直于AC的路径BE、DF去寻找奶酪.假设AC上堆满了奶酪,
哼哼和唧唧的速度相同,它俩谁最先寻找到奶酪?为什么?
28.(7分)如图,AB交CD于点0,AD、CB的延长线相交于点E,且OA=OC,AB=CD,你能说明∠A=∠C吗?点O在∠AEC的平分线上吗?
29.(8分)已知D是BC边上的一点,且CD=AB,∠ADB=∠BAD,AE是△ABD中线,
试说明AC=2AE
30.(10分)已知在△ABC中,∠A=90o,AB=AC,D为BC的中点.
(1)如图,E、F分别是AB、AC上的点,且BE=AF.试说明△DEF为等腰直角三
角形.
(2)若E、F分别为AB、CA延长线上的点,仍有BE=AF,在其他条件不变的情况
下,△DEF是否仍为等腰直角三角形?说明你的理由.
参考答案
一、1.D 2.C 3.B 4.B 5.D 6.B 7.C 8.A 9.B 10.D 11.A 12.C
二、13.∠DCD
14.95o15.8 16.ABC CDA17.90o
18.AB=DC(或AO=DO或BO=CO) 19.4 20.10
21.6 22.45o
三、23.∠BCD=20o解析:由已知条件可得∠BCE=60o,∠ACB=∠DCE=80o,所以
∠BCD=∠DCE-∠BCE=20o.
24.△ABC与△DEF全等理由:因为AC//DF,所以∠C=∠F.因为BF=CE,所以CB=FE又AC=DF,根据有两边及其夹角对应相等的两个三角形全等,
可以知道△ABC≌△DEF.
25.解析:连结AD,可以说明△ADB≌△ADC,则∠BAD=∠CAD,即AD平分∠BAC,又可以得到△ADE≌△ADF,所以AE=AF.
26.图中有3对全等三角形,分别为△ABF≌△DEC、△ABC≌△DEF、△BCF≌△EFC说明△ABF≌△DEC:因为AB//DE,所以∠A=∠D.又因为AB=DE,AF=DC,所以△ABF≌△DEC.
27.同时找到奶酪理由:由“ASA”可知AACD≌△CAB,因此AB=CD.又由“AAS”
可知△AB≌△CDF,因此BE=DF.哼哼和唧唧以相同的速度跑了相同的路程,因此它俩同时找到奶酪.
28.连结OE,可以说明△ADO≌△CBO,则∠A=∠C、∠ABE=∠CDE,可以说明△ABE≌△CDE,则有BE=DE、BO=DO,又可以得到△EBO≌△EDO所以∠AEO=∠CEO,即点O在∠AEC的平分线上.
29.如图,延长AE到点F,使EF=AE,连结DF.在△ABE与△FDE中,AE=FE,∠AEB=∠FED,BE=DE,所以△ABE≌△FDE,所以∠B=∠1.因为∠ADF= ∠ADB+∠1,∠ADC=∠BAD+∠B,∠ADB=∠BAD,所以∠ADF=∠ADC.因为AB=DF,AB=CD,所以DF=CD.在△ADF与△ADC中,AD=AD,
∠ADF=∠ADC,DF=DC,所以△ADF≌△ADC,所以AF=AC,又因为
AF=2AE,所以AC=2AE.
30.(1)连结AD,因为AB=AC,∠BAC=90o,D为BC的中点,所以AD⊥BC,BD=AD,所以∠B=∠DAC=45o.又BE=AF,所以△BDE≌△ADF,所以ED=FD、
∠BDE=∠ADF,所以∠EDF=∠EDA+∠ADF=∠EDA+∠BDE≌∠BDA=90o,
所以△DEF为等腰直角三角形.
(2)△DEF为等腰直角三角形理由:若E.F分别是AB、CA延长线上的点,如图
所示,连结AD.因为AB=AC,∠BAC=90o,D为BC的中点,所以AD=BD,AD⊥BC,所以∠DAC=∠ABD=45o,所以∠DAF=∠DBE=135o.又AF=BE,
所以△DAF≌△DBE.所以FD=ED、∠FDA=∠EDB,所以
∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90o,所以△DEF仍为等腰直
角三角形。
