Spin glass behaviour on random lattices
Quantum spin liquid emerging in 2D correlated Dirac fermions

Mean Field Critical Behaviour for a Fully Frustrated Blume-Emmery-Griffiths Model

Mean Field critical behaviour for a Fully Frustrated Blume-Emery-Griffiths Model
Francesco di Liberto∗ and Fulvio Peruggi
2
Mean field analysis
We will study the model defined by the Hamiltonian (1) by evaluating its free energy in a mean field approximation. For convenience we will set κ = K/J At each site i of the lattice we have to consider the variables Si = ±1 and ni = 0, 1. For notation purposes it is useful to introduce a new 4-state variable ν i such that {ν i } = {ni } ⊗ {Si } = {1 ↑, 1 ↓, 0 ↑, 0 ↓} ≡ {1, 2, 3, 4}. We can express the old variables in terms of this new variable by means of the relations: ni Si = δ ν i ,1 − δ ν i ,2 and ni = δ ν i ,1 + δ ν i ,2 . Moreover, using the index r to denote one of the four states of ν i , we can define pi r = δ ν i ,r , i.e. the probability that the site i will be found in the state ν i = r . Here the angular brackets represent, as usual, the average done with the Hamiltonian of Eq. (1). To obtain the free energy we evaluate first the internal energy of the system, which is the expectation value of our Hamiltonian: − βU ≡ −β H = −β Hij − β Hi = (3) δ ν i ,1 + δ ν i ,2 .
一些物理里面名词的中文对照(大部分是材料领域的)

Abelian group 阿贝尔群,又称Abel群ablation 烧蚀abnormal dispersion 反常色散Abrikosov vortex lattice 阿布里科索夫涡旋线格子Abrikocov vortex state 阿布里科索夫涡旋态absorber 吸收体absorption spectroscopy 吸收光谱abundance 丰度acceptor doping 受主掺杂acceptor impurity 受主杂质accumulation layer 累积层achromatic phase matching 消色差相位匹配achromatic wave plate 消色差波片achromatism 消色差[性]ac Josephson effect 交流约瑟夫森效应,又称交流Josephson效应acoustic compliance 声顺acoustic ohm 声欧[姆]acoustic stiffness 声劲[度]acoustic-optic tensor 声光系数张量acousto-optic effect 声光效应acousto-optic Q-switch 声光Q-开关acousto-optic signal processor 声光信号处理器acousto-optical tunable filter 声光可调滤波器actinide element 锕系元素activated tunneling 激活隧穿active device 有源器件active region 激活区addressing electrode 寻址电极adiabatic theorem,绝热定理adiabatic transformation 绝热变换adiabatic transport,绝热输运adiabaton 浸渐子,绝热子advection 平流aerodynamic sound 空气动力声aersol 气溶胶affinity potential 亲和势aggregate 聚集体aggregation 聚集Aharonov-Bohm (AB) effect AB效应,又称Aharonov-Bohm (AB) 效应Aharonov-Bohm (AB) flux AB磁通,又称Aharonov-Bohm (AB)磁通allowed state 容许态alpha decay ( -decay) 衰变alpha particle ( -particle) 粒子Altshular-Aronov-Spivak (AAS) effect AAS效应,又称Altshular-Aronov-Spivak效应amplification without inversion 无反转放大amplitude limiting 限幅amplitude transformer 变幅杆Andreev reflection 安德列也夫反射,又称Andreev反射Andreev mirror 安德列也夫镜[子],又称Andreev镜[子] Andreev scattering 安德列也夫散射,又称Andreev散射angular resolved photoemission spectroscopy 角分辨光电子谱[学] anisotropic confinement 各向异性限域anisotropic scatterer, 各向异性散射体anisotropy energy 各向异性能anomalon 反常子anomalous power laws 反常幂[次]率anomalous proximity effect,反常临近效应anomaly 反常antidot 同quantum antidot 反量子点antidodal point 腹点antigravity 反引力antihyperon 反超子anti-localization, 反局域化antimeson 反介子anti-exclusive principle 反不相容原理antiferromagnetic interaction 反铁磁相互作用antiferromagnetic semiconductor 反铁磁半导体anti-Stokes scattering 反斯托克斯散射anti-time ordered function, 反时序函数anyon 任意子aphelion 近日点, 远核点areal density 面密度armchair nanotube 扶手椅型纳米管arrayed waveguide gratings 阵列波导光栅artificial atom,人[工]构[造]原子artificial barrier 人工势垒artificial elment 人造元素atom laser 原子凝射器atom optics 原子光学atom trapping 原子陷俘,原子捕获atom waveguide 原子波导atomic clock原子钟atomic diffraction 原子衍射atomic fountain 原子喷泉atomic form factor 原子形状因子atomic time 原子时attenuation 衰减attosecond X-ray pulse 阿秒X射线脉冲Auger process 俄歇过程,又称Auger过程avalanche counter 雪崩计数器avalanche effect 雪崩效应avalanche photodiodes,apd 雪崩光电二极管azimuth 方位角back-action evasion 非干扰[测量]background radiation 本底辐射,背景辐射background temperature 本底温度, 背景温度balanced homodyne detection平衡零拍探测ballistic aggregate 弹道聚集体ballistic aggregation 弹道聚集ballistic electron injection 弹道电子注入ballistic transport弹道输运ballistics 弹道学band bending 带弯曲band index 带指标band of rotation-vibration 振转[谱]带band offset 带阶band repulsion 带排斥band theory 能带论bar 巴(压强单位),杆Barkhausen noise 巴克豪森噪声,又称Barkhausen噪声barn 巴恩(截面单位,10-24厘米2)barrier 势垒barrier curvature 势垒曲率barrier height 势垒高度barrier state 势垒态barrier tunneling 势垒隧穿base-centered orthorhombic lattice 底心正交格[子] base line 基线base material 基质base metal 碱金属basis vector 基矢beam 束,梁beam dump 束流捕集器beam focusing 束流聚焦behaviour 行为,性能Bell inequality贝尔不等式,又称Bell不等式bend resistance,弯曲电阻bent crystal 弯晶Berry phase 贝里相位,又称Berry相位βdecay β衰变βradioactivity β放射性βray β射线βspectum β谱βstability line β稳定线bevatron 吉伏质子加速器(高能质子同步稳相加速器)bicritical point 双临界点bicrystal junction 双晶结big bang model 大爆炸模型binary diffractive optical element 二元衍射光学元件bioastrophysics 天体生物物理学biochip 生物芯片bipolar junction transistor 双极[结]晶体管bit rate 比特率blackness 黑度blaze line 闪耀角bleaching effect 漂白效应blob 团迹,链滴Bloch electron 布洛赫电子,又称Bloch电子Bloch frequency,布洛赫频率,又称Bloch频率Bloch oscillation,布洛赫振荡,又称Bloch振荡Bloch theorem 布洛赫定理,又称Bloch定理blockade 阻塞Blonder-Tinkham-Klapwijk [BTK] model BTK模型body-centered cubic lattice 体心立方格[子]body-centered orthorhombic lattice 体心正交格[子]Bogoliubov [-de Gennes] equations 博戈留波夫[-得简斯]方程,又称Bogoliubov [-de Gennes]方程Boltzmann distribution 玻尔兹曼分布Boltzmann transport equation,玻尔兹曼输运方程bond-angle order 键角有序bond-orientational order 键取向有序bond polarizability 键极化性bond valence 键价boojum 布经(超流氦3中的取向织构)bosonization of field operators 场算符的波色化Bragg peak 布拉格峰,又称Bragg峰Bragg plane 布拉格平面,又称Bragg平面Bragg reflection 布拉格反射,又称Bragg 反射Bragg reflectors 布拉格反射器,又称Bragg 反射器Bragg waveguide 布拉格波导,又称Bragg 波导break junction 断裂结breathing mode呼吸模breeder 增殖反应堆breakup reaction 崩裂反应bright state 亮态brittleness 脆性buffer amplifier 缓冲放大器buffer gas 缓冲气体buffer layer, 缓冲层burn-up 燃耗Büttiker formula, 比特克公式,又称Büttiker公式buzzer 蜂鸣器C-15 structure C-15结构C[a]esium clock 铯钟calorie 卡【洛里】candle 烛光candescence 白热,又称白炽canonical commutation relation 正则对易关系canonical variable 正则变量cantact angle 接触角canted spin order倾斜自旋有序cantilever 悬臂(原子力显微镜中的)canthotaxie眼角[式]排列(另文说明)carbon cycle 碳循环(恒星内部的)carbon nanotube 碳纳米管carrier 载流子carrier concentration 载流子浓度carrier diffuse 载流子扩散carrier reservoir 载流子库Cartesian coordinates 笛卡儿坐标Cauchu-Schwarz inequality Cauchu-Schwarz不等式cavity dark state 腔暗态cavity dumping 腔倒空cavity quantum electrodynamics 腔量子电动力学cavity resonator [谐振]腔共振器14C dating 碳14测年celestial X-ray source 宇宙X 射线源center of inversion 反演中心center of moment 矩心central collision中心碰撞center-of-mass energy 质心系能量centrifuge 离心机centrifugal separation 离心分离ceramic 陶瓷chain folding 链折叠chain statistics 链统计学chalcogenide 硫属化物channel waveguide 沟道波导chaos synchronization 混沌同步chaotic communication 混沌通讯chaotic noise 混沌噪声characteristic impedance 特性阻抗characteristic curve 特征曲线charge-separated plasma 电荷分离等离子体(正负电荷在空间不同区域的等离子体) charge imbalance 电荷不平衡charge ordering 电荷有序charge parity effect,电荷宇称效应charge qubit 电荷量子比特(超导量子比特的一种)charge-phase qubit 电荷-相位量子比特(超导量子比特的一种)charge reservoir 电荷库charge stiffness 电荷劲度(衡量外场作用下电荷被自由加速的难易程度)charge-spin coupling电荷自旋耦合(用于自旋电子学)charge stripe phase 电荷条纹相charge-to-mass ratio 荷质比charge transfer insulator 电荷转移绝缘体charge transfer salt 电荷转移盐charge velocity 电荷速度(见于电荷-自旋分离现象)charging energy,充电能chemical shift 化学位移chiral liquid crystal 手征液晶chiral molecule手征分子,又称手性分子chiral symmetry broken 手征对称[性]破缺chirp啁啾chirped Gaussian pulse 啁啾高斯脉冲chirp filter 啁啾滤波器,又称线性调频滤波器,或色散延迟线chopper 斩波器circumlunar orbit 环月轨道circumsolar orbit 环日轨道circumterrestrial orbit 环地轨道cis-lunar space 月地空间clad 覆盖clamping 箝位classical fluid 经典液体clean limit [干]净极限cleaved coupling cavity 解理耦合腔cloning fidelity克隆保真度closed shell 满壳层,又称闭壳层,英文又称closure shellcluster state簇态CNO cycle 碳氮氧循环coalescence 聚合, 并合code 1,[代]码;2,密码;3,符号coding 编码codirectional coupling 同向耦合coefficient of correlation 关联系数coefficient of elasticity 弹性系数coexistence line 共存线(相图中的)coexisting phase 共存相coherence factor 相干因子coherence length,相干长度coherent atomic recoil 相干原子反冲coherent electron tunneling 相干电子隧道coherent peak 相干峰coherent photoassociation 相干光缔合coherent population oscillation相干布居振荡coherent population trapping相干布居囚禁coherent population transfer相干布居迁移coherent structure 拟序结构coherent terahertz waves相干太赫波coherent transient effects 相干暂态效应coherent trap 相干捕获cold finger 冷头cold fusion 冷聚变collective coordinate 集体坐标collective mode 集体模collective motion 集体运动collective pinning model 集体钉扎模型collinear phase matching 共线相位匹配colloid 胶体,胶质colloidal metal 胶体金属colored noise 色噪声colossal magnetoresistance [CMR] 庞磁电阻commensurate lattice 公度格子compact star 致密星compensated impurity 补偿杂质complementary metal oxide semiconductor [CMOS] 互补金属氧化物半导体complex 1,复合体;2,络合物complex analytical signal theory 复解析信号理论complex-conjugate pulses 复共轭脉冲compliance 1,柔度;2,顺度composite Fermion 复合费米子compression of ultrashort pulses 超短脉冲压缩compressor 压缩器,压机concurrence并发纠缠,又称量子并发condensate 凝聚体condensation energy 凝聚能condenser 冷凝器conductance fluctuation, 电导涨落conductance quantization 电导量子化conduction electron 传导电子confinement 1,约束(等离子);2,限域(凝聚态);3,禁闭(高能)congregating effect 聚集效应conjugate variable 共轭变量conservation of angular momentum 角动量守恒conservation of crystal momentum 晶体动量守恒conservative dislocation motion 保守位错运动(位错沿滑移面平行于Burgers矢量运动无净质量流)conservation of energy 能量守恒conservation law of flux 磁通守恒律conservation of momentum 动量守恒conservation of particle number粒子数守恒contact angle 接触角contact potential 接触势contact resistance 接触电阻continuation 延拓continuous group 连续群contour line 等值线contour map 等值线图contradirectional coupling反向耦合conventional unit cell 惯用单胞,简称单胞convergence factor 收敛因子conversion electron 内转换电子coolant moderator 载热减速剂cooperative diffusion 合作扩散Cooperon, 库珀子Cooper pair box 库珀对盒子coplanar waveguide 共面波导copolymer 共聚物core energy 芯能core nucleus 核芯[核]correlated spontaneous emission 关联自发发射correlation exponent 关联指数cosmic aerodynamics 宇宙气体动力学cosmic age 宇宙年龄cosmic constant 宇宙常量cosmic [microwave] background radiation [CMBR] 宇宙[微波]背景辐射cosmic microwave background 宇宙微波背景cosmic string 宇宙弦cosmochemistry 宇宙化学,天体化学cosmological nucleosynthesis 宇宙核合成cosmos 宇宙co-tunneling 共隧穿Couette flow 库埃特流Coulomb blockade 库仑阻塞Coulomb gap 库仑隙Coulomb interaction 库仑[相互]作用Coulomb island 库仑岛,又称单电子岛(single electron island)Coulomb potential 库仑势Coulomb repulsion 库仑斥力Coulomb staircase 库仑台阶counter telescope 计数器望远镜coupled-channels model 耦合道模型coupled mode theory 耦合模理论coupled waveguides,耦合波导coupled wells耦合阱coupling energy 耦合能coupling strength 耦合强度covalent bond 共价键creep wave蠕波,又称爬波critical assembly [核反应堆]临界装置critical density 临界密度critical dimension 临界维度cross-phase-modulation 交叉相位调制cross field 交叉场cross junction, 十字结crosstalk attenuation 串扰衰减crystal-field splitting 晶[体]场劈裂crystalline anisotropy晶态各向异性crystal symmetry class 晶体对称类cubic lattice 立方格子cuprate 铜氧化物curie 居里(非国际制放射性活度单位)current bias 电流偏置current operator 电流算符cutoff energy,截止能量cyclone 气旋cyclotron effective mass 回旋有效质量D/A converter 等于digital to analog converter 数模转换器damping radiation 阻尼辐射dark current 暗电流dark energy 暗能量dark state 暗态dark-state polariton 暗态光极化子date line 日界线dc Josephson effect 直流约瑟夫森效应,直流Josephson效应dc SQUID (superconducting quantum interference device) 直流超导量子干涉器Debye wave vector 德拜波矢decay heat 衰变热decay time,衰减时间deceleration 减速度decibel 分贝decoherence 退相干,又称消相干decoherence-free 无退相干,又称无消相干decontamination factor 去污因子decoupling epoch 退耦期decoy state 诱骗态deformation potential,形变势degeneracy collapse 简并塌缩degenerate pressure 简并压degenerate star 简并星de Gennes-Taupin length de Gennes-Taupin长度degree of order 有序度de Haas-Shubnikov effect de Haas-Shubnikov效应delay time,延迟时间demultiplexer 解复用器dendrite 1,枝晶;2,枝蔓;3,枝蔓体dense coding 密集编码dense wavelength division multiplexing 密集波分复用density correlation function,密度关联函数density distribution 密度分布density wave 密度波depairing 拆对dephasing length,退相位长度depinning 脱钉[扎]depleted Uranium 贫化铀deplation force 排空力(胶体物理用语)depletion layer 耗尽层descreening 去屏蔽deterministic equation 确定(论)的方程deuterium 氘, 即重氢deuterium oxide 重水dextrorotation 右旋diabatic approach 非绝热近似diagnostics 诊断学diagonal element 对角元diagonal matrix 对角矩阵diagonalization 对角化diamond structure 金刚石结构diblock copolymer 双嵌段共聚物dielectric response function 介电响应函数dielectric function,介电函数dielectric microcavity 介电[质]微腔dielectric reflector 介[电]质反射器differential conductance 微分电导differential input 差分输入differential rotation 较差自转(天文学用语)differential scanning calorimetry 差分扫描量热术diffraction-free beam 消衍射光束diffractive binary optics 衍射二元光学diffuseness [parameter] 弥散参数diffusion constant,扩散常数diffusion current 扩散电流diffusion region 扩散区diffusive transport,扩散输运digit 数字digital circuit 数字电路digital cross connect 数字交叉连接digit[al] to analog converter (DAC) 数模转换器digital micromirror device 数字微镜器件dilation 膨胀dilute phase 稀相dilation symmetry 伸缩对称dimensionless conductance 无量纲电导dimer 二聚体dimerization 二聚化dipole interaction 偶极相互作用dipole giant resonance 偶极巨共振Dirac braket 狄拉克括号Dirac picture 狄拉克绘景, 即相互作用绘景directed diffusion 定向扩散directional bond 定向键directional coupler 定向耦合器directional ordering 取向有序directional quantization 方向量子化direction of magnetization 磁化方向direct lattice 正格子,又称正点阵direct transition 直接跃迁dirty limit 脏极限dirty-metal regime,脏金属区discontinuity 1,不连续[性];2,突变[性] dislocation network 位错网络disordered alloy 无序合金disordered system 无序系统dispersion compensation 色散补偿dispersion-managed solitons 调控色散孤子dissipationless flow 无耗散流dissociation energy 离解能distillable entanglement 可萃取纠缠distinguishable states可区分态distributed Bragg reflector 分布布拉格反射器domain 1,畴;2,[定义]域;3,区域donor level 施主能级dopant 掺杂物doping 掺杂dosimetry 剂量学double-barrier tunneling,双势垒隧穿double exchange interaction 双交换相互作用double heterostructure DH 双异质结doublet state 双重态dressed atom 着衣原子,又称缀饰原子droplet model 小液滴模型Drude model,德鲁德模型duty ratio 占空比d-wave pairing d波配对dyad 并矢dynamical mass 动力学质量(08.02dynamic random access memory [DRAM] 动态随机存储器dynamic screening,动态屏蔽dynamically induced coherence 动态诱导相干dynamo theory 发动机理论dyne 达因early universe 早期宇宙eccentricity 偏心率eclipse 1,食;2,交食edge channel,边缘通道edge dislocation 刃[型]位错edge state,边缘态effective field theory 有效场理论effective Hamiltonian 有效哈密顿量effective mass approximation,有效质量近似Einstein-Podolsky-Rosen thought experiment EPR思想实验Einstein-Podolsky-Rosen effect EPR效应Einstein-Podolsky-Rosen pair EPR对Einstein-Podolsky-Rosen paradox EPR佯谬elastic compliance 弹性顺度elastic deformation 弹性形变electrical isolation 电绝缘electric breakdown 电击穿electric capacity 电容electric resistance 电阻electrical quadrupole moment 电四极矩electrochemical potential 电化学势electromagnetic absorption 电磁吸收electromagnetically induced absorption 电磁感生吸收electromagnetically induced transparency 电磁感生透明electromagnetic-environment effect,电磁环境效应electron backscattering pattern 电子背散射图样electron-beam lithography 电子束刻蚀electron configuration 电子组态electron density 电子密度electron-doped high temperature superconductor 电子掺杂的高温超导体electronegativity 电负性electron-electron interaction,电子-电子相互作用electron-hole pair 电子空穴对electron-hole recombination 电子-空穴复合electron hologram 电子全息术electron transition 电子跃迁electron pair 电子对electron pair tunneling 电子对隧穿electron-phonon coupling 电子声子耦合electron temperature,电子温度electron tunneling 电子隧穿electron waveguide,电子波导electron volt (eV) 电子伏electrorheological effect 电流变效应electrorheological fluid 电流变液Eliashberg equations Eliashberg方程Eliashberg theory of strong coupling Eliashberg强耦合理论elliptical orbit 椭圆轨道elliptic flow 椭圆流emittance 发射度empirical pseudopotential method 经验赝势方法empty lattice approximation 空晶格近似endohedral fullerene 内嵌原子富勒烯end-butt coupling 端面对接耦合energy relaxation length,能量弛豫长度energy transport velocity 能量传输速度ensemble average,系综平均entangled state 纠缠态entanglement 1,纠缠;2,纠缠度entanglement concentration 纠缠浓缩entanglement measure 纠缠度量entanglement monotone 单调纠缠量entanglement of formation 生成纠缠entanglement purification 纠缠纯化entanglement witness 纠缠见证entropy force 熵力envelope function,包络函数epithermal neutron 超热中子epoxy 环氧树脂erbium-doped fiber amplifier 掺饵光纤放大器error correction 纠错Esaki diode 江崎二极管evanescent state,衰逝态even-odd nucleus 偶奇核even parity 偶宇称evolution of inflation 暴涨演化Ewald construction Ewald作图法Ewald sphere Ewald球excess current 过剩电流excess neutron 过剩中子exchange-correlation hole 交换关联空穴exchange-correlation functional 交换关联泛函exchange hole 交换空穴exchange integral 交换积分excitation spectrum 激发谱excluded volume 排除体积exclusion of flux 磁通排斥exclusion principle 不相容原理exotic nucleus 奇特核expanding universe 膨胀宇宙extended [Brillouin] zone scheme 扩展[布里渊]区图式extraterrestrial life 地外生命extravehicular activity(EV A) [太空]舱外活动f-sum rule f求和规则face-centered orthorhombic lattice 面心正交格[子] face-on 正向facsimile 传真,英文简写为faxfacula 光斑Fahrenheit thermometer 华氏温度计faint object 暗天体fan diagram 扇形图F-center F中心Feno lineshape Feno线型Feno resonance Feno共振fan spin order 扇状自旋有序farad (F) 法拉(电容单位)Faraday depolarization 法拉第退偏振Faraday law of electrolysis 法拉第电解定律far-from-equilibrium system,远离平衡态系统far-side 背面(far-side of the moon, 月球背面)far-ultraviolet (FUV) 远紫外fast fission 快裂变fatigue crack 疲劳裂纹fatigue fracture 疲劳断裂fatigue strength 疲劳强度feed [source] 馈源feeder 馈线femto (f) 飞(=10-15)(01)femtosecond pulse shaping 飞秒脉冲成形Fermi age 费米[中子]年龄Fermi age-diffusion equation 费米年龄扩散方程Fermi arc 费米弧Fermi coupling constant 费米耦合常数Fermi energy 费米能量Fermi gas 费米气体Fermi golden rule 费米黄金定则Fermi liquid 费米液体Fermi liquid parameter 费米液体参数Fermi loop 费米环Fermi point 费米点Fermi transition费米跃迁Fermi vacuum 费米真空Fermi velocity 费米速度Fermi wavelength 费米波长Fermi wave vector,费米波矢Fermi’s golden rule费米黄金规则ferrielectric crystal 亚铁电晶体ferrimagnet 亚铁磁体ferroelectric 铁电体ferroelectric crystal 铁电晶体ferromagnet 铁磁体few-cycle pulse少周[期]脉冲few nucleon transfer 少[数]核子转移Feynman path,费曼路径Feynman path integral,费曼路径积分fiber cross connect 光纤交叉连接fiber grating 光纤光栅Fibonacci sequence 斐波那契序列fiducial confidence bar 置信棒fiducial point 基准点field intensity 场强field quantization 场量子化field quantum 场量子field strength 场强figure of merit,又称qualityfactor 品质因数filament 1,丝;2,丝极finite-amplitude wave 有限振幅波,又称大振幅波finite-difference method 有限差分方法finite element method 有限元法finite size effect 有限尺寸效应finite-size scaling 有限尺寸标度first approximation 一级近似first Brillouin zone 第一布里渊区first point of Aries 春分点,英文又称:vernal equinoxfirst point of Cancer 夏至点,英文又称:summer solsticefirst point of Capricornus 冬至点,英文又称:winter solsticefirst point of Libra 秋分点,英文又称:autumnal equinoxFiske steps 费斯克台阶,又称自感应台阶fissility 易裂变性fission 1,裂变;2,分裂fission isomer 裂变同质异能素fission nuclide 裂变核素fission reactor 裂变反应堆fission-spectrum neutron 裂变谱中子fission track dating 裂变径迹年代测定fitting curve 拟合曲线five-fold symmetry 5重对称fixed-range hopping 定程跳跃flash memory 闪速存储器,简称闪存flat spectrum 平谱flattening factor 扁率floating probe 浮置电极,又称浮置探针floating phase 浮置相Floquest theorem 弗洛开定理flow resistance 流阻fluctuating wall 涨落壁fluctuation 涨落(统计物理〕,又称起伏(声学〕fluence 注量fluorescence probe 荧光探剂flux,通量flux 1通量,又称流量;2,注量率;3,焊料;4 助熔剂flux bundle 磁通束flux flow amplifier (FFA) 磁通流放大器flux flow oscillator (FFO) 磁通流振荡器flux flow transistor(FFT)磁通流三极管,又称涡旋流三极管(vortex flow transistor) flux-line lattice 磁通线格子flux line 磁通线flux tube 磁流管flux quantum 磁通量子flux quantization 磁通量子化foam 泡沫focal point 焦点focal ratio 焦比focus 1,焦点;2,震源folding Brillouin zone 折叠布里渊区forbidden beta decay 禁戒b衰变forecast 预报forward bias 正向偏压four-Josephson junction logic (4JL) 四约瑟夫森结逻辑门Fourier analysis 傅里叶分析Fourier transform 傅里叶变换Fourier [transform] nuclear magnetic resonance 傅里叶[变换]核磁共振Fourier [transform] Raman spectroscopy 傅立叶[变换]拉曼谱学four probe method 四探针法four-terminal resistance,4端电阻fractional chain yield 相对链产额fractional cumulative yield 分积累产额fractional distillation 分馏fractional independent yield 分独立产额fractional statistics 分数统计法fragment 1,碎片;2,片段Franck-Condon principle弗兰克-康登原理free electron approximation 自由电子近似free electron gas 自由电子气体free energy 自由能free –free transition 自由-自由跃迁,又称自由态间跃迁freely falling body 自由落体free radical 自由基free spectral range 自由光谱范围freezing point 凝固点Frenkel exciton 弗仑克尔激子frequency conversion 频率转换Frequency division multiplexing 频分复用frequency jitter 频率抖动frequency multiplication 倍频friction 摩擦Friedel oscillation,Friedel振荡Friedel sum rule Friedel求和规则Frohlich interaction Frohlich相互作用front velocity波前速度frustrated magnet 窘组磁体fuel cell 燃料电池Fulde-Ferrell state Fulde-Ferrell态fullerene 富勒烯full moon 满月function 函数functional (1)泛函(2)功能(的)fundamental interaction 基本相互作用fundamental space-filling mode 基本空间填充模fuse (1)熔解(2)保险丝fused silica熔融石英fusion reactor 聚变[核反应]堆fuzzy information 模糊信息fussy mathematics 模糊数学gain-clamping 增益箝位gain efficiency 增益效率Galton plate 伽尔顿板-陈gamma(γ)伽马(地磁场强单位γ=nT)gamma rayγ射线gap 1,隙;2,能隙gap anisotropy 能隙各向异性gap parameter 能隙参数gaseous state 气态gate1,门;2,栅(极)gate voltage 门电压gauge symmetry 规范对称性gauss (G) 高斯(磁感应强度单位G=10-4T)Gaussian fluctuation 高斯涨落Gauss law 高斯定理Gauss surface 高斯面generalized Balmer formula 广义巴尔末公式generalized work 广义功general refractive index 广义折射率(量子信息)geomagnetic declination 地磁偏角geomagnetic inclination 地磁倾角geometrical structure factor 几何结构因子geometrization of gravitation 引力几何化German silver 德银g-factor g因子g-factor of electrons 电子的g因子g shift g移位ghost imaging 鬼成像giant magnetoresistance (GMR) 巨磁电阻Giaever tunneling 盖沃尔隧穿(单电(粒)子隧穿)Gibbs ensemble 吉布斯系综gilbert 吉尔(磁通势单位)Ginzburg-Landau coherence length 金兹堡-朗道(GL)相干长度Ginzburg-Landau equation 金兹堡-朗道(GL)方程Ginzburg-Landau-Abrikosov Go’rkov theory(GLAG)金兹堡-朗道-阿布里科索夫-高里科夫理论Glan-Thompson prism 格兰-汤普森棱镜Glan-Taylor prism 格兰-泰勒棱镜glass phase 玻璃相glassy ceramics 微晶玻璃glassy metal 玻璃态金属Glauber state Glauber态glide axis 滑移轴glide line 滑移线global phase 整体相位(量子信息)goniometer 测角器graded bandgap layer 缓变带隙层Gorter-Casimir two-fluid model 高特-卡西米尔二流体模型Graded index lens (GRIN) 梯度折射率透镜gradient of electric potential 电势梯度gram-molecule 克分子,摩尔(mole)grand free energy 巨自由能granular matter 颗粒物质granular superconductor 颗粒超导体granule 颗粒granularity 颗粒性granular metal 颗粒金属graphite 石墨graphite structure 石墨结构graph [线]图graph state 图态(量子信息)gravitational deflection of light 光线的引力偏折gravity acceleration 重力加速度Gray code 格雷码grazing angle 1,掠射角;2,擦边角greenhouse effect 温室效应group index of refraction 群折射率group theory 群论group velocity dispersion 群速度色散growth 生长growth model 生长模型guest host liquid crystal 宾主型液晶guided wave optics 导波光学gyroscopic effect 回转效应half metal 半金属half metallic magnet 半金属磁体half wave filter 半波滤波器half wave oscillator 半波振子half- wave zone method 半波带法half-wave voltage 半波电压Hall angle 霍尔角Hall coefficient 霍尔系数Hall field 霍尔电场[强度]Hall plateau 霍尔平台Hall resistance 霍尔电阻Hall voltage 霍尔电压halo nucleus 晕核halogen 卤素Hamiltonian matrix哈密顿[量]矩阵hard sphere 硬球hard sphere approximation 硬球近似harmonic generation 谐波产生Hartree-Fock electron 哈特里-福克电子H-center H心health physics 保健物理heat conductivity 1,导热性;2,热导率heat flow vector 热流矢量heat flux 热通量heat switch 热开关heavy electron 重电子heavy element 重元素heavy fermion superconductor 重费米子超导体heavy [fission] fragment 重【裂变】碎片heavy hole 重空穴heavy wall 重壁heavy water 重水hedgehog 猬缺陷height of potential barrier 势垒高度Heisenberg Hamiltonian 海森伯哈密顿量Heisenberg operators 海森伯算符Heisenberg uncertainty principle 海森伯不确定【性】原理Heitler-London theory 海特勒-伦敦理论Helfrich spontaneous curvature model 黑弗里希自发曲率模型helical spin order螺旋自旋有序helium liquefier 氦液化器heptahgedron 七面体Hermite polynomial 厄米多项式Hermitian matrix 厄米矩阵hertz (Hz) 赫兹, 频率单位heterotic superstring theory 杂化超弦理论Heusler alloy 霍伊斯勒合金hexadecapole 十六极hexahedron 六面体hexatic phase 六角相high coherence model 高相干模型high electron mobility transistor 高电子迁移率晶体管(简写:HEMT)high energy particle 高能粒子high-field domain 强场畴high-order dispersion 高阶色散high-order harmonic generation 高阶谐波产生high pass filter 高通滤波器high temperature reservoir 高温热源high temperature superconductor(HTS)高温超导体high vacuum 高真空high voltage electron microscopy 高压电子显微术Hohenberg-Kohn energy functional 霍恩伯格-科恩能量泛函hole-electron recombination 空穴-电子复合hole surface 空穴面(k空间中未占据态区的表面)hole-type high temperature superconductor 空穴型高温超导体holey fiber 多孔光纤hollow core optical fibers 空心光纤holon 空穴子homodyne零拍homodyne detection 零拍探测homolog[ue] 同系物homopolymer 单聚合物honeycomb photonic band gap fiber 蜂窝型光子带隙光纤hopping conductance 跳跃电导hopping energy,跳跃能hopping probability 跳跃概率hopping transport 跳跃输运host 基质host crystal 基质晶体,又称主晶hot carrier 热载流子h/e oscillation h/e振荡h/2e oscillation h/2e振荡Huang equations 黄[昆]方程组Huang-Rhys factor 黄昆-里斯因子Hubbard Hamiltonian 哈勃德哈密顿量Hubbard model 哈勃德模型Hubble time 哈勃时间hybrid bond 杂化键hybrid field effect 混合场效应hydrodynamics 流体[动]力学hydrodynamic mode 流体[动]力学模hydromagnetic disturbance 磁流体扰动hydromagnetic instability 磁流体不稳定性hydrophilic force 亲水力hydrophobic association 疏水缔合hydrophobic force 疏水力hyperbolic point 双曲点hypernucleus 超核hyper-Rayleigh scattering 超瑞利散射hyperspherical coordinate 超球座标hysteresis loop 1,滞后回线;2,磁滞回线hysteresis loss 1,滞后损失;2,磁滞损耗。
A Spin-Glass model of a Markov Random Field

A Spin-Glass model of a Markov Random FieldB.Caputo,J.Hornegger,D.Paulus and H.NiemannComputer Science Department,Chair for Pattern Recognition,University of Erlangen,Martensstrasse3,D-91058,Erlangen,GermanyIn the last few years there has been a growing interest within the machine learning comunity in Spin-Glass Theory(SGT)[8] and its possible applications in learning and recognition tasks[9],[2].SGT wasfirst used in physics to describe magnetic materials in which the interactions between the magnetic moments(spins)are random and conflicting[8].The attempt to understand the cooperative behaviour of such systems has led to the development of new concepts and techniques which have beenfinding applications and extensions in many areas such as attractor neural networks[1],combinatorial optimization problems,prebiotic evolution[8],and recently Gaussian Processes[9]and shape recognition[2].This contribution describes a new model that makes it possible to use SGT results in a Maximum A Posteriori-Markov Random Field(MAP-MRF,[7]) framework.Many vision problems can be posed as labeling problems;labeling is also a natural representation for the study of MRFs[7].Two major tasks in MRF modeling are how to define the neighborhood system for irregular sites,and how to choose the energy function for a proper encoding of constraints.How to define the neighbor relations between sites is related to their regularity;in the irregular case(i.e.object recognition problems,[7]),the neighborhood system must be defined by means of an“ad-hoc”distance that will be feature-dependent.If the application problem is3-D object recognition,we have the additional problem of choosing invariant features,or we should incorporate the pose parameters in the energy formulation and in the neighbor relations definition,with a dramatical increase in complexity.The energy function is a quantitative cost measure of the quality of a solution,which defines the best solution as its minimum.In the case of irregular sites,the energy function’s formulation can become something of an art,as it is generally done manually.SGT provides a way to deal with these problems in an elegant manner:full connectivity makes the neighborhood defi-nition irrelevant,and the energy function is defined independently from the considered application;this makes it possible tofind the analytical properties of the minima and may make it unnecessary to construct fast algorithms for seaching the absolute minima.To our knowledge,there are no previous works attempting to integrate SGT results in a MRF-MAP frame-work.Two basic properties of SG are disorder and frustration;these features are readily visualized in the energy function ,where is a generic configuration,the are random variables taking values in and is the connection matrix.It has been proved that(see[1],chap.4-6)choosing(while and hold),the(a chosen set of configurations)are the absolute minima of.These results can be extended from the discrete to the continuous case (i.e.,see[5]).With this choice for the connection matrix is straightforward to recognize that is a function of the scalar product between a generic configuration and a particular configuration which we want to be an absolute minima of.We propose to use SGT results as follows.Consider a generic pattern recognition problem:let be a set of sites corresponding to the features,and a continuous label set;then will be a labeling configuration in the configuration space;given the observed data,we define the optimal labeling to be the one which satisfy a MAP criterion.Now suppose we map the data from to a space,with, using a mapping.As is a function of the scalar product,this allows us to look for kernel functions such that,and thus to use the kernel without explicitly knowing.The Mercer’s condition [3]tells us for which kernels there exist a pair;the Gaussian kernel is a Mercer’s kernel[3],that is to say it is the scalar product between two generic vector in a space[3],which is the space where the SG energy lives.Thus,the kernel trick allows us to realize a Spin-Glass model of a Markov Random Field.We tested this model on two texture classification problems:in thefirst experiment we classifiedfive types of textures (see Figure1);for each class we had a sample set of64images,each of dimension.1Figure 1:Textures databases:on the top are five textures taken from the Meastex Database (available at .au/guy/meastex/meastex.html );on the bottom an example of radiographic image of periapical le-sion [4],and four regions of interest representing healtly and lesioned bone.The second experiment was done on a database of 228Regions Of Interest (ROIs)which were extracted from radio-graphic images of periapical lesions (see Figure 1,[4]).These ROIs represented regions of the image where the disease could be detected.The dimensions of these ROIs varied from to ;each region was selected on the basis of visual criteria and clinical results.Fea-tures were extracted in both cases by means of the co-occurrence matrices method [6],thus we obtained a vector of five features for each sample.The experiments were performed with a leave-one-out technique and prototypes were evaluated inmean value 85.1%90.3%gaussian mixture 86.8%Table 1:Experimental results three different ways:mean value,median value and Gaussian mixtures.Results reported in Table 1show that Gaussian mixtures give the best performance in both cases.References[1]D.J.Amit,“Modeling Brain Function”,Cambridge University Press,1989.[2]Y .Amit and M.Mascaro,“Attractor networks for shape recognition”Tech.Rep.no.495,Department of statistic,University of Chicago,available at /amit.[3]C.J.Burges,“A Tutorial on Support Vector Machines for Pattern Recognition”,Data Miniming and KnowledgeDiscovery ,V ol.2,N.2,1998.[4]B.Caputo,G.E.Gigante,“Analysis of Periapical Lesion Using Statistical Textural Features”,Proc.of MIE2000,pp1231-1234,August 2000.[5]T.Fukai,S.Shiino,“Large suppression of spurious states in neural networks of nonlinear analog neurons”,Phys.Rev.A ,V ol.42,N.12,Dec.1990.[6]R.M.Haralick,K.Shammugam,I.Dinstein.“Textural Features for Image Classification”,IEEE Trans.on Sys.,Manand Cyb.,Vol 3,No 6,1973.[7]S.Z.Li,“Markov Random Field Modeling in Computer Vision”,Computer Science Workbench,Springer,1995.[8]M.Mezard,G.Parisi,M.Virasoro,“Spin Glass Theory and Beyond”,World Scientific Singapore,1987.[9]M.Opper and O.Whinter,“Gaussian Processe for Classification:Mean Field Algorithms”,to appear in Neural com-putation ,vol 12,issue 11(2000).。
混凝土受压性能的非均质细观数值模拟

混凝土受压性能的非均质细观数值模拟作者:方志杨钻苏捷来源:《湖南大学学报·自然科学版》2010年第03期摘要:将混凝土看作是由骨料、砂浆及它们之间的界面组成的三相复合材料,在细观层次上建立了非均质混凝土棱柱体试件的随机骨料模型,分别赋予细观单元弹脆性损伤本构关系或弹塑性本构关系,研究了采用不同本构关系的混凝土棱柱体试件在单轴压缩荷载作用下的细观损伤演化过程,获得了相应的混凝土单轴受压宏观应力-应变曲线,并将计算结果与试验结果做了比较。
结果表明:混凝土试件的破坏是由于细观损伤的积累导致的;非均质模型计算所得的宏观应力应变曲线上升段与试验结果吻合相对较好,弹塑性本构模型计算所得的曲线下降段比弹脆性模型更接近于试验曲线。
关键词:混凝土, 单轴压缩,细观, 数值分析, 随机骨料模型, 本构模型中图分类号: 文献标识码:AMesoscopic Numerical Simulation on Compressive Behaviour of Heterogeneous ConcreteFANG Zhi†, YANG Zuan, SU Jie(College of Civil Engineering, Hunan Univ, Changsha, Hunan 410082, China)Abstract:In order to study the compressive behavior of concrete under uniaxial compressive load on mesoscopic level, considering the concrete as a three-phase composite material of aggregate, mortar and the interface between them, a random aggregate model at mesoscopic level with the usage of Monte Carlo method was developed. Mesoscopic numerical models for heterogeneous concrete were established, in which elastic brittle constitutive relationship for aggregate and the interface elements, and elasto-plastic constitutive relationship for motar elements were adopted, respectively. The results show that the failure of concrete is mostly due to the accumulation of damage at mesoscopic level, and the predicted macro-stress strain relationships of concreteunder uniaxial compression agree better with test results when considering the heterogeneity of concrete and using elasto-plastic relationship for motar element.Keywords: concrete; uniaxial compression; mesoscopic; numerical analysis; random aggregate model; constitutive relationship混凝土是工程中广泛应用的一种建筑材料,也是一种多相复合材料,内部结构非常复杂。
Metallic Spin Glass in Infinite Dimensions

a r X i v:con d -m a t /0003449v 1 [c o n d -m a t .s t r -e l ] 28 M a r 2000Metallic Spin Glass in Infinite Dimensions 1O.NarikiyoDepartment of Physics,Kyushu University,Fukuoka 810-8560,Japan(March,2000)Metallic spin glass is a new subject for theoretical stud-ies,while experimentally such a state has been recognized for a long time.Theoretical works by pioneers [2,3]have been done on the assumption of the presence of the metal-lic spin-glass state.However,the metallic spin-glass state remains to be derived from a microscopic medel.[4]In this Short Note we clarify the present status of the mi-croscopic theory and develop it in comparison with the theory of the Mott transition in infinite dimensions.[5]We will find a metal-insulator transition in the following and the transition is predominantly the Mott type but not the Anderson type.We consider the random spin-fermion model in infinite dimensions introduced in ref.2,H =−ijσt ij c †iσc jσ+J K iS z i σzi − ijJ ij S z i S z j ,(1)where c iσrepresents the conduction electron with thespin σ,σzithe spin density of the conduction electron and S zi the spin density of the localized spin at site i .The conduction electrons hop on the Bethe lattice.The density of states for bare conduction electrons is semicir-cular and the half-width is 2t where t ij =t/√Tδm,0,(3)in the spin-glass state of the mean field theory.[6]Here∆is the order parameter of the spin-glass state and the measure of broken ergodicity due to rugged energy land-scape.The mean field theory becomes exact in infinite dimensions.We can introduce the dynamics of localized spins [6]and the retarded dynamical spin susceptibility has imaginary part proportional to ωνwhere ωis a small real frequency and the exponent νis about 1/4at T =0.The Green function for conduction electrons is deter-mined asG 0(i ωn )−1=i ωn −t 2G (i ωn ),(4)in the same manner as in the case of the Mott transition [5]where G (i ωn )is the renormalized Green function for conduction electrons given byG (i ωn )−1=G 0(i ωn )−1−Σ(i ωn ).(5)In infinite dimensions G (i ωn )plays the role of the dy-namical mean field.Since we study the half-filled case,the chemical potential,µ,can be fixed as µ=0.We calculate the density of states ρ(ω)of conduction electrons by ρ(ω)=−Im G (ω+i0+)/π.The density of states at the Fermi energy,ρ(0),serves as the order parameter of the metal-insulator transition possible in our random spin-fermion model in infinite ly,the transition is predominantly the Mott type.Since our model is mapped onto a single-site model,[5]the localization character of the Anderson transition is apparently absent at the metal-insulator transition.In the case of the Anderson transition ρ(0)is uncritical.On the other hand,ρ(0)is critical at the Anderson-Mott transition in three dimensions.[8]Although our solution is obtained in infinite dimensions,it might be relevant to the three dimensional system.In our study the coupling J K plays the same role as the local repulsion U of the Hubbard model.If we neglect the dynamics of χ(ω),we obtain a metal-insulator transi-tion of the Hubbard type.[5]The transition obtained inref.3is this type.However,such a transition is an arti-fact due to insufficiency of the approximation.The Mott transition should beascribed to the quasiparticles of the Gutzwiller type [5]whose dynamics is drived by the dy-namics of localized spins.In our dynamical mean field theory both Hubbard type and Gutzwiller type charac-ters are taken into account.For simplicity,we approximate the dynamical suscep-tibility in eq.(2)by the static part in eq.(3).This ap-proximation favors the insulating state so that the actual λc is larger than the value obtained in the following.The dynamics is taken into account as the origin of the width of the density of states of quasiparticles around the Fermi energy [9]to be determined by the self-consistent proce-dure of the dynamical mean field theory.A self-consistent numerical solution for ρ(ω)using the fast Fourier transform is given in Fig.1where J K√∆.The presence of the quasiparticle peakestablishes the presence of a metallic state.When we increase the value of the parameter λ,we have a metal-insulator transition at a critical value λc where the quasiparticle peak vanishes.The transition point can be evaluated analytically in the same manner as in the case of the Hubbard model.[10]In the metallic state near the transition point the self-energy at a low energy is estimated asΣ(ω)=J 2K ∆ω2−ω20,(6)where ω20=t t ∗/[1+(4t 2/J 2K ∆)].Here t ∗is the renor-malized transfer integral for quasiparticles to be detrem-ined self-consistently.This self-energy serves as a good interpolation between weak and strong coupling limits.If ω0is finite,Σ(ω)∝−ωin the limit of ω→0so that the quasiparticle peak is obtained.If ω0vanishes,Σ(ω)∝1/ωat small ωso that the quasiparticle peak vanishes and the Hubbard bands are obtained.The self-consistently determined weight of the quasiparticle peak vanishes at λ=λc =1and this point corresponds to the metal-insulator transition.In summary,we have combined the dynamical mean field theories of the Mott transition and the spin glass in infinite dimensions and derived a metallic spin-glass state from the random spin-fermion model.Since our param-eter λis proportional to√[1]This paper has been submitted to the Short Note sectionof J.Phys.Soc.Jpn.[2]S.Sachdev,N.Read and R.Oppermann:Phys.Rev.B52(1995)10286.[3]A.M.Sengupta and A.Georges:Phys.Rev.B 52(1995)10295.[4]B.Rosenow and R.Oppermann:preprint (cond-mat/9811174).[5]A.Georges,G.Kotliar,W.Krauth and M.J.Rozenberg:Rev.Mod.Phys.68(1996)13.[6]K.H.Fischer and J.A.Hertz:Spin Glasses (CambridgeUniversity Press,Cambridge,1991).[7]R.Oppermann and B.Rosenow:Phys.Rev.Lett.80(1998)4767.[8]T.R.Kirkpatrick and D.Belitz:preprint (cond-mat/9609221).[9]A.Kawabata:Prog.Theor.Phys.54(1975)45.[10]M.J.Rozenberg,G.Kotliar and X.Y.Zhang:Phys.Rev.B 49(1994)10181.[11]D.Belitz and T.R.Kirkpatrick:Rev.Mod.Phys.66(1994)261.This figure "fig1.png" is available in "png" format from: /ps/cond-mat/0003449v1。
核磁共振波普仪器专业词汇英汉翻译

APT Attached Proton Test 质子连接实验ASIS Aromatic Solvent Induced Shift 芳香溶剂诱导位移BBDR Broad Band Double Resonance 宽带双共振BIRD Bilinear Rotation Decoupling 双线性旋转去偶(脉冲)COLOC Correlated Spectroscopy for Long Range Coupling 远程偶合相关谱COSY ( Homonuclear chemical shift ) COrrelation SpectroscopY (同核化学位移)相关谱CP Cross Polarization 交叉极化CP/MAS Cross Polarization / Magic Angle Spinning 交叉极化魔角自旋CSA Chemical Shift Anisotropy 化学位移各向异性CSCM Chemical Shift Correlation Map 化学位移相关图CW continuous wave 连续波DD Dipole-Dipole 偶极-偶极DECSY Double-quantum Echo Correlated Spectroscopy 双量子回波相关谱DEPT Distortionless Enhancement by Polarization Transfer 无畸变极化转移增强2DFTS two Dimensional FT Spectroscopy 二维傅立叶变换谱DNMR Dynamic NMR 动态NMRDNP Dynamic Nuclear Polarization 动态核极化DQ(C) Double Quantum (Coherence) 双量子(相干)DQD Digital Quadrature Detection 数字正交检测DQF Double Quantum Filter 双量子滤波DQF-COSY Double Quantum Filtered COSY 双量子滤波COSY DRDS Double Resonance Difference Spectroscopy 双共振差谱EXSY Exchange Spectroscopy 交换谱FFT Fast Fourier Transformation 快速傅立叶变换FID Free Induction Decay 自由诱导衰减H,C-COSY 1H,13C chemical-shift COrrelation SpectroscopY 1H,13C 化学位移相关谱H,X-COSY 1H,X-nucleus chemical-shift COrrelation SpectroscopY1H,X-核化学位移相关谱HETCOR Heteronuclear Correlation Spectroscopy 异核相关谱HMBC Heteronuclear Multiple-Bond Correlation 异核多键相关HMQC Heteronuclear Multiple Quantum Coherence异核多量子相干HOESY Heteronuclear Overhauser Effect Spectroscopy 异核Overhause效应谱HOHAHA Homonuclear Hartmann-Hahn spectroscopy 同核Hartmann-Hahn谱HR High Resolution 高分辨HSQCHeteronuclear Single Quantum Coherence 异核单量子相干INADEQUATE Incredible Natural Abundance Double Quantum Transfer Experiment 稀核双量子转移实验(简称双量子实验,或双量子谱)INDOR Internuclear Double Resonance 核间双共振INEPT Insensitive Nuclei Enhanced by Polarization 非灵敏核极化转移增强INVERSE H,X correlation via 1H detection 检测1H的H,X核相关IR Inversion-Recovery 反(翻)转回复JRES J-resolved spectroscopy J-分解谱LIS Lanthanide (chemical shift reagent ) Induced Shift 镧系(化学位移试剂)诱导位移LSR Lanthanide Shift Reagent 镧系位移试剂MAS Magic-Angle Spinning 魔角自旋MQ(C) Multiple-Quantum ( Coherence ) 多量子(相干)MQF Multiple-Quantum Filter 多量子滤波MQMAS Multiple-Quantum Magic-Angle Spinning 多量子魔角自旋MQS Multi Quantum Spectroscopy 多量子谱NMR Nuclear Magnetic Resonance 核磁共振NOE Nuclear Overhauser Effect 核Overhauser效应(NOE)NOESY Nuclear Overhauser Effect Spectroscopy 二维NOE谱NQR Nuclear Quadrupole Resonance 核四极共振PFG Pulsed Gradient Field 脉冲梯度场PGSE Pulsed Gradient Spin Echo 脉冲梯度自旋回波PRFT Partially Relaxed Fourier Transform 部分弛豫傅立叶变换PSD Phase-sensitive Detection 相敏检测PW Pulse Width 脉宽RCT Relayed Coherence Transfer 接力相干转移RECSY Multistep Relayed Coherence Spectroscopy 多步接力相干谱REDOR Rotational Echo Double Resonance 旋转回波双共振RELAY Relayed Correlation Spectroscopy 接力相关谱RF Radio Frequency 射频ROESY Rotating Frame Overhauser Effect Spectroscopy 旋转坐标系NOE谱ROTO ROESY-TOCSY Relay ROESY-TOCSY 接力谱SC Scalar Coupling 标量偶合SDDS Spin Decoupling Difference Spectroscopy 自旋去偶差谱SE Spin Echo 自旋回波SECSY Spin-Echo Correlated Spectroscopy自旋回波相关谱SEDOR Spin Echo Double Resonance 自旋回波双共振SEFT Spin-Echo Fourier Transform Spectroscopy (with J modulation)(J-调制)自旋回波傅立叶变换谱SELINCOR Selective Inverse Correlation 选择性反相关SELINQUATE Selective INADEQUATE 选择性双量子(实验)SFORD Single Frequency Off-Resonance Decoupling 单频偏共振去偶SNR or S/N Signal-to-noise Ratio 信 / 燥比SQF Single-Quantum Filter 单量子滤波SR Saturation-Recovery 饱和恢复TCF Time Correlation Function 时间相关涵数TOCSY Total Correlation Spectroscopy 全(总)相关谱TORO TOCSY-ROESY Relay TOCSY-ROESY接力TQF Triple-Quantum Filter 三量子滤波WALTZ-16 A broadband decoupling sequence 宽带去偶序列WATERGATE Water suppression pulse sequence 水峰压制脉冲序列WEFT Water Eliminated Fourier Transform 水峰消除傅立叶变换ZQ(C) Zero-Quantum (Coherence) 零量子相干ZQF Zero-Quantum Filter 零量子滤波T1 Longitudinal (spin-lattice) relaxation time for MZ 纵向(自旋-晶格)弛豫时间T2 Transverse (spin-spin) relaxation time for Mxy 横向(自旋-自旋)弛豫时间tm mixing time 混合时间τc rotational correlation time 旋转相关时间。
自旋玻璃与消息传递算法Spin Glass and Message-Passing 概要

自旋玻璃:无序与阻错系统的简单模型
• 3D regular lattice
(Edwards-Anderson, 1975)
• Complete graph
(Sherrington-Kirkpatrick 1975)
• Random Poisson graph
(Viana-Bray, 1985)
8
11
ergodic vs non-ergodic
?
12
repeated heating—annealing and the equilibrium Gibbs measure
Complexity (复杂度)
13
distribution of equilibrium free-energies
1
……
6
Equilibrium (static) and dynamical properties of complex systems are both difficult and interesting • Quenched randomness, frustration, nonself averaging, …, broken ergodicity. • NP-complete combinatorial optimizations, message-passing algorithms for information science (CDMA, for example!), econo-physics, …, biological systems.
23
How to calculate the grand free energy? The cavity approabrium dynamics of even a simple system may be difficult to understand
几何阻挫磁体简介000
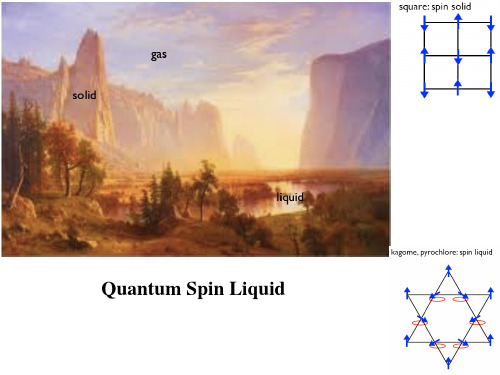
PM
阻挫磁体的判据: f
CW
TF
5
S0 / kB lnW
特征:基态存在很大的简并度 传统反铁磁体:
f
CW
TF
~1
Square Lattice:
Td ~ 2CW Td ~ 0.75CW
Triangular Lattice:
•多重简并基态
Triangular Lattice
三角晶格:6重简并 2重简并(FM) Kagome Lattice
→AFM+Spin
Liquid
→AFM
例2:ZnCr2O4
AFM → Quasispin Glass
问题1:几何阻挫磁体是否存在亚铁磁体?
First experimental realization of spin Ladder with FM Legs
问题2:几何阻挫自旋玻璃与传统自旋玻璃区别?
PRL,106, 247202 (2011
1.ACr2O4 (A=Zn,Cd,Hg) 几何阻挫磁体(Tetragonal Lattice)
•Cr3+ 占据四面体顶角
•Cr3+ 自旋占据t2g轨道, 只有自旋—晶格耦合
Cd
Cr
c
b
a
•强磁场诱导磁相变
强磁场调制“自旋—晶格”耦合
Orthorhombic(Fddd)
量子临界行为
磁场诱导量子相变
?
?
Magnetic Field-induced quantum phase transition: 概念:Noncollinear spin structure ———— Collinear spin Structure (First Order Transition) Example: Pyrochlore Lttice
Temperature Dependence of the Spin Polarization of a Quantum Hall Ferromagnet

1
A rapidly growing body of evidence, both theoretical [1{3] and experimental [4{7], strongly suggests that the lowest-lying charged excitation of the spin-polarized = 1 quantum Hall state is a spin-texture called a Skyrmion. This many-body state consists of radial spin density that is reversed at the center but gradually heals to the spin background over many magnetic lengths. The spin density distribution is determined by the interplay of the ferromagnetic exchange interaction and the Zeeman energy. The exchange interaction favors large Skyrmions while the Zeeman term favors smaller excitations. In GaAs samples presently under investigation the exchange energy can be up to two orders of magnitude larger than the Zeeman energy. Hartree-Fock calculations [2] predict that Skyrmions should consist of 3 4 spin ips per unpaired ux quantum for small excursions about = 1, a result consistent with early experimental work on the lling factor ( ) dependence of the zero temperature spin polarization near = 1 [4,6]. This dominance of the exchange interaction over the Zeeman energy has led theorists to refer to the = 1 quantum Hall state as the quantum Hall ferromagnet. In GaAs heterostructures experimentalists are presented an unprecedented opportunity to probe the physics of two-dimensional electron ferromagnetism in a well-characterized system. Thus insights gained from the thermodynamics of the spin polarization will be of interest not only to those studying many-body e ects in the integral quantum Hall regime, but also more generally, may elucidate the physics of 2D electron magnetism. In this communication we report on the experimental determination of the spin polarization as a function of temperature for such a = 1 quantum Hall ferromagnet. The system consists of a single-side n-modulation doped AlGaAs-GaAs single quantum well (SQW). The well thickness is 250 with an electron density of Ns = 1:8 10 cm and mobilA ity = 2:6 10 cm =V s. In order to perform absorption measurements the samples were mounted strain-free and thinned to 0:5m. The spin polarization is monitored through band-to-band absorption spectroscopy which distinguishes the occupancy of the two electron spin states. Band-gap absorption spectra show striking temperature dependence due to changes in the occupations of the spin-split states of the ground Landau level at lling factors
Ising spin glass under continuous-distribution random magnetic fields Tricritical points an

a r X i v :0804.1342v 1 [c o n d -m a t .s t a t -m e c h ] 8 A p r 2008Ising Spin Glass Under Continuous-Distribution Random Magnetic Fields:Tricritical Points and Instability LinesNuno Crokidakis ∗and Fernando D.Nobre †Centro Brasileiro de Pesquisas F´ısicasRua Xavier Sigaud 15022290-180Rio de Janeiro -RJ Brazil(Dated:April 8,2008)The effects of random magnetic fields are considered in an Ising spin-glass model defined in the limit of infinite-range interactions.The probability distribution for the random magnetic fields is a double Gaussian,which consists of two Gaussian distributions centered respectively,at +H 0and −H 0,presenting the same width σ.It is argued that such a distribution is more appropriate for a theoretical description of real systems than its simpler particular two well-known limits,namely the single Gaussian distribution (σ≫H 0),and the bimodal one (σ=0).The model is investigated by means of the replica method,and phase diagrams are obtained within the replica-symmetric solution.Critical frontiers exhibiting tricritical points occur for different values of σ,with the possibility of two tricritical points along the same critical frontier.To our knowledge,it is the first time that such a behavior is verified for a spin-glass model in the presence of a continuous-distribution random field,which represents a typical situation of a real system.The stability of the replica-symmetric solution is analyzed,and the usual Almeida-Thouless instability is verified for low temperatures.It is verified that,the higher-temperature tricritical point always appears in the region of stability of the replica-symmetric solution;a condition involving the parameters H 0and σ,for the occurrence of this tricritical point only,is obtained analytically.Some of our results are discussed in view of experimental measurements available in the literature.Keywords:Spin Glasses,Random-Field Systems,Replica Method,Almeida-Thouless Instability.PACS numbers:05.50+q,64.60.-i,75.10.Nr,75.50.LkI.INTRODUCTIONSpin-glass systems[1,2,3,4,5]continue to challenge many researchers in the area of magnetism.¿From the theoretical point of view,its simplest version defined in terms of Ising spin variables,the so-called Ising spin glass(ISG),represents one of the most fasci-nating problems in the physics of disordered magnets.The ISG mean-field solution,based on the infinite-range-interaction model,as proposed by Sherrington-Kirkpatrick(SK)[6], presents a quite nontrivial behavior.The correct low-temperature solution of the SK model is defined in terms of a continuous order-parameter function[7](i.e.,an infinite number of order parameters)associated with many low-energy states,a procedure which is usually denominated as replica-symmetry breaking(RSB).Furthermore,a transition in the presence of an external magneticfield,known as the Almeida-Thouless(AT)line[8], is found in the solution of the SK model:such a line separates a low-temperature region, characterized by RSB,from a high-temperature one,where a simple one-parameter solu-tion,denominated as replica-symmetric(RS)solution,is stable.The validity of the results of the SK model for the description of more realistic systems,characterized by short-range-interactions,represents a very polemic question[5].Recent numerical simulations claim the absence of an AT line in the three-dimensional short-range ISG[9],as well as along the non-mean-field region of a one-dimensional ISG characterized by long-range interactions [10].However,these results,obtained with rather small lattice-size simulations,do not rule out the possibility of a crossover to a different scenario at much larger lattice sizes, or also for smallerfields(and/or temperatures).One candidate for alternative theory to the SK model is the droplet model[11],based on domain-wall renormalization-group arguments for spin glasses[12,13].According to the droplet model,the low-temperature phase of anyfinite-dimensional∗E-mail address:nuno@cbpf.br†Corresponding author:E-mail address:fdnobre@cbpf.bra single thermodynamic state(together,of course,with its corresponding time-reversed counterpart),i.e.,essentially a RS-type of solution.Many important features of the ISG still deserve an appropriate understanding within the droplet-model scenario,and in par-ticular,the validity of this model becomes questionable for increasing dimensionalities, where one expects the existence of afinite upper critical dimension,above which the mean-field picture should prevail.Some diluted antiferromagnets,like Fe x Zn1−x F2,Fe x Mg1−x Cl2and Mn x Zn1−x F2,have been the object of extensive experimental research,due to their intriguing properties [14].These systems are able to exhibit,within certain concentration ranges,random-field,spin-glass or both behaviors,and in particular,the compounds Fe x Zn1−x F2and Fe x Mg1−x Cl2are characterized by large crystal-field anisotropies,in such a way that they may be reasonably well-described in terms of Ising variables.Therefore,they are usually considered as good physical realizations of the random-field Ising model(RFIM),or also of an ISG.For the Fe x Zn1−x F2,one gets a RFIM-like behavior for x>0.42,an ISG for x∼0.25,whereas for intermediate concentrations(0.25<x<0.42)one may observe both behaviors depending on the magnitude of the applied external magneticfield[RFIM (ISG)for small(large)magneticfields],with a crossover between them[15,16,17].In what concerns Fe x Mg1−x Cl2,one gets an ISG-like behavior for x<0.55,whereas for0.7< x<1.0one has a typical RFIM with afirst-order transition turning into a continuous one due to a change in the randomfields[14,18,19].Even though a lot of experimental data is available for these systems,they still deserve an appropriate understanding,with only a few theoretical models proposed for that purpose[20,21,22,23,24,25,26,27]. Within the numerical-simulation technique,one has tried to take into account the basic microscopic ingredients of such systems[20,21,22,23],whereas at the mean-field level, a joint study of both ISG and RFIM models has been shown to be a very promising approach[24,25,26,27].In the present work we investigate the effects of random magneticfields,following a continuous probability distribution,in an ISG model.The model is considered in the limit of infinite-range interactions,and the probability distribution for the random mag-neticfields is a double Gaussian,which consists of a sum of two independent Gaussian distributions.Such a distribution interpolates between the bimodal and the simple Gaus-sian distributions,which are known to present distinct low-temperature critical behavior, within the mean-field limit[24,25,26,27].It is argued that this distribution is more appropriate for a theoretical description of diluted antiferromagnets than the bimodal and Gaussian distributions.In particular,for given ranges of parameters,this distribu-tion presents two peaks,and satisfies the requirement of effective randomfields varying in both sign and magnitude,which comes out naturally in the identification of the RFIM with diluted antiferromagnets in the presence of a uniformfield[28,29];this condition is not fulfilled by simple discrete probability distributions,e.g.,the bimodal one,which is certainly very convenient from the theoretical point of view.Recently,the use a double-Gaussian distribution in the RFIM[30]yielded interesting results,leading to a candidate model to describe the change of afirst-order transition into a continuous one that occurs in Fe x Mg1−x Cl2[14,18,19].The use of this distribution in the study of the present model should be relevant for Fe x Mg1−x Cl2with concentrations x<0.55,where the ISG behavior shows up.In the next section we study the SK model in the presence of the above-mentioned random magneticfields;a rich critical behavior is presented,and in par-ticular,onefinds a critical frontier that may present one,or even two,tricritical points. The instabilities of the RS solution are also investigated,and AT lines presenting an in-flection point,in concordance with those measured in some diluted antiferromagnets,are obtained.Finally,in section4we present our conclusions.II.THE ISING SPIN GLASS IN THE PRESENCE OF A RANDOM-FIELDThe infinite-range-interaction Ising spin-glass model,in the presence of an external random magneticfield,may be defined in terms of the HamiltonianH=− (i,j)J ij S i S j− i H i S i,(1) where the sum (i,j)applies to all distinct pairs of spins S i=±1(i=1,2,...,N).The interactions{J ij}and thefields{H i}follow independent probability distributions,FIG.1:The probability distribution of Eq.(3)(the randomfields are scaled in units ofσ)for typical values of the ratio H0/σ:(a)(H0/σ)=1/3,1,5/2;(b)(H0/σ)=10.P(J ij)= N2J2 J ij−J0+exp −(H i+H0)22 12σ2[F({J ij,H i})]J,H= (i,j)[dJ ij P(J ij)] i[dH i P(H i)]F({J ij,H i}).(4) Now,one can make use of the replica method[1,2,3,4]in order to obtain the free energy per spin,−βf=lim N→∞1Nn([Z n]J,H−1),(5)where Z n represents the partition function of the replicated system andβ=1/(kT). Standart calculations lead toβf=−(βJ)22+limn→012 α(mα)2+(βJ)22ln Trαexp(H+eff)−12<Sα>++12<Sαβ>++1where <>±indicate thermal averages with respect to the “effective Hamiltonians”H ±effin Eq.(8).Assuming the RS ansatz [1,2,3,4],i.e.,m α=m (∀α)and q αβ=q [∀(αβ)],Eqs.(6)–(10)yieldβf =−(βJ )22m 2−1√212π ∞∞dze −z 2/2ln(2cosh ξ−),(11)m =1√212π +∞−∞dze −z 2/2tanh ξ−,(12)q =1√212π +∞−∞dze −z 2/2tanh 2ξ−,(13)whereξ±=β{J 0m +JGz ±H 0},(14)G = q + σJ 2=1√212π +∞−∞dze −z 2/2sech 4ξ−.(16)Let us now present the phase diagrams of this model.Since the random field induces the parameter q ,there is no spontaneous spin-glass order,like the one found in the SK model.However,there is a phase transition related to the magnetization m ,in such a waythat two phases are possible within the RS solution,namely,the Ferromagnetic (m =0,q =0)and the Independent (m =0,q =0)ones.The critical frontier separating these two phases is obtained by solving the equilibrium conditions,Eqs.(12)and (13),whereasinthecase of first-order phase transitions,the free energy per spin,Eq.(11),will be analyzed.Expanding the magnetization [Eq.(12)]in power series,m =A 1(q )m +A 3(q )m 3+A 5(q )m 5+O (m 7),(17)whereA 1(q )=βJ 0{1−ρ1(q )},(18)A 3(q )=−(βJ 0)315{2−17ρ1(q )+30ρ2(q )−15ρ3(q )},(20)andρk (q )=12π +∞−∞dze −z 2/2tanh 2k βJGz +H 01−(βJ )2Γm 2+O (m 4),(22)with Γ=1−4ρ1(q 0)+3ρ2(q 0),(23)where q 0corresponds to the solution of Eq.(13)for m =0.Substituting Eq.(22)in the expansion of Eq.(17),one obtains the m -independent coefficients in the power expansionof the magnetization;in terms of the lowest-order coefficients,one gets,m=A′1m+A′3m3+O(m5),(24)A′1=A1(q0),(25)A′3=−(βJ0)31−(βJ)2Γ Γ.(26)The associated critical frontier is determined through the standard procedure,taking into account the spin-glass order parameter[Eq.(13)],as well.For continuous transitions, A′1=1,with A′3<0,in such a way that one has to solve numerically the equation A′1=1,together with Eq.(13)considering m=0.If A′3>0,one may havefirst-order phase transitions,characterized by a discontinuity in the magnetization;in this case,the critical frontier is found through a Maxwell construction,i.e.,by equating the free energies of the two phases,which should be solved numerically together with Eqs.(12)and(13) for each side of the critical line.When both types of phase transitions are present,the continuous andfirst-order critical frontiers meet at a tricritical point that defines the limit of validity of the series expansion.The location of such a point is determined by solving numerically equations A′1=1,A′3=0,and Eq.(13)with m=0[provided that the coefficient of the next-order term in the expansion of Eq.(24)is negative,i.e.,A′5<0].Considering the above-mentioned phases,the AT instability of Eq.(16)splits each of them in two phases,in such a way that the phase diagram of this model may present four phases,that are usually classified as[24,25,26]:(i)Paramagnetic(P)(m=0;stability of the RS solution);(ii)Spin-Glass(SG)(m=0;instability of the RS solution);(iii) Ferromagnetic(F)(m=0;stability of the RS solution);(iv)Mixed Ferromagnetic(F′) (m=0;instability of the RS solution).Even though in most cases the AT line is computed numerically,for large values of J0[i.e.,J0>>J and J0>>H0]and low temperatures,one gets the following analytic asymptotic behavior,kT312π12J2G2 +exp−(J0−H0)2FIG.2:Phase diagrams of the infinite-range-interaction ISG in the presence of a double-Gaussian randomfield;the phases are labelled according to the definitions in the text.AT1and AT2 denote AT lines,and all variables are scaled in units of J.Two typical examples[(a)(σ/J)=0.2;(b)(σ/J)=0.6]are exhibited,for which there are single points(represented by black dots) characterized by A′1=1and A′3=0,defining the corresponding threshold values H(1)0(σ).For the particular caseσ=0,i.e.,the bimodal probability distribution for thefields [25],it was verified that the phase diagrams of the model change qualitatively and quan-titatively for incresing values of H0.Herein,we show that the phase diagrams of the present model change according to the parameters of the distribution of randomfields [Eq.(3)],which may modify drastically the critical line separating the regions with m=0 and m=0,defined by the coefficients in Eq.(24).In particular,onefinds numerically a threshold value,H(1)0(σ),for which this line presents a single point characterized by A′1=1and A′3=0;all other points of this line represent continuous phase transitions, characterized by A′1=1and A′3<0.Typical examples of this case are exhibited in Fig.2, for the dimensionless ratios(σ/J)=0.2and(σ/J)=0.6.As will be seen in the next figures,for values of H0/J slightly larger than H(1)0(σ)/J,this special point splits in two tricritical points,whereas for values of H0/J smaller than H(1)0(σ)/J,this critical frontier is completely continuous.Therefore,one may interpret the point for which H0=H(1)0(σ) as a collapse of two tricritical points.Such an unusual critical point is a characteristic of some infinite-range-interaction spin-glasses in the presence of random magneticfields [25,26],and to our knowledge,it has never been found in other magnetic models.¿From Fig.2,one notices that the threshold value H(1)0(σ)/J increases for increasing values ofσ/J,although the corresponding ratio H(1)0(σ)/σdecreases.Apart from that,this pecu-liar critical point always occurs very close to the onset of RSB;indeed,for(σ/J)=0.6, this point essentially coincides with the union of the two AT lines(AT1and AT2).At least for the range of ratiosσ/J investigated,this point never appeared below the AT lines,i.e.,in the region of RSB.Therefore,an analysis that takes into account RSB,will not modify the location of this point in these cases.In Fig.3we exhibit phase diagrams for afixed value ofσ(σ=0.2J),and increasing values of H0.In Fig.3(a)we show the case(H0/J)=0.5,where one sees a phase diagram that looks like,at least qualitatively,the one of the SK model;even though the random-field distribution[cf.Eq.(3)]is double-peaked(notice that(H0/σ)=2.5in this case),the effects of such afield are not sufficient for a qualitative change in the phase diagram of the model.As we have shown above[see Fig.2(a)],qualitative changes only occur in the corresponding phase diagram for a ratio(H(1)0(σ)/σ)≈5,or higher.It is important to remark that a tricritical point occurs in the corresponding RFIM for any (H0/σ)≥1[30],in agreement with former general analyses[31,32,33].If one associates the tricritical points that occur in the present model as reminiscents of the one in the RFIM,one notices that such effects appear attenuated in the present model due to the bond randomness,as predicted previously for short-range-interaction models[34,35].In Fig.3(b)we present the phase diagram for(H0/J)=0.993;in this case,one observes two finite-temperature tricritical points along the critical frontier that separates the regions with m=0and m=0.The higher-temperature point is located in the region where the RS approximation is stable,and so,it will not be affected by RSB effects;however,the lower-temperature tricritical point,found in the region of instability of the RS solution, may change under a RSB procedure.In Fig.3(c)we exhibit another interesting situation of the phase diagram of this model,for which the lower-temperature tricritical point goes down to zero temperature,defining a second threshold value,H(2)0(σ).This threshold value was calculated analytically,through a zero-temperature approach that follows below,for arbitrary values ofσ/J.Above such a threshold,only the higher-temperature tricritical point(located in the region of stability of the RS solution)exists;this is shown in Fig.3(d), where one considers a typical situation with H0>H(2)0(σ).It is important to notice that in Fig.3(d)the two AT lines clearly do not meet at the critical frontier that separates theFIG.3:Phase diagrams of the infinite-range-interaction ISG in the presence of a double-Gaussian randomfield with(σ/J)=0.2and typical values of H0/J;the phases are labelled according to the definitions in the text.AT1and AT2denote AT lines,and all variables are scaled in units of J.By increasing the value of H0/J,the phase diagram changes both qualitatively and quantitatively and,particularly,the critical lines separating the regions with m=0and m=0are modified;along these critical frontiers,the full(dotted)lines represent continuous (first-order)phase transitions and the black dots denote tricritical points;for the values of H0/J chosen,one has:(a)continuous phase transitions;(b)two tricritical points atfinite temperatures;(c)the lower tricritical point at zero temperature,defining the corresponding threshold value H(2)0(σ);(d)a single tricritical point atfinite temperatures.regions with m=0and m=0;such an effect is a consequence of the phase coexistence region,characteristic offirst-order phase transitions,and has already been observed in the SK model with a bimodal random-field distribution[25].The line AT1is valid up to the right end limit of the phase coexistence region,whereas AT2remains valid up to theFIG.4:Phase diagrams of the infinite-range-interaction ISG in the presence of a double-Gaussian randomfield with(σ/J)=0.6and typical values of H0/J;the phases are labelled according to the definitions in the text.AT1and AT2denote AT lines,and all variables are scaled in units of J.Along the critical lines separating the regions with m=0and m=0,the full(dotted)lines represent continuous(first-order)phase transitions and the black dots denote tricritical points; for the values of H0/J chosen,one has:(a)two tricritical points atfinite temperatures;(b)the lower tricritical point at zero temperature,defining the corresponding threshold value H(2)0(σ).left end limit of such a region;as a consequence of this,the lines AT1and AT2do not meet at the corresponding Independent-Ferromagnetic critical frontier.Additional phase diagrams are shown in Fig.4,where we exhibit two typical cases for the random-field width(σ/J)=0.6.In Fig.4(a)we show the equivalent of Fig.3(b), where two tricritical points appear atfinite temperatures;now one gets qualitatively a similar effect,but with a random-field distribution characterized by a smaller ratio H0/σ. From the quantitative point of view,the following changes occur,in the critical frontier Independent-Ferromagnetic,due to an increase inσ/J:(i)such a critical frontier moves to higher values of J0/J,leading to an enlargement of the Independent phase[corresponding to the region occupied by the P and SG phases of Fig.4(a)];(ii)the two tricritical points are shifted to lower temperatures.In Fig.4(b)we present the situation of a zero-temperature tricritical point,defining the corresponding threshold value H(2)0(σ);once again,one gets a physical situation similar to the one exhibited in Fig.3(c),but with a much smaller ratio H0/σ.Qualitatively similar effects may be also observed for other values ofσ,but with different threshold values,H(1)0(σ)and H(2)0(σ).We have noticedFIG.5:Evolution of the threshold values H(1)0(σ)(lower curve)and H(2)0(σ)(upper curve)with the widthσ(all variables are scaled in units of J).Three distinct regions(I,II,and III)are shown,concerning the existence of tricritical points andfirst-order phase transitions along the Independent-Ferromagnetic critical frontier.The dashed straight line corresponds to H0=σ, above which one has a tricritical point in the corresponding RFIM[30].that such threshold values increase withσ/J,even though one requires less-pronounced double-peaked distributions[i.e.,smaller values for the ratios H0/σ]in such a way to get significant changes in the standard SK model phase diagrams[as can be seen in Figs.2, 3(c),and4(b)].The evolution of the threshold values H(1)0(σ)and H(2)0(σ)with the dimensionless widthσ/J is exhibited in Fig.5.One notices three distinct regions in what concerns the existence of tricritical points andfirst-order phase transitions along the Independent-Ferromagnetic critical frontier.Throughout region I[defined for H0>H(2)0(σ)]afirst-order phase transition occurs atfinite temperatures and reaches the zero-temperature axis;a single tricritical point is found atfinite temperatures[a typical example is shown in Fig.3(d)].In region II[defined for H(1)0(σ)<H0<H(2)0(σ)]onefinds twofinite-temperature tricritical points,with afirst-order line between them[typical examples are exhibited in Figs.3(b)and4(a)].Along region III[H0<H(1)0(σ)]one has a completely continuous Independent-Ferromagnetic critical frontier[like in Fig.3(a)].The dashed straight line corresponds to H0=σ,which represents the threshold for the existence of a tricritical point in the corresponding RFIM[30].Hence,if one associates the occurrenceFIG.6:The zero-temperature phase diagram H0versus J0(in units of J)for two typical values of the dimensionless widthσ/J.The critical frontiers separating the phases SG and F′is continuous for small values of H0/J(full lines)and becomefirst-order for higher values of H0/J(dotted lines);the black dots denote tricritical points.Although the two critical frontiers become very close near the tricritical points,they do not cross each other;the tricritical point located at a higher value of J0/J corresponds to the higher dimensionless widthσ/J.of tricritical points in the present model with those of the RFIM,one notices that such effects are attenuated due to the bond randomness,in agreement with Refs.[34,35]; herein,the bond randomness introduces a spin-glass order parameter,in such a way that one needs stronger values of H0/J for these tricritical points to occur.Let us now consider the phase diagram of the model at zero temperature;in this case, the spin-glass order parameter is trivial(q=1),in such a way that the free energy and magnetization become,f=−J02 erfJ0m+H02 −erf J0m−H02−J2πG0 exp −(J0m+H0)22J2G20 ,(28)m=1JG0√2erf J0m−H02 ,(29)whereG0= 1+ σ2G0 J02J2G20 ,(32)a3=12G30 J0G20H02J2G20 ,(33)a5=12G50 J0G40H0G20 H02J2G20 .(34)For[H0/(JG0)]2<1[i.e.,a3<0],we have a continuous critical frontier given by a1=1,J0π2J2G20 .(35) This continuous critical frontier ends at a tricritical point(a3=0),1J 2=1⇒H0J=1+ σJ= 2 1+ σFIG.7:Typical phase diagrams of the infinite-range-interaction ISG in the presence of a double-Gaussian randomfield with(σ/J)=0.4are compared with those already known for some particular parisons of qualitatively similar phase diagrams are presented,essentially in what concerns the critical frontier that separates the regions with m=0and m=0.(a) Phase diagrams for the single Gaussian[(H0/J)=0.0and(σ/J)=0.4]and the double Gaussian [(H0/J)=0.8and(σ/J)=0.4]distributions for the randomfields.(b)Phase diagrams for the bimodal[(H0/J)=0.9573]and the double Gaussian[(H0/J)=1.0447]distributions for the randomfields.(c)Phase diagrams for the bimodal[(H0/J)=0.97]and the double Gaussian [(H0/J)=1.055]distributions for the randomfields.(d)Phase diagrams for the bimodal [(H0/J)=1.0]and the double Gaussian[(H0/J)=1.077]distributions for the randomfields. The phases are labelled according to the definitions in the text.AT1and AT2denote AT lines, and all variables are scaled in units of J.FIG.8:Instabilities of the replica-symmetric solution of the infinite-range-interaction ISG(cases J0=0)in the presence of a double-Gaussian randomfield,for two typical values of distribution widths:(a)(σ/J)=0.2;(b)(σ/J)=0.6.In each case the AT line separates a region of RS from the one characterized by RSB(all variables are scaled in units of J).Hence,Eqs.(36)and(37)yield the coordinates of the tricritical point at zero temperature. In addition to that,the result of Eq.(36)corresponds to the exact threshold value H(2)0(σ) (as exhibited in Fig.5).The above results are represented in the zero-temperature phase diagram shown in Fig.6,where onefinds a single critical frontier separating the phases SG and F′.In order to illustrate that the present model is capable of reproducing qualitatively the phase diagrams of previous works,namely,the Ising spin glass in the presence of random fields following either a Gaussian[24],or a bimodal[25]probability distribution,in Fig.7 we compare typical results obtained for the Ising spin-glass model in the presence of a double Gaussian distribution characterized by(σ/J)=0.4with those already known for such particular cases.In these comparisons,we have chosen qualitatively similar phase diagrams,mainly taking into account the critical frontier that separates the regions with m=0and m=0.In Fig.7(a)we exhibit the phase diagram of the present model [(H0/J)=0.8]together with the one of an ISG in the presence of randomfields described by a single Gaussian distribution;both phase diagrams are qualitatively similar to the one of the standard SK model.In Fig.7(b)we present phase diagrams for the bimodal and double Gaussian distributions,at their corresponding threshold values,H(1)0(σ).Typical situations for the cases of the bimodal and double Gaussian distributions,where two tricritical points appear along the critical frontier that separates the regions with m=0and m=0,are shown in Fig.7(c).Phase diagrams for the bimodal and double Gaussian distributions,at their corresponding threshold values,H(2)0(σ),are presented in Fig.7(d).Next,we analyze the AT instability for J0=0;in this case,Eq.(16)may be written askT√J ,(38)which corresponds to the same instability found in the case of a single-Gaussian random field[24].In Fig.8we exhibit AT lines for two typical values of distribution widths;in each case the AT line separates a region of RS from the one characterized by RSB.One notices that the region associated with RSB gets reduced for increasing values ofσ;however,the most interesting aspect in these lines corresponds to an inflection point,which may be identified with the one that has been observed in the experimental equilibrium boundary of the compound Fe x Zn1−x F2[15,24].Up to now,this effect was believed to be explained only through the ISG in the presence of a single-Gaussian randomfield,for which the phase diagrams in the cases J0>0are much simpler,with all phase transitions being continuous, typically like those of the SK model.Herein,we have shown that an inflection point in the AT line may also occur in the present model,for which one has a wide variety of phase diagrams in the corresponding case J0>0,as exhibited above.Therefore,the present model would be appropriate for explaining a similar effect that may be also observed experimentally in diluted antiferromagnets characterized byfirst-order phase transitions, like Fe x Mg1−x Cl2.III.CONCLUSIONSWe have studied an Ising spin-glass model,in the limit of infinite-range interactions and in the presence of random magneticfields distributed according to a double-Gaussian probability distribution.Such a distribution contains,as particular limits,both the single-Gaussian and bimodal probability distributions.By varying the parameters of this distri-。
船海专业OA资源-wk

船海专业OA资源简介:是一个收录科学文献预印本的在线数据库,目前包含了超过50万篇文章,并且以每个月5000篇的速度增长着。
目前,这个数据库包含:数学,物理,计算机,非线性科学,定量生物学,定量财务以及统计学几大分类。
其最重要的特点就是“开放式获取”,每个人都可以免费地访问全文数。
覆盖的领域包括:物理学、数学、非线性科学、计算机科学四个学科共计17万篇预印本文献。
该站点的全文文献有多种格式(例如PS、PDF、DVI等),需要安装对应的全文浏览器才能阅读,尤其是PS格式。
优点:Computational Complexity与Numerical Analysis用于船舶仿真数值模拟,计算机辅助设计船舶是船海专业的研究热点,目前的瓶颈在于计算量大与计算非线性。
Computational Complexity这个模块有很多关于提高计算性能的全文文献,对于解决并行计算问题有很好帮助。
Numerical Analysis模块研究很多非线性问题,尤其是边界元和流体粘性等船舶方面结构与流体问题研究起到很好的帮助。
并且这个数据库可以访问全文。
缺点:关注船舶仿真,不关注船舶设计这个数据库没有并没有关注船舶行业的总体性能,它的目标主要集中在船舶性能仿真方面,对于船舶设计等问题很少涉及,所以对于船海专业的人来说如果需要学习船舶仿真计算可以关注这个数据库。
2.中国科技论文在线简介:中国科技论文在线是经教育部批准,由教育部科技发展中心主办,针对科研人员普遍反映的论文发表困难,学术交流渠道窄,不利于科研成果快速、高效地转化为现实生产力而创建的科技论文网站。
作者所投论文遵守国家相关法律,为学术范围内的讨论,有一定学术水平,基本理论正确,且符合中国科技论文在线的基本投稿要求,一般可在7个工作日内发布。
优点:论文新颖,实船设计资料丰富,该数据库论文主要来源于船舶设计一线工作人员,论文内容主要集中与船舶实际设计中存在的问题与改良,该数据库文献发表时间较快,基本上涵盖了国内船舶设计一线的最新成果,且提供全文。
开启片剂完整性的窗户(中英文对照)

开启片剂完整性的窗户日本东芝公司,剑桥大学摘要:由日本东芝公司和剑桥大学合作成立的公司向《医药技术》解释了FDA支持的技术如何在不损坏片剂的情况下测定其完整性。
太赫脉冲成像的一个应用是检查肠溶制剂的完整性,以确保它们在到达肠溶之前不会溶解。
关键词:片剂完整性,太赫脉冲成像。
能够检测片剂的结构完整性和化学成分而无需将它们打碎的一种技术,已经通过了概念验证阶段,正在进行法规申请。
由英国私募Teraview公司研发并且以太赫光(介于无线电波和光波之间)为基础。
该成像技术为配方研发和质量控制中的湿溶出试验提供了一个更好的选择。
该技术还可以缩短新产品的研发时间,并且根据厂商的情况,随时间推移甚至可能发展成为一个用于制药生产线的实时片剂检测系统。
TPI技术通过发射太赫射线绘制出片剂和涂层厚度的三维差异图谱,在有结构或化学变化时太赫射线被反射回。
反射脉冲的时间延迟累加成该片剂的三维图像。
该系统使用太赫发射极,采用一个机器臂捡起片剂并且使其通过太赫光束,用一个扫描仪收集反射光并且建成三维图像(见图)。
技术研发太赫技术发源于二十世纪九十年代中期13本东芝公司位于英国的东芝欧洲研究中心,该中心与剑桥大学的物理学系有着密切的联系。
日本东芝公司当时正在研究新一代的半导体,研究的副产品是发现了这些半导体实际上是太赫光非常好的发射源和检测器。
二十世纪九十年代后期,日本东芝公司授权研究小组寻求该技术可能的应用,包括成像和化学传感光谱学,并与葛兰素史克和辉瑞以及其它公司建立了关系,以探讨其在制药业的应用。
虽然早期的结果表明该技术有前景,但日本东芝公司却不愿深入研究下去,原因是此应用与日本东芝公司在消费电子行业的任何业务兴趣都没有交叉。
这一决定的结果是研究中心的首席执行官DonArnone和剑桥桥大学物理学系的教授Michael Pepper先生于2001年成立了Teraview公司一作为研究中心的子公司。
TPI imaga 2000是第一个商品化太赫成像系统,该系统经优化用于成品片剂及其核心完整性和性能的无破坏检测。
Absence of an equilibrium ferromagnetic spin glass phase in three dimensions

a r X i v :c o n d -m a t /0208566v 2 [c o n d -m a t .d i s -n n ] 4 N o v 2002Absence of an equilibrium ferromagnetic spin glass phase in three dimensionsF.Krzakala 1and O.C.Martin 1,21Laboratoire de Physique Th´e orique et Mod`e les Statistiques,bˆa t.100,Universit´e Paris-Sud,F–91405Orsay,France.2Service de Physique de l’´Etat Condens´e ,Orme des Merisiers —CEA Saclay,91191Gif sur Yvette Cedex,France.(February 1,2008)Using ground state computations,we study the transition from a spin glass to a ferromagnet in 3-d spin glasses when changing the mean value of the spin-spin interaction.We find good evidence for replica symmetry breaking up till the critical value where ferromagnetic ordering sets in,and no ferromagnetic spin glass phase.This phase diagram is in conflict with the droplet/scaling and mean field theories of spin glasses.We also find that the exponents of the second order ferromagnetic transition do not depend on the microscopic Hamiltonian,suggesting universality of this transition.75.10.Nr,75.40.Mg,02.60.PnThe nature of the frozen phase in finite dimensional spin glasses [1]is still not understood.Many studies seem to support the many valley picture predicted by the mean field approach [2,3]in which replica symmetry is broken (RSB).Nevertheless other approaches [4,5]are not excluded;one open question is whether spin glass or-dering can co-exist with ferromagnetism.The different theoretical predictions here are in conflict.Moreover,this question is of experimental relevance:it may be possible to test for the co-existence of the two types of orderings in doped ferromagnets that show glassy behavior.In this paper we study the transition from a spin glass to a ferromagnet at zero-temperature for Ising spin mod-els having nearest and next-nearest neighbor interactions in d =3.First,we find that RSB,which is associated with system-size excitations having O (1)energies,per-sists in the presence of an excess of ferromagnetic over anti-ferromagnetic bonds.Second,our order parameter for RSB vanishes at the same concentration as where fer-romagnetism sets in;in fact it seems that ferromagnetic and spin glass orderings,with or without RSB,do not co-exist.These properties are in conflict with the mean field and droplet/scaling theories [4,5],the main theo-retical frameworks for spin glasses.Finally,the critical exponents and Binder cumulant at criticality for the fer-romagnetic transition are the same for our two models,and fully compatible with those found in a similar sys-tem [6],giving evidence for universality in this transition.Theoretical expectations —In the mean field picture,based on the infinite range Sherrington-Kirkpatrick (SK)model [7],one has the following sequence at low temper-ature when the concentration of ferromagnetic interac-tions is increased (see Fig.1):(a)an RSB phase with no magnetization (m =0);(b)a “mixed”phase with both RSB and m >0;(c)a standard ferromagnetic phase.The same phase diagram arises in the Random Energy Model [8].In these models the mixed phase fol-lows from the existence of a spin glass phase in a mag-netic field;indeed,a non zero magnetization creates an effective magnetic field,and thus mixed phases seem un-avoidable in mean field.One can also consider finite con-TemperatureρFIG.1.Left:Phase diagram in a mean-field model (ρis the excess concentration of ferromagnetic bonds,c.f.eq.1).A mixed (M)phase,with both ferromagnetic (F)ordering and replica symmetry breaking (RSB),is present.At larger temperature the system is paramagnetic (P).Right:The role of the coordination on the presence of such a mixed phase in the mean field picture at temperature T =0(artist’s view).nectivity generalizations [9,10]of the SK model where a spin is connected at random to a finite number of other spins.A study of the associated phase diagram has been performed [11]for connectivity 3and again shows the presence of a mixed phase,while the limit of large con-nectivities brings us back to the SK model.Now the com-bination of spin glass ordering and very low connectivity most likely inhibits ferromagnetism,so the size of the mixed phase should grow as the connectivity increases.This is what we illustrate in Fig.1.If mean field is a good guide for three dimensions,then a mixed phase should be easier to observe on lattices with large connectivities;for this reason we shall consider lattices with next-nearest neighbor interactions.Within the droplet or scaling theories,the phase dia-gram is very different because any magnetic field destroys the spin glass ordering.For instance,within the droplet picture [4],the mixed phase is incompatible with compact droplets.Similarly,within the scaling picture [5],having a mixed phase would require a line of neutral fixed points connecting two unstable fixed points under the renormal-ization group,i.e.,highly singular and non generic flows.Not surprizingly,the absence of a mixed phase is ex-plicitly confirmed in the Migdal-Kadanoffbond-moving approach [12,13].This picture works very well in low dimensions,and in particular it agrees with the consen-0.511.5m Lβ/ν(ρ-ρc )L1/νFIG.2.Scaling plot of m as a function of ρin the First Neighbor Model;ρF =0.385,ν=0.9and β=0.3.The inset shows the Binder cumulant of m J .sus of no mixed phase in dimensions d ≤2[14,15].Our focus in this work is the case d =3where the question of a mixed phase remains open.Note that high temper-ature series cannot address this problem as the mixed phase resides beyond the first boundary of singularities.A good way to tackle it is via Monte Carlo;unfortunately,such studies have systematically avoided the question of the mixed phase,focusing instead on ordering from the paramagnetic side.The only attempt to search for an equilibrium mixed phase we are aware of is that of Hart-mann [6]who worked at zero-temperature but was not able to estimate precisely the boundary of the spin glass phase and thus made no claims about the existence or not of a mixed phase.The models —We consider Edwards-Anderson-like Hamiltonians on a L ×L ×L cubic lattice:H J ({S i })=(1−ρ)<ij>J ij S i S j −ρ <ij>S i S j (1)where S i =±1are Ising spins and ρcontrols the amount of frustration in the system.The sums are over all nearest neighbor spins in the First Neighbor Model (FNM),and over nearest and next-nearest neighbor spins (a total of 18)in the Second Neighbor Model (SNM).The quenched couplings J ij are independent random variables,taken from a Gaussian distribution of zero mean and unit vari-ance and we impose periodic boundary conditions.This Hamiltonian has both a spin glass term and a ferromag-netic term;for ρ=0we recover the standard spin glass model while for ρ=1we have the usual Ising ferro-magnet.We use sizes up to L =12for the FNM and up to L =8for the SNM.At these sizes,the heuristic algorithm [16]we use gives the ground state with very high probability so that our systematic errors are much smaller than our statistical ones.Ferromagnetic ordering —We first focus on the tran-sition from a state where the magnetization per spin m is zero to a ferromagnetic state (m =0).Note that the0.511.522.5m Lβ/ν(ρ-ρc )L1/νFIG.3.Scaling plot of the mean value of m as a function of ρin the Second Neighbor Model;ρF =0.236,ν=0.9and β=0.3.The inset shows the Binder cumulant of m J .Hamiltonian has the global symmetry {S i }→{−S i },so m is an order parameter for the transition.For each instance,we determine the magnetization density ±m J (since the J ij are independent continuous random vari-ables,there are only two ground states,related by sym-metry).Our order parameter is thenm =·denotes the average over the disorder variables{J ij }.For a large excess of ferromagnetic interactions (ρ≈1),m will be close to 1,while for a small excess (ρ≈0),m will go to zero in the large volume limit.For both the FNM and SNM,the transition appears to be of second order;indeed our distributions of |m J |always have a sin-gle peak whereas a first order transition should lead to two peaks at the transition point,one at m >0and one at m =0.(These two peaks would be generated by those samples that are magnetized and those that are not.)To determine the critical value ρF ,we have computed the Binder cumulant associated with the distribution of m J :g (ρ,L )=1m 4J m 2J 2 .(3)The different L curves cross very well for both mod-els,giving ρF NMF=0.385(5)and ρSNM F =0.236(5).Moreover,applying finite size scaling,we should have g (ρ,L )=˜g L 1/ν(ρ−ρF ) .Doing so for the order pa-rameter,we expect m (ρ,L )=L −β/νF L 1/ν(ρ−ρF ) .The corresponding data collapse is very satisfactory as can be seen in Fig.2and 3.Furthermore,the values of the critical exponents are close for the two models:we find β=0.3(1)and ν=0.9(2).These values are within the error bars of those found by Hartmann who studied the case where J ij =±1[6],obtaining β=0.2(1)and ν=1.1(3).Last but not least,the values of the Bindercumulant at the critical point are all close to one-another. These results give evidence in favor of universality in spin glasses,at least for this particular transition.Replica symmetry breaking and sponges—RSB lit-erally means that P(q),the probability distribution of spin overlaps taken between equilibrium configurations is not concentrated as in a ferromagnet.Unfortunately, estimations of P(q)are plagued byfinite size effets.Hart-mann[6]measured the width of P(q)among ground states of the±J model but,because of subtleties intrin-sic to that model,he was not able to determine the lo-cation of the spin glass phase boundary and thus made no claims about the existence of a mixed phase.In our work we use a different probe of RSB that seems to suffer far less fromfinite size effects.The starting point is to remark that in the presence of RSB several macroscop-ically different valleys dominate the system’s partition function,having O(1)differences in free-energy.Extrap-olating such behavior to zero-temperature,we expect to have system-size excitations above the ground state cost-ing only O(1)in energy.In our models,we characterize the system-size excitations by their topology,following the procedures developped in[17].First,we produce an excitation by taking at random2spins in the ground state,forcing them to change their relative orientation, and recomputing the new ground state with that con-straint.By definition,the spins that areflipped in an excitation form a connected cluster;if it and its comple-ment“wind”around in all three(x,y,z)directions,we call it a sponge.(For instance a cluster winds in the x di-rection if there exists a closed walk on it having non-zero winding number in x.)We use the proportion of such sponge-like(topologically non-trivial)events as an order parameter for RSB.In the droplet model,this quantity decays as L−θso asymptotically there are no large scale O(1)excitations.As in[17],we increased the signal to noise ratio byfirst ranking the spins according to their localfield;then we took the two spins at random from the list’s top25%(or50%,both led to the same conclusions). We have measured this order parameter as a function ofρand L.Our results are very similar in the FNM and the SNM.Looking at the plot in Fig.4,there seems tobe a phase transition in the FNM atρF NMRSB ≈0.380(5).Fitting these curves leads unambiguously to a non-zero large L value for the order parameter whenρ=0.37and to a zero value whenρ=0.39.In the SNM(see inset ofFig.4),wefindρSNMRSB ≈0.235(5)and the extrapolationsaway from this point behave as in the FNM.Note that, within statistical errors,the curves have a common cross-ing point.Furthermore,just as forρ=0,up to the tran-sition point the fraction of sponge-like events increases with L.It thus seems most likely that these excitations survive as L→∞ifρ<ρRSB.This is as expected in the meanfield approach,but not in the droplet/scaling pic-tures.However,the transition pointρRSB is close if not equal toρF in both of our models,so it seems to us that0.10.20.3spongeratioρFIG.4.Fraction of sponge-like excitations versusρin the FNM.(The inset shows the data for the SNM.)ρF NMRSB=0.380(5)(ρSNMRSB=0.235(5)).there is no mixed phase having both sponge excitations and positive magnetization.This would be in contrast to the meanfield prediction.Domain wall wandering andθDW—We now study directly the spin glass ordering,be-it with or without RSB,so we no longer resort to O(1)energy sponges.It is well known that spin glass ordering is sensitive to pertur-bations;the standard probe for this consists in compar-ing periodic and anti-periodic boundary conditions[5], thereby creating an interface in the system.The typical energy change for such a modification of boundary con-ditions should grow more slowly than L2in the spin glass phase,with O(1)energy changes arising not too rarely, for instance with a probability going as an inverse power of L.Another important aspect of such an interface is associated with its position space properties:in a spin glass phase,it is“space spanning”.This can be made precise algorithmically by considering whether the inter-face winds around the whole lattice.We take this behav-ior to be an indication of the“fragility”of the ground state;we thus consider that we are in a spin glass phase when there is a positive probability that the interface is “spongy”,i.e.,winds around the lattice.We begin with the FNM.In Fig.5we show the frac-tion of instances where the interface is spongy.The data suggest a transition atρDW≤0.4.However there is a systematic drift of the crossing points to the left so the most straight-forward interpretation of our results is ρRSB=ρF=ρDW;then the spin glass ordering disap-pears when the ferromagnetic ordering appears,the two orderings do not co-exist and there is no mixed phase. If on the other hand one really believes meanfield to be a good guide,one can assume that the mixed phase is present but only in a very small window,something like ρ∈[0.38,0.40].To make such a window larger and thus to give creadence in favor of a mixed phase,we increase the connectivity of the lattice from6to18by going to the SNM.There,our analysis leads toρDW≤0.255;thus00.10.20.30.40.50.60.70.80.9s p o n g e r a t i oρFIG.5.Fraction of spongy interfaces versus ρin the FNM.(The inset shows the data for the SNM.)The crossing points drift to the left,suggesting ρDW ≈ρRSB .in this “improved”model,the most optimistic estimate for the window would be ρ∈[0.236,0.255].However just as in the FNM,the crossing points of the curves drift and again ρDW −ρRSB is very small if not zero,a result quite puzzling from the mean field perspective,not to mention the fact that RSB seems to be excluded in this window.To pursue the search for a mixed phase,we have stud-ied the FNM in d =4for sizes L ≤5.The behavior is similar to the case d =3,and in particular we obtain ρF =0.315(5)and ρRSB =0.325(5)(data not shown).But the crossing points of the Binder cumulant which determine ρF now shift towards larger values as L in-creases.As a result,there is no compelling evidence for a mixed phase and probably ρDW =ρF =ρRSB .Discussion and conclusions —In spite of our at-tempts to render finite dimensional models mean-field-like,we are unable to confirm the mean field prediction that RSB and ferromagnetic order can co-exist.Since we also find quite clear signals for RSB via the existence of spongy clusters having O (1)energies in the whole un-magnetized region,we cannot explain our results using the droplet/scaling theories either.(There is no RSB in those approaches.)Interestingly,all the results we obtain are compatible with the “Trivial-Non-Trivial”or TNT picture [17,18].In that picture,there are system-size excitations whose energies are O (1);this leads to RSB,i.e.a non-trivial distribution of spin overlaps.Fur-thermore,they are also compact,with a surface fractal dimension d s <d ,leading to a trivial distribution of link overlaps.This TNT picture forbids a mixed phase as fol-lows.Assume that the local magnetization density (in a big enough sub-volume of the whole)is self-averaging and equal to the global magnetization density.Activat-ing compact system-size excitations will not affect the local magnetization but will change the global one unless m =0.A well behaved magnetization with TNT then forces m =0,i.e.,no mixed phase.Other numerical studies,in particular based on Monte-Carlo simulations,are needed.On the analytical side,a computation of the phase diagram on the Bethe lattice with RSB [19],or field theoric approaches for the mixed phase in the spirit of [20],would be welcome.Finally,ex-perimentally,it may be possible to test whether magneti-zation and spin glass ordering can co-exist in equilibrium ;however this will require careful checks that equilibrium is indeed reached.Acknowledgements —We thank M.M´e zard,E.Vin-cent,O.White and A.P.Young for very useful discus-sions.FK acknowledges support from the MENRT.The LPTMS is an Unit´e de Recherche de l’Universit´e Paris XI associ´e e au CNRS.。
《材料科学与工程基础》英文影印版习题及思考题及答案

《材料科学与工程基础》英文习题及思考题及答案第二章习题和思考题Questions and Problems2.6 Allowed values for the quantum numbers ofelectrons are as follows:The relationships between n and the shell designationsare noted in Table 2.1.Relative tothe subshells,l =0 corresponds to an s subshelll =1 corresponds to a p subshelll =2 corresponds to a d subshelll =3 corresponds to an f subshellFor the K shell, the four quantum numbersfor each of the two electrons in the 1s state, inthe order of nlmlms , are 100(1/2 ) and 100(-1/2 ).Write the four quantum numbers for allof the electrons inthe L and M shells, and notewhich correspond to the s, p, and d subshells.2.7 Give the electron configurations for the followingions: Fe2+, Fe3+, Cu+, Ba2+,Br-, andS2-.2.17 (a) Briefly cite the main differences betweenionic, covalent, and metallicbonding.(b) State the Pauli exclusion principle.2.18 Offer an explanation as to why covalently bonded materials are generally lessdense than ionically or metallically bonded ones.2.19 Compute the percents ionic character of the interatomic bonds for the followingcompounds: TiO2 , ZnTe, CsCl, InSb, and MgCl2 .2.21 Using Table 2.2, determine the number of covalent bonds that are possible foratoms of the following elements: germanium, phosphorus, selenium, and chlorine.2.24 On the basis of the hydrogen bond, explain the anomalous behavior of waterwhen it freezes. That is, why is there volume expansion upon solidification?3.1 What is the difference between atomic structure and crystal structure?3.2 What is the difference between a crystal structure and a crystal system?3.4Show for the body-centered cubic crystal structure that the unit cell edge lengtha and the atomic radius R are related through a =4R/√3.3.6 Show that the atomic packing factor for BCC is 0.68. .3.27* Show that the minimum cation-to-anion radius ratio for a coordinationnumber of 6 is 0.414. Hint: Use the NaCl crystal structure (Figure 3.5), and assume that anions and cations are just touching along cube edges and across face diagonals.3.48 Draw an orthorhombic unit cell, and within that cell a [121] direction and a(210) plane.3.50 Here are unit cells for two hypothetical metals:(a)What are the indices for the directions indicated by the two vectors in sketch(a)?(b) What are the indices for the two planes drawn in sketch (b)?3.51* Within a cubic unit cell, sketch the following directions:.3.53 Determine the indices for the directions shown in the following cubic unit cell:3.57 Determine the Miller indices for the planesshown in the following unit cell:3.58Determine the Miller indices for the planes shown in the following unit cell: 3.61* Sketch within a cubic unit cell the following planes:3.62 Sketch the atomic packing of (a) the (100)plane for the FCC crystal structure, and (b) the (111) plane for the BCC crystal structure (similar to Figures 3.24b and 3.25b).3.77 Explain why the properties of polycrystalline materials are most oftenisotropic.5.1 Calculate the fraction of atom sites that are vacant for lead at its meltingtemperature of 327_C. Assume an energy for vacancy formation of 0.55eV/atom.5.7 If cupric oxide (CuO) is exposed to reducing atmospheres at elevatedtemperatures, some of the Cu2_ ions will become Cu_.(a) Under these conditions, name one crystalline defect that you would expect toform in order to maintain charge neutrality.(b) How many Cu_ ions are required for the creation of each defect?5.8 Below, atomic radius, crystal structure, electronegativity, and the most commonvalence are tabulated, for several elements; for those that are nonmetals, only atomic radii are indicated.Which of these elements would you expect to form the following with copper:(a) A substitutional solid solution having complete solubility?(b) A substitutional solid solution of incomplete solubility?(c) An interstitial solid solution?5.9 For both FCC and BCC crystal structures, there are two different types ofinterstitial sites. In each case, one site is larger than the other, which site isnormally occupied by impurity atoms. For FCC, this larger one is located at the center of each edge of the unit cell; it is termed an octahedral interstitial site. On the other hand, with BCC the larger site type is found at 0, __, __ positions—that is, lying on _100_ faces, and situated midway between two unit cell edges on this face and one-quarter of the distance between the other two unit cell edges; it is termed a tetrahedral interstitial site. For both FCC and BCC crystalstructures, compute the radius r of an impurity atom that will just fit into one of these sites in terms of the atomic radius R of the host atom.5.10 (a) Suppose that Li2O is added as an impurity to CaO. If the Li_ substitutes forCa2_, what kind of vacancies would you expect to form? How many of thesevacancies are created for every Li_ added?(b) Suppose that CaCl2 is added as an impurity to CaO. If the Cl_ substitutes forO2_, what kind of vacancies would you expect to form? How many of thevacancies are created for every Cl_ added?5.28 Copper and platinum both have the FCC crystal structure and Cu forms asubstitutional solid solution for concentrations up to approximately 6 wt% Cu at room temperature. Compute the unit cell edge length for a 95 wt% Pt-5 wt% Cu alloy.5.29 Cite the relative Burgers vector–dislocation line orientations for edge, screw, andmixed dislocations.6.1 Briefly explain the difference between selfdiffusion and interdiffusion.6.3 (a) Compare interstitial and vacancy atomic mechanisms for diffusion.(b) Cite two reasons why interstitial diffusion is normally more rapid thanvacancy diffusion.6.4 Briefly explain the concept of steady state as it applies to diffusion.6.5 (a) Briefly explain the concept of a driving force.(b) What is the driving force for steadystate diffusion?6.6Compute the number of kilograms of hydrogen that pass per hour through a5-mm thick sheet of palladium having an area of 0.20 m2at 500℃. Assume a diffusion coefficient of 1.0×10- 8 m2/s, that the concentrations at the high- and low-pressure sides of the plate are 2.4 and 0.6 kg of hydrogen per cubic meter of palladium, and that steady-state conditions have been attained.6.7 A sheet of steel 1.5 mm thick has nitrogen atmospheres on both sides at 1200℃and is permitted to achieve a steady-state diffusion condition. The diffusion coefficient for nitrogen in steel at this temperature is 6×10-11m2/s, and the diffusion flux is found to be 1.2×10- 7kg/m2-s. Also, it is known that the concentration of nitrogen in the steel at the high-pressure surface is 4 kg/m3. How far into the sheet from this high-pressure side will the concentration be 2.0 kg/m3?Assume a linear concentration profile.6.24. Carbon is allowed to diffuse through a steel plate 15 mm thick. Theconcentrations of carbon at the two faces are 0.65 and 0.30 kg C/m3 Fe, whichare maintained constant. If the preexponential and activation energy are 6.2 _10_7 m2/s and 80,000 J/mol, respectively, compute the temperature at which the diffusion flux is 1.43 _ 10_9 kg/m2-s.6.25 The steady-state diffusion flux through a metal plate is 5.4_10_10 kg/m2-s at atemperature of 727_C (1000 K) and when the concentration gradient is _350kg/m4. Calculate the diffusion flux at 1027_C (1300 K) for the sameconcentration gradient and assuming an activation energy for diffusion of125,000 J/mol.10.2 What thermodynamic condition must be met for a state of equilibrium to exist? 10.4 What is the difference between the states of phase equilibrium and metastability?10.5 Cite the phases that are present and the phase compositions for the followingalloys:(a) 90 wt% Zn–10 wt% Cu at 400℃(b) 75 wt% Sn–25wt%Pb at 175℃(c) 55 wt% Ag–45 wt% Cu at 900℃(d) 30 wt% Pb–70 wt% Mg at 425℃(e) 2.12 kg Zn and 1.88 kg Cu at 500℃(f ) 37 lbm Pb and 6.5 lbm Mg at 400℃(g) 8.2 mol Ni and 4.3 mol Cu at 1250℃.(h) 4.5 mol Sn and 0.45 mol Pb at 200℃10.6 For an alloy of composition 74 wt% Zn–26 wt% Cu, cite the phases presentand their compositions at the following temperatures: 850℃, 750℃, 680℃, 600℃, and 500℃.10.7 Determine the relative amounts (in terms of mass fractions) of the phases forthe alloys and temperatures given inProblem 10.5.10.9 Determine the relative amounts (interms of volume fractions) of the phases forthe alloys and temperatures given inProblem 10.5a, b, and c. Below are given theapproximate densities of the various metalsat the alloy temperatures:10.18 Is it possible to have a copper–silveralloy that, at equilibrium, consists of a _ phase of composition 92 wt% Ag–8wt% Cu, and also a liquid phase of composition 76 wt% Ag–24 wt% Cu? If so, what will be the approximate temperature of the alloy? If this is not possible,explain why.10.20 A copper–nickel alloy of composition 70 wt% Ni–30 wt% Cu is slowly heatedfrom a temperature of 1300_C .(a) At what temperature does the first liquid phase form?(b) What is the composition of this liquid phase?(c) At what temperature does complete melting of the alloy occur?(d) What is the composition of the last solid remaining prior to completemelting?10.28 .Is it possible to have a copper–silver alloy of composition 50 wt% Ag–50 wt%Cu, which, at equilibrium, consists of _ and _ phases having mass fractions W_ _0.60 and W_ _ 0.40? If so, what will be the approximate temperature of the alloy?If such an alloy is not possible, explain why.10.30 At 700_C , what is the maximum solubility (a) of Cu in Ag? (b) Of Ag in Cu?第三章习题和思考题3.3If the atomic radius of aluminum is 0.143nm, calculate the volume of its unitcell in cubic meters.3.8 Iron has a BCC crystal structure, an atomic radius of 0.124 nm, and an atomicweight of 55.85 g/mol. Compute and compare its density with the experimental value found inside the front cover.3.9 Calculate the radius of an iridium atom given that Ir has an FCC crystal structure,a density of 22.4 g/cm3, and an atomic weight of 192.2 g/mol.3.13 Using atomic weight, crystal structure, and atomic radius data tabulated insidethe front cover, compute the theoretical densities of lead, chromium, copper, and cobalt, and then compare these values with the measured densities listed in this same table. The c/a ratio for cobalt is 1.623.3.15 Below are listed the atomic weight, density, and atomic radius for threehypothetical alloys. For each determine whether its crystal structure is FCC,BCC, or simple cubic and then justify your determination. A simple cubic unitcell is shown in Figure 3.40.3.21 This is a unit cell for a hypotheticalmetal:(a) To which crystal system doesthis unit cell belong?(b) What would this crystal structure be called?(c) Calculate the density of the material, given that its atomic weight is 141g/mol.3.25 For a ceramic compound, what are the two characteristics of the component ionsthat determine the crystal structure?3.29 On the basis of ionic charge and ionic radii, predict the crystal structures for thefollowing materials: (a) CsI, (b) NiO, (c) KI, and (d) NiS. Justify your selections.3.35 Magnesium oxide has the rock salt crystal structure and a density of 3.58 g/cm3.(a) Determine the unit cell edge length. (b) How does this result compare withthe edge length as determined from the radii in Table 3.4, assuming that theMg2_ and O2_ ions just touch each other along the edges?3.36 Compute the theoretical density of diamond given that the CUC distance andbond angle are 0.154 nm and 109.5°, respectively. How does this value compare with the measured density?3.38 Cadmium sulfide (CdS) has a cubic unit cell, and from x-ray diffraction data it isknown that the cell edge length is 0.582 nm. If the measured density is 4.82 g/cm3 , how many Cd 2+ and S 2—ions are there per unit cell?3.41 A hypothetical AX type of ceramic material is known to have a density of 2.65g/cm 3 and a unit cell of cubic symmetry with a cell edge length of 0.43 nm. The atomic weights of the A and X elements are 86.6 and 40.3 g/mol, respectively.On the basis of this information, which of the following crystal structures is (are) possible for this material: rock salt, cesium chloride, or zinc blende? Justify your choice(s).3.42 The unit cell for Mg Fe2O3 (MgO-Fe2O3) has cubic symmetry with a unit celledge length of 0.836 nm. If the density of this material is 4.52 g/cm 3 , compute its atomic packing factor. For this computation, you will need to use ionic radii listed in Table 3.4.3.44 Compute the atomic packing factor for the diamond cubic crystal structure(Figure 3.16). Assume that bonding atoms touch one another, that the angle between adjacent bonds is 109.5°, and that each atom internal to the unit cell is positioned a/4 of the distance away from the two nearest cell faces (a is the unit cell edge length).3.45 Compute the atomic packing factor for cesium chloride using the ionic radii inTable 3.4 and assuming that the ions touch along the cube diagonals.3.46 In terms of bonding, explain why silicate materials have relatively low densities.3.47 Determine the angle between covalent bonds in an SiO44—tetrahedron.3.63 For each of the following crystal structures, represent the indicated plane in themanner of Figures 3.24 and 3.25, showing both anions and cations: (a) (100)plane for the rock salt crystal structure, (b) (110) plane for the cesium chloride crystal structure, (c) (111) plane for the zinc blende crystal structure, and (d) (110) plane for the perovskite crystal structure.3.66 The zinc blende crystal structure is one that may be generated from close-packedplanes of anions.(a) Will the stacking sequence for this structure be FCC or HCP? Why?(b) Will cations fill tetrahedral or octahedral positions? Why?(c) What fraction of the positions will be occupied?3.81* The metal iridium has an FCC crystal structure. If the angle of diffraction forthe (220) set of planes occurs at 69.22°(first-order reflection) when monochromatic x-radiation having a wavelength of 0.1542 nm is used, compute(a) the interplanar spacing for this set of planes, and (b) the atomic radius for aniridium atom.4.10 What is the difference between configuration and conformation in relation topolymer chains? vinyl chloride).4.22 (a) Determine the ratio of butadiene to styrene mers in a copolymer having aweight-average molecular weight of 350,000 g/mol and weight-average degree of polymerization of 4425.(b) Which type(s) of copolymer(s) will this copolymer be, considering thefollowing possibilities: random, alternating, graft, and block? Why?4.23 Crosslinked copolymers consisting of 60 wt% ethylene and 40 wt% propylenemay have elastic properties similar to those for natural rubber. For a copolymer of this composition, determine the fraction of both mer types.4.25 (a) Compare the crystalline state in metals and polymers.(b) Compare thenoncrystalline state as it applies to polymers and ceramic glasses.4.26 Explain briefly why the tendency of a polymer to crystallize decreases withincreasing molecular weight.4.27* For each of the following pairs of polymers, do the following: (1) state whetheror not it is possible to determine if one polymer is more likely to crystallize than the other; (2) if it is possible, note which is the more likely and then cite reason(s) for your choice; and (3) if it is not possible to decide, then state why.(a) Linear and syndiotactic polyvinyl chloride; linear and isotactic polystyrene.(b) Network phenol-formaldehyde; linear and heavily crosslinked ci s-isoprene.(c) Linear polyethylene; lightly branched isotactic polypropylene.(d) Alternating poly(styrene-ethylene) copolymer; randompoly(vinylchloride-tetrafluoroethylene) copolymer.4.28 Compute the density of totally crystalline polyethylene. The orthorhombic unitcell for polyethylene is shown in Figure 4.10; also, the equivalent of two ethylene mer units is contained within each unit cell.5.11 What point defects are possible for MgO as an impurity in Al2O3? How manyMg 2+ ions must be added to form each of these defects?5.13 What is the composition, in weight percent, of an alloy that consists of 6 at% Pband 94 at% Sn?5.14 Calculate the composition, in weight per-cent, of an alloy that contains 218.0 kgtitanium, 14.6 kg of aluminum, and 9.7 kg of vanadium.5.23 Gold forms a substitutional solid solution with silver. Compute the number ofgold atoms per cubic centimeter for a silver-gold alloy that contains 10 wt% Au and 90 wt% Ag. The densities of pure gold and silver are 19.32 and 10.49 g/cm3 , respectively.8.53 In terms of molecular structure, explain why phenol-formaldehyde (Bakelite)will not be an elastomer.10.50 Compute the mass fractions of αferrite and cementite in pearlite. assumingthat pressure is held constant.10.52 (a) What is the distinction between hypoeutectoid and hypereutectoid steels?(b) In a hypoeutectoid steel, both eutectoid and proeutectoid ferrite exist. Explainthe difference between them. What will be the carbon concentration in each?10.56 Consider 1.0 kg of austenite containing 1.15 wt% C, cooled to below 727_C(a) What is the proeutectoid phase?(b) How many kilograms each of total ferrite and cementite form?(c) How many kilograms each of pearlite and the proeutectoid phase form?(d) Schematically sketch and label the resulting microstructure.10.60 The mass fractions of total ferrite and total cementite in an iron–carbon alloyare 0.88 and 0.12, respectively. Is this a hypoeutectoid or hypereutectoid alloy?Why?10.64 Is it possible to have an iron–carbon alloy for which the mass fractions of totalferrite and proeutectoid cementite are 0.846 and 0.049, respectively? Why orwhy not?第四章习题和思考题7.3 A specimen of aluminum having a rectangular cross section 10 mm _ 12.7 mmis pulled in tension with 35,500 N force, producing only elastic deformation. 7.5 A steel bar 100 mm long and having a square cross section 20 mm on an edge ispulled in tension with a load of 89,000 N , and experiences an elongation of 0.10 mm . Assuming that the deformation is entirely elastic, calculate the elasticmodulus of the steel.7.7 For a bronze alloy, the stress at which plastic deformation begins is 275 MPa ,and the modulus of elasticity is 115 Gpa .(a) What is the maximum load that may be applied to a specimen with across-sectional area of 325mm, without plastic deformation?(b) If the original specimen length is 115 mm , what is the maximum length towhich it may be stretched without causing plastic deformation?7.8 A cylindrical rod of copper (E _ 110 GPa, Stress (MPa) ) having a yield strengthof 240Mpa is to be subjected to a load of 6660 N. If the length of the rod is 380 mm, what must be the diameter to allow an elongation of 0.50 mm?7.9 Consider a cylindrical specimen of a steel alloy (Figure 7.33) 10mm in diameterand 75 mm long that is pulled in tension. Determine its elongation when a load of 23,500 N is applied.7.16 A cylindrical specimen of some alloy 8 mm in diameter is stressed elasticallyin tension. A force of 15,700 N produces a reduction in specimen diameter of 5 _ 10_3 mm. Compute Poisson’s ratio for this material if its modulus of elasticity is 140 GPa .7.17 A cylindrical specimen of a hypothetical metal alloy is stressed in compression.If its original and final diameters are 20.000 and 20.025 mm, respectively, and its final length is 74.96 mm, compute its original length if the deformation is totally elastic. The elastic and shear moduli for this alloy are 105 Gpa and 39.7 GPa,respectively.7.19 A brass alloy is known to have a yield strength of 275 MPa, a tensile strength of380 MPa, and an elastic modulus of 103 GPa . A cylindrical specimen of thisalloy 12.7 mm in diameter and 250 mm long is stressed in tension and found to elongate 7.6 mm . On the basis of the information given, is it possible tocompute the magnitude of the load that is necessary to produce this change inlength? If so, calculate the load. If not, explain why.7.20A cylindrical metal specimen 15.0mmin diameter and 150mm long is to besubjected to a tensile stress of 50 Mpa; at this stress level the resulting deformation will be totally elastic.(a)If the elongation must be less than 0.072mm,which of the metals in Tabla7.1are suitable candidates? Why ?(b)If, in addition, the maximum permissible diameter decrease is 2.3×10-3mm,which of the metals in Table 7.1may be used ? Why?7.22 Cite the primary differences between elastic, anelastic, and plastic deformationbehaviors.7.23 diameter of 10.0 mm is to be deformed using a tensile load of 27,500 N. It mustnot experience either plastic deformation or a diameter reduction of more than7.5×10-3 mm. Of the materials listed as follows, which are possible candidates?Justify your choice(s).7.24 A cylindrical rod 380 mm long, having a diameter of 10.0 mm, is to besubjected to a tensile load. If the rod is to experience neither plastic deformationnor an elongation of more than 0.9 mm when the applied load is 24,500 N,which of the four metals or alloys listed below are possible candidates?7.25 Figure 7.33 shows the tensile engineering stress–strain behavior for a steel alloy.(a) What is the modulus of elasticity?(b) What is the proportional limit?(c) What is the yield strength at a strain offset of 0.002?(d) What is the tensile strength?7.27 A load of 44,500 N is applied to a cylindrical specimen of steel (displaying thestress–strain behavior shown in Figure 7.33) that has a cross-sectional diameter of 10 mm .(a) Will the specimen experience elastic or plastic deformation? Why?(b) If the original specimen length is 500 mm), how much will it increase inlength when t his load is applied?7.29 A cylindrical specimen of aluminumhaving a diameter of 12.8 mm and a gaugelength of 50.800 mm is pulled in tension. Usethe load–elongation characteristics tabulatedbelow to complete problems a through f.(a)Plot the data as engineering stressversusengineering strain.(b) Compute the modulus of elasticity.(c) Determine the yield strength at astrainoffset of 0.002.(d) Determine the tensile strength of thisalloy.(e) What is the approximate ductility, in percent elongation?(f ) Compute the modulus of resilience.7.35 (a) Make a schematic plot showing the tensile true stress–strain behavior for atypical metal alloy.(b) Superimpose on this plot a schematic curve for the compressive truestress–strain behavior for the same alloy. Explain any difference between thiscurve and the one in part a.(c) Now superimpose a schematic curve for the compressive engineeringstress–strain behavior for this same alloy, and explain any difference between this curve and the one in part b.7.39 A tensile test is performed on a metal specimen, and it is found that a true plasticstrain of 0.20 is produced when a true stress of 575 MPa is applied; for the same metal, the value of K in Equation 7.19 is 860 MPa. Calculate the true strain that results from the application of a true stress of 600 Mpa.7.40 For some metal alloy, a true stress of 415 MPa produces a plastic true strain of0.475. How much will a specimen of this material elongate when a true stress of325 MPa is applied if the original length is 300 mm ? Assume a value of 0.25 for the strain-hardening exponent n.7.43 Find the toughness (or energy to cause fracture) for a metal that experiences bothelastic and plastic deformation. Assume Equation 7.5 for elastic deformation,that the modulus of elasticity is 172 GPa , and that elastic deformation terminates at a strain of 0.01. For plastic deformation, assume that the relationship between stress and strain is described by Equation 7.19, in which the values for K and n are 6900 Mpa and 0.30, respectively. Furthermore, plastic deformation occurs between strain values of 0.01 and 0.75, at which point fracture occurs.7.47 A steel specimen having a rectangular cross section of dimensions 19 mm×3.2mm (0.75in×0.125in.) has the stress–strain behavior shown in Figure 7.33. If this specimen is subjected to a tensile force of 33,400 N (7,500lbf ), then(a) Determine the elastic and plastic strain values.(b) If its original length is 460 mm (18 in.), what will be its final length after theload in part a is applied and then released?7.50 A three-point bending test was performed on an aluminum oxide specimenhaving a circular cross section of radius 3.5 mm; the specimen fractured at a load of 950 N when the distance between the support points was 50 mm . Another test is to be performed on a specimen of this same material, but one that has a square cross section of 12 mm length on each edge. At what load would you expect this specimen to fracture if the support point separation is 40 mm ?7.51 (a) A three-point transverse bending test is conducted on a cylindrical specimenof aluminum oxide having a reported flexural strength of 390 MPa . If the speci- men radius is 2.5 mm and the support point separation distance is 30 mm ,predict whether or not you would expect the specimen to fracture when a load of 620 N is applied. Justify your prediction.(b) Would you be 100% certain of the prediction in part a? Why or why not?7.57 When citing the ductility as percent elongation for semicrystalline polymers, it isnot necessary to specify the specimen gauge length, as is the case with metals.Why is this so?7.66 Using the data represented in Figure 7.31, specify equations relating tensilestrength and Brinell hardness for brass and nodular cast iron, similar toEquations 7.25a and 7.25b for steels.8.4 For each of edge, screw, and mixed dislocations, cite the relationship between thedirection of the applied shear stress and the direction of dislocation line motion.8.5 (a) Define a slip system.(b) Do all metals have the same slip system? Why or why not?8.7. One slip system for theBCCcrystal structure is _110__111_. In a manner similarto Figure 8.6b sketch a _110_-type plane for the BCC structure, representingatom positions with circles. Now, using arrows, indicate two different _111_ slip directions within this plane.8.15* List four major differences between deformation by twinning and deformationby slip relative to mechanism, conditions of occurrence, and final result.8.18 Describe in your own words the three strengthening mechanisms discussed inthis chapter (i.e., grain size reduction, solid solution strengthening, and strainhardening). Be sure to explain how dislocations are involved in each of thestrengthening techniques.8.19 (a) From the plot of yield strength versus (grain diameter)_1/2 for a 70 Cu–30 Zncartridge brass, Figure 8.15, determine values for the constants _0 and ky inEquation 8.5.(b) Now predict the yield strength of this alloy when the average grain diameteris 1.0 _ 10_3 mm.8.20. The lower yield point for an iron that has an average grain diameter of 5 _ 10_2mm is 135 MPa . At a grain diameter of 8 _ 10_3 mm, the yield point increases to 260MPa. At what grain diameter will the lower yield point be 205 Mpa ?8.24 (a) Show, for a tensile test, thatif there is no change in specimen volume during the deformation process (i.e., A0 l0 _Ad ld).(b) Using the result of part a, compute the percent cold work experienced bynaval brass (the stress–strain behavior of which is shown in Figure 7.12) when a stress of 400 MPa is applied.8.25 Two previously undeformed cylindrical specimens of an alloy are to be strainhardened by reducing their cross-sectional areas (while maintaining their circular cross sections). For one specimen, the initial and deformed radii are 16 mm and11 mm, respectively. The second specimen, with an initial radius of 12 mm, musthave the same deformed hardness as the first specimen; compute the secondspecimen’s radius after deformation.8.26 Two previously undeformed specimens of the same metal are to be plasticallydeformed by reducing their cross-sectional areas. One has a circular cross section, and the other is rectangular is to remain as such. Their original and deformeddimensions are as follows:Which of these specimens will be the hardest after plastic deformation, and why?8.27 A cylindrical specimen of cold-worked copper has a ductility (%EL) of 25%. Ifits coldworked radius is 10 mm (0.40 in.), what was its radius beforedeformation?8.28 (a) What is the approximate ductility (%EL) of a brass that has a yield strengthof 275 MPa ?(b) What is the approximate Brinell hardness of a 1040 steel having a yieldstrength of 690 MPa?8.41 In your own words, describe the mechanisms by which semicrystalline polymers(a) elasticallydeform and (b) plastically deform, and (c) by which elastomerselastically deform.8.42 Briefly explain how each of the following influences the tensile modulus of asemicrystallinepolymer and why:(a) molecular weight;(b) degree of crystallinity;(c) deformation by drawing;(d) annealing of an undeformed material;(e) annealing of a drawn material.8.43* Briefly explain how each of the following influences the tensile or yieldstrength of a semicrystalline polymer and why:(a) molecular weight;。
spin glass

spin glass
Spin glass 中文名称自旋玻璃态。
定义
自旋玻璃最初主要是在合金中发现的,它是指一些含大量局域磁矩的金属或合金,在这类磁系统中,磁矩之间存在着铁磁相互作用与反铁磁相互作用的竞争。
随着温度的降低,整个磁矩系统的取向状态经历一个较为复杂的过程,最终冻结为自旋玻璃态。
从时间坐标上看,各个磁矩的冻结方向是无序的。
原理
这种稀释合金系统往往在某特定温度Tf以下,其杂质磁矩将混乱地被冻结起来,宏观磁矩等于零,系统的这一状态称之为自旋玻璃态。
重要特征
自旋玻璃的磁特性有两个重要特征:
1. 低场磁化率在冻结温度时出现一尖峰,峰值的尖锐度随磁场的减低而愈加显著;
2. 在冻结温度以下,自旋玻璃不具有自发磁化,其磁化过程是不可逆的,且存在剩磁影响及时间效应。
玻色-爱因斯坦凝聚态和相变

玻色-爱因斯坦凝聚态和相变
玻色-爱因斯坦凝聚(Bose-Einstein Condensates,简称BEC)是量子物理中的一种现象,其中遵从玻色–爱因斯坦统计且总粒子数守恒的理想气体,在温度低于一个极低但非零的转变温度 T_c 时,占全部粒子数有限百分比的(宏观数量的)部分将聚集到单一的粒子最低能态上。
这种现象是1924年由印度物理学家玻色和德国物理学家爱因斯坦独立提出的。
BEC的形成可以通过增加粒子浓度(压缩体积)或降低温度来实现。
如果是通过压缩体积达到的BEC,那么这是一种1阶相变,具有相变潜热;而如果是通过降低温度达到的BEC,那么这是一种三阶相变,此时在相变点位置比热容连续但比热容对温度导数不连续。
尽管BEC的概念已经存在了近百年,但相关的研究和探索至今仍在进行中,无论是在数学还是物理领域。
Dynamic phase diagram of the Number Partitioning Problem

1
arXiv:cond-mat/0408484v1 [cond-mat.dis-nn] 23 Aug 2004
We study the dynamic phase diagram of a spin model associated with the Number Partitioning Problem, as a function of temperature and of the fraction K/N of spins allowed to flip simultaneously. The case K = 1 reproduces the activated behavior of Bouchaud’s trap model, whereas the opposite limit K = N can be mapped onto the entropic trap model proposed by Barrat and M´ ezard. In the intermediate case 1 ≪ K ≪ N , the dynamics corresponds to a modified version of the Barrat and M´ ezard model, which includes a slow (rather than instantaneous) decorrelation at each step. A transition from an activated regime to an entropic one is observed at temperature Tg /2 in agreement with recent work on this model. Ergodicity breaking occurs for T < Tg /2 in the thermodynamic limit, if K/N → 0. In this temperature range, the model exhibits a non trivial fluctuation-dissipation relation leading for K ≪ N to a single effective temperature equal to Tg /2. These results give new insights on the relevance and limitations of the picture proposed by simple trap models.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Spin glass behaviour on random lattices
M O Hase1,2,a, J R L de Almeida2,b and S R Salinas1,c 1 Instituto de F´ isica, Universidade de S˜ ao Paulo Caixa Postal 66318 05315-970, S˜ ao Paulo, SP, Brazil 2 Departamento de F´ isica, Universidade Federal de Pernambuco 50670-901, Recife, PE, Brazil a mhase@p.br, b almeida@df.ufpe.br and c ssalinas@p.br February 6, 2008
Using the replica method, the variational free energy is written as c c n 1 2 f [G] = br qα − lim + 1 ,··· ,αr n → 0 2 2 r=0 β
(α1 ,··· ,αr ) n
− ln Tr{σ} exp G({σα }) + βH
Abstract The ground-state phase diagram of an Ising spin-glass model on a random graph with an arbitrary fraction (w) of ferromagnetic interactions is analysed in the presence of an external field. Using the replica method, and performing an analysis of stability of the replica-symmetric solution, it was shown that w = 1/2, correponding to an unbiased spin glass, is a singular point in the phase diagram, separating a region with a spin glass phase (w < 1/2) from a region with spin glass, ferromagnetic, mixed, and paramagnetic phases (w > 1/2).
and J0 is a positive parameter. According to the distribution (2), two sites are connected (disconnected) with a probability c/N (1 − c/N ), where c is the mean connectivity of the lattice. In this diluted ±J model, parameter w weighs the fraction of ferromagnetic bonds. 2
(x,x′ )∈ΛN
Jx,x′ σx σx′ − H
σx ,
x∈ΛN
(1)
where σx ∈ {−1, 1} is an Ising spin on the site x, belonging to a finite lattice ΛN of N sites and H is the external magnetic field. The first sum is over all distinct pairs of lattice sites. The exchange integrals {Jx,x′ } are independent and identically distributed random variables, associated with the distribution c c pJ (Jx,x′ ) = 1 − δ (Jx,x′ ) + ρ(Jx,x′ ) , (2) N N where ρ(Jx,x′ ) = wδ (Jx,x′ − J0 ) + (1 − w )δ (Jx,x′ + J0 ) , (3)
σα
,
(4)
α=1
where br =
R
dJρ(J ) coshn (βJ ) tanhr (βJ ) ,
(5)
and
n
G({σα }) = c
r =0 (α1 ,··· ,αr )
br qα1 ,··· ,αr σα1 · · · σαr
(6)
is the global order parameter[6, 11], which takes into account the 2n order parameters of this problem (in contrast to the Sherrington - Kirkpatrick (SK) model[1], which has just two order parameters). The stationary free energy comes from the minimization of the variational free energy (4) with respect to the set {qα1 ,··· ,αr }, which leads to the stationary conditions qα1 ,··· ,αr = Tr{σ} σα1 · · · σαr exp [G({σα }) + βH n α=1 σα ] . n Trσ exp [G({σα }) + βH α=1 σα ] (7)
model of Viana and Bray (VB), which is tractable by the replica method, leads to a glassy phase in the ground state. However, due to the subtleties of the problem, there are just a few available analytical results, and a complete solution remains an open question. Also, in spite of some efforts, there are no satisfactory solutions for the field behavior of the SG problem on random graphs[8]. In contrast to earlier results, more recent analytical calculations for the ground state of a dilute ferromagnet, with a specific choice of random fields, do not indicate the existence of replica breaking [9, 10]. In this article, some results for the ground state of a frustrated ±J Ising spin-glass on a random graph, in the presence of an external magnetic field, and with an arbitrary fraction of ferromagnetic interactions are reported. A parameter w that gauges the concentration of these ferromagnetic (J0 > 0) interactions is introduced. For w = 1/2, this model is a pure, unbiased, spin glass; ferromagnetic (antiferromagnetic) interactions are favoured for w > 1/2 (w < 1/2). It is known that the presence of an external field always increases the technical complexity of the solutions of these problems. In this analysis, the phase diagram in the ground state for external fields that are multiples of J0 is obtained, which resembles the choice of random fields that was already adopted in a previous work [8]. The topology of the random network favours the appearance of a spin glass phase for w < 1/2. For w ≥ 1/2, the usual spin glass, ferromagnetic, mixed, and paramagnetic phases are obtained. It should be emphasized that even in the presence of overall antiferromagnetic interactions (w < 1/2) the inherent disorder of the lattice still yields a spin-glass phase. Consider the Hamiltonian H({σx }) = −
