正弦和余弦定理
正弦定理和余弦定理

正弦定理和余弦定理正弦定理是什么正弦定理是三角学中的一个基本定理,它定义了在任意三角形中,角A、B、C所对的边长a、b、c与它们的正弦值之比相等,都等于外接圆的直径,即a/sinA = b/sinB = c/sinC = 2r=D(r为外接圆半径,D为直径)。
这个定理也可以表达为在任意一个平面三角形中,各边和它所对角的正弦值的比相等且等于外接圆的直径。
正弦定理的应用非常广泛,在解决三角形问题时非常有用。
例如,可以用正弦定理来求解三角形的边长或角的大小,或者判断一个三角形是否可能存在等。
余弦定理是什么余弦定理是描述三角形中三边长度与一个角的余弦值关系的数学定理,是勾股定理在一般三角形情形下的推广。
余弦定理中角条件是唯一的,所以角的对边在等式左边,两邻边及角的余弦在等式右边。
等式右边除夹角余弦值外的部分,可以看作是差的完全平方公式,可以辅助我们记忆。
正弦定理的证明方法方法1、直接过三角形一顶点如C作对边AB的垂线(设垂线长为h),则sinA=h/b,sinB=h/a,所以,sinA/a=sinB/b,同理可得sinC/c=sinB/b,因此a/sinA=b/sinB=c/sinC。
方法2、利用三角形面积公式:S=1/2absinC=1/2bcsinA=1/2casinB,整理即得:a/sinA=b/sinB=c/sinC。
方法3:作三角形的外接圆,过B作边BC的垂线交圆于D,连接CD,因圆周角为直角,则CD长为直径(不妨直径长度设为d)。
因圆周角相等,即角D=角A,所以sinA=sinD=BC/CD=a/d,同理可证sinB=b/d,sinC=c/d.所以,a/sinA=b/sinB=c/sinC。
方法4.还有一种向量的方法,在旧版课本上。
正弦定理证明具体步骤步骤1.在锐角△ABC中,设BC=a,AC=b,AB=c。
作CH⊥AB垂足为点HCH=a·sinBCH=b·sinA∴a·sinB=b·sinA得到 a/sinA=b/sinB同理,在△ABC中, b/sinB=c/sinC步骤2.证明a/sinA=b/sinB=c/sinC=2R:如图,任意三角形ABC,作ABC的外接圆O.作直径BD交⊙O于D.连接DA.因为直径所对的圆周角是直角,所以∠DAB=90度因为同弧所对的圆周角相等,所以∠D等于∠C.所以c/sinC=c/sinD=BD=2R 类似可证其余两个等式。
正弦,余弦定理

正弦,余弦定理正弦和余弦定理是三角函数中的重要概念,它们在解决三角形相关问题时起到了关键作用。
本文将分别介绍正弦和余弦定理的含义、推导过程以及应用场景。
一、正弦定理正弦定理是指在任意三角形中,三边的长度与其对应的角的正弦值之间存在一定的关系。
设三角形的三边分别为a、b、c,对应的角为A、B、C,则正弦定理可以表示为:a/sinA = b/sinB = c/sinC正弦定理的推导过程如下:假设有一个三角形ABC,分别连接AB、AC的垂线,垂足分别为D、E。
根据几何性质,可以得到以下关系:AD = b * sinCAE = c * sinB再根据三角形的内角和等于180°的性质,可以得到:∠B + ∠C + ∠AED = 180°∠B + ∠C + ∠ADE = 180°将上述两个等式代入,得到:∠ADE + ∠AED = 180°∠ADE + ∠ABC = 180°由此可以得出∠ABC = ∠AED,进而得到以下等式:sinA/sinB = AD/AE = b/c通过类似的推导过程,可以得到其他两个等式:sinA/sinC = c/asinB/sinC = a/b由此可以看出,正弦定理实际上是三个比例关系的等式,可以用来求解未知边长或角度的问题。
例如,已知一个三角形的两边和夹角,可以利用正弦定理求解第三边的长度或另外两个角的大小。
二、余弦定理余弦定理是指在任意三角形中,三边的长度与其对应的角的余弦值之间存在一定的关系。
设三角形的三边分别为a、b、c,对应的角为A、B、C,则余弦定理可以表示为:c² = a² + b² - 2abcosCb² = a² + c² - 2accosBa² = b² + c² - 2bccosA余弦定理的推导过程如下:假设有一个三角形ABC,分别连接AC、BC的垂线,垂足分别为D、E。
(完整版)解三角形之正弦定理与余弦定理

正弦定理与余弦定理教学目标掌握正弦定理和余弦定理的推导,并能用它们解三角形正余弦定理及三角形面积公式.教学重难点掌握正弦定理和余弦定理的推导,并能用它们解三角形.知识点清单一. 正弦定理:1. 正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,并且都等于外接圆的直径,即a b c2R( 其中R 是三角形外接圆的半径)sin A sinB sinC2. 变形:1)a b c a b csin sin sinC sin sin sinC 2)化边为角:a:b:c sin A:sin B:sinC;a sin A;b sin B a sin Ab sinBc sinC c sin C3)化边为角:a 2Rsin A, b 2Rsin B, c 2RsinC4)化角为边:sin A a;sin B b ; sin A asin B b sinC c sinC c5)化角为边:sin A a sinB b,sinC c2R2R2R3. 利用正弦定理可以解决下列两类三角形的问题:①已知两个角及任意—边,求其他两边和另一角;例:已知角B,C,a ,解法:由A+B+C=18o0 ,求角A,由正弦定理 a sinA; b sinB; b sin B c sin C a sin A; 求出 b 与cc sinC ②已知两边和其中—边的对角,求其他两个角及另一边。
例:已知边a,b,A,解法:由正弦定理 a sin A求出角B,由A+B+C=18o0 求出角C,再使用正 b sin B 弦定理 a sin A求出c边c sinC4. △ABC中,已知锐角A,边b,则① a bsin A 时,B 无解;② a bsin A 或 a b 时, B 有一个解;③ bsinA a b 时, B 有两个解。
如:①已知 A 60 ,a 2,b 2 3,求 B (有一个解 )②已知 A 60 ,b 2,a 2 3,求 B (有两个解 ) 注意:由正弦定理求角时,注意解的个数。
正弦定理和余弦定理

正弦定理(Sine theorem)1.内容:在△ABC中,角A、B、C所对的边分别为a、b、c,则有a/sinA=b/sinB=c/sinC=2R(其中R为三角形外接圆的半径)2.正弦定理的应用领域在解三角形中,有以下的应用领域:(1)已知三角形的两角与一边,解三角形(2)已知三角形的两边和其中一边所对的角,解三角形(3)运用a:b:c=sinA:sinB:sinC解决角之间的转换关系直角三角形的一个锐角的对边与斜边的比叫做这个角的正弦。
余弦定理余弦定理是揭示三角形边角关系的重要定理,直接运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个边求角的问题,若对余弦定理加以变形并适当移于其它知识,则使用起来更为方便、灵活。
1.余弦定理性质对于任意三角形,任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的两倍积,若三边为a,b,c 三角为A,B,C ,则满足性质——a^2 = b^2 + c^2 - 2·b·c·cosAb^2 = a^2 + c^2 - 2·a·c·cosBc^2 = a^2 + b^2 - 2·a·b·cosCcosC = (a^2 + b^2 - c^2) / (2·a·b)cosB = (a^2 + c^2 - b^2) / (2·a·c)cosA = (c^2 + b^2 - a^2) / (2·b·c)(物理力学方面的平行四边形定则中也会用到)第一余弦定理(任意三角形射影定理)设△ABC的三边是a、b、c,它们所对的角分别是A、B、C,则有a=b·cosC+c·cos B,b=c·cosA+a·cos C,c=a·cosB+b·cos A。
正弦定理的变形公式(1) a=2RsinA, b=2RsinB, c=2RsinC;(2) sinA : sinB : sinC = a : b : c;(条件同上)在一个三角形中,各边与其所对角的正弦的比相等,且该比值都等于该三角形外接圆的直径已知三角形是确定的,利用正弦定理解三角形时,其解是唯一的;已知三角形的两边和其中一边的对角,由于该三角形具有不稳定性,所以其解不确定,可结合平面几何作图的方法及“大边对大角,大角对大边”定理和三角形内角和定理去考虑解决问题(3)相关结论:a/sinA=b/sinB=c/sinC=(a+b)/(sinA+sinB)=(a+b+c)/(sinA+sinB+sinC)c/sinC=c/sinD=BD=2R(R为外接圆半径)(4)设R为三角外接圆半径,公式可扩展为:a/sinA=b/sinB=c/sinC=2R,即当一内角为90°时,所对的边为外接圆的直径。
正弦定理和余弦定理

返回
[研一题] [例 2] B、b. π 在△ABC 中,c= 6,C=3,a=2,求 A、
返回
[自主解答] π 3 ∴A=4或4π.
a c asin C 2 ∵sin A=sin C,∴sin A= c = 2 .
π 又∵c>a,∴C>A.∴A=4. 5π 6· sin 1n C = π = 3+1. sin 3
第四章
三角函数
四
正弦定理和余弦定理
• 1、正、余弦定理
定理 正弦定理
a b c = = sin A sin B sin C =2R
余弦定理 a2= a2+c2-2accos B b2=a2+b2-2abcosC c2 =
b2+c2-2bccos A
内
; ; .
容
定理
变 形 形 式
正弦定理 余弦定理 ①a= 2Rsin A , b= 2Rsin B , c= 2Rsin C ; b2+c2-a2 cosB= a b 2bc ②sin A=2R,sin B=2R, 2 a +c2-b2 c 2ac sin C=2R; cos B= ; 2 2 2 a + b - c (其中 R 是△ABC 外接圆半径) cos C= 2ab . ③a∶b∶c=sinA∶sin B∶sin C ④asin B=bsin A,bsin C=csin B, asin C=csin A.
(2)由正弦定理知sin A∶sin B∶sin C=a∶b∶c正确,即
(2)正确.
返回
2.在△ABC中,若A>B,是否有sin A>sin B?反之,是 否成立?
提示:∵A>B,∴a>b. a b 又∵sin A=sin B,∴sin A>sin B. 反之,若 sin A>sin B, 则 a>b,即 A>B. 故 A>B⇔sin A>sin B.
正弦定理、余弦定理知识点

正弦定理、余弦定理1. 三角形常用公式:A +B +C =π;S =21ab sin C =21bc sin A ==21ca sin B ;2.三角形中的边角不等关系:A>B ⇔a>b,a+b>c,a-b<c ;; 3.正弦定理:A asin =Bb sin =Ccsin =2R (外接圆直径);正弦定理的变式:⎪⎩⎪⎨⎧===C R c B R b AR a sin 2sin 2sin 2;a ∶b ∶c =sin A ∶sin B ∶sinC .4.正弦定理应用范围:①已知两角和任一边,求其他两边及一角. ②已知两边和其中一边对角,求另一边的对角.③几何作图时,存在多种情况.如已知a 、b 及A ,求作三角形时,要分类讨论,确定解的个数.已知两边和其中一边的对角解三角形,有如下的情况: (1)A 为锐角a=bsin A bsin A<a<b a b ≥ 一解 两解 一解(2)A 为锐角或钝角 当a>b 时有一解.5.余弦定理 a 2=b 2+c 2-2bccosA .c 2=a 2+b 2-2abcosC .b 2=a 2+c 2-2accosB . 若用三边表示角,余弦定理可以写为、6.余弦定理应用范围:(1)已知三角形的三条边长,可求出三个内角; (2)已知三角形的两边及夹角,可求出第三边.知识点1 运用判断三角形形状例题1在△ABC 中已知acosB=bcosA,试判断△ABC 的形状.【分析】利用正弦定理或余弦定理判断三角形形状,可以将三角形中的边用角表示,也可将角用边来表示.从中找到三角形中的边角关系,判断出三角形的形状. 【答案】解法1:由扩充的正弦定理:代入已知式 2RsinAcosB=2RsinBcosAsinAcosB-cosAsinB=0 , sin(A-B)=0A-B=0 ∴A=B 即△ABC 为等腰三角形解法2:由余弦定理: 22222222bca cb b ac b c a a -+⋅=-+⋅ 22b a = ∴ b a = 即△ABC 为等腰三角形.巩固练习1.在中,若2222sin sin 2cos cos b C c B b B C +=,试判断三角形的形状.2.在ABC ∆中,已知a 2tanB=b 2tanA,试判断这个三角形的形状.3.已知ABC ∆中,有cos 2cos sin cos 2cos sin A C BA B C+=+,判断三角形形状.知识点2 运用正、余弦定理解三角形解三角形问题中正、余弦定理的选择:(1)在下述情况下应首先使用余弦定理:①已知三条边(边边边),求三个角;②已知两边和它们的夹角(边角边),求其它一边和两角;(2)在下述情况下应首先使用正弦定理:①已知两边和一边的对角(边边角),求其它一边和两角;②已知两角和任一边(角角边、角边角),求其它两边和一角. 例题2 在△ABC 中,已知3=a ,2=b ,B=45︒ 求A 、C 及c .【分析】在解斜三角形应用过程中,注意要灵活地选择正弦定和余弦定理,解得其它的边和角【答案】解法1:由正弦定理得:23245sin 3sin sin === b B a A ∵B=45︒<90︒ 即b <a ∴A=60︒或120︒当A=60︒时C=75︒ 22645sin 75sin 2sin sin +===BC b c 当A=120︒时C=15︒ 22645sin 15sin 2sin sin -===B C b c 解法2:设c =x 由余弦定理 B ac c a b cos 2222-+=将已知条件代入,整理:0162=+-x x 解之:226±=x当226+=c 时2)13(231226223)226(22cos 22221=++=+⋅⋅-++=-+=bc a c b A 从而A=60︒ ,C=75︒ 当226-=c 时同理可求得:A=120︒ 巩固练习1.已知在ABC ∆中,2,6,45==︒=∠BC AB A在ABC ∆中,213,2tan tan +=-=c b bb c B A ,求三内角2.在ABC ∆中,已知B C A 2=+,32tan tan +=⋅C A ,求A 、B 、C 的大小,又知顶点C 的对边C 上的高等于34,求三角形各边a 、b 、c 的长.知识点3 解决与三角形在关的证明、计算问题例题3 已知A 、B 、C 为锐角,tanA=1,tanB=2,tanC=3,求A+B+C 的值.【分析】本题是要求角,要求角先要求出这个角的某一个三角函数值,再根据角的范围确定角.本题应先求出A+B 和C 的正切值,再一次运用两角和的正切公式求出A+B+C .【答案】 A B C 、、为锐角 ∴<++<0270°°A B C 又,,由公式可得tan tan A B ==12tan()tan tan tan tan A B A B A B +=+-⋅=+-=-112123[]tan()tan ()A B C A B C ++=++=++-+⋅tan()tan tan()tan A B C A B C 1 =-+--⨯33133() =0所以A+B+C=πsin sin sin sin cos cos cos cos 2222221336ααββααββ-++-+=221336-+=(cos cos sin sin )αβαβ --=-25936cos()αβ∴-=cos()αβ5972巩固练习1.在∆ABC 中,a 、b 、c 分别是角A 、B 、C 的对边,设a+c=2b,A-C=3π,求sinB 的值.2.在中,a ,b ,c 分别是的对边长,已知a ,b ,c 成等比数列,且,求的大小及的值.3.在ABC ∆中,若4,5==b a且3231)cos(=-B A ,求这个三角形的面积.例题4 在ABC ∆中,角A 、B 、C 的对边分别为a 、b 、c,证明:C B A cb a sin )sin(222-=-.【分析】在用三角式的恒等变形证明三角形中的三角等式时,其解题的一般规律是:二项化积、倍角公式,提取公因式,再化积.遇有三角式的平方项,则利用半角公式降次.【答案】证法一:由正弦定理得C A B C B A c b a 2222222sin 22cos 2cos sin sin sin -=-=-=C A B A B 2sin 2)sin()sin(2-+-=CB AC 2sin )sin(sin -=C B A sin )sin(-.证法二:由余弦定理得a 2=b 2+c 2-2bccosA,则222c b a -=22cos 2cA bc c -=1-c b 2∙cosA,又由正弦定理得c b =C Bsin sin ,∴222cb a -=1-C B sin sin 2∙cosA=C A B C sin cos sin 2sin -=C A B B A sin cos sin 2)sin(-+=C A B B A sin cos sin cos sin -=C B A sin )sin(-. 证法三:C B A sin )sin(-=CAB B A sin cos sin cos sin -. 由正弦定理得cbC B c a C A ==sin sin ,sin sin ,∴CB A sin )sin(-=cAb B a cos cos -,又由余弦定理得C B A sin )sin(-=cbc a c b b ac b c a a 22222222-+⋅--+⋅=22222222)()(c a c b b c a -+--+=222c b a -.巩固练习1.已知锐角三角形ABC 中,3sin()5A B +=,1sin()5A B -=. (1)求证tan 2tan A B =;(2)设3AB =,求AB 边上的高.参考答案课堂互动例题1 巩固练习1.【答案】[解法1]:由正弦定理2sin sin sin a b cR A B C===,R 为外接圆的半径,将原式化为22228sin sin 8sin sin cos cos R B C R B C B C =,sin sin 0B C ≠,sin sin cos cos B C B C ∴=. 即cos()0B C +=,90B C ∴+=,90A =.故为直角三角形[解法2]:将已知等式变为2222(1cos )(1cos )2cos cos b C c B b B C -+-=,由余弦定理可得22222222222222a b c a c b b c b c ab ac ⎛⎫⎛⎫+-+-+-⋅-⋅ ⎪ ⎪⎝⎭⎝⎭222222222a c b a b c bc ac ab+-+-=⋅⋅,即22b c +22222222()()4a b c a c b a ⎡⎤+-++-⎣⎦=也即222b c a +=,故为直角三角形.2.【答案】解法1:由已知得A A b B B a cos sin cos sin 22=,由正弦定理得AAB B B A cos sin sin cos sin sin 22=,∵sinAsinB ≠0,∴sinAcosA=sinBcosB,即sin2A=sin2B,∴2A=2B 或2A=1800-2B,即A=B 或A+B=900.∴ABC ∆是等腰三角形或直角三角形.解法2: 由已知得A A bB B a cos sin cos sin 22=,由正弦定理得A a b b a cos cosB 22=,即Ab a cos cosB =,又由余弦定理得bcac b b a 22ac b -c a 222222-+=+,整理得(a 2-b 2)(a 2+b 2-c 2)=0,∴a=b,或a 2+b 2=c 2, ∴ABC ∆是等腰三角形或直角三角形. 3.解:由已知得例题2 巩固练习1.【答案】解法1:由正弦定理,得2345sin 26sin =︒=C 因3226sin =⨯=⋅A AB 6,2==AB BC 由623<<,则有二解,即︒=∠60C 或︒=∠120C︒=︒-︒-︒=∠754560180B 或︒=︒-︒-︒=∠1545120180B故13sin sin +=⇒⋅=AC B ABC AC 或13-=AC ,︒=∠︒=∠15,120B C ︒=∠︒=∠75,60B C 解法2:令AC=b ,则由余弦定理222245cos 62)6(=︒-+b b 1302322±=⇒=+-b b b又C b b cos 222)6(222⋅-+=︒=∠±=⇒60,21cos C C 或︒=∠120C ︒=︒+︒-︒=∠⇒75)6045(180B 或︒=︒+︒-︒=∠15)12045(180B . 2【答案】由已知有bc B A 21tan tan =+,化简并利用正弦定理:B C B A B A B A sin sin 2sin cos sin cos cos sin =+ BCB A B A sin sin 2sin cos )sin(=+0cos sin 2sin =-A C C由0sin ≠,故︒=⇒=6021cos A A 由213+=cb,可设k c k b 2,)13(=+=,由余弦定理,得 k a k k k a 6)13(24)13(22222=⇒+-++=由正弦定理Cc A a sin sin =得 226232sin sin =⋅==kk a A c C 由b c <则C 是锐角,故︒=--︒=︒=75180,45C A B C3.【答案】由已知,得2C A B +=,又由︒=++180C B A ︒=⇒60B 故4160cos sin sin 2=︒=C A ①又由B c a S ABC sin 2134⋅⋅==∆164334=⇒=⇒ac ac ② 故64)sin ()sin (sin sin 22===C c A a C A ac 8sin sin ==⇒Cc A a由3460sin 8sin 8sin sin =︒⋅=⋅==B AB a b 则21260cos cos 222=-+=︒=ac b c a B即964848)(3)(222=+=+⇒=-+c a ac b c a 64=+⇒c a ③ 把③与②联立,得)26(2),26(2-=+=c a 或)26(2),26(2+=-=c a4.【答案】由已知B C A 2=+,及︒=+︒=⇒︒=++120,60180C A B C B A由CA C A C A tan tan 1tan tan )tan(-+=+及32tan tan ,3)tan(+=⋅-=+C A C A得33tan tan +=+C A ,以C A tan ,tan 为一元二次方程032)33(2=+++-x x 的两个根,解方程,得⎩⎨⎧+==32tan 1tan C A 或⎩⎨⎧=+=1tan 32tan C A ⎩⎨⎧︒=︒=⇒7545C A 或⎩⎨⎧︒=︒=4575C A 若︒=︒=75,45C A ,则860sin 34=︒=a ,6445sin 34=︒=b ,)13(445sin 75sin 8sin sin +=︒︒==A C a c 若︒=︒=45,75C A ,则︒=60sin 34a ︒==75sin 34,8b )13(64-=)623(4-=)13(8sin sin -==B C b c 例题3 巩固练习1.【答案】由正弦定理和已知条件a+c=2b,得sinA+sinC=2sinB.由和差化积公式,得2sin 2C A +cos 2C A -=2sinB. 由A+B+C=π得sin2C A +=cos 2B .又A-C=3π,得2cos 23B =sinB.∴2cos 23B=2sin 2B cos 2B ,∵0<2B <2π,∴cos 2B ≠0,∴sin 2B =43.∴cos 2B =2sin 12B -=413,∴sinB=2sin 2B cos 2B =2∙43∙413=839. 2.【答案】(I )成等比数列 又 在中,由余弦定理得(II )在中,由正弦定理得 .3.【答案】解法1:由余弦定理得c c bc a c b A 892cos 2222-=-+= cc ac b c a B 1092cos 2222+=-+= 由正弦定理得:B A B A sin 45sin sin 4sin 5=⇒= 3231)cos 1(4510989222=-++⋅-⇒B c c c c 3231])109(1[4580812224=+-+-c c c c 63632318016282222=⇒=⇒=-⇒c c cc 故1694893689cos 2=-=-=c c A 7165sin =A 4715sin 21=⋅⋅=∆A c b S ABC解法2:如图,作B A CAD -=∠,AD 交BC 于D ,令x CD =则由5=a 知,x AD x BD -=-=5,5,在CAD ∆中 由余弦定理3231)5(84)5()cos(222=--+-=-x x x B A 化简得199=⇒=x x ,在CAD ∆中由正弦定理)sin(4)sin(sin )sin(sin B A B A CD AD C B A CD C AD -=-⋅=⇒-=783)(cos 142=--=B A 74158735421sin 21=⨯⨯⨯=⋅⋅=∆C BC AC S ABC例题4 巩固练习1.【答案】(1)证明:因为3sin()5A B +=,1sin()5A B -=, 所以3sin cos cos sin 51sin cos cos sin 5A B A B A B A B ⎧+=⎪⎪⎨⎪-=⎪⎩,2sin cos 51cos sin 5A B A B ⎧=⎪⎪⇒⎨⎪=⎪⎩,tan 2tan A B ⇒=.所以tan 2tan A B =(2)因为2A B ππ<+<,3sin()5A B +=, 所以3tan()4A B +=-,即tan tan 31tan tan 4A B A B +=--, 将tan 2tan A B =代入上式并整理得 22tan 4tan 10B B --=.解得2tan 2B =,舍去负值得2tan 2B +=,从而tan 2tan 2A B ==. 设AB 边上的高为CD.则tan tan CD CD AB AD DB A B =+=+=AB=3,得CD= 2AB 边上的高等于2。
正弦定理和余弦定理

正弦定理和余弦定理1.正弦定理和余弦定理定理正弦定理余弦定理内容a sin A =b sin B =c sin C =2R (R 为△ABC 外接圆半径)a 2=b 2+c 2-2bc cos A ; b 2=c 2+a 2-2ac cos B ; c 2=a 2+b 2-2ab cos C 常见变形a =2R sin A ,b =2R sin B ,c =2R sin C ; sin A =a 2R ,sin B =b 2R ,sin C =c2R;a ∶b ∶c =sin A ∶sin B ∶sin C ; a +b +c sin A +sin B +sin C =asin Acos A =b 2+c 2-a 22bc ;cos B =a 2+c 2-b 22ac ;cos C =a 2+b 2-c 22ab2.三角形中常用的面积公式 (1)S =12ah (h 表示边a 上的高);(2)S =12bc sin A =12ac sin B =12ab sin C ;(3)S =12r (a +b +c )(r 为三角形的内切圆半径).3.三角形解的判断A 为锐角A 为钝角或直角 图形关系式 a =b sin A b sin A <a <b a ≥b a >b 解的个数 一解两解一解一解| 微 点 提 醒 |1.三角形中的三角函数关系 (1)sin(A +B )=sin C ; (2)cos(A +B )=-cos C ; (3)sin A +B 2=cos C 2;(4)cos A +B 2=sin C 2.2.三角形中的射影定理 在△ABC 中,a =b cos C +c cos B ; b =a cos C +c cos A ;c =b cos A +a cos B .3.利用正、余弦定理解三角形时,要注意三角形内角和定理对角的范围的限制.‖易错辨析‖判断下列结论是否正确(请在括号中打”√”或“×”)(1)在△ABC 中,已知a ,b 和角B ,能用正弦定理求角A ;已知a ,b 和角C ,能用余弦定理求边c .(√)(2)在三角形中,已知两角和一边或已知两边和一角都能解三角形.(√) (3)在△ABC 中,sin A >sin B 的充分不必要条件是A >B .(×)(4)在△ABC 中,“a 2+b 2<c 2”是“△ABC 为钝角三角形”的充分不必要条件.(√) (5)在△ABC 的角A ,B ,C ,边长a ,b ,c 中,已知任意三个可求其他三个.(×)‖自主测评‖1.(教材改编题)在△ABC 中,已知a =5,b =7,c =8,则A +C =( ) A .90° B .120° C .135°D .150°解析:选B cos B =a 2+c 2-b 22ac =25+64-492×5×8=12.所以B =60°,所以A +C =120°.2.(教材改编题)在非钝角△ABC 中,2b sin A =3a ,则角B 为( ) A.π6 B.π4 C.π3D.π2解析:选C 由正弦定理得b sin A =a sin B , 所以2a sin B =3a ,即sin B =32,又B 为非钝角,所以B =π3,故选C. 3.在△ABC 中,若a =18,b =24,A =45°,则此三角形( ) A .无解 B .有两解C .有一解D .解的个数不确定解析:选B 因为a sin A =b sin B,所以sin B =b a ·sin A =2418×sin45°=223.又因为a <b ,所以B 有两解.4.(教材改编题)已知△ABC 的三边之比为3∶5∶7,则最大角为( ) A.2π3 B.3π4C.5π6D.7π12解析:选A 由三边之比为a ∶b ∶c =3∶5∶7,可设a =3k ,b =5k ,c =7k (k >0),由余弦定理得cos C =a 2+b 2-c 22ab =(3k 2)+(5k )2-(7k )22×3k ×5k=-12,又0<C <π,所以C =2π3.5.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,cos2A =sin A ,bc =2,则△ABC 的面积为________.解析:由cos2A =sin A ,得1-2sin 2A =sin A ,解得sin A =12(负值舍去),由bc =2,可得△ABC的面积S =12bc sin A =12×2×12=12.答案:12………………考点一 利用正、余弦定理解三角形……|多维探究型|……………|多角探明|角度一 求三角形的边长【例1】 (2018届贵阳模拟)在△ABC 中,内角A ,B ,C 的对边a ,b ,c 成公差为2的等差数列,C =120°. (1)求边长a ;(2)(一题多解)求AB 边上的高CD 的长. [解] (1)由题意得b =a +2,c =a +4,由余弦定理cos C =a 2+b 2-c 22ab 得cos120°=a 2+(a +2)2-(a +4)22a (a +2),即a 2-a -6=0,∴a =3或a =-2(舍去),∴a =3.(2)解法一:由(1)知a =3,b =5,c =7,由三角形的面积公式得12ab sin ∠ACB =12c ×CD ,∴CD =ab sin ∠ACBc=3×5×327=15314,即AB 边上的高CD =15314. 解法二:由(1)知a =3,b =5,c =7,由正弦定理得3sin A =7sin ∠ACB =7sin120°,即sin A =3314,在Rt △ACD 中,CD =AC sin A =5×3314=15314,即AB 边上的高CD =15314.角度二 求三角形的角或角的三角函数值【例2】 (1)在△ABC 中,B =π4,BC 边上的高等于13BC ,则cos A =( )A.31010B.1010C .-1010D .-31010(2)(2018届河北“五个一名校联盟”模拟)已知a ,b ,c 分别是△ABC 的内角A ,B ,C 所对的边,且c =2,C =π3,若sin C +sin(B -A )=2sin2A ,则A =________.[解析] (1)设△ABC 中角A ,B ,C 的对边分别是a ,b ,c ,由题意可得13a =c sin π4=22c ,则a =322c .在△ABC 中,由余弦定理可得b 2=a 2+c 2-2ac =92c 2+c 2-3c 2=52c 2,则b =102c .由余弦定理,可得cos A =b 2+c 2-a 22bc=52c 2+c 2-92c 22×102c ×c=-1010,故选C.(2)在△ABC 中,由sin C +sin(B -A )=2sin2A 可得sin(A +B )+sin(B -A )=2sin2A ,即sin A cos B +cos A sin B +cos A sin B -sin A cos B =4sin A cos A ,∴cos A sin B =2sin A cos A ,即cos A (sin B -2sin A )=0,即cos A =0或sin B =2sin A , ①当cos A =0时,A =π2;②当sin B =2sin A 时,根据正弦定理得b =2a ,由余弦定理c 2=b 2+a 2-2ab cos C ,结合c =2,C =π3,得a 2+b 2-ab =4,∴a =233,b =433,∴b 2=a 2+c 2,∴B =π2,∴A =π6.综上可得,A =π2或π6.[答案] (1)C (2)π2或π6『名师点津』………………………………………………|品名师指点迷津|应用正弦、余弦定理的解题技巧(1)求边:利用公式a =b sin A sin B ,b =a sin B sin A ,c =a sin Csin A或其他相应变形公式求解.(2)求角:先求出正弦值,再求角,即利用公式sin A =a sin B b ,sin B =b sin A a ,sin C =c sin Aa 或其他相应变形公式求解.(3)已知两边和夹角或已知三边可利用余弦定理求解.(4)灵活利用式子的特点转化;如出现a 2+b 2-c 2=λab 形式用余弦定理,等式两边是关于边或角的正弦的齐次式用正弦定理.|变式训练|1.(2018届福建莆田联考)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,若a sin B cos C +c sin B cos A =12b ,且a >b ,则B =( )A.π6B.π3C.2π3D.5π6解析:选A ∵a sin B cos C +c sin B cos A =12b ,∴根据正弦定理可得sin A sin B cos C +sin C sin B cos A=12sin B ,即sin B (sin A cos C +sin C cos A )=12sin B .∵sin B ≠0,∴sin(A +C )=12,即sin B =12.∵a >b ,∴A >B ,即B 为锐角,∴B =π6,故选A.2.(2019届黄冈模拟)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c . (1)若23cos 2A +cos2A =0,且△ABC 为锐角三角形,a =7,c =6,求b 的值; (2)若a =3,A =π3,求b +c 的取值范围.解:(1)∵23cos 2A +cos2A =23cos 2A +2cos 2A -1=0, ∴cos 2A =125,又A 为锐角,∴cos A =15,a 2=b 2+c 2-2bc cos A ,即b 2-125b -13=0, 得b =5(负值舍去),∴b =5.(2)解法一:由正弦定理可得b +c =2(sin B +sin C )=2⎣⎡⎦⎤sin B +sin ⎝⎛⎭⎫2π3-B =23sin ⎝⎛⎭⎫B +π6, 又0<B <2π3,∴π6<B +π6<5π6,∴12<sin ⎝⎛⎭⎫B +π6≤1,∴b +c ∈(3,23]. 解法二:由余弦定理a 2=b 2+c 2-2bc cos A 可得b 2+c 2-3=bc , ∴(b +c )2-3=3bc ≤34(b +c )2,当且仅当b =c 时取等号,∴b +c ≤23,又由两边之和大于第三边可得b +c >3, ∴b +c ∈ (3,23].………………考点二 判断三角形的形状…………|重点保分型|……………|研透典例|【典例】 (一题多解)在△ABC 中,若a 2+b 2-c 2=ab ,且2cos A sin B =sin C ,试判断△ABC 的形状.[解] 解法一:利用边的关系来判断 由正弦定理得sin C sin B =cb,由2cos A sin B =sin C ,有cos A =sin C 2sin B =c2b .又由余弦定理得cos A =b 2+c 2-a 22bc ,所以c 2b =b 2+c 2-a 22bc,即c 2=b 2+c 2-a 2,所以a 2=b 2,所以a =b . 又因为a 2+b 2-c 2=ab .所以2b 2-c 2=b 2,所以b 2=c 2, 所以b =c ,所以a =b =c . 所以△ABC 为等边三角形. 解法二:利用角的关系来判断 因为A +B +C =180°, 所以sin C =sin(A +B ), 又因为2cos A sin B =sin C ,所以2cos A sin B =sin A cos B +cos A sin B , 所以sin(A -B )=0.又因为A 与B 均为△ABC 的内角,所以A =B , 又由a 2+b 2-c 2=ab ,由余弦定理,得cos C =a 2+b 2-c 22ab =ab 2ab =12,又0°<C <180°, 所以C =60°,所以△ABC 为等边三角形.『名师点津』………………………………………………|品名师指点迷津|判定三角形形状的两种常用途径[提醒]“角化边”后要注意用因式分解、配方等方法得出边的相应关系;“边化角”后要注意用三角恒等变换公式、三角形内角和定理及诱导公式推出角的关系.|变式训练|在△ABC 中,若(a 2+b 2)sin(A -B )=(a 2-b 2)sin(A +B ),则△ABC 的形状是( ) A .等腰三角形B .直角三角形C .等腰直角三角形D .等腰三角形或直角三角形 解析:选D 因为(a 2+b 2)sin(A -B )=(a 2-b 2)sin(A +B ),所以b 2[sin(A +B )+sin(A -B )]=a 2[sin(A +B )-sin(A -B )], 所以2sin A cos B ·b 2=2cos A sin B ·a 2, 即a 2cos A sin B =b 2sin A cos B .解法一:由正弦定理知a =2R sin A ,b =2R sin B , 所以sin 2A cos A sin B =sin 2B sin A cos B , 又sin A ·sin B ≠0,所以sin A cos A =sin B cos B ,所以sin2A =sin2B . 在△ABC 中,0<2A <2π,0<2B <2π,所以2A =2B 或2A =π-2B .所以A =B 或A +B =π2.所以△ABC 为等腰三角形或直角三角形,故选D. 解法二:由正弦定理、余弦定理得: a 2bb 2+c 2-a 22bc =b 2a a 2+c 2-b 22ac, 所以a 2(b 2+c 2-a 2)=b 2(a 2+c 2-b 2),所以(a 2-b 2)(a 2+b 2-c 2)=0, 所以a 2-b 2=0或a 2+b 2-c 2=0, 即a =b 或a 2+b 2=c 2.所以△ABC 为等腰三角形或直角三角形.故选D.………………考点三 三角形面积的计算………………|多维探究型|……………|多角探明|角度一 求三角形的面积【例1】 (2018届武汉调研)在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,且2b cos C =2a +c . (1)求B ;(2)若b =2,a +c =5,求△ABC 的面积. [解] (1)由正弦定理,知2sin B cos C =2sin A +sin C , 由A +B +C =π,得2sin B cos C =2sin(B +C )+sin C , 化简,得2sin B cos C =2(sin B cos C +cos B sin C )+sin C , 即2cos B sin C +sin C =0. 因为sin C ≠0,所以cos B =-12.因为0<B <π,所以B =2π3.(2)由余弦正理b 2=a 2+c 2-2ac cos B ,可知b 2=(a +c )2-2ac -2ac cos B , 因为b =2,a +c =5,所以22=(5)2-2ac -2ac cos 2π3,得ac =1.所以S △ABC =12ac sin B =12×1×32=34.角度二 已知三角形的面积解三角形【例2】 (2018届沈阳教学质量监测(一))在△ABC 中,已知内角A ,B ,C 的对边分别是a ,b ,c ,且2c cos B =2a +b . (1)求C ;(2)若a +b =6,△ABC 的面积为23,求c . [解] (1)由正弦定理得2sin C cos B =2sin A +sin B , 又sin A =sin(B +C ),∴2sin C cos B =2sin(B +C )+sin B ,∴2sin C cos B =2sin B cos C +2cos B sin C +sin B , ∴2sin B cos C +sin B =0, ∵sin B ≠0,∴cos C =-12.又C ∈(0,π),∴C =2π3.(2)∵S △ABC =12ab sin C =23,∴ab =8,由余弦定理,得c 2=a 2+b 2-2ab cos C =a 2+ab +b 2=(a +b )2-ab =28, ∴c =27.角度三 求有关三角形面积或周长的最值(范围)问题【例3】 (2018届沈阳市教学质量检测(一)) 已知△ABC 的三个内角A ,B ,C 的对边分别为a ,b ,c ,面积为S ,且满足4S =a 2-(b -c )2,b +c =8,则S 的最大值为________. [解析] 由题意得:4×12bc sin A =a 2-b 2-c 2+2bc ,又a 2=b 2+c 2-2bc cos A ,代入上式得:2bc sin A =-2bc cos A +2bc ,即sin A +cos A =1,2sin ⎝⎛⎭⎫A +π4=1,又0<A <π,所以π4<A +π4<5π4,所以A +π4=3π4,所以A =π2,S =12bc sin A =12bc ,又b +c =8≥2bc ,当且仅当b =c 时取“=”,所以bc ≤16,所以S 的最大值为8. [答案] 8『名师点津』………………………………………………|品名师指点迷津|与三角形面积有关问题的解题策略(1)求三角形的面积.对于面积公式S =12ab sin C =12ac sin B =12bc sin A ,一般是已知哪一个角就使用含哪个角的公式.(2)已知三角形的面积解三角形.与面积有关的问题,一般要利用正弦定理或余弦定理进行边和角的互化.(3)求有关三角形面积或周长的最值(范围)问题.一般转化为一个角的一个三角函数,利用三角函数的有界性求解,或利用余弦定理转化为边的关系,再应用基本不等式求解.|变式训练|1.(2018年全国卷Ⅲ)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .若△ABC 的面积为a 2+b 2-c 24,则C =( )A.π2B.π3C.π4D.π6解析:选C 根据题意及三角形的面积公式知12ab sin C =a 2+b 2-c 24,所以sin C =a 2+b 2-c 22ab =cos C ,所以在△ABC 中,C =π4.2.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知△ABC 的面积为a 23sin A .(1)求sin B sin C ;(2)若6cos B cos C =1,a =3,求△ABC 的周长. 解:(1)由题设得12ac sin B =a 23sin A ,即12c sin B =a3sin A .由正弦定理得12sin C sin B =sin A3sin A .故sin B sin C =23.(2)由题设及(1)得cos B cos C -sin B sin C =-12,即cos(B +C )=-12.所以B +C =2π3,故A =π3.由题设得12bc sin A =a 23sin A,即bc =8.由余弦定理得b 2+c 2-bc =9,即(b +c )2-3bc =9,得b +c =33. 故△ABC 的周长为3+33.。
正弦余弦定理

正弦定理在一个三角形中,各边和它所对角的正弦的比相等。
即a/sinA=b/sinB=c/sinC=2R(2R在同一个三角形中是恒量,是此三角形外接圆的半径的两倍)这一定理对于任意三角形ABC,都有a/sinA=b/sinB=c/sinC=2RR为三角形外接圆半径余弦定理是揭示三角形边角关系的重要定理,直接运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个边求角的问题,若对余弦定理加以变形并适当移于其它知识,则使用起来更为方便、灵活。
对于任意三角形三边为a,b,c三角为A,B,C满足性质(注:a*b、a*c就是a乘b、a乘c。
a^2、b^2、c^2就是a的平方,b的平方,c的平方。
)a^2=b^2+c^2-2*b*c*CosAb^2=a^2+c^2-2*a*c*CosBc^2=a^2+b^2-2*a*b*CosCCosC=(a^2+b^2-c^2)/2abCosB=(a^2+c^2-b^2)/2acCosA=(c^2+b^2-a^2)/2bc正弦是sin是xx的锐角的对边比斜边的值xxcos是xx的锐角的邻边比斜边的值正切是tan是xx的锐角的对边比邻边的值反正切的cot是xx的锐角的邻边比对边的值在△ABC中,∠C=90°,把锐角A的邻边与对边的比,叫做∠切,记作cotA 在△ABC中,∠C=90°,把锐角A的邻边与斜边的比,叫做∠弦,记作cos A.在△ABC中,∠C=90°,把锐角A的对边与邻边的比,叫做∠切,记作tanA在△ABC中,∠C=90°,把锐角A的对边与斜边的比,叫做∠弦,记作sinAA的余A的正。
正弦定理和余弦定理
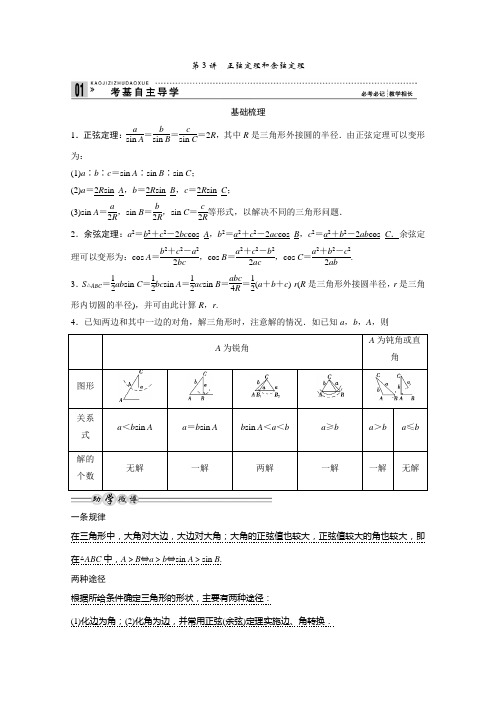
第3讲 正弦定理和余弦定理基础梳理1.正弦定理:a sin A =b sin B =csin C =2R ,其中R 是三角形外接圆的半径.由正弦定理可以变形为:(1)a ∶b ∶c =sin A ∶sin B ∶sin C ;(2)a =2R sin_A ,b =2R sin_B ,c =2R sin_C ;(3)sin A =a 2R ,sin B =b 2R ,sin C =c2R等形式,以解决不同的三角形问题.2.余弦定理:a 2=b 2+c 2-2bc cos_A ,b 2=a 2+c 2-2ac cos_B ,c 2=a 2+b 2-2ab cos_C .余弦定理可以变形为:cos A =b 2+c 2-a 22bc ,cos B =a 2+c 2-b 22ac ,cos C =a 2+b 2-c 22ab.3.S △ABC =12ab sin C =12bc sin A =12ac sin B =abc 4R =12(a +b +c )·r (R 是三角形外接圆半径,r 是三角形内切圆的半径),并可由此计算R ,r .4.已知两边和其中一边的对角,解三角形时,注意解的情况.如已知a ,b ,A ,则A 为锐角A 为钝角或直角图形关系 式 a <b sin Aa =b sin Ab sin A <a <b a ≥ba >ba ≤b解的 个数无解 一解 两解 一解 一解 无解一条规律在三角形中,大角对大边,大边对大角;大角的正弦值也较大,正弦值较大的角也较大,即在△ABC 中,A >B ⇔a >b ⇔sin A >sin B . 两种途径根据所给条件确定三角形的形状,主要有两种途径:(1)化边为角;(2)化角为边,并常用正弦(余弦)定理实施边、角转换.双基自测1.(人教A 版教材习题改编)在△ABC 中,A =60°,B =75°,a =10,则c 等于( ). A .5 2 B .10 2 C.1063D .5 6解析 由A +B +C =180°,知C =45°, 由正弦定理得:a sin A =c sin C ,即1032=c 22.∴c =1063.答案 C2.在△ABC 中,若sin A a =cos B b ,则B 的值为( ).A .30°B .45°C .60°D .90° 解析 由正弦定理知:sin A sin A =cos Bsin B ,∴sin B =cos B ,∴B =45°. 答案 B3.(2011·郑州联考)在△ABC 中,a =3,b =1,c =2,则A 等于( ). A .30° B .45° C .60° D .75° 解析 由余弦定理得:cos A =b 2+c 2-a 22bc =1+4-32×1×2=12,∵0<A <π,∴A =60°. 答案 C4.在△ABC 中,a =32,b =23,cos C =13,则△ABC 的面积为( ).A .3 3B .2 3C .4 3 D. 3 解析 ∵cos C =13,0<C <π,∴sin C =223,∴S △ABC =12ab sin C=12×32×23×223=4 3.答案 C5.已知△ABC 三边满足a 2+b 2=c 2-3ab ,则此三角形的最大内角为________. 解析 ∵a 2+b 2-c 2=-3ab , ∴cos C =a 2+b 2-c 22ab =-32,故C =150°为三角形的最大内角. 答案 150°考向一 利用正弦定理解三角形【例1】►在△ABC 中,a =3,b =2,B =45°.求角A ,C 和边c .[审题视点] 已知两边及一边对角或已知两角及一边,可利用正弦定理解这个三角形,但要注意解的判断.解 由正弦定理得a sin A =b sin B ,3sin A =2sin 45°,∴sin A =32. ∵a >b ,∴A =60°或A =120°.当A =60°时,C =180°-45°-60°=75°, c =b sin C sin B =6+22;当A =120°时,C =180°-45°-120°=15°, c =b sin C sin B =6-22.(1)已知两角一边可求第三角,解这样的三角形只需直接用正弦定理代入求解即可.(2)已知两边和一边对角,解三角形时,利用正弦定理求另一边的对角时要注意讨论该角,这是解题的难点,应引起注意.【训练1】 (2011·北京)在△ABC 中,若b =5,∠B =π4,tan A =2,则sin A =________;a =________.解析 因为△ABC 中,tan A =2,所以A 是锐角, 且sin Acos A=2,sin 2A +cos 2A =1,联立解得sin A =255,再由正弦定理得a sin A =bsin B ,代入数据解得a =210. 答案255210 考向二 利用余弦定理解三角形【例2】►在△ABC 中,a 、b 、c 分别是角A 、B 、C 的对边,且cos B cos C =-b2a +c .(1)求角B 的大小;(2)若b =13,a +c =4,求△ABC 的面积. [审题视点] 由cos B cos C =-b2a +c,利用余弦定理转化为边的关系求解. 解 (1)由余弦定理知:cos B =a 2+c 2-b 22ac ,cos C =a 2+b 2-c 22ab.将上式代入cos B cos C =-b2a +c 得:a 2+c 2-b 22ac ·2ab a 2+b 2-c 2=-b 2a +c , 整理得:a 2+c 2-b 2=-ac . ∴cos B =a 2+c 2-b 22ac =-ac 2ac =-12.∵B 为三角形的内角,∴B =23π.(2)将b =13,a +c =4,B =23π代入b 2=a 2+c 2-2ac cos B ,得b 2=(a +c )2-2ac -2ac cos B , ∴13=16-2ac ⎝⎛⎭⎫1-12,∴ac =3. ∴S △ABC =12ac sin B =334.(1)根据所给等式的结构特点利用余弦定理将角化边进行变形是迅速解答本题的关键.(2)熟练运用余弦定理及其推论,同时还要注意整体思想、方程思想在解题过程中的运用. 【训练2】 (2011·桂林模拟)已知A ,B ,C 为△ABC 的三个内角,其所对的边分别为a ,b ,c ,且2cos 2 A2+cos A =0.(1)求角A 的值;(2)若a =23,b +c =4,求△ABC 的面积. 解 (1)由2cos 2 A2+cos A =0,得1+cos A +cos A =0, 即cos A =-12,∵0<A <π,∴A =2π3.(2)由余弦定理得,a 2=b 2+c 2-2bc cos A ,A =2π3,则a 2=(b +c )2-bc , 又a =23,b +c =4, 有12=42-bc ,则bc =4, 故S △ABC =12bc sin A = 3.考向三 利用正、余弦定理判断三角形形状【例3】►在△ABC 中,若(a 2+b 2)sin(A -B )=(a 2-b 2)sin C ,试判断△ABC 的形状. [审题视点] 首先边化角或角化边,再整理化简即可判断. 解 由已知(a 2+b 2)sin(A -B )=(a 2-b 2)sin C , 得b 2[sin(A -B )+sin C ]=a 2[sin C -sin(A -B )], 即b 2sin A cos B =a 2cos A sin B ,即sin 2B sin A cos B =sin 2A cos B sin B ,所以sin 2B =sin 2A , 由于A ,B 是三角形的内角. 故0<2A <2π,0<2B <2π. 故只可能2A =2B 或2A =π-2B , 即A =B 或A +B =π2.故△ABC 为等腰三角形或直角三角形.判断三角形的形状的基本思想是;利用正、余弦定理进行边角的统一.即将条件化为只含角的三角函数关系式,然后利用三角恒等变换得出内角之间的关系式;或将条件化为只含有边的关系式,然后利用常见的化简变形得出三边的关系. 【训练3】 在△ABC 中,若a cos A =b cos B =c cos C;则△ABC 是( ). A .直角三角形 B .等边三角形 C .钝角三角形D .等腰直角三角形解析 由正弦定理得a =2R sin A ,b =2R sin B ,c =2R sin C (R 为△ABC 外接圆半径). ∴sin A cos A =sin B cos B =sin C cos C. 即tan A =tan B =tan C ,∴A =B =C . 答案 B考向三 正、余弦定理的综合应用【例3】►在△ABC 中,内角A ,B ,C 对边的边长分别是a ,b ,c ,已知c =2,C =π3.(1)若△ABC 的面积等于3,求a ,b ;(2)若sin C +sin(B -A )=2sin 2A ,求△ABC 的面积.[审题视点] 第(1)问根据三角形的面积公式和余弦定理列出关于a ,b 的方程,通过方程组求解;第(2)问根据sin C +sin(B -A )=2sin 2A 进行三角恒等变换,将角的关系转换为边的关系,求出边a ,b 的值即可解决问题.解 (1)由余弦定理及已知条件,得a 2+b 2-ab =4.又因为△ABC 的面积等于3,所以12ab sin C =3,得ab =4,联立方程组⎩⎪⎨⎪⎧a 2+b 2-ab =4,ab =4,解得⎩⎪⎨⎪⎧a =2,b =2. (2)由题意,得sin(B +A )+sin(B -A )=4sin A cos A , 即sin B cos A =2sin A cos A . 当cos A =0,即A =π2时,B =π6,a =433,b =233;当cos A ≠0时,得sin B =2sin A , 由正弦定理,得b =2a .联立方程组⎩⎪⎨⎪⎧a 2+b 2-ab =4,b =2a ,解得⎩⎨⎧a =233,b =433.所以△ABC 的面积S =12a b sin C =233.正弦定理、余弦定理、三角形面积公式对任意三角形都成立,通过这些等式就可以把有限的条件纳入到方程中,通过解方程组获得更多的元素,再通过这些新的条件解决问题. 【训练3】 (2011·北京西城一模)设△ABC 的内角A ,B ,C 所对的边长分别为a ,b ,c ,且cos B =45,b =2.(1)当A =30°时,求a 的值;(2)当△ABC 的面积为3时,求a +c 的值. 解 (1)因为cos B =45,所以sin B =35.由正弦定理a sin A =b sin B ,可得a sin 30°=103,所以a =53.(2)因为△ABC 的面积S =12ac ·sin B ,sin B =35,所以310ac =3,ac =10.由余弦定理得b 2=a 2+c 2-2ac cos B ,得4=a 2+c 2-85ac =a 2+c 2-16,即a 2+c 2=20.所以(a +c )2-2ac =20,(a +c )2=40. 所以a +c =210.第7讲 正弦定理、余弦定理应用举例基础梳理1.用正弦定理和余弦定理解三角形的常见题型测量距离问题、高度问题、角度问题、计算面积问题、航海问题、物理问题等. 2.实际问题中的常用角 (1)仰角和俯角在视线和水平线所成的角中,视线在水平线上方的角叫仰角,在水平线下方的角叫俯角(如图(1)).(2)方位角指从正北方向顺时针转到目标方向线的水平角,如B点的方位角为α(如图(2)).(3)方向角:相对于某正方向的水平角,如南偏东30°,北偏西45°,西偏东60°等.(4)坡度:坡面与水平面所成的二面角的度数.一个步骤解三角形应用题的一般步骤:(1)阅读理解题意,弄清问题的实际背景,明确已知与未知,理清量与量之间的关系.(2)根据题意画出示意图,将实际问题抽象成解三角形问题的模型.(3)根据题意选择正弦定理或余弦定理求解.(4)将三角形问题还原为实际问题,注意实际问题中的有关单位问题、近似计算的要求等.双基自测1.(人教A版教材习题改编)如图,设A,B两点在河的两岸,一测量者在A所在的同侧河岸边选定一点C,测出AC的距离为50 m,∠ACB=45°,∠CAB=105°后,就可以计算出A,B 两点的距离为().A.50 2 m B.50 3 m C.25 2 m D.2522m解析由正弦定理得ABsin∠ACB=ACsin B,又∵B=30°∴AB=AC·sin∠ACBsin B=50×2212=502(m).答案 A2.从A处望B处的仰角为α,从B处望A处的俯角为β,则α,β的关系为().A .α>βB .α=βC .α+β=90°D .α+β=180° 解析 根据仰角与俯角的定义易知α=β. 答案 B3.若点A 在点C 的北偏东30°,点B 在点C 的南偏东60°,且AC =BC ,则点A 在点B 的( ). A .北偏东15° B .北偏西15° C .北偏东10° D .北偏西10°解析 如图.答案 B4.一船向正北航行,看见正西方向相距10海里的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西60°,另一灯塔在船的南偏西75°,则这艘船的速度是每小时( ). A .5海里 B .53海里 C .10海里D .103海里解析 如图所示,依题意有∠BAC =60°,∠BAD =75°,所以∠CAD =∠CDA =15°,从而CD =CA =10(海里),在Rt △ABC 中,得AB =5(海里), 于是这艘船的速度是50.5=10(海里/时).答案 C5.海上有A ,B ,C 三个小岛,测得A ,B 两岛相距10海里,∠BAC =60°,∠ABC =75°,则B ,C 间的距离是________海里.解析 由正弦定理,知BC sin 60°=AB sin (180°-60°-75°).解得BC =56(海里).答案 5 6考向一 测量距离问题【例1】►如图所示,为了测量河对岸A ,B 两点间的距离,在这岸定一基线CD ,现已测出CD =a 和∠ACD =60°,∠BCD =30°,∠BDC =105°,∠ADC =60°,试求AB 的长. [审题视点] 在△BCD 中,求出BC ,在△ABC 中,求出AB .解 在△ACD 中,已知CD =a ,∠ACD =60°,∠ADC =60°,所以AC =a .∵∠BCD =30°,∠BDC =105°∴∠CBD =45°在△BCD 中,由正弦定理可得BC =a sin 105°sin 45°=3+12a .在△ABC 中,已经求得AC 和BC ,又因为∠ACB =30°,所以利用余弦定理可以求得A ,B 两点之间的距离为AB =AC 2+BC 2-2AC ·BC ·cos 30°=22a . (1)利用示意图把已知量和待求量尽量集中在有关的三角形中,建立一个解三角形的模型.(2)利用正、余弦定理解出所需要的边和角,求得该数学模型的解.【训练1】 如图,A ,B ,C ,D 都在同一个与水平面垂直的平面内,B 、D 为两岛上的两座灯塔的塔顶,测量船于水面A 处测得B 点和D 点的仰角分别为75°,30°,于水面C 处测得B 点和D 点的仰角均为60°,AC =0.1 km.试探究图中B 、D 间距离与另外哪两点间距离相等,然后求B ,D 的距离.解 在△ACD 中,∠DAC =30°,∠ADC =60°-∠DAC =30°,所以CD =AC =0.1 km.又∠BCD =180°-60°-60°=60°,故CB 是△CAD 底边AD 的中垂线,所以BD =BA . 又∵∠ABC =15°在△ABC 中,AB sin ∠BCA =AC sin ∠ABC , 所以AB =AC sin 60°sin 15°=32+620(km), 同理,BD =32+620(km). 故B 、D 的距离为32+620km. 考向二 测量高度问题【例2】►如图,山脚下有一小塔AB ,在塔底B 测得山顶C 的仰角为60°,在山顶C 测得塔顶A 的俯角为45°,已知塔高AB =20 m ,求山高CD .[审题视点] 过点C 作CE ∥DB ,延长BA 交CE 于点E ,在△AEC 中建立关系.解如图,设CD =x m ,则AE =x -20 m ,tan 60°=CD BD , ∴BD =CD tan 60°=x 3=33x (m). 在△AEC 中,x -20=33x , 解得x =10(3+3) m .故山高CD 为10(3+3) m.(1)测量高度时,要准确理解仰、俯角的概念;(2)分清已知和待求,分析(画出)示意图,明确在哪个三角形内应用正、余弦定理.【训练2】 如图所示,测量河对岸的塔高AB 时,可以选与塔底B 在同一水平面内的两个测点C 与D ,现测得∠BCD =α,∠BDC =β,CD =s ,并在点C 测得塔顶A 的仰角为θ,求塔高AB .解 在△BCD 中,∠CBD =π-α-β, 由正弦定理得BC sin ∠BDC =CD sin ∠CBD , 所以BC =CD sin ∠BDC sin ∠CBD =s ·sin βsin (α+β)在Rt △ABC 中,AB =BC tan ∠ACB =s tan θsin βsin (α+β). 考向三 正、余弦定理在平面几何中的综合应用【例3】►如图所示,在梯形ABCD 中,AD ∥BC ,AB =5,AC =9,∠BCA =30°,∠ADB =45°,求BD 的长.[审题视点] 由于AB =5,∠ADB =45°,因此要求BD ,可在△ABD 中,由正弦定理求解,关键是确定∠BAD 的正弦值.在△ABC 中,AB =5,AC =9,∠ACB=30°,因此可用正弦定理求出sin ∠ABC ,再依据∠ABC 与∠BAD 互补确定sin ∠BAD 即可. 解 在△ABC 中,AB =5,AC =9,∠BCA =30°.由正弦定理,得AB sin ∠ACB =AC sin ∠ABC, sin ∠ABC =AC ·sin ∠BCA AB =9sin 30°5=910. ∵AD ∥BC ,∴∠BAD =180°-∠ABC ,于是sin ∠BAD =sin ∠ABC =910. 同理,在△ABD 中,AB =5,sin ∠BAD =910, ∠ADB =45°,由正弦定理:AB sin ∠BDA =BD sin ∠BAD, 解得BD =922.故BD 的长为922. 要利用正、余弦定理解决问题,需将多边形分割成若干个三角形,在分割时,要注意有利于应用正、余弦定理.【训练3】 如图,在△ABC 中,已知∠B =45°,D 是BC 边上的一点,AD =10,AC =14,DC =6,求AB 的长.解 在△ADC 中,AD =10,AC =14,DC =6,由余弦定理得cos ∠ADC =AD 2+DC 2-AC 22AD ·DC=100+36-1962×10×6=-12,∴∠ADC =120°,∴∠ADB =60°. 在△ABD 中,AD =10,∠B =45°,∠ADB =60°,由正弦定理得AB sin ∠ADB =AD sin B, ∴AB =AD ·sin ∠ADB sin B =10sin 60°sin 45°=10×3222=5 6.。
正弦定理、余弦定理应用

余弦定理的定义
总结词
余弦定理是三角形中另一个重要的定 理,它描述了三角形各边与其对应角 的余弦值之间的关系。
详细描述
余弦定理指出,在任何三角形ABC中,边 长a、b、c与对应的角A、B、C的余弦值 之比都相等,即:a/cosA = b/cosB = c/cosC。这个定理可以通过三角形的相似 性质和直角三角形的勾股定理来证明。
计算三角函数值
已知三角形的两边和夹角,可以利用正弦定理求出其他角的正弦值。
在物理问题中的应用
计算振动频率
在振动问题中,可以利用正弦定理求 出振动的频率。
解决波动问题
在波动问题中,可以利用正弦定理分 析波的传播规律。
03
余弦定理的应用
在几何问题中的应用
确定三角形形状
01
通过余弦定理可以判断三角形是否为直角三角形、等腰三角形
物理问题中的综合应用
1 2
振动和波动问题
利用正弦定理和余弦定理,可以解决一些与振动 和波动相关的物理问题,如简谐振动、波动传播 等。
交流电问题
通过正弦定理和余弦定理,可以解决一些与交流 电相关的物理问题,如电流、电压、功率等。
3
光学问题
利用正弦定理和余弦定理,可以解决一些与光学 相关的物理问题,如光的反射、折射等。
02
正弦定理的应用
在几何问题中的应用
确定三角形形状
通过正弦定理可以判断三角形是直角三角形、等 腰三角形还是一般三角形。
计算角度
利用正弦定理可以求出三角形中未知的角度。
计算边长
已知三角形的两边和夹角,可以利用正弦定理求 出第三边的长度。
在三角函数问题中的应用
求解三角函数方程
利用正弦定理可以将三角函数方程转化为代数方程,从而求解。
正弦定理余弦定理

03
正弦定理与余弦定理的关 联
正弦定理与余弦定理的相似之处
01
两者都是关于三角形边角关系的定理,是三角学中 的基本定理之一。
02
它们都可以用来解决与三角形相关的问题,如求角 度、边长等。
03
正弦定理和余弦定理在形式上具有一定的对称性, 反映了三角形的内在规律。
正弦定理与余弦定理的不同之处
01
02
03
正弦定理主要应用于求解三角形 的角度,特别是当已知两边及其 夹角时;而余弦定理则更常用于 求解三角形的边长,特别是当已 知两角及一边时。
正弦定理中的角度是通过正弦函 数来表达的,而余弦定理中的角 度则是通过余弦函数来表达的。
正弦定理和余弦定理在应用上有 一定的互补性,可以根据具体问 题选择使用。
总结词
余弦定理是三角形中一个重要的定理,它描述了三角形各边与其对应角余弦值之间的关系。
详细描述
余弦定理是三角学的基本定理之一,它指出在任意三角形ABC中,任意一边的平方等于其他两边的平 方和减去两倍的另一边的长度与相邻两边的乘积。数学公式表示为:a^2 = b^2 + c^2 - 2bc cos(A) 。
交流电
交流电的电压和电流是时间的正 弦函数,这使得正弦定理在电力 系统中有着广泛的应用。
声学
声音的传播和反射可以用正弦和 余弦函数来描述,这使得余弦定 理在声学中有重要应用。
三角函数在工程中的应用
1 2
结构设计
在建筑和机械设计中,正弦和余弦定理常被用来 计算角度、长度等参数,以确保结构的稳定性和 安全性。
余弦定理的应用
总结词
余弦定理在解决三角形问题中具有广泛 的应用,包括求解角度、判断三角形的 形状以及解决实际问题等。
(完整版)解三角形之正弦定理与余弦定理

正弦定理与余弦定理教学目标掌握正弦定理和余弦定理的推导,并能用它们解三角形正余弦定理及三角形面积公式.教学重难点掌握正弦定理和余弦定理的推导,并能用它们解三角形知识点清单一.正弦定理:1. 正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,并且都等于外接圆的直径,即a b c2R(其中R是三角形外接圆的半径)sin A sin B si2.变形:1) a b c a b csin sin si nC sin sin si nC2)化边为角:a :b: c sin A: sin B :s in C -a si nA.b sin B a sin AJb sin Bc sin C c sin C '3)化边为角:a 2Rsin A, b 2Rsi nB, c 2Rs inC4)化角为边:sin A a ;J sin B b ; si nA aJ7sin B b sin C c sin C c5)化角为边:sin A a sin B b si nC c2R‘2R'2R3.利用正弦定理可以解决下列两类三角形的问题:①已知两个角及任意一边,求其他两边和另一角; 例:已知角B,C,a,解法:由A+B+C=18°0,求角A,由正弦定理-Sn) - Sn^; b sin B c sin C a sin A;求出b与cc sin C②已知两边和其中一边的对角,求其他两个角及另一边。
例:已知边a,b,A,解法:由正弦定理旦血求出角B,由A+B+C=180求出角C,再使用正b sin B弦定理旦泄求出c边c sin C4. △ ABC中,已知锐角A,边b,贝U①a bsin A时,B无解;②a bsinA或a b时,B有一个解;③ bsin A a b 时,B 有两个解。
如:①已知A 60 ,a 2,b2, 3 ,求B (有一个解) ②已知A 60 ,b 2,a23,求B (有两个解)注意:由正弦定理求角时,注意解的个数。
正弦定理、余弦定理及其应用

4.7正弦定理、余弦定理及其应用1.正弦定理(1)正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,即.其中R是三角形外接圆的半径.(2)正弦定理的其他形式:①a=2R sin A,b=____________,c=____________;②sin A=a2R,sin B=,sin C=;③a∶b∶c=______________________.2.余弦定理(1)余弦定理:三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍.即a2=,b2=,c2=.若令C=90°,则c2=,即为勾股定理.(2)余弦定理的推论:cos A=,cos B=,cos C=.若C为锐角,则cos C>0,即a2+b2______c2;若C为钝角,则cos C<0,即a2+b2______c2.故由a2+b2与c2值的大小比较,可以判断C为锐角、钝角或直角.(3)正、余弦定理的一个重要作用是实现边角____________,余弦定理亦可以写成sin2A=sin2B+sin2C-2sin B sin C cos A,类似地,sin2B=____________________;sin2C=__________________.注意式中隐含条件A+B+C=π.3.解三角形的类型(1)已知三角形的任意两个角与一边,用____________定理,只有一解.(2)已知三角形的任意两边与其中一边的对角,用____________定理,可能有__________________.如在△ABC(3)已知三边,用____________定理.有解时,只有一解.(4)已知两边及夹角,用____________定理,必有一解.4.三角形中的常用公式及变式(1)三角形面积公式S△=====.其中R ,r 分别为三角形外接圆、内切圆半径.(2)A +B +C =π,则A =__________,A2=__________,从而sin A =____________,cos A =____________,tan A=____________;sin A 2=__________,cos A 2=__________,tan A2=__________.tan A +tan B +tan C =____________.(3)若三角形三边a ,b ,c 成等差数列,则2b =____________⇔2sin B =____________⇔2sin B2=cos A -C 2⇔2cos A +C 2=cos A -C 2⇔tan A 2tan C 2=13.(4)在△ABC 中,a =b cos C +c cos B ,b =____________,c =____________.(此定理称作“射影定理”,亦称第一余弦定理)自查自纠1.(1)a sin A =b sin B =csin C=2R (2)①2R sin B 2R sin C ②b 2R c2R③sin A ∶sin B ∶sin C2.(1)b 2+c 2-2bc cos A c 2+a 2-2ca cos B a 2+b 2-2ab cos C a 2+b 2(2)b 2+c 2-a 22bc c 2+a 2-b 22ca a 2+b 2-c 22ab > <(3)互化 sin 2C +sin 2A -2sin C sin A cos B sin 2A +sin 2B -2sin A sin B cos C 3.(1)正弦(2)正弦 一解、两解或无解 ①一解②两解 ③一解 ④一解 (3)余弦 (4)余弦 4.(1)12ab sin C 12bc sin A 12ac sin B abc 4R 12(a +b +c )r(2)π-(B +C ) π2-B +C2 sin(B +C )-cos(B +C )-tan(B +C ) cos B +C 2 sin B +C21tanB +C 2tan A tan B tan C (3)a +c sin A +sin C (4)a cos C +c cos A a cos B +b cos A在△ABC 中,a =1,b =2,cos C =14,则c =( )A .1 B. 3 C.322D .2解:c 2=1+4-2×2×14=4,c =2.故选D .(2017·山东)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .若△ABC 为锐角三角形,且满足sin B (1+2cos C )=2sin A cos C +cos A sin C ,则下列等式成立的是( ) A .a =2b B .b =2a C .A =2B D .B =2A解:sin(A +C )+2sin B cos C =2sin A cos C +cos A sin C ,所以2sin B cos C =sin A cos C ⇒2sin B =sin A ⇒2b =a .故选A .(2017·全国卷Ⅰ)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知sin B +sin A (sin C -cos C )=0,a =2,c =2,则C =( ) A.π12 B.π6 C.π4 D.π3 解:由题意sin(A +C )+sin A (sin C -cos C )=0, 得sin A cos C +cos A sin C +sin A sin C -sin A cos C =0,即sin C (sin A +cos A )=2sin C sin ⎝⎛⎭⎫A +π4=0, 所以A =3π4.由正弦定理a sin A =c sin C ,得2sin 3π4=2sin C,即sin C =12,得C =π6.故选B .(2015·北京)在△ABC 中,a =4,b =5,c =6,则sin2A sin C=________.解:sin2A sin C =2sin A cos A sin C =2a c ×b 2+c 2-a 22bc =2×46×25+36-162×5×6=1.故填1.(2017·浙江)我国古代数学家刘徽创立的“割圆术”可以估算圆周率π,理论上能把π的值计算到任意精度.祖冲之继承并发展了“割圆术”,将π的值精确到小数点后七位,其结果领先世界一千多年,“割圆术”的第一步是计算单位圆内接正六边形的面积S 6,S 6=________.解:将正六边形分割为6个等边三角形,则S 6=6×⎝⎛⎭⎫12×1×1×sin60°=332.故填 332.类型一 正弦定理的应用(2016·全国卷Ⅱ)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若cos A =45,cos C =513,a =1,则b=________.解:在△ABC 中由cos A =45,cos C =513,可得sin A =35,sin C =1213,sin B =sin(A +C )=sin A cos C +cos A sin C =6365,由正弦定理得b =a sin B sin A =2113.故填2113.【点拨】先根据条件得到至少两个角的正弦值,再利用正弦定理,实现边角互化.(2017·全国卷Ⅱ)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .若2b cos B =a cos C +c cos A ,则B =________.解:由正弦定理可得2sin B cos B =sin A cos C +sin C cos A =sin(A +C )=sin B ⇒cos B =12⇒B =π3.故填π3.类型二 余弦定理的应用(2017·山东)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .已知b =3,AB →·AC →=-6,S △ABC =3,求A 和a .解:因为AB →·AC →=-6,所以bc cos A =-6. 又S △ABC =3,所以bc sin A =6,因此tan A =-1.又0<A <π,所以A =3π4.又b =3,所以c =2 2.由余弦定理a 2=b 2+c 2-2bc cos A ,得a 2=9+8-2×3×22×⎝⎛⎭⎫-22=29,所以a =29.【点拨】正、余弦定理是应用极为广泛的两个定理,它将三角形的边和角有机地联系起来,从而使三角与几何产生联系,为求与三角形有关的量(如面积、外接圆与内切圆半径和面积等)提供了理论依据,也是判断三角形形状、证明三角形中有关等式的重要依据.其主要方法有:化角法,化边法,面积法,运用初等几何法.注意体会其中蕴涵的函数与方程思想、等价转化思想及分类与整合思想.(2016·全国卷Ⅲ)在△ABC 中,B =π4,BC 边上的高等于13BC ,则cos A =( )A.31010B.1010 C .-1010 D .-31010解:由题意可得13a =c sin π4=22c ,则a =322c .在△ABC 中,由余弦定理可得b 2=a 2+c 2-2ac =92c 2+c 2-3c 2=52c 2,则b =102c .由余弦定理,可得cos A =b 2+c 2-a 22bc =52c 2+c 2-92c 22×102c ×c=-1010.故选C . 类型三 正、余弦定理的综合应用△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知a =b cos C +c sin B . (1)求B ;(2)若b =2,求△ABC 面积的最大值.解:(1)由已知及正弦定理得sin A =sin B cos C +sin C sin B .① 因为A =π-(B +C ),所以sin A =sin(B +C )=sin B cos C +cos B sin C .② 由①,②和C ∈(0,π)得sin B =cos B .又B ∈(0,π),所以B =π4.(2)△ABC 的面积S =12ac sin B =24ac .由已知及余弦定理得b 2=a 2+c 2-2ac cos B , 即4=a 2+c 2-2ac cos π4,又a 2+c 2≥2ac ,所以ac ≤42-2,当且仅当a =c 时,等号成立. 因此△ABC 面积的最大值为2+1.【点拨】(1)化边为角与和角或差角公式的正向或反向多次联用是常用的技巧;(2)已知边及其对角求三角形面积最值是高考中考过多次的问题,既可用三角函数求最值,也可以用余弦定理化边后用不等式求最值.(2016·山东)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知2(tan A +tan B )=tan A cos B +tan Bcos A.(1)证明:a +b =2c ; (2)求cos C 的最小值.解:(1)证明:由题意知2⎝⎛⎭⎫sin A cos A +sin B cos B =sin A cos A cos B +sin Bcos A cos B,化简得2(sin A cos B +sin B cos A )=sin A +sin B ,即2sin(A +B )=sin A +sin B ,因为A +B +C =π,所以sin(A +B )=sin (π-C )=sin C ,从而sin A +sin B =2sin C ,由正弦定理得a +b =2c .(2)由(1)知c =a +b 2,所以cos C =a 2+b 2-c 22ab=a 2+b 2-⎝⎛⎭⎫a +b 222ab=38⎝⎛⎭⎫a b +b a -14≥12,当且仅当a =b 时等号成立,故cos C 的最小值为12.类型四 判断三角形的形状在三角形ABC 中,若tan A ∶tan B =a 2∶b 2,试判断三角形ABC 的形状.解法一:由正弦定理,得a 2b 2=sin 2A sin 2B ,所以tan A tan B =sin 2Asin 2B,所以sin A cos B cos A sin B =sin 2A sin 2B,即sin2A =sin2B .所以2A =2B ,或2A +2B =π,因此A =B 或A +B =π2,从而△ABC 是等腰三角形或直角三角形.解法二:由正弦定理,得a 2b 2=sin 2A sin 2B ,所以tan A tan B =sin 2A sin 2B ,所以cos B cos A =sin A sin B ,再由正、余弦定理,得a 2+c 2-b 22ac b 2+c 2-a 22bc =ab,化简得(a 2-b 2)(c 2-a 2-b 2)=0,即a 2=b 2或c 2=a 2+b 2. 从而△ABC 是等腰三角形或直角三角形.【点拨】由已知条件,可先将切化弦,再结合正弦定理,将该恒等式的边都化为角,然后进行三角函数式的恒等变形,找出角之间的关系;或将角都化成边,然后进行代数恒等变形,可一题多解,多角度思考问题,从而达到对知识的熟练掌握.(2016·济南一中检测)在△ABC 中,内角A ,B ,C 对边的边长分别为a ,b ,c ,A 为锐角,lg b +lg 1c=lgsin A =-lg 2,则△ABC 为( )A .锐角三角形B .等边三角形C .钝角三角形D .等腰直角三角形解:由lg b +lg 1c =lg b c =-lg 2=lg 22,得b c =22,即c =2b .由lgsin A =-lg 2,得sin A =22,又A 为锐角,所以cos A =22.由余弦定理:a 2=b 2+c 2-2bc cos A 得a =b , 故B =A =45°,因此C =90°.故选D .类型五 解三角形应用举例(2015·湖北)如图,一辆汽车在一条水平的公路上向正西行驶,到A 处时测得公路北侧一山顶D 在西偏北30°的方向上,行驶600 m 后到达B 处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD =________m.解:设此山高h (m),则BC =3h ,在△ABC 中,∠BAC =30°,∠CBA =105°,∠BCA =45°,AB =600(m).在△ABC 中,根据正弦定理得BC sin A =ABsin C,即3h sin30°=600sin45°,解得h =1006(m).故填1006. 【点拨】①解三角形的方法在实际问题中,有广泛的应用.在物理学中,有关向量的计算也常用到解三角形的方法.②不管是什么类型的三角应用问题,解决的关键都是充分理解题意,将问题中的语言叙述弄明白,画出帮助分析问题的草图,再将其归结为属于哪类可解的三角形.如图,从气球A 上测得正前方的河流的两岸B ,C 的俯角分别为75°,30°,此时气球的高是60m ,则河流的宽度BC 等于________m.解:因为tan15°=tan(60°-45°)=tan60°-tan45°1+tan60°tan45°=2-3,所以BC =60tan60°-60tan15°=120(3-1)m.故填120(3-1).1.已知两边及其中一边的对角解三角形时,要谨防漏解.2.在判断三角形的形状时,一般将已知条件中的边角关系利用正弦定理或余弦定理转化为角的关系(注意应用A +B +C =π这个结论)或边的关系,再用三角变换或代数式的恒等变形(如因式分解、配方等)求解,注意等式两边的公因式一般不要约掉,而要移项提取公因式,否则有可能漏掉一种形状.3.要熟记一些常见结论,如三内角成等差数列,则必有一角为60°;若三内角的正弦值成等差数列,则三边也成等差数列;内角和定理与诱导公式结合产生的结论:sin A =sin(B +C ),cos A =-cos(B +C ),sin A2=cos B +C 2,sin2A =-sin2(B +C ),cos2A =cos2(B +C )等. 4.应用正、余弦定理解斜三角形应用题的一般步骤: (1)分析:理解题意,分清已知与未知,画出示意图;(2)建模:根据已知条件与求解目标,把已知量与求解量尽量集中到一个三角形中,建立一个解斜三角形的模型;(3)求解:利用正、余弦定理有序地解出三角形,求得数学模型的解; (4)检验:检验上述所求得的解是否符合实际,从而得出实际问题的解.5.正、余弦定理是应用极为广泛的两个定理,它将三角形的边和角有机地联系起来,从而使三角与几何产生联系,为求与三角形有关的量(如面积、外接圆、内切圆半径和面积等)提供了理论依据,也是判断三角形形状、证明三角形中有关等式的重要依据.其主要方法有:化角法,化边法,面积法,运用初等几何法.注意体会其中蕴涵的函数与方程思想、等价转化思想及分类讨论思想.1.(北京丰台2017届期末)在△ABC 中,C =π4,AB =2,AC =6,则sin B 的值为( )A.12B.22 C .-12 D.32解:由正弦定理得2sin C =6sin B ,解得sin B =32.故选D .2.(2016·天津)在△ABC 中,若AB =13,BC =3,∠C =120°,则AC =( ) A .1 B .2 C .3 D .4 解:由余弦定理得13=9+AC 2+3AC ⇒AC =1.故选A .3.设△ABC 的内角A, B, C 所对的边分别为a, b, c, 若b cos C +c cos B =a sin A, 则△ABC 的形状为( ) A .锐角三角形 B .直角三角形 C .钝角三角形 D .不确定解:由已知和正弦定理可得sin B cos C +sin C cos B =sin A ·sin A ,即sin(B +C )=sin A sin A ,亦即sin A =sin A sin A .因为0<A <π,所以sin A =1,A =π2.所以△ABC 为直角三角形.故选B .4.(2016·山东)△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,已知b =c ,a 2=2b 2(1-sin A ),则A =( ) A.3π4 B.π3 C.π4 D.π6 解:在△ABC 中,由余弦定理得a 2=b 2+c 2-2bc cos A , 因为b =c ,所以a 2=2b 2(1-cos A ), 又因为a 2=2b 2(1-sin A ), 所以cos A =sin A ,所以tan A =1,因为A ∈(0,π),所以A =π4.故选C .5.(2015·天津改编)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知△ABC 的面积为315,b -c =2,cos A =-14,则a 的值为( )A .2B .4C .6D .8解:由cos A =-14得sin A =154,所以△ABC 的面积为12bc sin A =12bc ×154=315,解得bc =24,又b -c =2,所以a 2=b 2+c 2-2bc cos A =(b -c )2+2bc -2bc cos A =22+2×24-2×24×⎝⎛⎭⎫-14=64,得a =8.故选D . 6.(2016·长春质检)在△ABC 中,D 是BC 中点,已知∠BAD +∠C =90°,则△ABC 的形状为( ) A .等腰三角形 B .直角三角形 C .等腰直角三角形 D .等腰三角形或直角三角形解:如图,由题可知,∠BAD +∠C =∠B +∠CAD =90°,在△ABD 中,BD sin ∠BAD =BD cos C =ADsin B ,在△ADC 中,CD sin ∠CAD =AD sin C =CD cos B,所以sin B cos C =sin Ccos B ,即sin2B =sin2C ,所以B =C 或2B +2C =π,则此三角形为等腰三角形或直角三角形.故选D .7.(2016·北京)在△ABC 中,∠A =2π3,a =3c ,则bc=________.解:由正弦定理知sin A sin C =a c =3,所以sin C =sin2π33=12,则C =π6,所以B =π-2π3-π6=π6,所以b =c ,即bc =1.故填1.8.(2017·浙江节选)已知△ABC ,AB =AC =4,BC =2.点D 为AB 延长线上一点,BD =2,连接CD ,则△BDC 的面积是________.解:取BC 中点E ,由题意,AE ⊥BC .△ABE 中,cos ∠ABC =BE AB =14,所以cos ∠DBC =-14,sin ∠DBC =1-116=154,所以S △BCD =12×BD ×BC ×sin ∠DBC =152.故填152.9.(2017·全国卷Ⅱ)△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c .已知sin(A +C )=8sin 2B2.(1)求cos B ;(2)若a +c =6,△ABC 的面积为2,求b . 解:(1)由题设A +B +C =π,得sin B =8sin 2B2,故sin B =4(1-cos B ). ①将①两边平方,整理得17cos 2B -32cos B +15=0,解得cos B =1(舍去),cos B =1517.(2)由cos B =1517,得sin B =817,故S △ABC =12ac sin B =417ac .又S △ABC =2,则ac =172.由余弦定理及a +c =6得b 2=a 2+c 2-2ac cos B =(a +c )2-2ac (1+cos B )=36-2×172×⎝⎛⎭⎫1+1517=4.所以b =2.10.(2015·全国卷Ⅱ)△ABC 中,D 是BC 上的点,AD 平分∠BAC ,△ABD 面积是△ADC 面积的2倍.(1)求sin ∠B sin ∠C;(2)若AD =1,DC =22,求BD 和AC 的长.解:(1)S △ABD =12AB ·AD sin ∠BAD ,S △ADC =12AC ·AD sin ∠CAD ,因为S △ABD =2S △ADC ,∠BAD =∠CAD ,所以AB =2AC .由正弦定理可得sin ∠B sin ∠C =AC AB =12.(2)因为S △ABD ∶S △ADC =BD ∶DC ,所以BD = 2. 在△ABD 和△ADC 中,由余弦定理得AB 2=AD 2+BD 2-2AD ·BD cos ∠ADB ,AC 2=AD 2+DC 2-2AD ·DC cos ∠ADC ,AB 2+2AC 2=3AD 2+BD 2+2DC 2=6.由(1)知AB =2AC ,故AC =1.(2016·北京)在△ABC 中,a 2+c 2=b 2+2ac . (1)求角B 的大小;(2)求2cos A +cos C 的最大值.解:(1)由a 2+c 2=b 2+2ac 得a 2+c 2-b 2=2ac .由余弦定理得cos B =a 2+c 2-b 22ac =2ac 2ac =22.又0<B <π,所以B =π4.(2)A +C =π-B =π-π4=3π4,所以C =3π4-A ,0<A <3π4.所以2cos A +cos C =2cos A +cos ⎝⎛⎭⎫3π4-A =2cos A +cos 3π4cos A +sin 3π4sin A=2cos A -22cos A +22sin A=22sin A +22cos A =sin ⎝⎛⎭⎫A +π4. 因为0<A <3π4,所以π4<A +π4<π,故当A +π4=π2,即A =π4时,2cos A +cos C 取得最大值为1.1.(2016·大兴区模拟)在△ABC 中,a =2,b =3,∠B =π3,则∠A 等于( )A.π6B.π4C.3π4D.π4或3π4解:因为b >a ,由正弦定理得到sin A =a sin B b =22,所以∠A =π4.故选B .2.(2016·湖南四校联考)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若(a 2+b 2-c 2)tan C =ab ,则角C 为( )A.π6或5π6B.π3或2π3C.π6D.2π3解:由题意得a 2+b 2-c 22ab =12tan C ,则cos C =cos C 2sin C ,且cos C ≠0,所以sin C =12,所以C =π6或5π6.故选A .3.(2016·郑州一测)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若b 3cos B =asin A ,则cos B =( )A .-12 B.12 C .-32 D.32解:因为b 3cos B =a sin A ,所以由正弦定理得sin B 3cos B =sin A sin A,所以tan B =3,又0<B <π,所以B =π3,所以cos B=12.故选B . 4.(北京通州2017届期末)在△ABC 中,a =2,B =π3,△ABC 的面积等于32,则b 等于( )A.32B .1 C. 3 D .2 解:由△ABC 面积公式可得S =12ac sin B =32,12×2c ×32=32,c =1,由余弦定理得b 2=a 2+c 2-2ac cos B =22+12-2×2×1×cos π3=3,b = 3.故选C .5.(2016·厦门期中测试)如图,D ,C ,B 在地平面同一直线上,DC =10 m ,从D ,C 两地测得A 点的仰角分别为30°和45°,则A 点离地面的高AB 等于( )A .10 mB .5 3 mC .5(3-1) mD .5(3+1) m解:直角三角形中,根据三角函数的定义得AB tan30°-ABtan45°=10,解得AB =5(3+1) (m).故选D . 6.(2016·河南三市调研)△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若c 2=(a -b )2+6,C =π3,则△ABC的面积为( )A .3 B.932 C.332D .3 3解:由c 2=(a -b )2+6,可得a 2+b 2-c 2=2ab -6,由余弦定理得2ab cos C =2ab -6,因为C =π3,所以ab =6,所以△ABC 的面积为12ab sin C =12×6×32=332.故选C .7.在△ABC 中,角A ,B ,C 所对应的边分别为a ,b ,c ,已知b cos C +c cos B =2b ,则ab =________.解法一:由正弦定理sin B cos C +sin C cos B =2sin B ,即sin(B +C )=sin A =2sin B ,有a b =sin Asin B =2.解法二:由余弦定理得b ·a 2+b 2-c 22ab +c ·a 2+c 2-b 22ac =2b ,化简得a =2b ,因此,ab =2.解法三:由三角形射影定理,知b cos C +c cos B =a ,所以a =2b ,所以ab=2.故填2.8.(武汉市2018届高三起点调研)在钝角△ABC 中,内角A ,B ,C 的对边分别是a ,b ,c ,若a =4,b =3,则c 的取值范围是________.解:在钝角△ABC 中,a =4,b =3,则4-3<c <4+3,即1<c <7,若C 是钝角,则cos C <0,则a 2+b 2-c 22ab<0,即c 2>a 2+b 2=25,所以c >5,即5<c <7;若A 是钝角,则cos A <0,则b 2+c 2-a 22bc <0,即c 2<a 2-b 2=7,所以c <7,又1<c <7,则1<c <7.综上可知,c 的取值范围是(1,7)∪(5,7). 故填(1,7)∪(5,7).9.(2016·浙江)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知b +c =2a cos B . (1)证明:A =2B ;(2)若△ABC 的面积S =a 24,求角A 的大小.解:(1)证明:由正弦定理得sin B +sin C =2sin A cos B ,故2sin A cos B =sin B +sin(A +B )=sin B +sin A cos B +cos A sin B ,于是sin B =sin(A -B ). 又A ,B ∈(0,π),故0<A -B <π,所以B =π-(A -B )或B =A -B , 因此A =π(舍去)或A =2B ,所以A =2B .(2)由S =a 24得12ab sin C =a 24,故有sin B sin C =12sin2B =sin B cos B ,因为sin B ≠0,所以sin C =cos B .又B ,C ∈(0,π),所以C =π2±B .当B +C =π2时,A =π2;当C -B =π2时,A =π4.综上,A =π2或A =π4.10.(2016·四川)在△ABC 中,角A ,B ,C 所对的边分别是a ,b ,c ,且cos A a +cos B b =sin Cc .(1)证明:sin A sin B =sin C ;(2)若b 2+c 2-a 2=65bc ,求tan B .解:(1)证明:根据正弦定理,可设a sin A =b sin B =csin C=k (k >0),则a =k sin A ,b =k sin B ,c =k sin C .代入cos A a +cos B b =sin C c 中,有cos A k sin A +cos B k sin B =sin C k sin C ,变形可得sin A sin B =sin A cos B +cos A sin B =sin(A +B ).在△ABC 中,由A +B +C =π,有sin(A +B )=sin (π-C )=sin C .所以sin A sin B =sin C .(2)由已知,b 2+c 2-a 2=65bc ,根据余弦定理,有cos A =b 2+c 2-a 22bc =35,所以sin A =1-cos 2A =45.由(1),sin A sin B =sin A cos B +cos A sin B ,所以45sin B =45cos B +35sin B ,即sin B =4cos B .故tan B =sin Bcos B=4.(2017·福建漳州质检)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,其中b ≠c ,且b cos B =c cos C ,延长线段BC 到点D ,使得BC =4CD =4,∠CAD =30°.(1)求证:∠BAC 是直角;(2)求tan ∠D 的值.解:(1)证明:因为b cos B =c cos C ,由正弦定理,得sin B cos B =sin C cos C ,所以sin2B =sin2C .又b ≠c ,所以2B =π-2C ,所以B +C =π2,所以∠A =90°.即∠BAC 是直角.(2)设∠D =α,由题意知CD =1,BC =4, 在△ABC 中,因为∠BAC =90°,∠ACB =30°+α,所以cos(30°+α)=ACBC ,所以AC =4cos(30°+α).在△ACD 中,AC sin α=CD sin ∠CAD,即AC sin α=112=2,所以AC =2sin α,所以4cos(30°+α)=2sin α,即2⎝⎛⎭⎫32cos α-12sin α=sin α,整理得3cos α=2sin α,所以tan α=32,即tan ∠D =32一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.函数y =cos ⎝⎛⎭⎫2x -π6的最小正周期是( ) A.π2B .πC .2πD .4π 解:函数y =cos ⎝⎛⎭⎫2x -π6的最小正周期T =2π2=π.故选B . 2.若tan α>0,则( )A .sin2α>0B .cos α>0C .sin α>0D .cos2α>0解:因为tan α>0,所以α∈⎝⎛⎭⎫k π,k π+π2(k ∈Z ),即α是第一、三象限角.所以2α∈(2k π,2k π+π)(k ∈Z ),再根据三角函数值在各象限的符号知,sin2α>0.故选A .3.(2015·厦门模拟)已知角θ是第二象限角,sin θ=34,那么角2θ为( )A .第一象限角B .第二象限角C .第三象限角D .第四象限角解:因为sin θ=34且角θ为第二象限角,所以cos θ=-1-sin 2θ=-74,cos2θ=cos 2θ-sin 2θ=-18,sin2θ=2sin θcos θ=-378.所以角2θ为第三象限角.故选C .4.(2016·江西三校联考)函数y =sin 2x 的图象的一个对称中心为( )A .(0,0) B. ⎝⎛⎭⎫π4,0 C.⎝⎛⎭⎫π4,12 D.⎝⎛⎭⎫π2,1 解:因为y =sin 2x =1-cos2x 2,令2x =π2+k π,k ∈Z ,所以x =π4+k π2,k ∈Z ,所以函数y =sin 2x 的图象的一个对称中心为⎝⎛⎭⎫π4,12.故选C .5.(2016·全国卷Ⅱ)函数f (x )=cos2x +6cos ⎝⎛⎭⎫π2-x 的最大值为( )A .4B .5C .6D .7解:因为f (x )=1-2sin 2x +6sin x =-2⎝⎛⎭⎫sin x -322+112,而sin x ∈[-1,1],所以当sin x =1时,f (x )取最大值5.故选B .6.(2016·淮南二模)已知函数f (x )=sin(2x +φ)满足f (x )≤f (a )对x ∈R 恒成立,则函数( ) A .f (x -a )一定为奇函数 B .f (x -a )一定为偶函数 C .f (x +a ) 一定为奇函数 D .f (x +a )一定为偶函数解:由题意得f (a )=sin(2a +φ)=1,则2a +φ=2k π+π2,k ∈Z ,所以f (x +a )=sin(2x +2a +φ)=sin(2x +2k π+π2)=cos2x ,此时函数为偶函数.故选D .7.(2016·南开模拟)△ABC 中三个内角为A ,B ,C ,若关于x 的方程x 2-x cos A cos B -cos 2C2=0有一根为1,则△ABC 一定是( )A .直角三角形B .等腰三角形C .锐角三角形D .钝角三角形解:依题意,可得1-cos A cos B -cos 2C 2=0,因为cos 2C 2=1+cos C 2=1-cos (A +B )2=1-cos A cos B +sin A sin B2,所以1-cos A cos B -1-cos A cos B +sin A sin B2=0,整理得:cos(A -B )=1,又A ,B 为△ABC 的内角,所以A =B ,所以△ABC 一定为等腰三角形.故选B .8.已知sin ⎝⎛⎭⎫α+π3+sin α=-435,-π2<α<0,则cos ⎝⎛⎭⎫α+2π3=( ) A .-45 B .-35 C.45 D.35解:因为sin ⎝⎛⎭⎫α+π3+sin α=32sin α+32cos α=-435,所以32sin α+12cos α=-45.所以cos ⎝⎛⎭⎫α+2π3=cos αcos 2π3-sin αsin 2π3=-12cos α-32sin α=45.故选C .9.(2016·湖南师大附中二模)设f (x )=1+cos2x +sin2x 2sin ⎝⎛⎭⎫π2+x +a sin ⎝⎛⎭⎫x +π4的最大值为3,则常数a =( ) A .1 B .1或-5C .-2或4D .±7解:f (x )=2cos 2x +2sin x cos x 2cos x+a sin ⎝⎛⎭⎫x +π4=2cos x +2sin x +a sin ⎝⎛⎭⎫x +π4=2sin ⎝⎛⎭⎫x +π4+a sin ⎝⎛⎭⎫x +π4=(a +2)sin ⎝⎛⎭⎫x +π4,则|a +2|=3,所以a =1或a =-5.故选B . 10.(2017·天津)设θ∈R ,则“⎪⎪⎪⎪θ-π12<π12”是“sin θ<12”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充要条件D .既不充分也不必要条件解:根据条件,由⎪⎪⎪⎪θ-π12<π12得0<θ<π6,推出sin θ<12,而当sin θ<12时,取θ=-π6,⎪⎪⎪⎪-π6-π12=π4>π12.故选A .11.(2015·郑州模拟)已知函数f (x )=cos ⎝⎛⎭⎫2x +π3-cos2x ,其中x ∈R ,给出下列四个结论: ①函数f (x )是最小正周期为π的奇函数; ②函数f (x )图象的一条对称轴是直线x =2π3;③函数f (x )图象的一个对称中心为⎝⎛⎭⎫5π12,0;④函数f (x )的递增区间为⎝⎛⎭⎫k π+π6,k π+2π3,k ∈Z . 则正确结论的个数是( )A .1B .2C .3D .4 解:f (x )=cos ⎝⎛⎭⎫2x +π3-cos2x =cos2x cos π3-sin2x sin π3-cos2x =-sin ⎝⎛⎭⎫2x +π6,不是奇函数,①错;f ⎝⎛⎭⎫2π3=-sin ⎝⎛⎭⎫4π3+π6=1,②正确;f ⎝⎛⎭⎫5π12=-sin π=0,③正确;令2k π+π2≤2x +π6≤2k π+3π2,k ∈Z ,得k π+π6≤x ≤k π+23π,k ∈Z ,④正确.综上知正确结论的个数为3.故选C . 12.(2015·重庆)若tan α=2tan π5,则cos ⎝⎛⎭⎫α-3π10sin ⎝⎛⎫α-π5=( )A .1B .2C .3D .4解:cos ⎝⎛⎭⎫α-3π10sin ⎝⎛⎭⎫α-π5=cos αcos 3π10+sin αsin 3π10sin αcos π5-cos αsin π5=cos 3π10+tan αsin 3π10tan αcos π5-sin π5=cos 3π10+2tan π5sin 3π102tan π5cos π5-sinπ5=cos π5cos 3π10+2sin π5sin 3π10sin π5cos π5=⎝⎛⎭⎫cos π5cos 3π10+sin π5sin 3π10+cos ⎝⎛⎭⎫π2-π5sin 3π1012sin 2π5=3cosπ10cos π10=3.故选C .二、填空题:本题共4小题,每小题5分,共20分.13.已知sin α=13,则sin(2 019π-α)=________.解:sin (2 019π-α)=sin (π-α)=sin α=13.故填13.14.cos43°cos77°+sin43°cos167°的值为________.解:cos43°cos77°+sin43°cos167°=cos43°cos77°+sin43°(-sin77°)=cos120°=-12.故填-12.15.(2015·广东模拟)已知角φ的终边经过点P (3,-4),函数f (x )=sin(ωx +φ)(ω>0)的图象的相邻两条对称轴之间的距离等于π3,则f ⎝⎛⎭⎫π12的值为________. 解:根据题意,T =2π3,ω=2πT =3,sin φ=-45,cos φ=35,f ⎝⎛⎭⎫π12=sin ⎝⎛⎭⎫3×π12+φ=sin ⎝⎛⎭⎫π4+φ=22(sin φ+cos φ)=-210.故填-210.16.(2017·全国卷Ⅲ)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知C =60°,b =6,c =3,则A =________.解:由题意,b sin B =c sin C ,即sin B =b sin C c =6×323=22,结合b <c ,可得B =45°,则A =180°-B -C =75°.故填75°.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)(北京西城2017届期末)已知函数f (x )=sin(2ωx -π6)+2cos 2ωx -1(ω>0)的最小正周期为π.(1)求ω的值;(2)求f (x )在区间⎣⎡⎦⎤0,7π12上的最大值和最小值. 解:(1)因为f (x )=sin ⎝⎛⎭⎫2ωx -π6+(2cos 2ωx -1) =⎝⎛⎭⎫sin2ωx cos π6-cos2ωx sin π6+cos2ωx =32sin2ωx +12cos2ωx =sin ⎝⎛⎭⎫2ωx +π6, 所以f (x )的最小正周期T =2π2ω=π,解得ω=1.(2)由(1)得f (x )=sin ⎝⎛⎭⎫2x +π6. 因为0≤x ≤7π12,所以π6≤2x +π6≤4π3.所以,当2x +π6=π2,即x =π6时,f (x )取得最大值为1;当2x +π6=4π3,即x =7π12时,f (x )取得最小值为-32.18.(12分)(2017福建三明质检)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且B =60°,c =4,b =6. (1)求sin C ;(2)求△ABC 的面积.解:(1)B =60°,c =4,b =6,在△ABC 中,由正弦定理b sin B =csin C ,得sin C =c sin B b =4×326=33.(2)由于b >c ,所以B >C ,则C 为锐角,所以cos C =63, 则sin A =sin(B +C )=sin B cos C +cos B sin C =32×63+12×33=32+36,所以△ABC 的面积S =12bc sin A =12×32+36=62+2 3. 19.(12分)(2016·长沙模拟)已知向量a =(2sin x ,3cos x ),b =(-sin x ,2sin x ),函数f (x )=a ·b . (1)求f (x )的单调递增区间;(2)在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边且f (C )=1,c =1,ab =23,a >b ,求a ,b 的值.解:(1)由题意得f (x )=-2sin 2x +23sin x cos x =3sin2x +cos2x -1=2sin ⎝⎛⎭⎫2x +π6-1, 令2k π-π2≤2x +π6≤2k π+π2(k ∈Z ),得k π-π3≤x ≤k π+π6(k ∈Z ).所以f (x )的单调递增区间是⎣⎡⎦⎤k π-π3,k π+π6,k ∈Z . (2)由(1)和条件可得f (C )=2sin ⎝⎛⎭⎫2C +π6-1=1, 则sin ⎝⎛⎭⎫2C +π6=1. 因为0<C <π,所以2C +π6=π2,即C =π6.所以cos C =a 2+b 2-c 22ab =32,又c =1,ab =23,所以a 2+12a 2=7,解得a 2=3或a 2=4,所以a =3或2,所以当a =3时,b =2,当a =2时,b = 3. 因为a >b ,所以a =2,b = 3.20.(12分)(2015·福建)已知函数f (x )的图象是由函数g (x )=cos x 的图象经如下变换得到:先将g (x )图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图象向右平移π2个单位长度.(1)求函数f (x )的解析式,并求其图象的对称轴方程;(2)已知关于x 的方程f (x )+g (x )=m 在[0,2π)内有两个不同的解α,β,求实数m 的取值范围.解:(1)将g (x )=cos x 的图象上所有点的纵坐标伸长到原来的2倍(横坐标不变)得到y =2cos x 的图象,再将y =2cos x 的图象向右平移π2个单位长度后得到y =2cos ⎝⎛⎭⎫x -π2 的图象,故f (x )=2sin x ,从而函数f (x )=2sin x 图象的对称轴方程为x =k π+π2(k ∈Z ).(2)f (x )+g (x )=2sin x +cos x =5⎝⎛⎭⎫25sin x +15cos x =5sin(x +φ)(其中sin φ=15,cos φ=25). 依题意,sin(x +φ)=m5在区间[0,2π)内有两个不同的解α,β,当且仅当⎪⎪⎪⎪m 5<1,故m 的取值范围是(-5,5).21.(12分)(2015·山东)设f (x )=sin x cos x -cos 2⎝⎛⎭⎫x +π4. (1)求f (x )的单调区间;(2)在锐角△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .若f ⎝⎛⎭⎫A 2=0,a =1,求△ABC 面积的最大值. 解:(1)由题意知f (x )=sin2x2-1+cos ⎝⎛⎭⎫2x +π22=sin2x 2-1-sin2x 2=sin2x -12.由-π2+2k π≤2x ≤π2+2k π,k ∈Z ,可得-π4+k π≤x ≤π4+k π,k ∈Z ;由π2+2k π≤2x ≤3π2+2k π,k ∈Z , 可得π4+k π≤x ≤3π4+k π,k ∈Z .所以函数f (x )的单调递增区间是⎣⎡⎦⎤-π4+k π,π4+k π (k ∈Z );单调递减区间是⎣⎡⎦⎤π4+k π,3π4+k π(k ∈Z ). (2)由f ⎝⎛⎭⎫A 2=sin A -12=0,得sin A =12,由题意知A 为锐角,所以cos A =32. 由余弦定理得a 2=b 2+c 2-2bc cos A , 可得1+3bc =b 2+c 2≥2bc ,即bc ≤2+3,当且仅当b =c 时等号成立.所以S △ABC =12bc sin A ≤2+34.所以△ABC 面积的最大值为2+34.22.(12分)(武汉2018届调研)在锐角△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,满足cos2A -cos2B +2cos(π6-B )cos ⎝⎛⎭⎫π6+B =0. (1)求角A 的值;(2)若b =3且b ≤a ,求a 的取值范围.解:(1)由已知cos2A -cos2B +2cos ⎝⎛⎭⎫π6-B cos ⎝⎛⎭⎫π6+B =0,得2sin 2B -2sin 2A +2⎝⎛⎭⎫34cos 2B -14sin 2B =0, 化简得sin A =32,又△ABC 为锐角三角形,故A =π3.(2)若b =3≤a ,所以c ≥a ,因而π3≤C <π2,π6<B ≤π3,12<sin B ≤32.由正弦定理得,a sin A =b sin B ,即2a 3=3sin B,即a =32sin B ,由12<sin B ≤32,知a ∈[3,3).所以a 的取值范围是[3,3).。
余弦定理与正弦定理

余弦定理与正弦定理余弦定理和正弦定理是解决三角形中边长和角度之间关系的重要定理。
它们在三角学中有着广泛的应用,能够帮助我们计算未知边长或角度。
本文将介绍余弦定理和正弦定理的定义、公式以及应用,并探讨它们的区别和联系。
一、余弦定理的定义和公式余弦定理是在三角形中,通过已知边长和夹角计算其他边长的定理。
它的定义如下:在三角形ABC中,设三条边分别为a、b、c,对应的夹角分别为A、B、C,则余弦定理的公式为:c² = a² + b² - 2abcosC其中,c为三角形对应于角C的边长,a和b为与角C相邻的两条边长,cosC为角C的余弦值。
二、正弦定理的定义和公式正弦定理是在三角形中,通过已知两个角度和一个边长计算其他边长的定理。
它的定义如下:在三角形ABC中,设三条边分别为a、b、c,对应的夹角分别为A、B、C,则正弦定理的公式为:a/sinA = b/sinB = c/sinC其中,a、b、c为三角形的边长,A、B、C为对应的角度。
三、余弦定理和正弦定理的应用1. 通过余弦定理计算未知边长或角度:- 已知两边长和夹角:可以使用余弦定理计算第三条边长,或者计算其他两个角度。
- 已知三边长:可以使用余弦定理计算其中一个角度。
2. 通过正弦定理计算未知边长或角度:- 已知两角度和一个边长:可以使用正弦定理计算其他两条边长。
- 已知一个角度和两边长:可以使用正弦定理计算另外两个角度。
四、余弦定理与正弦定理的区别和联系余弦定理和正弦定理在解决三角形问题时具有不同的应用场景。
余弦定理适用于已知边长和夹角的情况,可以求解缺失的边长或角度。
而正弦定理适用于已知两个角度和一个边长的情况,同样可以求解其他边长或角度。
此外,两个定理之间也存在一定的联系。
通过余弦定理可以推导出正弦定理,而正弦定理也可以推导出余弦定理。
在解决问题时,可以根据具体情况选择使用其中一个定理进行计算。
总结:余弦定理和正弦定理是解决三角形中边长和角度之间关系的重要定理。
几何中的正弦定理与余弦定理

几何中的正弦定理与余弦定理几何学是一门研究空间和形状的学科,其中涉及到许多重要的定理和公式。
正弦定理和余弦定理是几何学中两个基础而重要的定理,它们在解决三角形的边长和角度方面起着至关重要的作用。
一、正弦定理正弦定理是指在一个任意三角形中,三条边与其对应的角之间的关系。
根据正弦定理,我们可以得到以下公式:a/sin A = b/sin B = c/sin C其中,a、b和c分别代表三角形的三条边的长度,A、B和C分别代表三角形的三个对应角的度数。
通过正弦定理,我们可以求解一个未知边长或未知角度,只需知道其他两条边长或角度即可。
例如,当我们知道三角形的两条边长a和b,以及它们夹角C的度数,我们可以利用正弦定理计算第三条边c的长度:c = (sin C * a) / sin B通过正弦定理,我们可以方便地解决一些与三角形相关的几何问题,比如寻找缺失的边长或角度。
二、余弦定理余弦定理是描述一个三角形中的边长和角度之间的关系。
与正弦定理类似,余弦定理也是解决三角形问题的重要工具。
根据余弦定理,我们可以得到以下公式:c^2 = a^2 + b^2 - 2abcos C其中,a、b和c分别代表三角形的三条边的长度,C代表三角形的夹角的度数。
通过余弦定理,我们可以求解一个未知边长或未知角度,只需知道其他两条边长或角度即可。
例如,当我们知道三角形的两条边长a和b,以及它们夹角C的度数,我们可以利用余弦定理计算第三条边c的长度:c = √(a^2 + b^2 - 2abcos C)除了求解边长,余弦定理也可以用来求解角度。
例如,当我们已知三角形的三条边长a、b和c时,我们可以利用余弦定理求解夹角A的余弦值:cos A = (b^2 + c^2 - a^2) / 2bc通过计算余弦值的反函数,我们可以得到夹角A的度数。
综上所述,正弦定理和余弦定理是解决几何学中三角形问题的重要工具。
它们可以帮助我们计算未知的边长和角度,解决各种与三角形相关的几何问题。
(完整版)正弦定理、余弦定理知识点

正弦定理、余弦定理讲师:王光明【基础知识点】1. 三角形常用公式:A +B +C =π;S =ab sin C =bc sin A ==ca sin B ;2121212.三角形中的边角不等关系: A>B a>b,a+b>c,a-b<c ;;⇔3.【正弦定理】:===2R (外接圆直径);A a sin B b sin Ccsin 正弦定理的变式:; a ∶b ∶c =sin A ∶sin B ∶sin C .⎪⎩⎪⎨⎧===C R c B R b AR a sin 2sin 2sin 24.正弦定理应用范围: ①已知两角和任一边,求其他两边及一角. ②已知两边和其中一边对角,求另一边的对角.③几何作图时,存在多种情况.如已知a 、b 及A ,求作三角形时,要分类讨论,确定解的个数.已知两边和其中一边的对角解三角形,有如下的情况:(1)A 为锐角AABa=bsin A bsin A<a<b a b ≥ 一解 两解 一解(2)A 为锐角或钝角当时有一解.a>b 5.【余弦定理】 a 2=b 2+c 2-2bccosA .c 2=a 2+b 2-2abcosC .b 2=a 2+c 2-2accosB .若用三边表示角,余弦定理可以写为、6.余弦定理应用范围:(1)已知三角形的三条边长,可求出三个内角;(2)已知三角形的两边及夹角,可求出第三边.【习题知识点】知识点1 运用判断三角形形状例题1在△ABC 中已知acosB=bcosA,试判断△ABC 的形状.【分析】利用正弦定理或余弦定理判断三角形形状,可以将三角形中的边用角表示,也可将角用边来表示.从中找到三角形中的边角关系,判断出三角形的形状.【解析】解法1:由扩充的正弦定理:代入已知式2RsinAcosB=2RsinBcosAsinAcosB-cosAsinB=0 , sin(A-B)=0A-B=0 ∴A=B 即△ABC 为等腰三角形解法2:由余弦定理: 22222222bc a c b b ac b c a a -+⋅=-+⋅ 22b a = ∴ b a =即△ABC 为等腰三角形.知识点2 运用正、余弦定理解三角形解三角形问题中正、余弦定理的选择:(1)在下述情况下应首先使用余弦定理: ①已知三条边(边边边),求三个角;②已知两边和它们的夹角(边角边),求其它一边和两角;(2)在下述情况下应首先使用正弦定理:①已知两边和一边的对角(边边角),求其它一边和两角;②已知两角和任一边(角角边、角边角),求其它两边和一角.例题2 在△ABC 中,已知,,B=45︒ 求A 、C 及c .3=a 2=b 【分析】在解斜三角形应用过程中,注意要灵活地选择正弦定和余弦定理,解得其它的边和角【解析】解法1:由正弦定理得:23245sin 3sin sin === b B a A ∵B=45︒<90︒ 即b <a ∴A=60︒或120︒当A=60︒时C=75︒ 22645sin 75sin 2sin sin +===BCb c当A=120︒时C=15︒ 22645sin 15sin 2sin sin -===B C b c 解法2:设c =x 由余弦定理将已知条件代入,整理:解之:B ac c a b cos 2222-+=0162=+-x x 226±=x 当时 从而A=60︒ ,C=75︒226+=c 2)13(231226223)226(22cos 22221=++=+⋅⋅-++=-+=bc a c b A 当时同理可求得:A=120︒ C=15︒.226-=c 知识点3 解决与三角形在关的证明、计算问题例题3 已知A 、B 、C 为锐角,tanA=1,tanB=2,tanC=3,求A+B+C 的值. 【分析】本题是要求角,要求角先要求出这个角的某一个三角函数值,再根据角的范围确定角.本题应先求出A+B 和C 的正切值,再一次运用两角和的正切公式求出A+B+C .【解析】 A B C 、、为锐角∴<++<0270°°A B C 又,,由公式可得tan tan A B ==12tan()tan tan tan tan A B A B A B +=+-⋅=+-=-112123[]tan()tan ()A B C A B C ++=++=++-+⋅tan()tan tan()tan A B C A B C 1 =-+--⨯33133() =0所以A+B+C=π知识点4 求三角形的面积例题4 △ABC 中,D 在边BC 上,且BD =2,DC =1,∠B =60o ,∠ADC =150o ,求AC 的长及△ABC 的面积.【解析】在△ABC 中,∠BAD =150o -60o =90o ,∴AD =2sin60o =3.A在△ACD 中,AD 2=(3)2+12-2×3×1×cos150o =7,∴AC =7. ∴AB =2cos60o =1.S △ABC =21×1×3×sin60o =343.知识点4 解决实际为题例题4 如图,海中有一小岛,周围3.8海里内有暗礁。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正弦定理和余弦定理一、目标与策略明确学习目标及主要的学习方法是提高学习效率的首要条件,要做到心中有数!学习目标:● 使学生掌握正弦、余弦定理的推导过程,能初步运用正弦、余弦定理解斜三角形; ● 熟记正弦、余弦定理及其变形形式;● 通过正弦、余弦定理的推导体现数形结合的思想、分类讨论的思想。
重点难点:● 重点:正、余弦定理的推导及应用。
● 难点:正、余弦定理的向量证明,两个定理的综合运用。
学习策略:● 从特殊到一般:从熟悉的直角三角形的边角关系出发,概括出直角三角形中的正、余弦定理,再推广到一般,探究任意三角形中的边角关系。
二、学习与应用(一)三角形ABC ∆中(1)一般约定:ABC ∆中角A 、B 、C 所对的边分别为 ; (2)A B C ++= ;(3)大边对 ,大角对 ,即B C b c >⇔>;等边对 ,等角对 ,即B C b c =⇔=; (4)两边之和 第三边,两边之差 第三边,即............a c b +,...........a c b -.“凡事预则立,不预则废”。
科学地预习才能使我们上课听讲更有目的性和针对性。
我们要在预习的基础上,认真听讲,做到眼睛看、耳朵听、心里想、手上记。
知识回顾——复习学习新知识之前,看看你的知识贮备过关了吗? 详细内容请参看网校资源ID :#tbjx6#208608(二)Rt ABC∆中,090C∠=(1)..................B A+=;(2)22..................a b+=(3)..................sin A=,..................sin B=,..................sin C=;..................cos A=,..................cos B=,..................cos C=。
知识点一:正弦定理正弦定理:(一)直角三角形中的正弦定理的推导证明:(二)斜三角形中正弦定理的推导法一:构造直角三角形(1)当ABC∆为锐角三角形时如图,作AB边上的高线CD交AB于D,则知识要点——预习和课堂学习认真阅读、理解教材,尝试把下列知识要点内容补充完整,带着自己预习的疑惑认真听课学习。
课堂笔记或者其它补充填在右栏。
预习和课堂学习更多知识点解析请学习网校资源ID:#tbjx7#208608在Rt CBD ∆中, sin CD B a=,即sin CD a B =,在Rt ACD ∆中, sin CD A b=,即sin CD b A =,∴sin sin a B b A =,即sin sin a b A B=.同理可证sin sin b cB C =∴sin sin sin a b cA B C ==(2)当ABC ∆为钝角三角形时法二:圆转化法(1)当ABC ∆为锐角三角形时如图,圆O 是ABC ∆的外接圆,直径为2AD R =, 则C D ∠=∠,∴sin sin 2c C D R ==,∴2sin c R C=(R 为ABC ∆的外接圆半径) 同理,2sin a R A =,2sin b R B=故2sin sin sin a b c R A B C=== (2)当ABC ∆为钝角三角形时法三:面积法(详细内容请参考知识导学,ID :#tbjx9#208608) 法四:向量法(1)当ABC ∆为锐角三角形时过A 作单位向量j 垂直于AC , 则+= 两边同乘以单位向量,得j ⋅ (AC +)=j ⋅ ,即j AC j CB j AB ⋅+⋅=⋅∴0||||cos90||||cos(90)j AC j CB C ⋅+⋅-||||cos(90)j AB A =⋅-, ∵0j AC ⋅= ,||1j = ,||CB a = ,||AB c =, cos(90)sin C C -= ,cos(90)sin A A -=∴A c C a sin sin=,∴sin sin a c AC=,同理:若过C 作垂直于CB 得:sin sin b c B C=∴sin sin sin a b c A B C==,(2)当ABC ∆为钝角三角形时说明:(1)正弦定理适合于 三角形; (2)设R 为ABC ∆的外接圆半径,可以证明:_____sin sin sin a b cA B C=== (3)每个等式可视为一个方程:知三求一。
(三)利用正弦定理可以解决下列两类三角形的问题:(1) (2)知识点二:余弦定理余弦定理:即:(一)余弦定理的推导已知:ABC ∆中,BC a =,AC b =及角C ,求角C 的对应边c . 方法一:几何法(1)当ABC ∆为锐角三角形时如图,作BC 边上的高AD 根据勾股定理有:222AC AD CD =+,222AB AD BD =+,∵Rt ADC ∆中,cos CD AC C = ,∴2222()AB AC CD BD =-+222(cos )()AC AC C CB CD =-+-2222cos (cos )b b C a b C =-+-=222cos b a ab C +-即:2222cos c a b ab C =+-.(2)当ABC ∆为钝角三角形且C 为钝角时(3)当ABC ∆为直角三角形且C 为直角时方法二:向量法(1)当ABC ∆为锐角三角形时(如图),∵AC CB AB +=,∴()()AB AB AC CB AC CB =++222AC CB AC CB =++ 22||2||||cos()||AC CB AC C CB π=+-+222cos b ba C a =-+即:2222cos c a b ab C =+- (*)同理可得:2222cos b a c ac B =+-,2222cos a b c bc A =+- (2)当ABC ∆为钝角三角形且C 为钝角时(如图)注意:(1)推导(*)中,AC 与CB的夹角应通过平移后得到,即向量的起点应重合,因此AC 与CB的夹角应为C π-,而不是C .(2)对于直角三角形中2π=C 时,cos 0C =,则222c a b =+,恰好满足勾股定理。
方法三:解析几何方法——利用两点间距离公式(详细内容请参考知识导学,ID :#tbjx12#208608) (二)余弦定理的变形公式:cos __________________cos __________________cos __________________A B C ===(三)利用余弦定理可以解决下列两类三角形的问题:(1) (2)知识点三:解三角形一般地, 叫作解三角形。
类型一:正弦定理的应用例1.已知在ABC ∆中,10c =,45A = ,30C = ,解三角形. 解:总结升华: 举一反三:【变式1】在∆ABC 中,已知032.0=A ,081.8=B ,42.9a cm =,解三角形。
经典例题-自主学习认真分析、解答下列例题,尝试总结提升各类型题目的规律和技巧,然后完成举一反三。
课堂笔记或者其它补充填在右栏。
更多精彩内容请学习网校资源ID: #jdlt0#208608【变式2】在∆ABC 中,已知075B =,060C =,5c =,求a 、A .☆【变式3】在∆ABC 中,已知sin :sin :sin 1:2:3A B C =,求::a b c 。
例2.在60,1ABC b B c ∆== 中,,求:a 和A ,C .解:总结升华: 举一反三:【变式1】在ABC ∆中,c 2a =,45A = ,求b 和,B C .【变式2】在ABC ∆中20a =, 210b =,45A = , 求B 和c ;【变式3】在ABC ∆中,60B = ,14a =, b =求A ∠.类型二:余弦定理的应用例3.已知ABC ∆中,3AB =、BC =4AC =,求ABC ∆中的最大角。
解:总结升华: 举一反三:【变式1】已知ABC ∆中3a =, 5b =, 7c =, 求角C .【变式2】在ABC ∆中,角,,A B C 所对的三边长分别为,,a b c ,若::a b c =2:1),求ABC ∆的各角的大小.☆【变式3】在ABC ∆中,若222a b c bc =++,求角A .类型三:正、余弦定理的综合应用例4.在ABC ∆中,已知=a c 045B =,求b 及A .解:总结升华: 举一反三:【变式1】在ABC ∆中,已知3b =, 4c =, 0135A =.求B 和C .【变式2】在ABC ∆中,已知角,,A B C 所对的三边长分别为,,a b c ,若2a =,b =c =A 和sin C三、总结与测评要想学习成绩好,总结测评少不了!课后复习是学习不可或缺的环节,它可以帮助我们巩固学习效果,弥补知识缺漏,提高学习能力。
(一)利用正弦定理,可以解决以下两类有关三角形的问题:(1)(2) (二)利用余弦定理,可以解决以下两类有关三角形的问题:总结规律和方法——强化所学相关内容请参看网校资源ID :#tbjx16#208608(1) (2)特别说明:(详细内容请参考知识导学,ID :#tbjx19#208608) (四)判断三角形形状判断三角形形状的常用方法:(1) (2) (3)成果测评现在来检测一下学习的成果吧!请到网校测评系统和模拟考试系统进行相关知识点的测试。
知识点:正弦定理和余弦定理测评系统分数: 模拟考试系统分数:如果你的分数在80分以下,请进入网校资源ID :#cgcp0#20868做基础达标部分#cgcp1#208608的练习,如果你的分数在80分以上,你可以进行能力提升题目#cgcp2#208608的测试。
注:本表格为建议样式,请同学们单独建立错题本,或者使用四中网校错题本进行记录。
○网○校○重○要○资○源知识导学:正弦定理和余弦定理(#208608)自我反馈学完本节知识,你有哪些新收获?总结本节的有关习题,将其中的好题及错题分类整理。
如有问题,请到北京四中网校的“名师答疑”或“互帮互学”交流。
视听课堂:正弦定理和余弦定理(#214034)若想知道北京四中的同学们在学什么,请去“四中同步”看看吧!和四中的学生同步学习,同步提高!更多资源,请使用网校的学习引领或搜索功能来查看使用。
对本知识的学案导学的使用率:□好(基本按照学案导学的资源、例题进行复习、预习和进行课堂笔记等,使用率达到80%以上)□中(使用本学案导学提供的资源、例题和笔记,使用率在50%-80%左右)□弱(仅作一般参考,使用率在50%以下)学生:_______________ 家长:______________ 指导教师:_________________请联系北京四中网校当地分校以获得更多知识点学案导学。
