高考数学椭圆与双曲线的经典性质50条
椭圆、双曲线、抛物线知识总结

一.椭圆二.双曲线四.椭圆、双曲线及抛物线的性质对比(焦点在x轴上)名称椭圆双曲线抛物线定义|PF1|+|PF2|=2a(2a>|F1F2|)||PF1|-|PF2||=2a(2a<|F1F2︱)|PF|= 点F不在直线l上,PM⊥l于M标准方程12222=+byax(a>b>0)12222=-byax(a>0,b>0)y2=2px(p>0)图象几何性质范围byax≤≤,ax≥0≥x顶点),0(),0,(ba±±)0,(a±(0,0)对称性关于x轴,y轴和原点对称关于x轴对称焦点(±c,0 ))0,2(p轴长轴长2a,短轴长2b实轴长2a,虚轴长2b准线cax2±=2px-=通径abAB22=pAB2=渐近线xaby±=...——知识就是力量,学海无涯苦作舟!——不要担心知识没有用,知识多了,路也好选择,也多选择。
比如高考,高分的同学,填报志愿的时候选择学校的范围大,而在分数线左右的就为难了,分数低的就更加不要说了。
再比如,有了知识,你也可以随时炒老板。
高考数学椭圆与双曲线的经典性质50条

数学备课组椭圆1.点P处的切线PT平分△PF1F2在点P处的外角.2.PT平分△PF1F2在点P处的外角,则焦点在直线PT上的射影H点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3.以焦点弦PQ为直径的圆必与对应准线相离.4.以焦点半径PF1为直径的圆必与以长轴为直径的圆内切.5.若在椭圆上,则过的椭圆的切线方程是.6.若在椭圆外,则过Po作椭圆的两条切线切点为P1、P2,则切点弦P1P2的直线方程是.7.椭圆(a>b>0)的左右焦点分别为F1,F 2,点P为椭圆上任意一点,则椭圆的焦点角形的面积为.8.椭圆(a>b>0)的焦半径公式:,(, ).9.设过椭圆焦点F作直线与椭圆相交P、Q两点,A为椭圆长轴上一个顶点,连结AP 和AQ分别交相应于焦点F的椭圆准线于M、N两点,则MF⊥NF.10.过椭圆一个焦点F的直线与椭圆交于两点P、Q, A1、A2为椭圆长轴上的顶点,A1P和A2Q交于点M,A2P和A1Q交于点N,则MF⊥NF.11.AB是椭圆的不平行于对称轴的弦,M为AB的中点,则,即。
12.若在椭圆内,则被Po所平分的中点弦的方程是.13.若在椭圆内,则过Po的弦中点的轨迹方程是.双曲线1.点P处的切线PT平分△PF1F2在点P处的内角.2.PT平分△PF1F2在点P处的内角,则焦点在直线PT上的射影H点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3.以焦点弦PQ为直径的圆必与对应准线相交.4.以焦点半径PF1为直径的圆必与以实轴为直径的圆相切.(内切:P在右支;外切:P在左支)5.若在双曲线(a>0,b>0)上,则过的双曲线的切线方程是.6.若在双曲线(a>0,b>0)外,则过Po作双曲线的两条切线切点为P1、P2,则切点弦P1P2的直线方程是.7.双曲线(a>0,b>o)的左右焦点分别为F1,F 2,点P为双曲线上任意一点,则双曲线的焦点角形的面积为.8.双曲线(a>0,b>o)的焦半径公式:(,当在右支上时,,.当在左支上时,,9.设过双曲线焦点F作直线与双曲线相交P、Q两点,A为双曲线长轴上一个顶点,连结AP 和AQ分别交相应于焦点F的双曲线准线于M、N两点,则MF⊥NF.10.过双曲线一个焦点F的直线与双曲线交于两点P、Q, A1、A2为双曲线实轴上的顶点,A1P和A2Q交于点M,A2P和A1Q交于点N,则MF⊥NF.11.AB是双曲线(a>0,b>0)的不平行于对称轴的弦,M为AB的中点,则,即。
高中数学高考几何解析(椭圆双曲线抛物线)课本知识讲解及练习(含答案)
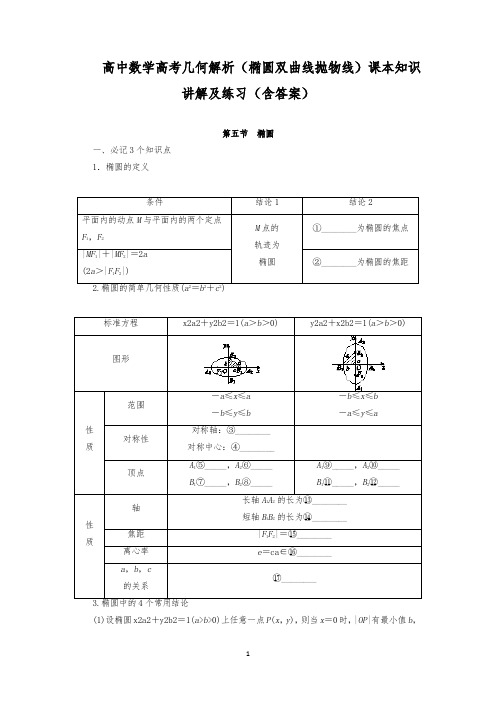
高中数学高考几何解析(椭圆双曲线抛物线)课本知识讲解及练习(含答案)第五节椭圆一、必记3个知识点1.椭圆的定义(1)设椭圆x2a2+y2b2=1(a>b>0)上任意一点P(x,y),则当x=0时,|OP|有最小值b,这时,P在短轴端点处;当x=±a时,|OP|有最大值a,这时,P在长轴端点处.(2)椭圆的一个焦点、中心和短轴的一个端点构成直角三角形,其中a是斜边长,a2=b2+c2.(3)已知过焦点F1的弦AB,则△ABF2的周长为4a.(4)若P为椭圆上任一点,F为其焦点,则a-c≤|PF|≤a+c.二、必明3个易误点1.椭圆的定义中易忽视2a>|F1F2|这一条件,当2a=|F1F2|其轨迹为线段F1F2,当2a<|F1F2|不存在轨迹.2.求椭圆的标准方程时易忽视判断焦点的位置,而直接设方程为x2a2+y2b2=1(a>b>0).3.注意椭圆的范围,在设椭圆x2a2+y2b2=1(a>b>0)上点的坐标为P(x,y)时,则|x|≤a,这往往在求与点P有关的最值问题中特别有用,也是容易被忽略而导致求最值错误的原因.三、技法1.求椭圆标准方程的2种常用方法(1)直接求出a,c来求解e.通过已知条件列方程组,解出a,c的值.(2)构造a,c的齐次式,解出e.由已知条件得出关于a,c的二元齐次方程,然后转化为关于离心率e的一元二次方程求解.(3)通过取特殊值或特殊位置,求出离心率.提醒:在解关于离心率e的二次方程时,要注意利用椭圆的离心率e∈(0,1)进行根的取舍,否则将产生增根.3.求解最值、取值范围问题的技巧(1)与椭圆几何性质有关的问题要结合图形进行分析,即使画不出图形,思考时也要联想到一个图形.(2)椭圆的范围或最值问题常常涉及一些不等式.例如,-a≤x≤a,-b≤y≤b,0<e<1,在求椭圆的相关量的范围时,要注意应用这些不等关系.(3)最值问题,将所求列出表达式,构造基本不等式或利用函数单调性求解.4.判断直线与椭圆位置关系的四个步骤第一步:确定直线与椭圆的方程.第二步:联立直线方程与椭圆方程.第三步:消元得出关于x(或y)的一元二次方程.第四步:当Δ>0时,直线与椭圆相交;当Δ=0时,直线与椭圆相切;当Δ<0时,直线与椭圆相离.5.直线被椭圆截得的弦长公式设直线与椭圆的交点坐标为A(x1,y1),B(x2,y2),则|AB|=(1+k2)[(x1+x2)2-4x1x2])=(y1+y2)2-4y1y2])(k为直线斜率).参考答案①F1,F2②|F1F2|③x轴,y轴④坐标原点⑤(-a,0)⑥(a,0)⑦(0,-b)⑧(0,b)⑨(0,-a)⑩(0,a)⑪(-b,0)⑫(b,0)⑬2a⑭2b⑮2c⑯(0,1)⑰c2=a2-b2第六节双曲线一、必记3个知识点1.双曲线的定义(1)平面内与两个定点F1、F2(|F1F2|=2c>0)的距离①________________为非零常数2a(2a<2c)的点的轨迹叫做双曲线.这两个定点叫做双曲线的②________,两焦点间的距离叫做③________.(2)集合P={M|||MF1|-|MF2||=2a},|F1F2|=2c,其中a,c为常数且a>0,c>0.(ⅰ)当④________________时,M点的轨迹是双曲线;(ⅱ)当⑤________________时,M点的轨迹是两条射线;(ⅲ)当⑥________________时,M点不存在.2.双曲线的标准方程和几何性质⑧________x ∈对称轴:⑪________对称中心:⑫________顶点坐标:A 1⑮______,A 2⑯________⑱____________c =⑳________|=21________;线段________;a 叫做双曲线的虚半轴长>b >0)(1)双曲线为等轴双曲线⇔双曲线的离心率e =2⇔双曲线的两条渐近线互相垂直.(2)渐近线的斜率与双曲线的焦点位置的关系:当焦点在x 轴上时,渐近线斜率为±ba,当焦点在y 轴上时,渐近线斜率为±ab.(3)渐近线与离心率.x2a2-y2b2=1(a >0,b >0)的一条渐近线的斜率为ba=e2-1.(4)若P 为双曲线上一点,F 为其对应焦点,则|PF |≥c -a .二、必明4个易误点1.双曲线的定义中易忽视2a <|F 1F 2|这一条件.若2a =|F 1F 2|,则轨迹是以F 1,F 2为端点的两条射线,若2a >|F 1F 2|则轨迹不存在.2.双曲线的标准方程中对a ,b 的要求只是a >0,b >0,易误认为与椭圆标准方程中a ,b 的要求相同.若a >b >0,则双曲线的离心率e ∈(1,2);若a =b >0,则双曲线的离心率e =2;若0<a <b ,则双曲线的离心率e >2.3.注意区分双曲线中的a ,b ,c 大小关系与椭圆a ,b ,c 关系,在椭圆中a 2=b 2+c 2,而在双曲线中c2=a2+b2.4.易忽视渐近线的斜率与双曲线的焦点位置关系.当焦点在x轴上,渐近线斜率为±ba,当焦点在y轴上,渐近线斜率为±ab.三、技法1.双曲线定义的应用(1)判定满足某条件的平面内动点的轨迹是否为双曲线,进而根据要求可求出曲线方程;(2)在“焦点三角形”中,常利用正弦定理、余弦定理,经常结合||PF1|-|PF2||=2a,运用平方的方法,建立|PF1|与|PF2|的关系.[注意]在应用双曲线定义时,要注意定义中的条件,搞清所求轨迹是双曲线,还是双曲线的一支,若是双曲线的一支,则需确定是哪一支.2.求双曲线标准方程的一般方法(1)待定系数法:设出双曲线方程的标准形式,根据已知条件,列出参数a,b,c的方程并求出a,b,c的值.与双曲线x2a2-y2b2=1有相同渐近线时,可设所求双曲线方程为:x2a2-y2b2=λ(λ≠0).(2)定义法:依定义得出距离之差的等量关系式,求出a的值,由定点位置确定c的值.3.求双曲线离心率或其范围的方法(1)求a,b,c的值,由c2a2=a2+b2a2=1+b2a2直接求e.(2)列出含有a,b,c的齐次方程(或不等式),借助于b2=c2-a2消去b,然后转化成关于e的方程(或不等式)求解.4.求双曲线的渐近线方程的方法求双曲线x2a2-y2b2=1(a>0,b>0)的渐近线的方法是令x2a2-y2b2=0,即得两渐近线方程为:xa±yb=0.参考答案①之差的绝对值②焦点③焦距④2a<|F1F2|⑤2a=|F1F2|⑥2a>|F1F2|⑦x≥a或x≤-a⑧y≥a或y≤-a⑨x轴,y轴⑩坐标原点⑪x轴,y轴⑫坐标原点⑬(-a,0)⑭(a,0)⑮(0,-a)⑯(0,a)⑰y=±ba x⑱y=±ab x⑲ca⑳a2+b2212a222b23a2+b2第七节抛物线一、必记2个知识点1.抛物线定义、标准方程及几何性质x轴⑤________y轴⑥________O(0,0)O(0,0)O(0,0)O(0,0)F⑦________⑧________⑨________设AB是过抛物线y2=2px(p>0)的焦点F的弦,若A(x1,y1),B(x2,y2),则(1)x1x2=p24,y1y2=-p2.(2)弦长|AB|=x1+x2+p=2psin2α(α为弦AB的倾斜角).(3)以弦AB为直径的圆与准线相切.(4)通径:过焦点且垂直于对称轴的弦,长等于2p.二、必明2个易误点1.抛物线的定义中易忽视“定点不在定直线上”这一条件,当定点在定直线上时,动点的轨迹是过定点且与直线垂直的直线.2.抛物线标准方程中参数p易忽视,只有p>0,才能证明其几何意义是焦点F到准线l 的距离,否则无几何意义.三、技法1.应用抛物线定义的2个关键点(1)由抛物线定义,把抛物线上点到焦点距离与到准线距离相互转化.(2)注意灵活运用抛物线上一点P(x,y)到焦点F的距离|PF|=|x|+p2或|PF|=|y|+p2.2.求抛物线的标准方程的方法(1)求抛物线的标准方程常用待定系数法,因为未知数只有p,所以只需一个条件确定p值即可.(2)因为抛物线方程有四种标准形式,因此求抛物线方程时,需先定位,再定量.3.确定及应用抛物线性质的技巧(1)利用抛物线方程确定及应用其焦点、准线等性质时,关键是将抛物线方程化为标准方程.(2)要结合图形分析,灵活运用平面几何的性质以图助解.4.解决直线与抛物线位置关系问题的常用方法(1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似,一般要用到根与系数的关系.(2)有关直线与抛物线的弦长问题,要注意直线是否过抛物线的焦点,若过抛物线的焦点,可直接使用公式|AB|=x1+x2+p,若不过焦点,则必须用一般弦长公式.(3)涉及抛物线的弦长、中点、距离等相关问题时,一般利用根与系数的关系采用“设而不求”“整体代入”等解法.提醒:涉及弦的中点、斜率时,一般用“点差法”求解.参考答案①相等②y2=-2px(p>0)③x2=-2py(p>0)④x2=2py(p>0)⑤x轴⑥y轴⑦F(-p2,0)⑧F(0,-p2)⑨F(0,p2)⑩e=1⑪x=-p2⑫y=-p2⑬-y0+p2⑭y0+p2⑮y≤0⑯y≥0。
高考数学椭圆与双曲线的经典性质技巧归纳总结

椭圆的定义、性质及标准方程高三数学备课组 刘岩老师1. 椭圆的定义:⑴第一定义:平面内与两个定点12F F 、的距离之和等于常数(大于12F F )的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距。
⑵第二定义:动点M 到定点F 的距离和它到定直线l 的距离之比等于常数)10(<<e e ,则动点M 的轨迹叫做椭圆。
定点F 是椭圆的焦点,定直线l 叫做椭圆的准线,常数e 叫做椭圆的离心率。
说明:①若常数2a 等于2c ,则动点轨迹是线段12F F 。
②若常数2a 小于2c ,则动点轨迹不存在。
2. 椭圆的标准方程、图形及几何性质:标准方程)0(12222>>=+b a b y a x 中心在原点,焦点在x 轴上)0(12222>>=+b a b x a y 中心在原点,焦点在y 轴上图形范围x a y b ≤≤, x b y a ≤≤, 顶点()()()()12120000A a A a B b B b --,、,,、,()()()()12120000A a A a B b B b --,、,,、,对称轴x 轴、y 轴;长轴长2a ,短轴长2b ;焦点在长轴上x 轴、y 轴;长轴长2a ,短轴长2b ;焦点在长轴上焦点 ()()1200F c F c -,、, ()()1200F c F c -,、, 焦距 )0(221>=c c F F)0(221>=c c F F离心率)10(<<=e a ce )10(<<=e a ce 准线2a x c=±2a y c=±参数方程与普通方程22221x y a b +=的参数方程为 ()cos sin x a y b θθθ=⎧⎨=⎩为参数 22221y x a b +=的参数方程为 ()cos sin y a x b θθθ=⎧⎨=⎩为参数3. 焦半径公式:椭圆上的任一点和焦点连结的线段长称为焦半径。
2017高考数学必考点【椭圆的性质.doc

2017高考数学必考点【椭圆的性质数学是高考考试中最能拉分的学科,很多学生的数学成绩难以提高往往是因为没有掌握好大纲要求掌握的考点,为了帮助大家复习好这些考点,下面为大家带来2017高考数学必考点【椭圆的性质_顶点范围_对称性_离心率】整理,希望高考生能够认真阅读。
椭圆的离心率:椭圆的焦距与长轴长之比叫做椭圆的离心率。
椭圆的性质:1、顶点:A(a,0),B(-a,0),C(0,b)和D(0,-b)。
2、轴:对称轴:x轴,y轴;长轴长|AB|=2a,短轴长|CD|=2b,a为长半轴长,b为短半轴长。
3、焦点:F1(-c,0),F2(c,0)。
4、焦距:。
5、离心率:;离心率对椭圆形状的影响:e越接近1,c就越接近a,从而b就越小,椭圆就越扁;e越接近0,c就越接近0,从而b就越大,椭圆就越圆;6、椭圆的范围和对称性:(ab0)中-axa,-byb,对称中心是原点,对称轴是坐标轴。
利用椭圆的几何性质解题:利用椭圆的几何性质可以求离心率及椭圆的标准方程.要熟练掌握将椭圆中的某些线段长用a,b,c表示出来,例如焦点与各顶点所连线段的长,过焦点与长轴垂直的弦长等,这将有利于提高解题能力。
椭圆中求最值的方法:求最值有两种方法:(1)利用函数最值的探求方法利用函数最值的探求方法,将其转化为函数的最值问题来处理.此时应充分注意椭圆中x,y的范围,常常是化为闭区间上的二次函数的最值来求解。
(2)数形结合的方法求最值解决解析几何问题要注意数学式子的几何意义,寻找图形中的几何元素、几何量之间的关系.椭圆中离心率的求法:在求离心率时关键是从题目条件中找到关于a,b,c的两个方程或从题目中得到的图形中找到a,b,c的关系式,高考物理,从而求离心率或离心率的取值范围.2017高考数学必考点【椭圆的性质_顶点范围_对称性_离心率】整理为大家带来过了,希望高考生能够在记忆这些考点的时候多下功夫,这样在考试的时候就能熟练应用。
专题50 双曲线-高考数学复习资料(解析版)
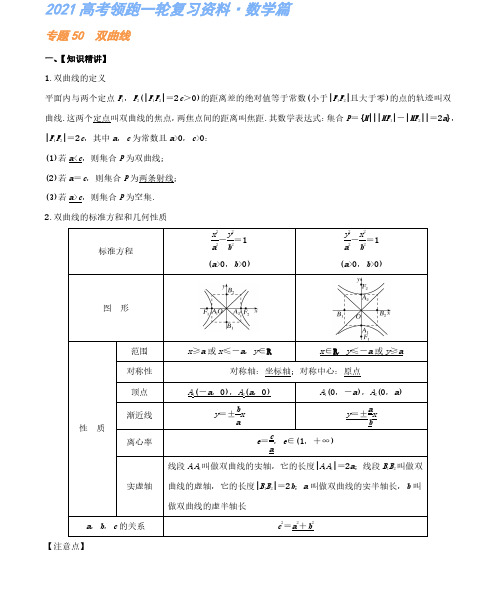
的取值范围是( )
33 -, A. 3 3
22 22 -, C. 3 3
33 -, B. 6 6
23 23 -, D. 3 3
【答案】 A
【解析】 因为 F1(- 3,0),F2( 3,0),x20-y20=1,所以M→F1·M→F2=(- 3-x0,-y0)·( 3-x0,-y0) 2
=x20+y20-3<0,即 3y20-1<0,解得-
a2 b2
的垂线,垂足为 A,且交 y 轴于 B,若 A 为 BF 的中点,则双曲线的离心率为( )
A. 2
B. 3
C.2
6 D.
2
【答案】 A
π -1
【解析】
由题易知双曲线
C
的一条渐近线与
x
π 轴的夹角为 ,故双曲线
C
的离心率
e=
cos
4
= 2.
4
x2 y2 3.(2019·宁夏模拟)设 P 是双曲线 - =1 上一点,F1,F2 分别是双曲线的左、右焦点,若|PF1|=9,则
b 2a,即 =
2,所以该双曲线
a
a
b 的渐近线方程为 y=± x=± 2x.
a
c 法二 由 e= =
a
b2
b
b
1+ a = 3,得 = 2,所以该双曲线的渐近线方程为 y=± x=± 2x.
a
a
(2)(2017
山东)在平面直角坐标系
xOy
中,双曲线
x2 a2
y2 b2
1(a
0,b
0)
的右支与焦点为 F
F1
的直线与双曲
线的上下两支分别交于点 B,A,若△ABF2 为等边三角形,则双曲线的渐近线方程为( )
高考数学复习考点知识与结论专题讲解54 双曲线的定义和性质

高考数学复习考点知识与结论专题讲解第54讲 双曲线的定义和性质【知识通关】通关一通关一、、双曲线的标准方程当焦点在x 轴上时,22221(0,0)x y a b a b −=>>,其中222c a b =+;当焦点在y 轴上时,22221(0,0)y x a b a b −=>>,其中222c a b =+.要点诠释:1. 这里的“标准”指的是中心在坐标原点,对称轴为坐标轴建立直角坐标系时,才能得到双曲线的标准方程;2. 在双曲线的两种标准方程中,都有0a >,0b >和222c a b =+;3. 双曲线的焦点总在实轴上:当焦点在x 轴上时,双曲线的焦点坐标为(),0c ,(),0c −;当焦点在y轴上时,双曲线的焦点坐标为()0,c ,()0,c −;4. 在两种标准方程中,可以根据系数的正负来判定焦点在哪一个坐标轴上.通关二通关二、、双曲线的几何性质图形通关三通关三、、求双曲线的方程的两种方法1. 定义法根据双曲线定义,确定2a ,2b 的值,再结合焦点位置,求出双曲线方程,常用的关系有: (1)222c a b =+;(2)双曲线上任意一点到双曲线两焦点的距离的差的绝对值等于2a .注意:求轨迹方程时,满足条件:122PF PF a −=()1202a F F <<为双曲线的一支,应注意条件合理取舍.2. 待定系数法(1)一般步骤①判断:根据已知条件,确定双曲线的焦点是在x 轴上,还是在y 轴上,还是两个坐标轴都有可能;②设:根据①中的判断结果,设出所需的未知数或者标准方程; ③列:根据题意,列出关于,,的方程或方程组; ④解:求解得到方程. (2)常见设法①与双曲线22221x y a b −=共渐近线的双曲线可设为()22220x y a b λλ−=≠;②若双曲线的渐近线方程为by x a =±,则可设为()22220x y a b λλ−=≠;③若双曲线过两个已知点,则可设为221(0)x y mn m n+=<; ④与双曲线22221x y a b −=共焦点的双曲线方程可设为()2222221x y b a a b λλλ−=−<<−+; ⑤与椭圆22221(0)x y a b a b +=>>有共同焦点的双曲线方程可设为()2222221x y b a a b λλλ+=<<−+. 结论一结论一、、双曲线定义的理解1. 设双曲线上的点M 到两焦点1F ,2F 的距离之差的绝对值为2a ,则有1202a F F <<,这一条①若122a F F =,则点M 的轨迹是分别以为端点的两条射线; ②若122a F F >,则点M 的轨迹不存在;③若20a =,则点M 的轨迹是线段12F F 的垂直平分线.2.若将双曲线的定义中“差的绝对值等于常数”中的“绝对值”去掉,则点的集合是双曲线的一支,具体是左支还是右支可借助图形来确定.【例1】到两定点()13,0F −,()23,0F 的距离之差的绝对值等于6的点M 的轨迹是() A. 椭圆B. 线段C. 双曲线D. 两条射线【答案】D【解析】到两个定点的距离之差的绝对值小于两个定点间距离的点的轨迹是双曲线,等于两个定点间距离时,双曲线退化成两条射线,分别以两个定点为射线的两个端点.12126F A F A F F −==时,这三点共线,且点A 在1F ,2F 之外.也可通过求轨迹方程的办法求出,此时要注意自变量的取值范围.【变式】已知点()2,0M −,()2,0N ,动点P 满足条件PM PN −=,则动点P 的轨迹方程为____.【答案】()221022x y x −=>【解析】由4PM PN MN −=<=,结合双曲线定义可知动点P 的轨迹为以M ,N 为焦点的双曲线右支,双曲线中2a =,24c =,所以a =,2c =,所以b =,轨迹方程为()221022x y x −=>. 结论二结论二、、双曲线上点的性质若P 为双曲线22221x y a b −=上一点,1F ,2F 为双曲线的左、右焦点,则122PF PF a −=.【例2】若双曲线E :221916x y −=的左右焦点分别为1F ,2F ,点P 在双曲线E 上,且13PF =,则2PFA. 11B. 9C. 5D. 3【答案】B【解析】由双曲线定义得1226PF PF a −==,即236PF −=,解得29PF =,故选B.【变式】P 是双曲线的右支上一点,M ,N 分别是圆和上的点,则的最大值为() A. 6B. 7C. 8D. 9【答案】D【解析】由题意得双曲线221916x y −=的焦点分别为()15,0F −,()25,0F ,且这两点刚好为两圆的圆心.由题意可得,当且仅当P 与M ,1F 三点共线,以及P 与N ,2F 三点共线时所求的值最大,此时()()1221639PM PN PF PF −=+−−=+= .故选D.结论三结论三、、焦点三角形周长拓展过双曲线22221x y a b −=上一个焦点作弦AB (交到同一支上),与另一个焦点F 构造三角形F AB ,则FAB 的周长等于42a AB +.【例3】如图,已知双曲线的左右焦点分别为1F ,2F ,过1F 的直线与左支交于A ,B 两点,若5AB =,且实轴长为8,则2ABF 的周长为____.【答案】26【解析】由双曲线的定义知,212F A F A a −=,212F B F B a −=,两式相加得22114F A F B F A F B a +−−=.又115AB F A F B ==+,28a =,故2211416521F A F B a F A F B +=++=+=,故2ABF 的周长为21526+= .【变式】设1F ,2F 为双曲线22221(0,0)sin 2x y b b πθθ−=<≤>的两个焦点,过1F 的直线交双曲线的同支于A ,B 两点,如果AB m =,则2AF B 的周长的最大值是() A. 4m − B. 4C. 4m + D. 42m +【答案】D【解析】由双曲线的定义有212sin AF AF θ−=,212sin BF BF θ−=,于是2AF B 的周长为22112sin 2sin 4sin 2AF BF m AF BF m θθθ++=+++=+,最大值当2πθ=时取得,最大值为42m +.故选D.结论四结论四、、双曲线的标准方程对于方程221x y m n+=, (1)表示双曲线的充要条件为0mn <;(2)表示焦点在x 轴上的双曲线的充要条件为0m >,0n <; (3)表示焦点在y 轴上的双曲线的充要条件为0m <,0n >.【例4】如果方程22121x y m m +=++表示双曲线,则m 的取值范围是()A. ()2,+∞B. ()2,1−−C. (),1−∞−D. ()1,2【答案】B【解析】由题意知,()()210m m ++<,解得21m −<<−,故m 的取值范围是()2,1−−.故选B.【变式】若方程2221523x y m m m +=−−−表示焦点在y 轴上的双曲线,求实数m 的取值范围. 【答案】()5,+∞【解析】由双曲线的焦点在y 轴上可知,m 需满足250,230m m m −> −−>,解得5m >.故实数m 的取值范围为()5,+∞.结论五结论五、、求双曲线的渐近线求双曲线22221(0,0)x y a b a b −=>>或22221(0,0)y x a b a b −=>>的渐近线方程的方法是令右边的常数等于0,即令22220x y a b −=得b y x a =±,或令22220y x a b −=得ay x b =±.【例5】双曲线2214y x −=的渐近线方程为()A. 12y x =± B. 2y x =± C. y = D. y =【答案】B【解析】令2204y x −=,得2y x =±,所以渐近线方程为2y x =±.故选B. 【变式】双曲线22149y x −=的渐近线方程是 A.32y x =± B. 23y x =± C. 94y x =± D. 49y x =±【答案】B【解析】渐近线方程为22049y x −=,即23y x =±.故选B.结论六结论六、、双曲线方程的设法1. 与双曲线22221(0,0)x y a b a b −=>>有相同渐近线的双曲线方程为2222(0)x y a b λλ−=≠2. 渐近线为ny x m =±的双曲线方程为2222(0)x y m nλλ−=≠3. 与双曲线22221(0,0)x y a b a b −=>>有共同焦点的双曲线方程为2222221()x y b a a b λλλ−=−<<−+ 4. 与椭圆22221(0)x y a b a b +=>>有共同焦点的双曲线方程为2222221()x y b a a b λλλ+=<<−+【例6】(1)与双曲线221169x y −=有相同的渐近线,且过点()3A −的双曲线方程是____. (2)与双曲线2211620x y −=有相同焦点,且经过点()5,2−的双曲线的标准方程是____.(3)与椭圆2214936x y +=有公共焦点,且经过点()2的双曲线的标准方程是____. 【答案】(1)224194y x −=(2)2212016x y −=(3)22194x y −= 【解析】(1)与双曲线221169x y −=有相同的渐近线方程的双曲线方程为()220169x y λλ−=≠,将点()3A −代入,得:()()22311694λ−=−=−.所以所求双曲线的方程为2211694x y −=−,即224194y x −=. (2)设所求双曲线方程为()22120161620x y λλλ−=−<<−+.因为双曲线过点()5,2−,所以25411620λλ−=−+,解得4λ=−或29λ=−(舍去),所以所求双曲线的方程为2212016x y −=.(3)设所求双曲线方程为()22136494936x y λλλ+=<<−−.因为双曲线过点(),所以18414936λλ+=−−,解得40λ=或23λ=(舍去),所以所求双曲线的方程为22194x y −=.【变式】已知双曲线过点(,且渐近线方程为12y x =±,则该双曲线的标准方程为____.【答案】2214x y −=【解析】设双曲线方程为()2204x y λλ−=≠,将点(代入得1λ=,所以双曲线方程为2214x y −=.结论七结论七、、点到线距离定值双曲线22221(0,0)x y a b a b −=>>的焦点到渐近线的距离等于虚半轴长b .【例7】双曲线22221(0,0)x y a b a b−=>>,则b 等于().A.1 C.2D.【答案】B【解析】焦点(,0)c 到0bx ay −=b =,故b ,故选B.【变式】已知双曲线2222:1(0,0)x y C a b a b−=>>的右焦点到渐近线的距离等于实轴长,则此双曲线的离心率为().【答案】C【解析】由题意可设双曲线C 的右焦点为(,0)F c ,渐近线的方程为by x a=±,可得2d b a ===,可得c ==,可得离心率ce a==故选C. 结论八结论八、、比值为定值双曲线22221(0,0)x y a b a b−=>>的焦点到渐近线的距离与顶点到渐近线的距离之比等于双曲线的离心率.【例8】已知双曲线22221(0,0)x y a b a b−=>>的焦点F 到渐近线距离与顶点A 到渐近线距离之比为3:1,则双曲线C 的渐近线方程为().A.y =±B.y =C.y =D.y = 【答案】A【解析】如图所示,双曲线顶点为A ,焦点为F ,过,A F 作渐近线的垂线,垂足为,B C ,所以OAB OFC ∆∆与相似(O 为坐标原点).又由题意知31CF AB =,所以3OF c OA a ==,即3c a =,又因为222c b a =+,所以228b a =,即ba=.所以渐近线方程为:y =±,故选A.【变式】设双曲线2222:1(0,0)x y C a b a b−=>>的两条渐近线互相垂直,顶点到一条渐近线的距离为1,则双曲线的一个焦点到一条渐近线的距离为().A.2C. D.4【答案】B【解析】因为双曲线2222:1(0,0)x y C a b a b−=>>的两条渐近线互相垂直,所以渐近线方程为y x =±,所以a b =,因为顶点到一条渐近线的距离为11=,所以a b ==,所以双曲线C 的方程为22122x y −=,焦点坐标为(2,0),(2,0)−,所以双曲线的一个焦点到一条渐近线的距离d ==故选B.结论九结论九、、等轴双曲线已知双曲线方程为22221(0,0)x y a b a b−=>>,当a b =时,称为等轴双曲线.(1)方程形式为22(0)x y λλ−=≠;(2)渐近线方程为y x =±,它们互相垂直;(3)离心率e =.【例9】关于渐近线方程为0x y ±=的双曲线有下述四个结论:①实轴长与虚轴长相等,②离心率是,③过焦点且与实轴垂直的直线被双曲线截得的线段长与实轴长相等,④顶点到渐近线与焦点到.其中所有正确结论的编号是().A.①②B.①③C.①②③D.②③④【答案】C【解析】①因为渐进线的斜率为11b aa b ±=±±=±或,所以①正确;②离心率e ,所以②正确;③设双曲线的方程为222x y a −=,将x c =代入双曲线方程可得2222y c a b =−=,过焦点且与实轴垂直的直线被双曲线截得的线段长为22b a =,与实轴长相等,同理,当焦点在y 轴上时此结论也成立,所以③正确;④因为顶点到渐近线的距离小于焦点到渐近线的距离,所以④不正确.故选C.【变式】已知双曲线2222:1(0,0)x y C a b a b−=>>的两条渐近线互相垂直,焦距为实轴长为().A.3B.6C.9D.12【答案】B【解析】因为两条渐进线互相垂直,故可得21b a−=−,又因为焦距为,故可得2c =,结合222a b c +=,解得3a =,3b =,c =,故实轴长26a =.故选B.结论十结论十、、离心率与渐近线斜率关系在双曲线方程为22221(0,0)x y a b a b −=>>中,c e a ====,所以双曲线的渐近线方程by x a=±可以表示为y =.【例10】设双曲线2222:1(0,0)x y C a b a b−=>>的一条渐近线方程为C 的离心率为__________.【解析】双曲线的渐近线方程为y ==,23e =,e =.【变式】在平面直角坐标系xOy 中,若双曲线2221(0)5x y a a −=>的一条渐近线方程为y x =,则该双曲线的离心率是__________. 【答案】32【解析】双曲线的渐近线方程为y ==,294e =,32e =. 结论十一结论十一、、过定点直线与双曲线相交问题1.若直线恒过的定点落在双曲线两支之内,当直线与双曲线只有一个交点时,该直线的斜率为bk a=±;如图(a )所示,1l ,2l 分别与渐近线平行,显然此时与双曲线只有一个交点; 2.若直线恒过的定点落在双曲线两支之内,当直线与双曲线的左右两支都有交点时,该直线的斜率满足(,)b bk a a∈−;如图(b )所示,1l ,2l 分别与渐近线平行,如果直线与双曲线的左右两支都有交点,则动直线只需按箭头方向旋转即可;3.若直线恒过的定点落在双曲线两支之内,当直线与双曲线的单支有两个交点时,该直线的斜率满足(,)(,)b bk a a∈−∞−∪+∞.如图(c )所示,1l ,2l 分别与渐近线平行,如果直线与双曲线的单支有两个交点,则动直线只需按箭头方向旋转即可.(a )(b )(c )【例11】斜率为2的直线l 过双曲线22221(0,0)x y a b a b−=>>的右焦点,且与双曲线的左、右两支分别相交,则双曲线的离心率的取值范围是__________.【答案】)+∞【解析】直线l 与双曲线的两支分别相交,满足2b b a a −<<(其中ba±为双曲线的两条渐近线的斜率),即2b a ==>,解得e >.所以双曲线的离心率的取值范围是)+∞. 【变式】已知双曲线22221(0,0)x y a b a b−=>>的右焦点为F ,若过点F 且倾斜角为60 的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是() A.(]1,2B.()1,2C.[)2,+∞D.()2,+∞【答案】C【解析】如图,1l 与2l 分别为与双曲线22221x y a b −=的渐近线平行的两条直线,直线l为过点F 且倾斜角为60°的直线,要使与双曲线的右支有且只有一个交点,则应使tan 60b a ≥°=,所以2e =≥.故选C.结论十二、双曲线的通径过焦点做实轴的垂线与双曲线22221x y a b −=()0,0a b >>垂的交点为A ,B ,则AB 即为双曲线的通径,22b AB a=.【例12】已知F 已为双曲线C :22221x y a b −=()0,0a b >>的右焦点,A 为C 的右顶点,B 为C 上的点,且BF 垂直于x 轴.若AB 的斜率为3,则C 的离心率为__________. 【答案】2【解析】由题意可得3BF AF =,而2b BF a =,AFc a =−,即23b a c a=−,变形得22233c a ac a −=−,化简可得2320e e −+=,解得2e =或1e =(舍去).【变式】已知双曲线22221x y a b −=()0,0a b >>的离心率为2,过双曲线的右焦点垂直于x 轴的直线被双曲线截得的弦长为m ,则ma=__________. 【答案】6【解析】双曲线的焦距为2c ,则2ca =,即2c a =,则b =,由题意知m ,故32b m a =,所以2226m b a a==. 结论十三结论十三、、焦点三角形的面积若点()00,P x y 在22221x y a b−=()0,0a b >>在上,设12F PF θ∠=,则12F PF ∆的面积120F PF S c y ∆=2121sin 2tan 2b PF PF θθ==i .【例13】设双曲线C :22221x y a b −=()0,0a b >>的左右焦点分别为1F ,2F ,.P 是C 上的一点,且12F P F P ⊥.若12F PF ∆的面积为4,则a =()A.1B.2C.4D.8【答案】A【解析】因为12F P F P ⊥,所以1290F PF ∠=°,1222124tan 2F PF b S b F PF ∆===∠.因为222222c a b e a a +==2215b a=+=,所以244a =,21a =,即1a =.故选A.【变式】设1F ,2F 是双曲线C :2213y x −=的两个焦点,O 为坐标原点,点P 是C 上且2OP =,则12F PF ∆的面积为(). A.72B.3C.52D.2【答案】B【解析】由已知,不妨设()12,0F −,()22,0F ,则1a =,2c =.因为12122OP F F ==,所以点P 在以12F F 为直径的圆上,即12F PF ∆是以点P 为直角顶点的直角三角形,1222123tan 2F PF b S b F PF ∆===∠,故选B.结论十四结论十四、、焦半径最值F 为双曲线22221x y a b −=()0,0a b >>的右焦点,若P 是双曲线右支上的动点,则PF c a ≥−;若P 是双曲线左支上的动点,则PF c a ≥+.【例14】若椭圆或双曲线上存在一点P 到两个焦点的距离之比为2:1,则称此椭圆或双曲线上存在“Γ点”的是().A.2211615x y += B.2212524x y += C.22115y x −= D.221x y −=【答案】D 【解析】在椭圆中,1221PF PF =>,122PF PF a +=,122PF PF =,即223aPF =,又2PF c a ≥−,故21333a a a c c e ≥−⇒≥⇒≥,又01e <<,故113e ≤<.在双曲线中,1221PF PF =>,22PF a =,2PF c a ≥−,故233a c a a c e ≥−⇒≥⇒≤,又1e >,所以13e <≤.A 选项:2211615x y +=,11,143e =∉ ,错误;B 选项:2212524x y +=,11,153e =∉,错误;C 选项:22115y x −=,(]41,3e =∉,错误;D 选项:221x y −=,(]1,3e =,正确.综上,故选D.【变式】已知双曲线C :22221x y a b −=()0,0a b >>的左右焦点分别为()1,0F c −,()2,0F c ,若双曲线上存在一点P 使得1221sin sin PF F aPF F c∠=∠,则双曲线的离心率的取值范围是__________.【答案】D【解析】在12PF F ∆中,由正弦定理可得211221sin sin PF PF PF F PF F =∠∠,则由已知得21a cPF PF =,即12c PF PF a =,由双曲线的定义可知122PF PF a −=,则222cPF PF a a −=,即222a PF c a =−,由双曲线的几何性质可知2PF c a >−,则22a c a c a >−−,即2220c ac a −−<,所以2210e e −−<,解得11e +<<+,又()1,e ∈+∞,故双曲线的离心率()1e ∈+.结论十五结论十五、、双曲线中的线段和差最值设双曲线方程为22221x y a b −=()0,0a b >>,1F ,2F 分别为双曲线的左、右焦点,()00,Q x y 为平面上一定点,M 为双曲线右支上任意一点.1.若定点()00,Q x y 与双曲线右焦点2F 在双曲线右支的同侧,则2MQ MF +的最小值是12QF a −,最大值不存在;2.若定点()00,Q x y 与双曲线右焦点2F 在双曲线右支的异侧,则2MQ MF +的最小值是2QF ,最大值不存在.【例15】已知F 是双曲线221412x y −=的左焦点,()1,4A ,P 是双曲线右支上的动点,则PF PA +的最小值为__________. 【答案】9【解析】设双曲线的右焦点为1F ,14PF PF =+,1min 1()5PF PF AF +==,则PF PA +的最小值为9.【变式】已知2F 是双曲线:C 221412x y −=的右顶点,动点A 在双曲线左支上,点B 为圆:E 22(2)1x y ++=上的一点,则2AB AF +的最小值为()A.9B.8C.D.【答案】A【解析】设双曲线C 的左焦点为1F ,则21126AF AF a AF =+=+,所以216AB AF AB AF +=++=115559AB AF BE F E +++≥+=+=,故选A结论十六结论十六、、黄金双曲线双曲线22221x y a b −=()0,0a b >>中,若a ,b ,c 成等比数列,即212290b ac F B A =⇔∠=°,离心率e =. 【例16】已知双曲线22221x y a b−=()0,0a b >>.(1)若实轴长、虚轴长、焦距成等差数列,则该双曲线的离心率为__________. (2)若实轴长、虚轴长、焦距成等比数列,则该双曲线的离心率为__________.【答案】(1)53(2【解析】(1)由题设可知2b a c =+,且222c a b =+,故2222a c c a +−=,得4a c c a +−=,即35c a =,所以53c e a ==. (2)由题设可知2b ac =,且222c a b =+,故22c a ac −=,即220c ac a −−=,由ce a=可得210e e −−=,解得e =或e =(舍去),所以e =. 【变式】设双曲线的一个焦点为F ,虚轴的一个端点为B ,如果直线FB 与该双曲线的一条渐近线垂直,那么双曲线的离心率是().【答案】D【解析】设双曲线的方程为22221x y a b−=(0,0)a b >>,不妨设一个焦点为(,0)F c ,虚轴的一个端点为(0,)B b ,则FB b k c =−.又渐近线的斜率为b a ±,所以由题意得1b b c a −⋅=−(b a−不符合,舍去),则2b ac =,又双曲线中222c a b −=,故22c a ac −=,即220c ac a −−=,由ce a=可得210e e −−=,解得e =或e =(舍去),故选D. 结论十七结论十七、、双曲线焦点弦弦长已知双曲线22221x y a b−=()0,0a b >>中,经过其焦点F 的直线交双曲线于A ,B 两点,直线AB的倾斜角为θ,双曲线的离心率为e ,则焦点弦长22221cos b a AB e θ=−. 【例17】过双曲线2214y x −=的右焦点为F 做A ,B 两点,则AB 为__________. 【答案】32【解析】由题知k =,所以1cos 2θ=,e =,由焦点弦长公式22221cos b a AB e θ=−得,2432AB ⋅=【变式】过双曲线22154x y −=的右焦点F 作一条斜率为2的直线与双曲线交于A ,B 两点,O 渐为坐标原点,则OAB ∆的面积为__________. 【答案】152【解析】由题意知2k =,所以cos θ=,e =,由焦点弦长公式22221cos b a AB e θ=−得AB ,O 到AB的距离d =,11522OAB S d AB ∆=××=.结论十八结论十八、、离心率的定义表示双曲线22221(0,0)x y a b a b −=>>中,121222F F c c e a a PF PF ===−.【例18】如图,已知ABCDEF 为正六边形,若以,C F 为焦点的双曲线恰好经过,,,A B D E 四点,则该双曲线的离心率为__________.1+【解析】设正六边形边长为1,则以FC 为x 轴,中垂线为y 轴建立直角坐标系,则(1,0)F −,(1,0)C ,故1c =.因为2FC =,1BC =,所以BF =,即12BF BC a −=−=,故a =.所以1ce a====.【变式】过双曲线22221(0,0)x y a b a b −=>>的左焦点(,0)(0)F c c −>,作圆2224a x y +=的切线,切点为E ,延长FE 交双曲线右支于点P ,若2OP OE OF =−,则双曲线的离心率是__________.【答案】√ଵଶ【解析】由ܱܲሬሬሬሬሬԦ=2ܱܧሬሬሬሬሬԦ−ܱܨሬሬሬሬሬԦ得 ܱܧሬሬሬሬሬԦ=ଵଶ(ܱܨሬሬሬሬሬԦ+ܱܲሬሬሬሬሬԦ),可知ܧ为ܲܨ的中点,令右焦点为ܨᇱ, 则ܱ为ܨܨᇱ的中点,ܲܨᇱ=2ܱܧ=ܽ.因为ܧ为切点,所以ܱܧ⊥ܲܨ,ܲܨᇱ⊥ܲܨ,ܲܨ−ܲܨᇱ=2ܽ,ܲܨ=3ܽ.又ܲܨଶ+ܲܨᇱଶ=ܨܨᇱଶ,则10ܽଶ=4ܿଶ,݁=√ଵଶ.结论十九结论十九、、离心率求值的正弦表示ܨଵ,ܨଶ为双曲线௫మమ−௬మమ=1(ܽ>0,ܾ>0)的左右焦点,ܲ是双曲线上的动点,若∠ܲܨଵܨଶ=ߙ,∠ܲܨଶܨଵ=ߚ,则双曲线的离心率为݁=ୱ୧୬(ఈାఉ)|ୱ୧୬ఈିୱ୧୬ఉ|.【例19】双曲线௫మమ−௬మమ=1(ܽ>0,ܾ>0)的左、右焦点分别是ܨଵ,ܨଶ,过ܨଵ作倾斜角为30∘的直线交双曲线右支于ܲ点,若ܲܨଶ垂直于ݔ轴,则双曲线的离心率为() A.√6B.√3C.√2D.√ଷଷ【答案】B【解析】解法一设|ܲܨଶ|=ݐ,|ܲܨଵ|=2ݐ,则|ܨଵܨଶ|=√3ݐ,即2ܽ=ݐ,2ܿ=√3ݐ,݁=ଶଶ=√3.故选B 解法二݁=ୱ୧୬ (ଽ∘ାଷ∘)ୱ୧୬ ଽ∘ିୱ୧୬ ଷ∘=√3故选B.【变式】已知ܨଵ,ܨଶ是双曲线ܧ:௫మమ−௬మమ=1的左、右焦点,点ܯ在ܧ上, ܯܨଵ与ݔ轴垂直,sin ∠ܯܨଶܨଵ=ଵଷ,则ܧ的离心率为() A √2B.ଷଶC √3D.2【答案】A【解析】解法一设ܯܨଵ=1,则ܯܨଶ=3,ܨଵܨଶ=2ܿ=2√2,2ܽ=ܯܨଶ−ܯܨଵ=2,݁=√2.故选A. 解法二݁=ୱ୧୬ (ଽ∘ା∠ெிమிభ)ୱ୧୬ ଽ∘ିୱ୧୬ ∠ெிమிభ=ୡ୭ୱ ∠ெிమிభଵିభయ=మ√మయమయ=√2.故选A.结论二十结论二十、、离心率的焦率的焦半半径比值表示若在双曲线௫మమ−௬మమ=1(ܽ>0,ܾ>0)上存在一点ܲ,使|ܲܨଵ|=ߣ|ܲܨଶ|(ߣ>1),则1<݁⩽ఒାଵఒିଵ. 【例20】双曲线௫మమ−௬మమ=1(ܽ>0,ܾ>0)的两个焦点分别为ܨଵ,ܨଶ若ܲ为其上一点,且 |ܲܨଵ|=2|ܲܨଶ|,则双曲线的离心率的取值范围是() A.(1,3)B (1,3]C (3,+∞)D.[3,+∞)【答案】B【解析】解法一由双曲线的定义知,||ܲܨଵ|−|ܲܨଶ||=2ܽ|ܲܨଵ|=2|ܲܨଶ|,即 |ܲܨଵ|=4ܽ,|ܲܨଶ|=2ܽ.又|ܲܨଵ|+|ܲܨଶ|⩾|ܨଵܨଶ|=2ܿ,故6ܽ⩾2ܿ,即݁⩽3.又݁>1,故1<݁⩽3.故选B解法二利用|ிభ||ிమ|的单调性,|ிభ||ிమ|=|ிమ|ାଶ|ிమ|=1+ଶ|ிమ|,随着∣ܲܨଶ|的增加,|ிభ||ிమ|减小,也就是说,当点ܲ右移时,|ிభ||ிమ|值减小,故要在双曲线上找到一点ܲ,使得 |ிభ||ிమ|=2,而当点ܲ在双曲线的右顶点上时,|ிభ||ிమ|⩾2,得ାି⩾2,即3ܽ⩾ܿ,则1<݁⩽3故选B解法三由题知ߣ=2,结合1<݁⩽ఒାଵఒିଵ,所以1<݁⩽3,故离心率的取值范围为(1,3]故选B. 【变式】已知双曲线௫మమ−௬మమ=1(ܽ>0,ܾ>0)的左、右焦点分别为ܨଵ,ܨଶ,点ܲ在双曲线的右支上,且|ܲܨଵ|=4|ܲܨଶ|,则此双曲线的离心率݁的最大值为________. 【解析】解法一由定义知|ܲܨଵ|−|ܲܨଶ|=2ܽ又已知|ܲܨଵ|=4|ܲܨଶ|,解得|ܲܨଵ|=଼ଷܽ,|ܲܨଶ|=ଶଷܽ.在△ܲܨଵܨଶ中,由余弦定理得ܿݏ∠ܨଵܲܨଶ=లరవమାరవమିସమଶ⋅ఴయ⋅మయ=ଵ଼−ଽ଼݁ଶ.要求݁的最大值,即求cos ∠ܨଵܲܨଶ的最小值.当ܲ为实轴的右端点时,cos ∠ܨଵܲܨଶ=−1,解得݁=ହଷ,即݁的最大值为ହଷ.解法二由定义知|ܲܨଵ|−|ܲܨଶ|=2ܽ,又已知|ܲܨଵ|=4|ܲܨଶ|,解得|ܲܨଵ|=଼ଷܽ,|ܲܨଶ|=ଶଷܽ,|ܲܨଶ|୫୧୬=ܿ−ܽ,从而只要ଶଷܽ⩾ܿ−ܽ,就能得到ܲ点存在,解得݁⩽ହଷ,等号可以取到,即݁的最大值为ହଷ解法三由题知ߣ=4,结合1<݁⩽ఒାଵఒିଵ,所以1<݁⩽ହଷ,故离心率的取值范围为ቀ1,ହଷቃ.结论二十一结论二十一、、双曲线焦半径比例模型1.已知双曲线௫మమ−௬మమ=1(ܽ>0,ܾ>0),经过其焦点ܨ的直线交双曲线于ܣ,ܤ两点,直线ܣܤ的倾斜角为ߠ,ܣܨሬሬሬሬሬԦ=ߣܨܤሬሬሬሬሬԦ,双由线的离心率݁满足:|݁cos ߠ|=ቚఒିଵఒାଵቚ或݁=√1+݇ଶቚఒିଵఒାଵቚ(其中݇=tan ߠ);2.已知双曲线௬మమ−௫మమ=1(ܽ>0,ܾ>0),经过其焦点ܨ的直线交双曲线于ܣ,ܤ两点,直线ܣܤ的倾斜角为ߠ,ܣܨሬሬሬሬሬԦ=ߣܨܤሬሬሬሬሬԦ,双曲线的离心率݁满足:|݁sin ߠ|=ቚఒିଵఒାଵቚ或 ݁=ට1+ଵమቚఒିଵఒାଵቚ(其中݇=tan ߠ)【例21】已知双曲线ܥ:௫మమ−௬మమ=1(ܽ>0,ܾ>0)的右焦点为ܨ,过ܨ且斜率为√3的直线交ܥ于ܣ,ܤ两点,若ܣܨሬሬሬሬሬԦ=4ܨܤሬሬሬሬሬԦ,则ܥ的离心率为() A.ହ B.ହC.ହ଼D.ଽହ【答案】A【解析】由题知ߣ=4,带入结论݁=√1+݇ଶቚఒିଵఒାଵቚ得݁=ට1+(√3)ଶቚସିଵସାଵቚ=ହ故选A .【变式】已知双曲线ܥ:௫మమ−௬మమ=1(ܽ>0,ܾ>0)的离心率为√3,过右焦点ܨ且斜率为݇(݇>0)的直线与ܥ相交于ܣ,ܤ两点.若ܣܨሬሬሬሬሬԦ=3ܨܤሬሬሬሬሬԦ,则݇=() A.√3B √10C √11D 2√3【答案】C【解析】由题知ߣ=3,带入结论݁=√1+݇ଶቚఒିଵఒାଵቚ得√3=√(1+݇^2)|(3−1)/(3+1)|,解得݇=±√11,因为݇>0,所以݇=√11,故选C.结论结论二十二二十二二十二、、斜率乘积定值模型(一)直线݈与双由线௫మమ−௬మమ=1(ܽ>0,ܾ>0)相交于ܣ,ܤ两点,若ܯ(ݔ,ݕ)为ܣܤ的中点,则 ݇⋅݇ைܯ=మమ,݇=మ௫బమ௬బ.【例22】已知双曲线ܧ的中心为原点,ܨ(3,0)是ܧ的焦点,过ܨ的直线݈与ܧ相交于ܣ,ܤ两点,且ܣܤ的中点为ܰ(−12,−15),则ܧ的方程为() A.௫మଷ−௬మ=1 B.௫మସ−௬మହ=1 C.௫మ−௬మଷ=1 D.௫మହ−௬మସ=1【答案】B【解析】解法一设双曲线方程为௫మమ−௬మమ=1,ܣ(ݔଵ,ݕଵ),ܤ(ݔଶ,ݕଶ),代人双曲线方程两式相减可得(௫భି௫మ)(௫భା௫మ)మ=(௬భି௬మ)(௬భା௬మ)మ,从而௫భା௫మమ=௬భି௬మ௫భି௫మ×௬భା௬మమ,即ଶ×௫ಿమ=݇×ଶ௬ಿమ,即ିଶସమ=ିଷమ,整理可得5ܽଶ=4ܾଶ,又ܽଶ+ܾଶ=9,两式联立可得 ܽଶ=4,ܾଶ=5.双曲线方程为௫మସ−௬మହ=1.故选B.解法二由݇⋅݇ைெ=మమ可得ିଵହିଵଶ×ି(ିଵହ)ଷି(ିଵଶ)=మమ,即5ܽଶ=4ܾଶ,ܿ=3.故选B【变式】已知直线ݔ−2ݕ+1=0与双曲线௫మమ−௬మమ=1(ܽ>0,ܾ>0)交于ܣ,ܤ两点,且线段ܣܤ的中点ܯ的横坐标为1,则该双曲线的离心率为() A.√2B √ଶC.√ହଶD.√3【答案】B【解析】解法一因为直线ݔ−2ݕ+1=0与双曲线௫మమ−௬మమ=1(ܽ>0,ܾ>0)交于ܣ,ܤ两点,且线段ܣܤ的中点ܯ的横坐标为1,所以݇ைெ=1.设ܣ(ݔଵ,ݕଵ),ܤ(ݔଶ,ݕଶ),则有ݔଵ+ݔଶ=2,ݕଵ+ݕଶ=2,௬భି௬మ௫భି௫మ=ଵଶ,௬భା௬మ௫భା௫మ=݇ைெ=1,ቐ௫భమమ−௬భమమ=1௫మమమ−௬మమమ=1,两式相减可化为ଵమ−ଵమ.௬భି௬మ௫భି௫మ⋅௬భା௬మ௫భା௫మ=0,可得మమ=ଵଶ,所以ܽ=√2ܾ,ܿ=√3ܾ,双曲线的离心率为=√ଷ√ଶ=√ଶ.故选B. 解法二由题知ܯ(1,1),由݇⋅݇ைெ=మమ得ଵଵ⋅ଵଶ=మమ,可得మమ=ଵଶ,所以ܽ=√2ܾ,ܿ=√3ܾ,双曲线的离心率为=√ଷ√ଶ=√ଶ.故选B 结论结论二十三二十三二十三、、斜率乘积斜率乘积定定值模值模型型(二)经过原点的直线݈与双曲线௫మమ−௬మమ=1(ܽ>0,ܾ>0)相交于ܯ,ܰ两点,ܲ是双曲线上的动点,直线ܲܯ,ܲܰ的斜率都存在,则݇ெ⋅݇ே为定值మమ=݁ଶ−1【例23】过原点的直线与双曲线௫మమ−௬మమ=1(ܽ>0,ܾ>0)交于ܯ,ܰ两点,ܲ是双曲线上异于ܯ,ܰ的一点,若直线ܯܲ与直线ܰܲ的斜率都存在且乘积为ହସ,则双曲线的离心率为________. 【答案】ଷଶ【解析】解法一由双曲线的对称性,可设ܲ(ݔ,ݕ),ܯ(ݔଵ,ݕଵ),则ܰ(−ݔଵ,−ݕଵ),由݇ெ⋅݇ே=ହସ,得௬బି௬భ௫బି௫భ⋅௬బା௬భ௫బା௫భ=ହସ,即ݕଶ−ݕଵଶ=ହସ(ݔଶ−ݔଵଶ),即ହସݔଶ−ݕଶ=ହସݔଵଶ−ݕଵଶ又 因为ܲ(ݔ,ݕ),ܯ(ݔଵ,ݕଵ)均在双曲线上,所以௫బమమ−௬బమమ=1,௫భమమ−௬భమమ=1,所以మమ=ହସ.所以 双曲线的离心率݁==ට1+మమ=ଷଶ.解法二݇ெ⋅݇ே=మమ=݁ଶ−1=ହସ,所以݁=ଷଶ【变式】ܲ(ݔ,ݕ)(ݔ≠±ܽ)是双曲线ܧ:௫మమ−௬మమ=1(ܽ>0,ܾ>0)上一点,ܯ,ܰ分别是双曲线ܧ的左、右顶点,直线ܲܯ,ܲܰ的斜率之积为ଵହ,则双曲线的离心率为________.【答案】√ଷହ【解析】解法一点ܲ(ݔ,ݕ)(ݔ≠±ܽ)在双曲线௫మమ−௬మమ=1上,有௫బమమ−௬బమమ=1.由题意又有௬బ௫బି⋅௬బ௫బା=ଵହ,可得ܽଶ=5ܾଶ,ܿଶ=ܽଶ+ܾଶ=6ܾଶ,则݁==√ଷହ解法二݇ெ⋅݇ே=మమ=݁ଶ−1=ଵହ,所以݁=√ଷହ.。
高考数学中的椭圆与双曲线相关知识点详解

高考数学中的椭圆与双曲线相关知识点详解椭圆和双曲线是高中数学中非常重要的概念,它们在解决几何问题和代数问题中都有广泛的应用。
在高考数学中,椭圆和双曲线都是重点考查的内容,因此对于这两个概念,学生需要掌握其相关知识点。
一、椭圆的定义与特征椭圆是平面上一点集合,其到两个不同定点的距离之和等于常数,这两个定点叫做椭圆的焦点。
椭圆上任意一点到这两个定点的距离之和等于椭圆上任意一点到其所在直线的垂足的距离之和。
根据椭圆的定义,我们可以得出以下特征:1. 椭圆上任意一点到两个焦点的距离之和等于常数2a;2. 椭圆的两个直径的长度之和为常数2a;3. 椭圆的两条焦弦的长度之和为常数2a;4. 椭圆的中心点位于两个焦点的中垂线上,中心到两个焦点的距离之和等于常数2a。
二、双曲线的定义与特征双曲线是平面上一点集合,其到两个不同定点的距离之差等于常数。
这两个定点叫做双曲线的焦点。
在双曲线上任意一点到这两个定点的距离之差等于椭圆上任意一点到其所在直线的垂足的距离之差。
双曲线的定义可以得出以下特征:1. 双曲线上任意一点到两个焦点的距离之差等于常数2a;2. 双曲线的两个直径的长度之差为常数2a;3. 双曲线的两条焦弦的长度之差为常数2a。
三、椭圆和双曲线的方程椭圆和双曲线都可以用方程表示。
以椭圆为例,如果椭圆的中心点为(h,k),椭圆的长轴长度为2a,短轴长度为2b,那么椭圆的标准方程为:(x-h)²/a² + (y-k)²/b² = 1而双曲线的标准方程为:(x-h)²/a² - (y-k)²/b² = 1其中,a和b分别代表长轴的长度和短轴的长度。
当a²> b²时,方程表示的是椭圆;当a² < b²时,方程表示的是双曲线;当a² = b²时,方程表示的是圆。
四、椭圆和双曲线的参数方程椭圆和双曲线的参数方程也可以帮助我们更好地了解它们的特征。
高考数学椭圆考点

高考数学椭圆考点高考数学中,椭圆是一个重要的考点。
椭圆是平面解析几何中的一个重要曲线,也是常见的二次曲线之一。
在椭圆的相关知识点中,包括椭圆的定义、性质、方程、参数方程以及椭圆的相关定理等。
首先,椭圆的定义是指平面上到两个给定点的距离之和等于常数的点的轨迹。
这两个给定点叫做椭圆的焦点,以及一个常数叫做椭圆的长轴长度。
椭圆的轨迹是一个闭合曲线,曲线的形状与其焦点和长轴的长度有关。
在解析几何中,我们通常使用坐标来描述椭圆。
椭圆的标准方程是x^2/a^2 + y^2/b^2 = 1,其中a和b分别是椭圆的长轴和短轴的长度。
这个方程表示了椭圆上的点到椭圆中心的距离与长轴和短轴长度的关系。
椭圆的一些基本性质也是我们需要了解的。
首先,椭圆有两个对称轴,分别是长轴和短轴。
长轴是连接两个焦点的直线段,而短轴是相互垂直于长轴的直线段。
椭圆的参数方程也是我们需要掌握的知识点。
通常我们可以使用参数方程x = a*cosθ,y = b*sinθ来描述椭圆上的点。
其中,θ是参数,a和b是椭圆的参数。
在高考数学中,椭圆的相关定理也是需要掌握的。
其中包括椭圆的切线定理和法线定理。
椭圆的切线定理是指,椭圆上任意一点的切线与该点的切线相关联,切线的斜率的倒数等于椭圆的斜率,而椭圆的法线是与切线相互垂直的直线。
除了切线和法线定理,另一个重要的定理是椭圆的离心率定理。
椭圆的离心率定义为焦点到椭圆中心的距离与椭圆长轴长度的比值。
椭圆的离心率决定了曲线的形状,当离心率小于1时,椭圆是闭合曲线;当离心率等于1时,椭圆是抛物线;当离心率大于1时,椭圆是双曲线。
在解题过程中,我们可以利用椭圆的性质和定理来解决各种与椭圆相关的问题。
例如,我们可以利用椭圆的切线定理来求椭圆上某一点的切线方程,或者利用椭圆的离心率定理来判断椭圆的形状。
椭圆还与其他数学内容有一定的联系。
例如,椭圆和三角函数之间存在一种关系,称为三角型。
通过椭圆的参数方程和三角函数的相关知识,我们可以深入研究椭圆与三角函数之间的关系。
有关椭圆的高考知识点

有关椭圆的高考知识点椭圆是数学中的一种几何形状,它是离心率小于1的圆的一种特殊情况。
在高考数学中,椭圆是一个重要的知识点,它涉及到椭圆的定义、性质、方程、参数方程等内容。
本文将从不同的角度探索有关椭圆的高考知识点,帮助大家更好地理解和应用该知识。
1. 椭圆的定义和性质椭圆的定义比较简单,它是离心率小于1的圆的一种特殊情况。
在平面直角坐标系中,椭圆的定义可以表达为:给定两个固定点F1和F2,以及一个正常数a,椭圆是到这两个点的距离之和等于常数2a的点的轨迹。
椭圆具有许多重要的性质。
首先,椭圆是对称图形,其中心是坐标原点,对称轴是x轴和y轴;其次,椭圆上的点到两个焦点的距离之和是常数2a;再次,椭圆上的点关于x轴和y轴的对称点也在椭圆上。
2. 椭圆的方程和参数方程在解决椭圆相关问题时,最常用的表达方式是椭圆的方程和参数方程。
椭圆的标准方程是:x^2/a^2 + y^2/b^2 = 1,其中a和b分别是椭圆的长半轴和短半轴。
通过椭圆的方程,我们可以了解椭圆的形状和位置。
a和b的大小关系决定了椭圆是瘦长椭圆还是矮胖椭圆,而a和b的值决定了椭圆的大小。
除了方程形式外,还可以使用参数方程来表示椭圆。
椭圆的参数方程为:x = a*cosθ,y = b*sinθ,其中θ是取值在0到2π之间的参数。
参数方程的优势在于可以直观地看出椭圆的运动轨迹。
当θ从0到2π变化时,椭圆的点会在平面上画出一圈完整的椭圆。
3. 椭圆的性质和应用椭圆有许多独特的性质和应用,对于理解和应用椭圆的知识点有很大的帮助。
首先,椭圆具有焦点性质。
椭圆上的每个点到两个焦点之间的距离之和是常数。
这个性质在实际生活中有很多应用,比如声波在焦点上的集中、行星的轨道等。
其次,椭圆还具有切线性质。
椭圆上的每个点的切线与该点到两个焦点的连线垂直。
这个性质在工程建模和物体运动的描述中常常使用,例如球体在椭球体内滚动的模型。
另外,椭圆还有与矩形和三角形面积相关的性质。
高考数学圆锥曲线必备50条

必背的经典结论椭 圆1. 点P 处的切线PT 平分△PF 1F 2在点P 处的外角.2. PT 平分△PF 1F 2在点P 处的外角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相离.4. 以焦点半径PF 1为直径的圆必与以长轴为直径的圆内切.5. 若000(,)P x y 在椭圆22221x y a b +=上,则过0P 的椭圆的切线方程是00221x x y y ab+=.6. 若000(,)P x y 在椭圆22221x y ab+=外 ,则过Po 作椭圆的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y y ab+=.7. 椭圆22221x y ab+= (a >b >0)的左右焦点分别为F 1,F 2,点P 为椭圆上任意一点12F PF γ∠=,则椭圆的焦点角形的面积为122tan2F P F S b γ∆=.8. 椭圆22221xya b+=(a >b >0)的焦半径公式: 10||M F a ex =+,20||M F a ex =-(1(,0)F c - , 2(,0)F c 00(,)M x y ).9. 设过椭圆焦点F 作直线与椭圆相交 P 、Q 两点,A 为椭圆长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的椭圆准线于M 、N 两点,则MF ⊥NF .10. 过椭圆一个焦点F 的直线与椭圆交于两点P 、Q, A 1、A 2为椭圆长轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P和A 1Q 交于点N ,则MF ⊥NF. 11. AB 是椭圆22221x y ab+=的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则22OM AB b k k a⋅=-,即0202y a x b KAB-=。
12. 若000(,)P x y 在椭圆22221x y a b +=内,则被Po 所平分的中点弦的方程是2200002222x x y y x y ab a b+=+.13. 若000(,)P x y 在椭圆22221x y ab+=内,则过Po 的弦中点的轨迹方程是22002222x x y y x y abab+=+.双曲线1. 点P 处的切线PT 平分△PF 1F 2在点P 处的内角.2. PT 平分△PF 1F 2在点P 处的内角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相交.4. 以焦点半径PF 1为直径的圆必与以实轴为直径的圆相切.(内切:P 在右支;外切:P 在左支)5. 若000(,)P x y 在双曲线22221x y a b -=(a >0,b >0)上,则过0P 的双曲线的切线方程是00221x x y y ab-=.6. 若000(,)P x y 在双曲线22221x yab -=(a >0,b >0)外 ,则过Po 作双曲线的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x xy y ab-=.7. 双曲线22221x y ab-=(a >0,b >o )的左右焦点分别为F 1,F 2,点P 为双曲线上任意一点12F PF γ∠=,则双曲线的焦点角形的面积为122t2F P F S b co γ∆=.8. 双曲线22221x yab-=(a >0,b >o )的焦半径公式:(1(,0)F c - , 2(,0)F c当00(,)M x y 在右支上时,10||M F ex a =+,20||M F ex a =-.当00(,)M x y 在左支上时,10||M F ex a =-+,20||M F ex a =--9. 设过双曲线焦点F 作直线与双曲线相交 P 、Q 两点,A 为双曲线长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的双曲线准线于M 、N 两点,则MF ⊥NF.10. 过双曲线一个焦点F 的直线与双曲线交于两点P 、Q, A 1、A 2为双曲线实轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF. 11. AB 是双曲线22221x y ab-=(a >0,b >0)的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则202y a x b KK ABOM =⋅,即0202y a x b K AB =。
高中数学高考总复习---双曲线及其性质知识讲解及考点梳理
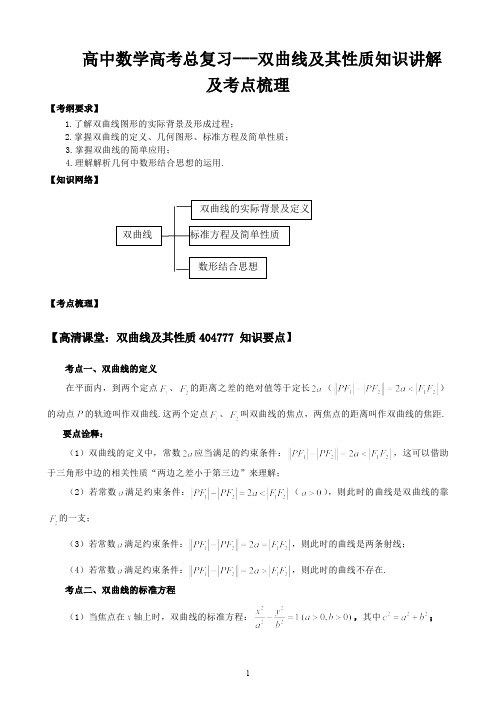
;
(4)渐近线:
.
考点四、有关双曲线的渐近线的问题 (1)已知双曲线方程求渐近线方程:
若双曲线方程为
渐近线方程
(2)已知渐近线方程求双曲线方程:
若渐近线方程为
双曲线可设为
2
(3)若双曲线与 ,焦点在 y 轴上)
(4)特别地当
有公共渐近线,可设为
(
,焦点在 轴上,
离心率
两渐近线互相垂直,分别为
,此时双曲线为
【解析】依题意设双曲线方程为
由已知得 又双曲线过点
, ,∴
∴
3
故所求双曲线的方程为
.
【总结升华】先根据已知条件确定双曲线标准方程的焦点的位置(定位),选择相应的标准方程, 再利用待定系数法确定 、 .
举一反三: 【变式】求中心在原点,对称轴在坐标轴上且分别满足下列条件的双曲线的标准方程.
(1)一渐近线方程为
,且双曲线过点
.
(2)虚轴长与实轴长的比为 【解析】
,焦距为 10.
(1)依题意知双曲线两渐近线的方程是
,故设双曲线方程为
,
∵点
在双曲线上,
∴
,解得
,
∴所求双曲线方程为
.
(2)由已知设 依题意
,
,则
,解得 .
()
∴双曲线方程为
或
.
类型二:双曲线的焦点三角形
例 2.中心在原点,焦点在 x 轴上的一个椭圆与双曲线有共同焦点 和 ,且
;
当 的系数为正时,焦点在 轴上,双曲线的焦点坐标为
,
.
考点三、双曲线的简单几何性质
双曲线
的简单几何性质
(1)范围:
(2)焦点
,顶点
高考数学复习:圆锥曲线

高考数学复习:圆锥曲线考点一:椭圆、双曲线、抛物线知识点1椭圆1、椭圆的定义(1)平面内与两个定点F 1,F 2的距离的和等于常数(大于|F 1F 2|)的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.(2)集合P ={M ||MF 1|+|MF 2|=2a },|F 1F 2|=2c ,其中a ,c 为常数且a >0,c >0.①当2a >|F 1F 2|时,M 点的轨迹为椭圆;②当2a =|F 1F 2|时,M 点的轨迹为线段F 1F 2;③当2a <|F 1F 2|时,M 点的轨迹不存在.2、椭圆的标准方程和几何性质标准方程x 2a 2+y 2b 2=1(a >b >0)y 2a 2+x 2b2=1(a >b >0)图形性质范围-a ≤x ≤a -b ≤y ≤b-b ≤x ≤b -a ≤y ≤a对称性对称轴:坐标轴;对称中心:原点顶点A 1(-a,0),A 2(a,0),B 1(0,-b ),B 2(0,b )A 1(0,-a ),A 2(0,a ),B 1(-b,0),B 2(b,0)离心率e =ca,且e ∈(0,1)a ,b ,c 的关系c 2=a 2-b 23、椭圆中的几个常用结论(1)过椭圆焦点垂直于长轴的弦是最短的弦,长为2b2a ,过焦点最长弦为长轴.(2)过原点最长弦为长轴长2a ,最短弦为短轴长2b .(3)与椭圆x 2a 2+y 2b 2=1(a >b >0)有共同焦点的椭圆方程为x 2a 2+λ+y 2b 2+λ=1(λ>-b 2).(4)焦点三角形:椭圆上的点P (x 0,y 0)与两焦点F 1,F 2构成的△PF 1F 2叫做焦点三角形.若r 1=|PF 1|,r 2=|PF 2|,∠F 1PF 2=θ,△PF 1F 2的面积为S ,则在椭圆x 2a 2+y 2b2=1(a >b >0)中:①当r 1=r 2,即点P 为短轴端点时,θ最大;②S =12|PF 1||PF 2|sin θ=c |y 0|,当|y 0|=b ,即点P 为短轴端点时,S 取得最大值,最大值为bc ;③△PF 1F 2的周长为2(a +c ).知识点2双曲线1、双曲线的定义(1)平面内与两个定点F 1,F 2(|F 1F 2|=2c >0)的距离之差的绝对值为非零常数2a (2a <2c )的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点.(2)集合P ={M |||MF 1|-|MF 2||=2a },|F 1F 2|=2c ,其中a ,c 为常数且a >0,c >0.①当2a <|F 1F 2|时,M 点的轨迹是双曲线;②当2a =|F 1F 2|时,M 点的轨迹是两条射线;③当2a >|F 1F 2|时,M 点不存在.2、双曲线的标准方程和几何性质标准方程x 2a 2-y 2b 2=1(a >0,b >0)y 2a 2-x 2b 2=1(a >0,b >0)图形性质范围x ≥a 或x ≤-a ,y ∈Ry ≤-a 或y ≥a ,x ∈R对称性对称轴:坐标轴,对称中心:原点顶点A 1(-a,0),A 2(a,0)A 1(0,-a ),A 2(0,a )渐近线y =±b axy =±a bx离心率e =ca,e ∈(1,+∞)实、虚轴线段A 1A 2叫做双曲线的实轴,它的长|A 1A 2|=2a ;线段B 1B 2叫做双曲线的虚轴,它的长|B 1B 2|=2b ;a 叫做双曲线的实半轴长,b 叫做双曲线的虚半轴长a ,b ,c 的关系c 2=a 2+b 2(c >a >0,c >b >0)3、双曲线中的几个常用结论(1)双曲线的焦点到其渐近线的距离为b .(2)若P 是双曲线右支上一点,F 1,F 2分别为双曲线的左、右焦点,则|PF 1|min =a +c ,|PF 2|min =c -a .(3)同支的焦点弦中最短的为通径(过焦点且垂直于长轴的弦),其长为2b2a ,异支的弦中最短的为实轴,其长为2a .(4)设P ,A ,B 是双曲线上的三个不同的点,其中A ,B 关于原点对称,直线PA ,PB 斜率存在且不为0,则直线PA 与PB 的斜率之积为b 2a2.(5)P 是双曲线上不同于实轴两端点的任意一点,F 1,F 2分别为双曲线的左、右焦点,则,其中θ为∠F 1PF 2.(6)等轴双曲线①定义:中心在原点,以坐标轴为对称轴,实半轴长与虚半轴长相等的双曲线叫做等轴双曲线.②性质:a =b ;e =2;渐近线互相垂直;等轴双曲线上任意一点到中心的距离是它到两焦点距离的等比中项.(7)共轭双曲线①定义:若一条双曲线的实轴和虚轴分别是另一条双曲线的虚轴和实轴,那么这两条双曲线互为共轭双曲线.②性质:它们有共同的渐近线;它们的四个焦点共圆;它们的离心率的倒数的平方和等于1.知识点3抛物线1、抛物线的定义:满足以下三个条件的点的轨迹是抛物线:(1)在平面内;(2)动点到定点F 的距离与到定直线l 的距离相等;(3)定点不在定直线上.2、抛物线的标准方程与几何性质焦半径(其中P (x 0,y 0))|PF |=x 0+p 2|PF |=-x 0+p 2|PF |=y 0+p 2|PF |=-y 0+p23、抛物线中的几何常用结论(1)设AB 是过抛物线y 2=2px (p >0)焦点F 的弦.①以弦AB 为直径的圆与准线相切.②以AF 或BF 为直径的圆与y 轴相切.③通径:过焦点垂直于对称轴的弦,长等于2p ,通径是过焦点最短的弦.(2)过x 2=2py 的准线上任意一点D 作抛物线的两条切线,切点分别为A ,B ,则直线AB 【题型1圆锥曲线的定义及应用】容易忽视圆锥曲线定义的限制条件,在椭圆的定义中,对常数加了一个条件,即常数大于12F F 。
高考数学 双曲线及其性质 讲解

16 9
例2 (2022广东茂名调研三,14)若双曲线经过点(1, 3 ),其渐近线方程为y
=±2x,则双曲线的方程是
.
x2 y2
13
解析 ①若双曲线的焦点在x轴上,则设 a2 - b2 =1(a>0,b>0),则 a2 - b2 =1且
b
1
a =2,联立解得a= 2 ,b=1,则双曲线的方程为4x2-y2=1;
③若Δ<0,则l与C相离.
综合篇
考法一 求双曲线的标准方程 1.定义法:由已知条件,若所求轨迹满足双曲线的定义,则利用双曲线的定 义求出参数a,b的值,从而得到所求的轨迹方程,求轨迹方程时,满足条件 “|PF1|-|PF2|=2a(0<2a<|F1F2|)”的轨迹为双曲线的一支,应注意合理取舍; 2.待定系数法:根据题目条件确定焦点的位置,从而设出所求双曲线的标 准方程,利用题目条件构造关于a,b的方程(组),解得a,b的值,即可求得方 程. 方程的常见设法:
高考 数学
专题九 平面解析几何
9.3 双曲线及其性质
基础篇
考点一 双曲线的定义及标准方程
1.定义
把平面内与两个定点F1,F2的距离之差的绝对值等于常数2a(0<2a<|F1F2|) 的点的轨迹叫做双曲线.
2.标准方程
焦点在x轴上: x2 - y2 =1(a>0,b>0);
a2 b2
焦点在y轴上: y2 - x2 =1(a>0,b>0).
双曲线C的渐近线方程为y=±
bx.∵
a
F1B·F2 B=0,∴F1B⊥F2B,
∴点B在☉O:x2+y2=c2上,如图所示,不妨设点B在第一象限,
高考数学知识点总结:双曲线知识汇总

高考数学知识点总结:双曲线知识汇总双曲线方程双曲线的第一定义:⑴①双曲线标准方程:. 一般方程:.⑵①i. 焦点在x轴上: 顶点: 焦点: ?准线方程渐近线方程:或ii. 焦点在轴上:顶点:. 焦点:. 准线方程:. 渐近线方程:或,参数方程:或 .②轴为对称轴,实轴长为2a, 虚轴长为2b,焦距2c. ③离心率. ④准线距(两准线的距离);通径. ⑤参数关系. ⑥焦点半径公式:对于双曲线方程(分别为双曲线的左、右焦点或分别为双曲线的上下焦点)“长加短减”原则:构成满足(与椭圆焦半径不同,椭圆焦半径要带符号计算,而双曲线不带符号)⑶等轴双曲线:双曲线称为等轴双曲线,其渐近线方程为,离心率.⑷共轭双曲线:以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线,叫做已知双曲线的共轭双曲线.与互为共轭双曲线,它们具有共同的渐近线:.⑸共渐近线的双曲线系方程:的渐近线方程为如果双曲线的渐近线为时,它的双曲线方程可设为.例如:若双曲线一条渐近线为且过,求双曲线的方程?解:令双曲线的方程为:,代入得.⑹直线与双曲线的位置关系:区域①:无切线,2条与渐近线平行的直线,合计2条;区域②:即定点在双曲线上,1条切线,2条与渐近线平行的直线,合计3条;区域③:2条切线,2条与渐近线平行的直线,合计4条;区域④:即定点在渐近线上且非原点,1条切线,1条与渐近线平行的直线,合计2条;区域⑤:即过原点,无切线,无与渐近线平行的直线.小结:过定点作直线与双曲线有且仅有一个交点,可以作出的直线数目可能有0、2、3、4条.(2)若直线与双曲线一支有交点,交点为二个时,求确定直线的斜率可用代入法与渐近线求交和两根之和与两根之积同号.⑺若P在双曲线,则常用结论1:P到焦点的距离为m = n,则P到两准线的距离比为m︰n.简证: =.常用结论2:从双曲线一个焦点到另一条渐近线的距离等于b.。
高中数学高考综合复习椭圆与双曲线

高中数学高考综合复习椭圆与双曲线(总30页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--高中数学高考综合复习专题二十一椭圆与双曲线一、知识网络二、高考考点 1.椭圆与双曲线的定义、标准方程与几何性质; 2.有关圆锥曲线的轨迹(或轨迹方程)的探求; 3.直线与圆锥曲线的问题:对称问题;最值问题;范围问题等;4.圆锥曲线的探索性问题或应用问题;5.以圆锥曲线为主要内容的综合问题;6.数形结合、等价转化、分类讨论等数学思想方法以及数学学科能力、一般思维能力等基本能力。
三、知识要点(一)椭圆Ⅰ定义与推论1、定义1的的认知设M为椭圆上任意一点,分别为椭圆两焦点,分别为椭圆长轴端点,则有(1)明朗的等量关系:(解决双焦点半径问题的首选公式)(2)隐蔽的不等关系:,(寻求某些基本量取值范围时建立不等式的基本依据)2、定义2的推论根据椭圆第二定义,设为椭圆上任意一点,分别为椭圆左、右焦点,则有:(d1为点M到左准线l1的距离)(d2为点M到右准线l2的距离)由此导出椭圆的焦点半径公式:Ⅱ标准方程与几何性质1、椭圆的标准方程中心在原点,焦点在x轴上的椭圆标准方程①中心在原点,焦点在y轴上的椭圆标准方程②(1)标准方程①、②中的a、b、c具有相同的意义与相同的联系:(2)标准方程①、②统一形式:2、椭圆的几何性质(1)范围:(有界曲线)(2)对称性:关于x轴、y轴及原点对称(两轴一中心,椭圆的共性)(3)顶点与轴长:顶点,长轴2a,短轴2b(由此赋予a、b名称与几何意义)(4)离心率:刻画椭圆的扁平程度(5)准线:左焦点对应的左准线右焦点对应的右准线椭圆共性:两准线垂直于长轴;两准线之间的距离为;中心到准线的距离为;焦点到相应准线的距离为 .Ⅲ挖掘与引申1、具特殊联系的椭圆的方程(1)共焦距的椭圆的方程且(2)同离心率的椭圆的方程且2、弦长公式:设斜率为k的直线l与椭圆交于不同两点,则;或。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
椭圆
1.点P处的切线PT平分△PF1F2在点P处的外角.
2.PT平分△PF1F2在点P处的外角,则焦点在直线PT上的射影H点的轨迹是以长轴为直径的圆,除去长轴的两个端点.
3.以焦点弦PQ为直径的圆必与对应准线相离.
4.以焦点半径PF1为直径的圆必与以长轴为直径的圆内切.
5.若在椭圆上,则过的椭圆的切线方程是.
6.若在椭圆外,则过Po作椭圆的两条切线切点为P1、P2,则切点弦P1P2的直线方程是.
7.椭圆(a>b>0)的左右焦点分别为F1,F 2,点P为椭圆上任意一点
,则椭圆的焦点角形的面积为
.
8.椭圆(a>b>0)的焦半径公式:
,(, ).
9.设过椭圆焦点F作直线与椭圆相交P、Q两点,A为椭圆长轴上一个顶点,连结AP 和AQ分别交相应于焦点F的椭圆准线于M、N两点,则MF⊥NF.
10.过椭圆一个焦点F的直线与椭圆交于两点P、Q, A1、A2为椭圆长轴上的顶点,A1P 和A2Q交于点M,A2P和A1Q交于点N,则MF⊥NF.
11.AB是椭圆的不平行于对称轴的弦,M为AB的中点,则
,即。
12.若在椭圆内,则被Po所平分的中点弦的方程是
.
13.若在椭圆内,则过Po的弦中点的轨迹方程是
.
双曲
1.点P处的切线PT平分△PF1F2在点P处的内角.
2.PT平分△PF1F2在点P处的内角,则焦点在直线PT上的射影H点的轨迹是以长轴为直径的圆,除去长轴的两个端点.
3.以焦点弦PQ为直径的圆必与对应准线相交.
4.以焦点半径PF1为直径的圆必与以实轴为直径的圆相切.(内切:P在右支;外切:P在左支)
5.若在双曲线(a>0,b>0)上,则过的双曲线的切线方程是
.
6.若在双曲线(a>0,b>0)外,则过Po作双曲线的两条切线切点为P1、P2,则切点弦P1P2的直线方
程是.
7.双曲线(a>0,b>o)的左右焦点分别为F1,F 2,点P为双曲线上任意一点,则双曲线的焦点角形
的面积为为.
8.双曲线(a>0,b>o)的焦半径公式:(,
当在右支上时,,.
当在左支上时,,
9.设过双曲线焦点F作直线与双曲线相交P、Q两点,A为双曲线长轴上一个顶点,连结AP 和AQ分别交相应于焦点F的双曲线准线于M、N两点,则MF⊥NF.
10.过双曲线一个焦点F的直线与双曲线交于两点P、Q, A1、A2为双曲线实轴上的顶点,A1P和A2Q交于点M,A2P和A1Q交于点N,则MF⊥NF.
11.AB是双曲线(a>0,b>0)的不平行于对称轴的弦,M为AB的中点,则,即。
12.若在双曲线(a>0,b>0)内,则被Po所平分的中点弦的方程
是.
13.若在双曲线(a>0,b>0)内,则过Po的弦中点的轨迹方程是
.
椭圆
1.椭圆(a>b>o)的两个顶点为,,与y轴平行的直线交椭圆于P1、P2时A1P1与A2P2交点的轨迹方程是.
2.过椭圆(a>0, b>0)上任一点任意作两条倾斜角互补的直线交椭圆于B,C两点,则直线BC有定向且
(常数).
3.若P为椭圆(a>b>0)上异于长轴端点的任一点,F1, F 2是焦点,
, ,则.
4.设椭圆(a>b>0)的两个焦点为F1、F2,P(异于长轴端点)为椭圆上任意一点,在△PF1F2中,记
, ,,则有.
5.若椭圆(a>b>0)的左、右焦点分别为F1、F2,左准线为L,则当0<e≤时,可在椭圆上求一点P,使
得PF1是P到对应准线距离d与PF2的比例中项.
6.P为椭圆(a>b>0)上任一点,F1,F2为二焦点,A为椭圆内一定点,则
,当
且仅当三点共线时,等号成立.
7.椭圆与直线有公共点的充要条件是
.
8.已知椭圆(a>b>0),O为坐标原点,P、Q为椭圆上两动点,且.(1);
(2)|OP|2+|OQ|2的最大值为;(3)的最小值是.
9.过椭圆(a>b>0)的右焦点F作直线交该椭圆右支于M,N两点,弦MN的垂直平分线交x轴于P,则.
10.已知椭圆(a>b>0) ,A、B、是椭圆上的两点,线段AB的垂直平分线与x轴相交于点, 则
.
11.设P点是椭圆(a>b>0)上异于长轴端点的任一点,F1、F2为其焦点记
,则(1)
.(2) .
12.设A、B是椭圆(a>b>0)的长轴两端点,P是椭圆上的一点,,
,,c、e分
别是椭圆的半焦距离心率,则有(1).(2) .(3)
.
13.已知椭圆(a>b>0)的右准线与x轴相交于点,过椭圆右焦点的直线与椭圆相交于A、B两点,点在
右准线上,且轴,则直线AC经过线段EF 的中点.
14.过椭圆焦半径的端点作椭圆的切线,与以长轴为直径的圆相交,则相应交点与相应焦点的连线必与切线垂直.
15.过椭圆焦半径的端点作椭圆的切线交相应准线于一点,则该点与焦点的连线必与焦半径互相垂直.
16. 椭圆焦三角形中,内点到一焦点的距离与以该焦点为端点的焦半径之比为常数e(离心率). (注:在椭圆焦三角形中,非焦顶点的内、外角平分线与长轴交点分别称为内、外点.)
17. 椭圆焦三角形中,内心将内点与非焦顶点连线段分成定比e.
18. 椭圆焦三角形中,半焦距必为内、外点到椭圆中心的比例中项.
双曲线
1.双曲线(a>0,b>0)的两个顶点为,,与y轴平行的直线交双曲线
于P1、P2时A1P1与A2P2交点的轨迹方程是.
2.过双曲线(a>0,b>o)上任一点任意作两条倾斜角互补的直线交双曲线于B,C两点,则直
线BC有定向且(常数).
3.若P为双曲线(a>0,b>0)右(或左)支上除顶点外的任一点,F1, F 2是
焦点, ,
,则(或).
4.设双曲线(a>0,b>0)的两个焦点为F1、F2,P(异于长轴端点)为双曲线上任意一点,在△PF1F2中,
记, ,,则有.
5.若双曲线(a>0,b>0)的左、右焦点分别为F1、F2,左准线为L,则当1
<e≤时,可在双曲线上
求一点P,使得PF1是P到对应准线距离d与PF2的比例中项.
6.P为双曲线(a>0,b>0)上任一点,F1,F2为二焦点,A为双曲线内一定点,则,当
且仅当三点共线且和在y轴同侧时,等号成立.
7.双曲线(a>0,b>0)与直线有公共点的充要条件是
.
8.已知双曲线(b>a >0),O为坐标原点,P、Q为双曲线上两动点,且
.
(1);(2)|OP|2+|OQ|2的最小值为;(3)的最小值是.
9.过双曲线(a>0,b>0)的右焦点F作直线交该双曲线的右支于M,N两点,弦MN的垂直平分线交x轴于P,则
.
10.已知双曲线(a>0,b>0),A、B是双曲线上的两点,线段AB的垂直平分线与x轴相交于点, 则
或.
11.设P点是双曲线(a>0,b>0)上异于实轴端点的任一点,F1、F2为其焦点记,则(1)
.(2) .
12.设A、B是双曲线(a>0,b>0)的长轴两端点,P是双曲线上的一点,
, ,
,c、e分别是双曲线的半焦距离心率,则有(1).
(2) .(3) .
13.已知双曲线(a>0,b>0)的右准线与x轴相交于点,过双曲线右焦点
的直线与双曲线相交
于A、B两点,点在右准线上,且轴,则直线AC经过线段EF 的中点.
14.过双曲线焦半径的端点作双曲线的切线,与以长轴为直径的圆相交,则相应交点与相应焦点的连线必与切线垂直.
15.过双曲线焦半径的端点作双曲线的切线交相应准线于一点,则该点与焦点的连线必与焦半径互相垂直.
16. 双曲线焦三角形中,外点到一焦点的距离与以该焦点为端点的焦半径之比为常数e(离心率).
(注:在双曲线焦三角形中,非焦顶点的内、外角平分线与长轴交点分别称为内、外点).
17.双曲线焦三角形中,其焦点所对的旁心将外点与非焦顶点连线段分成定比e.
18.双曲线焦三角形中,半焦距必为内、外点到双曲线中心的比例中项.。
