5×5方格被分成了五块;
五年级迎春杯备考必会题

36. 48 37. 4 38. 6 39. 684 40. 162 41. 34216 42. 256 43. 241365 44. 10 45. 44 46. 35 47. 144 48. 40 49. 1221 50. 20952 51. 231 52. 250 53. 28
× ×
×
×
× ×
△
×
× ☆
图1 图2
12. 计算: 82.54 835.27 20.38 2 2 6.23 390.81 9 1.03
13. 某班女同学人数是男同学的 2 倍,如果女同学的平均身高是 150 厘米,男同学的平均身高是 162 厘米. 那么全班同学的平均身高是 厘米.
25. 在长方形 ABCD 中,BE=5,EC=4,CF=4,FD=1,如图所示,那么 AEF 的面积为(
)
26.
2009 2009 2009 的个位数字是______.
2010 个 2009
27. 一个等差数列的第 3 项是 14,第 18 项是 23,那么这个数列的前 2010 项中有 1.2 倍.五年级共有 6
人.
48. 在右图中,共能数出
个三角形.
49. 一个电子钟表上总把日期显示为八位数,如 2011 年 1 月 1 日显示为 20110101.如果 2011 年最后 一个能被 101 整除的日子是 2011ABCD ,那么 ABCD .
45. 算式 101 2012 121 1111 503 的计算结果是
.
46. 在右图中,BC = 10,EC = 6,直角三角形 EDF 的面积比直角三角形 FAB 的面积小 5.那么长方形 ABCD 的面积是 .
北师大版五年级数学上册期中测试题(附答案)

五年级数学上册期中测试题一(附答案)时间:90分钟满分:100分一、填空(19分)1.4.6÷11用循环小数表示商是()。
2.从4里连续减()个0.06结果为1。
3.在自然数中,最小的数是(),最小的奇数是(),最小的偶数是(),最小的质数是(),最小的合数是()。
4.要画出某一图形平移后的图形,必须知道()和()。
5.如图有()条对称轴。
6.从0、4、5、8、9中选取三个数字组成能被3整除的数。
在这些数中最大的是(),最小的是()。
7.小贝在计算3.6除以一个数时,错把3.6看成了36,结果得15,这道题得数是()。
8.学校400米环形跑道每隔4米插一面小旗,现在要改成每隔5米插一面小旗,有()面小旗不要移动。
9.北京天安门前,每一天国旗与太阳是同时升起的。
旗杆长22米,升旗时间为2分零6秒,国旗每升高1米约需()秒。
(保留两位小数)10.在()里填上适当的数。
二、判断(5分)1.如果b是自然数,那么2b一定是偶数。
()2.轴对称图形中对应点连线垂直于对称轴。
()3.图形的平移运动只能是水平移动。
()4.已知自然数a只有两个因数,那么5a最多有3个因数。
()5.整数乘法的意义与小数乘法的意义不同,整数除法的意义与小数除法的意义也不同。
()三、选择(10分)1.94.6÷0.18的商是525时,余数是()。
A.1B.0.1C.102.以下图形的对称轴,正确的是()。
A. B. C.3.同一种毛巾,甲超市标价为6元3条,乙超市标价为7元4条,丙超市标价为8元5条那么毛巾在()超市最便宜。
A.甲B.乙C.丙D.无法确定4.如图所示中,图形A通过()得到图B。
A.向下平移3格,再向右平移5格B.向右平移3格,再向下平移3格C.向右下角平移3格D.向左平移3格,再向上平移3格5.迄今为止,数学家已经证明:任何一个比较大的偶数,都可表示成一个质数加上两个质数的积。
比如,16=7+3×3,再如,38=3+5×7,那么100=()A.9+7×13B.17+3×31C.1+3×33D.13+3×29四、按要求画一画(5分)(1)把平行四边形先向下平移6格,再向右平移2格,(2分)(2)画出三角形关于直线l对称的图形。
小学奥数题目-五年级-计算类-数独

数独数独源自于18世纪瑞士,之后流传到美国,再由日本发扬光大的一种数学游戏。
是一种运用纸、笔进行演算的逻辑游戏。
玩家需要根据9×9盘面上的已知数字,利用逻辑和推理,在其他的空格上填入1-9的数字。
1.概念简析:数独:是一种n×n的方阵,并满足每一行、每一列、每一个粗线宫内的数字都不相同,常见的形式:9×9数独。
2.解题方法:首先,从数字较多的行列对角线入手其次,排除法最后,分类讨论加入我的课程视频描述将1、2、3各3个分别放入下图3×3的表格中,使得各行各列以及两条对角线的三个数互不相同。
请问:有没有满足条件的填数方法?请在有和没有之间勾选合适的答案,如果有,请给出一种填数方法。
1.1.将1、2、3、4各4个分别放入下图4×4的表格中,使得各行各列以及两条对角线的四个数互不相同。
请问:有没有满足条件的填数方法?请在有和没有之间勾选合适的答案,如果有,请给出一种填数方法。
(回答“有”或“没有”)2.2.将10、20、30各3个分别放入下图3×3的表格中,使得各行各列以及两条对角线的三个数互不相同。
请问:有没有满足条件的填数方法?请在有和没有之间勾选合适的答案,如果有,请给出一种填数方法。
(回答“有”或“没有”)视频描述在下面5×5方格表中,将数字1、2、3、4、5填入小方格中,每个小方格内只允许填入一个数,使得每个数字在每行、每列都恰好出现一次,有些数已经先行填入其中。
请把方格表填满,并问x 应该填什么数?1.1.在图中每个小方格内填入一个数,使每一行、每一列都有1、2、3、4、5.那么,右下角的小方格(用粗线围出的方格)内填入的数应是________.2.2.将1、2、3、4、5、6这六个数字分别填入每个小方格中,如果要求每行、每列及每个对角线隔成的2×3方格内部都没有重复数字,则“▲”处填入的数字是___________.、5、4、2、33.3.如图,要在下列5×5的方格表中填入A、B、C、D、E五个英文字母,并且要求五个字母在每一行与每一列及对角在线,都只出现一次,则@所表示的英文字母为______.视频描述在下面7×7方格表的每个空格中填入1~7中的一个数字,使得每行、每列、每条对角线上的7个数字都互不相同,则其中A=_______.请在下图的每个空格内填入1~8中的一个数字,使得每行、每列、每条对角线上的8个数字都互不相同,问X 为多少?视频描述下图中9个3×3的小方格表合并成一个9×9的大方格表,每个格子中填入1~9中的一个数,每个数在每一行、每一列中都只出现一次,并且在原来的3×3的小方格表中也只出现一次,问10个五角星处所填数的总和是多少?1.如图是一个未完成的“数独”,给出A、B、C、D所在方格内应填的数字.问A、B、C、D四个数字之和为多少?(注:所谓“数独”即在9×9的方格中填入1~9中的数字,使得每个粗线3×3的方格中的数字及9×9的方格中每行、每列数字均不重复)。
走美杯四年级试题和答案
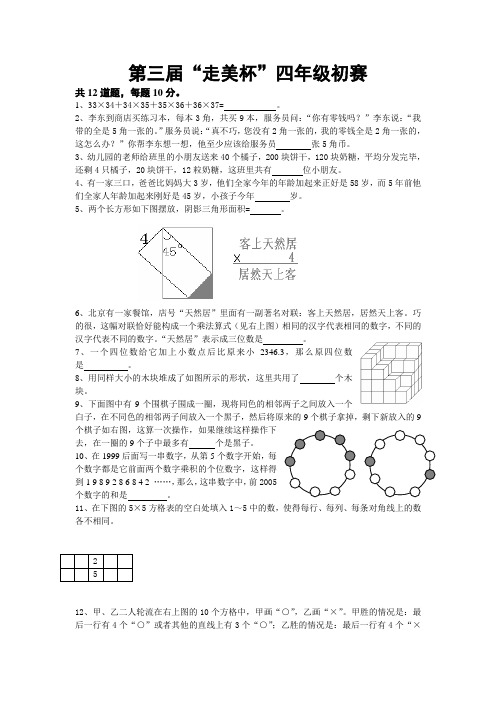
第三届“走美杯”四年级初赛共12道题,每题10分。
1、33×34+34×35+35×36+36×37= 。
2、李东到商店买练习本,每本3角,共买9本,服务员问:“你有零钱吗?”李东说:“我带的全是5角一张的。
”服务员说:“真不巧,您没有2角一张的,我的零钱全是2角一张的,这怎么办?”你帮李东想一想,他至少应该给服务员 张5角币。
3、幼儿园的老师给班里的小朋友送来40个橘子,200块饼干,120块奶糖,平均分发完毕,还剩4只橘子,20块饼干,12粒奶糖,这班里共有 位小朋友。
4、有一家三口,爸爸比妈妈大3岁,他们全家今年的年龄加起来正好是58岁,而5年前他们全家人年龄加起来刚好是45岁,小孩子今年 岁。
5、两个长方形如下图摆放,阴影三角形面积= 。
6、北京有一家餐馆,店号“天然居”里面有一副著名对联:客上天然居,居然天上客。
巧的很,这幅对联恰好能构成一个乘法算式(见右上图)相同的汉字代表相同的数字,不同的汉字代表不同的数字。
“天然居”表示成三位数是 。
7、一个四位数给它加上小数点后比原来小2346.3,那么原四位数是 。
8、用同样大小的木块堆成了如图所示的形状,这里共用了 个木块。
9、下面图中有9个围棋子围成一圈,现将同色的相邻两子之间放入一个白子,在不同色的相邻两子间放入一个黑子,然后将原来的9个棋子拿掉,剩下新放入的9个棋子如右图,这算一次操作,如果继续这样操作下去,在一圈的9个子中最多有 个是黑子。
10、在1999后面写一串数字,从第5个数字开始,每个数字都是它前面两个数字乘积的个位数字,这样得到1 9 8 9 2 8 6 8 4 2 ……,那么,这串数字中,前2005个数字的和是 。
11、在下图的5×5方格表的空白处填入1~5中的数,使得每行、每列、每条对角线上的数各不相同。
12、甲、乙二人轮流在右上图的10个方格中,甲画“○”,乙画“×”。
人教版小学数学五年级上学期期末模拟提高试卷测试卷

人教版小学数学五年级上学期期末模拟提高试卷测试卷一、填空题1.2.7×0.43的积是( )位小数。
5.08×0.49的积是( )小数,精确到百分位是( )。
2.王刚坐在教室的第3列第4行,用(3,4)表示,李红坐在第2列第6行,用( )表示。
用(5,2)表示的同学坐在第( )列第( )行。
3.在( )里填上“>”“<”或“=”。
5.4×0.99( )5.4 1.6×2.3( )2.30.8×2( )0.82 7.08×10( )7.08÷0.14.明明的平均步长是0.7米,他从图书室到实验室直线往返一趟走了约240步,图书室和实验室相距( )米。
5.一个盒子里有2个红球、3个白球和5个蓝球,现从盒中摸出一个球,有( )种可能,摸出( )球的可能性最大,摸出( )球的可能性最小。
6.仓库里原有货物56吨,每车能运走c 吨,今天运走了9车,运走了( )吨,仓库里还剩货物( )吨;当c 5=时,仓库里还剩货物( )吨。
7.一个平行四边形的面积是86平方厘米,和它等底等高的三角形的面积是( )平方厘米。
8.一个平行四边形的花坛,底为5米,高为7米,这个花坛的占地面积为( )平方米。
9.一个梯形的面积是34.2平方厘米,上、下底之和是18厘米,这个梯形的高是( )厘米。
10.一条步行街全长1350米,在步行街的一侧每隔50米张贴一张“社会主义核心价值观”的宣传画(两端都贴),一共要张贴( )张。
11.下面不是运用转化思想方法的是( )。
A .计算7.65÷0.85时,将其看成765÷85来算B .计算2.4×0.8时,先算24×8=192,再算192÷100=1.92C .推导平行四边形面积公式,把平行四边形沿着高剪拼成一个长方形D .计算“一个长是2.4dm ,宽是2dm”的长方形的面积”,列式为:2.4×212.下面关于运用转化方法的叙述错误的是( )。
四年级兴趣小组第三周每周一练解析

电子数字恢复,并将它写成横式形式:
.
×
图1
图2
【考点】数字谜
【难度】☆☆☆
【答案】224
【分析】被乘数的首位数只可能是 2、6、8;被乘数的个位数字只可能是 2、3、4、7、8、9、0;乘数
只可能是 2、6、8;积的百位数字只可能是 2 或 8;十位数字只可能是 2、3、5、8、9;个位只可 能是 1、3、4、7、8、9、0. 显然,积的百位数字不能是 8.而当积为 200 多时,只能被乘数为 20 多,乘数为 8, 经试: 288 224 符合条件.
显然只能令“北”、“京”分别表示 x 3 , x 4 ; 则 x (x 1) (x 2) (x 3) (x 4) x 4 ; 和为 4 5 6 7 8 30 .
3. 电子数字 0~9 如图 1 所示,图 2 是由电子数字组成的乘法算式,但有一些模糊不清,请将图 2 的
10. 在纸上写着一列自然数 1,2,…,98,99.一次操作是指将这列数中最前面的三个数划去,然后
把这三个数的和写在数列的最后面.例如第一次操作后得到 4,5,…,98,99,6;而第二次操作
后得到 7,8,…,98,99,6,15.这样不断进行下去,最后将只剩下一个数,最初的 99 个数连
同后面写下的数,纸上出现的所有数的总和是
2)上的棋子数均为偶数.那么“ 8 8 ”的方格中最多可以放
枚棋子.
图1
图2
【考点】组合,最值
【难度】☆☆☆☆☆
【答案】48
【分析】观察图 3,图 4,易发现其中标有 1~8 的斜线上各有奇数个格子,每条斜线上至少有一个格
子不能放棋子.又因为图 3 和图 4 标有 1~8 的斜线上的格子完全不同(如图 5),所以这 16 条斜
人教版小学三年级数学上册单元试卷全册
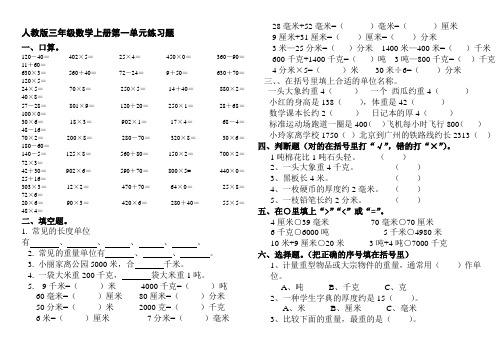
人教版三年级数学上册第一单元练习题一、口算。
120-40=402×5=25×4=450×0=360-90=11+60=630×3=560+40=72-24=9+50=630+70=120×5=24×5=70×8=250×5=14+40=880×2=40×8=57-28=801×9=120+20=250×1=28+68=100×0=30×6=18×3=902×1=17×4=68-4=48-16=70×2=200×8=280-70=320×8=30×6=180-60=140-5=125×8=560+80=150×2=700×2=72×3=42+30=902×6=590+70=800×5=440×0=25+16=303×3=12×2=470+70=64×0=25×8=72×6=20×6=90×3=420×6=280+40=55×5=48×4=二、填空题。
1. 常见的长度单位有、、、、。
2. 常见的重量单位有、、。
3. 小丽家离公园5000米,合千米。
4. 一袋大米重200千克,袋大米重1吨。
5. 9千米=()米4000千克=()吨60毫米=()厘米80厘米=()分米50分米=()米2000克=()千克6米=()厘米7分米=()毫米28毫米+52毫米=()毫米=()厘米9厘米+31厘米=()厘米=()分米3米—25分米=()分米1400米—400米=()千米600千克+1400千克=()吨3吨—800千克=()千克4分米×5=()米30米÷6=()分米三、、在括号里填上合适的单位名称。
小学思维数学讲义:计数之归纳法-带详解

计数之归纳法前面在讲加法原理、乘法原理、排列组合时已经穿插讲解了计数中的一些常用的方法,比如枚举法、树形图法、标数法、捆绑法、排除法、插板法等等,这里再集中学习一下计数中其他常见的方法,主要有归纳法、整体法、对应法、递推法.对这些计数方法与技巧要做到灵活运用.从条件值较小的数开始,找出其中规律,或找出其中的递推数量关系,归纳出一般情况下的数量关系.【例 1】 如图所示,在2×2方格中,画一条直线最多穿过3个方格;在3×3方格中,画一条直线最多穿过5个方可知;那么在5×5方格中,画一条直线,最多穿过 个方格。
【考点】计数之归纳法 【难度】2星 【题型】填空【关键词】希望杯,四年级,复赛,第14题,6分 【解析】 边长每多1,穿过的方格多2,那么5×5的最多穿过3+2+2+2=9个方格 【答案】9【例 2】 一条直线分一个平面为两部分.两条直线最多分这个平面为四部分.问5条直线最多分这个平面为多少部分?【考点】计数之归纳法 【难度】3星 【题型】解答 【解析】 方法一:我们可以在纸上试着画出1条直线,2条直线,3条直线,……时的情形,于是得到下表:由上表已知5条直线最多可将这个平面分成16个部分,并且不难知晓,当有n 条直线时,最多可将平面分成2+2+3+4+…+n =()12n n ++1个部分.方法二:如果已有k 条直线,再增加一条直线,这条直线与前k 条直线的交点至多k 个,因而至多被分成k +1段,每一段将原有的部分分成两个部分,所以至多增加k +1个部分.于是3条直线至多将平面分为4+3=7个部分,4条直线至多将平面分为7+4=11个部分,5条直线至多将平面分为11+5=16个部分.一般的有k 条直线最多将平面分成:1+1+2+…+k =()12k k ++1个部分,所以五条直线可以分平面为16个部分.例题精讲教学目标【答案】16【巩固】平面上5条直线最多能把圆的内部分成几部分?平面上100条直线最多能把圆的内部分成几部分? 【考点】计数之归纳法 【难度】4星 【题型】解答 【解析】 假设用a k 表示k 条直线最多能把圆的内部分成的部分数,这里k =0,1,2,……a 0=1a 1=a 0+1=2 a 2=a 1+2=4 a 3=a 2+3=7 a 4=a 3+4=11 ……故5条直线可以把圆分成16部分,100条直线可以把圆分成5051部分【答案】5051部分【例 3】 平面上10个两两相交的圆最多能将平面分割成多少个区域? 【考点】计数之归纳法 【难度】4星 【题型】解答 【解析】 先考虑最简单的情形.为了叙述方便,设平面上k 个圆最多能将平面分割成k a 个部分.141312111098765432187652134431221从图中可以看出,12a =,24221a ==+⨯,38422a ==+⨯,414823a ==+⨯,…… 可以发现k a 满足下列关系式:()121k k a a k -=+-.实际上,当平面上的(1k -)个圆把平面分成1k a -个区域时,如果再在平面上出现第k 个圆,为了保证划分平面的区域尽可能多,新添的第k 个圆不能通过平面上前()1k -个圆之间的交点.这样,第k 个圆与前面()1k -个圆共产生2(1)k ⨯-个交点,如下图:这2(1)k ⨯-个交点把第k 个圆分成了2(1)k ⨯-段圆弧,而这2(1)k ⨯-段圆弧中的每一段都将所在的区域一分为二,所以也就是整个平面的区域数增加了2(1)k ⨯-个部分.所以,()121k k a a k -=+-. 那么,10987292829272829a a a a =+⨯=+⨯+⨯=+⨯+⨯+⨯=12122...272829a =+⨯+⨯++⨯+⨯+⨯ ()2212...78992=+⨯+++++=.故10个圆最多能将平面分成92部分.【答案】92【例 4】 10个三角形最多将平面分成几个部分?【考点】计数之归纳法 【难度】4星 【题型】解答【解析】 设n 个三角形最多将平面分成n a 个部分.1n =时,12a =;2n =时,第二个三角形的每一条边与第一个三角形最多有2个交点,三条边与第一个三角形最多有236⨯=(个)交点.这6个交点将第二个三角形的周边分成了6段,这6段中的每一段都将原来的每一个部分分成2个部分,从而平面也增加了6个部分,即2223a =+⨯.3n =时,第三个三角形与前面两个三角形最多有4312⨯=(个)交点,从而平面也增加了12个部分,即:322343a =+⨯+⨯. …… 一般地,第n 个三角形与前面()1n -个三角形最多有()213n -⨯个交点,从而平面也增加()213n -⨯个部分,故()()222343213224213332n a n n n n ⎡⎤=+⨯+⨯++-⨯=++++-⨯=-+⎣⎦; 特别地,当10n =时,2103103102272a =⨯+⨯+=,即10个三角形最多把平面分成272个部分.【答案】272【例 5】 一个长方形把平面分成两部分,那么3个长方形最多把平面分成多少部分? 【考点】计数之归纳法 【难度】4星 【题型】解答【解析】 一个长方形把平面分成两部分.第二个长方形的每一条边至多把第一个长方形的内部分成2部分,这样第一个长方形的内部至多被第二个长方形分成五部分.同理,第二个长方形的内部至少被第一个长方形分成五部分.这两个长方形有公共部分(如下图,标有数字9的部分).还有一个区域位于两个长方形外面,所以两个长方形至多把平面分成10部分.第三个长方形的每一条边至多与前两个长方形中的每一个的两条边相交,故第一条边被隔成五条小线段,其中间的三条小线段中的每一条线段都把前两个长方形内部的某一部分一分为二,所以至多增加3×4=12个部分.而第三个长方形的4个顶点都在前两个长方形的外面,至多能增加4个部分. 所以三个长方形最多能将平面分成10+12+4=26.【小结】n 个图形最多可把平面分成部分数:直线:()112n n ⨯++;圆:()21n n +⨯-;三角形:()231n n +⨯⨯- ; 长方形:()241n n +⨯⨯-.【答案】26【例 6】 在平面上画5个圆和1条直线,最多可把平面分成多少部分? 【考点】计数之归纳法 【难度】5星 【题型】解答 【解析】 先考虑圆.1个圆将平面分成2个部分.这时增加1个圆,这个圆与原有的1个圆最多有两个交点,成为2条弧,每条弧将平面的一部分一分为二,增加了2个部分,所以2个圆最多将平面分成4个部分.当有3个圆时,第3个圆与原有的2个产生4个交点而增加4个部分,所以3个圆最多将平面分成8个部分.同样的道理,5个圆最多将平面分成22个部分.再考虑直线.直线与每个圆最多有2个交点,这样与5个圆最多有10个交点.它们将直线分成11条线段或射线,而每条线段又将平面的一部分一分为二,2条射线增加了一部分,因此5个圆和1条直线最多可将平面分成32个部分.【答案】32【例7】在一个西瓜上切6刀,最多能将瓜皮切成多少片?【考点】计数之归纳法【难度】4星【题型】解答【解析】将西瓜看做一个球体,球体上任意一个切割面都是圆形,所以球面上的切割线是封闭的圆周,考虑每一次切割能增加多少瓜皮片.当切1刀时,瓜皮被切成两份,当切第2刀时,由于切割线相交,所以瓜皮被切成4分,……,切第n次时,新增加的切割线与原来的切割线最多有()n-个交点.这21些交点将第n条切割线分成()21n-,所以21n-段,也就是说新增加的切割线使瓜皮数量增加了()在西瓜上切6刀,最多能将瓜皮切成11212223242532++⨯+⨯+⨯+⨯+⨯=片.【答案】32【例8】在一大块面包上切6刀最多能将面包切成多少块.(注:面包是一个立体几何图形,切面可以是任何方向)【考点】计数之归纳法【难度】5星【题型】解答【解析】题目相当于6个平面能将空间划分为多少个部分.通过找规律来寻找递推关系,显然的1个平面能将空间划分成2块,2个平面能将空间划分成4块,3个平面能将空间划分成8个平面,当增加到第四个平面时,第四个平面这能将原来空间中的8个部分中的其中几个划分.如图:注意到第四个平面与其他三个平面相交形成3条直线,这三条直线将第四个平面分割成7个部分,而每一部分将原来三个平面划分的8个空间中的7个划分成两份,所以4个平面能将空间划分成+=个部分.8715同样的第五个平面与前四个平面分别相交成4条直线,这四条直线能将第5个平面分割成++++=个部分,每一部分都划分原空间中的某一区域,所以第五个平面能使空间中的区1123411域增加到151126+==个部分.当增加到6个平面时,第六个平面共被划分成11234516+++++=个部分,所以第6个平面能将空间中的区块数增加到261642+=个部分.所以6刀能将面包切成42块.【答案】42。
六年级下册数学试题-奥数专题训练:数独人教版

数独数独源自于18世纪瑞士,之后流传到美国,再由日本发扬光大的一种数学游戏。
是一种运用纸、笔进行演算的逻辑游戏。
玩家需要根据9×9盘面上的已知数字,利用逻辑和推理,在其他的空格上填入1-9的数字。
1.概念简析:数独:是一种n×n的方阵,并满足每一行、每一列、每一个粗线宫内的数字都不相同,常见的形式:9×9数独。
2.解题方法:首先,从数字较多的行列对角线入手其次,排除法最后,分类讨论将1、2、3各3个分别放入下图3×3的表格中,使得各行各列以及两条对角线的三个数互不相同。
请问:有没有满足条件的填数方法?请在有和没有之间勾选合适的答案,如果有,请给出一种填数方法。
1. 1.将1、2、3、4各4个分别放入下图4×4的表格中,使得各行各列以及两条对角线的四个数互不相同。
请问:有没有满足条件的填数方法?请在有和没有之间勾选合适的答案,如果有,请给出一种填数方法。
(回答“有”或“没有”)2. 2.将10、20、30各3个分别放入下图3×3的表格中,使得各行各列以及两条对角线的三个数互不相同。
请问:有没有满足条件的填数方法?请在有和没有之间勾选合适的答案,如果有,请给出一种填数方法。
(回答“有”或“没有”)3. 3.将10、20、30各3个分别放入下图3×3的表格中,使得各行各列以及两条对角线的三个数的和都相等。
请问:有没有满足条件的填数方法?请在有和没有之间勾选合适的答案,如果有,请给出一种填数方法。
(回答“有”或“没有”)在下面5×5方格表中,将数字1、2、3、4、5填入小方格中,每个小方格内只允许填入一个数,使得每个数字在每行、每列都恰好出现一次,有些数已经先行填入其中。
请把方格表填满,并问x应该填什么数?1.2. 1.在图中每个小方格内填入一个数,使每一行、每一列都有1、2、3、4、5.那么,右下角的小方格(用粗线围出的方格)内填入的数应是________.3. 2.将1、2、3、4、5、6这六个数字分别填入每个小方格中,如果要求每行、每列及每个对角线隔成的2×3方格内部都没有重复数字,则“▲”处填入的数字是___________.A、5B、4C、2D、34. 3.如图,要在下列5×5的方格表中填入A、B、C、D、E五个英文字母,并且要求五个字母在每一行与每一列及对角在线,都只出现一次,则@所表示的英文字母为______.在下面7×7方格表的每个空格中填入1~7中的一个数字,使得每行、每列、每条对角线上的7个数字都互不相同,则其中A=_______.1.请在下图的每个空格内填入1~8中的一个数字,使得每行、每列、每条对角线上的8个数字都互不相同,问X为多少?下图中9个3×3的小方格表合并成一个9×9的大方格表,每个格子中填入1~9中的一个数,每个数在每一行、每一列中都只出现一次,并且在原来的3×3的小方格表中也只出现一次,问10个五角星处所填数的总和是多少?1. 1.如图是一个未完成的“数独”,给出A、B、C、D所在方格内应填的数字.问A、B、C、D四个数字之和为多少?(注:所谓“数独”即在9×9的方格中填入1~9中的数字,使得每个粗线3×3的方格中的数字及9×9的方格中每行、每列数字均不重复)。
高思导引六年级第12讲 计数综合三完整版

第12讲计数综合三内容概述建立递推的思想,将问题的复杂情形与简单情形联系起来;学会现察和发现递推关系;利用树形图、列表等方法处理某些递推关系.另外,综合运用各种方法处理与数字相关的复杂计数问题.兴趣篇1.一个楼梯共有10级台阶,规定每步可以迈一级台阶或二级台阶.走完这10级台阶,一共可以有多少种不同的走法?答案:89种。
解析:将台阶数和走台阶的方法数列成一张表格,如下所示:走1、2级台阶的方法数可以枚举得到.走3级台方法数可以分两类得到:如果第一步走1级台阶,那么参考数表可得,剩下2级有2种走法;如果第一步走2级台阶,同样参考数表可得,剩下1级有1种走法;因此3级合阶的走法总数为1+2=3,如上表箭头所示.以此类推便可填满整张表格.2.卡莉娅买了10块巧克力,她每天最少吃一块,最多吃3块,直到吃完,共有多少种吃法?答案:274种解析:将巧克力的数量与吃法数列成一张表格,如下所示:吃1、2、3块巧克力的方法数可以枚举得到,吃4块巧克力的方法数可以分三类得到:如果第一天吃1块,那么参考数表可得,剩下3块有4种吃法;如果第一天吃2块,同样参考数表可得,剩下2块有2种吃法;如果第一天吃3块,那么剩下1块还有1种吃法,因此4块巧克力的吃法总数为1+2+4=7,如上表箭头所示.以此类推便可填满整张表格.3.用1×2的小方格覆盖7×2的长方形,共有多少种不同的覆盖方法?答案:21种解析:找到左上角的方格,按照该方格是横着覆盖还是竖着覆盖分两类讨论即可得递推规则,从而得到如下所示的一张表格.4.如果在一个平面上画出4条直线,最多可以把平面分成几个部分?如果画20条线,最多可以分成几个部分?答案:11个;211个解析:由于新增直线被分为几部分,区域数量自然也就增加几部分,所以可以将情况写为如下的一张数表:所以20条直线的时候最多把平面分成2+2+3+4+…+20=211个部分.5.甲、乙、丙三名同学练习传球,每人都可以把球传给另外两个人中的任意一个.先由甲发球,经过6次传球后球仍然回到了甲的手中,请问:整个传球过程共有多少种不同的可能?答案:22种解析:采用“传球法”,甲拿球,所以最开始甲标1,乙、丙都标o,接着甲必须由乙、丙传球给他,所以他下方的数也必须由乙、两累加给他;其余两人同理——这就是传球规则决定累加规则,依据这一累加规则,我们不停地将数表向下累加,每传一次球就多累加一行,最后得到第“6”行.这一行的三个数分别为22、21和21.他们分别表示6次传球后,由甲、乙、丙拿球的传球方法数.由于题目要求最后球回到甲手中,因此答案为22种.6.如图12—1,用红、黄、蓝三种颜色给一个五边形的各个顶点染色,同一条边的两端点不能同色,且顶点A必须染红色,请问:有多少种不同的染色方式?图12—1答案:10种解析:采用“传球法”,A染红色,所以在红色的下方标1,黄色和蓝色下方标0.B 不能再染红色,所以红色下面的标O,黄色和蓝色下方标1.后面的C、D、E 按照传球规则进行累加,注意到E不能染红色,所以有5+5=10种染法.7.一个三位数,有相邻两个数字的和为16,那么这样的三位数共有多少个?答案:54个解析:首先要审清题,题目中说“有相邻两个数字的和为16”,并不是说所有相邻两个数字之和都是16.相邻两个数字之和为16有三种可能:79,97或88.(1)若百位和十位的数字之和为16,个位可以填O ~9,共3×10一30种填法.(2)若十位和个位的数字之和为16,百位可以填1~9,共3×9—27种填法,两种情况共计57种填法,考虑到797、979和888被算了两次,因此这样的三位数有57-3=54个.8.一个各位数字互不相等的五位数不含数字0,且数字和为18,这样的五位数共有多少个?答案:360个解析:满足条件的情况只有以下三种:1+2+4+5+6=18, l+2+3+4+8=18, 1+2+3+5+7=18,共计55A ×3=360个.9.一个十位数只含有数字1或2,且不含两个连续的数字1,一共有多少个这样的十位数?答案:144个解析:十位数中不含有1,有1种,十位数中含有一个1,有110C =10种.十位数中含有两个l ,有29C = 36种.十位数中含有三个l ,有38C = 56种.十位数中含有四个1,有47C =35种.十位数中含有五个1,有56C =6种.共计144种,10.一个六位数由1、2、3、4、5组成,而且任意相邻两个数位的数字之差都是1,这样的六位数有多少个?答案:72个解析:采用“传球法”,十万位可以填1、2、3、4、5,因此在下方分别填1.要求任意相邻两个数位之差都是1,因此万位1、2、3、4、5的下方分别填1、2、2、2、1.后面的数位同理,因此这咩的六位数共有9+18+18+18+9=72个,拓展篇1.老师给小高布置了12篇作文,规定他每天至少写1篇.如果小高每天最多能写3篇,那么共有多少种写完作文的方法?答案:927种解析:将作文数量与完成作文的方法数列成一张表格,如下所示:下面解释一下这张数表是如何累加得到的,写1、2、3篇作文的方法数可以枚举得到.写4篇作文的完成方法数可以分三类去数:如果第一天写1篇,那么参考数表可得,剩下3篇有4种完成方法;如果第一天写2篇,同样参考数表可得,剩下2篇有2种完成方法;如果第一天写3篇,那么剩下1篇还有1种完成方法,因此4篇作文的完成方法总数为1+2+4=7,如上表箭头所示.接着分析5篇作文的完成方法数,仍然分三类:第一天写1篇,那么参考数表可得,剩下4篇还有7种完成方法;第一天写2篇.那么剩下3篇还有4种完成方法:第一天写3篇,那么剩下2篇还有2种完成方法,因此5篇作文的完成方法数等于2+4+7=13……以此类推便可填满整张表格.2.用10个1×3的长方形纸片覆盖一个10×3的方格表.共有多少种覆盖方法?2.答案:28种解析:我们可以列出一个递推数表,将其表示如下:下面详细说明该问题的递推规律.覆盖1×3、2×3和3×3方格表的方法数可以枚举得到.接着分析覆盖4×3的表格有几种覆盖方法,如下匿所示,左上角的阴影方格在覆盖的时候有两种方法:竖着覆盖或横着覆盖.当竖着覆盖时,余下部分恰好是一个3×3的方格表,覆盖方法数为2;当横着覆盖时,其下方的方格只能被横放的纸片盖住,因此只剩下一个1×3的方格表需要覆盖,方法数为1.由此可得4×3的表格的覆盖方法数为2+1=3.用同样的方法分析5×3的方格表,可得其覆盖方法数等于4×3的方法数加上2×3的方法数,因此等于3+1=4.接着以此类推即可,余下部分恰好是一个3×3的方格表,覆盖方法数为2。
2022-2023学年苏教版三年级上册期末模拟测试数学试卷

………外………装…………○__姓名:___________班内…………○…………装订…………○…………绝密★启用前2022-2023学年苏教版三年级上册期末模拟测试数学试卷试卷副标题注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明一、选择题 1.王老师驾驶小轿车在笔直的公路上行驶,小轿车车厢的运动是( )。
A .旋转B .静止C .平移2.下面图( )中阴影部分的面积是整个正方形面积的23。
A .B .C .3.王爷爷家种了4行桃树,每行8棵。
如果想求出“梨树比桃树多几棵?”,需要选择( )作为补充条件。
A .梨树有5行 B .苹果树有40棵C .梨树的棵数是桃树的2倍4.下边的竖式计算中,箭头指的地方表示( )。
A .要分走48个十B .已经分走了48个十C .已经分走了48个一…○……………………………○……学校:__________:___________………○…………订…○…………………装…………○…A .①B .①或①C .①第II 卷(非选择题)请点击修改第II 卷的文字说明二、填空题 6.填合适的单位。
(1)一只鸭重2( ),一个鸭蛋重80( )。
(2)一罐奶粉的净含量是500( ),6罐这样的奶粉净含量是3( )。
7.170×5的积的末尾有_____个“0”,180×5的积的末尾有_____个“0”。
8.水果店有300个芒果,每8个装一盒,至少需要( )个盒子才能装完。
9.如图所示,整个图形表示200,涂色部分表示( )。
10.在如图的长方形中分出一个尽可能大的正方形.正方形的边长是_____厘米,周长是_____厘米.11.363 ,要使积是四位数,□中最小填( )。
要使□45÷9的商是三位数,□里可以填( )。
12.将一块饼平均分成6份,小刚吃了其中的2份,正好吃了这块饼的( ),小明吃了这块饼的16,剩下的都被小兵吃掉了,( )吃的多。
2022-2023学年山东省泰安市宁阳县蒋集镇青岛版(五年制)三年级上册期末考试数学试卷

2022-2023学年山东省泰安市宁阳县蒋集镇青岛版(五年制)三年级上册期末考试数学试卷学校:___________姓名:___________班级:___________考号:___________一、填空题1.832÷5的商是()位数,469÷7的商最高位是()位。
2.小明下午放学回到家的时间如图是(),在路上用了20分钟,小明下午放学的时间是()。
3.用分数表示涂色部分。
()()()()4.根据下面的描述,请在图中标出学校各场所的名称。
办公楼的南面正对着学校大门,北面是操场,东南面是教学楼,西南面是艺术楼,东北面是体育馆,西北面是餐厅。
5.填上合适的单位名称。
夏天午睡大约用了1()妈妈步行上班大约用15()6.珠子在算盘上上下移动属于()现象,大风车转动属于()现象。
(在括号里填“平移”或“旋转”。
)7.在括号里填上“>”“<”或“=”。
95分钟()1时20分钟160-74-26()160-(74+26)360÷2×3()360÷3×223×10()336÷38.180秒=()分钟7平方分米=()平方厘米600平方分米=()平方米2米=()厘米二、判断题9.数学课本封面的周长约是2900cm。
()10.这两个图形通过平移可以互相重合。
()11.计算316-60×3,要先算60×3再算316-180。
()12.35里面有5个13。
()13.最大的两位数与最小的两位数的乘积是三位数。
()三、选择题14.得数比1800大,比2800小的算式是()。
A.29×53B.37×65C.76×4915.一道除法算式中,除数是5,余数不可能是()。
A.3B.4C.516.用两个边长是6厘米的正方形,拼成一个长方形,这个长方形的周长和面积分别是()。
A.48厘米、36平方厘米B.42厘米、72平方厘米C.36厘米、72平方厘米17.一个披萨,张丽吃了它的14,刘静比张丽吃得少。
迎春杯初赛四年级年级题库

模块一、计算(一)、凑整【例 1】(2007年数学解题能力展示中年级初赛 1题)计算:98 +197 + 2996 + 39995 + 499994 + 5999993 + 69999992 + 799999991 = .(二)、提取公因数【例 2】(2008 年“数学解题能力展示”读者评选活动四年级组初赛 1 题)计算:l2345×2345 + 2469×38275 = 。
【例 3】(2009“数学解题能力展示"读者评选活动四年级初赛1 题)计算:2009 ÷ 37 + 300 ÷ (37 ×3) = .(三)、多位数计算【例 4】(2007年数学解题能力展示中年级初赛 2题)有一个2007位的整数,其每个数位上的数字都是9,这个数与它自身相乘,所得的积的各个数位上的数字的和是.(四)、公式法【例 5】(2010 年数学解题能力展示四年级初试1 题)计算:64×46 + 73× 37 + 82×28 + 91×19 = .【例 6】(2009“数学解题能力展示"读者评选活动四年级初赛10 题)老师在黑板上写了三个不同的整数,小明每次先擦掉第一个数,然后在最后写上另两个数的平均数,如此做了7 次,这时黑板上三个数的和为159.如果开始时老师在黑板上写的三个数之和为2008,且所有写过的数都是整数.那么开始时老师在黑板上写的第一个数是.(五)、等差数列【例 7】(2010 年数学解题能力展示四年级初试2 题)2010 个连续自然数由小到大排成一排,排在奇数个上的各数的平均数是2345,那么,排在偶数个上各数的平均数是.模块二、几何(一)一笔画问题【例 8】(2009“数学解题能力展示"读者评选活动四年级初赛 6 题)如图所示,某小区花园的道路为一个长480 米,宽200 米的长方形;一个边长为260 米的菱形和十字交叉的两条道路组成.一天,王大爷A 处进入花园,走遍花园的所有道路并从A 处离开.如果他每分钟走60 米,那么他从进入花园到走出花园最少要用分.(二)平面几何——等积变换【例 9】(2007年数学解题能力展示中年级初赛 7题)如图2,六边形ABCDEF 为正六边形,P为对角线CF 上一点,若PBC、PEF 的面积为3与4 ,则正六边形ABCDEF 的面积是.C DB P EF2(三)平面几何——周长与面积【例 10】(2008 年“数学解题能力展示”读者评选活动四年级组初赛12 题)如图,一个长方形被分成A、B、C三块,其中B 和C 都是长方形,A 的八条边的边长分别是l、2、3、4、5、6、7、8 厘米。
五年级奥数图形与面积A含详细答案

2010年五年级奥数题:图形与面积(A)一、填空题(共10小题,每小题3分,满分30分)1.(3分)如图,把三角形ABC的一条边AB延长1倍到D,把它的另一边AC延长2倍到E,得到一个较大的三角形ADE,三角形ADE的面积是三角形ABC面积的_________倍.2.(3分)如图,在三角形ABC中,BC=8厘米,AD=6厘米,E、F分别为AB和AC的中点.那么三角形EBF的面积是_________平方厘米.3.(3分)如图,,那么,三角形AED的面积是三角形ABC面积的_________.4.(3分)如图,三角形ABC的面积是30平方厘米,D是BC的中点,AE的长是ED的长的2倍,那么三角形CDE的面积是_________平方厘米.5.(3分)现有一个5×5的方格表(如图)每个小方格的边长都是1,那么图中阴影部分的面积总和等于_________.6.(3分)如图正方形ABCD边长是10厘米,长方形EFGH的长为8厘米,宽为5厘米.阴影部分甲与阴影部分乙的面积差是_________平方厘米.7.(3分)如图所示,一个矩形被分成A、B、C、D四个矩形.现知A的面积是2cm2,B的面积是4cm2,C的面积是6cm2.那么原矩形的面积是_________平方厘米.A BC D8.(3分)(2011•杭州模拟)有一个等腰梯形,底角为450,上底为8厘米,下底为12厘米,这个梯形的面积应是_________平方厘米.9.(3分)已知三角形ABC的面积为56平方厘米、是平行四边形DEFC的2倍,那么阴影部分的面积是_________平方厘米.10.(3分)(2012•中山市模拟)下图中,在长方形内画了一些直线,已知边上有三块面积分别是13,35,49.那么图中阴影部分的面积是_________.二、解答题(共4小题,满分0分)11.已知正方形的面积是50平方厘米,三角形ABC两条直角边中,长边是短边的2.5倍,求三角形ABC的面积.12.如图,长方形ABCD中,AB=24cm,BC=26cm,E是BC的中点,F、G分别是AB、CD的四等分点,H为AD上任意一点,求阴影部分面积.13.有两张正方形纸,它们的边长都是整厘米数,大的一张的面积比小的一张多44平方厘米.大、小正方形纸的边长分别是多少?14.用面积为1,2,3,4的四张长方形纸片拼成如图所示的一个长方形.问:图中阴影部分面积是多少?2010年五年级奥数题:图形与面积(A)参考答案与试题解析一、填空题(共10小题,每小题3分,满分30分)1.(3分)如图,把三角形ABC的一条边AB延长1倍到D,把它的另一边AC延长2倍到E,得到一个较大的三角形ADE,三角形ADE的面积是三角形ABC面积的6倍.考点:三角形面积与底的正比关系.分析:要求三角形ADE的面积是三角形ABC面积的多少倍,可连接BE,然后根据题意可得:AC=AE,根据△ABC和△ABE等高,即△ABC的面积是△ABE面积的,即△ABC有1份,则△ABE 有3份,因为AB=BD得出△ABE=△BDE,所以△BDE也有3份,然后根据问题解答即可.解答:解:(1×3×2)÷1,=6(倍);答:三角形ADE的面积是三角形ABC面积的6倍;故答案为:6.点评:此题应结合题意,作出一条辅助线,然后根据三角形的面积特点进行分析、解答即可.2.(3分)如图,在三角形ABC中,BC=8厘米,AD=6厘米,E、F分别为AB和AC的中点.那么三角形EBF的面积是6平方厘米.考点:组合图形的面积.分析:根据三角形的面积公式可先求出三角形ABC的面积,再根据F是边AC的中点,那么三角形ABF的面积等于三角形BCF的面积,即三角形ABF的面积等于三角形ABC的面积,又因为E是边AB的中点,那么三角形EFB的面积就等于三角形AEF的面积,即三角形EFB的面积等于三角形ABF的面积,即三角形EFB的面积等于三角形ABC的面积,列式解答即可得到答案.解答:解:三角形ABC的面积为:8×6÷2=24(平方厘米);三角形EBF的面积为:×24=6(平方厘米);答;三角形EBF的面积为6平方厘米.故答案为:6.点评:此题主要考查的是三角形的面积公式.3.(3分)如图,,那么,三角形AED的面积是三角形ABC面积的.考点:三角形面积与底的正比关系.分析:(1)先看△AEC和△ABC的面积关系:BC边上的高,既是△AEC的高也是△ABC的高,已知BE=BC,则EC=BC,根据三角形的面积公式可得:△AEC是△ABC的面积的;(2)同理,可以推理出△AED和△AEC的面积关系是:△AED是△AEC的面积的;由上述两个结论即可解决问题.解答:解:(1)已知BE=BC,则EC=BC,根据三角形面积公式可得:△AEC是△ABC的面积的;(2)已知CD=AC,则AD=AC,根据三角形面积公式可得:△AED是△AEC的面积的;所以△AED=△AEC=△ABC=△ABC.答:三角形AED的面积是三角形ABC面积的.故答案为:.点评:此题是考查了高相等的情况下,三角形的面积与这条高所在的底成正比关系的灵活应用.4.(3分)如图,三角形ABC的面积是30平方厘米,D是BC的中点,AE的长是ED的长的2倍,那么三角形CDE的面积是5平方厘米.考点:组合图形的面积.分析:因为等底等高的三角形的面积相等,所以三角形ADC的面积=三角形ABD的面积=三角形ABC 的面积的一半;又因AE:ED=2:1,所以S△CAE:S△CDE=2:1,从而可求三角形CDE的面积.解答:解:S△ABD=S△ADC=S△ABC=×30=15(平方厘米);S△CAE:S△CDE=2:1,S△CDE=S△ADC=×15=5(平方厘米);答:三角形CDE的面积是5平方厘米.故答案为:5.点评:此题主要考查等底等高的三角形的面积相等.5.(3分)现有一个5×5的方格表(如图)每个小方格的边长都是1,那么图中阴影部分的面积总和等于10.考点:组合图形的面积.分析:根据图形分别求出三个三角形的面积,相加即可求出图中阴影部分的面积总和.解答:解:2×3÷2+3×2÷2+4×2÷2,=3+3+4,=10.故答案为:10.点评:考查了组合图形的面积,解决此题的关键是分别得到三个三角形的面积.6.(3分)如图正方形ABCD边长是10厘米,长方形EFGH的长为8厘米,宽为5厘米.阴影部分甲与阴影部分乙的面积差是60平方厘米.考点:组合图形的面积.分析:根据题意可阴影部分甲的面积等于正方形ABCD的面积减去长方形EFMN;阴影部分乙的面积等于长方形EFGH减去长方形EFMN;再用阴影部分甲减去阴影部分乙就可得到答案,列式解答.解答:解:阴影部分甲的面积:10×10﹣(EF×EM),阴影部分乙的面积:8×5﹣(EF×EM),阴影部分甲﹣阴影部分乙的面积,=10×10﹣(EF×EM)﹣[8×5﹣(EF×EM)]=100﹣(EF×EM)﹣40+(EF×EM)=100﹣40,=60(平方厘米);答:阴影部分甲与阴影部分乙的面积差是60平方厘米.故填:60.点评:解答此题的关键是图形中的空白部分的即在正方形中也在长方形中,在计算中可以相互抵消.7.(3分)如图所示,一个矩形被分成A、B、C、D四个矩形.现知A的面积是2cm2,B的面积是4cm2,C的面积是6cm2.那么原矩形的面积是24平方厘米.A BC D考点:组合图形的面积.分析:图中的四个矩形是大矩形是被两条直线分割后得到的,矩形的面积等于一组邻边的乘积,从横的方向来看,两个相邻矩形的倍比关系是一致的,B是A的两倍,那么D也是C的两倍,从而求出D的面积,然后把A、B、C、D的面积加在一起即可.解答:解:由题意知:B是A的两倍,那么D也是C的两倍,所以D的面积是2×6=12(cm2),从而原矩形的面积是:2+4+6+12=24(cm2),故答案为:24.点评:此题考查组合图形的面积.8.(3分)(2011•杭州模拟)有一个等腰梯形,底角为450,上底为8厘米,下底为12厘米,这个梯形的面积应是20平方厘米.考点:梯形的面积.分析:根据等腰图形的面积公式可得,只要求出梯形的高就可以解决问题,作出梯形的两条高,根据等腰梯形的性质,可将这个底角为450的梯形分成了两个等腰直角三角形,由此可以得出梯形的高为2厘米.解答:解:梯形的高:(12﹣8)÷2,=4÷2,=2(厘米),梯形的面积:(8+12)×2÷2,=20×2÷2,=20(平方厘米),答:梯形的面积为20平方厘米.故答案为:20.点评:画出梯形的两条高将梯形分成两个直角三角形和长方形,是解决此类问题到的关键.9.(3分)已知三角形ABC的面积为56平方厘米、是平行四边形DEFC的2倍,那么阴影部分的面积是14平方厘米.考点:组合图形的面积.分析:①三角形ABC的面积为56平方厘米、是平行四边形DEFC的2倍,所以平行四边形DEFC的面积=56÷2=28(平方厘米);②△AED与平行四边形DEFC是等底等高的,根据三角形面积公式和平行四边形的面积公式可得,△AED的面积=平行四边形DEFC一半,由此即可计算得出阴影部分的面积.解答:解:根据分析可得:56÷2=28(平方厘米),28÷2=14(平方厘米),答:阴影部分的面积是14平方厘米.故答案为:14.点评:抓住图形中潜在的条件:得出等底等高的三角形与平行四边形的面积关系.10.(3分)(2012•中山市模拟)下图中,在长方形内画了一些直线,已知边上有三块面积分别是13,35,49.那么图中阴影部分的面积是97.考点:组合图形的面积.分析:因为长方形的面积等于△ABC与△ECD的面积和,所以△ABC与△ECD重叠部分的面积等于长方形未被这两个三角形盖住部分的面积和,即S=49+35+13=97.解答:解:如图:因为长方形的面积等于△ABC与△ECD的面积和,所以△ABC与△ECD重叠部分的面积等于长方形未被这两个三角形盖住部分的面积和,即:S=49+35+13=97.故答案为:97.点评:本题主要考查对三角形和长方形面积的计算及其之间关系的掌握,以及观察分析能力.二、解答题(共4小题,满分0分)11.已知正方形的面积是50平方厘米,三角形ABC两条直角边中,长边是短边的2.5倍,求三角形ABC的面积.考点:长方形、正方形的面积;三角形的周长和面积.分析:根据图形可知,正方形的边长是三角形的一条较长的直角边,设正方形的边长为a,三角形ABC 两条直角边中,长边是短边的2.5倍,则短边b=a÷2.5,然后利用三角形的面积公式解答.解答:解:正方形面积=a2=50平方厘米,即正方形的边长为a,那么三角形另一条直角边为b,长边是短边的2.5倍,a=2.5b,则b=a÷2.5,三角形面积=ab÷2;=a×a÷2.5÷2,=a2÷5,=50÷5,=10(平方厘米);答:三角形ABC的面积是10平方厘米.点评:此题主要考查正方形和三角形的面积计算方法,解答关键是利用等量代换来求出三角形的面积.12.如图,长方形ABCD中,AB=24cm,BC=26cm,E是BC的中点,F、G分别是AB、CD的四等分点,H为AD上任意一点,求阴影部分面积.考点:组合图形的面积.分析:此题是求图中组合图形的面积,可以利用辅助线将它转换成规则图形,如图,连接BH,将阴影部分分成了三个三角形,求出这三个三角形面积和即可解决问题.利用三角形面积公式进行解决.解答:解:如图,连接BH,AB=CD=24厘米,BC=AD=26厘米,因为F、G分别是四等分点,所以BF=AB==6(厘米),DG=24=6(厘米),S△BFH+S△DHG,=BF×AH DG×HD,=,=3×AH+3×DH,=3×(AH+DH),=3×AD,=3×26,=78(平方厘米),因为E是BC的中点,BE=13厘米,S△BEH=×13×24=156(平方厘米),78+156=234(平方厘米),答:阴影部分的面积为234平方厘米.点评:组合图形的面积计算,转化成规则图形的面积计算时解题的关键.13.有两张正方形纸,它们的边长都是整厘米数,大的一张的面积比小的一张多44平方厘米.大、小正方形纸的边长分别是多少?考点:长方形、正方形的面积.分析:可以分别设出这两个正方形的边长,然后进行讨论,如果有小数的情况就舍去,是整数的就保留,从而可以得到答案.解答:解:设大的正方形纸边长为a厘米,小的为b厘米,由题意b2﹣a2=44 (b+a)(b﹣a)=44 因其边长都是整厘米数,那么(b+a)与(b﹣a)也均为整厘米数而44分解成两个整数相乘只有3种情况,即44×1、22×2、11×4,由此可分别讨论:第一种情况:b+a=44 b﹣a=1 解得a=21.5,b=22.5,不符合题意,舍去;第二种情况:b+a=22 b﹣a=2 解得a=10,b=12,符合题意;第三种情况:b+a=11 b﹣a=4 解得a=3.5,b=7.5,不符合题意,舍去;综上所述,大的正方形纸边长为12厘米,小的为10厘米.答:大、小正方形纸的边长分别是12厘米、10厘米.点评:此题的关键是分情况讨论正方形的边长.14.用面积为1,2,3,4的四张长方形纸片拼成如图所示的一个长方形.问:图中阴影部分面积是多少?考点:组合图形的面积.分析:设面积为1的长方形长、宽分别为a、b,则ab=1,根据面积公式分别计算面积为2、3、4的长、宽,用a、b表示阴影部分的面积,即可解题.解答:解:设面积为1的长方形长、宽分别为a、b,则ab=1,面积为2的长方形宽为a,长为,面积为3的长方形和面积为4的长方形的长相等,则宽的比例为3:4,故面积为3的长方形的宽为,长为,BD=﹣b.阴影部分的面积为△ABD和△BCD面积之和,所以阴影部分的面积为,答:图中阴影部分面积是.点评:本题考查了长方形面积的计算,考查了三角形面积的计算,本题中求BD的长是解题的关键.====Word行业资料分享--可编辑版本--双击可删====源-于-网-络-收-集。
小学四年级数学思维专题训练—其他方法求面积(含答案解析)
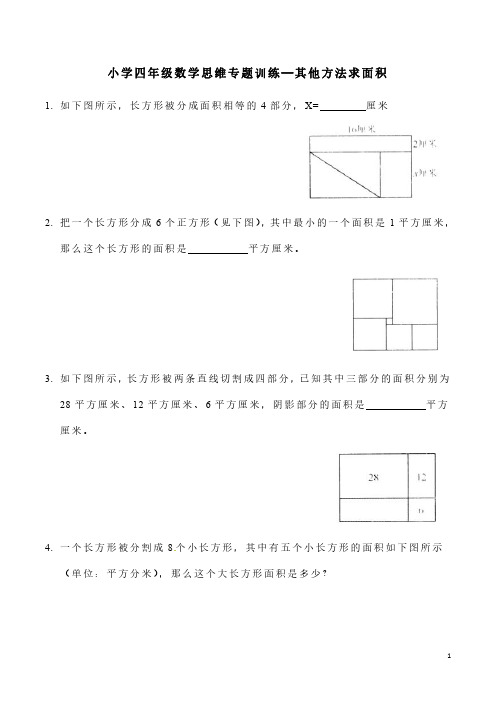
小学四年级数学思维专题训练—其他方法求面积1.如下图所示,长方形被分成面积相等的4部分,X=厘米2.把一个长方形分成6个正方形(见下图),其中最小的一个面积是1平方厘米,那么这个长方形的面积是平方厘米。
3.如下图所示,长方形被两条直线切割成四部分,已知其中三部分的面积分别为28平方厘米、12平方厘米、6平方厘米,阴影部分的面积是平方厘米。
4.一个长方形被分割成8个小长方形,其中有五个小长方形的面积如下图所示(单位:平方分米),那么这个大长方形面积是多少?5.如下图所示,在一块长24米、宽16米的长方形绿地上,有一条宽2米,请你列式计算出这条小路的面积。
6.如下图所示(单位:米),在大长方形中阴影部分的每个小长方形长相等,宽也相等,求空白部分的面积。
7.已知两个正方形的边长和为25厘米,大正方形面积比小正方形面积大125平方厘米,那么大正方形的面积是平方厘米。
8.正方形ABCD的边长为6米,E是BC的中点(见下图)。
四边形OECD的面积为平方米。
9.如下图所示,三角形ABC和三角形EFD是面积为2004平方厘米的全等的直角三角形,AB=EF,BC=FD,∠ABC=∠DFE=90°,点B在DE边上,点F在AC边上,形成长方形GBHF,求长方形ADEC的面积。
10.如下图所示,一大一小两个正方形拼在一起,若阴影部分的面积是10平方米,小正方形的面积是平方米。
11.如下图所示,AB=24厘米,长方形BDEF中的EF=15厘米,阴影△BCE的面积是60平方厘米,则△DCE的面积是平方厘米。
12.如下图所示,梯形ABCD中上底AB的长度是10厘米,梯形的高BE的长度是12厘米,且E是CD中点,BF将梯形ABCD分成面积相等的两部分。
那么,BF的长度是厘米。
13.如下图所示,A BCD是边长为18厘米的正方形,M、N分别是AB边上的点,已知:AM=2MB,CN=2NB,AN与CM相交于点O,则四边形AOCD的面积是平方厘米。
高思奥数导引小学四年级含详解答案第20讲 幻方与数阵图扩展部分
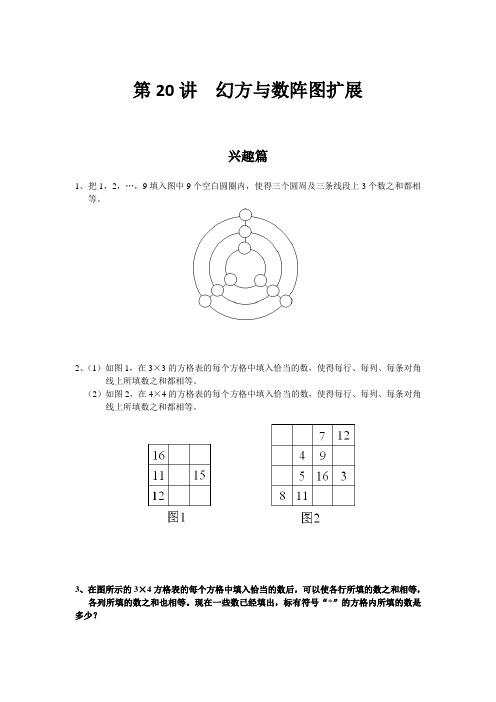
第20讲幻方与数阵图扩展兴趣篇1、把1,2,…,9填入图中9个空白圆圈内,使得三个圆周及三条线段上3个数之和都相等。
2、(1)如图1,在3×3的方格表的每个方格中填入恰当的数,使得每行、每列、每条对角线上所填数之和都相等。
(2)如图2,在4×4的方格表的每个方格中填入恰当的数,使得每行、每列、每条对角线上所填数之和都相等。
3、在图所示的3×4方格表的每个方格中填入恰当的数后,可以使各行所填的数之和相等,各列所填的数之和也相等。
现在一些数已经填出,标有符号“*”的方格内所填的数是多少?4、如图,请在空格中填入适当的数,组成一个三阶幻方。
5、请将图所示的5×5方格表补充完整,使得每个方格内都有一个数字,并且具有如下的性质:方格表中每行,每列和每条对角线的5个方格内所填的5个数中,1、2、3、4、5 恰好各出现一次。
请问:标有符号“△”,“▽”和“◯”的方格中所填的数分别是什么?6、请将1至9这9个数填入图中的方框内,使得所有不等号都成立。
所有满足要求的填法共有多少种?7、请在图所示的8个小圆圈内,分别填入1至8这8个数字,使得图中用线段连接的两个小圆圈内所填的数的差(大减小)恰好是1、2、3、4、5、6、7。
8、将1至5这5个数字填入图中的圆圈内,使得横线、竖线、大圆周上所填数之和都相等。
9、请在图中的六块区域内填入1、2、3、4、5、6,使得对每一个小圆圈来说,与它相邻的区域内的数之和都相等。
10、将0至9填入图的10块区域中(阴影区域除外),使得每个圆内的三个数之和都是相等的。
请问:这个和最小是多少?最大是多少?拓展篇1、将1,2,3,…,24,25分别填入图的各个方格中,使得每行、每列及两条对角线上的数的和相等。
现在已经填入了一些数,标有符号“*”的方格内所填的数是多少?2、请在图的每个空格内填入一个合适的数,使得每行、每列及两条对角线上的3个方格中的各数之和都相等。
江苏省苏州地区2023年三年级数学第二学期期末联考试题含解析

江苏省苏州地区2023年三年级数学第二学期期末联考试题一、我会选。
1.下列各式简便计算错误的是( )。
A .99×57=100×57-57B .25×32×125=25×4+8×125C .490÷14=490÷7÷22.下面有( )个图形是轴对称图形。
A .4B .5C .63.体育组买了50个篮球,付了3000元,找回了一些钱,体育组买的篮球的单价可能是( )。
A .60元B .62元C .59元D .41元4.20个最大两位数的和是( )。
A .200B .1800C .19805.一节课从9:25开始10:05下课,这节课共上了( ). A .40分钟 B .35分钟C .45分钟二、我会判断。
6.两个数相除,商一定小于这两个数。
(______) 7.最大的两位数是0.99. (_______) 8.长度单位的进率是10,面积单位的进率是100. ( )9.边长是4分米的正方形,它的周长和面积都相等。
(______) 10.下图中阴影部分占整个图形的。
(____)三、我能填。
11.下图的标志表示上午(______)时到晚上(______)时禁止机动车驶入。
12.□24÷6,如果商是三位数,□里最小是(______);如果商是两位数,□里最大是(______)。
13.找规律填数:2.4,3.0,3.6,4.2,(________)。
14.把一个蛋糕平均分成8块,小明吃了3块,小明吃了这个蛋糕的()(),剩下的爸爸吃了,爸爸吃了这个蛋糕的 ()()。
15.甲数×乙数=乙数(乙数不等于0),那么甲数是(________)。
16.下图计数器上的数写作(______),数中的“2”表示(______)。
17.把一个西瓜平均分成8块,丽丽吃了其中的3块,还剩下这个西瓜的() ()。
操作性试题

操作性试题安徽省庐江县新渡初级中学吴年生(邮编231524)操作性试题是指具有较强实践性与思辨性,能够有效考查学生的实践能力、创新意识和直觉思维能力、发散思维能力等综合素质的一类问题,通称为实践操作性试题。
解决实践操作性试题一般需要经历观察,操作,思考,想像,推理,交流,反思等实践活动过程,利用自己已有的生活经验、感知与发现结论,从而解决问题。
这类问题能够更好地促进学生对数学的理解,帮助他们提高用数学的语言、符号进行表达交流的能力。
在解决这类问题的过程中,学生能够感受到数学学习的情趣与价值,经历“数学化”和“再创造”的过程,不断提高自己的创新意识与综合能力,是《全日制义务教育数学课程标准(实验稿)》的基本要求之一。
近年来,实践操作性试题受到各命题单位的重视。
解答操作性试题,关键是要学会自觉地运用数学知识去观察、分析、抽象、概括所给的实际问题,揭示其数学本质,并转化为我们所熟悉的数学问题。
适合学生现有知识水平和实践能力。
近几年中考中的操作性试题大致可分为画图、图形的拼合、图形的分割、方案设计、猜想探索等几种类型。
一、画图型操作题例1.(2002”(两个圆、两个三角形、两条平行线)构建尽可能多的构思独特且有意义的图形,并写一两句诙谐的解说词。
分析:本题的答案千变万化,如:本题开放性、动手操作性强,答案多种多样。
其构思之巧妙,想象之丰富、语言之诙谐使人耳目一新。
例2.(2003年无锡市中考试题)用四块如下图①所示的瓷砖拼成的一个正方形,使拼成的图案成轴对称,请你在图②、图③、图④中各画出一种拼法(要求三种拼法各不相同,所画图案中的阴影部分用斜线表示)分析:本题的拼法很多,只要符合要求即可。
下面给出三种拼法。
评注:新精神和实践能力。
例3.(2003年泉州市中考题)如图,在四个正方形拼接成的图形中,以这十个点为顶点,共能组成___个等腰直角三角形。
你愿意把得到上述结论的探究方法与他人交流吗?若愿意,请在下方简要写出你的探究过程。
七年级数学上学期练习题(无答案)(人教新课标)
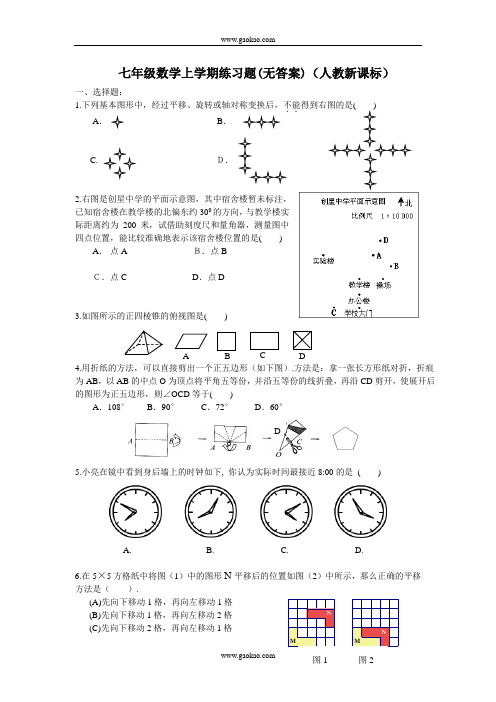
七年级数学上学期练习题(无答案)(人教新课标)一、选择题:1.下列基本图形中,经过平移、旋转或轴对称变换后,不能..得到右图的是( ) A.B.C.D.2.右图是创星中学的平面示意图,其中宿舍楼暂未标注,已知宿舍楼在教学楼的北偏东约300的方向,与教学楼实际距离约为200米,试借助刻度尺和量角器,测量图中四点位置,能比较准确地表示该宿舍楼位置的是()A.点AB.点BC.点C D.点D3.如图所示的正四棱锥的俯视图是( )4.用折纸的方法,可以直接剪出一个正五边形(如下图).方法是:拿一张长方形纸对折,折痕为AB,以AB的中点O为顶点将平角五等份,并沿五等份的线折叠,再沿CD剪开,使展开后的图形为正五边形,则∠OCD等于( )A.108°B.90°C.72°D.60°5.小亮在镜中看到身后墙上的时钟如下, 你认为实际时间最接近8:00的是( )A. B. C. D.6.在5×5方格纸中将图(1)中的图形N平移后的位置如图(2)中所示,那么正确的平移方法是().(A)先向下移动1格,再向左移动1格(B)先向下移动1格,再向左移动2格(C)先向下移动2格,再向左移动1格A C DO(1)(2)(3)(4)图5(D)先向下移动2格,再向左移动2格7.在下面图形中, 每个大正方形网格都是由边长为1的小正方形组成,则图中阴影部分面积最大的是 ( )A. B. C. D.8.如图①是一个正方形毛坯, 将其沿一组对面的对角线切去一半,得到一个工件如图②,对于这个工件,左视图、俯视图正确的一组的是( )① ②a b c dA.a 、bB.b 、dC.a 、cD.a 、d9.在右图中,将左边方格纸中的图形绕O 点顺时针旋转90°得到的图形是( )A. B.C. D.10.将一正方形纸片按图5中(1)、(2) 的方式依次对折后,再沿(3)中的 虚线裁剪,最后将(4)中的纸片打开铺平,所得图案应该是下面图案中的( )BACD11.用边长为1的正方形纸板,制成一幅七巧板(如图①),将它拼成“小天鹅”图案(如图②),其中阴影部分的面积为( ) A.38B.716C.12D.3412.下列个物体中, 是一样的为 ( )(1)(2) (3) (4)A. (1)与(2)B. (1)与(3)C. (1)与(4)D. (2)与(3)13.右图需再添上一个面,折叠后才能围成一个正方体,下面是四位同学补画的情况(图中阴影部分),其中正确的是 ( )A .C.14.下图中几何体的左视图是 ( )15.小丽制作了一个如下左图所示的正方体礼品盒,其对面图案都相同,那么这个正方体的平面展开图可能是 ( )正面第4题AC B DA16.某同学把下图所示的几何体的三种视图画出如下(不考虑尺寸),在这三种是图中,其正确的是( )A.①②B.①③C.②③D.①②③17.如图,是一个由若干个相同的小正方体组成的几何体的三视图,则组成这个几何体的小正方体的个数是 ( )主视图 左视图 俯视图A.7个B.8个C.9个D.10个18.由相同小正方体搭成的几何体如图,下列视图中不是这个几何体主视图(正视图)或俯视图或左视图的是 ( )19.如图是由几个小立方块所搭几何体的俯视图 ,小正方形中的数字表示在该位置的小立方块的个数,这个几何体的主视图是( )A BC D 20.一个几何体由一些小正方体摆成,其主(正)视图与左视图如图所示.其俯视图不可能是A B C D( )二、填空题:21.“◆”代表甲种植物,“★”代表乙种植物,为美化环境,采用如图所示方案种植. 按此规律第六个图案中应种植甲种植物_________株,第n 个图案中应种植乙种植物_________株.★ ★ ★ ★★ ★ ★ ◆ ◆ ◆★ ★ ◆ ◆ ★ ★ ★ ★ ◆ ★ ★ ★ ◆ ◆ ◆ ★ ★ ◆ ◆ ★ ★ ★ ★★ ★ ★ ◆ ◆ ◆★ ★ ★ ★22.如图,正方体表面上从A 点到C 1点的最短距离有________种。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如图,5×5方格被分成了五块;请你在每格中填入1、2、3、4、5中的一个,使得
每行、每列、每条对角线的五个数各不相同,且每块上所填数的和都相等.现有两个格子已分别填入1和2,请在其它格子中填上适当的数.那么,ABCDE这个五位数
是:
14523
.
考点:幻方.
分析:根据每行每列对角和=15,每块的和应该=15(总的和75分五块),所以:B (不是指B)上面格子的只能是2;
右下角4个格和是15,15=5+4+3+3=5+5+4+1=5+5+3+2=5+4+4+2,都有两个一样的,因为对角线5个数不一样,所以这相同的两个数,一个在D那列的最后一个,一个在E下面.又因为对角线上已经有2了,所以排除后面2个.如果是5433的话,那么左上右下这条对角线上已经有了2,4,5,即左上角那个格子是3,推出第2列最后那个格子也是3,但第4列最后那个格子也是3,矛盾了,所以右下角那4个是5541;
因为第4列第一个格子是1,所以D下面那个格子是4,右下角是1,如果C=3,那么第4列第二个格子和第5列第二个格子都必须是3,矛盾了,所以C=5 左上角是3,即第2列最后那个格子是3,所以D上面那个格子是3,E=3,D=2;
B下面格子是1,左下角是4,所以A=1,B=4.
所以ABCDE=14523.
解答:解:根据分析:B上面格子的只能是2;右下角那4个是5541;进而推出C=5;E=3;D=2;A=1,;B=4.
所以ABCDE这个五位数是14523.
故答案为:14523.
点评:分析题干,从使得每行、每列、每条对角线的五个数各不相同,且每块上所填数的和都相等以及已经填入的数字切入,逐步分析各字母所代表的数字,寻求答案.。
