2018-2019学年人教A版数学选修2-3全册课件：第一章 1.2 1.2.2 第二课时组合习题课

合集下载

人教a版数学【选修2-3】1.2.2《组合1》ppt课件

第一章
1.2
1.2.2
第1课时ቤተ መጻሕፍቲ ባይዱ
成才之路 · 高中新课程 · 学习指导 · 人教A版 · 数学 · 选修2-3
3．从 5 本不同书中取出 2 本并成一组和取出 3 本并成一组的组合数相同吗？为什么？ 4．从含有元素 a 的 n＋1 个不同元素中取出 m 个元素的组
m 合数 Cn ＋1，可以分成两类：一类不含元素 a，从剩余的 n 个元
成才之路 · 高中新课程 · 学习指导 · 人教A版 · 数学 · 选修2-3
组合数公式
思维导航 2．组合的本质是取出的 m 个元素不讲究顺序，也就是说元素没有位置的要求，因此这 m 个元素的全排列数只对应组合
m 数中的一个，由此你能得出求 Cn 的计算公式吗？你能不用列举
数数的方法求出前面 3 个问题中的票价种数、积的个数、线段条数吗？
第一章
1.2
1.2.2
第1课时
成才之路 · 高中新课程 · 学习指导 · 人教A版 · 数学 · 选修2-3
牛刀小试 1．C2 n＝10，则 n 的值为( A．10 C．3
[答案] B
) B．5 D．4
nn－1 [解析] 由题意得 2 ＝10，解得 n＝5 或 n＝－4(舍去)，故选 B.
第一章
1.2
1.2.2
第1课时
成才之路 · 高中新课程 · 学习指导 · 人教A版 · 数学 · 选修2-3
2．从 9 名学生中选出 3名参加“希望英语”口语比赛，有
( )种不同选法．( A．504 C．84 [答案] C
[解析] 只需从 9 名学生中选出 3 名即可，从而有 C3 9＝ 9×8×7 ＝84 种选法． 3×2×1

2018-2019学年人教A版数学选修2-3全册课件：第一章 1.

2 A 4 2 2 2 提示：能．因为 A2 ＝ C A ，所以 C ＝＝6. 4 4 2 4 A2 2
问题 4：你能把问题 3 的结论推广到一般吗？
提示：可以，从 n 个不同元素中取出 m 个元素的排列数可由以下两个步骤得到：第 1 步，从这 n 个不同元素中取出 m 个元素，共有 Cm n 种不同的取法；第 2 步，将取出的 m 个元素全排列，共有 Am m种不同的排法． m A n m m m 由分步乘法计数原理知，An ＝Cm · A ，故 C ＝ . n m n Am m
8×7×6 100×99 3 2 解：(1)原式＝C8＋C100×1＝＋＝56＋4 3×2×1 2× 1 ＝5 006. C5 19 14 3 n－1 5 (2)原方程可变形为 3 ＋1＝，Cn－1＝ Cn－3， 5 5 Cn－3 n－1n－2n－3n－4n－5 即 5！
m！5－m！ m！6－m5－m！即－ 5！ 6×5！ 7×m！7－m6－m5－m！＝， 10×7×6×5！ 6－m 7－m6－m ∴1－＝， 6 60 即 m2－23m＋42＝0，解得 m＝2 或 21. 而 0≤m≤5，∴m＝2.
－m m 2 3 3 ∴C8 ＋C5 ＝ C ＋ C ＝ C 8 8 8 9＝84.
1.2
1.2.2
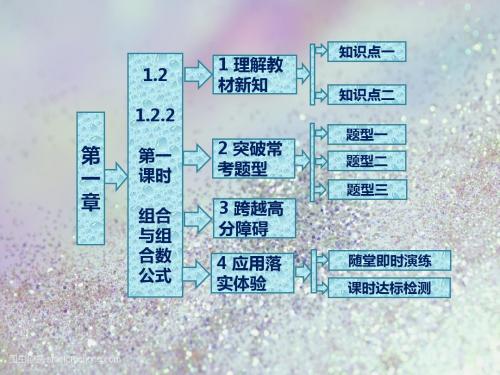
1 理解教材新知
知识点一
知识点二
题型一题型二题型三
第一章
第一课时
组合与组合数公式
2 突破常考题型 3 跨越高分障碍
4 应用落实体验
随堂即时演练课时达标检测
1.2
排列与组合
1．2.2
组合
第一课时
组合与组合数公式
组合与组合数 [提出问题]

2018-2019学年人教A版高中数学选修2-33 1.2-1.2.1 第1课时排列与排列数公式

栏目导引
第一章计数原理
2．判断下列问题是否是排列问题： (1)从 1 到 10 十个自然数中任取两个数组成直角坐标平面内的点的坐标，可得多少个不同的点的坐标？ (2)从 10 名同学中任抽两名同学去学校开座谈会，有多少种不同的抽取方法？ (3)某商场有四个大门，若从一个门进去，购买物品后再从另一个门出来，不同的出入方式共有多少种？
栏1)由于取出的两数组成点的坐标与哪一个数作横坐标，哪一个数作纵坐标的顺序有关，所以这是一个排列问题． (2)因为从 10 名同学中抽取两人去学校开座谈会的方式不用考虑两人的顺序，所以这不是排列问题． (3)因为从一门进，从另一门出是有顺序的，所以是排列问题．综上，(1)、(3)是排列问题，(2)不是排列问题．
栏目导引
第一章计数原理
2．排列数及排列数公式
排列从 n 个不同元素中取出 m(m≤n)个元素的所数定有义表示法全排列 n 个不同元素全部取出的一个排列，叫做 n 个元素的一个全排列，这时公式中 m＝n，即有 An n＝n×(n－1)×(n－2)×…×3×2×1
栏目导引
不同排列的个数叫做从 n 个不同元素
栏目导引
第一章计数原理
下面问题中，是排列问题的是(
)
A．由 1，2，3，4 四个数字组成无重复数字的四位数 B．从 60 人中选 11 人组成足球队 C．从 100 人中选 2 人抽样调查 D．从 1，2，3，4，5 中选 2 个数组成集合
答案：A
栏目导引
第一章计数原理
3 A2 ＝ ________ ， A 4 3＝________．
答案：12 6 若 Am 10＝10×9×…×5，则 m＝________．答案：6

人教A版高中数学选修2-3全册ppt课件

[一题多变] 1．[变条件]若本例条件变为个位数字小于十位数字且为偶数，那么这样的两位数有多少个．
解：当个位数字是 8 时，十位数字取 9，只有 1 个．当个位数字是 6 时，十位数字可取 7,8,9，共 3 个．当个位数字是 4 时，十位数字可取 5,6,7,8,9，共 5 个．同理可知，当个位数字是 2 时，共 7 个，当个位数字是 0 时，共 9 个．由分类加法计数原理知，符合条件的两位数共有 1＋3＋5 ＋7＋9＝25(个)．
用计数原理解决涂色(种植)问题
[ 典例 ] 如图所示，要给“优”、
“化”、“指”、“导”四个区域分别涂上 3 种不同颜色中的某一种，允许同一种颜色使用多次，但相邻区域必须涂不同的颜色，有多少种不同的涂色方法？
[解] 优、化、指、导四个区域依次涂色，分四步．
第 1 步，涂“优”区域，有 3 种选择．第 2 步，涂“化”区域，有 2 种选择．
利用分类加法计数原理计数时的解题流程
分步乘法计数原理的应用
[典例]
从 1,2,3,4 中选三个数字，组成无重复数字的整
数，则分别满足下列条件的数有多少个？ (1)三位数； (2)三位数的偶数．
[解] (1)三位数有三个数位，百位十位个位
故可分三个步骤完成：第 1 步，排个位，从 1,2,3,4 中选 1 个数字，有 4 种方法；第 2 步，排十位，从剩下的 3 个数字中选 1 个，有 3 种方法；
2．如果一个三位正整数如“a1a2a3”满足 a1<a2 且 a3<a2，则称这样的三位数为凸数(如 120,342,275 等)，那么所有凸数个数是多少？解：分 8 类，当中间数为 2 时，百位只能选 1，个位可选 1、0，由分步乘法计数原理，有 1×2＝2 个；当中间数为 3 时，百位可选 1,2，个位可选 0,1,2，由分步乘法计数原理，有 2×3＝6 个；同理可得：当中间数为 4 时，有 3×4＝12 个；当中间数为 5 时，有 4×5＝20 个；当中间数为 6 时，有 5×6＝30 个；当中间数为 7 时，有 6×7＝42 个；当中间数为 8 时，有 7×8＝56 个；当中间数为 9 时，有 8×9＝72 个．故共有 2＋6＋12＋20＋30＋42＋56＋72＝240 个．

人教a版数学【选修2-3】1.2.2《排列与组合习题课》ppt课件

成才之路 · 数学
人教A版 · 选修2-3
路漫漫其修远兮吾将上下而求索
成才之路 · 高中新课程 · 学习指导 · 人教A版 · 数学 · 选修2-3
第一章
计数原理
第一章
计数原理
成才之路 · 高中新课程 · 学习指导 · 人教A版 · 数学 · 选修2-3
第一章
1.2 排列与组合
1.2.2 组合第3课时排列与组合习题课
排列组合应用题
某校为庆祝 2014 年国庆节，安排了一场文艺演出，其中有 3 个舞蹈节目和 4 个小品节目，按下面要求安排节目单，有多少种方法： (1)3 个舞蹈节目互不相邻； (2)3 个舞蹈节目和 4 个小品节目彼此相间．
第一章
1.2
1.2.2
第3课时
成才之路 · 高中新课程 · 学习指导 · 人教A版 · 数学 · 选修2-3
[分析] 由题目可获取以下主要信息： ①题目中涉及3个舞蹈、4个小品共7个节目； ②是同类节目互不相邻的问题．解答本题的第 (1) 问可以先安排 4 个小品，然后让 3 个舞蹈
“插空”；第(2)问彼此相间时安排方式只能是小品占 1,3,5,7，
1.2
1.2.2
第3课时
成才之路 · 高中新课程 · 学习指导 · 人教A版 · 数学 · 选修2-3
[解析] (1)先在 6 个乒乓球中任取一个，作为一堆，有 C1 6种取法，再从余下的五个乒乓球中任取两个，作为一堆，有 C2 5种取法，再从余下三个中取三个作为一堆，有 C3 3种取法，故共有
成才之路 · 高中新课程 · 学习指导 · 人教A版 · 数学 · 选修2-3
1.巩固排列、组合的概念，排列数公式，组合数公式以及组合数的性质． 2 ．准确地应用两个基本原理，正确区分是排列问题还是组合问题．

2018-2019学年高中数学第一章计数原理 1.2.2 第1课时组合(一)讲义新人教A版选修2-3

含组合数的化简、证明或解方程、不
(1)对于含组合数的化简、证明或解方程、不等式等问题多利 ①组合数公式，即： Cnm＝m！nn！－m！＝nn－1…m！n－m＋1； ②组合数的性质，即 Cnm＝Cnn－m和 Cnm＋1＝Cmn ＋Cmn －1； ③排列数与组合数的关系，即 Anm＝Cmn Amm． (2)当含有字母的组合数的式子要进行变形论证时，利用阶乘便．
1．由 Cx1＋0 1＋C1170－x可得不相同的值的个数是
A．1
B．2
C．3
D．4
[解析]
x＋1≤10 ∵x1＋7－1≥x≤010，∴7≤x≤9，
17－x≥0
又 x∈Z，∴x＝7,8,9．
当 x＝7 时，C810＋C1100＝46
当 x＝8 时，C910＋C910＝20 当 x＝9 时，C1100＋C810＝46．
规律总结』 1.性质“Cnm＝Cnn－m”的意义及作用．反映的是组合数的对称性，即从n个不
意义 → 同的元素中取m个元素的一个组合与剩下的n－m个元素的组合相对应
作用 → 当m>n2时，计算Cnm通常转化为计算Cnn－m
2．与排列组合有关的方程或不等式问题要用到排列数、组组合数的性质，求解时，要注意由 Cnm中的 m∈N＋，n∈N＋，且的范围，因此求解后要验证所得结果是否适合题意．
序写出，即
• ∴所有组合为ABC，ABD，ABE，ACD，ACE BCD，BCE，BDE，CDE．
解法二：画出树形图，如图所示．
∴所有组合为 ABC，ABD，ABE，ACD，ACE，ADE，BCD CDE．
命题方向2 ⇨组合数公式
典例 2 (2018·江西玉山一中检测)若 20C5n＋5＝4(n＋4)Cnn＋－的值．

2019-2020年人教A版高中数学选修2-3：1.2排列与组合1.2.1排列课件 (共29张PPT)

课时作业
[自主梳理] 1．排列的有关概念 (1)定义：一般地，从 n 个不同元素中取出 m(m≤n)个元素，按照一定的顺序排成一列，叫作从 n 个不同元素中取出 m 个元素的一个排列． (2)相同排列：两个排列相同，当且仅当两个排列的元素完全相同，且元素的排列顺序也相同．
2．排列数与排列数公式
后面，则他可选的密码个数共有( )
A．A66
B．A68
C．A35＋A33
D．A35·A33
解析：分两步．第一步选 3 个数字安排在后三位，有 A35种方法，第二步把 3 个字母
安排在前三位，有 A33种方法，故共有 A35·A33个密码．
答案：D
探究三 “在”与“不在”的问题 [典例 3] 7 位同学站成一排． (1)若甲站在中间的位置，则共有多少种不同的排法？ (2)甲、乙只能站在两端的排法共有多少种？ (3)甲、乙不能站在排头和排尾的排法共有多少种？ (4)甲不能站排头、乙不能站排尾的排法共有多少种？ [解析] (1)先考虑甲站在中间，有 1 种排法，再在余下的 6 个位置排另外 6 位同学，共 A66＝720 种排法． (2)先考虑甲、乙站在两端，有 A22种排法，再在余下的 5 个位置排另外 5 位同学，有 A55种排法，共 A22A55＝240 种排法．
1.2 排列与组合 1.2.1 排列重点：排列的概念；排列数公
2.了解排列数的概念．
式；用排列知识解决简单的实
3.掌握排列数公式的推导方法．
际问题．
4.能用排列知识解决简单的实际问题. 难点：排列数公式的推导方法.
01 课前自主梳理 02 课堂合作探究 03 课后巩固提升
排列问题的实质是“元素”占“位子”问题，有限制条件的排列问题的限制条件主要表现在某元素不排在某个位子上或某个位子不排某些元素，解决该类排列问题的方法主要是按“优先”原则，即优先排特殊元素或优先满足特殊位子．

高中数学人教A版选修2-3第一章二项式定理各种题型归纳课件

题型7：求奇数(次)项偶数(次)项系数的和
例12 已知(3x 1)7 a0x7 a1x6 a6x a7
求(1)a1 a3 a5 a7 (2)a0 a2 a4 a6
(3) a0 a1 a2 a7
解 :设f (x) (3x 1)7
（3）f所f因 ((1以1)为 )a0aa01a,0aaa31a1,1a5aaa,222a7a是3 负 aa7数7 a7
解：原式化为[(x2 2) 3x]5
其通项公式为 Tr1 C5r (x2 2)5r (3x)r
要使x的指数为1,只需r 1
T2 C51(x2 2)4 3x
15x(x8 4 2x6 6 4x4 4 8x2 24 )
所以x的系数为15 24 240
例题点评括号里含有三项的情况可以把某两项合并为一项,合并时要注意选择的科学性.也可因式分解化为乘积二项式.
[(x 1) 1]5 1
x5 1
例题点评逆向应用公式和变形应用公式是高中数学的难点,也是重点,只有熟练掌握公式的正用,才能掌握逆向应用和变式应用
题型4 求多项式的展开式中特定的项(系数)
例8 (x 1) (x 1)2 (x 1)3 (x 1)4 (x 1)5
的展开式中,x2 的系数等于___________
注意(1)二项式系数与系数的区别.
(2) Tr1 Cnranrbr表示第 r 项.
题型3 二项式定理的逆用例6 计算并求值
(1) 1 2Cn1 4Cn2 2nCnn
(2) (x 1)5 5(x 1)4 10(x 1)3 10(x 1)2
5(x 1)
解(1):将原式变形
原式 Cn01n Cn11n1 2 Cn21n2 22 Cnn 2n

人教a版数学【选修2-3】第1章《计数原理》归纳总结ppt课件

2．(2012·浙江理，6)若从1、2、3、„、9这9个整数中同
时取4个不同的数，其和为偶数，则不同的取法共有( A．60种 C．65种 [答案] D B．63种 D．66种 )
[解析] 本题考查了排列与组合的相关知识．取出的 4 个数和为偶数，可分为三类．
4 2 2 四个奇数 C4 5，四个偶数 C4，二奇二偶，C5C4. 4 2 2 共有 C4 ＋ C ＋ C 5 4 5C4＝66 种不同取法． [点评] 分类讨论思想在排列组合题目中应用广泛．
1 n n ③各二项式系数的和：C0 ＋ C ＋„＋ C ＝ 2 . n n n
第一章
章末归纳总结
成才之路 · 高中新课程 · 学习指导 · 人教A版 · 数学 · 选修2-3
(4)解决二项式定理问题的注意事项
n－k k ①运用二项式定理一定要牢记通项 Tk＋1＝Ck a b ，注意(a n
＋b)n 与(b＋a)n 虽然相同，但具体到它们展开式的某一项时是不同的．另外，二项式系数与项的系数是两个不同概念，前者指
第一章
章末归纳总结
成才之路 · 高中新课程 · 学习指导 · 人教A版 · 数学 · 选修2-3
3．在(x2＋x＋1)(x－1)5的展开式中，含x4项的系数是(
)
A．－25
C．5 [答案] B
B．－5
D．25
[解析] (x2＋x＋1)(x－1)5＝(x3－1)(x－1)4，其展开式中 x4
中任何一种方法都不能完成这件事情，只能完成事件的某一部
分，只有当各步全部完成时，这件事情才完成．
第一章章末归纳总结
成才之路 · 高中新课程 · 学习指导 · 人教A版 · 数学 · 选修2-3
2．排列与组合 (1)排列与组合的定义

高中数学第一章计数原理 1_2 排列与组合 1_2_2_1课件新人教A版选修2-3

(仿照教材P23例6的解析过程)
【解析】(1)从口袋里的8个球中任取5个球,不同取法的种数是
8 7 6 C C 56. 3 2 1 5个球,其中恰有一个红球, (2)从口袋里的8个球中任取
5 8 3 8
可以分两步完成: 第一步,从7个白球中任取4个白球,有第二步,把1个红球取出,有
主题2:组合数公式与组合数性质从1,3,5,7中任取两个相除,
1.可以得到多少个不同的商?
提示: =4×3=12个不同的商.
A
2 4
2.如何用分步乘法计数原理求商的个数? 提示:第1步,从这四个数中任取两个数,有
第2步,将每个组合中的两个数排列,有
步乘法计数原理,可得商的个数为
2 C2 A 4 2
4.计算
CA
3 4
3 3
=________.
3 3 3 4
【解析】
答案:24
C A A 4 3 2 24.
3 4
5.一个口袋里装有7个白球和1个红球,从口袋中任取5 个球. (1)共有多少种不同的取法? (2)其中恰有一个红球,共有多少种不同的取法?
(3)其中不含红球,共有多少种不同的取法?
C 28得
2 n
n n 1 2
=28,所以n=8或n=-7(舍).
2.给出下面几个问题,其中是组合问题的是 ①某班选10名同学参加计算机汉字录入比赛;
(
)
②从1,2,3,4中选出2个数,构成平面向量a的坐标; ③从1,2,3,4中选出2个数分别作为实轴长和虚轴长,构
成焦点在x轴上的双曲线的方程;
4 种取法.C 7
种取法;
C1 1
故不同取法的种数是:
4 1 4 C7 C1 C7 C3 7 35. (3)从口袋里任取5个球,其中不含红球,只需从7个白球

人教版A版高中数学选修2-3：排列与组合_课件1

(2)方法 1：先把甲、乙作为一个“整体”，看作一个人，有 A55种站法，再把甲、乙进行全排列，有 A22种站法，根椐分步计数原理，共有 A55·A22＝240 种站法．
方法 2：先把甲、乙以外的 4 个人作全排列，有 A44种站法，再在 5 个空档中选出一个供甲、乙放入，有 A15种站法，最后让甲、乙全排列，有 A22种方法，共有 A44·A15·A22＝240 种．
三几何型排列组合问题
【例 3】已知平面 a∥β 在 a 内有 4 个点，在 β 内有 6 个点． (1)过这 10 个点中的 3 点作一平面，最多可作多少个
不同平面？ (2)以这些点为顶点，最多可作多少个三棱锥？ (3)上述三棱锥中最多可以有多少个不同的体积？
【解析】 (1)所作出的平面有三类： ①α 内 1 点，β 内 2 点确定的平面，有 C14·C26个； ②α 内 2 点，β 内 1 点确定平面，有 C24·C16个； ③α，β 本身，共 2 个．所以所作的平面最多有 C14·C26＋C24·C16＋2＝98(个)．
(2)要使六位数为奇数，其个位数字必须是 1 或 3 或 5，所以所求六位奇数的个数是 A13A14A44＝288.
(3)要使六位数能被 5 整除，个位数字必须是 0 或 5，当个位数字是 0 时，有 A55个；当个位数字是 5 时，有 4A44个，因此，能被 5 整除的六位数的个数是 A55＋4A44＝216.
相邻问题捆绑法；
不相邻问题插空法；
多排问题单排法；定序问题倍缩法；定位问题优先法；有序分配问题分步法；多元问题分类法；交叉问题集合法；至少(或至多)问题间接法；选排问题先取后排法；局部与整体问题排除法；复杂问题转化法.
3.解答组合应用题的总体思路 (1)⑥ 整体分类 .从集合的意义讲,分类要做到各类的并集等于全集,以保证分类的不遗漏，任何两类的交集等于空集，以保证分类的不重复,计算结果是使用分类计数原理. (2)⑦ 局部分步 .整体分类以后,对每一类进行局部分步,分步要做到步骤连续,以保证分步的不遗漏.同时步骤要独立,以保证分步的不重复.计算结果时用分步计数原理.

新人教A版高中数学(选修2-3)1.2《排列与组合》(组合)

例6．甲、乙、丙3位志愿者安排在周一至
周五的5天中参加某项志愿者活动，要求
每人参加一天且每天至多安排一人，并要
求甲安排在另外两位前面。不同的安排方
法共有（）
种方法，
所以，一共有90+360+90＝540种方法．
元素相同问题隔板策略
例.有10个运动员名额，再分给7个班，每班至少一个,有多少种分配方案？
解：因为10个名额没有差别，把它们排成一排。相邻名额之间形成９个空隙。
在９个空档中选６个位置插个隔板，可把名额分成７份，对应地分给７个班级，每一种插板方法对应一种分法将n个相同共的有元__素__分__成__m__份_种（分n，法m。为正整数）,每份至少一个元素,可以用m-1块隔板，插入n个元素排成一排的n-1个空隙中，所有分法数为
组合数性质1： 2：
特别地：
练习一
（1）（2）
（3）（4）（5）求
0 7
1,或5
的值 511
例题解读
求证：证明：因为
左边= =左边，所以等式成立
评注：注意阶乘的变形形式：
练习精选：证明下列等式：（1）
（2）
例题解读：
例1．6本不同的书，按下列要求各有多少种不同的选法：（1）分给甲、乙、丙三人，每人2本；
你发现ad了b bda dba
acd
什么ac?d cad dac
adc cda dca
bcd cbd dbc
bcd
bdc cdb dcb
（三个元素的）1个组合，对应着6个排列
对于，我们可以按照以下步骤进行
概念讲解
组合数公式
排列与组合是有区别的，但它们又有联系．一般地，求从n个不同元素中取出m个元素的

2019-2020学年人教A版高中数学选修2-3课件：第1章计数原理1.2.2(2)

第一章
计数原理
1.2 排列与组合 1.2.2 组合(二)
课前教材预案课堂深度拓展课末随堂演练课后限时作业
课前教材预案
要点求解组合问题的常用方法
• 常用的方法分直接法与间接法两大类．所谓直接法，就是利用分类或者分步计数原理，准确地分类或者分步，直接计算出结果；所谓的间接法，则是采用迂回战术，先求出不受限制条件下的组合数，再减去不符合题意的组合数的方法．
第一类，这 4 人全部入选，另一组 4 人由余下的 8 人中任选 4 人组成，有 C44C48＝70 种方法；
第二类，这 4 人中恰有 3 人入选日语翻译小组，必有 1 名“双面手”入选日语翻译小组，有 C34C12C47＝280 种方法；
第三类，这 4 人中恰有 2 人入选日语翻译小组，必有 2 名“双面手”都入选日语翻译小组，有 C24C22C46＝90 种方法；
• 【例题2】车间有11名工人，其中5名是钳工，4名是车工，另外2名既能做钳工又能做车工，从中选出4名钳工4名车工，问有多少种不同方法？
• 思维导引：可以从“既会钳工又会车工”的2名工人考虑分类求解，也可以从“只会钳工”的5名工人考虑分类求解．
解析方法一以“既会钳工又会车工”的 2 人(记为 A，B)来考虑分类，A，B 都不在内，有选法 C45C44＝5 种；A，B 都在内时又分“都做钳工”“都做车工”“一个做钳工一个做车工”三类，合计有选法 C22C25C44＋C22C45 C24＋A22C35C34＝120 种；A，B 仅有一人在内，又有“做钳工”和“做车工”两种选择，此时有选法 C12C35C44＋C12C45 C34＝60 种．由分类加法计数原理，合计共有不同的选法 185 种．
第三类：共线的 4 个点中没有点为三角形的顶点，共有 C38＝56 个不同的三角形．

高中数学选修2-3(人教A版)第一章计数原理1.2知识点总结含同步练习及答案

1 6 7 12 C0 12 < C12 < ⋯ < C12 > C12 > ⋯ > C12 ，所以 2x − 3 ⩾ 5 且 2x ⩽ 12 解得 4 ⩽ x ⩽ 6．
高考不提分，赔付1万元，关注快乐学了解详情。
− A5 9
= =
8 × 7 × 6 × 5 × (8 + 7) 8 × 7 × 6 × 5 × (24 − 9) = 1.
2×8×7×6×5×4+7×8×7×6×5 8×7×6×5×4×3×2×1−9×8×7×6×5
（3）根据原方程，可得
3x(x − 1)(x − 2) = 2(x + 1)x + 6x(x − 1).
0 10 （1）计算：C5 10 ⋅ C10 − C10 ； m−1 （2）证明：mCm n = nCn−1 ．
解：（1）原式= （2）证明：因为
10 × 9 × 8 × 7 × 6 × 1 − 1 = 252 − 1 = 251 ； 5×4×3×2×1
Cm n =
n! , m!(n − m)! (n − 1)! n(n − 1)! n m−1 n n! ⋅ = = . Cn−1 = m m (m − 1)!(n − m)! m ⋅ (m − 1)!(n − m)! m!(n − m)!
正整数 1 到 n 的连乘积，叫做 n 的阶乘，用 n! 表示．另外，我们规定 0! = 1 ．所以排列数公式还可以写成
Am n =
(n − m)！
n！
.
组合的定义一般地，从 n 个不同元素中取出 m （m ⩽ n ）个元素合成一组，叫做从 n 个不同元素中取出 m 个元素的一个组合（combination）．组合数及组合数的公式从 n 个不同元素中取出 m （m ⩽ n ）个元素的所有不同组合的个数，叫做从 n 个不同元素中取出 m 个元素的组合数，用符号 Cm n 表示．

人教a版数学【选修2-3】1.2.1《排列2》ppt课件

第一章
1.2
1.2.1
第2课时
成才之路 · 高中新课程 · 学习指导 · 人教A版 · 数学 · 选修2-3
2．5名同学排成一排，其中甲、乙、丙三人必须排在一起
的不同排法有(
A．70 C．36 [答案] C
)
B．72 D．12
[解析] 甲、乙、丙先排好后视为一个整体与其他 2 个同
3 学进行排列，共有 A3 A 3 3＝36 种排法．
3 ．间接法：先不考虑附加条件，计算出总排列数，再减
不合要求的排列数．去__________ 捆绑法，相离问题 ______ 插空法，定元、定位 4 ．相邻元素 ______ 优先排法，至多、至少______ 间接法，定序元素__________ 最后排法． ________
第一章
1.2
成才之路 · 数学
人教A版 · 选修2-3
路漫漫其修远兮吾将上下而求索
成才之路 · 高中新课程 · 学习指导 · 人教A版 · 数学 · 选修2-3
第一章
计数原理
第一章
计数原理
成才之路 · 高中新课程 · 学习指导 · 人教A版 · 数学 · 选修2-3
第一章 1.2 排列与组合
1.2.1 排列
1.2
1.2.1
第2课时
成才之路 · 高中新课程 · 学习指导 · 人教A版 · 数学 · 选修2-3
明确问题的限制条件，能够解决含有特殊元素 ( 或特殊位置)的排列问题，会用间接法求解有限制条件的排列问题．
第一章
1.2
1.2.1
第2课时
成才之路 · 高中新课程 · 学习指导 · 人教A版 · 数学 · 选修2-3
mAm n－1 __________

人教A版高二数学选修2-2：1.2类比推理课件 (共19张PPT)

圆的性质
球的性质
球的表面积 S = 4πR 2 球的体积 V = πR 3 3 球心与不过球心的截面(圆面) 的圆心的连线垂直于截面
与球心距离相等的两截面面积相等与球心距离不相等的两截面面积不相等,距球心较近的面积较大
4
圆的面积 S =πR 2 圆心与弦(非直径)中点的连线垂直于弦
与圆心距离相等的两弦相等与圆心距离不相等的两弦不相等,距圆心较近的弦较长
以点(x0,y0)为圆心, r为半径的以点(x0,y0,z0)为球心, r为半圆的方程为(x-x0)2+(y-y0)2 = r2 径的球的方程为 (x-x0)2+(y-y0)2+(z-z0)2 = r2
议 3、进行类比推理的步骤：
(1)找出两类对象之间可以确切表述的相似特征； (2)用一类对象的已知特征去猜测另一类对象的特征，从而得出一个猜想； (3)检验这个猜想.
所以A类事物具有P
导
3、归纳推理的步骤:
实验观察
大胆猜想
检验猜想
思情景引入：
1、据说春秋时代鲁国的公输班（后人称鲁班，被认为是木匠业的祖师）一次去林中砍树时被一株齿形的茅草割破了手，这桩倒霉事却使他发明了锯子.
鲁班的思路是这样的：茅草是齿形的；茅草能割破手. 我需要一种能割断木头的工具；它也可以是齿形的.
思考：平面几何中的哪一类图形可以作为四面体的类比对象
构成几何体的元素数目：三角形平面图形（二维）点
四面体
立体图形（三维）点或线
线
平面直角坐标系
线或面
空间直角坐标系
议
合作探究
A
探究一：类比平面内直角三角形的勾股定理，试给出空间中四面体性质的猜想．

新课标高中数学人教版选修2-3精品课件-【数学】1.3.1《二项式定理习题课》课件(新人教A版选修2-3)

(3)Cn1 2Cn2 3Cn3 ... nCnn
(4)Cn0

1 2
Cn1

1 3
Cn2

...

1 n
1
Cnn
6、（1-2x）6 a0 a1x a2 x2 a3x3 ... a6x6, 则 a0 a1 a2 ... a6 的值为（） A.1 B.64 C.243 D.729
⑷“第一盒中恰有三球”的概率。
P A
24 34

16 81
PB

C41 23 34

32 81
PC

C42 22 34

24 81
P
D

C43 34
2

8 81
如何产生［a,b］区间上均匀随机数呢？
利用计算器或计算机产生[0，1]上的均匀随机数
x=RAND,然后利用伸缩和变换，x x1 *(b a) a
7、若(2x 3)4 a0 a1x a2x2 a3x3 a4x4 , 则(a0 +a2 +a4 )2 (a1 a3 )2的值为（） A.1 B.-1 C.0 D.2
8、(2x3
+
1 x2
)n
(n

N
* )的展开式中，若存在
常数项，则n的最小值是（）
A.3 B.5 C.8 D.10
i=1
s=0
s=0
i<=100? 否输出s
结束
i=i+1
是
s=s+i
WHILE i<=100 s=s+i i=i+1