平面几何难题及解答

合集下载

高考数学压轴专题(易错题)备战高考《平面解析几何》难题汇编及答案解析

【高中数学】数学《平面解析几何》复习知识要点一、选择题1．已知椭圆22221(0)x y a b a b+=>>的焦点分别为1F ，2F ，点A ，B 在椭圆上，12AB F F ⊥于2F ，4AB =，12F F = ）A ．2213x y +=B ．22132x y +=C ．22196x y +=D ．221129x y +=【答案】C 【解析】【分析】利用椭圆的性质，根据4AB =，12F F =c =22 4b a=，求解a ，b 然后推出椭圆方程．【详解】椭圆2222 10x y a b a b +=>>（）的焦点分别为1F ，2F ，点A ，B 在椭圆上，12AB F F ⊥于2F ，4AB =，12F F =c =，22 4b a=，222c a b =-，解得3a =，b =，所以所求椭圆方程为：22196x y +=，故选C ．【点睛】本题主要考查椭圆的简单性质的应用，椭圆方程的求法，是基本知识的考查．2．已知椭圆C ：2212x y +=的右焦点为F ，直线l ：2x =，点∈A l ，线段AF 交椭圆C 于点B ，若3FA FB =u u u v u u u v，则AF u u u v ＝( )A B ．2C D ．3【答案】A 【解析】【分析】设点()2,A n ，()00,B x y ，易知F (1,0)，根据3FA FB =u u u v u u u v，得043x =，013y n =，根据点B 在椭圆上，求得n=1，进而可求得AF =u u u v【详解】根据题意作图：设点()2,A n ，()00,B x y ．由椭圆C ：2212x y += ，知22a =，21b =，21c =，即1c =，所以右焦点F (1,0)．由3FA FB =u u u v u u u v，得()()001,31,n x y =-．所以()0131x =-，且03n y =. 所以043x =，013y n =. 将x 0，y 0代入2212x y +=，得221411233n ⎛⎫⎛⎫⨯+= ⎪ ⎪⎝⎭⎝⎭.解得21n =，所以()2212112AF n u u u v =-+=+=故选A 【点睛】本题考查了椭圆的简单性质，考查了向量的模的求法，考查了向量在解析几何中的应用；正确表达出各点的坐标是解答本题的关键.3．已知直线:2l y x b =+被抛物线2:2(0)C y px p =>截得的弦长为5，直线l 经过2:2(0)C y px p =>的焦点，M 为C 上的一个动点，若点N 的坐标为()4,0，则MN 的最小值为（） A ．3B 3C ．2D ．22【答案】A 【解析】【分析】联立直线与抛物线方程利用弦长公式列方程，结合直线过抛物线的焦点，解方程可得2p =，再利用两点的距离公式，结合二次函数配方法即可得结果.【详解】由22224(42)02y x b x b p x b y px=+⎧⇒+-+=⎨=⎩， 121222,24b p b x x x x +=-=-，因为直线:2l y x b =+被抛物线2:2(0)C y px p =>截得的弦长为5，125x =-，所以()22222512424b p b ⎡⎤-⎛⎫=+-⨯⎢⎥ ⎪⎝⎭⎢⎥⎣⎦（1）又直线l 经过C 的焦点，则,22b pb p -=∴=- （2）由（1）（2）解得2p =，故抛物线方程为24y x =.设()20000,,4M x y y x ∴=.则()()()2222200000||444212MN x y x x x =-+=-+=-+，故当02x =时，min ||MN = 故选：A. 【点睛】本题主要考查直线与抛物线的位置关系，考查了弦长公式以及配方法的应用，意在考查综合应用所学知识解答问题的能力，属于中档题.4．设抛物线E ：26y x =的弦AB 过焦点F ，||3||AF BF =，过A ，B 分别作E 的准线的垂线，垂足分别是A '，B '，则四边形AA B B ''的面积等于( )A ．B ．C ．D ．【答案】C 【解析】【分析】由抛物线的方程可得焦点坐标及准线方程，设直线AB 的方程，与抛物线联立求出两根之和及两根之积，进而求出弦长AB ，由抛物线的性质可得梯形的上下底之和求出，求出A ，B 的纵坐标之差的绝对值，代入梯形的面积公式即可求出梯形的面积．【详解】解：由抛物线的方程可得焦点3(2F ，0)，准线方程：32x =-，由题意可得直线AB 的斜率存在且不为0，设直线AB 的方程为：32x my =+，1(A x ，1)y ，2(B x ，2)y ，联立直线与抛物线的方程：2326x my y x⎧=+⎪⎨⎪=⎩，整理可得：2690y my --=，所以126y y m +=，129y y =-，21212()363x x m y y m +=++=+，因为||3||AF BF =，所以3AF FB =uu u r uu r，即13(2x -，123)3(2y x -=-，2)y ，可得：123y y =-，所以可得：2222639y m y -=⎧⎨-=-⎩即213m =，由抛物线的性质可得： 21233166668223AA BB AB x x m ''+==+++=+=+=g ， 221212121||()436363636433y y y y y y m -=+-=+=+=g ，由题意可知，四边形AA B B ''为直角梯形，所以1211()||84316322AA B B S AA BB y y ''''=+-==gg g ，故选：C ．【点睛】本题考查抛物线的性质及直线与抛物线的相交弦长，梯形的面积公式，属于中档题．5．已知抛物线C ：212y x =的焦点为F ，A 为C 上一点且在第一象限，以F 为圆心，FA 为半径的圆交C 的准线于B ，D 两点，且A ，F ，B 三点共线，则AF =（）A ．16B ．10C ．12D ．8【答案】C 【解析】【分析】根据题意可知AD BD ⊥，利用抛物线的定义，可得30ABD ∠=︒，所以||||2612AF BF ==⨯=．解：因为A ，F ，B 三点共线，所以AB 为圆F 的直径，AD BD ⊥．由抛物线定义知1||||||2AD AF AB ==，所以30ABD ∠=︒．因为F 到准线的距离为6，所以||||2612AF BF ==⨯=．故选：C ．【点睛】本题考查抛物线的性质，抛物线的定义，考查转化思想，属于中档题．6．数学中的数形结合，也可以组成世间万物的绚丽画面.一些优美的曲线是数学形象美、对称美、和谐美的结合产物，曲线22322():16C x y x y =+恰好是四叶玫瑰线.给出下列结论：①曲线C 经过5个整点（即横、纵坐标均为整数的点）；②曲线C 上任意一点到坐标原点O 的距离都不超过2；③曲线C 围成区域的面积大于4π；④方程()223221)60(x y x y xy +=<表示的曲线C 在第二象限和第四象限其中正确结论的序号是( ) A ．①③ B ．②④ C ．①②③ D ．②③④【答案】B 【解析】【分析】利用基本不等式得224x y +≤，可判断②；224x y +=和()3222216x yx y +=联立解得222x y ==可判断①③；由图可判断④.()2223222216162x y xyx y ⎛⎫++=≤ ⎪⎝⎭，解得224x y +≤（当且仅当222x y ==时取等号），则②正确；将224x y +=和()3222216x y x y +=联立，解得222x y ==，即圆224x y +=与曲线C 相切于点()2,2，()2,2-，()2,2--，()2,2-，则①和③都错误；由0xy <，得④正确. 故选：B. 【点睛】本题考查曲线与方程的应用，根据方程，判断曲线的性质及结论，考查学生逻辑推理能力，是一道有一定难度的题.7．已知直线()0y kx k =≠与双曲线()222210,0x y a b a b-=>>交于,A B 两点，以AB 为直径的圆恰好经过双曲线的右焦点F ，若ABF ∆的面积为24a ，则双曲线的离心率为 A ．2 B ．3C ．2D ．5【答案】D 【解析】【分析】通过双曲线和圆的对称性，将ABF ∆的面积转化为FBF ∆'的面积；利用焦点三角形面积公式可以建立a 与b 的关系，从而推导出离心率. 【详解】由题意可得图像如下图所示：F '为双曲线的左焦点AB Q 为圆的直径 90AFB ∴∠=o根据双曲线、圆的对称性可知：四边形AFBF '为矩形12ABF AFBF FBF S S S ''∆∆∴== 又2224tan 45FBF b S b a ∆'===o，可得：225c a = 25e ∴= 5e ⇒=本题正确选项：D 【点睛】本题考查双曲线的离心率求解，离心率问题的求解关键在于构造出关于,a c 的齐次方程，从而配凑出离心率的形式.8．如图，设椭圆E ：22221(0)x y a b a b+=>>的右顶点为A ，右焦点为F ，B 为椭圆在第二象限上的点，直线BO 交椭圆E 于点C ，若直线BF 平分线段AC 于M ，则椭圆E 的离心率是（） A ．12B ．23C ．13D ．14【答案】C 【解析】如图，设AC 中点为M ，连接OM ，则OM 为△ABC 的中位线，于是△OFM ∽△AFB ，且OF OM 1FAAB2==，即c c a -=12可得e=c a =13．故答案为13．点睛：解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于a ，b ，c 的方程或不等式，再根据a ，b ，c 的关系消掉b 得到a ，c 的关系式，建立关于a ，b ，c 的方程或不等式，要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.9．已知直线21y kx k =++与直线122y x =-+的交点位于第一象限，则实数k 的取值范围是（）A ．12k >B ．16k <-或12k > C ．62k -<< D ．1162k -<< 【答案】D 【解析】【分析】联立21122y kx k y x =++⎧⎪⎨=-+⎪⎩，可解得交点坐标(,)x y ，由于直线21y kx k =++与直线122y x =-+的交点位于第一象限，可得00x y >⎧⎨>⎩，解得即可．【详解】解：联立21122y kx k y x =++⎧⎪⎨=-+⎪⎩，解得24216121k x k k y k -⎧=⎪⎪+⎨+⎪=⎪+⎩， Q 直线21y kx k =++与直线122y x =-+的交点位于第一象限， ∴2402161021kk k k -⎧>⎪⎪+⎨+⎪>⎪+⎩，解得：1162k -<<．故选：D ．【点睛】本题考查两直线的交点和分式不等式的解法，以及点所在象限的特征．10．已知双曲线2222:1(0,0)x y C a b a b-=>>，点()00,P x y 是直线40bx ay a -+=上任意一点，若圆()()22001x x y y -+-=与双曲线C 的右支没有公共点，则双曲线的离心率取值范围是（）． A ．(]1,2 B ．(]1,4 C ．[)2,+∞ D ．[)4,+∞ 【答案】B 【解析】【分析】先求出双曲线的渐近线方程，可得则直线bx ay 2a 0-+=与直线bx ay 0-=的距离d ，根据圆()()2200x x y y 1-+-=与双曲线C 的右支没有公共点，可得d 1≥，解得即可．【详解】由题意，双曲线2222x y C :1(a 0,b 0)a b-=>>的一条渐近线方程为b y x a =，即bx ay 0-=，∵()00P x ,y 是直线bx ay 4a 0-+=上任意一点，则直线bx ay 4a 0-+=与直线bx ay 0-=的距离224a 4a d ca b ==+， ∵圆()()2200x x y y 1-+-=与双曲线C 的右支没有公共点，则d 1≥， ∴41a c ≥，即4ce a=≤，又1e > 故e 的取值范围为(]1,4，故选：B ．【点睛】本题主要考查了直线和双曲线的位置关系，以及两平行线间的距离公式，其中解答中根据圆与双曲线C 的右支没有公共点得出d 1≥是解答的关键，着重考查了推理与运算能力，属于基础题．11．若函数1()ln (0,0)a a f x x a b b b+=-->>的图象在x ＝1处的切线与圆x 2＋y 2＝1相切，则a ＋b 的最大值是( ) A ．4 B ．2 C ．2 D ．【答案】D 【解析】()1ln (0,0)a a f x x a b b b+=-->>，所以()'a f x bx ＝－，则f ′(1)＝－ab为切线的斜率，切点为(1，－1a b+)，所以切线方程为y ＋1a b +＝－ab(x －1)，整理得ax ＋by ＋1＝0.因为切线与圆相切，所以22a b+＝1，即a 2＋b 2＝1.由基本不等式得a 2＋b 2＝1≥2ab ，所以(a ＋b )2＝a 2＋b 2＋2ab ＝1＋2ab ≤2，所以a ＋b ≤，即a ＋b 的最大值为.故选D.点睛：求曲线的切线方程是导数的重要应用之一，用导数求切线方程的关键在于求出切点00(,)P x y 及斜率，其求法为：设00(,)P x y 是曲线()y f x =上的一点，则以P 的切点的切线方程为：000'()()y y f x x x -=-．若曲线()y f x =在点00(,())P x f x 的切线平行于y 轴（即导数不存在）时，由切线定义知，切线方程为0x x =．12．已知抛物线24x y =的焦点为F ，准线为l ，抛物线的对称轴与准线交于点Q ，P 为抛物线上的动点，PF m PQ =，当m 最小时，点P 恰好在以,F Q 为焦点的椭圆上，则椭圆的离心率为（）A ．3-B ．2-CD 1【答案】D 【解析】由已知，(01)(01)F Q ，，，-，过点P 作PM 垂直于准线，则PM PF =．记PQM α∠=，则sin PF PM m PQPQα===，当α最小时，m 有最小值，此时直线PQ与抛物线相切于点P ．设204x P x ⎛⎫ ⎪⎝⎭，，可得(21)P ，±，所以2PQ PF ，==，则2PF PQ a +=，∴1a =，1c =，∴1ce a==，故选D ．13．已知曲线()2222:100x y C a b a b-=＞，＞的左、右焦点分别为12,,F F O 为坐标原点，P是双曲线在第一象限上的点，MO OP =u u u u v u u u v，直线2PF 交双曲线C 于另一点N ，若122PF PF =，且2120MF N ∠=︒则双曲线C 的离心率为（）A BC D【答案】B 【解析】【分析】由题意结合双曲线的定义可得124,2PF a PF a == ，在三角形12PF F 中，由余弦定理可得2224208c a a =+，据此计算双曲线的离心率即可. 【详解】由题意，122PF PF =，由双曲线的定义可得，122PF PF a -= ，可得124,2PF a PF a == ，由四边形12PF MF 为平行四边形，又2120MF N ∠=︒，可得12120F PF ∠=︒，在三角形12PF F 中，由余弦定理可得2224164242cos120c a a a a =+-⋅⋅⋅︒ ，即有2224208c a a =+，即227c a =，可得c =，即ce a==【点睛】双曲线的离心率是双曲线最重要的几何性质，求双曲线的离心率(或离心率的取值范围)，常见有两种方法：①求出a ，c ，代入公式c e a =； ②只需要根据一个条件得到关于a ，b ，c 的齐次式，结合b 2＝c 2－a 2转化为a ，c 的齐次式，然后等式(不等式)两边分别除以a 或a 2转化为关于e 的方程(不等式)，解方程(不等式)即可得e (e 的取值范围)．14．如图，12,F F 是双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点，过2F 的直线与双曲线C 交于,A B 两点．若11::3:4:5AB BF AF =，则双曲线的渐近线方程为（）A ．23y x =±B ．2y x =±C ．3y x =D ．2y x =±【答案】A【解析】【分析】设1123,4,5,AB BF AF AF x ====，利用双曲线的定义求出3x =和a 的值，再利用勾股定理求c ，由b y x a =±得到双曲线的渐近线方程. 【详解】设1123,4,5,AB BF AF AF x ====，由双曲线的定义得：345x x +-=-，解得：3x =，所以2212||46413F F =+=13c ⇒=因为2521a x a =-=⇒=，所以23b =所以双曲线的渐近线方程为b y x a=±=±. 【点睛】本题考查双曲线的定义、渐近线方程，解题时要注意如果题干出现焦半径，一般会用到双曲线的定义，考查运算求解能力.15．若圆1C ：2224100x y mx ny +---=（m ，0n >）始终平分圆2C ：()()22112x y +++=的周长，则12m n +的最小值为（） A ．92B ．9C ．6D ．3 【答案】D【解析】【分析】把两圆的方程相减，得到两圆的公共弦所在的直线l 的方程，由题意知圆2C 的圆心在直线l 上，可得()123,213m n m n +=∴+=，再利用基本不等式可求最小值. 【详解】把圆2C ：()()22112x y +++=化为一般式，得22220x y x y +++=，又圆1C ：2224100x y mx ny +---=（m ，0n >），两圆的方程相减，可得两圆的公共弦所在的直线l 的方程：()()12150m x n y ++++=. Q 圆1C 始终平分圆2C 的周长，∴圆心()21,1C --在直线l 上，()()12150m n ∴-+-++=，即()123,213m n m n +=∴+=. ()112225*********n m m n m n m n m n m n ⎛⎫⎛⎫∴+=+⨯=+⨯ ⎪ ⎪⎝⎭⎛⎫+=++ ⎪⎝⎝⎭⎭()115522333⎛≥+=+⨯= ⎝. 当且仅当2322m n n m mn +=⎧⎪⎨=⎪⎩即1m n ==时，等号成立. 12m n∴+的最小值为3. 故选：D .【点睛】本题考查两圆的位置关系，考查基本不等式，属于中档题.16．过坐标轴上的点M 且倾斜角为60°的直线被圆2240x y y +-=所截得的弦长为M 的个数为（）A ．1B ．2C ．3D ．4【答案】C【解析】【分析】设出直线方程，根据弦长公式，转化为圆心到直线的距离建立等量关系求解.【详解】由直线的斜率为tan 60k ︒==y b =+.圆2240x y y +-=可化为22(2)4x y +-=，圆心为(0,2)，半径为2r =，则由弦长公式得：圆心(0,2)到直线y b =+的距离为1d ===，即|2|12b -+=，解得0b =，4b =，故直线的方程为y =或4y =+.直线y =过坐标轴上的点(0,0)，直线4y =+过坐标轴上的点()0,4与3⎛⎫- ⎪ ⎪⎝⎭，故点M 的个数为3.故选：C.【点睛】此题考查直线与圆的位置关系，根据弦长公式将弦长问题转化为圆心到直线的距离求解.17．已知1F ，2F 是双曲线22221x y a b-=（0a >，0b >）的左、右焦点，点A 是双曲线上第二象限内一点，且直线1AF 与双曲线的一条渐近线b y x a=平行，12AF F ∆的周长为9a ，则该双曲线的离心率为（）A ．2B C ．3D ．【答案】A【解析】【分析】根据双曲线的定义，结合三角形的周长可以求出1AF 和2AF 的表达式，根据线线平行，斜率的关系，结合余弦定理进行求解即可.【详解】由题意知212AF AF a -=，2192AF AF a c +=-，解得21122a c AF -=，1722a c AF -=，直线1AF 与b y x a =平行，则12tan b AF F a ∠=，得12cos a AF F c∠=， 222121214cos 22AF c AF a AF F c AF c+-∠==⋅，化简得22280c ac a +-=，即2280e e +-=，解得2e =.故选：A【点睛】本题考查求双曲线的离心率，考查了双曲线的定义的应用，考查了余弦定理的应用，考查了数学运算能力.18．设椭圆22221(0)x y a b a b+=>>的右焦点为F ，过点F 作与x 轴垂直的直线l 交椭圆于P ，B 两点（点P 在第一象限），过椭圆的左顶点和上顶点的直线1l 与直线l 交于A 点，且满足AP BP <u u u v u u u v ，设O 为坐标原点，若(,)OP OA OB R λμλμ=+∈u u u v u u u v u u u v ，29λμ=，则该椭圆的离心率为（）A ．35B ．1213C ．35或1213D ．45【答案】A【解析】分析：根据向量共线定理及29λμ=，AP BP <u u u v u u u v ，可推出λ，μ的值，再根据过点F 作与x 轴垂直的直线l 交椭圆于P ，B 两点（点P 在第一象限），可推出P ，B 两点的坐标，然后求出过椭圆的左顶点和上顶点的直线1l 的方程，即可求得A 点的坐标，从而可得a ，b ，c 三者关系，进而可得椭圆的离心率. 详解：∵A 、P 、B 三点共线，(),OP OA OB R λμλμ=+∈u u u v u u u v u u u v∴1λμ+= 又∵29λμ= ∴1323λμ⎧=⎪⎪⎨⎪=⎪⎩或2313λμ⎧=⎪⎪⎨⎪=⎪⎩ ∵AP BP <u u u v u u u v∴2313λμ⎧=⎪⎪⎨⎪=⎪⎩∵过点F 作与x 轴垂直的直线l 交椭圆于P ，B 两点（点P 在第一象限） ∴2(,)b P c a ，2(,)b B c a - ∵过椭圆的左顶点和上顶点的直线1l 与直线l 交于A 点∴直线1l 的方程为为1x y a b +=- ∴()(,)a c b A c a+ ∵2133OP OA OB =+u u u r u u u r u u u r ∴222()1()33b a c b b a a a+=⋅+⋅-，即2b a c =+. ∴22224()2a c a ac c -=++，即223520a c ac --=.∴25230e e +-=∵(0,1)e ∈ ∴35e =故选A. 点睛：本题考查了双曲线的几何性质，离心率的求法，考查了转化思想以及运算能力，双曲线的离心率是双曲线最重要的几何性质，求双曲线的离心率(或离心率的取值范围)，常见有两种方法：①求出,a c ，代入公式c e a=；②只需要根据一个条件得到关于,,a b c 的齐次式，转化为,a c 的齐次式，然后转化为关于e 的方程(不等式)，解方程(不等式)，即可得e (e 的取值范围)．19．已知椭圆2221(1)x y a a+=>的左、右焦点分别为1F ，2F ，A 是椭圆在第一象限上的一个动点，圆C 与1F A 的延长线，12F F 的延长线以及线段2AF 都相切，且()3,0M 为其中一个切点．则椭圆的离心率为（）AB．3 C．2 D【答案】B【解析】【分析】设圆C 与1F A 的延长线相切于点N ，与2AF 相切于点T ，由切线长相等和椭圆的定义，解方程得出3a =，求出c ，进而可得离心率.【详解】设圆C 与1F A 的延长线相切于点N ，与2AF 相切于点T ，由切线长相等，得AN AT =， 11F N F M =，22F T F M =，1(,0)F c -，2(,0)F c ，由椭圆的定义可得，122AF AF a +=，()111223+22+F N F M c AF AN a AF AN a AN AT TF ==+==-+=+- 222(3)a F M a c =-=--，则26a =，即3a =，又1b =，所以2222c a b =-=，因此椭圆的离心率为223c e a ==. 故选：B.【点睛】本题主要考查求椭圆的离心率，熟记椭圆的定义，以及椭圆的简单性质即可，属于常考题型.20．已知平面向量,,a b c r r r 满足()()2,21a b a b a c b c ==⋅=-⋅-=r r r r r r r r ，则b c -r r 的最小值为（）A 75-B 73-C ．532-D 31- 【答案】A【解析】【分析】根据题意，易知a r 与b r 的夹角为60︒，设(=13a ，r ，()20b =，r ，(),c x y =r ，由()()21a c b c -⋅-=r r r r ，可得2212302x y x y +-+=，所以原问题等价于，圆221202x y x +-+=上一动点与点()20，之间距离的最小值，利用圆心和点()20，的距离与半径的差，即可求出结果.【详解】因为2a b a b ==⋅=r r r r ，所以a r 与b r 的夹角为60︒，设(=1a r ，()20b =，r ，(),c x y =r ，因为()()21a c b c -⋅-=r r r r ，所以221202x y x +-+=，又b c -=r r所以原问题等价于，圆221202x y x +-+=上一动点与点()20，之间距离的最小值，又圆221202x y x +-+=的圆心坐标为1⎛ ⎝⎭，所以点()20，与圆221202x y x +-+=上一动点距离的最小值为=. 故选：A.【点睛】本题考查向量的模的最值的求法，考查向量的数量积的坐标表示，考查学生的转换思想和运算能力，属于中档题．。

八年级数学下册平面几何经典难题训练沪科版

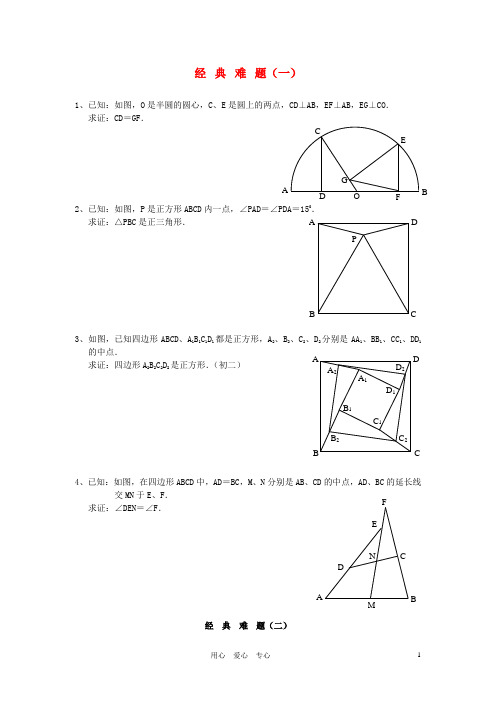
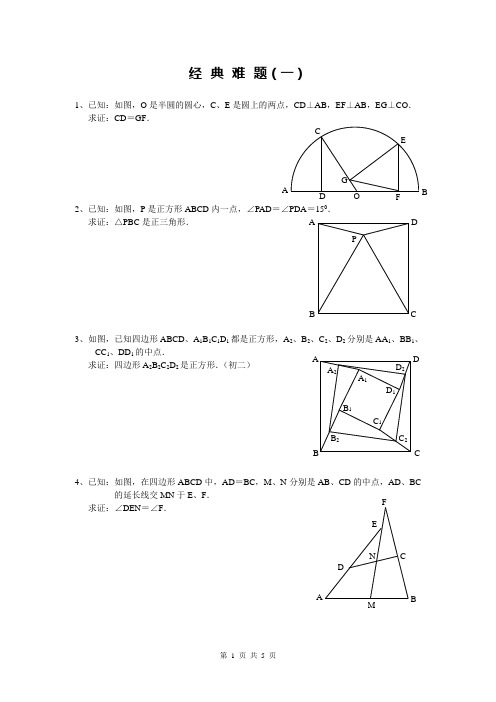
经典难题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．2、已知：如图，P 是正方形ABCD 内一点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．经典难题（二）A P C DB A FG CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 引圆的两条直线，交圆于B 、C 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．经典难1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）经典难题（四）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．P A D CB C B DAF PD E C B A A2、已知：P是边长为1的正方形ABCD内的一点，求PA＋PB＋PC的最小值．3、P为正方形ABCD内的一点，并且PA＝a，PB＝2a，PC＝3a，求正方形的边长．4、如图，△ABC中，∠ABC＝∠ACB＝800，D、E分别是AB、AC＝200，求∠BED的度数．经典难题解答:经典难题（一）1.如下图做GH⊥AB,连接EO。

平面几何难题解答

平面几何难题解答
如图 1，已知∠ABC=90° ，△ABE 是等边三角形，点 P 为射线 BC 上任意一点（点 P 与点 B 不重合），连接 AP，将线段 AP 绕点 A 逆时针旋转 60° 得到线段 AQ，连接 QE 并延长交射线 BC 于点 F．（1）如图 2，当 BP=BA 时，∠EBF= ，猜想∠QFC=
（2）如图 1，当点 P 为射线 BC 上任意一点时，猜想∠QFC 的度数，并加以证明；（3）已知线段 AB=2
3
，设 BP=x，点 Q 到射线 BC 的距离为 y，求关系式．
y 关于 x 的函数
解：（1）∠EBF=30° ； ∠QFC=60° ；（2）∠QFC=60° ．设 BP＞ √3AB，如图 1 所示． ∵∠BAP=∠BAE+∠EAP=60° +∠EAP， ∠EAQ=∠QAP+∠EAP=60° +∠EAP， ∴∠BAP=∠EAQ．在△ABP 和△AEQ 中 AB=AE，∠BAP=∠EAQ，AP=AQ， ∴△ABP≌△AEQ．（SAS） ∴∠AEQ=∠ABP=90° ． ∴∠BEF=180° -∠AEQ-∠AEB=180° -60° -90° =30° ． ∴∠QFC=∠EBF+∠BEF=30° +30° =60° ．（当 BP≤√ 3AB 时，如图 2 情形，不失一般性结论仍然成立）（3）在图 1 中，过点 F 作 FG⊥BE 于点 G． ∵△ABE 是等边三角形， ∴BE=AB=2√ 3．由（1）得∠EBF=30° ．在 Rt△BGF 中，BG= BE/2=√ 3， ∴BF= BG/cos30° =2． ∴EF=2． ∵△ABP≌△AEQ． ∴QE=BP=x， ∴QF=QE+EF=x+2．过点 Q 作 QH⊥BC，垂足为 H．在 Rt△QHF 中，y=QH=sin60°×QF=√ 3/2（x+2）（x＞0）．即 y 关于 x 的函数关系式是：y= √3/2x+ √3．

平面几何练习题及解答

平面几何练习题及解答一、直线与角度1. 给定一条直线L1和两条直线L2和L3，若L1与L2垂直，L2与L3平行，则L1与L3之间的夹角为多少度？解答：由于L1与L2垂直，可得出L2的斜率为无穷大，即L2为竖直线。

而L2与L3平行，说明它们具有相同的斜率。

因此，L3的斜率也为无穷大，即L3也是竖直线。

由此可知，L1与L3之间的夹角为90度。

2. 给定一条直线L和两点A、B，若L与AB的垂线相交于点M，且角AMB为40度，则角LMA的度数是多少？解答：由垂线的性质可得出，角LMA与角AMB互补，它们的度数和为90度。

已知角AMB为40度，因此角LMA的度数为90度减去40度，即50度。

二、三角形3. 已知三角形ABC，其中∠B = 90度，AB = 3 cm，BC = 4 cm，求AC的长度。

解答：根据勾股定理可得：AC² = AB² + BC²AC² = 3² + 4²AC² = 9 + 16AC² = 25AC = √25AC = 5 cm4. 已知三角形ABC，其中AB = 6 cm，BC = 8 cm，AC = 10 cm，求∠B的度数。

解答：根据余弦定理可得：BC² = AB² + AC² - 2 * AB * AC * cosB8² = 6² + 10² - 2 * 6 * 10 * cosB64 = 36 + 100 - 120 * cosB64 = 136 - 120 * cosB120 * cosB = 136 - 64120 * cosB = 72cosB = 72 / 120cosB = 0.6根据反余弦函数可得：∠B = arccos(0.6)∠B ≈ 53.13度三、圆的性质5. 在平面直角坐标系中，给定圆心为O(2, 3)，半径为5的圆C，点P(6, 7)是否在圆C上？解答：利用距离公式可计算OP的距离：OP = √((6-2)² + (7-3)²)OP = √((4)² + (4)²)OP = √(16 + 16)OP = √32OP ≈ 5.66由于OP的长度不等于圆C的半径，即5.66不等于5，因此点P不在圆C上。

2021年高中数学竞赛平面几何问题的解答及其它 (1)

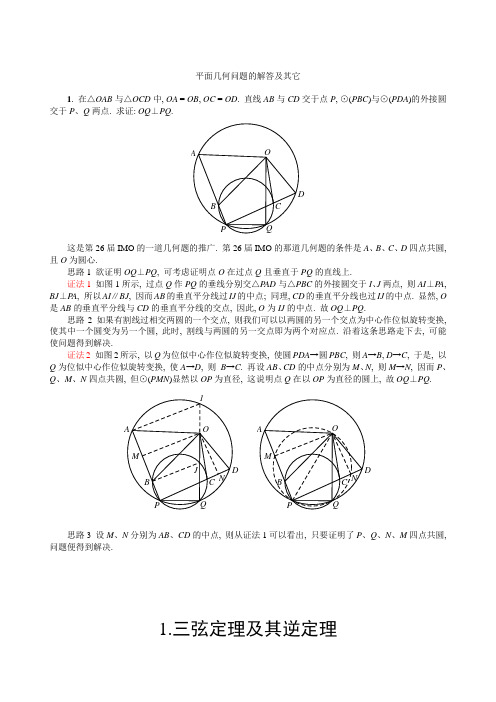
平面几何问题的解答及其它1. 在△OAB 与△OCD 中, OA = OB , OC = OD . 直线AB 与CD 交于点P , ⊙(PBC )与⊙(PDA )的外接圆交于P 、Q 两点. 求证: OQ ⊥PQ .A B CDPOQ这是第26届IMO 的一道几何题的推广. 第26届IMO 的那道几何题的条件是A 、B 、C 、D 四点共圆, 且O 为圆心.思路1 欲证明OQ ⊥PQ , 可考虑证明点O 在过点Q 且垂直于PQ 的直线上.证法1 如图1所示, 过点Q 作PQ 的垂线分别交△P AD 与△PBC 的外接圆交于I 、J 两点, 则AI ⊥P A , BJ ⊥P A , 所以AI ∥BJ , 因而AB 的垂直平分线过IJ 的中点; 同理, CD 的垂直平分线也过IJ 的中点. 显然, O 是AB 的垂直平分线与CD 的垂直平分线的交点, 因此, O 为IJ 的中点. 故OQ ⊥PQ .思路2 如果有割线过相交两圆的一个交点, 则我们可以以两圆的另一个交点为中心作位似旋转变换, 使其中一个圆变为另一个圆, 此时, 割线与两圆的另一交点即为两个对应点. 沿着这条思路走下去, 可能使问题得到解决.证法2 如图2所示, 以Q 为位似中心作位似旋转变换, 使圆PDA →圆PBC , 则A →B , D →C , 于是, 以Q 为位似中心作位似旋转变换, 使A →D , 则 B →C . 再设AB 、CD 的中点分别为M 、N , 则M →N , 因而P 、Q 、M 、N 四点共圆, 但⊙(PMN )显然以OP 为直径, 这说明点Q 在以OP 为直径的圆上, 故OQ ⊥PQ .A B C DPOQ NM1JM NQOPDC B A思路3 设M 、N 分别为AB 、CD 的中点, 则从证法1可以看出, 只要证明了P 、Q 、N 、M 四点共圆, 问题便得到解决.1.三弦定理及其逆定理—一个不可小觑的证明四点共圆的方法我们知道, 对于圆内接四边形来说, 有一个关于四边长与对角线长之间的一个度量等式, 这就是著名的Ptolemy 定理, 即设ABCD 是一个圆内接凸四边形, 则AB CD BC DA AC BD ⋅+⋅=⋅.Ptolemy 定理是处理圆内接四边形问题的一个有力工具, 其逆定理也是成立的, 即在凸四边形ABCD 中, 若AB CD BC DA AC BD ⋅+⋅=⋅, 则ABCD 是一个圆内接四边形.从表面上看来, Ptolemy 定理之逆可以证明四点共圆, 但在解题实践中, 欲用Ptolemy 定理之逆证明四点共圆似乎是一件奢侈的事件. 下面介绍Ptolemy 定理的一个等价定理——三弦定理.三弦定理设P A 、PB 、PC 是一圆Γ内有一公共端点的三条弦, BPC α=, APB β=, 则sin sin sin ()PA PC PB αβαβ+=+证明设圆Γ的半径为R , 由正弦定理, 2sin BC R α=, 2sin AB R β=, 2sin()AC R αβ=+, 于是sin sin sin ()PA PC PB αβαβ+=+⇔2sin 2sin 2sin ()PA R PC R PB R αβαβ⋅+⋅=⋅+⇔PA BC PC AB PB AC ⋅+⋅=⋅.而P ABC 是一个圆内接四边形, 由Ptolemy 定理, PA BC PC AB PB AC ⋅+⋅=⋅. 故三弦定理成立. 且三弦定理与Ptolemy 定理等价.三弦定理之逆设P A 、PB 、PC 是有一公共端点的三条线段,BPC α=,APB β=. 若sin sin sin ()PA PC PB αβαβ+=+.则P 、A 、B 、C 四点共圆.证明设过P 、A 、B 三点的圆与直线PC 交于P 、C ′两点, 由三弦定理, 有sin sin sin ()PA PC PB αβαβ'+=+. 比较条件, 得C ′=C , 故P 、A 、B 、C 四点共圆.PBACP( C' )BAC与Ptolemy 定理一样, 三弦定理可以用来处理有关圆内接四边形的问题, 而且因为三弦定理与三角函数联系在一起, 因此, 用三弦定理处理某些圆内接四边形问题比Ptolemy 定理还要方便. 我们在这里不准备论及. 而三弦定理之逆与Ptolemy 定理之逆就不一样了, 也就是说, 三弦定理之逆在证明四点共圆时表现得够大方的. 其原因也在于它与三角函数联系起来了, 我们可以充分利用三角函数这一工具.例1 设点P 、Q 、R 分别在锐角△ABC 的三条高AD 、BE 、CF 上, 且△PBC 、△QCA 、△RAB 的面积之和等于△ABC 的面积. 证明: P 、Q 、R 、H 四点共圆. 其中, H 为△ABC 的垂心.(2001, 第27届俄罗斯数学奥林匹克)证明如图所示, 不妨设R 在△HAB 内. 因PBC QCA RAB ABC HBC HCA HAB S S S S S S S ∆∆∆∆∆∆∆++==++, 所以()()HAB RAB PBC HBC QCA HCA S S S S S S ∆∆∆∆∆∆-=-+-即111222HR AB HP BC HQ CA ⋅=⋅+⋅, 再由正弦定理, 得sin sin sin HR C HP A HQ B =+. 而 180PHQ DHE C ∠=∠=︒-, RHQ A ∠=, PHR B ∠=,所以, sin sin sin HR PHQ HP RHQ HQ PHR ∠=∠+∠,故由三弦定理之逆, P 、Q 、R 、H 四点共圆.PAECBF DHRQBC例2设D 是△ABC 的边BC 上一点, DC 的垂直平分线交CA 于E , BD 的垂直平分线交AB 于F , O 是△ABC 的外心. 求证: O 、E 、A 、F 四点共圆. (第27届俄罗斯数学奥林匹克, 2001)证明设BC a =, CA b =, AB c =, 仍用A 、B 、C 表示△ABC 的三个对应的内角, 则2cos BD BF B =, 2cos DCEC C=,所以, 2cos BD AF c B =-, 2cos DCAE b C=-. 又由正弦定理, sin OA A a =, 于是再注意90FAO C =︒-, 90OAC B =︒-, 即得sin sin sin AF OAC AE BAO OA A +=⇔cos cos sin AF B AE C OA A +=⇔()cos ()cos 2cos 2cos 2BD DC a c B b C B C -+-=⇔cos cos c B b C a +=而最后一式即众所周知的三角形的射影定理, 因而等式sin sin sin AF OAC AE BAO OA A +=成立.由三弦定理之逆, O 、E 、A 、F 四点共圆.例3 设H 为△ABC 的垂心, D 、E 、F 分别为△ABC 的三边BC 、CA 、AB 上的点, 且DB = DF , DC = DE . 求证: E 、A 、F 、H 四点共圆.证明设BC a =, CA b =, AB c =, 仍用A 、B 、C 表示△ABC 的三个对应的内角, 则2cos BF BD B =, 2cos EC DC C =,所以, 2cos AF c BD B =-, 2cos AE b DC C =-.再设△ABC 的外接圆半径为R , 则不难知道, 2cos AH R A =. 又90HAE C =︒-, 90FAH B =︒-, 于是, 由正弦定理, 并注意cos cos()sin sin cos cos A B C B C B C =-+=-, 得sin sin sin AF HAE AE FAH AH A +=⇔cos cos cos AF C AE B a A +=⇔(2cos )cos (2cos )cos cos c BD B C b DC C B a A -+-=⇔cos cos (2cos cos cos )b B c C a B C A +=+⇔ cos cos (cos cos sin sin )b B c C a B C B C +=+⇔cos cos cos()b B c C a B C +=-而由正弦定理、倍角公式及和差化积公式, 有cos cos 2(sin cos sin cos )b B c C R B B C C +=+= (sin 2sin 2)2sin()cos()R B C R B C B C +=+-=BC2sin cos()cos ()R A B C a B C -=-.即cos cos cos ()b B c C a B C +=-成立, 因而sin sin sin AF HAE AE FAH AH A +=成立, 故由三弦定理之逆, E 、A 、F 、H 四点共圆.第1题的证法31 在△OAB 与△OCD 中, OA = OB , OC = OD . 直线AB 与CD 交于点P , △PBC 与△PDA 的外接圆交于P 、Q 两点. 求证: OQ ⊥PQ .证明设∠QPD = α, ∠CP A = β, 则由三弦定理, 有sin sin sin()PA PQ PD αβαβ+=+, sin sin sin()PB PQ PC αβαβ+=+, 两式相加, 得()sin 2sin (+)sin()PA PB PQ PC PD αβαβ++=+.设AB 与CD 的中点分别为M 、N , 则P A + PB = 2PM , PC + PD = 2PN , 所以sin sin sin()PM PQ PN αβαβ+=+.由三弦定理之逆, M 、P 、Q 、N 四点共圆. 但O 、M 、P 、N 四点共圆, 所以O 、M 、P 、Q 四点共圆. 而PM ⊥OM , 故OQ ⊥PQ .M NQOPDC B AB C第19题的证明19.设D 、E 、F 分别是△ABC 的边BC 、CA 、AB 上的点, 且DE ∥AB , DF ∥AC . 求证: (ⅰ) △AEF 的外接圆通过一个定点P .(ⅱ) 若M 为BC 的中点, 则∠BAM =∠P AC .证明设△AEF 的外接圆与△ABC 的A-陪位中线的另一交点为P , 由三弦定理, 有sin sin sin AP A AE BAP AF PAC =∠+∠.再设BD BC λ=, 则1DCBCλ=-, 所以, AE FD AC λ==, (1)AF ED AB λ==-, 于是 sin sin (1)sin AP A AC BAP AB PAC λλ=∠+-∠= sin (sin sin )AB PAC AC BAP AB PAC λ∠+∠-∠= sin (sin sin )AB BAM AC MAC AB BAM λ∠+∠-∠再注意M 是BC 的中点, 由分角线定理, sin 1sin BM AB BAMMB AC MAC∠==∠, 所以 sin sin AC MAC AB BAM ∠=∠因此, sin sin AP A AB BAM =∠, 从而sin sin AB BAMAP A∠=为定长. 故P 是一个定点, 且∠BAM =∠P AC .2. 圆过三角形的外心与一个顶点的条件2001年举行的第27届俄罗斯数学奥林匹克的一道几何题(例2)说明, 设O 是△ABC 的外心, D 是△ABC 的边BC 上一点, DC 的垂直平分线交CA 于E , BD 的垂直平分线交AB 于F , 则O 、E 、A 、F 四点共圆.我们可以证明, 如果一个过△ABC 的外心和顶点A 的圆与AC 、AB 分别交于E 、F 时, 一定在BC 上存在一点D , 使E 、F 分别在DC 的垂直平分线和BD 的垂直平分线上.事实上, 由三弦定理, sin sin sin AF OAC AE BAO OA A ∠+∠=. 而sin cos OAC B ∠=, sin cos BAO C ∠=,所以,1cos cos sin 2AF B AE C OA A BC +==. 设F 、E 在BC 上的射影分别为M 、N , 则1cos cos 2MN AF B AE C BC =+=是一个常数(与圆的位置无关), 且这个常数为边BC 的一半. 于是, 设点B 关于FM 的对称点为D , 则D 、C 关于EN 对称.这就证明了, 一个圆过△ABC 的外心和顶点A 的充分必要条件是: 这个圆与AC 、AB 分别交于E 、F 时, 线段EF 在BC 上的射影长等于BC 的一半.BCBC第17题的证明17. 设△ABC 的外心为O , 点P 、Q 分别在边AB 、CA 上, 且BP PQ QC CABCAB==. 求证: A 、P 、O 、Q 四点共圆.证明作△RQP , 使△RQP ∽△ABC , 且R 与A 在PQ 的两侧, 则PR PQ QR CA BC AB ==. 而BP PQ QC CA BC AB==, 所以RP =BP , QR =QC , 因此, ∠PRB =∠RBP , ∠CRQ =∠QCR . 这样∠CRQ +∠QRP +∠PRB =∠QCR +∠BAC +∠RBA .另一方面, 因(∠CRQ +∠QRP +∠PRB )+(∠QCR +∠BAC +∠RBA )=360︒, 所以∠CRQ +∠QRP +∠PRB =180°.这说明点R 在△ABC 的边BC 上. 因P 为BR 的垂直平分线与AB的交点, Q 为RC 的垂直平分线与AC 的交点, 故 A 、P 、Q 、O 四点共圆.附: 例2的另两个证法例2设D 是△ABC 的边BC 上一点, DC 的垂直平分线交CA 于E , BD 的垂直平分线交AB 于F , O是B C△ABC的外心. 求证: A、E、O、F四点共圆.（第27届俄罗斯数学奥林匹克）分析1 当E、F分别是外心O在CA、AB上的射影时, 点D为A在BC上的射影, 此时, 欲证结论显然成立. 以此为出发点, 我们可以得到如下的证明.证法1 过点A作BC的垂线,垂足为L, 再设M、N分别为CA、AB的中点, 则ML=MC, NL=NB, 所以LM∥DE, LN∥DE,进而EM MCDL LC=,DL BLFN BN=. 两式相乘, 得EM MC BL AC BN AC BNFN LC BN AB LC LC AB=⋅=⋅=⋅.但△ALC∽△BON, △ABL∽△COM, 所以AC OBLC ON=,BL OMAB OC=, 代入上式, 并注意OB=OC即得EM OMFN ON=. 于是△OME∽△ONF, 从而∠OEM=∠OFN, 故A、E、O、F四点共圆.分析2 如果E、A、F、O四点共圆. 因B、D、C三点在一直线上, 由Pascal定理, 直线DE与BO的交点则也应在这个圆上. 循着这个思路, 我们便得到证法2.证法2 设直线BO与DE交于P. 因∠BPD =∠CDE −∠CBP =∠ACB − (90°−∠BAC) = 90°−∠CBA. 又FD = FB, 所以, ∠BFD = 180°−2∠CBA = 2∠BPD, 再由FD = FB即知, 点F是△PBD的外心, 所以, FP = FD = FB, 因此, ∠FPD =∠EDF =180°−(∠FDB +∠EDC) = 180°− (∠CBA +∠ACB) =∠BAC, 这说明P、E、A、F四点共圆. 又∠FPB =∠PBF =∠BAO, 所以, O、P、A、F四点共圆. 故E、A、F、O四点共圆.B CC B3一类四点共圆问题揭秘象例2、例3这类四点共圆的问题还有更深刻的背景. 它们涉及到同向相似三角形的相似中心.两个同向相似三角形, 只要其相似系数不等于1, 则它们必有相似中心. 这个相似中心可以按如下方法作出.设△ABC与△A′B′C′同向相似. 当A′B′∥AB时, 直线A′A与B′B的交点O即△ABC与△A′B′C′的相似中心. 当A′B′╫AB时, 如图1和图2.所示, 设直线A′B′与AB交于点P, 则⊙(P AA′)与⊙(PBB′)的第二个交点O即△ABC与△A′B′C′的相似中心.A当三角形△的三个顶点在三角形△′的三边所在直线上时, 我们称三角形是三角形的内接三角形.定理设△PQR是△ABC的内接三角形, 则△ABC的所有与△PQR同向相似的内接三角形(对应顶点在△ABC的同一边所在直线上)都有同一个相似中心.这个定理的证明简单. 其相似中心即△PQR关于△ABC的密克点.根据这个定理, 如果我们确定了△ABC的内接△PQR的形状, 就可以确定其相似中心, 那么, △ABC 的顶点A, △PQR在AB、AC上的两个顶点, 相似中心, 这四点必然共圆. 但直接这样表现, 则太过明显, 于是, 我们作△PQR的外接圆与BC的另一交点, 再将条件转换, 一道四点共圆问题便出笼了.例1 如图所示, 设△PEF∽△ABC, 则可证△ABC的外心O是所有这样的△PEF的相似中心, 因此, O、E、A、F四点共圆. 再设△PEF的外接圆与BC的另一交点为D, 则∠FDB =∠FEP =∠CBA, ∠CDE =∠PFE =∠ACB, 所以, F、E分别是BD、DC的垂直平分线与AB、AC的交点, 于是便有第27届俄罗斯数学奥林匹克的那道几何题. 而第17题则是△PQR的外接圆与BC相切的情形.B CB C例2 如图所示, 设△XYZ是非直角△ABC的垂足三角形, △ABC的内接△PEF∽△XYZ, 则不难证明△PEF与△XYZ的相似中心是△ABC的垂心H. 再设△PEF的外接圆与BC的另一交点为D, 则∠FDB =∠FEP =∠ZYX = 180°−2∠CBA, ∠CDE =∠PFE =∠XZY =180°−2∠ACB, 所以, ∠BFD =∠CBA, ∠DEC =∠ACB, 因此, DF = DB, DE = DC. 于是有题1设H为△ABC的垂心, D、E、F分别△ABC的三边BC、CA、AB上的点, 且DB=DF, DC=DE. 求证: E、A、F、H四点共圆.B CB C容易看出, △AEF的外心在△PEF的外接圆上.事实上, 设△AEF的外心为O, 则∠FOE = 2∠BAC, 而∠EPF =180°−2∠BAC, 所以, ∠FOE +∠EPF =180°, 故O在△PEF的外接圆上. 因此, △PEF的外接圆即△OEF的外接圆.当△OEF的外接圆与BC相切时, P、D重合. 此时, 因为DB = DF, DC = DE, 而△DEF∽△XYZ, 这样便有DC XYDB XZ=. 于是有题2 设AD、BE、CF是锐角△ABC的三条高, H是△ABC的垂心. 过A、H两点的⊙O与AB、AC分别交于Q、P(均异于A). 求证: 若△OPQ的外接圆与BC相切于R, 则RC DE RB DF=.这正是美国国家队2006年选拔考试题.BB例3 如图所示, 设△PEF与△ABC反向相似, AL是高, M、N分别是AB、AC的中点, △MAL的外接圆与△NLC的外接圆交于L、K两点, 则可以证明K是所有这样的与△ABC反向相似的△PEF的相似中心. 再设△PEF的外接圆与BC的另一交点为D, 则∠FDB =∠FEP =∠ACB, ∠CDE =∠PFE =∠CBA, 所以, FD∥AC, ED∥AB, 于是, 我们有题3 △ABC中, 点A在直线BC上的射影为D, M、N分别为AB、AC的中点, △MBL的外接圆Γ1与△NLC的外接圆Γ2相交于D、K两点. 对BC边上的任意一点P, 过P作AB、AC的平行线分别与AC、AB交于E、F. 求证: K、E、A、F四点共圆.A BC DPEF LK NM MNKLFE D CBA Γ2Γ1这是2010年中国国家集训队测试题.又可以证明, K 在△ABC 的A-陪位中线上, 于是便得到第19题:设D 、E 、F 分别是△ABC 的边BC 、CA 、AB 上的点, 且DE ∥AB , DF ∥AC . 求证: (ⅰ) △AEF 的外接圆通过一个定点P .(ⅱ) 若M 为BC 的中点, 则∠BAM =∠P AC .BCC类似的与内心有关的问题是设I 是△ABC 的内心, D 、E 、F 分别边BC 、CA 、AB 上的点, 且BF = BD , CD = CE ,则E 、A 、F 、I 四点共圆.但这个问题太简单. 事实上, 由对称性, ∠IEC =∠CDI =∠IF A , 故E 、A 、F 、I 四点共圆.4 等角线及其性质给定一个角∠AOB ,OC 是它的角平分线,过O 点作两条关于OC 对称的直线OX 和OY ，则称OY 是OX 关于∠AOB 的等角线. 显然OX,OY 关于∠AOB 互为等角线.一个角的两边（所在直线）是本角的等角线;一个角的平分线是重合的等角线,即自等角线.一角的邻补角的平分线也是自等角线.ABOYXTOA BCDPNM定理1自∠AOB 的顶点O 引两条直线OC 、OD , P 是直线OC 上一点, 过P 作直线OA 、OB 作垂线, 垂足分别为M 、N , 则OC 、OD 是∠AOB 的两条等角线的充分必要条件是OD ⊥MN .CDPNMOABAB CD E定理2设D 、E 是△ABC 的边BC 上两点, 则∠BAD =∠EAC 的充分必要条件是:22AB BD BEAC DC EC⋅=⋅. 定理3设D 、E 是△ABC 的边BC 上两点, 且∠BAD =∠EAC , 则有AD ∙AE = AB ∙AC.最常见的等角线是三角形的同一顶点引出的三角形的高与外接圆的直径是该顶角的两条等角线. 实际上, 定理1已经包含了这一结果.利用等角线的性质可以简捷地处理一些竞赛中的平面几何问题.例1.设O 是△ABC 的外心, K 是△BOC 的外心, 直线AB 、AC 分别交△BOC 的外接圆于另一点M 、N , L 是点K 关于直线MN 的反射点. 求证: AL ⊥BC .(俄罗斯, 2000)证明因∠OMA =∠OCB =90︒-∠BAC , 即∠OMA +∠BAN =90︒, 所以MO ⊥AN . 同理, NO ⊥AM , 这说明O 为△AMN 的垂心, 于是△OMN 的外接圆与△AMN 的外接圆是等圆, 它们关于直线MN 对称. 由于K 为△OMN 的外心, 所以L 为△AMN 的外心, 从而AL 与AO 是∠BAC 的两条等角线, 但O 为△ABC 的外心, 故AL ⊥BC .第4题的证明4. 在锐角△ABC 中, AB ≠AC . 过A 作BC 的垂线AD , P 为AB 延长线上一点, Q 为AC 延长线上一点, 且P 、B 、C 、Q 四点共圆, DP = DQ . 求证: D 是△APQ 的外心.证明设O 为△ABC 的外心, 则AD 与AO 是∠BAC 的两条等角线, 而P 、B 、C 、Q 四点共圆, 所以△APQ 与△ACB 反向相似, 因此△APQ 的外心在直线AD 上.另一方面, 因AB ≠AC , 所以BC 与PQ 不平行,因此, PQ 的垂直平分线与直线AD 不重合. 而DP = DQ , 所以D 是PQ 的垂直平分线与直线AD 的交点. 而△APQ 的外心既在直线AD 上, 也在PQ 的垂直平分线上, 故D 是△APQ 的外心.N5 三角形的陪位中线三角形的中线的等角线称为陪位中线. 为方便计, 过△ABC 的顶点A 的中线的陪位中线称为△ABC 的A-陪位中线.下面的定理1是三角形的陪位中线的一个基本性质.定理1 设D 是△ABC 的边BC 上一点, 则AD 是△ABC 的A-陪位中线的充分必要条件是22BD AB DC AC. 定理2与定理3是三角形的陪位中线的两个判定定理.定理2 已知△ABC, Γ1是过A 、B 两点且与AC 相切的圆, Γ2是过A 、C 两点且与AB 相切的圆, 圆Γ1与圆Γ2交于A 、D 两点, 则AD 是△ABC 的A-陪位中线.FEDABCKΓ2Γ1ABCP定理3 设△ABC 的外接圆在B 、C 两点的切线交于P , 则AP 是△ABC 的A-陪位中线. 利用三角形的陪位中线的理论可以方便地处理有关平面几何问题.例1 圆Γ1与圆Γ2交于A 、B 两点. 点P 在圆Γ1上. 直线PA 与PB 分别交圆Γ2于C 、D (不同于A 、B ), 圆Γ1在A 、B 两点的切线交于Q . 如果P 在圆Γ2的外部, C 、D 均在Γ1的外部. 求证：直线PQ 平分线段CD . (圣彼德堡, 1997)证明因PQ 是△P AB 的P-对称中线, 而△P AB 与△PDC 反向相似, 所以PQ 为△PDC 的P-中线, 即直线PQ 通过CD 的中点. 换句话说, 直线PQ 平分线段CD .ΓΓAB21QP D CMABCΓC 1B 1TS例2 设Γ是△ABC 的外接圆, 圆Γ在B 、C 两点的切线交于T . 过A 且垂直于AT 的直线与直线BC 交于S , 点B 1、C 1在直线ST 上(B 1、B 在BC 的垂直平分线的同侧), 且TB 1 =TC 1 =TB . 求证: △AB 1C 1∽△ABC .(美国国家队选拔考试, 2006)证明设M 为BC 的中点, 则AM 、AT 是∠BAC 的两条等角线, 所以∠BAT =∠MAC . 又∠TBC =∠BAC , 所以∠TBA =∠TBC +∠CBA =∠BAC +∠CBA =180°−∠ACB . 于是, 由TC 1 = TB 及正弦定理, 得1sin sin sin sin TC TB BAT MAC MCAT AT TBA ACB AM∠∠====∠∠. 另一方面, 因∠TMS = 90°=∠TAS , 所以A 、M 、T 、S 四点共圆, 于是, ∠STA =∠SMA , 即 ∠C 1TA =∠CMA , 因此, △ATC 1∽△AMC . 同理, △AB 1T ∽△ABM . 故△AB 1C 1∽△ABC .第6题的证明6. 设△ABC 的A-中线关于∠BAC 的角平分线的对称直线与BC 交于D . △ADC 的外接圆与AB 的另一个交点为E , △ABD 的外接圆与AC 的另一个交点为F . 求证: EF ∥BC .证明因AD 是△ABC 的陪位中线. 于是22BD AB DC AC =.另一方面, 由圆幂定理, BD BC EB AB ⋅=⋅, DC BC FC AC ⋅=⋅. 因此,BD EB AB DC FC AC ⋅=⋅, 于是KB ABLC AC =, 故EF ∥BC .FABCDE第19题的证法219. 设D 、E 、F 分别是△ABC 的边BC 、CA 、AB 上的点, 且DE ∥AB , DF ∥AC . 求证: (ⅰ) △AEF 的外接圆通过一个定点P .(ⅱ) 若M 为BC 的中点, 则∠BAM =∠P AC .证明设过A 、B 两点且与AC 相切的圆和过A 、C 两点且与AB 相切的圆交于A 、P 两点, 则P 是一个定点. 且由定理2, AP 是△ABC 的A-陪位中线, 也就是说, ∠BAM =∠P AC .由弦切角定理, ∠P AC =∠PBA , ∠ACP =∠BAP , 所以△PCA ∽△P AB . 又DE ∥AB , DF ∥AC , 所以CE CD AFEA DB FB ==, 这说明E 、F 是两个相似三角形PCA 与P AB 的相似对应点, 因此, ∠PEC =∠PF A . 故E 、A 、F 、P 四点共圆. 换句话说, △AEF 的外接圆通过定点P .6 三角形的等角共轭点容易证明以下事实设P 是△ABC 所在平面上的一点, 则AP 、BP 、CP 分别关于∠BAC 、∠CBA 、∠ACB 的等角线交于一点或互相平行. 而且, 这三条等角线互相平行当且仅当点P 在△ABC 的外接圆上.这个事实的既可以用Ceva 定理的角元形式证明, 也可以用等角线的定理1和Ceva 定理证明. 如果AP 、BP 、CP 分别关于∠BAC 、∠CBA 、∠ACB 的等角线交于一点Q , 则点Q 称为点P 关于△ABC 的等角共轭点. 如, 三角形的外心和垂心即三角形的两个等角共轭点.定理1 设P 、Q 是△ABC 的两个等角共轭点,则sin sin AP BQCAQ BPC∠=∠. 定理2 设P 、Q 是△ABC 的两个等角共轭点,则BPC BQC BAC +=.定理3三角形的两个等角共轭点到各边的垂足在一个圆上, 且它的圆心是这两点连线的中点.定理4设P 、Q 是△ABC 的两个等角共轭点, D 、E 、F 是点P 分别关于BC 、CA 、AB 的对称点, 则点Q 是△DEF 的外心.证明如图所示, 因E 、F 是点P 分别关于CA 、AB 的对称点, 所以AE = AP = AF , 因此, 点A 在线段EF 的垂直平分线上. 设PE 与CA 交于M , PF 与AB 交于N , 则M 、N 分别为PE 、PF 的中点, 所以, EF ∥MN . 又PM ⊥CA , PN ⊥AB , 由性质1.2, AQ ⊥MN , 所以AQ ⊥EF , 因而AQ 即线段EF 的垂直平分线. 同理, BQ 是线段FD 的垂直平分线. 故点Q 是△DEF 的外心.ABCDPQ'P'Q定理5设P 、Q 是△ABC 的两个等角共轭点, 直线AP 关于∠BPC 的等角线为1l, 直线AQ 关于∠BQC 的等角线为2l , 则1l 与2l关于直线BC 对称. 事实上, 如图所示, 设P 、Q 两点关于BC 的对称点分别为P ′、Q ′, 则∠Q ′BC =∠CBQ =∠PBA , ∠BCQ ′ =∠QCB =∠ACP , 所以, Q ′、A 是△PBC 的两个等角共轭点, 因而PQ ′、P A 是∠BPC 的两条等角线. 同理, QP ′、QA 是∠BQC 的两条等角线. 显然, PQ ′与P ′Q 关于BC 对称, 因此, PQ ′与P ′Q 交于BC 上一点.由此即可得到美国2010年选拔考试的一道几何题:设P 、Q 是△ABC 内两点, 且∠ABP =∠QBC , ∠ACP =∠QCB , 点D 在BC 边上. 求证: ∠APB +∠DPC = 180°的充分必要条件是∠AQC +∠DQB =180°.事实上, 由条件知, P 、Q 是△ABC 的两个等角共轭点, PD 与P A 是∠BPC 的两条等角线. 由于QA 关于∠BQC 的等角线与P A 关于∠BPC 的等角线关于BC 对称, 它们的交点必在BC 上, 因此, QD 即QA 关于∠BQC 的等角线.可以证明: 三角形的外接圆与内切圆的内位似中心和外位似中心分别是三角形的Gergonne 点的等角共轭点和三角形的Nagel 点的等角共轭点.三角形的等角共轭点可以用来处理角的相等或互补、三线共点等问题.例1 设△ABC 的外接圆在B 、C 两点的切线交于P , 则AP 是△ABC 的A-陪位中线.证明设点A 关于BC 的中点M 的对称点为Q , 则ABQC 是一个平行四边形, 由此可知, BQ 、BP 是∠CBA 的两条等角线, CQ 、CP 是∠ACB 的两条等角线, 因而P 、Q 是△ABC 的两个等角共轭点, 所以AQ 、AP 是∠BAC 的两条等角线. 而AQ 过BC 的中点M , 故AP 是△ABC 的A-陪位中线.ABCPMQABPCMQ第51届波兰数学奥林匹克的一道试题为在△ABC 中, AB =AC , P 是三角形内部一点, 使得∠CBP =∠ACP , M 是边AB 的中点. 求证:∠BPM +∠CP A =180︒.这实际上就是上面这个问题. 只不过P 、A 换了个位置而已.例2 在凸四边形ABCD 中, 对角线BD 既不是平分∠ABC , 也不平分∠CDA , 点P 在四边形的内部, 满足∠PBC =∠DBA , ∠PDC =∠BDA . 证明: 四边形ABCD 内接于圆的充分必要条件是P A =PC . (第45届IMO, 2004)证明条件∠PBC =∠DBA , ∠PDC =∠BDA 表明A 、C 是△BDP 的等角共轭点, 所以sin sin PA BAD PC DCB ⋅∠=⋅∠.又由定理1, BAD BCD BPD +=,所以, ∠BAD −∠DCB =180°−∠DPB . 而∠BPD ≠180°, 因此, ∠BAD ≠∠DCB . 于是, P A =PC ⇔sin sin BAD DCB ∠=∠⇔∠BAD +∠BCD =180°⇔四边形ABCD 内接于圆.ABCDPBE'第15题的证明 15. 设P 、Q 是△ABC 的两个等角共轭点, 点P 在BC 、CA 、AB 上的射影分别为D 、E 、F . 求证: ∠EDF= 90°的充分必要条件是Q 为△AEF 的垂心.证明如图所示, 设点P 关于BC 、CA 、AB 的对称点分别为D ′、E ′、F ′, 则∠EDF =∠E ′D ′F ′. 由定理4, Q 是△D ′E ′F ′的外心. 因PE ⊥AE , PF ⊥AF , E 、F 分别为PE ′、PF ′的中点, 于是∠EDF = 90°⇔∠E ′D ′F ′ = 90°当且仅当E ′、Q 、F ′三点共线, 且Q 为E ′F ′的中点⇔PQ 与EF 互相平分⇔PEQF 是一个平行四边形⇔EQ ∥PF , 且FQ ∥EF ⇔EQ ⊥AF , FQ ⊥AE ⇔Q 为△AEF 的垂心.第16题的证明16．设△ABC 的内切圆与边BC 、CA 、AB 分别切于D 、E 、F , 点D 关于∠BAC 的外角平分线的对称点为P , 点E 关于∠CBA 的外角平分线的对称点为Q , 点F 关于∠ACB 的外角平分线的对称点为R , 则△PQR 与△ABC 是位似的.证明因AD 、BE 、CF 交于一点X , 而直线AP 与AD 是∠BAC 的两条等角线, BQ 与BE 是∠CBA 的两条等角线, CR 与CF 是∠ACB 的两条等角线, 所以AP 、BQ 、CR 三直线交于点X 关于△ABC 的等角共轭点Y .另一方面, 由正弦定理, sin sin AD C DC DAC =∠, sin sin BE CCE CBE=∠. 但DC = CE , ∠DAC =∠BAY , ∠CBE =∠YBA , 所以sin sin sin sin AD CBE YBA YABE DAC BAY YB∠∠==∠∠=. 又AP = AD , BQ = BE , 所以, YA AD AP YB BE BQ ==, 即YA YB APBQ=, 于是 PQ ∥AB . 同理, QR ∥BC , RP ∥CA . 故△XYZ 与△ABC 是位似的.RQA BCDPA 2B 2C 2C 1B 1A 1FLNME第20题的证明20．设AD 、BE 、CF 是△ABC 的三条高线(D 、E 、F 别在BC 、CA 、AB 上), P 为△ABC 所在平面上任意一点, 点P 在直线BC 、CA 、AB 、AD 、BE 、CF 上的射影分别为A 1、B 1、C 1、A 2、B 2、C 2. 求证: A 1A 2、B 1B 2、C 1C 2三线交于一点或互相平行.证明如图所示, 设L 、M 、N 分别为A 1A 2、B 1B 2、C 1C 2的中点. 因P A 1DA 2、PB 1EB 2、PC 1FC 2皆为矩形, 所以, L 、M 、N 也分别是PD 、PE 、PF 的中点, 于是, LM ∥DE , LN ∥DF . 而AD 、BC 为∠EDF 的内、外角平分线, 所以, 矩形P A 1DA 2的两条对称轴分别为∠MLN 的内、外角平分线. 但矩形P A 1DA 2的对角线A 1A 2与PD 关于其对称轴对称, 所以, 直线A 1A 2与PD 是∠MLN 的两条等角线. 同理, 直线B 1B 2与PE 是∠NML 的两条等角线, 直线C 1C 2与PF 是∠LNM 的两条等角线, 故A 1A 2、B 1B 2、C 1C 2三线交于一点或互相平行. 当点P 不在△ABC 的九点圆上时, A 1A 2、B 1B 2、C 1C 2三线交于一点, 此点即点P 关于△LMN 的等角共轭点.7 根轴与根心一、点对圆的幂设Г是平面上一个圆心为O 、半径为r 的圆, 对于平面上任意一点P , 令ρ(P )=PO 2 –r 2,则ρ(P )称为点P 对于圆Г的幂.显然, 当点P 在圆Г外时, ρ(P )＞0; 当点P 在圆Г内时,ρ(P )＜0; 当点P 在圆Г上时,ρ(P )=0. 且由勾股定理易得, 点P 在圆Г外时, ρ(P )即点P 到圆Г的切线长的平方; 点P 在圆Г内时, ρ(P )即以点P 为中点的弦的一半的平方的相反数.有了点对圆的幂的概念, 相交弦定理、割线定理、切割线定理就可以统一为定理1 (圆幂定理) 过定点任作定圆的一条割线交定圆于两点, 则自定点到两交点的两条有向线段之积是一个常数, 这个常数等于定点对定圆的幂. 即过点P 任作一条直线交圆Г于两点A 、B (A 、B 可以重合), 则ρ(P )=PA PB ⋅.定理2设A 、B 、C 、D 是一个已知圆上任意四点, 直线AB 与CD 交于点P , 直线AD 与BC 交于点Q , 则有2()()P Q PQ ρρ+=. 其中 ()X ρ表示点X 对已知圆的幂.PA定理3(Gergonne 定理) 设P 是△ABC 所在平面上任意一点, 过点P 作△ABC 的三边的垂线, 垂足分别为D 、E 、F , △ABC 与△DEF 的面积分别为S 、T , △ABC 的外接圆半径为R , 点P 对△ABC 的外接圆的幂为ρ, 则有2||4T S R ρ=.ABCDPFKEAPF DECBK例1 设I 为△ABC 的内心, D 、E 、F 分别为△ABC 的内切圆在边BC 、CA 、AB 上的切点. 过点A 作EF 的平行线分别与直线DE 、DF 交于P 、Q . 证明: ∠PIQ 为锐角. (第39届IMO, 1998)证明如图4,设△ABC 的内切圆半径为r , 因∠PQD =∠EFD =∠DEC , 所以, A 、Q 、D 、E 四点共圆, 于是有圆幂定理, 有 P A ⋅PQ = PE ⋅PD = PI 2–r 2; 同理, AQ ⋅PQ = FQ ⋅DQ = QI 2 –r 2. 两式相加, 得P A ⋅PQ + AQ ⋅PQ = PI 2 + QI 2 – 2r 2, 即PQ 2 = PI 2 + QI 2 – 2r 2＜PI 2 + QI 2.故∠PIQ 是一个锐角.例2 (Brocard 定理) 设⊙O 的内接四边形的两组对边的交点分别为P 、Q , 两对角线的交点为R . 求证:圆心O 为△PQR 的垂心.证明如图10, 因ρ(P ) = OP 2 –r 2, ρ(Q ) = OQ 2 –r 2, ρ(R ) = OR 2 –r 2, 由定理1.2, 有PR 2 = OP 2 +OR 2 –2r 2, PQ 2 = OP 2 + OQ 2 – 2r 2. 两式相减, 得 PR 2 –PQ 2 = OR 2 –OQ 2, 所以OP ⊥RQ ; 同理, OQ ⊥PR . 故圆心O 为△PQR 的垂心.BPP二、根轴可以证明, 如果动点到两定圆的幂相等, 则动点的轨迹是一条直线. 这条直线称为两定圆的根轴或等幂轴.如果两圆相切, 则两圆的根轴是过切点的公切线; 如果两圆相交, 则两圆的根轴是公共弦所在直线; 在任何情形, 两圆的根轴总是垂直于两圆连心线的一条直线. 设圆Γ1与圆Γ2的圆心分别为O 1、O 2, 半径分别为r 1、r 2. 如果圆外离, 则两圆的根轴在两圆之间; 如果两圆内含, 则两圆的根轴是在两圆之外(图14).两圆圆心O 1、O 2到两圆的根轴的距离分别为2221212122O O r r O O +-和2221212122O O r r O O -+.l Γ2Γ1l Γ2Γ1lΓ2Γ1l如果两圆相等, 则其根轴即连心线段的垂直平分线; 如果两圆同心, 则其根轴是无穷远直线. 如果两圆中有一圆退化为一点O (此时点O 称为点圆), 则其根轴仍然存在, 且除了点在圆上时其根轴为过这点的切线外, 其余情形根轴都在圆外；根轴上任意一点P 到圆的切线长PT 等于点P 到点O的距离.Pl根轴的作用主要可以用于证明三点共线和垂直问题. 而与垂心有关的问题很多时候都与根轴联系在一起, 这是因为有垂心就有三条垂线, .例1证明Steiner 定理: 四条直线相交成四个三角形, 则这四个三角形的垂心在一条直线上.证明如图18, 设四条直线相交成四个三角形分别为△BEC 、△CDF 、△AED 、△ABF , H 1、H 2、H 3、H 4分别为它们的垂心. 设直线H 1B 、H 1E 分别交EC 、BC 于K 、L , 则K 在以BD 为直径的圆Γ1上, L 在以EF 为直径的圆Γ2上, 由于L 、E 、K 、B 四点共圆, 所以, H 1L ⋅H 1E =H 1B ⋅H 1K , 这说明H 1在圆Γ1与圆Γ2的根轴上; 再设EH 3、DH 3分别交AB 、AD 与M 、N , 则M 在圆Γ1上, N 在圆Γ2上, 而E 、D 、N 、M 四点共圆, 所以H 3D ⋅H 3M =H 3E ⋅H 3N , 因此, H 3也在圆Γ1与圆Γ2的根轴上; 同理, H 2 、H 4也在圆Γ1与圆Γ2的根轴上. 故H 1、H 2、H 3、H 4四点共线.。

专题37平面解析几何解答题(第二部分)

专题37平面解析几何解答题（第二部分）一、解答题1．已知椭圆C 1：22221x y a b+=(a >b >0)的右焦点F 与抛物线C 2的焦点重合，C 1的中心与C 2的顶点重合.过F 且与x 轴垂直的直线交C 1于A ，B 两点，交C 2于C ，D 两点，且|CD |=43|AB |. （1）求C 1的离心率；（2）设M 是C 1与C 2的公共点，若|MF |=5，求C 1与C 2的标准方程.2．已知斜率为k 的直线l 与椭圆22143x y C +=：交于A ，B 两点，线段AB 的中点为()()10M m m >，．（1）证明：12k <-；（2）设F 为C 的右焦点，P 为C 上一点,且0FP FA FB ++=u u u r u u u r u u u r r ．证明：FA u u u r ，FP u u u r ，FB u u u r 成等差数列，并求该数列的公差．3．设O 为坐标原点，动点M 在椭圆C 22:12x y +=上，过M 作x 轴的垂线，垂足为N ，点P满足NP u u u v u u u v .（1）求点P 的轨迹方程；（2）设点Q 在直线3x =-上，且1OP PQ ⋅=u u u v u u u v .证明：过点P 且垂直于OQ 的直线l 过C 的左焦点F .4．已知椭圆E ：22221(0)x y a b a b+=>>的两个焦点与短轴的一个端点是直角三角形的三个顶点，直线l ：3y x =-+与椭圆E 有且只有一个公共点T ．（Ⅰ）求椭圆E 的方程及点T 的坐标；（Ⅱ）设O 是坐标原点，直线l '平行于OT ，与椭圆E 交于不同的两点A 、B ，且与直线l 交于点P ，证明：存在常数λ，使得2||||||PT PA PB λ=⋅，并求λ的值．5．如图，椭圆()222210x y a b a b+=>>的左、右焦点分别为12,,F F 过2F 的直线交椭圆于,P Q 两点，且1PQ PF ⊥（1）若1222PF PF ==（2）若1,PF PQ =求椭圆的离心率.e6．已知椭圆:E 22221x y a b+=（0a b >>）的半焦距为c ，原点O 到经过两点(),0c ，()0,b 的直线的距离为12c ．（Ⅰ）求椭圆E 的离心率；（Ⅱ）如图，AB 是圆:M ()()225212x y ++-=的一条直径，若椭圆E 经过A ，B 两点，求椭圆E 的方程．7．已知椭圆2222:1(0)x y E a b a b +=>>过点，且离心率e =.（1）求椭圆E 的方程；（2）设直:1()l x my m R =-∈交椭圆E 于,A B 两点，判断点9(,0)4G -与以线段AB 为直径的圆的位置关系，并说明理由.8．如图，椭圆E ：2222+1(0)x y a b a b =>>，过点P （0,1）的动直线l 与椭圆相交于A ，B 两点，当直线l 平行于x 轴时，直线l 被椭圆E 截得的线段长为（1）求椭圆E 的方程；（2）在平面直角坐标系xOy 中，是否存在与点P 不同的定点Q ，使得QA PA QB PB =恒成立？若存在，求出点Q 的坐标；若不存在，请说明理由.9．设椭圆E 的方程为()222210x y a b a b +=>>，点O 为坐标原点，点A 的坐标为 ()0a ，，点B 的坐标为()0b ，，点M 在线段AB 上，满足 2BM MA =，直线OM （Ⅰ）求E 的离心率e ；（Ⅱ）设点C 的坐标为()0b -，，N 为线段AC 的中点，点N 关于直线AB 的对称点的纵坐标为 72，求E 的方程.10．已知直线210x y -+=与抛物线2:2(0)C y px p =>交于,A B 两点，且||AB =(1)求p ；(2)设F 为C 的焦点，M ，N 为C 上两点，0FM FN ⋅=u u u u r u u u r ，求MFN △面积的最小值．11．已知抛物线()2:20C x py p =>的焦点为F ，且F 与圆22:(4)1M x y ++=上点的距离的最小值为4．（1）求p ；（2）若点P 在M 上，,PA PB 是C 的两条切线，,A B 是切点，求PAB V 面积的最大值．12．已知曲线C ：y =22x ，D 为直线y =12-上的动点，过D 作C 的两条切线，切点分别为A ，B .（1）证明：直线AB 过定点：（2）若以E (0，52)为圆心的圆与直线AB 相切，且切点为线段AB 的中点，求四边形ADBE 的面积.13．已知抛物线C ：22y x =的焦点为F ，平行于x 轴的两条直线12,l l 分别交C 于A B ，两点，交C 的准线于P Q ，两点．（Ⅰ）若F 在线段AB 上，R 是PQ 的中点，证明//AR FQ ；（Ⅱ）若PQF ∆的面积是ABF ∆的面积的两倍，求AB 中点的轨迹方程.14．设抛物线2:2(0)C y px p =>的焦点为F ，点(),0D p ，过F 的直线交C 于M ，N 两点．当直线MD 垂直于x 轴时，3MF =．(1)求C 的方程；(2)设直线,MD ND 与C 的另一个交点分别为A ，B ，记直线,MN AB 的倾斜角分别为,αβ．当αβ-取得最大值时，求直线AB 的方程．15．在直角坐标系xoy 中，曲线C ：y=24x 与直线(),0y kx a a =+>交与M,N 两点，（Ⅰ）当k =0时，分别求C 在点M 和N 处的切线方程；（Ⅱ）y 轴上是否存在点P ，使得当k 变动时，总有∠OPM =∠OPN ？说明理由. 16．抛物线C 的顶点为坐标原点O ．焦点在x 轴上，直线l ：1x =交C 于P ，Q 两点，且OP OQ ⊥．已知点()2,0M ，且M e 与l 相切．（1）求C ，M e 的方程；（2）设123,,A A A 是C 上的三个点，直线12A A ，13A A 均与M e 相切．判断直线23A A 与M e 的位置关系，并说明理由．17．已知抛物线C ：y 2=3x 的焦点为F ，斜率为32的直线l 与C 的交点为A ，B ，与x 轴的交点为P ．（1）若|AF |+|BF |=4，求l 的方程；（2）若3AP PB =u u u v u u u v ，求|AB |．18．设抛物线24C y x =：的焦点为F ，过F 且斜率为(0)k k >的直线l 与C 交于A ，B 两点，||8AB =．（1）求l 的方程；（2）求过点A ，B 且与C 的准线相切的圆的方程．19．已知抛物线C ：y 2=2x ，过点（2,0）的直线l 交C 于A ,B 两点，圆M 是以线段AB 为直径的圆.（1）证明：坐标原点O 在圆M 上；（2）设圆M 过点()4,2P -，求直线l 与圆M 的方程.。

专题08 平面解析几何(解答题)

专题08 平面解析几何（解答题）1．【2019年高考全国Ⅰ卷文数】已知点A ，B 关于坐标原点O 对称，│AB │=4，⊙M 过点A ，B 且与直线x +2=0相切．（1）若A 在直线x +y =0上，求⊙M 的半径；（2）是否存在定点P ，使得当A 运动时，│MA │−│MP │为定值？并说明理由．【答案】（1）M e 的半径=2r 或=6r ；（2）存在，理由见解析.【解析】（1）因为M e 过点,A B ，所以圆心M 在AB 的垂直平分线上.由已知A 在直线+=0x y 上，且,A B 关于坐标原点O 对称，所以M 在直线y x =上，故可设(, )M a a .因为M e 与直线x +2=0相切，所以M e 的半径为|2|r a =+.由已知得||=2AO ，又MO AO ⊥u u u u r u u u r，故可得2224(2)a a +=+，解得=0a 或=4a . 故M e 的半径=2r 或=6r .（2）存在定点(1,0)P ，使得||||MA MP -为定值. 理由如下：设(, )M x y ，由已知得M e 的半径为=|+2|,||=2r x AO .由于MO AO ⊥u u u u r u u u r ，故可得2224(2)x y x ++=+，化简得M 的轨迹方程为24y x =.因为曲线2:4C y x =是以点(1,0)P 为焦点，以直线1x =-为准线的抛物线，所以||=+1MP x . 因为||||=||=+2(+1)=1MA MP r MP x x ---，所以存在满足条件的定点P .【名师点睛】本题考查圆的方程的求解问题、圆锥曲线中的定点定值类问题.解决定点定值问题的关键是能够根据圆的性质得到动点所满足的轨迹方程，进而根据抛物线的定义得到定值，验证定值符合所有情况，使得问题得解.2．【2019年高考全国Ⅱ卷文数】已知12,F F 是椭圆2222:1(0)x y C a b a b+=>>的两个焦点，P 为C 上一点，O 为坐标原点．（1）若2POF △为等边三角形，求C 的离心率；（2）如果存在点P ，使得12PF PF ⊥，且12F PF △的面积等于16，求b 的值和a 的取值范围．【答案】（1）31-；（2）4b =，a 的取值范围为[42,)+∞.【解析】（1）连结1PF ，由2POF △为等边三角形可知在12F PF △中，1290F PF ∠=︒，2PF c =，13PF c =，于是122(31)a PF PF c =+=+，故C 的离心率是31ce a==-. （2）由题意可知，满足条件的点(,)P x y 存在．当且仅当1||2162y c ⋅=，1y yx c x c⋅=-+-，22221x y a b +=，即||16c y =，① 222x y c +=，②22221x y a b+=，③ 由②③及222a b c =+得422b y c =，又由①知22216y c=，故4b =．由②③得()22222a x c b c=-，所以22c b ≥，从而2222232,a b c b =+≥=故42a ≥.当4b =，42a ≥时，存在满足条件的点P ．所以4b =，a 的取值范围为[42,)+∞．【名师点睛】本题主要考查求椭圆的离心率，以及椭圆中存在定点满足题中条件的问题，熟记椭圆的简单性质即可求解，考查计算能力，属于中档试题.3．【2019年高考全国Ⅲ卷文数】已知曲线C ：y =22x ，D 为直线y =12-上的动点，过D 作C 的两条切线，切点分别为A ，B ．（1）证明：直线AB 过定点；（2）若以E (0，52)为圆心的圆与直线AB 相切，且切点为线段AB 的中点，求该圆的方程．【答案】（1）见解析；（2）22542x y ⎛⎫+-= ⎪⎝⎭或22522x y ⎛⎫+-= ⎪⎝⎭. 【解析】（1）设()111,,,2D t A x y ⎛⎫-⎪⎝⎭，则2112x y =．由于y'x =，所以切线DA 的斜率为1x ，故11112y x x t+=-．整理得112 2 +1=0. tx y -设()22,B x y ，同理可得222 2 +1=0tx y -．故直线AB 的方程为2210tx y -+=．所以直线AB 过定点1(0,)2．（2）由（1）得直线AB 的方程为12y tx =+．由2122y tx x y ⎧=+⎪⎪⎨⎪=⎪⎩，可得2210x tx --=．于是()21212122,121x x t y y t x x t +=+=++=+.设M 为线段AB 的中点，则21,2M t t ⎛⎫+⎪⎝⎭．由于EM AB ⊥u u u u r u u u r ，而()2,2EM t t =-u u u u r ，AB u u u r 与向量(1, )t 平行，所以()220t t t +-=．解得t =0或1t =±．当t =0时，||EM u u u u r =2，所求圆的方程为22542x y ⎛⎫+-= ⎪⎝⎭；当1t =±时，||2EM =u u u u r ，所求圆的方程为22522x y ⎛⎫+-= ⎪⎝⎭．【名师点睛】此题第一问是圆锥曲线中的定点问题和第二问是求圆的方程，属于常规题型，按部就班地求解就可以，思路较为清晰，但计算量不小.4．【2019年高考北京卷文数】已知椭圆2222:1x y C a b+=的右焦点为(1,0)，且经过点(0,1)A ．（1）求椭圆C 的方程；（2）设O 为原点，直线:(1)l y kx t t =+≠±与椭圆C 交于两个不同点P ，Q ，直线AP 与x 轴交于点M ，直线AQ 与x 轴交于点N ，若|OM |·|ON |=2，求证：直线l 经过定点．【答案】（1）2212x y +=；（2）见解析. 【解析】（1）由题意得，b 2=1，c =1．所以a 2=b 2+c 2=2．所以椭圆C 的方程为2212x y +=．（2）设P （x 1，y 1），Q （x 2，y 2），则直线AP 的方程为1111y y x x -=+．令y =0，得点M 的横坐标111M x x y =--．又11y kx t =+，从而11||||1M x OM x kx t ==+-．同理，22||||1x ON kx t =+-．由22,12y kx t x y =+⎧⎪⎨+=⎪⎩得222(12)4220k x ktx t +++-=．则122412kt x x k +=-+，21222212t x x k-=+．所以1212||||||||11x x OM ON kx t kx t ⋅=⋅+-+-()12221212||(1)(1)x x k x x k t x x t =+-++-22222222212||224(1)()(1)1212t k t kt k k t t k k-+=-⋅+-⋅-+-++12||1t t+=-．又||||2OM ON ⋅=，所以12||21tt+=-．解得t =0，所以直线l 经过定点（0，0）．【名师点睛】解决直线与椭圆的综合问题时，要注意：(1)注意观察应用题设中的每一个条件，明确确定直线、椭圆的条件；(2)强化有关直线与椭圆联立得出一元二次方程后的运算能力，重视根与系数之间的关系、弦长、斜率、三角形的面积等问题．5．【2019年高考天津卷文数】设椭圆22221(0)x y a b a b+=>>的左焦点为F ，左顶点为A ，上顶点为B .已知3||2||OA OB =（O 为原点）.（1）求椭圆的离心率；（2）设经过点F 且斜率为34的直线l 与椭圆在x 轴上方的交点为P ，圆C 同时与x 轴和直线l 相切，圆心C 在直线x =4上，且OC AP ∥，求椭圆的方程.【答案】（1）12；（2）2211612x y +=.【解析】（1）设椭圆的半焦距为c ，由已知有32a b =，又由222a b c =+，消去b 得22232a a c ⎛⎫=+ ⎪ ⎪⎝⎭，解得12c a =. 所以，椭圆的离心率为12. （2）由（1）知，2,3a c b c ==，故椭圆方程为2222143x y c c+=.由题意，(, 0)F c -，则直线l 的方程为3()4y x c =+，点P 的坐标满足22221,433(),4x y c cy x c ⎧+=⎪⎪⎨⎪=+⎪⎩消去y 并化简，得到2276130x cx c +-=，解得1213,7c x c x ==-. 代入到l 的方程，解得1239,214y c y c ==-.因为点P在x轴上方，所以3,2P c c ⎛⎫⎪⎝⎭.由圆心C在直线4x=上，可设(4, )C t.因为OC AP∥，且由（1）知( 2 , 0)A c-，故3242ctc c=+，解得2t=.因为圆C与x轴相切，所以圆的半径长为2，又由圆C与l相切，得23(4)242314c+-=⎛⎫+ ⎪⎝⎭，可得=2c.所以，椭圆的方程为2211612x y+=.【名师点睛】本小题主要考查椭圆的标准方程和几何性质、直线方程、圆等基础知识.考查用代数方法研究圆锥曲线的性质.考查运算求解能力，以及用方程思想、数形结合思想解决问题的能力. 6．【2019年高考江苏卷】如图，在平面直角坐标系xOy中，椭圆C:22221(0)x ya ba b+=>>的焦点为F1（–1、0），F2（1，0）．过F2作x轴的垂线l，在x轴的上方，l与圆F2:222(1)4x y a-+=交于点A，与椭圆C交于点D.连结AF1并延长交圆F2于点B，连结BF2交椭圆C于点E，连结DF1．已知DF1=52．（1）求椭圆C的标准方程；（2）求点E的坐标．【答案】（1）22143x y+=；（2）3(1,)2E--.【解析】（1）设椭圆C 的焦距为2c .因为F 1(−1，0)，F 2(1，0)，所以F 1F 2=2，c =1. 又因为DF 1=52，AF 2⊥x 轴，所以DF 2=222211253()222DF F F -=-=，因此2a =DF 1+DF 2=4，从而a =2. 由b 2=a 2−c 2，得b 2=3.因此，椭圆C 的标准方程为22143x y +=.（2）解法一：由（1）知，椭圆C ：22143x y +=，a =2，因为AF 2⊥x 轴，所以点A 的横坐标为1. 将x =1代入圆F 2的方程(x −1) 2+y 2=16，解得y =±4. 因为点A 在x 轴上方，所以A (1，4). 又F 1(−1，0)，所以直线AF 1：y =2x +2.由22()22116y x x y =+-+=⎧⎨⎩，得256110x x +-=，解得1x =或115x =-. 将115x =-代入22y x =+，得 125y =-，因此1112(,)55B --.又F 2(1，0)，所以直线BF 2：3(1)4y x =-.由221433(1)4x y x y ⎧⎪⎪⎨⎪+=-⎩=⎪，得276130x x --=，解得1x =-或137x =. 又因为E 是线段BF 2与椭圆的交点，所以1x =-. 将1x =-代入3(1)4y x =-，得32y =-. 因此3(1,)2E --.解法二：由（1）知，椭圆C：221 43x y+=.如图，连结EF1.因为BF2=2a，EF1+EF2=2a，所以EF1=EB，从而∠BF1E=∠B.因为F2A=F2B，所以∠A=∠B，所以∠A=∠BF1E，从而EF1∥F2A.因为AF2⊥x轴，所以EF1⊥x轴.因为F1(−1，0)，由221431xx y⎧⎪⎨+==-⎪⎩，得32y=±.又因为E是线段BF2与椭圆的交点，所以32y=-.因此3(1,)2E--.【名师点睛】本小题主要考查直线方程、圆的方程、椭圆方程、椭圆的几何性质、直线与圆及椭圆的位置关系等基础知识，考查推理论证能力、分析问题能力和运算求解能力.7．【2019年高考浙江卷】如图，已知点(10)F，为抛物线22(0)y px p=>的焦点，过点F的直线交抛物线于A、B两点，点C在抛物线上，使得ABC△的重心G在x轴上，直线AC交x轴于点Q，且Q在点F 的右侧．记,AFG CQG △△的面积分别为12,S S ．（1）求p 的值及抛物线的准线方程；（2）求12S S 的最小值及此时点G 的坐标．【答案】（1）p =2，准线方程为x =−1；（2）最小值为312+，此时G （2，0）．【解析】（1）由题意得12p=，即p =2. 所以，抛物线的准线方程为x =−1.（2）设()()(),,,,,A A B B c c A x y B x y C x y ，重心(),G G G x y .令2,0A y t t =≠，则2A x t =.由于直线AB 过F ，故直线AB 方程为2112t x y t-=+，代入24y x =，得()222140t y y t---=，故24B ty =-，即2B y t =-，所以212,B tt ⎛⎫- ⎪⎝⎭.又由于()()11,33G A B c G A B c x x x x y y y y =++=++及重心G 在x 轴上，故220c t y t-+=，得242211222,2,,03t t C t t G t t t ⎛⎫⎛⎫-+⎛⎫⎛⎫-- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. 所以，直线AC 方程为()222y t t x t-=-，得()21,0Q t-.由于Q 在焦点F 的右侧，故22t >.从而4224221244242222211|2|||322221222211|||1||2|23A ct t t FG y t S t t t t t S t t QG y t t t t-+-⋅⋅--====--+--⋅--⋅-.令22m t =-，则m >0，122113222134323424S m S m m m m m m=-=--=+++++⋅+…. 当3m =时，12S S 取得最小值312+，此时G （2，0）．【名师点睛】本题主要考查抛物线的几何性质，直线与抛物线的位置关系等基础知识，同时考查运算求解能力和综合应用能力.8．【2018年高考全国Ⅰ文数】设抛物线22C y x =：，点()20A ，，()20B -，，过点A 的直线l 与C 交于M ，N 两点．（1）当l 与x 轴垂直时，求直线BM 的方程；（2）证明：ABM ABN =∠∠．【答案】（1）y =112x +或112y x =--；（2）见解析. 【解析】（1）当l 与x 轴垂直时，l 的方程为x =2，可得M 的坐标为（2，2）或（2，–2）．所以直线BM 的方程为y =112x +或112y x =--．（2）当l 与x 轴垂直时，AB 为MN 的垂直平分线，所以∠ABM =∠ABN ．当l 与x 轴不垂直时，设l 的方程为(2)(0)y k x k =-≠，M （x 1，y 1），N （x 2，y 2），则x 1>0，x 2>0．由2(2)2y k x y x=-⎧⎨=⎩，得ky 2–2y –4k =0，可知y 1+y 2=2k ，y 1y 2=–4．直线BM ，BN 的斜率之和为1221121212122()22(2)(2)BM BN y y x y x y y y k k x x x x ++++=+=++++．① 将112y x k =+，222yx k=+及y 1+y 2，y 1y 2的表达式代入①式分子，可得121221121224()882()0y y k y y x y x y y y k k++-++++===．所以k BM +k BN =0，可知BM ，BN 的倾斜角互补，所以∠ABM =∠ABN ．综上，∠ABM =∠ABN ．【名师点睛】本题主要考查抛物线的标准方程与几何性质、直线与抛物线的位置关系，考查考生的化归与转化能力、运算求解能力，考查的数学核心素养是直观想象与数学运算.在设直线的方程时，一定要注意所设方程的适用范围，如用点斜式时，要考虑到直线的斜率不存在的情况，以免解答不严密或漏解.（1）求出直线l 与抛物线的交点，利用两点式写出直线BM 的方程;（2）由（1）知，当直线l 与x 轴垂直时，结论显然成立，当直线l 与x 轴不垂直时，设出斜率k ，联立直线l 与C 的方程，求出M ，N 两点坐标之间的关系，再表示出BM 与BN 的斜率，得其和为0，从而说明BM 与BN 两条直线的斜率互为相反数，进而可知两角相等.9．【2018年高考全国Ⅱ卷文数】设抛物线24C y x =：的焦点为F ，过F 且斜率为(0)k k >的直线l 与C 交于A ，B 两点，||8AB =．（1）求l 的方程；（2）求过点A ，B 且与C 的准线相切的圆的方程．【答案】（1）y =x –1；（2）22(3)(2)16x y -+-=或22(11)(6)144x y -++=．【解析】（1）由题意得F （1，0），l 的方程为y =k （x –1）（k >0）．设A （x 1，y 1），B （x 2，y 2）．由2(1)4y k x y x=-⎧⎨=⎩得2222(24)0k x k x k -++=． 216160k ∆=+=，故212224k x x k++=．所以212244(1)(1)k AB AF BF x x k+=+=+++=．由题设知22448k k +=，解得k =–1（舍去），k =1．因此l 的方程为y =x –1．（2）由（1）得AB 的中点坐标为（3，2），所以AB 的垂直平分线方程为2(3)y x -=--，即5y x =-+．设所求圆的圆心坐标为（x 0，y 0），则00220005(1)(1)16.2y x y x x =-+⎧⎪⎨-++=+⎪⎩，解得0032x y =⎧⎨=⎩，或00116.x y =⎧⎨=-⎩，因此所求圆的方程为22(3)(2)16x y -+-=或22(11)(6)144x y -++=．【名师点睛】本题主要考查抛物线与直线和圆的综合，考查考生的数形结合能力、运算求解能力，考查的数学核心素养是直观想象、数学运算.（1）利用点斜式写出直线l 的方程，代入抛物线方程，得到关于x 的一元二次方程，利用根与系数的关系以及抛物线的定义加以求解;（2）由题意写出线段AB 的垂直平分线所在直线的方程，设出圆心的坐标，由题意列出方程组，解得圆心的坐标，即可求解.10．【2018年高考全国Ⅲ卷文数】已知斜率为k 的直线l 与椭圆22143x y C +=：交于A ，B 两点．线段AB的中点为(1,)(0)M m m >．（1）证明：12k <-；（2）设F 为C 的右焦点，P 为C 上一点，且FP FA FB ++=0u u u r u u u r u u u r ．证明：2||||||FP FA FB =+u u u r u u u r u u u r．【答案】（1）见解析；（2）见解析.【解析】（1）设11()A x y ，，22()B x y ，，则2211143x y +=，2222143x y +=．两式相减，并由1212=y y k x x --得1212043x x y y k +++⋅=．由题设知1212x x +=，122y y m +=，于是34k m=-．由题设得302m <<，故12k <-．（2）由题意得F （1，0）．设33()P x y ，，则331122(1)(1)(1)(00)x y x y x y -+-+-=，，，，．由（1）及题设得3123()1x x x =-+=，312()20y y y m =-+=-<．又点P 在C 上，所以34m =，从而3(1)2P -，，3||=2FP u u u r ．于是222211111||(1)(1)3(1)242x x FA x y x =-+=-+-=-u u u r ．同理2||=22x FB -u u u r ．所以1214()32FA FB x x +=-+=u u u r u u u r ．故2||=||+||FP FA FB u u u r u u u r u u u r ．【名师点睛】本题主要考查椭圆的方程及简单几何性质、直线的斜率公式、直线与椭圆的位置关系、向量的坐标运算与向量的模等，考查运算求解能力、数形结合思想，考查的数学核心素养是数学抽象、数学运算.圆维曲线中与中点弦有关的问题常用点差法，建立弦所在直线的斜率与中点坐标间的关系，也可以通过联立直线方程与圆锥曲线方程，消元，根据根与系数的关系求解.11．【2018年高考北京卷文数】已知椭圆2222:1(0)x y M a b a b +=>>的离心率为63，焦距为22.斜率为k 的直线l 与椭圆M 有两个不同的交点A ，B . （1）求椭圆M 的方程；（2）若1k =，求||AB 的最大值；（3）设(2,0)P -，直线P A 与椭圆M 的另一个交点为C ，直线PB 与椭圆M 的另一个交点为D .若C ,D 和点71(,)44Q -共线，求k .【答案】（1）2213x y +=；（2）6；（3）1. 【解析】（1）由题意得222c =，所以2c =，又63c e a ==，所以3a =，所以2221b a c =-=，所以椭圆M 的标准方程为2213x y +=．（2）设直线AB 的方程为y x m =+，由2213y x m x y =+⎧⎪⎨+=⎪⎩消去y 可得2246330x mx m ++-=，则2223644(33)48120m m m ∆=-⨯-=->，即24m <，设11(,)A x y ，22(,)B x y ，则1232m x x +=-，212334m x x -=，则222212121264||1||1()42m AB k x x k x x x x ⨯-=+-=+⋅+-=，易得当20m =时，max ||6AB =，故||AB 的最大值为6．（3）设11(,)A x y ，22(,)B x y ，33(,)C x y ，44(,)D x y ，则221133x y += ①，222233x y += ②，又(2,0)P -，所以可设1112PA y k k x ==+，直线PA 的方程为1(2)y k x =+，由122(2)13y k x x y =+⎧⎪⎨+=⎪⎩消去y 可得2222111(13)121230k x k x k +++-=，则2113211213k x x k +=-+，即2131211213k x x k =--+，又1112y k x =+，代入①式可得13171247x x x --=+，所以13147y y x =+，所以1111712(,)4747x y C x x --++，同理可得2222712(,)4747x y D x x --++．故3371(,)44QC x y =+-u u u r ，4471(,)44QD x y =+-u u u r ，因为,,Q C D 三点共线，所以34437171()()()()04444x y x y +--+-=，将点,C D 的坐标代入化简可得12121y y x x -=-，即1k =．【名师点睛】本题主要考查椭圆的方程及几何性质、直线与椭圆的位置关系，考查考生的逻辑思维能力、运算求解能力，考查数形结合思想，考查的数学核心素养是直观想象、逻辑推理、数学运算.解决椭圆的方程问题，常用基本量法，同时注意椭圆的几何量的关系；弦长的计算，通常要将直线与椭圆方程联立，利用根与系数的关系求解.12．【2018年高考天津卷文数】设椭圆22221(0)x y a b a b+=>>的右顶点为A ，上顶点为B ．已知椭圆的离心率为53，||13AB =．（1）求椭圆的方程；（2）设直线:(0)l y kx k =<与椭圆交于,P Q 两点，l 与直线AB 交于点M ，且点P ，M 均在第四象限．若BPM △的面积是BPQ △面积的2倍，求k 的值．【答案】（1）22194x y +=；（2）12-．【解析】本小题主要考查椭圆的标准方程和几何性质、直线方程等基础知识．考查用代数方法研究圆锥曲线的性质．考查运算求解能力，以及用方程思想解决问题的能力．满分14分．（1）设椭圆的焦距为2c ，由已知得2259c a =，又由222a b c =+，可得23a b =．由22||13AB a b =+=，从而3,2a b ==．所以，椭圆的方程为22194x y +=．（2）设点P 的坐标为11(,)x y ，点M 的坐标为22(,)x y ，由题意，210x x >>，点Q 的坐标为11(,)x y --．由BPM △的面积是BPQ △面积的2倍，可得||=2||PM PQ ，从而21112[()]x x x x -=--，即215x x =．易知直线AB 的方程为236x y +=，由方程组236,,x y y kx +=⎧⎨=⎩消去y ，可得2632x k =+．由方程组221,94,x y y kx ⎧+⎪=⎨⎪=⎩消去y ，可得12694x k =+．由215x x =，可得2945(32)k k +=+，两边平方，整理得2182580k k ++=，解得89k =-，或12k =-．当89k =-时，290x =-<，不合题意，舍去；当12k =-时，212x =，1125x =，符合题意．所以，k 的值为12-．【名师点睛】高考解析几何解答题大多考查直线与圆锥曲线的位置关系，涉及轨迹方程问题、定值问题、最值问题、参数的取值或取值范围问题等，其中考查较多的圆锥曲线是椭圆与抛物线，解决此类问题要重视化归与转化思想及设而不求法的应用.13．【2018年高考江苏卷】如图，在平面直角坐标系xOy 中，椭圆C 过点1(3,)2，焦点12(3,0),(3,0)F F -，圆O 的直径为12F F ．（1）求椭圆C 及圆O 的方程；（2）设直线l 与圆O 相切于第一象限内的点P ．①若直线l 与椭圆C 有且只有一个公共点，求点P 的坐标； ②直线l 与椭圆C 交于,A B 两点．若OAB △的面积为267，求直线l 的方程．【答案】（1）椭圆C的方程为2214xy+=，圆O的方程为223x y+=；（2）①(2,1)；②532y x=-+．【解析】（1）因为椭圆C的焦点为12()3,0,(3,0)F F-，可设椭圆C的方程为22221(0)x ya ba b+=>>．又点1(3,)2在椭圆C上，所以2222311,43,a ba b⎧+=⎪⎨⎪-=⎩，解得224,1,ab⎧=⎪⎨=⎪⎩因此椭圆C的方程为2214xy+=．因为圆O的直径为12F F，所以其方程为223x y+=．（2）①设直线l与圆O相切于0000(),,(00)P x y x y>>，则22003x y+=，所以直线l的方程为000()xy x x yy=--+，即0003xy xy y=-+．由22001,43,xyxy xy y⎧+=⎪⎪⎨⎪=-+⎪⎩消去y，得222200004243640()x y x x x y+-+-=．（*）因为直线l与椭圆C有且只有一个公共点，所以222222000000()()(24)(44364820)4x x y y y x∆=--+-=-=．因为00,0x y>，所以002,1x y==．因此点P的坐标为(2,1)．②因为三角形OAB的面积为267，所以21267AB OP⋅=，从而427AB=．设1122,,()(),A x y B x y ，由（*）得2200022001,22448(2)2(4)x y x x x y ±-=+，所以2222121()()x B y y x A =-+-222000222200048(2)(1)(4)x y x y x y -=+⋅+．因为22003x y +=，所以22022016(2)32(1)49x AB x -==+，即42002451000x x -+=，解得22005(202x x ==舍去），则2012y =，因此P 的坐标为102(,)22．综上，直线l 的方程为532y x =-+．【名师点睛】本题主要考查直线方程、圆的方程、圆的几何性质、椭圆方程、椭圆的几何性质、直线与圆及椭圆的位置关系等知识，考查分析问题能力和运算求解能力. （1）利用椭圆的几何性质求圆的方程和椭圆的方程. （2）①利用直线与圆、椭圆的位置关系建立方程求解； ②结合①，利用弦长公式、三角形的面积公式求解.14．【2018年高考浙江卷】如图，已知点P 是y 轴左侧(不含y 轴)一点，抛物线C ：y 2=4x 上存在不同的两点A ，B 满足P A ，PB 的中点均在C 上．PMBAOyx（1）设AB 中点为M ，证明：PM 垂直于y 轴；（2）若P 是半椭圆x 2+24y =1(x <0)上的动点，求△P AB 面积的取值范围．【答案】（1）见解析；（2）1510[62,]4．【解析】本题主要考查椭圆、抛物线的几何性质，直线与抛物线的位置关系等基础知识，同时考查运算求解能力和综合应用能力.满分15分. （1）设00(,)P x y ，2111(,)4A y y ，2221(,)4B y y ．因为PA ，PB 的中点在抛物线上，所以1y ，2y 为方程202014()422y x y y ++=⋅即22000280y y y x y -+-=的两个不同的实数根．所以1202y y y +=．因此，PM 垂直于y 轴．（2）由（1）可知120212002,8,y y y y y x y +=⎧⎪⎨=-⎪⎩ 所以2221200013||()384PM y y x y x =+-=-， 21200||22(4)y y y x -=-．因此，PAB △的面积3221200132||||(4)24PABS PM y y y x =⋅-=-△．因为220001(0)4y x x +=<，所以2200004444[4,5]y x x x -=--+∈．因此，PAB △面积的取值范围是1510[62,]4．【名师点睛】圆锥曲线问题是高考重点考查内容之一，也是难点之一.椭圆、抛物线是其中常考内容，需要熟练地掌握椭圆和拋物线的定义、基本性质、标准方程等，对于处理有关问题有很大的帮助.同时还要注意运算能力的培养和提高.15．【2017年高考全国Ⅰ卷文数】设A ，B 为曲线C ：y =24x 上两点，A 与B 的横坐标之和为4．（1）求直线AB 的斜率；（2）设M 为曲线C 上一点，C 在M 处的切线与直线AB 平行，且AM ⊥BM ，求直线AB 的方程．【答案】（1）1；（2）7y x =+．【解析】（1）设A （x 1，y 1），B （x 2，y 2），则12x x ≠，2114x y =，2224x y =，x 1+x 2=4，于是直线AB 的斜率12121214y y x x k x x -+===-．（2）由24x y =，得2x y'=．设M （x 3，y 3），由题设知312x =，解得32x =，于是M （2，1）．设直线AB 的方程为y x m =+，故线段AB 的中点为N （2，2+m ），|MN |=|m +1|．将y x m =+代入24xy =得2440x x m --=．当16(1)0m ∆=+>，即1m >-时，1,2221x m =±+．从而12||=2||42(1)AB x x m -=+．由题设知||2||AB MN =，即42(1)2(1)m m +=+，解得7m =．所以直线AB 的方程为7y x =+．【名师点睛】本题主要考查直线与圆锥曲线的位置关系，主要利用根与系数的关系：因为直线的方程是一次的，圆锥曲线的方程是二次的，故直线与圆锥曲线的问题常转化为方程组关系问题，最终转化为一元二次方程问题，故用根与系数的关系及判别式是解决圆锥曲线问题的重点方法之一，尤其是弦中点问题，弦长问题，可用根与系数的关系直接解决，但应注意不要忽视判别式的作用．（1）设A （x 1，y 1），B （x 2，y 2），由两点斜率公式求AB 的斜率；（2）联立直线与抛物线方程，消y ，得12||=2||42(1)AB x x m -=+，解出m 即可．16．【2017年高考全国Ⅱ卷文数】设O 为坐标原点，动点M 在椭圆C 22:12x y +=上，过M 作x 轴的垂线，垂足为N ，点P 满足2NP NM =u u u ru u u u r.（1）求点P 的轨迹方程；（2）设点Q 在直线3x =-上，且1OP PQ ⋅=u u u r u u u r.证明：过点P 且垂直于OQ 的直线l 过C 的左焦点F .【答案】（1）222x y +=；（2）见解析.【解析】（1）设P （x ，y ），M （00,x y ），则N （0,0x ），00(,),(0,)NP x x y NM y =-=u u u r u u u u r ，由2NP NM =u u u ru u u u r 得0022x x y y ==，. 因为M （00,x y ）在C 上，所以22122x y +=.因此点P 的轨迹方程为222x y +=.（2）由题意知F （−1,0），设Q （−3，t ），P （m ，n ），则(3,),(1,),33OQ t PF m n OQ PF m tn =-=---⋅=+-u u u r u u u r u u u r u u u r， (,),(3,)OP m n PQ m t n ==---u u u r u u u r.由1OP PQ ⋅=u u u r u u u r得2231m m tn n --+-=，又由（1）知222m n +=，故330m tn +-=.所以0OQ PF ⋅=u u u r u u u r ，即OQ PF ⊥u u u r u u u r.又过点P 存在唯一直线垂直于OQ ，所以过点P 且垂直于OQ 的直线l 过C 的左焦点F .【名师点睛】定点、定值问题通常是通过设参数或取特殊值来确定“定点”是什么、“定值”是多少，或者将该问题涉及的几何式转化为代数式或三角问题，证明该式是恒成立的. 定点、定值问题同证明问题类似，在求定点、定值之前已知该值的结果，因此求解时应设参数，运用推理，到最后必定参数统消，定点、定值显现.（1）转移法求轨迹：设所求动点坐标及相应已知动点坐标，利用条件列两种坐标关系，最后代入已知动点轨迹方程，化简可得所求轨迹方程；（2）证明直线过定点问题，一般方法是以算代证：即证0OQ PF ⋅=u u u r u u u r，先设 P （m ，n ），则需证330m tn +-=，即根据条件1OP PQ ⋅=u u u r u u u r可得2231m m tn n --+-=，而222m n +=，代入即得330m tn +-=.17．【2017年高考全国Ⅲ卷文数】在直角坐标系xOy 中，曲线22y x mx =+-与x 轴交于A ，B 两点，点C的坐标为(0,1).当m 变化时，解答下列问题：（1）能否出现AC ⊥BC 的情况？说明理由；（2）证明过A ，B ，C 三点的圆在y 轴上截得的弦长为定值. 【答案】（1）不会，理由见解析；（2）见解析【解析】（1）不能出现AC ⊥BC 的情况，理由如下：设1(,0)A x ，2(,0)B x ，则12x x ，满足220x mx +-=，所以122x x =-. 又C 的坐标为（0，1），故AC 的斜率与BC 的斜率之积为121112x x --⋅=-，所以不能出现AC ⊥BC 的情况.（2）BC 的中点坐标为（2122x ，），可得BC 的中垂线方程为221()22x y x x -=-. 由（1）可得12x x m +=-，所以AB 的中垂线方程为2mx =-.联立22(21)22m x x y x x ⎧=-⎪⎪⎨⎪-=-⎪⎩，，又22220x mx +-=，可得212m x y ⎧=-⎪⎪⎨⎪=-⎪⎩，，所以过A 、B 、C 三点的圆的圆心坐标为（122m --，），半径292m r +=，故圆在y 轴上截得的弦长为22232m r -=（），即过A 、B 、C 三点的圆在y 轴上截得的弦长为定值. 【名师点睛】解答本题时，设()()12,0,,0A x B x ，由AC ⊥BC 得1210x x +=，由根与系数的关系得122x x =-，矛盾，所以不存在；求出过A ，B ，C 三点的圆的圆心坐标和半径，即可得圆的方程，再利用垂径定理求弦长.直线与圆综合问题的常见类型及解题策略：（1）处理直线与圆的弦长问题时多用几何法，即弦长的一半、弦心距、半径构成直角三角形．代数方法：运用根与系数的关系及弦长公式：222121212||1||1()4AB k x x k x x x x =+-=++-；（2）圆的切线问题的处理要抓住圆心到直线的距离等于半径，从而建立关系解决问题． 18．【2017年高考北京卷文数】已知椭圆C 的两个顶点分别为A (−2,0)，B (2,0)，焦点在x 轴上，离心率为32．（1）求椭圆C 的方程；（2）点D 为x 轴上一点，过D 作x 轴的垂线交椭圆C 于不同的两点M ，N ，过D 作AM 的垂线交BN 于点E .求证：△BDE 与△BDN 的面积之比为4:5．【答案】（1）2214x y +=；（2）见解析.【解析】（1）设椭圆C 的方程为22221(0)x y a b a b+=>>.由题意得2,3,2a c a=⎧⎪⎨=⎪⎩解得3c =.所以2221b a c =-=.所以椭圆C 的方程为2214x y +=.（2）设(,)M m n ，则(,0),(,)D m N m n -. 由题设知2m ≠±，且0n ≠.直线AM 的斜率2AM n k m =+，故直线DE 的斜率2DE m k n+=-. 所以直线DE 的方程为2()m y x m n +=--. 直线BN 的方程为(2)2ny x m=--. 联立2(),(2),2m y x m n n y x m +⎧=--⎪⎪⎨⎪=-⎪-⎩解得点E 的纵坐标222(4)4E n m y m n -=--+. 由点M 在椭圆C 上，得2244m n -=.所以45E y n =-. 又12||||||||25BDE E S BD y BD n =⋅=⋅△，1||||2BDN S BD n =⋅△，所以BDE △与BDN △的面积之比为4:5.【名师点睛】本题对考生计算能力要求较高，重点考查了计算能力，以及转化与化归的能力，解答此类题目，主要利用,,,a b c e 的关系，确定椭圆方程是基础，本题易错点是对复杂式子的变形能力不足，导致错漏百出.本题能较好地考查考生的逻辑思维能力、运算求解能力、分析问题与解决问题的能力等. （1）根据条件可知32,2c a a ==，以及222b a c =-，从而求得椭圆方程；（2）设(,)M m n ，则(,0),(,)D m N m n -，根据条件求直线DE 的方程，并且表示出直线BN 的方程，并求得两条直线的交点纵坐标，根据1212E BDE BDNN BD y S S BD y ⋅⋅=⋅⋅△△即可求出面积比值. 19．【2017年高考天津卷文数】已知椭圆22221(0)x y a b a b+=>>的左焦点为,()0F c -，右顶点为A ，点E的坐标为(0,)c ，EFA △的面积为22b ．（1）求椭圆的离心率；（2）设点Q 在线段AE 上，3||2FQ c =，延长线段FQ 与椭圆交于点P ，点M ，N 在x 轴上，PM QN ∥，且直线PM 与直线QN 间的距离为c ，四边形PQNM 的面积为3c ．（i ）求直线FP 的斜率；（ii ）求椭圆的方程．【答案】（1）12；（2）（ⅰ）34；（ⅱ）2211612x y +=．【解析】（1）设椭圆的离心率为e ．由已知，可得21()22b c a c +=．又由222b a c =-，可得2220c ac a +-=，即2210e e +-=．又因为01e <<，解得12e =．所以，椭圆的离心率为12．（2）（ⅰ）依题意，设直线FP 的方程为(0)x my c m =->，则直线FP 的斜率为1m．由（1）知2a c =，可得直线AE 的方程为12x yc c +=，即220x y c +-=，与直线FP 的方程联立，可解得(22)3,22m c c x y m m -==++，即点Q 的坐标为(22)3(,)22m c cm m -++．由已知|FQ |=32c ，有222(22)33[]()()222m c c c c m m -++=++，整理得2340m m -=，所以43m =，故直线FP 的斜率为34．（ii ）由2a c =，可得3b c =，故椭圆方程可以表示为2222143x y c c+=．由（i ）得直线FP 的方程为3430x y c -+=，与椭圆方程联立22223430,1,43x y c x y c c -+=⎧⎪⎨+=⎪⎩ 消去y ，整理得2276130x cx c +-=，解得137cx =-（舍去），或x c =．因此可得点3(,)2c P c ，进而可得2235|()()22|c c FP c c =++=，所以53||||||22c cFP FQ Q c P -=-==．由已知，线段PQ 的长即为PM 与QN 这两条平行直线间的距离，故直线PM 和QN 都垂直于直线FP ．因为QN FP ⊥，所以339||||tan 248c c QN FQ QFN =⋅∠=⨯=，所以FQN △的面积为2127||||232c FQ QN =，同理FPM △的面积等于27532c ，由四边形PQNM 的面积为3c ，得22752733232c c c -=，整理得22c c =，又由0c >，得2c =．所以，椭圆的方程为2211612x y +=．【名师点睛】圆锥曲线问题在历年高考中都是较有难度的压轴题，本题对考生的计算能力要求较高，是一道难题，重点考查了运算求解能力以及转化与化归的能力．求解此类问题时，利用,,,a b c e 的关系，确定椭圆离心率是基础，通过联立直线方程与椭圆（圆锥曲线）的方程，根据根与系数的关系进行解题，但本题需求解交点坐标，在求解过程要善于发现四边形PQNM 中的几何关系，从而易求其面积，进而使问题获解．（1）先根据题意得出21()22b c a c +=，然后结合222b a c =-，即可求得离心率；（2）（ⅰ）首先设直线FP 的方程为x my c =-，再写出直线AE 的方程，两方程联立得到点Q 的坐标，根据32FQ c =求得m 的值，即得直线FP 的斜率；（ⅱ）将直线FP 的方程和椭圆方程联立，可得点P 的坐标，再求,FP FQ ，确定直线PM 和QN 都垂直于直线FP ，根据平面几何关系求面积，从而可求得c 的值，进而得椭圆的方程．20．【2017年高考山东卷文数】在平面直角坐标系xOy 中，已知椭圆C :22221x y a b +=(a >b >0)的离心率为22，椭圆C 截直线y =1所得线段的长度为22. （1）求椭圆C 的方程；（2）动直线l :y =kx +m (m ≠0)交椭圆C 于A ，B 两点，交y 轴于点M .点N 是M 关于O 的对称点，⊙N 的半径为|NO |.设D 为AB 的中点，DE ，DF 与⊙N 分别相切于点E ，F ，求∠EDF 的最小值.【答案】（1）22142x y +=；（2）EDF ∠的最小值为π3. 【解析】（1）由椭圆的离心率为22，得2222()a a b =-，又当1y =时，2222a x a b =-，得2222a a b-=，所以224,2a b ==，因此椭圆方程为22142x y +=.（2）设1122(,),(,)A x y B x y ，联立方程2224y kx mx y =+⎧⎨+=⎩，得222(21)4240k x kmx m +++-=，由0∆>得2242m k <+.（*）且122421kmx x k +=+，因此122221my y k +=+，所以222(,)2121km mD k k -++，又(0,)N m -，所以222222()()2121km m ND m k k =-++++ 整理得2242224(13)(21)m k k ND k ++=+ ，因为NF m =，所以2422222224(31)831(21)(21)ND k k k k k NF+++==+++.令283,3t k t =+≥，故21214t k ++=，所以2221616111(1)2NDt t NFt t=+=++++ . 令1y t t=+，所以211y t'=-. 当3t ≥时，0y '>,从而1y t t =+在[3,)+∞上单调递增，因此1103t t +≥，等号当且仅当3t =时成立，此时0k =，所以22134ND NF≤+=，由（*）得 22m -<< 且0m ≠.故12NF ND ≥，设2EDF θ∠=，则1sin 2NF ND θ=≥ ，所以θ的最小值为π6，从而EDF ∠的最小值为π3，此时直线l 的斜率是0. 综上所述：当0k =，(2,0)(0,2)m ∈-U 时，EDF ∠取到最小值π3. 【名师点睛】圆锥曲线中的两类最值问题：①涉及距离、面积的最值以及与之相关的一些问题； ②求直线或圆锥曲线中几何元素的最值以及这些元素存在最值时确定与之有关的一些问题．常见解法：①几何法，若题目的条件和结论能明显体现几何特征及意义，则考虑利用图形性质来解决； ②代数法，若题目的条件和结论能体现一种明确的函数关系，则可先建立起目标函数，再求这个函数的最值，最值常用基本不等式法、配方法及导数法求解．解答本题时，（1）由22c a =得2a b =，由椭圆C 截直线y =1所得线段的长度为22，得2222a a b -=，求得椭圆的方程为22142x y +=；（2）由2224x y y kx m⎧+=⎨=+⎩，解得22(21)4k x kmx +++ 2240m -=，确定222(,)2121km m D k k -++，4222||3221m DN k k k =+++，结合22ND NF的单调性求EDF ∠的最小值.21．【2017年高考浙江卷】如图，已知抛物线2x y =，点A 11()24-，，39()24B ，，抛物线上的点13(,)()22P x y x -<<．过点B 作直线AP 的垂线，垂足为Q ．（1）求直线AP 斜率的取值范围；（2）求||||PA PQ ⋅的最大值．【答案】（1）(1,1)-；（2）2716. 【解析】本题主要考查直线方程、直线与抛物线的位置关系等基础知识，同时考查解析几何的基本思想方法和运算求解能力.满分15分. （1）设直线AP 的斜率为k ，2114122x k x x -==-+，因为1322x -<<，所以直线AP 斜率的取值范围是(1,1)-．（2）联立直线AP 与BQ 的方程110,24930,42kx y k x ky k ⎧-++=⎪⎪⎨⎪+--=⎪⎩ 解得点Q 的横坐标是22432(1)Q k k x k -++=+．因为|P A |=211()2k x ++=21(1)k k ++， |PQ |=222(1)(1)1()1Q k k k x x k -++-=-+，所以3(1)(1)k k PA PQ ⋅--+=．令3()(1)(1)f k k k =--+，因为2()(42)(1)f k k k '=--+，所以 f (k )在区间1(1,)2-上单调递增，1(,1)2上单调递减，因此当k =12时，||||PA PQ ⋅取得最大值2716．【名师点睛】本题主要考查直线方程、直线与抛物线的位置关系等基础知识，同时考查解析几何的基本思想方法和运算求解能力.（1）由斜率公式可得AP 的斜率为12x -，再由1322x -<<，得直线AP 的斜率的取值范围；（2）联立直线AP 与BQ 的方程，得Q 的横坐标，进而通过表达||PA 与||PQ 的长度，利用函数3()(1)(1)f k k k =--+的单调性求解||||PA PQ ⋅的最大值．22．【2017年高考江苏卷】如图，在平面直角坐标系xOy 中，椭圆2222:1(0)x y E a b a b+=>>的左、右焦点分别为1F ，2F ，离心率为12，两准线之间的距离为8．点P 在椭圆E 上，且位于第一象限，过点1F 作直线1PF 的垂线1l ，过点2F 作直线2PF 的垂线2l ．（1）求椭圆E 的标准方程；（2）若直线1l ，2l 的交点Q 在椭圆E 上，求点P 的坐标．【答案】（1）22143x y +=；（2）4737(,)77．【解析】（1）设椭圆的半焦距为c ．因为椭圆E 的离心率为12，两准线之间的距离为8，所以12c a =，228a c=，。

平面几何经典难题及解答

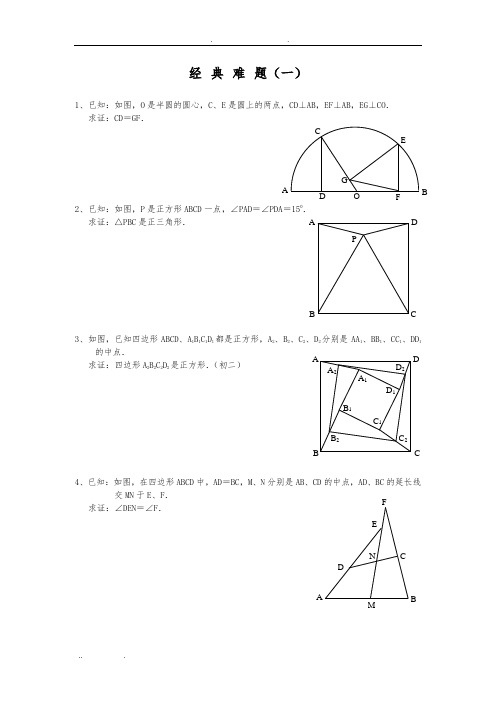
1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．2、已知：如图，P 是正方形ABCD 一点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．A P C DB A FG CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且OM ⊥BC 于M ．（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 引圆的两条直线，交圆于B 、C 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．经典难题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）经典难题（四）1、已知：△ABC 是正三角形，P 是三角形一点，PA ＝3，PB ＝4，PC ＝5．求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．4、平行四边形ABCD 中，设E 、F分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．2、已知：P 是边长为1的正方形ABCD 的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC DCA ＝300，∠EBA＝200，求∠BED 的度数．经典难题解答:APCBACBPDEDCB A A CBPD经典难题（一）1.如下图做GH⊥AB,连接EO。

高联难度平面几何100题第一题分析与解答

高联难度平面几何100题第一题分析与解答第一题：证明角平分已知PE 、PF 是⊙O 的切线，A 、B 是一组对径点，PB 交⊙O 于另一点C ，直线AF 、BE 交于D 点。

求证：PCE PCD ∠=∠。

法一、调和路线()1(2):(3):⎧⎪⇒⇒⎨⎪⎩方向:对边乘积相等两切一割调和四边形方向圆上再取一点与调和四顶点相连，得新的调和线束方向一组对顶点处的切线与另一组对角线，三线共点123⎧⎪⎪⎪⇔⎨⎪⎧⎪⎨⎪⎩⎩方向：用直线截得调和点列调和线束方向：用圆截得调和四边形垂直，角平分方向：特殊的调和线束平行，中点证明：由于PE ,PF 圆O 的切线，PBC 是圆O 的切线，所以四边形EBFC 是调和四边形.又因为，A 在圆O 上，所以，(AE ,AF ;AB ,AC )是调和线束设直线AC 与DE 交于点K ,则直线截调和线束(AE ,AF ;AB ,AC )于点E ,D ,B ,K . 于是(E ,D ,;B ,K )是调和点列，所以，(CE ,CD ,;CB ,CK )是调和线束.又因为AB 是圆O 的直径，所以，CK ⊥CB ，所以，CB 平分角ECD ,结论得证。

法二、角和边的推导1.整体思路：=EB AF D AB E F O P D C E F P PBO C =⎫⎧⎪⇒⇒⇔⎨⎬⇒=⎪⎩⎭图形基础，，，圆、、的关系结论切线切线2.关键步骤： ,,,.=EB AF DA B E F D P E F P PB O C =⎫⇒⎬⇒=⎭把的边和角的关系，推到至、切线切线3.难点突破：寻找点P 、D 的关系.证明过程：定调：,,90ABE ABF AEB AFB αβ∠=∠=∠=∠=︒.推演：+90BDF EBF BFD αβ∠=∠-∠=-︒90,90PEB PFB αβ∠=︒-∠=︒-，2+2180EPF EBF PEB PFB αβ∠=∠-∠-∠=-︒.突破：2,EPF EDF PE PF P ∠=∠=⇒是△EDF 的外心，所以，PDE PED ECP ∠=∠=∠,所以，P ,D ,E ,C 四点共圆.而PD =PE ,所以,PC 平分∠ECD . 结论：PCE PCD ∠=∠法三、角元塞瓦定理整体思路：AB E F P BEF CBA O D ⎫⎧⎪⇒⇒⇔⎨⎬⎪⎩⎭图形基础，，对圆周角元塞瓦对圆，圆圆转移角度联系两个赛周元塞瓦瓦角结论关键步骤：写出两个赛瓦定理，并选对点和三角形.难点突破：用圆连结两个塞瓦定理.证明过程：定调：设,ABE ABF αβ∠=∠=.由于AB 是圆的直径，所以，PEC EBA α∠=∠=. 推演：P 对△BEF 用赛瓦定理:()()sin 90sin sin sin cos sin sin sin sin 90cos PBE PEB PFE PBF PEF PFB ααββ︒-∠∠∠===∠∠∠︒- D 对ABC ∆用塞瓦定理:sin sin sin sin sin sin DCB DBC DAB DCA DBA DAC ∠∠∠=∠∠∠ 所以，()()sin 90sin tan sin 180sin DBC DCB DACβα︒-∠∠=︒-∠ 突破：因为,DBC PBE DCA PBF ∠=∠∠=∠，所以，sin cos cos costan cotsin sin cos sinPBEDCBDACβαβααβα∠∠===∠.结论：所以，PCE PCD∠=∠小结：角度一从调和角度，用全局的目光审视，是基于某个几何模型的做法，这需要一定的几何积累；方法二和方法三，都是从局部的观点去推到，结合综合法和分析法，按照作图的顺序逐步分析以及要证的结论逐步逆推，这就非常考验分析和发现能力，但是其更接近几何的本质.。

高考数学压轴专题(易错题)备战高考《平面解析几何》难题汇编及答案

【最新】高中数学《平面解析几何》专题解析一、选择题1．倾斜角为45︒的直线与双曲线22214x y b-=交于不同的两点P 、Q ，且点P 、Q 在x 轴上的投影恰好为双曲线的两个焦点，则该双曲线的焦距为（）A ．2B ．2C 1D 1【答案】B 【解析】【分析】方法一；由双曲线的对称性可知直线过原点，可得2Rt QOF △为等腰三角形且245QOF ∠=︒，根据勾股定理及双曲线的定义可得：1c =.方法二：等腰2Rt QOF △中，可得22b QF a=，且2b c a =.又根据222b a c =-，联立可解得1c =. 【详解】方法一；由双曲线的对称性可知直线过原点，在等腰2Rt QOF △中，245QOF ∠=︒，则122F F c =，2QF c =，1QF =.由双曲线的定义可得：122QF QF a-=，41c c -==，，故22c =.方法二：等腰2Rt QOF △中，22bQF a=，∴2b c a=. 又222b a c =-， ∴2240c c --=，得1c =.∴22c =. 故选：B . 【点睛】本题考查双曲线的性质，解题关键是将题目条件进行转化，建立等量关系求解，属于中等题.2．设D 为椭圆2215y x +=上任意一点，A （0，－2），B （0，2），延长AD 至点P ，使得|PD|＝|BD|，则点P 的轨迹方程为（）A ．x 2＋（y －2）2＝20B ．x 2＋（y －2）2＝5C ．x 2＋（y ＋2）2＝20D ．x 2＋（y ＋2）2＝5【答案】C 【解析】【分析】由题意得PA PD DA DB DA =+=+=，从而得到点P 的轨迹是以点A 为圆心，半径为【详解】由题意得PA PD DA DB DA =+=+，又点D 为椭圆2215y x +=上任意一点，且()()0,2,0,2A B -为椭圆的两个焦点，∴DB DA +=，∴PA =∴点P 的轨迹是以点A 为圆心，半径为 ∴点P 的轨迹方程为()22220x y ++=．故选C ．【点睛】本题考查圆的方程的求法和椭圆的定义，解题的关键是根据椭圆的定义得到PA =然后再根据圆的定义得到所求轨迹，进而求出其方程．考查对基础知识的理解和运用，属于基础题．3．已知双曲线2222:1(0,0)x y C a b a b-=>>)的左，右焦点分别为12,F F ，其右支上存在一点M ，使得210MF MF ⋅=u u u u r u u u r,直线:0l bx ay +=，若直线2//MF l 则双曲线C 的离心率为（）A B ．2C D ．5【答案】C 【解析】【分析】易得且1MF l ⊥，从而l 是线段1MF 的垂直平分线求出直线1MF 的方程与渐近线方程联立求出交点坐标，进而求得M 坐标，根据勾股定理即可求解离心率. 【详解】由120MF MF ⋅=u u u u v u u u u v可得12MF MF ⊥易知直线:0l bx ay +=为双曲线的一条渐近线，可知l 的方程为by x a=-，且1MF l ⊥，从而l 是线段1MF 的垂直平分线，且直线1MF 的方程为()ay x c b=+设1MF ，与l 相交于点(),N x y .由 ()a y x c b b y x a ⎧=+⎪⎪⎨⎪=-⎪⎩得2a x c aby c ⎧=-⎪⎪⎨⎪=⎪⎩即2,a ab N c c ⎛⎫-⎪⎝⎭，又()1,0F c -，由中点坐标公式，得222,.a ab M c c c ⎛⎫- ⎪⎝⎭由双曲线性质可得122MF MF a -=①，由12MF MF ⊥得222124MF MF c +=②，①②联立，可得2122MF MF b ⋅=所以点M 的纵坐标为2b c ，所以22b ab c c =即2b a =所以21 5.b e a ⎛⎫=+= ⎪⎝⎭故选：C 【点睛】本题考查双曲线性质的综合问题，考查数形结合思想，对于学生的数学运算和逻辑推理能力要求较高，属于一般性题目.4．直线3y kx =+与圆22(3)(2)4x y -+-=相交于M ，N 两点，若||3MN ≥k 的取值范围是（） A ．3,04⎡⎤-⎢⎥⎣⎦B ．30,4⎡⎤⎢⎥⎣⎦C ．3⎡⎤⎢⎥⎣⎦D ．2,03⎡⎤-⎢⎥⎣⎦【答案】A 【解析】【分析】可通过将弦长转化为弦心距问题，结合点到直线距离公式和勾股定理进行求解【详解】如图所示，设弦MN 中点为D ，圆心C(3,2),330y kx kx y =+⇒-+=Q∴弦心距222(1)1CD k k ==+-+，又2||23||33MN DN DN 厖?，∴由勾股定理可得222222231DN CN CD k ⎛⎫=-=-+…，222231|31|1(31)1(43)0041k k k k k k k k ⇒++++⇒+⇒-+剟剟答案选A 【点睛】圆与直线的位置关系解题思路常从两点入手：弦心距、勾股定理。

八年级数学下册平面几何经典难题训练沪科版

（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．2、已知：如图，P 是正方形ABCD 内一点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．A P C DB A FG CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且OM ⊥BC 于M ．（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 引圆的两条直线，交圆于B 、C 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）1、设P是边长为1的正△ABC内任一点，L＝PA＋PB＋PC，求证：≤L＜2．2、已知：P是边长为1的正方形ABCD内的一点，求PA＋PB＋PC的最小值．3、P为正方形ABCD内的一点，并且PA＝a，PB＝2a，PC＝3a，求正方形的边长．4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC＝200，求∠BED 的度数．经典难题解答:经典难题（一）1.如下图做GH ⊥AB,连接EO 。

平面几何经典难题及解答

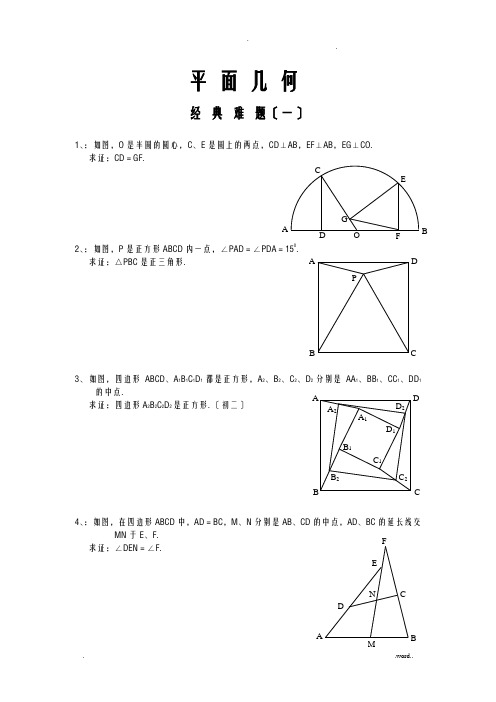
平面几何经典难题〔一〕1、：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．2、：如图，P 是正方形ABCD 内一点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．3、如图，四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．〔初二〕4、：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．A P C DB A F GC EBO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 B经典难题〔二〕1、：△ABC 中，H 为垂心〔各边高线的交点〕，O 为外心，且OM ⊥〔1〕求证：AH ＝2OM ；〔2〕假设∠BAC ＝600，求证：AH ＝AO ．〔初二〕2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A E，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．〔初二〕3、如果上题把直线MN 由圆外平移至圆内，那么由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设Q ．求证：AP ＝AQ ．〔初二〕4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．经典难题〔三〕1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．〔初二〕2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．〔初二〕3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．〔初二〕4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，BC ＝AD ．〔初三〕经典难题〔四〕1、：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．求：∠APB 的度数．〔初二〕2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．〔初二〕3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．〔初二〕经典难题〔五〕1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．2、：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．APCB APDA CBPD4、如图，△ABC中，∠ABC＝∠ACB＝800，D、E分别是AB、AC上的点，∠DCA＝300，∠EBA ＝200，求∠BED的度数．经典难题解答:经典难题〔一〕1.如下列图做GH⊥AB,连接EO。

平面几何练习题及答案

平面几何练习题及答案一、选择题1. 已知三角形ABC中，∠A=90°，AB=3cm，BC=4cm，求AC的长度。

A. 5cmB. 6cmC. 7cmD. √7cm2. 在矩形PQRS中，若PS=6cm，QR=8cm，求对角线PR的长度。

A. 10cmB. 12cmC. 14cmD. √(6²+8²)cm3. 圆O的半径为5cm，点A在圆上，点B在圆外，且OA=5cm，OB=10cm，求AB的长度。

A. 5cmB. 10cmC. 15cmD. √(10²-5²)cm二、填空题4. 已知等腰三角形的底边长为6cm，两腰长为5cm，求其面积。

答案：____cm²5. 已知直角三角形的两条直角边分别为3cm和4cm，求其外接圆的半径。

答案：____cm6. 已知正六边形的边长为a，求其内切圆的半径。

答案：____三、计算题7. 在三角形DEF中，DE=7cm，DF=8cm，EF=9cm，求三角形DEF的面积。

8. 已知圆的半径为r，圆心为O，点A在圆上，点B在圆外，OA=r，OB=2r，求AB的长度。

9. 已知矩形LMNP的长为10cm，宽为6cm，求其内切圆的半径。

四、证明题10. 证明：在直角三角形中，斜边的中线等于斜边的一半。

11. 证明：如果一个三角形的两边和其中一边上的高相等，那么这个三角形是等腰三角形。

12. 证明：在等边三角形中，每个内角都是60°。

五、解答题13. 已知圆的半径为r，求圆的周长和面积。

14. 已知矩形ABCD的长为a，宽为b，求对角线AC的长度。

15. 已知三角形ABC的三个顶点坐标分别为A(x1, y1)，B(x2, y2)，C(x3, y3)，求三角形ABC的面积。

答案：1. D2. D3. D4. 12cm²5. 2.5cm6. a/√37. 27cm²8. 5r9. 2cm10. 利用直角三角形斜边上的中线等于斜边的一半的性质证明。

平面几何经典难题

1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．2、已知：如图，P 是正方形ABCD 内一点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知：△ABC 中，H 为垂心（各边高线的交点），O（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 及D 、E ，直线EB及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·4、平行四边形ABCD 中，设E、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC 上的点，∠DCA ＝300，∠EBA ＝200，求∠BED 的度数．APCBACBPDEDA A CBPD。

初中平面几何经典,6种方法全面解答

方法六：作垂线构矩形
过点P作QM AC，作EN MQ于点N 易得PCQ PEN，EN QC，EN DM， QC PQ,故PQ DM；PM BM AQ 故APQ PDM，APQ PDM PDM DPM 900,故APQ DPM 900 故APD 900即有PA PD
学霸数学
ABC和BED都是等腰直角三角形，AB AC，E在BC上，D在BC下方，P是EC的中点，求证：PA PD
学霸数学
方法一：三线合一过A作AM BC，过D作DN BC MB MC、NB NC，PE PC
故PN PE NE 1 EC 1 BE 1 BC AM , PN AM
2
2
2
PN BM，故PM BN，故PM DN，得APM PDN
PAM DPN，PAM APM 900，故DPN APM 900
即PA PD，
学霸数学
方法二：类倍长中线
延长AP至M，使PM AP，连接AD、MD、ME 得APC MPE，PEM C 450可得DEM 900 EM AC AB，DE DB，故ABD MED，AD DM ADM 900，P为AM中点，故PA PD
学霸数学
方法五：作垂线构矩形
延长DE交AC于点M，连接PM 得EMC 900、C 450故ECM为等腰直角三角形 MP PE，PMA PED 1350，AM BD DE 故PAM PDE，APM DPE，APM APE 900 DPE APE 900即有PA PD
学霸数学
பைடு நூலகம்
学霸数学
方法三：旋转
将APC逆时针旋转900 至AMB BM PC PE，DB DE，MBD PED 1350 故MBD PED，DM DP，MDP 900 又MAP 900，故APD 900 故PA PD

平面几何应用题(含答案)

平面几何应用题(含答案)题目1：有一个圆形花坛，直径为10米。

现在要在花坛周围修建一条环形人行道，使得人行道的宽度为2米。

请问，环形人行道的面积是多少？解答：首先，我们需要计算出花坛的半径。

根据圆的直径和半径的关系，可以得知花坛的半径为5米。

接下来，我们计算环形人行道的外圆的面积和内圆的面积，然后两者相减即可得到环形人行道的面积。

外圆的半径为花坛的半径加上人行道的宽度，即5米+2米=7米。

内圆的半径为花坛的半径，即5米。

根据圆的面积公式，外圆的面积为π × 外圆半径的平方，内圆的面积为π ×内圆半径的平方。

所以，外圆的面积为49π平方米，内圆的面积为25π平方米。

最后，环形人行道的面积等于外圆的面积减去内圆的面积。

所以，环形人行道的面积为49π平方米减去25π平方米，即24π平方米。

题目2：一个直角三角形的两条直角边的长度分别为6厘米和8厘米，请问斜边的长度是多少？解答：根据勾股定理，直角三角形的斜边的长度等于直角边的平方和的平方根。

所以，斜边的长度等于√(6^2 + 8^2) = √(36 + 64) = √100 = 10厘米。

题目3：一个矩形花坛的长为12米，宽为8米。

现在要在花坛周围修建一个宽度均为3米的人行道，请问人行道的面积是多少？解答：首先，我们需要计算出花坛的长和宽分别加上人行道的宽度后的长度。

花坛的长加上人行道的宽度为12米+3米=15米，花坛的宽加上人行道的宽度为8米+3米=11米。

然后，我们计算人行道的面积。

人行道的面积等于花坛加上人行道的长度与宽度的乘积减去花坛的面积。

所以，人行道的面积等于(15米 × 11米) - (12米 × 8米) = 165平方米 - 96平方米 = 69平方米。

题目4：一个等边三角形的边长为10厘米，请问这个等边三角形的面积是多少？解答：根据等边三角形的面积公式，等边三角形的面积等于边长的平方乘以√3再除以4。

平面几何三大难题

平面几何三大难题平面何三大难难几目难难藏[]尺难作难的限定三大何难难几难难难明难明难难本段 []尺难作难的限定平面何作难限制只能用直尺、难难～而难里所难的直尺是指有刻度只能直难的尺。

几没画用直尺难难然可以做出难多难之难形～但有些难形如正七难形、正九难形就做不出。

有些难难看起好像难难～但难与当来来很真正做出却困难～难些难难之中最有名的就是所难的三大难难。

来很难难本段 []三大何难难几化难难方,求作一正方形使其面难等于一已知难～ 1.三等分任意角～ 2.倍立方,求作一立方使其难是一已知立方的二倍。

体体体3.难难本段 []难难难明难正方形都是常难的何难形～但如何作一正方形和已知难等面难,若已知难的半难与几个呢径难其面难难～1π²所以化难难方的难难等于去求一正方形其面难难～也就是用尺难做出难度难的难段;或者是的难段,。

三大难难ππ½π的第二是三等分一角的难难。

难于某些角如个个、三等分不难～但是否所有角都可以三等分,例如并呢～若90?180?60?能三等分难可以做出。

的角～那难正难形及正九难形也都可以做出了;注,难接一正十八难形每一难所难的难周角来内2018难,。

其难三等分角的难难是由求作正多难形难一难难难所引起的。

来360?/18?=20?第三难难是倍立方。

埃拉托塞尼;公元前个年公元前年,曾难难述一神难提到难有一先知者得到神难必个个276~195难立方形的祭难的难加倍～有人主难每难难加倍～但我难都知道那是难难的～因难难已难难成原的将体将体来倍。

难些难难困难数8学决家一千多年都不得其解～而难难上难三大难难都不可能用直尺难难难有限步难可解的。

年笛难建解析何以后卡儿几～1637难多何难难都可以难化难代难难难难究。

几数来研年旺策难难出三等分任一角及倍立方不可能用尺难作难的难明。

1837(Wantzel) 年林得曼;,也难明了的超越性;即不难任何整系多次式的根,～化难难方的不可能性数数1882Lindermanππ也得以立。

人教版初三数学竞赛专题：平面几何的定值问题(包含答案)

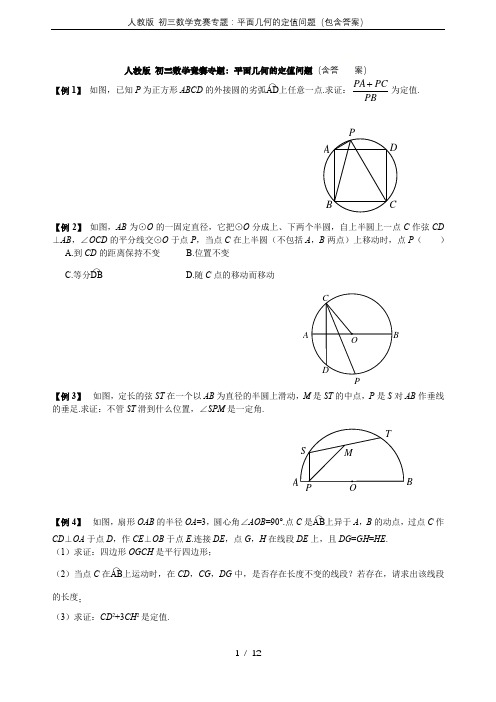
人教版初三数学竞赛专题：平面几何的定值问题（含答案）【例1】如图，已知P 为正方形ABCD 的外接圆的劣弧AD⌒上任意一点.求证：PA PC PB为定值.【例2】如图，AB 为⊙O 的一固定直径，它把⊙O 分成上、下两个半圆，自上半圆上一点C 作弦CD ⊥AB ，∠OCD 的平分线交⊙O 于点P ，当点C 在上半圆（不包括A ，B 两点）上移动时，点P （） A.到CD 的距离保持不变 B.位置不变C.等分DB⌒ D.随C 点的移动而移动【例3】如图，定长的弦ST 在一个以AB 为直径的半圆上滑动，M 是ST 的中点，P 是S 对AB 作垂线的垂足.求证：不管ST 滑到什么位置，∠SPM 是一定角.【例4】如图，扇形OAB 的半径OA =3，圆心角∠AOB =90°.点C 是AB⌒上异于A ，B 的动点，过点C 作CD ⊥OA 于点D ，作CE ⊥OB 于点E .连接DE ，点G ，H 在线段DE 上，且DG =GH =HE .（1）求证：四边形OGCH 是平行四边形；（2）当点C 在AB ⌒上运动时，在CD ，CG ，DG 中，是否存在长度不变的线段？若存在，请求出该线段的长度；（3）求证：CD 2+3CH 2是定值.P AB CDAPB【例5】如图1，在平面直角坐标系xOy 中，点M 在x 轴的正半轴上，⊙M 交x 轴于A ，B 两点，交y 轴于C ，D 两点，且C 为弧AE 的中点，AE 交y 轴于G 点.若点A 的坐标为（-2，0），AE =8. （1）求点C 的坐标；（2）连接MG ，BC ，求证：MG ∥BC ；（3）如图2，过点D 作⊙M 的切线，交x 轴于点P .动点F 在⊙M 的圆周上运动时，PFOF的比值是否发生变化？若不变，求出比值；若变化，说明变化规律.（图1）（图2）【例6】如图，已知等边△ABC 内接于半径为1的圆O ，P 是⊙O 上的任意一点.求证：P A 2+PB 2+PC 2为定值.【能力训练】1.如图，点A ，B 是双曲线xy 3上的两点，分别经过A ，B 两点向x 轴，y 轴作垂线段.若S 阴影=1，则BOACE HG D A=+21S S _______.（第1题图）（第3题图）（第4题图）2.从等边三角形内一点向三边作垂线段，已知这三条垂线段的长分别为1，3，5，则这个等边三角形的面积是__________.3.如图，OA ，OB 是⊙O 任意两条半径，过B 作BE ⊥OA 于E ，又作OP ⊥AB 于P ，则定值OP 2+EP 2为_________.4.如图，在菱形ABCD 中，∠ABC =120°，F 是DC 的中点，AF 的延长线交BC 的延长线于点E ，则直线BF 与直线DE 所夹的锐角的度数为（）A.30°B.40°C.50°D.60°5.如图，在⊙O 中，P 是直径AB 上一动点，在AB 同侧作A A '⊥AB ，AB B B ⊥'，且A A '=AP ，B B '=BP .连接B A ''，当点P 从点A 移动到点B 时，B A ''的中点的位置（） A ．在平分AB 的某直线上移动 B.在垂直AB 的某直线上移动 C.在弧AMB 上移动 D.保持固定不移动（第5题图）（第6题图） 6.如图，A ，B 是函数xky =图象上的两点，点C ，D ，E ，F 分别在坐标轴上，且分别与点A ，B ，O 构成正方形和长方形.若正方形OCAD 的面积为6，则长方形OEBF 的面积是（） A.3 B.6 C.9 D.127.（1）经过⊙O 内或⊙O 外一点P 作两条直线交⊙O 于A ，B 和C ，D 四点，得到如图①~⑥所表示的六种不同情况.在六种不同情况下，P A ，PB ，PC ，PD 四条线段之间在数量上满足的关系式可以用同一个式子表示出来.请你首先写出这个式子，然后只就如图②所示的圆内两条弦相交的一般情况给出它的证明.A ABCDEFAB'（2）已知⊙O 的半径为一定值r ，若点P 是不在⊙O 上的一个定点，请你过点P 任作一直线交⊙O 于不重合的两点E ，F . PE ·PF 的值是否为定值？为什么？由此你发现了什么结论？请你把这一结论用文字叙述出来.8.在平面直角坐标系中，边长为2的正方形OABC 的两顶点A ，C 分别在y 轴，x 轴的正半轴上，点O 在原点，现将正方形OABC 绕O 点顺时针旋转，当A 点第一次落在直线x y =上时停止旋转.旋转过程中，AB 边交直线x y =于点M ，BC 边交x 轴于点N .（1）求OA 在旋转过程中所扫过的面积；（2）旋转过程中，当MN 与AC 平行时，求正方形OABC 旋转度数；（3）设△MBN 的周长为P ，在正方形OABC 旋转的过程中，P 值是否有变化？请证明你的结论.⑥⑤④③②①P(B )A PB9.如图，AB 是半圆的直径，AC ⊥AB ，AC =AB .在半圆上任取一点D ，作DE ⊥CD ，交直线AB 于点E ，BF ⊥AB ，交线段AD 的延长线于点F .（1）设弧AD 是x °的弧，若要点E 在线段BA 的延长线上，则x 的取值范围是_______.（2）不论点D 取在半圆的什么位置，图中除AB ＝AC 外，还有两条线段一定相等.指出这两条相等的线段，并予证明.（第9题图）（第10题图）（第11题图）10.如图，内接于⊙O 的四边形ABCD 的对角线AC 与BD 垂直相交于点K ，设⊙O 的半径为R .求证：（1）2222DK CK BK AK +++是定值；（2）2222DA CD BC AB +++是定值.11.如图，设P 是正方形ABCD 外接圆劣弧弧AB 上的一点，求证：DPCP BPAP ++的值为定值.1.等腰△ABC 的底边BC 为定长2，H 为△ABC 的垂心.当顶点A 在保持△ABC 为等腰三角形的情况下改变位置时，面积S △ABC ·S △HBC 的值保持不变，则S △ABC ·S △HBC =________.2.已知A ，B ，C ，D ，E 是反比例函数xy 16=（x ＞0）图象上五个整数点（横、纵坐标均为整数），分别过这些点向横轴或纵轴作垂线段，以垂线段所在的正方形边长为半径作四分之一圆周的两条弧，组成如图所示的五个橄榄形（阴影部分），则这五个橄榄形的面积总和是__________（用含π的代数式表示）.P D CB A A折叠，使点A ，B 落在六边形ABCDEF 的内部，记∠C ＋∠D ＋）A. ∠1＋∠2＝900°－2α B. ∠1＋∠2＝1080°－2α C. ∠1＋∠2＝720°－α D. ∠1＋∠2＝360°－21α（第3题图）（第4题图）4.如图，正△ABO 的高等于⊙O 的半径，⊙O 在AB 上滚动，切点为T ，⊙O 交AO ，BO 于M ，N ，则弧MTN （）A.在0°到30°变化B.在30°到60°变化C.保持30°不变D.保持60°不变5.如图，AB 是⊙O 的直径，且AB =10，弦MN 的长为8.若MN 的两端在圆上滑动时，始终与AB 相交，记点A ，B 到MN 的距离分别为h 1，h 2，则∣h 1-h 2∣等于（）A.5B.6C.7D.8（第5题图） 12GF EDCHBAB6.如图，已知△ABC 为直角三角形，∠ACB =90°，AC =BC ，点A ，C 在x 轴上，点B 坐标为（3，m ）（m ＞0），线段AB 与y 轴相交于点D ，以P （1，0）为顶点的抛物线过点B ，D . （1）求点A 的坐标（用m 表示）（2）求抛物线的解析式；（3）设点Q 为抛物线上点P 至点B 之间的一动点，连接PQ 并延长交BC 于点E ，连接BQ 并延长交AC 于点F .试证明：FC （AC +EC ）为定值.7.如图，已知等边△ABC 内接于圆，在劣弧AB 上取异于A ，B 的点M .设直线AC 与BM 相交于K ，直线CB 与AM 相交于点N .证明线段AK 和BN 的乘积与M 点的选择无关.（第7题图）（第8题图）8.如图，设H 是等腰三角形ABC 两条高的交点，在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小，这时乘积S △ABC ·S △HBC 的值变小、变大，还是不变？证明你的结论.9.如图，在平面直角坐标系xOy 中，抛物线10941812--=x x y 与x 轴的交点为点A ，与y 轴的交点为点B .过点B 作x 轴的平行线BC ，交抛物线于点C ，连接AC .现有两动点P ，Q 分别从O ，C 两点同时出发，点P 以每秒4个单位的速度沿OA 向终点A 移动，点Q 以每秒1个单位的速度沿CB 向点B 移动.点P 停止运动时，点Q 也同时停止运动.线段OC ，PQ 相交于点D ，过点D 作DE ∥OA ，交CA 于E ，射线QE 交x 轴于点F .设动点P ，Q 移动的时间为t （单位：秒）. （1）求A ，B ，C 三点的坐标和抛物线的顶点坐标；（2）当t 为何值时，四边形PQCA 为平行四边形？请写出计算过程；（3）当290<<t 时，△PQF 的面积是否总是定值？若是，求出此值；若不是，请说明理由；（4）当t 为何值时，△PQF 为等腰三角形，请写出解答过程.NKMB AC HCBA（第9题图）（第10题图） 10.已知抛物线C 1：12121+-=x x y ，点F （1,1）. （1）求抛物线C 1的顶点坐标；（2）若抛物线C 1与y 轴的交点为A ，连接AF ，并延长交抛物线C 1于点B ，求证：211=+BFAF . （3）抛物线C 1上任意一点P （x P ，y P ）（0＜x P ＜1），连接PF ，并延长交抛物线C 1于点 Q （x Q ，y Q ），试判断211=+QFPF 是否成立？请说明理由.11.已知A ，B 是平面上的两个顶点，C 是位于AB 一侧的一个动点，分别以AC ，BC 为边在△ABC 外作正方形ACDE 和正方形BCFG .求证：不论C 在直线AB 同一侧的任何位置，EG 的中点P 的位置不变. 参考答案例 1 延长PC 至E ，使CE ＝AP ，连结BE ，则△BCE ≌△BAP ，及△PBE 为等腰直角三角形，故PA PC CE PC PEPB PB PB++=== 例2 B 提示：连结AC ，BC ，可以证明P 为APB 的中点．例3 ∵SP ⊥OP ，OM ⊥ST ，∴S ，M ，O ，P 四点共圆，于是∠SPM ＝∠SOM ＝12∠SOT 为定角．例4 (1)连结OC 交DE 于M ，则OM ＝CM ， EM ＝DM ，而DG ＝ HE ，则HM ＝GM 故四边形OGCH 是平行四边形． (2)DG 不变．DE ＝OC ＝OA ＝3 .DG ＝13DE ＝13×3＝1． (3)设CD ＝x ，延长OG 交CD 于N ，则CN ＝DN ＝12 x ，229CE x =- ， 2214DN x = .∴22394ON x =-，而ON ＝32CH ，∴22143CH x =-．故CD 2＋3CH 2＝x 2＋3(4－13x 2)＝x 2＋12－x 2为定值．例5 ⑴C (0，4) ⑵先求得AM ＝CM ＝5，连接MC 交AE 于N ，由△AO G ∽△ANM ，得OG AO MN AN =，O G ＝32，38OG OM OC OB ==，又∠BOC ＝∠G OM ，∴△G OM ∽△COB ，∠G MO ＝∠CBO ，得M G ∥BC ．⑶连结DM ，则DM ⊥PD ，DO ⊥PM ，DO 2＝OM •OP ，OP ＝163．动点F 在⊙M 的圆周上运动时，从特殊位置探求OFPF的值．当F 与点A 重合时，2316523OF AO PF AP ===-；当点F 与点B 重合时，8316583OF OB PF PB ===+；当点F 不与点A ，B 重合时，连接OF 、PF 、MF ，∴DM 2＝MO •MP ，∴FM 2＝MO •MP ，即FM MPOM FM=，又∠OMP ＝∠FMP ，∴△MFO ∽△MPF ，35OF MO PF MF ==，故OF PF 的比值不变，比值为35．例6 ∠BPC ＝120°，在△BPC 中，由余弦定理得BC 2＝PB 2＋PC 2－2PB •PC ＝BC 2，又由上托勒密定理得BC •P A ＋PC •AB ，而AB ＝BC ＝AC ，∴P A ＝PB ＋PC ，从而P A 2＋ PB 2＋ PC 2＝ (PB ＋PC )2＋ PB 2＋ PC 2＝2 (PB 2＋PC 2＋PB •PC )＝2BC 2＝2×()23＝6．故P A 2＋PB 2＋PC 2为定值．A 级 1．4提示：∵S 1＋S 阴＝ S 2＋S 阴＝xy ＝3，∴S 1＋S 2＝2xy －2S 阴＝6－2＝4．2．273 提示：1＋3＋5＝9是等边三角形的高． 3．r 2提示：先考查OB 与OA 垂直的情形．4．D 提示：延长BF 交DE 于点M ，连接BD ，则△BCD 为等边三角形，BF 平分∠CBD ．∵F 为CD 中点，且AD ∥CE ，∴△ADF 与△ECF 关于点F 中心对称．∴CE ＝AD ＝CD ，∴∠CEM=30°，∠DMF=60°，5．D 提示：A′B′的中点均在⊙O 的上半圆的中点处． 6．B 提示：S 正方形OCAD ＝OD •OC ＝A A x y k =＝6，∴S OEBF ＝OE •OF ＝x B •y B k =＝6． 7．⑴略⑵当点P在⊙O 内时，过P 作直径CD ，则PE •PF ＝PD •PC ＝r 2－OP 2为定值；当点P 在⊙O 外时，PE •PF 为定值22OP r -．结论：过不在圆上的一个定点任作一条直线与圆相交，则这点到直线与圆相交点的两条线段长的积为定值． 8．⑴2π⑵22.5° ⑶P 值无变化．理由如下：如图，延长BA 交y 轴于E 点，可证明△OAE ≌△OCN ，得OE ＝ON ，AE ＝CN ，又∠MOE ＝∠MON ＝45°，OM ＝ON ，∴△OME ≌△OMN ，得MN ＝ME ＝AM ＋AE ＝AM ＋CN ．∴P ＝MN ＋BN ＋BM ＝AM ＋CM ＋CN ＋BN ＋BM ＝AB ＋AC ＝4．9．⑴0＜x ＜90 ⑵BE ＝BF 提示：连接BD ，可证明△BDF ∽△ADB ，△BDE ∽△ADC ． 10．⑴作OP ⊥BD 于P ，OQ ⊥AC 于Q ，连接AO ，则AO 2＝()()221122BK DK CK AK ⎡⎤⎡⎤-++⎢⎥⎢⎥⎣⎦⎣⎦，又AK •CK ＝BK •DK ，得AK 2＋BK 2＋CK 2＋DK 2＝4R 2为定值． ⑵作直径DE ，连接AE ，BE ，CE ，AB 2＋CD 2＝4R 2，AD 2＋BC 2＝4R 2，故AB 2＋BC 2＋CD 2＋DA 2＝8K 2为定值． 11．设正方形的边长为a ，根据托勒密定理，对于四边形APBC 和四边形APBD ，有CP •a ＝AP •a ＋BP •2a ，DP •a ＝BP •a ＋AP •2a ，两式相加并整理得(CP ＋DP )a ＝(AP ＋BP )(a ＋2a )，从而21AP BPCP DP+=-+为定值．B 级1．1 提示：不妨设∠A 为锐角，AD ，BE ，CF 为△ABC 的三条高，H 为垂心，由AB ＝AC 知∠HBD ＝∠HCD ＝∠HAE ，∠HDC ＝∠CDA ＝90°，故R t △CHD ∽R t △ACD ．∴AD DC DC HD =，即AD •HD ＝DC 2＝14BC 2＝1．∴S △ABC •S △HBC ＝2111224BC AD BC HD BC ⎛⎫⎛⎫⋅⋅⋅= ⎪ ⎪⎝⎭⎝⎭＝1．当∠A ≥90°时，结论成立．2．13π－26 提示：∵A ，B ，C ，DE 是反比例函数y ＝16x(x ＞0)图象上五个整数点，由图象可知，这些点的横坐标分别为1，2，4，8，16．∴五个正方形的边长分别为1，3，4，2，1．∴这五人橄榄形的面积总和是2221111112211122222444424242πππ⎡⎤⎛⎫⎛⎫⎛⎫⨯-⨯⨯+⨯-⨯⨯+⨯-⨯⨯ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦＝5π－10＋8π－16＝13π－26． 3．B 提示：如图，设F A 的延长线与CB 的延长线交于点P ，G A ′的延长线与HB ′的延长线交于点P ′．由对称性可知∠1＝2∠APP ′，∠2＝2∠BPP ′．∴∠1＋∠2＝2∠APB ．∵∠APB ＝540°－α，∴∠1＋∠2＝1080°－2α． 4．D 5．B 提示：如图，设AB 与MN 交于点C ，过点O 作OD ⊥MN 于D ，连接FO 并延长交EB 于G ．由垂径定理，得OD ＝2254-＝3．由△AFO ≌△B G O ，得AF ＝B G ，即h 1＝B G ．由AF ⊥MN ，BE ⊥MN ，得△FOD ∽△F G E ．∴12OD FO GE FG ==．∴E G ＝2OD ＝6，∴12h h AF BE -=-＝E G ＝6． 6．⑴A (3－m ，0) ⑵y ＝x 2－2x ＋1 ⑶过点Q 作QM ⊥AC 于M ，过点Q 作QN ⊥BC 于N ，设Q 点的坐标为(x ，x 2－2x ＋1)，则QM ＝CN ＝(x －1)2，MC ＝QN＝3－x ．∵QM ∥CE ，∴PQM ∽△PEC ．∴QM PMEC PC=，即()2112x x EC--=，得EC ＝2(x －1)．∵QN ∥CF ，∴△BQN ∽△BFC ．∴QN BN FC BC =，即()24134x x FC ---=，得FC ＝41x +．又AC ＝4，∴FC (AC ＋EC )＝()44211x x +-⎡⎤⎣⎦+＝8为定值． 7．提示：易证△ABK ∽△BNA ，故AK •BN ＝AB 2为定值，即AK 与BN 的乘积与M 点的选择无关． 8．提示：S △ABC •S △HBC ＝116BC 4，由于BC 是不变的，所以当点A 至BC 的距离变小时，乘积S △ABC •S △HBC 保持不变． 9．⑴A (18，0)，B (0，－10)，顶点坐标为(4，－989)⑵若四边形PQCA 为平行四边形，由于QC ∥P A ，故只要QC ＝P A 185． ⑶即可，而P A ＝18－4t ，CQ ＝t ，故18－4t ＝t ，得t ＝设点P 运动t s ，则OP ＝4t ，CQ ＝t ，0＜t ＜4.5．说明P在线段OA 上，且不与点O ，A 重合．由于QC ∥OP 知△QDC ∽△PDO ，故144QD QC t DP OP t ===．同理QC ∥AF ，故14QC CE AF EA ==，即14t AF =，∴AF ＝4t ＝OP ．∴PF ＝P A ＋AF ＝P A ＋OP ＝18．又点Q 到直线PF 的距离d ＝10，∴S △PQF ＝12•PF •d ＝12×18×10＝90．于是S △PQF 的面积总为定值90． ⑷由前面知道，P (4t ，0)，F (18＋4t ，0)，Q (8－t ，－10)，0≤t ≤4.5．构造直角三角形后易得PQ 2＝(4t －8＋t )2＋102＝，FQ 2＝(18＋4t －8＋t )2＋102＝(5t ＋10)2＋100．①若FP ＝FQ ，即182＝(5t ＋10)2＋100，故25(t ＋2)2＝224，(t ＋2)2＝24425．∵2≤t ＋2≤6.5，∴t ＋2＝244414255=．∴t ＝ 4145－2． ②若QP ＝QF ，即(5t －8)2＋100＝(5t ＋10)2＋100，即(5t －8)2＝(5t ＋10)2，无0≤t ≤4.5的t 满足． ③若PQ ＝PF ，即(5t －8)2＋100＝182，∴(5t －8)2＝224．由于224≈15，又0≤5t ≤22.5，∴－8≤5t －8≤14.5，14.52＝22984124⎛⎫= ⎪⎝⎭＜224．故没有t (0≤t ≤4.5)满足此方程．综上所述，当t ＝4145－2时，△PQ R 为等腰三角形． 10．⑴C 1的顶点坐标为(1，12). ⑵略 ⑶作PM ⊥AB 于M ，作QN ⊥AB 交AB 延长线于N ，∴PM ＝1－y P ，FM ＝1－x P ．在R t △PMF 中，PF 2＝(1－y P )2＋(1－x P )2＝1－2y P ＋y P 2＋1－2x P ＋x P 2，又∵点P 在抛物线上，∴y P ＝12x P 2－x P ＋1，∴PF 2＝1－x P 2＋2x P －2＋y P 2＋1－2x P ＋x P 2＝y P 2，∴PF ＝y P ，同理，QF ＝y Q ，易证△PMF ∽△QNF ，则PM QN PF QF =，∴11Q P y y PF QF --=，即11PF QF PF QF --=，∴11PF QF+＝2． 11．先从特殊情况出发．当△ABC 是等腰直角三角形时，点P 与点C 重合，此时点P 的位置在AB 的中垂线上，且到AB的距离为12AB ，如图①所示．下面就一般情况来证明上面的结论(结论②所示)．过C ，E ，G 分别作直线AB 的垂线CH ，EM ，G N ，垂足分别是H ，M ，N ．容易证明△AEM ≌△ACH ，△B G N ≌△BCH ．从而有AM ＝CH ＝BN ，EM ＝AH ，G N ＝BH ．这样，线段AB 的中点O 也是线段MN 的中点，连接OP ，则OP 是梯形EMN G 的中位线，从而OP ⊥AB ，OP ＝12(EM ＋G N )＝ 12(AH ＋BH )＝12AB ．∴无论点C 在AB 同一侧的位置如何，E G 中点P 的位置不变．。

平面几何难题及解答

高考数学压轴专题(易错题)备战高考《平面解析几何》难题汇编及答案解析

八年级数学下册 平面几何经典难题训练 沪科版

平面几何难题解答

平面几何练习题及解答

2021年高中数学竞赛平面几何问题的解答及其它 (1)

专题37平面解析几何解答题(第二部分)

专题08 平面解析几何(解答题)

平面几何经典难题及解答

高联难度平面几何100题第一题分析与解答

高考数学压轴专题(易错题)备战高考《平面解析几何》难题汇编及答案

八年级数学下册平面几何经典难题训练沪科版

平面几何经典难题及解答

平面几何练习题及答案

平面几何经典难题

初中平面几何经典,6种方法全面解答

平面几何应用题(含答案)

平面几何三大难题

人教版 初三数学竞赛专题：平面几何的定值问题(包含答案)

八年级数学下册平面几何经典难题训练沪科版

人教版初三数学竞赛专题：平面几何的定值问题(包含答案)